|

La formation réticulée médiane :
un substrat
pour la sélection de l'action ? Modélisation
via
réseaux de neurones et
algorithmes
évolutionnistes.

Franck Dernoncourt
franck.dernoncourt@gmail.com
Supervisépar Stéphane Doncieux et
Benoàýt Girard

Table des matières
Table des matières i
Table des figures iii
1 Introduction 3
1.1 Remarques liminaires 3
1.2 Sélection de l'action 5
1.3 Données anatomiques internes 7
1.4 Démonstration de P(l) > 45 × P(p) 9
1.5 Modèles existants 10
1.5.1 Le modèle de Kilmer-McCulloch - 1969 10
1.5.2 Le modèle de Humphries - 2006 13
1.6 Démarche et objectifs de ce rapport 14
2 Matériel théorique 15
2.1 Les réseaux de neurones 15
2.2 Les algorithmes évolutionnistes 18
2.2.1 Définitions 18
2.2.2 Application 20
3 Tâche désincarnée : la tâche
vectorielle abstraite 23
3.1 Expérience 23
3.2 Résultats 26
4 Tâche incarnée : la tâche de survie
minimale 31
4.1 Expérience 31
4.2 Résultats 34
5 Discussions et perspectives 40
6 Conclusion 44
Bibliographie 46
TABLE DES MATI`ERES ii
A Notes techniques sur l'implémentation
51
B Exemple d'une mRF a` 4 clusters 53
C Exemple d'un cluster de la mRF 55
Table des figures
1.1 Tronc c'er'ebral chez un cerveau humain (partie en rouge)
4
1.2 Localisation de la mRF 4
1.3 Projections sur et depuis la mRF 4
1.4 Coupes du cerveau au niveau post'erieur du tronc c'er'ebral.
6
1.5 Coupe sagittale de la mRF 8
1.6 mRF et structures smallworld 11
1.7 Modèle de Humphries 13
2.1 Exemple d'un neurone avec 2 entr'ees 16
2.2 Exemple d'une mRF a` 4 clusters 17
2.3 Exemple d'un cluster de la mRF 17
2.4 Fonctionnement d'un algorithme 'evolutionniste 19
2.5 Exemple de front de Pareto de dimension 2 21
2.6 Mono vs multi-objectif 21
3.1 Tâche d'esincarn'ee 24
3.2 Front de Pareto de dimension 2 27
3.3 Front de Pareto de dimension 3 28
3.4 Front de Pareto 2D sans contraintes lors des mutations
29
3.5 Front de Pareto 2D de l''evolution sans aucune contrainte
30
4.1 Environnement de la tâche de survie minimale 32
4.2 Comparaison des contrôleurs al'eatoire et WTA dans la
tâche de survie 35
4.3 Front de Pareto 2D de l''evolution d'un
contrôleur mRF 36
4.4 Comparaison des contrôleurs dans la tâche de
survie 37
4.5 Comparaison des contrôleurs dans la tâche de
survie 37
4.6 Front de Pareto 2D de l''evolution d'un contrôleur
mRF avec modulation 38
4.7 Front de Pareto 2D de l''evolution d'un
contrôleur mRF sans saliences 39
A.1 Statistiques sur le code source 52
B.1 Exemple d'une mRF a` 4 clusters 54
C.1 Exemple d'un cluster de la mRF 56
Résumé
La formation r'eticul'ee m'ediane (mRF) est une r'egion du
tronc c'er'ebral recevant des entr'ees sensorielles très riches, en
mesure de controler les actions motrices via ses connexions vers la moelle
spinale et les nerfs cràaniens. Phylog'en'etiquement, la mRF est l'une
des plus anciennes structures nerveuses du tronc c'er'ebral, lui-même
'etant ce qu'on peut consid'erer comme un des centres les plus anciens du
système nerveux central. Elle semble donc constituer un proto
système de s'election de l'action.
Le premier modèle de la mRF a 'et'e propos'e par
[Kilmer et al., 1969], il interprète d'ejàle role de cette
r'egion comme un s'electeur de mode de fonctionnement. [Humphries et al., 2005]
ont voulu tester l'efficacit'e de ce modèle en tant que m'ecanisme de
s'election de l'action de bas niveau en le confrontant a` la tàache de
survie minimale propos'ee dans [Girard et al., 2003]. Le modèle original
s'est av'er'e peu efficace, ce qui a conduit [Humphries et al., 2006] a`
proposer un second modèle exprim'e dans un formalisme de r'eseau de
neurones et prenant quelques donn'ees anatomiques et physiologiques
suppl'ementaires. N'eanmoins, ce second modèle n'a qu'un succès
mitig'e sur la tàache de survie minimale et est assez peu plausible
anatomiquement en raison de sa forte abstraction.
Nous proposons dans ce rapport un nouveau modèle de la mRF
:
- contraint par les informations anatomiques quant a` sa
structuration;
- construit sur la base de r'eseaux de neurones g'en'er'es par
'evolution artificielle; - 'evalu'e sur des tàaches de s'election de
l'action.
Le modèle obtenu r'eussit avec succès les
tàaches de s'election, ce qui montre que la mRF peut servir de
système de s'election de l'action. Nous d'emontrerons 'egalement une
propri'et'e anatomique de la mRF qui coupl'ee aux r'esultats de l'article
[Humphries et al., 2006] montre qu'il est très probable que la mRF
r'eseau ait une structure de type small-world.
Ce projet est financ'e par l'ANR (ANR-09-EMER-005-01) dans le
cadre du projet EvoNeuro (http ://
pages.isir.upmc.fr/EvoNeuro).
Remerciements
Je souhaite tout d'abord exprimer ma plus profonde gratitude
envers mes deux encadrants, Stéphane Doncieux et Benoit Girard: outre
leurs précieux conseils indispensables pour mener a` bien ce projet, ils
ont suivi avec minutie l'avancée de mes travaux tout au long du stage et
leurs exigences élevées m'ont pousséa` donner le meilleur
de moi-même. La complémentaritéde leurs compétences,
Stéphane étant spécialiste de l'évolution
artificielle et Benoit expert en modeles neuro-computationnels de
sélection de l'action, revêtit une importance cruciale dans la
réalisation des travaux que nous allons présenter dans ce rapport
et m'a permis personnellement de gagner considérablement en
compétences sur ces deux problématiques en quelques mois
seulement.
Je tiens également a` remercier tres chaleureusement
Jean Liénard, Tony Pinville et Paul Tonelli, doctorants a` l'ISIR : leur
aide généreuse et leurs avis spontanés ont
orientémes réflexions vers des chemins plus fructueux, notamment
en partageant leurs diverses expériences de these.
Enfin, mes pensées de remerciements vont a` toutes les
autres personnes du CogMaster et de l'ISIR avec qui j'ai pu échanger sur
mon projet de stage et qui m'ont permis par leurs réflexions de
màurir ce projet et d'avancer dans mes recherches, et en particulier a`
mon tuteur du CogMaster et d'HEC, Philippe Mongin, dont la gentillesse, la
perspicacitéet l'ouverture d'esprit pour ne citer que quelques-unes de
ses qualités sont sans limite. Beaucoup de choses n'eurent pas
étépossibles sans lui.
Chapitre 1
Introduction
Ce chapitre présente une vue d'ensemble de la formation
réticulée médiane : après quelques remarques
préliminaires, nous résumerons des études qui tendent a`
montrer que la mRF est un proto-système de sélection de l'action.
Dans un second temps, nous présenterons de façon synoptique
l'ensemble des données anatomiques connues de la mRF permettant de la
modéliser. Enfin, nous étudierons les deux et uniques
modèles existants de la formation réticulée médiane
afin de voir leurs lacunes, tout en tirant parti de leurs points forts pour
construire le nôtre.
1.1 Remarques liminaires
La formation r'eticul'ee, dont fait partie la formation
r'eticul'ee m'ediane, est un composant du système nerveux central qui
doit son nom (tir'e du latin reticulum signifiant filet) a` sa pr'esentation
anatomique en r'eseau dense et intriqu'e. Situ'ee sur le plancher du tronc
c'er'ebral entre la moelle allong'ee et le m'esenc'ephale, elle projette et
reçoit des fibres nerveuses de toute la moelle spinale ainsi que de
nombreux autres composants du n'evraxe tels que le cortex c'er'ebral,
l'hypothalamus ou le cervelet (cf figures 1.1, 1.2 et 1.3).
Nous nous int'eresserons dans ce rapport a` une partie de la
formation r'eticul'ee appel'ee formation r'eticul'ee m'ediane (ou m'ediale),
que nous abrègerons par mRF dans la suite d'après la traduction
anglaise medial Reticular Formation.
FIGURE 1.1: Tronc c'er'ebral chez un cerveau humain (partie en
rouge)
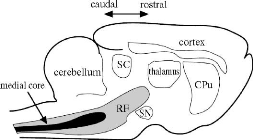
FIGURE 1.2: Localisation de la mRF (zone en noir) dans le
cerveau d'un chat. RF : reticular formation. CPu : caudate-putamen. SC :
superior colliculus. SN : substantia nigra. Source : [Humphries et al.,
2006]
La phylog'enèse du système nerveux montre que la
mRF est l'une des plus anciennes structures nerveuses du tronc c'er'ebral,
lui-même 'etant ce qu'on peut consid'erer comme un des centres les plus
anciens du système nerveux central. Ainsi, parmi les diff'erentes
espèces animales, la mRF est très comparable, comme le montre par
exemple [Ramón-Moliner and Nauta, 1966] entre les requins et les
humains, ce qui nous permettra d'agr'eger directement les donn'ees issues
d''etudes sur des animaux diff'erents.
1.2 S'election de l'action
La s'election de l'action d'esigne le problème crucial
que rencontre tout agent autonome, qu'il soit de nature animale ou robotique,
qui consiste a` choisir et coordonner continuellement ses comportements dans
l'optique de mener a` bien ses objectifs au long terme, tels que la survie, la
reproduction, ou tout autre tàache d'efinie par le concepteur dans le
cas d'un robot. Les animaux doivent donc n'ecessairement mettre en oeuvre des
solutions efficaces de s'election de l'action, d'o`u notre recherche au sein du
système nerveux d'un tel m'ecanisme.
Plusieurs donn'ees tendent a` montrer que la mRF est impliqu'ee
dans la s'election de l'action, nous allons les r'esumer succinctement dans
cette section.
Tout d'abord, la mRF semble disposer de toutes les
informations auxquelles ont accès les systèmes de monitoring et
sensoriels aussi bien externe qu'interne d'un animal : elle reçoit ainsi
une quantit'e consid'erable d'entr'ees sensorielles, comme le synth'etise
[Humphries et al., 2007], provenant notamment des sytèmes sensoriel,
respiratoire, visc'eral, vestibulaire, proprioceptif, nociceptif ou encore
cardio-vasculaire. Ces donn'ees sont corrobor'ees par les divers
enregistrements effectu'es sur la mRF montrant que cette dernière
r'eagit a` des stimuli très vari'es [Segundo et al., 1967, Bowsher,
1970, Langhorst et al., 1983].
De façon compl'ementaire, la mRF projette en masse sur
tous les niveaux de la moelle spinale ainsi que sur les nerfs cràaniens
[Torvik and Brodal, 1957, Eccles et al., 1976, Jones, 1995], ce qui lui donne
la capacit'e de contrôler aussi bien la musculature axiale que la face.
Par cons'equent, la mRF dispose des entr'ees et des sorties n'ecessaires a`
tout candidat de système de s'election de l'action.
Exp'erimentalement, il a 'et'e montr'e que des rats qui
avaient subi une coupe complète au niveau post'erieur du tronc
c'er'ebral, plus pr'ecis'ement post'erieur au thalamus et a` l'hypothalamus, en
enlevant toute la partie rostrale du cerveau par rapport a` cet axe de coupe
(cf les 3 axes de coupe sur la figure 1.4), pr'esentaient un comportement
surprenamment coh'erent [Woods, 1964], hormis les erreurs
engendr'ees par la perte de la vision, de l'odorat ainsi que des troubles de la
r'egulation hormonale. Les rats de l'exp'erience 'etaient toujours capable
d'effectuer des s'elections de l'action de bas niveau, tel manger, se mouvoir,
boire ou dormir en fonction des stimuli. Les r'esultats très importants
de cette exp'erience furent plus tard confirm'es par [Lovick, 1972, Berntson
and Micco, 1976, Berridge, 1989], mettant l'accent sur le fait que ces rats
peuvent effectuer des combinaisons d'actions coordonn'ees, tel tenir, ronger et
màacher de la nourriture, combinaisons plus complexes que de simples
r'eflexes qui pourraient 'emaner de la moelle spinale.
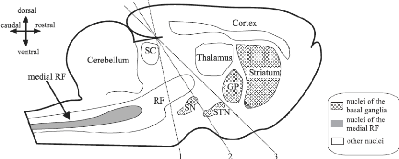
FIGURE 1.4: Coupes du cerveau au niveau post'erieur du tronc
c'er'ebral. Les lignes en pointill'es montrent 3 coupes, toute la partie du
cerveau situ'ee du côt'e rostral des lignes a 'et'e enlev'ee. GP : globus
pallidus. RF : reticular formation. SN : substantia nigra. STN : subthalamic
nucleus. SC : superior colliculus. Source : [Humphries et al., 2007]
Pour v'erifier le role de la mRF, des stimulations locales
'electriques et chimiques ont 'et'e faites sur des animaux normaux,
stimulations qui eurent pour r'eaction de les faire changer de comportement,
par exemple manger, dormir, boire, s'enfuir, chercher ou encore se laver
[Magoun and Rhines, 1946, Glickman and Schiff, 1967]. Ces r'esultats montrent
l'ampleur des diff'erents comportements que controle au moins en partie la
mRF.
A contrario, des 'etudes ont port'e sur l'impact de l'esions
a` la mRF. Elles t'emoignent de troubles s'evères du comportement,
notamment des troubles du sommeil, les sujets 'etudi'es montrant d'un
d'ephasage entre le sommeil c'er'ebral et le reste du corps [Birkmayer and
Pilleri, 1966], ou aussi des alternances fr'equentes entre sommeil pro-fond et
rage extreme [Jouvet, 1967]. [Parvizi and Damasio, 2003] ont meme montr'e
que des l'esions de certaines parties de la mRF peuvent provoquer
le coma, voire la mort chez un être humain.
Enfin, contrairement a` la plupart des structures neuronales,
les cellules de la mRF existent d`es la naissance [Hammer Jr et al., 1981], ce
qui peut repr'esenter une indication de l'importance de leur pr'esence pour la
survie de l'individu.
A` la lueur de ces diff'erentes 'etudes, il semble raisonnable
de supposer que la mRF constitue un proto-syst`eme de s'election de l'action,
proto car les actions en question semblent être d'un niveau assez
rudimentaire et en raison de l'anciennet'e phylog'en'etique.
1.3 Données anatomiques internes
Dans cette section, nous allons rassembler toutes les donn'ees
anatomiques qui seront utiles pour construire un mod`ele de la mRF.
Premi`ere remarque d'ordre g'en'eral, la litt'erature
neuroscientifique montre que les m'ecanismes de s'election de l'action sont
impl'ement'es suivant deux architectures diff'erentes dans le cerveau des
mammif`eres :
- une architecture de type centralis'ee, o`u chaque module
neuronal projette sur un syst`eme de d'ecision central. Les ganglions de la
base auraient ce type d'architecture [Redgrave et al., 1999, Prescott et al.,
1999].
- une architecture de type modulaire, o`u chaque module
neuronal est en comp'etition, inhibant ou excitant les autres modules. La mRF
aurait ce type d'architecture [Humphries et al., 2007].
Une des particularit'es de la mRF est son organisation en
clusters ('egalement appel'es stacks ou chips selon les articles) [Scheibel and
Scheibel, 1967], comme le montre la coupe sagitalle de la mRF pr'esent'ee sur
la figure 1.5.
La mRF d'un rat mesure environ 7 mm sur l'axe rostral-caudal
et contient entre 35 et 75 clusters [Humphries et al., 2006]. La mRF d'une
grenouille contient approximativement 0.75 million de neurones, tandis que
celle d'un être humain en contient 2 millions [Kilmer et al., 1969]. Les
clusters sont de la même taille en terme de dimension et de nombre de
neurones [Humphries et al., 2007]. Ils reçoivent tous les mêmes
entr'ees et projettent vers les mêmes zones [Humphries and Prescott,
2006].
Il existe deux cat'egories principales de neurones dans la mRF
:
- Les interneurones : de taille petite ou
moyenne, ils sont tous inhibiteurs (quelques exceptions
existent cependant) et projettent quasi exclusivement dans leur propre
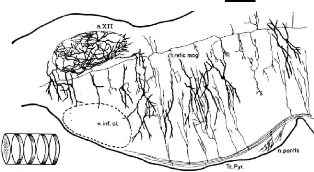
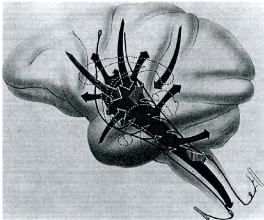
FIGURE 1.5: Coupe sagittale de la mRF sur un rat, montrant son
organisation en clusters. Source : [Scheibel and Scheibel, 1967]
cluster, aussi bien sur des neurones de projection que sur des
interneurones. Ils représentent environ 20% des neurones de la mRF
[Humphries et al., 2006].
- Les neurones de projection : de taille
moyenne a` très grande, ils sont tous excitateurs
(quelques exceptions existent cependant) et ils projettent quasi
exclusivement en dehors de leur propre cluster, vers d'autres clusters ou bien
en dehors de la mRF [Humphries et al., 2006]. Environ 45% des synapses en
entrée des neurones de projection sont GABAergiques, c'est-à-dire
inhibiteurs, donc provenant d'interneurones [Humphries et al., 2007]. Les
neurones de projection représentent environ 80% des neurones de la
mRF.
La probabiliténotée P(c) qu'un neurone de
projection projette sur un cluster donnéest l'objet de deux
modèles différents dans la littérature. Selon [Grantyn et
al., 1987],
P(c) = 0.25 quel que soit le cluster source (o`u se trouve le
noyau du neurone de projection) et le cluster destination (vers lequel projette
le neurone de projection). Selon [Kilmer et al., 1969], la
probabilitéP(c) dépend de la distance entre le cluster source et
le cluster destination : P(c) = d-a, o`u d est la distance et a un
paramètre supérieur ou égal a` 1.
La probabiliténotée P(p) qu'un neurone de
projection projette sur un neurone donné, sachant qu'il projette dans le
cluster de ce dernier, ainsi que la probabiliténotée P(l) qu'un
interneurone forme une connexion avec un neurone donnéde son cluster
sont toutes les deux faibles, probablement inférieures a` 0.1
d'après [Schuz, 1998, Albert and Barabási, 2002].
entièrement la structure du r'eseau :
- c : le nombre de clusters (entre 35 et 75);
- n : le nombre de neurones dans un cluster (environ 1500000/55
30000);
- p : le pourcentage de neurones de projection (environ 80%). Le
pourcentage d'interneurones est donc de 1 - p;
- P(c) : la probabilit'e qu'un neurone de projection projette
sur un cluster donn'e
(P(c) = 0.25 ou bien P(c) = d--a avec d la distance et
a un paramètre);
- P(p) : la probabilit'e qu'un neurone de projection projette sur
neurone donn'e,
sachant qu'il projette dans le cluster de ce dernier (P(p) <
0.1);
- P(l) : la probabilit'e qu'un interneurone forme une connexion
avec un neurone donn'e de son cluster (P(l) < 0.1).
Après avoir pr'esent'e les donn'ees anatomiques connues
sur la mRF, nous allons main-tenant pr'esenter une d'emonstration que nous
avons r'ealis'e au cours des recherches anatomiques montrant que P(l) > 45
× P(p).
1.4 D'emonstration de P(l) > 45 ×
P(p)
Soient, en plus des notations vues dans la section pr'ec'edente
:
- P(I ? I) la probabilit'e qu'un interneurone forme une
connexion avec un inter-neurone donn'e du même cluster (le signe ?
symbolise une connexion dans le graphe);
- P(I ? P) la probabilit'e qu'un interneurone forme une connexion
avec un neurone de projection donn'e du même cluster;
- nbI le nombre d'interneurones dans un cluster de la mRF;
- nbP le nombre de neurones de projection dans un cluster de la
mRF.
Supposons :
- qu'un interneurone ne projette que dans son propre cluster (le
nombre de projections d'interneurones en dehors de leur cluster est
n'egligeable);
- que P(c) = 0.25. C'est un des deux modèles
anatomiques connus pour P(c). Le second modèle, faisant d'ependre P(c)
de la distance entre le cluster source et le cluster destination, favorise une
structure de type small-world par rapport a` 0.25 comme le montre la figure
1.6. Par cons'equent, l'hypothèse prise ici permettra de g'en'eraliser
le r'esultat de la d'emonstration au second modèle, 'etant donn'e que
pour obtenir une structure small-world, intuitivement et comme le montre aussi
la figure 1.6, il faut un nombre 'elev'e de connexions dans un même
cluster (d'efini par P(l)) par comparaison au nombre de connexions
inter-cluster (d'efini par P(p)), ce que favorise le second modèle par
rapport au premier oiP(c) = 0.25.
Par construction :
- nous avons P(l) = P(I ? I) + P(I ? P) (car nous consid'erons
qu'un interneurone ne projette que dans son propre cluster);
- nous avons nbP/(nbP +nbI) = 80% (c'est la proportion de
neurones de projection, connue dans la litt'erature), donc nbP = 4 ×
nbI.
Comme nous l'avons vu pr'ec'edemment, 45% des synapses de
neurones de projection sont GABAergiques. Autrement dit, 45% des connexions
entrantes sur un neurone de projection proviennent d'un interneurone, car les
interneurones sont tous inhibiteurs et GABAergiques (il se peut qu'il y ait des
exceptions, mais n'egligeables).
nbI xP(I-+P)
Formellement, cela signifie que = 45%
nbIxP (I-+P )+nbP xP (p)xP (c)xc
ce qui est 'equivalent a` nbI × P(I ? P) = (45%/55%)
× (nbP × P(p) × P(c) × c) ce qui peut s''ecrire 'egalement
P(I ? P) = 4 × (45%/55%) × (P(p) × P(c) × c) (car nbP = 4
× nbI).
Remplaçons par les valeurs par P(c) = 0.25 et c = 55
(moyenne entre 35 et 75) : Cela donne donc P(I ? P) = 45 × P(p)
Or P(l) = P(I ? I) + P(I ? P)
D'o`u P(l) > 45 × P(p)
Ce r'esultat 'etaie fortement la thèse selon laquelle la
mRF a une structure de type small-world [Humphries et al., 2006], comme le
montre la figure 1.6.
Après avoir pr'esent'e la structure de la mRF, nous allons
maintenant analyser les deux uniques modèles publi'es de la mRF.
1.5 Modèles existants
1.5.1 Le modèle de Kilmer-McCulloch -
1969
Au cours des ann'ees 1960, W.L. Kilmer, W.S. McCulloch, and J.
Blum ont publi'e plusieurs articles proposant un premier modèle de la
mRF en se basant sur les 'etudes anatomiques de Scheibel & Scheibel. En
1969, ils ont synth'etis'e l'ensemble de leurs recherches dans un seul article,
qui devint un article de r'ef'erence sur le sujet [Kilmer et al., 1969].
Le fil conducteur de leur modèle est le concept de mode
de fonctionnement : un animal a` un instant donn'e suit un et un seul mode de
fonctionnement, comme par exemple manger ou dormir. La mRF a pour fonction de
passer d'un mode a` un autre. Pour appuyer cette hypothèse, lorsque la
RF est endommag'ee il est constat'e des changements de mode de fonctionnement
pathologique [Jouvet, 1967]. Il est pos'e comme hypothèse qu'àun
cluster est associ'e a` un et un seul mode de fonctionnement.
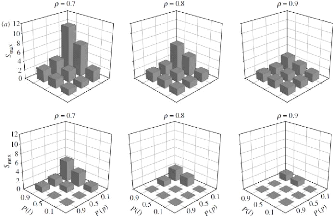
FIGURE 1.6: Cette figure montre a` quel degréla mRF
peut être considérée comme étant un réseau de
type small-world selon les valeurs de P(l), (P(p) et p. En hauteur, la valeur
Smax montre le degréde small-world : si elle est
supérieure a` 1, alors le réseau est considérécomme
étant small-world. Nous voyons clairement que la démonstration de
P(l) > 45 × P(p) accroàýt fortement les chances que la
mRF ait une structure de type small-world. Source : [Humphries et al., 2006]
Trois variantes du modèle sont propos'ees :
1. S-RETIC (S pour Simple, Retic pour Reticular) : Comme le
nom l'indique, ce premier modèle se veut simple et directement issu des
donn'ees anatomiques. Ce modèle est compos'e d'une douzaine de modules
recevant des stimuli et devant d'eterminer le mode a` choisir, un module
correspondant a` un cluster de la mRF. Ces modules reçoivent des
informations leur permettrant d'êtrea` la fois les g'en'eralistes, afin
de pallier toute d'efaillance de modules, et sp'ecialis'es afin d'être a`
même de prendre une d'ecision. Les modules sont plus ou moins li'es entre
eux en fonction de la distance qui les s'epare. Chaque module prend une
d'ecision et lui donne une probabilit'e, et la d'ecision finale prend en compte
l'ensemble des modules. Si le consensus pour un mode est assez grand, il y a
alors convergence vers ce mode. Ce modèle peut facilement être
'etendu a` davantage de modes et modules. Ce modèle donne des r'esultats
corrects, cependant il souffre de plusieurs manques, que la seconde variante va
essayer de combler.
discrimination, habituation et conditionnement. Pour
introduire ses propriétés, il faut fournir des informations
supplémentaires permettant d'indiquer si un stimuli ou un choix de mode
de fonctionnement est bon, neutre ou mauvais, a` l'instar de l'apprentissage
par renforcement. Cet apprentissage se fait au niveau de chaque module et de
façon coopérative entre les différents modules. Les
résultats pour ce modèle ne sont pas détaillés.
L'article souligne que STCRETIC a plusieurs caractéristiques peu
attrayantes : ses connexions ne respectent pas strictement le modèle
anatomique de la RF et il ne peut changer de mode que si un nouveau stimulus
arrive.
3. H-RETIC (H pour Hardware) : c'est une version hardware du
modèle, mais en cours d'élaboration au moment de
l'écriture de l'article, et jamais achevée par
la suite, STC-RETIC étant implémentéen un
software devenu trop compliquéa` maintenir et développer
efficacement avec les outils de l'époque.
Néanmoins, les résultats obtenus par les auteurs
avec ce modèle ne sont jamais vraiment exposés, et les
imprécisions concernant sa description font qu'il est difficile
d'implémenter le modèle pour l'analyser concrètement. En
outre, beaucoup de considérations de l'article sont certes
intéressantes, mais nullement explorées : ainsi exposé, le
modèle ne satisferait pas les exigences de publications scientifiques
actuelles. Il en résulte que ce premier modèle permet davantage
d'avoir une vue d'ensemble sur le mRF tout en donnant des pistes
intéressantes, a` défaut d'être précisément
décrit et réellement utilisable.
Pendant presque 40 ans, aucun nouveau modèle de la mRF
ne fut proposé. En 2005, Mark Humphries [Humphries et al., 2005] tenta
de reproduire le modèle de Kilmer-McCulloch et, afin d'évaluer
ses performances, il implémenta le modèle dans un robot
simuléainsi que dans un robot réel. Ce dernier fut
placédans le cadre une tàache de survie minimale inspirée
de [Girard et al., 2003] que nous détaillerons plus tard dans le
chapitre 4.1 : dans cette expérience, le robot a accès a` 4
variables (inputs de la mRF), a` partir desquelles il doit choisir une action
(output de la mRF) parmi 5 a` sa disposition, étant donnéque le
but pour le robot est de survivre le plus longtemps possible et que le temps de
survie reflète la qualitédu choix des actions.
Les résultats obtenus furent plutôt
décevants : certes le modèle de la mRF obtient des
résultat souvent meilleurs qu'un modèle purement aléatoire
(c'est-à-dire dans lequel les décisions sont prises
aléatoirement sans prendre en compte les variables en entrée),
néanmoins le modèle de la mRF est bien inférieur a` un
simple modèle de type Winner-Takes-All (WTA) dont la décision
prise correspond simplement a` la plus élevée des variables en
entrée.
1.5.2 Le modèle de Humphries - 2006
En 2006, Mark Humphries et ses collègues
présentèrent leur propre modèle de la mRF dans [Humphries
and Prescott, 2006], le second donc dans la littérature de la mRF. Ils
adoptèrent le formalisme classique des réseaux de neurones et
choisirent d'utiliser un modèle de population, o`u chaque neurone du
modèle représente un ensemble de neurones réels de la mRF,
comme le montre le schéma 1.7. Ils reprirent l'hypothèse de
Kilmer-McCulloch qui suppose qu'àun cluster est associée une et
une seule action.
Chaque cluster est composéde 2 neurones, modélisant
chacun l'activitémoyenne des neurones de chaque type de ce cluster :
- 1 neurone excitateur, projetant sur tous les autres neurones
hormis ceux de son cluster;
- 1 neurone inhibiteur, ne projetant que sur lui-même et
sur le neurone excitateur de son cluster.
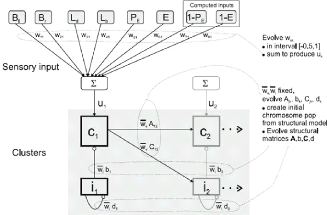
FIGURE 1.7: Modèle de Humphries. Ce schema montre deux
clusters, les entrees qu'il recoit ainsi que les connexions des
neurones du cluster de gauche. Chaque cluster contient un neurone inhibiteur
notei et un neuron excitateur notec. Source : [Humphries and Prescott, 2006]
Les poids des connexions reflètent d'une part les
probabilités des connexions issues des données anatomiques et
d'autre part le poids des connexions réelles dans la mRF, inconnues dans
la littérature.
[Girard et al., 2003] et certains paramètres ont 'et'e
optimis'es avec des algorithmes 'evolutionnistes, dont nous parlerons plus en
d'etail dans le chapitre 2.2. Les r'esultats s'av'erèrent 'egalement
plutôt d'ecevants en terme de dur'ee de survie, la plupart des
simulations de ce modèle ne furent que l'egèrement meilleures par
rapport au modèle purement al'eatoire.
1.6 Démarche et objectifs de ce
rapport
Bien que leurs r'esultats n'eurent pas de très bonnes
performances sur la tàache de survie en comparaison avec un
contrôleur al'eatoire, les deux modèles de la mRF ont eu le
m'erite de proposer des pistes de r'eflexion int'eressantes ainsi que, dans le
cas du second, des m'ethodes d''evaluation du modèle.
Notre d'emarche sera de construire un nouveau modèle de
la mRF, en observant strictement le formalisme des r'eseaux de neurones et en
respectant les donn'ees anatomiques, tout en diminuant le niveau d'abstraction
en augmentant le nombre de neurones par cluster. Nous avons d'ecid'e de
supprimer l'hypothèse pos'ee par les concepteurs des deux pr'ec'edents
modèles qu'un cluster correspond a` une et une seule action, car aucune
donn'ee anatomique n'appuie cette hypothèse et au vu de la diversit'e
des actions, il semble raisonnable de ne pas garder une telle contrainte.
Afin de ne pas avoir a` d'efinir tous les paramètres du
r'eseau a` la main et trouver les meilleurs r'eseaux, meilleur en terme de
tàaches de s'election de l'action et de respect des contraintes
anatomiques, nous utiliserons des algorithmes 'evolutionnistes a` l'instar de
Humphries. A` la diff'erence de ce dernier qui ne fixait qu'un seul objectif
dans ses 'evolutions, nous utiliserons un algorithme 'evolutionniste
multi-objectifs, ce qui nous permettra de mieux optimiser et 'etudier nos
r'eseaux.
Nous 'evaluerons notre modèle sur deux tàaches
de s'election de l'action : une tàache désincarnée
montrant de façon statique la capacit'e d'un r'eseau a` s'electionner
des actions, et une tàache incarnée mettant le modèle de
la mRF en situation r'eelle en s'inspirant de la tàache de survie
minimale qu'utilise 'egalement Humphries pour ses 'evaluations.
Le chapitre suivant expliquera en d'etail notre d'emarche et les
outils que nous avons utilis'es pour mener a` bien ce travail.
Chapitre 2
Matériel théorique
Pour commencer, nous allons expliquer comment la mRF dans
notre modèle sera formalisée en un réseau de neurones.
Puis, comme nous la ferons évoluer par algorithmes
évolutionnistes, nous allons présenter le fonctionnement de ces
derniers et voir ce qu'ils peuvent nous apporter. Les aspects techniques de
l'implémentation de ces outils théoriques seront
évoqués dans l'annexe A.
2.1 Les réseaux de neurones
Un r'eseau de neurones est compos'e d'un ensemble de neurones
et d'un ensemble de connexions orient'ees liant certains neurones d'entre eux.
Formellement, nous pouvons le consid'erer comme 'etant un graphe orient'e et
pond'er'e, chaque noeud correspondant a` un neurone.
Il existe diff'erents types de neurones : dans notre
modèle, nous utiliserons une variante des neurones a` taux de d'echarge
de type int'egrateurs a` fuite, appel'es lPDS (locally Projected Dynamical
Systems) car ils permettent de mod'eliser une population de neurones. Nous
avons choisi les lPDS en raison de leur propri'et'e de stabilit'e
int'eressante, puisqu'il a 'et'e montr'e, par exemple, que la stabilit'e (au
sens de la contraction) d'un système non lin'eaire compos'e de lPDS
d'ecoule directement de la stabilit'e du même système sans lPDS,
ce qui n'a pas 'et'e montr'e pour les int'egrateurs a` fuite standard [Girard
et al., 2008]. Comme nous cherchons ici a` construire un système
permettant la s'election de l'action, la stabilit'e est pr'ef'erable a`
l'instabilit'e.
Un neurone lPDS est caract'eris'e par 2 paramètres : -
ô, correspondant a` la constante de temps;
- threshold, correspondant au seuil d'activation.
Par simplicite, afin de ne pas multiplier les param`etres
libres, nous avons fixeô a` 5ms et mis le threshold a` 0. Nous avons
egalement fixele pas d'iteration dt, qui doit etre par construction toujours
inferieur a` ô, a` 1ms.
La premi`ere operation realisee par le neurone consiste en une
somme des grandeurs
recues en entrees, ponderees par les
coefficients synaptiques, c'est-`a-dire la somme
|
w1x1 + .. . + wmxm =
|
Xm
j=1
|
wjxj, o`u les xi etant les entrees et wi les coefficients
|
synaptiques.
(m
threshold +
Nous devons ajouter le seuil threshold a` cette formule :
Ewjxj
j=1
Nous utiliserons l'integration des lPDS par la methode
approchee d'Euler. La fonction d'activation sera donc la suivante,
an etant la valeur interne actuelle du neurone, an+1 sa
future valeur interne, egale a` la valeur de sortie :
an+1(x) = #177;max (1,min (0, (an + (x - an) * dt)))
ô
Comme x correspond a` la somme ponder'ee des grandeurs
recues en entrees, cela nous donne au final :
? an+1 = #177;max 1, min (0, an + (threshold + Ewjxj -
an) X dtô
j=1
Le #177; present dans la formule traduit le fait qu'un neurone
lPDS peut etre soit excitateur, soit inhibiteur.
La figure 2.1 montre un exemple de neurone, et le graphe B.1
represente un reseau de neurones issu de notre mod`ele correspondant a` une mRF
avec 4 clusters.
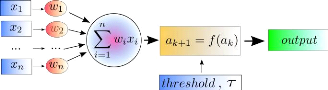
FIGURE 2.1: Exemple d'un neurone avec 2 entrées et une
fonction d'activation a` seuil.
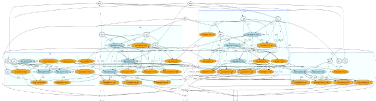
FIGURE 2.2: Exemple d'une mRF a` 4 clusters. Les neurones
oranges sont excitateurs, les neurones bleus foncésont inhibiteurs. Un
cluster correspond a` un rectangle bleu. Les neurones situés en dehors
des rectangles bleus représentent les entrées que
recoit la mRF ainsi que les neurones vers lesquels elle projette.
Cette figure se trouve également dans l'annexe B en version agrandie.
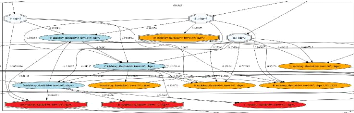
FIGURE 2.3: Exemple d'un cluster de la mRF. Les neurones
oranges sont excitateurs, les neurones bleus foncésont inhibiteurs.
Chaque connexion synaptique a` un poids entre 0 et 1. Les 3 neurones en bleu
clair sont les entrées (neurones d'entrée), les 3 neurones en
rouge sont les sorties de la mRF (neurones de sortie). Cette figure se trouve
également dans l'annexe C en version agrandie.
De même, chaque cluster de la mRF a le même nombre
de sorties. Au niveau global de la mRF, les valeurs de sorties correspondent a`
la moyenne des valeurs des sorties de chaque cluster. La figure C.1 montre un
cluster. Un cluster a un nombre de neurones et de connexions variables.
Ces réseaux comportant une quantitéimportante de
neurones, de connexions et de paramètres, il serait fastidieux de les
optimiser a` la main pour étudier en quelle mesure leur structure permet
la sélection de l'action. Par conséquent, nous avons choisi
d'utiliser les algorithmes évolutionnistes pour trouver des solutions
par cette méthode d'optimisation qui a des propriétés
particulièrement intéressantes pour notre problème comme
nous allons le voir dans la section suivante.
2.2 Les algorithmes 'evolutionnistes
2.2.1 D'efinitions
Les algorithmes 'evolutionnistes, 'egalement appel'es
algorithmes 'evolutionnaires, sont une famille d'algorithmes d'optimisation
s'inspirant du principe de s'election naturelle de la th'eorie
darwinienne. Dans le cadre de la s'election naturelle, un environnement donn'e
contient une population d'individus qui sont en concurrence pour la survie et
la reproduction. L'aptitude de chaque individu a` r'ealiser ces deux objectifs
d'etermine leur chance d'avoir des enfants, autrement dit de transmettre leurs
gènes a` des individus de la g'en'eration suivante, lesquels auront pour
des raisons g'en'etiques une chance accrue de bien r'eussir a` leur tour, voire
mieux, ces deux objectifs.
Ce principe d'am'elioration constante au cours des
g'en'erations est repris par les algorithmes 'evolutionnistes pour optimiser
des solutions a` un problème. A` la g'en'eration
initiale, une population compos'ee
d'individus diff'erents est g'en'er'ee, al'eatoirement ou bien
selon d'autres m'ethodes. Un individu correspond a` une solution au
problème, plus ou moins bonne : la qualit'e de l'individu par rapport au
problème est appel'ee fitness, le terme anglais
traduisant le degr'e d'ad'equation de la solution par rapport au
problème a` r'esoudre. Plus la fitness d'un individu est 'elev'ee, plus
ce dernier a des chances de transmettre une partie ou la totalit'e de son
g'enotype dans des individus de la g'en'eration suivante.
Un individu est cod'e sous la forme d'un
g'enotype, qui peut avoir n'importe quelle forme, telle une
chaàýne de caractères (algorithmes g'en'etique) ou bien un
vecteur de r'eels (strat'egies d''evolution). Chaque g'enotype est transform'e
en un ph'enotype au moment de l''evaluation de l'individu,
autrement dit lorsque que sa fitness est calcul'ee. Dans certains cas, le
ph'enotype est identique au g'enotype : on parle alors de codage
direct. Sinon, le codage est dit indirect. Par exemple, imaginons que
l'on souhaite optimiser la taille d'un parall'el'epipède rectangle
d'efini par sa longueur, sa hauteur et sa largeur. Pour simplifier l'exemple,
supposons que ces trois quantit'es soient des nombres entiers compris entre 0
et 15. On peut alors d'ecrire chacune d'elles en utilisant un nombre binaire de
4 bits. Un exemple de solution potentielle peut avoir pour g'enotype 0001 0111
01010. Le ph'enotype correspondant serait un parall'el'epipède de 1 de
long, 7 de haut et 10 de large.
Dernière d'efinition avant d'appliquer ces th'eories a`
notre modèle de la mRF, au moment du passage de l'ancienne a` la
nouvelle g'en'eration, sont appliqu'ees des op'erateurs de variation
dont le but est de manipuler les individus. Il existe deux types
d'op'erateurs de variation distincts :
- les op'erateurs de mutation, qui servent a`
introduire des variations au sein d'un même individu, a` l'instar des
mutations g'en'etiques;
- les opérateurs de croisement, qui
servent a` se faire croiser au moins deux génotypes différents,
a` l'instar des croisements génétiques issus de la
reproduction.
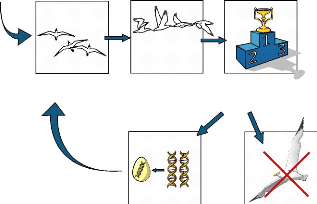
Population initiale La fitness du
phénotype est calculée
Les individus sont classés en fonction de leur fitness
Les descendants sont ajoutés à la population
Les individus avec les meilleurs fitness sont croisés
entre eux ; des mutations aléatoires sont ajoutées
Les individus avec les plus mauvaises fitness sont enlevés
de la population
FIGURE 2.4: Fonctionnement d'un algorithme
évolutionniste : a` partir d'une population initiale de solutions, ces
dernières sont classées selon leur fitness, les moins bonnes sont
éliminées et les meilleurs sont utilisées pour produire de
nouvelles solutions. Source : [Doncieux et al., 2004]
Nous avons choisi les algorithmes évolutionnistes car
ils ont fait leurs preuves dans des domaines divers tels la recherche
opérationnelle, la robotique, la biologie, la finance ou encore la
cryptographie. De plus, ils permettent d'optimiser plusieurs objectifs en
parallèle et nous pouvons les utiliser comme des boàýtes
noires car ils ne présupposent aucune
propriétémathématique sur le modèle a` optimiser,
permettant ainsi dans notre cas d'optimiser un système dynamique et non
linéaire tel un modèle neuronal. Leur seule réelle limite
est la complexitécomputationnelle, d'o`u la décision de coder
notre programme dans un langage rapide (C++), multi-threadé, et de
l'exécuter sur une grappe de serveurs. L'annexe A expose en
détail les aspects techniques de l'implémentation.
2.2.2 Application
Dans notre modèle, la mRF est modélisée
sous forme d'un réseau de neurones. Le génotype choisi lors de
l'implémentation est un ensemble de réseaux de neurones
correspondant chacun a` un cluster de la mRF ainsi qu'un vecteur contenant
l'ensemble des connexions entre les clusters, que nous appellerons
interconnexions. Le phénotype est obtenu a` partir du
génotype en copiant chacun de ces réseaux dont un grand
réseau, la mRF, sans oublier d'y rajouter les interconnexions.
Nos opérateurs de mutation sont :
- Ajout/suppression d'un neurone;
- Ajout/suppression/modification d'une connexion
(intra-réseau) ou d'une interconnexion (inter-réseau).
Nous aurions pu au cours des mutations modifier d'autres
paramètres, par exemple certaines propriétés des neurones
(e.g. inhibiteur/excitateur), néanmoins nous avons
préférélimiter le degréde libertéde
l'évolution. 'Egalement, nous n'avons pas choisi d'opérateurs de
croisement : bien qu'intuitivement nous pourrions penser qu'il serait
intéressant de croiser des mRF en leur permettant de mélanger
leurs clusters, une telle opération est d'une part très
délicate a` implémenter car les interconnexions sont propres a`
chaque cluster et chaque mRF, et d'autre part de tels croisements ne seraient
pas vraiment interprétables au niveau de l'évolution étant
donnéque le ràole de chacun des clusters n'est pas défini
a priori.
Une partie très délicate fut
l'implémentation des contraintes anatomiques de la mRF afin que
l'évolution produise des réseaux de neurones cohérents
avec les connaissances anatomiques. Nous l'avons implémentéa`
deux niveaux complémentaires :
- en amont, au niveau des opérateurs de mutation : a`
chaque mutation, nous veillons
a` rester aux alentours des données anatomiques;
- en aval, au niveau du calcul de la fitness : nous avons
utiliséun algorithme évolutionniste multi-objectif, ce qui nous
permet de définir un objectif de plausibilitéanatomique, poussant
ainsi les réseaux a` respecter les contraintes anatomiques.
La définition des objectifs impacte
considérablement les résultats. Nous avons mis en place un
objectif de plausibilitéanatomique, en plus des objectifs propres
tàaches de sélection de l'action que nous détaillerons
dans la section suivante.
Enfin, nous avons choisi d'utiliser l'algorithme
NSGA-II [Deb, 2001, Deb et al., 2002], qui est a` ce jour un
des plus performants algorithmes évolutionnistes multi-objectifs et de
loin le plus utilisé. Contrairement a` un algorithme mono-objectif o`u
il n'y a qu'un seul meilleur individu (avec possiblement des individus ex
æquo), les meilleurs individus issus d'une évolution
multi-objectif formeront un front appeléfront de Pa-
reto, d'une dimension égale au nombre d'objectifs
fixés. La figure 2.5 montre un front de Pareto de dimension 2 et la
figure 2.6 compare l'ensemble de résultats obtenus par un algorithme
mono-objectif par rapport a` l'ensemble de résultats obtenus par un
algorithme mono-objectif.
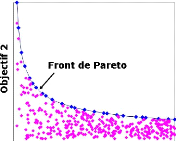

FIGURE 2.5: Exemple de front de Pareto de dimension 2 : sauf
mention contraire, les algorithmes évolutionnistes maximisent les
objectifs contrairement a` la majoritédes algorithmes d'optimisation
dont le but est de les minimiser.
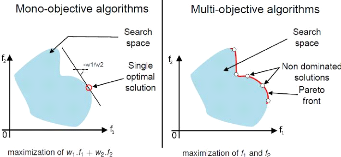
FIGURE 2.6: Mono vs multi-objectif. Un algorithme
mono-objectif donnera 1 résultat, tandis qu'un algorithme multi-objectif
donne un ensemble de résutat. Sur la figure de gauche, 11 et 12
correspondent respectivement aux scores obtenus pour l'objectif 1 et 2. w1 et
w2 sont des poids affectés aux deux scores, la combinaison
linéaire correspondant a` un objectif unique afin de pouvoir utiliser un
algorithme mono-objectif. Source: Stéphane Doncieux et Jean-Baptiste
Mouret.
A` présent que nous avons présentéd'une
part la mRF et d'autre part les outils théoriques que nous avons
utilisés pour le projet, tout en expliquant leur ràole dans la
modélisation de la mRF, nous allons dans le chapitre suivant
détailler les expériences de sélection de l'action
réalisées et analyser les résultats obtenus.
Chapitre 3
Tâche désincarnée : la
tâche
vectorielle abstraite
Dans ce chapitre, nous allons présenter la
première expérience pour évaluer notre modèle de la
mRF. Dans un premier temps, nous détaillerons l'expérience
réalisée, et dans un second temps nous analyserons les
résultats.
3.1 Expérience
La tàache d'esincarn'ee correspond a` une tàache
abstraite de s'election. Le principe est simple : nous donnons en entr'ee de la
mRF un vecteur de dimension 3, toutes les valeurs 'etant comprises entre 0 et
1. Ce vecteur d'entr'ee repr'esente un ensemble de valeurs issues de diverses
sources de donn'ees.
L'objectif de la mRF est de s'electionner une action. Pour
cela, nous avons d'ecid'e en nous inspirant de [Humphries et al., 2007] que
pour que la mRF choississe la bonne action, son vecteur de sortie, 'egalement
de dimension 3, doit avoir sa valeur maximum dans la même dimension que
celle contenant la valeur maximum du vecteur d'entr'ee. Par exemple, si le
vecteur d'entr'ee est (0.3, 0.5, 0.1), la mRF s'electionnera la bonne action si
et seulement si son vecteur de sortie est de la forme (a, b, c), o`u b > a
et b > c, comme le montre la figure 3.1.
Afin que l''evolution ne sur-apprenne pas un ensemble
restreint de vecteurs, ce qui empêcherait une bonne g'en'eralisation, la
mRF sera 'evalu'ee sur sa capacit'e a` s'electionner une action sur l'ensemble
de vecteurs de dimension 3 o`u nous faisons varier chaque 'el'ement d'un entre
0 et 1 d'un pas de 0.1, et en supprimant les vecteurs ayant plusieurs
composantes au maximum, afin d''eliminer les cas ambigus. Voici
contrast(X) = tu u u v
o`u k = arg max
n-1
i
xi.
?
??
(xi - xk
Xn
i=1
?
)2 ? ?
FIGURE 3.1: Ce schéma montre les deux premiers
objectifs de la tâche désincarnée : le réseau
recoit en entrée un vecteur de dimensions 3 dont les valeurs
sont entre 0 et 1, et il doit a` la fois prendre la bonne décision
(c'est-à-dire sélectionner la bonne dimension) et maximiser le
contraste.
cet ensemble de vecteurs 'ecrit formellement, ensemble qui
contient en tout 1155 { 'el'ements : }
X = (x1, x2, x3) | (x1, x2, x3) E S3 A (k = arg max
xi, -+ ((i =6 k A i E 1, 3K) -+ x > xi)
i
o`u S = {0.1 x i | i E [0, 10K}
N'eanmoins, ce premier objectif admet des solutions
inint'eressantes, comme par exemple un r'eseau de neurones qui copieraient
simplement les entr'ees en sortie. Afin d'op'erer une r'eelle s'election de
l'action, nous avons d'efini un second objectif forçant la mRF a`
maximiser le contraste entre la valeur maximum du vecteur de sortie et ses
autres valeurs. La formule g'en'erale pour calculer le contraste est la
suivante, en notant xi le ième 'el'ement du vecteur X et n sa
dimension :
/((0.6_0.5)2+(0.6_0.3)2)
contrast = 0.22. Plus le contraste est élevé,
plus l'action
2
est clairement sélectionnée.
Le troisième et dernier objectif sera de respecter les
contraintes anatomiques, pour que l'évolution produise des
réseaux se rapprochant le plus possible d'une structure de réseau
de type mRF. Le score de cet objectif de plausibilitéanatomiques
correspond a` une combinaison linéaire de scores de sous-objectifs, ces
derniers représentant chacun une des contraintes anatomique suivante
(nous reprenons les notations du chapitre 1.3) :
- p doit être égal a` 80%, la formule du score est
scorep = (-1) × (0.8 - p)2 ;
- P(c) doit être égal a` 25%, la formule du score
est scorepc = (-1) × (0.25 - pc)2 ; - les synapses
des neurones de projection sont a` 45% GABAergic, la formule du score
est scoregabaergic = (-1) × (0.45 -
percentgabaergic)2 ;
- les interneurones ne peuvent pas projeter en dehors de leur
cluster, nous notons nb interneuron not within chip le nombre d'interneurones
ne respectant pas cette contrainte;
- les neurones de projection ne peuvent pas projetter dans
leur cluster, nous no-tons nb projection within chip le nombre de projection ne
respectant pas cette contrainte.
Nous n'avons pas mis de contraintes sur P(p) et P(l) car les
données anatomiques connues a` leur sujet sont assez imprécises.
Comme nous l'avons soulignédans le chapitre 2.2, les algorithmes
évolutionnistes maximisent les objectifs, d'o`u les scores
négatifs puisque se rapprocher des contraintes équivaut a` un
score se rapprochant de la valeur 0.
La formule globale pour calculer le score du troisième
objectif est :
scoreanat =
8×(scorep+scorepc+scoregabaergic)-1×nb interneuron not within chip-
0.5 × nb projection within chip
Les pondérations 8, 1 et 0.5 ont
étéchoisies arbitrairement, le seul critère étant
que chacun des scores pondérés ait une valeur très
approximativement du même ordre de grandeur, afin de maximiser les
chances que l'évolution optimise chacun d'entre eux, et non juste de
certains potentiellement aux dépens des autres.
En résumé, voici les trois objectifs que nous avons
retenus :
- Objectif 1 : nombre de bonnes décisions. Minimum : 0,
maximum : nombre de vecteurs testés;
- Objectif 2 : importance du contraste. Minimum : 0, maximum : 1
(car toutes les valeurs des vecteurs sont comprises entre 0 et 1);
- Objectif 3 : plausibilitéanatomique. Minimum : -8,
maximum : 0.
En plus de ces trois objectifs situ'es en aval, nous avons
'egalement pos'e des contraintes anatomiques en amont, c'est-à-dire au
coeur de la d'efinition des op'erateurs de mutation, afin de pousser
l''evolution a` respecter le plus possible les donn'ees anatomiques. Nous
avions d'ejàmentionn'e dans le chapitre 2.2.2 cette double application
des contraintes. Voici les contraintes que nous avons mises dans les
op'erateurs de mutation :
- impossibilit'e pour un neuron de projection de projeter dans
leur cluster;
- impossibilit'e pour un internerneurone de projeter en dehors de
leur cluster; - P(c) doit être proche 25%;
- p doit être proche 80%.
Comme nous le voyons, ces contraintes ne contiennent qu'une
partie des donn'ees anatomiques connues : l'int'erêt de les ajouter dans
les op'erateurs de mutation est que l''evolution g'enère moins
d'individus manifestement non plausibles d'un point de vue anatomique. Mettre
trop de contraintes dans les op'erateurs des mutations serait n'eanmoins
risqu'e car, outre son coit computationnel, restreindre excessivement l'espace
de recherche peut rendre plus difficile l'obtention d'une bonne solution.
Nonobstant sa simplicit'e apparente, cette tàache
d'esincarn'ee permet de valider ou d'invalider la possibilit'e pour une
structure anatomiquement proche de la mRF d'effectuer des s'elections. Nous
allons analyser les r'esultats obtenus dans la section suivante.
3.2 Résultats
Tout d'abord, voici les paramètres que nous utiliserons
tout au long des exp'eriences, sauf indication contraire :
- taille de la population : 500 individus;
- nombre de g'en'erations : 500;
- nombre de clusters : 4;
- nombre de neurones initial par cluster (en plus des neurones
d'entr'ee et de sortie) : tirage al'etoire uniforme entre 3 et 10, les clusters
pouvant avoir un nombre de neurones diff'erents au sein de la même
mRF;
- probabilit'e d'ajouter/supprimer un neurone/une connexion
(inter ou intra-cluster) : 0.05;
- probabilit'e de modifier le poids d'une connexion (inter ou
intra-cluster) : 0.1; - nombre d'it'erations pour propager une entr'ee dans le
r'eseau : 100.
Les 'evolutions calcul'ees nous donnent des individus
pr'esentant au bout de 300 g'en'e-
rations plus de 95% de bonnes d'ecisions,
voire dans certains cas 100%, respectant
presque parfaitement les
contraintes anatomiques et dont les vecteurs de sortie ont
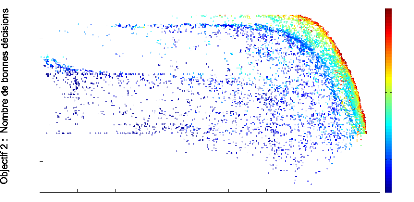
un contraste supérieur a` 0.6. Le graphique 3.2 montre
un front de Pareto 2D obtenu typiquement lorsque l'on représente les
scores des objectifs de bonnes décisions et de contaste obtenus par
chaque individu. Le graphique 3.3 montre un front de Pareto 3D montrant les
scores des 3 objectifs.
1200
Numéro de génération
500
1000
400
800
300
600
200
100
0
400
200
0
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Objectif 1 : contraste
FIGURE 3.2: Front de Pareto de dimension 2 repr'esentant les
scores des objectifs de contaste en abscisse et de bonnes d'ecisions en
ordonn'ee obtenus par chaque individu de chaque g'en'eration au cours de
l''evolution.
Prenons les 5 meilleurs individus présentant 1155 de
bonnes décisions et regardons la moyenne de leurs résultats :
- score de nombre de bonnes décisions : 1155 (ce qui
correspond au maximum théorique);
- score de contraste : 0.68761 (le maximum théorique est
1);
- score de plausibilitéanatomique : -1.20792e-15 (le
maximum théorique est 0).
Le tableau suivant résuméles statistiques
anatomiques moyennes de ces 5 individus.
Numéro de génération
0
0
-1
-2
-3
-4
-5
-6
-7
1200
1000
800
0.7
0.8
600
400
200
0.2
0.3
0.4 0.5
0.6
0
0
0.1
500
400
300
200
100
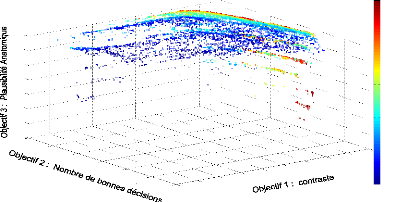
FIGURE 3.3: Front de Pareto de dimension 3 repr'esentant les
scores des objectifs de bonnes d'ecisions, de contaste ainsi que de
plausibilit'e anatomique obtenus par chaque individu de chaque g'en'eration au
cours de l''evolution.
|
Statistiques sur
les 5 meilleurs
individus
|
Contrainte
dans op'erateurs
de mutation
|
Contrainte
dans objectif
|
Données
anatomiques
connues
|
|
nombre total
de neurones
|
57
|
Aucune
|
Aucune
|
NA
|
|
nombre total
de connexions
|
117
|
Aucune
|
Aucune
|
NA
|
|
p
|
80%
|
80%
|
80%
|
80%
|
|
percentgabaergic
|
45%
|
Aucune
|
45%
|
45%
|
|
P(c)
|
25%
|
25%
|
25%
|
25%
|
|
P(p)
|
8.73626%
|
Aucune
|
Aucune
|
< 10%
|
|
P(l)
|
8.61552%
|
Aucune
|
Aucune
|
< 10%
|
|
Nombre de
interneurones
projettant en
dehors de
leur
cluster
|
0
|
0
|
0
|
0
|
|
Nombre de
neurones de
projection
projettant
dans
leur cluster
|
0
|
0
|
0
|
0
|
Ce résultat montre qu'en respectant les données
anatomiques connues de la mRF, cette dernière peut effectuer une
tàache de sélection de l'action. Pour comparaison, [Humphries et
al., 2007] dont cette tàache est inspirée obtient environ 75% de
bonnes décisions, sans se pencher sur le contraste, et considère
que cela suffit pour montrer la possibilitéd'une sélection de
l'action.
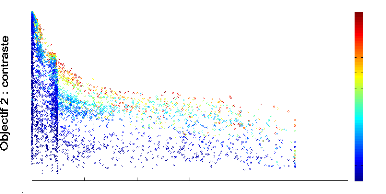
Nous avons également fait tourner le programme en
enlevant les contraintes situées dans les opérateurs de mutation.
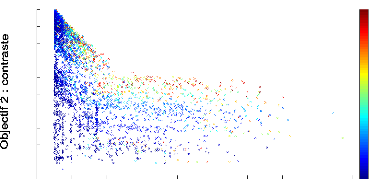
Comme le montre le graphique 3.4, cela a pour effet d'augmenter le nombre
d'individus ayant une faible plausibilitéanatomique, car nous voyons que
le front 2D représentant les scores des objectifs de bonnes
décisions et de contaste obtenus par chaque individu est beaucoup moins
nette que celui obtenu dans l'expérience initiale dont nous venons de
présenter les résultats. Cette observation correspond a`
l'intuition que nous avions. Néanmoins l'évolution
présente toujours des individus, certes plus rares que dans
l'expérience initiale, presque parfaitement plausibles anatomiquement,
de contraste supérieur a` 0.5 et dont le taux de bonnes décisions
est supérieur a` 95%.
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Numéro de génération
1200 400
1000
300
800
200
600
400
200
100
0
Objectif 1 : contraste
FIGURE 3.4: Front de Pareto 2D sans contraintes anatomiques
lors des mutations. Le front represente les scores des objectifs de bonnes
decisions et de contaste obtenus par chaque individu.
Une autre variante que nous avons essayée est d'enlever
les contraintes des opérateurs
des mutations et d'éliminer en
plus l'objectif de plausibilitéanatomique. Autrement
dit, nous avons
cherchéa` voir comment évoluerait un réseau sans
contrainte anato-
mique vis-à-vis de la tàache de
sélection.
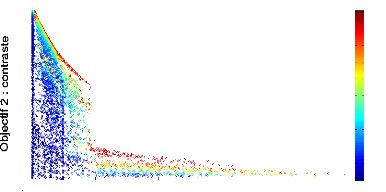
Les résultats montrent que d'une part les
réseaux obtenus ont des performances similaires a` celles obtenues avec
les réseaux contraints, voire légèrement meilleures (cf
graphique 3.5) si nous considèrons le contraste, et que d'autre part en
faisant des analyses statistiques sur la structure de ces réseaux, ils
ne tendent pas vers des structures de type mRF. Cela signifie que les
données anatomiques connues sur la mRF ne représentent ni un
avantage (car il existe d'autres structures de réseau tout aussi
performantes) ni un inconvénient pour la sélection.
1000
300
200
0
1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Numéro de génération
1200
800
200
600
100
400
Objectif 1 : contraste
FIGURE 3.5: Front de Pareto 2D de l''evolution sans aucune
contrainte anatomique (ni dans les mutations, ni dans un objectif). Le front
repr'esente les scores des objectifs de contaste en abscisse et de bonnes
d'ecisions en ordonn'ee obtenus par chaque individu de chaque g'en'eration au
cours de l''evolution.
Cette première série d'expériences
basées sur une tàache désincarnée a
montréla
capacitécomputationnelle de la mRF a` effectuer une
tàache de sélection. Notre modèle
est plus performant que celui de Humphries dans cette
tàache et nous y avons ajoutécomme contrainte
supplémentaire le contraste. Nous allons a` présent effectuer
une
seconde série d'expériences pour analyser les
performances de la mRF sur une tàache incarnée de simulation
robotique.
Chapitre 4
Tâche incarnee : la tâche de
survie minimale
A` l'instar du chapitre pr'ec'edent, nous allons dans ce
chapitre tout d'abord pr'esenter
l'exp'erience dans un premier temps, et
dans un second nous analyserons les r'esultats.
4.1 Experience
La tàache de survie minimale que nous utiliserons ici
est fortement inspirée de [Girard et al., 2003]. Il s'agit pour un robot
de sélectionner efficacement ses comportements afin d'assurer sa survie,
en maintenant ses variables d'état interne dans des intervalles
tolérables, sa zone de viabilité[Ashby, 1952]. Cette survie
dépend directement de la capacitédu robot a` se ravitailler
auprès de deux types de ressources différents, en un temps
limitépar son niveau de recharge. L'utilisation de deux ressources
différentes force le robot a` se déplacer dans l'environnement
pour accéder a` l'une puis a` l'autre et le met en situation de conflit
pour déterminer quelle ressource est prioritaire a` un instant
donné, susceptible de générer des oscillations
comportementales. Cette tàache sera simulée sur ordinateur.
Le robot sera placédans un environnement o`u il pourra
trouver deux types de ressources : des zones d'ingestion qui lui permettront de
faire des réserves et des zones de digestion o`u il pourra assimiler ses
réserves et les transformer en énergie utilisable. Sachant que
tous les comportements du robot consomment de l'énergie, il va donc
devoir alterner phases d'ingestion et de digestion pour survivre.
L'environnement expérimental est une surface plane de
400x400 unités entourée de
murs. Elle est recouverte de 25
carreaux de 80x80 unités, de trois types différents : 21
carreaux gris (zones neutres), 2 carreaux noirs (zones
d'ingestion), dont les ressources sont inépuisables, et 2 carreaux
blancs (zones de digestion). La figure 4.1 montre l'environnement.

FIGURE 4.1: Environnement de la tâche de survie
minimale. Nous y voyons 21 carreaux gris, 2 carreaux noirs et 2 carreaux
blancs, tous les carreaux étant de la même taille. Le cercle jaune
représente le robot.
Le robot est un disque de rayon 20 unités et
possède 2 variables internes :
- l'Energie Potentielle (EP) correspond aux
réserves puisées sur les zones d'ingestion, entre 0 et 1;
- l'Energie (E) est l'énergie
réellement utilisable pour survivre dans l'environnement, elle est
obtenue par digestion de l'EP sur les zones claires. Pour survivre, le robot
doit maintenir E au dessus de 0 et le maximum de E est 1.
Le robot a accès a` 4 capteurs externes :
- un pare-choc gauche (BL pour left bumper),
valeur binaire, a` 1 si contacts avec le mur, a` 0 sinon;
- un pare-choc droit (BR pour left bumper),
valeur binaire, a` 1 si contacts avec le mur, a` 0 sinon;
- un capteur de carreau noir (LD pour light
darkness), valeur binaire, a` 1 si sur un carreau noir, a` 0 sinon;
- un capteur de carreau blanc (LB pour light
brightness), valeur binaire, a` 1 si sur un carreau blanc, a` 0 sinon.
Le robot a 5 actions a` sa disposition :
- Explorer aléatoirement (wander) : le
robot se déplace aléatoirement (rotation aléatoire entre 0
et 9° suivie d'un déplacement vers l'avant de 5
unités). A` noter qu'en l'absence de capacités de navigation et
de mémoire sur l'environnement, seul ce comportement permet de trouver
des zones de recharges (carreaux blancs ou noirs). Cette action dure 2
unités de temps.
- 'Eviter un obstacle (avoid) : le robot
effectue une marche arrière de 60 unités suivie d'une rotation de
180°. Cette action dure 2 unités de temps.
- Recharger sur zone noire (reload on dark) :
le robot s'arrête et recharge son EP : äEP = 0.027 × LD. Nous
remarquons que le robot ne recharge réellement son EP que s'il se trouve
sur une zone noire. Cette action dure 1 unitéde temps.
- Recharger sur zone blanche (reload on
light) : le robot s'arrête et recharge son E : äE = 0.027 × LB
et äEP = -0.027 × LB. Nous remarquons que le robot ne recharge
réellement son E que s'il se trouve sur une zone blanche. Cette action
dure 1 unitéde temps.
- Se reposer (rest) : le robot ne fait rien.
Cette action dure 1 unitéde temps.
A` chaque unitéde temps, le robot consomme 0.002 de son
énergie, même lorsqu'il choisit de se reposer. Si l'énergie
devient négative ou nulle, alors le robot meurt.
Afin de choisir une action, la mRF reçoit en
entrée la salience de chacune des
actions
calculée a` partir des variables internes et externes. La
salience correspond au degréd'urgence ou de motivation a`
effectuer une action. Les formules utilisées ici pour le
calcul des saliences sont les mêmes que dans
l'évaluation du modèle de la mRF par [Humphries et al., 2005]
ainsi que dans l'évaluation d'un modèle des ganglions de la base
par [Girard et al., 2003].
- Swander = -BL - BR + 0.8(1 - PE) + 0.9(1 - E)
- Savoid = 3BL + 3BR
- Sreload on dark = -2LB - BL - BR + 3LD(1 - PE)/
- Sreload on light = -2LD - BL - BR + 3LB(1 - E) 1 - (1 -
PE)2
Si la mRF ne réussit pas a` converger avec les
saliences données en entrée, alors l'action de repos est
sélectionnée. Dans notre expérience, un nouveau vecteur de
salience est propagépendant 100 itérations (1 itération
durant 1ms) dans la mRF et nous considérons qu'il y a convergence
dès lors que sur les 50 dernières itérations la variation
de chacune des valeurs du vecteur de sortie de la mRF est inférieure a`
0.001. Lorsque la mRF converge, alors nous considérons que l'action
sélectionnée correspond a` la sortie la plus élevée
de la mRF. Nous testerons également une variante o`u l'action
sélectionnée est modulée en fonction du contraste du
vecteur de sortie de la mRF.
4.2 Résultats
Pour 'evaluer chaque contrôleur du robot, nous avons
simul'e 5 tàaches de survie mini-male dans la fonction fitness, en
plaçant a` chaque fois le robot a` un endroit al'eatoire sur la carte et
initialis'e avec comme valeurs 0.5 en 'energie et 1 en 'energie potentielle.
Comme a` chaque unit'e de temps le robot consomme 0.002 de son 'energie, sa
dur'ee de vie minimale est de 500 unit'es de temps. Afin que l''evaluation
prenne un temps raisonnable de calcul, nous avons limit'e les simulations a`
3000 unit'es de temps chacune.
Tout d'abord, afin de v'erifier une suffisante complexit'e de
la tàache, nous avons 'evalu'e un contrôleur al'eatoire, qui
d'ecidait au hasard une action parmi les cinq possibles. Les r'esultats de ce
contrôleur montre une survie moyenne entre 500 et 600 unit'es de temps,
ce qui confirme que la tàache ne peut être r'esolue par un
contrôleur al'eatoire et fournit une base de comparaison.
Une seconde v'erification pr'ealable que nous avons effectu'ee
fut de tester un contrôleur de type Winner-Takes-All (WTA), ce dernier
choisissant l'action en se basant sur la plus forte salience. Nos premiers
r'esultats ont montr'e que ces contrôleurs avaient une dur'ee de vie
approchant souvent les 3000 unit'es de temps, ce qui signifiait que la
tàache 'etait trop simple pour 'evaluer notre modèle de la mRF
correctement. Nous avons subs'equemment essay'e de trouver un facteur
complexifiant la tàache et nous avons trouv'e que la vitesse de
d'eplacement du robot, non sp'ecifi'ee dans [Humphries et al., 2005], influe
grandement sur les r'esultats. Initialement, dans notre exp'erience, lorsque le
contrôleur du robot choisit l'action a` explorer al'eatoirement, il se
d'eplace en avant de 10 unit'es après avoir effectu'e une rotation
al'eatoire. Lorsque nous diminuons la vitessse d'eplacement a` 5 unit'es, la
tàache devient plus difficile et un contrôleur WTA n'a plus qu'une
dur'ee de vie moyenne d'environ 1250 unit'es de temps, ce qui est loin de la
dur'ee de vie maximum (3000 unit'es de temps). Par cons'equent, la
tàache semble non triviale a` r'ealiser. La figure 4.2 compare les temps
de survie des contrôleurs al'eatoire et WTA sur 1000 tàaches de
survie.
Les r'esultats du contrôleur mRF montrent qu'en quelques
g'en'erations seulement le robot r'eussit a` vivre plus de 2500 unit'es de
temps, voire le maximum 3000. N'eanmoins, il faut plusieurs centaines de
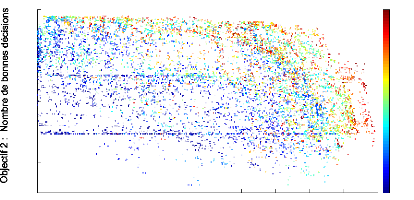
g'en'erations pour que le contraste devienne important. La figure 4.3 pr'esente
l''evolution du front de Pareto 2D d'un contrôleur mRF au bout de 500
g'en'erations : le temps de survie est proche ou 'egal a` la valeur maximum, le
contraste est d'environ la moiti'e du maximum th'eorique pour les meilleurs
individus. Les scores de l'objectif de plausibilit'e anatomique montrent que la
mRF respecte presque exactement les donn'ees connues sur la mRF. Concernant le
temps pass'e sur chacune des actions en moyenne pendant une tàache de
survie, la figure 4.5 montre qu'il n'y a pas de diff'erence notable entre les
diff'erents contrôleurs, a` l'exception
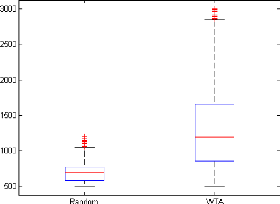
FIGURE 4.2: Comparaison des temps de survie des contrôleurs
aléatoire et WTA sur 1000 tâches de survie.
triviale du contrôleur aléatoire.
Nous avons essayéde forcer la mRF a` avoir un contraste
élevéen modulant les actions en fonction du contraste. A` cet
effet, nous avons redéfini chacune des 5 actions en incluant la valeur
du contraste, f étant la fonction de modulation du contraste :
- Explorer aléatoirement (wander) : le
robot se déplace aléatoirement (rotation
aléatoire entre 0 et f(contrast)x9° d'un
déplacement vers l'avant de f(contrast)x
5 unités).
- 'Eviter un obstacle (avoid) : le robot
effectue une marche arrière de f(contrast)x 60 unités suivie
d'une rotation de f(contrast) x 180°. Cette action dure 2
unités de temps.
- Recharger sur zone noire (reload on dark) :
äEP = f(contrast) x 0.027 x LD. - Recharger sur zone blanche
(reload on light) : äE = f(contrast) x 0.027 x LB et äEP =
-f(contrast) x 0.027 x LB.
- Se reposer (rest) : le robot ne fait rien.
En prenant comme fonction de modulation f(x) = /x et en
évaluant toujours chaque réseau sur 5 tàaches de survie,
les réseaux mRF obtenus présentent des durées de survie
similaires voire un peu inférieure aux contrôleurs WTA. Cependant,
le contraste est un peu meilleur que lorsque nous introduisons une fonction de
modulation, comme le
0.2
0
Numéro de génération
1
500
0.8
400
0.6
300
0.4
500 1000 1500 2000 2500 3000 3500
200
100
0
Objectif 1 : durée de survie
FIGURE 4.3: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution. Le contrôleur mRF a 'et'e 'evalu'e
sur 5 tâches de survie.
montre la figure 4.6. Par conséquent, la fonction de
modulation introduit une pression de sélection favorisant le contraste
aux dépens de la durée de survie. L'objectif de
plausibilitéanatomique a toujours un score entre -1 et 0, ce qui
signifie que les réseaux ont bien une structure de type mRF.
Autre variante de l'expérience initiale, nous avons
essayéde rendre la tàache plus
réaliste en supprimant
le calcul des saliences et donnant directement en entrée
des
réseaux les 4 variables externes (BL, BR, LD et LB) ainsi que les
2 variables internes
(E et EP), ce qui a pour effet de complexifier la
tàache. Nous avons également donnéen entrée 1-- E
et 1-- EP afin d'éviter que la tàache soit trop complexe, en
reprenant
ainsi la configuration de l'expérience de [Humphries and
Prescott, 2006]. Les réseaux ont donc dans cette variante 8
entrées et 4 sorties.
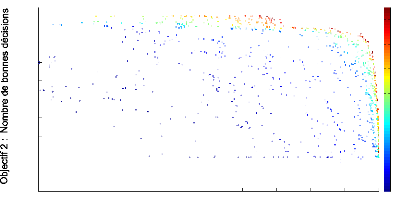
Le graphique 4.7 montre les fronts de Pareto obtenus au bout
de 1000 générations : nous voyons que certains réseaux ont
une durée de vie dépassant 2000 unités de temps,
néanmoins le contraste est très faible (inférieur a` 0.1).
Par comparaison avec les résultats obtenus avec le modèle de
Humphries [Humphries and Prescott, 2006], ce dernier indique que la plupart des
réseaux obtenus par évolution réussissent a` faire a`
peine mieux qu'un contrôleur aléatoire, mais les actions sont
modulées en fonction du contraste a` l'instar de ce que nous avons fait
dans l'expérience précédente. Ici,
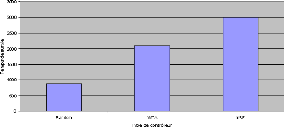
FIGURE 4.4: Comparaison des meilleures moyennes de temps de
survie sur 5 tâches obtenues par des contrôleurs aléatoire,
WTA et mRF. Pour chaque type de contrôleur, nous avons effectué20
000 évaluations, chacune d'entre elles consistant a` faire 5
tâches de survie et calculer la moyenne de la durée de survie.
Nous n'avons gardéici que la meilleure moyenne trouvée pour
chaque type de contrôleur.
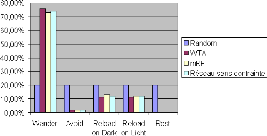
FIGURE 4.5: Comparaison du temps passésur chacune des
actions par les contrôleurs aléatoire, WTA et mRF. Ces
statistiques agrègent les données 500 tâches de survie pour
chacun des contrôleurs ayant les durées de survie les plus
élevées parmis 50 000 tâches de survie simulées.
nos réseaux réussissent clairement mieux qu'un
contrôleur aléatoire, cependant les actions ne sont pas
modulées.
Ces résultat montrent que la mRF est globalement plus
efficace qu'un simple réseau WTA et encore plus qu'un contrôleur
aléatoire, comme le résume la figure 4.4, contrairement aux
expériences de [Humphries et al., 2005] qui n'avaient pas réussi
a` évoluer la mRF de façon suffisamment optimale pour
dépasser le WTA. Cela signifie que la mRF est non seulement apte a`
faire de la sélection de l'action, mais que celleci peut faire face a`
des situations complexes o`u un réseau WTA ne suffirait pas.
Numéro de génération
500
400
300
200
100
0
400 600 800 1000 1200 1400 1600 1800 2000 2200
1
0.8
0.6
0.4
0.2
0
Objectif 1 : durée de survie
FIGURE 4.6: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution, avec modulation des actions en fonction
du contraste. La fonction de modulation est f(x) = /x et le contrôleur
mRF a 'et'e 'evalu'e sur 5 tâches de survie.
Néanmoins, dans les variantes o`u nous essayons de
rendre la tàache de survie plus réaliste, en modulant les actions
en fonction du contraste des vecteurs de sortie de la mRF ou en donnant a`
cette dernière directement les variables internes et externes sans
calcul préalable de saliences, les résultats que nous avons
obtenus sont moins probants : il faudrait approfondir davantage ces variantes.
Autre point a` creuser, il serait intéressant de quantifier la
propension de nos réseaux mRF a` généraliser leurs
performances en les évaluant sur un nombre plus important de
tàaches de survie.
Numéro de génération
1000
1
0.8
0.6
0.4
0.2
0
800
600
400
200
0
500 1000 1500 2000 2500 3000
Objectif 1 : durée de survie
FIGURE 4.7: Front de Pareto 2D de l''evolution d'un
contrôleur mRF repr'esentant les scores des objectifs de dur'ee de survie
(abscisse) et de contaste (ordonn'ee) obtenus par chaque individu de chaque
g'en'eration au cours de l''evolution. Le r'eseau recoit directement
en entr'ee toutes les variables externes et internes, et le contrôleur
mRF a 'et'e 'evalu'e sur 5 tâches de survie.
Chapitre 5
Discussions et perspectives
La nature de ce travail de modélisation de la mRF
était avant tout exploratoire. Seuls deux modèles existaient et
le nombre d'articles portant sur cette zone du cerveau est assez faible. Nous
avons donc forcément dàu faire un certain nombre de choix et
focaliser nos recherches sur certains points qui nous semblaient les plus
essentiels pour initier un tel travail de modélisation. Cependant de
nombreux axes d'études restent a` être explorés, nous
allons les évoquer brièvement dans ce chapitre.
Pour commencer, nous n'avons pas approfondi les
paramètres P(p) et P(l) du r'eseau : nous avons vu dans la
première partie de ce rapport que la litt'erature laissait supposer que
ces valeurs sont inf'erieures a` 0.1. Au cours de nos exp'eriences, nous
n'avons mis ni P(p) ni P(l) dans les contraintes anatomiques, n'eanmoins les
structures des meilleurs individus que nous avons obtenus montrent qu'en
moyenne les valeurs de P(p) et P(l) tournent toutes les deux autour de 0.09.
Cela est en coh'erence avec les donn'ees anatomiques connues de la mRF,
cependant nous avons d'emontr'e a` partir des donn'ees anatomiques connues que
P(l) > 45 × P(p), relation que nous ne retrouvons pas dans nos
r'esultats. Par cons'equent, il serait int'eressant de rajouter cette
contrainte afin de voir les performances des mRF ainsi 'evolu'ees.
Nous avons 'egalement laiss'e de côt'e l'analyse et
l'impact du modèle de population de neurones choisi, le lPDS, que nous
avons d'ecrit dans le chapitre 2.1 : en premier lieu, nous pourrions rendre
libres les paramètres que nous avons fix'es (ô a` 5ms et threshold
a` 0). En second lieu, il existe d'autres modèles de population de
neurones dont nous pourrions comparer l'efficacit'e dans notre modèle de
la mRF par rapport aux lPDS. Enfin, les r'eseaux que nous avons fait 'evoluer
sont de taille assez importante pour une mod'elisation, d'autant plus que nous
les faisons 'evoluer par algorithmes 'evolutionnistes, avec lesquels il est
pr'ef'erable de manipuler des r'eseaux de
faible taille pour des raisons de vitesse de calcul ainsi que
d'aisance d'interpr'etation : par cons'equent, il serait int'eressant de
quantifier l'impact du nombre maximum de neurones que peut contenir un
cluster.
Concernant la tàache incarn'ee, nous avons compar'e
indirectement nos r'esultats avec ceux de Humphries via la comparaison avec les
performances de contrôleurs WTA et al'eatoires. Il serait int'eressant de
comparer directement nos r'esultats avec ceux de Humphries en impl'ementant le
modèle de ce dernier dans notre programme.
En outre, la tàache incarn'ee comporte un certain
niveau d'abstraction : une 'evaluation encore plus pouss'ee de la mRF serait
par exemple de l'incorporer en tant que contrôleur d'une activit'e de
m'etabolisme connue d'un animal, tels les comportements alimentaires et
dipsiques de la souris [Guillot, 1988], et comparer les s'elections op'er'ees
par la mRF avec le comportement r'eel de l'animal.
Autre voie d'exploration, il serait int'eressant d'analyser
les r'eseaux de neurones obtenus suite a` l''evolution afin d'une part de mieux
comprendre comment ils r'eussissent a` r'esoudre une tàache de
s'election, et d'autre part d'essayer d'extraire les similarit'es entre les
r'eseaux obtenus. Dans ce même esprit, nous pourrions 'etudier les
propri'et'es de ces r'eseaux, comme par exemple la pr'esence de structures de
type small-world, scale-free ou autre.
Du côt'e neuro-'evolution, nous avons fait un usage
intensif des algorithmes 'evolutionnistes sans 'evaluer l'utilit'e de ces
derniers ainsi que leur impact sur les r'eseaux obtenus après
'evolution. Parmi les diff'erents aspects qu'il serait utile d'approfondir,
essayer d'introduire de nouveaux objectifs pourrait donner des r'esultats
int'eressants, en particulier :
1. un objectif de generalisation, permettant
de s'assurer que les d'ecisions prises par la mRF dans le cadre des
tàaches originales peuvent se g'en'eraliser a` d'autres tàaches
semblables. Plus pr'ecis'ement, dans la tàache d'esincarn'ee, cela
consisterait a` s'assurer que si nous donnons en entr'ee de la mRF un vecteur
non pr'esent dans l'ensemble de vecteurs d'entr'ee que nous avons utilis'e, par
exemple (0.3, 0.5, 0.68), la mRF donne 'egalement la bonne sortie (0, 0, 1).
Dans la tàache d'esincarn'ee, la g'en'eralisation pourrait se traduire
par 'evaluer la mRF dans des cartes dont la disposition est diff'erente que
celle que nous avons utilis'ee [Pinville et al., 2011].
2. un objectif de diversite, gràace
auquel l''evolution v'erifierait si au sein de chaque population les individus
(i.e. les mRF) ne sont pas tous semblables. Cet objectif permettrait de faire
face au genetic drift (convergence vers un optimum local) souvent constat'e, a`
l'instar de la s'election naturelle qui a vu se former des sous-groupes
gràace aux contraintes g'eographiques. On
peut ainsi trouver autant d'optima locaux que de sous-groupes,
permettant ainsi d'obtenir de meilleurs r'esultats en se rapprochant ainsi de
l'optimum global [Mouret and Doncieux, 2009a, Mouret and Doncieux, 2009b,
Doncieux and Mouret, 2009].
Une autre technique que nous pourrions utiliser pour essayer
d'am'eliorer les r'esultats obtenus par algorithmes 'evolutionnistes serait
d'effectuer l''evolution en plusieurs 'etapes. En effet, lorsque nous essayons
de faire r'ealiser au r'eseau une tàache difficile, l'espace de
recherche 'etant très important l''evolution peut rencontrer des
difficult'es a` franchir certains seuils. Par exemple, nous avons vu que la
variante de la tàache incarn'ee o`u nous nous donnions a` la mRF
directement les variables internes et externes sans calculer de salience
donnait des r'eseaux dont le contraste des vecteurs de sortie 'etait
très faible, même après plus de 1000 g'en'erations. Une
possibilit'e pour aider l''evolution a` optimiser davantage le contraste aurait
pu être dans un premier temps de faire apprendre le calcul des saliences
au r'eseau, et dans un second temps r'esoudre la tàache de survie.
'Etant donn'e que nous avons montr'e dans la tàache d'esincarn'ee que
des r'eseaux de type mRF pouvaient agir comme un WTA, et qu'un contrôleur
WTA peut effectuer la tàache de survie a` partir du calcul des saliences
de façon moyennement efficace (environ 1500 unit'es de temps de survie
sur un maximum de 3000) mais avec un contraste maximum, il est possible que
cette introduction d'un objectif temporaire (apprentissage le calcul des
saliences) dans l''evolution permette de franchir plus facilement des seuils
dans l'optimisation des objectifs de dur'ee de vie et de contraste.
Du côt'e neurophysiologique, la litt'erature donne un
certain nombre de pistes pour 'elaborer des modèles plus fins de la mRF,
en particulier pour mieux prendre en compte la diversit'e des noyaux et des
neurones, diviser la mRF selon ses 3 r'egions (m'esenc'ephalique, pontique,
bulbaire) et consid'erer davantage les fonctions de la mRF. Pour cela, les
diff'erentes 'etudes de l'activit'e neurophysiologique de la formation
r'eticul'ee (RF) repr'esentent une source d'inspiration utile, en particulier
la s'erie d''etudes physiologiques sur la RF r'ealis'ees par JM. Siegel dans
les ann'ees 1970 et 1980. Ainsi,
- [Siegel and McGinty, 1977] a trouv'e que les neurones de la
formation r'eticul'ee pontine (PRF) avaient un taux d'activit'e important en
phase de forte activit'e oculaire constat'ee par 'electro-oculographie, ce qui
est coh'erent avec les 'etudes ant'erieures. Les auteurs montrent 'egalement
l'existence d'un lien entre les d'echarges des neurones de la PRF et
l'activit'e motrice. Les donn'ees trouv'ees suggère un rôle majeur
des neurones de la PRF dans la r'egulation des activit'es motrices. L''etude
donne 'egalement une indication très int'eressante concernant les
projections 'emanant de la PRF : «The PRF's medial zone [...] is the
principal source of pontine reticular projections to the spinal cord; more than
half of its neurons send their axons
directly into the ventral, motor areas of the cord.».
- [Siegel, 1979] montre l'existence chez les chats de trois
classes de cellules dans la RF bulbaire (medullary reticular formation cells),
classification basée sur la corrélation entre leur
décharge et le type de mouvements effectués : une classe
décharge lorsque le mouvement est latéralement asymétrique
(54% des cellules), l'autre décharge lorsque le mouvement est
latéralement symétrique (38% des cellules). Les 8% de cellules
restantes correspondent a` la troisième classe et ne sont pas
liés a` un comportement moteur. Il n'existe pas de corrélation
entre la RF bulbaire et le mouvement oculaire, contrairement a` la RF
pontine.
- [Siegel et al., 1979] signale la présence chez les
chats d'une corrélation entre les décharges des neurones de la
mRF au niveau moelle allongée (appelée medial medullary reticular
formation, en français mRF bulbaire) et de certaines activités
motrices durant les phases d'activitéainsi que pendant le sommeil
paradoxal (REM sleep). L'étude remarque que les 3 types de cellules
précédemment évoquées peuvent également
être retrouvés dans le pont de Varole. Elle donne également
une estimation de leurs proportions ainsi que leur localisation.
A` plus long terme, un de nos objectifs est de connecter notre
modèle de la mRF avec les modèles de ganglions de la base
existants, connexion qui soulèvera a` son tour un nombre important de
problématiques : comment interagissent les réseaux, quel est le
role précis de chacun, etc. Pour anecdote historique, l'article original
présentant le premier modèle de la mRF s'achevait sur un dernier
chapitre de considérations cybernétiques évoquant
précisément ce genre de connexions entre zones du cerveau et en
imaginant leurs équivalents dans un controleur robotique [Kilmer et al.,
1969].
Chapitre 6
Conclusion
L'objectif de cette 'etude 'etait de proposer un nouveau
modèle de la mRF plus proche des donn'ees anatomiques que les deux
modèles pr'ec'edents existants dans la litt'erature et d''evaluer sa
capacit'e a` faire de la s'election de l'action. Notre d'emarche bas'ee sur les
algorithmes 'evolutionnistes nous a permis de montrer qu'un r'eseau pr'esentant
une structure de type mRF peut être capable d'une part de prendre les
d'ecisions attendues et d'autre part de les s'electionner de façon
franche :
- la première s'erie d'exp'eriences bas'ees sur une
tàache d'esincarn'ee a montr'e la capa-
cit'e computationnelle de la mRF a` effectuer une tàache
de s'election (chapitre 3);
- la seconde s'erie d'exp'eriences bas'ees sur
une tàache incarn'ee montre que la mRF
est capable d'effectuer une tàache de s'election de
l'action en condition simul'ee
(chapitre 4).
Les r'esultats que nous avons obtenus sont meilleurs que ceux
du modèle de Humphries dans les deux tàaches que nous avons
analys'ees : affiner le modèle en y ajoutant davantage de neurones et
supprimer l'hypothèse du modèle de Kilmer-McCulloch reprise par
modèle de Humphries qu'àchaque cluster correspond une action nous
a ainsi permis d'am'eliorer les performances en termes de s'election tout en
respectant davantage les donn'ees anatomiques connues sur la mRF.
N'eanmoins, la structure de type mRF ne semble pas
repr'esenter un avantage particulier par rapport a` un r'eseau de neurones sans
contrainte. Ainsi, pour r'epondre a` la question originale, la mRF peut
constituer un substrat pour la s'election de l'action, mais il ne semble pas
que sa structure repr'esente un atout en particulier.
En outre, la d'emonstration de P(l) > 45 × P(p) dans le
chapitre 1.4 nous permet
avec une certitude accrue d'affirmer que la mRF a
une structure de r'eseau de type
small-world, résultat pouvant s'avérer très
utile dans les analyses futures.
'Etant donnéla nature exploratoire de ce travail de
modélisation de la mRF, beaucoup d'axes de recherche que nous avons
évoqués dans la discussion restent toutefois a` être
explorés pour affiner le modèle et approfondir les
résultats. Cependant, les résultats de ce travail sont
encourageants et outre leurs implications sur les capacités
computationnelles de la mRF ils montrent l'apport potentiel des algorithmes
évolutionnistes aux neurosciences computationnelles.
Bibliographie
[Albert and Barabási, 2002] Albert, R. and
Barabási, A. (2002). Statistical mechanics of complex networks. Reviews
of modern physics, 74(1) :47-97. [cited at p. 8]
[Ashby, 1952] Ashby, W. (1952). Design for a brain. [cited at p.
31]
[Berntson and Micco, 1976] Berntson, G. and Micco, D. (1976).
Organization of brainstem behavioral systems. Brain Research Bulletin, 1(5)
:471-483. [cited at p. 6]
[Berridge, 1989] Berridge, K. (1989). Progressive degradation of
serial grooming chains by descending decerebration. Behavioural brain research,
33(3) :241-253. [cited at p. 6]
[Birkmayer and Pilleri, 1966] Birkmayer, W. and Pilleri, G.
(1966). The brainstem reticular formation and its significance for autonomic
and affective behavior. [cited at p. 6]
[Bowsher, 1970] Bowsher, D. (1970). Place and modality analysis
in caudal reticular formation. The Journal of Physiology, 209(2) :473-486.
[cited at p. 5]
[Deb, 2001] Deb, K. (2001). Multi-objective optimization using
evolutionary algorithms.
Wiley. [cited at p. 20]
[Deb et al., 2002] Deb, K., Pratap, A., Agarwal, S., and
Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm :
Nsga-ii. Evolutionary Computation, IEEE Transactions on, 6(2) :182-197. [cited
at p. 20]
[Doncieux and Mouret, 2009] Doncieux, S. and Mouret, J.
(2009). Single step evolution of robot controllers for sequential tasks. In
Proceedings of the 11th Annual conference on Genetic and evolutionary
computation, pages 1771-1772. ACM. [cited at p. 42]
[Doncieux et al., 2004] Doncieux, S., Mouret, J., Muratet, L.,
and Meyer, J. (2004). The robur project : towards an autonomous flapping-wing
animat. Proceedings of the Journées MicroDrones. [cited at p. 19]
[Eccles et al., 1976] Eccles, J., Nicoll, R., Rantucci, T.,
Taborikova, H., and Willey, T. (1976). Topographic studies on medial reticular
nucleus. Journal of Neurophysiology, 39(1) :109-118. [cited at p. 5]
[Girard et al., 2003] Girard, B., Cuzin, V., Guillot, A.,
Gurney, K., and Prescott, T. (2003). A basal ganglia inspired model of action
selection evaluated in a robotic survival task. Journal of integrative
neuroscience, 2 :179-200. [cited at p. 1, 12, 14, 31, 33]
[Girard et al., 2008] Girard, B., Tabareau, N., Pham, Q.,
Berthoz, A., and Slotine, J. (2008). Where neuroscience and dynamic system
theory meet autonomous robotics : a contracting basal ganglia model for action
selection. Neural Networks, 21(4) :628-641. [cited at p. 15]
[Glickman and Schiff, 1967] Glickman, S. and Schiff, B. (1967). A
biological theory of reinforcement. Psychological Review, 74(2) :81-109. [cited
at p. 6]
[Grantyn et al., 1987] Grantyn, A., Ong-Meang Jacques, V., and
Berthoz, A. (1987). Reticulo-spinal neurons participating in the control of
synergic eye and head movements during orienting in the cat. Experimental Brain
Research, 66(2) :355-377. [cited at p. 8]
[Guillot, 1988] Guillot, A. (1988). Contribution a` l'etude
des sequences comportementales de la souris : approches causale, descriptive et
fonctionnelle. Diplôme de Doctorat de lUniversitéParis 7,
SpécialitéBiomathématiques. [cited at p. 41]
[Hammer Jr et al., 1981] Hammer Jr, R., Lindsay, R., and
Scheibel, A. (1981). Development of the brain stem reticular core : an
assessment of dendritic state and configurationin the perinatal rat.
Developmental Brain Research, 1(2) :179-190. [cited at p. 7]
[Humphries et al., 2005] Humphries, M., Gurney, K., and
Prescott, T. (2005). Is there an integrative center in the vertebrate
brain-stem? a robotic evaluation of a model of the reticular formation viewed
as an action selection device. Adaptive Behavior, 13(2) :97-
113. [cited at p. 1, 4, 12, 33, 34, 37]
[Humphries et al., 2006] Humphries, M., Gurney, K., and
Prescott, T. (2006). The brainstem reticular formation is a small-world, not
scale-free, network. Proceedings of the Royal Society B : Biological Sciences,
273(1585) :503-511. [cited at p. 1, 4, 7, 8, 10, 11]
[Humphries et al., 2007] Humphries, M., Gurney, K., and
Prescott, T. (2007). Is there a brainstem substrate for action selection?
Philosophical Transactions of the Royal Society B : Biological Sciences,
362(1485) :1627-1639. [cited at p. 5, 6, 7, 8, 23, 29]
[Humphries and Prescott, 2006] Humphries, M. and Prescott, T.
(2006). Distributed action selection by a brainstem neural substrate : An
embodied evaluation. From Animals to Animats 9, pages 199-210. [cited at p. 7,
13, 36]
[Jones, 1995] Jones, B. (1995). Reticular formation:
cytoarchitecture, transmitters, and projections. The rat nervous system, pages
155-171. [cited at p. 5]
[Jouvet, 1967] Jouvet, M. (1967). Neurophysiology of the states
of sleep. Physiological Reviews, 47(2) :117-177. [cited at p. 6, 10]
[Kilmer et al., 1969] Kilmer, W., McCulloch, W., and Blum, J.
(1969). A model of the vertebrate central command system. International Journal
of Man-Machine Studies, 1(3) :279-
309. [cited at p. 1, 7, 8, 10, 43]
[Langhorst et al., 1983] Langhorst, P., Schulz, B., Schulz,
G., Lambertz, M., and Krienke, B. (1983). Reticular formation of the lower
brainstem. a common system for cardiorespiratory and somatomotor functions :
discharge patterns of neighboring neuronsinfluenced by cardiovascular and
respiratory afferents. Journal of the autonomic nervous system, 9(2- 3)
:411-432. [cited at p. 5]
[Lovick, 1972] Lovick, T. (1972). The behavioural repertoire of
precollicular decerebrate rats. The Journal of physiology, 226(2) :4P-6P.
[cited at p. 6]
[Magoun and Rhines, 1946] Magoun, H. and Rhines, R. (1946). An
inhibitory mechanismin
the bulbar reticular formation. Journal of
neurophysiology, 9(3) :165-171. [cited at p. 6]
[Mouret and Doncieux, 2009a] Mouret, J. and Doncieux, S.
(2009a). Overcoming the bootstrap problem in evolutionary robotics using
behavioral diversity. In Evolutionary Computation, 2009. CEC'09. IEEE Congress
on, pages 1161-1168. IEEE. [cited at p. 42]
[Mouret and Doncieux, 2009b] Mouret, J. and Doncieux, S.
(2009b). Using behavioral exploration objectives to solve deceptive problemsin
neuro-evolution. In Proceedings of the 11th Annual conference on Genetic and
evolutionary computation, pages 627-634. ACM.
[cited at p. 42]
[Mouret and Doncieux, 2010] Mouret, J. and Doncieux, S.
(2010). Sferesv2 : Evolving in the multi-core world. In Evolutionary
Computation (CEC), 2010 IEEE Congress on, pages 1-8. IEEE. [cited at p. 52]
[Parvizi and Damasio, 2003] Parvizi, J. and Damasio, A. (2003).
Neuroanatomical correlates of brainstem coma. Brain, 126(7) :1524-1536. [cited
at p. 6]
[Pinville et al., 2011] Pinville, T., Koos, S., Mouret, J., and
Doncieux, S. (2011). How to promote generalisation in evolutionary robotics:
the progab approach. [cited at p. 41]
[Prescott et al., 1999] Prescott, T., Redgrave, P., and Gurney,
K. (1999). Layered control
architectures in robots and vertebrates. Adaptive
Behavior, 7(1) :99-127. [cited at p. 7]
[Ramón-Moliner and Nauta, 1966] Ramón-Moliner, E.
and Nauta, W. (1966). The isodendritic core of the brain stem. The Journal of
Comparative Neurology, 126(3) :311-335.
[cited at p. 5]
[Redgrave et al., 1999] Redgrave, P., Prescott, T., and Gurney,
K. (1999). The basal ganglia: a vertebrate solution to the selection problem?
Neuroscience, 89 :1009-1024. [cited at p. 7]
[Scheibel and Scheibel, 1967] Scheibel, M. and Scheibel, A.
(1967). Anatomical basis of attention mechanisms in vertebrate brains. The
neurosciences : A study program, pages
577-602. [cited at p. 7, 8]
[Schuz, 1998] Schuz, A. (1998). Neuroanatomy in a computational
perspective. In The
handbook of brain theory and neural networks, pages
622-626. MIT Press. [cited at p. 8]
[Segundo et al., 1967] Segundo, J., Takenaka, T., and Encabo, H.
(1967). Somatic sensory properties of bulbar reticular neurons. Journal of
neurophysiology, 30(5) :1221-1238.
[cited at p. 5]
[Siegel, 1979] Siegel, J. (1979). Behavioral relations of
medullary reticular formation cells. Experimental Neurology, 65(3) :691-698.
[cited at p. 43]
[Siegel and McGinty, 1977] Siegel, J. and McGinty, D. (1977).
Pontine reticular formation neurons : relationship of discharge to motor
activity. Science, 196(4290) :678. [cited at p. 42]
[Siegel et al., 1979] Siegel, J., Wheeler, R., and McGinty, D.
(1979). Activity of medullary reticular formation neurons in the unrestrained
cat during waking and sleep. Brain Research, 179(1) :49-60. [cited at p. 43]
[Torvik and Brodal, 1957] Torvik, A. and Brodal, A. (1957).
The origin of reticulospinal fibers in the
cat. an experimental study. The Anatomical
Record, 128(1) :113-137.
[cited at p. 5]
[Woods, 1964] Woods, J. (1964). Behavior of chronic decerebrate
rats. Journal of Neurophysiology. [cited at p. 6]
Appendices
Notes techniques sur
l'implémentation
Nous tenons a` 'evoquer les outils informatiques que nous
avons utilis'es pour mener a` bien ce projet, car ils repr'esentèrent
d'une part un travail très important au cours du stage, et d'autre part
il est toujours int'eressant d'avoir une vision concrète des moyens
techniques utilis'es pour trouver les r'esultats du rapport, que ce soit par
curiosit'e, en vue de reproduire les exp'eriences ou bien encore pour trouver
des pistes de solutions pour impl'ementer ses propres modèles.
Nous voulons 'egalement mettre l'accent sur le fait que les
travaux r'ealis'es au cours du stage n'ont nullement pour but unique la
production de ce rapport mais aussi de donner la possibilit'e a` de potentiels
futurs successeurs d'être rapidement op'erationnels sans qu'ils aient
besoin de construire leurs propres outils informatiques a` partir de rien. Nous
rejoignons en cela l'initiative Plume du CNRS (http ://
www.projet-plume.org), dont le
but est de Promouvoir les Logiciels Utiles, Maàýtris'es et
'Economiques (d'o`u l'acronyme PLUME) a` destination de la communaut'e de
l'Enseignement Sup'erieur et de la Recherche.
A` cet effet, une attention particulière a 'et'e
port'ee sur la qualit'e du d'eveloppement et tout le code est disponible sous
la licence libre CeCILL (http ://www.cecill.info/) a` l'adresse TODO. Le
tableau A.1 montre quelques statistiques sur le code source ainsi que sur les
scripts 'ecrits afin d'automatiser certains processus et analyser les
r'esultats (contenus dans des fichiers de logs du programme principal).
Les r'eseaux de neurones ainsi que les algorithmes
'evolutionnistes ont 'et'e d'evelopp'es
en C++ pour des raisons de
rapidit'e, les algorithmes 'evolutionnistes deman-

FIGURE A.1: Statistiques sur le code source du programme et
des scripts d'analyse écrits en plus du framework Sferes2 et des
librairies existantes. La taille élevée des C/C++ headers
s'explique par l'utilisation intensive des templates.
dant des ressources computationnelles très importantes,
en s'appuyant sur le fra-
mework Sferes2 (http ://pages.isir.upmc.fr/
mouret/sferes2/) dévéloppéa` l'ISIR
[Mouret and Doncieux, 2010]. Pour les besoins du
développement, nous avons portéSferes2 sous Windows.
Le programme est multi-threadéet repose sur les libraires
Boost, notamment la Boost Graph Library qui permet de
gérer aisément les graphes, TBB (Intel Threading Building Blocks)
pour le multi-threading, Eigen2 pour les calculs matriciels et SDL pour le
rendu graphique de la tàache de survie minimale que nous verrons plus
tard.
Graphviz a étéutilisépour
générer graphiquement les réseaux de neurones
représentant les mRF, et le programme ffpmeg a
étéutilisépour générer des vidéos a`
partir de ces graphes. MATLAB a étéretenu pour analyser les
résultats.
Enfin, nous avons fait un usage intensif de la grappe de
serveurs du laboratoire ISIR pour exécuter notre programme, ce dernier
nécessitant une forte puissance de calcul. L'ensemble des programmes
utilisés dans ce projet tournent aussi bien sous Windows que sous
Linux.
L'ensemble du code source ainsi que des scripts d'analyse est
disponible a` l'adresse http ://
pages.isir.upmc.fr/evorob
db/moin.wsgi/mRF2011.
Miroir : http ://
bit.ly/mRF-xp
Exemple d'une mRF a` 4 clusters
Cf. page suivante.
FIGURE B.1: Exemple d'une mRF a` 4 clusters. Les neurones
oranges sont excitateurs, les neurones bleus foncésont inhibiteurs. Un
cluster correspond a` un rectangle bleu. Les neurones situés en dehors
des rectangles bleus représentent les entrées que
recoit la mRF ainsi que les neurones vers lesquels elle projette.
Exemple d'un cluster de la mRF
Cf. page suivante.
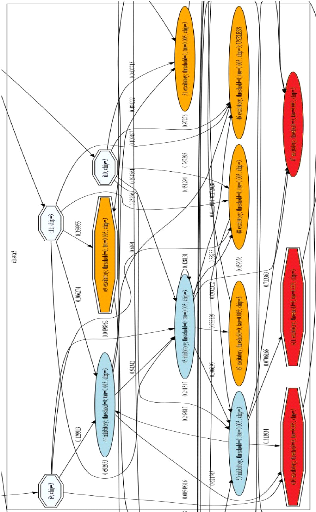
FIGURE C.1: Exemple d'un cluster de la mRF. Les neurones
oranges sont excitateurs, les neurones bleus foncésont inhibiteurs.
Chaque connexion synaptique a` un poids entre 0 et 1. Les 3 neurones en bleu
clair sont les entrées (neurones d'entrée), les 3 neurones en
rouge sont les sorties de la mRF (neurones de sortie).
| 


