1.5 Les communautés
1.5.1 Définition et choix de la terminologie :
clusters, communautés ou agrégats ?
Le terme « communauté »
provient d'une analogie avec les réseaux sociaux, un des champs
d'étude au coeur duquel les graphes sont très présents.
La communauté au sein d'un graphe est définie
par Santo Fortunato [Fortunato-2010] comme un «
ensemble autonome ». Ceci est l'expression d'un nombre de noeuds
connectés et regroupés (en communauté) de telle sorte que
le nombre de liens intracommunautaires soit le plus élevé
possible et le nombre de liens extracommunautaires soit le plus faible
possible.
La définition de la communauté induite devient
alors : « Une communauté forte est telle que le degré de
chaque noeud interne est supérieur à son degré externe
». La représentation de la figure 1.17 illustre cette
définition.
1.5. Les communautés 44
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
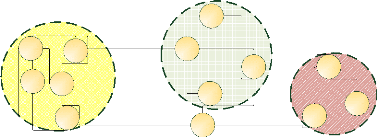
Figure 1.17 : Exemple de graphe où l'on peut
intuitivement détecter trois communautés telles que
définies par Santo Fortunato.
Pourtant, il n'existe pas de définition couramment
admise de ces ensembles. Le regroupement intuitif des noeuds selon leurs
connectivités, bien qu'ayant un grand succès, n'a pas
démontré son universalité. Fortunato lui-même,
déclare que « le premier problème dans la clusterisation
de graphe est la recherche d'une définition des caractéristiques
quantitatives d'une communauté »
[Fortunato-2010].
Dans ce contexte, le terme même de «
communauté » peut sans doute être considéré
comme abusif. En effet, hérité des réseaux sociaux, il
sous-tend un lien sémantique d'appartenance à une unité et
le partage d'éléments identitaires communs. Par exemple,
parlerions-nous facilement de communautés d'ordinateurs pour nommer un
ensemble de postes de travail sur un LAN au sein d'un WAN ?
La terminologie anglaise parfois utilisée, qui est
celle de « Cluster », possède, elle, des définitions
précises et contextuelles. Cependant, elle se réfère
autant à la structure inter-sommets, qu'aux sommets eux-mêmes.
Considérer l'ensemble à étudier (le cluster) comme un
ensemble de sommets participant d'une entité ayant sa propre
identité, nous semble abusif. C'est, pour utiliser une métaphore
courante, comme si pour définir un être humain on nommait un
ensemble d'organes liés par un réseau sanguin par le nom de ce
réseau sanguin. De plus, dans les réseaux sociaux, une fois la
communauté découverte, la structure porteuse n'a plus d'«
usage ». Ainsi, un groupe d'amis est indépendant de la relation
ayant servi à les repérer (SMS, emails, connexions
téléphoniques ou autres).
De plus, si la définition des clusters ou des
communautés retient comme caractéristique majeure la
proximité la plus importante possible en interne et la plus faible
possible en inter-communautés, l'appartenance d'objets à
plusieurs communautés devient alors une source naturelle de baisse de la
qualité. La communauté devant, par définition, être
le moins en interaction avec l'extérieur, la dénomination «
communauté avec recouvrements » devient un oxymore.
Il en est de même pour la terminologie de «
super-communauté ». Cette terminologie, utilisée pour
signifier des communautés de taille importante, associe alors le
préfixe « super » à un objet dont la qualité
peut être à priori jugé faible. La taille très
importante d'une
1.5. Les communautés 45
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
communauté est le plus souvent l'expression d'une
incapacité à déterminer des ensembles plus pertinents.
On peut aussi aisément concevoir que pour nommer les
ensembles de mots destinés à servir de moteurs à des
communautés dynamiques d'utilisateurs, le choix du terme «
communauté » ne soit pas judicieux. Il convient d'utiliser un
lexique différent pour nommer d'une part, les communautés
sociales, de l'autre, les ensembles de mots.
On peut enfin remarquer que Gregory Palla, au fil de ses
articles, a remplacé le mot « community »
[Palla&al-2005] par « module »
[Palla&al-2007]. Le terme de « module » ayant
déjà en mathématiques (module de nombre complexe, vecteur)
et en informatique (bloc de code) des définitions précises et
différentes, il ne semble pas approprié.
Toutes ces raisons nous encouragent à l'utilisation
d'un autre terme : celui d'agrégat. Bien qu'il soit
rarement utilisé [Botafogo&al-1991] [Cucala-2009], ce terme
semble pourtant le plus adapté.
Un agrégat est défini comme une «
réunion d'éléments matériels juxtaposés,
généralement hétérogènes, présentant
entre eux une certaine cohésion et formant un tout » (Larousse
2001). Tant que la nature du « tout » n'est pas
caractérisée comme ayant une identité propre, il ne nous
semble pas judicieux d'employer d'autres termes pour nommer ce regroupement.
Ainsi, tout travail de regroupement va-t-il créer un agrégat qui
est éventuellement une communauté. Un agrégat est
défini par Bayaly et Cunny, comme « un ensemble de noeuds
liés logiquement dans un graphe »
[Bailey&al-1986].
Pour conclure cette tentative de définition, je citerai
Filippo Radicchi et al [Radicchi&al-2004] : «
Cependant, pour analyser un réseau, il est nécessaire de
préciser quantitativement et sans ambiguïté ce qu'est une
communauté. ... Une communauté peut être vue comme un
ensemble d'éléments qui répondent à certaines
règles ». Ainsi, par exemple, la communauté des sommets
présentant les degrés les plus élevés devient
possible. De telles communautés seraient alors à l'opposé
des définitions données par Santo Fortunato
[Fortunato-2010].
Il nous faudra définir les règles de la
communauté. Une fois l'agrégat validé comme respectant les
règles caractérisant « notre définition » d'une
communauté, il pourra être éventuellement nommé
troupeau, ban, équipe, club, sous-réseau ou même
communauté en fonction de sa nature et de la nature des objets
regroupés. Cependant, pour respecter les terminologies habituelles et la
cohérence avec certains travaux, nous continuerons à nommer
« communautés » un ensemble de noeuds identifié comme
groupe constitué dans l'état de l'art de ce travail. Nous
réserverons le terme d'agrégat à la
deuxième partie de ce travail.
La création de communautés dans des graphes est
un sujet qui est de plus en plus abordé. Selon notre étude et
notre approche, identifier les communautés dans les grands graphes
revient à partitionner les grands graphes en sous-graphes et à se
poser la question suivante : recouvrement ou non recouvrement ?
1.5. Les communautés 46
Chapitre 1. État de l'art, notions, définitions et
vocabulaire sur les graphes
1. Les communautés sans recouvrement
Dans les communautés, les noeuds appartiennent au plus
à une seule communauté. Ce sont celles-ci qui sont
majoritairement étudiées. La figure 1.17
présente un exemple de découpage en
communautés sans recouvrement.
Dans la liste des travaux présentés au
paragraphe 3.4.3, les travaux Hagen et al. sont parmi les plus concrets
[Hagen&al-1992]. Ils utilisent des algorithmes de
partitionnement de graphes de façon à optimiser le regroupement
des liaisons entre composants sur une même couche du circuit
imprimé, afin de limiter le nombre de liaisons inter-couches, liaisons
qui sont à la fois chères et sources de défaillance.
2. Les communautés avec recouvrement
Dans les communautés avec recouvrement, les noeuds
peuvent appartenir à un nombre indéterminé de
communautés. Bien que représentant souvent des découpages
plus proches de la vie réelle, elles sont peu étudiées
(cf. figure 1.18). Une des raisons en est la difficulté de validation et
le caractère flou que peut présenter l'affectation d'un noeud
à plusieurs communautés si celle-ci est pondérée ou
relative.
Dans la liste des travaux présentés au
paragraphe 3.4.3, ceux de Palla et al. sont les plus célèbres.
Ils portent sur la création de communautés dans le domaine de la
biologie mais aussi dans celui des réseaux sociaux
[Palla&al-2005].
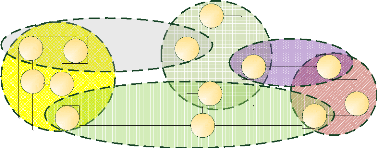
Figure 1.18 : Un exemple de graphe où l'on peut
observer six communautés avec recouvrement.
| 


