Analyse des séries chronologiques. les modèles ARCH et GARCH

Table des matières

Remerciements iii

Dédicaces iv

Résumé v

Abstract vi

Liste de figures vii

Liste d'abréviations viii

Introduction ix

1 Historique et Notions de base					1
1.1		Historique			1
1.2		Notions de base			4
		1.2.1		Les moments conditionnels	4
		1.2.2		La kurtosis et la skweness	6
		1.2.3		La volatilité	7
1.3		Modèle linéaire et non linéaire			8
		1.3.1		Notions de stationnarité	8
		1.3.2		Le processus bruit blanc (white noise process) . . . .	10
		1.3.3		Le processus d'innovation	10
		1.3.4		Modèle linéaire	11
		1.3.5		Opérateur de retard L	11
		1.3.6		Modèle ARMA	11
1.4		Méthodologie de Box-Jenkins			13
		1.4.1		Test sur les résidus	13
		1.4.2		Modèle non linéaire	16
2			TABLE DES MATIEEES
	Modèles ARCH et GARCH 2.1 Modèle ARCH 2.1.1 Définition et représentation 2.1.2 Propriétés des processus ARCH 2.2 Les modèles ARCH généralisées					23 23 23 28 37
			2.2.1 Modèle GARCH(p, q)			38
			2.2.2 Modèle GARCH (1, 1)			42
3	Estimation, prévision et tests					45
	3.1		Estimation			45
	3.2		La méthode de MV			46
			3.2.1 Estimation des paramètres du modèle ARCH . . . .			46
			3.2.2 Estimation des paramètres du modèle GARCH . . .			46
	3.3		La méthode de PMV			47
			3.3.1 Exemples			50
			3.3.2 Estimation du MV sous d'autres lois			51
	3.4		Prévision			54
			3.4.1 Modèle avec erreur ARCH			55
			3.4.2 Modèle avec erreur GARCH			57
			3.4.3 Erreur de prévision			58
	3.5		Identification et tests			59
			3.5.1 Tests d'effets ARCH/ GARCH			60
			3.5.2 La sélection d'un modèle			62
4	Extension du modèles (G) ARCH					64
	4.1		Modèles asymétriques			64
			4.1.1 Modèle EGARCH			65
			4.1.2 Modèles TGARCH			66
	4.2		Le modèle (G)ARCH en finance			66
			4.2.1 Les principales propriétés des séries financières . . . .			66
			4.2.2 La VaR			68
5	Application sur des données réelles					70
6	Conclusion					76

Remerciements

Je rends grace a Dieu qui m'a donné la volonté, la patience et le courage pour accomplir ce modeste travail.

Je remercie tout particuliêrement Madame Merzoughi Mouna, Docteur au département de mathématiques a l'université Badji-Mokhtar Annaba. Pour avoir encadré tout au long de notre travail et nous avoir appris qu'il y a soit et le monde et qu'il faut apprendre a s'imposer et imposer ses idées. Ce travail ne se serait pas fait sans ces bases.

Nous remercions toutes celles et ceux qui, de prés ou de loin par leurs ouvrages, Leurs expériences, leurs avis, leurs opinions et leurs écrits ont contribué a la Réalisation de ce travail.

Mes respectueux remerciements au membre de jury pour avoir honoré par leur présence afin d'examiner et jury ce travail.

Dédicaces

A mes très chers parents qui ont toujours été là pour moi, et qui m'ont donné un magnifique modèle de labeur et de persévérance. J'espère qu'ils trouveront dans ce travail toute ma reconnaissance et tout mon amour.

A mes chers frères : Mohamed et Bilal.

A mes tantes et à mes oncles,pour leur soutien morale et leurs sacrifices le long de ma formation.

Et leurs petits enfants : Dhikra wissal, Yakine, Mohamed Rahim, Ahmed Fakhre Islam et nouveau venu Mehdi.

A chaque cousins et cousines.

A mes meilleurs amis.

Je dédie ce mémoire.

SAMIRA

Résumé

Les modèles linéaires a coefficients constants classiques, fondés sur l'hypothèse que la variance des erreurs est constante, ne peuvent pas gérer la volatilité instantanée qui caractérise, en particulier, les séries financières (taux de change, taux d'infiation, indices boursiers,...). La classe des modèles ARCH , introduite par Engle (1982) s'est alors imposée comme alternative attrayante et fructueuse. En effet, ces modèles ont vite connu un développement conséquent avec l'apparition des modèles GARCH (Bollerslev, 1986) et leur forme similaire a celle des modèles ARMA classiques. Ainsi, la famille ARCH est capable et adéquate pour capturer plusieurs caractéristiques non linéaires, comme en particulier la volatilité clustering, l'excès de kurtosis et l'asymétrie.

Mots dlés modèles ARCH, GARCH et séries financières.

Abstract

The linear models with constant coefficients classic, founded on the assumption that the variance of the errors is constant, cannot manage the instantaneous volatility which characterizes, in particular, the financial series (rate of exchange, rate of inflation, indexes of security prices...). The class of models ARCH, introduced by Engle (1982) then imposed itself like attractive and profitable alternative. Indeed, these models have therefore been developing rapidly with the appearance of models GARCH (Bollerslev, 1986) and their form similar to that of the models ARMA classic. Thus, the ARCH family is able and adequate to capture many nonlinear characteristics, especially as volatility clustering, excess kurtosis and asymmetry.

Keywords : ARCH, GARCH models and financial series.

Liste de figures

Figure 1.1 : Simulation d'un processus BL(0,0,2,1). Figure 1.2 : Simulation de processus TAR.

Figure 1.3 : Comparaison entre le processus AR et SETAR. Figure 2.1 : Simulation d'un processus AR(1).

Figure 2.2 : Simulation d'un processus ARCH(1).

Figure 2.3 : L'évolutions de processus E2 t .

Figure 2.4 : Comparaison entre les processus AR(1) et ARCH(1).

Figure 2.5 : Simulation de processus ARCH pour différente retards. Figure 2.6 : Simulation d'un processus Y et son corrélogramme. Figure 2.7 : Le test de Jarque-Bera.

Figure 2.8 : Le test ARCH.

Figure 3.1 : Comparaison entre les distributions de student et normale. Figure 4.1 : Exemple de VaR sous distribution normale.

Figue 5.1 : La série des redements.

Figure 5.2 : Le correlogramme simple et partiel.

Figure 5.3 : Le test de normalité.

Figure 5.4 : Le corrélogramme simple et partiel des résidus.

Figure 5.5 : Le corrélogramme simple et partiel des résidus au carrés. Figure 5.6 : Le test ARCH.

Figure 5.7 : Estimations des paramètres.

Figure 5.8 : Le graphe des valeurs actuelle, prédites dans l'échantillon et du résidus.

Liste d'abréviations

- AR : AutoregRessive.

- ARCH: AutorégRessive Conditional Heteroscedacty.

- ARMA : AutoregRessive Moving Average.

- BL : BiLinéaire.

- CAC40 : Compagnie des Agents de Change.

- EGARCH : Exponential Generalized AutorégRessive Conditional Heteroscedacty.

- GARCH : Generalized Autorégressive Conditional Heteroscedacty. - GED : Generalized Error Distribution.

- LM : Multiplicateur de Lagrange.

- MA : Moving Average.

- MV : Maximum de Vraisemblance.

- NASDAQ : National Association of Securities Dealers Automated Quotations.

- PMV : Pseudo-Maximum de Vraisemblance.

- QMV : Quasi-Maximum de Vraisemblance.

- RESET: Regression Error Specification Test.

- SETAR : Self Exciting Threshold Autoregressive.

- TAR: Thershold AutorégRessive.

- TGARCH : Thershold Generalized AutorégRessive Conditional Heteroscedacty.

Introduction

Depuis les travaux de Wold (1938), l'intérêt pour le développement de modèles de séries chronologiques, pouvant répondre aux besoins de l'utilisateur, a augmenté. Les modèles de séries chronologique linéaires a coefficients constants ont connu une ère de prospérité grace, en particulier, aux travaux de Box et Jenkins (1970) et leur fameux ouvrage qui les a popularisés avec, en particulier, leur methodologie : identification, estimation, validation. Ces modèles, qui supposent une variance des erreurs constante, ont vite montré leurs limites, en particulier, dans la modélisation des séries chronologiques macroéconomiques et financières on la focalisation sur les premiers moments conditionnels-les moments d'ordre supérieurs étant traités comme des paramètres de nuisance- supposés constants par rapport au temps, s'est révélée limitative. De plus, l'importance croissante motivée par les considérations sur le risque et sur l'incertitude dans la théorie économique moderne ont nécessité le développement de nouvelles techniques pour les séries chronologiques économétriques permettant a la variance et a la covariance de dépendre du temps. Ainsi est née, sous l'impulsion du génie d'Engle (1982), la classe des modèles ARCH (autorégressifs conditionnellement hétéroscédastiques) suggérés afin de saisir les caractéristiques particulières des séries de données d'observations financières. Les modèles ARCH font la distinction entre les moments du second ordre conditionnels et inconditionnels (marginaux). Alors que les covariances marginales des variables d'intérêt peuvent être invariantes par rapport au temps, les variances et les covariances conditionnelles dépendent souvent et de façon non triviale, des états du passé du processus. Comprendre la nature exacte de cette dépendance temporelle est crucialement important car la perte en effi cacité, si l'hétéroscédasticité sous jacente est négligée, peut se révélée importante, en particulier dans l'évaluation de prévisions.

Les formulations de type ARMA sont quasiment centrées sur la structure d'autocovariance des processus. Or de nombreuses séries, financières, en particulier, celles des rendements ne diffèrent pratiquement pas des

CHAPITRE 0. INTRODUCTION

bruits blancs. En revanche, les séries de carrés ou des valeurs absolues sont souvent fortement autocorrélées. Ces deux propriétés ne sont pas incompatibles mais montre que le bruit blanc n'est pas indépendant. De plus les grandes valeurs (en valeur absolue) des données d'observation tendent a être suivies des grandes valeurs, et les petites valeurs, de petites. On dit que le marché est fortement volatil ou faiblement volatil.

Malgré ce phénomène, le processus peut-être stationnaire et donc, en particulier, homoscedastique (de variance marginale constante). Seulement, puisqu'une forte valeur de la donnée d'observation, au temps (t - 1) tend a augmenter la probabilité d'observer une forte valeur (en valeur absolue) au temps t, la variance de la variable au temps t conditionnellement a ses valeurs passées (appelée volatilité) ne semble pas constante.

L'hétéroscédasticité conditionnelle n'est incompatible ni avec l'homoscédasticité marginale, ni avec la stationnarité.

Il est important de noter que lorsqu'on considère les distributions de fréquence de séries de rendements, de variations de prix ou du logarithme de ces variations de prix, on remarque qu'elles ne correspondent pas a une distribution gaussienne. Elles sont a queues épaisses, a décroissance plus

{~x2 }

lente que exp et présentent un pic en zéro : elle sont dites leptokur-

2

tiques, leur cceffi cient de kurtosis est nettement supérieur a 3. Les modèles hétéroscedastiques se sont révélés particulièrement adaptés a la prise en compte de ces caractéristiques.

Le document est organisé de la façon suivante :

Le premier chapitre est consacré a une représentation générale de quelques notions de bases et un bref historique sur les modèles ARCH , constituant comme un chapitre de base.

Le second chapitre est distiné a décrire les diverses modélisations que l'on peut classer sous la rubrique des modèles hétéroscédastiques univariés et certaines de leurs propriétés. Le chapitre suivant constitue a des problèmes d'estimation, de prévision et de tests.

Dans le quatrième chapitre, on va donner quelques extensions non linéaires des modèles (G) ARCH et ainsi présenter l'importance de ces modèles sur la finance ou le marché financier

Enfin le dernier chapitre porte une application sur un indice boursier pour bien voir l'effet ARCH.

Chapitre 1

Historique et Notions de base

1.1 Historique

La théorie financière recourt de façon significative aux outils statistiques depuis plus de trente ans. On peut ainsi mentionner le travail tout a fait remarquable réalisé par Louis Bachelier (1870-1949), qui, dans sa thèse de doctorat es sciences mathématiques, défendue en mars 1900 et intitulée << Théorie de la spéculation>>, introduisit le concept de marché efficient bien longtemps avant que cette notion soit développée avec l'intérêt que l'on connalt. Il utilisa a cet effet des modèles de marche aléatoire, des mouvements browniens et de martingales. Il se posa même la question de tester sa théorie empiriquement. Mais son uvre resta discrète jusqu'en 1960, date de la traduction anglaise de son travail.

Jusque dans les années 1950, les ouvrages consacrés a la finance furent très souvent descriptifs. Le but essentiel consistait a décrire et informer sur les instruments financiers, les institutions financières et, de façon générale, les pratiques financières des entreprises. Parmi les travaux qui bouleversèrent cette situation, il faut notamment mentionner ceux de Markowitz [1952, 1959] et Tobin [1958] sur les sélections des portefeuilles d'une part, ceux de Modigliani et Miller [1958] sur la structure du capital et l'évolution des firmes, d'autre part.

En ce qui concerne l'usage des méthodes statistiques en finance, plusieurs voies ont été suivies.

1. L'utilisation des modêles de régression et des modêles économétriques se trouve dans pratiquement tous les secteurs de l'analyse financière. La référence la plus marquant en la matière faisant l'état de la question pour les années 1960 a 1975 est certainement l'ouvrage écrit par

Fama en 1976 et intitulé Foundations of finance. Cette publication ne doit cependant pas nous faire oublier, comme indiqué ci-dessus, les travaux basés sur les publications de Markowitz [1959] dans la sélection des portefeuilles, qui ont débouché sur des modèles de marché relativement complexes et qui ont constitué un domaine de réfiexion théorique intéressant pour la recherche statistique.

2. L'analyse multivariée (analyse en composantes principales, analyse discriminante,...) a aussi constitué un outil de plus en plus utilisé dans de nombreuses études exploratoires. Citons en particulier les articles de Pinches et Mingo [1973] et ceux de Herbst [1974] qui recourent a la fois a une analyse factorielle et une modélisation par régression, sans oublier les travaux de bloyd et Lee [1976] sur des modèles d'équilibre des actifs financiers. L'analyse discriminante a aussi trouvé dans l'usage des modèles logis une alternative utilisée par les praticiens.

3. L'usage des modêles de séries chronologiques, et tout particulièrement ceux associés a la classe des processus ARMA, constitue un aspect important de l'application de la statistique en finance. Dés le milieu des années 1970, plusieurs auteurs ont recouru a la méthodologie de Box et Jenkins pour estimer ou prévoir gains et taux. Nous évoquerons l'usage de cette démarche ci-dessous. Il est cependant utile de mentionner aussi dans cette catégorie, les tentatives liées a l'usage de l'analyse spectrale, notamment appliquée a l'étude des taux d'intérêt ou pour tester l'effi cacité d'un marché (par exemple, Granger et Morgenstern [1970] et Percival [1975]).

4. La théorie de la décision constitue un quatrième outil, permettant a divers auteurs de recourir a une approche bayésienne dans leur démarche : citons en particulier les travaux de Winkler et Barry [1975] dans le choix d'un portefeuille et ceux de Vasicek dans l'estimateur des betas des actions [1973].

Le développement des modèles ARCH se place dans le contexte et la lignée des modèles des séries chronologiques évoqués ci-dessus. Ces modèles ont été essentiellement développés avec des objectifs des descriptions, de dessaisonalisation, de prévision ou de contrôle de systèmes. L'age d'or de cette modélisation se situe dans les années 1970 avec le développement des modèles autorégressifs-moyennes mobiles (ARMA) et de leurs généralisations, qui présentaient l'avantage de se prêter facilement a l'emploi. Comme nous l'avant déjà souligné plus haut, leur usage s'est trouvé facilité par recours a une méthodologie, due a G.E.P. Box et G.M. Jenkins, destinée a

1.1. HISTOPIQUE

aider l'utilisateur dans le choix d'un modèle, l'estimation de ses paramètres et sa validation, méthodologie qui depuis une vingtaine d'années a engendré des travaux aussi multiple qu'intéressants.

Parmi les domaines d'application on la modélisation ARMA se révèle insuffi sante, figurent certains problèmes financiers et monétaires. Les séries disponibles dans ce secteur présentent en effet souvent des caractéristiques de dynamique non linéaire, dont la plus significative est le fait que la variabilité instantanée de la série (appelé volatilité) dépend de façon importante du passé. Il existe d'autre part des théories financières basées sur des principes d'équilibre et de comportements rationnels des agents intervenant sur le marché qui conduisent naturellement a introduire et a tester des contraintes structurelles sur les paramètres.

Historiquement, les modèles ARCH (Autorégressifs Conditionnellement Hétéroscédastiques) ont été introduits par R.F. Engle en 1982. Dans son article, l'auteur ne suppose plus que (€t; t Z) est un bruit blanc mais envisage plutôt que ce processus est de la forme :

"t = ~ ht

on

71_t c" i.i.d.Af (0, 1)

h = c + X p çbi "2 _ti

i=1

Dans cette expression, on suppose que c > 0 et que çb_i ~ 0 (i = 1, ..., p). Cette façon de procéder permettait a Engle de tenir compte du fait que les variations de prix --fortes ou faibles--étaient suivies d'autres variations fortes ou faibles des signes imprévisibles. Certaines conditions étaient en outre imposées afin de réduire le nombre de paramètres du modèles.

En ce qui concerne les domaines d'application, on peut en distinguer deux grandes catégories. Les premiers consistent a tester des théories économiques relatives aux divers marchés (devises, obligations,...). Les seconds traitent des comportements d'interventions sur le marché des établissements financiers (détermination des portefeuilles optimaux, de portefeuilles de couverture,...). Ce dernier type d'application est plus <<sensible>> et, par la-même, généralement couvert par le <<secret bancaire>> .

1.2 Notions de base

1.2.1 Les moments conditionnels

La définition d'un processus ARCH fait intervenir la notion de variance conditionnelle. Nous avons vu que la variance conditionnelle permet de modéliser la variance locale du processus a chaque instant t, en fonction des observations antérieures.

Cette notion peut être étendue a tous les moments de la série chronologique. Ainsi, l'espérance conditionnelle du processus {Xt} au temps t est la valeur moyenne attendue du processus au temps t calculée en tenant compte des valeurs du processus observées dans le passé. Pour illustrer ce concept, considérons la marche aléatoire

xt = xt_1 + €t, €t i.i.d r' ,A/ (0, 2)

Calculons son espérance conditionnelle en Xt, tenant compte des observations passées _{{Xt_i,} i > 0} : par linéarité de l'espérance, on peut écrire :

E (Xt/It~1) = E _(Xt~1/It~1) + E ("t/It-i)

Le premier des deux termes de la somme est la valeur attendue de Xt sachant _{{Xt_i,} i > 0}. Comme on connait _{Xt_i,} ce terme est l'espérance d'une valeur fixée _{Xt_1} et donc :

E (Xt/It~1) = Xt~1 + E ("t/It-i)

En ce qui concerne le deuxième terme, il faut observer que "t ne dépend pas des réalisations passées du processus _{{Xt_i,} i > 0} (car le processus {€t} est IID). La connaissance du passé ne modifie donc pas la valeur attendue de "t et on peut écrire :

E (Xt/It~1) = Xt~1 + E (€t) = Xt~1:

L'espérance conditionnelle d'une marche aléatoire en t est donc la valeur du processus en t - 1. On peut interpréter ce résultat en énonçant que le meilleur prédicteur linéaire de la valeur moyenne d'une marche aléatoire est réalisé en répétant sa dernière valeur observée.

Rappelons a présent la définition générale de l'espérance conditionnelle en termes de variables aléatoires. Pour tout couple de variables aléatoires

(X, Y ) continues de densite f (., .), la densite conditionnelle de X sachant que Y = y est definie par

fX[1⁷ (x/y) = f (x, y)

fy (y)

pour autant que fy (y) > 0. Il est donc naturel de definir l'esperance conditionnelle de X par :

E (X/Y = y) = f_#177;:dx xfxly (x/y)

pour les valeurs de y telles que fy (y) > 0. Dans le contexte des series chronologiques, la variable aleatoire X est la valeur Xt du processus au temps t, alors que la variable Y represente l'ensemble des valeurs {Xt_i, i > 0} = {Xt_i, i > 1} prises par le processus avant le temps t. Dans la suite de cette section, nous noterons cet ensemble It_1 :

It1 = {Xt_i,i > 0}.

It1 represente donc l'ensemble de l'information disponible jusqu'au temps t--1 inclu. Lorsque t augmente, _It1 contient davantage de variables aleatoires, c'est pourquoi on peut ecrire :

It1 C ^I C It+1 C It+2 C . . .

Nous avions observe dans l'exemple ci-dessus de la marche aleatoire que l'esperance de Xt_1 calculee conditionnellement à It1 = {Xt_i, i > 0} revient a prendre l'esperance d'une valeur connue Xt_1 et est donc egale à cette valeur Xt_1. On peut ecrire formellement ce resultat comme suit :

E (Xt_i/It-1) = Xt_i.

On peut bien entendu generaliser cette propriete a l'esperance de Xt conditionnellement a tout ensemble I, contenant Xt, et nous obtenons la première propriete de l'esperance conditionnelle :

E (Xt/I₈) = Xt, sits

Une deuxieme propriete importante de l'esperance conditionnelle est la loi des esperances iterees :

E (Xt/I₇.) = E (E (Xt/I₈)/I_r) , si r et s sont tels que I_r C I_s

(alors si r s), et, en particulier :

E (Xi) = E (E (Xt/I₅)).

Ce résultat fondamental est très utilisé car il permet souvent de calculer assez facilement une espérance après avoir conditionné le processus par un ensemble 1₅.

La notion de variance conditionnelle est naturellement définie a partir de celle de l'espérance conditionnelle, par la définition de la variance en fonction de l'espérance.

2 t = V (Xt/It~1)

= E (X2 t /it1) -- E (Xt/It~1)2 . 1.2.2 La kurtosis et la skweness

Soit jUk le moment empirique d'ordre k du processus Xt

La kurtosis

k = E [Xt -- E [Xt]]^k = 1 XT T t=1

(Xt - ~X~k

Definition 1.2.1 On définit une nouvelle mesure : le degré d'excês de Kurtosis.

3.

Degr^,e d⁰exc^~es de Kurtosis = 4

2

2

Definition 1.2.2 La Kurtosis ou le coefficient d'aplatissement pour un échantillon de taille T s'écrit :

KU = 4 2 2

~! Ti--oo

\/ ) 24 A/ 3, . T

Sous l'hypothêse nulle de normalité, on montre que :

~!

,A/ (0,1).

Ti--oo

K -- 3

T

q24

La Kurtosis mesure le caractère pointu ou plat de la distribution de la série. La Kurtosis de la distribution normale est 3. Si la Kurtosis est superieur a 3 (queues épaisses), la distribution est plutôt pointu (distribution leptokurtique); si la Kurtosis est inférieur a 3, la distribution est plutôt plat (distribution est dite platikurtique).

La skweness

Définition 1.2.3 La skweness ou le coefficient d'asymétrie pour un échantillon de taille T s'écrit :

(Sk)1 2 = 3

3

~

_r )

6

N 0, .

T

~!

Ti--oo

2

2

Sous l'hypothêse nulle de distribution normale et donc par conséquent de symétrie, on montre que :

(Sk)1 2	~! Ti--oo	,A/ (0,1).
q 6 T

La Skewness est une mesure de l'asymétrie de la distribution de la série autour de sa moyenne. La Skewness d'une distribution symétrie, telle que la distribution normale est nulle. La Skewness positive signifie que la distribution a une queue allongée vers la droite et la Skewness négative signifie que la distribution a une queue allongée vers la gauche.

1.2.3 La volatilité

La volatilité est une mesure de l'instabilité du cours d'un actif financier. Elle mesure l'amplitude des variations d'une action, d'un produit dérivé ou d'un marché. Il s'agit d'un paramètre de quantification du risque de rendement et de prix. Les séries monétaires et financières sont caractérisées par le clustering de volatilité, a savoir les périodes de forte volatilité alternent avec les périodes de faible volatilité. Ce phénomène, que nous appelons aussi l'hétéroscédasticité conditionnelle, est particulièrement fréquent dans les données boursières, les taux de changes ou d'autres prix déterminés sur les marchés financiers. Nous allons présenter quelques méthodes pour me-surer la volatilité. Elles sont groupées selon leurs caractéristiques : mesurer la volatilité en utilisant les formules statistiques ou en utilisant les modèles.

Les mesures statistiques

Sur le marché financier, la volatilité est mesurée comme l'écart type de la rentabilité. L'estimation de l'écart type des rentabilités journalières servent comme une méthode utile pour caractériser l'évolution de la volatilité. Cette

statistique mesure la dispersion de la rentabilité :

~ = T - 1

qPT ~Rt ~ R2 t=1

on R^~ est la rentabilité moyenne de l'échantillon. L'écart type est une mesure simple mais utile de la volatilité. Quand l'écart type est grand, la chance d'avoir une rentabilité élevée positive ou négative est grande. Plusieurs études ont utilisé la modification de l'écart type pour mesurer la volatilité.

Les modèles

Les formules statistiques ne sont effi caces a mesurer la volatilité que dans les cas on la valeur de l'écart type en t ne dépend pas de celle dans le passé. Pour ces cas, les mesures en utilisant des modèles sont plus effi caces. D'après Engle, la volatilité sur le marché financier est prévisible. Cette afli rmation n'est justifiée que dans les cas l'effet ARCH existe. Dans les modèles, les statistiques des séries temporelles sont prises pour trouver la meilleure valeur anticipée de la volatilité. Et en utilisant les statistiques des séries temporelles, il est possible de déterminer si l'information récente est plus importante que celle dans le passé.

1.3 Modèle linéaire et non linéaire

1.3.1 Notions de stationnarité

Rappelons au passage les définitions de la stationnarité forte et de la stationnarité faible (ou stationnarité du second ordre). Soit un processus temporel aléatoire (Xi, t 2 Z).

Définition 1.3.1 Le processus X est dit strictement ou fortement stationnaire si quelque soit le n-uplet du temps t1 < t2 < .. < t_n, tel que t 2 Z et pour tout temps h 2 Z avec t + h 2 Z,Vi,i = 1,..,m, la suite (Xt1+h, .., _Xtn+h) a la même loi de probabilité que la suite _(Xt1, .., Xt_n).

Dans la pratique, on se limite généralement a requérir la stationnarité du second ordre (ou stationnarité faible) du processus étudié.

Definition 1.3.2 Un processus (Xt, t E Z) est dit stationnaire au second ordre, ou stationnaire au sens faible, ou stationnaire d'ordre deux si les trois conditions suivantes sont satisfaites :

(i) E (X?) < oo, Vt E Z.

(ii) E (Xi) = m,indépendant de t, Vt E Z.

(iii) coy (Xt, Xt+h) = E [(Xt+h -- m)(Xt -- m)] = 7(h), indépendant de t, V(t,h) E Z².

La première condition garantit tout simplement l'existence (ou la convergence) des moments d'ordre deux. La seconde condition porte sur les moments d'ordre un et signifie tout simplement que les variables aléatoires Xt doivent avoir la meme espérance quelle que soit la date t. Enfin, la troisieme condition, porte sur les moments d'ordre deux résumés par la fonction d'autocovariance.

Cette condition implique que ces moments doivent etre indépendants de la date considérée et ne doivent dépendre uniquement que de l'ordre des retards. En résumé, un processus est stationnaire au second ordre si l'ensemble de ses moments sont indépendants du temps. Par conséquent, il convient de noter que la stationnarité implique que la variance ry (0) du processus Xt est constante au cours du temps.

Theoreme 1.3.1 (Théoreme de Wold) Tout processus stationnaire d'ordre deux (Xi, t E Z) peut 'etre représenté sous la forme :

Xt =

1 X i=0

iEt-t + kt

ofi les parametres _i satisfont 0 = 1, _i E R, Vi E N^*, Er() 2i < oo et ofi Et N IID (0, cr²). On dit que la somme des chocs passés correspond a la composante linéaire stochastique de Xt .Le terme kt désigne la composante linéaire.
·

Theoreme 1.3.2 (Théoreme de Volterra) Tout processus stationnaire au sens fort (Xi, t E Z) peut 'etre représenté sous la forme :

Xt =

1 X i=0

Et-i +

1 X i=0

1 X i=0

ijEt-iEt-j +

1 X i=0

1 X i=0

1 X k=0

ijkEt-iEt-jEt-k + · · · .

ofi Et est bruit blanc gaussien.

1.3.2 Le processus bruit blanc (white noise process)

Definition 1.3.3 Soit (Et)tEZ un processus stochastique, on dit que lg

\--t,tEZ

est un processus stochastique hasard pure ou bruit blanc faible(resp fort) si les trois proprietes sont verifier :

i) E (Et) = 0,Vt E Z.

ii) V ar (Et) = U², Vt E Z.

iii) Coy (Et, E_s) = E(EtE_s) = 0, Vt _L s.

La propriété iii implique que les Et sont non corrélées entre eux (resp les Et sont i. i. d)

Notation :

- Si {Et} est un bruit blanc faible, on notera par : {Et} rs^, W N (0, o^-2).

- Si {Et} est un bruit blanc fort, on notera par : {Et} rs^, IID (0, cr²).

Ce processus est un processus stationnaire d'ordre deux telle que : toutes les variables sont de même moyenne nulle et de variance ^cr2 (constante finie) et non corrélées entre eux.

1.3.3 Le processus d'innovation

Nous introduisons un concept d'innovation adapte a l'analyse des dynamiques non linéaires. L'innovation d'un processus stochastique Xt sont habituellement définies comme

1. Les erreurs représentent comme différence entre la valeur prévu et réalisé

Et = Xt - E (Xt/It-1)

est une innovation au sens forte. On peut dire que Et est un bruit blanc si E (Et) = a² et "orthogonal" a toute fonction du

passé de It1

E (Et/It-1) = 0;

2. Le carré des erreurs représentent comme différence entre la valeur réalisée et la variance conditionnelle

E²_t = Xt - V (XvIt-1) ;

3. Le carré des erreurs normalisées définie

2 (Xt - E (Xt/It_1))

,VV (Xt/It-1) .

E_t =

1.3.4 Modèle linéaire

Définition 1.3.4 Un processus _(Xt)tEZest un processus linéaire (resp linéaire général)de moyenne s'il s'écrit sous la forme:

xt = , + _X1 k"t--k

k=oo

oh _{"t}tEZ est un bruit blanc fort (resp faible) avec variance cr² et oh la suite des coefficients _k est supposé telle que : P1 k=QQ 2 k < oc.

1.3.5 Opérateur de retard L

L'opérateur L décale le processus d'une unité de temps vers le passé

LX = Xt~i

Propriétés

1. Si on applique h foie cet opérateur, on décale le processus de h unité de temps :

L(L(...LXt...)) = L^'Xt = Xt_h.

2. Si Xt = c,Vt E Z avec c E R,LⁱXt = Lⁱc = c,Vi E Z.

3. Si a < 1

(1 - ~L)1Xt= xt

(1 - aL)= uim

j--+oo (1 + ~L + ~²L²+::: + ~^jL^j)X _t:

Cette derniêre propriété est particuliêrement utile pour inverser des polynômes d'ordre 1 définis en l'opérateur de retard.

1.3.6 Modèle ARMA

Les modèles ARMA s'appuient principalement sur deux principes mis en évidence par Yule et Slutsky, le principe autorégressif et moyenne mobile.

Puis en 1970, leur application a l'analyse et a la prédiction des séries temporelle fut généralisés Box et Jenkins en combinant les deux principes ARMA ils montrèrent que ce processus pouvait s'appliquer a de nombreux domaines et était facile a implémenter.

Modèle AR

Un processus autorégressif est un processus dont chaque valeur est décrite comme une combinaison linéaire des valeurs précédentes plus une composante aléatoire qu'on appelle un <<choc>> . Le nombre de valeurs précédentes considérées est appelé <<ordre>> du processus.

Definition 1.3.5 Le processus {Xt, t N (ou Z)}satisfait l'équation générale d'un processus AR d'ordre P :

Xt = 8 + X p cbjXt--j + "t (1.1)

j=1

Definition 1.3.6 ot

8 : le coefficient d'accroissement; çbj : les coefficients d'autorégressifs;

"t : un choc bruit blanc indépendant.

Modèle MA

Chaque valeur est décrite par une composante d'erreur aléatoire et une combinaison linéaire des erreurs aléatoires associées aux valeurs précédentes. De même, l'ordre du processus est défini par le nombre d'erreurs précédentes prises, en considération.

Definition 1.3.7 Le processus {Xt, t N (ou Z)}satisfait l'équation générale d'un processus MA d'ordre q :

Xt = ~ - X q j"t--j + "t (1.2)

j=1

Definition 1.3.8 ot

j : les coefficients de moyenne mobile.

"t--j : les chocs ou le processus purement aléatoire.

Modèle mixte

Le modèle linéaire le plus courant est le modèle ARMA qui combine simplement les deux principes AR et MA.

Définition 1.3.9 Le processus {Xt, t N (ou Z)} admet l'équation générale suivante qui définit un modéle ARMA(p, q)

Xt = , + X p cbj Xt_3 - X q j t_3 (1.3)

j=1 j=1

oli p est l'ordre de processus autorégressif et q l'ordre de processus moyenne mobile.

1.4 Méthodologie de Box-Jenkins

L'approche de Box-Jenkins (1976) consiste en une méthodologie rigoureuse d'étude systématique des série chronologique a partir de leur caractéristique. L'objectif est de déterminer le modèle le plus adapté a représenter le phénomène étudié. Il faut bien noter qu'il est tout a fait possible d'obtenir plusieurs modèles satisfaisants. Cette méthodologie suggère une procédure a trois étapes :

- Identification du modèle : dans cet étape, on va étudier le corrélogramme simple et partiel correspondant, tel que le corrélogramme simple correspondant l'ordre du processus MA et simple leprocessus AR.

- Estimation des paramètres du modèle.

- Validation du modèle par tests sur les coffi cients et sur les résidus.

1.4.1 Test sur les résidus

Il existe un grand nombre de tests d'autocorrélation, les plus connus sont ceux de Box et Pierce (1970) et Ljung et Box (1978).

Test de Box-Pierce ( Porte-monteau)

Soit une autocorrélation des erreurs d'ordre h( h > 1) :

t = Pi _{t_i} + P2 _{t_2} + ~~ ~ + Ph _{t_h} + Vt avec Vt J'f (0,cr2 )

~

Les hypothèses du test de Box-Pierce sont les suivantes :

J

H0 : P1 = P2 = ~ ~ ~ ~ ~ ~ = Ph = 0 H1 : il existe au moins un P =6 0 Pour effectuer ce test, on a recours a la statistique _QBP qui est donnée

par:

QBP = T _XH ^P2 h

h=1

on T est le nombre d'observations et ^{^}Ph est le coefficient d'autocorrélation d'ordre h des résidus estimés et.

Sous l'hypothèse H0 vraie, _QBP suit la loi du khi-deux avec (H - p - q) degrés de liberté :

QBP = T

XH h=1

^P2 h ~! x^2 (H -- p -- q) T--oo

Pour effectuer ce test il est conseillé de choisir H = T 4 (d'aprés Box-Jenkins).

La règle de decision

Si QBP > k^* on k^* est la valeur donnée par la table du khi-deux pour un risque fixé et un nombre (H - p - q) de degrés de liberté, on rejette H0 implique que les "t ne forment pas un bruit blanc. Sinon, on accepte H1 (autocorrélation des erreurs).i.e les €t forment un bruit blanc.

Test de Ljung-Box

Ce test est a appliquer, de préférence au test de Box-Pierce. La distribution de la statistique du test de Ljung-Box est en effet plus proche de celle de khi-deux en petit échantillon que ne l'est celle du test de Box-Pierce. La statistique de test s'écrit :

QLB = T (T + 2)	XH h=1	^P2 h
		T -- H .

Sous l'hypothése nulle d'absence d'autocorrélation :

^P2 1 = ^P2 2 = ~ ~ ~ = ^P2 h = 0.

La statistique _QLB suit une loi de khi-deux a (H - p - q) degrés de liberté.

Tests d'hétéroscédasticité (ARCH)

Le test ARCH consiste a effectuer une régression autorégressive des résidus carrés sur q retard :

e2 t = 0 + X q _j e2 t_3

j=1

on et désigne le résidu a l'instant t issu de l'estimation des paramètres du processus ARMA (p,q).

Pour déterminer le nombre de retards q, on étudie le corrélogramme des résidus au carré.

Les hypothèses du test ARCH sont les suivantes :

J

H0 : homoscédasticité et Oo = O1 = ~ ~ ~ = O_q = 0 H1 : hétéroscédasticité et il y a au moins un coefficient O =6 0

Pour mener le test, on utilise la statistique de test T x R² on T correspond au nombre d'observations de la série et et R² représente le coefficient de détermination associé a la régression.

Sous l'hypothèse H0 la statistique de test T x R² suit la loi du khi-deux a q degrés de liberté.

La règle de décision

- Si T x R² x²(q) on x²(q) désigne la valeur critique figurant dans la

table du khi-deux, on accepte ici l'hypothèse H0 d'homoscédasticité. - Si T x R² > x²(q), on rejette ici l'hypothèse H0 d'homoscédasticité

et on admet qu'il y a de l'hétéroscédasticité.

Tests de normalité

Pour vérifier si le processus des résidus {€t, t Z} est un bruit blanc gaussien, plusieurs tests peuvent être utilisés, mais le test le plus courant est celui de Jarque et Bera. Ce dernier est fondé sur la notion de skewness et de kurtosis.

Le test de Jarque et Bera regroupe ces deux tests en un seul test. On construit la statistique :

T

S = 6 Sk + ₂₄ (K_u - 3)² -!

T T i--oo x2 (2)

Donc si S ~ x2 1_a (2) on rejette l'hypothèse H0 de normalité des résidus au seuil de a%.

1.4.2 Modèle non linéaire

Par conséquent, l'hypothèse de processus ARMA stationnaire ne per-met pas de prendre en compte d'une part les mécanisme d'asymétrie et d'autre part les rupture de forte amplitude. D'oñ la nécessite d'aller vers des modélisations non linéaires. L'espérance conditionnelle E (Xt/Zt_1) est la meilleurs approximation au sens de l'erreur quadratique moyenne de t par une fonction des valeurs passés. Il existe une infinité de processus non linéaire susceptible de représenter les propriétés des séries financières. Compbell, Lo et Mackinlay [1997] ont proposé le cadre suivant pour décrire un processus non linéaire :

Xt = g ( t-1, t-2,...) + h ( t-1, t-2,...)

on la fonction g(.) correspondant a la moyenne conditionnelle du processus X et on la fonction h(.) correspondant a un coefficient de proportionnalité entre X et le choc _t cela permet de classifier les processus non linéaire en deux parties :

1) Processus non linéaire en moyenne pour lesquelles g(.) est non linéaire.

2) Processus non linéaire en variance pour lesquelles h(.)est non linéaire.

Cette classification permet de regrouper la plupart de modèles non linéaire. Dans ce domaine le papier de Engle [1982] << Autoregressive Conditional Heteroskedasticity with Estimates of the variance of UK inflation -Economica->> a ouvert la voie a la modélisation ARCH et a ses nombreux développements. C'est précisément sur cette voie que mon document portera par l'essentiel. Mais avant cela, on va présenter un modèle non linéaire portant proche des modèles ARCH.

Modèle BL <<Granger et Anderson [1978]>>

Les modèles bilinéaires présente la particularité d'être a la fois linéaire en X et mais de ne pas d'être a ces deux variables prise conjointement. Un modèle BL d'ordre, noté par le signe BL (p, q, P, Q), s'écrit ainsi sous la forme :

Xt = , + X p cbiXt_ + X q j t-j + _XP X Q ~ijXt~i tj (1.1)

i=1 j=0 i=1 j=1

'y (h) =

~ 2 + A2E (X2 ) .2 si h = 0 t_2 0 si h ~

1

avec 0 = 1, (c_p, q, APi, AiQ ) E ^*4, V (i, i) et on €t désigne un bruit blanc éventuellement gaussien, c'est a dire un bruit blanc fort, cette l'hypothése assure l'existance de la variance. Certain des processus bilinéaires ont des proprietés proches de celles des modèles ARCH que nous étudions dans ce document.

Exemple 1.4.1 Comsidéroms um cas particulier de processus BL (0, 0, 2, 1) de type:

Xt = €t + A Xt_2 €t_ (1.2)

on A E et €t est identiquement indépendante distribué (0, cr²). Ce

processus est centré, puisque le bruit est indépendant du passé (donc coy (€t_1,Xt_2) = 0),

E (Xt) = E (€t) + A E (Xt_2 €t-1)

= E (€t) + A E _{(Xt_2)} E (€t-1) = 0.

Sa fonction de d'autocovariance est donné par:

'y (h) = E (Xt Xt_h)

= E [(€t + AXt_2 €t-1) (€t--h + AXt_2_h €t_1_h)] = E (€t €t--h) + A²E (Xt_2 €t--i Xt_2_h €t_1_h) +AE (Xt_2 €t-1€t--h) + AE (Xt_2_h €t-1--h €t)

pour h > 1, il n'apparait aucun terme en €2 t_h et puisque l'opérateur espérance est linéaire, la fonction 'y (h) est par conséquant nulle. En revanche, pour h = 0, on a :

'y (0) = E (€2 ) + A2E (X2 )

) E (€2

t t_2 t_1

= a² + A2E (X2 ) a2

t2

Ainsi la fonction générale d'autocovariance s'écrit :

La variance marginale de ce processus est V (Xi) = 2

1_A2a2. Tl existe

une solution stationnaire du seconde ordre de l'équation (1.2) a condition A²cr² < 1. Paralelement, la variance conditionnelle du processus X se dérive directement a partir de l'équation (1.2) :

]

V (Xt/Xt_2) = 2 [1 + A2X2 t_2

La variance conditionnel le du processus X dépend des valeurs passées de ce processus. On retrouve un effet de type ARCH. Ceci illustre le fait que plusieurs modélisations non linéaires peuvent être envisagées si l'on souhaite modéliser la dynamique dans la volatilité conditionnelle.

Exemple 1.4.2 On vérifie sur le graphique (1.1) que le modêle BL BL(0, 0, 2, 1) avec A = 0.2 est capable de générer des cluster de volatilité comme ceux observés sur données financiêres.

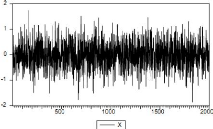
Figure 1.1 : Simulation d'un processus
BL(O,O,2,1).

Modèles TAR

Les modèles autorégressifs a seuil ou TAR ont été proposés par Tong [1978]. Tlles a introduits comme des approximations discrètes des modèles non linéaires. Tls permettent de reproduire des phénomènes tels qu'un cycle limite.

Supposons que le processus Yt vérifie au temps t une équation parmi plusieurs équations différente selon la valeur d'une variable (autre que Yt).

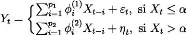
Chaque equation correspond a un regime. Dans le cas d'un seuil unique et d'une variable Xt,

Exemple 1.4.3 Considérons le cas de modeles AR (1) avec un seuil unique

{0⁽¹⁾Xt-i + Et, si Xt_i < a

Xt =

Tong a considers l'existance de plusieurs seuils. La variable Xt, est une variable exogene, soit une variable (Yt) retardée (Yt_d). Dans ce dernier cas, on parlera eventuellement de modele SETAR. Il est a noter que les bruits Et et n_t sont independants et peuvent etre de variance differente.

0⁽²⁾Xt-1 + Et, si Xt_1 > a

avec le même bruit. Une condition nécessaire et suc/cante d'existence d'une solution stationnaire et 0⁽¹⁾ < 1, 0⁽²⁾ < 1 et 0(1)0(2) < 1.

La série ci-dessous correspond a une simulation de la série

--0.2 Xt_1 + Et, si Xt_i < 1

Xt =

0.9 Xt_1 + Et, si Xt_i > 1

avec un bruit blanc gaussien, centré réduit,

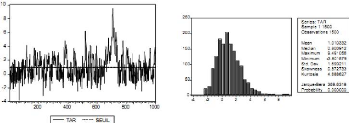
Figure 1.2 : Simulation de processus TAR.

Ce type de processus, la aussi, permet d'avoir des queues de distribution plus épaisses (en l'occurence ici pour les fortes valeurs de Yt - queue a droite).

Er 1 01) Xt__z + Et, si Xt < a

{ Xt

Yt =

r 4

²⁾Xt

_

i +

n

_t, si > a

Une écriture équivalente du modèle a seuil a deux régimes, avec un seul reatard, ou une seule variable exogène ( Xt ou Yt_i), est la suivante

Y=

+

0

⁽²⁾Xt

_

i + si Xt >

a,

{

6 ^.₁ #177; 0¹⁾ Xt_i #177; E_t, Si X_t <

cela équivalent a

Yt = (81 + 0⁽¹⁾Xt-i 1 lix_t<_a + (82 + 0⁽²⁾Xt-i 1 lix_t>_a + ut,

on (ut) est une séquence de bruits indépendants, dont la variance est de la forme

V (ut) = cr,²1Ex_t<_a + o-²,₇1Ex_t>_a.

Les modeles SETAR

Toutefois, dans cette classe de modèles, les travaux ont dans leur trés grande majorité portè sur la sous-classe des processus TAR et tout particulièrement celle des SETAR certainement en raison de moindres dificultés d'estimation. Ainsi, un SETAR a un seul changement de régime aura pour écriture :

61 + Er 1 0(¹⁾ Xt--i €it, si Xt_d < ~

Xt = 2

+ (2)

i Xt~i + E2t, si Xt_d > ~

et plus généralement, un SETAR (K, p1,..., pk, d) s'écrira :

Xt =

XK k=1

+

Pk i=i

)^,0^1°) iXt--i + Ekt x E (Xt-d E Rt)

on

{1 si Xt_d < ~

lit =

0 si Xt_d > a

Exemple 1.4.4 La Figure représente le graphique des données simulées provenant du modèle AR (1) et du modèle SETAR. Il s'agit de modèles simulés avec 200 observations et avec les paramètres suivants :

- pour le modèle AR (1) : Xt = 0:5 Xt_i + Et

- pour le modèle SETAR : Xt = -- 0.3Xt_1 (1 -- + Et

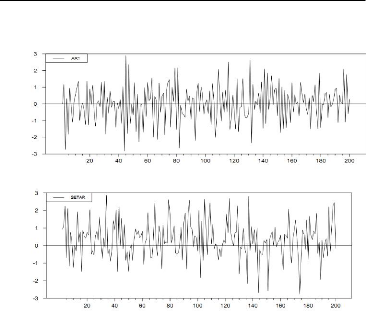
Figure 1.3 : Comparaison entre le processus AR et SETAR.

Exemple 1.4.5 Si on fait une analyse visuelle des deux graphiques, on constate que le pattern de ces deux modéles est différent. Une première différence est l'échelle des valeurs simulées qui est plus grande pour le modéle AR (1). Une deuxiéme différence vise la moyenne et la variance de la variable dépendante des modéles. L'analyse descriptive présentée au Tableau suivant permet de constater que la moyenne du modéle AR (1) est trés proche de zéro et plus petite que celle le modéle SETAR, mais sa variance est plus grande que celle du modéle SETAR. Les valeurs de skewness et d'excés de kurtosis permettent de rejeter l'hypothése de normalité pour les deux modéles.

	AR(1)	SETAR
Moyenne	0.0483*	0.4069*
Variance	1.8619*	1.0854*
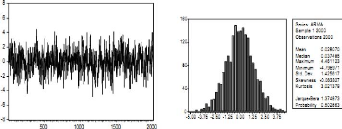
Skewness	-0.1607*	0.3703*
Kurtosis(Exc.)	-0.2268*	-0.0043*

Table 4.1 : Analyse descriptive pour les modéle AR (1) et SETAR.

Note : *indique que les tests sont significatifs a un niveau de con/lance de 95%.

Chapitre 2

Modèles ARCH et GARCH

2.1 Modèle ARCH

Dans le but de palier aux insuffi sance des représentations ARMA(p, q) pour les problèmes monétaires et financiers, Engle propose une nouvelle classe de modèles autorégressifs conditionnellement hétéroscédastiques (ARCH) apte à capter le comportement de la volatilité dans le temps. Le modèle

est formé de deux équations. La première met en relation le rendement et certaines variables qui l'expliquent et la seconde modélise la variance conditionnelle des résidus. Le principe proposé par Engle consiste à introduire une dynamique dans la détermination de la volatilité en supposant que la variance est conditionnelle aux informations dont nous disposons. Il avance une spécification ARCH(p) on le carré des innovations, c'est-à-dire la variance du terme d'erreur au temps t, dépend de l'importance des termes d'erreur au carré des p périodes passées. Le modèle ARCH(p) permet de générer des épisodes de volatilité importante suivis d'épisodes de volatilité plus faibles.

2.1.1 Definition et representation

Soit (Xi) un processus AR(1), tel que X = 8+a Xt_1 +"t, avec a < 1 et "t ~ Al (0, cr²) est un bruit blanc gaussien.

Alors, La moyenne et la variance inconditionnelles de X s'écrivent :

8

E (Xi) = 1 - a

₈2

et

V (Xt) = 1 - a2

Aussi :

( )

E Xt/Xt_1= Et_1 [Xi] = 8 + a Xt_1

La moyenne conditionnelle de Xt dépend de l'information disponible au temps t - 1 et n'est pas nécessairement constante. Par contre, la variance conditionnelle est fixe et ne dépend de l'information disponible au temps t - 1 en raison de l'hypothèse de constance de la volatilité :

( ) ( )

V Xt/Xt_1 = E (Xi - E (Xt))² /Xt_i

( )

= E €2 t /Xt_i = 2

En fait, l'hypothèse que les résidus soient des bruits blancs forts nous amène a ce résultat. Un bruit blanc fort implique que les residus ont une moyenne nulle et ils sont non correlés dans le temps. De plus, tout comme la variance inconditionnelle, la variance conditionnelle est constante. Cette dernière condition est peu réaliste parce que la variabilité dans le temps des variances est un fait stylisé bien établi en finance.

Exemple 2.1.1 La figure suivante présente une simulation d'un processus AR(1) :

Figure 2.1 : Simulation d'un processus AR (1).

En effet, le processus AR(1) est un processus gaussien : les queues de distribution sont moins épaisse que les queues observées sur la variance de l'indice CAC40 et on n'observe pas de période de haute volatilité. Les modêles ARCH (simulé ci-dessous) permettent, eux, de mieux prendre en compte ce genre de comportement :

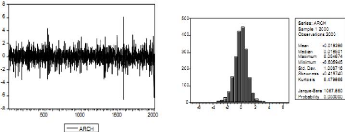
Figure 2.2 : Simulation d'un processus ARCH (1).

Les queues de distribution peuvent être plus épaisse que celle des lois normales (kurtosis de 6,47 avec les paramétres choisis), et on observe, comme sur les données empiriques, des zones de forte variabilité (volatilité).

Commançant par présenter le modèle ARCH(1).

Modèle ARCH(1)

Supposons que la variable Yt peut être expliqué dans un modèle dynamique linéaire avec les variables prédéterminée X et le vecteur de paramétres /,

Yt = X⁰ _t + "t (2.1)

on X est le vecteur des variables exogènes et correspond aux variables expliquant les rendements, inclus les valeurs décalé de variable dépendante et _t est un vecteur d'espérance nulle et de variance cr². On suppose que "2 _t suit un processus autorégressif AR(p)

"2 t = o + çb1€2 _t1 + ~ ~ ~ + p"2 _tp + Vt (2.2)

avec vt est un bruit blanc. L'ensemble d'information _It1 contient tout les informations qui est disponible a savoir les donnees de rendements à l'instant t -- 1, ainsi It1 = {Y_1, Yt-2, _;Xt_1, Xt_2, --}. Si le vecteur des parametres est connu, cet ensemble d'information contient egalement tous les residus a l'instant t -- 1, puisque

st-i = Yt-t -- Yt_t_r3, i = 1, 2, ...

La variance conditionnelle de 4, _{t ;}peut etre ecrit comme suit :

ht = V = E [E? (2.3)

donc Et/It_1 s Al (0, hi) :

L'idee d'Engle, mettait la variance conditionnelle de la serie des carrees des erreurs comme une fonction des erreurs retarde, de temps, de parametre et variables previsible :

{01 = 0^-2 (Et-1, Et-2, ... , t, 13) Et = nt ht, nt est i.i.d

avec E (rat) = 0 et V (rat) = 1. Il choisit une forme de fonction pour 14 tel que 4 = c+Eⁱ:_₁ cbiE?_i, avec c > 0 et cbi > 0 pour i = 1, 2, ... ,p et c, {ci}P₁ sont des constantes. Cette condition est necessaire pour 4 soit non negative. On obtient le modele ARCH(p) , suivant :

Et nt ht = nt

u uc v +

X p i=i

i"2 ti

on nt est bruit blanc faible, tel que E (ra_t) = 0 et V (rat) = ² ~: Definition 2.1.1 Un processus Et satisfait une representation ARCH(1) si

Et =lit ht (2.4)

avec

ht = c + 1"² (2.5)

t1

et oit _lit est bruit blanc faible, tel que E (ra_t) = 0 et V (rat) = ² ~:

Dans ce systeme, le processus Et est caracterise par des autocorrelations nulle E (EtE₈) = 0 pour t =6 s ce qui signifie que les termes d'erreurs Et sont non correles dans le temps. En effet, Et reste un bruit blanc mais dit faible. Un bruit blanc faible implique que les residus ont une moyenne nulle et ils

sont non corrélés dans le temps. Ainsi, la variance conditionnelle varie dans le temps, mais Et est non conditionnellement homoscédastique, c'est-à-dire qu'il y a l'existence d'une variance inconditionnelle finie.

On peut établir des résultats intéressants, nous pouvons écrire le modele ARCH sous deux autres formes. Prenons un modele ARCH (1) pour les illustrer.

1. Forme d'équilibre :

4 = .² + 01 (4_1 - a²)

Sachant que a² = 1-01, c nous retrouvons la forme habituelle du modele ARCH (1) ainsi :

14 = 1 + 01 (Et-1 C C 01 1 -- 01 )

C

2

= + 01Et-1 ~

1 -- 01 1 1C -- 01

= C + 014_1.

2. Autorégressive dans les erreurs au carré

"2 t = h2 t + Vt

oil vt = 4 - N.

Et en ayant les informations disponibles jusqu'au temps t-1 : E [vt/It_i] = E [Et/1^-t_1] -- E [ht/1-t_1] = ht2 -- ht2 = 0 est processus d'innovation pour

E?. Ainsi cette écriture précédente correspondant çà celle d'un processus AR (1) sur le carré E?

Et² = C + 01E²t--1 + Vt- (2.6)

On sait que ce processus Et est stationnaire au seconde ordre si et seulement si 1011 < 1, c'est à dire que la variance marginale est constante. Exemple 2.1.2 Les graphiques montrent l'évolution des processus Et dans

le cas d'un modèle ARMA a gauche, d'un modèle ARCH (1) au centre, et du rendement de l'indice CAC40 a droite.

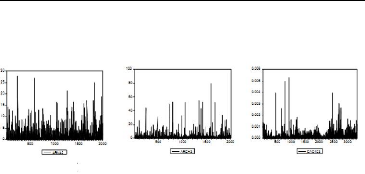
Figure 2.3 : L'^~evolutions de processus E2 t .

Exemple 2.1.3 Les graphiques ci-dessous permettent de comparer un processus AR (1) et un processus ARCH (1)

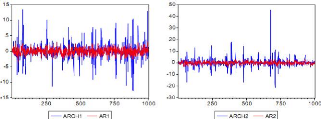
Figure 2.4 : Comparaison entre les processus AR (1) et ARCH
(1).

On peut déduire de ces différentes écritures, un certain nombre de propriétés qui pourront être étendues au cas des processus ARCH (p).

2.1.2 Propriétés des processus ARCH

Propriété 2.1 On peut noter que pour tout s > 1 : E (€t/It~s) = 0, cela signifie que le processus ARCH est orthogonale a tout passé.

Preuve. Pour demontrer cela on utilise la propriete des esperances iterees. En effet, on montre

E [Et/It-₈] = E [E /It-₅]

= E [0/1^-t_₈]

= 0

Propriete 2.2 La variance conditionnelle du processus Et, ARCH (1) , definit par l'equation (2.5) est non constante dans le temps et verifie :

V [Et/it,' = C

1 ~ s ~ 1 + ^s 1"2 ts; 8t: 1 -- 01

C'est la propriete centrale des processus ARCH : le processus Et a une variance conditionnelle depend du temps. On a l'idee que la liaison temporelle passe par l'intermediaire de l'equation autoregressif definie sur le carre du processus (2.6).

Preuve. On sait que E [Et/It__s] = 0 des lors, V [Et/it-s] = E [4/¹t-8] : Considerons le processus Et definie par la relation (2.6) on vt est un bruit blanc faible. Par iteration successive, on a :

E? = c + 01 + 2 1 +
·
·
· + s1 ~ + vt + ~1vt~1

1

+0204_2 + ~ ~ ~ +0,91 -174_5+1 +os1"2t-8

En considerant l'esperance conditionnelle de chacun de ces nombre, il vient :

_Xs ~ 1

E "2 t Its ~ = c 1 ~ s ~

1 + ^j 1E [vt~j~It~s]

1 ~ ₁

i=o

~ :

+^s 1E "2 tsIts

Puisque par definition du bruit blanc, on a

E[vt_i/lt,]= 0, Vj = 0, 1, , s-1, et par definition E [Et²_,/it-8] =

Et_,, on obtient ainsi la formule de la variance

Lorsque s tend vers l'infinie, ces variance conditionnelle converge vers la variance non conditionnelle, et l'on retrouve alors la formule :

V ["t] = uim

8--+oo

V [€t/7t-s]

_L L1 ~ qs ] ]

1

= uim + q^s 1"2 ts

s!1 1 - qi

C

=

1 - q1 .

Propriété 2.3 Les autocovariances conditionnelles du processus €t, ARCH (1), définit par l'équation (2.5) sont nulle

Cov ["t_; Et+k/1t_s] = 0.

Le processus est donc un processus sans mémoire.
Preuve. Cette propriété s'obtient de la façon suivante :

Cov ["t_; Et+k/1t_s] = E [EtEt+k/It_s] = E _["t/It-s] E [Et+k/It_s]

= E ["t"t+k/It_8]

= E [E ("t"t+k/IJt+k_1) /Zt-8] = E [€tE ("t+k/Zt+k_1) /Zt-8] = E ["t 0/Zt_8]

= 0

car _€t+k est connu en t + k - 1, on a donc

E ["t 0/Zt_8] = 0 ~

L'absence de corrélations entre les valeurs d'un processus ARCH est une caractéristique très importante de cette famille de modèle, qui les rend utiles pour modéliser certaines séries financières¹, comme le font remarquer Bera et Higgins [1993].

Propriété 2.4 La variance marginale du processus Et existe si et seulement si C > 0 et 0 < q < 1, d'oit le processus _t est stationnaire au seconde ordre.

¹Remarquons néanmoins que l'absence de corrélations entre les valeurs d'un processus ARCH n'implique pas que ces valeurs soient indépendantes. Comme nous le verrons

plus loin, des corrélations non linéaires peuvent en général exister entre les observations. Ce phénomène est possible puisque la distribution du processus n'est pas gaussienne mais seulement conditionnellement gaussien.

v u u ht = tc +

X p i=i

0i"2 t_i

En effet, il convient de vérifier notamment que V [4] et V [Et] sont définies de façons positive. Sous la condition c > 0 et 0 < 01 < 1, la variance marginale de Et existe et elle est constante dans le temps, donc le processus Et est stationnaire au seconde ordre.

On peut en outre établir les moment conditionnelle et non conditionnelle d'ordre quatre existe du processus Et.

Propriété 2.5 Le moment conditionnelle centre d'ordre quatre du processus Et verifie

E [4/1^-t_s] = 3 (c + 014_0²

Sous l'hypothese 30² 1< 1, le moment non conditionnelle centre d'ordre quatre du processus Et est egale à

E [Et] = 3 [c2 201c2 + 021E [Et2_1]]

1-- 01

= 3

c2 (¹ + 01)

(1 -- 30T) (1 -- 01)

La kurtosis (ou le coefficient d'applatissement de Ficher) non conditionnelle associee au processus ARCH(1) est

Ku =	E [E:]	= 3 I 1 --^-1 > 3 L1 -301JJ
	E^2 [4]

Sous l'hypothése de positivité du paramétre, 0i, la kurtosis non conditionnelle est toujours positive a celle de la loi normale : elle traduit l'aspect leptokurtique de la distribution du processus Et. C'est donc la deuxieme raison avec la variance conditionnelle dépendante du temps pour laquelle les processus ARCH sont trés utilisé pour représenter les séries financieres ou les résidus de modele linéaire définis sur série financiere.

Tout ces propriétés peuvent etre généralisées du cas d'un processus ARCH(p) .

Modèle ARCH(p)

Définition 2.1.2 Un processus Et satisfait une representation ARCH(p) si

Et = ht (2.7)

avec

et ofi ij_t désigne un bruit blanc faible, tel que E [_t] = 0 et

V [_t] = o² ~.

Les caractéristiques distinguée de ce modèle n'est pas seulement que la variance conditionnelle est une fonction de temps mais aussi c'est la forme particulière est spécifier. Les épisodes de la volatilité sont généralement caractérisés comme les chocs pour la variance dépendante. Dans le modèle de régression, un choc grave est présenté par un grand écart type, d'oñ présenter par une grande valeur positive ou négative de €t. Dans les modèles ARCH, la variance de l'erreur courante, conditionnelle sur l'erreur réalisée "t_1est un fonction croissante de l'ampleur des erreurs retardées sans tenir compte leur signe. p détermine la duré de temps avec laquelle les chocs persistent a faire conditionner la variance des erreurs.

Exemple 2.1.4 Ce phénoméne est illustré a la figure (2.5) oh des processus ARCH (p) sont simulés pour différentes valeurs de p :

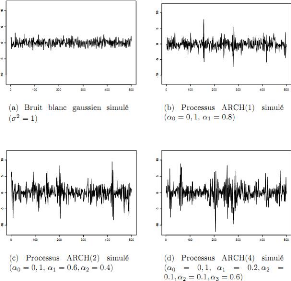
Figure 2.5 : Simulation de processus ARCH pour diff^~erente
retards.

Exemple 2.1.5 Donc, la volatilité a la date t est alors une fonction des carrées des écarts a la moyenne observés dans le passé proche. Si les coefficients P_i sont tous positives (assez grands), il y a un persistance des niveaux de volatilité : on observe des périodes de forte volatilité suivies des périodes de faible volatilité.

Plus généralement, les moments centrés d'ordre impaire, s'ils existent sont nulle, par symétrie. En supposant que le processus demeure infiniment loin dans le passé avec les 2r premiers moments finis, les moments d'ordre 2r existe si et seulement si (Engle [1982])

_Pr

1

_Yr
i=1

(2i - 1) < 1.

Modèle avec erreur ARCH

On considére dorénavant non plus un processus ARCH pour modéliser directement la série financière, mais les résidus d'un modèle linéaire. Prenant l'exemple d'un modèle linéaire autorégressif avec résidus de type ARCH (p).

On procéde la définition générale d'un processus autorégressif et d'un processus autorégressif linéaire <<Gouriéroux [1992]>> .

Definition 2.1.3 1) Un processus stochastique X est un processus autorégressif, AR, d'ordre k si et seulement si :

[ ]

X = E Xt/Xt~i + "t

= E [Xt/Xt_1, Xt_2,..., Xt_k] + €t

2) Un processus stochastique Xt est un processus autorégressif linéaire, AR, d'ordre k si et seulement si :

[ ]

X = EL _Xt/Xt~1+ Et

= EL [Xt/Xt_1, Xt_2,..., Xt_k] + "t

ofi EL (.) désigne l'espérance linéaire, avec € est un bruit blanc faible, tel que

E [€t "₅] = 0, si t =6 s

et

E ["t] = 0

satisfaisant la condition

E = 0.

On suppose que ce résidu admet un représentation autorégressif de type ARCH (p)

Et = pit ht

avec

,\Iht = c +

X p i=i

0t E?-t

et oft pi_t désigne un bruit blanc faible.

On a un modele qui décrit a la fois l'évolution de l'espérance conditionnelle et la variance conditionnelle du processus Xt dans le temps. Envisageons le cas le plus simple d'un processus de type AR (1) avec erreur ARCH (1)

Xt = S + aXt_i #177; Et, lad < 1 Et = \/c + 014-1

Dans ce cas les résidus satisfont les principales propriétés étudiées précédemment² :

i) le processus (Et) est orthogonal aux valeurs passées, pour quelque soit le retard

E [Et/It_₈] = 0, pour tout s > 1,

la variance conditionnelle

V [Et/it-i] = c + 014-i et suit un processus ARCH (1)

2 2

Et = c 0lEt-1 #177; pit.

ii) la propriété d'orthogonalité implique que les corrélations conditionnelles sont nulle : coy [Et, Et+k/it_8] = 0.

Il y a donc une absence de corrélation entre les valeurs présentes et futures du processus, quels que soient les retards s et k. Mais si la variance

²Les propriétés de processus d'innovation vt
·

conditionnelle de Et n'est pas constante, la variance non conditionnelle est constante.

On peut, en outre, en déduire un certain nombre de conclusion quant au processus Xt lui même. On peut montrer tout d'abord que l'espérance conditionnelle de Xt vérifie :

E [Xt/ Xt_s] = S + a E [Xt_i/ Xt_s] ;

ce qui montre que les prévisions non linéaires de Xt s'obtient comme les prévisions linéaires d'un processus AR (1). Plus généralement

Xt = ~ 1 ~ ~s + ~^sXt~s + "t + ~"t1 + ~ ~ ~ + ~^s1"ts+1

1 ~ ~

En prenant l'espérance conditionnelle de deux cotés, on obtient

1

E [Xt/ Xt_s ] = -- + a^sXt-.9
·

1 --a

De même façon, on peut montrer que la variance conditionnelle de Xt dépend du temps. En effet, on montre qu'elle dépend du processus EL de la façon suivante.

Propriete 2.6 La variance conditionnelle du processus AR (1) avec erreur ARCH (1), Xt, s'ecrit

[1

1 01_

v [xt/xt_d 1

= -- 6. 01 1 -- a2 a25 01 01 -- a2a28 +0

~

s 1 ~ ~2s ₂

2 Et^-8

01 -- a

Ainsi, la variance conditionnelle d'un erreur de prevision a l'horizon 1, s'ecrit

V [Xt/ Xt_s] = S + 014,

Preuve.

v [xt/xt_s ] = V [6

a^s-8+1/Xt-8

1 -- a + as Xt-8 + Et +

= V [Et/Et-9] + a²V [Et-i/Et_s] _a2(5-1)T ₇

V [Et-5#177;1/fit-s]

1 -- a^s

=

_Xs _ 1
J=0

~

1- 01

[ (1 1 _-- a2 8) ₀₁ (₀₁ __ _aa2₂8 #177;

=

-- a25 2

1

E.

-- _a2 .-8

1 [ ₀

₁

"

~ 1 ~ sj

_~2j 1 + sj

₁ "2 _ts

1 -- 01

En conclusion, si l'on désire prévoir le processus X dans le cas d'erreur ARCH (1), l'erreur de prévision a une horizon d'une période admet une

[ ]

variance V _{Xt/Xt_5qui} varie dans le temps en fonction de la valeur de

[ ]

"2 t_s; autrement dit V _{Xt/Xt_5=} I (st_S).

Exemple 2.1.6 Le graphe ci-dessous correspond a la simulation d'un tel processus, avec a droite son corrélogramme,

Figure 2.6 : Simulation d'un processus Y et son
corr^~elogramme.

Le corrélogramme partial suggére de tester un modéle autorégressif d'ordre 1 sur X . Toutefois, si l'on étudie la distribution des résidus du modéle X = 8 + aXt_1 + €t, l'hypothêse de normalité est clairement rejetée

Figure 2.7 : Le test de Jarque-Bera.

Le corrélogramme ne permet pas de rejeter l'hypothêse de bruit blanc, mais le corrélogramme ne permet de ne mesurer qu'une dépendance linéaire

entre € et _{"t_1.} L'idée peut alors être de tester le caractére ARCH des résidus obtenus, pour expliquer cette forte kurtosis,

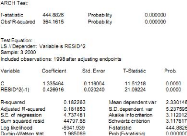
Figure 2.8 : Le test ARCH.

Ce test est alors clairement significatif, et l'on valide l'hypothêse de modêle ARCH pour les résidus. Le modêle est

alors

JX = 0:79404 Xt_1 + "t oh t = _t 1:335464 + 0:42691"2 t_1 et oh (_t) est un bruit blanc gaussien.

2.2 Les modêles ARCH généralisées

Pour de nombreuses applications, l'introduction d'un grand nombre de retards p dans l'équation de la variance conditionnelle du modèle ARCH (p) est nécessaire pour tenir compte de la longue mémoire de la volatilité qui caractérise certaines séries monétaires et financières. Ce nombre important de paramètres peut conduire a la violation de la contrainte de non-négativité de la variance et poser des problèmes d'estimations. Dans cette perspective, une extension importante, le modèle autorégressif conditionnellement hétéroscédastique généralisé (GARCH), est suggérée par Bollerslev [1986]. Cette approche exige moins de paramètres a estimer que la formulation ARCH (p) pour modéliser les phénomènes de persistance des chocs. La variance conditionnelle de la variable étudiée est déterminée par le carré des p termes d'erreur passés et des q variances conditionnelles retardées.

2.2.1 Modèle GARCH(p, q)

On continue de considérer un modèle autorégressif exprimé sous la forme

[ ]

X = E _{Xt/Xt_1+} €t avec _t est un bruit blanc faible et satisfaisant la

propriété E ["t/Zt_i] = 0.

Ces modèles ont été introduits avec une dynamique autorégressive,

"t = ~ h (2.7)

l'équation de la variance conditionnelle d'un processus GARCH s'écrit :

ht =

u u tc v +

X p i=1

çbiE2 t_i +

X q j=1

jh2 t--j

on ij_t .,A/ (0, cr²), et avec les conditions c > 0, çb > 0, pour i = 1,

2,..., p et j > 0, pour j = 1, 2,..., q satisfaisante pour garentir la posivité de h2 t .

Definition 2.2.1 1) Drost et Nijman [1993] ont convenu d'appeler GARCH faible weak GARCH .> tout bruit blanc faible Et si

i) E ("t/Zt_1) = 0, pour t E Z.

Cette propriété appelée différence de martingale (tout au moins par rapport a la filtration naturelle).

ii) Il existe des constantes c, _i, i = 1,2,... ,p et _j, j = 1,2,... q telles que :

h t = V ("t/Zt_1) = c + X p çbiE2 _{t_i} + X q jh2 _tj, pour t E Z.

i=1 j=1

2) Lorsque le processus d'innovation Vt et E² est lui même seulement supposé être un bruit blanc faible, alors qu'ils appellent GARCH semi-fort «semi-strong GARCH .> le même processus €t lorsqu'il s'agit d'une différence de martingale avec un processus d'innovation Vt qui est lui même une différence de martingale. Les processus GARCH semi-forts ainsi définis coIncident bien avec l'idée initiale de Engle et Bollerslev puisqu'il est clair réciproquement que si l'on suppose que Vt est une différence de martingale, on en déduit que :

Vt = 2 t - h2 _t

oh h _t est bien la variance de €t conditionnelle a l'information passée.

Definition 2.2.2 On dit que le processus GARCH (p, q) fort dans le cas
d'un GARCH semi-fort tel que l'innovation standardisée Vt = €t/h soit
un bruit blanc fort (suite de variables indépendantes et de même loi) et

_t ' JV (0, 1).

En fait, la popularité des processus GARCH faibles dans la littérature récente, à la suite des articles fondateurs de Drost et Nijman [1993], Drost et Werker [1996] et Nijman et Sentana [1996], s'analyse sans aucun doute comme le résultat d'une prise de conscience d'un risque de modèle <<GARCH semi-fort>> d'autant plus manifeste qu'il est aisé de montrer que la classe des processus GARCH semi-forts n'est robuste vis à vis d'aucun type d'agrégation. Plus précisément, ils ont d'abord montré que si des rendements quotidiens sont conformes à un modèle GARCH semi-fort, les mêmes rendements considérés sur un horizon plus long (par exemple hebdomadaire) ne peuvent pas l'être. Autrement dit, la classe des processus GARCH semi-forts n'est pas robuste vis-à-vis de l'agrégation temporelle et c'est pourquoi ils ont proposé de l'étendre à tous les processus qu'ils appellent GARCH faibles pour récupérer cette robustesse. De façon générale, dans la mesure on il n'existe aucune norme d'agrégation, ni temporelle ni contemporaine, qui s'impose à l'utilisateur, le concept de <<GARCH faible >> peut apparaitre comme la panacée pour évacuer un risque de modèle trop patent.

Pour motiver l'introduction des processus GARCH, on peut réécrire (2.7) à l'aides des opérateurs 1' (.) et W (.). Dans ce nouveau contexte, ces opérateurs sont définis par

~ (L) = ~ L + b2L + ~ ~ ~ + ~_pL^p

et

W (L) = 1L + 2L² + ~ ~ ~ + _qL^q. On peut donc écrire

q"t = _t + (L)"2 _t + W (L) h²_t

on L est l'opérateur de retard.

On a donc,

h2 t = c + '(L)s2 _t + W(L)h2 _t . (2.8)

Si toutes les racines de 1 -- (L) sont en dehors du cercle unité, on a :

2

c 0 (L) 2

h_t +

^t 1 - (L) 1 -- (L)Et .

Si la fonction rationnelle de l'opérateur de retard est développé en série, propriété (3), on se trouve :

00

h2 t = c + i=i 'i"2 ti

avec c^* > 0 et (pi > 0, pour i = 1, 2, ....

Cette dernière relation montre qu'un processus GARCH (p, q) est un processus ARCH d'ordre infini. On voit donc que les processus GARCH peuvent formellement représenter de façon plus parcimonieuse des processus ARCH contenant un nombre élevé de paramètres.

Dans la suit, on montre que le modèle GARCH peut être représenté comme une modèle ARMA dans les erreurs au carré. Posant que vt = E? -- h4 avec E (vt) = 0, E (vt v₅) = 0 pour t =6 s et E[vt/It_i] = E [E? -- h_t²/1^-t_1] = 0. Il satisfait la condition de bruit blanc, on peut écrire E? = h2 t + vt, cela donne :

2 Et = c +		X p i=i		i"2 ti +	X q J=1	~"2 t~i^- vt_i) + vt. j
Il s'ensuit que, 2 Et = c +	Xn i=i		(Oz + z) -				X q J=1	jvt~j + vt, t 2 Z

avec n = max (p, q).

Proprietes des processus GARCH

Les propriétés théoriques des processus GARCH se déduisent de la

même façon que nous avon développé les propriétés des processus ARCH. Propriete 2.6 Le processus Et est un bruit blanc si E (E?) < oo.

On a

E(Et) = E [E(Et/It_i)] = 0

et

cov(Et, Et-k) = E(EtEt-k) = E(Et_kE(Et/it_i)) = 0, k > 0.

Lien avec les propriétés des séries financières : non autocorrélation de €t (quelle que soit la spécification de h2 t ), autocorrélation de €² (ici ARMA).

Le calcul de la variance dans le cas général n'est pas direct. Bollerslev a montré que, dans le cas général, la variance du processus reste finie si la somme des paramètres est plus petite que 1.

Propriété 2.7 Une condition nécessaire de l'existence de la variance d'un processus GARCH (p, q) est

~ (1) + W(1) = X p ~i + X q 3 < 1 (2.9)

i=1 j=1

Si cette condition vérifie avec les contraintes de non négativité donnée ci-dessus, elle est également suffisante. Donc le processus GARCH est faiblement stationnaire ou stationnaire au seconde ordre.

Dans le cas on (2.9) est saturée, c'est a dire que Pp i=1 cb + Pq j-_i ., = 1, on dira alors que le processus GARCH est intégré, et on parlera de processus IGARCH.

Propriété 2.8 Le processus €² d'une représentation GARCH (p, q) peut être représenté sous la forme d'un processus ARMA (max (p, q), q) définie dans une innovation vt = €2 t - h2 t , tel que :

€2 t = c + _Xn (çb_i + i)€2 _{t_i} - X q jvt_3 + vt (2.10)

i=1 j=1

avec la conversion çb = 0 si i > p et j = 0 si j > q.

Cette observation amène deux conditions immédiates :

1. Bien que les valeurs €t d'un processus GARCH soient non corrélées, il existe une dépendances non linéaires entre les observations, puisque que le carré des observations se comporte formellement comme un processus ARMA;

2. Pour identifier le nombre des paramètres p et q d'un processus €t ~ GARCH(p, q), on peut utiliser les fonctions d'autocorrélation et d'autocorrélation partielle du processus €² suivant la même procédure utilisée pour trouver le nombre de paramètres d'un processus ARMA.

Dans la section suivante, on définit un cas particulier de ce processus, processus GARCH (1, 1), et ses propriétés.

2.2.2 Modele GARCH (1, 1)

Pour modéliser les données empirique sur le marché, financiere, un modele GARCH (1,1) est souvant suf fisante. Il est donne par l'équation

Yt = X_t^' 0 + Et, Et = Ti_t ht et ht = \/c + 0"²t_1 + h²t-1

avec c > 0, 0 > 0 et > 0. Dans ce modele, les carrés des résidus suit un processus ARMA (1,1),

"2t = c + (0 + ) "²t-1 -- vt-1 + vt

Il est stationnaire pour 0 < 0 + < 1, oft vt = E²_t -- h²_t est un processus d'innovation pour "²_t. Sous la condition de stationnarité de second ordre, la variance inconditionnelle du processus Et existe et constante au cours du temps. Sachant que V (Et) = E (E²_t) , il suffit a partir de la forme ARMA (1,1) sur E²_t de définir la variance du processus : V (Et) = c 0^-1 (1) =

c

1-(q+ ).

Selon Jurgen Franke, Wolfgang Hardle et Christian Hafner [2004] , la kurtosis existe si

30² + 20 + 2 < 1

et donne par : Ku =

E (4) = 3 [1 -- (0 + )2] (E (€t ))2 ^1 -- (0 + )2 --^20^2

Elle est toujours supérieur a trois. Ainsi, si 0 tend vers zéros, l'hétéroscédasticité est disparu et la valeur de la kurtosis tend vers trois. Enfin, on peut montrer que pour un processus GARCH la kurtosis est directement liée a l'hétéroscédasticité conditionnelle.

Considérons le cas de la kurtosis associée a la loi non conditionnelle dans un processus GARCH conditionnellement gaussien tel que Ti_t rs^, Ai (0, 1) . Dans ce cas, les moments conditionnels d'ordre 2 et 4 du processus Et sont liés :

E 4/It-1] = 3 [E [4/It-1]] 2 .

En effet, on rappelle que si une variable centrée x suit une loi normale, alors

E (x⁴) = 3 (V (x))² = 3 (E (x²))² .

Si on applique l'espérance sur les deux cotés de l'équation précédent, il devient

E [E [4 /1^-t_i]] = E [4]

3E [[E [4/1t-1 ]]2] 3 _[E [E [4/1t-i]]] 2

= 3E [4] .

On peut déduire que la loi marginale de Et a des queues de distribution plus épaisse (distribution leptokurtique) qu'une loi normale puisque

E [Et] 3E [4] .

(E (€i ))²

De plus, on peut calculer la kurtosis comme suit : K_u = 3 [E [E [4/1t_1]]]²

= 3(E (4))2 + (E (€i ))^2

3 (E (E?))^2 [ [E [4/It-1 ]] 2 - (E (ED)2]

= 3 + 3 (E (4))2 [[E [4/Z-1 ] ] 2 - E (E (4/1t-1))2]

3 + ₃V [E [E? /It-i]]

=

(E (4))²

la kurtosis est donc liée a une mesure de l'hétéroscédasticité conditionnelle.

Modeles ARMA-GARCH

C'est Weiss [1986] qui a introduit dans la variance conditionnelle des effets additionnels de variables expliquées. En effet, la modélisation GARCH peut être appliquée non au processus initial, mais au processus d'innovation. Ceci permet alors d'introduire divers effets additionnels de variables explicatives soit dans la moyenne conditionnelle, soit dans la variance conditionnelle. Par exemple, on peut considérer un modele de régression linéaire avec erreurs GARCH :

fYt = a Xt + Et

lEt ' GARCH (p, q)

Ce modèle est appelé modèle de régression avec erreurs GARCH. Dans le deuxième cas, le modèle consiste en un processus ARMA avec un processus d'innovation GARCH :

~

~ (L) Xt = ~ (L) "t €t ~ GARCH (p, q) Ce modèle est appelé modèle ARMA - GARCH.

Chapitre 3

Estimation, prevision et tests

3.1 Estimation

Dans cette section, nous allons traiter l'estimation des paramètres d'un modèle (C) ARCH, et, plus généralement, d'un modèle de régression avec erreur (C) ARCH. Les modèles introduits reposent sur des formulations des moyennes et variances conditionnelles.

En pratique celle-ci souvent paramétrées de façon que la moyenne conditionnelle mt (0) et la variance conditionnelle h _t (0) apparaissent comme des fonctions de paramètres inconnus et de valeurs passées du processus. La connaissance de, ces moments ne suffit cependant pas sans hypothèse supplémentaire a caractériser la loi conditionnelle du processus les méthodes d'estimations sont envisagées :

- La méthode de MV,

- La méthode de PMV,

- La méthode MV sous d'autres lois.

Estimation lorsque les moments sont paramètes

Dans la suite, nous indexons par o les espérances et les variances calculées par rapport a la vraie loi du processus. Nous reprenons ici la représentation de Gouriérous. Soit un modèle tel que :

~E ( )
it/it~1, xt = E (it/7t~1) = mt (0)
( )
V _{it/it_1,} xt = V₀ (it/7t~1) = h²_t (0^°) on 0⁰ est la vraie valeur inconnu du paramètre 0 appartenant a e inclus dans k:

Nous notons :

f M3t (0) = E. (Y³/It-1)

t K_u (0) = Ea (Y⁴/It-1)

les moments d'ordre supérieure.

Nous commencons par présenter les méthodes du MV et PMV.

3.2 La methode de MV

Pour comprendre cette approche, nous allons tout d'abord considérer le cas le plus simple d'un processus ARCH pur pour Y. Nous étudierons ensuite le cas des processus GARCH, et enfin des modeles de régression aves erreur (G) ARCH et des modele ARMA -- GARCH.

3.2.1 Estimation des parametres du modele ARCH

L'estimateur des parametres de modele ARCH se base tres souvent sur la maximisation de la fonction de vraisemblance. Nous supposons que le processus Yt est conditionnellement gaussien. La vraisemblance associée a Yt conditionnellement au passé it_1 est donc

(Yt/it-i ⁰) = 1

exp ( (yt -- rat (⁶))²)_-- r ,

ht Or 2h²_t

,

et dépend du vecteur 0 = (00, . . . , O_p) . La fonction de vraisemblance de (yi, y2, ... , yT)conditionnelle a /0 = 0 et par conséquent

T

r (yi, y2, - - - , ^{yT, 0}) = ₁₁ G (yt/it-1, 0)

t=1

L'estimateur est alors défini comme le vecteur 6¹7^-, = (00,..., 0p) qui maximise le logarithme de cette fonction vraisemblance :

BT = arg max log r (yi, y2, - - - , ^{yT, 0})

3.2.2 Estimation des parametres du modele GARCH

Nous avions observé que l'estimation par MV d'un modele ARMA est rendue plus dif ficile que celle d'un processus autorégressif pur, puisque

le processus d'innovation n'est pas directement observé. Le meme phénomène survient lorsqu'on tente de maximiser la vraisemblance d'un processus GARCH. En effet, la vraisemblance associée a Y conditionnellement au passé s'écrit

exp (Yt rat (0))2)

G 0) = 1

ht 2h²_t

mais cette fois, la variance 14 suit un processus ARMA et dépend donc des valeurs passée de la variance conditionnelle hi, , hT. Ces valeurs n'étant pas observé en pratique, la maximisation on directe de la vraisemblance est rendue impossible. En pratique, on estime successivement les

valeurs de hi, , 14^, avant de calculer la vraisemblance. Ainsi, pour un

vecteur 0^° = _;c;, _1;..., Q) fixé de paramètres, on calcul récur-

sivement

11,82 =co #177;

X p i=i

~~ i Y 2 si +

X q j=1

^^h^2 js~j

avec la convention Y = 0 et h? = 0 si i < 0. On remplace donc la fonction de vraisemblance par

exp (Yt rat (0))2)

G 0^°) = 1

htV'2ir 2h?

et la fonction de vraisemblance totale est

r (Yi, y2) YT, °°) = 11 L (yt~It~1;0^°)

t=1

Cette fonction de vraisemblance peut etre calculée pour différentes valeurs du vecteur 0^° et sa maximisatin livre l'estimateur de MV .

3.3 La methode de PMV

Dans cette approche, l'utilisation de la méthode du QMV ou PMV est particulièrement intéressante pour les modèles GARCH car elle est valide, asymptotiquement, pour tout processus GARCH strictement stationnaire (sous des conditions de régularité mineures), sans hypothèse de moments

sur le processus observe. Par consequent, la fonction de vraisemblance definissant l'estimateur du MV sous l'hypothese de normalite et la fonction de pseudo-vraisemblance de l'estimateur PMV (ou QMV ) sont les memes.

Les conditions de regularite sont toujours de trois types :

1. des conditions de stationnarite forte du processus,

2. des conditions d'existence des derivees et des moments apparaissant dans les diverses formules,

3. des conditions d'indentifiabilite des parametres 0, qui doit pouvoir etre retrouve, sans ambigüite a partir des deux premiers moments conditionnels.

Definition 3.3.1 La fonction de log-vraisemblance associée a un échantillon de T observations (yi, y2, .., yT) de Yt^- sous l'hypothese de normalité de la loi conditionnelle de Yt sachant s'écrit :

log LT (0) = - 2 log (27r) -- x-N t=1	1 x-N log (4 (0)) -- 2 t=1	(Yt int (0))^2
		h? (0) :

L'estimateur du PMV OT du parametre 0 est une solution du probleme :

max 0E0

log LT (^0) '

Exemple 3.3.1 Appliquons cette formule au cas d'un modele de régression linéaire avec erreur ARCH (p) :

f y_t = + Et

1 Et =ratht (⁰)

avec n_t est JV .d. (0, 1) et

E (Et/Et-1) = 0; V (Et/Et-1) = c +			x-N p i=i	Oz "2 ti:
V (Yt/it-1) = ht (0) = c +	x-N p i=i	(Yt^-i OXit-i)2

Dans ce cas, on a donc :

E (Yt/It_i) = mt (0) = QXt;

oI ~= (0,c, OD
·
· _;O_p) E IR^P+2 La log-vraisemblance s'écrit :

T log LT (0) = -- 2 log (27r) -- E t=1

log c +

X p t=i

(Y^-i OXt-i)^2)

1

2

~

_XT
t=i

2 2

(^Y-t /3Yt-z) x [C E oz (Yt_i - oxt-z)1 ^-1

i=1

Definition 3.3.2 Les estimateurs du MV sous l'hypothèse de normalité ou du PMV, notés OT, des paramètres 0 E R^k, satisfont un système non linéaire a K équations :

~~~~~=^{^}~T = 0

0 log LT (0)
00

avec

0 log LT (0) 00

~~~~~=^^~T

= 2

XT t=i

1 Oht (0) h? (0) 00

~~~~~=^^~T

+E t=i

(Yt -- mt (6))^2 Oht (0) N (0) ae

~~~~~=^^~T

+E t=i

Yt -- nit (0) h? (0)

amt (0) 00

~~~~~=^^~T

Remarque : On peut montrer que ce systeme peut se décomposer en deux sous systemes lorsque les parametres 0 interviennent de façon séparée dans l'écriture de l'espérance et de la variance conditionnelle. Ainsi, si l'on a 0 = (a, 0) oft a n'apparait que dans l'espérance conditionnelle et dans la variance conditionnelle, on peut décomposer ce systeme en deux sous systeme puisque :

0 log LT (a) 0a

~~~~~=^^~T

=

XT t=i

Yt -- nit (&) h? (S)

amt (a) as

a a

a log LT (0) 00

~~~~~=^^~T

= 2

XT t=i

1

aht (^3) 00

~~~~~=^^~T

+E t=i

OYt -- nit CO^2

aht (^3) 00

h? C4)

N C4)

s="4

Dans, le cas général du PMV, on sait que l'estimateur 0 est asymptotiquement normal et que sa matrice de variance covariance est définie par la formule suivante.

Propriete 3.1 Sous conditions de régularité, l'estimateur du PMV est asymptotiguement convergent et normal.

^-VT (Bt -- 0^°) --> Ai (0,J^-1/J^-1)

T--K:o

ofi la matrice de variance covariance asymptotigue de l'estimateur du PMV est calculée a partir de :

I_ J = Eo 1 0^2 log LT (0) 1, I = EE°10 log LT (0) a log LT (0)1 I_ 00 00^' 00 00^' i

·

Naturellement dans la pratique les matrice I et J sont directement estimées en remplacant l'espérance E₀ par la moyenne empirique et le parametre inconnu 0 par son estimateur convergent 0. Ainsi, on utilise :

J = _1 T		T E t=1		0^2 log LT (0)		^~~~~0=^.T
				00 00'
I = 1 T	T E t=1		0 log LT (0) 00		^~~~~=^.T		0 log LT (0) 00^'	=^.6T

et la variance estimée de OT vérifie alors

V (/T (et -- 61) = k1i j-1 3.3.1 Exemples

Les formules donnant les précisions asymptotiques des estimateurs du PMV peuvent se simplifier pour certains modeles particuliers.

i) Modeles conditionnellement normaux

La méthode coincide avec la méthode de MV. On a K_u (0^°) = 3, Mat (0^°) = 0, et on vérifie directement que I = J et

V (VT (6 1 t -- 19^°)) = j-1 = I-1.

ii) Parametrages independants de la moyenne et de la variance Un autre cas simple est celui on le parametre 0 peut de décomposer en

0= ( 0) '

a n'apparaissant que dans la moyenne et 0 que dans la variance :
mt (0) = mt (a) et ht (0) = ht (0) .

Nous avons alors :

2 h 1 i @mt(~^~) @mt(~^~) E 0 h2 t (~~) @~ @~^0 J = 4h 1 i @ht(^~) @ht(^~) 0 E 2h2 t (~~) @~ @~~

3 5

₃

5 -

E0 L

F 1 amt(a⁰) aht(0 0) m3t (0⁰)]

I = (0) as as r

E° [ 2h3 t / 2 (3°) as aa.

E₀ [ 3 [ /4¹ 0 amt (a^° ) amt (a° ) ]

1 ° as ^aS. amt(a⁰) aht(0°) mu (0°)]

/ 2 E

2h_t 0³ ) r 1 aht(0^°) aht(0°) ( K, (0^°) -- 1)]

° L⁴h1(0^°) as as^' \

Les matrices de variance-covariance asymptotiques des estimateurs sont :

~ ~

p ~ 1 @mt (~~) @mt (~~) ~~~1

V T (^{^}~T ~ ~~) = E ;

h2 t (~~) @~ @~~

et

~ ~

p ~ 1

^{^}~T ~ ~~~~ @ht (~~) @ht (~~) ~~~1

V T = E ~

2h2 _t (~~) @~ @~~

~ 1 ~

@ht (~~) @ht (~~)

E @~~ (K_u (~~) ~ 1) ~

4h2 _t (~~) @~

[^Eo [

1 014 (1^3°) aht (1^3°)11 2h^2t (0^°) 00 00

-1

Plus les queues de distributions conditionnelles sont épaisses (au sens kurtosis grande), moins les estimateurs des parametres figurant dans la variance conditionnelle sont précis.

3.3.2 Estimation du MV sous d'autres lois

En pratique, l'hypothese de normalité des rendements ne caractérise pas toujours le marché financier, en particulier pour des données de haute fréquence. En effet, les queues des distributions empiriques des rendements sont généralement plus épaisses que celles d'une loi gaussienne.

Nous voyons que le degré d'exces de kurtosis est largement et significativement positif. L'exces de kurtosis positif représente une distribution a queues épaisses. La valeur négative de skewness montre une distribution asymétrique (distribution vers la gauche). Le test de Jarque-Bera conduit

ici naturellement a rejeter l'hypothèse d'une distribution normale. Trois lois de distribution sont parfois imposées sur l'aléatoire ij_t en dehors de la loi normale : Student, skewed-student et GED.

Nous allons présenter ces différentes lois.

La distribution de Student

Bollerslev [1987] note que l'utilisation d'une distribution Student ayant des queues de distribution plus épaisses que la distribution gaussienne peut résoudre potentiellement ce problème. Avec une distribution Student. Sur le graphique (3.1), sont reportées les densités d'une loi normale et d'une loi de Student a 3 degrés de libertés. On vérifie que cette dernière admet des queues de distribution plus épaisses que celles de la loi normale : pour des degrés de liberté faibles, la distribution de Student est donc une distribution leptokurtique.

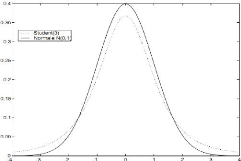
Figure 3.1 : Comparaison entre les distributions

de student et normale

Rappel Si x et y sont deux variables aléatoires indépendantes, telles que x suit une loi N(0, 1) et y suit une loi du chi-deux a 9 degrés de liberté,

alors la variable

x

t=
	py~9

Definition 3.3.3 Si la variable ij_t admet une distribution de Student a 9
degrés de libertés, oh 9 2 N vérifie 9 > 2, alors la log-vraisemblance associée

a une observation n_t et a l'ensemble de paramètres 0 s'écrit :

log r (0) = log [I' (^t9 #177; 2 ¹)1 - log [1^-1 (7 ₂ )1

~ ~ ~~

1 t

log [~ (# ~ 2)] + log ~h² 1 + 2

~ + (1 + #) log :

t

2 # ~ 2

ofi I' (.) désigne la fonction gamma.

La distribution de Student dissymetrique standardisee

Elle est introduite dans le cadre des divers processus GARCH par Lambert et Laurent [2001] qui se fondent sur une procedure de Fernandez et Steel [1998] . Ils l'appliquent a la loi de Student pour definir la Student dissymetrique qu'ils standardisent afin d'obtenir une densite ecrite en fonction de l'esperance et de la variance de l'aleatoire¹. La log-vraisemblance correspondance est alors :

log r (0) = log [r (V + 1 )] log [I' (2 V

)1 + log 2 )

1 + log (s)

2

~

2

(s nt + 771 )2 2/ )1

1 [log [71^- (V OD - 2)] + log + (1 + V) log 1 + - t

V - 2

avec :

M, =	F(9^1) 03 -- 2 ~~ ~ ~# 2 ~ ~ 1 ~ p ~ 2

S2 = (e + 2 -1 -m²

1

1 si _t ~ ~m

0 si n_t < --^m_s

s

It =

~ est un indicateur de dissymetrie tel que lorsque = 1, la distribution de Student dissymetrique standardisee est egale a la distribution de Student precedente.

¹Student dissymetrique est en effet definie sur un mode (qui n'est pas l'esperance) et une mesure de volatilite (qui n'est pas la variance) conditionnels.

La distribution GED

La distribution Generalized Error Distribution (GED) est définie par :

Definition 3.3.4 Si la variable n_t, telle que E(n_t) = 0 et V (n_t) = 1, admet une distribution GED de parametre 73 > 0, sa densite est definie par :

171 (nt) =

vexp [-^12 - 111 A2[(v+^1/^,9)]r (^19)

ofL A est une constante definie par :

A = [2^-(2/v)r (¹₀)]

^r (

³

9)

1

2

:

Si V = 2, alors A = 1 et l'on retrouve la densité d'une loi normale Ar(0,1). Si V < 2, les queues de distribution sont plus épaisses que celles d'une loi normale (distribution leptokurtique). Si V > 2, la distribution est platykurtique. Pour cette raison, elle est souvent utilisée afin de prendre en compte des effets de kurtosis. On note en particulier que :

A2⁽¹/^v)r (²)

#

E Intl = ~ _~1 ~

#

Préconisée notamment par Nelson [1991], la log-vraisemblance associée a une distribution de type GED est la suivante :

Definition 3.3.5 Si la variable n_t admet une distribution GED avec 73 2 IV, alors la log-vraisemblance associee a une observation n_t et a l'ensemble de parametres 0 s'écrit :

log r (0) = log ^V () 2 1 nt _r 2 (1 +73^-1) log (2)--log (F (¹ --^I log ⁽4)

A A V)) ^k

ofL F 0 designe la fonction Gamma.

3.4 Prevision

Une application importante de la théorie des modeles ARCH consiste a évaluer la précision de prévision des valeurs futures d'une série chronologique. Dans le cas d'un processus ARMA, nous avons vu que la variance

des prévisions dépend de l'horizon de prédiction et de la variance inconditionnelle de la série. En particulier, cette variance est indépendante du comportement local de la volatilité du processus a l'instant on on s'apprête a calculer les intervalles de prévision. Par contre, en ajustant un modele GARCH, nous allons voir suivant Bera and Higgins [1993] comment il est possible d'utiliser cette volatilité locale pour mesurer les intervalles de prévision.

3.4.1 Modele avec erreur ARCH

Supposons un processus AR (1) sans constante pour modéliser la moyenne conditionnelle

Xt = 0Xt_i + Et

on Et/it_1 rs^, Ar(0, h_t²). L'erreur suit un processus ARCH (1) de variance conditionnelle tel que ht = c + 014_1. Nous avons dérivé précédemment les espérances et variances conditionnelles du processus ARCH. Nous connaissons aussi les formules pour les prévisions _XT+h et le erreurs de prévisions E4,_#177;h d'un modele AR (1) supposant un bruit blanc fort des résidus. Le prédicteur optimal XT+h est la moyenne de ces prévisions, conditionnellement a l'information it disponible a l'instant T. Plus spécifiquement,

E (XT#177;h//t) = 0^hXt

V (ET#177;h//t) = E _[4-Fh + 02E4-'#177;h-i +
·
·
· + (₀h-1)² E9 ₊₁

+ terme croises/It] (_oh-1)²

= E [E4,_#177;h/lt] + 0²E [4+h-1//t] E _[4+1/1-t] + 0.

Sachant que E [4+h/It] = E [4+h_1/It] =
·
·
· = E [4+1/1^-t] = o^-2 et la formule se simplifie ainsi :

V (ET#177;h/it) = (1 + 0² + . . . + ^(0h-1)2) 2.

Dans le cas d'un terme d'erreur ARCH (1), nous avons montré que les erreurs au carré suivent un processus AR (1)

"2 _t= c + 014-1 +vt on E(vt) = 0. Ainsi, nous avons

E (4_#177;h/lt) = c + 0iE (4+h-1/It)

E (4#177;1/1t) = c + 0iE (4/10 = c + 014

E (4+2//t) = c + 01E (4+1//t) = c + 01 (c + 014) = c 01c + 0T4

E (4_#177;h/lt) = c + 0ic +
·
·
· + 0^h1"²T

Il s'agit alors de remplacer les termes appropries dans l'equation suivante :

V (ET#177;h/lt) = _E [ET2 #177;h/it]+02E [4+h-1/z] +. . .+ (oh-1)2 E [4+1/1-t] .

Ainsi, les acteurs des marches financiers peuvent etablir leurs previsions de la volatilite a partir des informations les plus recentes dont ils disposent. Dans le cas du modele GARCH (1,1), nous avons :

ht = c + 014-1 + 1h²t-1

En supposant que les donnees jusqu'au temps T sont disponibles, la prevision de la variance conditionnelle d'une periode est

117+1 = _117,2 (1) = c + 01E7,2 + 1h²T

Il est possible d'ecrire la prevision d'une autre maniere et en particulier la prevision de plusieurs periodes. En mettant Et = ntht au carre, nous obtenons l'expression E? = 704. Remplagons cette expression dans la formulation du modele GARCH (1,1), nous avons

h? = c + oi (74_14_0 + 14-1

Inserons maintenant l'expression cbih_t²_1 -- cbih_t²_1 dans l'equation precedente

4 = c + oin?_14_1 + 1h²t_1 + olq_i -- olq_i
= c + _(cbi + l) 4_1 + 014_1 (alt-1 -- 1)

A partir de cette formulation, nous pouvons ecrire la prevision de la variance conditionnelle de plusieurs periodes. D'abord, la prevision d'une periode est

14 (1) = c + (01 + i) 14 + 014 (⁷4 -- 1) Pour la prevision de deux periodes, nous avons

114-^, (2) = c + (01 + 1) 4+1 + 014+1 (⁷4+1 -- 1) Sachant que E [(4₊1 -- 1) /It] = 0, alors

14 (2) = c + (01 + 1) 4+1

= c + (01 + 1) (c + (01 + 1)4 + 01¹4 (⁷4 -- 1))

Pour la prévision de trois périodes, nous avons

h2 T (3) = c + (1 + 1) h2 T +2

= c+(01+ 1)(+ (01 + _i)(C + (01 + 04 + 014 04, -- 1)))

Ainsi, en répetent les substitutions, pour la prévision de h périodes, nous avons

hT (h) =

[^1^~(°^1 + 1)11-1] 1 -- (01 #177; i) #177; (01 + i)^h-1 14 (1) .

Et quand h oo, la variance conditionnelle tend vers la valeur d'équilibre i_(0:+ ) .

3.4.2 Modele avec erreur GARCH

Partons du processus ARMA (r, s)

0 (L) Xt = 111 (L) Et (3.1)

on 0 (L) = 1-01L-02L²--
·
·
·--O_rL^r, w (L) = 1- 1L- 2L²--
·
·
·-- ₈L⁸ et Et est un processus GARCH (p, q). Supposons que l'on observe cette série jusqu'au temps T. Toute prévision _XT+h a l'instant T + h reproduisant la structure de la série est de la forme

XT+h =

r i=i

~iXT +hi ~

Xs j=1

jET-Fh--i + "T +h:

Le prédicteur optimal XT+h est de la forme :

XT+h = E [XT#177;h/lt]

=

r i=i

OiE [XT +hiIt] ~

Xs j=1

jE [ET-Fh-j/it] + E [ET#177;h/lt]

=

r i=i

OtE [XT +hiIt] ~

Xs j=1

jE [ET-Eh-J/1d

puisque E [ET#177;h/lt] = 0.

Considérons le cas du processus AR (1) on 101 < 1 et Et est un processus GARCH (1,1). En effet, dans le cas d'erreurs GARCH, nous savons que

les erreurs au carre suivent un processus ARMA (1,1) et les previsions des erreurs au carre sont :

4 = c +(01+ ¹⁾ 4-1 + vt ~ 1Vt-1

L'esperance conditionnelle par rapport a it de cette relation permet d'obtenir E [E4,_#177;h/lt] en fonction de E [E4,_#177;h__i/It] pour i > 0.

E [ET² #177;i/it] = c + (01+ 1) "2 T iVT on VT = hT² -- Et²

E [4+2/It] = c + (01 + 1) E [E7,² +1/1-t ]

= c + ₍₀₁ + 1) (c + (01 + 1) ET ² ivT)

E [4-Fh/lt] = c + (01 + 1) E [ET² #177;h-i/it]
·

3.4.3 Erreur de prevision

Calculons a present l'erreur de prevision dans le but de determiner les intervalles de prevision. En considerant que les parametres ai sont compatibles avec l'hypothese d'inversibilite du processus, le modele (3.1) peut se reecrire sous la forme d'un processus MA (oo), et on peut donc ecrire :

XT+h =

1 X i=0

"YiET-Fh-i

on est le coefficient du developpement de 0^-1 (L) W (L) . En utilisant cette representation pour calculer le predicteur optimal, on peut ecrire :

XT+h = _X1 jET-Fh-i
i=h

et on en deduite l'erreur de prevision :

ET (h) = XT _+h ~ XT+h

=

Xh _ 1 i=0

~i"T +hi:

La precision de la prevision peut a present etre mesuree par la variance de ET (h) conditionnellement a l'information it disponible a l'instant T :

_Xh _ 1
i=0

V [ET (h) /¹t] =

^-)/E [4+h-z/it]

Nous pouvons à présent voir la grande différence entre la prévision avec ou sans erreur ARCH dans le processus d'innovation : si un erreur ARCH est présent, alors E _{~"2T+h_i/It]} dépend en général le temps, donc du point de référence à partir duquel la prévision est effectuée. A l'inverse, dans le cas d'un modèle homoscédastique dans lequel E ["2 T +h_i/It ] = ², la variance de la prévision des erreurs se réduit à Ph_1

i=0 'y2 i a2 ne dépend pas

de l'ensemble d'informations contenues dans It.

3.5 Identification et tests

Nous avons déjà indiqué que l'analyse de la structure de corrélations du carré des observations d'un processus GARCH (p, q) permet de déceler l'ordre du modèle. Nous allons considérer dans cette section le problème plus général du choix de l'ordre d'un modèle ARMA-GARCH et nous verrons comment développer des tests pour les identifier. Nous savons que l'outil de base permettant d'identifier l'ordre d'un modèle ARMA est la fonction d'autocorrélation ou d'autocorrélation partielle des observations Xt. Cet outil est en réalité toujours valable dans le cas d'un modèle ARMA avec le processus d'innovation GARCH. En effet, par les propriétés des processus GARCH étudiées précédemment, les innovations du modèle sont de moyenne nulle et non corrélée. On en déduit facilement que le comportement des fonctions d'autocorrélation et d'autocorrélation partielle sont identiques aux modèles ARMA étudiés.

Cependant, les innovations GARCH imposent une modification pour la fonction d'autocovariance ^{^}h
·

Comme nous l'avons étudié précédents, le test porte-manteau permet à ce niveau de conclure si des corrélations linéaires persistent dans les résidus et. Par la propriété de non corrélation des processus GARCH, nous savons que ce test ne suffit pas pour conclure. En conséquence, le développement de méthodes pour tester si une composante GARCH est présente ou non dans le processus d'innovations est très important. Une méthode pour identifier une telle dépendance non linéaire des résidus consiste à utiliser à nouveau le test portemanteau sur le carré des résidus e2 t . La procédure pour tester s'il réside des corrélations sur e _t est alors la suivante :

- Calcul de la moyenne de e2 t :

^^vT =

1 T

XT t=1

e2 t

- Calcul de la fonction d'autocorrélation empirique de e2 t :

PT ~1 /e2 t+h - ^vT ~ (e2 _t - ^{^}vT )

t=1

^{^}PT (h) = PT t=1 (e2 _t - ^vT )2

- Calcul de la statistique du test porte-manteau :

) = QT (e2 t

XT t=1

(^^PT (h))^2

Sous l'hypothèse nulle selon laquelle les e2 t sont non corrélés, cette statistique est distribuée asymptotiquement selon une loi x² k
·

En cas de rejet de l'hypothèse nulle, il faudra donc envisager d'ajuster un modèle (G) ARCH au processus des innovations. Pour identifier quels ordres peuvent être ajustés a ce processus, si €t est un processus GARCH (p, q), alors le €² est un processus ARMA (m, q), on m = max (p, q). Ceci implique que l'analyse des autocorrélations du carré des résidus e2 t peut être mise en uvre afin de trouver m et q, et d'en déduire p.

3.5.1 Tests d'effets ARCH/ GARCH

Comment tester la présence des effets (G) ARCH dans la série X ou dans le résidu du modèle linéaire autorégressif?

Deux principaux tests existent :

- Tests d'autocorrélation sur les carrés €² : application des statistiques usuelles du type Q - stat (Box Pierce, Ljung Box etc..).

- Les tests contre un modèle non-linéaire spécifique (comme les tests du LM d'absence d'auto-corrélation sur €2 t ).

Les tests du ML

Puisque l'estimation de modèles non-linéaires est en général plus diffi cile que celle des modèles linéaires, il est naturel de considérer des tests qui, bien qu'avec des alternatives non-linéaires spécifiques, ne requièrent pas l'estimation de ces alternatives.

C'est a cette catégorie qu'appartiennent les tests du ML. Nous disposons ainsi de trois tests de ce type, chacun testant un type de non-linéarité : ARCH et BL.

AR(p) contre AR(p) a erreurs ARCH(p) Dans ce type de tests, on considere un processus (Et) bruit blanc gaussien, c'est-à-dire i.i.d. dont la loi est Ai (0, o^-2). Les hypotheses sont alors

{H0 : Xt = ~ + Pp i=1 ~iXt~i + "t

_q

H1 : Xt = ~ + Pp c + Pp

i=1 ~iXt~i + j=1 0.4-i

On estime le modele (Ho) par la methode de moindres carres, et on calcule les residus (&t) obtenus. On estime alors par la methode de moindres carres la regression

2 Et = c +

X p j=1

PT t=1 v2 j^"2 t tj + vt avec R^2 = 1 ~ Et=1 lit - ~"):

La statistique du ML est alors asymptotiquement equivalente à T x R². Si l'on pose LM0 = T x R² alors, sous (Ho), LM0 est asymptotiquement distribuee comme un chi-deux à p degres de libertes.

AR(p) contre BL(p, 0, P,Q) Dans ce type de tests, on considere un processus (Et) bruit blanc gaussien, c'est-à-dire i.i.d. dont la loi est .Af (0, cr²). Les hypotheses sont alors

~ H0 : Xt = ~ + Pp i=1 ~iXt~i + "t

H1 : Xt = 6^. + _Eli=1 aiXt_i + Et + _PP PQ j=1 ijXt~i"t~j

i=1

Là encore, on estime le modele (Ho) par moindre carres, ainsi que '6^-2, estimateur de o^-2. La statistique du test ML est

" XT #h i " XT #

LM1 = ^{^}~^{~2 ^}z1_;t^{^}"t ^{^}M11 ~ ^M10 ^M1

00 ^{^}M01 ^{^}z1_;t^{^}"t ;

t=1 t=i

oil

^{^}z0_;t = (^-1, Xt-1,
·
·
· , Xt^--p)

^{^}z1_;t = (e^.t-1Xt-1, e't-1Xt--P, e^.t-2Xt-1, et-2Xt--P, et--QXt-1, et--QXt

et

^^Mii =

XT t=i

zi,t

Zip pour i = 0, 1

^{^}z1_;t

^t zo,t.

_XT
t=i

¹C/^{1 -}01 = ¹0^-10 =

Il est possible de montrer que sous (H0), LA) est asymptotiquement distribuée comme un chi-deux a P Q degrés de

libertés.

Le test RESET

On estime ici les parametres du modele linéaire

1/0 : Xt = +

X p i=i

aiXt_i + Et

et on calcule les résidus obtenus &t, les valeurs ajustées f(t = +

E^p.=i ai

T- .kt_i et la somme des carrés des résidus SCR0 = Et_i Et. On estime

alors, par la méthode des moindres carrés, les parametres de

^^"t = cto +

X p i=i

aiXt_i +

h J=1

bj ^Xj t+ vt,

v-T -2

et on calcule SCR =2_ v_t . La statistique de test est

RESET =	[SCR0_SCR1] h-1
	SCRi/ (T h)

qui suit sous (H0) (hypothese de modele AR (p)) un loi de Fisher F (h-1, T-p-h).

Test de McLeod

Le test de McLeod qui est semblable au test de Ljung-Box

a la différence que ce sont les résidus au carré qui sont évalués :

Q (p) = T (T + 2)	X p i=i	PZ (h)
		T -- i :

3.5.2 La selection d'un modele

Dans la mesure on l'on compare des modeles dits emboités (ARCH (1), ARCH (2), GARCH (2, 1), . . . ), c'est-a-dire dans la mesure on un modele peut s'exprimer comme une forme restreinte d'un autre modele, la

sélection du modèle et le choix de l'ordre peut se faire par le test ratio de vraisemblance "log-likelihood ratio test" :

LR = --2 (log £R- log £U)

avec log £R est la log-vraisemblance du modèle restreint et log LU est la log vraisemblance du modèle non-restreint. LR suit (asymptotiquement) une loi du chi-deux avec un nombre de degré de liberté égal au nombre de restrictions.

Exemple 3.5.1 Soient les modêles emboItés suivants :

Yt = ~ 0 + "t

avec

_{q q}

"t = _t c + _{i"2t_i} ou t = _t c + 1"2t_ + 1h2t_1.

On dit que le modêle ARCH (1) est une forme restreinte du modêle GARCH (1, 1) avec comme restriction 1 = 0.

Chapitre 4

Extension du modèles (G)

ARCH

Un problème se pose quand on estime les paramètres des modèles (C) ARCH pour un ordre plus élevée : les coefficients estimées violer la contrainte de non négativité de la variance. Pour éviter ce problème, John Geweke [1986] a suggère d'utiliser une approche multiplicatif de la variance conditionnelle :

h t = exp (c) :"²¹

t1:"²²

t2: : : : E2~p

tp.

Cette expression est toujours positive, indépendamment du fait que les paramètres soient positifs ou négatives. En prenant les logarithmes, on obtient

ln (h2 ) + ₂ ln ("2 )

) = c + 1 ln (€2 ) + ~ ~ ~ + çb_p ln (€2

t t.1 t2 tp

Tout les modèles examinées jusqu'a ici présentent l'inconvénient que les chocs positifs est négatifs exercent le même impacte sur la variance conditionnelle et ces signes est disparus. D'autre part, il est bien connu que la réaction de la volatilité du cours des actions est différente si les chocs sont négatifs, c'est-à-dire elle produise de mauvaise nouvelle.

4.1 Modèles asymétriques

La seconde grande approche couvre les modèles ARCH non linéaires et plus particulièrement la prise en compte des phénomènes asymétries. L'idée est toute simple : l'effet hétéroscédastique n'est sans doute pas le même suivant que l'erreur précédente est positive ou négative. Deux grandes classes de modèles ont été proposées :

4.1. MODELES ASYMETPJQUES

- Nelson [1990] s'est intéressé aux évolutions asymétriques de la variance à l'aide des modèles EGARCH.

- Engle et Bollerslev [1986] ont étudié les modèles ARCH à seuils (TARCH) on la variance est une fonction linéaire définie par morceaux qui permet différentes fonctions de volatilité selon le signe et la valeur des chocs. Rabemananjara et Zakoian [1991] ont proposé une généralisation avec les modèles les modèles TGARCH.

4.1.1 Modèle EGARCH

Dans le cas du modèle GARCH, les résidus sont au carré avant les estimer. Mais, il est possible que les mouvements en baisse et les mouvements en hausse donnent des effets différents sur la prédiction de la volatilité. Nelson est le premier enquêteur du modèle de l'effet levier (c'est-à-dire les mouvements en baisse ont plus d'infiuences que les mouvements en hausse).

Definition 4.1.1 Un processus € satisfait une représentation EGARCH (p, q) si et seulement si :

{ "t = ~ ht q j"t_ij

log h2 t = c + Pq i=1 i log h2 t_i + Pp i=1 ~i t_i + Pp q "t_i

i=1 ~i

h2 h2

t_i

oh le résidu normalisé ij est un bruit faible.

En utilisant le modèle EGARCH, Black trouve que la volatilité sur le marché boursier a tendance à augmente après les rentabilités négatives et a tendance à baisser après les rentabilités positives. Le modèle EGARCH exploite cette régularité empirique en mettant la variance conditionnelle en fonction de la taille et le signe de résidus retardés. Etant différent par rapport au modèle GARCH (p, q).

Remarque

Le modêle EGARCH ne fait aucune hypothése sur les paramétres q et pour assurer la non négativité de la variance conditionnelle.

Les coefficients _i tel que i = 1, 2,..., p, est typiquement négatif, donc un choc positif des rentabilités entraine une volatilité moins élevée qu'un choc négatif. Le modèle EGARCH donne des différences par rapport au modèle GARCH :

- Premièrement, les bonnes et les mauvaises nouvelles ont des impacts différents sur la volatilité dans le modèle EGARCH mais elles ont des mêmes impacts dans le modèle GARCH.

- Deuxièmement, les nouvelles importantes ont des impacts plus importants dans le modèle EGARCH que dans le modèle GARCH standard.

4.1.2 Modèles TGARCH

Une autre façon de modéliser les asymétries consiste a retenir des modélisations a seuils dans la lignée des modèles TAR. Le modèle TGARCH (Zakoian, [1994]) est défini de la façon suivante.

Définition 4.1.2 Un processus €t satisfait une représentation TGARCH (p, q) si et seulement si :

~

"t = _t ht
h²_t = c + Pp i=1 ~+ _i E+ t - ~~ _i E~ t + Pq j=1 jh2 tj

oh le résidu normalisé ij est un bruit faible, avec, c > 0, ~+ i ~ 0, q~ i ~ 0 et j ~ 0.

4.2 Le modèle (G)ARCH en finance

4.2.1 Les principales propriétés des séries financières

Les séries de prix d'actif et de rendements présentent généralement un certain nombre de propriétés similaires suivant leur périodicité. Soit Pt le prix d'un actif a la date t et Tt le logarithme du rendement correspondant :

Tt = log (Pt) - log (Pt-i) = log (1 + Rt)

on

Rt = (Pt -- pt-i) /pt-i

désigne la variation relative des prix. Les séries de prix d'actif et de rendements sont d'ailleurs sans unité, ce qui pour facilite la comparaison entre elles.

Charpentier (2002) distingue ainsi 8 principales propriétés que nous allons successivement aborder.

Propriété 4.1 (Stationnarité) Les processus stochastiques Pt associés aux prix d'actif sont généralement non stationnaires au sens de la stationnarité du second ordre, tandis que les processus associés aux rendements sont compatibles avec la propriété de stationnarité au second ordre.

Autrement dit, les trajectoires de prix sont généralement proche de marche aléatoire sans terme constante. Et, en revanche, les séries des rendements ont des trajectoires compatibles avec la stationnarité au second ordre.

Propriété 4.2 (Autocorrélations des carrés des variations de prix) La série (r2 _t ) associée aux carrés des rendements présente généralement de fortes auto-corrélations . Ce qui n'est pas compatible avec une hypothése de bruit blanc. Néanomois, les auto-corrélation de la série (rt) sont sou-vent trés faibles . La série (rt) la rendent proche d'un bruit blanc¹.

Propriété 4.3 (Queues de distribution épaisses) L'hypothése de normalité des rendements est généralement rejetée. Les queues des distributions empiriques des rendements sont généralement plus épaisses que celles d'une loi gaussienne. On parle alors de distribution leptokurtique.

Propriété 4.4 (Clusters de Volatilité) On observe empiriquement que de fortes variations des rendements sont généralement suivies de fortes variations. On assiste ainsi a un regroupement des extrêmes en cluster ou paquets de volatilités.

Propriété 4.5 (Queues épaisses conditionnelles) Même une fois corrigée de la volatilité clustering (par exemple avec des modéles GARCH), la distribution des résidus demeure leptokurtique même si la kurtosis est plus faible que dans le cas non conditionnelle.

Propriété 4.6 (Effet de levier) Il existe une asymétrie entre l'effet des valeurs passées négatives et l'effet des valeurs passées positives sur la volatité des cours ou de rendements. Les baisses de cours tendent a engendrer une augmentation de la volatilité supérieure a celle induite par une hausse des cours de même ampleur.

Propriété 4.7 (Saisonnalité) Les returns présentent de nombreux phénoménes de saisonnalité (effets week end, effet janvie etc..).

Toutefois, certaines saisonnalité peuvent être spécifiques a un échantillon, une période.. Il est, par contre, deux types de saisonnalité qui ont acquis droit de cité dans la littérature, pour avoir été discernés sur des échantillons, des périodes et au moyen de méthodologies présentant suffisamment de variété pour en étayer la robustesse. Il s'agit de "l'effet janvier" et de "l'effet week-end".

Propriété 4.8 (Asymétrie perte/gain) La distribution des cours est généralement asymétrique : il y a plus de mouvements forts a la baisse qu'a

¹L'hypothése usuelle en théorie de la finance consistait effi ctivement a supposer que les processus de rendements sont i.i.d et de variance finie. Un hypothése plus forte est aussi souvent faite sur le caractère gaussien de ces rendements.

la hausse.

4.2.2 La VaR

La VaR (de l'anglais value at risk, mot à mot: << valeur sous risque >> ) est une notion utilisée généralement pour mesurer le risque de marché d'un portefeuille d'instruments financiers. La notion de VaR est apparue pour la première fois dans le secteur de l'assurance. A la fin des années [1980], la banque Bankers Trust fut l'une des premières institutions à utiliser cette notion sur les marchés financiers aux Etats-Unis, mais c'est principalement la banque JP Morgan qui dans les années 90 a popularisée ce concept notamment grace à son système RiskMetric.

De façon générale, la VaR est définie comme la perte maximale potentielle qui ne devrait être atteinte qu'avec une probabilité donnée sur un horizon temporel donné (Engle etManganelli, [2001]). La VaR est donc la pire perte attendue sur un horizon de temps donné pour un niveau de confiance donné. La VaR répond à l'affi rmation suivante : << Nous sommes certains, à a%, que nous n'allons pas perdre plus de V euros sur les N prochains jours >> . V correspond à la VaR, a% au seuil de confiance et N à l'horizon temporel.

Supposons que la distribution des pertes et profits associée à la détention d'un actif sur une période corresponde à une distribution normale standard. Sur la Figure 4.3 est reproduite cette distribution de perte et profit supposée normale : sur la partie gauche de l'axe des abscisses figurent les rendements négatifs (pertes) tandis qu'à droite figure les rendements positifs (profits). Dans ce cas, la VaR définie pour un niveau de confiance de 1 - a, donc il y a 1 - a de chances que le rendement de l'actif, noté rt, soit au moins égal à F ^~1 (a) sur la période de détention.

Pr [rt < V aR(a)] = Pr [rt < F ^~1 (a)] = a

car V aR(a) = F ^~1 (a) on F (.) désigne la fonction derépartition associée à la distribution de perte et profit.

Exemple 4.2.1 La VaR au seuil de confiance de 95% a 1 jour, que l'on notera, VaR (95%, 1j), égale a 1 million d'euros signifie qu'un jour sur cent en moyenne, le portefeuille est susceptible d'enregistrer une perte supérieure a cette somme de 1 million d'euros. En considérant que les variations de valeur d'un portefeuille sont normales, la VaR peut être exprimé graphique-

ment,

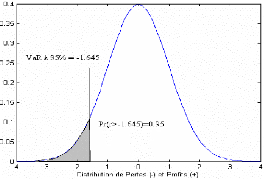
Figure 4.1 : Exemple de VaR sous distribution
normale.

Dans l'exemple ci-dessus, la VaR (95%, 1j) correspond approximativement a une perte de 1.65 millions d'euros et la VaR (99%, 1j) correspond a peu prés a une perte de 2.33 million d'euros.

Ainsi, la VaR correspond généralement a une perte (valeur négative). Toutefois, on trouve souvent une Value-at-Risk définie non pas a partir de la distribution de perte (-) et profit (+), mais a partir au contraire d'une distribution de profit(-) et perte(+). Dit autrement, une telle définition revient a omettre le signe moins devant la perte et donc a affi cher une VaR positive. Dans ce cas, la définition de la VaR correspond a l'opposé du fractile de la distribution de perte et profit :

V aR(a) = --F ^~1 (a).

Chapitre 5

Application sur des données

réelles

Nous avons présenté une application pratique sur des données réelles extraie d'un indice boursier et nous allons voir l'effet ARCH sur ce dernier. Et ensuite, nous pouvons appliquer la modélisation ARCH sur les données de cet indice.

Présentation de la série et analyse préliminaire

Les données sont des observations journalières de rendement sur l'indice boursier NASDAQ. Leur nombre est de 2261 observations. La période couverte s'étant de 2 janvier 2000 a décembre 2007

Logiciel utilisé

EViews (Vues économétriques) est un logiciel de statistiques, utilisé principalement pour les séries chronologiques orienté analyse économétrique. Elle est développée par Quantitative Micro Software (SMQ), fait maintenant partie de l'IHS .La version 1.0 a été publié en Mars 1994, et remplacé MicroTSP. La version actuelle de EViews est de 7,1, publié en avril 2010.

1) L'examen du graphe :

La première étape d'une série chronologique est la représentation graphique. Le graphe correspondant a cette série est le suivant :

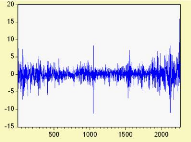
figue 5.1. : La s^~erie de redement.

L'analyse visuelle du graphe montre a première vue l'absance d'une tendance. D'oñ il y a lieu d'afiirmer une présomption du stationnarité de la série.

2) L examen du corrélogramme de la série

On obtient le correlograme simple et partiel calculée de cette série :

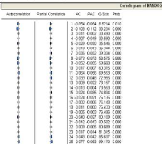
Figure 5.2 : Le correlogramme
simple et partiel.

Il faut s'intéresser au corrélogramme afin de procéder a l'identification des modèles.

L'autocorrélogramme simple (caractéristique des processus moyennes mobiles ), dans ce cas on obtenue l'ordre 2 de le processus MA. D'autre part, l'autocorrélogramme partiel (caractéristique des processus autorégressifs )

on a l'ordre 2 de le processus AR. Un troisième processus a analyser est celui qui combine les deux précédents processus (MA (2) et AR (2)) noté ARMA (2,2).

3. Validation du modèle ou les tests:

- - Le test de normalité :

Figure 5.3 : Le test de normalit^~e.

La valeur de test de Jarque-Bera (2944,783) est supérieure a 5.99 (la valeur de X²(2)), ce qui amène a l'absance de la normalité qui est également visible sur l'histogramme ci-dessus. Donc la série des résidus n'est pas un bruit blanc gaussien. Ainsi, la valeur de la kurtosis (8,59) assure cette resultat et aussi montre que la distribution de cette série est leptokurtique (supérieure a 3). En plus, on observe que la valeur de la skewness est égale a 0.0077 cela montre que la distribution est asymétrique et a une queue allogée vers la droite. On retrouve la propriété d'asymétrie aux gains.

- Corrélogramme simple et partiel des résidus

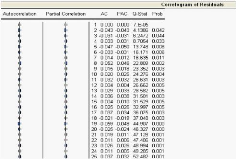
Figure 5.4 : Le corr^~elogramme simple et
partiel des r^~esidus.

On observe L'absence d'autocorrélation les résidus ou des rendements. Pour cette raison on va analyser les carrés des résidus.

- Corrélogramme simple et partiel des résidus au carrés

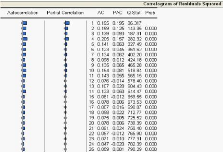
Figure 5.5 : Le corr^~elogramme simple et
partiel des r^~esidus au carr^~es.

A partir du corrélogramme, on remarque plusieurs termes significativement différents de zéro cela veut dire qu'il existe une autocorrélation et aussi il y a certainement un effet ARCH. Pour cela on est passé au test d'homoscédasticité dont le résultat ci-dessous.

- Le test ARCH d'hétéroscédasticité :

La détection de l'hétéroscédasticité par le processus ARCH se fait avec comme hypothese :

~

H0 : il y a homoscédasticité H1 : il y a hétéroscédasticité

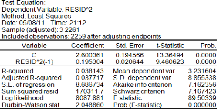
Figure 5.6 : Le test ARCH.

On a la statistique du ML (T * R²) = 86, 165 qui est supérieure a 5,99, on rejette l'hypothèse nulle d'homoscédasticité en faveur de l'hypothèse alternative d'hétéroscedasticité conditionnelle.

- Identification du modèle de type ARCH

On a eu plusieurs modèles ARCH avec des ordres p assez grands. Par conséquent on est passé au modèle GARCH (1, 1).

Les résultats obtenus dans la table ci-dessous montrent que les paramètres de l'équation de la variance conditionnelle sont significativement différents de zéro.

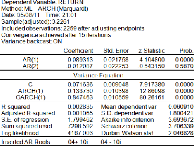
Figure 5.7 : Estimations des
param^~etres.

Le modèle retenu est un modèle AR (1) avec erreur GARCH (1, 1)

s'écrit sous la forme suivante :

X = 0:0893 Xt_i + €7 avec "t = ~tht on l'équation de la variance est

h t = 0:0716 + 0:1953"2 _{t_} + 0:8473h2 t_1.

- Graphique des séries résiduelles réelles et estimées

Le graphe de la valeur actuelle (actuel), prédite dans l'échantillon (fitted) et du résidus (résiduel).

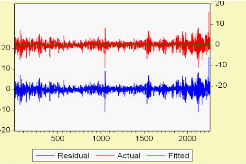
Figure 5.8 : Le graphe des valeurs actuelle,
pr^~edites dans l'^~echantillon et du r^~esidus.

L'observation du graphique montre bel et bien que les variables de la valeur actuelle sont collées avec celle de la variable projetée (fitted value) et que le résidu se comporte maintenant comme un bruit blanc.

Chapitre 6

Conclusion

Le but de ce document a été de mettre en évidence l'utilité des modèles non linéaires et l'hétéroscédasticité conditionnelle qui posséde, maintenant, des outils puissants d'analyse et de modélisation fondés sur des bases théoriques solides pour modéliser des séries chronologiques stationnaires présentant une dynamique non linéaire. Le concept de variance conditionnelle a commencé a jouer un grand role au début des années quatre vingt avec l'article fondateur de Engle (1982). Il caractérise les modèles venus élargir la classe des modèles classiques fondés essentiellement sur une structure de dépendance linéaire entre une variable a un instant t et ses valeurs passées et celles d'un bruit blanc et de ses valeurs passées.

Les modèles ARCH permettent de prendre en compte des faits stylisés inhérents a la volatilité comme, par exemple, un excès d'aplatissement, de faibles autocorrélations des rentabilités journalières des actifs considérés, et des autocorrélations positives et significatives pour le carré de ces rentabilités (i.e : non-stationnarité des variations de volatilité.

Avec l'existence de la volatilité, plusieurs chercheurs essayent d'étudier la raison de la volatilité du marché. La raison de volatilité n'est pas seulement les informations existantes sur le marché mais aussi les comportements des investisseurs, les bulles spéculatives et plusieurs autres facteurs. Avec ses influences, la volatilité fait stabiliser les marchés financiers et fait stabiliser aussi l'économie mondiale.

Les modèles ARCH et GARCH ont l'avantage de permettre de modéliser avec assez peu de paramètres des séries temporelles complexes et sont pour cette raison très utilisés pour certaines séries financières, en particulier pour prédire la volatilité. Il est cependant de plus en plus admis que la prise en compte de non-stationarités dans les séries financières est inévitable pour mettre en pratique ce type de modèles sur des données réelles

de longue durée.

Ces modèles ou des modèles qui s'en inspirent sont aussi employés dans d'autres contextes pour capturer d'autres propriétés des données. Ainsi, comme l'incertitude sur les rendements des actifs varie dans le temps avec la conjoncture, les événements politiques,. . . la décision de détenir de tels actifs de la part d'agents risquophobes doit être affectée par ces variations d'incertitude. Ces propriétés doivent se retrouver dans leurs rendements/prix. Lorsque l'incertitude est grande, l'agent demande une compensation pour le risque qu'il porte, il demande une prime de risque. Une famille de modèle inspirée des modèles ARCH tente de capturer les effets de cette incertitude sur les rendements d'actifs : ce sont les modèles ARCH-M.

Cependant, les modèles ARCH posent problème lorsque le nombre de données historiques devient extrêmement grand auquel cas les variances conditionnelles ont tendance a devenir négatives. En effet, le problème des modèles ARCH vient du fait que la volatilité est prédite par les carrés des innovations. Or, les rentabilités des actifs et la volatilité de ces actifs tendent a être négativement corrélées, phénomène que les modèles ARCH ne peuvent incorporer car ils restreignent la volatilité a être seulement affectée par les changements d'amplitude des innovations. En effet, le modèle EGARCH, tente de remédier a cet inconvènient, mais sa formulation reste complexe.

En plus, tous les modèles GARCH étudiés prennent la prime du risque des rendements des actifs sous-jacents comme constante. Cette hypothèse est critiquée dans l'article de Christoffersen-Jacobs (2004). Ces deux auteurs posent le problème de spécifier cette variable différemment. Dans cet essaie, on propose de la considérer comme une variable qui bouge dans le temps, en la modélisant par un processus GARCH.

Bibliographie

[1] Alami Ali et Renault Eric, <<Risque de modèle de volatilité>> , Février 2001, p 7-9.

[2] Charpentier Arthur, <<Cours de séries temporelles --Théorie et application-->>, volume 2, 2002, p 42-60.

[3] J.J. Daudin, C. Duby, S. Robin et P. Tr'ecourt, <<Analyse de S'eries Chronologiques>> , Mai 1996, p 26-38.

[4] Hurlin Christophe, <<Modèles ARCH-GARCH--application a la VaR>> , 2007, p 1-66.

[5] Ioana Teodora Mester, <<The volatility of the financial maeket--A quantitative approache-->> , p 895-898.

[6] Gouriéroux Christian, Joanna Jasiak, <<Non-linear innovations and impulse response>>, 3 juillet 1999, p 1-2.

[7] Kirchgassner et Jurgen Wolters, <<Intoduction to modern times series>>, avril 2007, p 241-261.

[8] Van Sacls Rainer et Van Bellegen, <<Séries chronologiques>> , 26 september 2005, 4^eédition, p 107-129.

[9] Wurtz Diethelm, Chalabi Yohan et Luksan Ladislav, <<Parameter estimation of ARMA model with GARCH/APARCH errors--An R and Splus software-->>, journal of statistical software, volume vv, p 4-12.