Analyse des séries chronologiques. les modèles ARCH et GARCH

3.3.2 Estimation du MV sous d'autres lois

En pratique, l'hypothese de normalité des rendements ne caractérise pas toujours le marché financier, en particulier pour des données de haute fréquence. En effet, les queues des distributions empiriques des rendements sont généralement plus épaisses que celles d'une loi gaussienne.

Nous voyons que le degré d'exces de kurtosis est largement et significativement positif. L'exces de kurtosis positif représente une distribution a queues épaisses. La valeur négative de skewness montre une distribution asymétrique (distribution vers la gauche). Le test de Jarque-Bera conduit

ici naturellement a rejeter l'hypothèse d'une distribution normale. Trois lois de distribution sont parfois imposées sur l'aléatoire ij_t en dehors de la loi normale : Student, skewed-student et GED.

Nous allons présenter ces différentes lois.

La distribution de Student

Bollerslev [1987] note que l'utilisation d'une distribution Student ayant des queues de distribution plus épaisses que la distribution gaussienne peut résoudre potentiellement ce problème. Avec une distribution Student. Sur le graphique (3.1), sont reportées les densités d'une loi normale et d'une loi de Student a 3 degrés de libertés. On vérifie que cette dernière admet des queues de distribution plus épaisses que celles de la loi normale : pour des degrés de liberté faibles, la distribution de Student est donc une distribution leptokurtique.

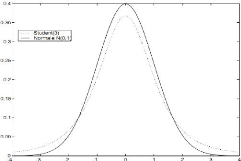
Figure 3.1 : Comparaison entre les distributions

de student et normale

Rappel Si x et y sont deux variables aléatoires indépendantes, telles que x suit une loi N(0, 1) et y suit une loi du chi-deux a 9 degrés de liberté,

alors la variable

x

t=
	py~9

Definition 3.3.3 Si la variable ij_t admet une distribution de Student a 9
degrés de libertés, oh 9 2 N vérifie 9 > 2, alors la log-vraisemblance associée

a une observation n_t et a l'ensemble de paramètres 0 s'écrit :

log r (0) = log [I' (^t9 #177; 2 ¹)1 - log [1^-1 (7 ₂ )1

~ ~ ~~

1 t

log [~ (# ~ 2)] + log ~h² 1 + 2

~ + (1 + #) log :

t

2 # ~ 2

ofi I' (.) désigne la fonction gamma.

La distribution de Student dissymetrique standardisee

Elle est introduite dans le cadre des divers processus GARCH par Lambert et Laurent [2001] qui se fondent sur une procedure de Fernandez et Steel [1998] . Ils l'appliquent a la loi de Student pour definir la Student dissymetrique qu'ils standardisent afin d'obtenir une densite ecrite en fonction de l'esperance et de la variance de l'aleatoire¹. La log-vraisemblance correspondance est alors :

log r (0) = log [r (V + 1 )] log [I' (2 V

)1 + log 2 )

1 + log (s)

2

~

2

(s nt + 771 )2 2/ )1

1 [log [71^- (V OD - 2)] + log + (1 + V) log 1 + - t

V - 2

avec :

M, =	F(9^1) 03 -- 2 ~~ ~ ~# 2 ~ ~ 1 ~ p ~ 2

S2 = (e + 2 -1 -m²

1

1 si _t ~ ~m

0 si n_t < --^m_s

s

It =

~ est un indicateur de dissymetrie tel que lorsque = 1, la distribution de Student dissymetrique standardisee est egale a la distribution de Student precedente.

¹Student dissymetrique est en effet definie sur un mode (qui n'est pas l'esperance) et une mesure de volatilite (qui n'est pas la variance) conditionnels.

La distribution GED

La distribution Generalized Error Distribution (GED) est définie par :

Definition 3.3.4 Si la variable n_t, telle que E(n_t) = 0 et V (n_t) = 1, admet une distribution GED de parametre 73 > 0, sa densite est definie par :

171 (nt) =

vexp [-^12 - 111 A2[(v+^1/^,9)]r (^19)

ofL A est une constante definie par :

A = [2^-(2/v)r (¹₀)]

^r (

³

9)

1

2

:

Si V = 2, alors A = 1 et l'on retrouve la densité d'une loi normale Ar(0,1). Si V < 2, les queues de distribution sont plus épaisses que celles d'une loi normale (distribution leptokurtique). Si V > 2, la distribution est platykurtique. Pour cette raison, elle est souvent utilisée afin de prendre en compte des effets de kurtosis. On note en particulier que :

A2⁽¹/^v)r (²)

#

E Intl = ~ _~1 ~

#

Préconisée notamment par Nelson [1991], la log-vraisemblance associée a une distribution de type GED est la suivante :

Definition 3.3.5 Si la variable n_t admet une distribution GED avec 73 2 IV, alors la log-vraisemblance associee a une observation n_t et a l'ensemble de parametres 0 s'écrit :

log r (0) = log ^V () 2 1 nt _r 2 (1 +73^-1) log (2)--log (F (¹ --^I log ⁽4)

A A V)) ^k

ofL F 0 designe la fonction Gamma.