Introduction générale
L
es séries temporelles constituent une branche de
l'économétrie dont l'objet est l'étude des variables au
cours de temps. Parmi ses principaux objectifs figurent la détermination
des tendances au sein de ces séries ainsi que la stabilité des
valeurs (et de leur variation) au cours de temps. On distingue notamment les
modèles linéaires (principalement " AR" et "MA"
pour Auto-Regressive et Moving Average) des modèles conditionnels
notamment "ARCH" pour Auto-Regressive conditional Heteroskedasticity).
L'analyse de ses séries touche
énormément des domaines de la vie professionnelles, et plus
précisément celui de la finance, l'image l'on pourrait se faire
de cette analyse rassemblerait à un homme très âgé
avec beaucoup d'expérience et une sagesse assez grande pour tirer des
événements passés des indications sur le future, une sorte
d'oracle.
En finance, ce serait plutôt une structure fondée
sur le marché financier, fournissant ainsi le volume nécessaire
d'information permettant de dresser une chronique historique des
événements passés et courante d'une perturbation
aléatoire .Dessus viendrait se greffer un protocole d'extraction des
données, intégré suivant un modèle judicieusement
adapté à l'analyse que l'on voudrait faire .Enfin, au sommet de
cette pyramide, la réponse à la question posé au
départ, qui sera la prévision. Afin de pouvoir bien
appréhender les séries temporelles, l'article débutera par
une première partie qui s'intéressera tout d'abord
à « l'analyse des processus stationnaire et les processus
"ARMA" », il poursuivra ensuite par « la
présentation de l'algorithme de Box et Jenkins » qui
décompose la modélisation "ARMA" en différentes
étapes : identification, estimation,
Validation et prévision .Enfin, on élabore
la méthode de lissage exponentielle. Ce pendant que la deuxième
partie se concentrera aux « travaux empiriques »nous
s'amuserons de jouer sur les informations passés et courantes d'une
série de US/Euro Foreign Echange Rate afin d'obtenir une meilleure
prévision.
D
e fait, le recourt à l'analyse en série
temporelle financière peut sembler pertinent lorsqu'on dispose d'un
nombre de données suffisamment important qui nous permettons d'obtenir
des prévisions à cour terme sans investir en temps et en
énergie dans la construction d'un modèle économique.
PREMIERE PARTIE
*LA PARTIE THEORIQUE*
Introduction de la première partie
C'est une partie
consacrée à l'étude théorique de l'analyse et
prévision des séries temporelles : nous commencerons par un
« premier chapitre » qui a le but d'introduire la notion du
processus temporel et plus particulièrement la classe de processus
"ARMA", cette présentation suppose qu'on définisse au
préalable un certain membre de notions essentielles à l'analyse
des séries temporelles, et en particulier la notion de
"stationnarité". En effet, il existe plusieurs forme d'un processus
stationnaire, la première représentait par la
décomposition de Wold qui permet d'exprimer le processus comme une somme
pondérés de bruit blanc ; et il existe certain processus
stationnaire peuvent être représenté par des processus
intégrant une partie "AR ","MA" et "ARMA". Nous allons donc
à présent poser la définition de la stationnarité
c'est pour cela nous attaquerons par la suite un « deuxième
chapitre »qui s'intéressera à étudier de
façon précise ce qui est un processus non stationnaire. Ainsi le
fait qu'un processus soit stationnaire ou non conditionne le choix de la
modélisation que l'on doit adopter, en règle
générale si l'on s'entendent notamment à la
méthodologie de "Box et Jenkins" ; c'est pour cela si le processus
est issue d'un processus non stationnaire, on doit avant toute les choses,
chercher à le "stationnariser" c'est-à-dire trouver une
transformation stationnaire de ce processus c'est le but de ce chapitre qui
permet d'étudier la méthode de moindre carrée
ordinaire(MCO) pour un processus "TS" (trend Stationnary) et la méthode
de filtre au différence si le processus est "DS" (defference
Stationnary) et par la suite on applique les tests de racine unitaire de Dickey
Fuller ,Phillips Perron et KPSS. En outre, nous arrivons à la
« troisième chapitre » qui nous donne une vision
sur les méthodes de prévision des séries
temporelles, il s'intéresse en premier lieu à la méthode
de "lissage exponentiel" qui se divise en trois méthode: lissage
exponentiel simple(LES), lissage exponentiel double et lissage exponentiel de
HoltWinters, ce chapitre jette la lumière en deuxième lieu
à la représentation de l'algorithme de Box-Jenkins (1976).
CHAPITRE1 :
Les processus aléatoires
stationnaires et les processus "ARMA"
Introduction :
P
armi l'ensemble des modèles stochastique, une classe
particulière des modèles appelée classe de processus
aléatoire stationnaire va permettre de caractériser la structure
de corrélation d'une série.
SECTION1:
Concepts des Séries Temporelles
1-Processus STOCHASTIQUE:
- Un processus aléatoire est une
application « x» qui associer au couple (w, t) la
qualité (w). Elle est telle que quelque soit t T fixé, xt est
une variable aléatoire définie sur un espace
probabilisé.
- Un processus stochastique est donc une famille
aléatoire indexé par t noté (, tT) ou
encore.
2-Processus STATIONNAIRE:
Nous commencerons par poser la définition d'un
processus stationnaire au sens strict (ou stationnarité forte) pour
ensuite étudier les propriétés de la stationnarité
de second ordre (ou stationnarité faible. Partant delà nous
étudierons des processus stationnaire particuliers qui sont les bruits
blancs.
2 -1-Définition d'un
processus stationnaire au sens strict
"La stationnarité
forte"
- Soit un
processus temporel aléatoire (, tZ) : le processus
est dit
strictement ou fortement stationnaire le n-uple temps
T et pour tout temps
hT avec
Z, i, avec i=1,..., n ; la suite () a la même loi de
probabilité que la suite ( ).
Une façon
équivalente de définir la stationnarité forte :
- Un processus
est dit stationnaire au sens strict si pour toute valeurs ()
- La
distribution jointe de la suite (dépend uniquement des intervalles de
temps () est indépendante de la période t.
2 - 2-Définition d'un
processus stationnaire d'ordre deux
"La stationnarité
faible"
Dans la pratique, on se limite
généralement à requérir la stationnarité de
second ordre si trois conditions suivantes sont satisfaites :
· t Z, E
()=m, indépendant de temps t
· t Z, V
()
· (t, h)
Z², cov (,)=E; indépendant de temps Pour
La première condition porte
sur les moments d'ordre un et signifier tout simplement que les variable
aléatoire doivent avoir la même espérance quelque soit la
date t. Autrement dit, l'espérance de processus doit être
indépendante de temps. Enfin, la troisième condition porte sur
les moments d'ordre deux résumé par la fonction d'autovariance
c'est-à-dire la fonction d'autovariance de processus doit être
indépendante du temps.
- En
résumé, un processus est stationnarité au second ordre si
l'ensemble de ses moments sont indépendants du temps.
2-3-Caractéristique d'une
série temporelle
Ø
Moyenne et Variance :
E ()=
V ()=
Ø La
fonction d'autocovariance :
La fonction d'autocovariance d'un
processus est donnée par :
= cov (,) = E
Elle mesure la covariance entre
deux valeurs de séparait par un certain délai h( retard), elle
fournit des informations sur la variabilité de la série et sur
les liaisons temporelles qui existe entre les différentes composantes de
la série.
- La fonction
d'autocovariance d'un processus stationnaire «»
vérifiés les propriétés suivantes :
= cov (=var (
-==
=:fonction symétrique
Ø La
fonction d'autocorrélation(FAC)
La fonction
d'autocorrélation d'un processus
stationnaire « »est donnée par :
=
Remarque :
Le graphique de la fonction
d'autocorrélation est appelé correlogramme, les sont calculer
pour h=0, 1 , ... , k ; avec k : le décalage maximum
admissible.
La fonction d'un processus
stationnaire « » vérifier les
propriétés suivantes :
=1
-1= 1
=:fonction paire
v Test
d'hypothèse et intervalle de confiance :
La variance des
autocorrélations est donnée par :
Var ( ) =
= (1+2)
- Pour T
grand :
=
- Pour
tester la significativité statistique de terme
d'autocorrélation :
ü :=0
ü : 0
v
Règle de décision :
- Si On ne rejette pas Le
coéfficient n'est statistiquement significative.
- Si:On rejette Le coefficient
est statistiquement significative
v Intervalle
de confiance :
()=
Ø La
fonction d'autocorrélation partielle (FAP) :
Cette fonction
d'autocorrélation partielle mesure la corrélation et ;
l'influence des autres variables décalés de H période (, )
ayant été retirée.
La fonction
d'autocorrélation partielle de « » est
donnée par :
=
Le calcule se complexe si on augmente la valeur de h,
on utilise donc l'algorithme de l'expression utilisée par
Durbin(1960)
v Test
d'hypothèse :
La statistique
suivante ;
= N (0, 1) ; est
utilisée pour tester la significativité de coefficient
ü
: =0
ü :
0
v Règle de décision :
- Si ; on ne rejette pas, le coefficient n'est pas
statistiquement significative.
- Si ; on rejette , le
coefficient est statistiquement significative
v Intervalle
de confiance :
Au niveau de confiance (1-)
l'intervalle de confiance est donnée par :
()=
Remarque : A la
différance de l'intervalle de confiance ; cet intervalle est
constant.
2- 4-Le Processus bruit
blanc
Parmi la classe des processus
stationnaires, il existe des processus particuliers. Ces processus sont
très souvent utilisés en analyse des temporelles, car ils
constituent en quelque sorte « les rubriques
élémentaire »de l'ensemble des processus temporelles.
En effet nous verrons par la suite que tout processus stationnaire peut
s'écrire comme une somme pondérée de bruit blanc
(théorème de Wold).
Un processus bruit blanc est un
processus stationnaire à accroissement indépendante. On parle
aussi de processus i.i.d (variable indépendante et identique
distribuée)
-Un processus est un bruit blanc
(,t Z ) ,il satisfait les deux conditions suivantes :
tZ ;
· E
()=0
· =E ()
=
En outre, on parle de bruit
blanc gaussien lorsque la loi de probabilité du processus est
elle-même gaussienne. iid N (m, )
SECTION2 :
Le théorème de Wold
Le théorème de Wold(1938) est le
théorème fondamentale de l'analyse des séries temporelles
stationnaire, nous commenceront par donner l'énoncer de ce
théorème, nous définirons l'opérateur retard.
1-Le théorème de
décomposition de Wold
L'énoncé du théorème de
Wold est le suivant:
=+
Ou :: Est une composante
déterministe
: Est une composante
stochastique (aléatoire)
On note quesont deux processus
orthogonaux (indépendant) et avec =; avec
2-Définition de l'opérateur
retard
L'énoncé du théorème de
Wold est souvent donné en introduisant « un
polynôme défini en l'opérateur retard ». Plus
généralement, les modèles des séries temporelles
sont souvent exprimés sous la forme de « polynôme
retard ».
- L'opérateur retard
(noté L pour Log ou B suivant les ouvrages) est défini de
façon suivante :
- On considère un
processus stochastique (Z), l'opérateur retard noté L, est
défini par la relation :
L=Z
Ø Les
propriétés :
ü
=jZ ; en particulier on a =
ü =c=c,
jZ ; si =c, tZ avec cR
ü () ==
(i, j)Z²
ü =
iZ
ü
(+)=+=(i ,j)Z²
ü == ()
si <1
Jusqu'à présent
nous avons vu que tout processus stationnaire pouvait s'écrire sous
forme d'une somme pondérée infinie de choc passés
(théorème de Wold). Pour toute cette classe de processus la
décomposition de Wold est une première représentation
n'est jamais la représentation optimale parmi toutes les
représentations possibles d'un même processus. Or par
définition, si l'on devait appliquer la décomposition de Wold,
cela supposerait que l'on estime une infinité de paramètre
(les). Donc dans la pratique, il convient de rechercher d'autres
représentations possibles pour les processus temporels.
§ Parmi
les représentations les plus utilisées figurent les
représentations "ARMA" pour AutoRegressive Moving Average. Cette
représentation consiste en l'adjonction d'ordre fini (AR) et d'une
composante moyenne mobile d'ordre fini(MA).
Nous allons donc commencer par
définir la classe de processus AR, MA, ARMA afin que nous
étudierons les conditions de la stationnarité.
SECTION3 :
Les processus "ARMA"
Définissons à présent la classe
AR, MA, ARMA
1-Définition des processus
« ARMA »
1-1-Les processus "AR"
La définition
générale d'un processus AR est la suivante :
§ Le
processus stationnaire (, t Z) satisfait une représentation
« AR » d'ordre "p" noté AR(p) si et seulement
si :
= avec = ou , R
On parle ici de
représentation autorégressive, dans le sens ou la variable est
déterminée par les valeurs passées :
1-2-LES PROCESSUS "MA"
La définition
générale d'un processus MA est la suivante :
Le processus satisfait une
représentation "MA" d'ordre « q » noté MA(q),
si seulement si :
; Le polynôme (L)
étant défini par (L)=;j<q
,(0, )
1-3- LES PROCESSUS "ARMA"
Naturellement, les
processus « ARMA » se définissent par
l'adjonction d'une composante moyenne mobile « MA »
§ Le
processus stationnaire satisfait une représentation
« ARMA » d'ordre p et q si et seulement si :
Avec : ; avec)
Ainsi, on constate que les
processus « AR » et « MA » ne sont
que des cas particuliers des processus "ARMA" ; Un
« AR(p) » correspond à un ARMA (p,0), de même
façon un « MA(q ) » correspond à
ARMA(0,q).
2-La stationnarité et
l'inversibilité des processus « ARMA »
La question est alors de savoir
sous quelles conditions sur les paramètres des polynômeset; Ces
processus sont-ils stationnaire ?
Nous allons en outre introduire
la notion d'inversibilité qui consiste à déterminer s'il
existe une représentation « MA » (respectivement
pour ``AR'') équivalente pour « AR »
(respectivement pour ''MA'').
Ø
Concernant les processus « AR » :
- U n processus AR(p) est
toujours inversible ; il est stationnaire lorsque les racines de
l'équation sont à l'extérieur de plan complexe.
- Un processus Stationnaire
AR(p) peut être représenté sous forme MA (:
Avec :
Ø
Concernant les processus « MA » :
- Un processus MA(q) est
toujours stationnaire, il est inversible si les racines de sont à
l'extérieur de "L)=0" cercle unité de plan complexe.
- Un processus inversible MA(q)
peut être représenté sous forme AR (:
Avec
Ø
Concernant les processus « ARMA » :
-Un processus ARMA (p, q) est
stationnaire et inversible si la partie « AR » est
stationnaire et la partie « MA » est inversible.
-Un processus ARMA (p, q)
stationnaire et inversible peut étre présenter sous forme un
processus MA () et AR ().
Avec est
stationnaire
Avec est
inversible
CONCLUSION :
D
ans ce premier chapitre ; nous avons introduit
la notion de la stationnarité du second ordre ou la stationnarité
faible .D'après cette définition, un processus est
stationnaire de second ordre si l'ensemble de ses moments d'ordre un et
d'ordre deux sont indépendant de temps.
CHAPITRE2:
Les processus aléatoires non
stationnaires
INTRODUCTION :
N
ous avons présenté dans le premier chapitre, la
notion de la stationnarité, mais les chroniques économiques sont
rarement des réalisations de processus aléatoires stationnaires,
c'est pour cela, nous étudierons dans ce chapitre les processus
aléatoires non stationnaires qui peuvent être observés
graphiquement soit à partir de la série d'origine( existence
d'une tendance, variabilité croissante au cour de temps), soit à
partir de la fonction d'autocorrélation et décroissante lente
.
La difficulté réside dans le fait qu'il existe
différentes sources de non stationnarité et qu'à chaque
origine du non stationnarité est associée une méthode
propre de stationnarisation. Nous commencerons donc par présenter deux
classe de processus non stationnaire, selon la terminologie de Nelson et
Plosser(1982):les processus TS (Trend Stationnary) et les processus DS
(Differency Stationnary); puis nous présenterons les méthodes de
stationnarisation pour chacune de classe de processus; ensuite, nous verrons
apparaitre les testes de racine unitaire de Dickey-Fuller, test de Phillips et
Perron et test de KPSS.
Enfin, il ne reste plus qu'introduire une sous classe de
processus «ARMA»;c'est la classe des processus "ARIMA"(Integrate
AutoRegressive Moving Average).
SECTION1 :
Les processus TS
1 -Définition :
Commençons par définir ce qu'est un processus
TS pour »Trend Stationnary», selon la terminologie proposée
par Nelson et Plosser(1982).
-(, t Z) est un processus TS s'il peut s'écrire sous la
forme suivante: avec f(t) est une fonction de temps et est
un BB (0,)
Le cas le plus fréquent rencontré dans les
séries économiques apparait lorsqu'on modélise f(t) par
polynôme d'ordre un soit :
Avec
On dit également que ce processus présente une
non stationnarité de type déterministe car seul le moment d'ordre
un dépend de temps.
· E ()=E ( ) = car E (t
· V ()= E t
· COV(,) =E-E()) (-E ( =E ()=0 ;
t
2- La stationnarité du processus
TS:
Le processus « TS » traduit l'existante de
fluctuations stationnaires représentées par sa variance autour
d'une tendance déterministe qui est sa moyenne. Afin de rendre ce
processus "stationnaire", il s'agit d'enlever la tendance du processus
après avoir estimé les coefficients de l'ordonnée à
l'origine et de la pente par LA MÉTHODE DE MOINDRE CARRÉE
ORDINAIRE(MCO).
= =
Le processus résultant « » est bien
stationnaire puisqu'il a les même propriétés que le terme
d'erreur « ».
SECTION2 :
Les processus DS
1 - Définition:
Comme nous l'avons précédemment
mentionné, il existe une autre forme de non stationnarité,
provenant non pas de la présence d'une composante déterministe
tendancielle, mais d'une source stochastique. C'est pourquoi nous allons
à présent introduire la définition de processus DS pour
Differency Stationnary.
- Un processus non stationnaire ( , t Z) est un processus DS
(Differency Stationnary) d'ordre « d » qui désigne
l'ordre de l'intégration, si le processus filtré défini
par :
; Avec L est l'opérateur retard, d
est l'ordre d'intégration et B est une constante encore appelée
dérive.
On dit également que ce processus présente une
non stationnarité de type stochastique car tendance aussi que la
variance sont variables dans le temps. Le cas le plus fréquemment
rencontré lors de l'étude des séries d'observation est
celui avec « d =1» : On parle de marché au
hasard avec dérive ;
Cas : Si B=0
Le processus donc comme suit :
(1-L)=C'est un processus AR(1) avec =1, on
appelle aussi DS sans dérive, marché au hasard qui a cette
représentation :
· E ()=E (+)=
· V ()=V (
· COV (
Le processus s'écrit donc comme suit:
(1-L) processus AR(1) avec dérive avec =1, on
appelle DS avec dérive, marche aléatoire qui a une
représentation équivalente :
· E () = E (+Bt
· V (
· COV (
2- La stationnarité de processus
DS:
Le processus DS de peut être rendre stationnaire
EN APPLIQUANT LE FILTRE AU DIFFÉRENCE
PREMIÈRE
SECTION3 :
Les tests de racine unitaire
- Il est important de pouvoir distinguer avant toute tentative
de modélisation «ARMA» si le processus
générateur d'une série d'observation appartient à
la classe TS ou DS. La littérature a sur ce sujet été
prolixe ces dernières années suite aux travaux pinières de
Dickey(1976) et Fuller(1976). On s'accorde néomoins pour reconnaitre
à trois tests particuliers, précisément ceux de Dickey et
Fuller(1979,1981), Phillips et Perron(1988) et Kwiatkowski et al(1989), la
capacité de donner de bonnes indications quant à la nature du non
stationnarité observée.
1-Test de Dickey-Fuller:
Le test de Dickey Fuller simple(1979) est un test de racine
unitaire (ou de non stationnarité) dont l'hypothèse nulle est la
non stationnarité d'un autorégressif d'ordre un.
Considérons un processus ( , t Z) satisfaisant la
représentation AR(1) suivante :
Avec
Le principe général du test de Dickey Fuller
consiste à tester l'hypothèse nulle de la présence d'une
racine unitaire.
Le test de Dickey Fuller se base à des 3 modèles
qui sont :
Donc le statistique de test est donnée par :
=Avec
Ø Règle de décision :
- Si ; alors on ne rejette pas le processus est non
stationnaire
- Si alors on rejettele processus est stationnaire
- Dickey et Fuller ont testé aussi la valeur de ( alors
on trouve ces trois modèles :
Donc
On aura les mêmes étapes de test
2- Test de Dickey Fuller Augmenté
(ADF):
C'est test est applicable dans le cas d'autocorrélation
des erreurs d'ou les articles de Dickey-Fuller(1981) étendent les
résultats des tests que l'erreur suit un processus AR(p) et ils sont
fondés sur l'estimation par MCO de trois modèles suivant.
Avec
Pour les trois modèles, on chercher à tester la
racine unitaire sous contre une racine en dehors du cercle unité.
Ceci revient à poser la stratégie
suivante :
La stratégie de test « ADF »
consiste en première étape à déterminer le nombre
de retard "p" nécessaire pour blanchir les résidus. Dans la
seconde étape, il suffit d'appliquer la stratégie
séquentielle du test de Dickey- Fuller simple.
Pour déterminer la valeur de "p", il suffit de
minimiser les critères d'information qui sont des critères
fondé sur le pouvoir prédictif du modèle
considéré et qui tiennent du nombre de paramètre à
estimer. Ces critères s'applique de façon générale
à tout type de modèle et pas uniquement aux modèles des
testes « ADF ».Nous retiendrons ; le critère
d'Akaike(1973) et le critère de Schwarz (1978).Pour un modèle,
incluant "p" paramètres, estimé sur "T" périodes et
dans la réalisation de l'estimateur de la variance des résidus
est :
- Le critère d'Akaike, ou AIC est :
AIC (p) =T Log () +2p
- Le critère de Schwartz(1978) est défini
par:
SIC(p)= T log () +p Log T
3- Test de Phillips et Perron:
Le test de Phillips et Perron(1988) est construit sur une
correction non paramétrique de la statistique de Dickey- Fuller pour
prendre en compte des erreurs hétéroscédastique et/ou
autocorrelées. Il se déroule en 4 étapes:
- Estimation par MCO des trois modèles de bases des
tests de Dickey- Fuller et calcule des statistiques associées, soit le
résidu estimé.
- Estimation de la variance dite de cour terme des
résidus :
- Estimation d'un facteur correctif «
»établit à partir de la structure des covariances des
résidus des modèles précédemment estimés de
telle sorte que les transformations réalisées conduisent à
des distributions identiques à celle de Dickey -Fuller
standard :
Calcule de la statistique de test :
=+ Avec K
=
4- Le test de KPSS:
Kwiatkowski, Phillips, Schmidt, et Shmin(1992) proposent un
test fondé sur l'hypothèse nulle de stationnarité.
Après l'estimation de modèles ; on calcule
la somme partielle des résidus : et on estime la
variance de long terme () comme pour le test de Phillips et Perron. La
statistique est alors :
LM=
- Si LM : on ne rejette pas l'hypothèse nul et on
conclu que la série est stationnaire.
- Si LM: on rejette l'hypothèse nul et on conclu que la
série n'est pas stationnaire.
SECTION 4 :
Les processus ARIMA
On a si le processus est de type
« DS » ; alors on emploie les filtres aux
différences pour le stationnariser. Le recours à ces filtres
permet de définir les processus ARMA intégrés notés
"ARIMA".
- Un processus (t Z) ARIMA (p, d, q) est un processus
stationnaire dont la différenciation est d'ordre
« d » :
Est un processus ARMA (p, q) stationnaire et
inversible
- Un modèle "ARIMA" est étiqueté comme
modèle ARIMA (p, d, q) dans le quel :
- L'estimation des modèles "ARIMA" suppose que l'on
travaille sur une série stationnaire. Ceci signifie que la moyenne de la
série est constante dans le temps, ainsi que la variance. La meilleur
méthode pour éliminer toute tendance est de différencier,
c'est-à-dire de remplacer la série originale par la série
des différences adjacentes. Une série temporelle qui a besoin
d'être différenciée pour atteindre la stationnarité
est considéré comme une version intégrée d'une
série stationnaire (d'où le terme Integrated).
N
CONCLUSION :
ous choisissons de faire une synthèse à ce
chapitre, on parle des tests de racine unitaire car ils sont les bases qui nous
permettons de savoir c'est le processus est « TS » ou
« DS » afin de recourir à une meilleur
méthode de stationnarisation pour suivre enfin l'algorithme de
Box-Jenkins qui ne se réalise que si la série
étudiée est issue d'un processus stationnaire.
CHAPITRE3 :
Méthode de prévision des séries
temporelles :
Lissage exponentiel-Méthodologie de Box
Jenkins
INTRODUCTION:
O
n cherche le plus souvent à prévoir une valeur
future mais aussi parfois à reconstituer une valeur manquante et
toujours à comprendre et expliquer les variations observées.
Les techniques mathématiques d'étude des
séries temporelles vont le plus simples comme le lissage exponentiel(qui
est une classe de méthode de lissage des séries chronologiques
dont l'objectif est la «prévision» qui consiste que chaque
observation à l'instant «t» dépend des observations
précédentes et d'une variation accidentelle et celle
dépendance est plus ou moins stable dans le temps)aux plus
élaborée comme l'algorithme de «Box&Jenkins»(qui
ont popularisé l'utilisation des modèles «ARMA» en
insistant sur les étapes nécessaires à la
modélisation d'une série temporelle qui est représenter
par quatre étapes qui sont d'abord, l'identification des modèles
ensuite, l'estimation des paramètres puis, l'étape de validation
des modèles et enfin, l'objectif visé c'est «la
prévision».
La prévision d'une série temporelle permet
à priori la planification et à posteriori, elle permet d'estimer
l'impact d'une perturbation sur la variable expliquée afin de trouver
des scénarios pour le future peuvent être réalisés.
SECTION1:
Le lissage exponentiel
Commercerons par représenter le lissage exponentiel qui
est un outil pour faire de la prévision des séries sans chercher
préalablement un modèle car il permet de faire varier le poids
relatif au passé récent et de passé le plus ancien. Il
existe trois méthodes de lissage exponentiel qui permet de prolonger une
série temporelle en vue de prévision à court terme. Nous
présenterons alors le lissage exponentiel simple(LES) quand
utilise lorsqu'on n'observe pas de tendance. Mais en générale,
les séries étudies contiennent des tendances ce qui nous
permettrons de recourir au lissage exponentiel double(LED) qui fait un
ajustement par droite et nous attaquerons par la suite le lissage qui donne un
poids plus grand pour les observations dans le voisinage de temps qui est le
lissage exponentiel généralisé(LEG) mais la mise en
oeuvre rigoureuse de ce dernier reste complexe sur le plan pratique, ce qui
nous permettrons enfin d'étudier l'approche de Hold & Winters
qui ont proposé des modèles voisin beaucoup plus
accessibles.
1-Le lissage exponentiel
simple(LES):
1-1-DÉFINITION :
Soit une série temporelle et nous somme à la
période T alors vous volons prédire «
» ou « h » est l'horizon de prévision,
pour ce faire, on fera intervenir à une méthode qu'on appelle le
lissage exponentiel simple. Cette méthode se base sur le fait que plus
les observations sont éloignées de la période
« T », plus leur influence sur la prévision est
faible. On considère que cette influence décroit de façon
exponentiel. La formule va comme suit :
= (1-
Selon cette formule, ne dépend pas de l'horizon de
prévision (et donc ). Cette formule tient donc seulement pour les
périodes de 1 à T. Elle nous indique également
que « » est une moyenne des observations
passées ou le poids de cette observation décroit de façon
exponentiel avec la distance. Le coefficient (0< <1) se nomme la
constante de lissage. L'inclusion de la constante (1- ) fait en sorte que la
somme du poids est inférieure par les observations
éloignées dans le temps. D'ailleurs, on dit que la
prévision est plus rigide à mesure que tend vers 1 dans la
mesure où la prévision n'est pas sensible aux fluctuations
à cour terme. Plus tend vers 0, plus la prévision est
influencée par les observations récentes.
1-2-Choix de la constante de
lissage :
- Pour choisir la constante de lissage, il s'agit de minimiser
le critère suivant qui correspond à la somme au carré de
l'erreur de prévision :
1.3- Limitation de la
méthode :
Parmi les limitations de cette méthode, on peut
citer :
- Qu'elle ne peut être appliquée à des
variations en forme rampe (tendance ou trend), ni à des variations en
échelon.
- Qu'il n'ya pas de règle idéale pour
déterminer la pondération appropriée, il s'agit de choisir
une valeur de la constante de lissage (). La plupart du temps, on
procède expérimentalement, en essayant deux ou trois valeur
différentes pour voir qu'elle est la plus appropriée.
2-Le lissage exponentiel
double (LED):
2-1-Définition:
- Le lissage exponentiel double (Broun1959) est une
méthode plus générale que le lissage exponentiel simple,
sauf que l'on fait un ajustement au voisinage de « T » non
plus par une constante, mais par une droite (a t+ b) ; on a donc :
Ceci suggère une prévision de la forme :
(h)=(T) +(T) h ; Pour choisir (T) et
(T), il faut minimiser cette fonction :
Q =
2.2- Propriété de la
méthode :
- Parmi les avantages de lissage exponentiel double c'est de
traité des séries présentant une tendance.
- La méthode de choix de la constante de lissage est
même que pour le lissage exponentiel simple.
3- Le lissage exponentiel
généralisé:
- Puisque les méthodes de lissage exponentiel simple et
double ajuste une constante ou une droite alors le lissage exponentiel
généralisé donne un poids plus grand aux observations dans
le voisinage de « T » on a :
Avec
Dont la prévision est donnée par :
=
Nous avons présenté que par un jeu des
coefficients, le lissage exponentiel permet de faire varier le poids relatif du
passé récent et de passé plus ancien mais il existe des
méthodes de prévision plus évaluées sont disponible
avec des progiciels de prévision. Il permet d'utiliser des
modèles plus complexes dont certains reposent sur une analyse
strictement statistique qui cherche le meilleur ajustement sans apporter
d'explication.
4- Le modèle de Holt&Winters
(1960) :
La méthode de Holt et Winters permet en effet
d'effectuer des prévisions sur des séries chronologiques assez
irrégulières et soumises ou non à des variations
saisonnières qui sont des variations dues à un effet
momentané se reproduisent régulièrement dans le temps
suivant non seulement un modèle additif qui est le plus simple
dans lequel la variation saisonnière s'ajoute simplement à la
tendance dans ce cas la chronique s'écrite :
Pour tout t=1,..., T
avec est une série chronologique qui se
décompose en une tendance notée ,des variations
saisonnières de période « p »(égale
,...., )et d'une composante accidentelle .
Mais aussi avec un modèle multiplicatif qui
introduit la composante saisonnière de manière multiplicative
dont la série s'écrit comme suit :
Pour tout t=1,..., T = (1+) + avec
=1+ ; coefficient saisonniers de modèle multiplicatif
L'approche de Holt et Winters consiste en trois lissages
exponentiels simultanés. On définit donc trois paramètre
notés. A chaque instant, elle donne une estimation :
· De la tendance
· Du coefficient saisonnier correspondant
· De la valeur observée
On peut choisir les coefficients arbitrairement : faible
si l'on considère que la valeur à l'instant
« t » dépend d'un grand nombre d'observations
antérieures, élever dans le cas contraire. On peut aussi calculer
les valeurs optimales en minimisant la somme des carrés des
différences entre les valeurs observées et estimées. On
procède ensuite aux prévisions, en considérant que la
tendance suit un modèle linéaire additif ou multiplicatif
à très court terme.
SECTION2 :
La méthodologie de "Box &
Jenkins"
Box et Jenkins(1976) ont promu une méthodologie
consistant à modéliser la série temporelle
univariées au moyen de processus « ARMA ». Ces
processus sont parcimonieux et constituent une bonne approximation de processus
plus généraux pourvu que l'on restreigne au cadre
linéaire.
Les modèles "ARMA" donne souvent de bon
résultats en prévision et ont bénéficié de
la vague de scepticisme quand l'intérêt des gros modèles
économétriques. La méthodologie de Box-Jenkins peut se
décomposer en quatre étapes :
Nous présenterons tout d'abord, l'étape de
l'identification ; ensuite nous jetterons la lumière à la
phase de l'estimation ; puis nous représenterons des tests de
diagnostic dans l'étape de validation ; enfin la dernière
étape consiste à utiliser le modèle
« ARMA » validé à des fins de
prévision.
1-L'identification:
Après avoir transformé la série
étudiée de manière à la stationnariser, ce qui est
déjà vu dans le deuxième chapitre ; on arrive
à l'étape de l'identification qui est une étape
délicate qui conditionne la prévision de la chronique, elle
consiste à déterminer les paramètres
« p » et « q » du modèle "ARMA"
à l'aide de la fonction d'autocorrélation simple et la fonction
d'autocorrélation partiel.
2- L'estimation:
L'estimation des paramètres d'un modèle ARMA (p,
q) lorsque les ordres «p» et «q» sont supposes connus par
la méthode de maximum de vraisemblance qui est réalisée
à l'aide d'algorithme d'optimisation non linéaire
(Newton-Raphson, méthode de Simplex).
3-Validation:
A l'étape de l'identification, les incertitudes
liées aux méthodes employées fond que plusieurs
modèles, en générale, sont estimés est c'est
l'ensemble de ces modèles qui subissent alors l'épreuve des
testes. Il en existe de très nombreux permettant d'une part de valider
le modèle retenu, d'autre part, de comparer les performances entre les
modèles.
3-1-Test de redondance :
Le but de ce test est de vérifier si les composantes
« AR » et « MA » de "ARMA" n'ont pas
des racines communes au moyen, par exemple, des algorithmes de Newton-Raphson.
Lorsque c'est le cas, on dit qu'il ya redondance et les coefficients
estimés du modèle sont instables et peuvent conduire à des
prévisions erronées. Il faut alors éliminer dans le
modèle "ARMA" la ou les variables responsables de cette redondance.
3-2-Test de significativité :
Ce test, nous permet d'effectuer le test de Student sur chacun
des paramètres de processus « ARMA » en divisant le
paramètre par son écart type. Il peut arriver qu'un ou plusieurs
paramètres ne soit pas significativement déférents
de « 0 » : le modèle est alors
rejeté et on retourne à l'étape d'estimation en
éliminant la variable dont le coefficient n'est pas significatif.
3-3-Test de recherche
d'autocorrélation :
· Test de Box-Pierce(1970)
On note « »
l'autocorrélation d'ordre « k » du processus,
pour un ordre « k », le test de Box et Pierce est :
Pour un processus ARMA (p, q) la statistique de test
est :
; SousQ(K-(p+q))
L'hypothèse est rejetée au seuil 5% si est
superieur à la quantité 0.95 de la loi ÷²de
correspondant.
· Test de Ljung-Box
Ce test est appliqué de préférence au
test de Box-Pierce lorsque « T » est faible:
Sous
3.4- Statistique de test :
Ø Test d'homoscidasticité :
· Test ARCH d'Engle(1982)
Ce test est très fréquemment utilisé de
série temporelle
= + +
· Test ou méthode de
Méland(1992)
Il s'intéresse à la représentation
graphiquement de la fonction d'autocorrelation de la série de
carré de résidu . Si ce terme est significativement 0 ; il
une héteroscédasticité.
Ø Test de normalité :
Le test le plus classique de Jarque et Berra est fondé
sur la notion de Skewness (asymétrie) et du Kurtosis (aplatissement)
· Les tests du Skewness et Kurtosis
Soit le moment empirique d'ordre K du processus
Le coefficient de Skewness :
Le coefficient de Kurtosis :
Alors les statistiques sont :
Avec (0, 3) sont les distributions normal de Skewness
et Kurtosis
· Test de Jarque et Berra
Le test de Jarque et Berra regroupe ces deux tests en un seul
test qui est :
S=
Si S; on rejette de normalité des résidus au
seuil de.
Ø Les critères de comparaison des
modèles :
Au-delà des critère standard (MSE,
MAE,...) ;on étudie les critères propre aux modèles
autorégressifs qui sont par exemple :
-Critère Akaîke(AIC)
-Critère Schwarz(SIC)
4-La Prévision:
Ø La transformation de la serie
Lorsqu'on identifier le processus étudier à un
processus «ARMA»; on a appliqué les déférentes
transformations, il est nécessaire lors de la phase de prévision
de prendre en compte la transformation retenue et de « recolorer la
prévision » ; plusieurs cas sont possible :
§ Si le processus contient une tendance
déterministe, on extrait cette dernière par régression
afin d'obtenir une série stationnaire lors de la phase de l'estimation.
Ensuite, lors de phase de prévision, on adjoint aux prévisions
réalisées sur la composante ARMA stationnaire, la projection de
la tendance.
§ Si la transformation résulte de l'application
d'un filtre linéaire (de type par exemple différance
première), on réalise la prévision sur la série
filtré stationnaire et l'on reconstruit ensuite par inversion de filtre
la prévision sur la série initiale.
Ø Prévision pour un processus
« ARMA » :
On considère un processus ARMA (p, q) telque :
Avec (et
Appliquons le théorème de Wold au processus et
considérons la forme MA () correspondante :
L'intérêt de l'utilisation de la forme MA () est
qu'il est possible de calculer facilement l'erreur de prévision comme
suit :
Avec
et
Donc l'intervalle de prévision se représente
comme suit :
Avec ?? (0, 1) au niveau
Ø Evaluation des
prévisions :
Pour évaluer les prévisions ; on peut
calculer (REQM, EAM, ERM et coefficient de Theil)
On dit que la prévision est bonne si ces mesures sont
proches de « 0 ».
· Racine de Erreur Quadratique
Moyenne(REQM)=
· Erreur Absolue Moyenne(EAM)=
· Erreur Relative Moyenne(ERM)=
· Coefficient de Theil(U)=
CONCLUSION :
La prévision a pour but d'estimer une
observation futur à partir de la connaissance historique, de
façon générale, une prévision est une
interprétation d'une historique lequel est constituer d'une série
d'observations effectuées à dates fixes et classer
chronologiquement.
En effet, nous avons utilisé dans ce
chapitre deux méthodes de prévisions qui sont le lissage
exponentiel et les techniques de Box& Jenkins. Nous avons tenons alors que
l'efficacité de la méthode de lissage exponentiel dépend
bien étendu de choix de la valeur de coefficient de lissage
qui pourra évaluer dans le temps ; il suffit aussi de se rappeler
que plus est grand, plus on privilégie les derniers résultats et
que l'influence des résultats antérieur décroit
exponentiellement avec leur éloignement de la date
considérée, d'où le nom de la méthode. En outre,
nous avons synthétisé que la méthode de Box-Jenkins(1976)
consiste à modéliser les séries temporelles au moyen de
processus « ARMA ». Ces processus sont parcimonieux
et constituent une bonne approximation de processus plus généraux
pourvu que l'on se restreigne au cadre linéaire. Les modèles
« ARMA » donnent souvent de bons résultats en
prévision et on bénéficier de la vague de scepticisme
quant à l'intérêt de grosses méthodes
économétriques.
Finalement, ces méthodes supposent que
le future rassemblera au passé, or, nous savons bien que dans la
conjoncture actuelle les changements sont plus en plus brutaux, les
évolutions sont plus en plus rapides. Dans le cadre de prévision
à cout terme, il nous utiliser ces méthodes avec
précaution. Pour le long terme, les résultats obtenus sont des
éventualités qui ne constituent qu'un élément de
prise de décision.
Conclusion de la première partie
L
'analyse des séries chronologiques est un objet
fondamentaux de la statistique, qui permet de connaitre les concepts des
séries temporelles en définissant toute les
caractéristiques de processus «ARMA»; nous insistons alors
sur le fait, que quelque soit la méthode utilisée, il faut
être vigilant sur les prévision effectuées qui peuvent
être dans certains cas totalement aberrantes.
En effet, la prévision par lissage exponentiel
dépend plus précisément du choix efficace de la constante
de lissage. Ce pendant que
L'algorithme de Box& Jenkins se
présente comme suit:
t=1,...,n
?
Transformation
? ?
TSpar la méthode d'estimation MCO
& DS par la méthode filtre au
différence première
?
Identification
?
Estimation
?
Test d'adéquation
Oui ?
Prévision
En résume enfin que par ces deux méthodes on
peut obtenir une comparaison entre les prévisions et que prévoir
le comportement futur d'une série chronologique ne nécessite
jamais l'utilisation de plusieurs
méthodes de prévisions; car nous ouvrons un
question à répondre dans la partie empirique qui nous permet
à constater la fiabilité de l'une de ces deux méthodes qui
ne dépend pas seulement de sa complexité théorique, mais
aussi des données, de l'information disponible et du champs
d'application.
DEUXIEME PARTIE
*LA PARTIE EMPIRIQUE*
Introduction de la deuxième partie

Dans cette partie « Empirique »,
on choisie d'utiliser le logiciel E-Views6 pour bien appréhender tout ce
qu'on avait vu dans la partie « Théorique ».
En effet, Eviews est un logiciel de système
d'exploitation Windows dans un des leaders mondiaux de logiciels
d'économétrie. Ce logiciel donne une prévision de
l'analyse des données scientifique, l'analyse financière, les
prévisions des ventes et les prévisions économiques. En
outre, les solutions logicielles Eviews matière de recherche et
d'enseignement, entreprise, organisme gouvernementaux et les utilisateurs des
étudiants à une analyse statistique puissant, de prévision
des outils de modélisation.
Pour ces raisons, nous utiliserons le logiciel Eviews
afin d'obtenir des résultats précises à propos de
modélisation de la série US/Euro Foreign Exchange Rate.
Introduction de la série US/Euro Foreign
Exchange Rate
L
es propriétés de long terme des
séries financières de prix de devise intéressent depuis
longtemps les financiers et les staticients. Dans ce travail empirique nous
réexaminons cette question à propos du taux de change à
partir de l'exemple de celui de l'Euro contre le Dollar.
En effet, le taux de change d'une devise (une monnaie)
est la cour (autrement dit le prix) de cette devise par rapport à une
autre. Dans notre travail le taux de change d'euro en dollar est le nombre de
dollar que l'obtient pour un euro. En outre, le taux de change est sans
contexte une macro-économique importante. Pour une petite
économique ouverte, l'ajustement de taux de change permet de lisser les
chocs affectant les termes de l'échange. Dans une économie moins
ouvert, il favorise l'ajustement des prix relatifs entre les secteurs des biens
échangeables et celui des biens non échangeables. Le taux de
change flottant varie alors en permanence et est déterminé par
l'offre et la demande de chacune des deux monnaies sur le marché des
changes.
L'objectif de notre étude alors de montrer
qu'il est possible de retrouver les bases théoriques fondamentale simple
permettant d'explique les déterminant à long terme de taux de
conversation US/Euro entre 1999 et 2010 afin d'avoir une prévision
à terme.
Ø Présentation des données : voir
ANNEXE 1
|
Title:
|
U.S. / Euro Foreign Exchange Rate
|
|
|
|
Series ID:
|
EXUSEU
|
|
|
|
|
|
Source:
|
Board of Governors of the Federal Reserve System
|
|
|
Release:
|
G.5 Foreign Exchange Rates
|
|
|
|
|
Seasonal Adjustment:
|
Not Applicable
|
|
|
|
|
|
Frequency:
|
Monthly
|
|
|
|
|
|
Units:
|
U.S. Dollars to One Euro
|
|
|
|
|
Date Range:
|
1999-01-01 to 2010-03-01
|
|
|
|
|
Last Updated:
|
2010-04-01 10:05 AM CDT
|
|
|
|
|
Notes:
|
Averages of daily figures. Noon buying rates in New York City
for
|
|
Cable transfers payable in foreign currencies.
|
|
|
|
|
|
|
|
|
Application par le logiciel Eviews
SECTION1 :
Prévision par la méthode de Lissage
exponentiel
Avant de pouvoir utiliser l'une des méthodes de lissage
exponentiel (simple, double, HoltWinters), nous devons tester
l'existence d'une éventuelle tendance ou/et d'une saisonnalité
dans notre série
Le Fisher calculé (8.530819) est largement
supérieur au Fisher tabulé (2.09), dans ce cas on rejette
l'hypothèse H0, la série est donc
saisonnière.
Notre série est à la fois affectée d'une
saisonnalité et d'une tendance, donc la méthode de lissage la
plus adéquate est celle de HoltWinters, allons opter pour le
modèle de Holt Winters additif.
1-Le modèle de Holt Winters additif
|
Date: 06/11/10 Time: 09:41
|
|
|
Sample: 1999M01 2010M03
|
|
|
|
Included observations: 135
|
|
|
|
Method: Holt-Winters Additive Seasonal
|
|
|
Original Series: VALUE
|
|
|
|
Forecast Series: VALUESM
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Parameters:
|
Alpha
|
|
1.0000
|
|
Beta
|
|
0.0000
|
|
Gamma
|
|
0.0000
|
|
|
|
|
|
Sum of Squared Residuals
|
|
0.122180
|
|
Root Mean Squared Error
|
|
0.030084
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
End of Period Levels:
|
Mean
|
1.356132
|
|
|
Trend
|
0.002721
|
|
|
Seasonals:
|
2009M04
|
-0.001826
|
|
|
|
2009M05
|
0.003471
|
|
|
|
2009M06
|
0.003077
|
|
|
|
2009M07
|
0.006083
|
|
|
|
2009M08
|
-0.001121
|
|
|
|
2009M09
|
-0.007087
|
|
|
|
2009M10
|
-0.010836
|
|
|
|
2009M11
|
-0.011539
|
|
|
|
2009M12
|
0.005040
|
|
|
|
2010M01
|
0.014847
|
|
|
|
2010M02
|
-0.000975
|
|
|
|
2010M03
|
0.000868
|
|
|
|
|
|
|
|
|
|
|
Les prévisions de notre série suivent la même
allure de tendance.
SECTION 2 : Prévision par la
méthode Box&Jenkins
1- Etude préliminaire de la
série :
1-1- l'examen du
graphe :
La première étape de l'étude d'une
série chronologique est la représentation graphique. Cette
visualisation donne des indications très précieuses pour choisir
un modèle
Pour illustre cette première phase de
modélisation, nous examinons le graphique
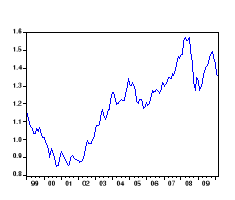
L'analyse visuelle du graphe montre à
première vue la présence d'une tendance. D'où il y a lieu
d'affirmer une présomption du non stationnarité
de notre série
1-2- L'examen du corrélogramme de la série
brute
· Corrélogramme de la série
brute
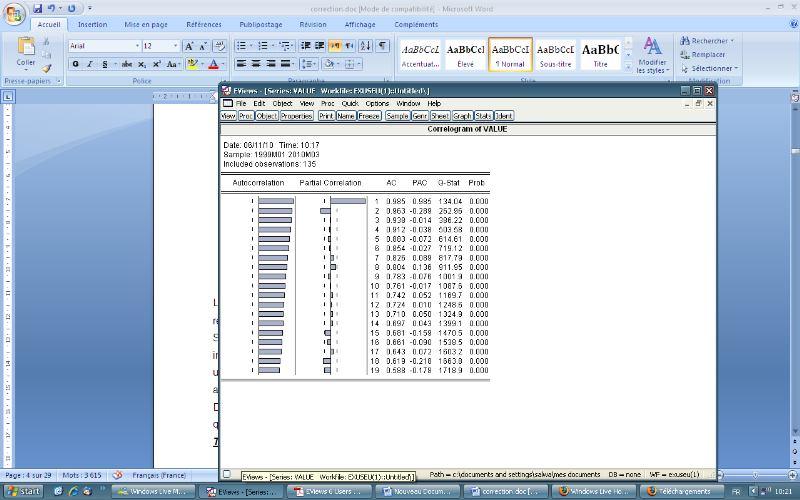
Le corrélogramme pressente (VALUE) est calculée
a l'aide du logiciel EVIEWS et sur 19 retard
Son examen pressente une décroissance de ses retards
(ce qui indique l'existence du facteur tendanciel). Les autocorrelation
s'annulent très lentement
Donc la série brute est effectuée de la
saisonnalité de la tendance, ce qui veut dire qu'elle est non
stationnaire on va confirmer avec le test qui suit :
|
Test for Equality of Means of VALUE
|
|
|
Categorized by values of VALUE
|
|
|
|
Date: 06/11/10 Time: 10:57
|
|
|
|
Sample: 1999M01 2010M03
|
|
|
|
Included observations: 135
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Method
|
df
|
Value
|
Probability
|
|
|
|
|
|
|
|
|
|
|
|
Anova F-test
|
(3, 131)
|
568.1851
|
0.0000
|
|
Welch F-test*
|
(3, 58.8123)
|
682.6354
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
*Test allows for unequal cell variances
|
|
|
|
|
|
|
|
Analysis of Variance
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Source of Variation
|
df
|
Sum of Sq.
|
Mean Sq.
|
|
|
|
|
|
|
|
|
|
|
|
Between
|
3
|
4.907427
|
1.635809
|
|
Within
|
131
|
0.377150
|
0.002879
|
|
|
|
|
|
|
|
|
|
|
|
Total
|
134
|
5.284577
|
0.039437
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Category Statistics
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Std. Err.
|
|
VALUE
|
Count
|
Mean
|
Std. Dev.
|
of Mean
|
|
[0.8, 1)
|
33
|
0.913230
|
0.042021
|
0.007315
|
|
[1, 1.2)
|
31
|
1.101381
|
0.063266
|
0.011363
|
|
[1.2, 1.4)
|
51
|
1.285882
|
0.053150
|
0.007443
|
|
[1.4, 1.6)
|
20
|
1.479645
|
0.055876
|
0.012494
|
|
All
|
135
|
1.181128
|
0.198588
|
0.017092
|
|
|
|
|
|
|
|
|
|
|
On teste les hypothèses suivantes :
Fc : Fisher calculée.
D'où on rejette H0. Ce qui veut dire que la
série est affectée d'une tendance.
On peut conclure que la série brute value est non
stationnaire, puisque les tests d'existence de la saisonnalité et de la
tendance sont retenus
1-3- dessaisonaliser la
série :
Nous présentons dans le tableau suivant les
coefficients saisonniers pour chaque mois
|
Date: 06/11/10 Time: 11:19
|
|
Sample: 1999M01 2010M03
|
|
Included observations: 135
|
|
Ratio to Moving Average
|
|
Original Series: VALUE
|
|
Adjusted Series: VALUESA
|
|
|
|
|
|
|
|
Scaling Factors:
|
|
|
|
|
|
|
|
1
|
1.010803
|
|
2
|
0.998782
|
|
3
|
1.000776
|
|
4
|
0.998398
|
|
5
|
1.003183
|
|
6
|
1.005573
|
|
7
|
1.005131
|
|
8
|
1.000898
|
|
9
|
0.996231
|
|
10
|
0.988611
|
|
11
|
0.986794
|
|
12
|
1.005089
|
|
|
|
|
|
|
· Le graphe de la série
désaisonnalisée :
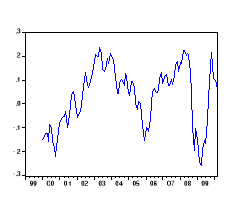
2-Etude de la stationnarité de la
série désaisonnalisée (valuesa)
** Test d'ADF sur la série
désaisonnalisée VALUESA** :
· Choix du nombre de retards optimal :
Avant de pouvoir appliquer le test de Dickey-Fuller, nous devons
déterminer le nombre de retards p qui minimise
les critères d'Akaike et Schwartz pour les trois modèles (avec
tendance et constante (trend and intercept), avec constante (intercept), sans
tendance ni constante (none)).
Les valeurs des critères d'Akaike et Schwartz sont
fournies par le logiciel Eviews et sont résumées dans le tableau
suivant :
|
Lags
|
Akaike
|
Schwarz
|
Lags
|
Akaike
|
Schwarz
|
Lags
|
Akaike
|
Schwarz
|
|
0
|
-4.233629
|
-4.288752
|
0
|
-4.312092
|
-4.246896
|
0
|
-3.977757
|
-3.999386
|
|
1
|
-4.364863
|
-4.277935
|
1
|
-4.319268
|
-4.221910
|
1
|
-4.127221
|
-3.982844
|
|
2
|
-4.349244
|
-4.240047
|
2
|
-4.288401
|
-4.178661
|
2
|
-4.109676
|
-3.912238
|
|
3
|
-4.332551
|
-4.200863
|
3
|
-4.266666
|
-4.134318
|
3
|
-4.070637
|
-3.994207
|
|
4
|
-4.312695
|
-4.158290
|
4
|
-4.250365
|
-4.095181
|
4
|
-4.108075
|
-3.952104
|
D'après le tableau nous constatons que le critère
d'Akaike est minimisé pour les trois modèles pour un nombre de
retard p = 1 tandis que le critère de Schwartz
est minimisé pour p = 0. En suivant le
principe de parcimonie nous retiendrons le nombre de retards qui permet
d'estimer le minimum de paramètres c'est-à-dire p = 0. Dans
ce cas on utilise le test de Dickey-Fuller simple (DF), donc il n'y a pas
d'autocorrélation des erreurs.
|
Null Hypothesis: VALUESA has a unit root
|
|
|
Exogenous: Constant, Linear Trend
|
|
|
Lag Length: 0 (Fixed)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t-Statistic
|
Prob.*
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller test statistic
|
-2.620864
|
0.2719
|
|
Test critical values:
|
1% level
|
|
-4.027959
|
|
|
5% level
|
|
-3.443704
|
|
|
10% level
|
|
-3.146604
|
|
|
|
|
|
|
|
|
|
|
|
|
*MacKinnon (1996) one-sided p-values.
|
|
|
|
|
|
|
|
|
|
|
|
|
Augmented Dickey-Fuller Test Equation
|
|
|
Dependent Variable: D(VALUESA)
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/11/10 Time: 12:12
|
|
|
|
Sample (adjusted): 1999M02 2010M03
|
|
|
Included observations: 134 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
VALUESA(-1)
|
-0.067131
|
0.025614
|
-2.620864
|
0.0098
|
|
C
|
0.057358
|
0.023058
|
2.487491
|
0.0141
|
|
@TREND(1999M01)
|
0.000347
|
0.000131
|
2.644404
|
0.0092
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.053536
|
Mean dependent var
|
0.001561
|
|
Adjusted R-squared
|
0.039086
|
S.D. dependent var
|
0.029396
|
|
S.E. of regression
|
0.028816
|
Akaike info criterion
|
-4.233629
|
|
Sum squared resid
|
0.108778
|
Schwarz criterion
|
-4.228752
|
|
Log likelihood
|
286.6531
|
Hannan-Quinn critter.
|
-4.207265
|
|
F-statistic
|
3.704956
|
Durbin-Watson stat
|
1.271757
|
|
Prob(F-statistic)
|
0.027216
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D'après ce tableau, on remarque que le coefficient de
la tendance est significatif, ce qui indique la présence de la
tendance.car la t-Statistique calculée est supérieur à
celle tabulée de DICKEY-FULLER (2.62)
Donc ça confirme qu'il y'a une non
stationnarité déterministe donc le type de la série
VALUESA est TS, et la meilleurs méthode pour la stationnarisée
est d'estimer la fonction de la tendance et de la retrancher de la série
VALUESA,
3-Stationnarisation de la série
valuesa
3-1- Estimation de la fonction de la
tendance :
|
Dependent Variable: VALUESA
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 16:04
|
|
|
|
Sample (adjusted): 2000M01 2010M03
|
|
|
Included observations: 123 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C
|
-0.012010
|
0.025537
|
-0.470286
|
0.6390
|
|
@TREND
|
0.000628
|
0.000315
|
1.996130
|
0.0482
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.031880
|
Mean dependent var
|
0.033831
|
|
Adjusted R-squared
|
0.023879
|
S.D. dependent var
|
0.125383
|
|
S.E. of regression
|
0.123877
|
Akaike info criterion
|
-1.322926
|
|
Sum squared resid
|
1.856812
|
Schwarz criterion
|
-1.277199
|
|
Log likelihood
|
83.35993
|
Hannan-Quinn critter.
|
-1.304352
|
|
F-statistic
|
3.984533
|
Durbin-Watson stat
|
0.133902
|
|
Prob(F-statistic)
|
0.048165
|
|
|
|
|
|
|
|
|
|
|
|
|
|
VALUESA = -0.0120096991311 +
0.000627953334795*@TREND
A présent il ne reste qu'à retrancher cette
équation de la série :
Stationnaire = Valuesa -
(0.0120096991311+0.000627953334795*(@TREND))
Donc notre série est stationnaire, on peu vérifier
par :
· Graphe de la série brute
désaisonnalisée et sans tendance VALUESA :
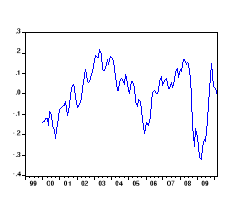
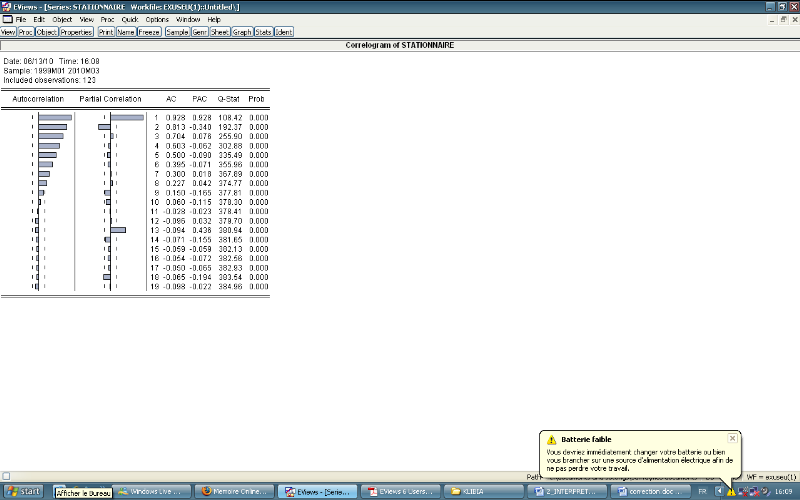
On remarque que les coefficients d'autocréation
qui s'annulent rapidement
Comme cette série est stationnaire
alors on effectue les 4 étapes de la méthodologie de Box
& Jenkins :
3-2-La méthodologie de Box &
Jenkins :
Ø Identification de modèle :
Cette étape consiste à identifier le modèle
susceptible de représenter la série
On va identifier à présent un model valide pour
faire notre prévisions, et pour cela on va estimer chaque model,
d'après les pics qui sont à l'intérieur de l'intervalle de
confiance
L'examen de ce corrélogramme montre deux pics
importants pour le terme « AR » dans
1,2,13 et six pics importants pour le terme «
MA » dans les retards 1,2,3,4,5,6.
Donc les modèles sont :
MA (1) AR(1) AR(2) MA(2) MA(3) MA(4) MA(5)
MA(6) MA(7) ARMA(1,1) ARMA(1.2) ARMA(1.3) ARMA(1.4)
ARMA(1.5)
ARMA(1.6) ARMA(1.7) ARMA(2.1) ARMA(2.2)
ARMA(2.3) ARMA(2.4) ARMA(2.5)
ARMA(2.6)
ARMA(2.7).
Pour pouvoir choisir un bon modèle parmi ceux
présenté ; on estime chaque modèle et en suite on
arrive à l'étape de validation ou applique le test de
L-JUNG BOX et les tests de normalité,
d'homogénéité.
Ø Estimation de modèle :
Nous estimons les paramètres de modèle qui
explique mieux nos observations.
Dans cet étape on test la signification des
coefficients des modèles par un simple test de Student
au seuil de 5% (on compare la statistique calculée avec la statistique
tabulée (1.96)). Si/ t-stat/>1.96 donc ce
modèle sera candidat à être valider.
|
Dependent Variable: STATIONNAIRE
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 16:18
|
|
|
|
Sample (adjusted): 2000M02 2010M03
|
|
|
Included observations: 122 after adjustments
|
|
|
Convergence achieved after 2 iterations
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
AR(1)
|
0.927749
|
0.032615
|
28.44562
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.869902
|
Mean dependent var
|
0.001160
|
|
Adjusted R-squared
|
0.869902
|
S.D. dependent var
|
0.123202
|
|
S.E. of regression
|
0.044438
|
Akaike info criterion
|
-3.381294
|
|
Sum squared resid
|
0.238940
|
Schwarz criterion
|
-3.358310
|
|
Log likelihood
|
207.2589
|
Hannan-Quinn critters.
|
-3.371958
|
|
Durbin-Watson stat
|
1.306086
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Inverted AR Roots
|
.93
|
|
|
|
|
|
|
|
|
|
|
|
|
On remarque que la t-statistique est supérieur
à 1.96 et les racines sont supérieures à
1 donc ce model est retenu, pour cela on va s'assurer avec des tests à
l'étape suivante :
Ø Validation de modèle :
Cette étape consiste à faire des tests de
validation qui sont comme suite :
1- test de L-Jung box (test d'absence
d'autocorrelation des résidus),
2- test de normalité (est ce que le
bruit blanc est gaussien ou pas)
3- test d'ARCH (l'homoscidasticité et
l'héteroscidasticité).
On commence par le test le plus utilisé qui est le test
de L-Jung box. Ce test est basé sur la comparaison
entre la dernière valeur de Q-stat calculée (sur
le corrélogramme) et la valeur tabulée de
Khi-deux de
(N-p-q) degré de liberté
/N : le nombre d'observation
p : l'ordre d'autorégressive
q : l'ordre de Moyen mobile
Si la statistique de Q-stat<X2 (N-p-q) on accepte
l'existante de l'absence d'autocorrelation des résidus, alors les
résidus constituent un bruit blanc ce qui nous donne un modèle
valide.
Apres avoir effectué ce
test on aura le résultat suivant :
1- test de L-Jung box
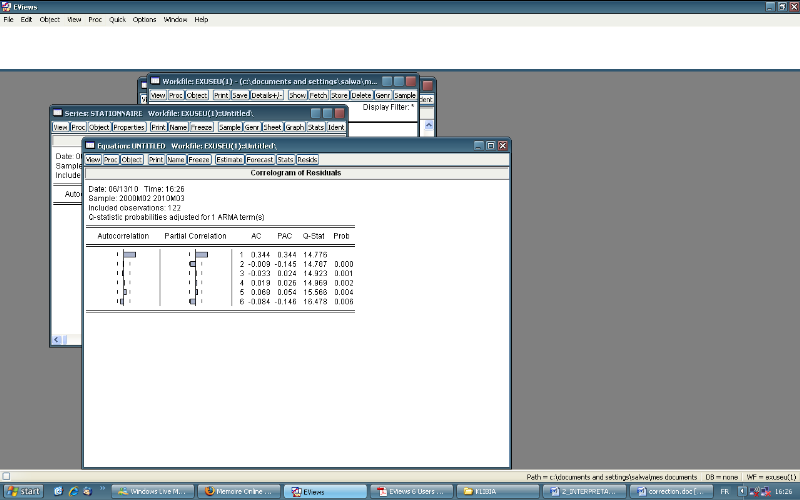
(View -Residual tests-corelogram Q-stat)
On remarque que tous les pics sont à l'intérieur
de l'intervalle de confiance c'est à dire ces résidus constituent
un bruit blanc, on confirme par le test de L-JUNG BOX, on
trouve Q-stat<X2(N-p-q).
Q-STAT=16.478<28.86=X (16) X
(16)=khi-deux de 16 degré de liberté.
2-test de Jarque et Berra :
Pour savoir si les résidus forment un bruit
blanc gaussien on applique le test de Jarques et
Berra.
· Le test de normalité :
S= suit une loi de Khi deux
Avec : Sk : le coefficient de Skewness
Ku : le coefficient de Kurtoisis
La statistique de Jarques et Berra (s=2.49)>x2 au
seuil de 5%
Par conséquent on rejette l'hypothèse de
normalité des résidus
On peut dire que le bruit blanc n'est pas gaussien
comme le montre
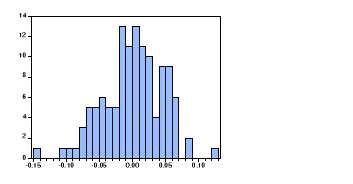
Le Jarque-Berra est une statistique de test pour examiner si la
série est normalement distribuée. La statistique mesure la
différence du Skewness et du Kurtosis de la série avec ceux de la
distribution normale
3- Test de l'effet ARCH:
|
Heteroskedasticity Test: ARCH
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F-statistic
|
3.024388
|
Prob. F(1,120)
|
0.0846
|
|
Obs*R-squared
|
2.999205
|
Prob. Chi-Square(1)
|
0.0833
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Test Equation:
|
|
|
|
|
Dependent Variable: RESID^2
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 16:40
|
|
|
|
Sample: 2000M02 2010M03
|
|
|
|
Included observations: 122
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C
|
0.001931
|
0.000268
|
7.198444
|
0.0000
|
|
RESID^2(-1)
|
0.035081
|
0.020172
|
1.739077
|
0.0846
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.024584
|
Mean dependent var
|
0.001959
|
|
Adjusted R-squared
|
0.016455
|
S.D. dependent var
|
0.002982
|
|
S.E. of regression
|
0.002958
|
Akaike info criterion
|
-8.792651
|
|
Sum squared resid
|
0.001050
|
Schwarz criterion
|
-8.746684
|
|
Log likelihood
|
538.3517
|
Hannan-Quinn critter.
|
-8.773981
|
|
F-statistic
|
3.024388
|
Durbin-Watson stat
|
1.201956
|
|
Prob(F-statistic)
|
0.084586
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D'après les probabilités de signification
(0.0846>0.05) et (0.0833>0.05) on déduire l'absence de l'effet
ARCH c'est à dire la variance des résidus sont
homogènes.
· Corrélogramme des résidus
au carrées :
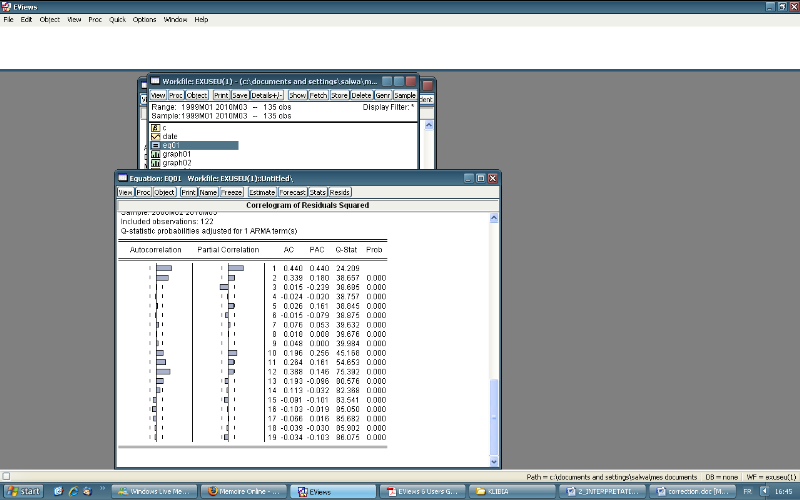
On remarque que tous les pics sont à
l'intérieur de l'intervalle de confiance ce qui confirme l'absence de
l'effet ARCH.
On peut aussi tester l'effet ARCH
d'après le coefficient de Kurtoisis, si Ku>3 il
existe l'effet ARCH, dans notre exemple KU=3.32>3.
Ø Prévision :
L'objectif de la méthode de Box & Jenkins est
de réaliser des prévisions. Une fois que le
modèle AR< M A (p, d, q) a été choisi, estime et valide
pour les observations X1, ...., Xt, on calcule les prévisions. On
suppose qu'on se trouve à l' instant t, et qu'on désir
prévoir la valeur de x t+ h, tel que alors on utilise l'estimateur
XX t(h) l'espérance conditionnelle de Xt+ h
Les valeurs de la prévision suivent une droite
linéaire.
ANNEXES
|
ANNEXE 1 :
|
|
|
|
|
DATE
|
VALUE
|
|
|
1999-01-01
|
1,1591
|
|
|
1999-02-01
|
1,1203
|
|
|
1999-03-01
|
1,0886
|
|
|
1999-04-01
|
1,0701
|
|
|
1999-05-01
|
1,0630
|
|
|
1999-06-01
|
1,0377
|
|
|
1999-07-01
|
1,0370
|
|
|
1999-08-01
|
1,0605
|
|
|
1999-09-01
|
1,0497
|
|
|
1999-10-01
|
1,0706
|
|
|
1999-11-01
|
1,0328
|
|
|
1999-12-01
|
1,0110
|
|
|
2000-01-01
|
1,0131
|
|
|
2000-02-01
|
0,9834
|
|
|
2000-03-01
|
0,9643
|
|
|
2000-04-01
|
0,9449
|
|
|
2000-05-01
|
0,9059
|
|
|
2000-06-01
|
0,9505
|
|
|
2000-07-01
|
0,9386
|
|
|
2000-08-01
|
0,9045
|
|
|
2000-09-01
|
0,8695
|
|
|
2000-10-01
|
0,8525
|
|
|
2000-11-01
|
0,8552
|
|
|
2000-12-01
|
0,8983
|
|
|
2001-01-01
|
0,9376
|
|
|
2001-02-01
|
0,9205
|
|
|
2001-03-01
|
0,9083
|
|
|
2001-04-01
|
0,8925
|
|
|
2001-05-01
|
0,8753
|
|
|
2001-06-01
|
0,8530
|
|
|
2001-07-01
|
0,8615
|
|
|
2001-08-01
|
0,9014
|
|
|
2001-09-01
|
0,9114
|
|
|
2001-10-01
|
0,9050
|
|
|
2001-11-01
|
0,8883
|
|
|
2001-12-01
|
0,8912
|
|
|
2002-01-01
|
0,8832
|
|
|
2002-02-01
|
0,8707
|
|
|
2002-03-01
|
0,8766
|
|
|
2002-04-01
|
0,8860
|
|
|
2002-05-01
|
0,9170
|
|
|
2002-06-01
|
0,9561
|
|
|
2002-07-01
|
0,9935
|
|
|
2002-08-01
|
0,9781
|
|
|
2002-09-01
|
0,9806
|
|
|
2002-10-01
|
0,9812
|
|
|
2002-11-01
|
1,0013
|
|
|
2002-12-01
|
1,0194
|
|
|
2003-01-01
|
1,0622
|
|
|
2003-02-01
|
1,0785
|
|
|
2003-03-01
|
1,0797
|
|
|
2003-04-01
|
1,0862
|
|
|
2003-05-01
|
1,1556
|
|
|
2003-06-01
|
1,1674
|
|
|
2003-07-01
|
1,1365
|
|
|
2003-08-01
|
1,1155
|
|
|
2003-09-01
|
1,1267
|
|
|
2003-10-01
|
1,1714
|
|
|
2003-11-01
|
1,1710
|
|
|
2003-12-01
|
1,2298
|
|
|
2004-01-01
|
1,2638
|
|
|
2004-02-01
|
1,2640
|
|
|
2004-03-01
|
1,2261
|
|
|
2004-04-01
|
1,1989
|
|
|
2004-05-01
|
1,2000
|
|
|
2004-06-01
|
1,2146
|
|
|
2004-07-01
|
1,2266
|
|
|
2004-08-01
|
1,2191
|
|
|
2004-09-01
|
1,2224
|
|
|
2004-10-01
|
1,2507
|
|
|
2004-11-01
|
1,2997
|
|
|
2004-12-01
|
1,3406
|
|
|
2005-01-01
|
1,3123
|
|
|
2005-02-01
|
1,3013
|
|
|
2005-03-01
|
1,3185
|
|
|
2005-04-01
|
1,2943
|
|
|
2005-05-01
|
1,2697
|
|
|
2005-06-01
|
1,2155
|
|
|
2005-07-01
|
1,2041
|
|
|
2005-08-01
|
1,2295
|
|
|
2005-09-01
|
1,2234
|
|
|
2005-10-01
|
1,2022
|
|
|
2005-11-01
|
1,1789
|
|
|
2005-12-01
|
1,1861
|
|
|
2006-01-01
|
1,2126
|
|
|
2006-02-01
|
1,1940
|
|
|
2006-03-01
|
1,2028
|
|
|
2006-04-01
|
1,2273
|
|
|
2006-05-01
|
1,2767
|
|
|
2006-06-01
|
1,2661
|
|
|
2006-07-01
|
1,2681
|
|
|
2006-08-01
|
1,2810
|
|
|
2006-09-01
|
1,2722
|
|
|
2006-10-01
|
1,2617
|
|
|
2006-11-01
|
1,2888
|
|
|
2006-12-01
|
1,3205
|
|
|
2007-01-01
|
1,2993
|
|
|
2007-02-01
|
1,3080
|
|
|
2007-03-01
|
1,3246
|
|
|
2007-04-01
|
1,3513
|
|
|
2007-05-01
|
1,3518
|
|
|
2007-06-01
|
1,3421
|
|
|
2007-07-01
|
1,3726
|
|
|
2007-08-01
|
1,3626
|
|
|
2007-09-01
|
1,3910
|
|
|
2007-10-01
|
1,4233
|
|
|
2007-11-01
|
1,4683
|
|
|
2007-12-01
|
1,4559
|
|
|
2008-01-01
|
1,4728
|
|
|
2008-02-01
|
1,4759
|
|
|
2008-03-01
|
1,5520
|
|
|
2008-04-01
|
1,5754
|
|
|
2008-05-01
|
1,5554
|
|
|
2008-06-01
|
1,5562
|
|
|
2008-07-01
|
1,5759
|
|
|
2008-08-01
|
1,4955
|
|
|
2008-09-01
|
1,4342
|
|
|
2008-10-01
|
1,3266
|
|
|
2008-11-01
|
1,2744
|
|
|
2008-12-01
|
1,3511
|
|
|
2009-01-01
|
1,3244
|
|
|
2009-02-01
|
1,2797
|
|
|
2009-03-01
|
1,3050
|
|
|
2009-04-01
|
1,3199
|
|
|
2009-05-01
|
1,3646
|
|
|
2009-06-01
|
1,4014
|
|
|
2009-07-01
|
1,4092
|
|
|
2009-08-01
|
1,4266
|
|
|
2009-09-01
|
1,4575
|
|
|
2009-10-01
|
1,4821
|
|
|
2009-11-01
|
1,4908
|
|
|
2009-12-01
|
1,4579
|
|
|
2010-01-01
|
1,4266
|
|
|
2010-02-01
|
1,3680
|
|
|
2010-03-01
|
1,3570
|
|
ANNEXE2:
|
Dependent Variable: STATIONNAIRE
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 17:28
|
|
|
|
Sample (adjusted): 2000M02 2010M03
|
|
|
Included observations: 122 after adjustments
|
|
|
Convergence achieved after 2 iterations
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
AR(1)
|
0.927749
|
0.032615
|
28.44562
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.869902
|
Mean dependent var
|
0.001160
|
|
Adjusted R-squared
|
0.869902
|
S.D. dependent var
|
0.123202
|
|
S.E. of regression
|
0.044438
|
Akaike info criterion
|
-3.381294
|
|
Sum squared resid
|
0.238940
|
Schwarz criterion
|
-3.358310
|
|
Log likelihood
|
207.2589
|
Hannan-Quinn criter.
|
-3.371958
|
|
Durbin-Watson stat
|
1.306086
|
|
|
|
ANNEXE3 :
|
Dependent Variable: STATIONNAIRE
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 16:12
|
|
|
|
Sample (adjusted): 2000M02 2010M03
|
|
|
Included observations: 122 after adjustments
|
|
|
Convergence achieved after 2 iterations
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
AR(1)
|
0.927749
|
0.032615
|
28.44562
|
0.0000
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.869902
|
Mean dependent var
|
0.001160
|
|
Adjusted R-squared
|
0.869902
|
S.D. dependent var
|
0.123202
|
|
S.E. of regression
|
0.044438
|
Akaike info criterion
|
-3.381294
|
|
Sum squared resid
|
0.238940
|
Schwarz criterion
|
-3.358310
|
|
Log likelihood
|
207.2589
|
Hannan-Quinn criter.
|
-3.371958
|
|
Durbin-Watson stat
|
1.306086
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Inverted AR Roots
|
.93
|
|
|
|
|
|
|
|
|
|
|
|
|
ANNEXE4:
|
Dependent Variable: VALUESA
|
|
|
|
Method: Least Squares
|
|
|
|
Date: 06/13/10 Time: 16:04
|
|
|
|
Sample (adjusted): 2000M01 2010M03
|
|
|
Included observations: 123 after adjustments
|
|
|
|
|
|
|
|
|
|
|
|
|
Variable
|
Coefficient
|
Std. Error
|
t-Statistic
|
Prob.
|
|
|
|
|
|
|
|
|
|
|
|
C
|
-0.012010
|
0.025537
|
-0.470286
|
0.6390
|
|
@TREND
|
0.000628
|
0.000315
|
1.996130
|
0.0482
|
|
|
|
|
|
|
|
|
|
|
|
R-squared
|
0.031880
|
Mean dependent var
|
0.033831
|
|
Adjusted R-squared
|
0.023879
|
S.D. dependent var
|
0.125383
|
|
S.E. of regression
|
0.123877
|
Akaike info criterion
|
-1.322926
|
|
Sum squared resid
|
1.856812
|
Schwarz criterion
|
-1.277199
|
|
Log likelihood
|
83.35993
|
Hannan-Quinn criter.
|
-1.304352
|
|
F-statistic
|
3.984533
|
Durbin-Watson stat
|
0.133902
|
|
Prob(F-statistic)
|
0.048165
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Conclusion générale
T
oute personne chargée de décrire et
d'analyser des séries chronologique et de mettre en ouvre des
méthodes simples de prévision à court terme de type Box
& Jenkins, de lissage exponentiel et méthode de HoltWinters.
L'objet des séries temporelle est
l'étude des variables au cour du temps, parmi ses principaux objectifs
figurent la détermination de tendance au sein de ces séries ainsi
que la stabilité des valeurs (et de leur variation) au cour de temps,
ainsi la formation présente des méthodes empiriques de
description et de prévision des séries financières c'est
le cas de notre travail qui s'intéresse au taux de conversion d'une
monnaie en une autre c'est le taux de change qui le prix, en monnaie
étrangère qu'il faut payer pour obtenir une de monnaie nationale
.La prise en compte d'une série stationnaire de taux de change US/Euro
signifie que ce dernier est de nature à absorber les chocs
économiques et qu'il existe une tendance de long terme que l'on peut
interpréter comme un niveau d'équilibre vers laquelle ce taux
revient en permanence, ce pendant que les études empiriques ne
permettent pas de conclure car le taux de conversion à terme est un
mauvais prédicteur de taux au comptant futur alors il existe une prime
de risque (charge, liquidité, imperfections, ...), mais elle est
instable et difficile à modéliser, donc à
prévoir.
Empiriquement, le taux de change demeure la bête
noire des financiers, le travail empirique montre qu'il est très
difficile de bien prévoir et expliquer les fluctuations de taux de
change.
Bibliographies
v Cour du
premier semestre de l'année, 2009-2010, 4ième Finance, de
Technique de prévision de mon professeur et encadreur « Dr
Jamel JOUINI »
v
Bourbonnais R., Terraza M. Analyse des séries temporelle en
économie, 1998, PUF
v
Bourbonnais R, Terraza M, Analyse des séries temporelles, Application
à l'économie et à la gestion, Ed. DUNOD, Paris, 2004*
G.E.P.Box, G.M.JENKINS, and
G.C.Reinsel. Time series. Analysis, Forecasting and Control. Prentice Hall,
Englewood Cliffs, New Jersey, third edition, 1994
v Box, G.,
ANDG.JENKINS (1976): Time series Analysis Forecasting and Control. San
Francisco
v
Gouréroux, C. ET Monfort, A. (1983), cour de séries temporelles,
Economica, Paris
v Dufour,
Jean-Marie(2003), Lissage exponentiel, Université de Montréal, 2
page
v Emmanuel
Cesar&Bruno Richard, les séries temporelles. Université de
Versailles Saint-Quentin-en-Yvelines. Module XML et Data Mining-Mars 2006
v Serge
Dégirine, cour de séries chronologique. Université Joseph
Fourier, 17 Septembre 2007
v Stein,
J.L. (2005). »the Fundamentals Determinants of the Real Exchange
Rate of the US Dollar Relative of the Other G-7 Currencies « , document de
travail n° 95/81 du Fonds Monétaire International
v Engel,
Charles, (2010). «Accounting for U.S. Real Exchange Rate Change «,
Journal of Polical Economy, vol. 107, p.507-508
| 


