|
MODELE DE RAMSEY & CONDITION DE
KEYNES-RAMSEY : Une explication rigoureuse et limpide
? Jean-Paul TSASA Vangu
Université Protestante au Congo
Centre Congolais-Allemand de Microfinance
Cellule de Réflexions Economiques et Sociales
Décembre 2009
Introduction
Qu'est ce que la croissance Economique ? Comment la
mesurer? Est-elle stable ? Quels sont ses composantes et la contribution
de chacune d'entre elles ? Quels sont les déterminants du
progrès technique ? Quelles sont les prédictions des
théories ayant étudié la croissance ? Etc. telles
sont les différentes questions que les théories de croissance se
propose de répondre. Au regard de ces préoccupations, cette
branche de croissance en sciences économiques apparait à la fois
très intéressante, captivant et surtout semble être
indispensable pour tout économiste.
Noter que, comme le soulignent d'ailleurs de nombreux
auteurs, la macro-dynamique exige une rigueur à tel enseigne que bon
nombre d'enseignants s'ingénient à faire comprendre aux
apprenants la complexité de différents modèles
plutôt qu'à se servir de ces recettes comme base pour apprendre
aux étudiants les politiques à mettre en oeuvre en vue de
détecter le sentier qui conduit à un croissance économique
robuste et durable.
Dans le souci de fournir aux économistes en herbe
un outil qui leur permet d'appréhender facilement le
développement de différents modèles de croissance
(susceptibles d'être enseignés au second cycle), cette note se
propos de présenter dans un langage simple et simplifié la
dérivation du modèle de Ramsey. Notez que la démarche
adoptée s'inscrit dans la logique du maître : la
simplicité dans la rigueur.
1. Pré-requis : ce qu'il faut connaitre pour
comprendre la dérivation du modèle de RAMSEY
Les concepts qu'il faut maîtriser avant de chercher
à dériver le modèle de Ramsey sont les suivants :
|
Á
|
Sais-tu que le modèle de Ramsey
endogénéise le taux d'épargne (contrairement au
modèle de Solow où le taux d'épargne est
exogène) ?
|
|
Â
|
Sais-tu que dans le modèle de Ramsey, le ménage
représentatif de l'économie est immortel et cherche à
maximiser son utilité intertemporelle ?
|
|
Comment s'écrit une fonction d'utilité
intertemporelle ?
Si tu ne sais pas, je peux t'aider ! Acceptes-tu mon
aide ?
Si non, OK ça ne dérange pas.
Si oui, la voici et retiens pour toujours cette
expression :

Où V : fonction d'utilité
intertemporelle ; U[C(t)] : utilité
instantanée ;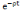 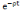 : facteur
d'actualisation psychologique ; : facteur
d'actualisation psychologique ;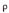 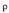 :
désigne la préférence pour le présent ou le taux
d'escompte psychologique :
désigne la préférence pour le présent ou le taux
d'escompte psychologique
Note : plus le taux d'escompte
psychologique est grand, plus l'argent valorise le présent plutôt
que l'avenir.
|
|
Ä
|
Elasticité de substitution intertemporelle (  ) : ) :
Elle correspond (dans le cas d'une fonction d'utilité
instantanée avec une élasticité de substitution
intertemporelle constante, notée :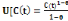
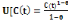 avec avec  ) à
l'inverse de l'aversion relative au risque. ) à
l'inverse de l'aversion relative au risque.
Soit :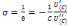 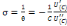
|
|
Å
|
En environnement risqué, 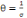 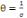 :
représente l'aversion relative au risque. :
représente l'aversion relative au risque.
Dans ce cas, la fonction d'utilité est dite
Constante Relative Risk Aversion (CRRA)
Note : plus l'aversion relative
au risque est grand, plus l'utilité marginale décroit vite quand
Ct augmente c'est-à-dire moins l'argent veut dévier par rapport
à un profil de consommation uniforme.
|
|
Æ
|
Optimisation dynamique et continue :
Comment se fait l'optimisation d'une fonction intertemporelle
par rapport à une variable de contrôle ? [Dans notre cas,
il s'agira de la maximisation de la fonction V par rapport à Ct]
La résolution d'un problème d'optimisation
dynamique et continue se fait en 4 étapes :
1. La formalisation du problème sous forme d'un
programme.
2. La détermination du Hamiltonien.
3. Les conditions du premier ordre.
4. les conditions de transversalité.
|
|
C'est peut-être cette logique qui manque soit
à certains enseignants, soit à certains étudiants pour
comprendre et faire comprendre, dans un langage facile mais rigoureux, de
concepts liés aux sciences dures !
|
2. Dérivation du modèle de
RAMSEY
Après avoir intériorisé ces
pré-requis, nous pouvons dès à présent
s'intéresser à la dérivation du modèle de
Ramsey.
2.1. Fonction d'utilité
intertemporelle
Elle s'écrit comme suit :
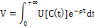
2.2. Maximisation de la fonction d'utilité
intertemporelle V
Nous allons maximiser la fonction V par rapport à la
variable de contrôle C(t) :
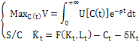
2.2.1. La détermination du
Hamiltonien
Le Hamiltonien de ce programme s'écrit comme
suit :
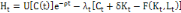
2.2.2. Les conditions du premier ordre
Les deux CPO s'expriment comme suit :
2.2.3. La condition de KEYNES-RAMSEY
La règle de KEYNES-RAMSEY consiste à
différentier par rapport au temps le logarithme de la première
CPO :
En dérivant la relation (3) par au temps, on
obtient :
En réaménageant la relation (3'), on
obtient :
En substituant l'équation (2) dans (3''), on
écrit :
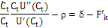
Cette expression nous permet donc de dégager le taux de
croissance de la consommation :
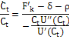
2.2.4. Détermination de l'équation
d'EULER
En considérant une fonction d'utilité CRRA
où l'aversion du risque est appréhendée à travers
le paramètre è et en admettant l'hypothèse selon laquelle
le facteur capital est rémunéré par sa productivité
marginale ;
|
* Aversion relative au risque :
|
:
|
|
|
* Elasticité de substitution intertemporelle
|
:
|
|
|
* Productivité marginale du capital
|
:
|
|
On obtient ainsi l'équation d'EULER. Elle exprime le
taux de croissance de la consommation choisi par l'agent
économique :
Il ressort de cette équation, une relation positive
entre le taux de croissance de la consommation et le taux
d'intérêt.
| 


