|
|
N°
d'ordre
08/2009
|
UNIVERSITE CADI AYYAD
N° d'ordre : 08/2009
FACULTE DES SCIENCES ET
TECHNIQUES- MARRAKECH
THÈSE
présentée à la Faculté des Sciences
et Techniques de Marrakech
pour obtenir le grade de :
Docteur
UFR : Gestion et valorisation des Géoressources
Spécialité : Hydrologie et
télédétection
Télédétection du manteau neigeux
et modélisation de la contribution des eaux de fonte des neiges aux
débits des Oueds du Haut Atlas de Marrakech
par :
Abdelghani BOUDHAR
(DESA: Risques Géologiques,
Télédétection et Cartographie)
soutenue le 21 Décembre 2009 devant la commission
d'examen :
Abdelghani CHEHBOUNIDirecteur de Recherche, IRD Toulouse,
France
Président
Lahcen BENAABIDATEPES, Fac. Sc. et Techniques, Fès,
Maroc
Rapporteur
Bouabid EL MANSOURIPES, Fac. Sc. Kénitra, Maroc
Rapporteur
Nour-Eddine LAFTOUHIPES, Fac. Sc. Semlalia, Marrakech, Maroc
Rapporteur
Jean-Emmanuel SICARTChargé de Recherche, IRD Grenoble,
France
Examinateur
Lahoucine HANICHPES, Fac. Sc. et Techniques, Marrakech, Maroc
Directeur de thèse
Gilles BOULETChargé de Recherche, IRD Toulouse, France
Co- Directeur
Brahim BERJAMYIngénieur d'état, ABHT, Maroc
Invité
|
|
Abdelghani BOUDHAR
|
|
Télédétection du manteau neigeux
et modélisation de la contribution des eaux de fonte des neiges aux
débits des Oueds du Haut Atlas de Marrakech
|
|
2009 (G)
|
|
Fiche de
présentation de la thèse
|
|
Auteur
|
|
Abdelghani BOUDHAR
|
|
Titre
|
|
Télédétection du manteau neigeux
et modélisation de la contribution des eaux de fonte des neiges aux
débits des Oueds du Haut Atlas de Marrakech.
|
|
Période
|
|
Décembre 2006 à décembre
2009
|
|
Directeur de thèse
|
|
Dr. Lahoucine HANICH
Professeur d'Enseignement
Supérieur
Université Cadi Ayyad. Faculté des Sciences
et Techniques (FST)-Marrakech, Maroc.
|
|
Co-directeur de thèse
|
|
Dr. Gilles BOULET
Chargé de Recherche (IRD (Institut de
Recherche pour le Développement)
CESBIO-UMR 5126 CNES-CNRS-IRD-UPS - Toulouse.
France.
|
|
Laboratoires
|
|
- Georessources, Département des Sciences de la
Terre, FST-Marrakech.
- CESBIO : Centre d'Etude Spatiale et de la
BIOsphère, Toulouse, France.
|
|
Cadres de coopération et de soutien
|
|
- Projet SUDMED: Collaboration entre l'Université
Cadi Ayyad, ABHT, ORMVA et DMN (Maroc) et l'Institut de Recherche pour le
développement (France).
http://www.irrimed.org/sudmed/presentation/;
-CREMAS : Centre de Recherche sur l'Eau en Milieu
Aride et Semi Aride à la (FST) de Marrakech. Jeune Equipe
Associée à l'IRD.
- Action Intégrée franco-marocaine n°/
MA/06/148 « Gestion durable des ressources en eau dans le bassin
versant de Tensift »
|
|
Articles publiés dans des revues internationales
à comité de lecture
|
|
|
Communications présentées dans des
colloques internationaux
|
|
REMERCIEMENTS
Il m'aura fallu de décembre 2006 à
décembre 2009 pour mener à bien cette thèse,
jonchée d'obstacles, poussant à la fatigue, voire dans les pires
cas à la démotivation. Ces épreuves ont toujours
été remplacées par un enthousiasme et un optimisme
débordant. J'ai vécu cette thèse comme un vrai parcours
personnel et humain, riche en rencontres. Heureusement, sur ce chemin, beaucoup
de personnes ont gravité autour de moi et m'ont donné
l'énergie d'aller de l'avant. Je vais donc prendre le temps de les
remercier chaleureusement.
Mes plus vifs remerciements s'adressent à mes
directeurs de thèse, Mr. Lahoucine HANICH de la Faculté des
sciences et Techniques de Marrakech et Mr. Gilles BOULET de l'Institut de
Recherche pour le Développement (IRD) à Toulouse, qui ont su me
lancer dans un domaine passionnant à la fois pour leurs patiences et
leurs disponibilités, leurs suivis attentifs et leurs conseils
avisés.
Cette thèse a été préparée
dans un cadre de collaboration de recherche Franco-Marocain. Je tiens à
remercier tous les organismes et les personnes pour le soutien financier de
cette thèse : Action Intégrée franco-marocaine
n°/ MA/06/148 « Gestion durable des ressources en eau dans le
bassin versant de Tensift », la jeune équipe associée
à l'IRD « CREMAS » et le programme de recherche
« SudMed ».
Je suis très reconnaissant à Lahcen BENAABIDATE,
Bouabid EL MANSOURI et Nour-Eddine LAFTOUHI, rapporteurs de ma thèse,
ainsi qu'à Jean-Emmanuel SICART et Brahim BERJAMY, examinateurs, d'avoir
accepté de participer au jury de thèse et de s'être rendu
à ma soutenance (malgré des lieux de résidence divers et
lointains !). Je les remercie des questions et remarques que leur a
inspirées ce travail et qui témoignent de l'intérêt
qu'ils y ont porté. Merci également à Abdelghani CHEHBOUNI
d'avoir présidé ce jury.
J'exprime aussi mes remerciements les plus sincères
à toute l'équipe du programme
« SudMEd » : A Monsieur Abdelghani CHEHBOUNI, le
responsable scientifique du projet pour ses encouragements et son soutien
scientifique et moral. Sur le volet
«télédétection», merci à Benoît
DUCHEMIN qui m'a beaucoup aidé à la découverte de
l'imagerie spatiale et pour son encadrement depuis mon stage de fin
d'étude de « DESA ». Merci à Vincent
Simmoneaux, Michel LE PAGE, Said KHABBA, Salah ERRAKI, Jamal EZZAHAR, Lionel
JARLAN, Bernard MOUGENOT pour leurs aides et leurs conseils. Merci à
mohammed KASBANI, Abdennacer KAMIL et Sonia THOMAS avec qui
j'ai passé des bons moments sur le terrain en montagnes du Haut
Atlas.
Merci à Mr. Yann KERR, Directeur du Centre d'Etude
Spatiale de la BIOsphère (CESBIO) à Toulouse de m'avoir accueilli
au sein de son laboratoire au cours zde mes missions à Toulouse. Merci
à tout le personnel du CESBIO.
Enfin, merci à tous mes collègues de
l'université Cadi Ayyad (Najib, Hicham, Youssef, Simohammed,
Abdelkarim...).
· RÉSUMÉ
Au centre du Maroc, la chaîne du Haut Atlas constitue
un véritable château d'eau pour les plaines arides avoisinantes.
C'est le cas de la plaine du Haouz dans la région de Marrakech où
les ressources en eau subissent une forte exploitation sous l'effet
conjugué de l'accroissement des besoins (due à l'expansion des
périmètres irrigués, à la démographie et au
développement du tourisme) et la réduction des ressources
(sécheresse passagère et/ou liée aux changements
environnementaux). Dans ce contexte, la gestion durable de ces ressources est
une priorité pour les autorités de la région et du pays.
C'est dans cet objectif global que nous avons entamé ce travail de
thèse.
L'objectif de notre travail est de modéliser,
comprendre et prédire l'apport de la fonte du manteau neigeux aux
débits des oueds des cinq sous bassins versants du Haut Atlas de
Marrakech. Afin de compenser l'absence des données in-situ dans
la zone, nous avons adopté une approche méthodologique
basée sur la combinaison des données hydro-climatiques
mesurées et les informations extraites à partir des images
satellites. Ces dernières ont été utilisées pour
déduire la répartition spatiotemporelle de deux paramètres
hydro-climatiques essentiels, l'extension du couvert nival et la
température de l'air. Les cartes d'enneigement sont produites à
partir des données issues de deux capteurs SPOT-VEGETATION et MODIS. Ces
cartes nous ont permis de comprendre la dynamique spatiale et temporelle du
couvert nival dans le Haut Atlas, par sous bassin versant, selon l'altitude et
l'exposition. À partir des données thermiques du capteur Landsat
ETM+, nous avons développé un modèle de spatialisation de
la température de l'air (MSPAT). Les résultats obtenus à
l'échelle ponctuelle (station météorologique) sont
comparables à ceux de modèle du gradient altitudinal. Tandis
qu'à l'échelle du bassin versant, les simulations des surfaces
des neiges sont nettement améliorées en utilisant la
température spatialisée par le modèle MSPAT.
Dans le but de comprendre les processus d'accumulation et
d'ablation du manteau neigeux dans la région d'étude, nous avons
testé le modèle de bilan d'énergie ISBA-ES à la
station nivale de l'Oukaimden située à 3200m d'altitude. Les
résultats obtenus montrent qu'une part importante de perte des eaux est
due à la sublimation (de 16 à 37%). En parallèle du
modèle ISBA-ES, nous avons utilisé des modèles simples de
type degré jour avec plusieurs formulations. A la fin de ce travail,
nous avons analysé l'apport des données de la
télédétection à la modélisation hydrologique
par le modèle Snowmelt Runoff Model « SRM ».
L'année 2005 a été choisie pour calibrer SRM et
étudier la sensibilité de ses paramètres. La validation du
modèle est effectuée sur les autres saisons entre 2002 et 2005.
Dans cette période, l'apport moyen des eaux de fonte de la neige aux
débits des principaux oueds atlasique est d'environ 25%.
Mots clés :
Hydrologie nivale, télédétection spatiale,
modélisation, manteau neigeux, semi-aride, Haut Atlas.
ÃÁÎÕ
ÇÁÑÓÇÁÜÜÜÉ
ÊÚÊÈÑ
ÓáÓáÉ
ÇáØáÓ
ÇáßÈíÑ æÓØ
ÇáãÛÑÈ ÎÒÇä
ÍÞíÞí
ááãíÇå
ÈÇáäÓÈÉ
ááÓåæá
ÇáãÍíØÉ ÐÇÊ
ÇáãäÇÎ ÇáÌÇ.
æåÐÇ íäØÈÞ
Úáì Óåá
ÇáÍæÒ í
ãäØÞÉ ãÑÇßÔ
ÍíË ÇáãæÇÑÏ
ÇáãÇÆíÉ ÊÚÑ
ÇÓÊÛáÇá ãßË
ÊÍÊ ÇáÊËíÑ
ÇáãÔÊÑß
ááÇÍÊíÇÌÇÊ
ÇáãÊÒÇíÏÉ
(æÐáß ÈÓÈÈ
ÇáÊæÓÚ í
ÇáãÓÇÍÇÊ
ÇáãÑæíÉ
æÒíÇÏÉ
ÇáÓßÇä) æ
ÇáäÞÕ í
ÇáãæÇÑÏ
(äÊíÌÉ ÇáÌÇ
æ/æ ÇáÊÛíÑÇÊ
ÇáÈíÆíÉ). í
åÐÇ ÇáÓíÇÞ
Åä ÇáÊÏÈíÑ
ÇáãÓÊÏÇã
áåÐå
ÇáãæÇÑÏ íÚÏ
æáæíÉ
ÈÇáäÓÈÉ
ááÓáØÇÊ í
ÇáãäØÞÉ
æÇáÈáÏ. ãä
ÇÌá åÐÇ ÇáåÏ
ÇáÚÇã ÈÏäÇ
åÐå ÇáØÑæÍÉ.
åÏäÇ
ÇáÓÇÓí ãä
åÐÇ ÇáÈÍË åæ
ÏÑÇÓÉ æ åã
ÐæÈÇä
ÇáËáæÌ ãä
ÇÌá ÊÍÏíÏ
ãÚÏá
ãÓÇåãÊåÇ í
ÇáÏæÑÉ
ÇáãÇÆíÉ
áÍæÖ ÊÇäÓíÊ.
áÊÚæíÖ
ÇáäÞÕ í
ÇáãÚØíÇÊ
ÇáãÞÇÓÉ
Úáì ÇáÑÖ
ÇÊÈÚäÇ
ãäåÌíÉ
ÊÚÊãÏ Úáì
ãÒÌ ßá ãä
ÇáÞíÇÓÇÊ
ÇáãÇÆíÉ
æÇáãäÇÎíÉ
æÇáãÚáæãÇÊ
ÇáãÓÊÎÑÌÉ
ãä ÕæÑ
ÇáÞãÇÑ
ÇáÕäÇÚíÉ.
åÐå ÇáÕæÑ
ãßäÊäÇ ãä
ÇáÍÕæá Úáì
ÈÚÖ
ÇáãÚÇííÑ
ÇáãäÇÎíÉ
ÇáÓÇÓíÉ í
ÏÑÇÓÉ
åíÏÑæáæÌíÇ
ÇáËáÌ
ßÇáÛØÇÁ
ÇáËáÌí
æÏÑÌÉ ÍÑÇÑÉ
ÇáåæÇÁ.
ÎÑÇÆØ
ÇáËáæÌ Êã
ÅäÔÇÄåÇ
ÈÇÓÊÎÏÇã
ÈíÇäÇÊ ÌåÒÉ
ÇáÇÓÊÔÚÇÑ
MODIS æ SPOT-VEGETATION
.åÐå
ÇáÎÑÇÆØ
ÓãÍÊ áäÇ Èåã
ÏíäÇãíßíÉ
ÇáÛØÇÁ
ÇáËáÌí í
ÇáØáÓ
ÇáßÈíÑ ÚÈÑ
ÇáãßÇä æ
ÇáÒãÇä áãÏÉ
8 ÓäæÇÊ
ãÇÖíÉ.
ÈÇÓÊÚãÇá
ÇáãÚØíÇÊ
ÇáÍÑÇÑíÉ
ááãÓÊÔÚÑLandsat
ETM+ æÖÚäÇ
äãæÐÌÇ
«MSPAT»
áÍÓÇÈ ÏÑÌÉ
ÍÑÇÑÉ
ÇáåæÇÁ
ÈÊÛííÑ
ÇáÇÑÊÇÚ
ÒÇæíÉ
ÇáãäÍÏÑÇÊ æ
ÒÇæíÉ
ÇáÊÚÑÖ Åáì
ÇáÔãÓ. ÊÔíÑ
ÇáäÊÇÆÌ Úáì
ãÓÊæì ãÍØÇÊ
ÇáÑÕÇÏ
ÇáÌæíÉäåÇ
ÞÇÈáÉ
ááãÞÇÑäÉ ãÚ
ÇáäãæÐÌ
ÇáãÈÓØ»Gradient»
í åÈæØ ÏÑÌÉ
ÍÑÇÑÉ
ÇáåæÇÁ ãÚ
ÇáÇÑÊÇÚ.
ÈíäãÇ Úáì
ãÓÊæì ÇáÍæÖ
ÇáãÇÆí
äáÇÍÙ ÊÍÓä
ßÈíÑ
ÈÇÓÊÎÏÇã
ÇáäãæÐÌ
«MSPAT» .
ãä Ìá åã
ÚãáíÉ ÊÑÇßã
æÊÐÑíÉ
ÇáËáæÌ í
ãäØÞÉ
ÇáÏÑÇÓÉ
ÞãäÇ
ÈÇÎÊÈÇÑ
äãæÐÌ áÊæÇÒä
ÇáØÇÞÉ
«ISBA-ES»Úáì
ãÍØÉ
ÇæßíãÏä
ÇáãÊæÇÌÏÉ
Úáì ÇÑÊÇÚ
3200ã. ÊÙåÑ
ÇáäÊÇÆÌ ä
ÍæÇáí 16
Åáì 37 í
ÇáãÇÆÉ ãä
ãíÇå ÇáËáæÌ
ÊÖíÚ ÈÓÈÈ
ÇáÊÈÎÑ.
ÈÇáãæÇÒÇÉ
ãÚ ÇáäãæÐÌ
ÇáãÚÞÏ
ÇÓÊÚãáäÇ
äãæÐÌ ÈÓíØ
ÈÚÏÉ ÕíÛ
íÍÓÈ ßãíÉ
ÇáÐæÈÇä ÈÚÏÏ
ÏÑÌÇÊ
ÇáÍÑÇÑÉ í
Çáíæã
ÇáæÇÍÏ. í
äåÇíÉ åÐÇ
ÇáÈÍË ÞãäÇ
ÈÏÑÇÓÉ
ãÓÇåãÉ
ãÚØíÇÊ
ÇáÇÓÊÔÚÇÑ
Úä ÈÚÏ í
ÇáäãÐÌÉ
ÇáåíÏÑæáæÌíÉ
ÈÇÓÊÚãÇá
ÇáäãæÐÌSRM . ÈÚÏ
ãÚÇíÑÉ åÐÇ
ÇáÎíÑÊã
ÊÞííã
ãÓÇåãÉ
ÐæÈÇä
ÇáËáæÌ í
ÇáãíÇå
ÇáÓØÍíÉ
ááÍæÇÖ
ÇáãÇÆíÉ
ÇáÑÚíÉ
ááØáÓ
ÇáßÈíÑ
áãÑÇßÔ. ÊÞÏÑ
åÐå
ÇáãÓÇåãÉ
ÈÍæÇáí 25%
Èíä 2002 æ 2005
.
ÇáßáãÇÊ
ÇáãÊÇÍ:
åíÏÑæáæÌíÇ
ÇáËáÌ
ÇáÇÓÊÔÚÇÑ
Úä ÈÚÏ
ÇáäãÐÌÉ
ÇáÛØÇÁ
ÇáËáÌí ÔÈå
ÇáÞÇÍáÉ
ÇáØáÓ
ÇáßÈíÑ.
· ABSTRACT
In the centre of Morocco, the High-Atlas mountain range
represents the most important water storage for the neighbouring arid plains.
It is the case of the Haouz plain, in the region of Marrakech, where water
resources are intensively exploited due to the combined effect of the
increasing needs (agriculture, demography and tourism) and the resources
reduction (temporary drought and/or linked to environmental changes). In this
context, sustainable management of these resources is a priority for the
authorities of the region and country. This is the overall objective of this
thesis.
The aim of this work is to model, understand and predict the
contribution of snowmelt to streamflow in the five sub-watersheds of the High
Atlas of Marrakech. To compensate the lack of in-situ data in the area, we have
adopted a methodological approach based on the combination of sparse
hydrometeorological in-situ data and information extracted from satellite
images. The later are used to provide the spatiotemporal fields of two
hydro-climatic parameters: snow cover area and air temperature. Snow maps are
produced using SPOT-VEGETATION and MODIS data. These maps have allowed us to
understand the spatial and temporal dynamics of snow cover in the High Atlas,
for each sub-watershed, depending on altitude and aspect. The thermal data
provided from Landsat ETM + sensor was used to develop a spatial model of air
temperature (MSPAT). The results at point scale (weather station) are
comparable with the lapse rate model, while at the watershed scale; simulations
of snow cover area are significantly improved using the temperature distributed
by MSPAT model.
In order to understand the accumulation and ablation process
of the snowpack in the study area, we tested an energy balance model
«ISBA-ES» in the Oukaimden station, located at the altitude of 3200m.
The results show that substantial water losses are due to sublimation (16 to
37%). We also used a simple degree day model with several formulations. At the
end of this work, we analyzed the contribution of remote sensing data for
hydrological modeling by the Snowmelt Runoff Model «SRM». The year
2005 was chosen for calibrating the SRM and the sensitivity studies of its
parameters. Model validation is performed on the other seasons between 2002 and
2005. In this period, the contribution of snowmelt to streamflow in the main
atlasique wadis is about 25%.
Key words: Snow hydrology,
remote sensing, modeling, snowpack, semi-arid, High Atlas.
TABLE DES MATIERES
Introduction
générale 10
Chapitre I
: Hydrologie spatiale 11
I.1Introduction
11
I.2Elément de la
télédétection spatiale 11
I.2.1Processus de la
télédétection 11
I.2.2Spectre
électromagnétique et réflectance 11
I.2.3Orbitographie 11
I.2.4Traitement des images
satellites 12
I.2.5Applications de la
télédétection en hydrologie 12
I.3L'Hydrologie et la
Modélisation 12
I.3.1Objet de l'hydrologie
12
I.3.2Modèles Hydrologiques
12
I.3.3Typologie des modèles
hydrologiques 13
I.3.4Critères
d'évaluation d'un modèle 13
I.3.5Modèles
utilisés dans ce travail 14
Chapitre II
: Présentation du bassin versant de Tensift et des données
utilisées 15
II.1Bassin versant de
Tensift 15
II.1.1Contexte
général 15
II.1.2Contexte Géologique
17
II.1.3Ressources hydriques
19
II.1.4Climat 19
II.2Sous bassins versants
atlasiques 23
II.2.1Caractéristiques
physiographiques 23
II.2.2Analyse Hydrologique
25
II.3Données
expérimentales 25
II.3.1Données
météorologiques 25
II.3.2Données nivales
25
II.3.3Données Hydrologiques
28
II.3.4Données satellitaires
28
Chapitre III :Analyse
de la dynamique spatio-temporelle du manteau neigeux dans les montagnes du Haut
Atlas de Marrakech à l'aide de la télédétection
31
III.1Introduction
31
III.2
Télédétection du manteau neigeux 31
III.2.1 Propriétés
optiques de la neige 31
III.2.2Données satellites
utilisées pour l'observation de l'enneigement 31
III.3Production des cartes
de surfaces enneigées 31
III.3.1Limitation des effets
géométriques 31
III.3.2Détection des nuages
31
III.3.3 Estimation des surfaces de
neige 32
III.4Analyse de la
variabilité spatiale et temporelle de l'enneigement
34
III.4.1Variabilité
interannuelle de l'enneigement sur le Haut Atlas 34
III.4.2Variabilité de
l'enneigement par bassin versant 36
III.4.3Caractéristiques de
l'enneigement selon l'altitude et l'exposition 36
III.4.4Relation entre
l'enneigement et les données hydro-climatiques 36
III.5Conclusion
37
Chapitre IV
:Spatialisation de la température de l'air dans les montagnes atlasique
à l'aide des données de l'infrarouge thermique
38
IV.1 Introduction
38
IV.2Techniques de
spatialisation de la température 38
IV.3 Méthodologie
38
IV.3.1Calcul de la
température de brillance 38
IV.3.2Dérivation de la
température de l'air 38
IV.3.3Analyse de la variation
spatiale de la température maximale de l'air 38
IV.3.4Modèle de
distribution spatiale de la température de l'air (MSPAT) 40
IV.4 Evaluation du
modèle MSPAT 40
IV.4.1A l'aide du réseau de
stations météorologiques 40
IV.4.2 A l'aide du modèle
de fonte et des surfaces enneigées observées par
télédétection 41
IV.5Conclusion
44
Chapitre V
: Modélisation de l'accumulation et de la fonte des neiges dans le
bassin versant de Rheraya 45
V.1Introduction
45
V.2Bilan d'énergie
et de masse du manteau neigeux 45
V.2.1Rayonnement net (Rnet)
45
V.2.2Flux turbulent 46
V.3Accumulation du manteau
neigeux 46
V.3.1Estimation de la
densité et l'équivalent en eau de la neige 46
V.3.2Reconstitution des
précipitations solides et liquides 47
V.4Modélisation de
la fonte des neiges 47
V.4.1Modèle de bilan
d'énergie 47
V.4.2Le modèle degré
jour 50
V.5Spatialisation de la
fonte à l'échelle du bassin versant de Rheraya
53
V.5.1Spatialisation des
données d'entrées et de la fonte 54
V.5.2Vérification du
modèle 54
V.6Conclusion
55
Chapitre VI
: Evaluation de l'apport de la fonte des neiges aux débits dans
principaux oueds du Haut Atlas de Marrakech 56
VI.1Présentation de
l'article (boudhar et al. 2009) 56
VI.2Introduction
56
VI.3Study area
56
VI.4Hydro-meteorological
data 56
VI.5Snow covers maps
57
VI.5.1From remote sensing data
57
VI.5.2From meteorological data
57
VI.5.3Comparison between simulated
and observed SCA on the days of satellite acquisition 57
VI.6Implementation and
calibration of SRM 60
VI.6.1Description of SRM
60
VI.6.2Sensitivity analysis and
parameters optimization 60
VI.6.3Analysis of model parameters
interdependence 60
VI.6.4Snowmelt contribution to
streamflow 61
VI.6.5Model validation
61
VI.7Conclusion
61
Conclusion et
Perspectives 63
Références
bibliographiques
64
ACRONYMES
ABHT
|
Agence du Bassin
Hydraulique du Tensift
|
AVHRR
|
Advanced Very
High Resolution
Radiometer
|
CAF
|
Club Alpin
Français
|
CESBIO
|
Centre d'Etudes
Spatiales de la BIOsphère
|
CNES
|
Centre National
d'Etudes Spatiales
|
CREMAS
|
Centre de Recherche sur
l'Eau en Milieu Aride et
Semi aride
|
DMN
|
Direction de la
Météorologie Nationale
|
DREF
|
Direction Régionale
des Eaux et Forêts
|
EOS
|
Earth Observing
System
|
ETM
|
Enhanced Thematic
Mapper
|
ISBA-ES
|
Interaction
Sol-Biosphre-Atmosphre-neige
explicite (Explicit Snow)
|
MNT
|
Modèle
Numérique de Terrain
|
MODIS
|
MODerate resolution Imaging
Spectroradiometer
|
MSPAT
|
Modèle de
SPAtialisation de la Température de
l'air
|
MSS
|
Multi-Spectral
Sensor
|
MVC
|
Maximum Value
Composite
|
NASA
|
National Aeronautics and
Space Administration
|
NDVI
|
Normalized Difference
Vegetation Index
|
ORMVAH
|
Office Régional de
Mise en Valeur Agricole du
Haouz
|
RMSE
|
Root Mean
Square Error
|
SCA
|
Snow Covered
Area
|
SPOT
|
Système Pour
l'Observation de la Terre
|
SRM
|
Snowmelt Runoff
Model
|
SRTM
|
Shuttle Radar
Topographic Mission
|
SWE
|
Snow Water
Equivalent
|
TOA
|
Top Of
Atmospher
|
UCAM
|
Université Cadi
Ayyad de Marrakech
|
|
LISTE DES
FIGURES
LISTE DES
TABLEAUX
· Introduction
générale
La neige peut couvrir à chaque instant une surface
d'environ 44% de la surface terrestre (Foster et Rango, 1982) et 53% de la surface de
l'hémisphère Nord. On peut distinguer deux types
d'évolution de la couverture neigeuse: une couverture permanente et une
couverture saisonnière. Généralement les couvertures
neigeuses saisonnières ne durent pas longtemps et commencent à
fondre à partir de la fin du printemps jusqu'à
l'été, alors que les couvertures neigeuses permanentes persistent
plusieurs années. Ces dernières se trouvent principalement dans
les régions Antarctiques et Groenland. Le volume d'eau stocké au
dessus de la surface terrestre sous la forme de glace et de neige constitue
environ 68% de l'eau douce de la planète (Shiklomanov, 1990).
Dans les zones arides et semi-arides, les
précipitations en montagne sont souvent la principale source d'eau pour
les populations vivant en aval. Les régions montagneuses jouent de ce
fait un rôle primordial car elles permettent l'alimentation en eau des
régions avoisinantes et contribuent d'une manière significative
à la recharge des nappes souterraines et des barrages. C'est le cas du
Maroc, qui se caractérise par de hautes altitudes de ses puissantes
chaînes montagneuses. Ces dernières occupent le Nord et le centre
du territoire marocain. La chaîne du Haut Atlas s'étend du
sud-ouest au nord-est, et comporte plusieurs sommets de plus de 3500 m dont
certains dépassent 4000 m. Son point culminant se situe au Jbel Toubkal
à 4165 m. Le Moyen Atlas, plus au Nord, compte également des
sommets dont l'altitude varie entre 2700m à 3300 m. A l'extrême
nord du Maroc la chaîne du Rif, avec son versant nord plongeant dans la
mer Méditerranée, culmine à 2456 m. L'Anti-Atlas, au sud
du Haut Atlas, atteint des altitudes dépassant 2500m. Ces montagnes
constituent un véritable château d'eau grâce à
l'augmentation des précipitations sous l'effet de l'altitude. Une part
importante de ces précipitions tombe sous forme de neige. A cet effet,
une quantité d'eau douce reste stockée temporairement sous forme
de neige avant d'être restituée à travers les
écoulements de surface pendant la période de fonte.
Au Maroc, peu de recherches ont été
menées sur l'importance de la neige dans le bilan hydrique des
régions avoisinantes des montagnes. La première étude du
manteau neigeux dans le Haut Atlas à commencé en 1989 avec le
programme « Al Ghait : Morocco Winter Snowpack Augmentation
Project », Programme de coopération entre le Royaume du Maroc
et les Etats-Unis (Matthews, 1989). Dans ce cadre, Abidi (1989) a
réalisé une modélisation des débits dans le bassin
versant de Tillouguit (2544 km²) à l'aide du modèle SRM
« Snowmelt Runoff Model ». Les surfaces de neiges
utilisées à l'entrée de SRM sont issues de deux
capteurs : Landsat Multispectral Scanner (MSS) et Advanced Very High
Resolution Radiometer (NOAA/AVHRR). Dix ans plus tard, deux grands projets de
recherche dans le secteur de la gestion des ressources en eau ont
été initiés dans deux grands bassins versants du Haut
Atlas. Le premier projet est intitulé GLOWA-IMPETUS, qui a
débuté en 2000, il a pour but de développer des solutions
pour les défis exceptionnels présentés par les
conséquences régionales du changement écologique global
pour les utilisateurs et les gestionnaires des ressources en eau dans deux
bassins versants au Bénin et au Maroc (
http://www.impetus.uni-koeln.de).
Le bassin marocain choisi par ce projet est le bassin versant de Drâa
(28428 Km²), situé sur le versant sud du Haut Atlas autour de la
ville d'Ouarzazate. Le second projet, SUDMED (
http://www.irrimed.org/sudmed/presentation/),
lancé en 2002, s'est concentré dans le bassin versant de Tensift
(20450 km²), situé sur le versant Nord du Haut Atlas, aux alentours
de la ville de Marrakech. Il s'agit d'un programme de coopération
Franco-marocain, qui a pour objectif de développer les
méthodologies permettant d'intégrer les informations de terrain,
les mesures satellites et les modèles physiques pour documenter,
comprendre et prévoir l'évolution hydro-écologique du
bassin versant du Tensift en vue d'une gestion durable (Chehbouni et al., 2003;
Chehbouni et al., 2008). Le présent travail de recherche rentre dans le
cadre de ce programme. Dans le cadre de ces deux projets, on note quelques
études concernant le manteau neigeux. Il s'agit essentiellement de
cartographier les surfaces de neige à l'aide des données de
télédétection. Les images issus des capteurs SPOT
VEGETATION, Landsat TM (Thematic Mapper) et MODIS on été
utilisées (Hanich et al., 2003; Chaponnière et al.,2005 ;
Schulz et De Jong, 2004; Leroux, 2006 ; Boudhar et al., 2007). Dans le
cadre d'IMPETUS, des travaux sur la modélisation de la fonte des neiges
(Schulz et De Jong ,2004) ont été effectués afin de
quantifier la part de la sublimation dans la perte de l'eau de la neige dans
les versants Sud à l'aide d'un modèle de bilan d'énergie.
Ainsi, Boudhar et al., 2009 ont effectué une quantification des apports
dus à la fonte des neiges dans cinq sous bassins versants du Haut Atlas
de Marrakech.
L'alimentation en eau de la ville de Marrakech et des
périmètres irrigués de la plaine du Haouz se fait
exclusivement à partir du château d'eau atlasique. En
période estivale notamment, une large part de la recharge des barrages
et des nappes souterraines situées en aval est issue de la fonte des
neiges à la fin du printemps. Sous l'effet conjugué de
l'augmentation de la demande en eau (due à l'expansion des
périmètres irrigués, à la démographie et au
développement du tourisme) et la réduction des ressources
(sécheresse passagère et/ou liée aux changements
environnementaux), les ressources en eau connaissent une forte exploitation.
Devant cette situation, la gestion durable de ces ressources est une
priorité pour les autorités de la région et du pays. C'est
dans cet objectif général de la caractérisation des
ressources hydriques de la région de Tensift que nous avons entrepris
cette thèse. Ce travail s'est déroulé au sein du centre de
recherche sur l'eau en milieu aride et semi aride (CREMAS1(*)) à la FST de Marrakech en
collaboration avec le CESBIO2(*) à Toulouse dans le cadre du projet de
recherche franco-marocain SUDMED. Ce projet a été lancé en
2002 en collaboration avec le CESBIO et l'UCAM3(*) avec l'appui des organismes
régionaux chargés de la gestion des ressources hydro-agricoles
dans le bassin de Tensift (ORMVAH4(*) et ABHT5(*)). Ainsi que le support du PAI (Programme d'Action
Intégrée du Comite Mixte Interuniversitaire Franco-Marocain,
`Volubilis' MA/06/148).
Parallèlement à la rationalisation de la gestion
de l'eau pour l'irrigation, qui consomme à elle seule 85% des ressources
en eau mobilisables dans le bassin, une meilleure caractérisation des
ressources en eau disponibles en amont est nécessaire. Pour cela, il est
important d'étudier les différents processus du manteau neigeux
du Haut Atlas afin de quantifier le stock de neige existant et de
prévoir les volumes d'eau qui seront disponibles lors de la fonte.
L'objectif de cette thèse est de comprendre
la dynamique spatio-temporelle du manteau neigeux en utilisant les
données issues de la télédétection,
analyser les processus de l'accumulation et de la fonte des neiges
dans le Haut Atlas à l'aide des mesures in-situ,
modéliser ces processus à l'échelle spatiale
(bassin versant), dans le but de prédire la
contribution de la fonte des neiges au débit des oueds du Haut Atlas de
Marrakech.
Pour atteindre cet objectif, nous avons suivi une approche
méthodologique basée sur la combinaison des données
expérimentales estimées in situ manuellement ou à
l'aide des stations météorologiques, et des données
satellitaires. Ces données ont été ensuite
assimilées dans un modèle hydrologique afin d'estimer l'apport
des eaux de fonte aux débits (
Figure ý0). Les axes de recherche sur
lesquels s'appuie ce travail sont:
i- Mesures de terrain : La première
étape consistait en la mise en place d'un protocole expérimental
limité au sous bassin versant de Rheraya, sous bassin montagneux pilote
du projet SUDMED. Le réseau de mesures météorologiques
présent dans la zone a été renforcé par
l'installation des stations climatiques. Ces dernières enregistrent
automatiquement les différents paramètres climatiques à
des pas de temps plus courts (30 min). A l'incertitude sur le forçage
climatique s'ajoute une large incertitude sur les débits
observés : avec un seul jaugeage par mois en moyenne, il est
très difficile de suivre l'évolution des barèmes lors de
la divagation des oueds après un épisode de pluie
particulièrement violent. Afin d'améliorer la précision de
la relation pluie-débit, mais aussi de la partition pluie/neige, les
mesures hydrométéorologiques (et nivologiques) ainsi que la
mesure des débits ont été renforcés pour une
année hydrologique test (sept. 2007- août. 2008). Au cours de
cette saison, nous avons aussi procédé à des mesures des
densités et des hauteurs du manteau neigeux dans le plateau d'Oukaimden.
ii- Observation satellitaire : Au cours
de cette étude, deux principales applications ont été
réalisées à l'aide de l'imagerie satellitaire. La
première est la cartographie de la couverture neigeuse et l'étude
de sa dynamique spatio-temporelle à l'échelle du Haut Atlas de
Marrakech. Cela a été fait en utilisant des séries
d'images issues des capteurs SPOT VEGETATION et MODIS couvrant la
période (de 1998 à 2006). La seconde application des
données de télédétection est la spatialisation de
la température de l'air avec des données d'infra rouge thermique
de l'instrument Landsat ETM+. Cela a pour but de corriger l'effet de la
faiblesse du réseau climatique pour spatialiser le modèle de
fonte de la neige.
iii- Modélisation : Deux types de
modèles ont été utilisés dans ce travail. Un
modèle de fonte de neige, simple dit « degré
jour » et un autre complexe à base physique
« ISBA-ES ». Ils sont utilisés pour comprendre les
processus d'ablation (fonte et sublimation) et d'accumulation des neiges. Ces
modèles sont validés avec les données enregistrées
par la station nivale d'Oukaimden et celles échantillonnées
manuellement lors des compagnes de mesures. Le deuxième modèle
testé dans ce travail est le modèle hydrologique SRM
(Snowmelt Runoff Model) qui utilise en entrée les données des
surfaces de neige obtenues par la télédétection. Il est
appliqué à l'échelle des cinq sous bassins versants
atlasiques afin d'estimer la contribution du manteau neigeux aux débits
des cours d'eau.
Ce mémoire est subdivisé en trois
parties :
La première partie est consacrée
à la présentation du contexte d'étude, des données
et d'une synthèse bibliographique sur la modélisation
hydrologique et la télédétection. Elle est
composée de deux chapitres. Le chapitre I est réservé
à une synthèse bibliographique sur la
télédétection et la modélisation hydrologique. Dans
le chapitre II nous avons présenté la zone d'étude
avec son contexte général, climatique et hydrologique. Nous avons
également présenté et analysé les données
hydrométéorologiques et satellitaires.
La deuxième partie est réservée
aux travaux liés à l'utilisation de la
télédétection pour la spatialisation des observations
(Surface d'enneigement et température de l'air). On
présente dans le chapitre III la méthodologie et les
différentes analyses et traitement effectués pour suivre la
dynamique spatio-temporelle du manteau neigeux dans le Haut Atlas de Marrakech.
Pour cela, Les produits issus des deux capteurs VEGETATION et MODIS ont
été utilisés. Dans le chapitre IV, on présente la
méthodologie suivie pour spatialiser la température de l'air
à l'aide des données infrarouge thermique Landsat ETM+ et les
résultats obtenus.
La troisième partie est consacrée
à la modélisation.
Les travaux de modélisation des processus de fonte des
neiges à l'échelle locale, au niveau du site d'Oukaimden,
et spatiale, au niveau du sous bassin versant de Rheraya, sont
présentés dans le chapitre V. Les deux modèles, simple
« degré jour » et à base physique
« ISBA-ES » sont utilisés. Le chapitre VI est
réservé à l'étude de la contribution de la fonte
des neiges aux débits des oueds des cinq sous bassins versants
atlasiques à l'aide du modèle hydrologique de fonte
« SRM ».
A la fin de ce mémoire, nous conclurons ce travail en
proposant des perspectives.
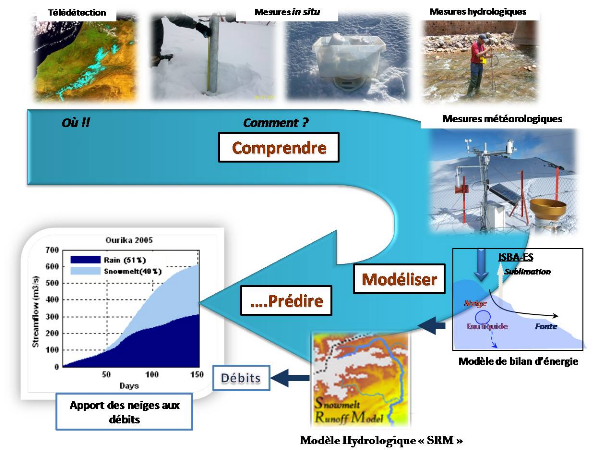
Figure ý0: Synthèse de l'approche
méthodologique utilisée dans ce travail pour étudier la
neige dans le Haut Atlas de Marrakech. Les questions clés posées
sont: Où sont les zones neigeuses? Qu'en est-il de ces
propriétés locales dans le temps (densité, hauteur...) ? -
Quelle quantité de neige ou de pluie en général est
disponible? Les réponses de ces questions sont apportées à
l'aide de la télédétection, des mesures climatologiques,
hydrologiques et mesures sur le terrain et par la
modélisation.
Chapitre I : Hydrologie
spatiale
·
Introduction
Les techniques de la télédétection
spatiale représentent un apport essentiel pour les études
hydrologiques. En hydrologie nivale en particulier, ces techniques sont
devenues ces dernières décennies plus appliquées pour le
suivi des ressources hydriques contenues dans le manteau neigeux. Les
données de la télédétection permettent l'obtention
des paramètres de terrain difficiles à mesurer en continue dans
des vastes zones. Différents paramètres nécessaires
à l'entrée des modèles hydrologiques distribués
peuvent être extraits à partir des images satellitaires. Ils sont
classés en deux types : paramètres
hydrométéorologiques d'état tels que l'humidité du
sol, la température de surface, l'extension du couvert nival et son
équivalent en eau, le couvert végétal et
l'élévation et paramètres
hydrométéorologiques de flux comme l'évapotranspiration.
Ces données sont très utiles pour modéliser les ressources
en eau dans le cas des bassins montagneux des zones arides et semi-arides peu
jaugées, et donc des bassins du Haut Atlas marocain.
Dans le présent chapitre, nous donnerons dans un
premier temps un aperçu général sur la
télédétection spatiale : ces processus, et la notion
du rayonnement électromagnétique, de refléctance et de
l'orbitographie des satellites. Nous présenterons ensuite quelques
étapes de traitement des images satellites et les différentes
applications de ces images en hydrologie. Dans une deuxième partie de ce
chapitre, nous fournirons une classification des différentes approches
en modélisation hydrologique. A la fin du chapitre, les modèles
utilisés au cours de ce travail sont présentés d'une
manière succincte.
I.1 Elément de la télédétection
spatiale
I.1.1 Processus de la télédétection
La télédétection est la technique qui,
par l'acquisition d'images, permet d'obtenir de l'information sur la surface de
la Terre sans contact direct avec celle-ci. La
télédétection englobe tous les processus qui consistent
à capter et à enregistrer l'énergie d'un rayonnement
électromagnétique émis ou réfléchi, à
traiter et à analyser l'information, pour ensuite mettre en application
cette information.
Le processus de télédétection peut
être divisé en sept étapes que nous allons décrire
succinctement et qui sont illustrées par le schéma
ci-après (
Figure ýI ).
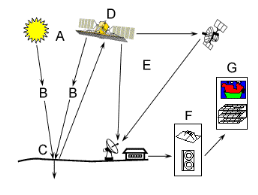
Figure ýI-: Le processus de la
télédétection ((c)CCRS/ CCT)
A: Source d'énergie ou d'illumination:
À l'origine de la majorité des processus de
télédétection se trouve une source d'énergie pour
illuminer la cible.
B: Rayonnement et atmosphère: Durant son
parcours entre la source d'énergie et la cible, le rayonnement interagit
avec l'atmosphère. Une seconde interaction se produit lors du trajet
entre la cible et le capteur.
C: Interaction avec la cible: Une fois parvenue
à la cible, l'énergie interagit avec la surface de celle-ci. La
nature de cette interaction dépend des propriétés de
réflexion, d'absorption et de transmission des éléments
présents à la surface (particules des sols, organes de la
végétation, cristaux de neige, molécule d'eau...), ainsi
que de leurs agencements (densité, structure et
géométrie).
D: Enregistrement de l'énergie par le
capteur: Une fois l'énergie diffusée ou
émise par la cible, elle doit être captée à distance
(par un capteur qui n'est pas en contact avec la cible) pour être enfin
enregistrée.
E: Transmission, réception et traitement:
L'énergie enregistrée par le capteur est transmise,
souvent par des moyens électroniques, à une station de
réception où l'information est transformée en images
(numériques ou photographiques).
F : Interprétation et analyse:
Une interprétation visuelle et/ou numérique de
l'image traitée est ensuite nécessaire pour extraire
l'information que l'on désire obtenir sur la cible.
G: Application: La dernière
étape du processus consiste à utiliser l'information extraite de
l'image pour mieux comprendre la cible, pour nous en faire découvrir de
nouveaux aspects ou pour aider à résoudre un problème
particulier.
I.1.2 Spectre électromagnétique et
réflectance
Le spectre électromagnétique varie des courtes
longueurs d'onde (dont font partie les rayons gamma et les rayons X) aux
grandes longueurs d'onde (micro-ondes et ondes radio). En raison des
propriétés de transparence de l'atmosphère, la
télédétection spatiale n'utilise qu'une partie du spectre
électromagnétique, on distingue les domaines solaire (ë=0.38
à 0.78 um), infrarouge thermique (ë=3 à 1000 um), et
micro-onde (ë = 10-3 m à 0.3 m) (
Figure ýI ). Le rayonnement est
réfléchi par la surface dans le domaine solaire, émis dans
l'infrarouge thermique; il peut être émis ou
réfléchi dans le domaine des micro-ondes en fonction du
caractère passif ou actif du système d'observation.
Le rayonnement qui n'est pas absorbé ou diffusé
dans l'atmosphère peut atteindre et interagir avec la surface de la
Terre. Lorsque l'énergie atteint la cible, la surface peut absorber
l'énergie, la transmettre ou réfléchir l'énergie
incidente. En mesurant l'énergie réfléchie ou émise
par la cible avec une variété de longueurs d'onde, nous pouvons
construire la signature spectrale pour un objet. Dans la
Figure ýI , quatre exemples de spectres de
réflectance très contrastés sont
présentés:
- La réflectance de la neige est très
élevée dans le visible et le proche infrarouge (> 90 %).
Elle diminue à partir de 1 um pour atteindre des valeurs très
faibles dans le moyen infrarouge à 1.55 um;
- L'eau absorbe la majorité du rayonnement reçu
quelle que soit la longueur d'onde (reflectance < ~10 %). La
réflectance diminue progressivement avec la longueur d'onde pour
atteindre des valeurs quasi-nulles dans le proche infrarouge après 0.9
um;
- La réflectance du sable, et plus
généralement celles de sols nus, est faible aux courtes longueurs
d'ondes, puis augmente quasi-linéairement (valeurs inférieures
à 5 % dans le bleu et autour de 20 % dans le proche infrarouge);
- Le comportement de la végétation
« verte » est typique, avec une forte absorption dans le
visible, et en particulier dans le rouge, pour la photosynthèse, et une
très forte reflectance dans le proche infrarouge (jusqu'à 50
%).
Les spectres présentés en
Figure ýI sont des cas typiques. Dans la
réalité les réflectances des surfaces varient en fonction
d'un grand nombre de facteurs, par exemple l'état de la surface manteau
neigeux, et notamment la proportion de neige fraîche et humide, où
la turbidité de l'eau, sa « couleur » et son
état de surface (vague, ondelettes, écumes...). Les
propriétés des sols et de la végétation seront
discutées ultérieurement.
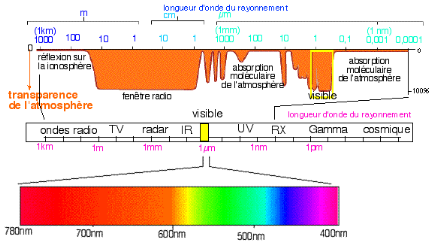
Figure ýI- :
Spectre du rayonnement et transparence de l'atmosphère.
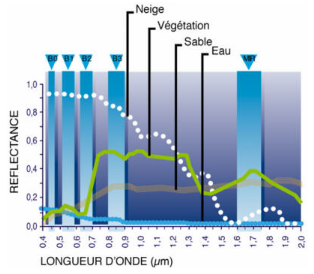
Figure ýI- :
Spectres typiques de réflectances de la neige, de l'eau, du sable et de
la végétation. Les bandes spectrales correspondent aux capteurs
embarqués sur SPOT : B1=Bleu, B2=rouge, B3=Proche Infrarouge,
MIR=Moyen Infrarouge. (
http://vegetation.cnes.fr).
I.1.3 Orbitographie
L'orbite d'un satellite est choisie en fonction de la
capacité des capteurs qu'il transporte et des objectifs de sa mission.
Le choix d'une orbite est déterminé par l'altitude (la hauteur du
satellite au-dessus de la surface de la Terre), l'orientation et la rotation du
satellite par rapport à la Terre.
Certaines plates-formes spatiales suivent une orbite allant
pratiquement du Nord au Sud ou vice-versa (c'est le cas des satellites dont il
est question par la suite). Ce type d'orbite est appelé orbite
quasi polaire à cause de l'inclinaison de l'orbite par rapport
à une ligne passant par les pôles Nord et Sud de la Terre (
Figure ýI ). La plupart des satellites sur
orbite quasi polaire ont aussi une orbite héliosynchrone,
de cette façon, ils observent toujours chaque région du
globe à la même heure locale
solaire. Pour une latitude donnée, la position du soleil dans
le ciel au moment où le satellite survole une certaine région au
cours d'une saison donnée sera donc toujours la même
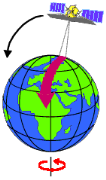
Figure ýI- : Orbite quasi polaire ((c)CCRS/
CCT)
Lorsqu'un satellite est en orbite autour de la Terre, le
capteur "observe" une certaine partie de la surface. Cette surface porte le nom
de couloir couvert ou fauchée (
Figure ýI ). Les capteurs
sur plate-forme spatiale ont une fauchée dont la largeur varie
généralement entre une dizaine et une centaine de
kilomètres. Pour les satellites à orbite quasi polaire, le
satellite se déplace selon une trajectoire Nord-Sud. Cependant, vue de
la Terre, la trajectoire du satellite semble avoir une composante vers l'Ouest
à cause de la rotation de la Terre. Ce mouvement apparent du satellite
permet à la fauchée du capteur d'observer une nouvelle
région à chacun des passages consécutifs
du satellite. L'orbite du satellite et la rotation de la Terre
travaillent donc de concert, permettant une couverture complète de la
surface de la planète après un cycle orbital complet.
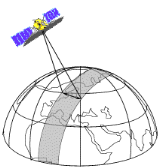
Figure ýI- : Fauchée d'un capteur
((c)CCRS/ CCT)
I.1.4 Traitement des images satellites
I.1.4.1 Pré-traitement
Afin qu'une image brute soit utilisable, il est
nécessaire d'appliquer des opérations de pré-traitement,
parfois appelées restauration et rectification d'image, pour corriger
les distorsions géométriques et radiométriques des
plates-formes et capteurs spécifiques.
Les distorsions géométriques (
Figure ýI ) peuvent être dues
à différents facteurs, notamment la perspective des capteurs
optiques, le mouvement du système de balayage, le mouvement de la
plate-forme, l'altitude, l'orientation et la vitesse de la plate-forme, le
relief du terrain, la courbure et la rotation de la Terre. Les corrections
géométriques sont appliquées pour compenser ces
distorsions afin que la représentation géométrique de
l'imagerie soit aussi proche que possible de la réalité.
Plusieurs de ces variations sont systématiques ou prévisibles, et
on peut en tenir compte par une modélisation précise du mouvement
de la plate-forme et du capteur, et par la relation géométrique
entre la plate-forme et la Terre. D'autres erreurs non systématiques, ou
aléatoires, ne peuvent pas être modélisées de cette
manière et on doit effectuer la correspondance géométrique
de l'imagerie à un système connu de coordonnées au sol.
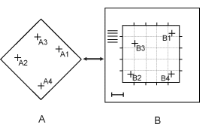
Figure ýI-: Exemple
de distorsions géométriques (A : image non
corrigée ;B : image corrigée et B, .B4 points de
contrôle) (
http://www.ccrs.nrcan.gc.ca/).
Les corrections
géométriques d'une image consistent à
identifier les coordonnées de l'image (ligne et colonne) de plusieurs
points clairement distincts, appelés points de contrôle au sol
(PCS), sur l'image à corriger et à les faire correspondre
à leur véritable position en coordonnées au sol (par
exemple en latitude et longitude). On peut également utiliser une image
déjà corrigée géométriquement (image de
référence) en lieu et place des points de contrôle au sol,
en sélectionnant des points remarquables et facilement
détectables (croisement de routes, de rivières, etc)
pour les faire correspondre avec des points de l'image à corriger. Cette
méthode est une rectification « image à image » (
http://www.ccrs.nrcan.gc.ca/).
Le nombre de points de contrôle dont on a besoin
dépend de l'ampleur des déformations de l'image à corriger
et de la complexité du modèle de transformation que l'on
désire appliquer. Les transformations polynomiales sont les plus
couramment utilisées.
Les corrections
radiométriques peuvent être nécessaires
à cause des variations dans l'illumination et dans la
géométrie de visée d'une scène, des conditions
atmosphériques, du bruit et de la réponse du capteur. Chacun de
ces facteurs variera selon le capteur et la plate-forme utilisés, et
selon les conditions d'acquisition des données. Trois étapes sont
nécessaires pour pouvoir disposer de données de
réflectance au sol: étalonnage, calcul de la réflectance
au sommet de l'atmosphère (TOA: Top of Atmosphere) et
corrections atmosphériques. Diverses méthodes de corrections
atmosphériques peuvent être appliquées, allant de
modèles très détaillés des conditions
atmosphériques durant l'acquisition des données, jusqu'à
un simple calcul basé seulement sur les données de l'image (
http://www.ccrs.nrcan.gc.ca/).
I.1.4.2 Rehaussement et transformation
Le rehaussement est appliqué afin d'améliorer
l'apparence d'une image pour faciliter son interprétation visuelle. Dans
une image brute, les informations utiles sont souvent contenues dans un
ensemble restreint de valeurs numériques parmi les valeurs possibles
(256 dans le cas de données à 8 bits). Le rehaussement des
contrastes se fait en changeant les valeurs initiales de façon à
utiliser toutes les valeurs possibles, ce qui permet d'augmenter le contraste
entre les cibles et leur environnement.
La transformation d'images est un procédé qui
implique la manipulation de plusieurs bandes de données, que ce soit
pour transformer une image provenant d'un capteur multispectral ou pour
transformer plusieurs images de la même région prises à des
moments différents (données multitemporelles). La transformation
d'images génère une "nouvelle" image en combinant les
différentes sources d'information de manière à rehausser
certaines caractéristiques ou certaines propriétés des
données qui sont moins évidentes dans l'image originale.
I.1.4.3 Classification et analyse
L'étape de classification a pour but d'assigner une
classe particulière ou thème (par exemple : eau, forêt de
conifères, maïs, blé, etc.) à chacun des pixels d'une
image. Il existe deux types de classification : manuelle et automatique.
On peut classer les méthodes de classification en deux
grandes catégories : les méthodes de classification
supervisée et les méthodes de classification non
supervisée. Une classification supervisée commence par
l'identification des classes d'information qui sont ensuite utilisées
pour définir les classes spectrales qui les représentent. Avec
cette méthode de classification, l'analyste identifie des
échantillons assez homogènes de l'image qui sont
représentatifs de différents types de surfaces (classes
d'information). Ces échantillons forment un ensemble de
données-tests. La sélection de ces données-tests est
basée sur les connaissances de l'analyste, sa familiarité avec
les régions géographiques et les types de surfaces
présents dans l'image. L'analyste supervise donc la classification d'un
ensemble spécifique de classes. Les informations numériques pour
chacune des bandes et pour chaque pixel de ces ensembles sont utilisées
pour que l'ordinateur puisse définir les classes et ensuite
reconnaître des régions aux propriétés similaires
à chaque classe. Avec la méthode de classification non
supervisée, les classes spectrales sont formées en premier,
basées sur l'information numérique des données seulement.
Ces classes sont ensuite associées, par un analyste, à des
classes d'information utile (si possible). Des programmes appelés
algorithmes de classification sont utilisés pour déterminer les
groupes statistiques naturels ou les structures des données.
Habituellement, l'analyste spécifie le nombre de groupes ou classes qui
seront formés avec les données. De plus, l'analyste peut
spécifier certains paramètres relatifs à la distance entre
les classes et la variance à l'intérieur même d'une classe.
Le résultat final de ce processus de classification itératif peut
créer des classes que l'analyste voudra combiner, ou des classes qui
devraient être séparées de nouveau. Chacune de ces
étapes nécessite une nouvelle application de l'algorithme.
L'intervention humaine n'est donc pas totalement exempte de la classification
non supervisée. Cependant, cette méthode ne commence pas avec un
ensemble prédéterminé de classes comme pour la
classification supervisée.
I.1.5 Applications de la télédétection en
hydrologie
En télédétection, les paramètres
de surface sont déduits à partir des mesures des rayonnements
électromagnétiques. Ces rayonnements sont à la fois
réfléchis et émis par la terre. Les premières sont
généralement les rayonnements solaires réfléchis
tandis que les seconds sont à la fois dans l'infrarouge thermique et les
micro-ondes du spectre électromagnétique. Les rayonnements
solaires réfléchis sont utilisés en hydrologie pour la
cartographie de la végétation et de la couverture de neige et des
études de qualité de l'eau. Les rayonnements émis dans
l'infrarouge thermique sont utilisés pour la température de
surface et les rayonnements émis dans le domaine des micro-ondes sont
utilisés pour les études de l'humidité du sol et de la
neige (Thomas et al., 2002). Les données Radars ou micro-ondes actives
sont aussi utilisées en hydrologie, on cite essentiellement son
application dans les études des précipitations (Krajewski et
Smith, 2002), dans l'estimation de l'équivalent en eau
de la neige (Bernier et al., 1999) et l'humidité.
Lorsque les données de
télédétection et les systèmes d'information
géographique (SIG) deviennent plus courants et plus accessibles, il
s'avéra utile, sinon impératif, de développer une nouvelle
génération de modèles ou d'adopter les modèles
existants pour qu'ils puissent prendre en compte ce nouveau type d'information.
Ainsi sont nés les modèles distribués, qui sont mieux
adaptés à la distribution spatiale de nouveau type de
données (Peck et al., 1981 ; Rango, 1985). Ainsi, par la suite les
modèles hydrologiques avec une structure spatiale basée sur des
modèles numériques de terrain (MNT) on été
développés (Moore et al., 1988 ; Palacios-Vélez et
Cuevas-Renaud, 1992 ; Vieux et Gaur, 1994) et des modèles tel que
SHE (système hydrologique européen) et TOPMODEL ont
été adaptés à ce nouveau type de données
(Quinn et al., 1991 ; Robson et al., 1993). En même temps, de
nouveau modèles compatibles avec les données de
télédétection et SIG sont émergé (Fortin et
al., 1995, Julien et al., 1990 ; Scheltz, 1990 ; Wigmosta et al.,
1994...). Par exemple, le modèle HYDROTEL (Fortin et al., 1995 ;
Fortin et al., 2001a) est développé dès le début
pour assurer sa compatibilité avec les données issus de la
télédétection et des SIG. Dans ce modèle, la
structure d'écoulement d'un bassin versant est évaluée par
PHYSITEL, un SIG spécialisé pour la mise en place des
modèles hydrologiques.
I.2 L'Hydrologie et la Modélisation
I.2.1 Objet de l'hydrologie
Il est assez difficile de définir l'hydrologie car ce
n'est pas une science unifiée. Etymologiquement "science qui traite des
eaux", la définition change d'une époque ou d'un hydrologue
à l'autre. Dans les dictionnaires, elle est parfois définie comme
la science qui étudie les eaux, leurs caractéristiques, leurs
propriétés, s'appuyant sur des considérations physiques,
météorologiques, géologiques ou chimiques. Le sujet
d'intérêt fondamental de l'hydrologie est le cycle de l'eau,
illustré à la
Figure ýI dans sa partie continentale (les
chiffres indiquent les flux moyens annuels en notant 100 le volume annuel total
des précipitations sur les terres émergées,
c'est-à-dire 119.000 km3, soit une lame d'eau annuelle
d'environ 800 mm sur les 149.400.000 km² de terres
émergées). Cet immense transfert d'eau naît des variations
spatiales et temporelles des flux journaliers d'énergie solaire, des
hétérogénéités de la surface du globe et de
la différence de mobilité de l'eau, qu'elle soit sous forme de
vapeur dans l'atmosphère, liquide à la surface de la Terre ou
dans le sous-sol, ou sous forme solide dans les neiges et les glaces.
Dooge (1988) mentionne que « l'affaire de
l'hydrologie est de résoudre l'équation du bilan de
l'eau ». L'hydrologie continentale, qui s'intéresse plus
particulièrement à la partie du cycle de l'eau sur ou proche des
terres émergées, peut être aussi définie comme la
science de l'eau qui traite de la circulation, de la distribution, de la
dynamique et des propriétés de l'eau sur Terre au travers du
cycle hydrologique (Eagleson, 1991). Ses thèmes d'étude sont les
précipitations, l'évaporation, l'infiltration, le ruissellement,
les écoulements dans les nappes et les cours d'eau, et le transport de
substances dissoutes ou en suspension.
Du fait de l'étendue de ces centres
d'intérêt, l'hydrologie est donc une science pluridisciplinaire
comprenant l'hydrologie de surface, la glaciologie, l'hydrogéologie, la
nivologie, la physico-chimie, en incluant aussi l'étude de
l'érosion ou du transport de sédiments. Mais elle est
également plus ou moins directement liée à la
météorologie, l'hydraulique, la géographie, la
géologie, la biologie ou l'écologie. Il est donc très
difficile d'assigner à l'hydrologie un but plus précis que la
lourde tâche de décrire et comprendre le cycle de l'eau, dans un
environnement éminemment complexe, hétérogène et
variable dans le temps. Kleme (1988) illustre d'ailleurs cette
complexité en disant que pour le scientifique, résoudre
l'équation du bilan de l'eau peut être considéré
comme l'un des Rubic Cubes les plus difficiles à résoudre de la
nature, pour lequel les facettes changent de couleur, de forme, de taille au
fur et à mesure qu'elles sont déplacées par
différentes forces, et dans lequel même les bases structurales
changent au cours du temps.
Bien que l'hydrologie vienne d'être
présentée comme une science, cette désignation n'est pas
la seule acceptée. En plus de la recherche fondamentale ou
appliquée, l'hydrologie inclut aussi l'ingénierie hydrologique ou
l'hydrologie opérationnelle. Pendant les années 80, certains
hydrologues se sont d'ailleurs interrogés sur la nature de l'hydrologie
en tant que science. Kleme (1986a), par exemple, a alarmé la
communauté scientifique sur ce qu'il a appelé le `dilettantisme
en hydrologie', mettant en garde les hydrologues sur la dangereuse tendance que
suivait l'hydrologie à devenir seulement une technologie mal
appliquée.
Le moteur de cette science réside principalement dans
le lien étroit qui existe entre l'homme et son environnement, et en
particulier dans la dépendance qu'il a vis-à-vis de la ressource
en eau, pour ses besoins d'alimentation ou dans ses activités. La
variabilité de cette ressource dans le temps est source de multiples
problèmes de gestion, auxquels l'hydrologie peut contribuer à
apporter des solutions (Michel, 1989).

Figure ýI-: Le cycle hydrologique, avec les
flux moyens annuels en pourcentage du volume annuel total des
précipitations sur les terres émergées (d'après
Maidment, 1992).
I.2.2 Modèles Hydrologiques
D'après le Dictionnaire de l'Environnement, le
modèle est "une représentation simplifiée,
relativement abstraite, d'un processus, d'un système, en vue de le
décrire, de l'expliquer ou de la prévoir". La
modélisation hydrologique est donc une représentation, partielle
ou totale, du cycle de l'eau. Cette représentation se fait
grâce à un ensemble d'équations mathématiques qui
sont appelées à reproduire le système.
Bien que connues depuis un certain temps, ce n'est qu'au
début des années 1960 que l'on a regroupé les
équations décrivant les écoulements de l'eau sur un bassin
versant dans un modèle mathématique. En effet, c'est seulement
avec l'arrivé des ordinateurs que les premiers modèles
hydrologiques capables de simuler un ensemble de processus hydrologiques ont
été développés (Stanford Watershed Model :
Crawford et Lindsey, 1966). Depuis lors, un nombre impressionnant de
modèles plus ou moins complexes ont été proposés.
Les éléments constitutifs d'un modèle
hydrologique sont représentés dans la
Figure ýI . Ils sont au nombre de cinq,
à savoir : la géométrie du système (bassin
versant), les entrées dans le système, les lois de formalisation
des processus, l'état initial et les conditions aux limites du
système et enfin les sorties.
Figure ýI- : Composants d'un modèle
(Singh, 1995)
I.2.3 Typologie des modèles
hydrologiques
Plusieurs auteurs ont proposé une classification des
modèles hydrologiques (Singh, 1995 ; Ambroise, 1999). A titre
d'exemple, Singh (1995) a proposé trois critères pour classer les
modèles hydrologiques qui sont : la description des processus,
l'échelle spatio-temporelle et la méthode utilisée pour
résoudre les équations. Selon la description des processus, on
peut avoir plusieurs niveaux de classification : modèle global ou
distribué (
Figure ýI ) déterministe ou
stochastique.
Refsgaard et Storm (1995) classent les modèles
hydrologiques en trois catégories : les modèles empiriques,
les modèles conceptuels et les modèles distribués à
base physique. D'après Refsgaard, les modèles hydrologiques
peuvent être classés selon la description des processus physiques
en tant que conceptuels ou physiques et selon la description spatiale des
processus au niveau du bassin versant en tant que globaux ou distribués.
En raison de l'ambiguïté de certains critères (notion de
conceptuel ou physique) une certaine confusion règne encore sur
l'appartenance de tel ou tel modèle à une famille donnée.
Chocat (1997) propose, quant à lui, de classer les
modèles hydrologiques par type d'utilisation (modèles cognitifs,
modèles prévisionnels, modèles décisionnels et
modèles normatifs) et par type d'approche
(physique/analogique/symbolique, axiomatique/heuristique,
déterministe/probabiliste (stochastique), microscopique
(réductionniste)/ macroscopique (holistique, conceptuelle),
empirique/théorique et spéculative/pragmatique).
Figure ýI- : Classification des
modèles proposée par Singh (1995)
Selon la description des processus hydrologiques dans le
modèle et sa liaison avec les caractéristiques du bassin versant,
le modèle peut être global ou distribué,
déterministe ou stochastiques ou mixte.
Dans un modèle global (lumped
model) le bassin est considéré comme une
entité géographique unique. Des relations empiriques (issues de
l'expérience) relient les entrées et les sorties. Les
équations sont souvent des équations différentielles
ordinaires (ODE, Ordinary differential equation) qui ne prennent pas en compte
la variabilité spatiale des processus, des entrées, des
conditions aux limites et les caractéristiques
géométriques du système (dans ce cas, le bassin versant).
Dans cette catégorie, on peut ranger les modèles GR
(Génie Rurale) (Edijanto et Michel,
1989; Makhlouf, 1994 ; Loumagne, 1988). SSARR (Speers, 1995).
L'utilisation de ces modèles empiriques nécessite une phase de
calage des paramètres, puisque ceux-ci ont une signification qui n'est
pas reliée à priori à des grandeurs mesurables du bassin
versant. L'avantage de ces modèles réside dans la
simplicité de leur structure et au rôle souvent bien
identifié de leurs paramètres.
Le modèle distribué (Distributed
model), prend explicitement en compte la variabilité
spatiale des processus et/ou des variables d'entrées et/ou des
conditions aux limites et/ou des caractéristiques du bassin versant. Ces
modèles spatialisés sont mis en oeuvre à
partir d'une unité élémentaire discrétisée,
cette unité élémentaire peut être une maille
carrée régulière, irrégulière (Girard et
al., 1981 ;Fortin et al., 1995), des triangles irréguliers, des tubes de
courant (Grayson et al., 1992). Ce sont souvent des modèles
mécanistes (le mécanisme de chaque processus est décrit de
manière réaliste) à base physique (les processus sont
décrits au moyen de lois physiques).
En pratique, le volume de données nécessaire
pour l'implémentation de ce modèle n'est en général
pas disponible en dehors de petits bassins versants expérimentaux bien
instrumentés, ce qui rend ce type de modèle peu
opérationnel. Le développement, la validation et l'utilisation
des modèles spatialisés ont été freinées par
la limitation des capacités informatiques. Elles sont aujourd'hui en
plein développement, encouragées par l'acquisition de
données spatialisées issues de l'imagerie satellitaire et
l'augmentation des performances des processeurs informatiques.
L'approche distribuée offre au moins deux
avantages : elle peut mieux capturer la variabilité
spatio-temporelle des composantes du cycle de l'eau et elle permet
d'étudier le changement d'échelle. Elle permet d'aborder par
exemple la question d'évolution du système (effet du changement
d'occupation du sol ou du changement climatique sur le bilan hydrologique) ou
d'étudier l'effet de la variabilité spatiale des facteurs
géographiques et météorologiques qui conditionnent la
réponse des bassins versants. Néanmoins, ce type de modèle
pose de nombreux problèmes. A titre d'exemple, nous pouvons citer le
problème de la surparamétrisation. Le nombre de paramètres
possibles est en effet croissant avec le nombre de mailles ou d'unités
de modèle (Beven et Kirkby, 1979), ce genre de problème pose
d'une part des difficultés métrologiques (acquisition des
données expérimentales pour renseigner les modèles) et
d'autre part des problèmes dans la phase de calage du modèle. A
titre d'exemple des modèles distribués, on cite : le
modèle SHE (Système Hydrologique Européen) (Abbott et al.,
1986a et b) développé à partir des années 1970 par
un regroupement de trois organismes (l'Institut d'hydraulique Danois,
l'institut d'hydrologie du Royaume Uni et Sogreah France), le modèle est
devenu opérationnel en 1982. Le modèle hydrologique CEQUEAU
(Morin, 1981) dont les premiers développements remontent au milieu des
années 1970.
Dans la majorité des cas, le modèle n'est pas
totalement distribué étant donné que certains composants
du système peuvent être globalisés. Le modèle est
alors de type semi distribué qui tient compte de la variabilité
spatiale à travers des classes ayant des comportements hydrologiques
supposés similaires. A titre d'exemple, nous pouvons citer TOPMODEL
(TOPography based hydrological MODEL) (Beven
et Kirkby, 1979), HBV (Hydrologiska Byrans
Vattenbalansavdelning) (Bergstrom, 1973), SRM
(Snowmelt Runoff Model)
(Martinec, 1975).
En fonction du niveau de description des processus, le
modèle peut être aussi déterministe, stochastique ou mixte.
Dans un modèle déterministe la
variabilité est décrite comme un ensemble de mailles
géographiquement localisées. Par contre dans un
modèle stochastique, ce sont plutôt des
distributions de probabilité qui sont associées à ces
grandeurs. La majorité des modèles sont
déterministes. L'approche probabiliste est utilisée soit parce
que le phénomène étudié est aléatoire soit
parce que nous cherchons à représenter des paramètres
difficilement explicitables physiquement.
I.2.4 Critères
d'évaluation d'un modèle
Pour analyser la performance d'un modèle, plusieurs
critères d'évaluation ont été
développés. Ils peuvent être utilisés aussi bien en
calibration qu'en validation.
Une simple analyse visuelle des résultats d'une
simulation n'est pas une évaluation objective du modèle. En
effet, l'oeil humain n'est pas capable de voir toutes les différences
qui peuvent exister entre deux courbes d'allure générale
similaire. Ainsi, nous avons besoin de nous doter de critères objectifs
(dénommés aussi fonctions objectives) pour comparer les
simulations aux observations et pour hiérarchiser des simulations qui
« ont l'air » équivalentes. Plusieurs critères
objectifs mathématiques existent pour quantifier la distance entre les
observations et la simulation.
Les principaux critères objectifs utilisés en
hydrologie sont :
- le critère de Nash-Sutcliffe (Nash et Sutcliffe,
1970) ou efficience E (
Équation ýI ):
Équation ýI-
Où simi est la variable simulée,
obsi est la variable observée, est la moyenne des
observations et n le nombre d'observations. Ce critère
quantifie la fraction de la variance observée qui est prise en compte
par le modèle. Il prend des valeurs entre-8 et 1. Plus l'efficience est
proche de 1, plus l'accord est meilleur entre la modélisation et
l'observation. Notons qu'une efficience négative signifie que les
valeurs simulées conduisent à de moins bons résultats.
Ce critère présente tout de même
l'inconvénient de donner beaucoup de poids aux valeurs moyennes. Nous
pourrons alors utiliser la même formulation sur le logarithme de la
variable (si celle-ci ne prend pas de valeur nulle) ou sur la racine de la
variable afin d'augmenter le poids des valeurs faibles. Par exemple, dans le
cas d'une application sur le débit, pour représenter correctement
les pics de crues, on utilise l'efficience classique. Dans le cas où on
s'intéresse plutôt au débit d'étiage, on utilisera
de préférence l'efficience sur les logarithmes ou sur les racines
afin de diminuer le poids des fortes valeurs de débit.
La mesure de l'erreur quadratique moyenne (RMSE) est
aussi un critère souvent utilisé pour mesurer l'écart
entre la simulation et l'observation, en donnant notamment une idée de
la dispersion entre les deux (
Équation ýI ). Plus elle sera faible
et plus l'écart entre la simulation et les observations sera faible.
Équation
ýI-
De la même façon qu'avec l'efficience, ce
critère peut être utilisé sur les logarithmes ou les
racines des variables puisque ce critère a tendance à donner
beaucoup de poids à la bonne représentation des fortes valeurs et
donc à biaiser par exemple la simulation des récessions de crues
(Boyle et al., 2000).
En s'appuyant sur la corrélation entre la série
simulée et la série observée, nous pourrons aussi chercher
à maximiser le coefficient de détermination R² (
Équation ýI ):
Équation
ýI-
Des bonnes valeurs d'efficience ou d'erreur quadratique
n'attestent pas de l'absence d'une erreur systématique. Pour
s'affranchir de cela, il est possible d'utiliser le critère de biais
« B » qui permet de mesurer la tendance du
modèle à sous-estimer ou surestimer les observations (
Équation ýI ). Comme pour l'erreur
quadratique ce critère devra être minimisé.
Équation
ýI-
Pour les mêmes raisons, Anderton et al. (2002a)
proposent d'utiliser le rapport V des volumes écoulés
simulés et observés pour estimer l'erreur sur le débit que
l'on cherchera à rendre le plus proche de 1 possible (
Équation ýI ) :
Équation
ýI-
Où est le débit simulé à
un temps t et est le débit observé pour ce même
temps t.
Tous ces critères sont utilisables à
différents pas de temps. Aussi une validation multi-critères
peut-elle être faite par exemple sur les débits horaires,
journaliers et décadaires, à l'aide du même critère
mais utilisé pour chaque pas de temps. A priori, plus le temps
d'intégration est long, meilleure est la simulation. L'efficience sur
les débits décadaires devrait donc être meilleure que
l'efficience sur les débits horaires.
L'utilisation de plusieurs critères objectifs ne
résout pas complètement le problème de
détermination des jeux de paramètres optimum. En premier lieu,
même si nous utilisons plusieurs critères, il va être
difficile de définir lequel est le plus important. Avec une
détermination fine des paramètres, il vient toujours un moment
où l'un des critères est amélioré au
détriment d'un autre. Comment choisir ? Ensuite, les paramètres
peuvent varier quelquefois dans des gammes importantes.
En phase de calage, des méthodes automatiques ont
été développées pour explorer plus largement les
gammes de valeur des paramètres. L'avantage principal de ces
méthodes automatiques est de pouvoir considérer l'ensemble des
critères et donc de trouver un équilibre entre les
différents objectifs de représentation des composantes
hydrologiques du bassin versant. Par contre, dans un contexte
d'équifinalité (Ce phénomène peut être
engendré lorsque des jeux de paramètres significativement
différents conduisent aux mêmes résultats de simulation),
elles ne permettent pas d'accéder à la modélisation
optimale, mais à un ensemble de jeux de paramètres conduisant
à des simulations équivalentes. Les deux méthodes les plus
connues sont la méthode multi-objectifs (Yapo et al., 1998) et la
méthode GLUE (Generalised Likelihood
Uncertainty Estimation) (Beven et Binley,
1992).
I.2.5 Modèles utilisés
dans ce travail
Dans ce travail, on se limite à l'étude de deux
types de modèles :
Le premier type s'intéresse à l'étude de
la fonte des neiges. Dans cette classe, on a choisi deux modèles, un
modèle simple dit « degré-jour » qui simule
la variation des équivalents en eau en n'utilisant que la
température de l'air et les précipitations comme variables
d'entrées et un modèle de fonte de bilan d'énergie,
ISBA-ES. En plus de la variation des équivalents en eau, Ce dernier
modèle simule d'autres processus qui interviennent dans le manteau
neigeux, tel que la sublimation, la quantité d'eau liquide contenue dans
le manteau...etc.
Le second type de modèle est un modèle
d'écoulement de la fonte (SRM) (Martinec, 1975). SRM est un model de
type degré-jour conçu pour simuler et calculer les débits
à l'exutoire des bassins versants montagneux où la fonte de neige
contribue significativement au débit. SRM est un modèle
hydrologique opérationnel, il a été appliqué
dès 1975 aux petits bassins européens et, jusqu'à
maintenant, il a été utilisé avec succès dans
environ 80 bassins montagneux dans 25 pays du globe (Martinec et al., 1998).
Afin de calculer la contribution de la fonte des neiges à
l'échelle du bassin, composante qui nous intéresse plus
particulièrement dans cette étude, SRM utilise comme
données d'entrée les surfaces de neige issues de la
télédétection. Ce sont donc les principales
caractéristiques sur lesquelles nous nous sommes appuyés pour
choisir SRM parmi les autres modèles.
Les applications de ces modèles sont
multiples, et permettent de simuler l'impact d'aménagements
anthropiques sur l'hydrologie d'un bassin versant (construction d'un
barrage), de gérer les ressources en eau disponibles sur les bassins
versants ou encore de reconstituer des chroniques de débits sur
des bassins sur lesquels on ne dispose que de chroniques de pluies. Ceci
constitue une donnée importante pour le gestionnaire et une aide
à la décision.
Chapitre II : Présentation du bassin versant de Tensift et
des données utilisées
II.1 Bassin versant de Tensift
II.1.1 Contexte général
Le bassin versant du Tensift est situé au centre Ouest
du Maroc entourant la région de Marrakech. Il occupe une superficie de
20450 km² (
Figure ýII ). Ce large domaine continental
est situé entre les latitudes 32° 10' et 30° 50' Nord et les longitudes
9° 25' et 7° 12' Ouest. Il est limité au Sud par la ligne de crête
de la chaîne du Haut Atlas, au Nord par le massif de petites montagne
nommé « Jbilet » avec des altitudes
inférieurs à 1000 mètres, à l'Est par la ligne de
partage des eaux, peu marquée, séparant le bassin du Tensift de
celui du Tessaout, affluant d'Oum Er R'bia et à l'Ouest par
l'océan Atlantique où se situe son exutoire. Les altitudes sont
donc très contrastées, varient de 0 mètre au niveau de son
exutoire à 4167 mètres au Jbel Toubkal.
Le bassin versant de Tensift peut êtres
subdivisée en deux parties dont le fonctionnement hydrologique est plus
contrasté, à savoir :
i. Montagnes du Haut Atlas : C'est la principale zone
d'étude, elle sera décrite en détail dans les sections
suivantes. Elles constituent la zone de production des eaux
caractérisée par une hydrologie de surface très active et
des précipitations importantes. Sous l'effet de l'altitude, les
précipitations sont sous deux formes, liquide et solide. Les oueds qui
drainent ces versants Nord des montagnes atlasique constituent la seule source
de l'alimentation des nappes dans la plaine du Haouz. A cet effet, ces
montagnes constituent donc un véritable château d'eau pour la
région.
ii. Plaine centrale semi-aride du Haouz : C'est une zone
de transit et de consommation des eaux. L'irrigation y consomme plus de 85 %
des ressources en eau disponibles.
Les oueds les plus importants prennent tous naissance dans le
Haut Atlas. Sur ce relief montagneux à structures géologiques
hétérogènes, des ruissellements à caractère
torrentiel interviennent et sont collectés par le réseau
hydrographique du Tensift qui les évacue vers l'océan. Les
principaux cours d'eau de la zone sont indiqués dans la
Figure ýII .
Figure ýII-: Bassin
versant du Tensift : sa situation dans la carte du Maroc et son
modèle numérique de terrain. Localisation des stations
hydrométriques et météorologiques utilisées dans
cette étude.
II.1.2 Contexte Géologique
Dans cette section, la géologie du bassin versant du
Tensift sera décrite par son aspect lithologique, le plus important
pour l'hydrologie. Les formations constituants le bassin de Tensift sont
diversifiés (
Figure ýII ). Dans la plaine, qui se
présente sous forme d'une dépression, on trouve des formations
détritiques issues du démantèlement de la chaîne
atlasique. Elles sont accumulées au Néogène et au
Quaternaire récent, recouvrant ainsi les formations primaires
secondaires et tertiaires. Les schistes sont largement répandus dans les
Jbilets avec des faciès et de couleurs très variés. On y
distingue des schistes sombres souvent lités, des schistes argileux et
des schistes gréseux avec des bancs épais de grès ou de
quartzites. Par ailleurs, d'autres formations moins étendues peuvent
être distinguées notamment des conglomérats, des
affleurements calcaires et siliceux, des roches éruptives comme les
granites et les gabbros. Dans la chaîne atlasique, les affleurements
lithologiques sont dominés par les faciès suivants : des roches
éruptives et métamorphiques précambriennes notamment les
granites, diorites, dolérites, andésites et rhyolites, des
schistes primaires, des formations secondaires fortement colorées en
rouge et largement dominées par des calcaires, des grès, des
marnes et des argiles. Bien que qualifiées d'imperméables, les
formations métamorphiques ou éruptives comportent des zones
d'altérations dont la capacité de rétention est
significative étant donné la pérennité de plusieurs
cours d'eau qui ne peut pas être attribuée au seul stock neigeux
(Huvelin 1973 ; Moukhchane, 1983 ; Sinan, 2000).
Figure ýII- :
Formations géologiques du bassin versant de Tensift (d'après la
carte géologique 1/500000 de Marrakech)
II.1.3 Ressources hydriques
II.1.3.1 Eaux de surface
Les ressources en eau de surface du bassin du Tensift sont
très irrégulières et inégalement réparties.
La grande partie des eaux de surface du bassin du Tensift est drainée
par les cours amont montagneux des affluents de rive gauche atlasiques de
l'oued Tensift qui prennent naissance dans le Haut Atlas. La rive droite donne
lieu à des ruissellements temporaires et de faible importance à
caractère torrentiel, qui se produisent suite aux orages ou aux
précipitations intenses. La zone de piedmonts et de plaines est
considérée comme une zone de consommation des eaux issues des
montagnes suite aux prélèvements par un réseau dense et
ramifié de seguias (Canaux traditionnels d'irrigation).
Sur la période 1970-2002 les apports moyens annuels,
drainés par les différents oueds du bassin versant du Tensift
sont évalués à près de 767.9 Mm3. Ces
apports varient entre un minimum de l'ordre de 72 Mm3 et un maximum
de l'ordre de 2467 Mm3. Ces apports moyens annuels présentent
une baisse moyenne de 6% par rapport aux apports moyens annuels
calculés sur la période 1935-2002. En outre, la région
bénéficie d'un transfert d'eau à partir du bassin de l'Oum
Er Rbia, via le canal de Rocade de 300 Mm3 en année moyenne,
destinés à l'alimentation en eau potable de la ville de Marrakech
et à l'irrigation dans le Haouz Central (
Tableau ýII ).
 Tableau ýII- :
Apports en eau de surface affectés aux sous bassins versants de Tensift
sur la période 1970-2002 (Source, ABHT) Tableau ýII- :
Apports en eau de surface affectés aux sous bassins versants de Tensift
sur la période 1970-2002 (Source, ABHT)
Les apports d'eau des oueds de la région sont en grande
partie prélevés par des séguias, particulièrement
dans la zone du Haouz Central et du N'Fis (
Tableau ýII ). Le taux des
prélèvements à partir de ces oueds varie de 60% dans le
bassin de l'Ourika, à 20 % dans le bassin du Ksob. Il est estimé
en moyenne à 44 %.
|
SOUS BASSIN
|
Prélèvement au fil de l'eau en
?m3
|
% de mobilisation
|
|
DAT
|
53
|
51
|
|
ZAT
|
54
|
41
|
|
OURIKA
|
93
|
67
|
|
RHERHAYA
|
34
|
67
|
|
N'FIS
|
136
|
82
|
|
EL MAL
|
23
|
40
|
|
CHICHAOUA
|
40
|
47
|
|
KSOB
|
9.5
|
20
|
|
AUTRES
|
260
|
-
|
|
TOTAL
|
602
|
|
Tableau ýII- : Prélèvement
des eaux par les seguias au niveau des sous bassin versant du Tensift (Source,
ABHT)
II.1.3.2 Eaux souterraines
Concernant les ressources en eaux souterraines, les
réservoirs dans lesquels s'accumulent ou transitent les eaux pluviales
infiltrées sont, eux aussi, d'inégale importance et leur
répartition géographique dans la région est quasi analogue
à celle des eaux de surface. Parmi les nappes les plus importantes, on
distingue:
· La nappe du Haouz-Mejjat, limitée par la
chaîne atlasique au Sud et les chaînons des Jbilet au Nord. Elle
s'étend d'Est en Ouest entre les reliefs des Jbilet et l'Oued Chichaoua
sur une superficie de 6.000 km² avec une largeur moyenne de 40 km (
Figure ýII ); Les écoulements
souterrains s'établissent dans les alluvions plio-quaternaires et les
formations du Néogène dont la puissance globale varie entre 50 et
80 mètres et pouvant atteindre localement 120 mètres. La surface
libre de la nappe s'établit en moyenne à 30 mètres sous le
niveau du sol et varie de 10 m à plus de 80m le long du piémont
de l'Atlas.
· La nappe du Bahira, allongée de l'Est à
l'Ouest entre le massif des Jbilet au Sud et les plateaux des Rehamna et du
Gantour au Nord et s'étend sur une superficie d'environ 5.000
km2. La zone d'action de l'ABHT n'en compte que 3000 Km2
renfermant les parties occidentale et centrale de la Bahira. Au niveau de
cette partie de la nappe, l'aquifère a une puissance moyenne de 50 m
avec une productivité variable et liée au degré de
fracturation.
Depuis 1970, les prélèvements d'eau pour
l'irrigation ont connu une forte extension. Actuellement, Les
potentialités de recharge des nappes phréatiques sont totalement
mobilisées, voire surexploitées par ces
prélèvements. La
Figure ýII montre que le niveau d'eau de
la nappe a enregistré une baisse généralisée
atteignant plus de 20 m au niveau des zones fortement exploitées, le
rythme de baisse avoisine les 1 m/an entre 1986 et 2002 (Berrazouk et al.,
2004).
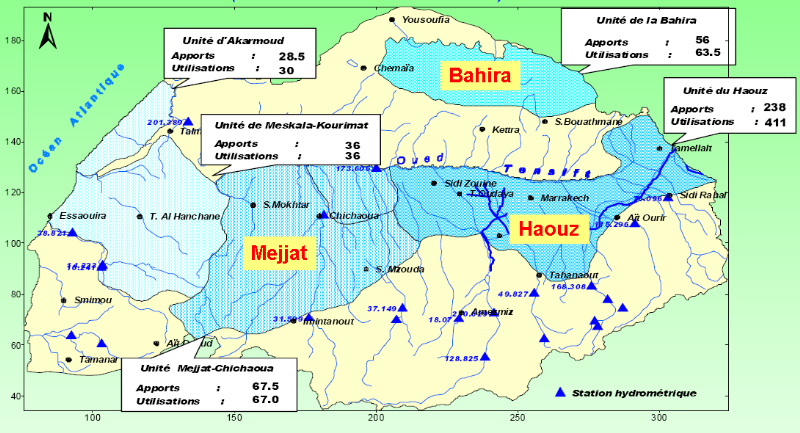
Figure ýII- : Principales nappes
phréatiques du bassin versant du Tensift (les valeurs des apports et
d'utilisations des eaux sont en Mm3/an) (Limam,
2005).
Figure ýII- : Variation du niveau de la nappe
du Haouz entre 1986 et 2002 (données : ABHT).
II.1.4 Climat
Le climat de la zone d'étude est
caractérisé par l'influence de l'Océan Atlantique. Cette
influence diminue d'autant plus qu'on s'éloigne vers l'intérieur.
Ainsi, le climat est semi aride influencé par le courant froid des
Canaries dans la zone côtière, semi aride chaud dans les Jbilet et
continental de type aride dans le Haouz et le Mejjate. La zone du bassin du
Tensift Est, est influencée par la présence du relief et
notamment le Haut Atlas.
Les données climatiques issues des différentes
sources (Direction des Ressources Hydrauliques, Office Régional de Mise
en Valeur Agricole du Haouz -organisme de gestion de l'irrigation, Office
National des eaux et Forets) ont été exploitées pour
analyser l'historique de la répartition spatio-temporelle des
précipitations et les températures. La localisation des stations
utilisées est représentée dans la
Figure ýII . Les précipitations sont
en général faibles et caractérisées par une grande
variabilité spatio-temporelle. La pluviométrie moyenne annuelle
est de l'ordre de 200 mm dans la plaine contre plus de 800 mm sur les sommets
de l'Atlas (
Figure ýII ). L'importance des
précipitations à ce niveau (hautes altitudes) est liée aux
baisses des températures et à l'orographie, avec une part
importante des chutes des neiges. Au niveau de la station d'Oukaimden CAF (Club
Alpin Français), La proportion annuelle des neiges peut atteindre 80%
des précipitations totales (
Figure ýII ). Pour cela, la chaine du Haut
Atlas forme un château d'eau pour cette région.
Les précipitations et les températures
mensuelles moyennes enregistrées entre 1972 et 2002 au niveau trois
stations Abadla, Takerkoust et sidi Rahal et entre 1988-2007 pour la station
Oukaimden CAF sont représentées dans la
Figure ýII . L'examen de la
répartition moyenne des pluies mensuelles montre l'existence de
deux saisons nettement différenciées :
· d'Octobre à Avril, une saison humide
où interviennent la quasi-totalité des épisodes pluvieux,
soit près de 80 à 93 % de la pluviométrie annuelle ;
· de Mai à Septembre, une saison sèche
avec seulement 7 à 17 % de la pluviométrie annuelle.
Figure ýII- : Carte de répartition
des précipitations moyennes annuelles dans le bassin versant de Tensift,
enregistrées entre 1972 et 2002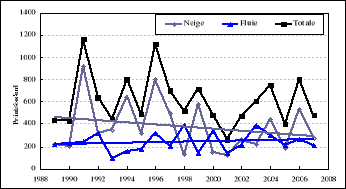
Figure ýII- : Variations des
quantités annuelles des pluies et neiges mesurées dans la station
d'Oukaimden CAF depuis 1988.
A l'inverse des précipitations, la température
est un facteur climatique beaucoup plus régulier à
l'échelle temporelle. Les écarts entre les températures
journalières sont assez importants avec un maximum d'environ 45°C
dans la plaine et un minimum de -17 °C en montagne (à la station de
CAF). Les températures moyennes mensuelles enregistrées dans
quelques stations de la zone d'étude, Sidi Rahal, Takerkoust et Abadla
pour la période de 1972 à 2001 et la station CAF pour la
période de 1988 à 2007, sont consignées dans les
graphiques de la
Figure ýII . Les températures
moyennes mensuelles varient entre 13°C et 28°C dans la plaine et
entre 2°C et 18°C en haute montagne. Les mois les plus chauds sont
généralement Juillet et Août. Le mois le plus froid est
Janvier.
L'hygrométrie est très faible. La moyenne
mensuelle au niveau de la station de sidi Rahal et Abadla varie de 45 %
(durant les trois mois d'été) à 70 % (pendant les mois
d'octobre à juin). A la station Lalla Takerkoust, l'humidité
reste presque constante toute l'année (entre 50 et 60%).
L'évaporation potentielle moyenne annuelle varie de 1
800 mm sur le versant atlasique à 2600 mm dans la plaine du Haouz. Elle
est minimale pendant le mois de Janvier alors que la maximale intervient
pendant les mois d'été. Près de 50% de
l'évaporation potentielle totale est enregistrée durant les mois
de Juin à Septembre.
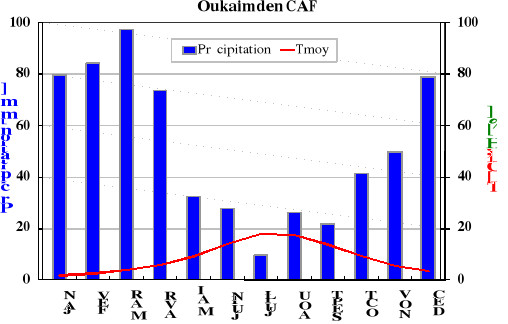 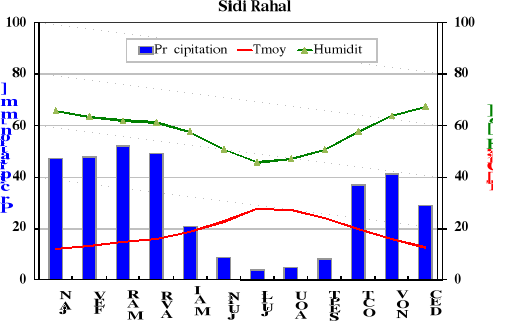 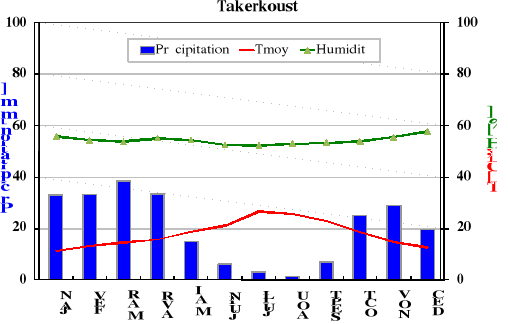 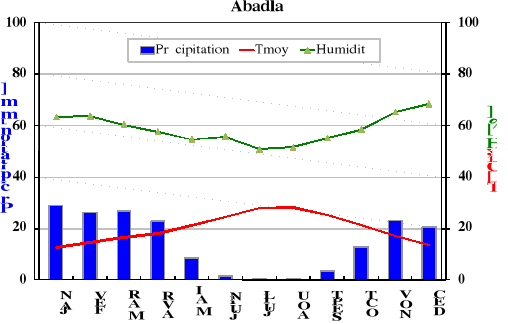
Figure ýII- :
Variation mensuelles des précipitations, température et
humidité au niveau des quatre stations de différentes
altitudes : 250, 630, 690 et 2600 m respectivement pour Abadla,
Takerkoust, Sidi Rahal et Oukaimden CAF.
II.2 Sous bassins versants atlasiques
La chaîne montagneuse du Haut-Atlas marocain est
d'environ 60 km de large sur 800 km de long orientée NE-SW. Dans le
cadre de cette étude, les sous bassins versants
sélectionnés sont les cinq principaux bassins actifs qui
alimentent la plaine du Haouz (
Figure ýII ). Ils se situent à
quelques dizaines de kilomètres au Sud et à l'Est de la ville de
Marrakech entre les latitudes 30°87' à 31°66' Nord et les
longitudes 7°22' à 8°67' Ouest. Ils constituent la limite Sud
du bassin versant de Tensift, avec d'Ouest en Est, le Nfis, la Rheraya,
l'Ourika, le R'Dat et le Zat.
II.2.1 Caractéristiques physiographiques
L'analyse de la physiographie et de la géomorphologie
d'un bassin versant constitue un élément indispensable pour la
compréhension de son fonctionnement hydrologique. Ces
caractéristiques ont une importance majeure car elles interviennent, et
souvent d'une façon combinée, dans les modalités de
l'écoulement superficiel. Les caractéristiques physiques d'un
bassin versant influencent fortement sa réponse hydrologique, et
notamment le régime des écoulements en période de crue ou
d'étiage.
Les principales caractéristiques physiographiques
utilisées dans cette étude sont extraites à partir
d'un MNT (Model Numérique de Terrain) de 90m de résolution.
La surface : Correspond
à l'aire délimitée par l'ensemble des points les plus
hauts qui constituent la ligne de partage des eaux. La surface (A) du bassin
versant, exprimée en km2, peut être
déterminée à l'aide d'un planimètre ou mieux par
les techniques de la digitalisation.
Le périmètre : Il
représente toutes les irrégularités du contour ou de la
limite du bassin versant, il est exprimé en km. Le contour du bassin est
constitué par une ligne joignant tous les points les plus
élevés. Il n'influence pas l'état d'écoulement du
cours d'eau au niveau du bassin versant. Le périmètre peut
être mesuré à l'aide d'un curvimètre ou
automatiquement par des logiciels.
Les altitudes : Ils
reflètent la morphologie du bassin versant. L'altitude joue un
rôle non négligeable sur l'intensité et sur la nature des
précipitations ayant par conséquent un lien avec le débit
à l'exutoire du bassin.
Les courbes hypsométriques sont un outil pratique pour
comparer plusieurs bassins entre eux ou les diverses sections d'un seul bassin.
Elles peuvent en outre servir à la détermination de la pluie
moyenne sur un bassin versant et donnent des indications quant au comportement
hydrologique et hydraulique du bassin et de son système de drainage.
La
Figure ýII représente une
comparaison de la variation des altitudes des cinq sous bassins versants
étudiés. C'est une comparaison de la répartition des
tranches d'altitudes de 100 mètres en fonction de surface. Cette figure
nous fournit une vue synthétique de la pente de l'ensemble des sous
bassins versants. On peut constater que les tranches d'altitudes
supérieures à 2000 m sont plus représentées dans
les trois premiers sous bassins Nfis, Rheraya et Ourika que dans les deux sous
bassins de Rdat ou Zat. Egalement, on note que les altitudes supérieures
à 3000 m sont plus représentées dans les deux sous bassins
de Rheraya et Ourika.
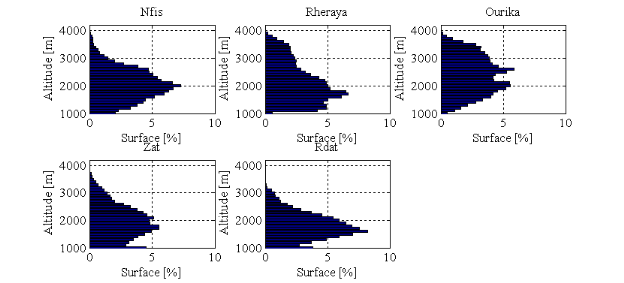
Figure ýII- : Variation des tranches
d'altitudes dans les sous bassins versant de Nfis, Rheraya, Ourika, Zat et
R'Dat.
La pente : La pente des cours
d'eau détermine la vitesse avec laquelle l'eau se rend à
l'exutoire du bassin et donc le temps de concentration. Elle influence sur
l'état d'écoulement du cours d'eau au niveau du bassin versant.
En effet, la pente peut se traduire par l'infiltration de l'eau (pour des
pentes faibles) ou au contraire un ruissellement de nature torrentielle (pour
des pentes fortes) suivant la lithologie des roches rencontrées.
Les classes des pentes reparties dans les cinq sous bassins
sont représentées dans la
Figure ýII . Ces variations des pentes sont
très liées aux altitudes. Dans les sous bassin versant les plus
élevées (Nfis, Rheraya et Ourika), on note que les classes des
pentes les plus répondues sont supérieures à 20
degrés. Par contre, dans les deux sous bassins les moins
élevés, les classes des pentes de moins de 20 degrés sont
plus représentées que les autres classes.
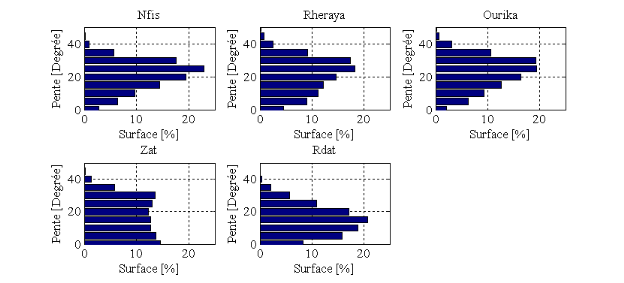
Figure ýII- : Variation des classes de
pente au niveau des sous bassin versant de Nfis, Rheraya, Ourika, Zat et
R'Dat.
Expositions des versants : Dans le cas
du Haut Atlas de Marrakech, il existe un contraste dans la durée de
l'ensoleillement et dans l'intensité calorifique des radiations
reçues au sol par unité de surface. Ceci est d'autant plus
accusé que les pentes des versants sont importantes, où les
vallées sont profondes et les versants exposés pour la plupart
vers le Nord ou le Nord-Ouest. Ces versants ne reçoivent pas les rayons
solaires sous de forts angles d'incidence, et certaines vallées sont
dans l'ombre très tôt le soir et assez tard le matin. Les plus
profondes perdent même tout ensoleillement pendant quelques semaines en
hiver. Cette atténuation du rayonnement solaire permet au sol de
conserver longtemps l'humidité et diminue le pouvoir évaporant de
l'air. Alors que les versants Sud sont relativement abrités des flux
humides du Nord-Ouest, il en résulte des hauteurs de
précipitations beaucoup plus faibles et ils font des adrets plus
exposés aux rayonnements solaires, ce qui accentue davantage
l'aridité.
Dans notre étude, ce paramètre est plus
déterminant en termes de fonte des neiges. Les graphes de la
Figure ýII illustrent les pourcentages des
orientations Nord, Est, Sud, et Ouest pour les cinq sous bassin
étudiés. On note ici que les expositions Nord sont les plus
représentées pour tout les sous bassin versant, et varient entre
27% pour le Nfis et 37% dans le Zat.
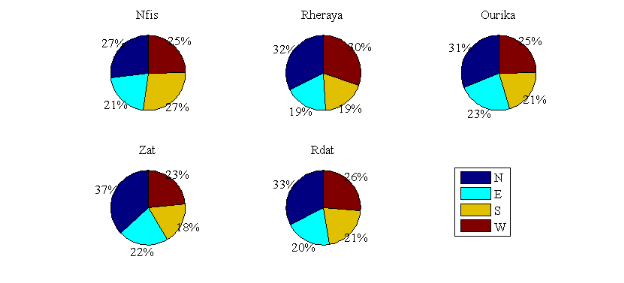
Figure ýII- : Répartition des
expositions des versants des cinq sous bassin versant de Nfis, Rheraya, Ourika,
Zat et R'Dat. N = Nord, E = Est, S = Sud et
W=Ouest.
L'indice de compacité
(KG) : Cet indice nous renseigne sur la forme du
bassin versant qui a une grande influence sur l'écoulement global des
cours d'eau et surtout sur l'allure de l'hydrogramme à l'exutoire du
bassin, résultant d'une pluie donnée. Il est établi en
comparant le périmètre du bassin à celui d'un cercle qui
aurait la même surface. Il s'exprime par la formule suivante (ROCHE,
1963) (
Équation ýII ):
Équation ýII-
Avec
KG : Indice de
compacité de Gravelius ;
P : Périmètre
stylisé en km du bassin versant, mesuré au curvimètre en
estompant les irrégularités de la limite réelle qui n'ont
aucune influence sur les écoulements.
A : Superficie du bassin
versant en km2.
Cet indice se détermine à partir d'une carte
topographique en mesurant le périmètre du bassin versant et sa
surface. Il est proche de 1 pour un bassin versant de forme quasiment
circulaire et supérieur à 1 lorsque le bassin est de forme
allongée. Un bassin versant circulaire est mieux drainé qu'un
bassin allongé. Les indices de compacité des bassins versants
atlasiques étudiés ici sont supérieurs à 1 (
Tableau ýII ), donc ils ont tous une forme
allongée.
Le rectangle équivalent ou rectangle de
Gravelius : Il correspond à une transformation purement
géométrique du bassin versant. Il prend alors une forme
rectangulaire tout en gardant la même superficie, le même
périmètre, le même indice de compacité et donc par
conséquent la même répartition hypsométrique. Dans
ce cas, les courbes de niveau deviennent parallèles aux cotés du
rectangle équivalent. La climatologie, la répartition des sols,
la couverture végétale et la densité de drainage restent
inchangées entre les courbes de niveau.
Plus un rectangle équivalent est allongé moins
il sera drainé. Les dimensions du rectangle équivalent sont
déterminées par les formules suivantes (ROCHE, 1963) (
Équation ýII et
Équation ýII ).
La longueur L et la largeur l sont
exprimées par les deux équations ci-dessous:
Équation ýII-
Équation ýII-
Avec :
KG : Indice de compacité de
Gravelius
A : Superficie du bassin
versant en km2
L : Longueur du rectangle
équivalent en km
l : Largeur du rectangle
équivalent en km.
Le tracé des droites de niveau du rectangle
équivalent découle directement de la répartition
hypsométrique cumulée.
La densité de drainage :
il s'agit de la longueur totale du réseau hydrographique par
unité de surface du bassin versant. Elle correspond pour un bassin
versant donné de superficie A comme étant la longueur totale des
cours d'eau d'ordre quelconque ramenée à la superficie totale A
du bassin versant. La densité de drainage est exprimée en km/km2
selon la formule suivante (
Équation ýII )
Équation ýII-
Avec :
Li : Longueur
totale des cours d'eau en km
A : Superficie du bassin versant en
km².
La densité de drainage dépend de la
géologie (structure et lithologie) des caractéristiques
topographiques du bassin versant et, dans une certaine mesure, des conditions
climatologiques et anthropiques. En effet, les secteurs situés en zones
de roches perméables ont en général des densités de
drainage faibles, alors que les secteurs de roches imperméables ont des
densités plus élevées.
Les conditions climatiques jouent également un
rôle important : les climats ayant des précipitations
réparties également tout au long de l'année auront des
densités de drainage plus faibles que les régions à climat
très contrasté comme les zones semi-arides. Les activités
humaines ont parfois un rôle important sur l'évolution
hydrologique. Cette influence peut avoir un effet régulateur mais aussi
un effet accélérateur du ravinement.
Les caractéristiques physiographiques
précédentes permettent de calculer le temps de concentration de
l'eau écoulée dans le bassin versant par la relation suivante (
Équation ýII ) :
Équation
ýII-
Avec: TC : temps de concentration en
heure
S : surface du bassin versant en
km²
L : longueur du rectangle
équivalent en km
Hmoy : altitude moyenne
du bassin versant en m
Hmin : altitude de
l'exutoire en m
Le temps de concentration représente le temps maximal
nécessaire au ruissellement en provenance du point le plus lointain du
bassin pour atteindre l'exutoire. Ce temps de concentration est très
important pour l'alerte d'un risque de crue dans un bassin versant.
A partir des valeurs de TC
calculées (
Tableau ýII ), Nous pouvons constater que
les bassins versants réagissant le plus vite à de fortes
précipitations sont les bassins de l'Ourika et de Rhéraya avec
des temps de concentrations de 5h7min et de 4h9min. Les crues, dans ces bassins
versants, seront plus dangereuses que dans les autres bassins versants,
où les temps de concentrations sont plus élevés.
Le tableau ci-dessous (
Tableau ýII ) synthétise les
caractéristiques physiographiques des cinq sous bassins versants
atlasiques qu'on peut regrouper en deux ensembles:
- Les bassins versants des oueds N'Fis, Rhéraya et
Ourika avec des altitudes moyenne au dessus de 2000 m et des pentes importantes
(pente moyenne de l'ordre de 20 %) laissant présager une fortes
érosion et un relief très accentué. Les
précipitations devraient être solides sur les hautes altitudes
impliquant un écoulement plus important lors de la fonte des neiges.
- Les bassins versants des oueds Zat et R'Dat sont plus bas en
altitudes (altitude moyenne autour de 1500 m avec des minima en dessous des
1000 m) et ont des pentes moyennes moins importantes (de l'ordre de 14-15 %).
Le régime des précipitations devrait être moins
influencé par la part des précipitations que les bassins versants
précédents.
La différence entre ces bassins se fait donc,
essentiellement, au niveau des reliefs et des pentes.
|
Bassin versant
|
Surface en (Km²)
|
Périmètre (Km)
|
Altitude moyenne (m)
|
Altitude min (m)
|
Altitude max (m)
|
Pente moyenne (%)
|
Altitudes importantes (m)
|
|
N'Fis
|
1288
|
200
|
2300
|
750
|
4088
|
19.3
|
1500-3000
|
|
Rheraya
|
225
|
78
|
2154
|
1036
|
4167
|
19.1
|
>2500
|
|
Ourika
|
507
|
104
|
2550
|
974
|
4001
|
19.9
|
1500-3500
|
|
Zat
|
540
|
135
|
1960
|
720
|
3847
|
15.5
|
1500-2500
|
|
R'Dat
|
557
|
130
|
1700
|
645
|
3476
|
13.8
|
<2500
|
|
Bassin versant
|
Indice de compacité
|
L (km)
|
l (km)
|
LOG (Km)
|
Long tot. des cours d'eau
|
Densité de drainage
|
TC
|
|
N'Fis
|
1,57
|
90,5
|
14,3
|
82
|
2887
|
2,24
|
8h 52 min
|
|
Rheraya
|
1,47
|
34
|
6,6
|
32
|
865
|
3,84
|
4h 9 min
|
|
Ourika
|
1,30
|
48,1
|
10,4
|
45.5
|
1550
|
3,06
|
5 h7 min
|
|
Zat
|
1,64
|
58,5
|
9
|
55
|
1664
|
3,08
|
6 h 25 min
|
|
R'Dat
|
1,55
|
50,1
|
11
|
50
|
1374
|
2,47
|
6h 31min
|
Tableau ýII- : Caractéristiques
physiographiques des cinq sous bassins versants atlasiques.
« L » et «l » sont les Longueurs et les
largeurs de rectangle équivalent, « LOG » est la
longueur des cours d'eaux principales et « TC »
représente le temps de concentration.
II.2.2 Analyse Hydrologique
Pour étudier le régime hydrologique des sous
bassins versants atlasiques, nous avons utilisé les données des
débits et des précipitations mesurées à
l'exécutoire de chaque bassin.
II.2.2.1 Régime des
débits
La
Figure ýII présente les variations
des débits moyens annuels aux exutoires des cinq sous bassins atlasiques
étudiés. A partir de cette figure, on constate que les
régimes d'écoulement dans ces bassins ont une très grande
irrégularité d'une année à l'autre. En effet, on a
une alternance des années sèches et humides. Par exemple, de 1980
à 1986, s'installe un long épisode de sécheresse sur
l'ensemble des bassins correspondant à la période de
sécheresse qui a sévi dans tout le Maroc. Cette période
est caractérisée par des débits moyens très faibles
qui dépassent rarement 2 m3/s. Ainsi, nous constatons que
plusieurs années sont marquées par de forts débits sur les
cinq stations comme les années 1991/92, 1993/94, 1995/96 et 1999/00.
Ces années particulières sont visibles sur les
cinq stations mais les réponses à l'exutoire sont
différentes. Les variations interannuelles des débits aux
exutoires de Tahanout, Taferiat et Sidi Rahal sont similaires. Au contraire, la
station d'Aghbalou enregistre des intensités importantes dans les
débits pour les années 1979/80, de 1989/90 à 1991/92 et
1993/94. La station d'Imin Lhammam enregistre des pics de débits pour
les années de 1977/78 à 1978/79, de 1987/88 à 1989/90, en
1991/92 et de 1995/96 à 1997/98.

Figure ýII-: Débits moyens annuelles au
niveau des exutoires des sous bassin atlasiques.
Le graphique de la
Figure ýII présente la variation
des débits moyens mensuels aux cinq stations implantées aux
exutoires des sous bassins versants étudiés. Ces débits
ont été obtenus par le calcul de la moyenne arithmétique
des données des débits mensuels de chaque année. La
période d'études a été définie afin de
prendre en compte le maximum de données compatible sur les cinq
stations. Cette période s'étend de 1970/71 à 2005/06.
De septembre à février, les débits
augmentent de 0.55 à 11 m3/s pour la station d'Imin Hammam.
Tandis que pour les autres stations, les débits connaissent une moindre
augmentation. Les débits maximums sont enregistrés au mois de
mars au niveau des stations d'Imin Hammam (15 m3/s) et Sidi Rahal
(5,8 m3/s). Alors que dans les stations de Taferiat et Aghbalou,
les maximums sont enregistrés au mois d'avril avec des débits de
8 m3/s et 14 m3/s respectivement. Dans la station de
Tahanaout, les débits maximums sont d'environ 5,5 m3/s durant
le mois de mai. Le régime d'écoulement diminue ensuite pour
reprendre un régime inférieur à 1,5 m3/s aux
mois de juillet et Août.
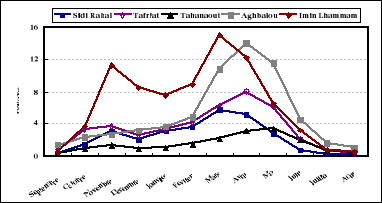
Figure ýII- : Débits moyens
mensuels mesurés au niveau des cinq stations exutoires des sous bassins
atlasiques entre 1970 et 2006.
Le sous bassin versant de N'Fis, du fait de sa superficie plus
grande que les autres sous bassins, reçoit d'octobre à
février une grande quantité d'eau, expliquant ainsi la forte
augmentation du débit pendant cette période non visible dans les
autres bassins versants ayant une superficie moindre. Le décalage du pic
de débits dans les différents bassins versants peut être
expliqué par la morphologie des bassins versants. En effet, nous pouvons
constater que les pics interviennent aux mois d'avril à mai dans les
sous bassins versants d'Ourika, de Rheraya et de Zat. Les tranches d'altitudes
supérieures à 3000 m sont plus importantes dans ces trois bassins
versants que dans les bassins de N'Fis et de R'Dat (
Figure ýII ). Ce décalage dans la
réponse hydrologique dans ces sous bassins est peut être
expliqué par la fonte du manteau neigeux stocké en hautes
altitudes. Aussi la lithologie et l'occupation du sol interviennent dans ce
processus hydrologique.
On conclut que le régime hydrologique présente
de même des variations mensuelles et saisonnières avec une
période humide répartie de septembre à mai et une
période sèche de juin à août avec des orages
d'été exceptionnels. Le régime hydrologique a un
caractère nival dans ces bassins.
II.2.2.2 Corrélation
précipitations débits
L'objectif de ce paragraphe est de mettre en évidence
la corrélation entre les précipitations et les débits et
d'analyser qualitativement la contribution de la pluie et de la neige sur les
débits à l'exutoire. Pour cela, nous allons étudier les
interactions entre la pluie et le débit à des pas de temps
annuel.
La
Figure ýII montre la relation
pluie-débits annuels au niveau des exutoires de cinq sous bassins
versants étudiés. On remarque que les pluies et les débits
sont plus corrélés dans les deux sous bassins de R'Dat et Zat
avec des coefficients de corrélation « R² » de
0.7 et 0.42, respectivement. Ce coefficient est assez faible pour les bassins
de Nfis, Ourika et Rheraya (R²<0.2). Ce décalage entre pluie et
débits peut être expliqué par différents points. Le
premier élément affectant cette relation est les pertes des eaux
à l'intérieur de chaque bassin. Ces pertes sont liées
essentiellement à l'évaporation directe et aux
prélèvements des eaux par les petites cours d'eau nommés
« seguia » destinée à l'irrigation (
Tableau ýII ). La quantité d'eau
destinée à l'irrigation par des seguias peut atteindre plus de
80% des eaux mobilisées. Le sous bassin versant de Nfis connait plus de
perte d'eau due à la grande superficie des surfaces irriguées par
rapport aux autres sous bassins. Le second effet de décalage entre les
pluies et les débits peut être lié aux stocks neigeux
installés aux hautes altitudes. Cela est surtout plus marqué dans
les deux sous bassins versants de Rheraya et d'Ourika.
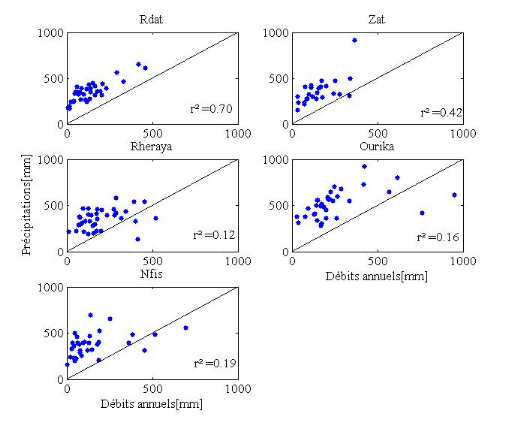
Figure ýII- : Corrélation entre les
précipitations et les débits moyens annuels au niveau des cinq
sous bassins versants atlasiques étudiés
II.3 Données expérimentales
II.3.1 Données météorologiques
Les données climatiques utilisées lors de cette
étude ont été collectées par le réseau de
stations pluviométriques et météorologiques de plusieurs
organismes, tels que l'ORMVAH, l'ABHT, le CAF et la DREF (voir page vi pour la
signification de ces acronymes). Dans la zone montagneuse, ce réseau a
été considérablement renforcé au cours du projet
SudMed par l'installation de six stations (OukaSM, Tachdert, Armed, Neltner,
Imskerlbour et Asni) reparties dans le bassin versant de Rheraya (
Figure ýII ). Les données
météorologiques issues de ces stations (température de
l'air, précipitations, vitesse du vent, rayonnement global et
humidité de l'air) ont été utilisées pour plusieurs
études :
i- Calibration et validation du modèle de
spatialisation de la température de l'air. Les stations
utilisées ici sont les six stations distribuées dans le bassin
versant de Rheraya, c'est-à-dire la station CAF et les cinq stations
installées dans le cadre du projet SudMed. Deux stations existent depuis
2003, Armed et OukaSudMed et trois autres depuis 2007 (Imskerlbour, Tachdert et
Neltner) (Chapitre III).
ii- Etudier les processus de fonte de neige à
l'échelle locale (station Oukaimden SudMed) à l'aide du
modèle de bilan d'énergie ISBA-ES et le modèle
degré jour, ainsi que pour la spatialisation du modèle de fonte
degré-jour (Chapitre V).
iii- Estimation de l'apport des neiges aux
débits des cinq sous bassins versants étudiés
à l'aide du modèle hydrologique de fonte
« SRM » sur la période de 2002 à 2005
(Chapitre VI).
II.3.2 Données nivales
I.1 Données
d'entrée et de validation du modèle de fonte
Le
Tableau ýII présente une
description détaillée des données climatiques et
nivologiques disponibles nécessaires pour la modélisation des
processus de fonte du manteau neigeux. Ces données sont classées
en deux types :
i) Données enregistrées en temps continu depuis
l'année 2003 à la station d'Oukaimden.
ii) Données ponctuelles mesurées in situ dans le
plateau d'Oukaimden, acquises en 2007/2008.
|
|
Données
météorologiques
|
Instrument
|
Unité
|
|
Données d'entrée des
modèles
|
Hauteurs de neige
|
Sonde ultrasonique
|
m
|
|
Température de l'air
|
Thermosonde (vaissala HM45)
|
°C
|
|
Rayonnement solaire incident
|
Pyranométre Skye
|
W/m2
|
|
Vitesse du vent
|
Anémométre A100
|
m/s
|
|
Albédo
|
2 Pyranométres (CM7)
|
|
|
Humidité relative
|
Hygromètre à condensateur (vaissala HMP45)
|
%
|
|
Données de validation
|
Données en continues
|
|
|
|
Hauteurs de neige
|
Sonde ultrasonique
|
m
|
|
Données ponctuelles
|
|
|
|
Epaisseurs de neige
|
manuel
|
cm
|
|
Equivalent en eau
|
manuel
|
mm
|
|
Densités
|
manuel
|
kg/m3
|
Tableau ýII- : Données disponibles pour
la modélisation de la fonte des neiges dans le site de
l'Oukaimden
I.1.1 La station nivale de
l'Oukaimden
Depuis l'hiver 2003, la station
nivo-météorologique d'Oukaimden est installée sur le
sommet de l'Oukaimden, à 3200 mètres d'altitude environ (
Figure ýII ). Celle-ci comprend des
instruments de mesure de la température et de l'humidité de l'air
à 2 mètres au dessus de surface du sol (thermo-sonde et
hygromètre à condensateur), de la vitesse du vent à 2
mètres au dessus de la surface du sol (anémomètre à
coupelles), du rayonnement solaire global (pyranomètre), des cumuls de
précipitations (pluviomètre à augets basculeurs) et de la
hauteur de neige (capteur acoustique). Les mesures, réalisées
à chaque minute, sont moyennées sur 30 minutes. Les
données semi-horaires sont ensuite sauvegardées localement. Nous
disposons, pour ainsi dire, de données brutes. Dans les conditions
météorologiques rencontrées à la station (Ta
[-20°C, 20°C], va < 20 m.s-1) (Ta est la
température de l'air, va est la vitesse du vent), les outils
utilisés pour mesurer la température, l'humidité de l'air,
la vitesse du vent et le rayonnement global sont relativement fiables et
robustes. La qualité de ces données peut être
qualifiée de bonne sauf pour les relevés de hauteur de neige et
de cumul de précipitations qui présentent des artefacts, qu'il
convient de corriger. Les mesures de l'albédo ne sont disponibles que
pour les deux saisons 2004/2005 et 2005/2006.

Figure ýII- : Station
météorologique de l'Oukaimden à 3200m
d'altitude
I.1.2 Protocole
d'échantillonnage manuel
Afin de transformer les hauteurs de neige mesurées dans
la station météorologique en équivalent en eau (Epaisseur
de la lame d'eau qu'on obtiendrait en faisant fondre un couvert de neige), un
modèle simulant les densités en continu est nécessaire. Ce
dernier doit être calibré avec des mesures in situ. A cet
effet, des mesures ponctuelles des densités et des hauteurs de neige on
été effectuées durant la saison 2007/2008 dans le plateau
d'Oukaimden à environ 3200m d'altitude (
Figure ýII ). Les points de mesures ont
été choisis selon leurs accessibilités et aussi qu'ils
soient loin des pistes de ski. Ils sont numérotés de 1 à
8, les six premiers sont alignés Nord-Sud et les deux autres points (7
et 8) se situent à proximité de la station
météorologique. Les densités sont mesurées, selon
des profils verticaux, au niveau du point 4, point situé dans un petit
talweg où les hauteurs de neige sont approximativement plus
élevées par rapport aux autres points. Les relevés ont
été effectués avec un intervalle de temps variant de 19
jours au début de saison à 8 jours pendant la période de
fonte avec une moyenne de 12 jours durant toute la période de mesure.
Les relevés de neige ont été
effectués à l'aide d'un cylindre métallique. À
chaque point d'échantillonnage, trois carottes de neige sont
prélevées dans un rayon d'environ 2 m autour du point original.
L'échantillon est pesé sur place à l'aide d'une balance et
l'équivalent en eau est obtenu directement (produit du poids et de la
hauteur de l'échantillon). Le cylindre carottier utilisé nous
permet aussi de mesurer l'épaisseur du couvert de neige, et sa
densité peut être calculée.
Les données de fonte journalière ont
également été recueillies au moyen d'un lysimètre
installé près de la station. Ce système n'a pas
fonctionné comme prévu, les eaux gelées à
l'intérieur de l'entonnoir collecteur ont empêché la
circulation des eaux de fonte. Ces données n'ont donc pas
été utilisées dans les analyses qui suivent. Cependant,
elles sont utiles pour connaitre la date de drainage des eaux de fonte.

Figure ýII- : Situation des points de
mesures des densités et des hauteurs dans le plateau d'Oukaimden
à 3200m d'altitude
Les valeurs moyennes des densités, hauteurs de neige et
équivalent en eau à chaque point de mesure on été
analysées. Ces valeurs sont très variables d'un point à un
autre avec des hauteurs minimales de 10 à 28 cm et maximales de 120 cm
(point 1). Les valeurs de densités sont faibles au début de
saison (variant de 250 (point 6) à 300 kg/m3 (point 1)) et
deviennent plus élevées à la fin de saison (entre 370
(point 2) et 450 kg/m3 (point 6)). Ces variations sont
présentées dans le
Tableau ýII sous forme de matrice de
corrélation entre tous les points d'échantillonnage sur toute la
saison entre les trois paramètres, densité, hauteurs et
équivalent en eau. On note ici, une très faible
corrélation (R²<0.2) entre les points 7 et 8 d'une part et le
point 1 d'autre part. Ce dernier point est aussi faiblement
corrélé avec la majorité des autres points
(R²<0.6) sauf pour la hauteur avec le point 4 (R²=0.96). Cette
différentiation du point 1 avec les autres points peut être
expliquée par deux éléments, le premier sa situation
près d'une piste de ski, ce qui provoque le tassement du manteau neigeux
et par la suite l'augmentation de la densité et de l'équivalent
en eau, le deuxième effet revient à la formation d'une grande
masse de neige sous l'effet du vent lors des premiers événements
neigeux, cette masse est restée gelée pendant une longue
période. On remarque que la meilleure corrélation existe entre
les points 3, 5 et 6 avec une corrélation moyenne de 0.72 pour les
densités, de 0.79 pour les hauteurs et de 0.77 pour les
équivalents en eau. Cette analyse de corrélation nous confirme le
caractère hétérogène du manteau neigeux même
à petite échelle.
|
Densités
|
|
|
|
|
|
|
|
|
|
|
Point1
|
Point2
|
Point3
|
Point4
|
Point5
|
Point6
|
Point7
|
Point8
|
|
Point 1
|
1,00
|
|
|
|
|
|
|
|
|
Point 2
|
0,37
|
1,00
|
|
|
|
|
|
|
|
Point 3
|
0,50
|
0,66
|
1,00
|
|
|
|
|
|
|
Point 4
|
0,96
|
0,37
|
0,47
|
1,00
|
|
|
|
|
|
Point 5
|
0,58
|
0,63
|
0,93
|
0,55
|
1,00
|
|
|
|
|
Point 6
|
0,57
|
0,66
|
0,92
|
0,56
|
0,99
|
1,00
|
|
|
|
Point 7
|
0,26
|
0,90
|
0,61
|
0,23
|
0,47
|
0,50
|
1,00
|
|
|
Point 8
|
0,12
|
0,72
|
0,45
|
0,12
|
0,27
|
0,28
|
0,72
|
1,00
|
|
Hauteurs
|
|
|
|
|
|
|
|
|
|
|
Point1
|
Point2
|
Point3
|
Point4
|
Point5
|
Point6
|
Point7
|
Point8
|
|
Point 1
|
1,00
|
|
|
|
|
|
|
|
|
Point 2
|
0,23
|
1,00
|
|
|
|
|
|
|
|
Point 3
|
0,40
|
0,91
|
1,00
|
|
|
|
|
|
|
Point 4
|
0,47
|
0,66
|
0,56
|
1,00
|
|
|
|
|
|
Point 5
|
0,64
|
0,87
|
0,90
|
0,75
|
1,00
|
|
|
|
|
Point 6
|
0,55
|
0,92
|
0,93
|
0,68
|
0,96
|
1,00
|
|
|
|
Point 7
|
0,05
|
0,86
|
0,88
|
0,38
|
0,69
|
0,77
|
1,00
|
|
|
Point 8
|
-0,03
|
0,87
|
0,87
|
0,39
|
0,67
|
0,74
|
0,99
|
1,00
|
Tableau ýII- : Matrices de
corrélation des paramètres mesurés entre les huit points
de mesure des hauteurs et des densités.
I.1.3 Correction des
hauteurs de neige
Dans la station d'Oukaimden, la hauteur de neige est
mesurée à l'aide d'un sondeur ultra-sonique SR-50 (Campbell,
2003) qui mesure la distance entre l'instrument et le sol, à partir de
la durée qui s'est écoulée entre l'émission d'une
impulsion ultrasonore dans un cône de 22° et le retour d'un
écho. Or, la vitesse du son dans l'air varie avec la température.
Il est donc impératif de corriger cet effet. Dans ce but, on a recours
aux mesures de la thermo-sonde et on applique la formule fournie par le
constructeur (Campbell, 2003) (
Équation ýII ).
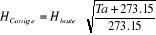 Équation ýII- Équation ýII-
Où Hbrute est la hauteur de neige non
corrigée et Ta est la température de l'air en
(°C).
En plus de la température, de nombreux facteurs
environnementaux altèrent les performances de la sonde : la neige peu
dense réfléchit moins le signal ; les averses de neige peuvent
atténuer fortement l'impulsion sonore ; par fort vent, l'écho
peut être rejeté hors de portée du capteur ; etc.
(Campbell, 2003 ; Brazenec, 2005). Il en résulte un signal bruité
par des variations de faibles amplitudes (quelques mm) et des pointes de
l'ordre de 1.50 mètres qui se produisent lorsque le capteur ne
reçoit pas de signal réfléchi. Pour corriger ces erreurs,
nous avons mis en place un protocole de contrôle des données,
conformément aux recommandations de Brazenec (2005) :
o Les pointes sont détectées en comparant chaque
donnée à la moyenne glissante d'amplitude 24 heures
centrée sur l'observation. Si l'écart entre ces deux valeurs est
supérieur à 2 fois l'écart type associé, la mesure
est considérée comme aberrante et remplacée par une valeur
obtenue par interpolation linéaire ;
o Toutes les valeurs négatives sont filtrées
;
o On applique finalement une moyenne glissante centrée
d'amplitude 1 heure pour lisser les données.
Cette méthodologie est effectuée pour les
saisons 2003-2004 à 2007-2008. La
Figure ýII illustre un exemple de
résultats pour la saison 2007-2008.

Figure ýII- : Hauteurs de neige brutes vs
corrigées (2003/2004)
II.3.3 Données Hydrologiques
II.3.3.1 Débits disponibles
Les débits mesurés à l'exutoire de chaque
sous bassin versant sont fournis par l'Agence de Bassin Hydraulique du Tensift
(ABHT). Chaque station est équipée d'un pluviomètre
cumulateur (relevé quotidiennement) et d'une échelle
liminimétrique. La hauteur d'eau y est relevée trois fois par
jour (8h, 12h et 18h), et plus fréquemment en cas de crue éclair.
Les jaugeages sont idéalement mensuels et réalisés par la
technique de l'exploration des champs de vitesse. Cependant, dans l'Atlas, les
campagnes de jaugeage sont peu fréquentes et non exhaustives pour des
raisons logistiques. Ainsi, l'ABHT manque souvent de points en hautes eaux et
de points en général pour tracer une courbe de tarage
satisfaisante.
Avec cette fréquence des jaugeages, il est notamment
très difficile de suivre l'évolution des barèmes lors de
la divagation des oueds après un épisode de pluie
particulièrement violent. Afin d'améliorer la précision
des mesures des débits à la station de Tahanaout, exutoire du
sous bassin versant pilote « Rheraya », nous avons
effectué une campagne de jaugeage complémentaire en moyenne tous
les 15 jours pendant l'année hydrologique 2007/2008. Pour les autres
saisons, nous avons recalculé les débits en utilisant les
jaugeages effectués par l'ABHT.
II.3.3.2 Technique de mesure des
débits
Lors des compagnes de jaugeage, les débits ont
été mesurés à l'aide de la technique d'exploration
des champs de vitesse. Rappelons que la vitesse d'écoulement n'est
jamais uniforme dans la section transversale d'un cours d'eau. Le principe de
cette méthode consiste donc à calculer le débit à
partir du champ de vitesse déterminé dans une section
transversale du cours d'eau (en un certain nombre de points de mesure,
situés le long de verticales réparties sur la largeur du cours
d'eau). La vitesse moyenne de l'eau a été
déterminée par la méthode de micro moulinet. Le micro
moulinet hydrométrique permet de mesurer la vitesse ponctuelle de
l'écoulement. Le nombre de mesures sur une verticale est choisi de
façon à obtenir une bonne description de la répartition
des vitesses sur cette verticale. De manière générale, on
fera entre 1, 3 ou 5 mesures suivant la profondeur du lit (
Figure ýII ).
Parallèlement à cette exploration du champ de
vitesse, et pour déterminer la section d'écoulement, on
relève le profil en travers du cours d'eau en mesurant sa largeur et en
effectuant des mesures de profondeur d'eau.
Le débit Q [m3/s] s'écoulant
dans une section d'écoulement S [m2] peut être
défini à partir de la vitesse moyenne V [m/s]
perpendiculaire à cette section par la relation (
Équation ýII ):
Q = V.S
Équation ýII-
Finalement, le calcul de la vitesse moyenne de
l'écoulement sur l'ensemble de la section S de longueur
L se fait par intégration des vitesses vi
définies en chacun des points de la section de profondeur
pi (variant pour chaque verticale de 0 à une
profondeur maximale P) et d'abscisse xi (variant
pour chaque verticale de 0 à L) (
Équation ýII ):
Équation
ýII-
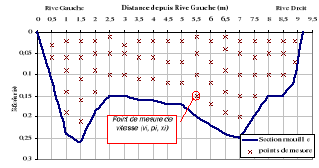
Figure ýII- : Exemple de point de mesure
dans la station hydrologique de Tahanaout en 08 janvier 2008.
Avec ces mesures des débits (jaugeage) on
détermine donc la courbe de tarage qui relie les hauteurs d'eau aux
débits. L'établissement de cette courbe nécessite au moins
dix mesures avec une fréquence élevée. Dans le cas de la
station de Tahanaout en 2007/2008 on remarque l'existence de deux
périodes avec deux courbes de tarages différentes. Cela est
dû au changement de la section du lit de l'oued. Par
l'intermédiaire des hauteurs prélevées quotidiennement par
l'operateur sur place et qui constitue le limnigramme, on transforme ces
hauteurs aux débits journaliers (Hydrogramme) (
Figure ýII ).
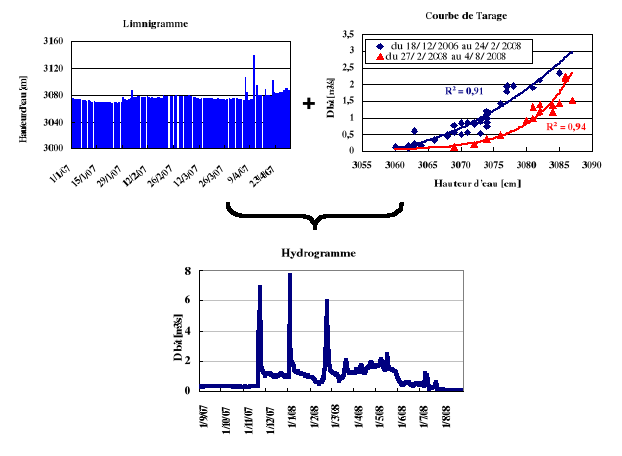
Figure ýII- : Transformation d'un
limnigramme en un hydrogramme par l'intermédiaire de la courbe de tarage
de deux périodes de différentes sections
II.3.4 Données satellitaires
II.3.4.1 Images SPOT VEGETATION
Les capteurs VEGETATION (Archard et al. 1994; Arnaud and Leroy
1991; Saint 1994), lancés à bord des satellites SPOT 4 et 5,
comprennent un système imageur dans quatre bandes spectrales
(bleu : 0,43 - 0,47 ìm, rouge: 0,61 - 0,68 ìm, PIR: 0,78 -
0,89 ìm et MIR : 1,58 - 1,75 ìm). Le champ d'ouverture est
de 0 à 55° de part et d'autre de la trace du satellite, permettant
l'acquisition de données sur une largeur de bande au sol
(fauchée) d'environ 2200 km. La taille du pixel au nadir est de 1,15 x
1,15km. VEGETATION est doté d'un système qui compense en partie
la perte de résolution spatiale en visée oblique. Les satellites
SPOT 4 et 5 suivent une orbite héliosynchrone inclinée de 98,72
degrés par rapport à l'équateur à une hauteur
d'environ 830 km. Leur durée de révolution est de 101 minutes (
Tableau ýII et
Tableau ýII ). Ces caractéristiques
techniques et orbitales font que l'instrument VEGETATION voit 90% de
l'équateur chaque jour, les 10% restant étant vus le lendemain.
Le capteur VEGETATION utilise un système à barrettes dont
l'optique compense en partie la perte de résolution spatiale en
visée latérale. Cette différence, ajoutée à
la capacité de navigation des plateformes SPOT explique l'excellente
qualité géométrique des images VEGETATION. Des
compléments d'informations sont disponibles sur les sites
suivants :
www.spot-vegetation.com,
www.vgt.vito.be,
www.spotimage.fr/. Depuis le
lancement du capteur VEGETATION-1 (1998), deux types de produits sont
proposés aux utilisateurs (Maisongrande et al. 2004):
- Produits P (utilisés dans cette étude):
ils correspondent à une acquisition (quasi-instantanée) par le
capteur lors du passage du satellite. Les luminances enregistrées sont
étalonnées et normalisées par rapport à
l'éclairement solaire. Les comptes numériques représentent
la réflectance apparente au sommet de l'atmosphère dans les
quatre bandes spectrales précitées.
- Produit S : ils sont obtenus en faisant une
synthèse de plusieurs images de la même zone acquises sur une
période de 10 jours, ceci afin de limiter la présence de nuages.
Le procédé de synthèse consiste en la sélection,
pendant cette période, de la meilleure observation (technique du Maximum
Value Composite, (Holben, 1986 ; Tarpley, 1984) ou de toutes les
observations non nuageuses, qui sont ensuite moyennées après
normalisation dans une configuration soleil-cible-capteur fixe (BiDirectional
Compositing) (Duchemin et al. 2002). Ces données ne sont pas
adaptées à l'étude des surfaces enneigées dans les
régions ou la couverture neigeuse présente une forte
variabilité spatio-temporelle.
Les deux types de produits sont corrigés des effets
géométriques et fournis dans un système de
représentation géographique «plate-carrée»
où chaque pixel correspond à un `carré' dont le
coté mesure 1/112°. Lors de cette étude, nous avons
utilisées les produits P à un pas de temps journalier. Ces
données couvrent la période allant de septembre 1998 à
Juin 2005.
|
Lancement
|
1998
|
|
Altitude
|
830 km
|
|
Orbite
|
polaire héliosynchrone
|
|
Heure de passage à
l'équateur
|
10:30 a.m (descendant)
|
|
Champ de vue
|
~2250 km
Angle d'observation (off-nadir) de l'ordre de 50.5°
|
|
Résolution spatiale au nadir
|
1.15 km
|
|
Période de revisite
|
1 jour
|
Tableau ýII-: Caractéristiques du
capteur SPOT VEGETATION (
http://vegetation.cnes.fr).
|
Bande
|
|
Bandes spectrales
|
|
Longueur d'ondes
|
|
Résolution spatiale (m)
|
|
1
|
|
Bleu
|
|
0.43-0.47 ?m
|
|
1000
|
|
2
|
|
Rouge
|
|
0.61-0.68 ?m
|
|
1000
|
|
3
|
|
Proche Infrarouge
|
|
0.78-0.89 ?m
|
|
1000
|
|
4
|
|
Moyen Infrarouge
|
|
1.58-1.75 ?m
|
|
1000
|
Tableau ýII- : Bandes spectrales du
capteur SPOT VEGETATION (
http://vegetation.cnes.fr/).
II.3.4.2 Les produits MODIS
L'instrument MODIS6(*), (Justice and Townshend 2002; Justice et al. 1998;
Justice et al. 1987; Running et al. 1994) est un capteur à large champ
embarqué sur la mission d'observation TERRA en 1999. Il observe la
totalité de la surface terrestre tous les un à deux jours depuis
des orbites quasi-polaires héliosynchrones (10h30 à
l'équateur). Ce capteur a des fauchées de plus de 2200 km et un
champ de vue de l'ordre de 110° (angle zénithal de visée
compris entre -55° et +55°). Un pixel d'une scène est ainsi
observé selon plusieurs configurations géométriques, ces
configurations étant rythmées par le cycle orbital du satellite
(16 jours) et le cycle annuel associé à l'évolution de la
position du soleil (
Tableau ýII ).
Le capteur MODIS utilise un miroir à balayage
double-face qui tourne de façon continue (Xiong et al. 2005). Le capteur
MODIS observe la terre dans 36 bandes spectrales de 0.4 à 14.4 um.
Dans notre étude, nous avons utilisé le produit
journalier «MOD09GHK» à la résolution spatiale de 500
m. Ce produit est généré à partir des observations
instantanées de réflectance MOD09 corrigées des effets
atmosphériques (Vermote et al. 2002). Il s'agit d'un produit de sept
bandes (de 1 à 7) dans les domaines visibles et proche infrarouge. (
Tableau ýII ). Les images
journalières sont commandées depuis septembre 2003 à juin
2006 via le site web de EOS7(*) (
https://wist.echo.nasa.gov ).
|
Lancement
|
1999
|
|
Altitude
|
705 km
|
|
Orbite
|
Héliosynchrone descendante
|
|
Heure de passage à
l'équateur
|
10:30 a.m.
|
|
Champ de vue
|
2330 km
|
|
Résolution spatiale au nadir
|
· 250 m (bande #1-2)
· 500 m (bande #3-7)
· 1 km (bande #8-36)
|
|
Période de revisite
|
(+/-2jours)
|
Tableau ýII- : Caractéristiques du
capteur MODIS TERRA (
http://modis.gsfc.nasa.gov/).
|
Bande
|
|
Bandes spectrales
|
|
Longueur d'onde
|
|
Résolution spatiale(m)
|
|
1
|
|
Rouge
|
|
0.62-0.67 ?m
|
|
250
|
|
2
|
|
Infrarouge
|
|
0.84-0.87 ?m
|
|
250
|
|
3
|
|
Bleu
|
|
0.45-0.47 ?m
|
|
500
|
|
4
|
|
Vert/Jaune
|
|
0.54-0.56 ?m
|
|
500
|
|
5
|
|
Infrarouge
|
|
1.23-1.25 ?m
|
|
500
|
|
6
|
|
Infrarouge
|
|
1.62-1.65 ?m
|
|
500
|
|
7
|
|
Infrarouge
|
|
2.10-2.15 ?m
|
|
500
|
Tableau ýII- : Les 7 premières bandes
spectrales de MODIS/TERRA (
http://modis.gsfc.nasa.gov/).
II.3.4.3 Données Landsat ETM+
Landsat, programme américain de
télédétection spatiale (NASA), a été le
premier programme civil d'observation de la Terre par satellite. Il a
commencé avec le lancement du premier LANDSAT en 1972. Les trois
premières missions étaient équipées de capteurs
à résolution hectométrique MSS8(*). A partir de 1982 et de l'envoi
de Landsat 4, les missions embarquent les capteurs TM9(*). La dernière
génération des satellites LANDSAT a commencé par un
échec. LANDSAT 6 a été perdu juste après son
lancement le 3 octobre 1993. LANDSAT 7 a été lancé en 1999
et est équipé d'un capteur multispectral (ETM+10(*)) (
Tableau ýII ). Le capteur ETM +
possède sept bandes spectrales avec une bande panchromatique
complémentaire à la résolution de 15 m et une
amélioration de la bande thermique de 120 à 60 m de
résolution par rapport à l'ancien capteur TM (
Tableau ýII ).
Nous avons utilisé six images ETM+ couvrant le bassin
versant de Rheraya reparties sur les deux années 2002 et 2003.
|
Lancement
|
1999
|
|
Altitude
|
705 km
|
|
Orbite
|
Quasi-polaire héliosynchrone
|
|
Heure de passage à
l'équateur
|
9 :35 a.m.
|
|
Champ de vue
|
185 km
|
|
Résolution spatiale au nadir
|
· 30 m en multispectral
· 15 m panchromatique
[60 m dans le thermique]
|
|
Période de revisite
|
15 jours
|
Tableau ýII- : Caractéristiques du
capteur Landsat 7ETM+ (
http://landsat.gsfc.nasa.gov/).
|
Bande
|
|
Bandes spectrales
|
|
Longueur d'ondes
|
|
Résolution spatiale (m)
|
|
1
|
|
Bleu
|
|
0.45-0.52 ?m
|
|
30
|
|
2
|
|
Vert
|
|
0.53-0.61 ?m
|
|
30
|
|
3
|
|
Rouge
|
|
0.62-0.69 ?m
|
|
30
|
|
4
|
|
Proche Infrarouge
|
|
0.78-0.91 ?m
|
|
30
|
|
5
|
|
Moyen Infrarouge
|
|
1.57-1.78 ?m
|
|
30
|
|
6
|
|
Infrarouge Thermique
|
|
10.4-12.6 ?m
|
|
60
|
|
7
|
|
Moyen Infrarouge
|
|
2.10-2.35 ?m
|
|
30
|
|
8
|
|
Panchromatique
|
|
0.50-0.90 ?m
|
|
15
|
Tableau ýII- : Bandes spectrales du capteur
Landsat 7 ETM+ (
http://landsat.gsfc.nasa.gov/).
II.3.4.4 Le
Modèle Numérique de Terrain
Le Modèle Numérique de Terrain (MNT)
utilisé dans cette étude (
Figure ýII ) provient des données
altimétriques recueillies au cours de la mission de 11 jours de la
navette spatiale SRTM11(*) en utilisant l'interférométrie radar.
Il est disponible depuis 2004 sur l'Afrique du Nord à la
résolution de 90m gratuitement sur (
http://seamless.usgs.gov/Website/Seamless/).
Il est de bonne qualité notamment car il décrit bien les pentes
contrairement à beaucoup de MNT issus d'interpolation de courbes de
niveau.
Il a été utilisé pour calculer les
caractéristiques topographiques telles que la pente, les expositions des
versants. Les différents calculs effectués sur le MNT ont
été réalisés à l'aide du module ENVI DEM
((c) 2008 ITT Visual Information Solutions) et l'application
« Spatial Analyst » du logiciel ArcGIS 9.1.
Chapitre III :
Analyse de la dynamique spatio-temporelle du manteau neigeux dans les montagnes
du Haut Atlas de Marrakech à l'aide de la
télédétection
· Introduction
La couverture neigeuse est une importante composante du
système climatique global, exerçant une influence
considérable sur la température et la circulation
atmosphérique des moyennes et hautes latitudes. Par les effets de
rétroaction de l'albédo des zones gelées et
enneigées et par les quantités d'eau potentiellement disponibles
dans ces zones et pouvant être libérées, ces régions
ont un rôle prépondérant à jouer dans
l'équilibre climatique du globe (Groisman and Davies, 2001). Le manteau
neigeux constitue un stock d'eau pour le printemps et l'été, dont
l'évolution peut être considérée comme un indicateur
des changements environnementaux (Bloschl, 1999, Liston 1999, Dennis, 2002).
Par conséquent, la connaissance de sa dynamique spatio-temporelle est
nécessaire pour modéliser correctement le bilan hydrique à
l'échelle d'un bassin versant (Martinec and Rango 1981, Kane et al.
1991, Hartman et al.1999).
En milieu semi-aride, les régions montagneuses
constituent souvent la principale source d'eau pour les populations vivant en
aval. Elles jouent de ce fait un rôle primordial car elles permettent
l'alimentation en eau des régions avoisinantes et contribuent d'une
manière significative à la recharge des nappes d'eau souterraine.
Dans certaines régions méditerranéennes, une part
importante de l'eau douce est stockée temporairement sous forme de neige
avant d'être restituée à travers les écoulements de
surface pendant la période de fonte. Au Liban par exemple, l'eau de
fonte de neige contribue approximativement aux deux tiers du volume total
annuel des débits (Shaban et al., 2004). Au Maroc, dans les massifs du
Moyen et Haut Atlas une part importante des précipitations tombe sous
forme de neige. Lors de la fonte, une quantité non négligeable de
l'eau s'écoule dans les cours d'eau. Cependant, la contribution de cette
eau de fonte aux débits des cours d'eau reste encore mal connue. C'est
ainsi que la caractérisation de la dynamique spatio-temporelle de
l'enneigement constitue le premier pas pour évaluer l'influence du stock
neigeux dans le bilan hydrique dans la région.
Dans le présent chapitre on présentera dans un
premier temps, un aperçu des données satellites les plus
utilisées dans la cartographie des surfaces enneigées. Ensuite on
expliquera les prétraitements appliqués aux données
satellitaires utilisées, suivi par une présentation de
l'algorithme développé pour cartographier les surfaces neigeuses
dans la chaîne montagneuse du Haut-Atlas marocain. Les variations
spatiales et temporelles de la couverture neigeuse sont étudiées
à l'échelle du Haut-Atlas (par tranche altitudinale et par
exposition) ainsi qu'au niveau des cinq grands bassins versants qui alimentent
la plaine du Haouz de Marrakech. Dans la dernière partie de ce chapitre,
ces variations sont enfin confrontées avec les mesures
météorologiques et hydrologiques disponibles
(précipitations, températures et débits) aux
échelles saisonnières et interannuelles.
III.1 Télédétection du manteau
neigeux
L'imagerie satellitaire est un outil particulièrement
adapté à la cartographie du couvert nival à grande
échelle, ce qui n'est pas facilement réalisable à partir
des observations locales conventionnelles. Elle permet d'obtenir des
observations régulièrement distribuées dans le temps et
dans l'espace. Grâce à ses propriétés
électromagnétiques, la neige est facilement détectable par
les systèmes embarqués. Pour cela, divers produits issus de
plusieurs capteurs sont disponibles pour les études de la neige.
III.1.1 Propriétés optiques de la neige
Les propriétés optiques de la neige, sa
réflectance élevée dans le domaine du visible et du proche
Infra-Rouge et une absorption élevée dans le domaine du Moyen
Infra-Rouge, sont très contrastées par rapport à la
plupart des autres surfaces terrestres (
Figure ýI ; Chapitre I), à
l'exception des nuages.
Ces propriétés rendent relativement aisée
la détection des surfaces enneigées à partir des
données satellite. L'image de la
Figure ýIII montre les bassins versants du
Haut Atlas et la plaine du Haouz vus le 10 février 2005 par le capteur
MODIS dans le domaine visible. La présence de la neige se traduit par
des refléctances élevées (comptes numériques (CN)
jusqu'à 10000) par rapport aux surfaces dépourvues de neige
(CN<2000) (Courbe de la
Figure ýIII ).
Figure ýIII- : Observation des neiges du
Haut Atlas par le capteur MODIS (bande B4 : Longueur d'onde 0.54-0.56 ?m)
le 10 février 2005, les courbes bleu délimitent les cinq sous
bassins versants du Haut Atlas. En bas de l'image les variations des
réfléctances du profil N-S (trait rouge) sont
présentées.
III.1.2 Données satellites utilisées pour
l'observation de l'enneigement
Depuis 1972, avec le lancement de NOAA-AVHRR (National Oceanic
and Atmospheric Administration-Advanced Very High Resolution Radiometer)
(Rango, 1986,1996), plusieurs types de capteurs ont été
utilisés pour cartographier les surfaces neigeuses de la terre à
différentes échelles et à différentes
résolutions. En 1986, des images de 1 km² de résolution
couvrant les états Unis et une partie de Canada ont été
produites par NOHRSC (National Operational Hydrologic Remote sensing Center)
(Hartman et al. 1996 ; Hall et al. 2000 ; Bitner et al. 2002).
Après, des produits de cartographie de la neige ont été
produites à l'aide de plusieurs capteurs, par exemple : Interactive
Multisensor Snow and Ice Mapping System (IMS) du NOAA avec 23 km² (Ramsay,
2000), des cartes de couverture de neige de 5 km² de résolution
produites par NESDIS (National Environmental Satellite, Data, and Information
Service) avec l'utilisation du satellite GOES (Geostationary Operational
Environmental Satellite) (Romanov et al., 2000; Bitner et
al., 2002). Le
Tableau ýIII résume les capteurs
les plus utilisés dans la cartographie des surfaces de neige et qui
opèrent dans les longueurs d'onde du visible et du proche infra rouge
|
Satellite
|
Capteur
|
résolution spatiale
|
largeur de fauchée
|
Année de lancement
|
|
NOAA
|
AVHRR
|
1100 m
|
2400-3000 km
|
1972
|
|
Landsat
|
MSS
|
80 m
|
185 km
|
1972
|
|
Landsat
|
TM
|
30 m
|
185 km
|
1982
|
|
Landsat
|
ETM+
|
15 m
|
185 km
|
1999
|
|
NOAA
|
GOES
|
1100 m
|
Geostationnaire
|
1975
|
|
DMSP
|
OLS
|
600 m
|
3000 km
|
1982
|
|
Terra/Aqua
|
MODIS
|
250,500,1000 m
|
2300 km
|
1999
|
|
Terra/Aqua
|
ASTER
|
15,30 m
|
60 km
|
1999
|
|
SPOT
|
VGT
|
1000
|
2200 km
|
1998
|
Tableau ýIII- : Capteurs spatiales les
plus applicables dans la cartographie de la surface neigeuse avec les
données acquises dans le visible et le proche
infrarouge
Durant la dernière décennie, une
génération de capteurs opérant dans le domaine solaire a
été mise en orbite et acquièrent des images avec une
répétitivité journalière. Citons par exemple
l'instrument VEGETATION (VGT) à bord du Système Pour
l'Observation de la Terre (SPOT)-4 lancé en 1998 et le capteur
Moderate-resolution Imaging Spectroradiometer (MODIS à bord de la
plateforme Earth Observing System (EOS) Terra en 1999). Ces capteurs ont
plusieurs bandes spectrales et offrent une résolution spatiale de 500
à 1000 mètres (
Tableau ýIII ). Dans le Haut Atlas
marocain, où le climat est semi aride, le manteau neigeux se
caractérise par une grande variabilité spatiale et temporelle.
Ainsi, la neige peut tomber et fondre en quelques jours. Ainsi, les produits
offerts par ces deux capteurs (MODIS et VGT) sont particulièrement
adaptés au suivi adéquat de la dynamique du manteau neigeux. Ils
acquièrent des images avec une haute répétitivité
temporelle, un pas de temps quasi journalier en dépit d'une basse
résolution spatiale.
III.2 Production
des cartes de surfaces enneigées
Les données issues de deux capteurs SPOT- VEGETATION et
MODIS ont été utilisées pour étudier les chroniques
spatio-temporelles des surfaces de neige dans la chaîne du Haut Atlas
marocain. On présente ici les traitements qu'elles ont subis et les
algorithmes développés pour cartographier les surfaces
enneigées.
III.2.1 Limitation des effets géométriques
Les images sont considérées comme
superposables : aucun traitement géométrique
supplémentaire n'a été mis en oeuvre. En revanche les
données MODIS ont été
géo-référencées et converties d'une projection
Sinusoïdal à la projection Lambert Nord Maroc, datum Merchich.
Le relief très accidenté de la zone
d'étude rend difficile l'interprétation des images acquises en
visée très oblique. L'angle de visée pour les deux
capteurs, VEGETATION et MODIS, peut atteindre plus de 55°. Cependant, les
cameras de l'instrument VEGETATION sont équipées d'un
système qui compense la dégradation de la résolution
spatiale dans les cas des forts angles de visée. Ce n'est pas le cas
pour le capteur MODIS qui utilise un miroir rotatif, et les images prises
à des angles de visées élevées subissent une forte
déformation géométrique. Pour éviter cette
distorsion, nous avons éliminé toutes les images acquises avec un
angle de visée supérieur à 23°, ce qui permet de
conserver environ 4 images par mois. Cette sélection permet de limiter
les effets relatifs aux variations de la géométrie
soleil-cible-capteur.
III.2.2 Détection des nuages
A cause de la barrière orographique, les masses d'air
atmosphériques sont contraintes de s'élever pour franchir des
chaînes de montagnes. Elles voient donc leurs températures chuter
ce qui provoque la saturation de la vapeur d'eau et la condensation sous forme
de nuages. Les zones montagneuses sont donc fréquemment sous les nuages,
ce qui empêche les observations par satellite dans le domaine optique.
Par ailleurs, les nuages ont une signature spectrale voisine de la neige dans
le domaine Visible (Konig, et al. 2001a), ce qui complique leur
identification.
Pour détecter les nuages, nous avons dans un premier
temps repéré les images présentant des réflectances
dans le bleu supérieures à 20% sur le piémont atlasique
(altitudes inférieures à 1000 m). A ce niveau
d'élévation, les fortes réflectances peuvent être
due à la présence des nuages. Cette méthode nous a permis
de sélectionner les images acquises dans des conditions nuageuses. Ce
premier tri est relativement grossier mais possède l'avantage
d'être automatisable. Il permet d'éliminer un grand nombre
d'images nuageuses sur le piedmont de l'Atlas, donc très probablement
nuageuses sur les sommets de l'Atlas. Dans une deuxième étape,
nous avons repéré visuellement les nuages sur les images
restantes en se basant sur la différence de signature spectrale dans le
bleu et le MIR (Moyen Infra
Rouge) sous le logiciel de traitement d'images ENVI.
Le nombre d'images VEGETATION retenues après ces deux
phases de traitement est respectivement de 36, 34, 23, 24, 35, 37 et 34 pour
les saisons 1998-1999, 1999-2000, 2000-2001, 2001-2002, 2002-2003, 2003-2004 et
2004-2005. Cette analyse ramène la fréquence des observations
à un ratio d'environ 30 images sur 300 par an, c'est-à-dire 1/10
comme les produits S10. A l'inverse de ces derniers les données du
produit P utilisées permettent d'augmenter la fréquence des
observations au moment même où la neige peut fondre. Dans le cas
des images MODIS, le nombre d'images finalement sélectionnées est
de 44, 52 et 96 pour les saisons 2003-2004, 2004-2005 et 2005-2006 ;
respectivement.
Après cette analyse, une série d'images basse
résolution, sans nuages et prises à des angles de visée
faibles sont disponibles pour cartographier les surfaces de neige dans le Haut
Atlas de Marrakech.
III.2.3 Estimation des surfaces de neige
III.2.3.1 Indices
de neige utilisés
Afin d'augmenter les contrastes au niveau d'un thème
(type de sol, eau, végétation,...) et de réduire les
autres thèmes, plusieurs indices ont été
développés. Ces indices se basent sur la combinaison de plusieurs
canaux. Par exemple pour mettre en évidence la végétation
chlorophyllienne, l'indice le plus fréquemment utilisé est les
NDVI12(*), défini
comme le ratio entre la différence des réflectances proche
infrarouge et rouge et la somme de ces réflectances. Pour identifier les
surfaces neigeuses plusieurs indices de neige ont été
développés.
Dans le cas des données VEGETATION, on a utilisé
un indice de neige (SI) qui utilise les réflectances des canaux bleu,
rouge et MIR (
Équation ýIII ) (Lissens et al.,
2000). Cet indice a été retenu après avoir
été comparé avec d'autres dans le cas du Haut Atlas
marocain (Hanich et al., 2003; De Solan et al., 2002), puis
amélioré pour réduire l'influence des variations de
signature spectrale du sol par le calcul d'un indice de neige modifié
(MSI,
Équation ýIII ) (Chaponnière
et al., 2005). L'indice de neige normalisé (NDSI) (
Équation ýIII ) est le plus
utilisé pour les données MODIS (Hall et al., 1995). Cet indice a
été appliqué dans le Haut Atlas marocain, et pour
réduire l'effet du sol, il a été comparé avec un
indice modifié (MNDSI) (
Équation ýIII ). Ce dernier minimise
les erreurs d'estimation des surfaces de neige.
Équation
ýIII-
Équation
ýIII-
Équation
ýIII-
Équation
ýIII-
Avec :
B0, B2 et B4 sont les réflectances dans le
visible.
MIR et B6 sont les réflectances dans le
Moyen Infra Rouge.
SI0 et NDSI0 sont les indices de neige
du pixel avec une couverture neigeuse de 0% ;
SI100 et NDSI100 est l'indice de neige
du pixel totalement couvert par la neige (100%).
La fraction de la surface enneigée dans chaque pixel a
été calculée en appliquant l'équation exponentielle
(
Équation ýIII )
pour les données VEGETATION et l'équation
linéaire (
Équation ýIII ) pour les
données MODIS. Ces deux formules on été obtenues
après l'analyse combinée de données basses
résolution (VEGETATION et MODIS) d'une part et des images à haute
résolution spatiale Landsat-TM (Chaponnière et al., 2005 ;
Leroux, 2006).) :
Équation ýIII-
Équation ýIII-
Où S est le taux d'enneigement en chaque
pixel.
III.2.3.2
Correction des effets topographiques
Pour tenir compte des effets de la topographie, on a
procédé à une correction des estimations 2D des surfaces
enneigées. Cette correction est réalisée au moyen de l'
Équation ýIII après
extraction de la pente moyenne correspondant à chacun des pixels de
l'image. Cette pente moyenne provient du produit pente fabriqué à
la résolution nominale du MNT (environ 90 m) puis dégradée
à la résolution des images SPOT-VEGETATION (1 km²) et MODIS
(0.5 km²) à l'aide du logiciel ENVI. Cette méthodologie est
généralisée sur une chronique d'images VEGETATION de 7 ans
(de septembre 1998 à juin 2005, Boudhar et al. 2007) et une série
d'images MODIS de 3 années (de septembre 2003 à juin 2006).
Équation
ýIII-
Où le taux d'enneigement réel est la proportion
de neige dans chaque pixel corrigé des effets de pente et S est le taux
d'enneigement vu du ciel pour chaque pixel calculée par les
équations (
Équation ýIII et
Équation ýIII ).
Les différentes étapes suivies pour obtenir les
surfaces de la couverture neigeuse à partir des données
VEGETATION et MODIS sont résumées dans l'organigramme de la
Figure ýIII .

Figure ýIII-: Organigramme synthétisant les étapes
suivies pour calculer les surfaces neigeuses à partir des données
VEGETATION et MODIS
La
Figure ýIII montre un exemple d'images de
l'extension du manteau neigeux sur le Haut Atlas de Marrakech obtenu par les
données SPOT VEGETATION. Ces surfaces sont à première vue
concentrées au centre de la chaîne, zone des hautes altitudes.
L'analyse détaillée de la variation spatio-temporelle de ces
surfaces sera discutée dans les sections qui suivent.
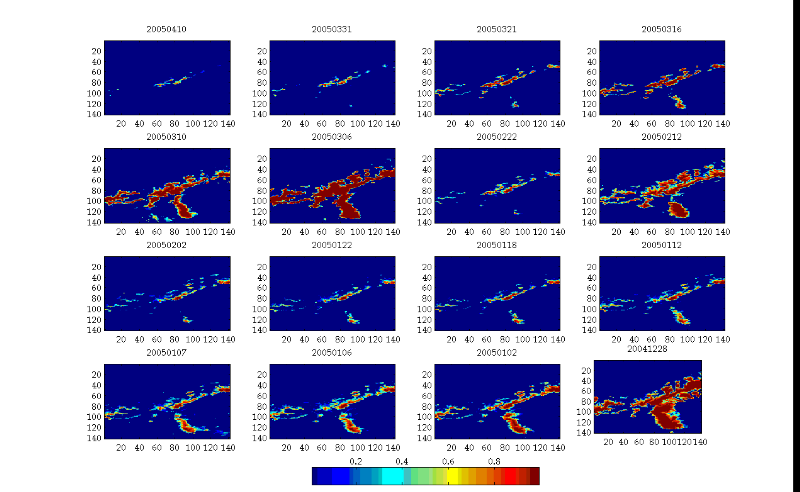
Figure ýIII- : Exemple d'images de
couverture de neige du Haut Atlas de Marrakech calculées à
partir des données SPOT VEGETATION durant la saison
2004/2005
III.2.3.3
Comparaison des surfaces enneigées MODIS et VEGETATION
Dans ce paragraphe, on compare les résultats de
cartographie des surfaces neigeuses obtenues par les deux instruments,
VEGETATION et MODIS. Cette comparaison est faite durant les périodes
2003/2004 et 2004/2005, pendant lesquelles les deux types de produit sont
disponibles. Pour comparer pixel par pixel les images de surface neigeuses des
deux capteurs, on a dégradé la résolution des produits
MODIS à la même résolution que les images VEGETATION (de
500m à 1km). La
Figure ýIII montre la relation globale sur
toute la période étudiée entre les surfaces issues des
deux capteurs à l'échelle du Haut Atlas de Marrakech. Les deux
produits sont bien corrélés avec un coefficient de
corrélation de 0.92 et une erreur quadratique (RMSE) de 0.7%. Cette
corrélation varie d'une date à autre, la
Figure ýIII montre la relation entre les
surfaces MODIS et VEGETATION pour quelques dates et le
Tableau ýIII résume les
statistiques relatives à l'enneigement de chaque date. Les RMSE
calculées entres les deux types de surfaces varient de 0.01 à
2.5% avec une moyenne de 1.3%. Cette différence est peut être due
aux différences des deux indices utilisés MSI et MNDSI et aussi
la différence de la résolution spatiale. Afin de comprendre
l'effet de ce dernier, on a comparé les deux surfaces selon les tranches
d'altitude (
Figure ýIII ). Cette figure montre que pour
toutes les altitudes on a une forte similitude entre les deux produits, MODIS
et VEGETATION, à l'exception des altitudes supérieures à
3800 mètres pour lesquelles on a un RMSE de 9.4%. A ce niveau, les
erreurs de l'effet de pente sont plus corrigées à la
résolution de 0.5 km² des images MODIS qu'à 1 km² des
images VEGETATION.
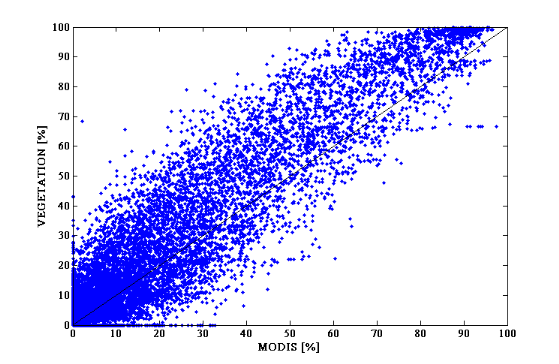
Figure ýIII- :
Corrélation entre les pourcentages d'enneigement issus des images
VEGETATION et MODIS dans le Haut Atlas durant la période (2003-2005)
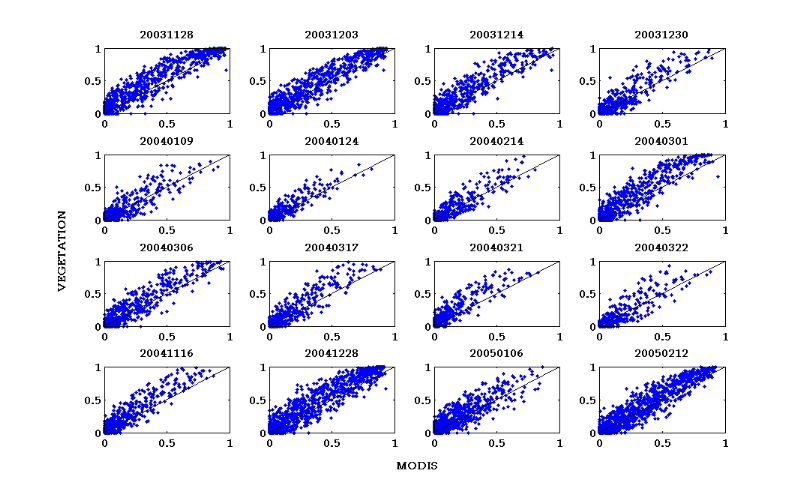 Figure
ýIII- : Corrélation entre les taux d'enneigement issus des
images VEGETATION et MODIS dans le Haut Atlas pour les dates les plus
enneigées Figure
ýIII- : Corrélation entre les taux d'enneigement issus des
images VEGETATION et MODIS dans le Haut Atlas pour les dates les plus
enneigées
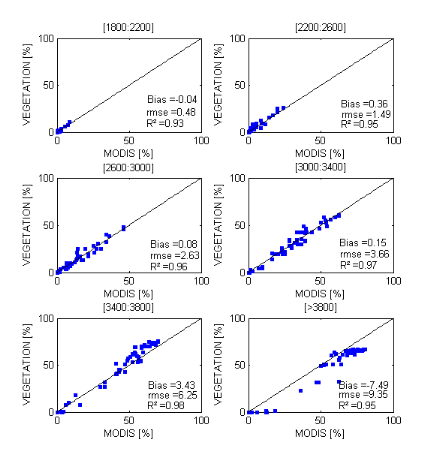
Figure ýIII- : Comparaison des proportions
des surfaces neigeuses estimées par VEGETATION et MODIS en pourcentage
au niveau de chaque tranche d'altitude du Haut Atlas
|
Date
|
RMSE(%)
|
Ecart moyen
(%)
|
R²
|
Equation de régression Y=a X+b
|
|
a
|
b
|
|
20050507
|
0,04
|
0,00
|
0,63
|
2,61397
|
0,00003
|
|
20050421
|
0,27
|
-0,02
|
0,56
|
0,91789
|
0,00031
|
|
20050410
|
0,39
|
0,00
|
0,81
|
0,87087
|
0,00020
|
|
20050331
|
1,07
|
0,09
|
0,67
|
0,56605
|
0,00040
|
|
20050212
|
2,22
|
0,28
|
0,95
|
0,85010
|
0,00084
|
|
20050202
|
1,14
|
0,07
|
0,83
|
0,72033
|
0,00082
|
|
20050122
|
1,42
|
0,04
|
0,69
|
0,71479
|
0,00100
|
|
20050106
|
1,87
|
0,23
|
0,87
|
0,77368
|
0,00022
|
|
20041228
|
2,72
|
0,46
|
0,95
|
0,83828
|
0,00031
|
|
20041218
|
1,63
|
0,23
|
0,89
|
0,67411
|
0,00006
|
|
20041116
|
1,57
|
0,24
|
0,92
|
0,71613
|
-0,00004
|
|
20040623
|
0,01
|
0,00
|
0,89
|
2,20146
|
0,00000
|
|
20040423
|
0,73
|
0,00
|
0,70
|
0,75916
|
0,00060
|
|
20040322
|
1,02
|
0,04
|
0,87
|
0,79645
|
0,00068
|
|
20040321
|
1,23
|
0,18
|
0,88
|
0,67735
|
-0,00017
|
|
20040317
|
1,35
|
0,14
|
0,90
|
0,73754
|
0,00045
|
|
20040306
|
1,62
|
0,18
|
0,92
|
0,80415
|
0,00029
|
|
20040301
|
2,35
|
0,37
|
0,93
|
0,74599
|
0,00031
|
|
20040214
|
0,91
|
0,06
|
0,90
|
0,80106
|
0,00040
|
|
20040124
|
0,78
|
0,08
|
0,89
|
0,77929
|
0,00004
|
|
20040109
|
1,14
|
0,05
|
0,86
|
0,81671
|
0,00049
|
|
20031230
|
1,25
|
0,11
|
0,90
|
0,77440
|
0,00042
|
|
20031214
|
1,81
|
0,25
|
0,92
|
0,79536
|
0,00001
|
|
20031203
|
2,17
|
0,34
|
0,95
|
0,85142
|
-0,00019
|
|
20031128
|
2,54
|
0,46
|
0,95
|
0,82909
|
-0,00063
|
|
20031030
|
0,35
|
0,03
|
0,53
|
0,53029
|
0,00003
|
|
Moyenne
|
1,29
|
0,15
|
0,84
|
0,89061
|
0,00026
|
Tableau ýIII- : Sommaire des statistiques
calculées entres les surfaces de neige MODIS et
VEGETATION
On constate que les
résultats de la cartographie des surfaces des neiges issues des deux
capteurs VEGETATION et MODIS sont comparables. Ils peuvent être donc
utilisés en même temps pour étudier la dynamique de
l'enneigement dans le Haut Atlas Marocain.
III.3 Analyse de la variabilité spatiale et temporelle
de l'enneigement
III.3.1 Variabilité interannuelle de l'enneigement sur
le Haut Atlas
Les surfaces de neige sont calculées sur la
fenêtre comprise entre les coordonnées géographiques
suivantes : Latitudes comprises entre 30.5N à 32.2N et Longitudes
comprises entre -9.5 E et -7 E. La
Figure ýIII présente la variation
saisonnière des surfaces enneigées calculées pour tout le
Haut Atlas sur la période 1998 à 2005 en utilisant les
données VEGETATION et 2005-2006 avec les données MODIS. Le
Tableau ýIII dresse les principales
caractéristiques de l'enneigement à partir de ces variations.
Cette figure permet de mettre en évidence la forte variabilité
saisonnière et interannuelle des précipitations solides. Les
épisodes de chute de neige sont marqués par des augmentations
brutales des surfaces calculées, alors que les forts épisodes de
fontes y compris en plein coeur de l'hiver, sont marqués par une
diminution importante de la surface neigeuse calculée (exemple :
surface passant de 2600 km² à 350 km² entre 17 et 27 janvier
2003). L'analyse du
Tableau ýIII permet de conclure
que :
Ø La présence de surfaces enneigées est
toujours détectée en hiver, mais sur des superficies très
variables (2512 km² le 20 janvier 2001 contre 4620 km² le 28
décembre 2005).
Ø La période d'enneigement (calculée
depuis la date d'apparition des surfaces neigeuses jusqu'à sa
disparition) est également très variable : la date du
1er épisode neigeux détecté fluctue entre fin
septembre (1998-1999) et fin décembre (2000-2001), tandis que les
dernières chutes de neige sont enregistrées entre fin janvier
(2000-2001) et début avril (2003-2004). Le manteau neigeux n'est pas
toujours continu en hivers.
Ø Le nombre d'épisodes neigeux
détectés par saison varie de un (1999-2000) à cinq
(2002-2003 et 2004-2005).
A partir de cette analyse on distingue deux groupes de
saisons : quatre saisons humides (1998-1999, 2003-2004, 2004-2005 et
2005-2006), marquées par une superficie moyenne de la couverture
neigeuse de l'ordre de 670 Km², contre quatre saisons sèches
(1999-2000, 2000-2001, 2001-2002 et 2002-2003) caractérisées par
une superficie plus faible (environ 430 Km²). Cependant, ces
résultats sont à relativiser car ils dépendent en partie
de la disponibilité des données non nuageuses (en moyenne quatre
données par mois, mais avec de longues périodes sans
observations, par exemple de septembre à décembre 2000). Ainsi,
étant donné que les épisodes de fonte peuvent être
relativement courts, il est possible que certains évènements de
précipitations solides ne soient pas détectés par manque
de données (pas d'image satellite). D'autre part, ceux-ci ne sont
détectés que s'ils correspondent à une augmentation de la
superficie des surfaces enneigées, ce qui n'est pas le cas lorsqu'il
neige sur le manteau neigeux déjà installé.
Néanmoins, cette classification en saison sèche ou humide est
cohérente avec le régime climatique de la région. En
effet, pour les saisons humides, la pluviométrie cumulée
enregistrée à la station de Tahanaoute, exutoire du bassin
versant de Rheraya, est de 500 mm/an, tandis que lors des saisons sèches
elle ne dépasse guère 280 mm/an. La moyenne des
températures maximales mesurée à la station d'Oukaimden
entre le 1er septembre et le 30 juin de chaque saison varie entre 11
et 11.4°C pour les saisons humides et de 11.4 à 12.2°C pour
les saisons sèches. Les débits moyens enregistrés
à l'exutoire du bassin versant de Rheraya est de 0.60 m3/s lors des
saisons humides et de 0.40 m3/s lors des saisons sèches. On peut
d'ailleurs noter que le rapport des débits (0.4/0.6) correspond
exactement au rapport des superficies d'enneigement moyennes du Haut Atlas
(430km2/670km2).
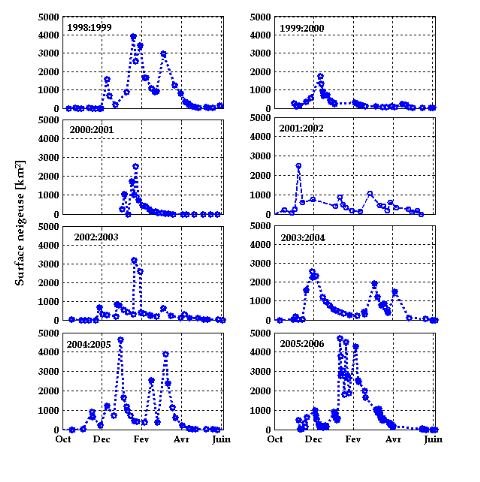
Figure ýIII- : Variation temporelle des
surfaces de neige au niveau du Haut Atlas de Marrakech entre 1998 et 2006. De
1998-1999 à 2004/2005 avec les données VEGETATION et en 2005/2006
avec les données MODIS.
|
Saison
|
Début de chute
|
Nombre d'événements
|
Période de présence de neige
|
Max
|
Surface moyenne(Km²)
|
Observations
|
|
Surface (km²)
|
date
|
|
|
1998-1999
|
07-déc.
|
4
|
07 décembre-10 avril
|
3900
|
16-janv.
|
779
|
-
|
|
1999-2000
|
20-sept
|
2
|
20 septembre-18 février
|
1745
|
11-oct.
|
312
|
Surfaces très faibles à partir du premier
novembre (moins de 300 km²)
|
|
2000-2001
|
30-déc.
|
3
|
30 décembre-19 février
|
2512
|
20-janv.
|
385
|
Images indisponibles avant le 30
décembre
|
|
2001-2002
|
16-oct.
|
4
|
16 octobre-22 avril
|
2518
|
07-nov.
|
431
|
Surface inferieure à 200 km² entre 27
janvier et 08 février
|
|
2002-2003
|
21-nov.
|
5
|
21 novembre-29 mars
|
3168
|
16-janv.
|
379
|
Surface inférieure à 100 km² du 03
à 14 mars
|
|
2003-2004
|
02-nov.
|
3
|
02 novembre-23 avril
|
2564
|
28-nov.
|
671
|
-
|
|
2004-2005
|
15-nov.
|
5
|
15 novembre-11 avril
|
4620
|
28-déc.
|
750
|
-
|
|
2005-2006
|
07-nov.
|
4
|
07 novembre- fin avril
|
4700
|
08-janv.
|
800
|
-
|
Tableau
ýIII-:Caractéristiques de l'enneigement dans le Haut Atlas de
Marrakech estimés à partir des données SPOT VEGETATION
pendant la période 1998-2005 et MODIS pour 2005-2006.
III.3.2 Variabilité de l'enneigement par bassin
versant
L'analyse de la variabilité des surfaces de la neige
par bassin versant est très utile. Elle permet d'étudier la
contribution de la fonte aux débits des cours d'eau. Les deux figures (
Figure ýIII et
Figure ýIII ) présentent les profils
de variation des surfaces enneigées calculées en pourcentage de
l'aire totale de chaque bassin versant du Haut Atlas pendant les saisons
1998/1999 à 2005/2006. Ces profils sont comparables car il s'agit de
l'enneigement sur les versants Nord du Haut Atlas. Le taux moyen d'enneigement
sur chaque bassin versant a été calculé sur la
période de présence de neige pour les huit saisons
étudiées. Les deux bassins versants Rheraya et Ourika ont les
taux d'enneigement moyen les plus élevés, 11 à 30% en
moyenne sur la Rheraya et 13 à 32% sur l'Ourika. Les trois autres
bassins présentent des taux moyens d'enneigement qui varient entre 4 et
20% pour le Zat, de 2 à 18% pour le R'Dat, et de 4 à 10% pour le
N'Fis. Le taux maximal de couverture neigeuse lors des huit saisons varie de
30% (1999-2000) à près de 80% (1998-1999 et 2005-2006) sur le
premier groupe, alors que pour le deuxième groupe le taux maximal
d'enneigement varie de 13% (2000-2001) à 62% (1998-1999). Cette
classification des cinq bassins versants selon le critère enneigement
est cohérente avec les caractéristiques topographiques ; les
bassins de hautes altitudes (Ourika et Rhéraya) sont plus
enneigés que les bassins de basse altitude (N'Fis, Zat et R'Dat).
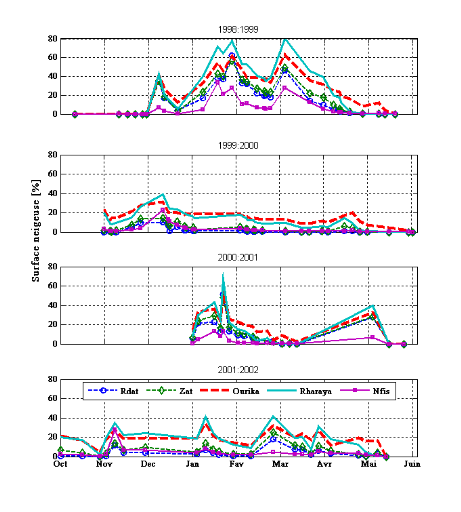
Figure ýIII- : Pourcentage de l'extension
du manteau neigeux dans les cinq sous bassins principaux du Haut Atlas de
Marrakech à l'aide des données VEGETATION pour la période
1998/1999 à 2001/2002.
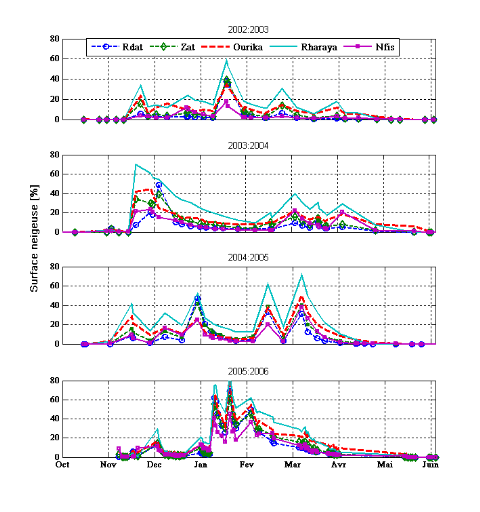
Figure ýIII- : Pourcentage de l'extension
du manteau neigeux dans les cinq sous bassins principaux du Haut Atlas de
Marrakech à l'aide des données VEGETATION (2002/2003 à
2004/2005) et MODIS (2005/2006).
III.3.3 Caractéristiques de
l'enneigement selon l'altitude et l'exposition
La
Figure ýIII montre la variation des
surfaces enneigées par tranche d'altitude sur l'ensemble du Haut Atlas
de Marrakech, durant les saisons allant de 1998-1999 à 2004-2005. Le
taux d'enneigement croit avec l'altitude, tout comme le caractère non
permanent du manteau neigeux : pendant la période hivernale, le
taux d'enneigement est toujours supérieur à 50% pour les
altitudes supérieures à 3000 m, alors qu'aucune neige
pérenne n'est observée en dessous de 2600 m. La période de
fonte peut être très courte aux faibles altitudes (par
exemple : du 7 au 13 novembre 2001, la surface enneigée passe de 57
à 3 % au dessus de la tranche d'altitude 2200-2600 m). Les altitudes
d'enneigement minimales durant la saison sont de l'ordre de 1400 m pour les
saisons humides contre 1800 m pour les saisons sèches. Les
premières précipitations solides tombent sur les points
culminants (altitudes supérieures à 3400 m).
Figure ýIII-: Proportion de la couverture
neigeuse par tranche d'altitude à l'échelle du Haut Atlas. De
1998-1999 à 2004/2005 avec les données VEGETATION et en 2005/2006
avec les données MODIS.
Les versants Nord du Haut Atlas sont exposés aux
perturbations pluvieuses provenant de l'Océan Atlantique avec une
direction Nord-Ouest. Ces perturbations sont en partie arrêtées
par les sommets centraux du Haut-Atlas et donc moins actives sur les versants
Sud qui par ailleurs connaissent également une influence saharienne plus
prononcée. Selon l'orientation des versants du Haut Atlas (vers le Sud
ou vers le Nord), il existe un contraste dans la durée de
l'ensoleillement. En effet, ces facteurs contrôlent fortement la
distribution de la couverture neigeuse selon l'exposition des versants. Sur la
Figure ýIII , les surfaces de neiges sont
représentées selon les expositions des versants du bassin versant
de Tensift. Cette figure met bien en évidence que les versants
orientés Nord reçoivent plus de neige par rapport à ceux
orientés Sud. Cette différenciation n'est vraiment nette que pour
les expositions au dessus de 2600m d'altitude. Dans cette partie du Haut Atlas
les versants sont plus pentus et les rayons du soleil sont proches des normales
à la surface. En fonction de la position du soleil, la durée
d'ensoleillement au cours de l'année est plus élevée au
Sud qu'au Nord. Les zones orientées Sud sont plus chauffées par
rapport à celles exposées Nord. Cela influence donc l'enneigement
entre les deux parties de l'Atlas et même dans un bassin versant
où les proportions des couvertures de neige sont plus importantes au
Nord qu'au Sud.
Figure ýIII- : Extension du manteau
neigeux selon l'exposition des versants Nord ou Sud en deux tranches
d'altitudes entre 1000 et 2600m et supérieurs à 2600m en
utilisant les données MODIS.
III.3.4 Relation entre l'enneigement et les données
hydro-climatiques
Dans cette section, nous confrontons les données de
surfaces enneigées estimées avec les données de
télédétection spatiale (MODIS et VEGETATION) aux mesures
hydro-climatiques disponibles sur les cinq bassins versants
étudiés : température, pluviométrie, hauteur
de neige et débit. Les séries temporelles de surfaces
enneigées calculées sur le bassin versant de Rheraya sont
comparées avec les précipitations mesurées à la
station de Tahanaout (exutoire du bassin de Rheraya), les hauteurs de neige et
les températures mesurées à la station d'Oukaimden (CAF)
localisée à 2760 mètres et à la station Oukaimden
SudMed située à 3200 mètres d'altitude à la limite
des bassins de la Rheraya et de l'Ourika. Les figures (
Figure ýIII et
Figure ýIII ) présentent le cas de
deux saisons particulièrement contrastées (1998-1999 et
2001-2002).
L'influence de la température de l'air est peut
être considérée comme le principal facteur pour la
formation et le chute de neige. En fin d'accumulation de neige, la couche
neigeuse formée au sol devient aussi très sensible à la
fluctuation de la température de l'air. On remarque que la variation des
surfaces enneigées est cohérente avec celle des
températures. Les pics de surfaces enneigées coïncident avec
des minima de températures (exemple du 7 décembre 1998 et du 7
janvier 2002), tandis que les périodes de fontes hivernales
correspondent à des épisodes de réchauffement temporaire
(cas du 2 à 5 février 1999 : la température passe de
-2 à 8 °C et la surface enneigée diminue de 106
à 86 km². Afin de montrer cette relation, les proportions des
surfaces d'enneigement dans le bassin versant de Rheraya ont été
comparées avec les températures de l'air moyen
enregistrées dans deux stations de montagne (
Figure ýIII ). Il s'agit de la station du
CAF et de la station SudMed (OukaSM) à Oukaimden, situées
à 2600m et 3200m d'altitude respectivement. Les surfaces de neige ont
une corrélation négative avec la température de l'air, les
coefficients de corrélation sont de -0.59 pour la station CAF et -0.49
pour la station Oukaimden SudMed.
On constate aussi la forte corrélation entre les
pluies, les hauteurs de neige mesurées et les variations de surfaces
enneigées calculées (exemple des événements
enregistrés le 7 décembre, 16, 26 janvier et le 3 mars au cours
de la saison 1998-1999 et le 10 novembre, 12 janvier et 17 mars de la saison
2001-2002) (
Figure ýIII et
Figure ýIII ). On remarque que cette
relation disparaît logiquement lors de la période de fonte
(exemple des précipitations enregistrées du 11 au 19 mars 1999).
En revanche, d'importantes chutes de neige enregistrées début
janvier 2002 ne correspondent à aucune pluie à Tahanaoute. La
croissance des surfaces enneigées permet donc parfois de pallier
à la faiblesse du réseau d'observations pluviométriques de
la région.
Les débits mesurés aux exutoires des cinq
bassins versants ont été comparés avec les surfaces
enneigées calculées sur la période 1998 à 2005.
Dans le cas de la Rheraya illustré ici (
Figure ýIII d et
Figure ýIII d), le contraste
pluviométrique se retrouve sur l'amplitude des débits de base et
sur celle des surfaces enneigées. Pour l'année 1998-1999, on note
également le rôle joué par le manteau en tant que stock
d'eau (décalage entre le maximum de surface enneigée et le
maximum de débit de base d'environ deux mois). Le caractère nival
du régime hydrologique du Haut-Atlas, ainsi que l'utilité du
suivi de l'enneigement pour la prévision des ressources en eau
estivales, sont ici mis en évidence.
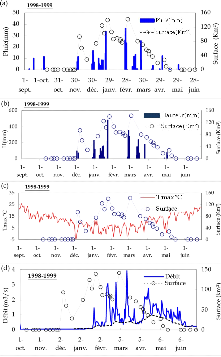
Figure ýIII-: Comparaison des surfaces
enneigées calculées à partir des données
SPOT-VEGETATION sur le bassin versant de Rheraya avec les données
hydro-climatiques (saison 1998-1999) : Précipitations
journalières (mm) mesurées à la station de Tahanaout,
exutoire du bassin de Rheraya (a), chutes de neige (mm) (b) et
températures maximales journalières (°C) (c)
mesurées à la station d'Oukaimden (CAF), débits
mesurés à la station de Tahanaout (débit de base
estimé en trait pointillé) (d).
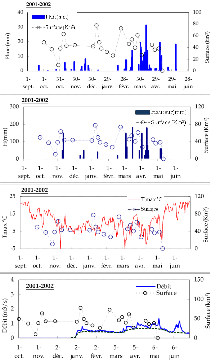
Figure ýIII-: Comparaison des surfaces
enneigées calculées à partir des données
SPOT-VEGETATION sur le bassin versant de Rheraya avec les données
hydro-climatiques (saison 2001-2002) : Précipitations
journalières (mm) mesurées à la station de Tahanaout,
exutoire du bassin de Rheraya (a), chutes de neige (mm) (b) et
températures maximales journalières (°C) (c)
mesurées à la station d'Oukaimden (CAF), débits
mesurés à la station de Tahanaout (débit de base
estimé en trait pointillé) (d)
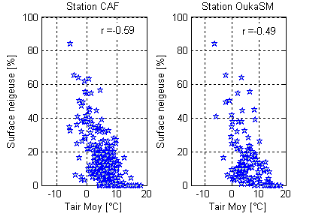
Figure ýIII- : Corrélation entre les
pourcentages d'enneigement au niveau du bassin versant de Rheraya et les
températures de l'air enregistrées à la station du CAF
(2600m) et OukaSM (3200m)
· Conclusion
Dans ce chapitre, on a constaté qu'il est possible
d'observer à partir de longues séries d'images satellitaires
(SPOT-VEGETATION et MODIS, 1998 à 2006) la dynamique de l'enneigement
dans le Haut Atlas et en particulier sur les cinq bassins versants les plus
actifs hydrologiquement dans la région de Marrakech (Nfis, Rheraya,
Ourika, Zat et R'Dat). Outre l'identification de saisons sèches et
humides, l'intérêt de la télédétection est
d'autant plus grand que la variabilité spatiale et temporelle du
manteau neigeux est particulièrement importante. La production de cartes
d'enneigement a permis ici de quantifier les variations temporelles du taux
d'enneigement d'un bassin versant à un autre, selon l'exposition et par
tranche d'altitude. Les taux de variations de l'enneigement sont
cohérents avec les données hydro-climatiques disponibles sur la
région. Ces informations peuvent renforcer de manière
significative les réseaux d'observation hydro-climatiques et peuvent
aider à la spatialisation de la pluie en hautes montagnes semi-arides.
Il apparaît ainsi que les données acquises par
les capteurs optiques à large champ (SPOT-VEGETATION et MODIS dans cette
étude) fournissent un indicateur de qualité pour le suivi de la
ressource neigeuse. On a également montré que les chroniques
d'enneigement dérivées des données VEGETATION et MODIS
sont un bon indicateur de la variabilité interannuelle de l'enneigement
qui doivent permettre, dans le cadre d'observation à long terme, de
sélectionner certaines années typiquement sèches ou
typiquement humides pour des études de processus plus
détaillées. Le suivi à long terme des surfaces
enneigées prend également toute son importance pour
évaluer l'impact des changements climatiques sur la ressource en eau
(évolution et variations de la distribution des précipitations
sous forme liquide et solide).
Dans le cadre de cette étude, les surfaces neigeuses
obtenues seront utilisées comme donnée d'entrée dans les
prochains chapitres. On va notamment étudier l'intérêt de
l'assimilation de ces surfaces enneigées dans un modèle
hydrologique de fonte (SRM) afin d'affiner notre compréhension du cycle
hydrologique de ces régions, et d'estimer l'apport nival dans les
débits de bassins versants du Haut Atlas.
Chapitre IV : Spatialisation de la température de
l'air dans les montagnes atlasique à l'aide des données de
l'infrarouge thermique
· Introduction
Les extensions neigeuses cartographiées à l'aide
des données satellites (chapitre III) constituent une information
importante pour caler les modèles de fonte (degré jour) à
l'échelle du bassin versant. Ces modèles n'utilisent à
l'entrée que deux paramètres météorologique:
la température de l'air et les précipitations. Afin de bien
simuler la distribution de la fonte des neiges et la répartition
pluie/neige dans les hautes altitudes, il est important de spatialiser la
température de l'air d'une manière efficace. C'est dans cet
objectif qu'on va utiliser les données infrarouges thermiques de
capteurs Lansat ETM+ pour spatialiser la température de l'air.
La température de l'air, contrôlée par le
bilan d'énergie de surface, l'état de l'atmosphère et les
propriétés thermiques de la surface, est un paramètre
météorologique important dans plusieurs domaines environnementaux
tel que la climatologie où elle est utilisée dans des
modèles de prévisions météorologiques et elle sert
aussi à l'étude des changements climatiques à
différentes échelles spatiales. En hydrologie nivale, la
température de l'air est le principal facteur de partition des
précipitations liquides et solides. Ainsi, la température de
l'air constitue le facteur majeur qui contrôle les échanges
énergétiques à la surface et dans le manteau neigeux. Elle
est donc une variable importante de l'estimation de la fonte des neiges
(Martinec, 1975; Bloschl, 1991; Brubaker et al., 1996, Richard and Gratton,
2001). A cet effet, une connaissance optimale de sa distribution
spatio-temporelle est primordiale dans la modélisation hydrologique.
Plusieurs techniques de spatialisation des données
climatiques ont été développées dans
différentes zones du monde (section IV-2). Ces méthodes
deviennent plus complexes pour les zones montagneuses où le climat est
lié à différents facteurs (altitude, pente et exposition).
Ainsi, l'application de ces méthodes nécessite un réseau
de stations météorologiques dense et bien représentatif
à l'échelle spatiale. Cela n'est pas le cas pour le Haut Atlas
où le nombre de stations météorologiques est très
faible. C'est dans ce contexte que nous avons étudié la
possibilité de spatialiser la température de l'air à
partir des données satellite de l'infrarouge thermique et un
modèle numérique de terrain pour prendre en considération
les différents facteurs topographiques.
Dans ce chapitre, on va
présenter la méthodologie développée pour
spatialiser la température de l'air dans les montagnes du haut Atlas.
Les données infrarouges thermiques issues des images Landsat ETM+ et un
MNT on été combinées pour proposer un modèle de
spatialisation de température de l'air, nommé MSPAT. L'apport du
modèle MSPAT par rapport au modèle de gradient d'altitude (GRAD)
sera ensuite analysé en comparant la qualité de la
prévision de la température par les deux méthodes pour des
stations de mesure de température de l'air installées
récemment et la qualité de la restitution des surfaces de neige
(SCA) à l'échelle du sous bassin versant de Rheraya.
IV.1 Techniques de
spatialisation de la température
Les techniques d'interpolation spatiale représentent
actuellement les méthodes les plus utilisées pour obtenir les
estimations des températures de l'air en tout point d'une zone
d'intérêt. Ces méthodes diffèrent par leurs
hypothèses, échelle d'application et leur nature
déterministe ou stochastique. Les techniques les plus utilisées
pour interpoler les données climatiques sont les suivantes: techniques
de Krigeage (Matheron, 1963), IDW (Inverse Distance Weighting) (légats
et Willmont, 1990), Splining (Eckstein, 1989; Gessler et Hutchinson, 1994), et
la méthode de régression polynomiale (Myers, 1990). Plusieurs
investigations ont été effectuées pour estimer la
distribution de la température de l'air en utilisant ces méthodes
d'interpolation. Dans une échelle régionale d'une zone
d'étude au Japon, Ishida et Kawashima (1993) ont trouvé des
erreurs comprises entre 1 et 3 °K par l'interpolation des données
horaire des températures avec l'altitude par la méthode de
co-krigeage. Hudson et Wackernagel (1994) également utilisé le
co-krigeage avec l'altitude pour la prévision des températures de
l'air en Ecosse, ils ont montré que cette technique est plus
performante qu'un simple algorithme d'interpolation. A l'échelle locale,
Soederstroem et Magnusson (1995) ont trouvés des erreurs entre 0,4
°K et 1,6 °K, en utilisant une approche d'interpolation par la
technique de krigeage sur une zone d'étude en Suède de 8
km2. Toutes ces études et bien d'autres, ont fait remarquer
que les résultats de krigeage sont fortement dépendants de la
distribution spatiale des stations météorologiques.
Dans les zones montagneuses, la température de l'air
est contrôlée par différents facteurs liés à
l'emplacement et la topographie (Hudson et Wackernagel, 1994). Par
conséquent, l'utilisation des méthodes d'interpolation
précitées peut générer des erreurs et des biais
élevés (Willmott et al., 1991; Robeson et Willmott, 1993).
Généralement, dans ces zones de reliefs, la méthode de
gradient d'altitude est la plus utilisée pour estimer les
températures à différentes altitudes (Colohan & Dunn,
1999, Singh & Singh, 2001). D'autres méthodes ont été
développées telles que la méthode géostatistique
AURELHY (Bénichou et al., 1987) qui prend en considération les
effets d'autres facteurs topographiques (pente, exposition des versants...).
Cependant, pour étalonner ces méthodes, il est nécessaire
d'avoir un réseau dense de stations météorologiques. Dans
la majorité des zones montagneuses du monde et en particulier dans les
pays en développement, on ne peut pas retrouver cette condition. Les
prévisions météorologiques peuvent offrir une alternative,
mais la grille des modèles météorologiques est trop
grossière (de 1 à 10 km) pour pouvoir correctement
désagréger la température de l'air à une
résolution plus fine des zones à relief complexe.
Les données satellite de l'Infrarouge thermique
permettent d'obtenir les températures de surface avec une
résolution spatiale plus élevée et sur des régions
plus étendues. Plusieurs études visant à utiliser cette
information pour cartographier la température de l'air à
l'échelle régionale reposent sur des données à une
résolution grossière. Par exemple, la température maximum
de l'air peut être inversée avec une précision d'environ
2,0 à 2,5 °K, en utilisant les températures de surface de la
terre provenant de NOAA-AVHRR (Vogt et al. 1996, 1997). En raison de la faible
résolution spatiale de ces données (1km), ces méthodes
semblent difficiles à mettre en oeuvre dans les régions
montagneuses.
IV.2 Méthodologie
Dans le but de proposer un modèle de spatialisation de
la température de l'air à partir des images landsat ETM+, nous
avons suivi la démarche méthodologique suivante :
- Calcul de la température de brillance à partir
des images landsat ETM+ ;
- Dérivation de la température de
l'air ;
- Analyse de la variabilité spatiale de la
température maximale de l'air ;
- Proposition du Modèle de distribution spatiale de la
température de l'air (MSPAT) ;
IV.2.1 Calcul de la
température de brillance
Le calcul de la température de brillance à
partir des données Landsat ETM+ bande 6 nécessite la conversion
du code numérique (CN) de chaque pixel de l'image en radiance
(L()).Pour cela, nous avons utilisé
la formule de l'
Équation ýIV
développé par la NASA (National Aeronautics and Space
Administration) d'après Markham & Barker 1986.
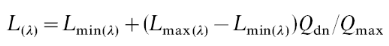 Équation
ýIV- Équation
ýIV-
L() est la radiance
spectrale reçue par le capteur exprimée en
mWcm-2sr-1m-1.
Qmax est la valeur maximale du
CN, Qmax=255. Qdn
est le niveau de gris pour le pixel ETM+ analysé.
Lmin() et
Lmax() sont les radiances
spectrales minimales et maximales détectées pour Qdn=0
et Qdn=255 respectivement. Pour les données Landsat ETM+,
Lmin() = 0.1238 pour
Qdn=0 et Lmax() =
1,56 mWcm-2sr-1m-1 pour Qdn=255
(Schneider and Mauser 1996). Donc, l'
Équation ýIV peut
être simplifiée sous la forme suivante (
Équation ýIV ):
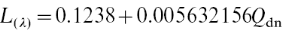 Équation
ýIV- Équation
ýIV-
Une fois la radiance spectrale calculée, la
température de brillance au niveau du satellite est
évaluée directement en utilisant la formule ci-dessous similaire
à l'équation de Planck (
Équation ýIV ) (Schott and Volchok
1985, Wukelic et al. 1989, Goetz et al. 1995):
Équation
ýIV-
Où L est la radiance spectrale à la
température TB. K1 et
K2 sont deux paramètres calibrés avant le
lancement, avec K1= 60.776
mWcm-2sr-1m-1, K2=1260.56
K.
IV.2.2
Dérivation de la température de l'air
Les cartes de la température maximale de l'air (Tam)
sont établies sur le bassin versant de Rheraya par la combinaison des
images ETM+ et les mesures locales, en supposant que les températures de
l'air et de brillance son reliées linéairement. Pour chaque image
ETM+, la température de brillance
(Tb) des pixels incluant les stations
météorologiques ont été extraits et
comparées avec les températures maximales de l'air
enregistrées in situ. La
Figure ýIV représente la
localisation des stations météorologiques utilisées dans
cette étude. Six images ETM+ réparties sur la saison (2002/2003)
ont été utilisées, le 07 novembre et le 25 décembre
2002 et le 26 janvier, le 11, 27 février et le 18 mai 2003. Les
données correspondant à ces dates sont disponibles sur trois
stations en montagne : Oukaimden CAF (toutes les dates), Armed (4 dates de
2003) et Oukaimden SudMed (une seule date en mai 2003). La
Figure ýIV représente la
corrélation entre les températures Tb versus
Tam de chaque date ETM+, et pour chaque station
météorologique. On note que les deux températures sont
fortement liées, avec un coefficient de corrélation proche de 1
(R²=0.82). Les cartes de température Tam seront par la
suite calculées directement à l'aide de la relation (
Équation ýIV ) que nous avons
appliquée pour chaque image ETM+.
Équation ýIV-
Figure ýIV-: Localisation des stations
météorologiques dans le bassin versant de
Rheraya
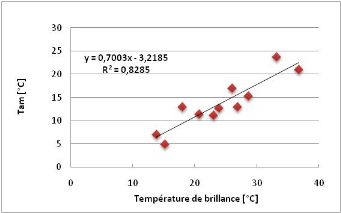
Figure ýIV- : Températures maximale
de l'air mesurées dans les stations météorologiques
disponibles versus les températures de brillance extraites des images
ETM°+ au pixel de chaque station
IV.2.3 Analyse de
la variation spatiale de la température maximale de l'air
IV.2.3.1 Effet de la topographie
i. Altitude
Dans les zones montagneuses, l'altitude est le premier facteur
de variation des températures. Il est bien connu que la montée en
altitude s'accompagne d'une baisse de la température de l'air. Ceci peut
être par exemple mis en évidence par le fait que la neige tient
plus longtemps en haute altitude qu'en basse altitude. Le gradient de
température désigne généralement la quantité
de variation de température de l'air avec l'altitude. Il s'exprime
généralement en °C/100m (degrés Celsius par 100
mètres).
La
Figure ýIV représente un exemple de
la variation de la température maximale de l'air en fonction de
l'altitude dans le bassin de Rheraya obtenue en appliquant la régression
linéaire (
Figure ýIV ) sur l'image acquise le
27/02/2003. Les deux variables (altitude et température) sont
très corrélées, avec une diminution de 18°C
associée à 3000 mètres de différence en
élévation. Cela correspond à une valeur de gradient de
0.60°C/100m. Dans le
Tableau ýIV , le gradient de
température moyen calculé entre les stations disponibles est
comparé avec celui calculé de chaque image ETM+. Les deux
gradients, extraits des images ETM+ et calculés à partir des
stations météorologiques, sont comparables. Ils varient entre
0.43 et 0.75°C/100m. Ces valeurs apparaissent comparables avec celles
obtenues à partir des stations météorologiques en
2007/2008 (
Figure ýIV ) et avec le gradient standard
international atmosphérique (-0.65°C) selon l'Organisation
Internationale de l'Aviation Civile.
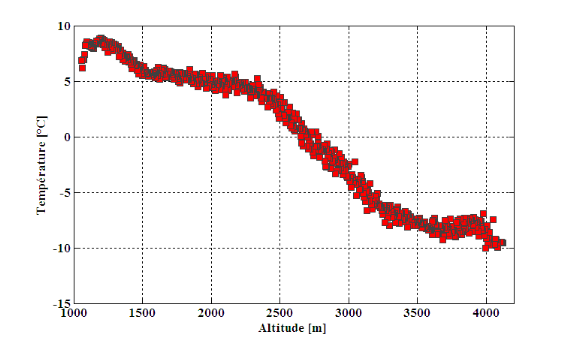
Figure ýIV- : Variation simulée de
la température maximale de l'air en fonction de l'altitude dans le
bassin de Rheraya le 27/02/2003(relation linéaire de la
température de brillance)
|
Gradient d'Altitude (°C/100m)
|
|
|
Date
|
Image TM
|
Station metéorologique
|
Ecart moyen
|
|
|
Saada-CAF
|
Saada-Armed
|
Moyenne
|
|
|
11/7/2002
|
-0.43
|
-0.65
|
-
|
-0.65
|
-0.22
|
|
12/25/2002
|
-0.51
|
-0.47
|
-
|
-0.47
|
0.04
|
|
1/26/2003
|
-0.53
|
-0.6
|
-0.51
|
-0.555
|
-0.025
|
|
2/11/2003
|
-0.51
|
-0.47
|
-0.53
|
-0.5
|
0.01
|
|
2/27/2003
|
-0.68
|
-0.69
|
-0.62
|
-0.655
|
0.025
|
|
5/18/2003
|
-0.75
|
-0.78
|
-0.7
|
-0.74
|
0.01
|
Tableau ýIV-: Comparaison des gradients de
température moyenne calculés entre les stations disponibles est
les images ETM+.
ii. Exposition des versants
L'orientation d'un versant, c'est, tout simplement, la
direction vers laquelle il regarde. Géométriquement,
l'orientation correspond à la direction vers l'aval de la ligne de plus
grande pente à chaque point. Les valeurs d'orientation exprimées
en degrés étant l'expression d'une variable de type circulaire.
La valeur 0° correspond à la valeur 360°, orientation plein
Nord, 90°, 180° et 270° correspondent à l'exposition Est,
Sud et Ouest, respectivement.
L'exposition des versants doit se voir d'abord comme un
facteur d'exposition au rayonnement solaire, donc au réchauffement dans
le cas d'une exposition Sud (mais aussi une illumination matinale dans le cas
des versants Est, tardive pour les versants Ouest).
L'exemple de la
Figure ýIV montre la variation de la
température maximale de l'air en fonction de l'exposition des versants
du bassin de Rheraya le 27 février 2003. On note dans cet exemple une
différence de 10°C de température entre les versants plein
Sud et plein Nord. Aussi, on constate que le changement de la
température selon les expositions des versants suit un modèle
sinusoïdal. Dans ce cas, la sinusoïde est centrée à
environ 140°, en cohérence avec le cycle diurne du soleil (l'angle
azimutal du soleil à l'heure d'acquisition est de 165°).
Figure ýIV- : Température moyenne
journalière enregistrée au niveau des stations montagneuses dans
le bassin de Rheraya (partie haute) et le gradient moyen annuel (partie basse)
en (2007/2008).
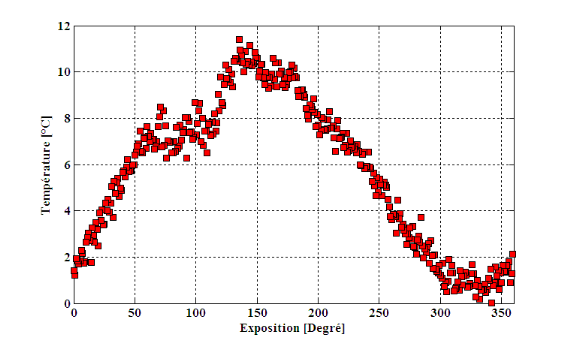
Figure ýIV- :
Variation de la température maximale de l'air en fonction d e
l'exposition des versants du bassin de Rheraya le 27 février
2003.
Une étude plus approfondie montre que la
dépendance de Tam avec l'exposition des versants est fonction
de la pente et de l'élévation solaire, mais aussi de l'altitude
puisque les pentes sont évidemment inégalement réparties
en altitude. La
Figure ýIV présente l'amplitude de
la variation de Tam avec l'exposition de sept bandes altitudinales de
1000 à 4200 mètres (bandes de 400m de haut), ainsi qu'avec les
pentes. L'analyse de cette figure montre que la variation de Tam
avec l'exposition est en accord avec la distribution altitudinale
des pentes, surtout durant l'hiver où l'élévation solaire
est faible. Cet effet est limité pour l'image acquise au mois de mai
avec une élévation solaire de 77°.
Figure ýIV- : Amplitude de la variation de
la température maximale de l'air avec l'exposition et les pentes de
sept bandes altitudinales à partir de 1000 à 4200 mètres.
IV.2.3.2 Effet de l'angle d'élévation solaire
L'angle d'élévation solaire au niveau d'un point
de la terre est l'angle entre la direction du soleil et l'horizontale au point (
Figure ýIV ). Il est fonction du temps, du
jour de l'année et de la latitude. Pour calculer cet angle, nous avons
utilisé un algorithme sous matlab développé par (Reda et
Andreas, 2003). Les valeurs des deux angles, élévation solaire et
azimut, sont présentées dans le
Tableau ýIV .
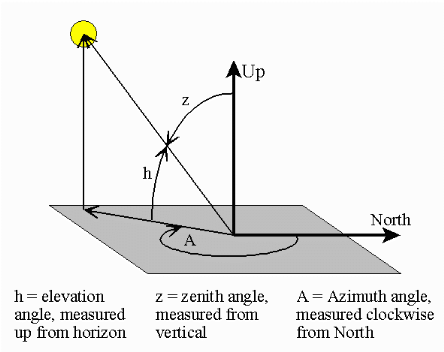
Figure ýIV- : Schéma des angles
Solaire
|
Date
|
Azimut
|
Elévation
|
|
07 Novembre 2002
|
176
|
42
|
|
25 Décembre 2002
|
172
|
35
|
|
26 Janvier 2003
|
167
|
39
|
|
11 Février 2003
|
166
|
44
|
|
27 Février 2003
|
164
|
49
|
|
18 Mai 2003
|
153
|
77
|
Tableau ýIV- : Angles solaire dans le Haut
Atlas au moment d'acquisition des images ETM+ disponibles
Les deux cartes de la
Figure ýIV représentent la
variabilité spatiale de la température maximale de l'air dans le
bassin versant de Rheraya à deux dates ETM+ : le 26/01/2003
et le 18/05/2003, acquises avec un angle d'élévation solaire de
39,12 et 77°, respectivement. A partir de ces deux images, il
apparaît clairement que l'angle solaire a un effet sur la distribution
spatiale de la température de l'air. Avec un angle faible, on a une
distinction nette entre les versants d'orientation Sud et Nord (Couleur
bleu : versant Nord et Couleur rouge : versant Sud) (Janvier par
exemple) et lorsque cet angle augmente (en mai par exemple) cette distinction
est beaucoup moins marquée (hors c'est à cette époque que
la fonte est maximale).

Figure ýIV- : Exemple de l'effet l'angle
solaire sur la variabilité de la température de l'air en
(°C) à deux dates différentes dans le bassin versant de
Rheraya.
IV.2.4
Modèle de distribution spatiale de la température de l'air
(MSPAT)
La température maximale de l'air dans chaque point
Tam(i,j) du bassin versant de Rheraya est
calculée à partir de la température enregistrée
dans la station météorologique de référence
(Tam(Iref,Jref)) et les différences topographiques
entre ce point et la station de référence. Ces différences
sont prises en compte pour l'utilisation du modèle MSPAT avec
l'altitude, l'exposition et la pente extraite pour le pixel (i,j) et la
localisation de la station de référence (
Équation ýIV ). Le modèle
MSPAT est établi pour obtenir des images de température maximale
de l'air à une résolution spatiale équivalent à
celle du MNT disponible (90m). En parallèle, la méthode
classique du gradient altitudinal est appliquée.
Équation
ýIV-
Avec : G est le gradient de
température calculé entre la station de référence
(Armed) et la station OukaSudMed, deux stations automatiques pour lesquelles
nous disposons de l'historique le plus long.
est la différence d'altitude entre la station de
référence et le pixel pour lequel on cherche à calculer la
température.
AS (i,j) et AS réf sont les
expositions des versants du pixel(i,j) et la station de
référence, respectivement.
Le modèle MSPAT est proposé pour reproduire la
variation de la température de l'air selon l'analyse
présentée ci-dessus. Pour une altitude donnée, le
modèle se base sur l'exposition, la pente et l'altitude selon les
équations suivantes (
Équation ýIV et
Équation ýIV ). En détails,
la température de l'air a été calculée en se basant
sur la température moyenne de chaque bande d'altitude avec une
correction de l'effet de l'exposition basée sur le cosinus (
Équation ýIV ). L'amplitude du
cosinus est ajustée en fonction du rapport pente locale et l'angle
d'élévation solaire (coefficient A dans l'
Équation ýIV et
Figure ýIV ).
Équation ýIV-
Équation ýIV-
Avec :
Tam(i,j) est la
température maximale de l'air du point (i,j) à l'altitude z et
l'exposition AS en degré.est la moyenne de la
température maximale de l'air de la bande altitudinale
z. A(i,j) est un
coefficient dépendant de la date et de la zone d'altitude.
SE et SL sont
respectivement l'angle d'élévation solaire et la pente, les deux
en degré. Le rapport SE/SL est limité à un seuil
égal à 5.5°.
Figure ýIV- : Relation entre le
coefficient « A » et le rapport angle
d'élévation solaire (SE) et la pente moyenne (SL) de chaque
tranche d'altitude pour les dates ETM+
IV.3 Evaluation du modèle MSPAT
IV.3.1 A l'aide du réseau de
stations météorologiques
Les températures journalières maximales
modélisées à l'aide du modèle MSPAT à la
localisation de chaque station météorologique ont
été évaluées par rapport aux mesures disponibles
sur le bassin versant de Rheraya. Ainsi, et en parallèle de cette
évaluation, les résultats obtenus avec MSPAT sont comparés
avec la méthode du gradient altitudinal (GRAD). L'évaluation
comparable des deux modèles a été effectuée en
utilisant les variables statistiques classiques (erreur quadratique moyenne
« RMSE », biais « BIAS », coefficient
de corrélation « R² »). La
Figure ýIV présente les
températures journalières maximales de l'air simulées
versus observées durant la saison 2007/2008, année où on a
un grand nombre de stations météorologiques en montagne. Les
variables statistiques obtenues en comparant les températures
journalières maximales de l'air simulées et observées sont
présentées dans la
Tableau ýIV . Ces statistiques sont
exprimées pour chaque saison. Armed étant la station de
référence, les valeurs de BIAS et RMSE sont nulles. Les biais
sont aussi nuls pour la station d'OukaSM que nous avons utilisée pour
calculer le gradient altitudinal moyen de température. A partir de ce
tableau on note que les performances des deux modèles, GRAD et MSPAT,
sont similaires. Les corrélations sont modérées à
excellentes (R² de 0.35 à 0.94), les biais sont faibles variant de
-0.5 à 1.2 °C et les erreurs quadratiques vont de 1 à
3.2°C. Le modèle MSPAT donne des résultats
légèrement supérieurs à ceux de GRAD pour les deux
stations CAF et Neltner, alors que c'est l'inverse pour les deux autres
stations (Imsker et Tachdert). Comme indiqué dans la
Figure ýIV , l'altitude reste le principal
facteur qui contrôle la température entre les stations
disponibles. Par conséquent, dans notre cas et avec un réseau
faible des stations météorologiques, on ne peut pas corriger les
effets des expositions et des pentes par le modèle MSPAT à la
localisation de chaque station.
|
Période d'acquisition
|
Stations
|
GRAD
|
MSPAT
|
|
R²
|
RMSE
|
BIAS
|
R²
|
RMSE
|
BIAS
|
|
2003/2004
|
Armed
|
1,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
|
CAF
|
0,56
|
3,14
|
-0,31
|
0,56
|
3,12
|
-0,10
|
|
OukaSM
|
0,77
|
2,51
|
0,00
|
0,77
|
2,51
|
0,00
|
|
2004/2005
|
Armed
|
1,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
|
CAF
|
0,91
|
2,00
|
-0,25
|
0,91
|
1,97
|
-0,05
|
|
OukaSM
|
0,87
|
2,44
|
0,00
|
0,87
|
2,44
|
0,00
|
|
2005/2006
|
Armed
|
1,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
|
CAF
|
0,85
|
2,23
|
-0,50
|
0,86
|
2,18
|
-0,26
|
|
OukaSM
|
0,76
|
2,90
|
0,00
|
0,76
|
2,90
|
0,00
|
|
2007/2008
|
Imsker
|
0,93
|
1,17
|
0,61
|
0,89
|
1,56
|
-1,24
|
|
Armed
|
1,00
|
0,00
|
0,00
|
1,00
|
0,00
|
0,00
|
|
Tachdert
|
0,94
|
1,00
|
0,10
|
0,92
|
1,16
|
0,56
|
|
Neltner
|
0,40
|
3,05
|
1,05
|
0,35
|
3,07
|
-0,31
|
|
OukaSM
|
0,74
|
2,27
|
0,00
|
0,74
|
2,27
|
0,00
|
Tableau ýIV- : Statistiques des
simulations de la température maximale de l'air au niveau des stations
de montagnes disponibles.
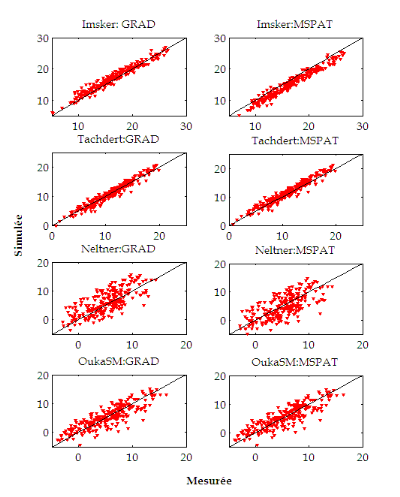
Figure ýIV- : Comparaison entre la
température mesurée et simulée par les deux
modèles, gradient « GRAD » et MSPAT en 2007/2008
IV.3.2 A l'aide du modèle
de fonte et des surfaces enneigées observées par
télédétection
Nous allons évaluer la performance des deux
modèles à l'échelle du sous bassin versant de Rheraya,
zone où les caractéristiques topographiques des versants sont
variées. La seule information observée dont on dispose à
cette échelle est celle concernant les surfaces des neiges (SCA)
calculées à partir des images satellitaires. On va choisir les
surfaces neigeuses calculées à partir des données MODIS,
produits qui coïncident avec la disponibilité des données
météorologique. Le calcul des SCA à partir des
données météorologiques en utilisant un modèle de
fonte de neige simple sera détaillé dans le Chapitre V. Les
températures spatialisées utilisées à
l'entrée du modèle de fonte, sont celles calculées par les
deux techniques GRAD et MSPAT.
Les surfaces enneigées observées par
télédétection et simulées avec les données
climatiques en utilisant les deux modèles de spatialisation de la
température GRAD et MSPAT sont comparées pour trois saisons
d'étude (2003/2004 à 2005/2006). Les courbes de variations
temporelles des SCA moyennées sur le bassin versant de Rheraya sont
présentées sur la
Figure ýIV . Les SCA simulées par
les deux methodes sont comparables avec les SCA observées. Cependant, en
2004/2005 le modèle GRAD sous-estime les simulations des SCA par rapport
aux données MODIS. Au début de la saison 2003/2004, pendant la
période de fonte entre décembre et janvier, on note une
surestimation des SCA avec le modèle GRAD, tandis que les deux SCA sont
semblables durant le reste de la saison. Par contre, à la fin de
2005/2006, on a une légère surestimation par le modèle
MSPAT. Les pics des SCA sont bien simulés avec les deux modèles,
mais avec toujours une légère sous estimation des SCA
après des événements de chutes des neiges plus
généralisés. Cette sous estimation est due à la
formulation de type asymptotique entre le SCA et l'équivalent en eau
utilisée au calcul, dans laquelle les SCAmax ne
dépassent pas 95% (
Équation ýV ,
Modélisation de l'accumulation et de la fonte
des neiges dans le bassin versant de Rheraya).
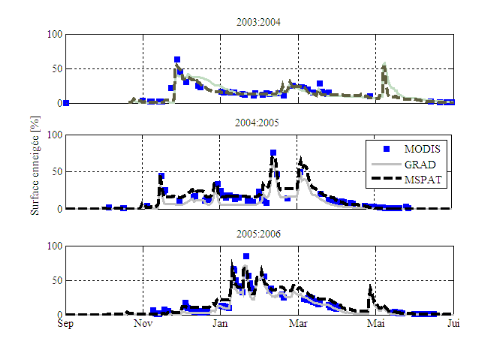
Figure ýIV- : courbes de variation des
surfaces enneigées estimées avec les deux modèles
climatiques, GRAD et MSPAT et calculées à partir des
données MODIS.
La
Figure ýIV montre un exemple de cartes des
SCA obtenues avec les deux modèles climatiques et dérivées
des produits MODIS. Les trois dates choisies sont situées durant la
période de fonte du 03 au 30 décembre 2003. La distribution des
SCA apparaît plus réaliste avec le modèle MSPAT. Cela est
évident sur les deux premières dates (03 et 12 décembre)
lorsqu'on observe les parties Ouest et Nord-Est du bassin versant.
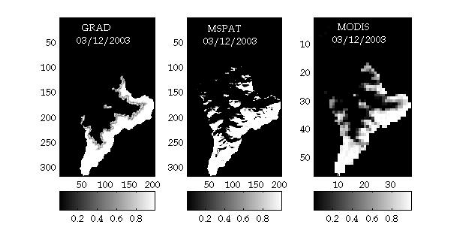 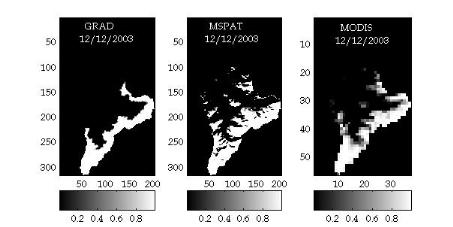 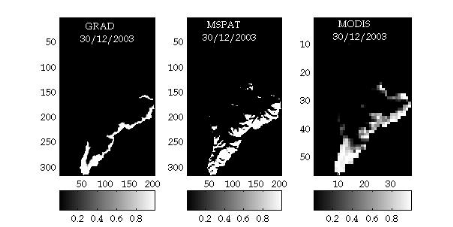
Figure ýIV- : Distribution spatiale des
surfaces neigeuses simulées avec les deux modèles de
spatialisation climatique (MSPAT et GRAD) comparées avec celles
observées avec MODIS. Les trois dates représentent une
période de fonte en décembre 2003.
Afin de quantifier les résultats obtenus ci dessus,
nous avons présenté les SCA simulées avec les deux
modèles climatiques versus les SCA observées (
Figure ýIV ). Cette comparaison est
effectuée sur une résolution spatiale dégradée
à 2 km². On note qu'avec le modèle MSPAT les nuages de
points sont plus centrés sur l'axe (100 :100). Les statistiques
détaillées de cette comparaison pour les trois saisons sont
résumées dans le
Tableau ýIV . Comme nous avons vu avec les
courbes de variation temporelle des SCA dans la
Figure ýIV , la comparaison pixel par pixel
montre globalement une amélioration nette des SCA simulées par le
modèle MSPAT par rapport au modèle GRAD. Cela est très
significatif pour les deux saisons 2004/2005 et 2005/2006 avec une diminution
du biais de 2.9 et 2.2%, respectivement.
|
|
Nombre d'images
|
Pixels
|
Efficience
|
GRAD
|
MSPAT
|
|
2003/2004
|
42
|
117
|
RMSE (%)
|
6,84
|
5,20
|
|
BIAS (%)
|
-0,17
|
-0,21
|
|
Equation de Régression
|
R²
|
0,80
|
0,88
|
|
a
|
0,89
|
0,96
|
|
b
|
0,01
|
0,00
|
|
2004/2005
|
52
|
117
|
RMSE (%)
|
9,66
|
6,08
|
|
BIAS (%)
|
-3,35
|
-0,42
|
|
Equation de Régression
|
R²
|
0,63
|
0,83
|
|
a
|
1,27
|
0,97
|
|
b
|
0,03
|
0,01
|
|
2005/2006
|
82
|
117
|
RMSE (%)
|
8,07
|
7,60
|
|
BIAS (%)
|
-2,28
|
0,11
|
|
Equation de Régression
|
R²
|
0,75
|
0,78
|
|
a
|
1,08
|
0,93
|
|
b
|
0,02
|
0,00
|
Tableau ýIV- : Comparaison des performances des
deux modèles GRAD et MSPAT pour estimer les surfaces de neige sur une
taille de pixel de 2*2 km.
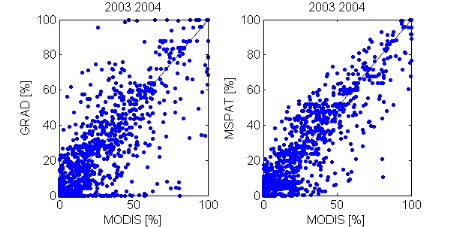 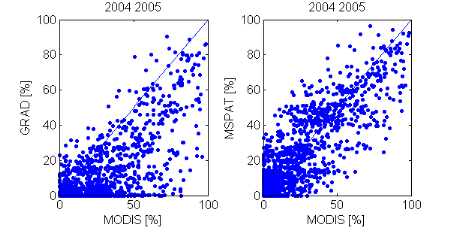 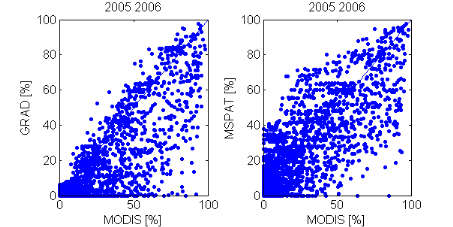
Figure ýIV- : SCA simulées avec les
deux modèles de spatialisation de la température de l'air, GRAD
et MSPAT, vs SCA calculées à partir des données MODIS.
Comparaison sur un pixel de 2*2km.
· Conclusion
L'étude présentée dans ce chapitre s'est
focalisée sur le test d'une méthode de spatialisation de la
température maximale de l'air, principalement développée
pour les zones montagneuses avec des données
météorologiques peu nombreuses vis-à-vis de la
variabilité spatiale attendue. La bande thermique des images Landsat
ETM+ a été utilisée pour calculer les températures
de brillance. Ces dernières données sont comparées avec
les températures maximales de l'air mesurées dans les stations
météorologiques disponibles. La relation linéaire entre la
température de brillance « Tb » et la
température maximale de l'air « Tam » obtenue permet
de généraliser le calcul des températures maximales de
l'air dans tous les pixels pour chaque image ETM+. Cette information est
utilisée pour caractériser la variation spatiale de la
température de l'air en fonction des facteurs topographiques (altitude,
pente et exposition) et l'angle d'élévation solaire. A partir de
cela, nous avons initialisé le modèle de variation spatiale de la
température de l'air (MSPAT) à l'échelle temporelle en
utilisant les données enregistrées dans une station de
référence.
Les simulations des températures de l'air par le
modèle MSPAT sont comparées avec celles obtenues avec le
modèle de gradient d'altitude (GRAD). Les résultats obtenus avec
les deux modèles à l'échelle des stations
météorologiques disponibles sont similaires. A l'échelle
spatiale, dans le bassin versant de la Rheraya qui présente une
importante hétérogénéité topographique, les
modèles sont validés par les surfaces de neige (SCA)
estimées. Ces dernières sont comparées avec les SCA
calculées à partir des données MODIS. Les résultats
montrent que le modèle MSPAT améliore significativement les
simulations des SCA. L'approche développée ici peut être
intéressante pour des applications hydrologiques, spécialement
pour la modélisation de la fonte des neiges à l'échelle du
bassin versant.
Chapitre V : Modélisation de
l'accumulation et de la fonte des neiges dans le bassin versant de Rheraya
· Introduction
Les modèles décrivant les processus
associés à l'accumulation et à la fonte des neiges ont des
degrés de complexité très contrastés et sont
utilisés pour répondre à plusieurs objectifs. Ceux-ci vont
de la prévision des débits dans des modèles hydrologiques
opérationnels (Melloh et al., 1997, Gomez et al., 2002) ou dans des
modèles de circulation atmosphériques (Essery, 1997; Beniston et
al. 2003) jusqu'à la prévision des impacts de processus de neige
dans des études écologiques (Groffman et al., 1999), en passant
par la prédiction d'avalanche (Essery et Yang, 2001).
Le degré de complexité de ces modèles va
du simple produit d'un facteur de fonte et de la température moyenne de
l'air (méthode degré-jour) jusqu'aux modèles à base
physique décrivant les échanges d'eau et d'énergie sous
toutes ses formes entre le sol, les différentes couches du manteau
neigeux et l'atmosphère. Généralement, on classe les
modèles de fonte de neige en deux grandes catégories: les
modèles conceptuels empiriques simples de type degré jour et les
modèles complexes de bilan d'énergie à base physique. Les
modèles degré jour (Martinec, 1985) sont adaptés à
l'utilisation en hydrologie nivale à des fins opérationnelles
dans les grands bassins, tandis que les modèles de bilan
énergétique (Bloschl et al.,1991a,b; Tarboton et al., 1995; Marks
et al., 1999b, Boone, 2000) sont adaptés aux études de processus
et à l'assimilation de données de
télédétection active ou passive dans le domaine
micro-onde. Même s'ils sont compliqués et nécessitent une
grande quantité de données d'entrée, ils
représentent de manière la plus exhaustive et mécaniste
possible les interactions entre les processus physiques au sein du couvert
nival : l'accumulation, la fonte et la métamorphose de la neige.
Certaines études dans des petits bassins versants expérimentaux
bien instrumentés ont montré que ces modèles pouvaient
fournir une représentation réaliste de la distribution spatiale
de l'évolution du couvert nival, pour peu que les
phénomènes les plus difficiles à représenter, tels
que l'ablation par le vent soient pris en compte (Daly et al., 2000 ;
David et Danny, 2005 ; Shamir et Georgakakos, 2006).
Nous nous intéressons dans ce chapitre avant tout
à la fonte des neiges dans un contexte de prévision du
débit. Le premier objectif est de comprendre les processus physiques qui
contrôlent l'ablation des neiges dans notre zone. Considérant le
fait que l'utilisation d'un indice de température pour prédire
l'apport de la fonte de neige est acceptée comme une simplification
considérable du bilan énergétique. Cette méthode
utilise la température et les précipitations pour résumer
l'accumulation puis la fonte de la neige. La température de l'air
étant le seul indice qui traduise les facteurs agissant sur les
échanges d'énergie à travers l'interface neige-air. Le
second objectif est de tester la validité des paramétrisations du
modèle simple calibrées à l'échelle locale pour
spatialiser la fonte à l'échelle du bassin versant. En d'autres
termes : les paramètres des relations conceptuelles de fonte
calibrés à l'échelle locale sont-ils suffisamment robustes
pour être appliqués au reste du massif?
Dans ce chapitre nous allons présenter dans un premier
temps les bases théoriques du bilan d'énergie et de masse du
manteau neigeux. Ensuite nous décrirons la méthode suivie pour
reconstituer les séries de précipitations au site d'Oukaimden qui
seront utilisées comme données d'entrée des modèles
de fonte appliqués. Le premier est un modèle à base
physique (ISBA-ES13(*) ; Boone, 2000)) qui nous a permis d'analyser les
différents processus physiques au sein du manteau neigeux. Le second est
basé sur une approche simple dite degré-jour avec deux
formulations de facteur de fonte, une utilisée sans aucune calibration
(Martinec, 1960) et la deuxième appliquée après
calibration (Kuustisto, 1980). En raison du manque des données
représentatives à l'échelle du bassin versant, on
n'évaluera les résultats de la spatialisation qu'avec le
modèle degré jour par comparaison des surfaces de neige
simulées avec celles obtenue avec la télédétection,
la seule information dont on dispose à cette échelle.
V.1 Bilan d'énergie et de masse du manteau neigeux
La description physique des processus de fonte repose sur le
bilan énergétique qui tient compte des modes les plus importants
d'échange de chaleur. Les premiers travaux de recherches abordés
sur le bilan d'énergie du manteau neigeux ont été
réalisés il y a environ cinq décennies (US Army Corps of
Engineers, 1956) succédés par plusieurs études
publiés dans un ensemble de revue et des livres (Male et Dranger,
1981 ; Male et gray, 1981; Moris, 1989; et Singh ,2001 ; Dewalle et
Rango 2008). Bien que les processus d'échanges d'énergie dans le
manteau neigeux sont assez bien identifiés en zone
tempérée ou nordique, les processus dominants dans les zones
arides sont plus difficiles à identifier et décrire, notamment en
raison du manque de données in situ disponibles et
particulièrement de dispositifs complets de mesures nivales à
l'image de ce qui se fait ailleurs (réseau SNOTEL aux Etats-Unis, NIVOSE
en France etc). Les instruments installés au site de l'Oukaimdem ont
permis de décrire un peu mieux les processus de fonte en milieu
semi-aride méditerranéen.
Durant les périodes d'accumulation et de la fonte des
neiges, la métamorphose de la neige est contrôlée par
l'énergie interne du manteau neigeux. L'état thermique du manteau
neigeux dépend étroitement des échanges avec
l'atmosphère. L'énergie incidente transmise à la neige est
issue du rayonnement solaire et du rayonnement atmosphérique.
L'énergie perdue par la surface de neige se fait par le transfert de la
chaleur convective de l'atmosphère, par l'échange de chaleur
latente de vaporisation dans l'atmosphère et par le rayonnement grande
longueur d'onde. Il y a un apport relativement faible de chaleur dû
à la pluie ainsi que d'une quantité généralement
négligeable de chaleur provenant du terrain sous-jacent (
Figure ýV ).
L'équation générale qui regroupe le bilan
d'énergie et de masse du manteau neigeux peut être écrite
sous la forme suivante (Male, 1981) (
Équation ýV ):
Équation
ýV-
Où est le rapport de l'échange d'énergie
(jm-2s-1) dans le manteau neigeux, et les deux termes
à droite représentent le transfert net d'énergie et de
masse vers et à partir du manteau. Le flux d'énergie net ()
inclus les rayonnements de toute longueurs d'onde absorbé par le
manteau neigeux, les transferts turbulents de chaleur latente et sensible
à la surface du manteau et le transfert convectif de la chaleur à
la base du manteau. Tandis que le transfert de masse () intègre
l'énergie équivalente de la sublimation, des
précipitations et de la fonte. Le transfert net de l'énergie peut
être écrit comme suit (
Équation ýV ):
Équation
ýV-
Avec :
Q* : Rayonnement net de toute longueurs d'onde
(W/m2);
QH : Flux de chaleur sensible
(W/m2);
QE : flux de chaleur latente
(W/m2);
QP : chaleurs apportée par les
précipitations (W/m2);
QG : Flux de chaleur du
sol (W/m2);
Les rayonnements constituent la composante dominante dans le
bilan d'énergie du manteau neigeux (Zuzel et Cox, 1975; Marks et Dozier,
1992). La quantité de chaleur transférée à la
couverture de neige par cette principale source d'énergie à la
surface de la terre varie avec la latitude, l'exposition, la pente, la saison,
l'heure du jour, les conditions atmosphériques, la couverture
forestière et la réflectivité de la surface de neige
(albédo). Les rayonnements de grande longueur d'onde sont aussi un
facteur important d'échange énergétique dans le manteau
neigeux. Les échanges de rayonnement de grande longueur d'onde entre
l'atmosphère et la surface de neige sont très variables et
dépendent essentiellement des conditions nuageuses, de la
quantité de vapeur d'eau dans l'atmosphère, du refroidissement
nocturne et de la densité de végétation (présence
d'un couvert forestier notamment).
Généralement, les processus d'échange
turbulents est le second facteur en termes d'importance pour les
transformations du manteau neigeux. En effet, il peut avoir des influences
significatives sur le rapport de fonte en raison de sa capacité à
amplifier ou compenser les flux de rayonnements. Les échanges de chaleur
turbulente entre la surface neigeuse et l'atmosphère sont liés
à la température de l'air et à la pression de vapeur
juste au-dessus de la de surface neige. Ces processus sont
particulièrement importants dans des conditions de tempête avec
des airs d'advection chauds et des humidités faibles. Les chutes de
pluie au dessus du manteau neigeux ont également une influence sur la
quantité d'eau de rétention et sur la circulation de l'eau au
sein du manteau, mais cela reste un facteur mineur par rapport aux autres flux
énergétiques.
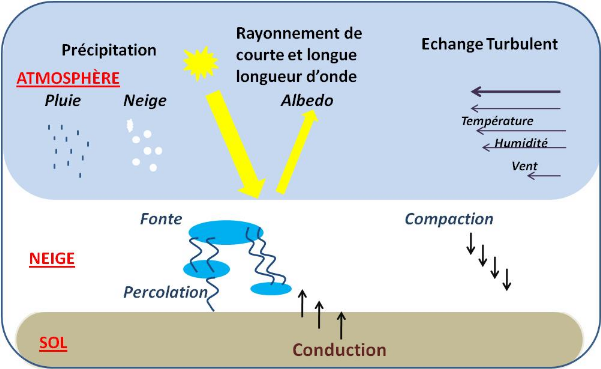
Figure ýV- : Diagramme schématique des
échanges d'énergie du manteau neigeux
V.1.1 Rayonnement net (Rnet)
Le rayonnement est constitué de deux composantes
distinctes : le rayonnement de courte longueur d'onde
provenant du soleil, ce dernier émettant quasi exclusivement dans la
gamme des longueurs d'onde de 0.3 à 2.2 ìm et du
rayonnement de grande longueur d'onde provenant du ciel et du
terrain environnant, qui se situent entre 6.8 et 100 ìm. Le rayonnement
net sur une surface de neige est décrit par les équations
ci-dessous (
Équation ýV et
Équation ýV ).
Équation
ýV-
Équation
ýV-
Avec :
Rnet, est la somme du rayonnement solaire net,
Snet, et du rayonnement net de grandes longueurs d'ondes,
Lnet. SI est la somme des rayonnements incidents direct
et diffus de courte longueur d'onde, á est le rayonnement de courte
longueur d'onde réfléchi, Li et Lo sont les
rayonnements de grande longueur d'onde incidents et émis ou
réfléchis, respectivement. Les nuages et la couverture de
forestière influencent radicalement les importances relatives des flux
de courte et de grande longueur d'onde, mais Rnet reste toujours le
flux incident. La composante net de courte d'onde (Snet)
régit principalement la durée et la quantité de la fonte;
le flux net des grandes longueurs d'ondes (Lnet) affecte la
période du dégagement de l'eau depuis le manteau neigeux en
raison de son influence sur la recongélation pendant la nuit et ainsi
sur le bilan d'énergie interne du manteau (Granger et Gray, 1990).
Rayonnement solaire net
Le rayonnement solaire net, Snet, est égal
au flux incidents de courte longueur d'onde (SI) reçu par la
surface moins la quantité réfléchie par la surface
(á) (
Équation ýV ) ;
Équation
ýV-
Le flux total des rayonnements incidents de courte longueur
d'onde (rayonnement global, SI) au niveau de la surface de neige est
fait de deux composantes, un faisceau direct avec d'évidentes
propriétés directionnelles, et une fraction diffusée par
l'atmosphère. Pendant que le faisceau direct traverse
l'atmosphère il est atténué par absorption et diffusion.
Les rayonnements solaires arrivant à la surface de la
terre sont partiellement réfléchis et partiellement
absorbés, en fonction de la réflectivité de la surface. Le
rapport entre les rayonnements réfléchis et incidents est
nommé albédo, qui varie considérablement
avec les conditions et l'âge de la neige. Les surfaces les plus
foncées ont un albédo faible et absorbent plus d'énergie
solaire que les surfaces les plus claires. Les valeurs d'albédo varient
de 0% (aucune réflexion) à 100% (réflexion totale). Le
Tableau ýV montre des valeurs typiques
d'albédo pour différentes surfaces.

Tableau ýV-: valeurs d'albédo pour
différentes surfaces
Rayonnement net de grandes longueurs
d'ondes
Le rayonnement net de grande longueur d'onde est la
différence entre le rayonnement émis par l'atmosphère (
Équation ýV ) dont on a soustrait la
part (1- ås) réfléchie par la surface (
Équation ýV ) et le rayonnement
émis par la surface (
Équation ýV ).
Équation
ýV-
Équation
ýV-
Équation ýV-
Avec :
Li est le rayonnement de grande longueur d'onde
incident ;
Lo est le rayonnement de grande longueur d'onde
sortant, (en W/m2),
åa est l'émissivité
atmosphérique, ås est l'émissivité de
surface, ó est la constante de Stefan-Boltzmann (5.67 x 10-8
W m-2 K-4), Ta et Ts sont les
températures de l'air et de surface (K) respectivement.
Le rayonnement incident de grande longueur d'onde
(Li) est émis essentiellement par la vapeur d'eau dans
l'atmosphère, ainsi que le dioxyde de carbone et l'ozone. La variation
de Li est ainsi en grande partie un résultat de la variation
de la nébulosité et de la température de la vapeur d'eau.
Puisque les couches de l'atmosphère près de la surface terrestre
ont la teneur en eau et la température les plus élevées,
elles ont la plus grande influence sur ce rayonnement.
Le rayonnement sortant (Lo) émi et
réfléchi par la surface de neige est calculé par l'
Équation ýV
L'émissivité de l'air dans le cas d'un ciel clair est
calculée par l'
Équation ýV ci dessous.
L'émissivité de la surface varie généralement entre
0.97 pour une neige ancienne et 0.99 pour la neige fraiche.
De nombreux travaux se sont attachés au
développement de méthodes de calcul de
l'émissivité. Les méthodes les plus précises
requièrent en général les profils verticaux
d'humidité et de température de l'atmosphère (Brutsaert,
1982). Ces données étant rarement disponibles, des
méthodes de calcul plus simples ont été
développées et on été comparées (Crawford et
Duchon, 1999; Maidment, 1992). La plupart d'entre elles sont strictement
empiriques mais il est aussi possible de dériver
l'émissivité sur des bases physiques. Le point de départ
de cette dérivation est l'équation de transfert radiatif dans une
atmosphère plane stratifiée. Cette dérivation aboutit
à la formulation de Brutsaert (1975) (
Équation ýV ).
Équation
ýV-
Où ea est la
pression de vapeur (kPa)
V.1.2 Flux turbulent
Les flux turbulents de chaleur sensible (H)
et de chaleur latente (LvE) sont des termes
importants d'échange d'énergie entre la surface de neige et la
couche basse de l'atmosphère (Morris, 1989). Le flux de chaleur latente
correspond à une perte de masse par sublimation. Le flux de chaleur
sensible est un résultat du contact entre la surface et l'air
sus-jacent ; les différences de température entre ces deux
éléments déterminent la direction et l'intensité du
flux (réchauffement de l'élément le plus froid).
L'énergie calorifique latente est gagnée par la condensation de
la vapeur d'eau dans l'air près de la neige ou perdue si la neige
sublime ou l'eau liquide contenue dans la neige s'évapore.
Les transferts de chaleur par turbulence sur le manteau
neigeux sont exprimés à l'aide de la formule aérodynamique
(Brock et al., 2000b; Oerlemans, 2000) (
Équation ýV et
Équation ýV ):
Équation
ýV-
Équation ýV-
Où
H et LvE sont respectivement les flux de
chaleur sensible et latente. air est la densité de
l'air en kg.m-1, Ta et Ts sont les
températures de l'air et de la surface (K) respectivement, ea
et es sont la pression de la vapeur d'eau (mb) au dessus de la
surface et à la surface respectivement et u est la vitesse du
vent en (m/s). CH est le coefficient d'échange de chaleur
sensible et CE celui de chaleur latente. Ces deux coefficients ont
des valeurs très voisines ; en pratique ils sont souvent pris comme
identiques. Cair est la chaleur spécifique de l'air,
exprimée en (J.Kg-1.K-1). Ces paramètres
spécifient l'efficacité des tourbillons à dissiper
l'énergie et dépendent de la rugosité aérodynamique
de la surface de la neige et de la stabilité atmosphérique
(tendance de la couche dense d'air proche de la neige à résister
aux mouvements d'inversion ou de mélange). Lv est la chaleur
latente de sublimation (J.kg-1).
V.2 Accumulation du manteau neigeux
V.2.1 Estimation de la densité et
l'équivalent en eau de la neige
L'équivalent en eau du manteau neigeux (Snow Water
Equivalent, SWE) est l'une des propriétés de la neige les plus
importantes pour les hydrologues. SWE représente la quantité
d'eau liquide du manteau neigeux que produirait la fonte complète de ce
dernier. Cette grandeur (SWE) peut être mesurée directement ou
à partir des hauteurs et des densités de neige. Autant la mesure
de la hauteur de neige est aisée, autant les mesures de densité
et de SWE sont plus complexes à mettre en oeuvre. Dans cette
étude, le SWE a été calculé à la base des
épaisseurs de neige mesurées régulièrement par la
station automatique d'Oukaimden à un pas de temps semi horaire et les
densités calculées au même intervalle de temps. Ces
dernières sont simulées à l'aide du modèle
empirique de Verseghy (1991) (
Équation ýV ).
La neige fraîche se tasse et se transforme sous l'effet
de divers processus (Sommerfeld et LaChapelle, 1970), ce qui entraîne une
augmentation graduelle de la densité avec le temps. Des mesures in situ
ont permis à Verseghy (1991) d'établir une loi exponentielle
décrivant le compactage global du manteau (
Équation ýV ):
Équation
ýV-
Où est la densité, () est la valeur asymptotique
de la densité due au vieillissement, et / le temps
caractéristique (0.24/4800 s-1). La densité moyenne
maximale utilisée par Verseghy ne peut pas excéder, elle est
fixée originellement à 300 kg-m-3. Cette densité est
appropriée pour la plupart des types de terrain et de
végétation.
Après chaque chute de neige, la densité moyenne
du manteau est calculée à partir d'une pondération de
masse de la densité du manteau neigeux précédent et de
celle de la nouvelle neige. Cette dernière est simulée à
l'aide de la formule de (Pomeroy et al., 1998), elle est liée à
la température de l'air par l'
Équation ýV . Quand la
température est au-dessus de 0 °C, la densité est
augmentée de 0,5 kg/m3/°C/h pour tenir compte
de l'augmentation de densité résultant de l'infiltration de l'eau
de fonte dans le manteau neigeux et de la recongélation de cette eau.
Si la densité est supérieure à, l'algorithme de
vieillissement de la neige n'est pas utilisé, mais la densité
peut quand même augmenter ou diminuer s'il y a d'autres épisodes
de fonte ou de chute de neige. La densité est toutefois limitée
à une valeur maximale de 450 kg/m-3, valeur obtenue à
partir des mesures de terrain.
Équation
ýV-
Où Ta est la température de l'air en
°C.
Le SWE est calculé chaque demi-heure comme le produit
de la densité calculée (
Équation ýV et
Équation ýV ) et de la hauteur de
neige mesurée dans la station d'Oukaimden (
Équation ýV ).
Équation
ýV-
Les graphes de la
Figure ýV illustrent la variation
temporelle des densités simulées et des équivalents en eau
reconstitués pour l'année 2007/2008. Les valeurs calculées
sont comparées avec celles obtenues lors des campagnes de mesures
effectuées pendant la même année. Globalement les
variations temporelles des densités et des équivalents en eau
simulés sont proches de ceux mesurés in situ et suivent
les mêmes variations temporelles. Les densités mesurées et
observées ont une corrélation moyenne (R²=0.32) et une
erreur quadratique moyenne (RMSE) de l'ordre de 41 kg/m3, ce qui
correspond à une erreur de 9%. Les équivalents en eau
simulés et mesurés sont fortement corrélés
(R²=0.72) et montrent une erreur quadratique moyenne de 40 mm soit une
erreur de 13% (
Figure ýV ). Ce décalage entre les
valeurs des équivalents en eau mesurés en chaque point de mesure
(voir §
Données ) et estimées à la
station peut être expliqué par les erreurs de mesure de hauteurs
de neige par la sonde lors des périodes de vent violent qui
déplacent la neige et ont tendance à l'accumuler près du
grillage qui entoure la station, créant ainsi un artefact de mesure.
Lors de la période de fonte, l'effet d'abri des mats de la station peut
également expliquer cette différence.
L'hétérogénéité de la couverture neigeuse en
fin de saison, évaluée à partir des points de mesure,
explique également cette différence: la neige a tendance à
s'accumuler vers les bas fonds plutôt que les crêtes.
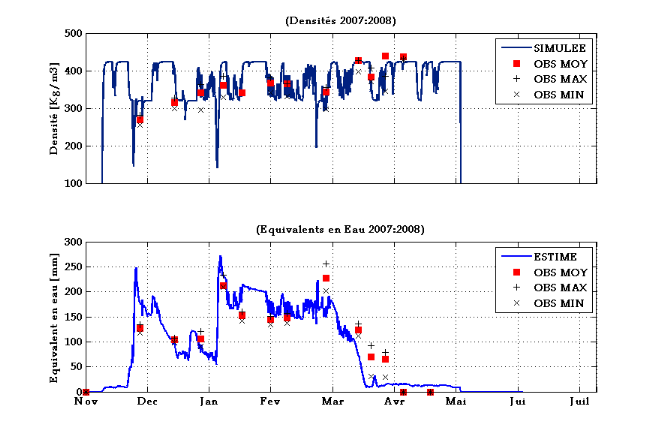
Figure ýV- :
densités et équivalents en eau reconstitués en temps
continue au niveau de la station d'Oukaimden comparés à des
points de mesures moyennes (OBS MOY), maximales (OBS MAX) et minimales (OBS
MIN) obtenues en 2007/2008.
Après la validation de cette méthodologie de
calcul des densités et des équivalents en eau de neige dans la
station de l'Oukaimden sur l'année 2007/2008, le calcul est ensuite
généralisé pour les autres saisons 2003/2004, 2004/2005 et
2005/2006. Le
Tableau ýV résume les principales
caractéristiques du manteau neigeux dans la station de l'Oukaimden lors
des ces dernières saisons. Ce tableau montre clairement la
variabilité saisonnière des caractéristiques du manteau
neigeux. Les dates de début de l'enneigement varient de mi-novembre au
20 décembre et la fin de saison varie entre 10 avril (en 2005) et le 15
mai (en 2003). Cela constitue une période d'enneigement moyenne variant
de 136 à 183 jours. L'épaisseur moyenne de la neige dans la
station atteint des maxima saisonniers variant de 70 cm, le 10/03/2005 à
122 cm, le 16/03/2006. Les équivalents en eau sont aussi très
variables, les valeurs maximales varient de 224 à 380 mm.
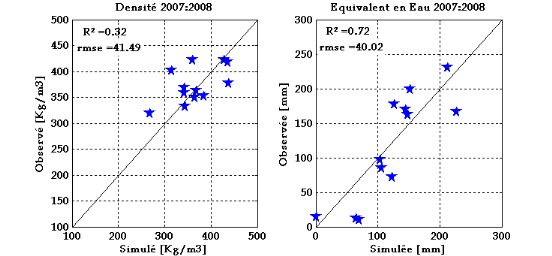
Figure ýV- : les valeurs des
densités et des équivalents en eau estimés versus
observés en 2007/2008.
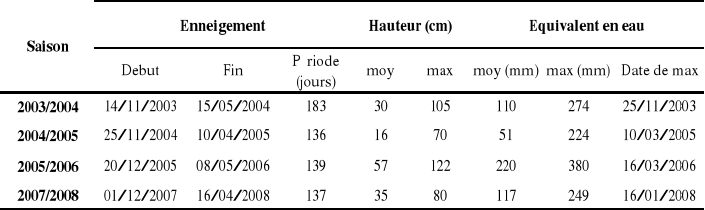
Tableau ýV- : Caractéristiques du
manteau neigeux à Oukaimden pour les quatre saisons
d'étude.
V.2.2 Reconstitution des
précipitations solides et liquides
Le pluviomètre à augets basculeurs qui
équipe la station d'Oukaimden n'est pourvu d'aucun système de
chauffage. Aussi, est-il impossible de déterminer
précisément l'occurrence d'une chute de neige et
l'équivalent en eau correspondant. La fonte de la neige dans l'entonnoir
dépend des conditions météorologiques et le
pluviomètre peut rapidement s'obstruer. Le dispositif instrumental n'est
donc pas adapté à la mesure des précipitations solides. En
plus d'une résistance chauffante ou d'un dispositif de mesure par
pesée, le pluviomètre devrait être muni d'un brise-vent
pour réduire les sous-estimations des cumuls dues au vent (Goodison et
al., 1981 ; Goodison et al., 1998 ; Larson et Peck, 1974).
Pour reconstituer les cumuls de précipitations
neigeuses, nous avons utilisé les hausses d'équivalent en eau
reconstituées présentées précédemment. Afin
de relier les hausses mesurées à un événement de
précipitation solide, les pluies et les températures de l'air
enregistrées par la station ont également été
utilisées selon la procédure d'identification et de
répartition des précipitations solides et liquides
suivante :
L'accumulation de neige au sol consécutive à une
précipitation entraîne la croissance de la hauteur de neige
mesurée. Cependant, la réciproque n'est pas vraie. Pour s'assurer
qu'une augmentation de la hauteur de neige n'est pas le fait du vent ou d'un
artefact (bruit), il est judicieux d'imposer les deux conditions suivantes :
a) la somme des variations positives de hauteur de
neige doit être supérieure à 1 mm dans un jour.
b) le pluviomètre doit détecter un
cumul dans les 24 heures qui suivent une augmentation du signal.
c) La température de l'air joue un rôle
essentiel dans la séparation des chutes des neiges et de pluies. Des
observations détaillées par le Corps of Engineers de
l'armée américaine (US Army Corps of Engineers, 1956) montre que
les fréquences de distribution des événements neigeux,
pluvieux et mixtes sont fortement liées à la température
de l'air (
Figure ýV ). En se basant sur cette figure,
la température moyenne de l'air doit être inférieure
à 3°C pour qu'un événement neigeux soit
enregistré (Fassnacht et Soulis, 2002). On calcule ensuite
l'équivalent en eau associé à une chute de neige en
multipliant la hauteur accumulée par la densité de la neige
fraîche, qui peut être estimée grâce à la
formule de l'
Équation ýV .
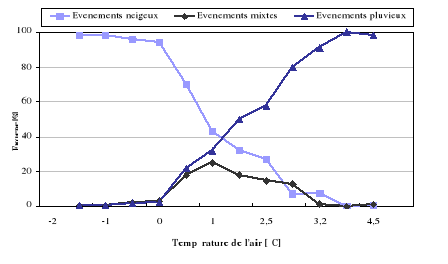
Figure ýV- : Variation de la
Fréquence d'occurrence des événements neigeux, mixtes et
pluvieux en fonction de la température de l'air (données :
US Army Corps of Engineers, 1956)
On peut raisonnablement envisager que l'entonnoir puisse
être rempli de neige pendant un épisode pluvieux et que le
pluviomètre collecte alors l'eau de pluie et l'eau de la neige qui a
déjà été prise en compte. De même pour les
épisodes de pluie et de neiges mêlées, entre -1 et 3°C
environ, il paraît impossible de les appréhender. Nous avons donc
décidé de ne conserver que les mesures du pluviomètre
effectuées en période de fonte et aux températures
supérieures à 3°C, autrement dit quand on peut être
sûr que le réceptacle ne contient pas de neige.
Les graphes de la
Figure ýV représentent une
comparaison de la répartition des précipitations liquides et
solides à l'Oukaimden (3200 mètres d'altitude) à un pas de
temps semi horaire et mesuré au site CAF à un pas de temps
journalier. Dans ce dernier, situé à 2600m d'altitude, les
hauteurs de neige tombées en une journée sont mesurées
manuellement. Les équivalents en eau de chaque chute sont
calculés par le produit de la hauteur et la densité de la neige
fraiche fixée à 100 kg/m3. Les cumuls de pluie au niveau de la
station OukaSM sont inférieurs à ceux de la station du CAF. De
même, les précipitations sous forme de neige sont plus importantes
dans la station d'OukaSM que dans la station de CAF. Cet écart entre ces
deux stations est cohérent avec la différence d'altitude
d'environ 600 mètres.
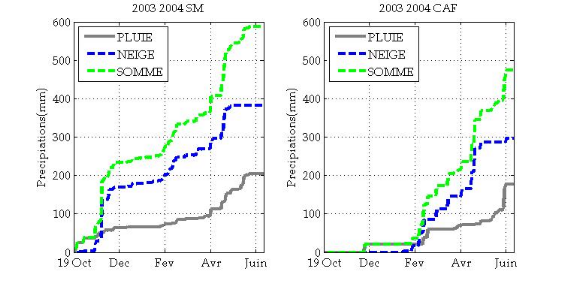 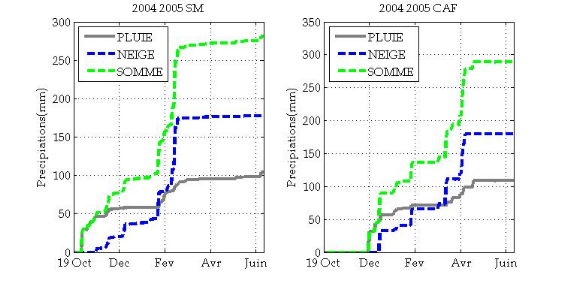 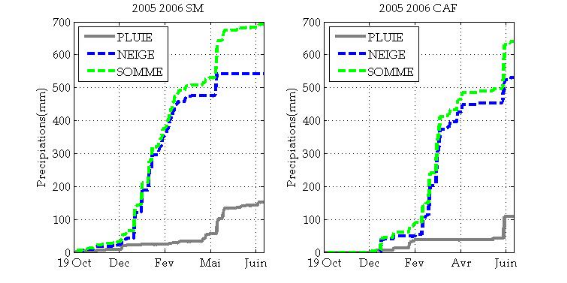
Figure ýV-: Comparaison de la
répartition des précipitations liquides et solides dans le site
d'Oukaimden SudMed (SM) (3200m) et au CAF (2600m)
V.3 Modélisation de la fonte des neiges
Les différentes données traitées
ci-dessus seront utilisées pour modéliser la fonte des neiges
à l'échelle locale. Deux approches ont été mises en
oeuvre, une approche physique pour bien comprendre les divers processus
influençant la fonte des neiges (le modèle ISBA-ES) et une
approche simple de type degré jour.
V.3.1 Modèle de bilan
d'énergie
V.3.1.1 Le
modèle ISBA-ES
Le modèle ISBA-« Explicit Snow » est un
modèle multicouches qui simule les processus affectant le manteau
neigeux (Boone, 2000; Boone et Etchevers, 2001). ISBA-ES a été
développé afin d'améliorer les performances du
modèle hydrologique distribué ISBA-MODCOU (Douville et al.,
1995). Basé sur l'approche de bilan d'énergie, ISBA-ES simule
donc la plupart des processus physiques présentés dans la
Figure ýV .
La coordonnée verticale z dans la neige est prise
égale à zéro à l'interface neige-atmosphère
et elle s'accroît vers le bas : les indices numérotant les couches
commencent à 1 pour la couche supérieure et augmentent avec la
profondeur jusqu'à un maximum de N = 3. N est le nombre de couches
minimum permettant de simuler correctement les gradients thermiques entre le
haut et le bas du manteau neigeux (Sun et al.1999).
Trois variables pronostiques sont utilisées dans
ISBA-ES pour décrire l'état du manteau neigeux
discrétisé en trois couches : l'équivalent en eau du
manteau neigeux (Ws(i) i=1-3), la quantité
d'énergie requise pour faire fondre intégralement la neige
(Hs) et l'épaisseur de la couche
(D(i), i=1-3). Par ailleurs, il traite les
propriétés thermiques de la neige de façon
indépendante des propriétés thermiques du sol et de la
végétation.
L'équation de conservation de masse pour le contenu en
eau total du manteau neigeux s'écrit comme suit (
Équation ýV ):
Équation
ýV-
Où WS est l'équivalent en
eau du manteau neigeux, ñw la masse volumique de
l'eau, En le flux d'évaporation et de sublimation,
Pn le flux de précipitations neigeuses,
Pr le flux de précipitations liquides et
Qn est le flux d'écoulement à la base du
manteau neigeux. Tous les flux sont exprimés en
kg.m-2.s-1.
La température moyenne de la couche de neige peut
être calculée à partir de l'équation de conservation
d'énergie suivante (
Équation ýV ):
Équation
ýV-
où j représente la couche de neige (j=1 : 3),
cnj la capacité calorifique de la neige de la couche j, Ds,j.
l'épaisseur de neige de la couche j, Ts,j la
température de la neige de la couche j, t le temps, Gs,j
représente le terme de transfert de chaleur du au gradient
thermique, RGs,j le flux de chaleur du aux changements de phase et
enfin Si est un terme représentant le réchauffement du
manteau neigeux suite à l'absorption du rayonnement solaire.
Le flux de chaleur à la surface de la neige (z = 0)
Gs0, orienté positivement vers le
bas est déterminé par l'
Équation ýV :
Équation
ýV-
Où Gs0 est le flux
de chaleur nette à l'interface neige /atmosphère,
ån est l'émissivité
(supposée égale à 1),
RA est le rayonnement infrarouge
descendant, ó est la constante de Stefan-Boltzmann,
Ts1 la température de la neige en
surface, Hn le flux de chaleur sensible,
LEn le flux de chaleur latente. Le dernier
terme de l'équation représente l'apport de chaleur latente par la
pluie lorsque celle-ci est à une température supérieure
à la température de surface de la neige:
cw est la capacité calorifique de
l'eau (4187 J kg-1 K-1),
Tr la température de la pluie et
Tf la température de fusion de
l'eau (273.16K).
Le flux de chaleur latente à la surface de la neige
(LEn) comprend les contributions de
l'évaporation de l'eau liquide contenue dans la couche de surface et la
sublimation; il s'écrit en fonction du gradient d'humidité selon
l'
Équation ýV identique à l'
Équation ýV .
Équation
ýV-
Où ña est
la densité de l'air, Va sa vitesse,
qa son humidité,
qsat(Ts1)
son humidité à saturation à la température
Ts1. et
CH le coefficient d'échanges
turbulents.
Le flux de chaleur sensible est donné par l'
Équation ýV .
Le flux d'eau liquide,
Qj, est calculé à la base de
chaque couche comme la différence entre le contenu en eau liquide de la
couche et son contenu en eau maximum. Le taux d'écoulement à la
base du profil de neige, Qn est
égal à ce flux d'eau pour la dernière couche de neige.
V.3.1.2 Etalonnage
du modèle ISBA-ES
Les différents prétraitements effectués
pour préparer les données d'entrée du modèle ont
été décrites dans les sections précédentes.
Ces données sont:
o La température de l'air, la vitesse du vent, le
rayonnement solaire global incident et l'humidité de l'air sont
mesurées à 2 m du sol dans la station pendant toute la
période de 2003 à 2008.
o Les hauteurs de neige sont mesurées pendant les
périodes hivernales de 2003 à 2008.
o Les précipitations neigeuses sont calculées
à partir des hauteurs de neige.
o Le rayonnement grandes longueurs d'onde émis par
l'atmosphère calculé à l'aide de la formule de Brutsaert
(1975) (
Équation ýV ). Cette équation
a été retenue après l'avoir comparée avec d'autres
formulations. Ces dernières supposent certaines hypothèses non
vérifiées dans notre cas d'étude (Chaponnière,
2005).
Les simulations d'étalonnage du modèle ISBA-ES
ont été menées au cours de la saison 2007/2008, pendant
laquelle des données in situ de densité sont
disponibles. Dans un premier temps on a testé le modèle en
reprenant les paramètres de neige par défaut (Boone, 2000).
Ensuite on a varié les deux paramètres jugés sensibles, la
rugosité (z0) du manteau neigeux et
la valeur maximale de l'albédo. Etant donnée la latitude du site,
une forte sensibilité de l'albédo sur les simulations est
attendue.
L'albédo est modélisé dans ISBA-ES
suivant la méthode présentée par Douville et al. (Douville
et al., 1995). Un taux de décroissance linéaire est
utilisé pour la neige sèche et un taux de décroissance
exponentielle est employé pour modéliser le métamorphisme
d'humidification de la neige. Dès qu'un nouvel épisode neigeux a
lieu, albédo de la neige tombée est celui d'une neige
fraîche, donc un albédo maximal qui réfléchit
quasiment l'intégralité du rayonnement incident. La fonction
d'estimation de l'albédo est bornée par un albédo minimum
de 0,5 et un albédo maximal de 0,85 (Douville et al., 1995). Cependant,
ces deux bornes d'albédo sont variables d'un endroit à un autre,
par exemple sur un site des Alpes (Boone and Etchevers, 2001) des mesures
d'albédo supérieures au seuil maximal d'albédo ont
été observées : l'albédo mesuré y a atteint
0,95. Dans le site de l'Oukaimden, les mesures de l'albédo pour les deux
saisons 2004/2005 et 2005/2006 montrent que les valeurs minimales sont de 0.4
à la fin de chaque épisode de neigeux et les valeurs maximales
peuvent atteindre 0.8, mais elles fluctuent généralement entre
0.7 et 0.8 et elles sont liées aux nouvelles neiges qui se
déposent au début de chaque événement.
La valeur de la rugosité du manteau neigeux
(z0) reportée dans la
littérature varie généralement entre 0.001 et 0.02m pour
les surfaces très lisses et des surfaces rugueuses respectivement
(Anderson, 1976 ; Moore, 1983 ; Morris, 1989). Cette rugosité
dépend de la hauteur de végétation lorsque la surface est
couverte. En haute montagne, sur sol nu, des phénomènes de
turbulence importants peuvent néanmoins avoir lieu alors que la
rugosité de surface est très faible. Ceci est dû au relief.
Un modèle de bilan d'énergie appliqué en montagne est de
ce fait systématiquement confronté au problème de la
turbulence générée non pas par la rugosité de
surface mais par le relief. Ainsi, c'est le paramètre z0 qui
est modifié afin de prendre en compte cet effet du relief. Sur notre
site (sommet sans végétation), la modification du
paramètre de rugosité a un fort impact (
Figure ýV ).
Dans les figures (
Figure ýV et
Figure ýV ) les équivalents en eau
simulés avec des valeurs maximales et minimales des deux
paramètres (albédo et rugosité) sont
présentés. Ces figures confirment la très grande
sensibilité du modèle aux deux paramètres. Le
Tableau ýV résume les statistiques
des différentes simulations de sensibilité. On note ici que la
meilleure restitution des équivalents en eau est obtenue avec un
albédo maximal moyen sur toute la saison de 0.8 et une rugosité
de 0.02m.
Figure ýV- : Sensibilité du
modèle ISBA-ES à la variation de la rugosité de neige en
2007/2008.
Figure ýV- : sensibilité du
modèle ISBA-ES à la variation de l'albédo de neige en
2007/2008.
|
Albédo
|
Rugosité (m)
|
R2
|
RMSE (mm)
|
BIAS (mm)
|
|
0,8
|
0,001
|
0,86
|
51,18
|
20,57
|
|
0,8
|
0,005
|
0,87
|
41,68
|
12,62
|
|
0,8
|
0,010
|
0,87
|
35,72
|
6,29
|
|
0,8
|
0,020
|
0,86
|
30,88
|
-2,88
|
|
0,7
|
0,020
|
0,66
|
49,71
|
-21,59
|
|
0,8
|
0,020
|
0,86
|
30,88
|
-2,88
|
|
0,9
|
0,020
|
0,85
|
40,64
|
12,69
|
Tableau ýV- : résultats des
simulations de sensibilité d'ISBA-ES à l'albédo et de la
rugosité en 2007/2008
Par la suite, l'évaluation du modèle pour
l'ensemble des simulations des autres saisons est effectuée avec les
valeurs de paramètres calibrés pour l'année 2007/2008. Les
graphes de la
Figure ýV illustrent les variations des
équivalents en eau obtenues pour les quatre saisons (2003/2004,
2004/2005, 2005/2006 et 2007/2008) et le
Tableau ýV résume les statistiques
obtenues. Généralement le modèle reproduit bien les
équivalents en eau (SWE) et les hauteurs pour les quatre saisons. Les
erreurs (RMSE) calculées entre les SWE simulés et mesurés
varient entre 50 mm en 2005/2006 et 19 mm en 2004/2005. Les coefficients de
corrélation (R²) sont supérieurs à 0.86 pour toutes
les saisons. A l'inverse des modèles simples de types degré jour,
les processus hivernaux sont bien simulés par ISBA-ES. Les variations
temporelles des SWE et les hauteurs sont sous estimées en fin de saison
(après le mois d'avril) pour les deux saisons 2005/2006 et 2003/2004.
Cette période de l'année est caractérisée par des
températures de l'air élevées, et des hauteurs de neige
faibles tombant souvent sur des sols nus. A cet effet, le modèle simule
des fontes rapides des neiges, alors qu'au niveau de la station on a des neiges
qui persistent. Ces dernières neiges sont dans la plupart du temps
bloquées par le grillage autour de la station qui induit un artefact de
mesure.
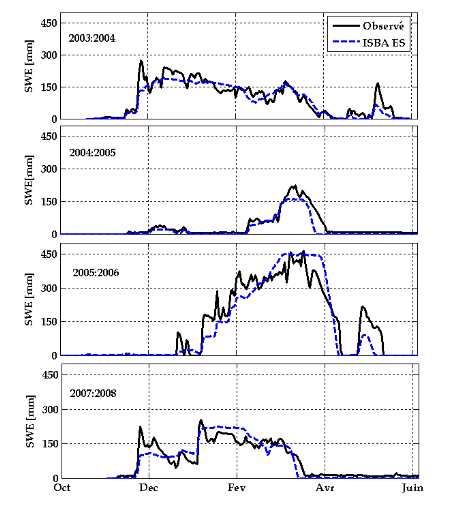
Figure ýV- : comparaison des variations des
équivalents en eau annuelles simulés par ISBA-ES et
observés à la station de l'Oukaimden.
|
|
Saison
|
R²
|
RMSE
|
BIAIS
|
|
SWE (mm)
|
2003/2004
|
0,86
|
29,98
|
-8,69
|
|
2004/2005
|
0,89
|
19,00
|
-8,83
|
|
2005/2006
|
0,91
|
48,61
|
-7,59
|
|
2007/2008
|
0,86
|
30,88
|
-2,88
|
|
HAUTEUR (m)
|
2003/2004
|
0,84
|
0,10
|
-0,05
|
|
2004/2005
|
0,89
|
0,05
|
-0,02
|
|
2005/2006
|
0,94
|
0,14
|
-0,06
|
|
2007/2008
|
0,76
|
0,13
|
-0,02
|
Tableau ýV- : Performances des simulations
des équivalents en eau obtenues par ISBA-ES
Tous les processus internes au manteau neigeux, tels que
l'absorption du rayonnement solaire incident, la rétention d'eau
liquide, les transferts de chaleur et la compaction de la neige, sont
déterminés en fonction de la densité de la neige. Cette
dernière est modélisée par ISBA-ES comme une fonction
exponentiellement croissante et bornée. Sur la
Figure ýV les densités
simulées par le modèle au niveau des trois couches sont
comparées avec celles mesurées in situ. Les couches sont
numérotées de 1 à 3 selon la profondeur, L3 est la couche
depuis la surface, L2 est l'intermédiaire et L1 la profonde. Les
densités simulées sont cohérentes avec les densités
mesurées en dehors des périodes de fonte. En revanche, les
densités simulées augmentent rapidement au milieu de la saison en
fonction de l'eau liquide stockée dans le manteau. La densité
« effective » du mélange neige et eau liquide est
largement supérieure à celui de la neige sèche. Il semble
que le modèle surestime le stockage d'eau liquide en milieu de saison
(février - mars). Cependant, une seule mesure de densité
(début février) est réellement incohérente avec la
densité simulée.
Figure ýV- : Variation des densités
de neige des trois couches simulées par ISBA-ES à la station
d'Oukaimden en 2007/2008. Les points représentent les mesures in
situ.
Sur les figures (
Figure ýV et
Figure ýV ) les valeurs simulées de
l'albédo sont comparées avec les valeurs mesurées et avec
les hauteurs de neige. Dans ISBA-ES l'albédo est calculé pour
une fraction de sol couvert par la neige égal à 100 % durant tout
l'hiver. Au niveau de la station météorologique, l'albédo
mesuré correspond à l'albédo total (tout le couvert du
sol). Les faibles valeurs (albédo égal à 0.2) sont celles
du sol nu et les valeurs maximales sont celles de la neige fraiche. Lorsque la
hauteur de neige est faible, on peut supposer qu'une partie de l'albédo
mesuré est aussi celui du sol nu émergeant par endroits. Afin de
vérifier l'impact du vieillissement de la neige sur l'albédo, les
valeurs simulées et mesurées sont comparées dans le cas
des hauteurs de neige supérieurs à 20 cm (
Figure ýV ).
Le modèle surestime les simulations de l'albédo,
tout en sous-estimant ses variations (Boone, 2000). Cela est plus important
pour les faibles hauteurs de neige (ex, début de chaque saison)
où les albédos mesurés sont très faibles sous
l'effet de la fraction du sol couverte de neige. .En revanche, ISBA-ES
reproduit bien les albédos au cours des phases de décroissance
à la fin de l'hiver des deux saisons et pour certaine périodes de
diminution des hauteurs de neige (ex, fin décembre 2004 et 2005 ;
février 2006).
En plus du vieillissement du manteau neigeux, d'autres
facteurs peuvent affecter les valeurs de l'albédo. Les faibles valeurs
enregistrées dans la station sont dues à la contamination du
manteau neigeux par la poussière en provenance des zones arides du sud
du Haut Atlas, à la fin de l'hiver.
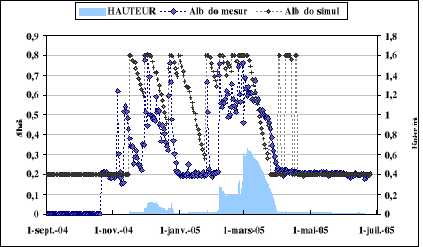
Figure ýV- : Comparaison de
l'albédo simulé par ISBA-ES et l'albédo et les hauteurs de
neige mesurés dans la station d'Oukaimden en 2004/2005
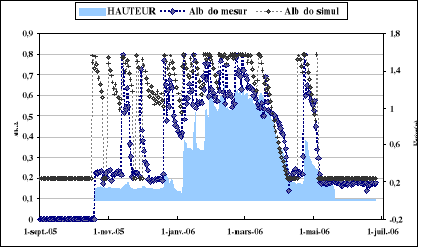
Figure ýV- : Comparaison de
l'albédo simulé par ISBA-ES et l'albédo et les hauteurs de
neige mesurés dans la station d'Oukaimden en 2005/2006
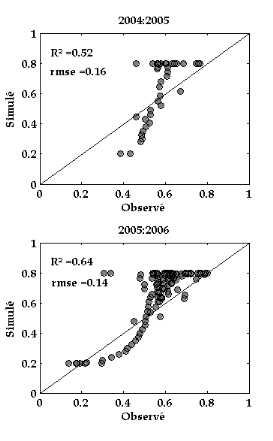
Figure ýV- : Corrélation de
l'albédo simulé et mesuré dans le cas des hauteurs de
neige supérieurs à 0.2 mètres
V.3.1.3 Processus
d'ablation de la neige
L'ablation de la neige est caractérisée par deux
processus importants : la fonte et la sublimation. La fonte est la
transformation de phase solide en
liquide par apport
d'énergie. La
sublimation
est le passage de l'
état
solide à l'
état gazeux avec
libération d'énergie.
Les deux processus ont lieu partout dans le monde où le
climat est froid et sec, mais ils sont accentués dans les montagnes des
régions arides et semi-arides. Des signes visibles de la sublimation
sont les pointes de neige communément appelés
«pénitents ». Ces derniers indiquent le niveau initial de la
neige et semblent s'élever de la couverture de la neige alors que ce
niveau de neige est gravé entre les pointes lors de l'ablation de la
neige. Des « pénitents » de neige ont été
observés à haute altitude dans le site d'Oukaimden indiquant des
conditions climatiques stables, favorables pour la sublimation pendant
plusieurs semaines (
Figure ýV ). Plusieurs théories ont
été développées pour expliquer la formation des
« pénitents ». Selon Llboutry, 1954 et Corripio,
2004, les processus de formation des « pénitents »
dans les zones froides et arides nécessitent un point de rosée
inferieur à zéro et des rayonnements solaires
élevés. Ces formes sont aussi toujours orientées vers le
soleil.

Figure ýV- : formes en
« Pénitents » Observées sur les versants
orientés vers le Sud du plateau d'Oukaimden le
30/01/2008
Les variations journalières des pertes d'eau due
à la fonte et à la sublimation sont illustrées dans la
Figure ýV en parallèle avec les
taux moyens des équivalents en eau, température, vitesse du vent
et rayonnement globale. On note que les pertes de l'eau au début de la
saison (entre novembre et février) sont dues essentiellement à la
sublimation. Cela est peut être expliqué par l'importance des
vitesses des vents moyennes, avec des maximas variant entre 5 et 10 m/s,
combinées parfois avec des températures élevées (
Figure ýV ). Dans cette figure la
quantité de l'eau sublimée par pas de temps de deux heures est
représentée en fonction des paramètres
météorologiques enregistrés dans la station
météorologique de l'Oukaimden. La sublimation de la neige reste
présente tout au long de la saison. A partir du mois de février,
le manteau neigeux libère des quantités importantes d'eau sous
l'effet de la fonte. Les facteurs principaux de la fonte sont l'augmentation de
température de l'air et aussi le changement de l'état du manteau
neigeux. L'apport de la sublimation dépend du déficit de la
pression de vapeur d'eau et de la vitesse du vent à la surface du
manteau (Sverdrup, 1936).
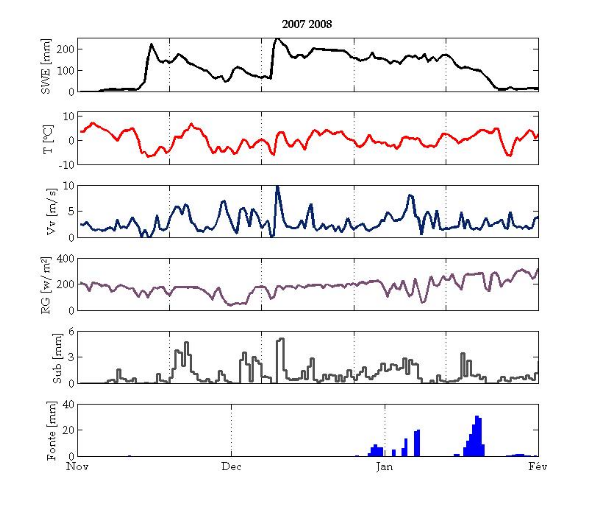
Figure ýV- : Variation journalières
des équivalents en eau, température de l'air, vitesse du vent,
Rayonnement global et de l'ablation des neiges (sublimation et fonte) dans le
site de l'Oukaimden en 2007/2008.
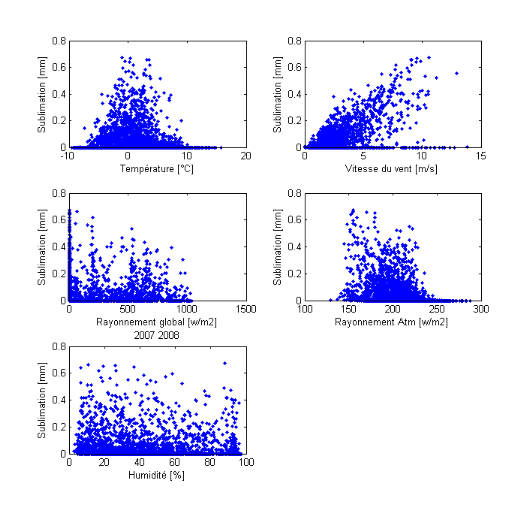
Figure ýV- : Corrélation entre la
quantité d'eau sublimée vs les paramètres
météorologiques mesurés à la station nivale de
l'Oukaimden en 2007/2008 à un pas de 2 heures.
La
Figure ýV illustre les cumuls saisonniers
des pertes par la fonte et la sublimation estimés pour le site
d'Oukaimden à l'aide du modèle ISBA ES. La majeure partie de
l'ablation des neiges au cours des quatre saisons est due à la fonte.
Cependant, une partie non négligeable des pertes de l'eau est
liée à la sublimation. La proportion de ce dernier
phénomène varie de 17% pendant la saison 2005/2006 à 38%
pendant la saison 2007/2008. On remarque que la fonte est
généralement caractérisée par la libération
brutale de l'eau pendant de courtes périodes, de façon
concomitante à l'augmentation de la température de l'air, tandis
que la sublimation se manifeste de façon régulière tout le
long de la saison. Dans les versants Sud du Haut Atlas, Schulz et Carmen, 2004
ont simulés une perte par sublimation de 45% dans le site de Tichki
(3250m) et de 43% dans le site de Tounza (2960m). Ces proportions sont
calculées à l'aide du modèle monocouche à base
physique « UEB » (Tarboton et Luce, 1996).
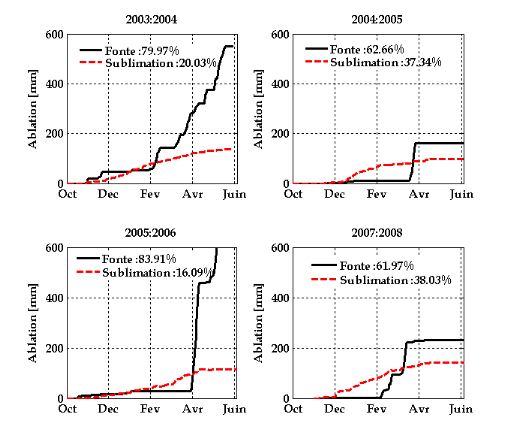
Figure ýV- : Proportions des processus de
la fonte et la sublimation modélisé par ISBA-ES dans le site de
l'Oukaimden
V.3.2 Le modèle degré
jour
La méthode la plus généralement
appliquée pour évaluer la fonte dans des modèles
hydrologiques consiste à utiliser les facteurs de degré jour.
Cela s'explique par la plus grande disponibilité des données de
température de l'air et à la possibilité de les interpoler
spatialement, ainsi que la simplicité de la méthode. La
majorité des modèles opérationnels utilisent la
méthode de degré jour pour simuler la fonte: le modèle HBV
(Bergstrom, 1976), le modèle SRM (Martinec et Rango, 1986), le
modèle UBC (Quick et Pipes, 1977), le modèle HYMET (Tangborn,
1984). Malgré la simplicité de cette méthode, elle
améliore la performance de ces modèles.
Le degré jour est défini ici comme 1°C de
différence entre la température moyenne journalière et une
température de référence, souvent égal à
0°C. A l'inverse des méthodes qui reposent sur de bilan
d'énergie du manteau neigeux et qui demandent une grande quantité
de variables d'entrées, la méthode basée sur l'approche
degré jour nécessite seulement des données sur la
température de l'air qui sont habituellement disponibles, et on peut
généralement déterminer les variations de la
température dans un bassin versant, tant pour déterminer les
fonctions degré jour que pour en faire l'application.
La méthode du degré jour repose sur deux
principes fondamentaux. Premièrement, la température de l'air
à proximité de la neige est dans l'ensemble une
intégration physique des mêmes modes d'échange de chaleur
que ceux qui provoquent la fonte de la neige. Deuxièmement, chacun des
modes d'échange de chaleur peut être mis en relation avec la
température de l'air, sauf pendant les périodes de vents
anormaux. Par exemple, la température minimale quotidienne de l'air est
fortement liée à la température du point de rosée,
qui détermine le gradient de tension de vapeur pour la fonte par
condensation. La température journalière maximale, ou l'amplitude
maximale de la variation de la température, constitue un indice du
rayonnement solaire. A l'intérieur de la plage de ses valeurs
habituelles, le rayonnement de grandes longueurs d'onde peut s'exprimer sous
forme d'une fonction linéaire de la température de l'air
(Brubaker et al., 1996).
Depuis son introduction la méthode du degré jour
a largement fait la preuve de sa robustesse et de la largeur de sa palette
d'utilisation, à condition qu'une réflexion préalable sur
les valeurs à attribuer au facteur de fonte soit menée (Martinec
et al., 1994). Elle est employée avec succès aussi bien pour la
modélisation des couverts temporaires dans le Middle West
américain (Kongoli et Bland 2000) que pour l'étude de l'ablation
sur les glaciers himalayens (Singh et al., 2000) ou la simulation des
écoulements dans un bassin de haute montagne de Colombie Britannique
(Moore, 1993) ou dans un petit bassin arctique (Hinzman et Kane 1991).
V.3.2.1 Description
du modèle
Pour estimer la quantité d'eau issue de la fonte des
neiges, nous avons construit un modèle simple qui simule les hauteurs et
les équivalents en eau du manteau neigeux au pas de temps semi horaire.
Ce dernier est basé essentiellement sur les variations de la
température de l'air par la méthode des degrés-jour et
l'apport de chaleur apporté par la pluie:
L'organigramme de la
Figure ýV illustre l'algorithme du
modèle d'accumulation et d'ablation utilisé. Après les
corrections effectuées sur les précipitations et la
séparation des pluies aux neiges, Deux cas sont possibles selon la
température de l'air :
· Si la température de l'air est
supérieure à 0°C, la fonte
« M » est calculée selon l'
Équation ýV . S'il tombe une hauteur
de pluie P sur la neige, une quantité d'eau de fonte égale
à FP est produite par l'apport de chaleur par
la pluie (
Équation ýV ).
Équation
ýV-
M est la quantité de l'eau
libérée par le manteau neigeux (mm/unité temps) et englobe
tout les processus d'ablation. Ta est la température moyenne
de l'air au pas de temps choisi en °C. T0 est la
température de référence, fréquemment égale
à 0°C. Le coefficient « FDF » est le facteur
degré jour (mm/ °C/jour). La principale difficulté dans ce
modèle réside dans la détermination de FDF, qui doit
être optimisé ou fixé judicieusement par des mesures sur le
terrain. Dans notre cas, le FDF est calculé par différentes
manières qui seront détaillées ci après.
Équation
ýV-
Avec :
X un coefficient estimé à 0.3 selon (Makhlouf,
1994) ;
P est la hauteur de pluie en mm.
La fonte totale est sera donc la somme des deux types de fonte
(
Équation ýV ):
Équation
ýV-
· Si la température de l'air est
inferieure à 0°C et si les précipitations
tombent sous forme neigeuse, la quantité tombée () s'additionne
au manteau neigeux.
Comme indiqué dans la
Figure ýV deux types de stockage sont
nécessaires pour continuer le calcul pour chaque pas de temps : la
hauteur de neige (H) et l'équivalent en eau
(SWE).
La hauteur du manteau neigeux à l'instant t+1
(H(t+1)) est reliée à la
hauteur à l'instant (t) H(t) par les
variations des chutes de neige entre les deux pas de temps et la
quantité de la fonte calculée par l'
Équation ýV .
Équation
ýV-
Les équivalents en eau sont calculés comme le
produit des hauteurs et des densités (
Équation ýV ).

Figure ýV- : Organigramme des étapes de calcul du
modèle degré jour
V.3.2.2 Calibration
et validation du modèle
Dans un modèle simple d'indice de température le
principal paramètre qui détermine la fonte est le facteur de
fonte (FDF). Ce dernier est affecté essentiellement par les
températures de l'air et aussi par plusieurs variables qui sont
spatialement ou temporellement reliées à l'énergie
nécessaire pour la fonte. Les valeurs de FDF, trouvées dans la
littérature varient entre 1 et 8 mm/°C/jour (Singh, P. et al.,
2000 ; Hock et al., 2003). Suite aux changements des
propriétés de la neige au cours de la saison, FDF varie aussi
selon la période de fonte.
La méthode degré jour n'est donc robuste qu'avec
un facteur de fonte variable (Rango et Martinec, 1995). De multiples approches
ont été tentées pour évaluer la variabilité
saisonnière de ce facteur :
En 1964, l'Organisation mondial de météorologie
(WMO) propose l'emploi des valeurs de FDF présentées dans le
Tableau ýV (en mm.
°C-1.j-1) sur la base de nombreuses mesures au
lysimètre. Ces valeurs varient suivant la nature de la surface (sol nu,
couvert forestier...).
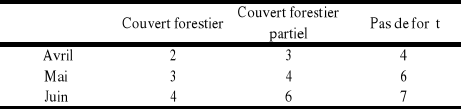
Tableau ýV- : Facteur de fonte selon
WMO
Anderson (1968) propose de prendre en compte la
variabilité saisonnière en posant (
Équation ýV ):
Équation ýV-
Où FDFmax et FDFmin sont les
valeurs saisonnières maximales et minimales du facteur de fonte et n le
numéro du jour d'une année commençant le 21 mars. Les
valeurs limites présentées dans le
sont proposées (en mm.
°C-1.j-1):
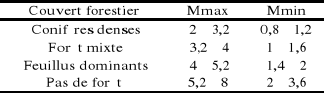
Tableau ýV-: Valeurs limites pour le facteur de
fonte selon Anderson (1968)
Des essais d'indexation du facteur de fonte
ont également été réalisés afin de pouvoir
calculer le facteur de fonte à partir de mesures de densité :
Martinec (1960) propose la relation suivante (
Équation ýV )
Équation ýV-
Kuustisto (1980) suggère plutôt les deux
équations (
Équation ýV et
Équation ýV ) pour les zones
forestières et les zones ouvertes respectivement.
Équation
ýV-
Équation
ýV-
Des études ont été menées afin de
comparer la méthode degré jour avec une approche radiative simple
(Brubaker et al.,1996 ; Cazorzi et al., 1996). Nous allons donc tester un
modèle qui tient compte de l'effet du rayonnement sur la fonte. Ce
modèle s'écrit comme suit (
Équation ýV ):
Équation
ýV-
Avec
FDF est le Facteur de fonte,
cm°C-1J-1 ; la densité de neige, Kg/
m3 ; la densité de l'eau liquide égale à
103 kg/ m3 et Rnet le flux radiatif en
W.m-2.
Afin d'obtenir une simulation réaliste de la fonte, il
est fortement recommandé de calculer des valeurs locales du FDF. Cela
est faisable avec des mesures journalières de température et de
quantité de l'eau perdue par la fonte depuis le manteau neigeux. FDF est
donc comme la moyenne des températures positives de l'air. Dans notre
site d'étude on ne dispose pas de mesures de neige à la
précision journalière pour estimer le facteur de fonte, mais il
existe des mesures d'équivalent en eau espacées de 1 à 3
semaines entre novembre 2007 et avril 2008 au sommet d'Oukaimden à 3200
mètres d'altitude. En se basant sur des couples de dates de mesure de
SWE sur des épisodes de fonte clairement identifiés (i.e. sans
accumulation entre les deux dates du couple), le FDF calculé de proche
en proche varie de 2.5 en hivers à 5.0 mm/°C/jour au printemps. A
cet intervalle de temps, plusieurs erreurs peuvent êtres commises pour
estimer FDF. Ces erreurs sont dues essentiellement à des variations
diurnes des températures de l'air.
La
Figure ýV illustre la variation du facteur
de fonte dans le plateau d'Oukaimden lors de la saison 2007/2008. Elles
confirment les tendances prévues : les valeurs de FDF sont faibles
au début de la saison (environ de 3 mm/°C/J) lorsque la neige est
fraîche et augmentent avec le temps après que le manteau neigeux
eu subi des transformations et contient une proportion d'eau liquide.
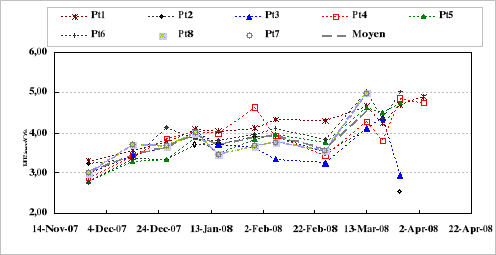
Figure ýV- : Variation du facteur de fonte
calculé à partir des densités mesurées sur sept
points nommés (Pt1, Pt2...Pt7) dans le plateau d'Oukaimden lors de la
saison 2007/2008.
Dans ce travail on va tester trois formules largement
utilisées pour obtenir le facteur de fonte
(FDF). Il s'agit ici de la relation empirique de
Martinec (1960) représentée par l'
Équation ýV , la relation
linéaire du FDF avec la densité suggérée par
Kuustisto (1980) selon l'
Équation ýV et la relation
intégrant le rayonnement net comme facteur de fonte, appelé par
la suite « RAD » (
Équation ýV ).
La calibration des modèles a été
effectuée avec les données de l'année 2007/2008 et la
validation sur les autres saisons (2003/2004, 2004/2005 et 2005/2006). Dans un
premier temps les simulations des équivalents en eau ont
été réalisées avec les valeurs initiales
proposées pour chaque méthode. La
Figure ýV montre les différentes
simulations effectuées avec les trois modèles. Une simulation
très éloignée des valeurs observées est obtenue
avec les deux modèles de Kuustisto et RAD. Par
contre, le modèle de Martinec simule mieux les équivalents en eau
sans aucune calibration avec un coefficient de détermination
égale à 0.81 et un RMSE de 43 mm.

Figure ýV- : simulation des équivalents
en eau en 2007/2008 par la méthode degré jour à l'aide de
trois modèles de calcul de facteur fonte
Puisque les trois modèles utilisés ici ont des
formulations empiriques, une calibration des paramètres est
nécessaire. Chaque formule est liée avec deux coefficients qu'on
va nommés « A » et « B ». Le but
recherché lors de la phase de calibration est de minimiser l'erreur
quadratique moyenne (RMSE) entre les valeurs observées et
calculées. La gamme de variation du paramètre
« A » a été fixée à
l'intervalle [0 30] avec un pas de 0.1 pour les deux modèles
Kustistio et RAD. La gamme du paramètre « B » a
été fixée à [-6 10] avec un pas de 0.1 et à
[-0.006 0.01] avec un pas de 0.001 pour les modèles Kustistio et RAD
respectivement. Ainsi, la gamme des deux paramètres donnant 95% de
l'efficience a été recherchée. La variation de l'erreur
quadratique moyenne en fonction des deux paramètres
« A » et « B » obtenues pour les
deux modèles est représentée dans les deux figures (
Figure ýV et
Figure ýV ). Le
Tableau ýV montre la comparaison de
l'efficience entre les trois modèles avant et après calibration.
Sur la saison 2007/2008, après calibration, les simulations des
équivalents en eau obtenues par les trois modèles sont largement
améliorées. L'ajout des effets du rayonnement solaire dans le
modèle RAD améliore nettement les simulations hivernales,
processus non simulés avec les deux autres modèles. Le
modèle RAD a donné l'efficience optimale, avec une
corrélation de 0.86 et un Bias de 2.32 mm.
|
Modèle
|
|
R²
|
RMSE (mm)
|
BIAS (mm)
|
|
Martinec
|
Non Calibré
|
0,76
|
40,00
|
-17,00
|
|
Calibré
|
0,76
|
40,00
|
-17,00
|
|
kustusto
|
Non Calibré
|
0,41
|
86,57
|
-62,59
|
|
Calibré
|
0,80
|
35,66
|
-13,00
|
|
RAD
|
Non Calibré
|
0,27
|
99
|
-72,97
|
|
Calibré
|
0,86
|
30
|
-2,32
|
Tableau ýV-: Performances des modèles
degré-jour dans l'estimation des équivalents en eau sans
calibration et sans calibration en 2007/2008
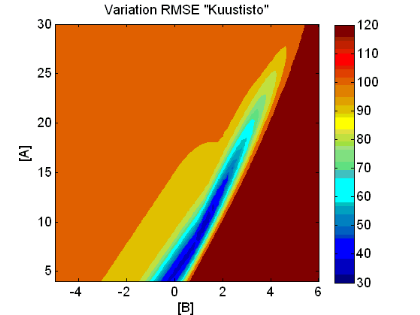
Figure ýV-:
variation de RMSE selon les deux paramètres A et B du modèle de
Kustisto en 2007/2008
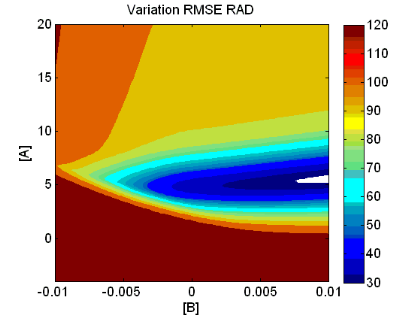
Figure ýV- : Variation du RMSE selon les
deux paramètres A et B du modèle avec rayonnement
« RAD » en 2007/2008
La gamme des paramètres donnant 95% de l'efficience
obtenues lors de phase de calibration, correspond à la bande bleue
foncée des deux figures (
Figure ýV et
Figure ýV ). Cette gamme est
appliquée pour valider les modèles sur les saisons 2003/2004,
2004/2005 et 2005/2006. Le
Tableau ýV résume les
résultats de simulation des équivalents en eau et des hauteurs de
neige obtenus en utilisant les modèles degré jour et ISBA-ES. En
2003/2004, les équivalents en eau (SWE) et les hauteurs de la neige sont
bien simulés avec le modèle ISBA-ES (erreur quadratique moyen
(RMSE) des SWE est de 30 mm) qu'avec les autres modèles degré
jour (RMSE des SWE dépasse 39 mm). Les résultats des simulations
des SWE et des hauteurs de la neige avec les différents modèles
sont semblables pour les autres saisons (2004/2005, 2005/2006 et 2007/2008),
sauf pour l'année 2005/2006 où les RMSE des SWE varient de 41
à 48 mm en utilisant les modèles Kuustusto, RAD et ISBA-ES et un
RMSE de 70 mm obtenu par le modèle de Martinec. La
Figure ýV monte la dynamique des
équivalents en eau simulés avec les trois modèles
degré jour. Ces dernières restituent bien les variations des
équivalents en eau sur l'année de calibration. Par contre en
validation le modèle Martinec n'arrive à bien simuler les
équivalents en eau qu'au début de la saison. Alors que les deux
modèles Kuustisto et RAD donnent une meilleure simulation sur toutes les
saisons.
|
|
Hauteurs(m)
|
Equivalent en eau (mm)
|
|
|
|
2003/2004
|
2004/2005
|
2005/2006
|
2007/2008
|
2003/2004
|
2004/2005
|
2005/2006
|
2007/2008
|
|
R²
|
Martinec
|
0,53
|
0,91
|
0,85
|
0,69
|
0,54
|
0,90
|
0,85
|
0,76
|
|
Kuustisto
|
0,84
|
0,91
|
0,92
|
0,71
|
0,87
|
0,94
|
0,95
|
0,80
|
|
RAD
|
0,75
|
0,93
|
0,93
|
0,85
|
0,80
|
0,94
|
0,94
|
0,86
|
|
ISBA-ES
|
0,84
|
0,89
|
0,94
|
0,76
|
0,86
|
0,89
|
0,91
|
0,86
|
|
RMSE
|
Martinec
|
0,22
|
0,06
|
0,22
|
0,14
|
71,95
|
22,97
|
70,02
|
40,13
|
|
Kuustisto
|
0,16
|
0,05
|
0,13
|
0,13
|
39,31
|
18,25
|
41,05
|
35,66
|
|
RAD
|
0,13
|
0,05
|
0,15
|
0,16
|
41,02
|
16,72
|
42,50
|
29,56
|
|
ISBA-ES
|
0,10
|
0,05
|
0,14
|
0,13
|
29,98
|
19,00
|
48,61
|
30,88
|
|
BIAS
|
Martinec
|
-0,09
|
-0,03
|
-0,15
|
-0,05
|
-39,79
|
-9,70
|
-34,41
|
-17,09
|
|
Kuustisto
|
0,04
|
-0,01
|
-0,07
|
-0,04
|
3,62
|
-5,01
|
-11,06
|
-13,00
|
|
RAD
|
-0,05
|
-0,01
|
-0,10
|
0,08
|
-19,83
|
-4,15
|
-17,00
|
2,32
|
|
ISBA-ES
|
-0,05
|
-0,02
|
-0,06
|
-0,02
|
-8,69
|
-8,83
|
-7,59
|
-2,88
|
Tableau ýV- : Performances des trois
modèles degré-jour et le modèle ISBA-ES à la
simulation des hauteurs et des équivalents en eau dans la station
d'Oukaimden.
Figure ýV- : Equivalent en eau
modélisé par trois modèles degré-jour et
observés à la station de l'Oukaimden en
2007/2008.
Les deux types de modèles, à base physique et
simple avec les différentes formulations, abordés ci-dessus sont
appliqués à la station météorologique de
l'Oukaimden. A ce niveau, on constate que le modèle ISBA-ES reste le
plus performant pour identifier les différentes grandeurs de variation
de la fonte et la sublimation. La mise en ouvre de ce type de modèle
à l'échelle spatiale nécessite la disponibilité de
plusieurs paramètres climatiques qui sont très rares dans notre
zone. Pour cela, on va tester dans la section suivante la performance du
modèle degré jour à l'échelle du bassin versant de
Rheraya.
V.4 Spatialisation de la fonte à l'échelle du
bassin versant de Rheraya
L'estimation de la fonte à l'échelle du bassin
versant constitue une étape déterminante pour la simulation des
débits. En 1986, l'Organisation météorologique Mondiale
« OMM » a comparée 11 modèles de fonte
différents appliqués sur plusieurs pays (Martinec et Rango,
1989 ; Tarboton et Luce 1996). Les résultats de cette
comparaison sont :
- La majorité des modèles utilisent l'approche
dégrée jour ;
- La subdivision du bassin versant en tranches d'altitudes est
importante ;
- La détermination du gradient de température
doit être analysée avec précisons ;
- L'interception des neiges par les forêts est aussi
importante à estimer.
Dans notre cas, on ne dispose que d'une seule station
météorologique nivale mesurant les différents
paramètres nécessaires pour appliquer un modèle de bilan
d'énergie. Pour cela, on a retenu la méthode degré jour
pour évaluer la fonte à l'échelle du bassin versant. Les
données de température et les précipitations sont
habituellement disponibles et on peut les spatialiser.
La vérification du modèle de fonte des neiges
est effectuée en comparant les surfaces de neige issues de la
télédétection avec celles simulées.
V.4.1 Spatialisation des données
d'entrées et de la fonte
Dans un modèle de fonte de type degré jour, il
faut spatialiser les températures et les précipitations. A cette
fin, nous avons utilisé un modèle numérique de terrain
(MNT) de 90 m de résolution (voir section
Le Modèle Numérique de Terrain).
Tous les calculs menés dans cette étape ont été
effectués sur des cartes de même résolution que le MNT.
Les températures de l'air sont spatialisées par
deux méthodes, en appliquant le modèle du gradient altitudinal
(GRAD), généralement appliqué pour les zones
montagneuses, et notre modèle de spatialisation de la
température (MSPAT) qui prend en compte les effets topographiques
(expositions et pentes des versants) et l'effet de l'angle solaire (
Spatialisation de la température de l'air dans
les montagnes atlasique à l'aide des données de l'infrarouge
thermique).
Pour calculer le gradient moyen des précipitations, les
données enregistrées au niveau des deux stations d'Oukaimden
(2600 m d'altitudes) et de Tahanaout (1040 m) sur la période (1998-2005)
ont été utilisées. La valeur moyenne obtenue est
égale à 0,03 mm/100 m. Afin d'obtenir les précipitations
séparées par phase solide ou liquide, nous avons appliqué
sur chaque pixel les seuils des températures illustrés dans la
Figure ýV .
Après la spatialisation des précipitations et
des températures de l'air sur tout le bassin versant, les
densités et les équivalents en eau sont ensuite calculés
pour chaque pixel en appliquant l'algorithme de la
Figure ýV .
Les deux modèles de fonte avec deux différentes
formules déterminant le facteur degré jour appliqués
à l'échelle locale sont ensuite généralisés
sur le bassin versant de Rheraya. Il s'agit ici de la formule utilisée
sans calibration de Martinec, 1975 et le modèle calibré de
Kuustisto, 1980) (
Équation ýV et
Équation ýV ).
V.4.2 Vérification du
modèle
V.4.2.1 Simulation
des surfaces de neige
Les cartes obtenues à l'aide du modèle de fonte
sont des équivalents en eau (SWE). Afin de pouvoir quantifier
l'efficience des modèles de fonte à l'échelle du bassin
versant, les seules informations disponibles sont les cartes de surface de
neige (SCA) obtenues à partir de la télédétection
(carte MODIS et VEGETATION). A cet effet, il faut transformer les cartes des
équivalents en eau en cartes des surfaces de neige.
La dérivation des surfaces de neige (SCA) sans
donnée de télédétection dans un bassin versant
quelconque requiert des observations des équivalents en eau (SWE) et des
SCA sur plusieurs années au cours de la période de fonte. Par
exemple les études effectués par (Luce et al., 1999; Luce et
Tarboton, 2004) pour dériver les courbes de variation des surfaces de
neige sont issues de campagnes intensives de mesure pour des petits bassin
expérimentaux. Ces données plus détaillées sont
indisponibles dans plusieurs endroits du monde, c'est le cas de notre zone. Les
fractions des SCA dans cette étude sont donc calculées selon une
approche asymptotique au SWE donnée par l'
Équation ýV et la
Figure ýV selon Anderson (1976).
SCAMAX est la fraction maximale de SCA, fixée à 0.95.
Équation ýV-
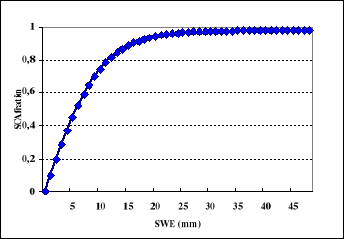
Figure ýV- : Surface de neige en fonction
des équivalents en eau selon Anderson (1976)
V.4.2.2 Effet de la
sublimation
Nous avons montré dans les sections
précédentes qu'une quantité importante de l'eau du manteau
neigeux est sublimée (jusqu'à 40%) (
Figure ýV ).Ainsi, ce
phénomène est lié principalement à la vitesse du
vent (
Figure ýV et
Figure ýV ). Cependant, pour des raisons de
disponibilité des stations météorologiques bien reparties
à l'échelle du bassin versant, il est difficile de
déterminer la distribution spatiale des quantités de l'eau
sublimée. Aussi, pour simplifier le calcul, nous avons
considéré que la proportion calculée par ISBA-ES dans le
site d'Oukaimden est la même sur tout le bassin versant. Pour faciliter
l'utilisation de ce paramètre, on retranche la perte due à la
sublimation dès l'observation de précipitations solides, comme si
la sublimation se produisait instantanément lorsque la neige se
dépose.
La
Figure ýV montre une comparaison des
simulations des surfaces de neige dans le bassin versant de Rheraya par les
deux modèles de fonte utilisés sans (colonne de gauche) et avec
(colonne de droite) la prise en compte l'effet de sublimation. Les SCA
simulées avec un coefficient de sublimation sont plus proche des SCA
observées par MODIS, dans ce cas les nuages des points sont plus
centrés. Dans le
Tableau ýV on a résumé les
statistiques des résultats relatives à cette comparaison. Avec
les deux modèles on note une amélioration de l'estimation des SCA
en éliminant la partie sublimée.
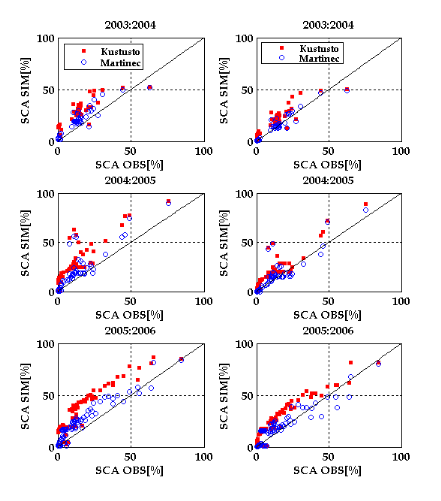
Figure ýV- : SCA calculées à
partir des données MODIS et simulées par les deux modèles
de fonte Kuustisto et Martinec sans (colonne de gauche) et avec sublimation
(colonne de droite) dans le bassin versant de Rheraya
|
|
|
Kuustisto
|
Martinec
|
|
Efficience
|
Sans sublimation
|
Avec sublimation
|
Sans sublimation
|
Avec sublimation
|
|
2003/2004
|
RMSE (%)
|
14,98
|
8,66
|
7,70
|
3,93
|
|
BIAIS (%)
|
13,18
|
6,32
|
5,40
|
0,68
|
|
Equation de Regression Y= aX+b
|
R²
|
0,69
|
0,77
|
0,81
|
0,89
|
|
a
|
0,79
|
0,86
|
0,86
|
1,01
|
|
b
|
-7,30
|
-3,40
|
-2,54
|
-0,78
|
|
2004/2005
|
RMSE (%)
|
19,51
|
11,46
|
12,75
|
8,80
|
|
BIAIS (%)
|
16,43
|
8,33
|
7,59
|
2,64
|
|
Equation de Régression Y= aX+b
|
R²
|
0,73
|
0,80
|
0,73
|
0,75
|
|
a
|
0,62
|
0,73
|
0,63
|
0,73
|
|
b
|
-4,90
|
-2,34
|
0,24
|
1,73
|
|
2005/2006
|
RMSE (%)
|
19,50
|
12,17
|
9,54
|
7,43
|
|
BIAIS (%)
|
17,61
|
10,40
|
7,65
|
3,20
|
|
Equation de Régression Y= aX+b
|
R²
|
0,85
|
0,88
|
0,90
|
0,85
|
|
a
|
0,76
|
0,88
|
0,92
|
1,01
|
|
b
|
-9,74
|
-7,31
|
-5,85
|
-3,42
|
Tableau ýV- : Statistiques relatifs
à l'estimation des SCA à l'échelle du bassin versant de
Rheraya sans et avec l'élimination de la perte par sublimation en
utilisant deux modèles de fonte Kuustisto et Martinec
La
Figure ýV illustre les courbes de
variation des SCA générées par les deux modèles en
appliquant les corrections expliquées ci-dessus. Le modèle
Kuustisto surestime les SCA (bias=7%), alors que le biais n'est que de 2% pour
le modèle de Martinec. Cette distinction est surtout nette en
période de fonte, du 1er décembre 2003 à mi
février 2004, à partir de mars 2005 et depuis février 2006
jusque la fin de saison. On remarque ici qu'avec le modèle de Martinec
sans calibration à l'échelle locale on reproduit des SCA proches
de celles observées par la télédétection.
Figure ýV- :
courbes de variation des surfaces de neige observées par MODIS et
calculées par les deux modèles simples de fonte, Kuustusto et
Martinec.
· Conclusion
Dans ce chapitre on a analysé les processus de perte et
d'accumulation de la neige au niveau de la station d'Oukaimden à 3200
mètres d'altitude à l'aide de deux types de modèle. Un
modèle de bilan d'énergie (ISBA-ES) et des modèles plus
simples dites degré jour. Pour ces derniers, on a testé trois
types de formulation : Un modèle utilisé sans calibration
(Martinec), le modèle de Kuustisto calibré et un modèle
intégrant le rayonnement net(RAD).
A l'échelle locale, les équivalents en eau (SWE)
simulés sur toutes les saisons par les deux formules de Kuustisto et RAD
après calibration sur 2007/2008 sont plus efficaces que la formule de
Martinec. Ces résultats sont comparables avec ceux obtenus pour le
modèle ISBA-ES. Ce dernier simule en revanche mieux les
équivalents en eau pour les saisons à longue période
hivernale où le manteau neigeux subit plus de transformations (exemple
des deux saisons 2003/2004 et 2007/2008). Les densités de la neige sont
globalement bien simulées avec une surestimation à la fin de mois
de février 2008 due à la forte quantité d'eau liquide
contenue dans le manteau neigeux. Les albédos modélisés
par ISBA-ES sont surestimés par rapport à ceux enregistrés
dans la station météorologique et surtout dans les
périodes de faibles hauteurs de neige où la fraction sol peut
influencer la réflexion des rayonnements. Le modèle ISBA-ES nous
a permis de mieux comprendre l'interaction des processus d'ablation de neige
dans le Haut Atlas. Les pertes par sublimation constituent une part non
négligeable d'eau, soit 16 à 37% du total. Le
phénomène de sublimation se produit d'une manière stable
le long de la saison, alors que la libération des eaux par le processus
de la fonte a lieu pendant de courtes périodes.
D'après cette étude on constate qu'un
modèle de bilan d'énergie est préférable lorsqu'on
s'intéresse aux processus physiques du manteau neigeux. Dans notre zone,
vu la rareté des données cela n'est plus applicable à
l'échelle du bassin. Dans ce contexte, les modèles degré
jour restent la meilleure façon d'estimer la fonte. Les surfaces de
neige issues de la télédétection sont utilisées
pour estimer les performances de deux modèles simples à
l'échelle du bassin versant. Les pertes par sublimation obtenues dans le
site d'Oukaimden à l'aide d'ISBA-ES sont retranchées directement
des précipitations solides, cela améliore la cohérence
entre les surfaces de neige simulées et observées. On conclue
aussi qu'une calibration d'un modèle simple à l'échelle
locale n'est pas nécessaire pour une application à
l'échelle spatiale. La formule de Martinec est performante pour
générer des SCA dans notre zone. Cette formule est celle
utilisée par le modèle hydrologique SRM souvent appliqué
à des fins opérationnelles. Dans le chapitre qui suit on va
évaluer la relation entre fonte et débit à l'aide du
modèle SRM dans cinq sous bassins versants du Haut Atlas.
Chapitre VI : Evaluation de l'apport de
la fonte des neiges aux débits dans principaux oueds du Haut Atlas de
Marrakech
Dans ce chapitre, on va analyser l'apport des données
de télédétection à la modélisation
hydrologique. La contribution de la fonte des neiges aux débits des
oueds atlasiques sera évaluée à l'aide du modèle
hydrologique de fonte « SRM ». Les différents
traitements relatifs à ce travail sont détaillés dans
l'article (Boudhar et al., 2009) à paraître en décembre au
journal des sciences hydrologiques. Une synthèse de cet article est
présentée au début de ce chapitre.
VI.1
Présentation de l'article (boudhar et al. 2009)
Les eaux de fonte des neiges jouent un rôle important
dans le bilan hydrique des bassins versants du Haut Atlas. Cependant, la
contribution respective des précipitations liquides et solides aux
débits des oueds reste encore mal connue. Les données
hydro-climatiques mesurées in situ dans la région sont rares et
les stations météorologiques sont souvent installées dans
les basses altitudes. Vu le manque de données in-situ
représentatives sur l'ensemble des bassins versants montagneux du Haut
Atlas, la télédétection satellitaire reste une source
d'information attractive et complémentaire aux mesures de terrain et en
particulier la cartographie de l'enneigement.
L'utilisation des observations de superficies neigeuses pour
prévoir les débits a débuté en 1930 par l'usage de
photographies aériennes (Potts, 1937). Depuis 1972, les informations
issues du capteur NOAA-AVHRR (National Oceanic and Atmospheric
Administration-Advanced Very High Resolution Radiometer) ont été
utilisées pour modéliser la fonte de neige (Rango, 1986,1996).
Parmi les modèles de fonte utilisant la couverture neigeuse en
entrée, le modèle conceptuel de fonte de neige
« SRM » (Martinec, 1975) est largement utilisé dans
le monde, soit pour mieux comprendre les estimations du bilan hydrique du
bassin versant pour des chroniques connues (mode
« réanalyse ») , Rango et Fourgon Katwijk,
1990 ; Songweon Lee, 2005, soit pour la prévision des débits
(mode « prédiction ») en quasi temps réels
(Rango et Martinec, 1979 ; Shafer et al., 1982, Martinec, 1985, Martinec
et Rango, 1995 ; Rango et Martinec, 1997 ; Klaus Seidel, 1998, Jesko
et Schaper, 1999 ; Gomez et Landesa, 2002 ; Thomas et al., 2008).
Les données issues de la
télédétection permettent d'accéder à la
variabilité spatio-temporelle de l'enneigement, et ce pour de grandes
superficies. Cependant, l'acquisition de ces données par les satellites
se fait dans des conditions météorologiques diverses. Par
exemple, les images prises en présence de nuage ne sont pas utilisables
pour cartographier la neige. Ce cas est plus fréquent dans les
régions montagneuses où la nébulosité est
généralement élevée. Dans le Haut Atlas marocain,
la chute de neige et sa fonte peuvent avoir lieu en une seule semaine. Dans ces
conditions et pour mieux étudier le couvert nival, il faut avoir des
séries d'images avec une fréquence élevée (en
moyenne, deux images par semaine). Afin de compenser le manque de
continuité dans les observations satellites, des informations
supplémentaires sur les variables d'états de l'extension
neigeuses peuvent être obtenues à partir des modèles
forcés avec des données mesurées à la surface
(températures de l'air, humidité, vitesse du vent, rayonnement
solaire, ...). La méthode qui combine les deux informations,
obtenues à partir de la télédétection et de la
modélisation et qui prend en compte les limites de chaque type de
donnée, reste la plus recommandée. Elle est connue sous le nom
d'assimilation des données (McLaughlin, 1995).
Dans ce chapitre nous avons utilisé le modèle
hydrologique « SRM » pour simuler les débits dans
les exutoires des cinq sous bassins versants atlasiques. Deux méthodes
d'estimation des SCA sont utilisés à l'entrée pour
évaluer la potentialité du modèle SRM : 1) surfaces
issues des images satellite et 2) surfaces simulées à l'aide d'un
modèle de fonte simple degré jour. Dans une première
étape nous avons effectué une analyse de sensibilité des
paramètres du modèle en deux modes : MOD1 avec des surfaces
de neige de télédétection et MOD2 avec des surfaces de
neige simulées. Cette étude de sensibilité permet ainsi
d'identifier les paramètres sur lesquelles la plus grande attention
devra être portée. Dans une deuxième étape, nous
avons procédé à la calibration du modèle en
introduisant le concept d'équifinalité des paramètres. Ce
phénomène peut être engendré lorsque des jeux de
paramètres significativement différents conduisent aux
mêmes résultats de simulation. Pour mettre en évidence le
phénomène de l'équifinilité nous avons produit des
contours de variation de l'efficience pour chaque paire de paramètres.
Cet exercice a été appliqué pour les cinq sous bassins
versants sur l'année 2005. Le choix de cette année est
conditionné par la disponibilité des données plus fiables
que les autres années (débits et pluies). Les jeux de
paramètres donnant 90% de l'efficience maximale ont été
sélectionnés comme « paramètres
acceptables » et utilisés pour la validation du
modèle.
Généralement, les simulations des débits
avec le modèle SRM en utilisant les deux types de surface de neige en
entrée sont satisfaisantes et comparables à l'échelle
saisonnière. Cependant, pour certains événements
localisés, on note une différence significative entre les
débits observés et simulés. Cela se produit lorsque le
réseau des pluviomètres est trop dispersé pour enregistrer
tous les événements pluvieux ou lorsque des erreurs des
estimations de la température influence la partition pluie/neige. Dans
les deux cas, la méthode utilisant les données interpolées
de télédétection (MOD1) améliore la
prévision des débits à court terme. Les observations des
surfaces de neiges peuvent être utilisées pour détecter les
événements pluvieux ou neigeux non enregistrés par les
stations météorologiques. La contribution du manteau neigeux aux
débits des oueds des cinq sous basins versants a été
déterminée. On distingue deux bassins (Rheraya et Ourika)
où le régime nival est très marqué avec un apport
de neige important qui peut atteindre 50% pour les saisons humides et plus de
20% pour les saisons sèches. Dans les exutoires des deux bassins de Nfis
et Zat, cet apport varie de 7 à 38 % et de 6 à 44%,
respectivement. Le bassin versant de R'dat est moins influencé par la
fonte des neige que les autres bassins cités, la neige contribue
à environ 2% à 15%. L'apport moyen de la fonte de la neige dans
ces oueds calculée entre 2002 et 2005 est d'environ 25%.
|
Evaluation of the snowmelt runoff model in the Moroccan
High Atlas Mountains using two snow-cover estimates
ABDELGHANI BOUDHAR1, LAHOUCINE
HANICH1, GILLES BOULET2, BENOIT DUCHEMIN2,
BRAHIM BERJAMY3 & ABDELGHANI CHEHBOUNI2
1 Faculté des Sciences et Techniques de
Marrakech, Avenue A. Khattabi, BP 549, Marrakech, Morocco
boudhar22@yahoo.fr
2 CESBIO, (Université de Toulouse, CNRS, CNES,
IRD), 18 Avenue Edouard Belin, bpi 2801, F-31401 Toulouse Cedex 9,
France
3 Agence du Bassin Hydraulique de Tensift, Marrakech,
Morocco
Hydrological Sciences-Journal-des Sciences
Hydrologiques, 54(6) December 2009
|
RÉSUMÉ
Au centre du Maroc, La chaîne montagneuse du Haut Atlas
constitue un véritable château d'eau pour les plaines arides
avoisinantes, et ce à la fois grâce aux précipitations
liquides et solides. Dans ce contexte, on a évalué la performance
du Snowmelt Runoff Model (SRM) dans les cinq principaux sous bassins versants
du Haut Atlas. En raison de la très faible densité des stations
climatiques dans le Haut Atlas, les processus de chute et de fonte des neiges
sont difficiles à contrôler avec seulement des données
météorologiques. Afin de compenser l'absence des données
in-situ, des cartes d'enneigement sont aussi dérivées à
partir des données issues de la télédétection. Nous
avons comparé la performance de SRM avec les deux types de cartes. Les
surfaces enneigées déduites par ces deux méthodes sont
généralement comparables dans tous les sous bassins versants, et
des simulations satisfaisantes des débits ont été obtenues
à l'échelle saisonnière en utilisant les deux types de
surface de neige. En revanche, des différences significatives peuvent
être observées pour certaines crues, avec une meilleure
prévision des débits lorsque les données de la
télédétection sont utilisées.
Mots clés : Cartographie de
neige ; SPOT-VEGETATION ; Modélisation de la fonte de
neige ; Haut Atlas ; Maroc.
ABSTRACT
In the centre of Morocco, the High-Atlas mountain range
represents the most important water storage for the neighbouring arid plains
through liquid and solid precipitation. In this context, we evaluated the
performance of the Snowmelt Runoff Model (SRM) on the five main tributary
watersheds of the High-Atlas range. Due to the very low density of climate
stations in the High Atlas, snowfall and snowmelt processes are difficult to
monitor with the sole meteorological data. In order to compensate for the lack
of in-situ data, snow maps are also derived from remotely-sensed data. We
compared the streamflow forecasting performance when the model is driven by one
or the other snow cover area estimates. Both estimates are generally comparable
in all watersheds, and satisfactory streamflow simulations are obtained at
seasonal timescales using both snow-cover products. But significant differences
can be observed for selected storms, with more accurate streamflow predictions
when the remotely-sensed data is used.
Keywords: Snow mapping;
SPOT-VEGETATION; Snowmelt runoff modelling; High-Atlas Mountains,
Morocco
·
Introduction
In most arid and semi arid regions of the world, water
resources are limited, and under severe and increasing pressure due to
expanding needs for populations, tourism, industry and agriculture. Water
resources are also affected by any succession of droughts. Several very dry
years have been observed in the Mediterranean region over the last decade, and
their frequency could increase due to climate change (Ceballos-Barbancho et
al., 2008). In these regions, mountains may obviously play an important role in
the regional water balance (Flerchinger & Cooley, 2000; Khazaei et al.,
2003; Pitlick 1994; Viviroli et al., 2003), but the contribution of snow and
rain to the annual and multi-annual water balance is still largely unknown.
This is the case in the centre of Morocco, where the High-Atlas mountain range
represents the most important water storage for the neighbouring arid plains
through liquid but also solid precipitation (Matthews, 1989, Chaponniere et
al., 2005; Boudhar et al., 2007). Snowfall usually occurs from November to May
at altitudes above 1400m, but the snow cover is rarely continuous: snow can
fall and melt within one week. However, in the highest parts of the High Atlas
range, snow is stored during several weeks to several months. High melting
rates contribute to baseflow from late winter to early summer, which can be
beneficial to the agriculture.
Remote sensing observations are particularly useful for
providing spatially distributed input data for snowmelt runoff modelling (e.g.
Dozier, 1989; Matson, 1991; Hall et al., 2002), and, in particular, snow cover
areas in the High-Atlas mountains (Hanich et al., 2003; Chaponnière et
al., 2005; Leroux, 2006; Boudhar et al., 2007). However, current satellites do
not acquire cloud free images with a satisfying (optimally, daily) frequency,
especially in mountainous regions where cloudiness is generally high. In order
to compensate for the lack of continuity in remote sensing observations,
additional information about snow state variables can be obtained from land
surface models that are forced with surface meteorological (precipitation, air
temperature and humidity, wind) and radiative variables (downward solar and
longwave radiation). Ideally, a system that optimally combines snow information
from both remote sensing observations and modelling predictions and at the same
time accounts for the limitations of each should provide estimates that are
superior to those derived from either models or remote sensing alone. This
method is commonly known as data assimilation (McLaughlin, 1995).
Data assimilation is a way to integrate data from a variety of
sources with different resolutions and accuracies with model prediction to
improve deterministic model accuracy (McLaughlin et al., 2005). It has been
applied in hydrology with increasing frequency in recent years. Data
assimilation is used not only to update the hydrological model states that
optimally combine model outputs with observation, but also to quantify
observational and hydrological model errors. Various data assimilation
techniques are used in hydrologic application. Brasnett (1999) used statistical
interpolation to assimilate global synoptic snow depth observations into a
simple snow accumulation/snowmelt model. Sun et al. (2004) used an extended
Kalman filter to assimilate synthetically generated snow water equivalent
observations into a catchment-based land surface model. Andreadis &
Lettenmaier (2006) assimilated snow cover area (SCA) estimates derived from the
MODIS sensor as well as snow depth derived from the AMSR sensor into a
macroscale hydrological model. Clark et al. (2006) also used SCA observations
as part of an ensemble Kalman filter to modify the statistical distribution of
snow in a mountainous watershed. They applied a simple, lumped
snowpack/water-balance model and carried out synthetic experiments that showed
that SCA assimilation does not result in significative improvement of simulated
streamflow. However, they acknowledge that «satellite SCA information will
be most useful in basins where snow cover is ephemeral», which is the case
in the High Atlas range.
The most widely used model designed to integrate SCA
information directly as an input is the Snowmelt Runoff Model (SRM, Martinec et
al., 1975). This approach is equivalent to the «direct insertion»
method and is very efficient when model errors are larger than observation
errors. Most other approaches simulate SCA and, when a satellite observation is
available, they readjust the Snow Water Equivalent (SWE) to minimize the
difference between simulated and observed SCA by mean of a Kalman Filter (Clark
et al., 2006, Slater & Clark., 2006) or a variational assimilation scheme
(Seo et al., 2003). Between two image acquisitions, they simulate the evolution
of the snowpack with a snowfall/snowmelt model that uses detailed distributed
meteorological data. These approaches are rather difficult to implement and
perform accurately in well instrumented catchments where observation and model
errors have comparable orders of magnitude. For most mountainous regions,
partly due to accessibility constraints, rainfall/snowfall and other
meteorological information are often lacking, especially in the highest parts
of the catchments. It is the case in the High Atlas range where most of the
meteorological stations, which measure routinely only bulk precipitation and
air temperature, are located close to the catchment's outlet. The more complex
models and assimilation methods are likely to fail or underperform in such
poorly instrumented environments. This explains why many operational streamflow
forecasting methods favour the simple and robust SRM model as well as the
direct insertion method. Of course, driving models such as SRM with good SCA
estimates remains a challenge in mountainous regions where spatially
distributed climatic data is lacking and where remote sensing data cannot be
acquired with a sufficient temporal resolution.
In this context, the first objective of this paper is to
compare snow cover area estimated by remote sensing and simulated by spatially
interpolated meteorological data. The second objective is to test the
performance of the SRM model for five sub-catchments of the High Atlas range
during the years 2002-2005 and to study the impact of choosing either of the
two SCA estimation methods on this performance: (1) snow depletion curves
obtained from a temporal interpolation of SPOT-VEGETATION SCA estimates, and
(2) a snowfall/snowmelt degree day model forced with spatially interpolated
meteorological data.
VI.2 Study area
The study area takes place in the Tensift watershed in central
Morocco (
Figure ýII ). This watershed covers
20 450 km2 and is composed by three parts: the northern
`Jbilet' hills, the `Haouz' plain and the northern side of the high Atlas
mountain range. The Tensift wadi flows sporadically from east to west and is
supplied mainly from the basin's south bank: the Atlas north hillsides.
The High-Atlas is mainly composed by metamorphic and eruptive
formations, which are impervious and generate overland flow. Some pervious
zones are still present, due to calcareous and marly sandstone formations or
local weathering of the impervious formations. These pervious zones are
probably responsible for an additional delay in lateral subsurface flow. The
Atlas's relief is very sharp with steep slopes. Land cover consists in sparse
trees below 2000m above sea level (coniferous and juniper), and bare rocks
above. Soils are almost non-existent on the slopes because of high erosion
rates. In the very narrow valleys, where the eroded sediments accumulate,
deeper soils are present on which crops are grown. This mountain range, about
800 km long and 60 km wide, is oriented NE-SW. The highest peak in the region
is the Jbel Toubkal (4167 metres above mean sea level), the highest summit of
North Africa. The High Atlas range is the region's water tower, supplying
several big irrigated areas in the surrounding plains of Haouz in the north, as
well as Souss, Drâa and Dades in the south. In these regions, more than
85% of the available water is used by agriculture.
Located in the surroundings of Marrakech city (
Figure ýII ), the Tensift watershed was
intensively monitored as a pilot site of the SUDMED program (Chehbouni et al.,
2008). The annual rainfall ranges from around 150 mm in the driest part of the
plain to about 800 mm in the mountain. Both rain and snow are very irregular in
time and space. There is no glacier in the area; therefore meltwater originates
totally from snow.
The main five tributary sub-catchments of the Tensift
watershed are located at south and east of the Marrakech city, between
latitudes 30°87 ' to 31°66' North and longitudes 22°7 'to
8°67' West. They form the southern boundary of the Tensift basin. They are
from West to East: Nfis, Rheraya, Ourika, Zat and R'Dat (
Figure ýII ). To run the SRM model, the
sub-catchments were subdivided into eight elevation zones. This partition was
done using a Digital Elevation Model (DEM) at 90m spatial resolution provided
by the Shuttle Radar Topography Mission (SRTM) after an 11-day mission in
February of 2000.
Figure ýVI illustrates the hypsometric
variation of the study area and the main geographic characteristics of each
sub-catchment are summarized in
Table ýVI . The eight 400m elevation bands
of
Figure ýVI are chosen as individual
hydrological response units for the SRM model. Relevant climatic input data
will thus be required for each of these bands. The sub-catchments can be
classified in two groups: basins with high altitudes (Ourika and Rheraya) and
basins with lower elevations (Nfis, Zat and R'Dat).
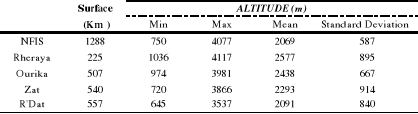
Table ýVI- :
Geographic characteristics of the study sub-catchments.
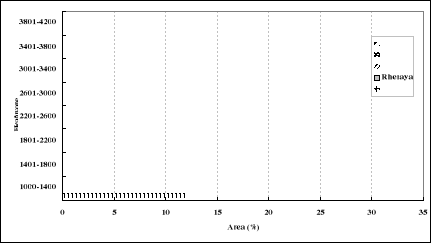
Figure ýVI-: Hypsometric variations for the
five study sub-catchments.
VI.3
Hydro-meteorological data
In addition to daily snow cover area (SCA), daily estimates of
air temperature and precipitation are needed to run the SRM for each
altitudinal band. These data were obtained from meteorological stations inside
or around the five sub-catchments (
Figure ýII ). For this study, daily average
air temperature data recorded at the Oukaimden (2760 m) and Sâada (411 m)
weather stations over the period (1998-2005) were used to calculate a global
mean lapse rate of 0.56°C/100m. Mean daily temperature at each elevation
zone is then obtained from the Oukaimden station data using this constant lapse
rate.
To determine zonal daily precipitation, the average daily
precipitation from all the available stations was assigned to the elevation
band corresponding to the mean altitude of all climate stations. Daily
precipitation was then extrapolated from this reference elevation band to all
surrounding bands with an average observed elevation gradient of 0.03 mm/100m.
The later was calculated from 1990 to 2006 between two stations: Marrakech
(450m) and Oukaimden (2600m).
Daily runoff measurements were collected at the sub catchments
outlet stations by the regional water agency (Agence du Bassin Hydraulique de
Tensift). These data were used to compare the observed and the simulated outlet
hydrographs.
VI.4 Snow covers
maps
VI.4.1 From remote sensing data
Snow cover areas (SCA) maps were available at 1km spatial
resolution after our previous work (Boudhar et al., 2007). SCAs maps were
established from SPOT-VEGETATION blue and middle infrared (MIR)
top-of-atmosphere reflectances (physical product, see Maisongrande et al.,
2004), using the modified snow index (Chaponnière et al., 2005). The
dates when snow cover maps are available (Table 2) corresponds to cloud-free
conditions and limited viewing angles (view zenith angles below 23°). The
mean interval between two successive clear sky images is one week, but there
are some longer periods without observations.
Based on this multitemporal dataset and the DEM, snow cover
areas of each elevation zone were successively derived from each
SPOT-VEGETATION snow map. Between two successive observations, depletion curves
of snow coverage were interpolated at a daily step using a linear model.

Table ýVI-: Availability of SPOT-VEGETATION
data and snow-cover estimates during the snowfall/snowmelt period (January to
June).
VI.4.2 From meteorological data
To estimate the daily SCA (snow cover area) without satellite
data, it is necessary to account for rainfall/snowfall partition (accumulation
processes) as well as snow drift, melting and sublimation (ablation processes).
For this purpose a relation between SCA and the Snow Water Equivalent (SWE) was
derived. The model elements consist of 30-m grid cells.
SWE is calculated from mean daily precipitation and mean daily
surface air temperature for each grid cell. Precipitation is modelled as snow
if the temperature is below 0°C, otherwise precipitation is rain.
Snowmelt is calculated according to Makhlouf (1994) through a
classical temperature index method described in Rango & Martinec (1995) (
Équation ýVI ):
Équation ýVI-
Where Ms is the daily bulk loss of water from the
snowpack (mm/unit time) and accounts for all the ablation processes;
Td is the mean daily air temperature (°C); T0 is the
base temperature (usually, 0°C); and a, the degree-day factor
(mm/°C/day). The later was computed with an empirical relationship based
on snow () and water () densities classically used in SRM model applications
(Martinec, 1960):
Équation ýVI-
The degree-day factor is low at the beginning of the season
(fresh snow) with a general trend of increase at the end of the season when
significant snow transformation and compaction has occurred and the snowpack
contains a large proportion of liquid water. In order to provide time-series of
snow density estimates, snow height and snow density measurements were carried
out from November 2007 to March 2008 at eight locations on the upper plateau of
the Oukaimden ski resort at 3200 metres above mean sea level. The resulting
degree-day factor was averaged over each month. It varies between 2.5 and 5.0
mm/°C/day from November to March. The same monthly values were used to
generate the SCA estimates for 2002-2005. To check whether the empirical
formulation (
Équation ýVI ) is realistic for the
High Atlas of Morocco, the observed degree-day factor was derived from the
2007-2008 measurement campaign for individual ablation periods. The values
ranged from 0.2 (late January) to 4.7 mm/°C/day (late March). Due to the
low space-time sampling resolution of those campaigns, we considered that the
degree-day factor obtained by
Équation ýVI was realistic, and
decided to keep this model to generate SWE time-series for each cell.
From the daily SWE we estimate a daily SCA using the following
empirical relationship (
Équation ýVI ):
Équation ýVI-
VI.4.3 Comparison between simulated and
observed SCA on the days of satellite acquisition
Figure ýVI illustrates an example of
SPOT-VEGETATION and modelled snow-cover maps for four selected dates in the
Rheraya sub-catchment. There is a large consistency in spatial patterns of snow
area between these two SCA estimates.
In
Figure ýVI , scatter plots of SCA values
derived from SPOT-VEGETATION and generated with the degree day method in all
sub-catchments are shown for the period 2002-2005. The difference between the
two snow products is quantified in
Table ýVI using the correlation
coefficient (R²), the root mean squared error (RMSE) and the Bias.
Although there is a large scatter in
Figure ýVI , there is little bias between
observed and simulated SCA estimates for all sub-catchments, except the Ourika
watershed which exhibits a small underestimation of SCA by the model (bias=
-9%).
Globally, there is a good correlation between the two snow
cover products in all sub-catchments with an exception in the season 2002 when
the SCA are poorly correlated. During that year, drier than usual, maximum SCA
is rather small (8, 35, 40, 25 and 18 % of the total area in Nfis, Rheraya,
Ourika, Zat and R'Dat, respectively).
|
Date
|
SPOT-VEGETATION
|
Degree day
|
|
09/01/2004
|
|
|
|
15/02/2004
|
|
|
|
16/03/2004
|
|
|
|
18/05/2004
|
|
|
Figure ýVI-: Examples of snow maps derived from
SPOT-VEGETATION (left), represented by gray levels (black: 0% SCA to white:
100% SCA), and simulated using the degree day method (right), binary product
(white: Snow; black: no snow)
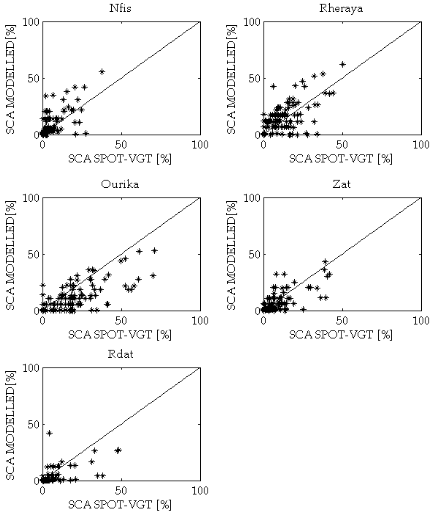
Figure ýVI-: Comparison between the snow cover
area calculated from SPOT- VEGETATION and that simulated by the degree day
method in five sub-catchments from 2002 to 2005.
|
|
Year
|
R²
|
BIAS (%)
|
RMSE (%)
|
|
NFIS
|
2002
|
0,0
|
8,6
|
14,9
|
|
2003
|
0,6
|
0,7
|
3,4
|
|
2004
|
0,5
|
1,0
|
7,0
|
|
2005
|
0,9
|
2,6
|
5,6
|
|
RHERAYA
|
2002
|
0,04
|
-10,3
|
15,8
|
|
2003
|
0,8
|
-1,5
|
4,1
|
|
2004
|
0,8
|
5,1
|
7,9
|
|
2005
|
0,8
|
9,1
|
11,9
|
|
OURIKA
|
2002
|
0,03
|
-9,8
|
17,8
|
|
2003
|
0,8
|
-9,6
|
13,4
|
|
2004
|
0,6
|
-7,0
|
14,2
|
|
2005
|
0,9
|
-1,0
|
7,0
|
|
ZAT
|
2002
|
0,02
|
-2,0
|
8,6
|
|
2003
|
0,5
|
-2,8
|
7,6
|
|
2004
|
0,8
|
-1,9
|
5,2
|
|
2005
|
0,7
|
1,2
|
6,5
|
|
RDAT
|
2002
|
0,03
|
-1,9
|
5,6
|
|
2003
|
0,9
|
-3,3
|
8,2
|
|
2004
|
0,8
|
-2,3
|
4,9
|
|
2005
|
0,4
|
-1,4
|
8,7
|
Table ýVI-:
statistics of the simulated vs. remote sensing SCA estimates comparison for
each year and each subcatchment.
VI.5 Implementation
and calibration of SRM
VI.5.1 Description of SRM
Among many snowmelt runoff models that use snow-cover
information, the deterministic SRM is one of the most widely used models in
both diagnostic (Rango & van Katwijk, 1990; Songweon et al., 2005), and
prognostic modes (Rango & Martinec, 1979; Shafer et al., 1982; Martinec,
1985; Martinec & Rango, 1995; Rango & Martinec, 1997; Klaus, 1998;
Jesko et al., 1999 ; Gomez, 2002; Thomas et al., 2008). It was first applied to
small European basins in 1975 and since then has been successfully used in
approximately 80 mountainous basins in 25 countries worldwide (Martinec, 1975;
Martinec et al., 2005). SRM is a degree-day-based model for daily runoff
simulations and forecasts in the mountainous areas in which snowmelt is the
major runoff contributor (Rango & Martinec, 1981; Martinec et al., 2005;
Mitchell & DeWalle, 1998). The degree-day method employed by the SRM model
has been used in different ways for more than 60 years (Clyde, 1931; Collins,
1934), and Rodriguez (1994) points out that the SRM and the Hydrologiska Byrans
Vattenbalansavdelning (HBV) model (Bergstrom, 1975) are the two most widely
used models based on the degree-day method (Rango and Martinec, 1995).
Assuming that there is an 18h time lag between the
meteorological inputs on day n and the resulting streamflow on day n+1, the SRM
calculates the daily streamflow separately for each elevation band as follows (
Équation ýVI )
Équation
ýVI-
In
Équation ýVI Qn+1
(m3/s), the daily average discharge on day n+1, is calculated as the sum of
three quantities from the preceding day n:
Snowmelt calculated as the product of the degree-day factor a
(cm/°C/d), the representative zonal degree-days (T+ ÄT) (°C
day), the ratio S of the SCA to the total basin area A (km²), and the
snowmelt runoff coefficient Cs;
Precipitation contributing to runoff (cm), calculated as the
product of measured precipitation P and the rainfall runoff coefficient Cr;
Discharge on the previous day Qn, weighted by the
recession coefficient where x and y are two empirical parameters.
(T+ ÄT) represents the extrapolated degree day
calculated at the hypsometric average elevation of the zone from the
degree-days measured at the meteorological stations. The snowmelt and rainfall
runoff coefficients Cs and Cr are defined, respectively, as those fractions of
snowmelt and rainfall that become streamflow. The recession coefficient on day
n+1, kn+1, is defined, as the ratio of streamflow on day n+1 to that
on day n when there is no input of runoff (see
Équation ýVI ). The factor 10 000/86
400 converts cm km2 / day to m3/s.
Équation ýVI is applied separately
to each zone and the discharges are summed. In addition to the five parameters
(Cs, a, Cr, x and y) and input data appearing in
Équation ýVI , the other parameters
are the critical temperature for melting (Tf) and for the snowfall/snowmelt
partition (Tc), i.e. the temperatures above which snow starts melting and
precipitation falls as snow (respectively).
VI.5.2 Sensitivity analysis and
parameters optimization
Separate model calibration is
performed for the two SCA products, i.e. the one computed from SPOT VEGETATION
(MOD1) and the other generated with the degree day method (MOD2). In order to
perform a classical split-sample analysis, 2005 was chosen, where relatively
good hydrometeorological data is available. In contrast to other years, in 2005
the measured runoff/rainfalls are consistent and they are continuously
available in all sub-catchments. An automatic approach was carried out for
model calibration by varying randomly each parameter value over a specified
realistic searching interval (
Table ýVI ). The objective of the
calibration procedure was to maximize the Nash & Sutcliffe (1970)
efficiency (
Équation ýVI ) but the volume error
(Dv) (i.e. mean difference between simulated and observed runoff) was also
computed (
Équation ýVI
Équation ýVI ).
Équation ýVI-
Équation ýVI-
Where Qi is the measured daily streamflow,
Q'i is the modelled daily streamflow and is the average of measured
streamflow over the calibration period, VR is the measured
cumulative streamflow volume and V'R is the simulated cumulative
streamflow volume.
A sensitivity analysis was carried out separately for each
sub-catchment to identify the most sensitive model parameters, i.e. the
parameters for which the Nash criteria is varying the most when the parameter
increases from the minimum to the maximum value of the searching interval.
Parameters are listed in
Table ýVI in decreasing sensitivity order.
The variation of the NASH efficiency (E) when the number of
optimized parameters increases has also been investigated. The adopted
iterative approach consists in: i) optimizing the most sensitive parameter
first and fix the other six parameters to values corresponding to the middle of
the realistic ranges given in
Table ýVI , plot the resulting Nash, then
ii) optimize the two most sensitive parameters and fix the other five, plot the
Nash and iii) repeat this operation for each parameter in decreasing
sensitivity order until all seven parameters are optimized. An example for the
Rheraya sub-catchment is illustrated on
Figure ýVI for MOD1 and MOD2. In order to
quantify the importance of the snowfall/snowmelt processes in the modelling
performance, E was also computed when all precipitation falls as snow (i.e.
SCA=0 for all altitudinal bands). The graphs indicate that the performance
increases rapidly when the number of parameters increases from one (x) to three
(x, y, Cr). The Nash function varied from 0.33 to 0.84 in MOD1, from 0.22 to
0.75 in MOD2 and from 0.12 to 0.69 in the simulation without snow cover. 0.69
is the overall Nash maximum in the later case since there are only 3 parameters
in the model without the snow module. Whereas for MOD2 a fourth (Cs) and fifth
parameter (a) still brings some improvement, the first guess values of the snow
module parameters are sufficient for the MOD1 configuration. This means that
the first guess values of a, Tf and Tc provide a reasonable estimate of the
daily melting quantities for a given remotely sensed SCA. Performances in both
configurations then reach a plateau when a sixth (Tc) and seventh (Tf)
parameters are calibrated and show no significant gain.
|
Parameters
|
|
No.
|
Value:
|
|
|
|
|
|
Min.
|
Interval
|
Max.
|
|
Recession coefficient, k
|
x
|
1
|
0.1
|
0.01
|
1
|
|
y
|
2
|
0.01
|
0.01
|
0.1
|
|
Rainfall runoff coefficient, Cr
|
|
3
|
0.01
|
0.02
|
0.99
|
|
Snowmelt runoff coefficient, Cs
|
|
4
|
0.01
|
0.02
|
0.99
|
|
Degree-day factor, a (cm °C-1
d-1)
|
|
5
|
0.05
|
0.05
|
1
|
|
Critical temperature, Tc (°C)
|
|
6
|
0
|
0.2
|
6
|
|
Melt temperature, Tf (°C)
|
|
7
|
0
|
0.2
|
6
|
Table ýVI-:
Parameter searching intervals for model calibration.
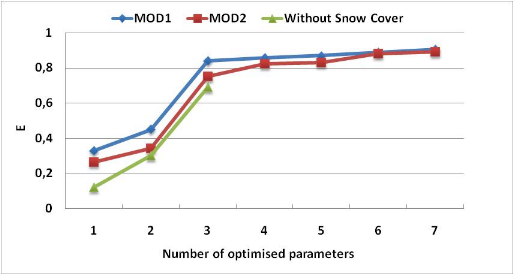
Figure ýVI-: Variation of the NASH efficiency
«E» according to the number of optimized parameters using VEGETATION
snow maps (MOD1), generated snow maps (MOD2) and when SCA is artificially kept
as zero.
VI.5.3 Analysis of model parameters
interdependence
The traditional concept of model calibration is built on the
hypothesis that a unique optimum set of parameter values exists; however there
is a multitude of parameter combinations that are «equally good» for
a particular objective. In most rainfall-runoff modelling exercises,
calibration is performed on the only observation that is available, i.e.
streamflow at the outlet. Streamflow integrates the various interactions
between the different intermediate storage, loss and redistribution processes.
The relative intensity of each of these processes is usually poorly known, and
a satisfying match between the observed and the simulated streamflow can be
achieved for a large range of parameters values. Beven & Binley (1992),
Beven (1993) and Beven (2008) call this the «equifinality issue».
This means that, for instance, a low value for one parameter that positively
affects one redistribution process (e.g. surface runoff) combined with a high
value of a second parameter governing a second redistribution process (e.g.
subsurface flow) will give a similar value for the performance criteria as a
higher value of the first parameter combined with a lower value of the second
one. The resulting parameters values deemed as «acceptable» can span
a very large range of values in the solution ensemble, even within realistic
boundaries. A method to check whether such equifinality problem is to produce
the contour plot of the Nash performance criteria for all pairs of parameters.
If two parameters can be calibrated independently, the resulting contour plot
peaks around one solution couple. This is the case for the Cr and
Cs parameters of SRM in the MOD2 configuration (
Figure ýVI , top) and, in a lesser extent,
in MOD1, even though both parameters contribute to surface runoff. The same
conclusion can be drawn for the Cr and degree-days factor parameters
(
Figure ýVI , top centre). If the contour
lines are either horizontal or vertical, one of the two parameters is rather
insensitive to streamflow prediction. This is the case for the critical
temperature that initiates melting (
Figure ýVI , bottom centre). If the contour
lines are organized diagonally, parameter dependence is high and the two
parameters cannot be calibrated independently. This is partly the case for the
x and y parameters that govern the recession (
Figure ýVI , Bottom).
Because the SRM model is rather simple and parsimonious,
equifinality is limited to the above-discussed examples. After the analysis of
the
Figure ýVI , we conclude that only
Tmelt could be fixed at an arbitrary value, and that a narrow
optimum range can be found for most parameters. Because the Nash criteria is
reaching a plateau when the less sensitive parameters are successively
calibrated, we decided to retain as «acceptable» all the parameter
sets that produce a Nash efficiency above 90% of the overall maximum. These
parameter sets will be used to generate an ensemble of streamflow time series
in the validation period for each model configuration (MOD1 or MOD2). The
ranges of model parameters of these subsets are shown in
Table ýVI . Because (1) streamflow is not
that sensitive to the parameter values of the snowmelt processes and (2) we
expect that the climate is less variable from one sub-catchment to the next
than the lateral redistribution of rain and meltwater, the model parameters
related to temperature (a, Tf and Tc) are considered to
be the same for the five sub catchments, while the parameters generating runoff
or recession are catchment-dependent.
As expected, the calibrated values for the parameters that
govern runoff or the redistribution of water are more variable from one
catchment to the other than from one configuration to the other. Performance of
the model during the calibration period (from January 1st to Mai 31, 2005)
indicate good efficiencies for Nfis, Rheraya and Ourika sub catchments where
E>0.79 for MOD1 and E>0.70 for MOD2 (
Table ýVI ) and satisfactory for Zat and
R'dat sub-catchments where E>0.63 for MOD1 and E>0.68 for MOD2.
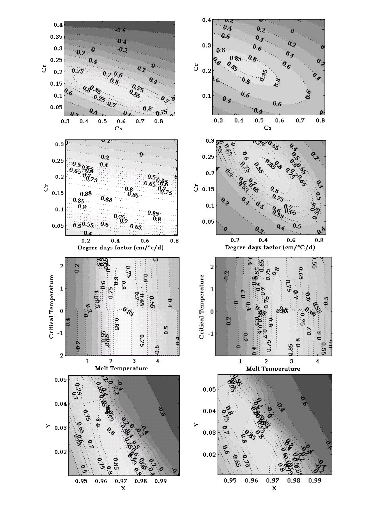
Figure ýVI-: Variations of Nash efficiencies
depending on the model parameters (2D analysis). The model is driven by snow
maps derived from SPOT- VEGETATION (MOD1, left) and simulated using the degree
day method (MOD2, right).
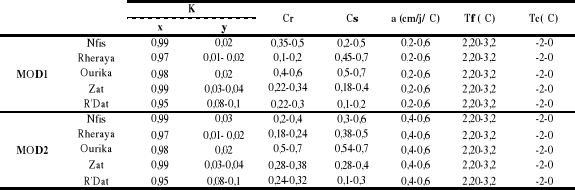
Table ýVI-:
Range of optimal model parameters giving 90% of the overall maximum of
NASH.
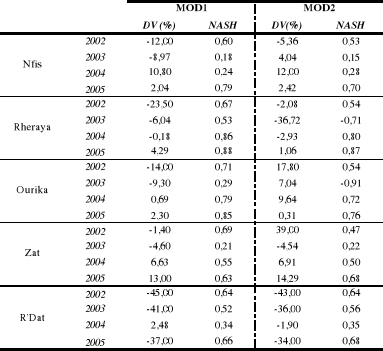
Table ýVI-:
Statistics associated to streamflows simulations.
VI.5.4 Snowmelt contribution to
streamflow
Once the SRM model is calibrated against streamflow
observations, it is interesting to look at the computed meltwater production
and thus at the relative contribution of snowmelt to streamflow. In this
exercise, the snow extents computed from SPOT-VEGETATION are used. The relative
contribution of snowmelt and rainfall are summarized in
Table ýVI from 2002 to 2005 for each
sub-catchment. Following the interannual and interbasin variability in observed
snow cover area, the fractions of snowmelt contributing to streamflow are also
variable from one year to the other and from one sub-catchment to another.
Except for 2005, where snowmelt contributes significantly in all sub-catchments
(varying from 15% in R'Dat to 51% in Ourika), the proportion of snowmelt in the
total runoff is more important in the Rheraya and Ourika sub-catchments (up to
38% in 2004), than in the other sub-catchments.
Figure ýVI and
Figure ýVI illustrate the cumulative curve
of the computed daily snowmelt and rainfall proportions to the runoff in two
distinct sub-catchements, Ourika and R'Dat, during the 2005 snowfall/snowmelt
season. From the satellite imagery, snow can be observed each year above 1400m
but persists at altitudes larger than 2600m. According to the area-elevation
curve for each sub-catchment (
Figure ýVI ), this represents 18%, 25%,
40%, 13% and 6% of the Nfis, Rheraya, Ourika, Zat and R'Dat sub-catchments
respectively. Consequently, as expected, the mean snowmelt contribution is more
important in the Ourika and Rheraya sub-catchments than in the Nfis, Zat and
R'Dat respectively. Almost the whole snowmelt contribution to runoff occurs in
February through May. Globally, from 2002 to 2005, this contribution is 25% on
average.
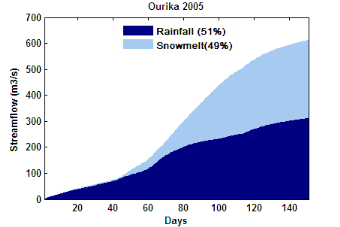
Figure ýVI-: Cumulative curves of snowmelt and
rainfall contributions to streamflow in the Ourika sub-catchment for 2005
snowfall/snowmelt season.
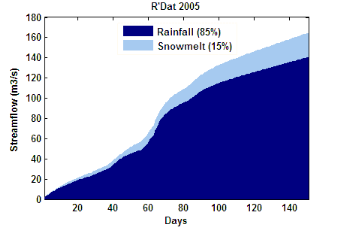
Figure ýVI-: Cumulative curves of snowmelt and
rainfall contributions to streamflow in the R'Dat sub-catchment for 2005
snowfall/snowmelt season.
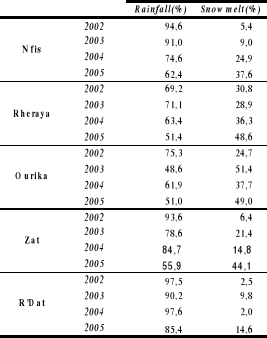
Table ýVI-:
Relative contribution of snowmelt and rainfall to streamflows
VI.5.5 Model validation
The model validation was conducted in the snowmelt season from
2002 to 2004 in the five sub catchments using representative SRM parameter
values adopted at the calibration test.
Figure ýVI illustrates the daily runoff
simulations using the two snow products MOD1 and MOD2, along with measured
discharges, and
Table ýVI summarizes the simulation result
statistics for fives sub-catchments.
At seasonal scale, the streamflow simulations using the two
snow products are comparable. The model efficiency with the two snow cover area
estimates varies widely from one year to the other and a basin to another,
reflecting the variation in climatic and topographic conditions of the region.
In decreasing order, without taking into account the year 2003 when the model
efficiency is very low for all sub-catchments, the streamflow simulations with
MOD1 are good in Ourika and Rheraya (E>0.72), acceptable in Zat (E> 0.50)
where snowmelt is significantly contributing to runoff but poor in Nfis and
RDat (E> 0.24). With MOD2, the model shows a good efficiency in 2004 (E>
0.72), acceptable in 2002 (E=0.54) and poor in 2003. However, in the other
sub-catchments, the performance of the model is acceptable for 2002 (E>0.47)
and lower in 2003 and 2004. The simulated average peak discharge was often
lower than observed (example, peak after Day 60, in 2004, cf.
Figure ýVI ). This can be explained by the
local intense rainfall events that are not captured by the available
raingauges. During recessions, the streamflow simulations are acceptable in all
sub-catchments.
The inability of the model to simulate the daily runoff in
Nfis, Rdat and Zat sub-catchments might be due to several factors. First, the
spatio-temporal variability of the rainfall could not be captured with the
available network. Local intense rainfall events occur mostly during the
summer; however, patchy rainfall events during the winter might explain the
poor prediction performance of peakflow discharge. This poor performance could
be due to the model itself and has been reported in many other studies
(Songweon et al. 2005 and Xingong L. & Mark W.W. (2008)). Second,
streamflow measurement is a difficult task in the wadi bed: the gauging
frequency (once a month on average) is not always adjusted for quickflow (high
flow) occurrence, and wadi beds often undergo drastic modifications after a
storm, preventing discharge measurement when the scale is isolated or when the
charge-discharge rating curve is no longer valid. This may cause that runoff
peaks are missed. This problem is less tricky during recessions and low flow
with more stable daily runoff. Third, the runoff generation mechanisms during
intense rainfall events in such area, where stream flow tends to be dominated
by rapid responses, are too complex for this relatively simple conceptual
model. Fourth, in a semi arid area, water losses via evapotranspiration for the
vegetation and via sublimation for snow are important, but they are perhaps not
properly taken into account by a simple conceptual model such as SRM. On the
southern slopes of the High Atlas, Schulz et De Jong (2004) found with an
energy balance model that on average 44% of snow ablation was attributed to
sublimation, and snow penitents were observed. Finally, the mechanisms of
groundwater redistribution are also unrecognizable and are difficult to be
modelled (Duclaux, 2005, Chaponnière et al., 2008).
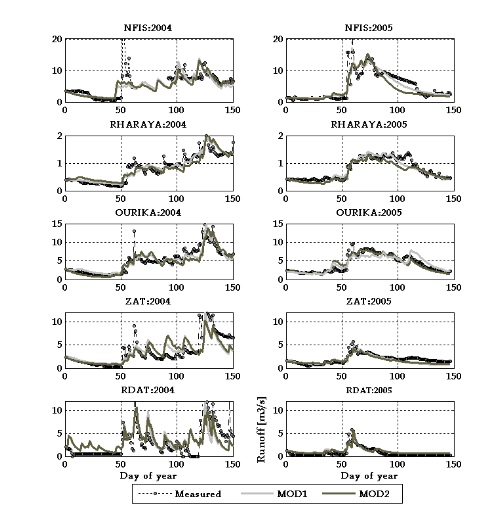
Figure ýVI-: Simulated and observed streamflows
for the calibration and validation periods in the fives
sub-catchments.
Finally, and more importantly, it must be stressed that if the
performance at the seasonal scale is satisfying for both SCA estimation methods
MOD1 and MOD2, significant differences can be observed for selected
storm/interstorm events. This occurs when the raingauge network is too sparse
to catch all precipitation events or when errors in temperature estimates
affect the rainfall/snowfall partition. In both cases the Remote Sensing method
improves the short term streamflow prediction.
Figure ýVI and
Figure ýVI , illustrate these two cases of
streamflow underestimation with MOD2, in the Ourika sub-catchment: the first
one from days 80 to 90 in 2002 (
Figure ýVI ), due to missing rainfall
events in the higher altitudes. In this period, the large SCA difference (about
30%) translates into 20% of streamflow difference that remains up to three
weeks. The second case represents an underestimation of the SCA with MOD2 from
day 63 to 69 in 2005, certainly due to an incorrect temperature lapse rate.
Because of the low redistribution of snowmelt process, the difference of SCA
during one week has an influence on streamflow for about 3 weeks.
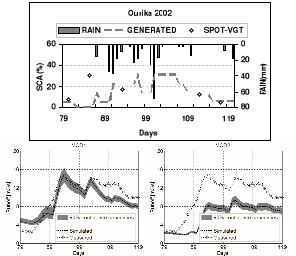
Figure ýVI-: Example of underestimation of
streamflow by MOD2 when a rainfall event occurs only in the ungauged upper part
of the Ourika subcatchment in 2002.
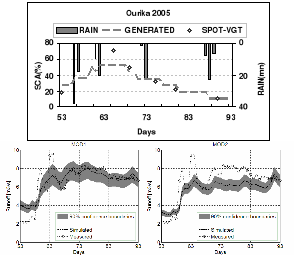
Figure ýVI-: Example of underestimation of
streamflow by MOD2 caused by an underestimation of the SCA generated by the
degree day model in the Ourika subcatchment in 2005.
·
Conclusion
The aim of the study was to investigate the relative
performance of the Snowmelt Runoff Model (SRM) to simulate streamflow in five
sub-catchments of the High Atlas Mountain range when using two snow extent
products of limited precision: i) a snow cover information derived from the
VEGETATION sensor onboard the SPOT satellite with a mean weekly interval, ii)
snow cover information computed solely from the meteorological data acquired at
a few climate stations.
At the seasonal scale, snow cover information obtained from
SPOT-VEGETATION and generated with the degree day method is quite comparable
for the five tributary sub-catchments. In general, streamflow simulation is
good in the Rheraya and Ourika sub-catchments where snow processes are
important and hydrometeorological data are relatively good. In the other hand,
SRM performances were poorer in the Nfis, Zat and R'Dat sub-catchments where
snow plays a smaller role in the hydrological budget.
In this study, the snowmelt contribution to streamflow was
computed in all sub-catchments from 2002 to 2005 using snow maps derived from
SPOT-VEGETATION sensor. Generally, it was shown that 25 % of streamflow
arriving from the North sides of High Atlas is derived from snowmelt.
At annual timescales, the simulated and observed hydrograph
using the two snow products in all sub-catchments are similar. Due to local
intense rainfall events not measured by the weather stations, where streamflow
tends to be dominated by rapid responses, the multiple peak discharge simulated
was often lower than observed. During recessions, the streamflow simulations
are acceptable. However, using snow cover information derived from remote
sensed data can significantly improve streamflow prediction for individual
interstorm periods were rainfall events are not observed by the given network
or when the temperature lapse rate is badly estimated.
Finally, the Remote Sensing and the meteorological data were
used separately to compute snow cover extent as an input in the SRM model.
Since the results with either data sources are encouraging, combining both
products to estimate the snowpack evolution between two image acquisitions
(instead of linearly interpolated snow depletion curves, as it is classically
done in most SRM applications) should improve the streamflow prediction
performance in the High Atlas. This has not been tested in this study but will
be done in the next future.
ACKNOWLEDGEMENTS
This study was supported by the research projects SUDMED
(IRD-UCAM), PAI (`Programme d'Action Intégrée du Comite Mixte
Interuniversitaire Franco-Marocain, Jeune Equipe IRD (CREMAS), `Volubilis'
MA/06/148) and PLEADeS see
http://www.pleiades.es/ project
funded by the European Commission (6th PCRD). The authors are
grateful to ABHT (Agence du Bassin hydraulique de Tensift, Marrakech, Morocco)
for the acquisition of the hydro-meteorological data on the Tensift watersheds.
We also thank the SPOT-VEGETATION program for provided the series of satellites
images.
· Conclusion et Perspectives
Une grande partie du territoire Marocain est soumise à
un climat aride à semi-aride. En conséquence, les ressources en
eau sont limitées et subissent une forte exploitation sous l'effet des
changements environnementaux dus essentiellement aux périodes de
sécheresse et à la croissance des besoins en eau. C'est le cas de
la région de Tensift où l'accroissement démographique
très fort des villes et l'extension des périmètres
irrigués et ainsi que le développement du tourisme sont à
l'origine d'une grande mobilisation des ressources hydriques. C'est donc vers
une optimisation de la gestion de l'eau qu'il faut tendre. Ce travail de
thèse s'inscrit dans ce contexte global de caractérisation des
ressources hydriques de la région de Tensift mené dans le cadre
du projet de recherche franco-marocain SUDMED. Ce projet, coordonné par
le CESBIO et l'UCAM, a été lancé en 2002 avec l'appui des
organismes régionaux chargés de la gestion des ressources
hydro-agricoles (ORMVAH et ABHT). La région d'étude principale de
ce projet est le bassin versant semi-aride du Tensift autour de la ville de
Marrakech, région où les enjeux relatifs à la gestion de
la ressource hydrique sont particulièrement forts.
Notre travail s'est focalisé sur les sous bassins
versants de la chaîne montagneuse du Haut Atlas de Marrakech. Grâce
à ses hautes altitudes, cette chaîne constitue une barrière
orographique naturelle face aux masses d'air chaud venues du Sud (Sahara) et
reçoit plus du triple des précipitations habituellement
enregistrées en plaine. Ces grandes altitudes représentent le
principal facteur qui contrôle les variations des paramètres
climatiques (température et précipitations). Une part importante
des précipitations tombe sous forme neigeuse et constitue un manteau qui
reste stocké temporairement avant d'être libéré dans
les cours d'eau et participer ainsi à soutenir les étiages. Ces
montagnes constituent donc un château d'eau pour la région et sont
aussi la principale zone de production des ressources hydriques.
La problématique abordée au cours de cette
thèse consiste en une meilleure caractérisation des ressources en
eau disponibles en montagne et en particulier l'apport de la fonte des neiges
aux débits. Pour cela, nous avons utilisé une approche
méthodologique combinant les données issues des images satellites
et les données mesurées in situ lors des compagnes de
mesures et collectées par les stations météorologiques.
Ces données ont été utilisées pour calibrer et
valider les différents modèles appliqués au cours de cette
étude.
Les images satellites basse résolution issues des
capteurs MODIS et VEGETATION nous ont permis de cartographier les surfaces de
neige dans le Haut Atlas. Les cartes de neige produites à la base d'un
indice de neige modifié sont utilisées pour décrire la
variabilité spatio-temporelle de l'enneigement dans le Haut Atlas et en
particulier sur les cinq sous bassins versants les plus actifs hydrologiquement
dans la région de Marrakech (Nfis, Rheraya, Ourika, Zat et R'Dat). Ces
cartes d'enneigement ont permis de quantifier les variations temporelles du
taux d'enneigement d'un bassin versant à un autre, selon l'exposition et
par tranche d'altitude. La chute de neige commence généralement
aux mois d'octobre ou novembre et la fonte totale se fait au mois d'avril ou
mai avec des périodes de fonte au milieu de la saison. Les altitudes qui
reçoivent plus de neige sont supérieures à 2600
mètres et les premières neiges tombent sur les altitudes
supérieures à 3800 mètres et persistent jusqu'à la
fin de la saison. On a classé les cinq sous bassins versants en deux
catégories : deux bassins (Ourika et Rheraya) dont le
fonctionnement a une forte composante nivale, se caractérisant par des
surfaces neigeuses maximales importantes (60 à 80% de l'aire totale) et
des périodes de présence de neige qui dépasse parfois cinq
mois, et les bassins de Zat, R'Dat et Nfis à la composante nivale moins
marquée, avec des surfaces neigeuses maximales qui ne dépassent
pas 60% et des périodes de présence de neige comprises entre un
et quatre mois. Les versants orientés vers le Nord reçoivent plus
de neige par rapport aux versants orientés vers le Sud. Les taux de
variations de l'enneigement sont comparables avec les données
hydro-climatiques disponibles sur la région (précipitation,
hauteurs de neige, température et débit à l'exutoire). Ces
informations sont un indicateur de qualité pour le suivi des ressources
hydriques neigeuses et peuvent renforcer de manière significative les
réseaux d'observation hydro-climatiques et aider à la
spatialisation de la pluie en haute montagne semi-aride.
Ces cartes d'enneigement constituent la seule information
disponible pour analyser les résultats des modèles de fonte via
une simulation des surfaces de neige. Afin de valider ces modèles
à l'échelle du bassin versant, une meilleure spatialisation des
paramètres climatiques est nécessaire. Vu la faible
densité du réseau hydro-climatique dans notre zone et la
complexité de la topographie, les méthodes d'interpolation
classiques sont difficiles à appliquer. Pour cela, nous avons
développé un modèle de spatialisation de la
température de l'air (MSPAT). La bande thermique des images
Landsat ETM+ a été utilisée pour calculer les
températures maximales de l'air dans tous les pixels pour chaque image
ETM+. Cette information est utilisée pour caractériser la
variation spatiale de la température de l'air en fonction des facteurs
topographiques (altitude, pente et exposition) et l'angle
d'élévation solaire. A partir de cela, nous avons
initialisé le modèle MSPAT à l'échelle temporelle
en utilisant les données enregistrées dans une station
météorologique de référence. Les résultats
obtenus par les deux modèles MSPAT et le gradient d'altitude (GRAD) sont
similaires à l'échelle des stations météorologiques
disponibles. Tandis qu'à l'échelle du bassin versant de Rheraya,
dont le relief est très contrasté, les modèles sont
évalués par les surfaces de neige (SCA) estimées. Ces
dernières sont comparées avec les SCA calculées à
partir des données MODIS. Les résultats montrent que le
modèle MSPAT améliore significativement les simulations des
SCA.
Comprendre les processus de fonte et d'accumulation des neiges
à l'échelle locale constitue une étape intéressante
vers une modélisation des débits à l'échelle du
bassin versant. La seule station nivale dont on dispose dans la région
est la station d'Oukaimden localisée à 3200 mètres
d'altitude. Celle-ci comprend des instruments de mesures des différents
paramètres nécessaires à une modélisation de fonte
des neiges à un pas de temps semi-horaire (température et
l'humidité de l'air, vitesse du vent, rayonnement solaire global, cumuls
de précipitations et de hauteur de neige). La qualité de ces
données peut être qualifiée de bonne sauf pour les
relevés de hauteur de neige et de cumul de précipitations qui
présentent des artefacts, qu'il convient de corriger. En plus des
mesures continues de la station nivale, des mesures ponctuelles des
densités et des hauteurs de neige on été effectuées
durant la saison 2007/2008 au sommet d'Oukaimden à environ 3200m
d'altitude. Ces données ont été utilisées pour
calibrer le modèle de transformation des hauteurs des neiges en
équivalent en eau par un modèle simulant l'évolution
temporelle des densités.
Deux types de modèle ont été
utilisés pour étudier les processus de la fonte des neiges dans
la station d'Oukaimden. Il s'agit d'un modèle à base physique de
bilan d'énergie (ISBA-ES) et de plusieurs modèles simples de type
degré-jour. Pour ces derniers, nous avons testé trois formules
largement utilisées pour obtenir le facteur de fonte ; la relation
empirique de Martinec, la relation linéaire
suggérée par Kuustisto et la relation intégrant
le rayonnement comme facteur de fonte « RAD ». La
calibration des modèles a été effectuée avec les
données de l'année 2007/2008 et la validation sur les autres
saisons. Les résultats des simulations des équivalents en eau
(SWE) à l'échelle locale montrent que la formule
Kuustusto est plus efficace que les deux autres modèles
degré jour. Ces résultats sont comparables avec ceux obtenus par
le modèle ISBA-ES. Ce dernier reproduit bien les équivalents en
eau pour les saisons à longue période hivernal où le
manteau neigeux subis plus de transformation (exemple des deux saisons
2003/2004 et 2007/2008). Les densités de la neige sont globalement bien
simulées avec une surestimation à la fin du mois de
février 2008 due à la forte quantité d'eau liquide
contenue dans le manteau neigeux. Les albédos modélisés
par ISBA-ES sont surestimés par rapport à celles
enregistrées dans la station météorologique et surtout
dans les périodes de faibles hauteurs de neige où la fraction sol
peut influencer la réflexion des rayonnements. ISBA-ES nous a permis de
mieux comprendre l'interaction des processus d'ablation de neige dans le Haut
Atlas. Les pertes par sublimation constituent une part non négligeable
d'eau, variant de 16 à 37%. Le phénomène de sublimation se
produit d'une manière stable le long de la saison. La libération
des eaux par le processus de la fonte se fait pendant des courtes
périodes.
A l'échelle locale, le modèle ISBA-ES est plus
efficace pour caractériser les processus influençant la dynamique
et l'état du manteau neigeux. En raison de la difficulté à
spatialiser certaines données d'entrée d'ISBA-ES, notamment le
vent et l'humidité, il est très difficile d'utiliser ce
modèle pour évaluer la fonte à l'échelle
régionale. Dans ce contexte, les modèles degré-jour,
basés sur des variables climatiques plus facilement spatialisables
(température et rayonnement) restent privilégiés pour
estimer la variabilité spatiotemporelle de la fonte. La comparaison des
différentes formules à l'échelle du bassin versant de
Rheraya, montre que l'utilisation du taux de perte due à la sublimation
obtenue par ISBA-ES dans la station nivale améliore les surfaces de
neige simulées. On conclue aussi qu'une calibration d'un modèle
simple à l'échelle local n'est pas nécessaire pour une
application à l'échelle spatiale. La formule de Martinec
est performante pour générer des SCA (surface de neige) dans
notre zone. Cette formule est d'ailleurs celle utilisée par le
modèle hydrologique Snowmelt Runoff Model « SRM »
souvent appliqué à des fins opérationnelles.
Les surfaces des neiges obtenues par la
télédétection et celles simulées par le
modèle degré-jour simple ont été utilisées
à l'entrée du modèle SRM. La performance de ce
modèle a été analysée au niveau des cinq sous
bassins versants atlasiques. En générale, les simulations sont
bonnes pour les sous bassins versant de Rheraya et Ourika où les
processus nivaux sont importants et les données
hydrométéorologiques sont relativement disponibles. De l'autres
coté, les simulations des débits sont moins efficaces pour les
sous bassins de Nfis, Zat et R'Dat où la neige joue un rôle moins
important dans le bilan hydrologique. Les réponses rapides des
débits générées par des événements
pluvieux à caractère torrentiel non mesurés par les
stations météorologiques sont mal simulées par SRM.
L'utilisation des surfaces de neige issues de la
télédétection améliore la prédiction des
débits par rapport aux surfaces simulées par le modèle
degré-jour. Cela est peut être expliqué par les
précipitations tombées aux hautes altitudes et difficiles
à enregistrer par le manque de stations de mesures. Ce type
d'événement peut être vu par les satellites sous forme
d'extension neigeuse. En utilisant les surfaces neigeuses issues de la
télédétection à l'entrée du modèle
SRM, nous avons montré qu'environ 25% des ressources hydriques
écoulées depuis les versants nord du Haut Atlas de Marrakech sont
proviennent de la fonte des neiges.
La voie de recherche initiée dans cette thèse,
qui n'avait d'ailleurs pas été employée jusqu'à
présent au Maroc, a débouché sur des résultats qui
sont primordiaux pour les gestionnaires des ressources en eau du bassin versant
de Tensift. Nous avons mis en évidence l'intérêt d'utiliser
les données de télédétection pour estimer l'apport
des eaux de fonte de neige aux débits à l'exutoire des bassins
versants du Haut Atlas de Marrakech. Ainsi, nous avons attaché, au cours
de cette thèse, beaucoup d'importance au caractère
opérationnel du travail. Les images satellite basses résolution,
nécessaires pour cartographier l'extension du manteau neigeux, sont
accessibles gratuitement. Cette information est utilisable à
l'entrée de plusieurs modèles hydrologiques comme SRM,
utilisée dans ce travail. Les modèles de fonte utilisés
ont été adaptés aux caractéristiques de notre
région concernant la faiblesse du réseau d'acquisition des
données hydro-climatiques. Cette démarche méthodologique
peut être appliquée dans des bassins versants montagneux non
jaugés. Nous espérons que la méthodologie
développée ici pourra être mise en oeuvre dans d'autres
sous bassins versants montagneux du Maroc à caractère nival.
En perspective de ce travail et pour une connaissance
approfondie du cycle hydrique et plus particulièrement la relation fonte
des neiges et débits, il reste certainement des voies de recherche
à explorer. Une prospection plus détaillée à
l'échelle spatiale et temporelle de la dynamique du manteau neigeux par
l'utilisation d'autres produits satellitaire à haute résolution
et haute répétitivité, par exemple les données du
capteur FORMOSAT (<10m de résolution et revisite de quatre jour) sera
envisagée. Ces données seront utilisées afin
d'améliorer l'estimation des surfaces d'enneigement à l'aide d'un
modèle de fonte. Le suivi à long terme des surfaces
enneigées prend également toute son importance pour
évaluer l'impact des changements climatique sur la ressource en eau
(évolution de la distribution des précipitations sous forme
liquide et solide).
La disponibilité des données in situ et
ses qualités représentent une limite de ce travail. Pour une
meilleure connaissance des processus d'ablation des neiges à
l'échelle du bassin par un modèle physique, nous recommandons
à la mise en place des stations météorologiques à
différentes altitudes représentatives du bassin. Ainsi que la
mise en place d'un système de mesure des quantités de neige
tombées qui permet de quantifier le taux de fonte et de sublimation
(coussin à neige, pluviomètre à pesée,
lysimètre à neige...). Vu la nature irrégulière des
précipitations, parfois torrentielles, et la géomorphologie
(hautes altitudes, pentes élevées..), de la région, la
section et les lits des oueds se modifient plusieurs fois dans une saison. Dans
ce contexte, l'entretien des sections de mesure des hauteurs d'eau dans chaque
station hydrologique est prioritaire. La fréquence des jaugeages des
débits des Oueds des différents bassins versants avec un pas
court et régulier sont également un point intéressant dans
des études de modélisation hydrologique.
Références bibliographiques
Abbott M.B., Bathurst J.C, Cunge J.A., O'Connell P.E.,
Rasmussen J. (1986a). An introduction to the European Hydrological System-
Système Hydrologique Européen "SHE". Journal of
Hydrology, 87, 45-77.
Abbott M.-B., Bathurst J.-C. , Cunge J.-A. , O'Connell P.-E. ,
Rasmussen. J. (1986b). An Introduction to the European Hydrological
SystemSystème hydrologique européen (SHE), Part 2: Structure of a
physically based, distributed modelling system. Journal of Hydrology,
87, 61-77.
Akyürek Z, Sorman A., (2002).Monitoring snow-covered
areas using NOAAAVHRR data in the eastern part of Turkey.Hydrological
Sciences Journal des Sciences Hydrologiques; 47(2):243-252.
Ambroise, B., (1999). La Dynamique du Cycle de l'Eau dans un
Bassin Versant. -Processus, Facteurs, Modèles-.
*H*G*A, 200 pp.
Anderson, E. A., (1968). Development and testing of snow pack
energy equations. Water Resources Research 4(1): 19-37.
Anderson, E.-A., (1976). A point energy and mass balance model
of a snow cover. Silver Spring, MD US. National Oceanic and Atmospheric
Administration (NOAA), Technical Report NWS 19.
Anderton, S., Latron, J. and Gallart, F., (2002a). Sensitivity
analysis and multi response, multicriteria evaluation of a physically based
distributed model. Hydrological Processes, 16: 333-353.
Andreadis, K.M., Lettenmaier, D.P., (2006). Assimilating
remotely sensed snow observations into a macroscale hydrology model. Adv.
in Water Resour. 29, 872-886.
Archard, F., Malingreau, J.P., & Phulpin, T., (1994). A
mission for global monitoring of the continental biosphere. VEGETATION
International Users Committee Secretariat, Joint Research Center, Institute for
Remote Sensing Application. I-21020 ISPRA (Va), Italy,
http://www.vegetation.cnes.fr/.
Arnaud, M., & Leroy, M. (1991). Spot-4 - a New Generation
of Spot Satellites. Isprs Journal of Photogrammetry and Remote Sensing,
46, 205-215.
Benichou P., Le Breton O., (1987). Prise en compte de la
topographie pour la cartographie des champs pluviométriques
statistiques, La Météorologie 7ème série,
1987, 14 p.
Bergstrom S., (1975). The development of a snow routine for
the HBV-2 model. Nordic Hydrology. 6, 73-92.
Bergstrom, S. (1973) The HBV model. Dans: Computer Models of
Watershed Hydrology (Editeur V.P Singh), 443-476, Water resources publications,
Highland Ranch,Colorado, USA.
Bergstrom, S., (1976). Development and application of a
conceptual runoff model for Scandinavian catchments.(Department of Water
Resources Engineering, Lund Institute of Technology/University of Lund,
Bulletin Series A, No. 52,134 pp.).
Bernier, M., J.P. Fortin, Y. Gauthier, R. Gauthier, R. Roy and
P. Vincent (1999). Determination of Snow Water Equivalent using RADARSAT SAR
data in eastern Canada. Hydrological Processes, 13: 3041-3051.
Berrazzouk S., Guemouria N., Chehbouni A., Simonneau V.
(2004). Historique de l'occupation du sol à Marrakech et impact sur les
ressources en eau, IMPETUS workshop, Ouarzazate, Morocco. 1-3 avril 2004.
Beven K.J., Kirkby, M.J.(1979). A physically based variable
contributing area model of basin hydrology. Hydrol. Sci. Bull., 24(1),
43-69.
Beven, K., Binley, A. (1992) the future of distributed models:
model calibration and uncertainty prediction. Hydrological Processes
6, 279-298.
Beven, K.J. (1993) Prophecy, reality and uncertainty in
distributed hydrological modelling. Advances in Water Resources
16, 41-51.
Beven, K.J. (2008) Environnement Modelling: an uncertain
future? Routledge, London, UK.
Bitner D, Carroll T, Cline D, Romanov R. (2002). An assessment
of the differences between three satellite snow cover mapping techniques.
Hydrological Processes 16: 3723-3733.
Bloschl G. (1991). The influence of uncertainty in the air
temperature and albedo on snowmelt. Nordic Hydrology 22: 95-108.
Bloschl G. (1999).Scaling issues in snow hydrology. Hydrol
Process ; 13 : 2149-2175.
Boone, A. (2000). "Modélisation des processus
hydrologiques dans le schéma de surface ISBA: Inclusion d'un
réservoir hydrologique, du gel et modélisation de la neige,"
Thèse de doctorat, Université P.Sabatier, Toulouse III, Toulouse,
France.
Boone, A., and P. Etchevers, (2001). An intercomparison of
three snow schemes of varying complexity coupled to the same land surface
model: local-scale evaluation at an Alpine site. J. Hydrometeorology,
2, 374-394.
Boudhar, A., Duchemin, B., Hanich, L., Chaponnière, A.
, Maisongrande, P., Boulet, G. , Stitou, J. and Chehbouni, A. (2007). Analyse
de la dynamique des surfaces enneigées du Haut Atlas Marocain à
partir des données SPOT-VEGETATION. Sécheresse
18 (4): 278-88.
Boudhar, A., Hanich, L., Boulet, G., Duchemin B., Berjamy B.
and Chehbouni, A. (2009). Sciences-Journal-des Sciences Hydrologiques,
54(6) December 2009.
Boyle, D.P., Gupta, H.V. and Sorooshian, S., (2000). Toward
improved calibration of hydrologic models: Combining the strengths of manual
and automatic methods. Water Resources Research, 36(12): 3663-3674.
Brasnett, B. (1999) A global analysis of snow depth for
numerical weather prediction. J Appl Meteorol.
38:726-40.
Brazenec, W.A., (2005). Evaluation of ultrasonic snow depth
sensors for Automated Surface Observing Systems (ASOS). M.S. thesis, Colorado
State University, Fort Collins, CO, Fall 2005.
Brock, B.W., Willis, I.C., Sharp, M.J. and Arnold, N.S.
(2000b) Seasonal and spatial variations in the surface energy balance of Haut
Glacier d'Arolla, Switzerland, Annals of Glaciology, 31, 53-62.
Brubaker K, Rango A, Kustas W. (1996). Incorporating radiation
inputs into the snowmelt runoff model. Hydrological Process 10:
1329-1343.
Brutsaert, W. (1975). On a derivable formula for long-wave
radiation from clear skies, Water Resources Research, 11,
742-744.
Brutsaert ,W., (1982). Evaporation into the atmosphere,
299pp., D.Reidel, Kluwer Academic Publishers.
Campbell Scientific Inc., (2003). Campbell Scientific Online
SR-50 Manual (
http://www.campbellsci.com/documents/manuals/sr50.pdf).
Cazorzi F., et Dalla Fontana G.(1996).Snowmelt modelling by
combining air temperature and a distributed radiation index. Journal of
Hydrology 181 (1996) 169-187.
Ceballos-Barbancho, A., Mora'n-Tejeda, E.,Luengo-Ugidos, M.A.,
Llorente-Pinto, J.M. (2008) Water resources and environmental change in a
Mediterranean environment: The south-west sector of the Duero river basin
(Spain). Journal of Hydrology. 351:126- 138
Chaponnière, A., Boulet, G., Chehbouni, A. and
Aresmouk, M. (2008) Understanding hydrological processes with scarce data in a
mountain environment, Hydrol. Process. 22,
1908-1921.
Chaponnière, A., Maisongrande, P., Duchemin, B.,
Hanich, L., Boulet, G., Halouat, S., Escadafal, R. (2005) A combined high and
low spatial resolution approach for mapping snow covered area in the Atlas
Mountain. International Journal of Remote Sensing 26:
2755-2777.
Chehbouni A. et al. Integrated modelling and remote sensing
approach: toward a sustainable management of water resources in a semi-arid
region. International Conference on Remote Sensing and Geo-information
Processing. September 7th to 9th, 2005, Trier (Germany).
Chehbouni, A., Escadafal, R., Boulet, G., Duchemin, B.,
Simonneaux, V., Dedieu, G., Mougenot, B., Khabba, S., Kharrou, H., Merlin, O.,
Chaponnière, A., Ezzahar, J., Erraki, S., Hoedjes, J., Hadria, R.,
Abourida, H., Cheggour, A., Raibi, F., Boudhar, A., Hanich, L.,Guemouria, N.,
chehbouni, Ah., Olioso, A., Jacob, F. and Sobrino, J. (2008) An integrated
modelling and remote sensing approach for hydrological study in semi-arid
regions: the SUDMED Program. International Journal of Remote Sensing.
29:5161-5181.
Chocat, B., (1997). Encyclopedie de l'hydrologie urbaine. ,
Tec et Doc Lavoisier Publishers, Paris, France 1136 pp.
Clark, M.P., Slater, A.G., Barrett, A.P., Hay L.E., McCabe,
G.J., Rajagopalan, B., Leavesley G.H. (2006) Assimilation of snow covered area
information into hydrologic and land surface models. Advances in Water
Resources. 29, 1209-1221.
Clyde, GD. (1931) Snow melting characteristics. Utah
Agricultural Experiment Station, Bulletin No. 231.
Collins, EH. (1934) Relationship of degree-days above freezing
to runoff. Transactions of the American Geophysical Union, Reports and
Papers, Hydrology: 624-629.
Corripio, J.G, Durant, Y., Guyomarc'h, G., Merindol, L.,
Lecorps, D. and Pugliese, P., 2004. Land-based remote sensing of snow for the
validation of a snow transport model. Cold Regions Sci. Techno., 39,93-104.
Crawford , N.H., and Linsley, R.K. (1966), `Digital Simulation
in Hydrology: Stanford Watershed Model IV,' Technical Report 39, Dept. of Civil
Engineering, Stanford University, California.
Crawford T.M. and C.E. Duchon. (1999). An improved
parameterization for estimating effective atmospheric emissivity for use in
calculating daytime downwelling longwave radiation, J. Appl. Meteorol.
38 (1999), pp. 474-480
Daly, S.-F., Davis, R.-E., Ochs, E., Pangburn, T., (2000) An
approach to spatially distributed snow modeling of the Sacramento and San
Joaquin basins, CA. Hydrol. Proces. 14, 3257-3271.
David C. Garen, Danny Marks, (2005). Spatially distributed
energy balance snowmelt modeling in a mountainous river basin: estimation of
meteorological inputs and verification of model results. Journal of
Hydrology 315 (2005) 126-153
De Solan et al. Cartographie de l'enneigement par
télédétection à partir d'images SPOT-VEGETATION et
Landsat-TM: application a` l'Atlas marocain. Séminaire international,
Hydrologie nivale en méditerrané, Décembre 2002, Beyrouth,
Lebanon.
Dennis G. Dye, (2002) Variability and trends
in the annual snow-cover cycle in Northern Hemisphere land areas,
1972-2000. Hydrol. Process. 16, 3065-3077 (2002).
Dewalle D. R.& Rango A. (2008) Principle of snow
hydrology. Cambridge university press.pp410.
Douville, H., Royer, J. F., et Mahfouf, J. F. (1995) "A new
snow parametrization for the Météo- France climate model."
Clim. Dyn., 12, 21-52.
Dozier, J. (1989) Spectral Signature of Alpine Snow Cover from
the Landsat Thematic Mapper. Remote Sensing of Environment
28,9-22
Duchemin B., Berthelot B., Dedieu G., Leroy M., Maisongrande
P. (2002) Normalisation of directional effects in 10-day global syntheses
derived from VEGETATION/SPOT: II. Validation of an operational method on actual
data sets". Remote Sensing of Environment ;81:101-113.
Duclaux, A., (2005). Modélisation hydrologique de 5
Bassins Versants du Haut-Atlas Marocain avec SWAT (Soil and Water Assessment
Tool), Master's Thesis, Institut National Agronomique de Paris-Grignon,
France.
Dunn, S. M., & Colohan, R. J. E. (1999). Developing the
snow component of a distributed hydrological model: A step-wise approach based
on multiobjective analysis. Journal of Hydrology, 223, 1-16.
Eckstein, B.A., (1989). Evaluation of spline and weighted
average interpolation algorithms, Computers & Geosciences, 15, No.
1, p79-94.
Edijatno C., Michel, C., (1989). Un modèle
pluie-débit à trois paramètres. La Houille
Blanche, 2, 113-121.
Fassnacht, S. R., and E.D. Soulis, (2002). Implications during
transitional periods of improvements to snow processes in the land surface
scheme - hydrological model WATCLASS. Atmosphere-Ocean, 40 (4),
389-403.
Flerchinger, G.N. & Cooley, K.R. (2000). A ten-year water
balance of a mountainous semi arid watershed. Journal of Hydrology
237, 86-99.
Fortin F, Bernier M, Battay A, Gauthier Y, Turcotte R.
(2000).Estimation of surface variables at the sub-pixel level for use as input
to climate and hydrological models. Proceedings of VEGETATION 2000 Symposium,
3-6 April 2000, Lake Maggiore, Italy.
Fortin J.P., Turcotte R., Massicotte S., Moussa R. et Fitzback
J. (2001a). A distributed watershed model compatible with remote sensing and
GIS data. Part 1: Description of the model. Journal of Hydrologic
Engineering - ASCE, 6(2): 91-99.
Fortin, J.P., R. Moussa, C. Bocquillon Et J.P. Villeneuve
(1995). Hydrotel, un modèle hydrologique distribué pouvant
bénéficier des données fournies par la
télédétection et les systèmes d'information
géographique. Revue des Sciences de l'Eau, 8 : 97-124.
Foster, J and Rango, A. (1982). Snow covers conditions in the
northern hemisphere during the winter of 1981. J. Clim., 20, 171-83.
Girard G., Ledoux E., Villeneuve, J.P., (1981). Le
modèle couplé - simulation conjointe des écoulements de
surface et des écoulements souterrains sur un système
hydrologique, Cahiers de l'ORSTOM, série HYDROLOGIE, 18(4),
195-280.
Goetz, S. J., Halthore, R. N., Hall, F. G., and Markham, B.
L., (1995), Surface temperature retrieval in a temperate grassland with
multiresolution sensors. Journal of Geophysical Research,
100, 25 397-25 410.
Gomez, L. & Rango, A. (2002) Operational snowmelt runoff
forecasting in the Spanish Pyrenees using the snowmelt runoff model.
Hydrological Processes. 16, 1583-1591.
Goodison, B. E., P. Y. T. Louie, and D. Yang, (1998). WMO
solid precipitation measurement intercomparison final report. WMO Instruments
and Observing Methods. Report No. 67, WMO/TD No. 872.
Goodison, B.E., H.L. Ferguson and G.A. McKay, (1981).
Measurement and Data Analysis, Chapter 6 in Handbook of Snow, Gray, D.M. and
D.H. Male, Eds., Pergamon Press Canada Ltd., pp. 191-274.
Granger, R.J. and Gray, D.M. (1990) A net radiation model for
calculating daily snowmelt in open environments, Nordic Hydrology, 21,
217-234.
Grayson R.-B., Moore I.-D., Mc Mahon T.-A., (1992).
Physically-based modelling.2. Is the concept realistic? Water Resources
Research, 26, 2659-2666.
GROISMAN, P. Y., and DAVIES, T. D., (2001). Snow cover and the
climate system. In Snow Ecology, edited by J. G. Jones, J. W. Pomeroy, D. A.
Walker and R. W. Hoham (New York: Cambridge University Press) pp. 1-44.
Hall DK, Riggs GA, Salomonson VV, DiGirolamo NE, Bayr KJ.
(2002). MODIS snow-cover products. Remote Sensing of Environment
83: 181-194.
Hall, D. K., Riggs, G. A., & Salomonson, V. V. (1995).
Development of methods for mapping global snow cover using moderate resolution
imaging spectroradiometer data. Remote Sensing of Environment, 54(2),
127-140.
Hanich, L., de Solan, B., Duchemin, B., Maisongrande, P.,
Chaponnière, A., Boulet,G. and Chehbouni, G. (2003) Snow cover mapping
using SPOT-VEGETATION with high resolution data: application in the Moroccan
Atlas Mountains. Proceedings of IEEE International Geoscience and Remote
Sensing Symposium (IGARSS), 21-25 July 2003, Toulouse, France.
Hartman RK, Rost AA, Anderson DM. (1996). Operational
processing of multi-source snow data. In Third International
Conference/Workshop on Integrating Geographic Information Systems and
Environmental Modeling, National Center for Geographic Information and
Analysis, Santa Barbara, CA.
Hartman, M. D., Baron, J. S., Lammers, R. B., Cline, D. W.,
Band, L. E., Liston, G. E., and Tague, C., (1999), Simulations of snow
distribution and hydrology in a mountain basin. Water Resources Research, 35,
1587-1603.
Hinzman, L. D. and D. L. Kane (1991). «Snow hydrology of
a headwater arctic basin. Conceptual analysis and computer modelling.»
Water Resources Research 27: 1111-1121.
Hoinkes, H. (1967). Glaciology in the international
hydrological decade. Presented at AIHS Commission on snow and ice, Report and
discussion (IAHS publication N° 79, PP. 7-16)
Holben B.N. (1986). Characteristics of maximum-value composite
images from temporal AVHRR data. Int. J. Remote Sensing,
7:1417-1434.
Hudson, G. and Wackernagel, H. (1994). Mapping temperature
using kriging with external drift: theory and an example from Scotland,
Int. J. Climatol. 14, 77#177;91.
Hutchinson, M.F., and P.E. Gessler, (1994), Splines - more
than just a smooth interpolator, Geoderma, Vol. 62, p45-67.
Huvelin P. (1973). Mouvements pré-atlasiques et
récents dans les Jbilets et sur leurs pourtours. Notes Serv.
Géol. Maroc, t.33, N°249, pp. 83-123.
Ishida, T. and Kawashima, S. (1993). Use of cokriging to
estimate surface air temperature from elevation, Theor. Appl.
Climatol., 47,147#177;157.
Jesko, S., Martinec, J., and Klaus, S. (1999) Distributed
mapping of snow and glaciers for improved runoff modelling. Hydrological
Processes. 13, 2023-2031.
Justice C, Vermote E, Townshend JRG, Defries R, Roy DP, Hall
DK, Salomonson VV, Privette J, Riggs G, Strahler A, Lucht W, Myneni R,
Knjazihhin Y, Running S, Nemani R, Wan Z, Huete A, van Leeuwen W, Wolfe R,
Giglio L, Muller J-P, Lewis P, Barnsley M. (1998). The Moderate Resolution
Imaging Spectroradiometer (MODIS): land remote sensing for global change
research. IEEE Transactions on Geoscience and Remote Sensing
36: 1228-1249.
Justice, C., & Townshend, J. (2002). Special issue on the
moderate resolution imaging spectroradiometer (MODIS): a new generation of land
surface monitoring. Remote Sensing of Environment, 83, 1-2
Justice, C., Townshend, J.R.G., & Salomonson, V. (1998).
The Moderate Resolution Imaging Spectroradiometer (MODIS): land remote sensing
for global change research. Ieee Transactions on Geoscience and Remote
Sensing, 36, 1228-1249.
Justice, C.O., Townshend, J.R.G., & Markham, B.L. (1987).
Modis Spatial-Resolution Study. International Journal of Remote Sensing,
8, 1119-1121.
KANE, D. L., HINZMAN, L. D., BENSON, C. S., and LISTON, G. E.,
(1991). Snow hydrology of a headwater Arctic basin 1. Physical measurement and
process studies. Water Resources Research, 27, 1099-1109.
Khazaei, E., Spink, A.E.F., and Warner, J. W. (2003) a
catchment water balance model for estimating groundwater recharge in arid and
semi-arid regions of south-east Iran. Hydrogeology Journal
11(3), 333-342.
Klaus, S. (1998). Effects of climate change on water resources
and runoff in an Alpine basin, Hydrological Processes.
12, 1659-1669.
Kleme, V. (1986b). Operational testing of hydrological
simulation models. Hydrological Sciences Journal, 31(1), 13-24.
Kleme, V. (1988). A hydrological perspective. Journal of
Hydrology, 100, 3-28.
Kongoli, C. E. and W. L. Bland (2000). «Long-term snow
depth simulations using a modified atmosphere-land exchange model.»
Agricultural and Forest Meteorology 104: 273-287.
Konig, M. Winther, J.-G, et Isaksson, E., (2001a). Measuring
snow and glacier properties from satellite. Rev. Geophys., 39 (1).
Krajewski, W. F. and Smith, J. A. (2002). Radar hydrology:
rainfall estimation. Advances in Water Resources. Volume 25, Issues
8-12, August-December 2002, Pages 1387-1394
Kuusisto, E. (1980). «On the values and Variability of
degree-day melting factor in Finland.» Nordic hydrology
11: 235-242.
Larson, L.W., and E.L. Peck, 1974 : Accuracy of precipitations
measurements for hydrological modeling. Water Resourc. Res., textbf10,
857-863.
Legates, D.R. and C.J. Willmott, (1990), Mean Seasonal and
Spatial Variability in Global Surface Air Temperature, Theor. Appl.
Climatol., vol. 41, p11-21.
Leroux, J. (2006) Optical remote sensing of snow cover
dynamics in the High-Atlas mountains of Morocco : application to the
hydrological modelling of the rheraya sub catchment. Master Thesis in
«Radio Astronomy and Space Science», Chalmers University of
Technology, Göteborg, Sweden, 92 pp.
Limam, N. (2005). Perspectives de développement des
ressources en eau dans le bassin du Tensift. Assemblée
générale du Réseau Méditerraneen des Organismes de
Bassin REMOB.Marrakech, Maroc, 23-26 mai 2005.
Lissens G, Kempeneers P, Fierens F. Development of a cloud,
snow and cloud shadow mask for VEGETATION imagery. Proceedings of VEGETATION.
Symposium, 3-6 April 2000, Lake Maggiore, Italy.
Liston, G. E., (1999). Interrelationships among snow
distribution, snowmelt, and snow cover depletion: implications for atmospheric,
hydrologic, and ecologic modeling. Journal of Applied Meteorology. 38,
1474-1487.
Llboutry, L. 1954 . The origin of penitents. J. Glaciolo.,
2(1952-56),331-338.
Loumagne C., Chkir N., Normand M., Ottlé C.,
Vidal-Madjar D., (1996). Introduction of the soil/vegetation/atmosphere
continuum in a conceptual rainfall/runoff model. Hydrological
Sciences, 41(6), 889-902.
Luce, C.-H., Tarboton, D., (2004). The application of
depletion curves for parameterization of subgrid variability of snow.
Hydrol. Proces. 18, 1409-1422.
Luce, C.-H., Tarboton, D.-G., Cooley, K.-R., (1999). Sub-grid
parameterization of snow distribution for an energy and mass balance snow cover
model. Hydrol. Proces. 13, 1921-1933.
Maidment, D.R. (1992). Hydrology. In:
Applied Hydrology, D. R. Maidment (Ed.), McGraw
Hill, New-York, 1412 p.
Maisongrande, P., Duchemin, B., Dedieu, G. (2004)
VEGETATION/SPOT - An Operational Mission for the Earth Monitoring: Presentation
of New Standard Products". International Journal of Remote Sensing
25,9-14.
Makhlouf Z., (1994). Compléments sur le modèle
pluie-débit GR4J et Essai d'estimation de ses paramètres.
Thèse de doctorat, Université Paris XI Orsay, CEMAGREF, Grenoble,
426 pages.
Male, D.H. and Granger, R.J. (1981) Snow surface energy
exchange, Water Resources Research, 117 (3), 609-627.
Male, D.H. and Grey, D.M. (1981), Snow cover ablation
and runoff, Snow cover ablation and runoff, D.H. Male and D.M. Grey (eds.).
Toronto, Ontario, Pergamon Press: 360-436
Markham, B. L., and Barker, J. L., 1986, Landsat-MSS and TM
post calibration dynamic ranges, atmospheric reflectance and at-satellite
temperature. EOSAT L andsat T echnical Notes 1, (Lanham,
Maryland: Earth Observation Satellite Company), pp. 3-8.
Marks, D. and Dozier, J. (1992) Climate and energy exchange at
the snow surface in the alpine region of the Sierra Nevada. 2. Snow cover
energy balance, Water Resources Research, 28 (11),
3043-3054.
Martinec J, Rango A, Robert R. (1998). Snow Runoff Model
(SRM) User's Manual. http://hydrolab.arsusda.gov/cgi-bin/srmhome [13 July
2003].
Martinec J. (1960). The degree-day factor for snowmelt runoff
forecasting. In IUGG General Assembly of Helsinki, IAHS Commission of
Surface Waters, IAHS: number 51, pp. 468-477.
Martinec J. (1975) Snowmelt-runoff model for stream flow
forecasts. Nordic Hydrology 6: 145-154.
Martinec J. (1985) Snowmelt runoff models for operational
forecasts. Nordic Hydrology 16: 129-136.
Martinec, J. & Rango, A. (1989). Merits of staistical
criteria for the performance of hydrological models. Water Ressour.
Bull., 25(2),421-32.
Martinec, J. & Rango, A. (1995) Seasonal runoff forecasts
for hydropower based on remote sensing. In Proceedings of the 63rd Western
Snow Conference, Reno, NV, USA, 10-20.
Martinec, J., A. Rango, et al. (1994). The Snowmelt Runoff
Model user's manual. Washington, D. C., NASA Reference Publ. No. 1100.
Martinec, J., and Rango, A., (1981), Areal distribution of
snow water equivalent evaluated by snow cover monitoring. Water Resources
Research, 17, 1480-1488.
Martinec, J., Rango, A., Robert R. (2005) Snow Runoff Model
(SRM) User's Manual. http://hydrolab.arsusda.gov/cgi-bin/srmhome [January,
2005].
Matheron, G., (1963). Principles of geostatistics?, Economic
Geology, 58, p. 1246-1266.
Matson, M. (1991) NOAA satellite snow cover data.
Palaeo-geog. and Paleoecol. 90,213 218.
Matthews, D.A. (1989) Programme Al Ghait - Morocco winter
snowpack augmentation project. Final report. Department of the
Interior, Washington D.C.
Matthews, D.A. (1989) Programme Al Ghait - Morocco winter
snowpack augmentation project. Final report. Department of
the Interior, Washington D.C.
McLaughlin, D. (1995) Recent advances in hydrologic data
assimilation, US Natl Rep Int Union Geod Geophys 1991-1994. Rev
Geophys. 33, 977-84.
McLaughlin, D., O'Neill, A., Derber, J., Kamachi, M.
(2005) Opportunities for enhanced collaboration within the
data assimilation community. Quarterly Journal of the Royal Meteorological
Society, 131, 3683-3693.
Michel, C. (1989). Hydrologie appliquée aux petits
bassins versants ruraux, Cemagref, Antony.
Mitchell, KM., DeWalle, DR. (1998) Application of the snowmelt
runoff model using multiple-parameter landscape zones on the Towanda Creek
basin, Pennsylvania. Journal of the American Water Resources Association
34: 335-346.
Moore, I. D, O'Loughlin, E. M. et Burch, G. J. (1988) A
contour-based topographic model for hydrological and ecological applications.
Earth Surface Processes Landf. 13, 305-320.
Moore, R. D. (1983). On the use of bulk aerodynamic formulae
over melting snow, Nordic Hydrology, 14(4), 193-206.
Moore, R. D. (1993). «Application of a conceptual
streamflow model in a glacierized drainage basin.» Journal of Hydrology
150: 151-168.
Morin, G., Fortin, J. P., Lardeau, J. P., W., S., et Paquette,
S. (1981). "Modèle CEQUEAU: Manuel d'utilisation." n° 93,
INRS-Eau, Sainte-Foy, Canada.
Morris, E.M. (1989) Turbulent transfer over snow and ice,
Journal of Hydrology, 105 (3-4), 205-223.
Moukhchane M. (1983). Contribution à l'étude des
réservoirs profonds de la bordure nord de l'Atlas entre Demnate et
Imintanoute (Maroc). Thèse de 3ème cycle.
Besançon. 119p.
Myers, R.H., (1990). "Classical and Modern Regression with
Applications", PWS-Kent Publishing, Boston, MA, p488.
Nash, J.E. and Sutcliffe, J.V., (1970). River flow forecasting
through conceptual models: 1. A discussion of principles. Journal of
Hydrology, 10: 282-290.
Oerlemans, J. (2000). Analysis of a three year meteorological
record from the ablation zone of Moteratschgletscher, Switzerland: energy and
mass balance, Journal of Glaciology, 46 (155), 571-579.
ORSTOM. (1976).Hydrologie du bassin du Tensift. Royaume du
Maroc, Ministère des travaux publics et communications, Direction de
l'Hydraulique, Division des Ressources en Eau..
Palacios-Vélez, O. L. et Cuevas-Renaud, B
(1992)SHIFT : A distributed runoff model using irregular triangular
facets. J. Hydrol. 134.35-55.
Peck, E.L., Keefer, T.N. et Johnson, E.R. (1981). Strategies
for using remotely sensed data in hydrologic models, Rapport NASA-CR
66729.
Pitlick, J. (1994) Relation between peak floods, precipitation
and physiography for five mountainous regions in the western USA. Journal
of Hydrol. 158 (3-4):219-240.
Potts HL. 1937. Snow surveys and runoff forecasting from
photographs. Transactions of the American Geophysical Union, South
Continental Divide Snow-Survey Conference: 658-660.
Pomeroy, J.W., D.M. Gray, K.R. Shook, B. Toth, R.L.H. Essery,
A. Pietroniro and N. Hedstrom. (1998). An evaluation of snow accumulation and
ablation processes for land surface modelling. Hydrological Processes, 12,
2339-2367
Quick, M.C., Pipes, A., (1977). UBC watershed model. Hydrol.
Sci.Bull. 221, 153-161.
Ramsay B. (2000). Prospects for the interactive multisensor
snow and ice mapping system (IMS). In Proceedings of the 57th Eastern Snow
Conference, Syracuse, NY, USA; 161-170.
Rango A. (1985). Assessment of remote sensing input to
hydrologic models. AWRA Water Ress. Bull. 212, 423-432.
Rango A. (1986). Progress in snow hydrology remote-sensing
research. IEEE Transactions on Geoscience and Remote Sensing
24: 47-53.
Rango A. (1996). Spaceborne remote sensing for snow hydrology
applications. Hydrological Science Journal 41:
477-494.
Rango, A, van Katwijk, V. (1990) Development and testing of a
snowmelt-runoff forecasting technique. Water Resources Bulletin
26, 135-144.
Rango, A. & Martinec, J. (1997) Water storage in mountain
basins from satellite snow cover mapping. In Remote Sensing and
Geographical Information Systems for Design and Operation for Water Resources
System, Baumgartner MF, Schultz GA, Johnson AI (eds). IAHS Publication No.
242. IAHS Press: Wallingford, 83-91.
Rango, A. & Martinec, J. (1979) . Application of a
snowmelt-runoff model using Landsat data. Nordic Hydrology
10: 225-238.
Rango, A. & Martinec, J. (1981) Accuracy of snowmelt
runoff simulation. Nordic Hydrology 12,
265-274.
Rango, A. & Martinec, J. (1995) Revisiting the degree-day
method for snowmelt computations. Water Resources Bull 1995.
31,657-69.
Rango, A. and J. Martinec (1994). «Model accuracy in
snowmelt runoff forecasts extending from 1 to 20 days.» Water Resources
Bulletin 30 (3): 463-470.
Reda, I., Andreas, A. (2003) Solar position algorithm for
solar radiation application. National Renewable Energy Laboratory (NREL)
Technical report NREL/TP-560-34302.
Refsgaard, J.C. et Storm, B. (1995): MIKE SHE. Dans V.P Singh
éditeur : Computer models of watershead hydrology. Water
resources publications, 809-846.
Richard C. and Gratton D. J. (2001). The importance of the air
temperature variable for the snowmelt runoff modelling using the SRM.
Hydrol. Process. 15, 3357-3370
Robeson, S. M. and Willmott, C. J. 1993. `Spherical spatial
interpolation and terrestrial air temperature variability', Proceedings Second
International Conference on Integrating GIS and Environmental Modeling,
Breckenridge, CO, pp. 111#177;115.
Roche, M., (1963). Hydrologie de surface. Gauthier-Villars
Editeur-Paris, 429 p., 204 fig.
Rodriguez, E., C.S. Morris, J.E. Belz, E.C. Chapin, J.M.
Martin, W. Daffer, S. Hensley, (2005). An assessment of the SRTM topographic
products, Technical Report JPL D-31639, Jet Propulsion Laboratory, Pasadena,
California, 143 pp.
http://www2.jpl.nasa.gov/srtm/srtmBibliography.html
Rodriguez, JY. (1994) an operational forecasting snowmelt
model with objective calibration. Nordic Hydrology
25: 79-100.
Romanov P, Gutman G, Csiszar I. (2000). Automated monitoring
of snow cover over North America with multispectral satellite data. Journal
of Applied Meteorology 39: 1866-1880.
Rosenthal W, Dozier J. (1996). Automated mapping of montane
snow cover at subpixel resolution from the Landsat Thematic Mapper. Water
Resour Res. 32(1): 115-130.
Running, S.W., Justice, C.O., Salomonson, V., Hall, D.,
Barker, J., Kaufmann, Y.J., Strahler, A.H., Huete, A.R., Muller, J.P.,
Vanderbilt, V., Wan, Z.M., Teillet, P., & Carneggie, D. (1994). Terrestrial
Remote-Sensing Science and Algorithms Planned for Eos Modis. International
Journal of Remote Sensing, 15, 3587-3620
Saint, G. (1994). VEGETATION onboard SPOT-4: mission
specifications version 3. VGT/PS/940518/1 document (39 pp.) available at
http://vegetation.cnes/fr./
and at the VEGETATION International Users Committee Secretariat at Joint
Research Centre (Ispra, Italy), e-mail: iuc.vegetation@ cen.jrc.it.
Schneider, K., andMauser, W., (1996). Processing and accuracy
of Landsat ThematicMapper data for lake surface temperature measurement.
International Journal of Remote Sensing, 17, 2027-2041.
Schott, J. R., and Volchok, W. J., (1985). Thematic Mapper
thermal infrared calibration. Photogrammetric Engineering and Remote
Sensing, 51, 1351-1357.
Schulz O. and De Jong C. (2004).snowmelt and sublimation:
field experiments and modelling in the High Atlas Mountains of Morocco.
Hydrology and earth system sciences; 8(6): 1076-1089.
Seo, D., Koren, V., Cajina, N. (2003) Real-Time Variational
Assimilation of Hydrologic and Hydrometeorological Data into Operational
Hydrologic Forecasting. J. of Hydromet., 4,
627- 641.
Shaban A, Faour G, Khawlie M, Abdallah Ch. (2004).Remote
sensing application to estimate the volume of water in the form of snow on
Mount Lebanon. Hydrological Sciences Journal des Sciences
Hydrologiques; 49(4): 611-621.
Shafer, BA., Jones, EB., Frick, DM. (1982) Snowmelt runoff
simulation using the Martinec Rango model on the South Fork Rio Grande and
Conejos River in Colorado. AgRISTARS Report. CP-G1-04072, Goddard Space
Flight Center, Greenbelt, MD, USA.
Shamir, E., Georgakakos, K.-P., (2006). Distributed snow
accumulation and ablation modeling in the American River basin. Adv.Water
Resour. 29 (4), 558-570.
Shiklomanov, I. A. (1990). Global water resources. Nature and
resources, 26 (3),343-343.
Simpson J, Stitt J, Sienko M. (1998).Improved estimates of the
areal extent of snow cover from AVHRR data. Journal of Hydrology, 204
: 1-23.
Sinan M. (2000). Méthodologie d'identification,
d'évaluation et de protection des ressources en eau des aquifères
régionaux par couplage des SIG, de la géophysique et de la
géostatistique. Application à l'aquifère du Haouz de
Marrakech (Maroc). Thèse Univ. Mohammed V. Rabat,
Maroc.
Singh, P., & Singh, V. P. (2001). Snow and glacier
hydrology. Dordrecht: Kluwer.
Singh, P., N. Kumar, et al. (2000). Degree-days factors for
snow and ice for Dokriani Glacier, Garhwal Himalayas. Journal of
Hydrology. 235: 1-11.
Singh, V.P., (1995). Computer models of watershead hydrology.
Water resources publications, 809-846.
Slater, A.G. and Clark, M.P. (2006) Snow Data Assimilation via
an Ensemble Kalman Filter. J. of Hydromet.
7,478-493.
Soederstroem, M. and Magnusson, B. 1995. `Assessment of local
agroclimatological conditions Ð a methodology', Agric. For. Meteorol., 72,
243#177;260.
Sommerfeld, R.A. and E. LaChapelle (1970). The classification
of snow metamorphism. J. Glaciol., 9, No.55, 3-17.
Songweon, L., Andrew, G. K., and Thomas, M.O. (2005) a
comparison of MODIS and NOHRSC snow-cover products for simulating streamflow
using the Snowmelt Runoff Model. Hydrol. Process. 19,
2951-2972.
Sospedra, F., V. Caselles, and E. Valor. (1998). Effective
wave number for thermal infrared bands--application to Landsat-TM. Int. J.
Remote Sensing, Vol. 19, No. 11, 2105-2117.
Speers, D.D. (1995) SSARR model. Dans: Computer Models of
Watershed Hydrology (Editeur V.P Singh), 367-394, Water resources
publications, Highland Ranch, USA.
Sun, C., J. Jin, and Y. Xue, 1999: A simple
snow-atmosphere-soil transfer (SAST) model. J. of Geophys. Res, 104,
19587-19579.
Sun, C., J. P. Walker, and P. R. Houser (2004), a methodology
for snow data assimilation in a land surface model, J. Geophys. Res.,
109, D08108,
doi:10.1029/2003JD003765.
Sverdrup HU. (1936). The eddy conductivity of the air over a
smooth snow field. Geofysiske Publikasjoner 11(7): 1-69.
Tangborn, W.V., (1984). Prediction of glacier derived runoff
for hydro-electric development. Geogr. Ann. 66A (3), 257-265.
Tarboton, D.G. and Luce, C.H. (1996) Utah Energy Balance Snow
Accumulation and Melt Model (UEB) Computer model technical description and
users guide, Utah Water Research Laboratory and USDA Forest
Service Intermountain Research Station: 64.
Tarpley J.P., S.R. Schneider and R.L. Money. (1984).Global
vegetation indices from NOAA-7 meteorological satellite. Journal of Climate
Applied Meteorology; 23:491-494.
Thomas J. Schmugge , William P. Kustas,
Jerry C. Ritchie, Thomas J. Jackson and Al Rango (2002). Remote sensing in
hydrology. Advances in Water Resources Volume 25, Issues 8-12,
August-December 2002, Pages 1367-1385
Thomas, N., Helmut, R., Petra, M., Florian, M. (2008)
Assimilation of meteorological and remote sensing data for snowmelt runoff
forecasting, Remote Sensing of Environment, 112(4),
1408-1420.
U.S. Army Corps of Engineers (1956). Snow Hydrology. North
Pacific division, Portland, Oregon, USA.
Vermote, E.F., El Saleous, N.Z., & Justice, C.O. (2002).
Atmospheric correction of MODIS data in the visible to middle infrared: first
results. Remote Sensing of Environment, 83, 97-111.
Verseghy, D.L., (1991). Class - a Canadian land surface scheme
for GCMS. Part I: Soil model. Int. J. Climatol., 11,
111-133.
Vieux, B.E. et Gaur, N. (1994) Finite element modelling of
storm water runoff using GRAS GIS. Microcomp. Civ. Eng. 9, 263-270.
Viviroli, D., Weingartner, R, and Messerli, B. (2003)
Assessing the hydrological significance of the world's mountains. Mountain
Research and Development, 23, 32-40.
Vogt, J.V., (1996). Land surface temperature retrieval from
NOAA AVHRR data. Dans : G. D'Souza., A. Belward & J.P. Malingreau
(eds.). Brussels & Luxembourg, 125-151.
Vogt, J.V., Viau, A.A. & Paquet, F., (1997). Mapping
Regional Air Temperature Fields Using Satellite Derived Surface Skin
Temperatures. International Journal of Climatology, 17, 1559-1579.
Wukelic, G. E., Gibbons, D. E., Martucci, L. M., and Foote, H. P., 1989,
Radiometric calibration of Landsat Thermatic Mapper Thermal Band. Remote
Sensing of Environment, 28, 339-347.
Willmott, C. J., Robeson, S. M. and Feddema, J. J. (1991).
Influence of spatially variable instrument networks on climatic averages,
Geophys. Res. Lett., 18, 2249#177;2251.
Winther, J-G, and D.K. Hall. (1999). Satellite deriver snow
coverage related to hydropower production in Norway: present and future. Int.
J. Of Rem. Sens. 20(15): 2991-3008.
WMO (1964). Guide for Hydrometeorological Practices, World
Meteorological Organisation, Geneva, Switzerland.
WMO (1986). Intercomparison of models of snowmelt runoff,
Operational Hydrology Report No 23, WMO n°646. World Meteorological
Organisation, Geneva, Switzerland.
World Bank. kingdom of morocco, a water sector review, Report
No. 14750-MOR 1995.
Wukelic, G. E., D. E. Gibbons, L. M. Martucci, and H. P.
Foote. (1989). Radiometric calibration of Landsat Thematic Mapper thermal band.
Remote Sens. Environ. 28: 339-347.
Xingong Li & Mark W. Williams (2008). Snowmelt runoff
modelling in an arid mountain watershed,Tarim Basin, China. Hydrol.
Process. 22, 3931-3940.
Xiong, X.X., Che, N.Z., & Barnes, W. (2005). Terra MODIS
on-orbit spatial characterization and performance. Ieee Transactions on
Geoscience and Remote Sensing, 43, 355-365.
Yapo, P.O., Gupta, H.V. and Sorooshian, S., (1998).
Multi-objective global optimization for hydrologic models. Journal of
Hydrology, 204: 83-97.
Zuzel, J. F., and L. M. Cox (1975), Relative Importance of
Meteorological Variables in Snowmelt, Water Resour. Res., 11(1),
174-176.
* 1 _ Centre de Recherche sur
l'Eau en Milieu Aride et Semi Aride : Equipe associée à
l'IRD
* 2 _ Centre d'Etudes
Spatiales de la BIOsphère
* 3 _ Université Cadi
Ayyad de Marrakech
* 4 _ Office Régional
de Mise en Valeur Agricole du Haouz
* 5 _ Agence du Bassin
Hydraulique du Tensift
* 6 _ MODerate resolution
Imaging Spectroradiometer
* 7 _ Earth Observing
System
* 8 _ Multi-Spectral
Sensor
* 9 _ Thematic Mapper
* 10 _ Enhanced Thematic
Mapper Plus
* 11 _ Shuttle Radar
Topographic Mission
* 12 _ Normalized Difference
Vegetation Index
* 13 _ Interaction
Sol-Biosphre-Atmosphre-neige explicite (Explicit Snow)
|
|



