Etude et modelisation des supercondensateurs

Universite Claude Bernard Lyon 1

Direction de la Recherche et des Etudes Doctorales

Service des Etudes Doctorales

Ba'timent l'Atrium

43, Bd du 11 Novembre 1918 69622 VILLEURBANNE cedex

N° ordre 042-2009

RAPPORT D'APRES SOUTENANCE

relatif a la these de Doctorat soutenue le 13 mars 2009
par Monsieur DIAB Yasser

Monsieur Yasser DIAB a presente ses travaux de these de doctorat avec clarte, peciagogie et enthousiasme.

Il a confirme qu'il avait realise un travail de grande ampleur sur ensemble des problemes de modelisation des supercondensateurs, et la pertinence de ses reponses aux questions du jury a montre sa tres bonne maitrise du sujet.

Le jury a egalement apprecie les nombreux couplages modelisation-experimentation ainsi que sa volonte de lier les modelisations electriques aux phenomenes physicochimiques.

II tient egalement a souligner l'originalite de la modelisation des phenomenes d'autodecharge. Enf in, le membre industriel du jury a particulierement apprecie le realisme des travaux.

Pour toutes ces raisons, le jury unanime decerne a Monsieur Yasser DIAB, le grade de docteur de l'Universite Claude Bernard de Lyon 1, specialite « Genie E lectrique ».

0 .-;.7VEPE T SIEGE : Universite Claude Bernard Lyon 1 - 43, Boulevard du 11 Novembre 1918 - 69 622 Villeurbanne Cedex, France.

N° education nationale : 069 1774 D ; SIRET : 196 917744 000 19 ; code NAF : 85.42Z

TP LYON 10071 69000 00001004330 72
http: / / www.univ-lyonl.fr ; telephone : [phone] ; telecopie : 04 72 43 10 20

N° d'ordre Année 2009

THESE
présentée
devant l'UNIVERSITE CLAUDE BERNARD - LYON 1
pour l'obtention
du DIPLOME DE DOCTORAT
(arrêté du 7 août 2006)

Spécialité : Génie Électrique
préparée au sein de

L'ECOLE DOCTORALE

ELECTRONIQUE, ELECTROTECHNIQUE, AUTOMATIQUE

DE LYON

présentée et soutenue publiquement le 13 Mars 2009
par

M. DIAB Yasser

(Ingénieur en énergie électrique de l'Université de Damas, Syrie)

ÉTUDE ET MODELISATION DES SUPERCONDENSATEURS : APPLICATIONS AUX SYSTEMES DE PUISSANCE

Après avis de :

M. COQUERY Gérard Directeur de Recherche, INRETS-LTN

M. OUSTEN Yves Professeur des Universités, Université de Bordeaux

Devant la commission d'examen formée de :

M. CAUMONT Olivier Responsable développement supercondensateurs, société

BATSCAP

M. COQUERY Gérard Directeur de Recherche, INRETS-LTN

M. GUALOUS Hamid Maître de Conférences (HDR), Université Franche-Comté

M. MULTON Bernard Professeur des Universités, ENS-Cachan

M. OUSTEN Yves Professeur des Universités, Université de Bordeaux

M. ROJAT Gérard Professeur des Universités, Université Lyon 1

M. VENET Pascal Maître de Conférences (HDR), Université Lyon 1

A mes parents
A la mémoire de mes grands-parents
A ma femme et mes enfants
A tous ceux qui me sont Chers

Résumé

Etude et modelisation des

supercondensateurs : applications aux

systèmes de puissance

Ce travail a pour objectif d'analyser quantitativement les performances (capacité, ESR, autodécharge, ...) des supercondensateurs issus de différentes technologies lorsqu'ils sont soumis aux contraintes électriques et thermiques. Les différents paramètres de ces supercondensateurs sont caractérisés par les techniques de spectroscopie d'impédance, de cycles de charge/décharge et de voltampérométrique.

La modélisation des supercondensateurs a été effectuée par plusieurs modèles complémentaires. Les résultats de simulation de ces derniers sont comparés avec ceux expérimentaux dans le domaine temporel et fréquentiel. Nous avons mis au point un modèle innovant de l'autodécharge dans les supercondensateurs.

L'ensemble de ce travail a permis d'étudier le comportement des supercondensateurs mis en série en mettant en évidence leur fiabilité, le temps d'équilibrage et le rendement énergétique global du système.

Mots-clés

Supercondensateur, caractérisation, modélisation, autodécharge, thermique, fiabilité, circuit d'équilibrage.

Abstract

Studying and modelling of supercapacitors :

Applications in power systems

The aim of this work is to analyze quantitatively the supercapacitors performance (capacitance, ESR, self-discharge ...), which are made by different technologies under constraints; thermal and electrical. Different supercapacitors parameters are characterized by the help of different techniques as impedance spectroscopy, voltamperometry, and charging/discharging cycles.

The supercapacitors modelling have been conducted by several complementary models. These models are compared in time and frequency domain with various experimental tests. A new model of the self-discharge was established.

All the life expectancy, energetic efficiency and balancing time are compared for different balancing circuits and typical applications.

The whole of this work has helped to investigate the supercapacitors behaviour applied in series demonstrating their reliability, the balancing time and the total energy efficiency of the system.

Key-words

Supercapacitor, characterization, modelling, self-discharge, thermal, reliability, balancing circuit.

Remerciements

Je tiens à remercier en tout premier lieu M. Gérard Rojat et M. Pascal Venet pour l'honneur qu'ils m'ont fait d'avoir acceptés l'encadrement de ma thèse.

J'exprime ma gratitude à l'Université de Damas en Syrie d'avoir financé ce travail. Je tiens à remercier M. Hamid Gualous pour ses encouragements et son aide pertinente à la réalisation de ce travail.

Je tiens à remercier chaleureusement M. Bernard Multon qui a bien voulu en être le président du jury. Je tiens à remercier également M. Gérard Coquery et M. Yves Ousten, qui ont accepté d'être les rapporteurs de ma thèse de doctorat. Je tiens à remercier également, M. Hamid Gualous et M. Olivier Caumont, qui ont bien acceptés d'examiner cette thèse.

Je tiens aussi à remercier M. Frédéric Ferreyre et Siméon Diampeni pour l'aide précieuse qu'ils m'ont apportée dans la correction de ce manuscrit.

Je tiens à remercier très particulièrement le technicien Younes Zetouni pour ses aides lors de mes expérimentations.

Je tiens à remercier les personnes qui m'ont aidé dans la recherche bibliographique : M. Stéphane Raël de l'INP de Loraine, M. Gianni Sartorelli de Maxwell technologie, M. Peter Kurzweil de l'Université de science appliquée à Amberg/Allemagne et M. Khaled Al-Cheikh Hamoud de l'INP de Grenoble.

J'adresse mes sincères remerciements à l'ensemble des membres de l'équipe du laboratoire Ampère pour l'ambiance chaleureuse qu'ils font régner au laboratoire.

Enfin, je remercie ma famille pour son aide et son soutien précieux durant ces années bien chargés.

Liste de matières

Liste de matières

1. INTRODUCTION GÉNÉRALE 21

2. PRINCIPES PHYSIQUES, TECHNOLOGIE ET APPLICATIONS DES SUPERCONDENSATEURS 27

2.1. INTRODUCTION 27

2.2. PRINCIPES PHYSIQUES 27

2.2.1. Double couche électrique 27

2.2.2. Pseudocapacitance 29

2.3. TECHNOLOGIE 30

2.3.1. Electrodes 30

2.3.2. Électrolytes 31

2.3.3. Séparateurs 32

2.3.4. Technique d'assemblage du supercondensateur 33

2.4. TECHNOLOGIE ET RECHERCHE ACTUELLES 35

2.4.1. Etat actuel de la technologie 35

2.4.2. Développement et recherches futures 39

2.5. APPLICATIONS 40

2.5.1. Domaine informatique 40

2.5.2. Domaine du transport 40

2.5.3. Couplage réseau-supercondensateurs 41

2.6. PRÉSENTATION DES SUPERCONDENSATEURS ÉTUDIÉS 41

2.7. CONCLUSION 43

3. CARACTÉRISATION ET MODÉLISATION ÉLECTRIQUE, FRÉQUENTIELLE ET THERMIQUE DES SUPERCONDENSATEURS 45

3.1. INTRODUCTION 47

3.2. MÉTHODES DE CARACTÉRISATION DES SUPERCONDENSATEURS 49

3.2.1. Charge/décharge 49

3.2.1.1. Outil de manipulation et principe 49

3.2.1.2. Essai à courant constant 50

3.2.1.3. Essai à tension constante 52

3.2.1.4. Essai à puissance constante et plan de Ragone 53

3.2.1.4.1 Détermination de la capacité en fonction de la puissance 53

3.2.1.4.2 Plan de Ragone 55

3.2.1.4.3 Comparaison énergétique des supercondensateurs 56

3.2.2. Voltampérométrie cyclique 56

3.2.2.1. Principe de la voltampérométrie cyclique 56

3.2.2.2. Essai de voltampérométrie cyclique 57

3.2.2.3. Définition du rendement coulombien 58

3.2.2.4. Effet du nombre de cycles de charge/décharge sur le rendement coulombien 59

3.2.3. Spectroscopie d'impédance électrochimique 60

3.2.3.1. Définition et principe 60

3.2.3.2. Essai de spectroscopie d'impédance 61

3.2.3.3. Dépendance des paramètres du supercondensateur avec la tension 65

3.2.3.3.1. Origine de la non-linéarité de la capacité du supercondensateur 65

3.2.3.3.2. Plan de mesure 65

3.2.3.3.3. Effet du protocole de caractérisation sur les paramètres du

supercondensateur 67

3.2.3.4. Capacité des supercondensateurs étudiés 69

3.3. MODÉLISATION ÉLECTRIQUE ET FRÉQUENTIELLE DES SUPERCONDENSATEURS 70

3.3.2. Modélisation temporelle du supercondensateur : modèle classique RC 70

3.3.2.1. Circuit équivalent 70

3.3.2.2. Identification des paramètres du modèle 71

3.3.2.2.1 Détermination des éléments du modèle (ESR et C) 71

3.3.2.3. Validation expérimentale et limitation 71

3.3.2.4. Effet du courant de la décharge sur les éléments du circuit classique 72

3.3.3. Modélisation temporelle du supercondensateur : modèle à deux branches 72

3.3.3.1. Non-linéarité de la capacité de la double couche du supercondensateur 73

3.3.3.2. Circuit équivalent 73

3.3.3.3. Identification des paramètres de la branche rapide 74

3.3.3.4. Identification des paramètres de la branche lente 75

3.3.3.5. Effet du courant de la charge/décharge 78

3.3.3.6. Comparaison du rendement coulombien des supercondensateurs étudiés 79
3.3.3.7. Comparaison des résultats obtenus par différentes méthodes 80

3.3.3.7.1. Présentation de la non-linéarité de la capacité obtenue par les

différentes techniques 80

3.3.3.7.2. Comparaison de la capacité nominale obtenue par différentes techniques

81

3.3.3.7.3. Comparaison des résistances par différentes techniques 82

3.3.3.8. Validation expérimentale et limitation 83

3.3.4. Modélisation dynamique du supercondensateur 84

3.3.4.1. Analyse du spectre d'impédance d'un modèle d'électrode poreuse 84

3.3.4.2. Modèle équivalent de la topologie du supercondensateur 85

3.3.4.3. Modèle à dérivée non-entière 86

3.3.4.4. Circuit électrique équivalent de l'impédance de diffusion 87

3.3.4.4.1 Modèle du réseau ladder (ligne de transmission) 87

3.3.4.4.2 Modèle des réseaux séries d'éléments de Zarc 88

3.3.4.4.3 Réponse en fréquence du circuit équivalent du supercondensateur 89

3.3.4.5. Approximation par élément à phase constante (CPE) à basses fréquences 92

3.3.4.5.1 Principe d'un élément à phase constante 92

3.3.4.5.2 Validation expérimentale 93

3.3.4.6. Représentation de la distribution de l'impédance de diffusion par un circuit

équivalent 94

3.3.4.7. Comparaison des modèles établis avec des essais expérimentaux 96

3.3.4.7.1. Comparaison des modèles établis avec un essai charge/décharge à courant constant 96
3.3.4.7.2. Comparaison des modèles établis avec un essai par voltampérométrie cyclique 96

3.3.4.7.3. Comparaison des modèles établis dans le cas d'une application

industrielle 97

3.3.4.8. Origine et modélisation du phénomène inductif 98

3.4. MODÉLISATION ET CARACTÉRISATION THERMIQUE DES SUPERCONDENSATEURS 100

3.4.1. Influence de la température lors de charge/décharge à courant constant 101

3.4.1.1. Essai de charge/décharge à différentes températures 101

3.4.1.2. Variation des paramètres de la branche rapide 103

3.4.1.3. Variation des paramètres de la branche lente 105

3.4.2. Variation thermique lors d'un essai par voltampérométrie cyclique 106

3.4.2.1. Essai par voltampérométrie à différentes températures 106

3.4.2.2. Rendement coulombien à différentes températures 107

3.4.3. Variation caractérisée par spectroscopie d'impédance 108

3.4.3.1. Dépendance en température des paramètres du supercondensateur BCAP010 108

3.4.3.1.1 Variation de la capacité en fonction de la température 108

3.4.3.1.2 Variation des résistances en fonction de la température 109

3.4.3.2. Approximation de la variation thermique de la dynamique des supercondensateurs 110
3.4.3.3. Dépendance en température et en tension des caractéristiques électriques du

supercondensateur 111

3.4.4. Modèle thermique du supercondensateur 112

3.4.4.1. Source de chaleur 112

3.4.4.1.1. Génération de chaleur irréversible 112

3.4.4.1.2. Génération de chaleur réversible 112

3.4.4.2. Impédance thermique 113

3.4.4.3. Réponse thermique du supercondensateur 115

3.4.4.3.1. Outil de mesure 115

3.4.4.3.2. Essai expérimental 116

3.4.4.3.3. Simulation et validation du modèle thermique 117

3.5. EFFET DU VIEILLISSEMENT SUR LES PARAMÈTRES DE SUPERCONDENSATEUR 119

3.5.1. Vieillissement accéléré 120

3.5.1.1. Vieillissement accéléré à la tension nominale et à la température limite d'utilisation 120
3.5.1.2. Vieillissement accéléré à la tension nominale et au-delà de la température

limite d'utilisation 121

3.6. CONCLUSION 122

4. ÉTUDE, CARACTÉRISATION ET MODÉLISATION DE L'AUTODÉCHARGE DES SUPERCONDENSATEURS 125

4.1. INTRODUCTION 127

4.2. MESURE DE L'AUTODÉCHARGE 128

4.2.1. Outil de mesure 128

4.2.2. Procédures de mesure 128

4.3. MÉCANISMES DE L'AUTODÉCHARGE 130

4.3.1. Autodécharge due à la dispersion des charges dans les pores 130

4.3.2. Autodécharge par diffusion liée au processus d'oxydoréduction 130

4.3.3. Autodécharge due au courant de fuite 130

4.3.4. Autodécharge due à la surtension 131

4.4. MODÉLISATION DE L'AUTODÉCHARGE 132

4.4.1. Modèle du courant de fuite 132

4.4.2. Modèles prenant en compte l'autodécharge due au processus de diffusion lié à

l'oxydoréduction 134

4.4.2.1. Modèle analytique 134

4.4.2.2. Circuit série 136

4.4.2.3. Circuit parallèle 139

4.4.3. Comparaison des modèles de l'autodécharge avec un essai de charge/décharge à
courant constant 144

4.5. VARIATION DES PARAMÈTRES DE L'AUTODÉCHARGE EN FONCTION DE LA TENSION INITIALE ET DE LA TEMPÉRATURE 145

4.5.1. Effet de la tension initiale 145

4.5.1.1. Variation des éléments du modèle liés au courant de fuite 145

4.5.1.2. Variation des éléments du modèle liés au processus de diffusion lors de l'oxydoréduction 146

4.5.2. Effet de la température ambiante 147

4.5.2.1. Variation des éléments du modèle liés au courant de fuite 148

4.5.2.2. Variation des éléments du modèle liés au processus de diffusion lors de l'oxydoréduction 149

4.6. COMPARAISON DE L'AUTODÉCHARGE DE DIFFÉRENTS SUPERCONDENSATEURS 151

4.6.1. Détermination des paramètres nominaux de l'autodécharge 151

4.6.2. Autodécharge des supercondensateurs du fabricant MAXWELL 152

4.6.3. Autodécharge des supercondensateurs des autres fabricants 155

4.7. EFFET DU VIEILLISSEMENT SUR L'AUTODÉCHARGE 157

4.8. DÉTERMINATION DES PARAMÈTRES DE L'AUTODÉCHARGE PAR SPECTROSCOPIE D'IMPÉDANCE 159

4.8.1. Réponse en fréquence de l'impédance de l'autodécharge 159

4.8.2. Essai de spectroscopie d'impédance à très basse fréquence 160

4.9. PHÉNOMÈNE DE LA RÉCUPÉRATION DE TENSION 162

4.10. IMPÉDANCE ÉLECTROCHIMIQUE DE L'AUTODÉCHARGE DE DIFFUSION 163

4.11. CONCLUSION 166

5. ÉVALUATION DES PERFORMANCES DES MODULES DE SUPERCONDENSATEURS 169

5.1. INTRODUCTION 171

5.2. CONCEPTION ET PERFORMANCE DES MODULES DE SUPERCONDENSATEURS 172

5.2.1. Dimensionnement des modules 172

5.2.2. Origine de la dispersion des paramètres des supercondensateurs d'un module173

5.2.2.1. Dispersion de fabrication des supercondensateurs 173

5.2.2.1.1. Gas de la dispersion de la résistance de fuite 174

5.2.2.1.2. Gas de la dispersion de la capacité 175

5.2.2.1.3. Gas de la dispersion de l'ESR 176

5.2.2.2. Différence de température entre les cellules du module 177

5.2.2.3. Effet de non-similitude du vieillissement sur les cellules du module 177

5.2.3. Performance du circuit d'équilibrage de tension 177

5.2.3.1. Définition du rendement énergétique des systèmes d'équilibrage 178

5.2.3.2. Détermination de l'espérance de vie d'un module 178

5.3. MODÉLISATION ET SIMULATION DU MODULE DE SUPERCONDENSATEURS AVEC PARAMÈTRES DISPERSÉS 181

5.3.1. Profils de courant des applications types 181

5.3.1.1. Applications avec un rapport cyclique élevé 181

5.3.1.1.1. Gycles de forts courants de charge/décharge 181

5.3.1.1.2. Projet Thalès [113, 159] 182

5.3.1.2. Applications avec un rapport cyclique bas 185

5.4. ÉTUDE COMPARATIVE DE SYSTÈMES D'ÉQUILIBRAGE 186

5.4.1. Systèmes d'équilibrage dissipatifs 186

5.4.1.1. Système d'équilibrage passif 186

5.4.1.1.1. Galcul du nouveau facteur de dispersion de la résistance de fuite 187

5.4.1.1.2. Galcul du temps d'équilibrage 188

5.4.1.1.3. Résultats de la simulation des applications 193

5.4.1.2. Diodes Zener 196

5.4.1.3. Résistances commandées 196

5.4.1.3.1. Résultats de la simulation des applications ayant un rapport cyclique élevé 197

5.4.1.3.2. Nouvelle génération de résistances commandées 199

5.4.1.4. Transistors MOSFET linéaires 200

5.4.2. Systèmes d'équilibrage non dissipatifs 200

5.4.2.1. Convertisseur Buck-Boost 200

5.4.2.1.1. Détermination de la fréquence de découpage et de l'inductance 201

5.4.2.1.2. Simulation du module de supercondensateurs 204

5.4.2.2. Convertisseur Flyback à secondaires distribués 205

5.4.2.3. Convertisseur Forward à bobinage distribués 206

5.5. CONCLUSION 207

6. CONCLUSIONS GÉNÉRALES ET PERSPECTIVES 209

7. RÉFÉRENCES 215

8. ANNEXES 229

1. Introduction générale

1. Introduction générale

Le développement technologique et la maîtrise de fabrication de nouveaux matériaux ont permis la réalisation des systèmes modernes de stockage d'énergie électrique comme les supercondensateurs. Grâce à leurs caractéristiques électriques intéressantes et leur nombre de cycles de charge/décharge élevé par rapport aux batteries, ils ont connu une grande évolution au cours de ces dernières années. De part, leur capacité de plusieurs milliers de Farads et leur faible résistance série, ces nouveaux composants sont adaptés pour le stockage d'énergie à forte puissance. Ils peuvent être utilisés de façon complémentaire aux batteries ou aux piles à combustible. Cette injection de puissance aux systèmes d'énergie électrique continue améliore les sources d'alimentation dans les applications, comme par exemple les applications terrestres et maritimes.

Ce travail a pour objectif d'analyser quantitativement les performances (capacité, ESR, autodécharge, rendement de décharge/charge...) des supercondensateurs commercialisés issus de différentes technologies lorsqu'ils sont soumis aux contraintes électriques et thermiques en vue de leur intégration dans les systèmes électriques de forte puissance. Les supercondensateurs étudiés sont symétriques à électrolyte organique et à électrodes de charbon.

L'étude proposée dans ce travail sur les propriétés électriques, dynamiques, thermiques et sur le vieillissement de ces nouveaux dispositifs de stockage d'énergie nécessite une compréhension de leur principe physique et de la technologie utilisée pour les fabriquer. Une présentation de ces derniers est faite en détail dans le premier chapitre de ce mémoire. De même, nous présentons les divers secteurs d'applications.

Afin d'évaluer les caractéristiques de ces composants, il est absolument indispensable d'utiliser des techniques de mesure particulières compte tenu de leur faible impédance et des phénomènes physiques et électrochimiques complexes qui régissent leur fonctionnement. De ce fait différentes techniques de caractérisation sont mises en oeuvre : cycle de charge/décharge à courant constant, (à tension constante et à puissance constante), spectroscopie d'impédance

et voltampérométrie. Une étude approfondie sur la comparaison de ces techniques est détaillée dans la première partie du deuxième chapitre.

La représentation du fonctionnement des supercondensateurs dans les systèmes électriques nécessite l'utilisation de modèles élaborés qui peuvent être incorporés dans les logiciels du type circuit. Dans la deuxième partie du deuxième chapitre, nous nous proposons d'analyser les différents modèles existant du supercondensateur. Chaque modèle met en évidence des phénomènes physiques différents comme la redistribution de charges, la répartition des charges dans la double couche, etc. Les éléments de ces modèles sont caractérisés par les techniques mentionnés ci-dessus en fonction de la tension et la température. Ainsi, l'ensemble du travail présenté sur ces modèles permet de démontrer leurs avantages et leurs inconvénients et nous a permis d'extraire un nouveau modèle représentant fidèlement le comportement dynamique du supercondensateur. Une étude électrothermique est envisagée. La modélisation électrique proposée est complétée par un modèle thermique permettant d'estimer l'augmentation de la température dûe à l'autoéchauffement.

Quand les supercondensateurs sont chargés et puis laissés en circuit ouvert, de la même manière que d'autres dispositifs de stockage d'énergie électrique, un phénomène d'autodécharge est observé. Il est important de quantifier cette autodécharge car elle conduit à une diminution de leurs performances en termes d'énergie et de puissance. Celle-ci est un paramètre très important dans les applications nécessitant le stockage de charges à long terme. De plus, elle permet aussi d'indiquer la qualité des matériaux utilisés pour la fabrication des supercondensateurs.

L'ensemble des mécanismes liés à l'autodécharge n'est pas totalement connu. Ces mécanismes sont complexes et ils ne peuvent pas être expliqués uniquement par le courant de fuite. Nous proposons, dans le troisième chapitre d'une part, d'analyser le phénomène d'autodécharge des supercondensateurs, en fonction des contraintes électrique et thermique et du vieillissement, et d'autre part de trouver un nouveau modèle de type circuit électrique capable de représenter l'autodécharge lors des simulations.

L'inconvénient majeur d'exploiter ces composants est lié à leur tension faible. Il est nécessaire d'en mettre un nombre important en série afin d'obtenir une tension donnée appropriée aux applications. Dans les applications industrielles, des dizaines à des centaines de supercondensateurs sont associés en série pour atteindre la tension souhaitée. Lors du fonctionnement d'un module de supercondensateurs, la dispersion des caractéristiques électriques et thermiques de chaque cellule du supercondensateur conduit à une distribution

non uniforme de tension sur celles-ci. Ceci est préjudiciable en termes de durée de vie des cellules.

La solution pour éviter les surtensions et cette réduction de durée de vie consiste à connecter un système d'équilibrage en parallèle aux bornes des cellules.

Nous proposons, dans le quatrième chapitre, une analyse comparative du point de vue énergie et durée de vie de divers systèmes d'équilibrage utilisés. Certaines définitions telles que le rendement énergétique du système d'équilibrage, le temps d'équilibrage sont proposées dans ce travail pour quantifier l'analyse effectuée. Généralement, les mécanismes du vieillissement des composants de stockage d'énergie électrique sont complexes. Les mécanismes de vieillissement du supercondensateur sont relativement simples, comparés à ceux des batteries, ils sont influencés essentiellement par la tension et la température du composant. Une estimation de la durée de vie des supercondensateurs est effectuée en fonction de la tension et de la température.

2. Principes physiques,

technologie et applications

des supercondensateurs

2. Principes physiques, technologie et applications

des supercondensateurs

2.1. Introduction

Les supercondensateurs offrent des performances en densité de puissance supérieures à celles des batteries et simultanément, des densités énergétiques plus élevées que les condensateurs classiques. Leur structure anode-cathode à base de charbon actif, permet de disposer d'une surface active importante ce qui permet d'obtenir des valeurs de capacité très élevées (plusieurs milliers de Farad) avec des courants de fonctionnement pouvant être supérieurs aux centaines d'Ampère et donc une puissance spécifique instantanée importante. Ils peuvent être combinés avec un accumulateur électrochimique classique et cette association offre alors l'ensemble des propriétés des deux solutions individuelles : d'une part, une puissance acceptable pour conserver la longévité des batteries et d'autre part une puissance instantanée élevée pour des demandes occasionnelles [1].

2.2. Principes physiques

Les supercondensateurs peuvent stocker l'énergie par deux processus. Le premier est la séparation des charges positives et négatives à l'interface entre l'électrode solide et l'électrolyte liquide (stockage électrostatique). Ce phénomène s'appelle la capacité de double couche. Le deuxième emmagasine les charges par des réactions faradiques réversibles (réactions de transfert d'électrons entre les électrodes et l'électrolyte) (stockage électrochimique comme dans les batteries) [2, 3].

2.2.1. Double couche électrique

Un supercondensateur est composé de deux électrodes, d'un électrolyte et d'un séparateur (cf. fig. 2-1). Lorsqu'il chargé, la répartition des charges entre une électrode (conducteur ou semi-conducteur) et un électrolyte (liquide ou solide ) permet la création de deux couches : une composée de charge positives dans l'électrode et des charges négatives (anions) dans l'électrolyte, et une autre composée des charges négatives (électrons) dans l'électrode et des charges positives (cations) dans l'électrolyte.

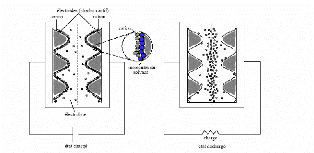
Fig. 2-1 : Structure interne des supercondensateurs à double couche électrique [4]

Le principe de base des supercondensateurs repose sur les propriétés capacitives de l'interface entre un conducteur électronique solide et un conducteur ionique. Le stockage d'énergie s'effectue par distribution des ions d'électrolyte au voisinage de la surface de chaque électrode, sous l'influence électrostatique de la tension appliquée. Il se crée ainsi aux interfaces une zone de charge d'espace, appelée double couche électrique, d'épaisseur limitée à quelques nanomètres, et dans laquelle règne un champ électrique relativement intense [4, 5].

Pour comprendre les processus électriques qui se produisent dans une double couche électrique, plusieurs modèles sont développés pour expliquer ce phénomène.

Le modèle de Helmholtz modélise la nature capacitive de l'interface entre un condensateur électrique solide et un conducteur ionique liquide et considère que les charges accumulées à l'interface forment un plan parallèle à celle-ci (cf. fig. 2-2-a) : nous parlons de plan de Helmholtz. Le calcul de la capacité surfacique C de la double couche est calculé par C=å/d avec å la permittivité diélectrique du solvant et d l'épaisseur de la double couche assimilable dans ce cas au diamètre moléculaire du solvant. Cependant, ce modèle est linaire et ne prend pas en compte la variation de capacité en fonction de la tension appliquée, ce qui induit une valeur de C supérieure d'un ordre à la valeur mesurée réellement [5].

Avec le modèle de Gouy-Champman, la double couche ne se limite pas au seul plan de Helmholtz, mais prend en compte une distribution volumique de charges dans l'électrolyte connue aujourd'hui sous le nom de couche diffusée (cf. fig. 2-2-b). Il est établi que dans le cas d'un profil unidirectionnel de champ électrique, la capacité surfacique de l'interface entre électrode et électrolyte est donnée par la relation suivante [5] :

2 qn å ? Ø

z . 0 2-1

0

C z

= .

d

?

. ch ? ?

u T ? 2 . u T ?

avec, ø0 le potentiel de surface, z la valence des ions, n0 la concentration en anions et cations à l'équilibre thermodynamique, å la permittivité diélectrique de l'électrolyte, q la charge électrique élémentaire, k la constante de Boltzmann, è la température et uT l'unité de potentiel thermodynamique (uT = k.è/q) [5] .

Le modèle le plus utilisé est celui de Gouy-Chapman-Stern qui combine les deux modèles en faisant intervenir la couche dense de Helmholtz (appelée alors couche de Stern) et la couche diffusée de Gouy-Chapman (cf. fig. 2-2-c). La capacité surfacique C de la couche double électrique est alors donnée par :

1 1 1

= + 2-2

C C _c Cd

C_c étant la capacité associée à la couche compacte, de même nature que celle préconisée par Helmholtz et Cd la capacité de la couche diffusée de Gouy et Chapman. Ces deux couches forment la double couche électrochimique.

(a)

(b) (c)

Fig. 2-2 : La double couche, modèles de Helmholtz (a), Gouy-Champn (b) et Stern (c) [5]

2.2.2. Pseudocapacitance

La pseudo-capacitance est créée par des réactions faradiques réversibles qui se produisent sur les électrodes. Elle est appelée pseudo-capacité afin de la différencier de celle de la capacité électrostatique. Le transfert de charges mené par ces réactions dépend de la tension [6]. Il existe deux types des réactions qui peuvent provoquer un transfert de charges avec une dépendance en tension : le premier est lié aux réactions d'oxydoréduction et le deuxième à l'adsorption des ions [7].

2.3. Technologie

2.3.1. Electrodes

Les trois catégories de supercondensateurs en fonction de la nature des électrodes sont les suivantes :

· les supercondensateurs à stockage d'énergie électrostatique : technologie d'électrodes au charbon actif,

· les supercondensateurs à stockage d'énergie électrochimique : technologie d'électrodes aux oxydes métalliques ou aux polymères conducteurs,

· les supercondensateurs à stockage d'énergie électrochimique et électrostatique : technologie d'électrodes hybride.

Supercondensateurs à stockage d'énergie électrostatique

Actuellement, la technologie la plus répandue est celle au charbon actif, dont les surfaces spécifiques dépassent 1000 m².g^-1 et peuvent atteindre 3000 m².g^-1. Ces supercondensateurs fonctionnent selon un principe de type électrostatique : l'électricité est stockée par accumulation d'ions dans la double couche électrique existant à l'interface électrodeélectrolyte. L'absence de véritables réactions chimiques permet une excellente réversibilité et une durée de vie importante (de plus de 1000 000 cycles). Citons deux autres particularités de ces supercondensateurs [8,9] :

· le faible coût des procédés de fabrication et surtout de la matière première.

· le stockage d'énergie principalement électrostatique leur confère une puissance spécifique potentiellement élevée, typiquement d'un seul ordre de grandeur inférieure à celle des condensateurs électrolytiques,

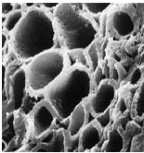
Fig. 2-3 : Structure microscopique d'une électrode à charbon actif [8]

Supercondensateurs à stockage d'énergie électrochimique

Cette technologie utilise des matériaux d'électrodes permettant d'obtenir une interface électrode électrolyte pseudo-capacitive. Deux types de matériaux sont utilisés [10,11] : les oxydes métalliques conducteurs électroniques ou les polymères conducteurs électroniques. Concernant les oxydes métalliques, il est impératif que ceux-ci ne se dissolvent pas dans l'électrolytique, ce qui limite le nombre de candidats possibles. C'est principalement l'oxyde ruthénium ou l'oxyde d'iridium en milieu acide sulfurique qui est utilisé [12]. Cette technologie est relativement onéreuse, aussi bien au niveau de la matière première qu'à celui des procédés de fabrication. Le comportement électrique de ces supercondensateurs est complexe.

Quant aux polymères conducteurs électroniques, tels que le polypole [13], le polythiophène polyaniline, ils permettent d'obtenir des capacités spécifiques élevées, de l'ordre de 200 F.g^-1 et pouvant atteindre 400 F.g^-1. De nombreux problèmes restent cependant à résoudre, notamment ceux liés à la stabilité en température, ainsi qu'à une puissance et une cyclabilité limitées.

Supercondensateurs à stockage d'énergie asymétrique

Ce type de supercondensateur dispose de deux électrodes de nature différente, par exemple une de carbone poreux et une d'oxyde de nickel mais nous pouvons aussi en trouver avec des polymères. Le but est d'exploiter les propriétés de la double couche et l'effet pseudo-capacitif. La densité d'énergie obtenue est supérieure à celle des composés carbonés toutefois les caractéristiques de charge/décharge sont non-linéaires [14].

2.3.2. Electrolytes

Dans les supercondensateurs, la résistance interne est composée de deux termes. Le premier est associé à la conduction électronique et est donc dépendant de la qualité électrique des électrodes. Le second, associé à la conduction ionique, dépend de la conductivité de l'électrolyte, ainsi que de l'aptitude des ions à migrer plus ou moins aisément dans la porosité de l'électrode jusqu'à la couche double. Il est par conséquent essentiellement lié aux caractéristiques de l'électrolyte, telles que [15,16] :

· la concentration en porteurs de charges libres (fonction de la solubilité du sel dans le solvant et du taux de dissociation du sel),

· la mobilité de ces porteurs (fonction de la viscosité du solvant et de la taille effective des ions en solution),

· la solvatation des ions,

· la valence des ions.

Rappelons de plus que la densité d'énergie des supercondensateurs dépend fortement de leur tenue en tension, paramètre étroitement lié à la stabilité électrochimique du solvant électrolytique. C'est le second critère majeur, guidant le choix des électrolytes utilisés dans la fabrication des supercondensateurs. Ainsi trouve-t-on deux types d'électrolyte pour supercondensateurs [4] :

· les électrolytes aqueux, tels que l'acide sulfurique ou la potasse,

· les électrolytes organiques, tel que le carbonate de propylène et l'acétonitrile.

Les électrolytes aqueux furent historiquement les premiers employés [15,16] pour la réalisation industrielle des supercondensateurs, en raison de leur excellente conductivité ionique (de l'ordre de 1 S.cm^-1). Les dispositifs associés présentent des puissances spécifiques élevées, typiquement de quelques kW.kg^-1. De plus, les ions sont de taille relativement faible (1 à 2 nanomètres) et accèdent facilement à la microporosité de la matière active de l'électrode. Aussi observe-t-on des capacités plus élevées en milieu aqueux qu'en milieu organique (pour lequel les ions, de taille généralement plus importante, voient une surface effective plus faible). En revanche, la tenue en tension des supercondensateurs à électrolyte aqueux est limitée à 1,2 V, tension d'électrolyse de l'eau. Par conséquent, l'énergie spécifique de ces dispositifs est faible, typiquement de 1 Wh.kg^-1. En outre, la nature corrosive de l'électrolyte aqueux impose des restrictions dans le choix des matériaux d'électrode.

L'utilisation d'électrolytes organiques a eu pour but l'obtention de tensions de polarisation, sans effets faradiques, plus importantes. Actuellement, la tension nominale des dispositifs à électrolyte organique est de 2,5 V à 2,7 V. La densité d'énergie, de l'ordre de 5 Wh.kg^-1, est donc considérablement accrue. Cependant, la conductivité ionique de ces composés étant médiocre (elle dépasse difficilement 0,03 S.cm^-1), le gain en tension de service ne se traduit que par une augmentation modérée de la puissance spécifique. Plusieurs travaux, tels que ceux présentés par G. Herlem et al [17], sont actuellement menés pour améliorer la conductivité des électrolytes organiques.

2.3.3. Séparateurs

La construction des supercondensateurs demande la mise en place d'une membrane isolante poreuse conductrice ionique pour séparer les deux électrodes imprégnées d'électrolyte. Un séparateur très utilisé est sans doute le Celgard mais il en existe d'autre comme le papier

cellulosique avec des fibres polymères de renfort, le polypropylène ou le polytetrefluorethylene (PTFE) (cf. fig. 2-4). En raison des propriétés inertes du PTFE, il est couramment utilisé avec les électrolytes ce qui allonge la durée de vie des supercondensateurs. Ces membranes séparatrices sont minces et robustes, elles occupent peu d'espace, ainsi les supercondensateurs peuvent fournir une densité d'énergie très élevée. Toutefois elles introduisent un terme supplémentaire dans le calcul de la résistance totale du composant qui est fonction du taux de porosité [9, 18].

Property Range Thickness (ì) : 7-35, Pore Size (ì) : 0.05-15, Porosity : 50-70 percent, Water Wet-able : Yes, Thermal Stability : to 250^oC, Resistance : 3-6cm^2, in 1.250 Specific Gravity H2SO4.

Fig. 2-4 : Séparateur de type PTFE de la gamme GORE [18]

2.3.4. Technique d'assemblage du supercondensateur

La figure 2-5 montre les différents constituants d'un supercondensateur. Nous y trouvons, outre les éléments déjà mentionnés, des collecteurs métalliques (généralement en aluminium) servant d'amenées de courant pour la matière active. La puissance spécifique du produit final dépendra aussi de la qualité du contact collecteur-électrode.

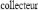
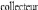
Fig. 2-5 : Principe d'assemblage des supercondensateurs [4]

Actuellement plusieurs procédés visent à optimiser le rapport coût de production/surface de carbone activé par unité de poids et de volume. Les techniques d'assemblage sont variées. Deux techniques principales le bobinage et l'empilement sont utilisés par plusieurs fabricants.

Pour la fabrication de ses composants, EPCOS utilisait comme MAXWELL aujourd'hui des électrodes en charbon actif, des collecteurs en aluminium, un séparateur en polypropylène et un électrolyte organique liquide (cf. fig. 2-6). Les collecteurs sont plongée dans un mélange fait de poudre de charbon actif imprégné de liant (téflon ou cellulose) et de solvant organique, puis ensuite bobinés avec le séparateur et séchés à 150 °C durant 12 h afin d'éliminer les résidus d'eau. Ensuite cette cellule est imprégnée dans l'électrolyte et placée dans une gaine en caoutchouc puis dans un boîtier cylindrique en aluminium, les connections étant soudées aux électrodes [4, 19].

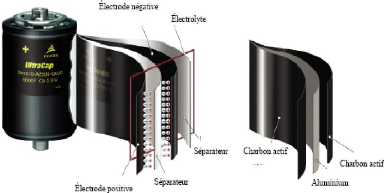
Fig. 2-6 : Structure d'un supercondensateur EPCOS et de son électrode [20,19]

D'autres fabricants utilisent auparavant les mêmes éléments de base mais avec des procédés de fabrication et d'assemblage différents. Les électrodes sont réalisées à base de tissu activé obtenu à partir de lin et de charbon brûlé puis activé, ce qui est plus coûteux. Le supercondensateur est réalisé par la mise en série de cellules séparées par le collecteur de courant, comme montré sur la figure 2-7. Cette disposition est dite bipolaire, car la cellule de base contient deux électrodes de polarité contraire. La forme finale du supercondensateur est généralement prismatique [4, 21].

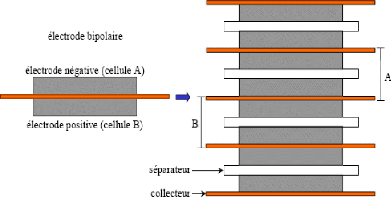
Fig. 2-7 : Électrode bipolaire et supercondensateur de Maxwell [4]

Finalement, le tableau 2-1 indique les caractéristiques des divers types de supercondensateurs. Outre les paramètres énergie et puissance déjà discutés, nous remarquons que c'est dans le cas d'électrodes de type polymère conducteur et d'un électrolyte organique que nous observons les meilleures performances [22].

Électrode	Charbon actif	Charbon actif	Matériau d'insertion		Polymère conducteur	Électrolyte
Acide sulfurique	Électrolyte organique	Acide sulfurique	Électrolyte organique		Énergie massique (Wh/kg)
de 0,2 à 1,1	de 2 à 4,2	de 2,7 à 5,5	11		Puissance massique (kW/kg)
de 1 à 10	de 0,1 à 1	de 10 à 100	100		Tension (V)
de 0,8 à 1,2	de 2 à 2,7	de 0,8 à 1,2	2,5

Tab. 2-1 : Comparaison des caractéristiques des supercondensateurs [22]

2.4. Technologie et recherche actuelles

2.4.1. Etat actuel de la technologie

Les premiers supercondensateurs avaient une résistance sériée élevée, ce qui induisait un

rendement moyen et une puissance spécifique limitée. Au cours des dernières années, nous avons assisté à un très grand effort de la part des fabricants afin de diminuer la résistance interne et d'augmenter la capacité de stockage ainsi que la tension nominale de fonctionnement. Le tableau 2-2 donne l'illustration de l'évolution des performances des supercondensateurs [23].

Tension nominale (V)	Capacité (F)	Volume (L)	Résistance série (m?)	Puissance spécifique	Énergie spécifique		Courant (A)	2,3
100	0,031	8	4,5kW/kg ; 5,4kW/l	2,0Wh/kg ; 2,4 Wh/l	30
	0,183	2	2,3kW/kg ; 3,6kW/l	1,5Wh/kg ; 2,4 Wh/	300
	0,26	0,4	10,7kW/kg ; 12,8kW/l	4,5Wh/kg ; 5,1Wh/l	-
	0,59	0,5	3,6 kW/kg ; 4,5 kW/l	2,3 Wh/kg ; 2,9Wh/l	400
	0,6	0,6	3,0 kW/kg ; 3,7kW/l	2,7Wh/kg ; 3,3 Wh/l	400
	0, 59	0,59	1,7 kW/kg ; 1,9kW/l	4,1Wh/kg ; 4,5 Wh/l	200		2,5
200	0,047	1,8	16kW/kg ; 18 kW/l	3,2Wh/kg ; 3,7Wh/l	50
	0,14	0,6	16,3kW/kg ; 18,8 kW/l	3,3Wh/kg ; 3,8Wh/l	300
	0,23	0,4	13kW/kg ; 17,3 kW/l	3,5Wh/kg ; 4,6Wh/l	300
	0,52	0,23	11,3kW/kg ; 13kW/l	3,9Wh/kg ; 4,5Wh/l	500
	0,64	0,2	11,2kW/kg ; 12,3kW/l	4,5Wh/kg ; 4,9Wh/l	500
	0,80	0,25	7,4kW/kg ; 7,8kW/l	5,1 Wh/kg ; 5,4 Wh/l	500		2,7
2600	0,36	0,28	4,1 5 kW/kg	5,6 Wh/kg	500

Tab. 2-2 : Évolution des caractéristiques des supercondensateurs de MAXWELL [23]

Les premières gammes de tension des supercondensateurs utilisés dans le commerce étaient de l'ordre de 2,3 V, leur capacité maximale de 3600 F et le courant maximal de 400 A. La seconde gamme avait une tension nominale de 2,5 V ce qui engendrait une augmentation importante de l'énergie stockée et de la puissance spécifique (la résistance série était plus faible).

Ces supercondensateurs ont plusieurs atouts pour les applications de traction électrique [24]. Leur utilisation comme système de puissance secondaire permet de fournir une source de puissance rapidement disponible lors des phases d'accélération et de freinage. En effet, leur constante de temps étant plus faible que celle des générateurs électrochimiques classiques

(charge ou décharge possible en quelques secondes) les supercondensateurs sont capables de fournir une puissance importante sur un temps très court [1]. De plus, l'utilisation d'un supercondensateur associé à une batterie permet d'augmenter la durée de vie de cette dernière en évitant les décharges profondes lors des appels de puissance. Enfin ce genre de dispositif possède une bonne cyclabilité (plus de 5.10⁵ cycles).

Comme nous pouvons le voir sur le tableau 2-3, les supercondensateurs se positionnent entre les batteries et les condensateurs classiques [25]. Ils sont caractérisés par leur énergie spécifique bien plus élevée que celle des condensateurs classiques. Par contre , l'énergie stockée est 10 fois plus faible que l'énergie stockée dans une batterie. Le problème des batteries classique réside dans leur faible puissance spécifique qui représente un dizaine de pourcents de la puissance classique d'un supercondensateur.

	Condensateur classique	Supercondensateurs		Batteries	Énergie spécifique (Wh.kg^-1)
<0.1	1 à 10	10 à 150		Puissance spécifique (W.kg^-1)
<100000	<10000	<1000		Durée de vie (cycles)
>500000	>500000	1000		Durée de la charge nominale
10^-6 à 10^-3	1 à 30 secondes	1 à 5 heures		Durée de la décharge nominale
10^-6 à 10^-3	1 à 30 secondes	0,3 à 3 heures		Rendement décharge/charge (%)
>95%	85% à 98%	70% à 85%

Tab. 2-3 : Comparaison des différents systèmes de stockage [1]

Le tableau 2-4 donne une liste non exhaustive de supercondensateurs ou de modules commerciaux. Quelques valeurs caractéristiques sont données à titre indicatif pour un modèle donné [26].

					Exemple de valeurs caractéristiques				Société Pays
Nom commercial	Electrolyte /Electrodes	Gammes Tensions Capacités	Tension Capacité Résistance série		Masse Volume	Energie spécifique	Puissance spécifique	BATSCAP France
SC	Organique	-	2,7 V 0,35 m?		500 g	5,3 Wh /kg	20 kW/kg	ELNA Japon
Dynacap	Organique	2,5 à 6,3 V	2,5 V		-	>0,97 Wh/l	0,4kW/l	EPCOS Allemagne/Japon
UltraCap	Organique	2,3 à 56 V	2,3 V		725 g	2,74 Wh/kg	3,04 kW/kg
	/carbone	7 à 2 700 F	2 700 F 0,6 mW		590 cm^3	3,36 Wh/l	3,74 kW/l	Evans Corp Etats-Unis Evans Corp États-Unis
Capattery	H2 SO4 /H2 O	5,5 et 11 V	5,5 V		-	-	-
	/carbone	0,47 à 1,5 F	1 F		14,2 cm^3 *	0,3 Wh/l	1 kW/l
			0,5 W
	H2 SO4 /H2 O ou KOH/H2 O	7 à 20 V	14 V		5 000 g	0,35 Wh/kg	2,5 kW/kg
	/carbone	8 à 420 F	65 F		2 709 cm^3	0,66 Wh/l	4,6 kW/l
			9 W
	H2 SO4 /H2 O	3 à 125 V	54 V		57 g	0,128 Wh/kg	426 kW/kg
	/Ta, Ta2 O5	10- ^3 à 200 mF	18 mF		19,4 cm^3	0,376 Wh/l	1 253 kW/l
	/RuO2		30 mW					Maxwell États-Unis
PowerCache	Organique	2,3 et 4,6 V	2,7 V		725 g	2,53 Wh/kg	3,04 kW/kg
	/carbone	4 à 2 500 F	2 500 F		614 cm^3	2,99 Wh/l	3,59 kW/l
			0,6 mW

Société Pays	Nom commercial	Electrolyte /Electrodes	Gammes Tensions Capacités	Tension Capacité Résistance série	Masse Volume	Energie spécifique		Puissance spécifique	Tokin/NEC États-Unis/Japon
Super-capacitor	H2 SO4 /H2 O	5,5 et 11 V	5,5 V	65 g	0,065 Wh/kg	0,046 kW/kg
	/carbone	0,01 à 1 F	1 F	28,8 cm^3 *	0,15 Wh/l	0,105 kW/l
			2,5 W					Panasonic Japon
Gold Capacitor	Organique	2,3 à 5,5 V	2,5 V	1,8 g*	0,48 Wh/kg	0,87 kW/kg
	/carbone	0,0022 à 22 F	1 F	1,1 cm^3 *	0,79 Wh/l	1,42 Wh/l
			1?					Samyoung Corée
PRO-CAP	Organique	5,5 V	5,5 V	-	-	-
	/carbone	0,022 à 1 F	1 F	1,42 cm^3 *	3 Wh/l	0,18 kW/l

Tab. 2-4 : Supercondensateurs ou modules commerciaux [26]

2.4.2. Développement et recherches futures

Au cours des dernières années, les travaux de recherche se sont multipliés pour améliorer les performances des supercondensateurs. Les challenges du développement des supercondensateurs sont les suivants :

· augmentation de la durée de vie en nombre de cycles,

· augmentation de la tension de fonctionnement,

· augmentation des densités de puissance et d'énergie,

· élargissement de la plage de fonctionnement de la température,

· optimisation de la relation prix-capacité.

Actuellement, des efforts particuliers se focalisent sur les supercondensateurs asymétriques, sur la diminution de la résistance série ESR, l'optimisation de l'électrolyte et sur l'autodécharge, etc.

Plusieurs méthodes pour réduire l'ESR ont déjà été élaborées, dont le polissage de la surface du collecteur de courant, l'amélioration de la liaison chimique de l'électrode au collecteur de courant et l'utilisation de couches minces colloïdales. En outre, la corrélation entre la structure poreuse des électrodes et la résistance série est en cours de recherche.

L'impact des propriétés de l'électrolyte sur la performance des supercondensateurs (la

résistance d'un électrolyte peut limiter la densité de puissance, sa concentration en ions et la tension de fonctionnement permet de limiter la densité d'énergie ...) est énorme. Les efforts de recherche, pour améliorer l'électrolyte, doivent être aussi importants que ceux consacrés à l'amélioration des électrodes [27].

Il y a quelques années le fabricant MAXWELL a annoncé son objectif : un supercondensateur fonctionnant à une tension de 3 V dans une plage de température de -35 à 105 °C. Les fabricants envisagent aussi d'atteindre une densité de puissance et d'énergie respectivement de 10 kW/kg et 10 Wh/kg [21].

2.5. Applications

Les supercondensateurs sont utilisés en remplacement et surtout en complément des piles et accumulateurs électrochimiques afin d'assurer la fonction puissance qui leur fait défaut. Nous trouvons ces composants dans les systèmes nécessitant une importante énergie délivrée en un temps bref. Les principaux secteurs concernés par les supercondensateurs sont :

· l'informatique et la télécommunication pour les petits composants à faible énergie spécifique,

· les alimentations de secours et le secteur du transport concernant les composants à haute énergie et haute puissance spécifiques.

2.5.1. Domaine informatique

A l'heure actuelle le supercondensateur est utilisé dans le domaine de l'électronique grand public pour les alimentations des circuits mémoires des télévisions vidéo, des systèmes audio, des récepteurs satellite, des horloges, des téléphones portables, des calculatrices... [21, 28].

2.5.2. Domaine du transport

Un des principaux domaines d'utilisation des supercondensateurs est le transport. Le couplage des supercondensateurs avec les batteries est une solution pour obtenir un système plus puissant et plus fiable pour le démarrage des moteurs et pour fournir plus de courant pour un préchauffage des catalyseurs et des bougies, pour les systèmes d'assistance électrique, pour faciliter le démarrage des moteurs diesels, etc. Les véhicules qui en tirent le plus de bénéfices

sont ceux qui font de fréquents arrêt tels que les bus, les navettes d'aéroport, les véhicules de transports, les taxis, etc. car les supercondensateurs sont rechargés lors des arrêts ou/et stockent l'énergie récupérée lors du freinage pour l'utiliser lors des phases d'accélération.

2.5.3. Couplage réseau-supercondensateurs

Les supercondensateurs peuvent jouer le rôle de compensateur de puissance instantanée en permettant de lisser la puissance. Nous pouvons citer l'utilisation de supercondensateurs pour l'alimentation des ascenseurs [29]. Dans cette application, les supercondensateurs jouent un double rôle : la récupération d'énergie et le lissage de la puissance prise ou fournie par le réseau [30].

2.6. Présentation des supercondensateurs étudiés

Nous avons choisi une large gamme de supercondensateurs pour les analyser dans notre étude. Ils sont fabriqués par plusieurs fabricants et appartiennent à différentes générations. Une photo de ces composants est montrée sur la figure 2-8. Leurs caractéristiques données par le constructeur sont détaillées dans le tableau ci-dessous. Ils possèdent des caractéristiques électriques différentes.

B49410 SC806 M600 BCAP010 BCAP013 BCAP350

Fig. 2-8 : Photo des supercondensateurs étudiés

Dans la suite de ce rapport, nous référencerons ces composants comme indiqué le tableau cidessous.

Fabricant	MAXWELL				BATSCAP		EPCOS	Numéro de série
BCAP010	BCAP013	BCAP350	M600	SC806	B49410		CN (F)
2600	450	350	2600	2600	3600		UN (V)
2,5	2,5	2,5	2,7	2,7	2,5		ESR (DC) (m?)
0,7	2,4	3,2	0,4	0,35	0,3		ESR (AC) (m?)
0,3 (1kHz)	0,8 (1kHz)	1,6 (1kHz)	0,28 (100Hz)	0,2	0,16		IN (A) (courant de charge/décharge)
600	180	30	-	600	500		IfN (mA) (courant de fuite)
5	3	1	5	-	-		Plage de températures
-35°C à 65°C	-35°C à 65°C	-40°C à 65°C	-40°C à 65°C	-30°C à 60°C	-30°C à 70°C		Température de stockage
-40°C à 70°C	-40°C à 70°C	-40°C à 70°C	-40°C à 70°C	-30°C à 70°C	-40°C à 70°C		Énergie spécifique Wh/kg
4,3	-	5,1	5,6	5,3	3,6		Puissance spécifique kW/kg
2,04	1,64	1,675	10,4	20	2,9		Nombre de cycles de charge/décharge
500 000	500 000	500 000	1000 000	-	500 000

Tab. 2-5 : Caractéristiques techniques des supercondensateurs étudiés [31-34]

Des images aux rayons X permettent de visualiser les détails de constitution de manière non intrusive comme le montre la figure 2-9, et notamment la reprise des collecteurs de courant vers les bornes qui est un point clé dans les performances des supercondensateurs. Ainsi, l'image (a) de la figure 2-9 correspond au composant BCAP010 de MAXWELL. Les collecteurs de courant correspondant à l'électrode positive sont reportés sur la borne par une soudure électrique où la densité de courant sera particulièrement importante. Nous pouvons également noter une perte de place importante liée à cette connexion. Les images (b) et (c) correspondent respectivement à un supercondensateur EPCOS B49410 et à un composant M600 [35] .

Fig. 2-9 : Images aux rayons X de supercondensateurs commercialisés [35]

2.7. Conclusion

En se basant sur les références bibliographiques présentées dans de ce chapitre, nous trouvons que les supercondensateurs présentent donc une technologie complètement différente des batteries. Au lieu d'un stockage de type faradique, le stockage de l'énergie est capacitif : le nombre de cycles obtenus est très élevé. La technologie mise en oeuvre est très souvent similaire à celle des batteries sur le principe des procédés (collecteurs, deux électrodes, ...) mais est moins lourde. Cependant, les supercondensateurs n'ont pas connu l'essor marketing escompté actuellement, d'où leur cantonnement à des marchés de niche. Néanmoins, sur le plan conceptuel, l'étude de ces systèmes électrochimiques entraîne celle de l'interface électrochimique, assez méconnue, et donc le développement d'idées extrêmement intéressantes et fructueuses.

3. Caractérisation et

modélisation électrique,

fréquentielle et thermique

des supercondensateurs

3. Caractérisation et modélisation électrique,

fréquentielle et thermique des supercondensateurs

3.1. Introduction

Pour stocker l'énergie électrique, les supercondensateurs sont de plus en plus employés dans différents secteurs tels que des communications, le transport, etc. L'étude de l'évolution de leurs paramètres lorsqu'ils sont soumis à des conditions recréées en laboratoire permet de prédire leur comportement dans le cas d'applications industrielles. La connaissance du comportement des supercondensateurs en fonction des contraintes industrielles est obtenue grâce à différentes méthodes de caractérisation. Trois techniques de caractérisation complémentaires sont réalisées :

o une caractérisation par cycle de charge/décharge à courant constant, à tension constante, ou à puissance constante.

o une caractérisation par spectroscopie d'impédance permettant le tracé du diagramme de Nyquist de l'impédance,

o une caractérisation par voltampéremétrie cyclique, la capacité étant montrée comme une dynamique en fonction de la tension appliquée.

Ces caractérisations permettent de déterminer les variations de l'impédance des supercondensateurs en fonction de la tension, du courant, de la fréquence et de la température.

Le supercondensateur engendre des phénomènes physiques complexes et couplés en temps, tension et température. Les méthodes de caractérisation des supercondensateurs ne sont pas jusqu'à présent normalisées et il est difficile de comparer les résultats obtenus avec ceux des fabricants. C'est pourquoi, afin d'obtenir des résultats expérimentaux fiables et reproductifs, nous avons défini, au début de chaque mesure, des méthodologies de mesure adéquates et adaptées aux méthodes de caractérisation. Par ailleurs, nous effectuerons une comparaison des résultats obtenus par les différentes méthodes et avec les données issues du fabricant.

Le développement à long terme des supercondensateurs nécessite des modèles élaborés capables de décrire leurs comportements temporels et dynamiques. Les supercondensateurs stockent les charges par des processus très différents de ceux qui surviennent dans les condensateurs classiques. Les modèles traditionnels utilisés pour décrire le comportement d'un condensateur sont insuffisants. Il est donc important d'établir des modèles plus avancés et précis permettant de décrire leurs comportements en fonctionnement.

Les recherches bibliographiques ont montré qu'il existe plusieurs modèles de

supercondensateur. Ils se basent sur deux principes :

· microscopique, ces modèles pouvant représenter précisément les phénomènes électrochimiques et physiques du composant [36-40].

· circuit électrique équivalent, ils sont peut-être moins précis mais plus facile à intégrer dans les logiciels de simulation de circuits [41-43].

Nous nous intéressons dans ce travail à des modèles de type circuit électrique équivalent pour représenter les supercondensateurs lors de simulation. Nous en présentons trois entre- autres : le modèle classique RC, le modèle à deux branches, et le modèle à simple pore. Ces modèles peuvent représenter les principaux phénomènes du supercondensateur par des cellules RC, tels que l'impédance complexe de pores, la redistribution de charges, etc. Une étude de ceux-ci montrant leurs avantages, leurs limites ainsi que l'indentification des leurs éléments sera présentée en détail. Finalement, leur comparaison permettra d'extraire un modèle général du supercondensateur.

Le comportement inductif des supercondensateurs dans le spectre d'impédance à haute fréquence est souvent observé. Ce comportement est généralement attribué aux connexions ainsi qu'au profil du parcours du courant au sein du composant. L'effet inductif dans le supercondensateur est souvent modélisé par une simple inductance, mais ceci ne correspond pas tout à fait à son comportement haute fréquence [44-47]. C'est pourquoi, nous proposons dans ce chapitre une interprétation plus large et une modélisation du phénomène inductif.

La température peut influencer les différents critères de performance d'un supercondensateur, à savoir la capacité, l'ESR, l'énergie stockable et la puissance maximale déchargeable. L'efficacité de cycle charge/décharge, qui sera représentée par le rendement coulombien, peut dépendre aussi de la température. A l'aide des différentes méthodes de caractérisation présentées, l'étude de la variation des performances représentées par les éléments des modèles sera effectuée.

Grâce à un modèle thermique composé des deux constantes de temps, une estimation de la température au coeur du supercondensateur est possible. La variation de la température engendre une variation des éléments du circuit électrique équivalent. Pour mieux représenter, le supercondensateur un couplage d'un modèle thermique avec le modèle électrique est envisagé dans ce chapitre. L'établissement analytique de la variation des paramètres du supercondensateur étant très difficile en fonction de la température, nous proposons une détermination de lois expérimentales reliant les différents paramètres du supercondensateur à la température.

Lors du fonctionnement des supercondensateurs, dans un environnement réel, ceux-ci sont soumis à des contraintes, thermiques, électriques, etc. ce qui engendre malheureusement une perte progressive de leurs performances tout en diminuant leur durée de vie. Nous présentons à la fin de ce chapitre une évolution des éléments de circuits électriques équivalents lors d'un vieillissement accéléré réalisé par "floating".

3.2. Méthodes de caractérisation des supercondensateurs

La connaissance des performances de supercondensateurs pour des applications de forte puissance est importante. Il existe trois méthodes principales pour analyser les supercondensateurs : le cycle de charge/décharge, la spectroscopie d'impédance et la voltampérométrie cyclique. Elles conduisent à l'acquisition de paramètres qui sont considérés suffisants pour décrire les propriétés générales du supercondensateur dans une large gamme de fréquence ainsi que dans le domaine temporel.

Les caractérisations testées sont toujours précédées par un court-circuit du supercondensateur pendant 24 heures afin de décharger complètement le supercondensateur.

3.2.1. Charge/décharge

3.2.1.1. Outil de manipulation et principe

Le banc réalisé permettant de caractériser le supercondensateur est composé de deux contacteurs pour changer la polarité du supercondensateur, qui peut se charger et se décharger via une alimentation et des plans de charge. Ainsi, dans le cas d'une charge, le supercondensateur est branché comme indiqué sur le schéma montré sur la figure 3-1, alors que pour un essai de décharge il est nécessaire d'inverser la polarité du supercondensateur en utilisant les contacteurs. Le courant maximal fourni par ce banc est de #177;400 A et la plage de tension est de 0 à 5 V. Les caractéristiques techniques de ce dispositif ainsi que son principe de fonctionnement sont données en détail dans le document référencé [48].

Alimentation

Plans de charge

Fig. 3-1 : Schéma du banc de caractérisation pendant la charge

Ce banc donne la possibilité d'effectuer des essais à une tension constante, à un courant constant et à une puissance constante. Nous allons aborder les différentes méthodes de caractérisation de supercondensateur en présentant leur principe ainsi qu'une comparaison des résultats obtenus [49-52].

3.2.1.2. Essai à courant constant

La charge ou la décharge à courant constant est la méthode la plus connue et la plus utilisée pour déterminer assez facilement la résistance et la capacité d'un supercondensateur. En première approximation, le supercondensateur peut être considéré comme un condensateur de capacité linéaire C avec une résistance en série ESR. La valeur de la capacité peut être déterminée par l'équation 3-1.

C I

=

Ät

c

. 3-1

Ä U c

où, (cf. fig. 3-2)

I est le courant de charge ou décharge,

ÄU_c est la différence de tensions entre UN et UN/2, Ät_c est la durée équivalente.

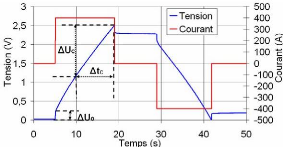
Fig. 3-2 : Détermination des paramètres du supercondensateur

La résistance équivalente série ESR est déterminée au début de la charge (ou de la décharge) par la variation brusque de la chute de la tension aux bornes du supercondensateur ÄU0 lors du passage du courant de charge de zéro à la valeur constante, comme le montre l'équation suivante :

ESR Ä 0

U

= 3-2

I

La capacité C et la résistance ESR peuvent être déterminées aussi bien lors de la charge que lors de la décharge.

Les constructeurs comme MAXWELL et EPCOS nous proposent des méthodes différentes de caractérisation du supercondensateur basées sur la charge/décharge à courant constant [28, 53, 54]. Nous nous proposons de présenter celle utilisée dans les fiches techniques de MAXWELL [28, 53]. Cette technique sera appelée par la suite méthode de MAXWELL. Dans cette méthode, nous déchargeons le supercondensateur par un courant constant à partir de sa tension UN jusqu'à la tension UN/2. La capacité C peut être calculée par l'équation 3-1 où ÄU_c et Ät_c sont déterminées et représentées sur la figure 3-3. La résistance ESR est déterminée par le rapport de la chute de tension ÄU0 et du courant de décharge I cinq secondes après l'arrêt du courant (cf. fig. 3-3).

Notons que le constructeur ne détermine pas comment charger le supercondensateur pour atteindre sa tension nominale et le temps de maintien de cette tension. Lors de notre étude expérimentale, nous avons maintenu chargé le supercondensateur pendant une heure. Le courant d'alimentation, pour maintenir la tension constante, devient alors très faible et sa valeur est alors de l'ordre du courant d'autodécharge (cf. chapitre consacré à l'autodécharge). De plus, une heure de charge nous permet de comparer les différentes méthodes de caractérisation présentées avec la spectroscopie d'impédance.

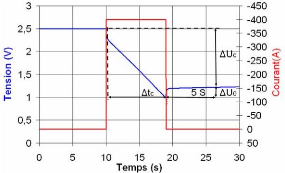
Fig. 3-3 : Détermination de la capacité et la résistance de supercondensateur
suivant la méthode du constructeur MAXWELL

A noter que la différence de tension ÄU_c est la fenêtre d'utilisation de tension du supercondensateur car entre les deux tensions UN et UN/2 nous pouvons récupérer 75% de l'énergie stockée dans le supercondensateur [55].

3.2.1.3. Essai à tension constante

Nous chargeons le supercondensateur via une résistance déterminée R par une tension constante. La figure 3-4 montre l'allure de la tension et du courant du supercondensateur durant la charge. Si la capacité est supposée constante, la tension aux bornes du supercondensateur s'accroît d'une manière exponentielle comme le met en évidence l'équation suivante :

? ?- t ?

u ( t ) U 1 exp ?

= ? - ?? ?? ? 3-3

? ô ?

où,

ô est la constante de charge,

U est la tension de charge souhaitée.

La capacité du supercondensateur C peut être calculée par la constante de temps déterminée et la résistance de charge R comme indiqué par l'équation 3-4 [49].

La valeur de l'ESR est très inférieure à celle de la charge R et peut être négligée dans le calcul de la capacité C comme indiqué sur l'équation 3-4.

ô

C=

ESR R R

+

ô

3-4

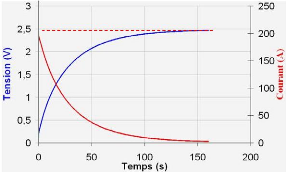
U

Fig. 3-4 : Allure de la tension et du courant du supercondensateur pendant l'essai à tension constante

Finalement, dans le tableau 3-1, nous comparons les résultats expérimentaux obtenus par les méthodes de caractérisation présentées pour le supercondensateur BCAP010 (2600 F ; 0,7 m? (DC) ; 2,5 V) (cf. § 2.6) pour un courant de charge ou de la décharge de 400 A et à une température de 25 °C. Ces résultats sont présentés en valeur réduite par rapport aux paramètres

donnés par le fabricant.

Le phénomène de la redistribution de charge peut influencer la caractérisation de la capacité de supercondensateur. Pour cela, nous l'avons caractérisé avec un courant de charge ou de décharge le plus élevé possible (400 A).

Les valeurs de la capacité C déterminée par ces méthodes de caractérisation sont un peu différentes. La valeur de la capacité de la décharge est inférieure à celle de la charge à cause de la présence des phénomènes faradiques. La résistance ESR caractérisée par la procédure de MAXWELL est élevée par rapport aux autres valeurs car cette méthode prend en compte la pénétration de charges dans les pores (liée à la durée de cinq seconds). Ceci sera détaillé ultérieurement après la présentation de certains phénomènes.

Paramètre	C (F)	C/ CN (%)	ESR (u?)		ESR/ ESRN(DC) (%)	Charge à courant constant
2724	105	445	67		Décharge à courant constant
2572	99	422	60		Décharge à courant constant (MAXWELL)
2645	102	508	76		Charge à tension constante
2720	105	-	-

Tab. 3-1 : Comparaison des résultats de différentes méthodes de caractérisation

3.2.1.4. Essai à puissance constante et plan de Ragone

Dans de nombreuses applications, les supercondensateurs travaillent à puissance constante. Il est donc important de caractériser les paramètres du supercondensateur dans ce cas.

3.2.1.4.1 Détermination de la capacité en fonction de la puissance

La détermination de la capacité C est basée sur le calcul de l'énergie déchargée du supercondensateur durant la décharge (où la charge) entre deux tensions données [56]. Dans ce type de caractérisation, nous supposons maintenir le produit u(t).i(t) à une valeur constante et donc d'assurer une augmentation du courant qui compense la diminution de la tension entre la valeur d'origine U2 et une autre valeur U1.

L'échange de l'énergie ?W durant la charge ou la décharge dans l'intervalle du temps _t2-t1 peut être exprimée par la forme la suivante :

t₂

Ä = ?

W u t i t dt 3-5
( ) . ( )

t 1

En intégrant l'équation 3-5 pour un intervalle donné de tension et pour une capacité constante, cette dernière est donnée par la relation suivante :

C

3-6

2.Ä W

2 2

( U 2 U

- )

1

Pour une décharge à puissance constante P la capacité peut être écrite comme le montre l'équation ci-dessous :

C

Ät

3-7

2 . .

P

2

( U 2 U 2

- )

1

En pratique, nous avons réalisé des essais à puissance constante de 25, 50, 100, 200, 300, 400, 500 W et à une température de 25 °C avec le protocole suivant : charger le supercondensateur par un courant élevé, ensuite maintenir la tension nominale UN aux bornes du supercondensateur pendant un certain temps (une heure pour notre étude), et enfin le décharger à puissance constante jusqu'à la tension UN/2.

La figure 3-5 représente l'évolution de la capacité du supercondensateur en fonction de la puissance déchargée. Nous constatons que la capacité équivalente du supercondensateur diminue fortement avec l'augmentation de la puissance. Ceci est dû à la dissipation de l'énergie dans la résistance ESR, qui augmente avec la puissance.

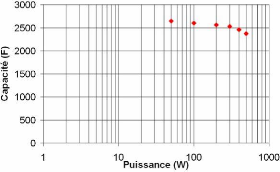
Fig. 3-5 : Capacité du supercondensateur déterminée en fonction de la puissance de la décharge

L'équation 3-7 montre que pour un intervalle donné de tension la capacité est proportionnelle à l'énergie déchargée. Pour les applications du supercondensateur, nous avons toujours besoin de déterminer la puissance et l'énergie maximales disponible. Il est donc intéressant de montrer l'énergie stockée dans le supercondensateur en fonction de la puissance, dans le plan dit de Ragone.

3.2.1.4.2 Plan de Ragone

Le plan de Ragone a pour but de déterminer la limite de la puissance disponible d'un supercondensateur et la région optimum de fonctionnement, c'est-à-dire la zone où l'énergie et la puissance disponibles sont élevées.

La forme spécifique de la courbe de Ragone dépend fortement de la perte thermique sur l'ESR mais faiblement de l'autodécharge. L'ESR conduit à limiter la puissance maximale lors des décharges [57, 58].

Des approximations linéaires nous permettent d'estimer le plan de Ragone [59, 60]. L'équation 3-8 montre l'évolution de l'énergie déchargée d'un supercondensateur de capacité C et de résistance ESR calculée pour une décharge de UN à UN/2 [35].

C ? ? ? ?

ESR P

.

? 2

?? ?

Ä =

W ??

ESR . P . ln + U ESR P

- . 3-8

? 2

2 N ?

? ? N ?

U ?

Le grand souci de caractérisation en puissance constante est de définir un protocole de mesure adéquat aux applications. Certains auteurs ont proposé des protocoles tels que celui de MILLER et al. [61] mais malheureusement ces protocoles sont spécifiques pour des types précis d'applications de supercondensateurs.

Nous traçons sur la figure 3-6 dans le plan de Ragone la courbe d'approximation calculée p r l'équation 3-8 avec la capacité déterminée précédemment et montrée sur la figure 3-5 avec a

ESR = 508 u?, et celle trouvée expérimentalement. A partir de cette figure, nous constatons que la relation puissance-énergie ne peut pas être calculée précisément par une simple approximation, car les paramètres du superc ondensateur varient en fonction des puissances de andées.

m

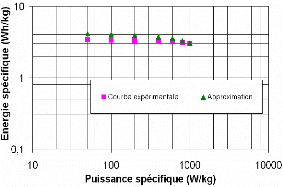
Fig. 3-6 : Plan de Ragone du supercondensateur BCAP010 déterminé par différentes méthodes

Pour conclure, nous avons vu dans ce paragraphe comment évaluer les énergies et les puissances disponibles en tenant compte de la chute ohmique dans la résistance interne. Il est important de noter que le plan de Ragone d'un supercondensateur dépend aussi de l'intervalle de tension. En fait, plusieurs autres effets sont à prendre en considération pour une évaluation complète du bilan énergétique d'un supercondensateur [26] : capacité non constante en fonction de la tension, distribution de résistances et de capacités, variations locales de conductivité de l'électrolyte, des phénomènes faradiques, etc.

3.2.1.4.3 Comparaison énergétique des supercondensateurs

A titre d'exemple, nous comparons sur les figures 3-7 la capacité et le plan de Ragone de deux supercondensateurs MAXWELL M600 (2600 F ; 2,7 V) et BCAP010 (2600 F ; 2,5 V). La figure 3-7-a illustre que le composant M600 a une capacité supérieure à celle du composant BCAP010 pour toute la plage de la puissance. Par conséquent, l'énergie déchargée du composant M600 est plus élevée que celle de l'autre composant (cf. fig. 3-7-b).

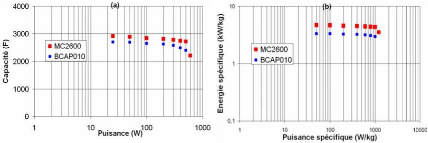
Fig. 3-7 : Comparaison capacitive et énergétique de deux supercondensateurs M600 et BCAP010

3.2.2. Voltampérométrie cyclique

La technique voltampérométrie cyclique est souvent utilisée par les électrochimistes pour l'étude des mécanismes des réactions d'oxydoréduction sur les électrodes. En fonction de la forme de leur dépendance à la vitesse de balayage, il est possible d'en déduire certaines caractéristiques des réactions, comme leur réversibilité ou l'intervention d'espèces adsorbées et aussi pour établir les limites du potentiel de fonctionnement réversible [62, 63].

3.2.2.1. Principe de la voltampérométrie cyclique

Cette méthode repose sur la mesure du courant résultant d'un balayage linéaire en potentiel

dU /dt entre deux limites U1 et U2 choisies. La réponse en courant pour un circuit série R, C(u) reconnaît deux régimes. Le régime transitoire qui dure un temps de l'ordre de la constante de temps RC, le courant, dans ces cas, peut être exprimé par la forme suivante [62, 63] :

dU ? ?- t ? ?

i ( t ) C ( u ) 1 exp

= - 3-9

?? ?? RC ??

dt ??

En régime permanent, le courant peut être calculé en supprimant l'exponentielle, qui représente le régime transitoire par l'équation suivante :

dU

i(t)=C(u) 3-10

dt

Le courant mesuré est la somme de deux contributions aux interfaces électrodes-électrolyte : le courant capacitif (non faradique) lié à l'existence de la double couche électrique et le courant associé aux phénomènes faradiques.

3.2.2.2. Essai de voltampérométrie cyclique

Nous avons réalisé un essai de voltampérométrie cyclique à l'aide de l'impédancemètre Zahner IM6+PP240 avec un balayage dU/dt de 10 mV/s dans l'intervalle [0 ; 2,5] V et pour le supercondensateur BCAP010 à 25 °C. La figure 3-8 montre la courbe de voltampérométrie cyclique, soit le courant en fonction de la tension aux bornes du supercondensateur.

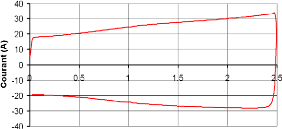
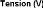
Fig. 3-8 : Voltampérométrie cyclique pour le supercondensateur BCAP010

La capacité du supercondensateur C est proportionnelle au courant mesuré (cf. eq. 3-10). Nous pouvons donc déduire la valeur de la capacité du supercondensateur à partir de la courbe de la figure 3-8. Sur la figure 3-9 nous présentons la capacité du supercondensateur durant la

charge et la décharge en fonction de la tension U. Nous trouvons que pendant la charge la capacité varie approximativement linéairement en fonction de la tension aux bornes du supercondensateur, tandis que durant la décharge la capacité est moins dépendante de la tension.

La différence entre la capacité de la charge et de la décharge est probablement due au courant faradique (lié aux réactions d'oxydoréduction) et non faradique des pores de différentes accessibilités [64-66]. Selon l'hypothèse envisagée, ces phénomènes engendrent des faibles valeurs de capacités. Ces dernières se chargent pendant la charge et continuent à se charger pendant la décharge, et ce n'est qu'à une faible valeur qu'elles commencent à se d charger.

é

Fig. 3-9 : Evolution de la capacité du supercondensateur durant la charge et la décharge

3.2.2.3. Définition du rendement coulombien

Afin de quantifier l'écart entre la capacité de la charge et de la décharge, nous définissons un nouveau paramètre de qualité qui est le rendement coulombien, qui représente en quelque sorte la charge récupérée pendant la décharge par rapport à celle stockée pendant la charge dans un supercondensateur pour un intervalle donné de tension [67]. En considérant une tension aux bornes du supercondensateur (par exemple la tension nominale), le rendement coulombien ç_c peut être défini par le pourcentage de la capacité de la décharge _Cdech à la tension nominale sur celle de la charge _Cch. C'est un facteur important pour montrer la qualité de supercondensateur, sachant qu'il vaut, dans le cas idéal, 100 %.

Le rendement coulombien peut donc être défini par la relation suivante :

ç_c = Cdech( UN)/ Cch(UN) 3-11

3.2.2.4. Effet du nombre de cycles de charge/décharge sur le rendement coulombien

L'écart entre la capacité de la charge et la décharge peut diminuer progressivement en fonction du nombre de cycles de charge/décharge et donc le rendement coulombien peut augmenter. Initialement la capacité de la charge diminue pendant quelques cycles, mais après plusieurs cycles de charge/décharge la capacité s'approche d'une valeur constante. La diminution initiale de la capacité de la charge peut-être due à la consommation irréversible des charges par des réactions faradiques d'oxydoréduction aux interfaces électrodes-électrolytes [68-70].

Cette précision est corroborée par voltampérométrie cyclique après vingt cycles de charge/décharge avec un balayage de 10 mV/s pour les composants BCAP010, M600 et SC806, et de 5 mV/s pour le composant B49410. Le balayage pour ce dernier est faible par rapport à sa capacité, car le courant d'alimentation maximale de notre spectromètre est limité à 40 A. Nous avons réalisé également la même voltampérométrie sur les deux supercondensateurs (BCAP013 et BCAP0350) de faible capacité avec un balayage de 1, 7 mV/s et 1,3 mV/s consécutivement (cf. fig. 3-10).

L'autoéchauffement dû au courant de charge/décharge peut être négligé car le courant parcourant le supercondensateur est relativement faible.

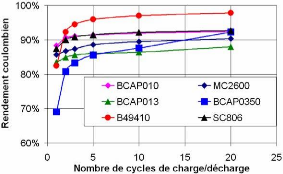
Fig. 3-10 : Rendement coulombien des supercondens ateurs étudiés

Nous comparons sur la figure 3-11 les valeurs de la capacité du supercondensateur BCAP010 obtenues par voltampérométrie pour le premier cycle avec celles obtenues pour le vingtième cycle. Nous trouvons que la capacité de la charge du premier cycle est supérieure à celle du vingtième cycle, tandis qu'elle reste quasiment constante pour la décharge. La capacité

de la charge du vingtième cycle devient très proche de celle de la décharge pour une tension au-delà d'un volt.

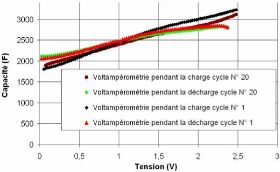
Fig. 3-11 : Comparaisons des valeurs de la capacité obtenues
par voltampérométrie pour le cycle N° 1 et N° 20

3.2.3. Spectroscopie d'impédance électrochimique

La spectroscopie d'impédance électrochimique est une méthode puissante de l'évaluation de la performance d'un supercondensateur dans le domaine fréquentiel. Celle-ci permet de caractériser les composants à stockage faradique et non- faradique [71] à savoir : résistance de l'électrolyte, capacité de la double couche, résistance de polarisation, résistance de transfert de charge, élément à phase constante (CPE), impédance de diffusion de charge, inductance virtuelle, etc.

Avec cette technique, le supercondensateur peut être caractérisé par ses différents éléments ; la capacité et les diverses contributions de l'ESR peuvent être déterminées séparément.

3.2.3.1. Définition et principe

Le principe de sp ectroscopie d'impédance électrochimique est basé sur la mesure d'une fonction de transfert suite à la perturbation imposée du système électrochimique étudié. Couramment, la perturbation est sinusoïdale. Le si gnal appliqué est donc de la forme suivante [72] :

e ( t ) = E _max .sin(ù.t) 3-12

La réponse en courant parcourant le composant électrochimique est de la même forme avec un déphasage ö comme l'illustre l'équation suivante :

i ( t ) = I _max . sin(ù.t -?) 3-13

L'impédance électrochimique se définie comme étant le nombre complexe Z(ù) résultant du rapport :

E(ù)

Z=
( ) ù 3-14
I ( )

ù

où, en mode potentionstatique, E(ù) est la perturbation imposée à un potentiel maximal choisiEmax et I(ù) la réponse en courant du composant étudié.

3.2.3.2. Essai de spectroscopie d'impédance

^õEn mode de caractérisation potentiostatique, le supercondensateur est polarisé par une tension continue U durant un certain temps avant le lancement des mesures de l'impédance. La durée de cette polarisation est fixée à une heure pour notre étude. Ce temps est certainement suffisant pour charger tous les éléments du supercondensateur notamment ceux de faibles accessibilités.

Un signal sinusoïdal de 10 m V (cette grandeur de tension permet d'avoir un bon compromis entre la précision de mesure et la perturbation électrochimique) est ensuite superposé à la tension stabilisée U. Le principe de spectroscop ie d'impédance électrochimique est présenté sur la figure 3-12. Les câbles de mesure et de puissance sont torsadés afin de minimiser l'effet des perturbations électromagnétiques. L'impédancemètre IM6+PP240 de Zahner est nécessaire pour appliquer une faible tension alternative et mesurer l' évolution du module et de la phase de l'impédance sur une plage de fréquences [73]. Les caractéristiques techniques du spectromètre sont détaillées dans l'annexe A.

Partie de puissance Partie de mesure

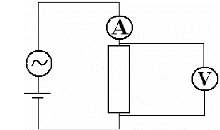
e(t)

U

Z

Fig. 3-12 : Schéma du principe de la caractérisation par spectroscopie d'impédance

En variant la réponse du signal alternatif, nous obtenons un spectre de l'impédance en fonction de la pulsation ù. La plage de fréquence a été choisie entre 10 mHz à 10 kHz, ce ^quipeut inclure la plupart des applications du supercondensateur. L'impédance obtenue peut être représentée sous plusieurs formes grâce aux tracés de Bode ou de Nyquist.

L a figure 3-13 pré sente le diagramme de Bode pour le supercondensateur BCAP010 mesurée à une tension continue de 2,5 V et à une température ambiante de 25 °C. Cette représentation permet de mettre en évidence l'existence de certains paramètres du supercondensateur, tels que la résistance ESR, la capacité C et l'inductance L.

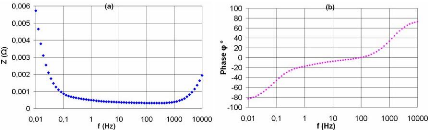
Fig. 3-13 : Module et phase de l'impédance du supercondensateur BCAP010 en fonction de la fréquence

La figure 3-14 montre que la partie imaginaire de l'impédance mesurée par spectroscopie d'impédance peut être interprétée par deux zones (capacitive et inductive) suivant le comportement fréquentiel du supercondensateur [74].

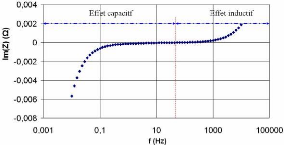
Fig. 3-14 : Partie imaginaire de l'impédance du supercondensateur BCAP010

> Pour une fréquence supérieure à celle de résonance (45 Hz pour le composant BCAP010), dit hautes fréquences, nous rencontrons l'effet inductif due à l'inductance propre du supercondensateur et à l'inductance parasite des câbles de connections.

> Pour une fréquence inférieure à celle de résonance (fréquences intermédiaires entre 55 mHz et 45 Hz pour le composant BCAP010), c'est l'effet capacitif qui prédomine, la capacité augmente avec la diminution de la fréquence à cause de la nature poreuse des électrodes (cf. fig. 3-15). Les électrodes sont fabriquées avec une surface poreuse très élevée, les pores ayant un diamètre de l'ordre du nanomètre.

> A basse fréquence (<10 mHz) la réactance, principalement attribuable à la capacité, est à son minimum. Dans ces conditions, les ions ont le temps de pénétrer dans la profondeur des pores et la surface maximale de l'électrode est utilisée pour contribuer à la capacité de la double couche ( Cdl) [75].

La réactance X_c permet de déterminer la capacité du composant comme le montre l'équation 3-15.

1

C ù = -

( ) 3-15

c

ùX

La figure 3-15 illustre l'augmentation de la capacité avec la décroissante de la fréquence, nous pouvons voir qu'à très basse fréquence (55 mHz) la capacité commence à se stabiliser à des valeurs comparables à celles qui résultent de la méthode précédente de charge/décharge.

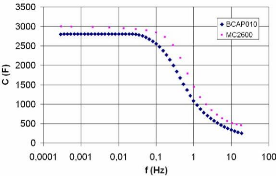
Fig. 3-15 : Evolution de la capacité des supercondensateurs BCAP010 et M600 vis-à-vis de la fréquence

> A très basse fréquence (<< 10 mHz), les phénomènes lents tels que la redistribution de charges et l'autodécharge dominent le comportement du supercondensateur. Des essais expérimentaux permettant la détermination des éléments propre ces phénomènes seront décrits ultérieurement.

La spectroscopie d'impédance électrochimique nous permet de connaître, les diverses

contributions résistives de l'ESR [26, 76]. Elles sont mises en évidence sur la figure 3-16.

> La résistance série R_s représente l'ensemble de la résistance de l'électrolyte, des électrodes, des collecteurs de courant et du séparateur. Cette résistance peut être déterminée à la fréquence de résonance.

> La résistance de l'électrolyte dans les pores est appelée résistance équivalente distribuée EDR : elle intervient à plusieurs niveaux et est difficile à évaluer. Elle est fonction du transfert ionique dans les pores du matériau d'électrode, éventuellement à l'interface électrolyte/électrode, des transferts électroniques à l'interface électrode/collecteur de courant, etc.

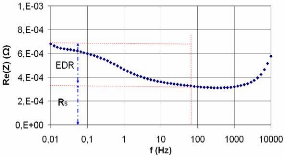
Fig. 3-16 : Contribution d'ESR du supercondensateur

A basse fréquence tous les éléments résistifs sont présents alors qu'à fréquence élevée seule la résistance R_s intervient.

Les erreurs de mesure pour un essai de spectroscopie d'impédance peuvent être déterminées pour le module et la phase. Sur la figure 3-17, nous montrons les erreurs faites en fonction de la fréquence pour l'essai présenté. Nous observons que ces erreurs sont variables suivant l'impédance mesurée.

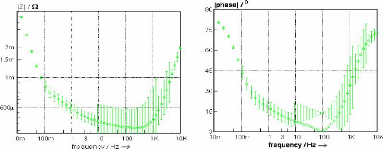
Fig. 3-17 : Erreurs de mesure provoquées par spectroscopie d'impédance

3.2.3.3. Dépendance des paramètres du supercondensateur avec la tension 3.2.3.3.1. Origine de la non-linéarité de la capacité du supercondensateur

La capacité est proportionnelle à la surface de l'interface et proportionnelle à l'inverse de la distance entre les charges. L'augmentation de la capacité due à l'augmentation de la tension peut être expliquée par la réduction de la distance entre les charges électrostatiques en raison de la compression électrostatique. Cette variation est aussi due à la variation de la constante diélectrique attribuable à l'électrostriction ou à la variation de la surface accessible [65, 77].

3.2.3.3.2. Plan de mesure

La spectroscopie d' impédance permet, comme énoncé auparavant, de caractériser les paramètres du supercondensateur pour une tension de polarisation donnée.

Nous avons caractérisé le supercondensateur BCAP010 à une température de 25 °C pour une tension de 0 à UN en suivant les étapes suivantes (illustration faite sur la figure 3-18) :

· court-circuit du supercondensateur pendant 24 h,

· court-circuit deux heures avant chaque mesure pour une tension donnée,

· chargement pendant une heure à une tension constante avant le lancement de la mesure,

· mesure de l'impédance (environ 30 minutes),

· court-circuit deux heures avant la mesure suivante, etc.

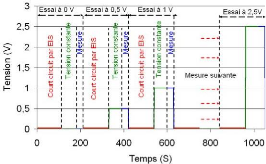
Fig. 3-18 : Protocole de mesure de l'impédance du supercondensateur en fonction de la tension

Ce plan de caractérisation a été choisi pour pouvoir caractériser le supercondensateur avec pratiquement le même état initial quelque soit la tension. Nous présentons sur la figure 3-19 le tracé de Nyquist du supercondensateur BCAP010 obtenu pour l'intervalle de fréquence de 10 mHz à 10 kHz et pour des tensions de polarisation de 0 ; 0,5 ; 1 ; 1,5 ; 2 et 2,5 V.

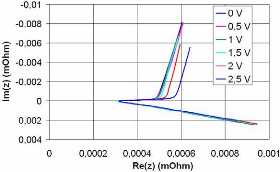
Fig. 3-19 : Tracé de Nyquist du supercondensateur pour un intervalle de tension [0 ; 2,5] V

A partir des résultats montrés sur la figure 3-20, nous pouvons observer que la capacité de la double couche du supercondensateur dépend fortement de la tension appliquée à ses bornes. Ceci est observé à partir des fréquences inférieures à 1 Hz et surtout pour des tensions supérieur à 0,5 V.

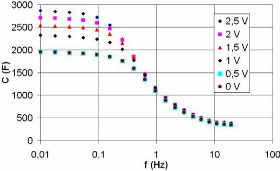
Fig. 3-20 : Evolution de la capacité du supercondensateur BCAP010 en fonction de la fréquence et de la tension à ses bornes

Nous montrons sur la figure 3-21 l'évolution de la partie réelle de l'impédance du supercondensateur en fonction de la tension et de la fréquence. La résistance du supercondensateur en haute fréquence est indépendante de la tension appliquée. Elle commence à s'accroître faiblement avec l'augmentation de la tension en dessous de la fréquence de résonance.

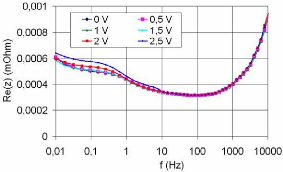
Fig. 3-21 : Évolution de l'ESR du supercondensateur en fonction de la tension et de fréquence

La dépendance de la capacité du supercondensateur C avec la tension U est montrée sur la figure 3-22 pour une fréquence de 10 mHz. La résistance R_s déterminée à la fréquence de résonance est invariable en fonction de la tension. En revanche, la résistance que présente la résistance de l'électrolyte EDR augmente avec l'augmentation de la tension. La figure 3-22 montre la variation de l'EDR déterminée pour une fréquence de 55 mHz en fonction de la tension. Cette dernière est l'image de la résistance de l'électrolyte distribuée liée au phénomène de diffusion sans tenir compte de celle liée au phénomène de redistribution de charge.

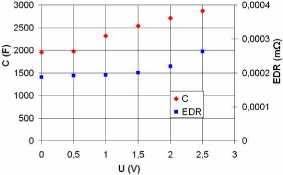
Fig. 3-22 : Évolution de la capacité et de l'EDR du supercondensateur en fonction de la tension

Dans la suite de ce rapport les deux fréquences de 10 mHz pour la capacité et de 55 mHz pour l'EDR sont considérées pour étudier la dépendance thermique, potentielle, etc. du supercondensateur.

3.2.3.3.3. Effet du protocole de caractérisation sur les paramètres du supercondensateur Nous avons proposé dans le paragraphe précèdent un protocole de caractérisation du spectre

d'impédance du supercondensateur pour différentes tensions. Nous proposons dans ce paragraphe un autre plan de mesure de l'impédance afin d'une part d'étudier l'influence de la méthode du chargement du supercondensateur sur ses paramètres et d'autre part, de simplifier la caractérisation du spectre d'impédance, qui était relativement longue auparavant.

Nous présentons sur la figure 3-23 le nouveau protocole de caractérisation par spectroscopie d'impédance. Dans ce nouveau plan, nous avons supprimé le temps du court-circuit effectué entre deux mesures.

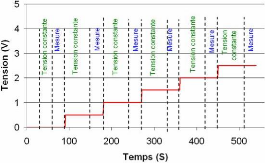
Fig. 3-23 : Deuxième protocole de mesure de l'impédance
du supercondensateur en fonction de la tension

Les résultats obtenus par le deuxième protocole sont comparés avec ceux du premier protocole (cf. fig. 3-24). Nous montrons sur cette figure la capacité déterminée à 10 mHz et 25 °C. Les valeurs de la capacité déterminées par les deux protocoles sont proches.

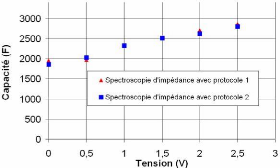
Fig. 3-24 : Evolution de la capacité du supercondensateur BCAP010
vis-à-vis de la tension déterminée par deux protocoles différents

Nous comparons sur la figure 3-25 la variation de la résistance EDR en fonction de la tension. Contrairement aux résultats précédents, nous trouvons qu'il y a un petit écart entre les

valeurs de l'EDR obtenues par les deux protocoles pour des tensions supérieures à 1 V. La caractérisation par le deuxième protocole conduit à accumuler des charges dans les pores du supercondensateur au fur et à mesure et donc la résistance EDR diminue.

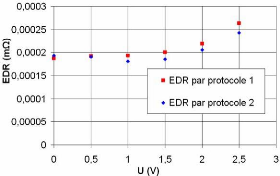
Fig. 3-25 : Evolution de la capacité du supercondensateur BCAP010
vis-à-vis de la tension déterminée par deux protocoles différents

3.2.3.4. Capacité des supercondensateurs étudiés

Pour terminer, nous présentons sur la figure 3-26 l'évolution de la capacité des supercondensateurs déterminée par le deuxième protocole à 25 °C et pour une fréquence de 10 mHz. Ces résultats confirment la dépendance de la capacité des supercondensateurs sur la tension et que la relation n'est pas exactement une droite.

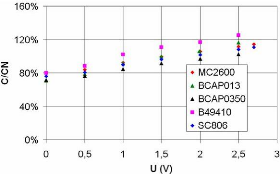
Fig. 3-26 : Evolution de la capacité des supercondensateurs étudiés en fonction de la tension

3.3. Modélisation électrique et fréquentielle des

supercondensateurs

L'utilisation des supercondensateurs a connu un développement important dans beaucoup d'applications ces dernières années. Il est donc important d'établir des modèles précis permettant d'évaluer le comportement de supercondensateurs en fonctionnement.

Nous présentons dans ce chapitre trois modèles de supercondensateurs. La méthode d'indentification de leurs éléments basée sur les techniques présentées précédemment et leur variation en fonction de la tension appliquée, du courant, etc., sera détaillée. Chaque modèle peut montrer certains avantages lors de la modélisation. Donc, une comparaison sera effectuée entre autre dans les deux domaines temporel et fréquentiel.

3.3.2. Modélisation temporelle du supercondensateur : modèle classique

RC

Dans certaines applications, comme celle d'une décharge lente de l'ordre d'une dizaine de secondes, le circuit équivalent classique d'un supercondensateur, composé d'une capacité C et d' une résistance série équivalente ESR peut être convenable pour décrire ses performances [50,78].

3.3.2.1. Circuit équivalent

En première approximation, les supercondensateurs peuvent être modélisés, comme un condenseur, par le modèle représenté sur la figure 3-27. La capacité C est fixe et une résistance série Rsérie représente les pertes électriques, résultant de l'autoéchauffement durant la charge et la décharge et limitant le courant passant dans le supercondensateur. Notons que pour atteindre une puissance élevée, il est absolument nécessaire d'avoir des composants avec une _Rsérie le plus faible [78, 77, 79]. En outre, la résistance en parallèle Rf permet de décrire le comportement du composant lors de l'autodécharge. Cette dernière sera présentée en détail dans le chapitre suivant. En négligeant, l'effet, la résistance de fuite Rf intervenant qu'aux très basses fréquences, la résistance série peut être assimilée à la résistance équivalente ESR.

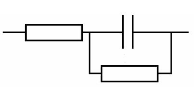
Rsérie ESR

Rf

C

Fig. 3-27 : Circuit classique équivalent du supercondensateur [77]

3.3.2.2. Identification des paramètres du modèle

Il existe plusieurs méthodes pour la détermination d'éléments du circuit équivalent (ESR et C). Ces méthodes sont basées sur différents principes. Certaines de ces méthodes ont été présentées plus haut. Par ailleurs, nous nous proposons d'utiliser la norme IEC 62391 [51, 52, 79].

3.3.2.2.1 Détermination des éléments du modèle (ESR et C)

Le supercondensateur est entièrement chargé à sa tension nominale pendant une heure. Ensuite, la source d'énergie est coupée et le supercondensateur est déchargé à un courant constant.

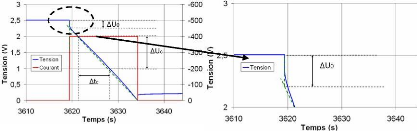
Fig. 3-28 : Détermination des éléments du circuit équivalent classique

Sur la courbe expérimentale, deux droites tangentes à la courbe expérimentale de la tension sont tracées pour déterminer ESR avec la chute de tension ÄU0. Cette dernière est mesurée comme indiqué sur la figure 3-28. La résistance ESR peut être calculée avec la chute de tension ÄU0 et le courant de charge, comme montré par l'équation 3-2 [59, 66, 80]. La capacité C est déterminée par l'équation 3-1, pour une durée ÄtC durant laquelle la tension aux bornes du supercondensateur décroit de 80% à 40% de sa valeur nominale UN (ÄU_c).

3.3.2.3. Validation expérimentale et limitation

Nous comparons sur la figure ci-dessous (cf. fig. 3-29) un essai expérimental de charge/décharge à 400 A effectué à 25 °C avec la simulation du circuit RC. Les résultats expérimentaux montrent qu'il y a un écart important entre la simulation du modèle RC et la courbe expérimentale, ce modèle montre donc son imprécision. En effet, ce modèle ne permet ni de représenter les variations de capacité qui apparaissent quand la tension change (non linéarité de la capacité du supercondensateur), ni la répartition lente des charges à la fin d'une charge ou d'une décharge [4]. En conséquence, un modèle qui prend en compte ces phénomènes est donc nécessaire pour une étude plus approfondie.

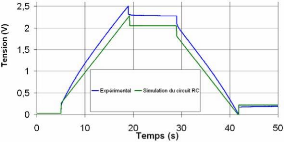
Fig. 3-29 : Comparaison de la réponse potentielle du circuit équivalent classique RC
avec un essai expérimental

3.3.2.4. Effet du courant de la décharge sur les éléments du circuit classique

Notons que les éléments du circuit classique RC (C et ESR) déterminés par la caractéristique de la décharge dépendent fortement du courant de décharge et de l'intervalle de tension dans lequel fonctionne le supercondensateur [80]. Sur les figures 3-30-a et b, nous présentons les valeurs de la capacité et de l'ESR des supercondensateurs BCAP010 (2600 F ; 0,7 m? (DC) ; 2,5 V) et M600 (2600 F ; 0,4 m? (DC), 2,7 V) déterminées à des valeurs de courants de décharge de 50, 100, 200, 300, et de 400 A et à une température de 25 °C. Nous observons que la capacité C varie très faiblement avec la variation du courant de la décharge tandis que la ré sistance ESR augmente fortement avec la diminution du courant. En conséquence, les paramètres du modèle varient suivant la dynamique de la décharge du supercondensateur.

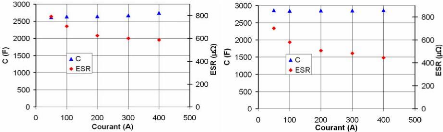
(a) BCAP010

(b) M600

Fig. 3-30 : Effet du courant de décharge sur la détermination de la capacité C et de la résistance ESR

3.3.3. Modélisation temporelle du supercondensateur : modèle à deux

branches

Nous avons trouvé qu'un simple circuit équivalent RC ne suffit pas à caractériser le comportement des supercondensateurs compte tenu de phénomènes qui comptent beaucoup dans leur comportement tels que la non-linéarité de la capacité de la double couche, la

redistribution de charge, etc. Nous avons donc besoin d'un modèle complet, qui prend en compte les différents phénomènes particuliers des supercondensateurs avec simplicité. Dans la suite, nous présenterons un modèle qui répond à ces questions tel que celui établi par Zubieta et al. [41, 81-83]. Ce modèle repose sur la répartition de l'énergie électrostatique des supercondensateurs en deux : une énergie rapidement stockée et une énergie lentement stockée.

3.3.3.1. Non-linéarité de la capacité de la double couche du supercondensateur

L'étude de la physique de la double couche montre que la capacité de la double couche n'est pas une constante, mais dépend fortement de la tension appliquée aux bornes du supercondensateur. Dans le paragraphe 3.2.2, l'étude expérimentale par le cycle de voltampérométrie a mis en évidence cette dépendance. Une modélisation de cette propriété est donc nécessaire afin d'obtenir des résultats précis lors de la simulation. Sur la base de la physique de la double couche, la capacité différentielle peut être modélisée en première approximation par une capacité d'une valeur constante C0 et une capacité dont la valeur varie de manière linéaire (k.u) en fonction de la tension u à ses bornes comme indiqué dans l'équation ci-dessous [41,82] :

Cdiff ( u) = C₀ + k.u 3-16

3.3.3.2. Circuit équivalent

Le circuit équivalent du supercondensateur, dit modèle à deux branches, est composé de deux cellules RC : une branche rapide _R1C1, qui intervient dans le régime transitoire, et une branche lente _R2, qui représente la redistribution des charges (cf. fig.3-31). Afin de tenir compte de la non-linéarité de la capacité du supercondensateur, la capacité de la branche rapide C1 est choisie variable en fonction de la tension à ses bornes (cf. eq. 3-17).

R1 R2

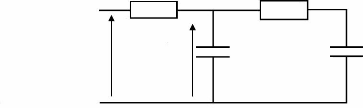
u

u 1

C1 C2

Fig. 3-31 : Modèle à deux branches du supercondensateur [41, 82]

C₁ ( u ₁) = C0+k.u 1 3-17

La propriété de la non-linéarité de la capacité de la double couche a pour conséquence que l'énergie stockée dans le supercondensateur est plus importante que dans le cas d'une capacité constante C0. La forme de l'énergie peut être écrite comme suit [41, 82] :

C k

0 3

W = u +

2

. . u 3-18

1 1

2 3

3.3.3.3. Identification des paramètres de la branche rapide

La méthode de caractérisation des éléments du circuit équivalent consiste à charger le supercondensateur par un courant constant d'une valeur élevée jusqu'à la tension nominale, et ensuite de laisser le supercondensateur en circuit-ouvert un certain temps. La procédure d'identification est basée sur l'hypothèse simplificatrice que les phénomènes rapides et lents se succèdent (rapide ensuite lent). Celle-ci doit s'opérer à courant élevé dont l'ordre de grandeur est celui du courant nominal du supercondensateur. Pour un seul cycle l'effet de l'autoéchauffement qui sera montré ultérieurement a une influence faible et négligeable sur la caractérisation par courant constant.

Vu que les deux branches possèdent des constantes de temps largement distinctes (R2C2

>> R

1 1 C ), pendant la phase de charge, la branche lente reste quasiment inactive. Le circuit

équivalent sera donc réduit comme suit :

I R1

u

C1

		u1

Fig. 3-32 : Circuit équivalent de la branche rapide

La résistance du supercondensateur R1 est déterminée par la formule présentée par l'équation 3-2.

Identification de la capacité C0

La capacité con stante C0 dans l'équation 3-17 peut être déterminée à partir de la définition de

la capacité différentielle à l'état initiale de la charge comme suit :

dq

I dt I

C0 = = = 3-19

du

(0) (0) (0) /

du du dt

avec,

q la charge stockée dans le supercondensateur.

Le rampe du(0)/dt est mesuré au voisinage de l'instant initial comme le montre la figure 3-33.

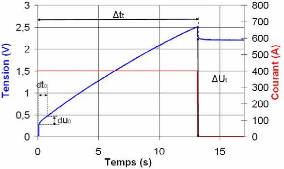
Fig. 3-33 : Principe de l'identification des éléments de la branche rapide

Identification de la constante k

L 'expression de la charge totale Qt stockée dans le supercondensateur à la fin de la charge en fonction de la durée totale Ätt de la charge et du courant de la charge I peut être donnée par l'équation ci-dessous :

Q t = I Ät t 3-20

Avec ÄUt l'évolution totale de la tension aux bornes du supercondensateur, nous pouvons obtenir la charge totale :

1

Q t = C Ä U _t + k Ä U t 3-21

2

0 2

A partir des deux expressions précédentes (3-20) et (3-21) nous pouvons écrire :

2 ( I. t - C · U )

Ä t 0 Ä t 3-22

ÄU t

k = 2

3.3.3.4. Identification des paramètres de la branche lente

Lorsque la tension aux bornes du supercondensateur atteint sa valeur nominale, le courant

d'alimentation s'annule et le phénomène prédominant dans le composant est celui de la redistribution de la charge entre les branches ra ide et lente. Le circuit équivalent schématisé

p

sur la figure 3-34 représente le supercondensateur durant cette phase oü R2 et C2 sont les éléments de la branche lente.

R2

I

C1

u2

u1

C2

Fig. 3-34 : Modèle équivalent durant la phase de redistribution

Identification de R2

Au moment de l'annulation du courant d'alimentation, le courant (initial) parcourant l'élément C2 est considéré nul, ce qui permet d'écrire l'équation suivante :

I (0) = Udébut / R₂ 3-23

De plus, la relation entre le courant de la capacité C1 et la tension à ses bornes à ce momentci peut être donnée par la formule suivante :

du

I = - C

(0) 1 (0) 3-24

1 dt

Pour le calcul de R2, nous approximons la pente initiale observée sur la tension du supercondensateur par une quantité ÄU/Ät, comme l'illustre la figure 3-35 et nous évaluons le terme I(0) pour le niveau médian de tension, à savoir _Udébut-ÄU /2 [4].

Ainsi R s'exprime par :

2

3-25

U - Ä U / 2 début Ät

C Ä U

1

R=
2

oü, _Udébut est la tension au début de la phase de redistribution.

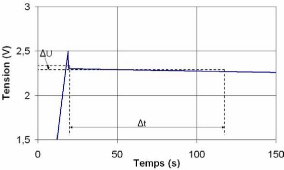
Udébut

Fig. 3-35 : Evolution de la tension aux bornes du supercondensateur pendant la phase de redistribution

Identification de la capacité C2 :

La capacité C2 peut être calculée à la fin de cette période oil les tensions sur C1 et C2 sont

supposées égales à la même valeur Ufi_n. En appliquant l'équation de conservation de la charge sur la charge stockée au début et à la fin de la phase de redistribution, nous pouvons écrire l'équation suivante :

C1 . U début = C ₂.U Cl + 3-26

fin fin

soit,

C2 = C1 . ( U début - U fin) / U fin 3-27

oil Ufi_n est la tension à la fin de la phase de redistribution.

Ce phénomène de redistribution interne, auquel sont associées des constantes de temps généralement très longues, met bien en évidence le problème de la disponibilité de l'énergie stockée dans les supercondensateurs. La majeure partie de celle-ci peut, certes, être qualifiée de rapide mais il reste une partie considérablement liée aux phénomènes lents [5,43].

Dans le tableau 3-2, nous donnons les valeurs des éléments du modèle à deux branches pour le supercondensateur BCAP010 déterminés à courant de charge de 400 A et à une température de 25 °C.

C1		R1 (u?)	C2 (F)		R2 (?)	C0 (F)
k (F/V)					1882
523	447	172	1,92

Tab. 3-2 : Eléments du modèle à deux branches pour le supercondensateur BACAP010 à 25 °C

3.3.3.5. Effet du courant de la charge/décharge

Afin de montrer l'influence du courant de charge/décharge sur la caractéristique électrique du supercondensateur, nous avons réalisé un essai de charge/décharge avec cinq courants différents 50, 100, 200, 300, et 400 A pour le supercondensateur BCAP010 à 25 °C. Le tableau 3-3 présente les résultats expérimentaux des éléments de la capacité C1 (C0 et k) et la résistance R1 déterminées au début de la charge et de la décharge. Nous trouvons que le choix de la valeur du courant de charge a une influence assez importante sur les résultats obtenus par cette technique : la capacité C1 calculée à la tension nominale varie de #177;4% et la résistance R1 de - 6% à +2% par rapport à leurs valeurs moyennes.

Courant (A)		k (F/V)	C0 (F)	C1 (F) à 2,5 V		R1 (u?)	400
Charge	523,2	1882	3190	447
	408	2165	3185	422		300
Charge	540	1832	3182	450
	431	2120	3178	420		200
Charge	550	1850	3225	450
	427	2084	3152	430		100
Charge	556	1857	3247	440
	414	2048	3083	450		50
Charge	595	1838	3326	410
	395	2075	3063	440		Moyenne
			3192	436

Tab. 3-3 : Éléments de la branche rapide déterminée à différents courant de charge/décharge

Sur la figure 3-36, nous représentons les résultats obtenus de la capacité C1 en tension nominale. D'après cette figure, nous observons que la capacité C1 déterminée durant la charge augmente avec la diminution du courant, tandis qu'elle diminue durant la décharge. La différence entre la capacité de charge et de décharge s'accroît donc avec la diminution du courant de charge.

L'écart existant entre la capacité de charge et de décharge a déjà été évoqué dans le paragraphe 3.2.2 qui traite de la méthode voltampérométrie ; la capacité de la charge est toujours supérieure à celle de la décharge.

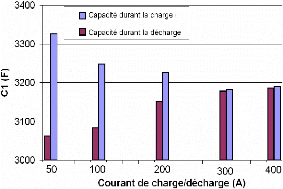
Fig. 3-36 : Capacité du supercondensateur BCAP010 déterminée à des différents courants de charge

Sur la figure 3-37, nous présentons le rendement oulombien vis-à-vis

c du courant de la

charge/décharge. No const

us atons ue l

q e rendement coulombien augmente avec

l'augmentation du courant de charge. Lors de la charge d'un supercondensateur par un faible courant les capacités liées aux phénomènes lents corre

sont ctement chargées, mais ces mêmes

capacités ne sont pas déchargée s pendan la dé arge l (à faib urant), car leurs charges

t ch ente le co

sont alors piégées dans les pores étroits.

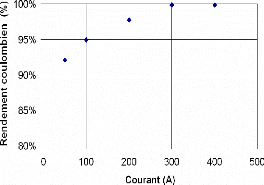
Fig. 3-37 : Rendement coulombien vis-à-vis du courant de charge/décharge

3.3.3.6. Comparaison du rendement coulombien des supercondensateurs étudiés

Dans le tableau ci-dessous, nous présentons les paramètres principaux R1 et C1 et le rendement coulombien pour des composants de différents fabricants MAXWELL, BATSCAP et EPCOS. Ces paramètres sont déterminés avec une valeur de courant de charge/décharge par Farad constante (0,15 A/F) pour les composants BCAP010, BCAP013, M600, et SC806.

Pour le composant B49410, cette valeur est de 0,11 A/F car la valeur nominale du courant de 540 A est supérieure à celle fournie par notre banc de manipulation. Pour le composant BCAP0350 cette valeur est de 0,09 A/F à cause de son faible courant nominal.

Nous trouvons d'après ces résultats que le rendement coulombien varie suivant le composant. Ce paramètre donne des informations importantes sur le niveau des phénomènes faradiques dans les supercondensateurs.

	Numéro de série	CN (F)	UN (V)	I (A)	I/CN (A/F)		R1 (m?)	k (F/V)	C0 (F)	C1 (UN) (F)		ç, (%)	MAXWELL
BCAP0350	350	2,5	30	0,09	Charge	4,3	57	239	389	96
						3,3	45	260	373
	450	2,5	70	0,15	Charge	2,120	113	309	590	97
						1,685	93	338	571
SC806	2600	2,7	400	0,15	Charge	0,912	551	2025	3512	81*
						0,462	324	1964	2840
B49410	3600	2,5	400	0,11	Charge	0,210	1065	2649	5311	96
						0,210	850	2997	5122
BCAP010	2600	2,5	400	0,15	Charge	0,447	523	1882	3190	100
						0,422	408	2165	3185
	2600	2,7	400	0,15	Charge	0,360	546	2024	3390	95
						0,317	321	2407	3210

Tab. 3-4 : Paramètres des supercondensateurs de différents fabricants

* Cette faible valeur n'a été mesurée que sur un élément BATSCAP. Elle serait à confirmer sur
d'autres éléments de ce même fabricant.

3.3.3.7. Comparaison des résultats obtenus par différentes méthodes

3.3.3.7.1. Présentation de la non-linéarité de la capacité obtenue par les différentes techniques

Nous nous intéressons à comparer les résultats obtenus temporellement par charge/décharge

à courant constant (procédure de Zubieta [41]) avec ceux obtenus par voltampérométrie et ceux donnés par spectroscopie d'impédance (à une température de 25 °C) (cf. fig. 3-38). Nous présentons sur cette figure les résultats de la mesure de la capacité du supercondensateur en fonction de la tension.

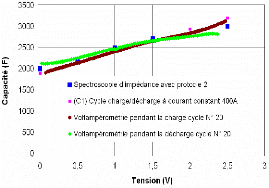
Fig. 3-38 : Comparaison des mé thodes tér on par la mesure

de carac isati

de la capacité en c

fon tion de la nsion

te

Les différentes techniques donnent des résul t ats diffé rents.

> Pendant la charge : les valeurs de la capacité m esurée par les méthodes temporelles (c harge/d éc harge à c o ura n t con s tant et voltampérométrie) sont assez proches. Celles obtenues par spectrométrie d'impédance sontinférieures à celles obtenu es par les méthodes temporelles.

> Pendant la écharge es v leurs e la cap cité o tenu s par ltamp

d l a d a b e vo erométrie

sont pratiquement identiques à celles obt enues par spec tr osco p ie d' im pédance, mais différentes de celles obtenues par charge/décharge à courant constant.

3.3.3.7.2. Comparaison de la capacité nominale obtenue par différentes techniques

Nous avons vu précédemment (cf. § 3.2.1) qu'il existe différentes méthodes permettant de déterminer la capacité du supercondensateur. Ces méthodes déterminent la capacité en supposant que celle-ci est indépendante de la tension appliquée dans l'intervalle de tension [UN/2 ; UN]. La détermination de cette capacité, dite capacité nominale, peut être réalisée par d'autres techniques en calculant la moyenne des capacités dans l'intervalle de tension mentionnée ci-dessus [84].

Nous comparons dans le tableau 3-5 la valeur de ces capacités à celle donnée par le fabricant pour les deux supercondensateurs BCAP010 et M600. Nous observons, comme prévu, que cette valeur obtenue par spectroscopie d'impédance et par voltampérométrie (décharge à 20 cycles) est très proche de celle de la méthode normalisée et de celle de MAXWELL, tandis que la méthode à charge/décharge à courant constant (C1) et par voltampérométrie (charge à 20 cycles) donnent des valeurs élevées.

	Capacite (F)	Courant constant (C1)		EIS à 10 mHz	Voltampérométrie (20 cycles)		Méthode norme IEC 6239			Méthode MAXWELL 400 A
		Décharge à 50 A			Décharge	400 A	50 A
	2600	2600	2600	2600	2600	2600	2600		2600	BCAP010
C	2863	2816	2614	2792	2596	2750	2623		2645
	110%	108%	101%	107%	100%	106%	101%		102%	M600
C	3130	-	2842	2956	2869	2857	2861		2902
	120	-	109	114	110	110	110		112

Tab. 3-5 : Détermination expérimentale de la capacité nominale
des supercondensateurs BCAP010 et M00

3.3.3.7.3. Comparaison des résistances par différentes techniques

Nous comparons dans le tableau 3-6 les valeurs de la résistance ESR obtenues par différentes méthodes de caractérisation à 25 °C et pour les deux supercondensateurs BCAP010 et M600.

Nous pouvons distinguer dans la documentation du fabricant comme MAXWELL deux résistances : la résistance DC (déterminée par décharge à courant constant) et la résistance AC (déterminée par une fréquence donnée). Nous présentons dans le tableau les valeurs réduites par rapport aux résistances DC et AC.

Nous pouvons constater que les valeurs de la résistance sont dispersées chaque méthode donnant une valeur différente des autres, mais les mesures par la méthode de MAXWELL, par la norme IEC 6239 et par spectroscopie d'impédance (à basse fréquence) donnent de s valeurs proches.

	Resistance (An)	EIS		Norme IEC 6239		MAXWELL à 400 A		Courant constant à 400 A
		ESR (55mHz;UN)	400 A	50 A
ESR	322	620	587	792	508	447
	700	700	700	700	700	700
	46	89	84	113	73	64
	300	300	300	300	300	300
	107	201	196	264	169	149		M600
ESR	272	439	422	701	405	360
	400	400	400	400	400	400
	69	110	106	175	101	90
	280	280	280	280	280	280
	97	157	150	250	145	129

Tab. 3-6 : Comparaison des valeurs de résistance obtenues par différentes méthodes

3.3.3.8. Validation expérimentale et limitation

Pour vérifier que le modèle à deux b ch

ran es étudié est précis, nous avons simulé ce modèle

grâce au log l S

icie implore ous p entons sur la figure 3-39, o

r. N rés la c mparaison du résultat de

simulation avec la réponse expérimentale. Cette figur ontre

e m d'une manière générale que le

modèle à d x ches sente c une nne p ision compo ement trique

eu bran repré ave bo réc le rt élec du
supercondensateu

r.

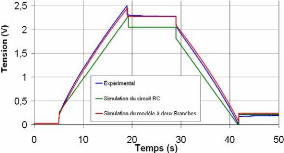
Fig. 3-39 : Comparaison du modèle à deux branches avec un essai expérimental

Cependant, un petit écart apparaît entre les résultats simulés et expérimental en fin de la charge, au début de la phase de redistribution et lors de la décharge (cf. fig. 3-40). Ceci résulte de la nature distribuée de la résistance et de la capacité du supercondensateur dûe à la structure poreuse des électrodes de structure volumique. L'effet de cette dernière peut être observé sur la courbe de charge/décharge et surtout après l'annulation du courant de charge/décharge (cf. fig. 3-40-a). De plus, la variation des éléments de la branche rapide de ce modèle en fonction du courant de la charge ou de la décharge n' st pas prise e

e n compte.

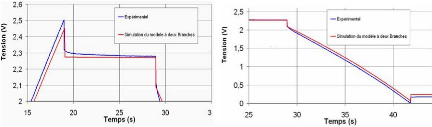
(a)

(b)

Fig. 3-40 : Présentation de l'écart entre le mo dèle à b

deux ranch l'ess

es et ai expérimental

Pour confirmer les résultats obtenus ci-dessus, nous avons réalisé un essai fréquentiel à 25 °C et à une tension de polarisation de 2,5 V sur le supercondensateur BCAP010. Nous

comparons sur la figure 3-41 le tracé de Nyquist du modèle à deux branches avec celui expérimental. Nous pouvons constater à partir de cette figure que la résistance R1 est supérieure à R_s. Par conséquent, pour la raison mentionnée ci-dessus le modèle à deux branches est limité et ne peut donc constituer un bon modèle dynamique du supercondensateur.

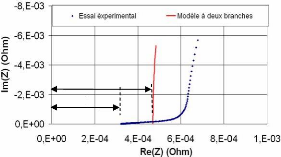
R_s

R1

Fig. 3-41 : Comparaison de la réponse en fréquence du modèle à deux branches avec l'essai fréquentiel

D'autres modèles temporels tels que celui proposé dans la référence [42] s ont présentés dans la littérature, mais le calcul complexe des éléments du modèle ainsi que le temps de simulation lent limite considérablement l'utilisation de ce type de modèle [85, 86].

3.3.4. Modélisation dynamique du supercondensateur

Les modèles présentés précédemment ne peuvent pas prédire avec précision les comportements dynamiques du supercondensateur tels que ceux trouvés dans certaines applications comme dans les véhicules hybrides, dans les asc enseurs [87, 88]. Ainsi, des modèles d'électrodes poreuses ont été proposés et sont décrits ci-dessous.

3.3.4.1. Analyse du spectre d'impédance d'un modèle d'électrode poreuse

Sur la figure 3-42, nous présentons le tracé de Nyquist de l'impédance du supercondensateur BCAP010 mesurée à 25 °C et à une tension constante de 2,5 V. Nous observons que le tracé de l'impédance à des fréquences intermédiaires de 55 mHz à 45 Hz est une droite d'un angle de 45 °C et que pour les basses fréquences (autours de 10 mHz), il tend approximativement vers une droite verticale.

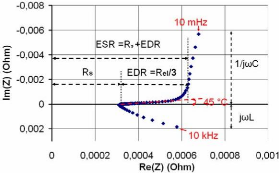
Fig. 3-42 : Tracé de Nyquist de l'impédance du supercondensateur

La région autours de l'angle de 45 °C (région de Warburg) est la conséquence de la capacité et de la résistance distribuées dans une électrode poreuse [89-91]. La résistance et la réactance augmente avec la diminution de la fréquence. Seule une partie de la double couche poreuse active est accessible aux fréquences intermédiaires [92]. Par contre, en basse fréquence, la plus grande partie de celle-ci est utilisée pour contribuer à la capacité de la double couche. La résistance distribuée EDR est également maximale [93]. Nous présentons dans le tableau 3-7 la valeur des paramètres pour le composant BCAP010.

EDR=Rel/3 (55 mHz)	Rs(ö =0 °)		Cdl (10 mHz)	(u?)
(u?)	(kF)		263
322	2,80

Tab. 3-7 : Paramètres principales du supercondensateur

3.3.4.2. Modèle équivalent de la topologie du supercondensateur

Un circuit équivalent convenable de la topologie des supercondensateurs peut être dérivé (cf. fig. 3-43) à partir de l'analyse du spectre d'impédance du supercondensateur présenté ci-dessus et dans le paragraphe 3.2.3.2. Le circuit équivalent se compose d'une inductance L, d'une résistance ohmique R_s et de l'impédance complexe des pores Z_p (représentée par la capacité de la double couche _Cdl et la résistance d'accessibilité aux pores _Rel). Ainsi, seuls quatre paramètres (L, R_s, Cdl, Rel) sont nécessaires pour établir un modèle, qui représente la physique d'un supercondensateur [94-97].

Le comportement inductif est simplifié ici par une inductance linéaire représentant l'inductance des connexions et de la géométrie du supercondensateur. L'effet inductif ainsi qu'une modélisation plus adéquate seront présentés dans le paragraphe 3.3.3.8.

L R_s Zp

Fig. 3-43 : Modèle équivalent de la topologie du supercondensateur [96]

L'impédance complexe du pore Z_p d'un supercondensateur (appelé aussi impédance de Warburg ou impédance de diffusion) peut être décrite par l'équation suivante (développée à partir de la théorie de Levie [98]) :

où

( )

ù = 3-28

C j ùô dl .

ô . coth( )

j ùô

Z_p

ô = × 3-29

dl R _el C dl

3.3.4.3. Modèle à dérivée non-entière

Le système à dérivée non entière est présenté afin de développer le terme coth de l'équation 3-28 pour les basses fréquences et pour les hautes fréquences comme suit [99] :

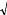
1+

2

x

coth(

x ) x ? 0 ? 3-30

x

coth( x ) x

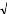
1 + x 2

?8 ? 3-31

x

En substituant la relation 3-30 dans l'équation 3-28, l'impédance de pore est alors égale à :

ù

ù 0

1 .

+ j

3-32

Z ù ?

p ( )

j C

ù . dl

avec ù0 = 1/ôdl. d'où,

pour les basse fréquences,

1 Z 3-33 p ( ù ) ? j C ù. dl

et pour les fréquences intermédiaires,

1

Z (ù) ? 3-34

^p C jù.ù

dl

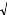
0

Ainsi, l'impédance de Warburg est un exemple typique d'élément à phase constante (CPE) pour lequelle l'angle de phase est une constante de 45 O indépendante de la fr équence [100,

101]. L'amplitude de l'impédance de Warburg est proportionnelle à l'inverse de la racine carrée de la fréquence (cf. eq. 3-34).

Nous comparons sur la figure 3-44 la simulation du modèle à dérivée non entière présenté par l'équation 3 -34 pour le supercondensateur BCAP010 avec l'essai expérimental qui a permis de tracer la figure 3-42. Nous observons que ce modèle est capable de modéliser précisément le comportement dynamique du supercondensateur concernant la distribution de la capacité et de la résistance. L'écart manifeste à très basse fréquence sera présenté ultérieurement.

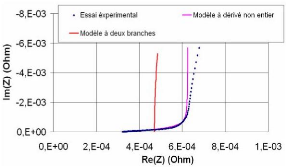
Fig. 3-44 : Comparaison du modèle à dérivé non entière avec un essai expérimental

L'inconvénient de ce modèle est qu'il ne peut pas être intégré dans un logiciel de simulation de type circuit électrique en électronique de puissance. En plus, il est difficile à établir dans le domaine réel. Il est donc nécessaire de trouver un autre modèle aussi précis mais assez facile à établir et à intégrer dans un logiciel de simulation.

3.3.4.4. Circuit électrique équivalent de l'impédance de diffusion

L'impédance d'accès aux pores ou bien l'impédance de diffusion représente les composants de stockage à nature distribuée non-faradique comme les supercondensateurs et faradique comme les batteries. En 1952 e a noté que cette ce ne peut pas être présentée

Graham impédan

par des réseaux électriques. Plus récemment Taylor et Gileadi ont tenté de la remplacer par des réseaux RC [66, 102]. Nous abordons dans la suite les deux circuits électriques équivalents employés pour remplacer l'impédance de diffusion par des réseaux RC : réseau de ladder et réseaux séries RC de Zarc [103].

3.3.4.4.1 Modèle du réseau ladder (ligne de transmission)

Généralement, le modèle de la ligne de transmission est un modèle très utilisé du supercondensateur [66, 86, 104, 105]. Les matériaux poreux utilisés pour former les électrodes

provoquent une résistance et une capacité distribuées dans l'espace de la double couche. Ceci donne un comportement correspondant à celle d'une ligne de transmission. La figure 3-45 illustre le circuit équivalent du supercondensateur avec l'impédance de diffusion présentée par une ligne de transmission avec N branches en parallèles.

Zp

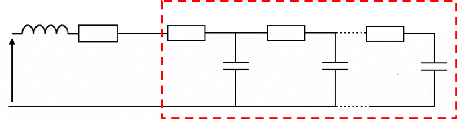
u

L R_s Rel/N Rel/N Rel/N

Cdl/N Cdl/N Cdl/N

Fig. 3-45 : Circuit électrique équivalent tenant compte l'impédance de diffusion
par un réseau ladder du supercondensateur [96, 98]

La précision de ce modèle dépend fortement du nombre des cellules RC en parallèle [96].

3.3.4.4.2 Modèle des réseaux séries d'éléments de Zarc

Il est proposé une autre représentation de l'impédance de diffusion par des réseaux séries d'éléments de Zarc [95, 96], déjà très utilisés pour représenter l'impédance de Warburg dans la simulation de batteries [40].

L'expression mathématique de l'impédance de diffusion de l'équation 3-28 peut être réécrite comme suit :

3-35

Rel

Z ( ù ) = coth( j R C

ù el dl )

p jùCdl

Cette expression peut être remplacée par l'expression suivante dans le domaine temporel :

1 2 Z ( ) t = + . p C C dl dl

N=8 ? N 2 2 ð ? ? exp ?? . t ?? N = ? R C 1 el dl . ?

3-36

Ainsi, l'expression mathématique de Z_p se traduit par une série de circuits RC comme représenté sur la figure 3-38.

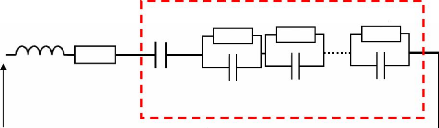
Cdl

Cdl /2 Cdl/2 Cdl/2

Rel1 R el2 RelN

L R_s

u

Zp

Fig. 3-46 : Circuit électrique équivalent tenant compte de l'impédance de diffusion par des réseaux de
Zarc du supercondensateur [95, 96]

La résistance _RelN peut être calculée par la formule suivante :

2R el

R = 3-37

elN N ð

2 2

Nous avons étudié le nombre optimum des cellules RC à placer en série. Nous représentons sur la figure 3-47 le pourcentage de la résistance _RelN par rapport à celle déterminée pour N = 1. Nous remarquons que sa valeur devient négligeable pour une valeur de N en dessus de dix. Ainsi, le nombre optimum de cellules à placer en série pour obtenir une bonne précision est aux alentours de dix.

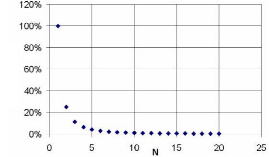
Ren

Rem/

Fig. 3-47 : Détermination du nombre optimum des cellules RC en série

3.3.4.4.3 Réponse en fréquence du circuit équivalent du supercondensateur

Pour le supercondensateur BCAP010, nous comparons sur la figure 3-48 le tracé de Nyquist du circuit électrique équivalent avec dix cellul es RC en série représenté sur la figure 3-46 (appelé aussi modèle à simple pore) avec l'essai expérimental. Les éléments du modèle à

simple pore sont tirés du tableau 3-7. A partir de cette figure, nous pouvons constater que le modèle présenté peut prédire le comportement dynamique du supercondensateur lié à la distribution de la capacité et de la résistance et qu'il donne des résultats assez proches de ceux du modèle à dérivé non-entière.

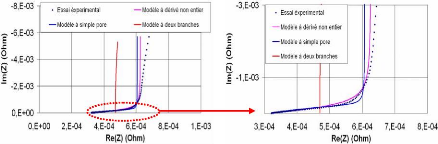
Fig. 3-48 : Comparaison du tracé de Nyquist du circuit électrique équivalent avec l'essai expérimental

Compte tenu l'hypothèse sur la similitude des pores constituants la double couche, le modèle à simple pore ne suit pas complètement l'essai expérimental dans la zone de Warburg. Une amélioration du modèle peut être proposée en considérant des pores non-homogènes. Le schéma à considérer est alors celui représenté sur la figure 3-49 avec CdlN ? Cdl/2 et RelN ? 2.R_el/(N².ð²).

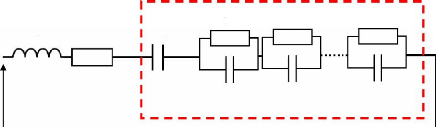
L R_s

u

Cdl

Cdl1 Cdl2 CdlN

Rel1 R el2 RelN

Zp

Fig. 3-49 : Circuit électrique équivalent du supercondensateur avec pores non-homogènes

Un nombre fini de cellules RC peut être déterminé par "fitting" grâce à l'utilisation d'un logiciel spécifique [106, 107]. Le "fitting" utilisé pour déterminer nos éléments est basé sur l'algorithme de minimisation d'erreur quadratique [73, 108, 109].

Nous présentons dans le tableau 3-8 les éléments du modèle avec une cellule Rel1Cdl1 déterminés comme mentionné ci-dessus. Nous remarquons que l'erreur est assez faible.

	Cdl kF	Rs uÙ	Rel1 uÙ		Cdl1 kF	Valeur
2,81	319	180	2,02		Erreur %
2	0,6	8,1	8,1

Tab. 3-8 : É

Le tracé de l'impédance du nouveau circuit est représenté sur la figure 3-50. Elle démontre l'importance du "fitting" pour améliorer la représentation du circuit équivalent du modèle.

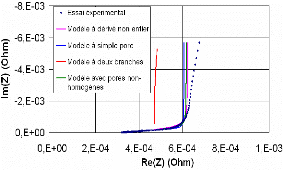
Fig. 3-50 : Comparaison du tracé de Nyquist du circuit électrique équivalent
du supercondensateur (modèle avec pores non-homogènes) avec l'essai expérimental

Dans le modèle à simple pore, les pores sont assimilés à des cylindres infinis et la double couche qui s'établit à la surface de leur paroi est associée à une capacité [72]. Ce modèle peut être réduit à basse fréquence à un simple circuit RC avec une capacité _Cdl et une résistance ESR (cf. eq. 3-38), ce qui explique la pente verticale sur le plan de Nyquist pour ces bases fréquences.

Z R R = + ( ) s el / 3

+

1/

jùCdl

3-38

Z ESR =

+

1/

jùCdl

Pour valider le modèle avec pores non-homogènes à basse fréquence, nous avons réalisé un e sai fréquentiel sur le supercondensateur BCAP010 dans l'intervalle de fréquence [0,3mHz ; s

10kHz] à une tension de polarisation de 2,5 V et à une température de 25 °C. La fréquence basse proposée de 0,3 mHz correspond à un temps réel supérieur à celui lié au phénomène de redistribution de charge. A noter que le supercondensateur avant cet essai a été court-circuité pendant plus de 24 heures pour s'assurer d'une complète décharge.

Nous comparons sur la figure 3-51 le tracé de q d

Ny uist u circuit schématisé sur la figure 3- 49 (avec les valeurs obtenues par fitting) avec l'essai fréquentiel. Nous observons que ce modèle est limité, car il ne tient pas mpte des pore les

co s plus difficilement accessibles

(phénomène de redistribution de charges).

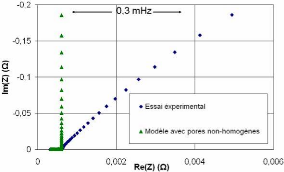
Fig. 3-51 : Comparaison du modèle avec pores non-homogènes
avec un essai expérimental en basse fréquence

3.3.4.5. Approximation par élément à phase constante (CPE) à basses fréquences

3.3.4.5.1 Principe d'un élément à phase constante

Les résultats expérimentaux effectués par spectroscopie d'impédance en basse fréquence montrent une non-concordance entre le modèle et les mesures. Cette dispersion, due à la distribution de charge et aux processus faradiques, peut être décrit comme étant une variation de capacité et exprimée en terme d'un élément à phase constante. Dans l'expression 3-38 de l'impédance, _jùCdl est remplacé par l'élément "CPE" comme suit [47, 110, 111] :

Z ESR = +	1	3-3		9

où, Q est un coefficient de proportionnalité et î (= 1) est la puissance de l'élément à phase constante, qui traduit l'intensité de la déviation par rapport à un systè me idéal.

Un élément à phase constante (CPE) permet de bien représenter le comportement du supercondensateur en basse fréquence (cf. fig. 3-52).

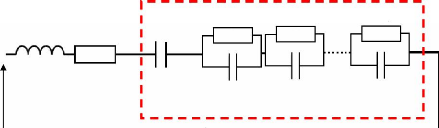
CPE

CPE1 CPE2 CPEN

Rel1 R el2 RelN

L R_s

u

Zp

Fig. 3-52 : Circuit électrique équivalent du supercondensateur avec pores non-homogènes et CPE

3.3.4.5.2 Validation expérimentale

Nous présentons dans le tableau 3-9 les éléments du CPE obtenus par "fitting".

	Q	î	Rs	Rel1	Q1		î1
kF		uÙ	uÙ	kF			Valeur
2,47	0,99	326	178	0,85	0,98		Erreur %
2,9	0,08	0,9	0,89	4,47	0,35

Tab. 3-9 : Élément du CPE à basse fréquence

Le tracé de Nyquist du modèle avec pores non-homogènes et CPE est montré sur la figure 3- 53. Nous remarquons que la combinaison réalisée avec CPE (cf. fig. 3-53) permet d'améliorer la modélisation du supercondensateur en basse fréquence. L'écart qui apparaît encore entre la courbe expérimentale et le tracé du modèle est dû aux processus faradiques tels que ceux liés à l'autodécharge. Ces derniers phénomènes seront abordés dans le chapitre suivant.

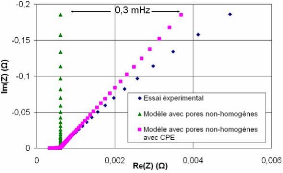
Fig. 3-53 : Comparaison du tracé de Nyquist du modèle représenté sur la figure 3-52
avec l'essai expérimental

3.3.4.6. Représentation de la distribution de l'impédance de diffusion par un circuit

équivalent

L'apparition du comportement d'un élément à phase constante (CPE) est liée à la présence d'une distribution de constantes de temps à basse fréquence. Au vue des différentes significations physiques du CPE présentées ci-dessus, les distributions de constantes de temps peuvent se classer en deux groupes distincts. Le premier groupe est lié à la distribution surfacique de l'électrode. Le second est lié à la distribution volumique. Pour les deux types de distribution, l'impédance conventionnelle, mesurée sur toute la surface de l'électrode, c respond à l'intégration de l'ensemble des impédances locales. Elle peut être modélisée p or ar une association, en parallèle, des différentes impédances locales Z_p1,..., _ZpNp, formant ainsi le réseau en échelle représenté sur la figure 3-54 [112].

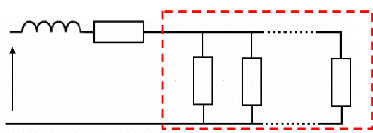
u

L R_s

Zp1

Zp2

Zp

ZpNp

Fig. 3-54 : Circuit électrique équivalent représentant la distribution d'impédance de diffusion [112]

· Circuit électrique équivalent général

Certains auteurs proposent de remplacer, dans la modélisation des composants électrochimiques, l'élément "CPE" par des circuits électriques équivalents en parallèle, chaque branche reproduisant le circuit électrique équivalent d'une gamme de pores d'électrode poreuse donnée [113]. Les différents éléments du circuit équivalent sont déterminés par "fitting". Cependant, le nombre élevé d'éléments passifs en série et/ou en parallèle rend difficile leur détermination.

Afin de simplifier la représentation des circuits électriques liés à la branche de redistribution des charges dans le schéma équivalent du supercondensateur, nous proposons comme d'autres auteurs [4, 35, 104] de considérer les branches lentes proposées par Zubieta [82] (cf. fig. 3-55).

3. Caractérisation et modélisation électrique, fréquentielle et thermique des supercondensateurs

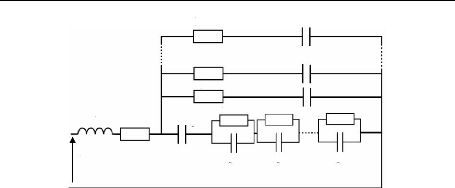
CNp

RNp

R3

C3

C2

Rel1 Rel2 RelN

Cdl

L R_s

R2

u

Cdl/2 Cdl/2 Cdl/2

Fig. 3-55 : Circuit électrique équivalent représentant
l'impédance de diffusion et la distribution d'impédances

Afin de valider ce circuit (cf. fig. 3-55), nous considérons deux branches en parallèle. L'utilisation d'un "fitting" nous permet de trouver le tableau 3-10 ci-dessous. D'après ce tableau, nous observons que malgré l'utilisation de deux branches lentes, les erreurs restent élevées.

	C2	C3	R2		R3
(F)	(F)	(?)	(?)		Valeur
97,5	624	1,23	24		Erreur %
106	Non déterminée	50	Non déterminée

Tab. 3-10 : Éléments de redistribution de charge déterminés par fitting

Cependant, comme nous pouvons le voir sur la figure 3-56, l'ajout de ces branches améliore la réponse en fréquence du modèle du supercondensateur dans le plan de Nyquist.

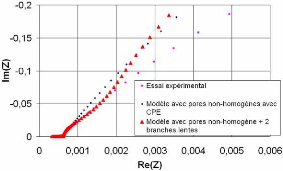
Fig. 3-56 : Comparaison du tracé de Nyquist du circuit schématisé
sur la figure 3-55 avec l'essai fréquentiel

Notons que nous avons validé ce modèle sur plusieurs composants et que nous avons trouvé des résultats similaires.

L'effet de la redistribution de charges ne peut donc être considéré avec précision (cf. les erreurs sur C2 et C3 dans le tableau 3-10). Nous proposons de le prendre en compte par un essai temporel.

3.3.4.7. Comparaison des modèles établis avec des essais expérimentaux

3.3.4.7.1. Comparaison des modèles établis avec un essai charge/décharge à courant constant

Nous comparons sur la figure 3-57 la simulation du modèle avec pores non-homogènes avec l'essai de charge/dé charge à courant constant présenté précédemment et ce pour le supercondensateur BCAP010. Nous observons que le modèle avec pores non-homogènes représente avec précision les phénomènes physiques du supercondensateur

Finalement, nous pouvons conclure que le modèle à simple pore est un modèle "dynamique" et celui à deux branches un modèle "statique". Malgré cela, un faible écart subsiste entre eux en fonctionnement en cycle de charge/décharge à courant constant.

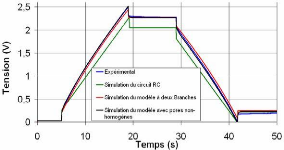
Fig. 3-57 : Comparaison des modèles
avec un essai de charge/décharge à courant constant de 400 A à 25 °C

3.3.4.7.2. Comparaison des modèles établis avec un essai par voltampérométrie cyclique

Nous comparons sur les figures 3-58 (a et b) les deux modèles établis du supercondensateur BCAP010 (modèle avec pores non-homogènes et modèle à deux branches) avec un essai voltampérométrique réalisé à 25 °C avec un balayage de 10 mV/s. Nous observons que la simulation du modèle à deux branches est très proche de la courbe expérimentale pour le cycle N° 1, mais un écart important apparaît après 20 cycles, tandis que pour le modèle avec pores non-homogènes c'est l'inverse.

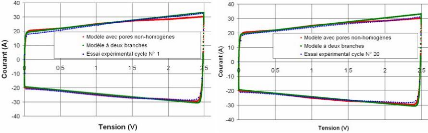
(a)

(b)

(a) Comparaison avec le cycle n° 1 (b) Comparaison avec le cycle n° 20

Fig. 3-58 : Comparaison de la simulation des modèles établis avec un essai voltampérométrie

3. 3.4.7.3. Comparaison des modèles établis dans le cas d'une application industrielle

Nous proposons ici de valider les modèles établis sur un profil de courant qui peut correspondre à celui rencontré dans certaines applications industrielles. Ce profil est composé de deux étapes comme illustré sur les figures 3-59 : Charge/décharge à plusieurs niveaux de courant pendant 500 secondes pour un intervalle de tension [UN/2 ; UN] (cf. fig. 3-59-a) puis le composant est laissé en circuit-ouvert trente minutes (cf. fig. 3-59-b).

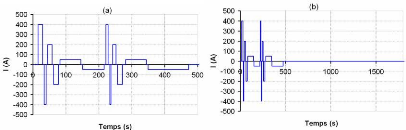
Fig. 3-59 : Profil du courant proposé pour comparer les modèles du supercondensateur

Nous comparons sur la figure 3-60 (a, b) entale en tension du

la réponse expérim

supercondensateur BCAP010 effectué à 25 °C avec la simulation des deux modèles (avec pores non-homogènes et à deux branches). Nous observons d'une manière générale que les deux modèles restent assez précis lors des temps de charge/décharge (plus de huit minutes) (cf. fig. 3-60-a). Après cette durée (décharge complète du supercondensateur), le modèle à deux branches est plus précis que le modèle avec pores non-homogènes (cf. fig. 3-60-b).

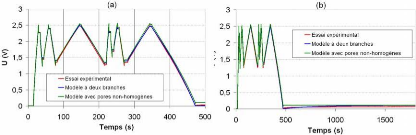
Fig. 3-60 : Comparaison de la réponse expérimentale du supercondensateur
avec la simulation des deux modèles établis

Cela est dû au fait que le modèle avec pores non-homogènes est obtenu grâce à un essai fréquentiel qui ne prend pas en compte le phénomène de redistribution des charges. En ajoutant une branche lente au modèle avec pores non-homogènes, le modèle devient alors plus précis (cf. fig. 3-61-a et b)).

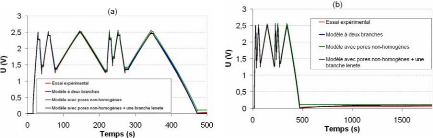
Fig. 3-61 : Comparaison du modèle à simple pore avec la branche lente avec l'essai expérimental

Le modèle à deux branches, quant à lui, est capable, en plus de sa simplicité, de représenter les phénomènes du supercondensateur précisément. Par conséquent, dans la suite de notre étude c'est le modèle à deux branches qui sera utilisé pour modéliser le supercondensateur.

Lors de ce denier essai expérimental la température du supercondensateur à ses bornes a augmenté de 4,5 °C. Nous nous proposerons donc, ultérieurement, d'étudier la variation des éléments des deux modèles du supercondensateur en fonction de la température.

3.3.4.8. Origine et modélisation du phénomène inductif

Comme nous l'avons montré auparavant, le diagramme de l'impédance en haute fréquenc e d'un supercondensateur peut être déformé par l'effet inductif. Le comportement inductif à haute fréquence est principalement causé par la connectique et par la géométrie du supercondensateur. Cet effet peut affecter la mesure d'impédance des composants de stockage d'énergie [97, 114].

Nous présentons sur la figure 3-62 le tracé du Nyquist du supercondensateur BCAP010 à 25 °C en haute fréquence. Le modèle avec pores non-homogènes et une simple inductance L en série ne suffit pas à caractériser correctement le comportement en haute fréquence du composant.

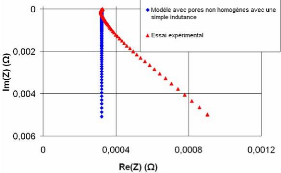
Fig. 3-62 : Tracé de Nyquist expérimental et du modèle avec des pores non-homogènes
et une inductance en série

Plusieurs travaux ont été consacrés à l'explication des comportements inductifs observés dans les composants de stockage d'énergie. Le comportement inductif peut être expliqué entre autres par les processus de relaxation présents dans la double couche électrique [47, 115-117].

La représentation de ce phénomène dans le modèle du supercondensateur par une inductance linéaire comme illustré sur la figure 3-49 ne suffit pas pour prendre en compte ce phénomène. Nous proposons donc de considérer des réseaux LR en série avec l'inductance série L_s de connexion pour modéliser en haute fréquence le comportement fréquentiel du supercondensateur (cf. fig. 3-63).

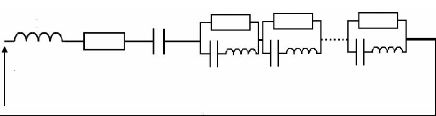
L_s

R_s

Rel1 R el2 RelN

Cdl Lp1 _C Lp2 C LpN

u Cdl1 dl2 dlN

Fig. 3-63 : Modèle du supercondensateur prenant en compte du phénomène inductif

Ces éléments inductifs peuvent être déterminés par fitting (cf. tab. 3-11).

	Ls (nH)	Lp1 (nH)		Lp2 (nH)	Valeur
27,3	4,6	2		Erreur %
4,8	3,6	7,8

Tab. 3-11 : Éléments inductifs déterminés par fitting

Nous comparons sur la figure 3-64 le tracé de Nyquist du circuit équivalent du supercondensateur schématisé sur la figure 3-63 avec les mesures expérimentales. Nous observons que le modèle proposé améliore considérablement la modélisation fréquentielle du supercondensateur.

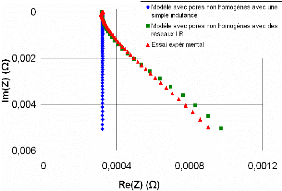
Fig. 3-64 : Comparaison du modèle tenant compte du phénomène inductance avec un essai fréquentiel

Cette étude a été appliquée sur l'ensemble des supercondensateurs étudiés. Nous avons remarqué que les valeurs des inductances sont toujours faibles par rapport à d'autres composants de stockage électrochimiques comme la pile à combustible, les batteries, etc. [71, 118].

3.4. Modélisation et caractérisation thermique des supercondensateurs

De nombreuses applications utilisent des supercondensateurs à des températures négatives ou positives. Les supercondensateurs peuvent fonctionner dans une large plage de température sachant que l'électrolyte utilisé possède une conductivité élevée dans cette plage.

La plage de température dans les documentations techniques des constructeurs est de [- 35°C ; 65°C] pour le supercondensateur BCAP010 de MAXWELL, de [-40°C ; 65°C] pour le s autres supercondensateurs de MAXWELL, de [-30°C ; 70°C] pour le supercondensateur d'EPCOS et de [-30°C ; 60°C] pour le composant de BATSCAP. C'est la stabilité de

l'électrolyte qui limite la température de f tio

onc nnem nt c

e ar à des températures élevées,

l'électrolyte se décompose.

Vu que la température de fonctionnement d'un supercondensateur peut avoir un effet significatif sur ses performances et que les éléments des modèles sont très dépendants de la température, nous nous proposons d'étudier dans ce paragraphe la variation thermique des paramètres des supercondensateurs.

3.4.1. Influence de la température lors de charge/décharge à courant

constant

Dans ce paragraphe, nous allons effectuer des cycles charge/décharge à courant constant pour différentes valeurs et à différentes températures sur deux supercondensateurs BCAP010 et M600 afin de montrer l'effet de la température sur deux générations de supercondensateurs.

3.4.1.1. Essai de charge/décharge à différentes températures

Pour des températures de -25, 0, 25, 45, et de 65 °C et pour les deux supercondensateurs étudiés BCAP010 et M600, nous avons effectué des essais de charge/décharge à courant constant de 400 A. Les résultats des essais sont présentés sur les figures 3-65-a et b.

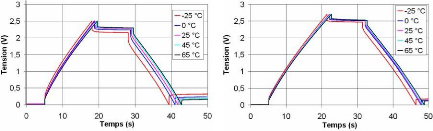
(a) BCAP010

(b) M600

Fig. 3-65 : Évolution de la tension aux bornes des supercondensateurs pendant le cycle charge/décharge à
courant constant de 400 A et à des différentes températures

D'après ces figures, nous constatons que durant la charge il existe un léger écart entre les courbes d'évolution de tension aux bornes du supercondensateur surtout pour la courbe mesurée à -25 °C, cet écart devenant plus important à partir de l'arrêt du courant de charge.

Nous présentons sur la figure 3-66 la variation de la résistance R1 du modèle à deux branches, déterminée en début de charge, des deux supercondensateurs vis-à-vis de la température ambiante. Nous observons que la résistance des deux supercondensateurs diminue avec l'augmentation de la température et que les variations sont importantes pour des

températures négatives.

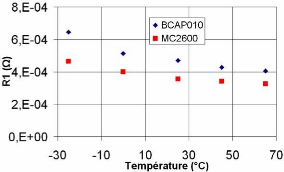
Fig. 3-66 : Evolution de la résistance R1 pour les composants
BCAP010 et M600 en fonction de la température

Nous présentons sur les figures 3-67-a et b la variation de la capacité C1 du modèle à deux branches de la charge et celle de la décharge déterminée pour une tension nominale à un courant de charge/décharge de 400 A en fonction de la température ambiante. La variation des éléments de la capacité C1 (C0 et k) en fonction de la température est montrée dans l'annexe B.

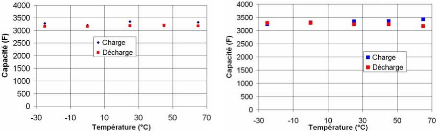
(a) BCAP010

(b) M600

Fig. 3-67 : Variation de la capacité de charge et celle de décharge en fonction de la température pour
BCAP010 et M600

Par conséquent, la capacité C1 varie faiblement quand la température varie. L'écart progressif manifeste sur les figures 3-65-a et b entre les courbes de tension aux bornes du supercondensateur durant le cycle de charge/décharge est donc dû à la variation de la ré sistance équivalente série.

D'après la figure 3-67- b, nous remarquons que la différence entre la capacité de charge et de décharge s'accroît avec l'augmentation de la température. Ceci nous à amener à réexaminer la variation de la capacité pour un cycle de charge/décharge avec un courant faible (50 A). Les

résultats expérimentaux présentés sur la figure 3-68 illustrent bien que cette différence s'accroît avec l'augmentation de la température. À température élevée la capacité liée aux réactions d'oxydoréduction augmente et cela surtout pour les faibles courants de charge/décharge (cf. § 3.3.3.5).

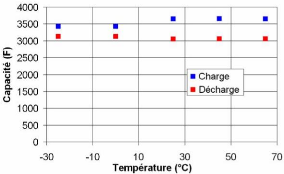
Fig. 3-68 : Variation de la capacité de charge et de décharge en fonction de la température
pour un composant M600 et pour un courant de charge/décharge de 50 A

La capacité des supercondensateurs BCAP010 et M600 déterminée temporellement n'est influencée que faiblement par la température.

Dans l'objectif d'établir une loi de la variation en fonction de la température des éléments du modèle à deux branches permettant d'estimer leur variation lors de la simulation, nous avons effectué un essai de charge/décharge à courant constant (400 A) sur le composants BCAP010 pour des températures de -25, 0, 10, 25, 35, 45, 55, et de 65 °C, les éléments du modèle, la branche rapide ₁ et C1, et la branche lente R2 et C2 ayant été caractérisés suivant la procédure

R

de Zubieta évoquée précédemment.

3.4.1.2. Variation des paramètres de la branche rapide

La figure 3-69 montre la variation en valeur réduite de la capacité C1 déterminée à la tension no inale (2,5 V) et celle de la résistance de la branche rapide R1 en fonction de la température.

m

E lle démontre que la capacité n'est pas tributaire de la température et que la variation peut être négligée pour le composant BCAP010.

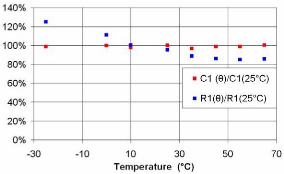
Fig. 3-69 : Variation en valeur réduite des éléments de la branche rapide en fonction de la température

Par ailleurs, la résistance R1 augmente fortement en températures négatives et diminue faiblement en températures positives. La variation de la résistance en fonction de la température est liée directement aux variations de la conductivité électrique des électrodes et à la conductivité ionique de l'électrolyte [20, 62].

Expérimentalement, les mesures de la résistance pour différentes températures (cf. fig. 3-69) montrent que la loi de variation peut être modélisée par une loi polynomiale ou exponentielle [20, 105, 119]. Nous proposons de modéliser la variation de la résistance R1 par une loi exponentielle de la forme suivante :

è?è

? 0

- ?

R ₁ ( ) R ₁ ( ₀ )

è = è á + â ô è

? ?

. e 3-40

? è è ?

? ?

où,

è est la température du supercondensateur,

è0 est la température de référence du supercondensateur, 25 °C dans notre étude, R1(è) est la valeur de la résistance du supercondensateur à la température è, R1(è0) est la valeur de la résistance à la température de référence è0,

ôè, áè, et âè sont des constantes liées aux caractéristiques thermiques du supercondensateur déterminées expérimentalement.

A partir des résultats expérimentaux, nous avons pu déterminer les constantes des caractéristiques thermiques des supercondensateurs BCAP010 et M600 avec une erreur relative moyenne faible comme le montre le tableau 3-12. Notons que la loi proposée a été celle qui a donné une erreur moyenne relative la plus faible par rapport à d'autres lois exponentielles ou polynomiales.

Composant	ôè (C^-1)	áè	âè		Erreur relative moyenne %	BCAP010
40	0, 81	0, 16	1,5		M600
48	0,85	0,16	1,0

Tab. 3-12 : Constantes de caractéristiques thermiques des supercondensateurs BCAP010 et M600

Nous présentons sur la figure 3-70 la comparaison entre la courbe expérimentale de la résistance R1 et celle trouvées par l'équation 3-40 (avec les paramètres du tableau 3-12) pour le composant BCAP010. La loi proposée est limitée à la plage de température donnée par le fabricant, pour des températures au-delà de cette limite, un processus du vieillissement commence à apparaître sur le supercondensateur et donc une autre fonction peut être utilisée.

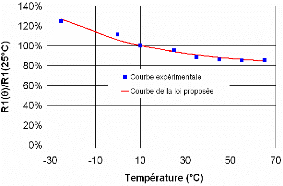
Fig. 3-70 : Comparaison entre la courbe expérimentale et celle obtenue par la loi proposée

3.4.1.3. Variation des paramètres de la branche lente

Nous nous intéressons dans ce paragraphe à déterminer la loi d'évolution des éléments de la branche lente en fonction de la température. Ces éléments que sont la capacité C2 et la résistance R2 ont été caractérisés à différentes températures. Nous représentons sur la figure 3- 71 l'évolution de ces éléments en fonction de la température ambiante. Nous observons que la capacité C2 augmente quand la température ambiante augmente alors que la résistance R2 diminue. Ces résultats sont liés à l a propriété thermique de l'électrolyte.

Fig. 3-71 : Variation des éléments de la branche rapide en fonction de la température

Les lois proposées pour représenter la variation en fonction de la température des éléments de la branche lente sont des fonctions polynomiales du deuxième ordre comme montré dans le système d'équations ci-dessous :

C ( ) è = C 2 2

( ) . è 0

2 ( a ) + + è 1 . 1, c è 1 . 1

( 2

2

a 2 )

2 . +

è 1, c

. è +

3-41

2 0

R ₂ ( è

) ( ).

= R è

où,

a, b et c sont des constantes thermiques, déterminées expérimentalement.

D'après les résultats montrés sur la figure 3-71, nous avons pu déterminer les constantes li ées aux caractéristiques thermiques de l'équation 3-41 (cf. tab. 3-13). Nous avons choisi un polynôme du deuxième ordre, car les autres fonctions telles que les polynômes d'ordre différent et les exponentielles ont donnée une erreur relative moyenne plus élevée.

Elément	a (C^-2)	b(C^-1)	C		Erreur relative moyenne %	C2
1,4.10^-4	16.10^-4	0,85	9,7		R2
-6,23. 10^-5	-4,4.10^-3	1,11	7,4

Tab. 3-13 : Coefficients thermiques des éléments de la branche lente pour le supercondensateur BCAP010

3.4.2. Variation thermique lors d'un essai par voltampérométrie cyclique

3.4.2.1. Essai par voltampérométrie à différentes températures

Les figures 3-72-a et b montre le voltampérogramme mesuré à une température de -25, 0, 25, 45, et de 65 °C obtenu avec un balayage de 10 mV/s pour les supercondensateurs BCAP010 et M600. A l'exception du régime transitoire, nous trouvons que l'évolution du courant en fonction de la tension est approximativement indépendante de la température ; il en

est de même pour la capacité puisque C=i/(du/dt) [35, 44].

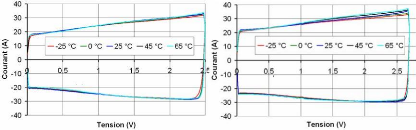
(a) BCAP010

(b) M600

Fig. 3-72 : Voltampérogramme à différentes températures
du supercondensateur BCAP010 et M600

3.4.2.2. Rendement coulombien à différentes températures

Nous avons calculé le rendement coulombien à partir des résultats présentés pour le supercondensateur M600 en fonction de la température ambiante. Sur la figure 3-73-a, nous représentons le rendement coulombien pour la tension nominale vis-à-vis de la température. Nous constatons que le rendement coulombien est plus élevé à des températures négatives qu'à des températures positives. Cela s'explique par le fait que les processus faradiques sont moins actifs aux températures négatives.

Par ailleurs, nous comparons sur la figure 3-73-b le rendement coulombien pour différentes températures pour les deux supercondensateurs M600 et BCAP010. Nous constatons que le rendement du composant BCAP010 est, comme montré précédemment, supérieur à celui du composant M600 notamment à des températures positives, et qu'il est moins influencé par les variations de température.

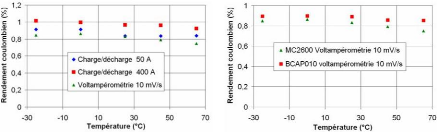
(a) M600 (b) Comparaison BCAP010 et M600

Fig. 3-73 : Evolution du rendement coulombien vis-à-vis de la température

3.4.3. Variation caractérisée par spectroscopie d'impédance

Nous avons réalisé des mesures par spectroscopie d'impédance sur les différents supercondensateurs BCAP010, M600, SC806 etc. à différentes températures afin de déterminer leur dépendance vis-à-vis de la température.

3.4.3.1. Dépe ndance en température des paramètres du supercondensateur BCAP010

Nous allons montrer la variation des paramètres du supercondensateur BCAP010 en fonction de la température à savoir les différentes résistances et la capacité totale à basses fréquences et à des fréquences intermédiaires. Des essais fréquentiels à tension nominale (2,5 V) et pour les températures de -25, 0, 15, 25, 35, 45, 55, et 65 °C sont réalisés par spectroscopie d'impédance. A noter que ces essais sont effectués après 24 h de court-circuit. Nous présentons sur la figure 3-74 le tracé de Nyquist du supercondensateur pour différentes températures.

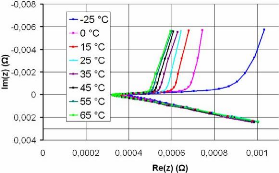
Fig. 3-74 : Tracé de Nyquist du supercondensateur BCAP010
pour différentes températures et pour une tension de 2,5 V

3.4.3.1.1 Variation de la capacité en fonction de la température

La figure 3-75-a représente l'évolution de la capacité du supercondensateur (évaluée à partir de la partie imaginaire) en fonction de la fréquence pour différentes températures. Nous présentons sur la figure 3-75-b la variation de la capacité C pour des fréquences de 10 mHz, 55 mHz et de 1 Hz vis-à-vis de la température.

D'après ces deux figures, nous constatons que la capacité à des fréquences intermédiaires augmente quand la température augmente notamment pour les températures négatives. Par contre, la capacité à basse fréquence est pratiquement indépendante de la température. Ce résultat correspond à celui obtenu par les autres techniques de mesures. Cela signifie qu'à

basse fréquence la contribution sur la capacité des ions pénétrant les pores de la double couche est identique pour les températures faibles et les températures élevées [120].

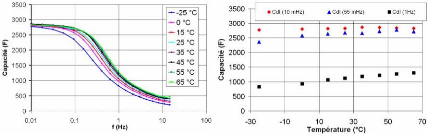
(a) pour une plage de fréquence (b) pour des fréquences de 10 mHz, 55 mHz et 1 mHz

Fig. 3-75 : Evolution de la capacité du supercondensateur BCAP010
en fonction de la fréquence pour plusieurs températures à tension nominale

3.4.3.1.2 Variation des résistances en fonction de la température

La figure 3-76-a représente l'évolution de la partie réelle de l'impédance du supercondensateur en fonction de la fréquence pour de différentes températures. Comme l'illustre la figure, la partie réelle de l'impédance augmente légèrement, lorsque la température diminue de 65 °C à 15 °C. Ensuite, pour les températures négatives, l'augmentation est plus importante. De même, l'augmentation à basse fréquence est plus importante qu'à haute fréquence.

Nous montrons sur la figure 3-76-b les différentes résistances du supercondensateur en fonction de la température ; la résistance équivalente série ESR pour plusieurs fréquences et la résistance équivalente distribuée EDR et la résistance série R_s.

La caractérisation en fonction de la température montre que la résistance équivalente série ESR augmente fortement lorsque la température diminue. La résistance liée à l'électrolyte EDR est aussi fortement influencée par la température. Pour une température supérieure à 0 °C cette ré sistance varie peu et pour des températures négatives, elle croît très rapidement lorsque la température diminue. Ceci est dû à la viscosité de l'électrolyte qui augmente pour les basses températures ce qui accroît la résistance de l'électrolyte [105, 121, 120]. La résistance série R_s ne varie que légèrement dans la plage de température considérée.

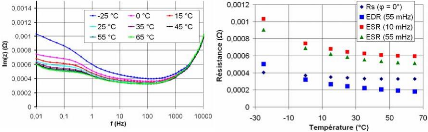
(a)

(b)

Fig. 3-76 : Evolution de la partie réelle de l'impédance du supercondensateur et des résistances R_s, EDR
et ESR en fonction de la fréquence pour plusieurs températures à la tension nominale

D'une manière générale, la variation de l'impédance en fonction de la température est fortement li ée à la nature du supercondensateur et à la concentration de l'électrolyte utilisé. Pour un type d'électrolyte, plus la concentration en ions est grande, moins la résistance augmente et la capacité diminue aux basses températures [122].

Nous avons étudié également la variation thermique par spectroscopie d'impédance des paramètres des autres supercondensateurs. Nous avons trouvé que pour tous les composants la dépendance avec la température est pratiquement similaire (cf. annexe C).

3.4.3.2. Approximation de la variation thermique de la dynamique des supercondensateurs

Afin de compléter l'étude thermique des modèles du supercondensateur, nous estimons dans le tableau 3-14 la variation des éléments du modèle avec pores non-homogènes en fonction de la température. La détermination d'une loi de variation, en fonction de la température, des éléments du modèle avec pores non-homogènes permet d'estimer l'évolution thermique du supercondensateur. Notons qu'il est plus difficile de déterminer ces lois pour les éléments du modèle à deux branches compte tenu d'un passage de courant élevé dans le composant créant un autoéchauffement.

L'évolution de la résistance ESR est représentée par ses deux éléments EDR et R_s. L'évolution de l'EDR est représentée par la loi exponentielle présentée par l'équation 3-40. La variation de R_s est représentée par la loi polynomiale présentée par l'équation 3-41. La capacité du supercondensateur _Cdl, déterminée par fitting, est pratiquement indépendante de la température ambiante. Seules les capacités _CdlN, présentes à des fréquences intermédiaires, sont variables en fonction de la température. Nous en présentons un exemple (pour _Cdl1) dans le tableau 3-14.

Composant	Élément	ôè (C^-1)	áè	âè		Erreur relative moyenne %	BCAP010
EDR	22	0,89	0, 12	1,6		M600
EDR	25	0,87	0,16	1,0		Composant
Élément	a (C^-2)	b(C^-1)	c	Erreur relative moyenne %		BCAP010
R5	3,2.10^-3	-3,8.10^-3	1,1	1,0		M600
R5	4,0.10^-3	-1,5.10^-	1,0	1,6		Composant
Élément	a (C^-2)	b(C^-1)	c	Erreur relative moyenne %		BCAP010
Cdl1	-5 -1,4.10	-3 4,9.10	0,87	2,0		M600
Cdl1	-2,9.10^-5	5,6.10^-3	0,87	1,0

Tab. 3-14 : Coefficients thermiques des supercondensateurs BCAP010 et M600

3.4.3.3. Dépendance en température et en tension des caractéristiques électriques du supercondensateur

Nous avons présenté auparavant la variation des paramètres du supercondensateur en fonction de la température ambiante et pour la tension nominale. Ceci nous a conduit à étudier et valider des résultats obtenus pour l'intervalle de tension [0 ; UN]. Nous nous intéressons donc à montrer, dans ce paragraphe, la variation des performances du supercondensateur en fonction de la température ambiante et en fonction de la tension.

Les figure 3-77 a et b illustrent l'évolution de la capacité du supercondensateur BCAP010 pour une température de -25, 0, 15, 25, 35, 45, 55, et de 65 °C et dans l'intervalle de tension [0V ; 2,5V]. Pour des fréquences basses (autour de 10 mHz), il est toujours observé que la capacité du supercondensateur est faiblement affectée par la variation de la température quelque soit la tension à ses bornes (cf. fig. 3-77-a), tandis que, pour des plus hautes fréquences la capacité diminue quand la température diminue surtout à des fréquences intermédiaires (à 1 Hz par exemple (cf. fig. 3-77-b)).

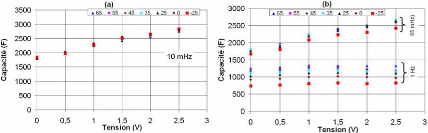
Fig. 3-77 : Évolution de la capacité du supercondensateur en fonction de la tension et de la température

A partir des figure 3-78-a et b, il est évident que la diminution de la température accroît la résistance EDR et donc l'ESR. Nous remarquons que la résistance R_s dépend faiblement de la

température et ne dépend pas de a tensio l pe re c clu que la température la

l n. I ut êt on plus basse

modifie d'une manière gnifica le f e cou nt dan

si tive lux d ra s la structur reuse.

e po

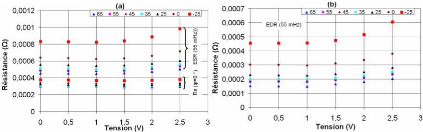
Fig. 3-78 : Evolution des résistances du supercondensateur en fonction de la tension et en fonction de la
température ambiante

3.4.4. Modèle thermique du supercondensateur

La température due à l'autoéchauffement est une grandeur importante dans un supercondensateur, elle est à l'origine du vieillissement. L'objectif de cette partie est de présenter une étude simple de l'origine de l'autoéchauffement et une modélisation simplifiée du comportement thermique.

3.4.4.1. Source de chaleur

Nous pouvons constater dans un supercondensateur que la production de chaleur est la superposition de générations irréversible et réversible de chaleur [96, 123, 124].

3.4.4.1.1. Génération de chaleur irréversible

La génération irréversible de chaleur, due à l'effet Joule, est la puissance dissipée dans les résistances ohmiques. La puissance dissipée peut être estimée pour une fréquence donnée à partir du modèle à simple pore (cf. eq. 3-42) en considérant _Ieff courant efficace dans le composant.

P th = ESR . Ieff ²3-42

3.4.4.1.2. Génération de chaleur réversible

Trois causes pour une génération de chaleur réversible sont possibles : des réactions chimiques d'oxydoréduction, l'effet Peltier et la variation de l'entropie [123-126]. L'autoéchauffement lié aux réactions d'oxydoréduction est dépendant de la tension. Les ions dans l'électrolyte d'une double couche sont organisés par le champ électrique pendant la charge

et se répandent à nouveau pendant la décharge : l'entropie peut être interprétée comme une mesure d'agitation. L'effet de Peltier pour les contacts entre l'aluminium et le charbon se traduit par une variation de température de quelques uK, qui est proportionnelle au courant appliqué. Ce dernier dans un supercondensateur à base de charbon et électrolyte organique peut être négligé [123, 124].

3.4.4.2. Impédance thermique

Fondamentalement, la propagation de la chaleur issue d'un composant peut s'effectuer de trois manières : par conduction, par convection, et par radiation [20, 123, 124].

Le circuit équivalent de l'impédance de diffusion de la chaleur se base sur la théorie des lignes de transmission [20, 127]. Il décrit correctement la distribution de la température interne du système et permet une corrélation claire entre éléments équivalents et éléments physiques. Il existe d'autres réseaux capables de décrire correctement le comportement thermique et plus facile à identifier mais la structure interne du réseau n'a pas de correspondance physique évidente [128, 127]. La figure 3-79 montre le circuit équivalent considéré.

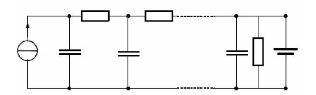
Pth

è1 è2

Rth1 Rth2 è_n

Cth 1 Cth2 Cthn

Rthn

è 0

Fig. 3-79 : Modèle thermique du supercondensateur à base de ligne de transmission

Il est clair, que l'identification de tous ces éléments par des mesures de température diverses à la surface et à l'intérieur du composant n'est pas envisageable. Le modèle équivalent devrait alors être simplifié pour obtenir un modèle identifiable. Le modèle simplifié proposé est basé sur l'hypothèse simplificatrice suivante : la température aux bornes et au coeur du supercondensateur est identique en régime permanent [129].

La température des bornes peut représenter la température à l'intérieur du supercondensateur car elles sont reliées directement aux collecteurs de courant en aluminium de conductivité thermique élevée. Des mesures ont été effectuées par l'Institut Paul Scherrer pour Maxwell en plaçant un thermocouple au centre du supercondensateur et un autre sur la borne positive. Les ré sultats ont montré que ces deux températures étaient pratiquement identiques [20].

La figure 3-80 représente un modèle thermique simplifié composé de deux constantes de temps. Ce modèle considère les températures du boîtier et des bornes [130].

Le flux thermique _Pth représente la puissance provenant de l'effet Joule en négligeant la source de chaleur réversible. La source de chaleur réversible peut être négligée pour une simple modélisation d'un supercondensateur, car sa constante de temps thermique est très supérieure aux périodes de charge/décharge [35, 131]. Ce flux de chaleur s'écoule dans les résistances thermiques _Rth1 ^et _Rth2 (en °C/W) et les capacités _Cth1 ^et _Cth2 (en J/°C) pour provoquer la chute de la température Äè (en °C) sur le composant. La température ambiante è_o est assimilée, dans le circuit équivalent, à une source de tension constante.

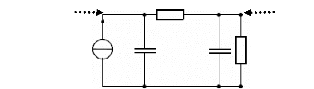
Cth1 Cth2

Pth

Rth2

Coeur (bornes) è_c Rth1 èb Boîtier

è0

Fig. 3-80 : Modèle thermique simplifié du supercondensateur

L'impédance thermique peut être écrite par la relation suivante à partir du circuit équivalent :

Z = R C + R

th ( ( th 2 // th 2 ) th 1 ) // th 1

C3-43

Avec le formalisme en p (variable de Laplace) _Zth peut exprimée ainsi :

1 + R th 1

R th 1

ô . p 1 + ô .

th 2 th 2

p

ô 2th p )

Z = ( R R

+

th th 1 th 2

3-44

)

1+

R R

+ R R

+

th 1 th 2 th 1 th 2

? ( R R

ô + ô +

1 p + ô ô

2 p R C p

2 1 1 2 p

th th th th th th

+ )

p

2 th 1 th 2 (1 + ô )(1

1 p +

th

avec

ô th 1

)C th 1 3-45

= ( R R

+

th 1 th 2

ô =

th 2 ( ₂ ) 2

R C

th th

L'expression 3-44 utilise l'hypothèse simplificatrice que la constante de temps thermique ôth2 est très grande par rapport à _ôth1 [132].

La montée en température entre le coeur (bornes) du composant et l'ambiance est donc :

Äè_c = P thZ th 3-46

L'évolution temporelle de la température du coeur du composant est alors gouvernée par cette expression :

? ? t ? ? ? t ? ? ?

?-

Ä ( )

t P R

= 1 exp ?-

è ?

th ? ? - ? ? ?? + R ? 1 exp

- ? ? ?? 3-47

1

c th th 2

? ? ? ? ô 1 ? ? ? ? ô2 ? ? ? ?

L'évolution de la température sur le boîtier, quant à elle, est donnée comme suit :

? t ? t

1

- ??- + ?-

ô

Ä è t P _th R th

= ? ? exp

b ( ) 2 1 exp ?

? ? ô2 ? ô 2 ? ô 1

? ?

?? 3-48

? ?

3.4.4.3. Réponse thermique du supercondensateur

3.4.4.3.1. Outil de mesure

La mesure de la température sur la surface du supercondensateur a été effectuée à l'aide de thermocouples de type K liés au système d'acquisition multivoies de National Instrument (NI 9211). Les caractéristiques techniques du système d'acquisition sont données dans l'annexe D. Ce système est programmé sous le logiciel LabView. L'acquisition de données est effectuée en temps réel.

Nous présentons sur la figure 3-81 la position des cinq thermocouples employés pour la mesure. Sur un composant BCAP010, trois sont collés sur l'extérieur du boîtier et deux sur les bornes. Un sixième thermocouple pour la température ambiante de la salle de manipulation est loin du composant (sachant que la convection est naturelle et que la salle climatisée est à 25 °C).

Fig. 3-81 : Position des thermocouples sur le supercondensateur

3.4.4.3.2. Essai expérimental

Le dispositi

f expérimental employé pour effectuer la charge/décharge est un banc Arbin (cf. annexe E) permettant d'effectuer des charges décharges à courant constant, puissance constante, ...

Le comportement thermique pendant la charge (exothermique) est différent de celui pendant la décharge (exothermique et endothermique). Afin de mesurer la température aussi précisément que possible, des pauses ont été ajoutées après chaque étape.

Nous avons chargé et déchargé le supercondensateur par à courant constant de 100 A avec un rapport cyclique de 0,83 à partir d'une tension initiale de UN/2 un

pendant

peu plus d'une heure. Ensuite, nous l'avons laissé se refroidir. Le profil du courant est montré sur la figure 3- 82-a et l'évolution de la tension aux bornes du supercondensateur pendant l'essai expérimental sur la figure 3-82-b.

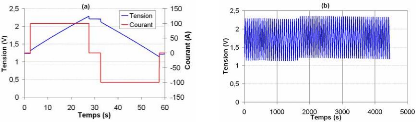
Fig. 3-82 : Evolution de la tension aux bornes du supercondensateur durant l'essai thermique

La réponse thermique du supercondensateur présentée sur la figure 3-83 montre les différente s températures dans le supercondensateur en fonction de tem

ps. La température aux

bornes du supercondensateur est supérieure aux autres. Les te

mpératures mesurées à

différentes positions du boîtier sont pratiquement les mêmes. Les résultats de la fi

gure

montrent que le régime permanent est atteint au bout d'une heure environ.

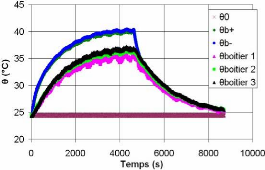
Fig. 3-83 : Evolution des températures du supercondensateur pour le profil présenté

3.4.4.3.3. Simulation et validation du modèle thermique

Les résultats expérimentaux montrés sur la figure 3-83 nous permettent de déterminer les éléments du modèle établi sur la figure 3-80. En régime permanant les résistances thermiques peuvent être e stimées par la puissance dissipée et l'augmentation des températures (cf. eq. 3- 49 ).

Äè Ä è

b c

R 2 = , R R

+ = 3-49

th th 1 th 2

P P

th th

Les capacités thermiques peuvent être calculées à partir des constantes de temps déterminées par un logiciel de "fitting" avec une erreur de moins de 1% (cf. eq. 3-50).

1

ô

th

1

Cth

3-50

R R

+

th 1 th 2

ô th 2

Rth 2

Cth

2

Ces éléments sont présentés dans le tableau 3-15 ci-dessous.

Elément	Rth1^(°C/W)	Rth2^(°C/W)	Cth1^(J/°C)		Cth2 (J/°C)	Valeur
0,7	2,88	172	433

Tab. 3-15 : Eléments du modèle thermique du supercondensateur

Par ailleurs, nous avons couplé le modèle thermique avec le modèle électrique avec des pores non-homogènes. Les valeurs de la résistance électrique ESR(è) sont ajustées suivant la température du composant par la loi établie auparavant. Le modèle à été implanté dans le logiciel Simplorer. La comparaison entre la simulation du modèle et les résultats expérimentaux est montrée sur la figure 3-84. Le modèle thermique établi représente avec une bonne précision pour un profil de courant donné l'évolution de la température du supercondensateur aux bornes (coeur) et à l'extérieur du boîtier.

Par contre il est bien évident que ce modèle n'est pas capable de modéliser les régimes transitoires thermiques rapides (de l'ordre de quelques secondes à quelques minutes) du supercondensateur. Pour prédire le comportement thermique en régime transitoire une modélisation analytique est nécessaire comme celle basé sur la méthode des différences finies [133].

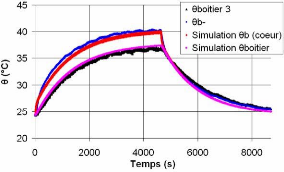
Fig. 3-84 : Réponse thermique du modèle du supercondensateur schématisé sur la figure 3-84

Un autre essai thermique sévère avec un courant de charge/décharge de 400 A a été effectué dans l'objectif de montrer les points les plus chauds sur la surface du supercondensateur. La figure 3-85 montre que la température aux bornes dépasse la température maximale limite du supercondensateur.

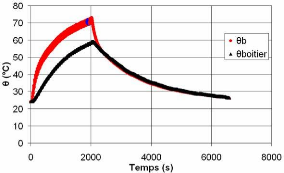
Fig. 3-85 : Evolution des températures aux bornes et sur le boîtier du composant

A l'aide d'une caméra infrarouge, nous avons relevé des images thermiques du supercondensateur. La figure 3-86 correspond à l'image thermique obtenue quelques instants avant l'annulation du courant de charge/décharge (instant indiqué de couleur différente sur la figure 3-85). Nous constatons sur la figure que les points les plus chauds, comme prévus sont les bornes et qu'il y a une légère augmentation de la température du centre du boîtier vers l'extérieur du boîtier (prés des bornes).

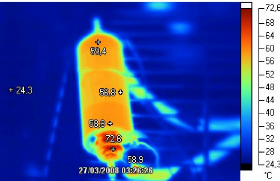
Fig. 3-86 : Thermographie du supercondensateur

3.5. Effet du vieillissement sur les paramètres de supercondensateur

Les mécanismes de vieillissement du supercondensateur peuvent être dûs à des contraintes électriques, mécaniques ou l'environnementales [77] :

· Les vibrations et les chocs mécaniques conduisent à affaiblir les connexions.

· Le vieillissement dû à l'environnement est également très important. Une température élevée accélère de façon importante la perte de performance du supercondensateur.

· Les contraintes électriques (comme une surtension) peuvent conduire aussi à une perte de performances du supercondensateur. Ce phénomène est accéléré par la température et son effet est augmenté par les impuretés et par l'eau contenu dans l'électrolyte. A température plus élevée, le processus de vieillissement est accéléré par une réactivité forte de la composition chimique et à des tensions élevées plus d'impuretés participent aux réactions d'oxydoréduction. Des conditions extrêmes peuvent conduire aussi à une évaporation de l'électrolyte.

La plupart des mécanismes de vieillissement engendre une diminution de la capacité C et une augmentation de l'ESR.

L'évolution des caractéristiques du supercondensateur nous donne une idée de la durée de vie du composant. Cette dernière représente un critère primordial pour l'utilisation de ces composants dans les applications de puissance. Différents essais de vieillissement accélérés sont habituellement employés pour étudier la durée de vie tels que les tests cycliques et des essais par "floating". Les tests cycliques consistent à charger et décharger le supercondensateur sous une température donnée avec un courant constant entre deux valeurs de potentiel [35, 104, 113, 121, 134]. Le vieillissement par floating consiste à contraindre le supercondensateur sous sa tension nominale et température maximale d'utilisation.

3.5.1. Vieillissement accéléré

Dans le cadre d'une collaboration avec H. Gualous et G. Alcicek du SET (laboratoire systèmes et transports) de Belfort, G. Alcicek a fait subir à cinq supercondensateurs M600 des vieillissements accélérés à la tension nominale et à des températures différentes [135]. Nous nous intéressons dans ce qui suit à analyser l'évolution des caractéristiques électriques lors de vieillissements effectués au SET dans le cadre du Master Recherche de G. Alcicek.

3.5.1.1. Vieillissement accéléré à la tension nominale et à la température limite d'utilisation

Le premier vieillissement a été effectué sur trois supercondensateurs à 2,7 V et à 65 °C (par G. Alcicek). Les figure 3-87-a et b illustrent le pourcentage de la variation des résistances des supercondensateurs en fonction du temps par rapport à leur valeur initiale ; la résistance ESR à 55 mHz, la résistance EDR à 55 mHz et la résistance R_s pour ö = 0 ° en fonction du temps. Nous observons bien une augmentation de ces résistances et que la variation de la résistance R_s est plus importante que celle de l'ESR. Ceci est dû à la faible augmentation de la résistance liée aux accès aux pores EDR.

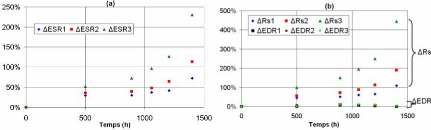
Fig. 3-87 : Evolution des résistances des supercondensateurs en fonction de temps

Sur la figure 3-88, nous présentons également le pourcentage de la diminution de la capacité de s supercondensateurs C à 10 mHz en fonction du temps.

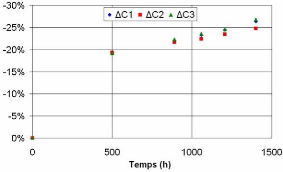
Fig. 3-88 : Evolution de la valeur de la capacité C des supercondensateurs en fonction de temps

3.5.1.2. Vieillissement accéléré à la tension nominale et au-delà de la température limite d'utilisation

Deux supercondensateurs ont été vieillis par G. Alcicek à la tension nominale de 2,7 V et à la température de 70 °C. Cette dernière est supérieure à celle maximale d'utilisation prisée par le fabricant.

Les figures 3-89-a, b, c et d ci-dessous illustrent l'évolution des paramètres de deux supercondensateurs en fonction de temps. Nous constatons que la résistance EDR, la résistance R _S augmente plus fortement en fonction du temps que lors du vieillissement précédent. La diminution de la capacité C est aussi plus rapide.

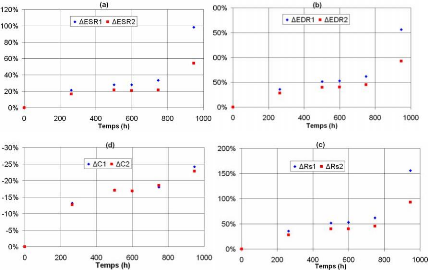
Fig. 3-89 : Evolution des paramètres des deux supercondensateurs en fonction de temps

La variation de la capacité du supercondensateur en fonction de la tension appliquée avant et après le vieillissement est montrée sur la figure 3-90 (ces essais ont été effectués au laboratoire Ampère). La capacité diminue de plus de 20 % pour la tension nominale (2,7 V), tandis que la diminution est plus faible pour des tensions plus faibles. Cela peut s'expliquer par la diminution de micropores accessibles du charbon actif surtout en tension élevée, et par une déformation de la structure du charbon actif [136].

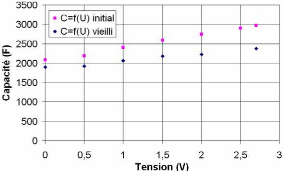
Fig. 3-90 : Capacité du supercondensateur vieilli N° 2 en fonction de la tension pour un composant sain et
vieilli

De nombreuses causes peuvent être responsable s du vieillissement du supercondensateur et ainsi de la diminution progressive de sa performance [137] :

· la saturation ionique de la surface des électrodes,

· l'augmentation de la résistance de contact de l'électrode,

· la diffusion d'eau dans l'électrolyte,

· la dégradation de l'électrolyte,

· des réactions d'oxydoréduction dûes aux impuretés.

3.6. Conclusion

Pour conclure sur la caractérisation, nous pouvons noter qu'il est nécessaire, pour mieux intégrer un supercondensateur dans les applications, de connaître ou de déterminer un certain nombre de paramètres essentiels : C(u), ESR, puissance et énergie disponibles, caractéristiques thermiques et qualité (vieillissement, rendement coulombien, etc.). Pour cela, des méthodes de caractérisation sont mises en oeuvre et sont appliquées sur des supercondensateurs commercialisés : charge/décharge à courant constant, à tension constante, à puissance

constante, voltampéremétrie, spectroscopie d'impédance.

Nous avons trouvé que la valeur des paramètres des supercondensateurs dépend de la technique de caractérisation ceci à cause de la non-linéarité de la capacité du supercondensateur, du phénomène de redistribution et des phénomènes faradiques tels que les réactions d'oxydoréduction. Plusieurs supercondensateurs commercialisés ont été étudiés par ces techniques de mesure. La capacité et la rési stance sont définies comme une quantité dynamique dépendant de la tension et du courant de charge/décharge du supercondensateur. La capacité mesurée est liée à la double couche et aux réactions électrochimiques [80].

Pour conclure sur les méthodes de mesure, vu que les paramètres des supercondensateurs peuvent dépendre des techniques de caractérisation, des mesures ont été effectuées afin de minimiser les perturbations faradiques, comme une charge/décharge du composant plusieurs fois. Cela donne des résultats très proches et fiables que peuvent être employés dans les applications industrielles.

Dans ce chapitre, nous avons présenté quelques circuits équivalents du supercondensateur. Ces circuits ont été utilisés pour interpréter les mesures obtenues. Les éléments des modèles établis sont identifiés à l'aide des techni ques de mesure présentées précédemment.

Le modèle classique RC donne une première approximation du comportement du supercondensateur. Le modèle à deux branches RC avec une capacité non-linéaire est un modèle assez simple et précis, mais il est limité et incapable de modéliser le comportement dynamique du composant. Les comportements résultant de la structure poreuse des électrodes du supercondensateur ont été modélisés par des réseaux RC en s érie avec le modèle à simple pore [96].

Le comportement inductif de la cellule peut être modélisé par des réseaux RL en série avec l'inductance L_s. Cet effet est provoqué par des réactions électrochimiques, par la dispersion de la porosité des électrodes et par la connectique du composant. L'expérience montre néanmoins que l'effet inductif est négligeable pour les cellules de forte valeur [114].

Nous avons étudié dans ce chapitre les variations des caractéristiques électriques des supercondensateurs en fonction de la température ambiante et les avons corrélées aux modèles à deux branc hes et avec pores non-homogènes.

Une augmentation de la température améliore les performances en termes d'énergie et de puissance, car la capacité augmente légèrement et les résistances (EDR et R_s) diminuent mais cette augmentation de température diminue le rendement coulombien. Notons qu'aux basses températures les supercondensateurs présentent globalement un meilleur comportement que les

accumulateurs.

Le supercondensateur a été modélisé thermiquement par des circuits _RthCth avec deux constantes de temps thermique. Le modèle thermique nous a permis d'estimer l'évolution de la température du composant due à l'autoéchauffement lors de son fonctionnement.

Malheureusement, en cours d'utilisation, les performances des supercondensateurs diminuent. Les symptômes majeurs rencontrés sont une diminution de la capacité liée à la quantité de charges stockées et une augmentation de résistance.

4. Étude, caractérisation

et modélisation

de l'autodécharge

des supercondensateurs

4. Étude, caractérisation et modélisation de

l'autodécharge des supercondensateurs

4.1. Introduction

Les supercondensateurs sont employés pour stocker l'énergie électrique pour des périodes s'étendant de quelques secondes à plusieurs jours. L'autodécharge permet de déterminer la durée du maintien de l'énergie stockée, en particulier pour les applications ayant un rapport cyclique bas. Une application typique est le démarrage d'un moteur de voiture après une semaine de stationnement dans un parking. Dans ce cas, il est nécessaire que le dispositif de stockage maintienne son énergie stockée le plus longtemps possible [55]. Dans les accumulateurs classiques, l'autodécharge reste très faible par rapport à celle des supercondensateurs et la durée de maintien de la plus grande part de l'énergie (shelf-life) est de l'ordre de quelques dizaines de mois à quelques années [138].

L'amplitude de l'autodécharge peut être déterminée soit en mesurant directement le courant de l'alimentation nécessaire à maintenir une tension constante (méthode appelée floating), ou soit par l'enregistrement de la tension aux bornes du supercondensateur en fonction du temps [1 39].

Dans notre travail, l'autodécharge est caractérisée par la mesure de la décroissance de la tension des supercondensateurs en circuit ouvert. La diminution graduelle en circuit ouvert de la tension d'un supercondensateur chargé peut être due à deux mécanismes différents: l' autodécharge ou la redistribution de charges. La redistribution de charges correspond à la répartition de charges entre les pores ayant des accessibilités différentes. Afin d'éviter celle-ci, nous allons commencer par définir une méthodologie à suivre pendant toute la caractérisation de l'autodécharge.

Plusieurs phénomènes peuvent se produire dans un supercondensateur chargé en circuit ouvert du fait de la nature chimique du supercondensateur. En effet, l'autodécharge est une fonction complexe du temps, de la tension et de la température. Certaines conditions, telles que la valeur de la tension, le type des impuretés dans l'électrolyte, etc., déterminent la nature des mécanismes de l'autodécharge et leur durée. La simple mise en parallèle d'une résistance de fuite avec la capacité totale du supercondensateur n'est donc pas suffisante pour modéliser convenablement l'autodécharge avec toute sa complexité. Pour cela, nous envisageons dans ce chapitre de déterminer un nouveau circuit électrique équivalent de l'autodécharge nous permettant de mieux la représenter et surtout de quantifier l'énergie dissipée dans le

supercondensateur lors de l'autodécharge.

Tout d'abord, l'autodécharge s'accélère fortement en fonction de la tension initiale et de la température ambiante ce qui réduit l'énergie emmagasinée dans le supercondensateur . Nous décrirons ainsi la dépendance des paramètres du modèle de l'autodécharge vis-à-vis de la tension et de la température.

Pour évaluer les paramètres de l'autodécharge en fonction de la tension et la température, et généraliser notre étude expérimentale, nous allons étudier l'autodécharge de supercondensateurs commerciaux issus de différents fabricants ayant des capacités et des tensions nominales différentes et étant produits. Les paramètres de l'autodécharge sont présentés en valeur réduite afin, d'une part, de les comparer par rapport à ceux donnés par le constructeur, et d'autre part, de montrer comment l'autodécharge peut varier suivant la capacité et les technologies de fabrication.

Le phénomène de récupération de tension apparaît, pour des faibles autodécharges. Une présentation expérimentale et une interprétation de celui-ci seront présentées.

Finalement, les éléments du modèle de l'autodécharge s ont déterminés en utilisant la sp ectroscopie d'impédance et comparés avec ceux trouvés par la mesure de la décroissance de la tension aux bornes du supercondensateur.

4.2. Mesure de l'autodécharge

4.2.1. Outil de mesure

La mesure de la tension aux bornes de plusieurs supercondensateurs en circuit ouvert se fait à l'aide du système d'acquisition multivoies de National Instrument (NI 9205) (cf. annexe E). Nous avons utilisé le logiciel LabView pour réaliser les acquisitions de données. Ce système nous a permis de mesurer simultanément l'autodécharge de plusieurs composants.

4.2.2. Procédures de mesure

Nous plaçons le supercondensateur dans une enceinte climatisée à une température constante de 25 °C durant plusieurs heures. Le supercondensateur est ensuite chargé par une source de tension constante pendant une heure puis est laissé en circuit ouvert pendant sept jours. Suite à la longue durée de charge (1 heure), les différents pores du supercondensateur sont

approximativement chargés à la même tension. En conséquence, quand le courant de charge s' arrête, la décroissance de la tension aux bornes du supercondensateur suit seulement l'effet de l'autodécharge, et l'effet de redistribution devient négligeable. L'identification proposée des paramètres d'autodécharge consiste à observer la tension aux bornes du supercondensateur. Dès que le courant de charge s'annule, nous mesurons la tension aux bornes du composant pendant sept jours. A la fin de la mesure, nous déchargeons les supercondensateurs et nous les court-circuitons pendant deux jours. Le plan d'essai de mesure est illustré sur la figure 4-1.

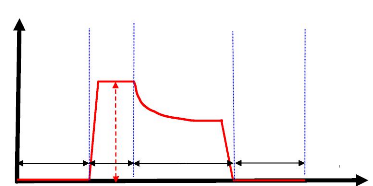
Tension

2 jours 2 jours

1 heure 7 jou rs

Essai N° 1

Court circuit

Chargement par
une source de
tension constante

U0

Mesure

nsion

de to

2

Essai N°

Court circuit

Temps

Fig. 4-1: Plan d'essai de mesure de l'autodécharge pour une tension initiale et une température
données

Sur la figure 4-2, nous présentons à titre d'exemple l'autodécharge d'un supercondensateur BCAP010 mesuré à 25 °C et pour une tension initiale de 2,5 V. Nous constatons une dé croissance rapide de la tension pendant les huit premières heures, et lente par la suite.

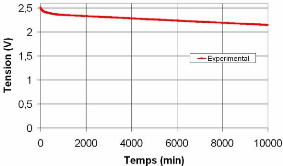
Fig. 4-2 : Tension lors de l'autodécharge du supercondensateur BACAP010

4.3. Mécanismes de l'autodécharge

L'énergie libre des supercondensateurs est plus élevée à l'état chargé qu'à l'état déchargé. Cependant, d'un point de vue de stabilité thermodynamique, il existe en permanence une force qui tend à ramener le système vers l'état déchargé [116]. Tous les supercondensateurs perdent lentement leur charge et, par conséquent, leur énergie stockée.

Quatre mécanismes distincts d'autodécharge peuvent être trouvés dans un supercondensateur [140] :

4.3.1. Autodécharge due à la dispersion des charges dans les pores

Une autodécharge du supercondensateur visible durant quelques secondes après l'interruption de courant de charge apparaît dans les électrodes poreuses. Celle-ci a été observée expérimentalement lors d'un cycle charge et décharge à courant constant. Elle a été interprétée et simulée dans le chapitre précédent (cf. § 3.3.4) et n'est pas considérée dans ce chapitre, sachant que le composant est chargé très lentement.

4.3.2. Autodécharge par diffusion liée au processus d'oxydoréduction

Quand la tension d'un supercondensateur dépasse une tension de seuil, une accumulation de concentrations d'espèces ioniques peut avoir lieu à l'interface électrode-électrolyte. Après l'arrêt du courant de charge dans le compostant, la majorité des charges restent en place formant la double couche, mais une part des charges compte tenu de la présence des impuretés se recombine ce qui entraîne une autodécharge. Quelques espèces ioniques vont se diffuser

vers l'électrolyte et d'autres à la surface du

charbon. Ce type d'autodécharge est le type

prédominant durant les premières heures de l'autodécharge. La nature de ces réactions n'est pas connue avec précision, mais il est probable que la présence d'eau dans l'électrolyte organique en soit la source [138]. Cette autodécharge est affectée par la quantité, la concentration et le type des impuretés existantes dans l'électrolyte.

4.3.3. Autodécharge due au courant de fuite

Le transfert d'électrons entre les électrodes dû à la présence des impuretés et à l'imperfection du séparateur engendre un faible courant entre les deux électrodes d'un supercondensateur.

4.3.4. Autodécharge due à la surtension

Enfin, nous allons présenter le dernier type d'autodécharge. Il est lié à certaines conditions : quand le supercondensateur est chargé à une tension supérieure à la tension seuil de la décomposition de l'électrolyte et quand des impuretés existent, des réactions irréversibles peuvent avoir lieu, la décomposition de l'électrolyte s'accompagnant généralement d'un dé gagement gazeux sous surtension (O2, H2, etc.). La décroissance de la tension du supercondensateur peut être exprimée par l'équation de Tafel. Cette dernière décrit la vitesse d'une réaction électrochimique non réversible due à une surtension (cf. eq. 4-1). L'équation de Tafel a été déduite expérimentalement et par suite sa justification théorique a été démontrée [116] :

u t b

( ) ln 0 - ln( + â )

= - ? ? b t

? i ?

? bC dl ? 4-1

u(t) est la tension aux bornes du supercondensateur, b est la pente de Tafel, â est une constante liée à la pseudocapacitance et i0 est le courant d'échange déterminant la vitesse du processus faradique de l'autodécharge dans ce cas [141]. La pente de Tafel et â peuvent être déterminés expérimentalement ou théoriquement.

Nous avons répertorié les différents mécanismes de l'autodécharge liés avec certaines conditions, notamment l'existence d'impuretés et la valeur de la tension. Si l'électrolyte du supercondensateur contient des impuretés, elles peuvent être oxydées ou réduites au-delà d'un certain potentiel. Dans le cas de concentrations faibles, l'autodécharge par processus d'oxydoréduction est contrôlée par la diffusion. Dans le cas de concentrations assez importantes, nous assistons à un effet de navette électrochimique entre les électrodes positives et négatives du supercondensateur [142].

Lorsque l'électrolyte contient des impuretés en concentration élevée et lorsque les valeurs des potentiels d'électrode le permettent, nous pouvons avoir oxydation à l'anode, engendrant des ions qui peuvent être réduits à la cathode, pour former à nouveau des ions, et ainsi de suite. Une partie du courant s'écoule donc en pure perte à cause de cette réaction parasite qui peut se dérouler indéfiniment. Dans ce cas, nous disons que la cellul e est le siège d'une boucle d' oxydoréduction, appelée aussi navette électrochimique [143].

4.4. Modélisation de l'autodécharge

Nous nous intéressons dans ce travail à l'étude de l'autodécharge conduisant à la décharge du supercondensateur en circuit ouvert, quand il est chargé à une tension inférieure ou égale à la tension nominale. Dans ce cas, nous pouvons rencontrer deux mécanismes d'autodécharge. Le premier est lié à la diffusion des espèces ioniques résultant de réactions faradiques d'oxydoréductions parasites aux interfaces charbon électrode. Il sera appelé par la suite l'autodécharge par processus de diffusion lié à l'oxydoréduction. Le deuxième est dû au courant de fuite. L'autodécharge sera ici interprétée et modélisée par ces deux mécanismes.

4.4.1. Modèle du courant de fuite

S'il existe des contacts électrode positive-électrode négative, l'autodécharge prendra place sous la forme d'un effet de couple galvanique [137].

La décroissance de la tension aux bornes d'un supercondensateur chargé et déconnecté illustre, durant une période de temps prolongé, l'existence d'un courant If, appelé courant de fuite. Pour tenir compte de l'autodécharge due au courant de fuite dans la modélisation d'un supercondensateur, il est courant d'ajouter au circuit équivalent une résistance de fuite Rf en parallèle avec la capacité totale du supercondensateur (cf. fig. 4-3) [144]. La valeur de ce courant de fuite dépend essentiellement de la concentration des impuretés et de l'épaisseur de la membrane poreuse [62].

R1 R2

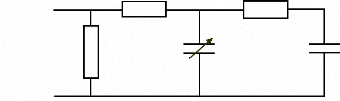
Rf

C1

C2

Fig. 4-3 : Circuit équivalent du supercondensateur
(développé à partir du modèle de Zubieta) tenant compte du courant de fuite

Dans ce cas, la décroissance de la tension aux bornes du supercondensateur peut être modélisée sous forme d'une fonction exponentielle comme dans l'équation suivante :

?? - t ???

exp 4-2

0 ? ? ô f ?

u ( t ) U

=

où,

U0 est la tension initiale aux bornes du supercondensateur en circuit ouvert au moment de

l'arrêt du courant de charge, t est le temps écoulé, ôf est la constante de temps représentant le courant de fuite.

Nous tenons à signaler que ôf est simple à déterminer, puisqu'il suffit d'approximer la décroissance du potentiel du supercondensateur par une exponentielle comme le montre la figure 4-4.

La constante de temps ô et la capacité du supercondensateur C sont utilisées pour calculer la

f 1

résistance de fuite Rf par la formule 4-3. La capacité totale du supercondensateur peut être représentée seulement par la capacité C1, car l'effet du phénomène de la redistribution est relativement faible dans ce cas.

ô _f

R = 4-3

1 ( U 0

^fC )

Par exemple, pour le composant BCAP010, Rf =1,34 k?.

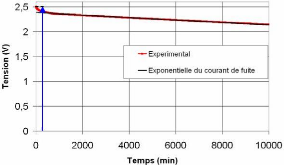
U0

Fig. 4-4 : Exponentielle représentative du courant de fuite
par rapport à la courbe expérimentale pour le composant BCAP010

Le circuit équivalent schématisé sur la figure 4-3 ainsi que les paramètres du supercondensateur BCAP010 ont été implantés dans le logiciel Simplorer. La comparaison des résultats de la simulation avec un essai expérimental, montrée sur la figure 4-5, illustre une

erreur importante due à la représentation de l'autodécharge par une simple résistance Rf. En conséquence, les mécanismes de l'autodécharge ne peuvent pas être complètement modélisés par une seule résistance Rf en parallèle avec la capacité C1. En effet, les deux mécanismes de l'autodécharge sont couplés, notamment au cours des premières heures oü le processus de diffusion lié à l'oxydoréduction gouverne fortement l'autodécharge [138].

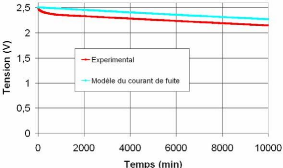
Fig. 4-5 : Comparaison du modèle de courant de fuite avec un essai expérimental

4.4.2. Modèles prenant en c ompte l'autodécharge due au processus de

diffusion lié à l'oxydoréduction

4. 4.2.1. Modèle analytique

Nous avons constaté auparavant que la décroissance de la tension du supercondensateur pendant l'autodécharge n'est pas uniquement liée au courant de fuite, mais aussi au processus de diffusion lié à l'oxydoréduction. Ce dernier contrôle l'autodécharge durant les premières heures (de quelques heures à quelques dizaines d'heures) [116].

Fig. 4-6 : Courbe expérimentale de l'autodécharge tracée en fonction de
la racine carrée du temps pour le composant BCAP010

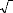
Pendant cette phase d'autodécharge du supercondensateur, la diminution de la tension du supercondensateur peut être modélisée moyennant certaines hypothèses simplificatrices par une équation fonction de la tension initiale et de la racine carrée du temps (cf. eq. 4-4 et fig. 4- 6) [138] :

u t U 0 - m t

( ) 4-4

où,

m est le paramètre de diffusion, qui peut être calculée par l'équation 4-5 :

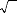
C q D

m R 0

= 4-5

C1 2

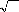
D est le coefficient de diffusion des ions dans l'électrolyte,

C12 est la capacité surfacique des deux doubles couches (positive et négative) du supercondensateur,

CR0 est la concentration initiale des espèces ioniques à l'interface électrode - électrolyte, q est la charge portée à la surface du charbon par ion.

Par exemple, pour le composant BCAP010 m = 7 mV/ s^1/2.

L'équation 4-4 décrit l'autodécharge du processus de diffusion lié à l'oxydoréduction pendant les premières heures, où le courant de fuite est faible et peut être négligeable [144]. La simulation complète de l'autodécharge consiste à associer les deux modèles : le modèle de courant de fuite et le modèle analytique de l'autodécharge due au processus de diffusion lié à l'oxydoréduction. Comme le montre la figure 4-7, il existe une faible erreur entre les résultats expérimentaux et la simulation. En effet, ce modèle est capable de modéliser parfaitement l'évolution de l'autodécharge du processus de diffusion lié à l'oxydoréduction avec le temps (erreur relative moyenne de 0,3%). Cependant, la difficulté de la construction du modèle est que les paramètres physiques requis pour calculer le paramètre de diffusion m, notamment CR0, sont difficile à déterminer. Par ailleurs, ce modèle ne peut pas être représenté par un circuit électrique équivalent.

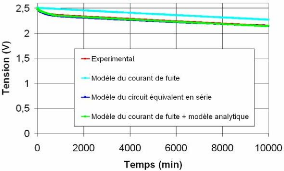
Fig. 4-7 : Comparaison du modèl analytique avec l'expérimental

e

4.4.2.2. Circuit série

Puisque le modèle analytique est difficile à ablir et limité par la quantité d'impuretés, un

ét

autre modèle est utilisable. Il se présente par deux circuit s RC en série modélisant les deux phénomènes de l'autodécharge (cf. fig. 4-8) [145]. La capacité totale du supercondensateur C1 est divisée en deux c apacités en série _Cfs ^et Crs.

u

R1

		Rfs		uf
	Rrs	ur

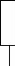
Cfs

R2

Crs C2

Fig. 4-8 : Circuit électrique équivalent du supercondensateur
prenant en compte l'autodécharge ; le courant de fuite par _Rfs ^et Cfs,
l'autodécharge du processus de diffusion lié à l'oxydoréduction par _Rrs ^et Crs

Pour identifier les nouveaux éléments du circuit électrique Rfs, Rrs, Cfs ^et _Crs, nous supposons que la courbe de la décroissance de la tension du supercondensateur u(t) est composée de deux exponentielles superposées avec deux constantes du temps différentes (cf. éq. 4-6). La première uf(t) représente l'autodécharge du courant de fuite et la deuxième u_r(t) (r pour redox) représente l'autodécharge du processus de diffusion lié à l'oxydoréduction. Cette dernière peut être déterminée par la différence de la courbe expérimentale de l'autodécharge avec

l'exponentielle liée au courant de fuite (cf. fig.4-9). Nous pouvons donc écrire :

u t u

( ) ( ) ( )

= t u t

+

f r

- t t 4-6

-

u t

( )

Ue

f 0

ô f + U_r 0 e ô_r

où,

Uf0 est la tension initiale de l'autodécharge du courant de fuite,

Ur0 est la tension initiale de l'autodécharge du processus de diffusion lié à l'oxydoréduction. Les deux tensions initiales sont déterminées à partir des résultats expérimentaux, comme illustré sur les figures 4-9.

ô_r est la constante de temps de l'exponentielle représentant l'autodécharge du processus de diffusion lié à l'oxydoréduction, elle est déterminée à partir des résultats expérimentaux. Le calcul de la deuxième constante de temps ôf est déjà présenté dans le paragraphe 4.4.1.

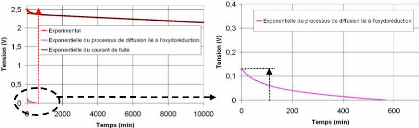
Uf0

Ur0

Fig. 4-9 : Courbe des exponentielles du courant de fuite et de
l'autodécharge du processus de diffusion lié à l'oxydoréduction

L'identification des deux capacités _Cfs ^et _Crs est basée sur l'hypothèse simplificatrice suivante : pendant la charge du supercondensateur le circuit électrique équivalent schématisé sur la figure 4-8 peut être réduit à deux condensateurs en série _Cfs ^et _Crs avec la résistance R1 (c f. fig. 4-10). Cette simplification est possible car les autres branches du circuit ont une constante de temps très élevé par rapport à celle de ce circuit. Ceci permet d'appliquer la loi de conservation de la charge : la charge totale stockée dans deux condensateurs en série est égale à la charge stockée dans chacun.

u

R

1

Cfs

Crs

uf ur

Fig. 4-10 : Circuit équivalent du supercondensateur pendant la charge

Ceci nous permet d'écrire l'équation suivante :

U 0

C = C 4-7

fs 1 U f 0

avec C1, capacité totale (équivalent à _Cfs en série avec Crs)

Ainsi, la valeur de la résistance de fuite peut être calculée par la relation ci-dessous :

ô f

R = 4-8

fs C

fs

Les paramètres de l'autodécharge du processus de diffusion lié à l'oxydoréduction sont calculés par la même méthode comme le montre les équations suivantes :

U₀

C = C 4-9

rs 1 U r 0

ô r

R = 4-10

rs C

rs

Dans le tableau ci-dessous nous présentons les valeurs des éléments du circuit série de l'autodécharge pour le supercondensateur BCAP010.

Cfs (kF)	Crs (kF)	Rfs (k?)		Rrs (?)	3,41
50	1,16	0,21

Tab. 4-1 : Eléments du circuit série de l'autodécharge du supercondensateur BCAP010

La comparaison des résultats expérimentaux avec la simulation est illustrée par la figure cidessous (cf. fig. 4-11). Nous constatons qu'il existe qu'une très légère différence entre la simulation du circuit série et la courbe expérimentale (erreur relative moyenne de 1,5%). La modélisation de l'autodécharge par un circuit électrique améliore nettement la simulation de l'autodécharge par rapport au modèle du courant de fuite. Cependant, l'erreur est légèrement supérieure à celle trouvée avec le modèle analytique notamment pendant les premières heures de l'autodécharge.

Le circuit série est un concept simple et assez facile à mettre en place par rapport au modèle analytique. Son intégration dans un logiciel de circuit électrique est aisée. Cependant, à partir du tableau 4-1, nous observons que les capacités _Cfs ^et _Crs possèdent des valeurs très élevées non représentatives du fonctionnement physique du composant.

Fig. 4-11 : Comparaison du modèle du circuit série avec un essai expérimental

4.4.2.3. Circuit parallèle

Nous avons montré précédemment que la représentation de l'autodécharge par un circuit série engendre des valeurs élevées non représentatives des deux capacités _Cfs ^et Crs.

Établir un nouveau modèle de l'autodécharge représentant mieux les mécanismes physiques qu'elle engendre est donc souhaitable.

Nous proposons de modéliser l'autodécharge par une résistance Rf en parallèle avec la capacité totale du superc ondensateur C1 pour le courant de fuite intrinsèque à celle-ci et une capacité _Crp en série avec une rési stance R _rp pour l'autodécharge due au processus de diffusion lié à l'oxydoréduction, comme schématisé sur la figure 4-12. Ce circuit n'est qu'une extension de celui montré sur la figure 4-3 en ajoutant une branche _RrpCrp. De ce fait, la résistance de fu e Rf peut être calculée comme montré dans le paragraphe 4.4.1. Ainsi sa valeur reste

it

inchangée.

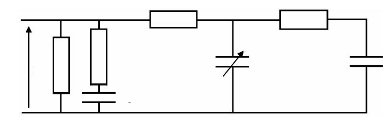
u

Rf

Rrp

Crp

R1 R2

C1 C2

Fig. 4-12 : Circuit équivalent du supercondensateur avec le circuit parallèle de l'autodécharge

Pour identifier les deux nouveaux éléments _Rrp ^et _Crp du circuit, nous simplifions le circuit équivalent ci-dessus à partir du comportement temporel du supercondensateur durant l'autodécharge :

· A l'instant zéro, au moment de l'arrêt du courant de charge, le circuit peut être simplifié par le schéma suivant :

U0

C1

Fig. 4-13 : Circuit équivalent de supercondensateur à l'état initial (fin de charge à une tension constante)

Dans ce cas, la charge initiale Q0 emmagasinée dans la capacité C1 peut être calculée par la formule suivante :

Q₀ = C₁. U₀ 4-11

· Après l'état initial, la différence des tensions des deux capacités C et C , due à

1 rp

l'accumulation de charge près des interfaces des électrodes-électrolyte, conduit à diffuser une partie de la charge stockée Q0 dans la double couche (représentée par C1) vers les interfaces électrodes-électrolyte (représentées par _Crp). Le circuit à considérer est celui de la figure 4-14, bien entendu en négligeant l'effet du courant de fuite.

Rrp

Uc1=U0

Crp

UCrp = 0

U0

C1

Fig. 4-14 : Répartition des tensions des éléments du circuit à l'état initial

· A la fin de la période d'autodécharge par processus de diffusion lié à l'oxydoréduction, le courant de diffusion s'annule, les tensions des deux capacités C1 et _Crp sont égales et valent la tension aux bornes du supercondensateur _Urf. La charge totale Q_r stockée est égale la charge initiale Q0.

Rrp

Uc1 =Urf

Crp

UCrp =Urf

Urf

C1

Fig. 4-15 : Répartition des tensions sur les éléments du circuit
à la fin de la phase du processus de diffusion lié à l'oxydoréduction

Nous pouvons donc écrire les équations suivantes :

Q_r = Q₀ = U0 . C₁( U 0) 4-12

Q r = Urf.( C1 (Urf )+C_rp) 4-13

où,

Urf est la tension aux bornes du supercondensateur à la fin de la période de l'autodécharge du processus de diffusion lié à l'oxydoréduction.

Nous pouvons donc écrire :

C₁ ( U₀). U₀ -C₁ ( U,f ) U_rf )

C = 4-14

rp

Urf

Par ailleurs, à partir de la figure ci-dessous (cf. fig. 4-16), nous pouvons écrire les équations suivantes :

u ( t ) = i (t ) .R _rp + u _crp (t)

du t

( ) 4-15

rp du t

( )

i t C

( ) = = - 1

C

rp

dt dt

u(t)

C1

uc1(t)

Crp

Rrp

i (t)

uCrp(t)

Fig. 4-16 : Circuit équivalent du supercondensateur lors de l'autodécharge
du processu s de diffusion lié à l'oxydoréduction

D'où, nous pouvons déduire l'équation différentielle suivante :

d u t C + C rp du t

2 ( ) 1 ( )

C R = 0 4-16

1 rp dt 2 + C dt

rp

La résolution de cette équation avec la condition initiale présentée précédemment permet de

calculer la tension instantanée aux bornes

du supercondensateur pendant la durée de

l'autodécharge par processus de diffusion lié à l'oxydoréduction par la fonction exponentielle suivante :

??

u t U

( ) 0 exp ??- t

= 4-17

? r ?

ô

avec,

U0 la tension initiale aux bornes du supercondensateur,

T_r la constante du temps de la charge de la capacité C_rp, qui peut être calculée par l'équation suivante :

C C R 1

rp rp

4. Etude, caractérisation et modélisation de l'autodécharge des supercondensateurs

ô = 4-18

r C C

+

1 rp

En supposant que la capacité C1 _>>Crp la constante du temps peut être donc réduite comme suit :

ô r = C _rp R rp 4-19

La résistance _Rrp, qui représente l'évolution des réactions faradiques aux interfaces électrodesélectrolyte, peut être calculée par l'équation suivante :

ô r

R = 4-20

^rp C

rp

Crp (kF)	Rrp (?)		Rf (k?)	0,2
85	1,34

Tab. 4-2 : Valeurs des éléments du circuit parallèle de l'autod arge

éch

pour le supercondensateur BCAP010

La comparaison entre la simulation des modèles réalisés avec les résultats expérimentaux, effectuée sur la figure 4-17, montre que le modèle du circuit parallèle est aussi précis que les autres modèles : analytique et circuit série (erreur relative moyenne de 1,2%).

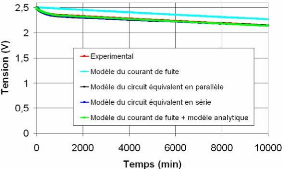
Fig. 4-17 : Comparaison de la simulation du circuit parallèle de l'autodécharge
avec la courbe expérimentale et les autres modèles réalisés

En fait, la valeur de la résistance _Rrp peut augmenter avec le temps ainsi que la résistance de fuite Rf, selon l'état thermodynamique de supercondensateur, ralentissant ainsi la charge dans

la capacité _Crp. Malgré cela, ce modèle montre qu'une partie de la charge de la capacité Crp peut se décharger dans la résistance de fuite Rf en tenant compte de l'effet de navette.

4.4.3. Comparaison des modèles de l'autodécharge avec un essai de

charge/décharge à courant constant

Le calcul des éléments de différents modèles est basé sur certaines hypothèses simplificatrices, telle que la supposition que le courant de fuite est négligeable pendant la durée où le phénomène lié au processus de diffusion lié à l'oxydoréduction domine.

Afin de vérifier les modèles établis, nous avons réalisé un essai de charge/décharge à courant constant avec un courant de 400 A et à une température de 25 °C pour le supercondensateur BCAP010. La valeur de courant de charge a été choisie la plus élevée possible, car pour cette valeur de courant (400 pouvons o

A) nous btenir un écart maximal entre la simulation et la

mesure (cf. § 3.3).

Malgré les hypothèses simplificatrices utilisées, la figure 4-18 illustre que nous pouvons tenir compte, lors de la modélisation du supercondensateur, de l'autodécharge due au processus de diffusion lié à l'oxydoréduction par un circuit électrique en parallèle ou en série sans avoir une influence importante sur le comportement du supercondensateur pendant la charge ou la décharge.

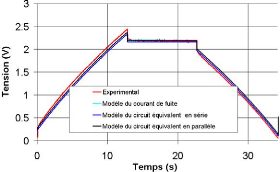
Fig. 4-18 : Comparaison des différents modèles établis lors de l'essai charge/décharge à courant constant

En conséquence, l e modèle du circuit parallèle représente le mieux les phénomènes de l' autodécharge. Ses paramètres seront utilisés par la suite pour montrer l'évolution de l' autodécharge en fonction des conditions de tension, thermiques et de la technologie de fabrication.

4.5. Variation des paramètres de l'autodécharge en fonction

de la tension initiale et de la température

4.5.1. Effet de la tension initiale

Nous avons présenté précédemment la dépendance de la capacité du supercondensateur vis-à-vis du potentiel. La capacité est non linéaire et varie en fonction de la tension à ses bornes. ^Iisera donc intéressant d'étudier l'influence de la variation de la tension appliquée sur la caractéristique de l'autodécharge des supercondensateurs. La figure 4-19 montre l'autodécharge du supercondensateur BCAP010 à 25 °C pour cinq tensions initiales différentes (0,5 ; 1,0 ; 1,5 ; 2,0 et 2,5 V).

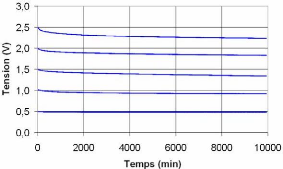
Fig. 4-19 : Caractéristique de l'autodécharge
pour différentes tensions initiales pour un supercondensateur BCAP010

A partir de cette figure, nous constatons que l'autodécharge s'accélère fortement avec l'augmentation de la tension initiale, et que pour des tensions faibles, l'autodécharge par processus de diffusion lié à l'oxydoréduction n'apparaît quasiment plus sur la caractéristique. En conséquence, quand la tension initiale diminue, l'autodécharge diminue aussi.

Nous allons mettre en évidence par la suite la variation des éléments liés à l'autodécharge pour le circuit électrique schématisé sur la figure 4-12 en fonction de la tension initiale.

4.5.1.1. Variation des éléments du modèle liés au courant de fuite

Pour la température et les tensions initiales mentionnées ci-dessus, nous avons déterminé la résistance de fuite du circuit parallèle de l'autodécharge, en suivant la méthode décrite dans le paragraphe 4.4.1. D'après la figure ci-dessous, nous constatons que l'augmentation de la

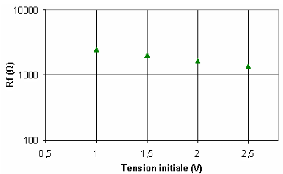
tension initiale conduit à diminuer la résistance de fuite. Le courant de fuite est plus important quand le supercondensateur est complètement chargé. Ceci est dû à la mobilité des charges, qui est proportionnelle à la tension appliquée [138].

Fig. 4-20 : Résistance de fuite vis-à-vis de la tension initiale

Pour une faible valeur de la tension initiale (0,5 V), le phénomène de récupération de tension apparaît comme dominant dans le comportement du supercondensateur. Ceci rend la détermination des paramètres de l'autodécharge moins précise. C'est pour cette raison que les paramètres de l'autodécharge pour cette tension initiale n'ont pas été déterminés. Ce phénomène sera présenté en détail à la fin de ce chapitre.

4.5.1.2. Variation des éléments du modèle liés au processus de diffusion lors de l' oxydoréduction

L'augmentation de la tension aux bornes du supercondensateur accélère le processus de diffusion lié à l'oxydoréduction compte tenue de l'augmentation de concentration initiale des espèces ioniques _CR0 à l'interface électrode/électrolyte. Dans la relation 4-5 une augmentation du paramètre _CR0 conduit à une augmentation du paramètre de diffusion m, qui conduit également à une augmentation de la rapidité de la décroissance de la tension aux bornes du supercondensateur (cf. eq. 4-4) [138]. Les résultats expérimentaux reportés sur les figures 4- 21-a, et b l'illustrent. La capacité _Crp en valeur réduite par rapport à la valeur nominale (CN) augmente avec l'augmentation de la tension initiale à la suite de l'accroissement de la concentration d'espèces ionique alors que la résistance _Rrp diminue faiblement.

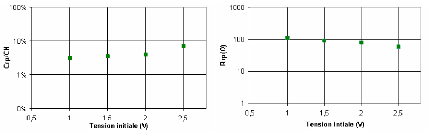
(a)

(b)

Fig. 4-21 : Capacité _C,. et résistance _R,. vis-à-vis de la tension initiale

Nous avons déterminé que la variation des éléments du modèle de l'autodécharge en fonction de la tension initiale peut être modélisée avec précision par la loi représentée par l'équation 3-40 (cf. 4-21).

0

u U

-

??

ô

R ( ) R ( )

u = U á â e

? + . u

f f 0 u u

?

?

u U

- 0

ô

C ( ) C ( ₀ )

u = U ? á â

+ . e u ? 4-21

rp rp u u

?

?

?

?

?

u U

- 0

ô_u

? ?

R u R U

( ) ( )

= 0 ? á â

+ .

rp e

rp u u

?

Nous présentons dans le tableau 4-3 les coefficients des paramètres de la loi pour ces éléments pour une tension initiale U0 de 2,5 V.

Composant	ôu (V^-1)	áu	âu		Erreur relative moyenne %	Rf
2,40	0,06	0,94	0,1		Crp
-0,32	0,45	0,55	1,5		Rrp
-5,02	4,37	-3,36	3,0

Tab. 4-3 : Paramètres des éléments du circuit équivalent de l'autodécharge

4.5.2. Effet de la température ambiante

Le supercondensateur BCAP010 peut fonctionner dans la plage de température de -35 °C à 65 °C. Nous avons démontré précédemment que la capacité d'un supercondensateur C1(u) ne

dépend que faiblement de la température ambiante. Par conséquent, la variation de la capacité C1(u) en fonction de la température est négligée dans la détermination des paramètres de l'autodécharge. L'autodécharge a été étudiée pour des températures de -25, 0, 25, 45 et 65 °C et pour une tension de 2,5 V. La figure ci-dessous indique l'allure de la dépendance vis à vis de la température. Nous constatons que l'autodécharge s'accéléré fortement avec l'augmentation de la température notamment pour les températures positives.

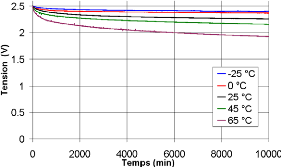
Fig. 4-22 : Autodécharge du supercondensateur BCAP010
pour différentes températures

4.5.2.1. Variation des éléments du modèle liés au courant de fuite

La figure 4-23 illustre la variation de la résistance de fuite en fonction de la température. L'augmentation de la température conduit à une diminution forte de la résistance de fuite, notamment pour les températures positives. Ceci est du à la mobilité des espèces ioniques, qui dépend de la température du supercondensateur [138].

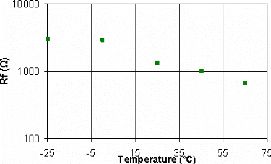
Fig. 4-23 : Résistance de fuite vis-à-vis de la température

4.5.2.2. Variation des éléments du modèle liés au processus de diffusion lors de l'oxydoréduction

Il semble donc que l'augmentation de la température du supercondensateur accélère fortement le processus faradique conduisant à un excédent de la concentration ionique près des électrodes (cf. fig. 4-22). Par conséquent, l'autodécharge du processus lié à l'oxydoréduction augmente beaucoup avec l'augmentation de la température ce qui engendre une augmentation de _Crp. De plus, l'augmentation de la température prolonge la durée de cette autodécharge, ce qui accroit la constante de temps alors que la résistance _Rrp diminue.

Sur les figures ci-dessous, nous mettons en évidence la variation de la capacité _Crp et de la résistance _Rrp en fonction de la température.

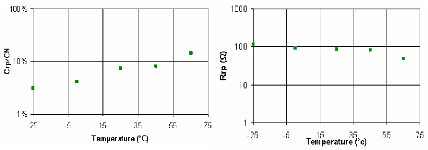
(a)

(b)

Fig. 4-24 : Capacité _C,. et résistance _R,. vis-à-vis de la température

Nous avons trouvé que la variation des paramètres du modèle de l'autodécharge en fonction de la température peut être représentée par la loi de l'équation 3-40. Cette représentation donne de meilleurs résultats que ceux obtenus avec d'autres lois.

2

R ( ) ( ) . .

( )

è = R è 1 . è

0 1

a + +

è b c

f f 1

( )

è

Crp

Crp

( )

è

Rrp

R rp

4-22

2

( ) . .

( )

è 2 . è

0 2 è

a + b c

+ 2

( ) . .

è ( 2

2 . 2 )

0 2 è

a + b c

è +

Les valeurs des coefficients de cette loi sont présentées dans le tableau ci-dessous avec leur erreur relative moyenne.

Élément	a (C^-2)	b (C^-1)	C		Erreur relative moyenne %	Rf
1,81	-0,02	2,67. 10^-5	20		Crp
2. 10^3	-2. 10^3	1.32. 10^6	19		Rrp
0,55	8,4. 10^3	1.8.10^4	11

Tab. 4-4 : Paramètres des lois polynomiales des éléments du circuit équivalent de l'autodécharge

Finalement, afin de généraliser les résultats trouvés auparavant, nous avons effectué des essais en fonction de différents couples (tension, température) comme l'illustre la figure 4-25 ci-dessous. Nous observons que l'augmentation de la température, même à faible tension, accélère l'autodécharge.

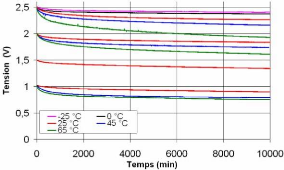
Fig. 4-25 : Autodécharge vis-à-vis de temps pou différentes tensions initiales et températures

r de

Nous détaillons sur les figures 4-26 et 4-27 les résultats présentés sur la figure 4-25. Nous trouvons que nos résultats obtenus précédemment sont toujours valables quelles que soient la tension et la température, même si l'effet de la température semble un peu moins prépondérant lorsque la tension est faible.

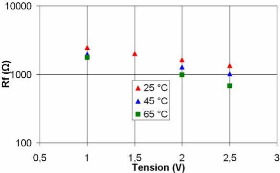
Fig. 4-26 : Variation de la résistance de fuite en fonction de tension et de la température

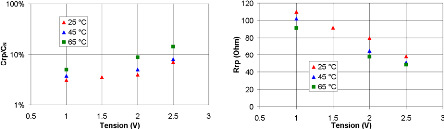
(b)

(a)

Fig. 4-27 : Variation des éléments _C,, ^et _Rrp en fonction de tension et de la température

Pour conclure, des tensions et des températures élevées accroissent largement l'autodécharge et par conséquence, le supercondensateur perd une partie importante de son énergie stockée par l'autodécharge. Pour maintenir l'énergie stockée à long terme dans les supercondensateurs, il est donc préférable que ceux-ci fonctionne à des températures inférieures à 25 °C.

4.6. Comparaison de l'autodécharge de différents

supercondensateurs

4.6.1. Détermination des paramètres nominaux de l'autodécharge

A fin de comparer les résultats obtenus expérimentalement avec ceux donnés par le fabricant et d'évaluer les paramètres de l'autodécharge en fonction de différents facteurs tels que la capacité du supercondensateur, la technologie de fabrication, etc., nous définissons et calculons certains paramètres liés aux caractéristiques de l'autodécharge.

Le premier est la résistance de fuite du fabricant _RfN. Elle peut être calculée en fonction du courant de fuite et de la tension nominale, qui sont données dans la documentation constructeur pour une température de 25 °C (cf. eq. 4-23). Le deuxième est la résistance de fuite par Farad (cf. eq. 4-24). Notons que nous avons indicé ces paramètres par N (courant de fuite _IfN, tension nominale UN, et capacité du supercondensateur CN).

RfN

UN = 4-23 I fN

R _fN Ù

( )

Résistance de fuite par Farad = 4-24

C ( )

N F

Afin de montrer l'effet de la technologie de fabrication sur les caractéristiques de

l'autodécharge, nous avons distingué deux types de supercondensateurs, les
supercondensateurs produ ts par le fabricant MAXWELL et ceux produits par d'autres

i

fabricants (EPCOS et BATSCAP).

4.6.2. Autodécharge des superco ndensateurs du fabricant

MAXWELL

Nous résumons dans le tableau 4-5 les caractéristiques des quatre supercondensateurs MAXWELL étudiés. Ils possèdent des capacités et des tensions nominales différentes. Les composants BCAP010, BCAP013 et BCAP350 sont issus de la même technologie (ancienne génération de supercondensateurs), alors que le composant M600 plus récent est fabriqué par une autre technologie (qualité de charbon actif et épaisseurs différentes). Nous constatons d'après le tableau 4-5 que la résistance de fuite _RfN et la résistance de fuite par Farad augmentent lors de la diminution de la capacité totale du composant.

Fabricant MAXWELL	Capacité Nominale	Tension nominale	Courant de fuite		Résistance de fuite		Résistance de fuite par Farad	Paramètre
CN (F)	U N (V)	I fN (mA)	Délai de mesure	R fN (?)	R /C fN N (?/F)		BCAP010
2600	2,5	5	72 h	500	0,19		M600
2600	2,7	5	72 h	540	0,21		BCAP013
450	2,5	3	72 h	833	1,85		BCAP350
350	2,5	1	72 h	2500	7,14

Tab. 4-5 : Paramètres nominaux de l'autodécharge des supercondensateurs Maxwell

La figure 4-31 montre la caractéristique de l'autodécharge des quatre composants étudiés. Cette caractéristique a été déterminée par la méthodologie présentée précédemment à une température de 25 °C. Tous les composants sont chargés initialement à la même tension (2,5 V). Nous constatons qu'ils n'ont pas les mêmes caractéristiques d'autodécharge surtout pendant les premières heures.

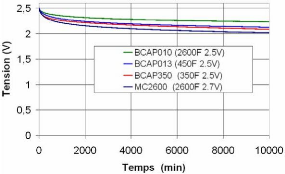
Fig. 4-28 : Caractéristique de l'autodécharge des supercondensateurs MAXWELL

Dans le tableau 4-6, nous comparons les résultats expérimentaux avec ceux du fabricant. Nous trouvons que la valeur obtenue de la résistance de fuite est supérieure à celle du fabricant. En effet, d'une part le fabricant l'a déterminée après 72 heures d'alimentation et sans séparer les deux phénomènes de l'autodécharge. De notre coté, nous l'avons déterminé pour une période de mesure très ngue (un

lo e se maine) et de pl nous tenon ompte, da

us s c ns la détermination de la résistance de fuite, de l'autodécharge du processus de diffusion lié à l'oxydoréduction. D'autre part, la résistance de fuite donnée par le fabricant celle-ci est donnée pour un courant ite n

de fu ominale maximale (donc résistance de fuite minim

ale).

Maxwell	Capacité Nominale	Résistance de fuite du fabricant	e fu Résistance d ite déterminée expérimentalement	Résistance de fuite norm alisée	Résistance de fuite par Farad du fabrica nt		Résistance de fuite par Farad déterminée expérimentalement	Paramètre
C N (F)	(?)	R fN R f (?)	R f/ R fN (%)	R fN / C N (?/F)	R f / C N (?/F)		BCAP010
2600	500	1345	269	0,19	0,52		M600
2600	540	729	135	0,21	0,28		BCAP013
450	833	4990	599	1,85	11,1		BCAP350
350	2500	8025	321	7,14	23,0

Tab. 4-6 : Comparaison des paramètres de l'autodécharge
donnés par le fabricant avec ceux expérimentaux

D'après les résultats expérimentaux dans le tableau ci-dessus et sur les figure 4-29-a et b,

nous trouvons que la résistance de fuite augmente lors de la diminution de la capacité du supercondensateur. Ceci est dû à la quantité des impuretés et à la surface du séparateur, qui augmentent avec les valeurs de capacité.

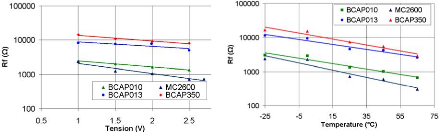
(a)

(b)

Fig. 4-29 : Résistance de fuite des supercondensateurs Maxwell
en fonction de la tension initiale et de la température

Nous pouvons constater sur la figure 4-28 que pendant les premières heures (pendant le processus de diffusion lié à l'oxydoréduction) l'autodécharge du supercondensateur BCAP350 et celle du BCAP013 est supérieure à celle BCAP010. Ceci peut être constaté aussi sur la figure 4-30-a et b : le pourcentage de la capacité _Crp du supercondensateur BCAP350 et celle du BCAP013 est supérieure à celle BCAP010 et pour toutes les tensions initiales et toutes les températures ambiantes. Ceci est explicable car les réactions d'oxydoréduction se multiplient dans les s perconden ateurs de

u s faible capacité [116 ]. En revanche, nous remarquons que le

composants M600 a la capacité _Crp (en valeur réduite) la plus grande ; l'énergi e dissipée par l'autodécharge due au pr ssus

oce de diffusion lié à l'oxydoréduction est plus la

importante,

technologie de fabrication est différente.

BCAP010 M600

BCAP013 BCAP350

-25 -5 15 35 55 7 5

Tem perature (DC)

(b)

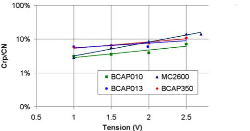
Crp/CN

100%

10%

1%

(a)

Fig. 4-30 : Capacité _Crp des supercondensateurs Maxwell
en fonction de la tension initiale de la température

(a)

(b)

Fig. 4-31 : Résistance _Rrp des supercondensateurs MAWELL
en fonction de la tension initiale et de la température

D'après les résultats expérimentaux des figures ci-dessus (cf. fig. 4-29 à 4-31), nous constatons que les paramètres du composant M600 sont plus influençables par la tension initiale et la température que les autres composants.

4.6.3. Autodécharge des supercondensateurs des autres fabricants

Dans ce paragraphe, nous allons comparer les paramètres de l'autodécharge des supercondensateurs pour différents fabricants, MAXWELL, BATSCAP et EPCOS. Tout d'abord, nous comparons deux composants de mêmes caractéristiques nominales (2600 F ; 2,7 V), à savoir le M600 de MAXWELL et le SC806 de BATSCAP. La comparaison de leur capacité et de leur résistance est effectuée dans le chapitre précédent.

Nous présentons sur la figure 4-32 la caractéristique de l'autodécharge pour les deux supercondensateurs M600 et SC806 et pour des tensions initiales de 0,5 ; 1 ; 1,5 ; 2 ; 2,5 et 2,7 V et à une température de 25 °C.

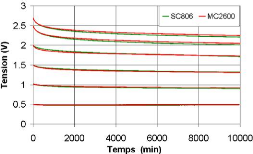
Fig. 4-32 : Caractéristi que de l'autodécharge des deux supercondensateurs M600 et SC806 pour une
température de 25 °C et pour des différentes tensions initiales

La caractéristique de l'autodécharge des ces composants en fonction de la température ambiante et pour une tension initiale de 2,7 V est montrée sur la figure 4-33.

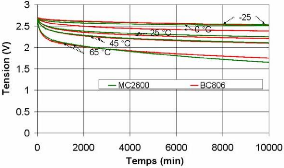
Fig. 4-33 : Caractéristique de l'autodécharge des deux supercondensateurs M600 et SC806
pour une tension initiale de 2,7 V et pour des différentes températures

D'après les figures 4-32 et 4-33, nous constatons qu'il a y une faible différence entre les caractéristiques de l'autodécharge des deux supercondensateurs. Ceci peut être constaté sur les figures 4-34 (a et b) et 4-35 (a et b).

La figure 4-34-b illustre la résistance de fuite par Farad. La résistance de fuite du composant B49410 (3600 F ; 2,5 V) est plus faible par rapport aux composants M00 et SC806 de capacité plus faible (2600 F).

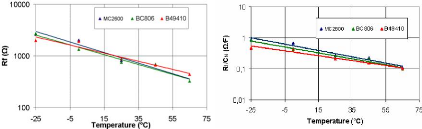
(a)

(b)

Fig. 4-34 : Résistance de fuite et résistance de fuite par Farad des supercondensateurs
en fonction de la température

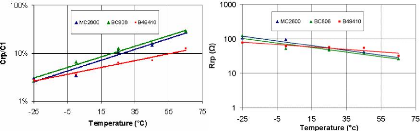
(a)

(b)

Fig. 4-35 : Capacité _Crp (normalisée à la capacité de la branche rapide C1) et résistance Rrp
des supercondensateurs en fonction de la température

Nous observons, à partir des figures 4-34 (a et b) à 4-35 (a et b), que d'une part le supercondensateur B49410 possède une autodécharge du processus de diffusion lié à l'oxydoréduction très faible par rapport à d'autres supercondensateurs malgré sa grande capacité et que d' autre part ses caractéristiques de l'autodécharge (courant de fuite et processus de diffusion lié à l'oxydoréduction) sont moins influencées par la variation de la température.

4.7. Effet du vieillissement sur l'autodécharge

L'autodécharge n'affecte pas seulement le rendement énergétique du supercondensateur mais est aussi liée à la durée de vie des supercondensateurs [116]. Il est probable que les supercondensateurs ayant une faible autodécharge ont aussi une durée de vie plus élevée, car une autodécharge élevée indique un niveau important d'impuretés et de réactions faradiques sur les électrodes. Avec le temps, il y a une dégradation des matériaux réduisant ainsi la capacité et augmentant la résistance de supercondensateur mplitude de l'autodécharge peut donc être

. L'a

un bon indicateur de la qualité du supercondensateur [14].

Nous avons montré précédemment l'évolution des paramètres des supercondensateurs M600, que sont la capacité et la résistance, en fonction de l'état du vieillissement. Le vieillissement considéré est obtenu en maintenant la tension aux bornes du supercondensateur à 2,7 V pendant une durée déterminée à une température de 65 °C ou de 70 ° C. Une diminution de la capacité de plus de 20% et une augmentation de 100% de la résistance sont observées. Ces variations proviennent vraisemblablement de la dégradation de l'électrolyte et d'une mauvaise accessibilité des pores par l'électrolyte.

Composant	Crp ^(F)	Crp / C1 (%)	Rrp (?)		Rf (?)	Composant neuf
377	11	44	714		M600 vieilli à 65 °C et 2,7 V
3 22	19	76	529		M600 vieilli à 70 °C et 2,7 V
7 29	58	136	359

Tab. 4-7 : Elément de l'autodécharge d s supercondensateurs M600 vieillis

e

L'autodécharge de supercondensateurs vieillis à 65 °C et 70 °C a été mesurée avant et après le vieillissement (cf. fig. 4-36-a). L'autodécharge évolue avec le vieillissement. Cette évolution dépend certainement du temps de maintien de la tension aux bornes du composant précèdent la mesure de l'autodécharge. Dans notre cas, ce temps est fixé à 1 heure (cf. § 4.2.2) ce qui engendre une amplitude sur la tension lors de l'autodécharge importante.

Une étude plus approfondie sur l'évolution de l'autodécharge lors du vieillissement serait à réaliser avec plusieurs composants et en considérant des points de mesure intermédiaires

Néanmoins, dans le cas de notre étude réalisée sur deux composants, nous observons une amplification de l'autodécharge. La capacité _Crp et la résistance _Rrp augmentent avec le vieillissement, tandis que la résistance de fuite Rf diminue (cf. tab. 4-7). Le vieillissement augmente l'autodécharge du processus de diffusion lié à l'oxydoréduction et prolonge sa durée (cf. fig. 4-37-b). En effet, la constante de temps ô_r= Crp.Rrp augmente, ce qui conduit à l'augmentation de ses deux éléments _(Crp ^et _Rrp). L'augmentation de l'autodécharge avec le vieillissement est due à la décomposition de l'électrolyte. Cette dernière amplifie les réactions d' oxydoréduction et peut produire des groupes oxygénés de surfaces [137].

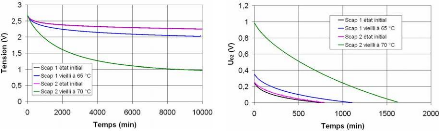
(a)

(b)

Fig. 4-36 : Autodécharge des supercondensateurs M600 vieillis par rapport à l'état initial

4.8. Détermination des para mètres de l'a todé harg

u c e par

spectroscop ie d'impédance

4.8.1. Réponse en fréquence de l'impédance de l'autodécharge

Les phénomènes électrochimiques rapides se produisent à haute fréquence et correspondent aux transferts de charges. Les phénomènes lents correspondant à des transports de matière par diffusion se produisent à basse fréquence.

L'impédance électrochimique de l'autodécharge par processus de diffusion lié à l'oxydoréduction _Zrp représentée par le circuit _RrpCrp sur la figure 4-12, peut être caractérisée, ainsi que l'impédance de la double couche, par spectroscopie d'impédance électrochimique.

Selon la nature des impuretés, le processus de diffusion lié à l'oxydoréduction est quasiréversible [137], c'est-à-dire que les charges diffusées vers les électrodes pendant cette autodécharge ne sont pas dissipées parfaitement mais elles peuvent être récupérées. Ceci nous permet en principe de caractériser l'impédance équivalente. La fréquence f correspond au phénomène de l'autodécharge par diffusion est comprise entre 30 uHz à 0.3 mHz (une heure à une dizaine d'heure).

Le schéma donné sur la figure 4-12 représente le comportement temporel du supercondensateur. En très basse fréquence, le circuit de la figure 4-12 p eut être réduit au schéma montré sur la figure 4-37, car les circuits ont une constante de temps très faible par rapport à la branche constituée f C1 :

par R

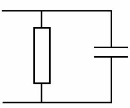
Rf

C1

Fig. 4-37 : Circuit équivalent du supercondensateur à très basse fréquence

La réponse en fréquence du circuit équivalent peut être déduite comme suit :

4-25

1 1 j C

= + ù 1

f

Z R

? - 1 2

? 1 R f ù R _f C 1

Z = ?? + ù

j C ?? = - j 4-26

1 1 2 2 2 2 2 2

? R R C 1 R C

f ? + ù + ù

f 1 f 1

R_f

Re( )

Z = 4-27

2 2 2

1 + ù f

R C 1

- ùR 2C

f 1

Im( )

Z = 4-28

2 2 2

1 + ù R C

f 1

Nous montrons sur la figure 4-38 le tracé de Nyquist correspondant au circuit _RfC1 à très basse fréquence. Nous constatons que la réponse en fréquence du circuit équivalent du supercondensateur à une fréquence de l'ordre de quelques nHz, est un demi-cercle de rayon de Rf/2. La fréquence correspondant au centre du demi-cercle est égale à ff = 1/(2ðRfC1). Nous constatons donc qu'il y a deux limites de l'impédance : à basse fréquence Z = Rf et à haute fréquence Z = 0. La fréquence intéressante qui permet théoriquement de déterminer la valeur de la résistance de fuite est de l'ordre de la fréquence ff.

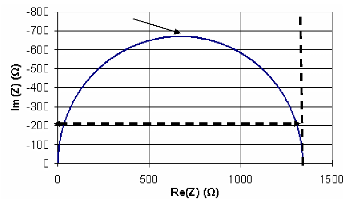
2.5 nHz

Rf

Fig. 4-38 : Simulation du circuit RfC ₁ en tracé de Nyquist

4.8.2. Essai de spectroscopie d'impédance à très basse fréquence

Pour caractériser l'autodécharge du supercondensateur BCAP010 à une température de 25 °C, nous avons réalisé un essai fréquentiel par spectroscopie d'impédance. D'abord, le

supercondensateur est court-circuité pendant plusieurs jours. Il est ensuite chargé sous tension continue de 2,5 V pendant une heure, puis une tension alternative d'une amplitude de 10 mV avec un balayage en fréquence de 10 kHz à 10 uHz (cf. § 3.2.2) lui est appliqué. Cette mesure a duré plus de 16 jours. Le résultat expérimental est représenté sur la figure 4-39 dans le plan de Nyquist.

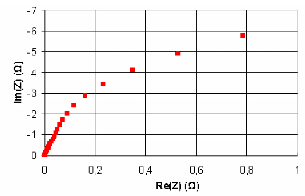
Fig. 4-39 : Tracé de Nyquist du supercondensateur BCAP010 jusqu'une fréquence basse de 10 uHz

Les valeurs des paramètres du circuit électrique équivalent du supercondensateur obtenues par "fitting" du circuit de la figure 4-12 sont données dans le tableau 4-8.

	C1	C2	R1	R2	Crp	Rrp		Rf
kF	F	mÙ	Ù	kF	Ù	kÙ		Valeur
2,8	106	0,64	2,2	0,95	51	0,3		Erreur %
2,8	87	2,6	99	374	115	453		Importance %
100	40	48	1	2	6	2

Tab. 4-8 : Paramètres de l'autodécharge caractérisés par EIS

Nous présentons sur la figure 4-40 le tracé de Nyquist du circuit électrique équivalent du supercondensateur schématisé à la figure 4-12 avec les paramètres caractérisés par spectroscopie d'imp édance. Il montre que la caractérisation de l'autodécharge par spectroscopie d'impédance est proche de la simulation fréquentielle du supercondensateur à très basse fréquence.

Par contre, les valeurs trouvées sont différentes de celles obtenues par caractérisation temporelle. Les erreurs de détermination par cette méthode sont importantes. En très basses fréquences, vue la durée très importante de la mesure, les caractérisations des paramètres des

supercondensateurs sont peu précis. De plus, nous avons trouvé que la fréquence optimum de mesure f requise pour déterminer la résistance de fuite est de l'ordre de quelques nHz ce qui est très inférieure aux possibilités en basse fréquence du spectromètre (10 uHz).

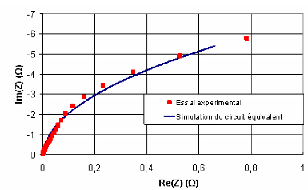
Fig. 4-40 : Comparaison de la simulation du circuit équivalent du supercondensateur
avec l'essai expérimental

4.9. Phénomène de la récupération de tension

A une température de 25 °C et pour une tension initiale de 0,5 V, l'autodécharge conduit pendant les premières heures à diminuer la tension aux bornes des supercondensateurs comme le montre la figure 4-41. Un phénomène de récupération de tension est ensuite observé. Un accroissement lent de la tension a lie e t probablem û ersion de la taille des

u. C ci es ent d à la disp

pores [116] : une redistribution de la charge entre les pores se produit lorsque les potentiels des différents pores ne so nt pas égaux. De plu , la quasi-réversibilité du processus de diffus

s ion due

aux impuretés peut être l'une des causes de la récupération de charge.

La remontée de la tension observée sur la figure est de l'ordre de plusieurs dizaines de jours et est très supérieure à celle de la redistribution de charges. Ceci nous a conduit à réétudier la théorie de l'autodécharge du processus de diffusion dû à l'oxydoréduction.

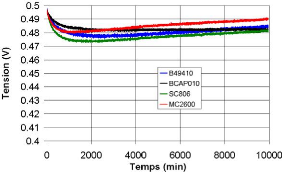
Fig. 4-41 : Tension aux bornes des supercondensateurs étudiés à une tension initiale de 0. 5V

4.10. Impédance électrochimique de l'autodécharge de diffusion

Nous proposons dans ce paragraphe d'étudier d'un point de vue théorique le comportement temporel et fréquentiel de l'impédance électrochimique de l'autodécharge due au processus de diffusion. Ceci va nous permettre de mieux comprendre les phénomènes observés expérimentalement tels que la récupération de tension.

A partir de l'équation de diffusion de concentration de charges aux interfaces charbon- électrolyte, nous pouvons déduire le courant et la tension de diffusion dus à l'oxydoréduction. Le courant parcourant les surfaces charbon-électrolyte d'épaisseur 2.h dû à la diffusion à l' instant t peut être écrit par l'équation suivante [138] :

idiff D ( t ) = m .C . exp

-

D t ?4-29

2

où,

m et D sont respectivement le paramètre et le coefficient de diffus ion (cf. eq. 4-5), C la capacité totale du supercondensateur.

du

C . = - diff 4-30

i ( t )

dt

A partir de l'équation 4-30 en considérant une capacité C non dépendante de la tension, la tension aux bornes du supercondensateur peut donc être donnée par la relation suivante [138] :

? ? ? - h 2 ? ? ? h ? ?

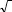
u t U m t

( ) 0

= - ? ?? 1 exp

- ? ? ?? + h D erfc ?? ?? ? 4-31

? D t ?

? ? ? ? D t

? ? ? ?

erfc étant la fonction erreur de Gauss (Error Function)

Pour expliquer le phénomène d'autodécharge dû au processus de diffusion, nous présentons l'évolution du courant et de la tension sur les figures 4-42-a et b avec un paramètre h donné dans le document [138].

(a)

(b)

Fig. 4-42 : Evolution du courant et de la tension de l'autodécharge de diffusion

D'après ces figures, nous observons d'une part que la durée de cette autodécharge est de quelques heures (cf. fig. 4-42-b) comme nous l'avons déterminé expérimentalement, d'autre part que la tension aux bornes du supercondensateur remonte très lentement après être descendue. Ce phénomène de récupération de tension n'est pas visible expérimentalement à court terme pour les tensions initiales élevées (cf. fig. 4-19). En effet les équations 4-29 et 4-31 ne considèrent que le courant et la tension de diffusion dus à l'oxydoréduction. Le courant de fuite intrinsèque important pour des tensions élevées n'est pas pris en compte dans ces équations. Ce phénomène de récupération de tension est donc masqué expérimentalement par le courant de fuite intrinsèque. Par contre, pour une tension initiale de 0,5 V (cf. fig. 4-42) le courant de fuite intrinsèque est faible et donc ce phénomène visible.

Nous proposons de calculer l'impédance de diffusion électrochimique de l'autodécharge. L'impédance temporelle z(t) (cf. eq. 4-32) peut être déduite de l'expression de la tension et du courant 4-29, 4-31, en négligeant l'erreur de Gauss erfc.

2

u t

( ) ?? ?? + h ?? ??

z t

( ) = t

= - . exp -1 4-32

i( t ) ? ? Dt ? ?

Nous réécrivons l'impédance de l'équation 4-29 dans le domaine fréquentiel en employant la transformation de Laplace.

4. Etude, caractérisation et modélisation de l'autodécharge des supercondensateurs

??

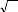
? 2 . ù ??

h j ù ? h j

2 .

? 1, ? jh BesselI

2 . 0 ,

?? D ?? ?? D ? ?

-

h BesselI .

jù.

= - 4-33

C

z ( )

ù

D

D . ù

h Dirac j

2 . ( ù

D

)

+

Nous présentons sur les figures 4-43 la partie imaginaire et réelle de l'impédance électrochimique de l'autodécharge du processus de diffusion en fonction de la fréquence

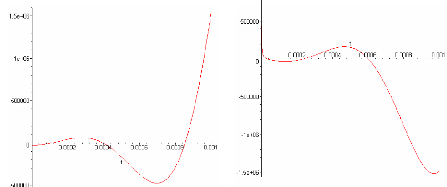
Re(Z'

Im(Z)

f (Hz)

f (Hz)

Fig. 4-43 : Partie imaginaire et réelle de l'impédance électrochimique de l'autodécharge de diffusion

Ces différents résultats montrent qu'il n'est pas aisé de modéliser finement l'ensemble des comportements lors d'une autodécharge du supercondensateur avec des circuits électriques équivalent RC.

Le circuit équivalent que nous avons établi dans ce chapitre (cf. fig. 4-12) ne prend pas en compte le phénomène de la récupération de tension.

4.11. Conclusion

Durant des périodes longues de stockage d'énergie, le supercondensateur en circuit ouvert se décharge lentement en perdant une partie importante de sa capacité. Cette décroissance dépend de la quantité et du type des impuretés et de la propriété du séparateur. L'étude présentée dans ce chapitre concerne la compréhension physique et la modélisation des mécanismes qui sont à l'origine du phénomène d'autodécharge dans un supercondensateur chargé. Nous rencontrons dans un supercondensateur chargé à une tension égale ou inférieure à la tension nominale deux principaux mécanismes. Le premier est lié au processus d'oxydoréduction de diffusion. Le deuxième est lié au courant de fuite.

Les phénomènes de l'autodécharge, le courant de fuite et le processus d'oxydoréduction de diffusion, sont représentés par différents modèles, analytique et par circuits électriques équivalents. Ces derniers sont basés sur la représentation des phénomènes de l'autodécharge par des circuits électriques RC soit en série ou en parallèle avec deux constantes de temps différentes : la constante de temps de courant de fuite et celle du processus d'oxydoréduction de diffusion. Un nouveau modèle représentant l'autodécharge par un circuit RC en parallèle avec la capacité du supercondensateur a été établi. Ce modèle est facile à établir, il suffit de mesurer la décroissance de la tension aux bornes du supercondensateur en circuit ouvert. Enfin, les modèles présentés sont comparés lors d'un essai d'autodécharge et de la charge/décharge à courant constant.

Nous nous sommes focalisés dans ce chapitre aussi sur l'effet de la variation des paramètres de l'autodécharge du supercondensateur en fonction de la tension initiale et de la température ambiante. Ces dernières ont une influence importante sur l'autodécharge. Elles conduisent à accélérer ses processus. Pour des tensions et des températures élevées, les pertes de l'énergie stockée dans les supercondensateurs augmentent fortement. Les paramètres de l'autodécharge en fonction de la tension initiale et de la température ont été trouvés expérimentalement et ensuite une approximation de cette fonction par des lois a été déterminée. Le nouveau modèle (c f. fig. 4-12), en plus de représenter finement le phénomène de l'autodécharge, nous donne des bases utiles pour l'interprétation des résultats expérimentaux : évolution des paramètres de l'autodécharge en fonction de la tension initiale, de la température et de la technologie de fabrication.

La durée prolongée de mesure, sept jours, nous a permis de démontrer que la rapidité de l'autodécharge diminue avec le temps quelque soit la tension initiale et la température du fait du retour de supercondensateur à l'état stable du point de vue thermodynamique. Ainsi, la résistance de fuite augmente avec le temps. Nous l'avons déterminée pour des durées différentes, sa valeur pour une semaine est très supérieure à celle de 24h. De plus, grâce à cette longue durée de mesure le phénomène de la récupération de tension à été observé. Ce phénomène nous démontre l'hypothèse de la réversibilité du processus de diffusion lié à l'oxydoréduction mais avec deux constantes de temps différentes. Celle de la récupération de la tension aux bornes du supercondensateur est très élevée par rapport à celle de la décharge du supercondensateur (cf. § 4-10).

Les paramètres d'autodécharge de supercondensateurs étudiés sont comparés. L'utilisation d'une nouvelle technologie pour fabriquer le nouveau composant M600 a toutefois été accompagnée d'une augmentation indésirable de la capacité du processus d'oxydoréduction de diffusion et du courant de fuite. Les fabricants pourraient utiliser un séparateur épais pour améliorer la diminution de tension, mais cette opération augmente en même temps, la résistance ESR.

5. Évaluation des

performances des modules de

supercondensateurs

5. Évaluation des performances des modules de

supercondensateurs

5.1. Introduction

La tension maximale des supercondensateurs étant limitée pour des raisons physiques à une tension de 3 V, une mise en série des supercondensateurs est indispensable. En effet, l'utilisation des supercondensateurs dans des applications de forte puissance ne peut se faire qu'en associant plusieurs éléments en série et/ou en parallèle pour pouvoir atteindre des tensions et des courants importants. Nous pouvons rencontrer cette association dans les véhicules électriques, les véhicules hybrides, les alimentations sans interruption, ...

La mise en série de cellules (supercondensateur élémentaire) ne peut être réalisée simplement à cause des dispersions des paramètres de chaque cellule. Ces dispersions sont dues aux températures différentes, aux vieillissements différents et aux paramètres de fabrication pouvant exister sur chaque cellule. Ces trois raisons conduisent à des déséquilibres de tensions entre chaque cellule. De plus, la non-linéarité de la capacité du supercondensateur peut influencer indirectement le déséquilibre. Ainsi, les tensions aux bornes de supercondensateurs lors des cycles de charge/décharge peuvent être déséquilibrées. Pour palier ce problème, il faut utiliser un système d'équilibrage des tensions. Afin d'analyser et d'évaluer ces systèmes, nous proposons de définir quelques concepts liés à leur performance tel que le rendement énergétique.

Une estimation de la durée de vie du supercondensateur en fonction des diverses contraintes appliquées est possible. Nous allons présenter dans ce chapitre une évolution de la durée de vie basée sur les résultats du vieillissement mené par le fabricant EPCOS en fonction des contraintes électrique et thermique.

Dans l'objectif de généraliser les résultats des performances du système d'équilibrage et de proposer des solutions d'équilibrage adéquates aux applications, nous définissons quelques applications types. Ces dernières peuvent représenter deux types principaux d'applications du supercondensateur : avec un rapport cyclique bas et avec un rapport cyclique élevé.

5.2. Conception et performance des modules de

supercondensateurs

5.2.1. Dimensionnement des modules

Pour dimensionner un système de supercondensateurs correctement un certain nombre de facteurs doivent être connus : les tensions maximum _(Umax) et minimum _(Umin), les courants moyen _(Imon) et de crête, la puissance, la durée de fonctionnement, etc. [146-148].

La capacité totale d'un module _Cmod peut être calculée par les grandeurs mentionnées cidessus. Le nombre de cellules à mettre en parallèle n_p et en série n est calculé comme suit :

n = Umax/UN 5-1
n_p = Cmod. n / C 5-2

où,

Umax est la tension maximum du module,

C est la capacité d'une cellule de supercondensateur.

Nous présentons sur la figure 5-1 des exemples de module de supercondensateurs pour divers fabricants.

Fig. 5-1 : Photo des systèmes et modules des supercondensateurs

Afin d'analyser la théorie de la performance du module de supercondensateurs, nous considérons que le système de supercondensateurs est composé de n cellules en série (cf. fig. 5-2). Pour la modélisation, nous considérons que le supercondensateur est modélis é par ses trois paramètres : C, une résistance série approximée à ESR et une résistance de fuite Rf.

Rf1 Rf2 Rfn

ESRl Cl ESR2 C 2 ESR C n n

Usc1 Usc2 Uscn

Umod

Fig. 5-2 : Module de supercondensateurs avec n cellules en séries

5.2.2. Origine de la dispersion des paramètres des supercondensateurs

d'un module

La tension totale _Umod sur le système de supercondensateurs est la somme des tensions de chaque cellule _Usci. Cette tension _(Umod) et le courant parcourant les cellules sont normalement co trôlés et ne doivent pas dépasser les

n limites prédéterminées. Généralement, la tension de

l'

chaque cellule n'est pas contrôlée. Or, la stabilité du fonctionnement de ce système dépend de état de cellules qui le composent, c'est-à-dire de la distribution de la tension sur les cellules. Dans le cas où toutes les cellules ont des paramètres égaux, elles ne subiront pas de contrainte locale, car l a distribution de la tension est homogène. Par contre dans le cas réel où les paramètres des cellules de supercondensateurs sont dispersés, une surtension sur une cellule peut apparaître. Cette dispersion est due à la température et au vieillissement non homogène, et à la dispersion de fabrication.

5.2.2.1. Dispersion de fabrication des supercondensateurs

Bien que des améliorations continues des techniques de production des supercondensateurs chez les fabricants soient mises en oeuvre, comme une grande automatisation des équipements de production, une dispersion importante peut se manifester sur les différents paramètres des composants produits dans une série.

La dispersion des paramètres des supercondensateurs produits par le même fabricant comme MAXWELL peut atteindre #177; 20% pour la capacité, #177; 25% pour la résistance série [28] et #177; 30% pour la résistance de fuite [129, 149].

Nous nous proposons d'analyser les divers cas de dispersion des paramètres des supercondensateurs et de voir leurs effets sur le nombre des cellules à mettre en série (n).

5.2.2.1.1. Cas de la dispersion de la résistance de fuite

Dans les applications avec un rapport cyclique bas, la rapidité de l'autodécharge peut conduire à une distribution non uniforme de la tension des cellules. A la fin de charge, toutes les cellules de supercondensateur d'un module ont la même tension à leurs bornes si la résistance ESR et la capacité C de chaque cellule sont similaires. Malgré cela, des autodécharges différentes peuvent avec le temps déséquilibrer les tensions aux bornes des cellules. En effet, la tens ion aux bornes des cellules ayant une autodécharge élevée décroît plus rapidement que la tension des autres cellules. Plus la valeur de la résistance de fuite Rfi est élevée plus la tension de la cellule sera élevée.

En supposant le nombre de cellule n très élevé, la résistance de fuite totale du module est

donnée par n R f (avec R f moyenne des résistance Rfi) . La tension Uscmax de la cellule ayant la

résistance de fuite la plus élevée _Rfmax peut être donnée en fonction de la tension du module Umod et du nombre de cellules n par la relation suivante [149] :

U sc

= ma x Umod

R fmax . 5-3 n.R f

Nous exprimons la résistance de fuite Rf_max par l'équation suivante [149] :

R _fmax= Rf. (1 +K_f)

5-4

Kf étant le facteur relatif de la dispersion de la résistance de fuite par rapport à la moyenne des résistances de fuite du module. Ce facteur peut être donc donné par la formule suivante [149] :

R f max-Rf

K f = 5-5

Rf

Pour une tension du module et une tension de cellule i données le nombre requis de cellules peut être calculé par la relation suivante :

n = Umod . (1 )

U_sci

+ K_f 5-6

Pour un facteur de dispersion Kf variant entre 0% à 60% [149] et pour un composant d'une tension nominale de 2,5 V, nous présentons sur la figure 5-3 le nombre de cellules en série en fonction de la tension du module. Nous constatons qu'à tension élevée et pour une dispersion importante de la résistance de fuite, il est nécessaire d'augmenter le nombre de cellules en série par rapport au cas idéal (sans dispersion). Afin de réduire le nombre de cellules, la dispersion de la résistance de fuite doit donc être la plus faible possible.

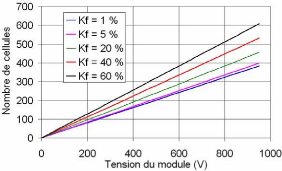
Fig. 5-3 : Nombre de cellules en fonction de la tension du module et du facteur de dispersion Kf

5.2.2.1.2. Cas de la dispersion de la ^capacitéNous nous intéressons ici à la dispersion de la capacité. Pendant la charge/décharge les

tensions aux bornes des cellules deviennent différentes. La cellule qui a une faible capacité Cmin se charge plus vite que les autres. La tension du module est égale à la somme des tensions aux bornes de chaque cellule et pendant la charge/décharge, peut être exprimée par l'équation 5-7.

i

=n i n =

5-7

U = ? ( ) (

U = ? +

U ESR I

. )

mod sc i

i

i = i = 1 i

c

1

En négligent la chute de tension sur les résistances ESR, l'équation 5-7 peut être simplifiée à l'équation 5-8.

i n =

i n =

U mod ( _sc ) ( ) 5-8

= ? U ? ? U c

i=

i i = 1 i

1

La capacité minimum peut être exprimée par l'équation suivante [149] :

C min = C . (1 + K_c ) 5-9

oü,

oü K_c est le facteur relatif à la dispersion de la capacité par rapport à la moyenne des capacités du module.

La chute aux bornes de la cellule ayant la capacité minimum peut être exprimée par la relation ci-après [149] :

C

U i = U 5-10

sc mod . n.Cmin

En remplaçant la capacité _Cmin de l'équation 5-9 dans l'équation 5-10, nous pouvons alors trouver le nombre de cellules n en série (cf. eq. 5-11).

n=

U 1

mod . 5-11

Usci +

1 K c

Comme dans le cas de dispersion de la résistance de fuite, nous présentons sur la figure 5-4 le nombre de cellule n vis-à-vis de la tension de module pour une dispersion de la capacité de 0 à -20%. Nous constatons que le nombre de cellules à placer en série augmente avec la dispersion.

Notons que l'influence de la dispersion de la résistance de fuite sur le nombre de cellules n est plus importante que celle liée à la dispersion de la capacité.

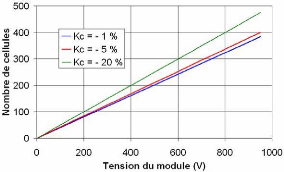
Fig. 5-4 : Nombre de cellules en fonction de la tension du module et du facteur de dispersion K_c

5.2.2.1.3. Cas de la dispersion de l'ESR

La dispersion sur l'ESR n'est pas étudiée car ce paramètre influence peu les différences de tension entre chaque cellule.

5.2.2.2. Différence de température entre les cellules du module

Les résultats expérimentaux montrent que les températures sur les cellules d'un même module sont non-homogènes [104, 150]. Ceci est dû à diverses raisons comme la nonhomogénéité de la ventilation forcée (cf. fig. 5-5).

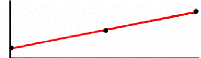
è_n

è 1

è1 è n

Flux d'aire forcé

Vue de coté Face

Fig. 5-5 : Exemple de gradient de température dans un module de supercondensateurs

La dispersion en température des cellules même avec une faible valeur peut conduire à des tensions de cellules non égales à long terme, car la résistance ESR et l'autodécharge varient considérablement en fonction de la température.

5.2.2.3. Effet de non-similitude du vieillissement sur les cellules du module

Nous avons vu auparavant que le vieillissement a un effet direct sur les paramètres internes du supercondensateur : augmentation de l'ESR, de l'autodécharge et aussi diminution de la capacité. Des essais de vieillissement ont été réalisés avec la même tension mais avec une différence de température de 5 °C. Les résultats de ces essais ont montré qu'une faible augmentation de la température conduit à des vieillissements très différents sur les cellules. Le même phénomène peut apparaître en cas de dispersion de la tension de cellules même en l'absence de surtension (cf. § 5.2.2.5).

5.2.3. Performance du circuit d'équilibrage de tension

La tolérance sur les paramètres des cellules de supercondensateur peut provoquer une surtension durant la charge/décharge. Par conséquent, il est indispensable de réduire la valeur de la charge délivrée à ces composants. A défaut, la surtension qui apparaît localement sur ces composants peut engendrer so it la dégradation progressive de la cellule qui affecte la durée de vie de ce composant, soit la destruction du composant (l'électrolyte organique dans la cellule

commence à se décomposer, produisant des produits gazeux ainsi qu'une accumulation de pression jusqu'à la destruction du composant).

Pour éviter ce phénomène, des circuits d'équilibrage sont ajoutés aux supercondensateurs, afin d'équilibrer les tensions et de redistribuer les surtensions sur les cellules [151-153]. Ces circuits permettent d'optimiser l'énergie stockée [1 51] et de prolonger la durée de vie des supercondensateurs.

L'étude des différents systèmes d'équilibrage nous conduit à proposer la définition de concepts permettant de les comparer en vue de sélectionner le système le plus performant et le plus fiable.

5.2.3.1. Définition du rendement énergétique des systèmes d'équilibrage

Afin d'évaluer la performance des systèmes d'équilibrage en terme d'énergie, nous définissons le rendement énergétique du circuit d'équilibrage d'un module par la relation 5-12. Il donne le pourcentage d'énergie stockée dans les supercondensateurs à la fin de l'équilibrage par rapport à l'énergie stockée au début d'équilibrage [154].

n n

i

? W i - ? W eq

i = 1 i = 1

ç = 5-12

n

? W_i

i= 1

où,

Wi est l'énergie utile stockée dans la cellule i (égale à l'énergie fournie par la source d'alimentation au supercondensateur moins celle _WESR dissipée dans la résistance ESR),

Weqi est l'énergie dissipée dans le circuit d'équilibrage lié à la cellule i.

5.2.3.2. Détermination de l'espérance de vie d'un module

Les supercondensateurs possèdent un nombre de cycles de charge/décharge très important par rapport aux accumulateurs classiques. Il s'agit en effet d'une technologie mettant en oeuvre des phénomènes sans modification physique des électrodes (théoriquement pas de réaction d'oxydoréduction). Cependant, l'espérance de vie des supercondensateurs est réduite pour des températures ou/et des tensions élevées, etc. Il est donc important d'établir un modèle qui permet d'estimer l'espérance de vie pour différentes conditions de tension et/ou de température.

Les processus faradiques dans les supercondensateurs engendrant un vieillissement sont accélérés par deux contraintes principales la tension et la température. Comme le montre la

figure 5-6, le vieillissement du supercondensateur est fonction de la tension et la température de fonctionnement.

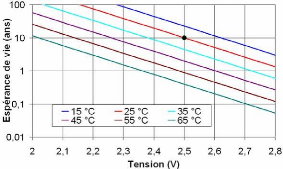
Fig. 5-6 : Espérance de vie du supercondensateur en fonction
de la tension et la température pour un composant d'EPCOS (2,5 V ; 65 °C) [19]

Nous pouvons constater d'après de cette courbe que l'espérance de vie du supercondensateur aux valeurs nominale (2,5 V et 25 °C) est de 10 ans.

U è

( + )

L'espérance de vie _Texp s'exprime par une fonction exponentielle de la tension U et de la température è (c.f. eq. 5-13) [155] suivant la loi d'Eyring [156, 157].

5-13

exp ( , ) .

è = C _t e v

C C

T U è

où,

Ct _v, et Cè sont des constantes de vieillissement qui peuvent être d

, C éterminées à partir de

la figure 5-6 : Ct =1,46.10 ans, C_v = -149 mV, Cè = -12,4 °C.

9

A côté de l'espérance de vie, un facteur de dégradation peut être utilisé pour une évaluation de l'espérance de vie avec des conditions variables (cf. eq. 5-14). La valeur de ce facteur varie de 0% à 100% (pour les composants vieillis (la capacité a diminué de 20% et l'ESR de 100%) [124].

dã

1 = dt 5-14 T u t ( ( ) ( )) + è t exp

A partir d'une dégradation initiale ã0 et l'intégration de l'équation 5-14 d'un état initial t0 à un état t, nous pouvons calculer la dégradation instantanée.

t 1

ã = ? dt + ã 5-15

0

t 0 T u t + t

exp ( ( ) è ( ))

L'espérance de vie moyenne _Tav pour un profil de la tension u(t) et une dynamique de la température è(t) peut être estimée par l'équation 5-16.

t t

Tav

- 0

( ( ), ( )) u t t

è = 5-16

t 1

dt

? T u t t

t 0 ( ( ) , ( ))

è

exp

Dans notre étude, le supercondensateur étant considéré comme sain initialement la dégradation présentée par l'équation 5-15 peut être réduite à celle de l'équation suivante :

t 1

ã = ? dt 5-17

0 T _exp (u( t ) è ( t ))

+

Pour un profil donné (u(t), è(t)) de période _Ttot app liquée durant N périodes, la dégradation du composant pendant l'utilisation peut être calculée par l'équation 5-18.

ã = ? dt + ? dt + +

T 2 T NT

tot 1 tot 1 tot 1

0 exp ( ( ) ( )) exp ( ( ) ( )) (1 ) exp ( ( ) ( ))

T u t + è t T u t + è t +

T - N T T u t t

... ? dt 5-18

è

Comme les dynamiques de u(t) et de è(t) sont périodiques d'une durée _Ttot, les dégradations provoquées à chaque période sont égales. Nous pouvons donc écrire :

Ttot 1

ã = N ? dt 5-19

0 exp ( ( ) ( ))

T u t + è t

L'espérance de vie moyenne _Tav pour un profil de u(t) et de è(t) de période _Ttot peut donc être donnée par l'équation 5-20.

NT tot

T tot

( ( ), è ( ))

u t t=

Tav

= 5-20

1 dt

T T

tot 1 tot

N? dt ?

T u t t

( T u t t

0 exp ( ), ( ))

è 0 exp ( ( ), ( ))

è

Par conséquent, il suffit de calculer la dégradation liée à un certain profil du courant durant une période _Ttot, pour déterminer l'espérance de vie.

Le courant de charge/décharge n'est pas pris en compte directement dans l'estimation de l' espérance de vie, mais son effet sur l'autoéchauffement (A0) est considéré dans la détermination de la température du composant 0 (0 = 00 +A0).

Notons que l'espérance de vie totale d'un module de supercondensateurs est égale à la plus faible espérance de vie de la cellule la plus critique.

5.3. Modélisation et simulation du module de

supercondensateurs avec paramètres dispersés

Nous pouvons trouver dans un module de supercondensateurs trois types principaux de déséquilibre de tension selon son origine :

· Déséquilibre dû aux supercondensateurs de résistance de fuite différente

· Déséquilibre dû aux supercondensateurs de capacité différente

· Déséquilibre dû aux supercondensateurs de résistance série différente

5.3.1. Profils de courant des applications types

Comme la performance et la fiabilité des systèmes d'équilibrage peuvent varier suivant l'application, nous avons choisi différentes applications typiques.

5.3.1.1. Applications avec un rapport cyclique élevé

5.3.1.1.1. Cycles de forts courants de charge/décharge

Dans cette application comme l'illustre la figure 5-7, le courant présente deux régimes : un courant transitoire (I1) qui charge initialement les supercondensateurs autour de leur valeur de tension nominale et un courant permanent périodique (I2), pour décharger/charger à courant constant les supercondensateurs. Ces courants ont été choisis de valeurs élevées afin de générer des surtensions sur les supercondensateurs et pour ainsi mettre en évidence l'efficacité des systèmes d'équilibrage.

L'application de récupération d'énergie par freinage dans un véhicule est une des applications qui peut engendrer une surtension sur des supercondensateurs. En effet, un freinage extrême peut faire appel à un courant de charge très élevé et provoquer instantanément une surtension locale sur quelques cellules [158].

Les caractéristiques "constructeur" des supercondensateurs font apparaître deux tensions. La première, appelée tension de travail, peut être appliquée pendant la durée de vie du supercondensateur sans dommage. La seconde _Umax, préjudiciable aux composants, appelée tension de crête ou "Surge Voltage", peut être appliquée seulement pendant quelques centaines de millisecondes. Quand un supercondensateur est soumis à une tension de crête, l'électrolyte organique dans la cellule se décompose rapidement [55]. Pour le supercondensateur étudié BCAP010, cette tension est de 2,8 V.

Fig. 5-7 : Profil du courant de charge/décharge à courant constant

5.3.1.1.2. Projet Thalès [113, 159]

Le principe du projet THALES (Tram-train Hybride à Alimentation Électrique par Supercondensateurs) consistait à alimenter un train-tram sans caténaire par un système de stockage d'énergie électrique à supercondensateurs embarqué. Entre deux stations consécutives les supercondensateurs fournissent l'énergie indispensable au roulement et la puissance en accélération. A l'arrêt en station un autre dispositif de stockage d'énergie relié au réseau de distribution d'électricité de faible puissance recharge rapidement le système embarqué. Le système embarqué peut rencontrer quatre phases de fonctionnement : accélération au départ de la station, roulement entre deux stations, récupération d'énergie par freinage à l'arrivée, et recharge par une alimentation dans la station (c.f. fig.5-8) [113, 159].

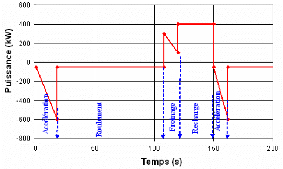
Fig. 5-8 : Profil théorique du projet THALES [113,159]

Afin de pouvoir utiliser un profil proche de celui du projet THALES et pour pouvoir comparer les résultats obtenus au profil précèdent, nous avons simplifié le profil par celui représenté sur la figure 5-9. Ce profil du courant a un bilan énergétique identique au profil de courant précèdent.

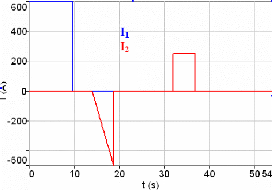
Fig. 5-9 : Profil du courant simplifié du projet THALES
(I1 est le courant transitoire et I2 est le courant permanent périodique)

L'espérance de vie d'un module composé de n cellules en série est égale à celle de la cellule la plus contrainte, c'est-à-dire présentant une dispersion sur l'une de ses caractéristiques la plus élevée, (par exemple une diminution de 20% de la capacité ou une augmentation de 60% de la résistance de fuite). Il suffit donc d'estimer l'espérance de vie de cette cellule pour obtenir celle du module.

La dispersion des paramètres (par exemple de la capacité) est toujours déterminée par rapport à leur valeur moyenne. C'est pourquoi, nous utiliserons l'hypothèse simplificatrice

d'un module de supercondensateurs se composant de deux cellules en série SC1 et SC2 : la première cellule représente une cellule moyenne de la capacité alors que la deuxième cellule présente une forte dispersion sur l'un de ses paramètres intrinsèques.

Pour les applications à rapport cyclique élevé, nous ne considérons que la dispersion sur la capacité car l'influence de la résistance de fuite sur les tensions est négligeable.

Dans le cas d'une dispersion sur la capacité, leurs valeurs peuvent être données par le système d'équations suivant :

C1 = C=C 5-21

C = C + K = C + K 5-22

2 . (1 ) . (1 )

c c

En considérant K_c = - 20%, les allures de la tension obtenues par simulation de ce module sont représentés sur les figures 5-10-a et b. La figure 5-10-a représente les tensions aux bornes des deux cellules pour un profil de fort courant de charge/décharge (cf. fig. 5-7) et la figure 5- 10-b pour le profil représenté sur la figure 5-9.

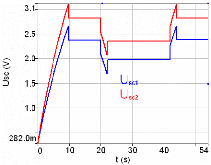
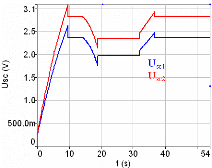
(b)

(a)

Fig. 5- 10 : Allure de la tension des supercondensateurs (sans système d'équilibrage)

La simulation du module avec un couplage électrothermique pour le premier profil de courant (cf. fig. 5-10-a) a montré que la température des supercondensateurs au bout d'une heure atteignait la température limite de 65 °C (pour une température ambiante de 25 °C). Notons que l'espérance du module a diminué de 93% avec l'effet de l'autoéchauffement par rapport au cas où nous le négligeons.

Quant au deuxième profil (cf. fig. 5-10-b) la température des composants a augmenté jusqu'à 47 °C (pour la même température ambiante) et l'espérance de vie a diminué de 64% par

rapport au cas oü l'autoéchauffement est négligé.

Dans ce type d'applications un système de refroidissement comme une ventilation forcée est nécessaire.

5.3.1.2. Applications avec un rapport cyclique bas

Dans certaines applications les supercondensateurs restent chargés long temps avant d'être déchargés par un courant relativement faible. Nous intitulerons ce type d'application `'application avec rapport cyclique bas». Les alimentations sans interruption par exemple en font partie.

Nous représentons sur la figure 5-11 un profil de courant typique pour simuler ce genre d'application.

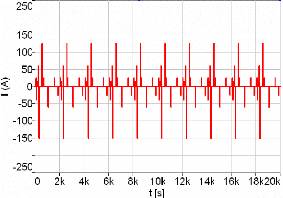
Fig. 5-11 : Profil de courant typique d'applications ayant un rapport cyclique bas

Dans ce type d'applications, le déséquilibre des tensions des supercondensateurs est engendré lentement, avec une constante de temps élevée. La dispersion de la capacité et/ou de la résistance de fuite est la cause de ce déséquilibre.

Nous avons simulé sur la figure 5-12 le deuxième cas par une augmentation de 60% de la résistance de fuite et une diminution de 20% de la capacité.

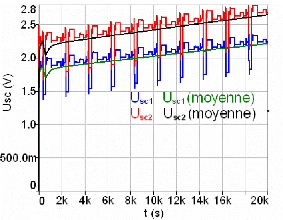
Fig. 5-12 : Allure des tensions des supercondensateurs

Dans ces applications, l'effet de l'autoéchauffement est faible.

Dans l'objectif d'évaluer les circuits d'équilibrage indépendamment de l'effet de l'autoéchauffement, nous supposons que la température du composant est fixée à 25 °C dans toutes les simulations qui suivent.

5.4. Etude comparative de systèmes d'équilibrage

Nous avons vu que la mise en série des supercondensateurs ayant différents paramètres conduit à un déséquilibre de leur tension. Nous présentons dans la suite différents types de systèmes d'équilibrage. Ces systèmes d'équilibrage sont de deux concepts : les circuits dissipatifs et non dissipatifs.

5.4.1. Systèmes d'équilibrage dissipatifs

La solution d'équilibrage dissipative consiste à dissiper une partie de l'énergie stockée dans le supercondensateur à tension élevée. La dissipation de cette énergie excessive ramène la surtension à une valeur de fonctionnement correcte.

5.4.1.1. Système d'équilibrage passif

Dans la solution passive, nous plaçons en parallèle aux bornes de chaque cellule des résistances d'équilibrage d'une valeur _Req comme représenté par le schéma sur la figure 5-13 [160, 154]. Le mécanisme de ce type d'équilibrage est simple par son principe : un courant parcourt toujours la résistance d'équilibrage connectée à ses bornes. Plus la tension est forte

plus le courant dans la résistance d'équilibrage est important, ce qui permet d'homogénéiser les tensions aux bornes des différents composants.

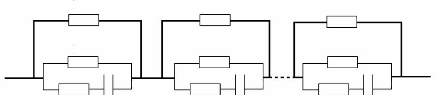
Req1 Req2 Reqn

Rf1

Rf2 Rfn

ESRl ESR2 ESR_n

Cl C2 C_n

Usc1 Usc2 Uscn

U_mod

Fig. 5-13 : Module de supercondensateurs avec un système d'équilibrage passif

Nous définissons le facteur d'équilibrage _Keq par la relation 5-23. Ce dernier donne la proportionnalité de la résistance d'équilibrage _Req par rapport à la moyenne des résistances de

fuite R f . D'après la référence [149], sa valeur peut être comprise entre 5% à 10%.

R eq

K = 5-23

eq

R_f

5.4.1.1.1. Calcul du nouveau facteur de dispersion de la résistance de fuite

Nous montrons dans ce paragraphe l'effet de l'emploi des résistances d'équilibrage R_eq aux bornes des supercondensateurs sur la dispersion de ses paramètres. Pour simplifier l'analyse, la dispersion de la résistance d'équilibrage est négligée.

Dans le cas de la dispersion de la résistance de fuite, la résistance équivalente R_pmax des deux résistances en parallèle Rfmax (la plus élevée) et R_eq peut être calculée par la formule suivante :

R R

. R . (1 )

eq f + K

eq f

max

R = = 5-24

max R R

+ K K

+ +

eq f eq f

max

1

p

En raison du nombre n de cellules en série élevé, la moyenne des résistances (R_p) en parallèle peut être approximée avec une faible erreur comme suit :

1 nn R R R R

1 e f

. .

q eq f R

i eq

R = ? =

R =

p ? ?

p 5-25

n i n 1

1 1 R R

i + + K +

= i = eq f R R

eq f eq

i

En considérons les résistances d'équilibrage, un nouveau facteur liée à la dispersion de la résistance de fuite peut être défini par l'équation suivante :

R -R

p p

max

K 5-26

f ' =

R p

d'où, en considérant les équations 5-24, 5-25 et 5-26 :

K K

f eq

.

K f K K

' = 5-27

+ + 1

f eq

Nous montrons sur la figure 5-14 le facteur de dispersion (calculé par l'équation 5-27) en fonction du facteur d'équilibrage pour certai es valeurs du facteur de dispersion de la

n

résistance de fuite Kf. Nous remarquons que l'utilisation d'une résistance d'équilibrage diminue largement la dispersion de la résistance de fuite et par conséquent le nombre de cellules requis en série pour une tension donnée (cf. eq. 5-6). En conclusion, pour un facteur d'équilibrage faible (entre 5% à 10%) la dispersion peut pratiquement disparaître entre les cellules d'un module. La durée de vie des cellule s est alors quasiment égale (si les différences de température entre cellules sont exclues).

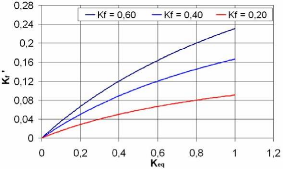
Fig. 5-14 : Evolution de la dispersion de la résistance en fonction du facteur d'équilibrage

5.4.1.1.2. Calcul du temps d'équilibrage

Dans le cas d'une dispersion de la capacité et de la résistance de fuite, le calcul de la performance du système d'équilibrage est difficile et dépend du profil de courant. Nous nous proposons donc de le simuler.

Définissons un nouveau paramètre lié à l'équilibrage à savoir le temps d'équilibrage. Nous distinguerons en fait deux temps d'équilibrage lors de l'étude de ces systèmes. Le premier est le temps Teq pour que les tensions instantanées des cellules du module s'égalent. Le deuxième le temps TU est le temps nécessaire pour que la tension aux bornes d'une cellule présentant une surtension atteigne la tension nominale UN.

Dans les applications ayant un rapport cyclique bas, les temps d'équilibrage sont principalement dûs à la valeur de la capacité du supercondensateur et à la résistance d'équilibrage. Reprenons le module présenté dans le paragraphe 5.2.1 et considérons seulement la dispersion de la capacité. Les résistanc es ESR des différents composants sont négligées.

En fin de la charge, la tension aux bornes de la capacité C2 peut être exprimée en fonction de la tension de la capacité C1 et du facteur de la dispersion K_c à partir de la loi de la conversation de charge par la formule suivante :

U sc = Usc 1 5-28

°' 1 + K c

02

Au moment de l'équilibrage (temps Teq), les tensions des cellules sont égales et peuvent être écrites par le système d'équations suivant en remplaçant la résistance R_p par sa valeur de l'équation 5-25 :

usc ( _eq)= U _s. .exp _1T eq =U

T

.

R_p C

[ Jsc01.exp [- T _eq. (1 + K eq 5-29

)j

Req. C

? T ? ? T + K ?

eq . (1 )

eq eq

u T

( ) = U . exp ?? - ?? = U . exp ?? - ?? 5-30

sc₂ eq sc sc

02 02

R C K

. (1 )

+ R C K

. . (1 )

+

? p C ? ? eq C ?

A noter que les deux tensions ci-dessus sont données sans la dispersion sur les résistances de fuite.

Le temps d'équilibrage peut être obtenu par l'équation ci-après en égalisant les deux dernières équations et en considérant l'équation 5-28 :

eq 5-31

ln(1 ) . (1 )

+ K + K

c c

T = . .

C R

eq K _c. (1 + Keq)

Dans certaines applications, il n'est pas nécessaire d'équilibrer les tensions instantanées des cellules mais seulement de réduire la surtension _Umax à la tension nominale. Ce dernier équilibrage permet de limiter la dissipation d'énergie dans les systèmes d'équilibrage. Si le supercondensateur SC2 de capacité C2 présente une surtension _Umax, nous pouvons identifier l'instant TU où la tension nominale est atteinte à partir de l'équation suivante :

?T.? ? T . (1 )

+ K ?

U U eq

1 1

u T U

( ) = . exp ?? - ?? = U . exp ?? - ?? = U 5-32

sc U max max N

2 ¹ R C R C K

. (1 )

+

? p 2 ? ? eq c ?

D'où,

eq

T (1 ) . ln ^max .

? U ? R

= + K ? ? . C

U c 5-33

? U 1 + K

N ? eq

Nous montrons sur les figures 5-15-a et b ces temps en fonction de la résistance d'équilibrage et pour différents facteurs de dispersion. Il est bien évident que le temps TU requis pour atteindre la tension nominale est inférieur à celui d'équilibrage _Teq. Plus le facteur de dispersion de la capacité est élevé, plus les temps requis _Teq et TU pour atteindre l'équilibrage sont faibles. Ceci s'explique car avec une forte dispersion sur le facteur K_c, la capacité correspondante est faible et donc la constante de temps de charge ou décharge est faible.

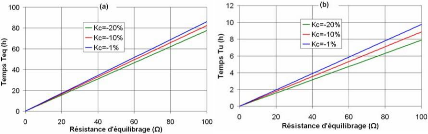
Fig. 5-15 : Temps d'équilibrage en fonction de la valeur de résistance d'équilibrage

Ces résultats sont obtenus avec comme seule dispersion sur les paramètres du composant la dispersion sur la capacité.

Dans le cas d'application où le rapport cyclique est bas, il est préférable de considérer une dispersion sur la capacité (K_c) et sur la résistance de fuite (Kf). Les tensions des cellules sont alors exprimées par les équations 5-34 et 5-35.

? +

t K

. (1 ) ?

eq

u t U

sc 1 ( ) 01 . exp

= ?? - ??

sc 5-34

R C

? eq . ?

?t K K
. (1 + eq f

+ ) ?

u t U

sc 2 ( ) 02 . exp

= ?? ??

sc - 5-35

R C K

. . (1 ) . (1 )

+ + K

? eq C f ?

De la même manière que ci-dessus, nous trouvons les nouveaux temps d'équilibrage (cf. eq. 5-36 et 5-37).

ln(1 + K_c ) . (1+ K _f + K _c K_c .Kf ^Teq K K K K K K K K

) .C. R

eq 5-36

+ . + . + _eq K _c . K f

.

c + c f eq f eq c

.

? U ?R

max eq

T = + +

(1 K K K K

+ ? ? . C

U c f c f

. ) . ln . 5-37

1

eq

U +K +Kf

La proportionnalité des deux temps d'équilibrage (sans (Teq1) et avec la dispersion (Teq2) sur la résistance de fuite) est donnée par l'équation 5-38. La figure 5-16-a donne cette relation en fonction du facteur de la dispersion avec K_c=-20%. Elle démontre que la dispersion de la résistance de fuite (avec la dispersion de la capacité) ralentit l'équilibrage des tensions.

Ceci peut être obtenu de la même façon pour le temps d'équilibrage TU (cf. eq. 5-39 et fig. 5- 16-b).

K_c . (1 + K _f + K _c + Kc.

)

5-38

K _f ) . (1 +K

eq

T eq 2

K _c + K_c . K _f + K_eq + K_eq . K_c+

.K f

Keq .K _c . K _f ) . (1 + K_c

T eq 1 (

)

T U 2

)

5-39

eq

1 + K _c +Kf.K

c + K_f ) . (1 + K

TU1 1 + K f +Keq )(1 +K_c )

où,

TU1 ^et _TU2 sont les temps d'équilibrage respectivement sans et avec la dispersion sur la résistance de fuite.

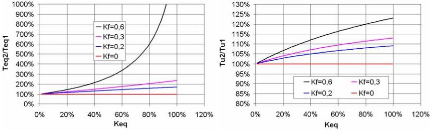
(a) (b)

Fig. 5-16 : C omparaison des temps d'équilibrage sans et avec la dispersion de résistance de fuite

La dispersion de la résistance de fuite augmente le temps d'équilibrage et peut donc réduire l'espérance de vie du composant et du module.

Dans les applications ayant un rapport cyclique élevé, il est difficile d'équilibrer la tension instantanée. Nous définissons donc un nouveau temps d'équilibrage correspondant au temps pour équilibrer les tensions moyennes.

Nous représentons sur la figure 5-17 le profil du courant et la réponse en tension d'un module de supercondensateurs utilisé dans une application avec rapport cyclique élevé. Pour une période T, le module est chargé à courant constant I pendant un temps áT/2 et déchargé pendant le même temps.

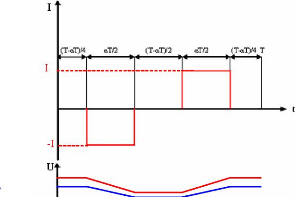
Umax

(1+Kc)Umax

-Usc2
-Usc1

Fig. 5-17 : Profil général du courant

Nous pouvons déduire le temps d'équilibrage des tensions moyennes à partir de la définition

de la valeur moyenne. En considérant des valeurs de capacité fixe (non dépendante de la tension), les tensions moyennes sans système d'équilibrage peuvent être écrites par les équations ci-dessous :

1

=

Usc

U sc 2

). C

5-40

á +

T I U

4 . . (1 + K c

max

4 . C

- á + max +

T I U

4 . . (1 c ).

K C

5-41

K_c )

4 . . (1

C +

Les évolutions des tensions moyennes pendant l'équilibrage sont données par le système d'équations suivant :

- á

. exp

t

5-42

T I U

+ 4 . max . (1 ).

+ K C

u =

sc 1

-

c

4 . C .

R C
p .

u

2

á T I U

+ 4 . max . (1 + K c

). C

. exp

? t ?

?? - ??

. . (1 )

+

? ?

c p c

5-43

sc 4 . . (1 )

C K

+ R C K

A l'équilibre, les deux tensions moyennes exprimées ci-dessus sont égales. D'où, nous pouvons calculer le temps d'équilibrage par l'équation 5-44.

eq 5-44

ln(1 ) . (1 )

+ K + K c c

T = . .

C R

eq K K

c . (1 + _eq )

A titre de comparaison, nous constatons que les deux temps d'équilibrage, celui de la relation 5-31 et de la relation de 5-44 sont identiques.

Dans le cas où la capacité et la résistance de fuite du supercondensateur SC2 sont dispersées, nous trouvons un temps d'équilibrage des tensions moyennes égal à celui donné par la relation 5-36.

5.4.1.1.3. Résultats de la simulation des applications

Nous comparons sur la figure 5-18-a et b l'espérance de vie, le rendement énergétique et le temps d'équilibrage pour les de ux profils du courant avec un rapport cyclique élevé (cf. fig. 5- 7 et 5-9). Ces résultats sont calculés par le logiciel Simplorer (méthode de Monte Carlo) pour Ttot= 1 h et K_c= -20%. Nous remarquons que les deux profils énergétiquement identiques

donnent des résultats identiques.

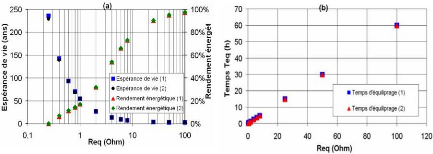
Fig. 5-18 : Comparaison de performance des applications à rapport cyclique ^élevé(1) profil de fort courant de charge/décharge (cf. fig. 5-7), (2) profil du projet THALES (cf. fig. 5-9)

Nous montrons sur la figure 5-19 l'espérance de vie vis-à-vis de la dispersion de la capacité K_c du supercondensateur. Nous remarquons que, quelle que soit la résistance de fuite, l'espérance de vie est supérieure à celle sans système d'équilibrage et qu'une résistance d'équilibrage faible, qui va rapidement supprime les surtensions, améliore cette espérance de vie.

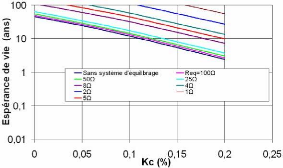
Fig. 5-19 : Espérance de vie en fonction du facteur de dispersion avec système d'équilibrage passif

D'après ces résultats pour des applications à rapport cyclique élevé, nous constatons qu'une résistance autour de 5 ? donne un résultat équilibré : une espérance de vie de l'ordre de 10 ans et un rendement énergétique de l'ordre de 60%. Nous représentons sur la figure 5-20 la tension aux bornes des supercondensateurs pour cette valeur de résistance pour l'application à fort courant (cf. fig. 5-7).

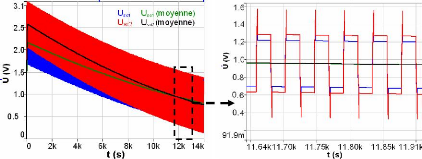
Fig. 5-20 : Tension aux bornes des supercondensateu avec une résistance d'équilibrage de l'ordre de 5?

rs

Notons que les performances de ce type d'équilibrage peuvent varier suivant le profil de l' application et que les résultats présentés sont donnés à titre indicatif.

Nous représentons sur la figure 5-21-a la performance du système d'équilibrage vis-à-vis de la résistance d'équilibrage pour une application à rapport cyclique bas (cf. § 5.3.1.2). Nous présentons sur la figure 5-21-b le profil de la tension aux bornes de supercondensateurs résultant des données du paragraphe 5.3.1.2 et pour une résistance d'équilibrage de 50 ?. D'après ces résultats, nous constatons qu'une telle valeur de résistance d'équilibrage de 50 ? est capable de limiter la tension au-dessous de sa valeur nominale et donne une espérance de vie et un rendement acceptables (espérance de vie de l'ordre de 10 ans et rendement de l'ordre de 60%).

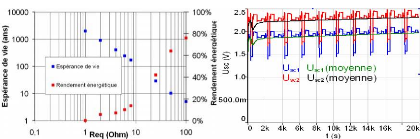
(a) (b)

Fig. 5-21 : Résultats de la simulation d'une application ayant un rapport cyclique bas

Ce type d'équilibrage passif est intéressant dans les applications ayant un rapport cyclique bas car sont coût est faible et les résistances d'équilibrage de relativement forte valeur conviennent [161]. Pour ce type d'application, nous n'étudierons pas les autres systèmes d'équilibrage plus coûteux

5.4.1.2. Diodes Zener

La deuxième solution consiste à utiliser des diodes Zener, en remplacement des résistances dans le système d'équilibrage passif [155]. Celles-ci doivent équilibrer la tension des supercondensateurs selon leur tension Zener. La figure 5-22 représente le circuit équivalent de ce système, dans lequel les diodes Zener sont liées en parallèle aux supercondensateurs. Le mécanisme de cet équilibrage est lié toujours à une perte d'énergie dans les diodes Zener. La difficulté majeure de ce système d'équilibrage est essentiellement de trouver les diodes Zener qui conviennent pour une application donnée comme les applications présentées précédemment [154].

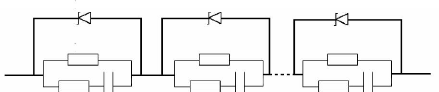
D1 D2 D_n

Rf1

Rf2 Rfn

ESRl Cl C2

ESR2 ESRn Cn

Usc1 Usc2 Uscn

Ucn

Fig. 5-22 : Système d'équilibrage à diodes Zener

5.4.1.3. Résistances commandées

Dans ce système d'équilibrage, un interrupteur actif est mis en série avec la résistance d'équilibrage. Ce dispositif est relié en parallèle à chacune des cellules du supercondensateur (c.f fig.5-23). Lorsque la tension du composant dépasse une valeur donnée, l'interrupteur est fe é, ce qui permet à un courant de parcourir la résistance d'équilibrage (comme dans le cas

rm

de l'équilibrage passif). Ensuite, l'interrupteur est ouvert lorsque la tension aux bornes de la cellule surveillée revient à une valeur de référence [56, 162, 153].

S 1 Req1 S2 Req2 S_n Reqn

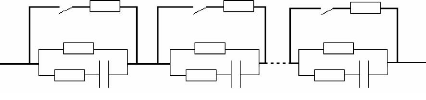
ESRl ESR2 ESR_n

Cl C2 C_n

Rf1 Rf2

Rfn

Usc1 Usc2 Uscn

Umod

Fig. 5-23 : Système d'équilibrage à résistances commandées

C

e système d'équilibrage se compose d'un circuit actif principal comprenant un dispositif actif de commutation tel qu'un transistor bipolaire ou MOSFET associé à la résistance d'équilibrage, un circuit de commande, et un autre de détection (cf. fig. 5-24). La commande de l'interrupteur est choisie de la telle façon qu'un minimum d'énergie soit dissipée dans les résistances d'équilibrage. L'interrupteur est fermé quand la tension du supercondensateur dépasse une valeur seuil. A titre d'exemple, le transistor (IRLI3705NPbF ; VDSS= 55 V ; R

DS(on)=0,01? ; ID=52 A) du fabricant International Rectifier a été choisi dans le système de la figure 5.24).

Fig. 5-24 : Schéma de la carte électronique d'équilibrage et sa photo [162]

5.4.1.3.1. Résultats de la simulation des applications ayant un rapport cyclique élevé

Nous présentons sur les figures 5-25-a et b les résultats de la simulation des deux profils du courant à rapport cyclique élevé (cf. fig. 5-7 et 5-9). Nous remarquons que cette solution d'équilibrage permet de contrôler l'énergie dissipée dans les résistances d'équilibrage, ce qui améliore fortement le rendement énergétique du système d'équilibrage (ç ? 87%).

Sur les figures 5-25-a et b, la résistance d'équilibrage _Req est limité à 5 ? car au-delà le temps d'équilibrage (TU) est supérieur au temps total simulé (Ttot).

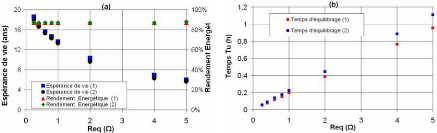
Fig. 5-25 : Comparaison de performanc des applications à rapport cyclique bas
e
avec les résistances commandées

L'intérêt de cette solution est de prendre des valeurs faibles de résistances d'équilibrage pour réaliser l'équilibrage le plus rapidement possible, car le rendement énergique ne peut pas descendre au-dessous d'une valeur limite. Cependant, pour des considérations de puissance dissipée dans cette résistance, la valeur de cette dernière ne pourra pas être trop faible.

Une résistance d'équilibrage de l'ordre de 2 ? peut donc, en plus d'un rendement élevé, assurer une espérance de vie d'environ 10 ans pour les deux profils, quelque soit la dispersion de la capacité (cf. fig. 5-25). La figure 5-26 montre la tension aux bornes des supercondensateurs (SC1 et SC2) avec un facteur de dispersion (KC) de -20% pour des résistances commandées de 2 ?.

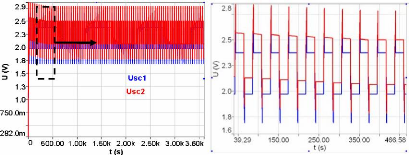
Fig. 5-26 : Tension aux bornes des supercondensateurs pour résistances commandées de 2 ?

Nous pouvons conclure que le système d'équilibrage à résistances commandées e st bien adapté aux applications à rapport cyclique très élevée [163].

La commande du transistor peut être réalisée par différentes méthodes. A titre d'exemple, dans notre exemple, nous fermons l'interrupteur quand la chute de la tension U_c sur la capacité du supercondensateur dépasse la valeur nominale limite ; U_c est donc la tension du supercondensateur moins la chute de tension sur la résistance ESR . Ceci permet d'améliorer la

performance du système d'équilibrage pour les applications à rapport cyclique élevé et de réduire le temps d'équilibrage TU.

La validation expérimentale de l'estimation de la résistance ESR par un circuit supplémentaire connecté en parallèle au supercondensateur est envisageable [164].

5.4.1.3.2. Nouvelle génération de résistances commandées

Nous pouvons trouver différentes configurations du circuit d'équilibrage avec résistances commandées. Le fabricant MAXWELL propose actuellement le circuit d'équilibrage donné sur la figure 5-27. Ce circuit se place entre deux supercondensateurs. Pour un nombre de cellules n, il faut n-1 circuits d'équilibrage. Son principe est basé sur la comparaison entre la tension des deux cellules de supercondensateurs ; le signal à la sortie du comparateur commande les transistors complémentaires Q1 et Q2 [55]. Il y a deux types de ces circuits selon la valeur désirée du courant d'équilibrage ; à faible et à fort courant.

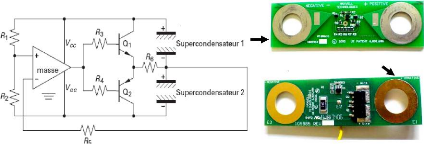
Circuit avec faible
courant d'équilibrage

Circuit avec fort
courant d'équilibrage

Fig. 5-27 : Schéma de principe d'un circuit d'équilibrage à résistance commandée de MAXWELL [55]

Le transistor Q1 est fermé quand la tension aux bornes du supercondensateur 1 est supérieure à celle du supercondensateur 2 et inversement.

La commande de ce type de circuit est très simplifiée, ce qui impacte le prix de celui-ci. L'av antage principal de ce système est qu'il permet d'équilibrer les tensions moyennes assez

r pidement et de stabiliser leur valeur avec le temps. A long terme cela peut aider à limiter a

l'apparition de la surtension sur le composant critique. La fi gure 5-28 présente la tension aux bornes des supercondensateurs avec ce type de commande (KC=-20%).

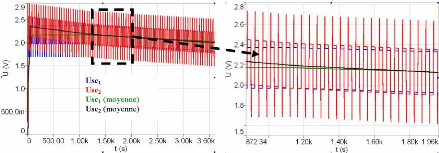
Fig. 5-28 : Tension aux bornes des supercondensateurs avec une résistance d'équilibrage de 5,5 ?

5.4.1.4. Transistors MOSFET linéaires

Nous pouvons aussi utiliser comme système d'équilibrage des MOSFET en remplacement du transistor et de la résistance d'équilibrage des circuits présentés précédemment. L'énergie de la surtension est alors dissipée dans la ré sistance interne du transistor. Ce dernier est commandé dans sa zone linéaire. La tension de commande grille source _Vgs est variable et proportionnelle à l'inverse de la surtens ion.

5.4.2. Systèmes d'équilibrage non dissipatifs

Pour pallier aux problèmes des solutions citées précédemment en l'occurrence l'énergie perdue dans le système d'équilibrage, des structures basées sur l'utilisation de convertisseurs statiques permettent de transvaser le surplus d'énergie aux supercondensateurs en surtensions sur les supercondensateurs sous alimentés.

5.4.2.1. Convertisseur Buck-Boost

Le principe général est de transférer l'énergie du supercondensateur présentant une tens ion él evée vers celui présentant une tension base, en passant par l'intermédiaire d'une inductance. La figure 5-29 illustre le montage d'un système d'équilibrage qui utilise une association de convertisseurs Buck-Boost (DC-DC) [165, 151].

D1 D2 D_n

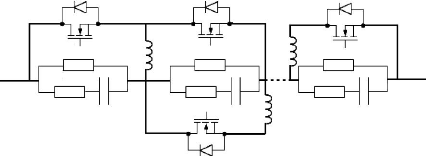
ESRl ESR2 C2 ESR_n C_n

Cl

Rf1

T1 T2

Rf2

Rfn

T_n

Usc1 Usc2 Uscn

Umod

Fig. 5-29 : Système d'équilibrage avec convertisseur Buck-Boost associée

5.4.2.1.1. Détermination de la fréquence de découpage et de l'inductance

Le principe de ce système consiste à redistribuer l'énergie stockée dans les supercondensateurs par l'utilisation des sources de courant auxiliaire. Afin d'expliquer le fonctionnement du système d'équilibrage et de pouvoir déterminer les paramètres du convertisseur proposé, nous utilisons deux cellules en série, les supercondensateurs SC1 et SC2. En négligeant les résistances de fuite, ces derniers sont simulés par une résistance ESR avec une capacité C en série [166, 165] (cf. fig. 5-30).

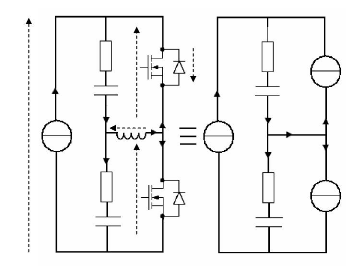
(a) (b)

ESRl

Usc1

Cl

iL1

L

I2

ESR2

C2

I

ESRl

Ud

Cl

T1

D1

I

I1

UL iL

I1

iL2

I

2

Usc2

ESR2

T2

D2

C2

2Ieq Ieq

Ieq

Umod

Fig. 5-30 : Principe du système d'équilibrage avec convertisseur Buck-Boost associé [165]

La commande des transistors se réalise selon la logique suivante :

· si Usc1>Usc2 : le transistor T2 est ouvert et T1 commute à la fréquence f,

· si Usc1< Usc2 : le transistor T1 est ouvert et T2 commute à la fréquence f.

Pour égaliser les tensions des supercondensateurs le rapport cyclique des transistors est fixé à 50% ; de ce fait le convertisseur Buck/Boost fonctionne en conduction discontinue. Nous remarquons, par cette logique de commande, qu 'il existe 3 séquences différentes [165].

Dans le cas oil Usc2> Usc1, nous représentons le courant et la tension dans l'inductance L sur la figure 5-31.

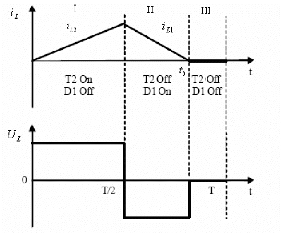
Fig. 5-31 : Séquence du système d'équilibrage
( i_L , U _L ) sont respectivement le courant et la tension de l'inductance L

Ces séquences correspondent aux événements suivants :

· phase I : T2 ON, D1 OFF, les supercondensateurs SC1 se charge avec le courant I, SC2 se charge avec le courant I- iL2 (cf. fig. 5-30),

U sc 2

i i

= 2 = . t

L L 5-45

L

· phase II : T2 OFF, D1 ON, le composant SC1 se charge avec le courant I+ iL1, le supercondensateur SC2 se charge avec le courant I,

5-46

Usc 1 +Ud T Usc2 T

iL ) +

- .( t -

1 L 2 L

2

iL = =

avec U la chute de la tension sur la diode D .

d 1

· phase III : T1 OFF, D2 OFF, SC1 se charge avec I, SC2 se charge avec I.

iL = iL1 = iL2 =0 5-47

A partir de la condition discontinue, nous pouvons déterminer le temps pour lequel le courant de l'inductance s'annule (t0) (cf. eq. 5-48)

.

Usc₂

t₀

Usc ₁

+

Ud

?

= 1+

?

)T

5-48

2

A partir de ces considérations, nous obtenons la relation du courant moyen dans l'inductance (cf. eq. 5-49).

U ? U ?

sc sc

2 2

I = . 1

?? + ?? 5-49

L 8 . .

L f U U

+

? sc d

1 ?

Comme l'illustre la figure 5-30-b, l'expression de l'évolution de la tension de cellule en fonction du courant I et _Ieq en négligeant la chute de tension sur la résistance peut être donnée par le système d'équations suivant :

I + I eq

u sc = . t

u = .t 5-50

sc₂

I-IeqC C

1 2

où,

I est le courant fourni par la source de courant chargeant les supercondensateurs, 2.Ieq est le courant d'équilibrage passant dans l'inductance (cf. fig. 5-30-b).

La valeur et le signe du courant Ieq dépendent de la différence de l'impédance qui existe entre les deux supercondensateurs (SC1, SC2).

Le but du système d'équilibrage étant d'égaliser des deux tensions _(usc1=usc2), ^à p artir de la dynamique de la tension aux bornes des supercondensateurs (cf. eq. 5-50), nous pouvons déduire l'expression du courant _Ieq (cf. eq. 5-51).

I = c

.I 5-51

eq K

-- 2 - K_c

K_c étant le facteur de dispersion sur la capacité.

L'inductance L et la fréquence (f =1/T) de découpage sont déterminées p our obtenir une

valeur moyenne du courant dans l'inductance égale à _2Ieq. En remplaçant le courant moyen de l'inductance donné par l'équation 5-49 par _2Ieq, nous obtenons la formule suivante :

L . f = U sc 2 - 2 - Kc .?1 + sc 2?5-52

Usc1 + U_d

1 6.I Kc

U ?

Par conséquent, en remplaçant les paramètres (I, K_c, U_sc, Ud = 0,3 V) donnés précédemment dans l'équation 5-52, nous obtenons la valeur de l'inductance et de la fréquence de découpage. Par exemple, nous trouvons pour le supercondensateur étudié BCAP010 ; f =10 kHz, L =0,5 uH.

Nous montrons sur la figure ci-dessous la carte de ce circuit d'équilibrage vendu par le fabricant MAXWELL.

Fig. 5-32 : Photo du convertisseur Buck-Boost

5.4.2.1.2. Simulation du module de supercondensateurs

Nous avons simulé le module de supercondensateurs (SC1+SC2) avec ce système d' équilibrage sous Simplorer pour une application à rapport cyclique élevé (cf. fig. 5-7). Les résultats sont présentés sur la figure 5-33. Ils montrent que la tension aux bornes des supercondensateurs s'équilibre très rapidement. C eci permet d'obtenir une espérance de vie et un rendement énergétique élevés (19 ans ; 92%). Nous remarquons que ce système

d'équilibrage améliore le rendement énergétique et qu'il prolonge l'espérance de vie du module de supercondensateurs par rapport aux autres systèmes d'équilibrage.

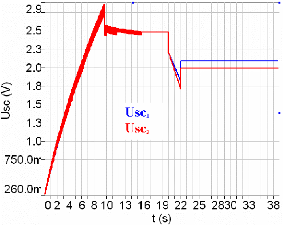
Fig. 5-33 : Tension aux bornes des supercondensateurs pendant l'équilibrage

Cependant, l'effet de la transmission d'énergie par les supercondensateurs peut devenir un inconvénient en terme d'énergie dissipée, lorsqu'un grand nombre de supercondensateurs sont en série.

L'inconvénient principal de ce circuit est son coût très élevé (pratiquement le même coût qu'un supercondensateur) [55].

5.4.2.2. Convertisseur Flyback à secondaires distribués

Cette solution est basée sur le transfert de l'énergie du supercondensateur ayant une tension élevée directement vers celui ayant la tension la plus basse. La figure 5-34 illustre le montage de ce système : un convertisseur statique principal centralisé (flyback multi-sorties) est lié avec un transformateur. Ce convertisseur fonctionne dès qu'une différence de tension est détectée, le transistor T conduit d'abord, permettant au primaire du transformateur de stocker l'énergie. Par la suite cette énergie magnétique va être distribuée au s econdaire du transformateur relié au supercondensateur présentant la tension la plus basse lorsque le transistor est ouvert (l'énergie stockée entraîne la conduction des diodes au secondaire) [151].

5. Evaluation des performances des modules de supercondensateurs

N T

p

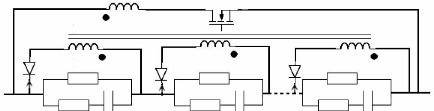
i1

D1

Ns1 Ns2

Rf1

D2

i2 i_n

Rf2

D_n

Rfn

Nsn

n

ESRl ESR2 ESR_n

C C2 C

l

Usc1 Usc2 Uscn

Umod

Fig. 5-34 : Système d'équilibrage Convertisseur Flayback à secondaires distribués

5.4.2.3. Convertisseur Forward à bobinage distribués

Une autre solution combine les deux circuits décrits précédemment. L'énergie est transférée directement sans passer par des supercondensateurs intermédiaires.

La figure 5-35 montre le schéma de ce système d'équilibrage. Dès qu'une différence importante de tension entre les supercondensateurs est détectée, le transistor correspondant est fermé. L'énergie va alors passer vers les autres supercondensateurs via les diodes et le transformateur. [151].

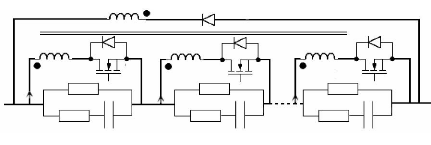
i1

N1

ESRl

Cl

Rf1

N D

D2

T T

1 2

Rf2

D1

i2

N2

ESR2 ESR_n

C2 C_n

i_n

N_n

Rfn

D_n T_n

Usc1 Usc2 Uscn

Umod

Fig. 5-35 : Système d'équilibrage avec convertisseur Forward à bobinage distribués

Les deux dernières solutions équilibrent les tensions instantanément, comme la solution présentée dans le paragraphe 5.4.2.1. La simulation du dernier système d'équilibrage et pour le module des supercondensateurs présenté auparavant est montrée sur la figure 5-36. Les ré sultats de ces dernières solutions sont relativement proches de ceux de la solution pour le système présenté au paragraphe 5.4.2.1, car nous avons simulé le transformateur par son

modèle idéal. Cependant, les pertes dans le transformateur sont assez importantes. Elles diminuent fortement le rendement énergétique du système global. Les deux dernières solutions ne sont pas employées avec les supercondensateurs car elles sont coûteuses en termes de composants magnétiques et de com nt.

posa

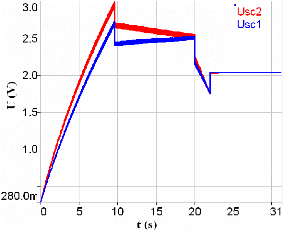
Fig. 5-36 : Evolution de tension aux bornes des supercondensateurs du système d'équilibrage ci-dessus

Il existe encore d'autres solutions d'équilibrage que celles que nous avons exposées [160, 167-169] mais celles-ci sont très complexes et coûteuses. Elles sont donc très rarement utilisées.

5.5. Conclusion

Nous avons montré qu'il existe deux paramètres principaux (Rf et C) pouvant être la cause de déséquilibres de tensions dans un module de supercondensateurs. Nous avons traité les cas essentiels : la dispersion de la capacité et/ou la dispersion de la résistance de fuite Rf.

Le remède au déséquilibre de tension consiste à ajouter aux bornes de chaque cellule élémentaire un circuit d'équilibrage intervenant lorsqu'une différence de tension apparaît. Les recherches bibliographiques ont montré qu'il existait plusieurs circuits d'équilibrage commercialisés, par résistances, diodes Zener, résistances commandées, convertisseurs statiques Buck-Boost sans ou avec transformateur), etc. Nos résultats montrent que ces circuits d'équilibrage diffèrent par leur rendement et par leur espérance de vie :

· Le circuit d'équilibrage avec résistance simple améliore l'espérance de vie du supercondensateur, mais participe à la dissipation d'une partie importante de l'énergie stockée, ce qui diminue le rendement énergétique.

· Le circuit d'équilibrage avec diodes Zener n'est plus commercialisé actuellement à cause de leur tensions et courant limités.

· Le circuit d'équilibrage de résistances avec interrupteurs commandées permet de contrôler l'énergie dissipée, tout en améliorant les contraintes de tension aux bornes du composant, ce qui contribue à une augmentation importante de l'espérance de vie du composant. L'inconvénient principal est que son coût est un peu élevé.

· Le circuit Buck-Boost équilibre la tension des supercondensateurs en transférant instantanément l'excédant d'énergie dû aux surtensions à des composants moins chargés. Ce circuit augmente l'espérance de vie du supercondensateur ainsi que le rendement énergétique du système d'équilibrage mais son encombrement ainsi que son coût élevé limitent son utilisation industrielle. Pour la même raison le système d'équilibrage des tensions des supercondensateurs avec transformateur n'est pas utilisé.

La constante de temps de l'autodécharge est élevée et est d'au moins quelques heures. Ce cas de déséquilibrage statique peut être parfaitement résolu par l'utilisation de résistances d'équilibrage en parallèle avec chaque cellule de supercondensateur.

Nous avons constaté que la performance et l'espérance de vie dépend essentiellement du ty p e d'application ; c'est-à-dire du profil de tension et de courant. Ceci rend chaque système d'équilibrage approprié à une application donnée.

L'équilibrage passif est plus approprié pour des applications à faible rapport cyclique. Dans ce s applications, la grandeur de la résistance d'équilibrage est généralement fixée à 1/10 de la valeur de résistance de fuite moyenne de la cellule. Les avantages de cette méthode d'équilibrage sont la simplicité et un faible coût.

Le système d'équilibrage par résistances commandées est requis pour les applications à rapport cyclique élevé. Dans ce type d'équilibrage, un certain nombre de commandes peut être utilisé pour atteindre l'équilibre de tension. La grandeur des résistances d'équilibrage peut être de l'ordre de 1/100 de la résistance de fuite. Dans ces applications un système de refroidissement est nécessairement installé, pour minimiser l'effet de la température sur l'espérance de vie du supercondensateur.

6. Conclusions générales et

perspectives

6. Conclusions générales et perspectives

Plusieurs méthodes de caractérisation sont utilisées pour évaluer les performances des supercondensateurs dans les plages de température et de tension d'utilisation. Ces méthodes de caractérisation des supercondensateurs sont des cycles de charge/décharge à courant constant (tension constante ou puissance constante), la spectroscopie d'impédance, la voltampérométrique.

Ces différentes méthodes donnent des résultats largement différents sur l'identification de l' ESR et légèrement différents sur l'évaluation de la capacité. Les mesures par méthodes temporelles donnent une capacité totale du supercondensateur qui se repartie entre celle de la double couche et une pseudo-capacité dûe à des processus électrochimiques lents. La pseudocapacité et la nature complexe du supercondensateur ont pour effet de rendre les résultats des techniques de caractérisation différents. La technique de spectroscopie d'impédance permet elle, de déterminer avec précision la dépendance en tension de la capacité de la double couche du supercondensateur _Cdl et de la résistance EDR du supercondensateur.

Les méthodes temporelles ont permis de déterminer le rendement coulombien et sa variation en fonction des différentes conditions. Il est remarqué que sa valeur diminue avec la diminution du courant de charge/décharge notamment aux températures élevées à cause de l'influence de la pseudo-capacité.

L'ensemble du travail effectué a permis d'établir des comparaisons entre les différents supercondensateurs de différentes technologies.

Les différents comportements des supercondensateurs sont modélisés par plusieurs modèles présentant tous certains avantages et inconvénients : le modèle classique RC est très simplifié mais aussi très imprécis ; et le modèle à deux branches est simple et relativement facile à identifier, mais sa précision dépend du profil du courant d'application ; le modèle avec pores non-homogènes représente bien le comportement dynamique des composants mais est assez complexe. Cependant, le supercondensateur est un dispositif complexe, il peut être intéressant de combiner les différents modèles afin d'obtenir un modèle général décrivant avec beaucoup de précision les différents phénomènes. Par exemple le modèle avec pores non-homogènes peut être complété avec les branches lentes du modèle à deux branches et le modèle de l'autodécharge.

S achant que l'autodécharge est un indicateur important pour quantifier les performances du supercondensateur. Nous avons étudié en détail celle-ci. Une méthodologie de mesure a été étudiée et adaptée pour mesurer celle-ci. Cette dernière a été représentée par plusieurs modèles. Un circuit électrique équivalent série a été proposé. Le calcul des ses éléments a été fait par la mesure de la décroissance de la tension aux bornes du supercondensateur, mais ses éléments ne représentent pas tout à fait les comportements physiques de l'autodécharge. Pour cela, un nouveau modèle d'autodécharge représentant mieux les mécanismes physiques engendrant celle-ci, a été proposé. Dans celui-ci, l'autodécharge est modélisée par une résistance en parallèle avec la capacité totale du supercondensateur pour le courant de fuite intrinsèque à celle-ci et une capacité série avec une résistance pour les réactions d'oxydoréduction. Ce modèle donne des résultats intéressants, notamment, il a permis de quantifier, pour la première fois, une capacité des réactions d'oxydoréduction dûe aux impuretés. Cependant, les processus d'autodécharge dépendent du type et de la quantité d'impuretés, ce qui rend la précision du modèle proposé tributaire de ces facteurs.

Nous avons constaté que les deux mécanismes d'autodécharge varient fortement en fonction de la température ambiante et de la tension initiale. Ainsi, l'énergie stockée dans le supercondensateur est dissipée lentement à température et tension faibles et rapidement à température et tension élevées.

Ces phénomènes lents tels que la redistribution de charges et l'autodécharge ne peuvent pas être caractérisés d'une manière fiable par sp ectroscopie d'impédance. Par conséquent, la mesure de la décroissance de la tension en circuit ouvert reste la méthode la plus précise pour les caractériser.

Pour diverses applications, il est nécessaire que le supercondensateur puisse fonctionner dans une vaste plage de température. Il est observé qu'une augmentation de la température améliore les performances en termes d'énergie et de puissance, ESR diminue. Par contre, l'autodécharge est plus importante et la durée de vie du dispositif diminue. L'étude en température a montré qu'il existe un fonctionnement optimal pour des températures se situant aux alentours de 25 °C où l'ESR approche sa valeur minimale en fonction de la température, l'autodécharge est assez faible et la durée de vie est convenable.

Un modèle thermique simple a été présenté. Il donne une estimation de la température du supercondensateur. Cependant, ce modèle est limité et il ne permet pas de prédire la

répartition avec précision de la température dans le supercondensateur ni d'optimiser la gestion thermique du composant.

L'évolution des performances des supercondensateurs lors du vieillissement accéléré a été représentée, d'un point de vue électrique global, par la diminution de la capacité, l'augmentation de l'ESR et de l'autodécharge.

Les différents circuits d'équilibrage sont simulés et leur influence sur la dynamique de la tension de cellules est montrée à long terme. Les résultats sont analysés sur plusieurs applications. Il est constaté que l'utilisation de circuits d'équilibrage améliore la performance du module de supercondensateurs vis-à-vis de la fiabilité. Le type du circuit d'équilibrage à considérer dépond du type d'application. Il sera important de valider expérimentalement les résultats obtenus sur les différents circuits d'équilibrage notamment sur des profils de tension et de courant industriels.

Les processus d'autodécharge dans les deux électrodes, positive et négative, peuvent être différents. La mesure de la décroissance de la tension des deux électrodes prises séparément serait important à réaliser pour mieux comprendre les mécanismes d'autodécharge.

Une autre méthode de caractérisation d'autodécharge, appelée `'floating», consisterait à appliquer une tension constante (polarisation potentiostatique) et de mesurer le courant d'alimentation. Il serait intéressant de comparer les résultats par cette méthode de caractérisation avec ceux obtenus par la méthode utilisée dans ce mémoire.

Les principaux inconvénients des supercondensateurs sont leur autodécharge élevée, leur faible densité d'énergie, leur faible tension nominale et la grande partie de l'énergie irrécupérable en dessous de 1 V. Ces facteurs limitent l'utilisation des supercondensateurs. La nouvelle génération de supercondensateurs asymétriques avec des électrodes hybrides limite certains de ces inconvénients [170]. Une étude complète de ce nouveau composant serait à envisager.

.

7. Références

7. Références

[1 ] A. Rufer, «Le supercondensateur et la batterie se marient pour fournie de l'énergie'`,

Electronique, vol. 100, février. 2000, pp. 81-84.

[2] M. Williams and J.L. Davis, Mixed-valence complex electrodes for a rechargeable electrical energy storage device, United States Patent 5383089, 1995.

[3] K.H. An et al., «High-Capacitance supercapacitor using a nanocomposite electrode of single-walled carbon nanotube and polypyrrole'`, Journal of The Electrochemical Society, vol. 149, 2002, p. A1058.

[4] F. Belhachemi, «Modélisation et caractérisation des supercondensateurs à couche double électrique utilisés en électronique de puissance'`, thèse de doctorat à l'INPL, Nancy, 2001.

[5] S. Rael, B. Davat, and F. Belhachemi, «Supercondensateurs à couche double électrique: principes de fonctionnement et comportement électrique'`, Journées Electrotechniques du Club EEA sur le thème : Énergie portable : autonomie et intégration dans l'environnement humain, Cachan/France, 2002.

[6] A.M. Namisnyk, «A survey of electrochemical supercapacitor technology «, University of Technology, Sydney/Australie , 2003.

[7] B.E. Conway, V. Birss, and J. Wojtowicz, «The role and utilization of pseudocapacitance for energy storage by supercapacitors'`, Journal of Power Sources, vol. 66, 1997, pp. 1-14.

[8] X. Andrieu, L. Moreau, and B. Pichon, «Etude comparative d'électrodes de carbone pour supercapacités à électrolyte organique'`, Journées d'Etudes sur les Supercondensateurs, Paris/France, 1998.

[9] «Quelques informations sur des techniques de stockage de l'énergie'`, documentation internet pl.legoff.free.fr.

[1 0] M. Rose, «Performance characteristics of large surface areas chemical double-layer capacitors'`, Proceedings of the 33rd International Power Sources Symposium, Penningham/UK. 1988, pp. 572-591.

[1 1] A. Burke and T. Murphy, «Material characteristics and the performance of electrochemical capacitors for electric/hybrid vehicle applications'`, Materials for Electrochemical Energy Storage and Conversion--batteries, Capacitors, and Fuel Cells: Symposium Held April 17-19, 1995, San Francisco, California, USA, 1995.

[1 2] D. Evans, J. Zheng, and S. Roberson, «Improved capacitor using amorphous RuO 2'`, doc. internet www. evanscap.com/technical.html.

[1 3] H. Kuzmany, M. Mehring, and S. Roth, «Electronic Properties of Conjugated Polymers III, Basic Models and Applications, Proc'`, Int. Winter School, Kirchberg, Austria, 1989.

[14] A. Burke, «Ultracapacitors: why, how, and where is the technology'`, Journal of Power Sources, vol. 91, 2 000, pp. 37-50.

[15] M. Tournoux and R. Durand, «Materiaux pour le stockage et la transformation électrochimique de l'énergie'`, Rapport de l'Institut des Matériaux de Nantes, pp. 40- 42.

[16] T. Morimoto et al., «Electric double-layer capacitor using organic electrolyte'`, Journal of Power Sources, vol. 60, 1996, pp. 239-247.

[17] G. Herlem, B. Fahys, and M. Herlem, «Nouveaux électrolytes non aqueux liquides pour supercapacités'`, Journées d'Etudes sur les Supercondensateurs, Paris/France, Février. 1998.

[18] Site internet : www.gore.com.

[19] Epcos, «UltraCapTM Double Layer Capacitors, A New Energy Storage Device for Peak Power Applications'`, Product Profile EPCOS, 2002.

[20] H. Gualous, «Stockage et gestion de l'énergie électrique dans des systèmes hybrides : applications au transport terrestre'`, HDR à l'Université de Franche-Comté, décembre, 2005.

[21] A. Schneuwly et al., «BOOSTCAP Double-Layer Capacitors for Peak Power Automotive Applications'`, Proceedings of the Energy Storage Association, Spring Meeting, 2001.

[22] A. Lagrange, «Condensateur'`, doc. N° E2060, techniques-ingenieur, 1996.

[23] Maxwell Technologies , «Boostcap Ultracapacitor Module Operating Manual'`, doc. internet www.maxwell.com , 2003.

[24] P. Mestre, «Utilization of ultracapacitors as a auxiliary power source in electric vehicle'`, Proceeding of the EPE, vol. 97, pp. 8-10.

[25] C. Raible and H. Michel, «High energy density with ultracapacitors. Bursting with power'`, Siemens Matsushita Components doc. internet http://www. epcos.
com/inf/20/35/articles.

[26] J. Lassègues, «Supercondensateurs'`, doc. N° D3334, techniques-ingenieur, , 2001.

[27] M. S. Halper and J. C. Ellenbogen, «Supercapacitors: A Brief Overview'`, The MITRE Corporation, McLean, Virginia, USA. doc. internet
http://www.mitre.org/work/tech_papers/tech_papers_06/06_0667/06_0667.pdf, Mar. 2006.

[ Maxwell Technologies, «Ultracapacitor p

28] roduct guide'`, doc. internet

www.maxwell.com.

[29] W. Koczara, Z. Chodnicki, and B Dakyo, «Power-energy management in lift drive system with supercapacitor compensator'`, ESSCAP, Belfort/ France. 2004.

[30] A. Marquet, «Application des supercondensateurs dans les réseaux de distribution électrique'`, JESC' 98, Paris/France, 1998.

[31] Batscap, «Les supercapacités, caractéristiques techniques «, doc. internet
www.batscap.com/supercapacite/conception.php.

[32] Maxwell Technologies, «M600 BOOSTCAP Ultracapacitor Cell'`, doc. internet www.maxwell.com.

[33] Maxwell Technologies, «Series BCAP'`, doc. internet www.b-l-
l.com/maxweel/contents/ultracapacitors/datasheets/BCAP_Series.pdf.

[34] «Ultracapacitors B49410B2366Q000'`, doc. internet
Epcos,

www.epcos.com/inf/20/35/ds/B49410B2366Q000.pdf.

[35] W. Lajnef, «Modélisations des supercondensateurs et évaluation leur vieillissement en cyclage actif à fort niveaux de courant pour des applications véhicules électriques et hybrides'`, thèse de doctorant, à l'université de Boréaux , 20 06.

[36] J. Bisquert et al., «Impedance of constant phase element (CPE)-blocked diffusion in film electrodes'`, Journal of Electroanalytical Chemistry, vol. 452, 1998, pp. 229-234.

[37] J. Bisquert et al., «Theoretical models for ac impedance of finite diffusion layers exhibiting low frequency dispersion'`, Journal of Electroanalytical Chemistry, vol. 475, 1999, pp. 152-163.

[38] J. Bisquert, G. Garcia-Belmonte, and A. Pitarch, «An explanation of anomalous diffusion patterns observed in electroactive materials by impedance methods.'`, Chemphyschem, vol. 4, 2003, pp. 287-92.

[39] M.W. Verbrugge and P. Liu, «Microstructural Analysis and Mathematical Modeling of Electric Double-Layer Supercapacitors'`, Journal of The Electrochemical Society, vol. 152, 2005, p. D79.

[40] A. Lasia , «Electrochemical Impedance Spectroscopy and its Applications Département de chimie'`, thèse de doctorat à l'Université de Sherbrooke, Québec/Canada, 1999.

[41] L. Zubieta and R. Bonert, «Characterization of double-layer capacitors for power electronics applications'`, Industry Applications, IEEE Transactions on, vol. 36, 2000, pp. 199-205.

[42] F. Belhachemi, S. Rael, and B. Davat, «Supercapacitors electrical behaviour for Power electronics applications'`, PEMC, vol. 200, pp. 3.195-3.200.

[43] achemi, S. Rael, and B. Davat, «A physical based model of power electric
F. Belh

double-layers supercapacitors'`, Industry Applications Conference, Industry Applications Conference IEEE, pp. 3069 - 3076.

[44] W. Lajnef et al., «Characterization methods and modelling of ultracapacitors for use as peak power sources'`, Journal of Power Sources, vol. 168, 2007, pp. 553-560.

[45] J. Bisquert, H. Randriamahazaka, and G. Garcia-Belmonte, «Inductive behaviour by charge-transfer and relaxation in solid-state electrochemistry'`, Electrochimica Acta, vol. 51, 2005, pp. 627-640.

[46] B. Bozzini, C. Mele, and I. Sgura, «On the observation of inductive high-frequency impedance behaviour during the electrodeposition of Au-Sn alloys'`, Journal of Applied Electrochemistry, vol. 34, 2004, pp. 277-281.

[47] X. Wu et al., «General Equivalent Circuits for Faradaic Electrode Processes under Electrochemical Reaction Control'`, Journal of The Electrochemical Society, vol. 146, 1999, p. 1847.

[48] F. Bretton, «Caractérisation et modélisation de supercondensateurs via un banc des essais'`, Stage de longue durée l'Université Claude B ernard , 2003.

[49] P. Kurzweil, «ac Impedance Spectroscopy-A Powerful Tool For The Characterization Of Materials And Electrochemical Power Sources'`, 14th International seminar on double layer capacitors, USA, 2004.

[50] R.L. Spyker and R.M. Nelms, «Classical equivalent circuit parameters for a doublelayercapacitor'`, Aerospace and Electronic Systems, IEEE Transactions on, vol. 36, 2000, pp. 829-836.

[51] D. IEC, «62391-1, Fixed electric double layer capacitors for use in electronic equipment'`, Part I: Gen eric specification (IEC 40/1378/CD, 2003), June, 2004.

[52] D. IEC, «62391-2, Fixed electric double layer capacitors for use in electronic equipment'`, Part I: Sectional specification: Electric double layer capacitors for power application (IEC 40/1379/CD, 2003), June, 2004.

[53] Maxwell Technologies , «Representative Test Procedure for Customer Evaluations'`, Application Note, doc. 1007239 doc internet www.maxwell.com, 2002.

[54] Epcos, «UltraCap Double Layer Capacitors Data Sheet Collection'`, doc. internet www.epcos.com, 2005.

[55] H. Gualous and R. Gallay, «applications des supercondensateurs'`, 2007.

[56] R. Spyker and R.M. Nelms, «Evaluation of double layer capacitor technologies for high power and hi gh energy storage applications'`, ieee- Industrial Electronics, 1997, pp. 1086-1091.

[57] B.E. Conway and W.G. Pell, «Power limitations of supercapacitor operation associated with resistance and capacitance distribution in porous electrode devices'`, Journal of Power Sources, vol. 105, 2002.

[58] W.G. Pell and B.E. Conway, «Quantitative modeling of factors determining Ragone plots for batteries and electrochemical capacitors'`, Journal of Power Sources, vol. 63, 1996, pp. 255-266.

[59] T. Christen and C. Ohler, «Optimizing energy storage devices using Ragone plots'`, Journal of Power Sources, vol. 110, 2002, pp. 107-116.

[60] T. Christen and M.W. Carlen, «Theory of Ragone plots'`, Journal of Power Sources, vol. 91, 2000, pp. 210-216.

[61] J. Miller and A. Burke, «Electric Vehicle Test Procedures Manual'`, Idaho National Engineering Laboratory Report No DOE/ID-10491, 1994.

[62] J.P. Zheng and T.R. Jow, «High energy and high power density electrochemical capacitors'`, Journal of Power Sources, vol. 62, 1996, pp. 155-159.

[63] B.E. Conway, «Analysis of power limitations at porous supercapacitor
W.G. Pell and

electrodes under cyclic voltammetry modulation and dc charge'`, Journal of Power Sources, vol. 96, 2001, pp. 57-67.

[64] P. Kurzweil, M. Chwistek, and R. Gallay, «Electrochemical and Spectroscopic Studies on Rated Capacitance and Aging Mechanisms of Supercapacitors Based on Acetonitrile'`, Proc. 2nd European Symposium on Super Capacitors & Applications.

[65] P. Kurzweil, M. Chwistek, and R. Gallay, «Capacitance Determination and Abusive Aging Studies of Supercapacitors Based on Acetonitrile and Ionic Liquids'`, The 16th International Seminar On Double Layer Capacitors,, Dec. 2006.

[66] P.L. Moss et al., «Transmission Line Model for Describing Power Performance of Electrochemical Capacitors'`, Journal of The Electrochemical Society, vol. 154, 2007, p. A1020.

[67] S.K. Tripathi, A. Kumar, and S.A. Hashmi, «Electrochemical redox supercapacitors using PVdF-HFP based gel electrolytes and polypyrrole as conducting polymer electrode'`, Solid State Ionics, vol. 177, 2006, pp. 2979-2985.

[68] M. Hahn et al., «Gas evolution in activated carbon/propylene carbonate based double-layer capacitors'`, Electrochemistry Communications, vol. 7, 2005, pp. 92 5-930.

[69] C.T. Hsieh and H. Teng, «Influence of oxygen treatment on electric double-layer capacitance of activated carbon fabrics'`, Carbon, vol. 40, 2002, pp. 667-674.

[70] S.A. Hashmi, R.J. Latham, and R. Schlindwein, «Studies on all solid state electric double layer capacitors using proton and lithium ion conducting polymer electrolytes'`, Journal of the Chemical Society, Faraday Transactions, vol. 93, 1997, pp. 4177-4182.

[71] uments, «Electrochemical Impedance Spectroscopy Theory: A Primer'`,
Gamry Instr

doc. internet www. gamry. com/App_Notes/EIS_Primer/EIS_Primer. htm.

[72] J. Jorcin, «Spectroscopie d'impedance electrochimique locale : caracterisation de la delamination des peintures et de la corrosion des alliages Al-Cu'`, Thèse de doctorat à INP de Toulouse/France , 2007.

[73] W. Adiran, «electrochemical impedance spectroscopy using the Bas-Zahner IM6 and IM6e impedance Analyzers'`, Current Separations, 1998, pp. 53-59.

[74] R.M. Nelms, D.R. Cahela, and B.J. Tatarchuk, «Modeling double-layer capacitor behavior using ladder circuits'`, Aerospace and Electronic Systems, IEEE Transactions on, vol. 39, 2003, pp. 430-4 38.

[75] J.R. Miller and D.A. Evans, «Design and performance of high-reliability double-layer capacitors'`, Electronic Components and Technology Conference, 1990. Proceedings., 40th, 1990, pp. 289-297.

[76] C. Portet et al., «Modification of Al current collector surface by sol-gel deposit for carbon-carbon supercapacitor applications'`, Electrochimica Acta, vol. 49, 2004, pp. 905-912.

[77] R.G.V. Hermann, «High performance double-layer capacitor for power electronic applications'`, Second Boostcap meeting, Montena Components SA, Fribourg, Switzerland, Mar. 2001.

[78] R.M. Nelms et al., «A comparison of two equivalent circuits for double-layer capacitors'`, Applied Power Electronics Conference and Exposition, 1999. APEC'99. Fourteenth Annual, vol. 2, 1999.

[79] N. Khan et al., «Transient analysis of pulsed charging in supercapacitors'`, TENCON 2000. Proceedings, vol. 3, 2000.

[80] P. Kurzweil , B. Frenzel , and R. Gallay, «Capacitance Characterization Methods and Ageing Behaviour of Supercapacitors'`, The 15th International Seminar On Double Layer Capacitors, 2005.

[81] L. Zubieta and R. Bonert, «Characterization of double-layer capacitors (dlcs) for power electronics applications'`, Industry Applications Conference, IAS Annual Meeting IEEE, vol. 2, 1998, pp. 1149-1154.

[82] L.E. Zubieta , «Characterization of double-layer capacitors for power electronics applications.'`, thèse de doctorat at University of Toronto/Canada, 1999.

[83] R. Bonert and L. Zubieta, «Measurement techniques for the evaluation of double-layer powercapacitors'`, Industry Applications Conference, 1997. Thirty-Second IAS Annual Meeting, IAS'97., Conference Record of the 1997 IEEE, vol. 2, 1997.

[84] E. Harzfeld,, R. Gallay, and M. Hahn, «Capacitance and Series Resistance determination in high power ultracapacitors'`, ESSCAP, Belfort/France, 2004.

[85] H. Gualous, R. Gallay, and A. Berthon, «Utilisation des supercondensateurs pour le stockage de l'énergie embarquée: applications transport: Le stockage de l'énergie au service du transport'`, REE. Revue de l'électricité et de l'électronique, 2004.

[86] W. Lajnef et al., «Ultracapacitors modeling improvement using an experimental characterization based on step and frequency responses'`, Power Electronics Specialists Conference, 2004. PESC 04. 2004 IEEE 35th Annual, vol. 1, 2004.

[87] Z. Chlodnicki and W. Koczara, «Supercapacitor storage application for reduction drive negative impact on supply grid'`, Compatibility in Power Electronics, 2005. IEEE, 2005, pp. 78-84.

[88] R. Kötz et al., «Supercapacitors for peak-power demand in fuel-cell-driven cars'`, ECS Electro-Chemical Society, 52nd Meeting,, San Francisco, Sept, 2001, pp. 2-7.

[89] E. Warburg, Ann. Physik, vol. 67, 1899, p. 493.

[90] S.R. Taylor and E. Gileadi, «Physical interpretation of the Warburg impedance'`, Corrosion, vol. 51, 1995.

[91] D. Grahame, «Mathematical theory of the Faradic admittance'`, Journal of Electrochemical Society, vol. 99, 1952, p. 370C.

[92] R. Kötz and M. Carlen, «Principles and applications of electrochemical capacitors'`, Electrochimica Acta, vol. 45, 2000, pp. 2483-2498.

[93] F. Rafik et al., «Supercapacitors characterization for hybrid vehicle applications'`, Power Electronics and Motion Control Conference, 2006. IPEMC'06. CES/IEEE 5th International, vol. 3, 2006.

[94] S. Buller et al., «Simulation of supercapacitors in highly dynamic applications'`, 18th International Electric Vehicle Symposium, Berlin, Germany, October, 2001.

[95] S. Buller et al., «Modeling the dynamic behavior of supercapacitors using impedance spectroscopy'`, Industry Applications Conference, 2001. Thirty-Sixth IAS Annual Meeting. Conference Record of the 2001 IEEE, vol. 4.

[96] S. Buller, «Impedance-based simulation models for energy storage devices in advanced automotive power systems'`, Thesis, Institute for Power Electronics and Electrical Drives ISEA Aachen/Germany, 2002.

[97] E. Karden, S. Buller, and R.W. De Doncker, «A frequency-domain approach to dynamical modeling of electrochemical power sources'`, Electrochimica Acta, vol. 47, 2002, pp. 2347-2356.

[98] R. de Levie, «On porous electrodes in electrolyte solutions'`, Electrochimica Acta, vol. 8, 1963, pp. 751-780.

[99] D. Riu, N. Retiere, and D. Linzen, «Half-order modelling of supercapacitors'`, Industry Applications Conference, 2004. 39th IAS Annual Meeting. Conference Record of the 2004 IEEE, vol. 4, 2004.

[100] V.S. Muralidharan, «Warburg impedance-basics revisited'`, Anti-Corrosion Methods and Materials, vol. 44, 1997, pp. 26-29.

[1 01] A. Lasia, «Impedance of porous electrodes'`, Journal of Electroanalytical Chemistry, vol. 397, 1995, pp. 27-33.

[102] W.G. Pell and B.E. Conway, «Voltammetry at a de Levie brush electrode as a model for electrochemical supercapacitor behaviour'`, Journal of Electroanalytical Chemistry, vol. 500, 2001, pp. 121-133.

[103] E. Surewaard et al., «Advanced Electric Storage System Modeling in Modelica'`, Proceedings of the 3 rdInternational Modelica Conference, pp. 95-102.

[1 04] N. Rizoug, « Modélisation électrique et énergétique des supercondensateurs et méthodes de caractérisation : Application au cyclage d'un module de supercondensateurs basse tension'`, thèse de doctorat à l' Ecole Centrale de Lille - Université des sciences et technologies de Lille/France, 2006.

[1 05] W. Lajnef et al., «Ultracapacitor electrical modelling using temperature dependent parameters'`, Belfort/France, pp. ESSCAP, novembre 2004.

[1 06] M. Yang et al., «A hybrid genetic algorithm for the fitting of models to electrochemical
impedance data'`, Journal of Electroanalytical Chemistry, vol. 519, 2002, pp. 1-8.

[1 07] P. Zoltowski, «The power of reparametrization of measurement models in electrochemical impedance spectroscopy'`, Journal of Electroanalytical Chemistry, vol. 424, 1997, pp. 173-178.

[1 08] E.C. Levy, «Complex curve fitting'`, IRE Transactions on Automatic Control, vol. 4, 1959, pp. 37-43.

[1 09] Zahner, «Thales Software Package'`, doc. internet www.zahner.de. .

[110] P.J. Mahon et al., «Measurement and modelling of the high-power performance of carbon-based supercapacitors'`, Journal of Power Sources, vol. 91, 2000, pp. 68-76.

[111] C. Hitz and A. Lasia, «Experimental study and modeling of impedance of the her on porous Ni electrodes'`, Journal of Electroanalytical Chemistry, vol. 500, 2001, pp. 213-222.

[112] J.B. Jorcin et al., «CPE analysis by local electrochemical impedance spectroscopy'`, Electrochimica Acta, vol. 51, 2006, pp. 1473-1479.

[1 13] A. Hammar, « Modélisation du supercondensateur et étude de son vieillissement : utilisation dans les applications de transports ferroviaire'`, thèse de doctorat à l'université Claude Bernard - Lyon 1, 2006.

[114] E. Karden, «Using low-frequency impedance spectroscopy for characterization, monitoring, and modeling of industrial batteries'`, RWTH Aachen, Diss, 2001.

[1 15] D. Harrington and B. Conway, «Ac impedance of faradaic reactions involving electrosorbed intermediates. I: Kinetic theory'`, Electrochimica acta, vol. 32, 1987, pp. 1703-1712.

[116] B.E. Conway, Electrochemical Supercapacitors: Scientific Fundamentals and Technological Applications , Kluwer Academic/Plenum Publishers, 1999.

[117] C.A. Schiller et al., «Relaxation impedance as a model for the deactivation mechanism of fuel cells due to carbon monoxide poisoning'`, Physical Chemistry Chemical Physics, vol. 3, 2001, pp. 211 3-2116.

[118] B. Savova-Stoynov and Z.B. Stoynov, «Analysis of the inductance influence on the measured electrochemical impedance'`, Journal of Applied Electrochemistry, vol. 17, 1987, pp. 1150-1158.

[119] H. Gualous et al., «Experimental study of supercapacitor serial resistance and capacitance variations with temperature'`, Journal of Power Sources, vol. 123, 2003, pp. 86-93.

[120] F. Rafik et al., «Frequency, thermal and voltage supercapacitor characterization and modeling'`, Journal of Power Sources, vol. 165, 2007, pp. 92 8-934.

[121] F. Rafik, «Modélisation des comportements des supercondensateurs, études de leur vieillissement dans des milieux contraints, applications aux systèmes d'automatisation Picke and Place'`, thèse de doctorat à l'Université de Franche-Comté/France, 2007.

[122] R. Kötz, M. Hahn, and R. Gallay, «Temperature behavior and impedance fundamentals of supercapacitors'`, Journal of Power Sources, vol. 154, 2006, pp. 550-555.

[123] J. Schiffer, D. Linzen, and D.U. Sauer, «Heat generation in double layer capacitors'`, Journal of Power Sources, vol. 160, 2006, pp. 765-772.

[124] A. Sarja, "Reliability based life cycle design and maintenance planning, " Workshop on Reliability Based Code Calibration, March 21-22, 2002, Zurich, Suisse

[125] O. Bohlen, J. Kowal, and D.U. Sauer, «Ageing behaviour of electrochemical double layer capacitors Part II. Lifetime simulation model for dynamic applications'`, Journal of Power Sources, vol. 173, 2007, pp. 626-632.

[126] , J. Kowal, and D.U. Sauer, «Ageing behaviour of electrochemical double O. Bohlen

layer capacitors Part I. Experimental study and ageing model'`, Journal of Power Sources, vol. 172, 2007, pp. 468-475.

[1 27] M. Correvon, «Modélisation thermique des composants de puissanc'`, doc. internet www.files.iai.heig-vd.ch.

[128] W. Lajnef et al., «First step in the reliability assessment of ultracapacitors used as power source in hybrid electric vehicles'`, Microelectronics and reliability, vol. 44, 2004, pp. 1769-1773.

29]

[1

[1
[1

[1

L. Zubieta and R. Bonert, «Experimental 400 kW sec double-layer capacitor energy storagesystem'`, Industry Applications Conference, 1999. Thirty-Fourth IAS Annual Meeting. Conference Record of the 1999 IEEE, vol. 4, 1999.

30] W. Lajnef et al., «Specification and use of pulsed current profiles for ultracapacitors power cycling'`, icroelectronics Reliability, vol. 45, 2005, pp. 1746-1749. M

31] P. Guillemet, Y. Scudeller, and T. Brousse, «Multi-level reduced-order thermal modeling of electrochemical capacitors'`, Journal of Power Sources, vol. 157, 2006, pp. 630-640.

32] J. Didier , «Thermique pour l'électricien'`, doc. internet www.stielec.ac-aixmarseille.fr, 2001.

[133] H. Gualous et al., «Supercapacitor Thermal Characterization in Transient State'`, Industry Applications Conference, 2007. 42nd IAS Annual Meeting. Conference Record of the 2007 IEEE, 2007, pp. 722-729.

[134] A. Schneuwly and R. Gallay, «Properties and applications of supercapacitors-From the state-of-the -art to future trends'`, PCIM2000 Power Quality, Nürnberg, Germany.

[135] G. ALCICEK, «Étude et amélioration de la sûreté de fonctionnement des supercondensateurs.'`, Master recherche : procédé et traitement de l' énergie électrique Université de Franche Comté. 2006.

[136] T. Umemura et al., «Life expectancy and degradation behavior of electric double layer capacitor part I'`, Properties and Applications of Dielectric Materials, 20 03. Proceedings of the 7th International Conference on, vol. 3, 2003.

[137] P. Azais, «Recherche des causes du vieillissement de supercondensateurs à électrolyte organique à base de carbones activés'`, thèse doctorat, Université d'Orléans/France, 2003.

[1 38] B.W. Ricketts and C. Ton-That, «Self-discharge of carbon-based supercapacitors with

organic electrolytes'`, Journal of Power Sources, vol. 89, 2000, pp. 64-69.

[1 39] «Simple measurement of supercapacitor parameters'`, Application Note AN1005

revision .0, doc. internet www.cap-xx.com. .

[140] B.E. Conway, W.G. Pell, and T.C. Liu, «Diagnostic analyses for mechanisms of self-discharge of electrochemical capacitors and batteries'`, Journal of Power Sources, vol. 65, 1997, pp. 53-59.

[141] D.R. Crow, Principles and Applications of Electrochemistry, CRC Press, 1994.

[142] M. Hahn et al., «Supercapacitors based on glassy carbon and sulfuric acid-mechanisms of self-discharge'`, Electro chemistry , pp. 67-68 .

[143] D. Devilliers and É. Mahé, «Cellules électrochimiques: aspects thermodynamiques et cinétiques'`, l'actualité chimique, 2003, p. 31.

[1 44] R. Rosser, «Conduction, processus Faradique faradique s et non faradique s'`, doc. N° J1802, techniques-ingenieur, 2005.

[145] Z. Ding, et al., «Modeling of the supercapacitors and influence of the temperature during selfdischarge'`, ESSCAP, Belfort/France, 2004.

[146] H. Douglas and P. Pillay, «Sizing ultracapacitors for hybrid electric vehicles'`, Industrial Electronics Society, 2005. IECON 2005. 32nd Annual Conference of IEEE, 2005, pp. 1599-1604.

[147] ., «Contribution to the sizing of supercapacitors and their applications'`, F. Rafik et al

ESSCAP, Belfort/France, 2004.

[148] M. Ayad et al., «Association de convertisseurs multiniveaux et de supercondensateurs dans une alimentation continue réversible isolée'`, EPF'00, pp. 233-238.

[149] A.S. Gianni and A. Schneuwly, «Role and utilization of voltage balancing device for EDLC stacks'`, ESSCAP, Lausanne/Suisse, 2006.

[150] N. Rizoug et al., «Voltage sharing in supercapacitor modules: experimental study'`, Power Electronics Specialists Conference, 2004. PESC 04. 2004 IEEE 35th Annual, vol. 1, 2004.

[151] P. Barrade, S. Pittet, and A. Rufer, «Energy storage system using a series connection of supercapacitors, with an active device for equalizing the voltages'`, IPEC, 2000, pp. 3- 7.

[152] A. Rufer and P. Barrade, «Key Developments for Supercapacitive Energy Storage: Power Electronic Converters, Systems and Control'`, Second Boostcap Meeting, vol. 29, 2001.

[153] arie Françoise, «Contribution à la commande neuronale et à la gestion d'énergie

J.N. M

d'un système hybride batterie-supercondensateurs (Application aux transports terrestres)'`, thèse doctorat à l'Université de Franche-Comté, Belfort/France, 2004.

[1 54] Y. Diab, P. Venet, and G. Rojat , «Comparison of the Different Circuits Used for Balancing the Voltage of Supercapacitors: Studying Performance and Lifetime of Supercapacitors'`, ESSCAP, Lausanne/Suiss e, 2006.

[155] D. Linzen et al., «Analysis and evaluation of charge-balancing circuits on performance, reliability, and lifetime of supercapacitor systems'`, Industry Applications, IEEE Transactions on, vol . 41, 2005, pp. 1135-1141.

[156] Y. Kobayashi, «Acceleration coefficient of the molded electric double layercapacitor'`, Electronic Components and Technology Conference, 1992. Proceedings., 42nd, 1992, pp. 617-623.

[1 57] O. Tebbi, «Estimation des lois de fiabilité en mécanique par les essais accélères», thèse de doctorat, Université d'Angers, 2005.

[1 58] S.W. Moore and P.J. Schneider, «A Review of Cell Equalization Methods for Lithium
Ion and Lithium Polymer Battery Systems'`, SAE Publication, 2001, pp. 01-0959.

[1 59] A. Hammar et al., «Assessment of electrothermal model of supercapacitors for railway applications'`, Power Electronics and Applications, 2005 European Conference on, 2005, p. 8.

[160] V.V. Harri and E. Egger, «All-purpose circuitry concept SAM applications and networking for supercapacitors «, 2nd Boostcap Meeting, Fribourg/Switzerland, 2001.

[1 61] B. Maher, «A backup power system using ultracapacitors'`, Power Electronics Technology, 2004, pp. 44-49.

[162] Y.H.K. Do Yang Jung, «Development of Ultracapacitor Modules for 42 Volt Automotive Electrical Systems'`, Journal of Power Sources, vol. 114, Mar. 2003, pp. 366-373.

[163] «application and balancing circuit «, doc. internet www.engineerlive.com. .

[164] P. Venet, «Amélioration de la sûreté de fonctionnement des dispositifs de stockage d'énergie''`, HDR à l'Université Claude Bernard-Lyon 1, 2007.

65]

[1
[1
[1

P. Barrade, «Series Connection of Supercapacitors: Comparative Study of Solutions for the Active equalization of the Voltages'`, PCIM 2000: International Conference on Power, Conversion and Intelligent Motion, Nürnberg/Germany, June 2000, p. 4.

66] J. Lachaize, «Étude des stratégies et des structures de commande pour le pilotage des systèmes énergétiques à Pile à Combustible (PAC) destinés à la traction», Thèse de doctorat à l'ENSEEIHT Toulouse/ France, 2004.

67] Ph. Desprez, G. Barrailh, P. Lavaur, M. Bariand, C. Jehoulet, S. Raël , B. Davat,, « SAFT Supercapacitors cells and batteries'`, Proc. EPE'03, Toulouse/France, 2003.

[168] P. Desprez et al., Supercapacitor balancing method and system, Brevet US 2003/0062876 A1 déposé le 17 juin 2002 et publié le 3 avril 2003, équivalent européen : brevet EP 1 274 106 A1 déposé le 10 juin 2002 et publié le 8 janvier 2003, équivalent français : brevet FR 2 826 202 déposé le 18 juin 2002 et publié le 20 décembre 2002., .

[1 69] P. Thounthong, «Conception d'une source hybride utilisant une pile à combustible et des super-condensateurs'`, thèse de doctorat à l'l'Institut National Polytechnique de Lorraine, Nancy/France, 2005.

[170] H. Gualous G. Alcicek, Y. Diab, A. Hammar, P. Venet, K. Adams, M Akiyama, C. Marumo, `' Lithium Ion capacitor characterization and modelling», ESSCAP 2008, Rome, Italy.

8. Annexes

8. Annexes

A. Caractéristiques techniques de spectroscopie d'impédance (photo)

		PC+IM6	PC+IM6+PP240
Mode de fonctionnement		Potentiostatique, Galvanostatique	Potentiostatique, Galvanostatique
Plage de tensions		#177;10V	#177;4V
Précision sur la tension		#177;500uV	#177;0,1%/#177;1mV
Plage de courants		#177;3A	0A à #177;40A
Précision sur le courant		0,1% à 1%	#177;0,25%
Puissance de sortie		36W max	400W
Plage de fréquences		10uHz à 8MHz	10uHz-100kHz
Plage d'impédances		1m?-30 M?	1u?-1k?
Température ambiant		0°C à 30°C	0°C à 30°C
Amplitude du signal alternatif		1mV à 1V	1mV à 1V
Précision sur la phase		#177;0,1° à #177;0,3°	#177;0,1° à #177;0,3°
PP240 IM6

B. Variation des éléments de la capacité de la branche rapide en fonction de la température ambiante

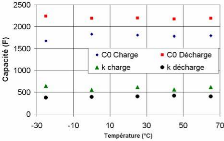
Figure 1 : Evolution des éléments de la capacité C1 en fonction de la température pour le composant
BCAP010

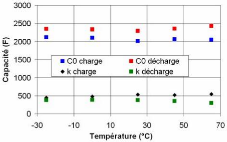
Figure 2 : Evolution des éléments de la capacité C1 en fo nction de la température pour le composant
M6 00 déterminée à u n courant de charge/décharge de 400 A

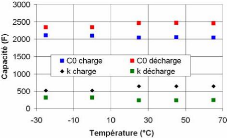
Figure 3 : Evolution des éléments de la capacité C1 en fonction de la température pour le composant
M600 déterminée à un courant de charge/décharge de 50 A

C. Dépendance en température des paramètres des supercondensateurs Nous présentons sur les figures ci-dessous la variation des caractéristiques électriques des

deux supercondensateurs M60 0 et SC806 en fonction de la température.

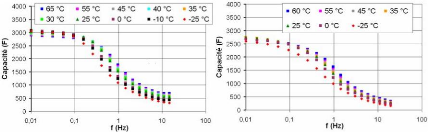
(a) M600

(b) SC806

Figure 4: Evolution de la capacité du supercondensateur M600 et SC806 en fonction de la fréquence

pour plusieurs températures à la tension nominale

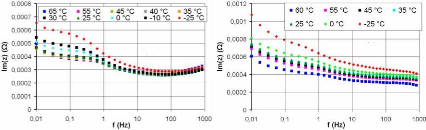
(a) M600

(b) SC806

Fig. 8-1 : Évolution de la partie réelle de l'impédance des composants M600 et SC806
en fonction de la fréquence pour plusieurs températures à la tension nominale

D. Caractéristiques du module NI 9211

· Températures de fonctionnement de -40 à 70 °C,

· 4 entrées de thermocouples ou de tension de #177;80 mV,

· Résolution de 24 bits, réjection du bruit 50/60 Hz.

E. Caractéristiques du banc Arbin

· de 0 V à 3 0V

· de -500A à +500A en charge et de décharge.

· puissance max :15 KW

· 3 gammes de courant : à 500 A, précision : 500mA 0 à 50 A, précision : 50mA 0 à 1 A, précision : 1mA

F. Caractéristiques du module NI 9205

· Résolution de 16 bits, fréquence d'échantillonnage rassemblé de 250 Kéch./s,

· Températures de nt de -40 à 70 °C,

fonctionneme

· Gammes d'entrée programmables de #177;200 mV, #177;1 V, #177;5 V et #177;10 V,

· 32 entrées analogiques asymétriques ou 16 différentielles.

Résumé :

Etude et modelisation des supercondensateurs : applications aux systèmes de puissance

Ce travail a pour objectif d'analyser quantitativement les performances (capacité, ESR, autodécharge, ...) des supercondensateurs issus de différentes technologies lorsqu'ils sont soumis aux contraintes électriques et thermiques. Les différents paramètres de ces supercondensateurs sont caractérisés par les techniques de spectroscopie d'impédance, de cycles de charge/décharge et de voltampérométrique.

La modélisation des supercondensateurs a été effectuée par plusieurs modèles complémentaires. Les résultats de simulation de ces derniers sont comparés avec ceux expérimentaux dans le domaine temporel et fréquentiel. Nous avons mis au point un modèle innovant de l'autodécharge dans les supercondensateurs.

L'ensemble de ce travail a permis d'étudier le comportement des supercondensateurs mis en série en mettant en évidence leur fiabilité, le temps d'équilibrage et le rendement énergétique global du système.

Mots-clés : Supercondensateur, caractérisation, modélisation, autodécharge, thermique, fiabilité, circuit d'équilibrage.

Abstract :

Studying and modelling of supercapacitors : Applications in power systems

The aim of this work is to analyze quantitatively the supercapacitors performance (capacitance, ESR, self-discharge ...), which are made by different technologies under constraints; thermal and electrical. Different supercapacitors parameters are characterized by the help of different techniques as impedance spectroscopy, voltamperometry, and charging/discharging cycles.

The supercapacitors modelling have been conducted by several complementary models. These models are compared in time and frequency domain with various experimental tests. A new model of the self-discharge was established.

All the life expectancy, energetic efficiency and balancing time are compared for different balancing circuits and typical applications.

The whole of this work has helped to investigate the supercapacitors behaviour applied in series demonstrating their reliability, the balancing time and the total energy efficiency of the system.