|

DECREMER Renaud
Université Paul Verlaine de Metz
UFR Droit, Economie, Administration

Mémoire de M1 en Sciences Economiques

Sous la direction de Monsieur Philippe CASIN
« L'université Paul Verlaine de METZ
n'entend donner ni approbation, ni
improbation aux opinions émises dans ce
mémoire. Celles-ci doivent être
considérées
comme personnelles à son auteur. »
PREFACE ET REMERCIEMENTS
Cette partie a vocation à retranscrire
brièvement la manière dont le mémoire a vu le jour ainsi
que mes impressions personnelles avant, pendant, et après la
réalisation de ce dernier. Si seul le sujet en lui-même vous
intéresse, vous pouvez sans problème passer outre cette partie et
vous rendre directement au sommaire.
Le mémoire, pour un étudiant de master,
constitue probablement, dans la majorité des cas, le travail le plus
abouti, le plus long, le plus complexe, le plus intéressant et le plus
personnel auquel il n'a jamais eu l'occasion de prendre part. C'est bien
entendu mon cas, et c'est pour cela que je tiens à m'exprimer sur le
déroulement de celui-ci.
Il est important de rappeler que le mémoire constitue
un choix pour un étudiant, dans la mesure où celui-ci est libre
de choisir le sujet qui lui convient le mieux parmi ceux qui lui sont
proposés. Mon choix s'est porté sur ce sujet (la
régression PLS), pour plusieurs raisons. La première est que j'ai
toujours été attiré par l'analyse de données, les
statistiques, et les chiffres en général. Mais bien que ce
domaine me fascine, il m'a, à plusieurs reprises, posé des
problèmes (difficultés de compréhension notamment) tout au
long de mon cursus. J'ai donc tenu, en choisissant ce sujet, à essayer
de renverser certaines de ses difficultés, d'autant plus que je pense
être amené à me spécialiser en Expertise Statistique
dans le cadre de la dernière année de ma filière. Il
était donc très important, à ce titre, pour moi, de
réaliser par moi-même un travail où je puisse
développer ma propre approche, à partir des
éléments avec lesquels j'étais à l'aise, d'un sujet
qui m'était jusqu'alors inconnu, et qu'il allait falloir comprendre par
moi-même, avec pour seule aide les diverses recherches que j'allais
devoir mener, et quelques explications venant de la part du responsable du
sujet que j'ai choisi. C'est dans ce contexte que le choix d'un tel sujet m'est
apparu comme étant la meilleure solution. Bien entendu, il est
évident que le choix de ce sujet ne s'est pas fait sans tenir compte
d'autres facteurs, notamment l'imposante demande, de la part des autres
étudiants, pour certains sujets faisant une plus grande
unanimité, n'ayant pas trait au domaine de l'analyse de données.
Il était alors évident que mon choix allait se porter sur ce
sujet.
Le sujet étant choisi, j'ai eu toute liberté
pour mener ce travail dans la direction qui me convenait le mieux. J'ai alors
décidé d'adopter la démarche qui est
généralement la mienne lorsque je suis amené à
traiter un sujet auquel je ne suis pas encore familiarisé, à
savoir celle qui consiste à « comprendre pour expliquer ». Je
pense que certains étudiants auraient abordé ce mémoire en
lançant un maximum de recherches sur le sujet, en faisant un immense
effort de synthèse et de réorganisation des idées, et en
retranscrivant, dans une formulation qui leur est plus ou moins propre, le
compte- rendu de leurs recherches. Cela n'a pas été ma
démarche, car un tel effort ne m'aurait pas permis d'approfondir
à ma guise ma connaissance du sujet. J'ai donc effectué un
certain nombre, limité, de recherches, sans chercher à me
documenter de manière exhaustive. Le but n'était pas de
réunir tous les ouvrages accessibles traitant du sujet,
mais simplement de trouver une base de réflexion me
permettant de situer le sujet, et de me renseigner sur ses principaux enjeux.
Par la suite, le travail de recherche a pris une proportion très
marginale par rapport au travail de réflexion personnelle, car c'est
avant tout ce travail qui m'a permis d'avancer dans ce mémoire. C'est ce
travail qui m'a donné la possibilité de vérifier que
l'enjeu de la méthode était bien réel, et ne se justifiait
pas qu'à travers les dires des auteurs qui ont eu le loisir de s'y
intéresser.
Le lecteur que vous êtes notera assez rapidement et
aisément que mon approche fut assez littéraire. En effet, selon
moi, les diverses formules et propriétés mathématiques ne
trouvent leur sens qu'en tant qu'outil permettant de raisonner et de tirer des
conclusions, qui doivent rester compréhensibles par la majorité,
et donc littéraires. De plus, de très nombreux travaux ayant
déjà été menés sur ce sujet, il était
inutile de se focaliser sur les formules et les démonstrations
mathématiques, auxquelles je ne pouvais, personnellement, rien apporter.
J'ai donc simplement retranscrit les formules à la base de la
méthode, principalement en utilisant les notations de l'ouvrage de
Michel Tenenhaus (« La Régression PLS -- Théorie et Pratique
»), qui d'ailleurs fut l'ouvrage central autour duquel s'est construit mon
mémoire, sans pour autant lui avoir emprunté une part très
importante de contenu (exception de la brève présentation
historique du sujet faite en tout début de première partie, et de
la faite démonstration sur l'indépendance des composantes PLS).
J'ai donc tâché de rester le plus littéraire et le plus
compréhensible possible, afin ceux qui n'ont que des connaissances
limitées en statistiques (dont je fais partie) puissent décemment
comprendre ce la majorité de ce qu'ils pourront lire dans ce
mémoire, et se familiariser avec les notions les plus importante de
celui-ci. Si mon approche avait été trop
mathématisée, ou trop complexe, je n'aurais pas pu
prétendre avoir apporté quoi que ce soit au lecteur, car je
n'aurais fait que rendre compte des travaux de personnes nettement plus
connues, expérimentées et très probablement plus
compétentes que moi, et j'aurais été incapable de me
retrouver dans ce mémoire, pas plus que je n'aurais été
capable de comprendre et de m'imprégner de la plupart des notions que
j'aurais été amené à utiliser.
Bien entendu, cela ne m'a pas empêché
d'évoquer les formules dont sont issues les composantes de la
régression PLS, ni d'évoquer certaines propriétés
mathématiques de l'analyse, parfois sous forme de formules, car il
aurait été déplacé de parler d'un sujet dont les
fondements (les formules mathématiques) ne sont pas abordés.
Aussi, je n'ai pas la prétention d'affirmer qu'un lecteur n'ayant aucune
notion statistique sera capable de suivre l'intégralité des
raisonnements qui sont développés tout au long de ce
mémoire (que ce soit dans les parties mathématiques ou dans les
parties littéraires). Néanmoins, je garde l'espoir qu'elles
puissent trouver, dans ce mémoire, une présentation plus
abordable de la méthode et de son utilité, que ce qu'il est
généralement coutume de rencontrer dans la plupart des travaux
traitants du sujet (que ce soit dans les livres ou sur internet).
Etant donné l'approche utilisée pour
réaliser ce travail, il m'a été très difficile
d'établir un plan dès le départ. Plusieurs idées me
sont venues à l'esprit, mais il m'était pratiquement impossible
de retenir un plan qui soit trop précis avant d'avoir abordé les
différents aspects que je tenais à traiter. C'est pour cela que
le plan a beaucoup évolué (sans jamais avoir existé dans
une version qui soit un tant soit peu détaillée) jusqu'à
ce que le mémoire ne soit terminé, car sa structure
dépendait de l'évolution de ma perception du sujet,
elle-même conditionnée par l'avancée de ce mémoire.
C'est notamment pourquoi, pendant longtemps, j'ai pensé intégrer
à ce mémoire une partie « Application à la
réalité », faisant la démonstration d'une utilisation
de la régression PLS sur un jeu de données réelles, avant
d'avoir l'idée, qui m'a semblée plus intéressante, de
créer une partie « Simulations », faisant elle aussi la
démonstration d'une utilisation de la méthode, mais sur
données fictives, créées de toutes pièces à
l'aide de Microsoft Excel 2003 et de sa fonction permettant de
générer une composante aléatoire. Au départ, je ne
souhaitais pas que la partie « Simulations » écarte totalement
la partie « Application à la réalité », mais la
différence d'intérêt entre les deux méthodes,
combinée au fait que le mémoire devait toucher à sa fin
(pour des raisons de temps), a fait que j'ai préféré
totalement délaisser cette idée initiale, pour ne pas risquer de
compromettre l'intérêt de celle que j'ai finalement
décidé de retenir. Naturellement, j'aurais souhaité que
cette partie soit tout de même intégrée à ce
mémoire, mais elle ne m'aurait que très difficilement permis de
me prononcer sur l'efficacité de la méthode, sauf à
disposer de suffisamment de données que pour être en mesure de
former une population mère, sur laquelle j'aurais pu testé les
qualités de prédictions des modèles établis sur
base d'un échantillon réduit de cette population. Mais même
si tel avait été le cas, je n'aurais que très
difficilement pu disposer de données desquelles j'étais
suffisamment informé des propriétés que pour pouvoir tirer
des conclusions générales sur l'efficacité de la
méthode, et sur les meilleures conditions d'efficacité de
celle-ci. Dans une certaine mesure, les différentes simulations que j'ai
pu mener lors des différents tests m'ont permis d'isoler l'influence de
certains facteurs, et de tenter des conclusions sur l'impact de ces derniers
sur l'efficacité de la méthode. Voila pourquoi j'ai
privilégié cette partie.
Le fait de ne pas avoir pu intégrer cette partie «
Application à la réalité » constitue mon plus grand
regret, car le but de toute méthode statistique reste probablement de
pouvoir servir dans un cadre réel, le contraire leur enlevant tout
intérêt. De ce point de vue, une application sur des séries
réelles, dans le but de modéliser des relations liant des
variables réelles, est nettement moins abstraite que ne le seront jamais
des données fictives, ce qui aurait pu être plus parlant aux yeux
de certains lecteurs.
Ce n'est pas mon seul regret. J'aurais également
aimé pouvoir approfondir les tests, en faire davantage, et faire
davantage de simulations pour chaque test, afin qu'en ressortent des
conclusions plus précises, plus ciblées, plus exhaustives.
Toutefois, je n'aurais pas souhaité que ce soit au prix d'une
transparence amoindries des simulations réalisées, qui ont
été volontairement très détaillées.
Je regrette également de ne pas avoir
évoqué le cas de la régression PLS multivariée
(c'est-à-dire : avec de multiples variables expliquées), ou
encore de ne pas avoir traité le cas de la régression PLS avec
présence de données manquantes. Ces deux cas existent pourtant et
représentent deux avantages considérables de cette
méthode.
Toutefois, il faut garder à l'esprit que ces divers
approfondissements auraient probablement rendu le mémoire nettement
moins compréhensible, et nettement plus fastidieux à aborder dans
son intégralité.
Finalement, je m'estime satisfait de ce mémoire,
à plusieurs titres. Il m'a tout d'abord permis d'améliorer ma
compréhension générale du domaine statistique, et plus
particulièrement ma compréhension du sujet. Ensuite, le travail
qu'il a nécessité m'a permis d'améliorer ma méthode
de travail, ma capacité à m'organiser, à gérer le
facteur temps, à mieux cerner les qualités et les défauts
inhérents à ma manière de travailler, et à mener
à bien un travail de plus grande ampleur que ceux que j'ai pu
connaître jusqu'à présent. Il m'a également permis
de m'épanouir à travers une démarche personnelle, et donc
adaptée à moi-même, me permettant par la même
occasion d'aborder les aspects du sujet auxquels je suis le plus sensible.
J'en viens donc à la fin de ce préambule et j'en
profite pour remercier ceux qui ont, directement ou indirectement,
contribué à ce mémoire. La première personne qui me
vient à l'esprit est Monsieur Philippe Casin, maître de
conférence dans ma faculté (UFR Droit, Economie et Administration
de l'université Paul Verlaine de Metz), et responsable de la direction
de ce mémoire (et à l'origine de la présence du sujet
parmi les sujets disponibles). Son aide, ses conseils et indications m'ont
notamment permis de mieux cerner le sujet et d'en déduire l'orientation
que je souhaitais lui donner. Je remercie également Christine
Stachowiak, également enseignante de ma faculté et responsable
méthodologique des mémoires de ma promotion. Je remercie ces deux
professeurs à la fois pour leur apport au mémoire, mais
également pour leurs enseignements auxquels j'ai pu assister. D'autres
professeurs me viennent également à l'esprit, dans la mesure
où ils m'ont permis d'acquérir certaines connaissances
mathématiques (ou autres ayant servi à ce mémoire) et
m'ont permis de maitriser certaines notions. Je remercie donc, de
manière générale, tous les professeurs dont j'ai pu
assister aux cours, plus particulièrement Monsieur François
Marque (enseignant en mathématiques, statistiques, et informatique),
Monsieur Marius Marchal (enseignant en mathématiques et statistiques) et
Monsieur Pierre Morin (enseignant en Macroéconomie appliquée, et
ayant eu la délicatesse d'expliquer efficacement la signification de
certaines statistiques utilisées dans le cadre des différents
modèles économétriques vu en cours).
Bien entendu, je ne pourrais conclure cette section sans citer
Michel Tenenhaus, omniprésent et incontournable s'agissant de la
régression PLS, et dont l'ouvrage (évoqué plus haut)
m'aura permis de disposer d'une base solide de réflexion. J'en remercie
donc l'auteur, en saluant l'exhaustivité dont il a su faire preuve.
INTRODUCTION
GENERALE
L'analyse statistique est un large domaine recouvrant des
techniques d'analyse de plus en plus nombreuses. Ces nouvelles techniques se
développent continuellement, pour faire face à différents
problèmes. Les attentes envers ces analyses sont de plus en plus
élevées, et on cherche à les rendre de plus en plus
efficaces, et de plus en plus adaptées à des situations
concrètes, parfois très spécifiques. Ainsi, lorsque l'on
tente d'expliquer une variable par plusieurs autres variables (la
première étant la variable expliquée, ou endogène,
et les autres étant les variables explicatives, ou exogènes), on
ne cherche pas seulement à obtenir un modèle minimisant les
erreurs d'estimations des individus actifs (individus à partir desquels
le modèle a été construit), on cherche également
à obtenir un modèle qui soit facilement interprétable, et
qui permette d'effectuer des prévisions sur des individus (ou des
entrées) pour lesquels on ne connaît pas la valeur de la variable
explicative. Il faut, bien évidemment, que ces prévisions soient
les plus proches possibles de la réalité. Il faut
également que les modèles soient stables, c'est-à-dire que
les chances d'obtenir un modèle trop éloigné de la
réalité soient minimales, car on ne peut pas toujours comparer
les valeurs estimées aux valeurs réelles, dont on ne dispose pas
(à priori), puisqu'on cherche à les estimer. Il faut parfois
même que ce modèle remplisse ces conditions alors que l'on dispose
de très peu d'individus actifs, alors même que le nombre de
variables explicatives est très élevé, ce qui rend
pourtant, d'un point de vue théorique, la construction d'un
modèle, représentatif de la réalité, très
délicate. C'est précisément ce à quoi tente de
répondre la régression PLS.
Comme nous allons le constater tout au long de ce
mémoire, la régression linéaire simple ou multiple,
répondant au simple critère des MCO (moindres carrés
ordinaires), est souvent prise à défaut lorsqu'il s'agit
d'applications de ce type. Soit, tout simplement, parce que les conditions
initiales, à cause des propriétés mêmes de cette
méthode, rendent son calcul impossible, ce qui est notamment le cas
lorsque le nombre de variables explicatives devient inférieur au nombre
d'individus actifs, puisqu'il existe alors une infinité de solutions au
problème de la minimisation du critère des MCO, toutes
répondant à une égalisation à zéro de ce
critère (et donc impossibles à discerner les unes des autres).
Soit, sans rentrer dans des cas aussi extrêmes, parce que cette
méthode est peu efficace sur des situations tendant à approcher
ce cas limite. La multicolinéarité des variables explicatives
pose également d'importants problèmes de stabilité de
cette méthode. La régression PLS, en contournant ces
problèmes, parvient à proposer des modèles parfois
étonnants de précision et de stabilité, compte tenu de
conditions initiales qui sont parfois, à priori, très peu
propices à l'établissement d'un modèle (échantillon
de taille réduite, de mauvaise qualité, grand nombre de variables
explicatives, ...). C'est ce que nous allons tenter d'expliquer, et
d'apprécier, au cours de ce mémoire, en comparant et en opposant
les deux approches.
Dans la première partie de ce mémoire, nous
présenterons et définirons la méthode. Nous exposerons les
formules qui permettent de construire ce modèle. Bien que la
régression PLS puisse être multivariée (c'est-à-dire
avec des modèles présentant plusieurs variables explicatives) et
s'appliquer sur des échantillons présentant des données
manquantes, nous ne nous intéresserons qu'au cas de la régression
PLS univariée sans données manquantes, notamment afin de ne pas
compliquer la compréhension et l'interprétation des formules.
Nous verrons également que la régression PLS étant un
processus itératif, dont les résultats varient en fonction du
nombre d'étapes choisies, il est nécessaire de
s'intéresser à des critères, plus ou moins objectifs,
permettant de retenir un certain nombre d'étapes. Dans la seconde
partie, nous nous intéresserons à quelques cas «
extrêmes », mettant en valeur les qualités et défauts
inhérents à l'approche PLS, de sorte à permettre au
lecteur de mieux cerner l'enjeu de l'utilisation correcte de cette
méthode. Nous verrons également que la régression PLS, en
réalité, constitue une forme de généralisation de
la régression linéaire au sens des MCO, et peut
s'appréhender en termes de « moindres carrés partiels »
(Partial Least Squares, dont les initiales sont à l'origine de
l'appellation de la méthode). Enfin, dans la troisième partie,
nous ferons de vrais simulations sur des jeux de données fictives
(présentant un certain degré d'aléa) afin de faire une
démonstration des qualités d'estimation de la régression
PLS, particulièrement dans certaines conditions, tout en expliquant
comment retenir le nombre correct d'étapes au regard des
critères. Nous pourrons ainsi comparer les différents
modèles obtenus et nous prononcer sur l'utilité de la
méthode et de l'application des critères qui lui sont
indissociables, tout en nous prononçant sur l'influence des
propriétés de l'échantillon.
Il est important de noter que plusieurs logiciels ont
été utilisés dans le cadre de ce mémoire. Les plus
utilisés ont été Microsoft Word (rédaction du
mémoire) et Microsoft Excel (réalisation de divers calculs, des
tableaux, et de la partie simulations) dans leurs versions 2003 et 2007. Paint
a été utilisé afin de convertir les tableaux Excel au
format image. Certaines équations ont été
générées à l'aide du complément Microsoft
Equations 3.0. Les régressions PLS ont toutes été
effectuées avec StatBox Pro 6.40. Les régressions
linéaires des moindres carrés ordinaires ont été
effectuées avec Eviews 5.0.
SOMMAIRE
Introduction GénéraleFFFFFFFFFFFFFFFFFFFFFFFFFF..
8
Partie 1 : Présentation de la régression
PLS
I. Contexte historiqueFFFFFFFFFFFFF.FFFFFFFFFF... 13
II. Qu'est-ce que la régression PLS 7
FFFFFFFFFFFFFFFFFF. 13
III. Principes d'une régression
linéaireFFFFF...FFFFFFFFFFFF 14
IV. Les avantages de la régression PLS 15
V. Le principe de la régression PLS
univariéeFFFFFFFFFFFF.FF 16
VI. Les étapes de calcul de la régression PLS1
19
VII. Indépendance des
composantesFFFFFFFFFFFFFFFFFFF. 24
VIII. Centrage et réduction des
donnéesFFFFFFFFFFFFFF.FFF 26
IX. Le critère de validation croisée
FFFFFFFFFFFFFFFFFF 28
X. Les critères liés à la covariance
composante - variable expliquéeFFFFF 32
Partie 2 : Utilisation de la régression PLS sur
des cas limites
I. Régression PLS avec une seule variable
explicativeFFFFFFFFFFF. 35
II. Un exemple à trois variables
explicativesFFFFFFFFFFFFFF.F 38
III. La régression linéaire et le critère
des moindres carrésFFFFFFF...FF 48
IV. La régression PLS comme généralisation
des MCOFFFFFFFFFFF 48
V. Le critère de la régression
PLSFFFFFFFFFFFFFFFFFFF 53
Partie 3 : Simulations
I. Test n°1FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 64
II. Test n°2FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 82
III. Test n°3FFFFFFFFFFFFFFFFFFFFFFFF.FFFF 102
IV. Conclusions sur les simulations réalisées
119
Conclusion généraleFFFFFFFFFFFFFFFFFFFFFFFFFF.
121
Bibliographie 124
Table des matières 125
AnnexesFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF. 127
PARTIE 1
Présentation de la régression
PLS
I. Contexte historique1
La régression PLS (Partial Least Squares
regression) est une technique d'analyse et de prédiction
relativement récente. Elle a été conçue pour faire
face aux problèmes résultants de l'insuffisance de l'utilisation
de la régression linéaire classique, qui trouve ses limites
dès lors que l'on cherche à modéliser des relations entre
des variables pour lesquelles il y a peu d'individus, ou beaucoup de variables
explicatives en comparaison au nombre d'individus (le nombre de variables
explicatives pouvant excéder très largement le nombre
d'individus), ou encore lorsque les variables explicatives sont fortement
corrélées entre elles.
La méthode PLS répond précisément
à ses problèmes. Cette méthode fut proposée par
Wold S., Albano C., Dunn III W.J., Esbensen K., Hellberg S., Johansson E. et
Sjôstrôm M. en 1983, et connu de grands succès dans le
domaine de la chimie, où, souvent, les données répondent
à ce type de propriétés. La méthode PLS fut
principalement développée autour de Svante Wold, qui a
dirigé de nombreuses thèses portant sur le sujet. De plus, ce
dernier, associé à Nouna Kettaneh-Wold et à plusieurs
collaborateurs, ont développé le logiciel d'analyse des
données SIMCA-P, logiciel centré sur la régression PLS.
En France, Michel Tenenhaus s'est beaucoup
intéressé à cette méthode et a
réalisé de nombreux travaux à ce sujet. Son ouvrage «
La régression PLS -- Théorie et Pratique » (2002,
éditions TECHNIP) a énormément contribué à
la réalisation de ce mémoire, notamment dans la partie
théorique de ce dernier.
Par ailleurs, Tenenhaus M. pense que la régression PLS
pourrait connaître les mêmes succès qu'en chimie si elle
était utilisée dans d'autres domaines.
Voyons à présent en quoi consiste cette
méthode.
II. Qu'est-ce que la régression PLS ?
La régression PLS est une méthode statistique
permettant d'identifier des relations entre plusieurs variables. Il y a
toujours, d'une part, les variables explicatives (notées
généralement x1, ..., xp), et les variables expliquées
(notées généralement y1, ..., yq). Ces variables sont,
dans une régression PLS, toutes étudiées sur les
mêmes « individus ». On distingue la régression PLS
univariée, ou « régression PLS1 », de la
régression PLS multivariée, appelée également
« régression PLS2 ». Dans le premier cas, la régression
ne porte que sur une seule variable expliquée. Dans le second, il peut y
avoir plusieurs variables expliquées (et, même si l'algorithme de
la régression PLS multivariée est présenté
différemment de celui de la version simple, il constitue une
généralisation de
1 D'après Tenenhaus M. (2002). La
Régression PLS-- Théorie et Pratique, Editions TECHNIP
ce dernier dans la mesure où les résultats sont
équivalents lorsque la régression PLS multivariée ne porte
que sur une seule variable expliquée).
La régression PLS s'inscrit dans la catégorie des
régressions linéaires. Il convient donc, avant de rentrer dans le
coeur du sujet, de comprendre ce qu'est une régression
linéaire.
III. Principes d'une régression
linéaire
Le but de la régression est donc d'expliquer les
valeurs et les variations d'une ou plusieurs variables expliquées (les
« y ») par les valeurs et les variations d'une ou plusieurs variables
explicatives (les « x »). Par exemple, on peut chercher à
expliquer le poids d'un individu (variable expliquée) par sa taille
(variable explicative). Dans ce cas, on a une régression PLS
univariée avec une seule variable explicative. Naturellement, il
paraît difficile d'admettre, dans la pratique, que le poids d'un individu
puisse être seulement expliqué par sa taille. En effet, plusieurs
individus de même taille peuvent avoir un poids différent, et,
plus généralement, on peut dire que le poids des individus n'est
pas strictement fonction de leur taille. Cela ne veut pourtant pas dire que la
taille d'un individu ne peut pas constituer un facteur explicatif de son poids.
Il s'agit donc d'une « variable explicative » potentielle parmi
d'autres. On peut affiner l'analyse en ajoutant, dans la liste des variables
explicatives, le montant du budget de cet individu consacré à
l'alimentation. Cela devrait donc nous permettre, en partie, de comprendre
pourquoi deux individus de même taille peuvent avoir un poids
différent (la seconde variable explicative, c'est-à-dire la part
de budget consacrée à l'alimentation, pouvant d'expliquer
certaines divergences). Evidemment, cela ne suffira pas à expliquer
entièrement les écarts que l'on peut observer d'un individu
à l'autre. Il est bien entendu possible de trouver des variables
supplémentaires susceptibles d'expliquer mieux encore les variations de
la variable « poids » d'un individu à l'autre. Mais le fait
d'intégrer de plus en plus de variables rend l'analyse plus
compliquée et les résultats plus difficiles à
interpréter. En fait, on attend de l'analyse qu'elle nous renseigne
à la fois sur l'importance des différentes variables «
explicatives », et sur le bienfondé de l'intégration de
chaque variable dans l'analyse.
Il est important de signaler que l'analyse ne doit jamais
porter sur un seul individu. En effet, ce qu'on attend de la régression,
c'est qu'elle nous fournisse les coefficients (associés à chaque
variable explicative) les plus pertinents possibles. On cherche (lorsque la
régression se limite à une seule variable expliquée) une
fonction linéaire permettant d'estimer une valeur de « y » en
fonction de chaque valeurs prises par les x1, ...,xp. Cela passe donc par la
recherche de coefficients, de sorte à trouver une fonction du type y =
a*x1 + b*x2 +... Si la régression porte sur un seul individu, les
coefficients seront infiniment instables dès lors qu'il y a plus d'une
variable explicative. En effet, si on prend le cas d'un individu de 80 kg,
mesurant 180 cm et consacrant 1.000 € chaque année à
l'alimentation, il existe une infinité de combinaisons permettant de
retranscrire cette relation. Par exemple, on pourrait dire que le poids en kg
de cet individu est égal à
0,444 fois sa taille en centimètres, ou bien à
0,08 fois son budget alimentation en euros, ou encore à 0,222 fois sa
taille en centimètres auxquels on additionne 0,04 fois son budget
alimentation en euros. Cela nous donnerait une infinité de
modèles impossibles à départager. Et, plus important
encore, ce modèle ne serait probablement pas pertinent s'agissant d'un
autre individu. Il faut donc, de préférence, un nombre
d'individus assez conséquent, de sorte à avoir une
régression plus pertinente, susceptible de correspondre à
n'importe quel individu, avec une marge d'erreur dont on peut se faire une
idée raisonnable. Naturellement, le fait d'intégrer toujours plus
d'individus à l'analyse ne supprimera pas la marge d'erreur. Mais cela
permettra d'avoir les coefficients les plus précis possibles, et d'avoir
une idée précise de la marge d'erreur (qu'on peut estimer, par
exemple, à l'aide du coefficient de corrélation).
En fait, le but premier de la régression n'est pas de
s'intéresser à un individu particulier, mais à un individu
« abstrait », pour lequel les relations entre les variables sont des
relations valables « en moyenne », peu importe les valeurs prises par
les variables explicatives. Lorsqu'on a estimé les coefficients de la
régression, on attend que celle-ci nous donne un modèle qui, pour
chaque valeurs que peuvent prendre les différentes variables
explicatives, renvoi une valeur de la variable expliquée qui, en
moyenne, doit correspondre à la réalité, avec la marge
d'erreur la plus faible possible.
Ceci est donc l'objet de la régression PLS. Mais c'est
aussi celui de la régression linéaire simple ou multiple (avec,
dans ce cas, toujours une seule variable expliquée « y »).
Cette régression linéaire à un objectif simple : trouver
les coefficients, pour chaque variable explicative, qui minimisent les
écarts, pour la variable expliquée, entre les valeurs
estimées par le modèle, et les valeurs observées dans la
pratique, pour l'échantillon donné sur lequel est effectué
la régression. Il s'agit de minimiser la somme des résidus (mis
au carré, dans le simple but d'éviter la compensation
systématique des erreurs positives et négatives), ou, dit
autrement, de maximiser le coefficient de corrélation (ce qui est un
objectif propre à la régression linéaire, qui ne
s'applique pas forcément à la régression PLS, du moins pas
dans toutes ses étapes).
Voyons à présent quel est l'intérêt de
la régression PLS par rapport aux autres modèles
linéaires.
IV. Les avantages de la régression PLS
Etant donné que la régression linéaire
permet de traiter le type de problème que nous avons
précédemment abordé, pourquoi donc chercher à
utiliser la régression PLS ? Qu'est-ce qu'elle apporte de plus que la
régression linéaire ?
Partie 1: Présentation de la régression PLS
En fait, les avantages de la régression PLS sont nombreux :
- Tout d'abord, dans le cas régression PLS
multivariée (régression PLS2), il peut y avoir plusieurs
variables expliquées. Nous n'évoquerons malheureusement pas ce
cas.
- Dans le cas où une des variables explicatives serait
une stricte combinaison linéaire des autres, la régression
linéaire ne peut avoir lieu sans enlever au moins une variable
explicative de l'analyse. La régression PLS ne présente pas cet
inconvénient.
- La régression PLS peut traiter des cas où les
individus seraient moins nombreux que les variables explicatives. La
régression linéaire ne peut le faire.
- La régression PLS, étant basée sur
l'algorithme NIPALS, permet de travailler sur des échantillons
même si certaines données manquent pour certains individus pour
certaines variables, et ce sans même à avoir à estimer au
préalable les données en question. Néanmoins, nous nous
limiterons dans ce mémoire aux formules de la régression sans
données manquantes, car elles sont plus faciles à
interpréter.
- Lorsque les variables explicatives sont fortement
corrélées entre-elles, la régression linéaire
devient très peu pertinente, au sens où les coefficients qui en
ressortent deviennent très instable lorsque l'on « bruite »
les données (on fait varier, de manière aléatoire et
très légère, les données de l'échantillon).
La régression PLS, basée sur des critères de covariance,
est considérée comme étant plus robuste. Les coefficients
demeurent stables et gardent une certaine significativité, même en
présence de corrélations fortes entres les variables.
Voyons donc comment fonctionne cette méthode qui semble si
avantageuse.
V. Le principe de la régression PLS
univariée
Le principe de la régression PLS est assez simple, bien
que se déroulant en un nombre d'étapes à priori non
défini (se construisant toutes de la même manière, à
partir des résidus des précédentes étapes).
On a d'une part une variable qu'on cherche à expliquer
« y », et d'autre part des variables explicatives « x1, x2, ...,
xp ». Les valeurs de ces variables (les yi, x1i, x2i, ..., xpi) sont
observées sur « n » individus.
Remarque : Les données associées aux variables
y, x1, x2, ..., xp seront centrées et réduites, ce qui est
obligatoire et indispensable dans le cadre de la régression PLS. Les
coefficients de corrélation entre ces variables seront donc égaux
à leur covariance. Pour centrer les données, on soustrait
à chaque donnée de la série la moyenne de la série.
Pour les réduites, on divise chaque donnée de la série par
l'écart type de cette dernière. Au final, on a donc une moyenne
nulle pour chaque série, et un écart-type égal à 1
(et donc une variance elle aussi égale à 1). Nous reviendrons
plus tard sur le centrage et la réduction des données, qui sont
des étapes assez simples, n'altérant pas la structure de variance
des différentes données.
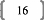
La régression va consister à chercher des
composantes ti, t2, ..., s'exprimant en fonction des variables explicatives xi,
x2, ..., xp, en trouvant une série de coefficients (pour chaque
composante : un coefficient associé directement ou indirectement
à chaque variable) pour chaque composante, à la manière
d'une régression linéaire, à la différence
près que les coefficients sont calculés sur base d'un
critère de covariance.
On procède par étape. D'abord, on défini
ti en cherchant des coefficients w11, wi2, ..., wip pour chaque variable
explicative. On obtient donc une équation du type : t1 = wMM*xM +w12*x2
+ ... + w1p*xp.
Ensuite, on effectue une régression linéaire de
ti sur y. Ainsi, on peut exprimer y en fonction de ti, à l'aide d'un
coefficient ci (9- = ci*ti)2. En fait, cela permet tout d'abord
d'obtenir de manière rapide un coefficient de corrélation, afin
d'estimer la qualité de la régression à l'étape 1.
Ensuite, cela permet d'exprimer directement y en fonction de xi, x2, ..., xp,
en « transformant » les coefficients wMM, wM2, ..., wip, en les
multipliant par une constante, afin de réorienter la régression
sur l'échelle de la variable y.
A l'étape 1, l'équation sera donc la suivante : 9-=
cM*wMM*xM + ci*wi2*x2 + ... + cl*w1p*xp. (1)
On a donc une régression s'exprimant de manière
similaire à une régression simple, mais avec un critère de
covariance. On connaît la qualité de la régression
grâce au coefficient de corrélation de ti avec y.
Néanmoins, si la qualité de la régression
n'est pas satisfaisante, on peut l'améliorer en ajoutant des composantes
supplémentaires.
Dans la deuxième étape, on va
s'intéresser à la fraction de variance des variables qui
échappe à la première étape de la
régression, c'est-à-dire les résidus. On va donc effectuer
les régressions des variables y, xi, x2, ..., xp sur ti et obtenir des
séries statistiques correspondant aux résidus de ces
séries de base, séries que nous nommerons respectivement yi, xii,
xM2, ..., xlp.
Ensuite, la même méthode qu'à
l'étape 1 sera appliquée pour déterminer une composante
t2, mais cette fois à partir des séries y1, x11, x12, ..., xlp.
On obtient alors des coefficients w2i, w22, ..., w2p qui permettent d'exprimer
t2 en fonction de xMM, xM2, ..., xip. Nous verrons qu'il est possible, à
partir de là, et des régressions des variables explicatives sur
ti, d'exprimer directement t2 en fonction des variables initiales
2 Pour chaque modèle, 9- est la
notation employée pour désigner l'estimation de la variable y par
le modèle en question. Pour obtenir la valeur de y correspondante (dans
le cas d'un individu connu), il suffit d'ajouter à 9- les
résidus de la régression du modèle en question.
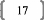
centrées-réduites (plutôt qu'en fonction de
leurs résidus, ce qui facilite le calcul et l'interprétation),
avec des coefficients recalculés.
Ensuite, on effectue une régression linéaire
multiple de y sur ti et t2. Comme c'est une régression linéaire,
la qualité de la régression ne peut qu'en être
améliorée (du moins au niveau du coefficient de
corrélation).
On obtient alors l'équation suivante : y = ci*ti + c2*t2.
Nous verrons par la suite pourquoi le coefficient ci n'est pas modifié
par rapport à la régression de la première
étape.
Si on détaille cette équation, obtient :
y = ci*Wii*xi + ... + cl*W1p*xp + c2*W21*x11 + ... + c2*W2p*xlp
(2)
Nous verrons qu'il est possible de simplifier cette
équation de sorte à exprimer directement y en fonction des
variables explicatives initiales, c'est-à-dire en éliminant les
séries correspondant aux résidus des régressions des
variables initiales sur ti. Une telle simplification sera possible à
chaque étape, de sorte à conserver, à chaque étape,
un modèle linéaire s'exprimant directement en fonction des
variables initiales.
Cette équation, à l'étape 2, paraît
déjà fort complexe sous forme de formule. Néanmoins, dans
le cas d'un exemple concret, elle est écrite de manière tout
à fait similaire à une régression linéaire multiple
(lorsque les coefficients sont connus numériquement). Seuls les
coefficients affectés à chaque variable varient.
Naturellement, on peut encore ajouter des étapes
supplémentaires pour affiner la qualité de la régression,
selon le même principe. Cela ne compliquera pas vraiment l'étude
du modèle définitif car il sera toujours aussi facile à
analyser (un seul coefficient définitif pour chaque variable
explicative, même si ce coefficient s'obtient par un calcul de plus en
plus long au fur et à mesure que l'on ajoute des étapes).
Notons qu'il est possible de retenir un certain nombre
d'étapes en fonction de critères objectifs quant à la
significative de chaque étape. Nous nous intéresserons par la
suite à quelques critères permettant de déterminer, plus
ou moins objectivement, le nombre d'étapes à retenir.
Il est maintenant temps de passer aux étapes de calcul
à proprement parler.
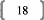
VI. Les étapes de calcul de la régression
PLS1
Comme expliqué précédemment, nous nous
contenterons des formules de la régression PLS sans données
manquantes, afin d'éviter de compliquer l'interprétation de ces
dernières. Néanmoins, il est bon de savoir que, en cas de
régression PLS avec données manquantes, les formules changent,
même si elles sont équivalentes à celle de la
régression PLS sans donnée manquantes lorsqu'il ne manque aucune
donnée.
Dans un premier temps, il s'agit de trouver une composante
qu'on nommera t1, qui, à l'instar de la variable expliquée dans
la régression linéaire, sera exprimée en fonction des
variables explicatives à l'aide de coefficients qui seront
calculés au cours de cette étape. « y » sera par la
suite exprimé directement en fonction de cette composante « t1
».
Ces coefficients, notés w1j (dans le cas de celui
associé à la « jème variable explicative
», le « 1 » étant associé à la
première composante « t1 ») vont être
déterminés selon un critère de covariance, et leur
méthode de calcul est très simple et facilement
interprétable, surtout en l'absence de données manquantes.
La formule, pour le jème coefficient, est la
suivante :
Y
~
Cov(x ~
~ ~
~
(3)
~
Y
~
Cov2(x ~ ~

19
(Naturellement, il ne faut pas confondre le « j
» de la somme des « covariances-carré » de tous les
« xj » avec y, avec le « j » présent dans le terme
« w1j » et au dénominateur de l'expression du membre de
droite, qui signifie que l'on s'intéresse uniquement au cas de
lajème variable)
Ce sont donc les covariances, pondérées par la
racine de la somme de leurs carrés, qui vont déterminer les
coefficients de la composante « t1 », et donc indirectement la
relation entre les variables explicatives et « y ». Le fait que la
pondération s'effectue par rapport à des covariances dont les
valeurs sont mises au carré indique qu'on souhaite éviter la
neutralisation des covariances positives et négatives, et qu'on veut
pondérer chaque covariance par l'importance totale de toutes les
covariances entre les variables explicatives et « y ».
Le fait que la covariance d'une variable explicative avec la
variable « y » détermine directement le coefficient qui sera
affecté à cette variable dans le modèle explicatif de la
variable « y », signifie que quoi qu'il arrive, plus cette covariance
sera élevée, et plus le coefficient sera important, et ce quelque
soient les corrélations relatives des différentes variables
explicatives. On a donc ici une première idée de la «
robustesse » de la régression PLS.

20
Une fois les coefficients wMj obtenus, il devient très
facile d'obtenir la composante ti :
p
t1 1 ixi ~(4)
i 1
Dit autrement :
tl = wMM*xM + w12*x2 + ... + wip*xp (5)
Ensuite, on effectue une régression simple de y sur ti, et
on obtient donc :
."= cM*tM (6)
." correspondant à la série des estimations des
valeurs dey selon cette régression.
Et donc y = ci*ti + yi (7)
yi correspondant naturellement à la série des
résidus de cette régression simple.
On peut donc exprimer y directement en fonction des variables
explicatives xi, ..., xp. ."= cl*w11*x1 + cl*w12*x2 + ... + cl*w1p*xp (8)
Il s'agit là d'une manière de réajuster les
coefficients wMj à l'échelle de y, en les multipliant par la
constante ci.
Les « p » coefficients wij*ci nous donnent des
indications claires sur l'importance de la prise en compte de chaque variable
sur la régression. En outre, ces coefficients seront du même signe
que les coefficients de corrélation et que les covariances des variables
auxquelles ils sont associés avec y. Ils seront d'ailleurs directement
proportionnels aux covariances. Il n'en va pas de même dans une
régression linéaire multiple. Il en résulte une
interprétation des coefficients beaucoup plus simple.
Cette régression simple, de y sur ti, nous permet
d'obtenir un coefficient de corrélation, qui nous permet
d'apprécier la qualité de la régression à
l'étape 1, ainsi qu'une série de résidus yl, qui s'obtient
en calculant la différence suivante :
y1 = y -- cM*ti (9)
Si on estime la qualité de la régression
insuffisante, on peut passer à l'étape 2, qui se déroule
de manière comparable à l'étape 1, mais qui porte non plus
sur les variables initiales (centrées-réduites) y, xi, ..., xp
mais sur les résidus de leur régression simple sur ti, qu'on
appellera donc yi, xMM, ..., xip. Ces nouvelles séries,
créées en effectuant autant de régression simples que de
variables, sont donc indépendantes de la première composante ti.
Le pouvoir explicatif de la composante t2, qui sera créée sur
base de ces
variables, sera donc complètement nouveau et pourra donc
venir s'additionner à celui de la composante ti.
A l'étape 2, nous allons obtenir une série de
coefficients W2; (W2i, W2p), qui nous
permettront d'exprimer t2 en fonction des variables xMM, F, xip,
résidus des régressions des variables y, xi, F, xp sur ti.
La formule de ces coefficients est strictement identique
à celle de leurs équivalents de l'étape 1. Seules les
variables sur lesquelles ils sont calculés changent (on passe des
variables de départ aux séries de résidus) :
)
w2
~
)
Cov(x1i ,
~ 1
(10)
i 1
i

Cov2(x1i ,
~ 1

21
Et, de manière équivalente à l'étape
1 :
~
i 1
On effectue une régression de y sur ti et t2 et on obtient
la relation suivante : y = ci*ti + c2*t2 + y2 (12)
Le coefficient ci restera identique à celui de
l'étape 1 car, les variables ti et t2 étant indépendantes,
la prise en compte de la variable t2 dans la régression ne modifie pas
la relation initiale définie dans la régression entre y et ti.
Néanmoins, cette formulation pose problème, puisque
cette fois, y est fonction des variables initiales, mais aussi des variables
résiduelles (obtenue par régression sur ti) :
[= cl*W11*x1 + F+ cl*W1p*xp + c2*W21*x11 + F+ c2*W2p*xlp (13)
Les équations deviennent plus chargées, et
l'interprétation plus compliquée. Les estimations deviennent
également nettement plus laborieuses, si on donne des valeurs arbitraire
aux variables xi et si on cherche à connaître la valeur
correspondante pour y estimée par le modèle.
Mais il y a moyen de ré-exprimer l'équation de
t2 directement en fonction des variables initiales xi. Pour se faire, il suffit
de se rappeler comment celles-ci ont été construites : à
partir des variables xi et de ti, lors des régressions des variables xi
sur ti.

22
Ainsi, on a effectué, pour chaque valeur de j allant de 1
à p, la régression linéaire simple suivante :
x; = cii*ti + xM+ (14) Le coefficient « ci; »
étant le coefficient de régression de la variable x; sur
tM.
Les xi; peuvent donc s'exprimer de la manière suivante
:
xi; = xi -- ci+*ti (15)
Donc, il est possible d'exprimer t2 en fonction des coefficients
cii, et des variables xi et de la composante ti.
P
t2 = E W2J . * (X J
. -- c 1J . * t ) .(=> (16)
J . 1
Sachant que la composante ti peut elle aussi s'exprimer en
fonction des variables xj. L'équation devient donc :
P P
t2 W2 J .*
(X -c1J . EW1J . X ) (17 )
J .1 J .1
Si on détaille l'équation, cela nous donne :
t2 = w21*[xl -- ciM*(wiM*xi+ +wip*xp)] + + w2p*[xp -- cip*(wiM*xi
+ + wip*xp)]
Equation que l'on peut réécrire :
t2 = W21 *X1 --
(EP c1J . W2J .
W11)* #177;
·
·
·+ W2P
P X (P c1J . * W2J . *
P )* X P
J .1J .1
Ou encore :
P P
(18)
t2 (w21
2 W *
11 c1J .
W )*X (W *E )*X
2J . 1 "' 2P -W C W
1P 1J . 2J . P
J .1 J .1
On peut donc définir des coefficients que nous appelleront
« w2i' » permettant d'exprimer t2en fonction des variables xi :
|
W2
|
P
J .I=W2J .-W Ec
*W
2j
1J . 1J . 2j
|
(19)
|
J . 1

23
Partie 1: Présentation de la régression PLS
Ainsi, on peut résumer t2 à l'équation suivante :
p
/ . 1
C'est-à-dire :
t2 = w21'*x1 + ... + w2p'*xp (20) L'équation de y devient
alors :
p p
Y*
J
* *w
1
c1
. X/ . #177;c2
*Ew2/ . X q (21)
/ . 1 / . 1
Où y* est une autre notation pour .3
Ou:
[= c1*w11*x1 + ... + c1*w1p*xp + c2*w21'*x1 + ... + c2*w2p'*xp
Equation qui peut se réécrire :
[= (c1*w11+c2*w21')*x1 + ... + (c1*w1p+c2*w2p')*xp
(22) ou encore
y = (c1*w11+c2*w21')*x1 + ... + (c1*w1p+c2*w2p')*xp + y2 (23)
y2 étant la série des résidus de la régression
de y sur (t1,t2).
y peut donc s'écrire directement en fonction des variables
xj.
La régression de y sur t1 et t2 nous donne le
coefficient de corrélation de la régression à
l'étape 2. Il nous permet également, par déduction, de
connaître l'amélioration du coefficient de corrélation du
fait de l'ajout de la 2ème étape.
On peut bien évidemment envisager une
3ème étape, en travaillant à partir des
résidus de l'étape 2. Pour se faire, on peut soit effectuer une
régression multiple de y, x1, ..., xp sur (t1,t2) et calculer les
résidus, soit effectuer une régression simple de y1, x11, ...,
x1p sur t2, et calculer les résidus. La seconde méthode semble
être la plus simple étant donné qu'à
3 Les différences de notations sont dues
à l'utilisation de Microsoft Equations 3.0, logiciel permettant
d'insérer des équations notamment dans des documents Word mais ne
présentant pas les mêmes possibilités en matière
d'insertion de caractères spéciaux.
ce stade des calculs, on connaît normalement
déjà les variables yi, xii, ..., xMp puisqu'on a
été obligé de les calculer lors de la seconde
étape.
Nous allons maintenant nous intéresser à une
propriété très intéressante des composantes, il
s'agit de l'orthogonalité (indépendance) des composantes entre
elles.
VII. Indépendance des composantes
L'une des propriétés primordiales d'une
régression PLS est l'indépendance des composantes ti, t;, ..., tH
formées à partir des variables explicatives.
En effet, la première composante ti est formée
à partir des variables explicatives, en leur donnant certains
coefficients sur base de leur covariance avec la variable expliquée
« y » (ou de leur coefficient de corrélation avec la variable
y si les variables sont centrées réduites). Pour se faire, la
variable ti sera représentative d'une partie de la variance des
variables explicatives. Bien entendu, si y n'est pas une combinaison
linéaire des variables explicatives, et qu'il y a plus d'une variable
explicative dans l'analyse (et qu'aucune de ces variables n'est combinaison
linéaire des autres), la variable ti sera insuffisante pour expliquer
toute la variance de y, de même qu'elle sera insuffisante pour expliquer
toute la variance des variables explicatives, et toute la covariance des
variables explicatives avec y.
Il en demeurera un résidu. La variance de y ne sera pas
totalement expliquée par la variance de ti. Il y a moyen
d'améliorer le pouvoir explicatif du modèle. Pour cela, on
s'intéresse aux résidus, qui ont été «
oubliés » par la première composante. Cette première
composante est indépendante des résidus. Or, on se sert de ces
résidus pour construire la seconde composante t;, qui sera par la
même occasion indépendante de ti. La composante t;
s'intéressera donc à la variance de y qui n'est pas
expliquée par ti. Les résidus qui en résulteront, qui sont
donc indépendants de t;, et indépendants de ti (ils sont le
résultat d'une régression sur des résidus qui sont
déjà indépendants de ti), serviront à la
création de t3. t3 sera donc indépendante de ti et t;. Il en ira
de même pour toutes les composantes, qui seront toutes
indépendantes entre elles.
Cette indépendance peut se démontrer assez
facilement d'un point de vue mathématique. Voici la démonstration
telle qu'elle est présentée dans l'ouvrage « La
Régression PLS Théorie et Pratique » de Michel TENENHAUS,
avec quelques précisions supplémentaires :
L'argument avancé est le suivant : th'tl = 0 pour l_h.
th est le vecteur formé des « n » valeurs que
prend la hième composante pour les « n » individus.
th' est la transposée du vecteur th.
tl est le vecteur formé des « n » valeurs que
prend la lième composante pour les « n »
individus.
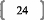
Le fait que le produit th'tl soit égal à 0
traduit covariance nulle entre les deux composantes, et donc une
indépendance de celles-ci, pour autant que les variables de
départ soient centrées (ce qui donne également des
composantes centrées). Si les composantes sont centrées, leur
moyenne est nulle. Les écarts à la moyenne deviennent donc
égaux aux valeurs prises. La covariance, qui est la moyenne des produits
des écarts à la moyenne, devient donc égale à la
moyenne des produits des valeurs des composantes. Si th'tl = 0, cela veut dire
que la somme des produits des valeurs des composantes h et l est nulle. Donc,
la moyenne de ces produits est également nulle. La covariance est donc
nulle, et les variables sont donc indépendantes.
On a ti't2 = ti'Xiw2 = 0 puisque ti'Xi = 0.
Xi étant la matrice des résidus des
régressions des variables xi sur ti. w2 est le vecteur de coefficients
associés aux résidus xi; pour former la composante t2.
Le fait que ti'Xi = 0 vient du fait que la matrice Xi est la
matrice des résidus des régressions des variables xi sur ti.
Supposons ti, ..., th orthogonaux, alors les vecteurs ti, ...,
th#177;i sont orthogonaux. Montrons que th#177;i est orthogonal aux vecteurs
ti, ..., th :
t'hth#177;i = t'hXhwh#177;i = 0 puisque t'hXh = 0
t'h-fth#177;1 = t'h-1Xhwh#177;1
= t'h-1[Xh-1- thp'h]wh#177;i
= [t'h-iXh-i -- t'h-ithp'h]wh#177;i
= 0 puisque t'h-iXh-i = 0 et t'h-lth = 0 par l'hypothèse
de récurrence.
Sachant que ph=X'h-ith/t'hth, c'est à dire que ph est le
vecteur des coefficients de régression entre la composante th et les
xh-1j.
t'h-2th#177;1 = t'h-2Xhwh#177;1
= t'h-2[Xh-2 -- th-ip'h-i -- thp'h]wh#177;i = 0
Puisque t'h-2Xh-2 = 0, t'h-2th-i = t'h-2th = 0, et ainsi de
suite, d'où le résultat.
Cette indépendance entre les composantes entraîne
mécaniquement l'impossibilité de construire un nombre de
composantes supérieur au nombre de variables explicatives comprises dans
la régression, puisqu'elles sont formées à partir de ces
variables. De plus, si certaines variables explicatives sont strictement
combinaisons linéaires les unes des autres, cela entraînera
d'autant une réduction du nombre maximal possible d'étapes.
On peut, par un raisonnement similaire, penser que la
présence de variables fortement autocorrélées (sans
être forcément combinaisons linéaires les unes des autres)
réduit d'autant l'intérêt d'intégrer un trop grand
nombre de composantes dans l'analyse.
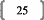
Nous allons, à présent, nous intéresser
brièvement au centrage et à la réduction des
données, deux notions capitales en analyse statistique, et
incontournable en régression PLS (du moins s'agissant du centrage des
données).
VIII. Centrage et réduction des
données
Il est important, avant d'interpréter une
régression, de savoir si elle porte sur des données
centrées ou non, réduites ou non. L'interprétation du
modèle obtenu en est complètement modifiée.
Le fait de centrer les données permet notamment de ne
retenir que les variations des variables autour de la moyenne. Cela facilite en
outre les calculs de covariance et des coefficients de corrélation. Le
centrage des données ne modifie en aucun cas la variance (et
l'écart-type) mais ramène la moyenne de la série à
O. Pour centrer une série, on retranche à chacune de ses
données la moyenne de la série.
La réduction des données permet
d'éliminer les effets d'échelle. Une série de grands
nombres, telle que le PIB d'un pays, aura tendance à varier très
fortement (en valeur absolue), alors qu'une série de nombre faibles,
comme par exemple des taux d'intérêts, aura tendance à
varier très peu (toujours en valeurs absolue). La réduction des
données permet de prendre équitablement en compte les variations
relatives autour de la moyenne, et non les variations absolues. Le fait de
réduire une série de données ramène la valeur de
l'écart-type (et donc de la variance) de la série à 1.
Lors d'une régression, la réduction des données va peser
sur l'ordre de grandeur des coefficients.
La réduction des données n'affecte pas la
qualité d'une régression. En revanche, le centrage l'affecte
généralement. En effet, centrer les données revient
à considérer les données non centrées auxquelles on
ajoute une constante.
En régression PLS, les données doivent
être impérativement centrées, sans quoi les
propriétés mathématiques de la régression seraient
modifiées. Il serait en outre impossible de régresser sur des
données non centrées avec constante (car les coefficients,
basés sur des critères de covariance, seraient
systématiquement nuls pour une constante). Cela affecterait la
qualité de la régression.
La réduction des données n'est par contre pas
nécessaire. Elle influence seulement l'ordre de grandeur des
coefficients. Le fait de ne pas réduire les données permet une
interprétation plus directe des coefficients. Le fait de travailler sur
un modèle réduit permet en revanche d'obtenir des coefficients
qui représentent mieux la part « d'explication » de la
variance de y par chaque variable explicative.
Note : Normalement, lorsqu'on centre et on réduit les
données, on commence d'abord
par les centrer, puis on les
réduit dans un second temps. L'inverse est possible, mais

27
après la réduction, il faut retrancher des
données la « moyenne réduite » (la moyenne des
données réduites) et non la moyenne de la série initiale.
Ceci vient du fait que la réduction des données affecte à
la fois la variance et la moyenne, alors que le centrage n'affecte que la
moyenne (donc, réduire en second lieu n'impose pas de recalculer la
variance des données centrées). Quoi qu'il en soit, centrage des
données et réduction des données sont deux concepts
indépendants.
Bien qu'il ne soit pas possible d'effectuer une
régression PLS sur des variables non - centrées, et qu'il soit
impossible de calculer une constante, il est possible de passer, après
obtention des résultats, d'un modèle centré à un
modèle non-centré avec constante.
Notons qu'il est également possible (et facile) de passer
d'un modèle centré, réduit, à un modèle
centré, non réduit.
Prenons par exemple trois variables. A comme variable
expliquée, B et C comme variables explicatives. Notons Acr, Bcr et Ccr
les variables A, B et C centrées et réduites, et Ac, Bc et Cc les
variables centrées non-réduites.
Si on travaille sur modèle centré-réduit, on
aura une relation du type :
Acr = b*Bcr+c*Ccr, où b et c sont les coefficients obtenus
par régression (quelle qu'elle soit) associés respectivement aux
variables B et C.
Pour passer aux variables centrées, non réduites,
il suffit de remplacer Acr, Bcr et Ccr par leur expression en fonction de Ac,
Bc et Cc.
Acr = Ac/a(A), Bcr = Bc/a(B) et Ccr = Cc/a(C).
Le modèle devient donc :
Ac/a(A) = b*Bc/a(B) + c*Cc/a(C)
« Ac = [b*Bc/a(B) + c*Cc/a(C)^*a(A)
Ce qui nous donne :
Ac
*(a)1 *Bc [c *
(a)
o-
(b)
o- (c) *Cc(24)
Les coefficients de la régression centrée
(non-réduite) peuvent être obtenus en multipliant ceux de la
régression centrée-réduite par le rapport de
l'écart type de la variable expliquée sur l'écart type de
la variable explicative (a(Y)/a(X) si Y est la variable expliquée et X
la variable explicative considérée).
Le passage d'un modèle simplement réduit
(non-centrée) à un modèle non-centré et
non-réduit se fait bien entendu de la même manière.

28
On annule donc la réduction en multipliant les
coefficients par le rapport des écarts types de la variable
expliquée et de la variable explicative.
Pour décentrer des données, il suffit
d'établir un raisonnement similaire. Si nous sommes en présence
d'un modèle centré du type Ac = b*Bc + c*Cc (où Ac, Bc et
Cc représentent les variables A, B, C une fois centrées), on peut
le réécrire de la manière suivante :

)
A
(A--A)=b*(B--B)+c*(C--C
A=b*(B--B)+c*(C--C)

A b*B+c*C--b*B--c*C+ A
(25)

Sachant que A , B et C sont les
moyennes calculées initialement sur les séries A, B et C.
La manipulation est la même si l'on souhaite passer d'un
modèle centré-réduit à un modèle non
centré et réduit, à la différence près qu'il
faut retrancher les moyennes réduites en lieu et place des moyennes
initiales.
IX. Le critère de validation croisée
La validation croisée se base sur la qualité
d'approximation du modèle des valeurs de la variable expliquée
pour les individus sur lequel il se fonde.
On cherche à prendre en compte deux
éléments, qu'on va ensuite comparer. Il s'agit des
critères RSS (Residual Sum of Squares) et PRESS (PRediction Error Sum of
Squares). Les deux prennent normalement des valeurs différentes pour
chaque étape de la regression (ils diminuent à chaque
étape).
Le premier, le critère RSS, n'est autre que la somme du
carré des résidus (SCR), calculé en comparant les
prédictions de la valeur expliquée (y) par le modèle pour
chaque individu, aux valeurs initiales de la valeur y pour ces mêmes
individus.
A l'étape h, la formule de RSS est :
n
RSSh =E(yi- (y *) hi
)2 (26)
i ~
Où yi est la valeur initiale
(centrée-réduite) pour l'individu i. (y*)hi = Shhi= ci*tii +
+ ch*thi (27)
On peut résumer ce critère en disant qu'il s'agit
de la somme des erreurs
d'approximation du modèle mises au
carré. De la connaissance de ce critère, et de la
connaissance
de la variance de la variable y, on peut aisément retrouver le
coefficient
de détermination de la régression. Plus le
coefficient de détermination de la régression est faible, et plus
la somme des carrés des résidus est élevée. En
effet, le modèle est d'autant plus efficace qu'il commet peu d'erreurs.
Un modèle « parfait », dans cette optique, est un
modèle pour lequel où les écarts des prédictions
sont nuls, donc où SCR (RSS) est nul, et donc le coefficient de
détermination (R2) égal à 1.
Le critère RSS nous donne donc une idée de la
qualité du modèle. Mais le problème est qu'il n'est pas
suffisant car il délivre une information « absolue » sur les
résidus et non « relative » (relative à la variance de
la variable à expliquer). C'est pourquoi le R2 lui est
préférable.
Quoi qu'il en soit, plus la régression PLS comporte
d'étapes, et plus la qualité d'approximation du modèle est
bonne (ou, au moins, aussi bonne qu'aux étapes
précédentes). Le critère RSS diminue donc d'étape
en étape.
Ainsi, RSS1 RSS2 RSS3 ...
L'autre critère, le PRESS, lui est assez similaire. La
différence est qu'il s'attache à mesurer la qualité de
prédiction du modèle sur les individus lorsqu'ils sont exclus de
ce modèle. Pour cela, on effectue, pour chaque individu, une
régression PLS (à « h » étapes, car on cherche
à mesurer la pertinence de la hème étape) en
excluant cette individu des calculs du modèle. Ensuite, on estime la
valeur de la variable expliquée pour cet individu, à l'aide des
valeurs de ses variables explicatives et des coefficients obtenus dans la
régression qui ne prenait pas en compte la présence de cet
individu. On compare cette valeur à la valeur effective de « y
» pour cet individu, et on obtient un résidu. On renouvelle
l'étape avec tous les autres individus, et puis on fait la somme du
carré de ces résidus.
Par exemple, on commence en prenant le premier individu d'une
régression qui comporte « n » individu. On effectue la
régression PLS sur les (n-1) derniers individus, et on estime, à
l'aide des coefficients de cette régression, et des valeurs des
variables explicative pour ce 1er individu, la valeur de la variable
expliquée, donnée par le modèle. On la compare avec la
valeur effective de y et on garde le résidu. On répète
ainsi l'opération avec le 2ème individu, en effectuant
la régression sur le 1er et les (n-2) derniers individus.
L'opération, au final, a été répétée
autant de fois que la régression ne comporte d'individu, chacune de ces
régressions visant à prédire la valeur de y de l'individu
qui a été exclu de leur calcul4.
4 On peut également exclure des individus
« bloc par bloc », par exemple deux par deux, et les prédire
simultanément. La taille des blocs dépend avant tout de la
quantité totale d'individus, car exclure systématiquement les
individus un par un demande un nombre considérable de calculs.
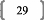
PRESSh 0.95 * RSSh_i
a (33)

30
Partie 1: Présentation de la régression PLS
Voici la formule du PRESS de la régression PLS à
l'étape h :
n
PRESS h = E (Yi - (Y*)
h( i) )2 (28)
i i
Où y*h(-i) est mis pour ÿh(-i), c'est-à-dire
l'estimation de « yi » par la régression PLS à h
étapes qui ne prend pas en compte le ième individu.
On a donc deux estimateurs de la qualité de la
régression. Le premier, le RSS, en prenant en compte 100% de
l'information de la régression que l'on cherche à estimer, sera
forcément plus faible (car l'estimation de meilleure qualité) que
le PRESS, qui se prive, pour l'estimation de chaque individu, de la
présence de l'individu en question dans les calculs.
Pour l'étape h, le PRESS sera donc supérieur au
RSS. On sait également que le PRESS, à l'étape h, est
inférieur au PRESS à l'étape h-1. Il en va de même
pour le RSS.
On peut donc écrire les relations suivantes :
PRESSh z RSSh (29)
RSSh s RSSh-1 (30)
PRESSh s PRESSh-1 (31)
L'inconnue est la relation qui lie le critère PRESS
à l'étape h au critère RSS de l'étape (h-1). Le
PRESS de l'étape h sera forcément inférieur ou égal
à ce qu'il était à l'étape h1. Il sera
également forcément supérieur ou égal au RSS de
l'étape h. En revanche, s'il parvenait à être
inférieur au RSS de l'étape (h-1), cela voudrait dire que la
qualité d'estimation du modèle s'est considérément
améliorée, puisqu'il peut désormais estimer, avec plus de
précision, les valeurs « yi » des individus, sans les
connaître au préalable, que le modèle de l'étape
précédente ne le peut, en les connaissant.
Donc, par exemple, le fait que la composante « h »
ait une importance significative dans la régression pourrait se traduire
par le fait que PRESSh soit inférieur à RSSh-1. On peut aussi
être plus ou moins exigeant en donnant un coefficient différent de
1 à RSSh-1 :
PRESSh s x*RSSh-1 (32)
Si x est inférieur à un, on accentue la contrainte,
on aura moins tendance à retenir des étapes
supplémentaires.
Dans le logiciel SIMCA-P, par exemple, la composante th est
retenue si :

31
Le fait que l'équation soit mise sous forme de racine
est simplement la conséquence du fait qu'on cherche à se replacer
à l'échelle des résidus, et non à l'échelle
des résidus au carré. Cela rend le critère de choix mieux
interprétable. Cela veut dire, à peu de choses près, que
les résidus tels qu'ils sont calculés dans le PRESSh, pris en
valeur absolue, ne doivent pas, en moyenne, excéder 95% des
résidus tels qu'ils sont calculés dans le critère
RSSh-1.
On peut se passer des racines et revenir à une
équation de la même forme que la précédente (30),
mais le coefficient doit être mis au carré.
PRESSh s 0.9025*RSSh-1 (34) Ou encore :
PRESSh < 0.9025 (35) RSS
h 1
Ceci est également retranscris de la manière
suivante dans l'ouvrage « La Régression PLS : Théorie et
pratique » de Michel Tenenhaus :
PRESS
Q2(h) --1--
h 0.0975 (36)
RSS h1
On peut passer de la forme précédente (35) à
celle-ci (36) de la manière suivante :
PRESS
(35) <=> h 1 0.0975
RSS h1
PRESS
<=> h 0.0975 --1
RSS h 1
RSS
h 1
1 (36)
PRESSh
<=> h 0.0975
Tout ceci est donc strictement équivalent, mais certaines
formes se prêtent mieux au calcul et d'autres mieux à
l'interprétation.
Le principal problème du critère de validation
croisée est qu'il fait appel à un nombre considérable de
calculs. Il faut en effet effectuer, pour chaque étape, autant de
régression PLS que d'individus présents dans la régression
initiale, afin d'être en mesure de calculer le PRESS de l'étape en
question.

32
De plus, la valeur du coefficient que nous avons appelé
« x » est complètement arbitraire, et s'en tenir strictement
à ce critère pourrait se révéler dangereux, dans la
mesure où cela pourrait donner des résultats assez
aléatoires (il arrive parfois que certaines composantes apportent plus,
en terme de prédiction, que celles qui les précèdent), et
on n'a pas vraiment le loisir de se prononcer sur la structure des
composantes.
C'est pourquoi nous allons nous intéresser à
l'utilisation conjointe de deux autres critères.
X. Les critères liés à la covariance
composante - variable expliquée
Chaque étape de la régression PLS peut se
résumer comme étant le produit de la maximisation de la
covariance (au carré, car ce qui importe, c'est la covariance en valeur
absolue) entre la variable à expliquer (ou les résidus de la
projection de celle-ci sur le modèle tel qu'il était à
l'étape précédente) et la nouvelle composante, avec pour
contrainte que celle-ci soit formée linéairement à partir
des variables explicatives (ou des résidus de leur projection sur le
modèle tel qu'il était à l'étape
précédente), la somme des coefficients au carré
(associés à chaque variable explicative) étant
égale à 1.
Nous reviendrons sur ce critère lors de la deuxième
partie de ce mémoire, lorsque nous comparerons l'approche PLS et
l'approche des MCO.
Cette covariance au carré, peut s'écrire,
à la première étape « Cov2(Y,ti) » (Y
étant la variable expliquée). Il s'agit en réalité
du produit du coefficient de détermination entre Y et ti
(R2(Y,ti)) et de la variance de ti. Dit autrement :
Cov2(Y,ti) = R2(Y,ti)*Var(ti). Il s'agit donc de
maximiser ce produit, en jouant sur les deux termes, qui sont les deux
critères que nous allons retenir dans le cadre du choix du nombre de
composantes.
Le premier terme, R2(Y,ti), n'est autre que le
critère normal que l'on cherche à maximiser lorsque l'on effectue
une régression linéaire multiple au sens des MCO. Il s'agit en
réalité de la faculté « pure » du modèle
à prédire la variable Y sur les individus actifs5. Il
est donc important que les composantes retenues apportent toutes une part
significative en termes de corrélation par rapport à la variable
Y, sous peine de risquer de n'avoir aucune vertu explicative.
Le second terme, Var(ti), représente, en quelques
sortes, la fraction de la structure interne de l'ensemble formé par les
variables explicatives (ensemble X) expliquée par la composante ti, Il
s'agit donc de la prise en compte de la structure propre à l'ensemble X,
et, en lui-même, ce terme n'a pas vocation à expliquer la variable
Y.
5 On entend, par individus actifs, les individus se
trouvant à la base de la création du modèle.
Chaque composante répond donc au compromis d'expliquer
au mieux la fraction de la variance de Y non prise en compte par les
composantes précédentes, tout en rendant au mieux compte de ce
qui est propre à l'ensemble des variables explicatives et qui n'a pas
encore été pris en compte par les composantes
précédentes.
Ces deux critères doivent être les plus
élevés possibles s'agissant des composantes retenues.
L'idéal est que les deux, pour toute composante retenue, soient
significatifs. Mais, parfois, on peut justifier la conservation d'une
étape supplémentaire sur base d'un seul des deux critères.
Le tout est de comparer ce qu'apporte chaque composante supplémentaire
par rapport à ce qu'il reste à expliquer, sachant que chaque
critère, pris individuellement, peut être plus élevé
pour des étapes pourtant précédées par d'autres
étapes pour lequel le critère est moins élevé.
Il se peut donc même, parfois, qu'il soit
nécessaire de retenir une étape intermédiaire dans le but
d'être en mesure de retenir les étapes qui la suivent, même
si cette étape, en elle-même, au regard des critères pris
isolément, n'est pas suffisamment significative que pour justifier sa
retenue. Par exemple, la 3ème étape peut sembler
non-significative, mais si la 4ème étape l'est
davantage au regard de l'un des deux critères, il est
préférable de se poser la question de retenir les 4
premières étapes, et dans ce cas on ne pourra pas passer outre la
3ème. Mais dans ce cas, il faut être sûr que
l'importance de la 4ème étape est capitale au regard
de ce qu'il reste à expliquer.
Ces précisions étant faites, il est maintenant
temps de passer à la seconde partie, durant laquelle nous allons pouvoir
mettre en oeuvre la méthode et l'appliquer à des cas simples,
atypiques et extrêmes, permettant de mieux comprendre
l'intérêt de la méthode et de mieux cerner les
pièges à éviter.
PARTIE 2
Utilisation de la régression
PLS sur des cas limites
Nous allons tout d'abord nous attaquer au cas le plus simple,
c'est-à-dire celui de l'application de la régression PLS
univariée sur un modèle à une variable explicative.
I. Régression PLS avec une seule variable
explicative
Prenons un tableau de données simples et fictives, avec
deux variables : le poids et la taille. On essaye d'expliquer le poids en
fonction de la taille.
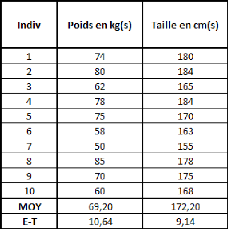
La covariance entre ces deux variables est de 87,36, le
coefficient de corrélation (R) est de 89,84%, et le coefficient de
détermination (R2) est de 80,71%.
Comme il n'y a qu'une seule variable explicative (la taille), la
régression PLS ne comportera pas plus d'une étape.
Si on effectue une régression PLS sur les variables
centrées-réduites (pour chaque donnée de la série,
on retranche la moyenne de la série, et on divise la différence
par l'écart-type de la série), cela nous donne la relation
suivante :
Poidscr = 0,898*Taillecr
Où Poidscr et Taillecr sont respectivement les
séries des données des séries Poids et Taille
centrées-réduites.
Sur les données non-centrées et
non-réduites, avec l'intégration d'une constante, la relation est
la suivante :
Poids = 1,045*Taille -- 110,831
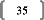
Dans un cas comme dans l'autre, le coefficient de
détermination (R2) de la régression vaut
approximativement 0,81.
Voyons donc comment utiliser ce modèle. Prenons une taille
au hasard : 180 cm.
Le modèle avec variables non-centrées et
non-réduites s'applique directement. Le poids de cet individu de 180cm
devrait donc être de 1,045*180 -- 110,831 = 77,27 kg approximativement.
Bien entendu, il s'agit de la valeur extrapolée par le modèle,
qui est théorique. Il y a une marge d'erreur, mais le fait que le
coefficient de corrélation soit assez élevé (81%) laisse
présager d'une assez bonne capacité à prédire du
modèle.
Concernant le modèle « centré-réduit
», il faut d'abord centrer et réduire les la valeur « 180cm
» en utilisant la moyenne et l'écart type calculés sur la
série « Taille » (même si cette série ne comprend
pas cette valeur) : (180-172,2)/9,14 = 0,8534...
Pour cette valeur, la variable « Poidscr » prend
donc la valeur 0,898*0,8534, soit 0,7664... Pour obtenir le Poids non
centré et non réduit, il faut multiplier cette valeur par
l'écart-type de la série Poids et y ajouter la moyenne de la
série : 0,7664*10,64 + 69,2 = 77,35 kg. Naturellement, ce « 77,35
kg » calculé à l'aide de ce modèle devrait être
égal à la valeur calculée par le modèle
précédent. La différence s'explique par des erreurs
d'arrondis. Il aurait fallu prendre davantage de décimales en compte
pour arriver au même résultat.
Ces deux modèles donnent donc exactement les
mêmes résultats. Le premier permet simplement un calcul plus
direct, plus rapide et plus simple, de même qu'une interprétation
plus rapide.
Si on s'attarde sur le coefficient de détermination de
la régression (0,81), on s'aperçoit qu'il est strictement
égal au coefficient de détermination entre les deux variables
(Poids et Taille). Cela veut dire que la régression prend en compte de
manière optimale la corrélation entre les deux variables. Hors,
c'est également le cas lorsqu'on effectue une régression
linéaire simple, où le R2 de la régression est
égal au R2 entre la variable explicative et la variable
expliquée (lorsque les variables sont centrées ou qu'une
constante a été intégrée). Hors, il ne peut pas
exister deux résultats différents (deux séries de
coefficients différents), pour une régression de ce type, qui
aboutiraient au meilleur coefficient de détermination possible pour
cette analyse. Donc, cela veut nécessairement dire que les coefficients
trouvés sont les mêmes que les coefficients qui auraient
été trouvés dans le cadre d'une régression
linéaire simple.
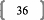
En effet, si on effectue une régression linéaire
simple, c'est-à-dire si on cherche à calculer les coefficients
« a » et « b » par régression linéaire simple
sur un modèle du type Poids = a*Taille + b, on obtient les
résultats suivants :
,
36
87
a Cov(Poids, aille ) Var(
aille)
1,0455
83,56

37
Y ax b b Y ax 69,2 --1,0455 *172, 2 b 110 ,
8351
On a donc finalement le modèle suivant : Poids =
1,0455*Taille -- 110,8351
On constate donc, à quelques décimales près
là encore, que les modèles sont identiques.
Si on fait la régression linéaire simple sans
constante, mais avec variables centrées - réduites, on obtient
les mêmes résultats que pour la régression PLS à une
composante sur variables centrées-réduites. Nous ne
détaillerons pas les calculs mais le résultat donné par
Eviews 5.0 pour une telle régression (régression linéaire
simple sur variables centrées-réduites) est le suivant : Poidscr
= 0,898394*Taillecr.
Dans les deux cas, les modèles donnent les mêmes
résultats.
Il faut néanmoins se garder d'affirmer qu'une
régression PLS et une régression linéaire donnent
forcément les mêmes résultats. Néanmoins, on
constate ici qu'une régression linéaire simple (avec centrage des
données ou constante), et qu'une régression PLS à une
étape pour une seule variable explicative (avec centrage des
données ou constante), donnent les mêmes résultats. Comme
il n'y a qu'une seule étape possible lorsqu'il n'y a qu'une seule
variable, nous pouvons dire que régression PLS1 pour une seule variable
explicative et régression linéaire simple (ou régression
linéaire multiple à une seule variable explicative) donnent les
mêmes résultats et s'équivalent donc en tout points (si ce
n'est pas la différence d'approche pour ce qui en est des calculs).
Nous allons essayer de voir sous quelles conditions une
régression PLS (à plus d'une variable explicative) et une
régression linéaire multiple peuvent donner les mêmes
résultats.
II. Un exemple à trois variables
explicatives
Reprenons le même exemple mais en ajoutant deux
séries fictives supplémentaires (qui seront utilisées
comme variables explicatives supplémentaires) :
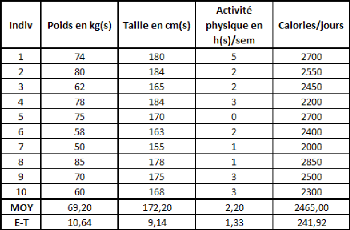
La matrice des corrélations correspondantes est la
suivante :
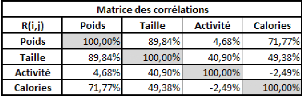
Et la matrice des variances-covariances :
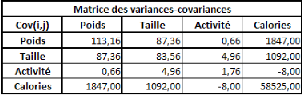
Ces séries supplémentaires ont volontairement
été créées de manière à diminuer les
résidus, c'est-à-dire à améliorer le pouvoir
explicatif du modèle, même si une part aléatoire a
été volontairement conservée. Les 5 séries
étant purement fictives, il sera inutile d'appliquer quelque
modèle que ce soit, qui soit fondé sur ces séries,
à la réalité.
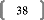
Effectuons tout d'abord une régression linéaire
simple sur ce modèle. Avec Eviews 5.0, on obtient :
- En travaillant sur les données non-centrées et
non-réduites et avec intégration
d'une constante :
Poids = 1.039*Taille
-- 2.5*Activité +
0.012*Calories -- 133.426. Les 4 coefficients sont
jugés significatifs au seuil de 1%, ce qui est plutôt
étrange quand on regarde la corrélation Poids/Activité
(corrélation apparemment très faible). Le signe du coefficient
« Activité » est également surprenant, à priori,
étant donné qu'il est opposé à celui du coefficient
de corrélation Poids/Activité.
On obtient un coefficient de détermination de la
régression de 98,08%.
- En travaillant sur les données
centrées-réduites :
Poidscr = 0.893*Taillecr --
0.296*Activitécr + 0.255*Caloriescr
Le coefficient de détermination est toujours de 98,08%.
Les 3 coefficients sont jugés significatifs au seuil de 1%.
- Si on travaille sur les données
initiales sans constante, on obtient la relation :
Poids = 0.221*Taille - 0.603*Activité + 0.013*Calories.
Cette fois, le coefficient de corrélation n'est plus que de 58,81%, et
aucun coefficient n'est significatif au seuil de 1% (le coefficient
associé à la variable Activité n'est pas non plus
significatif au seuil de 5%, ce qui n'est toutefois pas le cas des autres). On
comprend donc ici tout l'intérêt d'intégrer une constante
dans la régression ou de centrer les données (la réduction
n'importe pas).
Effectuons à présent une régression PLS
univariée sur le modèle en question : II.1.
Régression PLS à 1 étape
- Modèle normal :
Poids = 0.694*Taille + 0.249*Activité +
0.021*Calories -- 102.603 - Modèle centré-réduit
:
Poidscr = 0.597*Taillecr +
0.031*Activitécr + 0.477*Caloriescr
Le coefficient de détermination (R2) de la
régression de Y sur t1 est de 87,97%. On ne peut donc pas dire qu'il
soit identique à celui de la régression multiple, puisqu'il lui
est inférieur.
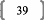
A la vue de ce premier modèle, on peut dors et
déjà tirer quelques conclusions, et on peut se poser plusieurs
questions :
- Le coefficient de régression est inférieur
à celui de la régression linéaire simple. La
régression PLS serait-elle une méthode moins efficace que la
régression linéaire simple ?
- Les coefficients affectés aux différentes
variables ne sont pas du tout les mêmes d'un modèle à
l'autre. Parfois même, on observe un changement de signe : c'est le cas
pour la variable Activité. La régression PLS serait-elle plus
« objective » que ne l'est la régression linéaire
simple ?
- On constate cette fois que la variable Activité observe
un coefficient de signe similaire à son coefficient de
corrélation avec la variable poids.
- Les deux derniers points découlent directement du
fait que les variables étant centrées, et n'ayant retenu qu'une
seule étape, les coefficients sont directement proportionnels aux
coefficients de corrélation des différentes variables
explicatives par rapport à la variable Poids.
Comparons les deux modèles (non-centrés,
non-réduits, avec constante) en utilisant leurs prévisions des
valeurs de la variable expliquée (Poids) :
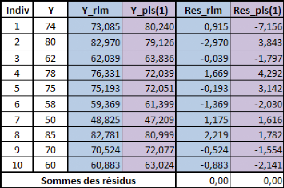
Y correspond à la variable Poids (variable
expliquée)pour les 10 individus.
Y_rlm correspond à la prédiction de la variable
Poids pour les mêmes individus par le modèle de régression
linéaire simple, Res_rlm correspond aux résidus de cette
régression.
Y_pls(1) correspond à la prédiction de la
variable Poids pour les mêmes individus par le modèle de
régression PLS1 à une étape, la colonne Res_pls(1)
correspondant aux résidus.
SCT (somme des carré totale, c'est la somme des
carrés des écarts à la moyenne de Y) = 1131.6 SCR_rlm
(somme des carrés résidus pour la régression
linéaire multiple) = 21.715 SCR_pls(1) (somme des carrés
résidus pour la régression PLS à une étape) =
114.402
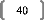
Partie 2 : Utilisation de la régression PLS sur des
cas limites Plusieurs remarques :
- La somme des résidus (sans les élever au
carré) de la régression multiple est égale à 0, car
les résidus s'annulent, et c'est également le cas de la
régression PLS à une étape.
- La somme du carré des résidus de la
régression PLS(1)6 est très nettement
supérieure à celle de la régression linéaire
simple. Cela ne nous apprend rien, puisque le coefficient de la
régression PLS(1) était nettement inférieur à celui
de la régression multiple.
- La prévision de la régression PLS(1) n'est
meilleure que dans le cas du 8ème individu. -
Généralement, les erreurs de prévisions vont dans le
même sens, exception faite des individus 1, 2 et 5.
- Les écarts de prévisions (entre les deux
méthodes) les plus marqués (en valeur absolue) concernant les
individus 1, 2, 4 et 5, plus particulièrement l'individu n°1 et
l'individu n°2. L'individu n°1 est très mal prédit par
le modèle PLS(1).
Ceci étant dit, passons à la régression PLS
à 2 étapes. II.2. Régression PLS à 2
étapes
- Modèle normal :
Poids = 0.844*Taille + -2.225*Activité +
0.019*Calories -- 119.039 - Modèle centré-réduit
:
Poidscr= 0.725*Taillecr
+ -0.277*Activitécr +
0.442*Caloriescr
Le coefficient de la régression passe de 87,97%
à 95,52%. La part de la variance expliquée par t1 est de 87,97%
(normal, puisque t1 n'a pas changé) et celle expliquée par t2 est
de 7,55% (on l'obtient directement par différence, les composantes
étant indépendantes).
Plusieurs conclusions s'imposent :
- Les coefficients sont tous modifiés, tous de
manière assez importante, exception faite du coefficient lié
à la variable Calories.
- Les coefficients se rapprochent tous de leur valeur en
régression linéaire multiple. Exemple : dans le modèle
normal, le coefficient lié à la variable Taille passe de 0.694
à 0.844 et se rapproche ainsi fortement du coefficient de la
régression linéaire (1.039). La différence la plus
flagrante concerne le coefficient lié à la variable
Activité. Il était de 0.249 dans le modèle normal PLS(1),
il est maintenant de -2.225 dans le modèle normal
6 Les notations PLS(1), PLS(2), ... PLS(p) seront
couramment utilisées pour désigner respectivement les
modèles PLS à 1, 2, ..., p étape(s). Il est important de
ne pas les confondre avec les notations PLS1 et PLS2, désignant
respectivement des modèles de régression PLS univariée et
multivariée.
PLS(2). Il s'est considérablement rapproché de la
valeur du modèle de régression linéaire (-2.5).
- Ce dernier coefficient, justement, a changé de signe,
et n'est donc plus du même signe que le coefficient de corrélation
Poids/Activité. Son ordre de grandeur est également
significativement modifié. Il était très faible, notamment
s'agissant du modèle centré-réduit. Il possède
à présent un ordre de grandeur qui se chiffre en dixième,
à l'instar des coefficients des autres variables. Pourtant, si on
regarde les coefficients de corrélation, le coefficient de la variable
Activité devrait rester insignifiant en comparaison aux autres. Comment
ceci peut-il s'interpréter ?
- La qualité de la régression s'est nettement
améliorée, tendant subitement vers celle de la régression
linéaire simple, bien qu'elle lui reste inférieure.
Afin de mieux se rendre compte de l'amélioration de la
qualité de la régression,
reprenons le précédent
tableau et ajoutons-y les prédictions et les résidus du
modèle
PLS (2)
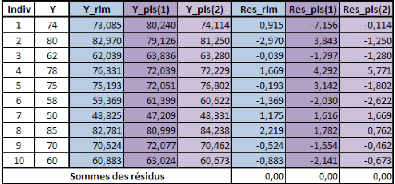
Ce que l'on peut remarquer :
- La somme des carrés des résidus
s'élève à 50.669 pour le modèle PLS(2), ce qui est
nettement inférieur à ce qu'il en était à
l'étape 1 (114.402), et qui se rapproche de ce que l'on observe
s'agissant de la régression linéaire (21.715).
- Les erreurs d'estimation les plus fortes concernent les
individus 4, et 6, plus particulièrement l'individu 4. Ces erreurs
tendent même à s'aggraver, alors que dans tous les autres cas,
elles diminuent (exception faite de l'individu 7 pour lequel la
prévision reste stable). On pourrait penser que le modèle PLS(2)
ignore « volontairement » l'individu n°4, car si on
l'enlève de l'analyse, la somme des résidus tendrait vers une
valeur plus faible.
- De plus, si on enlevait l'individu 4 de l'analyse, la somme
des résidus au carré (SCR)
plongerait de 50.669 à
17.367. La somme des résidus au carré du modèle de
régression
linéaire passerait quant à elle de 21.715
à 18.929, soit une sensibilité nettement plus
faible (ce qui est normal, l'individu 4 est nettement mieux
prédit par le modèle de régression linéaire). Le
modèle PLS(2) serait alors meilleur prédicateur des valeurs
actives que le modèle de régression linéaire. La
régression PLS pourrait-elle donc être une analyse plus pertinente
que la régression linéaire simple, exception faite de certains
individus ?
- Seul l'individu 1 fait l'objet d'une opposition du signe des
résidus. En revanche, les individus 2 et 5, qui faisaient l'objet d'un
désaccord de signe à l'étape 1, ne le font plus à
l'étape 2 (le désaccord restant néanmoins assez
prononcé en valeur absolue).
Il est très intéressant de noter que si on pratique
une régression linéaire simple en enlevant le
4ème individu de l'analyse, on obtient les résultats
suivants :
- Modèle normal avec constante :
Poids = 0.878*Taille -- 2.265*Activité + 0.017*Calories --
120.171 - Modèle centré-réduit :
Poidscr = 0.708*Taillecr -- 0.288*Activitécr +
0.381*Caloriescr
Le coefficient de détermination passe à 98.78%.
La somme du carré des résidus passerait de 21.715
à 12.74, pour seulement un individu (sur 10) ôté.
On remarque que les coefficients se rapprochent très
nettement de leur valeur calculée par le modèle PLS(2).
Ceci nous amène à une double conclusion :
- Le retrait de l'individu 4 des individus actifs
améliore sensiblement la qualité de l'analyse. Bien que
l'individu 4 était assez bien prédit par la régression
linéaire, son retrait a permit de « relâcher » la
régression, au sens où la prise en compte forcée de cet
individu atypique empêchait le modèle de prédire
correctement certains des autres individus.
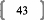
Partie 2 : Utilisation de la régression PLS sur des
cas limites Le tableau suivant illustre ce phénomène :
Res2 rlm représente la série des résidus
au carré de la régression linéaire pour chaque
individu.
Res2 rlm(-4) représente cette même
série pour la régression linéaire avec le
4ème individu ôté de l'analyse. La colonne «gain
» représente le gain apporté par le retrait du
4ème individu dans l'analyse en termes de résidu au
carré Il se calcule par soustraction suivante : Res2 rlm - Res2
rlm(-4).
Globalement, on observe un gain sur le critère des MCO
de 8.975 (21.715 -- 12.74). Ce gain est expliqué à 31% par la
disparition du résidu lié au 4ème individu, et
à 69% par l'amélioration des prédictions des autres
individus.
On note néanmoins que c'est l'individu 2 qui profite au
mieux de ce retrait, et que les individus 3, 5, 6 et 7 sont à
présent moins bien estimés. On peut donc penser que l'individu 2
et l'individu 4 sont dans une certaine mesure opposés car ils ne
s'analysent pas de la même manière, étant donné que
la prise en compte de l'individu 4 fausse énormément la
prédiction de l'individu 2.
- L'analyse se rapproche de celle établie par la
régression PLS à l'étape 2. Les coefficients se
rapprochent de ceux du modèle PLS(2). Cela nous confirme, dans une
certaine mesure, que le modèle PLS(2) a négligé l'individu
n°4, et que d'une certaine manière, c'est un point positif, puisque
ce dernier faussait les prévisions des autres individus.
Néanmoins, il est important de signaler que si le
retrait de l'individu 4 fait passer le R2 de la régression
linéaire de 98.08% à 98.78%, le retrait de l'individu 2 (en
laissant l'individu 4) fait passer le R2 de la régression de
98.08% à 99,2%, ce qui serait encore plus significatif.
Le tableau suivant résume les différents
coefficients de corrélation (en régression linéaire)
résultant du retrait de chaque individu :
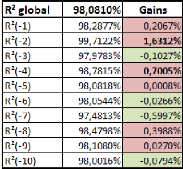
On remarque que 4 individus (les individus 3, 6, 7 et 10)
n'ont pas intérêt à être retirés en termes de
R2. Leur retrait détériorerait la qualité de la
régression. Ces 4 individus présentent très probablement
des caractéristiques « dans la moyenne » des autres. Les
retirer ne ferait que mettre encore plus en évidence le caractère
inconciliable de l'analyse des autres individus. Cela ne modifierait pas outre
mesure les coefficients, mais rendrait la qualité de la
régression plus mauvaise.
Note : Il n'est pas inconcevable que le retrait d'un
individu altère le coefficient de régression. Normalement, cela
devrait l'améliorer, car moins il y a d'individu, plus il est possible
d'ajuster les coefficients des variables afin d'expliquer les autres. C'est
particulièrement le cas lorsqu'il y a presque autant de variables
explicatives que d'individus. Néanmoins, si l'individu est bien
prédit par le modèle, son retrait risque de réduire
très peu la somme des carrés résiduels, et de
réduire fortement la somme des carrés totale. Si le terme SCR
diminue moins, en proportions, que le terme SCT, la qualité de la
régression se détériorera.
En revanche, les individus dont le retrait améliorerait
significativement la qualité de l'analyse sont les individus 2, 4 et 8.
On peut penser qu'ils sont quelques peu atypiques, et, de ce fait, «
tirent » vers eux l'analyse, influençant ainsi fortement les
coefficients.
Il serait difficile d'aller plus loin dans l'analyse, dans la
mesure où l'on ne dispose pas d'une population sur laquelle on puisse
tester les différents modèles, et ainsi s'apercevoir de la
qualité des différents individus actifs.
Passons donc à la régression PLS à 3
étapes.
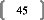
Partie 2 : Utilisation de la régression PLS sur des
cas limites II.3. Régression PLS à 3
étapes
Les deux modèles sont les mêmes qu'en
régression linéaire simple :
- Poids = 1.039*Taille -- 2.5*Activité +
0.012*Calories -- 133.426 pour le modèle non centré,
non-réduit.
- Poidscr = 0.893*Taillecr -- 0.296*Activitécr +
0.255*Caloriescr pour le modèle centré réduit.
Toutes les statistiques associées sont donc similaires.
La troisième composante apporte un gain de 2.56% et porte donc le
coefficient de corrélation à 98.08%, comme dans la
régression linéaire simple.
Il est inutile de calculer les valeurs de Y ainsi que les
résidus, puisqu'ils sont nécessairement les mêmes qu'en
régression linéaire.
La seule chose que nous pouvons conclure est la convergence de
la régression linéaire simple et de la régression PLS
à 3 étapes, soit quand on retient autant d'étapes que de
variables explicatives (le maximum d'étapes possibles). Il est inutile
de tenter d'exploiter les résidus de l'étape 3 pour une
4ème étape, cela n'apporterait aucun gain, ces
résidus n'étant plus du tout corrélés, la
4ème composante serait nulle, ainsi que toutes celles qui
suivraient.
Dans ces conditions, si on considère la dernière
étape possible comme étant la version la plus aboutie de la
régression PLS, quel peut-être l'apport de la régression
PLS par rapport à la régression linéaire simple, si les
résultats sont les mêmes ?
Conclusions sur cette régression à 3 variables
explicatives :
Nous allons essayer de synthétiser tout ce que nous avons
observé au cours des 3 étapes, et nous tâcherons ensuite
d'expliquer point par point ce qui a aboutit à ces résultats.
Au cours de cette régression, nous avons observé
plusieurs choses :
- La régression linéaire simple est celle qui
obtient les meilleurs résultats en termes de coefficient de
régression et donc de SCR sur l'ensemble des individus actifs.
- En régression linéaire simple, comme en
régression PLS (à quelque étape que ce soit),
résidus positifs et négatifs se compensent parfaitement.
- La qualité, en termes de R2 et de SCR, de la
régression PLS, s'améliore d'étape en étape.
- L'ordre de grandeur des différents coefficients peut
fortement varier d'une étape à
une autre, ainsi que leur
signe. Dans un premier temps, lors du modèle PLS(1), ces
coefficients
sont strictement proportionnels aux corrélations entre la variable
expliquée
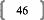
et les différentes variables explicatives. Ensuite, les
résultats se rapprochent progressivement de ceux trouvés à
l'aide de la régression linéaire.
- De manière générale, on observe une
convergence de la régression PLS vers la régression
linéaire simple lorsque le nombre d'étapes augmente, pour obtenir
des résultats égaux lorsqu'il y a autant d'étapes que de
variables.
- Selon le modèle PLS(1), la relation
Poids/Activité est positive, ce qui n'est pas le cas dans les autres
modèles.
- De manière générale, les résidus
ont tendance à aller dans le même sens s'agissant des trois
modèles calculés, exception faite de quelques individus.
- Le modèle PLS(2) voit ses coefficients se rapprocher
de ceux de la régression linéaire simple (par opposition au
modèle PLS(1)), pratiquement dans tous les domaines (coefficients,
coefficient de corrélation, résidus, ...). Le modèle
PLS(2) semble donc être une sorte de compromis entre le modèle
PLS(1) et le modèle de régression linéaire (ou
modèle PLS(3)).
- Dans un premier temps, les résidus de la
régression PLS(1) sont nettement plus élevés que ceux de
la régression linéaire. A la première étape, la
régression PLS est un beaucoup plus mauvais prédicateur (en terme
de résidus) que ne l'est la régression linéaire,
concernant tous les individus, exception faite du 2ème
individu.
- Si on enlève l'individu n°4, les
résultats de la régression PLS(2) sont nettement meilleurs et on
observe qu'ils surpassent ceux de la régression linéaire
(calculée sur les 10 individus actifs, ce n'est bien entendu plus le cas
si on enlève l'individu 4 de l'analyse, puisque la régression
linéaire est celle qui, par définition, minimise la somme des
carrés des résidus). L'individu 4 est donc probablement vu comme
un individu atypique, que la régression PLS(2) a jugé bon de
négliger.
- Nous avons vu que l'individu 4 s'oppose à l'individu
2. Si la régression PLS(2) a choisi de le négliger, ce n'est pas
le cas de la régression linéaire, qui, au contraire, laisse un
peu plus de coté l'individu 2. On a donc constaté que l'exclusion
de l'individu 2 de la régression permettait une nette
amélioration des résultats selon le critère des MCO.
Plusieurs phénomènes permettent en
réalité d'expliquer ou de résumer ces conclusions :
- Le modèle de régression linéaire est par
définition celui qui obtient le meilleur résultat par rapport
à son propre critère.
- La régression PLS est une forme de
généralisation de la régression linéaire simple ou
multiple.
- La régression PLS, dans sa première
étape, et, dans une moindre mesure, dans les quelques étapes qui
suivent (en cas de grand nombre d'étapes), prend avant tout en compte
les corrélations simples entre les variables, alors que la
régression linéaire va au-delà de ce simple
critère.
Nous allons donc nous attarder sur ces trois points.
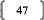
III. La régression linéaire et
critèredesmoindrescarrésle
Bien sûr, la régression linéaire au sens
des MCO n'est pas le sujet du mémoire. Néanmoins, il est bon de
savoir qu'il est impossible d'obtenir, via un modèle linéaire, un
meilleur résultat en termes de SCR que celui obtenu par la
régression linéaire, puisque c'est le critère sur lequel
se fonde cette méthode.
On peut éventuellement trouver un meilleur
modèle, mais seulement sous une forme qui ne soit pas linéaire.
Ce n'est pas le cas de la régression PLS, qui est elle aussi un
modèle linéaire.
La régression PLS ne peut donc, en aucun cas, toute
chose égale par ailleurs, fournir un modèle qui soit un meilleur
prédicateur de l'ensemble des variables actives en termes de SCR,
que celui fourni par la régression linéaire simple ou
multiple.
Le résultat peut au mieux égaler celui obtenu
par la régression linéaire simple, notamment en utilisant le
nombre maximal d'étapes, ce qui n'est pas l'intérêt initial
de la méthode.
IV La régression PLS comme
généralisation des MCO
La régression PLS, comme nous l'avons constaté
à l'étape 3, et comme nous l'avons constaté dans l'analyse
à une seule variable explicative, converge parfaitement vers la
régression linéaire.
A la première étape, les coefficients sont
strictement proportionnels aux coefficients de corrélation de la
variable explicative concernée par rapport à la variable
expliquée.
Mais dès la seconde étape, on s'éloigne de
ce schéma en tentant d'expliquer les relations entre les
résidus.
Souvent, les relations entre la variable expliquée et
les variables explicatives dépassent les simples coefficients de
corrélation. Il est possible d'avoir, par exemple, une relation
très faible entre la variable expliquée et les différentes
variables explicatives prises indépendamment, et au final,
d'obtenir une relation très forte entre la variable expliquée et
les différentes variables explicatives. C'est le cas lorsque les
relations entre les variables explicatives sont fortes.
Si les variables explicatives étaient orthogonales
entre elles, la variable expliquée pourrait s'expliquer, dans le cadre
d'une régression linéaire, directement en fonction des
coefficients de corrélation variable expliquée/variable
explicative concernée. Nous verrons ainsi que, pour une
régression portant sur des variables explicatives
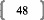
orthogonales (c'est-à-dire que les coefficients de
corrélation des variables explicatives prises deux à deux sont
nuls), il n'y a aucune différence entre une régression PLS
à une ou plusieurs étapes et une régression
linéaire simple ou multiple au sens des moindres carrés.
Ce qui peut provoquer une différence entre les deux
méthodes, c'est la multicolinéarité des variables
explicatives (en d'autres termes, lorsque les variables explicatives sont
corrélées entre elles).
Lorsque les variables explicatives présentent des
relations entre elles, la régression PLS, à l'étape 1, les
néglige. A l'étape 2, ce n'est déjà plus le cas.
Pourquoi ? Parce que la régression PLS(1) ne suffit pas à
expliquer toute la relation entre la variable expliquée et l'ensemble
des variables explicatives. Elle prend en compte la relation entre la variable
expliquée et chacune des variables explicatives prise
indépendamment, mais néglige le fait que plusieurs variables
explicatives peuvent expliquer une même partie de la variance de la
variable expliquée, et qu'une combinaison linéaire de ces
variables explicatives peut aussi expliquer davantage que le pourront jamais le
faire les variables explicatives additionnées.
Prenons un cas extrême pour nous en convaincre.
IV.1. Un exemple d'inefficacité de la
régression PLS à une étape
Nous choisissons une variable à expliquer Y étant
fonction linéaire de deux variables explicatives x1 et x2. Y est
créée selon une relation linéaire exacte Y = x1 - x2.
Volontairement, nous avons créé les séries de sorte
à ce que la variable Y n'ait une très faible variance. Nous avons
toutefois évité le cas extrême, pour des raisons
mathématiques, où Y aurait une variance nulle.
Voici donc les trois séries générées
:
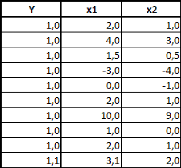
Naturellement, la série Y ne variant pratiquement pas,
elle ne peut pas non plus « covarier » avec l'une ou l'autre des
autres séries. Nous sommes donc en présence d'un cas où
les coefficients de corrélation R(Y,xi) et R(Y,x2) sont pratiquement
nuls et surtout non significatifs.
Par conséquent, la régression PLS à une
étape affectera des valeurs pratiquement aléatoires aux
coefficients des variables xi et x2, et ne sera pas du tout pertinente,
puisqu'elle tentera d'expliquer les quasi-inexistantes variations de Y par ses
quasi - inexistantes « covariations » avec xi et x2.
La régression PLS(1) nous donne donc un modèle Y
= 0.045*xi + 0.04*x2, ce qui n'a rien à voire avec la relation que nous
avons créée. Le coefficient de détermination en
témoigne : 0.72% !
Si on passe à l'étape 2, ou si on pratique une
régression linéaire, on obtient bien entendu la relation que l'on
attend : Y = 1 *xi -- M*x2. Le coefficient de régression est bien
entendu de 100%.
Nous voici donc en présence de variables où
aucune des variables explicatives n'est significativement
corrélée à Y, et où il existe pourtant une relation
linéaire exacte entre Y et l'ensemble des variables explicatives.
Prenons maintenant un tout autre exemple avec une variable
expliquée Y et trois variables explicatives xi, x2 et x3.
IV.2. Un exemple de régression PLS sur variables
explicatives orthogonales
La relation entre Y et les trois variables explicatives
importe peu. Mais en revanche, nous avons choisi trois variables explicatives
complètement orthogonales les unes par rapport aux autres.


Partie 2 : Utilisation de la régression PLS sur des
cas limites Voici les statistiques des différentes séries
:

Et la matrice des corrélations :
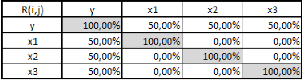
On observe donc que la variable Y est corrélée
à 50% à chacune des trois variables explicatives, qui elles ne
sont pas du tout corrélées entre elles.
Si on effectue une régression PLS à une
étape, on obtient le modèle suivant : y = 0.5*x1 + 0.5*x2 +
0.5*x3 -- 0.75
Le coefficient de détermination de la régression
est de 75%.
On constate que le modèle reste inchangé et que
le résultat ne s'améliore pas selon que l'on passe à une
régression PLS(2), PLS(3), ou qu'on pratique une régression
linéaire multiple.
On constate également que le coefficient de la
régression (75%) est égale à la somme des coefficients de
corrélation des différentes variables explicatives avec la
variable expliquée, élevés au carré :
(0.5)2 + (0.5)2 + (0.5)2 = 0.75. Cela ne peut
être le cas que lorsque les variables explicatives sont orthogonales, ou
du moins quand chaque variable explicative explique sa propre part de la
variance de Y, sans empiéter sur l'explication livrée par les
autres. Chaque variable explique donc 25% distincts de la variance de
Y.
IV.3. Conclusions
Si les variables explicatives étaient liées les une
aux autres, il y a de fortes chances que plusieurs de ces variables
expliqueraient des fractions identiques de la variance de Y.
Prenons un cas extrême qu'il n'est pas besoin
d'illustrer pour comprendre : Soit Y une variable expliquée,
corrélée à 100% à ses deux variables explicatives,
elles-mêmes alors forcément corrélées entre elles
à 100%. Le coefficient de régression ne saurait dépasser
100% et être égal à 200%. Les deux variables expliquent
parfaitement Y individuellement. L'ajout de l'autre variable n'apporte donc
rien en qualité de la
régression, puisqu'elle explique exactement la même
fraction (ici, 100%) de la variance de Y.
Si on reprend notre analyse «
Poids/Taille/Activité/Calories », on s'aperçoit que si on
fait la somme des corrélations au carré variable
expliquée/variable explicatives, on obtient : 89.84%2 +
4.68%2 + 71.77%2 = 132.44%. Il est donc évident
que les variables explicatives sont corrélées entre elles, et
qu'il y a des « recoupements » au niveau de leur pouvoir explicatif
respectif de la variance de la variable Poids, puisque, dans le meilleur des
cas (régression linéaire multiple), on obtient un coefficient de
détermination de la régression de 98.08%.
On voit donc que le coefficient de la régression peut
être supérieur ou inférieur à la somme des
coefficients de détermination variable expliquée/variables
explicatives :
- Supérieure lorsqu'il y a une compensation d'effets de
plusieurs variables explicatives.
- Inférieure quand les variables explicatives expliquent
des fractions identiques de la variance de la variable expliquée.
Bien entendu, les deux phénomènes peuvent se
produire conjointement et il est alors très difficile de s'y
retrouver.
Toujours est-il que la régression PLS, à
l'étape 1, passe complètement outre la
multicolinéarité des variables. A l'étape 2, c'est plus
délicat, car on commence à s'intéresser aux relations
entre les résidus, délaissés par la «
régression brutale » de la première étape. On
n'explique pas encore toute la relation (sauf s'il n'y a que deux étapes
possibles), puisqu'on ne s'intéresse qu'aux covariances des
résidus des variables explicatives par rapport à la variable
expliquée (on ne s'intéresse pas aux relations des résidus
des différentes variables explicatives entre eux). On procède
étape par étape. Lorsqu'il y autant d'étapes que de
variables explicatives, il n'est pas possible de trouver des relations
supplémentaires entre les résidus.
Pourquoi cette convergence entre régression PLS(p) et
régression linéaire multiple ? Parce qu'il est impossible de
former plus de « p » composantes indépendantes à partir
d'un sous-espace comprenant « p » variables. Lorsqu'on en arrive
à « p » composantes, on a forcément pris en compte
toute l'inertie des variables explicatives. Comme, à la «
pième » étape, toute l'inertie a été prise en
compte, et qu'aucun pouvoir explicatif supplémentaire n'a
été créé (chaque composante étant
formée à partir des « p » variables, elle ne peut
apporter aucun pouvoir explicatif n'existant pas dans ces « p »
variables), on ne peut obtenir résultat qui soit meilleur ou moins bon
que celui obtenu par la méthode des MCO, puisque finalement, on utilise
la méthode des MCO pour régresser Y par rapport aux composantes
t1, F, tp.

53
Le résultat sera forcément égal. La
régression PLS(p) est l'équivalent strict d'une régression
linéaire multiple au sens des MCO. Les étapes
précédentes peuvent donc être vues comme des
régressions linéaires multiples partielles, puisqu'on prend
progressivement en compte l'inertie des variables explicatives. En fait, on la
prend « partiellement » en compte, avant de faire une
régression par la méthode des moindres carrés ordinaires.
D'où la signification des initiales de la régression PLS :
Partial Least Squares, c'est-à-dire les « moindres carrés
partiels ».
La régression PLS est donc une forme de
généralisation de la méthode des MCO.
V. Le critère de la régression PLS
Le critère de la régression PLS se distingue du
critère de la régression linéaire classique.
En régression linéaire classique, on se contente
de minimiser les erreurs d'estimations sur variables actives, entendues aux
sens des carrés des résidus. On minimise la somme du carré
des résidus. On a ainsi un modèle qui colle « au plus
près » du « nuage de points ».
La régression PLS n'a pas le même objectif, et
l'approche n'est pas la même non plus. On crée pour chaque
étape, une composante qui est fonction des variables explicatives
étudiées*, en lui imposant la contrainte selon laquelle la somme
des carrés des coefficients de la composante (par rapport aux variables
explicatives) doit être égale à 1. Cette contrainte
étant prise en compte, on maximise la covariance élevée au
carré (ce qui revient au même que de maximiser la covariance en
valeur absolue) de la variable Y par rapport à ti.
*(qui changent à chaque étape, sachant
qu'à la première étape il s'agit des variables initiales
centrées-réduites, qu'à la seconde il s'agit des
résidus des régressions des variables explicatives sur ti, et
ainsi de suite, comme expliqué en première partie)
Ce programme d'optimisation, à l'étape 1, peut donc
s'écrire de la manière suivante : Max Cov2(Y,ti)
~
2
s.c. W i ~
i ~
~
t, Xi Wi
i
~
Sachant que Cov2(Y,ti) = R2(Y,ti)*Var(ti),
Var(Y) étant égal à 1 puisque Y est une variable
centrée-réduite.
Notons qu'aux étapes suivantes, on peut remplacer ti par
tj et Y par les résidus de la régression de Y sur tj-1.
Il s'agit donc de maximiser à la fois la variance de ti
(plus la variance de ti est importante, et plus l'inertie de l'ensemble
formé par les variables explicatives est expliquée, la variable
ti ne pouvant pas comporter de fraction de variance expliquant autre chose que
l'inertie des variables explicatives) et le coefficient de détermination
de Y avec ti, c'est-à-dire l'explication de Y par tM.
En d'autres termes, on cherche à trouver une variable qui
représente au mieux « l'ensemble X », tout en étant
capable d'expliquer au mieux les variations de Y.
Il ne s'agit donc pas simplement de trouver des coefficients
qui expliquent au mieux la variance de Y (il ne s'agit là que d'un seul
des deux critères), il faut également que les variables
explicatives soient « bien représentées ».
C'est là toute la différence avec la
régression linéaire simple ou multiple, qui ne considère
que le critère d'explication de la variance de Y, et néglige
à priori complètement la représentation des variables
explicatives.
La régression PLS n'est, bien entendu, pas insensible
à l'explication de la variance de Y, mais est obligée de trouver
un compromis puisqu'elle doit aussi prendre en compte la représentation
de l'ensemble X. Si la variance de ti est trop faible, la covariance de Y et ti
le sera également, et le critère ne sera pas maximisé.
V.1. Régression PLS et MCO : Différence entre
objectivité et opportunisme
La régression linéaire, en cherchant «
à tout prix » à passer au plus près du nuage de
points, peut-être amenée à effectuer une sorte de «
surparamétrage » et à livrer une explication qui finalement
ne rend plus compte des caractéristiques des variables explicatives, et
de leur réel pouvoir d'explication de la variable endogène*.
C'est particulièrement le cas lorsque les variables
explicatives sont fortement corrélées entre-elles, et que le
nombre d'observations (individus) est faible. A ce moment là, il existe
une multitude de modèles possibles permettant de passer assez
près du nuage de points, avec des combinaisons de coefficients
très variables. Les coefficients associés au modèle «
optimal » (celui retenu au sens des MCO) deviennent alors très
instables, car une faible variation aléatoire des séries (on
appelle cela « bruiter » les données) peut engendrer de fortes
variations des coefficients, rendant par la même occasion le
modèle presque impossible à interpréter dès lors
que l'on prend en compte l'importance de l'instabilité des
coefficients.

55
Le fait que le nombre d'individus soit faible aggrave ce
phénomène de surparamétrage7 dans la mesure
où un nombre d'individus qui n'est pas significativement
supérieur au nombre de variables a tendance à engendrer un
ajustement parfait ou quasi-parfait du modèle, qui bien sûr ne
peut rendre compte du potentiel réel de prédiction du
modèle (au-delà des individus actifs). On se retrouve donc, dans
de pareilles circonstances, avec un modèle sur-ajusté, trop
opportuniste car cherchant à tout prix à expliquer la variance de
Y, au détriment des relations objectives liant Y aux autres variables
individuellement, et, par la même occasion, au détriment de la
stabilité des coefficients.
D'ailleurs, ces deux problèmes, à savoir
multicolinéarité des variables et faiblesse du nombre
d'individus, trouvent leur cas limite mathématiquement, puisqu'il est
impossible de pratiquer une régression linéaire lorsqu'une des
variables est combinaison linéaire des autres (c'est-à-dire qu'on
assiste à la présence d'une relation linéaire exacte liant
les variables, ce qui constitue en fait un cas extrême de
corrélation des variables entre elles), et puisqu'il est
également impossible de pratique une régression linéaire
dès lors que le nombre d'individus devient inférieur au nombre de
variables.
D'ailleurs, ces deux problèmes, à savoir
multicolinéarité des variables et faiblesse du nombre
d'individus, trouvent leur cas limite mathématiquement, puisqu'il est
impossible de pratiquer une régression linéaire lorsqu'une des
variables est combinaison linéaire des autres (c'est-à-dire qu'on
assiste à la présence d'une relation linéaire exacte liant
les variables, ce qui constitue en fait un cas extrême de
corrélation des variables entre elles), et puisqu'il est
également impossible de pratique une régression linéaire
dès lors que le nombre d'individus devient inférieur au nombre de
variables (si c'est le cas, il existe alors une infinité de combinaisons
permettant d'atteindre un modèle expliquant 100% de la variance de
Y).
La régression PLS, à l'étape 1 du moins,
elle, ne souffre pas de ces problèmes. Elle isole les variables
explicatives dans leur capacité à expliquer Y. On obtient ainsi
un modèle décrivant une relation « factuelle »,
objective, entre Y et les variables explicatives, isolée de toute prise
en compte des relations liant les variables explicatives entre elles.
La multicolinéarité n'est alors plus un
problème car les coefficients ne sont pas influencés par les
relations entre les variables explicatives. De même, on peut alors se
permettre de travailler sur un échantillon où les individus sont
inférieurs au nombre de variables explicatives, puisque tout ce qui
importe est désormais de dégager les différentes
covariances entre Y et les différentes variables explicatives, ce qui
est toujours possible dès lors qu'il y a au moins 2 individus et que Y
varie un minimum (une variable ne variant pas ne covarie pas non plus, et il
est alors impossible de
~Le terme surparamétrage désignant un
phénomène selon lequel le modèle tente de modéliser
les fractions les moins objectives de l'ensemble formé par les variables
explicatives. On peut simplifier cette assertion en disant qu'il y a
surparamétrage dès lors que le modèle prend en compte les
« erreurs » dans ses estimations.
s'exprimer quant aux relations qui régissent sa variance).
Contrairement à la régression linéaire, cela nous donne un
résultat unique.
Il y a donc deux choses qui, notamment en étant
réunies, peuvent faire coïncider, plus ou moins fortement, les
résultats de la régression linéaire et de la
régression PLS à une seule étape :
- Un nombre considérable d'individus actifs en comparaison
avec le nombre de variables actives.
- Une faible multicolinéarité des variables
explicatives.
Un nombre important d'individus actifs a fortement tendance
à réduire les possibilités de surparamétrage
opportuniste de la régression linéaire. Il faut alors que le
modèle détermine une relation capable d'expliquer l'ensemble du
nuage de points, forcément d'autant plus représentatif d'une
population globale que ne l'est un échantillon plus réduit. Les
probabilités d'erreurs sont alors plus faibles. Les individus atypiques,
au sein de l'échantillon, sont « noyés dans la masse »,
et ont d'ailleurs généralement tendance à se compenser.
Dans ces conditions, il devient inutile, lorsqu'on cherche à minimiser
la somme du carré des résidus, de s'attarder à expliquer
des individus qui présentent des caractéristiques incompatibles
avec « la moyenne », sous peine de voir l'ensemble des
prévisions devenir complètement faussées.
Une faible multicolinéarité des variables
explicatives fait mécaniquement converger les deux méthodes. La
régression linéaire, qui normalement prend en compte les
relations entre les variables explicatives, en devient réduite à
obtenir un résultat similaire à celui d'une régression PLS
à une étape (qui ne prend pas en compte ces relations), ces
relations étant inexistantes.
V.2. Régression PLS à étapes multiples
: Compromis entre objectivité et opportunisme
L'opportunisme n'est en général pas une
qualité, sauf lorsqu'il rime avec réalisme. Cette loi vaut aussi
pour le domaine de l'économétrie.
Ainsi, le fait de dépasser la simple notion de «
covariance pure » entre Y et chaque variable explicative, et de montrer
que cette notion ne suffit pas, est le point fort de la régression
linéaire.
A deux reprises dans ce mémoire, nous avons pu observer
que la régression PLS à une seule étape était trop
loin de la réalité :
- Dans l'exemple traité dans le point IV.1. de cette
partie (page 49), nous avions nous
même créé la
série Y, et elle était conçue de telle sorte à
être égale à xi -- x2. La
régression PLS(1) a
testé la covariance entre Y et xi, puis entre Y et x2,
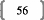
indépendamment de la considération selon
laquelle il était peut-être envisageable que xi et x2
étaient fortement corrélées entre elles et que Y pouvait
peut-être s'expliquer, non pas par les variations individuelles de xi et
x2, mais par leurs variations conjointes, c'est-à-dire par les
variations formées par l'ensemble (xi,x2). Le modèle PLS(1)
conclu alors à une relation insignifiante. Nous sommes dans le cas type
où il ne fallait justement pas maximiser la variance de ti (la variance
de Y étant pratiquement inexistante), mais se focaliser sur le
coefficient de corrélation (Y,ti). La relation était parfaite, et
on ne peut plus simple à retrouver, mais inexistante au sens de la
régression
PLS(1).
- Dans notre exemple «
Poids/Taille/Activité/Calories » du point II de cette partie (plus
exactement à la page 39 s'agissant de la régression PLS à
une seule étape), les variables « Activité physique »
et « Calories » avaient justement été
créées de sorte à expliquer les résidus de la
régression de la variable Poids sur la variable Taille. Ce fut d'autant
plus le cas de la variable Activité, qui fut créée en
première, uniquement sur base de ce critère (la variable Calories
étant volontairement corrélée au Poids et à la
Taille, sa construction dépassait ce critère).
En d'autres termes, pour expliquer décemment
l'influence de la variable Activité, il fallait raisonner «
à Taille égale », c'est-à-dire qu'il fallait
éliminer l'impact de la valeur Taille sur la valeur Poids,
c'est-à-dire à prendre en considération les résidus
de la régression « Poids sur Taille ». Hors, la
régression PLS(1) ne tient pas compte de ces éléments.
Elle a simplement relevé le fait que la variable Activité
était très peu corrélée à la variable Taille
(positivement), et a donc affecté un coefficient très faible
à cette variable dans le modèle (et s'est par la même
occasion trompée sur le signe de la relation).
La régression linéaire, elle, n'est pas
tombée dans le piège, et a remarqué qu'en affectant un
coefficient plus important à la variable Taille, et en affectant un
coefficient élevé et négatif à la variable
Activité, on arrivait à un meilleur résultat.
C'était le résultat espéré, puisqu'il rend
nettement mieux compte des conditions qui sont à la base de la
création des variables.
Dans ces deux cas, on peut être pratiquement sûr
que si on avait créé d'autres individus satisfaisants aux
mêmes conditions que les individus actifs, ils auraient été
nettement mieux prédits par le modèle de régression
linéaire.
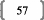
Partie 2 : Utilisation de la régression PLS sur des
cas limites Je vois principalement deux enseignements à tirer de
ces exemples :
- Considérer des relations «
séparées » entre une variable expliquée et des
variables explicatives ne revient pas au même que de considérer la
relation liant la variable expliquée à l'ensemble des
variables explicatives. Les deux analyses se distinguent l'une de l'autre
dès lors qu'il existe des relations liant les variables explicatives
entre elles. La régression PLS(1), en tenant des analyses
séparées, n'est pas toujours capable de rendre compte de la
réalité.
Cette explication est parfaitement illustrée par
l'exemple où Y = x1 -- x2. Y ne peut ni s'expliquer par x1 ni par x2,
mais par l'ensemble des deux, c'est-à-dire par la meilleure combinaison
linéaire possible de x1 et x2 capable d'expliquer Y, en l'occurrence
(dans le cas présent) la différence entre x1 et x2.
- Il existe une différence notable entre «
corrélation simple » et « corrélation partielle ».
La corrélation simple mesure le pourcentage de variation conjointe de
deux variables sans tenir compte de l'influence possibles d'autres facteurs. La
corrélation partielle mesure le pourcentage de variation conjointe de
deux variables « toute chose étant égale par ailleurs
». C'est-à-dire qu'elle cherche à mesurer l'influence de la
variation d'une variable sur la variation d'une autre variable, les autres
variables étant fixées. La régression PLS à une
seule étape ne s'intéresse qu'à la corrélation
simple, alors que la régression linéaire, en cherchant à
passer au plus près du nuage de points, est forcée de prendre en
compte les relations entre variables explicatives, et les coefficients qui en
découlent sont donc conditionnés par les corrélations
partielles entre les variables explicatives et la variable expliquée.
C'est particulièrement le cas dans l'exemple «
Poids/Taille/Activité/Calories », où la variable
Activité présente un coefficient de corrélation non
significatif avec la variable Taille, mais où la corrélation
partielle Poids/Activité, notamment pour Taille fixée, est
très élevée et négative, ce qui se ressent dans le
coefficient affecté par la régression linéaire, mais
absolument pas dans le coefficient affecté par la régression
PLS(1).
Pour ces raisons, on peut dire que la régression PLS(1)
est irréaliste, et a de fortes chances d'être surpassée par
la régression linéaire, que ce soit en termes d'explication des
individus actifs, ou en termes de prévisions d'autres individus.
Dans la majorité des cas, la régression PLS(1)
n'est donc pas suffisante. Faut-il pour autant se rabattre
systématiquement sur la régression linéaire, sachant que
les étapes supplémentaires ne sont que des compromis entre une
régression PLS(1) irréaliste et une régression
linéaire rendant mieux compte des relations entre les variables ?
Ce n'est pas forcément le cas. En fait, en augmentant le
nombre d'étapes de la
régression PLS, on vise essentiellement
à mieux rendre compte de la réalité, en prenant
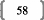
en compte en premier lieu les relations les plus objectives
entre les variables. Dès lors que l'on passe à l'étape 2,
et que l'on se rend compte que des covariances demeurent dans les
résidus ignorés par l'étape 1, on en est indirectement
amené à prendre en compte les relations entre les variables
explicatives (puisque les résidus de la régression de chaque
variable explicative sur ti sont conditionnés par les relations
existantes entre les autres variables et ti, puisqu'elles ont elle aussi
contribué à sa formation).
Mais cette prise en compte se fait progressivement,
étape par étape, en privilégiant les relations les plus
objectives, et non les plus « marginales », qui ne conduisent
qu'à un surparamétrage du modèle en cherchant à
prendre en compte des relations qui n'existent pas vraiment. On arrive donc
ainsi à isoler, avec plus ou moins d'efficacité, la partie
purement « opportuniste » d'une régression linéaire.
Le but est de s'arrêter à la bonne étape,
avant que n'ait lieu le phénomène de surparamétrage. La
régression PLS n'est en fait qu'une sorte de régression
linéaire par des « moindres carrés contraints », la
contrainte étant plus ou moins renforcée selon le nombre
d'étapes.
Cette contrainte génère alors un biais dans le
modèle. On entend par là que l'espérance de l'estimateur
diverge de la moyenne observée sur la population (pour les valeurs de la
variable expliquée). Les moindres carrés ordinaires constituent
les « meilleurs estimateurs linéaire non biaisés » (on
les appelle aussi « B.L.U.E. », qui vient de la traduction
anglaise « Best Linear Unbiased Estimators »). Quand on
cherche à comparer deux estimateurs non-biaisés, on dit que le
meilleur est celui qui présente la variance la plus faible. C'est le cas
des M.C.O. Néanmoins, cela n'exclu pas la possibilité de trouver
un estimateur biaisé qui soit meilleur. C'est précisément
ce qu'on cherche à déterminer en régression PLS.
Cela peut paraître impossible, la méthode des
moindres carrés ordinaires étant celle qui, par
définition, minimise la somme des résidus au carré... Mais
il faut savoir que l'on cherche, non pas à prédire au mieux les
valeurs des individus actifs (ce qui est inutile en soit, puisqu'elles sont
connues), mais à estimer les valeurs que sont sensés prendre
d'autres individus pour la variable expliquée, en fonction des valeurs
(connues) qu'ils présentent au niveau des variables explicatives.
Il s'agit donc d'effectuer de l'estimation, et non d'expliquer
au mieux des relations sur des individus que l'on connaît
déjà. Dans ce contexte, le surparamétrage qui
résulte du critère de la régression linéaire est
à éviter.
L'autre avantage de la régression PLS réside
dans une plus grande lisibilité du modèle. Les coefficients
étant plus stables (pour autant que le bon nombre d'étapes ait
été retenu), l'interprétation du modèle en est
rendu plus aisé. En cas de régression linéaire par les
M.C.O. sur des variables fortement corrélées, et
particulièrement sur un faible nombre d'individus actifs, on doit faire
face à une grande instabilité des coefficients,
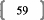
plusieurs relations faisant intervenir des combinaisons de
coefficient très variées donnant des résultats très
proches. Dans ce contexte, il devient impossible de tenir une
interprétation correcte du modèle.
Quoi qu'il en soit, la question que l'on doit se poser,
généralement, lorsque l'on tente d'établir une analyse,
est la suivante « Comment un obtenir un modèle, formé
à partir d'un échantillon plus ou moins réduit, qui soit
représentatif de la population mère ? ».
C'est ce que nous allons tenter d'établir dans la
prochaine partie. Nous allons avoir l'occasion de construire des modèles
sur base d'un échantillon, d'en choisir un, avant de le tester sur le
reste de la population mère, et de vérifier le bienfondé
de ce choix, en comparant ses résultats à ceux des autres
modèles.
Passons donc, sans plus attendre, à la partie «
Simulations ».
PARTIE 3
Simulations
Au cours de cette section, nous allons tenter de comprendre
comment retenir, en régression PLS, le nombre d'étapes optimal
(sachant qu'on se réserve le droit de choisir autant d'étapes que
de variables et de déboucher ainsi sur une régression
linéaire) permettant d'effectuer la meilleure estimation possible sur un
nombre d'individus « important », en travaillant avec un nombre plus
réduit d'individus actifs.
Nous allons pour cela créer nous-mêmes les
données de la « population mère », et établir un
modèle sur un échantillon réduit de cette population
initiale. Nous tenterons ensuite de voir dans quelle mesure les
différents modèles que nous allons calculer permettront d'estimer
le reste de la population.
Pour mettre en évidence l'utilité de la
régression PLS, nous choisirons un nombre assez faible d'individus
actifs, et des variables considérablement corrélées
entre-elles (sinon, le nombre d'étapes n'influencera pas le
modèle, pour des raisons vues dans la partie précédente).
Nous tenterons également, dans une certaine mesure, de faire varier ces
paramètres, afin d'essayer de mettre en évidence les conditions
pour lesquelles les conséquences engendrées par le choix du
nombre d'étapes sont significatives.
Naturellement, il ne s'agit pas de dresser des conclusions qui
se voudraient exhaustives quant aux propriétés de la
régression PLS, qui délimiteraient clairement des seuils
d'efficacités de la méthode en fonction de chaque
paramètre. Il s'agit uniquement de faire des tests, de traiter quelques
cas différents, avec des données qui ont des
propriétés connues, afin de mettre en évidence certaines
tendances, et de prouver empiriquement que, sous certaines conditions, la
régression PLS est une méthode qui se justifie pleinement.
Afin d'éviter tout manque d'objectivité dans la
création des données, celles-ci seront
générées sous Excel, avec une composante
prédéfinie et une composante aléatoire. Toutes les
données de la population mère seront
générées simultanément, y compris celles des
individus actifs, qui seront choisi « au hasard » dans la population
mère.
Pour générer une composante aléatoire, la
fonction « ALEA() » d'Excel sera utilisée. Cette fonction ne
possède peut-être pas toutes les propriétés d'une
vraie fonction aléatoire au sens pur (l'aléa pur, en
informatique, n'existe pas, puisque tout y est toujours fonction de quelque
chose), mais ses propriétés sont probablement suffisantes que
pour se livrer à un exercice de ce type sans que les conclusions ne
soient excessivement faussées. De plus, pour éviter autant que
possible tout problème, l'exercice sera répété
plusieurs fois avec des données régénérées
à chaque fois.
Cette fonction ALEA() génère aléatoirement
un nombre à 16 décimales compris entre 0
et 1. La distribution
de ce nombre au sein de cet intervalle est supposée
équiprobable
pour chaque sous-intervalle de même amplitude
défini au sein de l'intervalle (quelque
soit l'amplitude choisie). En théorie, notons que
l'espérance de la fonction ALEA() est sensée être la
suivante : E[ALEA()]=0.5
Naturellement, on peut obtenir un nombre aléatoire de
l'ordre grandeur que l'on souhaite en multipliant cet aléa par une
constante. On peut aussi créer une relation aléatoire entre deux
variables, ou une relation partiellement aléatoire.
Nous allons ainsi définir un jeu de 5 variables
explicatives xi, x2, x3, x4 et x5, et une variable expliquée Y. Nous
choisissons un nombre 5 variables dans l'optique d'un compromis. D'une part, il
faut un minimum de variables pour pouvoir observer des effets de
multicolinéarité et pouvoir juger de la pertinence d'une
méthode dans le cadre d'un jeu de relations suffisamment complexes.
D'autre part, il ne faut pas non plus choisir un nombre trop
élevé de variable sous peine de compliquer le problème
plus qu'il ne l'est nécessaire et de se détourner de l'objectif
initial qui est de tester la régression PLS.
Les relations entre les variables seront toutes
définies de manière linéaire. On part de xi, fonction
éventuelle d'un aléa et d'une constante. Ensuite, on envisage x2,
qui peut éventuellement être fonction de xi. x3 pourra quant
à elle être fonction de xi et x2, et ainsi de suite, chaque
variable pouvant être fonction de toutes les variables dont l'indice est
inférieur au sien. La variable Y peut logiquement être fonction de
toutes les variables explicatives. Les relations entre les variables sont ainsi
hiérarchisées afin de pouvoir être facilement
encodées avec Excel.
Naturellement, chaque variable peut également
intégrer des constantes ou des fonctions aléatoires de
constantes.
Chaque test effectué fera l'objet de 4 simulations, afin
de voir si les résultats sont significativement modifiés, et de
tenir des conclusions moins hasardeuses.
Notons également que le nombre d'individus étant
important, les tableaux contenant les données brutes se trouvent dans la
partie « Annexes » (ces tableaux s'étalant de la page 127
à la page 138).
I. Test n°1
Prenons les relations suivantes :
xi = 200 + 100*ALEA()
x2 = 100 + 100*ALEA() + 2*ALEA()*xi + 0.5*xi
x3 = 2*ALEA()*xi + 2*ALEA()*x2
x4 = -50 - 3*ALEA()*xi + 2*ALEA()*x3
x5= 100 + 100*ALEA() + 5*ALEA()*xi + x2 + ALEA()*x4
Y = 2*xi +2*ALEA()*xi + ALEA()*x3+ 0.5*x4 + ALEA()*x4+ x5+
0.5*ALEA()*x5 On peut résumer ces
relations via le tableau suivant :
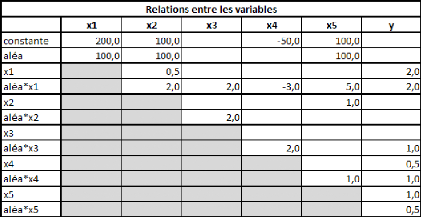
50 individus sont générés selon ces
formules (avec Excel), dont les 10 premiers serviront d'individus actifs pour
la création des modèles, et les 40 autres serviront à
mettre à l'épreuve la capacité à estimer de chaque
modèle.
4 simulations différentes seront effectuées.
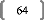
Il peut-être intéressant, au préalable, de
s'intéresser aux caractéristiques des séries qui vont
être ainsi générées :
Pour mieux comprendre ce tableau, prenons deux exemples :
- La variable xi est la somme d'un terme constant d'une valeur
de 200, qui ne fait l'objet d'aucun aléa, mais aussi d'un terme
aléatoire, pouvant varier de 0 à 100 et d'espérance 50. On
a donc une espérance totale de 250, qui se décompose
structurellement en 200 unités constantes et de 50 unités
aléatoires.
- La variable x2 est fonction de 4 termes :
o Un terme constant, d'une valeur de 100.
o Un terme aléatoire d'espérance 50.
o Un terme fonction aléatoire de xi, pouvant varier entre
0 et 500, d'espérance 250, espérance qui se décompose en
:
n Un terme constant dans xi qui devient aléatoire dans
x2, comptant pour une espérance de 200.
n Un terme aléatoire dans xi qui devient aléatoire
de 2nd degré dans x2, comptant pour une espérance de
50.
o Un terme fonction directe de xi, pouvant varier entre 100
et 150 (xi pouvant varier entre 200 et 300), d'espérance 125, qui se
décompose de la manière suivante :
n Un terme constant dans xi, qui reste constant dans x2,
comptant pour dans l'espérance de x2 pour 100 unités.
n Un terme aléatoire dans xi, qui reste aléatoire
dans x2, comptant pour 25 unités.
Au final, l'espérance de la variable x2 se
décompose donc en :
o 200 unités constantes (dont 100 issues de xi)
o 275 unités aléatoires (dont 225 issues de xi)
o 50 unités « doublement aléatoires »,
qui proviennent toutes de xi.
Avec le phénomène d'enchevêtrement des
variables les unes dans les autres, on remarque que l'on arrive à
obtenir jusqu'à 6 degrés d'aléa dans une variable. Tout
ceci semble fort complexe, mais une fois chaque degré d'aléa
clairement identifié pour chaque variable, le tableau permet d'avoir une
vue d'ensemble de la structure qui est à la base de la
génération des différentes variables. Notons
néanmoins que ce tableau ne nous renseigne pas sur les relations des
variables entre elles.
On s'aperçoit donc que, dans l'ensemble, le terme
constant n'est pas celui qui domine, et que de très fortes variations
peuvent affecter plus ou moins aléatoirement l'ensemble des variables,
avec des aléas qui peuvent se répercuter sur plusieurs variables
à la fois (ce qui peut perturber ou au contraire renforcer la relation
entre ces variables).
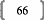
I.1. Simulation n°1
Les statistiques observées (moyenne et écart-type)
sur les individus actifs (les 10 premiers individus) sont les suivantes :

La matrice des coefficients de corrélation sur ces
individus donne :
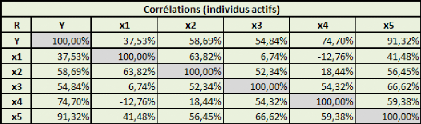
On observe donc des coefficients assez élevés
(en moyenne), que ce soit entre la variable expliquée et les variables
explicatives, ou entre les variables explicatives entre elles.
Voyons à présent les mêmes tableaux, pour la
population mère (les 50 individus) :
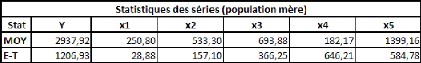
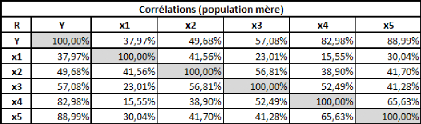
Les statistiques sur échantillon ne sont bien sûr
pas ce qu'elles sont sur la population
mère, mais, toute proportion
gardée, on constate des similitudes conséquentes. Notons
au passage que la population mère englobe les individus
actifs et que cela a un léger impact sur la similitude des
données.
Voici ce que nous donnent les différents modèles
PLS que nous pouvons calculer sur le modèle :
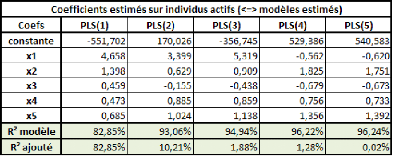
On remarque que les coefficients sont peu stables lorsque l'on
ajoute des étapes.
Remarquons également qu'en termes de R2
ajouté, seules les deux premières étapes semblent
significatives.
Regardons à présent les coordonnées des
composantes ainsi que leur variance :
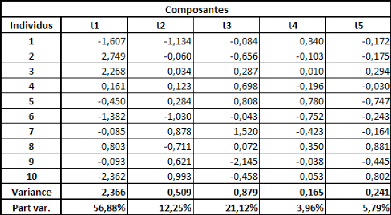
On remarque que les 3 premières composantes sont
significatives en termes de variance.
Au regard des deux critères, il serait donc judicieux
de retenir 2 ou 3 composantes, la première n'étant pas
suffisante, et les deux dernières n'étant pas significatives. La
troisième composante ne se justifie que parce que sa variance est
considérable et apporte probablement une part importante d'explication
des variables x.
On retiendra donc, assez arbitrairement, 3 composantes.
Regardons à présent les résultats de
l'application des différents modèles sur les 40 individus
non-actifs :
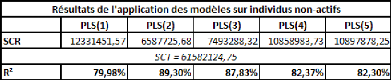
On remarque donc que c'est le modèle à 2
composantes qui obtient le meilleur score (89.30%), le modèle à 3
composantes obtenant un score assez proche de ce dernier.
Si nous effectuons une régression linéaire
multiple sur les 40 individus non-actifs, ce qui correspond au meilleur
résultat possible en termes de SCR et donc de R2, nous
obtenons les résultats suivants :
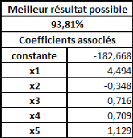
On remarque que le modèle PLS(2), ainsi que le
modèle PLS(3) que nous avons retenu, sont nettement plus proches de ce
« meilleur score possible » que ne l'est la régression PLS(5),
c'est-à-dire la régression linéaire multiple sur les
individus actifs.
La régression PLS, combinée aux
critères utilisés pour la sélection du nombre
d'étapes, est donc, ici, un meilleur estimateur que ne l'est la
régression linéaire.
Mais cette unique simulation ne saurait suffire, nous allons donc
en faire plusieurs autres afin de voir si cette tendance se vérifie.
1.2. Simulation n°2
La population mère et les individus actifs étant
tous régénérés (selon les mêmes formules que
pour la première simulation), voici ce que deviennent les nouvelles
statistiques.
Pour les individus actifs :

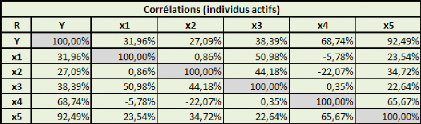
Pour la population mère :
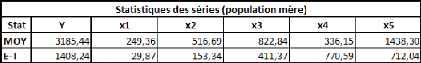
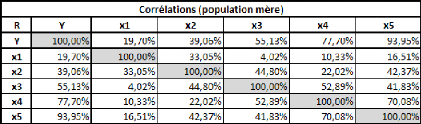
Par rapport à la précédente simulation,
il faut noter une forte instabilité des corrélations des
individus actifs, et une instabilité significative des
corrélations de la population mère.
Intéressons nous à présent aux composantes
PLS et aux différents modèles selon le nombre d'étapes
:
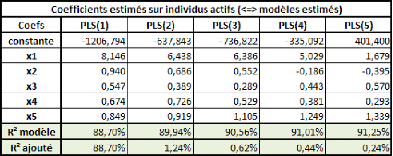
Au regard de ce tableau, il semble inutile de retenir davantage
de 1 étape. On note une grande instabilité des coefficients,
à l'exception de la variable x5.
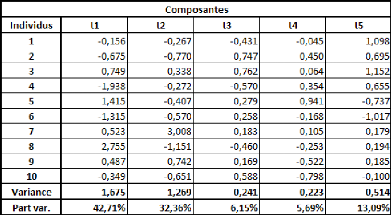
L'interprétation est plus délicate s'agissant de
la variance des composantes. Il faut, au regard de ce critère, retenir
au moins 2 étapes. Mais les 3 dernières étapes semblent
également significatives, notamment la toute dernière, qui nous
obligerait à retenir les deux autres si on souhaitait la prendre en
compte.
A la vue du premier tableau, et dans l'optique de trouver un
compromis, nous allons nous contenter de deux étapes.
Voyons à présent les résultats de
l'application des différents modèles sur les individus non-actifs
:
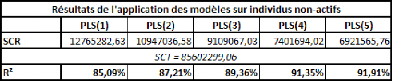
Nous sommes ici dans un cas plus délicat. Tous les
modèles, sans exception, donnent des résultats satisfaisants, et
ce malgré une amplitude conséquente des coefficients.
Néanmoins, dans ce cas-ci, la qualité des
résultats semble fonction croissante du nombre d'étapes retenues.
C'est ce que pouvait nous laisser imaginer le deuxième critère.
Mais ce n'est pas le cas du premier critère, qui nous aurait
plutôt poussés à ne retenir qu'une seule étape.
Néanmoins, on peut noter que l'amélioration des
résultats n'est pas si importante que cela, et que le choix du second
modèle, dans l'optique de compromis, n'était pas un si mauvais
choix.
Voyons ce que nous donne la régression linéaire
multiple sur les individus non-actifs :
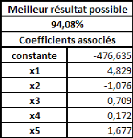
On remarque là aussi, par rapport à la
précédente simulation, une forte instabilité des
coefficients (ce qui est surprenant lorsqu'il s'agit de comparer deux
populations de taille presque aussi importante que leur population mère
respective).
On constate que les 5 modèles approchent raisonnablement
ce résultat optimal (au sens des moindres carrés), et que le
modèle PLS(5) (ou de régression linéaire) est le
meilleur.
1.3. Simulation n°3
Données des individus actifs :

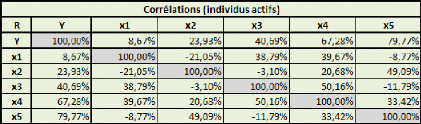
Données de la population mère :
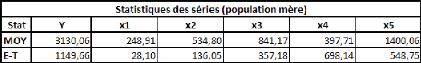
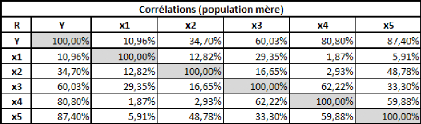
On note toujours des instabilités conséquentes par
rapport aux deux précédentes simulations.
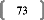
Passons sans attendre à l'étude des modèles
et composantes :
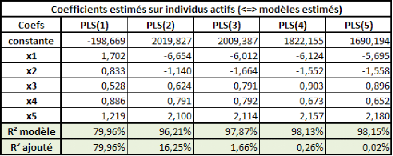
On remarque que le modèle à 5 composantes
explique très bien la population active. Néanmoins, le
modèle à 2 composantes semble suffire, avec un R2 de
96.21%, les 3 autres étapes n'apportant rien de significatif.
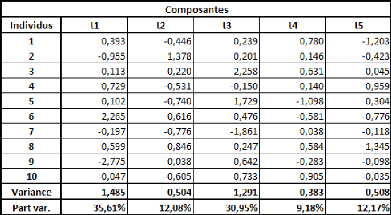
Ici, le choix semble nettement plus délicat. Il semble
inconcevable de retenir moins de 3 composantes, et les deux dernières
composantes semblent également importantes, mais nettement moins que ne
l'est la troisième.
D'après les deux tableaux, le mieux semblerait être
de retenir 3 composantes.
Voyons à présent les résultats des
modèles sur le reste de la population mère :
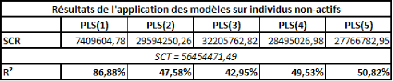
Cette fois, la contradiction est de taille. Les
critères nous on poussé à choisir le moins bon
modèle, et le seul « bon » modèle qui le soit vraiment
(quand on connaît les résultats obtenus lors des deux autres
simulations) est le modèle PLS(1).
Malheureusement, peu de choses laissaient présager que
le modèle 1 était le bon, excepté le fait que la
première composante suffisait à expliquer 79.96% de la variance
de Y s'agissant des individus actifs. On aurait hélas pu penser que, le
second axe apportant 16.25% d'explication de la variance de Y, et le
troisième axe présentant une inertie considérable (presque
aussi importante que celle du premier axe), il était indispensable de
retenir 3 axes.
Ce n'était malheureusement pas le cas. On peut
probablement expliquer cela par le fort degré d'aléa, qui soumet
la qualité de l'échantillon à un hasard
considérable.
Notons néanmoins que la régression linéaire
multiple n'aurait pas, elle non plus, atteint des résultats
intéressants
Voici les données et les résultats du meilleur
modèle possible :
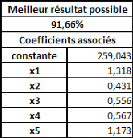
On constate ici que le modèle PLS(1) était d'une
bonne qualité. La régression PLS n'était donc pas une
mauvaise méthode sur cet exercice (bien au contraire, elle surpasse
complètement la régression linéaire), mais le choix du
nombre correct d'étapes était impossible au regard des
critères, ce qui rend ici l'utilité de la méthode
nettement moins intéressante (à quoi bon détenir le bon
modèle si on ne sait pas le distinguer des autres lorsqu'on ne peut pas
le tester sur la population mère ?).
I.4. Simulation n°4
Données des individus actifs :

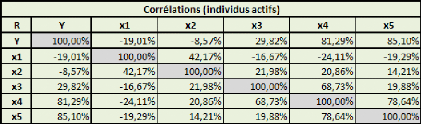
Données de la population mère :
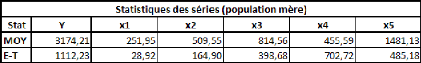
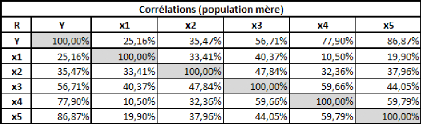
Il n'y a rien à ajouter sur ces données, quand on a
déjà vu (dans les précédentes simulations) à
quel point les séries étaient instables.
Partie 3: Simulations
Passons aux
caractéristiques des modèles et composantes afin de discuter des
critères :
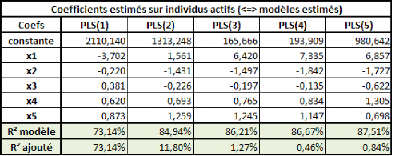
Au regard de ce critère, il semble intéressant de
retenir deux composantes, les 3 dernières n'apportant rien
d'intéressant en terme d'explication de la variance de Y.
Voyons à présent l'inertie des composantes :
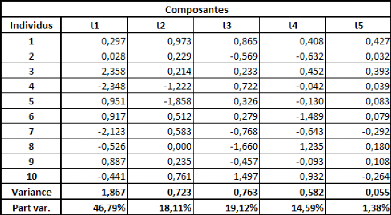
Ici, il semblerait qu'il soit préférable de retenir
4 composantes.
Dans une optique de compromis, nous retenons arbitrairement 3
composantes (2 ou 4 composantes auraient également pu se
justifier).

Voyons donc les résultats des différents
modèles :
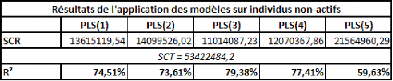
Dans l'ensemble, les modèles ont des résultats
plutôt moyens. Néanmoins, cette fois, les critères nous ont
conduits au choix du meilleur modèle.
La régression linéaire est celle qui obtient le
plus mauvais résultat. Les meilleurs résultats possibles
étaient les suivants :
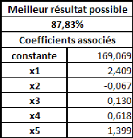
Le modèle choisi est bien entendu celui qui s'en approche
le plus.
De toutes les simulations effectuées, celle-ci est
celle qui présente la population mère la moins bien
modélisable. Il est donc normal que les résultats des
différents modèles testés soient moins bons dans
l'ensemble que ceux des simulations précédentes.

I.5. Conclusions sur le test n°1
Il est à présent temps de conclure sur l'ensemble
des simulations effectuées dans le cadre de ce premier test.
Le tableau suivant nous donne pas mal d'indications :
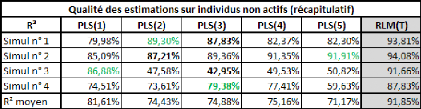
La colonne RLM(T) représente le R2
obtenu par régression linéaire multiple sur les individus non
actifs pour chaque simulation. Il s'agit du meilleur score possible à
obtenir, en termes de R2, par une régression de type
linéaire.
En vert est systématiquement indiqué, pour
chaque simulation, le meilleur modèle (parmi les 5 modèles
proposés par la régression PLS) obtenu àpartir de
l'échantillon.
En gras est systématiquement indiqué le
modèle PLS correspondant au nombre d'étapes retenues au regard
des critères.
On remarque plusieurs choses :
- Le meilleur modèle n'est jamais le même sur deux
simulations différentes.
- Le meilleur modèle n'a été choisi
qu'à une seule reprise à l'aide des critères.
- En général, le meilleur modèle se situe
environ à 5% du meilleur résultat possible. - Le modèle de
régression linéaire n'est le meilleur qu'à une seule
reprise.
- En moyenne, les résultats obtenus à l'aide du
modèle choisi (sur base des critères utilisés) est
meilleur que ne le sont les résultats de la régression
linéaire. C'est notamment le cas pour la simulation n°4, sans
laquelle cette remarque ne tiendrait plus. - En moyenne, c'est le modèle
PLS(1) qui obtient les meilleurs résultats.
- En moyenne, c'est le modèle PLS(5) qui obtient les plus
mauvais résultats.
- Les résultats varient peu, aussi bien au cas par cas
qu'en moyenne, s'agissant des modèles à 2, 3 et 4 composantes. On
pourrait facilement inclure la 5ème composante à ce
raisonnement si on ne tenait pas compte de la 4ème
simulation.
Les résultats sont donc très nuancés pour
cet exercice. L'utilité de la méthode semble pourtant
réelle, puisqu'en moyenne, la régression linéaire est
celle qui présente les moins bons résultats, et qu'en moyenne, le
modèle choisi est meilleur que le modèle de régression
linéaire. Mais ces résultats tiennent trop à la
présence de la 4ème simulation que pour être
jugés fiables.
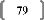
On note néanmoins une certaine robustesse de l'approche
PLS vu les résultats obtenus à la première
étape.
Notons aussi que si on observe les coefficients trouvés
par les modèles, quels qu'ils soient, on se trouve devant un souci
évident d'interprétation, et il semble difficile de savoir si un
modèle est plus fiable ou non qu'un autre.
Voici un tableau retranscrivant les écarts-types
observés par les coefficients sur l'ensemble des simulations :
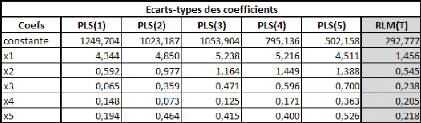
On note qu'excepté s'agissant de la constante, les
écarts-types sont nettement plus faibles pour la régression
PLS(1). Plusieurs d'entre eux sont même inférieurs aux
écarts - types observés pour les régressions faites sur
les individus non-actifs, ce qui est réellement impressionnant vu que la
taille de l'échantillon est 4 fois inférieure à la taille
de la population formée par les individus non-actifs.
Il est important de noter que la régression
linéaire (ou PLS(5)) est celle qui présente les coefficients les
plus instables, constante exceptée. Il s'agit là d'une relative
illustration de l' « opportunisme » de la méthode.
Pour en conclure sur ce test, nous retiendrons surtout que les
composantes aléatoires qui sont à l'origine de la création
des séries sont probablement nettement trop élevées que
pour obtenir des résultats suffisamment représentatifs de
l'efficacité des méthodes.
Ce tableau, confrontant les moyennes observées sur les
séries et les espérances de ces mêmes séries, le
confirme :
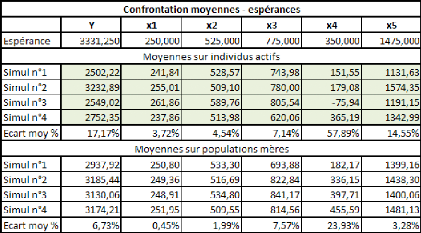
La colonne «Ecart moy 96 » calcule l'écart
relatif moyen (en valeur absolue) des moyennes considérées par
rapport à l'espérance de la série.
On note une forte instabilité générale
des séries. Les séries x1 et x2 sont les seules à
présenter une instabilité relativement faible. La série x5
présente quant à elle une instabilité acceptable. En
revanche, les séries x3, x4 et y sont considérablement instable,
particulièrement la série x4, ce qui est normal si l'on se
réfère à sa répartition en terme de degrés
d'aléa (le terme constant y est résiduel).
S'il est normal de constater des écarts significatifs sur
un échantillon de 10 individus, il l'est moins s'agissant d'une
population mère de 50 individus.
Le deuxième test que nous allons effectuer se fera en
conséquences avec des composantes aléatoires amoindries.
II. Test n°2
Comme il l'a été expliqué à la fin
du premier test, il est nécessaire de travailler avec des données
moins aléatoires, et notamment avec des relations moins
aléatoires entre les séries. Ce sera donc l'objet de ce second
test.
La seule différence avec le premier test va donc
résider dans les relations génériques entre les variables.
Le nombre de variables, d'individus actifs, d'individus au sein de la
population mère, et de simulations ne changeront donc pas.
Prenons donc, cette fois, les relations suivantes :
xi = 225 + 50*ALEA()
x2 = 125 + 50*ALEA() + ALEA()*xi + xi
x3 = 0.5*xi + ALEA()*xi + 0.5*x2 + ALEA()*x2
x4 = -50 -- 0.75*xi -- 1.5*ALEA()*xi + 0.5*x3 + ALEA()*x3
x5 = 125 + 50*ALEA() + 1.25*xi + 2.5*ALEA()*xi + x2 + 0.25*x4 +
0.5*ALEA()*x4
Y = 2.5*xi + ALEA()*xi + 0.25*x3 + 0.5*ALEA()*x3 + 0.75*x4 +
0.5*ALEA()*x4 + 1.125*x5 + 0.25*ALEA()*x5
Les relations semblent certes légèrement plus
complexes, mais en fait, la part d'aléa a été
divisée par deux dans chaque relation liant une variable à une
autre variable ou à une constante, et cette diminution a
été compensée par une hausse des relations directe entre
les variables entre-elles ou des relations entre les variables et les termes
constants. L'espérance des séries demeure ainsi inchangée
par rapport au premier test effectué.
Voici le tableau synthétisant les relations entre les
variables :
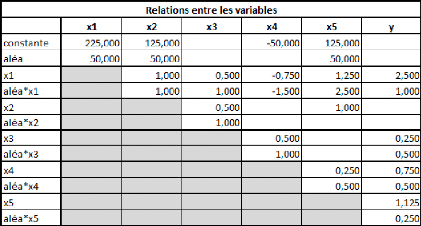
Et voici le tableau résumant les nouvelles
caractéristiques des séries :
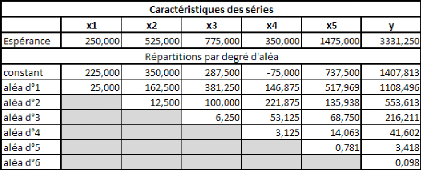
Il est bon de noter qu'en divisant par deux la composante
aléatoire qui fondait toute relation directe entre les variables, et en
divisant par deux l'aléa des termes constants, on a fait bien plus que
diviser par deux l'influence de l'aléa dans l'ensemble des
séries. Mais cela n'empêche pas l'ensemble des séries de
conserver une forte composante aléatoire.
Si l'on observe le tableau, on s'aperçoit que les
espérances des séries restent inchangées. Seules les
proportions des différents degrés d'aléa sont
modifiées. Elles sont à présent plus raisonnables. Les
termes constants prennent une importance beaucoup plus conséquente. Les
aléas de degrés élevés prennent quant à eux
une importance nettement moindre.
On peut donc s'attendre à des séries plus
prévisibles, des relations entre les variables plus stables, et donc des
données moins aléatoires au sein des individus actifs et de la
population mère.
On a donc plus de chances d'avoir un échantillon de
qualité décente, et plus de chances d'avoir une population
mère représentant fidèlement les caractéristiques
des séries.
Passons donc à présent aux simulations, qui, comme
dans l'exemple précédent, seront au nombre de 4.
II.1. Simulation n°1
Voyons tout d'abord les caractéristiques des individus
actifs :

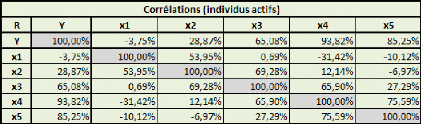
On observe que les écarts types des séries sont
nettement plus faibles que ceux que l'on a pu constater dans les simulations du
premier test. Les moyennes des séries sont raisonnablement proches de
leur espérance.
Caractéristiques de la population mère :
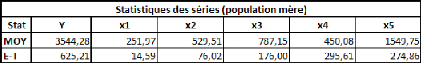
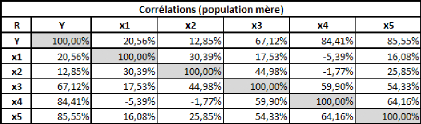
Naturellement, les moyennes enregistrées sur la
population mère sont encore plus proches des espérances
théoriques des séries. On observe néanmoins que la
série x4 est toujours fortement instable et que sa moyenne reste assez
éloignée de l'espérance.
Pour ce qui en est des corrélations, on peut dire que
l'échantillon représente assez moyennement la population
mère.
Attardons nous à présent sur les critères de
décision quant au choix du modèle, et observons pour cela les
caractéristiques des modèles et des composantes :
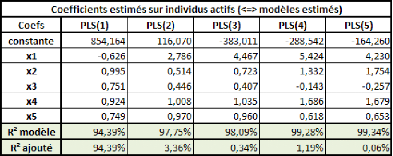
On s'aperçoit que les coefficients sont assez instables
d'un modèle à l'autre, et que même les variables
théoriquement les plus stables ne sont pas épargnées (bien
au contraire). Cela tient à la complexité du jeu des variables
entre-elles.
Notons également que les individus actifs sont nettement
mieux prédits (globalement) que dans les simulations du test
précédent.
On remarque que les 3 dernières composantes apportent
très peu en termes de prédiction des individus actifs. Ce
critère nous incite à ne retenir que 2 composantes.
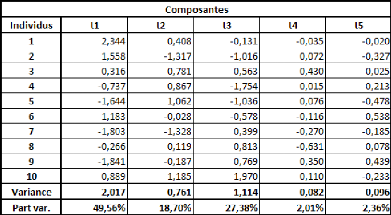
Le critère de la variance des axes nous incite
clairement à retenir 3 composantes. C'est ce que nous ferons, afin
d'éviter de perdre une partie importante de la représentation des
axes.
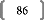
Notons que les deux derniers axes sont jugés
complètement inutiles par les deux critères. Nous retenons
donc 3 composantes.
Voyons à présent les résultats des
estimations des différents modèles sur les 40 autres individus
:
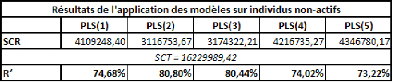
On remarque que les modèles à 2 et 3 composantes
sont considérablement meilleurs que les autres.
Les modèles recommandés par les deux
critères sont donc ici les meilleurs. Le modèle que nous avons
retenu (celui à 3 composantes) n'est pas le meilleur mais est
très proche de celui qui l'est.
Regardons à présent le meilleur résultat
possible :
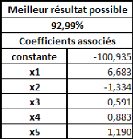
On s'aperçoit que les modèles en sont assez
loin, ce qui est paradoxal. En effet, dans les simulations du
précédent test, les meilleurs modèles s'approchaient en
moyenne à 5% du meilleur résultat possible. Cette fois-ci,
l'écart est de 12%, alors que nous avons réduit l'impact du
facteur aléatoire.
Cela relève probablement d'une mauvaise qualité
de l'échantillon, pas suffisamment représentatif de la population
mère. On peut raisonnablement qu'il s'agisse d'une exception et que les
prochains individus actifs seront plus représentatifs des prochaines
populations mères (dans les simulations suivantes).
Quoi qu'il en soit, cette simulation est plutôt positive
car les critères ont retenu les bons modèles.
11.2. Simulation n°2
Voyons tout de suite quelles sont les caractéristiques des
séries. Tout d'abord celles des individus actifs :
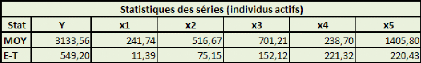
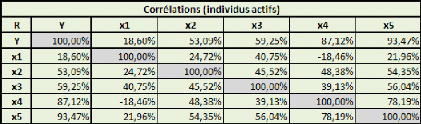
Et voici celles de la population mère :
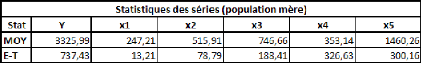
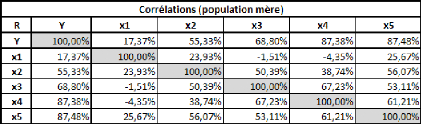
1l semblerait les coefficients de corrélations des
séries issues des individus actifs soient un peu plus
représentatifs de ceux de celles issues de la population mère que
dans la simulation précédente.
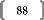
Etudions à présent la construction des
modèles et des composantes, avec, tout d'abord, les modèles en
question :
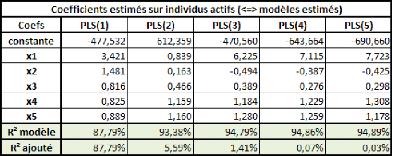
Notons que les coefficients évoluent de manière
assez stable d'étape en étape, si l'on ne tient pas compte de
l'étape n°2 qui marque une sorte de « coupure »
s'agissant du coefficient de la constante et de celui de x1.
Ce critère nous incite, sans équivoque, à
retenir les deux premières composantes.
Notons par contre que les individus sont moins bien
prédictibles que dans la simulation précédente (94.89% au
mieux contre 99.34% dans la simulation n°1).
Etudions à présent les variances des axes :
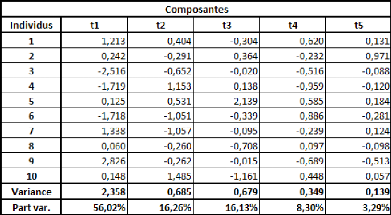
Ce critère nous conduit à conserver 3 ou 4 axes. A
nouveau, nous choisissons le compromis et retiendrons 3 axes.
Les résultats des modèles sont les suivants :
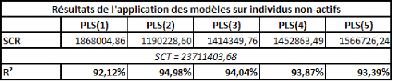
Les résultats semblent assez indifférents quant
au modèle choisi. C'est à nouveau le modèle à 2
composantes qui sort légèrement du lot, tel que le
préconisait le premier critère (c'était déjà
le cas dans la simulation précédente). Le choix de 3 axes
constitue le 2ème meilleur choix possible.
Voyons quels sont les données du résultat optimal
sur les 40 individus concernés :
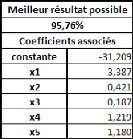
On s'aperçoit que le modèle PLS(2) était
vraiment proche du résultat optimal. Pourtant, les coefficients, pour
certains d'entre eux, sont loin d'être les mêmes.
On remarque cette fois-ci que, contrairement à
l'exemple précédent, qui voyait un écart de + de 12% entre
le meilleur modèle et le résultat optimal, ici, cet écart
est inférieur à 1%. Cela tend à confirmer que la
simulation précédente constituait une exception. On peut penser
que les individus actifs représentaient un échantillon de
meilleure qualité (plus représentatif) de la population
active.
Pour ce qui en est de l'efficacité de la méthode
PLS, nous pouvons dire qu'elle est ici difficilement démontrable
étant donné la proximité des modèles en terme de
qualité d'estimations.
Néanmoins, le fait que les critères nous aient
amenés à choisir le deuxième meilleur modèle (le
modèle PLS(3)), et le fait que l'hésitation portait sur les
modèles PLS(2), PLS(3) et PLS(4) (les 3 meilleurs modèles), nous
laisse à penser que la méthode est satisfaisante.
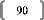
11.3. Simulation n°3
Les caractéristiques des individus actifs et de la
population mère sont les suivantes. Pour les individus actifs :
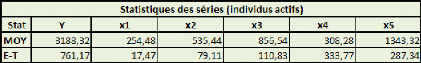
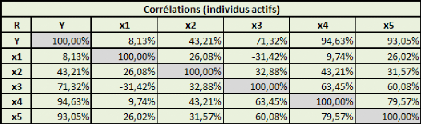
Pour la population mère :
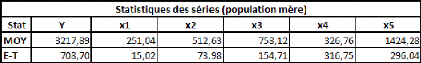
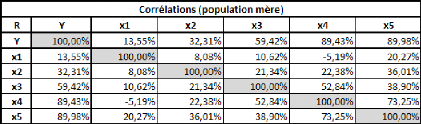
Comme dans la première simulation, les
caractéristiques des individus actifs représentent moyennement
celles de la population mère.
Intéressons nous à présent aux
modèles et composantes :
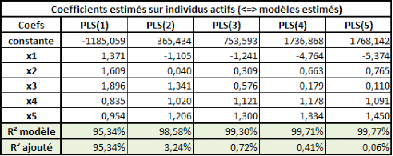
Les individus actifs semblent facilement modélisables. Ce
critère nous invite à retenir une, ou éventuellement deux
composantes.
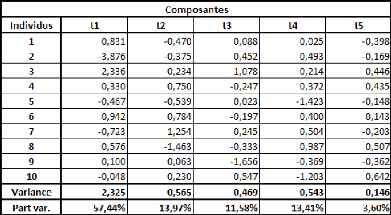
Le critère de la variance des axes semble nous inviter
à retenir 4 composantes, mais nous indique clairement que la
première composante est de loin la plus représentative.
Nous retiendrons 3 composantes, et ce pour deux raisons
:
- Parce que les coefficients semblent hautement instables
à partir de l'étape 4.
- Parce qu'il serait trop dangereux de se priver d'une partie
trop importante de l'inertie des axes. Les deux premiers axes, à eux
seuls, ne suffisent peut-être pas. Bien sûr, l'idéal serait
de retenir 4 axes au regard du critère d'inertie, mais cela reviendrait
à ignorer complètement le premier critère. Le choix de 3
composantes relève donc encore du principe de compromis.
Passons à présent aux résultats des
estimations des modèles :
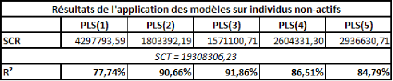
Cette fois, il semblerait que nous ayons choisi le bon nombre
d'axes.
Notons que le premier critère, à lui seul, nous
aurais dangereusement tenté de ne retenir qu'un seul axe. Il
était important de se fier au second critère. Néanmoins,
ce dernier, à lui seul, nous aurait poussé à retenir 4
axes, dont un aurait été de trop. Il est donc important de se
fier aux deux critères en relativisant l'importance d'un seul
critère pris isolément.
Notons que, dans l'ensemble, les prévisions sont
meilleures qu'elles ne l'étaient lors de la première simulation,
et moins bonnes qu'elles ne l'étaient pour la seconde.
Le résultat optimal était le suivant :
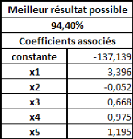
Contrairement à la première simulation, le
meilleur modèle (qui fut d'ailleurs le modèle choisi) s'approche
considérablement du meilleur résultat possible. La
régression linéaire, quant à elle, était nettement
plus loin du résultat.
Bien que l'on craignait, au départ, d'avoir un
échantillon peu représentatif de la population mère, et
d'avoir des résultats semblables à ceux de la première
simulation, ce fut moins le cas ici. Les prévisions des
différents modèles ne sont pas aussi bonnes qu'elles ne
l'étaient dans la seconde simulation, mais cette fois, les
critères nous ont poussés à choisir le bon modèle,
qui lui était tout à fait correct.
La régression PLS, dans ce cas-ci, était donc
utile.
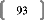
11.4. Simulation n°4
Voici les caractéristiques des individus actifs :

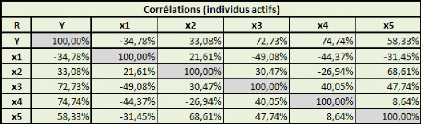
Et les caractéristiques de la population mère :
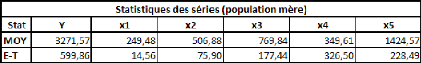
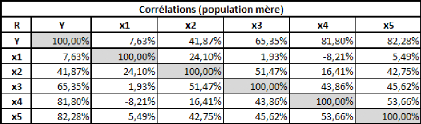
Les caractéristiques de l'échantillon semblent
assez peu représentatives de celles de la population mère,
à l'instar de ce que l'on a pu constater lors des simulations 1 et 3.
L'instabilité de la variable X4 semble y être pour beaucoup.
Les différents modèles obtenus à partir de
l'échantillon sont les suivants :
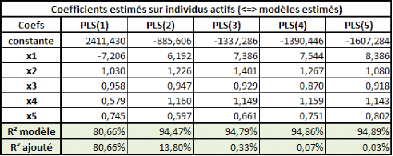
Le critère du « R2 ajouté »,
sans équivoque, nous recommande de retenir 2 étapes. Notons que
les coefficients sont assez stables à partir de l'étape 2
jusqu'à l'étape 5.
Etudions à présent les variances des
différentes composantes :
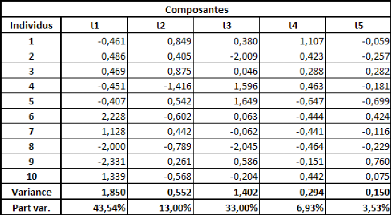
Ce critère nous incite à retenir 3 étapes,
la 3ème étant apparemment presque aussi importante que
la première.
Nous allons donc, en quelques sortes, privilégier,
cette fois, le second critère, et choisir 3 composantes, surtout
parce que la troisième composante semble très importante au
regard du second critère, et aussi parce que les coefficients semblent
raisonnablement stables entre l'étape 2 et l'étape 3. Un
phénomène de surparamétrage ne semble donc pas trop
à craindre. Il s'agit au contraire de tenir davantage compte de
l'inertie de l'ensemble des variables explicatives.
Les résultats donnés par les modèles sont
les suivant :
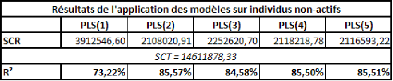
Cette fois, il y a vraiment très peu de
différences entre les 4 derniers modèles. La stabilité
relative des coefficients s'agissant des 4 dernières étapes
aurait pu nous le suggérer.
Dans cette simulation, le plus important était de ne
pas retenir le premier modèle, qui est le seul dont les résultats
se démarquent (dans le mauvais sens) du lot. Le choix du nombre
d'étapes importait peu, pourvu qu'on en retienne au moins deux. Nous en
avons retenu 3, sur base des critères, et avons ainsi pu éviter
le seul danger possible.
Notons que, dans l'ensemble, les prévisions ne semblent
pas très bonnes. Voyons donc quel était le résultat
optimal :
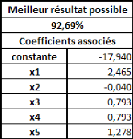
Le meilleur modèle était à un peu plus de
7% du meilleur résultat possible. La qualité de
l'échantillon était donc probablement moyenne. La population
mère, quant à elle, devait également être de
qualité moyenne, puisqu'elle est la moins bien modélisable sur
les 4 simulations que nous avons pu faire.
Ce n'est pas pour autant que le bilan de la méthode PLS
soit mauvais sur cet exemple, car même si la régression
linéaire aurait donné de meilleurs résultats que ceux
donnés par le modèle choisi, la différence était
négligeable.
II.5. Conclusions sur le test n°2
Il est maintenant temps de conclure sur ce second test, dont
l'originalité, par rapport au premier test, était de travailler
sur des relations moins aléatoires.
Voici le tableau retraçant les résultats des
différents modèles pour chaque simulation :
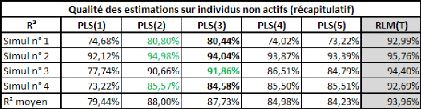
On s'aperçoit que notre choix s'est invariablement
porté sur la conservation des 3 premières étapes.
On remarque aussi que la régression PLS(1) était
dans tous les cas celle qui donnait les moins bons résultats, alors que,
le plus souvent, il suffisait d'ajouter la seconde composante que pour obtenir
le meilleur résultat possible.
Néanmoins, le choix systématique de 3
étapes n'était pas si mauvais en soi. Il constitue, dans 1 des 4
cas, le meilleur choix possible, et dans les autres cas, montre des
résultats presque aussi bons que ceux du meilleur choix possible.
Sur l'ensemble des 4 simulations, l'apport de la
méthode PLS est considérable, car il donne, en moyenne des
résultats plus proches du « résultat optimal » que ne
le fait la régression linéaire (PLS(5)).
On note, sur l'ensemble des simulations, que la population
formée par les individus non-actifs était
légèrement mieux modélisable que ce n'était le cas
dans le test précédent (le meilleur résultat possible
donne à présent un R2 en moyenne de 93.96%, contre
91.85% lors du premier test).
On peut également constater que, dans l'ensemble, les
modèles établis sur les individus actifs prédisent
nettement mieux le reste de la population.
En revanche, ce que l'on constate moins, c'est un
éventuel rapprochement entre le résultat du meilleur des 5
modèles et le « résultat optimal ». Cet écart
reste, en moyenne, d'environ 5%.
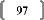
On constate d'ailleurs une sorte de convergence des
résultats, comme si chaque modèle (excepté le
modèle PLS(1)) était aussi bien capable d'estimer le reste de la
population mère que les autres ne le sont.
Les prédictions s'améliorent donc nettement,
mais l'écart du meilleur modèle (et également du
modèle choisi) par rapport au meilleur résultat possible ne
diminue pas en moyenne. De plus, les résultats semblent être moins
sensibles par rapport au choix du modèle.
On remarque néanmoins que cette différence par
rapport au premier test s'explique principalement par la simulation n°3 de
ce dernier, qui avait complètement bouleversé les
résultats. Sans elle, les conclusions du premier test ressembleraient
davantage à celle du second. Mais la probabilité d'obtenir une
simulation aussi atypique était bien entendu plus élevée
dans le premier test, étant donné l'instabilité des
séries.
Regardons à présent les écarts-types
enregistrés sur les coefficients :
On observe cette fois que les modèles PLS(2) et PLS(3)
sont les plus stables. Le modèle PLS(1) est aussi relativement stable
constante exceptée.
De manière générale, la stabilité
des modèles est légèrement meilleure que celle
constatée lors du modèle précédent. On note
également que le meilleur modèle possible sur individus ne
faisant pas partie de l'échantillon est de loin le plus stable.
Etudions à présent les moyennes enregistrées
sur les séries :
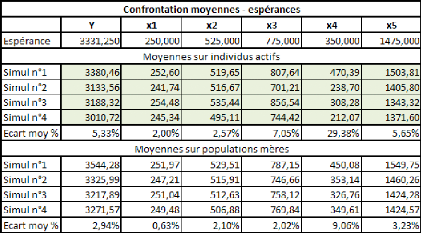
Par rapport au précédent test, on note que les
séries sont devenues nettement plus stables, que ce soit au niveau de
l'échantillon qu'au niveau de la population mère. Les
écarts par rapport à l'espérance sont devenus acceptables,
excepté s'agissant de la variable x4, qui reste hautement instable.
La question que l'on peut légitimement se poser est la
suivante : Est-ce que la réduction du facteur aléatoire avantage
l'approche PLS ou l'approche des MCO ?
En fait, la réponse théorique à cette
question est assez délicate, car plusieurs effets entrent en jeu :
- S'il n'y avait aucun facteur aléatoire, les individus
actifs seraient à 100% représentatifs de la population
mère, et la régression linéaire serait avantagée,
car en passant au plus près du nuage de points formé par les
individus actifs, elle passerait forcément au plus près de celui
formé par le reste de la population. Une réduction du facteur
aléatoire avantage donc, de ce point de vue, l'approche des MCO.
- Une réduction du facteur aléatoire,
compensée par une hausse des relations directes entre les variables
explicatives, peut renforcer la nécessité d'utiliser la
méthode PLS, qui, comme nous l'avons vu, permet en partie de faire face
au phénomène de multicolinéarité. Toutefois, cet
effet semble nettement moins évident que le premier.
Si l'on observe les résultats moyens des modèles
au cours des deux tests, on s'aperçoit que, visiblement, c'est la
régression linéaire qui est avantagée par la
réduction du facteur aléatoire, puisque ses résultats
s'améliorent en moyenne.
Ce tableau permet de comparer les résultats moyens
enregistrés au cours des 2 tests :

On s'aperçoit que tous les résultats sont en nette
progression, excepté pour le modèle à une composante.
L'approche PLS pure semble donc affaiblie et l'approche des
MCO semble renforcée. Mais la nécessite d'utiliser la
méthode PLS, combinée aux critères utilisés, quant
à elle, reste bien réelle, car bien que l'écart
enregistré entre le modèle choisi et le modèle PLS(5) est
faible, il est assez stable d'une simulation à l'autre.
En réalité, la diminution du facteur
aléatoire n'avait pas pour but d'avantager l'une ou l'autre
méthode (même si l'approche PLS semble s'en trouver
désavantagée), mais d'avoir des résultats qui nous
permettent des conclusions plus stables, étant donné le nombre de
simulations limitées que nous avons le loisir de pratiquer.
Si nous avions pu faire plusieurs dizaines de simulations,
nous aurions probablement pu nous contenter des relations utilisées dans
le premier test. Ce n'est malheureusement pas le cas car j'ai personnellement
choisi de détailler un maximum le déroulement de chaque
simulation, dans le but de rester le plus transparent possible (le manque de
transparence pouvant, en statistiques, couvrir une éventuelle
manipulation des résultats dont je ne souhaite pas être
soupçonné, sous peine d'enlever toute crédibilité
aux résultats trouvés lors des simulations).
Le fait de travailler avec des séries plus stables
permet de compenser, dans une certaine proportion, le faible nombre de
simulations. Cet objectif semble être atteint, dans une certaine mesure,
car les résultats ont assez peu varié d'une simulation à
l'autre :
- Le nombre d'étapes choisi au regard des critères
fut toujours le même.
- Le meilleur modèle était dans 3 cas le
modèle PLS(2), et dans l'autre cas le modèle PLS(3), sachant que
même dans ce cas, le modèle PLS(2) donnait des résultats
très satisfaisants.
- Les résultats des différents modèles sont
plus stables.
- La prévisibilité de la population mère
était plus stable.
L'autre but était tout de même de savoir si une
réduction du facteur aléa affectait plus particulièrement
un modèle qu'un autre. Apparemment, c'est le cas. Il faut retenir, en
moyenne, plus d'étapes que dans le premier test, pour obtenir un bon
modèle. Mais cette conclusion, basée sur seulement 4 simulations
par test, est à relativiser à cause de l'instabilité des
résultats du premier test.
Pour en finir sur les conclusions de ce deuxième test,
nous dirons que la régression PLS fut efficace dans presque 100% des
cas, car les résultats du modèle retenu étaient toujours
meilleurs que ceux du modèle PLS(5) équivalent à la
régression linéaire selon le critère des MCO,
excepté lors de la dernière simulation où les deux
modèles se valent (avec un léger avantage pour le modèle
des MCO).
Par rapport au précédent test, on note des
conditions plus stables. Le modèle choisi creuse, en moyenne, un
écart moins important par rapport au modèle PLS(5), mais un
écart qui est plus constant que dans le test précédent.
On peut penser que le modèle PLS retenu est, pour les
deux tests, globalement meilleur que le modèle PLS(5), et que cet
écart est plus conséquent lorsque l'aléa prédomine,
mais qu'il est plus constant lorsque l'aléa est plus faible.
Il est maintenant temps de procéder à un
troisième et dernier test. Le but va être de mettre en valeur la
capacité de la régression PLS à fonctionner sur un nombre
d'individus actifs à peine supérieur au nombre de variables.
III. Test n°3
Par rapport au précédent test, les relations
génériques entre les variables ne changeront pas. Il suffit donc
de retourner au début du second test pour connaître les
propriétés exactes des variables.
Pour rappel, voici les espérances théoriques des
séries :

La seule modification portera sur le nombre d'individus
actifs. Le nombre d'individus actifs passera de 10 à 7. La taille de la
population mère choisie sera toujours de 50 individus, ce qui nous
laisse 43 individus sur lesquels nous mettrons à l'épreuve les
qualités d'estimation des modèles.
Le but est de mettre en évidence les qualités
d'estimation de la régression PLS sur faible échantillon.
Nous choisissons une telle approche car l'intérêt
de la régression PLS se justifie surtout dans ce genre de cas de
figures. Sur un échantillon trop élevé, les individus
atypiques se compensent et on obtient souvent des caractéristiques trop
représentatives de la population mère, ce qui élimine
mécaniquement, en grande partie, le danger de surparamétrage de
la régression linéaire au sens des MCO.
Néanmoins, afin de « laisser une chance »
à la régression multiple, nous conservons un nombre d'individus
actifs légèrement supérieur au nombre de variables, sans
quoi ce test serait totalement inutile.
Ainsi, le fait de passer de 10 à 7 individus semble
peut-être anodin, mais en réalité, cela change
énormément la donne, puisque le nombre d'individus
supplémentaires par rapport au nombre de variables explicatives passe de
5 à 2.
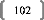
III.1 Simulation n°1
Observons les données des individus actifs :

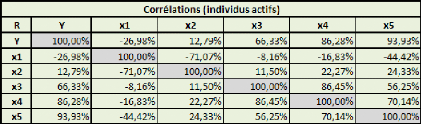
Et les données de la population mère :
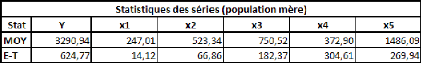
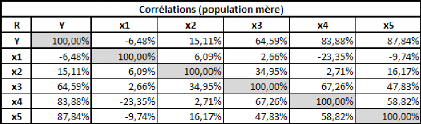
On s'aperçoit, cette fois, que les relations entre Y et
chaque variable explicative sont assez comparables au sein des individus actifs
et de la population mère, mais que les relations entre les variables
explicatives sont mal représentées par l'échantillon.
Quant aux moyennes des séries, elles sont, pour certaines,
s'agissant des individus actifs, loin de correspondre aux espérances
théoriques.
Intéressons nous à présent aux
critères de décisions
Tout d'abord, les prévisions des modèles retenus
:
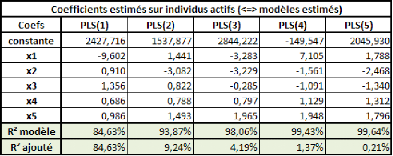
On remarque une instabilité assez forte des
coefficients.
Ce critère nous incite plutôt à retenir 2,
éventuellement 3 composantes. Mais compte tenu du faible nombre
d'individus actifs, on peut s'attendre à un surparamétrage
rapide. La troisième composante, n'apportant que 4.19% d'explication de
la variance de Y, ne semble donc pas intéressante. Le fait de retenir
une seule composante pourrait également se justifier.
Voyons à présent ce qu'il en est des variances des
axes :
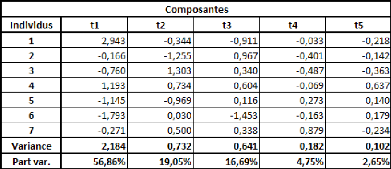
Ce critère nous incite à retenir 2 ou 3
composantes.
Dans les simulations précédentes, nous en
aurions probablement retenu 3, mais ici, nous allons nous contenter de 2
composantes, étant donné le faible nombre d'individus actifs et
la contribution modérée de la 3ème composante
à l'explication de la variance de Y.
Notre choix se portera donc sur la conservation de 2
composantes.
Partie 3: Simulations Confrontons à
présent les modèles au reste de la population mère :
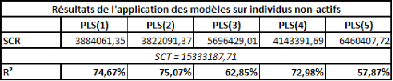
Nous sommes en présence d'un cas assez particulier. Il
fallait avant tout éviter de retenir 3 ou 5 composantes.
S'il est clair que nous n'aurions pas retenu 5 composantes,
nous avons douté quant au choix du 3ème modèle,
ce qui, ici, aurait été une erreur. Par contre, si nous avions
retenu 4 composantes, cela n'en aurait pas été une au regard des
résultats empiriques. Néanmoins, le score réalisé
par le modèle PLS(4) tient probablement davantage au hasard. Nous avons
donc bien fait de retenir un faible nombre d'étapes. Le nombre
d'individus actifs étant faible, il aurait été quelque peu
dangereux de retenir une troisième composante. Mais cela aurait pu se
justifier.
Dans tous les cas, le résultat obtenu aurait
été meilleur qu'en régression linéaire. Voyons
à présent quel était le meilleur résultat possible
sur les 43 individus non-actifs :
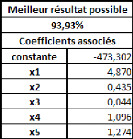
Bien évidemment, avec un échantillon aussi
faible, il aurait été très chanceux d'arriver à
prédire aussi bien la population active que ce n'était le cas
dans les simulations du test précédent.
On constate que la régression linéaire
s'éloigne complètement du résultat. La régression
PLS, dans ses premières étapes, parvient à compenser, dans
une certaine mesure, la mauvaise qualité de l'échantillon. Mais
cette compensation est loin d'être intégrale.
Il est important de faire d'autres simulations pour voir dans
quelle mesure ces résultats se vérifient.
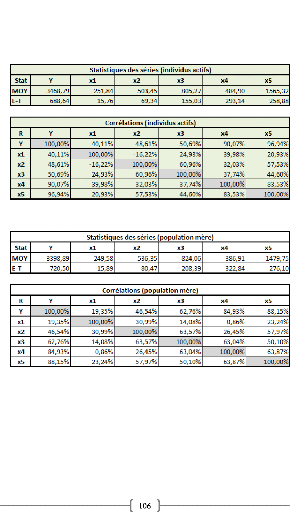
Partie 3: Simulations
111.2 Simulation n°2
Les statistiques des individus actifs sont les suivantes :
Et voici celles de la population mère :
Les corrélations de la population formée des 7
individus actifs semblent assez peu représentatives de celles de la
population mère.
1ntéressons nous à présent aux
différents modèles qui s'offrent à nous.
Tout d'abord, les modèles en eux-mêmes :
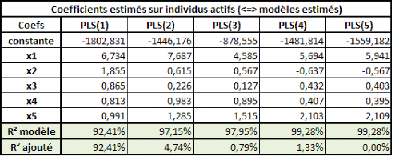
Le critère du R2 nous invite à retenir
une composante, éventuellement 2. Voyons ce que nous dit le
critère de la variance des composantes :
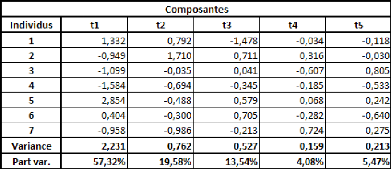
Le critère nous suggère de retenir 3 étapes.
Selon le même principe que pour la précédente simulation,
il semblerait néanmoins bon de sacrifier la 3ème
composante.
Les deux critères étant pris en
considération, le plus sage semble être de retenir 2
étapes, le premier axe ne présentant pas une variance
suffisante.
Nous retenons donc 2 composantes.
Voici les résultats de la confrontation des modèles
avec les autres individus :
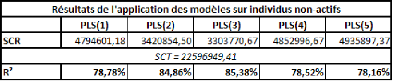
Notre choix s'est porté sur un des deux meilleurs
modèles.
Il est étonnant de constater que le troisième
axe, n'apportant presque rien en termes de R2 ajouté (sur les
individus actifs), corresponde au meilleur modèle. Néanmoins, sa
variance était importante.
Ce qu'il fallait avant tout éviter, ici, était
de retenir 1, 4 ou 5 axes. C'est ce que les critères, combinés
l'un à l'autre, nous ont conduit, bien que le premier critère,
pris isolément, nous aurait peut-être conduit à ne retenir
qu'un seul axe.
Voyons à présent quel était le meilleur
résultat possible :
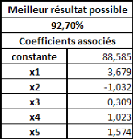
Par rapport à la simulation précédente,
on peut dire que les modèles sont nettement plus proches du meilleur
résultat possible. Ce n'est probablement pas la population mère
qui est en cause, mais la capacité de représentation de
l'échantillon, qui est probablement meilleure dans ce cas-ci.
Pour en conclure sur cette simulation, nous pouvons dire que
la méthode de régression PLS obtient des résultats
significatifs. Cette fois encore, le modèle PLS(5), correspondant au
critère des MCO, était le moins bon. Le modèle que nous
avons retenu lui a été meilleur.
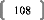
Partie 3: Simulations
111.3 Simulation n°3
Les données des individus actifs sont les suivantes :
Et voici les données de la population mère :
Les données des individus actifs semblent assez peu
représentatives de celles de la population mère.
Passons maintenant en revue les critères des
différents modèles qui s'offrent à nous. Tout d'abord, les
modèles en eux-mêmes :
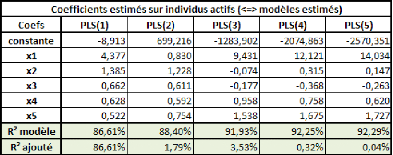
Le critère du R2 ajouté par chaque
composante semble nous indiquer de ne retenir qu'une seule étape.
Voyons ce qu'indiquent les variances des axes :
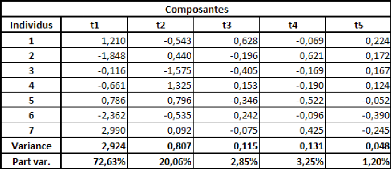
Ce critère nous indique de retenir deux composantes.
Bien que la deuxième composante semble ne pas
être significative quant à l'estimation de la variable Y pour les
individus actifs, et qu'il soit dangereux de retenir trop de composantes sur un
aussi faible échantillon, cette composante représente à
elle seule une variance considérable.
Nous retenons donc 2 composantes.
Voyons si les résultats donnés par les estimations
des différents modèles nous ont donné raison :
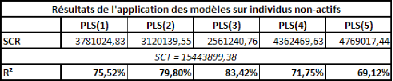
Apparemment, nous aurions mieux fait de retenir 3 composantes.
Mais les critères ne nous indiquait nullement de procéder de la
sorte, et le risque de surparamétrage était élevé.
Choisir trois 3 composantes aurait donc été, ici, le meilleur
choix à postériori, mais ca n'aurait pas été un bon
choix au regard des critères. Choisir 3 composantes aurait probablement
été irrationnel, ce qui, ici, n'aurait pas empêché
la chance de couronner ce choix de réussite.
Nous avons hésité entre retenir 1 ou 2
composantes, et le choix de 2 composantes était meilleur. Ca aurait pu
ne pas être le cas. Mais, force est de constater que, sur le nombre de
simulations que nous avons fait jusqu'ici, les choix que nous avons fait se
sont dans l'ensemble montré bon, et c'est cela qui importe. Bien
sûr, on ne peut pas contrôler le facteur « chance »,
mais, sur un grand nombre de simulations, ce facteur importe peu. L'important
est donc, dans ces conditions, que le choix se porte le plus souvent possible
sur l'un des meilleurs modèles. C'est le cas ici.
Voyons à présent ce qu'il en était du
meilleur résultat possible :
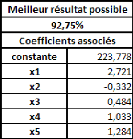
Le modèle que nous avons choisi était assez loin
de ce résultat. Mais nous n'aurions pas pu faire beaucoup mieux. Il a
l'air de se confirmer, au fil des simulations, que la faible taille de
l'échantillon se traduise par une moins bonne qualité de ce
dernier (en moyenne et toute chose égale par ailleurs), ce qui est tout
à fait logique, et nous amène forcément à avoir des
modèles qui soient moins représentatifs de la «
réalité ».
Le bilan de cette simulation est donc, somme toute, assez
positif.
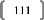
111.4 Simulation n°4
Les caractéristiques des individus actifs pour cette
dernière simulation sont les suivantes :

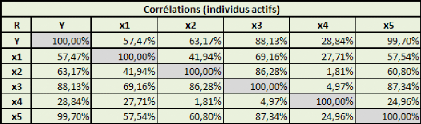
Et voici les données équivalentes pour ce qui en
est de la population mère :
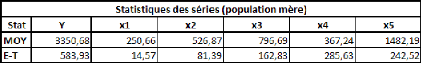
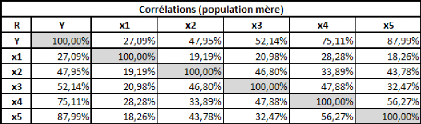
Comme pour les précédentes simulations de ce test,
les caractéristiques de la population mère sont assez mal
représentées par l'échantillon.
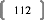
Passons à présent à l'étude des
différents modèles PLS possibles :
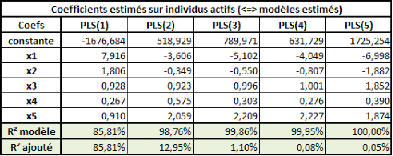
Ce critère nous incite à retenir 1 ou 2 axes.
Voyons ce que l'on peut dire des variances des axes :
Ce critère nous incite à retenir, selon
différentes interprétations possibles, 1, 2, 3 ou 4 axes.
Nous sommes en présence d'un choix délicat.
Retenir 1 seul axe est probablement insuffisant. Retenir un deuxième axe
nous apporte moyennement peu en termes de variance, mais l'apport est
significatif en termes de R2 ajouté. Globalement, il faut
donc retenir le deuxième axe.
Mais dès lors que l'on retient deux axes, on est
forcément tenté de retenir le troisième qui comporte une
variance non négligeable. Sachant que le 4ème axe
détient lui aussi une certaine variance, se priver à la fois du
3ème et du 4ème axe peut paraitre
dangereux.
Nous choisirons donc, pour cette fois, de retenir 3
axes. Nous n'en retenons pas moins
dans l'espoir d'éviter le
danger qui consiste à avoir un modèle trop peu
représentatif de
l'ensemble X. Nous n'en retenons pas plus dans l'espoir
d'éviter le surparamétrage. C'est le seul choix qui ne nous
expose que modérément à chaque risque pris
individuellement.
Voyons dès lors quels sont les résultats de la mise
à l'épreuve des modèles sur les autres individus de la
population mère :
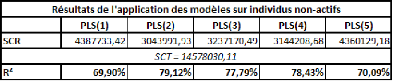
Les résultats semblent assez indifférents quant au
choix de retenir 2, 3 ou 4 composantes.
Parmi les trois modèles concernés, nous avons
choisi le moins bon, mais nous avons probablement évité certains
risques (qui ne se sont pas vraiment vérifiés ici).
De plus, l'écart par rapport aux deux autres
modèles est relativement infime. Voyons ce qu'il en est du meilleur
résultat possible :
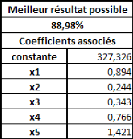
Apparemment, la population mère était, cette fois,
légèrement moins bien modélisable qu'elle ne
l'était lors des précédentes simulations.
Cela explique peut-être, en partie, les faibles
résultats obtenus par les modèles établis sur base de
l'échantillon.
Quoi qu'il en soit, les critères nous ont permis à
nouveau de retenir un modèle se situant dans la bonne « tranche
» de résultats.
Il est à présent temps de conclure sur le
troisième test.
111.5 Conclusions sur le test n°3
Le but de ce troisième test était de voir si la
régression PLS était bel et bien une méthode
intéressante sur un échantillon faible, et, plus
particulièrement, de voir si une réduction de la taille de
l'échantillon permet à l'approche PLS de « creuser
l'écart » par rapport aux autres modèles.
Voyons donc le tableau résumant les résultats
obtenus :
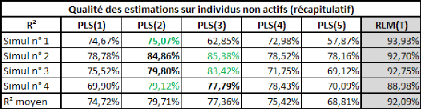
On s'aperçoit que dans 3 cas sur 4, notre choix s'est
porté sur le modèle à 2
composantes. Dans le dernier
cas, notre choix s'est porté sur le modèle à 3
composantes.
Même si nous n'avons choisi le meilleur qu'à une
seule reprise, notre choix s'est toujours porté sur les deux
modèles (PLS(2) et PLS(3)) qui cumulent à eux deux tous les
meilleurs résultats sur les 4 simulations. Parmi ces deux
modèles, le plus important était de ne pas choisir le
modèle 3 lors de la première simulation.
On observe aussi qu'en moyenne, le modèle PLS(2) est le
meilleur, suivi de près par le modèle PLS(3). Le modèle
PLS(5) est quant à lui nettement moins bon puisqu'il se situe à
plus de 10% (en moyenne) des meilleurs modèles.
La régression linéaire au sens des MCO est donc
clairement désavantagée par la faiblesse de l'échantillon,
puisque dans le test précédent, l'écart avec les meilleurs
modèles n'était en moyenne que de 4%.
Le test semble donc, dans une certaine mesure, doublement
concluant :
- Nous constatons, comme nous l'avons expliqué d'un point
de vue théorique, que la régression PLS est plus utile sur un
échantillon faible.
- Les modèles choisis au regard des critères sont
constamment parmi les meilleurs.
Notons qu'en moyenne, les modèles retenus sur base des
critères sont 10 à 11% meilleurs que le modèle de
régression linéaire des MCO.
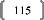
Il est également positif de constater que les
résultats du modèle retenu sont assez stables. Ils oscillent
entre 75.07% et 84.86% (9.79% d'amplitude), alors que le modèle PLS(5)
oscille entre 57.87% et 78.16% (20.29% d'amplitude).
Néanmoins, cette conclusion serait clairement ternie si
par malchance nous avions retenu le modèle à 3 composantes pour
la première simulation. Mais quoi qu'il en soit, même dans ce cas
de figure, les résultats auraient été meilleurs que ceux
obtenus par la régression PLS(5) pour chaque simulation.
Voyons à présent les différents
écarts-types des coefficients enregistrés sur les 4 simulations
pour chaque modèle :
La première chose que l'on remarque, c'est qu'il semble
extrêmement pénalisant de passer d'un échantillon de 10
individus à un échantillon de 7 individus, toutes choses
égales par ailleurs. Tous les modèles présentent, dans
l'ensemble, des coefficients très peu stables, en comparaison avec ce
que l'on a pu voir précédemment.
On s'aperçoit que le meilleur modèle possible
sur les 43 individus non actifs (dont les écarts-types se trouvent dans
la colonne de droite du tableau ci-dessus) est nettement plus stable que ne le
sont les différents modèles estimés sur base des 7
individus actifs, ce qui est parfaitement normal.
On s'aperçoit également que le modèle
PLS(1), sur l'ensemble des coefficients, est probablement le plus stable (les
écarts-types sont les plus faibles excepté s'agissant des
coefficients affectés à la constante et aux variables x1 et x4,
bien que restant très faible pour la variable x4). Le modèle
PLS(2) est également l'un des plus stables.
On s'aperçoit également que le modèle
PLS(5) est hautement instable, exception faite de certains coefficients. Cela
tend à souligner, dans une certaine mesure, la faible robustesse de
l'approche des MCO sur un échantillon trop de taille faible. Ce qui
n'est, bien entendu, pas surprenant, étant donné les nombreuses
explications fournies à ce sujet tout au cours du mémoire,
notamment s'agissant de « l'opportunisme » de la méthode des
MCO.
On constate néanmoins qu'aucun modèle n'a le
« monopole » de la stabilité de l'ensemble des coefficients.
C'était déjà le cas dans nos précédents
tests. Le nombre de simulations est trop faible que pour que ce ne soit le
cas.
Quoi qu'il en soit, globalement, les coefficients sont plus
instables que dans le test n°2, ce qui est normal, puisqu'on travaille sur
des séries qui ont les mêmes caractéristiques, avec un
échantillon plus faible, donc moins représentatif des
caractéristiques intrinsèques des variables, et dont la
modélisation est donc fortement soumise au facteur aléatoire.
Voyons à présent ce qu'il en est des
différences constatées entre la moyenne des séries (au
niveau des individus actifs comme au niveau de la population mère) et
les espérances des variables :
Par rapport au précédent test, il est logique de
constater que les écarts à l'espérance s'équivalent
dans une certaine mesure, étant donné que la population
mère est de même taille dans les deux tests, et étant
donné que les séries gardent les mêmes
propriétés.
On constate une relative hausse de l'instabilité des
caractéristiques des individus actifs. Il est étonnant de
constater que cette hausse reste modérée, après avoir
amputé l'échantillon de 30% des ses individus (10 dans le test
n°2, 7 dans le test n°3). On aurait pu s'attendre à ce que les
moyennes soient nettement plus instables. Ce n'est pas complètement le
cas. Nous aurions peut-être dû travailler avec seulement 6
individus afin de diminuer encore davantage la qualité de
l'échantillon (5 auraient été insuffisants car le
modèle linéaire établi sur le critère des MCO
aurait systématiquement trouvé la
présence d'une relation linéaire exacte,
excessivement instable d'un échantillon à l'autre).
De manière à conclure sur ce test, comparons
à présent les résultats moyens obtenus par les
différents modèles lors des tests n°2 et n°3.

On constate que l'effet de la diminution de l'échantillon
est réel, car les résultats sont en chute libre.
Mais il est fort intéressant de constater que les
modèles à faible nombre d'étapes sont ceux qui souffrent
le moins de ce changement. Si on s'en tient aux extrêmes, on
s'aperçoit que, sur 10 individus, le modèle PLS(5)
(équivalent au critère des MCO) est meilleur d'à peu
près 5% que le modèle PLS(1). Mais lors du passage à 7
individus, les résultats du modèle PLS(5) plongent de plus de
15%, alors que le modèle PLS(1) pers moins de 5%. Le modèle
PLS(1) surpasse alors le modèle PLS(5) de presque 6%.
S'agissant des autres modèles à 2, 3 et 4
étapes, les pertes semblent assez semblables. Le modèle PLS(2)
est le moins affecté des 3. Il était déjà le
meilleur (en moyenne) lors du 2ème test, et l'écart se
creuse davantage ici, excepté par rapport au modèle PLS(1) qui
est le seul à tendre à le rattraper.
Cela nous confirme donc que l'approche PLS,
représentée par les premières étapes de la
construction d'un modèle PLS, est particulièrement utile
lorsqu'il y a peu d'individus actifs, car ses résultats sont moins
sensibles au nombre d'individus actifs et au facteur aléa. Il semble
donc s'agir bel et bien d'une approche plus robuste que ne l'est l'approche des
MCO.
On pourrait se demander ce qu'il en serait si l'on augmentait
considérablement le nombre d'individus actifs. On peut penser que les
dernières étapes s'amélioreraient considérablement,
alors que les premières étapes auraient plutôt tendance
à stagner.
Quoi qu'il en soit, cela ne veut pas dire que l'approche des
MCO au sens stricte soit à privilégier. Tout dépendrait
bien entendu de l'efficacité des critères que nous avons
utilisés au cours de nos 12 simulations.
Il est à présent temps de conclure sur cette
troisième et dernière partie.
IV. Conclusions sur les simulations
réalisées
Ce qu'il est primordial de retenir sur l'ensemble de ces
tests, c'est que l'important n'est pas vraiment de comparer une approche
à une autre. Certes, il est bon de savoir que les premières
étapes sont à priori meilleures sur faible échantillon, et
que les dernières étapes seraient plutôt à
privilégier en cas d'échantillon de grande taille. Mais ce qui
compte avant tout, c'est que les critères nous permettent de retenir, en
moyenne, dans tout type de circonstances, le meilleur nombre possible
d'étapes à priori.
C'est plutôt ce que l'on a pu constater au cours des
tests que nous avons effectué. Les critères nous ont souvent
amené à retenir un des meilleurs modèles, souvent meilleur
que ne l'est le modèle associé au critère des MCO, et
souvent parmi les meilleurs modèles.
L'approche en termes de MCO stricts de la régression
linéaire multiple n'est donc, à elle seule, pas suffisante,
puisqu'une approche PLS avec sélection du nombre d'étapes au
regard des critères lui est généralement
préférable, d'après les tests que nous avons pu mener en
tout cas.
Il est important de signaler que ces tests n'ont de sens que
pour tester l'efficacité de la méthode dans l'absolu. Ils ne sont
pas tout à fait réalistes, puisque, dans la
réalité, lorsqu'on étudie un échantillon, on ne
connaît ni les caractéristiques intrinsèques des variables,
ni les caractéristiques de la population mère. L'approche que
nous avons utilisée ne fonctionne que pour tenter de démontrer
certaines propriétés théoriques de la régression
PLS.
Dans la réalité, lorsque l'on étudie un
échantillon, et qu'on tente d'établir des prévisions qui
ont vocation à s'appliquer au-delà de l'échantillon, on ne
peut pas vérifier quels sont en effet les résultats des
différents modèles.
Voila pourquoi il est important de déterminer, dans un
cadre théorique, si la méthode PLS, combinée à
l'utilisation des critères, permet de connaître le meilleur
modèle à utiliser (ou l'un des meilleurs). Pour plus de
réalisme, nous avons volontairement fait abstraction des
résultats obtenus par les modèles sur le reste de la population
mère, de sorte à faire un choix sur seule base des
caractéristiques des modèles établis, comme c'est le cas
dans une situation réelle où l'on ne dispose pas des
données permettant de vérifier si l'approche est juste ou non.
Le fait que les résultats, dont nous n'avons tenu
compte qu'après avoir choisi un modèle, donnent plutôt
raison aux critères nous amène à penser qu'il pourrait en
être de même dans la réalité.
Néanmoins, étant donné le fait que, dans
la réalité, les propriétés des variables ne sont
pas connues, il est impossible d'être sûr du bienfondé du
choix d'un modèle. Mais il s'agit avant tout, non pas de choisir le
« meilleur modèle », qui dans la réalité est
souvent impossible à déterminer, mais plutôt le
modèle qui, à priori, offre l'espérance de résultat
la plus élevée. Etant donné le fait que les
résultats, obtenus au cours de nos tests, concordent assez bien avec les
critères, on peut raisonnablement penser que les critères
puissent également s'appliquer à des modèles
établis sur base d'un échantillon réel.
Ces tests nous ont également permis de savoir, de
manière très générale, que tout chose égale
par ailleurs, les modèles à faible nombre d'étapes
trouvent davantage leur utilité en présence d'aléa fort et
d'échantillon de taille réduite, c'est-à-dire lorsque la
population a peu de chances de se modéliser au mieux suivant un
modèle qui modéliserait les individus actifs au mieux.
La corrélation des variables explicatives entre-elles
est également très importante, même si nous ne l'avons pas
démontré au cours de ces tests (mais nous avions vu
précédemment que plus les variables explicatives sont
orthogonales entre elles, et plus les étapes de la régression PLS
se confondent).
Mes principaux regrets, s'agissant de cette partie, sont,
d'une part, de ne pas avoir pu effectuer davantage de simulations par test, et
d'autre part, de ne pas avoir pu mener d'autres tests, notamment en augmentant
la taille de l'échantillon ou en décorrélant fortement les
variables.
CONCLUSION
GENERALE
Il est maintenant temps de conclure sur ce mémoire. Au
cours de ce dernier, j'ai tenté de présenter la régression
PLS de la manière la plus littéraire possible, dans le but
d'expliquer la méthode et ses justifications à ceux qui ne la
connaissent pas.
Dans un premier temps, le but a été de situer la
méthode historiquement, et au sein de la vaste discipline formée
par l'ensemble des analyses statistiques. Ainsi, nous avons vu en quoi
consistait une régression linéaire sur le principe, avant de voir
en quoi consistait la régression PLS en elle-même.
Ensuite, nous avons détaillé un minimum les
formules nécessaires à la mise en pratique de la
régression PLS univariée, sans données manquantes, sur
laquelle s'est focalisé le mémoire. Nous avons ainsi voir comment
se calculent les composantes, comment se construit le modèle, et
dégager de cela quelques propriétés théoriques
(critère de covariance, indépendance des composantes, centrage et
réduction des données, ...). Nous avons également vu les
critères qui permettent de savoir combien d'étapes il est
préférable de retenir.
Nous avons pu constater que la régression PLS peut
s'appliquer à des échantillons présentant moins
d'observations que de variables explicatives.
Nous sommes ensuite passés à quelques exemples
théoriques extrêmes, desquelles nous avons pu déduire
quelques propriétés s'agissant de l'usage pratique de la
méthode. Nous avons ainsi pu constater que la méthode est
d'autant plus efficace en cas de multicolinéarité des variables
explicatives, cas sur lequel nous nous sommes longuement attardés. C'est
de cette manière que nous avons pu distinguer la différence
d'approche entre la méthode des MCO et la méthode de
régression PLS, tout en montrant que la seconde constituait une
généralisation de la première.
Nous sommes ensuite passés à des tests
basés sur des simulations à partir de données fictives
avec des propriétés connues à l'avance, que nous avons
détaillé. Nous avons ainsi pu faire trois tests. Le
deuxième s'est différencié du premier par une part
nettement amoindrie du facteur aléatoire, et le troisième s'est
différencié du deuxième par un échantillon de
taille réduite. Nous en avons conclu que la régression
linéaire est avantagée lorsque l'échantillon est fortement
représentatif de la population mère. Au contraire, un
échantillon de taille réduite, et des séries comportant
une forte part d'aléa (l'aléa se traduisant concrètement
par « tout ce qui n'est pas fonction de l'ensemble des variables »),
sont autant d'éléments qui favorisent les régressions PLS
à faible nombre d'étapes.
Nous avons également pu démontrer, dans une
certaine mesure, que la régression PLS, utilisée judicieusement
(c'est-à-dire combinée comme il se doit aux critères
retenus), permet de dépasser la simple approche des MCO, parfois trop
« opportuniste » (ce qui est un danger lorsque l'échantillon
est réduit).
Au regard de l'ensemble du mémoire, il semble que la
régression PLS peut se caractériser comme étant une
méthode robuste, fiable, s'appliquant dans de nombreux cas, et
étant plus générale que ne l'est la régression
linéaire.
Ses principaux avantages, lorsque le nombre d'étapes est
adroitement choisi, peuvent se résumer ainsi :
- La régression PLS fonctionne bien sur un
échantillon de taille faible, pouvant même être
inférieur au nombre de variables explicatives.
- La régression PLS permet de compenser, partiellement,
une baisse de qualité de l'échantillon.
- La régression PLS permet d'éviter certains
problèmes engendrés par la multicolinéarité des
variables.
A cela, on peut ajouter deux avantages, que nous n'avons pas eu
l'occasion de démontrer :
- La régression PLS, dans son approche multivariée,
permet d'expliquer plusieurs variables endogènes.
- La régression PLS, dans un algorithme plus
général, permet de créer un modèle en tenant compte
des individus présentant certaines données manquantes, sans avoir
recours à des méthodes d'estimation des données
manquantes.
Ces avantages justifient donc l'utilisation de la
méthode. Bien entendu, elle se justifie plus particulièrement
dans les conditions que nous avons exposé, mais, de manière
générale, cette méthode semble pouvoir se justifier en
toutes circonstances, pour autant que l'on soit prêt à retenir le
nombre d'étapes maximal si les critères le justifient.
Par conséquence, bien que cette méthode ait
connu la plupart de ses succès dans le domaine de la chimie, on peut
penser qu'elle pourrait facilement être transposée à
d'autres domaines, particulièrement dans ceux où le nombre
d'individus actifs est faible (en comparaison au nombre de variables
explicatives) et où les variables explicatives sont significativement
corrélées entre-elles.
BIBLIOGRAPHIE
Références internet :
Druilhet P., Mom A., « Régression PLS: Une
nouvelle approche »
http://www.agro-montpellier.fr/sfds/CD/textes/druilhet1.pdf
AI ACCESS, Glossaire de la modélisation
:
http://www.aiaccess.net/French/Glossaires/GlosMod/f_gm_correlation_partielle.htm
http://www.aiaccess.net/French/Glossaires/GlosMod/f_gm_pls.htm
Revue de statistique appliquée :
Cazes P. (1995), tome 43, n°1 :
http://archive.numdam.org/article/RSA_1995__43_1_5_0.pdf
http://archive.numdam.org/article/RSA_1995__43_1_7_0.pdf
http://archive.numdam.org/article/RSA_1995__43_1_65_0.pdf
Palm R., Iemma A.F., tome 43, n°2 :
http://archive.numdam.org/article/RSA_1995__43_2_5_0.pdf
Bry X., Antoine P., « Application à l'analyse
biographique», Explorer l'explicatif :
http://www.cairn.info/article.php?ID_REVUE=POPU&ID_NUMPUBLIE=POPU_406&ID_ARTICLE=POPU
_406_0909
Bastien P., Tenenhaus M. (2003), « Régression PLS
et données manquantes », Club SAS STAT :
http://club-sas-stat.jeannot.org/journees/docs20031204/PLSetDonneesManquantes.pdf
Bastien P., Vinzi V.E., Tenenhaus M. (2002), «
Régression linéaire généralisée
PLS», Groupe HEC :
http://www.hec.fr/hec/fr/professeurs_recherche/upload/cahiers/CR766.pdf
http://www.iut-lannion.fr/LEMEN/MPDOC/STAT/chap3/estim.htm
Chavent M., Patouille B. (2003), « Calcul des
coefficients de régression et du PRESS en régression PLS1
» :
http://www.math.u-bordeaux.fr/lchavent/Publications/2003/press-pls-preprint.pdf
Goupy J., « La régression PLS1, cas particulier
de la régression linéaire séquentielle orthogonale
(RLSO) » :
http://www-rocq.inria.fr/axis/modulad/archives/numero-33/goupy-33/goupy-33.pdf
Techniques statistiques récentes pour l'analyse des
données :
http://www.univ-lille2.fr/cerim/recherche/stats/axe3.html
Ces liens sont directement « clicables » à
l'adresse suivante :
http://www.renaudloup.be/refinternet.htm
Livres :
Tenenhaus M. (2002), « La Régression PLS:
Théorie et Pratique», Editions TECHNIP
TABLE DES MATIERES
Introduction GénéraleFFFFFFFFFFFFFFFFFFFFFFFFFF.. 8
Sommaire 11
Partie 1 : Présentation de la régression
PLS
I. Contexte historiqueFFFFFFFFFFFFF.FFFFFFFFFF 13
II. Qu'est-ce que la régression PLS 7
FFFFFFFFFFFFFFFFFF 13
III. Principes d'une régression
linéaireFFFFF...FFFFFFFFFFFF 14
IV. Les avantages de la régression PLS 15
V. Le principe de la régression PLS
univariéeFFFFFFFFFFFF.FF 16
VI. Les étapes de calcul de la régression PLS1
19
VII. Indépendance des composantesFFFFFFFFFFFFFFFFFFF.
24
VIII. Centrage et réduction des
donnéesFFFFFFFFFFFFFF.FFF 26
IX. Le critère de validation croisée
FFFFFFFFFFFFFFFFFF 28
X. Les critères liés à la covariance
composante - variable expliquéeFFFFF 32
Partie 2 : Utilisation de la régression PLS sur
des cas limites
I. Régression PLS avec une seule variable
explicativeFFFFFFFFFFF. 35
II. Un exemple à trois variables
explicativesFFFFFFFFFFFFFF.F 38
II.1. Régression PLS à 1 étape 39
II.2. Régression PLS à 2
étapesFFFFFFFFFFFFFFFFFFFFF 41
II.3. Régression PLS à 3
étapesFFFFFFFFFFFFFFFFFFFFF 46
III. La régression linéaire et le critère
des moindres carrésFFFFFFF...FF 48
IV. La régression PLS comme généralisation
des MCOFFFFFFFFFFF 48
IV.1. Un exemple d'inefficacité de la régression
PLS à une étapeFFFFFFFFFF. 49
IV.2. Un exemple de régression PLS sur variables
explicatives orthogonalesFFFFFF. 50
IV.3. Conclusions.FFFFFFFFFFFFFFFF...FFFFFFFFF 51
V. Le critère de la régression
PLSFFFFFFFFFFFFFFFFFFF 53
V.1. Régression PLS et MCO : Différence entre
objectivité et opportunismeFFFF...F 54
V.2. Régression PLS à étapes multiples :
Compromis entre objectivité et opportunismeFF 56
Partie 3 : Simulations
I. Test n°1FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 64
I.1. Simulation n°1FFFFFFFFFFFFFFFFFFFFFFFFF 67
1.2. Simulation n°2FFFFFFFFFFFFFFFFFFFFFFFFF 70
1.3. Simulation n°3FFFFFFFFFFFFFFFFFFFFFFFFF 73
1.4. Simulation n°4FFFFFFFFFFFFFFFFFFFFFFFFF 76
1.5 Conclusions sur le test n°1 79
II. Test n°2FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 82
II.1. Simulation n°1FFFFFFFFFFFFFFFFFFFFFFFFF 85
11.2. Simulation n°2FFFFFFFFFFFFFFFFFFFFFFFFF 88
11.3. Simulation n°3FFFFFFFFFFFFFFFFFFFFFFFFF 91
11.4. Simulation n°4FFFFFFFFFFFFFFFFFFFFFFFFF 94
11.5. Conclusions sur le test
n°2FFFFFFFFFFFFFFFFFFFFFF 97
III. Test n°3FFFFFFFFFFFFFFFFFFFFFFFF.FFFF 102
III.1. Simulation n°1FFFFFFFFFFFFFFFFFFFFFFFF... 103
111.2. Simulation n°2FFFFFFFFFFFFFFFFFFFFFFFF... 106 111.3. Simulation
n°3FFFFFFFFFFFFFFFFFFFFFFF...F 109 111.4. Simulation
n°4FFFFFFFFFFFFFFFFFFFFFFFF... 112 111.5. Conclusions sur le test
n°3FFFFFFFF..FFFFFFFFFFFF. 115
IV. Conclusions sur les simulations réalisées
119
Conclusion généraleFFFFFFFFFFFFFFFFFFFFFFFFFF.
121
Bibliographie 124
AnnexesFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF. 127
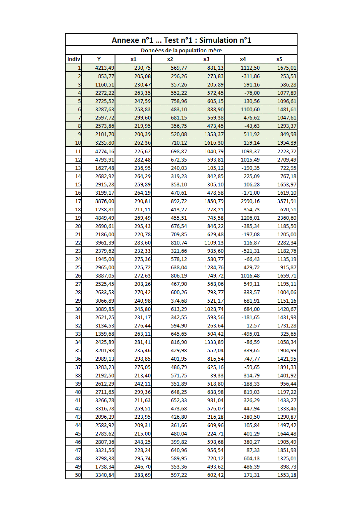
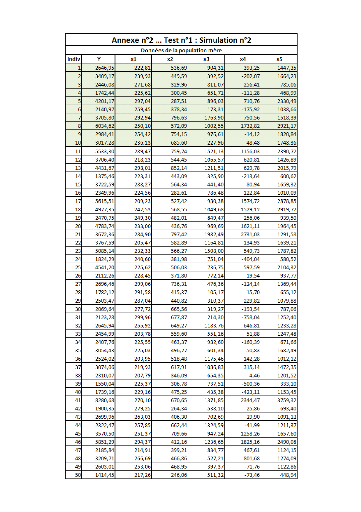
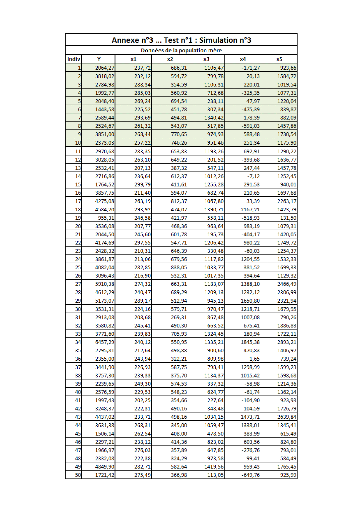
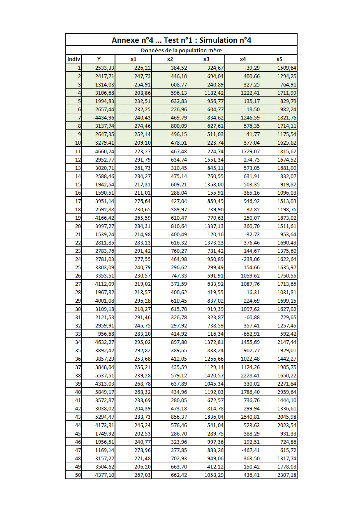
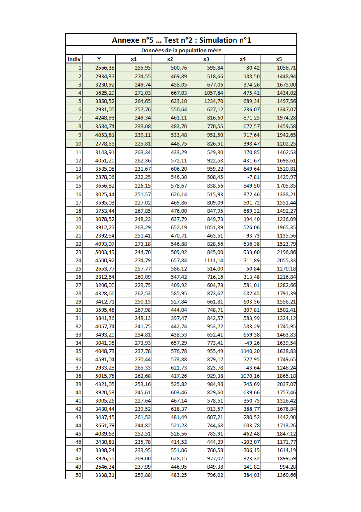
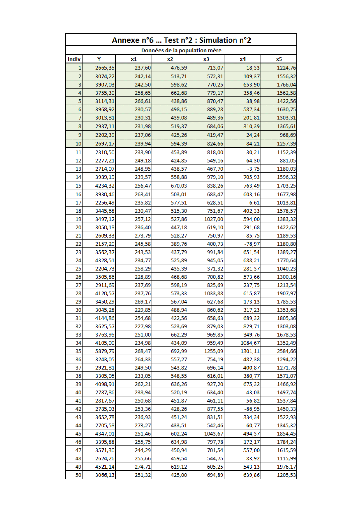
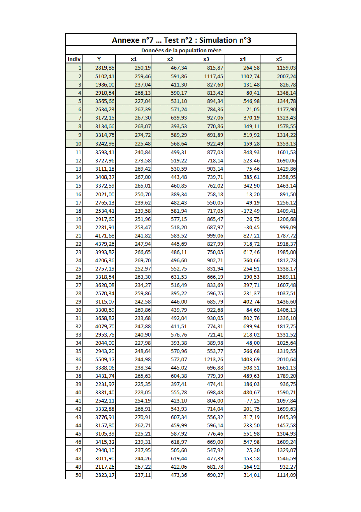
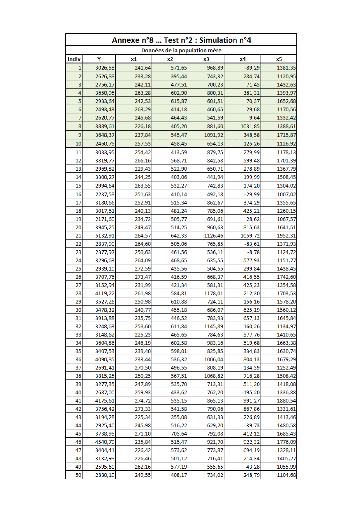
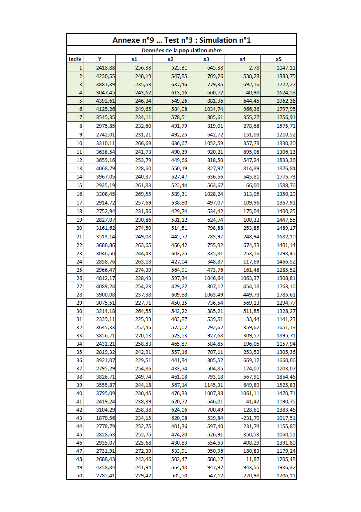
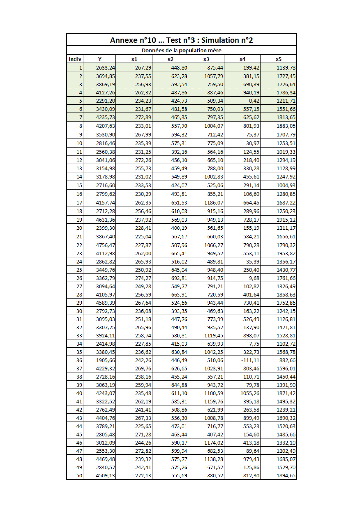
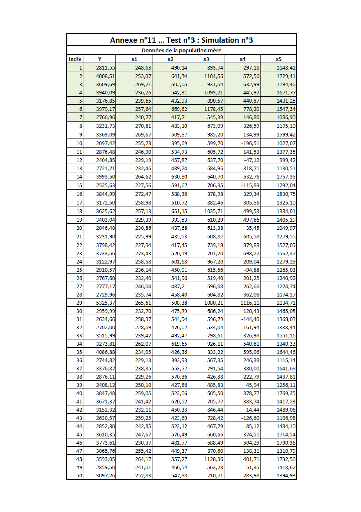
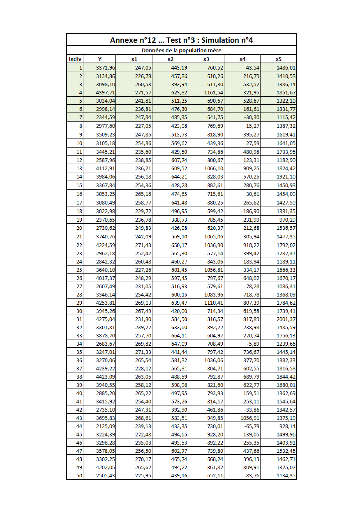
| 


