SOMMAIRE
Introduction GénéraleFFFFFFFFFFFFFFFFFFFFFFFFFF..
8
Partie 1 : Présentation de la régression
PLS
I. Contexte historiqueFFFFFFFFFFFFF.FFFFFFFFFF... 13
II. Qu'est-ce que la régression PLS 7
FFFFFFFFFFFFFFFFFF. 13
III. Principes d'une régression
linéaireFFFFF...FFFFFFFFFFFF 14
IV. Les avantages de la régression PLS 15
V. Le principe de la régression PLS
univariéeFFFFFFFFFFFF.FF 16
VI. Les étapes de calcul de la régression PLS1
19
VII. Indépendance des
composantesFFFFFFFFFFFFFFFFFFF. 24
VIII. Centrage et réduction des
donnéesFFFFFFFFFFFFFF.FFF 26
IX. Le critère de validation croisée
FFFFFFFFFFFFFFFFFF 28
X. Les critères liés à la covariance
composante - variable expliquéeFFFFF 32
Partie 2 : Utilisation de la régression PLS sur
des cas limites
I. Régression PLS avec une seule variable
explicativeFFFFFFFFFFF. 35
II. Un exemple à trois variables
explicativesFFFFFFFFFFFFFF.F 38
III. La régression linéaire et le critère
des moindres carrésFFFFFFF...FF 48
IV. La régression PLS comme généralisation
des MCOFFFFFFFFFFF 48
V. Le critère de la régression
PLSFFFFFFFFFFFFFFFFFFF 53
Partie 3 : Simulations
I. Test n°1FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 64
II. Test n°2FFFFFFFFFFFFFFFFFFFFFFFFFF...FF 82
III. Test n°3FFFFFFFFFFFFFFFFFFFFFFFF.FFFF 102
IV. Conclusions sur les simulations réalisées
119
Conclusion généraleFFFFFFFFFFFFFFFFFFFFFFFFFF.
121
Bibliographie 124
Table des matières 125
AnnexesFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF. 127
PARTIE 1
Présentation de la régression
PLS
I. Contexte historique1
La régression PLS (Partial Least Squares
regression) est une technique d'analyse et de prédiction
relativement récente. Elle a été conçue pour faire
face aux problèmes résultants de l'insuffisance de l'utilisation
de la régression linéaire classique, qui trouve ses limites
dès lors que l'on cherche à modéliser des relations entre
des variables pour lesquelles il y a peu d'individus, ou beaucoup de variables
explicatives en comparaison au nombre d'individus (le nombre de variables
explicatives pouvant excéder très largement le nombre
d'individus), ou encore lorsque les variables explicatives sont fortement
corrélées entre elles.
La méthode PLS répond précisément
à ses problèmes. Cette méthode fut proposée par
Wold S., Albano C., Dunn III W.J., Esbensen K., Hellberg S., Johansson E. et
Sjôstrôm M. en 1983, et connu de grands succès dans le
domaine de la chimie, où, souvent, les données répondent
à ce type de propriétés. La méthode PLS fut
principalement développée autour de Svante Wold, qui a
dirigé de nombreuses thèses portant sur le sujet. De plus, ce
dernier, associé à Nouna Kettaneh-Wold et à plusieurs
collaborateurs, ont développé le logiciel d'analyse des
données SIMCA-P, logiciel centré sur la régression PLS.
En France, Michel Tenenhaus s'est beaucoup
intéressé à cette méthode et a
réalisé de nombreux travaux à ce sujet. Son ouvrage «
La régression PLS -- Théorie et Pratique » (2002,
éditions TECHNIP) a énormément contribué à
la réalisation de ce mémoire, notamment dans la partie
théorique de ce dernier.
Par ailleurs, Tenenhaus M. pense que la régression PLS
pourrait connaître les mêmes succès qu'en chimie si elle
était utilisée dans d'autres domaines.
Voyons à présent en quoi consiste cette
méthode.
II. Qu'est-ce que la régression PLS ?
La régression PLS est une méthode statistique
permettant d'identifier des relations entre plusieurs variables. Il y a
toujours, d'une part, les variables explicatives (notées
généralement x1, ..., xp), et les variables expliquées
(notées généralement y1, ..., yq). Ces variables sont,
dans une régression PLS, toutes étudiées sur les
mêmes « individus ». On distingue la régression PLS
univariée, ou « régression PLS1 », de la
régression PLS multivariée, appelée également
« régression PLS2 ». Dans le premier cas, la régression
ne porte que sur une seule variable expliquée. Dans le second, il peut y
avoir plusieurs variables expliquées (et, même si l'algorithme de
la régression PLS multivariée est présenté
différemment de celui de la version simple, il constitue une
généralisation de
1 D'après Tenenhaus M. (2002). La
Régression PLS-- Théorie et Pratique, Editions TECHNIP
ce dernier dans la mesure où les résultats sont
équivalents lorsque la régression PLS multivariée ne porte
que sur une seule variable expliquée).
La régression PLS s'inscrit dans la catégorie des
régressions linéaires. Il convient donc, avant de rentrer dans le
coeur du sujet, de comprendre ce qu'est une régression
linéaire.
III. Principes d'une régression
linéaire
Le but de la régression est donc d'expliquer les
valeurs et les variations d'une ou plusieurs variables expliquées (les
« y ») par les valeurs et les variations d'une ou plusieurs variables
explicatives (les « x »). Par exemple, on peut chercher à
expliquer le poids d'un individu (variable expliquée) par sa taille
(variable explicative). Dans ce cas, on a une régression PLS
univariée avec une seule variable explicative. Naturellement, il
paraît difficile d'admettre, dans la pratique, que le poids d'un individu
puisse être seulement expliqué par sa taille. En effet, plusieurs
individus de même taille peuvent avoir un poids différent, et,
plus généralement, on peut dire que le poids des individus n'est
pas strictement fonction de leur taille. Cela ne veut pourtant pas dire que la
taille d'un individu ne peut pas constituer un facteur explicatif de son poids.
Il s'agit donc d'une « variable explicative » potentielle parmi
d'autres. On peut affiner l'analyse en ajoutant, dans la liste des variables
explicatives, le montant du budget de cet individu consacré à
l'alimentation. Cela devrait donc nous permettre, en partie, de comprendre
pourquoi deux individus de même taille peuvent avoir un poids
différent (la seconde variable explicative, c'est-à-dire la part
de budget consacrée à l'alimentation, pouvant d'expliquer
certaines divergences). Evidemment, cela ne suffira pas à expliquer
entièrement les écarts que l'on peut observer d'un individu
à l'autre. Il est bien entendu possible de trouver des variables
supplémentaires susceptibles d'expliquer mieux encore les variations de
la variable « poids » d'un individu à l'autre. Mais le fait
d'intégrer de plus en plus de variables rend l'analyse plus
compliquée et les résultats plus difficiles à
interpréter. En fait, on attend de l'analyse qu'elle nous renseigne
à la fois sur l'importance des différentes variables «
explicatives », et sur le bienfondé de l'intégration de
chaque variable dans l'analyse.
Il est important de signaler que l'analyse ne doit jamais
porter sur un seul individu. En effet, ce qu'on attend de la régression,
c'est qu'elle nous fournisse les coefficients (associés à chaque
variable explicative) les plus pertinents possibles. On cherche (lorsque la
régression se limite à une seule variable expliquée) une
fonction linéaire permettant d'estimer une valeur de « y » en
fonction de chaque valeurs prises par les x1, ...,xp. Cela passe donc par la
recherche de coefficients, de sorte à trouver une fonction du type y =
a*x1 + b*x2 +... Si la régression porte sur un seul individu, les
coefficients seront infiniment instables dès lors qu'il y a plus d'une
variable explicative. En effet, si on prend le cas d'un individu de 80 kg,
mesurant 180 cm et consacrant 1.000 € chaque année à
l'alimentation, il existe une infinité de combinaisons permettant de
retranscrire cette relation. Par exemple, on pourrait dire que le poids en kg
de cet individu est égal à
0,444 fois sa taille en centimètres, ou bien à
0,08 fois son budget alimentation en euros, ou encore à 0,222 fois sa
taille en centimètres auxquels on additionne 0,04 fois son budget
alimentation en euros. Cela nous donnerait une infinité de
modèles impossibles à départager. Et, plus important
encore, ce modèle ne serait probablement pas pertinent s'agissant d'un
autre individu. Il faut donc, de préférence, un nombre
d'individus assez conséquent, de sorte à avoir une
régression plus pertinente, susceptible de correspondre à
n'importe quel individu, avec une marge d'erreur dont on peut se faire une
idée raisonnable. Naturellement, le fait d'intégrer toujours plus
d'individus à l'analyse ne supprimera pas la marge d'erreur. Mais cela
permettra d'avoir les coefficients les plus précis possibles, et d'avoir
une idée précise de la marge d'erreur (qu'on peut estimer, par
exemple, à l'aide du coefficient de corrélation).
En fait, le but premier de la régression n'est pas de
s'intéresser à un individu particulier, mais à un individu
« abstrait », pour lequel les relations entre les variables sont des
relations valables « en moyenne », peu importe les valeurs prises par
les variables explicatives. Lorsqu'on a estimé les coefficients de la
régression, on attend que celle-ci nous donne un modèle qui, pour
chaque valeurs que peuvent prendre les différentes variables
explicatives, renvoi une valeur de la variable expliquée qui, en
moyenne, doit correspondre à la réalité, avec la marge
d'erreur la plus faible possible.
Ceci est donc l'objet de la régression PLS. Mais c'est
aussi celui de la régression linéaire simple ou multiple (avec,
dans ce cas, toujours une seule variable expliquée « y »).
Cette régression linéaire à un objectif simple : trouver
les coefficients, pour chaque variable explicative, qui minimisent les
écarts, pour la variable expliquée, entre les valeurs
estimées par le modèle, et les valeurs observées dans la
pratique, pour l'échantillon donné sur lequel est effectué
la régression. Il s'agit de minimiser la somme des résidus (mis
au carré, dans le simple but d'éviter la compensation
systématique des erreurs positives et négatives), ou, dit
autrement, de maximiser le coefficient de corrélation (ce qui est un
objectif propre à la régression linéaire, qui ne
s'applique pas forcément à la régression PLS, du moins pas
dans toutes ses étapes).
Voyons à présent quel est l'intérêt de
la régression PLS par rapport aux autres modèles
linéaires.
IV. Les avantages de la régression PLS
Etant donné que la régression linéaire
permet de traiter le type de problème que nous avons
précédemment abordé, pourquoi donc chercher à
utiliser la régression PLS ? Qu'est-ce qu'elle apporte de plus que la
régression linéaire ?
Partie 1: Présentation de la régression PLS
En fait, les avantages de la régression PLS sont nombreux :
- Tout d'abord, dans le cas régression PLS
multivariée (régression PLS2), il peut y avoir plusieurs
variables expliquées. Nous n'évoquerons malheureusement pas ce
cas.
- Dans le cas où une des variables explicatives serait
une stricte combinaison linéaire des autres, la régression
linéaire ne peut avoir lieu sans enlever au moins une variable
explicative de l'analyse. La régression PLS ne présente pas cet
inconvénient.
- La régression PLS peut traiter des cas où les
individus seraient moins nombreux que les variables explicatives. La
régression linéaire ne peut le faire.
- La régression PLS, étant basée sur
l'algorithme NIPALS, permet de travailler sur des échantillons
même si certaines données manquent pour certains individus pour
certaines variables, et ce sans même à avoir à estimer au
préalable les données en question. Néanmoins, nous nous
limiterons dans ce mémoire aux formules de la régression sans
données manquantes, car elles sont plus faciles à
interpréter.
- Lorsque les variables explicatives sont fortement
corrélées entre-elles, la régression linéaire
devient très peu pertinente, au sens où les coefficients qui en
ressortent deviennent très instable lorsque l'on « bruite »
les données (on fait varier, de manière aléatoire et
très légère, les données de l'échantillon).
La régression PLS, basée sur des critères de covariance,
est considérée comme étant plus robuste. Les coefficients
demeurent stables et gardent une certaine significativité, même en
présence de corrélations fortes entres les variables.
Voyons donc comment fonctionne cette méthode qui semble si
avantageuse.
V. Le principe de la régression PLS
univariée
Le principe de la régression PLS est assez simple, bien
que se déroulant en un nombre d'étapes à priori non
défini (se construisant toutes de la même manière, à
partir des résidus des précédentes étapes).
On a d'une part une variable qu'on cherche à expliquer
« y », et d'autre part des variables explicatives « x1, x2, ...,
xp ». Les valeurs de ces variables (les yi, x1i, x2i, ..., xpi) sont
observées sur « n » individus.
Remarque : Les données associées aux variables
y, x1, x2, ..., xp seront centrées et réduites, ce qui est
obligatoire et indispensable dans le cadre de la régression PLS. Les
coefficients de corrélation entre ces variables seront donc égaux
à leur covariance. Pour centrer les données, on soustrait
à chaque donnée de la série la moyenne de la série.
Pour les réduites, on divise chaque donnée de la série par
l'écart type de cette dernière. Au final, on a donc une moyenne
nulle pour chaque série, et un écart-type égal à 1
(et donc une variance elle aussi égale à 1). Nous reviendrons
plus tard sur le centrage et la réduction des données, qui sont
des étapes assez simples, n'altérant pas la structure de variance
des différentes données.
La régression va consister à chercher des
composantes ti, t2, ..., s'exprimant en fonction des variables explicatives xi,
x2, ..., xp, en trouvant une série de coefficients (pour chaque
composante : un coefficient associé directement ou indirectement
à chaque variable) pour chaque composante, à la manière
d'une régression linéaire, à la différence
près que les coefficients sont calculés sur base d'un
critère de covariance.
On procède par étape. D'abord, on défini
ti en cherchant des coefficients w11, wi2, ..., wip pour chaque variable
explicative. On obtient donc une équation du type : t1 = wMM*xM +w12*x2
+ ... + w1p*xp.
Ensuite, on effectue une régression linéaire de
ti sur y. Ainsi, on peut exprimer y en fonction de ti, à l'aide d'un
coefficient ci (9- = ci*ti)2. En fait, cela permet tout d'abord
d'obtenir de manière rapide un coefficient de corrélation, afin
d'estimer la qualité de la régression à l'étape 1.
Ensuite, cela permet d'exprimer directement y en fonction de xi, x2, ..., xp,
en « transformant » les coefficients wMM, wM2, ..., wip, en les
multipliant par une constante, afin de réorienter la régression
sur l'échelle de la variable y.
A l'étape 1, l'équation sera donc la suivante : 9-=
cM*wMM*xM + ci*wi2*x2 + ... + cl*w1p*xp. (1)
On a donc une régression s'exprimant de manière
similaire à une régression simple, mais avec un critère de
covariance. On connaît la qualité de la régression
grâce au coefficient de corrélation de ti avec y.
Néanmoins, si la qualité de la régression
n'est pas satisfaisante, on peut l'améliorer en ajoutant des composantes
supplémentaires.
Dans la deuxième étape, on va
s'intéresser à la fraction de variance des variables qui
échappe à la première étape de la
régression, c'est-à-dire les résidus. On va donc effectuer
les régressions des variables y, xi, x2, ..., xp sur ti et obtenir des
séries statistiques correspondant aux résidus de ces
séries de base, séries que nous nommerons respectivement yi, xii,
xM2, ..., xlp.
Ensuite, la même méthode qu'à
l'étape 1 sera appliquée pour déterminer une composante
t2, mais cette fois à partir des séries y1, x11, x12, ..., xlp.
On obtient alors des coefficients w2i, w22, ..., w2p qui permettent d'exprimer
t2 en fonction de xMM, xM2, ..., xip. Nous verrons qu'il est possible, à
partir de là, et des régressions des variables explicatives sur
ti, d'exprimer directement t2 en fonction des variables initiales
2 Pour chaque modèle, 9- est la
notation employée pour désigner l'estimation de la variable y par
le modèle en question. Pour obtenir la valeur de y correspondante (dans
le cas d'un individu connu), il suffit d'ajouter à 9- les
résidus de la régression du modèle en question.
centrées-réduites (plutôt qu'en fonction de
leurs résidus, ce qui facilite le calcul et l'interprétation),
avec des coefficients recalculés.
Ensuite, on effectue une régression linéaire
multiple de y sur ti et t2. Comme c'est une régression linéaire,
la qualité de la régression ne peut qu'en être
améliorée (du moins au niveau du coefficient de
corrélation).
On obtient alors l'équation suivante : y = ci*ti + c2*t2.
Nous verrons par la suite pourquoi le coefficient ci n'est pas modifié
par rapport à la régression de la première
étape.
Si on détaille cette équation, obtient :
y = ci*Wii*xi + ... + cl*W1p*xp + c2*W21*x11 + ... + c2*W2p*xlp
(2)
Nous verrons qu'il est possible de simplifier cette
équation de sorte à exprimer directement y en fonction des
variables explicatives initiales, c'est-à-dire en éliminant les
séries correspondant aux résidus des régressions des
variables initiales sur ti. Une telle simplification sera possible à
chaque étape, de sorte à conserver, à chaque étape,
un modèle linéaire s'exprimant directement en fonction des
variables initiales.
Cette équation, à l'étape 2, paraît
déjà fort complexe sous forme de formule. Néanmoins, dans
le cas d'un exemple concret, elle est écrite de manière tout
à fait similaire à une régression linéaire multiple
(lorsque les coefficients sont connus numériquement). Seuls les
coefficients affectés à chaque variable varient.
Naturellement, on peut encore ajouter des étapes
supplémentaires pour affiner la qualité de la régression,
selon le même principe. Cela ne compliquera pas vraiment l'étude
du modèle définitif car il sera toujours aussi facile à
analyser (un seul coefficient définitif pour chaque variable
explicative, même si ce coefficient s'obtient par un calcul de plus en
plus long au fur et à mesure que l'on ajoute des étapes).
Notons qu'il est possible de retenir un certain nombre
d'étapes en fonction de critères objectifs quant à la
significative de chaque étape. Nous nous intéresserons par la
suite à quelques critères permettant de déterminer, plus
ou moins objectivement, le nombre d'étapes à retenir.
Il est maintenant temps de passer aux étapes de calcul
à proprement parler.
VI. Les étapes de calcul de la régression
PLS1
Comme expliqué précédemment, nous nous
contenterons des formules de la régression PLS sans données
manquantes, afin d'éviter de compliquer l'interprétation de ces
dernières. Néanmoins, il est bon de savoir que, en cas de
régression PLS avec données manquantes, les formules changent,
même si elles sont équivalentes à celle de la
régression PLS sans donnée manquantes lorsqu'il ne manque aucune
donnée.
Dans un premier temps, il s'agit de trouver une composante
qu'on nommera t1, qui, à l'instar de la variable expliquée dans
la régression linéaire, sera exprimée en fonction des
variables explicatives à l'aide de coefficients qui seront
calculés au cours de cette étape. « y » sera par la
suite exprimé directement en fonction de cette composante « t1
».
Ces coefficients, notés w1j (dans le cas de celui
associé à la « jème variable explicative
», le « 1 » étant associé à la
première composante « t1 ») vont être
déterminés selon un critère de covariance, et leur
méthode de calcul est très simple et facilement
interprétable, surtout en l'absence de données manquantes.
La formule, pour le jème coefficient, est la
suivante :
Y
~
Cov(x ~
~ ~
~
(3)
~
Y
~
Cov2(x ~ ~

19
(Naturellement, il ne faut pas confondre le « j
» de la somme des « covariances-carré » de tous les
« xj » avec y, avec le « j » présent dans le terme
« w1j » et au dénominateur de l'expression du membre de
droite, qui signifie que l'on s'intéresse uniquement au cas de
lajème variable)
Ce sont donc les covariances, pondérées par la
racine de la somme de leurs carrés, qui vont déterminer les
coefficients de la composante « t1 », et donc indirectement la
relation entre les variables explicatives et « y ». Le fait que la
pondération s'effectue par rapport à des covariances dont les
valeurs sont mises au carré indique qu'on souhaite éviter la
neutralisation des covariances positives et négatives, et qu'on veut
pondérer chaque covariance par l'importance totale de toutes les
covariances entre les variables explicatives et « y ».
Le fait que la covariance d'une variable explicative avec la
variable « y » détermine directement le coefficient qui sera
affecté à cette variable dans le modèle explicatif de la
variable « y », signifie que quoi qu'il arrive, plus cette covariance
sera élevée, et plus le coefficient sera important, et ce quelque
soient les corrélations relatives des différentes variables
explicatives. On a donc ici une première idée de la «
robustesse » de la régression PLS.

20
Une fois les coefficients wMj obtenus, il devient très
facile d'obtenir la composante ti :
p
t1 1 ixi ~(4)
i 1
Dit autrement :
tl = wMM*xM + w12*x2 + ... + wip*xp (5)
Ensuite, on effectue une régression simple de y sur ti, et
on obtient donc :
."= cM*tM (6)
." correspondant à la série des estimations des
valeurs dey selon cette régression.
Et donc y = ci*ti + yi (7)
yi correspondant naturellement à la série des
résidus de cette régression simple.
On peut donc exprimer y directement en fonction des variables
explicatives xi, ..., xp. ."= cl*w11*x1 + cl*w12*x2 + ... + cl*w1p*xp (8)
Il s'agit là d'une manière de réajuster les
coefficients wMj à l'échelle de y, en les multipliant par la
constante ci.
Les « p » coefficients wij*ci nous donnent des
indications claires sur l'importance de la prise en compte de chaque variable
sur la régression. En outre, ces coefficients seront du même signe
que les coefficients de corrélation et que les covariances des variables
auxquelles ils sont associés avec y. Ils seront d'ailleurs directement
proportionnels aux covariances. Il n'en va pas de même dans une
régression linéaire multiple. Il en résulte une
interprétation des coefficients beaucoup plus simple.
Cette régression simple, de y sur ti, nous permet
d'obtenir un coefficient de corrélation, qui nous permet
d'apprécier la qualité de la régression à
l'étape 1, ainsi qu'une série de résidus yl, qui s'obtient
en calculant la différence suivante :
y1 = y -- cM*ti (9)
Si on estime la qualité de la régression
insuffisante, on peut passer à l'étape 2, qui se déroule
de manière comparable à l'étape 1, mais qui porte non plus
sur les variables initiales (centrées-réduites) y, xi, ..., xp
mais sur les résidus de leur régression simple sur ti, qu'on
appellera donc yi, xMM, ..., xip. Ces nouvelles séries,
créées en effectuant autant de régression simples que de
variables, sont donc indépendantes de la première composante ti.
Le pouvoir explicatif de la composante t2, qui sera créée sur
base de ces
variables, sera donc complètement nouveau et pourra donc
venir s'additionner à celui de la composante ti.
A l'étape 2, nous allons obtenir une série de
coefficients W2; (W2i, W2p), qui nous
permettront d'exprimer t2 en fonction des variables xMM, F, xip,
résidus des régressions des variables y, xi, F, xp sur ti.
La formule de ces coefficients est strictement identique
à celle de leurs équivalents de l'étape 1. Seules les
variables sur lesquelles ils sont calculés changent (on passe des
variables de départ aux séries de résidus) :
)
w2
~
)
Cov(x1i ,
~ 1
(10)
i 1
i

Cov2(x1i ,
~ 1

21
Et, de manière équivalente à l'étape
1 :
~
i 1
On effectue une régression de y sur ti et t2 et on obtient
la relation suivante : y = ci*ti + c2*t2 + y2 (12)
Le coefficient ci restera identique à celui de
l'étape 1 car, les variables ti et t2 étant indépendantes,
la prise en compte de la variable t2 dans la régression ne modifie pas
la relation initiale définie dans la régression entre y et ti.
Néanmoins, cette formulation pose problème, puisque
cette fois, y est fonction des variables initiales, mais aussi des variables
résiduelles (obtenue par régression sur ti) :
[= cl*W11*x1 + F+ cl*W1p*xp + c2*W21*x11 + F+ c2*W2p*xlp (13)
Les équations deviennent plus chargées, et
l'interprétation plus compliquée. Les estimations deviennent
également nettement plus laborieuses, si on donne des valeurs arbitraire
aux variables xi et si on cherche à connaître la valeur
correspondante pour y estimée par le modèle.
Mais il y a moyen de ré-exprimer l'équation de
t2 directement en fonction des variables initiales xi. Pour se faire, il suffit
de se rappeler comment celles-ci ont été construites : à
partir des variables xi et de ti, lors des régressions des variables xi
sur ti.

22
Ainsi, on a effectué, pour chaque valeur de j allant de 1
à p, la régression linéaire simple suivante :
x; = cii*ti + xM+ (14) Le coefficient « ci; »
étant le coefficient de régression de la variable x; sur
tM.
Les xi; peuvent donc s'exprimer de la manière suivante
:
xi; = xi -- ci+*ti (15)
Donc, il est possible d'exprimer t2 en fonction des coefficients
cii, et des variables xi et de la composante ti.
P
t2 = E W2J . * (X J
. -- c 1J . * t ) .(=> (16)
J . 1
Sachant que la composante ti peut elle aussi s'exprimer en
fonction des variables xj. L'équation devient donc :
P P
t2 W2 J .*
(X -c1J . EW1J . X ) (17 )
J .1 J .1
Si on détaille l'équation, cela nous donne :
t2 = w21*[xl -- ciM*(wiM*xi+ +wip*xp)] + + w2p*[xp -- cip*(wiM*xi
+ + wip*xp)]
Equation que l'on peut réécrire :
t2 = W21 *X1 --
(EP c1J . W2J .
W11)* #177;
·
·
·+ W2P
P X (P c1J . * W2J . *
P )* X P
J .1J .1
Ou encore :
P P
(18)
t2 (w21
2 W *
11 c1J .
W )*X (W *E )*X
2J . 1 "' 2P -W C W
1P 1J . 2J . P
J .1 J .1
On peut donc définir des coefficients que nous appelleront
« w2i' » permettant d'exprimer t2en fonction des variables xi :
|
W2
|
P
J .I=W2J .-W Ec
*W
2j
1J . 1J . 2j
|
(19)
|
J . 1

23
Partie 1: Présentation de la régression PLS
Ainsi, on peut résumer t2 à l'équation suivante :
p
/ . 1
C'est-à-dire :
t2 = w21'*x1 + ... + w2p'*xp (20) L'équation de y devient
alors :
p p
Y*
J
* *w
1
c1
. X/ . #177;c2
*Ew2/ . X q (21)
/ . 1 / . 1
Où y* est une autre notation pour .3
Ou:
[= c1*w11*x1 + ... + c1*w1p*xp + c2*w21'*x1 + ... + c2*w2p'*xp
Equation qui peut se réécrire :
[= (c1*w11+c2*w21')*x1 + ... + (c1*w1p+c2*w2p')*xp
(22) ou encore
y = (c1*w11+c2*w21')*x1 + ... + (c1*w1p+c2*w2p')*xp + y2 (23)
y2 étant la série des résidus de la régression
de y sur (t1,t2).
y peut donc s'écrire directement en fonction des variables
xj.
La régression de y sur t1 et t2 nous donne le
coefficient de corrélation de la régression à
l'étape 2. Il nous permet également, par déduction, de
connaître l'amélioration du coefficient de corrélation du
fait de l'ajout de la 2ème étape.
On peut bien évidemment envisager une
3ème étape, en travaillant à partir des
résidus de l'étape 2. Pour se faire, on peut soit effectuer une
régression multiple de y, x1, ..., xp sur (t1,t2) et calculer les
résidus, soit effectuer une régression simple de y1, x11, ...,
x1p sur t2, et calculer les résidus. La seconde méthode semble
être la plus simple étant donné qu'à
3 Les différences de notations sont dues
à l'utilisation de Microsoft Equations 3.0, logiciel permettant
d'insérer des équations notamment dans des documents Word mais ne
présentant pas les mêmes possibilités en matière
d'insertion de caractères spéciaux.
ce stade des calculs, on connaît normalement
déjà les variables yi, xii, ..., xMp puisqu'on a
été obligé de les calculer lors de la seconde
étape.
Nous allons maintenant nous intéresser à une
propriété très intéressante des composantes, il
s'agit de l'orthogonalité (indépendance) des composantes entre
elles.
VII. Indépendance des composantes
L'une des propriétés primordiales d'une
régression PLS est l'indépendance des composantes ti, t;, ..., tH
formées à partir des variables explicatives.
En effet, la première composante ti est formée
à partir des variables explicatives, en leur donnant certains
coefficients sur base de leur covariance avec la variable expliquée
« y » (ou de leur coefficient de corrélation avec la variable
y si les variables sont centrées réduites). Pour se faire, la
variable ti sera représentative d'une partie de la variance des
variables explicatives. Bien entendu, si y n'est pas une combinaison
linéaire des variables explicatives, et qu'il y a plus d'une variable
explicative dans l'analyse (et qu'aucune de ces variables n'est combinaison
linéaire des autres), la variable ti sera insuffisante pour expliquer
toute la variance de y, de même qu'elle sera insuffisante pour expliquer
toute la variance des variables explicatives, et toute la covariance des
variables explicatives avec y.
Il en demeurera un résidu. La variance de y ne sera pas
totalement expliquée par la variance de ti. Il y a moyen
d'améliorer le pouvoir explicatif du modèle. Pour cela, on
s'intéresse aux résidus, qui ont été «
oubliés » par la première composante. Cette première
composante est indépendante des résidus. Or, on se sert de ces
résidus pour construire la seconde composante t;, qui sera par la
même occasion indépendante de ti. La composante t;
s'intéressera donc à la variance de y qui n'est pas
expliquée par ti. Les résidus qui en résulteront, qui sont
donc indépendants de t;, et indépendants de ti (ils sont le
résultat d'une régression sur des résidus qui sont
déjà indépendants de ti), serviront à la
création de t3. t3 sera donc indépendante de ti et t;. Il en ira
de même pour toutes les composantes, qui seront toutes
indépendantes entre elles.
Cette indépendance peut se démontrer assez
facilement d'un point de vue mathématique. Voici la démonstration
telle qu'elle est présentée dans l'ouvrage « La
Régression PLS Théorie et Pratique » de Michel TENENHAUS,
avec quelques précisions supplémentaires :
L'argument avancé est le suivant : th'tl = 0 pour l_h.
th est le vecteur formé des « n » valeurs que
prend la hième composante pour les « n » individus.
th' est la transposée du vecteur th.
tl est le vecteur formé des « n » valeurs que
prend la lième composante pour les « n »
individus.
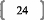
Le fait que le produit th'tl soit égal à 0
traduit covariance nulle entre les deux composantes, et donc une
indépendance de celles-ci, pour autant que les variables de
départ soient centrées (ce qui donne également des
composantes centrées). Si les composantes sont centrées, leur
moyenne est nulle. Les écarts à la moyenne deviennent donc
égaux aux valeurs prises. La covariance, qui est la moyenne des produits
des écarts à la moyenne, devient donc égale à la
moyenne des produits des valeurs des composantes. Si th'tl = 0, cela veut dire
que la somme des produits des valeurs des composantes h et l est nulle. Donc,
la moyenne de ces produits est également nulle. La covariance est donc
nulle, et les variables sont donc indépendantes.
On a ti't2 = ti'Xiw2 = 0 puisque ti'Xi = 0.
Xi étant la matrice des résidus des
régressions des variables xi sur ti. w2 est le vecteur de coefficients
associés aux résidus xi; pour former la composante t2.
Le fait que ti'Xi = 0 vient du fait que la matrice Xi est la
matrice des résidus des régressions des variables xi sur ti.
Supposons ti, ..., th orthogonaux, alors les vecteurs ti, ...,
th#177;i sont orthogonaux. Montrons que th#177;i est orthogonal aux vecteurs
ti, ..., th :
t'hth#177;i = t'hXhwh#177;i = 0 puisque t'hXh = 0
t'h-fth#177;1 = t'h-1Xhwh#177;1
= t'h-1[Xh-1- thp'h]wh#177;i
= [t'h-iXh-i -- t'h-ithp'h]wh#177;i
= 0 puisque t'h-iXh-i = 0 et t'h-lth = 0 par l'hypothèse
de récurrence.
Sachant que ph=X'h-ith/t'hth, c'est à dire que ph est le
vecteur des coefficients de régression entre la composante th et les
xh-1j.
t'h-2th#177;1 = t'h-2Xhwh#177;1
= t'h-2[Xh-2 -- th-ip'h-i -- thp'h]wh#177;i = 0
Puisque t'h-2Xh-2 = 0, t'h-2th-i = t'h-2th = 0, et ainsi de
suite, d'où le résultat.
Cette indépendance entre les composantes entraîne
mécaniquement l'impossibilité de construire un nombre de
composantes supérieur au nombre de variables explicatives comprises dans
la régression, puisqu'elles sont formées à partir de ces
variables. De plus, si certaines variables explicatives sont strictement
combinaisons linéaires les unes des autres, cela entraînera
d'autant une réduction du nombre maximal possible d'étapes.
On peut, par un raisonnement similaire, penser que la
présence de variables fortement autocorrélées (sans
être forcément combinaisons linéaires les unes des autres)
réduit d'autant l'intérêt d'intégrer un trop grand
nombre de composantes dans l'analyse.
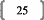
Nous allons, à présent, nous intéresser
brièvement au centrage et à la réduction des
données, deux notions capitales en analyse statistique, et
incontournable en régression PLS (du moins s'agissant du centrage des
données).
VIII. Centrage et réduction des
données
Il est important, avant d'interpréter une
régression, de savoir si elle porte sur des données
centrées ou non, réduites ou non. L'interprétation du
modèle obtenu en est complètement modifiée.
Le fait de centrer les données permet notamment de ne
retenir que les variations des variables autour de la moyenne. Cela facilite en
outre les calculs de covariance et des coefficients de corrélation. Le
centrage des données ne modifie en aucun cas la variance (et
l'écart-type) mais ramène la moyenne de la série à
O. Pour centrer une série, on retranche à chacune de ses
données la moyenne de la série.
La réduction des données permet
d'éliminer les effets d'échelle. Une série de grands
nombres, telle que le PIB d'un pays, aura tendance à varier très
fortement (en valeur absolue), alors qu'une série de nombre faibles,
comme par exemple des taux d'intérêts, aura tendance à
varier très peu (toujours en valeurs absolue). La réduction des
données permet de prendre équitablement en compte les variations
relatives autour de la moyenne, et non les variations absolues. Le fait de
réduire une série de données ramène la valeur de
l'écart-type (et donc de la variance) de la série à 1.
Lors d'une régression, la réduction des données va peser
sur l'ordre de grandeur des coefficients.
La réduction des données n'affecte pas la
qualité d'une régression. En revanche, le centrage l'affecte
généralement. En effet, centrer les données revient
à considérer les données non centrées auxquelles on
ajoute une constante.
En régression PLS, les données doivent
être impérativement centrées, sans quoi les
propriétés mathématiques de la régression seraient
modifiées. Il serait en outre impossible de régresser sur des
données non centrées avec constante (car les coefficients,
basés sur des critères de covariance, seraient
systématiquement nuls pour une constante). Cela affecterait la
qualité de la régression.
La réduction des données n'est par contre pas
nécessaire. Elle influence seulement l'ordre de grandeur des
coefficients. Le fait de ne pas réduire les données permet une
interprétation plus directe des coefficients. Le fait de travailler sur
un modèle réduit permet en revanche d'obtenir des coefficients
qui représentent mieux la part « d'explication » de la
variance de y par chaque variable explicative.
Note : Normalement, lorsqu'on centre et on réduit les
données, on commence d'abord
par les centrer, puis on les
réduit dans un second temps. L'inverse est possible, mais

27
après la réduction, il faut retrancher des
données la « moyenne réduite » (la moyenne des
données réduites) et non la moyenne de la série initiale.
Ceci vient du fait que la réduction des données affecte à
la fois la variance et la moyenne, alors que le centrage n'affecte que la
moyenne (donc, réduire en second lieu n'impose pas de recalculer la
variance des données centrées). Quoi qu'il en soit, centrage des
données et réduction des données sont deux concepts
indépendants.
Bien qu'il ne soit pas possible d'effectuer une
régression PLS sur des variables non - centrées, et qu'il soit
impossible de calculer une constante, il est possible de passer, après
obtention des résultats, d'un modèle centré à un
modèle non-centré avec constante.
Notons qu'il est également possible (et facile) de passer
d'un modèle centré, réduit, à un modèle
centré, non réduit.
Prenons par exemple trois variables. A comme variable
expliquée, B et C comme variables explicatives. Notons Acr, Bcr et Ccr
les variables A, B et C centrées et réduites, et Ac, Bc et Cc les
variables centrées non-réduites.
Si on travaille sur modèle centré-réduit, on
aura une relation du type :
Acr = b*Bcr+c*Ccr, où b et c sont les coefficients obtenus
par régression (quelle qu'elle soit) associés respectivement aux
variables B et C.
Pour passer aux variables centrées, non réduites,
il suffit de remplacer Acr, Bcr et Ccr par leur expression en fonction de Ac,
Bc et Cc.
Acr = Ac/a(A), Bcr = Bc/a(B) et Ccr = Cc/a(C).
Le modèle devient donc :
Ac/a(A) = b*Bc/a(B) + c*Cc/a(C)
« Ac = [b*Bc/a(B) + c*Cc/a(C)^*a(A)
Ce qui nous donne :
Ac
*(a)1 *Bc [c *
(a)
o-
(b)
o- (c) *Cc(24)
Les coefficients de la régression centrée
(non-réduite) peuvent être obtenus en multipliant ceux de la
régression centrée-réduite par le rapport de
l'écart type de la variable expliquée sur l'écart type de
la variable explicative (a(Y)/a(X) si Y est la variable expliquée et X
la variable explicative considérée).
Le passage d'un modèle simplement réduit
(non-centrée) à un modèle non-centré et
non-réduit se fait bien entendu de la même manière.

28
On annule donc la réduction en multipliant les
coefficients par le rapport des écarts types de la variable
expliquée et de la variable explicative.
Pour décentrer des données, il suffit
d'établir un raisonnement similaire. Si nous sommes en présence
d'un modèle centré du type Ac = b*Bc + c*Cc (où Ac, Bc et
Cc représentent les variables A, B, C une fois centrées), on peut
le réécrire de la manière suivante :

)
A
(A--A)=b*(B--B)+c*(C--C
A=b*(B--B)+c*(C--C)

A b*B+c*C--b*B--c*C+ A
(25)

Sachant que A , B et C sont les
moyennes calculées initialement sur les séries A, B et C.
La manipulation est la même si l'on souhaite passer d'un
modèle centré-réduit à un modèle non
centré et réduit, à la différence près qu'il
faut retrancher les moyennes réduites en lieu et place des moyennes
initiales.
IX. Le critère de validation croisée
La validation croisée se base sur la qualité
d'approximation du modèle des valeurs de la variable expliquée
pour les individus sur lequel il se fonde.
On cherche à prendre en compte deux
éléments, qu'on va ensuite comparer. Il s'agit des
critères RSS (Residual Sum of Squares) et PRESS (PRediction Error Sum of
Squares). Les deux prennent normalement des valeurs différentes pour
chaque étape de la regression (ils diminuent à chaque
étape).
Le premier, le critère RSS, n'est autre que la somme du
carré des résidus (SCR), calculé en comparant les
prédictions de la valeur expliquée (y) par le modèle pour
chaque individu, aux valeurs initiales de la valeur y pour ces mêmes
individus.
A l'étape h, la formule de RSS est :
n
RSSh =E(yi- (y *) hi
)2 (26)
i ~
Où yi est la valeur initiale
(centrée-réduite) pour l'individu i. (y*)hi = Shhi= ci*tii +
+ ch*thi (27)
On peut résumer ce critère en disant qu'il s'agit
de la somme des erreurs
d'approximation du modèle mises au
carré. De la connaissance de ce critère, et de la
connaissance
de la variance de la variable y, on peut aisément retrouver le
coefficient
de détermination de la régression. Plus le
coefficient de détermination de la régression est faible, et plus
la somme des carrés des résidus est élevée. En
effet, le modèle est d'autant plus efficace qu'il commet peu d'erreurs.
Un modèle « parfait », dans cette optique, est un
modèle pour lequel où les écarts des prédictions
sont nuls, donc où SCR (RSS) est nul, et donc le coefficient de
détermination (R2) égal à 1.
Le critère RSS nous donne donc une idée de la
qualité du modèle. Mais le problème est qu'il n'est pas
suffisant car il délivre une information « absolue » sur les
résidus et non « relative » (relative à la variance de
la variable à expliquer). C'est pourquoi le R2 lui est
préférable.
Quoi qu'il en soit, plus la régression PLS comporte
d'étapes, et plus la qualité d'approximation du modèle est
bonne (ou, au moins, aussi bonne qu'aux étapes
précédentes). Le critère RSS diminue donc d'étape
en étape.
Ainsi, RSS1 RSS2 RSS3 ...
L'autre critère, le PRESS, lui est assez similaire. La
différence est qu'il s'attache à mesurer la qualité de
prédiction du modèle sur les individus lorsqu'ils sont exclus de
ce modèle. Pour cela, on effectue, pour chaque individu, une
régression PLS (à « h » étapes, car on cherche
à mesurer la pertinence de la hème étape) en
excluant cette individu des calculs du modèle. Ensuite, on estime la
valeur de la variable expliquée pour cet individu, à l'aide des
valeurs de ses variables explicatives et des coefficients obtenus dans la
régression qui ne prenait pas en compte la présence de cet
individu. On compare cette valeur à la valeur effective de « y
» pour cet individu, et on obtient un résidu. On renouvelle
l'étape avec tous les autres individus, et puis on fait la somme du
carré de ces résidus.
Par exemple, on commence en prenant le premier individu d'une
régression qui comporte « n » individu. On effectue la
régression PLS sur les (n-1) derniers individus, et on estime, à
l'aide des coefficients de cette régression, et des valeurs des
variables explicative pour ce 1er individu, la valeur de la variable
expliquée, donnée par le modèle. On la compare avec la
valeur effective de y et on garde le résidu. On répète
ainsi l'opération avec le 2ème individu, en effectuant
la régression sur le 1er et les (n-2) derniers individus.
L'opération, au final, a été répétée
autant de fois que la régression ne comporte d'individu, chacune de ces
régressions visant à prédire la valeur de y de l'individu
qui a été exclu de leur calcul4.
4 On peut également exclure des individus
« bloc par bloc », par exemple deux par deux, et les prédire
simultanément. La taille des blocs dépend avant tout de la
quantité totale d'individus, car exclure systématiquement les
individus un par un demande un nombre considérable de calculs.
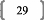
PRESSh 0.95 * RSSh_i
a (33)
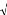
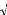

30
Partie 1: Présentation de la régression PLS
Voici la formule du PRESS de la régression PLS à
l'étape h :
n
PRESS h = E (Yi - (Y*)
h( i) )2 (28)
i i
Où y*h(-i) est mis pour ÿh(-i), c'est-à-dire
l'estimation de « yi » par la régression PLS à h
étapes qui ne prend pas en compte le ième individu.
On a donc deux estimateurs de la qualité de la
régression. Le premier, le RSS, en prenant en compte 100% de
l'information de la régression que l'on cherche à estimer, sera
forcément plus faible (car l'estimation de meilleure qualité) que
le PRESS, qui se prive, pour l'estimation de chaque individu, de la
présence de l'individu en question dans les calculs.
Pour l'étape h, le PRESS sera donc supérieur au
RSS. On sait également que le PRESS, à l'étape h, est
inférieur au PRESS à l'étape h-1. Il en va de même
pour le RSS.
On peut donc écrire les relations suivantes :
PRESSh z RSSh (29)
RSSh s RSSh-1 (30)
PRESSh s PRESSh-1 (31)
L'inconnue est la relation qui lie le critère PRESS
à l'étape h au critère RSS de l'étape (h-1). Le
PRESS de l'étape h sera forcément inférieur ou égal
à ce qu'il était à l'étape h1. Il sera
également forcément supérieur ou égal au RSS de
l'étape h. En revanche, s'il parvenait à être
inférieur au RSS de l'étape (h-1), cela voudrait dire que la
qualité d'estimation du modèle s'est considérément
améliorée, puisqu'il peut désormais estimer, avec plus de
précision, les valeurs « yi » des individus, sans les
connaître au préalable, que le modèle de l'étape
précédente ne le peut, en les connaissant.
Donc, par exemple, le fait que la composante « h »
ait une importance significative dans la régression pourrait se traduire
par le fait que PRESSh soit inférieur à RSSh-1. On peut aussi
être plus ou moins exigeant en donnant un coefficient différent de
1 à RSSh-1 :
PRESSh s x*RSSh-1 (32)
Si x est inférieur à un, on accentue la contrainte,
on aura moins tendance à retenir des étapes
supplémentaires.
Dans le logiciel SIMCA-P, par exemple, la composante th est
retenue si :

31
Le fait que l'équation soit mise sous forme de racine
est simplement la conséquence du fait qu'on cherche à se replacer
à l'échelle des résidus, et non à l'échelle
des résidus au carré. Cela rend le critère de choix mieux
interprétable. Cela veut dire, à peu de choses près, que
les résidus tels qu'ils sont calculés dans le PRESSh, pris en
valeur absolue, ne doivent pas, en moyenne, excéder 95% des
résidus tels qu'ils sont calculés dans le critère
RSSh-1.
On peut se passer des racines et revenir à une
équation de la même forme que la précédente (30),
mais le coefficient doit être mis au carré.
PRESSh s 0.9025*RSSh-1 (34) Ou encore :
PRESSh < 0.9025 (35) RSS
h 1
Ceci est également retranscris de la manière
suivante dans l'ouvrage « La Régression PLS : Théorie et
pratique » de Michel Tenenhaus :
PRESS
Q2(h) --1--
h 0.0975 (36)
RSS h1
On peut passer de la forme précédente (35) à
celle-ci (36) de la manière suivante :
PRESS
(35) <=> h 1 0.0975
RSS h1
PRESS
<=> h 0.0975 --1
RSS h 1
RSS
h 1
1 (36)
PRESSh
<=> h 0.0975
Tout ceci est donc strictement équivalent, mais certaines
formes se prêtent mieux au calcul et d'autres mieux à
l'interprétation.
Le principal problème du critère de validation
croisée est qu'il fait appel à un nombre considérable de
calculs. Il faut en effet effectuer, pour chaque étape, autant de
régression PLS que d'individus présents dans la régression
initiale, afin d'être en mesure de calculer le PRESS de l'étape en
question.

32
De plus, la valeur du coefficient que nous avons appelé
« x » est complètement arbitraire, et s'en tenir strictement
à ce critère pourrait se révéler dangereux, dans la
mesure où cela pourrait donner des résultats assez
aléatoires (il arrive parfois que certaines composantes apportent plus,
en terme de prédiction, que celles qui les précèdent), et
on n'a pas vraiment le loisir de se prononcer sur la structure des
composantes.
C'est pourquoi nous allons nous intéresser à
l'utilisation conjointe de deux autres critères.
| 


