

Faculté des Sciences et
Ingénierie
Science de la Planète et de
l'Environnement
Master 1 Eau, Sol, Environnement
Rapport de stage
MODELISATION HYDROLOGIQUE CONCEPTUELLE GR :
CAS DU
BASSIN VERSANT DE NSIMI AU CAMEROUN
Présenté par :
BWIRA Jean Paul
Dirigé par :
Mr. David LABAT
Maitre de conférence
Responsable Master 2 Surveillance et Gestion de
l'Environnement
Mars 2016
Université Paul Sabatier
Master Eau, Sol, Environnement
Stage effectué au Laboratoire Géosciences
Environnement Toulouse
II
Résumé
Un modèle hydrologique est un outil numérique de
représentation des relations pluies-débits à
l'échelle du bassin versant. Les modèles conceptuels
présentent le bassin versant sous forme d'un ensemble des
réservoirs interconnectés après avoir simplifier le cycle
de l'eau. La modélisation présentée dans ce rapport a
été fait à l'aide des modèles GR4J et GR2M.
Le but de cette étude a été de
vérifier l'adéquation des modèles utilisés sur le
bassin versant. Nous avons appliqué ces modèles sur le bassin
versant expérimental de Nsimi au Caméroun. Les résultats
de simulation sont jugés satisfaisants lorsqu'elles donnent des
coefficients de Nash de plus de 75%. Les résultats obtenus avec le GR4J,
nous a donné des coefficients de Nash très faibles. Suite
à ces coefficients de Nash de l'ordre d'une dizaine de pourcent, nous
pouvons alors dire que le bassin versant de Nsimi est inadapté au
modèle GR4J. Contrairement au modèle GR4J, le modèle GR2M
nous a donné des coefficients de Nash de plus de 50%, il répond
mieux que GR4J mais ces résultats ne nous permettent pas encore de
conclure de l'adaptation du modèle au bassin. Il sera important pour les
prochaines études de procéder à un contrôle des
données en amont pour juger de la qualité et de la
fiabilité pour avoir des conclusions définitives sur l'adaptation
du bassin aux modèles GR4J et GR2M.
Abstract
A hydrological model is a digital representation tool of
rainfall-runoff relations throughout the watershed. Conceptual models represent
the watershed as a set of interconnected sub-basins after the simplification of
the water cycle. The hydrological modelling presented in this report was done
with the GR4J and GR2M models.
The aim of this study was to check the adequacy of the above
mentioned models on the experimental watershed of Nsimi in Cameroun. Modelling
results are satisfactory when the they have Nash coefficients greater than
75%.
When used on our experimental watershed, the GR4J model gave a
weak Nash coefficient of a 10%-magnitude, which shows that Nsimi watershed is
unsuitable to GR4J model. Nevertheless GR2M model gave a greater Nash
coefficient of 50%. But we can't conclude of the adaptedness of GR2M model as
its Nash coefficient falls short of the cut-off of 75%.
III
Table des matières
Résumé ii
Abstract ii
Table des matières iii
Liste des figures v
Liste des tableaux v
Remerciement vi
Introduction 1
PREMIERE PARTIE : SYNTHESE BIBLIOGRAPHIQUE 3
I. LE CYCLE DE L'EAU 3
II. CONCEPT DE MODELISATION 4
II.1. TYPOLOGIE DES MODELES HYDROLOGIQUES 5
II.1.1. Les modèles conceptuels 5
II.1.2. Le modèle empirique 6
II.1.3. Le modèle statistique 7
II.1.4. Les modèles à base physique 8
II.1.5. Les modèles continus et les modèles
événementiels 9
II.1.6. Les modèles linéaires 9
II.1.7. Les modèles « boite noire » 10
II.2. CHOIX DU MODELE 10
II.2.1. La problématique 10
II.2.2. La possibilité de détermination des
paramètres 10
II.2.3. La possibilité de simulation 11
II.2.4. La facilité d'utilisation 11
II.3. MISE AU POINT DU MODELE 11
II.3.1. Le calage des paramètres 11
II.3.2. La validation du modèle 12
II.3.3. L'exploitation et l'interprétation 12
DEUXIEME PARTIE : MODELISATION DU BASSIN DE NSIMI
13
I. PRESENTATION DE LA ZONE D'ETUDE 13
I.1. Situation géographique 13
I.2. Contexte climatique 14
I.3. Contexte géologique 14
I.4. Hydrologie et couverture végétale 15
II. PRESENTATION DES MODELES 18
II.1. Le modèle GR4J 18
II.2. Le modèle GR2M 19
III.
iv
RESULTATS 19
III.1. Les résultats du modèle GR4J 20
III.2. Les résultats du modèle GR2M 22
IV. SYNTHESE DES RESULTATS ET DISCUSSION
23
V. CONCLUSION 25
VI. REFERENCES BIBLIOGRAPHIQUES : 26
VI. ANNEXES 27
Les données mensuelles du bassin de Nsimi 27
V
Liste des figures
Figure 1: Répartition mondiale de l'eau douce
(UNFAO, Word Ressources Institut, 2001) 1
Figure 2: Les grands réservoirs d'eau (Jacques
Beauchamp, Université de Picardi, 2008) 3
Figure 4: Représentation d'un bassin versant
(ALSACE NATURE, tirée sur
http://sermnon.fr/définition-d-un-bassin-versant.htm)
4
Figure 3: Le cycle de l'Eau (tirée sur Internet)
4
Figure 5: Les composants d'un modèle hydrologique
(GNOUMA P., Etat de l'art : Modélisation
hydrologique et typologie de modèles, 2006)
4
Figure 6: Schéma de la structure d'un
modèle conceptuel (Perrin et al.2001) 6
Figure 7.2. Carte de situation géographique de
Nsimi (Jean-Loup GOEDLIN et al., Les Bassins
Versants du Centre et Sud Cameroun) 13
Figure 8.1: Situation géographique du Cameroun
13
Figure 9: Les Isohyètes (mm) interannuels du
bassin de Nyong (Tirée sur le site l'ORE-BVET) 14
Figure 10: Géologie du bassin de Nyong
(Tirée sur le site de l'ORE-BVET) 15
Figure 11: Evolution du débit dans le temps du
bassin de Nsimi (1994-2013) 17
Figure 12: Variation des précipitations de Nsimi
(1994-2013) 17
Figure 13: Structure générale du
modèle GR4J, (Perrin et al., Modèles hydrologiques du
Génie
Rural, 2007) 18
Figure 15: Structure générale du
modèle GR2M (C. Perrin et al., 2007) 19
Figure 16: Hydrogramme unitaire du modèle GR4J
(1994-2013) 21
Figure 17: Hydrogramme unitaire du modèle GR2M
(1994-2013) 22
Liste des tableaux
Tableau 1: Quelques paramètres hydrologiques du
bassin de Nyong 16
Tableau 2: Pluie moyenne annuelle (mm/an), ETP (mm/an),
16
Tableau 3:Résultats du modèle GR4J
(1994-2013) 20
Tableau 4: Résultats du modèle GR2M
(1994-2013) 22
Tableau 5: Résultats du modèle GR4J de
trois années en fonction de la saison (1999, 2003, 2012)
21
Tableau 6: Résultats du modèle GR2M en
fonction de la saison (1999, 2003, 2012) 23
vi
Remerciement
Au terme de ce modeste travail, je tiens à remercier
d'une manière particulière mon tuteur de stage, Monsieur David
LABAT, Maitre de conférence et Responsable de Master 2 Surveillance et
Gestion de l'environnement à l'Université Paul Sabatier, pour
avoir consacrer son temps à la réussite de ce travail. Je le
remercie également pour le climat favorable de collaboration et de suivi
de qualité pendant toute la période de stage.
Mes remerciements s'adressent également à
Monsieur Stéphane AUDRY, Responsable du service d'observation «
Bassins Expérimentaux Tropicaux », pour nous avoir fourni les
données qui nous ont permis de produire ce travail.
Je ne serai pas ingrat à l'égard de mes
très chers parents, pour leur soutien moral et matériel qu'ils ne
cessent de me fournir chaque jour de ma vie.
Merci également à la famille du Professeur
Berthollet BWIRA KABORU, Dr. Jacques SHEBEHE, Jonas MUBAWA, Pacifique
KUNJIRAKWINJA, qui m'ont toujours inspiré le sens du devoir et du
travail bien fait.
Je ne saurai pas finir sans remercier, mes deux camarades
Corneille HOUNGUE et Adrien LAVELLE avec qui la collaboration et le climat de
travail a été impeccable tout au long de ce stage.
1
Introduction
L'eau est indispensable à l'existence, au
développement et à la vie des êtres vivants. Elle
intervient dans le geste quotidien de l'homme. Moteur du développement
économique et social, l'eau est également un
élément essentiel à la préservation de
l'environnement naturel.
Dans les activités économiques, une grande
quantité d'eau est utilisée dans l'agriculture, dans les
productions industrielles, les transports et beaucoup d'autres
activités.
Selon le Ministère de l'Environnement, sur les
trente-quatre milliards de m3 prélevés en 2001en
France, six milliards que l'on appelle « part consommée »
c'est-à-dire ne retournant pas en milieu naturel est répartit
comme suit :
- 48% pour l'irrigation (2,88 milliards de m3)
- 24% pour les usages domestiques (1,44 milliards de
m3) - 22% pour la production d'énergie (1,32 milliards de
m3) - 6% pour l'industrie (hors énergie) (0,36 milliards de
m3)
L'eau douce étant inégalement répartie
à travers le globe et son utilisation étant parfois
gérée inadéquatement, certaines régions sont
caractérisées par une rareté de l'eau ou sont
déjà en pénurie (Afrique sub-saharienne, Proche-Orient,
Midwest américain). Le manque d'eau sera de toute évidence un des
problèmes les plus importants du 21e siècle [Figure
1]. Le prélèvement dans certaines rivières est tel que le
débit n'est plus suffisant pour alimenter les deltas. Ces
pénuries causées d'origine anthropiques pourraient par ailleurs
être amplifiées par le réchauffement climatique
(sécheresses, modifications du régime de précipitations).
Celui-ci pourrait par ailleurs amplifier les inondations et autres
événements extrêmes.
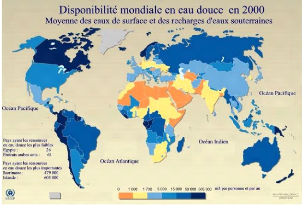
Figure 1: Répartition mondiale de l'eau douce
(UNFAO, Word Ressources Institut, 2001)
Afin de pallier aux difficultés liées à
la ressource en eau, plusieurs études ont été
menées depuis la fin des années 1960 dans le domaine de
l'hydrologie, qui est donc une science de la terre qui s'intéresse au
cycle de l'eau, c'est-à-dire aux échanges entre
l'atmosphère, la surface terrestre et son sous-sol, dans l'objectif
d'assurer une meilleure gestion des ressources en eau, la
2
prévision des crues ou des étiages, la lutte
contre les catastrophes naturelles (inondation), etc. Ces études ont
abouti au développement de plusieurs modèles hydrologiques pour
tenter de représenter le comportement hydrologique à
l'échelle du bassin versant.
Dans le cadre de notre stage au Laboratoire Géoscience
Environnement de Toulouse (GET), nous avons travaillé sur la
modélisation hydrologique conceptuelle GR (Génie Rural) avec le
modèle GR4J et GR2M sur le bassin versant expérimental de Nsimi
au Cameroun. L'objectif de cette modélisation est de vérifier si
les deux modèles sont adaptés à l'étude du bassin
versant de Nsimi. Les modèles GR proposent des relations
comportementales simples à l'échelle du bassin versant d'une
façon empirique sans lien direct avec les bases de la physique
(Ambroise, 1991).
3
PREMIERE PARTIE : SYNTHESE BIBLIOGRAPHIQUE
I. LE CYCLE DE L'EAU
Le cycle hydrologique ou cycle de l'eau est un modèle
qui représente le parcours de l'eau entre les grands réservoirs.
Ces réservoirs peuvent être sous forme d'eau liquide, solide ou de
vapeur d'eau sur Terre. On a par exemple les océans,
l'atmosphère, les lacs, les cours d'eau, les nappes d'eaux souterraines
et les glaciers [Figure 2]. Le moteur de ce cycle est l'énergie solaire
qui, en favorisant l'évaporation de l'eau, entraîne tous les
autres échanges. Le cycle de l'eau est composé des
phénomènes d'évaporation, de l'évapotranspiration,
des précipitations, de ruissellement, d'infiltration, de percolation
[Figure 3].
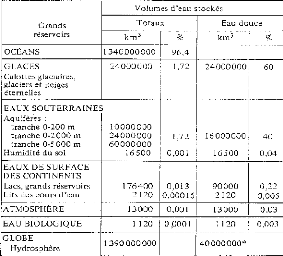
Figure 2: Les grands réservoirs d'eau (Jacques
Beauchamp, Université de Picardi, 2008)
L'hydrologie étudie généralement le cycle
de l'eau à l'échelle du bassin versant. Un bassin versant est une
portion de territoire dont l'ensemble des eaux convergent vers un même
point de sortie appelé exutoire qui peut être la mer,
l'océan, une rivière, etc. Le bassin versant est limité
par des frontières naturelles appelées lignes de crêtes ou
lignes de partage des eaux [Figure 4]. De part et d'autre de ces lignes de
crêtes s'écoulent les eaux des précipitations et des
sources, ainsi que tous les éléments dissous ou en suspension
tels que les sédiments et les pollutions.
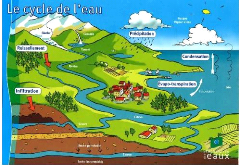
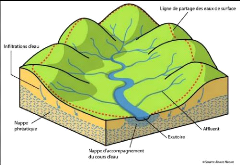
Figure 4: Le cycle de l'Eau (tirée sur
Internet)
Figure 3: Représentation d'un bassin versant
(ALSACE
NATURE, tirée sur
http://sermnon.fr/définition-d-un-
bassin-versant.htm)
4
II. CONCEPT DE MODELISATION
Un modèle hydrologique, ou modèle
pluie-débit, est un outil numérique de représentation de
la relation pluie-débit à l'échelle d'un bassin versant.
Il permet de transformer des séries temporelles décrivant le
climat d'un bassin versant donné (séries de précipitations
et de températures par exemple, séries qui sont les
entrées du modèle hydrologique) en une série de
débits (sortie du modèle hydrologique).
Un modèle hydrologique est caractérisé
par cinq éléments qui le constitue [Figure 5] : la
géométrie du bassin versant (le système), les
entrées du système, les lois de formalisation des processus,
l'état initial et les conditions aux limites du système et les
sorties du modèle (Singh, 1995).
Les équations de
processus
|
Les entrées
|
|
Bassin versant
(Processus, caractéristiques)
|
|
Les sorties
|
|
|
Etat initial et conditions
aux limites
Figure 5: Les composants d'un modèle hydrologique
(GNOUMA P., Etat de l'art : Modélisation hydrologique et typologie de
modèles, 2006)
5
Le principe de la modélisation se présente sous
plusieurs approches :
? La représentation des processus hydrologiques par des
lois physiques qu'on appelle modélisation à base physique : On
cherche à reproduire le monde réel dans sa complexité par
les lois physiques expérimentales. Cette approche exige la
qualité et la représentativité des données. Elle
permet d'identifier et d'expliquer les facteurs déterminants.
? La reproduction des écoulements sans chercher
à représenter les processus : la modélisation
conceptuelle. Dans ce genre de modélisation, on simplifie au maximum la
représentation du monde réel. Ce type de modélisation
possède un nombre de paramètres réduit et une mise en
oeuvre facile.
? La spatialisation ou non des paramètres (les
modèles globaux et les modèles spatialisés ou
distribués)
II.1. TYPOLOGIE DES MODELES HYDROLOGIQUES
Il existe plusieurs modèles hydrologiques qui sont
choisis par rapport aux objectifs de modélisation, des paramètres
du modèle et aux données d'entrée. On peut trouver
plusieurs classifications de modèles hydrologiques dans la
littérature en fonction des auteurs. Par exemple Refsgaard et Storm
(1996) classent les modèles hydrologiques en trois grandes
catégories : les modèles empiriques, les modèles
conceptuels et les modèles à base physique. La notion de la
classification des modèles est très complexe et en raison de
l'ambiguïté de certains critères (notion de conceptuel ou
physique) une certaine confusion règne encore sur l'appartenance de tel
ou tel autre modèle à une catégorie donnée
(Payraudeau, 2002). Nous avons énuméré dans cette partie
quelques types de modèles sans pouvoir les classer forcement comme
certains auteurs peuvent les faires dans plusieurs ouvrages. La liste de
modèles cités ci-dessous n'est pas exhaustive.
II.1.1. Les modèles conceptuels
Les modèles conceptuels considèrent
généralement le bassin versant comme étant un ensemble de
réservoirs interconnectés, après quelques simplifications
du cycle de l'eau. Un modèle hydrologique conceptuel tente de reproduire
la réponse hydrologique d'un bassin versant en remplaçant la
réalité de l'écoulement par une idéalisation
simplifiée de la situation réelle tant de la
géométrie du bassin versant que de l'écoulement
lui-même. Les données hydrologiques et
météorologiques servent alors à faire des estimations
seulement des paramètres. Les modèles hydrologiques conceptuels
sont basés sur un aspect perceptuel du comportement de l'eau dans le
bassin versant et sont par conséquent des modèles
déductifs.
Parmi le modèle à réservoir, on a le
modèle d'hydrogramme unitaire instantané de Nash (1957). Dans ce
modèle, les réservoirs représentent l'évolution du
ruissellement de surface due à la circulation de l'eau dans le bassin
versant, tant le long des pentes que dans le réseau hydrographique. Le
modèle de Nash permet de simuler les crues de beaucoup des bassins
versants avec succès. La validation des résultats des simulations
est conditionnée par les hypothèses de l'hydrogramme unitaire qui
doivent être vérifiées de toute évidence quel que
soit le modèle utilisé. Le modèle de réservoir a
été développé par plusieurs chercheurs avec
différentes approches tels que des modèles GR3J1
(Michel et Edijatno, 1988), les modèles
1 GR3J : modèle Génie Rural à pas
de temps journalier et à trois paramètres.
6
GR4J2 [Figure 6] (Edjatino et Michel,1994), (Perrin
et al. 2003), les modèles GR2M3 (Kabouya, 1990 et
Michel, 1994) également. La figure ci-dessous donne la structure
générale du modèle GR4J.
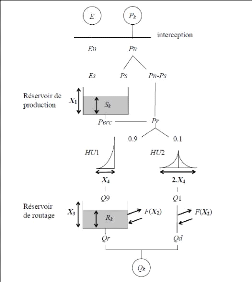
Figure 6: Schéma de la structure d'un
modèle conceptuel (Perrin et al.2001)
II.1.2. Le modèle empirique
Le modèle empirique cherche à reproduire la
dynamique des variables de sortie en fonction des variables d'entrée
sans tenter de décrire les processus élémentaires. Le
modèle empirique utilise une représentation des formules et des
équations qui calculent par exemple un débit en utilisant une
information minimale du bassin versant. Deux exemples sont les plus
utilisés, on a la formule rationnelle et les courbes enveloppes.
L'expression de la formule rationnelle s'écrit :
Q=C*i*A
Avec Q : Débit (m3/s)
I : intensité de la pluie (m/s)
C : coefficient de ruissellement A : surface du bassin
(m2)
Dans la représentation graphique, une courbe enveloppe
est le lieu géométrique des points les plus extérieurs au
graphique. La courbe enveloppe est modélisée par une
équation du type :
2 GJ4J : modèle Génie Rural à pas
de temps journalier et à quatre paramètres.
3 GR2M : modèle Génie Rural à pas
de temps mensuel et à deux paramètres.
7
qs=áAn
Avec á et n étant des paramètres
définis à partir des observations. Par contre le modèle
empirique représente des inconvénients comme par exemple, les
résultats dépendent de coefficients locaux, non transposables
directement ; Beaucoup de paramètres ne sont pas pris en compte
explicitement. Les autres processus ne peuvent pas être rattachés
aux crues calculés, comme le transport des solides, le
phénomène érosif des berges, ...
Le modèle empirique caractérise globalement la
relation Pluie-Débit par des traitements des séries
chronologiques (Ambroise, 1991).
II.1.3. Le modèle statistique
Le modèle statistique utilise des fonctions de
distribution statistiques par exemple la loi Normale, la loi de Gumbel, la loi
de Poisson, ...
Ce modèle permet de prédire ou de faire une
évaluation d'un comportement observé en utilisant les fonctions
de distribution. Ces fonctions permettent l'analyse des variables sous forme
d'échantillon d'une population statistique soit dans l'objectif de faire
une régionalisation en vue de la prédiction de certaines
grandeurs statistiques dont l'analyse fréquentielle.
Généralement, dans le modèle statistique, la variable
qu'on étudie la plus, est l'estimation du débit à
l'exutoire d'un bassin versant dont les caractéristiques sont le
débit maximum ou minimum instantané, journalier, mensuel ou
annuel. A partir de plusieurs études effectuées, il a
été démontré que la loi Normale représente
correctement le comportement de la moyenne de la caractéristique prise
en considération, alors que le comportement des débits maximum ou
minimum est mieux appréhendé par une loi dite de type
extrême (Loi de Gumbel, loi de log Peaeson III, ...). L'utilisation de la
loi appropriée, le calcul des quantiles avec leurs incertitudes et
l'estimation des grandeurs de ses paramètres relèvent du domaine
de la statistique.
Les modèles statistiques sont utilisés dans les
domaines du Génie Civil pour le dimensionnement des ouvrages
hydrauliques. Ils permettent d'estimer des débits de projet pour des
différentes probabilités d'apparition. Ils font intervenir la
notion du temps de retour. Le temps de retour est la probabilité qu'un
événement apparaisse une fois soit tous les 10 ans ou 50 ans,
...
Cependant, les modèles statistiques présentent les
points négatifs qui sont :
? Estimation d'une seule valeur caractéristique
(débit de pointe par exemple)
? Pas de prise en compte explicite de plusieurs
paramètres
? Impossibilité de rattacher d'autres processus aux
crues calculées comme l'érosion des berges
Les résultats obtenus sont complétement
dépendants des données utilisées (les modèles
statistiques proposent un contrôle de l'extrapolation des valeurs
observées vers des valeurs plus rares sous l'hypothèse d'une loi
statistique)
Les valeurs obtenues pendant le calcul et leurs temps de
retour comportent des erreurs de simulation qui ne sont pas facilement
calculables et les intervalles de confiance aussi sont estimés avec
incertitude.
8
Les études actuelles portent sur l'amélioration
de ces aspects car les modèles statiques sont incontournables en
hydrologie et ils sont ainsi couplés à d'autres modèles
comme le modèle conceptuel.
II.1.4. Les modèles à base physique
Les modèles à base physique reposent sur la
résolution d'un grand nombre d'équation de continuité et
de quantité de mouvement liée soit au processus de transport
d'eau ou des substances soit d'énergie. Ces équations doivent
décrire les différents phénomènes dans d'un bassin
versant. On a par exemple le système d'équation de Barré
de Saint Venant qui ressoude les écoulements en surface libre et celui
de Darcy qui résout les écoulements souterrains. En
matière d'écoulement, le modèle à base physique qui
serait le plus complet est celui qui pourra résoudre l'équation
de Barré de Saint Venant en deux dimensions pour les écoulements
en surface libre et celui de Darcy à trois dimensions pour les
écoulements souterrains.
Ce type de modèle a besoin de trois éléments
complexes :
Etablir la description du bassin versant plus en détail
par un maillage fin à trois dimensions Des schémas
numériques robustes
Des valeurs de paramètres pour chaque maille et dans
chaque direction
Ces trois éléments présentent une
difficulté pour l'application de ce type de modèle et explique
leur nombre restreint dans la modulation hydrologique. Le SHE4 est
le modèle le plus utilisé parmi le modèle à base
physique en hydrologie.
Le SHE résout le bilan hydrique sur le bassin versant
en se basant sur des équations physiques et des paramètres
spatialisés.
La plus grande difficulté dans ce type de modèle
est la détermination des paramètres. Les paramètres ayant
un sens physique comme la conductivité hydraulique, les
paramètres de friction devraient être mesurable in situ mais en
pratique, on constate que la mesure de ces paramètres et la
détermination de leur répartition spatiale induit le plus souvent
à des difficultés d'utilisation rigoureuse des modèles
à base physique tel que le SHE. Les distorsions des modèles
même pour les plus détaillés sont inévitables. Pour
calculer un débit à l'exutoire d'un bassin versant, les
paramètres du modèle doivent endosser les incertitudes
liées aux simplifications. Ces simplifications sont inévitables
et elles impliquent que certains processus ne sont pas très bien
simulés.
Après de test de simulation, on constate le plus
souvent que les valeurs des paramètres ne correspondent plus à
leurs valeurs mesurées même si elles pouvaient être exactes.
A partir de ce constat on peut alors affirmer que le modèle à
base physique qui donne une réponse très proche des observations
n'a pas des paramètres physiques ; et donc un modèle à
base physique qui utilise les paramètres mesurés devraient
normalement donner une réponse inexacte. Ce modèle est plus
adapté dans la recherche sur des bassins test ou pour simuler des
expériences en laboratoire mais difficile à appliquer dans le cas
pratique.
4 Le SHE « Système Hydrologique
Européen » est un modèle développé vers les
années 1980 (Abbot et al. 1986)
9
II.1.5. Les modèles continus et les
modèles événementiels
Dans le domaine des aménagements des infrastructures
hydrauliques, l'application d'un modèle hydrologique consiste à
déterminer une crue de projet à partir d'une pluie de projet.
Dans ce genre d'étude, l'objectif de la modélisation sera alors
la recherche d'un événement unique : le modèle à
choisir sera ainsi un modèle événementiel. Un tel
modèle ne prend en compte que qu'une seule entrée (les
précipitations) pour calculer une seule crue (crue du projet). Les
modèles de simulation continus visent la simulation en continue du
comportement hydrologique du bassin versant. La simulation peut être
menée sur des longues périodes de temps, couvrant toute une
variété de situations hydrométéorologiques, allant
de crues aux étiages. Ces modèles doivent considérer tous
les processus influençant de façon significative la
réponse du bassin versant et pas les seuls processus impliqués
dans un phénomène hydrologique particulier. Ils
nécessitent aussi l'estimation des conditions initiales. L'existence des
équations permettant de calculer le débit de base et en tenant
compte de facteurs météorologiques à la pluie est la
principale différence entre les modèles continus et les
modèles événementiels. Les exemples des modèles
continus sont tous des modèles à base physique et certains
modèles conceptuels.
II.1.6. Les modèles linéaires
Les modèles linéaires pluie-débit sont
parmi les plus utilisé par les services d'annonce des crues (la
météo). Il propose une relation linéaire entre les
entrées du modèle qui sont les précipitations et les
sorties qui sont les débits. Les autres modèles comme les
modèles à base physique, bon nombre des modèles
conceptuels, ils sont non linéaires. Les modèles non
linéaires interviennent très souvent dans la relation entre le
stockage et le débit :
S= a*Qc
On peut avoir une possibilité d'exprimer cette relation
en fonction du temps de réponse k du bassin versant, du débit et
de l'intensité de la pluie :
K= a*Qb ou k= a*id
Ces types de modèles possèdent beaucoup des
simplifications en hydrologie. Les modèles de transfert typique sont des
hydrogrammes unitaires. Dans ce type de modèle si certaines
hypothèses sont vérifiées, ce modèle s'applique
bien sans grande perte de précision mais n'oublions pas qu'à la
base, il n'existe pas un écoulement linéaire. Les lois
fondamentales de circulation des fluides sont régies par les relations
non linéaires de Reynolds qui prennent en compte la turbulence et les
phénomènes dynamiques du fluide. Certains indices indiquent que
tous les bassins versants ne peuvent pas accepter une relation linéaire.
Les phénomènes qui peuvent expliquer le comportement non
linéaire d'un bassin versant sont :
La variation du temps de parcours en fonction du débit
d'écoulement
La diminution des effets de stockage en fonction de
l'augmentation de la crue (temps de réponse bas et forte augmentation du
débit)
Les variations du débit de pointe avec le volume de
crue
Les variations de certains paramètres en fonction de
certains éléments (comme le coefficient de ruissellement,
intensité maximale de la pluie) lors de la simulation.
Un autre phénomène de la non
linéarité est du comportement hydrologique vient de l'existence
de seuils dans la réponse hydrologique. Les phénomènes le
plus directs sont les débordements
10
qui induisent à un ralentissement important d'une partie
de volume de crue. On peut avoir beaucoup d'autres phénomènes du
non linéarité du comportement hydrologique d'un bassin.
II.1.7. Les modèles « boite noire
»
Les modèles boite noire qu'on appelle encore ARMAX
(Auto-Regressive Moving Average with eXogenous input) tente de
représenter la relation pluie-débit par une formulation
mathématique de type auto régressif (Box et Jenkins, 1976).
L'expression mathématique de ce modèle est
donnée par la formule :
p r q
??(??) = - ? ??i??(?? - ??) + ???????(?? - ??) + ?
??????(?? - ??) + ??(??)
i=1 ??=1 ??=1
Y(t) est le débit simulé ; p,r,q sont les ordres
du modèle ; a,b,c sont les paramètres du modèle ; x(t-j)
est une variable explicative (pluie) ; e(t) est le bruit blanc et t l'indice de
temps (jour).
Dans les modèles boite noire, le bassin est
considéré comme étant une entité unique. Ces
modèles utilisent des relations empiriques qui relient les
entrées et les sorties du modèle sans pour autant chercher
à se rapprocher d'une loi physique. En 1972, Chow a subdivisé les
modèles boite noire en deux classes : les modèles
déterministes et non déterministe. Les modèles non
déterministes regardent les variables d'entrés et de sorties du
système hydrologique comme des variables aléatoires et essaie de
trouver une relation mathématique soit statistique entre ces variables.
L'hydrogramme unitaire peut être pris comme un exemple type du
modèle déterministe.
II.2. CHOIX DU MODELE
Comme nous l'avons dit précédemment, il existe
une grande diversité de modèle en hydrologie et souvent on a des
difficultés à choisir un modèle pour une étude
donnée. Le choix d'un modèle se fait en générale en
fonction de l'objectif de l'étude hydrologique qu'on aura à
effectuer et en fonction des composantes hydrologiques du bassin versant qu'on
cherche à représenter. Il est important de choisir un
modèle qui est adéquat à la problématique
posée. Le choix du modèle doit vérifier ces quatre
principes :
II.2.1. La problématique
Les études hydrologiques sont faites pour
résoudre les problèmes d'aménagement hydrauliques de cours
d'eau et des ouvrages dans le domaine d'urbanisme et des problèmes de
sécurité des populations pour éviter les inondations et
d'autres catastrophes liées à l'eau. Ces études peuvent
servir à dimensionner des ouvrages de régulations des crues, les
ouvrages d'évacuation des eaux des pluies, les pollutions ponctuelles,
... Par exemple, pour ce type de problématique, le modèle
à choisir devra prendre en compte quelques paramètres tels que
l'évaporation, les variations du niveau de la nappe, etc et
négliger ou au moins simplifier la formation des crues. Pour ces
études de bilan hydrologique on peut recourir aux modèles
linéaires et les modèles non linéaires.
II.2.2. La possibilité de détermination
des paramètres
Les données hydrométéorologiques et la
taille du bassin versant sont les deux aspects qui expliquent cette contrainte
de possibilité à déterminer les paramètres. Par
exemple pour les modèles conceptuels on a besoin d'une longue
série des données pluie-débit pour assurer un
11
bon calage. Pour la plupart des modèles beaucoup plus
complexes, il faut apporter des données supplémentaires de
conductivité hydraulique par exemple qui doit être estimée
ou mesurée. On peut aussi se retrouver dans le cas où on doit
faire des estimations des paramètres du modèle par
régionalisation, c'est-à-dire faire des interpolations qui
permettront de transporter des paramètres estimés sur un bassin
versant jaugés vers un bassin non jaugé. Dans ce cas, il faudra
trouver un modèle qui offre cette possibilité. On peut retenir
dans ce cas le modèle de Nash qui, ses paramètres peuvent
être reliés à la description géomorphologique du
bassin versant.
II.2.3. La possibilité de simulation
L'utilisation de certains modèles présente des
avantages du fait qu'ils donnent la possibilité de fonctionner
automatiquement d'une manière itérative.
II.2.4. La facilité d'utilisation
On peut aussi avoir certains modèles qui
présentent des difficultés pour les utilisateurs. Même en
possédant le manuel d'utilisation, la lecture des fichiers de sortie
rend le logiciel une source de travail pénible. Il est conseillé
d'utiliser des programmes récents qui possèdent les idées
de base sur les anciens modèles. On doit éviter d'utiliser les
modèles dont les modules ne peuvent pas être compris et
maitrisés. Les difficultés hydrologiques restent les mêmes
quel que soit les programmes mais elles restent inaperçues grâce
à la facilité d'usage.
II.3. MISE AU POINT DU MODELE
La mise au point d'un modèle se fait en suivant 3
grandes étapes qui sont la calibration du modèle (le calage), la
validation du modèle, l'exploitation et l'interprétation.
II.3.1. Le calage des paramètres
D'une façon très générale, la
calibration consiste à évaluer les paramètres inconnus du
modèle de manière à simuler des réponses qui soient
très proches de la réalité (les observations). Ceci permet
l'exploitation du modèle avec les valeurs estimées des
paramètres pour simuler des crues qui n'ont pas servi au calage tout
comme des crues hypothétiques passées ou futures. La
première étape du calage consiste à sélectionner
les événements et en suite l'estimation des paramètres
proprement dits. Le choix des événements est simplifié
dans le cas de la simulation en continu ; sur les n années existantes,
on ne prend qu'une moitié pour le calage et une autre pour la
validation.
Les modèles qui comportent plus de trois
paramètres inconnues sont difficiles à caler. Les modèles
conceptuels simples qui sont plus facile à caler. Ces modèles
contiennent souvent une équation d'infiltration globale à un ou
deux paramètres et un hydrogramme unitaire à deux
paramètres (Par exemple le nombre de réservoirs et le temps de
montée pour l'hydrogramme de Nash).
Les méthodes de calage plus rigoureuses et automatiques
nécessitent l'adoption d'une fonction d'erreur et d'un algorithme
d'optimisation. La fonction d'erreur est la valeur absolue de la
différence entre les débits de pointe observés et
simulés. Les plus complexes prennent en compte l'ensemble de
l'hydrogramme. Parmi les fonctions d'erreur, on peut avoir par exemple :
o La différence des débits de pointe
12
?? = ??????- ??????
Avec e la fonction d'erreur, ?????? le débit de pointe
observé et ?????? le débit de pointe simulé
o La somme des carrées des erreurs
??
?? = ?(????(??) - ????(??))2
??=1
????(??) est le débit observé au pas de temps i et
????(??) le débit simulé au pas de temps i.
o La fonction de Nash-Suttcliffe
??= 1
|
-
|
? ?? (????(??) -
??=1
|
????(??))2
|
|
- ??)2
|
|
La fonction de Nash exprime le rapport entre l'erreur du
modèle donné et l'erreur d'un modèle de
référence, apprécié à la moyenne des
débits. Il existe beaucoup d'autres fonctions d'erreur qu'on n'a pas
mentionnées.
L'algorithme d'optimisation est représenté par
la surface décrite par la fonction critère dans l'espace des
paramètres qu'on appelle la surface de réponse. La recherche de
paramètres optimaux revient à trouver le minimum global de cette
surface.
Il existe plusieurs algorithmes, comme par exemple :
- Algorithme de Rosenbrock-Palmer (Rosenbrock 1960, Palmer 1969)
- Méthode de Simplex (Singh 1995)
- Méthode des gradients basée sur les
équations de Lagrange
II.3.2. La validation du modèle
La validation du modèle a pour objectif de
déterminer si le modèle est adapté à la simulation
et estimer l'erreur à craindre en simulation. On peut estimer ces
erreurs en appliquant le modèle sur des événements autre
que ceux utilisés pour le calage. Pour faire la validation du
modèle, il faut faire le choix final des valeurs des paramètres
du modèle ; appliquer le modèle sur les événements
autre que ceux qui ont été prise pour le calage ;
apprécier les résultats et calculer les erreurs
résultantes.
II.3.3. L'exploitation et l'interprétation
L'exploitation et l'interprétation des
résultats est l'étape finale d'une modélisation
hydrologique. En définitive, il faut prendre quelques précautions
à ce niveau :
o Eviter un modèle pour des extrapolations très
importantes.
o Les résultats obtenus de la modélisation
doivent être vérifiés et comparés à d'autres
études similaires.
o Les erreurs calculées doivent être
reportées dans les résultats finals.
o Faire des représentations graphiques de
résultats à l'image de la qualité des simulations.
13
DEUXIEME PARTIE : MODELISATION DU BASSIN DE
NSIMI
Nous sommes parvenus à acquérir les
données hydrologiques, géologiques et
météorologiques du bassin de Nsimi grâce à
l'ORE-BVET5. Le Projet ORE-BVET a été financé
par le Ministère de la Recherche et des Nouvelles Technologies,
l'Institut National des Sciences de l'Univers, l'Institut de Recherche pour le
Développement et l'Observatoire Midi-Pyrénées.
I. PRESENTATION DE LA ZONE D'ETUDE
I.1. Situation géographique
Le Bassin versant expérimental de Nsimi est un petit
sous bassin du Nyong dans le sud du Cameroun. Le Cameroun est un pays de
l'Afrique Centrale, ayant comme capitale politique Yaoundé (3° 52'N
et 11°31'E). C'est un pays situé entre le Nigéria à
l'Ouest et le Tchad au nord, la RCA à l'Est et le Gabon au Sud. Sa
superficie est de 475 442 Km2. Nsimi se trouve dans le sud du
Cameroun avec une superficie de 0,6 ha et déversant dans le lac Olama
[Figure 7.2].
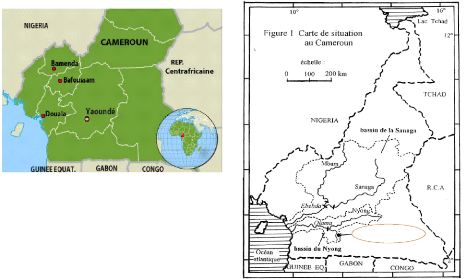
Figure 7.1: Situation géographique du
Cameroun
BVET de Nsimi
Figure 8.2. Carte de situation géographique de
Nsimi (Jean-Loup GOEDLIN et al., Les Bassins Versants du Centre et Sud
Cameroun)
5 ORE-BVET « Observatoire de Recherche en
Environnement sur les Bassins Versants Expérimentaux ».
I.2. 14
Contexte climatique
Le climat du Cameroun est formé par deux domaines. Le
domaine équatorial et le domaine tropical. Le domaine équatorial
est caractérisé par des précipitations abondantes, des
températures élevées et stables, et une
végétation qui se dégrade au fur et à mesure qu'on
s'éloigne de l'équateur. Dans ce domaine du Cameroun, on a quatre
saisons : la saison de pluie allant de mars à juin, une petite saison
sèche en juillet et août, la saison de pluie allant de septembre
à novembre et la grande saison sèche allant de décembre
à février).
Sur le bassin expérimental de Nsimi
c'est-à-dire sous bassin du Nyong, on a un climat équatorial du
type guinéen à 4 saisons sur la plus grande partie de la zone. La
petite saison va de mars à mai, la grande saison des pluies de septembre
à novembre et est séparée par une courte saison plus
sèche, la grande saison sèche s'étendant de
décembre à février. Les pluviométries annuelles
sont comprises entre 1500 et 2000 mm, la température moyenne annuelle
est de l'ordre de 25°C. Toutefois, dans la frange côtière
limitée aux 80-100 km du cours inférieur du Nyong, le climat est
du type camerounien ; ici, il n'existe plus qu'une saison relativement
sèche, de décembre à février. La
pluviométrie annuelle est comprise entre 2000 et 3500 mm [Figure 6], la
température annuelle moyenne est de 26°C, dans cette zone
très chaude et très humide, l'hygrométrie annuelle moyenne
dépasse 85%.
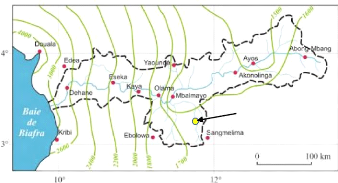
BVERT de Nsimi
Figure 9: Les Isohyètes (mm) interannuels du
bassin de Nyong (Tirée sur le site
l'ORE-BVET)
I.3. Contexte géologique
D'après la récente synthèse de Vicat
(1998), le substratum du bassin du Nyong est constitué par deux
ensembles principaux.
Dans la partie nord, on a la zone mobile fortement
affectée par l'orogénèse panafricaine (600500 Milliards
d'années), qui représente la terminaison occidentale de la
chaîne des Oubanguides. Dans la partie la plus au nord (a) ; on retrouve
la série de Yaoundé qui est caractérisée par la
formation de gneiss et de migmatites à grenats, venant d'anciens
sédiments granitisés et métamorphisés dans le
faciès granulite, et (b) au contact avec le craton, la série
15
d'Ayos-Mbalmayo-Bengbis, fomée de chloritoschistes et
de quartzites, interprétée comme la semelle
rétrométamorphisée de la nappe panafricaine.
Dans la partie Sud, on a le groupe du Ntem qui correspond
à la bordure septentrionale du craton du Congo, stable depuis environ
2000 Milliards d'années. Ce complexe comprend d'Est en Ouest les
séries d'Ayina, du Ntem et du Nyong. Les formations plutoniques sont
constituées de granitoïdes appartenant à deux lignées
mises en place au cours d'épisodes successifs : les charnockites
libériennes (vers 2900 Milliards d'années), et les granites plus
potassiques et leucocrates (2700-2600 Milliards d'années). On peut
remarquer des fréquentes intrusions au sein de ces formations rocheuses.
Ces intrusions sont en relation avec différents épisodes
tectoniques qui ont été décrites : ceintures de roches
vertes, particulièrement abondantes à l'Ouest avec les sillons
ferrifères, série rubanée à gneiss, corps de
dolérites, gabbro et rarement de péridotites.
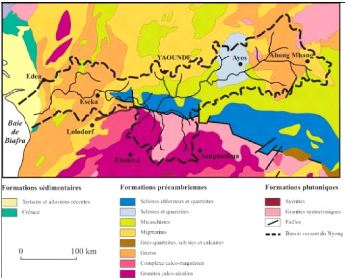
Figure 10: Géologie du bassin de Nyong
(Tirée sur le site de l'ORE-BVET)
I.4. Hydrologie et couverture
végétale
Le tableau 1 présente la synthèse de quelques
paramètres hydrologiques du bassin de Nyong tout en sachant que nous
avons travaillé sur les données du bassin expérimental de
Nsimi uniquement. Ces chiffres sont des valeurs moyennes recueillies entre 1999
et 2002.
16
Tableau 1: Quelques paramètres hydrologiques du
bassin de Nyong
(Tiré sur le site de l'ORE-BVET, 2002)
|
Nsimi
|
Messam
|
Pont So'o
|
Mbalmayo
|
Olama
|
|
Surface
(km2)
|
0,60
|
206
|
3,070
|
13,555
|
18,510
|
|
Pluie
(mm/an)
|
1,779#177;254
|
1,779
|
1,749#177;225
|
1,579#177;159
|
1,636#177;181
|
|
DébitX10-3
(m3/s)
|
7,6#177;2,6
|
3,60#177;1,48
|
43,9#177;15,7
|
133,8#177;31,5
|
201,3#177;47,0
|
|
Lame6
(mm/an)
|
397#177;133
|
551#177;226
|
451#177;161
|
311#177;73
|
343#177;80
|
|
Ke* (%)
|
22,3
|
31,0
|
25,8
|
19,7
|
21,0
|
Coefficient d'écoulement7*
Tableau 2: Pluie moyenne annuelle (mm/an), ETP
(mm/an),
Q(mm/an) du bassin de Nsimi de 1994 à 2013
|
Année
|
Pluie (mm)
|
ETP8(mm)
|
Q (mm)
|
|
1994
|
1339
|
5,8366
|
358,56
|
|
1995
|
1498
|
5,8366
|
263,52
|
|
1996
|
1788,3
|
5,8366
|
475,2
|
|
1997
|
1783,2
|
5,8366
|
371,52
|
|
1998
|
1815,4
|
5,8366
|
362,88
|
|
1999
|
2161,1
|
5,8366
|
95,04
|
|
2000
|
1724,1
|
5,8366
|
375,84
|
|
2001
|
1428,9
|
5,8366
|
211,68
|
|
2002
|
1568
|
5,8366
|
263,52
|
|
2003
|
947
|
5,8366
|
125,28
|
|
2004
|
1612,2
|
5,2341
|
293,76
|
|
2005
|
1477,8
|
5,5441
|
185,76
|
|
2006
|
1625
|
5,8554
|
185,76
|
|
2007
|
1688,1
|
6,4255
|
220,32
|
|
2008
|
1818,5
|
6,1643
|
311,04
|
|
2009
|
1733,65
|
5,8366
|
289,44
|
|
2010
|
1722,9
|
5,8366
|
298,08
|
|
2011
|
1317,97
|
5,8366
|
164,16
|
|
2012
|
1606,5
|
5,8366
|
151,2
|
|
2013
|
1469,3
|
5,8366
|
181,44
|
A partir des séries pluie-débit que l'on a
obtenu grâce à la base des données de l'ORE-BVET, on peut
voir l'évolution du débit et de la pluie au cours des
années de Nsimi.
6 La lame d'eau est la quantité d'eau
précipitée par unité de temps
7 Le coefficient d'écoulement est le rapport,
exprimé en pourcentage, entre la quantité d'eau
écoulée par la quantité d'eau précipitée
8 L'évapotranspiration est la somme de la
transpiration du couvert végétal et de l'évaporation des
sols
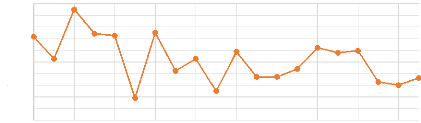
Evolution du débit dans le temps (1994-2013)
Débit (mm)
450
400
250
200
500
350
300
150
100
50
0
1994 1996 1998 2000 2002 2004 2006 2008 2010 2012
Années
17
Figure 11: Evolution du débit dans le temps du
bassin de Nsimi (1994-2013)
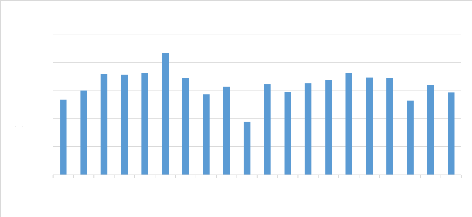
Variation des précipitations (mm)
2500
1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006
2007 2008 2009 2010 2011 2012 2013
Années
Pluie (mm)
2000
1500
1000
500
0
Figure 12: Variation des précipitations de Nsimi
(1994-2013)
La figure 12 présente l'évolution des
précipitations sur 20 ans. Nous remarquons sur cette chronologie que
1999 est l'année qui enregistre des fortes précipitations
(année la plus humide), les précipitations les plus faibles
s'enregistrent en 2003.
Sur le bassin de Nyong, les collines et les versants sont
recouverts par la forêt secondaire, la forêt « vierge »
ne subsistant plus qu'en de rares lambeaux à l'échelle de la
région ; certaines zones ont été déboisées
pour laisser la place aux cultures traditionnelles essentiellement
vivrières (manioc, macabo9, banane plantain, arachide,
maïs...). Ces parcelles, sur lesquelles n'est utilisé aucun
engrais, retournent en friche au bout de quelques années, tandis que
d'autres
9 Le macabo est un tubercule consommé par les
populations du Cameroun et des pays voisins, principalement le Gabon qui est
à grande majorité de culture bantou.
18
sont à leur tour déboisées et mises en
culture. Le bas fond marécageux est le domaine des
raphiales10.
II. PRESENTATION DES MODELES
Pour notre étude, on a utilisé le modèle
GR4J et le modèle GR2M II.1. Le modèle GR4J
Le modèle GR4J est un modèle pluie-débit
global à 4 paramètres permettant de faire de simulation au pas de
temps journalier. Ce modèle a pour objectif de faire des simulations
pluies-débits robustes et fiables pour l'utilisation dans l'application
de la gestion des ressources en eau et d'ingénierie. Il
été développé au Cemagref11 par Perrin
(2002) et al. (2003) sous une version excel en libre accès sur
internet.
Schéma de la structure d'un modèle GR4J
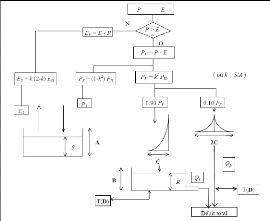
Figure 13: Structure générale du
modèle GR4J, (Perrin et al., Modèles hydrologiques du
Génie Rural,
2007)
Les entrées du modèle:
- Nom du bassin
- Superficie du bassin
- Paramètres du modèle (X1 : capacité de
réservoir de production, X2 : paramètre d'échange, X2 : la
capacité de réservoir de routage, X4 : temps de base de
l'hydrogramme unitaire)
- Taux de remplissage
10 Les Raphiales sont des forêts
marécageuses des bords de marigots et de rivières.
11 CEMAGREF « Centre d'Étude du Machinisme
Agricole et du Génie Rural des Eaux et Forêts »
-
19
Période de mise en route et durée de la
période de test
- Date, Pluie (mm), ETP (mm) et le débit
(m3/s)
Pour juger de la qualité de simulation, on se base sur
le critère d'efficacité de Nash qui est calculé sur les
débits. Pour l'optimisation des paramètres, il faudra alors se
mettre dans une cellule cible c'est-à-dire la cellule Q de Nash
présente dans le logiciel et lancer la fonction solveur d'Excel.
A la sortie du modèle, on a des graphiques
présentant l'évolution du taux de remplissage du réservoir
de production, l'évolution du taux de remplissage du réservoir de
routage, un hydrogramme unitaire qui présente les chroniques de
débits observés et simulés et autre graphique qui
présente les débits observés et simulés pour
pouvoir les comparés.
II.2. Le modèle GR2M
Le GR2M est un modèle qui permet de faire de
simulation pluies-débits au pas de temps mensuel. Il a aussi
été mis développé par Mouehli et al.
(2006). Le logiciel GR2M présente presque la même interface
que le GJ4R. Le GR2M possède deux paramètres, X1
représente le taux de remplissage de réservoir du production et
X2 le taux de remplissage du réservoir de routage. Il utilise aussi le
critère d'efficacité de Nash pour évaluer la
qualité de la simulation. A la sortie du modèle, on a les
chroniques de débits simulés et observés,
l'évolution du taux de remplissage de deux réservoirs.
Schéma de structure d'un modèle GR2M
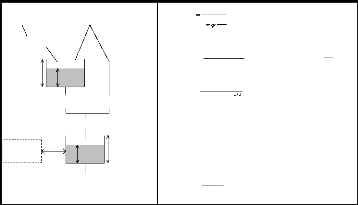
Production
store
Outside of
the basin
evaporation
E
X1
(4)
(7)
(8)
X2
(3)
(5)
P2
S
(1) (2)
P3
Q
R
P
(6)
P1
Routing
store
60 mm
(1)
(2)
(3)
(4)
(6)
(7)
(8)
(5)
S1
S ? X ?
P ?
S2 P2?S2?S
1/ 3
R1 ?R?P3
S2
?
S ?
R2 ? X5.R1
P1 ?P?S?S1
P3 ? P1 ?
P2
?
? S ?
2
1 ?? ? ?
2
Q ?
?
? ?
1
R2 ?
3 ?
? X?
1 ? ?
1?
S1
60
X1
?1???
Figure 14: Structure générale du
modèle GR2M (C. Perrin et al., 2007) III. RESULTATS
- Calcul de l'ETP
L'ETP est l'un des paramètres que possèdent les
deux modèles. Nous l'avons calculé avec l'une
des formules de Turc (Valérie Borrel, Cours
Evapotranspiration 2011).
ETP=0.40*(Rg+50)* (T
T+15) * (1+50-hr
70 ) (1)
20
|
ETP=0.40*(Rg+50)* ( T
T+15)
|
(2)
|
T : la température moyenne (°C)
Hr : l'humidité relative (%)
Rg : le rayonnement solaire moyen (cal/cm2/jour)
La formule (1) pour une humidité inférieure
à 50% et (2) pour une humidité supérieure ou
égale
à 50%.
Pour GR2M, l'entrée du modèle requiert des
débits en mm/mois et donc sommes par une
conversion de la série des débits par la relation
:
?? ( mm
mois) = ??(??3
A (m2) ??1000??30??24??3600
?? )
III.1. Les résultats du modèle GR4J
Tableau 3:Résultats du modèle GR4J
(1994-2013)
|
Calage du modèle
|
|
|
Période de mise en route
|
Période test
|
Paramètres du modèle
|
Critère
d'efficacité
|
|
Années
|
Nbre de
jours
|
Années
|
Nbre de
jours
|
x1(mm)
|
x2(mm)
|
x3(mm)
|
x4(jours)
|
Nash (%)
|
|
1994-1995
|
720
|
1995-2013
|
6584
|
-18,50
|
5,24
|
6,20
|
-0,69
|
9,7
|
|
1994-1996
|
1085
|
1996-2013
|
6219
|
-18,50
|
5,19
|
6,16
|
-0,69
|
9,8
|
|
1994-1997
|
1450
|
1997-2013
|
5854
|
-18,50
|
5,15
|
6,12
|
-0,69
|
9,7
|
|
1994-1998
|
1815
|
1998-2013
|
5489
|
-18,50
|
5,09
|
6,05
|
-0,69
|
9,7
|
|
1994-1999
|
2180
|
1999-2013
|
5124
|
-18,50
|
5,16
|
6,14
|
-0,69
|
10,3
|
|
1994-2000
|
2545
|
2000-2013
|
4759
|
-18,50
|
5,03
|
5,94
|
-0,69
|
10,3
|
|
1994-2001
|
2910
|
2001-2013
|
4394
|
-18,50
|
4,99
|
5,87
|
-0,69
|
10,1
|
|
1994-2002
|
3275
|
2002-2013
|
4029
|
-18,50
|
4,95
|
5,83
|
-0,69
|
10,4
|
|
1994-2003
|
3640
|
2003-2013
|
3664
|
-18,50
|
4,97
|
5,82
|
-0,69
|
10,5
|
Débit (mm/j)
468
1600,0
1400,0
1200,0
1000,0
200,0
00,0
00,0
00,0
0,0
Débit observé Débit simulé Pluie
200
250
0
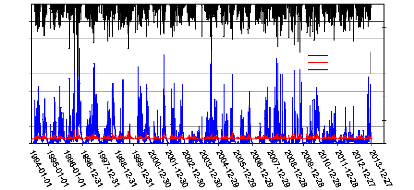
50
300
100
150
Pluie (mm)
21
Figure 15: Hydrogramme unitaire du modèle GR4J
(1994-2013)
Le tableau 3 présente les résultats obtenus par
les modèles GR4J. Ces résultats de simulation sont obtenus sur
différente périodes de calage et de validation. La figure 16 est
une hydrogramme unitaire qui présente les chroniques de pluie, de
débits simulés et observés pour le coefficient de Nash le
plus élevé pour le modèle.
Tableau 4: Résultats du modèle GR4J de
trois années (1999, 2003, 2012) en fonction de la saison
|
Calage du modèle
|
|
|
Période de mise en
route
|
Période test
|
Paramètres du modèle
|
Critère
d'efficacité
|
|
Année
|
Saison
|
Années
|
Saison
|
x1(mm)
|
x2(mm)
|
x3(mm)
|
x4(jours)
|
Nash (%)
|
|
1999
|
Humide
|
2003/2012
|
Sèche/Semi-humide
|
-18,50
|
0,13
|
4,90
|
-4,90
|
14,3
|
|
2003
|
Sèche
|
1999/2012
|
Humide/Semi-humide
|
-18,50
|
3,95
|
4,51
|
-4,35
|
9,2
|
22
III.2. Les résultats du modèle GR2M
Tableau 5: Résultats du modèle GR2M
(1994-2013)
|
Calage du modèle
|
|
|
Période de mise en route
|
Période test
|
Paramètres du
modèle
|
Critère
d'efficacité
|
|
Années
|
Nbre de mois
|
Années
|
Nbre de mois
|
x1(mm)
|
x2(mm)
|
Nash (%)
|
|
00-1994
|
12
|
1995-2013
|
227
|
7,11
|
0,30
|
51,0
|
|
1994-1995
|
24
|
1996-2013
|
215
|
7,08
|
0,30
|
50,7
|
|
1994-1996
|
36
|
1997-2013
|
203
|
7,02
|
0,29
|
50,6
|
|
1994-1997
|
48
|
1998-2013
|
191
|
6,97
|
0,29
|
48,8
|
|
1994-1998
|
60
|
1999-2013
|
179
|
6,95
|
0,28
|
47,9
|
|
1994-1999
|
72
|
2000-2013
|
167
|
7,02
|
0,30
|
61,7
|
|
1994-2000
|
84
|
2001-2013
|
155
|
7,07
|
0,29
|
59,6
|
|
1994-2001
|
96
|
2002-2013
|
143
|
7,22
|
0,29
|
57,9
|
|
1994-2002
|
108
|
2003-2013
|
131
|
7,20
|
0,29
|
60,1
|
|
1994-2003
|
120
|
2004-2013
|
119
|
7,18
|
0,29
|
62,0
|
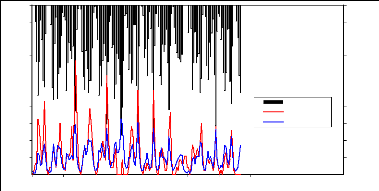
Le tableau 4 présente les résultats obtenus de
l'application du modèle GR2M sur le bassin versant. Ces résultats
ont été obtenus sur différentes périodes de mise en
route et de test. La validation des résultats est faite sur le
coefficient de Nash le plus élevé et les paramètres
retenus du modèle sont pour le Nash le plus élevé. La
figure 17 présente les chroniques de pluies, de débits
observés et simulés du modèle GR2M.
)
140
1
1
mo
120
Débit (mm/mois)
mm
100
200
180
160
40
80
60
20
janv.-94 janv.-96 janv.
0
-98 janv.-00 janv.-02 janv.-04 janv.-06 janv.-08 janv.-10
janv.-12
Pluie
Débit observé Débit simulé
0 50 100 150 200 250 300 350 400 450 500
P l u ie (mm/mois)
|
Figure 16:
|
Hydrogramme unitaire du modèle GR2M
(1994-2013)
|
23
Tableau 6: Résultats du modèle GR2M sur
trois années (1999, 2003, 2012) en fonction de la saison
|
Calage du modèle
|
|
|
Période de mise en route
|
Période test
|
Paramètres du modèle
|
Critère
d'efficacité
|
|
Année
|
Saison
|
Année
|
Saison
|
x1(mm)
|
x2(mm)
|
Nash (%)
|
|
1999
|
Humide
|
2003/2012
|
Sèche/Semi-humide
|
7,39
|
0,24
|
27,7
|
|
2003
|
Sèche
|
1999/2012
|
Humide/Semi-humide
|
5,77
|
0,14
|
0,6
|
IV. SYNTHESE DES RESULTATS ET DISCUSSION
La simulation pluie-débit de deux modèles
appliqués sur le bassin versant expérimental de Nsimi nous a
donné des résultats assez différents sur les deux
modèles. Pour le modèle GR4J, le coefficient de Nash le plus
élevé est de 10,5%. Par contre, le modèle GR2M donne le
Nash le plus élevé de 62%, ce qui nous permet de confirmé
que ce dernier est mieux adapté au bassin versant de Nsimi par rapport
au modèle GR4J. En calculant les erreurs associées aux
débits observés et simulés avec le GR4J, on se retrouve
avec des erreurs de 80,5% qui sont extrêmement importantes. Le GR2M nous
donne des erreurs de 2,12% sur les débits observés et
simulés.
Nous avons aussi vérifié si ces deux
modèles sont sensibles aux saisons. Pour cela, nous avons
sélectionné sur toute l'ensemble de la série de
données l'année la plus humide, l'année la plus
sèche et celle qui est plus ou moins humide. Nous avons alors fait
tourner les modèles en calant la période humide sur
l'année sur la période sèche et vice versa. L'année
la plus humide de la série est 1999, l'année sèche est
2003 et 2012 l'année semi-humide. Le tableau 5 présente les
résultats de simulation de GR4J en fonction de la saison. Nous
remarquons que ces résultats ne sont toujours pas satisfaisants. Les
coefficients de Nash sont toujours faibles, on peut alors conclure que le
modèle GR4J n'est pas sensible sur le bassin de Nsimi en fonction de la
saison.
Le tableau 6 présente les résultats de
simulation avec GR2M de trois années en fonction de la saison. Nous
remarquons aussi que ces résultats ne sont pas aussi meilleurs que pour
GR4J, du coup on peut conclure que la saison n'a pas d'impact sur la
qualité de simulation.
La validation d'un modèle sur un bassin versant est
jugée meilleure, lorsqu'on atteint des critères
d'efficacité sur le coefficient de Nash de plus de 75%. Avec le GR2M, on
a atteint 62%, ce qui n'est pas très loin de 75%. On peut alors
émettre les hypothèses sur la qualité de simulation :
? 1ère hypothèse : la non
représentativité des données
On peut se poser ici la question de savoir si les hauteurs de
pluies du bassin versant sont représentatives par rapport à la
superficie du bassin. Mais aussi, si on ne possède qu'une seule station
pluviométrique on n'aura pas une meilleure estimation de la pluie
moyenne du bassin versant tout en sachant que la quantité de
précipitations qui tombe n'est pas égale sur toute la superficie
du bassin.
? 2ème hypothèse : les données
manquantes
24
Dans la série des données de précipitions
du bassin de Nsimi, nous avons eu certaines périodes sans valeur de
précipitation et de débit. Il se pourrait que pendant ces
périodes la station connaisse des problèmes par exemple suite
à des forts orages car la partie sud du Cameroun est une région
exposée à des fortes précipitations et des forts moussons.
Dans la série des données météorologiques, nous
avions également des périodes sans données et donc pour le
calcul de l'évapotranspiration, nous avons fait des estimations de
température moyenne, humidité et de rayonnement solaire moyen
[Annexe] pour combler les lacunes dans la série des données.
Nous supposons que ces deux hypothèses peuvent
influencer fortement la qualité de simulation.
Critique des données
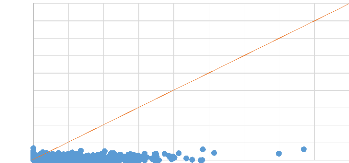
La figure 17 présente la distribution de pluie et de
débits du bassin versant de Nsimi. Comme la figure l'illustre, nous
remarquons une distribution très hétérogène des
pluies aux débits correspondants. Cette distribution confirme la non
représentativité des données que l'on a
évoqué ci-haut. Elle peut avoir plusieurs origines parmi
lesquelles une mauvaise définition des limites du bassin versant, une
sous-estimation ou une surestimation de débits et de pluies. Pour
corriger cela, il faudrait chercher à ramener toutes ces observations
dans le domaine de définition. Il faudra alors recourir à de test
statistique qui devront montrer que cette série de données suit
une loi statistique déterminer ce qui reviendra à forcer la
réalité. Donc faire de la modélisation sur ces genres de
donner signifie faire de la modélisation sur des données
déjà modélisées c'est qui ne reflètera pas
la réalité de la modélisation du bassin.
Plan (Q,P)
0,0 20,0 40,0 60,0 80,0 100,0 120,0 140,0 160,0 180,0
Pluie (mm)
Débit (mm)
180
160
140
120
100
40
20
60
80
0
Figure 17: Distribution des observations
pluie-débit
25
V. CONCLUSION
Comme nous l'avons dit précédemment, la
modélisation hydrologique cherche à représenter de
manière simplifiée le comportement hydrologique et le
fonctionnement d'un bassin versant. Dans notre cas du bassin versant
expérimental de Nsimi, le modèle GR4J nous donne des mauvais
résultats de simulation. En conclusion, le modèle GR4J n'est pas
adapté au bassin versant de Nsimi. Il ne sera donc pas possible
d'appliquer ce modèle dans le domaine par exemple de la gestion et de
l'estimation de la ressource en eau pour ce bassin. Par contre, le
modèle GR2M est plus ou moins adapté au bassin avec 62%
d'efficacité de la simulation. Nous pensons que si ces deux
hypothèses évoquées ci haut étaient
vérifiées, on devrait aller au-delà de 62%. On devrait
aussi comparer nos résultats à d'autres résultats des
études précédentes sur la modélisation hydrologique
du bassin de Nsimi mais hélas!! On a été le premier
à travailler sur ce sujet dans le cas de Travail pratiqué
Encadré de Master 1. Pour les prochaines études sur la
modélisation du bassin de Nsimi, il sera important de procéder
à un contrôle des données en amont pour juger de la
qualité et de la fiabilité des données pour avoir des
conclusions définitives sur l'adaptation du bassin aux modèles
GR4J et GR2M.
26
VI. REFERENCES BIBLIOGRAPHIQUES :
Charles Perrin (2000), Vers une
amélioration d'un modèle global pluie-débit au travers
d'une approche comparative, Thèse de doctorat, p. 351-p.
370
Safouane Mouelhi (2006), vers une chaine
cohérente de modèles pluie-débit conceptuels aux pas de
temps pluriannuel, annuel, mensuel, et journalier, Thèse de
doctorat, p. 31-p. 33
Andre Musy (1998), Hydrologie
appliquée, Ecole Polytechnique de Lausane, 1998,
p.231-Benoit Hingray et al. (2009), Hydrologie
générale
Tarik Benkaci ali & Nourredine Dechemi
(2004), Modélisation pluie-débit journalière
par des modèles conceptuels et boite ; test d'un modèle
neuroflou, Article
27
VI. ANNEXES
Les données mensuelles du bassin de Nsimi
|
Date
|
Pluie (mm)
|
Q
(mm/mois)
|
Radiation
globale
(KW/m2)
|
Température
(°C)
|
Humidité
(%)
|
|
janv-91
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
févr-91
|
119,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
mars-91
|
201,00
|
21,60
|
0,13
|
22,53
|
85,97
|
|
avr-91
|
193,00
|
30,24
|
0,13
|
22,53
|
85,97
|
|
mai-91
|
198,90
|
56,16
|
0,13
|
22,53
|
85,97
|
|
juin-91
|
88,90
|
43,20
|
0,13
|
22,53
|
85,97
|
|
juil-91
|
130,90
|
38,88
|
0,13
|
22,53
|
85,97
|
|
août-91
|
113,30
|
25,92
|
0,13
|
22,53
|
85,97
|
|
sept-91
|
104,10
|
25,92
|
0,13
|
22,53
|
85,97
|
|
oct-91
|
270,30
|
43,20
|
0,13
|
22,53
|
85,97
|
|
nov-91
|
110,60
|
25,92
|
0,13
|
22,53
|
85,97
|
|
déc-91
|
42,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
janv-92
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
févr-92
|
0,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-92
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
avr-92
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
mai-92
|
0,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juin-92
|
0,00
|
30,24
|
0,13
|
22,53
|
85,97
|
|
juil-92
|
0,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
août-92
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
sept-92
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
oct-92
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
nov-92
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
déc-92
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
janv-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
avr-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mai-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
juin-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
juil-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
août-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
sept-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
oct-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
nov-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
déc-93
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
janv-94
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-94
|
0,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-94
|
47,40
|
12,96
|
0,13
|
22,53
|
85,97
|
|
avr-94
|
165,50
|
12,96
|
0,13
|
22,53
|
85,97
|
28
mai-94
|
266,80
|
64,80
|
0,13
|
22,53
|
85,97
|
|
juin-94
|
166,00
|
56,16
|
0,13
|
22,53
|
85,97
|
|
juil-94
|
43,50
|
34,56
|
0,13
|
22,53
|
85,97
|
|
août-94
|
101,50
|
12,96
|
0,13
|
22,53
|
85,97
|
|
sept-94
|
223,30
|
34,56
|
0,13
|
22,53
|
85,97
|
|
oct-94
|
241,30
|
86,40
|
0,13
|
22,53
|
85,97
|
|
nov-94
|
83,70
|
34,56
|
0,13
|
22,53
|
85,97
|
|
déc-94
|
0,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
janv-95
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-95
|
0,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
mars-95
|
57,30
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-95
|
243,70
|
17,28
|
0,13
|
22,53
|
85,97
|
|
mai-95
|
277,90
|
34,56
|
0,13
|
22,53
|
85,97
|
|
juin-95
|
113,50
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juil-95
|
34,40
|
8,64
|
0,13
|
22,53
|
85,97
|
|
août-95
|
274,50
|
30,24
|
0,13
|
22,53
|
85,97
|
|
sept-95
|
202,20
|
30,24
|
0,13
|
22,53
|
85,97
|
|
oct-95
|
182,90
|
60,48
|
0,13
|
22,53
|
85,97
|
|
nov-95
|
89,60
|
34,56
|
0,13
|
22,53
|
85,97
|
|
déc-95
|
22,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
janv-96
|
32,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
févr-96
|
43,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-96
|
252,30
|
21,60
|
0,13
|
22,53
|
85,97
|
|
avr-96
|
170,80
|
21,60
|
0,13
|
22,53
|
85,97
|
|
mai-96
|
109,60
|
21,60
|
0,13
|
22,53
|
85,97
|
|
juin-96
|
134,70
|
25,92
|
0,13
|
22,53
|
85,97
|
|
juil-96
|
158,00
|
56,16
|
0,13
|
22,53
|
85,97
|
|
août-96
|
121,10
|
17,28
|
0,13
|
22,53
|
85,97
|
|
sept-96
|
372,50
|
69,12
|
0,13
|
22,53
|
85,97
|
|
oct-96
|
312,70
|
133,92
|
0,13
|
22,53
|
85,97
|
|
nov-96
|
71,60
|
73,44
|
0,13
|
22,53
|
85,97
|
|
déc-96
|
9,80
|
21,60
|
0,13
|
22,53
|
85,97
|
|
janv-97
|
0,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
févr-97
|
11,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-97
|
136,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-97
|
211,60
|
25,92
|
0,13
|
22,53
|
85,97
|
|
mai-97
|
250,40
|
30,24
|
0,13
|
22,53
|
85,97
|
|
juin-97
|
133,50
|
30,24
|
0,13
|
22,53
|
85,97
|
|
juil-97
|
186,80
|
30,24
|
0,13
|
22,53
|
85,97
|
|
août-97
|
259,40
|
51,84
|
0,13
|
22,53
|
85,97
|
|
sept-97
|
222,80
|
77,76
|
0,13
|
22,53
|
85,97
|
|
oct-97
|
223,00
|
60,48
|
0,13
|
22,53
|
85,97
|
|
nov-97
|
126,30
|
38,88
|
0,13
|
22,53
|
85,97
|
|
déc-97
|
22,20
|
12,96
|
0,13
|
22,53
|
85,97
|
|
janv-98
|
3,00
|
4,32
|
0,13
|
22,53
|
85,97
|
29
févr-98
|
38,40
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-98
|
101,70
|
4,32
|
0,13
|
22,53
|
85,97
|
|
avr-98
|
266,60
|
17,28
|
0,13
|
22,53
|
85,97
|
|
mai-98
|
177,30
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juin-98
|
238,50
|
21,60
|
0,13
|
22,53
|
85,97
|
|
juil-98
|
163,40
|
38,88
|
0,13
|
22,53
|
85,97
|
|
août-98
|
113,00
|
30,24
|
0,13
|
22,53
|
85,97
|
|
sept-98
|
148,70
|
17,28
|
0,13
|
22,53
|
85,97
|
|
oct-98
|
350,20
|
116,64
|
0,13
|
22,53
|
85,97
|
|
nov-98
|
167,00
|
69,12
|
0,13
|
22,53
|
85,97
|
|
déc-98
|
47,60
|
25,92
|
0,13
|
22,53
|
85,97
|
|
janv-99
|
29,70
|
8,64
|
0,13
|
22,53
|
85,97
|
|
févr-99
|
124,90
|
8,64
|
0,13
|
22,53
|
85,97
|
|
mars-99
|
116,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-99
|
275,00
|
21,60
|
0,13
|
22,53
|
85,97
|
|
mai-99
|
233,80
|
30,24
|
0,13
|
22,53
|
85,97
|
|
juin-99
|
141,80
|
0,00
|
0,13
|
22,53
|
85,97
|
|
juil-99
|
157,10
|
0,00
|
0,13
|
22,53
|
85,97
|
|
août-99
|
204,50
|
0,00
|
0,13
|
22,53
|
85,97
|
|
sept-99
|
384,10
|
0,00
|
0,13
|
22,53
|
85,97
|
|
oct-99
|
301,20
|
17,28
|
0,13
|
22,53
|
85,97
|
|
nov-99
|
163,50
|
0,00
|
0,13
|
22,53
|
85,97
|
|
déc-99
|
29,30
|
0,00
|
0,13
|
22,53
|
85,97
|
|
janv-00
|
23,60
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-00
|
65,90
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-00
|
190,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-00
|
141,80
|
34,56
|
0,13
|
22,53
|
85,97
|
|
mai-00
|
230,70
|
56,16
|
0,13
|
22,53
|
85,97
|
|
juin-00
|
220,00
|
51,84
|
0,13
|
22,53
|
85,97
|
|
juil-00
|
57,90
|
25,92
|
0,13
|
22,53
|
85,97
|
|
août-00
|
56,50
|
17,28
|
0,13
|
22,53
|
85,97
|
|
sept-00
|
237,80
|
21,60
|
0,13
|
22,53
|
85,97
|
|
oct-00
|
379,90
|
99,36
|
0,13
|
22,53
|
85,97
|
|
nov-00
|
119,80
|
47,52
|
0,13
|
22,53
|
85,97
|
|
déc-00
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
janv-01
|
2,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
févr-01
|
29,70
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-01
|
154,40
|
12,96
|
0,13
|
22,53
|
85,97
|
|
avr-01
|
127,80
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mai-01
|
209,80
|
12,96
|
0,13
|
22,53
|
85,97
|
|
juin-01
|
98,40
|
8,64
|
0,13
|
22,53
|
85,97
|
|
juil-01
|
19,50
|
4,32
|
0,13
|
22,53
|
85,97
|
|
août-01
|
68,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
sept-01
|
198,50
|
8,64
|
0,13
|
22,53
|
85,97
|
|
oct-01
|
376,10
|
99,36
|
0,13
|
22,53
|
85,97
|
|
nov-01
|
119,60
|
38,88
|
0,13
|
22,53
|
85,97
|
30
déc-01
|
25,10
|
8,64
|
0,13
|
22,53
|
85,97
|
|
janv-02
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-02
|
63,50
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-02
|
207,80
|
25,92
|
0,13
|
22,53
|
85,97
|
|
avr-02
|
235,10
|
21,60
|
0,13
|
22,53
|
85,97
|
|
mai-02
|
114,80
|
30,24
|
0,13
|
22,53
|
85,97
|
|
juin-02
|
137,80
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juil-02
|
116,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
août-02
|
70,50
|
4,32
|
0,13
|
22,53
|
85,97
|
|
sept-02
|
170,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
oct-02
|
307,80
|
51,84
|
0,13
|
22,53
|
85,97
|
|
nov-02
|
119,60
|
73,44
|
0,13
|
22,53
|
85,97
|
|
déc-02
|
25,10
|
17,28
|
0,13
|
22,53
|
85,97
|
|
janv-03
|
4,20
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-03
|
64,20
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-03
|
112,80
|
0,00
|
0,13
|
22,53
|
85,97
|
|
avr-03
|
140,10
|
8,64
|
0,13
|
22,53
|
85,97
|
|
mai-03
|
154,20
|
4,32
|
0,13
|
22,53
|
85,97
|
|
juin-03
|
159,50
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juil-03
|
166,80
|
17,28
|
0,13
|
22,53
|
85,97
|
|
août-03
|
145,20
|
12,96
|
0,13
|
22,53
|
85,97
|
|
sept-03
|
0,00
|
12,96
|
0,13
|
22,53
|
85,97
|
|
oct-03
|
0,00
|
21,60
|
0,13
|
22,53
|
85,97
|
|
nov-03
|
0,00
|
21,60
|
0,13
|
22,53
|
85,97
|
|
déc-03
|
0,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
janv-04
|
80,80
|
8,64
|
0,13
|
22,53
|
85,97
|
|
févr-04
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
mars-04
|
67,90
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-04
|
249,10
|
34,56
|
0,14
|
23,27
|
87,75
|
|
mai-04
|
170,80
|
30,24
|
0,13
|
22,40
|
91,00
|
|
juin-04
|
78,60
|
12,96
|
0,12
|
21,90
|
91,30
|
|
juil-04
|
170,60
|
25,92
|
0,11
|
21,60
|
92,40
|
|
août-04
|
151,20
|
30,24
|
0,11
|
21,60
|
91,80
|
|
sept-04
|
143,00
|
21,60
|
0,13
|
21,60
|
91,20
|
|
oct-04
|
257,90
|
38,88
|
0,13
|
21,60
|
91,60
|
|
nov-04
|
216,10
|
60,48
|
0,14
|
22,60
|
89,10
|
|
déc-04
|
26,20
|
21,60
|
0,13
|
22,90
|
88,10
|
|
janv-05
|
0,80
|
4,32
|
0,14
|
22,20
|
82,10
|
|
févr-05
|
33,00
|
4,32
|
0,13
|
24,30
|
83,80
|
|
mars-05
|
179,40
|
17,28
|
0,14
|
23,60
|
85,80
|
|
avr-05
|
220,50
|
17,28
|
0,14
|
23,50
|
87,00
|
|
mai-05
|
108,70
|
12,96
|
0,14
|
23,00
|
86,90
|
|
juin-05
|
152,10
|
17,28
|
0,10
|
22,40
|
90,30
|
|
juil-05
|
81,70
|
12,96
|
0,09
|
21,80
|
91,20
|
|
août-05
|
40,10
|
4,32
|
0,09
|
21,70
|
88,70
|
|
sept-05
|
205,50
|
12,96
|
0,12
|
22,20
|
89,90
|
31
oct-05
|
356,00
|
56,16
|
0,13
|
21,80
|
90,00
|
|
nov-05
|
76,30
|
17,28
|
0,13
|
22,70
|
88,00
|
|
déc-05
|
23,70
|
8,64
|
0,10
|
22,10
|
89,10
|
|
janv-06
|
32,60
|
0,00
|
0,11
|
23,28
|
85,32
|
|
févr-06
|
101,10
|
4,32
|
0,12
|
23,28
|
84,01
|
|
mars-06
|
65,00
|
0,00
|
0,12
|
23,14
|
84,16
|
|
avr-06
|
198,20
|
8,64
|
0,12
|
22,94
|
85,06
|
|
mai-06
|
252,70
|
21,60
|
0,12
|
22,49
|
90,16
|
|
juin-06
|
199,50
|
25,92
|
0,11
|
22,17
|
90,47
|
|
juil-06
|
70,00
|
8,64
|
0,11
|
22,36
|
89,31
|
|
août-06
|
69,50
|
8,64
|
0,13
|
22,53
|
85,97
|
|
sept-06
|
225,20
|
17,28
|
0,13
|
22,53
|
85,97
|
|
oct-06
|
291,00
|
51,84
|
0,13
|
22,53
|
85,97
|
|
nov-06
|
120,20
|
34,56
|
0,14
|
22,40
|
85,09
|
|
déc-06
|
0,00
|
4,32
|
0,13
|
22,50
|
79,99
|
|
janv-07
|
0,00
|
0,00
|
0,15
|
21,95
|
70,41
|
|
févr-07
|
47,00
|
0,00
|
0,14
|
24,26
|
72,25
|
|
mars-07
|
96,60
|
0,00
|
0,16
|
24,03
|
75,83
|
|
avr-07
|
208,00
|
0,00
|
0,15
|
23,33
|
82,70
|
|
mai-07
|
258,40
|
0,00
|
0,14
|
22,63
|
85,66
|
|
juin-07
|
160,60
|
25,92
|
0,13
|
21,95
|
86,83
|
|
juil-07
|
66,90
|
4,32
|
0,10
|
21,44
|
87,16
|
|
août-07
|
136,90
|
4,32
|
0,11
|
21,54
|
89,13
|
|
sept-07
|
302,10
|
30,24
|
0,14
|
21,96
|
88,53
|
|
oct-07
|
237,90
|
69,12
|
0,13
|
22,53
|
85,97
|
|
nov-07
|
164,30
|
64,80
|
0,13
|
22,51
|
85,95
|
|
déc-07
|
9,40
|
21,60
|
0,14
|
22,38
|
80,62
|
|
janv-08
|
59,60
|
21,60
|
0,13
|
22,52
|
80,66
|
|
févr-08
|
35,80
|
0,00
|
0,16
|
22,95
|
71,33
|
|
mars-08
|
171,10
|
8,64
|
0,15
|
22,63
|
83,41
|
|
avr-08
|
242,80
|
38,88
|
0,13
|
22,53
|
85,97
|
|
mai-08
|
265,20
|
51,84
|
0,13
|
22,53
|
85,97
|
|
juin-08
|
212,10
|
47,52
|
0,13
|
22,53
|
85,97
|
|
juil-08
|
67,10
|
25,92
|
0,13
|
22,53
|
85,97
|
|
août-08
|
190,70
|
21,60
|
0,13
|
22,53
|
85,97
|
|
sept-08
|
228,30
|
30,24
|
0,13
|
22,53
|
85,97
|
|
oct-08
|
185,10
|
25,92
|
0,13
|
22,53
|
85,97
|
|
nov-08
|
96,30
|
25,92
|
0,13
|
22,53
|
85,97
|
|
déc-08
|
64,40
|
12,96
|
0,13
|
22,53
|
85,97
|
|
janv-09
|
8,20
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-09
|
109,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-09
|
26,40
|
0,00
|
0,13
|
22,53
|
85,97
|
|
avr-09
|
213,70
|
8,64
|
0,13
|
22,53
|
85,97
|
|
mai-09
|
300,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juin-09
|
271,80
|
69,12
|
0,13
|
22,53
|
85,97
|
|
juil-09
|
51,26
|
17,28
|
0,13
|
22,53
|
85,97
|
32
août-09
|
218,69
|
25,92
|
0,13
|
22,53
|
85,97
|
|
sept-09
|
136,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
oct-09
|
322,00
|
64,80
|
0,13
|
22,53
|
85,97
|
|
nov-09
|
124,40
|
64,80
|
0,13
|
22,53
|
85,97
|
|
déc-09
|
2,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
janv-10
|
0,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
févr-10
|
63,70
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-10
|
209,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
avr-10
|
176,20
|
8,64
|
0,13
|
22,53
|
85,97
|
|
mai-10
|
241,40
|
25,92
|
0,13
|
22,53
|
85,97
|
|
juin-10
|
98,80
|
12,96
|
0,13
|
22,53
|
85,97
|
|
juil-10
|
93,40
|
21,60
|
0,13
|
22,53
|
85,97
|
|
août-10
|
84,90
|
17,28
|
0,13
|
22,53
|
85,97
|
|
sept-10
|
199,20
|
43,20
|
0,13
|
22,53
|
85,97
|
|
oct-10
|
350,10
|
73,44
|
0,13
|
22,53
|
85,97
|
|
nov-10
|
202,70
|
60,48
|
0,13
|
22,53
|
85,97
|
|
déc-10
|
3,50
|
8,64
|
0,13
|
22,53
|
85,97
|
|
janv-11
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-11
|
91,70
|
12,96
|
0,13
|
22,53
|
85,97
|
|
mars-11
|
121,77
|
8,64
|
0,13
|
22,53
|
85,97
|
|
avr-11
|
74,00
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mai-11
|
80,10
|
21,60
|
0,13
|
22,53
|
85,97
|
|
juin-11
|
164,70
|
17,28
|
0,13
|
22,53
|
85,97
|
|
juil-11
|
110,60
|
25,92
|
0,13
|
22,53
|
85,97
|
|
août-11
|
100,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
sept-11
|
216,80
|
17,28
|
0,13
|
22,53
|
85,97
|
|
oct-11
|
249,50
|
25,92
|
0,13
|
22,53
|
85,97
|
|
nov-11
|
108,80
|
21,60
|
0,13
|
22,53
|
85,97
|
|
déc-11
|
0,00
|
0,00
|
0,13
|
22,53
|
85,97
|
|
janv-12
|
15,20
|
0,00
|
0,13
|
22,53
|
85,97
|
|
févr-12
|
86,80
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-12
|
127,80
|
4,32
|
0,13
|
22,53
|
85,97
|
|
avr-12
|
115,50
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mai-12
|
276,20
|
12,96
|
0,13
|
22,53
|
85,97
|
|
juin-12
|
255,20
|
43,20
|
0,13
|
22,53
|
85,97
|
|
juil-12
|
39,20
|
12,96
|
0,13
|
22,53
|
85,97
|
|
août-12
|
104,00
|
8,64
|
0,13
|
22,53
|
85,97
|
|
sept-12
|
185,70
|
17,28
|
0,13
|
22,53
|
85,97
|
|
oct-12
|
199,60
|
12,96
|
0,13
|
22,53
|
85,97
|
|
nov-12
|
173,80
|
21,60
|
0,13
|
22,53
|
85,97
|
|
déc-12
|
27,50
|
8,64
|
0,13
|
22,53
|
85,97
|
|
janv-13
|
46,40
|
4,32
|
0,13
|
22,53
|
85,97
|
|
févr-13
|
40,90
|
4,32
|
0,13
|
22,53
|
85,97
|
|
mars-13
|
167,90
|
12,96
|
0,13
|
22,53
|
85,97
|
|
avr-13
|
222,00
|
17,28
|
0,13
|
22,53
|
85,97
|
|
mai-13
|
155,60
|
8,64
|
0,13
|
22,53
|
85,97
|
33
juin-13
|
76,70
|
8,64
|
0,13
|
22,53
|
85,97
|
|
juil-13
|
75,50
|
8,64
|
0,13
|
22,53
|
85,97
|
|
août-13
|
48,90
|
4,32
|
0,13
|
22,53
|
85,97
|
|
sept-13
|
100,90
|
8,64
|
0,13
|
22,53
|
85,97
|
|
oct-13
|
294,30
|
43,20
|
0,13
|
22,53
|
85,97
|
|
nov-13
|
193,00
|
38,88
|
0,13
|
22,53
|
85,97
|
|
déc-13
|
47,20
|
21,60
|
0,13
|
22,53
|
85,97
|
|
|
Changeons ce systeme injuste, Soyez votre propre syndic

"L'ignorant affirme, le savant doute, le sage réfléchit"
|



