Chapitre I
Modélisation du
système
de puissance
1.1- Introduction.
Un grand réseau électrique (appelé aussi
système de puissance) se compose d'éléments
(générateurs, transformateurs, lignes,...), plus ou moins
nombreux selon la taille du réseau, interconnectés, formant un
système complexe capable de générer, de transmettre et de
distribuer l'énergie électrique à travers de vastes
étendues géographiques, figure (1). Un modèle
mathématique typique non-réduit d'un "grand" système peut
contenir jusqu'à 15000, voire plus, variables d'état (Farmer,
2006). Ainsi, les systèmes de puissance modernes sont
caractérisés par taille et complexité croissantes. Plus la
dimension d'un système de puissance augmente, plus les processus
dynamiques et l'analyse des phénomènes physiques sous-jacents
sont complexes. Outre leur taille et leur complexité, les
systèmes de puissance présentent un comportement
non-linéaire et variant dans le temps. Les non-linéarités
peuvent être introduites par des éléments à
fonctionnement discontinu tels relais, thyristors, ..., par des
éléments avec hystéré sis ou saturation,... . De
nos jours, cette complexité structurelle impacte de plus en plus
l'évolution des problèmes de stabilité et des
phénomènes dynamiques dans les systèmes de puissance
interconnectés.
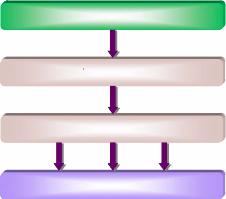
Distri bution
Production
Transport
Charges
Figure 1. Les différents niveaux
d'un système de puissance.
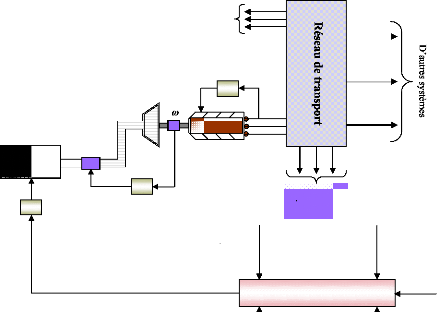
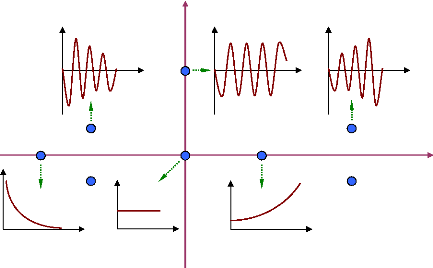
Les grandes composantes d'un système de puissance
peuvent être représentées par un schéma blocs comme
le montre la figure (2), (Sauer et al., 1998). Cette
représentation ne montre pas toutes les interactions dynamiques entre
les éléments et leurs contrôles, mais elle peut servir
à une description générale pour les structures
dynamiques.
L'étude de la performance dynamique d'un système
de puissance est très importante pour les opérateurs du
système (point de vue économique) et la société en
général (point de vue de fiabilité). Une étape
essentielle dans ce type d'étude est de comprendre physiquement et
mathématiquement les phénomènes dynamiques
d'intérêt. Ensuite, la modélisation et la simulation
effectuées du système peuvent refléter son comportement
critique.
Source
d'énergie
Contrôle de
la source
d'énergie
Signaux de contrôle de la
puissance de
génération désirée
Système de la
force motrice
Régulateur
de fréquence
D'autres
générateurs
Générateur
Régulateur
de tension
Puissance de
génération
Système de contrôle central
V
Charges
Puissance
transmise
Fréquence du
système
Fréquence de
référence
du
système
|
Programmation de puissance de transmission
|
Figure 2. Structure générale
d'un système de puissance. 1.2- Les
phénomènes dynamiques.
Dans un système de puissance une grande
variété de phénomènes dynamiques différents
est susceptible de se produire. Ces phénomènes dynamiques ont des
caractéristiques et des origines physiques diverses et se produisent
dans des gammes de temps différentes.
Un phénomène dynamique est
généralement initié par une perturbation, une action d'un
contrôleur, une manoeuvre de protection,... .
Selon le niveau de la perturbation d'origine, nous pouvons
distinguer deux classes de phénomènes dynamiques :
- les "petites" perturbations. Il s'agit de fluctuations
normales, de faible amplitude, des grandeurs électriques ou
mécaniques ; (par exemple, variation continue de charge). Ces
phénomènes se manifestent habituellement dans le système
par de faibles oscillations transitoires souvent peu amorties.
- les "grandes" perturbations. Ce type de perturbation
correspond, par exemple, à un court-circuit sur une ligne de
transmission, à la perte d'un générateur,... . Elles
exciteront par contre des oscillations importantes.
Afin de mieux comprendre les mécanismes
d'instabilité des systèmes de puissance, les divers
phénomènes dynamiques doivent être définis et
classés. Si l'on tient compte de leurs
caractères physiques ainsi que de leurs plages de
réponse temporelles, les phénomènes dynamiques sont
habituellement divisés en quatre groupes (Machowski et al.,
1998).
1.2.1- Les phénomènes de
propagation.
Ils se produisent dans les lignes de transmission haute
tension de grande longueur et correspondent à la propagation des ondes
électromagnétiques provoquées par des coups de foudre ou
des opérations de coupure/fermetures. La gamme de temps de la dynamique
de ces phénomènes va de la microseconde à la milliseconde.
Ils possèdent les dynamiques les plus rapides.
1.2.2- Les phénomènes
électromagnétiques.
Ils ont lieu principalement dans les enroulements des
générateurs et des moteurs (enroulements armatures et
amortisseurs) et dans les dispositifs électroniques de puissance. Ils
découlent d'une perturbation (tel un court-circuit), d'une
opération d'un système de protection, d'une commutation
(thyristors, ...), ou d'une interaction entre les machines électriques
et le réseau.
Ces phénomènes génèrent des
courants et des couples élevés à l'intérieur des
générateurs, sur une échelle de temps typique de plusieurs
millisecondes. Au-delà de ce laps de temps, les inerties de la turbine
et du générateur sont suffisantes pour empêcher toute
variation importante de vitesse de rotor.
1.2.3- Les phénomènes
électromécaniques.
Les phénomènes électromécaniques
impliquent principalement les champs de rotors, les enroulements amortisseurs
et les inerties des rotors. Ils sont principalement dus aux mouvements des
masses tournantes des générateurs et des moteurs. Ils se
produisent à la suite d'une perturbation, d'une opération de
commande sur le système de contrôle de tension ou sur le
contrôle de la turbine. La gamme de temps de ces phénomènes
s'étend environ d'une seconde à plusieurs secondes. Cette
échelle de temps est considérée suffisamment grande pour
que les phénomènes soient influencés par la turbine et les
systèmes de commande de générateur. Dans cette gamme de
temps, les variations de vitesse de rotor couplées aux variations
électromagnétiques produisent alors des effets
électromécaniques.
1.2.4- Les phénomènes
thermodynamiques.
Les phénomènes thermodynamiques se
développent dans les chaudières des centrales thermiques lors de
la demande de commande automatique de génération, mise en
application suite à une perturbation d'équilibre entre la
production et la consommation de puissance. Ils s'étendent de quelques
dizaines de secondes à quelques dizaines de minutes : ils
présentent ainsi les dynamiques les plus lentes.
La figure (3) montre la classification des
phénomènes dynamiques expliquée ci-dessus.
Une "bonne" compréhension physique et
mathématique du système et des phénomènes
associés permet de mieux comprendre la modélisation et la
simulation du système à refléter les comportements
critiques de ce dernier. Le paragraphe suivant définit le modèle
mathématique utilisé et ses éléments.
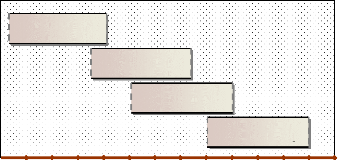
Dynamiques de
propagation
Dynamiques
électromagnétiques
électromécaniques
Dynamiques
Dynamiques
thermodynamique
s
microsecondes millisecondes secondes minutes
Figure 3. Caractéristiques des
phénomènes dynamiques rencontrés
dans les
systèmes de puissance.
1.3- Le modèle général
non-linéaire.
1.3.1- Introduction.
La première étape, lorsqu'on veut analyser et
commander un système électrique de puissance, consiste à
trouver un "bon" modèle mathématique. Généralement,
un modèle, dans l'analyse des systèmes, est un ensemble
d'équations ou de relations, qui décrit convenablement les
interactions entre les différentes variables étudiées,
dans la gamme de temps considérée et avec la précision
désirée, pour un élément ou un système. Par
conséquent selon le but de l'analyse, un élément ou un
même système physique, peut donner lieu à des
modèles différents.
Dans de nombreux cas, le choix du modèle correct est
souvent la partie la plus difficile de l'étude. Le point essentiel est
de trouver le "bon modèle" qui réalise un compromis entre la
fidélité du comportement qualitatif et quantitatif et la
simplicité de mise en oeuvre à des fins d'analyse et de
synthèse. Les modèles complexes ont généralement
besoin d'un nombre plus important de paramètres. En outre, l'obtention
de valeurs fiables pour ces paramètres exige un travail important. Enfin
si des méthodes trop complexes sont utilisées, l'analyse et les
calculs sont inutilement "volumineux" et l'interprétation du
résultat exige également un travail très important
(Andersson, 2006).
Généralement, pour établir un
modèle de réseau électrique pour les études
dynamiques, on tient compte uniquement des équipements en
activité pendant la plage temporelle du phénomène
dynamique considéré. Le résultat est donc le modèle
de connaissance complet du système : il se compose d'équations
différentielles ordinaires non-linéaires et d'équations
algébriques (Kundur, 1994).
Les modèles présentés dans ce chapitre
concernent les éléments suivants :
- les unités de production : générateurs
électriques, systèmes d'excitation, turbines et systèmes
de contrôle associés.
- les transformateurs et les lignes de transmission du
réseau de transport.
- les charges enfin pour la partie consommation.
1.3.2- Les éléments du
modèle.
1.3.2.1- Modèle du
générateur.
L'énergie électrique est
généralement produite par les machines synchrones. Ces
dernières sont caractérisées par une vitesse de rotation
de l'arbre de sortie de chaque machine égale à la vitesse de
rotation du champ tournant. Pour obtenir un tel fonctionnement, un couple
mécanique issu d'une énergie primaire source, comme
l'énergie hydraulique, l'énergie nucléaire ou
l'énergie chimique, est appliqué à l'axe de la machine
synchrone via un lien mécanique intermédiaire, à savoir la
turbine. Le champ magnétique rotorique est généré
habituellement par un circuit d'excitation alimenté par courant continu.
La position du champ magnétique rotorique est alors fixe par rapport au
rotor : ceci impose en fonctionnement normal une vitesse de rotation identique
entre le rotor et le champ tournant statorique. Ainsi, les enroulements du
stator sont soumis à des champs magnétiques qui varient
périodiquement. Une f. é.m. de courant alternatif est
donc induite dans le stator.
Les générateurs synchrones participent de
façon extrêmement importante aux phénomènes
dynamiques et à la qualité globale de l'alimentation en
énergie. Il est donc nécessaire de développer des
modèles pratiques et réalistes des machines synchrones. Dans ce
chapitre, nous présenterons et discuterons un modèle
adapté à l'analyse de la stabilité dynamique.
1.3.2.1.1- Modèle de la machine synchrone dans
le repère de Park.
Dans la machine idéale, le stator est muni de trois
enroulements repérés a, b et c,
décalés de 120 degrés. Le rotor comporte un certain nombre
d'enroulements, répartis sur deux axes: l'axe-d, (axe
direct) qui coïncide avec celui de l'enroulement d'excitation et
l'axe-q (axe quadratique) situé en quadrature avance
par rapport à l'axe direct (Custem, 2002, II).
Pour supprimer la non-linéarité entre les
grandeurs du stator et celles du rotor, les enroulements de la machine doivent
être ordonnés selon deux axes perpendiculaires, chaque machine est
modélisée dans sa référence locale (d-q)
tournant avec son rotor (Andersson, 2006). Pour formaliser le couplage entre
les équations du système et établir les équations
décrivant le comportement du système global, toutes les tensions
et tous les courants doivent être représentés dans une
seule référence commune à toutes les machines.
Généralement, une référence tournant à la
vitesse synchrone sert de référence commune. Une telle approche
peut être réalisée par la transformation de Park. Le
développement de cette transformation est donnée à
l'annexe A.
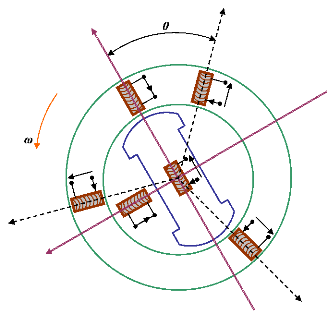
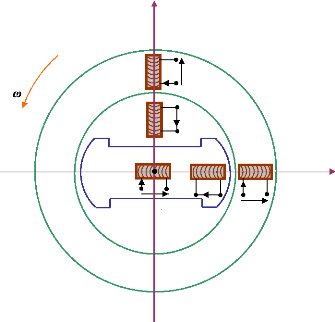
La figure (4) montre schématiquement les enroulements
et les sens des courants dans une machine synchrone. La figure (5) donne le
modèle équivalent dans le repère de Park (d-q).
Les différents enroulements dans les deux représentations sont
les suivants :
- Les trois enroulements statoriques notés a,
b et c, et leurs enroulements équivalents notés
d5 et q5.
- L'axe direct comporte l'enroulement d'excitation noté
f, et un enroulement amortisseur noté
da.
- L'axe en quadrature comporte un enroulement amortisseur
noté qa.
Notons enfin que l'enroulement d'excitation est soumis à
une tension Vf tandis que les circuits da, qa sont
court-circuités en permanence.
d
iD a
D
ia va
vb
ib
Q
f
vf
if
c
b
vc
iQ
ic
q
c
b
a
Figure 4. Modélisation de la machine
synchrone idéalisée.
q
if
qh iqh vqh
qa iqa
f
vf
da
ida
idh
vdh
dh
d
Figure 5. Modèle de la machine
synchrone dans le repère de Park.
1.3.2.1.2- Les hypothèses du
modèle.
Le modèle du générateur et de ses
contrôles se limite habituellement aux équations
différentielles ordinaires couplées entre elles via les
équations algébriques du réseau de transport. Chaque
équation différentielle exprime la dérivée d'une
variable d'état (tels l'angle de rotor, la tension d'excitation, ...) en
fonction d'autres variables d'état et variables algébriques. Le
nombre d'équations différentielles décrivant le
modèle du générateur définit l'ordre du
modèle. Il existe plusieurs modèles, allant du plus simple, le
modèle classique représentant seulement les
caractéristiques électromécaniques du
générateur, au plus complexe, à savoir le modèle du
huitième ordre tenant compte de tous les circuits de rotor, de stator,
d'amortissement et de champ de saturation (Anderson et al., 2003).
Dans les études des oscillations électromécaniques, le
modèle du générateur doit représenter deux
caractéristiques fondamentales : les caractéristiques
électriques des enroulements d'excitation et les caractéristiques
mécaniques de l'arbre du générateur.
Les hypothèses considérées pour
établir ce modèle sont basées en négligeant
l'influence : - des résistances rotoriques et statoriques.
- des enroulements amortisseurs.
- du champ de saturation.
- des phénomènes transitoires dans le stator.
- de la variation de vitesse dans les équations de
tensions du stator (ainsi, ùr =
ùo = 1 [p.u]), (cette supposition est faite pour
compenser l'effet de l'annulation des phénomènes transitoires
dans le stator).
Ce modèle néglige également
l'amortissement produit par les courants de Foucault dans le corps du rotor (on
suppose que la f. é.m. transitoire suivante l'axe d,
à savoir E'd, est constante). Ainsi, comme il n'y a aucun
enroulement sur l'axe en quadrature pour représenter le corps du rotor,
nous aurons:
Ed ' = , X q = X q
0 '
E'd : f.é.m. du générateur
induite suivante l'axe d, en p.u. X'q :
réactance synchrone d'axe q, en p.u.
Xq : réactance transitoire d'axe
q, en p.u.
Enfin, nous supposerons que l'angle de rotor ä
(position angulaire du rotor par rapport à la référence
tournante au synchronisme) coïncide avec l'angle de la tension interne du
générateur.
Le modèle résultant est le modèle du
troisième ordre. Il est décrit par les variables d'état
suivants (Anderson et al., 2003) :
E'q : f.é.m. du
générateur induite suivante l'axe q, en p.u.
ù : vitesse angulaire du rotor, en p.u.
ä : angle de rotor, en rad.
Ce modèle, bien adapté à l'étude
de la stabilité dynamique, est le plus simple. Il est largement
utilisé dans l'analyse des valeurs propres et le réglage des
paramètres des stabilisateurs de puissance (Sauer et al.,
1998).
1.3.2.1.3- Equations
électriques.
Considérons une ième machine
d'un réseau multimachines, nous allons déterminer dans de ce
paragraphe les équations algébriques du stator de cette machine :
à savoir les équations concernant les tensions suivant les axes
d et q et les puissances électriques.
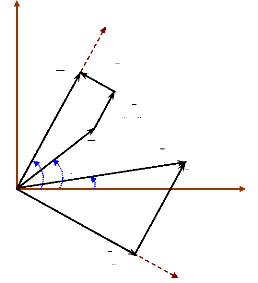
Les grandeurs électriques de cette machine sont
représentées sur la figure (6). Avant de débuter le
calcul, nous pouvons faire les remarques suivantes :
- le repère (di, qi) concerne la
ième machine seule, alors que le repère
(D, Q) est commun à toutes les machines du
système.
- l'angle de couple äi, vu entre D et
qi, représente la position du repère (d,q) de
la ième machine par rapport au repère commun
(D,Q) : il varie constamment dans le temps et peut être positif
ou négatif (Yu, 1983).
Q
qi
Eqi jXqiIqi
'
jXdi Idi
Ii
Iqi
Idi
di
äi
Vi
ái
èi
D
Figure 6. Phaseurs relatifs à la
ième machine d'un système multimachines.
D'après la figure (6), la tension terminale
Vi de la ième machine du
système peut se déterminer par l'équation suivante :
Vi = E ' qi - jX '
di Idi - jXqiIqi (1)
Notons, dans le repère commun (D-Q), les
expressions suivantes :
E ' qi= E ' qi e
ä
j i
|
Iqi I qi e ä
= , ( - 90 ° )
j i I di I di e
ä
= j i
|
(2)
|
Vi i Ve j á i
=
En introduisant les relations (2) dans la relation (1), nous
obtenons :
j á ä ä ä
i i i i
' ( 90 )
j j + °
V e E e X I e jX I e
= - -
j (3)
i qi di di qi qi
Qui devient après arrangement :
V e i i = E - X I - jX I
- ( ä - á ) '
j (4)
i qi di di qi qi
V jV E X I jX I (5)
i i i i i i qi di di qi qi
- - - = - -
'
cos( ä á ) sin( ä á
)
En séparant partie réelle et partie imaginaire,
nous obtenons les expressions de Vd et Vq
suivantes :
ç ??
V X I
di qi qi
=
Vqi
' ' (6)
E X I
qi di di
-
En considérant les relations (2) et la relation suivante :
Ii = Idi + Iqi,
l'équation (1) peut être donc réécrite comme suit
:
|
V E e jX I jX e jX I e
' ä - ' + ' ä - ä
j i i i
j j
i qi
= di i di qi qi
|
(7)
|
Pour n machines d'un système multimachines,
l'équation (7) peut s'écrire sous la forme matricielle suivante
:
[ ] [ ][ ] [ ] [ ] [ ][ ][ ]
V E e j X I j X X I e
= - + -
' ' '
j ä j ä (8)
q d d q q
Dans cette dernière équation, les termes
[V] , [ ' ]
Eq , [I] et [Iq
] sont des vecteurs colonnes
de dimension n et les coefficients [
jä ]
e, [ ' ]
X d et [ ' ]
X d - X q sont des matrices
diagonales.
Les puissances électriques (apparente, active et
réactive) de la ième machine sont
données par :

)
S P jQ V I V j V I jI
*
i ei ei i i di qi di qi
= + = = + -
( ) (
(V di
- V di Iqi )
I V I j V I
di qi qi qi di
+ +
) (
? ??
??
Pei
Qei
V di
I V I
di qi qi
+
V qi I di - V di I qi (9)
Etant donné que les phénomènes transitoires
dans le stator sont négligés, le couple électrique est
dons égal à la puissance électrique active en per-unit.
Ainsi Tei = Pei.
1.3.2.1.4- Equations
mécaniques.
Les propriétés mécaniques des machines
synchrones se modélisent généralement à l'aide de
l'équation du mouvement basée sur le théorème du
moment cinétique (Andersson, 2006). Cette équation
présente une importance fondamentale dans l'étude des
oscillations électromécaniques, car ces oscillations
représentent un phénomène important dans la plupart des
systèmes de puissance, en particulier ceux qui contiennent de lignes de
transmission longues (Andersson, 2006). Dans le fonctionnement à
l'état d'équilibre, toutes les machines synchrones du
système tournent à la même vitesse angulaire
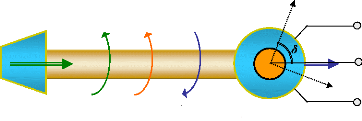
électrique. Le couple mécanique
Tm est de même sens que le sens de
la rotation de l'axe du générateur. Le couple électrique
Te est de sens opposé à la rotation et ce
couple équilibre le couple mécanique (Basler et al.,
2005), figure (7). Lors d'une perturbation, un ou plusieurs
générateurs peuvent être accélérés ou
ralentis et il y a donc risque de perdre le synchronisme. Ceci peut avoir
impact important sur la stabilité du système et les
générateurs perdant le synchronisme doivent être
débranchés, sinon ils pourraient être
sévèrement endommagés.
Turbine
Rotor
Te
Tm ù
Pm
q
Pe d
Générateur
Figure 7. Couples mécanique et
électrique agissant sur l'axe d'un générateur.
Pour un système multimachines, s'il y a un
déséquilibre des couples agissants sur le rotor de la
ième machine, cette dernière va
accélérer ou ralentir selon l'équation du mouvement
suivante :
Äù& =
i T T
2 H i
1
( )
mi ei
- (10)
Avec Hi constante d'inertie (en secondes)
représentant l'inertie totale de toutes les masses tournantes
connectées à l'arbre du générateur.
Pour des oscillations à faibles fréquences, le
courant induit dans les enroulements amortisseurs est négligeable. Par
conséquent les enroulements amortisseurs peuvent être
complètement négligés dans la modélisation du
système. Si les enroulements amortisseurs sont ignorés, le couple
d'amortissement produit par ces enroulements amortisseurs est donc
également négligeable. Pour tenir compte de la composante du
couple négligée, on introduit dans l'équation du mouvement
un terme de compensation D (nommé aussi coefficient
d'amortissement) en p.u, (Sauer et al., 1998). Ce coefficient
représente l'amortissement naturel du système : il empêche
l'accroissement des oscillations, à moins qu'une source d'amortissement
négatif soit introduite (tel le régulateur de tension du
système d'excitation). L'équation du mouvement peut être
donc réécrite comme suit :
|
ù& H ù
i T T D
1 ? ? Ä
Ä = ( (
mi ei i i
2 i
|
-1)) (11)
|
L'équation de l'angle de rotor de la
ième machine est donné par :
ä& i = ù o
(Äù i -1) (12)
Avec :
Äùi : déviation de la vitesse
angulaire du rotor de la ième machine, en p.u.
ùo : vitesse de synchronisme (vitesse de base), en
rad/s.
(ùo = 2ðf , f :
fréquence nominale, en Hz).
Tmi : couple mécanique fourni par la turbine, en
p.u.
Tei : couple électromagnétique
associée à la puissance électrique Pei
produite du
|
générateur, (
|
T ei
|
P
= ), en p.u.
ei
ù i
|
Di : coefficient d'amortissement du
générateur, en p.u. ä : angle de rotor, en rad.
1.3.2.1.5- Régulation du
générateur.
Les machines synchrones du système doivent être
capable de maintenir l'équilibre des puissances actives et des
puissances réactives dans des conditions de fonctionnement diverses.
Ainsi, des tensions sinusoïdales équilibrées sont garanties
avec des amplitudes et des fréquences constantes.
Si l'équilibre des puissances actives n'est plus
assuré, la fréquence de synchronisme dans le système sera
changée, alors qu'un déséquilibre des puissances
réactives entraînera une variation des tensions du système
par rapport à leurs valeurs de référence (Andersson,
2006).
Pour assurer une génération satisfaisante
d'énergie électrique, pour un grand nombre de points de
fonctionnement, le couple mécanique Tm
appliqué au rotor et la tension d'excitation Efd doivent
être réglés systématiquement pour s'accommoder de
toute variation du système.
Le système responsable de la génération
du couple mécanique et ainsi de l'entraînement du rotor du
générateur est appelé "système de force motrice".
Le contrôle de la fréquence (ou contrôle de la puissance
active) associé à ce système maintient la vitesse nominale
des générateurs en assurant de ce fait une fréquence
constante. Par ailleurs, le système d'excitation est responsable de la
tension d'excitation fournie au générateur. Le régulateur
de tension (ou régulateur de la puissance réactive)
associé modifie les valeurs du système d'excitation pour enfin
obtenir les tensions désirées aux bornes du
générateur (Anderson et al., 2003).
Nous présentons par la suite successivement les principes
généraux :
- de la génération de la puissance mécanique
avec la régulation de fréquence
- du système d'excitation avec la régulation de
tension et leurs modèles mathématiques.
1.3.2.1.5.1- Régulateur de fréquence et
modèle de la turbine.
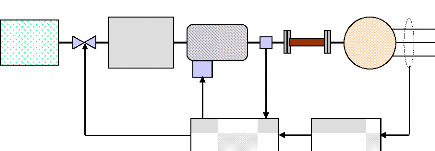
Un système de force motrice, figure (8), se compose de
la source d'énergie primaire, de la turbine (équipé d'un
servomoteur) et du régulateur de fréquence (gouverneur) (Farmer,
2006).
La turbine transforme l'énergie potentielle de la
source en énergie de rotation de l'arbre (rotor) sur lequel est
placé l'alternateur. L'alternateur convertit la puissance
mécanique fournie par la turbine en puissance électrique de
sortie. La vitesse de l'arbre de la turbine est mesurée
précisément et comparée à la vitesse de
référence. Le régulateur de fréquence (vitesse)
agit ensuite sur le servomoteur pour ouvrir et fermer les vannes de
contrôle et modifier par conséquent la vitesse du
générateur. Ainsi, le rôle de la turbine est
d'entraîner le rotor du générateur à la vitesse
synchrone correspondant à la fréquence du système de
puissance.
Source de
l'énergie
primaire
Valve de
contrôle
Conversion
de l'énergie
Turbine
Régulateur de
fréquence
Servo -
moteur
Capteur de
vitesse
Arbre de
transmission
Référence de
puissance
Générateur
Réseau de
transport, 3Ö
Figure 8. Structure générale
d'un système de force motrice - générateur.
Les turbines à vapeur utilisées dans les
centrales thermiques (charbon, gaz, pétrole, nucléaire) sont
constituées d'un certain nombre de roues, successivement fixes et
mobiles, portant des ailettes le long desquelles la vapeur se déplace.
Au fur et à mesure que la vapeur progresse axialement dans la turbine,
sa pression diminue et la taille des ailettes augmente. Ces différentes
roues sont généralement groupées en plusieurs
étages, particulièrement dans les centrales de grande puissance.
La division de la turbine en étages permet de resurchauffer la vapeur
entre les étages en assurant, par conséquent, un meilleur
rendement au cycle thermique (Custem, 2002, I).
Le gouverneur forme une boucle de retour qui surveille la
vitesse du rotor à chaque instant. Considérons par exemple une
perturbation de l'équilibre des puissances actives. Dans les toutes
premières secondes, l'énergie correspondante va être
prélevée sur l'énergie cinétique des masses
tournantes des unités de production. Ceci va entraîner une
perturbation de la vitesse de rotation de ces unités. Cet écart
de vitesse doit être détecté et corrigé
automatiquement par les gouverneurs. Ces gouverneurs doivent changer
l'admission de fluide (vapeur, gaz ou eau) dans les turbines de manière
à ramener les vitesses et donc la fréquence du réseau,
autour de leurs valeurs nominales.
Dans tout système de puissance, il très
important de maintenir la fréquence dans une plage étroite autour
de sa valeur nominale (50 ou 60 Hz). Le respect strict de cette valeur est non
seulement nécessaire au fonctionnement correct des charges mais il est
également l'indicateur d'équilibre entre puissances actives
produites et consommées (Custem, 2002, I).
Dans l'analyse de la stabilité transitoire ou
dynamique, la réponse temporelle du système de la force motrice
à une perturbation est considérée comme plus lente que la
plage d'étude de la stabilité concernée (typiquement entre
10 et 20 secondes). Ainsi, le modèle du système de la force
motrice peut être extrêmement simplifié. Pour une analyse de
stabilité transitoire d'une durée de quelques secondes, le
modèle du système de la force motrice peut être
supprimé en considérant que le couple mécanique de la
turbine reste constant (Farmer, 2006). Sa faible influence sur le comportement
des oscillations électromécaniques associées à la
stabilité aux petites perturbations peut aussi être
négligée. Ainsi, il n'est pas utilisé lors de
l'établissement du modèle linéaire du système de
puissance associé à ce type de stabilité.
Dans quelques cas, le modèle peut être
employé pour calculer les fréquences naturelles de torsion du
système de rotor. Il peut être également employé
dans la simulation dynamique du
système de puissance pour obtenir des informations sur les
couples de rotor se produisant lors d'un défaut (Machowski et
al., 1998).
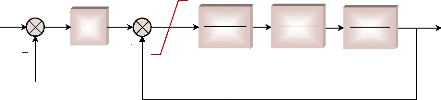
Le modèle de l'ensemble turbine à vapeur/gouverneur
utilisé en simulation dynamique du modèle non-linéaire est
représenté par la figure (9), (Milano, 2005).
T max
Tm
1
ùréf
1 +
KR
sT 4
1 3
+sT
+
1+
+
sT5
1+s TC
1+ sTS
ù
Tmin
Régulateur
Servomoteur
Réchauffeur
Figure 9. Modèle de la turbine et du
gouverneur. 1.3.2.1.5.2- Régulateur de tension et modèle
du système d'excitation.
Le système d'excitation est un système
auxiliaire qui alimente les enroulements d'excitation de la machine synchrone
afin que cette dernière puisse fournir le niveau de puissance
demandé. En régime permanent, ce système fournit une
tension et un courant continu mais il doit être capable également
de faire varier rapidement la tension d'excitation en cas de perturbation sur
le réseau (Custem, 2002, I).
Actuellement, des systèmes d'excitation variés sont
employés. Trois principaux types peuvent être identifiés
(IEEE, 2005) :
a)- Les systèmes d'excitation à courant
continu -CC- :
Ils utilisent une génératrice à courant
continu avec collecteur comme source de puissance du système
d'excitation.
b)- Les systèmes d'excitation à courant
alternatif -CA- :
Ils utilisent un alternateur et des redresseurs statiques ou
tournants pour produire le courant continu nécessaire dans l'enroulement
d'excitation de la machine synchrone.
c)- Les systèmes d'excitation statiques
(systèmes ST) :
Dans ce cas, le courant d'excitation est fourni par un
redresseur commandé. Sa puissance est fournie soit directement par le
générateur à travers un transformateur donnant le niveau
approprié de tension, soit par des enroulements auxiliaires
montés dans le générateur.
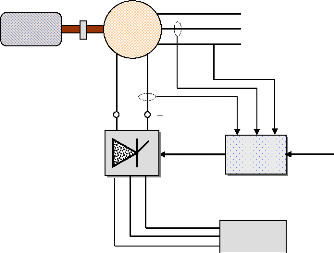
Les systèmes d'excitation sont équipés de
contrôleurs, appelés habituellement régulateurs de tension
(Automatic Voltage Regulator : AVR), figure (10). Ces derniers sont très
importants pour l'équilibre de la puissance réactive qui sera
fournie ou absorbée selon les besoins des charges. En outre ces
contrôleurs représentent un moyen très important pour
assurer la stabilité transitoire du système de puissance. Le
régulateur de tension agit sur le courant d'excitation de l'alternateur
pour régler le flux magnétique dans la machine et "ramener" la
tension de sortie de la machine aux valeurs souhaitées. Une
caractéristique très importante d'un régulateur de tension
est sa capacité à faire varier rapidement la tension
d'excitation.
Vt
It
If
+
Système
d'excitation
statique
Vf
Vref
AVR
Turbin
Générateur
Source
auxiliaire
Figure 10. Structure générale
d'un système d'excitation statique avec son AVR.
Le groupe IEEE task forces présente
périodiquement des recommandations pour la modélisation des
éléments d'un système de puissance dont les
systèmes d'excitation. Plusieurs modèles sont
suggérés pour chaque type de système d'excitation (IEEE,
2005). Les systèmes d'excitation statiques étant les plus
installés actuellement, nous avons donc choisi dans notre étude
d'utiliser le modèle du système IEEE-ST1A, modèle le plus
utilisé dans la littérature. Ce type de système
d'excitation se caractérise par sa rapidité et sa
sensibilité (IEEE, 2003) :
- sa constante de temps Ta est faible,
normalement de l'ordre de quelques millisecondes - son gain
Ka est élevé, généralement
entre 200 et 400 per-unit.
La figure suivante montre le modèle du système
d'excitation et de son régulateur de tension utilisé dans notre
étude.
Vt
Efd _ max
Vréf
+
+

K a
1+sT a
Efd
Efd _ min
VS
Figure 11. Modèle simplifié
du système d'excitation IEEE-type ST1A.
La grandeur Vref, est la consigne de
tension déterminée pour satisfaire les conditions de
l'état équilibré. Le régulateur de tension compare
le signal Vt (un signal continu proportionnel à la valeur
efficace de la tension alternative du générateur) à la
tension de consigne Vref .Un signal complémentaire
VS peut être ajouté au noeud de comparaison : il s'agit
d'un signal issu de certains dispositifs spécifiques de commande comme
les stabilisateurs de puissance (PSS). Ensuite, le signal d'erreur est
amplifié pour donner la tension d'excitation demandée
Efd. La constante de temps et le gain de l'amplificateur sont
respectivement Ta et Ka. Les valeurs
extrémales de la tension d'excitation (Efd _max,
Efd_min) sont fixées par un système de limitation.
E & = - + -
( ( ) )
K V V V E (13)
fd a réf t S fd
T a
La relation suivante décrit, tous calculs faits, le
fonctionnement du modèle : 1
La relation entre la tension d'excitation Efd
et la tension interne du générateur
E'q est donnée comme suit :
|
1
E & ' = ( ( ) )
E X X I E
- - ' - '
q fd d d d q
T ' do
|
(14)
|
1.3.2.2- Réseau de transport.
Le réseau de transport relie toutes les centrales
électriques dans un système de puissance et distribue la
puissance aux différents consommateurs. Les éléments
principaux du réseau sont les lignes aériennes à haute
tension, les câbles souterrains, les transformateurs et les jeux de
barres. Des éléments auxiliaires peuvent être
trouvés : des condensateurs en série, des réactances
shunts et des systèmes compensation, des systèmes de
protection..., (Machowski et al., 1998).
Pour la modélisation de notre système de
puissance, nous nous intéressons à établir le
modèle de transformateurs et le modèle de lignes de
transmission.
1. 3. 2. 2. 1- Modèle de
transformateurs.
Le transformateur permet d'élever l'amplitude de la
tension alternative disponible à la sortie de l'unité de
production pour l'amener aux niveaux requis pour le transport. A l'autre
extrémité de la chaîne, côté consommateurs,
les transformateurs sont utilisés pour abaisser la tension et la ramener
aux valeurs utilisées dans les réseaux de distribution -BT-.
Outre la transmission de l'énergie électrique
avec modification des tensions, les transformateurs peuvent être
utilisés pour contrôler les tensions de noeuds des réseaux
(Custem, 2002, I). Ce contrôle de tension utilise la variation du nombre
de spire des transformateurs. La figure (12) montre le schéma
équivalent du transformateur (sans circuit magnétique) : il est
doté de plusieurs prises (côté haute tension) permettant de
modifier le nombre de spires du primaire. L'impédance ZT
correspond à l'impédance équivalente totale vue du
primaire.
Dans certains transformateurs, la modification de spires
requiert de mettre l'appareil hors service et de changer manuellement les
connexions. Plus généralement, cette modification peut être
effectuée en charge c.-à-d. sans interrompre le courant qui
parcourt l'enroulement dont on modifie le nombre de spires. Le dispositif
correspondant, appelé régleur en charge, comporte un
contacteur conçu pour éviter la formation d'arcs
électriques (susceptibles d'endommager les contacts) et un moteur
électrique pour entraîner ce contacteur.
V1 ZT N1 N2 V2
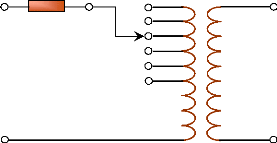
Figure 12. Modèle simplifié
de transformateur.
Si N1 est le nombre de spires côté haute
tension et N2 est le nombre de spires côté basse tension,
le rapport de transformation M est défini par :
N
M = (15)
1
N 2
La relation entre la tension du côté primaire
V1 et la tension du côté secondaire V2 à
vide
est :
V V 1
2 = (16)
M
Si la tension du primaire diminue, la tension du secondaire
peut être maintenue constante en diminuant le rapport M,
c.-à-d. en effectuant un changement de prise du côté
primaire. En charge, l'équation (15) n'est plus applicable à
cause de l'impédance ramenée au primaire du transformateur
ZT, mais le principe de fonctionnement reste le même (Andersson,
2006).
La figure (13) représente le schéma
équivalent en ð du transformateur sans circuit
magnétique (Milano, 2005). Dans notre étude, les régleurs
en charge ne sont pas modélisés : ainsi le rapport de
transformation reste fixe pendant les simulations dynamiques. Toutefois, nous
en tenons compte lors du calcul d'écoulement de puissance, de
manière à ce que les tensions restent dans leurs limites
autorisées et que la convergence de l'algorithme de l'écoulement
de puissance reste assurée (Tolba, 2005).
1. 3. 2. 2. 2- Modèle des lignes de
transmission.
Les réseaux de transport assurent la liaison entre les
centres de production et les zones de consommation. Ils permettent aussi
d'échanger de la puissance à travers les lignes d'interconnexion,
entre pays ou grandes zones relevant de gestionnaires de réseaux
différents (Bornard et al., 2005).
Les modèles des lignes de transmission utilisés
dans l'analyse dynamique des réseaux électriques sont
habituellement classés en trois groupes, en fonction des longueurs des
lignes, (longues, moyennes, courtes) (Sauer et al., 1998). Compte tenu
des longueurs et de la fréquence de fonctionnement, typiquement 50-60
Hz, une ligne de transmission se caractérise par un modèle
à constantes localisées (les phénomènes de
propagation sont négligés car L << ë / 2ð,
où ë est la longueur d'onde associée à la
fréquence f). La structure la plus

employée pour ce modèle est le schéma
équivalent en ð, figure (14). Il se caractérise par
trois paramètres principaux (Kundur, 1994) :
- une résistance série R.
- une réactance constituée d'une inductance de
série L due au couplage par champ magnétique entre les
conducteurs.
- une capacité de shunt C due au couplage par
champ électrique entre les conducteurs.
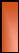
V1 Z / M V2


(1-M) / Z M (M-1) / Z


Figure 13. Modèle en ð du
transformateur.
V1 R jX V2
B / 2 B / 2
Figure 14. Modèle en ð d'une
ligne de transmission. 1.3.2.3- Modèle des
charges.
La charge représente :
- soit une charge matérielle réelle
- soit l'impédance d'entrée équivalente d'un
système de puissance, non explicitement représenté dans le
modèle du système.
En conséquence, lorsque les systèmes de
puissance sont analysés, seuls les réseaux et les
sous-réseaux de transport sont modélisés, tandis que les
réseaux de distribution ne le sont habituellement pas : ils sont
simplement remplacés par des charges équivalentes. Pour l'analyse
de la stabilité, chaque charge représente habituellement une
partie relativement importante du système comportant typiquement des
réseaux de distribution de basse et moyenne tension, de faibles sources
d'énergie fonctionnant au niveau de la distribution, les
régulateurs de tension de distribution, ... . Elle inclut
également les différentes charges réelles tels les
moteurs, les éclairages et les appareils électriques (Machowski
et al., 1998).
Les caractéristiques des charges ont une influence
importante sur la stabilité et la dynamique du système. En raison
de la complexité et la variation continuelle des charges et de la
difficulté d'obtenir des données précises sur leurs
caractéristiques, une modélisation précise des charges est
très difficile. Ainsi, des simplifications sont indispensables selon le
but de l'étude demandée. Pour les études de
stabilité dans lesquelles la gamme de temps considérée est
de l'ordre de 10 secondes après la perturbation, les modèles de
charges les plus utilisés sont généralement des
modèles statiques. Le caractère statique est lié à
la description de la charge par des équations purement
algébriques (Andersson, 2004).
Soit un noeud de tension VL, auquel une charge
consommant une puissance PL + jQL est reliée. Cette
charge peut être représentée par des admittances statiques
GL = PL/ VL2 et BL = QL/ VL 2 comme le
montre la figure (15), (Custem, 2002, I).

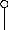

VL
PL , QL
GL
- jBL


Figure 15. Modélisation d'une
charge par son admittance équivalente.
L'admittance équivalente de charge est calculée
après avoir déterminé les données
nécessaires de l'étude de l'écoulement de puissance :
P Q
Y = - (17)
L L
L V
j
V 2 2
L L
1.3.2.4- Mise en équations du réseau de
transport.
L'établissement du modèle
généralisé du réseau de transport et des charges
implique de déterminer les équations algébriques
représentant les interconnexions entre les circuits des
générateurs et l'ensemble des transformateurs, des lignes de
transmission et des charges du
système. Le problème est ainsi de
déterminer et de mettre en équations le fonctionnement du
macro-modèle du réseau de transport. Le réseau
électrique peut être décrit sous la forme matricielle
suivante :
[I]=[Y]·[V] (18)
Où : [I] : le vecteur des courants
injectés aux noeuds du réseau.
[V] : le vecteur des tensions aux noeuds du
réseau.
[Y] : la matrice d'admittance du réseau de
transport.
Les simplifications du réseau de transport permettent
d'utiliser les modèles d'éléments du réseau
précédent à savoir :
- les transformateurs, représentés par un
schéma équivalent en ð.
- les lignes de transmission, représentés
également par un schéma équivalent en ð.
Ces différents schémas en ð sont
assemblés conformément à la topologie du réseau. A
cet ensemble, nous ajoutons les admittances shunt représentant les
charges ainsi que les réactances provenant des machines (Custem, 2002,
II).
Commençons par la "construction" de la matrice admittance
[Y]. Cette matrice se compose de termes diagonaux [Y]
ii et des termes non-diagonaux [Y]
ij , (Custem, 2002, I) :
- les termes [Y] ii , (self
admittance), représentent la somme de toutes les admittances
connectées aux noeuds i.
- les termes [Y] ij , (l'admittance mutuelle),
représentent la somme de toutes les
admittances joignant les noeuds i et j, au
signe près.
Partant de l'idée que tous les noeuds du réseau
sauf les noeuds internes des générateurs n'ont pas d'injection de
courant, le principe de la méthode de Kron peut ainsi être
appliqué pour la réduction du réseau (Arthur R. Bergen
et al., 2000).
Sachant que la somme de tous les courants dans chaque noeud de
charge vaut zéro, les noeuds des charges dans l'équation (18)
peuvent donc être éliminés. L'équation (18)
s'écrit alors comme suit (Yu, 1983) :

? ?
? ?
=
? ?
? ?
? ?
L
? ? ?
??
In
0
Y Y
nn nr
M
Yrn
L L L
M
Yrr
?
?
?
? ?
·
? ? ?
??
L
V n
Vr
? ? ?
? ?
(19)
Où : n : l'indice des noeuds de
générateurs.
r : l'indice des noeuds restants.
m : l'indice de tous les noeuds du réseau.
En décomposant l'équation matricielle (19), nous
obtenons le système d'équations suivant :
· [ V r ]
(20)
[ ] [ ] [ ] [ ]
I Y V Y
n nn n nr
= · +

·
[ ] [ ]
+
0
]
· [ V n
Y V
rr r
[ ]
Y rn
Ce système d'équations peut être
reformulé comme suit :

[ ] [ ] [ ] [ ] 1 [ ]
Y bus = Y nn - Y nr · Y rr
- · Y rn (22)
Où : [Ybus ] est la matrice d'admittance
réduite du réseau électrique, car la dimension de cette
matrice a été ramenée de m×m à
n×n.
En introduisant l'équation (8) dans l'équation
(21), nous obtenons :
[ ] [ ] [ [ ][ ] [ ][ ][ ]]
I Y E e j X X I e
= · + -
' '
j ä j ä (23)
m q d q q
Avec : [ ] 1
[ ] [ ] 1 [ ' ] -
Y m = Y bus - + j X d (24)
Où [ ] [ ] [ jâ ]
Y m = Y m e représente la
matrice de l'admittance totale du réseau électrique
réduit.
Le courant de la ième machine du
réseau à n machines s'écrit dans le
référentiel (D-Q) comme suit :
|
Ii
|
n
j â ij
?= Y e
mij
j 1
|
( )
' ä ( ' ) ä
j
E e j X X I e
j j
j
+ -
qj dj qj qj
|
(25)
|
y compris le terme j = i.
Dans le référentiel (d-q)i de la
ième machine, cette dernière équation
devient :
|
n
I I e Y e jE X X I
- - ° +
= = + -
j ä â ä
( 90 ) ( ) ' '
i ij ij
?= ( )
j
qj qj dj qj
( )
dqi i mij
j 1
|
(26)
|
Avec ä ij = ä j-
ä i
En décomposant l'équation (26), nous obtenons les
expressions du courant de la ième machine suivant les axes
direct et en quadrature :
n
Idi
Y mij
?
Re( )
I dqi
1
j
n
Iqi
Y mij
?
Im( )
I dqi
1
j
( )
- + -
S E X X C I
' '
ij qj qj dj ij qj
(27)
( )
( )
C E X X S I
' '
ij qj qj dj ij qj
+ -
( )
= +
cos( )
â ä
ij ij
Avec :
C ij
S ij
(28)
L'ensemble de ces équations de courants
complété par les équations de tension correspondantes (6)
des machines, représente les équations de la partie
algébrique du modèle d'état général
présenté ultérieurement.
1.3.3- Les équations d'état
généralisé du modèle.
Comme nous l'avons présenté dans la
première partie de ce chapitre, un système de puissance est un
système dynamique non-linéaire, qui peut être décrit
par un ensemble d'équations différentielles ordinaires
non-linéaires couplées du premier ordre et un ensemble
d'équations algébriques, où les formes
générales de ces ensembles d'équations
différentielles et algébriques peuvent être
exprimées comme suit :
x i f i x x x n i n
& K K
= =
( 1 , 2 , , ) ; 1,2, ,(29)
|
0 ( 1 , 2 , , )
= K
h j x x x m
|
; 1,2, ,
j m
= K(30)
|
Les équations différentielles correspondent aux
fonctionnements dynamiques des générateurs, des systèmes
d'excitation et des autres éléments du système. Les
équations algébriques correspondent aux équations des
réseaux de transport et des stators des générateurs. La
solution de ces deux groupes d'équations détermine l'état
électromécanique du système à chaque instant.
Nous rappelons ci-dessous les équations décrivant
le modèle déduit du système de puissance :
1
ù& i T T D
= ( ( 1))
mi - ei - i i -
ù (31)
2 H i
ä& i =
ù0(ùi -1) (32)
E & = - - -
1 ' '
' ( ( ) )
E E X X I (33)
qi ' fdi qi di di di
T d i
0
E & = - + -
1 ( ( ) )
K V V U E (34)
fd a réf t S fd
T a
T = E ' I + ( X - X
' ) I I (35)
ei qi qi qi di di qi
V di = XqiIqi (36)
qi - X ' di I di (37)
'
V qi = E

V ti = V di +V
qi (38)
2 2

?
Idi
))
C I
ij qj
· - ·
( S ij
E X X
' + - '
qj qj dj
(
· ·
Yï
n
· ' + - '
E X X
qj qj dj
(
ij qj
I qi ? Yï · ( C ij j 1
· ·
La figure (16) représente les éléments du
modèle du système de puissance avec leurs interactions.
L'approche finale de la modélisation du système
de puissance implique une présentation de l'ensemble des
équations de ce système sous forme d'équations
d'état généralisées comme suit :
x & = f(x, u) (40)
y=g(x,u) (41)
Une telle forme représente un système invariant
dans le temps (système autonome). Où :
,
? ? ? ? ? ?
?
1 ?
?
?
?
?
,
?
1 ?
2
n
2
m
&
x1
&
& 2
x
?
x = M
&
xn
? x
? x
x M
= ?
?
? ? x
? u ? f ?
1 ? 1
?u f 2 ? 2 = ? ? ? ? ? ?
? ? ? ?
u M
= , f M
? ? ? ?
? ur ? ? fn ?
? y
? y
y M
= ?
?
? ? y
? g
? g
2
?
1 ?
(42)
g M
= ?
?
m
? ? g
x : vecteur d'état du système de
n variables.
x& : vecteur dérivé du vecteur
x par rapport au temps.
u : vecteur de r signaux d'entrée du
système.
f : vecteur de n fonctions non-linéaires
reliant les variables d'état xi et les signaux d'entrée
ui aux dérivées des variables d'état
x& i .
y : vecteur de m signaux de sortie du
système.
g : vecteur de m fonctions non-linéaires reliant
les signaux d'entrée ui et les variables d'état
xi aux variables de sortie yi.
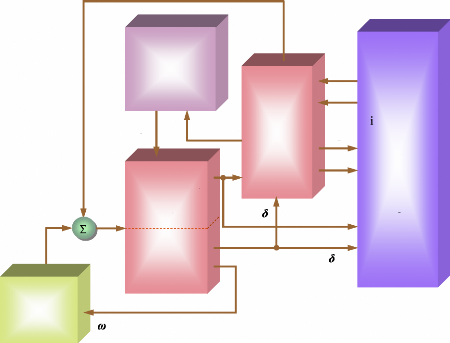
Turbine &
Gouverneur
Pm
Fm
+
Fe
_
Fa
Efd
Equations de
circuit du rotor
d'excitation &
Equations du
mouvement
Systèm e
AVR
k&
ù&
ä&
k& fd
q
'
Vt
E'q
Equations
de circuit
du stator
Pe
Vd
Vq
Vt
E'q
Vq
Iq
Vd
Id
Equations de
réseau de
transport
ncluant les
charges
statiques
Id
Iq
Figure 16. Digramme de l'ensemble des
blocs du système de puissance.
Les variables d'état permettent de décrire
complètement l'évolution dynamique du système par
n équations différentielles de premier ordre.
L'état et la sortie du système peuvent ainsi être
calculés, à tout instant, pour des conditions initiales
quelconques.
Quand les dérivées des variables d'état
x sont égales à zéro, (c.-à-d.
x& = 0), le système est à l'équilibre. Ainsi,
ce point d'équilibre est le point auquel toutes les variables
d'état sont constantes et le fonctionnement du système autour de
ce point est dit linéaire. La détermination de modèle
linéaire fait l'objet du paragraphe suivant.
1.4- Le modèle linéaire.
1.4.1- Introduction : Linéarisation du
modèle.
La quasi-totalité des systèmes dynamiques
réels possède des caractéristiques non- linéaires.
Le comportement dynamique d'un système de puissance peut être
décrit par un ensemble d'équations différentielles et
algébriques (EDA). Compte tenu que le système de puissance,
évolue généralement autour d'un point de fonctionnement
donné lors des petites perturbations, il est possible de
linéariser ses équations EDA autour de ce point.
Comme nous l'avons vu précédemment, le point de
fonctionnement normal du système se définit comme un point
d'équilibre ou une condition initiale. Les dérivées des
variables d'état en ce point sont donc égales à
zéro. L'équation (40) devient ainsi :
x&0
=f(x0,u0)=0 (43)
Où : x0 est le vecteur des variables
d'état correspondantes au point d'équilibre. u0 est le
vecteur d'entrée correspondant au point d'équilibre.
Si une petite perturbation se superpose aux valeurs
d'équilibre, l'équation (43) s'écrit : x x x f x x u
u
& = & + Ä & = + Ä + Ä
0 ( 0 , 0 ) (44)
Puisque ces perturbations sont petites, l'équation (44)
peut être développée en série de Taylor
limitée aux termes de premier ordre.
Alors, nous obtenons pour chaque variable d'état :
? f f ? i i
(45)
r
?
i i
? f f
x x x f x u
& & & L L
= + Ä = +
0 ( 0 , 0 ) ? Ä + +
x ? Ä +

x ? Ä + +
u ? Ä u
x 1
x n
i i i i 1 n 1
u 1
? ? ? ? u r
Avec : i = 1,2, K , n .
Etant donné que, x & i 0 = f
i ( x 0 , u 0 ) = 0 ,
l'équation précédente peut être mise sous la forme
suivante :
? f ? f
i f i ? i i
? f
Ä =
x & L L
? Ä + +
x ? Ä +
x ? Ä + +

u ? Ä u (46)
x x
1 n
i 1 n 1 r
1
u r
? ? ? u ?
? g
?
?
?
Nous pouvons appliquer les mêmes étapes de
linéarisation sur l'équation de la sortie (41) :
r (47)
j j
g g j j
g
Ä =
y ? Ä + +
x L 1 L
x
j 1 n
? ? ? ?
x u
1 n 1
u
? Ä +
x ? Ä + +

u ? Ä u
r
Avec : j = 1,2, K , m
Si le système fonctionne avec de petites perturbations au
voisinage du point d'équilibre,
? f i
nous pouvons supposer que toutes les dérivées
premières (,...) sont constantes dans le
? x i
domaine de fonctionnement.
Par conséquent, le système linéarisé
peut être représenté par les deux équations
suivantes:
Ä = ? Ä + + ? Ä + ? Ä + + ? Ä =
x a x a x b u b u i n
& L L K (48)
i i in n i ir r
1 1 1 1 , 1,2, ,
Ä = ? Ä + + ? Ä + ? Ä + + ? Ä =
y c x c x d u d u j m
j j jn n j jr r
1 1 1 1 , 1,2, , (49)
L L K
En écrivant ces deux équations sous forme
matricielle, nous obtenons le modèle d'état linéaire final
suivant :
Äx&=AÄx+BÄu
(50)
Äy=CÄx+DÄu
(51)
Avec:
1
L
1
1 L
? f ? f
1 1
L
r
? u
?u
M
1
L
M
? f n n
? f
L
r
m m
?g
,
,
? g
? u
M
? u r
?u
1
? u?u
r
A
C
Où:
? f 1 ? f 1
?
?
?
M ?
?
?
? ?
L
? x n
?x1
M L
? f n n
? f
? x
n
L
? x 1
? g 1 1
L ? g
? g m m
1
? x?x
n
?g
? ? ? ? ? ?
??
B
D
?g
?u
M
?g
?
?
?
?
?
?
??
?
1 ?
?
?
?
?
??
(52)
(53)
A: matrice d'état (n×n).
B : matrice d'entrée (n× r).
C : matrice de sortie (m× n).
D : matrice de contrôle (m× r).
- Le nombre des variables d'état n
définit la longueur du vecteur d'état Äx, le nombre
de lignes et de colonnes de la matrice A, le nombre de lignes de la matrice B
et le nombre des colonnes de la matrice C.
- Le nombre r des variables d'entrées choisies
définit la longueur du vecteur d'entrée Äu et le
nombre de colonnes des matrices B et D.
- Le nombre des variables de sorties choisies m
définit la longueur du vecteur de sortie Äy et le nombre
de lignes des matrices C et D.
- La matrice A est appelée matrice
d'état ou matrice d'évolution, car elle contient la
description du comportement dynamique du système. Elle rend compte aussi
de l'évolution du système en régime libre, c.-à-d.
à commande nulle.
- La matrice B est appelée matrice de commande ou
matrice d'entrée. Elle rend compte du comportement dynamique du
système en réponse à une commande.
- La matrice C est appelée matrice d'observation.
Elle permet de relier la sortie à l'état.
- La matrice D est enfin appelée matrice d'action
directe qui relie directement la
commande à la sortie. Elle est en général
nulle dans les systèmes physiques ; le
système est dit "strictement propre" (Allenbach et
al., 2005, II).
1.4.2- Application au système de
puissance.
Lorsque le système de puissance est soumis aux petites
perturbations, les variables d'état du système restent au
voisinage de leurs valeurs initiales et la linéarisation du
système peut être aisément appliquée (CIGRE,
1999).
Les variables d'état proposées pour notre
système de puissance de n machines, représenté
par l'ensemble des équations (31) à (34), sont :
x E E
[ , , ' , ] T
Ä = Ä ù Ä ä Ä
Ä
i i i qi fdi
, 1, ,
i n
= K
(54)
Le développement du modèle linéaire de notre
système, explicité dans l'annexe B, nous donne l'ensemble des
équations suivantes :
? n n
1 ? 1
? D K K E '
ù& ù 1
ä
Ä = ? Ä ? ? = Ä ? ? = Ä T (55)
i i i ij j
( ) ( ) ? + Ä
2 ij qj mi
2 H 2 H
i ? j 1 j 1 ? i
Ä ä i = ù0Äù
i
& (56)
|
? ?
'
& 1 ä
n n 1
Ä = ? ? = Ä ? ? = Ä + Ä
E ' ?? ( ) ( E E
K ) ??
qi ' 4 ij j qj fdi
T K
doi ? j 1 3
j 1 ij ?
|
(57)
|
? n n ? ai
Ä = ? ? = Ä ? ? = Ä ? Ä
& 1 ä K
? K K K K E E
'
E ? + Ä U (58)
fdi ai ij j
( 5 ) ( )
ai ij qj
6 fdi Si
T T
ai ? j 1 j 1 ? ai
Les constantes de linéarisation
K1ij...K6ij sont des matrices carrées
d'ordre n. Les valeurs de ces constantes dépendent des
paramètres des générateurs, du réseau de transport
et des conditions initiales du système. Les éléments
diagonaux des matrices des constantes déterminent les
propriétés dynamiques des machines, tandis que les
éléments non-diagonaux représentent les interactions
dynamiques entre les machines (Yu, 1983).
L'ensemble d'équations ci-dessus peut être
représenté sous la forme de modèle linéaire
correspondant à l'équation (50).
Ce modèle d'état linéaire sera donc
utilisé pour analyser la stabilité du système.
1.4.3- Analyse du modèle linéaire. 1.4.3.1-
Introduction.
L'analyse des valeurs propres et l'analyse modale du
système de puissance linéarisé sont des outils "puissants"
pour étudier les propriétés dynamiques du système.
L'évaluation précise de la fréquence des oscillations
électromécaniques et de l'amortissement de ces oscillations peut
être déterminée à partir de l'analyse des valeurs
propres ; l'analyse modale permet quant à elle d'obtenir des
informations supplémentaires plus approfondies telle la nature des modes
(dominants ou non, ...).
1.4.3.2- Valeurs propres.
Après avoir établi le modèle
d'état linéaire correspondant à l'équation (47), la
caractérisation de la stabilité du système peut se faire
à partir de la matrice dynamique A et de ses valeurs propres
(première méthode de Lyapunov).
Considérons un système linéaire
défini par le modèle d'état (50), (51). En appliquant la
transformation de Laplace à ces équations, nous obtenons
l'ensemble d'équations suivant dans le domaine fréquentiel
complexe :
sÄx(s) =
AÄx(s) + BÄu(s)
(59)
Äy(s) =
CÄx(s) + DÄu(s)
(60)
La solution explicite de cet ensemble d'équations est
donnée comme suit :
Ä = ? ? Ä + Ä (61)
y ( s ) C ( sI A )
1 B u ( s ) D u ( s ) Où
: I est la matrice d'identité.
Ainsi, la réponse dynamique du système est
déterminée par l'équation caractéristique de la
matrice d'état A définie par :
det(ë·I-A)=0 (62)
Les valeurs ë qui satisfont l'équation
précédente sont appelées les valeurs propres du
système. Une valeur propre définit le mouvement du système
lié à une fréquence propre.
Une valeur propre -un mode- est caractérisée par
une fréquence d'oscillation et un amortissement. Elle est
représentée généralement par le nombre complexe
suivant :
ë=ó#177;jù (63)
Cette relation est équivalente à la relation
définissant les valeurs propres d'un système du deuxième
ordre (Brogan et al., 2000). Par suite :

ë=-ù n æ
#177;jù n 1 - æ (64)
2
Où : ó est la partie réelle de la
valeur propre (abscisse de convergence). ù est la pulsation
propre d'oscillation (rad/s).
ùn est la pulsation naturelle
d'oscillation (rad/s).
æ est le facteur d'amortissement d'oscillation.
Une matrice d'état de dimension n× n est
associée à n valeurs propres.
L'analyse des valeurs propres permet d'obtenir tout d'abord la
fréquence d'oscillation et le facteur d'amortissement.
La fréquence naturelle d'oscillation est donnée par
la relation suivante :
ù
f = (65)
2 ð
Le facteur d'amortissement détermine la
décroissance de l'amplitude d'oscillation. Il est donné par :
ó
-
=
(66)
ó 2 ù
2
+

æ
Dans un modèle linéaire, la solution des
équations linéaires du système décrit
l'évolution exponentielle au cours du temps de la perturbation. Ainsi,
cette solution peut être représentée par une combinaison de
fonctions d'exponentielles eëit représentant
les caractéristiques
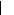
temporelles associées à chaque valeur propre
ëi. Les constantes de temps ô =
1/ói caractérisent de façon
générale l'amortissement du système.
L'interprétation physique des signaux correspondants
aux fonctions de la forme eëit est simple. Elle est
illustrée par la figure (17) qui représente dans le plan complexe
l'allure des variations de tels signaux en fonction du temps, suivant la
position du point représentatif de ëi.
t
t
t
jù
t
ó
t
t
Figure 17. Analyse par lieu des
pôles de la stabilité d'un système.
- Une valeur propre réelle correspond un mode
non-oscillatoire. Si la valeur propre réelle est négative, les
exponentielles apparaissant dans la réponse temporelle sont des
fonctions décroissantes du temps. La rapidité de
décroissance est liée à la constante de temps
d'amortissement. Plus la valeur de l'abscisse de convergence ó est
grande, plus la constante de temps est faible et l'amortissement rapide.
- Par contre, si la valeur propre réelle est positive, le
mode présente une instabilité apériodique.
- En revanche, les valeurs propres complexes, en paires
conjuguées, correspondent aux modes oscillatoires. Le mode oscillatoire
peut être divergent, c.-à-d. instable, si la partie réelle
de la valeur propre est positive, il est au contraire amorti, c.-à-d.
stable, si la partie réelle est négative.
Cette analyse révèle qu'il est possible de
déterminer la nature (stable ou instable) d'un système
linéaire à partir d'une "inspection" de la position des
pôles de la fonction de transfert du système dans le plan
complexe. En outre, la connaissance de la position des pôles peut fournir
des renseignements sur le comportement du système lors de régimes
transitoires typiques tels que la réponse à une impulsion,
à un échelon, ... .
Des modes instables ou mal amortis peuvent être dominants :
leurs contributions déterminent alors l'allure de la réponse
temporelle globale du système.
Dans les réseaux électriques, il est
évidemment nécessaire que tous les modes du système soient
stables c.-à-d. placés dans la partie gauche du plan complexe.
1.4.3.3- Analyse modale.
Comme nous l'avons vu, les valeurs propres du système
déterminent les caractéristiques dynamiques du système
(fréquences et facteurs d'amortissement) ainsi que l'état de
stabilité du système.
L'analyse des vecteurs propres, qui découle de l'analyse
des valeurs propres, peut aussi fournir d'autres informations importantes.
Lorsqu'une instabilité ou un mode mal amorti prend
naissance dans un système de puissance, il est très
intéressant d'examiner les points suivants (Custem, 2002, I; Breulmann
et al., 2000) :
- les variables d'état liées aux modes
dominants.
- les éléments du système permettant
d'agir efficacement pour le stabiliser. - les groupes cohérents de
générateurs présentant des oscillations couplées. -
les signaux les plus efficaces à appliquer aux contrôleurs.
- les paramètres des contrôleurs réalisant un
"meilleur" amortissement.
L'analyse modale présentée par la suite concerne
les vecteurs propres, les facteurs de participation et les résidus.
1.4.3.3.1- Vecteurs propres.
Le modèle linéaire d'un système de
puissance peut être représenté, comme nous l'avons
déjà expliqué, par un modèle d'état
décrit par l'équation (50). Les vecteurs propres, à droite
et à gauche, de la matrice d'état du système peuvent
être calculés par les équations suivantes :
A? i = i ë? i (67)
ø i A= i
ëø i (68)
Où : ëi est une
ième valeur propre (toutes les valeurs propres
étant supposées distinctes). öi est le
ième vecteur propre à droite associé
à ëi.
øi est le ième vecteur
propre à gauche associé à ëi.
Pour une matrice d'état de dimension nx n, le
vecteur propre à droite est un vecteur colonne de dimension nx
1, tandis que le vecteur propre à gauche est un vecteur ligne de
dimension 1x n. Les deux vecteurs sont définis comme suit :
|
? ?1i
? ? ?2i
? M
=
i ?
? ? ?ni
|
?
?
?
?
?
?
|
, øi = [ø1i
ø2i L ø n i ] (69)
|
La relation caractéristique entre les vecteurs propres
à droite et à gauche est déterminée par leur
produit matriciel. Le produit matriciel entre deux vecteurs propres, à
droite et à
gauche, associés à deux valeurs propres
différentes vaut zéro. Par contre, lorsque les deux vecteurs
propres correspondent à la même valeur propre, leur produit
matriciel normalisé vaut 1. Ces propriétés peuvent se
résumer de la façon suivante :
?? 0 ; i j
?
ø ? (70)
i j 1 ;
= i j
? =
L'ensemble des vecteurs propres à droite du système
forme la matrice modale à droite, donnée comme suit :
Ö = [ ? 1 L ? i L? n ]
(71)
De même, la matrice modale à gauche est
formée des vecteurs propres à gauche :
Ø = ø 1 T L ø L
ø
[ ]T
T T
i n (72)
Le vecteur propre à droite, q'i, montre
l'influence relative de chaque variable d'état dans un mode
excité donné. Ainsi, pour un vecteur propre à droite
complexe, l'amplitude relative des éléments du vecteur indique le
degré de participation des variables d'état au mode
considéré. Quant à la phase des éléments du
vecteur, elle donne le déphasage des variables d'état dans le
mode donné.
En ce qui concerne le vecteur propre à gauche,
Ji, il détermine l'ensemble des variables d'état
participant relativement à la composition du
ième mode. Il indique également la
contribution de chaque variable d'état dans l'évolution du mode
considéré.
Dans le plan complexe, le diagramme représentant les
composantes d'un vecteur propre à droite, q'i, relatives aux
différentes variables d'état est appelé le "mode shape"
(Custem, 2002, II). Dans un système de puissance multimachines, le mode
shape indique la façon dont les générateurs oscillent les
uns par rapport aux autres, les deux cas limites étant les oscillations
cohérentes et les oscillations en opposition de phase (Bragasson, 2005).
Ainsi, les modes shapes du système peuvent identifier les groupes
cohérents des générateurs. En outre, le mode shape peut
confirmer le type de chaque mode. (Local ou interrégional).
1. 4.3. 3.2- Facteur de
participation.
L'approche standard, habituellement employée pour
évaluer la participation d'une variable d'état xk dans
le ième mode, étudie les
éléments correspondants du vecteur propre à droite
q'i. Bien que cette méthode soit simple à employer, elle
présente un défaut très sérieux, à savoir
les valeurs numériques des éléments des vecteurs propres
à droite dépendent des unités des variables d'état
correspondantes. Il est donc difficile de comparer les valeurs obtenues pour
des variables d'état différentes. Par conséquent cette
méthode est seulement exploitable pour des variables d'état ayant
les mêmes unités et jouant les mêmes rôles
(PérezArriaga, 1981).
Rappelons qu'un vecteur propre à droite q'i
mesure l'influence relative de chaque variable d'état xk dans
un ième mode et qu'un vecteur propre à gauche
Ji indique la contribution de l'activité de xk dans le
ième mode. Par conséquent, une
"quantité" caractéristique d'un mode donné peut être
obtenue par produit, élément par élément, d'un
vecteur propre à droite et d'un vecteur propre à gauche
correspondant. Cette quantité, appelée le facteur de
participation, est calculée par la relation suivante :
Ainsi, le facteur de participation peut fournir des
informations fines sur le problème : il représente une mesure
relative de la participation de la kème variable
d'état dans le ième mode, et vice versa (Hsu
et al., 1987; Kundur, 1994).
Etant donné que les matrices modales, à droite
et à gauche, Ö et Ø sont inverses, le facteur de
participation est donc une grandeur sans dimension. Ceci veut dire que le
facteur de participation, au contraire du vecteur propre à droite, est
indépendant des unités des variables d'état.
Les facteurs de participation peuvent être regroupés
dans une matrice, appelée matrice de participation P telle que :
Ñ = [ p 1p2 L
pi L p n ] (74)
Avec :
M
ö ø
ni in
M ?
?
?
p1 i
Ñi
p2 i
pni
ö1
ö2
ø ii
ø ii
?
1 ?
2
(75)
?
?
?
?
Dans la matrice de participation P, comme le montre
l'équation (76), la jème colonne indique
comment un jème mode participe relativement à
l'évolution des variables d'état du système tandis que la
ième ligne indique comment les différents
modes participent relativement à l'évolution de la
ième variable d'état (Custem, 2002, II).

p1
m
x1
M
M (76)
?
?
?
?
?
?
M
p11
L L
O
O
M
Ñi
O
O
M
M
p p
n nm
L L
1
xn
Une autre propriété intéressante du
facteur de participation pij s'interprète souvent
comme la sensibilité du jème mode aux
changements des termes diagonaux aii de la matrice
d'état du système A, (Van Ness et al.,
1994).
Pour les études de stabilité aux petites
perturbations, l'influence d'une source d'amortissement appliqué
à un générateur peut être déterminée
par les facteurs de participation, comme suit (Rogers, 2000) :
- si, pour n'importe quel mode, le facteur de participation
correspondant à la vitesse du générateur est nul,
l'introduction d'une source d'amortissement au générateur n'aura
aucun effet sur le mode.
- si le facteur de participation est réel positif, l'ajout
d'amortissement à ce générateur augmentera l'amortissement
du mode.
- en revanche, si le facteur de participation est réel
négatif, l'amortissement ajouté au générateur
réduira l'amortissement du mode.
En outre, les facteurs de participation, par leur
propriété de pouvoir déterminer les variables
d'état responsables des modes indésirables, peuvent être
employés pour trouver les points les plus efficaces pour installer des
contrôleurs de stabilisation.
La matrice de participation peut montrer aisément les
variables d'état les plus impliquées dans le mode
indésirable : les termes de la matrice P de plus grande amplitude de la
colonne relative au mode considéré indiqueront la participation
en question.
1.4.3.3.3- Résidus.
L'efficacité du signal d'entrée d'un
contrôleur de stabilisation ou l'emplacement optimal de ce dernier dans
un système de puissance multimachines peuvent être
identifiés par la méthode des résidus. Cette
méthode est dérivée de la relation entre la fonction de
transfert et le modèle d'état.
Le modèle d'état d'un système
représente à la fois les propriétés
d'entrée/sortie du système et le comportement interne du
système. A l'inverse, la fonction de transfert du système ne
concerne que la relation entrée-sortie du système.
Pour déterminer la relation entre la fonction de
transfert et le modèle d'état, nous prenons les équations
(50) et (51) pour un système monovariable (Single Input- Single Output
system), et nous considérons la fonction de transfert entre les
variables y et u.
Supposons que D = 0, les équations d'état
s'écrivent comme suit :
Äx&=AÄx+BÄu
(77)
Äy=CÄx (78)
y s
La fonction de transfert Ä s'écrit de la façon
suivante :
( )
Ä u s
( )
(79)
( ) -
Ä y s
( )
G s C sI A B
1
= = -
( )
Ä u s
( )
Pour un système en boucle ouverte, la fonction
G(s) peut être décomposée en
éléments simples comme suit :
n n
R R R R R
1 2 n i
G s
( ) = + + +
L = ? ?
i = (80)
( ) ( ) ( ) ( ) ( )
s s
- s s
- s s
- = = -
s s
-
n i i i ë i
s
1 2 1 1
Où :
s : l'opérateur de Laplace.
s1, s2, ...,sn : les pôles de
G(s) - les valeurs propres du système-. Ri :
le résidu de G(s) au pôle si.
Le résidu peut s'exprimer par la relation suivante
(Kundur, 1994):
R i =C Ö i
Ø i B (81)
D'après cette relation, nous remarquons que le
résidu Ri pour un mode ëi donné mesure la
sensibilité de ce mode à un signal de contre-réaction
sortie-entrée. Ainsi, les résidus peuvent déterminer les
modes les plus affectés par un signal de retour.
La figure (18) montre un système G(s)
équipé d'un contrôleur en contre-réaction de
fonction de transfert H(s).
Système
u(s) +
-
G(s)
H(s)
Régulateur
y(s)
Figure 18. L'ensemble
système-contrôleur en boucle fermée.
Lorsqu'on ferme la boucle par un régulateur
H(s), les valeurs propres du système initial
G(s) vont se déplacer. Le déplacement de ces
valeurs propres peut être calculé par l'équation suivante
(Aboul-Ela et al., 1996) :
Äë i = RiH(ë
i ) (82)
Cette équation montre que le déplacement des
valeurs propres, créé par le contrôleur, est proportionnel
aux amplitudes des résidus correspondants.
Pour un système multivariables, l'influence du
même contrôleur H(s), (sans se soucier de sa
structure et de ses paramètres) peut être étudiée en
différents emplacements. Si le résidu, associé à un
mode ëi donné, est calculé pour chaque emplacement,
le résidu le plus élevé indique donc l'emplacement le plus
efficace du contrôleur (Pagola et al., 1989). De même, en
changeant le signal d'entrée du contrôleur, différentes
valeurs des résidus vont être obtenues. Par conséquent, le
résidu le plus élevé indique le signal d'entrée le
plus efficace.
1.5- Conclusion.
Dans ce chapitre, nous avons présenté la
modélisation du système de puissance pour les études de la
stabilité aux petites perturbations. Nous avons aussi
présenté la linéarisation du système avec l'analyse
modale du modèle linéaire du système. Les points
d'étude principaux de ce chapitre sont présentés
ci-dessous :
- Le modèle choisi pour chaque machine synchrone du
système est du troisième ordre. Les équations
différentielles de la machine sont décrites par les trois
variables d'état : ä, ù et
E'q. Ce modèle convient bien pour les études
de stabilité angulaire aux petites perturbations.
- Le système d'excitation et la turbine et leurs
régulateurs sont aussi modélisés.
- Le modèle généralisé du
réseau de transport et des charges est déterminé. Dans ce
modèle, les circuits de stators des machines, les transformateurs, les
lignes de transmission et les charges sont représentées sous
forme d'équations algébriques.
- le système est représenté par un ensemble
d'équations, couplées, différentielles et
algébriques. Ce modèle décrit le comportement
non-linéaire du système de puissance.
- Le système de puissance est souvent soumis à
des petites perturbations qui se produisent continuellement sous l'influence de
faibles variations de charges et des sources. Ces perturbations sont
considérées comme suffisamment petites pour permettre de
linéariser les équations du modèle général
du système. La représentation d'état du système est
ensuite déduite.
- La stabilité du système est uniquement
définie par le lieu des pôles, dans le plan complexe, de sa
fonction de transfert.
- L'analyse modale du système donne des informations
importantes concernant les caractéristiques des modes d'oscillations,
les variables d'état participant à l'évolution de ces
modes, ... .
Après avoir enfin présenté les
modèles linéaire et non-linéaire du système, nous
présentons dans le chapitre suivant les différents types de
stabilité du système de puissance et plus particulièrement
la stabilité angulaire aux petites perturbations objet de notre
travail.
| 

