Approche de résolution par régularisation des problèmes de programmation mathématique à deux niveaux dans le cas de la non unicité de la solution du problème du suiveur

Année Académique 2007/2008

APPROCHE DE RÉSOLUTION PAR
RÉGULARISATION DES PROBLÈMES DE
PROGRAMMATION MATHÉMATIQUE À DEUX
NIVEAUX DANS LE CAS DE LA NON UNICITÉ DE
LA SOLUTION DE LA SOLUTION DU PROBLÈME DU
SUIVEUR.

MÉMOIRE

Présenté et soutenu en vue de l'obtention du Diplôme d'Études Approfondies (D.E.A.) Option : ANALYSE NUMÉRIQUE

Par :

FOUODJI DEDZO FRANCISQUE
Matricule 02W026

Sous la direction de :

PAULINE LAURE FOTSO Maître de Conférence

Dédicaces

Je dédie ce travail

? A mon père,

? A ma mère,

? A la famille Tsapi,

? A mes frères et soeurs.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Remerciements

Ce travail n'aurait pu être réalisé sans le concours, le soutien et les encouragements de plusieurs personnes que je tiens à remercier particulièrement. Il s'agit de :

? Professeur Pauline Laure Fotso, qui malgré ses nombreuses occupations à accepté d'encadrer ce travail, et ainsi guider mes pas dans ce premier travail de recherche;

? mr Calixte.O.Pieume, dont la disponibilité infinie et les conseils avisés m'ont permis d'éviter bien d'écueils;

? le Dr Guy Merlin Mbakop, qui m'a ouvert généreusement sa bibliothèque personnelle;

? les enseignants du département de mathématiques de l'université de Yaoundé I et de l'école normale supérieure de Yaoundé, à qui je doit la majeure partie de mes connaissances en mathématiques;

? mon père Mr Dedzo André et ma mère Mme Kamené Marie, qui m'ont transmis le goût de l'effort, et qui n'ont jamais cessé de m'apporter leurs support tant matériel que psychologique;

? les familles Tsapi, Nzangué et Zietchou, pour leur aide matérielle et leur encouragements;

? mes frères aînées Theophile, Merlin et Gustave, qui ont été mes guides éclairés durant mes premières années d'université et dont l'apport à ma formation universitaire et intellectuelle ne saurait être quantifié.

? mes camarades de promotion: Daoussa Daniel, Tchouaké Hervé, Kenfac Brice, Ngongang Eric, Ekwadi cyrille, Moualeu Dany, Batkam cyrille, Kenmogne Marcelin;

? mes amis Chassep Joel, Tagne Takam Cyrille, Mbah .N.Serge, Tewa Jean Claude, Meta-gheu Gisèle, Pokouo Sandrine, Tagne.K.Steve william;

? tous ceux que je n'ai pas cité ici et qui m'ont apporté leur aide durant ce travail.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Table des matières

Dédicaces i

Remerciements ii

Table des matières iv

Table des figures v

Résumé vi

Abstract vii

Introduction générale viii

1	Genéralités sur la programmation mathématique à deux niveaux		1
	1.1	Formulation générale des PBN	2
		1.1.1 Définition et présentation	2
	1.2	Quelques propriétés des PBN	3
	1.3	Quelques résultats d'optimisation paramétrique	6
	1.4	Conditions d'optimalités	12
		1.4.1 Cas des PBN linéaires	12
		1.4.2 Cas général	13
	1.5	Algorithmes et méthodes de résolution des PBN	14
		1.5.1 Algorithme de descente	14
		1.5.2 L'algorithme du paquet	15
	1.6	Les applications de la PBN	16
		1.6.1 Production agricole , production de biocarburant	16
		1.6.2 Le problème principal-agent [10] 18
2	Non unicité de la solution du problème du suiveur : les différentes techniques
	d'approches.		20
	2.1	Position du problème	21
	2.2	L'approche optimiste	22
	2.3	L'approche pessimiste	24

TABLE DES MATIÈRES iv

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

3 Approche de résolution par régularisation des PBN dans le cas de la non

unicité. 30
3.1 La régularisation de Tykhonov ............................ 30 3.2 régularisation par l'élément de plus petite norme .................. 37

3.2.1 première méthode ............................... 37

3.2.2 Deuxième méthode .............................. 41

3.3 Algorithme de résolution d'un PBN dans le cas de la non unicité ......... 43

3.3.1 La methode du paquet ............................ 43

3.3.2 Présentation de l'algorithme ......................... 44
3.4 Convergence de l'algorithme du paquet modifié ................... 47

Conclusion et perspectives 50

Bibliographie 51

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Table des figures

1.1 Sur les effets du transfert de la contrainte x = 0 du premier niveau dans (BLP1)

au second niveau dans (BLP2). ........................... 4

1.2 Sur l'importance de l'ordre du jeu .......................... 5

2.1 Sur les difficultés rencontrées dans le cas de la non unicité ............ 22

2.2 Fonction objectif du leader .............................. 27

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Résumé

Les approches classiques de résolution des PBN (Problème de programmation mathématique à deux-niveaux) dans le cas de la non unicité de la solution du problème du suiveur qui sont : l'approche optimiste et l'approche pessimiste présentent de nombreux défauts. Parmi lesquels le problème d'instabilité des solutions optimiste et pessimiste ainsi que celui de leurs l'éloignement, par rapport à la solution réelle du problème [11]. Dans ce document, nous présentons une approche de résolution des PBN dans le cas de la non unicité qui permet de contourner ces défauts : l'approche de résolution par régularisation des problèmes de programmation à deux-niveaux dans le cas de la non unicité de la solution du problème du suiveur. Cette méthode consiste à introduire dans le problème du suiveur un paramètre (le paramètre de régularisation) de sorte que le nouveau problème du suiveur (le problème du suiveur régularisé) admette une solution unique fortement stable. Lorsque le paramètre de régularisation tend vers zero, la solution du problème régularisé converge vers une approximation de la solution du problème original qui présente de meilleures propriétés de régularité que les solutions obtenues par les approches classiques (approches optimiste et pessimiste) de résolution des PBN de ce type. Nous présentons également un algorithme de S.Dempe issu de cette approche, dont nous étudions la convergence théorique.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Abstract

Optimistic and pessimistic approaches are classical methods uses for solving bilevel programming problems with non-unique lower level solutions. But, both the optimistic and pessimistic solutions can in general not be assumed to be good approximations of realized solutions in practice, and small changes in the problem data can result in drastic changes of theses solutions [11]. We present in this document an approach which circumvents these difficulties : the regularization approach for solving bilevel problems with non-unique lower level solutions. This approach consists (in general) of introducing a regularization parameter in the lower level problem such that the new problem (regularized problem) has a unique lower level solution which is strongly stable. This solution converges (when the regularization parameter converges to zero) to an approximation of the original problem which is more regular (and even better) than optimistic and pessimistic solutions respectively. We present also an algorithm by S.Dempe resulting from regularization approach and show the convergence of this algorithm.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Introduction générale

Les Hommes recherchent en général ce qu'il y'a de meilleur, et lorsqu'ils sont face à un problème de prise de décision, tous voudraient prendre la décision optimale.

Un des traits caractéristiques de notre époque est l'intérêt croissant porté aux problèmes de planification économique, de gestion, et de contrôle de systèmes. Comme jamais dans l'histoire, on ressent de nos jours la nécessité d'une gestion fructueuse et efficace des ressources naturelles et humaines, des moyens matériels et techniques.

Ainsi se pose le besoin de disposer d'outils objectifs susceptibles d'aider à prendre face à un problème, la meilleure décision.

Le domaine des mathématiques qui permet de modéliser les processus de prise de décision est la programmation mathématique. Au fil du temps et en fonction des besoins, se sont développées la programmation linéaire (PL), la programmation non linéaire (PNL), la programmation multiobjectif (POM) et la programmation à deux-niveaux.

La PL et la PNL permettent de modéliser des processus de prise de décisions dans les systèmes centralisés; c'est-à-dire dans les systèmes où un seul décideur est préoccupé par l'optimisation d'une fonction objectif soumise à des contraintes éventuelles. La POM quant à elle permet d'aborder les problèmes d'optimisation dans lesquels le décideur voudrait atteindre plusieurs objectifs simultanément.

Pour ce qui est de la programmation à deux-niveaux (PBN), elle permet de modéliser des processus de prises de décision dans un système décentralisé. Ici, deux décideurs ne pouvant agir indépendamment l'un de l'autre, mais suivant une certaine hiérarchie, souhaitent prendre chacun la meilleure décision par rapport à des objectifs généralement différents. La stratégie choisie par l'un des décideurs (le leader ou décideur du premier niveau) influence la fonction objectif et/ou la région réalisable de l'autre (le suiveur ou décideur du second niveau). Par conséquent, la décision de ce dernier est fortement liée à celle du leader. Ainsi un PBN est constitué de deux problèmes d'optimisation qu'on ne peux résoudre séparément.

La PBN suscite depuis quelques décennies déjà un grand intérêt dans la communauté de la programmation mathématique; ceci grace à ses nombreuses applications en économie, en ingénierie et dans plusieurs autres domaines des sciences.

La plupart des méthodes de résolution des PBN développées dans la littérature suppose au préalable que le problème du second niveau admet une solution unique; ceci dans le but de transformer le PBN en un problème d'optimisation à un niveau classique. Mais il se trouve que la majorité des problèmes modélisés sous forme de PBN sont tels que le problème du suiveur n'admet pas une solution unique [11].

C'est pourquoi la recherche depuis plus d'une décennie déjà, est tournée vers la résolution des PBN dans le cas de la non unicité de la solution du problème du second niveau.

Notre travail consiste à présenter une approche de résolution des PBN qui fait actuellement l'objet de recherches profondes : l'approche de résolution par régularisation des PBN dans le

TABLE DES FIGURES 0

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

cas de la non unicité de la solution du problème du suiveur.

Ce travail est organisé ainsi qu'il suit :

? au chapitre un, nous présentons les généralités sur la PBN dans le cas de l'unicité de la solution du problème du second plan;

? au chapitre deux nous présentons les différentes techniques d'approches des PBN dans le cas de la non unicité;

? enfin au chapitre trois nous présentons l'approche par régularisation, ainsi qu'un algorithme de résolution basé sur cette approche développé par S.Dempe, dont nous étudions la convergence.

CHAPITRE PREMIER

Genéralités sur la programmation

mathématique à deux niveaux

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Introduction

La programmation mathématique à deux niveaux (PBN) est une branche de la programmation mathématique qui résoud des problèmes ayant une structure hiérarchique constituée de deux unités indépendantes de prise de décision. Chaque unité de la hiérarchie souhaite minimiser (ou maximiser) sa fonction objectif, en tenant compte du contrôle partiel exercé à l'autre niveau de prise de décision. La PBN modélise des problèmes de prise de décision qui exigent des compromis parmi les objectifs de deux individus ou entités qui interagissent. Un décideur se voit assigner le rôle de meneur (ou leader ou décideur du premier plan) et prend sa décision en fonction de la (ou des) décision(s) éventuelle(s) d'un décideur de second plan appelé suiveur. La première utilisation d'un modèle hiérarchique date de 1934 et a été faite par H.V Stackelberg [2] dans une monographie sur l'économie de marché, pour décrire la situation de plusieurs décideurs qui veulent réaliser leurs objectifs respectifs mais ne peuvent le faire indépendamment les uns des autres. Cependant les toutes premières formulations liées aux PBN proprement dit sont l'oeuvre d'auteurs tels que Kornaj et Liptack [3] en 1965, Ross [4], Simaan et Cruz [5] ou Bracken et McGill [6]. Toutefois, Candler et Norton [7, 8] furent les premiers à utiliser la terminologie programmation à deux niveaux ou à plusieurs niveaux dans un rapport de la banque mondiale. C'est finalement au début des années 1980 que, vu ses applications dans la résolution d'une multitude de problèmes concrets (problèmes de gestion, de planification économique, de contrôle de systèmes, de chimie, de sciences environnementales,....), la PBN a commencé à susciter une attention particulière. Motivés par la théorie des jeux de H.V Sta-ckelberg [2], plusieurs auteurs se sont lancés dans l'étude de la PBN; ce qui a permis son essor dans la communauté de la programmation mathématique.

Dans ce chapitre, après avoir donné une présentation générale et quelques propriétés des PBN, nous présenterons des résultats d'optimisation paramétrique généralement utilisés pour leur résolution. Ensuite, nous donnerons quelques conditions sous lesquelles les PBN admettent des solutions dans le cas de l'unicité de la solution du problème du suiveur; ce qui nous permettra de présenter des algorithmes développés afin de construire de manière effective ces solutions. Nous terminerons en donnant quelques unes des nombreuses applications de la PBN.

Genéralités sur la programmation mathématique à deux niveaux 2

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

1.1 Formulation générale des PBN

1.1.1 Définition et présentation

Un problème de programmation mathématique à deux niveaux peut être défini comme un problème d'optimisation dont l'une des contraintes est un autre problème d'optimisation. La formulation générale d'un PBN est la suivante :

min F(x,y)	(1.1)
y
sujet à : G(x,y) = 0	(1.2)
min f(x,y) x	(1.3)
sujet à : g(x,y) = 0	(1.4)

La fonction F : Rⁿ × R^m -? R ; n, in ? N représente la fonction objectif du leader tandis que la fonction f : Rⁿ × R^m -? R ; n, in ? N représente celle du suiveur.

Les fonctions G : Rⁿ ×R^m -? Rp et g : Rⁿ ×R^m -? Rq sont respectivement les contraintes du problème du leader et du problème du suiveur.

Le leader est le décideur qui à la possibilité de prendre une décision sans tenir compte des opinions d'autres décideurs que lui. Mais étant donné (comme c'est le cas dans plusieurs problèmes d'optimisations concret) que la possibilité de prendre une décision optimale (i.e celle qui minimise sa fonction objectif) ne dépend pas uniquement de sa personne, le leader se voit contraint de prendre en compte les réactions d'un autre décideur qu'on appelle le suiveur.

les vecteurs x et y qui apparaissent dans le problème (1.1) - (1.4) sont respectivement appelés variable du problème du suiveur et variable du problème du leader.

La structure hiérarchique du problème (1.1) - (1.4) suggère que le problème du leader (1.1) - (1.2) ne peut être résolu si l'on ne connaît pas la (ou les ) solutions du problème du suiveur (1.3) - (1.4); ce qui permet de définir une autre formulation du PBN comme suit :

«min y

{ } » F (x, y) : G(x, y) = 0 et x ? (y) (1.5)

avec pour y fixé dans R^m :

{ }

(y) := Argmin f(x, y) : g(x, y) = 0 (1.6)

x

(y) représente l'ensemble des solutions du problème d'optimisation paramétrique (1.3) - (1.4). Les guillemets dans (1.5) expriment l'incertitude de la définition du PBN dans le cas où (y) n'est pas réduit à un singleton ( non unicité de la solution du problème du suiveur) La formulation (1.5) - (1.6) est celle que nous utiliserons tout au long de cet exposé.

Pour y fixé dans R^m , l'ensemble M(y) := {x ? Rⁿ : g(x, y) = 0} représente l'ensemble des

décisions admissibles du suiveur ( ou encore la région réalisable du suiveur ).

{ }

L'ensemble R := (x, y) ? Rⁿ × R^m : G(x, y) = 0 et x ? (y)est la région réalisable du

leader.

Le PBN peut encore se mettre sous la forme :

min (x,y)?R

F(x,y)

Définissons à présent ce qu'on entend par solution d'un PBN

Genéralités sur la programmation mathématique à deux niveaux 3

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

_{n o}

Définition 1.1.1. On considère le problème (1.5) - (1.6) On pose Y = y E 1[8^m : G(y) < 0 .

On suppose que Ø(y) est réduit à un singleton pour tout y E Y .

Un point (x^*, y^*) E 1[8ⁿ x 1[8^m est appelé solution optimale locale du problème (1.5) - (1.6) si y^* E Y, x^* E Ø(y^*) et il existe une boule ouverte centrée en y^* (Uä(y^*), 8 > 0) avec F(x, y) > F(x^*, y^*) pour tout (x, y) satisfaisant y E Y n Uä(y^*) , x E Ø(y).

(x^*, y^*) est solution optimale globale si 8 = oo.

Remarques 1.1.1.

1) Si le problème (1.3) - (1.4) admet une solution unique x(y) pour chaque paramètre y vérifiant les contraintes du leader, alors sous des hypothèses de régularité sur les fonctions contraintes du second plan [ 9,10 ], la fonction

x : 1[8^m -? 1[8ⁿ y H x(y)

est continue. avec {x(y)} = Ø(y) .

2) Si le problème (1.3) - (1.4) n'admet pas une solution unique pour tout paramètre y vérifiant les contraintes du premier niveau, alors le leader se trouve face à un dilemme [11] en ce sens que même s'il connaît sa région réalisable, il ne sait pas quelle sera la décision du suiveur. L'analyse des différentes approches permettant d'attaquer (1.1) - (1.4) dans ce cas de figure fera l'objet du chapitre suivant.

3) Les contraintes du leader sont dites couplées lorsque la fonction contrainte du premier niveau G dépend effectivement de la variable x contrôlée par le suiveur. Rechercher les solutions réalisables qui vérifient ces contraintes en étant compatibles avec la reaction du suiveur est aussi difficile que la résolution du PBN lui même [10].

Nous allons maintenant présenter quelques propriétés caractéristiques des PBN :

1.2 Quelques propriétés des PBN

Propriété 1.2.1. Dans la formulation du PBN (1.1) - (1.4), la position des fonctions contraintes n'est pas arbitraire. En effet, en transférant les contraintes du leader au problème du suiveur, la région réalisable de celui-ci s'en trouve réduite (ou restreinte) ; ce qui peut modifier la solution (si elle existe ) du problème du suiveur, et partant la solution du problème (1.1) - (1.4). Il en est de même si on transfère plutôt les contraintes du suiveur au problème du leader. Nous illustrons cette propriété par cet exemple tiré de [13] :

On considère le PBN linéaire :

(BLP1) :

max

y

y

sujet à : 0 < y < 1

{w:w<y}

x = 0

x E Argmax

w

et le problème : (BLP2) :

max y

y

Genéralités sur la programmation mathématique à deux niveaux 4

sujet à : 0 < y < 1

x E Argmax w

{w : w < y et w = 0}

Les problèmes (BLP1) et (BLP2) ont les mêmes contraintes excepté le fait que la contrainte du premier niveau dans (BLP1) est transféré au deuxième niveau dans (BLP2).

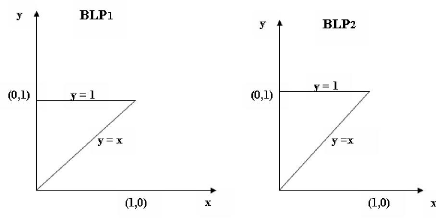
Comme le montre la figure ci-dessous, les deux problèmes ont une même région réalisable.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

FIG. 1.1 Sur les effets du transfert de la contrainte x = 0 du premier niveau dans (BLP1) au second niveau dans (BLP2).

{ }

On a 1 = (0, y) : 0 < y < 1

pour les deux problèmes; mais pour y fixé dans R, on a pour (BLP1) : Ø(y) = {y} tandis que (

{0} si y = 0

pour (BLP2) : Ø(y) = w sinon .

Il s'ensuit que pour (BLP1) la seule solution réalisable et qui s'avère être la solution optimale est y = 0. La solution optimale pour (BLP2) est y = 1.

Propriété 1.2.2. La solution optimale du PBN change en général lorsque l'ordre du jeu

est changé (i.e lorsque le problème du leader est décalé au second plan tandis que le suiveur devient le leader). 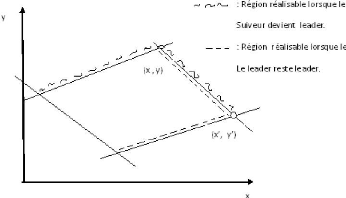Ceci est dû au fait que le problème étant hiérarchique, les deux décideurs ne peuvent prendre leurs décisions simultanément; ce qui signifie que le leader se doit d'anticiper sur le choix du suiveur sous réserve que celui-ci à le droit et la possibilité de choisir une solution optimale sous les conditions posées par les choix du leader [11]. Nous illustrons cet exemple par la figure 1.2 tirée de [11], sur laquelle (x, y) et (x^', y^') représente respectivement la solution

Genéralités sur la programmation mathématique à deux niveaux 5

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

FIG. 1.2 Sur l'importance de l'ordre du jeu

optimale lorsque le i^eme décideur à le premier choix.

Propriété 1.2.3. La solution optimale d'un PBN n'est pas en général indépendante des

{ }

min (x - 1)² + (y - 1)² : x E Ø(y) .

y

contraintes inactives ajoutées au problème du suiveur. L'exemple suivant tiré de [14] illustre bien cette propriété :

Soit le PBN :

{ }

avec Ø(y) = Argmin 0.5x² + 500x - 50xy .

x

{ }

. Ce problème est équivalent à : min (x-1)² +(y -1)² : x+500-50y = 0 . La solution

x, y

unique de ce problème est (x^*, y^*) = (0.82; 10.02) et la valeur optimale de la fonction objectif est F(x^*, y^*) = 81.33.

Ajoutons la contrainte x ~ 0 au problème du suiveur; alors (x^*, y^*) est un point réalisable pour le problème et x^* ~ 0; mais la solution optimale du suiveur est :

₁

50y - 500 si y ~ 0

En introduisant cette fonction dans fonction objectif du leader, on a :

₁

(50y - 501)² + (y - 1)² si y ~ 0

F (x(y), y) =

x(y) = 1 + (y - 1)² si y ~ 10

.

1 + (y - 1)² si y ~ 10

La valeur minimale de cette fonction est 1 et est atteinte en (x^°, y^°) = (0, 1). Une condition nécessaire et suffisante garantissant au PBN l'existence d'une solution optimale globale indépendante par ajout ou suppression de contraintes inactive peut-être trouvé dans [14].

Genéralités sur la programmation mathématique à deux niveaux 6

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Dans toute la suite, nous ne considérerons que les PBN dans lesquels les contraintes du leader ne sont pas couplées ; i.e la fonction contrainte du leader ne dépend pas de la variable du problème du suiveur. Ainsi les contraintes du leader s'écriront : G(y) < 0 au lieu de G(x, y) < 0.

Dans le but de prendre en compte les contraintes du type égalité, les contraintes du deuxième plan seront désormais de la forme g(x, y) < 0 et h(x, y) = 0 où h : 1[8ⁿ x 1[8^m -> 1[8^k

le problème (1.1) - (1.4) devient donc :

{ }

min F(x, y) : G(y) < 0, x E Ø(y) . (1.7)

y

avec Ø(y) = Argmin x

{ } f(x, y) : g(x, y) < 0 et h(x, y) = 0 .

Ø(y) représente l'ensemble des solutions du problème d'optimisation paramétrique :

{ }

min f(x, y) : g(x, y) < 0 et h(x, y) = 0 . (1.8)

x

comme nous l'avons indiqué précédemment, la résolution de (1.7) - (1.8) suppose la résolution au préalable du problème d'optimisation paramétrique que constitue le problème du suiveur (1.8). Par ailleurs, la plupart des méthodes de résolution des PBN exploitent des conditions nécessaires et suffisantes permettant de montrer l'équivalence du PBN à un problème d'optimisation à un niveau classique de la forme :

min y

{F(x(y),y). : G(y) < 0}. (1.9)

Où x(y) représente la solution de (1.8) pour le paramètre y. La résolution de (1.9) nécessite outre la régularité des fonctions F et G, la continuité au moins de la fonction à valeur optimale x : y i-> x(y). Ainsi donc, la résolution d'un PBN est fortement lié à la résolution d'un problème d'optimisation paramétrique.

Dans le paragraphe à venir, nous présentons les résultats d'optimisation paramétrique nécessaires à la résolution des PBN.

1.3 Quelques résultats d'optimisation paramétrique

On considère le problème (1.8) pour y fixé dans 1[8^m ; avec les fonctions f, g et h suffisamment régulières.

On considère l'application M : 1[8^m -> 2' définie par :

{ }

M(y) := x E 1[8ⁿ : g(x, y) < 0 et h(x, y) = 0 pour tout y E 1[8^m.

M(y) est l'ensemble réalisable de (1.8) pour le paramètre fixé y. On défini l'ensemble des minimaux locaux de (1.8) par

{ }

Øloc(y) = x E M(y) : ?E > 0 avec f(x, y) < f(z, y) Vz E M(y) n V_å(x) ;

{ }

où V_å := z E Rⁿ : 11x - z11 < E est la boule ouverte centré en x et de rayon E.

Soit L(x, y, À, u) := f(x, y) + À^Tg(x, y) + u^Th(x, y) , le lagrangien du problème (1.8).

Genéralités sur la programmation mathématique à deux niveaux 7

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

On pose :

{ }

A(x, y) := (À, u) E 1[8^p x 1[8^q : À > 0, À^Tg(x, y) = 0, V_xL(x, y, À, u) = 0

{ }

L'ensemble SP(y) = x E M(y) : A(x, y) =6 0 est appelé l'ensemble des points station-

naires du problème (1.8)

Dans la suite, nous utiliserons abondamment l'assertion suivante :

{ }

(C) : l'ensemble (x,y) E 1[8ⁿ x 1[8^m : g(x, y) < 0, h(x, y) = 0 est non vide et compact

Définition 1.3.1. Soit y0 E 1[8^m, x0 E M(y0)

On dit que lescontraintes de qualification de Mangasarian-Fromowitz (MFCQ) sont satisfaites au point (x0, y0) s'il existe une direction d E 1[8ⁿ satisfaisant :

Vxgi(x0, y0)d < 0 pour tout i E I(x0.y0) := {j : gj(x0, y0) = 0}

Vxhj(x0, y0) = 0 pour tout j = 1, ...., q

}, , q sont linéairement indépendants.

{et les gradients Vxhj(x0,y0) : j = 1

Définition 1.3.2. soit y0 E 1[8^m et x0 E SP(y0)

On dit que les conditions suffisantes d'optimalités forte (SSOC) sont satisfaites au point (x0, y0) si pour tout (À, u) E A(x0, y0) et pour tout d =6 0 satisfaisant :

(i) Vxgi(x0, y0)d = 0 pour tout i E J(À) := {j : Àj > 0}

(ii) Vxhj(x0, y0) = 0 pour tout j = 1, ..., q on a dTV _xxL(x0, y0, À, u)d > 0.

Définition 1.3.3. On dit que les contraintes de constance de rang (CRCQ) sont satisfaites au point (x0, y0) si il existe une boule ouverte centrée en (x0, y0) de rayon e > 0 W_å(x0, y0)

tel que pour tout sous ensembles I Ç I(x0, y0) := {i : gi(x0, y0) = 0} ; J Ç {1, ...., q} , la

{ } { }

famille de gradients V_xgi(x,y) : i E I U Vxhj(x0,y0) : j E J ait le même rang pour tout (x, y) E W_å(x0, y0).

Définition 1.3.4. Une fonction f : 1[8^k -- 1[8 est dite semi-continue inférieurement au point

zn = z on a lim inf n?oo

f(zn) > f(z) .

z E 1[8^k si pour toute suite {zn}^oon°1 Ç 1[8^k avec lim

n?oo

f est dite semi-continue supérieurement au point z E 1[8^k si pour toute suite {zn}oon°1 Ç 1[8^k

avec lim n?oo

zn = z on a lim sup n?oo

f(zn) < f(z) .

Genéralités sur la programmation mathématique à deux niveaux 8

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Définition 1.3.5. Une fonction F : R^k -? 2^Rl est dite semi-continue supérieurement au point z ? R^k si pour tout ensemble ouvert Z avec F(z) ? Z , il existe une boule ouverte centrée en z, Uä(z); 8 > 0 telle que F(z^') ? Z pour tout z^' ? Uä(z).

F est dite semi-continue inférieurement au point z ? R^k si pour tout ensemble ouvert Z avec F(z) n Z =6 Ø , il existe une boule ouverte centrée en z, Uä(z); 8 > 0 telle que F(z^') n Z =6 Ø pour tout z^' ? Uä(z).

Définition 1.3.6. Une fonction F : R^k -? 2^R1 telle que F(y) est non vide et compact pour tout y ? R^k est dite Lipchitz-continue supérieurement en un point z ? R^k si il existe une boule ouverte centrée en z, (Uä(z); 8 > 0) et une constante K < 8 telle qu'on a pour tout z^' ? Uä(z), l'inclusion F(z^') ? F(z) + Kkz - z^'kB^l ; où B^l désigne la boule unité de R^l.

F est dite Lipschtz-continue inférieurement en un point z ? R^k si il existe une boule ouverte centrée en z,( Uä(z); 8 > 0) et une constante L < 8 telles que pour tout z', z^'' ? Uä(z), on a l'inclusion F(z^') ? F(z^'') + Kkz^'' - z^'kB^l.

Définition 1.3.7. L'optimum local x0 ? Øloc(y0) est dit fortement stable s'il existe une boule ouverte centré en y0 (Uä(y0), 8 > 0) , une boule ouverte centré en x0 (V_å(x0), å > 0) et une fonction continue

x : Uä(y0) -? V_å(x0) tel que x(y) soit l'unique optimum local du problème (1.8) dans V_å(x0) pour tout y ? Uä(y0).

Théorème 1.3.1. [16] Soit y0 ? R^m. On suppose que les assertions (MFCQ) et (SSOC) sont satisfaites pour (1.8) en (x0, y0) avec x0 ? Øloc(y0). Alors l'optimum local x0 est fortement stable.

La preuve originale de ce théorème dans [16] utilise une théorie que nous n'avons pas abordé dans ce travail : la théorie du degré. Dans [11], ce résultat est démontré autrement en supposant qu'en plus, ( 1.8) satisfait les contraintes d'indépendance linéaire (LICQ) en (x0, y0).

Définition 1.3.8. On dit que (1.8) satisfait les contraintes d'indépendance linéaire (LICQ) en (x0, y0) si la famille de gradients :

_{n o} [ _{n o}

?xgi(x0, y0), i ? I(x0, y0) ?xhj(x0,y0),j = 1, ..., q est linairement independante.

Où I(x0, y0) := i : gi(x0, y0) = 0

Définition 1.3.9. Une fonction f : Rp -? Rq est dite localement Lipschitz-continue au point x0 ? Rp s'il existe une boule ouverte centré en x0, (V_å(x0), å > 0) et une constante K < 8 tel que

f(x) - f(x^') . = Kkx - x0k pour tout x, x^' ? V_å(x0)

F est dit localement Lipschitz-continue supérieurement en x0 si pour toute boule ouverte centrée en x0 ? V_å(x0), å > 0 et pour une certaine constante K < 8, on a l'égalité :

f(x) - f(x0) = Kkx - x^'k pour tout x ? V_å(x0)

Genéralités sur la programmation mathématique à deux niveaux 9

Définition 1.3.10. Une fonction f : 1[8p -? 1[8q est appelé PC-function (piecewise continuously differentiable function) en x0 s'il existe une boule ouverte centrée en x0 (V_å(x0) , e > 0) et un nombre finie de fonctions continûment différentiables

fi :V_å(x0) -? 1[8^q, i = 1, ..., t

tel que f est continue sur V_å(x0) et f(w) ? {f1(w), ..., ft(w)}. pour tout w ? V_å(x0).

Théorème 1.3.2. [17] Les PC-functions sont localement Lipschitz-continues avec pour constante de Lipschitz la plus grande constante de Lipschitz de la famille de fonction qui définit la PC-function.

La preuve de ce théorème nécessite le lemme suivant :

Lemme 1.3.1. [24]

Soit g : [0,1] -? 1[8p une fonction continue et soit la famille d'ensemble non vide fermé {Ai}qi=1 ? 1[8^m telles que

[ g([0,1]) := x?[0,1]

{g(x)} ?

[ ^qi=1

Ai

alors, il existe une suite de réels {ti}^r+1

i=0 avec t0 = 0, tr+1 = 1, ti < ti+1 ?i et la suite {ji}ri=0

i = 0, ...,r telle que

{g(ti), g(ti+1)} ? Aji i = 0, ..., r.

La preuve de ce lemme ce fait par induction sur le nombre r des différents ensembles Ai pour lesquels il existe des points t tels que g(t) ? Ai. On peut la trouver dans [11].

Preuve (du théorème) :

Soit f : 1[8p -? 1[8q une PC-function. Soit x0 ? 1[8p ; f est une PC-function en x0.

Par définition, il existe une boule ouverte V_å(x0) centrée en x0 de rayon e > 0 et un nombre finie de fonctions continûment différentiables

fi : V_å(x0) -? 1[8^q, i = 1, ..., k

telles que f est continue sur Vå(x0 et

f(u) = {f1(u), ..., fk(u)} ?u ? V_å(x0)

soit x, y ? V_å(x0) Posons :

w(t) = f(x + t(y - x)), t ? [0, 1]

wi(t) := w(t) si fi (x + t(y - x)) = f(x + t(y - x))

x.

_{n o}

Ai = x ? V_å(x0) : fi(x) = f(x) .

Puisque f est continue sur V_å(x0), Ai est fermé.

En effet, soit {xk}k ? Ai une suite de points telle que xk ?

k?+8

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Genéralités sur la programmation mathématique à deux niveaux 10

Il suffit de montrer que x ? Ai. On a :

(xk ? k?+8

x) =f(xk) ? f(x) (car f est continue sur Vå(x0)) k?+8

De même, puisque fi est continue sur V_å(x0), on a

(xk ? k?+8

x) fi(xk) k?+8 fi(x)

Étant donné que xk ? Ai ?k ? N, on a fi(xk) = f(xk) ?k ? N d'où

f(xk) ? f(x) et f(xk) ? fi(x)

k?+8 k?+8

et par unicité de la limite, on a f(x) = fi(x)

d'où x ? Ai. et par suite, Ai est fermé.

D'après le lemme 1.3.1, il existe des points t0 = 0 < t1 < ... < t_r < tr+1 = 1 tels que :

w(ti), w(ti+1) ? Ajz, i = 0, ..., r (i)

on a

f(y) - f(x) 1 1 = 1 lw(1) - w(0)Il=

r i=0

w(ti+1) - w(ti)

=

r i=0

wjz(ti+1) - wjz(ti)

(d'après (i))

r = E i=0 r = E i=0

wjz(ti+1) - wjz(ti)11 fjz (x + ti+1(y - x) - fjz(x + ti(y - x) 11

r = E i=0

Kjz x - ti+1(y - x) - ti(y - x) (car fjz est lip sur Vå(x0))

r = E i=0

Kji (ti+1 - ti)(y - x)

= max 1=j=k

Kjzky - xk

r i=0

|ti+1 - ti|

= Kky - xk

Où K = max j

Kjz est la plus grande constante de lipschitz des fonctions fi, i = 1, ... , k

Donc f est localement lipschitzienne.
·

L'intérêt des PC-function est qu'elles possèdent un grand nombre de propriétés qui sont d'une grande utilité dans l'optimisation paramétrique. Nous allons maintenant définir la notion de gradient généralisé au sens de Clarke.

Définition 1.3.11. Soit f : Rp -? R une fonction localement Lipschitz- continue. Le gradient généralisé au sens de Clarke de f en x0 est défini par :

?f(x0) = convn lim _k?8 ?f(xk) : k J

xk = xo, V f (xk) existeVk ?

00

où conv désigne l'enveloppe convexe.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Genéralités sur la programmation mathématique à deux niveaux 11

Théorème 1.3.3. [11] Soit f : 118p -> 118 une PC-function alors

_{n o}

?f(x0) = conv ?fi(x0) : x0 E cl int supp(f, fi)

où supp(f, fi) = {x : f(x) = fi(x)} ; cl int supp(f, fi) est l'adhérence de l'intérieur de l'ensemble supp(f, fi).

La preuve de ce théorème peut être trouvé dans [11]

Définition 1.3.12. Une fonction f : 118p -> 118 est dite différentiable en x0 dans la direction r E 118p si la quantité suivante existe et est finie :

f^0(x0, r) := lim t?o+

[f(x0 + tr) - f(x0)] t

f⁰(x0, r) est la dérivé de f dans la direction r en x0.

Définition 1.3.13. Une fonction directionnellement différentiable f : 118p -> 118 est dite Bouligand-différentiable (B-différentiable) en x0 si la dérivée directionnelle d'ordre 1 de f en x0 ; i.e

lim

x?x0

= 0

f(x) - f(x0) - f⁰(x0, x - x0)

kx - x0k

. Une fonction f localement Lipschitz-continue, directionnellement différentiable est B-différentiable

[20] et f⁰(x0, .) est une sélection continue de fonction linéaires :

_{n o}

f⁰(x0, r) E ?fi(x0)r : i E Io f(x0)

_{n o}

où Io f(x0) = i : x0 E supp(f, fi)

Définition 1.3.14. Une fonction f : 118p -> 118 est dite pseudodifférentiable en x0 si il existe une boule ouverte centrée en x0, (V_å(x0), å > 0) et une fonction semi-continue supérieurement Pf : V_å -> 2^Rp avec Pf(y) non vide, convexe et compact pour tout y E V_å(x0) telles que

f(x) = f(x0) + g(x - x0) + o(x, x0, g) Vx E V_å(x0)

où g E Pf(x) et lim ^o(xk,x0,gk)= 0 Pour toute suite {xk}k _i , {gk}k ₁ avec lim xk = 0, gk E

k?0 kxk-x_ok -- _k--

Tf(xk)

.

Le théorème suivant est fondamental en ce sens qu'il permet de transformer (1.7)-(1.8) en un problème d'optimisation à un niveau.

Théorème 1.3.4. Considèrons le problème (1.8) en y = y0 et supposons que les assertions (MFCQ), (SSOC), et (CRCQ) sont satisfaites en un point stationnaire x0 E sp(y0). alors x0 est fortement stable et l'unique fonction x(y) avec {x(y)} = Øloc(y) n V_å(x0) est une PC-function.

La preuve de ce théorème nécessite des notions que nous n'avons pas jusqu'ici abordées ; elle peut être néanmoins trouvée dans [11].

Le corollaire suivant découle des propriétés des PC-functions.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Genéralités sur la programmation mathématique à deux niveaux 12

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Corollaire

Sous les hypothèses du Théorème 1.3.4 on a que la solution optimale locale x(y) est

? Localement Lipschitz-continue de jacobien généralisé au sens de Clarke donné par :

{ }

Ox(y0) = conv Vxi(y0) : i E Io x(y0)

? Directionnellement différentiable avec

{ }

x^'(y0, r) = Vxi(y0)r : i E Io x(y0)

? B-différentiable

? Pseudodifférentiable de différentielle

{ }

_x(y0) = conv Vxi(y0) : i E I_x(y0)

Nous allons maintenant présenter quelques conditions sous lesquelles le problème (1.7)-(1.8) admet une solution locale ou globale. Nous ne traiterons dans le paragraphe suivant par soucis de clarté de notre exposé , que le cas où le problème du suiveur (1.8) admet une solution pour chaque paramètre y ; le cas de la non unicité qui constitue le coeur de notre travail sera traité au chapitre suivant.

1.4 Conditions d'optimalités

1.4.1 Cas des PBN linéaires

Définition 1.4.1. Un PBN est dit linéaire si toutes les fonctions contraintes et les fonctions objectifs du leader et du suiveur respectivement sont linéaires. La formulation générale d'un PBN linéaire est la suivante :

{ }

min < d1,x > + < d2,y >: A3y = b,y = 0,x E Ø(y) . (1.10)

y

avec Ø(y) = Argmin x

{ } < c,x >: A1x < a - A2y,x = 0 où x E IIB^n,y E IIB^ma E IIBp,b E IIB^let

les matrices A1, A2,A3 ainsi que le vecteur c sont de dimensions appropriées. Ø(y) est l'ensemble des solutions du problème du suiveur donné par :

{ }

min < c,x >: A1 < a - A2y,x = 0 (1.11)

x

Définition 1.4.2. Une fonction : IIBp -? 2^Rq est dit polyédrique si son graphe

{ }

grph() := (x, y) E IIBp x IIBq : x E (y) s'écrit comme réunion finie d'ensemble convexes

polyédriques.

Un ensemble convexe polyédrique est une intersection finie de démi-espaces [15].

Théorème 1.4.1. La fonction

Ø(.) : IIB^m -? 2Rn

y H Argmin x

{ } < c, x >: A1x < a - A2y, x = 0 est polyédrique.

Genéralités sur la programmation mathématique à deux niveaux 13

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Corollaire

{ }

(x,y) : A1 + A2 < a, A3y = b, x > 0, y > 0

Si le problème (1.11) admet une solution unique pour chaque paramètre y, alors le problème (1.10) - (1.11) admet une solution optimale qui est le sommet du polyèdre que constitue l'ensemble

.

Si le problème du suiveur admet une solution unique pour chaque paramètre y alors, ces solutions définissent une application y i- " x(y) linéaire ; le PBN se reformule de la façon

suivante :

Preuve :

{ }

min < d1, x(y) > + < d2, y >: A3y = b, y > 0 y

ce qui est un problème de programmation linéaire simple dont on sait que la solution optimale est atteinte sur les sommets du polyèdre que constitue l'ensemble des contraintes.
·

1.4.2 Cas général

Définition 1.4.3. On suppose que card Ø(y) = 1 pour tout y E Y . On appelle fonction à valeur optimale la fonction

? : 1[8^m - " 1[8ⁿ

{ }

y i- " ?(y) = Argmin f(x, y) : g(x, y) < 0 et h(x, y) = 0

x

On convient de noter ?(y) = x(y) pour tout y E Y .

Théorème 1.4.2. Si les assertion (C), et (MFCQ) sont satisfaites, alors la fonction ø(.) est semi-continue supérieurement et la fonction à valeur optimale ?(.) est continue.

Ce theorème est démontré dans [11]

Théorème 1.4.3. On considère le PBN (1.7) - (1.8) et on suppose que les assertions (C) et (MFCQ) sont satisfaites en tout point (x, y) E 1[8ⁿ x Y , avec x E M(y) ; on suppose en plus que R =6 0 et que card Ø(y) = 1 pour tout y E Y . Alors le PBN admet une solution optimale globale.

Preuve :

Puisque card Ø(y) = 1 pour tout y E Y le problème (1.7) - (1.8) est équivalent au problème :

{F(x, y) = F(x(y), y), y E Y}

min . (1.12)

y

où Vy E Y, x(y) = ?(y) est la solution du problème du suiveur. La fonction F est continue et d'après le lemme, ?(.) est continue. D'autre part Y est un fermé borné de 1[8^m donc est compact ; d'où , (1.12) admet une solution optimale globale.

Genéralités sur la programmation mathématique à deux niveaux 14

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

D'autres conditions d'optimalités des PBN peuvent être trouvées dans [11].

Maintenant que nous sommes en possession de quelques résultats nous permettant d'affirmer sous certaines conditions l'existence de solutions globales ou locales du PBN (1.7) - (1.8), il se pose la question de savoir : comment déterminer de façon effective ces solutions ?

1.5 Algorithmes et méthodes de résolution des PBN

La littérature nous propose dans le cas de l'unicité de la solution du problème du suiveur, plusieurs algorithmes permettant le calcul de la (ou des) solution(s) de (1.7) - (1.8). Nous présentons dans ce paragraphe un algorithme inspiré de la méthode de descente connue en optimisation à un niveau et un algorithme dit du paquet.

1.5.1 Algorithme de descente

Si le problème du suiveur admet une solution unique pour tout paramètre y alors (1.7) - (1.8) est equivalent à (1.12).

Supposons que (1.8) est un problème d'optimisation paramétrique convexe et que les assertions (MFCQ), (CRCQ) et (SSOC) sont satisfaites en tout point (x, y) tel que

x E Ø(y), G(y) < 0. Alors, d'après le théorème 1.3.1 l'unique solution optimale de ce problème est fortement stable. Par le théorème 1.3.5 elle est une PC-function et par conséquent la dite solution est localement Lipschtz-continue . Il s'ensuit que la fonction objectif de (1.12) est di-rectionnellement différentiable.

Ce qui motive à envisager un algorithme de descente[11]. La méthode consiste en : étant donné un point réalisable x chercher une direction de descente d E Rⁿ suivant laquelle F(.) décroît. Un nouveau point x + Ed (E > 0) est déterminé de façon à assurer une décroissance raisonnable de F(.) tout en demeurant réalisable pour le PBN. On construit ainsi une suite qui converge vers une solution stationnaire au sens de Clarke.

Définition 1.5.1. Soient f E C(Rp, R) et x E Rp.

1. On dit que d E Rp\{0} est une direction de descente en x s'il existe E_o > 0 tel que

f(x + Ed) < f(x) VE E [0, E0].

2. On dit que d E Rp\{0} est une direction de descente stricte en x s'il existe E_o > 0 tel que f(x + Ed) < f(x) VE E [0, E_o].

Définition 1.5.2. Soit f : Rp -> R une fonction et z E Rp. Si f est localement Lipschtz-continue, z est dit stationnaire au sens de Clarke si 0 E ?f(z) ; si f est pseudodifférentiable, le point z est dit pseudostationnaire si 0 E (z).

Genéralités sur la programmation mathématique à deux niveaux 15

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Algorithme de descente

Entrée : Les paramètres du PBN (1.7) - (1.8). Sortie : Une solution stationnaire au sens de Clarke.

1. Choisir y⁰ satisfaisant G(y⁰) < 0;

2. Initialiser k := 1

3. Déterminer une direction r^k, 1r^k1 > 1 satisfaisant F(y^k, x^k) < s^k V_yGi(y^k)r^k < -Gi(y^k) + s^k, Z = 1, ..., l et s^k < 0;

4. Choisir un pas de longueur t^k tel que F(y^k + t^kr^k) < F(y^k) + Et^ks^k, G(y^k + t^kr^k) < 0

5. Initialiser x^k+1 := x^k + t^kr^k , déterminer x^k E ø(y^k) ; incrementer k := k + 1;

6. Si un critère d'arrêt est satisfait, arrêter ; sinon aller à l'étape 2.

On se donne en général un critère d'arrêt de la forme x^k+1 - _xk ~< E. De plus, puisque la convergence n'est pas toujours assuré, une règle de base est de fixer le nombre d'itérations maximale K^max.

Sous certaines conditions de régularité, on montre [11] que chaque point d'accumulation de la suite (x^k, y^k) obtenue au moyen de l'algorithme est un point stationnaire de (1.7) - (1.8) au sens de Clarke.

1.5.2 L'algorithme du paquet

On considère le problème (1.8) en y = y0 et on suppose que les assertions (MFCQ), (SSOC) et (CRCQ) sont satisfaites en x0 E SP(y0) . Alors (1.12) est un problème de minimisation d'une fonction Lipschtz-continue.

Nous présentons l'algorithme dans le cas où la contrainte G(y) < 0 est absente.

Soit v(y) le gradient généralisé au sens de Clarke de F ; la méthode du paquet s'inspire de la méthode dite de découpage de plan (cutting plane method) pour la minimisation de fonctions convexes.

Soit {yi}ki=1 ; {zi}ki=1 des points d'essaie et des itérées déjà évalués. La méthode de découpage du plan consiste à minimiser la fonction :

mia _k nv(yi)d + v(yi)(zk - yi) + F(yi)o (1.13)

La direction d qui minimise ce modèle est une direction de descente si y n'est pas un point stationnaire. Mais il s'avère que l'utilisation du modèle (1.13) pour trouver une direction de descente à une vitesse de convergence très lente; c'est pourquoi à (1.13) on ajoute le terme de

régularisation quadratique (2tkjd^T d pour obtenir le modèle

^e1<^rm

1

nv(yi)d - áik > + F(zk) + (2t )dTd (1.14)

-- = J k

Avec áik = F(zk) - v₍yi)₍zk - yi) - F(yi)

La solution optimale d de (1.14) est une direction de descente pour F(y) en y = zk sous réserve que le modèle donne une approximation suffisamment bonne de F(y) dans un voisinage du point non stationnaire zk. Une nouvelle itérée est zk+1 = zk + d est calculée de manière à faire décroître de façon considérable la fonction modèle ; i.e F(zk + d) < F(zk).

Genéralités sur la programmation mathématique à deux niveaux 16

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Si dans le voisinage de zk la direction de descente n'est pas assez bonne, alors aucune nouvelle itérée n'est calculée mais les nouveaux points d'essaie yk+1 et zk seront utilisés pour rechercher une nouvelle direction de descente dans (1.14) après ajout d'un gradient généralisé ?..F(yk+1).

Algorithme du paquet

Entrée : Suite d'itérée {zi}k _i=1 et des points d'essaie {yi}k _i=1, le paramètre de régularisation tk

Sortie : Une meilleure itérée zk+1 ou un modèle amélioré.

1. Calculer une solution optimale dk de (1.14); initialiser : yk+1 := zk + dk

2. Si ..F(yk+1) est suffisamment petit comparé à ..F(zk) alors :

a) Agrandir tk et retourner à 1 ou

b) Poser zk = yk+1 . Si ..F(yk+1) n'est pas suffisamment petit comparé à ..F(zk) alors

c) réduire tk et retourner à 1 ou

d) poser zk+1 = zk calculer v(yk+1) E ?..F(yk+1)

Il existent plusieurs critères pour le choix de tk à l'étape 2; ils peuvent être trouvés dans [11].

Pour terminer ce chapitre , nous allons présenter quelques unes des nombreuses applications de la PBN.

1.6 Les applications de la PBN

1.6.1 Production agricole , production de biocarburant

Nous présentons ici un modèle qui nous a été inspiré par la lecture de [18] et dont la résolution permettrait non seulement d'augmenter la production agricole du Cameroun (jugulant ainsi la crise alimentaire dont est sujet le pays), mais aussi de réduire la pollution de l'air par les gaz d'échappement d'automobiles et la pollution du sol et des eaux par les engrais chimiques.

Gêné dans sa politique de développement par la faiblesse de la production agricole, face à la nécessité de réduire la pollution associé à l'émission des gaz d'échappement des automobiles et la pollution des sols et des eaux par les engrais chimiques, le gouvernement Camerounais décide d'explorer les possibilités afin d'encourager l'industrie pétrochimique à utiliser les produits agricoles pour produire du biocarburant. Différents produits agricoles tels que le tournesol, le soja, les graines de coton, ou l'arachide peuvent être utilisés à cette fin [18]. Mais il s'avère que le coût de production de biocarburant est plus élevé que le coût de production de carburant en utilisant les hydrocarbures. Dans le but d'encourager les industriels à utiliser les produits agricoles, le gouvernement leurs accordent une réduction de taxe suffisante. En contrepartie, l'industrie s'engage à être neutre (i .e à ne pas spéculer sur les prix) et à produire du biocarburant.

Le secteur agricole est représenté par un ensemble d'exploitations agricoles; nous décrivons le modèle pour une seule exploitation agricole; il pourra être facilement généralisé dans le cas de plusieurs exploitations.

L'exploitant peut librement laisser une partie de sa plantation en jachère (au quel cas plus tard cette partie pourra être cultivé sans usage d'engrais chimiques) ou l'utiliser à la production de plantes pour biocarburant. Dans les deux cas, il engrange des revenues sous forme de

Genéralités sur la programmation mathématique à deux niveaux 17

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

prime du gouvernement pour avoir laissé une partie de ses terres au repos ou sous forme de subventions de l'État plus les bénéfices faits après la vente de sa production à l'industrie.

Pour maximiser son profit, le fermier décide par lui même quelle surface de terre il va laisser en jachère, quelle surface il va utiliser pour la culture de plantes destinées à la production de biocarburant et quelle surface utiliser pour la production des autres produits.

Soit xj E IR, x_n E 1[8p, xd E 1[8q respectivement la surface de terre laissée en jachère, utilisée pour la production de produits pour biocarburant et utilisée pour la production des autres denrées. On considère les vecteurs ep = (1, ....,1)^T E 1[8p ; eq = (1, ....,1)^T E 1[8q. (Les entiers p et q representant le nombre de produits agricoles utilisés pour la productions de biocarburants et le nombre de produits destinés à la consommation. Chaque composante des vecteurs x_n et xd representant la surface utilisée pour la culture d'un produit fixé.)

Le problème du fermier consiste à maximiser l'argent qu'il gagne grace à son exploitation :

< pd + u - cd,xd > + < pn + s - cn,xn > + ãxj --* max	(1.15)
xj,xd,xn
< e^p, xn > + < e^q, xd > +xj C t	(1.16)
< e^p, xn > + xj C ó1t	(1.17)
< e^p, xn > + < e^q, xd > C ó2t	(1.18)
xd C t', xn > 0, xd > 0 , xj > 0	(1.19)

Où :

D pn,pd désignent respectivement le vecteur argent gagné par unité de surface cultivé de produits pour biocarburant et le vecteur bénéfice par unité de surface cultivés pour les autres produits.

D s est le vecteur subventions accordées par l'État pour les produits pour biocarburant ; c_n le coût de la production de ces plantes.

D ã est la prime par unité de surface de terre laissée en jachère.

D u est la subvention accordée par unité de surface de terre utilisée à la production d'autres produits ; cd leurs coût de production.

D t est la surface de terre arable que dispose le fermier.

D ó1 et ó2 sont des proportions fixé par le gouvernement.

D (1.15) est la fonction objectif du fermier.

D (1.16) est la contrainte sur la surface de terre arable disponible dans l'exploitation agricole. En effet, on ne peut utiliser que ce que l'on possède.

D (1.17) les restrictions de l'État sur la proportion de terre laissée en jachère ou utilisée à la production de plantes pour biocarburant. Car il faut encourager la production des produits agricole destinées à la consommation.

D (1.18) les considérations agronomique visant à limiter la surface de terre cultivé (pour éviter

Genéralités sur la programmation mathématique à deux niveaux 18

la pollution du sol).

D La première inégalité de (1.19) représente la contrainte sur certaines denrées qu'on ne veut pas produire au delà de certaines quantités.

Le gouvernement joue le rôle de leader dans ce problème. Son objectif est de minimiser le total des primes et des subventions accordées aux exploitants. Soit k_r le vecteur volume de biocarburant r, r = 1, ..., w produit par unité de surface ; Soit T_r la réduction de taxe (proportionnelle au volume de biocarburant produit) accordée à l'industrie pour le biocarburant r.

Alors le gouvernement doit résoudre le problème :

Xw r=1

Tr < kr, xn > + ãxj + < ue^q, xd > + < se^p, xn >? « min ô,ã,u,s

» (1.20)

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

< e^p, x_n > < t^' (1.21)

_Xw < k_r, x_n > < H (1.22)

r=1

p_n = p_n(T) > 0, T > 0, ã > 0, u > 0 (1.23)

où x_n, xj, x_c résolvent(1.15) - (1.19) (1.24)

Où

D t^' et H sont des données fixés par le gouvernement

D (1.20) est la fonction objectif du gouvernement

D (1.21) est la contrainte sur la surface de terre utilisé pour la production de biocarburant.

D (1.22) la contrainte sur la quantité de biocarburant produit.

D (1.23) traduit la neutralité de l'industrie, le prix du biocarburant est fonction des réductions de taxes T et est fixé une fois pour toute.

Nous obtenons ainsi un PBN. Ce modèle peut être élargie à un problème d'optimisation à trois niveaux en y incluant le problème de l'industrie pétrochimique.

1.6.2 Le problème principal-agent [10]

Ceci est un cas particulier des problèmes de la théorie du principal - agent.

Un décideur appelé le principal engage un autre l'agent pour le représenter dans l'une de ses structures. Les décideurs signent un contrat ou il est consigné que le principal délègue (une partie de) son autorité à l'agent ; en lui donnant ainsi la liberté de choisir ses actions (de façon limitée ou non) en fonction de ses propres objectifs seulement. Ainsi, uniquement dans l'espoir d'atteindre ses objectifs, l'agent cherche à maximiser l'impact de son action a E A en résolvant le problème :

Z max a?A X

G(s(x), ag(x|a)dx .

Genéralités sur la programmation mathématique à deux niveaux 19

Où la fonction d'utilité G : 118 x A -? 118 permet de mesurer la valeur de la rémunération s(x) à recevoir du principal représentant la contrepartie des efforts consentis pour son action a et X est l'ensemble des résultats possibles des actions a E A de l'agent. La densité désignée par la fonction g(x|a) est utilisée pour décrire les probabilités de réalisation des résultats x E X si l'agent mène une action a E A. La remuneration s(x) est payée à l'agent si le résultat x est obtenu. La fonction s : X -? 118 fait aussi partie du contrat signé par les deux parties. Du point de vue du principal, la fonction s représente aussi un ensemble de primes servant à motiver l'agent à agir afin qu'il puissent atteindre ses objectifs. Ainsi, le principal doit choisir cette fonction de façon à approcher son but au maximum. En supposant que le principal utilise la fonction d'utilité H : 118 -? 118 pour mesurer son profit x - s(x) provenant des activités de l'agent et qu'il utilise la même densité g pour évaluer les probabilités requises pour la réalisation du résultat x, il aura besoin pour la réalisation de ses objectifs de résoudre le problème :

msESax J X

H(x - s(x))g(x|a^')dx).

où S désigne l'ensemble de tous les systèmes de remuneration possible et a^' une solution du problème de l'agent pour une fonction fixé s(.). Le modèle obtenu ne saurait être complet sans la condition

_J G(s(x), a^')g(x|a^')dx > c

X

,où a^' résoud le problème de l'agent. Si cette inégalité n'est pas satisfaite, l'agent n'acceptera pas de signer le contrat avec le principal. Cette inégalité représente donc une contrainte que doit respecter le leader. Ce problème peut être résumé par :

max JsES X				H(x - s(x))g(x|a^')dx).
Jsujet : X					G(s(x), a^')g(x|a^')dx > c
a' E Argmin aEA	J X	G(s(x), a)g(x|a)dx).

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

D'autres applications de la PBN peuvent être trouvés dans [11] ou [10].

Conclusion

Nous avons dans ce chapitre donné une présentation générale de la programmation mathématique à deux niveaux et présenté quelques algorithmes de résolution dans le cas de l'unicité de la solution du suiveur. Mais il se trouve que dans la plupart des cas, les problèmes modélisés sous formes de PBN sont tels que le problème du second plan admet plus d'une solution ; ce qui complique considérablement le problème. Dans le chapitre suivant, nous allons présenter les différentes techniques développées pour attaquer les PBN dans ce cas ; ce qui nous permettra par la même occasion de définir la notion de problèmes d'optimisation mal posés.

CHAPITRE DEUX

Non unicité de la solution du problème du

suiveur : les différentes techniques

d'approches.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Dans toute la suite, lorsque nous dirons "cas de la non unicité", ce sera pour dire "cas de la non unicité de la solution du problème du suiveur".

Introduction

Au chapitre un, nous avons présenté quelques résultats d'optimalité et quelques algorithmes de résolution des PBN dans le cas de l'unicité de la solution du suiveur. Il se trouve cependant que dans la plupart des applications, le problème du suiveur n'admet pas une solution unique; d'où la nécessité d'explorer de nouvelles techniques afin de résoudre les PBN dans ce cas plus général.

Les PBN dans le cas de la non unicité font partie d'une classe plus large de problèmes de programmation mathématique : les problèmes de programmation mathématique mal-posés.

Définition 2.0.1. Soit E un espace de Banach reexif, ó une topologie sur E, K un convexe fermé non vide de E et h : K -* R U {+oo}

Le problème de programmation mathématique :

inf v?K

h(v) (2.1)

est dit bien-posé au sens de TIKHONOV (resp bien-posé au sens général) suivant la topologie ó, s'il existe une solution unique u0 à (2.1) et toute suite minimisante ¹ de (2.1) ó-converge vers u0 (resp (2.1) a au plus une solution et toute suite minimisante admet une sous suite qui ó-converge vers la solution unique.)

Un problème de programmation mathématique est dit mal-posé s'il n'est pas bien-posé.

Commençons par présenter la position du problème dans la resolution des PBN dans le cas de la non unicité.

^1Une suite (un)n ? K est appelé suite minimisante si uim n?+8

h(un) = inf h(v). v?K

Par définition de l'infimum, une telle suite existe toujours.

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 21

2.1 Position du problème

Considérons une nouvelle fois le PBN :

«min y		{ } » F(x, y) : G(y) < 0, x E Ø(y) (2.2)
Où	Ø(y) = Argmin x		{ } f(x, y) : g(x, y) < 0, h(x, y) = 0 (2.3)

Pour y fixé, Ø(y) est l'ensemble des solutions du problème.

{ }

min f(x, y) : g(x, y) < 0, h(x, y) = 0 (2.4)

x

F : Rⁿ X R^m -? R, f : Rⁿ X R^m -? R, G : Rⁿ X R^m -? Rp,

g : Rⁿ X R^m -? Rq sont des fonctions suffisamment² régulières.

{ }

Posons Y = y E R^m : G(y) < 0 et supposons que Y est fermé.

Les guillemets dans (2.2) expriment l'incertitude de la définition de (2.2) dans le cas de la non unicité; car lorsque Ø(y) n'est pas réduit à un singleton pour tout y E R^m, le leader se trouve face à un dilemme.

En effet, pour prendre sa décision (qu'il souhaite optimale), le leader doit savoir qu'elle sera la décision du suiveur. Dans le cas où il existe plusieurs décisions possibles pour le suiveur, le leader se trouve dans l'embarras (car il ne sait sur laquelle portera le choix de celui-ci).

La question qu'on se pose ici est celle de savoir : comment aborder le PBN (2.2)-(2.3) dans le cas de la non unicité de la solution de (2.4) ?

L'exemple suivant illustre les difficultés qu'on peut rencontrer dans le cas de la non unicité.

Exemple 2.1.1. On considère le PBN :

«min y					{ } » x^2+ y^2: x E Ø(y), -1 < y < 1
Où Ø(y) = Argmin x On a :			{-xy : 0 < x < 1}
Ø(y) :=	{	{0} si y < 0 {1} si y > 0 [0,1] si y = 0

Ainsi,

F(x(y), y) =

{

y2 si y < 0 1 + y^2si y > 0 E [0,1] si y = 0

. (2.5)

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Le tracé de F est le suivant :

²Suivant les résultats que nous énoncerons, nous exigerons que ces fonctions satisfassent des propriétés de régularité parfois différentes

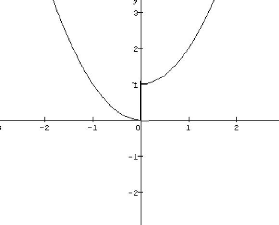
Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 22

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

FIG. 2.1 Sur les difficultés rencontrées dans le cas de la non unicité

pour y = 0; on a W(y) = [0, 1]. Donc pour ce paramètre, W(y) contient une infinité d'éléments. On se trouve donc ici dans le cas de la non unicité.

d'après (2.5), l'expression de la fonction objectif n'est connue que si le suiveur annonce clairement son choix; la solvabilité du problème du leader dépend de ce choix. En effet, si le suiveur fait le choix x(0) = 0 E W(0) alors le problème du leader est solvable; la solution optimale du PBN est (0, 0) et la valeur de la fonction objectif du leader est 0.

{ F (x(y), y) = y² : -1 y < 0 }

min

y

le PBN n'admet pas de solution dans ce cas car F(x(y), y) = y² est dérivable et on a

Si le choix du suiveur se porte sur x(y) = 0 E W(y), avec y < 0 alors le problème du leader devient :

VF(x(y),y) = (0,2y)

VF(x(y),y) = 0 =' y = 0

Or y = 0 ne satisfait pas à la contrainte -1 y < 0 donc le problème du leader n'admet pas de point critique et par conséquent n'admet pas de solution.

Jusqu'ici, trois approches ont été développées dans la littérature pour résoudre les PBN dans le cas de la non unicité : l'approche optimiste, l'approche péssimiste et l'approche par régularisation sur laquelle porte notre travail.

2.2 L'approche optimiste

Cet approche est envisageable dans le cas où le leader à la possibilité de persuader le suiveur de prendre une décision qui lui sera favorable (favorable est compris ici au sens ou la dite décision permet au leader d'atteindre son objectif).

la formulation optimistique de (2.2)-(2.3) est la suivante :

min

y

{ }

?_o(y) : y E Y (2.6)

Où

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 23

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

{ }

?_o(y) = min F(x, y) : x E W(y) (2.7)

x

Définition 2.2.1. Un point (x^*, y^*) E 1[8ⁿx1[8^m est appelé solution optimiste locale de (2.2)-(2.3) si y^* E Y, x^* E W(y^*) avec

F(x^*, y^*) < F(x, y^*) Vx E W(y^*)

et il existe Uä(y^*), 8 > 0 boule ouverte centrée en y^* de rayon 8 telle que

?_o(y^*) < ?_o(y) Vy E Uä(y^*) n Y

(x^*, y^*) est appelé solution optimiste globale si 8 = o0

Énonçons maintenant un théorème d'existence de solution optimiste :

Théorème 2.2.1. Si les assertions (C) et (MFCQ) sont satisfaites en tout points (x, y) E 1[8ⁿ x Y avec x E M(y), alors

Le problème (2.2)-(2.3) admet une solution optimistique globale.

Preuve :

Considérons le problème

{ }

min F(x, y) : y E Y, x E W(y) (2.8)

x,y

Les solutions globales de (2.8) et le problème optimiste (2.4)-(2.6)-(2.7) coincident.

En effet si (x^*, y^*) vérifie (2.8) alors (x^*, y^*) vérifie (2.4)-(2.6)-(2.7).

réciproquement, si (x^*, y^*) vérifie (2.4)-(2.6)-(2.7) alors par définition de solution optimiste globale, on a :

F(x^*, y^*) < F(x, y^*) Vx E W(y)

et

?_o(y^*) < ?_o(y) Vy E Y

{ }

F (x^*, y^*) < F (x, y^*) Vx E W(y^*) = F (x^*, y^*) < min F (x, y^*) : x E W(y^*)

x

Or

{ } { }

?_o(y^*) < ?_o(y)Vy E Y ? min F(x, y^*) : x E W(y^*) < min F(x, y) : y E Y, x E W(y)

x x

{ }

Ce qui implique que min F(x, y^*) : x E W(y^*) < F(x, y) Vy E Y, Vx E W(y)

x

d'où F(x^*, y^*) < F(x, y) Vy E Y, Vx E W(y) autrement dit,

(x^*, y^*) E Argmin x,y

{ } F(x,y) : y E Y,x E W(y)

donc (x^*, y^*) est optimum global de (2.8).

D'autre part, puisque les assertions (C) et (MFCQ) sont satisfaites, la fonction à valeur optimale

(voir définition 1.4.4) est continue ; ce qui permet de montrer que l'ensemble

{ }

(x, y) : x E W(y) est fermé. D'autre part, étant donné que Y est fermé, l'assertion (C) nous

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 24

.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

garanti que l'intersection de {(x, y) : x E Ø(y)} avec Rⁿ x Y est compact (comme fermé dans un compact).

D'où puisque F est continue sur Rⁿ x R^m, le problème (2.8) admet un optimum global. En vertu de l'équivalence que nous avons établie entre (2.8) et le problème optimiste, on conclut que (2.4)-(2.6)-(2.7) admet une solution optimistique globale.
·

Exemple 2.2.1. Reconsidérons le PBN de l'exemple 2.1.1 :

« min y		n o » x^2+ y^2: x E Ø(y), -1 < y < 1
Où Ø(y) = Argmin x	n o - xy : 0 < x < 1

Comme trouvé précédemment, on a ?0(y) = minnx² + y² : x E Ø(y)=(1 + y² si y > 0

x

siy < 0

y2

Le problème optimiste s'écrit donc :

_{n o}

min ?0(y) : -1 < y < 1

y

et la solution optimiste globale est (x0, y0) = (0, 0).

L'un des défauts de l'approche optimiste est qu'elle n'est pas envisageable dans la plupart des cas concrets. En effet, en économie par exemple, dans le but de faire régner une concurrence loyale entre des entreprises concurrentes, la législation interdit le plus souvent une quelconque coopération entre les dites entreprises et leurs éventuels clients.

Aussi, dans grand nombre de problèmes modélisés en PBN, le suiveur ne constitue que rarement une personne physique avec qui le leader pourrait envisager une coopération. En plus, même si la coopération est permise, le leader n'a pas de garanti sur le fait que le suiveur respectera ses engagements.

Ceci constitue quelques limites de l'approche optimiste.

2.3 L

'approche pessimiste

Lorsqu'il est impossible au leader d'influencer les choix du suiveur, une décision optimale du leader, étant donné qu'il n'a aucun contrôle sur le problème, est celle qui limite au mieux les dégâts lorsque le suiveur prend des décisions qui lui sont nuisibles.

Mathématiquement, la formulation pessimiste de (2.2)-(2.3) s'écrit :

_{n o}

min ?_p(y) : y E Y (2.9)

y

?p(y) = max x

n o F(x, y) : x E Ø(y) (2.10)

Définition 2.3.1. Un point (x^*, y^*) E Rⁿ x R^m est appelé solution pessimiste locale de (2.2)(2.3) si y^* E Y, x^* E Ø(y^*) avec

F(x, y^*) < F(x^*, y^*) V x E Ø(y^*)

et il existe Uä(y^*), 8 > 0 boule ouverte centrée en y^* de rayon 8 telle que

?_p(y^*) < ?_p(y) Vy E Uä(y^*) n Y

(x^*, y^*) est appelée solution pessimiste globale si 8 = +oo.

Le problème 2.4)-(2.9)-(2.10) est appelée formulation péssimistique de (2.2)-(2.3)).

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 25

Énonçons un théorème d'existence de solution pessimiste.

Théorème 2.3.1. Considérons le PBN 2.4)-(2.9)-(2.10). Supposons que Ø(.) est semi-continue inférieurement (Sci) en tout point de Y et que l'assertion (C) est satisfaite. Supposons que (2.9) admet une solution admissible, alors 2.4)-(2.9)-(2.10) admet une solution optimale globale.

Preuve :

{ }

Posons K = (x,y) ? Rⁿ × R^m : g(x, y) = 0 et h(x, y) = 0 . L'assertion (C) nous garanti que K est compact.

Soit P2 : Rⁿ × R^m -? Rm

(x, y) 7-? y la deuxième projection.

P2(K) n Y est l'ensemble des solutions admissible de (2.9). P2 étant continue, P2(K) est compact ; d'où P2(K) n Y est compact comme intersection d'un fermé et d'un compact.

Montrons que : cp_p est semi-continue inférieurement (Sci).

Soit y0 ? R^m, montrons que cp_p est Sci en y0.

soit _(yk)k?N une suite de R^m telle que (y^k)k -? y0

k?+8

Il suffit de montrer que lim inf cp_p(y^t) = cp_p(y0)

k?+8

i.e

sup

k?N

inf cp_p(y^t) = cp_p(y0)

t=k

On a F(x, y^t) = cp_p(y^t) ?x ? Ø(y^t) d'où

inf

t=k

F(x, y^t) = inf cp_p(y^t) ?x ? Ø(y^t) ?k ? N

t=k

et

F(x, y^t) = sup

k?N

inf

t=k

inf

cp_p(y^t) ?x ? Ø(y^t)

t=k

sup

k?N

i.e

lim inf t?+8

F(x, y^t) = lim inf cpp(y^t) t?+8

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Or F est continue sur Rⁿ × R^m ;

d'où F(x,.) est continue sur R^m ?x ? Rⁿ fixé ; il vient alors que :

lim inf t?+8

F(x, y^t) = lim t?+8

F(x, y^t) = F(x, y0) ?x ? Rn

Donc

liminf cp_p(y^t) = F(x, y0) ?x ? Ø(y0) ? Rn t?+8

d'où

lim inf cp_p(y^t) = max

_x {F(x, y0) : x ? Ø(y0)}

t?+8

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 26

i.e

lim inf ?_p(y^t) > ?_p(y0)

t?+8

Donc ?_p est Sci.

Comme l'ensemble des solution admissibles de (2.9) P2(K) n Y est compact, le problème 2.4)-(2.9)-(2.10) admet un minimum global.
·

Exemple 2.3.1. On considère une nouvelle fois le PBN de l'exemple 2.1.1. La formulation pessimiste de ce problème est :

_{n o}

min ?_p(y) : -1 < y < 1

y

Où

(

2 1+ y² si y > 0

?_p(y) = max{x + y² : x E Ø(y) y

}= si <0

y

avec

Ø(y) =	{	{0} si y < 0 {1} si y > 0 [0,1] si y = 0		.
Où			Ø(y) =			{	[-1,1] si y = 0 {-y - 1} si y > 0 {-y + 1} si y < 0

(x0, y0) = (1, 0) est une solution pessimiste locale et la valeur péssimistique de la fonction objectif est 1.

Mais la résolution des PBN en utilisant l'approche pessimiste présente également des défauts :

En effet les solutions pessimiste sont en général instables, dû [11] au manque possible de semi-continuité de la fonction Ø(.) qui à chaque paramètre du problème du leader associe l'ensemble des solutions du problème du suiveur correspondant.

Ce défaut conduit à deux conséquences majeures :

r Les solutions péssimiste ne sont pas en général de bonnes approximations des solutions réalisables en pratique.

r Une petite perturbation sur les données du problème peut conduire à un changement drastique de la solution du suiveur. Ainsi, si le leader ne résolvait pas son problème réel mais une approximation (ce qui est le cas la plupart du temps), ses solutions peuvent être éloignées des solutions réelles.

Les exemples 2.3.2 et 2.3.3 suivants illustrent bien ces défauts :

Exemple 2.3.2. Considérons le PBN

min

y

{(x - y)² + y² : ?20 < y < 20, x E Ø(y)}

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 27

Pour y = 0; on a Ø(y) = [-1,1] et le problème du suiveur admet pour ce paramètre une infinité de solutions.

Posons F(x, y) = (x - y)² + y² ; en introduisant dans F la solution du suiveur , on obtient :

F(x(y), y) =

{

(-2y - 1)^2+ y^2si y > 0 (-2y + 1)^2+ y^2si y < 0 E [-1,1] si y = 0

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

FIG. 2.2 Fonction objectif du leader la formulation optimiste du problème est la suivante :

min y

n o ?0(y) : -20 < y < 20

Où

_{n o}

?0(y) = min (x - y)² + y² : x E Ø(y)

x

Il est clair que la solution optimiste du problème est (x0, y0) = (0, 0). Le graphe de F nous permet d'ailleurs de confirmer ce résultat.

Une fois de plus, d'après le graphe de F, quelque soit le signe de y, y =6 0 , la fonction F

atteint son infimum lorsque y --* 0 et on a : lim y?0

F(x(y), y) = 1.

Ainsi, la solution réalisable en pratique du problème est atteinte lorsque y --* 0 et la valeur de la fonction objectif est 1; ce qui est bien éloigné de la valeur optimistique qui est 0 .

Exemple 2.3.3. Considérons le PBN

_{n o}

min - x + y² : -0.5 < y < 0.5, x E Ø(y)

y

Où

Ø(y) = Argmin x

{xy^2: -1 < x < 1}

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 28

On a alors

(

{-1} si y =6 0

W(y) =

[-1,1] si y = 0

Pour y = 0, le problème du suiveur admet une infinité de solutions; on est donc dans le cas de la non unicité. La formulation optimiste du problème est :

min

y

{?0(y) : -0.5 < y < 0.5}

Où	n o ?0(y) = min (-x + y^2: x E W(y) x

L'unique solution optimiste est (x0, y0) = (0, 1) ; et la valeur optimiste de la fonction objectif du leader est -1

Supposons maintenant que le problème du suiveur soit perturbé de telle sorte que l'ensemble des solutions du problème du suiveur se réécrivent :

Wá(y) = Argmin x Où á > 0 et suffisamment petit. Posons fá(x, y) = xy^2+ áx^2On a Vxfá(x, y) = y^2+ 2áx

{xy^2+ áx^2: -1 < x < 1}

2

V_xf_á(x,y) = 0 = x = -₂

On a

V2 xxfá(x,y) = 2á > 0

d'où pour y admissible, x = -y2

_2á est solution du problème du suiveur. Ainsi,

(

{-1} si y² > 2á

- y2_2á

2á

si y2 <

W_á(y) =

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

En insérant cette solution dans la fonction objectif du leader, on obtient :

(

F(xá(y), y) = y2 + 1 si y² > 2á

y2 - y2

_2á si y² < 2á

Le problème devient donc

n F (xá(y), y) : -0.5 < y < 0 o

min

y

L'unique solution de ce problème est y_á = 0 Vá > 0

Lorsque á --* 0 , la solution du problème perturbé est (0, 0) et la valeur de la fonction objectif tend vers 0; valeur qui est éloigné de la valeur optimiste-1.

Ainsi, la solution optimiste est instable.

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 29

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

L'étude tant du point de vue théorique que numérique d'un problème d'optimisation instable est très difficile. Néanmoins une possibilité d'éviter ce problème d'instabilité existe. Elle consiste à prolonger (une sorte de prolongement par continuité) la fonction W(.) de façon à obtenir une nouvelle fonction W^' : R^m -? 2^R7 continue. D'après les résultats énoncés dans [23], le nouveau problème "réagira" de façon régulière aux perturbations "régulières" (i.e pour de petites perturbations, la solution du problème perturbé ne sera pas éloignée de la solution du problème non perturbé) ; et ainsi, le problème d'instabilité sera résolu.

L'approche pessimiste de résolution des PBN dans le cas de la non unicité à été intensive-
ment étudié par P.Loridan, J.Morgan et leurs Co-auteurs. Dans plusieurs articles, ils étudient le PBN (2.2)-(2.3) dans un cas plus général, en ce sens que les fonctions f, g, h, F, et G qui définissent le problème sont perturbées et la convergence vers un problème non perturbé est étudiée. (voir par exemple les articles [19, 20, 21]). Dans [22], le concept de å-optimalité est utilisé pour régulariser le problème pessimiste.

Malgré tous ces résultats, certains problèmes demeurent :

? l'approche optimiste est très peu souvent envisageable;

? les solutions péssimistes, même lorsqu'elles sont stables sont le plus souvent éloignées des solutions réelles;

? comment discriminer entre l'approche péssimiste et optimiste? Autrement dit dans une situation donnée, comment savoir quelle approche (optimiste ou péssimiste) est la plus adéquate?

Afin de contourner ces difficultés, il serait préférable pour le leader, non pas de calculer la solution "réelle" optimiste ou péssimiste de son PBN mal-posé qui dans ce cas cours de grands risque d'être instable (donc inutilisable), mais d'en calculer une approximation dans un voisinage des solutions admissibles qui aurait la propriété d'être fortement stable. L'approche par régularisation permet de calculer de telles solutions.

Dans le chapitre suivant, après avoir présenté les différentes techniques de régularisation développées jusqu'ici dans la littérature, nous exposons un algorithme de résolution des PBN dans le cas de la non unicité développé par S.Dempe en 2000 basé sur l'approche par régularisation. Nous-nous pencherons enfin sur l'étude de la convergence de cet algorithme.

CHAPITRE TRIS

Approche de résolution par régularisation

des PBN dans le cas de la non unicité.

Où

(y) = Argmin

x

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Soit le PBN :

\ min y

{ } » F (x, y) : y ? Y, x ? (y) (3.1)

{ }

f(x, y) : g(x, y) = 0, h(x, y) = 0 (3.2)

Y est un fermé deR^m

F : Rⁿ × R^m -? R, f : Rⁿ × R^m -? R
g : Rⁿ × R^m -? R^q, h : Rⁿ × R^m -? Rk

Nous voulons résoudre (3.1 - 3.2) dans le cas où le problème du suiveur

{ }

min f(x, y) : g(x, y) = 0, h(x, y) = 0 (3.3)

x

n'admet pas une solution unique.

Au chapitre deux, nous avons vu qu'on peut pour ce faire utiliser l'approche optimiste ou l'approche pessimiste; mais il nous a été donné de constater que ces deux approches présentent de graves défauts dont certains (par exemple le problème d'instabilité de la solution) peuvent être contournés tandis que d'autres, (par exemple le problème d'éloignement de la solution optimiste ou péssimiste de la solution optimale du PBN) n'ont pas encore pu être résolus.

Pour éviter ces défauts, une autre approche a été développée dans la littérature et fait actuellement l'objet de nombreuses recherches : c'est l'approche par régularisation. A ce jour on distingue deux techniques de régularisation : la régularisation de Tykhonov et la régularisation par l'élément de plus petite norme.

3.1 La régularisation de Tykhonov

Cette technique consiste à introduire un paramètre (dit de régularisation) dans le problème du suiveur de façon à ce que le nouveau problème (le problème du suiveur régularisé) admette pour chaque paramètre de régularisation une solution unique fortement stable. Cette solution unique converge vers une solution du problème du suiveur original lorsque le paramètre de régularisation tend vers zéro (sous l'hypothèse que les fonctions qui définissent le problème

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 31

satisfont certaines conditions de régularité).

Par cette technique, la solution obtenue est une approximation de la solution du PBN original, mais qui a l'avantage d'être stable et qui parfois est même meilleure que la solution optimiste ou péssimiste.

Lemme 3.1.1. Si le problème du suiveur (3.3) est convexe, (i.e les fonctions f(. , y), gi(. , y) i = 1, ... ,p sont convexes et les fonctions hj(. , y) j = 1, ... ,q sont affines linéaires sur Rⁿ pour y fixé dans R^m.)

Si en plus F(., y) est strictement convexe pour y fixé dans R^m, alors :

(i) la fonction f(. , y) + áF(. , y) est strictement convexe Vá > 0 Vy E R^m ;

(ii) le problème

{ }

min f(x, y) + áF(x, y) : g(x, y) < 0, h(x, y) = 0 (3.4)

x

admet une solution unique pour tout á > 0 tel que l'ensemble des solutions admissibles de (3.4) est non vide.

preuve :

(i) Montrons que f(. , y) + áF(. , y) est strictement convexe Vá > 0 Vy E R^m. Soient y E R^m , á > 0, x, z E Rⁿ, t E [0, 1]

on a :

f(tx + (1 - t)z, y) < tf(x, y) + (1 - t)f(z, y) (car f(. ,y) est convexe)

~áF(tx + (1 - t)z, y) < á~tF(x, y) + (1 - t)F(z, y) (car F(. ,y) est strictement convexe ) < átF(x, y) + á(1 - t)F(z, y).

d'où

f(tx+(1-t)z, y)+áF(tx+(1-t)z, y) < t(f(x, y)+áF(x, y))+(1-t)(f(z, y)+áF(z, y)) Donc f(., y) + F(., y) est strictement convexe.

(ii) Soit á > 0 tel que l'ensemble des solutions admissibles de (3.4) est non vide.

Montrons que (3.4) admet une solution unique ;

Supposons que (3.4) admet deux solutions distinctes {x(y)}et{z(y)}. g étant convexe et h affine linéaire, pour y fixé dans R^m, 2x(y) + 2z(y) est une solution admissible de (3.4). En effet,

g (¹x(y) + ₂z(y),y) ~ ₂g(x(y),y) +¹₂g(z(y),y) ~ ₂.₀+ ¹₂.0 = 0

h (x(y) + ₂z(y),y) = ₂h(x(y),y) + ₂h(z(y),y) = ₂.0+ ¹₂.0 = 0

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 32

Puisque f(. , y) + áF(. , y) est strictement convexe,

f (x(y) + ₂z(y), y + áF (2x₍y) + 2z(y), y) < 2 (f(x(y), y) + áF(x(y), y))+

1 ~f(z(y), y) + áF(z(y), y)

2

<

2min { f(x, y) + áF(x, y) : x E M(y)}+

x

1

2

{ }

min f(x, y) + áF (x, y) : x E M(y)

x

{ }

< min f(x, y) + áF (x, y) : x E M(y)

x

ce qui est absurde.

Si les assertion du theorème1.3.1 sont satisfaites, alors

Øá(y) = Argmin x

{ } f(x, y)+áF(x, y) : g(x, y) < 0 , h(x, y) = 0 est semi-continue supérieurement.

La régularisation de Tykhonov consiste à remplacer le problème (3.1)-(3.2) par :

{ }

min F(x, y) : y E Y, x E Ø_á(y) (3.5)

y

Où

Øá(y) = Argmin x

{ } f(x,y) + áF(x,y) : g(x,y) < 0 ,h(x,y) = 0 (3.6)

F : 1[8ⁿ x 1[8^m -? 1[8 est strictement convexe par rapport à la première variable; f : 1[8ⁿ x 1[8^m -? 1[8 ainsi que toutes les fonctions composantes de g : 1[8ⁿ x 1[8^m -? 1[8^p sont convexes par rapport à la première variable; h : 1[8ⁿ x 1[8^m -? 1[8^kest affine linéaire sur 1[8ⁿ par rapport à la première variable. Le problème du suiveur régularisé est défini par :

min

x

{ }

f(x,y) + áF(x,y) : g(x, y) < 0, h(x, y) = 0 (3.7)

L'idée d'utiliser cette méthode est due à A.N.Tykhonov [25]. On a le résultat suivant :

Théorème 3.1.1. Si les assertions (C), (MFCQ) sont satisfaites pour (3.5)-(3.6) en y = y° et si V _xxF(x, y) est définie positive en tout point (x, y), alors :

(i) l'unique solution optimale x_á(y) E Ø_á(y) est fortement stable pour tout á > 0 et est directionnellement différentiable.

(ii) Pour tout á > 0, on a les inégalités suivantes :

F(xá(y), y) < min { }

F (x, y) : x E Ø(y)

x

f(xá(y), y) > ?(y) = min { }

f(x, y) : g(x, y) < 0, h(x, y) = 0

x

(iii) Pour y fixé dans 1[8^m ,

{ }

lim ~x_á(y)~ = Argmin F(x, y) : x E Ø(y)

á?)+ x

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 33

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Preuve :

On se place sous les hypothèses du théorème.

(i) Puisque (3.4) est un problème d'optimisation paramétrique convexe et que V _xxF(x, y) est définie positive, les conditions du théorème 1.3.1 sont satisfaites [26] ; d'où x_á(y) est fortement stable pour tout á > 0 et est directionnellement différentiable.

(ii) On a g(xá(y), y) < 0 et h(xá(y), y) = 0

d'où

f(xá(y), y) >_ min {f(x,y) : g(x, y) < 0, h(x, y) = 0} = ?(y).

Montrons que F(xá(y), y) < min { }

F (x, y) : x E Ø(y)

x

Supposons que

F(xá(y), y) > min { }

F (x, y) : x E Ø(y)

x

alors

x E Ø(y) = {?(y), y E R^m} : F(xá(y), y) > F(x, y)

d'où

?y0 E IIB^m : áF (x_á(y0), y0) > áF (?(y0), y0) (car á > 0)

Or on a

f(xá(y), y) >_ ?(y) Vy E 118^m

donc

f(x_á(y0), y0) + áF(x_á(y0), y0) > ?(y0) + áF(x, y0) ce qui contredit le fait que x_á(y) E Ø_á(y).

(iii) D'après (ii), on a F(xá(y), y) < min { }

F (x, y) : x E Ø(y)

x

Puisque F est continue, on a :

lim

á?0+

d'où

F(xá(y), y) = F (áli _ô+ xa(y), y) = min {F(x, y) : x E Ø(y)}

x

{ }

lim ~x_á(y)~ = Argmin F (x, y) : x E Ø(y)
·

á?0+ x

L'assertion (iii) de ce théorème peut être interprétée comme suit : pour y fixé dans R^m, lorsque á tend vers 0⁺, l'unique solution du problème du suiveur régularisé par la méthode de Tykhonov converge vers la solution du problème original du suiveur, qui permet au leader de minimiser sa fonction objectif.

Ainsi, {x_á(y)} tend (lorsque á --* 0⁺) vers la solution du problème du suiveur recherchée dans l'approche optimiste. L'avantage ici est que x_á(y) est fortement stable et même lorsque l'approche optimiste n'est pas envisageable, cette approximation de la solution du PBN pourra être atteinte.

En utilisant le concept de å-optimalité, S.Addoune dans [27] énonce une autre version du théorème précédent. Avant d'y arriver, Commençons par définir la notion de solution å-optimale.

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 34

Définition 3.1.1. Soit e > 0

Une solution e-optimale du problème du suiveur (3.7) est un élément de l'ensemble

{ }
Tá,E(y) := x E M(y) : f(x, y) + áF(x, y) < ?_á(y) + e

Où M(y) est l'ensemble des solutions admissible de (3.7) et

{ }

?_á(y) := min f(x, y) + áF (x, y) : x E M(y)

x

Théorème 3.1.2. Soit á > 0 , e > 0

Si l'assertion (C) est satisfaites pour le problème du suiveur (3.4), alors il existe une constante c telle que

Tá,E(y) C _T0,E+ác(y) pour tout y E Y

Preuve :

{ }

D'après (C) K = (x, y) E Rⁿ x Y : x E M(y) est compact. Puisque F est continue, il existe des réels b et c tels que

b < F(x, y) < b + c V(x, y) tels que y E Y et x E M(y)

Ceci implique que

f(x, y) + áF(x, y) > ?(y) + áb V(x, y) tels que y E Y et x E M(y)

{ }

Où ?(y) = ?0(y) = min f(x, y) : x E M(y) .

x

Soit x E _Tá,E(y) alors,

f(x, y) + áb < f(x, y) + áF(x, y) < ?á(y) + e (par definition de Tá,E(y))

i.e

f(x,y) + áb < min

x

< min

x

{ }

= min f(x, y) : x E M(y) + á(b + c) + e

x

{ }

f(x,y) + áF(x,y) : x E M(y) + e

{ }

f(x,y) + á(b + c) : x E M(y) + e

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

d'où

f(x, y) < ?(y) + ác + e

i.e x E T0,E+ác(y) donc

Tá,E(y) C _T0,E+ác(y) pour tout y E Y

Dans le théorème précédent, _T0,E+ác(y) représente l'ensemble des solutions (e+ác)-optimale du problème du suiveur original pour le paramètre fixé y, donc plus rigoureusement, on devrait écrire _TE+ác(y) au lieu de T0,E+ác(y).

Le théorème que nous allons à présent énoncer permet de comparer la solution du problème régularisé et celle du problème original.

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 35

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Théorème 3.1.3. Si les hypothèses du théorème 3.1.2 sont satisfaites, alors pour tout x ? Wá,å(y), y ? Y on a :

min {F(x, y) : x ? W(y)} + a = F(x, y) = min {F(x, y) : x ? W0,å+ác(y)}

x x

Ceci implique que :

et

x,y

min {F(x, y) : x ? W(y)} + á = min {F(xá,å(y), y) : x ? W(y)} y
min {F(x_á,å(y),y) : x ? W(y)} = min {F(x, y) : x ? W0,å+ác(y), y ? Y}

y x,y
Où xá,å(y) ? W0,å+ác(y) ?y

Preuve :

Soit y ? Y, x ? Wá,å(y) alors,

{ } {F(x(y), y) : x ? W0,å+ác(y)}

F(x, y) = min F(x, y) : x ? Wá,å(y) = min

x y

(car Wá,å(y) ? W0,å+ác(y) pour tout y ? Y )

D'autre part, on a par définition :

{ }

f(x, y) + áF(x, y) = ?_á(y) + å = min f(x, y) + áF(x, y) : x ? M(y) + å

x

= min

{} + å (carW(y) ? M(y)) f(x,y) + áF(x, y) : x ? W(y) { }

x

= min

x

= ?(y) + min

x

= f(x, y) + á min

?(y) + áF(x,y) : x ? W(y) + å

{ }

áF(x,y) : x ? W(y) + å

{ }

x

d'où donc

F(x, y) : x ? W(y) + å

F(x, y) = min {F (x, y) : x ?Ø(y)} + a

min {F(x, y) : x ? W(y)} + a = F(x, y) = min {F(x, y) : x ? W0,å+ác(y)}

x x

En prenant le minimum de chaque membre de ces inégalités, on obtient la dernière implication du théorème.
·

Le corollaire suivant découle de la dernière implication du théorème 3.1.3 :

Corollaire 3.1.1. Sous les hypothèses du théorème 3.1.2, si á?0⁺å?0⁺tel que ^å_á?0, alors

{ } { }

min F(x, y) : x ? Wá,å(y) -? min F(x,y) : x ? Ø(y)

x x

et	{ } { } min F(x, y) : x ? Wá,å(y), y ? Y -? min F(x,y) : x ? W(y), y ? Y x,y x,y

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 36

Notons que les assertions du théorème 3.1.1 ne sont pas toujours vérifiés lorsque simultanément on fait tendre á vers 0⁺ et y vers y⁰. L'exemple 3.1.1 illustre ce fait :

Exemple 3.1.1. Soit le PBN

_{n o}

y

min (x - y)² + y² : -20 < y < 20, x E Ø(y)

Où	Ø(y) = Argmin nxy : -y - 1 < x < -y + 1o x

Le problème régularisé correspondant par la méthode de Tykhonov est :

_{n o}

min (x - y)² + y² : -20 < y < 20, x E Ø_á(y)

y

où

Øá(y) = Argmin x

n o xy + á(x - y)^2+ áy^2: -y - 1 < x < -y + 1

Posons

F(x, y) = (x - y)²
f(x, y) = xy

f_á(x, y) = xy + á(x - y)² + áy²

On a

V2 _xxF(x, y) = 2 > 0 d'où F est strictement convexe.

V²_xxf(x, y) = 0 d'où f est convexe.

Donc le problème régularisé admet une solution unique pour chaque paramètre de régularisation.

On a

V_xf_á(x, y) = y + 2á(x - y) = 2áx + y(1 - 2á) V_xf_á(x,y) = 0 ~x = y(1 - 2a)

Dont le seul point critique est x = y(1 - 12á), pour á fixé. posons 0 < á < 41

-y - 1 < x < -y + 1 ~-y - 1 < y(1 -21á) < -y + 1

?	2á	< y <	2á
	4á - 1		4á - 1

Si y > - 2á

4á-1^,

alors puisque 0 < á < ¹₄, y>0

on a

Argmin

x

nxy + á(x - y)² + áy² : -y - 1 < x < -Y+11=--Y-- 1

y+1}=--y-1

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Si y < 2á

4á-1 alors y < 0 d'où

Argmin x

n o xy + á(x - y)^2+ áy^2: -y - 1 < x < -y + 1 = -y + 1

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 37

donc pour 0 < á < ^14, Pour y = 2á, on a

xá(y) =

{

- y - 1 si y > - 2á 4á-1 y(1 - 1 2á) si ^2á 4á-1 = y = - 2á 4á-1 - y + 1 si y < 2á 4á-1

2á

= y =

2á

4á - 1

4á - 1

d'où x_á(y) = y - y2á = y - 1 Or on a

lim

á?0+

x_á(y) = lim y - 1 = -1 =6 0 = Argmin {x² : x ? Ø(0)}

x

y?0

Malgré ce défaut, la solution du problème du suiveur régularisé est plus régulière que les solutions du problème du suiveur original. En plus {x_á(y)} étant directionnellement différen-tiable, on peut envisager l'application de l'algorithme de descente pour la détermination de la solution du PBN [11].

3.2 régularisation par l'élément de plus petite norme

3.2.1 première méthode

Si la fonction objectif du leader F ne possède pas toutes les propriétés requises pour que puisse être appliquée la régularisation de Tykhonov, une autre méthode dénommée régularisation par l'élément de plus petite norme peut être appliquée.

Cette méthode consiste à prendre comme approximation de la solution du problème du suiveur

{x(y)} = Ø⁰(y) ; (sous réserve que Ø⁰(y) est un singleton)

Où pour tout y ? 1[8^m

Ø^0(y) = Argmin x

{kxk : x ? Ø(y)}

Cette technique de régularisation à été utilisée pour la première fois par P.Loridan et J.Morgan en 1992 dans [28] en appliquant une idée de V.F.Solohovic émise en 1970 dans [29].

Mais il se trouve malheureusement que l'utilisation de cette approche ne permet pas de contourner toutes les difficultés rencontrées dans les approches optimiste et péssimiste respec-

tivement. En effet, la fonction Ø^0(.) : y 7? Argmin x

{kxk : x ? Ø(y)} n'est pas en général

semi-continue inférieurement. Ceci peut être observé dans l'exemple suivant :

Exemple 3.2.1. [28] On considère le PBN :

min

y

{ - xy : x ? Ø(y)}

Où

Ø(y) = Argmin {(y - 0.5)x : 0 = x = 1}

x

Ø(y) =

{

{0} si y > 0.5 [0,1] si y = 0.5 {1} si y < 0.5

On a

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 38

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

°(y) ={{0}

si y = 0.5

{1} si y < 0.5

d'où

(

0 si y = 0.5

F(x(y), y) =

-y si y < 0.5

Où {x_á(y)} = Ø^°(y)

L'infimum de F sur [0,1] est égal à -0.5 Pourtant, il n'existe pas de y appartenant à [0,1] tel que F(x(y),y) = -0.5

donc Ø^°(.) n'est pas semi-continue inférieurement.

Il est tout de même possible de contourner cette difficulté. Ceci se fait en utilisant à nouveau le concept de solution å-optimale.

On pose :

Ø^°E(y) = Argmin x

n o kxk : x ? ØE(y)

Où

_{n o}

Ø_E(y) = x ? M(y) : f(x, y) = ?(y) + å

Si le problème (3.4) est convexe, alors Ø_E(y) est réduit à un singleton sous réserve que Ø(y) =6 Ø [11]. On alors note x_E(y) l'unique élément de Ø_E(y).

On a le théorème suivant :

Théorème 3.2.1. [28]

On considère le problème d'optimisation paramétrique convexe (3.3) en y = y^°.

Si les assertions (C) et (MFCQ) sont satisfaites en tout point (x, y^°) avec x ? M(y^°), alors

E?°+

lim x_E(y) = x°(y)

preuve : On a

_{n o n o}

x ? M(y) : f(x,y) = ?(y) ? x ? M(y) : f(x,y) = ?(y) + å ?å > 0

i.e

Ø°(y) ? Ø_E(y) ? å > 0

ainsi

x°(y) ? Ø_E(y)

d'où

x_E(y) = min kxk, x ? Ø_E(y) = x°(y) < +8, ? å > 0

x _{n o}

Donc la suite {x_E(y)}_E est borné et par conséquent admet un point d'accumulation x.

Ainsi, la suite {x_E(y)}_E admet une sous suite que nous notons encore {x_E(y)}_E qui converge vers x

Or

x_E(y) ? M(y) et f(xE(y), y) = ?(y) + å ?å > 0

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 39

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

d'où lorsque å ? 0⁺, x ? M(y) et f(x, y) = ?(y) i.e

x ? Ø0(y) = Ø(y)

Par ailleur, on a i.e

kxk = lô å

Ilxå(y) Ilx0(y) Il

kxk = Ilx0(y) avec x, x0(y) ? Ø(y)

d'où x = x0(y) par unicité de l'élément de plus petite norme de Ø(y) = Ø0(y) (grace à la convexité du problème (3.3))
·

Ainsi, le PBN régularisé par la méthode de la plus petite norme s'écrit :

_{n o}

min F (x_å(y), y) : y ? Y

y

Où {xå(y)} = Argmin x		n o kxk : x ? Øå(y) ,å > 0
Posons	S = {(x,y) : y ? Y, x ? Ø(y), F(x, y) = inf ?p(z) }

Où

_{n o}

?_p(z) = max F (x, z) : x ? Ø(z)

x

S est l'ensemble des solutions admissibles du problème du leader qui sont plus bonnes que la solution péssimistique du PBN (3.1)-(3.2). On l'appelle ensemble des sous-solutions optimales de (3.1)-(3.2).

On a le résultat suivant :

Théorème 3.2.2. [28]

On suppose que le problème du suiveur (3.3) est convexe et que les assertions (C) et (MFCQ) sont satisfaites en tout point (x, y), x ? M(y) et y ? Y .

Pour toute suite (å^k)_k (å^k > 0 ?k) convergeant vers 0⁺, on considère la suite (y^k)_k tel que

yk ? Argmin y

n o F(x, y) : x ? Ø^0åk(y), y ? Y ?k.

Tout point d'accumulation (x, y) de la suite {xåk(yk), yk}8k=1 est une sous-solution optimale du PBN (3.1)-(3.2) ; i.e (x, y) ? S.

Preuve :

_{n o}

Posons K = (x, y) ? Rⁿ × Y : x ? M(y) ; d'après (C), K est compact.

Soit (x, y) un point d'accumulation de {xåk(yk), yk}k=1 ( qui existe car (xåk(yk), y^k) ? K ?O ;

On veut montrer que (x, y) ? S, i.e F(x, y) = inf z		?p(z).
Supposons que F(x, y) > v = inf z	?p(z).

{x_åk(y^k),y^k}⁸_k=1 admet une sous-suite que nous notons encore {x_åk(y^k),y^k}⁸_k=1 qui converge

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 40

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

vers (x, y). Soit

(F (x, y) - v)

0 < ä <

3

Puisque F est continue,

F (xåk(yk), y^k) -?

k--00 F(x, y)

d'où

~~ < ä

?K1 ? N : k > K1 = ~~F(xåk(yk), y^k) - F(x, y)

= -F(xåk(yk), y^k) + F(x, y) < ä

= F (xåk(yk), y^k) > F(x, y) - ä > 3ä + v - ä

= F(xåk(yk), y^k) > v + 2ä

Puisque K est compact et ?_p semi-continue inférieurement, v est fini et ?z ? P2(K) : v = ?_p(z)

z

z ? P2(K) = ?(z^t) ? P2(K) : z^t -?

t--00

= ?(z^t) ? P2(K) : ?_p(z^t) -??_p(z) = v

t--00

d'où ?t1 ? N : t > t1 = ?_p(z^t) = v + ä.

z^t.

Soit t > t1 fixé. Puisque z^t ? P2(K),

?(v^k)k ? P2(K) : v^k -?

k--00

Soit la suite (u^k)k définie par u^k ? Ø_åk(v^k) ?k

{ }

F(x, z^t) : x ? Ø(z^t)

Soit u un point d'accumulation de (u^k)k (qui existe car (u^k)k ? P2(K)) ; d'après le theorème 3.2.1, u ? Ø(z^t) ;

d'où

F(u, z^t) = ?_p(z^t) = max

x

(u^k)k admet une sous-suite que nous notons encore (u^k)k qui converge vers u ; étant donné que F est continue, on a :

d'où

F(u^k, v^k) -? k--00

F(u, z^t)

?K2 ? N : k > K2 = F(u^k, v^k) = F (u, z^t) + ä = F(u^k, v^k) = ?_p(z^t) + ä

Ainsi pour t > t1 et k > max (K1, K2), on a

F(u^k, v^k) = ?_p(z^t) + ä = v + 2ä < F(x_åk(y^k), y^k)

Ce qui contredit le fait que y^k? Argmin y		{ } F(x, y) : x ? Ø^0åk(y^k), y ? Y .
donc F(x, y) = inf z	?p(z). ·

Ce théorème montre qu'en résolvant le PBN (3.1)-(3.2) en utilisant cette méthode, on aboutit à une solution qui est meilleure que la solution pessimiste.

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 41

3.2.2 Deuxième méthode

Si la fonction objectif du leader ne possède pas les propriétés nécessaires pour l'application de la régularisation de Tykhonov, une autre méthode de régularisation de(3.1)-(3.2) consiste à remplacer le problème du suiveur par :

{ }

min f(x, y) + á11x11² : x E M(y) pour á > 0 (3.8)

x

Soit W_á l'ensemble des solutions de (3.8)pour y fixé; Le PBN régularisé s'écrit alors :

{ }

min F(x, y) : y E Y, x E W_á(y) (3.9)

y

Où

Wá(y) = Argmin x

{ } f(x, y) + á11x11^2: x E M(y) (3.10)

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Des relations entre le problème régularisé (3.9)-(3.10) et le problème original (3.1)-(3.2) sont présentées dans [28].

On a le théorème suivant :

Théorème 3.2.3. Considérons les problèmes (3.3) et (3.8). Si les assertions (C) et (MFCQ) sont satisfaites, alors :

1) Pour toute suite (y^k)k avec y^k E Y Vk et (á^k)k C 1[8+ convergeant vers y et á respectivement, toute suite (x^k)k satisfaisant x^k E W_ák(y^k) V k, admet un point d'accumulation x tel que x E W_á(y)

2)

lim

yk?y ák&0

Pour á = 0, on a :

x_ák(y^k) = x(y)

Sous réserve que W(y) = {x(y)}

Preuve :

1)

xk E W_ák(y^k) Vk = g(x^k, y^k) < 0 et h(xk, y^k) = 0

{ }

= (x^k, y^k)_k C K := (x,y) E 1[8ⁿ X 1[8^m : g(x,y) < 0, h(x, y) = 0

d'après l'assertion (C), K est compact.

Si on note P1(K) la première projection de K sur 1[8ⁿ, puisque P1 est continue, P1(K) est compacte.

(x^k)_k C P1(K) = (x^k)_k admet un point d'accumulation x

montrons que x E W_á(y)

D'après le théorème 1.4.2, W_.(.) est semi-continue supérieurement. (x^k)k admet x comme point d'accumulation implique que (x^k)k admet une sous-suite que nous notons encore (x^k)k qui converge vers x.

xk E W_ák(y^k) Vk = x E W_á(y) (car W_.(.) est semi-continue sup)

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 42

D'après le théorème 1.4.2, x_.(.) est continue d'où

lim

yk?y ákN0

x_ák(y^k) = x(y)
·

Notons qu'en général, sans l'hypothèse Ø(y) = {x(y)} ; on n'a pas

lim yk?y ák&0

xák(y^k) = x(y) ? Argmin x

{ } kxk : x ? Ø(y)

L'exemple suivant illustre ce fait :

Exemple 3.2.2. On considère le problème :

{ }

min xy : x ? [-1, 1]

x

on a

Ø(y) =

{ [-1,1] si y = 0 {-1} si y > 0 {1} si y < 0

Le problème régularisé est

{ }

min xy + áx² : x ? [-1, 1]

x

On a ?_x(xy + áx²) = y + 2áx ?_x(xy + áx²) = 0 ? x = -y2á en plus, ?2 xx(xy + áx²) = 2á > 0

-1 = x = 1 ? -1 = - y = 1

2á

?-2á = y = 2á

donc

{

Ø_á(y) =

{-^y_2á} si y ? [-2á, 2á]

{1} si y = -2á
{-1} si y = 2á

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

la suite (x_ák(y^k))k = (-k) n'admet pas de limite dans [-1,1] lorsque y^k ? 0 et á^k ? 0

{ }

alors que Argmin _x |x| : x ? Ø(0) = {0}

On montre que si (3.3) est convexe, alors pour á > 0 fixé, le problème (3.8) admet une solution unique et le fonction x_á(.) est continue [28]

pour á > 0 fixé et Sous certaines conditions (que nous mentionnerons par la suite) l'unique solution optimale de (3.8) est Lipschitz-continue par rapport à á et y.

Il s'ensuit que le PBN régularisé

min

y

{F_á(y) := F(xá(y), y) : y ? Y} (3.11)

est un problème de minimisation d'une fonction Lipschitz-continue, et par conséquent peut être résolu par un algorithme du paquet.

Nous allons dans la paragraphe qui suit présenter un algorithme développé par S.Dempe [12] qui résoud les PBN dans le cas de la non unicité en se basant sur cette méthode de régularisation.

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 43

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

3.3 Algorithme de résolution d'un PBN dans le cas de la non unicité

Nous allons présenter l'algorithme lorsque le problème du suiveur n'est pas soumis à la contrainte h(x, y) = 0. Le problème du suiveur régularisé est alors donné par

{ }

min f(x, y) + ákxk² : g(x, y) = 0 (3.12)

x

On suppose que les assertions (C), (MFCQ) et (CRCQ) sont satisfaites. Ceci nous garanti que la fonction x_.(.) qui à (á,y) associe la solution de (3.10) pour le paramètre á > 0 et y fixé est une PC-function; et par conséquent est Lipschitz-continue. Le problème consiste donc à minimiser la fonction Lipschitz-continue F_á(y).

3.3.1 La methde du paquet

L'algorithme que nous présentons dans cette section est un algorithme du paquet. Cet algorithme se construit à partir de la méthode du paquet, qui est une généralisation de la méthode de descente (connue en optimisation diérentiable) à des fonctions qui ne sont pas diérentiables, mais au moins Lipschitz-continue.

F(y)

Rappelons qu'une méthode de descente pour la recherche de y telle que F(y) = min

y

consiste à construire la suite _(yn)n vérifiant :

1. initialisation : y0 donné;

2. n^ime itération : on suppose y1, y2, ..., y_n connus;

a) chercher dⁿ une direction de descente stricte en y_n ; i.e chercher dⁿ tel que ? p0 > 0 avec

F(y_n + pdⁿ) < F(y_n) ?p ?]0, p0]

b) prendre yn+1 = y_n + pdⁿ (avec p bien choisi). On a le Lemme suivant :

Lemme 3.3.1. Soit y ? R^m.

Si F ? C¹(R^m, R) et si ?F(y) =6 0; alors w = -?F(y) est une direction de descente stricte en

y.

Preuve :

Soit ? la fonction de R dans R définie par

?(p) = F(y + pw)

Puisque F est C¹,

? ? C¹(R,R) et ?^'(p) = w.?F(y + pw)

.

Supposons que ?F(y) =6 0.

On veut montrer que ?p0 > 0 tel que si p ?]0, p0] alors F(y + pw) < F(y); ou encore que ?(p) < ?(0).

On a

?^'(0) = w.?F(y) = - |?F(y)|² < 0

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 44

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

d'où comme ?^' est continue, il existe ä0 > 0 tel que si ñ E [0,ä0] alors ?^'(ñ) < 0.

Soit ñ E]0, ä0]. Alors f

?(ñ) - ?(0) = J

cp^'(t)dt < 0 (car Vt E]0, ñ], ?^'(t) < 0)

o

donc on a

?(ñ) < ?(0) Vñ E]0, ä0]

Il suffit donc de prendre ñ0 = ä0 pour conclure.
·

Ce lemme nous montre que lors de la minimisation d'une fonction différentiable F, pour trouver une direction de descente stricte en un point y il suffit de considerer la direction

d = -VF(y). Le prototype de l'algorithme de descente pour la minimisation des fonctions différentiables est donc :

Entrée : y0 donné ;

Sortie : la suite (yn)n

On suppose y1, y2, ..., y_n connus ;

a) calculer dⁿ = -VF(y_n)

b) prendre yn+1 = y_n + ñdⁿ (avec ñ bien choisi).

Supposons à présent que F est juste Lipschitz-continue ; alors le gradient de F n'existe pas en tous points y, mais on peut calculer en ces points un gradient généralisé (par exemple le gradient généralisé au sens de Clarke). On montre [30] que si v(y) est le gradient généralisé au sens de Clarke de F en y, alors d = -v(y) n'est pas forcément une direction de descente stricte de F en y.

Dans la méthode du paquet, on commence par calculer le gradient généralisé de F en y; si la direction opposée à celle de ce gradient (d = -v(y)) est une direction de descente stricte, on construit un nouveau point z = y + ñd qui améliore la fonction F.

Sinon on cherche une autre direction de descente. On montre [11] qu'en général, si {yi}ki=1 et {zi}ki=1 sont des points d'éssaie et des itérées déjà évalués, la direction d qui minimise le modèle

max¹

_ik {v(yi)d - áik} + F(zk) + (2t )d^T d (3.13)

1< k

Avec áik = F(zk) - v(yi)(zk - yi) - F(yi) est une direction de descente stricte de F en zk. Nous avons déjà présenté le prototype de l'algorithme du paquet à la section 1.5.1 du chapitre un.

3.3.2 Présentation de l'algorithme

Le principe de l'algorithme est le suivant : pour la valeur fixée á0 du paramètre de régularisation et pour å0 > 0, utiliser l'algorithme du paquet que nous avons présenté au chapitre un pour calculer la solution å0-optimale z⁰ du problème régularisé de paramètre á0 ; ensuite considerer un nouveau paramètre á1 < á0 et å1 < å0 et calculer la solution å1-optimale z¹. Si z1 est meilleure que z⁰, alors z¹ est une itérée; sinon y¹ = z¹ est un point d'éssaie (ce point sera utilisé pour le calcul d'une nouvelle direction de descente en z⁰). Ainsi de suite jusqu'à ce que soit satisfait un certain critère d'arrêt (qui ici portera sur å).

le prototype de cet algorithme est le suivant :

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 45

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

étape1 : Choisir å0, á⁰ et un point de départ z0

initialiser s := 0

étape2 : Avec comme point de départ z^s, calculer en utilisant l'algorithme du paquet une solution ås-optimale z^s+1 du problème (3.11)

étape3 : Poser å^s+1 := ås2 , á^s+1 := ás2 , s := s + 1 et répéter l'étape 1 jusqu'à ce qu'un critère d'arrêt soit satisfait.

On montre [30] que si la valeur de á^s n'est pas très petite, l'étape 2 peut s'effectuer en un nombre fini d'itérations ; ceci est également garanti si la suite _(zs)sEN obtenue en appliquant l'algorithme converge vers un point z où l'unique solution x0(z) du problème du suiveur est fortement stable.

Utilisant ce prototype, K.C.Kiwiel dans [30] construit un algorithme qui consiste en une suite d'applications de l'algorithme du paquet à différents problèmes. Lors de l'utilisation de cet algorithme, les itérées z^s calculées sont réutilisées même lorsqu'elles ne permettent pas d'avoir une décroissance significative de F_á par rapport aux itérées calculées précédemment ; ce qui peut conduire au pire des cas à un recommencement infini de l'algorithme(on dit que l'algorithme boucle).

C'est face à ce défaut de l'algorithme de K.C.Kiwiel que S.Dempe dans [12] a proposé un nouvel algorithme : l'algorithme du paquet modifié.

Cet algorithme consiste à : étant donné le paramètre á^s à la s^me itération, déterminer l'itérée z^s qui permet à F_ás(z^s) = F(x_ás(z^s), z^s) d'approximer au mieux F(x(z^s), z^s) ; ensuite faire décroître á^s et ne considérer que les z^s significatifs.

On note v(y) le gradient généralisé de F_ás(y). D'après [30] ; on a

{?_xF~x_á(y), y~d + ?yF~xá(y), y : d E ?_yx_á(y)}

v(y) E

Soit {yk}sk=1 une suite de points d'essaie; {z^k}^s_k=1la suite d'itérées calculées jusqu'à l'étape s. On considère le modèle suivant :

{ } + F_á(z^s) + u^sd^T d

max v(y^k)^Td - âk,s

2 (3.14)

kEJs

Où J_s ? {1,...,s};u^s > 0 et

âk,s = F_á(z^s) - v₍y^k)(z^s - y^k) - F_á(y^k)

Comme nous l'avons déjà mentionné au chapitre un, le réel d qui minimise le modèle (3.14) est une direction de descente pour F_á(y) en y = z^s.

Soit å > 0 le réel positif tel que ?å^' = å , (3.12) n'admet pas de solution å^'-optimale. å est appelé seuil d'optimalité. Soit %^s > 0 le rayon de la région de confiance (c'est le rayon de la plus petite boule dans laquelle on est sûr de trouver une solution). Soit mL un paramètre positif (paramètre de recherche en ligne [12]). Soit u^s = umin > 0 , á^s le coefficient de régularisation et d^s le réel qui minimise (3.14).

On pose

s - 1

ås := max m_p(IIu^sd^sII _+Eçsjâj,s) , _jEmax₀{IIy^j - z^jII+EIIz^k+1 - z^kII}

jEJ_s k=j

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 46

Où (7^s_j)j sont les multiplicateurs de lagrange du problème de minimisation de (3.14) et

J_s ? {j : 7s j =6 0}

Es est utilisé pour mesurer la qualité de l'approximation z^s de la solution du PBN calculé à la s^eme iteration. Durant la procédure E^s doit tendre vers 0 ; mais pour des raisons pratiques, (impossibilité de trouver des solutions E^'-optimale pour les valeurs de E^' plus petite qu'une certaine valeur seuil) on arrête l'algorithme si E^s < E.

Soit k = 1 une certaine constante utilisée pour borner le changement de la région de confiance. 81 un paramètre donné.

Les principales étapes de l'algorithme sont les suivantes :

Algorithme du paquet modifié

Entrée : Suite d'itérée {zk}sk=1, les points d'essaie {yk}sk=1, les paramètres ás > 0, E^s > 0, us, Ss

Sortie : Une meilleure itérée z^s+1. Etape1 :

a) Calculer en augmentant si nécessaire la valeur de u^s, le réel d^s qui minimise le modèle (3.13) ainsi que les multiplicateurs de Lagrange ç^s_j, j E J_s tel que M^sII < Os

b) Tester le critère d'arrêt E^s < E, réduire E^s et J_s si nécessaire. Si E^s < S^s alors

Ss := ùS^s

Etape2 :

_{n o}

Si F_ás(z^s + d^s) < F_ás(z^s) + mL max v(yk)T d^s - âk,s alors

k?J_s

zs+1 := z^s + d^s, t_s := 1

Sinon

a) Rechercher t_s > 0 tel que

F_ás(z^s + t_sd^s) < F_ás(z^s) + _mLts max {v(y^k)^Td^s ? âk,s}

k?J l

et faire z^s+¹ := z^s + t_sd^s

b)Ou considerer que l'étape est nulle et calculer un nouveau point d'essaie yk+1 := z^s + td^s avec t > 0

t_s := 0

Si t > 0, calculer un nouveau coefficient de régularisation á^s+1 E]0, á^s] tel que

F_ás+1(z^s+1) - F_ás(z^s) < 0.5 (F_ás(z^s+¹) - F_ás(z^s)~ , ys+1 := zs+1

Sinon

ás+1 := ás

Etape3 : Choisir un nouveau rayon de la région de confiance O^s < êS^s Réactualiser l'ensemble J_s et les autres paramètres. Calculer le gradient généralisé de la fonction F_ás+1(y) au point y = ys+1 Faire S^s+¹ := S^s,s := s + 1 et répéter l'étape 1.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 47

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

La méthode pour la recherche de t_s à l'étape 2 et la méthode utilisé pour le choix de la région de confiance peuvent être trouvées dans [30].

Pour l'étude théorique, on choisi le seuil d'optimalité å = 0. L'algorithme précédent génère une suite (á^s, x_ás(z^s))_s qui théoriquement est infinie. Si (á^s)_s converge vers zero, alors le problème est résolu avec succès.

La modification apporté par ce nouvel algorithme réside dans le contrôle de la région de confiance, en posant que %^s < êä^s ave ê > 1. L'ajout de ce contrôle garanti que que toutes les itérées et points d'essaie générés durant l'exécution de l'algorithme ont toujours un intérêt.

Étant donné que l'algorithme génère une suite (z^s)_s ayant une infinité de termes (du point de vu théorique), il est impossible de le dérouler manuellement sur un exemple de PBN donné. Néanmoins, dans le paragraphe qui suit, nous allons étudier la convergence théorique de l'algorithme du paquet modifié afin de montrer que la suite (z^s)_s calculée converge vers une approximation de la solution du PBN original qui est stationnaire au sens de clarke. Ce qui permettra de conclure puisque la solution du problème du suiveur est fortement stable, que l'approximation de la solution du problème original calculée via l'algorithme est également fortement stable [11].

3.4 Convergence de l'algorithme du paquet modifié

Définition 3.4.1. Soit ë⁰ E Ë_á(x_á(y⁰), y⁰)

On dit que l'assertion (NE) est satisfaite si la matrice

~ V²_xxL(x_á(y⁰), y0, ë⁰) + 2áE VTxgJ0(xá(y0), y0) ~

VxgI0(xá(y0), y⁰) 0 VygI0(xá(y0), y0)
est de rang maximal : n + I(x_á(y⁰), y⁰)

}où J⁰ = j : ë0 j > 0 et I⁰ = I(xá(y0), y⁰) = { j : gj (xá(y0), y⁰) = 0 , E est la matrice
identité.

On suppose que les assertions (C), (MFCQ), (CRCQ) et (NE) sont satisfaites pour le problème (3.12). Alors [11] la différentielle au sens de Clarke F_á en y⁰ E Y est donné par {V_xF(x_á(y⁰), y⁰)?_yx_á(y⁰) + VyF(xá(y0), y0)}

?F_á(y⁰) =

posons Y = 1[8^m, et supposons également que la suite (z^s)_s généré par l'algorithme est infini et borné.

Si le seuil d'optimalité å = 0 est choisi, alors [30] le critère d'arrêt de l'algorithme est {V_xF(x_ás(z^s), z^s)d + VyF(xás(zs), z^s) : d E ?_yx_ás(z^s)}

0 E .

i.e dès que z^s est stationnaire au sens de Clarke.

Montrer que l'algorithme converge revient à montrer que la suite (z^s)_s converge vers un

point stationnaire au sens de Clarke. C'est-à-dire qu'il faut montrer que :

{V_xF (x_á(y), y)d + V_yF(x_á(y), y) : d E ?_yx_á(y)}

0 E .
où (xá(y), y, á) est un point d'accumulation de la suite {x_ás(z^s), zs, ás}8s=1 . On a le résultat suivant :

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 48

Théorème 3.4.1. Soit {x_ás(z^s), z^s, ás}00s=1 la suite généré par l'algorithme du paquet modifié pour å = 0. Supposons que la suite _(ás)s est borné par á⁰ > 0, alors tout point d'accumulation (xá(y), y, á) de cette suite satisfait

}.

{ ?_xF (x_á(y), y)d + ?_yF (x_á(y), y) : d ? ?yxá(y)

0 ?

preuve :

Rappelons que dans l'algorithme du paquet modifié, la modification apporté à l'algorithme de Kiwiel consiste à contrôler le renouvellement de la région de confiance à chaque itération ; ainsi certains résultats de [30] reste vraies pour l'algorithme modifié.

Soit y un point d'accumulation de la suite (z^s)_s. La solution optimale d^s du problème de minimisation de (3.13) vérifie [30] :

ds ? ?Fás (z^s; max {ky^j- z^jk + \ jEJs,ç^sj 0

Es - 1 k=1

}~kz^k+1- z^kk

Si l'assertion (SSOC) est satisfaite en (x0(y), y),

alors

{?_xF(x0(y), y)d + ?_yF(x0(y), y) : d ? ?yx0(y) }

0 ?

Où ?F_á(z; å) est l'å-sous différentielle de Goldstein définie par

{ }

?F_á(z; å) = conv ?F_á(y) : kz - yk = å

?F_á(z; å) est semi-continue supérieurement et localement borné [31]. D'où si (á, y, 0,0) est un point d'accumulation de la suite

s- 1 00

{á^s, z^s, d^s, max {y^j -- z'k + E kz^k+1 _ zkk } ,

jEJs,çs j

k=1 s=1

alors 0 ? ?F_á(y) et le théorème 3.9 de [30] nous permet de conclure que

{ ?_xF (x_á(y), y)d + ?_yF (x_á(y), y) : d ? ?yxá(y) }

0 ? .
·

Si la suite (á^s)_s converge vers zero, alors la condition suffisante d'optimalité forte (SSOC) aux points d'accumulations de {x_ás(z^s), zs}00s=1 est nécessaire pour garantir que l'algorithme du paquet modifié sera à mesure de calculer toutes les données nécessaire a la résolution du PBN.

Si cette condition d'optimalité (SSOC) est satisfaite, le théorème précédent montre que les points d'accumulations de la suite {x_ás(z^s), z^s}:₁ sont des points stationnaires au sens de Clarke.

Notons que la suite (z^s)_s converge grace à la modification apporté par l'algorithme du paquet modifié.

Le corollaire suivant découle du théorème précédent.

Corollaire 3.4.1. Soit {x_ás(z^s), zs, ás}00s=1 la suite générée par l'algorithme du paquet modifié, où {ás}00s=1 converge vers zero. Soit y = lim z^s et x0(y) ? Ø(y)

s?00

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Approche de résolution par régularisation des PBN dans le cas de la non unicité. 49

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Ce résultat nous garanti que en résolvant le PBN (3.1)-(3.2) par régularisation (utilisant l'algorithme du paquet modifié), on aboutit à une approximation de la solution de la solution du problème original qui est stationnaire au sens de Clarke (par consequent fortement stable). Donc plus régulière que les solutions optimiste et péssimiste respectivement qui sont le plus souvent instables.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Conclusion et perspectives

Notre travail consistait à présenter l'approche par régularisation de résolution des PBN dans le cas de la non unicité de la solution du problème du suiveur, qui fait actuellement l'objet de nombreuses recherches.

Après avoir présenté les approches optimiste et pessimiste qui sont les techniques classiques de résolution des PBN dans le cas de la non unicité, nous avons montré que la solution du PBN régularisé, même si elle n'est qu'une approximation de la solution du PBN original, possède de meilleures propriétés de régularité que les solutions optimiste et pessimiste. Nous avons pour terminer présenté un algorithme de résolution basé sur cette approche développé par S.Dempe, dont nous avons étudié la convergence théorique.

Mais il se trouve que la convergence théorique d'un algorithme n'implique pas forcément sa convergence numérique (i.e après l'implementation de l'algorithme). Nous envisageons dans un travail futur implementer cet algorithme et étudier sa convergence numérique. Nous pourrons également voir dans quelle mesure généraliser les résultats que nous avons présentés dans les espaces Rⁿ aux espaces de Hilbert, afin qu'ils puissent être utilisés dans les applications en ingénierie par exemple.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

Bibliographie

[1] I.D.Prete, M.B.Lignola, And J.Morgan. New concept of well-posedness for optimization problems with variational inéquality constraints.Journal of Inequalities in Pure and Applied Mathématics, 2002.

[2] H.V.Stackelberg. Marktform und Gleichgewicht. Springer-Verlag, Berlin, 1934. Engl transl : The theory of the market economy, Oxford University press, 1952.

[3] Kornaj,J et Liptak,T. Two-level planning. Econometrica, 33 :141-169, 1965.

[4] Ross, S.A .The economic theory of agency : the principal's problem. AER, 63 :134-139, 1973.

[5] Simaan, M et Cruz,J.B. On the stackelberg strategy in non zero-sum games.Journal of optimization theory and applications, 11 : 533-555, 1973.

[6] Bracken, J et McGill, J. Mathematical programs with optimization problems in the constraints. Operations reseach, 21 :37-44, 1973.

[7] Candler, W et Norton, R. Multi-level programming . World Bank developement research center discussion paper.20.Washington.DC, 1977.

[8] Candler, W et Norton, R. Multi-level programming and development policy. World Bank developement research center discussion paper.258. Washington.DC, 1977.

[9] A.Auslander. Regularity theorems in sensivity theory with nonsmooth data. In J.Guddat, H.Th.Jongen, F.Nozicka, and B.Kummer, editors, Parametric optimisation and related topics, page 9-15. Akademic Verlag, Berlin, 1987.

[10] A.B.Zemkoho. Approche multicritère de résolution des problèmes de programmation à deux niveaux. Memoire de DEA, Université de Yaoundé I, 2006.

[11] S.Dempe. Foundation of bilevel programming. Kluwer Academic Publishers, Dor-drecht/Boston/London, 2002.

[12] S.Dempe. A bundle algorithm applied to bilevel programming problems with non-unique lower level solutions.

[13] C.Audet, J.Haddad, G.Savard. A note on the definition of the linear bilevel solu-tion.Elsevier Science, 2005.

[14] C.M.Macal and A.P.Hurter. Dependence of bilevel mathematical programs on irrelevant constraints. Computer and Operations Research, 24 :1129-1140, 1997.

[15] R.T.Rockafellar. Convex analysis. Princeton University press, Princeton, 1970.

[16] M.Kojima. Strongly stable stationary solutions in non linear programs. In S.M.Robinson,editor,Analysis and computation of fixed points, pages 93-138; Academic press, new york, 1980.

[17]

BIBLIOGRAPHIE 52

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

W.W.Hager. Lipschitz continuity for constrained processes. SIAM Journal on control and optimization, 17 : 251-269, 1979.

[18] J.F.Bard, J.Plummer and J.C.Sourie. Determining tax credit for converting nonfood crops to biofuels : an application of bilevel programming. In A.Migdalas, P.M.Pardalos and P.Varbrand, editors, multilevel optimization : Algorithm and applications, Page 23-50. Kluwer Academic Punlishers, Dordrecht,1998.

[19] P.Loridan and J.Morgan.Approximate solutions for two-level optimization problems.In K.Hoffman.J.Hiriart-Urruty,C.Lemarchal and J.Zowe,editor,trends in mathematical opti-mization,volume 84 of international series of numerical mathematics.Pages 181-196. Bir-khäuser Verlag,Basel,1988.

[20] P.Loridan and J.Morgan.New results on approximate solutions in two-level optimization. Optimization.20 : 819-836, 1989.

[21] P.Loridan and J.Morgan. å-regularized two-level optimization problems : approximation and existence results.In optimization-fifth French-German conference (Varez), page 99-113. Lecture notes in mathematics, Springer Verlag, Berlin,No.1405.1989.

[22] P.Loridan and J.Morgan. On strict å-solutions for two level optimization problem.In proceedings of the international conference on operations research 90, pages 165-172. Spriger Verlag, Berlin, 1992.

[23] B.Bank, J.Guddat, D.Klatte, B.Kummer, and K.Tammer. Non-linear parametric optimi-zation.Akademic Verlag, Berlin,1988.

[24] S.Scholtes.Introduction to piecewise differentiable equations. Technical report, Universität Karlsruhe, Institut für Statistick und mathematische Wirtschaftstheorie,1994.No.53/1994.

[25] A.N.Tykhonov.Methods for the régularization of optimal control problems. Soviet Mathematical Doklady,6 :716-763,1965.

[26] D.Klatte and B.Kummer.Strong stability in nonlinear programming revisited. Journal of the australian Mathematical society, Ser.B, 40 :336-352,1999.

[27] S.Addoune.Optimisation à deux-niveaux : condition d'optimalité, approximation et stabilité. PhD thesis. Université de Bourgogne, Département de Mathématique,1994.

[28] P.Loridan and J.Morgan. Least-norm régularization for weak two-level optimization problems. In optimization, optimal control and partial Differential Equations, volume 107 of International Series of Numerical Mathematics, page 307-318. Birkhäuser Verlag, Basel, 1992.

[29] V.F.Solohovic. Unstable extremal problem and geometric properties of Banach Spaces. Soviet Mathematical Doklady. 11 :1470-1472, 1970.

[30] K.C.Kiwiel. Restricted step and Levenberg- Marquard techniques in proximal bundle method for nonconvex nondifferentiable optimization. SIAM Journal on Optimization, 6 :227-249, 1996.

[31] K.C.Kiwiel. Method of descent for nondifferentiable optimization. Springer-verlag, 1985.