Approche de résolution par régularisation des problèmes de programmation mathématique à deux niveaux dans le cas de la non unicité de la solution du problème du suiveur

2.2 L'approche optimiste

Cet approche est envisageable dans le cas où le leader à la possibilité de persuader le suiveur de prendre une décision qui lui sera favorable (favorable est compris ici au sens ou la dite décision permet au leader d'atteindre son objectif).

la formulation optimistique de (2.2)-(2.3) est la suivante :

min

y

{ }

?_o(y) : y E Y (2.6)

Où

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 23

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

{ }

?_o(y) = min F(x, y) : x E W(y) (2.7)

x

Définition 2.2.1. Un point (x^*, y^*) E 1[8ⁿx1[8^m est appelé solution optimiste locale de (2.2)-(2.3) si y^* E Y, x^* E W(y^*) avec

F(x^*, y^*) < F(x, y^*) Vx E W(y^*)

et il existe Uä(y^*), 8 > 0 boule ouverte centrée en y^* de rayon 8 telle que

?_o(y^*) < ?_o(y) Vy E Uä(y^*) n Y

(x^*, y^*) est appelé solution optimiste globale si 8 = o0

Énonçons maintenant un théorème d'existence de solution optimiste :

Théorème 2.2.1. Si les assertions (C) et (MFCQ) sont satisfaites en tout points (x, y) E 1[8ⁿ x Y avec x E M(y), alors

Le problème (2.2)-(2.3) admet une solution optimistique globale.

Preuve :

Considérons le problème

{ }

min F(x, y) : y E Y, x E W(y) (2.8)

x,y

Les solutions globales de (2.8) et le problème optimiste (2.4)-(2.6)-(2.7) coincident.

En effet si (x^*, y^*) vérifie (2.8) alors (x^*, y^*) vérifie (2.4)-(2.6)-(2.7).

réciproquement, si (x^*, y^*) vérifie (2.4)-(2.6)-(2.7) alors par définition de solution optimiste globale, on a :

F(x^*, y^*) < F(x, y^*) Vx E W(y)

et

?_o(y^*) < ?_o(y) Vy E Y

{ }

F (x^*, y^*) < F (x, y^*) Vx E W(y^*) = F (x^*, y^*) < min F (x, y^*) : x E W(y^*)

x

Or

{ } { }

?_o(y^*) < ?_o(y)Vy E Y ? min F(x, y^*) : x E W(y^*) < min F(x, y) : y E Y, x E W(y)

x x

{ }

Ce qui implique que min F(x, y^*) : x E W(y^*) < F(x, y) Vy E Y, Vx E W(y)

x

d'où F(x^*, y^*) < F(x, y) Vy E Y, Vx E W(y) autrement dit,

(x^*, y^*) E Argmin x,y

{ } F(x,y) : y E Y,x E W(y)

donc (x^*, y^*) est optimum global de (2.8).

D'autre part, puisque les assertions (C) et (MFCQ) sont satisfaites, la fonction à valeur optimale

(voir définition 1.4.4) est continue ; ce qui permet de montrer que l'ensemble

{ }

(x, y) : x E W(y) est fermé. D'autre part, étant donné que Y est fermé, l'assertion (C) nous

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 24

.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

garanti que l'intersection de {(x, y) : x E Ø(y)} avec Rⁿ x Y est compact (comme fermé dans un compact).

D'où puisque F est continue sur Rⁿ x R^m, le problème (2.8) admet un optimum global. En vertu de l'équivalence que nous avons établie entre (2.8) et le problème optimiste, on conclut que (2.4)-(2.6)-(2.7) admet une solution optimistique globale.
·

Exemple 2.2.1. Reconsidérons le PBN de l'exemple 2.1.1 :

« min y		n o » x^2+ y^2: x E Ø(y), -1 < y < 1
Où Ø(y) = Argmin x	n o - xy : 0 < x < 1

Comme trouvé précédemment, on a ?0(y) = minnx² + y² : x E Ø(y)=(1 + y² si y > 0

x

siy < 0

y2

Le problème optimiste s'écrit donc :

_{n o}

min ?0(y) : -1 < y < 1

y

et la solution optimiste globale est (x0, y0) = (0, 0).

L'un des défauts de l'approche optimiste est qu'elle n'est pas envisageable dans la plupart des cas concrets. En effet, en économie par exemple, dans le but de faire régner une concurrence loyale entre des entreprises concurrentes, la législation interdit le plus souvent une quelconque coopération entre les dites entreprises et leurs éventuels clients.

Aussi, dans grand nombre de problèmes modélisés en PBN, le suiveur ne constitue que rarement une personne physique avec qui le leader pourrait envisager une coopération. En plus, même si la coopération est permise, le leader n'a pas de garanti sur le fait que le suiveur respectera ses engagements.

Ceci constitue quelques limites de l'approche optimiste.

2.3 L

'approche pessimiste

Lorsqu'il est impossible au leader d'influencer les choix du suiveur, une décision optimale du leader, étant donné qu'il n'a aucun contrôle sur le problème, est celle qui limite au mieux les dégâts lorsque le suiveur prend des décisions qui lui sont nuisibles.

Mathématiquement, la formulation pessimiste de (2.2)-(2.3) s'écrit :

_{n o}

min ?_p(y) : y E Y (2.9)

y

?p(y) = max x

n o F(x, y) : x E Ø(y) (2.10)

Définition 2.3.1. Un point (x^*, y^*) E Rⁿ x R^m est appelé solution pessimiste locale de (2.2)(2.3) si y^* E Y, x^* E Ø(y^*) avec

F(x, y^*) < F(x^*, y^*) V x E Ø(y^*)

et il existe Uä(y^*), 8 > 0 boule ouverte centrée en y^* de rayon 8 telle que

?_p(y^*) < ?_p(y) Vy E Uä(y^*) n Y

(x^*, y^*) est appelée solution pessimiste globale si 8 = +oo.

Le problème 2.4)-(2.9)-(2.10) est appelée formulation péssimistique de (2.2)-(2.3)).

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 25

Énonçons un théorème d'existence de solution pessimiste.

Théorème 2.3.1. Considérons le PBN 2.4)-(2.9)-(2.10). Supposons que Ø(.) est semi-continue inférieurement (Sci) en tout point de Y et que l'assertion (C) est satisfaite. Supposons que (2.9) admet une solution admissible, alors 2.4)-(2.9)-(2.10) admet une solution optimale globale.

Preuve :

{ }

Posons K = (x,y) ? Rⁿ × R^m : g(x, y) = 0 et h(x, y) = 0 . L'assertion (C) nous garanti que K est compact.

Soit P2 : Rⁿ × R^m -? Rm

(x, y) 7-? y la deuxième projection.

P2(K) n Y est l'ensemble des solutions admissible de (2.9). P2 étant continue, P2(K) est compact ; d'où P2(K) n Y est compact comme intersection d'un fermé et d'un compact.

Montrons que : cp_p est semi-continue inférieurement (Sci).

Soit y0 ? R^m, montrons que cp_p est Sci en y0.

soit _(yk)k?N une suite de R^m telle que (y^k)k -? y0

k?+8

Il suffit de montrer que lim inf cp_p(y^t) = cp_p(y0)

k?+8

i.e

sup

k?N

inf cp_p(y^t) = cp_p(y0)

t=k

On a F(x, y^t) = cp_p(y^t) ?x ? Ø(y^t) d'où

inf

t=k

F(x, y^t) = inf cp_p(y^t) ?x ? Ø(y^t) ?k ? N

t=k

et

F(x, y^t) = sup

k?N

inf

t=k

inf

cp_p(y^t) ?x ? Ø(y^t)

t=k

sup

k?N

i.e

lim inf t?+8

F(x, y^t) = lim inf cpp(y^t) t?+8

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Or F est continue sur Rⁿ × R^m ;

d'où F(x,.) est continue sur R^m ?x ? Rⁿ fixé ; il vient alors que :

lim inf t?+8

F(x, y^t) = lim t?+8

F(x, y^t) = F(x, y0) ?x ? Rn

Donc

liminf cp_p(y^t) = F(x, y0) ?x ? Ø(y0) ? Rn t?+8

d'où

lim inf cp_p(y^t) = max

_x {F(x, y0) : x ? Ø(y0)}

t?+8

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 26

i.e

lim inf ?_p(y^t) > ?_p(y0)

t?+8

Donc ?_p est Sci.

Comme l'ensemble des solution admissibles de (2.9) P2(K) n Y est compact, le problème 2.4)-(2.9)-(2.10) admet un minimum global.
·

Exemple 2.3.1. On considère une nouvelle fois le PBN de l'exemple 2.1.1. La formulation pessimiste de ce problème est :

_{n o}

min ?_p(y) : -1 < y < 1

y

Où

(

2 1+ y² si y > 0

?_p(y) = max{x + y² : x E Ø(y) y

}= si <0

y

avec

Ø(y) =	{	{0} si y < 0 {1} si y > 0 [0,1] si y = 0		.
Où			Ø(y) =			{	[-1,1] si y = 0 {-y - 1} si y > 0 {-y + 1} si y < 0

(x0, y0) = (1, 0) est une solution pessimiste locale et la valeur péssimistique de la fonction objectif est 1.

Mais la résolution des PBN en utilisant l'approche pessimiste présente également des défauts :

En effet les solutions pessimiste sont en général instables, dû [11] au manque possible de semi-continuité de la fonction Ø(.) qui à chaque paramètre du problème du leader associe l'ensemble des solutions du problème du suiveur correspondant.

Ce défaut conduit à deux conséquences majeures :

r Les solutions péssimiste ne sont pas en général de bonnes approximations des solutions réalisables en pratique.

r Une petite perturbation sur les données du problème peut conduire à un changement drastique de la solution du suiveur. Ainsi, si le leader ne résolvait pas son problème réel mais une approximation (ce qui est le cas la plupart du temps), ses solutions peuvent être éloignées des solutions réelles.

Les exemples 2.3.2 et 2.3.3 suivants illustrent bien ces défauts :

Exemple 2.3.2. Considérons le PBN

min

y

{(x - y)² + y² : ?20 < y < 20, x E Ø(y)}

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 27

Pour y = 0; on a Ø(y) = [-1,1] et le problème du suiveur admet pour ce paramètre une infinité de solutions.

Posons F(x, y) = (x - y)² + y² ; en introduisant dans F la solution du suiveur , on obtient :

F(x(y), y) =

{

(-2y - 1)^2+ y^2si y > 0 (-2y + 1)^2+ y^2si y < 0 E [-1,1] si y = 0

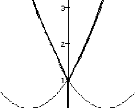
Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

FIG. 2.2 Fonction objectif du leader la formulation optimiste du problème est la suivante :

min y

n o ?0(y) : -20 < y < 20

Où

_{n o}

?0(y) = min (x - y)² + y² : x E Ø(y)

x

Il est clair que la solution optimiste du problème est (x0, y0) = (0, 0). Le graphe de F nous permet d'ailleurs de confirmer ce résultat.

Une fois de plus, d'après le graphe de F, quelque soit le signe de y, y =6 0 , la fonction F

atteint son infimum lorsque y --* 0 et on a : lim y?0

F(x(y), y) = 1.

Ainsi, la solution réalisable en pratique du problème est atteinte lorsque y --* 0 et la valeur de la fonction objectif est 1; ce qui est bien éloigné de la valeur optimistique qui est 0 .

Exemple 2.3.3. Considérons le PBN

_{n o}

min - x + y² : -0.5 < y < 0.5, x E Ø(y)

y

Où

Ø(y) = Argmin x

{xy^2: -1 < x < 1}

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 28

On a alors

(

{-1} si y =6 0

W(y) =

[-1,1] si y = 0

Pour y = 0, le problème du suiveur admet une infinité de solutions; on est donc dans le cas de la non unicité. La formulation optimiste du problème est :

min

y

{?0(y) : -0.5 < y < 0.5}

Où	n o ?0(y) = min (-x + y^2: x E W(y) x

L'unique solution optimiste est (x0, y0) = (0, 1) ; et la valeur optimiste de la fonction objectif du leader est -1

Supposons maintenant que le problème du suiveur soit perturbé de telle sorte que l'ensemble des solutions du problème du suiveur se réécrivent :

Wá(y) = Argmin x Où á > 0 et suffisamment petit. Posons fá(x, y) = xy^2+ áx^2On a Vxfá(x, y) = y^2+ 2áx

{xy^2+ áx^2: -1 < x < 1}

2

V_xf_á(x,y) = 0 = x = -₂

On a

V2 xxfá(x,y) = 2á > 0

d'où pour y admissible, x = -y2

_2á est solution du problème du suiveur. Ainsi,

(

{-1} si y² > 2á

- y2_2á

2á

si y2 <

W_á(y) =

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

En insérant cette solution dans la fonction objectif du leader, on obtient :

(

F(xá(y), y) = y2 + 1 si y² > 2á

y2 - y2

_2á si y² < 2á

Le problème devient donc

n F (xá(y), y) : -0.5 < y < 0 o

min

y

L'unique solution de ce problème est y_á = 0 Vá > 0

Lorsque á --* 0 , la solution du problème perturbé est (0, 0) et la valeur de la fonction objectif tend vers 0; valeur qui est éloigné de la valeur optimiste-1.

Ainsi, la solution optimiste est instable.

Non unicité de la solution du problème du suiveur : les différentes techniques d'approches. 29

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

L'étude tant du point de vue théorique que numérique d'un problème d'optimisation instable est très difficile. Néanmoins une possibilité d'éviter ce problème d'instabilité existe. Elle consiste à prolonger (une sorte de prolongement par continuité) la fonction W(.) de façon à obtenir une nouvelle fonction W^' : R^m -? 2^R7 continue. D'après les résultats énoncés dans [23], le nouveau problème "réagira" de façon régulière aux perturbations "régulières" (i.e pour de petites perturbations, la solution du problème perturbé ne sera pas éloignée de la solution du problème non perturbé) ; et ainsi, le problème d'instabilité sera résolu.

L'approche pessimiste de résolution des PBN dans le cas de la non unicité à été intensive-
ment étudié par P.Loridan, J.Morgan et leurs Co-auteurs. Dans plusieurs articles, ils étudient le PBN (2.2)-(2.3) dans un cas plus général, en ce sens que les fonctions f, g, h, F, et G qui définissent le problème sont perturbées et la convergence vers un problème non perturbé est étudiée. (voir par exemple les articles [19, 20, 21]). Dans [22], le concept de å-optimalité est utilisé pour régulariser le problème pessimiste.

Malgré tous ces résultats, certains problèmes demeurent :

? l'approche optimiste est très peu souvent envisageable;

? les solutions péssimistes, même lorsqu'elles sont stables sont le plus souvent éloignées des solutions réelles;

? comment discriminer entre l'approche péssimiste et optimiste? Autrement dit dans une situation donnée, comment savoir quelle approche (optimiste ou péssimiste) est la plus adéquate?

Afin de contourner ces difficultés, il serait préférable pour le leader, non pas de calculer la solution "réelle" optimiste ou péssimiste de son PBN mal-posé qui dans ce cas cours de grands risque d'être instable (donc inutilisable), mais d'en calculer une approximation dans un voisinage des solutions admissibles qui aurait la propriété d'être fortement stable. L'approche par régularisation permet de calculer de telles solutions.

Dans le chapitre suivant, après avoir présenté les différentes techniques de régularisation développées jusqu'ici dans la littérature, nous exposons un algorithme de résolution des PBN dans le cas de la non unicité développé par S.Dempe en 2000 basé sur l'approche par régularisation. Nous-nous pencherons enfin sur l'étude de la convergence de cet algorithme.