Approche de résolution par régularisation des problèmes de programmation mathématique à deux niveaux dans le cas de la non unicité de la solution du problème du suiveur

1.2 Quelques propriétés des PBN

Propriété 1.2.1. Dans la formulation du PBN (1.1) - (1.4), la position des fonctions contraintes n'est pas arbitraire. En effet, en transférant les contraintes du leader au problème du suiveur, la région réalisable de celui-ci s'en trouve réduite (ou restreinte) ; ce qui peut modifier la solution (si elle existe ) du problème du suiveur, et partant la solution du problème (1.1) - (1.4). Il en est de même si on transfère plutôt les contraintes du suiveur au problème du leader. Nous illustrons cette propriété par cet exemple tiré de [13] :

On considère le PBN linéaire :

(BLP1) :

max

y

y

sujet à : 0 < y < 1

{w:w<y}

x = 0

x E Argmax

w

et le problème : (BLP2) :

max y

y

Genéralités sur la programmation mathématique à deux niveaux 4

sujet à : 0 < y < 1

x E Argmax w

{w : w < y et w = 0}

Les problèmes (BLP1) et (BLP2) ont les mêmes contraintes excepté le fait que la contrainte du premier niveau dans (BLP1) est transféré au deuxième niveau dans (BLP2).

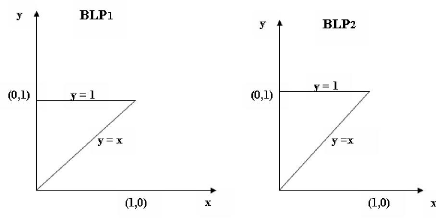
Comme le montre la figure ci-dessous, les deux problèmes ont une même région réalisable.

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

FIG. 1.1 Sur les effets du transfert de la contrainte x = 0 du premier niveau dans (BLP1) au second niveau dans (BLP2).

{ }

On a 1 = (0, y) : 0 < y < 1

pour les deux problèmes; mais pour y fixé dans R, on a pour (BLP1) : Ø(y) = {y} tandis que (

{0} si y = 0

pour (BLP2) : Ø(y) = w sinon .

Il s'ensuit que pour (BLP1) la seule solution réalisable et qui s'avère être la solution optimale est y = 0. La solution optimale pour (BLP2) est y = 1.

Propriété 1.2.2. La solution optimale du PBN change en général lorsque l'ordre du jeu

est changé (i.e lorsque le problème du leader est décalé au second plan tandis que le suiveur devient le leader). 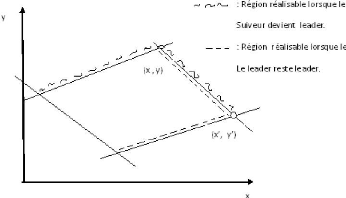Ceci est dû au fait que le problème étant hiérarchique, les deux décideurs ne peuvent prendre leurs décisions simultanément; ce qui signifie que le leader se doit d'anticiper sur le choix du suiveur sous réserve que celui-ci à le droit et la possibilité de choisir une solution optimale sous les conditions posées par les choix du leader [11]. Nous illustrons cet exemple par la figure 1.2 tirée de [11], sur laquelle (x, y) et (x^', y^') représente respectivement la solution

Genéralités sur la programmation mathématique à deux niveaux 5

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji c~UYI 2007-2008

FIG. 1.2 Sur l'importance de l'ordre du jeu

optimale lorsque le i^eme décideur à le premier choix.

Propriété 1.2.3. La solution optimale d'un PBN n'est pas en général indépendante des

{ }

min (x - 1)² + (y - 1)² : x E Ø(y) .

y

contraintes inactives ajoutées au problème du suiveur. L'exemple suivant tiré de [14] illustre bien cette propriété :

Soit le PBN :

{ }

avec Ø(y) = Argmin 0.5x² + 500x - 50xy .

x

{ }

. Ce problème est équivalent à : min (x-1)² +(y -1)² : x+500-50y = 0 . La solution

x, y

unique de ce problème est (x^*, y^*) = (0.82; 10.02) et la valeur optimale de la fonction objectif est F(x^*, y^*) = 81.33.

Ajoutons la contrainte x ~ 0 au problème du suiveur; alors (x^*, y^*) est un point réalisable pour le problème et x^* ~ 0; mais la solution optimale du suiveur est :

₁

50y - 500 si y ~ 0

En introduisant cette fonction dans fonction objectif du leader, on a :

₁

(50y - 501)² + (y - 1)² si y ~ 0

F (x(y), y) =

x(y) = 1 + (y - 1)² si y ~ 10

.

1 + (y - 1)² si y ~ 10

La valeur minimale de cette fonction est 1 et est atteinte en (x^°, y^°) = (0, 1). Une condition nécessaire et suffisante garantissant au PBN l'existence d'une solution optimale globale indépendante par ajout ou suppression de contraintes inactive peut-être trouvé dans [14].

Genéralités sur la programmation mathématique à deux niveaux 6

Mémoire de DEA * Laboratoire d'analyse numérique * UYI Francisque.D.Fouodji (c)UYI 2007-2008

Dans toute la suite, nous ne considérerons que les PBN dans lesquels les contraintes du leader ne sont pas couplées ; i.e la fonction contrainte du leader ne dépend pas de la variable du problème du suiveur. Ainsi les contraintes du leader s'écriront : G(y) < 0 au lieu de G(x, y) < 0.

Dans le but de prendre en compte les contraintes du type égalité, les contraintes du deuxième plan seront désormais de la forme g(x, y) < 0 et h(x, y) = 0 où h : 1[8ⁿ x 1[8^m -> 1[8^k

le problème (1.1) - (1.4) devient donc :

{ }

min F(x, y) : G(y) < 0, x E Ø(y) . (1.7)

y

avec Ø(y) = Argmin x

{ } f(x, y) : g(x, y) < 0 et h(x, y) = 0 .

Ø(y) représente l'ensemble des solutions du problème d'optimisation paramétrique :

{ }

min f(x, y) : g(x, y) < 0 et h(x, y) = 0 . (1.8)

x

comme nous l'avons indiqué précédemment, la résolution de (1.7) - (1.8) suppose la résolution au préalable du problème d'optimisation paramétrique que constitue le problème du suiveur (1.8). Par ailleurs, la plupart des méthodes de résolution des PBN exploitent des conditions nécessaires et suffisantes permettant de montrer l'équivalence du PBN à un problème d'optimisation à un niveau classique de la forme :

min y

{F(x(y),y). : G(y) < 0}. (1.9)

Où x(y) représente la solution de (1.8) pour le paramètre y. La résolution de (1.9) nécessite outre la régularité des fonctions F et G, la continuité au moins de la fonction à valeur optimale x : y i-> x(y). Ainsi donc, la résolution d'un PBN est fortement lié à la résolution d'un problème d'optimisation paramétrique.

Dans le paragraphe à venir, nous présentons les résultats d'optimisation paramétrique nécessaires à la résolution des PBN.