Chapitre 3
Stabilité et stabilisation des systèmes
hybrides
3.1 Stabilité des systèmes à
commutations non linéaires sur le plan [MS.9]
Un système à commutations est une famille
de systèmes dynamiques équipée d'une loi qui
détermine à tout moment quelle dynamique est responsable de
l'évolution temporelle.
Dans le cas des systèmes en temps continu, un
système à commutations peut s'écrire sous la forme
qÿ =
fá(q), q ? M,
á ? I, (3.1)
où I est un sous-ensemble mesurable de
R, M est une variété différentielle et
F = {fá | á ? I} est
une collection de champs de vecteurs sur M. Si la forme est la
même que celle d'un système de contrôle,
l'interprétation est différente : nous voulons déterminer
des propriétés sur l'évolution du système qui ne
dépendent pas de la loi de commutation, qui est une fonction
á : [0, 8) ? I
appartenant à un sous-ensemble G de
L8([0, 8), I)
(cf. [73]).
Dans cette section, nous nous intéressons en
particulier au problème suivant : si un point q0 de
M est globalement asymptotiquement stable pour chaque
fá, quelles autres conditions sur F
sont nécessaires pour garantir que q0 soit
globalement asymptotiquement stable pour (3.1) indépendamment et
uniformément par rapport au choix de la loi de commutation
á ? G ?
Plus précisément, nous nous intéressons ici
aux systèmes à commutations non linéaires du type
qÿ = á
X(q) + (1 - á)Y
(q), q ? R2 ,
á ? {0,1}, (3.2)
où les deux champs de vecteurs X et
Y sont lisses et G =
L8([0, 8),
{0, 1}). Nous supposons que
X(0) = Y (0) = 0 et que les deux
systèmes dynamiques qÿ =
X(q) et qÿ = Y
(q) sont globalement asymptotiquement stables
à l'origine. Nous cherchons des conditions sur X et
Y (faciles à vérifier et invariantes par petites
perturbations) telles que le système (3.2) soit globalement
uniformément asymptotiquement stable à l'origine par rapport
à á ? L8([0,
8), {0, 1}) (GUAS
dans la suite), c'est-à-dire si, (i) pour tout ä >
0 il existe å > 0 tel que toute trajectoire
de (3.2) démarrant d'un point de norme inférieure à
å reste dans la boule de centre l'origine et rayon
ä et (ii) pour tous ä1,
ä2 > 0, il existe T > 0
tel que l'évaluation au temps T d'une quelconque
trajectoire de (3.2) démarrant d'un point de norme inférieure
à ä1 ait norme inférieure à
ä2.
Notons
Z = {q ?
R2 |
dim(span(X(q),Y
(q))) < 2}.
Un premier résultat que nous pouvons démontrer est
le suivant.
Théorème 3.1 Si Z
est compact, alors (3.2) est uniformément stable par
rapport à á. Si, en plus,
Z = {0} alors (3.2)
est GUAS.
D'autres conditions peuvent être obtenues en tenant compte
de la position relative de X et
Y le long de Z. En
particulier, il est facile de voir que s'il existe une composante connexe de
Z \ {0} sur laquelle X
et Y pointent de façon opposée, alors
(3.2) n'est pas GUAS.
Introduisons l'hypothèse suivante, qui est
générique dans la classe des couples de champs de vecteurs
globalement asymptotiquement stables à l'origine (au sens de la
topologie C2) : nous disons que (X, Y
) satisfait l'hypothèse (h0) si (i)
Z \ {0} est une sous-variété
immergée de R2, (ii) X et Y
changent orientation en traversant Z et (iii)
X et [X, Y ] ne sont pas colinéaires
aux points de Z \ {0} auxquels X
est tangent à Z.
Théorème 3.2 Soit
(X, Y ) une couple de champs de vecteurs globalement
asymptotiquement stables à l'origine satisfaisant l'hypothèse
(h0). Alors : (A) si l'origine est isolée dans
Z et X n'est nulle part
tangent à Z \ {0}, alors
(3.2) est GUAS; (B) si Z \ {0}
contient une composante connexe non bornée sur laquelle
X et Y pointent de
façon opposée, alors (3.2) admet des trajectoires qui
divergent.
La figure 3.1 donne, graphiquement, la clé de la preuve
de l'énoncé (A). Les courbes Tj indiquent les
composantes connexes de Z \{0}. Nous
considérons les deux trajectoires démarrant de q
et qui commutent à chaque croisement de Z.
Nous montrons qu'elles convergent vers l'origine et que le champ de vecteurs
X + Y pointe toujours à
l'intérieur de la région bornée qu'elles délimitent
(sauf, éventuellement, à l'origine). Nous pouvons ainsi exclure
toute intersection des deux trajectoires en dehors de la composante connexe de
R2 \ ?jTj qui contient l'origine.
Nous concluons en utilisant la structure ainsi caractérisée de
l'ensemble des points atteignables à partir de q par
des trajectoires admissibles de (3.2).
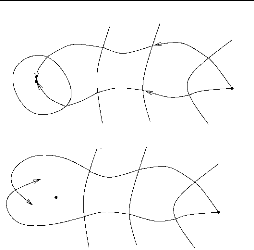
T4
0
X
Y
X
Y
0
Y
X
T3
Y
T3
X
Y
X
T2
X
T2
X
Y
Y
Y
Y
X
q
X
q
T1
T1
FIGURE 3.1 Idée de la preuve du théorème
3.2, énoncé (A)
3.2 Systèmes soumis à une condition
d'excitation persistante [MS.6,23]
Nous étudions dans cette section des systèmes de
contrôle du type
xÿ = Ax +
á(t)bu, x ?
Rd, (3.3)
oh A est une matrice n ×
n, b est un vecteur de
Rd, (A, b) est un couple
commandable, la commande u est scalaire et á
est une loi de commutation dépendant du temps à valeurs
dans l'intervalle [0, 1] qui satisfait une condition
d'excitation persistante du type
|
Z t+T
t
|
á(s)ds = 1a,
pour tout t = 0, (3.4)
|
oh 0 < 1a = T sont indépendants de
t.
A 1a et T donnés, notons
G(T, 1a) l'ensemble des á
: [0, 8) ? [0, 1]
mesurables qui satisfont (3.4). Un élément de
G(T, 1a) est dit un (T,
1a)-signal.
Nous disons qu'un vecteur K est un
(T, 1a)-stabilisateur si le retour d'état
u = -Kx stabilise (3.3) à l'origine,
uniformément par rapport à tous les éléments de
G(T, 1a). Plus précisément,
K ne peut dépendre que de A, b, T, 1a
et pas de á. La question de l'existence d'un
(T, 1a)-stabilisateur a son origine dans des problèmes
d'identification et commande adaptative (cf. [12]). La condition d'excitation
persistante peut aussi modéliser des contraintes sur l'action de
stabilisation qui dépendent de phénomènes
périodiques ou quasi-périodiques. Elle peut aussi être
utilisée pour étudier des situations dans lesquelles le
contrôleur n'a pas la possibilité, par moments, d'agir sur le
système (par exemple, à cause d'interruptions de la transmission
entre le contrôleur et l'actionneur) et il n'est pas possible de savoir
a priori à quels instants cela arrivera, mais seulement de
garantir que cela n'arrivera pas « trop souvent ».
Nous nous intéressons en particulier au cas oh la
matrice A n'est pas stable. Il paraît difficile dans
cette situation d'utiliser des méthodes de type Liapounov. Nous avons
donc développé une méthode démonstrative par
contradiction qui permet d'associer, par une procédure asymptotique, un
système à commutations au système excité. En
démontrant que ce système limite est stabilisable, nous obtenons
la (T, 1a)-stabilisabilité du système
excité. La stabilisabilité du système à
commutations est prouvée en généralisant un
résultat d'observabilité uniforme obtenu par Gauthier et Kupka
dans [60].
Nous obtenons ainsi le résultat suivant.
Théorème 3.3 Soit
(A, b) commandable et supposons que toutes les
valeurs propres de A sont à partie
réelle inférieure ou égale à zéro. Alors,
pour tout T, 1a avec T = 1a >
0 il existe un (T, 1a)-stabilisateur de
(3.3).
Pour tout (A, b) commandable, pour tout
K dans Rd, pour tous T, 1a
avec T = 1a > 0, et pour tout á ?
G(T, 1a), soit
ë+(á, K) l'exposant
maximal de Liapounov associé à xÿ =
(A - ábKT)x, à
savoir :
|
ë+(á,
K) = sup lim sup
11x011=1
t?+8
|
log(kx(t; 0,
x0, K, á)I)
|
|
|
t
|
.
|
Ici x(t; 0,
x0, K, á) indique l'évaluation au temps
t de la solution de xÿ = (A -
ábKT)x avec condition initiale
x0 au temps 0.
Le taux de convergence associé à
(A, b, T, 1a, K) est défini par
tc(A,b,T,1a,K) = - sup
ë+(á,
K).
á?G(T,u)
Les changements de variables linéaires n'affectent pas les
exposants de Liapounov et donc tc(A, b, T, 1a, K) =
tc(PAP -1, Pb, T, 1a,
(P-1)TK),
(3.5)
pour toute matrice inversible P.
Le taux maximal de convergence associé
à xÿ = Ax +
ábu, á ? G(T, pi), est
défini par
|
TC(A, T, pi) = sup
K?Rd
|
tc(A, b, T, pi, K).
|
Il ne dépend pas de b à cause de
(3.5) (on peut toujours transformer le système en forme compagnon par un
changement linéaire des variables).
Proposition 3.4 Il existe
ñ* ? (0, 1) (ne
dépendant que de d) tel que pour tout
(A, b) commandable, pour tout T >
0 et tout ñ ?
(ñ*,1] nous avons TC(A,T,
ñT) = +8.
La proposition précédente peut être
démontrée par un argument de type grand gain. Dans le cas
d = 2, nous pouvons obtenir le résultat complémentaire
suivant.
Proposition 3.5 Soit d
= 2. Il existe ñ* ?
(0, 1) tel que pour tout (A, b)
commandable, pour tous T > 0 et
ñ ? (0, ñ*), nous
avons TC(A,T, ñT) <
+8.
Nous ne sommes pas en mesure d'établir si la
proposition 3.5 peut être généralisée au cas
d > 2. La technique à la base de notre preuve n'est
pas facilement généralisable, reliant sur la construction
explicite de certaines courbes dans le plan. Nous croyons, néanmoins,
qu'il soit raisonnable de conjecturer l'extensibilité du résultat
au-delà de la dimension deux.
Une conséquence de la proposition 3.5 est l'existence
d'une matrice A telle que, si pi/T <
ñ*, le système (3.3) n'admet pas de
(T, pi)-stabilisateur. Nous pouvons prendre, par exemple,
( ë 1 ) 0
)
A = , b =
0 ë 1
avec ë suffisamment grand.
L'intérêt de cette propriété vient de sa
compatibilité avec les trois faits suivants : primo, toute limite
faible-? dans
L8([0,
+8), [0, 1]) d'une suite
(án)n?N avec
án ? G(Tn,
ñTn) et limn?+8
Tn = 0 est à valeurs dans
[ñ,1]; deuxio, la topologie faible-?
rend l'application entrée-sortie á 7?
x(t; 0, x0, K,
á) continue ; tertio, le système à
commutations
xÿ =
0 1 )
x + á?bu
0 0
peut être stabilisé, uniformément par
rapport à á? ?
L8([0,
+8), [ñ, 1]), avec un
taux de décroissance arbitrairement grand. Une conjecture à
priori plus faible (mais probablement équivalente) de celle concernant
l'extensibilité de la proposition 3.5 au cas d > 2
est qu'il existe, en toute dimension supérieure à deux, un couple
commandable (A, b) et des valeurs 0 < pi =
T tels que (3.3) n'admet pas de (T,
pi)-stabilisateur.
La constante qui discrimine entre taux de convergence
arbitrairement grand et taux de convergence borné peut être
étudiée en fonction de A et T.
Soit
ñ(A,T) =
inf{ñ ? (0,1] |
TC(A, T, T ñ) = +8}. (3.6)
Remarquons que ñ(A,T)
est égal à ñ(A/T, 1) et
ne dépend pas de la trace de A. La définition
de ñ et le résultat qui suit sont valables
pour d ? N quelconque.
Lemme 3.6 La fonction T 7?
ñ(A, T) est localement Lipschitz sur
(0, +8). Les deux limites
limT?+8
ñ(A,T) et
limT?0+ ñ(A,T)
existent et sont égales, respectivement, à
supT>0
ñ(A,T) et
infT>0
ñ(A,T).
Le comportement de la fonction ñ est
loin d'être complètement compris et suscite des nombreux
problèmes ouverts et conjectures. Par exemple : quelles sont les
matrices A pour lesquelles T 7?
ñ(A,T) est constante ? Est-ce que la valeur
constante de ces fonctions dépend de A? Si oui, comment
? La même question de l'éventuelle dépendance par rapport
à A se pose pour les limites
limT?0+ ñ(A,T) et
limT?+8 ñ(A,T).
3.3 Analyse de stabilité des systèmes
linéaires à commutations à temps discret par le biais de
fonctions de Liapounov quadratiques [MS.27]
Nous considérons dans cette section la stabilité
uniforme de systèmes a commutation linéaires a temps discret du
type
x(k + 1) =
Aî(k)x(k),
k ? N, (3.7)
où la suite x est a valeurs dans
Rd. Les matrices Aî, de
taille d × d, dépendent d'un paramètre
î ? ? RM qui varie en
fonction du temps (discret).
L'intérêt principal de ce type de systèmes
est son aptitude a modéliser des situation où la dynamique est
sujette a perturbations dépendantes du temps trop difficiles a
décrire précisément, mais que l'on peut borner (cf. [73,
96]).
La stabilité d'un système du type (3.7) peut
être caractérisée grâce au rayon spectral conjoint
([32, 93]). Celui-ci n'étant pas calculable exactement en un nombre fini
de pas, il en résulte que l'analyse de stabilité de (3.7) reste
un problème ouvert, même dans le cas d = 2. (La
situation est différente dans le cas des systèmes a temps continu
: voir [34] et [14] pour une classification des systèmes globalement
uniformément stables et aussi [5] pour la réduction au cas
d = 2 d'une classe de systèmes de dimension
supérieure.)
La recherche de critères viables pour tester la
stabilité de ces systèmes a donné lieu récemment a
une intense activité scientifique (cf., par exemple, [28, 61] et les
références qui y sont citées).
Un des critères les plus populaires est celui de la
stabilité dite quadratique, qui correspond a l'existence d'un
fonction de Liapounov quadratique V (x) =
xTPx commune a toutes les dynamiques
Aî (cf. [20]). Nous appellerons dans la suite cette
stabilité quadratique statique. L'avantage pratique de ce type
de critère est qu'il peut être reformulé de façon
équivalente en termes d'inégalités matricielles
linéaires (LMI dans l'acronyme anglais utilisé habituellement)
qui peuvent être testées par des solveurs classiques ([38]).
Le critère de stabilité quadratique statique
peut être étendu au cas où la fonction de Liapounov
dépend du paramètre î, prenant la forme
V (x, î) =
xTP(î)x
(cf. [56]). On parle alors de stabilité quadratique
dépendant des paramètres. Dans le cas où les matrices
Aî appartiennent a un polytope, î 7?
Aî est une paramètrisation affine et l'application
î 7? P(î) est contrainte a
être affine, l'existence d'une telle fonction de Liapounov peut a nouveau
se tester grâce a des LMI ([50]).
La contribution présentée ici a pour but de
garantir que la structure imposée a î 7?
P(î) dans [50] n'est pas contraignante par
rapport a celle plus général de la stabilité quadratique
dépendant des paramètres, dans le sens que si A(
) est un polytope convexe et une fonction de Liapounov dépendante de
î existe, alors il en existe une qui est affine (et sa
recherche peut donc être effectuée par le biais d'une LMI). Nous
montrons aussi que, même en rajoutant une dépendance explicite de
P par rapport au temps k, la classe de
systèmes dont la stabilité peut être testée
grâce a P ne croît pas.
Definition 3.7 Nous disons que (3.7) est
uniformément asymptotiquement stable si, pour tout
x0 ? Rd,
la solution de (3.7) avec condition initiale x(0) =
x0 converge à zéro uniformément par
rapport à {î(k)}k?N
? et si, pour tout R > 0, il existe
r > 0 tel que, pour tous
Ix(0)I < r,
{î(k)}k?N ?
et k ? N, nous avons
Ix(k)I <
R.
Une condition suffisante pour la stabilité uniforme
asymptotique de (3.7) est la suivante.
Definition 3.8 Nous disons que (3.7)
satisfait la propriété de stabilité quadratique
dépendant des paramètres (SQDP) s'il existe
á0,á1,á2
> 0 et
V (x, î) =
xTP(î)x
(3.8)
tels que
á1IxI2 =
V (x, î) =
á2kxk2
et, pour tous x(0) ?
Rd,
{î(k)}k?N ?
et k ? N, nous avons
V (x(k +
1), î(k + 1)) - V
(x(k),
î(k)) =
-á0Ix(k)I2.
La souplesse de la propriété SQDP est
donnée par le fait qu'elle autorise P à
dépendre du temps, par le biais du paramètre de commutation
î. Nous pouvons obtenir une autre condition suffisante,
a priori plus générale, pour la stabilité uniforme
asymptotique de (3.7) en ajoutant dans P la dépendance
explicite par rapport au temps.
Définition 3.9 Nous disons que (3.7)
satisfait la propriété de stabilité quadratique
dépendant des paramètres et du temps (SQDPT) s'il existe
á0,á1,á2
> 0 et
V (k, x,î) =
xTP(k,
î)x
tels que
á1IxI2 =
V (k,x, î) =
á2kxk2
et, pour tous x(0) ?
Rd,
{î(k)}k?N ?
et k ? N, nous avons
V (k + 1,
x(k + 1), î(k
+ 1)) - V (k,
x(k),
î(k))=-á0
Ix(k)
12.
Soit le simplexe conv{e1,... , eM}
de RM, où
{e1,... , eM} dénote la base
canonique. Nous supposons dans la suite que A est de la
forme
A(î) =
XM îiAi.
i=1
Nous disons que V , définie par (3.8),
est polyquadratique si P(î)
est linéaire par rapport à î.
Remarque 3.10 Le système (3.7) est
uniformément asymptotiquement stable si et seulement si cela est vrai
pour le système où est remplacé par
{e1,... , eM}. En effet, en
utilisant la convexité de la norme des matrices, il est possible de
vérifier que le rayon spectral conjoint des deux systèmes est le
même.
L'équivalence entre les différentes notions de
stabilité quadratique est énoncée dans le
théorème suivant.
Théorème 3.11 Soient =
conv{e1,...,eM} et
A(î) = PM i=1
îiAi pour î ? .
Alors (3.7) satisfait la propriété de SQDPT si et seulement s'il
satisfait la propriété de SQDP avec V
polyquadratique.
Nous pouvons aussi montrer que la stabilité asymptotique
uniforme n'est pas équivalente à la stabilité quadratique,
dans le sens suivant.
Proposition 3.12 Il existe des
systèmes du type (3.7) qui sont uniformément asymptotiquement
stables mais qui ne satisfont pas la propriété de SQDP.
L'équivalent de la proposition 3.12 dans le cas
à temps continu avait déjà été
remarqué (cf. [53, 78]). Le passage au cas du temps discret peut se
faire en discretisant un système à commutions à temps
continu vérifiant GUAS et n'admettant pas de fonction de Lyapounov
quadratique commune et en faisant tendre le pas de discretisation temporelle
vers zéro.
| 

