Chapitre troisième : GEOMETRIE
NON-EUCLIDIENNE
Tout ce qui précède nous aide à
introduire la notion de géométrie non-euclidienne. Dans un
premier temps nous présenterons les limites de la
géométrie euclidiennes qui ont conduit à
l'élaboration d'un autre type de géométrie. Les notions de
géodésique et d'espaces de Riemann nous aideront à
définir la géométrie non-euclidienne en prenant comme
exemples concrets les cas de la géométrie sphérique et de
la géométrie hyperbolique.
3.1. Limites de la géométrie
euclidienne
Au début du chapitre premier, nous avons
souligné que l'objet de la géométrie euclidienne est
l'étude des formes et des propriétés des corps naturels.
Longtemps considérée comme l'archétype du raisonnement
logico-déductif, elle présentait, en effet l'avantage de
définir les propriétés intuitives des objets
géométriques dans une construction mathématique
rigoureuse. Pour les anciens Grecs, la géométrie euclidienne
avait un intérêt pratique et aujourd'hui encore, elle est
très utilisée dans des domaines tels que l'architecture et la
topographie.
Tant que nos calculs et manipulations s'effectuent dans le
plan, la géométrie euclidienne reste valable. Cependant, dans des
espaces dites courbes, par exemple, les principes de la
géométrie euclidienne doivent être complétées
par ceux de la géométrie noneuclidienne. Pour décrire la
surface de la sphère, notamment calculer la distance entre deux points
se trouvant sur une sphère, on doit faire nécessairement appel
à la géométrie noneuclidienne. La géométrie
euclidienne est aussi prise à défaut quand le postulat des
parallèles n'est pas accepté.
3.2. Géodésique et équation
métrique
Définition 3.1.
Considérons la surface bidimensionnel d'une sphère
de rayon R. Etant donnés deux points B et C
diamétralement opposés, nous cherchons la plus courte
distance s mesurée sur la sphère entre B et
C. La courbe obtenue est une géodésique.
Remarque 3.1.
Cette notion généralise, pour une surface
arbitraire, la notion de droite du plan.
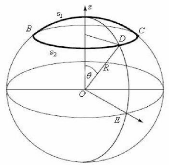
Fig. 3.1. Une sphère de centre 0, avec
géodésiques.
Remarque 3.2.
Nous supposerons comme intuitif que la longueur d'une courbe
de l'espace tridimensionnel euclidien est toujours supérieure ou
égale à la longueur de toute projection plane de cette courbe.
Le rayon entre l'axe Oz et l'un des points B ou
C est trivialement donné par :
r = Rsin è (3.1.)
Et donc la
moitié du périmètre du cercle à hauteur de
B et C sera donné par :
P 2 sin
ð è
R
s = =
2 = ð è
R sin (3.2.)
2 2 2
Le périmètre d'un cercle en fonction de l'angle
d'ouverture de ce dernier étant donnée par:
L = R.á (3.3.)
Il vient donc
automatique :
s 2 = R(2è ) (3.4.)
? ?
Comme ð sin è = 2 è sur l'intervalle ??
0, ð alors s 2 = s 1 (il y a
égalité en è = 0
?? 2
ð
et è = ).
2
Définition 3.2.
Les géodésiques de la sphère sont donc
les arcs de grands cercles, trajets empruntés par les avions pour les
vols intercontinentaux, et correspondent aux lignes obtenues entre la surface
de la sphère et un plan passant par le centre de celle-ci.
Les propriétés géométriques des
figures tracées sur la surface d'une sphère ne sont donc plus
celles de la géométrie euclidienne. Ainsi, le plus court chemin
d'un point B à un point C, sur la surface
sphérique, est constitué par un arc de grand cercle passant par
les points B et C. Les arcs de grand cercle jouent le
même rôle pour la sphère que les droites dans le plan. Ce
sont les géodésiques de la sphère.
Considérons maintenant deux surface bidimensionnelles :
la surface de la sphère et celle du cylindre. Etant donnés deux
points B et C, nous traçons la courbe
géodésique entre ces points :
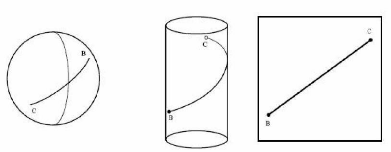
(3.5.)
Le cylindre peut être découpé
parallèlement à son axe et déplié à plat. La
géodésique apparaît ainsi comme une droite du plan. Nous
disons alors que le cylindre est "intrinsèquement plat" (même si
sa topologie diffère de celle du plan, il faut en particulier ici
éviter que la coupure ne traverse la géodésique). Ce n'est
évidemment intuitivement pas le cas de la surface de la
sphère.
Dans le cas de la surface cylindrique, nous pouvons
définir les coordonnées cartésiennes du plan B (
y1, z 1 ) et C(
y2, z2 permettant d'écrire la
longueur s de la courbe (droite) BC sous la forme du
théorème de Pythagore :
s 2 = ( y - y ) + z -
z (3.6.)
2 ( 2
2 1 2 1
La métrique du plan est euclidienne et sous
infinitésimale nous obtenons l'équation métrique
euclidienne :
ds 2 = dx2 + dy2
(3.7.)
Sur le cylindre, le changement de variable y =
rè donne :
|
2 2
s r r
2 ( 2
= è è
- + - =
2
( ( è è
- + -
z z
2 1 ) z z r
2 1 2 1 2 1
Ou sous forme locale :
|
(3.8.)
|
La surface du cylindre peut ainsi être
représentée par des coordonnées cartésiennes
analogues à celles du plan, la métrique de la surface du cylindre
étant euclidienne sous forme infinitésimale et sous forme
globale.
Remarque 3.3.
La relation précédente (3.9) correspond à
celle de l'équation métrique en coordonnées polaires.
Pouvons-nous nous intéresser à écrire
l'analogue du théorème de Pythagore pour une surface
sphérique ? L'impossibilité de découper la sphère
et de l'aplatir pour épouser un plan rend cette tâche
difficile.
Voilà pourquoi l'équation de la métrique ne
peut s'écrire sous forme générale comme le
théorème de Pythagore.
Cependant, localement (c'est-à-dire dans une
région de petite dimension devant le rayon de la sphère), les
propriétés de la sphère peuvent être décrites
par des coordonnées cartésiennes d'un plan tangent à sa
surface (c'est la propriété essentielle des espaces de Riemann)
tel que l'équation métrique soit localement euclidienne :


ds 2 = r2dè
2+r2 sin 2 èd ö
2 (3.10.)
En posant dî =
gèè dè, dç =
gèè dè il vient alors :
ds g d
2 ( ) 2 ( ) 2 2 2
= èè è + g d
öö ö î ç
= +
d d (3.11.)
Avec : gèè =
R2 g öö = R2 sin
2 èds2 (3.12.)
Alors que è ,
ö sont les coordonnées de Gauss, î , ç sont les
coordonnées du plan
localement tangent.
Cette petite présentation ayant été faite
dans un cadre plus général, nous allons nous intéresser
aux espaces de Riemann.
| 

