Chapitre 1 : La détermination des besoins en eau
des cultures
Dans un premier temps, la détermination des besoins en
eau d'une culture nécessite la connaissance de divers paramètres
concernant, aussi bien la plante elle-même que les données
climatiques ou pédologiques de la région.
Selon Doorenbos et Pruitt (1975) le climat est l'un des
facteurs qui influe le plus sur le volume d'eau que la culture perd par
évapotranspiration. Les pratiques agronomiques, les techniques
d'irrigation, les engrais, les infestations dues aux insectes et aux maladies
peuvent aussi influencer le taux d'évapotranspiration.
1.1. Pourquoi déterminer les besoins en eau des
cultures ?
Connaître la valeur des besoins en eau des cultures est
à la base de :
- projet d'irrigation : conception des réseaux
d'irrigation (calcul du débit de dimensionnement des ouvrages),
- gestion des réseaux d'irrigation : prévision
à court terme (programmation des apports d'eau), - pilotage des
irrigations,
- planification de l'utilisation des ressources hydrauliques :
volume d'eau nécessaire pour l'irrigation, surfaces irrigables au vu des
ressources, etc.
1.2. Comment déterminer les besoins en eau des
cultures ?
D'après Doorenbos et Pruitt (1975) l'estimation de
l'évapotranspiration en vue de la programmation de l'irrigation doit se
faire en se fondant sur le calcul de l'évapotranspiration maximale et de
la pluie efficace (Pe).
1.2.1. Besoin en eau d'irrigation
Le besoin d'irrigation, noté (BI) est définit
comme étant le volume d'eau qui déverra être apporté
par irrigation en complément à la pluviométrie et
éventuellement d'autres ressources telles que les remontées
capillaires (l'apport d'une nappe phréatique), la réserve en eau
initiale dans le sol, et la fraction de lessivage (lorsque la salinité
influe sur la disponibilité en eau pour les plantes).Le calcul de ces
besoins d'irrigation repose sur un bilan hydrique, qui exprime la
différence entre les besoins en eau de la culture et les apports d'eau
d'origine naturelle, donné par la formule :
( ETc Pe Ac S
- - - Ä
BI =
)
( )
I LR
-
Avec :
BI : besoin d'irrigation (mm),
ETc : évapotranspiration de la culture (mm),
Pe : précipitation efficace (mm), calculée en
retirant à la précipitation totale les pertes par ruissellement
ou par percolation profonde,
Ac : ascension capillaire (mm), due aux flux ascensionnels
à partir des eaux souterraines,
AS : variation de la réserve d'eau du sol (mm),
différence entre les quantités d'eau disponible dans la zone
racinaire au début et à la fin de la saison
végétative,
LR : fraction de lessivage.
BI étant un besoin net, pour calculer la
quantité réelle d'eau à apporter à la culture il
faut tenir compte des efficiences de transport, de distribution et
d'application de l'eau. Si on considère une efficience globale, produit
entre les 3 efficiences décrites, le besoin brut en eau d'irrigation
(BI brut) est :
BI brut = BI / eff
Où eff : l'efficience d'irrigation, exprime le rapport
adimensionnel entre la hauteur d'eau d'irrigation effectivement requise par la
culture et celle qu'on doit prélever à la source.
Pour arriver à calculer les besoins d'irrigation il faut
connaître d'abord les besoins en eau maximums des cultures (ETm).
1.2.2. Besoin en eau de culture (ETm)
En matière d'irrigation, on cherche à placer les
plantes dans des conditions de production optimales et on base l'irrigation sur
la valeur de l'évapotranspiration maximale (ETm) qui est une
valeur ponctuelle liée à l' ET0 qui est relative
à une région par un coefficient cultural, donnée par la
formule de base de l'approche climatique :
ETm = kc × ET0
ETm : évapotranspiration maximale d'une culture (mm),
kc : coefficient cultural,
ET0 : évapotranspiration de référence
(mm).
1.2.2.1. Choix du coefficient cultural
Par définition, le coefficient cultural (kc) est le
rapport entre l'évapotranspiration de la culture (ETc) et
l'évapotranspiration potentielle (ET0), il intègre les effets des
4 caractéristiques primaires qui distinguent une culture de la culture
de référence qui sont : la hauteur de la culture, la
résistance de surface sol - végétation, l'albédo,
l'évaporation de sol (Allen et al, 1998).
Les facteurs qui influent sur la valeur de kc sont : les
caractéristiques de la culture, les dates de plantation ou de semis, le
rythme de son développement et la durée de son cycle
végétatif, les conditions climatiques, en particulier au
début de la croissance et la fréquence des pluies ou des
irrigations.
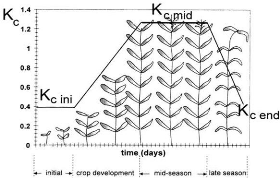
Figure 7 : Courbe de coefficients culturaux et
définition des phases
(Doorenbos et Pruitt, 1975)
La courbe de kc sur l'ensemble de la période de
croissance a été présentée initialement par
Doorenbos et Pruitt (1975). Elle permet de distinguer les 3 valeurs de kc
(initial, mi-saison, et d'arrière saison). Les valeurs les plus
élevées du kc sont observées au printemps et en automne,
lorsque le sol est encore humide. Les valeurs les plus basses sont
notées en été (Allen et al, 1998 in traité
d'irrigation).
En choisissant le kc approprié pour une culture
donnée et pour chaque mois du cycle végétatif, il faut
tenir compte du rythme de son développement, l'époque de
plantation ou de semis, les conditions climatiques notamment le vent et
l'humidité, et également la particularité de la
formule utilisée pour le calcul de l'ET0, ce qui pose
un problème d'harmonisation et d'utilisation des valeurs publiées
dans la littérature d'après Puech et Hernandez (1973) cité
par Choisnel (1989).
Selon Tuzet et Perrier (1998) in traité d'irrigation,
le kc varie essentiellement avec les caractéristiques propres de la
culture et seulement un peu avec le climat. Cela permet le transfert des
valeurs standard de kc (comme celles proposées dans les Bulletins FAO-24
et 56) d'un endroit à l'autre entre les zones climatiques. Mais pour
avoir plus de précision dans la détermination de l'ETc, il est
toujours préférable d'utiliser les valeurs de kc
déterminés expérimentalement dans la région
elle-même.
1.2.2.2. Les méthodes d'estimation de
l'ET0
L'ET0 est considérée comme une
donnée climatique, ne dépend que des conditions
atmosphériques, de l'énergie disponible à la surface
évaporante et la résistance aérodynamique de couvert
végétal. Ils existent des méthodes expérimentales
pour la mesure directe de l'ET0, basées sur le bilan hydrique, le bilan
d'énergie et la méthode lysimétrique. Devant la
difficulté de la mise en place de ces dispositifs, différentes
formules avec des degrés d'empirisme variables ont été
développées depuis ces 50 dernières années pour
estimer indirectement cette grandeur à partir de données
climatiques. Elles sont classées en 4 groupes selon les
paramètres utilisés, parmi ces formules on peut citer :
- Les formules combinées :
- de Penman originale (1963),
- de FAO Penman-Monteith (1994).
- Les formules basées sur la température :
- Blaney-Criddle (1950),
- Turc,
- Jensen-Haise,
- Hargreaves,
- Thornwaite.
- Les formules basées sur la radiation :
- FAO-Radiation,
- Christiansen - Hargreaves (1969),
- Christiansen - Samani (1985).
- Les formules basées sur l'humidité relative de
l'air :
- d'Ivanov (1954),
- d'Eagleman (1967), - FAO Class A.
1.2.3. Formule de FAO Penman - Monteith
La formule de Penman-Monteith se distingue parmi les
différentes formules par son origine théorique
dérivée du bilan de flux énergétique à la
surface de couvert végétal, dans un souci de normalisation, la
FAO, à travers son groupe d'experts opérants dans
différents contextes climatiques, a adapté la formule de
Penman-Monteith aux conditions d'un couvert de gazon et propose la formule
dérivée comme la nouvelle définition de
l'évapotranspiration de référence.
Allen et al (1994) cité in traité d'irrigation
(1998) ont définit l'ET0 comme «l'évapotranspiration d'un
couvert végétal "hypothétique" de référence
ayant une hauteur de 12 cm, une résistance du couvert de 70 s/m et un
albédo de 23%. Un couvert de gazon se développe activement sur
une grande étendue régulièrement tendu, bien
alimenté en eau et indemne de maladies ».
L'évapotranspiration de référence peut
s'écrire selon la formule (Allen et al, 1994):
ET =
0 Ä + +
ã (1 0,34 )
U 2
900
0,408 (Rn - G)
Ä + ã U2 s
(
T 273
+
e
-
e a
)
Avec :
ETo : évapotranspiration de référence
journalière (mm/j),
Rn : rayonnement net à la surface de culture (M
J/m2/j),
G : flux de chaleur échangé avec le sol (M
J/m2/j),
T : température moyenne journalière (°C),
U2 : vitesse moyenne journalière du vent mesuré
à 2 mètres (m/s),
es et ea : respectivement la pression de
vapeur saturante et la pression réelle de l'air à la même
hauteur (kPa),
A : pente de la courbe de pression de vapeur saturante à
la température T (kPa /°C), ã : constante
psychrométrique (kPa /°C),
900 coefficient pour la culture de référence (kg K/
kJ) liées aux unités utilisées a la distribution de
variables ñ, cp et ra,
0,34 : coefficient de vent pour la culture de
référence (kg K/ kJ) résultant du rapports rs /
ra, 0,408 inverse de ë = 2,45 MJ/ kg.
Sur la base des résultats de plusieurs études,
notamment celles de Jensen et al (1990) cité par Kassam et Smith (2001),
la consultation d'experts mené par la FAO sur la méthodologie
d'estimation des besoins en eau des cultures a conduit à recommander la
méthode de Penman-Monteith comme méthode
privilégiée d'estimation de ET0 du gazon, et donc pour servir de
base à la détermination des coefficients culturaux.
Pour confirmer la validité de cette formule dans notre
région d'étude, nous avons essayé de la comparer avec
d'autres formules telles que celles de Turc et Blaney - Criddle (détails
de calculs en annexe 1).
ETO (mm/j)
4
2
7
6
5
3
1
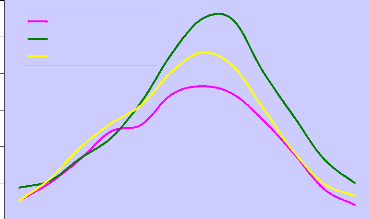
Turc
Blaney-Criddle Pen-Month (cropwat)
Janv. Fév. Mars Avril Mai Juin Juill. Août Sept.
Oct. Nov. Déc.
Figure 8 : L'évapotranspiration
potentielle calculée par différentes formules
dans la wilaya
de Tipaza
La figure ci-dessous montre bien la différence des valeurs
de l'ET0 durant l'année entre chaque formule utilisée :
- La formule de Blaney-Criddle surestime
généralement l'ET0 durant toute l'année,
- la formule de Turc sous estime l' ET0 pendant
l'été, alors qu'elle reste proche de la formule de FAO Penman -
Monteith durant l'hiver et l'automne,
- au printemps ces 2 formules sous estimes l' ET0 par rapport
à la formule de FAO Penman - Monteith,
- en fin la formule de FAO Penman - Monteith est celle qui a
permet une estimation moyenne de l' ET0.
Tableau 7 : Total annuel de l' ET0 pour chaque
formule de calcul
|
Formules
|
ET0 (mm/an)
|
|
Blaney-Criddle
|
1408
|
|
Pen-Month
|
1243
|
|
Turc
|
1113
|
Donc la formule de FAO Penman - Monteith donne la meilleure
estimation de l'ET0 dans la région de Tipaza. Selon les travaux de
Jensen et al (1990) citée par Kassam et Smith (2001), l'erreur commise
sur la valeur de l'ET0 par cette formule n'est que de l'ordre de 0,49.
Vu la complexité de cette formule qui nécessite
la détermination de différents paramètres climatiques, la
FAO la informatisée dans son logiciel Cropwat pour éviter la
manipulation manuelle.
1.4. La détermination des besoins en eau des
cultures sous serre
Les besoins en eau des cultures sous serre varient, bien
évidemment, de ceux en plein champ. Ils dépendent plus
particulièrement de l'importance du rayonnement parvenant au niveau de
la culture, et des caractéristiques optiques de transmission du
matériau de couverture, qui modifieront essentiellement les
échanges de chaleur et de vapeur avec l'atmosphère. L'importance
de ces échanges dépendra également des apports
énergétiques représentés par le chauffage et de la
fréquence du renouvellement de l'air à l'intérieur de la
serre ainsi que de la ventilation à l'extérieur. Mais la
méthode de calcul des besoins en eau reste la même.
ETms = ET0s × kc ETms : besoins en eau
max. des cultures (mm),
ET0s : évapotranspiration potentielle sous serre (mm),
kc : coefficient cultural sous serre.
Les besoins en eau d'irrigation sous serres sont : BI serre =
ETms (pluie = 0).
Les besoins en eau des cultures sous serre peuvent être
approchés également par une corrélation qui a
été établie par Menier et al en 1970
(cité par Boussaid et Kaced, 1996) liant
l'évapotranspiration max. sous serre et celle en conditions
naturelles.
ETms = 0,56 ETm + 0,7
Ces mêmes collaborateurs ont établi une autre
relation entre l' ETms et le rayonnement global hors serre (G) :
ETms = 0,44 G - 0,35
1.4.1. Modèles de détermination de
l'évapotranspiration sous serre (ET0s)
Il existe plusieurs formules pour approcher
l'évapotranspiration sous serre, dont :
a) formule de De Villele (1970) Donnée
par la relation suivante : ET0s = 0, 67 × Gs - 0, 2
Avec :
ET0s : évapotranspiration sous serre (mm/j),
Gs : rayonnement global sous serre
(cal/cm2/j) et obtenu par :
Gs = G × t
G : rayonnement global estimé (cal/cm2/j),
t : coefficient de transmission de la couverture de la serre.
Selon De Villele, dans la région
méditerranéenne t est égal a : - 60 à 65 % en cas
d'une serre plastique en PVC armé, - 80 % en cas d'une serre plastique
en polyéthylène,
- 65 % en cas d'une serre plastique en
polyéthylène double, - 75 % en cas d'une serre en verre.
L'estimation du rayonnement global se fait à partir de
l'équation :
G = G ° × (0,62 i + 0,17)
G : rayonnement global estimé (cal/cm2/j),
G ° : rayonnement global aux confins de l'atmosphère
(cal/cm2/j), i : fraction d'insolation relative.
b) Modèle de Bouchet
Qui estime l'ET0 serre à partir de deux mesures :
température et évaporation.
ET0s = á × k × ev
á : coefficient dépendant du type d'abri
météorologique,
k : coefficient dépendant de la température moyenne
journalière (° C), ev : évaporation de la décade
considérée (mm/j).
Pour le calcul de l'évapotranspiration sous serre dans
la wilaya de Tipaza nous avons préféré d'utiliser la
formule de De Villele qui a été déterminé
d'après les travaux de ce dernier dans de nombreux pays
méditerranéens particulièrement en Tunisie.
| 


