Mesure du risque de marché et théorie des valeurs extrêmes

INSTITUT DES HAUTES ÉTUDES ÉCONOMIQUES ET COMMERCIALES
MÉMOIRE DE RECHERCHE APPLIQUÉE
PEUT-ON EVITER LES CRISES?
MESURE DU RISQUE DE MARCHÉ ET THÉORIE DES VALEURS EXTRæMES:

UNE VISION QUANTITATIVE DU RISQUE EXTRæME APPLIQUÉE Ë LA CRISE DES
SUBPRIMES



MASTER : FINANCE DE MARCHÉ [SMT]

AUTEUR : J. MEILHOC

TUTEUR : A. AUBRY, QUANTITATIVE FUND MANAGER DATE : 2 JUIN 2012

RÉSUMÉ

Les récentes crises financières et monétaires ont conduit le développement de nouveaux outils de protection contre le risque de marché. Le théorème de la limite centrale, qui décrit le comportement asymptotique de la moyenne d'un grand nombre de variables indépendantes, ne semble plus adéquat lorsque des événements rares ou extrêmes deviennent normes, comme lors de la crise des Subprimes. A ce titre, la Value-at-Risk, qui peut se définir comme le quantile déterminant la plus grande perte que peut subir un portefeuille avec une probabilité d'occurrence déterminé, permet de mesurer ce risque extrême. La théorie des valeurs extrêmes (TVE), étudiée dans le cadre de la recherche d'évènements rares d'une suite de variable s aléatoires indépendantes, associée à la Value-at-Risk peut être un excellent indicateur. Ce mémoire de recherche prend son essence dans la recherche des valeurs extrêmes appliquées à la Value-at-Risk, afin d'y élaborer un modèle de prévention du risque cohérent.

MOTS-CLÉS : FINANCE QUANTITATIVE; MODÉLISATION MATHÉMATIQUE; PROBABILITÉS ET STATISTIQUES ; RISK MANAGEMENT ; THÉORIE DES VALEURS EXTRæMES ; VALUE-AT-RISK (VAR)

ABSTRACT

Financial crises have become a principal concern to lead the development of new market risk indicators. The central limit theorem, which describes the average asy mptotic behavior of a random process, does not characterize rare or extreme events, like subprime mortgage crises do. Value at Risk (VaR) is defined by risk exposure at a given probability level at a specified time horizon. Computing extreme value theory (EVT), focusing on the tails of the sample distribution, is an excellent approach for its use in managing risks. This research paper presents an application of extreme value theory to compute to Value-at-Risk of a market position in order to provide a consistent risk measurment.

KEY-WORDS: QUANTITATIVE FINANCE; MATHEMATICAL MODELING; PROBABILITY AND STATISTICS; RISK MANAGEMENT; EXTREME VALUE THEORY ; VALUE-AT-RISK (VAR)

Introduction 6

I. Section theorique 10

I.I. Modele de frequence des rentabilites anormales 10

I.I.1 Taux de rentabilites normales et anormales 11

I.I . 1 . 1 Processus d'évaluation 11

I.I . 1 .2 Procédure de test 12

I.I.2 Calcul des rentabilites anormales 12

I.I .2 . 1 Modèles théoriques 12

I. I .2 . 1 . 1 Modèle de moyenne 13

I. I .2 . 1 . 2 Modèle de marché 13

I.I .2 .2 Évaluation des paramètres 14

I.I.3 Rentabilites anormales 16

I.I.4 Test de significativite 17

I.I .4. 1 Moindres carrés ordinaires 17

I.I .4.2 Rentabilités anormales transversales et cumulés 19

I.I .4. 3 Méthode de Brown et Warner 19

I.I .4.4 Méthode de Pattel 20

I.I .4. 5 Méthode de Bohemer, Musumeci et Poulsen 20

I.II. Mesure du risque 22

I.II.1 Mesure du risque gaussien 25

I.II. 1 . 1 Distribution de gauss 25

I. II. 1 .2 . 1 Loi des grands nombres 25

I. II. 1 .2 .2 Loi de Gauss 26

I.II. 1 . 2 Value-at-Risk classique 27

I.II.2 Distribution des valeurs extremes 29

I.II.2 1 Études fondamentales 30

I.II.2 . 2 Lois des maxima : résultat exacts 31

I.II.3 Mesure du risque extreme 33

I.II. 3 . 1 Théorème de Fisher-Tippet 33

I. II. 3 . 1 . 1 Modélisation paramétrique des maxima par blocs 36

I. II. 3 . 1 .2 Sélection de la taille des blocs 36

I. II. 3 . 1 . 3 Estimation du modèle BM par le maximum de vraisemblance 36

I.II. 3 . 2 Théorème de Balkema-de Haan -Picklands 39

I. II. 3 .2 . 1 Modélisation paramétrique de la distribution des excès 42

I. II. 3 .2 .2 Estimation du modèle de seuil par le maximum de vraisemblance 43

I.II. 3 . 3 4 Value-at-Risk extreme 43

3

II. Section empirique 46

II.I Mesure des fréquences anormales 46

II.I.1 Processus 46

II.I.2 Taux de rentabilités normales et anormales 52

II. I.2 . 1 Fréquences normales 52

II. I.2 . 2 Fréquences anormales 53

II.I.3 Résultat des fréquences anormales 54

II. I. 3 . 1 Rentabilités anormales stationnaires 54

II. I. 3 . 2 Rentabilités anormales cumulées 55

II.I.4 Test de significativité 56

II.II. Théorie des valeurs extremes et Value-at-Risk 58

II.II.1 Analogie statistique de la distribution des rendements et maximum

de vraisemblance 59

II. II. 1 . 1 Analogie statistique de la distribution des rendements 60

II . II. 1 . 1 . 1 Comportement limite de la loi exponentielle 60

II . II. 1 . 1 .2 Comportement limite de la loi de Pareto 62

II . II. 1 . 1 . 3 Comportement limite de la loi normale 63

II. II. 1 .2 Maximum de vraisemblance 65

II.II.2 Modèle de sélection de maxima 66

II. II. 2 . 1 Réalité erratique 66

II. II. 2 .2 Sélection de seuil 69

II.II.3 Value-at-Risk 71

II. II. 3 . 1 Couverture conditionnelle 72

II. II. 3 .2 Modèle de rentabilité ajustée du risque 75

Conclusion 78

Bibliographie 81

Annexes 85

A. Graphiques : Sélection de seuil 86

B. Stratégie : Synthèse générale 87

C. Graphiques : VaR 88

D. Stratégie 89

E. Visual Basic Application : Loi de valeurs extremes 91

F. Visual Basic Application : Loi de probabilité 93

G. Origines macroéconomiques de la crise des subprimes 97

4

Nous tenons à remercier sincèrement M^r Aubry pour avoir accepté d'encadrer ce mémoire. Ses orientations, ses conseils et ses contacts nous ont permis de mener à bien cette recherche. Je remercie aussi tout particulièrement Mr Assemat, directeur du pTMle finance de marché, pour avoir su transmettre sa passion et son esprit d'analyse. Enfin, nous souhaitons remercier également M^r Rudelle, professeur d'économie et M^r Viar, professeur de mathématiques, sans qui tout cela n'aurait été possible.

INTRODUCTION

<< [ÉJ Les idées, justes ou fausses, des philosophes de l'économie et de la politique ont plus d'importance qu'on ne le pense en général. Ë vrai dire le monde est presque exclusivement mené par elles. Les hommes d'action qui se croient parfaitement affranchis des influences doctrinales sont d'ordinaire les esclaves de quelque économiste passé. Les illuminés du pouvoir qui se prétendent inspirés par des voies célestes distillent en fait des utopies nées quelques années plus tTMt dans le cerveau de quelque écrivailleur de Faculté.È

John Maynard Keynes

<< Théorie générale de l'emploi, de l'intérêt et de la monnaieÈ Chapitre 24, 1936

Les récentes crises financières et monétaires sont indubitablement une préoccupation majeure des acteurs des marchés financiers, des banques, des pouvoirs politiques et des instances de régulation. Les fluctuations extrêmes des cours de bourse sont importantes pour l'activité économique réelle. La hausse de la volatilité en temps de crise, corrélée à la chute des marchés financiers est particulièrement inquiétante. Nous pouvons donner à ce titre l'exemple de la crise des Subprimes, qui a annoncé la chute de la banque américaine Lehman-Brothers disparue le 15 septembre 2008. Ce climat pousse les acteurs du marché, comme les régulateurs bancaires, à développer de nouveaux outils de protection contre le risque de marché. La finance moderne met en avant les mathématiques du hasard et de la statistique, conceptualisées par des lois mathématiques probabilistes capables de mesurer le risque de marché. Celui-ci se matérialise par l'espérance de pertes auxquelles les investisseurs sont impliqués. Les variations des marchés financiers : marchés des instruments de base Ð actions, obligations, devises, matières premières Ð mais aussi les marchés des produits dérivés Ð contrats à terme, options Ð sont par définition risquées et instables. Il faut par conséquent déterminer ce risque de manière précise pour mieux l'appréhender. Parmi ces outils, il existe deux mesures générales : la mesure de sensibilité et la mesure de variance.

La première peut être théorisée en fonction de la sensibilité que représente un produit financier par rapport à son indice de référence. Ainsi, le risque de marché est la probabilité de perte liée aux évolutions des marchés. Na
·vement, si nous possédons une action du Dow Jones Industrial Average et que l'ensemble du marché subit une baisse, il semble naturel de considérer qu'il va en être de même pour notre action. Cette première mesure s'assimile à la sensibilité relative d'un actif détenu par rapport aux facteurs de risque de marché. Ainsi, des modèles de risque se sont

1

développés comme le << Capital Asset Pricing M odel (CAPM)pour le plus connu. Ils mesurent la variance de la rentabilité implicite du marché par un coefficient de régression à des facteurs de risque par rapport au marché dans son ensemble. Cependant, le <<risk manager a besoin d'une mesure pragmatique du risque d'exposition. En effet, lorsqu' un nombre important d'instruments très différents compose le portefeuille, il est difficile d'adjoindre l'ensemble des covariances pouvant exister. C'est pour cette raison qu'il est décisif d'appréhender le risque à partir de profils à la fois différents et complémentaires : la dispersion des pertes et profits des actifs.

La deuxième met en exergue deux mesures de risque venant de la distribution des rentabilités des actifs : la volatilité et la Value-at-Risk (VaR). Ces mesures ne se concentrent pas sur les mêmes paramètres: La volatilité mesure les variations d'un actif autour de la tendance centrale. Cette mesure accorde le même poids aux gains espérés qu'aux pertes potentielles. Or la notion de risque est directement liée aux pertes émanant d'un actif détenu, lequel implique un revenu aléatoire. Une mesure asymétrique pouvant juger du risque de perte est nécessaire. La volatilité prend donc en compte toutes les rentabilités, positives ou négatives, extrêmes ou modéré. La Value-at-Risk peut se définir comme le quantile déterminant la plus grande perte que peut subir un portefeuille avec une probabilité d'occurrence et sur un horizon de temps déterminé: C'est un indicateur pouvant estimer le risque extrême. Ces deux indicateurs donnent une information différente. D'une part, la volatilité peut enregistrer un taux élevé et seulement capturer des risques moyens, certes significatifs, mais pas extrêmes. Tout l'enjeu d'une mesure du risque synthétique pertinente est d'estimer convenablement la perte éventuelle que peut subir un actif. D'autre part, déterminer le risque par la volatilité, moment² d'ordre 2,

¹ Voir : W F. Sharpe

² Pour tout n ? N d'une variable aléatoire réelle X est défini par m_n =ö E(Xⁿ)

3 4

présuppose que les moments suivants, le skewness et le kurtosis , ne nécessitent pas d'être ajoutés dans une mesure de risque viable. La théorie sous- jacente en est la normalité des rentabilités. La loi Normale est en effet caractérisée par les deux premiers moments. La volatilité n'est assurément pas la meilleure mesure de risque extrême. Utiliser la Value-at-Risk permet de passer outre ces difficultés dans la mesure oü le quantile de la distribution ne représente pas un équilibre moyen mais prend en compte les pertes extrêmes. Ce mémoire de recherche prend son essence dans la recherche des valeurs extrêmes appliquées à la Value-at-Risk, afin d'y élaborer une mesure de performance ajustée du risque cohérente. La prévention des évènements extrêmes est aujourd'hui en plein essor. Nous le constatons régulièrement:

· Dans l'étude du vent: à près de 650 km de rayon, ayant atteint un

5

maximum de 280 km/h, l'ouraganKatrina fut le plus puissant et le plus meurtrier des phénomènes naturels qu'ont connu les Etats-Unis, prenant près de 1836 vies et causant plus de 108 milliards de dollars à la collectivité locale⁶.

· Dans l 'étude des plaques tectoniques: le tremblement de terre Crustal, touchant Ha
·ti le 12 janvier 2010, était d'une magnitude de 7.0 - 7.3. Il a causé blessés ⁷

la perte de 230 000 vies, faisant 300 000 . 1.2 million

d'hommes et de femmes furent privés de ressources vitales.

· Dans l'étude séismologique: le séisme de la côte pacifique de Töhoku, oü le japon fut impliqué, le 11 mars 2011, dans l'une des plus importantes catastrophes de son histoire: Le Tsunami de Fukushima. Cet accident majeur a impacté les réacteurs d'une centrale nucléaire laissant un important volume de rejet radioactif.

³ Le coefficient d'asymétrie (Skewness) correspond à une mesure la distribution d'une variable aléatoire réelle. En termes généraux, l'asymétrie d'une distribution est positive si la queue de droite est plus longue ou épaisse, et négative si la queue de gauche est plus longue ou dense.

⁴ Le coefficient d'aplatissement ou coefficient de Pearson (kurtosis) correspond à une mesure leptokurtique de la distribution d'une variable aléatoire réelle.

⁵ Ouragan de catégorie 5

⁶ Chiffre officielle publié par Knabb Richard D, Ç Tropical Cyclone Report: Hurricane Katrina: 23-30 August 2005, NHC (National Hurricane center), 20 décembre 2005.

⁷ Soit plus de 2.5% de la population

L'ensemble de ces évènements, dont l'espérance mathématique d'en conna»tre la manifestation est mince, est de nature extrême. Ils existent effectivement et doivent être pris en compte.

Les statisticiens ont mis en place des mesures de prévention de ces mouvements, utilisant la Ç théorie des valeurs extrêmes È. Aujourd'hui les domaines d'applications utilisant ces analyses sont nombreux. En hydrologie, par exemple, les données excessives sont particulièrement utiles pour la prévision des crues. Dans le domaine assuranciel, elles sont utilisées dans l'évaluation des grands sinistres. En finance, les marchés financiers connaissent eux aussi des mouvements erratiques extrêmes liés à l'incertitude de l'environnement macro-économique. Faire appel à la théorie des valeurs extrêmes appliquées à la Value-at-Risk dans un tel climat est un bon point d'appui quant à la recherche de la vérité. Expérimenter ces analyses pendant la crise des S ubprimes est intéressant: un investisseur aurait-il pu contrTMler son risque en mesurant le risque de perte extrême?

Ce mémoire met en évidence les méthodes théoriques et empiriques d'évaluations des valeurs extrêmes conditionnelles appliquées à la Value-atRisk afin d'émettre une stratégie performante ajustée du risque. Celui -ci est divisé en deux sections:

Dans la première section, nous verrons l'aspect théorique de la fréquence des rentabilités anormales sur les 30 composantes du DJIA. Cette fréquence nous permettra d'apprécier la vélocité et l'ampleur avec laquelle les rendements d'un actif se meuvent d'un niveau de stabilité donné vers un niveau supposé par la crise, transformant ainsi le discernement qu'ont les investisseurs du risque d'un actif. Puis, nous étudierons la mesure du risque appliquée à la VaR liée aux théories des valeurs extrêmes.

Dans la deuxième section, à travers la partie empirique, nous pourrons nous intéresser à leurs applications sur le DJIA en période de crise des Subprimes.

I. SECTION THÉORIQUE

« Imaginez une regle tenue verticalement sur votre doigt : cette position tres instable devrait conduire à sa chute, au moindre mouvement de la main ou en raison d'un tres leger courant d'air. La chute est liee fondamentalement au caractere instable de la position ; la cause immediate de la chute est, elle, secondaire »

Didier Sornette, 2002

I.I. MODéLE DE FRÉQUENCE DES RENTABILITÉS ANORMALES

Les aspects macroeconomiques montrent de façon indubitable les consequences d'une crise, particulièrement celle des Subprimes, qui fut, pour les observateurs les plus avertis, aussi importants que celle qui a vu le jour du jeudi noir de 1929⁸. Cependant, lorsqu' on se situe sur un marche financier, dans notre exemple le Dow Jones Industrial Average (DJIA), comment considerer l'impact qu'a eu cette crise sur les actifs le composant ? Évaluer la hausse de la volatilite, sur un intervalle de temps representant la crise, afin d'y extraire des rentabilites anormales, peut etre un bon point d'appui. Mais comment pouvons-nous juger de ce que peut representer le niveau de la volatilite dite normale à titre de comparaison ?

La technique de l' « etude d'evenement », initie par E. Fama⁹, a precisement
pour objectif d'apprecier la precipitation et la profusion avec laquelle un

⁸ Le « krach de 1929 » est une crise financière qui se deroula à la Bourse de New-York entre le jeudi 24 octobre et le mardi 29 octobre 1929. Cet evenement marque le debut de la « Grande depression », la plus grande crise economique du XX^e siècle. Les jours-cles du krach ont herite de surnoms distincts : le 24 octobre est appele « jeudi noir », le 28 octobre est le « lundi noir », et le 29 octobre est le « mardi noir », dates obscures de l'Histoire des bourses de valeurs.

⁹ Hypothèse d'efficience des marches enseignee par E. Fama dans «Market effifiency, long-term returns and behavioural finance », journal of finance economics, 1998, dans lequel il quantifie les effets que peuvent impliquer un evènement de nature à changer la perception qu'ont les investisseurs de la valeur theorique d'un titre.

actif se déplace, transformant ainsi le discernement qu'ont les investisseurs du risque d'un actif.

Nous allons pour ce faire nous focaliser sur la recherche des rentabilités anormales, puis juger de leur significativité à travers des tests statistiques.

I.I.1 TAUX DE RENTABILITÉS NORMALES ET ANORMALES

Les crises financières et monétaires occasionnent donc des mouvements particuliers sur le cours d'un titre. L'approche utilisée pour isoler ceux-ci des fluctuations liées à l'influence de facteurs exogènes à la crise des Subprimes repose ainsi sur le calcul de rentabilités anormales. Par définition, ces taux de rentabilités sont obtenus par différence entre les rentabilités observées, influencées par l'incertitude qui règne sur les marchés en période de crise, et les rentabilités dites normales, données par l'absence de perturbations majeures.

Les rentabilités anormales sont nécessairement calculées en fonction d'un modèle de calcul. A ce titre, nous avons choisi d'en présenter deux dans notre étude:

· Le modèle de moyenne

· Le modèle de marché.

I.I.1.1 PROCESSUS D'ÉVALUATION

Les variables du modèle permettant le calcul des rentabilités anormales font l'objet d'une évaluation préalable. Cette estimation doit être conduite sur une période de temps antérieure dans laquelle il n'y eu aucune représentation de crise ou d'évènements extraordinaires capables de biaiser l'étude¹⁰.

1 0 Pour l'étude de la crise des subprimes, il est important d'éviter les mouvements de bourse liés au choc du 11 septembre 2001 et du scandale d'Enron en 2003 par exemple.

I.I.1.2 PROCÉDURE DE TEST

C'est lorsque nous avons calculé les rentabilités anormales que nous pouvons juger de la robustesse de ceux-ci.

· Une première étape consiste à calculer la somme des taux de rentabilités anormaux obtenue à partir des différents titres de l'échantillon.

· Une deuxième étape sera également réalisée pour calculer les rentabilités anormales cumulées (RAC) des titres pendant la crise. Cette information nous permet de conna»tre la véritable intensité d'un évènement par rapport à ses fluctuations exogènes.

· Une troisième étape montre statistiquement comment, à un seuil de risque octroyé , la crise des subprime agit sur le cours.

I.I.2 CALCUL DES RENTABILITÉS ANORMALES

I.I.2.1 MODéLES THÉORIQUES

Dans ce mémoire de recherche, nous allons analyser deux méthodes couramment utilisées dans la littérature financière. Ces méthodes repèrent de facon efficiente la présence de trajectoire de cours anormaux. Selon Stephen J. Brown et Jerold B. Warner¹¹, il s'agit du:

· Modèle de moyenne (constant mean return model, Ç CMRM È)

· Modèle de marché (market modele, Ç MM È)

1 1 Dans leur ouvrage ÇMeasuring security price performance È, journal of financial economics, publié en 1980.

I.I.2.1.1 Modèle de moyenne

Attachée à l'évaluation du modèle de moyenne, l'évolution des taux de rentabilité de l'action i est formulée par:

Ri,t = 11_i + i,t

Oü R
·, indique le taux de rentabilité de l'action i à la période t, u1, le taux
de rentabilité moyen de l'action i, est e!,! l'innovation en date t,
hypothétiquement homoscédastique a²(er) et d'espérance nulle. Un modèle

ARCH - GARCH¹² peut également être étudié afin d'estimer une variance non constante dans le temps.

I.I.2.1.2 Modèle de marché

13

Le modèle de marché fut initié par Sharpeen 1963. Ce modèle postule

pour une relation linéaire entre le taux de rentabilité R
·, d'un actif et le taux
de rentabilité Rm,t de l'indice de référence, mesuré à partir de l'action i. Ce

1 2 (( (Generalized) Auto Regressive Conditional Heteroskedasticity . Créé par Robert F. Engle en 1982. Ce modèle est un outil statistique qui mesure le comportement de la volatilité dans le temps. Son créateur voulait un outil plus précis que l'ARMA (( Auto Regressive Moving Average , utilisant une volatilité constante. A travers ce principe, une dynamique est introduite dans la détermination de la volatilité. Pour cela, on admet que la variance est conditionnelle aux renseignements dont nous disposons. Le modèle ARCH est

composé de deux équations: = z_t E(z_t ) = 0var(z_t ) =1 Dans l'équation,

t t t

est une fonction non constante, mesurable et positive de l'information disponible en t -1. Tim Bollerslev, en 1986, proposa une extension au modèle ARCH, le modèle GARCH. Il sert à modéliser

les phénomènes de persistance des chocs de variance. C'est une solution alternative qui permet de ne retenir un nombre limité de retards q, par rapport à un modèle ARCH (q) linéaire. Il se présente de la manière suivante:

2 t

q p 2 2 = + + i t i i t i

=+ (L) ^t2 +(L) ^t2

i=1 i =1

¹³ Estimation de la valeur théorique d'un actif financier exprimé dans le ((Capital Asset Pricing Model (CAPM)

modèle s'inscrit donc dans le cadre d'une mesure de sensibilité du titre étudié. Expressément, nous avons:

Ri,t = +iRm,t +

i i,t

Oü a! et f.? sont les deux éléments du modèle de marché, et !!, et une
perturbation homoscédastique a²(e1) d'espérance nulle. Comme pour le

modèle de moyenne, la variance peut être calculée selon des critères hétéroscédastique avec ARCH - GARCH.

I.I.2.2 ÉVALUATION DES PARAMéTRES

En ce qui concerne le modèle de moyenne, nous devons calculer un simple paramètre donné par la rentabilité moyenne 4u de l'action i sur N, la période pour laquelle nous tirons nos taux de rentabilités normales. Le modèle de marché quant à lui requière l'intervention de deux paramètres distincts, à

savoir a et f.? de i sur les mêmes périodes.

Pour ce faire, nous pouvons estimer l'ensemble des paramètres liés à chaque modèle à l'aide d'une représentation matricielle de la période N. A ce titre, nous pouvons consulter les études de John Y. Campbell, Andrew W. Lo et Craig MacKinlay, publiées en 1997¹⁴.

Deux composantes sont à calculer. Soit Ri, le vecteur composer des N taux de rentabilité et Xi :

· Un vecteur de N lignes égales à 1 pour le modèle de moyenne

· Une matrice à deux colonnes et N lignes dans le cas du modèle de marché dans laquelle les lignes de la première colonne sont égales à 1 et celles de la deuxième colonne prennent pour valeur le taux de rentabilité du marché en N.

1 4 Ouvrage: Ç The econometrics of financial markets È, Princeton University Press, Chapitre 4.

· Enfin, nous avons un vecteur 8
· de paramètre agrégé au modèle utilisé,

soit ji. pour le modèle de moyenne, soit (a1,f3!) pour le modèle de

marché.

Cette représentation donne formellement l'équation suivante:

R_i = X_i +

i i

Pour chaque modèle, l'appréciation des paramètres peut aussi s'effectuer par le calcul des moindres carrés ordinaires (MCO). On peut observer à présent l'expression des différents estimateurs comme suit:

ö = i

¹X_i^'R_i

(X_i^'X_i)

'

ö 2( _i) = (N k ö 1

iö i )

ö _i

2( i)

= R_i Xi i

1

2( _i) =

(X_i^'X_i)

Oü k désigne le nombre de paramètres du modèle utilisé.

· k = 1 pour le modèle de moyenne

·

15

k = 2 pour le modèle de marché

I.I.3 RENTABILITÉS ANORMALES

Énoncées précédemment, les rentabilités anormales sont obtenues par
différence entre les rentabilités étudiées en Ai et les rentabilités dévoilées
par le modèle en Ni. Estimé à partir d'une reproduction matricielle des

données, le vecteur ö des A rentabilités anorm ales estimées est décrite par

7

la relation:

ö _i = R_i X_i ö i

Dans lequel R_!^! et X_!⁴ sont les corollaires de R et X respectivement. Le

vecteur des taux anormaux sur Ai peut s'analyser de telle sorte qu'il existe une ' erreur È commise dans la prévision de la rentabilité du titre i. Mathématiquement, cette ' perturbation È réelle s'exprime comme:

i

Xi ( i

ö i) i

L'espérance mathématique des taux de rentabilités anormales, liés aux valeurs Xj^!, elles-mémes tirées des variables explicatives sur la période de crise, est donnée par:

E ö _i





Xi = E ( ö Xi ) i i

Xi

Avec 8_L, calculé précédemment, l'équation donnée par !_L - !! =

(X!^!X1 ) ! 'X!^! . Celle-ci montre une espérance nulle dans la mesure oü la
perturbation est supposée indépendante et identiquement identifiée sur Ni et Ai.

I.I.4 TEST DE SIGNIFICATIVITÉ

Comment pouvons-nous juger de la significativité des tests réalisés selon les modèles théoriques réalisés précédemment? Plusieurs étapes peuvent être mise en Ïuvre pour en tirer une hypothèse viable. Afin de montrer la véracité du raisonnement utilisé dans cette étude, nous allons dans un premier temps étudi er, en passant par la technique des moindres carrés ordinaires, un actif considéré indépendamment avant d'initier une analyse sur données associées.

I.I.4.1 MOINDRES CARRÉS ORDINAIRES

Dans la littérature économétrique, une rentabilité anormale est assimilable à un point aberrant par rapport à une suite de variables iid. Dans notre étude, nous usons des hypothèses classiques dans laquelle les moindres carrés ordinaires sont donnés par le vecteur des espérances des Ai lignes et de la matrice de variances-covariances des Ai lignes et des Ai colonnes de cette erreur. Nous avons :

E ö_i X_i = 0

2 Vi ö i

' Xi = ^2( i) + ^2( i) Xi (Xi^'Xi) ^1Xi

vi, ^MM
vi, ^MM

1

(Rm, Rm)2

Oü I montre formellement la matrice identifiée par les Ai lignes et des Ai colonnes. Parce qu'il prend en compte un élément additionnel lié à l'étude de l'indice de référence, les indicateurs v!,, de la diagonal Vi dans le modèle de marché prend l'expression suivante:

= ²( _i) 1+ +

N

(Rm,t Rm)2

N

t

=2( i).Cm,

Oü R_m se rapporte au taux de rentabilité moyen de l'indice de référence sur Ni. Nous le verrons dans la sous-section suivante lorsque Pattel dans son ouvrage publié en 1976 et Boehmer dans sa publication de 1991, utilisent cette expression dans leurs tests statistiques. En outre, cette formule permet de dissocier la hausse de la volatilité, exprimée par l'écart-type des fluctuations des cours, et la perturbation liée aux rentabilités anormales. Logiquement, l'accroissement de la variance est une fonction décroissante du nombre d'observations N utilisé pour estimer les valeurs des paramètres. Cela a pour effet de lisser la volatilité de l'étude des rentabilités normales. C'est pour cette raison qu'il est justifié d'utiliser un laps de temps N équilibré entre stabilité et précision. L'augmentation sera d'autant plus forte que les conditions de marché dans lesquelles sont calculées les rentabilités anormales s'écartent de celles qui avaient cours lors de la phase

d'estimation des paramètres. Dans les faits, la valeur de a²(E1) est inconnue. Nous utiliserons alors l'estimateur sans biais noté a²(E1). Pour ce faire, nous serons amenés à utiliser l'estimateur 11_L de la matrice de variances-covariances des taux anormaux dont la formule est donnée par¹⁵:

^öV_i ö 2( _i) + ö 2( _i) X_i ^'(X_i^'X_i) ¹X_i

Exprimé par la quantité, calculé avec :

övi, MM = ö 2( i) 1+ N1	+		(Rm, Rm)2

t

övi, ^M M = ö 2( i).Cm,

1 5 Nous devons savoir si l'analyse de cette dernière donnée est homoscédastique. En cas contraire, le risque spécifique peut biaiser les calculs. Boehmer se propose d'étudier se corollaire à travers une étude statistique.

I.I.4.2 RENTABILITÉS ANORMALES TRANSVERSALES ET CUMULÉS

L'analyse des rentabilités anormales transversale permet de juger de la signification d'un échantillon donné à une période T. Une quantité importante de travaux de recherche a été réalisée en fonction du comportement des rentabilités sélectionnées. Parce que nous travaillons sur les queues de distribution, ces statistiques vont avoir pour propriétés d'être asymptotiquement normales, d'espérance nulle et de variance égale à 1. La convergence vers la normalité étant vérifiée dès lors que le nombre de données est important (Brown et Warner) ou que le nombre d'actifs étudié soit supérieure ou égale à 30 (Pattel, Boehmer et al.). Les rentabilités anormales cumulées (RAC) permettent de juger de l'effet de la crise sur les différents actifs que peut détenir un actionnaire. C'est la représentation de l'amplitude des rentabilités anormales d'un échantillon sur une période donnée.

I.I.4.3 MÉTHODE DE BROWN ET WARNER

La méthode de Brown et Warner, notée, est la plus couramment utilisée dans l'industrie financière. Cette statistique s'exprime:

1 N

N ö i, i =1

1 N2

N ö 2( i) i=1

Nous avons donc les rentabilités anormales équipondérées de l'ensemble des titres sur la volatilité que peuvent générer celles-ci. C'est donc la rentabilité Ai obtenue divisée par le risque que celle-ci génère par ses variations erratiques en période de crise. Il est à noter que cette statistique implique une constance de la volatilité dans le temps. Nous pouvons aussi remarquer que cette hypothèse n'est plus vérifiée en phase de Ç partitionnement des données È ou Ç Clustering È dans lequel deux ou plusieurs titres réagissent, sur un intervalle de temps i, à un évènement lambda. Cette corrélation est exprimée à travers de nombreux exemples sur les marchés financiers.

I.I.4.4 MÉTHODE DE PATTEL

La méthode de Pattel peut se conceptualiser en deux parties. Les rentabilités anormales appartenant à la période de crise sont pris un à un afin d'être calculées par l'écart-type (soit le risque) de l'erreur d'estimation. Cet écart- type correspond au T^ème élément de la dia gonale de la matrice V, donné par

l'expression öVi, MM = ö ( _i).Cm, , vu précédemment. Pour la méthode de Pattel, nous avons la formule de la rentabilité anormale standardisée, telle que:

ö _i,

i, ^övi,

Le poids que peut donner un titre à forte volatilité historique dans le portefeuille est diminué. La statistique de Pattel prend la forme de:

I=1

N

,

I



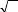
N



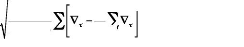
1

2

N

N

1

N(N 1)

N i =1

i =1

20

UNE VISION QUANTITATIVE DU RISQUE EXTRæME APPLIQUÉE Ë LA CRISE DES
SUBPRIMES

I.I.4.5 MÉTHODE DE BOHEMER, MUSUMECI ET POULSEN

Faisant foi d'une robustesse plus importante lorsque la variance augmente, cette statistique cherche à valider ou non l'hypothese selon laquelle A tend vers 0 pendant la période d'échantillonnage. La méthode de Bohemer, Musimeci et Poulsen s'exprime des lors comme:

1 N
N i =1

L'incertitude est au cÏur de la logique financière. Le profil de risque que les investisseurs prennent à travers leurs positions est par conséquent déterminant. Le test des rentabilités anormales prend en compte deux paramètres: l'espérance mathématique et l'écart-type. Lorsque les marchés sont en équilibre, il est alors possible d'envisager une relation entre la rentabilité attendue et son risque intrinsèque, déterminé à partir de l'écart qu'il peut exister entre la rentabilité moyenne historique amenée par cette dernière. Le test des fréquences anormales sur un temps long a donc pour objet de conna» tre l'ampleur, mais aussi la durée, que peut amener de telles rentabilités en période d'incertitude. Nous pouvons désormais reconna» tre, de facon plus rigoureuse, l'état de crise, la quantifier, peut-être la comparer.

Cette introduction nous amène à penser qu'il est nécessaire d'établir une solide gestion de mesure des risques.

I.II. MESURE DU RISQUE

Ç Les influences qui déterminent les mouvements de la Bourse sont innombrables, des événements passés, actuels ou même escomptables, ne présentant souvent aucun rapport apparent avec ses variations, se répercutent sur son cours. [ÉJ Mais il est possible d'étudier mathématiquement l'état statique du marché à un instant donné, c'est -à-dire d'établir la loi de probabilité des variations de cours qu'admet à cet instant le marché. Si le marché, en effet, ne prévoit pas les mouvements, il les considère comme étant plus ou moins probables, et cette probabilité peut s'évaluer mathématiquement È

Louis bachelier

Ç Théorie de la spéculation È. Annales scientifiques de l'E.N.S. 3ème série, tome 17 (1900), p 21-86

La finance moderne met en avant les statistiques. Ceux-ci rationalisent le mouvement de prix des marchés financiers. Le risque en est par conséquent mesurable et gérable. Les travaux en ce domaine ont débuté selon la connaissance générale en 1900, quand un jeune mathématicien, Louis Bachelier, eut la curiosité d'étudier la fluctuation des cours des marchés financiers dans sa thèse : Ç Théorie de la spéculation È. Inspiré par Pascal et Fermat, qui avait initié le concept de probabilité, L. Bachelier étudia dans sa thèse les bons du trésor francais. Considéré comme le précurseur de la théorie moderne du portefeuille et des mathématiques financières, L. Bachelier met en avant un concept nouveau : les prix montent et descendent avec des probabilités égales. Pour ainsi dire, si le nombre de données augmente à un rythme élevé, les échanges boursiers se fondent en un bruit stationnaire. Le risque de marché matérialise l'espérance de pertes auxquelles les investisseurs sont impliqués. Pour le gérer , il faut donc l'évaluer de manière pr écise. A ce titre, parmi ces outils, existe:

· Les mesures de sensibilité

· Les mesures de variance

Une première mesure du risque est en fonction de la sensibilité que représente un actif par rapport à son indice de référence. Cette première mesure s'assimile à la sensibilité relative d'un actif détenu par rapport aux facteurs de risque de marché. Elle mesure la variance de la rentabilité implicite du marché par un coefficient de régression à des facteurs de risque, tel le marché dans son ensemble. Formellement, nous avons:

cov(R_p, R_m)

=

var(R_m)

16

Oü R_p est le taux de rentabilité de l'action et R_m , celui du marché .

Cependant, le <<risk manager È a besoin d'une mesure pragmatique du risque d'exposition. En effet, lorsqu'un nombre important d'instruments très différents compose le portefeuille, il est difficile d'imbriquer de facon cohérente l'ensemble des covariances pouvant exister. C'est pour cette raison qu'il est décisif de capturer le risque à partir de profils différents : La dispersion des pertes et profits des actifs.

Nous pouvons mettre en exergue deux mesures de risque venant de la distribution des rentabilités des actifs : la volatilité et la Value-at-Risk (VaR). Ces mesures ne se concentrent pas sur les mémes paramètres:


· La volatilité mesure les variations d'un actif autour de la tendance centrale. En effet son expression en fonction du vecteur des taux de rentabilités R est¹⁷ :



= E (RE(R))²

1 6 Le modèle de marché, vu dans la sous-section précédente, n'est qu'une relation statistique utilisant la môme notification <<bôta È,

¹⁷ Regnault nous enseigne en 1863 qu'il existe une loi mathématique qui règle les variations
et l'écart moyen des cours de la Bourse: L'écart des cours est en raison directe de la racine

carrée du temps. Cette écart se définit dans la pratique par: t. , oü t représente la fenôtre de temps pour laquelle la volatilité Ç historique È est calculée.

Cette mesure accorde le même poids aux gains espérés qu'aux pertes potentielles. Or la notion de risque est directement liée aux pertes émanant d'un actif détenu, lequel implique un revenu aléatoire. Une mesure asymétrique pouvant juger du risque de perte est nécessaire. La volatilité prend donc en compte toutes les rentabilités, positives ou non, extrêmes ou non.


· la Value-at-Risk peut se définir comme le quantile déterminant la plus grande perte que peut subir un portefeuille avec une probabilité d'occurrence donné sur un horizon déterminé à l'avance : nous sommes en présence d'un indicateur pouvant estimer le risque extrême.

Ces deux indicateurs donnent une information différente. D'une part, la volatilité peut enregistrer un taux élevé et seulement capturer des risques moyens, certes significatifs, mais pas extrêmes. Tout l'enjeu d'une mesure du risque synthétique pertinente est d'estimer convenablement la perte éventuelle que peut subir un actif. Or un titre ' a peut avoir une volatilité de 10% mais ne pas observer d'extremum très important, avec un maximum de 5% de perte sur une journée par exemple . Au contraire, un actif ' b comptant une volatilité de 5%, peut conna»tre des pertes, certes rares, de plus de 20%. Le titre ' b nous semble donc plus risqué, même si ses risques Ç moyens s'avèrent être moins importants que ceux du premier.

18

D'autre part, d éterminer le risque par le momentd'ordre 2, la volatilité,

19

présu ppose que les kurtosis ²⁰

moments suivants, le skewness et le , ne nécessitent pas d'être ajoutés dans une mesure de risque viable. La théorie sous- jacente en est la normalité des rentabilités. La loi Normale est en effet caractérisée par les deux premiers moments. Utiliser la Value-at-Risk permet de passer outre ces difficultés dans le sens oü le quantile de la distribution ne représente pas un équilibre moyen mais prend en compte les pertes extrêmes. En outre, nous pouvons souligner le fait que la volatilité n'est assurément pas la meilleure mesure de risque extrême. Nous allons

1 8 Pour tout n ? N d'une variable aléatoire réelle X est défini par m_n =ö E(Xⁿ)

¹⁹ Le coefficient d'asymétrie (Skewness) correspond à une mesure la distribution d'une variable aléatoire réelle. En termes généraux, l'asymétrie d'une distribution est positive si la queue de droite est plus longue ou épaisse, et négative si la queue de gauche est plus longue ou dense.

²⁰ Le coefficient d'aplatissement ou coefficient de Pearson (kurtosis) correspond à une mesure leptokurtique de la distribution d'une variable aléatoire réelle.

dans cette partie étudier plus en détail cette mesure de risque en utilisant la théorie des valeurs extremes.

I.II.1 MESURE DU RISQUE GAUSSIEN

I.II.1.1 DISTRIBUTION DE GAUSS

I.II.1.2.1 Loi des grands nombres



D'un point de vue théorique, une variable continue prend une infinité de
valeurs à l'intérieur de son intervalle de définition. La loi des grands
nombres compte pour ce faire un
échantillon assez important de
variables aléatoires. En ce sens, la
théorie des grands nombres est
simple: Si la taille de l'échantillon est
assez importante, la moyenne
empirique de la variable étudiée tend
vers celle théorique de somme unitaire .
Par conséquent, considérons un

échantillon d'observation x₁, x₂...x_n d'une variable aléatoire X₁ ,

d'espérance u et d'écart-type finis. Des lors, la loi des grands nombres

Nous avons alors: P(lim Mn = u) =1. La loi

n

énonce que, quand n , l

converge en direction de u .

a moyenne empirique

+...

M_n = (x₁ + x₂ + x_n)

n

des grands nombres est une loi asymptotique qui assure ainsi que la moyenne empirique est un estimateur convergent de l'espérance mathématique.

I.II.1.2.2 Loi de Gauss

La loi normale de la lois continues ²¹

partie

fait famille des . Elle est associée

aux noms de Carl Friedrich Gauss et de Pierre Simon Laplace. Appelé, le théorème central limite, celui-ci indique que la somme des variables est distribuée de facon aléatoire et indépendante lorsque le nombre de données dans la somme augmente. Cette loi est définie par la moyenne u , et la

2

variance parce qu'elle est symétrique par rapport à la tendance centrale.

Nous exprimons la fonction de densité de probabilité de la loi normale avec X + comme:

1 P(x) = 2

e

1X m ( )2 22

La loi normale a une tendance centrale nulle et un écart typeégale à 1.
Nous avons donc par définitionN (0,1). Puisque P( x) = P(x), pour toute

variable centrée et réduite, la médiane, la moyenne et le mode sont confondus. Pour exprimer la continuité de ce théorème, nous pouvons écrire la fonction de distribution cumulée pour P(x) = P(X x):

x
P(x) = P(t)dt

2 1 Une loi de probabilité est dite continue lorsqu'elle se rapporte à une mesure de Lebesgue. Pour plus d'explication, se référer à l'ouvrage de G. Saporta: Ç Probabilités, analyse des données et statistiques È.

Si les différents écarts-types pris un à un sont dérisoire s par rapport à
l'ensemble, le théorème de la limite centrale reste valide. La distribution
gaussienne d'écart-type proportionnel

Nb of standard deviations

Number 4000 of data

in

interval

3000

2000

1000

0

-6.0 -4.0 -2.0 0.0 2.0 4.0 6.0





1



à représente la différence entre le

n

moyenne empirique Mde

n

l'échantillon et l'espérance ude la

variable aléatoire X . L'approximation
de la moyenne théorique upar la

moyenne empirique M_n permet de

contrôler l'erreur énoncée

précédemment. La probabilité que M_n

soit dans l'intervalle [ u t ,u + t ] se retrouve représentée par l'aire sous
la courbe comprise entre les abscisses t et + t . Sur les marchés

financiers, la plupart des mouvements sont inférieurs à une fois l'écart-type. Cette mesure représente 68% des amplitudes à la hausse comme à la baisse. 95% doivent être à moins de deux écarts-types et 98% à moins de trois écarts-types. Selon cette loi de probabilité, il existe très peu de grands mouvements.

La thèse de L. Bachelier fut largement ignorée par ses contemporains. Cependant, ses travaux furent traduits, réédités, puis développés pour aboutir au grand édifice de l'économie et de la finance moderne²².

I.II.1.2 VALUE-AT-RISK CLASSIQUE

La Value at Risk est une mesure de risque statistique popularisée dans les années 1990 par JP Morgan. La Value-at-Risk peut se définir par la perte maximale que peut engranger un portefeuille sur un laps de temps et un niveau de confiance donnée.Ç The greatest benefit of Value-at-Risk lies in the imposition of a structured methodology for critically thinking about risk. Institutions that go through the process of computing their VAR are forced to confront their exposure to financial risks and to set up a proper risk management function. Thus the process of getting to Value-at-Risk may be as important as the number itself È souligne P. Jorion dans son ouvrage: Ç Value at Risk: The New Benchmark for Controlling Market Risks È, paru

²² Développée initialement par H. Markowitz en 1954

23



3000

2000

0

4000

Number
of data

in
interval

1000

VaR(q)

-6.0 -4.0 -2.0 0.0 2.0 4.0 6.0

Nb of standard deviations

en 1996. P. Jorionnous enseigne que
la valeur W^!_T du portefeuille est donnée



par W exp( R_T ) avec W0, la valeur

T

initiale d'un portefeuille de titres et R^!_T son taux de rentabilité continu sur un

P_'

horizon T donné par ln( ) . Dès lors,

P' 1

nous notons l'équation

W =W₀ exp(R ) , représentant la

valeur minimale du portefeuille que l'on étudiera avec une probabilité égale au seuil q, le seuil de risque dont nous voulons étudier la représentativité. La valeur de la VaR est donnée par:

W W₀ =W₀ exp(R ) 1

De manière plus formelle, notons f(w), la distribution des valeurs du

portefeuille à la date T, la valeur W^* est analogue à q = f (w)dw. A ce

w

titre, si nous notons la probabilité p=Prob(w=W^*), l'espérance

mathématique de la valeur du portefeuille se situe au-dessus de W^*, nous obtenons:

W

p = f (w)dw =1 q

²³ P. Jorion est professeur de finance à l'université de Californie à Irvine. Ingénieur de formation, il obtient un Ph.D en Çfinance internationaleÈ à l'université de Chicago en 1983.

28

_pème

D'un point de vue économétrique , W^* se défini t comme le percentile

de la distribution de l'échantillon à la date T. La Value-at-Risk s'intègre pleinement dans le cadre de la gestion de portefeuille, pouvant signifier précisément au gérant ou aux institutions financières à quelle valeur peut être estimée le risque économique et réglementaire²⁴.

I.II.2 DISTRIBUTION DES VALEURS EXTRæMES

Ç Les théoriciens classiques ressemblent à des géomètres euclidiens qui, dans un monde non-euclidien découvrant par l'expérience que des lignes droites parallèles se rencontrent souvent, reprocheraient aux lignes de ne pas rester droites - comme seule remède aux collisions malheureuses qui se produisent. Pourtant, en vérité, il n'existe pas d'autre remède que de se débarrasser de l'axiome des parallèles et de travailler dans une géométrie non-euclidienne. C'est une chose similaire qui est requise aujourd'hui en économie È

John Maynard Keynes

La théorie des valeurs extrêmes (TVE) est étudiée dans le cadre de la recherche d'évènements rares d'une suite de variables aléatoires indépendantes et identiquement identifiées. L'observation des cours des actifs financiers montre que ceux-ci sont hypothétiquement influencés par leurs cours passés, auquel l'aléa est souvent modélisé par un mouvement brownien géométrique. La théorie des valeurs extrêmes est donc un cas particulier de ce mouvement. L'intérêt concret de l'étude des extrêmes se trouve dans l'analyse des maxima et des minima des séries statistiques concernées.

Sur les marchés financiers, nous gardons toujours à l'esprit les grandes crises qui ont marquées notre histoire, poussant les actifs à atteindre des valeurs extrêmes comme pour la crise des Subprimes. En outre, bien conna»tre la distribution maximum et minimum se révèle être un excellent

²⁴ Notamment avec les directives B%ole II, III.

outil d'aide à la décision, voire une opportunité de gestion en temps de crise.



La Théorie des Valeurs Extremes s'intéresse non pas à la modélisation totale d'une distribution mais seulement aux queues des lois spécifiques²⁵.

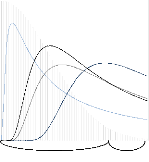
N (x)

Deux théorèmes sont indispensables pour une bonne compréhension de la Théorie des Valeurs Extremes : celui de Fisher- Tippet et celui de Balkema - de Haan-Picklands. Deux méthodes

principales de modé lisation des

0%

3.0 4.0 5.0 6.0 7.0

évènements rares sont possibles : La méthode <<Block Maxima>> (BM) qui modélise la distribution des extremes par la Generalized Extreme Value Theory (GEV) dérivant explicitement du théorème de Fisher-Tipett, et la méthode <<Peaks Over Theshold>> (POT) qui modélise la distribution des excés au-dessus d'un seuil élevé (faisant appara»tre les queues de distribution) par la Generalized Pareto Distribution (GPD) estimé par le théorème de Balkema-de Haan-Picklands. Cette dernière méthode sera modélisée en fréquence des rentabilités anormales afin d'estimer le paramètre u de la crise des Subprimes.

I.II.2 1 ÉTUDES FONDAMENTALES

Concernant la loi faible des grands nombres, rappelons cependant les études fondamentales permettant de lier la théorie fondée sur le comportement asymptotique de la distribution d'une somme de variable aléatoire et celui de la distribution du maximum et du minimum.

²⁵ Voir Embrechts, Kluppelberg, Mikosch et Beirlant, Goegebeur, Segers, Teugels pour plus d'approfondissements.

Soit X une variable aléatoire appartenant au domaine d'attraction d'une
fonction D(G ) avec (0,2) et (b_n) une suite croissante de nombre R

telle que P(X > b_n) ~ 1 , F1 = X1 et F_n = max(X₁, X₂,..., X_n),n > 2 , alors n

lim P(Y_n > bnxn) = lim P(Y_n > bnxn) =1

n nP(X > bnxn) n nP(F_n > bnxn)

Cela nous permet de conna»tre la probabilité, pour un nombre n grand, du dépassement d'un seuil x par l'ensemble de la composition d'une suite de n variables aléatoires. Lorsqu'une de ces variables se présente de facon extreme par rapport aux valeurs prises par chacun des autres éléments de la suite, nous considérons que le seuil x a été franchi. Ceci caractérise l'événement rare dont nous cherchons à étudier la distribution.

I.II.2.2 LOIS DES MAXIMA : RÉSULTAT EXACTS

Le phénomène empirique suit une marché aléatoire, mesuré par une variable X, décrivant l'évolution du prix d'un actif financier. La variable aléatoire X présente la rentabilité logarithmique. Nous dénommons

· g_X la fonction de densité notée [l, u ]

· G_X la fonction de répartition de probabilité de la variable aléatoire X. Soit X1, X2,É, X une suite de variables aléatoires aux dates 1, 2 É, n .

n Nous

écrivons F_n la rentabilité maximum et f_n le minimum, dont ceux-ci observées sur n séances boursières. Dans la suite de notre mémoire de recherche, nous traiterons les résultats ne concernant que le maximum (F_n), car ceux obtenus au minimum (f_n) s'en déduisent en considérant la série opposée X₁, X₂,..., X_n, démontrée par l'équation suivante :

f_n(X)Min(X₁, X₂,..., X_n)

= Max( X₁, X₂,..., X_n) F_n( X)

Si les cours suivent une marche aléatoire P_t+1 = P_t + X1, X2,É,

t+1 .de variable

X_n indépendamment, alors les distributions du maximum F_n sont conférées
parG_Fn (x) = [ G_X (x)]ⁿ. Les propriétés statistiques du maximum dépendent de

GX pour les grandes valeurs de x. En ce qui concerne les autres valeurs de x, l'influence de GX(x) se révèle être de moins en moins important avec n. C'est donc dans les queues de distribution de X, par définition synonymes d'extrême, que nous allons nous pencher dans cette étude. Nous pouvons en déduire la forme de la loi limite de F_n en faisant tendre n vers l'infini et en se servant de la formule. La fonction de répartition x < u = 0 et x > u =1 . Dans ce cas, la loi limite est dégénérée parce qu'elle se réduit à une masse de Dirac²⁶ portée en u. Toutefois, les formules présentées ci-dessus présentent un intérêt limité. La loi de la variable X est rarement connue précisément en pratique, ainsi que la loi du terme maximum. Nonobstant, même si la loi de la variable X est exactement connue, le calcule de F_n peut être vecteur de difficulté. Dépossédée d'expression analytique, la distribution d'une variable normale se révèle être une intégrale incalculable.

_nème

Sa puissance nous conduit à de sérieux problèmes numériques que ce

soit pour les grandes valeurs de n ou de x. C'est pour ces différentes raisons que nous sommes astreints à étudier le compor tement asymptotique du terme maximum FnÕ.

Cependant, Il existe deux théorèmes distincts capables de contourner le problème de dégénérescence. Selon la méthode employée, il s'agit du théorème de Fisher-Tippet et du Théorème Balkema-de Haan-Picklands. Nous allons rentrer dans les détails dans la section suivante.

²⁶ Dans une masse de Dirac, mesuré a partir d'un espace (X,) et un point a dans X, tel que A ,( _a(A) =1 si a A et _a(A)=0 si a A.

I.II.3 MESURE DU RISQUE EXTRæME

I.II.3.1 THÉORéME DE FISHER-TIPPET

Théorème Fisher-Tippet: Si pour une distribution G non connue, l'échantillon des maxima normalisés converge en loi vers une distribution non dégénérée, alors il est équivalent de dire que G est dans le MDA de la GEV Hî

A partir des données de prix traitées de façon journalière lors de la crise de Subprimes, nous supposons avoir une suite première d'observations X1, X2, É , X_n issue d'une fonction de distribution inconnue F²⁷. Cet échantillon peut être séparé en k blocs²⁸ disjoints de même longueur s. Les données

X₁⁽¹⁾,X₂⁽¹⁾,...,X_!⁽¹⁾, i = 1, É, k sont de natures indépendantes et

identiquement identifiées avec comme fonction de distribution F. Nous nous attachons à conna»tre les maxima de ces k blocs comme:

Y S = max(X₁ , X₂ ,..., X_s )
Qui agence la base de ce qui sera notre échantillon de données supposées

indépendante Y_!^!,Y_!^!,...,Y,^!. La loi fondamentale à la modélisation des

maxima est la Generalized Extreme Value (GEV) définie par la fonction de répartition suivante:

!1

)

si

0

!

exp( (1+ x)

H ! (x) =



si

= 0

exp( e ^x)

²⁷ A ce stade, aucune hypothèse n'est présupposée

33

²⁸ Un bloc peut correspondre à un mois, un an, etc.

Oü x est tel que 1+ x > 0. est le paramètre de forme. La GEV rassemble

trois distributions particulières:



§? Si >0, la loi de Fréchet (Type I):

(x) = G1 k

x 1 ( 1

0 x 0 ) = exp( x ^k) x > 0

k



!

§? Si <0, la loi de Weibull (Type II):

(x) = G 1 k

x 1 ( 1+

exp( x ^k) x 0 ) = 1 k > 0

k



			§? Si =0, la loi de Gumbel (Type III): (x)= G0(x)= exp( e ^x^)



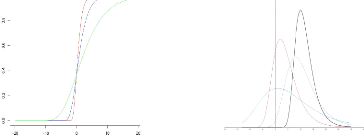
Ainsi, nous avons exposé sur les graphiques correspondant à chaque
itération deux paramètres²⁹ : Le paramètre de localisation 4u et celui de

x u

dispersion o>0. La GEV prend alors la forme de : H ! (x) = H ! ( )

,u,

La démonstration fondamentale de la modélisation des maximas est celui de
Fisher-Tippet³⁰. Supposons que nous ayons deux suites d'entiers réels tel

que a >0 et b
· tel que :

!

a_i ¹(Y_i^s b_i) H P { a_i ¹(Y b_i) y}= F^s(a_iy+b_i) H(y)

Avec H, une loi non dégénérée. a_i ¹(Y_i^s b_i), et Pour s?8, les k maxima

normalisés. Alors, F est dans le Çmaximum domain of attraction È (MDA)

de H, que nous pouvons écrire plus formellement par F?MDA(H).

Fisher-Tippet montre alors que F?MDA(H) si, et seulement si, H est du

type de H ! . La GEV est donc la seule distribution limite non dégénérée

²⁹ Les paramètres .i et a peuvent également s'écrire respectivement et

³⁰ Démontré en 1928

35

pour un échantillon de maxima normalisé. Nous obtenons alors une méthode simple de sélection de forme F. Le tableau ci-joint souligne quelles distributions sont associées aux lois de la GEV.

TAB: MDA

Gumbel Fréchet Weibull

Normale Cauchy Uniforme

Exponentielle Pareto Beta

Lognormale Student

Gamma

I.II.3.1.1 Modélisation paramétrique des maxima par blocs

La modélisation issue du théorème Fisher-Tippet, suppose que l'échantillon de maxima suive exactement une loi GEV.

I.II.3.1.2 Sélection de la taille des blocs

La littérature financière classique et l'exercice des statistiques en finance ne définissent pas une dimension standard dans la sélection des blocs. Il faut cependant que s soit de taille suffisamment importante pour que la condition asymptotique vue précédemment soit considérée. L'ingénierie financière dans les faits prend en compte un nombre de maxima caractéristique pour que l'estimation des paramètres de la GEV soit assez précise. Il est donc usuel de prendre s = 21, soit un mois boursier, ou s = 254, soit un an.

I.II.3.1.3 Estimation du modèle BM par le maximum de vraisemblance

C'est à partir de l'échantillon lié à la sélection des maximas précédente que nous pouvons estimer les paramètres de la GEV. La méthode utilisée pour l'évaluation du modèle BM se réfère au maximum de vraisemblance initié pour la première fois par Fisher au début du siècle dernier. Soit l'échantillon

de maxima supposé indépendant Y=(Y₁,Y₂,...,Yk) et h! , la densité de

,u,

x u !

la loi GEV H ! (x) = H ! ( ) pour ?0 :

,u,

1 ! Y u h! (y) = 1+ ( ) ,u,

! 1+ ! exp 1+

! y u ( )

1 !

" La vraisemblance de l'échantillon Y est : !(

n ,u, ,Y)= ^h" (Yi) ,u, i=1

. Il fait

31

appel à des procédures numériques pour la maximisation de la
vraisemblance. Il est alors aisé de calculer les estimateurs dans le cadre de la
loi des grands nombres. En revanche, il est difficile de donner un estimateur

asymptotique efficace et normal, particulièrement lorsque l'échantillon est

!

de petite taille. R. Smith³² montre qu'il suffit que =-0.5 pour que les

états de régularité du maximum de vraisemblance soient conformes. Pour le

!

cas oü = 0, la log-vraisemblance est égale à:

^n Yi /1 l(0,/1, ,Y)= nln exp( i= 1

^nYi /1 ) i=1

Plus précisément, en dérivant cette fonction afin de mettre en scène les deux paramètres exposés antérieurement nous obtenons le système d'équations suivant.

3 1 En réalité l'Algorithme de quasi-Newton

³² Dans son ouvrage: ÇExtreme Value Analysis of environnemental Time series: an Application to Trend Detection of Ground-Level ZoneÈ

37

Il est à noter pour conclure qu'il n'existe pas de solution à ces équations de maximisation³³.

) = 0

ⁿ Y_i u

n exp(

i =1

n+

n

Yi u

Yi u exp( ) 1 = 0

i= 1

3 3 Utilisation de méthodes numériques, type algorithmes de Newton-Raphson

I.II.3.2 THÉORéME DE BALKEMA-DE HAAN-PICKLANDS

Théorème Balkema-de Haan-Picklands: Il s'en déduit que
la distribution des excès au-dessus d'un seuil élevé converge

vers la GPD G!? lorsque le seuil tend vers la lmite

,!(!)

supérieure du support de G.

Supposons que X1, X2, É, X_n sont des variables aléatoires de prix indépendantes appartenant à une distribution appelée F(X). Soit xF, l'extrémité finie ou infinie de la distribution F. Alors, la fonction de distribution dépassant Xi après un seuil donné u, quand y = 0, est donné par:

y Fu(y) = P(X u X > u

+ = F(y u) F(u) 1 F(u)

Belkema et de Haan en 1974, ou encore Pickands en 1975, ont théorisé la fonction de Pareto généralisée en montrant qu'elle s'apparente à une distribution limite F _u(y) quand le seuil u tend vers l'extrémité de la fonction. Il s'agit d'une découverte statistique majeure. Si F ? MDA (Hî), il est alors possible de trouver une fonction positive mesurable par f.?(u) de telle sorte

que :

lim >

u xF

= 0

F_u(y) G ! (u)(y)

Pour 0=y=XF-u, ou G ! (u)(y) correspond à la distribution Pareto

G ! (U)(Y) = ,

!' 1 (1+ ) (u) !y 1 exp( ) (u)

si si

0 = 0

Ou y=0 pour î^?=0 et 0=y=-^!(!)_!? pour î^?<0. Néanmoins, le choix

du seuil u est primordial pour la réussite de cet exercice de modélisation de la distribution Pareto généralisée. Comme pour le test de fréquence anormale, oü nous devions choisir préalablement une fenétre de test de plus ou moins longue distance, la valeur représentative est généralement choisie en fonction d'un compromis, capable de biaiser l'étude.

î? se révèle être un paramètre de forme particulièrement important, quant à

f.?(u), il s'apparente à un paramètre d'échelle. Nous pouvons dès à présent



émettre une conc ordance avec le

théorème précédant, respectivement 4u

et a. La GPD intègre par sa

particularité d'autres formes de

distribution. En considérant que î^? > 0,

la version paramétrique de G se rapporte à la distribution originaire de Pareto, laquelle est souvent utilisée en actuariat dans l'approche des

probabilités d'erreurs. Vilfredo
Pareto³⁴ décrivit la répartition de la
richesse selon la notation suivante:

P(u) = (u / m) . En outre, Quelle est la proportion P des ménages gagnant

plus qu'un niveau de revenu u? V. Pareto estimait -! à -3/2. La puissance

est donc en premier lieu élevée au cube

puis à la racine carrée divisé par 1.

Ceci fut la base des premières lois !-stable de Lévy ³⁵

Paul , repris quelques

années plus tard par B. Mandelbrot³⁶ dans son étude sur les variations du prix du coton. A contrario, si î^? < 0 prend la forme d'une loi de Gumbel. Enfin, lorsque î^? = 0, sa correspondante est une distribution exponentielle. Le premier cas ( î^? > 0) se retrouve pertinent dans le cadre d'une distribution réelle possédant des queues de distribution épaisses. Les estimations de î?

et de f.?(u) sont calculées à partir de l'expression G!?,!(U)y par la méthode

du maximum de vraisemblance³⁷. Lorsque î^? > 0.5, Hosting et Wallis

³⁴ Né en 1848, V. Pareto était un industriel, un économiste et un sociologue italien. Son héritage en tant qu'économiste fut ample, particulièrement en terme de recherches scientifiques et d'équations mathématiques, recourant de manières intensives aux données. Son étude la plus connue concerne la répartition de la richesse correspondant à une loi de puissance.

³⁵ Paul. Lévy, né en 1886, est un mathématicien francais. Il fait partie des fondateurs modernes des probabilités. On lui doit les lois stables stochastiques: << La distribution de Lévy È. Il fut professeur à l'école polytechnique et enseigna les probabilités à B. Mandelbrot.

³⁶ Né en 1924 à Varsovie, B. Mandelbrot fut professeur de mathématiques à l'Université Yale et membre émérite du Ç Thomas L. Watson Laboratory È d'IBM. Il a notamment publié <<Les objets fractalesÈ

³⁷ Nous pouvons nous conférer à l'étude d'Embrechts paru en 1997.

montrent que l'estimation tirée du maximum de vraisemblance tend à être asymptotiquement normalement distribué.

I.II.3.2.1 Modélisation paramétrique de la distribution des excès

Cette modélisation de queue de distribution engage un échantillon au-dessus du seuil u, lequel conduit à une forme de loi GPD.



Dans la littérature financière et statistique, les méthodes utilisées reposent sur le comportement graphique des valeurs considérées supérieures à un seuil donné. Cette méthode porte le nom de Ç Peak-Over-Threshold È. Initialement développé par Picklands en 1975, ce concept fut étudié par de

38

nombreux auteurs. Cependant, cette méthode reste arbitraire. En réalité, u, doit être assez grand pour que l'estimation de la distribution de Pareto généralisée soit valide, mais pas trop

élevée pour garder une certaine cohérence avec le modèle. Cet arbitrage est

analogue à la méthode BM vue postérieurement.

3 8 Tel que Smith en 1987, Davison et Smith en 1990 ou Reiss et Thomas en 2001, pour ne citer qu'eux.

42

I.II.3.2.2 Estimation du modèle de seuil par le maximum de vraisemblance



Supposons que notre échantillon des

excès !=(!!,!!,...,!!_U) est

indépendante et identiquement

identifiée avec comme fonction de
distribution la GPD. La fonction de

densité g de G est alors pour î^??0 :

1

1 x 1

g(x) = (1+ ) .

Nous pouvons dès lors estimer la log-

vraisemblance:

N u 1 l( , , X)= Nu ln ( +1) ln(1+ i= 1

Xi). Hosking et Wallis montre que

lorsque nous dérivons et , nous obtenons les équations de

maximisation à partir desquelles nous calculons les estimateurs du maximum de vraisemblance.

I.II.3.3 4 VALUE-AT-RISK EXTREME

Nous pouvons reconna»tre qu'il existe une similitude certaine entre le concept de Value-at-Risk et la méthode d'approche des queues de distribution des lois de valeurs extrêmes. Unir ensemble ces deux fondements pourrait indubitablement donner un véritable outil de contrôle du risque. Formulé précédemment, la propriété des extrêmes peut être faite de deux facons distinctes:

· Par la méthode des maximums d'une série de variable aléatoire dans le temps : La méthode BM

· Par la méthode du seuil en prenant l'ensemble des valeurs se situant

entre [#177;u; #177;8] : La méthode POT

Dans ce papier de recherche, nous utilisons la dernière méthode énoncée qui
représente la plus récente, mais aussi la plus efficace des méthodes connues

43

sur ce sujet. De plus, ce modèle se révèle être pratique dans le fait qu'il considère un nombre limité de donnée.

Afin de construire le modèle de Pareto généralisée, nous allons donner un
seuil u important. Soit Y1, Y2, É, Y_n, les données supérieures au seuil défini

comme Y1=X -u. Belkema et de Haan en 1974 comme Picklands en



1975 nous enseignent que F!y=G!,13 y est une estimation assez

importante de u. A partir de !_!y, prenons x=u+y, nous pouvons

approximer F(x), pour x > u. Nous obtenons:

F(x) = (1 F(u))G F(u)

^, (u)(y)+

La fonction F(u) peut être estimée empiriquement de facon nonparamétrique par la fonction de distribution cumulative:

n

öF(u) Nu

=

n

Oü N représente le nombre d'occurrence supérieure au seuil u et n



l'échantillon. En corroborant G!,! y et Fu à Fx, nous pouvons ainsi

écrire:



^ö

ö

ö

xu

ö

(

)

N _u

F x

ö ( ) 1

= 1 +

1

n



Les paramètres î et f.? sont estimés à partir de î et f.? respectivement, obtenus

à partir du maximum de vraisemblance.

44

Pour q > F(u), la VaR_q peut être calculé en résolvant x :

VaRq = uö +

ö nö ( (1 q) ) 1 ö Nu

Dans lequel u est le seuil défini, f.? est l'estimation du paramètre d'échelle et î est l'estimation du paramètre de localisation.

Le principal avantage de cette mesure non-paramétrique réside dans le fait

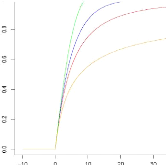
0.4 qu'elle se concentre exclusivement sur



VaR(q) VaR 1/2(1-q)

les queues de distribution. Cependant, 0.35 nous pouvons en conclure que cette ^0.3 méthode ne considère pas les 0.25 rendements comme indépendants et 0.2 identiquement distribués les uns des 0.15 autres.

0.1

0.05 0

45

II. SECTION EMPIRIQUE

Ce mémoire de recherche appliquée fut réalisé à partir de données diffusées sur Bloomberg®. L'estimation des taux de rentabilités anormales et le calcul des lois de valeurs extremes appliquées à la Value-at-Risk font l'objet de deux sous-parties. Nous distinguerons donc d'une part l'estimation des fréquences anormales, représentant sta tistiquement l'état de crise, et d'autre part la performance ajustée du risque liée aux valeurs extremes.

II.I MESURE DES FRÉQUENCES ANORMALES

II.I.1 PROCESSUS

Nous nous sommes intéressés aux cours journaliers spot des 30 valeurs composant le Dow Jones Industrial Average. La première chronique dans laquelle nous calculons les taux de rentabilités normales avant crise couvre la période du 13/06/2006 au 15/06/2007, soit 7 620 observations alors que la deuxième, d'oü sont évaluées les rentabilités anormales, se déploie sur une période allant du 02/07/2007 au 01/02/2010, soit 19 560 observations. Nous aurons donc à étudier 27 180 données totales.



Ce choix est justifié pour trois raisons:


· La période d'échantillonnage avant crise représente une année boursière. Plus le nombre d'observations augmente, plus la représentation graphique de la variance s'aplatira, ce qui aura pour effet de donner une

39

volatilité moyenne biaisée , que l'on utilise l'un ou l'autre des modèles .

3 9 Nous avons étudié le modèle de moyenne et le modèle de marché. Pour plus d'information, voir section I.I.2.1 Modèles théoriques

Il est justifié d'user de pragmatisme quant à la précision et la représentation des données utilisées. De plus, il serait hâtif de se précipiter sur un nombre de données plus important dans le sens oü il n'est pas très adéquate d'y incorporer l'instabilité de variance dü à une autre crise antérieure.

· Les tests de cohérence statistiques ont tous pour particularités d'être asymptotiquement normales avec N ~ (0, 1). Cette convergence est qualifiée à partir du moment oü le nombre de jours post-crise est grand et que le nombre N de valeur étudiée est supérieur ou égal à 30⁴⁰. Ainsi, les 30 valeurs du DJIA et le nombre important de données sont en accord avec les statisticiens.

· Pour des raisons de programmation en Visual Basic, nous avons préféré laisser un espace-temps de 10 séances boursières entre la période de temps dite normale et celle de la crise des Subprimes. Ce laps de temps fut fixé de facon arbitraire.

· La crise des Subprimes a véritablement commencé entre juillet et aoüt 2007. Pour des raisons de cohérence et parce que les experts semblent divergents quant à la date précise de commencement

de la crise, et parce que cela ne peut être absolument incontestable, notre étude commence le 02/07/2007 et fini début 2010. Il s'agit d'une période particulièrement volatile sur l'ensemble des marchés financiers, ce qui nous conforte dans le choix de cet échantillonnage.

⁴⁰ Ces indications ont été mises en place par Brown, Warner, Pattel et Boehmer afin d'assurer la fiabilité et la robustesse de l'étude.

6/13/2006 6/13/2007 6/13/2008 6/13/2009 6/13/2010

100 10

N A (T)

Statistiques préliminaires

Nous avons réalisé une étude statistique préalable sur 4 titres de natures différentes, afin de mieux appréhender nos rentabilités anormales. Nous allons étudier 651 observations par titre, du 02/07/2007 au 01/01/2010, soit 2 604 données. Impacté par la crise des Subprimes et par une forte volatilité des cours, nous avons sélectionné:

· Le DJIA

· Bank Of America

· IBM

· Exxon

Le DJIA est calculé en fonction de la moyenne des fluctuations des 30 titres le composant. Il peut être un bon indicateur de moyenne pour l'ensemble du marché. Cependant, ces variations sont par définition lissées en fonction des différentes sensibilités des titres concernés. Bank Of America, IBM et Exxon ont été choisis d'une part, par leur importance en terme de capitalisation et d'autre part, par leurs différences sectorielles les unes des

autres. Nous avons donc un échantillon restreint, mais représentatif du marché américain. Les tableau x ci-dessous permettent de résumer les principaux états statistiques des différents titres :

TAB 1: Statistiques DJIA

Rentabilités Rentabilités Rentabilités de

anormales normales l'étude

Stat.

Distr.

Ecart (A)

Stat.

Distr.

Nobs Moyenne

Médiane Ecart-Type Maximum Minimum

Skewness
Kurtosis
Jarque-Bera

AMoyenne - Médiane

AN(x) Moyenne

AN(x) Ecart-Type

AN(x) Skewness

AN(x) Kurtosis

TAB 2: Statistiques BOfA

Nobs Moyenne

Médiane Ecart-Type Maximum Minimum

Skewness
Kurtosis
Jarque-Bera

AMoyenne - Médiane

AN(x) Moyenne

AN(x) Ecart-Type

AN(x) Skewness

AN(x) Kurtosis

651 -0,04% 0,03% 1,84% 10,51% -8,20%	253 0,09% 0,08% 0,62% 1,96% -3,35%		905 -0,01% 0,06% 1,59% 10,51% -8,20%	0,11355
-0,62499	0,05665		5,39216
4,05181	7,67157		1,57E+02
2,81E+01	8,23E+02		-0,08%
0,01%	-0,06%		0,044%
-0,090%	0,008%		-0,837%
0,378%	-0,593%		-0,11355
0,62499	-0,05665		-2,39216
-1,05181	-4,67157
			Rentabilités
Rentabilités	Rentabilités de		anormales
normales	l'étude		651
253	905		-0,17%
0,03%	-0,12%		-0,13%
0,06%	-0,04%		6,26%
0,83%	5,33%		30,21%
3,07%	30,21%		-34,21%
-3,84%	-34,21%		-0,11217
-0,21515	-0,15918		6,87582
3,31565	10,53018		4,09E+02
3,00E+00	2,14E+03		-0,04%
-0,03%	-0,09%		0,174%
-0,033%	0,123%		-5,261%
0,172%	-4,327%		0,11217
0,21515	0,15918		-3,87582
-0,31565	-7,53018

Ecart (A)

49

TAB 3: Statistiques IBM

Nobs Moyenne

Médiane Ecart-Type Maximum Minimum

Skewness
Kurtosis
Jarque-Bera

AMoyenne - Médiane

AN(x) Moyenne

AN(x) Ecart -Type

AN(x) Skewness

AN(x)Kurtosis

Stat.

Distr.

Ecart (A)

TAB 4: Statistiques Exxon

Nobs Moyenne

Médiane Ecart-Type Maximum Minimum

Skewness
Kurtosis
Jarque-Bera

Ecart (A)

AMoyenne - Médiane AN(x) Moyenne AN(x) Ecart-Type AN(x) Skewness AN(x) Kurtosis

Stat.

Distr.

Rentabilités anormales

Rentabilités normales	Rentabilités de l'étude	651 0,04% 0,05% 1,93% 10,90% -6,10%
253 0,16% 0,08% 1,13% 8,96% -3,35%	905 0,06% 0,06% 1,73% 10,90% -6,10%	0,22614
1,80300	0,28681	3,11525
14,92480	4,51118	5,91E+00
1,64E+03	9,85E+01	-0,02%
0,08%	0,00%	-0,037%
-0,156%	-0,062%	-0,934%
-0,127%	-0,732%	-0,22614
-1,80300	-0,28681	-0,11525
-11,92480	-1,51118
		Rentabilités
Rentabilités	Rentabilités de	anormales
normales	l'étude	651
253	905	-0,04%
0,17%	0,02%	-0,01%
0,20%	0,06%	2,39%
1,21%	2,13%	15,86%
3,64%	15,86%	-15,03%
-4,85%	-15,03%	0,17919
-0,39195	0,11030	9,46848
0,84258	11,30631	1,14E+03
5,55E+01	2,60E+03	-0,02%
-0,03%	-0,04%	0,036%
-0,172%	-0,019%	-1,387%
-0,211%	-1,126%	-0,17919
0,39195	-0,11030	-6,46848
2,15742	-8,30631

Nous pouvons établir plusieurs commentaires:


· La loi normale standard défend l'idée que la moyenne et la médiane sont confondues. Il existe une différence de 0.08 pour DJIA montrant que les

50

critères ne sont pas respectés. Il en va de méme pour les autres titres présentés.

§? L'écart-type moyen ne para»t pas très élevé. Pourtant, nous assistons à des extremes importants:

· DJIA: De +10.51% pour le maximum et de -8.20% pour le minimum

· Bank Of America : De +30.21% pour le maximum et de -34.21% pour le minimum

· IBM: De +10.90% pour le maximum et de -6.10% pour le minimum

· Exxon: De +15.86% pour le maximum et de -15.03% pour le minimum

§? Il est intéressant de noter que les mesures d'asymétrie (Skewness) et d'aplatissement (Kurtosis), sous l'hypothèse de normalité, prennent respectivement les valeurs 0 et 3. Ici, ces deux paramètres sont respectivement ?0 et >3, laissant apparaitre un caractère leptokurtique des cours et la formation empirique de queue de distribution épaisse par rapport à la loi normale. Le skewness est positif pour l'ensemble des titres à l'ex ception de Bank of America, montrant qu'il y a une quantité importante de petits mouvements à la hausse et de grands déplacements à la baisse.

· Le test de normalité de Jarque-Bera⁴¹ est différent de 0 pour l'intégralité des valeurs. Il rejette donc l'hypothèse nulle de normalité pour n'importe quel niveau de pertinence.

En résumé, cette première étape nous permet de rejeter l'hypothèse de normalité et de comprendre qu'il existe effectivement des extremes conséquents.

4 1 Le test de Jarque Bera cherche à déterminer si une suite de variables aléatoires suit une

2

loi de distribution normale. Cette statistique suit asymptotiquement une loi du ֈ deux

!!!

₆(s +!!!!!),

degrés de liberté. Nous avons JB= ou n est le nombre d'observations, k

le nombre de variables explicatives, s le skewness (moment d'ordre 3 d'une variable centrée-réduite) et K le kurtosis (moment d'ordre 4 d'une variable centrée-réduite). La statistique de JB indique qu'une suite de variable suit une loi normale lorsqu'elle s'approche de 0.

II.I.2 TAUX DE RENTABILITÉS NORMALES ET ANORMALES

II.I.2.1 FRÉQUENCES NORMALES

180 La période post-crise fut faste pour les

investisseurs. D'un point de vue



160

macroéconomique, on constate une

140

hausse de la liquidité au niveau

120

100 2007, le rapport entre la masse

⁸⁰ monétaire et le PIB se situe à 30%,

⁶⁰ alors qu'entre 1980 et 2000, celui-ci

40 n'était que de 18% à 20%. En l'espace

de 6 années, il augmente donc de 10 à

20

12%. Sous l'égide des différentes

6/13/06 8/13/06 10/13/06 12/13/06 2/13/07 4/13/07 6/13/07

0



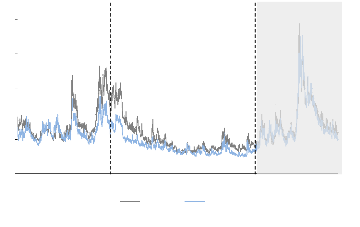
Enron

11 Sept. 2001

1/3/00 1/3/03 1/3/06 1/3/09

V2X Index VIX Index

Subprimes

Corée du
Nord

100

90

80

70

60

50

40

30

20

10

0

52

banques centrales, garant de la stabilité des prix, cette liquidité abondante n'a pas entra»né d'inflation. Bien entendu, si toutes ces liquidités n'ont aucun effet sur les prix des biens et des services, elles en ont sur les prix des actifs dont l'offre est peu importante. Cet aspect, associé à une baisse des indicateurs de risque, tel que la prime de risque ou la volatilité implicite, majoré d'une forte croissance mondiale, a eu pour conséquence la hausse des cours de bourse, notamment du DJIA. En outre, nous constatons le parcours linéaire croissant des 30 titres du DJIA sur la période énoncé précédemment.

Bien que la crise des Subprimes émane sans doute de cette apparente stabilité, c'est dans un climat avantageux que nous calculons nos rentabilités dites << normales È, qui ne dévoilent pas de perturbations apparentes.

II.I.2.2 FRÉQUENCES ANORMALES

180
160



La crise des Subprimes démarre durant l'été 2007 aux États-Unis. Celle-ci remet en cause fondamentalement le système bancaire dans son ensemble.

140

120

100 Le problème se trouve dans la capacité

des établissements

80 financiers à gérer

leurs risques, tant dans leurs transferts

60

que dans le suivi qui en découle.

40

D'autre part, l'octroi de crédit

20

hypothécaire à une clientèle non-

7/2/07 11/2/07 3/2/08 7/2/08 11/2/08 3/2/09 7/2/09 11/2/09 3/2/10 7/2/10 11/2/10 solvable a mis à mal la titrisation

dépourvu de fonds propres. C'est aussi le fonctionnement même des agences de notation qui semble être problématique. Cette crise mondiale fut liée aux crédits hypothécaires à risque aux États-Unis, ne représentant pourtant qu'un marché de 1000 milliards de dollars. Nous pouvons visualiser, en base 100, l'impact qu'a eu cette crise sur les cours des 30 titres composants le DJIA. La crise des Subprimes se révèle être complexe dans les faits. Nous allons dans cette étude exprimer des résultats quantitatifs pouvant, peut-être, donner une réponse quant à l'origine de cette crise, à posteriori. Pour plus d'informations, nous vous invitons à consulter le rapport du conseil d'analyse économique⁴².

⁴² Rapport écrit par P. Artus, J-P Betbèze, C. Boissieu et G. Capelle-Blancard, intitulé: «La crise des subprimes» publié par <<La documentation françaiseÈ en 2008. Celui-ci donne une analyse complète de la situation micro et macro-économique de la crise des subprimes.

II.I.3 RÉSULTAT DES FRÉQUENCES ANORMALES

II.I.3.1 RENTABILITÉS ANORMALES STATIONNAIRES

Les résultats produits par chacun des modèles sont intéressants. Il est à noter qu'il existe peu de différence entre les résultats tirés des deux modèles d'un point de vue globale, bien que le modèle de marché semble, à première vue, apporter un appoint d'information manifeste lié à la sensibilité des titres par rapport à leur indice de référence. Dans le cadre d'un travail de simulation, Brown et Warner aboutissent à la méme interprétation lorsqu'ils comparent la force des deux modèles.

Nous avons donc un modèle de moyenne donnant -82.80% et un modèle de marché estimé à 82.95%, soit 0.15% de différence.

Il existe cependant des rentabilités proches de la normalité, comme l'atteste le graphique présenté ci-dessous :



-0.5%

-1.0%

0.5%

0.0%

1.0%

15.0%

10.0%

5.0%

0.0%

-5.0%

-10.0%

-15.0%





Rentabilité anormale

Rentabilité anormale

Cependant, en ce qui concerne la réaction des cours dans leur globalité, les résultats nous prouvent statistiquement que nous sommes bien sur une période d'instabilité. Comme en atteste la majorité des rentabilités anormales significativement différentes de 0.

II.I.3.2 RENTABILITÉS ANORMALES CUMULÉES

Ce test exprime l'écart-type des fluctuations des cours lié à la perturbation des rentabilités anormales. Nous avons ici un pic, partant du début de l'expérience jusqu'au 3/10/2009, lequel enregistre un taux anormalement bas cumulé de -115,20%.



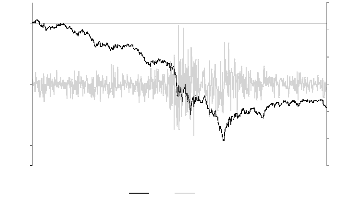
20.0%

0.0%

10.0%

15.0%

-20.0%

5.0%

-40.0%

-60.0%

-115,20%

7/2/07 2/2/08 9/2/08 4/2/09 11/2/09

RAC Rentabilité

anormale

-80.0%

-100.0%

-120.0%

-140.0%

0.0%

-5.0%

-10.0%

-15.0%

P&L

Les rentabilités anormales progressent
de facon croissante jusqu'au point bas
puis semblent stagner jusqu'à la fin de



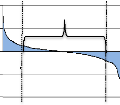
95%

10.00%

5.00%

l'étude. Le retour vers la normalité 2.5% semble loin. Les stratégies basées sur

0.00% le retour à la moyenne (mean-

-5.00%

2.5%



Rentabilité anormale

reversion-model) semblent être difficile à réaliser. Ce test montre que -10.00% les anormalités ont été statistiquement multipliées par 5 au sommet de la crise. Les statistiques préliminaires nous ont informés de la non-normalité

des cours étudiés. Nous en avons ici un exemple plus concret.

55

II.I.4 TEST DE SIGNIFICATIVITÉ

Il convient de noter par ailleurs que les trois statistiques de représentativité
fournissent des conclusions globalement convergentes. Celles-ci deviennent

de plus en plus significative au milieu
1.00 de l'étude, autour du 3/10/2009, date à



laquelle les rentabilités anormales
0.50 cumulées sont les plus importante s. Il

existe cependant plusieurs phases
0.00 quant à la validité de ce test. Certaines

valeurs semblent être plus

-0.50 significatives que d'autres. Les statistiques proches de 0, comprises entre [ -1 ; 1], rejette nt l'hypothèse

-1.00

8/6/07 1/3/08 6/1/08 10/29/08 3/28/09 8/25/09

Test de Brown et Warner

Test de Boehmer Musumeci et Poulsen

Test de Pattel



d'anomalie statistique. D'autres sont,
sans nul doute, incontestables au seuil

de [-10 ; -50] et [10; 60]. Cela nous laisse penser qu'il y a des mouvements plus calmes et d'autres plus agités.

60.00



40.00 20.00 0.00 -20.00 -40.00



-60.00

8/6/07 1/3/08 6/1/08 10/29/08 3/28/09 8/25/09

Test de Brown et Warner

Test de Pattel

Test de Boehmer Musumeci et Poulsen

56

60.00 55.00 50.00 45.00 40.00		-10.00 -15.00 -20.00 -25.00
				20.00 15.00
				10.00

Test de Brown et Test de Test de Boehmer Warner Pattel Musumeci et Poulsen

La statistique fréquentielle de Boehmer, ayant une propension plus importante à accepter l'hypothèse selon laquelle les rentabilités anormales sont nulles , est distinctement supérieure de 0, élevé à 10.69 et 10.77 en valeur absolue, respectivement pour le modèle de moyenne et celui de marché. Ce tableau résume les observations menées dans cette étude:

TAB 5: Fréquences anormales									Nobs
Moy		Ecart type	Max	Min	Modèle de moyenne	Modèle de marché		Rentabilités
								anormales
19560	0%	2,02%	11%	-9%	-83.80%	-83.95%		Test de Brown et
								Warner
19560	-0,59	9,4	50,29	-43,75	-15,11	-15,19		Test de Pattel
19560	-0,6	10,01	52,27	-47,06	-15,43	-15,5		Test de Boehmer
19560	-0,41	5,05	19,15	-13,54	-10,69	-10,77		RAC
19560	-52%	34%	3%	-115%				BWC
19560	-239,98	157,29	14,35	-536,74				PC
19560	-245,55	163,15	13,68	-562,12				BC
19560	-170,67	107,6	19,08	-315,39

Ce test est par conséquent concluant dans sa globalité. Les rentabilités anormales calculées précédemment montrent l'ampleur de la crise des Subprimes et la nécessité d'instaurer une politique de mesure du risque viable. Il nous montre également qu'il existe des taux de rentabilités extremes dont la distribution asymptotique normale ne prévoit pas les effets.

II.II. THÉORIE DES VALEURS EXTRæMES ET VALUE-AT-RISK

V. Pareto XIX ^e

s'intéresse la

à fin du siècle à la distribution des revenus

dans la société. Il en conclut que la société humaine est fondée sur une loi mathématique de forme décroissante, dans laquelle la distribution statistique prend une forme hyperbolique, laissant appara»tre des queues épaisses. Nous avons pu souligner l'importance des lois issues de la famille Ç parétienne È, dont les applications en sciences sociales sont croissantes au fil des années. L'abondante littérature disponible sur le sujet en témoigne.

Le succès rencontré par ces lois nous a incités à examiner leur apport sur le marché du DJIA en période de crise des Subprimes. Cette application met en perspective différents raisonnements en termes de rentabilité ajustée du risque sur le marché des actions. La performance d'un investisseur sur une période donnée est souvent liée à quelques journées exceptionnelles. La distribution empirique de forme leptokurtique en témoignant (La grande majorité des cours se concentre vers la moyenne historique proche de 0). La plupart des journées d'activité ne contribue donc que marginalement au résultat. Les activités de marché témoignent d'une forte instabilité, révélant des mouvements violents et soudains. C'est dans cet état statistique, oü le nombre de rentabilités anormale s est important, que nous pouvons parler de crise. La réalité erratique des cours de bourse est quantifiable. Nous allons donner une image de cette réalité statistique dans un premier temps avant de calculer notre loi de valeurs extremes.

II.II.1 ANALOGIE STATISTIQUE DE LA DISTRIBUTION DES RENDEMENTS ET MAXIMUM DE VRAISEMBLANCE

Cette section a pour objet d'exposer la

100000% Distribution logarithmique du DJIA



100% Lorsque la loi de valeurs extrêmes est

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

DJIA



identifiée, les conditions de distribution théorique pe uvent être utilisées pour obtenir le type de loi limite. Nous avons pu constater dans la section théorique que certaine s lois convergent vers différentes lois parente s. En effet, les lois à support borné, comme la loi uniforme,

appartienne nt au domaine d'a ttraction maximum de Weibull, avec î^?>0.

Les lois dont les queues décroissent de facon exponentielle appartiennent au

MDA de Gumbel, avec î^?=0. Nous pouvons citer à ce titre la loi normale

et la loi exponentielle. Le s lois dont le paramètre de libe rté est égal à î^?, faisan t appara» tre des queues de distribution épaisse s appartiennent, comme la loi de student ou celle de Pareto, au MDA de Fréchet. Dans cet exercice, nous avons choisi d'analyser quatre lois théoriques :

· La loi normale

· La loi de Laplace

· La loi de Pareto

·

59

La loi de student



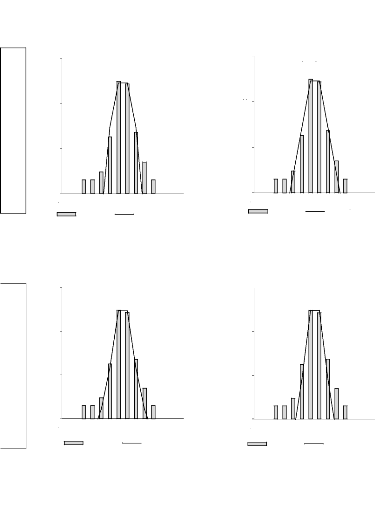
II.II.1.1 ANALOGIE STATISTIQUE DE LA DISTRIBUTION DES RENDEMENTS

II.II.1.1.1 Comportement limite de la loi exponentielle

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

Laplace

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

DJIA LAPLACE

GUMBEL

100000%

Normale

100000%

DJIA NORMAL

10000%

1000%

100%

10000%

1000%

100%

100000%

10000%

1000%

100%

Student

Pareto

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

DJIA PARETO

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

DJIA STUDENT

100000%

10000%

1000%

100%

FRECHET

La fonction de répartition de la loi exponentielle de paramètre A.=1 est

x

F(x) =1 e pour x=0. Avec b log(n) et a =1, nous pouvons

résoudre l'équation donnée par le théorème de Fisher-Tippet avec :

60

MESURE DU RISQUE DE MARCHÉ ET THÉORIE DES VALEURS EXTRæMES
Fn (a_nx + b_n) = (1 -- e^-x-k'g(n))ⁿ

₎n

e^-x

Fⁿ(a_nx + b_n) = (1

n

Fn (a_nx + b_n) --> exp { --e ^-x}

Fⁿ(a_nx + b_n) =

La loi de Laplace, ici représentée, et une loi double exponentielle car sa densité peuvent etre vue comme l'association de deux lois exponentielles indépendantes, situées de part et d'autre de la tendance centrale.

Le maximum normalisé et le MDA de la loi exponentielle convergent vers une loi de Gumbel. C'est pour cette raison que la loi de Gumbel est aussi appelée « loi de type exponentiel ».

Prenons le théoreme de Balkema-de Haan-Picklands, en prenant i_u.=1, oil

u correspond au seuil défini. Alors :

Fu(y)= F(u + y) -- F(u)

y 0

e

=

u _e-u -y

_eu

1 F(u)

Fu(y)= F(u+ y) F(u)

F(u)

¹

Fu(y)= F(u+ y) F(u) 1 F(u)

= 1 -- e^-y

Par conséquent, pour tout y>0, la GPD s'accorde à etre une loi exacte

pour tout u pour le parametre î^?=0 avec i_u.=1.

Nous pouvons constater une nette amélioration graphique entre le DJIA et la loi de probabilité concernée. Nous retenons donc la loi de Laplace pour cette raison.

61

II.II.1.1.2 Comportement limite de la loi de Pareto

La fonction de répartition de Pareto s'écrit F(U) =1 Um , oü U > 0 et

!

a>0. Pour le théorème des BM, nous posons f3₃=0 et a =(nU)a. Pour

x > 0=

Fⁿ(a_nx + b_n) = (1 U(a_nx) = (1 Ua_n x )n

₎n

x

Fⁿ(a_nx + b_n) = (1

n

Fⁿ(a_nx + b_n) exp { x }

Fⁿ(a_nx +b_n) = (X)

La loi de Pareto appartient au MDA de la loi de Fréchet. Communément, la loi de Fréchet est appelée loi de type Pareto.

Concernant la méthode POT, nous posons f3₃=ub pour /3>0. On obtient:

uby)

F_u(y) = F(u+ F(u) y 0

1 F(u)

uby) Fu(y) = F(u+ F(u) 1 F(u) uby) Fu(y) = F(u+ F(u) 1 F(u)

uby) = Uu U(u+ Uu =1 (1+ by)

La limite est alors la loi GPD de paramètre î^? pour î^?=^! !

et /3=î^?.

Remarquons les extremes qui sont d'avantages compris sous la courbe, particulièrement du cTMté des valeurs négatives.

62



II.II.1.1.3 Comportement limite de la loi normale

La fonction de répartition de la loi normale quand N~(0,1) est F x =



. Nous avons donc 1-Fx~¹

x21r

!!

e^!2 quand x?+8,

alors⁴³. En ce qui concerne la méthode des blocks, nous aurons:

lim u +	z 1 F(u+ u	) =	lim u +		z1 z (1+ ) exp e 21 (u+ ^zu)^2 + 21 u2 = u2

si on suppose que f3,=¹, nous avons pour x?+8 :

!

1	z 1 F(u+ u	) F(u) = F(u + uz)		z 1 e

1 F(u) 1 F(u)

En ce qui concerne la méthode d'excès de seuil, celle-ci convergera vers une

loi de type exponentielle. D'autre part, si b donne Fb =1-¹et a =

!

!, on aura:

b_!

F(a_nx

n { 1 F(a_nx + b_n }= { 1 b_n)

+ } x

e

1 F(b_n)

lim n +

lim F^n(anx +bn) = n +

x e (1 n

x ) = exp { e }

qui converge vers la loi de Gumbel. Smith nous enseigne en 2003 qu'il est
préférable d'utiliser les lois GEV et GPD pour chaque théorème les

43 1 W. Feller démontre en 1968 que 1 Ð F(x) équivaut à x21r

!! e^!2 quand x?+8

63

concernant, plutôt que la loi de Gumbel et la loi exponentiel le, bien qu'elles soient toutes deux de formes exactes. L'aspect propre des lois généralisées semble être plus en accord avec les méthodes vues précédemment.

La convergence avec la distribution réelle est concordante graphiquement pour x [-4.2 ; 4.2]. Cependant, nous pouvons constater, de part et d'autre de la courbe, qu'il existe des extrêmes non pris en compte par la densité de probabilité normale. Cette loi est alors également rejetée empiriquement par cette méthode. Si l'on suppose une distribution gaussienne pour les rendements journaliers, la probabilité qu'un rendement observé dévie de sa moyenne de 4 écarts-types est inférieure à 0,01%, soit un évènement observé en moyenne tous les 62 ans.

Le tableau ci-dessous nous montre la probabilité de s'écarter de la moyenne
de écarts-types, tel que 1 P( X ) La dernière colonne

représente le nombre d'années (sur 254 séances) assimilée à l'apparition d'un événement:

TAB 6 : Probabiité normale
Probabiité	Années		1
0,31731050786291410283	0,012		2
0,0455002638963584144	0,086		3
0,0026997960632601891	1,46		4
0,00006334248366623984	62,20		5
0,00000057330314375839	6 867,3		6
0,00000000197317529008	1 995 265		7
0,00000000000255962509	1,5x10^9		8
0,00000000000000124419	3,22x10^12		9
0,00000000000000000023	16 1,7x10		10
1,52x10 -23	2,58x1020

La probabilité de s'éloigner de plus de 5 écarts-types de la moyenne
convient à un évènement extrêmement rare, lequel n'a peut-être jamais été
observé. Or les variations réelles retenues sur notre fenêtre de test prouvent

que la théorie gaussienne néglige les variations extremes. Une autre approche est donc nécessaire pour assurer une rentabilité ajustée du risque.

Il existe des modalités essentielles pour l'existence de constantes de normalisation. Remarquons que les extremes sont tirés asymptotiquement d'une loi non-conditionnelle, alors que la variable sortie des lois de valeurs extremes est tirée d'une loi conditionnelle. Il est donc important d'estimer la convergence la plus proche. Dès lors, l'indice de queue représentera le poids des extrêmes dans la distribution.

TAB 7: Intervalle de confiance et probabiités

Intervalle	DJIA	NORMALE	STUDENT	PARETO		LAPLACE	-10,83
0,00	0,00	0,00	0,11	0,00		-9,17
0,00	0,00	0,00	0,07	0,00		-7,50
2,00	0,00	0,01	0,16	0,02		-5,83
2,00	0,00	0,06	0,43	0,24		-4,17
3,00	0,27	0,44	1,65	2,57		-2,50
18,00	29,93	8,13	14,52	27,09		-0,83
310,00	285,80	307,35	299,05	286,07		0,83
272,00	285,80	307,35	299,05	286,07		2,50
23,00	29,93	8,13	14,52	27,09		4,17
5,00	0,27	0,44	1,65	2,57		5,83
2,00	0,00	0,06	0,43	0,24		7,50
0,00	0,00	0,01	0,16	0,02		9,17
1,00	0,00	0,00	0,07	0,00		10,83
0,00	0,00	0,00	0,11	0,00		Total
638,00	638,00	638,00	638,00	638,00

II.II.1.2 MAXIMUM DE VRAISEMBLANCE

Supposons que notre échantillon des excès X=(X1,X2,...,XN_!) est

indépendante et identiquement identifiée avec comme fonction de distribution la GPD. Nous obtenons les équations de maximisation à partir desquelles nous calculons les estimateurs du maximum de vraisemblance. Nous avons donc la log-vraisemblance de chaque loi estimée à partir de la distribution réelle. Ces données sont présentées dans le tableau suivant:

TAB 8: MDA

NORMALE STUDENT PARETO LAPLACE

DJIA 41,85 75,77 86,54 82,83

Le maximum de vraisemblance le plus proche est celui de la loi de Pareto avec 86.54. Le domaine d'attraction maximum est donc celui de la loi de Fréchet.

II.II.2 MODéLE DE SÉLECTION DE MAXIMA

II.II.2.1 RÉALITÉ ERRATIQUE

La théorie de la normalité des marchés financiers est spécifiquement remise en cause avec la théorie des valeurs extremes. Particulièrement en haute fréquence oü la stationnarité des cours est plus erratique. L'étude menée précédemment nous a permis de com prendre que le développement de la gestion du risque dans un univers gaussien, introduit par la normalité des rendements, est inadapté à l'appréhension des comportements extremes.

44



L' << homme moyen >> de A. Queteletn'existe pas en finance. Dans ce préambule sur les extremes de marché, nous étudions les variations du DJIA sur la période de test. Cette étude comprend 1 148 données de prix, du 13/06/2006 au 31/12/2010. Nous avons choisi d'illustrer nos propos en sélectionnant le maximum |Dt| des variations Intra-Day⁴⁵ en valeur absolue en t, à partir d'un seuil s prédéfini.

Placé sur une fenétre glissante D₁,D₂,...,D_! de taille F, lorsque le seuil s
est supérieure à |Dt|, la rentabilité réelle du DJIA en t en valeur absolue est donnée par:



+

P_t

b

1

1

;

P_t

1

1

P_t

+

P_t

?? P_t

= 1; c=

P_t

D = max a =

t

⁴⁴ A. Quetelet est un mathématicien, astronome, naturaliste et statisticien belge du XIXème siècle. Il présenta dans son ouvrage: << Sur l'homme et le développement de ses facultés, essai d'une physique social>> la notion d'homme moyen. << L'homme moyen d'une population est un individu dont les caractéristiques physiologiques sont chacune égale à la moyenne des autres caractéristiques physiologiques de la population>>

⁴⁵ Ensemble des variations comprises dans une journée boursière.

Oü et !!! est le plus haut du jour, P_!^! est le plus bas et P!_1 est le cours de

clTMture du jour précédent. Nous indiquons le dépassement relatif.



0.00% 5.00% 10.00% 15.00%

6/13/2006

2/13/2007 10/13/2007 6/13/2008 2/13/2009 10/13/2009 6/13/2010

True Range

Soit IF, la fenétre de test, dont la série des violations définie par la variable dichotomique est la suivante:

1 siD > s

I_F =

0 si D < s



s est le seuil appartenant à la fenétre F compris entre 1 et F. Fest un
nombre > 1, pour lequel le nombre de donnée |D| est inférieure au nombre

t

total de données compris dans l'échantillon. Soit F < D_t Il s'agit de

2

déterminer jusqu'à quel point les variations du marché se sont rendues en Çintraday È. A ce stade, nous choisissons une fenêtre de 50 jours. Cette taille permet de lisser les variations erratiques sans biaiser les informations d'une part, tout en laissant appara»tre une légere variance d'autre part. Nous avons également choisi d'étudier plusieurs seuils s distincts. Nous avons donc :

TAB 9 : Seuil

S = 2% 3% 5% 8% 10% 12%

Nous donnons ci-après deux représentations graphiques qui permettent de visualiser les valeurs ayant dépassées s. Nous avons préféré les présenter à partir d'une échelle logarithmique, plutôt que sur échelle linéaire simple. Lorsque l'on exprime un nombre en logarithme, on effectue une mise à l'échelle ce qui permet, plutôt que de se concentrer sur la valeur absolue du nombre comme on le fait couramment, de le comparer aux autres nombres qui l'entourent. Ainsi, nous pourrons juger de la pertinence de chaque seuil sur la fenétre F = 50.

LN(D_t) > S

10						1

6/13/2006

2/13/2007

10/13/2007	6/13/2008	2/13/2009	10/13/2009	6/13/2010	2%
3%	5%	8%	10%	12%

Les résultats sont évocateurs. Les variations laissent appara»tre une majorité



LN(D_t) > S

10

1

1/17/2008 9/17/2008 5/17/2009

2% 3% 5%

8% 10% 12%

des variations journalières supérieures ou égales à 3%. Celles-ci se concentrent sur une période de 615 jours, du 17/01/2008 au 23/09/2009. Cela représente 53.57% des données de l'étude⁴⁶. Le DJIA, pendant la crise des Subprimes, a donc connu statistiquement une distribution des cours formant des queues de distribution épaisses en valeur absolue.

46 615

Le calcul est le suivant: .100=53.57, soit 53.57%

1148

Nous pouvons aussi émettre l'idée qu'il y a eu un effet <<Clustering>> et un effet <<Momentum⁴⁷ >> sur la période ventrale.

II.II.2.2 SÉLECTION DE SEUIL

Deux méthodes statistiques de modélisation des queues sont possibles:

· La méthode BM

· La méthode POT

En finance de marché, nous allons privilégier la méthode POT, plus adaptée, notamment parce qu'elle va en adéquation avec un phénomène couramment observé: Le <<clustering⁴⁸ >>. De plus, comparée à la méthode BM, qui ne considère pas toutes les valeurs susceptibles d'être extrêmes⁴⁹, cette méthode est à la fois plus flexible et plus réaliste.

P&L Distribution |P&L|



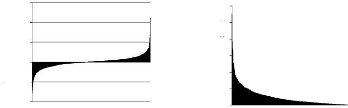
15.00%

10.00%

5.00%

0.00%

-5.00%

-10.00%

12.000%

10.000%

8.000%

6.000%

4.000%

2.000%

0.000%

P&L Distribution

|P&L|

⁴⁷ La Théorie des Marchés Efficients (Efficient Market Theory) soutient que les marchés fonctionnent de manière à retranscrire intégralement et instantanément l'ensemble des informations disponibles. Jegadeesh et Titman, en 1993, mettent en évidence l'effet <<momentum >>. Ils observent que la tendance des titres par rapport au marché semble se poursuivre dans une mouvance irrationnelle. Il en va de même pour la variance journalière dans ce contexte.

⁴⁸ Le phénomène de cluster, vu précédemment en section théorique, se défini comme une grappe de volatilités caractéristiques des rentabilités liées aux actifs financiers.

⁴⁹ La méthode BM extrait le maximum de chaque période définie préalablement. Elle ne prend donc pas en compte certaines données extrêmes liées aux cycles financiers et peut en revanche prendre des valeurs faibles lors des blocks précédents.

Cette modélisation de queue de distribution engage un échantillon au-dessus du seuil u, lequel conduit à une forme de loi GPD. Les méthodes utilisées reposent sur le comportement graphique des valeurs considérées supérieures à un seuil. Ces deux graphiques montrent d'une part la variation décroissante du DJIA pendant la crise des subprimes. D'autre part, la variation décroissante en valeur absolue. Remarquons le caractère asymptotique de la courbe. Le nombre de valeurs se réduisant lorsque l'on approche la valeur nulle de l'abscisse. Il est alors délicat de choisir un seuil u grand pour que l'estimation de la distribution de Pareto généralisée soit valide. Celui -ci ne peut également pas être trop élevé pour garder une certaine cohérence avec le comportement réelle du cours du DJIA. Le nombre de données supérieur à u défini est en rapport direct avec l'espérance future d'observer un tel évènement. Nous constatons au vu du tableau présenté ci-dessous qu'il existe très peu de variation supérieure à 5% (soit 4,86% des échanges). Environ la même quantité est observée pour les valeurs dépassant 4%. Les valeurs inférieures à 3% semblent cohérentes en terme de volume d'observations, cependant, celles-ci risque nt de biaiser le modèle, se rapprochant trop de la tendance centrale.

TAB 10: Nombre d'observation supérieure à u			Variation> u
Nobs		2%
149		3%
58		4%
28		5%
15		6%
9		7%
5		8%
2

Nous présentons donc un seuil u = 0.03. Nous obtenons 58 données. Le graphique ci-contre représente ce seuil, qui semble correspondre aux valeurs extrêmes présentées par la théorie.



12.00%

u = 3%

14.000%

MESURE DU RISQUE DE MARCHÉ ET THÉORIE DES VALEURS EXTRæMES

9.00%

DJIA Return u

0 20 40 60 80

u = 3% Puissance (u = 3%)

100000%

Queue de distribution (log)
u > 3%

Log

y = 1.3562ln(x) - 0.8559
R² = 0.74542

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Extreme Enreg. (Extreme)

-10.8 -7.5 -4.2 -0.8 2.5 5.8 9.2

DJIA

12.000%

10.000%

6.00%

3.00%

0.00%

8.000%

6.000%

4.000%

2.000%

0.000%

5

4

3

2

1

0

10000%

1000%

100%

Distribution

y = 0.129x^-0.353
R² = 0.98599

II.II.3 VALUE-AT-RISK

La TVE appliquée à la Value-at-Risk permet d'évaluer le degré de
résistance des variations des marchés, au méme titre que le degré de solidité
d'une voiture en phase de cra sh-test. Le comportement stochastique des
extremes issus d'un échantillon permet la mise en place d'un cadre
mathématique rigoureux. S'intéressant directement à la queue de
distribution, faisant appara»tre le degré d'importance statistique des
extremums, nous allons dans cette section présenter, à partir des résultats
obtenus précédemment, une stratégie de gestion basée sur le calcul de la
Value-at-Risk. Notre étude va porter sur la rentabilité ajustée du risque que
peut proposer la VaR déterminée à partir du quan tile des extremes sur le
DJIA pendant la crise des Subprimes. En proposant une telle stratégie, un
investisseur pouvait-il éviter les pertes liées à cette crise ? Pouvait-il
bénéficier d'un Tracking-Error avantageux en achetant lorsque la VaRt > Rt
et en vendant lorsque la VaRt < Rt au seuil de probabilité fixé ? Nous allons
71

mettre en avant deux mesures liées à la VaR: dans un premier temps, nous sélectionnerons un modèle adéquate quant à la validité du modèle présenté, puis dans un second temps, nous calculerons, à partir des résultats obtenus, la performance que pouvait développer une stratégie long-short du 13/06/2006 au 31/12/2010.

II.II.3.1 COUVERTURE CONDITIONNELLE

Afin d'étudier le risque que peuts dégager la VaR basée sur la théorie des

Valeurs Extremes pour p?(95%), avec t = 1, nous allons procéder à un

exercice de capable de les de violations ⁵⁰

backtesting montrer occurrences . Celui-ci consiste en réalité à confronter d'une part, la VaR calculée à l'aide du quantile des valeurs extrêmes et d'autre part, les pertes et profits réels. Pour valider cette méthode de prévision, les pertes effectives ne devraient

51

pas dépasser la VaR de plus de 5% des cas . Dans le cas contraire, nous devrions remettre en cause ce modèle. Nous proposons d'adapter la Valueat-Risk calculée de facon journalière sur une fenêtre plus lointaine, permettant ainsi de lisser les observations. Nous utilisons donc une fenétre

glissante x1,x2,...,x_! de taille F. Cette méthode nous présente le

dépassement de la Value-at-Risk lorsqu'elle est supérieure à x, la rentabilité réelle du DJIA en t en valeur absolue. Soit IF, la série des violations définie par la variable dichotomique suivante :

1 si R_t <VaR_t

Dg_t =

0 si R_t VaR_t 1 si x <VaR_t

I_F =

1 si R_t >VaR_t 0 si x > VaR_t

Dd_t =

0 si R_t VaR_t

5 0 Initialement développé par Campbell S. D, en 2005.

51 En d'autres termes, 95% des variations journalières seront contrôlées avec seulement 5% d'erreur de prévision



x est le rendement absolu sur la fenétre F compris entre 1 et F, symbolisant la fin du backtesting. Dg, les valeurs représentées par la distribution négative située à gauche et Dd, celles positives de droite. Ces deux dernières données sont présentées de facons indicatives. Le modèle de Value-at-Risk reste fiable lorsque les violations comprises sur la fenétre F

52

respectent la propriété du ratio de couverture conditionnelle . Il permet une
comparaison de la proportion p de violation au niveau de risque 1 - p. Ce
test est dit négatif lorsque le nombre d'observations diffère largement de p.

!!!! !

Ce ratio est donné par oü des VaR dépassan t x

! 'F est la somme sur

!

la fen étre. Il est à noter qu'un bon modèle ne doit ni sous-estimer, ni-sur- estimer le risque. L'avantage de cette technique réside dans le fait qu'elle permet de capturer les caractéristiques de la dynamique temporelle de l'échantillon à travers le temps. Nous avons sélectionné une fenétre F = 50 jours dans notre étude. Nous avons également choisi d'étendre nos observations de part et d'autre de la crise des Subprimes pour montrer l'exigence de la VaR des valeurs extremes par rapport à celle retenue par la loi normale. Nous aurons donc 1 147 observations.

TAB 11: Dépassement de VaR
VaR Loi Normale	VaR GPD		Nobs
1147	1147		Nombre de dépassement
112	12		Couverture conditionnelle
9,76%	1,05%		< 0,05
NON	OUI

5 2 Le ratio de couverture fut développé par Kupiec en 1995. Il fut ensuite repris par Christoffersen en 1998

Le modèle lié à la loi normale se révèle inadapté pour estimer le risque réel.
Il enregistre un taux de 9.91%, dépassant de 4.91 point le taux d'échec
accepté. Cet échec est attendu dans la

[Echelle logarithmique]

100 Dépassement de VaR (95%) mesure oü ce modèle de mesure du

(F = 50) risque ne permet pas de prendre en

compte le caractère leptokurtique des rendements.



10

1

6/13/2006 6/13/2009

VaR N(|x|) F=50 VaR GPD(|x|) F=50



En période de crise, la VaR GPD ne laisse appara»tre qu'une infinité de dépassements journaliers sur F = 50. Le ratio de couverture conditionnelle nous indique qu'il existe un taux de dépassement de 1,05% pour une Value-at-Risk acceptant 5% de risque. Ce modèle rempli donc les conditions pour un dépassement qui ne sous-estime, ni ne surestime le risque de marché. Ce modèle conditionnel fournit une quantification plus flexible de la VaR, qui tient compte de la dynamique de la volatilité. En effet, lorsque le taux de croissance dépasse le seuil u fixé à 3%, la VaR conditionnelle Ç vibre È, couvrant le risque de perte extreme (Cf. : graphique, éléments fléchés ). Le graphique ci -dessous souligne la différence qu'il peut exister entre la VaR classique et celle liée aux valeurs extremes.

Backtesting: Occurences de violations de VaR(95%)

12.00% 9.00% 6.00% 3.00% 0.00%

6/13/2006 6/13/2007 6/13/2008 6/13/2009 6/13/2010

|R| VaR N(|x|) VaR GPD(|x|)

En outre, nous retenons le modèle de VaR GPD conditionnée à partir d'un seuil fixé à 3%. Nous allons, dans la sous-section suivante, établir une stratégie long-short à partir des résultats obtenus ci-dessus.

II.II.3.2 MODéLE DE RENTABILITÉ AJUSTÉE DU RISQUE

Cette sous-section montre comment la théorie des valeurs extrême peut être utilisée comme stratégie de couverture du risque de marché. Celle-ci implique la distribution asymptotique univariée des taux de rendement minimum et maximum d'une position de marché. La VaR est calculée en fonction d 'une formule d'agrégation du risque, laquelle prend en compte

· Le facteur de sensibilité des extrêmes, à travers une méthode conditionnelle

· La corrélation entre les facteurs de risque et la position du marché

Nous suivrons l'évolution de la VaR analysée à partir cette hypothèse.

En pondérant celle-ci par la dynamique de prix de l'actif étudié, nous
déterminerons la mesure du risque que peut prendre la détention de l'actif
dans le portefeuille. Pour établir une gestion performante basée sur la VaR,

pour p?(95%), avec t = 1, nous allons préalablement, à travers l'étude des

extrême de la crise des Subprimes, confronter d'une part, la _MVaR calculée à l'aide du quantile des valeurs extrêmes et d'autre part, les pertes et profits réels du DJIA. Soit _MVaR, l'agrégation de la M à à la VaR, définie par les deux variables suivantes :

P_t.(1+VaR_t(q)) si R_t > 0

MVaR =

P_t si R_t < 0

(1+VaR_t(q))

Oü Rt, le taux de rentabilité du DJIA en t, Pt le prix auquel le DJIA est indexé en t et q le quantile de la probabilité de perte maximum, ici réduit à 95%.

Nous avons choisi de présenter un graphique exposant:

· L'évolution du cours du DJIA

· MVaR classique calculé à partir du quantile de distribution de la loi normale

· La _MVaR GPD initiée à partir des éléments calculés précédemment



26000

PVaR

21000

16000

11000

6000

1000

6/14/2006 6/14/2008 6/14/2010

Price Normale GPO

Nous remarquons que la VaR GPD est réactive. Conditionnée à partir du seuil u = 3%, elle tombe sous le cours en septembre 2008, lors de la chute de la banque américaine Lehman Brothers. Puis, passe au-dessus du cours lorsque la distribution cumulée des rendements se recentre vers la tendance centrale, en 2010. La VaR classique reste très proche du cours de l'indice en période de perte extrême. Elle ne permet donc

pas d'assurer une gestion de portefeuille sécurisée. La _MVaR ayant détectée une occurrence de perte extrême par le fait qu'elle soit inférieure au cours du DJIA, se révèle être un indicateur de décision intéressant dans une gestion de portefeuille mettant en avant le risque. Afin de simuler cette aversion au risque, nous pouvons alors prendre position à l'achat oü a la vente en fonction de cette dernière. Soit _WVaR, la variable déterminant l'achat ou la ve nte de Pt, tel que:

P_t si PVaR_t > R_t

WVaR =

Pt 1 si PVaR_t < R_t

Oü Rt, le taux de rentabilité du DJIA en t, Pt le prix auquel le DJIA est indexé en t.

Nous présentons dans le tableau ci-dessous les résultats empiriques de notre analyse:

Tab12: Résultats
Base 100	DJIA	Normale	GPD
Nobs	1148	1148	1148
Moyenne	98,20	88,83	98,87
Volatilité	19,14	17,18	14,08
Maximum	131,09	117,82	126,54
Minimum	55,58	59,92	69,65
Perte maximale	44,42	40,08	30,35
Skewness	-0,10	-0,02	0,27
Kurtosis	-1,21	-1,52	-1,38
Beta (MCO)	1,000	0,904	0,995

La performance relative du modèle lié 100% à la loi normale et celui évalué à l'aide



90%



de la GPD sont présentés par rapport

80%



70% aux résultats empiriques du DJIA



60% pendant la période de test. Nous



50%

pouvo ns noter que la VaR GPD



40%



30% garantie un seuil de perte maximal de -



20% 3 0,5%, quand le cours descend à -



10%

44,42% . Nous remarquons également

0%







VaR GPO VaR Normale Prix



SVaR: Performance

125
115

85

des modèles. On remarque que le

75

coefficient d'asymétrie est négatif pour

65

le DJIA et la VaR normale, alors que

55

6/14/2006 6/14/2009

Price Normale GPO



celui de la VaR GPD est positif à 0,27.
Ceci dénote que la loi des cours
comporte plus de mouvements à la
baisse pour les deux premiers et une tendance plus haussière pour le dernier.

77

CONCLUSION

Nous soulignons au terme de cette étude l'importance des mouvements extrêmes lors de la crise des Subprimes. B. Mandelbrot avait déjà émis des réserves en 1963 quant à la validité du comportement aléatoire du mouvement brownien caractérisé par les deux premiers moments de la loi normale. En effet, les hypothèses qui les soutiennent, peuvent corrompre leur validité intrinsèque dans le cas oü des événements imprévisibles influencent de facon prépondérante la moyenne de l'échantillon. La crise des Subprimes en est l'exemple type. Nous pouvons apprécier la fréquence du DJIA par l'exercice du calcul des rentabilités anormales, se déplacant d'un niveau de stabilité vers celui réalisé par la crise. Les résultats obtenus montrent que la crise des Subprimes a enregistré une fréquence journalière continue importante.

Le caractère imprévisible des évènements rares est omniprésent en économie, en finance et en assurance. Parallèlement aux travaux de P. Levy en 1920, le développement des études statistiques des valeurs extrêmes, mené par R. Fisher et L. Tippett en Grande- Bretagne, B. Gnedenko en Union soviétique, M. Fréchet et E. Gumbel en France et L. Mises en Autriche, a émergé. Ces études se concentrent sur le maximum et le minimum d'une suite d'événements dans un échantillon, événements d'occurrence faible, mais de grande importance. Ces Ç événements raresÈ forment ce que l'on nomme les queues de distributions. Ces statisticiens ont montré que la valeur maximale de l'échantillon ne peut obéir qu'à l'une parmi trois distributions différentes : les distributions de Fréchet, de Gumbel et de Weibull.

Il en est ainsi des étude s de fiabilité, oü, pour calculer la probabilité de défaut, nous cherchons à considérer la probabilité de défaillance de son Ç maillon le plus faible È. Par exemple, pour déterminer les caractéristiques d'un barrage, il faut connaitre la pression maximale que l'ouvrage pourra être amené à tolérer, et non sa pression moyenne qu'il supportera en situations normales. Pour cela, il faut caractériser les variables extrêmes de l'échantillon d'observations. C'est se que propose de quantifier la Value -at-Risk, qui mesure la perte potentielle maximale à un seuil de probabilité et à un horizon de temps fixés. L'analyse de cette dernière menée sur le DJIA nous a permis de comprendre qu'il est possible de la quantifier, de facon analytique, en utilisant la loi de distribution de Pareto généralisée, les

probabilités de pertes extrêmes. En pondérant la VaR GPD, nous avons mesuré le risque de marché, nous permettant de limiter les pertes encourues par la détention du DJIA. Il est à noter que cette méthode peut être facilement assimilable aux méthodes de gestion assurancielle de portefeuille OBPI⁵³ ou CPPI⁵⁴, dans laquelle la VaR GPD servirait de seuil dynamique de proportion au risque.

Paradoxalement, l'étude menée précédemment nous a permis de remarquer que les statistiques ne sont pas une science exacte. En modélisant statistiquement les valeurs extrêmes du DJIA, un problème est apparu de manière récurrente : La pertinence des données utilisées.

En effet, les méthodes de significativité de Brown et Warner , de Pattel et de Bohemer, Musumeci et Poulsen impliquent une constance de la volatilité dans le temps. Or nous savons que les marchés financiers sont hétéroscédastique et qu'il est nécessaire d'utiliser un processus ARCHGARCH afin de proposer un modèle adéquat. Nous pouvons également remarquer que cette hypothèse n'est plus vérifiée en phase de Ç partitionnement des données È ou Ç Clustering È dans lequel deux ou plusieurs titres réagissent, sur un intervalle de temps i, à un même évènement. Cette corrélation est souvent révélée à travers de nombreux exemples sur les marchés financiers, notamment lorsque Lehman Brothers disparue pendant la crise des Subprimes .

Aussi, il faut utiliser une fenêtre de taux de rentabilité équilibré s entre stabilité et précision afin de réduire l'effet de croissance de la variance estimée à partir du nombre d'observations. En ce qui concerne la théorie des valeurs extrêmes, le choix du seuil u de sélection des données maximum et minimum est primordial pour la validité de l'étude. Il s'agit d'une part de sélectionner un seuil grand, au dessus duquel nous conservons assez de données pour que l'approximation asymptotique soit à la fois applicable et précise. D'autre part pas trop élevé pour ne pas donner trop d'importance aux écart-types de l'estimateur. Cela révèle d'une certaine approximation.

5 3 <<Option Based Portfolio Insurance>> est une méthode d'assurance de portefeuille à base d'options, conceptualisée par Leland et Rubinstein en 1981.

⁵⁴ <<Constant Proportion Portfolio Insurance>> est la méthode du coussin. Initialement développée par P. Erold en 1986 et Black et Jones en 1978, elle vise à maintenir une proportion constante d'exposition au risque.

De plus, Selon N. Taleb, il n'est pas possible de mesurer le risque d'événements rares catastrophiques dont nous n'avons jamais connu d'exemple par le passé. Ces <<cygnes noirs >>, tels qu'il les appelle, invalideraient les approches statistiques de modélisation du risque. Mais il reste encore beaucoup à découvrir. La préface de la deuxième édition du livre << Une approche fractale des marchés È soulignait : Ç L'économie financière, en tant que discipline, en est là oil en était la chimie au XVI e siècle : c'était un ramassis de savoir-faire, de sagesse populaire fumeuse, d'hypothèses non confirmées et de spéculations grandioses È⁵⁵.

La crise financière des Subprimes est-elle un cygne noir au méme titre que l'accident subi par la centrale nucléaire de <<Three Mile Island >>⁵⁶, oü, malgré la prudence établie par les instances de régulation nucléaire, une erreur de nature non-quantifiable, mit en échec le système de süreté ? Ou pouvons-nous plutôt la comparer à la tempéte qui dévasta les Pays-Bas en 1953, événement anormal, mais dont on pouvait mesurer la probabilité ?

5 5 B. Mendelbrot et R. L Hudson: Une approche fractale des marchés Ð Risquer, perdre et gagner ; Editions Odile Jacob, Paris 2009, 358 pages.

⁵⁶ La central nucléaire de Three mile Island est situé dans l'est des Etats-Unis est connu pour avoir subi un accident classé au niveau 5 l'échelle international des évenements nucléaires (INES). C'était le 28 mars 1979.

BIBLIOGRAPHIE

BALKEMA A. A., DE HAAN L., 1974, "Residual life time at great age", Annals of Probability 2, p 792-804.

BEIRLANT J., GOEGEBEUR Y.,s "Segers J. et Teugels J., 2004, Statistics of Extremes - Theory and Applications", Wiley, England.

BERMAN S. M., 1963, "Limiting theorems for the maximum term in stationary sequences", Annals of Mathematical Statistics, p 502-516.

BOEHMER E., MUSUMECI J. ET POULSEN A., 1991, "Event-study methodology under conditionsof induced variance", Journal of Financial Economics, vol. 30, n°2, p 253-272.

BROWN S. ET WARNERJ., 1980, "Measuring security price performance", Journal of Financial Economics, vol. 8, n°3, p 205-258.

CAMPBELL J., LO A. ET MACKINLAY C., 1997, "The econometrics of financial markets", Princeton University Press.

CLAUSS P., 2011, "Gestion de portefeuille", Dunod.

DANIELSSON J., DE VRIES C.G., 1997, "Value at risk and extreme returns", Working Paper, London School of Economics, London, UK.

DEKKERS A. L. M., DE HAAN L., 1989, "On the estimation of the extreme value index and large quantile estimation", The Annals of Statistics, p 1795-1832.

EMBRECHTS P., KL†PPELBERG C., MIKOSCH T., 1997, "Modelling Extremal Events for Insurance and Finance", Springer-Verlag, Berlin.

ENGLE R.F., 1982, "Auto-regressive conditional heteroskedasticity with estimates of the variance of united kingdom inflation", Econometrica, p 987-1007.

Fama E., 1970, "Efficient capital markets: a review of theory and empirical work", The Journal of Finance, val. 25, n°1, p 383-417.

FISHER R., TIPPET L., 1928, "Limiting Forms of the Frequency Distribution of the Largest or Smallest Member of a Sample", Cambridge Philosophical Society, p 180-190.

GNEDENKO B.V., 1943. "Sur la distribution limite du terme maximum d'une série aléatoire". Annals of Mathematics, p 423-453.

GUMBEL E J., 1958, "Statistics of Extremes", Columbia University Press, New-York.

e

HAMON J., 2005, "Bourse et gestion de portefeuille" , Economica, 2edition.

HILL B M., 1975, "A simple general approach to inference about the tail of a distribution", Annals of Statistics, p 1163-1173.

HULL J., 2006, "Options, futures et autres actifs dérivés", 6^e edition, Pearson Education.

JORION P., 1996, "Risk: Measuring the risk in value at risk", Financial Analysts Journal, p 47-56.

JORION P., 1997, "Value at Risk: The New Benchmark for Controlling Market Risk", McGraw-Hill, Chicago.

e

JORION P., 2006, "Value -at-Risk" , McGraw -Hill, 3edition.

JP MORGAN, 1995. RiskMetrics^TM - Technical Document, 3rd ed

KUPIEC P. H., 1995, "Techniques for verifying the accuracy of risk measurement models", Journal of Derivatives, p 73-84.

LO A. W., MACKINLAY A. C., 1990, "An econometric analysis of nonsynchronous trading", Journal of Econometrics, p 181-211.

LONGIN F. M., 1997, "The threshold effect in expected volatility: A model based on asymmetric information", The Review of Financial Studies, 837-869.

LONGIN F., 1993, "Volatility and extreme movements in fianncial markets", Ph.D. Thesis, HEC.

LONGIN F., 1996, "The asymptotic distribution of extreme stock market returns", Journal of Business, p 383-408.

LONGIN F., 2000, "From VaR to stress testing: The extreme value approach". Journal of Banking and Finance, p 1097-1130

LONGIN F., SOLNIK, B., 2001, "Extreme correlation of international equity markets", Journal of Finance, p 651-678

82

LUX T., SORNETTE D., 1999, "On rational Bubbbles and fat tails", Journal of Monetary Economics.

MANDELBROT B., 196,. "The variation of certain speculative prices", Journal of Business, p 394-419.

MANDELBROT B., 1997, "Fractales, hasard et finance", Flammarion.

MANDELBROT B., 2001, "Stochastic Volatility, Power Laws And Long Memory", Quantitative finance, vol. 1, n°6, December, p 558-559.

MANDELBROT B.,1963, "The Variation Of Certain Speculative Prices", Journal of Business, vol. 36, n°4, p 394-419.

MCNEIL A. J., 1998, "Calculating quantile risk measures for financial return series using extreme value theory", Working Paper, ETH, Zurich, Switzerland.

PARKINSON M., 1980, "The Extreme Value Method For Estimating The Variance Of The Rate OfReturn", Journal of Business, Vol. 53, p 61-66.

PATTEL J., "Corporate forecasts earning per share and stock price behavior: empirical test", Journal of Accounting and Research, vol. 14, n°1, p 246-276.

PICKANDS J., 1975, "Statistical inference using extreme order statistics". Annals of Statistics, p 119-131.

RIVA F., 2008, "Application financieres sous Excel en Visual Basic", Economica, 3° edition.

SAPORTA G., 1990, "Probabilités, analyse des données et statistique", Editions Technip.

SHARPE W., 1963, "A simplified model for portfolio analysis", Management Science, vol. 9, n°1, p 277-293.

SIVERMAN B., 1986, "Density estimation for statistics and data analysis", Chapman and Hall, London.

SMITH R., 1989, "Extreme Value Analysis of Environmental Time Series: an Application to Trend Detection in Ground-Level Zone", Statistical Science, p 367- 3 93

SORNETTE D., 1998, "Multiplicative processes and Power laws", Physical review, p 4811-4814.

83

WHITE H., 1982, "Maximum Likelihood Estimation of Misspecified Models", Econometrica, p 1-16.

ANNEXES

A. Graphiques : Sélection de seuil 86

B. Stratégie : Synthèse générale 87

C. Graphiques : VaR 88

D. Stratégie 89

E. Visual Basic Application : Loi de valeurs extremes 91

F. Visual Basic Application : Loi de probabilité 93

G. Origines macroéconomiques de la crise des subprimes 97

85

A. GRAPHIQUES : SÉLECTION DE SEUIL



u > 3%

5

y = 1.3562ln(x) - 0.8559
R² = 0.74542

4

3

2

1

0



u > 4%

5

y = 1.268ln(x) - 0.7444
R² = 0.77269

4

3

2

1

0

Extreme Enreg. (Extreme)

Extreme Enreg. (Extreme)







u > 5%

u > 6%

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

5

4

3

y = 1.0948ln(x) - 0.5358
R² = 0.80069

y = 0.8955ln(x) - 0.3101
R² = 0.80966

5

4

3

2

1

0

2

1

0

Extreme Enreg. (Extreme)

Extreme Enreg. (Extreme)

86

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17

Si VaR (q) >

t Rt

Long



B. STRATÉGIE : SYNTHéSE GÉNÉRALE

Sélectionner un actif



Déterminer un période T

Choisir la fréquence des taux de rentabilités



Calculer les taux de rentabilités Rt



Sélectionner un seuil extreme u



L'hypothèse est
rejetée

Etablir un test d'ajustement sur les valeurs réelles
observées correspondant au seuil 1 - q

Calculer la VaR en fonction du quantile q sur une
période t

Estimé les paramètres !!,(3^!

asymptotique à partir du rendement u

de la distribution

L'hypothèse est
acceptée

Calculer la VaR pondérée par le prix de l'actif en t

Si VaR (q) <

t Rt

Short

87

125 115 105 95 85 75 65 55

C. GRAPHIQUES : VAR



DJIA

6/14/2006 6/14/2008 6/14/2010

Price

SVaR classique

125

115 105 95 85 75 65

55

6/14/2006 6/14/2008 6/14/2010

Normale



SVaR GPD

125

115

105

95

85

75

65

55

6/14/2006 6/14/2008 6/14/2010

88

GPD

D. STRATÉGIE

Nous vous présentons ici une stratégie basée sur plusieurs actifs différents. Il s'agit, comme dans l'exemple vu précédemment, d'une stratégie long-short basée sur l'achat de call et de put. Soit R1, R2,É,R_n, une suite de variables aléatoires indépendantes et identiquement distribuées, calculées par ln(Pt/Pt-1), oü P est le prix de l'actif en t. Pour

P_t.(1+VaR_t(q)) si R_t > 0

MVaR =

P_t si R_t < 0

(1+VaR_t(q))

oÜ _MVaR est la pondération de la VaR à l'actif, et la VaR est donnée par

VaRq = uö +

ö fl ( ö Nu

ö (1 q) ) 1. Lorsque la VaR (q = 95%) =R^2, alors le

risque est dit faible. Inversement, le risque est dit élevé. Nous avons donc

· L'achat d'un Call lorsque la VaR = cours

· L'achat d'un Put lorsque la VaR < cours.



DJIA; BOfA; IBM; Exxon

350

300

250

200

150

100

50

0

6/13/06 6/13/07 6/13/08 6/13/09

400



140

130

120

110

100

90

80

Call
ITM

Put

ITM

6/13/06 6/13/07 6/13/08 6/13/09

70

60

Cette étude nous permet de constater qu'il existe, sur les marchés financiers,
une volatilité plus importante en phase de baisse des cours. Il existe aussi

89

des effets "clusters" oü la corrélation des actifs se concentre en une période t, impliquant un risque de non-diversification statistique (risque de marché).



40.00%

Performance

50.00%

30.00%

20.00%

10.00%

0.00%

Call/Put

Enreg. (Call/Put)

100Moy. mobile sur per. (Call/ Put)

Nous enregistrons une performance de 40,1% en prés de 2 ans et 6 mois de gestion, avec un maximum de 47,18%. Cette stratégie met en avant le risque probabiliste pour en dégager une rentabilité. Le risque extrême "Black Swan" est également pris en compte.

Cependant, Un test "Out-of-Sample"
doit être établi pour confirmer cette
hypothèse. Les Calls et les Puts sont

ici hors premium. Il serait nécessaire de minorer l'effet de cette prime sur la performance de la stratégie.

Resultats	Données	Call	Put
Nobs	906
Moyenne	32.11%	122	90
Ecart-type	10.9%	8.80	10.88
Maximum	47.18%	140	100
Minimum	0.00%	100	65
Skewness	-0.94	-0.09	-0.59
Kurtosis	0.02	-0.77	-1.21
Jarque Bera	4.69	21.53	28.84
Performance	40.10%	20%	20%

90

E. VISUAL BASIC APPLICATION : LOI DE VALEURS EXTRæMES

'Indicateur de Hill (Pour Fréchet uniquement)

Function Hill(rank As Double, Nb As Double) As Double

medianrank = (1 / (1 - ((rank - 0.44) / (Nb + 0.12))))

Hill = WorksheetFunction.Ln(WorksheetFunction.Ln(medi anrank))

End Function 'Gumbel

Function Gumbel(x As Double, a As Double, b As Double) As Double

If b <= 0 Then

Call MsgBox("b doit tre strictement positif", vbExclamation, "Paramtre incorrect")

Exit Function End If

Gumbel = Exp(-(x - a) / b) * Exp(-Exp(-(x - a) / b)) / b

End Function 'Fréchet

Function Fréchet(x As Double, a As Double, b As Double) As Double

If x <= 0 Then

FrÉchet = 0 Exit Function End If

91

If b <= 0 Then

Call MsgBox("b doit être strictement positif", vbExclamation, "Parametre incorrect")

Exit Function End If

Fréchet = a / b * (b / x) ^ (a + 1) * Exp(-(b / x) ^ a)

End Function 'Weibull

Function Weibull(x As Double, a As Double, b As Double) As Double

If x <= 0 Then

Weibull = 0 Exit Function End If

Weibull = a / b ^ a * x ^ (a - 1) * Exp(-(x / b) ^ a)

End Function

92

F. VISUAL BASIC APPLICATION : LOI DE PROBABILITÉ

Option Explicit

'ETAPE 1: COPIER ET TRIER

'Dans cette section, nous allons copier le nombre de série pour les trier, dans le but de dessiner la fonction de distribution cumulée

' La variable "Total" nous donne le nombre de donnÉe existante

Public Sub Copy_and_Sort()

Dim Total As Integer

Let Total = Range("Total").Value

' Copier dans un tableau reconfiguré de Total lignes et de 1 colonne

Let Range("Y1").Resize(Total, 1) =

Range("Selection").Resize(Total, 1).Value

' Trier les données copiées

Call Range("Y1").Resize(Total, 1).Sort(Key1:=Range("Y1").Resize(Total, 1), Order1:=xlAscending, Header:=xlGuess, OrderCustom:=1, MatchCase:=False, Orientation:=xlTopToBottom, DataOption1:=xlSortTextAsNumbers)

End Sub

'ETAPE 2: DEFINIR L'INTERVAL DE DISTRIBUTION

'Dans cette section, l'intervalle est défini afin que celui-ci soit le plus large possible en aberrant les cases vides

'La variable "Interval" est donnée 10 quand la borne inférieure "borneinf" est Égale 0

'La fenêtre "step" est Égale à 0,1

93

'La variable "case_vide" est ici exprimée "as boolean", c'est ^ö dire soit "Vrai" Il n'y a pas de case vide, soit "Faux" il y a des cases vides

Public Sub Intervallecorrespondant ()

Const Interval = 10 Const borne_inf = 0 Const Step = 0.1

Dim intervalleconfiance As Double

Let intervalleconfiance = Interval

Dim case_vide As Boolean

' Montre la dimension de l'intervalle du plus grand au plus petit

' S'arrête lorsque l'ensemble des cases de sont pas vides, ou, par sécurité, lorsque la taille de l'intervalle est Égale ^ö 0

Do

Let Range("Intervalleconfiance").Value = intervalleconfiance

Call Application.Calculate

Dim minimum As Integer

Let minimum = Application.WorksheetFunction.Min(Ra

nge("Distributions"))

Let case_vide = (minimum > 0) ' Vrai si le minimum >= 1

Let intervalleconfiance = intervalleconfiance - Step '
Boucle

Loop Until case_vide Or

intervalleconfiance <= borne_inf

94

End Sub

'ETAPE 3: FONCTION DE DISTRIBUTION

'Dans cette section, nous allons créer une fonction afin de faciliter les calculs de fonction de distribution

' Somme des returns (Ln(t) / Ln(t-1))

' Les champs doivent être vertical avec le meme nombre de ligne

Public Function SumAbsLn(ByRef valeurscourrantes As Range, ByRef DJIA As Range) As Double

Dim size As Integer

Let size = valeurscourrantes .Rows.Count

If size <> DJIA.Rows.Count Then

Call MsgBox("La taille des séries ne corresponde pas !")

End If

Dim resultat As Double Let resultat = 0

Const petitesvaleurs = 0.01 Dim i As Integer

For i = 1 To size

Dim Borne As Double

' Si les données sont égales à 0, prendre la plus petite value

Let Borne = Application.WorksheetFunction.Max(v a l e u r s c o u r r a n t e s (i, 1).Value, petitesvaleurs)

' increment result with the absolute value of the log of the ratio between actual and model data

95

Let resultat = resultat + Abs(Log(Borne / DJIA(i, 1).Value))

Next i

96

Let SumAbsLn = resultat End Function

G. ORIGINES MACROÉCONOMIQUES DE LA CRISE DES SUBPRIMES

Comité de B%ole Ratio: Cooke, McDonough

Hausse des besoins en fonds propres



Recherche
de rentabilité

Exigence de
rentabilité

Baisse de la
prime de

risque

Etats

Confiance
Ç Paradoxe de
la
tranquillité »

Credibilité
des banques
centrales

Innovation
financiere

Concurrence

Baisse de
l^Õinflation

Baisse des
taux long
terme

Rel%ochement
des critéres

Excédent commerciaux des pays émergents

Titrisation

Hausse de la
liquidité

Hausse de lÕépargne dans les pays émergents

Expansion
du credit

Hausse de lÕinflation

Investissement

Hausse de la
consommation

Anticipation
des profits

Croissance

Hausse du
prix des
actifs

Choc de
productivité

Optimisme

Source : P. Artus, J-P Betbeze, C. Boissieu et G. Capelle-Blancard, «La crise des subprimes», Conseil d'analyse Cconomique, la documentation frangaise, 2008, p 60

97 UNE VISION QUANTITATIVE DU RISQUE EXTRæME APPLIQUÉE Ë LA CRISE DES

SUBPRIMES