Prévision de la consommation du gaz naturel pour la distribution publique par la méthode traditionnelle, lissage exponentiel et Box & Jenkins

	République Algérienne Démocratique et Populaire Ministère de l'Enseignement Supérieur et de la Recherche Scientifique Institut National de la Planification et de la Statistique MEMOIRE En vue de l'obtention du diplôme d'Ingénieur d'Etat en Planification et Statistique Option : Statistique Appliquée THEME
	Prévision de la consommation du gaz naturel pour la distribution publique par la méthode traditionnelle, lissage exponentiel et Box & Jenkins
	Présenté par : Encadré par :
	Ratiba MOULAÏ Mme KHERCHI Naima ZAKANE 1 9^ème promotion 2006-2007

i6d~cacee5

Je dédie ce travail, à la mémoire de mon père, à ma mère, à mon frère Riadh, à mes soeurs Lamia et amel, à mon neveu Mhamed, à mes nièces Zineb, Wafaa, Yasmine, Alaa, ainsi qu'à tous mes amis.

~atiEa

Je dédie ce travail à mes chers parents qui m'ont tout donné, à mes frères Ahmed et AEK, à mes soeurs Zineb et Yasmine ainsi qu'à mon oncle Ahmed sans oublier mon cher mari Hichem.

~a~~a

Sommaire

Introduction générale ..2

Chapitre 1 : Présentation de la SONELGAZ

1.1 Généralité sur le gaz naturel 4

1.1.1 Origine et Histoire .4

1.2.2 Description et caractéristiques techniques .4

1.2.3 Utilisation ...5

1.2 Présentation de la SONELGAZ ..5

1.2.1 Historique 5

1.2.2 Organisation du groupe SONELGAZ 7

1.2.3 Présentation de la direction Analyse et Prévision (DAP) ..8

1.2.4 Clientèle gaz 9

1.2.5 Plan national gaz 10

Chapitre 2 : Prévision par la méthode traditionnelle, lissage exponentiel et Box & Jenkins.

2.1 Prévision par la méthode traditionnelle 12

2.1.1 Etude de la série ..12

2.1.1.1 Définition d'une série chronologique ..12

2.1.1.2 Les composantes d'une série chronologique 12

2.1.1.3 Schémas de décomposition d'une série chronologique 13

2.1.1.3.1 Principe de conservation des aires 13

2.1.1.3.2 Procédure de choix d'un schéma de décomposition .14

2.1.2 Estimation des composantes de la série ..15

2.1.2.1 Estimation de la tendance ..15

2.1.2.1.1 Méthode des moindres carrés .15

2.1.2.1.2 Méthode des moyennes mobiles 15

2.1.2.1.3 Avantages et inconvénients des méthodes d'estimation 16

2.1.2.2 Estimation des coefficients saisonniers 16

2.1.2.2.1 Méthode pratique 17

2.1.2.2.2 Méthode analytique .18

2.1.2.2.3 Série désaisonnalisée ou série CVS 19

2.1.2.3 Estimation des variations accidentelles 19

2.1.3 Prévision 19

2.2 Prévision par la méthode de lissage exponentiel ..20

2.2.1 Lissage exponentiel simple .20

2.2.1.1 Choix de la prévision initiale .21

2.2.1.2 Choix optimal de la constante de lissage 21

2.2.1.3 Limitation de la méthode 21

2.2.2 Lissage exponentiel double .22

2.2.2.1 Présentation 22

2.2.2.2 Propriétés de la méthode 22

2.2.3 Lissage exponentiel de Holt-Winters 22

2.3 Prévision par la méthode de Box & Jenkins .25

2.3.1 Concepts des séries chronologiques 25

2.3.1.1 Processus stochastique	25
2.3.1.2 Processus aléatoires stationnaires	25
2.3.1.2.1 Caractéristiques d'un processus aléatoire stationnaires	..26
2.3.1.3 Les opérateurs de Box & Jenkins	28
2.3.1.3.1 Les effets des opérateurs de Box & Jenkins	29
2.3.2 Les processus ARMA	30
2.3.2.1 Le théorème de décomposition de Wald	30
2.3.2.2 Processus AutoRégressif d'ordre p : AR (p)	.30
2.3.2.3 Processus Moyenne Mobile (Moving Average) d'ordre q : MA (q)	.31
2.3.2.4 Processus mixte AutoRégressif Moyenne Mobile d'ordre p et q :
ARMA (p,q)	..32
2.3.3 Les processus aléatoires non stationnaires	..34
2.3.3.1 Description des processus TS et DS	..34
2.3.3.2 Processus mixte AutoRégressif Moyenne Mobile Intégré d'ordre (p, d, q) : ARIMA (p, d, q) .36 2.3.3.3 Processus Saisonnier AutoRégressif Moyenne Mobile Intégré d'ordre (p,d,q) * (P,D,Q)s : SARIMA (p,d,q) * (P,D,Q)s ...37 2.3.3.4 Etude de la non stationnarité d'une série chronologique 37 2.3.3.4.1 Test de tendance et de saisonnalité par la méthode des variances ..37
2.3.3.4.2 Tests de racine unitaire		39
2.3.3.4.2.1 Les tests de Dickey-Fuller simple (DF)		..39
2.3.3.4.2.2 Les tests de Dickey-Fuller Augmentés (ADF)		40
2.3.3.4.2.3 Le test de Philips et Perron		.45
2.3.4 La méthodologie de Box & Jenkins		45
2.3.4.1 Identification		..46
2.3.4.2 Estimation		..46
2.3.4.3 Validation		46
2.3.4.3.1 Le test de Student des paramètres		..46
2.3.4.3.2 Le coefficient de détermination		..47
2.3.4.3.3 Les tests sur les résidus		...47
2.3.4.3.4 Les critères de comparaison de modèles		.49
2.3.4.4 Prévision		..50
Chapitre 3 : Application des méthodes de prévision
3.1 Analyse descriptive		54
3.1.1 Historique des paramètres de la distribution publique		54
3.1.2 Présentation des données		55
3.2 Application de la méthode traditionnelle		..56
3.2.1 Etude de la série nord		..56
3.2.2 Etude de la série hauts plateaux (HP)		.62
3.2.3 Etude de la série sud		63
3.3 Application de la méthode de lissage exponentiel		65
3.3.1 Etude de la série nord		..65
3.3.2 Etude de la série hauts plateaux		..66
3.3.3 Etude de la série sud		67
3.4 Application de la méthode de Box & Jenkins		68
3.4.1 Etude de la série nord		..68
3.4.1.1 Analyse du corrélogramme		68

3.4.1.2 Etude de la stationnarité de la série « nordsa » .70

3.4.1.3 Identification et estimation du modèle ..72

3.4.1.4 Validation du modèle 73

3.4.1.5 Prévision 75

3.4.2 Etude de la série hauts plateaux .75

3.4.2.1 Analyse du corrélogramme 75

3.4.2.2 Etude de la stationnarité de la série « HPsa » 77

3.4.2.3 Identification et estimation du modèle ..78

3.4.2.4 Validation du modèle 79

3.4.2.5 Prévision 81

3.4.3 Etude de la série sud 81

3.4.3.1 Analyse du corrélogramme 81

3.4.3.2 Etude de la stationnarité de la série « sudsa » 83

3.4.3.3 Identification et estimation du modèle ..84

3.4.3.4 Validation du modèle 85

3.4.3.5 Prévision 87

3.4.4 Comparaison des résultats des méthodes de prévision 87

Conclusion générale 91

Bibliographie ..94

Annexes 95

Introduction générale

L'analyse des séries temporelles et plus particulièrement la prévision à court et moyen terme, a connu un développement important depuis trente ans. La diffusion de logiciels spécialisés la met à la portée de toutes les organisations. La prévision est fondamentale dans la mesure ou elle est à la base de l'action. La prise de décision doit en effet toujours reposer sur des prévisions, c'est ainsi que la Société Nationale de l'Electricité et du Gaz « SONELGAZ » (lieu de notre stage) s'intéresse aux prévisions de la consommation de l'électricité et du gaz afin de faire face à la demande de sa clientèle, mais aussi orienter sa politique commerciale (prix, marketing... etc).

C'est dans ce but que la compagnie nous a chargé de faire une étude scientifique et d'élaborer un modèle prévisionnel sur la consommation nationale du gaz naturel pour la distribution publique.

Afin de répondre aux attentes de la SONELGAZ, nous avons décider d'utiliser trois méthodes de prévisions à court terme à savoir : la méthode traditionnelle, la méthode de lissage exponentiel et la méthode de Box & Jenkins.

La première méthode est la plus simple et la plus facile à mettre en oeuvre, on suppose que la série est la juxtaposition par addition ou par multiplication des composantes, de tendance, de cycle conjoncturel, des variations saisonnières et des variations accidentelles. La méthode de lissage exponentiel regroupe l'ensemble des techniques qui ont pour caractéristiques communes d'accorder un poids plus important aux valeurs récentes de la chronique. Enfin la méthode de Box & Jenkins qui est la méthode de prévision la plus élaborée, sa caractéristique essentielle est d'effectuer une modélisation stochastique où l'évolution de la série est la réalisation d'un processus aléatoire déterminé. Contrairement aux autres méthodes de prévision, ce modèle n'est pas donné a priori mais sélectionné dans une classe très étendue de modèles, les modèles ARIMA (Auto Regressive Integrated Moving Average).

C'est ainsi que nous avons essayer de part ce travaille, de répondre à la question :

Quelle est la méthode de prévision la plus adéquate pour prévoir la consommation du gaz naturel pour la distribution publique ?

Afin de répondre à notre problématique nous avons structuré notre travaille en trois chapitres :

1- Le premier chapitre est consacré à la présentation de la SONELGAZ (généralités sur le gaz naturel, historique de l'entreprise, organisation, missions...etc).

2- Le deuxième chapitre quant à lui portera sur la présentation théorique des trois méthodes de prévision à savoir la méthode traditionnelle, la méthode de lissage exponentiel et la méthode de Box & Jenkins.

3- Enfin le troisième chapitre est consacré à l'application de ces méthodes et à la comparaison des résultats de prévision.

Pour clore ce travaille une conclusion générale est présentée à la fin.

Chapitre 1 : Présentation de la

SONELGAZ

1.1 Généralités sur le gaz naturel : 1.1.1 Origine et histoire¹ :

Le gaz naturel a été découvert au Moyen-Orient au cours de l'antiquité. Il y a de cela quelques milliers d'années, l'apparition soudaine de gaz naturel s'enflammant brutalement était assimilée à des sources ardentes. En Perse, en Grèce ou en Inde, les Hommes ont érigé des temples autour de ces feux pour leurs pratiques religieuses. Cependant ils n'évaluèrent pas immédiatement l'importance de leur découverte. C'est la Chine qui autour de 900 avant Jésus- Christ, comprit l'importance de ce produit et fora le premier puit aux alentours de 211 avant Jésus Christ.

En Europe, il fallut attendre jusqu'en 1659 pour que la Grande-Bretagne découvre le gaz naturel et le commercialise à partir de 1790. En 1821, à Fredonia (Etats-Unis), les habitants ont découvert le gaz naturel dans une crique par l'observation de bulles de gaz qui remontaient jusqu'à la surface. William Hart est considéré comme le "père du gaz naturel". C'est lui qui creusa le premier puit nord-américain.

Au cours du XIXème siècle, le gaz naturel a presque exclusivement été utilisé comme source de lumière. Sa consommation demeurait très localisée en raison du manque d'infrastructures de transport qui rendait difficile l'acheminement de grandes quantités de gaz naturel sur de longues distances. En 1890, un changement important intervint avec l'invention des joints à l'épreuve des fuites. Cependant, les techniques existantes n'ont pas permis de transporter le gaz naturel sur plus de 160 kilomètres et ce produit a été gaspillé pendant des années car brûlé sur place. Le transport du gaz naturel sur de longues distances s'est généralisé au cours des années 1920, grâce aux progrès technologiques apportés aux gazoducs. Après la seconde guerre mondiale, la consommation de gaz naturel s'est développée rapidement en raison de l'essor des réseaux de canalisation et des systèmes de stockage.

1.1.2 Description et caractéristiques techniques :

Le gaz naturel est incolore, inodore, insipide, sans forme particulière et plus léger que l'air. Il se présente sous sa forme gazeuse au dessus de -161°C. Pour des raisons de sécurité, un parfum chimique, le mercaptan, qui lui donne une odeur d'oeuf pourri, lui est souvent ajouté de sorte qu'une fuite de gaz puisse ainsi être détectée.

Le gaz naturel est un mélange d'hydrocarbures légers comprenant du méthane, de l'éthane, du propane, des butanes et des pentanes. D'autres composés tels que le CO2, l'hélium, le sulfure d'hydrogène et l'azote peuvent également y être trouvés. La composition du gaz naturel n'est jamais la même. Cependant, on peut dire que son composant principal est le méthane (au moins 90%). Il possède une structure d'hydrocarbure simple, composé d'un atome de carbone et de quatre atomes d'hydrogène (CH4). Le méthane est extrêmement inflammable. Il brûle facilement et presque totalement et n'émet qu'une faible pollution. Le gaz naturel n'est ni corrosif ni toxique, sa température combustion est élevée et il possède un intervalle restreint d'inflammabilité, ce qui en fait un combustible fossile sûr comparé à d'autres sources d'énergie. En outre, en raison de sa densité de 0,60, inférieure à celle de l'air (1,00), le gaz naturel a tendance à s'élever et peut, par conséquent, disparaître facilement du site où il se trouve par n'importe quelle fissure.

¹ http://www.unctad.org/infocomm/francais/gaz/descript.htm

On trouve du gaz naturel partout dans le monde, dans des réservoirs situés en profondeur sous la surface terrestre, ou des océans. Des poches de gaz peuvent se former au dessus des dépôts de pétrole brut, ou être emprisonnées au sein de roches poreuses. On qualifie le gaz naturel d'"associé" lorsqu'il est trouvé en présence de pétrole brut et "non associé" lorsqu'il est seul.

Le gaz naturel est considéré comme un combustible propre. Sous sa forme commercialisable, il ne contient presque pas de soufre et ne produit pratiquement aucun dioxyde de soufre (SO2). Ses émissions d'oxydes d'azote (NOx) sont plus faibles que celles du pétrole ou du charbon et celles de gaz carbonique (CO2) inférieures à celles des autres combustibles fossiles.

1.1.3 Utilisation 1:

Le gaz naturel est l'un des moyens énergétiques les moins polluants. En effet, lorsque sa combustion est complète, il n'émet que de l'eau et du dioxyde de carbone.

Il est utilisé comme source d'énergie dans l'industrie afin de produire de la chaleur (chauffage, fours...) et de l'électricité. En 2006, au niveau mondial, plus de 20 % de l'électricité est produite à partir de gaz naturel, et cette part ne cesse d'augmenter. Chez les particuliers, le gaz naturel est utilisé pour le chauffage, l'eau chaude et la cuisson des aliments. Enfin, depuis quelques années, le gaz naturel comprimé en bouteilles est utilisé en France comme carburant pour les véhicules (GNV). Mais déjà plus d'un million de véhicules au gaz naturel roulent déjà dans le monde, dans des pays comme l'Argentine et l'Italie.

Le gaz naturel est aussi la matière première d'une bonne partie de l'industrie chimique et pétrochimique : à la quasi-totalité de la production d'hydrogène, de méthanol et d'ammoniac, trois produits de base, qui à leur tour servent dans diverses industries.

1.2 Présentation de la SONELGAZ :

1.2.1 Historique :

1947 : Création de "ELECTRICITE et GAZ d'ALGÉRIE ": EGA

1969 : Création de la SOCIETE NATIONALE de l'ÉLECTRICITÉ et du GAZ : SONEL GAZ Par ordonnance

~6959 du 26 juillet 1969 parue dans le journal officiel du 1^er août 1969, la Société Nationale de l'Electricité et du Gaz (SONEL GAZ) est créée en substitution à EGA (1947,1969) dissout par ce même décret. L'ordonnance lui assigne pour mission générale de s'intégrer de façon harmonieuse dans la politique énergétique intérieure du pays. Le monopole de la production, du transport, de la distribution, de l'importation et de l'exportation de l'énergie électrique attribué à SONELGAZ a été renforcé. De même, SONELGAZ s'est vu attribuer le monopole de la commercialisation du gaz naturel à l'intérieur du pays, et ce pour tous les types de clients (industries, centrales de production de l'énergie électrique, clients domestiques). Pour ce faire, elle réalise et gère des canalisations de transport et un réseau de distribution.

1983 : Restructuration de SONELGAZ

¹ www.wikipedia.org

Toutes les unités de travaux et de fabrication de matériels, crées pour palier au manque de capacités nationales se sont transformées en 1983 en entreprise autonome, c'est ainsi que :

KAHRIF : Travaux d'électrification.

KAHRAKIB : Montage des infrastructures et installations électriques. KANAGAZ : Réalisation des canalisations de transport et de distribution du gaz. INERGA : Travaux de génie civil.

ETTERKIB : Montage industriel.

AMC : Fabrication des compteurs et des appareils de mesure et de contrôle. 1991 : Nouveau statut de SONELGAZ

SONELGAZ : Société Nationale d'Electricité et du Gaz change de nature juridique et devient un établissement Public à Caractère Industriel et Commercial (décret exécutif ~ 91-475 du 14 décembre 1991).

1995 : SONELGAZ (EPIC)

Le décret exécutif ~95-280 du 17 septembre 1995 confirme la nature de SONELGAZ en tant qu'établissement public à caractère industriel et commercial.

SONELGAZ est placé sous tutelle du Ministre chargé de l'énergie (article 2).

SONELGAZ est doté de la personnalité morale et jouit de l'autonomie financière (article 4).

SONELGAZ est régie par les règles de droit public dans ses relations avec l'Etat. Il est réputé commerçant dans ses rapports avec les tiers (article 5).

Le même décret défini en son article 6 les missions de SONELGAZ :

- Assurer la production, le transport et la distribution de l'énergie.

- Assurer la distribution public du gaz dans le respect des conditions de qualité, se sécurité et au moindre coût, dans le cadre de sa mission de service public.

2002 : Sonelgaz.Spa

Le décret présidentiel n02-195 du 1^er juin 2002, fixe les statuts de la société algérienne de l'électricité et du gaz Sonelgaz.Spa, ayant pour missions :

1- La production, le transport, la distribution et la commercialisation de l'électricité, tant en Algérie qu'à l'étranger

2- Le transport du gaz pour les besoins du marché national.

3- La distribution et la commercialisation du gaz par canalisation tant en Algérie qu'à l'étranger

4- Le développement et la fourniture de toutes formes et sources d'énergie.

5- L'étude, la promotion et la valorisation de toutes formes et sources d'énergie.

6- Le développement par tout moyen de toute activité ayant un lien direct ou indirect avec les industries électriques et gazière et de toute activité pouvant engendrer un intérêt pour « Sonelgaz.Spa » et généralement toute opération de quelque nature qu'elle soit pouvant se rattacher directement ou indirectement à son objet social, notamment la recherche, l'exploration, la production et la distribution d'hydrocarbures.

7- Le développement de toute forme d'activités conjointes en Algérie et hors d'Algérie avec des sociétés algériennes ou étrangères.

8- La création de filiales, les prises de participation et de détention de tous porte feuille d'action et autres valeurs mobilières dans toute société existante ou à créer en Algérie et à l'étranger.

Le même décret consacre la mission de service public confiée à Sonelgaz.Spa. Le groupe SONELGAZ l'expansion

Durant les années 2004 à 2006, devenant une holding ou groupe d'entreprises, Sonelgaz se restructure en filiales chargées de ses activités de base :

SONELGAZ Production Electricité (SPE) Gestionnaire Réseau Transport Electricité (GRTE) Gestionnaire Réseau Transport Gaz (GRTG)

En 2006 la fonction distribution est structurée en quatre filiales :

Alger

Région Centre Région Est

Région Ouest

Au delà de cette évolution assurer le service public reste la mission essentielle de SONELGAZ ; l'élargissement de ses activités et l'amélioration de sa gestion économique bénéficient en premier lieu à cette mission qui constitue le fondement de sa culture d'entreprise.

1.2.2 Organisation du groupe SONELGAZ :

Sonelgaz a adapté son organisation aux principes et dispositions de la loi n° 02-0 1 du 05/02/2002. Ses organes de direction se sont renforcés pour mettre en oeuvre sa stratégie et réaliser ses objectifs.

Le groupe Sonelgaz est constitué de la société mère (Administrateurs Délégués, Directions générales et Directions Exécutives) et de filiales.

La Sonelgaz est dotée des organes sociaux prévus par ses statuts (Assemblée Générale et Conseil d'Administration)

La présidence de SONELGAZ est dotée d'organes pour le management et le pilotage constituée :

· Du Comité Exécutif,

· Du Comité de Coordination Groupe,

· Des Comités de Groupe (de décision et ou de concertation) spécialisés (au nombre de huit).

Les Directions Générale et Directions Exécutives de la maison mère couvrent les fonctions dites groupe :

· Développement et stratégie,

· Systèmes d'information,

· Engineering,

· Ressources humaines,

· Finances et comptabilité,

· Audit technique,

· Audit de Gestion,

· Communication Corporate,

· Juridique,

· Relations Internationales.

Les filiales sont réparties par pôle de métiers :

· Filiales métiers (, production, transport de l'électricité, Transport du gaz, distribution de l'électricité et du gaz)

· Filiales métiers périphériques (logistique, soutien)

· Filiales travaux

Le groupe dispose de participations dans sept sociétés.

Principes d'organisation ayant présidé à la structuration du groupe :

· La stratégie industrielle et financière relève de la Maison Mère

· Les filiales sont chargées de la mise en oeuvre des stratégies chacune pour ce qui la concerne,

· Les filiales sont dotées de l'autonomie de gestion et elles ont une obligation de résultats

· Orientation et intervention sur les filiales via les organes sociaux (Assemblée Générale et Conseil d'Administration).

1.2.3 Présentation de la Direction Analyse et Prévision (DAP) :

La DAP est une sous-direction de la Direction Générale Développement et Stratégie (DGDS) Principales activités de la DAP :

Statistiques :

- Collecte des données traitement des données Publication (bulletin

statistique, bilan énergétique, rapports mensuels,...)

Analyse de la demande :

- Classification de la clientèle selon la forme de la courbe de charge :

· Panels Moyenne Tension (MT) / Âasse Tension (ÂÔ)

· Clientèle Haute Tension (HT)_?

- Modélisation macro-économique de la demande énergétique. - Analyse de la clientèle par commune / wilaya.

Prévision de la demande :

Prévision de la demande énergétique : une stratégie en trois piliers 1er pilier : Fiabilité des données

· Segmentation et connaissance de la clientèle,

· Optimisation de la segmentation des données selon les directions régionales de distribution,

· Meilleure organisation des données par type, nature,... à l'échelle régionale et nationale.

· Plus de coordination entre les structures régionales des filiales de distribution et de la DAP/DGDS (suite à la restructuration de l'entreprise)

2ème pilier : Outils de calculs performants

· Le choix de la méthode de prévision est décisif.

· Il dépend essentiellement de la qualité des données.

· Outil de calcul convivial (simple d'utilisation, dynamique, extensible,...).

3ème pilier : Efficacité de la ressource humaine

· Formation continue de la ressource humaine sur les outils de prévision de la demande énergétique.

· Préparation d'une ressource humaine compétitive par rapport à celle de concurrents potentiels.

· Encouragement et promotion de la ressource humaine.

1.2.4 Clientèle gaz :

Le groupe SONELGAZ distribue le gaz naturel qu'il achète à la SONATRACH, à ses différents clients à savoir :

- La Distribution Publique « DP » (Basse Pression) : elle représente les ménages et les artisans (boulangeries, restaurants,... etc.)

- Petites et moyennes industries (Moyenne Pression) : elles représentent les usines de production et de transformation tels que : les briqueteries, la cimenterie, ... etc.

- Grosses industries (Haute Pression) : elles représentent la production électrique, la production électrique en Algérie provient essentiellement du gaz naturel, on peut citer comme centrale électrique d'El Hamma.

1.2.5 Plan national gaz :

Le Gaz : une ressource à promouvoir¹

En trois décennies, la consommation industrielle et domestique de gaz a connu un essor appréciable grâce aux efforts de Sonelgaz qui a multiplié les actions de promotion de cette énergie.

Pour la période 1999 / 2015, un programme national gaz a été décidé par le gouvernement pour faire face à la croissance remarquable de la demande de gaz naturel enregistrée ces dernières années et concrétiser par la même occasion le modèle de consommation énergétique national affirmé dans la loi sur la maîtrise de l'énergie dont les options énergétiques ont trait, entre autres, à l'utilisation prioritaire et maximale des hydrocarbures gazeux (gaz naturel, gaz propane liquéfié) pour la couverture des usages thermiques finaux en raison de leur disponibilité et de leur qualité environnementale.

SONELGAZ fourni des efforts considérables pour améliorer le taux de pénétration en gaz naturel, afin de vulgariser l'accès à cette énergie dont l'Algérie dispose amplement. Les réalisations de la période 2000 / 2006 ont permis de hisser le taux de pénétration du gaz de 30% à 37%.

Sur la période 2000 / 2009, la consommation gaz (Distribution Publique) passera de 2 500 à 6 500 106 m3. La consommation gaz des clients industriels et des centrales de production passera de 8 600 à 13 700 106 m3.

Le nombre prévisionnel total de clients gaz passera d'environ 2,2 millions en 2006 à 4,5 millions en 2016, avec un taux d'accroissement annuel moyen de 7,47% et un taux de pénétration égal à 57% à l'horizon 2009.

Ces programmes rencontrent un énorme écho auprès des populations. Une très forte demande d'extension est enregistrée en permanence, imposant ainsi de fréquentes modifications de la consistance de ces programmes De même pour la clientèle industrielle qui, dans le sillage de la mise en oeuvre des réformes et de l'ouverture économique, exprime une demande de cette énergie de plus en plus importante.

¹ www.sonelgaz.dz

Chapitre 2 : Prévision par la méthode

traditionnelle,

lissage exponentiel et Box & Jenkins

Dans ce chapitre, on va présenter théoriquement l'essentiel de la méthode traditionnelle, la méthode de lissage exponentiel et la méthode de Box & Jenkins afin de pouvoir faire des prévisions.

2.1 Prévision par la méthode traditionnelle : 2.1.1 Etude de la série

2.1.1.1 Définition d'une série chronologique :

On appelle série chronologique (série temporelle ou encore chronique) une série statistique à deux variables ( , y ) avec t?i, i= {t1, t2, ..., tn} où la première composante du couple t est le

temps et la deuxième composante est une variable numérique y prenant ses valeurs aux instants t. Suivant la nature du problème étudié la chronique peut être journalière (cours d'une action en bourse), mensuelle (consommation mensuelle de gaz), trimestrielle (nombre trimestriel de chômeurs), annuelle (chiffre annuel des bénéfices des exportations)... etc.

L'étude des séries chronologiques est utile lorsque l'on cherche à analyser, comprendre ou encore prévoir un phénomène évoluant dans le temps. Le but est donc de tirer des conclusions à partir des séries observées.

2.1.1.2 Les composantes d'une série chronologique :

Dans un premier temps, l'examen graphique de la série étudiée permet de dégager, un certain nombre de composantes fondamentales de l'évolution de la grandeur étudiée.

Il faut alors analyser ces composantes, en les dissociant les unes des autres, c'est-à-dire en considérant une série comme résultant de la combinaison de différentes composantes.

La tendance ou « trend » notée ~ , censée décrire le mouvement de long terme, de fond ou encore structurel du phénomène. Ce mouvement est traditionnellement représenté par des formes analytiques simples : polynomiales, logarithmiques, exponentielles, cycliques, logistiques.

La composante cyclique notée C qui regroupe des variations à période moins précise autour de la tendance. Ces phases durent généralement plusieurs années, mais n'ont pas de durée fixe. Sans informations spécifiques, il est généralement très difficile de dissocier la tendance du cycle. Dans la plupart des travaux sur les séries temporelles la tendance regroupe aussi la composante cyclique.

La composante saisonnière ou variations saisonnières notées S sont des variations se reproduisant périodiquement à des moments bien déterminés et qui sont liées au rythme imposé par les variations météorologiques des saisons (production agricole, consommation de gaz, . . .), ou encore par des activités économiques et sociales (fêtes, vacances, solde, le ramadhan, etc.)

La composante résiduelle notée å . Elle rassemble tout ce que les autres composantes n'ont pu expliquer du phénomène observé. Elle contient donc de nombreuses fluctuations, en particuliers accidentelles, dont le caractère est exceptionnel et imprévisible, (catastrophes naturelles, grèves, guerres...). Comme par hypothèse ce type d'événement est censé être corrigé, le résidu présente en général une allure aléatoire plus ou moins stable autour de sa moyenne.

2.1.1.3 Schémas de décomposition d'une série chronologique :

La technique de décomposition d'une série chronologique, repose sur un modèle qui l'autorise. Ce modèle porte le nom de schéma de décomposition.

Il en existe essentiellement trois grands types :

Schéma additif :

Dans un modèle additif, on suppose que les 3 composantes : tendance, variations saisonnières et variations accidentelles sont indépendantes les unes des autres.

On considère que la série yt s'écrit comme la somme de ces 3 composantes :

y _t= ft + ^St + t

Graphiquement, l'amplitude des variations est constante autour de la tendance Schéma multiplicatif :

a) Première forme de modèle multiplicatif :

On suppose que les variations saisonnières dépendent de la tendance et on considère que yt s'écrit de la manière suivante :

y _t= ft × St + t

Graphiquement, l'amplitude des variations (saisonnières) varie.

b) Deuxième forme de modèle multiplicatif :

On suppose que les variations saisonnières et les variations accidentelles dépendent de la tendance et on considère que yt s'écrit de la manière suivante :

yt=ft ×St ×åt

Ce 2^ème modèle multiplicatif se ramène à un modèle additif en considérant la série ln(yt) :

ln yt = ln ft + ln St + ln Et

2.1.1.3.1 Principe de conservation des aires : Cas du modèle additif :

Le principe de conservation des aires se traduit par le fait que la somme des coefficients saisonniers ainsi que la somme des variations accidentelles, soit égale à 0 :

~ n

? Si = 0 , ?åt = 0

i= 1 t= 1

Cas du modèle multiplicatif :

Le principe de conservation des aires dans le cas multiplicatif se traduit par le fait que la

moyenne des coefficients saisonniers ainsi que le moyenne des variations accidentelles, soit

~ ~ ~ ~

? = 1 ,

~ ? = 1

E

3 ~

p = ~

i 1 ~ = ~

égale à 1 :

2.1.1.3.2 Procédure de choix d'un schéma de décomposition : a) La méthode de la bande :

La procédure de la bande consiste a partir de l'examen visuel du graphique de l'évolution de la série brute à relier, par une ligne brisée, toutes les valeurs « hautes » et toutes les valeurs « basses » de la chronique. Si les deux lignes sont parallèles, la décomposition de la chronique peut se faire selon un schéma additif ; dans le cas contraire le schéma multiplicatif semble plus adapté.

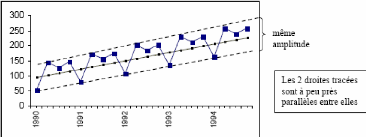
Figure 2.1 - Exemple de schéma additif

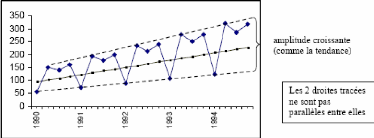
Figure 2.2- Exemple de schéma multiplicatif

b) Le test de Buys-Ballot :

On calcule, pour chacune des années, la moyenne (y ) et l'écart type (u ), puis on estime par MCO les paramètres á1 et á2 de l'équation u = a1y + a2 + E . Dans le cas, ou le paramètre á1 n'est pas significativement différent de 0 (test de Student) alors on accepte l'hypothèse d'un schéma additif ; dans le cas contraire, nous retenons un schéma multiplicatif.

2.1.2 Estimation des composantes de la série : 2.1.2.1 Estimation de la tendance :

2.1.2.1.1 Méthode des moindres carrés : Cas du modèle additif :

On utilise la méthode des moindres carrés pour ajuster la série chronologique Yt, avec

Yt = t + St . Le trend s'écrit t = at + b , la série sera donc ajustée par une droite d'expression :

Yt = at + b + S t

Le principe de la méthode des moindres carrés est de minimiser la quantité :

n

D=

? (Yt - (at+b)) ²

t= 1

a et b sont solutions des équations :

äD äD

= 0 et = 0.

äa äb

D'où :

n

tiYi-ntY

?

i

=

1

n

?

t2- nt 2 i

c0v(t,

>

)=

V(t)

et b = Y - at

i

=

1

avec :

i=1

1 ⁿ
Y = n ? Yi ,

1 n

t t

= ?

i

n i=1

Cas du modèle multiplicatif :

On a Yt = t ×St

Ce qui implique In Yt = In t + In St

Le calcul est ramené donc au calcul précédent. 2.1.2.1.2 Méthode des moyennes mobiles :

Le principe de cette méthode est de remplacer un certain nombre de données consécutives par leur moyenne arithmétique, mais on décale ce calcul de période en période, en réutilisant toutes les données du calcul précédent moins la première.

La moyenne mobile d'ordre p (p= 4 si données trimestrielles, p=12 si données mensuelles) relative à la date t est définie par :

Mp (t) = 1

P

? Yt+i

P i=1

a

Si p est impair (p= 2k+ 1) la moyenne mobile sera définie par :

Yt-k + _Yt-k+1 + + Yt+k

Mp (t)= = 2k + 1

Si p est pair (p= 2k) la moyenne mobile sera définie par :

Mp (t) =

Yt2k + - Yt+k

Ytk+1 + +

2

2 k

Remarque : À partir d'une série contenant n données, on perd (p-1) valeurs si p est impair et on perd p valeurs s'il est pair.

Définition des médianes mobiles :

La définition est analogue à celle des moyennes mobiles : on prend les mêmes valeurs de Yt , et on calcule la médiane au lieu de calculer la moyenne.

2.1.2.1.3 Avantages et inconvénients des méthodes d'estimation : Les moyennes mobiles :

· Les moyennes mobiles peuvent être influencées par des valeurs aberrantes.

Conséquence : Au lieu de calculer les moyennes mobiles, on peut choisir d'estimer ft à l'aide des médianes mobiles de même ordre.

· Perte de données : Si on dispose d'une série chronologique sur n années contenant p mois

chacune (np observations), alors on ne pourra calculer une estimation de la tendance que pour np - p + 1 ou np - p mois (selon la parité de p), soit une année de moins que la série.

· Malgré ces inconvénients, elles sont une bonne estimation.

· L'estimation par moyenne mobile donne une meilleure estimation que par les moindres

carrés, car cette méthode est plus générale, elle est utilisée lorsque l'équation de la tendance est inconnue, ft est proche des valeurs.

Les moindres carrés.

· L'estimation est moins bonne.

· Un ajustement correct n'est pas toujours possible.

L'avantage : facilité pour prévoir la tendance aux dates np + 1, np + 2. 2.1.2.2 Estimation des coefficients saisonniers :

Il existe deux méthodes d'estimation : la méthode pratique et la méthode analytique. Tout deux sont présentées ci-après :

Définition des coefficients saisonniers :

On sait que l'influence des variations saisonnières doit être neutre sur l'année et que ces variations ( St ) se répètent théoriquement à l'identique de période en période.

Dans toute série chronologique observée sur un cas réel, les variations saisonnières ne sont
jamais identiques. Donc, pour satisfaire aux exigences du modèle théorique, et pour pouvoir

étudier la série réelle, il faut estimer, à la place des St observées, des variations périodiques identiques chaque année(mois par mois, ou trimestre par trimestre) qu'on appelle coefficients saisonniers.

On les note S3 / j =1 à 12 pour des données mensuelles.

j=1 à 4 pours des données trimestrielles. 2.1.2.2.1 Méthode pratique :

La série yt est observée sur n année par période « p ». p = 12 mois (j=1, 2,..., 12) ou 4 trimestres (j= 1, 2, 3 ou 4). Les variations saisonnières St sont égales, par hypothèse du modèle additif à :

St = yt - t ou St = yt - _P(t)

On obtient donc n × 3 valeurs de St, qu'on peut écrire _S~3 . On retiendra 12 valeurs de S₃ (mois) ou 4 valeurs de S₃ (trimestres) comme coefficients saisonniers, en calculant, mois par mois, ou trimestre par trimestre, la moyenne arithmétique des St , sur l'ensemble des n années, on obtient :

1 ⁿ

S3=?Si3
ⁿ

i

=1

On peut remplacer le calcul de la moyenne par celui de la médiane de la série des Sij, pour éviter l'influence des valeurs aberrantes.

La somme sur l'année de ces coefficients saisonniers S₃ devrait en toute logique être égale à
0. En fait, bien souvent, les approximations des calculs conduisent à un résultat légèrement
différent. Dès lors, dans le cas où la somme des S₃ est différente de 0, on calcule un

coefficient correcteur « ñ » qui est la moyenne des S₃ sur l'année.

1 _v,

12 41 S3 ou ñ =

3=¹

1 _v,

4 LI S 3

3=¹

12

4

=

Et l'on retient en définitive, comme coefficient saisonnier corrigé la valeur :

S; =S3- ñ

Le principe théorique selon lequel la moyenne (ou la somme) des coefficients saisonniers est égale à zéro est respectée par les S. (coefficients saisonniers corrigés).

PP

? s; = 0 ou 1 ? s; = 0 .

3=1 P 3=1

Pour le modèle multiplicatif la moyenne des coefficients saisonniers doit être égale a 1.

Le calcul des coefficients saisonniers pour les modèles, additif et multiplicatif, est résumé comme suit :

Modèle additif Modèle multiplicatif

St = yt -St=ytlf

Si= moyenne ou médiane des St

P

Si ? Si? 0 ou S? 0 Si ? p ou S

i= 1 i= 1

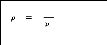
₁ ?P

S; = S - ñ S; = Si lñ

i

P P

? s=0 o ? s; = 1

=

1

P i=1

Figure 2.3-Calcul des coefficients saisonniers 2.1.2.2.2 Méthode analytique ¹:

L'estimation se fait par un calcul dérivé directement de la méthode des moindres carrés. Si les n années sont divisées en p périodes (1,2,..., j,...n), avec p = 12 mois ou p = 4

trimestres, et si l'on appelle _y.i la moyenne des n mois ou trimestres _(y.i =1 ~ ? yii ), on

P

~

obtient après calculs :

1 Bernard PY., Statistique descriptive, Nouvelle méthode pour bien apprendre et réussir. 4éme édition. Ed ECONOMICA, Paris, 1999.

Les p valeurs des coefficients saisonniers sont : S3 = y.3 -y -a[3-P +₂ 11 (j varie de 1 àp).

On peut, comme précédemment corriger ces S₃ en S; .

Cette valeur du « vecteur » S₃ , facilement calculable n'est valable en modèle additif que si le
trend est linéaire. On peut la trouver de la même manière en modèle multiplicatif sur un trend exponentiel (en passant par les logarithmes).

2.1.2.2.3 Série désaisonnalisée ou série CVS : Définition :

On appelle série désaisonnalisée ou série corrigée des variations saisonnières notée série CVS, la série chronologique yt à laquelle on a enlevé les variations saisonnières.

Dans le cas du modèle additif :

La série désaisonnalisée est : yt = yt - St ou encore yi; = ya3 - S3^' Dans le cas du modèle multiplicatif :

La série désaisonnalisée est : y; = yt ou encore ya = S'3

Intérêts :

- La particularité de la série CVS est que les données de y; sont directement comparables : on a enlevé l'effet des saisons et donc le caractère propre de chaque mois on peut par exemple comparer les données d'un mois de janvier et celle d'un mois de juillet.

- A partir de la série CVS, on peut réévaluer la tendance par ajustement ou lissage (moindres carrés ou moyennes mobiles sur y; ...), afin d'avoir une meilleure estimation de la tendance.

2.1.2.3 Estimation des variations accidentelles : Il suffit d'enlever à la série CVS l'influence du trend Pour un modèle additif : et = yt - j;

~

Pour un modèle multiplicatif :

yt

~

ft

åt =

2.1.3 Prévision : Série ajustée (y~t ):

Si l'on somme dans le modèle additif, ou si l'on multiplie, dans le modèle multiplicatif, les
deux composantes, trend et coefficient saisonniers, calculées on obtient la série ajustée, notée

y~t :

Modèle additif: ÿt = t + S.^' Modèle multiplicatif: ÿt = _t × S.'

La série ajustée t représente l'évolution qu'aurait subi le phénomène, si le mouvement saisonnier était parfaitement régulier d'année en année.

Les « p » coefficients saisonniers, identiques d'année en année, s'écrivent sous forme d'un vecteur lorsque l'on veut donner l'équation de t :

Exemple modèle additif par mois :

S ' S '

ût = at + b +

S.^'

S ' ~

La prévision de la chronique se ramène à poursuivre le calcul de la série ajustée pour les mois ou les trimestres qui suivent :

Ût+h = êt(t + h) + + S.; ~

Remarque :

- On fait des prévisions en supposant que la tendance va suivre la même évolution (linéaire,

exponentielle, polynomiale...), et que les variations saisonnières seront identiques.

On obtient ainsi une estimation de l'évolution de la grandeur observée, on ne peut pas tenir compte des variations accidentelles.

Intérêt :

· On peut faire des prévisions pour l'année qui suit la dernière année d'observation, afin de prévoir par exemple des investissements, la consommation de gaz naturel

· On peut faire des prévisions pour des années qui ont été observées, dans le but de comparer

les prévisions (faites à partir des années précédentes) et les données réelles. Cela permet de voir l'impact d'un événement (ex : campagne publicitaire, catastrophe naturelle, crise boursière...).

2.2 Prévision par la méthode de lissage exponentiel :

Le lissage exponentiel prend en compte les valeurs passées d'une série temporelle

afin de fournir une prévision. L'importance avec laquelle ces valeurs passées sont prises en compte décroît exponentiellement avec l'ancienneté de celles-ci par rapport à la valeur à prévoir.

Nous étudierons le lissage exponentiel simple employé pour des chroniques dépourvues d'une
tendance ou d'une saisonnalité, puis le lissage exponentiel double qui convient pour des séries
présentant une tendance, enfin le lissage de Holt-Winters, pour le cas ou la tendance et la

composante saisonnière sont juxtaposées soit de manière additive, soit de manière multiplicative.

2.2.1 Lissage exponentiel simple :

La prévision S_t+1fournie par la méthode de lissage exponentiel simple, est définie par :

St₊1 = Àyt + (1 - À)St

Où :

St₊1 : La prévision à l'instant (t+1).

yt : L'observation à l'instant (t).

St : La prévision à l'instant (t).

À : Constante de lissage comprise entre 0 et 1.

St₊1 = ÀE (1 - À)i yt-ii=o

2.2.1.1 Choix de la prévision initiale :

Une manière habituelle d'initialiser y~o (1) = S1 est de la choisir parmi les possibilités suivantes :

1)- Prendre S1 = y1 c'est surtout adéquat pour une série très fluctuante (cours de bourse, par exemple).

2)- Prendre pour S1 la moyenne de toutes les données, c'est surtout adéquat pour une série qui oscille autour d'une valeur constante, par exemple la vente d'un produit dont la demande est stable dans le temps.

3)- Prendre pour S1 la moyenne de quelques une des premières données. 2.2.1.2 Choix optimal de la constante de lissage :

La méthode la plus courante pour choisir la constante de lissage, consiste en les étapes suivantes :

1)- Choisir un des critère : MSE (carré moyen des erreurs), MAE (erreur absolue moyenne),...

2)- Choisir un ensemble de valeurs de À par exemple les valeurs de 0 à 1 par pas de 0,1 : (0, 0.1,...,0.9)

3)- Choisir la prévision initiale.

4)- Pour chaque valeur de À choisie, effectuer l'ensemble des calculs du lissage exponentiel.

5)- Choisir la valeur de À qui améliore le mieux le critère (par exemple qui fournit le plus petit MES).

2.2.1.3 Limitation de la méthode :

Parmi les limitations de cette méthode, on peut citer :

- Qu'elle ne peut être appliquée à des variations en forme de rampe (tendance ou trend), ni à des variations en échelon.

- Qu'il n'y a pas de règle idéale pour déterminer la pondération appropriée, il s'agit de choisir une valeur de A . La plupart du temps, on procède expérimentalement, en essayant deux ou trois valeurs différentes pour voir quelle est la plus appropriée.

2.2.2 Lissage exponentiel double : 2.2.2.1 Présentation :

Le lissage exponentiel double (Brown [1959]) est une méthode plus générale que le

lissage simple et particulièrement adaptée aux séries chronologiques présentant une tendance. Nous pouvons résumer les étapes du lissage exponentiel double comme suit :

On pose ~yt (h) = St (h)

~y_t(h) = [2 ,S; - s;]+ h_{1 -}^A _A (St-St ) ... (2.1)

Où :

A : constante de lissage exponentiel.

h : décalage de la prévision dans le futur, exprimé en nombre de périodes. St = A yt + (1 -A) S;-1 et St = A St + (1- A) St^'l1

St = A?(1- A) iyt-i et s;=A².?(i+1)(1-A) iyt-i

i=

~

i

=

~

On pose:

at = 2 _S;-1 - St^'' et bt = 1 A _A(St-1 - s;) -

L'équation (2.1) devient:

~yt (h) = at + h bt

2.2.2.2 Propriétés de la méthode:

- Parmi les avantages du lissage exponentiel double c'est de traiter des séries présentant une tendance.

- La méthode de choix optimal de A est la même que pour le lissage exponentiel simple.

- Le problème du choix des prévisions initiales, se pose avec autant d'acuité que pour le lissage simple. On peut, par exemple, choisir les valeurs initiales comme suit :

a1=y1, b1 = 0.

2.2.3 Lissage exponentiel de Holt-Winters :

La méthode de Holt-Winters est basée sur trois équations, dont chacune à pour objet de lisser une des trois composantes de le série à savoir : l'aléa, la tendance et le saisonnier.

Elle est comparable en cela au lissage exponentiel double, qui ajuste la tendance et lisse l'aléa, mais en plus elle introduit une composante St pour traiter la saisonnalité.

Dans la présente méthode, il y'a deux façons de combiner la tendance linéaire et la composante saisonnière :

1- Par multiplication, et c'est le cas du modèle de Holt-Winters multiplicatif.

2- Par addition, et c'est le cas du modèle de Holt-Winters additif.

Le modèle multiplicatif :

La composante saisonnière est introduite de manière multiplicative, la chronique s'écrit dans ce cas :

yt = (at + btt)St + Et .

Trois lissages distincts sont effectués :

- le lissage de la moyenne a avec un coefficient de lissage a, avec a ? [0 ; 1]. - le lissage de la tendance b avec un coefficient de lissage 13, avec 13 ? [0 ; 1]. - le lissage de la saisonnalité S avec un coefficient de lissage, y avec y ? [0 ; 1].

Formulation :

Lissage de la moyenne : at = a(yt _/St-p) + (1 - a)(at-1 + bt-1)

Lissage de la tendance : bt = 0(at - at-1) + (1 - 0)bt-1 Lissage de la saisonnalité : St = 7(yt /at) + (1 - 7)St-p

Prévision à un horizon de h périodes :

y^~t+h = (a_t + _hbt)St-p+h si 1< h < p

y^~t+h = (at + _hbt)St-4+h+h si p+ 1< h < 2p

avec:

at = moyenne lissée de la série en t.

yt = valeur observée de la série en t.

St = coefficient saisonnier en t.

p = périodicité des données (p=12 en mensuel, p= 4 en trimestriel). bt = tendance estimée en t.

Dans certaines écritures du modèle les coefficients saisonniers vérifient la propriété :

p

?Sa = p selon le principe de la conservation des aires, si ce n'est pas le cas, ces coefficients

i= 1

sont corrigés (S~^') de la même façon que dans la méthode traditionnelle.

Initialisation :

Initialisation de la saisonnalité : Les coefficients saisonniers pour la première année sont estimés par la valeur observée en t (yt) divisée par la moyenne y des p premières observations de la première année.

St yt pour t = 1,..., p

y

Initialisation de la moyenne lissée : a_p = y (y moyenne de la première année) Initialisation de la tendance : b_p = 0

Le modèle additif :¹

La composante saisonnière est introduite de manière additive, la chronique s'écrit dans

ce cas : yt = (at + btt) + St +fit

Formulation :

Lissage de la moyenne : at = a(yt - St-p) + (1 - a)( at- 1 + bt-1) Lissage de la tendance : bt = 0(at - at-1) + (1 - 0)bt-1

Lissage de la saisonnalité : St = 7(yt - at) + (1 - 7)St-p Prévision à un horizon de h périodes :

y^~t+h = (at+hbt)+St-p+h si 1< h = p

y^~t+h = (at+hbt)+St-2p+h si p+ 1< h < 2p

p

0

=

Si

?

1

i=

Dans ce cas le principe de la conservation des aires implique :

Initialisation :

Initialisation de la saisonnalité : St = yt - y (y moyenne de la première année), t = 1,..., p Initialisation de la moyenne lissée : a_p = y

Initialisation de la tendance : b_p = 0

1 Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004, P65

Choix des paramètres:

Les paramètres a, 13 et y sont optimisés comme pour les méthodes non saisonnières en minimisant la somme des carrés des erreurs prévisionnelles entre la valeur observée de la chronique et les valeurs prévues.

2.3 Prévision par la méthode de Box & Jenkins :

2.3.1 Concepts des séries temporelles

2.3.1.1 Processus stochastique

Un processus aléatoire est une application X qui associe au couple (w, t) la quantité yt (ù) . Elle est telle que ?t ? T fixé,yt est une variable aléatoire définie sur un espace probabilisé. Une processus stochastique est donc une famille de variables aléatoires indicées par t noté

(yt,t ? T) ou encore yt .

Dans la suite de l'exposé, l'espace des indices T est le temps, t est alors l'instant d'observation de la variable aléatoire y sur l'individu w . Si T est l'ensemble des réels, le processus est dit continu. Si T = Z ou N ou N* ou N* borné, le processus est dit discret.

On suppose, par la suite que la série temporelle notée yt, t ? Z (soit une succession d'observations régulièrement espacées dans le temps d'une valeur économique) est une réalisation d'un processus stochastique discret univarié¹.

2.3.1.2 Processus aléatoires stationnaires :

On dira qu'une série chronologique est stationnaire si elle est la réalisation d'un processus stationnaire, ceci implique que la série ne comporte pas de tendance ni de saisonnalité. Processus stationnaire au sens strict (stationnarité forte) :

On dit que ( yt ) est strictement (ou fortement) stationnaire si pour toute suite finie d'instant ti,t2,...,tk élément de Z et tout entier r ? Z, les lois jointes de _(yti ,...,y_tk ) et de _{(y4+r,...,ytk+r)} sont les mêmes (lois jointes invariantes par translation dans le

temps)².

~ y..ditk ) (y₄,...,yt_k) = ,y )(yti , . . . , ytk+r) k

Processus stationnaire au second ordre (stationnarité faible) :

Un processus aléatoire yt,t ? T est dit stationnaire au second ordre, si les moments d'ordre1 (moyenne ou espérance mathématique) et d'ordre 2 (variance et autocovariance) sont

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition 2004, P73.

² Master M2-AE2 PRO, Econométrie Bancaire et Financière, Analyse des séries temporelles, Mohamed Boutahar, octobre 2006

indépendants de t :

(i) E(e)? 8 ? t? Z.

(ii) E ( yt ) = m indépendante de t, ? t? Z.

(iii) cov (y_t , y_t+h) = 7(h) indépendante de t, ? t? Z.

Processus bruit blanc (White Noise) :

Un bruit blanc est une suite de variables aléatoires(E_t ,t ? Z) non corrélées et d'espérance et de

variance constante.

Un bruit blanc est donc tel que :

E(Et) = m ? t? Z.

V(E_t)=a²? t? Z. cov(Et ,Et+h) = 7(h) = 0 ? t? Z.

Si l'espérance m est nulle, on dit que le bruit blanc est centré.

Remarque : Dans la suite lorsqu'on parlera de stationnarité, cela sous-entendra une stationnarité au second ordre.

2.3.1.2.1 Caractéristiques d'un processus aléatoire stationnaire : Fonction d'autocovariance :

La fonction d'autocovariance mesure la covariance de la série avec elle-même décalée de h périodes. La fonction d'autocovariance d'un processus stochastique est définie par :

7(h) = cov(yt, yt+h) = E(yt - m)(yt+h - m) ? t? Z.

n-h

L'autocovariance estimée (empirique) est donnée par :

1

.

t

1

'5^,(h)= ?(yt - o(yt+h - y) n

=

1ⁿ

avec y y

= ? ~

n ~ = 1

Propriétés :

· V(yt) = 7(0) ? t? Z.

· 7(h) = 7(0) ? h ? Z.

· 7(h) = 7(-h) ? h ?

Fonction d'autocorrélation ACF (Auto Correlation Function) :

On appelle fonction d'autocorrélation simple notée p(h), la fonction qui mesure la corrélation de la série avec elle-même décalée de h périodes. Cette fonction est définie par :

p(h)=o c v(yt, yt+h) cov(yt , _yt+h ) 7(h)

V(y_t) V(yt+h) V(yt) 7(0)

? h ? Z.

L'autocorrélation empirique est donnée par :

n-h

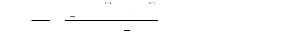
(yt -y)(yt+h - y)

?

1

=

t

=

n

2

(yt -y)

?

7 ~( )

h

b(h)=

'5(⁰)

? h ? Z.

t

=

1

Propriétés :

·	p(0) = 1		? h ? Z.	·
p(h) = p(0)	? h ? Z		·
p(h) = p(-h)	? h ? Z.

Dans le cas d'une série stationnaire, la fonction d'autocorrelation décroît exponentiellement vers zéro. La décroissance est davantage linéaire pour les séries non stationnaires rencontrées en pratique.

Fonction d'autocorrélation partielle PACF (Partiel Auto Correlation Function) : Régression affine :

Soit (yt_,t ? Z) un processus aléatoire stationnaire, on appelle régression affine de yt sur {y₈,8 = t - 1} , la variable y: vérifiant :

t 1

yt =

* a0+?a^,y t-, ou a0,a1,... ? R

,

=

1

On appelle fonction d'autocorrélation partielle les corrélations entre les différents couples(yt,yt₊h) , l'influence des variables _yt+h-, pour (0 < i < h) ayant été retirée. Elle est mesurée par le coefficient de corrélation partiel noté r (h) vérifiant :

* * , * * ,

r(h) =

cov(y_t - yt,yt-h - yt-h) cav(Yt - Yt ,Yt-h - Yt-h)

= ? h ? Z .

V(yV^,,, t Yt lv lyt-h-yt-h)

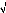
V(yt - yt )

Où y: régression affine de yt sur { yt-i, yt-2,...yt-h } .

y:-h régression affine de yt -h sur{yt-i, yt-2,...yt-h+i }.

Propriété :

Sous l'hypothèse de la stationnarité r(h) = ah, ou ah est le coefficient de _yt-h dans la régression de yt sur { yt _-i, yt _-2 ,...yt - h} .

Innovation d'un processus stationnaire :

Soit (yt, t ? z) un processus stationnaire.

On appelle innovation du processus (yt, t ? Z) à la date t la variable :

Et = yt - yt

~

Où y: est la régression affine de yt sur ys , S< t-1

E((y_t - yt )ys ) = ° ? S< t-1

~

Propriété :

La suite des innovations (Et, t ? Z) constitue un bruit blanc centré.

2.3.1.3 Les opérateurs de Box & Jenkins1 : Opérateur retard (B) :

L'opérateur B est défini comme agissant sur la série. A un instant t on fait correspondre la valeurs de la série à l'instant t-1, on définit ainsi une nouvelle série B y comme :

B yt = yt-i

On peut appliquer plusieurs fois cet opérateur, on définit ainsi de nouvelles séries :

B²y_t = B(By_t) = Byt-i = yt-2

Bm yt = yt-m

Cet opérateur est linéaire ; il est inversible et son inverse B^-i = F est défini par F yt = yt+i ; F est appelé opérateur avance.

Propriétés de l'opérateur retard :

- Ba = a , l'opérateur d'une constante a est une constante.

_-

--^°yt = yt .

- (Bⁱ + Bⁱ)yt = Bⁱyt+Bⁱyt = yt-t+yt-i . - Bⁱ(Bⁱyt) = B^i+jyt = yt-t-i

L'opérateur de différenciation ? :

L'opérateur ? (prononcé « nabla ») est défini par :

¹. Bernard Rapacchi, centre interuniversitaire de Grenoble 1993

?yt = yt - yt-1 .

Nous entrons maintenant dans des considérations de notation. En effet, par écriture purement formelle on peut écrire :

? yt = y_t - Byt = (1- B)y_t .

On peut écrire ? sous la forme d'un polynôme en B avec :

? = 1 - B

Ce mode d'écriture sous forme de polynôme en B est en fait très pratique mais totalement
formel. Il ne faut pas oublier que, quand on écrit (1- B)y , on définit à partir d'une série y une

nouvelle série qui à t, fait correspondre la différence entre la valeur de la série observée à l'instant t et celle observée à l'instant t-1.

L'opérateur de désaisonnalisation ?s : L'opérateur ?s est défini par :

?s = yt - yt-s .

En d'autres termes :

?s = (1 - B^s).

2.3.1.3.1 Les effets des opérateurs de Box & Jenkins : L'opérateur ? :

· Permet d'éliminer la tendance de la série.

· Peut être répété plusieurs fois, si la tendance n'est pas linéaire. Par exemple :

?²> = (1 - Br yt = (1 - 2B + B²)yt

· Permet d'éliminer une tendance quadratique. Le nombre de fois où on applique ? est appelé ordre de différentiation.

L'opérateur ?s :

· Permet d'éliminer la saisonnalité de période S.

· On peut également l'appliquer plusieurs fois :

?s = ?s(yt - yt-s)
·

Le nombre de fois où on applique ?s est appelé ordre de désaisonnalisation.

2.3.2 Les processus ARMA :

Il est possible de définir la classe des processus ARMA à partir du théorème de décomposition des processus de Wold.

2.3.2.1 Le théorème de décomposition de Wald :

Soit le processus centré réel ou complexe Zt stationnaire et de variance finie. Il existe trois processus Tt, Xt, Et , qui vérifient les propriétés suivantes :

Zt = Tt + Xt

Où Tt et Xt sont deux processus indépendants.

Le processus Tt est dit processus singulier (ou encore processus déterminable), Il s'agit

d'une composante dont chaque valeur peut se calculer à partir d'une combinaison linéaire finie ou infinie de ses valeurs passées. C'est donc un processus dont nous pouvons déterminer exactement la prévision. Par opposition au processus précédent, Xt porte le nom de processus indéterminable.

Et est un bruit blanc centré, E (Et) = 0

+8

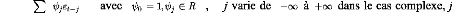
Xt =

? ei,-j avec eo =1,ei ? R , j varie de -8 à +8 dans le cas complexe, j

~ = { o

8

+8

varie de 0 à +8 dans le cas réel et ? e 2 ~ +8

~ = { o

8

2.3.2.2 Processus AutoRégressif d'ordre p : AR (p)

Définition :

Un modèle autorégressif est un modèle expliquant une variable par son passé, et éventuellement par d'autres variables. Un processus (X_t,t ? Z) est dit processus autorégressif d'ordre p, noté AR (p) s'il s'écrit sous la forme :

Xt = 01Xt-1 + _02Xt-2 +
·
·
· + 0pXt- _p + E t

X_t - 01Xt-1 - 02Xt-2 -
·
·
· - 0 _pXt -_p = E t
(1 01B 02B²
·
·
· pBpXt = EtÖ _p(B) Xt = Et

Où 01,02,
·
·
·,0_p ? R,0_p ?o .

(Et , t ? Z) est un bruit centré de variance 0^-2 .

Ö_p (B) polynôme caractéristique du processus(Xt,t ? Z).

Condition de stationnarité et d'inversibilité :

Un processus AR d'ordre p est stationnaire, si toutes les racines du polynôme caractéristique Ö _p(B) sont de module différent de 1 (les racines sont à l'extérieur du cercle unitaire).

Si toutes les racines du polynôme caractéristique sont de module supérieur à 1, alors le processus est inversible et (E_t,t ? Z) est l'innovation du processus (E(EtXt-h ) = o ?h = 1).

La fonction d'autocorrélation :

On a : -y(h) = E(XtXt-h) h »- 0 .

= ERO1Xt-1 + ... + OpXt-p + Et)Xt-h] h >- 0 .

= O1E(Xt-1Xt-h) + ... + _{OpE(Xt-pXt-h)} + _E(EtXt-h) h >- 0.

= O1-y(h -1) + ... + O_p-y(h - p) h .- 0. .... (2.2)

En divisant (2.2) par -y(0) , on obtient la fonction d'autocorrélation

p(h) = O1p(h -1) + ... + O_pp(h - p) h .- 0

D'autre part on a :

p(1) = O1 + O2p(1) + ... + O_p p(p - 1)

p(2) = O1p(1) + O2 + ... + Op p(p - 2)

:.

:

p(p) = O1p(p -1) + O2p(p - 2) + ... + O_p

En réécrivons ce système sous forme matricielle nous obtenons le système d'équations de Yule-Walker :

? ? ?

?p(1) 1 p(1) p(p - 1)O1

? ? ? ?

? ? ?

? _?p(2) p(1) 1 p(p - 2) O2

? ? ?

? ? ?

? ?

? ? ? ?

? ? ?

= ??

? ? ? ?

? ? ?

? ? ? ?

? ?

?

? ?

? ? ?

? ? ? ? ?

p(p)p(p-1)p(p-2)1O_p ? ?? ?

?

La fonction d'autocorrélation partielle :

Le problème lorsque l'on adopte une spécification autorégressive est de déterminer l'ordre du processus autorégressif, pour cela on va se référer à la fonction d'autocorrélation partielle :

- Le dernier coefficient O_p d'un AR (p) est égal à r(p) le coefficient d'autocorrélation partiel de même rang.

- La PACF d'un AR (p) à ses p premières valeurs différentes de 0 et les autres sont nulles.

Donc on reconnaît qu'une série suit un processus AR (p), si sa PACF s'annule à partir d'un décalage p.

2.3.2.3 Processus Moyenne Mobile (Moving Average) d'ordre q : MA (q) Définition :

Un processus (xt, t ? Z) satisfait une représentation Moyenne Mobile d'ordre q notée MA (q), s'il vérifie l'équation suivante :

x_t = E_t - B1Et-1 - B2Et-2 - ... - BqEt-q .

x_t = E_t - B1BEt - B2B² E_t - ... - B IP

q E_t .

xt = (1 - B1B - B2B² - ... - B_qB^q)Et .
x_t = È_q(B)E_t.

Où B1,B2,...,B_q ? R B_q ? 0 .

(E_t ,t ? Z) est un bruit centré de variance 0-² .

È _q(B) polynôme caractéristique du processus (x_t, t ? Z). Condition de stationnarité et d'inversibilité :

Un processus moyenne mobile est stationnaire par définition, car c'est une combinaison linéaire finie de processus stationnaire (E_t ,t ? Z).

Si toutes les racines du polynôme caractéristique sont de module supérieur à 1, alors le processus est inversible.

La fonction d'autocorrélation :

Si les conditions d'inversibilité sont respectées, la fonction d'autocovariance 7(h) d'un MA (q) s'écrit :

(1+++...+)0-² h = 0

1 2 q

7(h) = (-Bh + _B1Bh+1 + ... + Bq-hBq)⁰-² h = 1,..., q

0

h ? q

En divisant la fonction d'autocovariance par la variance on obtient la fonction

d'autocorrélation partielle :

q

{(-Bh + B1Bh+1 q + ... + Bq-hBq)

h = 1,...,

P

7(0) 0

(h) = ^7(h) = ⁽¹+ ^q +...+ Bq 2)

h ? q

Donc on reconnaît qu'une série suit un processus MA (q), si sa ACF s'annule à partir d'un décalage q.

2.3.2.4 Processus mixtes AutoRégressif Moyenne Mobile d'ordre p et q : ARMA (p, q) Définition

Un processus ARMA (p, q) résulte d'une combinaison d'un modèle AR (p) et d'un modèle MA (q).

Un processus (X1, 1 ? Z) satisfait une représentation ARMA (p, q), s'il vérifie l'équation suivante :

X 1 - ö X 1 - - ö X 1 -- - ö pX1-p = å 1 - è å 1 -- è å 1 -- ~~~ - è _q å 1 - q

~~~ 1 1 ~ ~

1 1 ~ ~

(1 ~~~ ) (1 1 ~ ~~~ )

- ö B - ö B - - ö B X = - è B - è B - - è _q B å 1

~ " ~ q

1 ~ J, 1

Ö ~ ( B ) X 1 = Èq(B)å 1

Où ö1,ö~,~~~,ö ~ ? R ö_~ ? O

è ₁ , è ~ ,~~~, è q ? R è_q ? O

(å ₁ , 1 ? Z) est un bruit centré de variance ²

ó .

Ö ~ (B) polynôme caractéristique du processus autorégressif.

È_q(B) polynôme caractéristique du processus moyenne mobile.

Condition de stationnarité et d'inversibilité :

Si toutes les racines du polynôme Ö ~ (B) sont de module supérieur à 1 et toutes les racines du polynôme È _q (B) sont de module supérieur à 1 alors le processus est stationnaire et inversible et (å ₁ , 1 ? Z) est son innovation.

Synthèse :

L'intérêt de l'étude des fonctions d'autocorrélations et d'autocorrélations partielle estimées et de leur représentation sous forme graphique est de pouvoir associer à une série observée un modèle théorique ARMA (p, q). Le tableau suivant propose un récapitulatif sur les formes des fonctions d'autocorrélations et d'autocorrélations partielle théoriques des processus AR (p), MA (q), ARMA (p, q).

Tableau (2.1) 1 : Résumé des propriétés des fonctions d'autocorrélation et d'autocorrélation
partielle

Processus	(ACF)	(PACF)
AR (p) : öp (B)X t = å t	Décroissance exponentielle et/ou sinusoïdale.	Pics significatifs pour les p premières retards, les autres coefficients sont nuls pour des retards >p.
MA (q) : X t = èq(B)åt	Pics significatifs pour les q premiers retard, les autres coefficients sont nuls pour des retards >q.	Décroissance exponentielle et/ou sinusoïdale.
ARMA (p, q) : ö p ( B ) X t = èq(B)å t	Décroissance exponentielle ou sinusoïdale amortie tronquée après (q-p) retards.	Décroissance exponentielle ou sinusoïdale amortie tronquée après (p-q) retards.

2.3.3 Les processus aléatoires non stationnaires :

Les processus stochastiques non stationnaires sont caractérisés par des propriétés stochastiques qui évoluent en fonction du temps.

On distingue deux types de processus stochastiques non stationnaires : une non stationnarité de nature déterministe (TS) et une non stationnarité de nature stochastique (DS)

2.3.3.1 Description des processus TS et DS : Processus TS :

Définition :

Un processus (Xt ,t ? Z) présente une non stationnarité de type déterministe TS (Trend Stationnary), s'il peut se décomposer en une somme de deux fonctions : X t = ft + å t

Tel que : åt est un processus stationnaire de type ARMA. Et ft : est une fonction polynomiale du temps.

¹REGIS BOURBOUNNAIS, MICHEL TERRAZA, Analyse des séries temporelles en économie, édition « PUF » juin 1998, page 192.

Le processus TS le plus simple et le plus utilisé en économie est représenté par une fonction polynomiale de degré 1, il s'écrit :

xt = ao + a1t + Et .

Où ao , a1 ? ]R

Et bruit blanc de moyenne nulle et de variance u² . Les caractéristiques de ce processus sont :

E(xt) = ao + a1t .

V(xt) = u2 .

cv(xt,xt-h) = o ?h ? o.

La non stationnarité de ce processus est dû au fait que son espérance dépend du temps.

La méthode pour stationnariser un processus TS est d'estimer les coefficients ao, a1 par MCO (Moindre Carrés Ordinaires) et de retrancher de la valeur de xt en t la valeur estimée de sa moyenne a~o + a~1t .

Processus DS :

DS sans dérive :

Soit le processus DS sans dérive (AR(1)) :

xt = xt - 1 + Et.
(1- B)xt = E_t .

La racine du polynôme caractéristique (1 - B) est égale à 1. On dit que le processus xt a une racine unité, il est donc non stationnaire.

Ce processus DS sans dérive peut se réécrire sous la forme :

xt = xt- 1 + Et = xt-2 + Et- 1 + Et = ~~~
= xt-h + _Et-h + ~~~ + Et .

t

= o x

+ .

1

=

~

Les propriétés d'un tel processus :

E(xt) = xo .

t

V(x_t) = E(x_t - E(x_t ))² = E(? Ei)² = tu 2 .

1

=

~

Un processus DS sans dérive est un processus stationnaire en moyenne et non stationnaire en variance.

DS avec dérive :

Considérons un processus DS avec dérive :

t

.

X_t Xt-1 +E_t +Xo +?Ei

1

=

i

Les propriétés sont les suivantes :

E(Xt) = t/, + Xo .

v(Xt) = t0-.

2

Un processus DS avec dérive est un processus non stationnaire en moyenne et en variance. Ces moments évoluent en fonction du temps t.

Un processus DS est un processus que l'on peut stationnariser par l'application du filtre aux différences :

Xt = Xt-1 + Et . (Xt - Xt-1) = Et . ? Xt = Et .

2.3.3.2 Processus AutoRégressif Moyenne Mobile Intégré d'ordre (p, d, q) :

ARIMA (p, d, q)

Définition 1 :

Un processus (Xt,t ? Z) est dit processus ARIMA d'ordre (p, d, q), s'il satisfait l'équation suivante :

Ö_p(B)(1- B)^d Xt = È_q(B)Et ... (2.3) Ö

p(B)? ^d X_t = È_q(B)E_t

Ou les racines des polynômes Ö _p (B) et È_q (B) sont de module supérieur à 1 et (Et, t ? Z) est

un bruit blanc centré de variance 0^-2 .

Le processus (Xt,t ? Z) n'est pas stationnaire, puisqu'il est stationnarisé en lui appliquant l'opérateur de différenciation.

En posant Y = (1- B)^d Xt

(2.3) devient Ö _p(B)Yt = È_q(B)E_t, (Y_t,t ? Z) est un processus ARMA (p, q) stationnaire.

Définition 2 :

Un processus (xt,t E Z) ARIMA (p, d, q), est un processus non stationnaire dont la différentiation d'ordre d : Yt = (1- B)^d x_t est un processus ARMA (p, q) stationnaire et inversible.

2.3.3.3 Processus Saisonnier AutoRégressif Moyenne Mobile Intégré d'ordre

(P,d,q)^* (¹³,D,Q)s : SARIMA(P,d,q)^* (1,D,Q)s

Une série xt suit un processus SARIMA (Seasonnal Autoregressive Integrated Moving Average) d'ordre(p, d, q) * (P, D, Q)s , si cette série a une saisonnalité de période S et qu'on peut écrire :1

(D _p(B)(D p (B^s) (1- B)^d (1- _Bs )D x_{1 1} = eq(B)eQ(Bs ^)åt

Où :

d : différence.

S : l'ordre de la saisonnalité ( S=12 données mensuelles, S=4 données trimestrielles). D : différence saisonnière.

(D _~(B) : polynôme autorégressif d'ordre p.

(Dp(B^s) : polynôme autorégressif saisonnier d'ordre P.

e_q(B) : polynôme moyenne mobile d'ordre q.

eQ(B^s) : polynôme moyenne mobile saisonnier d'ordre ^Q.(å_t,t E Z) e¹ st un bruit centré de variance ó².

2.3.3.4 Etude de la non stationnarité d'une série chronologique :

2.3.3.4.1 Test de tendance et de saisonnalité par la méthode des variances :

Cette méthode est basée sur le test de Fisher, on a recours à ce test pour détecter l'existence d'une éventuelle saisonnalité et/ou une tendance.

Le tableau ci-dessous résume cette méthode

1 Bernard Rapacchi, centre interuniversitaire de Grenoble 1993

Tableau 2.2- Analyse de la variance pour détecter une saisonnalité

et/ou une tendance¹

Somme des carrés	Degré de liberté	Désignation	Variance
SP=ND.i -x)^2 i	p-1	Variance Période _ P	=
			P p -1
SA=PE:i. -.)^2 i	N-1	Variance Année	V= SA
			A N --1
SR =Mxii^-x -x.i +X.)2 i i	(p-1) (N-1)	Variance Résidu	SR V R =
			(N - 1)(P - 1)
ST =??gi -x..)^2 i j	N p-1	Variance Totale	ST V
			T = N * P -1

Où :

N : le nombre d'années.

p : le nombres d'observations (la périodicité) dans l'année (trimestre p = 4, mois p = 12).

_v

= 1 N moyenne de la période j.

i=1

1 ^P

i. = ? xij moyenne de l'année i.

P i=1

N P

. .

=? ? xi, moyenne générale de la chronique sur les N*p observations.

i= 1 j=1

N * P

St = SA + SP + R (année) (Période) (résidus)

.

A partir du tableau (2.2) nous pouvons construire les tests d'hypothèses. Test de saisonnalité :

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004, P13

I	H0 : pas de saisonnalité H1 : existance d'une saisonnalité
Calcul du Fisher empirique : Fe^, = V P VR		que l'on compare au Fisher lu dans la table Fv^a1, v 2 à

v1= p-1 et v2 = (N-1) (p-1) degrés de liberté.

Si Fe, ? F(^c;,--1er --1)(P --1)) , alors on rejette l'hypothèse H0, la série est donc saisonnière.

Test de tendance :

I

H0 : pas de tendance.

H1 : existance d'une tendance.

Calcul du Fisher empirique : Fe^, = VA VR

que l'on compare au Fisher lu dans la table F^av~, v 2 à

v3= N-1 et v2 = (N-1) (p-1) degrés de liberté.

Si Fe, ? F(^aN--1,(N --1)(P --1)) , alors on rejette l'hypothèse H0, la série est don affectée d'une tendance.

2.3.3.4.2 Tests de racine unitaire :

Les structures DS et TS jouent un rôle très important dans le traitement statistique d'une chronique. Comment choisir entre l'une ou l'autre des structures ? Les tests de racine unitaire tentent de répondre à cette question.

2.3.3.4.2.1 Les tests de Dickey-Fuller simples :(DF)

Les tests proposés par DICKEY & FULLER (1969) ont pour but de vérifier la stationnarité de la série étudiée. Ils permettent de déceler le type de non stationnarité de la série.

L'application du test se fait en estimant par la méthode des moindres carrés ordinaires MCO trois modèle suivant que le processus qui représente la série xt contient ou non une constante et une tendance. Les modèles de bases sont :

Modèle [1] : (1 -- o1B)x_t = Et modèle autorégressif d'ordre 1 : AR (1). Modèle [2] : (1 -- O1B)(xt -- g ) = Et modèle AR (1) avec constante. Modèle [3] : (1 -- 01B)(xt -- a -- ,fit) = Et modèle AR (1) avec tendance.

Où (Et, t E Z) est un bruit centré de variance o^-2 . g, a, 0 sont des constantes.

Les hypothèses du test sont :

{

Ho : 101 = 1 H1: 101 ?1

- Si dans l'un des trois modèles l'hypothèse nulle est vérifiée, le processus est alors non stationnaire.

- Si dans les trois modèles en même temps, l'hypothèse nulle est vérifiée, le processus est donc non stationnaire. (la non stationnarité est de nature (stochastique)).

- Si dans le modèle [3], on accepte l'hypothèse H₁: ö -<1, et si le coefficient b est

significativement différent de zéro : alors le processus est un processus TS : on peut le rendre stationnaire en calculant les résidus par rapport à la tendance estimée par les moindres carrés ordinaires.

Pour des raisons statistiques DICKEY et FULLER ont choisi de tester la valeur ( - 1)

au lieu de 10^~1 , on obtient alors les modèles suivants :

Modèle [1] : ?.xt = p.xt-1 + Et b = (1-1)

Modèle [2] : ?X_t = ñàXt-1 + C + å_t C : constante.

Modèle [3] : ?X_t = ñàXt-1 + C + bt + å_t bt : tendance

Dans ce cas les hypothèses du test sont :

I

Ho
H1

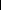
: ;9' = o :p ? o

DCKEY et FULLER ont tabulé les valeurs critiques pour chaque modèle et pour des échantillons de tailles différentes que l'on compare avec les différentes valeurs des t-statistiques obtenues par l'estimation des coefficients (les valeurs calculées par le logiciel « EVIEWS »).

On accepte H0 lorsque la valeur de t calculée est supérieure à la valeur tabulée, le processus n'est donc pas stationnaire.

2.3.3.4.2.2 Les tests de Dickey-Fuller Augmentés :( ADF) 1

1 .

. Reps Bourbonnais : Econométrie Edition DUNOD, 2000 , P232.

Dans ce test DF simple, on a supposé que Et un bruit blanc or il n'y a aucune raison pour que l'erreur soit non corrélée. Pour cette raison, Dickey et Fuller ont mis au point un nouveau test qui prend en considération cette hypothèse. Ils lui ont attribué le nom de test de Dickey - Fuller augmenté.

Ce test est fondé, sous l'hypothèse alternative 0i - i sur l'estimation par les MCO des trois

modèles suivants :

Modèle [4] : Vx_t = px" - i t i i

~

+ Et

.

i= 2

Modèle [5] : Vx_t = pXt-i - ?0i?xt-i+i

i=2

~

Modèle [6] : vx_t = pXt-i - ?0i?xt-i+i +C + Et .

i= 2

La valeur de p peut être déterminée selon les critères de Akaike ou Schwarz, ou encore en partant d'une valeur suffisamment importante de p, on estime un modèle à p-1 retards, puis à p-2 retards jusqu'à ce que le coefficient du ^piéme retard soit significatif (si p=0 on utilisera dans ce cas les tests DF)

Une Stratégie de Tests :

Nous allons à présent proposer une stratégie de tests de Dickey Fuller permettant de tester la non stationnarité conditionnellement à la spécification du modèle utilisé. On considère les trois modèles définis comme suit :

Modèle [1] : ?xt = pxt-i+Etp = (0i -i)

Modèle [2] : ?xt = pxt-i + C + Et

Modèle [3] : ?x_t = px" + C + bt + Et

{H0 : p = 0

Où Et iid (0, u²) . On cherche à tester l'hypothèse de racine unitaire :

Hi: p ?0

² Le principe général de la stratégie de tests est le suivant. Il s'agit de

partir du modèle le plus général, d'appliquer le test de racine unitaire en utilisant les seuils correspondant à ce modèle, puis de vérifier par un test approprié que

le modèle retenu était le »bon». En effet, si le modèle n'était pas le »bon», les seuils utilisés pour le test de racine unitaire ne sont pas valable. On risque alors de commettre une erreur de diagnostic quant à la stationnarité de la série. Il convient dans ce cas, de recommencer le test de racine unitaire dans un autre modèle, plus contraint. Et ainsi de suite, jusqu'à trouver le »bon» modèle, les »bons» seuils et bien entendu les »bons» résultats.

¹ U.F.R Economie Appliquée, Séries Temporelles, cours de Christophe Hurlin.

~

+C + Et .

Le déroulement de la stratégie de test est reportée sur la figure(2.1) . On commence par tester la racine unitaire à partir du modèle le plus général, à savoir le modèle 3. On compare

la réalisation de la statistique de Student _tp~=0aux seuils q³_c, ) tabulés par Dickey et Fuller, ou

McKinnon pour le modèle 3 Si la réalisation de _tp~=0est supérieure au seuil _C(c,) on accepte
l'hypothèse nulle de non stationnarité. Une fois que le diagnostic est établi, on cherche à
vérifier si la spécification du modèle 3, incluant une constante et un trend, était une
spécification compatible avec les données. On teste alors la nullité du coefficient b de la
tendance. Deux choses l'une :

· Soit on a rejeté au préalable l'hypothèse de racine unitaire, dans ce cas on teste la nullité de b par un simple test de Student avec des seuils standards (test symétrique, donc seuil de 1.96 à 5%). Si l'on rejette l'hypothèse b = 0, cela signifie que le modèle 3 est le »bon» modèle pour tester la racine unitaire, puisque la présence d'une tendance n'est pas rejetée. Dans ce cas, on conclut que la racine unitaire est rejetée, la série est TS, du fait de la présence de la tendance. En revanche, si l'on accepte l'hypothèse b = 0, le modèle n'est pas adapté puisque la présence d'une tendance est rejetée. On doit refaire le test de racine unitaire à partir du modèle 2, qui ne comprend qu'une constante.

· Soit, au contraire, on avait au préalable, accepté l'hypothèse de racine unitaire, et dans ce cas, on doit construire un test de Fischer de l'hypothèse jointe p = 0 et b = 0. On teste ainsi la nullité de la tendance, conditionnellement à la présence d'une racine unitaire:

He : (c, b, p) = (c, 0,0) contre HP

La statistique de ce test se construit de façon standard par la relation :

F3 =

SCR3

(SCR3,c - SCR3)/ 2

/(n - 3)

Où _SCR3,c est la somme des carrés des résidus du modèle 3 contraint sous He :

? xt = c + Et

et SCR3 est la somme des carrés des résidus du modèle 3 non contraint. Si la réalisation de F3 est supérieure à la valeur 03 lue dans la table à un seuil a%, on rejette l'hypothèse He . Dans ce cas, le modèle 3 est le »bon» modèle et la série xt est intégrée d'ordre 1, I (1) + c +T, le taux de croissance est TS, ?xt = c + bt + Et . En revanche, si l'on accepte He le coefficient de la tendance est nul, le modèle 3 n'est pas le »bon» modèle, on doit donc effectuer à nouveau le test de non stationnarité dans le modèle 2.

Si l'on a accepté la nullité du coefficient b de la tendance, on doit alors effectuer à nouveau les tests de non stationnarité à partir cette fois-ci du modèle 2 incluant uniquement

une constante. On compare alors la réalisation de la statistique de Student tp~ = 0 aux seuils

C(²c, ) tabulés par Dickey et Fuller, ou McKinnon pour le modèle 2 . Si la réalisation de tp=0est supérieure au seuil C(2c, ) on accepte l'hypothèse nulle de non stationnarité. Une fois que le

diagnostic est établi, on cherche à vérifier si la spécification du modèle 2, incluant une constante, est une spécification compatible avec les données. On teste alors

la nullité du coefficient c de la constante. Deux choses l'une :

· Soit on a rejeté au préalable l'hypothèse de racine unitaire, dans ce cas on teste la nullité de c par un simple test de Student avec des seuils standard (test symétrique, donc seuil de 1.96 à 5%). Si l'on rejette l'hypothèse c = 0, cela signifie que le modèle 2 est le »bon» modèle pour tester la racine unitaire, puisque la présence d'une constante n'est pas rejetée. Dans ce cas, on conclut que la racine unitaire est rejetée, la série est stationnaire I (0) + c. En revanche, si l'on accepte l'hypothèse c = 0, le modèle 2 n'est pas adapté puisque la présence d'une constante est rejetée. On doit refaire le test de racine unitaire à partir du modèle 1, qui ne comprend ni constante ni trend.

· Soit, au contraire, on avait au préalable, accepté l'hypothèse de racine unitaire, et dans ce cas, on doit construire un test de Fischer de l'hypothèse jointe p = 0 et c = 0. On teste ainsi

la nullité de la constante, conditionnellement à la présence d'une racine unitaire:

Hô : (,, p) = (0,0) contre H?

La statistique de ce test se construit de façon standard par la relation :

F2 = S CR2

(SCR2,, - SCR2)/ 2

/(n - 2)

Où SCR2_,, est la somme des carrés des résidus du modèle 2 contraint sous Hô , c'est à dire

n n

SCR2,, = ?EÎ = ?(?xt)² et SCR2 est la somme des carrés des résidus du modèle

t=1 t=1

2 non contraint. Si la réalisation de F2 est supérieure à la valeur 01 lue dans la table à un seuil a, on rejette l'hypothèse le, au seuil a%. Dans ce cas, le modèle 2 est le »bon» modèle et la série xt est intégrée d'ordre 1, I (1) + c. En revanche, si l'on accepte le, , le coefficient de la constante est nul, le modèle 2 n'est pas le »bon» modèle on doit donc effectuer à nouveau le test de non stationnarité dans le modèle 1.

Enfin, si l'on a accepté la nullité du coefficient c de la constante, on doit alors effectuer à nouveau les tests de non stationnarité à partir cette fois-ci du modèle 1 sans constante ni trend. On compare alors la réalisation de la statistique de Student _tp~=0 aux seuils Cta)

tabulés par Dickey et Fuller, ou McKinnon pour le modèle 1. Si la réalisation de tp~=0est supérieure au seuil Ct_a) , on accepte l'hypothèse nulle de non stationnarité. Dans ce cas la série

xt est I (1) et correspond à une pure marche aléatoire, xt = xt-1 + Et . Si l'hypothèse nulle est rejetée, la série est stationnaire, I (0) de moyenne nulle. xt = 01xt-1 + E_t 01 - 1

Estimation du modèle (3) ?Xt = pXt-1 + c + bt + Et p = ö 1 - 1

Test H0: p = 0 si tb ? C(a) H0 acceptée

Rejet H0

Test de Student b = 0 (seuils loi normale)

Test He : (c, b, p) = (c, 0,0)

Statistique F3 seuils Fuller

Rejet H0 H0 acceptée H0 acceptée Rejet H0

Estimation du modèle (2)

?Xt est TS Xt I(1) + T + c ? Xt = c + bt + E t

VjXt = p

Xt-1 + c + Et

t TS

GG

Xt es G

X_t = (pj+1)Xt-

+jcj+jbtj+jet

TestkH_o: pk= 0ksi t'p ?kC(a)kH_o acceptée

Rejet H0 H0 acceptée

Test de Student c = 0 (Seuis oi normae) lllllllllllllllllllllllll Rejet H0

Test Hg : (c, p) = (0,0) Statistique F2 seuils Fuller

H0 acceptée H0 acceptée Rejet H0

Estimation du modèle (1)

jfojfmjljkfjkfvk
?Xt = pXt-1 + Et

Xt est I(0) + c

Xt= (p +¹)Xt-1 + c + Et

Xt est I(1) + c

VX_t =jc + E t

Test H_o: p = 0 si tb ? C(a) H0 acceptée

Rejet H0 H0 acceptée

Xt est I (0)

Xt = (p +¹)Xt-1 + Et

XtI (1) ?Xt = E t

Figure 2.1- Stratégie de Tests de Dickey Fuller.

2.3.3.4.2.3 Le test de Phillips et Perron :1

Le test de Phillips et Perron (1988) est construit sur une correction non paramétrique des statistiques de Dickey-Fuller pour prendre en compte des erreurs hétéroscédastique et/ou autocorrélées. Il se déroule en quatre étapes :

- estimation par les moindres carrés ordinaires des trois modèles de base des tests de DickeyFuller et calcul des statistiques associées, soit et le résidu estimé ;

;

ⁿ

- estimation de la variance dite de court terme des résidus â^-2 = ¹?e?

t

1

n

=

- estimation d'un facteur correctif s? (appelé variance de long terme) établi à partir de la structure des covariances des résidus des modèles précédemment estimés de telle sorte que les transformation réalisées conduisent à des distributions identiques à celles du Dickey-Fuller standard :

i 1 n S? = 1? et^2 2? / 1) n ? etet-i t=1 i=1 t=i+1

. Pour estimer cette variance de long terme, il est

nécessaire de définir on nombre de retards l (troncature de Newey-West) estimé en fonction

2

du nombre d'observations n, 1 4(n / 100)⁹ ;

( qui est égal à 1 de

-

2
2

ó

k

avec

St

g_ -1) n(k -1)ó

- calcul de la statistique de PP : = k -

+ó- ₁

manière asymptotique si et est un bruit blanc. Cette statistique est à comparer aux valeurs critiques de la table de Mackinnon.

Il est à noter que les logiciels RATS et Eviews permettent directement l'utilisation de ces tests.

2.3.4 La méthodologie de Box & Jenkins :

Box & Jenkins (1976) ont promu une méthodologie consistant à modéliser les séries temporelles univariées au moyen des processus ARMA. Ces processus sont parcimonieux et constituent une bonne approximation de processus plus généraux pourvu que l'on se restreigne au cadre linéaire. Les modèles ARMA donnent souvent de bon résultats en prévision.

La méthodologie de Box & Jenkins peut se décomposer en quatre étapes:

Etape 1 : Indentification, c'est une étape délicate qui conditionne la prévision de la chronique, elle consiste à déterminer les paramètres p et q du modèle ARMA à l'aide de la ACF et la PACF.

Etape 2 : Estimation, elle consiste à estimer les paramètres du modèle identifié.

Etape 3 : Validation, on vérifie que le modèle retenu est valide ; on test la significativité des

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004 P 158-159.

paramètres estimés et que les résidus forment bien un bruit blanc, enfin à partir des critères d'information on choisit le modèle le plus adéquat.

Etape 4 : Prévision, on établit une prévision pour une certaine période du future.

2.3.4.1 Identification :

Cette étape consiste à déterminer les paramètres p, q du modèle ARMA, on utilise traditionnellement deux graphiques : ceux de la fonctions d'autocorrélation simple et de la fonction d'autocorrélation partielle. L'idée sous-jacente est que chaque modèle ARMA possède des fonctions d'autocorrélation théorique spécifiques. En comparant l'éventuelle similitude de ces fonctions théoriques et estimées, on peut alors choisir un ou plusieurs modèles théoriques. Cette étape est la partie la plus délicate car dans la pratique les corrélogrammes observés n'engendrent pas toujours un choix évident. Pour rappel les allures (théoriques) des fonctions ACF et PACF ont été présentées dans le tableau (2.1) du même chapitre.

2.3.4.2 Estimation1 :

L'estimation des paramètres d'un modèle ARMA (p, q) lorsque les ordres p et q sont supposés connus peut se réaliser par différentes méthodes dans le domaine temporel :

· Moindres Carrés Ordinaires (modèle sans composante MA, q = 0). Dans ce cas, on retrouve les équations de Yule Walker. En remplaçant les autocorrélations théoriques par leurs estimateurs, on peut retrouver les estimateurs des MCO des paramètres du modèle par la résolution des équations de Yule Walker.

· Maximum de Vraisemblance approché (Box & Jenkins 1970).

· Maximum de Vraisemblance exacte (Newbold 1974, Harvey et Philips 1979, Harvey 1981).

(Le logiciel Eviews nous fournit directement les résultats d'estimation)

2.3.4.3 Validation :

A l'étape de l'identification, les incertitudes liées aux méthodes employées font que plusieurs modèles, en général, sont estimés et c'est l'ensemble de ces modèles qui subissent alors l'épreuve des tests. Il en existe de très nombreux permettant d'une part de valider le modèle retenu, d'autre part de comparer les performances entre modèles.

2.3.4.3.1 Le test de Student des paramètres :

On effectue un test classique de Student sur chacun des paramètres du processus ARMA en divisant le paramètre par son écart type. Il peut arriver qu'un ou plusieurs paramètres soient pas significativement différent de 0 : le modèle est alors rejeté et on retourne à l'étape d'estimation en éliminant la variable dont le coefficient n'est pas significatif.

1 U.F.R Economie Appliquée, Séries Temporelles, cours de Christophe Hurlin.

Soit l'hypothèse :

Ho : _P=o
H1 : :i'P ? o

{

~

On calcule la statistique de Student : tc = OP

, avec O^~_P estimé au seuil a =5%.

(var(_P))

Si tc ? 1.96 (cas asymptotique) on rejette l'hypothèse H0 (les paramètres sont significativement différents de zéro), donc on accepte le modèle ARMA (p, q) , dans le cas contraire on rejette le modèle ARMA (p, q).

2.3.4.3.2 Le coefficient de détermination1 :

Les coefficients de détermination (R² normal ou R² corrigé) des modèles estimés sont :

n

~

2

E_t

?

R

2= 1-t=1

n

?

gt - X)^2

t

=

1

n

?

2 n - 1 t=1

n

n-P-4_?

R

=

1

gt - X)²

E²

t

( E~t = résidu d'estimation)

t

=

1

On utilise de préférence le R² puisqu'il permet de prendre en compte le nombre de variables explicatives, c'est à dire les p termes retardés de l'AR et les q retards de la composante MA. Bien entendu ces coefficients sont proches de 1 lorsque l'ajustement du modèle aux données

n

est parfaite, c'est à dire si Ee tend vers 0. La significativité de coefficient de détermination

t= 1

est testée à l'aide d'une statistique de Fisher classique

2.3.4.3.3 Les tests sur les résidus :

Le processus estimé est bien évidemment de bonne qualité si la chronique calculée suit les évolutions de la chronique empirique. Les résidus entre les valeurs observées et les valeurs calculées par le modèle, doivent donc se comporter comme un bruit blanc normal. Les résidus estimés sont notés : E~t

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004, P 230

Tests de recherche d'autocorrélation¹ :

Si les résidus obéissent à un bruit blanc, il ne doit pas exister d'autocorrelation dans la série. Les tests suivant peuvent être utilisés :

a) Le test de Box et Pierce :

K

Il est établi à partir de la statistique Q = n> ~ k (êt) qui est en fonction de la somme des carrés

1

=

k

???????

HO
· = p2 =...= pK = O
·

des autocorrélations bk² g ) de la ACF et du nombre d'observations n. Il permet de vérifier L'hypothèse :

H1 existe au moins unpi

1 i

"1

significativement différent de O.

Cette statistique Q en l'absence d'autocorrélation obéit à un x² à (v = K-(p+ q)) degrés de

liberté ou p est l'ordre de la partie autorégressive et q est l'ordre de la partie moyenne mobile, et K est el nombre de retards choisis pour calculer les autocorrélations.

Pour effectuer ce test, il est conseiller de choisir K proche du tiers du nombre d'observations. L'hypothèse H0 est rejetée au seuil de 5 % si Q est supérieur au quantile de 0.95 de la loi du x² .

b) Le test de Ljung et Box :

La statistique de Ljung et Box est donnée par :

k

~=n

(n+2)

Tests de normalité :

K

? agi)

n - k

1

Le test se déroule de manière identique à celui de Box et Pierce.

Dans la cas d'un résidu hétéroscédastique, il convient d'utiliser la statistique de Box-Pierce corrigée Q'.

a) Les tests du Skewness et de Kurtosis :

Soit Pk = 1 (Xi X)^k le moment d'ordre k, le coefficient de Skewness ( ^/2) est égal à :

i

(3/2 P3 = 3/2 P2

et le coefficient du Kurtosis (32 = P42 P 2

.

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004

Si la distribution est normale et le nombre d'observation grand :

0i^/2 ?

Et

N(0; n6 )

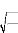
24

02 ? N(3; )

n

On construit alors les statistiques :

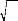
_0:/ 2 - 1

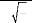
6

n

0 02 - 3

et v₂=

v1

=

24

n

que l'on compare à 1.96 au seuil de 5 %.

Si les hypothèse H0 : v1 = 0 (symétrie) et v2 = 0 (aplatissement normal) sont vérifiées alors v1 -1.96 et v2 -1.96 ce qui veut dire que l'hypothèse de normalité est vérifiée, dans le cas contraire, l'hypothèse de normalité est rejetée.

b) Le test de Jarque et Bera¹ :

Il s'agit d'un test qui regroupe les résultats précédents, si e² et 02 obéissent à des lois

normales alors la quantité S :

n n (02 S = 6 0₁^1/2 + 24 - 3)² suit un e_a (2) à 2 degrés de liberté.

Donc si S = e_a (2) , on rejette l'hypothèse H0 de normalité des résidus au seuil a .

2.3.4.3.4 Les critères de comparaison de modèles2 :

Il arrive fréquemment qu'à l'issue de tous les tests précédents plusieurs modèles se montrent résistants. Pour choisir le meilleur d'entre eux, on peut utiliser des critères de comparaison des modèles. Ces critères sont forts nombreux et jouent, parfois, un rôle important en économétrie.

Ces critères, que l'on cherche à minimiser sont fondés sur l'erreur de prévision, nous pouvons citer :

Le critère d'information de Akaike (AIC, Akaike Information Criterion) :

Présenté en 1973 pour un ARMA (p, q), Akaike a démontré que le meilleur des modèles ARMA non filtré est celui qui minimise la statistique :

¹ Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004, P 238

² Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition DUNOD, 2004, P 242

AIK (p, q) = n log ô^- + _2(p + q)

Le critère d'information bayésien (BIC, Bayesian Information Criterion) : Pour un ARMA (p, q), il s'écrit :

BIC (p, q) =

(p + q) I 6 n log ô1 - (n - p - q) log 1-n + (p + q) log n + log (p + e^l 3c 1 ^11 Ce - ] ]

De manière générale le critère BIC a des caractéristiques plus intéressantes que celles du critère AIK. Il est convergent et pénalise plus fortement les paramètres en surnombre que le critère AIK.

Le critère de Schwarz (1978) :

SC (p, q) = n log e + (p + q) log n .

Le critère de Hannan-Quin (1979) :

HQ (p, q) = log e+ (p + q)c log [ lo_ng n I

Où c est une constante à spécifier.

Le modèle est alors retenu pour le calcule des prévisions qui est la dernière étape de la méthode de BOX - JENKINS.

2.3.4.4 La prévision :

Transformation de la série :

Lorsque pour identifier le processus étudié à un processus ARMA, on a appliqué différentes transformations, il est nécessaire lors de la phase de prévision de prendre en compte la transformation retenue et de »recolorer la prévision». Plusieurs cas sont possibles:

· Si le processus contient une tendance déterministe, on extrait cette dernière par régression afin d'obtenir une série stationnaire lors de la phase d'estimation. Ensuite, lors de la phase de prévision, on adjoint aux prévisions réalisées sur la composante ARMA stationnaire, la projection de la tendance.

· Si la transformation résulte de l'application d'un filtre linéaire (de type par exemple différences premières), on réalise les prévisions sur la série filtrée stationnaire et l'on reconstruit ensuite par inversion du filtre les prévisions sur la série initiale.

Prédicateur pour un processus ARMA : Soit le modèle retenu ARMA (p, q) tel que :

ö_p(B)X_t = è_q (B)å_t Avec (ö_p,è_q ) ? à IR^*2 et et iid (0_' )

8

La forme MA (8) correspondante est : x ð₀ =1.

j 0

Il s'en suit que la meilleure prévision que l'on peut faire de _xt+1 compte tenu de toute l'information disponible jusqu'à la date t, noté xà_t(1) est donnée par :

à xt	(1)E(xt+1/ x , xt-2 , , x0)

E(xt+1 / åt,åt-Dåt-2, ,å ₀)

+8

ð å j t

+

1

-

j

j 1

Des lors, l'erreur de prévision est donnée par la réalisation en (t+1) de l'innovation qui en t n'est pas connu :

t+

x xà_t(1) = åt+1

Plus généralement pour une prévision à horizon k on a :

+8

t (k) -- = ? n E + -
i=k

k 1

t+k - xt (k) = ?niEt+k-i

0

=

i

Déterminons un intervalle de confiance sur la prévisionxà_t(k), sous l'hypothèse de normalité des résidus å_t . On montre alors que :

- xt+k îCt(k)

N(0,1) lorsque : t ?8

vark+k-2t(kg /2

Or, on sait que :

.

k

-12

k

-1_ )1= ?

₃^0-E

E {(xt+k-ît (k))² -- E i = 0

D'où : xt+k (k) l k-1 1/2 -?N(0'1) QE 1?n. ?? i=0

lorsque :t? 8.

On peut donc construire un intervalle de confiance sous la forme :

? ?(k-1 )1/2

IC = (k) #177; ta/2 ? ⁱi=0 ?

? ?

Synthèse de la méthodologie de Box & Jenkins :

Série Xt

Etude de la stationnarité

Test de racine unité

Série stationnaire Yt

Passage aux différences si
DS

Régression sur le temps si
TS

Analyse du corrélogramme simple et partiel

Détermination des ordres p et q du processus ARMA

Oui

Test de Student, les coefficients non significatifs sont
supprimés

Test sur les résidus sont -ils des
bruit blanc ?

Estimation des paramètres

Non
Ajout d'un ordre p ou q

Si plusieurs modèles « concurrents »
critères AIC, SC...

Prévision par
ARMA

Figure 2.2- Algorithme de traitement d'une chronique selon la
méthodologie de Box & Jenkins

Chapitre 3 : Application des méthodes

de prévision

DP

Dans ce chapitre, on va tout d'abord faire une analyse descriptive de la série consommation du gaz naturel pour la distribution publique, ensuite faire une présentation des données afin de se familiariser avec celle-ci, enfin nous allons appliquer les différentes méthodes de prévision vu dans le chapitre 2 et les comparer afin de dégager la méthode de prévision la plus performante.

3.1 Analyse descriptive :

3.1.1 Historique des paramètres de la distribution publique :

Le tableau ci-dessous représente l'évolution de la consommation de gaz naturel pour la distribution publique de 1980 à 2006 avec le nombre d'abonnés et les taux de croissance.

Tableau 3.1- Evolution de la consommation du gaz naturel DP 1980-2006

		1980		1981		1982	1983	1984	1985	1986		1987		1988
Nombre d'abonnés DP^1		501 320		482 511		522 130	565 422	601 471	608 589	657 698		710 518		762 480
DISTRIBUTION PUBLIQUE ( 10^6 thermies^2 )		5 504		5 795		6 829	7 424	8 669	9 520	10 871		11 048		11 939
Taux de croissance ( % )		-		^5,^3		17,8	8,7	16,8	9,8	14,2		1,6		8,1
		1989		1990		1991	1992	1993	1994	1995		1996		1997
Nombre d'abonnés DP		803 065		854 688		905 816	965 308	1 024 139	1 080 849	1 137 348	1	187 631	1	232 529
DISTRIBUTION PUBLIQUE ( 10^6 thermies )		12 015		13 531		16 311	17 023	18 908	18 593	19 957		21 530		20 970
Taux de croissance ( % )		0,6		12,6		20,5	4,4	11,1	-1,7	7,3		7,9		-2,6
		1998		1999		2000	2001	2002	2003	2004		2005		2006
Nombre d'abonnés DP	1	279 109	1	331 684	1	394 578	1 464 700	1 555 774	1 683 348	1 835 509	2	016 749	2	216 265
DISTRIBUTION PUBLIQUE ( 10^6 thermies )		22 633		24 122		24 456	25 845	27 201	31 014	34 790		38 355		38 785
Taux de croissance ( % )		7,9		6,6		1,4	5,7	5,2	14,0	12,2		10,2		1,1

Son graphe est représenté ci-dessous :

45 000 40 000 35 000 30 000 25 000 20 000 15 000 10 000 5 000 0

Figure 3.1- Evolution de la consommation du gaz naturel DP 1980-2006

1 Distribution publique

2

Thermie : unité de mesure de quantité de chaleur, valant un million de calorie. On mesure le gaz naturel par sa teneur énergétique

Nous remarquons sur la figure 3.1, que la consommation du gaz naturel pour la distribution publique évolue de façon exponentielle, ceci s'explique par l'augmentation du nombre d'abonnés d'année en année ainsi que l'augmentation du taux de pénétration en gaz naturel surtout à partir de 2002 ou l'Etat a mis en place un large programme publique pour permettre le raccordement des citoyens sur l'ensemble des wilayas. Les réalisations de la période 2000/2006 ont permis de hisser le taux de pénétration du gaz de 30% à 37%.

3.1.2 Présentation des données :

Toutes les données utilisées dans notre étude proviennent de la Direction Analyse et Prévision (DAP) de la Sonelgaz. Il s'agit de données mensuelles de janvier 2003 à décembre 2006 et cela pour chaque wilaya de l'Algérie.

Pour la distribution publique qui représente les ménages et les artisans, le gaz naturel est essentiellement utilisé pour le chauffage, l'eau chaude, la cuisson des aliments, et l'intensité de cette utilisation est liée au climat plus exactement à la température. Nous savons qu'en hiver où la température est en baisse la consommation du gaz naturel est nettement plus élevée qu'en été puisqu'on sollicite plus souvent le chauffage, le chauffe bain,... etc.

C'est sur cette base qu'on a divisé le territoire algérien en trois zones à savoir : le nord, les hauts plateaux et le sud.

Nord : le climat est de type méditerranéen, les hivers sont humides et doux et les étés chauds et secs. Sur les villes côtières les températures hivernales varient entre 8 et 15°C, elles grimpent à 25°C au mois de mai pour atteindre une moyenne de 35°C en juillet et août.

Hauts Plateaux : le climat est de type semi- aride, les étés y sont lourds et secs et les hivers très froids et humides. Les températures avoisines les 5°C voire -7°C en hiver ou la neige est fréquente, la température estivale varie de 35°C à 40°C.

Sud : le climat est de type saharien, la température varie entre 15 et 28°C pour atteindre 40 à 45°C voire plus en été.

Ainsi par rapport à notre découpage du territoire algérien et après avoir fait les totaux nous obtenons trois séries mensuelles de la consommation du gaz naturel pour la DP à savoir : nord, hauts plateaux (HP), sud.

Donc les données sur lesquelles nous allons travailler sont des données mensuelles allant de janvier 2003 à décembre 2006 ce qui nous fait 48 observations et ceci pour chaque série.

Dans ce qui suit nous allons représenter les différents graphes des trois séries :

2.8E+09 2.4E+09 2.0E+09 1.6E+09 1.2E+09 8.0E+08 4.0E+08

2003 2004 2005 2006

NORD

HP

5.E+09 4.E+09 3.E+09 2.E+09 1.E+09 0.E+00

2003 2004 2005 2006

2.8E+08 2.4E+08 2.0E+08 1.6E+08 1.2E+08 8.0E+07 4.0E+07 0.0E+00

2003 2004 2005 2006

SUD

Figure 3.2- Consommation du gaz naturel DP pour les séries nord, HP et sud.

Nous remarquons sur les graphes des trois séries nord, hauts plateaux, sud la présence d'une forte saisonnalité. En effet les mois de janvier et décembre présentent une augmentation de la consommation du gaz (diminution de la température) et les mois de juillet et août présentent une nette diminution de la consommation du gaz (augmentation de la température).

La consommation du gaz naturel a augmenté dans les trois séries entre 2003 et 2006 avec des taux de croissance de 4.81% pour le nord, 7.9% pour les hauts plateaux, 6.29% pour le sud. Cette augmentation est due à l'augmentation du nombre d'abonnés et au raccordement en gaz de plusieurs communes à titre d'exemple dans le nord les communes de Benni Tamou, Oued Djer (Blida) et de Bourkika, Ahmeur El Ain (Bouira) ont été raccordées, dans les hauts plateaux : Ain Chouhada (Médéa), El Hamel, Ouled Derradj (Djelfa) enfin dans le sud : Kantara, Rouidjel (Adrar).

3.2 Application de la méthode traditionnelle :

Comme nous avons trois chroniques (nord, hauts plateaux, sud) à analyser, et afin d'éviter toute répétition, nous allons présenter une analyse détaillée pour la série nord, puis nous donnerons seulement les résultats pour les séries hauts plateaux et sud.

3.2.1 Etude de la série Nord :

La sélection du schéma de décomposition :

Graphe de la série :

2.8E+09

2.4E+09

2.0E+09

1.6E+09

1.2E+09

8.0E+08

4.0E+08

2003 2004 2005 2006

2.8E+09 2.4E+09 2.0E+09 1.6E+09 1.2E+09 8.0E+08 4.0E+08

2003 2004 2005 2006

NORD

NORD

Figure 3.3- Graphique de la série nord Figure 3.4-Procedure de la bande

En premier lieu on procède à l'examen visuel du graphique de la série « nord » illustré par la figure 3.3, en reliant par une ligne toutes les valeurs hautes et toutes les valeurs basses de la série « nord » (figure 3.4), nous remarquons que les deux lignes sont à peu prés parallèles, ce qui nous pousse à supposer que le schéma est additif. Afin d'écarter le doute nous procédons au test de Buys-Ballot.

Le test de Buys-Ballot :

Le test de Buys-Ballot comme nous l'avons présenté dans le chapitre 2 est basé sur la régression suivante :

ai = a1yi + a2 + ei ... (3.1)

L'estimation de l'équation (3.1) faite sous Eviews nous donne les résultats suivants :

a_i = 0.690780 yi - 188778609.1 + ei (1.87)

n = 4

(1.87) = t de Student calculé pour n = 2.

Le coefficient á1 = 0.690780 n'est pas significativement différent de 0

(t_ca/ =1.87 < ter =4,3027), donc nous pouvons conclure à un schéma de type additif.

Donc notre série « nord » désignée par « y » peut s'écrire comme suit :

yt = ft + ^St + e t

Où

ft : représente la tendance ou trend

St : représente les variations saisonnières

et : représente les variations accidentelles Estimation des composantes de la série : Estimation de la tendance :

Comme le nombre d'observations n'est pas très importants (n = 48) et que la méthode d'estimation par moyenne mobile nous fera perdre 12 observations, nous optons alors pour la méthode des moindres carrés (MCO) pour estimer la tendance.

L'équation du trend linéaire est la suivante :

~t= at + b

Les calculs sont les suivants :

La somme des n premiers nombres entiers est :

n(n + 1) 48(49) = = 1176.

2 2

n

? ti=

i

=

1

La somme des carrés des n premiers nombres entiers est :

n

?= n(n + 1) (2n +1)₌ 48(49) (97) t 2= 38024.

i₆

=

6

i

¹

La moyenne de la variable temps est donc :

= ¹?ti = 24.5 et t 2 = 600.25. n

i=1

La moyenne des observations est :

y = 1 ?yi =1 185 430 847. n =

i 1

La pente du trend linéaire estimée par MCO est :

n

0317(

4

yt) V(t)

t ynty
-

i i

n

?

t2- nt 2 i

= 469863.7401

?

i

=

1

Et

i

=

1

b ~ = y - ât = 1173919186 a

L'équation du trend estimée par MCO est donnée par :

~^~t = 469863.7401 t [phone] ... (3.2)

Pour avoir la série ~^~t il suffit de remplacer t (t = 1,...48) dans l'équation (3.2) [voir annexe A tableau A1].

Estimation des coefficients saisonniers :

Avant de calculer les coefficients saisonniers nous devons tout d'abord calculer les variations saisonnières St qui sont obtenues en retranchant de notre série brute yt la tendance estimée précédemment ~~t (~~

St = yt - t ) [ voir annexe A tableau A1]

Les coefficients saisonniers S_i ( j = 1,...,12 données mensuelles) sont calculés par la méthode pratique de la manière suivante :

1 ⁿ

Si = Sii ?

ⁿ

i

=1

Les coefficients saisonniers pour la série « nord » sont consignés sur le tableau 3.2

Tableau 3.2- Calcul des coefficients saisonniers pour la série « nord »

S1	1036506605	S7	-574498900
S2	819333574	S8	-598817166
S3	425726265	S9	-560713568
S4	-80192075	S10	-482968910
S5	-331768947	S11	13546022
S6	-517520845	S12	851367945

12

La somme des coefficients saisonniers est égale à 0 ( ? Si = 0), donc on a pas

i=1

besoins de calculer les coefficients saisonniers corrigés Si^'( Si =S^'i ). Série désaisonnalisée ou série (CVS) :

La série corrigée des variations saisonnières (CVS) notée y; est la série yt à laquelle on a enlevé les variations saisonnières, elle exprime ce qu'aurait été la réalité du phénomène s'il n'y aurai pas eu de saisons. [voir annexe A tableau A1] :

yii = yii - Si i = 1,...,4 etj= 1,...,12

Le graphe de la série CVS est illustré ci-dessous :

1 600 000 000

1 400 000 000

1 200 000 000

1 000 000 000

800 000 000

600 000 000

400 000 000

200 000 000

1 800 000 000

0

Yt*(CVS)

Figure 3.5- Série CVS de la consommation du gaz naturel nord

Nous remarquons sur le graphe (figure 3.5) que l'effet saisonnier a disparu, nous n'avons plus de pics importants pour les mois de janvier et décembre (ou la consommation de gaz augmente) et les mois de juillet et août (ou la consommation de gaz diminue considérablement).

Estimation des variations accidentelles :

Les variations accidentelles (å~ ) sont obtenues en retranchant de la série CVS l'influence du trend [voir annexe A tableau A1]:

å ~ = ~ ~ - ~ ~

~ ~

n

La somme des variations accidentelles étant égale à 0 (

? = 0), donc il y'a bien å ~

~ = 1

conservation des aires (les hausses sont compensées par les baisses). La figure 3.6 illustre le graphe des variations accidentelles :

variations accientelles

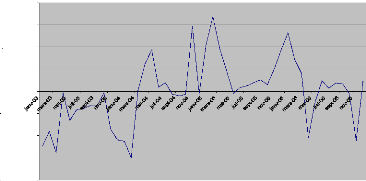
400 000 000

300 000 000

200 000 000

100 000 000

0

-100 000 000

-200 000 000

-300 000 000

-400 000 000

Et=Yt*-Ft

Figure 3.6- Graphe des variations accidentelles série nord Etablissement de la chronique ajustée et prévision :

La série ajustée ~~~ représente l'évolution qu'aurait subi le phénomène, si le mouvement saisonnier avait été parfaitement régulier d'année en année.

En modèle additif elle se calcule comme suit [voir annexe A tableau A1] :

~
~ ~~ = ~~ + s ~

L'équation de la chronique ajustée est donc ici :

~~~ = 469863.7401 t [phone] + s. (j= 1,...,12)

1500000000

1000000000

2000000000

500000000

Le graphe de la chronique ajustée apparaît ci-dessous :

2500000000

Yt(série ajustée)

Yt(série ajustée)

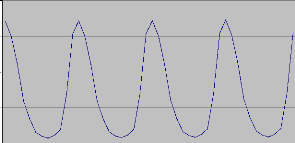
0

Figure 3.7- Série ajustée consommation de gaz naturel pour le nord On remarque bien sur le graphe la régularité de l'effet saisonnier d'année en année.

La chronique ajustée, permet d'effectuer des prévisions conjoncturelles (sous l'hypothèse d'un maintien de tendance) : ~ ~ h ~( ) ~

Y + = ~ + h+ + S ~ ' .

Ainsi les prévisions sur la consommation du gaz naturel pour la distribution publique pour l'année 2007 sont illustrées dans le tableau ci-dessous :

Tableau 3.3 -Prévision sur la consommation du gaz naturel région nord par la méthode
traditionnelle.

mois (2007)	Y ~~ +h
janv-07	2233449114
févr-07	2016745947
mars-07	1623608502
avr-07	1118160025
mai-07	867053017
juin-07	681770983
juil-07	625262791
août-07	601414389
sept-07	639987851
oct-07	718202373
nov-07	1215187168
déc-07	2053478955

La consommation de gaz naturel en 2007 pour la distribution publique région nord diminuera de 0.75% par rapport à 2006.

3.2.2 Etude de la série Hauts Plateaux (HP) : La sélection du schéma de décomposition :

Graphe de la série :

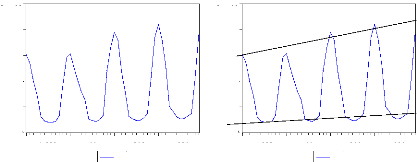
5.E+09

4.E+09

3.E+09

2.E+09

1.E+09

0.E+00

HP

HP

2003 2004 2005 2006

5.E+09

4.E+09

3.E+09

2.E+09

1.E+09

0.E+00

2003 2004 2005 2006

Figure 3.8- Graphique de la série HP Figure 3.9- Procédure de la bande

La figure 3.9 nous a pas permis de déceler le type de schéma, alors nous préférons écarter le doute en nous référons au test de Buys-Ballot.

Le Test de Buys-Ballot : L'estimation du modèle nous donne :

ó~ = 1.131342 y~ - 595214686+ å~ (3.65)

á~ = 1.131342 n'est pas significativement différent de 0 (( )a1= 3.65 < ~~~)

~~a~ = 4,3027), donc nous

pouvons conclure à un schéma de type additif.

Estimation des composantes de la série :

Estimation de la tendance :

L'équation du trend estimée par MCO est donnée par :

~~~ = 3862915,607t + 1523119524 ... (3.3 )

La série ~~~ , les variations saisonnières (Si), les coefficients saisonniers (Si), la série CVS

( ~

y ), enfin les variations accidentelles (å~ ), sont illustrées dans l'annexe A tableau A2. Prévisions :

Tableau 3.4 -Prévision sur la consommation du gaz naturel région HP par la méthode
traditionnelle.

mois (2007)	Y ~~ +h
janv-07	3670756733
févr-07	3228299481
mars-07	2365272433
avr-07	1510178124
mai-07	949929318,6
juin-07	647301352,6
juil-07	583252416,4
août-07	582290568,6
sept-07	653463784,3
oct-07	819751582,1
nov-07	2235685421
déc-07	3557599880

La consommation de gaz naturel en 2007 pour la distribution publique région HP diminuera de 2.2% par rapport à 2006.

3.2.3 Etude de la série Sud :

La sélection du schéma de décomposition : Graphe de la série :

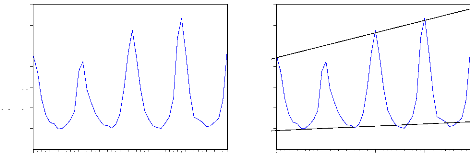
2.8E+08

2.4E+08

2.0E+08

1 .6E+08

1.2E+08

8.0E+07

4.0E+07

0.0E+00

2003 2004 2005 2006

2003 2004 2005 2006

2.8E+08

2.4E+08

2.0E+08

1 .6E+08

1.2E+08

8.0E+07

4.0E+07

0.0E+00

SUD		SUD

Figure 3.10- Graphique de la série sud Figure 3.11- Procédure de la bande

En utilisant la méthode de la bande (figure 3.11), nous remarquons que les deux lignes ne sont pas parallèles donc nous supposons que le schéma de décomposition est de type multiplicatif, laissons de test de Buys-Ballot nous confirmer notre supposition.

Test de Buys-Ballot :

49-_i= 1.313411y, - 63044534+ E_y (6.45)

= 1.313411 est significativement différent de 0 (( tca1= 6.45 > 4⁽2⁵ = 4,3027), donc nous pouvons conclure à un schéma de type multiplicatif.

Notre série s'écrit :

yt=~t × St × å _t ... (3.4)

Pour rendre la sérié « sud » additif on considère la série ( In~t ): In yt = In t + In St + In Et Donc nous allons procéder de la même manière que les séries précédentes :

Estimation des composantes de la série :

Estimation de la tendance :

L'équation du trend estimée par MCO est donnée par :

In t ~ = 0,001153477 t + 18,15630339

Pour les autres composantes de la série « sud », voir annexe A tableau A3. Prévision :

Afin d'avoir un modèle additif on a converti notre série « sud » qui est un modèle multiplicatif en un modèle additif à l'aide de la fonction (ln), donc pour avoir nos prévision nous devons avoir recours à la fonction inverse du (ln) qui est la fonction exponentielle (e), c'est-à-dire que nous devons appliquer la fonction exponentielle aux prévisions qu'on a obtenu avec la série ( In~t ) les résultats obtenus sont :

Tableau 3.5 -Prévision sur la consommation de gaz naturel région Sud par la méthode
traditionnelle

mois (2007)	Ût+ h
janv-07	212916279,9
févr-07	160521551,3
mars-07	106475413,3
avr-07	70858392,3
mai-07	58139761,6
juin-07	50296016,97
juil-07	44205437,49
août-07	43252731,13
sept-07	51422072,62
oct-07	64060353,98
nov-07	98596430,88
déc-07	190252329

La consommation de gaz naturel en 2007 pour la distribution publique région Sud diminuera de 4.5% par rapport à 2006.

3.3 Application de la méthode de lissage exponentiel : 3.3.1 Etude de la série nord :

Avant de pouvoir utiliser l'une des méthodes de lissage exponentiel (simple, double, HoltWinters), nous devons tester l'existence d'une éventuelle tendance ou/et d'une saisonnalité dans la série « nord ».

Test de saisonnalité :

???????

H° : pas de saisonnalité H1 : existance d'une saisonnalité

= 74.59

Calcul du Fisher empirique : F_c = V P

VR

La valeur de Fisher lue dans la table à p-1 [11] et (N-1) (p-1) [33] degré de liberté est égale à

Fa =

(P-1 F°.°

,(N-1)(p-1)) (11,3⁵ 3) = 2.09 .

Le FG^, est largement supérieur au Fisher tabulé, dans ce cas on rejette l'hypothèse H0, la série est donc saisonnière.

Test de tendance :

???????	H° : pas de tendance. H1 : existance d'une tendance.
Fisher empirique : FC = VA VR		= 5.94

Fisher tabulé
· Fa = F°.°5 = 2
· 89

· (P-1,(N-1)(P-1)) (11,33)

? Fe₎ donc on rejette H0 ce qui veut dire que notre série est affectée d'une tendance.

La série « nord » est à la fois affectée d'une saisonnalité et d'une tendance, donc la méthode de lissage la plus adéquate est celle de Holt-Winters, reste à choisir entre les deux types de composition additive ou multiplicative. On a vu dans la méthode traditionnelle que la série « nord » suivait un schéma de type additif, donc nous allons opter pour le modèle de HoltWinters additif.

Dans ce cas la chronique s'écrit : yt = at + btt + St + å t

Les valeurs de a, (3, 1, sont obtenues en essayant plusieurs combinaisons possibles de ces
paramètres et on prend les valeurs de a, (3,1^, qui minimisent la racine carrée de l'erreur

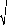
n

), c'est ainsi que nous obtenons les résultats

quadratique moyenne (RMSE = 1 ?(ût -.)²

n =

t 1

suivants :

?? ??????? ??

= = =

0.47 0 1

L'initialisation est effectuée par la méthode la plus simple (p=12) : a_p = a12 = moyenne de la première année = 1049586454.

b_p = b12 =0.

St = yt - 1049586454 t = 1,2,...,12

Les résultats détaillés de la méthode sont fournis dans l'annexe B tableau B 1. Prévision :

y^~t+h = (at+hbt)+St^*-p+h 1 = h = 12

Le tableau ci-dessous illustre les prévisions pour l'année 2007 par la méthode de Holt-Winters

Tableau 3.6 -Prévision par la méthode de Holt-Winters sur la consommation du gaz naturel
région nord

mois (2007)	y^~t+h
janv-07	2201703841
févr-07	1887692519
mars-07	1440620227
avr-07	802075626
mai-07	720804572
juin-07	597650686
juil-07	513420715
août-07	509508094
sept-07	549299882
oct-07	611327324
nov-07	1058360612
déc-07	2089168145

La consommation du gaz naturel en 2007 pour la distribution publique région nord diminuera de 10.48 % par rapport à 2006.

3.3.2 Etude de la série Hauts Plateaux (HP) : Test de saisonnalité :

FC = 77.63 > ee₃₎ = 2.09, donc la série est saisonnière.

Test de tendance :

FC = 4.069 > Fe₎ = 2.89, donc la série est affectée d'une tendance.

Ainsi, la méthode de lissage la plus adaptée pour cette série est la méthode de Holt-Winters additif.

Les paramètres estimés sont : a = 0.74, 0 = 0, ry = 1.

Les résultats détaillés de la méthode sont fournis dans l'annexe B tableau B2 Prévision :

Tableau 3.7 -Prévision par la méthode de Holt-Winters sur la consommation du gaz naturel
région HP

mois (2007)	y^~t+h
janv-07	3835824200
févr-07	3252725560
mars-07	2381979373
avr-07	1626496990
mai-07	1280048015
juin-07	984505971
juil-07	909927980
août-07	932188491
sept-07	1004949896
oct-07	1168207384
nov-07	2547879253
déc-07	3816386880

La consommation du gaz naturel en 2007 pour la distribution publique région HP augmentera de 11.6 % par rapport à 2006.

3.3.3 Etude de la série Sud :

Test de saisonnalité :

FC = 49.95 > F° °33) = 2.09, donc la série est saisonnière. Test de tendance :

FC = 3.38 > F(U53) = 2.89, donc la série est affectée d'une tendance.

Ainsi, la méthode de lissage la plus adaptée pour cette série est la méthode de Holt-Winters multiplicatif.

Dans ce cas la chronique s'écrit : yt = (at + btt)St + å t Les paramètres estimés sont : a = 0.62, 0 = 0, ry = 1.

Les résultats détaillés de la méthode sont fournis dans l'annexe B tableau B3. Prévisions :

Y ~ +h ( a hb ) S ~ + h

= + -= =

1 h 12

Tableau 3.9 -Prévision par la méthode de Holt-Winters sur la consommation du gaz naturel
région sud.

mois (2007)	Y ~ +h
janv-07	179379988
févr-07	205248932
mars-07	154396679
avr-07	101040251
mai-07	68432332,2
juin-07	61622715,9
juil-07	53188007,4
août-07	46160662,5
sept-07	46256300,4
oct-07	54426021,6
nov-07	66105614,1
déc-07	101663398

La consommation du gaz naturel en 2007 pour la distribution publique région Sud diminuera de 5.63 % par rapport à 2006.

3.4 Application de la méthode de Box & Jenkins

Dans ce qui suit nous allons appliquer la méthodologie de Box & Jenkins pour nos trois séries et cela pour effectuer des prévisions allant de janvier 2007 à décembre 2007.

La méthode de prévision de Box & Jenkins à l'instar des méthodes les plus anciennes (traditionnelle, lissage exponentiel) demande un nombre élevé de données, comme nous disposons seulement de 48 observations nous présageons obtenir des prévision de qualité inférieure.

Pour le traitement économétrique de nos séries on utilise le logiciel Eviews 4.1

3.4.1 Etude de la série nord :

3.4.1.1 Analyse du corrélogramme :

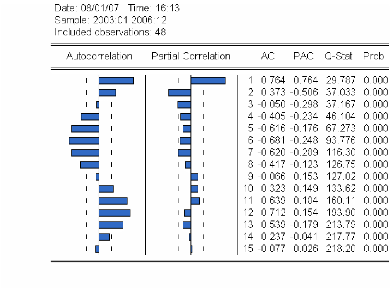
Comme nous le voyons sur le corrélogramme, la sérié initiale (nord) n'est pas stationnaire, on remarque plusieurs pics significatifs qui se répètent, il existe donc une forte saisonnalité, il convient alors de la désaisonnaliser à l'aide de l'opérateur de désaisonnalisation de Box & Jenkins 12

1 - ~ ) et de générer une nouvelle série « nordsa » telle que : nordsa (t) = 12

1 - ~ ) nord (t) = nord (t) - nord (t-12).

Cette méthode pour désaisonnaliser à un grand désavantage surtout dans notre cas, car elle nous fera perdre 12 observations ce qui fait que par la suit nous allons travailler avec 36 observations ce qui laisse à désirer sur la qualité de nos prévisions.

Après avoir effectuer la désaisonnalisation sur la série « nord » nous obtenons le corrélogramme suivant :

Nous remarquons bien sur le corrélogramme de la nouvelle série « nordsa » que l'effet saisonnier à disparu. Nous allons maintenant étudier la stationnarité de la série « nordsa ».

3.4.1.2 Etude de la stationnarité de la série « nordsa » : Le test de Dickey-Fuller :

Choix du nombre de retards optimal :

Avant de pouvoir appliquer le test de Dickey-Fuller, nous devons déterminer le nombre de retards p qui minimise les critères d'Akaike et Schwartz pour les trois modèles (avec tendance et constante (trend and intercept), avec constante (intercept), sans tendance ni constante (none)).

Les valeurs des critères d'Akaike et Schwartz sont fournies par le logiciel Eviews et sont résumées dans le tableau suivant :

Tableau 3.10- Critères d'Akaike et Schwartz pour la série nordsa

Modèles / Retards		0	1	2	3	4
MODELE 3	AIK	41.16626	41.16441	41 .25871	41 .27472	41 .26160
	SC	41.30093	41.34580	41.48773	41.55226	41.58854
MODELE 2	AIK	41.12688	41.10688	41.20017	41.21089	41.20407
	SC	41.21666	41.24292	41.38339	41.44218	41.48431
MODELE 1	AIK	41.06859	41.05299	41.14436	41.16120	41.14990
	SC	41.11348	41.14368	41.28177	41.34623	41.38343

D'après le tableau (3.10) nous constatons que le critère d'Akaike est minimisé pour les trois modèles pour un nombre de retard p = 1 tandis que le critère de Schwartz est minimisé pour p = 0. En suivant le principe de parcimonie nous retiendrons le nombre de retards qui permet

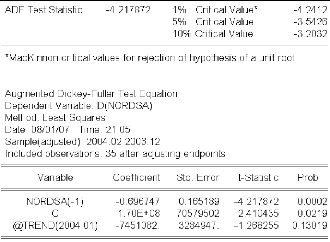
d'estimer le minimum de paramètres c'est-à-dire p = 0. Dans ce cas on utilise le test de Dickey-Fuller simple (DF), donc il n'y a pas d'autocorrélation des erreurs.

Le test de Dickey-Fuller simple :

On commence par tester la présence d'une racine unitaire à partir du modèle le plus général à savoir le modèle (3) incluant une constante et un trend :

A nordsa (t) = p nordsa (t - 1)+c+bt .

On test alors l'hypothèse nulle Ho : p = o de présence de racine unitaire (la série n'est pas stationnaire) contre l'hypothèse alternative de stationnarité H1 : p ? 0 .

Eviews nous fournit les résultats suivants :

La réalisation de Mckinnon pour le modèle (3) tp^, = -4.217872 est inférieure à la valeur
tabulée Cem = -3.5426, on rejette donc l'hypothèse nulle d'existence de racine unitaire au seuil a= 5%.

A présent nous allons tester la significativité du coefficient b de la tendance par un simple test de Student.

D'après les résultats précédents, le coefficient de la tendance b n'est pas significativement différent de 0 puisque la statistique calculée de Student égale à -1.268255 est inférieure à 1.96, donc le modèle (3) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (2) qui ne comprend qu'une constante : A nordsa (t) = p nordsa (t - 1) + c + å t

Les résultats d'estimation du modèle (2) sont résumés ci-dessous :

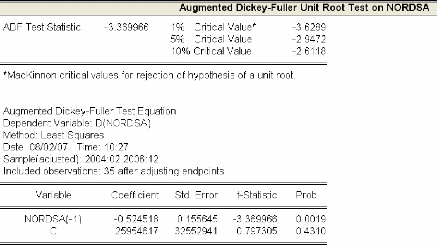
On rejette l'hypothèse nulle de présence de racine unitaire puisque tp~ = -3.369966 est

inférieure à la valeur tabulée du modèle (2) Cô.05 = -2.9472 au seuil a = 5%.

Dans ce cas on va tester la nullité du coefficient c de la constante. La présence d'une constante est rejetée puisque la statistique de Student calculée égale à 0.797305 est inférieure à 1.96 ce qui veut dire que le modèle (2) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (1) qui ne comprend ni constante ni trend :

A nordsa (t) = p nordsa (t - 1) + å t

Les résultas sont les suivants :

La réalisation de Mckinnon au seuil a= 5% ( tp~ = -3.295387) est inférieure à la valeur tabulée

(

1 .o5= -1.9507), donc nous pouvons conclure que la série « nordsa » est stationnaire. 3.4.1.3 Identification et estimation du modèle :

Comme notre série initiale « nord » est affectée d'une saisonnalité de période s =12 nous allons la modéliser par un modèle SARIMA (p, d, q) * (P,D,Q)12.

Pour identifier l'ordre des paramètres du modèle SARIMA nous allons nous référer au corrélogramme de la série « nordsa ».

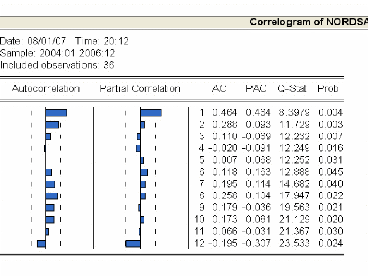
D'après le corrélogramme on peut identifier les modèles : SARIMA (1,0,1) * (1,1, ₀₎₁₂ , SARIMA (1,0,1) * (1,1,1)12 , SARIMA (1,0, 2) * (1, 1,0)12 .

D'après l'estimation des modèles identifiés précédemment qui sont représentés dans l'annexe C2 tableaux C.2.2 et C.2.3 les modèles SARIMA (1,0,1) * (1,1,1)12 et SARIMA (1,0,2) * (1, 1,0)12 ne sont pas valides, leurs coefficients ne sont pas significatifs tandis que les coefficients du modèle SARIMA (1,0,1) * (1, 1,0)12 (annexe C2 tableau C.2.1) sont significativement différents de 0. Il convient maintenant d'analyser le résidu de ce modèle afin de le valider.

3.4.1.4 Validation du modèle :

Le modèle estimé SARIMA (1,0,1)* (1,1,0)12 est de bonne qualité si son résidu se comporte comme un bruit blanc normal, c'est-à-dire que le résidu doit être non autocorrélé et normal.

Test d'autocorrélation du résidu (test de Ljung-Box) :

On test l'hypothèse nulle d'absence d'autocorrélation du résidu H0 : ñ1 = p2 = = p12 = 0 contre l'hypothèse alternative H1 : il existe au moins un ñi significativement différent de 0 .

Le corrélogramme du résidu du modèle estimé est représenté ci-dessous :

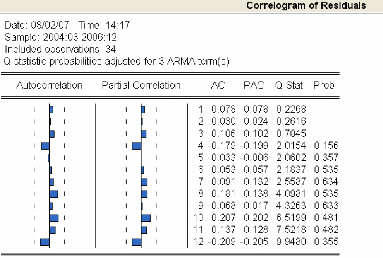
Le corrélogramme du résidu ne fait apparaître aucun terme en dehors de l'intervalle de confiance au seuil a= 5% (aucun terme n'est significatif) et la statistique de Ljung-Box Q = 9.9480 est inférieure à la valeur tabulée du khi-deux à 9 degrés de liberté A = 16.919, on accepte donc l'hypothèse nulle de non autocorrélation du résidu ce qui implique que le résidu peut être assimilé à un bruit blanc.

Test de normalité du résidu (test de Jarque et Bera) :

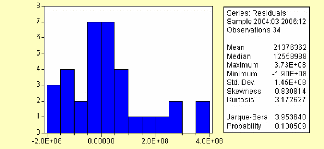
La statistique de Jarque et Bera S = 3.953640 est inférieure à la valeur tabulée du khi-deux à 2 degrés de liberté A = 5.991 au seuil a= 5%.

Donc notre résidu forme bien un bruit blanc normal.

On conclut que le modèle SARIMA (1,0,1) * (1,1,0)12 est valide et peut s'écrire :

(1 - 0B)(1 - 0'B¹²)(1 - Br (1 - B¹²)¹nord(t) = (1 - BB)E_t

(1 +1.040145B)(1 - 0.526545B¹²)(1 - B¹²)nord(t) = (1 - 1.340138B)E_t

3.4.1.5 Prévision :

La série « nord » a été modélisée par un processus SARIMA (1,0,1) * (1,1,0)12 qui s'écrit comme suit :

nord(t) = -1.040145nord(t-1) + 1.525645nord(t-12)+1.587828nord(t-13)- 0.525645nord(t-24)- 0.547683nord(t-25)- 1.340138 _åt-1 +E_t .

On calcul les prévisions pour 12 mois allant de janvier à décembre 2007. Pour la première valeur prévue on a :

nord 01_,2007 = -1.040145nord 12, 2006 + 1.525645nord01,2006 +1.587828nord _12,2005 - 0.525645nord 01, 2005 -0.547683nord 12, 2004 - 1.340138 E12_,2006 + E01_,2007 .

Le terme résiduel futur est inconnu, donc on va le considérer égale à 0 : E01_,2007 = 0.

nord 01_,2007 = -1.040145 (2 092 195 557)+ 1.525645(2 491 665 080)+1.587828(2 228 136 137)

- 0.525645 (2 431 015 764)-0.547683 (2 024 839 461)- 1.340138 (-2.6E+07)

nord 01_,2007 = 2811128725.

Les résultats des prévisions sont présentés dans le tableau suivant :

Tableau 3.10 -Prévision par la méthode de Box & Jenkins sur la consommation du gaz
naturel région nord.

mois (2007)	nord (t+h)
janv-07	2811128725
févr-07	1754127972
mars-07	1954664661
avr-07	425096492
mai-07	1133399104
juin-07	393505180
juil-07	994013944
août-07	256946608
sept-07	1055081082
oct-07	275100101
nov-07	1245108030
déc-07	1577538010

La consommation du gaz naturel en 2007 pour la distribution publique région nord diminuera de 4.32% par rapport à 2006.

3.4.2 Etude de la série Hauts Plateaux (HP) : 3.4.2.1 Analyse du corrélogramme :

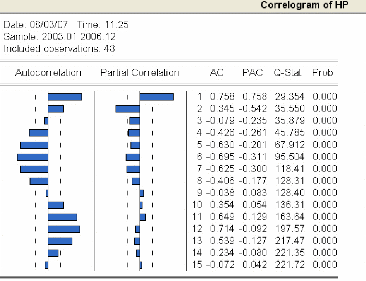
A partir du corrélogramme, nous constatons que la série « HP » n'est pas stationnaire, on remarque plusieurs pics significatifs, la série est donc saisonnière, nous devons la désaisonnaliser avec l'opérateur de désaisonnalisation. Nous obtenons alors une nouvelle série « HPsa » dont le corrélogramme est le suivant :

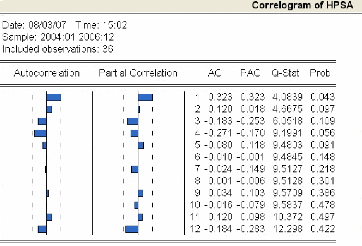
L'effet saisonnier a disparu, passons à présent à l'étape suivante qui est l'étude de la stationnarité.

3.4.2.2 Etude de la stationnarité de la série « HPsa » : Le test de Dickey-Fuller :

Choix du nombre de retards optimal :

Les critères d'information d'Akaike et Schwatz ont été minimisés pour un nombre de retards p = 0 (annexe C1 tableau C. 1.1). Dans ce cas on utilise le test de Dickey-Fuller simple.

Le test de Dickey-Fuller simple :

On commence par estimer le modèle (3), dont les résultats d'estimation sont les suivants :

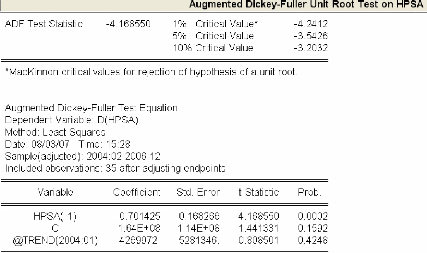
La réalisation de Mckinnon&_ñ = -4.168550 est inférieure à la valeur tabulée ~

~ O~O5 = -3.5426,

on rejette donc l'hypothèse nulle d'existence de racine unitaire au seuil á = 5%.

On test maintenant la nullité du coefficient b de la tendance. D'après les résultats d'estimation ce coefficient n'est pas significativement différent de 0 puisque la statistique calculée de Student égale à -0.808501 est inférieure à 1.96, donc le modèle (3) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (2) dont les résultas sont les suivants :

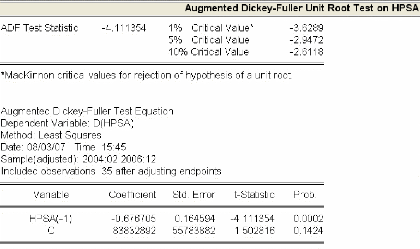
On rejette l'hypothèse nulle de présence de racine unitaire puisque&_ñ = -4.111354 est inférieure à la valeur tabulée du modèle (2) ~

C O5 = -2.9472 au seuil á = 5%.

La constante C n'est pas significative car la statistique de Student calculée égale à 1.502816 est inférieure à 1.96 ce qui veut dire que le modèle (2) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (1).

La réalisation de Mckinnon au seuil á= 5% (&_ñ = -3.758273) est inférieure à la valeur tabulée

(

~ C .05 = -1.9507), donc nous pouvons conclure que la série « HPsa » est stationnaire.

3.4.2.3 Identification et estimation du modèle :

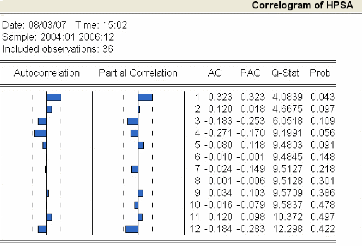
D'après le corrélogramme on peut identifier les modèles suivants : SARIMA(1,0,1)* (1,1, ⁰)12, SARIMA (1,0,1) * (0,1,2)12 , SARIMA (1,0,1) * (1, 1, ₂₎₁₂ .

Le modèle SARIMA (1,0,1) * (1,1,2)12 n'est pas valide, ces coefficients ne sont pas significatifs (annexe C2 tableau C.2.6), par contre les coefficients estimés des modèles SARIMA (1,0,1) * (1,1, ₀₎₁₂ et SARIMA (1,0,1) * (0,1,2)12 sont significatifs (annexe C2 tableaux C.2.4 et C.2.5). On applique les critères de pouvoir prédictif pour choisir entre ces deux modèles :

Tableau 3.11- Critères de pouvoir prédictif HPsa

Critères	R^2	SCR	AIK	SC
SARIMA (1,0,1)*(1,1,0)	0.103106	3.07E+18	42.05644	42.19112
SARIMA (1,0,1)*(0,1,2)	0.251307	2.63E+18	41.92433	42.10208

On opte pour le modèle SARIMA (1,0,1) * (0,1,2)12 du fait qu'il donne les plus petites valeurs du AIK et SC et du critère SCR et un plus grand R² .

3.4.2.4 Validation du modèle :

Test d'autocorrélation du résidu (test de Ljung-Box) :

Le corrélogramme du résidu de la série « HPsa » est représenté ci-dessous :

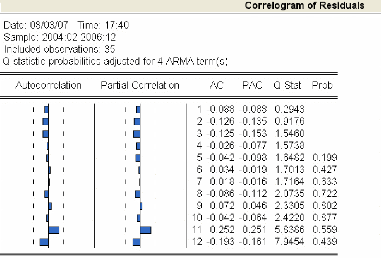
Le corrélogramme du résidu ne fait apparaître aucun terme en dehors de l'intervalle de confiance au seuil a = 5% et la statistique de Ljung-Box Q = 7.9454 est inférieure à la valeur tabulée du khi-deux à 8 degrés de liberté A = 15.507. Donc le résidu forme bien un bruit blanc.

Test de normalité du résidu (test de Jarque et Bera) :

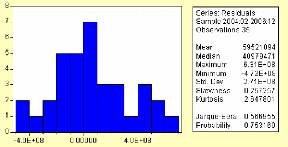
La statistique de Jarque et Bera S = 0.566955 est inférieure à la valeur tabulée du khi-deux à 2 degrés de liberté A = 5.991 au seuil a= 5%.

Donc notre résidu forme bien un bruit blanc normal.

On conclut que le modèle SARIMA (1,0,1)* (0,1,2)12 est valide et peut s'écrire :

(1 - OB)(1 - B)⁰ (1 - B¹²)¹ HP (t) = (1 - BB) (1 - B1B¹² - B2B²⁴)e_t .

(1 + 0.587746B)(1 - B¹²)HP(t) = (1 - 0.997493B)(1 - 0.169309B¹² - 0.610933B²⁴ )et .

3.4.2.5 Prévision :

La série « HP » a été modélisée par un processus SARIMA(1,0,1)* (0,1,2)12 qui s'écrit comme suit :

HP(t) = -0.587746HP(t-1) + HP(t-12) + 0.587746HP(t-13) - 0.997493 _Et-1 - 0.169309 Et_12+ 0.168884 Et_13 - 0.610933 _Et-24 + 0.609401 Et_25 + Et

Les résultats des prévisions sont présentés dans le tableau suivant :

Tableau 3.12 -Prévision par la méthode de Box & Jenkins sur la consommation du gaz
naturel région HP.

mois (2007)	HP (t+h)
janv-07	4127926249
févr-07	3706058639
mars-07	2549155013
avr-07	1092425308
mai-07	667040044
juin-07	742354688
juil-07	472133847
août-07	590249808
sept-07	566840838
oct-07	836848416
nov-07	2016070538
déc-07	3871507607

La consommation de gaz naturel en 2007 pour la distribution publique région HP diminuera de 0.16% par rapport à 2006.

3.4.3 Etude de la série sud :

3.4.3.1 Analyse du corrélogramme :

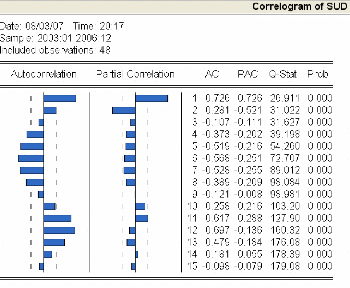
Le corrélogramme nous indique que la série « sud » n'est pas stationnaire, elle est affectée d'une saisonnalité. Nous devons procéder à sa désaisonnalisation. Nous obtenons alors une nouvelle série « sudsa », son corrélogramme est le suivant :

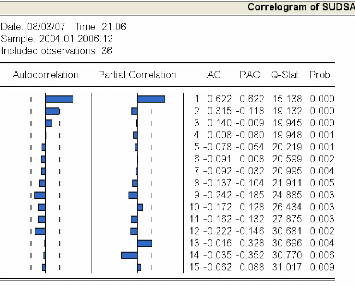
3.4.3.2 Etude de la stationnarité de la série « sudsa » : Le test de Dickey-Fuller :

Choix du nombre de retards optimal :

Les critères d'information d'Akaike et Schwatz ont été minimisés pour un nombre de retards p = 0 (annexe C. 1 tableau C. 1.2). Dans ce cas on utilise le test de Dickey-Fuller simple.

Le test de Dickey-Fuller simple :

On commence par estimer le modèle (3), dont les résultats d'estimation sont les suivants :

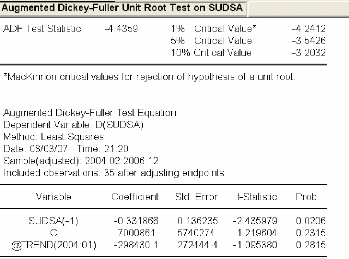
La réalisation de Mckinnon&_ñ = -4.43 59 est inférieure à la valeur tabulée ~

~ O~O5 = -3.5426, on rejette donc l'hypothèse nulle d'existence de racine unitaire au seuil á = 5%.

Le coefficient b de la tendance n'est pas significatif, la statistique calculée de Student égale à -1.095380 est inférieure à 1.96, donc le modèle (3) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (2) dont les résultas sont les suivants :

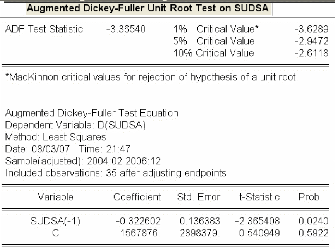
On rejette l'hypothèse nulle de présence de racine unitaire puisque &ñ = -3.3 6540 est inférieure à la valeur tabulée du modèle (2) ~

C O~O5 = -2.9472 au seuil á = 5%.

La constante C n'est pas significative car la statistique de Student calculée égale à 0.540949 est inférieure à 1.96 ce qui veut dire que le modèle (2) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (1).

La réalisation de Mckinnon au seuil á= 5% (&_ñ = -2.336270) est inférieure à la valeur tabulée

(

~ C O~O5 = -1.9507), donc nous pouvons conclure que la série « sudsa » est stationnaire. 3.4.3.3 Identification et estimation du modèle :

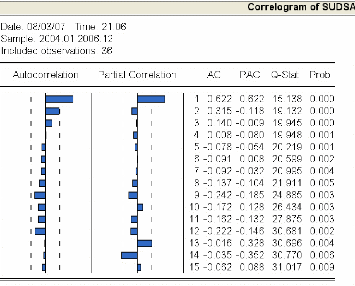
D'après le corrélogramme on peut identifier les modèles suivants : SARIMA (1,0,2) * (1,1, ⁰)12, SARIMA (1,0,2) * (0,1,2)12 , SARIMA (1,0,2) * (2,1,0)12 .

Les coefficients du modèle SARIMA (1,0,2)* (2,1,0)12 (annexe C.2 tableau C.2.9) ne sont pas significatifs, reste à choisir entre les deux modèles :

Tableau 3.13-Critères de pouvoir prédictif sudsa

Critères	R^2	SCR	AI K	SC
SARIMA(1,0,2)*(1,1,0)	0.461851	7.30E+15	36.07410	36.02405
SARIMA(1,0,2)*(0,1,2)	0.555944	6.80E+15	41.92433	36.24624

On conclut que le meilleur modèle est le modèle SARIMA (1,0,2) * (0,1,2)12 .

3.4.3.4 Validation du modèle :

Test d'autocorrélation du résidu (test de Ljung-Box) :

Le corrélogramme du résidu de la série « sudsa » est représenté ci-dessous :

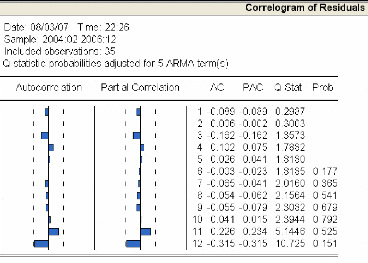
On remarque que tous les coefficients d'autocorrélation sont nuls, tous les termes sont à
l'intérieur de l'intervalle de confiance et la statistique de Ljung-Box Q = 10.725 9454 est
inférieure à la valeur tabulée du khi-deux à 7degrés de liberté xe = 14.067. Donc le résidu

forme un bruit blanc.

Test de normalité du résidu (test de Jarque et Bera) :

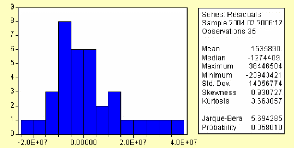
La statistique de Jarque et Bera S = 5.694285 est inférieure à la valeur tabulée du khi-deux à 2 degrés de liberté A = 5.991 au seuil a= 5%.

Donc notre résidu forme bien un bruit blanc normal.

On conclut que le modèle SARIMA (1, 0, 2) * (0,1, ₂₎₁₂ est valide et s'écrit :

(1 - OB)(1 - Br (1 - B^12)^1sud(t) = (1	- te - 02B^2) (1 - «B^12 -	0^24)Et
(1 + 0.469969B) (1 - B^12)sud(t) = (1 -	1.768860B - 0.943874B^2)	(1 + 0.279024B^12 -	0.632610B^24)Et

3.4.3.5 Prévision :

sud (t) = -0.469969sud(t- 1 )+sud(t- 1 2)+0.469969sud(t- 13)-1 .768860 Et - 1 -0.943874 Et - 2 + 0.279024 Et - 12 -0.493554 _Et-13 -0.895973 _Et-24 +1.118998 _Et-25 +0.597104 _Et-48 + Et

Tableau 3.14- Prévision par la méthode de Box & Jenkins sur la consommation du gaz
naturel région sud

mois (2007)	sud (t+h)
janv-07	265445183
févr-07	218658909
mars-07	123004612
avr-07	50952777
mai-07	75601628
juin-07	1571968
juil-07	108397826
août-07	63105743
sept-07	57476122
oct-07	62346570
nov-07	112732432
déc-07	131246130

La consommation du gaz naturel en 2007 pour la distribution publique région sud augmentera de 5.37 % par rapport à 2006.

3.4.4 Comparaison des résultats des méthodes de prévision :

La comparaison des résultats prévisionnels obtenus par les trois méthodes de prévision à savoir la méthode traditionnelle, la méthode de lissage exponentiel et la méthode de Box & Jenkins est basée sur la racine carrée de l'erreur quadratique moyenne RMSE telle que :

n

RMSE = 2

1 ~ ~ ~

? -

y y

t t

n 1

t=

ou y~t est la valeur prévue à l'instant t et

yt est la valeur réelle observée à l'instant t

Une méthode est jugée plus appropriée qu'une autre (ses résultats prévisionnels sont plus fiables) si son RMSE est plus petit par rapport à celui de l'autre méthode.

Faute de données réelles pour l'année 2007, le RMSE a été calculé à partir des valeurs prévues pour l'année 2006 obtenues à partir du modèle réestimé pour la circonstance.

Pour les trois série nord, Hauts Plateaux, sud la comparaison entre les prévisions et les valeurs réelles est représentée dans les tableaux suivants :

Pour le nord :

Tableau 3.15- Comparaison des résultats de prévision région nord

Méthode de Box & Jenkins

Méthode de lissage exponentiel de HW¹

Méthode traditionnelle

nord

Dates

janv-06 2 491 665 080
févr-06 2 153 245 146
mar-06 1 699 279 034

avr-06 904 128 877

mai-06 814 064 677

juin-06 724 000 478

juil-06 633 091 584

août-06 633 088 875

sept-06 667 852 433

oct-06 702 615 991

nov-06 986 852 808

déc-06 2 092 195 557

RMSE

Valeurs prévues		écart		Valeurs réelles
2227810749		-263854331		2 491 665 080
2011107582		-142137563,8		2 153 245 146
1617970137		-81308896,87		1 699 279 034
1112521661		208392783,1		904 128 877
861414652,5		47349975,47		814 064 677
676132618,4		-47867859,36		724 000 478
619624426,5		-13467157,5		633 091 584
595776024,3		-37312850,74		633 088 875
634349486,3		-33502946,74		667 852 433
712564008,5		9948017,46		702 615 991
1209548804		222695995,8		986 852 808
2047840590		-44354966,68		2 092 195 557
		128695419
Valeurs prévues	écart		Valeurs réelles			Valeurs prévues
2166185637	-325479442,7		2 491 665 080			4587273141
1955187720	-198057425,5		2 153 245 146			2860853970
1488364705	-210914329,3		1 699 279 034			3583864190
1018643974	114515096,9		904 128 877			1207660356
770690843,9	-43373833,13		814 064 677			2064835885
600307379,7	-123693098,1		724 000 478			453761200,7
560922861,8	-72168722,16		633 091 584			1628071426
545069638,5	-88019236,46		633 088 875			332817413,8
594940609	-72911823,98		667 852 433			1686471998
682042300,3	-20573690,72		702 615 991			418467931,8
1281910207	295057399,1		986 852 808			2320144777
2045088391	-47107166,29		2 092 195 557			2811377194
	165306916,6

écart

2 095 608 061 707 608 824 1 884 585 156 303 531 478 1 250 771 208 -270 239 277 994 979 842 -300 271 461 1 018 619 565 -284 148 059 1 333 291 969 719 181 637 1105550290

Valeurs
réelles

Pour les Hauts Plateaux :

Tableau 3.16- Comparaison des résultats de prévision région HP

HP

Méthode de Box & Jenkins

Méthode de lissage exponentiel de HW

Méthode traditionnelle

Valeurs prévues		écart		Valeurs réelles
3624401745		-585 764 939		4 210 166 685
3181944494		-443 317 082		3 625 261 575
2318917446		-281 923 594		2 600 841 040
1463823137		442 942 396		1 020 880 741
903574331,3		87 947 083		815 627 248
600946365,3		-10 027 390		610 973 755
536897429,1		7 832 719		529 064 711
535935581,3		-14 059 305		549 994 887
607108797		-36 008 135		643 116 932
773396594,8		37 157 617		736 238 978
2189330434		92 163 679		2 097 166 755
3511244893		-321 749 925		3 832 994 818
Valeurs prévues	écart		Valeurs réelles			Valeurs prévues
3741211325	-468 955 360		4 210 166 685			3024169222
3276178772	-349 082 803		3 625 261 575			4097659433
2458791569	-142 049 471		2 600 841 040			2130613042
1938996926	918 116 185		1 020 880 741			1590575581
1253257299	437 630 051		815 627 248			312964275
975390662,4	364 416 907		610 973 755			730815079
935322262,9	406 257 552		529 064 711			478230399
955474412,1	405 479 525		549 994 887			447510501
1020614664	377 497 732		643 116 932			451348269
1215668073	479 429 095		736 238 978			875978208,6
2577283523	480 116 768		2 097 166 755			1779364086
3675011720	-157 983 098		3 832 994 818			3669542378

Dates

janv-06 4 210 166 685

févr-06 3 625 261 575
mar-06 2 600 841 040

avr-06 1 020 880 741

mai-06 815 627 248

juin-06 610 973 755

juil-06 529 064 711

août-06 549 994 887

sept-06 643 116 932

oct-06 736 238 978

nov-06 2 097 166 755
déc-06 3 832 994 818

écart

-1 185 997
463

472 397 858 -470 227 998 569 694 840 -502 662 973 119 841 324 -50 834 312 -102 484 386 -191 768 663 139 739 231 -317 802 669 -163 452 440

RMSE 279600632 455201371,8 469001865

Valeurs
réelles

¹Holt-Winters

Pour le sud :

Tableau 3.17- Comparaison des résultats de prévision région sud

sud Dates janv-06 févr-06 mar-06 avr-06 mai-06 juin-06 juil-06 août-06 sept-06 oct-06 nov-06 déc-06 RMSE	Méthode traditionnelle
	Valeurs réelles	Valeurs prévues	écart
	253 940 738	210767140,1	-43 173 598
	186 869 959	158901274,7	-27 968 684
	108 213 521	105400669	-2 812 852
	62 494 535	70143160,02	7 648 625
	57 757 631	57552908,97	-204 722
	53 020 728	49788337,73	-3 232 390
	43 638 402	43759235,5	120 833
	45 421 698	42816145,59	-2 605 552
	52 637 649	50903027,17	-1 734 622
	59 853 601	63413739,92	3 560 139
	95 080 405	97601215,67	2 520 811
	186 861 187	188331955,1	1 470 768
			15149574,7

Méthode de lissage exponentiel de HW

Valeurs réelles			Valeurs prévues		écart		Valeurs réelles
253	940	738	196680030,7	-57	260	707	253	940	738
186	869	959	240929480,9	54	059	522	186	869	959
108	213	521	187141401,8	78	927	881	108	213	521
62	494	535	131266717,1	68	772	182	62	494	535
57	757	631	91503781,54	33	746	151	57	757	631
53	020	728	72533387,87	19	512	660	53	020	728
43	638	402	61342740,03	17	704	338	43	638	402
45	421	698	57094233,57	11	672	536	45	421	698
52	637	649	54067347,2	1	429	698	52	637	649
59	853	601	65686590,52	5	832	990	59	853	601
95	080	405	82479382,19	-12	601	023	95	080	405
186	861	187	119215224,8	-67	645	962	186	861	187

Méthode de Box & Jenkins

Valeurs prévues		écart
166201150	-87	739	588
178795900	-8	074	059
100552525	-7	660	996
140860818	78	366	283
43669290	-14	088	341
31286413	-21	734	315
7778789	-35	859	613
77476022	32	054	324
41822308	-10	815	341
51515563	-8	338	038
85150135	-9	930	270
280964211	94	103	024

44628570,77 46626287,4

Ainsi les RMSE des trois méthodes de prévision sont résumées dans le tableau suivant :

Tableau 3.18- Comparaison des RMSE des méthodes de prévision

Séries/ RMSE	RMSE1	RMSE2	RMSE3
nord	128695419	165306917	1105550290
HP	279600632	455201372	469001865
sud	15149575	44628570,8	46626287,4

Où RMSE1, RMSE2 et RMSE3 sont associées à la méthode traditionnelle, la méthode de lissage exponentiel et la méthode de Box & Jenkins respectivement.

Pour les trois série ; nord, Hauts Plateaux, sud RMSE1< RMSE2 < RMSE3, ce qui veut dire que la méthode traditionnelle est la méthode de prévision la plus fiable et la plus proche de la réalité dans notre cas.

Les prévisions obtenues par cette méthode sont en harmonie avec l'allure générale des séries étudiées puisque le phénomène de périodicité est reproduit mais avec une légère baisse.

En ce qui concerne les deux autres méthodes, les résultats obtenus sont loin de la réalité.

La méthode de lissage exponentiel de Holt-Winters a sous-estimé la consommation du gaz naturel pour le nord et l'a surestimée pour les Hauts Plateaux et le sud.

La méthode de Box & Jenkins est celle qui a donné les plus mauvaises prévisions, en effet l'écart entre les valeurs prévues et les valeurs réelles est assez important. Elle a surestimé la consommation du gaz pour le nord et l'a sous-estimée pour les Hauts Plateaux et le sud.

Conclusion générale

Le gaz naturel représente une des sources d'énergie, les plus utilisées dans le monde, voir la plus prometteuse puisqu'elle bénéficie avec la montée des préoccupations environnementales d'une considération importante. L'Algérie est un pays producteur et exportateur de cette énergie, il a été donc primordial pour la SONELGAZ, d'analyser et prévoir l'évolution temporelle de la consommation du gaz naturel, afin de comprendre le mécanisme qui gère cette consommation et de tirer par la suite des informations pertinentes qui serviront à la phase de prise de décisions.

Notre étude a porté sur l'analyse des séries chronologiques représentant l'évolution de la consommation mensuelle du gaz naturel pour la distribution publique. Dans la phase descriptive, nous avons remarqué que la consommation du gaz naturel pour la distribution publique est directement liée aux facteurs météorologiques. Partant de ce principe nous avons découpé le territoire algérien en trois zones : le nord, les hauts plateaux et le sud. Ce qui voulait dire que nous allions étudier trois séries chronologiques, chacune d'elle comprenant 48 observations.

En premier lieu nous avons appliqué la méthode de prévision traditionnelle. En suivant le principe de cette méthode, nous avons décomposer nos série en trois composantes : la tendance, les variations saisonnières et les variations accidentelles. Pour le nord et les hauts plateaux, le schéma de décomposition était de type additif, tant dis que pour le sud, il était de type multiplicatif. Après estimation de ces composantes, on a pu de façon très simple effectuer nos prévisions pour l'année 2007.

En second lieu, nous allions appliquer l'unes des méthodes de prévision de lissage exponentiel (simple, double, Holt-Winters additive, Holt-Winters multiplicative). Après des tests adéquats, nous avons opté pour la méthode Holt-Winters additive pour le nord et les hauts plateaux et la méthode de Holt-Winters multiplicative pour le sud. Apres avoir estimé les paramètres de lissage, nous avons pu aisément réaliser nos prévisions.

Enfin la méthode de Box & Jenkins a été appliquée sur nos données. Comme nos trois séries étaient affectées d'une forte saisonnalité, nous étions donc obligé de les désaisonnaliser à l'aide l'opérateur de désaisonnalisation, mais cette méthode nous avait fait perdre 12 observations, ce qui voulait dire que nous allions travailler par la suite avec de nouvelles séries contenant chacune d'elle 36 observations. Après avoir effectué la désaisonnalisation, les séries obtenues étaient stationnaires, nous avons donc choisi de les modéliser par les modèles SARIMA étant donné la présence de saisonnalité. Une fois le modèle choisi, estimé et validé, nous avons calculé nos prévisions.

Après avoir obtenu les résultats de prévision par les trois méthodes, nous avons constaté que la méthode la plus simple et la plus facile à mettre en oeuvre à savoir la méthode traditionnelle, avait donné les prévisions les plus fiables et les plus proches de la réalité, tant dis que les méthodes de lissage exponentiel et de Box & Jenkins avaient donné des prévisions de mauvaises qualités. La méthode de Box & Jenkins, malgré sa supériorité théorique par rapport aux deux autres méthodes a donné les prévisions les moins proches de la réalité, ce qui était prévisible, puisque nous avions travailler avec 36 observations et cette méthode requière au minimum une cinquantaine d'observations pour donner des prévisions de bonnes qualités.

Prévoir le comportement futur d'une série chronologique, nécessite l'utilisation pas d'une mais de plusieurs méthodes de prévision, car nous avons constaté que la fiabilité d'une

méthode de prévision, ne dépendait pas seulement de sa complexité théorique, mais aussi des données, de l'information disponible et du champs d'application.

Cependant si le nombre de données était plus élevé les résultats seraient sans doute différents, la méthode de Box & Jenkins avait donné des prévisons de mauvaises qualités étant donné le manque d'observations.

Toutefois, il serai intéressant de faire une étude explicative sur la consommation du gaz naturel pour la distribution publique, en utilisant une méthode de prévision économétrique incluant comme variables explicatives : les facteurs météorologiques, le nombre d'abonnés, le taux de pénétration du gaz naturel... etc.

Bibliographie

Bibliographie :

1- PY B., Statistique descriptive, Nouvelle méthode pour bien apprendre et réussir. 4éme édition. Ed. ECONOMICA, Paris, 1999.

2- BOURBOUNNAIS R., TERRAZA M., Analyse des séries temporelles en Economie, Ed. PUF, juin 1998.

3- BOURBOUNNAIS R., TERRAZA M., Analyse des séries temporelles, Application à l'économie et à la gestion, Ed. DUNOD, Paris, 2004.

4- BOURBOUNNAIS R., Econométrie, 3éme édition. Ed. DUNOD, Paris, 2000. Sites et adresses web :

1- www.sonelgaz.dz

2- www.wikipedia.org

3- http://www.unige.ch/ses/sococ/eda/bernard/box.pdf

Dur, dur ! Les séries chronologiques, RAPACCHI B., Centre Interuniversitaire de Calcul de Grenoble, 1993.

4- http://lumimath.univ-mrs.fr/~boutahar/AE2PRO.pdf

Master M2-AE2 PRO, Econométrie Bancaire et Financière, Analyse des séries chronologiques, BOUTAHAR M., octobre 2005.

5- http://www.unctad.org/infocomm/francais/gaz/descript.htm

Annexe A : Méthode traditionnelle

Tableau A1- Calcul des composantes de la série nord

Dates	y (nord)				~	S			S~	~ y (CVS)				å			y
janv-03	1	963	751	471	1174389050	789	362	421	1036506605		927	244	866	-247	144	183	2210895654
févr-03	1	813	699	681	1174858913	638	840	768	819333574		994	366	107	-180	492	806	1994192487
mars-03	1	323	756	619	1175328777	148	427	842	425726265		898	030	354	-277	298	423	1601055042
avr-03	1	088	519	916	1175798641	-87	278	725	-80192075	1	168	711	991	-7	086	650	1095606566
mai-03		713	831	545	1176268505	-462	436	960	-331768947	1	045	600	492	-130	668	013	844499558
juin-03		575	936	413	1176738368	-600	801	956	-517520845	1	093	457	257	-83	281	111	659217524
juil-03		526	357	244	1177208232	-650	850	988	-574498900	1	100	856	144	-76	352	088	602709332
août-03		514	482	788	1177678096	-663	195	308	-598817166	1	113	299	954	-64	378	142	578860929
sept-03		552	839	073	1178147959	-625	308	886	-560713568	1	113	552	641	-64	595	318	617434391
oct-03		688	574	175	1178617823	-490	043	648	-482968910	1	171	543	085	-7	074	738	695648914
nov-03	1	020	927	504	1179087687	-158	160	183	13546022	1	007	381	482	-171	706	205	1192633709
déc-03	1	812	361	016	1179557551	632	803	465	851367945		960	993	071	-218	564	480	2030925495
janv-04	1	990	980	491	1180027414	810	953	077	ÓSj=0		954	473	886	-225	553	528	2216534019
févr-04	1	700	081	599	1180497278	519	584	321			880	748	025	-299	749	253	1999830852
mars-04	1	610	123	737	1180967142	429	156	595		1	184	397	471	3	430	329	1606693407
avr-04	1	223	551	984	1181437006	42	114	978		1	303	744	059	122	307	053	1101244931
mai-04	1	037	802	844	1181906869	-144	104	026		1	369	571	791	187	664	921	850137923
juin-04		683	327	686	1182376733	-499	049	047		1	200	848	531	18	471	798	664855888
juil-04		646	673	662	1182846597	-536	172	935		1	221	172	562	38	325	965	608347697
août-04		572	905	389	1183316461	-610	411	071		1	171	722	556	-11	593	905	584499294
sept-04		602	915	806	1183786324	-580	870	519		1	163	629	374	-20	156	951	623072756
oct-04		688	165	645	1184256188	-496	090	543		1	171	134	554	-13	121	634	701287279
nov-04	1	490	974	188	1184726052	306	248	136		1	477	428	166	292	702	114	1198272074
déc-04	2	024	839	461	1185195916	839	643	546		1	173	471	517	-11	724	399	2036563860
janv-05	2	431	015	764	1185665779	1 245	349	985		1	394	509	159	208	843	380	2222172384
févr-05	2	343	573	713	1186135643	1 157	438	070		1	524	240	139	338	104	496	2005469217
mars-05	1	804	890	969	1186605507	618	285	462		1	379	164	704	192	559	197	1612331772
avr-05	1	200	055	675	1187075371	12	980	304		1	280	247	750	93	172	379	1106883296
mai-05		846	129	354	1187545234	-341	415	880		1	177	898	301	-9	646	933	855776287
juin-05		687	435	707	1188015098	-500	579	391		1	204	956	552	16	941	454	670494253
juil-05		638	545	026	1188484962	-549	939	936		1	213	043	926	24	558	965	613986061
août-05		628	796	855	1188954825	-560	157	970		1	227	614	021	38	659	196	590137659
sept-05		679	960	443	1189424689	-509	464	246		1	240	674	011	51	249	322	628711121
oct-05		737	070	033	1189894553	-452	824	520		1	220	038	943	30	144	390	706925643
nov-05	1	305	610	525	1190364417	115	246	108		1	292	064	503	101	700	086	1203910439
déc-05	2	228	136	137	1190834280	1 037	301	857		1	376	768	192	185	933	912	2042202225
janv-06	2	491	665	080	1191304144	1 300	360	936		1	455	158	475	263	854	331	2227810749
févr-06	2	153	245	146	1191774008	961	471	138		1	333	911	572	142	137	564	2011107582
mars-06	1	699	279	034	1192243872	507	035	162		1	273	552	769	81	308	897	1617970137
avr-06		904	128	877	1192713735	-288	584	858			984	320	952	-208	392	783	1112521660
mai-06		814	064	677	1193183599	-379	118	922		1	145	833	624	-47	349	975	861414652
juin-06		724	000	478	1193653463	-469	652	985		1	241	521	322	47	867	860	676132618
juil-06		633	091	584	1194123327	-561	031	743		1	207	590	484	13	467	158	619624426
août-06		633	088	875	1194593190	-561	504	315		1	231	906	041	37	312	851	595776024
sept-06		667	852	433	1195063054	-527	210	621		1	228	566	001	33	502	947	634349486
oct-06		702	615	991	1195532918	-492	916	927		1	185	584	901	-9	948	017	712564008
nov-06		986	852	808	1196002782	-209	149	974			973	306	786	-222	695	996	1209548804
déc-06	2	092	195	557	1196472645	895	722	912		1	240	827	612	44	354	967	2047840590

Tableau A2- Calcul des composantes de la série HP

Dates	y (HP)	~	S	S~	~ y (CVS)	å	y
janv-03	3 032 793 861	1526982439	1 505 811 422	1958354344	1 074 439 517	-452 542 922	3485336783
févr-03	2 696 191 658	1530845355	1 165 346 303	1512034177	1 184 157 481	-346 687 873	3042879531
mars-03	1 991 305 173	1534708270	456 596 903	645144213	1 346 160 960	-188 547 311	2179852484
avr-03	1 432 256 702	1538571186	-106 314 484	-213813011	1 646 069 713	107 498 527	1324758175
mai-03	619 068 546	1542434102	-923 365 556	-777924733	1 396 993 279	-145 440 823	764509369
juin-03	450 838 212	1546297017	-1 095 458 805	-1084415614	1 535 253 826	-11 043 191	461881403
juil-03	404 805 128	1550159933	-1 145 354 805	-1152327466	1 557 132 594	6 972 661	397832467
août-03	402 111 206	1554022848	-1 151 911 643	-1157152229	1 559 263 435	5 240 587	396870619
sept-03	431 526 933	1557885764	-1 126 358 831	-1089841929	1 521 368 862	-36 516 902	468043835
oct-03	667 697 672	1561748680	-894 051 008	-927417047	1 595 114 719	33 366 039	634331633
nov-03	1 868 510 063	1565611595	302 898 468	484653876	1 383 856 187	-181 755 409	2050265472
déc-03	2 937 315 402	1569474511	1 367 840 891	1802705420	1 134 609 982	-434 864 529	3372179931
janv-04	3 079 610 801	1573337426	1 506 273 375	ÓSj=0	954473886	-452 080 969	3531691770
févr-04	2 526 369 372	1577200342	949 169 030		1 014 335 195	-562 865 147	3089234519
mars-04	2 058 716 011	1581063258	477 652 753		1 413 571 797	-167 491 460	2226207471
avr-04	1 587 033 428	1584926173	2 107 255		1 800 846 439	215 920 266	1371113162
mai-04	1 271 839 009	1588789089	-316 950 080		2 049 763 741	460 974 653	810864356
juin-04	527 363 068	1592652004	-1 065 288 936		1 611 778 683	19 126 678	508236390
juil-04	465 179 781	1596514920	-1 131 335 140		1 617 507 246	20 992 326	444187454
août-04	433 977 864	1600377836	-1 166 399 972		1 591 130 093	-9 247 742	443225606
sept-04	505 954 400	1604240751	-1 098 286 351		1 595 796 329	-8 444 422	514398822
oct-04	673 604 325	1608103667	-934 499 342		1 601 021 372	-7 082 295	680686620
nov-04	2 422 533 049	1611966583	810 566 467		1 937 879 173	325 912 590	2096620459
déc-04	3 304 231 508	1615829498	1 688 402 010		1 501 526 088	-114 303 410	3418534918
janv-05	3 896 905 709	1619692414	2 277 213 295		1 938 551 365	318 858 951	3578046758
févr-05	3 601 825 444	1623555329	1 978 270 115		2 089 791 267	466 235 938	3135589506
mars-05	2 346 677 635	1627418245	719 259 390		1 701 533 422	74 115 177	2272562458
avr-05	1 536 991 751	1631281161	-94 289 409		1 750 804 763	119 523 602	1417468149
mai-05	629 632 597	1635144076	-1 005 511 479		1 407 557 330	-227 586 747	857219344
juin-05	536 480 500	1639006992	-1 102 526 492		1 620 896 114	-18 110 878	554591378
juil-05	470 410 172	1642869907	-1 172 459 735		1 622 737 638	-20 132 269	490542441
août-05	479 528 443	1646732823	-1 167 204 380		1 636 680 673	-10 052 150	489580594
sept-05	569 706 998	1650595739	-1 080 888 741		1 659 548 927	8 953 188	560753809
oct-05	737 915 480	1654458654	-916 543 175		1 665 332 527	10 873 872	727041607
nov-05	2 090 981 943	1658321570	432 660 373		1 606 328 067	-51 993 503	2142975446
déc-05	3 692 307 919	1662184485	2 030 123 433		1 889 602 499	227 418 013	3464889905
janv-06	4 210 166 685	1666047401	2 544 119 284		2 251 812 341	585 764 940	3624401745
févr-06	3 625 261 575	1669910317	1 955 351 259		2 113 227 399	443 317 082	3181944493
mars-06	2 600 841 040	1673773232	927 067 808		1 955 696 827	281 923 594	2318917446
avr-06	1 020 880 741	1677636148	-656 755 407		1 234 693 753	-442 942 395	1463823137
mai-06	815 627 248	1681499063	-865 871 815		1 593 551 981	-87 947 083	903574331
juin-06	610 973 755	1685361979	-1 074 388 224		1 695 389 370	10 027 391	600946365
juil-06	529 064 711	1689224895	-1 160 160 184		1 681 392 177	-7 832 718	536897429
août-06	549 994 887	1693087810	-1 143 092 924		1 707 147 116	14 059 306	535935581
sept-06	643 116 932	1696950726	-1 053 833 794		1 732 958 861	36 008 135	607108797
oct-06	736 238 978	1700813641	-964 574 664		1 663 656 025	-37 157 617	773396594
nov-06	2 097 166 755	1704676557	392 490 197		1 612 512 878	-92 163 679	2189330433
déc-06	3 832 994 818	1708539473	2 124 455 345		2 030 289 398	321 749 925	3511244893

Tableau A3- Calcul des composantes de la série sud

Dates	ln y (Sud)	~	S	S~	~ y (CVS)	å	y
janv-03	19,0080039	18,1574569	0,850547	0,96358583	18,044418	-0,11303883	19,1210427
févr-03	18,8245054	18,1586103	0,66589506	0,67996153	18,1445439	-0,01406647	18,8385719
mars-03	18,3901533	18,1597638	0,23038953	0,26829394	18,1218594	-0,03790441	18,4280578
avr-03	18,0143811	18,1609173	-0,14653617	-0,14009023	18,1544714	-0,00644594	18,0208271
mai-03	17,7641796	18,1620708	-0,39789119	-0,33907732	18,1032569	-0,05881388	17,8229935
juin-03	17,7144573	18,1632243	-0,44876693	-0,4851547	18,199612	0,03638777	17,6780696
juil-03	17,4911503	18,1643777	-0,67322743	-0,61538627	18,1065366	-0,05784116	17,5489915
août-03	17,5202257	18,1655312	-0,64530552	-0,63832717	18,1585528	-0,00697836	17,527204
sept-03	17,6809958	18,1666847	-0,48568884	-0,46647351	18,1474694	-0,01921533	17,7002112
oct-03	17,8583939	18,1678382	-0,30944428	-0,24786883	18,1062627	-0,06157545	17,9199693
nov-03	18,1155127	18,1689916	-0,05347893	0,18218709	17,9333256	-0,23566602	18,3511787
déc-03	18,8338766	18,1701451	0,6637315	0,83834979	17,9955268	-0,17461829	19,0084949
janv-04	18,9506924	18,1712986	0,77939376	ÓSj=0	17,9871065	-0,18419207	19,1348844
févr-04	18,5575796	18,1724521	0,38512751		17,8776181	-0,29483401	18,8524136
mars-04	18,3313337	18,1736055	0,15772815		18,0630398	-0,11056579	18,4418995
avr-04	18,0669308	18,174759	-0,10782825		18,207021	0,03226198	18,0346688
mai-04	17,8610179	18,1759125	-0,31489455		18,2000953	0,02418277	17,8368352
juin-04	17,6654453	18,177066	-0,51162071		18,1506	-0,02646601	17,6919113
juil-04	17,6403183	18,1782195	-0,53790116		18,2557046	0,0774851	17,5628332
août-04	17,5344532	18,1793729	-0,6449197		18,1727804	-0,00659254	17,5410458
sept-04	17,6928084	18,1805264	-0,487718		18,1592819	-0,02124449	17,7140529
oct-04	18,0393328	18,1816799	-0,1423471		18,2872016	0,10552172	17,9338111
nov-04	18,5943371	18,1828334	0,41150372		18,41215	0,22931663	18,3650204
déc-04	19,0434484	18,1839868	0,85946158		18,2050986	0,0211118	19,0223366
janv-05	19,2559134	18,1851403	1,07077312		18,2923276	0,10718729	19,1487261
févr-05	19,0093293	18,1862938	0,82303553		18,3293678	0,143074	18,8662553
mars-05	18,5741775	18,1874473	0,38673019		18,3058835	0,11843625	18,4557412
avr-05	18,1344571	18,1886007	-0,05414369		18,2745473	0,08594654	18,0485105
mai-05	17,8780606	18,1897542	-0,31169362		18,2171379	0,0273837	17,8506769
juin-05	17,6292325	18,1909077	-0,56167523		18,1143872	-0,07652053	17,705753
juil-05	17,5560995	18,1920612	-0,63596167		18,1714858	-0,02057541	17,5766749
août-05	17,5056871	18,1932147	-0,68752753		18,1440143	-0,04920037	17,5548875
sept-05	17,7311486	18,1943681	-0,46321953		18,1976221	0,00325398	17,7278946
oct-05	17,9577889	18,1955216	-0,23773275		18,2056577	0,01013607	17,9476528
nov-05	18,407682	18,1966751	0,21100691		18,2254949	0,02881982	18,3788622
déc-05	19,1938283	18,1978286	0,99599977		18,3554785	0,15764998	19,0361783
janv-06	19,3526115	18,198982	1,15362944		18,3890257	0,19004361	19,1625679
févr-06	19,0459235	18,2001355	0,84578801		18,365962	0,16582648	18,880097
mars-06	18,4996169	18,201289	0,29832789		18,2313229	0,03003395	18,4695829
avr-06	17,9505897	18,2024425	-0,2518528		18,0906799	-0,11176257	18,0623522
mai-06	17,871766	18,2035959	-0,33182991		18,2108434	0,00724741	17,8645186
juin-06	17,7861935	18,2047494	-0,41855593		18,2713482	0,06659877	17,7195947
juil-06	17,5914481	18,2059029	-0,6144548		18,2068344	0,00093146	17,5905166
août-06	17,63 15005	18,2070564	-0,5755559		18,2698276	0,06277 127	17,5687292
sept-06	17,7789422	18,2082099	-0,42926767		18,2454157	0,03720584	17,7417363
oct-06	17,9074122	18,2093633	-0,30195118		18,155281	-0,05408235	17,9614945
nov-06	18,3702335	18,2105168	0,15971665		18,1880464	-0,02247044	18,3927039
déc-06	19,0458766	18,2116703	0,8342063		18,2075268	-0,00414349	19,0500201

Annexe B : Lissage exponentiel

Tableau B1-Calcul des paramètres du lissage exponentiel de Holt-Winters
pour la série nord

Dates	Y (nord)					~	b	S	~ S
janv-03	1	963	751	471				914165017	914165017
févr-03	1	813	699	681				764113227	764113227
mars-03	1	323	756	619				274170165	274170165
avr-03	1	088	519	916				38933462	38933462,3
mai-03		713	831	545				-335754909	-335754909
juin-03		575	936	413				-473650041,5	-473650041
juil-03		526	357	244				-523229209,9	-523229210
août-03		514	482	788				-535103666,3	-535103666
sept-03		552	839	073				-496747380,6	-496747380
oct-03		688	574	175				-361012278,8	-361012279
nov-03	1	020	927	504				-28658950	-28658949,7
déc-03	1	812	361	016	1	049 586 454	0	762774561,8	762774562
janv-04	1	990	980	491		1062384093	0	928 596 398	907114470
févr-04	1	700	081	599		1002968704	0	697 112 895	675630967
mars-04	1	610	123	737		1159471592	0	450 652 145	429170217
avr-04	1	223	551	984		1171290649	0	52 261 335	30779407,1
mai-04	1	037	802	844		1266356188	0	-228 553 344	-250035272
juin-04		683	327	686		1214948312	0	-531 620 625	-553102553
juil-04		646	673	662		1193776955	0	-547 103 293	-568585221
août-04		572	905	389		1153466042	0	-580 560 653	-602042581
sept-04		602	915	806		1128178700	0	-525 262 894	-546744822
oct-04		688	165	645		1091048335	0	-402 882 690	-424364618
nov-04	1	490	974	188		1292483192	0	198 490 996	177009068
déc-04	2	024	839	461		1278186595	0	746 652 867	725170939
janv-05	2	431	015	764		1383575997	0	1 047 439 767	1023739448
févr-05	2	343	573	713		1507131863	0	836 441 850	812741531
mars-05	1	804	890	969		1435272135	0	369 618 834	345918516
avr-05	1	200	055	675		1300157571	0	-100 101 896	-123802215
mai-05		846	129	354		1194184381	0	-348 055 027	-371755345
juin-05		687	435	707		1205874198	0	-518 438 491	-542138809
juil-05		638	545	026		1196368035	0	-557 823 009	-581523327
août-05		628	796	855		1202473087	0	-573 676 232	-597376550
sept-05		679	960	443		1203765705	0	-523 805 262	-547505580
oct-05		737	070	033		1173773603	0	-436 703 570	-460403889
nov-05	1	305	610	525		1142446189	0	163 164 336	139464018
déc-05	2	228	136	137		1301793617	0	926 342 520	902642202
janv-06	2	491	665	080		1368736514	0	1 122 928 566	1119901154
févr-06	2	153	245	146		1344327902	0	808 917 244	805889832
mars-06	1	699	279	034		1337434082	0	361 844 952	358817540
avr-06		904	128	877		1180828527	0	-276 699 650	-279727061
mai-06		814	064	677		1172035380	0	-357 970 703	-360998115
juin-06		724	000	478		1205125067	0	-481 124 589	-484152001
juil-06		633	091	584		1198446144	0	-565 354 560	-568381972
août-06		633	088	875		1202356057	0	-569 267 182	-572294593
sept-06		667	852	433		1197327827	0	-529 475 394	-532502805
oct-06		702	615	991		1170063942	0	-467 447 951	-470475363
nov-06		986	852	808		1007267471	0	-20 414 663	-23442074,6
déc-06	2	092	195	557		1081802687	0	1 010 392 870	1007365458

Tableau B2-Calcul des paramètres du lissage exponentiel de Holt-Winters
pour la série HP

Dates		Y (HP)			~	b	S	~ S
janv-03	3	032	793	861			1621592148	1621592148
févr-03	2	696	191	658			1284989945	1284989945
mars-03	1	991	305	173			580103460	580103460
avr-03	1	432	256	702			21054989,02	21054989,02
mai-03		619	068	546			-792133167	-792133167
juin-03		450	838	212			-960363501	-960363501
juil-03		404	805	128			-1006396585	-1006396585
août-03		402	111	206			-1009090507	-1009090507
sept-03		431	526	933			-979674780	-979674780
oct-03		667	697	672			-743504041	-743504041
nov-03	1	868	510	063			457308350	457308350
déc-03	2	937	315	402	1411201713	0	1526113689	1526113689
janv-04	3	079	610	801	1445846249	0	1 633 764 552	1622650282
févr-04	2	526	369	372	1294540801	0	1 231 828 571	1220714301
mars-04	2	058	716	011	1430753896	0	627 962 115	616847844,9
avr-04	1	587	033	428	1530820058	0	56 213 370	45099100,22
mai-04	1	271	839	009	1925352625	0	-653 513 616	-664627886,3
juin-04		527	363	068	1601509344	0	-1 074 146 276	-1085260546
juil-04		465	179	781	1505358940	0	-1 040 179 159	-1051293429
août-04		433	977	864	1459263919	0	-1 025 286 055	-1036400325
sept-04		505	954	400	1478774212	0	-972 819 812	-983934082,2
oct-04		673	604	325	1433141486	0	-759 537 161	-770651431,2
nov-04	2	422	533	049	1826883064	0	595 649 986	584535715,4
déc-04	3	304	231	508	1790796783	0	1 513 434 725	1502320455
janv-05	3	896	905	709	2140331619	0	1 756 574 090	1739277891
févr-05	3	601	825	444	2310283907	0	1 291 541 537	1274245338
mars-05	2	346	677	635	1872523301	0	474 154 334	456858135,4
avr-05	1	536	991	751	1582632060	0	-45 640 309	-62936507,81
mai-05		629	632	597	1361012533	0	-731 379 936	-748676135,4
juin-05		536	480	500	1545727073	0	-1 009 246 573	-1026542772
juil-05		470	410	172	1519725144	0	-1 049 314 972	-1066611171
août-05		479	528	443	1508691266	0	-1 029 162 823	-1046459022
sept-05		569	706	998	1533729568	0	-964 022 571	-981318769,9
oct-05		737	915	480	1506884642	0	-768 969 162	-786265361,3
nov-05	2	090	981	943	1498335656	0	592 646 288	575350088,6
déc-05	3	692	307	919	2001933434	0	1 690 374 485	1673078286
janv-06	4	210	166	685	2336161213	0	1 874 005 472	1857397534
févr-06	3	625	261	575	2334354744	0	1 290 906 832	1274298894
mars-06	2	600	841	040	2180680395	0	420 160 645	403552706,7
avr-06	1	020	880	741	1356202480	0	-335 321 739	-351929676,4
mai-06		815	627	248	1497397961	0	-681 770 713	-698378651
juin-06		610	973	755	1588286513	0	-977 312 757	-993920695
juil-06		529	064	711	1580955458	0	-1 051 890 748	-1068498686
août-06		549	994	887	1579625124	0	-1 029 630 238	-1046238175
sept-06		643	116	932	1599985764	0	-956 868 832	-973476770,2
oct-06		736	238	978	1529850322	0	-793 611 345	-810219282,4
nov-06	2	097	166	755	1511106229	0	586 060 525	569452587,4
déc-06	3	832	994	818	1978426666	0	1 854 568 152	1837960214

Tableau B3-Calcul des paramètres du lissage exponentiel de Holt-Winters
pour la série sud

Dates	y (sud)	~	b	S	~ S
janv-03	179 916 582			2,150000852	2,150000852
févr-03	149 754 134			1,789559985	1,789559985
mars-03	96 993 386			1,159069721	1,159069721
avr-03	66 611 056			0,796001267	0,796001267
mai-03	51 866 288			0,619801478	0,619801478
juin-03	49 350 444			0,5897371 74	0,5897371 74
juil-03	39 473 902			0,47171 2624	0,471 71 2624
août-03	40 638 469			0,485629182	0,485629182
sept-03	47 726 428			0,570330199	0,570330199
oct-03	56 990 428			0,681034885	0,681034885
nov-03	73 699 952			0,88071 3483	0,88071 3483
déc-03	151 164 108	83682098	0	1,806409156	1,806409156
janv-04	169 895 203	80792213,11	0	2,102866062	2,113702277
févr-04	114 671 214	70429327,99	0	1,628174189	1,636564285
mars-04	91 452 813	75682327,86	0	1,208377379	1,214604232
avr-04	70 205 048	83441521,39	0	0,841368264	0,845703893
mai-04	57 140 171	88866251,11	0	0,642990677	0,646304053
juin-04	46 989 995	83170498,89	0	0,564983926	0,567895328
juil-04	45 823 989	91833987,94	0	0,498987249	0,501558565
août-04	41 220 787	87523258,55	0	0,470969519	0,473396458
sept-04	48 293 542	85758243,18	0	0,56313586	0,566037738
oct-04	68 294 021	94761589,22	0	0,720693074	0,724406855
nov-04	118 964 666	119757517,6	0	0,993379525	0,998498479
déc-04	186 408 008	109487251,7	0	1,702554453	1,711327835
janv-05	230 535 042	109575117,5	0	2,103899564	2,096345645
févr-05	180 155 211	110240682,9	0	1,634198975	1,628331486
mars-05	116 590 396	101712213,1	0	1,14627725	1,142161614
avr-05	75 109 459	93998419,81	0	0,79905023	0,796181291
mai-05	58 122 337	91763523,04	0	0,633392606	0,63111845
juin-05	45 318 798	84601916	0	0,53567106	0,533747766
juil-05	42 122 791	84487000,2	0	0,49857127	0,496781181
août-05	40 051 918	84830742,2	0	0,4721391 91	0,470444005
sept-05	50 181 079	87483928,87	0	0,573603399	0,571543912
oct-05	62 946 068	87395325,23	0	0,720245251	0,717659256
nov-05	98 708 537	94817385,18	0	1,041038379	1,037300596
déc-05	216 657 501	114928318,2	0	1,885153324	1,878384799
janv-06	253 940 738	118506778,8	0	2,142837234	2,149272483
févr-06	186 869 959	115929312,7	0	1,611930189	1,616771048
mars-06	108 213 521	102583815,4	0	1,054879082	1,058047036
avr-06	62 494 535	87472683,39	0	0,7144463	0,716591885
mai-06	57 757 631	89776009,41	0	0,643352622	0,645284702
juin-06	53 020 728	95482491,11	0	0,555292676	0,5569603
juil-06	43 638 402	90550029,96	0	0,48192587	0,4833731 63
août-06	45 421 698	94055516,68	0	0,482924337	0,484374628
sept-06	52 637 649	92636404,86	0	0,568217744	0,569924184
oct-06	59 853 601	86724884,56	0	0,690154865	0,6922275
nov-06	95 080 405	89581467,5	0	1,061 384767	1,064572258
déc-06	186 861 187	95496932,87	0	1,956724487	1,962600813

Annexe C : Méthode de Box & Jenkins

Annexe C1 : Critères d'Akaike et Schwartz

Tableau C. 1.1 - Critères d'Akaike et Schwartz pour la série HPsa

Modèles / Retards		0	1	2	3	4
MODELE 3	AIK	42.02582	42.07436	42.08306	42.12873	42.19157
	SC	42.15914	42.25393	42.30980	42.40356	42.51537
MODELE 2	AIK	41.98890	42.05571	42.08212	42.15042	42.16269
	SC	42.07778	42.19039	42.26351	42.37944	42.44024
MODELE 1	AIK	41.99796	42.06911	42.12479	42.21031	42.16337
	SC	42.04240	42.15890	42.26084	42.39353	42.39465

Tableau C. 1.2- Critères d'Akaike et Schwartz pour la série sudsa

Modèles / Retards		0	1	2	3	4
MODELE 3	AIK	36.12653	36.01651	36.10550	36.18746	36.28326
	SC	36.25985	36.19608	36.33224	36.46228	36.60706
MODELE 2	AIK	36.10620	36.06389	36.11960	36.20938	36.31326
	SC	36.19508	36.19857	36.30100	36.43840	36.59080
MODELE 1	AIK	36.05789	36.03971	36.07484	36.16598	36.26797
	SC	36.10232	36.12950	36.21089	36.34919	36.49926

Annexe C2 : Estimation des modèles identifiés

Tableau C.2.1-Estimation du modèle SARIMA(1,0,1)* (1,1,0)12 pour la série nordsa

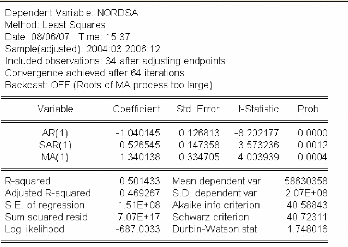
Tableau C.2.2- Estimation du modèle SARIMA(1,0,1)* (1,1,1)12 pour la série nordsa

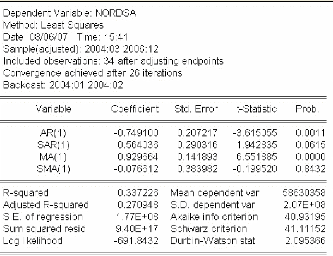
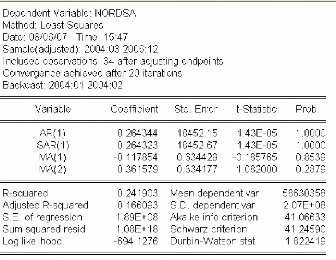
Tableau C.2.4- Estimation du modèle SARIMA(1,0,1)* (1,1,0)12 pour la série HPsa

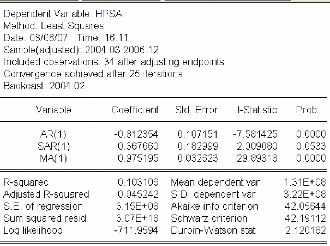
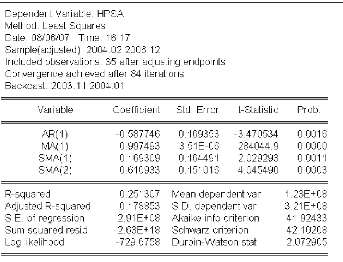
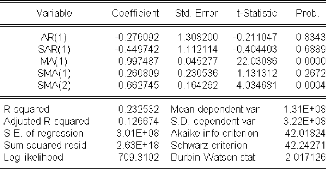
Tableau C.2.5- Estimation du modèle SARIMA(1,0,1)* (0,1,2)12 pour la série HPsa

Tableau C.2.6- Estimation du modèle SARIMA (1, 0,1) * (1,1,2)12 pour la série HPsa

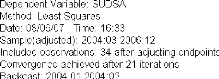
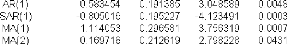
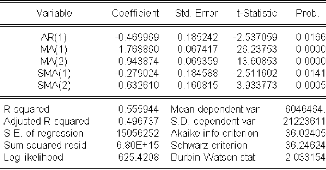
Tableau C.2.8- Estimation du modèle SARIMA(1,0,2)* (0,1, ₂₎₁₂ pour la série sudsa
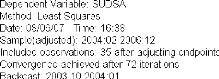
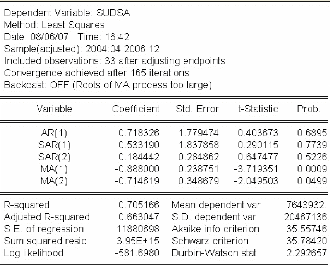