Prévision de la consommation du gaz naturel pour la distribution publique par la méthode traditionnelle, lissage exponentiel et Box & Jenkins

2.3 Prévision par la méthode de Box & Jenkins :

2.3.1 Concepts des séries temporelles

2.3.1.1 Processus stochastique

Un processus aléatoire est une application X qui associe au couple (w, t) la quantité yt (ù) . Elle est telle que ?t ? T fixé,yt est une variable aléatoire définie sur un espace probabilisé. Une processus stochastique est donc une famille de variables aléatoires indicées par t noté

(yt,t ? T) ou encore yt .

Dans la suite de l'exposé, l'espace des indices T est le temps, t est alors l'instant d'observation de la variable aléatoire y sur l'individu w . Si T est l'ensemble des réels, le processus est dit continu. Si T = Z ou N ou N* ou N* borné, le processus est dit discret.

On suppose, par la suite que la série temporelle notée yt, t ? Z (soit une succession d'observations régulièrement espacées dans le temps d'une valeur économique) est une réalisation d'un processus stochastique discret univarié¹.

2.3.1.2 Processus aléatoires stationnaires :

On dira qu'une série chronologique est stationnaire si elle est la réalisation d'un processus stationnaire, ceci implique que la série ne comporte pas de tendance ni de saisonnalité. Processus stationnaire au sens strict (stationnarité forte) :

On dit que ( yt ) est strictement (ou fortement) stationnaire si pour toute suite finie d'instant ti,t2,...,tk élément de Z et tout entier r ? Z, les lois jointes de _(yti ,...,y_tk ) et de _{(y4+r,...,ytk+r)} sont les mêmes (lois jointes invariantes par translation dans le

temps)².

~ y..ditk ) (y₄,...,yt_k) = ,y )(yti , . . . , ytk+r) k

Processus stationnaire au second ordre (stationnarité faible) :

Un processus aléatoire yt,t ? T est dit stationnaire au second ordre, si les moments d'ordre1 (moyenne ou espérance mathématique) et d'ordre 2 (variance et autocovariance) sont

1

Régis Bourbonnais, Michel Terraza, Analyse des séries temporelles, Edition 2004, P73.

² Master M2-AE2 PRO, Econométrie Bancaire et Financière, Analyse des séries temporelles, Mohamed Boutahar, octobre 2006

indépendants de t :

(i) E(e)? 8 ? t? Z.

(ii) E ( yt ) = m indépendante de t, ? t? Z.

(iii) cov (y_t , y_t+h) = 7(h) indépendante de t, ? t? Z.

Processus bruit blanc (White Noise) :

Un bruit blanc est une suite de variables aléatoires(E_t ,t ? Z) non corrélées et d'espérance et de

variance constante.

Un bruit blanc est donc tel que :

E(Et) = m ? t? Z.

V(E_t)=a²? t? Z. cov(Et ,Et+h) = 7(h) = 0 ? t? Z.

Si l'espérance m est nulle, on dit que le bruit blanc est centré.

Remarque : Dans la suite lorsqu'on parlera de stationnarité, cela sous-entendra une stationnarité au second ordre.

2.3.1.2.1 Caractéristiques d'un processus aléatoire stationnaire : Fonction d'autocovariance :

La fonction d'autocovariance mesure la covariance de la série avec elle-même décalée de h périodes. La fonction d'autocovariance d'un processus stochastique est définie par :

7(h) = cov(yt, yt+h) = E(yt - m)(yt+h - m) ? t? Z.

n-h

L'autocovariance estimée (empirique) est donnée par :

1

.

t

1

'5^,(h)= ?(yt - o(yt+h - y) n

=

1ⁿ

avec y y

= ? ~

n ~ = 1

Propriétés :

· V(yt) = 7(0) ? t? Z.

· 7(h) = 7(0) ? h ? Z.

· 7(h) = 7(-h) ? h ?

Fonction d'autocorrélation ACF (Auto Correlation Function) :

On appelle fonction d'autocorrélation simple notée p(h), la fonction qui mesure la corrélation de la série avec elle-même décalée de h périodes. Cette fonction est définie par :

p(h)=o c v(yt, yt+h) cov(yt , _yt+h ) 7(h)

V(y_t) V(yt+h) V(yt) 7(0)

? h ? Z.

L'autocorrélation empirique est donnée par :

n-h

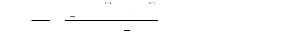
(yt -y)(yt+h - y)

?

1

=

t

=

n

2

(yt -y)

?

7 ~( )

h

b(h)=

'5(⁰)

? h ? Z.

t

=

1

Propriétés :

·	p(0) = 1		? h ? Z.	·
p(h) = p(0)	? h ? Z		·
p(h) = p(-h)	? h ? Z.

Dans le cas d'une série stationnaire, la fonction d'autocorrelation décroît exponentiellement vers zéro. La décroissance est davantage linéaire pour les séries non stationnaires rencontrées en pratique.

Fonction d'autocorrélation partielle PACF (Partiel Auto Correlation Function) : Régression affine :

Soit (yt_,t ? Z) un processus aléatoire stationnaire, on appelle régression affine de yt sur {y₈,8 = t - 1} , la variable y: vérifiant :

t 1

yt =

* a0+?a^,y t-, ou a0,a1,... ? R

,

=

1

On appelle fonction d'autocorrélation partielle les corrélations entre les différents couples(yt,yt₊h) , l'influence des variables _yt+h-, pour (0 < i < h) ayant été retirée. Elle est mesurée par le coefficient de corrélation partiel noté r (h) vérifiant :

* * , * * ,

r(h) =

cov(y_t - yt,yt-h - yt-h) cav(Yt - Yt ,Yt-h - Yt-h)

= ? h ? Z .

V(yV^,,, t Yt lv lyt-h-yt-h)

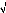
V(yt - yt )

Où y: régression affine de yt sur { yt-i, yt-2,...yt-h } .

y:-h régression affine de yt -h sur{yt-i, yt-2,...yt-h+i }.

Propriété :

Sous l'hypothèse de la stationnarité r(h) = ah, ou ah est le coefficient de _yt-h dans la régression de yt sur { yt _-i, yt _-2 ,...yt - h} .

Innovation d'un processus stationnaire :

Soit (yt, t ? z) un processus stationnaire.

On appelle innovation du processus (yt, t ? Z) à la date t la variable :

Et = yt - yt

~

Où y: est la régression affine de yt sur ys , S< t-1

E((y_t - yt )ys ) = ° ? S< t-1

~

Propriété :

La suite des innovations (Et, t ? Z) constitue un bruit blanc centré.