Prévision de la consommation du gaz naturel pour la distribution publique par la méthode traditionnelle, lissage exponentiel et Box & Jenkins

3.4.1.2 Etude de la stationnarité de la série « nordsa » : Le test de Dickey-Fuller :

Choix du nombre de retards optimal :

Avant de pouvoir appliquer le test de Dickey-Fuller, nous devons déterminer le nombre de retards p qui minimise les critères d'Akaike et Schwartz pour les trois modèles (avec tendance et constante (trend and intercept), avec constante (intercept), sans tendance ni constante (none)).

Les valeurs des critères d'Akaike et Schwartz sont fournies par le logiciel Eviews et sont résumées dans le tableau suivant :

Tableau 3.10- Critères d'Akaike et Schwartz pour la série nordsa

Modèles / Retards		0	1	2	3	4
MODELE 3	AIK	41.16626	41.16441	41 .25871	41 .27472	41 .26160
	SC	41.30093	41.34580	41.48773	41.55226	41.58854
MODELE 2	AIK	41.12688	41.10688	41.20017	41.21089	41.20407
	SC	41.21666	41.24292	41.38339	41.44218	41.48431
MODELE 1	AIK	41.06859	41.05299	41.14436	41.16120	41.14990
	SC	41.11348	41.14368	41.28177	41.34623	41.38343

D'après le tableau (3.10) nous constatons que le critère d'Akaike est minimisé pour les trois modèles pour un nombre de retard p = 1 tandis que le critère de Schwartz est minimisé pour p = 0. En suivant le principe de parcimonie nous retiendrons le nombre de retards qui permet

d'estimer le minimum de paramètres c'est-à-dire p = 0. Dans ce cas on utilise le test de Dickey-Fuller simple (DF), donc il n'y a pas d'autocorrélation des erreurs.

Le test de Dickey-Fuller simple :

On commence par tester la présence d'une racine unitaire à partir du modèle le plus général à savoir le modèle (3) incluant une constante et un trend :

A nordsa (t) = p nordsa (t - 1)+c+bt .

On test alors l'hypothèse nulle Ho : p = o de présence de racine unitaire (la série n'est pas stationnaire) contre l'hypothèse alternative de stationnarité H1 : p ? 0 .

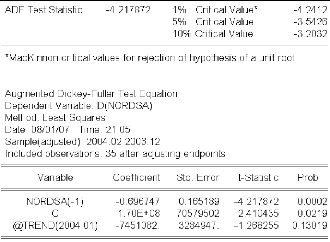
Eviews nous fournit les résultats suivants :

La réalisation de Mckinnon pour le modèle (3) tp^, = -4.217872 est inférieure à la valeur
tabulée Cem = -3.5426, on rejette donc l'hypothèse nulle d'existence de racine unitaire au seuil a= 5%.

A présent nous allons tester la significativité du coefficient b de la tendance par un simple test de Student.

D'après les résultats précédents, le coefficient de la tendance b n'est pas significativement différent de 0 puisque la statistique calculée de Student égale à -1.268255 est inférieure à 1.96, donc le modèle (3) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (2) qui ne comprend qu'une constante : A nordsa (t) = p nordsa (t - 1) + c + å t

Les résultats d'estimation du modèle (2) sont résumés ci-dessous :

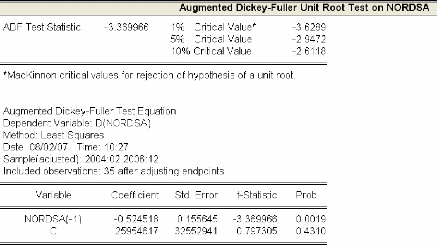
On rejette l'hypothèse nulle de présence de racine unitaire puisque tp~ = -3.369966 est

inférieure à la valeur tabulée du modèle (2) Cô.05 = -2.9472 au seuil a = 5%.

Dans ce cas on va tester la nullité du coefficient c de la constante. La présence d'une constante est rejetée puisque la statistique de Student calculée égale à 0.797305 est inférieure à 1.96 ce qui veut dire que le modèle (2) n'est pas adapté. On doit refaire le test de racine unitaire à partir du modèle (1) qui ne comprend ni constante ni trend :

A nordsa (t) = p nordsa (t - 1) + å t

Les résultas sont les suivants :

La réalisation de Mckinnon au seuil a= 5% ( tp~ = -3.295387) est inférieure à la valeur tabulée

(

1 .o5= -1.9507), donc nous pouvons conclure que la série « nordsa » est stationnaire. 3.4.1.3 Identification et estimation du modèle :

Comme notre série initiale « nord » est affectée d'une saisonnalité de période s =12 nous allons la modéliser par un modèle SARIMA (p, d, q) * (P,D,Q)12.

Pour identifier l'ordre des paramètres du modèle SARIMA nous allons nous référer au corrélogramme de la série « nordsa ».

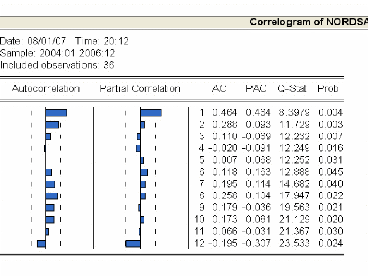
D'après le corrélogramme on peut identifier les modèles : SARIMA (1,0,1) * (1,1, ₀₎₁₂ , SARIMA (1,0,1) * (1,1,1)12 , SARIMA (1,0, 2) * (1, 1,0)12 .

D'après l'estimation des modèles identifiés précédemment qui sont représentés dans l'annexe C2 tableaux C.2.2 et C.2.3 les modèles SARIMA (1,0,1) * (1,1,1)12 et SARIMA (1,0,2) * (1, 1,0)12 ne sont pas valides, leurs coefficients ne sont pas significatifs tandis que les coefficients du modèle SARIMA (1,0,1) * (1, 1,0)12 (annexe C2 tableau C.2.1) sont significativement différents de 0. Il convient maintenant d'analyser le résidu de ce modèle afin de le valider.