Simulation de modèles de diffusion appliqués aux taux d'intérêts

4.5 Simulation du processus d'Ornstein-Uhlenbeck exponentiel

Ce processus fut etudie par Jean-Francois Begin dans son article paru en 2010 : "Analyse MCMC de certains modeles de diffusion avec application au marche europeen du carbone".

Ce modele ressemble au processus d'Ornstein-Uhlenbeck toutefois il est exponentiel. Il se presente sous la forme suivante :

d(log r) = k(19 -- (log rt))dt + o^-dWt (4.39)

La difference par rapport aux autres modeles est qu'ici on considere le logarithme du prix et non le prix en temps que tel, ce modele permet le retour a la moyenne.(voir [1])

Apres discretisation du temps :

log(rt+h) = log(P_t) + k(19 -- log(P_t))h + as/hZ (4.40)

Afin de simuler le processus, nous utiliserons les parametres obtenus par Begin en utilisons la methode MCMC (Markov chain monte carlo)

E = 0.0632

bk = --0.0240 a = 0.0573

Algorithme 34 Processus d'Ornstein-Uhlenbeck

1.Simuler n réalisations (zi...z_n) de la variable aléatoire z '-" N(0, 1) 2.Initialiser r0

3.Pour j = 1...m, calculer :

_V"

log(r3) = log(r3_i) + k(O - log(r3_i)) A t + cr A tz3 (4.41)

FIGURE 15.1 : Simulation d'un FIGURE 15.2 : Flux de 30 trajectoires

processus d'O-U exponentiel. du processus d'O-U exponentiel.

4.6 Simulation du modêle d'Eraker de volatilité stochastique

Le processus suivant a été proposé par Eraker dans son article paru en 2001 : "MCMC analysis of diffusion models with application to finance".

dr = (O_r + k_rrt)dt + _r exp(¹ ₂Vt)dW¹ (4.42)

t

dVt = k_vVtdt + avdW t 2 avec d(W1, W²) = pdt (4.43)

Aprés discrétisation du temps :

rt+h = Vt+h =

p ^brt + (Or + kr^brt)h + ar exp(^1 2Vt) hZ^1 / ^bVt + kv( ^bit)h + av hZ^2, avec Z^1'^2 JV(0, 1)

Afin de simuler le processus, nous utiliserons les paramètres obtenus par Eraker en utilisons la méthode MCMC.

^bO_r = 0.00127

^bk_r = 0.01271, k = 0.03873

^b;. = 0.24297, ^b = --0.38174

Algorithme 35 Modéle d'Eraker

1.Simuler m réalisatioms (zi...z_n) de la variable aléatoire z '-" .Af(0, 1)

2.Simuler m réalisatioms (z^' ₁...z^' _n) de la variable aléatoire z^' '-" .,A/(0, 1)

3.Imitialiser v0 4.imitialiser r0 5.Pour j = 1...m, calculer :

_s/ \/

vj = vj_i + kv(vj_1) A t + a A t(p * zj + 1 - p²*z^' _j) (4.44)

6.Pour j = 1...m, calculer :

_p

rj = rj_1 + (O_r + krrj_i) A t + _r exp(¹ _{2Vj_i)} A tzj (4.45)

(voir [9])

FIGURE 18.1 : Simulation de la volatilité FIGURE 18.2 : Flux de 30 trajectoires.

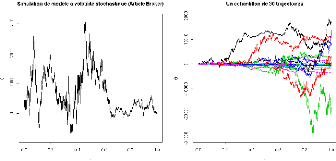
FIGURE 19.3 : Simulation du modèle FIGURE 19.4 : Flux de 30 trajectoires

4.7 Simulation du modêle de Heston de volatilité stochastique

Définition 36 Modéle de Heston de volatilité stochastique (SV)

Le modéle de Heston de volatilité stochastique est trés utilisé pour le pricing de produits dérivés

/

dS = rStdt + VtStdW ¹ (4.46)

t

/ t avec d (W 1, W ²⁾

dVt = k(O - Vt)dt + a VtdW ² = pdt (4.47)

Ici S représente l'actif sous-jacent de l'option (taux d'intérêt, taux de change, actions,...) et (St)t>o est le processus de son cours a la date t, (V)

t,t>o est le processus de sa volatilité. _{(Wt1)t>o,(Wt2)t>0} sont deux mouvements browniens standard corrélés, de paramétre de corrélation p.

W t 1 = 1 t

_p

W t 2 = 1 _t + 1 -- p²4q avec 01,4q v.a.i.i.d de loi .A1(0,1)

Le processus (Vt)t>0 est un processus du type CIR (Cox-Ingersoll-Ross).

(voir [14],[16])

Aprés discrétisation du temps :

St#177;h = St + (r St)h + St VVo/hz¹

+ k(19 --17t)h + av VVZ² avec Z¹'² Ji(0, 1)

Vt#177;h =

Afin de simuler le modele de Heston, nous utiliserons les parametres obtenus par Najed Ksouri dans le rapport technique qu'il publia en Mai 2007 intitulé "Méthodes d'approximation numérique pour le pricing des options vanilles et asiatiques dans le modele de Heston de volatilité stochastique".

	b = 0:04
	bk = 0:3
	^b = 0:15

Algorithme 37 Modele de Heston de volatilité stochastique 1.Simuler n réalisations (zi...z_n) de la variable aléatoire z J1(0,1)

2.Simuler n réalisations (z⁰₁:::z⁰ ) de la variable aléatoire J1(0,1)

3.Initialiser vo 4.initialiser so 5.Pour j =1...n, calculer :

6.Pour j = 1...m, calculer :

s3 = sj_1 + _{(rsi_1)} A t + sj_1\/vj_1\/A tz3 (4.49)

FIGURE 16.1 : Simulation volatilité FIGURE 16.2 : Flux de 30 trajectoires

FIGURE 17.1 : Simuation du modèle FIGURE 17.2 : Flux de 30 trajectoires