Méthodes de prévention des risques dues aux éboulements des roches dans les mines souterraines

I.2 MECANISME DE RUPTURE DES CORPS SOLIDES

I.2.1 RELATION ENTRE CONTRAINTE ET DEFORMATION A. La rhéologie

La rhéologie est l'étude du comportement des matériaux.

Il existe plusieurs modèles rhéologiques idéalisés pour l'étude du comportement des différents matériaux.

> Élasticité

On définie l'élasticité linéaire ou la loi de HOOKE et l'élasticité non linéaire ou formulation de CAUCHY.

a) Matériaux parfaitement linéaire ou matériaux Hookeen

La relation entre la contrainte ó et la déformation Ó pour un matériau parfaitement élastique s'écrit :

ó =E.Ó avec : E module d'élasticité Son modèle mécanique est un ressort.

b) Les matériaux non linéaires de Cauchy

L'élasticité linéaire des matériaux isotropes constitue une vieille et simple théorie pour la modélisation du comportement contrainte déformation du sol sous les conditions des moindres contraintes.

Cependant dans beaucoup de temps la courbe intrinsèque est généralement non linéaire. Les sols à comportement non linéaire doivent se caractériser par des modules variables de contraintes de déformation. La plus simple formulation de ce modèle est de remplacer les contraintes élastiques dans les relations linéaires des contraints-déformation par des modules tangents fonction des invariants de contraintes ou de déformation.

Ces contraintes élastiques sont obtenues expérimentalement sous forme de modules sécantes Ks et Gs exprimés en terme de contrainte ou déformation normales ou octaédriques.

> Matériaux ou matériaux Newtoniens

Un fluide idéal ne peut subir aucune contrainte cisaillant sans se déformer d'une manière permanente.

Le matériau newtonien peut présenter les déformations cisaillantes qui sont proportionnelles à la variation des contraintes cisaillantes.

La relation mathématique qui lie la déformation cisaillante à la contrainte cisaillante est donnée

par : ä=ì.ã

ã=3/2 Ó.t avec ì coefficient de viscosité

D'où ä= 3/2 ì. Ó.t

Ici le modèle mécanique est un amortisseur

La relation entre les contraintes normales et déformation est de la forme :

ó= 3ì. Ó.t

> Matériaux parfaitement plastique

Lorsqu'on soumet un matériau parfaitement plastique à une contrainte inférieure à ó 0 il ne se déforme pas.

Cependant il se déforme d'une manière permanente si la contrainte est égale à ó0.

Le modèle rhéologique est un patin ne pouvant se déplacer qu'avec un fortement solide. Le diagramme contrainte-déformation est une ligne parallèle à l'axe da déformation qui

intercepte l'axe des contraintes au point ó0.

> Matériaux élastoplastiques ou matériaux Saint Venante

C'est un matériau qui a un comportement parfaitement élastique par des contraintes inférieur à

ó0 et un comportement parfaitement plastique lorsque la contrainte est égale à ó0. Le modèle rhéologique est un ressort mis en série avec un patin à fortement solide.

> Matériaux viscoélastique ou matériaux de MAXWELL

La contrainte agit sur le matériau élastique qui à son tours agit sur l'élément visqueux.

Il lui correspond alors une déformation élastique Ó' et une déformation visqueuse Ó'' La déformation totale sera notée : Ó= Ó'+ Ó "

Ó= ó /E + ó/3 ì

Le modèle rhéologique est un ressort mis en série avec un amortisseur. B. Contrainte et déformation des corps solides

Déformation élastique des solides

1°) Exemple des ressorts

Le cas le plus simple de déformation élastique est celui des ressorts.

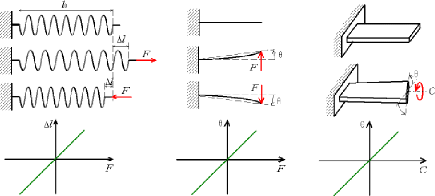
Trois exemples de ressorts : ressort à spires non-jointives sollicité selon son axe (fig. de gauche), ressort à lame sollicité en flexion (au centre), ressort à lame sollicité en torsion (à droite)

Sur les dessins, nous n'avons pas représenté la réaction du support auquel est accroché le ressort. Mais il faut bien voir que la déformation résulte de l'application de deux actions mécaniques opposées (forces et/ou couples) ; s'il n'y a qu'une seule force, en application du principe fondamental de la dynamique, la force accélère le ressort sans provoquer de déformation, on se ramène à la mécanique du point.

Lorsque les lois de déformation sont linéaires, le coefficient de proportionnalité est appelé raideur du ressort et est noté k :

· F = k1 · Äl pour une traction-compression ;

· F = k2 · è pour une flexion ;

· C = k3 · è pour une torsion.

On remarque que les coefficients k1, k2 et k3 ne sont pas homogènes (ils n'ont pas la même dimension). L'angle è doit être exprimé en radians.

Dans le cas d'un ressort à spires non-jointives, l'énergie de déformation élastique W est le travail de la force :

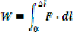
C'est donc la surface du triangle délimité par la droite dans le graphique (Äl,F), soit W = 1/2 k1 Äl 2 = 1/2 · F · Äl

				9

Illustration graphique de l'énergie de déformation élastique dans le cas d'un ressort à spires non-jointives

2°) Limite d'élasticité

La déformation élastique intervient pour les faibles sollicitations. Si l'on augmente les sollicitations, on change le mode de déformation :

· rupture (endommagement) pour les matériaux dits « fragiles » :

· déformation plastique (irréversible et non linéaire) puis rupture pour les matériaux dits « ductiles » ;

· éventuellement fluage pour les matériaux ductiles si la vitesse de déformation est lente ou la température élevée.

La contrainte délimitant le domaine élastique des autres domaines est appelée limite d'élasticité (yield strength en anglais).

3°) Contrainte et déformation

On utilise deux modèles de déformation élastique : la traction-compression et le cisaillement. La flexion peut se modéliser selon les cas comme une traction-compression ou comme un cisaillement, la torsion se modélise comme un cisaillement (voir plus bas).

a) Traction-compression uniaxiale

Prenons le cas de la traction ou de la compression d'une pièce cylindrique ou parallélépipédique selon son axe. La traction-compression correspond à des forces s'exerçant perpendiculairement aux sections de ces pièces ; elle est dite uniaxiale car les côtés de la pièce ne sont pas contraints, toutes les forces sont sur un même axe.

> Allongement dans l'axe

En prenant des pièces de différentes dimensions, on remarque que pour une force donnée :

· l'allongement Äl est proportionnel à la longueur initiale l0 du cylindre ;

ceci se conçoit bien : si l'on met deux ressorts identiques bout-à-bout, le premier ressort transmet intégralement la force au second ressort, les deux s'allongent donc de la même quantité ; donc si avec un ressort on a un allongement Äl1, avec deux ressorts l'allongement total est 2Äl1 ;

· l'allongement Äl est inversement proportionnel à la section du cylindre ;

on conçoit également aisément que si l'on met deux ressorts identiques en parallèle,
chaque ressort exercera la moitié de la force de traction, l'allongement final sera donc

Ä1/2 ; si l'on double la section de la pièce, c'est comme si l'on mettait deux pièces côte-àcôte.

Si l'on veut caractériser le matériau en faisant abstraction de la forme de la pièce et de ses dimensions, on définit donc :

· l'allongement relatif ou déformation (strain en anglais), noté å

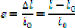
å est sans dimension, on l'exprime parfois en % (100×Äl/l0)

· la contrainte (stress en anglais), notée ó

ó est homogène à une pression ; du fait des valeurs énormes mises en jeu, on l'exprime généralement en mégapascal (MPa).

La loi élastique s'écrit alors : ó = E å

c'est la loi de Hooke ; E est le module de Young (Young's modulus en anglais), qui est une caractéristique du matériau. E est également homogène à une pression, du fait des valeurs très élevées qu'il prend, il est généralement exprimé en gigapascal (GPa).

On voit aisément que la densité d'énergie de déformation w, c'est-à-dire l'énergie élastique divisée par le volume de la pièce, vaut :

w = 1/2 · ó · å = 1/2 · E å²

> Élargissement

Lorsque l'on exerce une traction ou une compression, on constate que la largeur de la pièce varie également, à l'inverse de l'allongement. La variation relative de dimension est proportionnelle à l'allongement relatif å, le coefficient de proportionnalité s'appelle le coefficient de Poisson ou rapport de Poisson (Poisson's ratio en anglais) en hommage au mathématicien français Siméon Denis Poisson. Il est noté í et est sans unité :

· pour un cylindre :

· pour un parallélépipède rectangle :

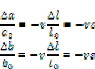
Considérons le volume de la pièce. Pour une pièce cylindrique, on a : V = l × ð r 2

Pour des petites variations, on a donc :