Notion de mécanique céleste classique

1

TABLE DES MATIERES

Introduction . 3

CHAPITRE I FORCES CENTRALES

I. Généralités 4

1. Définitions . ...4

2. Compléments mathématiques . 5

II. Mouvement à force centrale ..6

1. Définition de la force centrale 6

2. Loi de Newton 7

3. Propriétés des mouvements à force centrale . 7

a. Le moment cinétique . ..7

a.

. .8

a. Formules de Binet . 9

III. Champ Newtonien 10

1. Définition d'un champ Newtonien . 10

2. Trajectoire d'un mobile soumis à un champ Newtonien . 10

3. Etude dynamique des champs Newtoniens .12

a. Energie potentielle 12

b. Energie cinètique . 12

c. Energie mécanique . 13

..

Loi des aires

CHAPITRE II MOUVEMENT DES PLANETES AUTOUR

DU SOLEIL CAS DE LA TERRE
I. Les lois de Kepler .	14
1. Introduction aux lois de Kepler .	..14
2. La première et la seconde loi de Kepler .	14
3. Caractéristiques de la trajectoire d'une planète .	15
4. La troisième loi de Kepler	17
II. Le mouvement de la terre dans le système solaire .	18
1. Rappels sur les référentiels	18				2. Le mouvement de la Terre autour du soleil .
..19	3. Le mouvement de rotation de la Terre autour d'elle m me.
20
CHAPITRE III MOUVEMENT DES SATELLITES
I. Satellite circulaire quelconque	...21
II. Satellites Terrestres .	22
1. Satellites naturels	22					2. Satellites artificiels .
.23
a. Vitesse de libération VL	..23
b. Mise sur orbite d'un satellite	..24
III. Satellite géostationnaire	..26
IV. Domaines d'utilisation des satellites	29
1. Le domaine météorologique	29						2. Les domaines des télécommunications .
29

Conclusion 31

Références 32

3

INTRODUCTION

La mécanique céleste est un terme qui désigne la description du mouvement des objets astronomiques (les étoiles, les planètes ...) à l'aide des théories physiques et mathématiques, les domaines de la physique les plus directement concernés sont la cinématique et la dynamique.

L'alternance du jour et de la nuit, les phases de la Lune et la position changeante des planètes attirent l'attention de l'humanité, c'est le point de départ pour étudier le ciel, ainsi les savants se sont mis à étudier les mouvements des corps célestes dans l'espace, au début du XVI^ème siècle Copernic attribue au soleil le r le admis depuis cette époque (le soleil est le centre de notre galaxie), que Kepler vers la fin du siècle énonça les lois (qui portent son nom) constituant une étude cinématique de ce mouvement et qu'en 1666, Newton expliqua le résultant des efforts entre les corps par l'interaction gravitationnelle.

Dans ce mémoire, on va présenter les notions sur les forces centrales et à partir de ces notions on va élaborer les lois de Kepler et on termine par des applications de ces lois sur les planètes et les satellites.

CHAPITRE I FORCES CENTRALES

I. Généralités

1. Définitions

La gravitation : C'est l'une des quatre interactions fondamentales de la nature (les trois autres étant les interactions électromagnétiques, nucléaires fortes et nucléaires faibles). C'est une force attractive de longue portée et de faible amplitude.

Etude dynamique : C'est l'étude du mouvement des corps sous l'action des forces extérieures.

Une planète : Elle se distingue d'une étoile essentiellement par le fait qu'elle n'a pas de source d'énergie interne durable sur des milliards d'années. Une telle source durable d'énergie ne peut être que d'origine nucléaire.

Un satellite naturel : C'est un objet qui est en orbite autour d'une planète plus grande que lui l'opposition des satellites artificiels. Ils peuvent être de grosse taille et ressembler à des petites planètes. Un exemple important est la lune.

Un satellite artificiel : C'est un objet fabriqué par l'homme, envoyé dans l'espace à l'aide d'un lanceur et mis sur orbite autour d'une planète ou d'un satellite.

Le système solaire : C'est un système planétaire composé d'une étoile, le soleil, et des corps célestes ou objets définis gravitant autour de lui (autrement dit, notre système planétaire) : les dix planètes et leurs 165 satellites naturels connus (appelés usuellement des « Lunes »).

Un équateur : C'est l'intersection de la surface d'un objet céleste avec le plan perpendiculaire à son axe de rotation et contenant son barycentre. Dans le cas d'un objet de forme relativement sphérique, comme la Terre, il s'agit d'une ligne imaginaire quasiment circulaire, équidistante de son pôle Nord et de son pôle Sud.

2. Compléments mathématiques

- Gradient d'une fonction

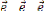
Considérons l'espace rapporté à un repère orthonormé {O, 1, 2, 3}. Soit f (x,y,z) une fonction des variables x, y et z.

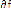
La différentielle de f s'écrit: df = dx + dy + dz

df représente la variation de f lorsque l'on passe du point M(x,y,z) au point M'(x+dx,y+dy,z+dz). Le vecteur correspondant à ce déplacement

s'écrit: = = dx ₁ + dy ₂ + dz 3

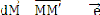
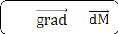
df = f .

df peut donc s'écrire:

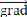
5

où le vecteur f (gradient de f) a pour expression:

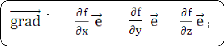
f = 1 + 2 + 3

- Résolution de l'équation différentielle de la forme : y»+y = a (avec a est une constante)

La solution générale de cette équation différentielle est : y = y1 + y2

avec y1 : c'est la solution de l'équation différentielle sans seconde membre
y''+y = 0

et y2 : c'est la solution particulière de cette équation différentielle

La solution de l'équation différentielle sans second membre est :

y1 = A cos (t - t0) telle que A et t0 sont des constantes La solution particulière y2 est :

y2 = a telle que a est une constante

Alors la solution générale de l'équation différentielle de la forme y1+ y2 = a

est :

y= a + A cos (t - t0)

II. Mouvement à force centrale

1. Définition de la force centrale

Une force est centrale si sa ligne d'action passe constamment par un point O appelé pôle.

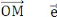
Le vecteur position et la force appliquée à la particule sont alors dirigées suivant le même vecteur unitaire relatif aux coordonnées polaires de M.

Nous avons alors, = r r

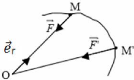
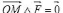
= - F r (Force radiale)

Donc le moment de la force par rapport au point O est : Exemple :

Force d'interaction gravitationnelle entre deux masses m et M distantes de r :

= -

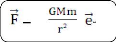
r

où G désigne la constante d'attraction universelle.

7

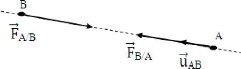
2. Loi de Newton

Soient deux particules A et B des masses respectivement m1 et m2

Les interactions entre les deux particules, représentées par _A/B et _B/A sont tel

que :

A/B= - _B/A= - AB

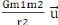
G est la constante de gravitation universelle G = 6 ,67 .10^-11 Nm² /kg² r est la distance entre A et B. (voir la figure suivante)

3. Propriétés des mouvements à force centrale

a. Le moment cinétique

Le moment cinétique de la particule M par rapport à un point fixe O, dans un repère R, est constant

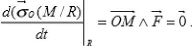
donc le moment cinétique de M s'écrit :

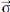
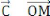
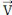
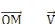
0(M/R) = Ë m (M/R) = m = 0 Ë m 0(M /R) Où 0 et 0(M /R) sont la position et la vitesse initiales de M dans R

- Si le vecteur est nul, alors le vecteur vitesse (M/R) et le vecteur position sont parallèles. Le mouvement est alors rectiligne.

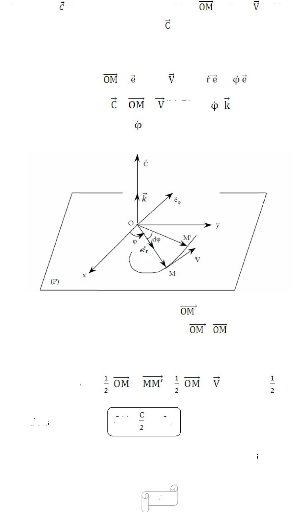
- Si le vecteur est non nul, les vecteurs positions et vitesse (M/R)

appartiennent à un plan perpendiculaire à . La trajectoire du point M est alors plane.

b. Loi des aires

En coordonnées polaires : = r _r et (M/R)= _r+ r ö

donc = Ë (M/R) = r²

alors C= r²

C est la constante des aires.

Examinons l'aire balayée par le rayon vecteur entre l'instant t et t + dt,

entre ces deux instants le rayon vecteur passe de à ', en effectuant une

rotation d'angle dö, l'aire hachurée dS est approchée par celle du triangle OMM' dont la mesure est :

alors

Où S0 est une constante déterminée à partir des conditions initiales et C la constante des aires.

dS = | Ë |= | Ë (M/R) dt|= Cdt

S(t)= t + S0

C. Formules de Binet

En coordonnées polaires : = r _r et (M/R)= _r+ r ö

- Dans le cas d'un mouvement à accélération centrale, le carré du module du vecteur vitesse est:

= =

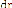
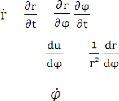
V² = ² + r^{2 2} et

On pose u = , donc du = - et = -

ce qui donne = - d'autre part, C=r²

peut s'écrire = Cu²

V² = [- ( )] ²C²u⁴ + ( ).C²u⁴

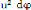
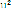
et

V² = C² [( ) ² + u²]

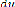
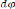
La première formule de Binet s'écrit:

et rö² = C²u⁴ = C²u

La deuxième formule de Binet s'écrit alors :

Dont la valeur algébrique est : = - r

On a

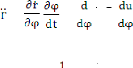
= = (-C ) C²u² = -C²u²

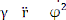
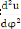
= -C²u² [ + u]

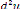
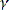
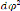
9

- La deuxième formule de Binet permet de déterminer l'accélération de la particule étudiée si l'on connaît l'équation polaire et inversement.

Le mouvement du point M étant à accélération centrale, on a :

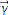
(M/R) = ( - r ) r

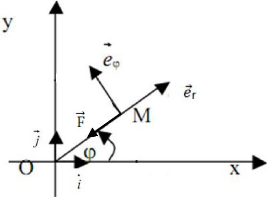
III. Champ Newtonien

1. Définition d'un champ Newtonien

On considère un axe polaire de référence pris dans le plan de la trajectoire, et

repérons la position du point matériel M par ses coordonnées polaires (r, ö).

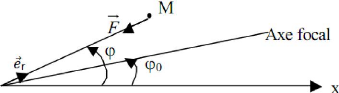
Un champ Newtonien est un champ de forces dont l'expression est de la forme:

= -

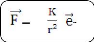
r

K est une constante.

10

Si la constante K est positive, la force est attractive. Si k est négative la force est répulsive.

2. Trajectoire d'un mobile soumis à un champ Newtonien

On considère le champ d'attraction universelle exercée par une masse M en O sur une particule M de masse m située à une distance r de O.

- Principe fondamentale de la dynamique : = m (M)

- L'interaction de la particule de masse M sur la particule de masse m

r

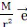
représentée par Newton est : = -G

par conséquent : (M) = -G

r

et à partir de la deuxième formule de Binet on a :

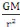
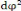
= GMu² = C²u² [ + u]

+ u =

ce qui donne :

donc = [ 1 + cos ö ]

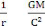
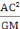
C'est l'équation différentielle du second ordre en u par rapport à O La solution génèrale de cette équation différentièlle est :

u( ) = = + A cos( - ö0)

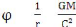
0 est determiné par les conditions initiales, on peut les choisir de sorte que 0 = 0

d'où ( ) =

On pose p = et e =

( ) =

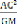
Il vient alors

C' est l'équation d'une conique d'excentricité e et de paramètre p. -Si e = 0. La conique est une cercle.

-Si 0 < e < 1. La conique de M est une ellipse.

-Si e = 1. La conique du point M est une parabole.

-Si e > 1. La conique de M est une hyperbole.

3. Etude dynamique des champs Newtoniens

a. Energie potentielle

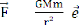
Le champ Newtonien est conservatif : la force = - r , dérive d'un

potentiel = -

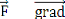
EP(M)

Lorsque la particule M est éloignée (voir la partie précédente) le potentiel est nul

donc E_p = -G

comme ( ) =

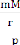
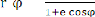
Ep= -GMm

Il vient alors

12

b. Energie cinètique

Par la definition classique de l'energie cinètique on a : E_c= m V2

En coordoonèes polaires (r, ) : (M/R)= _r+ r ö

avec ( ) = et = (C/r²)

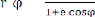
E_c= [1 + e² + 2e cos ]

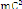
Il vient alors

c. Energie mécanique

L'energie mécanique est la somme des deux energies, l'energie potentielle et l'energie cinètique E = E_p + E_c

donc E = -GMm [

] + [ (1 + e² + 2e cos )]

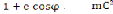
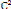
On sait que p= donc = GMm

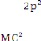
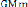
E= - (1 - e²)

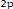
alors

On peut conclure que l'energie mécanique est constante

- Si 0 < e < 1. La trajectoire est une ellipse et l'énergie mécanique E < 0,

Sachant que E = Ep+Ec < 0 donc mV² < (GMm /r) , donc |E_c| < |E_p|

-Si e = 1. La trajectoire du point M est une parabole

donc E = 0 . Il vient alors |E_c|=|E_p|

-Si e > 1. La trajectoire de M est une hyperbole et E > 0 donc |E_c|>|E_p|.

14

CHAPITRE II

MOUVEMENT DES PLANETES

AUTOUR DU SOLEIL

CAS DE LA TERRE

I. Les lois de Kepler

1. Introduction aux lois de Kepler

Les lois de Kepler sont des lois mathématiques décrivent le mouvement des planètes.

Elles régissent le mouvement de la Terre et des autres planètes autour du Soleil, mais aussi de la Lune autour de la terre, des satellites, naturels ou artificiels, autour de leur planète, et par extension, de tout corps en orbite autour d'un autre.

2. La première et la seconde loi de Kepler

.La première loi de Kepler : Les centres d'inertie des planètes décrivent des ellipses dont le foyer est confondu avec le centre d'inertie du soleil.

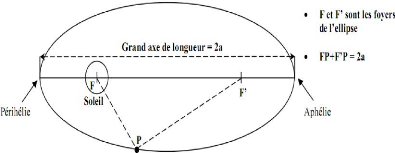
Le cercle est une ellipse dont les foyers sont confondus.

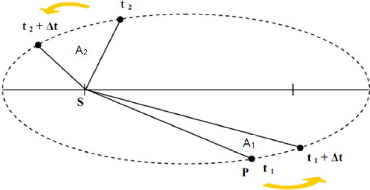
.La deuxième loi de Kepler : Ces ellipses sont parcourues selon la loi des aires ;

L'aire balayée par le rayon vecteur est proportionnelle à la durée du balayage

S(t)= t + S0

avec C est une constante des aires et S0 est une constante d'intégration.

La figure suivante explique bien cette loi :

Le segment de droite reliant le Soleil, S, à la planète, F, (le segment [SF]) balaie des aires A (A1 et A2) égales pendant des durées Ät égales.

3. Caractéristiques de la trajectoire d'une planète

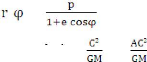
L'équation de la conique est :

( ) =

avec P et e sont des constantes respectivement égales et , où C : est

Les centres d'inertie des planètes décrivent des ellipses dans le foyer est confondu avec le centre d'inertie du soleil.

la constante des aires, G est la constante de gravitation, M est la masse d'une planète et A est une constante détermine par les conditions initiales (Voir chapitre -1- la partie du champ newtonien).

Soient O un point représentant le centre d'inertie du soleil, et le point M centre d'inertie d'une planète.

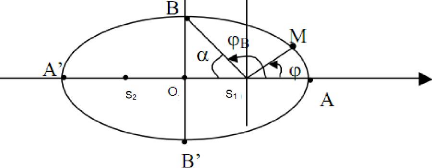
Soient a = OA = OA', b = OB = OB' et c = OS1 = OS2

A et A' sont deux points présents respectivement le périhélie et l'aphélie. Le périhélie : est le point de l'orbite le plus prés du soleil.

L'aphélie : est le point de l'orbite le plus éloigné du soleil.

Dans le cas d'un satellite de la terre, on parle de périgée et d'apogée.

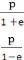
Si ö = 0 donc rmin=

et rmax - rmin = 2c =

p = (1 - e²)

d'o

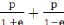
p = a ( 1 - e² )

Si ö = ð donc rmax= donc rmin+ rmax = 2a = Il vient alors

Finallement

e =

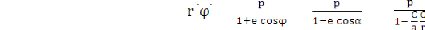
Pour ö = öB , donc : ( )

= = =

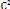
donc p = rB - donc rB = a (1 - e²) + ae² = a

alors rB= a et a² = b² + c²

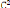
On en déduit encore que : = a - = a (1- ) = a (1-e²) = p

p =

Par consèquent

17

4. La troisième loi de Kepler

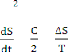
L'aire balayée par le rayon veteur est : S(t) = t + S0

La vitèsse aréolaire du point M est : A = = =

?S c'est la surface d'une ellipse donc ?S = ðab

a et b sont respectivement le demi-grand et le demi-petit axe de l'ellipse.

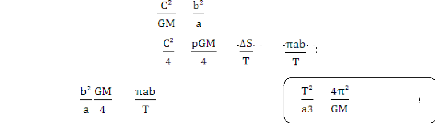
En tenant compte de p= =

Nous écrivons, A² = =

donc = ( )² finalement :

= ( )² = ( )²

= = constante

C'est la troisième loi de Kepler

La troisième loi de Kepler dit : le carré de la période de révolution T est

proportionnel au cube du demi-grand axe a de l'ellipse ; le rapport est le

m me pour toutes les planètes du système solaire.

II. Le mouvement de la terre dans le système solaire

1. Rappels sur les référentiels

- Un référentiel galiléen :

C' est un référentiel en translation rectiligne uniforme par rapport au référentiel de Copernic dont l'origine est au centre du soleil et des trois axes perpendiculaires les uns par rapport aux autre sont dirigés vers trois étoiles fixes dans notre galaxie.

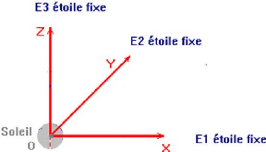
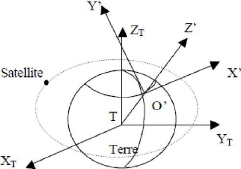
Les référentiels galiléens se rapportent tous, comme les autres au m me temps universeles. Les référentiel galiléen sont en translation rectiligne et uniforme les uns par rapport aux autres. Il forment ainsi un groupe appelé groupe de Galilée. - Le référentiel de kepler :

Nous admettons qu'il existe au moins trois étoiles E1, E2 et E3 considérées comme ponctuèlles qui, avec le centre O du Soleil, forment un tétraèdre indéformable. Soit (O,X ,Y ,Z) un repère orthonormé rigidement lié à ce tétraèdre ( voir la figure)

En munissant ce repère d'une base de temps, nous constituons le référentiel de Kepler que nous supposons galiléen.

19

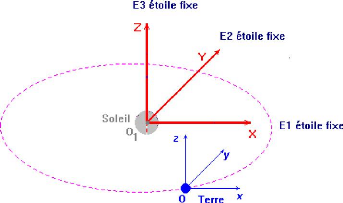
2. Le mouvement de la Terre autour du soleil

Etudions le mouvement de la Terre, de centre T de masse Mt, qui tourne autour du Soleil, de centre S de masse M_s , dans le référentiel de Kepler considérégaliléen.

La seule force extérieure qui s'applique sur la Terre est la force d'attraction gravitationnelle exercée par le Soleil notée .

= -G

Cette force est centrale, la trajectoire est plane.

A partir des lois de Kepler, la trajectoire qui d'écrit la Terre autour du Soleil est une ellipse (e ) et le Soleil occupe l'un du foyer de cette ellipse. Le plan de la trajectoire (XO1Y) sur la figure est le plan de l' écliptique.

L'équation de la trajectoire est r(ö) =

La péroide de rotation de la Terre autour du Soleil est TT = 1 an . Nous démontrerons dans la troisième loi de Kepler que

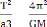
= = constante

avec a est le grand demi-axe de l'ellipse de la trajectoire.

Le repère d'origine O ( centre de la Terre ) et d'axes x , y et z parallèles aux axes de Kepler X , Y et Z est approximativement en translations rectiligne et uniforme au cours d'une durée limitée, par exemple un jour on peut considérer qu'un tel repère est galiléen.

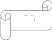
3. Le mouvement de rotation de la Terre autour d'elle

m me

Dans le repère (T, x, y, z) la Terre tourne autour d'un axe SN, de direction fixe, faisant un angle á = 23°27' avec la normale au plan de l'écliptique (voir la figure au dessous). S et N sont les pôles géographiques, (E) est le plan de l'Equateur.

La Terre effectue 365,25 tours par an ; la durée du jour solaire moyen est de ce fait, 86400s.

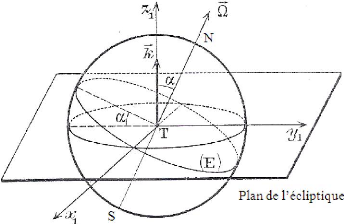
La rotation de la terre autour d'elle-même nous donne l'alternance du jour et de la nuit.

CHAPITRE III

MOUVEMENT DES SATELLITES

I. Satellite circulaire quelconque

Nous avons admis un référentiel lié à une planète de masse MF quelconque

R ( F, x, y, z ), la planète autour du Soleil par une trajectoire elliptique, et pour une durée plus court, ce référentiel supposons galiléen, un satellite de masse MS est soumis à une force de gravitation crée par une planète tel que :

= -G

Avec r la distance entre les centres d'inertie d'une planète et d'un satellite. Cette force étant centrale, qui a dont une trajectoire plane, l'équation de la trajectoire s'écrit sous la forme :

r( ) = (voir le chapitre 1)

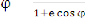
21

dans notre cas la trajectoire est circulaire (e = 0).

II. Satellites Terrestres

1. Satellites naturels

-La Terre possède un seul satellite naturel ; la Lune. Cette dernière se déplace sur une orbite circulaire de manière uniforme.

-La durée d'un jour la Lune décrit un angle de 0,23 radian par rapport à la Terre, ce qui donne la période de la Lune TL, avec TL correspond à 2ð radians.

d'o TL = = 27,3 jours

-Le schéma suivant représente les différentes phases de la Lune est nouvelle lorsque la face qu'elle présente à la Terre n'est pas éclairée (la nuit).

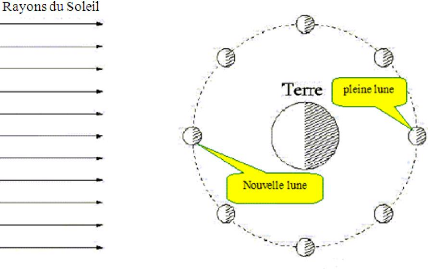
Le cycle des phases de la Lune, appelé lunaison, durée TN = 29,5 jours, pour expliquer la différence entre cette durée et la période du mouvement circulaire de la Lune autour de la Terre, on doit prendre en compte le mouvement de la terre autour du Soleil, et pour cela on étudie les différente positions de la Lune lors des nouvelles Lunes successives à l' instant t et t + TN (voir le schéma)

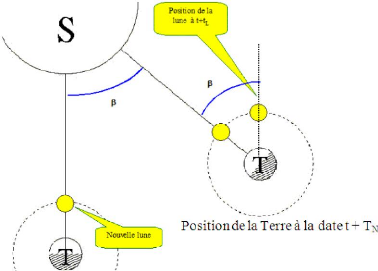
23

On sait que la Terre en orbite elliptique de période TT = 365,25 jours autours du soleil, en 27,3 jours, la Terre décrit autour du soleil â = 2ð = 0,47 rad

La Lune se retrouve à la position ·nouvelle lune· lorsqu'elle se déplace sur son orbite par un angle de â' = 2ð + â = 2ð + 0,47 = 6,75 rad

Il vient alors : TN = = 29,5 jours

2. Satellites artificiels

a. Vitesse de libération VL

Soit un satellite artificiel de masse MS autour de la Terre de masse Mt tel que son énergie mécanique E est :

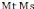
E = E_c + E_p = Ms V_o² + ( - G )

o r désigne la distance entre les centres d'inertie de la Terre et du satellite.

D'autre part, l'énergie mécanique s'écrit sous la forme suivante :

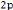
E = - G ( 1 - e² ) (voir le chapitre 1)

avec e et p sont respectivement l'excentricité et le paramètre du trajectoire. Sachant que :

-Si E_m 0, la trajectoire du satellite est circulaire ou elliptique.

-Si E_m 0, la trajectoire du satellite est hyperbolique.

-Si E_m = 0, la trajectoire du satellite est parabolique, ce qui correspond à une vitesse initiale V0 telle que :

MS V0² - G = 0

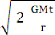
donc V0 = = VL

Cette vitesse ne dépend que du rayon de la trajectoire du satellite r.

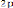
On sait que : E_m = MS V0² - G = - G ( 1 - e² )

donc MS V0² = - G e²

Finalement on obtient :

V0 = VL e

Par conséquent : -Si V0 VL c'est-à-dire e = 1

c'est la condition qui donne la trajectoire parabolique ou hyperbolique et donc celui-ci est s'éloigne indéfiniment de la Terre.

-Si V0 VL c'est-à-dire e 1

c'est la condition qui donne la trajectoire du satellite fermée, celle-ci est circulaire ou elliptique.

Cette dernière condition est nécessaire pour éviter la disparition du satellite.

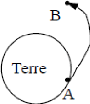
b. Mise sur orbite d'un satellite

C'est une opération qui se déroule en deux étapes:

i) Lancement à partir d'une station terrestre A.

En station terrestre A, le lancement se fait avec une vitesse 0 < V0 < VL

25

ii) La satellisation (mise sur orbite) se fait en B grâce à une deuxième accélération qui fournira l'accroissement nécessaire de la vitesse.

B est généralement le périgée de l'ellipse.

> Orbite de transfert géostationnaire (GTO)

Pour positionner un satellite en orbite géostationnaire il existe deux méthodes : Injection via orbite GTO : le lanceur n'a pas les capacités de monter en orbite géostationnaire. Il libère le satellite sur une orbite de transfert en attendant de l'amener sur l'orbite géostationnaire.

Injection directe en orbite GEO par le lanceur : une partie du lanceur peut atteindre l'orbite géostationnaire et injecter le satellite sur la bonne orbite L'insertion en GTO commence à partir de l'orbite basse : le lanceur fournit au satellite une vitesse supérieure à la vitesse de satellisation nécessaire à cette altitude et l'insère sur une trajectoire elliptique qui va croiser l'orbite géostationnaire. C'est cette orbite de transfert de basse altitude vers la géostationnaire que l'on appelle orbite de transfert géostationnaire (GTO).

Le timing de lancement doit être extrêmement précis. Le moment et l'endroit de l'injection sur l'orbite de transfert doit permettre au satellite :

- de se déplacer jusqu'à l'orbite géostationnaire

- et d'y arriver à l'endroit à peu près exact où le satellite doit se positionner, après un nombre révolutions bien défini

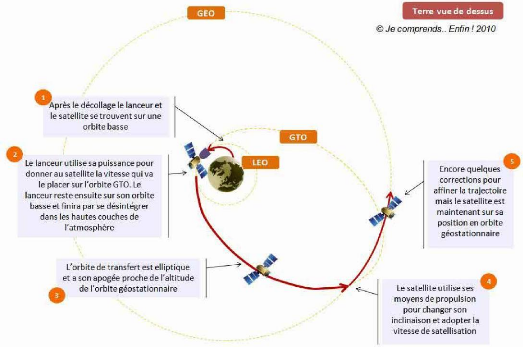
> Injection en orbite GEO via orbite GTO

L'injection finale sur l'orbite géostationnaire se fait par la propulsion du satellite :

- par un moteur qui sera utilisé ensuite pour le maintien à poste

- ou par un moteur dédié à cette tâche et qui ne sera plus utilisé ensuite (moteur à poudre, etc.)

III. Satellite géostationnaire

Les satellites géostationnaires sont des satellites fixes (stationnaire) par rapport à la Terre (géo).

Pour que ce soit le cas, il faut que :

-Ils décrivent un mouvement circulaire uniforme dans un plan perpendiculaire à l'axe des p les terrestres (SN), ils évoluent donc dans un plan contenant l'Equateur.

-Ils ont la m me sens de rotation que la Terre autour de l'axe de ses p les (SN). -Leur période de révolution T égale à la période de rotation de la Terre sur elle m me (24heurs environ).

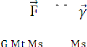
Comme un satellite géostationnaire est un satellite qui para t fixe pour un observateur terrestre, et de la m me vitesse de rotation que celle de la Terre. Le principe fondamental de la dynamique donne :

= MS

qui se traduit par = V0²

(la force de gravitation équilibre la force centrale)

V0 = = VL

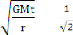
Elle donne alors :

27

ce qui correspond bien à V0 VL

Dans la pratique, la vitesse de libération est de l'ordre de 11 km/s.

On pose r = RT + h avec RT et h sont respectivement le rayon de la Terre et l'altitude à laquelle doit se trouver le satellite géostationnaire.

- Calculons l'altitude h :

On sait que la période de révolution du satellite est égale à la période de rotation de la Terre sur elle-m me qui est T = 24 heurs

et d'après la troisième loi de Kepler on a : donc r^3 = (RT + h)^3 = T^2
		=
d'o RT + h =

h = - RT

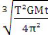
Finalement

tels que : RT = 5,98 .10²⁴ kg , T = 86164 s et G = 6,67 . 10^-11 N m² kg^-2

Donc les satellites géostationnaires se trouvent à une altitude d'environ (par une application numérique) h = 36000 km au dessus de surface terrestre.

Par conséquent la vitesse et la période de révolution des satellites sont indépendants de la masse des satellites mais dépendent de la masse de la Terre MT et de l'altitude h à laquelle ils se trouvent.

29

IV. Domaines d'utiisation des satellites

1. Le domaine météorologique

On peut observer par les satellites artificiels les mouvements des nuages, les vents... Leurs données permettent de traiter la structure de l'atmosphère (stabilité, température, vents et humidité) ce qui supplémente les données de stations terrestres et aérologiques pour alimenter les modèles de prévision numérique du temps.

Les autres informations qu'on peut mentionner :

-Mesure de la température de surface de la mer, de la couverture de glace en hiver et des déplacements des icebergs pour les marins et les pêcheurs -Études climatologiques de la progression des glaciers, des déserts pour l'hydrologie

-Étude de la pollution atmosphérique et des traînées de mazout en mer

2. Les domaines des télécommunications

- Téléphonie

Les téléphones mobiles satellitaires (depuis des bateaux, avions, etc.) eux se connectent directement au satellite. Ils doivent donc être en mesure d'émettre un signal et de le pointer vers le satellite même en cas de mouvements (vagues sur un bateau, déplacement et turbulences en avion) ou de lieux isolés (déserts...) .

- Télévision

L'antenne parabolique reçoit des signaux transmis par un satellite ^placégénéralement sur orbite géostationnaire (satellite géostationnaire), les signaux

captés par l'antenne parabolique sont ensuite envoyés vers le décodeur numérique afin d'être traités et décodés.

- GPS (Global Positioning System)

Le système Américain GPS comprend au moins 24 satellites artificiels orbitant à 36000 km d'altitude (ceinture de Clarke, Mathématicien Anglais, 1945). Ces satellites émettent en permanence un signal d'heure précis (grâce à leur horloge atomique), ainsi que leurs coordonnées exactes.

Ainsi un récepteur GPS qui capte les signaux d'au moins quatre satellites peut, en mesurant les écarts relatifs des horloges, connaître son éloignement par rapport aux quatre satellites et, par triangulation, situer précisément en trois dimensions n'importe quel point placé en dessous des satellites GPS (avec une précision de 15 à 100 mètres pour le système standard). Le GPS est ainsi utilisé pour localiser des véhicules roulants, des navires, des avions, des missiles et même des satellites évoluant en orbite basse.

Le GPS étant un système développé pour les militaires Américains, certaines informations peuvent être cryptées et priver les personnes qui ne disposent pas des codes de la précision maximale.

Pendant de nombreuses années, les civils n'avaient accès qu'à une précision faible (environ 100m). Le 1er mai 2000, le président Bill Clinton a annoncé qu'il mettait fin à cette dégradation volontaire du service. Depuis, il est courant d'avoir une position précise à 20 mètres ou mieux.

En 1957, les russes ont envoyé le premier satellite « Spoutnik ». Signalons qu'actuellement, les européens sont en train de concevoir un système << Galiléo » à 32 satellites.

31

CONCLUSION

Nous avons vu la mécanique céleste classique comme étant la résolution d'un problème de la mécanique Newtonienne. Cette étude, basée sur les lois de Kepler et la loi de la gravitation universelle de Newton, explique bien le mouvement des corps célestes.

Dans ce mémoire, nous avons présenté les grandes lignes des notions de force centrale avec quelques calculs sur ces notions (moment cinétique, énergies,...), ainsi que les applications des lois de Kepler et la loi de la gravitation (loi de Newton) sur la Terre qui sont discutées dans le chapitre 2. Et finalement nous avons terminé par des applications de toutes les lois que nous avons vues sur les satellites ainsi que les différentes utilisations des satellites artificiels dans certains domaines dans la vie.

REFERENCES

BIBLIOGRAPHIE

+ D. CHENOUNI, Cours de mécanique du point matériel SMP - S1 FSDM 2006-2007. + ANNEQUIN ET BOUTIGNY. Cours de physique MECANIQUE I mathématiques supérieures. Edition Paris (1978). Chap 8.

+ MHIRECH ABDELAZIZ. Cours de mécanique du point matériel SM-S1 et SMI-S1 FSR 2004-2005.

WEBOGRAPHIE

+ http :// aalem.free.fr/maths/c06-gradient-d'une-fonction.pdf

+ http://data0.eklablog.com/chiphys67/perso/mecatsobli/cours/chapitre%204%20mouv ement%20des%20satellites%20et%20des%20pla.pdf

+ http://montblancsciences.free.fr/terms/physique/cours/p14.htm

+ http://clubastronomie.free.fr/lois/mecanique_celeste.htm

+ http://lal.univ-lille1.fr/docpedago/CoursMPMDuriezS3.pdf

+ http://www.questmachine.org/article/Domaines_d_utilisation_des_satellites

+ I:\Références\wikipidya\Phys_ N° 07 Mouvement des satellites et des planètes.mht