Stochastic differential equations involving the two- parameter fractional brownian motion

1.2 Two-parameter Fractional Brownian Motion

1.2.1 The Main Definition

For technical simplicity we consider two-parameter fBm (fBm field) {B^H_t , t ? 118²₊}, where t = (t1, t2). We suppose that s = t if s = (s1, s2), t = (t1, t2) and si = ti, i = 1, 2.

1.2.2 Fractional Integrals and Fractional Derivatives of 14 Two-parameter Functions

Definition 1.2.1. The two-parameter process {B^H_t ,t ? R²₊} is called a (normalized) two-parameter fBm with Hurst index H = (H1, H2) ? (0,1)², if it satisfies the assumptions:

(a) B^H is a Gaussian field, Bt = 0 for t ? ?R²₊;

(b) EBtⁱ = 0, EBt ^HB^H = 1 11

4

(ti ^2Hi si 2Hi ti si

i=1,2

Evidently, such a process has the modification with continuous trajectories, and we will always consider such a modification. Moreover, consider "two-parameter" increments:Ä_sB^H_t := B^H_t - BHs1t2 - BHt1s2 + B^H_s for s = t. Then they are stationary. Note, that for any fixed ti > 0 the process B^H

(ti,.)

will be the fBm with Hurst index Hj, i = 1,2, j = 3 - i, evidently, nonnormalized.

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions

For á = (á1, á2) denote (á) =

(á1)¹(á2)

Definition 1.2.2. [12] Let f ? T := [a, b] := 11 [ai, bi], a = (a1, a2),

i=1,2

b = (b1, b2). Forward and backward Reimann-Liouville fractional integrals of orders 0 < ái < 1 are defined as

(I_a^á_r¹² f)(x) := (á) f (u) ?(x, u, 1 - á) du,

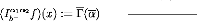
and

(Ir2 f)(x) := (á) f (u)

du

lx,b] ?(x, u, 1 - á) ,

correspondingly, where [a, x] = 11 [ai, xi], [x, b] = 11 [xi,bi],du = du1du2,

i=1,2 i=1,2

?(u, x, á) =| u1 - x1 |^á1| u2 - x2 |^á2, u, x ? [a, b].

Definition 1.2.3. Forward and backward fractional Liouville derivatives of orders 0 < ái < 1 are defined as

2

(Dr² f)(x) := (1 f (u) a) \ du

?x1?x2 ?(x, u, á)

and

?2 f (u) , du, x ? [a, b]

(Dr :á2 x)

:= (1 - á) ?x1?x2 i[x,b] ?(x, u, á)

1.2.2 Fractional Integrals and Fractional Derivatives of Two-parameter Functions 15

Definition 1.2.4. Forward fractional Marchaud derivatives of orders 0 < ái < 1 are defined as

~ f Ä_u xdu

( 15r² f)(x) :=(1 - á) f (x) +

?(x, u, á) á1á2 ./[a,x] ?(x, u,⁽ 1 )+ á)

+ E i=1,2,j=3-i	ái	áj	ix% f (x) - f (ui, x j) dui) a% (xi - ui)^1+^á%
	xj - aj

and the backward derivatives can be defined in a similar way

Let 1 = p = 8, the classes Iá1á2

+ (L_p(T )) := ~f|f = Iá1á2

_a+ ?, ? ? L_p(T )~,

_I

á1á2 - (L_p(T )) := ~f|f = Iá1á2 b- ?, ?? L_p(T)1 Further we denote Dá1á2

_a+ := Ia-+ á1á2). Of course, we can introduce the notion of fractional integrals and fractional derivatives on R² +. For exemple, the Riemann-Liouville left and Right sided fractional integrals and derivatives on R²₊ are defined by the formulas

(If+ l1á2 f)(x) := (á) L8 f(t) ,x] cp(x , u, á)^dt

f (t)

(I21á2 f)(x) := (á) 48) ?(x,u, á) dt,

2

(c^á

^(á12)f)(x) = (DT^á2 f)(x) := (1 - á) ? x1?x2

?I f(t)

(,_,x] (p(x ,t, á) dt

and

2

f ft)

(I^-(á1á2)f)(x) (D^á1á2f)(x)

:= (1 - á) ?x1?x2 _i[x,8) ?(x( t, á)^dt,

0 < ái < 1. Evidently, all these operators can be expanded into the product

of the form Iá1á2

+ = Iá+ 1 ? I^á2 +, and so on. In what follows we shall consider

only the case Hi ? (1/2, 1). Define the operator

YM#177; 1 H2 f := i=1,2

C(3) H%I^á1á2 #177; f.

1.2.3 Hölder Properties of Two-parameter fBm

We fix á = (á1, á2), ái ? (0,1] and let T = [a1, b1] × [a2, b2]. Let f the Riemann-Liouville fractional integral of order á i.e

1

x1 Ix2

₂ (x1 - t1) 1-- f (át1,t21 (x2 )- t2)--á2

f)(x1, x2) = (al)F(a2) dt1dt2, (x1, x2) ? T

vx1)^v.1^ritc:E2) a1 . a

p

The space Ëá,p = (I_a^á+)(L_p(T)) is called the Liouville space (or Besov space) and it becomes separable Banach space with respect to the norm WEc+fllá,p = IIfII

Proposition 1.2.3.1. [6] For every á, â

Iá _a+I^â a+= Iá+â

_a+ ,

If f ? C²_b (T) and f = 0 on ?1T = ([a1,b1] × {b1}) ? ({a1} × [a2,b2])then the function

1 f x1 14+ f (x1, x2) = r2 ?²f(t1,t2) dt1dt2

(1 - á1)(1 - á2) _L1 J_a2 ?t1?t2 (x1 - t1)^á1 (x2 - t2)^á2

(1.4)

is the unique function from L₈(T) such that

I^á_a+D^á_a+f = f.

For a rectangle D = [s1, t1] × [s2, t2] ? T we define the increment on D of the function f : T ? R by

f(D) = f(t1,t2) - f(t1, s2) - f(s1,t2) + ^f(s1, s2).

We denote by _C[ai,bi],ái the space of all ái-Hölder functions on [ai, bi] and

kfk[ai,bi],ái = sup u6=v,ai=u,v=bi

|f(u) - f(v)| (u - v)ái .

Also, we denote by CT,á1,á2 the space of all (á1, á2)-Hölder functions on T, i.e., f ? CT,á1,á2 if f is continuous,

If(a1, .)k[a2,b2],á2 < 8, f(., a2)k[a1,b1],á1 < 8

and

|f([u1, v1] × [u2, v2])|

< 8.

|u1 - v1|^á1|u2 - v2|^á2

kfkT,á1,á2 = sup

ui6=vi

Proposition 1.2.3.2. [4] Let 0 < â1 < á1,0 < â2 < á2 and p = 1. Then we have the continuous inclusions Ëá,p ? Ëâ,p,

Ëá,p ? Cá1-p^-1,á2-p^-1, Câ1,â2 ? Ëã,p if áip > 1, âi > ãi > 0

1.2.4 Fractional Generalized Two-parameter Lebesgue-Stieltjes Integrals 17