Modélisation et couverture des comptes courants postaux

ÉCOLE NATIONALE DE LA STATISTIQUE ET DE L'ADMINISTRATION ÉCONOMIQUE 3, AVENUE PIERRE LAROUSSE - 92245 MALAKOFF CEDEX, FRANCE



Mémoire d'Actuariat présenté
pour l'obtention du diplôme
de l'ENSAE
et l'admission à l'Institut des Actuaires

le

Par: GUILLAUME OMINETTI et MARIE TODD

Titre: Modélisation et couverture des Comptes Courants Postaux

Confidentialité: NON OUI (Durée: 1 an 2 ans)

Les signataires s'engagent à respecter la confidentialité indiquée ci-dessus

Membre présent du jury de l'Institut des Actuaires

Membres présents du jury de la filière Actuariat de l'ENSAE

Entreprise

Nom: LA BANQUE POSTALE Signature:

Directeurs de mémoire en entreprise Nom: CHRISTOPHE LUNVEN Signature:

Nom: LUDOVIC MERCIER Signature:

Invité Nom: Signature:

Secrétariat : Bibliothèque:

Autorisation de publication et de mise en ligne sur un site de diffusion de documents actuariels (après expiration de l'éventuel délai de confidentialité) Signature du responsable entreprise

Signature du candidat

1

Résumé

Une banque de détail effectue un service dit de transformation, ou d'intermédiation, c'est-à-dire qu'elle collecte les dépôts de ses clients et utilise ces ressources pour investir sur les marchés, en particulier pour prêter aux particuliers, aux entreprises ou sur le marché interbancaire. Cette position d'intermédiaire financier expose la banque à un risque majeur, appelé risque de liquidité : elle investit en général à long terme des ressources sans maturité définie, qui peuvent être potentiellement exigées par les clients du jour au lendemain. C'est la raison pour laquelle on parle de dépôts à vue. Ainsi, un retrait important et brutal par de nombreux clients peut créer un déséquilibre soudain dans le bilan de l'établissement. Dans un tel scénario, ce dernier ne dispose plus des liquidités pour faire face à la demande et se voit contraint de réemprunter sur les marchés et/ou de vendre une partie de ses actifs financiers d'échéance lointaine. Si le contexte de marché est défavorable à cet instant, avec des taux d'intérêts très élevés, la banque enregistre alors potentiellement une perte.

Pour diminuer son exposition à ce risque, elle doit donc placer une proportion suffisamment importante de l'encours à court terme. Cependant, il est aussi dans son intérêt de placer l'essentiel de ses ressources à long terme afin, d'une part, de profiter de taux d'intérêts plus avantageux et, d'autre part, de lisser sa rémunération au cours du temps. Un arbitrage doit être effectué entre les deux types d'investissement. L'établissement de crédit doit définir une politique de risque qui pilote ses stratégies de placement sur les marchés. Ce pilotage dépend étroitement des modèles statistiques utilisés pour effectuer les projections sur le niveau des taux et des encours futurs : on parle de gestion actif/passif. Cette gestion nécessite une analyse régulière de la situation du bilan et surtout de son évolution probable. L'estimation des besoins et des excédents de liquidité aux dates futures y revêt une importance capitale.

Ce mémoire explore la problématique de la gestion actif-passif d'une banque de détail en proposant d'abord une modélisation, puis une couverture, de l'encours des comptes courants de l'établissement de crédit dans le futur.

La première partie de l'étude a consisté à proposer des scénarios d'évolution de l'encours global des comptes à vue. Ce dernier est défini comme l'agrégat des sommes d'argent déposées par les clients sur leur compte courant.

Les articles académiques que nous avons lus, pour orienter notre démarche, ne proposaient que des modèles d'évolution macroéconomiques insuffisants à nos yeux. Nous pensons en effet que la dynamique de l'encours est un processus complexe intégrant des effets très variés, aussi bien économiques (le Produit Intérieur Brut, l'inflation) que démographiques (structure par âge de la clientèle) ou comportementaux (taux de sorties volontaires des clients). La littérature académique consultée ne tenait pas suffisamment compte de ces éléments.

Ainsi, nous avons bâti un cadre théorique microéconomique beaucoup plus fin. Le modèle probabiliste construit repose sur une ventilation de la clientèle par strates «financières» et par âges et reproduit les mouvements aléatoires sur les comptes courants de chacun des clients en intégrant des facteurs variés comme l'inflation ou les taux de mortalité par âge. Ensuite, nous avons implémenté informatiquement la modélisation mathématique innovante que nous avons construit. L'enjeu de ces simulations a été de valider le comportement du modèle et d'analyser sa sensibilité aux différents paramètres.

En particulier, nous y avons établi que le modèle retenu pour l'inflation conditionne fortement la dispersion de l'encours : une inflation aléatoire, et plus volatile, élargit les intervalles de confiance pour la valeur de l'encours, à une date future donnée.

2

Le degré de mobilité des clients, qui caractérise leur propension à changer facilement d'état et à sortir plus facilement, est un déterminant essentiel de la volatilité de l'encours. Cela signifie que, plus la base de clientèle est mobile, plus notre pouvoir prévisionnel sur l'évolution de l'encours aux pas de temps suivants est dégradé. De même, les taux de sortie des clients, utilisés dans la calibration du modèle, modifient de manière importante la durée de vie des dépôts dans une vision de vieillissement du stock existant, lorsque la banque arrête toute ouverture de compte.

La démographie actuelle de la clientèle est, quant à elle, un facteur déterminant de la croissance de l'encours sur le court-moyen terme. Nous y avons mis en évidence que, dans le cadre de notre modèle, l'arrivée de la génération du baby-boom dans des âges avancés est susceptible d'entraîner, dans un futur proche, une surperformance de l'augmentation de l'encours par rapport à ce que l'on pourrait s'attendre a priori, notamment parce que les personnes âgées détiennent en moyenne plus de liquidités. Par ailleurs, nous avons pu vérifier qu'une banque en ligne, qui se caractérise par une clientèle très jeune, connaît une surperformance sensible de la croissance de son encours. Cela est lié au vieillissement de sa clientèle actuelle et à l'augmentation de l'effectif de cette dernière. À l'inverse, une base de clientèle initialement âgée peut entraîner une stagnation de l'encours, voire une décroissance de celui-ci, sur le court-moyen terme en raison de la perte prochaine des clients les plus aisés.

La seconde partie de l'étude a consisté à analyser les performances de différentes stratégies d'investissement de l'encours bancaire. L'enjeu est d'y modéliser l'arbitrage, entre l'investisse-ment à court-terme et l'investissement à long-terme, qui se pose dans la recherche simultanée d'une rémunération lisse et pérenne mais avec une faible exposition au risque de liquidité. Pour atteindre cet objectif, nous avons considéré une stratégie de placement simple pour la banque de détail, consistant à investir à court terme une proportion constante de l'encours de clientèle et à investir le résiduel à long terme, sur des obligations à cinq ans. En nous appuyant sur un modèle financier classique sur les taux (celui de Hull et White), nous avons simulé des scénarios d'évolution des taux de marché de différentes échéances. Ainsi, chacune de ces simulations a fourni une trajectoire possible pour les prix des obligations et les rendements des deux supports. En couplant cette simulation avec celle sur l'encours bancaire effectuée en première partie, nous avons alors simulé la marge nette dégagée par l'établissement sur une période donnée. Cette marge nette est définie comme la rémunération qu'il perçoit à chaque date au titre de ses placements passés sur les marchés. Nous l'avons effectué pour différentes stratégies de placement, correspondant à une allocation plus ou moins importante d'investissement sur le support court-terme (respectivement long-terme). Pour analyser la robustesse de chaque stratégie, nous avons également simulé un scénario de stress, qui consiste en une sortie subite et massive de clients, couplée à une hausse des taux.

Nous avons mis en évidence que plus la banque place une part importante de l'encours des dépôts à vue à long terme, plus elle diminue la volatilité de sa marge mais plus elle s'expose à un fort risque de liquidité : sous le scénario catastrophe que nous générons, la banque s'expose à une perte d'autant plus lourde qu'elle a investi massivement à long terme. Nous avons alors été en mesure de tracer des graphes illustrant cet arbitrage entre lissage de rémunération et risque de liquidité. L'optimalité de l'investissement a été envisagée comme un problème de minimisation de la volatilité de la marge sous contrainte d'une perte plafond, en cas de scénario de stress. Ce programme d'optimisation doit être résolu par la banque au regard de la ligne de conduite sur le risque qu'elle s'est fixée. Toutefois, nous avons établi que la structure par âge de la clientèle conditionne le choix de stratégie de l'établissement de crédit. Ainsi, à volatilité de marge donnée (correspondant donc à une certaine allocation entre placements court-terme et long-terme), une banque présentant une clientèle jeune (respectivement âgée) s'expose à un risque de liquidité inférieur (respectivement supérieur) sur

3

le scénario catastrophe généré. La raison à ce résultat est le différentiel de croissance dans l'encours de ces banques.

Finalement, dans le cadre de notre modélisation, sous le problème de minimisation de volatilité avec contrainte sur la perte, la banque de détail va donc choisir d'investir une proportion d'autant plus importante de l'encours global sur le long terme que sa clientèle est jeune.

4

Abstract

A bank provides a so-called maturity transformation service: it gathers liquidity from its customers' demand deposits and trades this amount on the financial market, particularly to issue loans to individuals, to corporates or to other financial institutions. This unique role of financial middleman exposes the bank to a major risk, known as liquidity risk : indeed, it invests in long-term financial assets the liquidity held on «non-maturity» deposits, which have no stated maturity and where individual depositors have the right to add or substract balances without restriction. Therefore, an unexpected and massive withdrawal can result in a sudden mismatch between assets and liabilities of the retail bank. In fact, the latter becomes incapable of raising enough liquidity and is forced to borrow on the money market and /or to sell part of its long-term financial assets in order to face its customers' demand. If the market conditions are quite poor at this very moment, with very high interest rates, the institution can potentially carry a significant loss in the event of such a scenario.

In order to minimize its liquidity risk exposure, it has to invest in short-term assets an important enough proportion of its demand deposit liability. Nevertheless, it is more interesting to trade long-terme assets since they generally offer higher return rates and enable the bank to smooth its margin over time. Thus, the bank has to reach a relevant compromise between the two kinds of assets. It has to define its risk-appetite internal policy that will drive its investment strategies on the financial markets. This management is closely dependent on the statistical models used for predicting both the interest rates and the demand deposit liability : it is known as Asset-Liability Management (ALM). It requires a frequent analysis of assets and liabilities and of their probable evolution. Within this context, the estimation of both future liquidity needs and excess is of the utmost importance.

This paper explores the subject of asset-liability management for a retail bank by proposing first a theoretical evolution model, and then a hedging, of the demand deposit liability of the financial institution.

The first part of the study consists in proposing scenarios for the future evolution of the «non-maturity» deposit liability. The latter is defined as the total amount held by customers on their demand deposits.

The existing literature on the subject we have read only proposed macroecomic-oriented models, which appeared to be irrelevant from our point of view. Indeed, we believe that the stochastic evolution of the deposit liability is a complex process driven by various effects, ranging from economic ones (the Gross Domestic Product, the inflation rate) to demographical ones (the age structure of the customer base) or behavioral ones (the attrition rate). None of the papers we have consulted wak taking these different aspects into account.

Therefore, we have built a far more accurate microeconomic-oriented theoretical framework. This stochastic model relies on an apportionment, that is to say a breakdown, of the customer base both by strata (on a financial criterium) and by age and reproduces the random moves on individuals' demand deposits while integrating various exogenous factors such as inflation or mortality rates. Then we have implemented this innovative mathematical model on computer. The purpose of the conducted simulations was to analyze both the relevance of the results implied by our model and their sensibility to the different parameters.

We have notably proved that the underlying model used for inflation strongly influences the demand deposit dispersion: a random and more volatile inflation broadens the confidence intervals for the value of the demand deposit at a set date in the future.

5

The degree of mobility of customers, which characterizes their propensity to move easily from one financial state to another and to leave the bank, largely conditions the volatility of the deposit balance. This means that the more mobile the customers are, the more our predictive power on the evolution of the demand deposit liability is deteriorating. Similarly, the bank-leaving rate used to calibrate the model significantly modifies the duration of demand deposit liability in the situation where the bank stops issuing accounts.

The bank's customer base today's structure is the major driver of the growth of its demand deposit balance in the short and in the mid term. We have emphasized the fact, that within the framework of our model, the ageing of the baby-boom generation is likely to cause in the near future an overgrowth of the demand deposit balance compared to what we could expect first, given that elderly people generally hold more liquidity on their accounts. Besides, we have been able to prove that a bank whose customers are quite young (typically the case of recently-appeared online banks) will see the growth of its demand deposit balance overperform because of the ageing of its customers and the increase in the number of them. On the contrary, an elderly customer base can result in a stagnation or even a decrease in the demand deposit liability in the short and in the mid term, due to the loss of the wealthiest customers in the near future.

The second part of the study has aimed at analyzing the performance of different investment strategies. The stake was to modelize the compromise to reach (between investing in short-term and in long-term financial assets) that raises while trying to ensure both a smooth and sustainable margin and a low liquidity risk exposure. To achieve this goal, we have considered a simple investment strategy for the retail bank, that consists in trading a set and constant proportion of the demand deposit liability on short-term assets and to invest the remaining on five-year maturity state bonds. Thanks to the Hull and White classical financial model on market rates, we have generated future evolution scenarios for the term structure of the rate curve. Each of these simulations has provided a possible trajectory for the bonds prices and the returns of the assets the bank can buy. By coupling this implementation with the one on the stochastic evolution of the demand deposit balance built in the first part, we have simulated the net margin the bank perceives over a given period of time. The net margin is defined as the remuneration the bank gets at each date from its past investments, that is to say the interest rate cash-flows following its past trades. We have implemented this procedure for different investment strategies, each one matching a specific allocation in the demand deposit balance investment between short-term and long-term assets. What's more, in order to analyze the robustness of the different strategies, we have generated a stress test consisting in both a sudden and massive attrition and a dramatic increase in market rates.

We have emphasized the fact that the more the retail bank invests on long-term state bonds, the more it reduces the volatility of its net margin but the more it is exposed to an important liquidity risk too : thus, under the stress test we have simulated, the financial institution is all the more exposed to a major loss since it has massively invested in long-term securities. We were then able to plot graphs that give a visual illustration to the compromise between smooth remuneration and liquidity risk : the optimality of the investment is seen in the light of a margin volatility minimization program with condition on the loss incurred under the stress test. This optimality is then to be determined by each bank in regard of the risk-appetite policy it follows. However, we have been able to establish that the age structure of the retail bank's customer base impacts its investment choice. Thus, for a given margin volatility (matching a specific allocation between short and long-term investments), a bank whose customers are particularly young (resp. elderly) is exposed to a lower (resp. higher) liquidity risk under the simulated stress test. The reason for this result is the significant differential in the growth of the deposit balance of these banks. As a matter of fact, within

6

our model framework, under the margin volatility minimization program with condition on the loss incurred under the stress test, the retail bank invests an all the more important part of its demand deposit liability in long-term securities since its customers are young.

7

8

Table des matières

I Analyse de la problématique ALM et revue de la littérature 11

1 Le pilotage actif-passif 11

1.1 Notions autour du risque ALM 11

1.2 Objectifs 12

1.3 L'approche académique de la problématique : éléments de bibliographie . . 13

2 Démarche du projet 15

II Modélisation de l'évolution du niveau d'encours 16

3 Observations empiriques et orientation de la démarche 16

3.1 Analyse du niveau d'encours historique 16

3.2 Motivation de l'approche retenue 18

4 L'approche macroéconomique 19

4.1 Principe et choix des variables explicatives 19

4.2 Résultats 20

4.3 Un modèle pour l'inflation 21

5 L'approche probabiliste interne 23

5.1 La segmentation clientèle 23

5.2 Modélisation de la dynamique des encours 24

5.2.1 Notations 24

5.2.2 Dynamique des clients au sein de la banque 25

5.2.3 Dynamique de l'encours client moyen par cellule 26

5.2.4 Le modèle probabiliste et ses hypothèses 27

III Application informatique du modèle construit 32

6 Analyse de premières simulations 32

6.1 Les paramètres et les variables d'état initiales 32

6.1.1 Taux de transition et de sortie 32

6.1.2 Lois des processus d'arrivée 33

6.1.3 Inflation et encours client moyen par cellule 34

6.2 Résultats obtenus 34

7 Sensibilités aux paramètres et aux variables initiales 36

7.1 Influence de l'inflation et des taux de transition 37

7.2 Influence de la démographie initiale 42

7.2.1 Pyramide des âges et calibration des processus d'arrivée 42

7.2.2 Déséquilibre démographique initial vers le bas 46

7.2.3 Déséquilibre démographique initial vers le haut 47

7.3 Vision «mort» du bilan et durée de vie théorique des dépôts 48

8 Un modèle à «superstrates» 49

9

9 Vers une calibration du modèle sur les données

historiques? 56

IV Modélisation de l'évolution de la marge nette 57

10 Définition et principes 57

10.1 Une approche économique et comptable 57

10.2 Les stratégies de placement et le «compte d'intérêts» 57

11 Le modèle 59

11.1 La courbe des taux 59

11.2 Récapitulatif du modèle général 63

11.3 Les stratégies de placement 64

11.3.1 Position du problème 64

11.3.2 Métriques utilisées 65

11.3.3 Notations 66

11.3.4 L'investissement sur les marchés 67

12 Simulations de l'évolution de la marge nette

d'intérêts 69
12.1 Illustration des différences entre les stratégies d'investissement sur un cas très

simple 69

12.2 Volatilité de la marge et perte en situation de stress 71

12.3 Influence de la structure initiale de la base de clientèle 73

A Dynamique de l'encours des dépôts à vue 77

B Résolution détaillée du modèle de Hull et White 79

C Table INED utilisée pour la calibration des taux de mortalité 84

10

Introduction

Les banques de détail jouent principalement le rôle d'intermédiaire financier et rendent un service de liquidité: elles empruntent à court terme aux personnes ayant un excès de financement (par le biais de leurs dépôts) et prêtent, en général à long terme, aux personnes ayant un besoin de financement. Ce mécanisme fondamental s'appelle la transformation et fait des établissements de crédit des acteurs essentiels du paysage économique actuel. Cette opération d'intermédiation comporte néanmoins des risques substantiels pour les établissements bancaires.

Le principal d'entre eux est le risque de liquidité, qui traduit une incapacité de la part de l'établissement à rééquilibrer son bilan. L'origine de ce risque réside dans le fait que les sommes déposées par les clients sur leurs comptes, qui constituent le principal passif de long terme des banques de détail, sont intrinsèquement des ressources sans maturité contractuel-lement définie, à la différence des principaux postes figurant à l'actif (tels les obligations d'Etat ou les prêts immobiliers ainsi qu'à la consommation). Ainsi, un retrait soudain et massif des clients peut potentiellement excéder les réserves de liquidité de l'établissement et créer une insuffisance de trésorerie. Cela oblige dès lors la banque à réemprunter et rend nécessaire une liquidation dans l'urgence de ses actifs longs, avec le risque de marché que cela induit. On parle ainsi de passif sans échéance. Pour faire face à ce type de risque, la banque propose en interne des lois d'écoulement sur les dépôts à maturité incertaine pour définir ses stratégies de placements. D'autre part, les programmes de financement qu'elle adopte doivent lui permettre de réajuster au mieux son bilan en cas de déséquilibre de ce dernier et prennent en compte l'évolution des marchés, en particulier celle des niveaux des courbes de taux. Cette gestion est connue sous le nom de gestion du bilan bancaire ou gestion actif-passif (en anglais Asset Liability Management abrégé en ALM). Le second risque le plus important s'inscrivant dans ce cadre, et intimement lié à celui de liquidité, est le risque de taux (de change, d'intérêt et même d'inflation). En effet, un changement des courbes de taux induit, d'une part, une modification de la valeur des positions financières figurant au bilan et, d'autre part, une modification potentielle du comportement des clients. Le niveau des taux agit par ailleurs directement sur l'efficacité des stratégies financières visant à équilibrer le bilan de l'établissement de crédit. Il s'agit dès lors pour la banque de définir une politique de gestion des ressources figurant à son passif en vue d'optimiser la valeur économique de l'ensemble sur la durée. Ce pilotage dépend étroitement des modèles statistiques utilisés pour effectuer les projections sur le niveau des taux et des encours futurs.

La problématique de gestion des risques ALM, qui n'a pas encore été beaucoup explorée d'un point de vue théorique, revêt ainsi une importance capitale pour les banques de détail, surtout depuis la crise financière de 2008.

L'objectif de notre étude est d'explorer plus en détail les différents aspects des problèmes posés. Après une revue de la littérature existante sur le sujet, nous définirons un cadre théorique innovant pour la modélisation de l'évolution de l'encours des dépôts à vue, en l'envisageant sous un angle microéconomique. Après construction de ce modèle de prévision stochastique de l'encours, nous diffuserons les courbes de taux sur les marchés selon le modèle de Hull et White. Cela nous permettra dans une dernière partie d'analyser les performances de différentes stratégies de placement de l'encours bancaire, en étudiant notamment l'exposition qu'elles induisent aux risques de taux et de liquidité. Nous serons alors en mesure de discuter l'optimalité des différentes stratégies envisagées selon le point de vue adopté.

11

Première partie

Analyse de la problématique ALM et

revue de la littérature

1 Le pilotage actif-passif

1.1 Notions autour du risque ALM

Le bilan simplifié d'une banque de détail comprend les principaux postes suivants.

Actif	Passif
Immobilisations	Capitaux propres
Crédits immobiliers	Comptes-chèques (CCP)
Crédits à la consommation	CSL (comptes sur livrets)
Autres créances	LA/LDD/LEP (livrets réglementés)
Portefeuille de marché	PEL/CEL (épargne logement)
Trésorerie	Programmes de financement
	(émissions d'obligations/emprunts interbancaires)

Le passif, qui correspond aux ressources de la banque, est essentiellement constitué de l'épargne et des dépôts de la clientèle. Ces dépôts sont dits à vue, car ils peuvent être exigés à tout instant par le client (d'où le terme de passif sans échéance), et constituent la principale «raison d'être» de la gestion ALM. À l'exception des comptes courants, les dépôts sont rémunérés selon des taux qui évoluent'. Tous ces dépôts sont comptabilisés en couru, c'est-à-dire en coût amorti : on effectue une analyse période après période des flux d'intérêts et des décaissements qui seront amenés à les affecter aux différentes dates futures.

À l'actif, qui correspond aux emplois, figurent, notamment, les crédits distribués par l'établissement bancaire aux particuliers et aux entreprises. Environ 90% de ces crédits sont contractés à taux fixe. Les excédents de trésorerie sont généralement soit prêtés à d'autres établissements (sur le marché interbancaire) soit investis en des portefeuilles de titres, d'échéances similaires à la durée de vie moyenne estimée des postes au passif. Les titres sont soit affectés en trading et comptabilisés en valeur de marché, ou Marked-To-Market, soit détenus jusqu'à maturité (HTM pour Held To Maturity) et comptabilisés en coût historique.

La détention d'obligations souveraines, considérées comme des titres sûrs, permet à la banque de les mettre en garantie pour se refinancer auprès de la Banque Centrale en cas de stress de liquidité.

En fonction de l'adossement emplois-ressources, la banque de détail a un :

- Besoin de liquidités lorsqu'il y a insuffisance des dépôts pour faire face à la demande de crédits. Il lui faut alors trouver ces ressources, par exemple en émettant des titres ou en ayant recours au prêt interbancaire;

- Excédent de liquidités lorsque toute l'épargne liquide n'a pas été transformée. La banque peut alors utiliser ces ressources pour prêter sur le marché interbancaire ou investir en titres.

'Par exemple, le taux du livret A est actualisé tous les trois mois : réglementé, il tient compte du niveau de l'inflation et des taux courts

12

Ainsi, la banque de détail finance l'investissement en transformant l'épargne liquide des différents comptes clients en prêts à long terme (figurant à l'actif). Cette activité des banques, l'intermédiation, leur fait porter un risque de liquidité, en raison des différences de maturité entre les deux types d'engagements. La difficulté de la gestion bancaire, pour les établissements de crédit, réside essentiellement dans le fait suivant : les postes figurant au passif présentent en majorité une maturité incertaine et servent à financer les postes figurant à l'actif qui se caractérisent essentiellement par un échéancier connu. En pratique, le passif est globalement considéré comme un poste court terme alors que l'actif comprend essentiellement des crédits à long terme. Ainsi, l'établissement de crédit se retrouve engagé sur deux «terrains» à des niveaux opposés. Intuitivement, on comprend que toute la difficulté de ce service de transformation pour la banque est d'assurer une rentabilité a minima tout en contrôlant ses prises de risque afin de pouvoir tenir à tout instant ses engagements sur les deux «terrains».

La Banque Postale totalise actuellement plus de 11 millions de comptes courants actifs (comptes chèques), désignés en interne sous l'appellation Comptes Courants Postaux (CCP). Ces comptes courants, non rémunérés, représentent environ un tiers de son passif, soit approximativement 45 milliard d'euros actuellement. Cette banque n'est toutefois pas représentative de la plupart des autres établissements de crédit français dans la mesure où elle totalise un nombre bien plus élevé de dépôts de clientèle que la majorité d'entre eux. Cette spécificité lui permet de prêter massivement sur le marché interbancaire.

1.2 Objectifs

La gestion ALM a pour objectif d'estimer et de piloter l'équilibre entre les emplois et les ressources au regard de la politique de risque souscrite par l'établissement. Les risques les plus pris en compte dans son pilotage sont le risque de liquidité et les risques de taux (intérêts, change, inflation), qui demeurent très liés.

Cette gestion passe d'abord par une analyse régulière de la situation du bilan et de son évolution probable. Ainsi, la mesure des besoins et des excédents de liquidité aux dates futures s'inscrit dans la gestion du risque de liquidité. La mesure des déséquilibres entre les emplois et les ressources sensibles aux mouvements d'un même taux nécessite quant à elle une couverture spécifique de ce risque.

Le premier enjeu du pilotage du bilan bancaire est de viser un adossement actif/passif dans le temps, c'est-à dire un équilibre entre les cash flows générés dans le futur par l'actif et le passif. Le second consiste à définir une politique globale permettant de garantir un résultat pérenne et de lisser la rentabilité dans le temps pour s'affranchir des effets de cycle. Ceci est réalisé essentiellement au moyen de couvertures financières contre les mouvements de taux. L'utilisation de produits dérivés revêt ainsi un caractère indispensable.

Le pilotage ALM implique de pouvoir observer le comportement financier de la clientèle et de proposer des modèles d'évolution de ce dernier. Par ailleurs, il nécessite de travailler en coordination avec le département chargé de la politique marketing dans la mesure où le comportement clientèle modélisé est fortement lié aux stratégies commerciales et marketing proposées.

La gestion ALM s'appuie donc à la fois sur la modélisation statistique des comportements de la clientèle et sur les différentes méthodes de couverture sur les marchés financiers : les modèles de prévision retenus permettent de définir des stratégies financières d'achat de titres et de dérivés sur les marchés afin de se couvrir contre les risques modélisés.

13

1.3 L'approche académique de la problématique : éléments de bibliographie

La littérature académique sur la gestion ALM, ou sur la modélisation du niveau de l'encours de dépôts, est relativement peu étoffée. Certains articles ont particulièrement retenu notre attention. Nous les présentons succinctement ci-après.

Le premier d'entre eux, intitulé The arbitage-free valuation and hedging of demand deposits and credit card loans, fut écrit en 1997 par Robert A. Jarrow et Donald R. van Deventer. Ce papier vise à donner, sous certaines hypothèses, la «valeur» actuelle de la masse totale des dépôts à vue de la banque et à en déduire des stratégies de couverture. L'approche est successivement faite en temps discret et en temps continu, de manière complètement analogue. Nous nous contenterons ici de décrire leur démarche dans le cas discret.

Dans une économie à temps discret tE{0,1, ..., ô} munie d'une filtration naturelle Ft, les auteurs font l'hypothèse d'un marché segmenté : les individus, comme les banques, ont accès à un marché de titres du Trésor, mais seules les banques peuvent créer des comptes courants (sur lesquels les individus peuvent placer des dépôts). L'encours en t de l'ensemble des dépôts de la banque est noté D(t). Le marché du Trésor est supposé parfait ² et complet ³. Sur ce marché sont échangés un titre «cash» sans risque de valeur B(t) en t et des zéros-coupons. Le prix à la date t d'un zéro-coupon payant 1$ en T est noté P(t, T) avec

1

r(t)= P(t, t + 1) - 1

le taux d'intérêt spot. Sous l'hypothèse d'absence d'opportunités d'arbitrage, les auteurs déduisent l'existence d'une unique probabilité risque-neutre Q équivalente à la probabilité historique sous laquelle les zéros-coupons écrits dans le numéraire cash sont des martingales, soit

P(t, T)=EQ (P(t+

+r1,T) |Ft) =B(t)EQ (B(T)|Ft)

Les dépôts à vue sont quant à eux rémunérés au taux instantané i(t), c'est-à-dire qu'un dollar versé en t sur le compte est rémunéré par la banque 1 + i(t) dollars à la date t + 1. Les individus ne pouvant pas arbitrer, i(t) < r(t) pour tout t. L'inégalité stricte est autorisée car les auteurs laissent la possibilité d'opportunités d'arbitrage par les établissements de crédit.

Sous ces hypothèses, et en considérant que D(t) et i(t) sont adaptés à Ft, Jarrow et van Deventer écrivent la valeur actuelle nette en 0 des dépôts à vue de la banque comme étant égale à

VD(0)=EQ	ô-1E t=0	D(t)(r(t) - i(t))	)
		B(t + 1)

Il s'agit de l'espérance sous la probabilité risque-neutre de la somme actualisée des flux futurs affectant les dépôts. Les auteurs l'interprètent comme la valeur d'un swap vanille de taux durant ô périodes, recevant le taux variable r(t) et payant le taux variable i(t), de nominal variable D(t) en t. Ils en déduisent la couverture de l'encours, consistant à investir D(0) (l'encours initial) en zéros-coupons P(0, 1) et à vendre le swap représenté par VD(0).

²Les actifs sont divisibles à l'infini, le marché est infiniment liquide, il n'y a pas de coûts de transaction ni de dividendes, les ventes à découvert sont autorisées sans pénalités ni contraintes et les taux de prêt et d'emprunt sont les mêmes

³Tout flux en r est atteignable par un portefeuille autofinançant admissible

14

Pour mener à terme les calculs, les auteurs proposent plusieurs modèles pour D(t) et i(t). Citons notamment D(t)=a+br(t) ou ln(D(t))-ln(D(t-1))=a+br(t)+ct+d(r(t)-r(t-1)) où le temps est censé être un proxy de variables macroéconomiques pertinentes. En temps continu, l'article propose d'utiliser pour le taux spot r(t) le modèle de Vasicek et d'expliquer la variation de l'encours par le niveau des taux courts selon dln(D(t))=(a+br(t)+ct)dt+edr(t). Dans ces conditions, le logarithme de l'encours est donc une diffusion. Nous reviendrons sur ce dernier point ultérieurement.

Datant de 2009, l'article Hedging interest rate margins on demand deposits d'Alexandre Adam, Mohamed Houkari et Jean-Paul Laurent propose, quant à lui, une approche dite en «couru». Ils ne considèrent donc pas la valeur actuelle nette de l'encours mais directement la marge de taux d'intérêt générée par la banque, période après période. Celle-ci est définie comme la différence entre le taux d'intérêt auquel la banque prête et le taux qu'elle verse sur les dépôts. L'approche est en temps continu. Les auteurs de l'article modélisent le taux LIBOR forward Lt := L(t, T, T + 6T) à la date t, prévalant sur l'intervalle [T, T + 6T], par l'équation différentielle stochastique

dLt = Lt(pLdt + ULdWL(t))

avec /1L et UL constants. L'encours de dépôts à la date t, Kt, est supposé suivre la dynamique

dKt = Kt(aKdt + UKd

WK(t))

avec /1K et UK également constants. Leur idée est également de créer une dépendance entre le niveau d'encours et le niveau des taux. Ils supposent donc, en s'inspirant d'un article de Kalkbrener et Willing de 2004, que

_v'

d WK(t) = pdWL(t) + 1 - p²dWK(t)

où WK est un mouvement brownien orthogonal à WL, WK étant censé représenter d'autres sources de risques indépendantes des mouvements de la courbe des taux. Le taux versé sur les dépôts est modélisé par une fonction affine du taux sur le marché, soit g(Lt) = + /3Lt. Dans ces conditions, la marge de taux d'intérêt sur la période [T, T + 6T] est définie par

IRM_g(KT, LT)=6TKT(LT - g(LT))

Par la suite, les auteurs considèrent des stratégies de couverture qui consistent à signer des contrats à terme de gré à gré appelés FRA (pour Forward Rate Agreements). Ces derniers conduisent à la famille de pay-offs {9(L0 - LT), 9 R}. Par extension, ils définissent les stratégies admissibles comme les intégrales stochastiques relativement au processus d'Itô Lt,

soit

(Z T )

9tdLt, _(9t)0=t=T adapté

0

Les auteurs résolvent alors le problème de minimisation de la variance de la marge de taux d'intérêt sous contrainte d'espérance. Après calcul, ils en déduisent les stratégies optimales statiques, puis dynamiques, par des méthodes de contrôle stochastique.

Citons pour terminer l'article de thèse de Tanja Eronen intitulé Non-maturity Deposit Valuation and Hedging datant de 2008. Il offre un panorama relativement complet de la littérature existante sur le sujet et discute certaines hypothèses faites dans les modèles proposés. Il évoque en outre plusieurs méthodes et outils de couverture pour la gestion ALM : les floors (de taux d'intérêt) ainsi que différents swaps de taux.

15

2 Démarche du projet

Notre étude se divise en deux parties.

Elle commence par la modélisation de l'évolution future de l'encours des dépôts à vue.

Notre approche consistera dans un premier temps à régresser cette masse des encours ainsi que ses variations (ou une fonction de celles-ci) sur des variables macroéconomiques telles que le Produit Intérieur Brut, l'inflation ou encore le niveau des taux courts. Nous utiliserons pour cela les données de l'encours de La Banque Postale sur les dernières années. L'enjeu de cette première étape est d'analyser la sensibilité du niveau des dépôts à des grandeurs «globales», avant de nous consacrer à une modélisation plus fine de celui-ci. La démarche consistant à relier directement l'encours bancaire (ou ses variations) au niveau des taux, dans un cadre de séries temporelles, a été largement employée dans le passé, notamment par Jarrow et van Deventer comme nous l'avons précisé. Elle a également été reprise par Eronen. Nous pourrons confronter cette modélisation ad hoc aux données historiques de La Banque Postale

Dans un second temps, nous définirons un cadre théorique plus complet qui constitue l'innovation majeure de cette étude et en est sa principale motivation. Il est fondé sur l'idée que notre capacité prédictive d'évolution de l'encours est beaucoup plus forte lorsque nous nous basons sur la structure par âge des clients et que nous nous focalisons sur un segment de clientèle particulier. Ainsi, en découpant le portefeuille de clients de la banque puis en tenant compte des comportements caractéristiques à chaque groupe plus homogène ainsi formé, on espère augmenter notre pouvoir explicatif sur l'évolution de la masse des encours (partiels puis global par agrégation). En outre, cette approche a l'avantage de permettre une analyse plus fine du comportement des clients dans chaque segment et donc d'aider à la définition de politiques commerciales plus optimales adressées à chacun d'entre eux. Cette approche nécessitera la mise en place d'un modèle mathématique et d'hypothèses sous-jacentes, qui sont exposés en détail dans la partie dédiée. Pour inférer la distribution statistique de variables liées à l'encours clientèle, nous effectuerons des simulations Monte-Carlo sous divers choix de paramètres. Le principal enjeu de cette modélisation est de déterminer la sensibilité de la dynamique de l'encours à ces derniers.

La dernière partie de ce projet est le volet financier, qui consiste à exploiter les résultats de la première partie pour définir des stratégies de placement plus optimales. Il s'agira en premier lieu de modéliser l'évolution de la courbe des taux sur les marchés financiers. En croisant cette modélisation avec celle de l'évolution du niveau d'encours, nous serons en mesure de projeter les intérêts générés par les dépôts dans le cadre d'une politique de placement précise. Ils seront fonction du volume d'encours disponible, de l'allocation de cette ressource entre les placements potentiels et du niveau des taux d'intérêts à chaque date. La marge de taux d'intérêts a déjà été évoquée; nous rappelons qu'elle s'identifie simplement à la différence entre le taux de placement de la banque (ce qu'elle gagne) et le taux de rémunération des dépôts (ce qu'elle distribue à ses clients). L'objectif sera ensuite de couvrir cette marge, c'est-à-dire de l'insensibiliser le plus possible aux fluctuations de taux et de niveau d'encours, sous contrainte toutefois de pouvoir faire face à un stress de liquidité. Nous analyserons l'efficacité de différentes stratégies de placement, en recherchant celle(s) garantissant une marge nette la moins volatile possible et une prise de risque de liquidité limitée. Cette approche correspond à une vision plus pérenne de l'activité, qui s'emploie à s'affranchir des effets de cycle sans pour autant mettre en péril la santé financière de l'établissement. Ceci nous permettra de proposer des stratégies de pilotage ALM.

16

Deuxième partie

Modélisation de l'évolution du niveau

d'encours

3 Observations empiriques et orientation de la démarche

3.1 Analyse du niveau d'encours historique

Une observation de l'évolution de l'encours global⁴ des CCP à la Banque Postale appelle plusieurs remarques qualitatives. Nous avons tracé ci-dessous l'évolution de cette grandeur sur la période 1994-2010. Les relevés sont mensuels, avec interpolation affine.



FIG. 1 - Évolution historique des CCP

On constate déjà une tendance nette de croissance de la masse des dépôts. Les mesures étant mensuelles, le graphe ici capture en fait la dynamique globale des encours. En réalité, une étude de cette quantité à une échelle plus fine révèlerait des saisonnalités infra-mensuelles intimement liées à la période étudiée, d'un ordre de grandeur de deux à cinq milliards d'euros. Les flux importants représentés par le versement des salaires (en fin de mois), des allocations sociales ou encore des retraites en sont essentiellement à l'origine. Dans la cadre de cette étude, nous nous restreindrons à la partie dite «stable» de l'encours, c'est-à-dire celle représentée sur le graphique ci-dessus.

Ainsi, bien que les dépôts soient à vue, et donc, en théorie, sans maturité, on observe une forme de stabilité remarquable de l'encours, qui ne «s'évapore» jamais. Cette dernière remarque permet d'investir sur des actifs financiers les liquidités collectées en considérant que les dépôts ont une certaine durée de vie moyenne effective. En pratique, cette dernière est considérée comme étant de l'ordre de cinq ans. Les banques savent ainsi que les dépôts

⁴Nous désignons par cette expression la somme des dépôts correspondant à tous les comptes courants ouverts dans l'établissement

17

à vue restent relativement lontemps en base. Toutefois, précisons ici que La Banque Postale (à titre d'exemple, mais la remarque est vraisemblablement pertinente pour les autres établissements de crédit) ne l'a jamais mesuré précisément. En outre, l'encours total est continuellement «pollué» par la production nouvelle (arrivées de clients). Les différents effets (arrivées, sorties...) n'ayant jamais été isolés, on observe l'évolution de l'agrégat sans pouvoir connaître ce qui se passe aux échelles inférieures. Notre modèle permettra de définir une forme de benchmark précis pour l'appréhender plus finement.

Partant de ce graphe, deux approches ALM sont envisageables.

La première correspond à une vision surnommée «mort du bilan», dans laquelle la banque arrête toutes ses commercialisations de produits. Cette approche consiste à modéliser le vieillissement du stock existant sans aucune nouvelle arrivée extérieure. On y étudie l'évaporation progressive de la masse des encours dans le temps, consécutive aux départs des clients actuels (volontaires, vers la concurrence, ou par décès). L'établissement de crédit adopte alors une forme de convention d'écoulement pour décrire ce vieillissement, qui va conditionner sa stratégie d'achat de titres. Quatre scénarios possibles de cette «mort du bilan» sont représentés ci-après. Les courbes orange, jaune et mauve correspondent respectivement à une décroissance linéaire, à une décroissance linéaire après un premier choc, et à une décroissance de type exponentiel ou hyperbolique qui ralentit progressivement. L'adoption d'un scénario plus brutal, avec un écoulement plus rapide, correspond bien évidemment à une vision plus prudente. Les banques adoptent en général une convention d'écoulement standard parmi l'une de ces formes. L'idée est de retenir un scénario de crise dans lequel l'évolution est relativement simple, typiquement une diminution brutale de 10% (choc initial) suivie d'une décroissance linéaire jusqu'à une échéance T (10 ans, 15 ans...) où tout le stock aura disparu. Le modèle développé dans ce mémoire permettra a priori des modélisations de mort du bilan plus «réalistes» correspondant à une évolution plus stochastique (se rapprochant de l'évolution historique), tel que cela est suggéré par la courbe rouge. Ceci permettra de modifier la convention d'écoulement et par conséquent les stratégies d'achat de titres. À titre d'exemple, si la convention standard (décroissance linéaire sur T années) s'avère trop pessimiste, nous pourrons optimiser les placements en investissant sur des titres de maturité plus longue aux taux de rendement plus élevés.



FIG. 2 - Scénarios d'évaporation de la masse des encours de CCP

La seconde approche est quant à elle associée à une vision dite «dynamique». Ceci passe non seulement par la modélisation du vieillissement du stock existant mais également par la modélisation d'une production nouvelle correspondant aux arrivées progressives de nouveaux

18

clients. Dans cette vision, on opère une projection de l'encours des dépôts à vue de la banque dans le futur.



FIG. 3 - Dynamique future de la masse des encours de CCP

L'idée est de calculer (ou à défaut d'estimer) la distribution statistique du niveau d'encours à différents horizons. Nous pourrons en déduire des intervalles de confiance théoriques (ou empiriques) de la grandeur considérée, aux différentes dates.

Cette modélisation constituera le coeur de ce projet.

3.2 Motivation de l'approche retenue

Comme nous l'avons expliqué, nous souhaitons avant tout développer une nouvelle approche de modélisation des encours. Nous allons exposer ici la raison qui nous a amenés à rejeter les modèles que nous avons consultés dans la littérature académique.

Nous observons que dans l'ensemble des articles que nous avons lus sur le sujet, les auteurs considèrent que l'encours bancaire suit une dynamique très (trop) simple. En temps discret, leur démarche consiste généralement à l'écrire comme une fonction déterministe du temps, du Produit Intérieur Brut et/ou des taux courts. L'idée est de le décrire comme une fonction croissante du temps et de la richesse nationale et comme une fonction décroissante du niveau des taux (en raison de l'attrait supplémentaire induit pour les livrets rémunérés). Lorsque les auteurs raisonnent en temps continu, ils supposent généralement que le niveau Ät des dépôts de la banque est une diffusion. Autrement dit, ils considèrent que Ät est solution d'une équation différentielle stochastique (EDS) du type

d1Xt = lXt(adt + adWt)

avec /1 > 0 constant et o- constant. C'est notamment ce que suggèrent les auteurs sus-cités (Jarrow et van Deventer ainsi que Adam, Houkari et Laurent).

Notre conviction est que, dans un cas comme dans l'autre, la modélisation sous-jacente n'est absolument pas pertinente pour l'encours bancaire. Le plus gros reproche que nous faisons à ces deux approches est leur «pauvreté» explicative. En effet, l'ensemble de la dynamique des dépôts est résumé dans un cas par les variations des taux ou du PIB et dans l'autre par deux paramètres exogènes (à savoir le drift /1 et la volatilité a). Il est intuitivement improbable qu'un si petit nombre de paramètres ou de facteurs puisse expliquer une dynamique aussi complexe que celle de l'encours des dépôts à vue. Le premier cas correspond à une approche typiquement macroéconomique et ignore totalement les aspects microécono-miques, démographiques et comportementaux sous-jacents dans la dynamique des dépôts.

19

Pour illustrer notre propos, on peut remarquer qu'il pose implicitement une évolution identique pour toutes les banques quelle que soit leur structure actuelle. Or il apparaît plausible de considérer que les encours des comptes courants d'une banque en ligne, fondée il y a dix ans, et d'une banque implantée historiquement depuis des décennies, possédant une clientèle d'un âge avancé, soient amenés à évoluer différemment dans le futur. De même, les caractéristiques démographiques du pays d'implantation de l'établissement, qui apparaissent aussi comme des éléments déterminants, sont totalement ignorés. Par exemple, une baisse importante de la mortalité dans un pays donné suggère une croissance notablement supérieure de l'encours des banques présentes dans ce pays, au moins sur le moyen-long terme. Les mêmes remarques valent pour le modèle de diffusion de type Black-Scholes, qui est certes adapté pour des variations de cours de titre ou de taux, mais dont la pertinence ici est plus que discutable. Nous critiquons donc ce choix, probablement influencé par une certaine «culture» du pricing et de la finance quantitative, consistant à adopter pour le processus de l'encours des dépôts à vue une évolution similaire à celui d'un taux de change ou du cours du pétrole. Les processus sous-jacents sont en effet totalement différents! En outre, tout le pouvoir explicatif de ce dernier modèle réside dans une unique variable aléatoire, à savoir Lt lui-même. La diffusion crée par ailleurs une évolution très erratique et peut générer des trajectoires paraissant intuitivement très invraisemblables⁵ (fortes variations locales, décroissance vers 0 puis remontée importante. . .).

De notre point de vue, les approches présentées fournissent ainsi intrinsèquement des modélisations du comportement de l'encours très irréalistes. Les différents exemples invoqués ci-dessus prouvent que celui-ci est intimement lié à des données économiques (notamment l'inflation) et démographiques ainsi qu'à la structure de la base de clientèle actuelle ou au comportement des clients. Ce dernier varie d'ailleurs selon toute vraisemblance avec leur âge et leurs caractéristiques propres.

Nous proposons dès lors d'adopter une démarche plus économétrique. Nous reprendrons dans un premier temps l'approche macroéconomique suggérée dans les articles afin de nous faire une première idée du «lien» entre l'encours et certaines variables globales. Nous l'affinerons ensuite en construisant un cadre théorique fondé sur la segmentation du portefeuille de clientèle et intégrant des facteurs démographiques et comportementaux.

4 L'approche macroéconomique

4.1 Principe et choix des variables explicatives

Nous allons chercher ici à régresser la masse des encours Lt (ou une fonction de celle-ci) sur des variables macroéconomiques pertinentes. Par exemple, il est généralement admis que le niveau des taux courts influence fortement Lt. L'idée derrière cette constatation empirique est que, lors des périodes à fort taux d'intérêt sur les marchés, les personnes investissent plus de liquidités sur des produits rémunérés, tels que le livret A.

Ainsi, nous avons vu par exemple que Jarrow et van Deventer proposaient l'équation

ln(Lt) - ln(Lt_1)=a + br(t) + et + d(r(t) - r(t - 1))

qui relie les accroissements de l'encours à celui des taux courts. Ils y reconnaissent toutefois que la dynamique de la masse des dépôts est pilotée par d'autres facteurs, d'où le terme

⁵On peut se demander si l'observation de la trajectoire historique de l'encours des CCP de La Banque Postale permet de se prononcer sur la validité de l'hypothèse d'évolution selon dLt = Lt(pdt + adWt) et notamment de l'infirmer. Cela est l'objet d'une brève discussion menée en annexe A

20

linéaire en t. Le temps est censé être ici une approximation des autres variables macroéconomiques non incluses dans le modèle.

En 2000, James M. O'Brien a, quant à lui, proposé d'intégrer le revenu national dans les variables explicatives en écrivant : ln(Lt) - ln(Lt_1) = a + b(r(t) - i(t)) + cln(Y (t)) + f(t) avec E(f(t))=0 pour tout t, où i(t) est le taux de rémunération du dépôt et Y (t) le Produit Intérieur Brut (PIB) à la date t. Notons au passage que l'économiste reconnaît ici indirectement la complexité de l'évolution des dépôts en rajoutant un terme correctif d'erreur censé représenter un aléa non relié aux variables macroéconomiques.

Dans le cadre de cette étude, nous avons retenu plusieurs variables explicatives pour mener nos régressions linéaires simples et multivariées :

- l'inflation hors tabac : elle représente implicitement le coût de la vie et les variations de volume des agrégats monétaires;

- le PIB : il capture la vitesse de croissance de l'économie, que l'on peut légitimement corréler à la richesse des ménages et donc au niveau de leurs dépôts à vue;

- le niveau des taux courts (taux Pibor à 3 mois) : on s'attend à ce qu'il soit corrélé négativement au niveau des encours non rémunérés;

- le niveau des taux longs (taux des emprunts d'État à 10 ans).

Notre plage de données s'étend de janvier 1994 à décembre 2010. Le pas de temps est mensuel, hormis pour certaines variables (comme le PIB) pour lesquelles les données sont trimestrielles. Le logiciel statistique utilisé est SAS.

4.2 Résultats

En ce qui concerne les régressions simples, les variables macroéconomiques (PIB, inflation) se sont avérées être de très bonnes variables explicatives pour le niveau d'encours, avec des coefficients de détermination de l'ordre de 95%. A contrario, la régression de l'encours global sur le niveau des taux, que l'on prenne les taux courts ou les taux longs, n'a donné que des résultats médiocres. Pour tenir compte de décalages éventuels entre les mouvements des différentes variables, nous avons donc tenté de régresser l'encours sur les taux passés (en intégrant un retard variable) ainsi que sur leurs variations dans le passé proche (comme le suggèrent Jarrow et van Deventer). Aucune de ces tentatives n'a toutefois permis de déceler une telle relation. Ainsi, de manière assez surprenante, les régressions que nous avons menées sur l'évolution historique de l'encours des comptes courants à La Banque Postale ne nous ont pas permis de relever un lien avéré entre celui-ci (ou ses variations) et les mouvements de taux sur les marchés. Pour tenter de capter l'influence éventuelle des taux à un ordre plus élevé, nous avons donc déflaté l'encours (ou nous l'avons divisé par le PIB) puis nous avons tenté de mener une régression de cette nouvelle variable (ou de son logarithme) sur le niveau des taux. Toutefois, les résultats sont restés décevants avec des coefficients de détermination très faibles.

Par la suite, notre démarche a donc consisté à chercher une représentation de type AR(1)⁶ sur l'encours, puis sur l'encours déflaté, en tentant de régresser leurs variations mensuelles soit sur le niveau des taux, soit sur les variations de ces derniers sur les périodes précédentes. Ces méthodes plus sophistiquées n'ont malheureusement pas non plus permis de résultats probants. Les procédures de désaisonnalisation des différentes séries chronologiques n'ont en

⁶Pour AutoRegressive d'ordre 1. Il s'agit de chercher une représentation de la variable Lt - öLt-1, avec öER, en fonction des autres séries chronologiques. Nous avons essentiellement travaillé avec =1

21

rien changé la donne, dans la mesure où la série historique de la masse des dépôts des CCP présente une composante saisonnière quasi-inexistante.

Ainsi, le meilleur résultat obtenu, en tant que compromis entre qualité explicative et parcimonie du nombre de variables de régression, s'est finalement avéré être la régression simple du niveau des encours sur celui de l'inflation, correspondant à un excellent coefficient de détermination de R² = 0,973! Nous avons tracé ci-dessous la courbe correspondante.



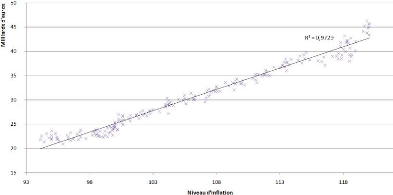
FIG. 4 - Régression du niveau de l'encours sur l'inflation hors tabac

L'inflation est donc un très bon indicateur du niveau moyen de l'encours dans la banque. Cela signifie implicitement que la richesse réelle détenue par les ménages sur leur compte courant (à vue) ne varie pas, ou très peu, au cours du temps. Dans la mesure où les CCP ne sont pas des produits d'épargne, mais des comptes servant aux retraits quotidiens pour les dépenses courantes (dont le montant suit par définition exactement le niveau de l'inflation), un tel résultat est relativement conforme à l'intuition.

4.3 Un modèle pour l'inflation

La régression précédente nous incite à intégrer l'inflation dans le modèle mathématique de dynamique des encours que nous allons construire. Il nous faut donc adopter un modèle pour cette grandeur économique. Nous allons commencer par définir les notations et le vocabulaire que nous utiliserons dans cette étude. Dorénavant, nous appellerons inflation mensuelle, ou plus simplement inflation, sur la période [t - 1, t] (où t N^" décompte le temps en mois) le taux itt d'augmentation des prix sur cette période. Cette variable capture localement, à une échelle mensuelle, la dynamique d'évolution des prix. Nous définissons le niveau d'inflation par ilt = (1 + lrt)llt_1 : il mesure la tendance au cours du temps de l'évolution des prix. En particulier, le niveau d'inflation est défini à multiplication par une constante près. Pour y remédier, on peut donc fixer son niveau à une certaine date de manière arbitraire (en général à 100). Il s'identifie alors à ce qui est appelé Indice des Prix à la Consommation (IPC). C'est sur cette dernière variable, publiée par l'Institut National de la Statistique et des Études Économiques (INSEE), que nous avons effectué la dernière régression.

Nous adopterons pour l'inflation un modèle similaire à celui proposé par Vasièek en 1977 pour la dynamique du taux spot sans risque. Nous considérons ainsi que l'inflation men-

suelle 7rt suit sur un espace (S2, IF, P) - où P désigne la probabilité historique - une équation différentielle stochastique d'Ornstein-Uhlenbeck, selon

d7rt = a(b - 7rt)dt + QdWt , t E R+

avec Wt un mouvement brownien standard unidimensionnel, dont la filtration naturelle sera dorénavant notée Gt =Q(Wt, 0<u<t).

Le modèle est spécifié par trois paramètres : a, b et la volatilité a ER^*₊. Il s'agit d'un modèle dit de retour à la moyenne car le processus 7rt oscille autour de b. Ainsi, a > 0 est un paramètre d'échelle qui mesure la vitesse de rappel vers b du processus 7rt.

Cette équation différentielle stochastique se résout explicitement par

t

7rt = 7r0e^-at + b (1 - e-at) + a

J e^-a(t-s)dW_s (1) 0

On a même plus généralement pour 0<t1 <t2

t2

\ _f

7rt2 = 7rt₁e^-a(t2-t1) + b (1 - e-a(t2-t1)/ + a _J e^--a(t2-s)dW_s (2)

t1

Par le théorème d'isométrie des intégrales stochastiques, l'intégrale de Wiener du membre de

2

droite dans (1) est une variable gaussienne centrée de variance Q2 _Ret, e-2a(t-s)ds = 2_a (1 - e-2at)

Par conséquent

² 1 7rt N (7r0e^-at + b (1 - e-at) 2_a (1 - e-2at))

En particulier, E^P(7rt) = 7r0e^-at + b (1 - e^-at) et VP(7rt) =

0.^2 2a

(1 - e-2at), qui convergent

22

0.²

respectivement lorsque t ? +oo vers b et 7.

2a

Par ailleurs, l'indépendance des accroissements du brownien, combinée à l'expression (2),

permet d'affirmer que la loi conditionnelle de 7rt sachant _7rt-1 est la gaussienne

2

N (7rt-1e^-a + b (1 - e^-a) , 2_a (1 - e-2a)/11

Cette remarque est de première importance pour la simulation informatique de l'inflation. En effet, même si sa dynamique est décrite ici de manière continue, nous la considèrerons uniquement à des instants discrets (t=0, 1, 2, ...). Ainsi, partant de 7r0, il suffira de générer des lois normales successives, dont les paramètres dépendent du niveau précédent de l'inflation, pour obtenir de proche en proche une trajectoire de cette dernière.

À titre illustratif, nous avons simulé puis tracé ci-après deux trajectoires pour un quadruplet de paramètres identiques (a, b, a, 7r0) = (0.2, 0.002, 0.0002, 0.002) sur un horizon h = 180 mois, correspondant à 15 ans. Sachant que l'objectif annoncé de la Banque Centrale Européenne est une inflation annuelle à 2%, le choix des paramètres s'est effectué a priori en cherchant à revenir en moyenne vers une valeur d'inflation mensuelle équivalente. Nous avons fait figurer entre parenthèses sur l'axe des ordonnées, à côté de ch9ue niveau 7r d'inflation mensuelle, le taux d'inflation annuel équivalent, défini par (1 + 7r)¹ - 1. Il s'agit du taux d'inflation annuel réalisé si 7rt =7r tout au long de l'année.

⁷On peut en fait montrer que dans ces conditions, le processus 1rt converge en loi quand t ? +oo vers un

processus stationnaire de loi normale N ~

b, a2

2a



23

Il convient de remarquer que des trajectoires avec des périodes déflationnistes, bien que n'arrivant que très rarement, sont également permises par ce modèle (pour la simple raison que P(rt<0) > 0 pour tout t).

Ce modèle sur l'inflation sera utilisé pour simuler des trajectoires d'évolution de l'encours. Nous reviendrons plus en détail sur ce point dans la section dédiée.

5 L'approche probabiliste interne

Cette section vise à conduire une analyse plus détaillée de l'évolution des encours afin d'affiner la prévision. La vision que nous adoptons ici n'est donc plus globale, mais revêt au contraire un caractère «microéconomique».

5.1 La segmentation clientèle

La clientèle de la banque présente une forte hétérogénéité selon plusieurs critères. Elle peut donc être stratifiée, afin de définir différentes catégories homogènes auxquelles correspondent des encours partiels. Les critères de classification envisageables sont par exemple le niveau de revenu, la surface financière (c'est-à-dire le niveau de patrimoine placé dans la banque), le nombre de produits contractés, la catégorie socio-professionnelle ou encore l'ancienneté dans l'établissement. Ces strates peuvent ensuite être croisées avec les âges pour obtenir des cellules de clientèle. L'intérêt attendu de cette segmentation de la base de clients est d'améliorer notre capacité prédictive des encours en tenant compte des comportements propres à chaque cellule ainsi définie. À titre d'exemple, le pouvoir d'achat du client est un indicateur de la stabilité de son encours personnel. En effet, les personnes à haut revenu présentent des mouvements sur leurs comptes plus importants et plus imprévisibles et sont plus susceptibles de quitter l'établissement que les clients ayant un revenu modeste, car ils cherchent plus à optimiser leurs placements : ils sont plus «volatiles» et leur probabilité de sortie est plus élevée. De même, la probabilité annuelle de clotûre d'un compte est beaucoup plus faible dans la première année qu'au bout de cinq ans d'ancienneté. Enfin, les personnes âgées ont également un comportement plus stable et donc plus prédictible que les jeunes, ce qui a son importance compte tenu du fait qu'ils détiennent en général des encours plus élevés.

5.2 Modélisation de la dynamique des encours

5.2.1 Notations

Le portefeuille de clientèle de l'établissement bancaire est ventilé par strates et par âges. Les strates, en nombre s, seront désignées par l'indice iEE={1, 2, ..., s}. Typiquement, nous aurons 3 < s < 8. Les âges seront, quant à eux, indicés par j E E = {á, ..., w} où á et w désignent les âges limites retenus. Ainsi, á est l'âge minimum légal pour obtenir un compte tandis que w correspond à l'âge maximum pour un client de la banque, dont la probabilité de sortie dans l'année est égale à 1. Cette segmentation correspond donc à |E| |E| cellules de clientèle, chacune d'entre elles étant indicée par un couple (i, j) E ExE. Le temps est indicé par tEN, l'instant 0 correspondant à aujourd'hui. Le pas de temps peut être mensuel, trimestriel ou annuel. Dans le cadre de cette étude, nous le décompterons mensuellement. Comme dans l'approche macroéconomique précédente, l'encours total des dépôts à vue à la date t de la banque est noté 0t. L'encours des clients appartenant à la strate i et l'encours des clients d'âge j à cette même date sont notés respectivement _0(i,:),t ^{et 0}(: j) t. Enfin, l'encours détenu par les clients de la strate i et d'âge j, correspondant à la cellule de clientèle (i, j), est spécifié de manière analogue par la variable _0(i,j),t. En particulier, pour toute date tEN,

0t =		Xs i=1		^0(i,:),t =				Xù j=á	^0(:,j),t
Comme par ailleurs V iEE, ^0(i,:),t =	Xù j=á		^0(i,j),t, on obtient à chaque date tEN
0t =					Xs i=1	Xù j=á	^0(i,j),t

comme ventilation de l'encours global des comptes courants en ses composantes par cellule de clientèle.

Le nombre de clients détenteurs de ces dépôts à vue à une date t, noté vt, est de manière analogue ventilé par strate, par âge et par cellule, avec les notations respectives v(i,:),t, í(:,j),t et _v(i,j),t. On a donc pour tout tEN,

Vt =

Xs i=1

v(i,:),t =

Xù j=á

v(:,j),t et V iEE, í(i,:),t =

Xù j=á

v(i,j),t

24

soit

Vt =

Xs i=1

Xù j=á

v(i,j),t

Les encours client moyens au niveau de la banque, de la strate i, de l'âge j et de la cellule (i, j) sont respectivements notés 0t, ⁰(i,:),t, ⁰(:,j),t ^et 0(i,j) t. Ils sont définis par la somme d'argent moyenne détenue par chaque client à l'échelle considérée, soit

0t 0t = vt

, ^0(i,:),t =

^0(i,:),t í(i,:),t

, ^0(:,j),t=

^0(:,j),t í(:,j),t

et ^0(i,j),t =

^0(i,j),t v(i,j),t

Afin d'obtenir des écritures plus condensées, nous introduisons des grandeurs vectorielles correspondant à ces différentes variables.

Pour tout tEN, nous définissons

vt =

? ? ? ?

v1,t v2,t . . . vs,t

? ? ?E N|Ó||Î| avec vi,t = ?

í(i,á),t í(i,á+1),t . . . í(i,ù),t

I

E N^|Î|, iEE

De même, nous posons

0t =

? ? ? ?

01,t 02,t . . . 0s,t

? ? ?E R|Ó||Î| avec 0i,t = ?

^0(i,á),t ^0(i,á+1),t . . . ^0(i,ù),t

? ? ? ?

E R^|Î|, i E E

On remarque alors que l'encours partiel de la strate i et que l'encours global de la banque à la date t s'expriment respectivement par

^0(i,:),t = (vi,t|0i,t) et At =

Xs i=1

^0(i,:),t = (vt|0t)

25

où (.|.) désigne le produit scalaire euclidien usuel.

Nous nous intéressons notamment à la structure par terme des différents encours, c'est-à-dire à leur évolution en fonction de l'horizon h de prévision. Il nous faut donc typiquement prévoir les lois de probabilités des variables aléatoires _Di,t+h ^et _Ot+h, pour hE{1, 2, ...,10}. La segmentation opérée, en plus d'affiner la prévision, permettra d'estimer la «valeur» des différentes strates du point de vue de la banque de détail.

5.2.2 Dynamique des clients au sein de la banque

Les clients de la banque, à un instant t, sont mobiles. Ainsi, un client particulier peut, au pas de temps suivant, avoir intégré une nouvelle strate ou même avoir quitté la banque (par décision volontaire ou par décès). Partant d'une répartition initiale v0, on suppose que chacun des í0 = IIv0II₁ clients évolue selon un processus identique, mais indépendamment de tous les autres. Décrivons ce processus.

Un client appartenant à la cellule (i, j) à la date t (c'est-à-dire appartenant à la strate i et d'âge j) se retrouvera en t + 1 dans l'une des s strates de la banque, avec un âge qui aura évidemment augmenté mécaniquement de un, ou aura quitté l'établissement. Il sera donc intégré dans l'une des cellules (l, j + 1), l EE ou ne sera plus client.

Plus précisément, on note ë(i,j)

k le taux de transition d'un client appartenant à la cellule (i, j) vers la cellule (k, j + 1), k E E et ^o(i,j) son taux de sortie à toute date. Cela signifie qu'un client dans la cellule (i, j), à une date quelconque, a une probabilité ë(i,j)

k d'être dans

la cellule (k, j + 1) et une probabilité ^o(i,j) d'avoir quitté l'établissement à la date suivante. On a donc l'identité

Xs k=1

ë(i,j) k + o(i,j) = 1 pour tout (i, j) E E x Î

Il pourrait être envisagé d'introduire des probabilités de transition évoluant au cours du temps. Toutefois, nous avons considéré que cela n'introduisait qu'un intérêt limité rapporté à la forte complexité supplémentaire que cela aurait induit. En outre, il apparaît plausible que de telles probabilités de transition restent très stables, indépendantes de la démographie

26

future du pays par exemple.

La dynamique des clients au sein de l'établissement est résumée dans le schéma suivant :



Par ailleurs, pour prendre en compte l'arrivée de nouveaux clients dans la banque étudiée, nous introduisons des processus d'entrée _é(i,j),t, ((i, j), t)EE x x N^*. La variable aléatoire é(i,j),t à valeurs dans N représente le nombre de nouveaux clients arrivés dans la banque entre les instants t - 1 et t et ayant plus précisément incorporé la cellule clientèle (i, j). Afin de garder une modélisation suffisamment riche pouvant intégrer des effets démographiques, nous n'imposons pas l'homogénéité dans le temps des processus d'arrivée. Ainsi, nous serons amenés à étudier des cas dans lesquels _é(i,j),t ^et _é(i,j),t/ ont des lois potentiellement différentes pour t =6 t^'. On supposera en revanche, et à l'instar de ceux de transition, que les processus d'arrivée sont indépendants les uns des autres. Nous pouvons donc écrire

V(((i,j),t), (i^',j^'),t^')) E (E x x N^*)² , ((i,j),t) =6 ((i^',j^'),t^') = é(i,j),t ^et _é(i/,j/),t/ indépendantes

5.2.3 Dynamique de l'encours client moyen par cellule

Nous nous référons ici au résultat de la partie précédente dans lequel l'inflation s'était révélée être l'indicateur essentiel du niveau de l'agrégat des encours à l'échelle de la banque. D'une manière analogue, il est légitime de supposer que l'encours client moyen par cellule (i, j) suit la même évolution. Il s'agit à nouveau, conformément à l'intuition, d'affirmer que la richesse réelle moyenne détenue sur le compte courant par les clients d'un certain âge j et d'une strate précise (reflétant leur surface financière ou le nombre de produits qu'ils détiennent...) est a priori une grandeur très stable dans le temps. Finalement, on s'attend à ce que la variable _(i,j),t capte la dynamique inflationniste et s'exprime en première approximation comme une fonction de celle-ci. Nous supposerons donc que l'encours moyen par cellule_Ä(i,j),t, à chaque date t~1, est une fonction déterministe du niveau de l'inflation ilt

27

sur la période [0, t] : ceci est réalisé en reliant l'évolution de _0(i,j),t sur la période [t - 1, t] à l'inflation mensuelle correspondante 7rt par l'opération simple suivante :

Ot = (1 + it)Ot-1

pour 1 < t < h, où h E N^* (en mois) est l'horizon d'étude. En revanche, 7rt (et IL) pourront être aléatoires.

5.2.4 Le modèle probabiliste et ses hypothèses

Nous détaillons dans cette section toutes les hypothèses mathématiques du modèle introduit ci-dessus. Rappelons que les strates, en nombre s, sont désignées par l'indice i E E= {1, 2, ..., s} et que les âges sont, quant à eux, indicés par j E E= {a, ..., w} où a et w désignent les âges limites retenus.

Cette segmentation définit |E| |E| cellules de clientèle, chacune d'entre elles étant indicée par un couple (i, j)EExE. Le temps est décompté mensuellement et indicé par tEN, l'instant 0 correspondant à aujourd'hui.

On considère sur l'espace probabilisé (52, W, P) trois familles dénombrables de variables aléatoires :

- {⁰(i,j),t} indicée par ((i, j), t) E E x E x N. La variable _0(i,j),t, à valeurs dans R,

représente l'encours client moyen de la cellule (i, j) à la date t;

- {7r(i,j),t,l} indicée par ((i, j),t,l)EE x E x N^* x N^*. L'idée est de numéroter à chaque date les clients présents dans chaque cellule; on note alors _7r(i,j),t,l la variable aléatoire, à valeurs dans EU{o}, qui associe au client numéro l de la cellule (i, j) à la date t - 1 l'endroit où il sera à la date suivante t (un indice k de E s'il reste dans la banque et intègre la cellule (k, j + 1) et o s'il quitte l'établissement) ;

- {t(i,j),t} indicée par ((i, j),t) E E x E x N^*. La variable _t(i,j),t, à valeurs dans N, représente le nombre d'arrivées depuis l'extérieur dans la cellule (i, j) entre t - 1 et t. Il s'agit donc du nombre de nouveaux clients arrivés en t dans cette cellule.

On note _(Ht)tEN la filtration canonique associée à ces trois familles de variables aléatoires et (Mt)tEN celle associée aux deux dernières⁸, qui concernent les mouvements de clients. Par définition, H0 =M0 = {0,52} et pour tout t E N^*,

1 _n o ~

Ht = ó Ä(i,j),u (i,j)EÓxÎ , {é(i,j),u } (i,j)EÓxÎ , {ð(i,j),u,l } ((i,j),l)EÓxÎxN*, 0 < u < t

~Mt = ó({é(i,j),u}(i,j)EÓxÎ , _{{ð(i,j),u,l}((i,j),l)EÓxÎxN*,} 0 < u < t

_{n o}

Remarquons ici que les variables _Ä(i,j),0 sont H0-mesurables (elles sont connues aujour-

d'hui et assimilées à des constantes).

Ces familles constituent les «briques» élémentaires à partir desquelles est construit tout le modèle. Le but est de définir (par récurrence) deux nouvelle familles de variables aléatoires {v(i,j),t} ^et _{0(i,j),t} indicées par ((i, j), t)EE x E x N modélisant respectivement le nombre de clients dans la cellule (i, j) à la date t et l'encours des dépôts à vue des clients de cette cellule à la même date. Remarquons qu'elles seront liées par

Vt EN, ⁰(i,j),t = v(i,j),t Ä(i,j),t

⁸Nous verrons l'utilité de ce découpage dans les hypothèses sous-jacentes au modèle

Vt E N, Dt =

(

D1,t D2,t . . . Ds,t

) E ^R|Ó||Î| avec Di,t =

Ä(i,á),t ^0(i,á+1),t . . . ^0(i,ù),t

I

E R^|Î|, i E E

Vt E N^*, tt =

(

t1,t t2,t . . . ts,t

? ? ?E N|Ó||Î| avec ti,t = ?

t(i,á),t t(i,á+1),t . . . t(i,ù),t

? ? ? ?

E N^|Î|, i E E

Vt E N^*, vt =

?v1,t ? ?gv2,t ? . . . vs,t

? ? ?E N|Ó|(|Î|-1) avec vi,t = ?

v(i,á+1),t v(i,á+2),t ^ . . . v(i,ù),t ^

I

E ^N|Î|-1, i E E

Vt E N, vt =

? ? ? ?

v1,t v2,t . . . vs,t

? ? ?E N|Ó||Î| avec vi,t = ?

v(i,á),t v(i,á+1),t . . . v(i,ù),t

? ? ? ?

E N^|Î|, i E E

28

~et que les variables ~í(i,j),0~ (i,j)?Ó×Î et ~Ä(i,j),0 (i,j)?Ó×Î sont considérées comme des constantes. Elles sont donc H0-mesurables (il s'agit respectivement des nombres de clients par cellule et des encours par cellule dans le portefeuille actuel). On construit alors pour tout ((i, j),t)EE x x N*

B(i,j),t =

í(i,j),t-1 X l=1

^1{ð(i,j),t,l = o4

également à valeurs dans N qui s'identifie au nombre de sorties (c'est-à-dire de clients perdus) de la cellule (i, j) entre t - 1 et t.

De même, soit pour (k, (i, j), t)EE x (E x (⁷.71 - {c4)) x N*

^ í(k,j-1),(i,j),t=

í(k,j-1),t-1 X l=1

^1{ð(k,j-1),t,l = i4

le nombre de clients de la banque présents en t - 1 dans la cellule (k, j - 1) et ayant migré dans la cellule (i, j) entre t - 1 et t. Dans ces conditions

v(i,j),t ^ = _Xs ^ í(k,j-1),(i,j),t

k=1

n'est autre que le nombre de clients de la banque déjà présents en t - 1 et ayant bougé dans la cellule (i, j) entre t - 1 et t.

Finalement, la nouvelle distribution de clients dans le portefeuille s'actualise selon

Vt E N, v(i,j),t+1 = í(i,j),t+1 + é(i,j),t+1

En particulier, il n'y a pas de problème de référence circulaire dans ces définitions, bien que chacune d'entre elles appelle une ou plusieurs des autres. Les définitions ci-dessus sont donc valides.

Pour finir, on définit, à partir de cet ensemble de variables, les variables aléatoires vectorielles suivantes sur (S2, W, P)

Avec ces notations, on a

Vt E N, vt+1 = vt+1 ] + 1t+1

L'encours de la strate i à la date t vaut ⁰(i,:),t =(vi,t|Äi,t) et l'encours global des dépôts à vue de la banque à cette même date s'exprime selon

_Xs i=1

At =

0(i,:),t = (vt|At)

On suppose que :

(1) les variables aléatoires {⁰(i
·

,3),t}((i,j),t)EÓxÎxN, {é(i,j),t}((i,j),t)EÓxÎxN* et

{ð(i,j),t,l}((i,j),t,l)EÓxÎxN*xN* sont toutes mutuellement indépendantes;

(2) V((i, j), t, l) E E x E x N^* x N^*, P (ð(i,j),t,l =k)=ë(i,j) _ksi k EE et
P (ð(i,j),t,l =o)=o^(i,j). On a donc

Xs k=1

ë(i,j) k + o(i,j) = 1 .

La présentation est ici axiomatique mais correspond à des hypothèses «naturelles».

L'hypothèse (1) garantit que les clients de la banque évoluent dans les cellules de manière indépendante les uns des autres et que le processus associé est markovien. L'hypothèse (2) assure que ce processus interne de transition des clients est même homogène dans le temps. Ainsi, on écrit simplement ici qu'à une date quelconque, un client dans la cellule (i, j) a une probabilité ë(i,j)

k d'être dans la cellule (k, j + 1) et une probabilité ^o(i,j) d'avoir quitté
l'établissement à la date suivante.

En particulier, compte-tenu des hypothèses précédentes, il est facile de voir que l'on peut explicitement décrire les lois conditionnelles suivies par certaines des variables que nous venons de définir. Ainsi, conditionnellement à l'information disponible à la date t E N, c'est-à-dire conditionnellement à la sous-tribu Ht, les hypothèses (1) et (2) assurent que :

- pour tout ((i, j), t)EE x E x N, è(i,j),t+1 suit une loi binomiale _{Bin(í(i,j),t} , o(i,j)) ;

- pour tout (k, (i, j),t)EE x (E x (E - {á})) x N, í(k,j-1),(i,j),t+1 ^ suit une loi binomiale

~ ~

Bin _í(k,j-1),t , ë(k,j-1) ;

i

Par conséquent, connaissant la décomposition

s k=1

^

í(i,j),t+1 ^ =

í(k,j-1),(i,j),t+1

29

on a, conditionnellement à Ht,

s

í(i,j),t+1 ^ ~ Bin(í(k,j-1),t , ë_i (k,j-1))
k=1

où toutes les binomiales sont mutuellement indépendantes.

En outre, sous l'ensemble de ces hypothèses, il est aisé de voir que la famille de variables aléatoires _(vt)tEN constitue une chaîne de Markov (inhomogène) à espace d'états discret

E ^=N|Ó||Î| et de valeur initiale v0. Ainsi, sous le modèle construit, si l'état de la banque vt est connu à la date t, la trajectoire strictement antérieure à cette date n'a pas d'importance pour le calcul probabiliste relatif à la dynamique future de cet état.

Nous allons à présent démontrer cette propriété. Il nous faut montrer l'identité suivante, notée (X)

Vt E N*, V(Su)0<u<t E E^t+1,P(vt = St | V0 < u < t - 1, v_u = S_u) = P(vt = St | vt-1 = St-1) Soit tEN^* et _(Su)0<u<t EEt+1.

Notons _{Bä,t_1} l'événement {V 0 < u < t - 1, v_u =S_u} et _Aä,t la quantité P(vt =St | Bä,t_1).

Aä,t = P(V(i,j)EE x , í(i,j),t=ä(i,j),t | Bä,t_1)

= P(ViEE, í(i,á),t =ä(i,á),t et Vj > á + 1, í(i,j),t =ä(i,j),t | Bä,t_1)

= P (ViEE, é(i,á),t =ä(i,á),t et Vj > á + 1, é(i,j),t +

Es k=1

í(k,j_1),(i,j),t^^ =ä(i,j),t | Bä,t_1

s

? = P n {é(i,á),t=ä(i,á),t} n _n n té(i,j),t +Eí(k,j_1),(i,j),t^{^}=ä(i,j),t | Bä,t_1

iEÓ iEÓj>á+1 k=1

s í(k,j-1),t-1

? n {é(i á),t=ä(i,á),t} n _n n té(i,j),t=ä(i,j),t - _E E ¹{ð(k,j-1),t,l = i} | Bä,t_1

iEÓ iEÓj>á+1 k=1 l=1

? ?n n n = P {é(i,á),t=ä(i,á),t} n iEÓ iEÓj>á+1

{

é(i,j),t =ä(i,j),t -

Es k=1

ä(k,j-1),t-1 E l=1

^1{ð(k,j-1),t,l = i}

} | Bä,t_1

Or l'hypothèse (1) formulée dans la partie de construction du modèle théorique assure }que toutes les variables _{{é(a,b),t}(a,b)EÓxÎ} et {ð(a,b),t,l ((a,b),l)EÓxÎxN* sont indépendantes de la tribu _{Ht_1} et donc en particulier de Bä,t_1 EHt_1.

Par conséquent

s ä(k,j-1),t-1

?

_{?n n E}

Aä,t = P {é(i,á),t =ä(i,á),t } n _{n E}

1t(i,j),t=ä(i,j),t - 1

iEÓ iEÓj>á+1 k=1 l=1

L'hypothèse (i) garantit également que les variables aléatoires _{{é(a,b),t}(a,b)EÓxÎ} et {ð(a,b),t,l}((a,b),l)EÓxÎxN* sont toutes mutuellement indépendantes et donc finalement

Aä,t = (H

iEÓ

_ls ä(k,j-1),t-1 P({é(i,á),t=ä(i,á),t}) I P _n n {é(i,j),t=ä(i,j),t - _E E 1

iEÓj>á+1



l=1

k=1

{ð(k,j-1),t,l = i}}

30

Dans cette dernière expression, la dépendance en l'événement _{Bä,t_1} n'intervient que par le biais des valeurs des _{ä(k,j_1),t_1} dans les sommes. En conséquence, si _(Su)0<u<t EE^t+1 et

~ ~

àS_u

0<u<t

EE^t+¹ sont tels que _{ät_1=St_1} et ät =St alors _{Aä,t=Aàä,t} (*).

( )

Pour conclure, on écrit que si C est l'ensemble des à6_u EE^t+¹ tels que _{6t_1=St_1} et

0<u<t

bt =

S_t

P({vt=6t} n {vt-1=6t-1})

P(vt=6t | vt-1=6t-1) =

P(vt-1 =6t-1)

( )

P

P(vt=6t | vt-1=6t-1) =

E (^$4)0<<t^EC

v 0 < u < t, v_u=^à6_u P(vt-1=6t-1)

( ) ( )

P E=

(^$4)0<<t^EC

E=

(^$4)0<<t^EC

vt=^à6t | v 0 < u < t - 1, v_u =^à6_u P v 0 < u < t - 1, v_u =^à6_u

P(vt-1=6t-1)

( )

Aàä,tP v 0 < u < t - 1, v_u= à6_u

P(vt-1=6t-1)

EC 0<<t

D'après (*), on a donc

EP(vt=6t | vt-1=6t-1) = Aä,t

($4)

( )

P v 0 < u < t - 1, v_u=à6_u

P(vt-1=6t-1)

31

E= Aä,t

(^84)0<<t^EC

( { } ) P nu<t_2 vu=^à6u n {vt-1=6t-1} P(vt-1 =6t-1)

P(vt-1=6t-1)

P(vt=6t | vt-1=6t-1) = Aä,t

P(vt-1=6t-1)

= Aä,t

Il s'agit exactement de l'identité (X).

32

Troisième partie

Application informatique du modèle

construit

L'objet de cette section est de mettre en application, par simulation informatique, le modèle mathématique que nous venons de développer.

Nous l'effectuerons sur un modèle «jouet», c'est-à-dire simplifié et non calibré sur des données historiques. Ainsi, la banque virtuelle que nous allons créer et faire évoluer n'a qu'un nombre limité de clients et les différents paramètres de la dynamique (tels que les différentes probabilités de transitions et de sortie ou encore les lois des processus d'arrivées) seront fixés a priori, en exploitant au maximum les données économiques ou démographiques de la population française, mais pas celles relatives à la clientèle de La Banque Postale. L'enjeu est plus ici de valider en première approche le modèle construit, de se faire une idée du comportement de l'encours sous celui-ci et d'analyser sa sensibilité aux différents paramètres par le biais de simulations.

Le logiciel utilisé pour cette implémantation informatique est Scilab.

6 Analyse de premières simulations

6.1 Les paramètres et les variables d'état initiales

Nous allons considérer une banque de détail comprenant E = s = 4 strates. Le pas de temps est mensuel, et les âges des clients, décomptés également mensuellement, sont compris entre á = 18 ans (et 0 mois) et ù = 80 ans (et 0 mois), correspondant donc à Î =(80 ? 18) * 12 + 1=745 classes d'âge pour un total de E Î =2980 cellules de clientèle. Chacune de ces cellules est supposée contenir initialement n = 10 clients. Il s'agit d'une hypothèse forte : la distribution initiale des clients est uniforme à l'échelle de la banque.

Bien que nous n'effectuions ici aucune calibration sur des données historiques, nous allons bien évidemment choisir des valeurs «raisonnables» pour les paramètres modulant les dynamiques des clients et de l'encours moyen.

6.1.1 Taux de transition et de sortie

Les cellules de clientèle correspondant aux clients les plus âgés sont caractérisées par un taux de sortie de 1 : toutes les personnes âgées de ù décèdent dans le mois suivant. Autrement dit

Vi E E,Vk E E, ë(i,ù) k = 0 et o(i,ù) = 1

Soit désormais j 6=ù. Le taux de sortie ^o(i,j) des clients de la cellule (i,j) est à la fois dû à la mortalité et aux départs volontaires vers la concurrence. Il paraît raisonnable de supposer ces deux phénomènes indépendants. Nous souhaitons en outre adopter des taux de transition reflétant la plus grande probabilité pour un client de rester dans sa strate que d'en bouger. Ainsi, au sein de la sous-population des _í(i,j),t clients de la cellule (i, j) qui sera vivante en

l - 1

t + 1, nous pouvons considérer que le taux de maintien dans la strate i est de _l où l ~ 2

est un paramètre mesurant la propension à rester dans sa strate.

33

Le taux de passage dans l'une des (s - 1) autres strates ou vers la concurrence (sortie volontaire) est quant à lui pris uniforme égal à ls ¹ _=4l 1 pour s = 4.

Pour calibrer la mortalité, nous nous référons à la plus récente table de taux de mortalité par âge publiée par l'Institut National des Études Démographiques (INED) en 2008. Cette table, que nous avons reportée en annexe C, fait figurer le nombre de décédés dans l'année pour 1000 personnes de chaque groupe d'âges dans les populations françaises masculine, féminine et totale. Nous noterons ÷j ce taux annualisé pour la population totale correspondant à l'âge j E FL exprimé en mois. Le taux mensuel ?j de décès pour une personne de cet âge j peut dans ces conditions être pris égal à

1 - ~1 - 10-3÷j ~ 1 12 soit ?j 10-3 ÷j

?j = 12 pour ÷j petit

Sous l'hypothèse d'indépendance entre la mortalité et les strates vers lesquelles les personnes seraient amenées à évoluer à la date suivante sans mortalité, nous avons donc finalement pour (i, j) E E x (FL - {ù})

{	ë(i,j) k = 1 - ?j ls si k E (E - {i}) ë(i,j) i= (l - 1) (1 - ?j) si k = i l o(i,j) = ?j + 1 - ?j ls

Une valeur du paramètre l plus faible correspond à une base clientèle plus mobile mais également à un taux de sortie plus élevé. Lorsque les sorties de clients sont importantes, on parle alors d'attrition forte.

6.1.2 Lois des processus d'arrivée

Les lois des processus d'arrivée _é(i,j),t doivent être a priori calibrées à dire d'expert, d'autant plus qu'elles sont directement influencées par la politique commerciale mise en oeuvre par l'établissement. Pour ces simulations d'essai, nous supposerons qu'elles sont de Poisson et qu'elles permettent globalement de garder une population constante au sein de la banque. Cette remarque est de première importance : couplée à celle concernant l'uniformité de la répartition en t = 0 des clients au sein de l'établissement, elle assure que les aspects démographiques n'entreront pas en jeu ici. Nous souhaitons en effet les écarter dans un premier temps.

De manière à assurer une entrée continue de jeunes clients, nous posons donc déjà

V (i, t) E xE x N^*, é(i,á),t ^ Poisson (n)

Pour j =6 á, il s'agit de paramétrer des entrées aléatoires qui équilibrent en moyenne les sorties de la banque (vers la concurrence ou par décès) à partir des cellules de l'âge j - 1. Ces sorties affectent en effet l'effectif des clients d'âge j. Les paramètres des lois de Poisson étant fixés comme nous venons de l'expliquer (compensation sorties/entrées en espérance), nous avons finalement

V (i, j, t) E Ex(FL - {á})xN^*, é(i,j),t ^ Poisson (no(i,j-1))^ Poisson (n (?j-1 +

1 - ?j-1 1 1 ls )

34

6.1.3 Inflation et encours client moyen par cellule

Nous supposons que les s =4 strates retenues reflètent la surface financière du client, et par conséquent le volume des liquidités détenues sur ses dépôts. Ce dernier sera pris décroissant en iEE={1,2,3,4}. De plus, nous prenons, à strate fixée, un encours moyen par client qui croît avec l'âge, ce qui est globalement conforme à la réalité.

L'encours moyen par client correspondant à la cellule la plus modeste de la banque (c'est-à-dire les jeunes de 18 ans dans la strate i=4) est normalisé, pris égal à 1 (soit _(4,á),0 =1). Nous ferons ensuite les hypothèses suivantes :

- pour chaque strate, l'encours moyen par client est identique dans les cellules correspondant au même âge en années;

- pour la strate i=4, _(4,á),0=1 et l'encours moyen par client augmente de 0.5 par an; - pour la strate i=3, _(3,á),0=2 et l'encours moyen par client augmente de 1 par an;

- pour la strate i=2, _(2,á),0=3 et l'encours moyen par client augmente de 2 par an;

- pour la strate i=1, (1,á),0 =4 et l'encours moyen par client augmente de 4 par an.

On peut représenter la matrice L0 répertoriant les encours moyens _(i,j),0 sur les comptes des clients par cellule (i, j) à la date initiale (t=0). Rappelons que les âges j sont décomptés mensuellement :

Strate	j = c = 216 (18 ans)	j = 217 (18 ans 1 mois)	... ...	j = 228 (19 ans)	j = 229 (19 ans 1 mois)	... ...	j = 959 (79 ans 11 mois)	j = w = 960 (80 ans)
i = 1	4	4	...	8	8	...	248	252
i = 2	3	3	...	5	5	...	125	127
i = 3	2	2	...	3	3	...	63	64
i = 4	1	1	...	1,5	1,5	...	31,5	32

Dans le cadre de notre modèle, l'inflation est, in fine, un déterminant essentiel du volume total des encours. L'encours moyen par cellule _(i,j),t à chaque date t ~ 1 est une fonction déterministe du niveau de l'inflation llt sur la période [0, t] avec

llt

Ät-1

Ät = ilt-1

pour 1<t<h, où hEN^* (en mois) est l'horizon d'étude.

Nous envisageons ici deux scénarios possibles d'évolution de l'inflation et donc a fortiori de l'encours moyen par cellule, compte tenu de la remarque précédente :

- le premier est complètement déterministe: l'inflation mensuelle itt reste constante jus-qu'à l'horizon h;

- le second correspond à l'adoption du modèle de type Ornstein-Uhlenbeck pour l'infla-

tion, à paramètres (a, b, a, it0). Le programme simulera donc une trajectoire de l'inflation (lrt)0<t<h selon cette dynamique.

6.2 Résultats obtenus

Nous avons généré plusieurs scénarios d'évolution de l'encours. Dans chaque simulation, et conformément aux hypothèses mathématiques de la modélisation adoptée, nous faisons évoluer indépendamment la base des clients d'une part et l'encours moyen des différentes cellules d'autre part. Nous sommes alors capables, par produit terme à terme à chaque date,

35

de générer la trajectoire correspondante de l'encours total dans la banque jusqu'à un certain horizon.

Inflation constante it et Ät =(1 + it) _Ät-1 pour 1<t<h, lE{2, 60} :

Prenons à titre d'exemple h = 120 mois, c'est-à-dire un horizon de 10 ans. Nous avons tracé ci-dessous les trajectoires typiques d'encours obtenues dans ces conditions avec les deux valeurs de l retenues. Nous y avons choisi it = 0.002 correspondant à une inflation annuelle de 2.4%.



FIG. 5 - Une trajectoire pour l = 2 (courbe bleue) et l = 60 (courbe rouge) de la dynamique de l'encours total avec une inflation constante

Les valeurs 60 et 2 du paramètre l correspondent respectivement à un changement de strate tous les cinq ans et tous les deux mois en moyenne. On obtient dans un cas une base clientèle stable et dans l'autre une base volatile caractérisée par un changement de strate beaucoup plus fréquent. La trajectoire correspondant à l=2 apparaît bien plus «erratique» en raison de la plus forte mobilité des clients (ce qui diminue notre pouvoir prévisionnel sur les encours futurs).

Rappelons ici que la population totale dans la banque est globalement constante car les entrées y équilibrent les sorties. La croissance globale de l'encours dans les deux cas est dûe à l'inflation. Les «sursauts» correspondent quant à eux aux mouvements aléatoires des clients au sein des strates. Leur amplitude apparaît logiquement d'autant plus prononcée que les clients sont mobiles.

36

Inflation à dynamique Ornstein-Uhlenbeck {lrt} et A =(1 + itt) Ä _-1 pour 1<t<h, lE{2, 60} :

Nous avons, toujours sur un horizon de h=120 mois, tracé deux trajectoires simulées (l'une avec l = 2 et l'autre avec l = 60) avec, cette fois-ci, une inflation aléatoire. Les paramètres adoptés pour la dynamique Ornstein-Uhlenbeck sont toujours

(a, b, a, it0)=(0.2,0.002,0.0002, 0.002).



FIG. 6 - Une trajectoire pour l=2 (courbe bleue) et l=60 (courbe rouge) de la dynamique de l'encours total avec une inflation suivant une évolution d'Ornstein-Uhlenbeck

Pour de tels paramètres, les «formes» obtenues sont à première vue similaires. Il nous faut générer un grand nombre de trajectoires pour tenter de déceler les différences potentielles induites par le changement dans l'évolution de l'inflation.

7 Sensibilités aux paramètres et aux variables initiales

Pour pouvoir formuler des remarques qualitatives valides et faire de l'inférence statistique, nous ne pouvons nous restreindre à une seule réalisation dans chaque configuration.

L'enjeu ici est d'apprendre qualitativement et quantitativement sur les lois de certaines variables, conformément à l'ensemble du modèle que nous avons construit et des hypothèses que nous avons posées. Parmi ces variables d'«intérêt», citons par exemple les encours à horizon donné (dans la banque, dans chaque strate...) ou encore la durée de vie de l'encours dans une vision «mort de bilan» où la banque arrête de commercialiser tout produit. Pour réaliser cet objectif, il nous faut, à jeu de paramètres et d'hypothèses fixé, simuler plusieurs trajectoires (il faut en réaliser le plus grand nombre possible, la vitesse de calcul à notre disposition étant ici le facteur limitant). Nous pourrons, dès lors, calculer certaines statistiques «naturelles»⁹ relatives aux variables d'intérêt. Une telle démarche correspond à des simulations de type Monte-Carlo. La raison du recours à la simulation est notre incapacité

⁹Par exemple l'espérance empirique (c'est-à-dire la moyenne des obsevations), la variance réalisée ou encore des quantiles empiriques

37

à calculer explicitement les lois des variables aléatoires auxquelles nous nous intéressons, en raison de la trop grande complexité du modèle sous-jacent. En effet, la connaissance des différents taux de transition et de sortie, des lois des processus d'entrée ainsi que de la dynamique inflationniste ne permet pas de décrire explicitement la distribution de probabilité de vt,, où t0 est un horizon donné. Nous sommes donc ramenés à générer le plus grand nombre de scénarios pour inférer les lois des variables¹⁰. Voici le résultat d'une simulation de différentes trajectoires dans un même sous-cas (jeu de paramètres fixé). Lorsque le nombre de trajectoires augmente, on voit apparaître une forme d'«enveloppe» typique, qui est la traduction visuelle des intervalles de confiance de l'encours total à chaque date.



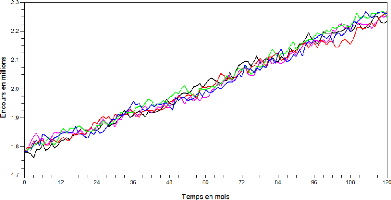
FIG. 7 - Un faisceau de trajectoire de l'encours total de la banque (l=2 et ir=0.002)

7.1 Influence de l'inflation et des taux de transition

Dans le cadre du modèle mathématique construit, l'inflation est l'unique déterminant de la croissance de l'encours moyen par cellule de clientèle dans la banque. Par conséquent, c'est cette grandeur qui est à l'origine de la tendance (haussière, baissière ou stable) de l'encours total dans l'établissement de crédit sur le moyen-long terme. Si l'on reprend ainsi les trajectoires simulées avec ii-=0.002 pour lE{2,60} (Figure 5 de la page 28), et que l'on calcule le

Ä120 - Ä0

taux de croissance de l'encours sur les 10 ans, on obtient respectivement 27.8%
Ä0

et 27.4%, sachant que le niveau d'inflation a augmenté de (1 + it)¹²⁰ - 1 = 27.1% sur cette même période. Les fluctuations obtenues sont dûes aux mouvements des clients au sein de la banque, et ce d'autant plus que les clients sont mobiles, c'est-à-dire que le paramètre l est faible. On observe donc dans le cas l =2 des irrégularités locales dans l'évolution de l'encours, qui peut même sur certaines périodes décroître.

En particulier, on remarquera ici que, bien que notre modèle suppose la relation déterministe Ät = (1 + ii-) _Ät-1 pour 1 < t < h entre encours moyen et inflation, l'encours total

¹⁰La loi forte des grands nombres et le théorème central limite sont implicitement «appelés» derrière cette procédure

38

dans la banque n'est pas pour autant une fonction déterministe du niveau de l'inflation sous celui-ci. La raison à cela réside dans la mobilité des clients au sein de l'établissement. Ainsi, si sur l'intervalle mensuel [t - 1, t], une proportion importante de clients passe dans des strates d'indice supérieur (correspondant à des encours plus modestes), l'encours total de la banque peut décroître sur cette même période alors que le niveau d'inflation aura été multiplié par 1 + it sur cet intervalle. Pour illustrer notre propos, nous avons simulé une trajectoire de l'encours global de la banque pour l=2 et it =0.002 sur un horizon de 17 ans (204 mois) et nous l'avons régressée sur le niveau d'inflation (normalisé à 100 en t = 0). Ce dernier est ici complètement déterministe, donné par ilt =100(1 + it)^t pour 1<t<204.



FIG. 8 - Régression du niveau de l'encours simulé sur le niveau d'inflation hors tabac

Nous disposons ainsi d'une base de comparaison avec la régression que nous avions effectuée à partir de l'encours des CCP de la Banque Postale en début d'étude. Le coefficient R² de détermination obtenu sur la trajectoire simulée est supérieur (nous avions obtenu R² =0,973 sur les données historiques). Toutefois, il est intéressant de noter que notre modèle, par la dynamique continuelle de la base de clients dans le temps, permet de rendre compte d'écarts de l'encours global par rapport au niveau d'inflation, même si l'encours moyen par cellule (donc, en fin de compte, le niveau moyen d'un dépôt de CCP) suit exactement ce niveau.

Pour saisir l'influence de la dynamique de l'inflation sur celle de l'encours, nous nous sommes intéressés, à titre d'exemple, à la distribution statistique de 60, qui n'est autre que l'encours bancaire global à un horizon d'observation de h = 60 mois. Nous reprenons pour cela, dans le cadre du modèle que nous avons construit, chacune des quatre configurations de base présentées précédemment (inflation constante ou à dynamique Ornstein-Uhlenbeck et l E{2, 60}). Nous avons généré 1000 trajectoires pour chacune de ces configurations.

Nous avons commencé par comparer les volatilités renormalisées des trajectoires d'encours sous les différents jeux de paramètres. La volatilité renormalisée Vol d'une trajectoire simulée

d'encours _{{At}tE{0,1,...,60}} est la variable aléatoire définie par

1 V ol({At}tE{0,1,...,60}) = A0

v X6 0 tt=1

(At - At-1)^2

39

Elle qualifie l'amplitude de ses variations locales (d'un mois à l'autre). Nous avons donc, dans chacun des quatre sous-cas, calculé la moyenne des 1000 volatilités empiriques associées aux trajectoires simulées. L'adoption de la valeur 60 pour le paramètre l se traduit ainsi par une diminution de 91.2% de cette volatilité par rapport au cas l = 2. L'adoption d'une dynamique inflationniste aléatoire augmente légèrement cette volatilité par rapport au cas d'une inflation constante, respectivement de 8.2% et de 8.7% pour l = 2 et l = 60. On confirme donc numériquement l'observation empirique sur les courbes tracées précédemment.

Nous faisons à présent figurer dans le tableau ci-après, pour chacun des quatre sous-cas (où nous disposons de 1000 données), la moyenne et l'écart-type empiriques, les valeurs minimale et maximale obtenues ainsi que l'intervalle empirique de confiance" à 95% de A60. Toutes les grandeurs sont exprimées en pourcentage de l'encours total initial A0 =1781050.

Statistique	At =(1 + ðt) At-1
	ðt constant ðt = ð = 0.002		dðt=a (b - rt) dt+ódWt (a, b, ó, ð0)=(0.2, 0.002, 0.0002, 0.002)
	l = 2	l = 60	l = 2	l = 60
Moyenne	112.76%	112.71%	112.65%	112.71%
Taux de croissance moyen sur la période	12.76%	12.71%	12.65%	12.71%
Ecart-type	0.90%	0.73%	2.35%	2.27%
Minimum	109.40%	110.57%	105.40%	106.46%
Maximum	115.32%	114.79%	119.28%	119.21%
[q5%, q95%]	[111.30%, 114.23%]	[111.51%, 113.89%]	[108.71%, 116.59%]	[109.11%, 116.50%]

Il convient d'abord de noter que les espérances empiriques obtenues dans les quatre sous-cas sont très proches (moins de 0.1% d'écart entre l'espérance empirique la plus élevée et la plus faible). On retrouve ici, à l'échelle d'un plus grand échantillon, que le taux de croissance moyen de l'encours sur la période est commandé par le niveau d'inflation, qui a crû de 12.73% sur la période, dans le cas de ðt =ð =0.002 que nous avons retenu.

En revanche, l'influence sur la variance des résultats apparaît très sensible à la valeur du paramètre l d'une part et au modèle retenu pour la dynamique de l'inflation d'autre part. On observe, en effet, des intervalles de confiance empiriques bien plus larges dans le cas de l'inflation aléatoire. Par ailleurs, dans le cas de l'inflation déterministe, l'écart-type obtenu est sensiblement supérieur avec la base de clientèle plus mobile. Ces remarques sont valables également dans les comparaisons des valeurs minimales et maximales.

"La notation qy avec xE[0, 1] désigne le quantile d'ordre x

40

Afin de disposer d'une base de comparaison plus «visuelle», nous faisons figurer ci-après les histogrammes des encours simulés _Ä60 à horizon h = 5 ans dans les cas l = 2 (bleu) et l=60 (rouge) avec une inflation d'abord déterministe.



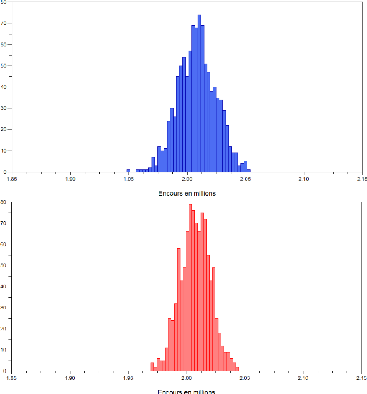
On retrouve graphiquement sur les deux histogrammes les résultats numériques figurant dans le tableau : si la valeur moyenne ne varie que très peu entre les deux cas, l'écart-type lui est totalement différent. Il est ainsi près de 25% plus élevé avec la base de clientèle plus mobile. On observe ainsi une plus grande «concentration» des réalisations dans le cas l =60 où la base de clientèle est plus «rigide» et change peu de strate.

41

En comparaison, voici ce que l'on obtient avec une inflation suivant une dynamique d'Ornstein-Uhlenbeck.



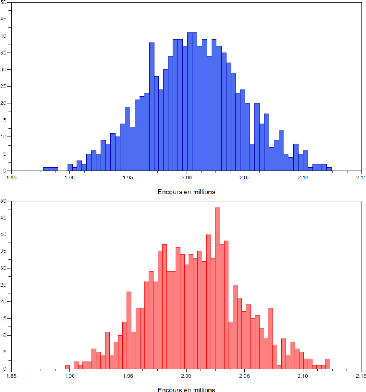
L'introduction d'une inflation aléatoire se traduit par une augmentation de l'écart-type empirique d'environ 160% dans le cas l =2 et d'environ 210% dans le cas l =60. La dispersion des résultats apparaît donc bien plus importante lorsque l'inflation est aléatoire.

Ce résultat est conforme à l'intuition : en effet, le taux de croissance local de l'encours moyen, et donc de l'encours, devient stochastique lorsque l'inflation est une variable aléatoire. Notre capacité prédictive sur le moyen-long terme s'en trouve donc sensiblement affectée.

Par conséquent, une plus grande mobilité de la base de clientèle, ainsi que le caractère stochastique du niveau d'inflation, sont des facteurs qui augmentent à la fois la volatilité de l'encours et sa dispersion, c'est-à-dire sa variance, à une date considérée. Alors que les taux de transition semblent être les déterminants essentiels de la volatilité, l'influence de l'inflation prédomine largement pour l'écart-type. Ce n'est en effet que dans le cas d'une inflation connue fixée que la mobilité des clients affecte sensiblement la variance.

42

7.2 Influence de la démographie initiale

Jusqu'à présent, nous avons adopté dans l'ensemble des simulations et analyses menées des hypothèses démographiques très simplificatrices : nous avons en effet considéré l'uniformité initiale de la répartition des clients et la constance en moyenne de cette répartition dans le temps, quel que soit l'horizon. L'enjeu était d'étudier les influences de la mobilité des clients et de la croissance du niveau d'inflation sur la dynamique de l'encours. Il nous fallait en conséquence «éliminer» tout aspect démographique dans cette dynamique.

Dans cette section, nous visons au contraire à explorer l'influence des facteurs démographiques sur l'évolution de l'encours. Nous pouvons notamment envisager de modifier l'uniformité de la répartition initiale de clients, en autorisant à la date t=0 des effectifs variables dans les différentes cellules de clientèle. En outre, nous ne chercherons plus à assurer la constance (en moyenne) de l'effectif Vt des clients au cours du temps. A contrario, la base de clients évoluera constamment et nous ferons vieillir le stock existant, en tâchant d'interpréter les différents types de «régimes» d'évolution de l'encours que nous mettrons ainsi en évidence.

7.2.1 Pyramide des âges et calibration des processus d'arrivée



La pyramide des âges¹² dans un pays est une représentation graphique qui permet de visualiser la répartition de sa population par sexe et par âge, à un moment donné. Elle est constituée de deux histogrammes, un pour chaque sexe (avec par convention les hommes à gauche et les femmes à droite), où les effectifs masculins et féminins sont portés en abscisse

¹²Ce type de graphique est apparu en 1874 dans le premier Atlas statistique des États-Unis. Son nom vient de sa forme lorsque la population a une forte natalité et une forte mortalité : il est élargi à la base et étroit au sommet. Mais cette forme peut varier. La pyramide des âges montre en un coup d'oeil le régime démographique et l'histoire d'un pays sur près d'un siècle

43

(axe horizontal) et les âges en ordonnée (axe vertical). Chaque barre associée à un sexe et à un âge précis a une longueur proportionnelle à l'effectif de la sous-population correspondante.

Come nous l'avons expliqué en début d'étude, notre conviction est que la composante démographique a potentiellement un impact significatif sur le niveau d'encours futur d'une banque donnée. À titre d'exemple, nous constatons sur la pyramide des âges actuelle de notre pays que l'ensemble de la génération du baby-boom est sur le point de rentrer dans l'âge de la retraite. Dans la mesure où ce flux générationnel suit la période de très faible natalité observée durant la Seconde Guerre Mondiale, le nombre de personnes âgées est vraisemblablement sur le point d'augmenter fortement dans un futur proche. Or les personnes âgées sont celles qui détiennent en général le plus d'encours. En conséquence, si une banque capte approximativement une part de marché constante et voit la population de ses clients de plus de 60 ans augmenter dans les mêmes proportions, on peut raisonnablement s'attendre à ce que cette singularité démographique assure une croissance future de l'encours probablement plus élevée que nous n'aurions pu le supposer a priori. Cette simple remarque montre la nécessité d'intégrer les aspects démographiques dont nous disposons dans la calibration du modèle que nous avons construit.

Afin de réaliser cet objectif, nous allons opérer une projection de la pyramide des âges actuelle dans le futur.

Pour décrire cette dernière, nous introduisons des paramètre _{(îj,t)(j,t)EÎXN} tels que _îj,t E [0, 1] est proportionnel à l'effectif de la sous-population d'âge j dans la pyramide des âges à la date t. Nous normalisons cette suite par rapport à la date actuelle (t=0) en posant _îá,0 =1. En ce qui concerne la description de la pyramide actuelle, nous souhaitons en pratique épouser sa forme globale et capter ses tendances, sans être excessivement pointilleux. Nous prendrons donc, avec j en mois,

f

îj,0 = 1 si 216 < j < 779 (de á = 18 ans jusqu'à 64 ans et 11 mois) îj,0 = 0.7 - 0.3 j_780 960_780 si 780 < j < 960 (de 65 ans jusqu'à ù = 80 ans) Autrement dit, nous avons retenu, pour décrire la pyramide actuelle, un paramètre îj,0

constant égal à 1 jusqu'à 64 ans et 11 mois, puis nous l'avons fait décroître linéairement entre 65 ans et 80 ans de 0.7 à 0.4.

Pour projeter cette description démographique dans le futur, nous utilisons les taux de mortalité annualisés pour 1000 personnes ÷j correspondant à l'âge j E exprimé en mois, que nous avions déjà introduits pour calibrer les sorties de la banque par décès. Nous poserons (

îá,t = 1 pour t E N*

îj,t+1 = îj_1,t(1 - 10_³÷j_1) si j E - {á} pour t E N

La projection opérée pour la pyramide des âges est ainsi très simple. D'une part, elle est déterministe : nous faisons l'hypothèse que les taux de mortalité moyens sont exactement réalisés à chaque date et qu'ils restent constants dans le temps. D'autre part, nous y supposons implicitement une immigration nulle ainsi qu'une natalité constante égale à celle d'aujourd'hui. En dépit de ces hypothèses très simplificatrices, cette projection est calquée, dans les grandes lignes, sur l'évolution probable de la population française et a le mérite d'être facile à calculer pour les simulations. Des raffinements sont évidemment envisageables, mais nous souhaitons à nouveau capter ici des tendances générales et illustrer des phénomènes typiques dont peut rendre compte notre modèle.

44

Nous allons en premier lieu utiliser cette pyramide et ses projections futures pour calibrer les processus d'entrée _{tt}tEN*, en faisant l'hypothèse que _é(i,j),t suit une loi de Poisson de paramètre (et donc d'espérance) dépendant de l'effectif dans la pyramide des âges de la sous-population d'âge j - 1 à la date t - 1. Plus précisément, nous supposerons donc que

V (i, j, t) EE x E - {á} x N^*, é(i,j),t ^ Poisson (nîj-1,t-1o^vol,(i,j-1)) V (i, t) E E x N^*,é(i,á),t ^ Poisson (n)

où n est un paramètre entier fixé et où ^ovol,(i,j) est le taux de sortie volontaire de la cellule (i, j), c'est-à-dire _ovol,(i,j) =o(i,j) - ?j . Si nous reprenons les notations déjà introduites dans

les parties précédentes, ^ovol,(i,j) vaut donc 1 - ?j

ls .

En fin de compte, nous posons des processus d'arrivée stationnaires pour les cellules correspondant à l'âge minimal á, afin d'assurer un renouvellement continu de la base de clientèle. En revanche, pour les autres cellules, les processus d'entrée sont pris inhomogènes dans le temps de manière à intégrer l'évolution de la pyramide des âges dans la dynamique de la base de clientèle. Nous souhaitons plus précisément paramétrer, à chaque date, des arrivées qui soient proportionnelles aux effectifs correspondants dans la pyramide des âges qui prévaudra à cet instant. On suppose donc ici implicitement que la banque tend à capter une part de marché constante! Le paramètre de la loi de Poisson suivie par é(i,j),t est donc pris proportionnel à deux grandeurs :

- l'effectif normalisé _îj-1,t-1 associé à l'âge immédiatement inférieur j - 1 au sein de la pyramide projetée de la date t - 1;

- le taux de sortie volontaire des clients de l'âge immédiatement inférieur j - 1.

L'intérêt de cette calibration réside dans le fait qu'elle «standardise» la distribution démographique donnée par les projections de la pyramide que nous avons calculées, dans le sens où elle tend à assurer un retour vers un effectif nîj,t pour chaque cellule (i, j) à la date t. Par conséquent, avec cette calibration des processus d'arrivée, la base de clientèle de la banque tend à se calquer, en terme de distribution d'âges, sur la pyramide qui évolue au cours du temps. n peut être interprété comme le nombre d'arrivées mensuelles moyennes dans chacune des cellules correspondant à l'âge á=18 ans et 0 mois. C'est un paramètre qui caractérise le nombre typique de personnes par cellule de clientèle, à multiplication par le facteur d'échelle démographique _îj,t près.

Dans les simulations que nous allons à présent effectuer, la distribution initiale de clients í0 a une importance capitale pour la dynamique future de l'encours comme nous allons le mettre en évidence. Nous dirons dorénavant que la banque est dans une situation initiale normale ou stable si :

- la typologie actuelle de ses clients est l'exact reflet démographique de la population française, dans le sens où la distribution de sa clientèle par âge respecte les proportions de la pyramide ;

- les s cellules correspondant à un même âge j sont toutes constituées initialement d'un nombre égal de clients.

La première condition impose qu'il existe p EN^* tel que í.,j,0 = Lpîj,0] pour tout j E FL, et la seconde que Vi E E, íi,j,0 = í',3,°

s . Autrement dit, dans un tel schéma, il existe n E N tel que í(i,j),0=Lnîj,0] (*) pour toute cellule (i, j).

A contrario, nous parlerons de déséquilibre démographique vers le bas (respectivement vers le haut) si la population initiale de la banque n'est pas représentative de la démographie

45

française, dans la mesure où elle présente un excès de jeunes personnes (respectivement de personnes âgées). La première situation est typique des banques en ligne, qui sont apparues relativement récemment et qui ont jusqu'à présent majoritairement séduit une clientèle jeune. La seconde situation est plus représentative de la clientèle actuelle de La Banque Postale, composée d'une proportion importante de personnes d'un âge avancé.

Commençons par analyser l'évolution de l'encours en partant d'une situation démographique normale. Afin de discerner le facteur démographique dans ces simulations, nous y prendrons toujours une inflation mensuelle constante it = 0.002. En outre, nous prendrons¹³ n=20. Voici ce que l'on obtient comme trajectoires respectivement avec l=2 et l=60.



FIG. 9 - Une trajectoire pour l=2 (courbe bleue) et l=60 (courbe rouge) de la dynamique de l'encours total avec une inflation constante et une situation démographique normale

À première vue, on ne décèle pas de différence dans la forme d'évolution par rapport à ce que nous avions déjà obtenu dans les simulations précédentes.

Toutefois, si l'on calcule le taux de croissance de l'encours sur les dix années obtenu respectivement avec ces deux trajectoires, on obtient 39.7% dans le cas l = 2 et 40.0% pour l = 60, alors que le niveau d'inflation a «seulement» augmenté de (1 + it)¹²⁰ - 1 = 27.1% sur cette même décennie. Ainsi, contrairement au cas où la population dans la banque était constante en moyenne et uniformément répartie entre les différentes cellules à chaque date, pour lequel la croissance obtenue était très voisine de celle du niveau d'inflation¹⁴, on obtient ici une surperformance sensible par rapport à l'inflation. La raison de ce différentiel est purement démographique : la singularité démographique du baby-boom visible sur la pyramide¹⁵ entraîne une augmentation continue et significative de la sous-population des clients de plus de 65 ans au sein de l'établissement dans les années à venir. Comme cette population détient en moyenne plus d'encours, ce décalage démographique interne à la banque

¹³Nous doublons n par rapport aux simulations précédentes afin de ne pas faire de troncature trop «brutale» dans la formule (*)

¹⁴Rappelons que nous avions obtenu respectivement des croissances de 27.8% et 27.4% sur les trajectoires de la Figure 5 page 28

¹⁵Et qui se retrouve dans la population de la banque puisque cette dernière a une base de clientèle qui en est le reflet en proportions

46

vient s'ajouter à l'inflation et augmente d'autant plus l'encours global.

7.2.2 Déséquilibre démographique initial vers le bas

Nous considérons à présent une banque dont la clientèle en t = 0 est essentiellement constituée de jeunes. La pyramide des âges de la sous-population des clients de la banque est donc particulièrement élargie vers le bas et étroite vers le haut. Pour étudier l'effet d'un

tel déséquilibre, nous considérons un établissement ayant une distribution démographique n

normale, puis nous retirons ₄ personnes de chaque cellule au-delà de 50 ans.



FIG. 10 - Une trajectoire pour l=2 (courbe bleue) et l=60 (courbe rouge) de la dynamique de l'encours total avec une inflation constante et un déséquilibre démographique vers le bas

On remarque que dans ces conditions, les deux valeurs du paramètre donnent des évolutions différentes. La forte mobilité des clients avec l = 2 se traduisant aussi par des entrées importantes depuis l'extérieur, l'ensemble du vide générationnel au-delà de 50 ans se remplit rapidement dans ce cas, au cours d'une période transitoire d'environ deux ans. Tout se passe comme si les personnes âgées extérieures éprouvaient soudainement autant d'attirance pour cette banque que pour une autre. Dit autrement, la pyramide des âges interne à la banque converge rapidement vers celle de l'ensemble de la population française. L'arrivée importante de personnes âgées, qui étaient en nombre déficitaire au début, constitue la période transitoire observée et explique la croissance forte à l'origine. A contrario, dans le cas l=60, il y a peu de sorties, mais également peu d'entrées, entraînant une rigidité de la base de clientèle. En conséquence, le vide générationnel existant initialement ne se comble que très modestement et très lentement. L'encours de la banque conserve donc en «mémoire» sa répartition initiale sur le long terme, ce qui pénalise durablement la croissance de l'encours! Pour l = 60, c'est l'effet vieillesse qui l'emporte : la croissance de l'encours est essentiellement due (inflation mise à part) à l'arrivée continuelle de jeunes clients et au vieillissement de la base clientèle existante, qui a tendance à s'enrichir. Le cumul de ces deux phénomènes permet, sur cette simulation, une croissance de l'encours de 67.5%! Pour l =2, la croissance obtenue est supérieure et égale à 83.1%, en raison du rapide rééquilibrage démographique. Dans tous les cas,

47

on retrouve donc ici une croissance très forte, surperformant l'inflation, typique de l'encours des banques en ligne.

7.2.3 Déséquilibre démographique initial vers le haut

Nous considérons à présent la situation inverse, à savoir une banque dont la clientèle actuelle est essentiellement constituée de personnes âgées aux encours élevés. La pyramide des âges de la sous-population des clients de la banque est donc ici en forme de toupie, étroite vers le bas et élargie vers le haut. Pour créer cette situation, nous avons pris la pyramide des âges française et nous l'avons «retournée», comme s'il fallait lire les âges de haut en bas sur la représentaion graphique de la page 35. Nous adoptons donc ici un cas extrême, en considérant un établissement pour lequel la pyramide des âges de la clientèle est exactement le négatif de la pyramide des âges de la France.



FIG. 11 - Une trajectoire pour l=2 (courbe bleue) et l=60 (courbe rouge) de la dynamique de l'encours total avec une inflation constante et un déséquilibre démographique vers le haut

Dans ce cas-ci, on observe à court terme une stagnation (voire une décroissance) très probable de l'encours total. Dans le cas l =2, à l'instar du cas précédent, la forte mobilité des personnes, aussi bien internes qu'externes à l'établissement, assure une forme de rééquilibrage démographique relativement rapide. On observe ainsi une période transitoire de décroissance nette de l'encours correspondant à la perte de clients âgés, remplacés par des jeunes apportant peu de liquidités. Ainsi, sur cette simulation, la base de clientèle met approximativement de un à deux ans pour se calquer plus conformément à la pyramide des âges, avant de croître selon la dynamique typique qu'on lui connaît. De même, dans le cas l =60, la forte rigidité de la base de clientèle crée une rémanence dans la structure de cette dernière, sur le moyen-long terme, avec une masse des dépôts croissant très faiblement (uniquement par l'inflation en fait). Il faut attendre dans ce cas plusieurs années avant de rééquilibrer la population des clients sur la pyramide des âges.

Les croissances de l'encours des dépôts sur cette décennie sont, dans ces simulations, respectivement de 13.8% et de 14.2%, soit bien inférieures à la croissance que l'on aurait projetée a priori, en se basant sur l'inflation modélisée! Un tel déséquilibre démographique

48

s'accompagne donc d'une sous-performance de la croissance de l'encours par rapport au niveau de l'inflation.

7.3 Vision «mort» du bilan et durée de vie théorique des dépôts

Il s'agit ici d'estimer, dans le cadre de notre modèle, la durée de vie théorique de l'encours des CCP, sous l'hypothèse que la banque ne commercialise plus de produits. Dans ce contexte, seuls les comptes des clients à l'heure actuelle continuent d'évoluer dans le futur, mais aucun nouveau compte ne sera ouvert. L'agrégat de dépôts s'éteindra donc définitivement lorsque tous les clients actuels auront quitté l'établissement par décision volontaire ou par décès.

Notre modèle étant fondé sur des taux de sortie, la décroissance de l'encours est exponentielle. La durée caractéristique de décroissance dépend directement de ces taux de sortie.

Voici par exemple ce que l'on obtient avec l = 2 dans les cas respectifs d'une situation démographique initiale stable, déséquilibrée vers le haut et déséquilibrée vers le bas. Afin de pouvoir les comparer, les trajectoires obtenues sont renormalisées afin de coïncider à l'origine.



FIG. 12 - Une trajectoire avec une situation initiale stable (courbe verte), un déséquilibre démographique vers le haut (courbe rouge) et un déséquilibre démographique vers le bas (courbe bleue) de la dynamique de l'encours total avec un encours moyen par cellule déterministe

On retrouve visuellement la décroissance exponentielle annoncée. Remarquons toutefois que la banque s'en sort d'autant mieux qu'elle a une population jeune à l'instant où toute commercialisation de produits est arrêtée, ce qui est très intuitif. Elle profite en effet du vieillissement de ses clients actuels et de la croissance de leur richesse. A l'inverse, une banque ayant une clientèle d'un âge avancé perd plus rapidement son agrégat de dépôts en raison du départ rapide de ses clients patrimoniaux.

Avec notre modèle, il faut attendre, même dans le cas l = 2 d'une grande mobilité des clients, des durées typiques de l'ordre de 60 ans pour épuiser totalement le stock. En d'autres termes, certains clients actuels d'âge resteront dans l'établissement jusqu'à avoir atteint l'âge maximum. En réalité, il faut bien sûr tenir compte de phénomènes que notre modèle ne

49

prend pas en compte ici, typiquement l'effet de réputation. Il est en effet légitime de penser qu'une banque arrêtant de commercialiser des produits ait de plus en plus de difficultés à retenir ses clients au fur et à mesure de son «déclin». Notre modèle peut donc être utilisé pour simuler des trajectoires de mort de l'encours sur le court-moyen terme (au plus quelques années). Pour des durées importantes de plus de 10 ans, il est raisonnable de penser que le modèle construit n'est plus valide et qu'il faut intégrer d'autres aspects. Par exemple, cela pourrait raisonnablement s'envisager avec des taux de sortie croissants avec le temps.

8 Un modèle à «superstrates»

Au vu de cette première analyse, il ressort que les valeurs typiques que nous avons adoptées pour l présentent toutes deux des avantages et des inconvénients.

Ainsi, dans le cas l = 60, on constate par comparaison avec la courbe d'évolution de l'encours des CCP sur les quinze dernières années, que cette valeur de paramètre fournit des courbes trop peu volatiles, comme si notre pouvoir explicatif sur l'encours était trop élevé. En revanche, dans le cas de déséquilibres démographiques, il permet de rendre compte d'un effet mémoire sur le moyen-long terme qui paraît satisfaisant.

A contrario, le paramètre l = 2 semble donner des résultats plus conformes à la réalité sous l'angle de la forme générale d'évolution, dans la mesure où il permet des «sauts» plus marqués qui sont nettement visibles sur la courbe historique. Cependant, nous avons vu que cette valeur de paramètre entraîne des réajustements démographiques que l'on a envie de qualifier de «trop» rapides : ainsi, tout déséquilibre démographique interne à la banque se résorbe en moyenne approximativement en un an, ce qui semble a priori peu plausible. En outre, le cas l = 2 correspond à un changement de strate tous les deux mois en moyenne. Une telle valeur de paramètre peut donc paraître artificielle, dans la mesure où la ventilation en strates est censée capturer la situation financière générale du client, que l'on ne s'attend évidemment pas à voir changer aussi fréquemment.

Le but de cette section est de proposer une forme d'amélioration de ce que nous avons considéré jusqu'ici, qui puisse concilier, dans la mesure du possible, les faits stylisés évoqués ci-dessus, tout en offrant une représentation plus crédible de la réalité.

Notre point de départ est le suivant : il est légitime de penser que l'encours d'un client (peu importe sa situation financière) puisse connaître de fortes fluctuations d'un mois sur l'autre, suite à des dépenses inhabituelles ou encore à des virements vers des supports d'épargne par exemple. Nous envisageons donc ici une amélioration dans la calibration du modèle en ventilant chaque strate en deux sous-strates. Ces dernières regroupent respectivement les clients de la strate considérée dont le compte est dans un état «haut» (fortement alimenté) et ceux dont le compte est dans un état «bas» (peu alimenté). Les clients ont alors une propension marquée à rester dans leur strate, mais une forte mobilité au sein de celle-ci entre les différentes sous-strates qui la composent. Cela correspond bien à l'idée selon laquelle la surface financière du client est une donnée relativement stable, tandis que l'état de son compte peut, quant à lui, être beaucoup plus volatile! De cette manière, on conserve un pouvoir explicatif sur l'encours du client sur le moyen-long terme (donné par la strate à laquelle il appartient) tout en introduisant des fluctuations «locales» mensuelles données par les mouvements internes à chaque strate entre les deux états. Une telle approche prend tout son sens si l'on pense à des périodes annuelles précises, comme les fêtes de fin d'année, où l'on peut observer des débits importants sur la majorité des comptes courants.

50

Nous allons à présent expliciter cette démarche. Considérons une banque de détail comprenant E = s = 8 strates. L'idée est de les voir groupées par paire (en tant qu'état «haut» et état «bas») au sein de quatre «superstrates» qui représentent la surface financière. La superstrate 1 correspond aux clients les plus aisés et regroupe les strates i = 1 et i = 2 qui sont respectivement ses états «haut» et «bas». La superstrate 4 correspond, quant à elle, aux clients les plus modestes et se compose des strates i = 7 («haut») et i = 8 («bas»). L'état complémentaire de la strate i au sein d'une «superstrate» sera appelé strate binôme. Les âges des clients sont toujours compris entre c=18 ans (et 0 mois) et w=80 ans (et 0 mois). Chacune des 5960 cellules est supposée contenir initialement n = 5 clients : on a réparti les clients de chacune des 2980 cellules précédentes uniformément entre les deux cellules-filles correspondant aux états «haut» et «bas».

Les cellules de clientèle regroupant les clients les plus âgés sont toujours caractérisées par un taux de sortie de 1 :

Vi E E, Vk E E, ë(i,ù) k = 0 et o(i,ù) = 1

Soit désormais j =6 w. Nous considérons que le taux de maintien dans chacune des (quatre)

l - 1

«superstrates» est de _l , où l ~2 caractérise la stabilité de la surface financière des clients.

Nous pourrons prendre typiquement l=60, correspondant à une sortie au terme de cinq ans (en moyenne) de la superstrate. Les sorties par décès sont par ailleurs toujours calibrées sur

celui de passage dans l'une des (s - 2) autres strates est pris uniforme égal à 1

les taux de mortalité publiés par l'INED. Le taux de sortie volontaire est pris égal à 1 2l et

2l(s - 2)^.

En particulier, nous supposons que les clients changeant de «superstrate» ont autant de chances de se retrouver dans les états «haut» et «bas» de la «superstrate» d'arrivée. En revanche, si le taux de maintien dans chaque «superstrate» est élevé, nous souhaitons autoriser des mouvements fréquents entre les deux strates qui la composent : pour spécifier ce mouvement potentiel, nous introduisons un nouveau paramètre uE[0, 1], qui mesure la propension à rester dans le même état («haut» ou «bas»). Plus précisément, le taux de transition vers

l'autre strate de la «superstrate» à laquelle le client appartient est (1 - u)l - 1

l et celui de

l - 1

maintien dans sa strate actuelle est u_l . En faisant varier le paramètre u, on contrôle la

dynamique de transition d'un état à un autre au sein d'une «superstrate». Pour u = 0.5, les deux états sont équiprobables; pour u faible, on assure une forme d'attirance vers la strate binôme et pour u élevé, on assure une plus grande stabilité du client au sein de son état actuel. Ainsi, un u proche de zéro correspond à une situation dans laquelle la présence du client dans un état («haut» ou «bas») au sein de sa «superstrate» entraîne une plus forte probabilité de le retrouver dans l'état binôme à la date suivante. Intuitivement, si l'on adopte un tel u, on postule implicitement que, si le client est dans son état «bas» à une date t, alors il y a de fortes chances pour qu'il alimente son compte et qu'il passe dans l'état «haut» en t+1. Réciproquement, s'il est dans l'état «haut» en t, il est probable qu'il fasse un virement de ce compte vers un livret d'épargne et donc qu'il passe dans l'état «bas» en t + 1. À l'inverse, pour u proche de un, on postule simplement qu'il est plus probable que chaque client reste dans son état.

51

Sous l'hypothèse d'indépendance entre la mortalité et les strates vers lesquelles les personnes seraient amenées à évoluer à la date suivante sans mortalité, nous avons donc pour

(i, j) E E x (FL - {ù}), et en notant i⁰ la strate binôme de i,

?

?????????

?????????

ë(i,j) k= 1 - ?j si k E (E - {i, i⁰}) 2l(s - 2)

ë(i,j) i=u(l - 1) (1 - ?j) si k = i

l

_ë(i,j)

i0=(1 - u)(l - 1) (1 - ?j) si k = i0

o(i,j) =?j + 1 - ?j

2l

l

Enfin, les entrées sont dans un premier temps calibrées de manière à équilibrer les sorties. En effet, nous voulons d'abord assurer une constance démographique moyenne dans la sous-population des clients de la banque.

V (i, j, t) E Ex(FL - {á})xN^*, é(i,j) t Poisson (no(i,j-1)) Poisson (n 1?j-1 +

~~ 1 - ?j-1 2l

L'encours moyen par client correspondant à la cellule la plus modeste de la banque est normalisé, pris égal à 1. Il s'agit des jeunes de 18 ans dans l'état «bas» de la «superstrate» 4, autrement dit des jeunes de 18 ans de la strate i = 8. Nous ferons ensuite l'hypothèse que l'état «haut» correspond à un encours moyen deux fois plus élevé que l'état «bas», et que l'état «bas» est repris de l'encours moyen que nous avions supposé lorsque s était égal à 4. Voici donc la matrice D_o. Nous avons fait figurer en vert les strates correspondant à des états «hauts» et en bleu celles correspondant aux états «bas».

Superstrate	Strate	j = á = 216	j = 217	...	j = 228	j = 229	...	j = 959		j = ù = 960	1
i = 1	8	8	...	16	16	...	496	504
	4	4	...	8	8	...	248	252		2
i = 3	6	6	...	10	10	...	250	254
	3	3	...	5	5	...	125	127		3
i = 5	4	4	...	6	6	...	126	128
	2	2	...	3	3	...	63	64		4
i = 7	2	2	...	3	3	...	63	64
	1	1	...	1,5	1,5	...	31,5	32

On obtient alors des formes générales d'évolution similaires à celles que nous avons déjà analysées, avec des variations locales d'encours assez nettes. La différence est que ces variations sont ici principalement dues aux mouvements des clients au sein de leur «superstrate» respective entre les états «hauts» et «bas».

Pour discerner ces cas, nous avons simulé des trajectoires de l'encours global de la banque pour différentes valeurs de u. Afin de saisir l'influence de ce paramètre seul, nous avons par ailleurs adopté une inflation constante ð=0.002. Nous avons pris uE{0.5, 0.1} correspondant à différents cas décrits dans le paragraphe précédent et nous avons simulé des trajectoires de l'encours sur 10 ans.



52

FIG. 13 - Une trajectoire pour u=0.5 (courbe verte) et u=0.1 (courbe rouge) de la dynamique de l'encours total avec un encours moyen par cellule déterministe

Nous avons alors calculé, dans le cas u = 0.5, la volatilité renormalisée moyenne de l'encours obtenue sur 1000 trajectoires. La volatilité correspondante s'est ainsi avérée être seulement 3% inférieure à celle obtenue dans le cas des strates «simples» (s=4) pour l =2! Nous sommes donc effectivement parvenus à obtenir des sursauts locaux de l'encours, similaires à ceux dans le modèle simple à 4 strates pour l = 2, et ce en dépit de la valeur l = 60! Ainsi, nous conservons ici un pouvoir explicatif fort sur chaque client, qui a une forte probabilité de rester au sein de sa «superstrate». Toutefois, grâce à la modélisation simple du caractère aléatoire de l'encours personnel de chacun d'entre eux d'un mois sur l'autre, nous créons une volatilité locale qui diminue notre pouvoir prévisionnel sur l'encours global. Par ailleurs, les deux trajectoires simulées ci-dessus permettent d'entrevoir les différences de dynamique imposées par le changement de valeur de u.

Pour u=0.1, on discerne ainsi des formes d'alternances fréquentes entre croissance locale et décroissance locale de l'encours d'un mois sur l'autre. Cet effet «balançoire» est dû à l'attirance pour la strate binôme: une situation de déséquilibre en t (plus de personnes dans l'état «haut» que dans l'état «bas») est suivie avec une très forte probabilité d'un déséquilibre inverse en t + 1. C'est cet effet que nous discernons dans les crêtes de la courbe d'évolution de l'encours. Nous avons entouré une telle évolution caractéristique en «dents de scie» (voir Figure 13 ci-dessus).

Toutefois, la formidable stabilité démographique que nous imposons ici (uniformité initiale et constance en moyenne dans le temps) ne permet pas de distinction encore très nette des types d'évolution de l'encours futur. Nous allons donc à présent réintroduire l'aspect démographique.

53

Les paramètres adoptés sont l =60 et u=0.5, correspondant à un changement de «super-strate» tous les 5 ans en moyenne et une équiprobabilité entre les deux états «haut» et «bas». Les entrées sont à nouveau calibrées conformément aux projections futures de la pyramide des âges. Nous prenons désormais n=10.

Nous avons fait figurer sur les graphes ci-après les évolutions respectives de l'encours avec une situation initiale stable de la base de clientèle puis avec les deux types de déséquilibre (vers le bas et vers le haut). Sur chaque graphe, nous avons également fait figurer en noir la courbe d'évolution de l'encours si celui-ci suit exactement le niveau d'inflation (qui croît de 2.4% par an) : cela fournit ainsi une base de comparaison pour les croissances des trajectoires simulées. En outre, toutes les trajectoires ont été renormalisées de manière à partir d'une origine commune, le but étant de discerner les formes d'évolution à partir d'un même point de départ actuel.



FIG. 14 - Une trajectoire avec une situation initiale stable (courbe verte) et un déséquilibre démographique vers le haut (courbe rouge) de la dynamique de l'encours total avec une inflation constante dans le modèle à «superstrates»

On retrouve le fait qu'un déséquilibre vers le haut entraîne une sous-performance par rapport à l'inflation. Dans une première phase, l'encours décroît faiblement en raison de la perte des clients âgés qui détiennent le plus d'encours. La tendance s'inverse cependant progressivement en quelques années. Cela est dû à l'inflation d'une part, mais aussi à l'augmentation du nombre de jeunes clients, au vieillissement de la base de clientèle d'un âge intermédiaire en t = 0 ainsi qu'à l'arrivée de la génération du baby-boom, qui fournit un nombre croissant d'entrées de clients d'un âge avancé. Lorsque la banque possède initialement une base de clients stable, c'est-à-dire calquée sur la pyramide des âges, elle surperforme l'inflation comme nous l'avons déjà constaté dans les modèles à strates. Cela est essentiellement lié au vieillissement de ses clients appartenant à la génération du baby-boom.



54

FIG. 15 - Une trajectoire avec une situation initiale stable (courbe verte) et un déséquilibre démographique vers le bas (courbe bleue) de la dynamique de l'encours total avec une inflation constante dans le modèle à «superstrates»

Dans le cas d'un déséquilibre démographique initial vers le bas caractéristique des banques en ligne, la surperformance par rapport à l'inflation est très nette. Elle provient essentiellement de la croissance du nombre de clients et au vieillissement de la clientèle existante. On obtient dans les deux cas un rééquilibrage progressif en plusieurs années, sans pour autant «tuer» toute volatilité locale comme cela était le cas avec l = 60 dans le modèle à strates simples.

Enfin, ce raffinement à «superstrates» permet également d'intégrer l'influence de déséquilibres de la démographie initiale de la base de clientèle entre les états «haut» et «bas», afin de mieux anticiper l'évolution de l'encours sur le court terme. Imaginons, à titre d'exemple, que l'on sache que u a une valeur faible. Autrement dit, l'attirance pour la strate binôme est forte : un compte bien alimenté a de fortes chances d'avoir beaucoup diminué au mois suivant (par virement vers les comptes d'épargne par exemple). Dès lors, si la distribution de clients présente un déséquilibre envers un état, on obtient une forme de rémanence locale de ce déséquilibre sur le court terme, avec un effet oscillant qui s'amortit sur plusieurs mois. Inversement, si u est fort, on s'attend à conserver ce biais vers les strates «hautes» sur les mois à venir.

Pour illustrer notre propos, nous avons simulé une trajectoire d'encours sur un an avec l= 60 et u=0.1. Nous avons créé un déséquilibre initial en partant de la situation démographique stable puis en transférant, pour chaque âge j et chaque «superstrate», un client de l'état «bas» vers l'état «haut». Sachant que n = 10, cela représente 10% de l'effectif de chaque cellule jusqu'à 65 ans.



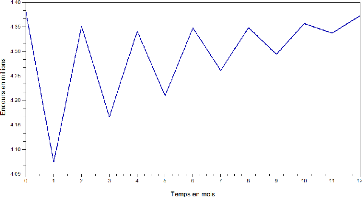
55

FIG. 16 - Une trajectoire avec déséquilibre démographique initial vers les strates «hautes»

On observe très clairement la rémanence annoncée, avec un effet balançoire qui s'amortit dans ce cas-ci sur une durée typique d'une année. Au-delà, le déséquilibre s'est effacé suite aux mouvements et arrivées de nouveaux clients. Cela permet d'une certaine manière de créer un mouvement de «masse» à court terme. Tout se passe ainsi comme si l'on créait artificiellement une corrélation entre les mouvements de clients dans le modèle à strates simples. On obtient dès lors une liberté de modélisation supplémentaire dont on ne disposait pas avant.

En conséquence, ce modèle peut être utile pour affiner la prévision à court terme de l'encours si l'on dispose de la distribution actuelle de la base des clients et si l'on a calibré (sur la base d'observations historiques) la valeur de u.

Finalement, ce modèle à «superstrates», qui nous donne la possibilité de «pianoter» sur les états «haut» et «bas», sur les probabilités de transition de l'un vers l'autre et sur les taux de transition de «superstrate» nous permet de générer, dans le cadre de valeurs de paramètres «réalistes»¹⁶, des trajectoires de l'encours qui respectent certains faits stylisés que nous posons a priori :

- un fort pouvoir prévisionnel sur l'état patrimonial de chaque client (c'est-à-dire la «superstrate» à laquelle il appartient)

- une volatilité locale (sur pas de temps mensuel) de l'encours

- une rémanence sur le moyen-long terme d'un déséquilibre démographique initial qui s'amortit en plusieurs années

D'un point de vue purement théorique, ce modèle, que nous avons appelé à «superstrates», est toutefois strictement identique aux cas analysés précédemment. Notre but ici était simplement de construire une structure pour notre banque virtuelle qui soit plus réaliste du point de vue des valeurs de paramètres et de prouver que l'on retrouvait toujours les faits stylisés soulevés.

¹⁶Dans le sens où les taux de transition et de sortie adoptés paraissent plausibles si l'on interprète les «superstrates» comme le reflet de la surface financière et les strates comme l'état du compte

56

9 Vers une calibration du modèle sur les données historiques?

Le modèle construit étant en mesure de générer de nombreux faits stylisés «réalistes», il est tentant de chercher à le calibrer sur les données historiques de La Banque Postale. Il serait intéressant d'analyser les scénarios d'évolution de l'encours bancaire qu'il génère dans un cadre concret, et éventuellement de confronter ses prédictions à la réalité.

Malheureusement, cette calibration se heurte à une difficulté (d'ordre «pratique») majeure : en effet, notre modèle présuppose que la banque ait ventilé sa clientèle en strates par surface financière et surtout qu'elle dispose d'un historique individuel suffisamment ancien de chacun de ses clients actuels. C'est une condition sine qua non à l'estimation des différents taux de transition et de sorties volontaires. En outre, même si ces informations individuelles étaient enregistrées, il faudrait encore retravailler l'ensemble de la base de données afin de calculer les effectifs des différentes cellules et le nombre de clients bougeant vers une cellule donnée à chaque date, pour pouvoir effectivement commencer le travail d'estimation.

C'est la raison pour laquelle nous n'avons pas été en mesure de calibrer notre modèle sur la clientèle de La Banque Postale.

Remarquons toutefois ici que, même si nous parvenions à estimer l'ensemble des paramètres du modèle (les )(i,j)

k et ^o(i,j) des matrices de transition) ainsi que les lois des processus é(i,j),t dans une première étape , il nous faudrait encore effectuer, dans une seconde étape, des simulations de type Monte-Carlo à partir de ces paramètres estimés. Ce procédé est dénommé «doublement stochastique» dans la littérature statistique car l'incertitude porte déjà sur les paramètres des lois simulées.

57

Quatrième partie

M odélisation de l'évolution de la

marge nette

10 Définition et principes

10.1 Une approche économique et comptable

Deux approches sont envisageables dans la «valorisation» économique des dépôts que la banque détient aujourd'hui.

La première d'entre elles, particulièrement utilisée aux États-Unis où le concept de juste valeur prédomine, est la valeur actuelle nette (VAN) des dépôts vus d'aujourd'hui, ou NPV (Net Present Value). Conforme à la vision financière classique du marked-to-market, elle consiste à actualiser la somme des cash flows futurs affectant les dépôts pour en donner la valeur économique actuelle. Le plus gros défaut de cette approche est sa sensibilité aux fluctuations des taux d'intérêt : des mouvements de la courbe des taux modifient profondément la valeur de la banque. C'est pourquoi cette approche, plutôt adaptée à la valorisation de titres amenés à être revendus à très court terme, est parfois considérée comme artificielle ou virtuelle pour valoriser un agrégat de dépôts.

En gestion ALM, et particulièrement en France, les banques de détail raisonnent plutôt en couru. On parle d'approche IRM (Interest Rate Margin) ou MNI ( pour Marge Nette d'Intérêts). Cela consiste à se focaliser sur l'évolution, au cours du temps, des flux générés par les dépôts, en les considérant au fil de l'eau, sans actualisation. Dans cette vision, c'est le concept de marge nette dégagée à chaque date qui prend toute son importance.

D'une manière générale, la marge nette d'intérêts dégagée par l'établissement à la date t, que nous noterons IRM(t), peut être définie comme le flux net d'intérêts perçu par la banque à cette même date. Ainsi, IRM(t) =I (t) - I (t) où I (t) désigne le flux d'intérêts perçu par la banque à la date t au titre de ses placements effectués avant cette date, alors que I (t) s'identifie au flux d'intérêts reversé aux clients en t en rémunération de leurs dépôts.

Dans le cadre de cette étude, nous aurons I (t)=0 pour tout t puisque les CCP ne sont pas rémunérés. Ainsi

IRM(t) = I (t)

10.2 Les stratégies de placement et le «compte d'intérêts»

Soit un horizon h en mois, pris supérieur ou égal à 60. À chaque date 0 < t < h - 1, la banque investit tout ou partie des dépôts clientèles sur les marchés. Plusieurs dimensions sont présentes dans ce processus de décision : le choix de la quantité d'encours à investir, le choix du ou des supports de placement et l'allocation à chacun d'entre eux.

Nous supposerons dorénavant que la banque a le choix, à chaque date, entre deux supports d'investissement, offrant des taux d'intérêts différents :

- le premier support correspond à des prêts interbancaires d'échéance un mois (court terme);

- le second support correspond à des investissements de plus long terme d'échéance 5 ans.

Les deux supports sont fondés sur des combinaisons de zéros-coupons de différentes échéances. Un zéro-coupon d'échéance T est un instrument financier qui rapporte 1 euro en T. On dit

58

alors qu'il a pour maturité T -t'⁷. Le prix en t d'un tel instrument financier est noté ZC(t, T). Le temps est décompté en mois dans ces notations. Nous adoptons les hypothèses de travail suivantes dans le cadre de notre étude :

- le support court-terme dans lesquel on peut investir en tE{0, 1,.. . , h - 1} est le zéro-

coupon d'échéance t + 1, donc de maturité 1 mois. Le prix à débourser en t pour un tel produit est ZC(t, t + 1);

- le support long-terme dans lequel on peut investir en tE{0, 1,.. . , h - 1} est l'obligation d'échéance 5 ans, de nominal 1 euro et reversant des coupons mensuels fixes de xt euros avec remboursement du nominal à échéance. Les flux reversés par ce produit financier acheté en t sont illustrés sur le schéma ci-dessous;



Cet instrument financier est en fait une combinaison de zéros-coupons de différentes échéances. Par absence d'opportunités d'arbitrage (AOA)'⁸, le prix d'achat en tE{0, 1,.. . , h - 1} de cette obligation s'écrit :

Bond(t, t + 60) = 1 =

6 0 X i=1

xtZC(t, t + i) + ZC(t, t + 60)

Son prix de revente, en une date t_v E{t + 1, t + 2,. .. , t + 59}, s'écrit :

Bond(tv,t + 60) =

t+60X i=tv+1

xtZC(tv, i) + ZC(tv, t + 60)

Remarquons que le montant du coupon est fixé en t à la date d'achat par l'équation

xt =

1 -ZC(t,t+60)

>60 ;
i=1 ZC(t, t + i) - à chaque date tE{1, 2,.. . , h}, la banque perçoit un flux I(t) au titre de ses placements passés, qui peut être divisé entre remboursement de capital K(t) et tombée de flux d'intérêts I⁺(t), avec donc I(t) = K(t) + I⁺(t). Le montant K(t) est réintégré à la masse des CCP et réinvesti sur les marchés. En revanche, I⁺(t) est reversé sur le «compte d'intérêts» destiné aux actionnaires de l'établissement. En conséquence, les

¹⁷L'échéance d'un produit financier est la date à laquelle il «expire» donc ici la date où l'on reçoit l'unique détachement de coupon de 1 euro alors que sa maturité est la distance à l'échéance

¹⁸Il n'est pas possible de gagner de l'argent à coup sûr à partir d'un investissement nul

59

tombées d'intérêts ne viennent pas alimenter l'encours de CCP et ne peuvent pas être réinvesties à des dates ultérieures;

- les marchés sont parfaits : on peut acheter et vendre toute proportion de titres, il n'y a pas de coûts de transaction, les marchés sont infiniment liquides¹⁹ et nous ignorons

le risque de contrepartie²⁰ (ainsi, les investissements considérés sont sans risque).

11 Le modèle

11.1 La courbe des taux

Comme les stratégies de placement considérées correspondent à des prêts de maturités différentes, il nous faut modéliser l'évolution des taux de marché correspondant à ces différentes maturités. L'objet de cette section est de modéliser la courbe des taux.

Plusieurs modèles classiques s'offrent à nous. Le modèle de Vasièek, qui a déjà été rencontré dans la section dédiée au taux d'inflation, est largement employé en raison de sa simplicité. Nous adoptons un modèle probabiliste de marché (i~, W, _(Ft')t'ER+ , P), où P désigne la probabilité historique que nous avions déjà rencontrée, lors du modèle de dynamique interne à la banque. Nous supposons l'absence d'opportunités d'arbitrage sur ce marché, garantissant l'existence d'une probabilité risque-neutre Q équivalente à la probabilité historique. Nous avons décidé de retenir le modèle de Hull et White qui constitue une extension du modèle de Vasièek sous lequel la diffusion du taux court (taux spot), sous la probabilité risque-neutre Q, se met sous la forme

drt' = (bt' - art') dt^' + ód Wt' , t^' E R+

où Wt' désigne un mouvement brownien standard (sous Q). On parle de modèle de taux à k facteurs si la dimension de ce brownien est k. Dans cette étude, nous nous restreindrons à un modèle à un facteur. En tant que solution d'une équation différentielle stochastique, le taux spot est markovien sous cette dynamique. Il est intéressant de noter que, dans le cas général, la probabilité que le taux court soit négatif sous Q est strictement positive.

Les paramètres a et óER + sont constants et correspondent respectivement à la force de rappel du processus et à sa volatilité. Le paramètre bt' est déterministe et il est choisi de manière à «fitter» la courbe des taux actuellement observée sur les marchés. Plus précisément, il est calibré implicitement de façon à ce que les taux forwards instantanés issus du modèle correspondent à ceux issus du marché. Nous allons expliciter cette démarche²¹.

Dans le cadre de l'écriture du modèle de Hull et White, le temps est décompté en années. C'est la raison pour laquelle nous le notons t^', la désignation t étant réservée aux durées mensuelles.

Il nous faut modéliser les déformations de la courbe des taux en écrivant les équations suivies par les zéros-coupons. Soit le zéro-coupon d'échéance T^' qui rapporte 1 euro en T^', dont le prix en t^' est noté B(t^', T^'). Toujours sous l'hypothèse d'AOA, tous les actifs du marché ont pour rendement rt' sous Q. Nous pouvons alors écrire

dB(t^', T^') = B(t^', T^') (rt'dt^' + a(t^', T^')d Wt') , t^' E R+

¹⁹Il y a toujours une contrepartie à l'achat et à la vente pour toute quantité de titres

²⁰Connu aussi sous le nom de risque de crédit, c'est le risque que la contrepartie (ici l'émetteur du zéro-coupon ou de l'obligation) fasse défaut et ne puisse être en mesure de nous verser le(s) flux initialement convenu(s)

²¹Plusieurs formules seront indicées par un numéro. La démonstration précise d'obtention de la formule correspondante figure en annexe B

Le taux zéro-coupon actuariel R(t^', T^') écrit en base annuelle²² prévalant en t^' pour un zéro-coupon d'échéance T^' est la variable aléatoire définie par

B(t^',T^') =

1

(1 + R(t', T'))T '-t'

La courbe T^' ?R(0, T^') définit la courbe zéro-coupon actuelle.

Il y a une infinité d'actifs sur ce marché (autant que d'échéances). En posant Ft' =ó(W_u, 0=u=t^'), le marché peut donc être supposé complet.

En effectuant le changement de variable Yt' = rt'e

at^'

, on intègre l'équation précédente

selon

rt' = r0e^-

at' +t' e a(t --3)bsds + Q J t e--te ^--s)dWs JJfo o

60

On a même plus généralement

rT' = rt'e

a(T'-t') + J T e a(T'-3)bsds + Q J ^T' e ^a^(T' 3)dWs (1) t' t'

compte tenu du caractère markovien.

Pour reconstruire la courbe des taux sous ce modèle, il nous faut déterminer le prix des zéros-coupons de différentes échéances. Par AOA et complétude du marché, nous avons

B(t^',T^') = _EQ [e-ft' ^rudu|Ft'] (*)

Comme nous connaissons la dynamique du taux spot sous la mesure Q, il nous est possible d'expliciter le prix des zéros-coupons en fonction des différents paramètres du modèle.

Notons I(t^', T^') l'intégrale du taux court sur l'intervalle [t^', T^'], soit I(t',T')= f T '

_t' r_udu.

Par application du théorème de Fubini stochastique, nous obtenons que, conditionnellement à Ft', I(t^', T^') suit une loi gaussienne dont les deux premiers moments sont donnés par

{

m(t^',T^') = EQ [I(t^',T^')|Ft'] = 1T' - e-a(T'-t')) - fT e^-^a(T'-s)bsds + J T bsds IaL ' t, V (t^', T^') = VQ [I(t^', T^')|Ft'] = â2[T' - t^' + âe-a(T'--t') - 12ae-2a(T'-t') - â] (2)

De la relation (*), nous obtenons B(t^',T^')=e^-m(t',T')+^12V(t',T').

Remarquons que jusqu'à présent, nous ne connaissons pas bt'. Nous allons le déterminer de façon à ce que les prix zéro-coupon du modèle correspondent à ceux observés aujourd'hui sur les marchés.

Considérons le taux spot (ou instantané) forward à la date T^' vu de la date t^' défini par

?ln(B(t^', T^'))

f(t^',T^') = ?T'

²²C'est une convention

Il s'agit du taux prévalant à la date T^' pour une durée infinitésimale, anticipé depuis la date t^'. Cette variable aléatoire Ft'-mesurable est donc une fonction déterministe de la courbe des taux T^' ? B(t^', T^') de la date t^'. Il est équivalent de connaître les taux spot forward et les prix zéros-coupons, car ils sont liés par

B(t^', T^') = e- RT0

t' f(t',s)ds

En particulier, compte tenu de la forme obtenue pour B(t^',T^'), les taux forward instantanés initiaux s'écrivent

f(0,T^') = - Dln(B(0, T')) = Dm(0, T') - 1 DV (0, T^')

DT' DT' 2 DT'

soit

_fT⁰2 ( _l

f(0,T^') = r0e^-aT0 + e^-a(T0-s)b_sds - 2a2 1 1 - 2e-FIT' + e 2âT'/

Par dérivation par rapport à T^', on obtient alors la calibration suivante pour bT0

bT0 = af(0,T^') + _DfDT,' + 2a (1 - e-2aT) (3)

En utilisant cette relation, l'expression donnant le taux court se réécrit alors

rT 0 =rte

T0 a(T'-t') + y(T^') - y(t^')e^-^a(T'-t') + df e-a(T^'-s)dWs (4) t'

2

où y(t^')=f(0, t^') + 2a2 (1 - e-at0) . À titre illustratif, nous faisons figurer ici la courbe des

taux zéros-coupons actuariels ainsi que la courbe des taux forwards instantanés actuelles. Elles se désuisent aisément l'une de l'autre, comme nous l'avons expliqué. Leur connaissance est indispensable à la calibration du modèle de Hull et White.



FIG. 17 - La courbe des taux actuelle

61

En utilisant l'expression trouvée pour bT' ci-dessus, l'espérance conditionnelle m(t⁰, T⁰) de I(t⁰, T⁰) peut se réécrire

m(t⁰, T⁰) = P(t⁰, T⁰) (rt' ? ã(t⁰)) + ln( B(0,t0)

B(0, T 0)) + ¹₂(V (0, T⁰) - V (0, t⁰)) (5)

1 - e- en notant P(t^0,T^0) =		â(T^'-t^')		. On en déduit finalement l'expression des prix zéro-

62

B(t⁰,T⁰) = B(ô_' ) exp {(f(0, t⁰) - rt') P(t⁰,T⁰) - 4a (1 - e-2at') P(t⁰ T⁰)²} (6)

Dans la mesure où B(t⁰,T⁰) s'écrit ^{eA(t',T')rt'+C(t',T'),} avec A et C fonctions déterministes, on dit que le modèle de Hull et White est un modèle affine de taux²³.

Le modèle de Hull et White présente l'énorme avantage d'être compatible avec la courbe des taux actuelle (ce qui n'est pas le cas du modèle de Vasicek). Il offre par ailleurs des expressions relativement simples pour les niveaux de taux et les prix des zéro-coupons, ce qui en fait un modèle «facile» d'utilisation.

Si l'on souhaite diffuser des taux courts et taux longs à partir de ce modèle, il faut se donner les jeux de paramètres suivants :

- les paramètres intrinsèques du modèle a et ó

- le paramètre observé bt'. On utilise la courbe des taux actuelle (les prix zéro coupons B(0, T⁰) pour l'ensemble des T nécessaires) pour calculer les taux forwards instantanés et implicitement calibrer la fonction pour l'ensemble des maturités.

Une simulation de taux d'intérêts correspond alors à la génération de l'ensemble de trajec-toires {t0?B(t0,T0)}T'?{1,2,...,h+59}.

Voici par exemple trois trajectoires simulées du taux spot sur les cinq prochaines années.



FIG. 18 - Des trajectoires du taux spot rt' sous Hull et White avec a=0.1 et ó =0.01

²³L'exposant dans l'exponentielle est une fonction affine du taux spot rt'

63

Nous avons construit ce modèle en «base» annuelle comme cela est de coutume, mais nous pouvons en déduire très facilement les grandeurs en «base» mensuelle que nous avons définies précédemment. Remarquons en effet que les variables «mensuelles» et «annuelles» définies sont très simplement reliées par

^,

12

12 )

ZC(t, t + n) = B(t t + n

avec tE{0, 1,...,h - 1} et nE{1, 2, ... , 60} entiers qui représentent le temps en mois.

Le taux de rémunération offert en t sur [t, t + 1] pour l'investissement mensuel de maturité 1 mois est le taux EURIBOR²⁴ un mois noté L(t). Il s'agit d'un taux linéaire post-compté exprimé en base annuelle. En conséquence, par absence d'opportunité d'arbitrage, nous avons immédiatement²⁵

1

ZC(t, t + 1) = 1

1+ ₁₂L(t)

où L(t) s'exprime à partir du modèle de Hull et White selon

~

L(t) = 12 _(t t-1 pour t E {0,1,...,h - 1}
12^, 12 + 12)

Nous supposerons dans cette étude que le niveau des taux est indépendant de tous les mouvements de clients. En reprenant les notations déjà introduites, nous affirmons donc que }les variables aléatoires {rt,}t,ER+, {é(i,j),t}((i,j),t)EÓxÎxN* et {7r(i,j),t,l ((i,j),t,l)EÓxÎxN*xN* sont toutes mutuellement indépendantes.

11.2 Récapitulatif du modèle général

Dans cette section, nous établissons un résumé de l'ensemble du cadre mathématique construit. L'ensemble des variables d'intérêt sont définies sur un espace probabilisé (S2, W, P) muni d'une tribu W. La probabilité historique est désignée par P. Voici l'ensemble de la démarche suivie :

- nous avons défini les variables aléatoires, avec t en mois,

_{n o}

Ä(i,j),t

((i,j),t)EExExN, {t(i,j),t}((i,j),t)EExsxN* ^et _{{7r(i,j),t,l}((i,j),t,l)EEx,=,xN*xN*,} ainsi que les écritures matricielles condensées _{Ot}tEN et _{tt}tEN* associées aux deux pre-

mières. La variable _0(i,j),t, à valeurs dans R, représente l'encours client moyen de la cellule (i, j) à la date t. La variable aléatoire _7r(i,j),t,l est, quant à elle, à valeurs dans EU{o} et associe au client numéro l de la cellule (i, j) à la date t - 1, l'endroit où il sera à la date suivante t (un indice k de E s'il reste dans la banque et intègre la cellule (k, j + 1) et o s'il quitte l'établissement). La variable _t(i,j),t, à valeurs dans N, représente le nombre d'arrivées extérieures (ie de nouveaux clients) dans la cellule (i, j) entre t - 1 et t.

Enfin, nous avons noté _(Ht)tEN la filtration canonique associée à ces trois familles de variables aléatoires et _(Mt)tEN celle associée aux deux dernières, qui concernent les mouvements de clients (on a donc Mt CHt) ;

- sous l'hypothèse d'AOA, nous avons défini une probabilité risque-neutre Q équivalente à P, puis un mouvement brownien standard (Wt,) _t,ER+ unidimensionnel sous Q. À

²⁴Euro Interbank Offered Rate

²⁵Rappelons que t est décompté en mois

64

partir de ce dernier, nous diffusons les taux spot selon le modèle de Hull et White qui s'écrit drt' =(bt' - art') dt^' + QdWt' avec t^' ER+ en années, ce qui permet de retrouver l'ensemble de la courbe des taux et ses déformations au cours du temps. Nous avons noté Ft' =ó( Wt', 0<u<t^') la filtration engendrée par ce brownien ;

- nous avons également défini, avec t en mois, un mouvement brownien standard unidimensionnel _(Wt)tER+ sous P, puis, à partir de celui-ci, l'inflation mensuelle ðt par l'équation différentielle stochastique dðt = a(b - rt) dt+ódWt pour t E R+. Nous avons noté Gt =ó(Wt, 0<u<t) la filtration engendrée par ce brownien.

Remarquons ainsi que les tribus ó(Ht, t E N), ó(Ft', t^' E R+) et ó(Gt, t E R+) sont toutes incluses dans W.

En ce qui concerne les lois de ces variables, nous avons posé les hypothèses suivantes :

_n o ~

(1) les variables aléatoires Ä(i,j),t _{((i,j),t)EÓxÎxN,} ~é(i,j),t ((i,j),t)EÓxÎxN* et ~ð(i,j),t,l }((i,j),t,l)EÓxÎxN*xN* sont toutes mutuellement indépendantes;

(2) d((i, j), t, l) E E x x N^* x N^*, P (ð(i,j),t,l =k)=ë(i,j)

k si k est dans E et

P (ð(i,j),t,l

=o)=^o(i,j) avec donc

Xs k=1

ë(i,j) k + o(i,j) = 1;

(3) les tribus ó(Mt, t E N) et ó(Ft', t^' E R+) sont indépendantes : les mouvements des clients sont donc indépendants des mouvements de taux sur les marchés

(4) les tribus ó(Mt, t E N) et ó(Gt, t E R+) sont indépendantes : les mouvements des clients sont donc indépendants de l'évolution de l'inflation

11.3 Les stratégies de placement

11.3.1 Position du problème

Nous avons vu que la banque de détail considérée investit à chaque date le montant d'en-cours dont elle dispose, soit en prêt interbancaire de rémunération EURIBOR pour le mois suivant, soit en obligations à 5 ans avec coupons mensuels fixes. Nous supposons dorénavant que l'établissement de détail choisit une proportion fixe y E [0, 1] pour spécifier cette allocation entre court-terme et long-terme. Plus précisément, notre hypothèse de travail pose que la banque investit sur les marchés à chaque date t un montant yLt sur le support court-terme et le montant résiduel en obligations. Ainsi, la banque effectue son allocation en terme de proportions fixes de l'encours des CCP à la date considérée. À titre d'exemple, un choix de y = 10% signifie que la banque souhaite garder en «rolling» court-terme exactement 10% de ce qu'elle doit à ses clients. Cela correspond à une vision moins prudente que y = 50% : en effet, si la banque doit faire face à un nombre important de sorties à un moment donné, elle sera plus en mesure, dans le second cas, de lever facilement les liquidités pour rendre l'argent aux clients qui la quittent. Il est toutefois plausible de considérer que le placement à long-terme offre une rémunération supérieure, dans la mesure où la courbe des taux est (en général) croissante.

Il y a ainsi deux stratégies caricaturales : d'une part, placer continuellement à long terme l'intégralité des dépôts (y=0) et d'autre part investir la totalité à court terme (y=1). Dans le premier cas, la volatilité de la marge est fortement réduite mais on est exposé à un très grand risque de liquidité; dans le second, la marge nette dégagée connaît de plus fortes variations et

65

suit les effets de cycle, mais on est en mesure à tout instant de faire face à un retrait massif. Un arbitrage rémunération/risque doit donc s'effectuer.

De plus, il apparaît plausible que cet arbitrage doive être considéré différemment suivant la structure de la base de clientèle existante. Par exemple, une banque en ligne, présentant un déséquilibre démographique vers le bas, est a priori moins exposée au risque de liquidité qu'un établissement présentant, à l'inverse, un déséquilibre démographique vers le haut. C'est en tout cas ce que suggèrent nos analyses de la partie précédente : dans le premier cas, la croissance de l'encours bancaire est en effet très nette alors que dans le second, des décroissances locales de celui-ci d'un mois sur l'autre (pouvant être à l'origine d'insuffisance de trésorerie) sont bien plus probables.

Nous nous posons donc ici la question du choix de la proportion optimale26 y^" d'allocation entre les deux supports pour une banque donnée.

11.3.2 Métriques utilisées

Suivant la stratégie de placement choisie et la masse d'encours disponible à chaque date, la banque dégage un flux continu de marges nettes d'intérêts _{{IRM(t)}tE{1,2,...,h}} venant alimenter le compte d'intérêts. Un des buts du pilotage actif-passif est de rendre ce processus le moins volatile possible, en lissant la rémunération perçue par l'établissement au cours du temps. La banque souhaite s'affranchir autant que possible des effets de cycle (taux bas et encours en baisse par exemple). Il faut en particulier chercher à insensibiliser le plus possible la marge nette d'intérêts aux fluctuations de taux.

Une première appoche naturelle peut donc consister à analyser, pour différentes stratégies y, la volatilité de la série t -+ IRM(t) et à retenir celle(s) qui la rend(ent) minimale. Cependant, cette démarche n'est pas complètement satisfaisante dans la mesure où l'on peut s'attendre intuitivement à ce qu'elle sélectionne la stratégie qui consiste à tout placer à long terme. Ce faisant, on ignore à nouveau totalement le risque de liquidité! Pour imposer une contrainte indirecte sur l'allocation des dépôts entre les deux placements, il nous faut donc simuler un scénario de stress consistant en une perte massive et brutale de clients (une diminution importante des CCP), concomitante à une forte élévation du niveau des taux sur les marchés. Dans ce scénario de stress, une banque ayant massivement investi à long terme se voit contrainte de vendre dans l'urgence tous ses actifs longs (afin de disposer des liquidités exigées par les clients quittant l'établissement) alors que le contexte de marché est très défavorable!

Au vu de la brève discussion menée précédemment, la définition de l'«optimalité» de la stratégie doit donc nécessairement intégrer un critère de lissage de la rémunération dans le temps et un critère de risque. Nous retenons ainsi une double métrique pour spécifier la performance de la stratégie associée à la proportion y E[0, 1] :

- la volatilité réalisée renormalisée de la série chronologique _{{IRM(t)}tE{1,2,...,h}} sur l'intervalle [61, h] avec pas mensuel, définie comme

1000 A = (h - 61)L0

v u u Xh tt=62

(IRM(t) - IRM(t - 1))^2

Le but est de la rendre minimale afin de lisser le processus de marge nette d'intérêts dans le temps. La raison du choix de l'intervalle [61, h], au lieu de [0, h] qui peut paraître

²⁶Dans un sens que nous allons définir à présent

66

plus naturel, vient du fait que l'on souhaite faire une comparaison en régime établi et non transitoire : en effet, sur [0,60], il n'y a aucun réinvestissement de capital provenant du portefeuille d'obligations. À l'inverse, sur [61, h], la stratégie adoptée est «mature» : la banque possède potentiellement des obligations d'échéance t pour tout t E [61, h] et a commencé à réinvestir des tombées en capital provenant du portefeuille d'obligations ;

- la perte réalisée renormalisée suite à l'application d'un scénario de stress, qui consiste à générer simultanément une forte attrition de la base clientèle existante (et donc une décroissance locale subite de l'encours) ainsi qu'un choc sur la courbe des taux. Il s'agit à nouveau d'un critère de risque qui permet d'analyser la robustesse de la stratégie adoptée en testant la perte à laquelle est exposée l'établissement sur un tel scénario catastrophe. Le stress créé consistera plus précisément en un départ subit, à

60 + h

la date t^* = 2 , de 10% de la base de clientèle et à un choc de taux simultané

ZC(t^* i)

ZC(t^*, i) ?^,consistant à décaler l'ensemble de la courbe zéro-coupon de la 1.03

date t^*, selon un même facteur multiplicatif. En adoptant la notation u_ =max(-u, 0) pour u E R, la perte renormalisée supportée par la banque dans ce stress test est alors définie par

= 100 (IRM(t^*)) .

La double métrique adoptée illustre donc bien le fait qu'un arbitrage doit être effectué par l'établissement de crédit entre ces deux approches extrêmes. En effet, il s'agit d'une part de placer le plus possible à long terme afin de lisser au maximum la marge nette dans le temps et de l'insensibiliser aux mouvements de taux et, d'autre part, de continuer à placer une part suffisamment importante à court terme. Cela permet de disposer à tout instant de liquidités suffisantes pour faire face à un stress potentiel de sortie des clients.

11.3.3 Notations

Rappelons que la banque perçoit à chaque date t E {1, 2, ... , h} un flux I(t) au titre de ses placements passés, qui peut être divisé entre remboursement de capital K(t) et tombée de flux d'intérêts I+(t) avec I(t) = K(t) + I+(t). À chaque date t E {0, 1, ... , h - 1}, notons

Ädisp _tle montant total de liquidités dont la banque dispose à la date t pour investir sur les
marchés. Il est a priori différent de l'encours Ät que nous avons modélisé, dans la mesure où la banque en a déjà investi une partie dans le passé. Ainsi, Ät est le volume d'encours en t en terme de passif (autrement dit, en terme de dette de l'établissement envers ses clients) alors que Ädisp

t est le montant de ce passif que la banque peut effectivement mobiliser et placer en t. Avec les notations déjà introduites, il est immédiat que

Ädisp _t= K(t) + (Ät ? Ät_1)

K(t) est la partie du capital précédemment investie que l'on récupère en t tandis que (Ät ? Ät_1) est la variation d'encours due à l'inflation et aux mouvements des clients. En particulier, si la tombée en capital est faible et si l'encours clientèle diminue entre les dates t - 1 et t, on se retrouve dans une situation dans laquelle Ädisp

t <0. Nous allons revenir sur ce point. y E[0, 1] est la proportion de Ät que la banque choisit d'avoir placé en t dans le support court-terme.

Enfin, nous définissons, pour tE{1, ... , h}, les variables ni(t)ER qui décrivent la quantité d'obligations d'échéance i E {60, 61, ... , h + 59} dans le portefeuille de l'établissement au terme de l'investissement de la date t - 1.

67

À titre d'exemple, imaginons que la banque prête, à chaque date, la totalité de l'encours disponible pour le mois suivant (rémunération EURIBOR 1 mois) dans une stratégie de «rolling» continu, afin de disposer à chaque date de la totalité des liquidités déposées sur leurs comptes par ses clients. Nous avons dans ces conditions y=1 et pour tout tE{0, 1,... ,h - 1}

?

????

????

Ädisp t = Ät K(t + 1) = Ät

IRM(t + 1) = I⁺(t + 1) = 12 L(t) = Ät (ZC(t,t + 1) ~1

On remarque donc que même dans ce cas «simple», la marge nette d'intérêts est instable. Elle est en effet exposée à la fois à la volatilité des taux et à la volatilité de l'encours des CCP.

11.3.4 L'investissement sur les marchés

Supposons que la banque ait choisi la proportion y pour régir ses investissements sur les marchés.

À la date initiale t = 0, la banque dispose de Ädisp

0 = Ä0. Elle investit alors I⁰₀ = yÄ0 en zéros-coupons d'échéance un mois et I¹₀ = (1 - y)Ä0 en obligations à 5 ans, qui lui rapporteront individuellement des coupons mensuels fixes de x0 dépendant de la courbe des taux actuelle.

Plaçons-nous à présent à une date intermédiaire tE{1,... , h - 1}. La banque perçoit déjà le flux relatif au prêt court-terme qu'elle a consenti à la date précédente. En t-1, nous savons

ZC(t - 1, t)

qu'elle a investi sur ce support un montant _yÄt-1, correspondant à une quantité yÄt-1

de zéros-coupons de maturité 1 mois. Elle perçoit donc un flux ^yÄt-1 en t qui se

ZC(t - 1, t)

partage entre remboursement de capital à hauteur de _yÄt-1 et tombée d'intérêts à hauteur de yÄt-1 (ZC(tl 1, t) - 11. Par ailleurs, la banque dispose de ni(t) obligations d'échéance

i E {60, 61, ... , h + 59} dans^/son portefeuille, à cet instant. Ce portefeuille d'obligations lui ramène en t un remboursement en capital de nt(t) (si t>60) et une tombée de flux d'intérêts

(dûe aux détachements de coupons) de

t+59X k=max(t,60)

x(k-60)nk(t).

Au final, on peut donc écrire provisoirement

????????

?

???????? K(t) = nt(t) + yÄt-1

Ädisp _t= K(t) + (Ät - Ät-1) = Ät - (1 - y)Ät-1 + nt(t)

IRMp^rovisoire(t) = yÄt-1 ZC(t - 1, t) - 1 + x(k-60)nk(t)
~ 1 ~ t+59_X

k=max(t,60)

Il se pose ensuite la question du nouvel investissement à réaliser.

Si Ädisp

t > yÄt, alors la banque investit en t un montant I⁰_t = yÄt en zéros-coupons

yÄt

d'échéance un mois, correspondant à une quantité ZC(t, t + 1) de ces titres. Elle investit

68

ensuite le montant résiduel I¹_t = Odisp

t - I⁰_t en obligations d'échéance t + 60, reversant des coupons fixes xt. Elle achète donc une quantité I¹_t de ces obligations. Le portefeuille d'obligations détenues s'actualise alors selon nt(t +1)=0, _nt+60(t +1)=I¹_t et ni(t + 1)=ni(t) pour i O{t, t + 60}. Finalement

t+59

IRM(t) = IRMp^rovisoire(t) = yOt-1 1 1 + x(k-60)nk(t)

ZC(t - 1, t)

k=max(t,60)

À l'inverse, si Odisp

t < yOt, la banque est en déficit de liquidités puisqu'elle n'a pas

récupéré suffisamment en capital pour s'en tenir à sa stratégie d'investissement qui impose de prêter à chaque date yOt pour le mois suivant. L'établissement est ainsi dans l'obligation de vendre une partie de ses actifs longs pour mobiliser ces liquidités. Afin de ne pas compliquer inutilement la procédure, nous supposerons que la banque vend ses obligations par échéances croissantes jusqu'à avoir recouvré le montant nécessaire en terme de capital. Il lui faut donc vendre exactement yOt - Odisp

t obligations, en commençant par celles d'échéance

max(t+1, 60), puis max(t+1, 60)+1 et ainsi de suite jusqu'à t+59. Si la vente de l'intégralité du portefeuille d'obligations ne permet pas de combler le déficit²⁷, la banque va chercher la partie manquante dans ses capitaux propres et l'inscrire en négatif dans sa marge nette de la date t. Pour illustrer notre propos, supposons qu'il existe i ? {max(t + 1, 60), ... ,t + 58}

i			i + 1
tel que yOt - Odisp t >	X k=max(t+1,60)	nk(t) et yOt - Odisp t =		X k=max(t+1,60)	nk(t). Dans ces

conditions, la banque vend toutes ses obligations d'échéance max(t + 1, 60), ... , i et une

i + 1

quantité mi+1(t) =

X k=max(t+1,60)

nk(t) - (yOt - Odisp t ) de ses obligations d'échéance i + 1.

Cela permet de récupérer exactement en capital le montant yOt - Odisp

t puis d'investir
I⁰_t = yOt en zéros-coupons d'échéance un mois. Évidemment, aucune obligation n'est alors achetée en t. Cependant, cette liquidation dans l'urgence des actifs longs impacte la marge nette selon

i

_X

IRM(t) = IRMp^rovisoire(t)+ nk(t)(Bond(t, k) - 1) + mi+1(t)(Bond(t,i + 1) - 1)

k=max(t,60)+1

Le portefeuille d'obligations détenues s'actualise alors selon nt(t + 1)=0, nk(t + 1)=0 pour k ?{max(t + 1, 60), ... , i}, _ni+1(t + 1)=ni(t) - mi(t) et nk(t + 1)=nk(t) pour les autres k.

À la date finale t=h, la banque dispose de liquidités à hauteur de

_Odisp

h =Oh - (1 - y)Oh-1 + nh(h) et du portefeuille d'obligations décrit par les données des

ni(h), i?{h + 1, ... , h + 59}. Elle perçoit sa dernière marge d'intérêts

h+59

k =h

IRM(h) = yOh-1 ZC(h - 1, h) 1 1) E + x(k-60)nk(h)

À terme, le portefeuille d'obligations s'actualise donc selon nh(h +1)=0 et nk(h +1)=nk(h) pour k 6=h.

²⁷Remarquons cependant que ce cas est hautement improbable

69

12 Simulations de l'évolution de la marge nette d'intérêts

Nous prendrons dorénavant pour l'ensemble de nos simulations h = 120, c'est-à-dire un horizon d'investissement de dix ans. Nous étudierons ainsi la marge nette générée par les différentes stratégies sur l'intervalle de temps [60, h].

12.1 Illustration des différences entre les stratégies d'investissement sur un cas très simple

Afin de comprendre les différences dans la marge nette dégagée entre différentes stratégies d'investissement, nous considérons une banque virtuelle dont l'encours reste constant sur [0, h], en fixant Ät = 1000 pour tout t {0,.. . , h}. Nous simulons ensuite une trajectoire de taux spot sous le modèle de Hull et White, toujours avec les paramètres a=0.1 et ó= 0.01, fournissant les trajectoires de tous les prix zéros-coupons {t'--+B(t', T')}T/E{1,2,...,h+59}. Pour cet ensemble de trajectoires, correspondant à une simulation de taux d'intérêts, nous étudions la marge nette dégagée par la banque sur [60, h] avec trois stratégies données respectivement par yE{0.1, 0.5, 1}. Voici les résultats obtenus.



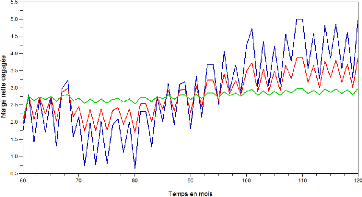
FIG. 19 - La marge nette d'intérêts dégagée _{{IRM(t)}tE{60,61,...,h}} pour y=1 (courbe bleue), y=0.5 (courbe rouge) et y=0.1 (courbe verte)

Dans le cas y =1, la banque place à chaque date la totalité de l'encours dont elle dispose pour le recouvrer le mois suivant. Dans ces conditions, dans la mesure où l'encours disponible est constant, la marge nette suit exactement l'évolution des taux d'intérêts. Elle est donc volatile. Dans le cas y =0.5, la banque place à chaque date la moitié de l'encours dont elle dispose à court terme. Comme il n'y a aucun choc de liquidité, elle n'est jamais obligée de revendre ses actifs longs et elle lisse plus sa rémunération dans le temps grâce aux coupons fixes reversés par son portefeuille d'obligations. La marge nette suit donc toujours l'évolution des taux d'intérêts, mais de manière moins nette que précédemment. Enfin, dans le cas y=0.1, la banque ne place que 10% de l'encours à court terme. La majorité de son actif est

70

constituée d'obligations, ce qui lui permet d'être beaucoup moins tributaire des mouvements de taux et de générer une marge nette d'intérêts très peu volatile. Remarquons toutefois que, dans ce cas précis, cette dernière stratégie se caractérise par un manque à gagner lorsque les taux sont élevés, typiquement après la date t = 100 dans notre simulation. On retrouve ici toute la dimension de cet arbitrage : lisser la rémunération dans le temps signifie s'affranchir des effets de cycle et donc a fortiori s'interdire de profiter pleinement des périodes à forts taux d'intérêts.

Pour comprendre à présent l'impact d'un stress de liquidité sur cette marge, nous créons un déséquilibre local de l'encours en posant _Ä100 =900 et Ät = 1000 pour t6=30. La banque se retrouve donc, en cette date intermédiaire, avec une perte (imprévue) de 10% de l'encours. Le stress généré ici a seulement lieu au niveau de la base de clientèle : nous ne touchons absolument pas aux taux. Le graphe ci-dessous illustre l'impact de ce scénario sur les marges calculées précédemment.



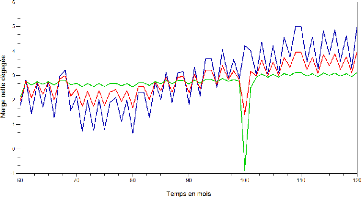
FIG. 20 - La marge nette d'intérêts dégagée _{{IRM(t)}tE{60,61,...,h}} pour y=1 (courbe bleue), y=0.5 (courbe rouge) et y=0.1 (courbe verte) avec un stress de sortie en t=100

On constate visuellement que le stress de liquidité que nous générons ici a des conséquences très différentes suivant la stratégie adoptée. Dans le cas y=1, comme la banque se contente de placer à chaque date la totalité de l'encours pour le mois suivant, le scénario ne fait, en fin de compte, que diminuer sa marge nette dégagée en t = 101 de 8% par rapport au cas précédent où l'encours était constant. En revanche, dans les cas y =0.5 et y =0.1, la banque se retrouve subitement en t = 100 en situation d'insuffisance de liquidités. En conséquence, elle se voit contrainte de vendre une partie de son portefeuille d'obligations. Comme le stress intervient à une date où les taux ont tendance à croître, cette revente a lieu dans un contexte plutôt défavorable : l'établissement vend donc à perte une partie de ses actifs longs. Dans le cas où elle a la moitié de l'encours placé à court terme, la marge dégagée en t = 100 est impactée mais reste largement positive du fait essentiellement des intérêts perçus au titre des prêts court-terme. A contrario, pour y =0.1, la perte engendrée par la revente des obligations dépasse le flux d'intérêts perçus (détachements de coupons et prêt court terme) : la marge nette devient donc négative à la date de stress!

71

En fin de compte, on retrouve sur cette simulation le fait que plus y est faible, plus la banque est exposée au risque de liquidité et donc à une perte importante en cas de scénario défavorable d'évolution de l'encours.

Dans le cas d'un stress concomitant sur la courbe des taux, le scénario catastrophe généré est encore plus brutal.

Cet exemple illustre la démarche poursuivie. Cependant, notre but reste d'étudier les marges nettes associées à des trajectoires stochastiques de l'encours générées par notre modèle. Nous allons donc à présent, pour différents choix de y E [0, 1], simuler indépendam-ment²⁸ :

- des scénarios d'évolution de l'encours selon le modèle sur la dynamique de la base de clientèle;

- des scénarios d'évolution des taux selon le modèle de Hull et White.

En les couplant, nous pourrons extraire des trajectoires de marges nettes perçues par l'établissement sur la période considérée. Nous en déduirons alors les «propriétés» des marges générées par les différentes stratégies du point de vue des deux critères que nous avons choisis d'adopter, ainsi que l'influence de la structure initiale de la base de clientèle sur ces «propriétés».

12.2 Volatilité de la marge et perte en situation de stress

Nous retenons pour nos simulations le modèle à «superstrates» en situation démographique stable²⁹ à la date initiale t=0. Nous simulons alors, pour différentes valeurs du paramètre y, p=150 trajectoires de marges nettes d'intérêts jusqu'en t=h=120. Nous calculons

ensuite les valeurs prises par les statistiques A=

1000 (h - 61)L0

v u u Xh tt=62

(IRM(t) - IRM(t - 1))^2

1000

et T= (IRM(t^*))^- sur chaque trajectoire de marge nette d'intérêts simulée.

Ä0

Nous analysons alors, pour chaque y choisi, la moyenne empirique des p valeurs simulées de

A et de T, que nous noterons  (y) et T à (y).

Valeur de y	Volatilité empirique moyenne de A (c'est-à-dire Â(y)) (x10^-3)	Écart-type empirique de A (x10^-3)
1	209.6	5.3
0.7	145.8	7.2
0.5	104.2	3.4
0.3	62.9	1.3
0.1	21.5	0.7
0.05	11.4	0.6
0.07	5.6	0.6

Nous constatons que la volatilité obtenue  (y) est quasiment proportionnelle à y. La raison à ce résultat réside dans le fait que la volatilité dans la marge dégagée est essentiellement «apportée» par les fluctuations de taux d'un mois sur l'autre. Dans ces conditions, c'est le processus de tombée des flux d'intérêts, au titre des placements court-terme, qui apporte l'es-

²⁸Conformément à l'hypothèse (3) du modèle global

²⁹Sa clientèle est le reflet de la pyramide en terme de distribution d'âges

moyenne empirique

72

sentiel de la volatilité de la marge {IRM(_t)}0<t<h. Par ailleurs, la dispersion des résultats empiriques obtenus est faible, avec un écart-typeempirique qui ne dépasse jamais 5% de la Ëà (y).

( Nous avons tracé ci-dessous le graphe obtenu en reportant les points de coordonnées ) à (y) , Ë^à (y)dans le plan «perte x volatilité», afin d'illustrer l'arbitrage à effectuer entre les deux grandeurs.



FIG. 21 - La volatilité de la marge nette d'intérêts et la perte moyenne engendrée par le scénario de stress pour différentes politiques de placement dans le cas d'une clientèle en situation démographique normale

Nous mettons bien en évidence sur cet échantillon de simulations qu'une diminution de y, c'est-à-dire une moindre proportion de l'encours placée à court terme, lisse la marge nette perçue mais accroît le risque de liquidité auquel la banque s'expose. Comme on pouvait s'y attendre, dans le cadre de ces p simulations, lorsque l'établissement place 100% de son encours total à court-terme, il s'immunise totalement contre le stress de liquidité et de taux généré : sa marge en t^* ne devient jamais négative. Dans les autres cas, suivant le scénario pour l'encours et les taux, la marge dégagée à cette même date peut être positive ou négative suivant le contexte de marché (c'est-à-dire la courbe des taux en t^*). à (y), qui fournit la moyenne empirique de la partie négative de IRM(t^*), est donc négatif pour yE{0.3,0.1,0.05,0.02}.

Il n'existe pas de stratégie «optimale», pour la simple et bonne raison que chaque banque a une définition individuelle du caractère optimal, fonction de la politique de risque à laquelle elle souscrit. Toutefois, il est légitime de se demander quelle influence la structure initiale de la base de clientèle peut avoir sur le processus de marge nette en termes de volatilité et de perte. Cette influence peut en effet conditionner le choix de la stratégie à adopter pour l'établissement. La section qui suit explore cette question.

73

12.3 Influence de la structure initiale de la base de clientèle

Toujours dans le cadre du modèle à «superstrates», nous considérons désormais une banque de détail présentant un déséquilibre démographique vers le bas (respectivement vers le haut)³⁰ à la date initiale t = 0. Nous simulons alors, pour chacun de ces établissements, et pour chacune des valeurs dey précédentes, p trajectoires de marges nettes d'intérêts jus-qu'en t=h=120. Nous notons ^àËbas (y) (respectivement ^àËhaut (y)) et ^àbas (y) (respectivement àhaut (y)) les moyennes empiriques des p valeurs simulées de Ë et de , respectivement pour les deux banques.

( )

Voici le graphe obtenu en reportant les points de coordonnées ^àbas (y) , ^àËbas (y)et

( )

àhaut (y) , ^àËhaut (y)dans le plan «perte x volatilité». Nous y faisons figurer également

)en noir les points précédents (^àË (y) , à (y)correspondants à l'établissement en situation démographique stable afin de disposer d'une base de comparaison visuelle.



FIG. 22 - La volatilité de la marge nette d'intérêts et la perte moyenne engendrée par le scénario de stress pour différentes politiques de placement dans le cas de déséquilibres dans la structure par âge de la clientèle : vers le haut (points ) et vers le bas (points )

Nous remarquons que la volatilité renormalisée de la marge ne varie que très faiblement entre les trois établissements. En revanche, la perte renormalisée engendrée par le scénario catastrophe est sensiblement différente suivant la structure par âge de la clientèle. Ainsi, la banque ayant une clientèle jeune (respectivement âgée) est en moyenne moins exposée (respectivement plus exposée) au stress de liquidité. Ce résultat numérique est relativement conforme à l'intuition : la banque ayant capté majoritairement des clients jeunes va en effet connaître une surperformance sensible de la croissance de son encours par rapport aux deux autres établissements. En conséquence, entre t^" - 1 et t^", son encours bancaire a tendance à plus augmenter que chez les autres banques. Le choc de liquidité qu'on lui impose en cette

³⁰Sa clientèle est particulièrement jeune (respectivement âgée)

date est donc mieux absorbé! En effet, comme Ät* est bien supérieur à _Ät*-1, la diminution de 10% de l'encours en t^" que nous imposons correspond à une diminution inférieure à 10% entre _{Ät*_1} et Ät* choc = 0.9Ät*. À l'inverse, la banque présentant une clientèle plutôt âgée connaît une forme de stagnation (voire de décroissance) de son encours sur la période considérée. La simulation d'un départ subit de 10% de sa clientèle vient s'ajouter à ce phénomène et l'impacte d'autant plus durement!

À la lumière de cette discussion, nous comprenons que la banque est en mesure de tenir compte de la structure par âge de sa clientèle actuelle pour décider de sa politique de placement. À volatilité de marge donnée (correspondant donc à une certaine stratégie y), une banque présentant un déséquilibre démographique vers le bas (respectivement vers le haut) s'expose à un risque de liquidité inférieur (respectivement supérieur). Dans le cadre d'un problème de minimisation de volatilité sous contrainte de seuil sur la perte³¹, la banque de détail va donc choisir d'investir, en terme de proportion de l'encours global, d'autant plus sur le long terme qu'elle a une clientèle jeune!

74

³¹Ou, de manière équivalente, de minimisation de la perte sous contrainte de seuil sur la volatilité

75

Conclusion

Cette étude sur la modélisation et la couverture des comptes courants a consisté à explorer les différentes facettes que revêt la gestion actif-passif du point de vue d'une banque de détail.

Le premier enjeu à relever était de proposer des scénarios d'évolution de l'encours global des comptes à vue. La description de la dynamique future de ce passif bancaire, sans maturité contractuellement définie, est essentielle dans l'optique d'équilibrer le bilan de l'établissement à chaque date. Les articles académiques traitant de ce sujet ne proposant, de notre point de vue, que des modélisations macroéconomiques, superficielles et ne tenant pas suffisamment compte des spécificités de cette variable, nous avons défini un cadre théorique bien plus fin en y intégrant simultanément des aspects macroéconomiques, comportementaux et démographiques. Le modèle probabiliste construit, de type markovien, est bâti sur des facteurs variés, tels que l'inflation, l'évolution future de la pyramide des âges, les taux de mortalité, la structure par âge de la base de clientèle ou encore les caractéristiques «financières» des clients. Il repose sur une ventilation de la clientèle par strates et par âges et permet de générer des trajectoires d'évolution de l'encours global en reproduisant les mouvements sur les comptes courants de chacun des clients de la banque de détail.

L'utilisation de l'outil informatique et de nombreuses simulations de type Monte-Carlo nous ont permis d'établir ou de retrouver de nombreux faits stylisés et de réaliser l'importance cruciale de certains paramètres du modèle.

En particulier, il s'est avéré que la modélisation retenue pour l'inflation conditionne fortement la dispersion de l'encours à une date future donnée : une inflation aléatoire et plus volatile élargit les intervalles de confiance pour la valeur de l'encours.

Le degré de mobilité des clients, qui caractérise leur propension à changer facilement d'état et à sortir plus facilement, est un déterminant essentiel de la volatilité de l'encours. Ainsi, plus la base de clientèle est mobile, plus notre pouvoir prévisionnel sur l'évolution de l'encours, aux pas de temps suivants, est dégradé. Enfin, les taux de sortie des clients modifient de manière importante la durée de vie des dépôts, dans une vision «mort du bilan» de vieillissement du stock existant lorsque la banque arrête toute commercialisation de produits.

La démographie actuelle de la clientèle est quant à elle un facteur déterminant de la croissance de l'encours sur le court-moyen terme. Nous y mettons en évidence que, dans le cadre de notre modèle, l'arrivée de la génération du baby-boom dans des âges avancés est susceptible d'entraîner, dans un futur proche, une surperformance de l'augmentation de l'encours par rapport à ce que l'on pourrait s'attendre a priori (car les personnes âgées détiennent en moyenne plus de liquidités). Nous avons aussi pu vérifier qu'une banque, typiquement en ligne, qui se caractérise par une clientèle très jeune, connaît une surperformance sensible de la croissance de son encours. Cela est lié au vieillissement de sa clientèle et à l'augmentation de l'effectif de cette dernière. À l'inverse, une base de clientèle initialement âgée peut entraîner une stagnation de l'encours, voire une décroissance de celui-ci, sur le court-moyen terme en raison de la perte prochaine des clients les plus aisés.

Afin d'inscrire ce modèle «innovant» d'évolution de l'encours dans le cadre de la gestion du bilan bancaire, il s'est agi ensuite de proposer des stratégies d'investissement de l'encours bancaire que nous avions modélisé. L'enjeu était d'illustrer, dans le cadre du modèle construit, le risque de liquidité dont doivent tenir compte les banques de détail dans leur allocation de capital entre les supports de taux court-terme et long-terme. Nous y avons donc intégré un modèle financier classique sur les taux. En nous appuyant sur le modèle de Hull et White, nous avons d'abord diffusé les taux spots et les courbes zéros-coupons associées à différentes échéances. Nous avons ensuite analysé les performances de stratégies financières

76

simples, consistant à placer à court terme une proportion constante fixée de l'encours et à placer le résiduel à long terme sur des obligations à cinq ans, et ce à chaque date. Nous avons retenu le concept de marge nette dégagée par l'établissement sur une période donnée, définie comme la rémunération qu'il perçoit à chaque date, au titre de ses placements passés sur les marchés. En simulant la marge générée sous différentes stratégies, nous avons vu que la banque de détail doit réaliser un arbitrage entre un critère de risque et un critère de lissage de la rémunération dans le temps dans le choix de sa stratégie «optimale». Ainsi, plus l'établissement place une part importante de son bilan à long terme, plus il diminue la volatilité de sa marge mais plus il s'expose à un fort risque de liquidité : en cas de situation de stress, caractérisée par une sortie subite et massive de clients, éventuellement couplée à une hausse des taux, l'établissement est obligé de liquider dans l'urgence, voire à perte, ses actifs longs. A contrario, plus la banque place à court terme, moins elle est exposée à ce risque, mais plus sa marge est tributaire des mouvements de la courbe des taux et a un caractère volatile. Dès lors, dans le premier cas, l'établissement s'affranchit, en partie, des effets de cycle (notamment des périodes où les taux chutent) alors que dans le second, sa rémunération les suit certes très fortement, mais l'optique d'investissement est bien plus prudente du point de vue du risque de liquidité. La définition de l'optimalité de la politique de placement doit donc s'apprécier au regard de la politique de risque souscrite par la banque. Néanmoins, nous y avons établi que la structure par âge actuelle de la clientèle de l'établissement est un facteur influençant le choix de la stratégie. Ainsi, à volatilité de marge donnée (correspondant donc à une certaine allocation entre placements court-terme et long-terme), une banque présentant une clientèle jeune (respectivement âgée) s'expose à un risque de liquidité inférieur (respectivement supérieur) sur le scénario catastrophe généré. La raison à ce résultat est le différentiel de croissance dans l'encours de ces banques. Finalement, dans le cadre de notre modélisation, la banque de détail va donc choisir d'investir une proportion d'autant plus importante de l'encours global sur le long terme que sa clientèle est jeune.

Des pistes d'amélioration de cette étude peuvent être suggérées. Une démarche de calibration du modèle sur les données historiques d'une banque de détail permettrait, notamment, d'inscrire celui-ci dans un cadre plus concret et de confronter ses capacités prédictives à la réalité. Cette calibration se heurte toutefois à la difficulté pratique de collecte des données : le modèle construit présuppose, en effet, que la banque ait compartimenté sa clientèle en strates, mais aussi et surtout qu'elle dispose d'un suivi individuel suffisamment long de chaque client, ceci afin d'estimer correctement les paramètres, tels que les taux de transition. Par ailleurs, nous avons été amenés à poser des hypothèses théoriques a priori pour de nombreux éléments du modèle, essentiellement dans un souci de ne pas trop le complexifier. Enfin, il faut garder à l'esprit que notre modèle est adapté pour capter des tendances, mais qu'il ne peut, bien évidemment, prétendre à une exhaustivité descriptive de la dynamique des encours bancaires. Ces derniers sont assujettis à de très nombreuses variables économiques, démographiques, financières et même comportementales que notre modèle ne peut reproduire dans leur intégralité. Enfin, le processus de choix de la stratégie financière, confiné dans notre travail au choix d'une proportion entre deux alternatives d'investissement (court terme et obligations à cinq ans), pourrait être enrichi d'une dimension, en intégrant également le choix de l'échéance des placements à long terme que l'on souhaite effectuer. Cette piste de recherche supplémentaire aurait l'avantage de tenir compte de la forme de la courbe des taux à chaque date afin d'optimiser la rémunération perçue.

77

A Dynamique de l'encours des dépôts à vue

L'objet de ce point d'annexe est de mener une discussion brève sur l'inférence statistique à laquelle nous pouvons prétendre sur la forme de l'évolution de l'encours At des dépôts de la banque, à partir de l'observation de sa trajectoire passée.

Soit T > 0. On considère le processus des encours _(At)tE[0,T] observé sur l'intervalle [0, T] à intervalles de temps discrets aux points 0, 6, 26, ..., n6 =T. Le résultat de l'observation est un vecteur _A(T ),ä = (A0, Aä, _A2ä, ..., AT).

Supposons que

dAt = At(udt + QdWt) (*)

avec u > 0 constant et o- constant et _(Wt)tE[0,T] un mouvement brownien standard.

Cette hypothèse est notés Hu,ó.

Si le processus suivait une telle dynamique, At suivrait à chaque date une loi log-normale

selon At = A0e(u- 2 )t+óWt

En particulier, l'espérance et la variance de la variable At croîtraient exponentiellement, respectivement selon

E(At) = A0eu^t

et

)Var(At) = A² 0e2ut (eó2t - 1

Une question naturelle vient à l'esprit : l'observation de la trajectoire historique permet-elle d'infirmer l'hypothèse _Hu,ó d'évolution de At selon l'EDS (*) ?

La réponse est (malheureusement) négative. Dans la mesure où nous disposons de la valeur de At à des dates discrètes (pas de temps mensuel), il est impossible d'infirmer l'hypothèse Hu,ó pour la simple raison que le support de la loi de A (T),ä est (R+)ⁿ+¹ tout entier!

On peut d'ailleurs préciser ici que même si l'on observait le processus At continûment, c'est-à-dire même si l'on disposait de la donnée A^(T) = (At,t E [0,T]), on ne pourrait pas pour autant se prononcer sur l'existence d'une tendance !

La raison tient en un argument mathématique sur les lois de probabilités des processus que nous développons brièvement ci-dessous³².

Notons P^Tó², u la loi de A^(T) si dAt=At(udt + QdWt).

Si l'on observe une trajectoire Z sur [0, T], dire si Z a été tiré selon P ou Q à coup sûr (risques de première et de deuxième espèces nuls) signifie qu'il existe un ensemble de trajectoires A tel que P(A)=0 et Q(A)=1 soit que PIQ.

De même, on ne peut pas distinguer P^Tó², u1 et P^Tó², u2 si les deux mesures sont équivalentes,

soit P^Tó², u1 << P^Tó², u2 et P^Tó², u2 << P^Tó², u1. Or c'est une conséquence immédiate du théorème de Girsanov que pour u1 #u2, P^Tó², u1 ^ P^Tó², u2.

³²Rappel : soient P1 et P2 deux mesures de probabilités définies sur un espace (S2, T). On dit que :

- P2 est absolument continue par rapport à P1 (notation P2 <<P1) si VA ET, (P1(A)=0) = (P2(A)=0)

- P2 est étrangère à P1 (notation P21P1) s'il existe AET tel que P1(A)=0 et P2(A^c)=0

- P1 et P2 sont équivalentes (notation P1 ,--, P2) si VA E T, (P1(A) = 0) q (P2(A) = 0) ce qui équivaut à P2 <<P1 et P1 <<P2

78

Autrement dit, pour T fini, on «peut supposer» u = ó2 2 ! Pour pouvoir se prononcer, il faudrait l'observation de la trajectoire complète, c'est-à-dire T = oc, dans la mesure où

P8 ó2, uI P8 2 si u6= ó2 33.

ó2, ó2 2

Ces considérations invitent donc à la prudence quant à toute interprétation trop hâtive suite à une observation limitée du processus étudié.

Toutefois, en dépit de cette remarque, on peut tout de même se demander s'il est «raisonnable» d'accepter l'hypothèse _Hu,ó. Pour ce faire, on peut par exemple remarquer que sous _Hu,ó, on a

_ó2

Vt E {ä, 2ä, . . . , nä} , ln(Ät) - ln(Ät_1) = u - 2 + ó(Wt - Wt_1)

c'est-à-dire ln(Ät)-ln(Ät_1)=m(t) où les _{{m(t)}tE{ä,2ä,...,nä}} sont des variables gaussiennes

indépendantes identiquement distribuées d'espérance u- ó2 2 et de variance ó². Une approche peut ainsi consister à tracer les valeurs prises par les variables m(t) au cours du temps. Voici ce que l'on obtient à titre d'exemple sur les données historiques mensuelles de La Banque Postale de janvier 1994 à décembre 2010.



À première vue, ce graphe ne suggère pas la stationnarité des variables (les fluctuations sont quasiment deux fois plus importantes au début de la période qu'à la fin).

_n }

³³Remarquer par exemple que si A = lim inf

t-.+oo |ln(Ät)|=+8 alors P8 ó2, _u(A)=1 alors que P⁸ (A)=0

ó2, ó2

2

B Résolution détaillée du modèle de Hull et White

Cette annexe détaille les étapes de calcul permettant d'obtenir les formules annoncées du modèle de Hull et White, numérotées de 1 à 6 dans le rapport.

Formule (1) : En posant Yt, = rt,e^at', la formule d'Itô donne dYt, = drt,e^at' + art,e^at'dt^'

soit

dYt,	=
dYt,	=
dYt,	=

drt,e^at' + art,e^at'dt^'

((b_t, - art') dt^' + ódWt,) ^eat' + aYt,dt^' e^at'bt0dt^' + óe^at'dWt,

T T

donc pour T^' >t^', on a YT0 = Yt' + _f e^asb_sds + ó _f e^asdW_s et donc

t' t'

rT0 = rt,e

a(T'-t') + f T e^-^a(T'-s)bsds + ó J T' e-a(T'-s)dWs t' t'

_T0

Formule (2) : Par définition, I(t^', T^')= Jr_udu d'où en tenant compte de la formule (1)

_t'

I(t^',T^') =

_IT0

r_t0e^-a(u-t') + e^-a(u-s)b_sds + ó ^J e^---s)dW_s} du

{ J_t' t' JJJ

(/ _{l f} r f l

I(t^',T^') = f

T rt0e-a(u-t')du +J^T 1fe^-a(u-s)_sds}du+ óJ^T {J~e^-a(u-s)dW_s}du

_t' lit' JJJ t' lit, JJJ

rt0 I(t^',T^') = (1 - e- a	a(T'-t')) + Z T0(f T0 e-a(u-s)du) bsds + ó 1T0 (rT 0e-a(u-s)du) d Ws s
rt0 I(t^',T^') = (1 - e- a	T0 1 - e a(T'-s) ó fT0 a(T'-t')) +Z bsds + (1 - e-a(T0-s)) dWs a a

L'indépendance des accroissements du brownien et l'isométrie d'Itô sur les intégrales stochastiques prouvent alors que la loi conditionnelle de I(t^', T^') sachant Ft, est la gaussienne

rt, N a

(1 - e-

T01 - e a(T^'-s) ó2L T0 2 a(T'-e)) + bsds , 2 (1 - e-a(T -s)) ds! ft, â a

Formule (3) : On dérive par rapport à T^' l'équation suivante

f(0,T^') = r0e^-^aT0 +

/'T^' J 0 e

2 -a(T'-s)bsds - 2a2 (1 - 2e-aT0 + e-2aT')

79

Cela donne alors

?f(0,T^') ?T'

ar0e

T aT0 + bT0 + r (-a)e^-^a(T'-s)bsds - 2~2 (2ae-aT' - 2ae-2aT0~ Jo

bT 0 =

80

?f(0, T^') ó2 ~ ó2+ af(0, T^') + 1 - 2e-aT0 + ^e-2aT' + (2e-6T -- 2e-2aT'

_{l l}

ar 2a / 2a (

~

bT 0 6-2

= af(0 T^') + ar 2 ago + 2 a _l - e-2aT'

Formule (4) : Les formules (1) et (3) assurent que

rT 0 =rte

a(T'-t')+Z T0 e-a(T'-s) {af(0 s) + ?f(0, s) + ó^2 (1 - e-2as) Ql ds+ T0 e-a(T'-s)dWs ?s 2a J t

ó²

Posons y(s)=ã(s)e-a(T'-s) = (f(0, s)+ 2a2 (1 - _e-as)²) e-a(T'-s) alors

' [?f(0,s) ó2 as) --as] --a(T'--s) _Q2 (1 -a(T'-s)

y (s) = ?s + (1 - e e e + â f (0, s) + _2a2 1-- e-as)2) e

y'(s) l

e a(T s) f ~fDs 2

s) + af (0, s) + 2â (2e--as -- 2e-2as + 1 -- 2e^--as + e-2as)]

[af(0 2

y^'(s) = _e-a(T -s) , s) + ?fâs, s) + 2a (1 - e-2as)l

On retrouve exactement l'intégrande dans la formule donnant rT 0 figurant ci-dessus. Par conséquent

rT 0 = rte rT 0 = rte rT 0 = rte

~T y^'(s)ds + ó fT0 e-a(T'-s)dWs t' ' fT0 a(T'-t') + y(T^') - y(t^') + ó e-a(T'-s)dWs t' fT0 a(T'-t') + ã(T^') - ã(t^')e^-^a(T'-t') + ó ^e-a(T'-s)d Ws t'

Formule (5) : On sait que

?

?

?

T' =

T' 2

T'

f(0,T^') = -

?ln(B(0,T^')) ?m(0,T^') 1 ?V (0, T^')

donc

' âm(0, s) - 1 ?V (0, s)} ds -ln(B(0, t^')) + ln(B(0,T')) L=

{ as 2 ?s

1

-ln(B(0,t^')) + ln(B(0,T^')) = m(0, t^') - m(0,T^') - 2 (V (0, t^') - V (0, T^'))

1

m(0,T^') - m(0,t^') = ln (B(0, ,T') ) + ₂ (V (0,T^') - V (0,t^')) (*)

Des formules (1) et (4) donnant rT', on déduit par identification que

_T'

Zt'

e^-a(T'-s)b_sds = ã(T^') - ã(t^')e^-a(T'-t')

En conséquence

rt' m(t^', T^') = (1 - e- a rt' m(t^', T^') = a (1 - e-

a(T'-t')) + f T { (u) - ã(t^')e^-^a(u-t')} du t' f a(T'-t')) +J'^T ã(u (u)du i(')1 - e-â(T -t^') -- t

Sachant que ã(0)=f(0, 0)=r0, la formule précédente s'écrit pour pE1I8+

r0 m(0,p) = (1 - e- a

fP ap) 1-- + ^J y(u)du -- y(0) âe

ap

_fP

m(0,p) = J y(u)du

0

1 - e-

Finalement, en posant P(t^', T^')=

a(T^'-t^')

, on obtient

a

81

rt' m(t^',T^') = (1 - e- a

a(T'-t')) + f ã(u)du - f ã(u)du - ã(t')1 a o

m(t^',T^') = rt'P(t^',T^') + m(0,T^') - m(0,t^') - ã(t^')P(t^',T^')

m(t^', T^') = P(t^', T^') [rt' - ã(t^')] + m(0, T^') - m(0, t^')

En réintégrant cette dernière expression dans (*), on obtient exactement

m(t^',T^') = P(t^',T^') (rt' - ã(t^')) + ln( B(0,t')

B(0, T '))+ 12 (V (0,T^') -V(0,t^'))

Formule (6) : La relation ^{B(t',T')=e-m(t',T')+12V(t',T')} couplée à la formule (5) donne

- B(t^',T^') = B(0,T')e B(0, t )

1 1 2 (V (0,T^') - V (0,t^')) - P(t^',T^') (rt' - ã(t^')) + 2V (t^',T^')

B⁽t^' T^') = B(0,T')e-P(t',T')rt'+S(t',T')

B(0, t')

1 1

en notant S(t^',T^')=-₂ (V (0,T ') - V (0,t^')) + ₂V (t^',T^') + P(t^',T^')ã(t^').

Partant de l'expression V (t^', T^') = peut écrire			ó2 fT' - t^' + 2e-a(T'-t') - 1 e-2a(T'-t') 3 on COL a 2a 2a1^, 2at'l
V (0,T^') - V (0,t^') =	2 + 2 (e aT' e at^' (e 2aT' e ó -t' - - - - - - [T' a \ / 2a \ /]
V (0,T^') - V (0,t^') = V (t^',T^') +		~ ó^2 a2 2 a(T'-t') + 12ae 2a(T'-t') + 32a+ 2 -

2

a

a (2e-aT' - e-at') -

_{l J}

1 re-2aT' - e-2at')]

V (0,T^') - V (0,t^') = V (t^',T^') +

2 ó^2 a a (1 - e-a(T'-t')) - 1 (1 - (T e-2a'-t')) + 2 / /

a (2e-aT' - e-at') - 2a (e-2aT' - e-2at')1

V (0, T^') - V (0,t^') = V (t^',T^') + a2 [:(1 - e-at'/ (1 - e -a(T'-t')) - 2a (1 - e-2at') (1 - e-2a(T'-t'))J

Dans ces conditions, nous avons

S(t^', T^') = P(t^', T^') (f(0,t^') + 2a2 (1 - 2e-at' + ^e-2a1) + ^2a2 h-2 (1 - e-at) P(t^' T^')+

21a(1 - e-2at') (1 - e-2a(T'-t'))J

S(t^',T^') = P(t^',T^')f(0,t^') + _2a2 hP(t^', T') (1 - 2e-at' + e-2at' - 2 (1 - e-at')) + 2a (11 - e-2at') (1 - e-2a(T'-t'))J

S(t^', T^') = P(t^', T^')f(0, t^') +

ó^2 2a^2

[P(t^', T') (e-2at' - 1) + 2a (1 - e-2at') (1 - e-2a(T'-t'))J

S(t^', T^') = P(t^', T^')f(0, t^') + 2a2 (1 e-2at') [-P(t^',T^') + 2a (1 - e 2a(T'-t'))J

S(t^', T^') = P(t^', T^')f(0, t^')

S(t^', T^') = P(t^', T^')f(0, t^') S(t^', T^') = P(t^', T^')f(0, t^')

(1 - e-2a(T'-t'))#

82

ó2 (1 e2 1 -- e-a(T'-t') 1

-- at) 2 '

" -

4a a² a²

ó2 (1 - e-2at') 1 _h 1 - _e- 2a(T^'-t^')~i
2 - 2e-a(T'-t') -

4a a²

- e-a(T'-t') i2

ó2 tat 1

4a (1 - e ) _a2 h1

83

S(t^',T^') = P(t^',T^')f(0,t^') -

ó2 (1 - e ^2at') P(t^' T^')^2 4a J

Pour conclure, on réinjecte cette formule dans l'expression

B(t^' T^') = B(0,T')e P(t',T')rt'+S(t',T')

, B(0, t')

pour obtenir

B(t^', T^') = B~ô_' ~ exp ^S (f(0, t^') - rt') P(t^', T^') - 4a (1 - e ^2at') P(t',T')2}

84

C Table INED utilisée pour la calibration des taux de mortalité



85

Références

[1] Jarrow, Van Deventer, 1998, The arbitrage-free valuation and hedging of demand deposits and credit card loans, Journal of Banking and Finance, Vol. 22, pp. 249-272.

[2] Eronen, 2008,Non-maturity Deposit Valuation and Hedging, Thesis, Helsinki University of Technology.

[3] Adam, Houkari, Laurent, 2009, Hedging interest rate margins on demand deposits.

[4] Kalkbrener, Willing, 2004, Risk management of non-maturing liabilities, Journal of Banking and Finance, Vol. 28, pp. 1547-1568.

[5] O'Brien, 2000, Estimating the Value and Interest Rate Risk of Interest-Bearing Transactions Deposits, Federal Reserve System.

[6] Site internet de l'Institut National des Études Démographiques, www.ined.fr

[7] Site internet de l'Institut National de la Statistique et des Études Économiques, www.insee.fr