Agrégats de mots sémantiquement cohérents issus d'un grand graphe de terrain

3.5 : Méthode 4 : Méthode d'enrichissement d'agrégats par gravité 115

Chapitre 3. Les méthodes d'agrégations proposées

Le but de l'évocation des espaces lexicaux n'est pas de rechercher une identité entre eux et les agrégats. En effet, un champ ou un réseau lexical se définissent dans l'espace restreint d'un texte, ce qui n'est pas le cas des agrégats qui doivent pouvoir être créés à partir de fichiers de log de plusieurs millions de mots. Il n'en reste pas moins que Fayaret manipule des objets de même nature que ceux qui nous intéressent (les mots et les utilisations conjointes), qui une fois regroupés présentent une architecture similaire fondée sur un emboitement d'espaces sémantiques : champ lexical inclus dans un réseau lexical et agrégats « noyaux » inclus dans agrégats augmentés. Les agrégats noyaux se doivent de présenter une cohérence sémantique particulièrement élevée.

Il est ainsi possible d'imaginer un certain nombre de cercles périphériques. Ces zones périphériques détermineraient des zones d'influences où des noeuds satellites seraient sémantiquement liés à l'agrégat. En partant de cette hypothèse, les noeuds « en attraction » sont donc soumis à l'équivalent d'une « force de gravité » par les noeuds de l'agrégat.

Création d'un agrégat augmenté par l'ajout d'un noeud à lien unique Augmentation des surfaces de recouvrement par la création d'agrégats augmentés Attachement de noeuds fortement liés à l'agrégat

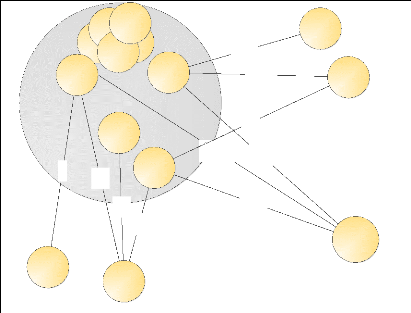
Figure 3.14 : Exemples de figures où des noeuds proches d'agrégats peuvent contribuer à la création d'un agrégat augmenté.

3.5 : Méthode 4 : Méthode d'enrichissement d'agrégats par gravité 116

Chapitre 3. Les méthodes d'agrégations proposées

3.5.2 Présentation de la méthode d'Enrichissements par gravité

La méthode proposée calcule un coefficient d'attraction du noeud externe par l'agrégat, puis ordonne les noeuds en fonction de ce coefficient (en cas d'égalité d'attraction, le poids du noeud permettra d'arbitrer ce classement). Pour éviter des agrégats de trop grande taille, on limitera ensuite le nombre de noeuds ayant rallié l'agrégat (à quelques dizaines par exemple).

Cette technique a plusieurs avantages :

· en premier lieu elle représente un coût computationnel faible. Une fois les agrégats noyaux calculés, elle ne nécessite qu'un calcul arithmétique et un classement sur des noeuds en attraction par chacun des agrégats ;

· en second lieu, elle augmente la couverture des zones en recouvrement ;

· en dernier lieu, elle permet de réintroduire dans les agrégats des noeuds exclus par les algorithmes d'agrégation (cf. figure 3.8).

Calcul du Coefficient d'Attraction (CA)

Notons CAX,A le CA pour le noeud X et l'agrégat A. La valeur de CAX,A est donnée par la formule ci-dessous :

1

k=1

Où PLk représente le poids de la liaison entre le noeud k interne à A et le noeud X externe à A. DX,A représente le degré du noeud X vers l'ensemble des noeuds de l'agrégat A et PX le poids affecté au noeud X.

Une opération de filtrage est alors effectuée pour ne pas créer de liens trop faibles. Pour cela nous ne considérons que les CA au-dessus d'une certaine valeur.

Enfin, nous pouvons effectuer une classification des noeuds dans des zones d'influence en fonction de leur CA, ceci permettant d'avoir rapidement une représentation visuelle exploitable.

Exemple de calcul et d'ordonnancement des noeuds dans la création d'un agrégat augmenté

Dans cet exemple (cf. figure 3.15) nous calculons d'abord le coefficient d'attraction CA des noeuds {V, W, X, Y, Z} du graphe de la figure 3.15 pour l'agrégat A1.

3.5 : Méthode 4 : Méthode d'enrichissement d'agrégats par gravité 117

Chapitre 3. Les méthodes d'agrégations proposées

³⁰⁰⁰

^W

²

¹⁵⁰⁰

⁵⁰

^A1

⁶⁰

⁵⁰⁰

²⁰

^X

²⁰⁰

³⁰⁰

²⁵⁰

¹⁰⁰⁰

²⁰⁰

¹⁵⁰

⁵⁰

³⁰⁰

²⁰⁰

⁵⁰⁰⁰

^Z

¹⁰⁰⁰

⁶⁰⁰

^Y

^V

⁰

Figure 3.15 : Graphe d'un agrégat et de noeuds possibles pour la formation d'un agrégat étendu.

Le niveau de seuil de validé du CA est ici fixé à 10% du poids du noeud.

Noeuds	? poids liens vers agrégat/poids du noeud	Degré du noeud vers l'agrégat	CA	Le noeud est-il valide pour appartenance à l'agrégat étendu ?
V	(200 + 1000 +150) / 6000	3	0.675	Oui
W	2/3000	1	3.3 E-4	Non [Filtré]
X	(50 + 20 + 200) / 300	3	2.7	Oui
Y	(300 +50) / 1000	2	0.35	Oui
Z	200 / 5000	1	0.04	Non

Tableau 3.2 : Enrichissement de l'agrégat du graphe étudié figure 3.15.

Les noeuds sont ensuite classés par ordre décroissant de la valeur du coefficient d'attraction. En cas d'égalité si l'on veut limiter le nombre de noeuds par agrégat étendu, on utilise le poids du noeud comme élément départageant. Les mots les plus usités sont préférés aux mots rares, car, statistiquement une part importante de mots rares n'est que le fruit d'erreurs de frappe ou de fautes orthographe. L'ordre des noeuds est donc le suivant : X puis V et enfin Y. La figure 3.16 représente le coefficient d'attraction des noeuds {V, W, X, Y, Z} par rapport à l'agrégat noyau A1 du graphe étudié dans cet exemple.

3.6 : Conclusion 118

Chapitre 3. Les méthodes d'agrégations proposées

³⁰⁰⁰

^W

²

¹⁵⁰⁰

⁶⁰

²⁵⁰

³⁰⁰

⁵⁰⁰

^X

⁶⁰⁰⁰

^V

¹⁰⁰⁰

^Y

²⁰⁰

⁵⁰⁰⁰

^Z

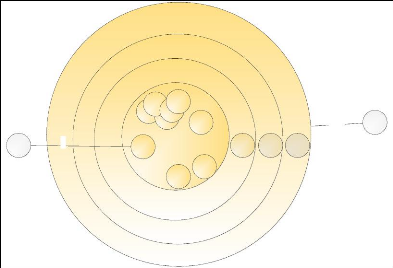
Figure 3.16 : Graphe d'un agrégat et noeuds sous attraction correspondant à l'agrégat étendu