II.9.valeurs expérimentale des temps de
relaxation du cobalt
II.9.1.mesure de T1 (temps de relaxation
spin-réseau).
Pour la mesure de T1, on utilise la méthode
`inversion-récupération', sur le pic encerclé en rouge de
la figure13 avec les paramètres
récapitulés sur le la figure ci-dessous :
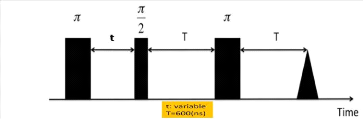
Figure II.8: paramètres de
la séquence `inversion-récupération' pour la mesure de T1
du Co2+.
II.10.1Etude du T1
La mesure du T1 a été faite en utilisant la
méthode « inversion-récupération ».
La courbe montrée ci-après est un exemple d'une
courbe de mesure de T1 obtenue a une température T=4K.
28
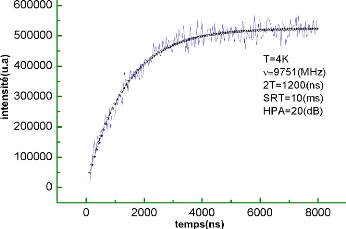
Figure II.9: la courbe
caractéristique de T1 du Cobalt a 4K .
En se servant du logiciel « originlab », on peut
aisément effectuer un fit (courbe noire) a l'aide de l'expression :
y=y0+A1.exp (-x/T1) , a partir de laquelle on aura une information sur la
valeur du temps de relaxation T1 qui vaut dans ce cas
1.33(us).
On enregistre pour la deuxième fois une courbe de mesure
de T1 mais a une température plus basse (T=1.7K).
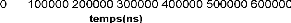
29
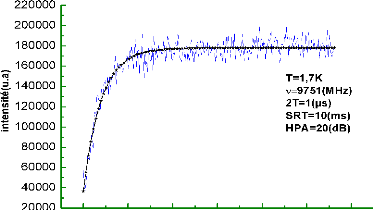
Figure II.10 : la courbe
caractéristique de T1 du Cobalt a 1.7 K.
En utilisant de la même manière que
précédemment le logiciel « originlab » pour fiter cette
courbe, on obtient un temps T1 égal a 39.82(us).
II.10.2.Etude du T2.
On passe maintenant à une autre manipulation qui consiste
à mesurer le temps de cohérence T2 du cobalt dans le ZnO.
Pour cela, on utilise la séquence dite de HAHN qui permet
de suivre l'évolution de l'amplitude de l'écho en fonction du
retard entre les deux pulses.
La courbe montrée sur la figure ci-dessous est un exemple
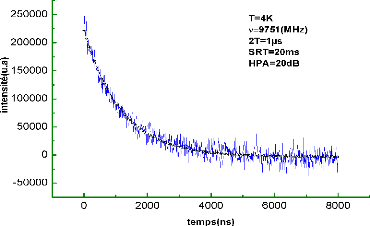
d'une courbe de mesure de T2 obtenue a une température T=4K.
30
Figure II.11 : courbe de décroissance
de T2 a 4 K . Le fit (montré en ligne noire ) a l'aide de
l'équation :
Y=A1.exp (-x/t2) +y0 (1)
Donne une valeur du temps de cohérence valant :
T2=1.17 (us).
Pour voir l'influence de la température sur le temps de
cohérence, on refait la même manipulation pour une
température plus basse (T=1.7K).
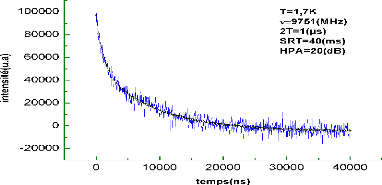
Figure II.12: courbe de décroissance
de T2 a 1.7 K.
Le meilleur fit de cette courbe a été
réalisé en utilisant l'équation :
Y=A1.exp(-x/t1)+A2.exp(-x/t2)+y0.
Voici un tableau récapitulatif des résultats de
mesures de T1 et T2 en fonction de la température.
|
Température(k)/temps(us)
|
T1
|
erreur
|
T2
|
erreur
|
|
4 k
|
1.33
|
0.047
|
1.17
|
0.018
|
|
2 k
|
39.86
|
1.64
|
1.09
8.85
|
0.1
0.3
|
Tableau II.1
Oscillations de RABI du Co2+ dans le
ZnO.
L'experience des oscillations de RABI s'effectue en utilisant
une séquence de pulses comme indiqué sur le schéma :

FigureII.13 : séquence pour
obtenir les oscillations de RABI .
L'evolution de l'echo de spin pour cette séquence donne
des oscillations comme indiquées sur la figure suivante :
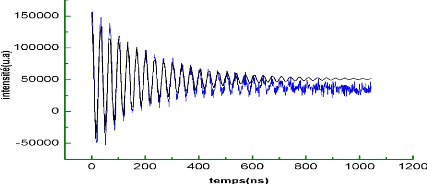
Figure II.14 :oscillations de RABI
avec fit .
31
32
Le fit des oscillations de RABI a l'aide de l'équation :
y=A1.cos(2ðx/A2).exp(-x/ôR)+y0 permet d'extraire la fréquence
de RABI ainsi que le temps d'amortissement des oscillations.
íRabi =1/TR =0.03 GHz.( TR=33.62ns).
ôR=223.96(ns).
Discussions :
On commence par noter que toutes les études de dynamique
de spin s=3/2 du Co2+ dans ZnO ont été réalisées
dans la configuration où B0//C.
Une étude précédente de la
décohérence d'un ion métallique dans le ZnO, a savoir
l'ion Fe3+ a montré 1? A . T
T 1( T )
que :
Où le premier terme correspond au processus de relaxation
du spin par le couplage direct avec le réseau (processus a 1phonon) et
où le deuxième terme correspond a un processus RAMAN à 2
phonons optiques dans ZnO.
? T 1(4 k ) 1
2 r T 1(4 k ) 1 _
?_I ? ? 0 . 5 = =
1 . 3 3 3 1 0 ( 2)
?? ??
T 1(2 k ) 4 T 1(2
k ) L] 40
theoique exp érimental
Nous commençons par étudier la pertinence de
chacun de ces deux processus de relaxation dans le cas du cobalt Co2+ :ZnO.
Hypothèse 1 :
Alors : et
1 T 0
? B . exp( ? )
T 1 ( T )
T
Les résultats théorique et expérimental
ne sont pas en accord , donc ce processus est exclu dans la gamme de
température étudiée.
Hypothèse 2 : où :
hùT.O =2ðkBT0
Les deux rapports expérimental et théorique ne sont
non plus égaux pour cette deuxième hypothèse et donc le
processus RAMAN a 2 phonos transverses optique exclu dans la gamme de
température étudiée.
rT1(4k)1
? 2 ?
?? ??
T 1 (2 k ) ?? =
4 ?
? T 1(4 k
) 3 1 0 ( ? 2 )
ln( 3 0. 3 0)
? ? 4.92 ?
5.
ln(2
Hypothèse 3 :dans la littérature sur la relaxation
de spin , on trouve qu'il existe d'autres processus RAMAN à deux phonons
acoustiques avec differentes dépendance en temperature selon la
configuration de l'ion paramagnétique considéré .
?? T 1(2 k
) ?] =
On cherche donc une relaxation gouvernée par : , où
:C et n des paramètres >1.
|
n
theoique
1 ?C.T
|
theoique
et
|
en égalant les deux expressions ci-dessus, on aboutit
à :
n
Une étude bibliographique montre, en effet, que dans le
cas d'un état fondamental avec plusieurs niveaux de spins, une
relaxation de spin de type RAMAN avec une dépendance en
température du type
|
5
|
|
|
|
|
peut être obtenu théoriquement en tenant compte de
la modulation du champ
|
|
T1(T)
|
|
33
cristallin produit sur l'ion Co2+ pour la matrice de znO , en
présence d'agitation thermique.
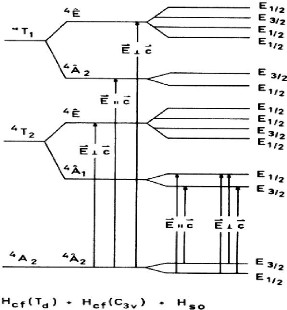
Figure II.15: les bas niveaux
d'énergie du Co2+ dans une symétrie
tétraédrique et trigonale.[15]
(? . )
S O ? kBT
? C . F
Il est également démontré
théoriquement que ce processus doit dominer les autres processus
RAMAN(en
dans le régime de température
T7,T9,...etc) dans le cas où le
critère suivant est vérifié :
2
34
étudié .
Où : est la constante du couplage spin orbite de l'ion
Co2+ et est le terme de champ cristallin pertinent.
Des études expérimentales
précédentes à la fois en RPE continue[16] et en
optique[15] ont permis d'établir les valeurs
suivantes de et de :
?
|
ORBACH/BLUME
|
SATI et al.
|
KOIDL
|
|
-143.3 (cm-1)
|
-143.3 (cm-1)
|
|
4000 (cm-1)
|
4010(cm-1)
|
Tableau II.2
35
Avec et kBT=25 meV pout T=300k, on peut évaluer la
pertinence du processus
RAMAN en T5 par rapport aux autres, via le
critère :
(ëS.O)2/?C.F=5.13cm-1>2cm-1(kBT
a 3K),valable dans la gamme de température étudiée.
L'analyse précédente des résultats
expérimentaux montre que très probablement c'est le processus
RAMAN a deux phonons acoustiques dans l'état fondamental (S=3/2) de
l'ion Co2+ dans le ZnO qui est responsable de la relaxation
longitudinale (T1) du pseudo spin s=1/2.
Le tableau II.2 fait apparaitre via le fit bi-exponentiel a 2k et
via le fit mono-exponentiel a 4k un même temps de cohérence court,
dans les deux cas de l'ordre de 1us. Ceci semble indiqué un processus de
déphasage très efficace a ces deux températures.
Ce premier processus de décohérence non
identifié mais qui est sans doute lié a la
décohérence partielle , non complète au temps court,est
analogue a ce qui est prédit théoriquement pour le qubit du
phosphore dans le Silicium[17].
Le deuxième temps de cohérence mesuré a 2k
de l'ordre de 8us , c.-à-d. 5 fois plus petit que T1(2k). ce
deuxième temps caractéristique n'est pas visible a 4k, ce qui
suggère que ce deuxième processus de décohérence
est fortement dépendant de la température comme le suggère
T1(T) mesuré a 4k .ce deuxième processus est probablement lui
aussi dû à des processus RAMAN .
Enfin, concernant les mesures des oscillations de RABI a 2k, les
résultats expérimentaux montre que :
ôR=223.9(ns)<<T2(2k)=8(us).
| 


