|

4 Juillet 2019
DÉPARTEMENT DE MATHÉMATIQUES ET
INFORMATIQUE
MASTER MéTHODES NUMéRIQUES ET
STATISTIQUES
APPLIQUéES
OPTION : MéTHODES STATISTIQUE POUR
LA
DISCRIMINATION ET LE SCORING
RAPPORT DE PROJET DE FIN D'éTUDES
Marche aléatoire, mouvement Brownien
et
applications
|
Réalisé par :
Taoufik SOUALI
|
Encadré par :
Mr. AHMED EL KHARROUBI
Devant le jury :
Mme. S.BOUJENNA Mme. H.CHAMLAL
Mr. A.EL KHARROUBI Mr. M.EL MAGHRI
Mr. T.OUDERAHMANE
|
1
Remerciements
Tout d'abord, je tiens à remercier Allah le tout
puissant et miséricordieux, qui m'a donné la force et la patience
d'accomplir ce modeste travail. Tous les membres de l'équipe
pédagogique et l'ensemble du corps enseignant de notre Faculté
des Sciences Ain Chock pour leurs aides, leurs remarques et leurs respect,
durant tout notre parcours universitaire.
Je tiens à remercier également mon encadrant le
Professeur Monsieur A.EL KHAR-ROUBI pour son judicieux encadrement, sa
disponibilité, son soutien et ses précieux conseils tout au long
de ces quatre mois de recherche, qu'ils m'ont apporté une
compréhension plus approfondie concernant les missions
évoquées dans ce rapport, lors des différents suivis.
Je tiens à exprimer mes remerciements les plus
sincères au Professeur Madame S.BOUJENA pour ses grands
efforts déployés et pour la continuation de cette formation. Je
vous remercie très chaleureusement de nous avoir continuellement
encouragé, pour votre soutien scientifique et humain, pour votre
gentillesse et votre hospitalité.
Je tiens également à remercier tous les membres
du jury pour leurs présence, leur lecture attentive de mon
mémoire ainsi que pour les remarques qu'ils m'adresseront lors de cette
soutenance afin d'améliorer mon travail.
Un grand merci à ma familles et mes amis, qui par leurs
prières et leurs encouragements, on a pu surmonter tous les
obstacles.
2
Table des matières
|
Remerciements Introduction
|
1
2
|
|
1
|
Les notions fondamentaux
|
5
|
|
1.1
|
Introduction aux processus stochastique
|
5
|
|
|
1.1.1 Généralités
|
6
|
|
|
1.1.2 Les processus gaussiens
|
8
|
|
|
1.1.3 Notion de temps d'arrêt d'un processus
|
9
|
|
|
1.1.4 Martingales en temps continu
|
9
|
|
1.2
|
Marche aléatoire
|
10
|
|
|
1.2.1 Marche aléatoire sur Z
|
10
|
|
|
1.2.2 Marche aléatoire sur Zd, d
~ 1
|
20
|
|
1.3
|
Mouvement brownien
|
23
|
|
|
1.3.1 Mouvement brownien uni-dimensionnel standard
|
23
|
|
|
1.3.2 Caractère gaussien du mouvement brownien
|
25
|
|
|
1.3.3 Quelques modifications du Mouvement Brownien
|
28
|
|
|
1.3.4 Mouvement Brownien multidimensionnel
|
29
|
|
|
1.3.5 Régularité des trajectoires Brownien
|
30
|
|
|
1.3.6 Probabilités de transition du mouvement brownien
|
32
|
|
2
|
Construction de l'intégrale
stochastique
|
34
|
|
2.1
|
Intégrale stochastique des processus
élémentaires
|
34
|
|
2.2
|
Les processus intégrants
|
37
|
|
|
2.2.1 Aspects hilbertiens de l'intégrale stochastique
|
37
|
|
2.3
|
L'intégrale stochastique comme processus
|
39
|
T.Souali TABLE DES MATIÈRES
3 Notions sur le calcul stochastique d'Itô
41
3.0.1 Notion de processus d'Itô 41
3.0.2 La formule d'Itô 42
3.1 Équations différentielles stochastiques 43
4 Applications 45
4.1 Mouvement brownien et Problème de Dirichlet 45
4.1.1 Problème de Dirichlet uni-dimensionnel 45
4.1.2 Problème de Dirichlet multi-dimensionnel 47
4.1.3 Interprétation probabiliste du problème de
Dirichlet 48
4.2 Modèle de Black-Scholes 49
4.2.1 Description du modèle de Black et Scholes 49
Conclusion 52
3
Annexe 53
4
Introduction
En mathématiques, en économie et en physique
théorique, une marche au hasard est un modèle mathématique
d'un système possédant une dynamique discrète
composée d'une succession de pas aléatoires, ou effectués
« au hasard ». On emploie également fréquemment les
expressions marche aléatoire, promenade aléatoire ou random walk
en anglais. Ces pas aléatoires sont de plus totalement
décorrélés les uns des autres , cette dernière
propriété, fondamentale, est appelée caractère
markovien du processus, du nom du mathématicien Markov. Elle signifie
intuitivement qu'à chaque instant, le futur du système
dépend de son état présent, mais pas de son passé,
même le plus proche. Autrement dit, le système « perd la
mémoire » à mesure qu'il évolue dans le temps. Pour
cette raison, une marche aléatoire est parfois aussi appelée
« marche de l'ivrogne ». L'idée de marche aléatoire a
été introduite en 1905 par le bio statisticien Karl Pearson
Cette modélisation mathématique permet de rendre
compte de certains phénomènes naturels, dont l'exemple le plus
fameux est le mouvement brownien, correspondant par exemple aux mouvements en
apparence aléatoires des particules présentes dans le fluide
intérieur d'un grain de pollen. Le mouvement brownien, ou processus de
Wiener, est une description mathématique du mouvement aléatoire
d'une « grosse » particule immergée dans un fluide et qui
n'est soumise à aucune autre interaction que des chocs avec les «
petites » molécules du fluide environnant. Il en résulte un
mouvement très irrégulier de la grosse particule, qui a
été décrit pour la première fois en 1827 par le
botaniste Robert Brown en observant des mouvements de particules à
l'intérieur de grains de pollen. La réalité des
observations de Brown a été discutée tout au long du xxe
siècle. Compte tenu de la médiocre qualité de l'optique
dont il disposait, certains ont contesté qu'il ait pu voir
véritablement le mouvement brownien, qui intéresse des particules
de quelques micromètres au plus. Les expériences ont
été refaites par l'An-glais Brian Ford au début des
années 1990, avec le matériel employé par Brown et dans
les conditions les plus semblables possibles. Le mouvement a bien
été observé dans ces conditions, ce qui valide les
observations de Brown (et justifie le nom de Mouvement Brownien).
En 1901, Louis Bachelier propose un premier modèle
mathématique du mouvement brownien et l'applique à la finance.
Mon mémoire de master est consacré à
l'étude des relations entre mouvement brownien et marches
aléatoires d'une part, problème de Dirichlet d'autre part,dans
des domaines bornés puis encore l'étude du modèle
Black-Scholes qui est un modèle mathématique du marché
pour une action, dans lequel le prix de l'action est un processus stochastique
en temps continu . Ce mémoire se divise en quatre chapitres. Le premier
chapitre est un chapitre introductif sur les notions fondamentaux. On
définit la marche aléatoire et le mouvement Brownien et on donne
quelques propriétés de ces processus. Dans le deuxième
chapitre, on définit les notions de l'intégrales stochastique. Le
troisième chapitre est consacré à l'étude du calcul
stochastique d'Itô. Et la dernière partie principale de ce
mémoire, on va établir les propriétés du mouvement
Brownien pour montrer une liaison ou une connexion avec le problème de
Dirichlet, et on donne une brève description du modèle de
Black-Scholes.
6
Les notions fondamentaux
1.1 Introduction aux processus stochastique
Un processus physique ou économique est
traditionnellement décrit par une fonction
X : t i-+ X(t) où
la variable t qui représente le temps peut être
discrète ou continue et X(t) est la valeur
numérique ou plus généralement à valeur dans
Rd mesurant l'état du processus à l'instant
t. Si la valeur de X dépend aussi du "hasard", on dit
que le processus est stochastique.
Depuis Kolmogorov, on modélise le hasard par un espace
(Q,F,P). Il est donc naturel d'essayer de décrire le
processus stochastique X par une fonction de deux variables
(t,w) i-+ X(t,w) où la nouvelle variable
w représente le "hasard" et appartient à Q. Mais la
fonction X définie sur l'espace produit T X Q
où T est l'ensemble des temps, doit vérifier certaines
conditions. Par exemple il est raisonnable de supposer que pour tout instant
t, l'application partielle X(t) : w i-+
X(t,w) état aléatoire du processus à
l'instant t fixé est une variable aléatoire
définie sur (Q,F,P).
On peut donc voir le processus X comme la famille de
variables aléatoires (X(t))tET.
Mais cette condition de mesurabilité individuelle de chaque
X(t) est insuffisante. En effet quand on observe un processus
dans la pratique, on constate que pour chaque instant t fixé, seuls
certains événements A E F peuvent survenir dans
l'intervalle de temps [0,t]. Ces événements constituent
une sous-tribu Ft de F appelée parfois l'informa-tion
disponible à l'instant t. La famille (Ft)tET
est croissante et s'appelle une filtration. Comme X(t)
décrit l'état du processus à l'instant t, il
convient donc de supposer que cette variable aléatoire est
Ft-mesurable. On est donc conduit à modéliser un
processus stochastique comme on va le voir ci-dessous.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
7
1.1.1 Généralités
Définitions
On appelle processus stochastique (resp.processus stochastique
adapté), la donné
X = (Q,F,(X(t))tET,P)
resp.
(Q,F,(Ft)tET,(X(t))tET,P)
où
· Q est un ensemble (univers des possibles).
· F est un tribu de parties de Q ou
u-algèbre.
· P est une mesure de probabilité sur
(Q,F).
· T est un sous-ensemble de R+ (qui
représente le temps).
· (Ft)tET une filtration indexée par T
i.e une famille croissante de sous tribus de F.
· (X(t))tET une famille de variables
aléatoire définies sur (Q,F), à valeurs
dans un espace topologique E muni de sa tribu borélienne
B(E).
Remarque 1.
1) Un processus stochastique modélise
l'état d'un système aléatoire au cours du temps. L'es-pace
E dans lequel les variables aléatoires X(t) prennent leurs valeurs, est
appelé l'espace des états du processus. La variable
aléatoire X(t) représente l'état du processus à
l'instant t.
2) Dans la plupart des cas, l'espace des états
(E,B(E)) est l'espace numérique(Rd,B(Rd))de
dimension d et l'ensemble des temps Test un intervalle [0,a] ou [0,+oc[. Dans
ce cas le processus X est dit à temps continu. Lorsque T est l'ensemble
N des entiers, le processus est à temps discret.
3) La filtration d'un processus est un objet important
qui contient l'essentiel des propriétés probabilistes du
processus comme nous le verrons bientôt. L'exemple le plus simple est la
filtration naturelle de la famille (X(t))tET, où pour tout t
E T, Ft = u(X(s),s < t) est la tribu engendrée par les variables
aléatoires X(s) pour s t. On notera que la filtration naturelle d'une
famille (X(t))tET de variables aléatoires, est la plus petite de toutes
les filtrations par rapport auxquelles la famille (X(t))tET est adaptée.
En effet une telle filtration contient toujours la filtration naturelle de
(X(t))tET comme sous-filtration. Un processus X sans précision de
filtration, est donc toujours adapté à sa filtration
naturelle.
4) L'application t -+ X(t,w) de T dans E est la
trajectoire du processus correspondant à l'éventualité w E
Q.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
8
Continuité et mesurabilité des
processus
On suppose dans cette partie que le temps est continu i.e. T
= [0,a] ou T = [0,+8[.
Définition 1.1.1. Un processus X est
dit continu (resp.P-p.s continu)si pour tout w ? Q (resp.pour
P-presque tout w ? Q), la fonction t -? X(t,w)
de T dans E est continue.
Processus à temps continu
Soit (Q,F,(Ft)t>0,P) un
espace probabilisé ~ltré.
Définition 1.1.2. Soit X =
(X(t))t>0 un processus défini sur
(Q,F,(Ft)t>0,P) 1) Le processus
X est dit mesurable si l'application
X : [0,+8[×Q -? (E,Ó)
(t,w) 7? X(t,w)
est mesurable par rapport à B([0,t]) ?
Ft .
2) Le processus X est dit adapté si ?t
= 0 X(t) est Ft-mesurable.
3) Le processus X est dit progressivement mesurable (ou
progressif) si ?t = 0 l'application
X : [0,+8[×Q -? E
(s,w) 7? X(s,w)
est mesurable par rapport à B([0,t]) ?
Ft.
Remarque 2. Un processus progressivement
mesurable est évidemment mesurable. D'autre part la condition de
mesurabilité progressive implique l'adaptation du processus à la
filtration (Ft)tET mais un processus adapté n'est pas
forcément progressivement mesurable.
Théorème 1.1. Si un
processus adapté X est continu à droite, il est progressivement
mesurable.
Définition 1.1.3. Soit X =
(X(t))tET un processus à valeurs dans E =
Wd. On dit que :
1) X est à accroissements indépendants si
pour toute suite finie d'instants t0 < t1 < ···
< tn, les variables aléatoires X(t1) -
X(t0),···
,X(tn) -
X(tn_1)sont indépendantes.
2) X est à accroissements stationnaires si pour
tous s < t ? T, la loi de la variable aléatoire
X(t) - X(s) ne dépend que de t
- s.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
1.1.2 Les processus gaussiens Loi gaussienne,
rappels
Les vecteurs aléatoires que nous considérons sont
supposés définis sur un espace probabilisé
(Q,F,P) que nous ne mentionnerons plus dans la suite.
Soit = (X1,···
,Xn) un vecteur aléatoire de Rn
centré 1, appartenant à
L2(Q,F,P) 2 et soit I' = (I'ij)(1 <
i,j < n) sa matrice des covariances 3.
Définition 1.1.4. Le vecteur est
gaussien si pour tous a1,a2,···
,an E R la variable aléa-
|
toire réelle
|
Xn i=1
|
aiXi est de loi normale.
|
9
Proposition 1. Le vecteur
aléatoire centré de matrice des covariances I' est
gaussien si et seulement si sa fonction caractéristique
Oæ(t) =
E(eihæ,ti) est de la forme
:
öæ(t) =
e-2ht,I' ti (t E
Rn)
1
où (.,.) désigne le produit
scalaire de Rn et I' t est le vecteur
transformé de t par la matrice
I '. On dit alors que suit la loi
Nn(0,I' ) (l'indice n indiquant que c'est
une loi de Gauss dans Rn).
Plus généralement, un vecteur aléatoire
Z de Rn suit la loi de Gauss
Nn(m,I' ) de moyenne m =
(m1,··· ,mn) et de matrice
des covariances I ', si le vecteur Z - m suit la loi
Nn(0,I' ). Sa fonction caractéristique est
alors égale à :
oZ(t) =
eihm,tie-21ht,I'ti (t
ERn)
.
Propriétés 1.
1) Lorsque la matrice I' est définie
positive(i.e. Vt E Rn
0,(t/I't) # 0), elle est
alors inversible et la loi gaussienne
Nn(m,I') admet une densité de
probabilité sur Rn de la forme
f(x) = 1 exp I --2 (x - m,
F-1(x - m))) .
(N/27)n Vdet(F) \ /
2) Les composantes Zi d'un vecteur gaussien Z =
(Z1,··· ,Zn) sont
indépendantes si et seulement si elles sont non-corrélées,
c'est à dire si sa matrice des covariances est diagonale.
1. i.e les Xi sont intégrables et E(X1)
= E(X2) = ··· = E(Xn) = 0
2. i.e pour tout i = 1,···
,n, E(X2i ) <
+oo
3. i.e I'ij = E(XiXj)
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
10
Processus gaussiens
Définition 1.1.5. Un processus
aléatoire à valeurs dans E = Rd est dit gaussien si
toutes ses lois de dimension finie sont gaussiennes.
Soit X = (X(t))tET un processus gaussien réel
i.e(E = R). Pour tous s,t ? T, on
pose
m(t) = E(X(t))
I'(s,t) = E((X(t) -m(t))(X(s)
-m(s))
Définition 1.1.6.
1) La fonction m : T 7-? R s'appelle la moyenne du
processus X.
2) La fonction I' : T × T 7-? R est
appelé la covariance du processus gaussien X.
1.1.3 Notion de temps d'arrêt d'un processus
Définition 1.1.7. Soit
(Ft)tET une filtration et = cr(?tETFt) sa tribu
terminale. Une variable aléatoire r : Q 7-? T ?
{+8} est appelée Ft-temps d'arrêt si pour
tout t ? T,on a {r = t} ? Ft. On pose
alors
Ft = {A ?
F8;?t ? T,An{r =
t} ? Ft} C'est la tribu des événements
antérieurs au temps r.
Définition 1.1.8. Soit X un processus
et A un sous-ensemble mesurable de l'espace des états E. Les variables
aléatoires définies sur Q par
DA(W) = inf{t = 0;X(t,w) ? A}
TA(W) = inf{t > 0;X(t,w) ? A}
(avec la convention inf(Ø) = +8)
sont respectivement le temps d'entrée dans A et le temps de retour dans
A.
1.1.4 Martingales en temps continu
Les martingales continues sont l'analogue des martingales
discrètes mais à temps continu, il s'agit d'un processus
stochastique dont l'espérance à l'instant t
dépend de l'information disponible à un certain temps s
= t .
Définition 1.1.9. Un processus
stochastique (M(t))t~0 à valeurs réelles,
Ft-adapté et intégrable est une martingale continue
si
E(M(t)/Fs) = M(s),s =
t
Sous-martingale si
E(M(t)/Fs) =
M(s)
Sur-martingale si
E(M(t)/Fs) =
M(s)
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
1.2 Marche aléatoire
1.2.1 Marche aléatoire sur Z
Définition 1.2.1. Soit
(Mn)n>0 une suite de variables aléatoires
indépendantes et identiquement distribuées toutes à
valeurs dans {-1,1} avec :
P{Mn = 1} = p et
P{Mn = -1} = 1-p = q
On pose :
S0 = 0
{
Sn =
Xn i=1
Mi
La suite (Sn)n>0 est
appelée marche aléatoire sur Z.
La marche aléatoire simple est dite symétrique
lorsque p = q = 21
Pour la suite on concentre sur la marche aléatoire
symétrique.
Proposition 2.
·
E(Sn) = 0
· V (Sn) = n
On a
Puisque
|
E(Sn) =
|
n i=1
|
E(Mi) = 0
|
|
E(M1) = E(M2) = ... =
E(Mn) = 0
Par calcul on trouve :
E(S2n) =
|
Xn i=1
|
Xn j=1
|
E(MiMj) = 0
|
|
Puisque
E(MiMj) =
|
{
|
1 sii=j
E(Mi)E(Mj) = 0 si i j
|
|
11
Définition 1.2.2. (Chemin)
Soit n > 0 ,m > 0 et a,b E Z
on appellera chemin du point (m,a) au point
(n,b) une ligne brisée, c'est-à-dire une suite
de segments joignant des points successifs du plan
(m0,a0),(m1,a1),
·
·
·
,(mr,ar), qui commence au point
(m0,a0) = (m,a) et se termine au point
(mr,ar) = (n,b).
Notation : On note un chemin pour une marche
aléatoire de n pas par
(S0,S1,
·
·
·
,Sn) E Zn+1. Pour la suite
nous nous concentrons surtout sur les chemins qui joignent ((m,a) =
(0,0) au point (n,b) = (n,Sn).
Notons nd : le nombre de fois où Mi =
+1 et ng : le nombre de fois où Mi = -1
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
12
alors
|
{ n = nd +ng sn
= nd - ng
|
donc
|
{ nd = 2
n+sn
n--sn
ng = 2
|
|
La position Sn = sn est
donnée par
sn = nd - (n -
nd) = 2nd - n
nd admet les valeurs
0,1,2,··· ,n ainsi
sn ?
{-n,-(n-2),···,n-2,n}
Proposition 3. La probabilité d'un
chemin (S0,S1,···
,Sn) pour une marche aléatoire à n pas
est égale à 2n1 .
Remarque 3. Tous les chemins sont
équiprobables.
Démonstration. Considérons un chemin
(S0 = s0,S1 =
s1,··· ,Sn =
sn).On a s0 = 0 et si - si_1 ?
{-1,+1} pour i = 1,2,···
,n. On a
P{S0 = s0,S1 =
s1,··· ,Sn =
sn}
Alors
P{S0 = s0,S1 =
s1,···,Sn =
sn} = P{M1 = s1 - s0,M2
= s2 - s1,···,Mn
= sn -sn_1}
= Yn
i=1
1
P{Mi = si - si_1}
=
2n
PuisqueP{Mi =si-si_1}=
12,?i ? {1,···
,n}
n+sn
2
Proposition 4. Considérons un point A
= (n,sn). Le nombre de chemins possibles entre l'origine et
le point A est
Nn,sn = Cnd
n = Cn
Le nombre de chemins di~érents avec n pas est
égale à 2n.
Proposition 5. Notons la probabilité
que la particule arrive au point Sn = sn
à l'instant n, par pn,sn.Ainsi :
1 1 n+sn
P{Sn = sn} = pn,sn
= 2n Nn, = 2n Cn 2
Démonstration. Si Sn =
sn,et s'il y a eu nd pas vers la droite et
ng pas vers la gauche, on a nd
-ng = sn et nd
+ng = n. On trouve nd =
n+sn
2 et ng = n_sn
2 . Le nombre de chemins
distincts est le nombre de manières de placer les nd
pas vers la droite parmi les n pas,
n+sn
soit Cnd
n = Cn . Tous les chemins ont la
même probabilité 1
2 2n , d'où le résultat.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
13
Principe de réfléxion
Théorème 1.2. Soient n,b
> 0 et sn > 0, alors le nombre de chemins
joignant (0,b) à (n,sn)
et touchant l'axe des abscisses est exactement le nombre de chemins
joignant (0,-b) à
(n,sn)
Théorème 1.3. Soit
n,sn ? Z +, le nombre de chemins
(s0,s1,···
,sn) de l'origine s0 = 0 au point
(n,sn) tel que
s1 > 0,s2 >
0,···,sn-1 >
0,sn > 0
est donné par
sn
Nn-1,sn-1 -
Nn-1,sn+1 = n
|
Nn,sn
|
|
Retour à l'origine
Remarque 4. Pour un retour à
l'origine à un instant n, l'instant n considéré doit
être nécessairement pair. Nous allons donc considérer des
instants de la forme 2n. On note u2n la probabilité
qu'il y ait un retour à l'origine à un instant
2n.
Lemme 1. la probabilité qu'il y ait
un retour à l'origine à un instant 2n est égale
à
= P{S2n = 0ll
1
u C
2n T I = P2n n
,0 = 2n 2n
u2n = 1 pour n = 0.
Démonstration. On applique la proposition 5 au
points (0,0) et (2n,0)
1 1 2n+0
2
P{î2n = 0} =
p2n,0 = 22n N2n,0 = 22n
C2n
d'où le résultat.
Approximation de u2n
par la formule de Stirling
Approximation de la probabilité d'un retour à
l'origine à l'instant 2n par la formule de Stirling pour un n
grand
1
Démonstration. Formule de Stirling n! '
v2ðn (ne ) n
On a donc (2n)! ' v4ðn
(2é) n et (n!)2 '
2ðnl(é)2n
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
alors
(2n)!
u2n = (n!)2 2-2n
(2n 1)2n
v4ðn e-2n
' 27rn (7,,,) 2n 2
eJl
1
Premier retour à l'origine
Définissons l'instant du Premier retour à
l'origine par
T0 = inf{n = 0, n = 0} avec
convention inf(Ø) = +8
La probabilité que le premier retour à l'origine
soit à l'instant 2n. Noté par f2n tel
que
f2n = P{T0 = 2n}
Relation entre u2n
et f2n
Pour n = 1
Théorème du retour à
l'origine
Théorème 1.4. La
probabilité qu'il y ait un retour à l'origine jusqu'à
l'instant 2n compris est égale à la probabilité
qu'il y ait un retour à l'instant 2n :
P{ 1 # 0, 2 # 0,··· ,
2n # 0} = P{ 2n = 0} = u2n (1.1)
Les i étant tous positifs ou tous
négatifs (avec la même probabilité), on a :
1 1
P{ 1 > 0, 2 >
0,··· , 2n > 0} =
2P{ 2n = 0} = 2u2n (1.2)
Démonstration. Nous démontrons
l'équation (1.2) On ana
P{ 1 > 0, 2 >
0,···, 2n > 0} =
14
00
P{ 1 > 0, 2 >
0,···, 2n =
2sn} sn=1
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
(Les termes de la somme avec sn > n sont
nuls). d'après le théorème(1.2)
l 1
P{ 1 > 0, 2 >
0,··· , 2n =
2sn} = 2n
N2n-1,2sn-1 -
N2n-1,2sn+1
Alors
|
P{ 1 > 0, 2 >
0,···, 2n > 0} =
|
00 sn=1
|
2n 1
{N2n-1,2sn-1 -
N2n-1,2sn+1}
|
|
Elle reste
|
1 2n
|
1 n 1
N2n-1,1 = 2nC2n-1
= 2u2n
|
|
D'après le théorème du retour à
l'origine, la particule n'est pas retournée à l'ori-gine
jusqu'à l'instant 2n - 2 compris avec la probabilité
u2n-2. Au temps 2n, soit elle revient à
l'origine (c'est donc pour la première fois) avec la probabilité
f2n, soit elle n'y revient pas avec la probabilité
u2n. Autrement dit, Pour n =
1,2,··· ,N
f2n = u2n-2 -
u2n
On particule
1n-1
f2n = 22n-1C2n-2
-u2n
Alors
1 (2n - 2)!
(( n - 1)!)2 - u2n
f2n =
22n-1
Donc
1 (2n)! 4n2
f2n =
22n ((n)!)2 (2n - 1)2n
- u2n
15
D'où
1
f2n = (2n -
1)u2n
Dernier retour à l'origine
Rappel La fonction de répartition de
la loi arc sinus standard est donnée par :
2 arcsin(vx) F (x) =
ð
Pour 0 < x < 1, et dont la densité de
probabilité est donnée par :
f(x) =
1
\I ð x(x -1)
sur ]0,1[ . La loi arc sinus est un cas particulier de
la loi bêta avec les paramètres á = â
= 12. Ainsi si X est de loi arc sinus
standard alors X ti Beta(12,
12)
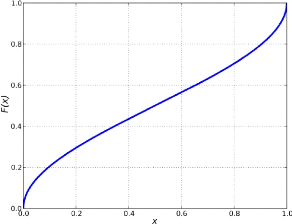
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
FIGURE 1.1 - Représentation graphique
de F(x)
Théorème 1.5. La
probabilité que la dernière visite à 0 avant le temps
2n se produise au temps 2k est donné par
á2k,2n =
P{î2k = 0,î2k+1 #
0,··· ,î2n # 0} =
u2ku2n-2k Théorème
1.6. Si î0 = 0, pour n = 0
P{î1 ×î2
×···×în #
0,în = sn} = |sn|
n
|
P{în = sn}
(1.3)
|
|
Par conséquent
P{î1 × î2
×···× î2n # 0} =
n
E{|în|}
1
X
snEZ
|
X
P{î1 ×î2
×···×în #
0,în = sn} =
snEZ
|
|sn|
n
|
P{în = sn}
|
|
16
Démonstration. Prenons d'abord sn
> 0. Le nombre de chemins dans l'événement
considéré par le théorème (1.2) snn
Nn,sn, et chaque chemin a n+sn
2 pas vers la droite et n-sn
2 vers
la gauche. Donc
P{tt tt tt
S1 ×
S2 × ··· × în
# 0,Sn = sn} =
sn
|
(
Nn sn G)2
n+sn)
(2)
1 12 (n )--sn
|
|
. Même our sn < 0 (on applique le
principe de réflexion) d'où le résultat. On a
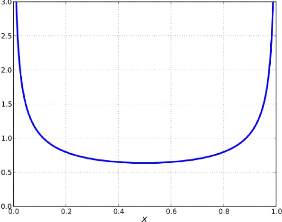
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
FIGURE 1.2 - Représentation graphique
de f(x)
Donc
1
P{?sn?Z (S1 × S2
× ··· × Sn # 0) n Sn
= sn} =
n
|
E{|Sn|}
|
|
P{S1 ×S2 × ···
×Sn # 0n(?snEgn =
sn)} =
n
1
E{|Sn|}
sn=2m
= E P{S1 ×S2 × ···
× S2m # 0,S2m =
sn} sn=-2m
=
|
sn=2m
E
sn=-2m
|
|sn|
2m
|
P{S2m = sn}
|
|
17
1
P{S1 × S2 × ···
× Sn # 0 n Ù} =
n
|
E{|Sn|}
|
1
P{S1 ×S2
×···×Sn # 0} = n
|
E{|Sn|}
|
|
Démonstration. (théorème 1.3)
tt
á2k,2n = P{S2k
= 0,S2k+1 # 0,···
,S2n # 0}
= P{S2k = 0}P{S2k =
0,S2k+1 # 0,···/S2n
# 0}
= P{S2k = 0}P{S2k =
0,S2k+1 # 0,···
,S2n-2k # 0}
On pose m = n- k montrons que
P{S2k = 0,S2k+1 #
0,··· ,S2m # 0} = P{S2m
= 0}
P{S2k = 0,S2k+1 #
0,··· ,S2m # 0} = P{S1
×S2 × ··· × S2m #
0}
T.Souali CHAPITRE 1. LES NOTIONS
FONDAMENTAUX
P{î1 X î2 X ··· X
î2m # 0} = 2
|
Xm k=1
|
2k 2m
|
P{î2m = 2k}
|
|
Xm k=1
= 2
2k 1
Cm+k
2m
2m22m
Montrons que
2k Cm+k
2m = Cm+k-1
2m-1 - Cm+k
2m-1
2m
On a
(2m - 1)! (2m - 1)!
Cm+k-1
2m-1 - Cm+k
(m+k -1)!((2m-1-(m+k
-1))! (m+k)!((2m-1-(m+k))!
2m-1 =
"= (2m -1)!
|
#
1 1
(m+k -1)!(m-k)!
-(m+k)!(m-k -1)!
|
|
= (2m -1)!
Lm+k)!(m-k)!]
(m+k)-(m-k
(2m -1)! =2k
(m+k)!(m
- k)!
2k 2m
(2m)!
=
(m+k)!(m - k)!
= 2k Cm+k
2m 2m
Donc
P{î1 X î2 X ··· X
î2m # 0} = 2
|
Xm k=1
|
2 1 rCm+k-1 - Cm+k
1
L 2m-1 2m-1]
|
|
1 m
= 2 X 22m C2m-1
1 =Cm = P{î2m = 0}
22m 2m
Alors
18
á2k,2n =
P{î2k = 0}P{î2m = 0}
= P{î2k = 0}P{î2n-2k}
= u2ku2n-2k
La représentation graphique de la distribution
discrète de l'arc-sinus à n = 50
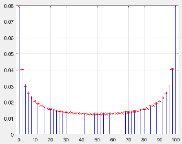
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
Remarque 5. La distribution
á2k,2n est symétrique par rapport à n,
on a donc :
á2k,2n =
á2n-2k,2n
On donne maintenant l'approximation de la probabilité
á2k,2n à l'aide de la formule de
Stirling.
Rappelons que :
1 1
P{î2k = 0} ' v et
P{î2n-2k = 0} ' q
ðkð(n - k)
Alors
1 1
Ck 2kCn-k
2n-2k ' q
22n ð
á2k,2n =
(n - k)
' 1
n
1
q k
ð n(1 -
kn)
Si on pose
1
f(x) =
qð x(1 - x)
On voit que
á2k,2n '
1 f(tk) avec tk = k
n n
si n -? 8 alors tk devient une variable
continue et t ? [0,1] On intégrant f
X
F(t) =
n<t
k
|
X
á2k,2n '
n<t
k
|
1 n
|
k !f n
|
|
19
ft f(x)dx = 2 arcsinvt
F(t) donnera la probabilité que le
dernier retour à l'origine arrive avant le temps relatif
k n
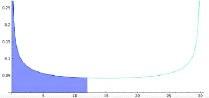
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
20
Interprétation de f(t) et
F(t) à l'aide d'un exemple Prenons une marche
aléatoire de 30 pas, c'est-à-dire n = 30. Choisissons
l'intervalle I = [0,12] et regardons la probabilité
que le dernier retour à l'origine soit dans l'intervalle
considéré. L'aire bleu foncée visualisé sur la
figure ci-dessus sous la courbe de f(t) et dans l'intervalle
I donne la probabilité approximée que le dernier retour à
l'origine soit avant le temps k = 12. La valeur approximative de
l'aire est donné par:
où t = k n
comme n = 30 et k = 12 on a t = 12
30 = 0.4. Ainsi
2
F (0.4) ' ð
|
J
arcsin 0.4 0.4359
|
|
La probabilité que le dernier retour à l'origine
soit avant le temps 12, dans une marche
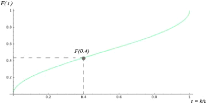
aléatoire de 30 pas, est d'environ 0,4359.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
1.2.2 Marche aléatoire sur Zd, d > 1
Définition 1.2.3. Soit
(e1,··· ,ed) la base
canonique de Zd.Soit (Mn)
une suite infinie de variables aléatoires indépendantes et
identiquement distribuées, à valeurs dans l'ensemble fini
{+e1,+e2,···
,+ed} tel que Vk E
{1,··· ,d} :
1
P{Mk = +ek} = P{Mk = -ek} =
2d
On pose :
0=0
{
Sn =
Xn i=1
Mi
21
La suite (cn)n>0 est
appelée marche aléatoire sur
Zd.
Dans la suite, on s'intéresse au cas d = 2 et
d = 3.
Considérons maintenant une marche aléatoire
à 2 dimensions. Dans ce cas, la particule aura 4 mouvements possibles :
en avant et en arrière (comme en dimension 1) et à droite et
à gauche.(voir la simulation)
On remarque que la probabilité pour chaque mouvement
possible mk pour k E 1,2,3,4
(m1 monter, m2 descendre, m3 à droite,
m4 à gauche) est égale à
P{6
1 =1
P{Si=mk} = 2.2 4
Considérons maintenant une marche aléatoire
à 3 dimensions. Dans ce cas, la particule aura 6 mouvements possibles :
en avant, en arrière, à droite et à gauche(comme en
dimension 2)et en haut et en bas. (voir la simulation)
On remarque que la probabilité pour chaque mouvement
possible mk pour k E
{1,2,3,4,5,6} est égale
à
P16
1 =1
P16 mk} 2.3 6
pour i = 1,2,···
,n
Théorème 1.7.
(Théorème de Polya) On considère une marche
aléatoire simple symétrique sur Zd.
Si d < 3 la marche aléatoire est récurrente. Si d
> 3 la marche aléatoire est tran-siente.
Simulation
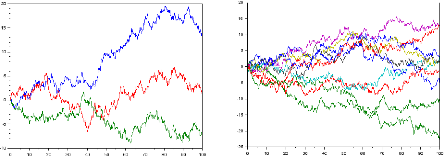
Les graphes suivants représentent respectivement la
simulation du marche aléatoire sur Z den = 1000 pour p
= 23
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
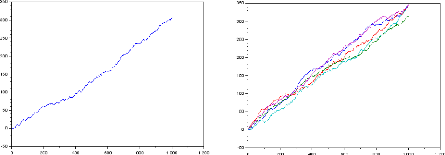
1
pour p = 3
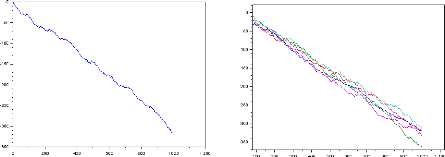
Les graphes suivants représentent respectivement la
simulation du marche aléatoire sur Z
den=1000pourp=q= 2 1
22
Conclusion :
· Lorsque p > q
la tendance est croissante.
· Si p < q la tendance est
décroissante.
Le graphe suivant représente la simulation du marche
aléatoire sur Z2
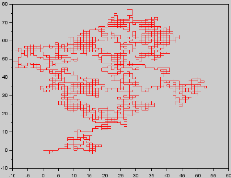
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
Les graphes suivants représentent respectivement la
simulation du marche aléatoire sur Z3 de n = 50 ,n =
100,1000
23
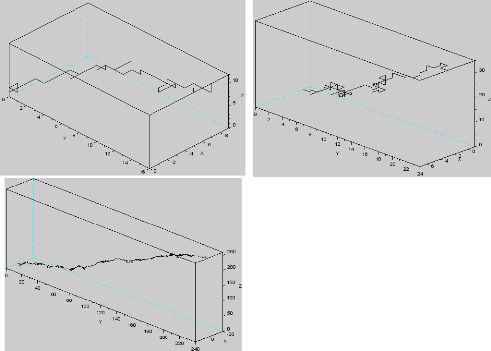
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
24
1.3 Mouvement brownien
Inroduction : Le mouvement brownien
décrit le déplacement, d'une particule en suspension dans un
liquide, par exemple celui d'un grain de pollen dans l'eau. Bien que plusieurs
scientifiques aient imaginé ou observé le mouvement brownien bien
avant Robert Brown, celui-ci est le premier à publier en 1827 des
résultats d'observation de ce mouvement au microscope. En 1905, Albert
Einstein présente une description quantitative du mouvement brownien qui
permet notamment d'estimer la dimension des molécules, et plus tard de
définir le nombre d'Avogadro, le mouvement dans n'importe quelle
direction donnée en fonction du temps est aussi alors décrit
comme n'ayant pas de tangente en tout point. Finalement, c'est Norbert Wiener
qui développe la théorie mathématique de ce mouvement en
1923, basée sur la théorie des probabilités, et confirme
que les trajectoires de ce mouvement sont presque sûrement continues,
mais nulle part différentiables. Le mouvement brownien est un processus
stochastique à temps continu
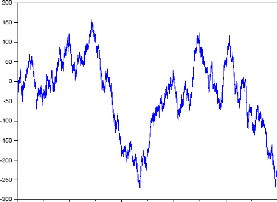
FIGURE 1.3 - Représentation du mouvement
brownien.
et à espace d'états continu. Il est aujourd'hui
appliqué dans une plusieurs de domaines, surtout en finance.
1.3.1 Mouvement brownien uni-dimensionnel standard
Ily a plusieurs présentations possibles du mouvement
brownien. Nous avons choisi de privilégier l'aspect processus à
accroissements indépendants.
Définition 1.3.1. (Mouvement
brownien uni-dimensionnel) Un processus B =
(Ù,F,(Ft)t>0,(B(t))t~0,P)
à valeurs réelles est appelé mouvement brownien
uni-dimensionnel si
1)
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
B(0) = 0 P -p.s.
2) V0 < s < t, la variable aléatoire B(t) -
B(s) est indépendante à Fs
3) V0 < s < t,B(t) - B(s) est de loi N(0,\/t -
s)
La propriété 1) le mouvement Brownien est
issu de l'origine c'est à dire que P(B(0) = 0) = 1. La
propriété 2) traduit que le mouvement Brownien est à
accroissements indépendants. La propriété 3) est la
stationnarité des accroissements du mouvement Brownien.
Théorème de Donsker
Le théorème de Donsker est l'un
des théorèmes qui ont une grande importance dans la
théorie des probabilité, qui découle du
théorème central limite, et qui consiste à établir
une convergence en loi d'une marche aléatoire vers un processus
stochastique gaussien.
Théorème 1.8.
(Théorème de Donsker) Soient (Un)n>1 une suite
i.i.d de variables aléatoires centrés, de carré
intégrable et de variance U2.
|
On définit la marche aléatoire
|
n
E
k=1
|
Uk de manière affine par morceaux en
considérant le
|
processus (Xn(t))t>0 défini par
?
Uk + (nt - [nt])U([nt]-1) ?
1
Xn(t) =
?[nt] E ? k=1
oVn
25
Pour tout t E [0,1] et [x] désigne la partie
entière de x.
Considérons l'espace C([0;1]) des fonctions
à valeurs réelles et continues sur [0,1]. On munit C([0;1]) de la
tribu borélienne B et de la norme ||.||0c. Ainsi
Xn est une variable aléatoire à valeurs dans
(C([0;1]),B).
La suite (Xn)n>1 converge en loi vers un mouvement
brownien standard B = (B(t))t>0 quand n tend vers l'infini.
Notation : FBt =
u(B(s),s < t) est la filtration naturelle associé à
B(t)t>0 Proposition 6. Soit B un mouvement
brownien et (FBt )t>0 sa filtration naturelle.
1) B est une (FBt)-martingale i.e pour
tout t < s E(B(t)/Fs) = B(s)
2) Si B est un mouvement brownien, le processus
(B2(t) - t)t>0 est une (FBt)-martingale i.e
pour tout t < s
E(B2(t) - t/Fs) = B2(s) -
s
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
26
Démonstration.
1)
· Pour tout t > 0 le processus
de brownien B(t) est
FBt-mesurable donc il est adapté
à la filtration naturelle a-(B(s),s < t)
· B est intégrable c'est à dire pour
tout t > 0, E(|B(t)D <
+oo.
· Soit t > s. Comme B(t) - B(s)
est indépendante à Fs alors
E(B(t) - B(s)/Fs) =
E(B(t) - B(s)) = 0
puisque B est centré. D'où le
résultat.
Théorème 1.9.
(caractérisation de P. Lévy du mouvement brownien) :
Soit (Ft)t>0 une filtration et M = (Mt)t>0
une Ft-martingale continue avec M(0) = 0. Si le processus
(M2(t) - t)t>0 est aussi une
Ft-martingale, alors M est un mouvement brownien.
1.3.2 Caractère gaussien du mouvement brownien
Théorème 1.10.
1) SoitB =
(0,F,(Ft)t>0,(B(t))t>0,P) un
mouvement brownien. Il satisfait les propriétés suivantes
:
i) B(0) = 0 P-p.s
ii) V 0 < t1 < t2 <
··· < tn,
(B(t1),B(t2),···
,B(tn))est un vecteur gaussien centré,
iii)
(Ft)t>0 la filtration natu-
Vs,t > 0,E(B(s)B(t)) = min(s,t) c'est
à dire B est un processus gaussien réel centré et de
fonction de covariance (s,t) = min(s,t).
2) Inversement,si un processus B vérifie i), ii), iii)
et si on note
|
relle de la famille(B(t))t>0, alors
(0,F,
|
(Ft)t>0,(B(t))t>0,P)
|
est un mouvement brownien (naturel).
Démonstration. Supposons que B soit
un mouvement brownien. Soient
a1,a2,··· ,an E R
et 0 < t1 < ··· <
tn.Montrons par récurrence sur n que
a1B(t1)+···+anB(tn)
est une variable aléatoire normale.Si n = 1
a1B(t1) = a1(B(t1) - B(0))
est de loi N(0,Jt1). Si on suppose l'assertion
démontrée pour n - 1, la variable
aléatoire a1B(t1) + ··· +
anB(tn) est alors normale comme somme des deux
variables aléatoires a1B(t1) +
··· + (an +an_1)B(tn_1)
et an(B(tn-B(tn_1)) qui sont
normales et indépendantes,d'où ii). Prenons maintenant
0 < s < t, on aE(B(s)(B(t)-B(s))
= E(B(s))E(B(t)-B(s)) = 0. On obtient alors
E(B(s)B(t)) = E((B(s)(B(t) - B(s)) +
B2(s)) = E(B2(s)) = s =
min(s,t)
.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
|
àBkAt = At
|
k
E
i=1
|
Zk, k E
{1,2,···,m}
|
27
La mesure de Wiener sur
C([0,oo[,R)
Considérons l'espace C =
C([0,oo[,R) des fonctions continues sur
[0,oo[ à valeurs réelles et pour tout t > 0,
considérons l'application X(t) : C i-+
R,définie pour tout w E C par
X(t,w) = w(t)
On munit l'espace C de la filtration naturelle
(gt)t>0 des X(t) Considérons
maintenant un mouvement brownien continu B =
(Q,F,(Ft)t>0,(B(t))t>0,P).
Proposition 7. L'application
0 : w i-+ {t i-+
B(t,w)}
de (Q,F) dans (C,g)
qui à w E Q associe la trajectoire brownienne t i-+
B(t,w), est mesurable.
Proposition 8.
1) Soit W = 0P la mesure image de
P, par l'application 0 prédéfinie en proposition
7. Cette mesure W sur la tribu de Borel g de
C([0,oo[,R),ne dépend pas du mouvement
brownien continu B qui a servi à la construction. On l'appelle la mesure
de Wiener de C([0,oo[,R)
2) Le processus W =
(C,g,(gt)t>0,(X(t))t>0,W)
est un mouvement brownien continu appelé processus de
Wiener.
Simulation
Pour simuler le mouvement brownien qui est un processus
à temps continus, il faut d'abord discrétiser le temps. Soit
At la longueur d'une période de temps.
On simulerons le mouvement brownien au temps
0,At,2At,3At,···
La propriété 2 de la définition du
mouvement brownien implique que
{BkAt-B(k-1)At : k E N}
est une suite de variable aléatoire i.i.d suit la loi
N(0,At)
Pour simuler une trajectoire du mouvement brownien jusqu'à
l'instant mAt, il suffit de générer m
variables aléatoires indépendants {Zk,k E
{1,2,··· ,m}} de loi N(0,1).
Puisque
B(0) = 0, et BkAt =
B(k-1)At + AtZk, k E
{1,2,··· ,m}
On simulerons
àB(0) = 0, et
àBkAt =
àB(k-1)At + AtZk
Par induction
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
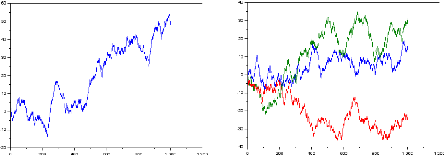
Les graphes suivants représentent respectivement la
simulation du mouvement brownien uni-dimensionnelle pour m = 50 ,
m = 100,m = 1000
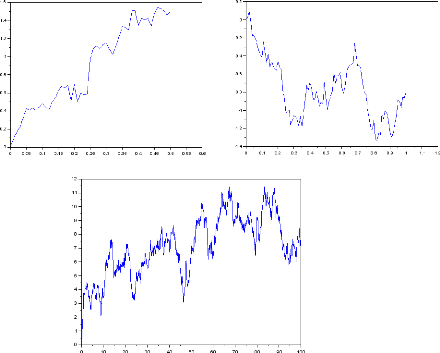
Les graphes suivants simulent respectivement plusieurs
trajectoires du mouvement brownien
28
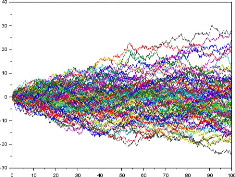
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
1.3.3 Quelques modifications du Mouvement Brownien
Le Mouvement Brownien absorbé
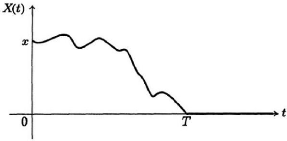
FIGURE 1.4 - Mouvement Brownien absorbé
Définition 1.3.2. On
s'intéresse du mouvement Brownien commencé en x.Désignons
par T le premier instant où ce mouvement brownien atteint la valeur
0
Le processus (Z(t))t~0 défini par:
|
Z(t) =
|
?
?
?
|
B(t), si t < T 0 si t > T
|
29
Ce processus est appelé mouvement brownien
absorbé. mouvement brownien à
dérivé
Définition 1.3.3. Soit (B(t))t~0
un mouvement brownien et /1 un nombre réel. Le proces-sus (Y
(t))t~0,où Y (t) = B(t) + ,it,est appelé mouvement brownien
à dérive;la constante
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
30
u est le paramètre de dérivé.
Le mouvement brownien
géométrique
Définition 1.3.4. Soit (B(t))t~0 un
mouvement brownien Le processus (X(t))t~0, où X(t) = eB(t), est
appelé mouvement brownien géométrique.
1.3.4 Mouvement Brownien multidimensionnel
Définition 1.3.5. Un processus B =
(Ù,F,(Ft)t>0,(B(t))t>0,P)
à valeurs dans Rd est appelé mouvement brownien
d-dimensionnel si
1) B(0) = 0 P -p.s.
2) V0 < s < t, la variable
aléatoire B(t) - B(s) est indépendante à
Fs.
\/3) V0 < s < t,B(t) -
B(s) est de loi gaussienne .,A/d(0, (t - s)Id) où
Id est la matrice identité de Rd.
Simulation
On simulera le mouvement Brownien en R2
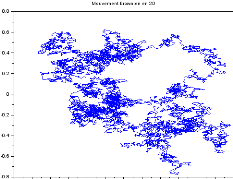
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
1.3.5 Régularité des trajectoires
Brownien Variation quadratique des trajectoires
Rappel : Soit f : [a,b] -+ R et
7r : a = t0 < t1 < t2 <
·
·
· < tn = b une
subdivisions de [a,b].
|
La variation (
resp.la variation quadratique) de f
est défini avec la formule Vð =
|
n-1X k=0
|
|f(tk+1-
|
|
n-1X
f(tk))| (resp.V (2)
ð =
k=0
|
(f(tk+1) - f(tk))2) et la
variation (Total) de f sur [a,b] est égale
|
à Vf a,b = sup
ð Vð.
· La fonction f est alors dite à variation
bornée sur [a,b] si V a,b
f < +oo (f est dite aussi
à variation finie sur [a,b]).
· Lorsque V a,b
f = +oo ,on dit que f est à variation
non bornée sur [a,b] (ou à variation infinie sue
[a,b]).
· On définit la variation quadratique (totale) des
processus comme la limite [f]a;b =
où |7r| = max (tk+1 - tk) est
le pas de la subdivision 7r. 0<k<n
· Si f est continue et à variation
borné, sa variation quadratique est nulle.
Soit maintenant B(t)t>0 un mouvement brownien.
On va étudier la variation quadratique de ses
trajectoires sur un intervalle de temps quelconque [s,t] pour une
subdivision 7r : s = t0 < t1 < t2 <
·
·
· < tn = t, on pose
:
|
V (2) ð =
|
n-1X k=0
|
(B(tk+1) - B(tk))2
|
|
Démonstration. On commence à remarquer
que h =
|
Xn i=1
|
(ti - ti-1)
|
31
V (2)
ð est une variable aléatoire dont on va
considérer la convergence au sens de L2.
Proposition 9.
lim
gðg-+0
i.e
V (2)
ð = t - s dans L2
lim
gðg-+0
E((V (2)
ð - (t - s)2) =
0
.
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
Xn i=1
Yn =
Xn i=1
Soit
|B(ti) - B(ti-1)|2
- (t - s)
h i
|B(ti) - B(ti-1)|2
- (ti - ti-1)
Où
Xi = |B(ti) -
B(ti-1)|2 - (ti - ti-1)
Et on note que
|
Y2 n
|
n
i=1
|
Xn j=1
|
XiXj =
|
n i=1
|
X
X2 i +2
i<j
|
XiXj
|
En utilisant le fait que les accroissement sont
indépendants et que E(|B(ti) -
B(ti-1)|2 - (ti - ti-1)) = 0
Alors
E(XiXj) = 0 pouri j
|
d'où
|
E(Yn2) =
|
n i=1
|
E(X2i )
|
On a
E(Xi) = E(B(ti) -
B(ti-1)4 - 2(ti -
ti-1)E(B(ti) - B(ti-1)2
+ (ti - ti-1)2
Puisque (B(ti) -
B(ti-1)) suit la loi .JV(0, -
ti-1)
Alors
E(X2i ) = 3(ti -
ti-1)2 - 2(ti - ti-1)2 +
(ti - ti-1)2 = 2(ti -
ti-1)2
|
D'où
|
E(Yn2) =
|
Xn i=1
|
E(X2i )
|
32
n
= 2 (ti - ti-1)2
i=1
|
< 2|'7|
|
Xn i=1
|
(ti - ti-1)
|
< 2(t-s)|7r|
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
|
Comme |7r| tend vers 0 alors lim
n-++oo
|
E(Yn2) = 0 alors
Yn tend vers 0 dans L2
|
lim |ð|-+0
D'où
V (2)
ð = t - s dans L2
.
Corollaire 1.1. Si
B(t)t>0 est un mouvement brownien réel
standard alors, pour P-presque tout w, la trajectoire t ?
B(t,w) est à variation infinie sur tout intervalle
[s,t] avec s,t ? R+,s < t.
Démonstration. Pour tout w ? Q et
toute subdivision 7r : s = t0 < t1
< t2 < ··· < tn =
t. On a
|
V (2) ð =
|
n-1E k=0
|
(B(w,tk+1) -
B(w,tk))2 ---?
|ð|-+0
|
t - s
|
On pose alors
Q0 = w : t ? B(t,w) soit
continue
Et pour s,t ? Q+ tels que s < t
Qs,t = w : V (2)
ð -? t-s
Donc si w ? Q0 n Qs,t et
Vs,t(w) désigne la variation totale de t ?
B(t,w) sur [s,t]
Alors on a l'inégalité
|
V (2) ð =
|
n-1E k=0
|
(B(w,tk+1) -
B(w,tk))2
|
|
= (sup
k
|
|B(w,tk+1) - B(w,tk)|)
|
n-1E k=0
|
(B(w,tk+1) - B(w,tk))
|
33
Comme t ? B(t,w) est une fonction
uniformément continue,on a
lim (sup |B(w,tk+1) -
B(w,tk)|) = 0 |ð|-+0k
V (2)
et si Vs,t(w) < +8 on doit avoir
lim ð = 0 contredisant le fait que w ? Qs,t.
|ð|-+0
Alors la trajectoire t ? B(t,w) est
à variation infinie sur [s,t].
Corollaire 1.2. Les trajectoires du
mouvement brownien sont P-p.s nulle part dérivable.
1.3.6 Probabilités de transition du mouvement
brownien Noyaux de transition
Définition 1.3.6. Une collection
{Ps,t;s,t ? R+ et s < t} d'application
de E × BE dans [0,1] est appelé famille
de noyaux de transition si :
1)
T.Souali CHAPITRE 1. LES NOTIONS FONDAMENTAUX
34
VA E BE, Vs < t, l'application x 7?
Ps,t(x,A) est mesurable.
2) VA E E, Vs < t, l'application x
7? Ps,t(x,A) est mesure de probabilité sur BE.
Définition 1.3.7. Un processus X =
(Ù,F,(Ft)t>0,(X(t))t>0,P)
de Markov à valeurs dans E et de famille de noyaux de transition
{Ps,t;s,t E R+et s < t} si pour toute fonction f
: E -+ R borélienne bornée et tout s < t dans
R+, on a :
E(f(X(t)/Ft)) = Pt_sf(X(s))P -
p.s. (1.4)
Les noyaux de transition Pt_s sont aussi appelés
probabilités de transition. La loi de X(0) i.e la mesure de
probabilité u sur BE défini par
u(A) = P(X(0) E A)
est appelé loi initiale du processus X.
Lorsque Ps,t = P0,t_s ne dépend que de la
différence t - s on dit que X est un processus de Markov
homogène.
Le semi-groupe du mouvement brownien
Soit B =
(Ù,F,(Ft)t>0,(B(t))t>0,P)
un mouvement brownien sur R.
Théorème 1.11. B est un
processus de Markov homogène sur R de loi initiale u = 80
et dont le semi groupe de la forme
Z
1 R f(y)exp(-(x -
y)2
Pt(f)(x) = v2ðt 2t )dy
La propriété de Markov forte
Théorème 1.12. Pour toute
fonction f : R -+ R borélienne bornée, pour tout h
~ 0 et tout temps d'arrêt r presque sûrement fini de la
filtration de B, on a
E(f(B(r + h)/Fô)) =
Phf(B(r)) P - p.s
35
Construction de l'intégrale
stochastique
Soit B = (B(t))t~0 un mouvement brownien standard
continu sur un espace de probabilité filtré
(Ù,F,(Ft)t>0,P)
.On considère des processus Y dont les accroissements
infinitésimaux (La notion de différentielle stochastique) dY
(t) pour t E [a,b] sont de la forme dY (t) =
X(t)dB(t) où dB(t) est l'accroissement
infinitésimal du mouvement brownien B et X un
processus adapté à la filtration (Ft)t>0 et
suffisamment régulière.
En sommant les accroissements pour bien définit
l'intégrale suivant:
Z b a
X(s,w)dB(s,w) (2.1)
La fonction s --+ B(s,w) n'est pas à
variation bornée donc on ne peut pas considérer (4.1)
comme une intégrale de Lebesgue-Stieltjes. On va commencer par
construire l'intégrale stochastique sur un ensemble de processus dits
élémentaires qui vont jouer le rôle des fonctions en
escalier (resp. des fonctions simples) dans l'intégration des fonctions
au sens de Riemann (
resp. au sens de Lebesgue).
2.1 Intégrale stochastique des processus
élémentaires
Définition 2.1.1. Un processus
élémentaire est une fonction aléatoire de la forme
X(t,w) = n-1X
Xi(w)1[ti,ti+1[(t) i=0
Vt E [a,b], Vw E Ù. Avec
a = t0 < t1 < t2 < ···
< tn = b est une subdivision de l'intervalle [a,b], et telle
que pour tout j E {0,1,··· ,n -
1} Xi soitFti-mesurable.
Notation :On notera alors I' (resp.
I'n,n > 0) l'ensemble des processus
élémentaires sur [a,b] (resp. le sous-ensemble des X
E I' tels que les variables aléatoires Xi ont un moment
d'ordre n,i.e E(|Xi|n) <
+oc).
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
36
Définition 2.1.2. On appelle
intégrale stochastique (au sens d'Itô) du processus X E I'
donné par (3.1) la variable aléatoire réelle
Z b n-1X
a X(t)dB(t) := Xi(Bti+1 - Bti).
i=0
Proposition 10. (Propriétés de
l'intégrale stochastique) 1) Linéarité : si X et Y E
I' et ë,u E R, on a
Z b Z b Z b
a (ëX(t)+uY (t)dB(t) = ë a X(t)dB(t)+u
a Y (t)dB(t).
b
2) Centrage : Si X E I'1, alors
f X(t)dB(t) E
L1(Q,F,P) et on a :
a
!
Z b
E a X(t)dB(t) = 0.
Z b
3) (Appartenance à L2) : Si X
E I'2, alors a X(t)dB(t) E
L2(Q,F,P) et
? !2? !
Z b Z b
E ? a X(t)dB(t) ? = E a
X2(t)dt . (2.2)
Démonstration.
1) Soit X et Y
de processus de subdivision commun a = t0
< t1 < t2 < ··· <
tn = b de l'intervalle [a,b].
Pour tout t E [a,b], ù E Q et
ë,u E R on a
Z b
a (ëX(t)+uY (t))dB(t) = ëX(t,w)+uY (t,w)
=
n-1X i=0
(ëXi(ù) +
uYi(ù))1[ti,ti+1[(t)
|
= ë
|
n-1X i=0
|
Xi(ù)1[ti,ti+1[(t)
+ u
|
n-1X i=0
|
Yi(ù))1[ti,ti+1[(t)
|
Z b Z b
= ë a XtdB(t)+u a YtdB(t).
2) Pour tout i E
{0,1,··· ,n - 1}, les
variables Bti+1 - Bti et Xi
sont indépendantes et sont dans
L1 donc leur produit et dans
L1 comme Bti+1 - Bti
est centrée, on a
E(Xi(Bti+1 - Bti)) =
E(Xi)E(Bti+1 - Bti)) = 0
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
37
Alors
jb) E XtdB(t)=
E? Xi(Bti+1 - Bti) ?
i=0
=
n-1X i=0
=
n-1X i=0
~ ~
E Xi(Bti+1 - Bti)
E(Xi)E(Bti+1 - Bti) = 0.
3) Soit i < j. La variable aléatoire
Xi(Bti+1 -Bti) est dans L2 comme
produit de deux variables de L2 indépendantes. Comme
Xj est dans L2,la variable aléatoire
XiXj(Bti+1 - Bti) est dans L1.
De plus étant Ft; mesurable, elle est indépendante de
Bti+1 - Bti. Le produit de ces deux dernières
variables est donc dans L1 et on a
E(XiXj(Bti+1 - Bti)(Bt;+1
-Bt;)) = E(XiXj(Bti+1 -
Bti))E(Bt;+1 - Bt;) b
On en déduit que f
XtdB(t) est dans L2 et que :
E [ f
b
X(t)dB(t))2 = E
(1XiXj(Bti+1 -
Bti)(Bt;+1 - Bt;) ?
i,j
|
?
n-1X
E ?
i,j
|
?Xi2(Bti+1 - Bti)2
?
|
=
n-1X i=0
=
n-1X i=0
E(Xi2)E((Bti+1 -
Bti)2) E(Xi2)(ti+1
- ti)
Z b
a E(X2(t))dt
= E fb2)
(la troisième égalité découlant de
l'indépendance de (Bti+1 - Bti)2 et de
Ft; donc de
X2i et la
quatrième du fait que Bti+1 - Bti est de variance
égale à ti+1 - ti. D'où le
résultat.
b
Corollaire 2.1. L'application X 7-?
I(X) := f X(t)dB(t)
est une isométrie de l'es-
a
pace vectoriel 2 muni de la norme de
L2([a,b] × 0,B[a,b]
? F,dt ? dP) dans l'espace
L2(0,F,P).
Démonstration. La linéarité de
X 7-? I(X) est donné dans 1) de la
proposition 10 et l'égalité
kI(X)kL2(0,P) =
kXkL2(0,dt®dP) est l'équation
(3.2)
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
38
Dans cette partie nous définissons les classes de
processus qu'on peut intégrer par rapport au mouvement brownien.
2.2 Les processus intégrants
Définition 2.2.1. Soit X =
(X(t))tE[a,b] un processus défini sur l'espace filtré
(Ù,F,Ftt>0,P).
1) On dit que X est dans la classe Ë2
si X est progressivement mesurable et si
Z b a
|
X2(t)dt < +8,P-p.s.
|
|
2) On dit que X est dans la classe M2 si X est
progressivement mesurable et si
( )
Z b
E a X2(t)dt < +8
Z b
où a X2(t)dt est la variable
aléatoire qui pour tout w ? Ù est égale à
l 'intégrale de Z b
Lebesgue a X2(t,w)dt.
Remarque 6.
· On a clairement
2 ? M2 ? Ë2
·
Ë2(resp.M2,) est un espace
vectoriel pour les opérations usuelles d'addition des processus
(?X,Y ? Ë2,X + Y = ((X(t) + Y
(t))tE[a,b]) et la multiplication d'un processus par un scalaire (?X
? R,Y ? À2,ÀX = (ÀX(t))t
? [a,b]).
· M2 c'est la structure la plus
intéressante car c'est un espace de Hilbert, on constate que tout X
? M2 s'identifie à un élément de
L2([a,b] × Ù,B[a,b] ? F,dt
? dP) puisque la condition (3.2) s'écrit
( )
Z b
kXkL2([a,b]xÙ,dt®dP) =
E a X2(t)dt
Z= [a,b]xÙ(X2(t,w))dtdP <
+8.
2.2.1 Aspects hilbertiens de l'intégrale
stochastique
Proposition 11. M2 est un sous
espace fermé de l'espace de Hilbert
L2([a,b] ×
Ù,B[a,b] ? F,dt ? dP)
Notation : Pour simplifier l'écriture,
on notera kXkL2([a,b]xÙ,dt®dP) =
kXkM2 norme du processus X de l'espace de
Hilbert M2.
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
39
Théorème 2.1. L'espace
1-2 des processus élémentaires de
carré intégrable est un sous-espace dense de l'espace de Hilbert
M2.
(i.e.VX E M2,?(X)n E
1-2 : lim 11Xn - X11M2 = 0)
n--+oo
f
b
Corollaire 2.2. L'isométrie X i-+
I(X) := X(t)dB(t) de 1-2 dans
L2(SZ,P) se pro-
longe de manière unique en une isométrie de
M2 dans L2(SZ,P) Pour
X E M2 on posera
b
I(X) = f X(t)dB(t)
a
et on l'appellera l'intégrale stochastique de X sur
l'intervalle [a,b].
Remarque 7. :Pour déterminer
pratiquement l'intégrale stochastique d'un processus X E
M2, on doit donc trouver une suite de processus
élémentaires Xn E 1-2 qui converge
vers X au sens de la norme 11.11M2.On a alors :
b
n lim fa Xn(t)dB(t) = f
bX(t)dB(t)
Toutes les propriétés de l'intégrale
stochastique des processus élémentaires de la proposition 7 sont
valables pour les processus de M2.
Z b
Proposition 12. L'application X i-?
a X(t)dB(t) est linéaire de M2 dans
L2(SZ,P) et
pour tout X E M2, on a
(fb)
= 0
?2
E (fbX(t)dB(t)) = E
(abX2(t)dt)
Exemple 1. (Calcul d'une intégrale
stochastique) Soit a > 0 On va calculer l'intégrale
a
stochastique f B(t)dB(t) où B est le
mouvement brownien restreint à l'intervalle [0,a].
0
Soit B E M2 . En effetB est à
trajectoires continues donc progressivement mesurable d'après le
théorème (3.1) et :
Z a ~ Z a
E 0 B2(t)dt =
0 E(B2(t)dt
= f atdt
0
a
= 2 < +oc
donc l'intégrale I a un sens. Considérons
alors la subdivision ðn de l'intervalle [0,a] constituée
des points,
tk =
ka
2n , k = 0,1,2,···,n
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
et les processus élémentaires
Xn = (Xn(t))tE[0,a]
définissent par :
|
Xn(t) =
|
2n-1
X
i=0
|
Bka 2n
|
1[ ka
2n ,(k+1)a
2n [(t)
|
La suite Xn converge vers B dans
M2. En effet
? ?
Z a ~ n-1X Z (k+1)a
E 0 (Xn(t) -
B(t))2dt = E ? 2n
(Xn(t) -
B(t))2dt
2n ?
ka
i=0
=
=
2n-1Z (k+1)a
X 2n E((B(t)
-Bka )2)dt
ka 2n
i=0 2n
2n-1Z (k+1)a
X 2n ka
(t - 2n )dt
ka
i=0 2n
1 a
2 2n+1 =
-? 0 (n ? +8)
a2
2n+1
40
Calculons maintenant l'intégrale stochastique de
Xn :
Z b 2n-1X
a Xn(t)dB(t) =
Bka
2n (B(k+1)a
2n -Bka
2n )
i=0
-B2ka
-(B(k+1)a -
Bka)21[B2(k+1)a
2n 2n 2n 2n
~ 2n-1X 2
1 2n-1~ ~
X
=
B2(k+1)a - 1
2n -B2ka
B(k+1)a
2n - Bka
2 2n 2 2n
i=0 i=0
La première des sommes ci-dessus est
télescopique et vaut Ba(car B0 = 0). La
deuxième somme est égale à la variation quadratique
Sðn de B sur l'intervalle [a,b], on sait
que
|
lim
n-++oo
|
Sðn = a (dans
L2)
|
Résultat : Il en
résulte que
Za
0 B(t)dB(t) =
12(B2a -
a).
2.3 L'intégrale stochastique comme processus La
martingale intégrale stochastique
Supposons que le mouvement brownien B =
(Ù,F,(Ft)t>0,(B(t))t>0,P)
qui définie les intégrales stochastiques a une filtration
complète i.e pour tout t = 0, la tribu Ft
T.Souali CHAPITRE 2. CONSTRUCTION DE L'INTÉGRALE
STOCHASTIQUE
41
contient les ensembles négligeables de F.
L'intervalle d'intégration sera [0,T] ,(T
> 0).Pour un processus X E
Ë2([0,T]), on
considère l'intégrale
Z t
I(t) = 0 X(s)dB(s) (t E [0,T])
Proposition 13. Le processus I =
(I(t))tE[0,T] est adapté à la filtration
(Ft)tE[0,T].
Théorème 2.2. Si X est un
processus de M2, alors le processus I = (I(t))tE[0,T] est une
martingale de carré intégrable, adaptée à la
filtration brownienne FBt =
cr(B(s),s t).
Corollaire 2.3. (théorème
d'arrêt) Soit X E M2([0,T]) et r un temps
d'arrêt de la filtration brownienne tel que r T. Alors le
processus
Z t?ô
I(t ? r) = 0 X(s)dB(s) (t E
[0,T])
est une martingale.
42
Notions sur le calcul stochastique
d'Itô
Soit B =
(Q,F,(Ft)t>0,(B(t))t>0,P)
un mouvement brownien continu , et T > 0 un temps
fixé.
On considère les espaces de processus intégrants
Ap([0,t]), p > 1 (i.e les processus X
progressivement mesurables tels que IP-p.s, t i-+ X(t,w)
est dans Lp([0,T]) (resp.l'espace
M2([0,T])).
3.0.1 Notion de processus d'Itô
Définition 3.0.1. Un processus X =
(X(t))tE[0,T] définie sur (Q,F,P) et
adapté à la filtration (Ft)tE[0,T] est
appelé processus d'Itô s'il est de la forme :
Z t Z t
X(t) = X(0) + 0 a(s)ds + 0
b(s)dB(s) (Vt E [0,T])
Où a E A1 et b E A2 sont deux
processus.
Le processus X admet la différentielle
stochastique
dX(t) = a(t)dt + b(t)dt
Remarque 8. On notera que ®
équivaut à dire que pour tous 0 < t1 <
t2 < T on a
X(t1) - X(t2) = f
t2 a(s)ds + f t2 b(s)dB(s).
t1 t1
-On peut définir la notion de processus d'Itô
sur n'importe quel intervalle de temps [c,d] 0 < c < d.
Ainsi un processus X = (X(t))tE[c,d] adapté à
la filtration est d'Itô, s'il est de la forme
Z t Z t
X(t) = X(c) + c a(s)ds + c b(s)dB(s)
(Vt E [c,d])
Où a E A1([c,d]) et b E A2([c,d])
sont deux processus.
T.Souali CHAPITRE 3. NOTIONS SUR LE CALCUL STOCHASTIQUE
D'ITÔ
Exemple 2. On sait que
Z t
0 B(s)dB(s) =
12(B2(t) - t)
i.e
Remarque 9. On a
Comme l'intégrale
t
B2(t) = t + 2 fo
B(s)dB(s)
t
B2(t) - t = 2 fo
B(s)dB(s)
Z t
0 B(s)dB(s)
est une martingale Alors
B2(t) - t
43
est une martingale.
qu'on peut récrire la sous forme di~érentielle
:
d(B2(t)) = dt + 2B(t)dB(t).
3.0.2 La formule d'Itô
Théorème 3.1. Soit X un
processus d'Itô sur l'intervalle [0,T] de di~érentielle
stochastique.
dX(t) = a(t)dt + b(t)dt
Soit f : (t,x) i- f f(t,x) une fonction définie de
R+ x R à valeurs dans R.
f est de classe C2 par rapport la
variable x et de classe C1 par rapport la variable t. Alors
: (f(X(t),t))tE[0,T] est un processus d'Itô qui a pour
di~érentielle stochastique :
?f ?f 1 ?2f
d(f(X(t),t)) = ?t (X(t),t)dt + ?x(X(t),t)dX(t) +
?x2 (X(t),t)b2(t)dt (3.1)
2
Le terme suivant 2 âx2
(X(t),t)(bt)2dt s'appelle le terme complémentaire
d'Itô.
l'équation (3.1) équivalent à
f(X(t),t) = f(X(0),0)+ f t (X(s),s)ds+lo?f
t (X(s),s)dX(s)+?f 2 lot ax
(X(s),s)b2(s)ds ?x
On peut généraliser le théorème
(3.1) à un nombre fini quelconque de processus d'Itô.
T.Souali CHAPITRE 3. NOTIONS SUR LE CALCUL STOCHASTIQUE
D'ITÔ
44
Théorème 3.2. Soient
(X1(t),X2(t),··· ,Xm(t)), des
processus d'Itô de di~érentielles respectives
dXi(t) = ai(t)dt + bi(t)dt, i = 1,···
,m
et soit f E
C1,2(1[8mx1[8+)
une fonction à valeurs réelles. Si on poseX(t) =
(X1(t),X2(t),··· ,Xm(t)), le
processus (f(X(t),t))tE[0,T] est d'Itô et il a une
di~érentielle stochastique donnée par :
m d(f(X(t),t)) = at (X(t),t)dt+E ax
(X(t),t)dXi(t)+ 1 E axe' (X(t),t)bi(t)bj(t)dt
i=1 a 7
(3.2)
|
Avec 21
|
Em i,j=1
|
?2f (X(t),t)bi(t)bj(t)dt est
le terme complémentaire d'Itô. ?xiyj
|
3.1 Équations différentielles
stochastiques
Définition 3.1.1. Soit 0 < a <
b. On appelle équation di~érentiable stochastique (EDS) sur
[a,b], avec donné initiale æa,tout relation de la forme
:
|
(EDS)
|
{ dX(t) = ó(X(t),t)dB(t) + u(X(t),t)dt X(a) =
æa,
|
où X : est un processus d'Itô sur [a,b] c'est
l'inconnue de EDS,
æa une variable aléatoire
donné, Fa-mesurable
ó(x,t) et u(x,t) sont deux fonctions
donnée,mesurables définies sur IR x [a,b] et à
valeurs
réelles
Résoudre l'EDS c'est trouver un processus d'Itô
X sur l'intervalle [a,b] tel que
a
X(t) = æa + ftó(X(s)
s)dB(s) + ft(X(s),s)ds Vt E [a,b]
Remarque 10. Comme pour les
équations di~érentielles, une EDS n'a pas forcément une
solution. Même si une solution existe, on ne pourra pas, en
général, l'exprimer simplement à l'aide du mouvement
brownien (B(t)). On va néanmoins donner un résultat d'existence
et d'unicité dans un cas intéressant qui ressemble en tout point
au théorème de Cauchy-Lipschitz pour les équations
di~érentielles ordinaires.
Un théorème d'existence et d'unicité
pour les EDS
Théorème 3.3. On suppose que
les fonction t ó(0,t) et t u(0,t) sont bornées sur
[a,b] et qu'il existe une constante C > 0 telle que pour
tout x,y E 1R et tout t E [a,b],on ait
|ó(x,t)-ó(y,t)| < C|x-y|, u(x,t)-u(y,t)|
< C|x-y|
i.e les fonctions ó et u sont lipschitziennes par
rapport à la variable x, uniformément en t E [a,b]. On suppose
aussi que la donnée initiale æa a un moment d'ordre
deux.
Alors il existe une solution X = (X(t))tE[a,b]
de l'EDS.
T.Souali CHAPITRE 3. NOTIONS SUR LE CALCUL STOCHASTIQUE
D'ITÔ
45
Exponentielle stochastique
Corollaire 3.1. L'EDS sur tout intervalle de
temps [0,T]
?
?
?
a une solution unique
dX(t) = X(t)dB(t) X(0) = 1
( )
B(t) - 1
X(t) = exp 2t
Démonstration. On suppose que la solution
X(t) est de la forme X(t) = eY (t),
pour
un certain processus d'Itô Y (t). Si tel
était le cas, en supposant que dY (t) = 1a(t)dt +
u(t)dB(t), la formule d'Itô montre que
X(t)dB(t) = d(eY (t))
= eY(t)dY(t) + 1
2eY(t)u2(t)dt
= X(t)dY (t) +
2X(t)u2(t)dt
1
D'où il résulte que dY(t) = dB(t) - 1
2u2(t)dt. Donc dY(t) = dB(t) -
1 2dt d'où Y(t) =
B(t)- 1 2t
On vérifions en suite que X(t) = exp(B(t) - 1
2t) est bien la solution unique de l'EDS.
Définition 3.1.2. On appelle
exponentielle stochastique du mouvement brownien un pro-
cessus de la forme
( )
B(t) - 1
ã(B(t)) = exp 2t .
Plus généralement on peut définir
l'exponentielle stochastique d'un processus d'Itô.
Théorème 3.4. Étant
donné un processus d'Itô Z de di~érentielle stochastique
dZ(t) = a(t)dt + b(t)dB(t), l'EDS
?
?
?
dX(t) = X(t)dZ(t) = a(t)dt+b(t)dB(t) (t E [0,T])
X(0) = 1
a une solution unique de la forme
)
Z t
ã(Z(t)) = exp(Z(t) - 1 0
b2(s)ds(t E [0,T])
2
On l'appelle exponentielle stochastique de Z.
Corollaire 3.2.
('y(Z(t)))tE[0,T] est une martingale si et
seulement si pour tout t,
E('y(Z(t))) = 1
.
On l'appelle la martingale exponentielle de Z.
46
Applications
4.1 Mouvement brownien et Problème de
Dirichlet
Dans ce chapitre on parlera du problème de Dirichlet
continue, en liaison avec le mouvement Brownien puis on déterminons la
solution de ce problème par la formule d'Itô. Puis en
étudiant le modèle de Black-Scholes. On commence tout d'abord par
l'étude du problème de Dirichlet uni-dimensionnel sur
l'intervalle borné [a,b].
4.1.1 Problème de Dirichlet uni-dimensionnel
Rappel
Définition 4.1.1. (temps
d'arrêt) Une variable aléatoire T à valeurs réelles
est un temps d'arrêt si :
Vt ~ 0, l'événement {T
t} et Jt - mesurable
Proposition 14. Si S et T sont deux temps
d'arrêts, alors le temps aléatoire S ? T défini
par S(w) ? T(w) = min(S(w),T(w) est un temps d'arrêt.
Théorème 4.1.
(théorème d'arrêt)
1) Soit M une martingale. Si T est un temps d'arrêt
borné, on a
E(MT) = E(M0)
2) Soit X un processus Jt adapté tel que
pour tout t, E(|X(t)|) < +oc. Alors X est une
martingale si et seulement si pour tout temps d'arrêt T borné, XT
E L1 et E(XT) = E(X0).
Proposition 15. Considérons une
martingale M et un temps d'arrêt T. Alors le processus Mt défini
par MTt = MT?t est une martingale,
appelée martingale arrêtée au temps T.
T.Souali CHAPITRE 4. APPLICATIONS
47
Temps d'atteinte des bornes d'un intervalle
Soit B un mouvement brownien, et introduisons pour a
> 0 le temps d'arrêt Ta = inf{t >
0,B(t) = a}.
Considérons la martingale
Më(t) = exp(ÀB(t)-
ë2 2 t) pour un À > 0
et N(t) = Më(Ta)
qui est la martingale, arrêter au temps Ta. Ainsi
nous avons N(t) = Më(Ta
? t), d'où nous déduisons 0 <
N(t) < eaë, ce qui entraîne que
N est bornée.
Nous pouvons donc appliquer le théorème
d'arrêt à la martingale N et au temps d'arrêt
Ta, ce qui donne
E(N(Ta)) = E(N(0)) = 1.
Puisque N(Ta) = exp(Àa -
ë2 2 Ta) et en posant =
ë2 2 , nous en déduisons que
"
E(e_èTa) =
e_a 2è.
En faisant tendre vers 0 et par théorème de
convergence dominée, il est facile d'obtenir P(Ta
< +oc) = 1.
On considère a > 0 et b > 0 et
soit T = min(Ta,Tb), on sait que T
< +oc P-p.s i.e P(T < +oc) = 1.
Proposition 16. Soit B un mouvement brownien
issu de 0 la probabilité de sortie de l'in-tervalle] -
b,a[ sont données par
b a
P(Ta < T_b) = a +
b ;P(T_b < Ta) =
a+b
et
E(T) = ab.
Démonstration. On sait que P(T <
+oc) = 1, donc
P(Ta < T_b)+P(T_b
< Ta) = 1.
Soit la martingale arrêtée Mt =
BT?t, on applique le théorème (4.1) au temps
T alors
0 = E(M0) = E(MT) = a
P(T = Ta) - b P(T =
T_b)
Puisque {T = Ta} = {Ta
< T_b} et {T = T_b} = {Tb <
Ta} on obtient le résultat
b a
P(Ta < T_b) = a+b
;P(T_b < Ta) = a+b.
T.Souali CHAPITRE 4. APPLICATIONS
?
?
?
48
Soit le problème :
u"(x) = 0 si x E [a,b]
u(x) = f(x) si x E
â[a,b]
avec [a,b] c R,[a,b] borné et u
: R -3 R de classe C2.
Théorème 4.2. Soit x E
[a,b], et soit r = inf{t >
0/B(t) E â([a,b])} est un temps
d'arrêt appelé temps de sortir de l'intervalle [a,b]
alors :
1) P(r < +oc) = 1.
2) u(x) =
Ex(f(B(r))) est solution du
problème de Dirichlet.
4.1.2 Problème de Dirichlet
multi-dimensionnel
Soit D un ouvert borné de Rd où
d E N*,puis soit f : âD --3 R une
fonction continue. Alors le problème de Dirichlet consiste à
trouver une fonction u tel que :
|
{
|
u E C(D,R) f1
C2(D,R) Äu = 0 si sur D
u = f si sur OD
|
Définition 4.1.2.
· La
fonction v : D -3 R de classe C2 est harmonique si
Äv = 0. Pour tout x E Rd et
r > 0, la boule et la sphère de centre x et de rayon r sont
notées
B(x,r) = {y E Rd :
|x - y| < r} et S(r,x) = {y
E Rd : |x - y| = r} et
la boule fermée de centre x et de rayon r est notée
B(x,r) = B(x,r) U
S(x,r) = {y E Rd : |x -
y| < r}
. On notera parfois OB(x,r) =
S(x,r).
· On dit que la fonction v : D -3 R
véri~e la propriété de la moyenne si pour tout x
E D et r > 0 tel que B(x,r) c D on
a
1
v(x) = u(S(x,r))
faB(x,r) v(z)du(z)
u : La mesure surfacique de Lebesgue sur
Rd.
T.Souali CHAPITRE 4. APPLICATIONS
49
4.1.3 Interprétation probabiliste du
problème de Dirichlet
Le problème de Dirichlet continu a été
étudié au dix-neuvième siècle et doit son nom au
mathématicien Peter Gustav Lejeune Dirichlet. La solution probabiliste
du problème de Dirichlet continu, due à Shizuo Kakutani, date du
milieu du vingtième siècle. Le problème de Dirichlet
continu se situe à la confluence des probabilités (mouvement
brownien), de la théorie du potentiel, de l'analyse harmonique, et des
équations aux dérivées partielles, elle sont
développée par Paul Lévy et Joseph Leo Doob au cours du
vingtième siècle. La thoérie de probabilité
permette de résoudre le problème de manière
approché.
· Soit B(t) un mouvement brownien avec B(0) =
x sur Rd et
r = inf{t > 0 : B(t) E
ÔD}
Le temps de sortie de l'intervalle D pour
(B(t))t~0.
· On note Ex l'espérance sachant
B(0) = x.
· Le mouvement brownien est un processus de Markov fort
et la formule d'Itô assure que si f est une fonction de classe
C2 sur Rd dans R à
dérivées borné, alors
Z t Z t
f(B(t)) = f(B(0)) + 0 Vf(B(s))dB(s) + 1 0
Äf(B(s))ds. (4.1)
2
Z t
L'intégrale stochastique 0
Vf(B(s))dB(s) est une martingale.
Le lien entre probabilités et analyse est contenue dans la
remarque suivante: Remarque 11. (f(B(t)))t~0 est une
martingale si f est une fonction harmonique.
Proposition 17. La fonction u : D 7?
R est harmonique, si et seulement si u vérifie la
propriété de la moyenne.
Nous prenons l'exemple du problème de Dirichlet sur
l'intervalle D =]0,1[x]0,1[ soit le problème:
|
?
?
?
|
Ä(x,y) = 0 si (x,y) E D
u(x,y) = b(x,y) si (x,y) E ÔD
|
|
Théorème 4.3. Soit (x0,y0)
E on a :
|
D, B(0) = (x0,y0) et r = inf{t ~ 0 : B(t)
E ÔD} alors
|
1) P(r < +oc) = 1
2) u(x0,y0) = E(b(B(r)/B(0) = (x0,y0))) est
solution du problème de Dirichlet.
Théorème 4.4.
(Harmonicité de la représentation
probabiliste)
La fonction v définie sur D par v(x) =
Ex(b(B(r))) est harmonique sur D.
T.Souali CHAPITRE 4. APPLICATIONS
50
Remarque 12. La représentation
probabiliste ci-dessus montre que la solution du problème de Dirichlet
en un point x de D s'écrit comme la moyenne des valeurs aux bords
pondérées par la loi du lieu de sortie d'un mouvement brownien
issu de x.
Démonstration. (théorème 4.3)
2) Supposons que u E
C2(R2) est une solution au
problème de Dirichlet sur D. La formule d'Itô (4.1)
vérifie que:
Z t?r Z t?r
u(B(t ? r)) = u(B(0)) + 0
Vu(B(s))dB(s) + 1 0 Äu(B(s))ds
2
Soit B E D,pour tout s E [0,t]
on a Äu(B(s)) = 0 Donc
1 Z t?r
0 Äf(B(s))ds = 0
2
Z t?r
L'intégrale stochastique 0 Vf(B(s))dB(s)
est une martingale pour t.
Alors pour tout (x0,y0) E
D
E(u(B(r ?t)/B(0) = (x0,y0))) =
E(u(B(0))/B(0) = (x0,y0)) = u(x,y) Puisque r
est nul et que u est borné sur D, lorsque t
tend vers +00 alors
u(x,y) = E(u(B(r))/B(0) = (x0,y0))) =
E(b(B(r))/B(0) = (x0,y0)))
4.2 Modèle de Black-Scholes
Comme exemple d'application du calcul stochastique aux
mathématiques financières on va présenter la
méthode de Black et Scholes de calcul du prix d'une option
européenne.
4.2.1 Description du modèle de Black et Scholes
L'évolution des cours
Sur l'espace probabilisé filtré
(Q,F,Ft,P) où Ft est la filtration
brownienne. Le modèle proposé par Black et Scholes pour
décrire l'évolution des cours est un modèle à temps
continu avec un actif risqué (une action de prix S(t) à
l'instant t) et un actif sans risque (de prix S0(t)
à l'instant t). On suppose l'évolution de
S0(t) régie par : l'équation
différentielle (ordinaire)
dS0(t) = rS0(t)dt
T.Souali CHAPITRE 4. APPLICATIONS
51
où r est une constante positive. Cela signifie
que le taux d'intérêt sur le marché des placements sans
risque est constant et égal à r (noter que r
est ici un taux d'intérêt instantané, à ne pas
confondre avec le taux annuel ou le taux sur une période des
modèles discrets). On pose S0(0) = 1, de sorte que
:
S0(t) = ert pour t >
0
On suppose que l'évolution du cours de l'action est
régie par l'équation différentielle stochastique
dS(t) = uS(t)dt + óS(t)dB(t) tel que S(0)
> 0 (4.2)
où :
· u :est un coefficient de croissance.
· ó :est un coefficient de
volatilité.
· B(t) : est un mouvement brownien standard.
· S(0) : est une valeur initiale pour
S(t).
Le modèle étudié sur l'intervalle
[0,T] ou T est la date d'échéance de l'option
à étudier. On s'intéresse aux solutions
(S(t))t>0 de l'équation
t
S(t) = x(0) + f
S(s)(uds + ódB(s)) (4.3)
Cet équation s'écrit sous la forme
{ dS(t) = S(t)(udt + ódB(t))
(4.4)
S(0) = x(0)
Cela signifie que l'on cherche un processus adapté
(S(t))t>0 tel que les intégrales f0t
S(s)ds et f0t S(s)dB(s) aient
un sens, et qui vérifie, pour chaque t.
Z t
S(t) = x(0) + 0 (uS(s)ds +
óS(s)dB(s)) IID - p.s
On pose Y (t) = log(S(t)) où S(t)
est une solution de l'équation (4.3).S(t) est un
processus d'Itô. Donc on peut appliquer la formule d'Itô à
f(x) = log(x)
f(X(t)) = f(X(0)) + t
Jo f'(X(s))dX(s) + 2 Jot
f"(X(s))d(S,S)s
On obtient en supposant que S(t) est positif :
log(S(t)) = log(S(0)) + ft S(()) + 21 Jot
(S;(1s))
d(S,S)s
T.Souali CHAPITRE 4. APPLICATIONS
52
En effet :
(,S)s = ( f t
óS(s)dB(s), f t
SóS(s)dB(s))
f t
= ( 0
óS(s)dB(s))
= I tó2S2(s)d(B,B)s
ot
= 0 ó2S2(s)ds 0
On a : dS(s) =
S(s)(uds+ódB(s)) Donc
log(S(t)) = log(S(0)) +
foot
S(s)(uds+ódB(s))
1 2 0 (82-(1s) f
t)2()S(s) +
82(s)ds
= log(S(0)) + f t uds + f t
ódB(s) + 21 f t -ó2ds
0 0 2 0
= log(S(0))+ ft(u -
2 )ds + ~t ódB(s)
Soit, en utilisant (4.4)
Y (t) = Y (0) + ft- 2
)ds + f tódB(s)
On en déduire que :
ó2
Y (t) = log(S(t)) =
log(S(0)) + (u - 2
)t+óB(t)
2
elog(S(t)) = elog(S(0))e(u-
2 )t+óB(t)
On a ainsi montré que, si
(S(t))t>0 est un processus strictement
positif vérifiant (4.3),on a bien
ó2
S(t) = x(0)exp((u - 2
)t + óB(s))
Vérifions maintenant que ce processus est bien une
solution. On a S(t) = f(t,B(t)),
où
ó2
f(t,x) = x(0)exp((u - 2
)t + óx)
La formule d'Itô donne : S(t) =
f(t,B(t))
= f(0,B(t)) +ft
f f(s, B(s))ds +
t fx(s,
B(s))dB(s) + 2 f t
f00xx(s,B(s)d(B,B)s
T.Souali CHAPITRE 4. APPLICATIONS
53
Mais comme la variation quadratique du mouvement brownien vaut
(s) ((B,B)s = s). Donc
S(t) = X(0) + f t S(s)(u - 2 )ds + f t
S(s)ódB(s) + 2 f t S(s)ó2ds
2
= S(t) = X(0) +fotuS(s)ds - f t 2
S(s)ds + otóS(s)dB(s) + f0t
2 S(s)ds
et finalement
S(t) = X(0) +f
tS(s)uds +
ftS(s)ódB(s)
Théorème 4.5. Soit ó,u
deux nombre réels, (B(t))to>0 un mouvement brownien et T
un réel strictement positif, pour tout réel x(0), il existe un
processus d'Itô unique (S(t))0<t<T qui véri~e, pour tout t
< T,
f t f t
S(t) = X(0) + 0 S(s)uds + 0
S(s)ódB(s)
Ce processus est donné par
2
S(t) = x(0)exp((u - 2 )t+óB(t))
Remarque 13.
· Le processus
S(t) que l'on vient d'expliquer servira de modèle standard pour le prix
d'un actif financier. On l'appelle modèle de Black et Scholes.
· Lorsque u = 0, S(t) est une martingale
exponentielle.
54
Conclusion
Le mouvement brownien est l'objet central du calcul des
probabilités moderne. Il intervient dans de très nombreux
modèles en physique, chimie, biologie, sciences économiques et
mathématiques financières. Il est tout à la fois une
martingale, un processus gaussien, un processus à accroissements
indépendants et un processus de Markov. Ces diverses
propriétés qui en font le processus stochastique par excellence,
sont présentées dans ce mémoire avec les deux outils
qu'ils permettent de développer : l'intégrale d'Itô et la
notion d'équation différentielle stochastique.
2
3
4
5
6
7
8
2
3
4
5
6
7
8
55
Annexe
code de simulation sous Scilab
Le code suivant représente un code Scilab de simulation
de la trajectoire Marche aléatoire sur Z.
1 function [ a]= marche ( n , p , x0 )
|
X=[ x0 ]
for k =1:n do
X=[X,X( $ ) +2*( rand ( ) <p ) -1]
end;
xset ( 'window ' ,1)
plot (X)
a=[X]
|
9 endfunction
Le code suivant représente un code Scilab de simulation
des plusieurs trajectoires Marche aléatoire sur Z.
1 function X = marche1D ( n , p , x0 ,N)
|
X = zeros ( n+1 ,N)
I = [ 1 : n+1] '
for i =1:N
a = marche ( n , p , x0 )
X ( : , i ) = a ' ;
end
plot ( I ,X)
|
9 endfunction

Le code suivant représente un code Scilab de simulation
de la trajectoire Marche aléatoire sur Z2.
1 function [X, Y] = chaine2 ( n , x0 , y0 , p1 , p2 , p3 )
Le code suivant représente un code Scilab de simulation
de la trajectoire Marche aléatoire sur Z3.
1 function [X, Y] = chaine3 ( n , x0 , y0 , z0 , p1 , p2 , p3 ,
p4 , p5 )
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
X( 1 ) = x0 ;
Y ( 1 ) = y0 ;
e1 = [ 1 ; 0 ] ; e2 = [ 0 ; 1 ] ;
e3 = -e1 ; e4 = -e2 ;
D = [ e1 e2 e3 e4 ] ;
P = [ p1 ; p2 ; p3 ] ;
fi g u r e
for i = 1: n do
a = grand (1 , " mul " ,1 ,P ) ;
X( i +1) = X( i ) +D( 1 , : ) * a ;
Z( i +1) = Y( i ) +D( 2 , : ) * a ;
end
for i = 1: n
plot (X( i : i +1) ,Y( i : i +1) , ' r ' )
sleep ( 1 )
end
e n d fun c t ion
X( 1 ) = x0 ;
Y ( 1 ) = y0 ;
Z ( 1 ) = z0 ;
e1 = [ 1 ; 0 ; 0 ] ; e2 = [ 0 ; 1 ; 0 ] ; e3 = [ 0 ; 0 ; 1 ] ;
e4 = -e1 ; e5 = -e2 ; e6 = -e3 ;
D = [ e1 e2 e3 e4 e5 e6 ] ;
P = [ p1 ; p2 ; p3 ; p4 ; p5 ] ;
fi g u r e
for i = 1: n do
a = grand (1 , " mul " ,1 ,P ) ;
X( i +1) = X( i ) +D( 1 , : ) * a ;
Z( i +1) = Y( i ) +D( 2 , : ) * a ;
BB( i +1) = Z( i ) +D( 3 , : ) * a ;
end
for i = 1: n
plot3d (X( i : i +1) ,Y( i : i +1) ,Z( i : i +1) , 'b ' )
sleep ( 1 )
end
e n d fun c t ion
Le code suivant représente un code Scilab de simulation de
la trajectoire Mouvement Brownien sur 1[8.
|
1
2
3
4
|
function B=simulbrown ( n ,m, Delta )
Z = grand (m, n , " nor " ,0 ,1) ;
/ / vecteur colonne compose de m v . a . iid N( 0 , 1 )
B = zeros (m+1 ,n ) ;
|
|
5
|
/ / initialisation : trajectoires du mouvement brownien
|
|
6
|
temps = zeros (m+1 ,1) ;
|
|
7
|
for i = 1 : m
|
|
8
|
B( i + 1 , : ) = B( i , : ) + sqrt ( Delta ) *Z( i , : )
|
|
9
|
temps(i+1,1) = temps ( i , 1 ) + Delta
|
|
10
|
end
|
|
11
|
a=B
|
|
12
|
plot (temps , B) ;
|
|
13
|
endfunction
|
Le code suivant représente un code Scilab de simulation de
la trajectoire Mouvement Brownien sur 1[82.
1 / / Parametres de la simulation
2 function a=simulbrown2d(T,N)
|
3
4
|
h = T/N;
sh = sqrt(T/N);
|
5 / / Initialisation des vecteurs de calcul
6 temps = h * [ 0 :N] ;
7 x = zeros ( size (temps)) ;
8 y = zeros ( size (temps)) ;
9 / / calcul des vecteurs de bruits sur x et y
10 bruitX = grand (N, 1 , " nor " ,0 , sqrt(T));
11 bruitY = grand (N, 1 , " nor " ,0 , sqrt (T) ) ;
12 / / calcul de la trajectoire
|
13
14
15
16
17
18
19
|
for i = 2:N+1
x ( i ) = x ( i -1) + sh * bruitX ( i -1) ;
y ( i ) = y ( i -1) + sh * bruitY ( i -1) ;
end
a=[x , y]
plot(x,y);
title ( 'Mouvement brownien en 2D ' ) ;
|
20 endfunction
58
Bibliographie
[1] B. Bercu, D. Chafaii, Modélisation
stochastique et simulation, mathématiques appliquées pour le
master/SMAI, Dunod, 2007.
[2] D. Chafaï, F. Malrieu, Recueil de modèles
aléatoires, springer-verlag Berlin Heidelberg, 1990.
[3] J. Chiasson, Introduction to Probability Theory and
Stochastic Processes, Wiley, 1 edition (April 8, 2013).
[4] D. Foata, A. Fuchs, Processus stochastiques :
Processus de Poisson,chaine de Markovet martingales Dunod, Paris, 2004,
236 pages.
[5] L. Gallardo, Mouvement Brownien et calcul
d'Itô, éditions Hermann, (September 17, 2008).
[6] G. Grimmett, D. Stirzaker, Probability and Random
Processes, Oxford University Press, Third Edition, Oxford, 2001, 608
pages.
[7] I. Karatzas, S. E. Shreve, Brownian Motion and
Stochastic Calculus, Springer Verlag, 2005.
[8] D. Lamberton, B. Lapeyre, Introduction au calcul
stochastique appliqué la finance, ellipses 3éme
édition marketing 2012.
[9] G. F. Lawler, V. Limic, Random Walk : A Modern
Introduction,first édition, Cambridge University Press, New York,
2010.
[10] R. Meester,A Natural Introduction to Probability
Theory, seconde édition, springer Basel 2003.
[11] S. Méléard,Modèles
aléatoires en Ecologie et Evolution, Springer-Verlag, Berlin
Heidelberg 2016
[12] G. H. Weiss, Random Walks and Their Applications:
Widely Used as Mathematical Models, Random Walks Play Important Role in Several
Areas ofPhysics, Chemistry, and Biology, American Scientist, vol. 71, n1,
1983, pp. 65-71.
| 



