1.3.2 Calcul de la capacité du réseau de
voies de circulation :
Notre raisonnement sera bâti sur la théorie des
graphes. Nous supposerons que tous les aéronefs peuvent emprunter toutes
les voies de circulation sans restriction aucune.
La théorie des graphes nous dit que la valeur du flot
maximal sur un réseau est égale à la capacité de la
coupe minimale sur ce réseau (théorème de Ford et
Fulkerson). La coupe se définie comme étant l'ensemble des arcs
déconnectant la source du puits.
Nous manipulerons dans la suite une (s, t)-coupe
(nous dirons simplement une coupe) comme une partition S ? T.
Il est clair que si nous enlevons tous les arcs (x, y) ayant leur
origine x dans S et leur destination y dans T,
il ne peut plus exister de chemin orienté allant de s
à t.
Prenons l'exemple du réseau ci-dessous :
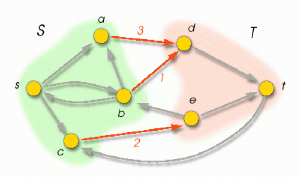
Figure 1 7:Coupe d'un graphe
La coupe ci-dessus est définie par la partition S= {
s, a, b, c } et T= { d, e, t }. Elle comporte les arcs (a,d)
(b,d) et (c,e). Sa capacité est de 6.
Le problème qui va nous intéresser est de
déterminer parmi toutes les coupes d'un réseau, celle de
capacité minimale. Cette capacité est égale à la
valeur du flot maximal, qui sort de la source ou qui est déversé
au puits. C'est en fait le flot maximal possible dans le réseau sans
goulots d'étranglements.
En outre, nous rappelons ceci :
Un réseau de transport est la donnée :
- d'un graphe orienté G(X, A),
- de deux sommets distincts e et s (entrée et sortie)
- chaque arc possède une certaine capacité
(débit maximum autorisé sur cet arc) donnée par la
fonction :
c : A - R+
Un flot sur le graphe G(X, A) est une fonction f : A -
R+ respectant les contraintes suivantes :
- V a E A, f(a) < c(a) (c(a) indique la limite
supérieure du flot admissible sur l'arc a)
- V xE X, ?yf(x,y)= ?yf(y,x) (Loi de noeuds)
Ainsi le flot total dans le graphe est F =?yf(e,y)= ?yf(y,s).
Notre problème revient à calculer Fmax. Sur la figure
ci-dessous F=f1 +f2 = f3 +f4 + f5.
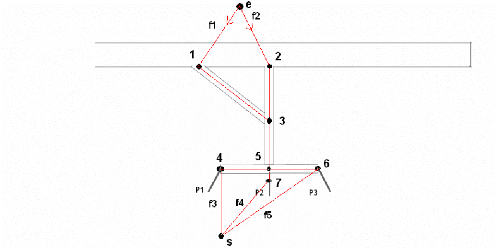
Figure 18: Flot dans un graphe de voies de
circulation
La plupart des algorithmes de calcul de flot maximum sont
basés sur l'idée selon laquelle partant d'un flot
déjà existant (au départ il peut être nul), on va
augmenter le flot allant de la source au puits en poussant littéralement
la commodité là où c' est possible. Les algorithmes se
distinguent seulement par la méthode utilisée afin de
déterminer par où et comment pousser du flot.
On définit pour cela un autre réseau dit
réseau auxiliaire ; ce graphe dépend du flot f déjà
établi, nous le notons N(f).
? Définition Réseau auxiliaire :
Étant donné un réseau de flot N = (G, s, p, c) et un flot
f, nous allons construire le réseau auxiliaire associé N(f) =
(G(f), s, p, cf ). Pour cela, on pose :
cf (u, v) = c(u, v) - f(u, v) + f(v, u) pour tout couple de
sommets (u, v), avec c(u, v), f(u, v) et f(v, u) égales à 0 si
elles ne sont pas définies. Le réseau G(f) est alors
défini comme suit :
X(G(f)) = X(G), (X(G)
est l'ensemble de sommets du graphe G.)
A(G(f)) = {(u, v)
| cf(u, v) > 0}, (A(G) est l'ensemble des arcs de
G)
L'algorithme le plus populaire pour la détermination
du flot maximal Fmax est dû à Ford et Fulkerson et fut
développé dans les années 60. Ils proposent de partir d'un
flot réalisable dans le réseau. A chaque étape,
l'algorithme cherche un chemin augmentant c'est-à-dire un chemin
orienté entre e et s dans le réseau auxiliaire. Si un tel chemin
existe, il est saturé et le flot additionnel est ajouté à
F (flot de sortie). S 'il n'existe plus de chemin augmentant, l'algorithme
s'arrête et le flot courant est retourné. En d'autres termes, Le
principe de cet algorithme est de trouver un chemin menant de la source au
puits capable d'améliorer le flot, de l'augmenter et de recommencer
jusqu'à ce qu'il n'existe plus de chemin pouvant être
maximisé.
? Enoncé de l 'Algorithme de Ford et Fulkerson :
Entrées : Graphe G, points d'entrée et sortie e et s Sorties
: Flot F de type réel.
- Initialiser F à zéro.
- Tant qu'il existe un chemin augmentant p de e à s
faire:
· Calculer le graphe auxiliaire N(f)
· Pousser un flot fp le long de p dans le réseau
résiduel
· à F on donne la valeur F+fp (F4--F+fp)
- Fin faire
- Retourner F.
Cet algorithme se termine après F-Fi itérations. (F
étant la valeur du flot à retourner et Fi la valeur flot
initiale)
A chaque itération, le flot est augmenté d'une
unité si les capacités sont rationnelles (si les capacités
sont irrationnelles, la vitesse de convergence est faible), il se terminera
donc après F itérations. L'algorithme de recherche d'un chemin
non saturé a une complexité de O(Card(A) +
Card(X)× log(card(X)). L'algorithme de Ford et Fulkerson a
donc pour complexité F× O( Card(A) +
Card(X)× log(card(X)).
Cet algorithme est convergent ; mais comme il est fonction de la
valeur du flot à retourner, le temps de calcul peut souvent être
très élevé.
En 1972, un autre algorithme a amélioré
l'algorithme précédent : il s'agit de l'algorithme d'Edmonds et
Karp. Il est presque identique à celui de Ford et Fulkerson, sauf que le
chemin augmentant à chaque fois est choisi le plus court :
Edmonds et Karp = Ford et Fulkerson + plus court
chemin.
? Algorithme d'Edmonds et Karp :
1. Débuter par le flot nul F = 0 ;
2. Calculer le réseau auxiliaire N(F) ;
3. Chercher un plus court chemin de s vers p
dans G(F) ;
4. S'il existe un tel chemin P, pousser du flot le long
de P, mettre F à jour (F4--F+fp) et aller au point 2
;
5. Sinon terminer et retourner F comme solution du
problème.
Sa complexité est O(card(A)× card(X))/2.
Il converge plus rapidement que l'algorithme de Ford et Fulkerson et
surtout il n'est pas fonction du flot à retourner. Nous avons retenu ce
dernier algorithme et l'avons programmé en Visual Basic.
| 


