5.3 Protection de la communication
Protéger la communication revient à
préserver la confidentialité et l'intégrité des
messages qui passent à travers le réseau ainsi que le secret du
flux. Quand des informations doivent être transmises entre deux
systèmes surtout hétérogènes par leurs
systèmes de sécurité, elles peuvent être
interceptées ou altérées par un intrus.
5.3.1 Approches de protection
On distingue essentiellement trois approches de protection des
messages en cours de communication
Sécurité orientée liaison
C'est la protection des messages qui circulent à
travers un lien de communication individuel entre deux noeuds (qu'il soit des
noeuds intermédiaires ou finaux) indépendamment de la source et
de la destination. Etant donné que l'information est
protégée sur les liaisons et pas au sein des noeuds qu'elles
relient, les noeuds eux-mêmes doivent être protégées
physiquement; d'ailleurs cette approche pose plusieurs problèmes.
Sécurité de bout en bout
Le but de cette approche est de protéger le message
pendant sa transmission entre source et destination de façon à ce
que la subversion de n'importe quel lien de communication ne peut
altérer le du message.
Sécurité orientée association
C'est un raffinement de l'approche de protection de bout en bout
qui offre aux utilisateurs une grande flexibilité dans le choix des
noeuds intermédiaires de communication.
Les méthodes de protection des messages se basent sur
l'idée de brouiller le message de manière à le rendre
incompréhensible et inintelligible pour l'attaquant. Pour ce faire, il
existe deux techniques différentes :
La stéganographie C'est un mot issu du grec
Stéganô, signifiant Je couvre et Graphô, signifiant
J'écris. Il s'agit de se servir d'un grand message pour cacher un autre
beaucoup plus petit. L'exemple le plus courant est de cacher le message dans
une image en utilisant les bits les moins significatifs de chaque pixel comme
bit de message. Ainsi, le message passe en clair dans le réseau, sans
personne en puisse trouver la composition du vrai message, sauf les personnes
concernées.
L'idée est de prendre un message et de le modifier de
manière aussi discrète que possible afin d'y dissimuler
l'information à transmettre. Le message original est le plus souvent une
image. La technique de base dite LSB pour Least Significant Bit consiste
à modifier le bit de poids faible des pixels codant l'image : une image
numérique est une suite de points, que l'on appelle pixel, et dont on
code la couleur à l'aide d'un triplet d'octets par exemple pour une
couleur RGB sur 24 bits. Chaque octet indique l'intensité de la couleur
correspondante rouge, vert ou bleu (Red Green Blue) par un niveau parmi 256.
Passer d'un niveau n au niveau immédiatement supérieur (n+1) ou
inférieur (n-1) ne modifie que peu la teinte du pixel, or c'est ce que
l'on fait en modifiant le bit de poids faible de l'octet, l'annexe 6.1 contient
un exemple explicatif.
Toutefois, la stéganographie s'avère peut
utilisée à cause du surcoût de communication qu'elle
engendre pour cacher le message. A cet effet, on s'intéresse
spécialement à la deuxième technique qui est la
cryptographie.
La cryptographie La cryptographie est l'étude des
méthodes permettant de transmettre des données de manière
confidentielle. Afin de protéger un message, on lui applique une
transformation qui le rend incompréhensible; c'est ce qu'on appelle le
chiffrement, qui, à partir d'un texte en clair, donne un texte
chiffré. Inversement, le déchiffrement est l'action qui permet de
reconstruire le texte en clair à partir du texte chiffré en
utilisant une clé particulière et un algorithme de
déchiffrement.
On distingue deux catégories de systèmes
cryptographiques:
· Systèmes de cryptographie symétrique:
Les algorithmes de chiffrement symétrique se fondent
sur une même clé pour chiffrer et déchiffrer un message
(Figure 4.4). Le problème de cette technique est que la clé, qui
doit rester totalement confidentielle, doit être transmise au
correspondant de façon sûre.
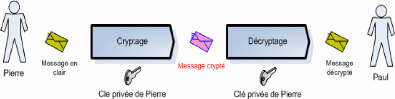
Figure 4.4 Système de cryptographie symétrique.
Le principe de fonctionnement du système
d'authentification à clés symétriques est le suivant :
Soit 'M' un ensemble de messages vérifiant une
propriété particulière (définie à l'avance
par les deux interlocuteurs) et soit 'm', appartenant à 'M', le message
à échanger. L'émetteur chiffre 'm' avec la clé
secrète 's' et envoie le résultat Es(m) au destinataire, ce
dernier déchiffre le message Ds(Es(m))= m et vérifie si le
message déchiffré appartient à 'M', si c'est le cas alors
l'authenticité du message est prouvée, sinon le message est
rejeté.
Parmi les algorithmes de cryptographie symétrique les plus
connus on cite :
a- DES (Data Encryption Standard) : C'est-à-dire
Standard de Chiffrement de Données est un standard mondial depuis plus
de 15 ans. Bien qu'il soit un peu vieux, il résiste toujours très
bien à la cryptanalyse et reste un algorithme très sûr.
Au début des années 70, le développement
des communications entre ordinateurs a nécessité la mise en place
d'un standard de chiffrement de données pour limiter la
prolifération d'algorithmes différents ne pouvant pas communiquer
entre eux. Pour résoudre ce problème, L'Agence Nationale de
Sécurité américaine (N.S.A.) a lancé des appels
d'offres. La société I.B.M. a développé alors un
algorithme nommé Lucifer, relativement complexe et sophistiqué.
Après quelques années de discussions et de modifications, cet
algorithme est devenu alors D.E.S.
Le D.E.S. est un système de chiffrement par blocs,
c'est a dire il ne chiffre pas les données à la volée
quand les caractères arrivent, mais il découpe virtuellement le
texte clair en blocs de 64 bits qu'il code séparément, puis qu'il
concatène. Un bloc de 64 bits du texte clair entre par un coté de
l'algorithme et un bloc de 64 bits de texte chiffré sort de l'autre
coté. L'algorithme est assez simple puisqu'il ne combine en fait que des
permutations et des substitutions. On parle en cryptologie de techniques de
confusion et de diffusion.
C'est un algorithme de cryptage à clef secrète.
La clef sert donc à la fois à crypter et à
décrypter le message. Cette clef a ici une longueur de 64 bits,
c'est-à-dire 8 caractères, mais seulement 56 bits sont
utilisés. On peut donc éventuellement imaginer un programme
testant l'intégrité de la clef en exploitant ces bits
inutilisés comme bits de contrôle de parité.
L'entière sécurité de l'algorithme repose
sur les clefs puisque l'algorithme est parfaitement connu de tous. La clef de
64 bits est utilisée pour générer 16 autres clefs de 48
bits chacune qu'on utilisera lors de chacune des 16 itérations du D.E.S.
Ces clefs sont les mêmes quel que soit le bloc qu'on code dans un
message.
En effet la sécurité du D.E.S. avec ses 16
rondes est grande et résiste à l'heure actuelle à toutes
les attaques linéaires, différentielles ou par clefs
corrélées, effectuées avec des moyens financiers et
temporels raisonnables (i.e. moins de 10 millions de dollars et moins d'un
mois). La grande sécurité repose sur ses tables de substitutions
non linéaires très efficaces pour diluer les informations. De
plus le nombre de clefs est élevé (256=7,2*1016) et peut
être facilement augmenté en changeant le nombre de bits pris en
compte. D'autres avantages plus techniques au niveau cryptanalyse existent. De
plus, cet algorithme est relativement facile à réaliser
matériellement et certaines puces chiffrent jusqu'à 1 Go de
données par seconde ce qui est énorme : c'est plus que ce qu'est
capable de lire un disque dur normal.
b-IDEA (International Data Encryption Algorithm) : Cet
algorithme a été conçu dans les années 90. C'est un
algorithme de chiffrement symétrique par blocs utilisé pour
chiffrer et déchiffrer des données. Il manipule des blocs de
texte en clair de 64 bits. Une clé de chiffrement longue de 128 bits
(qui doit être choisie aléatoirement) est utilisée pour le
chiffrement des données, et on a besoin de la même clé
secrète pour les déchiffrer. Comme tous les algorithmes de
chiffrement par blocs, IDEA utilise à la fois la confusion et la
diffusion. L'algorithme est basé sur le mélange
d'opérations de différents groupes algébriques(voir Annexe
6.1).
· Des systèmes de cryptographie
asymétrique
Ces systèmes ont été proposés par
Whitfield Diffie et Martin Hellman en 1976 marquant ainsi la naissance de la
cryptographie moderne. La cryptographie asymétrique (appelée
aussi
cryptoraphie à clé publique) utilise deux
clés : une clé publique et une clé privée. Les
clés publique et privée sont mathématiquement liées
par l'algorithme de cryptage de telle manière qu'un message
crypté avec une clé publique ne puisse être
décrypté qu'avec la clé privée correspondante. Mais
ces clés ont la propriété que si l'on connaît la
clé publique, il est impossible de trouver par calcul la clé
privée. Dans un système cryptographique à clé
publique, chaque partie communicante possède sa propre paire de
clés publique/privée. Comme son nom l'indique, la clé
publique est mise à la disposition de quiconque désire chiffrer
un message. Ce dernier ne pourra être déchiffré qu'avec la
clé privée, qui doit être confidentielle.
Voici comment un tel système peut assurer la
confidentialité des communications : deux sujets, Paul et Pierre,
désirent échanger des informations qu'il tiennent à garder
secrètes et intègres. Pierre va chiffrer l'information avec la
clé publique de Paul. La confidentialité de l'information est
maintenue, car seul Paul peut la déchiffrer au moyen de sa clé
privée (Figure 4.5).
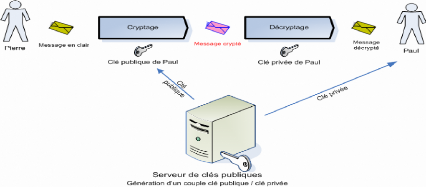
Figure 4.5 Système de cryptographie asymétrique.
Quelques algorithmes de cryptographie asymétrique
très utilisés :
a- RSA (Rivest, Shamir et Adleman) :
Cet algorithme est très largement utilisé, par
exemple dans les navigateurs pour les sites sécurisés et pour
chiffrer les emails. Il est dans le domaine public (Figure 4.5).
L'algorithme est remarquable par sa simplicité. Il est
basé sur les nombres premiers. Pour encrypter un message, on fait : c =
m^e mod n
Pour décrypter : m = c'd mod n
m = message en clair
c = message encrypté
(e,n) constitue la clé publique
(d,n) constitue la clé privée
n est le produit de 2 nombres premiers
^est l'opération de mise à la puissance (a'b : a
puissance b)
mod est l'opération de modulo (reste de la division
entière)
Créer une paire de clés : C'est très simple,
mais il ne faut pas choisir n'importe comment e, d et n. Et le calcul de ces
trois nombres est tout de même délicat (figure 4.6).
e n d n

Texte en clair
Texte codé
Décryptage
Texte en clair
Cryptage
n m
m c = m^e mod n c m = c^d mod
Figure 4.6 Principe de fonctionnement de l'algorithme RSA.
Voici comment procéder :
1. Prendre deux nombres premiers p et q (de taille à peu
près égale). Calculer n = pq.
2. Prendre un nombre e qui n'a aucun facteur en commun avec
(p-1)(q-1).
3. Calculer d tel que ed mod (p-1) (q-1) = 1
Le couple (e,n) constitue la clé publique. (d,n) est la
clé privée.
l'annexe6.2 contient un exemple bien detaillé de cet
algorithme.
b- DSA (Digital Signature Algorithm) :
Plus connu sous le sigle DSA, est un algorithme de signature
numérique standardisé par le NIST aux États-Unis, du temps
où le RSA était encore breveté. Le processus de cet
algorithme se fait en trois étapes :
1. Génération des clés
Leur sécurité repose sur la difficulté du
problème du logarithme discret dans un groupe fini.
· Choisir un nombre premier p de L-bit, avec 512 < L
< 1024, et L est divisible par 64
· Choisir un nombre premier q de 160 bits, de telle
façon que p - 1 = qz, avec z un entier
· Choisir h, avec 1 <h < p - 1 de manière
à ce que g = h^z mod p> 1
· Générer aléatoirement un x, avec 0
<x < q
· Calculer y = g^x mod p
· La clé publique est (p, q, g, y). La clé
privée est x
2. Signature
· Choisir un nombre aléatoire s, 1 <s < q
· Calculer s1 = (g's mod p) mod q
· Calculer s2 = (11(m) + s1xx)s'-1 mod q, où 11(m)
est le résultat d'un hachage cryptographique
· La signature est (s1,s2)
3. Vérification
· Rejeter la signature si 0<s1<q ou 0<s2<q
n'est pas verifié
· Calculer w = (s2) -1 (mod q)
· Calculer u1 = H(m)xw (mod q)
· Calculer u2 = s1 xw (mod q)
· Calculer v = [g^u1xy^u2 mod p] mod q
· La signature est valide si v = s1
| 


