|
Université Montpellier II
Sciences et Techniques du
Languedoc
THÈSE
pour obtenir le grade de
DOCTEUR DE L'UNIVERSITÉ MONTPELLIER II
Discipline : Biostatistique
Ecole doctorale : Information,
Structures, Systèmes
présentée et soutenue publiquement
le 22
Octobre 2009
par
Ciré Elimane SALL
Modélisation spatiale hiérarchique
bayésienne de l'apparentement
génétique et de l'héritabilité en
milieu
naturel à l'aide de marqueurs
moléculaires
Composition du jury:
|
M.
|
Jean-Noël Bacro
|
Université Montpellier II
|
Président du jury
|
|
Mme
|
Sophie Gerber
|
INRA
|
Rapporteur
|
|
Mme
|
Brigitte Mangin
|
INRA
|
Rapporteur
|
|
M.
|
Olivier Hardy
|
Université Libre de Bruxelles
|
Examinateur
|
|
M.
|
Ali Gannoun
|
CNAM
|
Directeur de thèse
|
|
M.
|
Frédéric Mortier
|
CIRAD
|
Co-directeur de thèse
|
Remerciements
Ce travail de thèse s'est inscrit dans le cadre d'une
collaboration scientifique entre l'ISRA, Institut Sénégalais de
Recherches Agricoles, et le CIRAD, Centre de coopération Internationale
en Recherche Agronomique pour le Développement. Il a été
principalement réalisé au sein de l'Unité de Recherche 39
"Diversité génétique et amélioration des
espèces forestières" du CIRAD. Pour mener ce travail à
terme, j'ai bénéficié de l'appui d'un certain nombre de
personnes à qui je souhaiterai témoigner toute ma gratitude.
Je voudrai, tout d'abord, remercier les membres de mon jury de
thèse qui ont bien voulu juger ce travail. Je remercie vivement
Frédéric Mortier qui a encadré avec enthousiasme et
générosité ce travail. Je tiens à lui
témoigner toute ma reconnaissance et toute ma gratitude pour son
investissement personnel dans l'aboutissement de cette thèse. Merci
Fred. Ces années de thèse ont été très
enrichissantes pour moi et j'espère que j'aurai l'opportunité de
collaborer avec toi sur d'autres projets. Je remercie Ali Gannoun pour avoir
bien voulu accepter d'être mon directeur de thèse. Sophie Gerber
et Brigitte Mangin ont accepté d'être les rapporteurs de mon jury
de thèse. Je les remercie pour leurs remarques et suggestions
constructives qui ont permis d'améliorer sensiblement une version
antérieure de ce manuscrit. Je remercie Olivier Hardy pour avoir bien
voulu examiner ce travail et Jean-Noël Bacro pour avoir accepté de
présider mon jury de thèse.
Je remercie également les membres de mon comité
de thèse. Philippe Letourmy a suivi mon travail de thèse avec
beaucoup d'intérêt. Il est, en outre, à l'origine du projet
de thèse. Je lui témoigne içi toute ma reconnaissance.
Catherine Trottier a, à chaque fois, épluché avec beaucoup
de rigueur le document de travail remis lors de la réunion de mon
comité de thèse. Ses observations et remarques ont permis
d'améliorer considérablement ces documents. Merci pour les
remarques avisées et l'intérêt manifesté à
l'égard de ce travail. Je remercie Avner Bar-Hen, Marie-Pierre Etienne
et Frédéric Hospital pour leurs critiques constructives et leurs
encouragements. J'ai bien apprécié l'humilité dont ils ont
fait montre.
J'ai partagé, durant ces années de
préparation de ma thèse, le bureau avec
Pierrette Chagneau. Nous nous sommes, je l'espère,
soutenus mutuellement. A mes moments de doute ou de déprime, je savais
que je pouvais toujours compter sur une oreille attentive. Merci Pierrette pour
les multiples coups de main. Merci aussi pour avoir souvent accepté,
dans la joie et la bonne humeur, d'être mon chauffeur. Bonne chance pour
la suite et attention à tes rotules.
Je remercie Philippe Vigneron qui s'est beaucoup
intéressé à l'avancée de mon travail de
thèse. Je n'oublierai pas les moments de pause studieuse durant lesquels
Philippe me faisait souvent bénéficier, avec une
générosité manifeste, de son savoir et de son
expérience dans le domaine de la génétique des
populations. Vivien Rossi m'a apporté son appui pour la
définition du modèle spatial hiérarchique bayésien
pour l'apparentement. Il a aussi relu de manière approfondie une version
antérieure de ce manuscrit. Je lui en suis très reconnaissant.
Jean-Marc Bouvet m'a accueilli au sein de l'Unité de Recherche 39
"Diversité génétique et amélioration des
espèces forestières". Je le remercie d'avoir bien voulu
m'accueillir dans cette unité de recherche et de m'avoir fourni les
données utilisées pour l'application pratique de ce travail.
Roselyne Lannes s'est occupée, avec gentillesse, de la gestion
administrative de mes séjours au CIRAD. Je tiens à lui exprimer
ma profonde gratitude.
Mes parents m'ont élevé dans un environnement
propice aux études et m'ont encouragé à poursuivre mes
études. Merci papa. Maman, "ô ma mère, toi qui me portas
sur le dos, toi qui m'allaitas, toi qui gouvernas mes premiers pas, toi qui la
première m'ouvris les yeux aux prodiges de la terre", merci. Je remercie
mes frères et soeurs qui m'ont fortement soutenu avant et durant la
préparation de cette thèse.
Je remercie enfin Papa Abdoulaye Seck, ancien Directeur
Général de l'ISRA, et Taïb Diouf, actuel Directeur
Général de l'ISRA, pour m'avoir encouragé à
préparer une thèse et avoir facilité, de manière
pratique, cette préparation.
Ce travail de thèse a été financé
grâce à une bourse d'étude accordée par le
Ministère français des Affaires Etrangères et un appui
complémentaire conséquent du CIRAD (DESI et UR 39).
A mes parents
A mes frères et soeurs
A mon défunt tonton, Lassana SYLLA
Table des matières
Introduction i
1 Apparentement spatial 1
1.1 Introduction 1
1.2 Modèle de Milligan 1
1.2.1 Estimation des paramètres 2
1.2.2 Propriétés statistiques 3
1.2.3 Limites du modèle de Milligan 3
1.3 Cas de plus de 2 génotypes 4
1.3.1 La vraisemblance composite 5
1.3.2 La vraisemblance composite par paires pour l'estima-
tion de l'apparentement 9
1.4 Prise en compte de l'information spatiale 9
1.4.1 Version hiérarchique bayésienne du
modèle de Milligan 10 1.5 Conclusion 14
2 Héritabilité en milieu naturel 15
2.1 Introduction 15
2.2 Covariance phénotypique et covariance
génétique 16
2.3 Revue bibliographique 17
2.3.1 Modèle de régression linéaire pour
l'estimation de l'héritabilité 18
2.3.2 Modèle de la
vraisemblance pour l'estimation de l'hé-
ritabilité 19
2.4 modèle pour l'apparentement et
l'héritabilité 20
2.4.1 Modèle bayésien hiérarchique 21
2.4.2 Lois a posteriori des paramètres 22
2.5 Conclusion 24
3 Estimation 26
3.1 Inférence bayésienne 26
3.1.1 Les méthodes de Monte Carlo 28
3.1.2 Les méthodes de Monte Carlo par chaînes de
Markov 29
3.2 Algorithmes d'estimation des paramètres 32
3.2.1 Version bayésienne du modèle de Milligan
32
3.3 Estimation dans le cas spatial 33
3.4 Estimation des paramètres génétiques
35
3.5 Conclusion 37
4 Applications 38
4.1 Application à des données sur le karité
38
4.1.1 Introduction 38
4.1.2 Analyse statistique des données 41
4.1.3 Résultats 44
4.2 Application du modèle spatial pour l'apparentement
55
4.2.1 Étude de l'effet du prior 56
4.2.2 Effet de la variance de dispersion sur les données
simulées 57 4.3 Discussions 60
Conclusion générale et perspectives 65
Bibliographie 68
Table des figures
1 Structure d'une molécule d'ADN iii
2 Transmission des allèles de deux parents à
leurs enfants. Les allèles A1 des enfants sont identiques par
descendance. (a) Les allèles A2 des enfants sont identiques par
état. (b) Les allèles A2 des enfants sont identiques par
descendance. x
3 Les modes d'identité par descendance des
allèles de deux individus : pour chacun des cas, les 2 points du haut
représentent les allèles de l'un des individus et ceux du bas les
allèles de l'autre individu; 2 allèles IBD sont reliés par
un trait. xi
3.1 Graphe acyclique orienté du modèle
bayésien hiérarchique . . . 32
4.1 Aire de répartition de l'arbre à karité
en Afrique 39
4.2 Distribution spatiale des arbres par classe de
diamètre 46
4.3 Histogramme du diamètre des arbres 46
4.4 Nombre d'allèles observés par locus 48
4.5 Eboulis des valeurs propres 49
4.6 Contribution à l'axe 1 50
4.7 Contribution à l'axe 2 50
4.8 Cercle des corrélations 50
4.9 Représentation des individus sur les axes principaux
50
4.10 Distribution de la statistique de Mantel; le trait vertical
(en
gras) représente la valeur observée de la
statistique de Mantel 51
4.11 Corrélogramme représentant l'indice de
Moran en fonction de la classe de distance spatiale (* : p - vallue < 5%; ns
: non significatif) 52
4.12 Estimation du coefficient d'apparentement moyen en
fonction de la distance entre les individus selon 3 méthodes
différentes (Lynch-Ritland, Wang et Milligan 53
4.13 Distribution des valeurs estimées du coefficient
d'apparente-
ment de Milligan 55
4.14 Boxplot des valeurs estimées du coefficient
d'apparentement
de Milligan 55
4.15 Corrélation entre l'apparentement réel et
l'apparentement estimé en fonction du nombre de locus et du prior (la
figure à gauche représente le cas avec une loi de Dirichlet dont
les paramètres sont égaux et très faibles
(10-5) et la figure de droite une loi de Dirichlet dont tous les
paramètres sont égaux à 0.1). 57
4.16 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 5 locus et une variance de dispersion égale à 0.1
58
4.17 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 5 locus et une variance de dispersion égale à 1
58
4.18 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 5 locus et une variance de dispersion égale à 10
59
4.19 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 5 locus et une variance de dispersion égale à 100
59
4.20 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 10 locus et une variance de dispersion égale à 0.1
60
4.21 Corrélation entre l'apparentement réel et
l'apparentement estimé 1) dans le cas non spatial et (2) dans le cas
spatial avec 10 locus et une variance de dispersion égale à 1
60
4.22 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 10 locus et une variance de dispersion égale à 10
61
4.23 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 10 locus et une variance de dispersion égale à 100
61
4.24 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 15 locus et une variance de dispersion égale à 0.1
62
4.25 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 15 locus et une variance de dispersion égale à 1
62
4.26 Corrélation entre l'apparentement réel et
l'apparentement estimé (1) dans le cas non spatial et (2) dans le cas
spatial avec 15 locus et une variance de dispersion égale à 10
63
4.27 Distribution du paramètre í associé
à la distance dans le mo-
dèle spatial pour l'apparentement 64
Liste des tableaux
1 Probabilités de 2,1, et 0 allèles IBD sachant
quelques relations
standards xvi
2 Probabilités conditionnelles des IBS sachant IBD,
dans le cas non-consanguin à un locus; fj est la fréquence de
l'allèle Aj et des allèles avec des indices différents
sont distincts xvii
1.1 Probabilités d'observer le mode d'IBS sachant le
mode d'IBD; fk est la fréquence de l'allèle Ak et des
allèles avec des indices différents sont distincts. 2
2.1 Probabilité d'observer un couple de
génotypes, à un locus chez des individus diploïdes,
conditionnellement à leur mode d'apparentement : non-apparentés
ou plein-frères. Les indices j, k et l représentent des
allèles mutuellement différents de l'allèle i. 20
4.1 Classes de diamètre des arbres 44
4.2 Fréquences alléliques aux locus 45
4.3 Caractéristiques des différents locus 47
4.4 Hétérozygotie moyenne sur les locus 47
4.5 Test de Mantel 51
Introduction générale
L'objectif de cette introduction est d'abord de rappeler
brièvement quelques notions élémentaires en
génétique et définitions telles que celle de la structure
de l'acide désoxyribonucléique (ADN) et celle d'un marqueur
génétique qui seront utiles pour la suite. Nous présentons
après la problématique des recherches en amélioration
génétique et le modèle théorique de la
génétique quantitative. Nous décrivons ensuite les
dispositifs de recherche en sélection participative qui constituent le
contexte dans lequel s'insère l'application de notre travail.
Après avoir présenté les différents modes
d'identité des allèles, nous définissons le coefficient
d'apparentement génétique entre deux individus qui mesure la
similarité génétique entre ces individus. Nous passons
ensuite en revue les principales méthodes d'estimation de
l'apparentement génétique et donnons enfin les objectifs de notre
travail et l'organisation de ce document.
Quelques notions de génétique
Caractère Un caractère est une
particularité, une caractéristique observable chez un individu;
un caractère héréditaire est un caractère transmis
par les ascendants à leur descendant.
Chromosome Un chromosome est un élément
microscopique constitué d'une molécule d'acide
désoxyribonucléique (ADN). Les chromosomes sont en nombre
variable selon chaque espèce; l'espèce humaine compte 46
chromosomes répartis en 23 paires.
Gène Un gène est une quantité
d'information concernant un caractère élémentaire qui est
transmise par un parent à son descendant. Les chromosomes portent les
gènes qui sont les supports de l'information
héréditaire.
Génôme L'ensemble des chromosomes d'un individu
constitue son génôme.
Locus Un locus correspond à une position précise
d'un gène sur un chromosome.
Allèle Un allèle est une des formes ou versions
d'un gène présent en un locus; par exemple, lorsqu'un gène
A se présente sous 2 formes différentes A1 et A2 ces
différentes formes sont appelées des allèles.
Génotype La combinaison des gènes
présents en un locus d'un individu constitue son génotype au
locus considéré, par exemple A1A1, A1A2 ou A2A2.
Phénotype Le phénotype est l'expression du
génotype dans un milieu donné; le phénotype est l'ensemble
des caractères apparents d'un individu et est fonction de son
génotype et du milieu environnemental dans lequel vit cet individu
Homozygote Un individu portant 2 copies du même
allèle à un locus, par exemple A1A1, est dit
homozygote.
Hétérozygote Un individu portant 2
allèles différents à un locus, par exemple
A1A2, est dit hétérozygote.
Polymorphisme Un locus est dit polymorphe lorsqu'il a plus de
deux allèles; l'existence de différents allèles possibles
à un locus définit le polymorphisme génétique.
Hétérozygotie moyenne
L'hétérozygotie moyenne est défini par le rapport de la
somme des proportions d'individus hétérozygotes à chaque
locus au nombre total de locus.
Diversité allélique La diversité
allèlique est donnée par le nombre moyen d'allèles par
locus.
Fréquence allélique La fréquence
allélique est une mesure de la fréquence relative d'un
allèle à un locus donné dans l'ensemble de la
population.
ADN et marqueurs génétiques
iii
deux brins et chaque brin est constitué de
l'enchaînement précis de quatre éléments de base,
les nucléotides (cf Figure 1) (Boichard et al., 1998). Ces
nucléotides diffèrent selon la base azotée qu'ils
contiennent : l'adénine notée A, la guanine (G), la thymine (T)
et la cytosine (C). Les successions des nucléotides sur les deux brins
sont complémentaires (la base C est complémentaire à la
base G et la base T est complémentaire à la base A). Cette
succession des nucléotides constitue la séquence de l'ADN. Un
marqueur génétique se
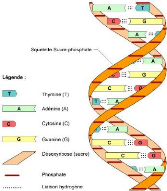
FIG. 1 - Structure d'une molécule d'ADN
trouve à des endroits précis du
génôme et est dans la suite synonyme de locus marqueur; un locus
marqueur est un locus polymorphe dont le génotype renseigne sur le
génotype d'un ou de plusieurs locus voisin(s) (De Vienne, 1998). Un
marqueur génétique de qualité "idéale" est :
1. polymorphe, c'est à dire qu'il possède
plusieurs allèles;
2. co-dominant, c'est à dire un locus pour lequel tous
les allèles présents peuvent être simplement déduits
de l'observation du phénotype; l'hétérozygote peut
être distingué de l'homozygote au locus;
3. non-épistasique, c'est à dire qu'il n'y a pas
d'interaction inter-locus; le génotype en un locus est
indépendant du génotype aux autres locus;
4. neutre, une substitution des allèles au locus marqueur
n'a pas d'autres effets phénotypiques que ceux qui permettent de
déterminer son gé-
notype; un marqueur neutre révèle directement les
modifications géné-
tiques qu'elles se traduisent ou non par
une modification phénotypique;
5. insensible au milieu, le génotype peut être
déduit du phénotype indépendamment du milieu.
Les plus courants des marqueurs génétiques sont
les marqueurs biochimiques, les marqueurs morphologiques et les marqueurs
moléculaires. Mais le plus souvent, ce sont les marqueurs
moléculaires qui ont, pour la plupart, toutes les qualités
citées ci-dessus, au moins lorsque les techniques appropriées
sont mises en oeuvre (De Vienne, 1998). Les marqueurs moléculaires
permettent une caractérisation du génome de manière
fiable, spécifique et rapide. Ainsi, nous nous intéresserons
essentiellement, dans la suite, aux marqueurs moléculaires. Les
marqueurs microsatellites ou SSR (Simple Sequence Repeats) sont des
séquences constituées de répétition en tandem
(toujours dans le même sens) d'un à quatre nucléotides
répétés de 10 à 20 fois en moyenne. Par exemple,
(A)Th , (TC)Th, (TAT)Th et (GATA)Th
avec ii le nombre de répétitions, sont des marqueurs
microsatellites couramment observés. Très nombreux et bien
répartis sur le génome, les microsatellites se
caractérisent par un important polymorphisme dû à la
variation du nombre de répétitions selon les allèles
(Boichard et al., 1998). Il s'agit ainsi d'un polymorphisme du nombre
d'unités de répétitions et l'importance de ce
polymorphisme constitue l'intérêt des marqueurs microsatellites.
Les microsatellites sont des marqueurs dits multialléliques, c'est
à dire qu'ils permettent de révéler une série de
plusieurs allèles par locus. Les locus ainsi mis en évidence sont
le plus souvent codominants et les deux allèles homologues sont
observables chez un individu hétérozygote. Pour que le marqueur
microsatellite puisse être repéré sans
ambiguïté , il doit être entouré de part et d'autre
par des séquences flanquantes uniques, appelées amorces,
permettant d'identifier le locus. En effet, bien qu'un microsatellite
donné ne soit pas spécifique d'un locus, les séquences
flanquantes par contre le sont et une paire d'amorces spécifiques de ces
régions flanquantes n'amplifiera que ce microsatellite. Ainsi, puisque
les séquences des régions flanquantes sont
généralement identiques pour les individus d'une même
espèce, un locus microsatellite particulier peut souvent être
identifié par ses séquences flanquantes (Selkoe et Toonen,
2006).
La mise en évidence du polymorphisme du marqueur est
réalisée par l'amplification par PCR (Polymerase Chain Reaction)
de la séquence entourant le microsatellite puis par
électrophorèse sur gel d'acrylamide dont la haute
résolution permet de distinguer des allèles dont la taille
diffère de deux bases seulement (Boichard et al., 1998). La PCR,
réaction de polymérisation en chaîne, est un
procédé de biologie moléculaire permettant d'amplifier in
vitro une zone spécifique de l'ADN (la séquence cible) comprise
entre deux
v
amorces connues. Cette technique permet, grâce a
l'utilisation de l'enzyme polymérase qui résiste a de très
hautes températures (thermo-résistante) et des amorces
spécifiques, de multiplier par un facteur 2 le fragment d'ADN cible a
chaque cycle et de le rendre ainsi facilement détectable après un
certain nombre de cycles. Chaque cycle est constitué des trois
étapes suivantes effectuées chacune a une température bien
précise :
1. dénaturation; la dénaturation de l'ADN a
94° consiste a dissocier les deux brins d'ADN (rupture des liaisons
hydrogènes entre les deux brins);
2. hybridation; la température est abaissée
rapidement durant 45s a une température définie selon le type
d'amorce et ainsi les amorces hybrident sur leur brin complémentaire;
3. élongation; une hausse rapide de la
température a 72° durant 1 mn permet a l'enzyme polymérase
(la Taq polymérase) d'ajouter des nucléotides aux amorces
hybridées en respectant la complémentarité des bases.
Problématique de l'amélioration
génétique
Les caractères soumis a l'étude
génétique peuvent présenter une variabilité soit
discrète soit continue (Verrier et al., 1998). Le nombre de
modalités différentes observées dans le premier cas est
fini et souvent faible; il peut s'agir par exemple de l'aspect lisse ou
ridé du grain chez le pois, la forme arrondie ou allongée d'un
fruit, la couleur des pétales des fleurs. Cependant les
caractères d'intérêt présentent, le plus souvent au
niveau d'une population, une distribution continue et ceci s'explique par le
fait que ces caractères sont soumis a la fois aux effets de plusieurs
gènes, aux effets du milieu et éventuellement a leurs
interactions (Boichard et al., 1998); c'est par exemple le cas pour la
croissance d'un arbre, la production de fruits, la précocité de
production, ou la teneur moyenne en matière grasse des graines. Les
variations phénotypiques observées pour un caractère
quantitatif donné sont imputables a la fois a des différences de
génotypes entre individus et a des différences de conditions du
milieu dans lequel se trouvent les individus. Le concept
d'héritabilité permet de quantifier l'importance de ces deux
sources de variation (Verrier et al., 1998).
L'hérédité est le phénomène
de transmission d'un caractère des ascendants aux descendants et, dans
le domaine de l'amélioration génétique des populations,
l'héritabilité des caractères d'intérêt est
un paramètre fondamental. En effet, le progrès
génétique ou réponse a la sélection qui est
défini
par l'écart entre la valeur des descendants issus de
parents sélectionnés et la valeur de descendants issus de parents
choisis aléatoirement permet d'évaluer la performance des
programmes de sélection et s'exprime en fonction de ce paramètre
(Verrier et al., 1998). La détermination de l'héritabilité
qui correspond à la part relative de la variance phénotypique due
aux effets génétiques nécessite de disposer d'information
sur la relation génétique entre les individus de la population et
donc le pedigree, c'est à dire l'arbre généalogique des
individus.
Modèle de génétique quantitative Un
modèle simple en génétique quantitative consiste à
considérer que la valeur phénotypique d'un individu est
expliquée par les allèles dont il a hérité et par
l'influence de l'environnement qu'il a subi durant son développement
(Frankel et Soule, 1981). La valeur phénotypique Y d'un individu peut
être décomposée en une part moyenne déterministe de
la valeur de la population u, une part due au génotype de l'individu G
et une part due aux facteurs environnementaux spécifiques à
l'individu considéré E :
Y = u + G + E (1)
Ainsi, la variance phénotypique totale peut être
décomposée en une composante due à la variation entre les
génotypes et une composante due à la variation environnementale
:
ó2 Y = ó2 G + ó2
E.
La variance génotypique peut se décomposer en une
part de variance génétique additive et une part de variance de
dominance:
ó2 G = ó2 a + ó2 d. (2)
Définition 1 (Epistasie) Lorsque le caractère
considéré est contrôlé par plusieurs gènes de
différents locus, un terme supplémentaire sera introduit dans
l'expression de la variance génétique; ce terme correspond
à la variance due à l'épistasie qui est l'effet de
l'interaction des allèles de différents locus (inter-loci).
La variance génétique additive ó2 a chez
un individu est la variance de la valeur génétique additive qui
correspond à la somme des effets moyens des gènes maternel et
paternel qu'il possède et représente la fraction de la valeur
génotypique dont on peut facilement prédire la transmission par
un parent à son descendant; elle s'exprime en fonction du degré
de parenté entre les individus. La variance de dominance correspond
à l'effet de l'interaction des gènes intra-locus (Verrier et al.,
1998).
vii
L'un des objectifs principaux de la génétique
quantitative est l'étude de la transmission héréditaire
des caractères à variation continue et la notion
d'héritabilité des caractères permet de mesurer la
ressemblance entre apparentés. L'héritabilité au sens
large, H2, est le rapport de la variance génétique
à la variance phénotypique :
H2 = ó2 G
ó2 Y (3)
L'héritabilité au sens étroit ou strict,
h2, d'un caractère est définie par le rapport de la
variance génétique additive à la variance
phénotypique du caractère :
h2 = ó2 a
ó2 Y (4)
"L'hérédité au sens strict est un
paramètre spécifique du caractère étudié et
de la population observée. L'hérédité au sens
étroit dépend en outre du milieu dans lequel se trouve la
population."
L'héritabilité au sens étroit
s'interprète comme le coefficient de régression de la valeur
phénotypique du descendant sur celle de son parent moyen. L'importance
relative du génotype considéré comme cause de la valeur
phénotypique observée est mesurée par
l'héritabilité au sens strict qui est un important
paramètre dans la description de la transmission
héréditaire des caractères quantitatifs. Le progrès
génétique est défini par l'écart entre la valeur
des descendants issus de parents sélectionnés et la valeur de
descendants qui seraient issus de parents choisis aléatoirement. Il
permet de mesurer l'efficacité de la sélection et est
proportionnel à l'héritabilité au sens étroit du
caractère d'intérêt.
Remarque 1 Le modèle défini par
l'équation 1 n'est cependant correct que lorsque les effets du
génotype et de l'environnement sont additifs et que l'interaction
génotypexenvironnement est supposée nulle. Cette hypothèse
d'absence d'interaction génotypexenvironnement est souvent valide en
sélection animale ou végétale lorsque les
sélectionneurs ont un certain niveau de contrôle de leur plan
d'expérience de telle sorte que l'association
génotypeenvironnement soit minimisée (Hartl et Clark, 1997). Le
modèle complet lorsque l'hypothèse d'absence d'interaction
génotype-environnement G * E n'est pas valide est donné par
Y = u + G + E + G * E (5)
Dispositif de sélection participative en milieu
naturel
L'un des objectifs principaux de la génétique
quantitative est l'étude de la transmission héréditaire
des caractères à variation continue (Verrier et al., 1998).
Classiquement, un dispositif expérimental de sélection en milieu
contrôlé permet de connaître le pedigree, donc
l'apparentement entre les individus et d'en déduire
l'héritabilité des caractères. Mais actuellement de plus
en plus de programmes de recherche reposent sur des dispositifs de
sélection participative en milieu naturel dans lesquels sont
impliquées les populations locales qui sont les utilisateurs potentiels
des résultats de recherche. Cette collaboration entre producteurs et
chercheurs permet de mieux prendre en compte les interactions génotype *
environnement, de mieux cerner les critères de choix des producteurs
dans leur diversité et de contribuer au maintien in situ de ressources
génétiques importantes pour les communautés locales
(Hocdé et al., 2001). Elle permet le développement d'une large
gamme de variétés performantes adaptées aux conditions
climatiques locales et aux besoins et préférences des
agriculteurs. Cependant en milieu naturel, l'information sur le pedigree n'est
souvent pas disponible ou est incomplète. L'apparentement
génétique n'est pas connu dans ce contexte. Aussi, les
croisements entre les individus ne sont souvent pas contrôlés et
donc le calcul de l'héritabilité des caractères et la
mesure du gain génétique constituent un enjeu majeur pour les
sélectionneurs. Les marqueurs moléculaires sont de plus en plus
utilisés pour estimer l'apparentement génétique sans
connaissance du pedigree et ensuite estimer l'héritabilité des
caractères d'intérêt pour déterminer le
progrès génétique des programmes de sélection. La
possibilité d'inférer la relation génétique parmi
les individus d'une population a permis l'expansion de divers domaines de
recherche comme ceux qui concernent l'évolution et la conservation du
patrimoine génétique (Blouin, 2003). Nous pouvons citer, par
exemple, l'estimation de l'héritabilité en milieu naturel,
l'estimation des flux de gènes dans une population et la minimisation du
taux de consanguinité dans une population en captivité (Blouin,
2003).
Modes d'identité des allèles et apparentement
génétique
Le coefficient de parenté joue un rôle
très important dans beaucoup de domaines de la biologie des populations
et de la génétique (Lynch et Ritland, 1999; Milligan, 2003). En
agriculture, des mesures faites sur des individus ap-
ix
parentés peuvent servir à estimer les
composantes additive et de dominance de la variance génétique et
prédire ensuite le gain génétique des programmes de
sélection et d'amélioration des plantes (Weir et al., 2006).
L'apparentement reflete l'histoire commune des membres d'une même famille
ou d'une même population et affecte ainsi tous les caracteres ayant une
composante génétique (Weir et al., 2006). L'existence de lien de
parenté entre deux individus correspond au fait que les deux individus
ont un ou plusieurs ascendants communs (Jacquard, 1970). Cependant
l'apparentement est seulement défini par rapport à une certaine
population de référence bien spécifiée (Lynch et
Walsh, 1998). En effet, tous les individus d'une même espece ou d'une
population sont apparentés selon un certain degré en ce sens
qu'ils ont des copies de genes qui étaient présents chez un
ancêtre plus ou moins lointain. Ce probleme est résolu en
considérant que la population de référence est
constituée d'individus non-apparentés (Lynch et Walsh, 1998;
Hardy, 2003).
Les modes d'identité des allèles
L'apparentement génétique est
caractérisé par les probabilités d'identité par
descendance des alleles de deux individus (Anderson et Weir, 2007). Deux
alleles sont dits identiques par descendance (IBD) lorsqu'ils sont, tous les
deux, la copie d'un même allele provenant d'une des
générations précédentes (Anderson et Weir, 2007).
Deux alleles sont dits identiques par état (IBS) en un locus, s'ils sont
du même type allélique au locus : c'est à dire les alleles
ont le même type de base pour un marqueur SNP ou le même nombre
d'unités de répétition pour un marqueur micro-satellite
(Weir et al., 2006). Deux alleles IBD sont IBS alors que le contraire n'est pas
toujours vrai. En effet, 2 alleles peuvent avoir la même séquence
nucléotidique alors qu'ils sont des copies de différents alleles
dans la population de référence. Ces deux alleles sont IBS et non
IBD. Par contre des alleles identiques par descendance sont
nécessairement identiques par état en l'absence de mutation
(Lynch et Walsh, 1998). La connaissance du mode d'identité par
état de deux alleles peut cependant permettre d'inférer, dans
certains cas, au sujet de leur mode d'identité par descendance : si nous
considérons, par exemple, deux parents de génotypes respectifs
A1A2 et A2A2 et qui ont deux enfants de
même génotype A1A2 les alleles A1 des deux enfants sont
nécessairement IBD car ils sont deux copies du même allele
parental; les alleles A2 des enfants sont IBS mais nous ne savons, par contre,
pas si ces alleles sont bien IBD (voir Figure 2). Il est aussi relativement
facile de calculer la probabilité que des individus aient un certain
type de génotypes lorsque leur relation parentale est connue mais par
contre il n'est pas aisé de pouvoir déterminer la
probabilité d'avoir une certaine relation parentale sachant leurs
génotypes (Weir et al., 2006)
Père Mère

A1
A1 A2
A2
A1 A2
A2 A2
Père Mère
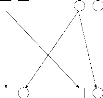
A1
A1
A2
A2 A1 A2
A2 A2
Enfant 1 Enfant 2 Enfant 1 Enfant 2
(a) (b)
FIG. 2 - Transmission des allèles de deux parents
à leurs enfants. Les allèles A1 des enfants sont identiques par
descendance. (a) Les allèles A2 des enfants sont identiques par
état. (b) Les allèles A2 des enfants sont identiques par
descendance.
xi
Des individus apparentés ont une tendance plus
importante d'avoir des génotypes similaires que des individus non
apparentés car ils ont une probabilité plus élevée
d'avoir des allèles IBD. En un locus donné, deux individus
diploïdes possèdent 4 allèles au total et il existe 15
possibilités d'identité par descendance des allèles de ces
individus (identité par descendance interindividus et intra-individus)
décrites par Jacquard (1970) et dont la définition est due
à Gillois (1964). Lorsque l'origine parentale des allèles de ces
individus n'est pas considérée, les différentes
possibilités d'identité par descendance des 4 allèles du
couple d'individus au même locus sont réduites à 9
configurations ou modes d'identité notés IBD1, . .. , IBD9
(Figure 3) (Anderson et Weir, 2007). De plus, si les deux individus ne sont pas
consanguins, c'est à dire que leurs parents ne sont pas
apparentés, il y a seulement 3 modes d'IBD possibles : IBD7, IBD8 et
IBD9.

IBD1 IBD2 IBD3

IBD4
IBD7
IBD5 IBD6

IBD8 IBD9

FIG. 3 - Les modes d'identité par descendance des
allèles de deux individus : pour chacun des cas, les 2 points du haut
représentent les allèles de l'un des individus et ceux du bas les
allèles de l'autre individu; 2 allèles IBD sont reliés par
un trait.
Le coefficient d'apparentement
Le coefficient d'apparentement de deux individus est
défini par la probabilité qu'un allèle pris au hasard chez
l'un des individus soit identique par descendance à un allèle
pris au hasard au même locus chez l'autre individu (Jacquard, 1970). En
notant Ä la probabilité que les 2 individus aient un mode
d'identité par descendance IBD , le coefficient d'apparentement est
donné par (Lynch et Walsh, 1998) :
1 1
è = Ä1 + 2(Ä3 + Ä5 + Ä7) +
4Ä8 (6)
Cette formule est obtenue en prenant la somme
pondérée des probabilités d'identité par
descendance des allèles conditionnellement au mode d'IBD du couple. Par
exemple sachant que les individus X et Y sont IBD1 tout allèle de X
tiré aléatoirement est IBD à tout allèle pris
aléatoirement chez Y et donc la probabilité conditionnelle vaut
1. Si les individus ont l'un des modes d'IBD IBD3, IBD5 ou IBD7 tout
allèle tiré aléatoirement de X a une chance sur deux
d'être IBD à tout allèle tiré de manière
aléatoire chez Y . Aussi, sachant que les individus sont IBD8, il y a
une chance sur deux de tirer l'allèle IBD chez l'individu X et aussi une
chance sur deux de tirer cet allèle chez l'individu Y , ce qui fait que
la probabilité conditionnelle correspondante vaut 1/4. Enfin, si les
individus sont IBD2, IBD4, IBD6 ou encore IBD9, ils n'ont pas d'allèle
IBD en commun. Donc la probabilité d'IBD conditionnellement à
l'un de ces 4 modes est nulle.
Lorsque deux individus sont par exemple plein-frères et
non consanguins ils ont une chance sur deux d'hériter du même
allèle paternel et aussi, de manière indépendante, une
chance sur deux d'hériter du même allèle maternel et
Ä7 = 0.25, Ä8 = 0.5, Ä9 = 0.25. Les autres modes d'IBD ne
peuvent pas être observés dans ce cas comme les individus sont
non-consanguins et leur coefficient d'apparentement est è = 0.25.
Méthodes d'estimation de l'apparentement en
l'absence du pedigree à l'aide des données
moléculaires
Différentes méthodes d'estimation de
l'apparentement par utilisation de marqueurs moléculaires sont
développées dans la littérature scientifique (Blouin,
2003). Celles-ci sont réparties, selon leur fondement théorique,
en deux familles : les méthodes d'estimation par maximum de
vraisemblance (Thompson (1975); Milligan (2003); Anderson et Weir (2007)) et
les méthodes des
xiii
moments (Queller et Goodnight (1989); Li et al. (1993);
Ritland (1996b); Lynch et Ritland (1999); Wang (2002)). Une revue
détaillée de ces méthodes peut être trouvée
dans Blouin (2003); Weir et al. (2006) et dans Hepler (2005). Parmi ces
méthodes, nous nous intéresserons plus particulièrement,
dans la suite, à l'étude de l'une des plus récentes
d'entre elles dans chacune des deux familles décrites ci-dessus : la
méthode des moments de Wang (2002) et celle du maximum de vraisemblance
de Milligan (2003). Nous décrivons dans la suite la méthode
d'estimation de l'apparentement de Wang et faisons une brève
présentation de la méthode par maximum de vraisemblance de
Milligan sachant qu'elle sera étudiée plus en détail au
chapitre suivant (section 1.2) car elle constitue la base de la méthode
qui sera développée dans ce travail.
Méthode des moments de Wang
Considérons que les observations portent sur le
génotype à un locus d'une paire d'individus diploïdes non
consanguins. Nous avons vu que dans une population composée d'individus
diploïdes non consanguins, un couple d'individus donné peut n'avoir
aucun allèle IBD (mode IBD9), avoir un unique allèle IBD (mode
IBD8) ou deux allèles IBD (mode IBD7) en un locus. Le coefficient
d'apparentement1 est donné par l'expression :
(7)
2
Ä8
r = 2è = Ä7 +
La méthode d'estimation de l'apparentement de Wang
(2002) est basée sur le calcul d'un indice de similarité, I,
entre les deux individus. Celui-ci correspond à la proportion moyenne
d'allèles présent chez un individus choisi comme
référant qui sont IBS aux allèles de l'autre individu. Le
choix du référant n'influence pas la valeur de l'indice. Wang
définit quatre catégories selon le degrés de
similarité entre les 2 individus :
- la catégorie 1 correspond au cas où l'individu
2 a ses deux allèles IBS avec l'individu 1. Cela correspond aux couples
de génotype de la forme AiAi - AiAi et AiAj - AiAj et I =
1;
la catégorie 2 correspond au cas où 3 des 4
allèles du couple sont IBS. Les couples de génotype sont de la
forme AiAi - AiAj et I = 3/4;
- la catégorie 3 correspond aux cas où les
individus ont en commun un seul allèle IBS. Les couple de
génotype sont de la forme AiAj - AiAk et I = 1/2;
1Il y a une certaine confusion terminologique dans
la littérature scientifique : en anglais è est souvent
appelé !!coefficient of coancestry!! et r est plutôt appelé
!!coefficient of relatedness!!
- enfin la catégorie 4 inclue les cas oil les deux
individus n'ont aucun allèle IBS en commun. Les couples de
généotype sont de la forme AiA3 -AkAl et I = 0.
Wang donne alors l'expression des probabilités
d'occurrence de chacune des catégories, notées Ps, s =
1, . . . , 4, en fonction de L7 et L8 et des fréquences
alléliques de la population. Dans cette approche, Wang se place
initialement dans le cas d'un seul locus. Dans le cas mono-locus, Wang
distingue encore 2 cas, le cas de locus bi-allélique et le cas de locus
multi-alléliques.
Dans le cas d'un locus à 2 allèles, la
catégorie 3 n'est pas observable. Il faut résoudre un
système de 3 équations (dont 2 indépendantes) à 2
inconnues pour obtenir l'estimation de L7 et L8 : il suffit donc de
résoudre seulement 2 des 3 équations. L'estimation de
l'apparentement dans ce cas est donnée par:
rà =
4 àP1 + 3
àP2 - 2(1 + a2) , (8)
2(1 - a2)
oil a2 = > 3 p2 j et p3 la fréquence de
l'allèle A3 dans la population. Comme un couple d'individus à un
locus donné ne peut appartenir qu'à une unique catégorie,
soit àP1 = 1 et àP2 = 0 soit
àP1 = 0 et àP2 = 1.
Pour un locus multi-allélique, nous nous retrouvons
confronté à un système de 4 équations à 2
inconnues dont 3 équations indépendantes. Il y a donc plus
d'équations indépendantes que de paramètres et les
solutions du système d'équations varient selon le couple
d'équations considéré. Il n'y a donc pas d'unicité
des solutions du système d'équations. Une solution est d'utiliser
la méthode des moindres carrés pondérés pour
estimer les paramètres. Le principe de la méthode des moindres
carrés pondérés consiste à procéder à
une transformation linéaire des observations de telle sorte que les
conditions du théorème de Gauss-Markov soient respectées.
Pour cela, chaque observation sera pondérée par sa variance
résiduelle. Cependant les poids optimaux nécessaires à la
mise en oeuvre de cette méthode dépendent de la matrice de
variance-covariance des résidus qui est fonction des paramètres
inconnus L7 et L8. La solution, pour estimer les poids optimaux,
proposée par Wang est de supposer que L7 et L8 sont nuls; en absence
d'information, Wang suppose donc les individus indépendants. Dans un
deuxième temps, il propose d'utiliser la méthode des moindres
carrés pondérés pour obtenir les estimations de L7 et de
L8 et en déduire l'estimation de r.
Par la suite, Wang discute du cas de plusieurs loci. Comme, la
variabilité de chacun des locus peut être forte, il explique
qu'une simple moyenne non pondérée des Pà et
des a (cf equation 8) sur l'ensemble des locus peut ne pas être efficace
et pertinente. Il teste alors différentes pondérations. Parmi
elle, il en choisit une qui apparaît être la plus adaptée au
plus grand nombre de
xv
situations qu'il rencontre.
Les valeurs prises par l'estimateur de l'apparentement de Wang
(2002) sont quelquefois en dehors de l'intervalle de définition du
coefficient de parenté, c'est à dire [0; 1]. Cette remarque est
aussi valable pour les valeurs données par d'autres estimateurs obtenus
par la méthode des moments comme ceux de Ritland (1996b) et de Lynch et
Ritland (1999). Ceci reflète l'importance de la variabilité
résiduelle des estimateurs basés sur la méthode des
moments (Thomas, 2005). Par exemple, lorsque les individus
considérés ne sont pas apparentés, près de la
moitié des valeurs estimées données par la méthode
de Wang (2002) sont négatives tandis que les estimations obtenues par la
méthode du maximum de vraisemblance sont toujours comprises dans
l'intervalle de définition du paramètre inconnu. Lorsque les
valeurs estimées sont en dehors de l'intervalle de définition du
paramètre elles ne peuvent pas être interprétées
comme des probabilités d'IBD. Il est possible d'imposer une contrainte
pour que l'estimation reste dans l'intervalle de définition du
paramètre mais ceci induit par contre un biais (Milligan, 2003; Thomas,
2005). L'importance de ce biais dépend du mode réel de
parenté des individus.
L'estimateur de l'apparentement de Wang (2002) est sans biais
lorsque les fréquences alléliques sont supposées connues.
Le biais reste faible lorsque les fréquences alléliques sont
estimées en utilisant un autre échantillon et ceci a
été vérifié par différentes simulations
(différentes fréquences alléliques, différents
nombres de loci et degrés de parenté).
L'expression analytique de la variance de l'estimateur de
l'apparentement de Wang n'est pas connue. Ainsi, c'est seulement par simulation
que la variance de l'estimateur peut être estimée. Wang a
comparé, par simulation, le comportement de l'estimateur qu'il propose
à d'autres estimateurs fondés sur les méthodes des moments
Lynch et Ritland (1999); Queller et Goodnight (1989). Lorsque les
fréquences alléliques sont supposées connues la variance
moyenne des erreurs d'échantillonnage en un locus est
indépendante du nombre de locus considéré pour tous les
estimateurs à l'exception de celui de Lynch et Ritland (1999). Il faut
noter que les estimateurs de Queller et Goodnight (1989), Ritland (1996b) et
Lynch et Ritland (1999) sont indéfinis pour certaines fréquences
alléliques (les dénominateurs étant nuls). Lorsque les
fréquences alléliques sont estimées, les variances des
estimateurs de l'apparentement de Wang (2002) et de Queller et Goodnight (1989)
sont plus faibles que celles de Lynch et Ritland (1999) et ne varient presque
pas en fonction de la taille de l'échantillon (nombre de locus) et du
type d'apparentement considéré.
|
`(<) =
|
XL
l=1
|
{ X9 }
êiP (IBSl )
log j|IBDi , j ? {1,...,9}
i=7
|
Méthodes du maximum de vraisemblance
Les méthodes d'estimation de l'apparentement par
maximum de vraisemblance ont été développées pour
diverses situations. Thompson (1975) propose une méthode qui permet
d'inférer, dans une population non consanguine, une relation existante
entre deux individus telle que non-apparenté, parents/enfants, 1/2
frères etc. Thompson (1975) décrit la vraisemblance des IBS
conditionnellement à une relation R, pour un locus, comme suit :
L(<; IBSj) = P(IBSj|R)
9
= X
i=7
9
= X
i=7
P(IBSj|IBDi)P(IBDi|<), j ? {1, . . . , 9}
êiP(IBSj|IBDi)
oil ê7, ê8 et ê9 désignent les
probabilités d'avoir 2, 1 et 0 allèles IBD sachant
une
relation R. Le tableau 1 donne les probabilités d'avoir 2, 1 ou 0
allèles IBD
sachant des relations standards et les
probabilités conditionnelles d'identités
|
Classe de parenté <
|
ê7
|
ê8
|
ê9
|
|
Vrais jumeaux
|
1
|
0
|
0
|
|
Parent-enfant
|
0
|
1
|
0
|
|
Plein-frères
|
0.25
|
0.50
|
0.25
|
|
Demi-frères
|
0
|
0.50
|
0.50
|
|
Grand-parent/petit-fils
|
0
|
0.50
|
0.50
|
|
Non-apparentés
|
0
|
0
|
1
|
TAB. 1 - Probabilités de 2,1, et 0 allèles IBD
sachant quelques relations standards
par état sachant les identités par descendance
sont des fonctions polynomiales des fréquences alléliques et sont
données dans le tableau 2. Lorsque les génotypes sont
observés sur L locus autosomaux (non liés au sexe) et
indépendants, l'expression de la vraisemblance est tout simplement
donnée par le produit des vraisemblances aux différents locus et
la log-vraisemblance est donc égale à
xvii
|
IBS
|
Etat allélique
|
IBD7
|
IBD8
|
IBD9
|
|
IBS1
|
AiAi, AiAi
|
f2
i
|
f3
i
|
f4
i
|
|
IBS2
|
AiAi, AjAj
|
0
|
0
|
f2i f2j
|
|
IBS3
|
AiAi, AiAj
|
0
|
f2i fj
|
2f3i fj
|
|
IBS4
|
AiAi, AjAk
|
0
|
0
|
2f2i fjfk
|
|
IBS5
|
AiAj, AiAi
|
0
|
f2i fj
|
2f3i fj
|
|
IBS6
|
AjAk, AiAi
|
0
|
0
|
2f2i fjfk
|
|
IBS7
|
AiAj, AiAj
|
2fifj
|
fifj(fi + fj)
|
4f2i f2j
|
|
IBS8
|
AiAj, AiAk
|
0
|
fifjfk
|
4f2i fjfk
|
|
IBS9
|
AiAj,AkAl
|
0
|
0
|
4fifjfkfl
|
TAB. 2 - Probabilités conditionnelles des IBS sachant
IBD, dans le cas nonconsanguin à un locus ; fj est la fréquence
de l'allèle Aj et des allèles avec des indices différents
sont distincts
On peut noter que P (IBSlj|IBDO)
dépend du locus, en revanche les êi, i = 7, 8, 9 n'en
dépendent pas.
De plus, d'après le tableau 1, il n'est pas toujours
possible de distinguer certaines classes de parenté entre elles sur la
base uniquement de l'information fournie par les données
génotypiques. Ainsi en l'absence de données sur l'âge des
individus il n'est pas possible de distinguer certaines relations : c'est le
cas, par exemple, entre la relation grand-parent/petit-fils et la relation de
demi-frères. Cette question est largement débattue dans l'article
de Thompson (1975).
Dans l'approche de Thompson (1975), l'apparentement est
essentiellement qualitatif, en ce sens qu'il s'agit d'affecter les couples
d'individus dans des classes de parenté. En revanche, l'approche
développée par Milligan (2003) permet d'estimer l'apparentement
sur une échelle continue et généralise celui de Thompson
(1975) au cas d'individus consanguins (Weir et al., 2006). Nous
étudierons plus particulièrement le modèle pour
l'estimation de l'apparentement de Milligan (2003) au chapitre suivant.
Objectifs de la thèse
L'objectif principal de cette thèse est de
développer un modèle statistique incorporant des covariables pour
l'estimation conjointe de l'apparentement génétique et de
l'héritabilité des caractères phénotypiques. En
effet, la prise en compte de covariables telle que l'information spatiale
permettrait éventuellement d'améliorer l'estimation de
l'apparentement génétique. Le modèle
statistique développé s'insère dans le
cadre des méthodes de la vraisemblance composite. La prise en compte de
l'information spatiale nous permettra de modéliser l'identité par
descendance avec un modèle linéaire
généralisé et une fonction de lien probit ordinal.
L'intérêt de la prise en compte du spatial en
génétique est que l'on considère que des individus proches
du point de vue spatial sont aussi génétiquement proches.
Organisation du document
Ce manuscrit de thèse est composé de 4
chapitres. L'objectif du chapitre 1 est de développer un modèle
statistique pour l'estimation de l'apparentement en considérant une
covariable. La covariable qui sera considérée est la distance
spatiale entre les individus. Nous proposons, au chapitre 2, un modèle
hiérarchique bayésien pour estimer à la fois
l'apparentement et l'héritabilité en milieu naturel. Les
algorithmes d'inférence bayésienne pour l'estimation des
paramètres génétiques, lorsque le pedigree n'est pas
connu, sont ensuite exposés au chapitre 3. Le chapitre 4 porte sur une
application à des données génétiques et spatiales
sur le karité. Enfin, nous récapitulons, dans la dernière
partie, les propriétés statistiques de l'estimation de
l'apparentement avec co-variables, les résultats obtenus, les
contraintes rencontrées, les problèmes non résolus et nous
donnons les perspectives et pistes de recherche envisagées.
Chapitre 1
Modélisation de l'apparentement :
prise en compte de l'information
spatiale
1.1 Introduction
L'objectif de ce chapitre est de développer un
modèle statistique pour l'estimation de l'apparentement en prenant en
compte l'information spatiale. La première partie décrit le
modèle pour l'estimation de l'apparentement par maximum de vraisemblance
lorsque les génotypes de deux individus sont observés et les
fréquences alléliques sont connues. Nous étudierons
ensuite le cas oil plus de deux individus sont observés et nous verrons
que l'approche de Milligan s'insère dans un cadre plus large qui est
celui de la vraisemblance composite. La vraisemblance composite ainsi que les
propriétés de l'estimateur du maximum de vraisemblance composite
seront ensuite présenté. Nous décrirons enfin le
modèle spatial hiérarchique pour l'apparentement. Nous avons
choisi, dans ce modèle, de considérer la distance spatiale entre
les individus comme une covariable mais d'autres covariables comme le site
expérimental ou la région pourraient aussi être
envisagées.
1.2 Modèle de Milligan pour l'apparentement :
approche par maximum de vraisemblance
Considérons que les observations portent sur le
génotype d'un couple d'individus donné et que la distribution des
fréquences alléliques est connue. Soit IBS ? {IBS1, IBS2, . . . ,
IBS9} le mode d'IBS observé en un locus et
A = (A1, . . . , A9) le vecteur des probabilités d'IBD du
couple d'individus. La vraisemblance est égale à :
9
|
L(A; IBS) =
|
X
i=1
|
P(IBSj|IBDi)Ai,, j ? {1, . . . , 9}. (1.1)
|
Les probabilités conditionnelles P(IBSj|IBDi) sont des
fonctions polynômiales des fréquences alléliques et sont
données au tableau 1.1. Pour L locus indépendants, la
vraisemblance est simplement donnée par le produit des vraisemblances
1.1 :
L(A; IBS) = 11L 9
P(IBSlj|IBDi)Ai, j ? {1, . . . , 9}
l=1 i=1
oil IBSl désigne le mode d'IBS
observé au locus l. Notons bien que la probabilité d'IBD, A, est
indépendante du locus considéré. En effet, le degré
d'apparentement entre deux individus, qui est déterminé par la
donnée des probabilités d'IBD A, est indépendant du locus
considéré bien que chaque locus soit caractérisé
par les fréquences alléliques à ce locus.
|
|
|
|
|
|
Mode d'IBD IBDj
|
|
|
|
|
Mode d'IBS
|
Etat allélique
|
IBD1
|
IBD2
|
IBD3
|
IBD4
|
IBD5
|
IBD6
|
IBD7
|
IBD8
|
IBD9
|
|
IBS1
|
AiAi, AiAi
|
fi
|
f2
i
|
f2
i
|
f3
i
|
f2
i
|
f3
i
|
f2
i
|
f3
i
|
f4
i
|
|
IBS2
|
AiAi, AjAj
|
0
|
fifj
|
0
|
fif2
j
|
0
|
f2 i fj
|
0
|
0
|
f2 i f2
j
|
|
IBS3
|
AiAi, AiAj
|
0
|
0
|
fifj
|
2f2i fj
|
0
|
0
|
0
|
f2i fj
|
2f3i fj
|
|
IBS4
|
AiAi, AjAk
|
0
|
0
|
0
|
2fifjfk
|
0
|
0
|
0
|
0
|
2f2i fjfk
|
|
IBS5
|
AiAj, AiAi
|
0
|
0
|
0
|
0
|
fifj
|
2f2i fj
|
0
|
f2i fj
|
2f3i fj
|
|
IBS6
|
AjAk, AiAi
|
0
|
0
|
0
|
0
|
0
|
2fifjfk
|
0
|
0
|
2f2i fjfk
|
|
IBS7
|
AiAj, AiAj
|
0
|
0
|
0
|
0
|
0
|
0
|
2fifj
|
fifj(fi + fj)
|
4f2i f2j
|
|
IBS8
|
AiAj, AiAk
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
fifjfk
|
4f2i fjfk
|
|
IBS9
|
AiAj, AkAl
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
4fifjfkfl
|
TAB. 1.1 - Probabilités d'observer le mode d'IBS
sachant le mode d'IBD ; fk est la fréquence de l'allèle Ak et des
allèles avec des indices différents sont distincts.
1.2.1 Estimation des paramètres
L'estimateur du maximum de vraisemblance Aà
de A est obtenu en maximisant la fonction de vraisemblance dans l'espace des
paramètres de dimension 8 en raison de la contrainte sur les
paramètres P9j=1 Aj = 1. Si nous supposons que les individus sont non
consanguins il n'est pas possible que les
individus aient reçus en un locus deux copies du
même allèle parental et ainsi un couple d'individus donné
ne peut avoir à locus qu'une unique possibilité d'avoir 2, 1 ou
aucun allèle(s) IBD et ces cas correspondent respectivement aux modes
d'IBD IBD7, IBD8 et IBD9 (voir figure 3). L'estimateur du maximum de
vraisemblance sera obtenu par optimisation de la fonction de log-vraisemblance
sur l'espace des paramètres (L7, L8, L9) qui est de dimension 2 en
raison de la contrainte P9 i=7 Li = 1. Comme le plus souvent il n'est pas
possible d'obtenir une solution analytique, la procédure d'optimisation
proposée par Milligan (2003) est basée sur une conversion de la
méthode du simplex qui est une technique d'optimisation numérique
avec contraintes (Press et al., 1992).
1.2.2 Propriétés statistiques
L'estimateur de l'apparentement de Milligan (2003) a, comme
tout estimateur du maximum de vraisemblance, de bonnes propriétés
statistiques à savoir la consistance, l'efficacité et la
normalité asymptotiques (en terme de nombre de locus) dans les
conditions de régularité standard (Tassi, 1985, chapitre 8). Ceci
explique pourquoi la méthode du maximum de vraisemblance est largement
utilisée en inférence statistique paramétrique. Cependant
à taille finie, l'estimation de l'apparentement par maximum de
vraisemblance de Milligan est biaisée. D'une manière
générale les méthodes d'estimation par maximum de
vraisemblance présentent un écart quadratique moyen plus faible
que celui des estimateurs obtenus par la méthode des moments mais
lorsque les données disponibles ne sont pas importantes, ce qui est le
cas si peu de marqueurs à différents loci sont disponibles, les
estimateurs du maximum de vraisemblance peuvent être fortement
biaisés (Thomas, 2005).
1.2.3 Limites du modèle de Milligan
L'estimateur de l'apparentement par maximum de vraisemblance
de Milligan peut présenter un biais lorsque les données
moléculaires ne sont pas abondantes. Mais son biais se rapproche de
celui des estimateurs des moments lorsque nous disposons d'un nombre important
de locus multi-alléliques (20 ou plus d'après Thomas (2005)).
D'une manière générale, les méthodes d'estimation
par maximum de vraisemblance donnent des estimateurs ayant une erreur
quadratique moyenne plus faible que celle des estimateurs obtenus par la
méthode des moments mais lorsque les données disponibles, c'est
à dire le nombre de locus marqueurs, ne sont pas abondantes, les
méthodes basées sur la vraisemblance fournissent des estimateurs
assez biaisés (Thomas, 2005). Ainsi, il faudrait disposer de beaucoup de
locus marqueurs poly-
morphes pour s'assurer de la possibilité d'avoir un
estimateur consistant de l'apparentement. Parmi les principaux
inconvénients ou limites du modèle de Milligan pour
l'apparentement, nous pouvons relever qu'il ne considère que les
génotypes d'un seul couple d'individus, que les fréquences
alléliques dans la population sont supposées connues et qu'il ne
prend pas en compte la disponibilité éventuelle d'une information
exogène.
1.3 Modèle lorsque plus de deux génotypes
sont observés
Considérons maintenant que n génotypes sont
observés et que les fréquences alléliques dans la
population sont connues. Nous avons n(71) couples de
génotypes. Dans la suite du chapitre, l'unité statistique,
très fréquemment utilisé, sera le couple et c = 1, . . . ,
C désignera l'indice du couple parmis les n(n - 1)/2 = C couples
disponibles. Ainsi si c = 1 le couple considéré est le couple (1,
2) si c = C le couple considéré est le couple (n - 1, n).
Considérons tout d'abord le cas où les
observations portent sur le génotype à un locus. Soient
IBSc le mode d'IBS en un locus du couple c, IBDc
le mode d'IBD du couple, Äc le vecteur des
probabilités d'IBD du couple c. Nous avons déjà
vu que
9
|
L (Äc; IBSc) =
|
X
i=1
|
P (IBSj,c|IBDi,c) Äi,c, où j ? {1, . . . , 9}.
|
|
L(Ä; IBS) =
|
11C
c=1
|
11L
l=1
|
9
X
i=1
|
P (IBSlj,c|IBDi,c) Äi,c où j ?
{1, . . . , 9}.
|
En notant, A le vecteur des probabilité d'IBD entre
tous les couples, une généralisation directe consisterait
à considérer l'ensemble des couples simultanément. Mais
cela conduirait à évaluer la probabilité suivante
P (IBS1, IBS2, . . . , IBSC|IBD) (1.2)
où IBD est le vecteur des modes d'identité par
descendance de l'ensemble des couples. Mais la difficulté réside
dans le fait que cette probabilité n'a généralement pas
une expression connue. D'autres solutions doivent être envisagées.
Ainsi, en notant IBSlc le mode d'IBS au locus l du couple
c; le modèle de Milligan pour C = n(n - 1)/2 couples est donné
par
sont indépendants. Le problème posé par
ce modèle vient du fait que les couples de génotypes ne sont pas
indépendants et donc la vraisemblance de Ä ne correspond pas
simplement au produit des vraisemblances de ses composantes Äc,
c = 1, . . . , C. Mais cette solution qui consiste à employer le
modèle de Milligan pour C couples et à considérer le
produit des vraisemblances des vecteurs des probabilités d'IBD des
allèles de chacun des couples d'individus s'insère, comme nous le
verrons dans la suite, dans le cadre théorique du modèle de la
vraisemblance composite par paires.
1.3.1 La vraisemblance composite
Les méthodes par vraisemblance sont largement
utilisées en inférence statistique paramétrique en raison
des bonnes propriétés asymptotiques de l'estimateur du maximum de
vraisemblance. Cependant, dans certains cas, il est difficile d'écrire
ou de calculer la vraisemblance. En effet, dans certaines applications, la
fonction de vraisemblance ne peut être calculée à cause de
la présence d'un important volume de données
corrélées ou d'un modèle statistique avec une structure
fortement hiérarchique. Une manière de contourner ces
difficultés est de remplacer la vraisemblance par une fonction
paramétrique plus facile à déterminer et c'est l'objet de
la vraisemblance composite qui permet de réduire la complexité
numérique des procédures d'optimisation même en
présence de données fortement corrélées ou d'un
modèle à structure hiérarchique (Varin et Vidoni, 2005).
La méthode de la vraisemblance composite qui appartient à une
classe plus large de modèles, qui est celle de la pseudo-vraisemblance,
consiste à calculer l'expression d'une combinaison de vraisemblances
relatives à une petite partie des données (Lindsay, 1988). Le
terme de pseudo-vraisemblance a été initialement introduit par
Besag (1974) et Lindsay (1988) a préféré plutôt
employer le terme vraisemblance composite en justifiant son choix par le fait
que ce nom décrit mieux la méthode de construction
considérée. L'idée de la vraisemblance composite est de ne
s'intéresser qu'à une partie de la vraisemblance complète.
En effet, nous pouvons décomposer, pour un modèle
paramétrique, la vraisemblance complète en un produit de
vraisemblances et ne considérer pour l'inférence statistique
qu'une partie de ces vraisemblances qui est relativement plus simple à
calculer. La définition générale de la vraisemblance
composite est donnée par Varin et Vidoni (2005).
Definition 2 Soit {f(Y ; ö), Y E 3), ö E Ö} un
modèle statistique paramé-
trique avec 3) c Rn,
Ö c Rd, n = 1 et d = 1. Considérons un
ensemble
d'événements {A : A E F, i E I} of F est une
u-algèbre de 3) et I c N.
Une vraisemblance composite est définie par:
Lcl( ; Y ) = fi f(Y E Ai; )w%,
i?I
avec f(Y E Ai;è) = f({Yj E Y : Yj E Ai}; ), où Y =
(Y1,Y2,...,Yn) et {wi,i E I} est un ensemble de pondérations
appropriées. La log-vraisemblance composite associée est
£cl( ; Y ) = log Lcl( ; Y ).
Une vraisemblance composite est un produit
pondéré de vraisemblances relatives à un ensemble
d'événements mesurables. La densité f(Y ; )
considérée dans cette définition peut, en effet,
être vu comme une densité conditionnelle ou une densité
marginale et chaque composante de la vraisemblance composite est
proportionnelle à une densité conditionnelle ou marginale. En
particulier, le modèle de la vraisemblance standard peut être vue
comme un cas particulier du modèle de la vraisemblance composite : en
effet, pour un ensemble d'événements indépendants,
l'expression de la vraisemblance standard est exactement égale à
celle de la vraisemblance composite avec des poids égaux à 1
Nous noterons, par la suite la fonction, de densité de
probabilité d'une variable aléatoire Y par fY (Y ; ) où un
vecteur de paramètres. Supposons que Y s'écrive comme Y = (Y1,
Y2) ainsi que = ( 1, 2). La vraisemblance complète est égale
à :
L( ; Y ) = fY1(Y1; )fY2|Y1(Y2; |Y1), (1.3)
|
et la log-vraisemblance complète £( ; y) = log{fY (Y
; )} est donnée par :
|
|
£( ; Y ) =
|
log{fY2|Y1(Y2; |Y1)} + log{fY1(Y1;
|
)}
|
(1.4)
|
|
=
|
£C( ;Y1) + £M( ;Y2)
|
|
(1.5)
|
|
où £C(
|
; Y1) est dénommée log-vraisemblance
conditionnelle et £M(
|
; Y2) log-
|
vraisemblance marginale.
Les méthodes d'estimation par maximum de vraisemblance
composite peuvent être réparties en 2 classes différentes :
les méthodes de vraisemblance composite par omission et celles de la
vraisemblance composite par sélection.
La vraisemblance composite par omission Elle consiste à
négliger les termes qui rendent délicat le calcul de la
vraisemblance complète. La vraisemblance composite par omission revient
à négliger la vraisemblance marginale dans l'expression de la
vraisemblance complète (équation 1.3). Ainsi, il s'agit
içi d'omettre certaines composantes de la vraisemblance complète,
en l'occurrence les vraisemblances marginales, pour ne retenir que les
vraisemblances
conditionnelles. Nous pouvons citer parmi les modèles de
vraisemblance composite obtenus par omission :
- le modèle de la pseudo-vraisemblance de Besag (1974)
appliqué à l'analyse de données spatiales (produit des
distributions conditionnelles d'un vecteur aléatoire Yi sachant tous les
autres points voisins)
Lcl(ö; y) = 11n
fYi|Y(-i)(Yi; ö|Y(-i))ùi,
i=1
oil Y(-i) est le vecteur des observations sans sa
ième composante et ùi = 0 ;
- la vraisemblance partielle de Cox (1975) ; considérons
un vecteur aléatoire Y transformé en une séquence
(X1, S1,. . . , Xm, Sm), la vraisemblance
peut s'écrire :
m m
Lcl(ö;Y ) = 11
fXi|X(i-1),S(i-1)(Xi;
ö|X(i-1), S(i-1)) 11
fSi|X(i),S(i-1)(Sj; ö|X(i),
S(i-1))
i=1 i=1
oil X(i) = (X1, . . . , Xi), S(i) =
(S1, . . . , Si) et m un réel ; le second membre du produit est
appelé la vraisemblance partielle basée sur S dans la
séquence {Xi, Si} ;
- la vraisemblance d'ordre m de (Azzalini, 1983) donnée
par
Lcl(ö; Y ) = fY1(Y1; ö)
|
11n
i=2
|
fYi|Y i-1
i-1 (Yi; ö|Y i-1
i-m),
|
|
oil Y i-1
i-m= (Yi-m, . . . , Yi-1) et m ? {1, . . . , n - 1}; la
log-vraisemblance
est dans ce cas approchée par une somme de
log-vraisemblances conditionnelles aux m dernières observations.
Ces différents exemples ont en commun le fait de
considérer les lois conditionnelles afin d'éliminer le facteur
à l'origine de la complexité des expressions de la vraisemblance.
La vraisemblance partielle de Cox (1975) est très utile lorsque son
expression est beaucoup plus simple que celle de la vraisemblance
complète, ce qui est le cas par exemple quand elle n'est fonction que du
paramètre d'intérêt et non du paramètre de
nuisance.
La vraisemblance composite par sélection La
vraisemblance compo-
site par sélection consiste à construire
les lois marginales d'un sous-ensemble
d'observations. Il peut s'agir par exemple d'écrire le
produit des lois marginales (la vraisemblance simple, singlewise likelihood),
le produit des lois jointes des couples (vraisemblance par paires, pairwise
likelihood) ou le produit des lois des triplets d'observations (vraisemblance
par triplet, tripletwise likelihood) qui sont basées respectivement sur
les événements marginaux, des couples et des triplets
d'observations. Nous aurons ainsi pour n observations
y1,...,yn :
- la vraisemblance par paires Lcl(ö; Y ) =
11n fYi,Yj(Yi, Yj; ö)ùij
i>j=1
- la vraisemblance par triplet Lcl(ö;Y) = 11
i>j>k=1
|
fYi,Yj,Yk(Yi,Yj,Yk;ö)ùijk
|
oil (ùij) et (ùijk) sont
des systèmes de pondération, positifs ou nuls. Aussi, il est
possible de considérer par exemple une combinaison de la vraisemblance
par paires et de vraisemblance simple ; ce qui correspondrait à la
méthode de la pseudo-vraisemblance de Cox et Reid (2004).
La log-vraisemblance composite,tcl(ö; Y ), est
donc une somme de logvraisemblances d'événements conditionnels ou
marginaux qui peuvent être calculées (Lindsay, 1988).
Estimation des paramètres du modèle En reprenant
les notations de la définition 2, l'estimateur du maximum de
vraisemblance composite est défini par :
|
àöcl = argmax
öEÖ
|
`cl(ö; Y )
|
et est solution de l'équation :
Vecl(ö; Y ) = E ùiV log{f(y ? Ai; ö)} = 0,
iEI
àöcl
appelée, fonction score composite
De plus, Varin et Vidoni (2005) démontrent le
théorème suivant :
Théorème 1 L'estimateur du maximum de la
vraisemblance composite du paramètre ö est consistant, a une
distribution asymptotique gaussienne de moyenne ö et de matrice
de variance-covariance
H(ö)-1J(ö)[H(ö)-1]1 :
àöcl ?N{ö,
H(ö)-1J(ö)[H(ö)-1]1},
L
avec H(ö) = Ef(y;ö0){V2tcl(ö; y)},
J(ö) = V{Vicl(ö; y)} et où ö0, le vrai
paramètre, appartient à l'intérieur de Ö.
1.3.2 La vraisemblance composite par paires pour
l'estimation de l'apparentement
Nous donnons maintenant la définition du modèle
de l'apparentement génétique pour n individus (C couples) ; ce
modèle généralise celui de Milligan. Nous
définissons ensuite l'estimateur de l'apparentement
génétique par maximum de vraisemblance composite par paires.
Définition 3 (Vraisemblance composite par paires pour
l'apparentement) Soient g = (g1, g2, . . . , gn) le
vecteur de n génotypes observés en L loci indépendants.
Soient IBSl cle mode d'IBS au locus l du couple c. Soit
IBDc
le mode d'IBD du couple c. Soit Ä = (Äc)c=1,...,C le
vecteur des paramètres dont chacune des composantes
Äc est le vecteur des probabilités d'IBD des
allèles du couple c. La vraisemblance composite par paires
Lcp du paramètre Ä est définie par
|
Lcp(Ä; IBS) =
|
11C
c=1
|
11L
l=1
|
9
X
i=1
|
P (IBSlj,c|IBDi,c) Äi,c, j ? {1, . .
. , 9}. (1.6)
|
et la log-vraisemblance composite par paires associée est
donnée par tcp(Ä; IBS) = log
(Lcp(Ä; IBS)) .
L'estimateur du maximum de vraisemblance composite par paires de
l'apparentement Ä noté 3Äcp est solution
de V (tcp(Ä; IBS)) et s'écrit
3Äcp = ( 3Ä71:c,...,3Äc9pc .
)c=1,...C
L'expression du coefficient d'apparentement donnée par
l'Equation 6 dans l'introduction et la propriété d'invariance
fonctionnelle (Saporta, 1990) garantissent que
|
3ècp
c
|
3,7, + 21 (++3Ä)+ 413'7,c
|
est l'estimateur du maximum de vraisemblance composite par paires
du coefficient d'apparentement èc du couple c.
1.4 Prise en compte de l'information spatiale
L'une des hypothèses fortes du travail réside
dans le fait que deux individus ont d'autant plus de chance d'avoir des
allèles IBD qu'ils sont spatialement proches.
Nous proposons, dans la suite, un modèle
hiérarchique bayésien pour l'apparentement en prenant en compte
l'information spatiale. L'intérêt de la modélisation
hiérarchique bayésienne est que cette approche permet de scinder
un problème complexe en une certaine série de problèmes
relativement plus simples à traiter (Wikle, 2003). Le principe de la
modélisation hiérarchique est basé sur le simple fait que
la loi jointe d'un certain nombre de variables aléatoires peut toujours
être décomposée en un produit de lois conditionnelles
(Wikle, 2003). Par exemple si on considère 3 variables aléatoires
X, Y Z, la distribution jointe de ces variables est
ðX,Y,Z(X, Y, Z) = ðX|Y,Z(X|Y, Z)ðY |Z(Y
|Z)ðZ(Z).
Cette formule constitue le noeud de la modélisation
hiérarchique. La modélisation d'un processus complexe ayant une
loi jointe qui est difficile à spécifier peut ainsi être
faite avec un modèle hiérarchique comportant au moins trois
niveaux de base (Wikle, 2003) :
1. niveau des données Y : ce niveau permet
d'expliciter la loi des observations conditionnellement à un process
latent et à un ensemble de paramètres ö1. Cela permet donc
d'expliciter la vraisemblance;
2. niveau du processus ç : ce niveau permet de stipuler
la loi du processus latent conditionnellement à un second ensemble de
paramètres ö2
3. niveau des paramètres ö : ce niveau permet de
décrire en terme de loi de probabilité, les connaissances a
priori que l'on a des paramètres, ö1 et ö2, définis
dans les deux premiers niveaux .
Dans le cadre Bayésien, nous nous intéressons
à la distribution jointe a posteriori du processus latent et des
paramètres sachant les données. D'après le
théorème de Bayes :
ðç,ö1,ö2|Y (ç, ö1, ö2|Y ) ?
ðY |ç,ö1(Y |ç,
ö1)ðç|ö2(ç|ö2)ðö1,ö2(ö1,ö2)
1.4.1 Version hiérarchique bayésienne du
modèle de Milligan
Le modèle de Milligan peut être décrit de
manière hiérarchique bayésienne.
Definition 4 Soit IBS = (IBS1, . . . ,
IBSL) le vecteur aléatoire du mode d'IBS pour L Locus
indépendants. Soit IBD = (IBD1, . . . , IBDL), le
vecteur aléatoire latent du mode d'IBD pour les L loci. Le modèle
hiérarchique bayésien de l'apparentement est donné par les
équations suivantes :
- niveau des données
ðIBS|IBD(IBS|IBD) = 11L
ðIBSl|IBDl(IBSl|IBDl) (1.7)
l=1
où ðIBSl|IBDl(IBSl|IBDl) désigne
une loi multinomiale M (1; pl 1,. . .
,pl9), pli sont les
probabilités d'IBS sachant le mode d'IBD au locus l donnés
dans le tableau 1.1. Ce premier niveau décrit l'indépendance
conditionnelle des modes d'IBS sachant les modes d'IBD.
- niveau du processus
ðIBD|Ä(IBD|A) = 11L
ðIBDl|Ä(IBDl|A) (1.8)
l=1
où ðIBDl|Ä(IBDl|A) est une loi
multinomial M (1, A1, . . . , A9). Ce deuxième niveau
reflète l'indépendance entre locus.
- niveau des paramètres
ðÄ(A) = D (u1, . . . , u9) (1.9)
où D est une loi de dirichlet et les u = u1, . . . , u9
sont donnés.
Dans l'approche bayésienne, un vecteur latente, mode
d'IBD, IBD = (IBD1,...,IBDL), est introduit et
dépend du locus.
La généralisation que nous proposons va consister
à modéliser différemment, le vecteur latent du mode
d'IBD.
Hypothèses Nous supposons que les individus de la
population ne sont pas consanguins, c'est à dire que leurs parents ne
sont pas apparentés. Ainsi, les modes d'IBD possibles des allèles
de 2 individus sont réduits uniquement aux 3 cas suivants :
- les individus n'ont aucun allèle IBD, ils sont IBD9 ;
c'est le cas s'ils n'ont par exemple aucun parent en commun
les individus ont 1 allèle IBD, ils sont IBD8 ; ceci
n'est possible que s'ils ont au moins un parent en commun (même
père ou même mère)
- les individus ont 2 allèles IBD, ils sont IBD7 ; ceci
n'est possible que lorsqu'ils ont deux parents en commun
Ce qui est important avec cette hypothèse, c'est qu'un
couple de génotypes donné ne présente donc qu'une seule
possibilité d'avoir aucun allèle, un allèle ou deux
allèles identiques par descendance (cf Figure 3). Cette hypothèse
nous permet de définir une structure d'ordre qui est relative à
la similarité
des allèles d'un couple d'individus. Avec
l'hypothèse que la similarité allélique de deux individus
est ordonnée et si nous supposons que le mode d'IBD suit une loi
multinomiale, nous proposons de modéliser le mode d'IBD avec un GLM
probit ordinal, décrit en terme de variable latente gaussienne (voir
(McCullagh et Nelder, 1989, Chapitre 5)).
Modèle spatial hiérarchique bayésien Nous
proposons un premier modèle spatial hiérarchique. Nous ne
présentons pas ici la loi a priori des paramètres, uniquement les
deux premiers niveaux de la modélisation hiérarchique :
- niveau des données
|
ðIBS|IBD(IBS|IBD) =
|
YC
c=1
|
YL
l=1
|
ðIBS|IBD(IBSl c|IBDl
c)
|
oil ðIBSlc|IBDlc(IBSl c|IBDl
c) est une loi multinomiale M(1,pl
1,pl 2, . . . ,pl 9) avec les
pl i, i = 1, . . . , 9 des fonctions polynômiales
des fréquences alléliques au locus l = 1, .. . , L donné
au Tableau 1.1. Ce premier niveau décrit l'indépendance
conditionnelle des modes d'IBS entre individus et entre locus sachant les modes
d'IBD.
niveau du processus
P (IBDl i,c|ak-1, ak,ç~ = P (Zl c ?]ak-1,
ak]|ç) , i = 7,8,9 ðZlc|ç(Zl c|ç) = N
[hç(dc),1]
oil les ak sont des seuils tels que ak-1 < ak et soient
égaux à -8, 0, a ou +8}. Comme la variable IBD est ordinale
à trois modalités, seul un seuil, nommé aussi a, est
inconnu.
Une première approche consiste à
modéliser hç(dc) comme une fonction
linéaire de la distance,
hç(dc) = ii + udc
avec ç = (ii, u) un vecteur de paramètres
inconnus. Le problème posé par ce modèle est que comme la
distance spatiale est la seule variable explicative dans l'expression de la
moyenne de la variable latente et donc la seule variable permettant de
distinguer les couples entre eux, nous risquons de la conserver dans le
modèle même si en réalité elle n'est pas
significativement discriminante. Nous proposons une autre approche de
modélisation qui consiste à introduire une couche
supplémentaire dans le modèle hiérarchique
bayésien. Cette couche correspond à un effet du couple
considéré et cet effet dépend de la distance entre les
individus constituant le couple. Le modèle spatial hiérarchique
bayésien pour l'apparentement est donné par la définition
suivante.
Définition 5 (Modèle spatial hiérarchique
pour l'apparentement) Soient (g1, . . . , gn), le
génotype de n individus issus d'une population non con-sanguine
et observés sur L locus indépendants. Soit c =
1, ...,C les C couples associés aux n individus. Soient I BDc
= (I BDc1, . . . , I BDcL) le
vecteur aléatoire des modes d'IBD du couple c au L
oùIBDlc est une variable aléatoire ordinale
à trois modalités. On note IBD le vecteur des modes d'IBD
pour tous les couples à tous les loci. Soient IBSc =
(IBS1 c,. . . , I BSS) le vecteur des modes
d'IBD du couple c aux différents locus L et IBS le vecteur des
modes d'IBS pour tous les couples à tous les loci. Soit d = (d1, .
. . , dC) le vecteur des distances géographiques
observées entre les couples. Le modèle spatial
hiérarchique bayésien de l'apparentement est donnés par
les équations (1.10), (1.11), (1.12) et (1.13)
ðIBS|IBD(IBS|IBD) = 11C
11L
ðIBSl|IBDl(IBSlc|IBDlc)
(1.10)
c=1 l=1
où ðIBSl|IBDl(IBSlc|IBDlc) est une loi
multinomial M(1,pl 1,pl 2,. . .
,pl9) avec les pli, i = 1,
. . . , 9 sont des fonctions polynômiales des fréquences
alléliques au locus l = 1, . . . , L qui sont donnés au
Tableau 1.1. Ce premier niveau décrit l'indépendance
conditionnelle des modes d'IBS entre individus et entre locus sachant
les modes d'IBD des couple d'individus à tous les locus. De
plus, Il existe un vecteur Z aléatoire latent gaussien, de longeur
L × C, tel que
P (IBDL|ák-1, ák, çc)
= P (Zlc ?] ák-1, ák]
|çc) , i = 7, 8, 9 (1.11)
avec
ðZlc|çc(Zlc|çc)
= N (çc, 1) (1.12)
et où les ák sont des seuils tels que
ák-1 < ák et soient égaux à -8, 0, á ou
+8}. Comme la variable IBD est ordinale à trois modalités, seul
un seuil, nommé aussi á, est inconnu.
ð(çc|u,í,
ó2ç) = N(u + ídc,
ó2ç) (1.13)
où ç = (u, í,
ó2ç) est un vecteur de paramètres
inconnus.
En particulier
e--(z-71.)2dz,
P(/BA,c177c) --
P(I BDl9,c|çc) =
c)2dz
et P(IBD,l7 = 1 e-v12ð
f0 8
,c c .0.71- f á (z-çc)2dz. v12
/r0 e--
(z-71 1
1.5 Conclusion
Dans ce chapitre nous avons présenté le
modèle de Milligan qui utilise les méthodes du maximum de
vraisemblance. Nous avons montré comment prendre en compte
simultanément n génotypes. Nous avons mis en évidence que
l'approche de milligan pour n individus pouvait se traiter en utilisant la
théorie de la vraisemblance composite. Nous avons alors
généralisé le modèle de Milligan en
définissant la vraisemblance composite par paires pour l'apparentement
et donné les propriétés statistiques de l'estimateur de
l'apparentement génétique par maximum de vraisemblance composite
par paires. Nous avons ensuite supposé que les individus sont
non-consanguins et que le mode d'IBD suit une loi multinomiale ordinale. Ces
hypothèses nous ont permis de modéliser l'identité par
descendance avec un GLM probit en terme de variable latente gaussienne. Nous
avons supposé que deux individus ont plus de chance d'avoir des
allèles identiques par descendance s'ils sont spatialement proches et
défini ensuite un premier modèle spatial hiérarchique
bayésien pour l'apparentement. Le problème posé par ce
modèle est que comme les couples d'individus ne se distinguent que par
la distance spatiale entre les individus, la distance spatiale risque
d'être conservée même si elle n'est pas significative. Nous
avons défini un second modèle spatial hiérarchique
bayésien pour l'apparentement qui prend en compte l'effet des couples
d'individus. Contrairement au premier modèle, la moyenne de la variable
latente dans ce second modèle ne dépend pas de la distance
spatiale mais c'est la moyenne de l'effet du couple qui est fonction de la
distance spatiale. Le modèle que nous avons développé
permet de prendre en compte de manière générale des
covariables pour estimer l'apparentement génétique entre
plusieurs couples d'individus. D'autres covariables pourraient aussi être
prises en compte. Nous citons, par exemple, la zone d'étude et le
producteur. En effet, on pourrait aussi considérer qu'au sein d'un
même site de production ou chez un producteur donné, les
génotypes des individus concernés sont plus ou moins
génétiquement similaires comparativement à des individus
ne provenant pas du même site ou du même producteur. Ce
modèle offre aussi la possibilité d'estimer les fréquences
alléliques et de prendre en compte la dépendance entre les
couples d'individus. Nous proposons au chapitre suivant un modèle
bayésien pour estimer à la fois l'apparentement
génétique et l'héritabilité des caractères
lorsque le pedigree n'est pas connu.
Chapitre 2
Modélisation des paramètres
génétiques en milieu naturel
2.1 Introduction
L'enjeu que constitue l'estimation de la variance
génétique et de l'héritabilité des
caractères dans le domaine de l'amélioration
génétique des plantes ou des animaux a déjà
été souligné dans l'introduction générale de
ce travail. L'héritabilité d'un caractère est un
indicateur de la possibilité, pour une population donnée, de
répondre à la sélection et reflète le potentiel
d'évolution de cette population (Thomas et al., 2000). La connaissance
de la covariance entre les caractères quantitatifs d'individus
apparentés permet d'estimer l'héritabilité d'un
caractère (Falconer, 1974; Ritland, 1996b). De manière classique,
des dispositifs expérimentaux bien précis sont mis en place et
les relations de parenté sont donc connues (Lynch et Walsh, 1998; Thomas
et al., 2000). Lorsque les relations généalogiques entre les
individus sont connues, il est possible de calculer les coefficients
d'apparentement puis d'estimer la variation génétique à
partir de mesures faites sur les individus (Moore et Kukuk, 2002). Mais en
milieu naturel, l'apparentement entre les individus est inconnu.
L'objectif dans cette partie est de proposer un modèle
qui permet d'estimer simultanément l'apparentement et
l'héritabilité sans connaissance du pedigree. Tout d'abord nous
rappelons le lien entre variance phénotypique et génétique
puis nous présentons rapidement les modèles existants pour
l'estimation de l'héritabilité en milieu naturel. La
dernière partie est consacré au développement d'un
modèle hiérarchique bayésien qui permet d'estimer
simultanément l'apparentement et l'héritabilité.
2.2 Covariance phénotypique et covariance
génétique
Les modèles de génétique quantitative
classiquement utilisés (Lynch et Walsh, 1998), sont exprimés en
terme de modèles linéaires mixtes :
Y = X3 + a + (2.1)
où Y = (Y1, .. . , Yn) est le vecteur
phénotypique de m individus, X une ma-trice m×q de co-variables, 3
les effets fixes associé, a = (a1, .. . , an) le vecteur des
effets génétiques additifs individuels supposé gaussien
d'espérance nulle et de matrice de variance covariance Va.
Enfin, = ( 1,.. . , n) est un vecteur de résidus
supposé gaussien d'espérance nulle et de matrice de variance
covariance Vå = ó2 åId
où Id désigne la matrice identité. En supposant que les
vecteurs a et ne sont pas corrélés, l'espérance et la
matrice de variance-covariance du vecteur des observations Y sont
E(Y) = X3
et
V2 Y = Va + ó2
å.
Le premier terme de cette dernière expression
correspond à la contribution de la variance des effets
génétiques additifs et le second terme correspond à celle
des résidus. Les effets fixes influence donc l'espérance des Y
tandis que les effets aléatoires influencent la variance et la
covariance des Y .
Dans le cas de populations diploïdes, l'effet
génétique individuel a se décompose en deux parties. La
première am correspond à la part
génétique héritée de la mère in, et la
seconde ap correspond à la part génétique
héritée du père p. Si les effets de dominance et
d'épistasie sont nuls, le modèle s'écrit
Y = X3 + am + ap +
Si les effets sont distribués selon une gaussienne
d'espérance nulle et de même variance (même population
d'effets), la covariance phénotypique entre les individus 1 et 2, est
égale à
CovY1,Y2 = Covam1+ap1+å1,am2+ap2+å2
= Covam1+ap1,am2+ap2
= Covam1,am2 + Covam1,ap2 + Covap1,am2 + Covap1,am2
Le calcul de CovY1,Y2 dépend du patrimoine
génétique commun que partage les deux individus et donc de leur
degrés d'apparentement (Lynch et Walsh, 1998). Les deux individus
partagent des gènes identiques par descendance avec la
probabilité è. Comme les effets sont issus de la même
distribution gaussienne, On en déduit que
CovY1,Y2 = 4èE(amap).
Or les parents ne transmettent que la moitié de leur
patrimoine génétique, 4èE(amap)
correspond au double de la variance génétique additive que
multiplie la probabilité que les gènes tirés
aléatoirement chez les deux individus soit IBD. Donc
CovY1,Y2 = 2è12ó2 a = ó2 ar12.
oil ó2 a désigne la variance additive,
è12 le coefficient d'apparentement ("co-ancestry") et r12 =
2è12 le coefficient de parenté (relatedness coefficient, cf
introduction). Ainsi, dans un modèle de génétique additif
Va = Ró2 a et les effets individuels sont
a = (a1,...,an) ~ N(0,ó2
aR)
oil R est la matrice des coefficients de parenté entre
tous les couples d'individus.
2.3 Revue des modèles classiques pour
l'estimation de l'héritabilité en milieu naturel
Nous avons déjà relevé que les
modèles pour l'estimation de l'apparentement génétique
à l'aide des données moléculaires pouvaient être
regroupées en deux catégories : ceux qui sont basés sur
les moments et ceux basés sur la vraisemblance. De même, les
méthodologies développées permettant de combiner à
la fois l'information apportée par les données
moléculaires et l'information phénotypique pour estimer
l'héritabilité, lorsque le pedigree n'est pas connu, peuvent
être classées en deux catégories (Ritland, 1996b; Mousseau
et al., 1998; Thomas et Hill, 2000; Thomas, 2005). La première approche,
développée par Ritland (1996b), est basée sur une
procédure de régression linéaire simple (Moore et Kukuk,
2002).La seconde famille, développée par (Mousseau et al., 1998;
Thomas et Hill, 2000), est basées sur des approches par maximum de
vraisemblance.
2.3.1 Modèle de régression linéaire
pour l'estimation de l'héritabilité
Soient Y = (Y1, . . . , Yn) le phénotype de n
individus. L'approche proposée par Ritland (1996b) repose sur la
similarité phénotypique Zc entre les C
couples d'individu et est définie par
|
(Yi--
Zc =
|
Y )(Yj --
|
Y )
|
|
ó2
Y
|
|
avec Y et ó2Y sont la
moyenne et la variance empirique des Y . Le modèle de régression
proposé par Ritland (1996b), pour l'héritabilité du
caractère, est
Zc = 2èch2 +
åc (2.2)
oil h2 est l'héritabilité au sens
strict, èc le coefficient d'apparentement entre les individus
du couple c et åc un terme résiduel. Dans ce
modèle, le coefficient d'apparentement est supposé connu. Il est
en fait substitué par la valeur de son estimation. Il s'agit d'un
modèle de régression linéaire oil h2
est le paramètre à estimer et è est la variable
indépendante. L'estimateur de l'héritabilité au sens
strict est donné par
h2 = Cov(Zc, èc) ,
2Vè
Vè étant la variance vraie du coefficient
d'apparentement moyen entre toutes les paires d'individus. La variance vraie de
l'apparentement est due à la présence de différents modes
d'apparentement dans la population (par exemple la présence à la
fois de couples de pleins-frères, de demi-frères et de
nonapparentés) (Ritland, 2000). L'expression de Vè dépend
de la méthode d'estimation utilisée. En utilisant l'estimateur
qu'il propose dans Ritland (1996a), Ritland (1996b) montre que l'estimateur de
Vè est égal à
|
bVè = 1
C
|
XC
c=1
|
?
? ?
|
{E
|
2
L l=1 -- El=1 ù2l
àèl,c
|
?
? ?
|
1
|
XC
c=1
|
2
àèc ) .
|
|
L (.02
1 -- El=1 l
|
C
|
oil àèc est l'estimateur
de l'apparentement entre les individus du couple c au locus L. Ce modèle
a été appliqué récemment pour l'estimation de
l'héritabilité dans une population de Karité au Mali
(Bouvet et al., 2008).
2.3.2 Modèle de la vraisemblance pour l'estimation
de l'héritabilité
Le modèle de la vraisemblance pour l'estimation de
l'héritabilité développé par (Mousseau et al.,
1998) est basé sur l'hypothèse que la distribution de
l'apparentement entre les individus est connue. (Mousseau et al., 1998)se place
dans le cadre oil les individus sont soit non-apparentés soit
plein-frères. De plus, la variabilité génétique est
aussi supposée purement additive et il n'y a pas d'effet d'environnement
ni d'effet maternel. Sous ces hypothèses, la corrélation attendue
entre les caractères quantitatifs de deux individus est égale
à 2èh2 ; la corrélation attendue entre les
caractères quantitatifs est nulle si les individus sont
non-apparentés et vaut 0.5h2 s'ils les individus sont
plein-frères comme è = 1/4 dans ce dernier cas (Mousseau et al.,
1998).
Soit Y le phenotype de m individus. On suppose que le
génotype g des individus à au moins un locus pour les m individus
est disponible. La distribution des caractères quantitatifs de deux
individus peut être définie selon trois approches
différentes. La première approche consiste à
considérer que le couple (Y1, Y2) a une distribution bivariée
dont l'apparentement et l'héritabilité affectent uniquement le
terme de covariance. La seconde approche revient à dire que le produit
Y1Y2 suit une distribution univariée dont seule la moyenne
est fonction de l'apparentement et de l'héritabilité. Une
dernière approche est de considérer que la somme Y1 + Y2 a une
distribution univariée dont seule la variance et non la moyenne est
fonction de l'apparentement et de l'héritabilité.
L'inconvénient de la seconde approche est que si nous considérons
que la distribution des Yi, i = 1, 2 est une gaussienne, la distribution des
Y1Y2 est asymétrique et donc il faudrait plutôt choisir
une distribution non gaussienne. Les deux autres approches (la première
et la troisième) présentent essentiellement les mêmes
avantages. En effet, elles exploitent toutes les deux essentiellement la
même information à partir des données et finalement la
dernière est retenue par (Mousseau et al., 1998). Mousseau et al. (1998)
donne les probabilités conditionnelles d'observer un couple de
génotype (g1, g2), à un locus, sachant que les individus ont soit
indépendants (ma) soit pleins frères (pf). Ces
probabilités sont données dans le Tableau 2.1. Notons P
(Gl 1, Gl 2|ma) et P (Gl 1,
Gl 2|pf) les probabilités d'observer à un
locus, l, d'un couple sachant que les individus sont respectivement
non-apparentés et plein-frères. La probabilité d'observer
des genotypes en plusieurs locus indépendants conditionnellement au mode
de parenté d'un couple est tout simplement le produit des
probabilités conditionnelles du couple de génotypes
observé à chaque locus. Notons u et ó2 la
moyenne et la variance de la variable aléatoire Y et considérons
maintenant Y 1 ' = (Y1--u)/ó la valeur phénotypique
centrée et réduite de Y pour l'individu 1. L'espérance
Probabilité des marqueurs sachant que les individus
sont
Génotype du couple non apparentés
plein-frères
AiAi - AiAi p i2 (1 + pi)2/4
AiAj - AiAj 4pipj (1 + pi + pj + 2pipj)/2
AiAi - AiAj 4pi 1 + pi
AiAj - AiAk 4pi (1 + 2pi)/2
AiAj - AkAl 1 1/4
TAB. 2.1 --- Probabilité d'observer un couple de
génotypes, à un locus chez des individus diploïdes,
conditionnellement à leur mode d'apparentement : non-apparentés
ou plein-frères. Les indices j, k et l représentent des
allèles mutuellement différents de l'allèle i.
de Y10 +Y20 est
nulle et sa variance est égale à 2 si les individus 1 et 2 ne
sont pas apparentés et est égale à 2 + h2 si le
couple est plein-frère. Mousseau et al. (1998) proposent un
modèle de mélange pour l'héritabilité :
L(h2) = 11 [(1 ? ë) 11 P
Wl1,Gl2|na)ö(Y 0
i + Yj0, 0,2)
i<j l=1
+ë 11L
l=1
P Gl2|p f) ö(Y 0i + Yj0, 0,
2 + h2)]
avec ö(Y, 0, ó2) est la fonction de
densité gaussienne centrée et de variance ó2,
ë la proportion de mélange qui est supposée connue.
Thomas et al. (2000) ont généralisé le
modèle de mélange proposé par Mousseau et al. (1998) pour
prendre en compte simultanément d'autres structures de parenté
prédéterminées, par exemple une population composée
de non-apparentés, de demi-frères et de plein-frères.
2.4 Modèle pour l'estimation de l'apparente-
ment et de l'héritabilité en milieu
naturel
Les modèles classiques permettent d'estimer
l'héritabilité en milieu naturel lorsque le coefficient
d'apparentement (Ritland, 1996b) ou le mode d'apparentement (Mousseau et al.,
1998) est supposé connu. Mais le plus sou-vent, en milieu naturel,
l'apparentement n'est pas connu et il est estimé à l'aide des
données moléculaires. Le modèle de régression
linéaire de Ritland (1996b) peut être utilisé en estimant
préalablement l'apparentement entre
les individus avant d'estimer l'héritabilité.
L'inconvénient est que l'effet de la variabilité de
l'apparentement sur l'estimation de l'héritabilité n'est pas
prise en compte. Le modèle de Mousseau et al. (1998) considère
par contre qu'un couple d'individus donné ne peut avoir qu'un certain
nombre de types de parenté; par exemple que deux individus sont soit
pleins-frères soit nonapparentés. En milieu naturel, il est
souvent difficile d'envisager que les individus ne peuvent avoir que certains
types de parenté. Le plus souvent, l'apparentement varie dans ces
conditions sur une échelle continue. Deux solutions sont possibles : la
première solution est d'estimer d'abord l'apparentement puis
l'héritabilité; une seconde solution consiste à estimer
simultanément l'apparentement et l'héritabilité en
utilisant les données moléculaires et les données
phénotypiques. L'inconvénient de la première solution est
qu'il est possible que la matrice d'apparentement estimée
préalablement ne soit pas une matrice définie- positive. La
seconde solution d'une part nous assure par contre que la matrice
d'apparentement obtenue est bien définie-positive et d'autre part elle
permet de tenir compte de la variabilité de l'estimation de
l'apparentement dans l'estimation de l'héritabilité. Nous
proposons un modèle pour estimer à la fois l'apparentement et
l'héritabilité en milieu naturel en utilisant les données
moléculaires. L'approche choisie est celle d'un modèle
bayésien hiérarchique. La raison du choix d'un modèle
bayésien hiérarchique est que, conditionnellement au vecteur des
probabilités d'IBD, donc de la connaissance de la matrice
d'apparentement, la loi du phénotype et du mode d'identité par
état est connue.
2.4.1 Modèle bayésien hiérarchique
Soient y le vecteur des n phénotypes, a = (a1,. . . ,
an) les effets génétiques additifs associés aux
n individus. Le modèle de génétique quantitative additif
(cf Equation 1 de l'introduction) peut être formulé de
manière hiérarchique :
Yi|u, ai, óå ~ N (u + ai,
ó2 å) a = (a1, . . . , an)
|ó2 a, R ~ N(0,ó2
aR),
oil ó2 å est la variance résiduelle, Id
désigne la matrice identité, ó2 a la variance additive et
R la matrice de parenté (R = 2È) entre tous les individus qui
dépend des probabilités d'IBD. Le modèle défini par
les equations suivantes permet d'estimer simultanément
l'héritabilité d'un caractère phénotypique et
l'apparentement entre les individus
Le modèle hiérarchique bayésien est
défini par les équations suivantes :
1. modèle des données (phénotype et
IBS)
ðY |u,a,ó2å(Y |u, a,
ó2å) = 11n N (u + ai,
ó2åId) (2.3)
i=1
|
ðIBS|0(IBS|Ä) =
|
11C
c=1
|
L 9
11
EP(IBSlj,c|IBDli,c)Äi,c}
(2.4)
l=1 i=1
|
pour j = 1, . . . , 9 et Id la matrice identité. Ce
premier niveau exprime le fait d'une part que conditionnellement aux effets
génétiques additifs, les phénotypes sont
indépendants et d'autre part que les phénotypes et les IBS sont
indépendants.
2. modèle du processus
ða|ó2a,R(a|ó2a,
R) = Nn(0,ó2aR)
|
|
(2.5)
|
3. modèle des paramètres
ð0(Ä)
= 11C ðÄc(Äc) =
11C D(u1, . .
c=1 c=1
ðu(u) = N(0,
ó2u)
|
|
. , u9)
|
(2.6)
(2.7)
|
|
|
ðóa(ó2a) =
IG(ma, sa)
|
|
(2.8)
|
|
ðó2å(ó2å)
= IG(må, så)
|
|
(2.9)
|
Nous supposons donc a priori que les Ä sont
indépendants entre individus et tous tirés selon la même
loi de Dirichlet oil les paramètres u sont fixés. De plus, nous
supposons que les paramètres Ä, u, ó2a
et ó2å sont indépendants. Enfin, IG
désigne une loi inverse Gamma oil les paramètres m. et
s. sont fixés.
2.4.2 Lois a posteriori des paramètres
La densité de la loi jointe a posteriori des
paramètres du modèle est
ða,0,u,óa,cl|y,IBS (a,
Ä, u, óa, óå|y, IBS) ?
ðy|u,a,ó1 (y|u, a,
óå)ðIBS|Ä(IBS|Ä)
2 2
ða|óa,R(a|óa, R)ð0
(Ä)ðu(u)ðóa(óa)ð4
(óå).
La densité de la loi conditionnelle complète a
posteriori de chacun des paramètres est déduite de la
densité de la loi jointe a posteriori en considérant cette
dernière comme une fonction du paramètre qui nous
intéresse, les données et les autres paramètres
étant fixés (Sorensen et Gianola, 2007).
La densité de la loi conditionnelle complète a
posteriori du vecteur des effets génétiques est
ða|y,IBS,R,u,óa,4 (a| y, IBS, R, u, ó,!,
óå2 \
) ? ðy|u,a,ó1 (y|u, a,
óå)ða|óa,R(a|óa, R)
~ ~
? ~ó2 -(y - u - a)0 (y - u - a)
~-n/2 exp ×
å 2ó2 å
~ ~
(det(ó2aR))-1/2 exp - 12
a'R-1a
2óa
? (óå21n/2 (det
(óa2R)) -1/2 × ~
~
-(y - u - a)0 (y - u - a) -
1
exp a0R-1a .
2ó2 2ó2
å a
En développant cette dernière expression, on peut
montrer que a|y, IBS, A, u,ó2a,
ó2å ~ N(ua|y, Óa|y)
avec
ua|y = óå 2Óa|y(y - u)
et
~ 2
óa ) -1
å R-1
Óa|y = óå I + 2
- La densité de la loi conditionnelle complète a
posteriori du vecteur A des probabilités d'IBD est
ðA|y,IBS,a,óa(A|y, IBS, a,
ó2a) ?
ðIBS|A(IBS|A)ða|óa,R(a|ó2a,
R)ðA(A)
?
ðIBS|A(IBS|A)ða|óa,R(a|ó2a, R)
? 11C 11L
c=1 l=1
9
E
P(IBSlj,c|IBDli,c)Äi,c
×
i=7
~
(det(óa2R)) 1/2 exp- 1 a'R-1a)
2ó2a pour j = 1, . . . , 9.
- En faisant le même raisonnement que pour a, la
densité de la loi conditionnelle complète a posteriori de la
moyenne u est
ó2 ó
ðu|y,a4(u|y, a, ó) = N { (Id + å )
(y ? a), ó (Id + ó:
u u
La densité de la loi conditionnelle complète a
posteriori de la variance génétique additive est
ðó2 a|a,R,ma,sa(ó2 a|a, R,
ma, sa) ? ða|ó2
a,R,ma,sa(a|ó2 a, R, ma,
sa)ðó2 a(ó2
a)
~
sma
a
? (det(óa2R)) 1/2 exp 2a' R-1 a)
× ó2a
(ma)(ó2a)-(ma+1) exp(-sa/ó2a)
~
?
~ó2 ~-n/2 (ó2
-a0R-1a + 2sa
a)-(ma+1) exp
a 2ó2
a
? (ó2)-( n+22 ma +1) (
afR-1a + 2sa
exp
2óa2


oil est la fonction gamma, Nous reconnaissons, dans cette
dernière expression, une loi inverse-gamma de paramètres
et
sa|y =
al R-1a
2 + sa.
- En procédant de la même manière, on
obtient la densité de la loi conditionnelle a posteriori complète
de ó2e qui est une inverse-gamma de
paramètres
et
(P - u - a)'(P - u - a)
så|y = 2 + så.
2.5 Conclusion
Nous avons, dans ce chapitre, d'abord présenté
les modèles classiques pour l'estimation de l'héritabilité
en milieu naturel à l'aide des données moléculaires. Le
premier modèle présenté, celui de Ritland (1996a), repose
sur une procédure de régression linéaire. Ce modèle
consiste à écrire la similarité génotypique des
couples d'individus en fonction de leur apparentement. Ce modèle est,
à première vue, bien adapté à l'estimation de
l'héritabilité en milieu naturel vu que dans ce contexte
l'apparentement varie sur une échelle continue. Cependant, comme en
milieu naturel, l'apparentement génétique n'est
justement pas connu, il est estimé, la
variabilité de l'estimation de l'apparentement doit être prise en
compte et le modèle de Ritland ne prend pas bien en compte cette
variabilité. Mousseau et al. (1998) ont développé un
modèle de la vraisemblance pour estimer l'héritabilité et
les corrélations génétiques. Ce modèle suppose que
la structure d'apparentement est connue : les individus sont soit
plein-frères soit non apparentés. Il a été
appliqué à une population de saumons en captivité
composée uniquement de familles de plein-frères. Ce modèle
a été généralisé par Thomas et al. (2000)
pour prendre en compte d'autres structures d'apparentement
prédéterminées (non-apparentés, demifrères,
plein-frères par exemple). L'application pratique de ces modèles
à des études réalisées en milieu naturel est
confrontée au fait qu'en milieu naturel l'apparentement varie, comme
nous l'avons déjà indiqué, sur une échelle
continue. Nous avons proposé une approche pour modéliser à
la fois l'apparentement et l'héritabilité. Il s'agit d'un
modèle bayésien hiérarchique pour l'apparentement et
l'héritabilité. L'intérêt de ce modèle est
d'une part, qu'il nous libère de devoir faire des hypothèses sur
la structuration de l'apparentement en un certain nombre de classes
prédéterminées, et d'autre part, qu'il permet de prendre
en compte l'effet de la variabilité de l'estimation du vecteur des
probabilités d'IBD sur l'estimation de la variance
génétique additive. Ce modèle nous assure enfin que la
matrice d'apparentement des couples d'individus est bien
définie-positive.
Chapitre 3
Estimation des paramètres
génétiques en milieu naturel
L'objectif dans ce chapitre est de proposer des
méthodes d'estimation des paramètres génétiques en
milieu naturel. Comme nous avons choisi de nous placer dans un cadre
bayésien, nous rappelons tout d'abord les outils nécessaires pour
l'inférence statistique bayésienne, notamment les méthodes
de Monte Carlo et les méthodes de Monte Carlo par Chaînes de
Markov (MCMC). Nous proposons ensuite trois algorithmes pour l'estimation de
l'apparentement en milieu naturel. Les 2 premiers algorithmes sont des
algorithmes de Metropolis-Hastings et la différence entre ces
algorithmes est principalement liée au choix de la loi de proposition.
Nous présentons ensuite un algorithme pour estimer à la fois
l'apparentement et l'héritabilité lorsque le pedigree n'est pas
connu.
3.1 L'inférence statistique bayésienne et
les méthodes de Monte Carlo par Chaînes de Markov
Les méthodes statistiques fréquentistes
considèrent les paramètres comme des quantités fixes alors
que les méthodes statistiques bayésiennes considérent les
paramètres comme des variables aléatoires. La différence
principale entre l'approche bayésienne et l'approche classique dite
fréquentiste est que la première propose une loi de
probabilité sur les paramètres (Robert, 1992). Les
paramètres ne sont donc plus considérés comme des
quantités fixes mais comme des variables aléatoires dont nous
avons une connaissance plus ou moins exacte. Cette connaissance est traduite
par le choix d'une distribu-
tion a priori sur les paramètres. On appelle
modèle statistique bayésien la donnée
d'un modèle statistique paramétré ayant pour fonction de
densité fY |ö(Y |ö) et d'une loi a priori sur les
paramètres notée ðö(ö) qui admet pour fonction de
densité fö(ö) (Robert, 1992). La loi a posteriori de ö
est obtenue par utilisation de la version continue de la formule de Bayes
(1763) :
fY |ö(Y |ö)fö(ö)
fö|Y (ö|Y ) =
f fY|ö(Y |ö)45(ö)dö. (3.1)
La principale différence entre l'approche
bayésienne et l'approche dite classique ou fréquentiste
basée sur la vraisemblance est que la vraisemblance est, avec l'approche
bayésienne, modifiée en une loi a posteriori donnée par la
formule 3.1 et représente l'actualisation de l'information a priori,
donnée par la loi a priori ðö(ö), au vu de l'information
contenue dans les observations, fY |ö(Y |ö) (Robert, 1992; Marin et
Robert, 2007).
Le choix de la loi a priori reste un problème
délicat en statistique bayésienne. Lorsque des connaissances a
priori sur les données ou le modèle sont disponibles, elles
pourront ou devront être utilisées pour le choix de la loi a
priori (Marin et Robert, 2007). Cependant, il faut bien souligner que
l'introduction d'une loi ðö sur les paramètres ö divisent
depuis de nombreuses années les statisticiens (Robert, 1992; Efron,
2005). L'inférence statistique bayésienne est basée sur
les distributions a posteriori des paramètres du modèle. Ainsi
l'inférence bayésienne est réalisée
conditionnellement aux observations et l'analyse bayésienne donne un
sens probabiliste bien précis à ce conditionnement en attribuant
une loi de probabilité aux paramètres (Parent et Bernier, 2007).
Le problème est de calculer les caractéristiques a posteriori
des paramètres ö, de certaines fonctions des paramètres
h(ö) ou des espérances, sous la loi a posteriori, de ces fonctions
de la forme :
I h(ö)fö|Y (ö|Y )dö.
Il peut s'agir, par exemple, de la moyenne a posteriori qui est
donnée par l'espérance de ö sous la loi a posteriori
Eö|Y (ö|Y ) = f öfö|Y (ö|Y
)dö
Le plus souvent, le paramètre ö est un vecteur
multidimensionnel de dimension K, de la forme ö = (ö1, ö2, ... ,
öK) et le calcul du dénominateur dans l'expression de la loi a
posteriori (Equation 3.1) fait intervenir une intégrale multiple. Ce
calcul pose souvent problème. Il faut généralement
prendre en compte l'impossibilité de calculer cette
expression quand on réalise la phase d'inférence
bayésienne (Parent et Bernier, 2007). Nous distinguons deux classes de
méthodes d'inférence bayésienne : les méthodes de
calcul analytique et les méthodes numériques. Les méthodes
de calcul analytique englobent celles basées sur les distributions a
priori dites conjuguées. Une famille de lois a priori, notée
Hö est dite conjuguée si, pour toute loi a priori ðö E
Hö, la loi a posteriori ðö|Y (ö|Y ) appartient
également à Hö (Robert, 1992). Le passage des lois a priori
aux lois a posteriori se réduit alors simplement à un changement
de paramètres (Robert, 1992). L'emploi des méthodes analytiques
ne peut être envisagé que dans des cas particuliers. Or en
pratique, pour réaliser l'inférence bayésienne des
modèles à plusieurs paramètres, donc plus complexes, la
loi a priori est généralement de structure quelconque et donc la
commodité que représente le calcul des lois conjuguées
naturelles ne peut pas être exploitée (Parent et Bernier, 2007).
Des méthodes numériques doivent donc être envisagées
pour la réalisation effective de l'inférence bayésienne
des modèles multiparamètriques plus complexes (Parent et Bernier,
2007). Parmi les méthodes numériques, nous pouvons citer les
méthodes de Monte Carlo et les méthodes de Monte Carlo par
Chaînes de Markov (MCMC pour Markov Chain Monte Carlo). Ces
méthodes sont des méthodes algorithmiques qui sont maintenant
largement utilisées pour évaluer les densités a posteriori
ðö|Y (ö|Y ) des paramètres (Chib et Greenberg, 1995;
Parent et Bernier, 2007).
3.1.1 Les méthodes de Monte Carlo
Les méthodes de Monte Carlo ont été
développées à l'origine dans le domaine de la physique
pour approcher des expressions de la forme
fEY (h(Y )) = h(Y )fY (Y )du(Y ) < 8, (3.2) oil fY est la
densité de la variable aléatoire Y par rapport à la mesure
u et h une fonction mesurable quelconque. La méthode de Monte carlo
consiste à réaliser des simulations numériques de
variables aléatoires pour obtenir une approximation d'intégrales
qui converge avec le nombre de simulations. Ceci est justifié par la loi
forte des grands nombres (Marin et Robert, 2007). Nous avons d'après la
loi forte des grands nombres,
1
Ti
Xn
i=1
h(Yi) p.s
-? EY (h(Y ))
En outre, si EY (h(Y )2) < 8, par l'emploi du
théorème central-limite, nous avons un résultat de
convergence asymptotique
|
vn ( 1n Eli h(Yi) - EY (h(Y )))
|
p.s
-? N(0, 1)
|
|
|
|
|
VY (h(Y ))
|
|
et nous pouvons construire un intervalle de confiance
asymptotique pour EY (h(Y )). Néanmoins, il n'est pas toujours possible
de simuler suivant la loi de Y , ðY . De plus, il peut s'avérer,
comme c'est le cas pour la simulation d'événements rares, que la
simulation suivant ðY n'est pas toujours optimale (Marin et Robert, 2007).
Lorsque la simulation selon la loi ðY n'est pas possible et en notant que
l'expression (3.2) peut aussi s'écrire d'une autre manière
comme
I
h(Y )fY (Y ) g(Y )du(Y ), g(Y )
où g est la densité d'une autre loi de probabilité dont le
support contient
celui de la loi associée à la densité fY
. Ainsi, un échantillon simulé selon la densité g permet
aussi d'approcher cette expression lorsque la fonction h(Y )fY (Y )/g(Y ) est
employée (Marin et Robert, 2007). Cette autre méthode de
Monte-Carlo est appelée méthode d'échantillonnage
préférentiel ou pondéré 1 : elle
consiste à simuler une suite Y1,. . . , Yn suivant la loi de
densité g et d'approcher EY (h(Y )) par
1
n
Xn
i=1
h(Yi)f(Yi) (3.3)
g(Yi)
La loi g est appelée la loi d'importance et le rapport
fY (Yi)/g(Yi) est le poids d'importance associé à la variable
aléatoire Yi. D'après la loi forte des grands nombres
|
1
n
|
Xn
i=1
|
h(Yi)f(Yi)
g(Yi)
|
ps ? I (h(Y ) 9(Y))
g(y) g(Y )du(Y ) = EY (h(Y ))
|
3.1.2 Les méthodes de Monte Carlo par chaines de
Markov
Les méthodes de Monte Carlo par chaînes de Markov
(MCMC) permettent d'obtenir un échantillon Y1, . . . , Yn de
loi ðY sans simuler directement suivant ðY . Le principe
général des méthodes MCMC repose sur l'utilisation d'une
chaîne de Markov (V)tEN ergodique de loi stationnaire ðY
;
1Cette méthode est appelée importance
sampling en anglais
ainsi, si Y t a comme distribution marginale ðY
, Y t+1 est aussi marginalement distribué selon ðY (Marin
et Robert, 2007). On appelle algorithme MCMC toute méthode
produisant une chaîne de Markov ergodique de loi stationnaire la
distribution d'intérêt (Robert, 1996). Le théorème
ergodique garantit la convergence presque sûre de
vers EY [h(Y )] = f h(Y )dðY (Y ) lorsque T tend vers
l'infini pour toute fonction h réelle dont l'espérance en valeur
absolue est finie et ceci quelque soit la distribution initiale (Marin et
Robert, 2007).
En inférence bayésienne, la méthode MCMC
la plus couramment utilisée pour simuler selon la loi a posteriori
ðö|Y (ö|Y ) est celle dite de Metropolis-Hastings (Parent et
Bernier, 2007). celle approche, décrite par l'Algorithme 1, repose sur
l'utilisation d'une loi dite loi instrumentale ou loi de proposition de
densité conditionnelle qö|öt-1(ö|öt-1) et
sur le calcul du ratio de MétropolisHasting suivant :
ñ=
fö|Y (ö|Y
)
föt-1|Y (öt-1|Y
)
qöt-1|ö(öt-1|ö)
qö|öt-1(ö|öt-1)
=
fY |ö(Y |ö)fö(ö)
qöt-1|ö(öt-1|ö)
fY |öt-1(Y
|öt-1)föt-1(öt-1)
qö|öt-1(ö|öt-1)
L'intérêt majeur de l'algorithme de
Metropolis-Hastings est qu'il n'est pas nécessaire de calculer les
constantes de normalisation. Il suffit donc pour mettre en oeuvre cet
algorithme de connaître la loi cible à la constante de
normalisation près. Cet algorithme a été d'abord
développé par Metropolis et al. (1953) et
généralisé plus tard par Hastings (1970). Cependant, bien
que, la convergence de l'algorithme de Metropolis-Hastings soit
théoriquement garantie pour un large choix de lois de proposition
(Roberts et Smith, 1994), le choix de la loi de proposition influence fortement
la vitesse de convergence de l'algorithme (Parent et Bernier, 2007). Un mauvais
choix de la loi de proposition peut entraîner soit un fort taux de rejet
des valeurs proposées et donc la chaîne de Markov bouge
difficilement soit une mauvaise exploration du support de la loi cible
ðö|Y car la chaîne reste dans un voisinage de la valeur
initiale ö0 (Marin et Robert, 2007). Un autre algorithme MCMC est celui de
l'échantillonnage de Gibbs qui a été initialement
développé par Geman et Geman (1984). Considérons un
vecteur ö = (ö1, ... , öK) de dimension K de loi
ðö|Y (ö|Y ). Supposons qu'il est possible de simuler selon toutes
les lois conditionnelles ðök|ö(-k),Y (ök|ö(-k), Y ), k
= 1, ... , K et oil ö(?k) désigne
Algorithme 1 Algorithme de Metropolis-Hastings
Initialisation : choisir ö0
for t from 1 to T do
générer ö ~
qö|öt1(ö|öt-1) et u ~ U[0,1]
fö|Y (ö|Y )
qöt-1|ö(öt-1|ö)
calculer ñ = föt-1|Y
(öt-1|Y
)qö|öt-1(ö|öt-1)
décider
if u = ñ then öt =
ö
else
öt = öt-1
end if end for
le vecteur ö privé de la composante k.
L'algorithme d'échantillonnage de Gibbs est donné par
l'Algorithme 2. Chaque étape de l'algorithme de Gibbs est en fait
scindée en K sous-étapes successives correspondant chacune
à la simulation suivant la distribution conditionnelle de l'une des
composantes du vecteur ö sachant toutes les autres composantes. La
distribution jointe est stationnaire à chacune des K sous-étapes
de l'itération t = 1, . . . ,T et si la chaîne est
irréductible, elle converge vers ðö|Y pour toute
valeur initiale (Marin et Robert, 2007). L'algorithme d'échantillonnage
de Gibbs est un cas
Algorithme 2 Algorithme d'échantillonnage de Gibbs
for t from 1 to T do
générer öt1 ~
ðöt 2 , . . . , öt-1
1|öt-1
2 ,...,öt-1
K ,Y (öt 1|öt-1 K ,Y )
générer öt 2 ~ ðöt K , Y )
2|öt
1,öt-1
3 ...,öt-1
K ,Y (öt 1, öt-1
3 . . . , öt-1
...
générer ötK ~
ðöt 3 . . . , öt
K|öt 1,öt
3...,öt K-1,Y (öt 1, öt K-1, Y )
end for
particulier de l'algorithme de Metropolis-Hastings
Alors que la mise en oeuvre de l'algorithme de
Metropolis-Hastings exige de connaître la loi a posteriori à une
constante multiplicative près, celle de l'algorithme
d'échantillonnage de Gibbs exige la connaissance des distributions
conditionnelles complètes. Ainsi, l'algorithme de Metropolis-Hastings
comparé à celui de l'échantillonnage de Gibbs est
générique en ce sens qu'il présente de plus larges
possibilités d'utilisation.
Paramètre inconnu
Variable latente
Variable observée
IBD


IBS

Ä
FIG. 3.1 - Graphe acyclique orienté du modèle
bayésien hiérarchique
3.2 Algorithmes d'estimation des paramètres
3.2.1 Version bayésienne du modèle de
Milligan
La version bayésienne du modèle de Milligan a
été présentée dans la définition 4 et la
figure 3.1 présente le graphe orienté acyclique du modèle.
Dans la version bayésienne du modèle, les paramètres
d'intérêt sont, les probabilités d'IBD, Ä et le
vecteur latent des modes d'IBD, IBD. D'un point de vue bayésien,
l'objectif est de pouvoir simuler selon la loi a posteriori
ðÄ,IBD|IBS(Ä, IBD|IBS)
Cela est possible en utilisant un algorithme de Gibbs. En effet,
la loi a posteriori du vecteur des probabilités d'identité par
états est
ðÄ|IBD,IBS(Ä|IBD, IBS) ?
ðIBS|IBD(IBS|IBD)ðIBD|Ä(IBD|Ä)ðÄ(Ä)
Comme, la loi du mode d'IBS conditionnellement au mode d'IBD est
indépendante de Ä,
ðÄ|IBD,IBS(Ä|IBD, IBS) ?
ðIBD|Ä(IBD|Ä)ðÄ(Ä)
La loi du mode d'identité par états, IBD est
ðIBD|Ä(IBD|Ä) = 11L
ðIBDl|Ä(IBDl|Ä)
l=1
oil ðIBDl|Ä(IBDl|Ä) est une loi
multinomiale de paramètres Ä1, . . . , Ä9. De plus, nous avons
supposé que la loi a priori de Ä était une loi de Dirichlet.
Comme la loi de Dirichlet est la conjuguée naturelle de la loi
multinomiale (Robert, 1992), la loi a posteriori
ðÄ|IBD(Ä|IBD) est donc une loi de Dirichlet
D(#IBD1 + á, #IBD2 + á, . . . , #IBD9 +
á).
oil #IBDi = ELl=1 1lIBDl=IBDl
idésigne le nombre total de locus sur l'ensemble des
différents loci de type IBDi,i = 1, . . . , 9.
La loi a posteriori de IBD sachant IBS et Ä est une loi
discrète qui est entièrement définie par les
probabilités a posteriori. Pour un locus l,
pli = P(IBDli|Ä,IBS) j
P(IBSlj|IBDli)Äi
= Ei9 1 P(IBSlj|IBDli)Äi ? {1,
pour i = 1, . . . , 9 et donc
ðIBDl|Ä,IBSl(IBDl|Ä,
IBSl) = M(1, pl 1,pl 2,.
. . ,pl9).
Ainsi, la loi a posteriori
ðÄ,IBD|IBS(Ä,IBD|IBS) peut être simulée avec
l'algorithme d'échantillonnage de Gibbs (Algorithme 3)
Algorithme 3 Algorithme de Gibbs pour l'apparentement
générer Ä0 ~ D(1,1,1) à
l'étape t, générer
IBDl,t+1 ~ M(1, Äl,t 1 ,Äl2 ,t ,
. . . , Äl,t
9 ), l = 1, . . . , L
Ät+1 ~ D(#IBDt1 +1 + á, #IBDt+1
2 + á, . . . , #IBDt+1
9 + á)
3.3 Estimation de l'apparentement en milieu naturel :
prise en compte de l'information spatiale
Le modèle de l'apparentement prenant compte de
l'information spatiale a été décrit dans la
définition 5. Les paramètres de ce modèle, sont les
modes
d'IBD, IBD, pour tous les locus L et tous les couples C, Z le
vecteur gaussien latent associé, le seuil á (variable ordinale
à trois modalités, il n'y a qu'un seuil), l'effet couple 77 ainsi
que les paramètre de régression lié à la distance,
í, au et 0-2ç. D'un point de vue
bayésien, l'objectif est de pouvoir simuler selon la loi a posteriori
ðIBD,Z,á,ç,u,í,ó2
ç|IBS(IBD,Z, á, 77, au, í,
0-2ç|IBS)
Nous donnons maintenant les lois conditionnelles
complètes a posteriori des paramètres à estimer. Comme
toutes les conditionnelles ne sont pas accessibles, nous utiliserons les
algorithmes de Gibbs et de Métropolis-Hasting (Metropolis-HAsting within
Gibbs). Nous nous plaçons désormais dans le cas d'une population
non-consanguine.
Loi a posteriori du mode d'IBD La loi conditionnelle a
posteriori du mode d'IBD du couple c au locus l est une loi discrète
définie par les probabilités
pli = P
(IBDli,c|Ä,IBSlj,c)
=
P(IBSlj,c|IBDli,c)P(Zlc
E]ák_1, ák]|77c)
P9 i=7
P(IBSlj|IBDli)P(Zlc
E]ák_1, ák]|77c)
pour i = 7, 8, 9 et
ák
P(Zlc E]ák_1, ák]
|77c) = j ö(Z, 77c, 1)
ak-1
oil ö(Z,77, 1) est la densité d'une loi gaussienne
d'espérance 77 et de variance 1.
Loi a posteriori de la variable latente En reprenant les
travaux de Chib et Greenberg (1998), la loi a posteriori de la variable latente
Z, sachant le mode d'IBD, les seuils associés et le paramètre 77,
est une loi gaussienne N(77, 1) tronquée sur l'intervalle
]ák_1, ák].
Loi a posteriori des seuils En reprenant les travaux de Chib et
Greenberg (1998), nous proposons de simuler le seuil á selon la loi
uniforme
á ~U[max(Z, IBD = 8), min(Z, IBD = 7)]
Loi a posteriori du paramètre ç En reprenant les
calcul presente dans le chapitre 2, la loi conditionnelle complète a
posteriori du paramètre ç est
ç|Z, u, í, óç~ N
ó2ç
(u + ídc +
ó2çZ
,ó2ç 1 +
óç2 1 +
Loi a posteriori du paramètre u La densite de la loi
conditionnelle complète a posteriori du paramètre u est
~ó2 ~
u0(ç - íd) , ó2
u0ó2 ç
u|ç, d, í, ó2 ç ~ N ó2 u0 +
ó2 ó2 u0 + ó2
ç ç
Loi a posteriori du paramètre í La loi
conditionnelle complète a posteriori du paramètre í est
~ó2 ~
í0d(ç - u)
óí20 óç2
,
ç d, u, óç2
ó20 ó2, ó2
d2 ó2 í
ç ç
Loi a posteriori du paramètre
ó2ç Nous choisissons come loi a priori du
paramètre ó2ç une inverse-gamma
IG(m, s), et la loi conditionnelle complète a posteriori de la variance
est donc une inverse-gamma
Cm + n (ç - u - ídY (ç - u -
íd)

+ s2,
2
Les lois conditionnelles a posteriori du mode d'IBD d'un
couple de genotypes et des paramètres ç, u, í, et
ó2ç sont connues mais la loi conditionnelle
a posteriori des seuils n'a pas une expression analytique connue. Nous
proposons un algorithme comportant une etape de Metropolis-Hastings pour la
mise à jour de la loi des seuils et une etape d'echantillonnage de Gibbs
pour les autres paramètres dont les lois a posteriori sont connues.
3.4 Estimation de l'apparentement et de
l'héritabilité en milieu naturel
Nous proposons maintenant un algorithme d'inference pour
estimer à la fois l'apparentement et l'heritabilite des
caractères lorsque le pedigree n'est pas connu. Les lois conditionnelles
complètes a posteriori des paramètres associes au modèle
statistique pour l'apparentement et l'heritabilite ont ete
déjà données précédemment
(voir section 2.4). Les lois conditionnelles complètes a posteriori des
effets génétiques additifs a, de la moyenne u, de la variance
génétique additive ó2a et de la
variance résiduelle ó2e sont des lois
connues conditionnellement à la connaissance de l'apparentement entre
tous les couples. Or en milieu naturel, Ä n'est pas connu. Nous avons
montré dans les chapitres précédents comment à
partir de l'information moléculaire, il était possible d'estimer
l'apparentement. L'idée maintenant est de combiner dans un même
algorithme l'estimation de la variance génétique et de
l'apparentement. La difficulté réside dans le fait que
désormais conditionnellement à l'effet additif et au mode
d'identité par état (ou par descendance) n'est plus connue. En
effets, la densité conditionnelle est
fÄ|a,IBS,ó2 a(Ä|a, IBS,
ó2 a) cc
fa|R,ó2a(a|R,ó2a)fIBS|Ä(IBS|Ä)
oil fa|R,ó2a est la densité d'une loi
gaussienne d'espérance nulle et de ma-trice de variance covariance
ó2aR et fIBS|Ä(IBS|Ä) est le produit de
densité de lois multinomiales, donnée dans la definition 4. Comme
cette loi n'a pas de forme classique connue, nous proposons d'employer un
algorithme de Metropolis-Hastings. Nous proposons une nouvelle valeur
d'apparentement pour le couple c, Ä*c, de la
manière suivante : soient m = min(Ä7,c, Ä8,c, Ä9,c),
ä ,,, 1.1[0,m] et soient k1 et k2 deux numéros d'indices
choisis par tirage sans remise dans l'ensemble {7, 8, 9}, :
Ä?c = (Ä7,c +
ä1l{k1=7} -- ä1l{k2=7}, Ä8,c +
ä1l{k1=8} -- ä1l{k2=8}, Ä9,c +
ä1l{k1=9} -- ä1l{k2=9}) .
Le ratio de Metropolis-Hastings est donné par
fÄ|a,IBS,ó2a(Ä|a, IBS,
ó2a) qÄ|Ä(Ä*|Ä)
ñ(Äc, Ä:) cc
fÄ*|a,IBS,ó2a (Äl a, IBS,
óa2) qÄ|Ä0,
(Ä| Äl
|
cc
|
fa|R?,ó2 a(a|R?, ó2
a)
fa|R,ó2 a(a|R, ó2
a)
|
fIBS|Ä*(IBS|Ä*)
|
|
min(Ä*)
|
|
|
fIBS|Ä(IBS|Ä)
|
|
min(Ä) .
|
oil min(Ä*) provient de la loi de
proposition. Ainsi, en estimant simultané-
min(Ä)
ment, la variance génétique et l'apparentement,
on constate que l'information phénotype contenu dans la valeur
génétique intervient dans l'estimation de l'apparentement. De
plus, il est possible de mettre des contraintes de sorte que seul des valeur
d'apparentement valides, au sens oil la matrice R soit définie
positive. Maintenant que l'apparentement est connu, on poursuit classiquement
par des étapes de Gibbs la mise à jour, des autres
paramètres (cf chapitre 2).
3.5 Conclusion
L'inférence statistique bayésienne est
basée sur la distribution a posteriori des paramètres du
modèle statistique considéré qui permet de calculer les
caractéristiques a posteriori de ces paramètres. Nous avons
d'abord décrit les outils nécessaires à l'inférence
statistique bayésienne que sont les méthodes de Monte Carlo et
plus particulièrement les méthodes de Monte Carlo par
chaînes de Markov. Une des caractéristiques essentielles d'un
algorithme MCMC est qu'il ne demande pas de connaître la constante de
normalisation de la loi cible, ce qui est le cas des lois a posteriori pour
l'approche bayésienne (Parent et Bernier, 2007). Une méthode MCMC
générique est celle de Metropolis-Hastings. La convergence de
l'algorithme de Metropolis-Hastings est théoriquement garantie pour un
large éventail de lois de proposition. L'emploi de l'algorithme de
Metropolis-Hastings permet de traiter différents problèmes parmi
les plus complexes (Parent et Bernier, 2007). Cependant, la rapidité
d'atteinte de l'état limite stationnaire de la chaîne de Markov
ainsi produite doit être considérée avec attention car elle
dépend du choix de la loi de proposition. Un second groupe de
méthodes MCMC est celui de l'algorithme d'échantillonnage de
Gibbs. L'algorithme d'échantillonnage de Gibbs permet de simplifier le
problème de l'inférence statistique bayésienne en
remplaçant la simulation d'une loi jointe d'un vecteur aléatoire
à n composantes par une suite de n tirages aléatoires à
une dimension (Parent et Bernier, 2007). La mise en oeuvre, en pratique, de
l'algorithme de Gibbs exige cependant de pouvoir écrire les lois
conditionnelles complètes a posteriori des paramètres. Nous avons
proposé un algorithme de Gibbs pour l'estimation de l'apparentement sans
prise en compte de l'information spatiale. Lorsqu'on considère le mode
d'IBD comme une variable latente et qu'on choisit une loi a priori de Dirichlet
pour le vecteur des probabilités d'IBD, nous avons montré que la
loi conditionnelle complète a posteriori du vecteur des
probabilités d'IBD est aussi une loi de Dirichlet et que la loi
conditionnelle complète a posteriori du mode d'IBD est une loi
multinomiale. Comme nous pouvons simuler selon ces deux lois conditionnelles
complètes a posteriori, nous pouvons utiliser un algorithme de Gibbs
pour l'estimation de l'apparentement et ceci correspond au troisième
algorithme proposé. Enfin deux algorithmes de Métropolis-Hastings
within Gibbs pour estimer d'une part l'apparentement en tenant compte de
l'information spatiale et d'autre part l'héritabilité a
été décrit.
Chapitre 4
Applications
4.1 Application à des données sur le
karité
4.1.1 Introduction
Les données utilisées pour cette application ont
été obtenues dans le cadre du projet INNOVKAR 1 dont
l'objectif principal est l'amélioration de la production du
karité (Vitellaria paradoxa) par une gestion durable et efficace des
systèmes agroforestiers. Il s'agit d'un projet INCO 2
financé par l'Union Européenne et dont la coordination est
assurée par le responsable de l'Unité de Recherche
"Diversité génétique et amélioration des
espèces forestières" du CIRAD.
Le karité est une espèce de la famille des
Sapotacea qui est très répandue dans les parcs agroforestiers en
zone sub-saharienne (Kelly, 2004). La notion de parc est
caractérisée par une présence régulière,
systématique et ordonnée d'arbres à l'intérieur des
champs et est le résultat d'un long processus d'évolution durant
lequel s'établit une association entre d'une part, les
éléments naturels c'est-à-dire les arbres et arbustes
conservés, entretenus et améliorés en raison de leur
utilité, et d'autre part, les productions végétales
annuelles à l'intérieur d'un espace régulièrement
exploité (Bagnoud et al., 1995; Sautter, 1968). Un parc comprend un
certain nombre de champs sur lesquels sont cultivées différentes
espèces (céréale, coton, sorgho, arachide) et qui sont
régulièrement laissés en jachère afin de restaurer
la fertilité des
1INNOVKAR : Innovative tools and techniques for
sustainable use of the shea tree in sudano-sahelian zone
2INCO : Specific international scientific cooperation
activities
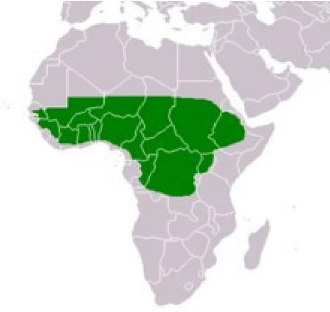
FIG. 4.1 - Aire de répartition de l'arbre à
karité en Afrique
sols. La durée de la période de jachère
varie d'un agriculteur à l'autre et peut s'étaler sur une
période de 3 ou 4 ans à 25 ou même 30 ans (Kelly et al.,
2004b). Les parcs agroforestiers sont dominés, le plus souvent, par une
à trois espèces d'arbres comme c'est le cas pour les parcs
agroforestiers à karité au Mali (Sanou et al., 2005). Le
karité occupe, par exemple, 4, 7 millions d'hectare au Mali et ceci
s'explique par l'importance de son rôle pour la sécurité
alimentaire et la génération de revenus (Cardi et al., 2005). En
effet, dans cette zone, les producteurs conservent et maintiennent dans leurs
champs les arbres à karité surtout en raison de l'importance
économique qu'ils représentent. Le fruit du karité est
aussi bien consommé par les populations humaines que par les animaux et
le beurre extrait de son noyau est utilisé pour la consommation locale
comme huile de cuisson et pommade et consti-
tue une importante source de devises étrangères
pour certains pays comme le Mali ou le Burkina Faso (Kelly et al., 2004a). Les
produits du karité sont en plus utilisés pour la médecine
traditionnelle. L'aire de répartition géographique du
karité en Afrique s'étend de l'est du Sénégal
à la région des hauts plateaux de l'Ouganda formant ainsi une
ceinture ininterrompue d'environ 6000 km de long et 500 km de large (Figure
4.1) (Cardi et al., 2005). La densité des populations de karité
varie fortement selon le mode d'occupation des sols, les localités et
les conditions écologiques. Le karité a, le plus sou-vent, un
système de reproduction sexuée et est principalement
pollinisé par les insectes (Cardi et al., 2005). La période de
floraison et de fructification s'étend de décembre à mai
avec quelques faibles variations en fonction de la zone géographique
considérée (Sanou et al., 2005; Cardi et al., 2005; Okullo et
al., 2004).
Le site de l'étude est le village de MPeresso
situé dans la zone dite Mali Sud qui couvre toute la région de
Sikasso et une partie des régions de Koulikoro et de Ségou; le
village MPeresso (12°16'N, 5°19'W) se trouve
dans la région naturelle du plateau de Koutiala et couvre une superficie
de 117 km2 (Kelly, 2004). Le climat est de type sud-soudanien et la
pluviométrie moyenne de 1991 à 2002 était de près
de 900 mm avec un minimum de 586 mm et un maximum de 1249 mm (Bouvet et al.,
2008). Trois parcelles ont été initialement retenues sur ce site
selon les deux critères suivants : le mode d'occupation du sol (champ
cultivé, jachère et forêt naturelle) et la densité
d'arbres adultes (arbres ayant une circonférence à 1, 30 m du sol
supérieure à 20 cm) (Kelly et al., 2004a). Dans le cadre de
l'application de ce travail, nous nous sommes intéressés
uniquement aux données collectées sur la parcelle qui
était en jachère. C'est une parcelle de 2, 10 ha contenant 222
arbres à karité avec une densité de 68.1 arbres à
l'hectare (Kelly et al., 2004b).
Différentes mesures ont été
réalisées : le diamètre du tronc à 1m30,
l'information moléculaire et les coordonnées
géographiques. Malheureusement, ces informations ne sont pas disponibles
pour l'ensemble des 222 arbres présents sur le cite de MPeresso. Le
diamètre n'est disponible que pour les individus dont la hauteur est
supérieure à 1m30, cela représente 161 arbres. Le
phénotype des autres individus, les 61 juvéniles restants, est
égal à 0. L'information moléculaire, pour 12
microsatellittes, n'est disponible que pour 193 individus, les 29 restants
présentent à un ou plusieurs locus des données manquantes.
Ils ne seront donc pas utilisés pour les analyses
génétiques. Enfin, les coordonnées géographiques
sont disponibles pour 131 arbres parmi les 222. Les coordonnées
géographiques sont, pour des raisons pratiques sur le terrain,
exprimées en coordonnées azimut z (ou coordonnées
angulaires). Par la suite nous travaillerons avec les coordonnées
cartésiennes obtenues directement des
coordonnées azimut en utilisant la transformation
suivante
x1,i = x1,i_1 + di cos(zi)
x2,i = x2,i_1 + di sin(zi)
oil x1,0 = 0 et x2,0 = 0 sont les coordonnées d'un arbre
référant, x1,i, x2,i les coordonnées de l'arbre i.
Finalement, pour l'analyse génétique/spatiale
seul 58 individus sont géoréférencés et ne
présentent aucune donnée génétique manquante. Ce
dernier jeu de donnée sera utilisé pour l'application du
modèle développé dans les chapitres
précédents
4.1.2 Analyse statistique des données
Nous avons étudié la diversité
génétique du karité avec les logiciels POP-GENE (Yeh et
Boyle, 1997) et FSTAT (Goudet, 2001). Les paramètres standards mesurant
la diversité génétique ont été
calculés. Ces paramètres sont le nombre d'allèles
observés par locus, l'hétérozygotie observée et
l'estimation sans biais de l'hétérozygotie attendue sous
l'hypothèse de Hardy-Weinberg (Nei, 1987). La similarité
génotypique des individus et l'association entre les locus ont
été étudiées en effectuant une analyse en
composantes principales. En effet, l'analyse en composantes principales (ACP)
est une méthode statistique multidimensionnelle qui permet de
synthétiser un ensemble de données. Avec un tableau de
données constitué de n individus et p variables, l'ensemble des
données forme un nuage de m points dans un espace de dimension p et le
principe de l'ACP est d'obtenir une représentation approchée du
nuage des individus dans un sous-espace de dimension faible k m (Saporta,
1990); ceci s'effectue par projection sur des axes bien choisis en maximisant
l'inertie du nuage projeté. L»utilisation de l'ACP nous a permis
d'étudier l'association entre les génotypes aux différents
locus et l'existence éventuelle de groupes d'individus ayant des
génotypes similaires. L'ACP a été réalisée
avec le package ade4 du langage de programmation R (Chessel et al., 2004; R
Development Core Team, 2008). L'étude de la structuration spatiale est
faite, d'une part, selon le phénotype et, d'autre part, selon le
génotype. La structure spatiale au niveau phénotypique est
caractérisée en donnant la distribution spatiale des arbres en
fonction de leur classe de diamètre. La structuration spatiale au niveau
génotypique est d'abord évaluée par les FIS. Le
paramètre FIS, appelé indice de fixation, mesure la
consanguinité intra-population définie par Cockerham (1969) et
son expression est :
Ha - Ho
FIS = ,
Ha
avec Ha le taux d'hétérozygotes
attendu sous l'hypothèse d'équilibre de Hardy-Weinberg et
Ho le taux d'hétérozygotes observé. Cet indice
permet donc d'évaluer le déficit d'hétérozygotes
dû à l'écart à la panmixie. Le FIS est
calculé selon la méthode de Weir et Cockerham (1984) et la valeur
critique associée est obtenue par permutations aléatoires des
allèles des individus à l'intérieur des
échantillons. Le niveau de signification est évalué selon
la méthode de correction séquentielle de Bonferroni pour les
tests multiples (Rice, 1989). Un FIS significatif est
interprété comme un indicateur de la consanguinité dans
une population et/ou d'une sous-structuration de la population. La structure
génétique spatiale dans un second temps est évaluée
à la fois par le test de Mantel, par le corrélogramme de Moran et
par l'étude de la relation entre l'apparentement estimé et la
distance spatiale. Nous avons, à cet effet, défini 15 classes de
distance avec un pas de 10 m par classe. Le coefficient d'apparentement moyen
entre les individus de chacune des classes est alors calculé selon trois
méthodes différentes (méthode de Lynch et Ritland (1999),
méthode de Wang (2002) et méthode de Milligan (2003)). Nous avons
étudié la relation entre le coefficient d'apparentement moyen
estimé selon ces deux méthodes des moments et le logarithme de la
distance entre les individus. Le test de signification de l'estimateur du
coefficient d'apparentement moyen par classe de distance est
réalisé par permutations aléatoires (1000 permutations)
des positions géographiques des génotypes des individus en
utilisant le programme SPAGEDI (Hardy et Vekemans, 2002) ; ceci concerne
uniquement les estimations données par les deux méthodes
basées sur le calcul des moments (Lynch et Ritland (1999),
méthode de Wang (2002)). L'estimation de l'apparentement par maximum de
vraisemblance (modèle de Milligan (2003)) a été
réalisée avec le programme ML-Relate (Kalinowski et al., 2006).
L'utilisation du programme SGS (Degen et al., 2001) nous a permis de calculer,
pour chaque classe de distance, l'indice d'agrégation (p) qui est
basé sur celui de Clark et Evans (1954) afin de déterminer la
structure spatiale du karité dans la parcelle en jachère (Ripley,
1981; Degen, 2000). Une valeur de p < 1 indique que la distribution est
agrégée, p = 1 pour une distribution aléatoire et lorsque
p > 1 la distribution est dite régulière (Hardesty et al.,
2005). Le nombre de classes de distance est ajusté pour garantir qu'il y
ait un minimum de 30 paires d'individus dans chacune des classes. Ce choix est
justifié en raison de la robustesse des tests de permutation (Hardesty
et al., 2005). L'indice d'autocorrélation de Moran est calculé
pour chaque classe de distance; cet indice est l'une des statistiques de test
d'autocorrélation spatiale la plus utilisée (Hardy et Vekemans,
1999). Il est défini pour chaque classe
de distance d par
I(d) =
2 E (ds,ij - ds) (dg,ij -
dg)
(n(n - 1) - 2) i<j ós
g
ñm =

nE1 Enjùij(d)(fi - f)(fj - f)
(E7 ETI ùij (d)) (Eni(fi
- f)2)
oil n est le nombre d' arbres, fi et fj sont respectivement
les valeurs observées aux sites i et j, f est la moyenne des
fi et ùij(d) sont les poids associés qui valent 1 si le site i et
le site j sont séparés d'une distance comprise dans d et
0 sinon (Hardy et Vekemans, 1999). Pour décrire la structure
génétique, la variable f considérée
représente la fréquence d'un allèle A donné et
cette fréquence peut être définie à
différents niveaux : une sous-population, un individu, ou un
allèle. Dans la plupart des applications, l'indice I de Moran est
utilisé pour décrire la structure génétique d'une
population continue et les fréquences alléliques sont
définies au niveau individuel. Pour un individu diploïde, les
fréquences alléliques sont 0 , 0.5 et 1 pour, respectivement, les
génotypes aa, aA, et AA, oil a représente tout autre
allèle différent de l'allèle A (Hardy et Vekemans, 1999).
L'indice de Moran ainsi calculé correspond à l'estimation moyenne
par classe de distance du coefficient d'apparentement de Wright (Cockerham,
1969; Hardy et Vekemans, 1999) qui est la corrélation entre les
fréquences alléliques moyennes entre deux individus . Le
coefficient d'apparentement de Wright, ñij, entre deux
individus diploïdes, i et j, est
ñij =
2èij
v1 + FiV1 + Fj
oil èij est le coefficient d'apparentement et
Fi est le coefficient de consanguinité de l'individu i (Hardy et
Vekemans, 1999).
L'existence d'une association entre les distances
génétiques et les distances géographiques est
évaluée par le test de Mantel. Ce test permet de calculer la
corrélation entre deux matrices de distance (Rossi, 1996). Dans le cas
précis qui nous intéresse, il s'agit des matrices de distance
génétique et de distance spatiale et nous voulons savoir si des
individus spatialement proches ont tendance à être aussi
génétiquement proches. La matrice des distances
génétiques qui permet d'estimer la similarité
génétique entre les individus a été calculée
selon la méthode de Nei (1972). La statistique normalisée de
Mantel est donnée par
d'individus (Arnaud et al., 1999). La corrélation
obtenue avec les données est comparée aux correlations obtenues
lorsque les lignes et les colonnes d'une des deux matrices sont
permutées aléatoirement. Il s'agit de simuler des
réalisations de l'hypothèse nulle : absence de corrélation
linéaire entre les deux
matrices. il est possible tester
l'hypothèse nulle avec la statistique de Mantel, calculée pour
chaque permutation (Rossi, 1996). 1000 permutations seront
effectuées.
4.1.3 Résultats
Répartition spatiale des arbres selon le
diamètre
L'étude de la répartition spatiale des arbres
selon leur diamètre à 1, 30 m de hauteur a donc été
effectuée sur l'échantillon réduit composé de 131
arbres. Les arbres sont regroupés en 6 classes diamétriques. Ces
classes de diamètre sont définies au Tableau 4.1). La Figure 4.2
représente la distribution spatiale
|
Diamètre à 1, 30 m de hauteur
|
0
|
]0,10[
|
[10,20[
|
[20,30[
|
[30,65[
|
=65
|
|
Classe de diamètre
|
C1
|
C2
|
C3
|
C4
|
C5
|
C6
|
TAB. 4.1 - Classes de diamètre des arbres
des arbres selon leur classe de diamètre. Comme les
coordonnées spatiales des arbres juvéniles (il s'agit des 91
arbres des classes C1 et C2 ne sont disponibles), ces arbres ne sont donc pas
représentés sur cette figure. Nous pouvons noter que les arbres
de plus faible diamètre (les arbres de la classe C3) ont une
distribution plutôt concentrée sur un seul coté de la
parcelle alors que les individus appartenant aux classes C4, C5 et C6 ont une
distribution assez régulière. L'histogramme du diamètre du
tronc à 1, 30 m est donné par la Figure 4.3. La distribution des
arbres est asymétrique négative. En effet, 146 arbres (soit plus
de 75% de l'effectif total) ont un diamètre inférieur à 40
cm et 154 arbres (soit près de 80% des arbres) ont un diamètre
inférieur à 60 cm. Ainsi, il s'agit plutôt d'une population
d'arbres essentiellement juvéniles. La distribution des arbres par
classe de diamètre présente deux modes; le premier mode (0--20
cm) correspond plutôt aux arbres en régénération
depuis que la parcelle est mise en jachère et le second mode (100--120
cm) représente la distribution des arbres adultes qui se trouvaient
déjà sur la parcelle lorsque celle-ci était encore en
culture (Kelly, 2004; Kelly et al., 2004b).
Locus Allèles Fréquences
157 0.219
B5 161 0.781
E4
114 0.006
116 0.063
119 0.060
120 0.099
121 0.741
123 0.026
125 0.003
127 0.003
201 0.626
F5 205 0.045
209 0.330
224 0.676
E11 228 0.301
230 0.023
E6a
120 0.023
122 0.249
124 0.590
126 0.139
E6b
101 0.033
103 0.280
106 0.293
108 0.105
114 0.155
116 0.135
151 0.027
B3 155 0.973
H4
214 0.186
216 0.745
218 0.065
222 0.003
D10
218 0.030
220 0.248
222 0.252
224 0.321
226 0.076
228 0.073
G7
136 0.013
140 0.029
142 0.006
144 0.400
148 0.510
150 0.042
D6
116 0.071
117 0.081
118 0.155
119 0.612
120 0.071
124 0.009
F1
302 0.003
304 0.474
306 0.513
314 0.010
EffectIf
0 20 40 60 80 100
0
50 100 150
Diamètre à 1,30 m
0 20 40 60 80 100 120 140
X
V
-100 -80 -60 -40 -20 0
?
?
?
?
?
? ? ? ??
? ? ?
? ?
? ?
? ?
?
?
?
?
?
?
?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
? ?
?
?
? ?
?
?
?
?
?
?
?
?
?
?
??
? ?
? ? ?
?
?
? ? ?
?
?
? ??
?
?
?
?
?
?
?
?
?
? ???
?
? ? ? ?
?
?
C 3
C 4
C 5
C 6
?
? ?
?
FIG. 4.2 - Distribution spatiale des arbres par classe de
diamètre
FIG. 4.3 - Histogramme du diamètre des arbres
Mesure de la diversité génétique
L'étude de la diversité génétique
a été réalisée sur le sous échantillon
constitué des 193 individus génotypés. Le Tableau 4.2
donne les fréquences alléliques observées aux 12 locus.
Tous les locus sont polymorphes et le nombre total d'allèles varie de 2
pour le locus B5 à 8 pour le locus E4 (Figure 4.4). La proportion des
locus polymorphes pour lesquels la fréquence allélique la plus
élevée ne dépasse pas 95% est de 85.7% (Tableau 4.4);
ainsi près de 86% des locus présentent des variations
alléliques importantes. Les paramètres mesurant le polymorphisme
des différents locus et les FIS associés à
chaque locus sont présentés au Tableau 4.3. L'indice de fixation
varie de --0.287 (pour le locus F1) à 0.555 (pour le locus G7) (Tableau
4.3). Le taux, Ho, d'hétérozygotes observé
varie de 0.258 (pour le locus G7) à 0.660 (pour le locus F1) et le taux
moyen d'hétérozygotie pour l'ensemble des locus est 0.421
(Tableau 4.3 et Tableau 4.4). Nous notons pour certains locus (les locus E4,
E6b, D10, G7 et D6) une déviation significative par rapport à
l'hypothèse d'équilibre de Hardy-Weinberg au seuil nominal de a =
5%, ce qui correspond à un seuil ajusté de a/12 = 0.00417
(Tableau 4.3). Lorsque nous considérons, non plus individuellement mais
globalement, l'ensemble des locus, l'indice de fixation FIS est
significativement différent de 0.
Analyse en composantes principales
L'ACP a été donc réalisé sur le sous
jeu de données réduit à 193 individus. La Figure 4.5
représente l'éboulis des valeurs propres. Le premier axe
TAB. 4.3 - Caractéristiques des différents locus
|
Locus
|
N
|
na
|
Ho
|
Ha
|
FIS
|
P-value
|
|
B5
|
178
|
2
|
0.337
|
0.342
|
0.018n8
|
0.4500
|
|
E4
|
176
|
8
|
0.318
|
0.432
|
0.266n8
|
0.0042
|
|
F5
|
179
|
3
|
0.430
|
0.498
|
0.139n8
|
0.0250
|
|
E11
|
176
|
3
|
0.466
|
0.452
|
_0.029n8
|
0.6167
|
|
E6a
|
173
|
4
|
0.561
|
0.571
|
0.021n8
|
0.4333
|
|
E6b
|
152
|
6
|
0.500
|
0.782
|
0.363n8
|
0.0042
|
|
B3
|
185
|
2
|
0.373
|
0.406
|
_0.0025n8
|
1.0000
|
|
H4
|
161
|
4
|
0.373
|
0.406
|
0.084n8
|
0.1125
|
|
D10
|
165
|
6
|
0.612
|
0.760
|
0.197n8
|
0.0042
|
|
G7
|
155
|
6
|
0.258
|
0.577
|
0.555n8
|
0.0042
|
|
D6
|
161
|
6
|
0.485
|
0.585
|
0.175n8
|
0.0042
|
|
F1
|
156
|
4
|
0.660
|
0.512
|
_0.287n8
|
1.0000
|
|
Total
|
|
|
|
|
0.1568
|
0.0042
|
N nombre d'individus, na nombre d'allèles au
locus, Ho hétérozygotie observée ;
Ha : hétérozygotie attendue sous
l'hypothèse d'Hardy-Weinberg ;
ns indique que le test d'équilibre d'Hardy-Weinberg est
non significatif au seuil nominal ajusté de 0.0042
TAB. 4.4 - Hétérozygotie moyenne sur les locus
|
Ha
|
H8b
|
Ho
|
P(0.95)
|
P(0.99)
|
Nma
|
|
Population
|
0.497
|
0.499
|
0.421
|
0.917
|
1.000
|
4.500
|
|
Ecart-type
|
0.192
|
0.193
|
0.167
|
|
|
|
Ha : hétérozygotie attendue sous
l'hypothèse d'Hardy-Weinberg ; Ho hétérozygotie
observée ; Hsb hétérozygotie calculée sans biais ;
Nma nombre moyen d'allèles par locus;
P(0.95) et P(0.99) polymorphisme au seuil 95% et 99%
respectivement.
0 2 4 6 8
Nombre d'allele,s
B5 E4 F5 E11 E6a E6b B3 H4 D10 G7 D6 F1
Locus
FIG. 4.4 - Nombre d'allèles observés par locus
principal explique près de 12% de l'inertie et les deux
premiers axes n'expliquent qu'un peu plus de 20% de l'inertie totale. La
première composante principale oppose d'une part, les locus F5 et E6, et
d'autre part, les locus D10 et D6 (Figure 4.6). La seconde composante oppose,
dans une moindre mesure, les locus H4 et F1 d'une part, aux locus E11 et G7
d'autre part (Figure 4.7). L'observation du cercle des corrélations
permet aussi de confirmer cette opposition entre ces 2 groupes de variables
(Figure 4.8). La projection des individus sur le plan principal est
donnée par la Figure 4.9. Nous pouvons ainsi distinguer le groupe des
individus plutôt semblables du point de vue de leurs génotypes aux
locus F5 et E6 des individus qui sont plutôt semblables aux locus D10 et
D6.
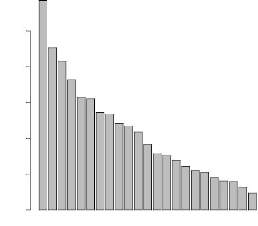
11.7 8.29 6.31 5.44 4.83 4.35 3.14 2.77 2.2 1.8 1.57 0.95
% d'inertie
0 2 4 6 8 10
FIG. 4.5 Eboulis des valeurs propres
Structure génétique spatiale
Test de Mantel Le test de Mantel a été
effectué sur le sous-échantillon
constitué des 58
individus dont les coordonnées spatiales et les
génotypes
à tous les locus sont disponibles. Le test de Mantel
n'est pas significatif
50 CHAPITRE 4. APPLICATIONS
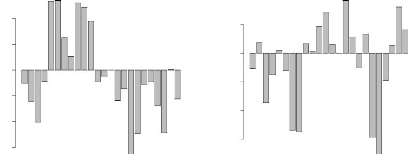
0.4
0.2
0.0
- 0.2
- 0.4
- 0.6
0.2
0.0
- 0.2
- 0.4
- 0.6
B58 B5b E4a E4b F5a F5b El la Ellb Eeaa Rah Elba Bibb B3a B3b
H4a H4b DlOa DlOb G7a G7b Dia Deb Fla Fib
B5a B5b E4a E4b F5a F5b El la Ellb Eeaa Rah Elba Bibb B3a B3b
H4a H4b DlOa DlOb G7a G7b Dia Deb Fla Fib
FIG. 4.6 - Contribution à l'axe 1 FIG. 4.7 ---
Contribution à l'axe 2
|
|
|
|
E6aa
F5a E6ab E6ba
|
|
H4a E6bb F1a
F1b
D10b H4b
D6b B5b B3a
|
|
|
D10a
|
D6a
E4a
|
B5a E4b
G7a G7b
|
B3b
E11bE11a
|
F5b
|
-1.0 -0.5 0.0 0.5 1.0
Axe 1
FIG. 4.8 - Cercle des corrélations
|
26
31
17
|
215
220
221
74
25
175 15 145 144 72 11
164 218
10
58
80 219 151
11416
8990 169 47
83 212
|
154
200
205
132 163
162 196 170
165
131
152 8 166 197
208 194 174
105
34
129
188
142 126 125
104
146 156 103
|
|
91
|
111
214
82
22
|
217 107108
23 112 109 168 182
187
124
213 81 157
2 97
77
87
158
117 41 192 48
70
|
18
120 106
75 128
51 84 119
113
186 11
153 210
147
101
12
33 130
118159
160
|
-6 -4 -2 0 2 4 6
Axe 1
FIG. 4.9 - Représentation des individus sur les axes
principaux
|
Axe 2
|
-1.0 -0.5 0.0 0.5 1.0
|
|
Axe 2
-2 4
2
0
(Figure 4.10). En effet, la statistique de Mantel
observée est ñm = --0.048 et la probabilité
d'observer une valeur supérieure ou égale à cette
dernière valeur sous l'hypothèse nulle, c'est à dire que
les distances génétiques ne sont pas linéairement
corrélées aux distances géographiques, vaut 0.805 (Figure
4.10 et Tableau 4.5).
Test de Mantel
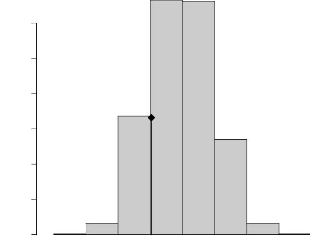
Frequence
0 50 100 150 200 250 300
-0.2 -0.1 0.0 0.1 0.2
Valeur simuléé
FIG. 4.10 - Distribution de la statistique de Mantel; le trait
vertical (en gras) représente la valeur observée de la
statistique de Mantel
Statistique de Mantel observée -0.048 p-value
simulée 0.805
1000 répétitions
TAB. 4.5 - Test de Mantel
Indice de Moran La relation entre la distance
génétique et la distance spatiale est donnée par le
corrélogramme de Moran (Figure 4.11) : il y a une structure
génétique spatiale significative au seuil de 5%. La classe de
distance inférieure à 15.3 m a une structure
génétique significativement différente de celle d'une
distribution spatiale aléatoire des génotypes. Les arbres qui
sont distants de moins de 15 m environ ont donc une structure spatiale
positive, c'est à dire qu'ils ont tendance à être
génétiquement similaires que ne le sont
.


.
.
.
.
.
* ns
-0.15 -0.10 -0.05 0.00 0.05
Incline de Moran
20 40 60 80 100 120 140
distance
FIG. 4.11 - Corrélogramme représentant l'indice de
Moran en fonction de la classe de distance spatiale (* : p - vallue < 5%; ns
: non significatif)
des individus tirés au hasard spatialement. La
structuration spatiale est aussi significative au delà de 140 in. La
population de karité ainsi étudiée présente une
structure spatiale agrégée (indice d'agrégation R = 0.86,p
- value < 0.01). Cette distribution agrégée jusqu'à une
distance d'environ 15 m serait expliquée, d'après Kelly (2004),
par le mode de distribution des semences de karité. En effet, comme le
karité est une espèce barochore, la plupart de ses fruits tombent
sous le houppier de l'arbre. Les résultats d'une étude portant
sur la distance de dispersion des graines de karité dans un parc
agroforestier à MPeresso montrent, en effet, que 95% des graines d'un
arbre donné se retrouvent à moins de 25 m de son houppier (Sanou
et al., 2005). Kelly et al. (2004a) montrent que la distribution spatiale du
karité sur le site de MPeresso devient de plus en plus
agrégée en passant du champ à la jachère et
à la forêt. Les activités agricoles menées au champ
(récolte des fruits, labour, élagage des arbres) expliquent que
la distribution des arbres est moins agrégée et que la structure
spatiale a plutôt tendance à devenir régulière
(Kelly et al., 2004a).
Apparentement en fonction de la distance La Figure 4.12
présente l'estimation de l'apparentement génétique moyen
en fonction de la distance spatiale entre les individus dans la parcelle en
jachère selon deux méthodes d'estimation de l'apparentement par
les moments (Wang (2002); Lynch et Ritland (1999)) et selon la méthode
par maximum de vraisemblance de Milligan (2003). Nous notons de manière
globale que le coefficient d'apparente-
Lynch-Ritland Wang Milligan
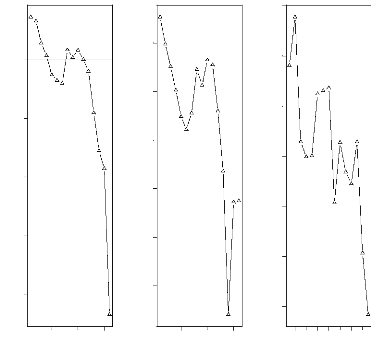
- 0.4 -0.3 -0.2 -0.1 0.0
coeffident dapparentement
coeffident dapparentement
- 0.30 -0.25 -0.20 -0.15 -0.10 -0.05
coeffident dapparentement
0.02 0.04 0.06 0.08 0.10 0.12 0.14
20 60 100 140
50 100 150
50 100 150
distance distance distance
(a) (b) (c)
FIG. 4.12 - Estimation du coefficient d'apparentement moyen en
fonction de la distance entre les individus selon 3 méthodes
différentes (Lynch-Ritland, Wang et Milligan
régression linéaire de l'apparentement en
fonction du logarithme de la distance est, dans les deux cas, significativement
négative (pente= --0.030 et la p-value associée vaut p=0.019 pour
la méthode de Wang; pente= --0.038 et la p-value associée est
inférieure à 10-4 pour la méthode de Lynch et
Ritland). Ces résultats sont cohérents avec ceux obtenus avec le
corrélogramme de Moran qui montrent qu'il y a une structure
génétique significative à faible et grande distances. Nous
n'avons, par contre, pas pu effectuer le test de signification du
paramètre de la régression linéaire du coefficient
d'apparentement estimé selon la méthode de (Milligan, 2003) en
fonction de la distance. Nous notons cependant des différences dans
l'allure générale des courbes présentées sur la
Figure 4.12. Tout d'abord certaines valeurs estimées de l'apparentement
par la méthode des moments sont négatives alors que celles
données par la méthode de Milligan sont toutes positives; alors
qu'avec la méthode de Lynch et Ritland, l'apparentement
décroît de manière graduelle de 0 à 100 m puis de
manière abrupte à partir de 120 m, l'estimateur de
l'apparentement de Wang décroît avec la distance jusqu'à
140 m mais a une tendance à croître au delà de cette
distance. Cependant un défaut majeur de ces deux dernières
méthodes est qu'elles fournissent des valeurs estimées
négatives. Ainsi respectivement près de 59% et 61% des valeurs
estimées du coefficient d'apparentement d'un couple d'individus par les
méthodes respectivement de Lynch et Ritland (1999) et Wang (2002) sont
négatives; ce qui n'a pas vraiment de sens du point de vue de
l'interprétation biologique (Milligan, 2003). Le coefficient
d'apparentement moyen estimé selon la méthode de Milligan (2003)
varie de 0.135 pour des individus distants de 10 à 20 m jusqu'à
0.017 pour des individus distants de plus de 150 m. La distribution des valeurs
estimées du coefficient d'apparentement de Milligan est
présentée aux Figures 4.13 et 4.14; la distribution est
asymétrique et l'apparentement moyen est faible (0.09). Aussi, il faut
souligner que contrairement aux méthodes d'estimation par les moments,
l'estimation de l'apparentement par maximum de vraisemblance de Milligan (2003)
est toujours comprise dans l'intervalle de définition du
paramètre. Cette contrainte induit par contre un biais pour les valeurs
du paramètre proches de 0; ceci est illustré par les Figures 4.13
et 4.14. Nous notons, en effet, qu'il y a un excès de valeurs
estimées de l'apparentement qui sont proches de 0.
4.2. APPLICATION DU MODÈLE SPATIAL POUR
L'APPARENTEMENT55
0.0 0.2 0.4 0.6 0.8
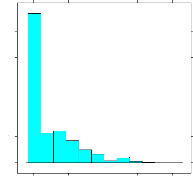
0.0 0.2 0.4 0.6 0.8
Frequence
40
20
50
30
10
0
?
?
?
?
?
?
? ? ? ?
? ? ? ?

coefficient d'apparentement
FIG. 4.13 - Distribution des valeurs estimées du
coefficient d'apparentement de Milligan
FIG. 4.14 - Boxplot des valeurs estimées du coefficient
d'apparentement de Milligan
4.2 Application du modèle spatial
développé
pour l'estimation de l'apparentement
Nous avons appliqué le modèle spatial pour
l'estimation de l'apparentement (voir Définition Modèle Spatial)
à des données simulées. Les données ont
été simulées de la manière suivante :
- nous avons d'abord simulé les fréquences
alléliques selon une loi de Dirichlet dont tous les paramètres
sont égaux à 1
- nous avons simulé ensuite les génotypes de 5
mères et 5 pères avec un nombre variable de locus (5, 10, 15, 20,
30, 50 et 100 locus) selon une loi multinomiale dont les probabilités
associées sont les fréquences alléliques au locus
- nous simulons après les génotypes de 20
enfants. Le nombre d'enfants pour chaque mère est obtenu par 20 tirages
aléatoires avec remise d'un élément parmi 5 et une fois
que le nombre d'enfants pour une mère est connue, l'assignation du
père est faite en fonction de la distance entre les pères et la
mère : le père d'un enfant est simulé selon une loi
multinomiale dont les probabilités associés sont égales
aux distances entre les pères et la mère
considérée. Le génotype d'un enfant à un
locus est ensuite obtenu par le tirage aléatoire d'un
allèle parmi les 2 allèles présents au locus
considéré chez sa mère et le tirage d'un allèle au
hasard parmi les 2 allèles présents au locus
considéré chez sont père. Les juvéniles sont enfin
positionnés autour de leur mère selon une gaussienne
centrée sur la mère et une variance de dispersion égale
à 0.1, 1, 10, 100 respectivement.
Nous nous proposons maintenant d'étudier d'abord
l'effet du choix des paramètres du prior, c'est à dire le choix
des paramètres de la loi de Dirichlet pour les deux modèles
(modèles spatial et non spatial), selon le nombre de locus
considéré avec 100 répétitions. Ensuite, nous
étudions l'effet de la variance de dispersion autour de la mère
pour le modèle spatial pour l'apparentement.
4.2.1 Étude de l'effet du prior
Comme pour tout modèle bayésien, le choix de la
loi a priori des paramètres est toujours délicat car il peut
influer sur la qualité de l'inférence des paramètres.
Classiquement, avec un modèle multinomial-Dirichlet, le prior qui est
choisi est une loi de Dirichlet D(1, 1, 1), qui correspond à un prior
uniforme. Cependant, avec peu d'observations, comme par exemple avec uniquement
5 locus, le choix de cette loi n'est pas approprié car les individus
non-apparentés sont sous-estimés et l'apparentement est donc
sur-estimé. En effet, si toutes les 5 observations ont un mode d'IBD qui
est S9 alors la loi a posteriori des probabilités d'IBD est une D(1, 1,
6), donc la moyenne a posteriori du paramètre d'intérêt qui
est le coefficient d'apparentement è vaut 1/8+ 1/16 donc 0.1875; ce qui
est assez élevé sachant que le coefficient d'apparentement entre
deux demi-frères par exemple vaut 0.12. Nous n'avons par
conséquent pas choisi ce prior. Nous nous proposons de comparer les
résultats obtenus pour deux lois a priori du vecteur des modes d'IBD :
une loi de Dirichlet D(10-5, 10-5, 10-5) et
une loi de Dirichlet D(0.1, 0.1, 0.1). La corrélation entre la vraie
valeur de l'apparentement et la valeur estimée en employant notre
modèle avec chacun des deux priors considérés est
présentée à la Figure 4.15. Nous notons d'abord que la
corrélation entre la vraie valeur et la valeur estimée de
l'apparentement croît avec le nombre de locus pour les deux priors.
Ensuite, il y a clairement un effet du prior sur la corrélation entre
l'apparentement réel et l'apparentement estimé. Lorsque le nombre
de locus est faible, (par exemple avec 10 locus, ce qui se rapproche du cas de
nos données sur le karité) la corrélation moyenne entre
les vraies valeurs et les valeurs estimées est de près de 75%
avec le prior D(0.1, 0.1, 0.1) et ce résultat est assez convenable. Par
contre, avec le prior D(10-5, 10-5, 10-5), la
corrélation vaut à peine 60%. Lorsqu'on choisit comme loi a
priori D(10-5, 10-5, 10-5),
le nombre d'individus non-apparentés est en fait
sur-estimé. Ce qui justifie alors le choix de la loi priori D(0.1, 0.1,
0.1). Nous n'avons cependant pas une explication précise du fait que le
prior D(0.1, 0.1, 0.1) donne des résultats meilleurs que ceux
donnés par le prior D(10-5, 10-5,
10-5).
0.2 0.4 0.6 0.8 1.0
0.4 0.5 0.6 0.7 0.8 0.9 1.0


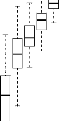
?
?
?
?
?
?
5 10 20 50 5 10 20 50
FIG. 4.15 - Corrélation entre l'apparentement
réel et l'apparentement estimé en fonction du nombre de locus et
du prior (la figure à gauche représente le cas avec une loi de
Dirichlet dont les paramètres sont égaux et très faibles
(10-5) et la figure de droite une loi de Dirichlet dont tous les
paramètres sont égaux à 0.1).
4.2.2 Effet de la variance de dispersion sur les
données simulées
Nous nous intéressons maintenant à
l'étude de l'effet de la prise en compte du spatial sur l'estimation de
l'apparentement génétique. Nous avons pour cela fait quelques
simulations pour comparer le comportement du modèle spatial et celui du
modèle non spatial pour l'apparentement. Nous avons simulé
0.4 0.5 0.8 0.7 0.8
à cet effet des données simulées avec un
nombre variable de locus (5, 10 et 15 locus) et une variance de dispersion de
0.1, 1, 10 et 100. La distribution de l'apparentement obtenue avec ces
simulations est donnée par les Figures 4.16 à 4.26 pour 5, 10 et
15 locus et des variances de dispersion de 0.1, 1, 10 et 100 locus. Nous notons
que la prise en compte du spatial améliore bien l'estimation de
l'apparentement. En effet, la variabilité est généralement
moins importante avec le modèle spatial qu'avec le modèle
non-spatial. Le modèle non spatial sur-estime l'apparentement. La
variabilité du modèle non-spatial est réduite lorsque le
nombre de locus augmente. Nous notons que modèle spatial donne d'une
manière générale de meilleurs résultats que le
modèle non-spatial et ceci même lorsque la variance de dispersion
est grande. Lorsque la variance de dispersion est faible ou moyenne le
modèle spatial donne de meilleurs résultats et lorsque la
variance de dispersion est forte les deux modèles (modèle spatial
et modèle non spatial pour l'apparentement) donnent des résultats
assez similaires. Donc la prise en compte de l'information spatiale
améliore la qualité de l'estimation de l'apparentement
génétique par utilisation des données
moléculaires.

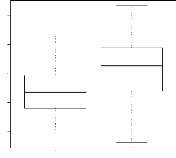
1 2
0.4 0.5 0.8 0.7 0.8
1 2
FIG. 4.16 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 5 locus et une variance de dispersion égale
à 0.1
FIG. 4.17 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 5 locus et une variance de dispersion égale
à 1
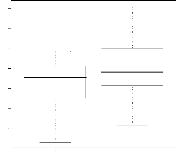
1 2
0.45 0.50 0.55 0.60 0.65 0.70 0.75
FIG. 4.18 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 5 locus et une variance de dispersion égale
à 10

1 2
0.2 0.3 0.4 0.5 0.6 0.7
FIG. 4.19 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 5 locus et une variance de dispersion égale
à 100
Application du modèle spatial développé
aux données sur le Karité Le seul caractère
phénotypique observé dans le jeu de donnés dont nous avons
disposé pour l'application de ce travail est le diamètre à
1, 30 mètre de hauteur. Comme ce caractère dépend de
l'âge des individus et que les individus observés n'ont pas tous
le même âge, l'estimation de l'héritabilité de ce
caractère avec ce jeu de données n'a pas de sens. Nous n'avons
donc pas pu appliquer le modèle spatial pour estimer à la fois
l'apparentement et l'héritabilité aux données
karité. Nous avons alors appliqué le modèle spatial pour
l'apparentement sur un jeu de données réduit seulement aux 58
individus pour lesquels le génotype était complet et dont on
disposait des coordonnées spatiales.
La distribution du paramètre í associé
à la distance spatiale (voir Définition 4)est donnée par
la Figure 4.27. La distribution de ce paramètre ne couvre pas la valeur
0 et donc nous en déduisons qu'il y a bien un effet de la distance
spatiale sur l'estimation de l'apparentement. Comme les valeurs estimées
du paramètre associé à la distance sont négatives,
plus la distance entre des individus est grande et moins ils sont
apparentés. Néanmoins cela reste à confirmer avec de plus
amples études.
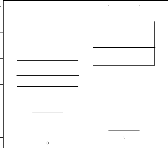
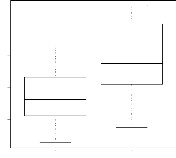
1 2
0.65 0.70 0.75 0.80
0.60 0.65 0.70 0.75 0.80 0.85
1 2
FIG. 4.20 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 10 locus et une variance de dispersion égale
à 0.1
4.3 Discussions
FIG. 4.21 - Corrélation entre l'apparentement
réel et l'apparentement estimé 1) dans le cas non spatial et (2)
dans le cas spatial avec 10 locus et une variance de dispersion égale
à 1
L'application pratique de notre travail a porté sur
l'étude de la diversité génétique et de la
structuration spatiale du karité dans une parcelle de jachère au
sud du Mali. Le génotype à 12 marqueurs microsatellites à
1, 30 m de hauteur de 222 arbres à karité ont été
prélevés dans une parcelle de jachère sur le site de
MPeresso. Les coordonnées géographiques de seulement certains de
ces arbres (132 arbres parmi) ont aussi été relevés. Le
nombre d'allèles par locus varie de 2 à 8 et l'indice de fixation
FIS observé varie entre --0.287 pour le locus F1 à
0.555 pour le locus G7. Le FIS global pour l'ensemble des locus est
significativement différent de 0 et ainsi la population de karité
étudiée sur le site en jachère de MPeresso est en
déséquilibre par rapport au modèle de Hardy-Weinberg. La
structuration spatiale a été étudiée aussi bien au
niveau phénotypique qu'au niveau génotypique. Au niveau
phénotypique, nous avons étudié la distribution des arbres
par classe de diamètre. Cette distribution observée
présente deux modes : le premier correspond aux jeunes arbres en
régénération et le second aux arbres déjà
présents lorsque la parcelle était encore en culture. Nous avons
effectué une analyse en composantes principales pour étudier
l'association entre les génotypes aux différents locus; nous
avons ainsi pu distinguer l'association des locus F5 et E6, d'une
|
0.80 0.85 0.70 0.75 0.80
|
|
|
1 2
|
FIG. 4.22 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 10 locus et une variance de dispersion égale
à 10

1 2
0.85 0.70 0.75
FIG. 4.23 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 10 locus et une variance de dispersion égale
à 100
part, et celle des locus D10 et D6 d'autre part; cependant le
pourcentage d'inertie totale expliquée par les deux premiers axes
principaux est relativement faible (à peine 20%). Aussi la
réalisation du test de Mantel ne nous permet pas de conclure à
l'existence d'une association significative entre les distances
génotypiques et les distances spatiales. Cependant, il ressort du test
de Moran que la structuration spatiale du karité est
agrégée à faible et grande distances. La structuration
spatiale à grande distance pourrait être dûe aux
activités humaines. En effet, la structuration à grande distance
en jachère pourrait s'expliquer par les pratiques des populations
locales, qui entraînent une dispersion une dispersion des graines et du
pollen. Aussi, les modèles théoriques prédisent
l'existence d'une structure génétique spatiale lorsque le flux de
gènes est restreint localement et une absence de structure spatiale
lorsque le flux de gènes par les graines est extensif (Hardesty et al.,
2005). L'apparentement moyen entre les individus en fonction des classes de
distance a été déterminé selon deux méthodes
d'estimation fondées sur le calcul des moments (celle de Wang (2002) et
celle de Lynch et Ritland (1999)) et aussi selon la méthode du maximum
de vraisemblance de Milligan (2003). L'apparentent moyen décroît
significativement avec le logarithme de la distance. Mais, d'une manière
globale, l'apparentement moyen de l'échantillon
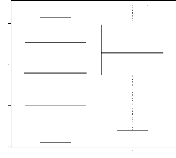
1 2
0.70 0.75 0.80 0.85
FIG. 4.24 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 15 locus et une variance de dispersion égale
à 0.1

1 2
0.70 0.75 0.80 0.85
FIG. 4.25 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 15 locus et une variance de dispersion égale
à 1
étudié est très faible. Nous avons aussi
noté l'existence d'une autocorrélation spatiale significative
jusqu'à une distance d'environ 15m. Cependant, le test de Mantel ne nous
permet pas de déceler une relation linéaire entre la distance
génétique et la distance géographique. Kelly et al.
(2004b) ont étudié la structuration spatiale du karité au
sud du Mali en comparant les résultats obtenus en jachère et en
forêt. Il ressort de leurs travaux que la structuration spatiale est plus
prononcée en jachère qu'en forêt. Parmi les facteurs
expliquant cela, nous pouvons relever le niveau de fructification plus
important dans la jachère dû à une moindre
compétition entre les arbres, ce qui favorise la
régénération naturelle des plants juvéniles autour
des arbres mères du fait que les graines de Vitelleria Paradoxa sont
principalement dispersées par la gravité. En forêt par
contre, le plus faible niveau de fructification qui est dû à une
compétition plus forte entre les arbres, réduit le nombre
d'arbres autour de l'arbre mère et affecte en conséquence la
structuration spatiale du Karité.
Nous avons effectué quelques simulations pour valider
le modèle spatial pour l'estimation de l'apparentement. Nous notons que
la prise en compte de l'information spatiale améliore sensiblement
l'estimation de l'apparentement génétique. Ceci est surtout
vérifié lorsque la variance de dispersion des juvéniles
autour du pied mère est faible, c'est à dire lorsque
l'hypothèse que
0.70 0.75 0.80 0.85
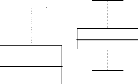

1 2
FIG. 4.26 - Corrélation entre l'apparentement
réel et l'apparentement estimé (1) dans le cas non spatial et (2)
dans le cas spatial avec 15 locus et une variance de dispersion égale
à 10
des individus plutôt proches spatialement sont proches
génétiquement est vérifiée.
Frequency
0 100 200 300 400 500 600
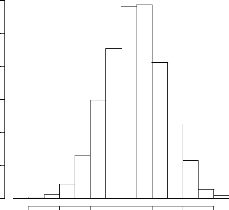
-0.007 -0.006 -0.005 -0.004 -0.003 -0.002
-0.001
IBDSpat$Bet[-c(1:100)]
FIG. 4.27 - Distribution du paramètre í
associé à la distance dans le modèle spatial pour
l'apparentement
Conclusion générale et
perspectives
La génétique quantitative s'intéresse
à l'étude de la transmission héréditaire des
caractères quantitatifs. Un caractère répond à la
sélection lorsque'il a une variabilité génétique
héritable et qu'il n'est pas contraint par les corrélations
génétiques avec d'autres caractères sous sélection.
De manière classique, des dispositifs expérimentaux oil les
croisements entre individus sont contrôlés sont mis en place et
permettent d'estimer l'héritabilité. Cependant,
l'héritabilité d'un caractère mesuré en laboratoire
ou en serre est différente de l'héritabilité de ce
même caractère mesuré en milieu naturel. Ceci s'explique
par les différences environnementales et l'interaction
génotype-environnement. Actuellement, des programmes de recherche sont
de plus en plus menés avec des dispositifs de sélection
participative en milieu naturel. Hors en milieu naturel, comme les croisements
ne sont pas contrôlés, l'apparentement n'est pas connu ou, au
mieux, il n'est connu que partiellement. La possibilité d'estimer
l'apparentement et l'héritabilité des caractères en milieu
naturel à l'aide des données moléculaires suscite un
intérêt croissant dans différents domaines liés
à l'amélioration génétique des populations.
Ce travail de thèse nous a permis tout d'abord de
généraliser le modèle de la vraisemblance de Milligan pour
l'apparentement. Nous avons montré que le modèle de Milligan
s'insère dans un cadre théorique plus large qui est celui de la
vraisemblance composite. En effet, le modèle de Milligan pour n
individus consiste à écrire le produit des lois jointes des
couples de génotypes et revient à écrire la vraisemblance
composite par paires. Nous avons défini le modèle de la
vraisemblance composite par paires pour l'estimation de l'apparentement.
Cependant, les approches classiques pour l'estimation de l'apparentement
génétique développées jusqu'ici ne permettent pas
de prendre en compte une information exogène comme l'information
spatiale. Or, il serait raisonnable de supposer que plus des individus sont
spatialement proches plus ils sont génétiquement proches. Nous
avons développé un modèle spatial bayésien
hiérarchique pour l'estimation de l'apparentement
génétique entre
des individus sans connaissance du pedigree à l'aide
des données moléculaires. L'avantage de la modélisation
bayésienne hiérarchique est qu'elle permet de scinder un
problème complexe en une série de problèmes plus faciles
à traiter. Nous avons supposé que les individus sont
non-consanguins et que le mode d'IBD suit une loi multinomiale et
proposé de modéliser le mode d'IBD avec un GLM probit ordinal.
L'idée est que deux individus proches spatialement sont aussi proches
génétiquement. La prise en compte de l'information spatiale
permet de modéliser le mode d'IBD en fonction d'une variable latente
gaussienne dont la moyenne dépend de la distance entre les individus.
Plus précisément, l'information spatiale permet de
discrétiser le mode d'identité par descendance.
Nous avons ensuite proposé un modèle
bayésien hiérarchique pour estimer à la fois
l'apparentement et l'héritabilité en milieu naturel à
l'aide des données moléculaires. L'intérêt de ce
modèle est qu'il ne suppose pas, contrairement aux modèles de la
vraisemblance pour l'héritabilité développés
d'abord par Mousseau et al. (1998) et ensuite par Thomas et al. (2000), que la
population a une structure d'apparentement prédéterminée
et connue. Un autre avantage du modèle est qu'il permet de bien prendre
en compte l'effet de la variabilité de l'estimation de l'apparentement
sur celle de l'estimation de l'héritabilité. Ce modèle
garantit en outre que la matrice d'apparentement estimée des couples
d'individus est une matrice symétrique définie positive, ce qui
est attendu comme propriété pour une matrice de
variance-covariance.
Trois algorithmes MCMC pour l'inférence
bayésienne des paramètres du modèle pour l'estimation de
l'apparentement sont proposés. Les deux premiers algorithmes sont de
type Métropolis-Hastings avec des lois de proposition
différentes. Mais comme la difficulté avec un algorithme de
MétropolisHastings réside souvent dans le choix de la loi de
proposition appropriée, le dernier algorithme pour l'estimation de
l'apparentement proposé est un algorithme de Gibbs qui a donc l'avantage
d'être plus facilement mis en oeuvre. Comme pour l'inférence des
paramètres du modèle spatial hiérarchique pour
l'apparentement, la loi a posteriori conditionnelle complète des seuils
n'a pas une forme analytique connue et que les lois a posteriori des autres
paramètres sont connues, nous ne pouvons pas employer un algorithme de
Gibbs pour l'inférence bayésienne. Un algorithme de
Métropolis-Hastings couplé à un algorithme de Gibbs pour
l'inférence des paramètres du modèle spatial
bayésien hiérarchique pour l'apparentement a été
proposé. Une difficulté rencontrée dans l'application du
modèle spatial pour l'estimation de l'apparentement, c'est qu'avec peu
d'observations, il peut arriver qu'aucun couple de génotypes partageant
deux allèles identiques par descendance, donc de mode d'IBD 87, ne soit
simulé. Le nombre de modalités observé est réduit
à 2, donc le modèle est non-identifiable et les seuils
associés sont non-estimables.
67
Pour l'application pratique, le jeu de données dont
nous disposons ne comporte qu'une seule variable phénotypique, le
diamètre des arbres à 1, 30 mètre de hauteur. Le
diamètre des arbres est mesuré sur des individus d'âges
différents et comme il varie évidemment en fonction de
l'âge de l'individu considéré, l'héritabilité
de ce caractère pour des individus mesurés à des
âges différents est difficilement interprétable. C'est
pourquoi nous n'avons pas appliqué le modèle
développé dans ce travail pour estimer à la fois
l'apparentement et l'héritabilité. Nous avons pu obtenir
finalement d'autres données phénotypiques sur le karité et
nous envisageons d'appliquer le modèle spatial pour l'estimation de
l'apparentement et de l'héritabilité en milieu natural et
valoriser ensuite ce travail par une publication. En outre, il nous faudra
effectuer plus de simulations pour pouvoir estimer à la fois
l'apparentement et l'héritabilité et bien mesurer l'apport du
modèle spatial sur l'estimation de ces paramètres. Il serait
aussi intéressant de développer un modèle spatial qui
prendrait en compte la dépendance entre les couples d'individus. Nous
avons considéré dans ce travail que les fréquences
alléliques sont connues. Comme en pratique, elles ne sont souvent pas
connues, nous allons développer un algorithme pour estimer à la
fois les fréquences alléliques, l'apparentement et
l'héritabilité. Nous avons supposé avec le modèle
spatial pour l'estimation de l'apparentement que la population est
composée d'individus non-consanguins. Cependant cette hypothèse
peut se révéler restrictive pour l'application pratique du
modèle. Il serait intéressant d'envisager le développement
d'un modèle spatial pour estimer l'apparentement génétique
d'individus issus d'une population consanguine. Dans ce cas, le modèle
ne serait plus ordinal comme tous les 9 modes d'identité par état
des allèles peuvent être observés. Le modèle
approprié est un modèle multinomial et non un modèle
probit. De plus, nous pourrions considérer que les observations sont les
génotypes d'un triplet et non d'un couple et employer le modèle
de la vraisemblance composite par triplets et non par paires. Cependant ceci
augmenterait considérablement le nombre de paramètres du
modèle.
Bibliographie
ANDERSoN, A. D. et WEiR, B. S. (2007). A maximum-likelihood
method for the estimation of pairwise relatedness in structured populations.
Genetics, 176:421-440.
ARNAuD, J.-F., MADEc, L., BELLiDo, A. et GuiLLER, A. (1999).
Micro-spatial genetic structure in the land snail Helix aspersa (gastropoda :
Helicidae). Heredity, 83:110-119.
AzzALiNi, A. (1983). Maximum likelihood estimation of order m for
stationary stochastic processes. Biometrika, (70):381-387.
BAGNouD, N., ScHiMiTHUSEN, F. et SoRG, J.-P. (1995). Les parcs
à karité et néré au Sud-Mali : analyse du bilan
économique des arbres associés aux cultures. Bois et Forêts
Des Tropiques, 244, 9Û23., (244):9-23.
BAyES, T. (1763). An essay toward solving a problem in the
doctrine of chances. Phil. Trans. Roy. Soc., 53:370-418.
BESAG, J. E. (1974). Spatial interaction and the statistical
analysis of lattice system (with discussion). Journal of the Royal Statistical
Society, Series B, 36(2):192-236.
BLouiN, M. S. (2003). DNA-based methods for pedigree
reconstruction and kinship analysis in natural populations. Trends in Ecology
and Evolution, 18(10):503-511.
BoicHARD, D., LE Roy, P., LEvEziEL, H. et ELSAN, J.-M. (1998).
Utilisation des marqueurs moléculaires en géntique animale. INRA
Prod. Anim., 11(1):6780.
BouvET, J.-M., KELLy, B.-A., SANou, H. et ALLAL, F. (2008).
Comparison of marker- and pedigree-based methods for estimating heritability in
an agroforestry population of vitellaria paradoxa c.f. gaertn. (shea tree).
Genetic resources and crop evolution, 55:1291-1301.
CArdi, C., VAiLLANt, A., SANou, H., KELLy, B. A. et BouvEt,
J.-M. (2005). Characterisation of microsatellite markers in the shea tree
(Vitellaria paradoxa c.f. gaertn) in mali. Molecular Ecology Notes,
(5):524-526.
ChEssEL, D., Dufour, A.-B. et ThiouLousE, J. (2004). The ade4
package-I- One-table methods. R News, 4:5-10.
Chib, S. et GrEENbErg, E. (1995). Understanding the
Metropolis-Hastings algorithm. The American Statistician, 49(4):327-335.
Chib, S. et GrEENbErg, E. (1998). Analysis of multivariate probit
models. Biometrika, 85(2):347-361.
CLArk, P. J. et EvANs, F. C. (1954). Distance to nearest
neighbour as a measure of spatial relationships in populations. Ecology,
35:445-453.
CockErhAm, C. C. (1969). Variance of gene frequencies. Evolution,
23:72- 84.
Cox, D. R. (1975). Partial likelihood. Biometrika,
(62):269-276.
Cox, D. R. et REid, N. (2004). A note on pseudolikelihood
constructed from marginal densities. Biometrika, 91(3):729-737.
DE ViENNE, D. (1998). Les marqueurs moléculaires et leurs
applications. INRA.
DEgEN, B. (2000). Sgs : Spatial genetic software. computer
program and user's manual. http ://
kourou.cirad.fr/genetique/software.html.
DEgEN, B., PEtit, R. et KrEmEr, A. (2001). Sgs-spatial genetic
software : a computer program for analysis of spatial genetic and phenotypic
structures of individuals and populations. Journal of Heredity, 92:447-448.
EfroN, B. (2005). Bayesians, frequentists, and scientists.
Journal of the American Statistical Association, 100(469):1-5.
FALcoNEr, D. S. (1974). Introduction à la
génétique quantitative. Masson et Cie, Paris.
FrANkEL, O. H. et SouLE, M. E. (1981). Conservation and
Evolution. Cambridge University Press, Cambridge.
GEmAN, S. et GEmAN, D. (1984). Stochastic relaxation, gibbs
distributions and the bayesian restoration of images. IEEE Transactions on
Pattern Analysis and Machine Intelligence, 6(6):721-741.
Gillois, M. (1964). La relation d'identité
génétique. Thèse de Doctorat, Faculté des sciences,
Paris.
GoudEt, J. (2001). FSTAT, a program to estimate and
test gene diversities and fixation indices (version
2.9.3).
http ://
www2.unil.ch/popgen/softwares/fstat.htm.
HARdEsty, B., Dick, C., KREmER, A. et BERmiNghAm, E. (2005).
Spatial genetic structure of Simarouba amara aubl. (simaroubaceae), a
dioecious, animal-dispersed neotropical tree, on barro colorado island, panama.
Heredity, 95:290-297.
HARdy, O. et VEkEmANs, X. (1999). Isolation by distance in a
continuous population : reconciliation between spatial autocorrelation analysis
and population genetics models. Heredity, 83:145-154.
HARdy, O. J. (2003). Estimation of pairwise relatedness
between individuals and characterization of isolation-by-distance processes
using dominant genetic markers. Molecular Ecology, 12:1577Û1588.
HARdy, O. J. et VEkEmANs, X. (2002). Spagedi : a versatile
computer program to analyse spatial gentic structure at the individual or
population levels. Molecular Ecology Notes, 2:618-620.
HARtl, D. L. et ClARk, A. G. (1997). Principles of population
genetics. Sunderland,Massachusetts, third édition.
HAstiNgs, W. (1970). Monte carlo sampling methods using markov
chains and their applications. Biometrika, 57:97-109.
HEplER, A. B. (2005). Improving forensic identification using
Bayesian networks and relatedness estimation. Phd thesis, North Carolina State
University, Raleigh, NC.
Hocdé, H., LANçoN, J. et TRouchE, G. (2001).
Pour une conception élargie de la sélection participative. In La
sélection participative : impliquer les utilisateurs dans
l'amélioration des plantes, pages 0817, Montpellier. CIRAD, MICAP.
JAcQuARd, A. (1970). Structures génétiques des
populations. Masson.
KAliNowski, S., WAgNER, A. et TApER, M. (2006). Ml-relate: a
computer program for maximum likelihood estimation of relatedness and
relationship. Molecular Ecology Notes, 6(6):576-579.
KELLY, B. A. (2004). Impact des pratiques humaines sur la
dynamique des populations et sur la diversité génétique de
Vitellaria Paradoxa (Karité) dans les systèmes agroforestiers au
Sud du Mali. Thèse de Doctorat, Université de Bamako.
KELLY, B. A., BOUVET, J.-M. et PiCARD, N. (2004a). Size class
and spatail pattern of Vitellaria Paradoxa in relation to farmer's practices in
mali. Agroforestry Systems, (60):3-11.
KELLY, B. A., HARDY, O. et BOUVET, J.-M. (2004b). Temporal and
spatial genetic structure in Vitellaria Paradoxa (shea tree) in an agroforestry
system in southern mali. Molecular Ecology, 13(5):1231-1240.
Li, C. C., WEEKS, D. E. et CHAKRAVATi, A. (1993). Similarity of
DNA fingerprints due to chance and relatedness. Hum. Hered., (43):45-52.
LiNDSAY, B. G. (1988). Composite likelihood methods. Contemporary
mathematics, 80:221-239.
LYNCH, M. et RiTLAND, K. (1999). Estimation of pairwise
relatedness with molecular markers. Genetics, 152:1753-1766.
LYNCH, M. et WALSH, B. (1998). Genetics and Analysis of
Quantitative Traits. Sinauer Associates.
MARiN, J.-M. et ROBERT, C. P. (2007). Bayesian Core : A Practical
Approach to Computational Bayesian Statistics. Springer.
MCCULLAGH, P. et NELDER, J. A. (1989). Generalized Linear Models.
Chapman& Hall/CRC, second édition.
METROPOLiS, N., ROSENBLUTH, A., ROSENBLUTH, M., TELLER, A. et
TELLER, E. (1953). Equations of state calculations by fast computing machines.
Journal of Chemical Physics, 21(6):1087-1091.
MiLLiGAN, M. G. (2003). Maximum-likelihood estimation of
relatedness. Genetics, 163(3):1153-1167.
MOORE, A. J. et KUKUK, P. F. (2002). Quantitative genetic
analysis of natural populations. Nature Reviews Genetics, 3:971978.
NEi, M. (1972). Genetic distances between populations. American
Naturalist, 106:283-292.
NEi, M. (1987). Molecular Evolutionary Genetics. Colombia
University Press, New York.
OkuLLo, J., HALL, J. et ObuA, J. (2004). Leafing, flowering
and fruiting of Vitelleria paradoxa subsp. nilotica in savanna parklands in
Uganda. Agroforestry Systems, 60:77-91.
PArEnt, E. et BErniEr, J. (2007). Le raisonnement
bayésien Modélisation et inférence. Statistique et
probabilités appliquées. Springer-Verlag, Paris.
PrEss, W., TEukoLsky, S., VEttErLing, W. et FLAnnEry, B.
(1992). Numerical Recipes in C. Cambridge University Press, Cambridge, UK, 2nd
édition.
QuELLEr, D. et Goodnight, K. (1989). Estimating relatedness using
molecular markers. Evolution, (43):258-275.
R DEvELopMEnt CorE TEAM (2008). R A Language and Environment
for Statistical Computing. R Foundation for Statistical Computing, Vienna,
Austria. ISBN 3-900051-07-0.
RicE, W. R. (1989). Analysing tables of statistical tests.
Evolution, 43:223- 225.
RipLEy, B. (1981). Spatial Statistics. Wiley Series in
Probability and Mathematical Statistics Wiley, New York.
RitLAnd, K. (1996a). Estimators for pairwise relatedness and
individual inbreeding coefficients. Genet. Res., 67:175-186.
RitLAnd, K. (1996b). A marker-based method for inferences about
quanti-
tative inheritance in natural populations. Evolution,
50(3):10621073.
RitLAnd, K. (2000). Adaptive genetic variation in the Wild,
chapitre Detecting Inheritance with Inferred Relatedness in Nature, pages
187-199. Oxford University Press, New York.
Roberts, G. et SMith, A. (1994). Simple conditions for the
convergence of the gibbs sampler and the metropolis-hastings algorithms.
Stochastic Processes and their Applications, 49(2):207-216.
Rossi, J.-P. (1996). Statistical tool for soil biology. xi.
autocorrelogram and mantel test. European Journal of Soil Biology,
32(4):195-203.
SAnou, H., Lovett, P. N. et Bouvet, J.-M. (2005). Comparison
of quantitative and molecular variation in agroforestry populations of the shea
tree (Vitellaria paradoxa C.F. Gaertn) in Mali. Molecular Ecology, 14:2601-
2610.
SAportA, G. (1990). Probabilités, analyse des
données et statistique. Editions Technip, Paris.
SAutter, G. (1968). Les structures agraires en Afrique tropicale.
Centre de documentation universitaire, Paris.
Selkoe, K. A. et Toonen, R. J. (2006). Microsatellites for
ecologist : a practical guide to use and evaluating microsatellite markers.
Ecology Letters, 9:615-629.
Sorensen, D. et GiAnolA, D. (2007). Likelihood, Bayesian and
MCMC Methods in Quantitative Genetics. Springer.
TAssi, P. (1985). Méthodes statistiques. Economica.
ThoMAs, S. C. (2005). The estimation of genetic relationships
using molecular markers and their efficiency in estimating heritability in
natural populations. Philos Trans R Soc Lond B Biol Sci,
360(1459):1457-1467.
ThoMAs, S. C. et Hill, W. G. (2000). Estimating quantitative
genetic parameters using sibships reconstructed from marker data. Genetics,
155(4):1961-1972.
ThoMAs, S. C., PeMberton, J. M. et Hill, W. G. (2000).
Estimating variance components in natural popualtions using inferred
relationships. Heredity, 84:427-436.
ThoMpson, E. A. (1975). The estimation of pairwise relationships.
Ann. Hum. Genet., 39:173188.
VERRIER, E., BRABAND, P. et GALLAIS, A. (1998). Faits et concepts
de base en génétique quantitative. Institut National Agronomique
Paris-Grignon.
WANG, J. (2002). An estimator for pairwise relatedness using
molecular markers. Genetics, 160:1203-1215.
WEIR, B. S., ANDERSON, A. D. et HEPLER, A. B. (2006). Genetic
relatedness analysis : modern data and new challenges. Nature reviews Genetics,
7:771- 780.
WEIR, B. S. et COCKERHAM, C. C. (1984). Estimating F-statistics
for the analysis of population structure. Evolution, 38(6):1358-1370.
WIKLE, C. K. (2003). Hierarchical bayesian models for predicting
the spread of ecological processes. Ecology, 84(6):1382-1394.
YEH, F. et BOYLE, T. (1997). Population genetic analysis of
co-dominant and dominant markers and quantitative traits. Belgian Journal of
Botany, pages 129-157.
Résumé La connaissance de
l'apparentement génétique entre individus permet d'estimer
l'héritabilité des caractères d'intérêt. La
possibilité d'estimer l'héritabilité en milieu naturel
suscite un intérêt croissant pour l'amélioration
génétique des populations. Mais en milieu naturel, le pedigree
n'est pas connu. L'utilisation des marqueurs moléculaires permet
d'estimer l'apparentement puis d'estimer l'héritabilité.
Néanmoins, les approches classiques ne permettent pas d'introduire une
information exogène comme l'information spatiale. Or, nous pouvons
supposer que deux individus proches géographiquement sont proches
génétiquement. L'objectif de ce travail est de développer
des modèles statistiques pour l'estimation de l'apparentement et de
l'héritabilité à l'aide des marqueurs moléculaires
en prenant en compte l'information spatiale. Premièrement, nous
construisons un modèle spatial hiérarchique bayésien de
l'apparentement. Comme la vraisemblance des observations, modes
d'identité par état entre génotypes, est complexe, le
modèle statistique pour l'apparentement considéré est
celui de la vraisemblance composite. Le lien entre le mode d'identité
par descendance et la distance spatiale se fait par l'intermédiaire d'un
GLM probit ordinal. Deuxièmement, nous proposons une modélisation
simultanée de l'apparentement et de l'héritabilité. Dans
la troisième partie, nous proposons différents algorithmes MCMC
pour l'inférence des paramètres des modèles. Finalement,
l'intérêt du modèle spatial pour l'apparentement est
illustré par une application à des données sur le
karité (Vitellaria paradoxa).
Mots Clés Bayésien hiérarchique, MCMC,
Vraisemblance Composite, Apparentement, Héritabilité, Spatial,
Marqueurs Moléculaires, Karité
Spatial hierarchical Bayesian Model for relatedness and
heritability based on
molecular markers.
Abstract The knowledge of genetic relatedness
between individuals combined with phenotypic information enables us to estimate
the heritability of character of interest. Estimating the heritability in
natural populations remains a real challenge for the obvious reason that, in
natural populations, the pedigree remains unknown. The use of molecular markers
allows the assessment first of relatedness and then of heritability. However,
classical approaches do not allow to introduce exogenous information such as
geographical information. Nevertheless, we can assume that the closer two
individuals are spatially, the more genetically close they are. The aim of this
study is to develop statistical models allowing the simultaneous estimation of
relatedness and heritability by using molecular markers as well as spatial
information. In the first part, we develop a hierarchical spatial Bayesian
model for relatedness taking into account spatial information. As the
likelihood of the data given by the identity-by-state mode of pairs of
genotypes, is not tractable, we propose the use of the composite likelihood
approaches. The link between the identity-bydescent mode and the spatial
distance is made using ordinal Probit models belonging to the generalized
linear models. In the second part, we propose to model relatedness and
heritability simultaneously. In the third part, we give different MCMC
algorithms for model inference. Finally, the spatial model for relatedness is
emphasized by an application on Shea tree (Vitellaria paradoxa) data.
Keywords Hierarchical Bayesian, MCMC, Composite Likelihood,
Relatedness, Heritability, Spatial, Molecular Markers, Shea Tree.
Discipline : Biostatistiques
CIRAD, UR 39 : Diversité génétique et
amélioration des espèces forestières.
TA A-39 / C. Campus international de Baillarguet. 34398
Montpellier Cedex 5 - France
| 


