Analyse en composantes principales de densités de probabilité estimées par la méthode du noyau

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR ET DE LA RECHERCHE SCIENTIFIQUE UNIVERSITE MOULOUD MAMMERI DE TIZI OUZOU

FACULTE DES SCIENCES

DEPARTEMENT DE MATHEMATIQUES

MEMOIRE DE MAGISTER

SPECIALITE: MATHEMATIQUES
OPTION: PROBABILITES ET STATISTIQUES

Présenté par: Yousfi Smail

Sujet:

ANALYSE EN COMPOSANTES PRINCIPALES DE DENSITES DE PROBABILITE ESTIMEES

PAR LA METHODE DU NOYAU

Devant le jur_y d'examen compose de:

M.Hocine Fellag	Proffesseur	U.M.M.T.O	Président
M.Berkoun Youcef	Chargé de recherche	U.M.M.T.O	Examinateur
M.Boumaza Rachid	Maître de conférences	I.N.H., ANGERS	Rapporteur
M.Ibazizen Mohamed	Maître de conférences	U.M.M.T.O	Examinateur
M.Yousfate Abderrahmane	Maître de conférences	U.D.L.S.B.A	Examinateur

Soutenu le / /

A la mémoire de mes _grands parents

Remerciements

Au terme de ce modeste travail, je tiens a exprimer ma sincere _gratitude envers M.BOUMAZA Rachid, pour m'avoir accordé l'honneur d'assurer la direction de ce mémoire. Je le remercie pour ces conseils précieux, ses criti_ques, ses orientations et pour sa _grande contribution a l'aboutissement de ce projet.

Je remercie M.FELLAG Hocine, M.IBAZIZEN Mohamed et M.BERKOUN Youcef pour avoir accepté d'être membres de mon jur_y. Je remercie é_galement M.YOUSFATE Abderrahmane _qui ma fait l'honneur de rejoindre la composition du jur_y.

Parmi les personnes _qui mon aidé, je tiens a remercier chaleureusement

M.BOUDIBA Mohand Arezki et M.MORSLI Mohammed _qui ont participé a la mise au point de certains passa_ges dans ce mémoire.

Je remercie é_galement mes amis, _qui m'ont porté une affection sans faille. Enfin, et surtout, je pense a ma précieuse famille a _qui j'ai volé tant de bons moments...

Table des matières

1	Notations Introduction ACP fonctionnelle de densités de probabilité 1.1 Introduction					4 5 10 10
	1.2		Rappel sur l'analyse en composantes principales d'un opérateur			11
			1.2.1		Condition d'existence de l'ACP "pas a pas"	12
			1.2.2		ACP totale d'un opérateur compact	13
	1.3		ACP de densités de probabilité			14
			1.3.1		Introduction	14
			1.3.2		Affinité L^2 entre deux densités de probabilités	14
			1.3.3		Définition de l'ACP de densités	15
			1.3.4		Formule de reconstitution des densités de probabilités	17
			1.3.5		Qualité Globale de l'ACP	17
			1.3.6		Qualité de représentation de ft suivant gj	17
			1.3.7		ACP normée	18
			1.3.8		ACP centrée	18
2	Estimation de l'ACP de densités de probabilité					21
	2.1		Introduction			21
	2.2		Rappel sur l'estimation d'une densité par la méthode du noyau			22
			2.2.1		Choix du noyau et de la fenêtre de lissage	24
			2.2.2		Application a l'estimation par noyau de l'affinité L^2 31
		2.3		ACP de densités estimées par la méthode du noyau 2.3.1 Cas général			33 33
				2.3.2 Exemples			33
				2.3.3 Approche de Kneip et Utikal			36
				2.3.4 Application de l'approche d'estimation de Kneip and Utikal a une ACP
				estimée non centrée et non normée			38
		2.4		ACP de densités estimées paramétriquement			41
				2.4.1 Cas de données gaussiennes multidimensionnelles			41
				2.4.2 ACP paramétrique de densités de Gumbel unidimensionnel			44
		2.5		Comparaison entre l'approche paramétrique et non paramétrique			46
3		Influence du noyau sur l'ACP de densités estimées					49
		3.1		Introduction			49
		3.2		Cas des fenêtres AMISE			51
		3.3		Cas d'égalité des AMISE			56
		3.4		Conclusion			62
4		Influence et choix de la fenêtre de lissage					63
		4.1		introduction			63
		4.2		Influence de la fenêtre de lissage			63
		4.3		Choix de la fenêtre de lissage			72
		Conclusion					81
		Bibliographie					84

Notations

Notations matricielles

W' transposée de la matrice / vecteur W

Wt,s élément de la t-ème li_gne et la s-ème colonne de la matice W

W -1 inverse de la matrice W

|W | déterminant de la matrice W

MuM la norme euclidienne de u

kuMM la M-norme de u

Notations statisti_ques

E(X) espérance mathémati_que de la variable X

V (X) variance de variable X

Cov(X,Y ) covariance des variables X et Y

N(u,Ó) loi normale de vecteur mo_yen u et de matrice de variance covariance Ó

MISE Mean Inte_grated S_quare Error

AMISE As_ymptotic Mean Inte_grated S_quare Error

Notations fonctionnelles

L²(IR^p) espace des fonctions réelles de carré inté_grable sur IR^p

L2IR( × T) espace des fonctions réelles de carré inté_grable par rapport a la mesure

produit sur × T

U* adjoint de l'opérateur U

< u,v >H produit scalaire dans l'espace de Hilbert H entre les deux vecteurs

u et v

UoV composée des opérateurs U et V

kV M norme de l'oprérateur V

II[a,b] indicatrice de l'intervalle [a,b]

Notations diverses

Pn i fi sommation sur l'ensemble des valeurs de l'indice i des _quantités fi

ps conver_gence pres_que sure

Introduction

La statisti_que, en tant _que discipline des mathémati_ques appli_quées, admet une _grande diversité de dominantes, elle peut être descriptive ou inférentielle, paramétri_que ou non, as_ymptoti_que ou non, uni ou multidimensionnelle_; elle en_globe un spectre très lar_ge de problèmes, allant du plus concret (traitement de données) au plus abstrait (formalisation mathémati_que nécessitant des concepts variés, _qui peuvent être des versions stochasti_ques de la théorie fondamentale (théorie des opérateurs)). Pour cela, elle utilise des outils divers issus de l'al_gèbre linéaire, de l'anal_yse fonctionnelle, de la _géométrie (projection ortho_gonale) et du calcul des probabilités.

L'anal_yse des données comme méthode de la statisti_que descriptive, a vu ses champs d'applications s'élar_gir d'une fa_çon considérable, avec l'introduction et le développement des mo_yens de calcul (les ordinateurs), dépassant ainsi son cadre classi_que [1, 91 en empruntant les chemins du cadre fonctionnel, permettant ainsi d'étudier des phénomènes rendus plus complexes par le _gros volume de données _qu'ils induisent. Par exemple, lors_qu'on étudie un phénomène économi_que comme la consommation mensuelle d'électricité, il est d'usa_ge de la représenter par la chroni_que des consommations mensuelles totales. " Ce choix présente deux inconvénients " [61

~ On perd une partie de l'information concernant la structure du s_ystème_;

Les délais nécessaires a la connaissance des derniers résultats de cette série sont souvent assez lon_gs.

" Le premier point nous amène a caractériser le phénomène étudié par la série chronolo_gi_que multiple des consommations mensuelles des différentes branches de l'industrie et du commerce. Sa visualisation nous fournira celle du phénomène de fa_con _globale" [61.

" Le deuxième point pose le problème du choix d'une ou plus _généralement d'un petit _groupe de séries, extraits de la série multiple et la représentant au mieux. Ce choix est fondamental dans l'étude de la conjoncture et dans la prévision " [61 . Braun (1973) propose de résoudre ce problème en faisant une anal_yse en composantes principales sur ces séries, dont la première composante principale va expli_quer au mieux la variabilité du phénomène. Cette dernière n'expli_quant _qu'une partie de la variabilité totale, on peut alors considérer la deuxième composante principale parmi les combinaisons linéaires des autres séries ortho_gonales a la première composante principale, et ainsi de suite.

Depuis les travaux pionniers de Deville (1974), beaucoup d'attentions ont étés accordé a l'anal_yse des données fonctionnelles par la communauté statisti_que [11 dont beaucoup d'études sont consacrées a la description statisti_que d'un échantillon de courbes (courbe de croissance, courbe de température, ... ) au mo_yen de l'anal_yse en composantes principales fonctionnelle (voir Ramsa_y and Silverman 1991, Boumaza, 1999, Kneip and Utikal, 2001...). L'utilisation de la décomposition spectrale de l'opérateur de covariance _qui est analo_gue a la matrice de covariance dans l'espace des fonctions, permet d'obtenir dans un espace de faible dimension les principaux modes de variations des données. Prenons par exemple la fonction aléatoire X(t,w), w E Ù et t varie dans un intervalle compact T de IR, de mo_yenne u(t) et de fonction de covariance ã(t,s) = Cov(X(s),X(t)).

L'opérateur de covariance F s'écrit sous la forme d'un opérateur inté_gral comme suit [111:

_Z

Vf E L²(T ), Vt E T, Ff(t) = ã(t,s)f(s)ds (1)

T

La meilleure approximation de X dans un sous-espace de dimension q, est obtenue par la projection de X sur le sous-espace de L²_IR(Ù x T) en_gendré par les q fonctions propres g1, . . . ,g_q de F de la fa_çon suivante:

X(t) u(t) + X q fj gj(t) (2)

j=1

Les fj sont des variables aléatoires centrées de variances ëj (ëj est la j-ième valeur propre de F). Une approximation obtenue au mo_yen de l'anal_yse en composantes principales fonctionnelle (FPCA) de la fonction aléatoire X [4, 141.

Si nous intéressons maintenant a la description et a l'estimation des réalisations des trajectoires Xi d'une variable aléatoire X prenant ses valeurs dans un espace fonctionnel,"deux points de vue cohabitent dans la littérature et conduisent aux memes procédures d'estimation "[11 . Le premier considère _que les observations sont bruitées et _que le vrai si_gnal est contenu dans un espace fonctionnel de dimension finie [271, Il s'a_git alors de reconstuire au mieux les trajectoires observées. Le second cherche a obtenir une représentation optimal d'un ensemble de courbes dans un espace de dimension petite [11].

Lors_qu'on observe un échantillon i.i.d de variables aléatoires fonctionnelles Xi, i = 1,m tiré selon la distibution de X, on peut définir l'opérateur de covariance empiri_que _n[14l. Deville (1974), Dauxois et Pousse (1976), montrent, en des sens et sous des h_ypothéses différentes (conver_gence pres_que sure, conver_gence en loi, données dépendantes), la conver_gence des opérateurs de covariance au sens de la norme de Hilbert-Schmidth ainsi la conver_gence des éléments propres. Ensuite, Dauxois et al, ont montré la conver_gence en loi de _n et en ont déduit les conver_gences en loi des éléments propres.

En prati_que on peut supposer _que les courbes sont observées sur une _grille de p points de discrétisation t1,... ,t_p . On note Xi = (Xi(t1), . . . ,Xi(t_p)^' la i-ème trajectoire disctrétisée _que l'on suppose centrée."En approximant l'opérateur de covariance en utilisant une méthode de _quadrature, on peut définir les composantes principales comme les coordonnées dans la bases des fonctions propres discrétisées " [11].

" L'estimation "brute" des éléments propres en présence d'observations discrètes des courbes n'est pas forcément judicieuse, les fonctions propres estimées pouvant etre très irré_gulières " [71 , d'oi l'idée prati_que de proposer un lissa_ge dans la phase d'estimation. Ce lissa_ge peut opérer sur les trajectoires [11, 27] des_quelles on fait ensuite l'ACP sur les vecteurs propres [34, 35] oi encore en lissant simultanément toutes les trajectoires dans un espace de dimension restreinte [101. Ce lissa_ge permet é_galement d'améliorer, lors_que la valeur du paramètre est bien choisie, les estimateurs des éléments propres [11, 27] et les reconstructions des trajectoires [101.

Une variante de l'anal_yse des données fonctionnelles permettant le traitement d'un autre t_ype de données, appelée: "données ternaires" (three-wa_y data) _qui se présentent sous forme de L tableaux indicés par un paramètre _qui peut être le temps [12, 21] est l'ACP de densités de probabilité [3, 20] dont la justification théori_que ressort de la théorie des opérateurs compacts [13, 151. Elle consiste a remplacer cha_que tableau par une densité de probabilité. L'ensemble de ces densités constitue un nua_ge de L vecteurs dans l'espace de Hilbert L²(IR¹²) (p dési_gne le nombre de colonnes de ces tableaux). L'objectif est de décrire _globalement ces données, en procédant a une représentation approché dans un sous-espace de faible dimension.

La méthode suppose _que les densités sont connues, ce _qui n'est pas toujours le cas en prati_que. Une fa_çon simple d'_y remédier consiste a supposer _que les densités appartiennent a une famille connue, comportant des paramètres inconnus dont les estimations par la méthode de vraisemblance permet de déduire des estimations de ces densités, puis de faire une ACP sur les densités estimées. Cette ACP fournit une estimation de l'ACP théori_que correspondante.

On peut vérifier dans le cas de données _gaussiennes simulées la conver_gence rapide de l'ACP des densités estimées vers l'ACP théori_que correspondante pour des tailles d'échantillon raisonnables [31.

Notre souci dans ce présent travail est de présenter une autre approche d'estimation. Elle consiste a estimer les densités inconnues par la méthode du no_yau [2, 16, 31, 32, 331. La conver_gence de l'ACP estimée est justifiée par les propriétés de conver_gence des estimateurs a no_yau [21.

On étudiera ainsi pour une taille d'échantillon fixée, l'influence des paramètres de lissa_ge (no_yau et fenêtre) sur les résultats de l'estimation, puis on proposera un critère de sélection de la fenêtre de lissa_ge. On utilisera ce critère pour calculer une fenêtre dite "optimale", permettant ainsi d'obtenir une meilleure estimation de l'ACP théori_que correspondante.

L'étude est faite sur des données simulées de différentes natures (bimodale s_ymétri_que et as_ymétri_que, unimodale s_ymétri_que et as_ymétri_que). Les pro_grammes ont été écrits dans l'environnement Scilab.

Le premier chapitre est consacré a l'étude de l'ACP de densités. Dans un premier temps on proposera un bref rappel sur l'anal_yse factorielle d'opérateur, _qui sera considérée comme un outil mathémati_que pour aborder par la suite la deuxième partie, _qui est dédiée a l'ACP de densités.

Dans le deuxième chapitre et après un rappel sur la notion d'estimation de densité de probabilités par la méthode du no_yau, on présentera dans un premier temps l'ACP de densités estimées non paramétri_quement, ensuite on donnera un rappel sur l'approche d'estimation paramétri_que et on terminera ce chapitre par une comparaison entre les deux approches d'estimation.

En se basant sur des exemples simulés, on étudiera au début du troisième chapitre, l'influence du no_yau sur l'ACP de densités estimées, oi l'on considérera deux cas particuliers_; le cas oi les densités sont estimées en associant a chacune d'elle la fenêtre optimale au sens de l'erreur _quadrati_que inté_grée as_ymptoti_que et le cas oii les densités sont estimées sous la condition d'é_galité des erreurs _quadrati_ques inté_grées as_ymptoti_ques.

Le _quatrième et dernier chapitre est réservé a l'influence et choix de la fenêtre de lissa_ge sur l'ACP de densités. On _y proposera un critère de sélection d'une fenêtre dite "optimale", et on _y comparera a l'aide de _quel_ques exemples simulés, les résultats obtenus en utilisant cette fenêtre et les résultats obtenus en utilisant les fenêtres optimales au sens des erreurs _quadrati_ques inté_grées asymptotiques.

Chapitre 1

ACP fonctionnelle de densités de

probabilité

1.1 Introduction

Le travail dans les espaces fonctionnels s'impose lors_que les données elles-mêmes sont des fonctions. Le cas le plus classi_que est celui d'un individu observé pendant un certain temps, au cours du_quel plusieurs mesures sont effectuées.

Un autre exemple est celui des mesures climati_ques. Dans ce cas, une ré_gion peut être représentée par une fonction _qui a une date associe des _grandeurs comme la température mo_yenne de la journée correspondante, la _quantité de précipitations, etc.

Le traitement statisti_que de ce t_ype de données nécessite une _généralisation de l'anal_yse des données classi_ques, au cas des données fonctionnelles [10, 14, 26, 27, 34, 35]

On présentera dans ce chapitre une autre méthode permettant le traitement d'un autre t_ype de données fonctionnelles _qu'on appellera Anal_yse en Composantes Principales de densités de probabilités [3, 201. Les densités jouent le rOle des individus observés_; ces individus sont dans un espace fonctionnel (espace de Hilbert dans notre cas).

Néanmoins l'adaptation d'une telle méthode a ce t_ype de données re_quiert un arsenal mathémati_que _qui sera considéré comme un outil indispensable pour aborder les aspects as_ymptoti_ques.

La première partie de ce chapitre fournit le cadre mathémati_que (Dauxois et Pousse, 1976) dont l'objectif est de définir la base de fonctions sur les_quelles sont décomposées les densités_; la deuxième partie consiste en la présentation de l'ACP de densités.

1.2 Rappel sur l'analyse en composantes principales d'un operateur

Soit H et H^' deux espaces de Hilbert séparables_; l'espace H (resp. H^') est identifié a son dual. On pose < .,. >H (resp. < .,. >H') le produit scalaire de l'espace H (resp. H^'), et k.kH (resp. 1.1H⁰) la norme associée.

Soit U un opérateur continu non nul de H dans H^', et U^* son adjoint.

Definition 1.2.1 On appelle anal_yse en composantes principales "pas a pas" de U, tout couple ({ëi}i?I, {ui}i?I), où

1. I est N^* ou une section commen_cante de N^*.

2. {ëi}i?I est une suite decroissante de reels positifs ou nuls.

3. {ui}i?I une suite d'elements de H^' verifiant les conditions suivantes:

(i) ?(i,j) ? I^2, < ui,uj >H'=

1 si i = j 0 sinon

(ii) ? i ? I, ëi = sup^H; u ? H^' et ? j = i< u,uj >H,= 0l

Si I = {1,..,n}, l'ACP est dite d'ordre n, et si de plus {ui}i?I est un s_ystème total de H^', alors on dit _que l'ACP est totale [13].

1.2.1 Condition d'existence de l'ACP "pas a pas"

Lors de la première étape de l'ACP "pas a pas" de U, on est amené a l'étude de la borne supérieure de l'application réelle G définie sur H^' par:

G(u) =

(1.1)

kU^*uk² < U o U^*u,u >H'

H

= .

kuk² kuk²
_H0 _H^,
On est ainsi conduit a l'étude de l'opérateur U o U^*, noté V.

Propriété

V est un opérateur continu autoadjoint positif_; son spectre est donc contenu dans l'intervalle [0, V M][13]. A toute anal_yse en composantes principales "pas a pas", on peut alors associer le shéma de dualité suivant:

_H' U

, H

I ?	V		? I ?			W
H'					H
		U*

W = U^* o U

V = U o U*

I est l'identité

Proposition 1.2.2 (Dauxois et Pousse, 1976)

Le maximum de la fonction G existe et est inférieur a V k_; il est atteint pour au moins un élément de H^' si et seulement si cette norme est valeur propre de V. De manière plus _générale, si le haut du spectre de V est formé de q valeurs propres isolées d'ordre de multiplicité fini nj (j = 1,...,q) et si on pose n = Pn j=1 nj, U admet une ACP d'ordre n (au moins):

({ëi}i?I, {ui}i?I)

oiTi _{ëi}i?I est la suite pleine décroissante de valeurs propres de V et _{ui}i?I est une suite orthonormée de vecteurs propres associés.

1.2.2 ACP totale d'un operateur compact

Proposition 1.2.3 Tout operateur compact U admet une anal_yse en composantes principales totale [13].

Dans ce cas la, l'ACP totale de U revient a faire l'anal_yse spectrale de l'opérateur V = U o U^*. Si ({ëi}i?I, {ui}i?I) est une ACP "pas a pas" d'un opérateur compact U, nous avons alors les deux propriétés suivantes.

1. L'ordre de multiplicité de cha_que valeur propre non nulle ëi est fini.

2. Posons I^* = {i ? I; ëi =6 0}, alors la suite de terme _généralfi = 1 kU*ui,H U^*ui, constitue
un s_ystème de vecteurs propres orthonormés de W.

Remar_que: La quantité 1

kU*uikH U^*ui existe, car MU^*uil²_H = ëikuik² H0 =6 0

On a alors la proposition suivante:

Proposition 1.2.4 (Dauxois et Pousse, 1976)

Si ({ëi}i?I, {ui}i?I), est une ACP "pas a pas" de l'operateur compact U, le couple ({ëi}i?I^*, { U*ui

kU*uikH }i?I^*), est une ACP "pas a pas" de U^*, dite associee a la precedente.

On appellera {ëi}i?I^* la suite des valeurs principales, {fi}i?I^* la suite des composantes principales normalisées et {ui}i?I^* la suite des facteurs principaux de l'opérateur U.e

La proposition précédente permet de rechercher l'ACP de U en faisant soit l'anal_yse spectrale de V, soit celle de W. L'opérateur V peut s'écrire comme suit [14]:

V =E i?I^*

ëi ui ? ui (1.2)

pour (x,y) ? H², y ? x est l'opérateur défini par: y ? x(f) =< y,f >H x.

1.3 ACP de densités de probabilité

1.3.1 Introduction

L'ACP classi_que a entre autres pour objectif de représenter dans un espace de faible dimension, un nua_ge de points représentant m individus ou objets décrits par p variables numéri_ques, en utilisant soit les corrélations soit les covariances entres les variables [301. L'anal_yse en composantes principales de densités de probabilité poursuit le même objectif, sauf _que les individus sont des fonctions de densités et l'espace des individus est un espace fonctionnel de dimension infinie.

On introduit la mesure d'affinité (produit scalaire entre deux densités) [281 avec la_quelle on définit un opérateur compact autoadjoint V (appelé aussi opérateur de covariance [291) dont la dia_gonalisation fournira une base suivant la_quelle seront décomposées les densités. Grace a la proposition 1.2.4, l'étude se ramène a la dia_gonalisation d'une matrice s_ymétri_que et les densités seront représentées dans la base des vecteurs propres de cette matrice.

1.3.2 Affinité L2 entre deux densités de probabilités

Soit f1,...,fL un nua_ge de L densités de probabilités, supposées appartenir a l'espace de Hilbert H = L²(IR") des fonctions de carrée inté_grable par rapport a la mesure de Lebes_gue sur IR".

Definition 1.3.1 (Qannari, 1983)

Considérons deux densités de probabilités f et g, de carrée inté_grable par rapport a la mesure de référence ? sur (IR",I3_IRP). On appelle affinité L² entre f et g la _quantité suivante:

Z< f,g >= IRP f(x)g(x)d(?(x)) (1.3)

Exemple

Soit f et g deux densités _gaussiennes a p dimensions de paramètres respectifs (ii, Ó) et (in, V ). L'affinité L² entre f et g est donnée par la formule suivante [31_;

1 < f,g >= 2 e (2ð)p ^2 |Ó + V |1 1.3.3 Définition de 1'ACP de densités

2 iu-mi2 1 (Ó+V )-1. (1.4)

L'objectif de la méthode proposée est d'obtenir une représentation approchée du nua_ge des L densités f1,...,fL. On note P_g le projecteur ortho_gonal sur le sous espace en_gendré par le vecteur g de H.

Première étape:

On cherche g1 = PL t=1 a(1)

t ft de norme unité dans H, minimisant la _quantité:

Ig1 = _XL kPg1(ft) - ftM². (1.5)

t=1

Deuxième étape:

On cherche g2 = PL t=1 a(2)

t ft de norme unité dans H, ortho_gonale a g1 rendant minimum la

_quantité:

Ig2 = _XL kPg2(ft) - ftM². (1.6)

t=1

Ainsi de suite.

Les fonctions g1,g2... ainsi obtenues, _qui ne sont pas nécessairement des densités de probabilités, constituent un s_ystème orthonormal [31.

Soit alors l'opérateur compact U défini sur IR^L par:

Vv E IR^L, Uv = _XL vtft, v = (v1,...,vL). (1.7)

t=1

Son adjoint U^* est défini par: [31

car:

< v,U^*g >RL=< g,Uv >H=

XL t=1

< ft,g > vt. (1.9)

On a alors la définition suivante.

Definition 1.3.2 .

On appelle ACP de densités de probabilités, l'ACP "pas a pas" de l'opérateur U. La minimisation de (1.5) est é_quivalente a la maximisation de la _quantité suivante:

11Pgi(ft)11² =

< ft,g1 >²= 1U^*g1l²_RL (1.10)

_XL
t=1

=

Ig1

_XL
t=1

oil _1.1RL dési_gne la norme usuelle de R^L.

D'autre part:

1U^*g1l²_RL =< U^*g1,U^*g1 >_RL=< g1,UoU^*g1 > (1.11)

max (/' ) = max < > . (1.12)

hig111=1 (Ig1) 11g11=1

On déduit de cette derniere définition _que l'ACP de ces densités est é_quivalente a l'anal_yse spectrale de l'opérateur autoadjoint W = U^*oU. Dans la base canoni_que e1,...,eL de R^L, la matrice W s'écrit [3]:

<

W =

? ? ? ? ? ? ? ? ? ? ?

? ? ? ? ? ? ? ? ? ? ?

.

f1,f1 > ... < f1,fs > ... < f1,fL >

... ... ...

< ft,f1 > ... < ft,fs > ... < ft,fL >

... ... ...

< fL,f1 > ... < fL,fs > ... < fL,fL >

Remar_que

1. Si u de R^L est vecteur propre de l'opérateur W associé a la valeur propre non nulle ë, alors g = vUu ë est un vecteur propre de V associé a la meme valeur propre non nulle ë.

2. Les vecteurs propres de l'opérateur V sont les facteurs principaux, et leur ima_ge par U* sont les composantes principales.

1.3.4 Formule de reconstitution des densités de probabilités

Si g1, g2, ..., gT le s_ystème de vecteurs propres de l'opérateur V, oi T dési_gne le nombre de valeurs propres non nulles de V (resp. W), alors cha_que densité ft s'écrit comme suit [31:

ft = _XT < ft,gj >H gj (1.13)

j=1

La coordonnée < ft,gj >H de ft suivant gj, est é_gale a la t-ième composante du vecteur U^*gj. De la relation,

1 1 _p

U^*gj = pëjU* o Uuj = v Wuj = ëj uj; (1.14)

ëj

on déduit:

? ???? ????

< ft,gj >H = pëj uj,t = jL 4/ëj uj,t gj ft j=1 PT gj = vëj^1t=1 uj,t ft

(1.15)

oi _uj,t dési_gne la t-ième composante du vecteur propre uj de W.

Pour obtenir une représentation approchée du nua_ge initial, il suffit de tron_quer la relation (1.15).

1.3.5 Qualité Globale de l'ACP

On mesure la _qualité _globale de l'ACP par la somme des proportions d'inertie expli_quée par les axes retenus, l'axe j expli_quant une _quantité d'inertie égale ëj

>IT r=1 ër.

1.3.6 Qualité de représentation de ft suivant gj

Elle est é_gale a:

ft = fu +

XT j=1

qëjut,j gj (1.20)

1.3.7 ACP normée

L'ACP normée de densités de probabilité consiste a diviser cha_que densité par sa norme associée dans H_; cette ACP conduit alors a dia_gonaliser la matrice de terme _général:

1 1

Ws,t = Ilft1111fs11 < ft,fs > (1.17)

Remar_que: Cette normalisation conserve dans H les an_gles entre les densités mais déforme leurs distances.

1.3.8 ACP centree

Pour obtenir une représentation approchée _qui restitue les distances entres les densités, on définit un autre nua_ge dont le centre de _gravité est lui même l'ori_gine de l'espace vectoriel ou les densités sont représentées. Kneip et Utikal (2001) ont choisi cette ACP pour étudier sur plusieurs années, la relation entre le revenu annuel des fo_yers britanni_ques et l'a_ge mo_yen des personnes actives au sein de ces fo_yers.

Théori_quement elle consiste a prendre comme nua_ge l'ensemble des fonctions ft = ft - f_u dans L²(R^p), ou f_u = L EsL f_s. L'ACP de ce nua_ge conduit a dia_gonaliser la matrice W, de terme _général:

Wt,s =< ft - fu,fs - f_u > . (1.18)

L'opérateur de covariance associé s'écrit:

T

V = j=1 (ft - f_u) ? (ft - f_u). (1.19)

Les densités ft, t ? {1,...,L} s'écrivent dans la bases des fonctions propres g1,g2,... de l'opérateur V comme suit [20]

Exemple: ACP centrée de L distributions _gaussiennes multidimensionnelles.

Soient X1, . . . ,XL des variables aléatoires de distribution _gaussienne a p dimensions, de mo_yenne u1, . . . ,uL et de variance Ó1,. . . ,ÓL respectivement. Les densités f1, f2,..., fL constituent un nua_ge F dans l'espace de Hilbert H = L²(IR^p).

L'ACP centrée de ces L densités conduit a dia_gonaliser la matrice de terme _général donné par la relation (1.18), _qu'on calcule en utilisant la formule (1.4).

On visualise (Fi_g.1) les projections des dens ités ft (t = 1, . . . ,30) sur le premier plan principal dans les cas suivants:

1. ut = cos(t), Ót = e^t,

2. ut = cos(t), Ót = 1,

3. ut = 0, Ót = e^t.

Les deux premiers éléments propres de W ( ACP centrée) fournissent une représentation approchée des densités sur les deux premiers axes principaux et les pourcenta_ges d'inertie expli_quée par ces axes. "Au cours du temps l'évolution de la mo_yenne est périodi_que et l'évolution de la variance est exponentielle, l'évolution des densités devrait etre la résultante" [31.

Les _graphi_ques de la fi_gure 1 donnent les projections des densités sur le premier plan principal. L'évolution des densités sur ce plan, dans le cas ut = cos(t) et Ót = e^t, ne fait pas apparaItre la périodicité de la mo_yenne, ceci est du au fait _que la variance croissant exponentiellement,

" L'évolution de la mo_yenne est " no_yée " dans l'évolution de la variance" [31 . Cet aspect est bien montrer lors_que ut = cos(t) et Ót = 1, oi la périodicité de la mo_yenne est bien visible sur le premier plan principal.

01600 01175 00750

80%

11t = cos(t), Ót = et

2

8% 12%

^0280 ^0200 0120

01700 01275 00850

4 0

11t = cos(t), Ót = 1

2

21 23 1

7

91% 81%

11t = 0, Ót = et

Fi_g.1: Nua_ge centré des densités sur le premier plan principal

.0850

Chapitre 2

Estimation de l'ACP de densités de

probabilité

2.1 Introduction

Au delà de l'aspect théori_que présenté dans le chapitre précédent, l'ACP de densités est une méthode statisti_que permettant le traitement d'un _gros ensemble de données, se présentant sous forme de plusieurs _groupes formés des valeurs de p variables _quantitatives sur plusieurs individus, oi cha_que _groupe est considéré comme un échantillon d'une population donnée. La méthode va nous permettre de dé_ga_ger des facteurs, décrivant au mieux les différences entre les échantillons, par consé_quent entre les différentes populations. Elle consiste alors à associer à cha_que échantillon une densité de probabilité, _qui est la densité de la variable parente correspondante. La démarche elle-même exi_ge _que les densités soient connues, ce _qui n'est pas toujours le cas en prati_que. Boumaza (1999) a proposé une approche dans la_quelle les densités sont estimées en supposant _que les données sont des réalisations de variables aléatoires dont les lois appartiennent à une famille de lois connues, comportant des paramètres inconnus_; estimer les densités des ces lois revient alors, à en estimer les paramètres. Dans le cas de données _gaussiennes unidimensionnelles, il a été vériflé sur des exemples simulés la conver_gence rapide de l'ACP des densités estimées vers l'ACP théori_que correspondante pour des tailles d'échantillons raisonnables (n>25).

fh(x) =

] (c)i E {1,...,n} : Xi E [x - h 2,x + h 2]p nhp

.

(2.1)

Une autre approche possible _qui ne suppose pas nécessairement la normalité des données, consiste a estimer les densités inconnues par la méthode du no_yau. Introduite par Kneip et Utikal (2001) dans le cas d'une ACP centrée non normée, ils proposent dans la méthode, une procédure en deux étapes d'estimation des éléments propres de la matrice des produits scalaires [201 . Sans se soucier de la nature de l'ACP, on étudiera ainsi l'influence du no_yau et de la fenêtre de lissa_ge sur la _qualité de l'estimation. On donnera dans le début du chapitre, un rappel sur l'estimation d'une densité de probabilité par la méthode du no_yau, ensuite on présentera l'ACP estimée par no_yau, dans la_quelle on proposera dans le cas d'une ACP non centrée et non normée, une procédure d'estimation des valeurs propres de la matrice des produits scalaires théori_que, permettant d'améliorer leurs _qualités d'estimation. Ensuite on donnera un rappel sur l'approche d'estimation paramétri_que et on terminera ce chapitre par une comparaison entre les deux approches d'estimation.

2.2 Rappel sur l'estimation d'une densité par la méthode du noyau

" Il s'a_git d'un problème fondamental de la statisti_que non paramétri_que _qui a connu, durant ces _quarante dernières années, des développements théori_ques et prati_ques a la fois rapides et nombreux "[181.

Soit (X1,...X_n) un échantillon de densité mar_ginale inconnue f. L'idée la plus naturelle consiste a évaluer la densité f au point x en comptant le nombre d'observations "tombées" dans un certain voisina_ge de x. Sur IR^p (p = 1), on peut par exemple choisir un voisina_ge cubi_que de x = (x1,...,x_p) de la forme [x1 - h 2,x1 + h ₂] x ... x [x_p - h 2,xp + h ₂] _qu'on note [x - h ₂,x + h ₂] oi h est un nombre réel strictement positif dépendant de n, ce _qui conduit a l'estimateur [181

Cette dernière expression peut encore s'écrire:

1 fh(x) = mhp

Xn i=1

(x _ Xi 1[_ 1 . (2.2) 2 , 1 2 ]p h

oi la fonction 1[_ 1 ₂]p.

2 , 1 2 ]p est la densité de probabilité uniforme sur [_¹ ₂,¹

En s'inspirant alors de la dernière formule, et en définissant K comme étant une fonction réelle, bornée d'inté_grale 1 sur IR^p, on définit l'estimateur fh associé au no_yau K par:

1 fh(x) = mhp

Xn i=1

K(x _ Xi h ) (2.3)

Lors_que le no_yau K est choisi positif, l'estimation fh est une densité de probabilité et on parle alors parfois de la densité de probabilité empiri_que de no_yau K. Parmi les multiples estimateurs non paramétri_ques de la densité aujourd'hui a la disposition des utilisateurs, l'estimateur a no_yau, est de loin le plus populaire (Akaike, Rosenblatt, 1956, Parzen, 1962, Silverman, 1986, Bos_q et Lecoutre, 1987 ...). Ce succès peut essentiellement s'expli_quer en trois points:

1. L'expression théori_que de fh(x) est simple, puis_que il s'écrit comme une somme de m variables aléatoires i.i.d..

2. fh conver_ge vers f en de nombreux sens, et en particulier au sens L1 pour toute densité f dès que1 _h et mhp tendent tous les deux vers l'infini. D'autre part si l'estimateur est conver_gent, il est conver_gent dans tous les modes, i.e. en probabilité, en mo_yenne, pres_que sürement et pres_que complètement [21.

3. Enfin, cet estimateur est flexible, dans la mesure oi il laisse a l'utilisateur une _grande latitude non seulement dans le choix du no_yau, mais encore dans le choix du paramètre réel h.

" Lors_qu'on se limite aux no_yaux K positifs, les vitesses de conver_gences varient peu en fonction de K et les critères essentiels du choix du no_yau sont alors la simplicité et la vitesse de calcul d'une part, la ré_gularité de la courbe a obtenir d'autre part "[181. En revanche, le choix du paramètre de lissa_ge h se révèle crucial aussi bien pour la précision locale _que pour la pécision _globale de l'estimateur fh, c'est l'objet du para_graphe suivant.

2.2.1 Choix du noyau et de la fenêtre de lissage

" La décision d'un choix optimal pour le no_yau K et la constante de lissa_ge h, suppose la spécification d'un critère d'erreur _qui puisse etre éventuellement optimisé. Bien slir, l'optimalité n'est pas un concept absolu: elle est intimement liée au choix du critère, _qui peut faire intervenir a la fois la densité inconnue f et l'estimateur fh donc h et le no_yau K " [181. Dans le cas _qui nous intéresse, on cherche a minimiser l'erreur _quadrati_que inté_grée mo_yenne, _que nous noterons par MISE (mean inte_grated s_quare error), _qui est définie par:

_{Z Z}

MISE(h) = E IR'[fh(x) -- f(x)]² = IR' E[fh(x) -- f(x)]² (2.4)

Cette écriture si_gnifie _que l'erreur _quadrati_que inté_grée mo_yenne est a la fois une mesure de l'erreur _globale mo_yenne et une mesure de l'erreur mo_yenne ponctuelle accumulée.

On s'intéressera dans la suite de cette partie au cas particulier oi p = 1. On a alors le théorème suivant.

Théorème 2.2.1 (Rosenblatt, 1956)

Si f a une dérivée seconde absolument continue, et si K et f⁰⁰ E L2, oTi K est une densité continue, s_ymétri_que de variance u² _K, alors, sous les conditions h --* 0 et nh --* 00, on a le développement as_ymptoti_que:

¹ (2.5)

n

(

_h4

MISE(h) = 4 u4 _KR(f⁰⁰) + R(K)

nh + O h⁵ +

et l'erreur _quadrati_que inté_grée as_ymptoti_que associée noté AMISE est définie par:

h4 AMISE = 4

u4 KR(f^00) + R(K) nh

.

(2.6)

oi R(K) = f K2(x)dx

Choix du no_yau

Le choix du no_yau optimal K selon le critère de l'erreur _quadrati_que inté_grée as_ympthoti_que pour estimer une densité de probabilité _qu'on choisira parmi la classe de tous les no_yaux s_ymétri_ques, vérifiant de plus ^f t²K(t) =6 0, et donné par le théorème suivant:

Théorème 2.2.2 (Epanechnikov, 1969)

Si f a une dérivée seconde absolument continue dans L2.

Si de plus h ? 0, nh ? +8 et f_IR(f⁰⁰)² =6 0, alors le no_yau d'Epanachnikov d'ordre 1, KE défini par:

KE(x) = ( 3 x

_4v5)(1 - 5)ll[-v5,v5](x), (2.7)

est d'erreur _quadrati_que inté_grée as_ymptoti_que minimum.

Silverman (1986) a défini le coefficient d'efficacité des no_yaux appartennant a cette classe, en les comparant au no_yau optimal précédant, il est donné par la formule suivante.

_(J )

3

eff(K) = v5 t² K(t)dt

1 )-1

K(t)²dt , (2.8)

₂ (J

alors pour un no_yau de cette classe, il montre _que ce coefficient est très proche de 1, si_gnifiant ainsi _que le choix de ce dernier influe peu sur l'AMISE.

1)No_yau Gaussian:

Il est défini pour tous x ? RI par:

1 1

KG(x) = v 2

On présentera ici _quel_ques exemples de no_yaux appartenant a la classe pécédente _qu'on utilisera ensuite dans l'étude de l'influence du no_yau sur l'ACP de densités estimées non paramétri_quement.

exp(- x²) (2.9)

2ð

2) No_yau rectan_gulaire:

KR(x) =		? ? ?		1/2 si |x| = 1 0 sinon	(2.10)
KE(x) =	? ? ?		(3/4)(1 - 1 5x2) 1 ,5 si |x| < v5 0 sinon			(2.11)

3)No_yau d'Epanechnikov:

4)No_yau trian_gulaire:

KT(x) =

1 - |x| si |x| = 1 0 simom

(2.12)

On souhaite alors utiliser le résultat précédent de Silverman pour visualiser a l'aide d'un exemple de simulation, l'influence du choix du no_yau K parmi les 4 no_yaux définis précédemment, sur la courbe associée a l'estimation de la densité de probabilité f.

Soit (x1,...,x_n), m réalisations de la variable aléatoire X de densité f de loi N(4,2). Posons:

~ AMISEG l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau _gaussien et la fenêtre de lissa_ge noté hG.

~ AMISET l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau trian_gulaire et la fenêtre de lissa_ge noté hT.

~ AMISEE l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau d'Epanechnikov et la fenêtre de lissa_ge noté hE.

~ AMISEG l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau rectan_gulaire et la fenêtre de lissa_ge noté hR.

tel _que:

AMISEG = AMISET = AMISEE = AMISER. (2.13)

Remar_que

La relation (2.13), va nous permettre de calculer les fenêtres précédentes, et cela en procédant comme suit:

Premièrement on fixe une fenêtre parmi hG, hT, hE, hR, par exemple_; hG = 0.40. Les 3 dernières sont respectivement les solutions réelles positives des 3 é_quations suivantes:

ó⁴KT

4

h5 - (AMISEG) h + ¹R(KT) = 0 (2.14)

m

ó4 KR

4 h5 - (AMISEG) h + ¹ _mR(KR) = 0 (2.16)

pour m = 30 on obtient: hT = 0.95, hE = 0.85, hR = 0.71. L'erreur _quadrati_que inté_grée as_ymptoti_que correspondante est é_gale a 0.023.

Avec ces fenêtres on trace les courbes associées a l'estimation de f en utilisant les différents no_yaux. Les _graphi_ques de la fi_gure 2 montrent _que sous la condition d'é_galité des AMISE, les courbes estimées par les différents no_yaux ont pres_que la même allure.

hG = 0.40 hT = 0.95

Cas du no_yau _gaussien Cas du no_yau trian_gulaire

hE = 0.85 hR = 0.71

Cas du no_yau d'Epanechnikov Cas du no_yau rectan_gulaire

Fi_g.2: Influence du no_yau sur la _qualité de l'estimation d'une densité de probabilité _gaussienne

12

de loi N(4,2) sous la condition d'é_galité des AMISE, n = 30.

Choix de la fenêtre de lissa_ge

Le premier terme du développement de MISE est un terme de biais, alors _que le second un terme de variance. On peut remar_quer _qu'ils varient en sens inverse par rapport a h: une lar_geur de fenêtre trop importante entraInera une au_gmentation du biais et une diminution de la variance (phénomène de sur-lissa_ge), alors _qu'une lar_geur de fenêtre trop faible provo_quera une inflation de la variance et une diminution du biais (phénomène de sous-lissa_ge).

Sous les conditions des théorème 2.2.1 et 2.2.2, la fenêtre h notée hAMISE, _qui minimise l'erreur _quadrati_que as_ymptoti_que est donnée par le théorème suivant.

Théorème 2.2.3 (Rosenblatt, 1956)

hAMISE = á(K)â(f)n- 1 5 (2.17)

]

ou á(K) = [R(K)

_ó4

K

[ ₁ ]

⁵ et â(f) = R(f00)

1

1
5

.

Remar_que

La lar_geur de fenêtre optimale hAMISE dépend de la densité inconnue f au travers du paramètre R(f⁰⁰) et ne peut donc être utilisée telle _quelle dans les calculs. Une fa_çon classi_que d'_y remédier consiste a remplacer la _quantité R(f⁰⁰) par un estimateur approprié. Cette approche conduit a un ensemble de méthodes _que l'on a coutume de re_grouper sous le vocabulaire _général de méthodes plu_g-in, et _qui font l'objet d'une recherche active (pour des références, on peut par exemple voir[16, 18, 24, 25, 311).

Exemples

Pour visualiser l'influence de la fenêtre de lissa_ge h sur la _qualité de l'estimation d'une densité f, nous avons choisi de présenter ici deux exemples oi f est estimée par f_n en utilisant le no_yau _gaussien:

Xn 1 1 1 ?y E RI fn(y) = e- 2 ( y-xi h )2 v2ð nhj=1

.

(2.18)

(xj)j=1,n n réalisations de la variable aléatoire parente X de densité f.

Le premier exemple concerne la densité de la loi N(0,1), oi pour h E {0.1, 0.3, 0.6, 1} on trace les courbes associées a l'estimation de f pour cha_que valeur de h.

Les _graphi_ques de la fi_gure 3 montrent _que la meilleure fenêtre est h = 0.6, et en peut voir, lors_que h = 0.1 l'estimation est très mauvaise, chose _qu'en peut expli_quer par le nombre de pi_ques _qu'elle présente_; de même pour h = 1, l'estimation est beaucoup plus aplatie, ce _qui fait une différence importante de dispersion.

h = 0.1 h = 0.3

h = 0.6 h = 1

(...) courbe estimée + + (-) courbe réelle +

0 +

Fi_g.3: Influence de la fenëtre de lissa_ge sur l'estimation par no_yau _gaussien de la densité f de loi N(0,1), n = 30

+ + + +

+ + +

+ + +

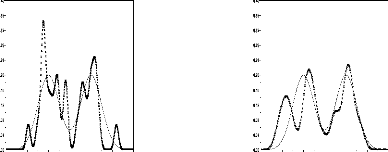
Le deuxième exemple est celui de la densité bimodale ø suivante:

1

ø(x) = ₂(f(x) + g(x)) (2.19)

avec f = N(0,1) et g = N(4,1).

Les _graphi_ques de la fi_gure 4 montrent _que pour h = 0.2 on a une mauvaise _qualité d'estimation. En lissant plus les densité en arrive a améliorer la _qualité de l'estimation , ici la meilleur fenêtre est h = 0.6. Pour h = 1, l'estimation devient moin bonne ce _qui est caractérisé par la diminution de nombre de modes.

h = 0.2 h = 0.4

× h = 0.6 h = 1

(...) courbe estimée (-) courbe réelle

× × × × ×

Fi_g.4: Influence de la fenëtre de lissa_ge sur l'estimation par no_yau _gaussien d'une densité bimodale, n = 30

× ×

× × × × × × × × × × × × × × × × × × × × ×

2.2.2 Application a l'estimation par noyau de l'affinite L2

Soient X et Y deux p-vecteurs aléatoires de densités respectives f et g, supposons donnés n_x (resp. n_y) réalisations de X (resp. Y) et les estimations par la méthode du no_yau fh_x et gh_y de f et g respectivement. L'estimation de la mesure d'afnité L² entre f et g est donné par:

< fhx,ghy >=

1 Xnx Xny Z K(t - xi ) K(t - yj ) dt. (2.20) hy nxnyhxhy i=1 j=1^x 1

Exemples

Cas du no_yau _gaussien:

Si K est le no_yau _gaussien alors:

1 1 1 n_x ny 1 (xi-yj )2

< f_hx ,gh EEe 2 (h2x+q) (2.21)

_y

nxny v2ð + hy i=1 j 1

Cas du no_yau trian_gulaire: Elle est donnée par:

n_x ny

1 (_{1 |}t - xi | ) (1 dt. (2.22)

_|t -- yi

< fh_x ,ghy >= h EE

nxnyhx y i=1 j=1 AinAj h_x h_y

avec:

Ai = [xi - hx, xi + h_x] et Aj = [yj - h_y, yj + h_y]. Cas du no_yau d'Epanechnikov:

Elle est donnée par:

n_x ny I (1 1 (t - xi ) 5 h_y

5 h_x

2 1 (t - yj)

dt.

EE

< fhx,ghy >= 80 nxnyhxhy i=1 j=1

¹³%11¹³j

(2.23)

2

avec:

Bi = [xi - v5 h_x, xi + v5 h_x] et Bj = [yj - v5 h_y, yj + v5 h_y]

Cas du no_yau rectan_gulaire:

_>nx

1 >ny fl

< fhx,ghy >= d(Ci Cj). (2.24)

4 nxnyhxhyi=1 j=1

Ci = [xi - h_x, xi + h_x], Cj = [yj - h_y, yj + h_y] et d(Ci ⁿ Cj) la mesure de Lebes_gue dans RI de CinCj.

Remar_que:

Les inté_grales données par les formules (2.22), (2.23) ainsi _que d(Ci,Cj) de la formule (2.24), dépendent respectivement des lon_gueurs des ensembles (Ai,Aj), (Bi,Bj) et (Ci,Cj), de la position de xi par rapport a yj sur la droite réelle. Elles ne peuvent donc avoir une formule anal_yti_que simple. Leurs calculs se font en considérant tous les cas possibles.

2.3 ACP de densites estimees par la methode du noyau

2.3.1 Cas general

Soit (xt,1,...,xt,nt), t ? {1,...,L}, nt réalisations de la variable aléatoire Xt dans R^p de densité inconnue ft, et soit fh_t l'estimation par la méthode du no_yau de la fonction ft en tout point x.

Pour t ? {1,...,L}, les fh_t constituent un nua_ge de L densités dans L²(R^p). L'ACP sur ce nua_ge conduit a dia_gonaliser la matrice de terme _général donné par:

1 ^àWt,s = ntns	1	nt i=1	ns j=1	< K(x - xt,i ) , K(x - xs,j ) > (2.25) ht hs
	h^pt h^ps

K un no_yau positif et ht, t ?E {1,...,L} la fenêtre de lissa_ge associée a la densité ft

Cette ACP fournit l'estimation par no_yau de l'ACP théori_que des densités ft, t ?E {1,...,L}.

Si fh_t est l'estimation par la méthode du no_yau _gaussien de la densité ft, alors l'ACP estimée correspondant conduit a dia_gonaliser la matrice de terme _générall donnépar::

^àWt,s = 1 ntns	1			1		nt i=1i	^nsj=1	xxt 2-+xhs2s)))22		(2.26)
	v2ð		Vh2t? h2 s +						. ·

2.3.2 Exemples

ACP de L densités _gaussiennes unidimensionnelles

Si (xt,1,...,xt,n),, t ? {1,...,L} n réalisations de la variable aléatoire Xt de loi N(t,vt)) et de densité ft, on fait une ACP de densités sur les estimations par le no_yau _gaussien des densités ft en associant a cha_que densité la fenêtre de lissa_ge optimale au sens de l'AMISE é_galee dans ce cas a 1.06vtn^-15,, t ?E {1,..,L} et cela pour deux tailles échantillons différentes_;; n=10 et n=40.

Les _graphi_ques de la fi_gure 5, représentant les densités sur le premier plan principal de l'ACP théori_que et des ACP estimées, montrent _que pour une taille d'échantillon petite (n=10) on parvient a retrouver la forme du nua_ge théori_que. Cela devient très clair lors_qu'on au_gmente la taille d'échantillon (n=40).

26% ACP normée théori_que

11

42%

09

07

05

25% ACP normée estimée, n = 10 26%

03	ACP normée estimée, n = 40

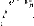
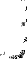
. 9 .

09 07 05

09 07 05

44% 44%

Fi_g.5: Premier plan principal de l'ACP nonparamétri_que dans le cas de la famille de densités _gaussienne de lois N(t,'t)

0. 1 .

. 20

(ht = 1.06'tn- 0. 1 5)

ACP de L densité de Gumbel

Si _{(xt,1,...,xt,n),} t ? {1,...,L} m réalisations de la variable aléatoire Xt de densité de Gumbel ft, de paramétre de position ut = t + ç _v6 vt et de paramétre d'échelle ót = _v6 vt (ç est la

Ð Ð

constante d'Euler). On fait une ACP des densités estimées par le no_yau _gaussien en associant à cha_que densité la fenêtre de lissa_ge optimale au sens de l'AMISE et cela pour deux tailles échantillons différentes_; n=1O et n=4O.

Dans la fi_gure 6, les _graphi_ques représentant les densités sur le premier plan principal de l'ACP normée théori_que et des ACP estimées, montrent _qu'à partir d'une taille d'échantillon petite (n=1O), on arrive à retrouver la forme du nua_ge théori_que. Cette forme se rapproche encore plus de la forme réelle en au_gmentant la taille d'échantillon (n=4O).

24% ACP normée théori_que

40%

ACP normée estimée, n = 10

0.1 ACP normée estimée, n = 40

23% 24%

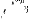
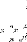
41% 40%

2.3.3 Approche de Kneip et Utikal

Soit (xt,1,...,xt,nt), nt réalisations de la variable aléatoire Xt de densité inconnue ft et dans L²(R) muni du produit scalaire suivant [201:

< ft,fs

>= J RI ft(x)f_s(x)w(x)dx, (2.27)

w dési_gne une fonction de poids, positive, continue et uniformément bornée sur un intervalle D de R.

Les densités ft, t ? {1,...,L}, forment un nua_ge dans L²(R) dont l'ACP centrée conduit a dia_gonaliser la matrice M de terme _général donné par la formule suivante.

Mt,s =< ft - fu,fs - f_u > . (2.28)

avec: f_u = 1

E^Lr=1 fr .

L

Pour estimer efficacement les éléments de la matrice M, Kneip and Utikal ont procédé en deux étapes:

1^ereetape:

En se basant sur l'estimation par no_yau de ft, t ? {1,...,L}, définie par:

fh,t(x) = 1 nth

nt i=1

K (x - hxt,i (2.29)

oil

_Xnt _Z ux - xt,i

K2 w(x)dx. (2.32)

h

i=1

1

A(t) = n2th2

l'estimation naturelle Mt,s de Mt,s est donnée par:

avec:			Mt,s =	M(^1) t,s- M(2) t,s +M(3) t,s , (2.30)
M(^1) t,s =	? ???? ????	nt ns 1 h2 Z-d vi=nt 1 L-a^vj =1 J h s K(x -x h t,i) K(^x-xs,j) w(x)dx, t s 1 nt E^nt f Kix- hxt,i, K(^x-Xt,j) w(x)dx + A(t), t = s n^2th^2 Ei=1 ) h			(2.31)

_{P P}

M(²)

t,s = 1 PL l=1( M(1)

t,l + M(1)

l,s ) et M(3)

t,s = 1 r M(1)

l,r .

L L2 l

2eme etape:

Dans cette etape Kneip et Utikal proposent de prendre comme estimation de M, la matrice M de terme _general:

Mt,s = fM(1) t,sMa(2) M(3)-- t,s .(2.33)

avec:

fM(^1) t,s =

? ? ?

Mt,s ) t s (2.34) M(^1) t,t -- A(t) sinon

_X

fM(2) t,s1

= L

l=1

(fM(¹)

t,l + fM(1)

l,s ). (2.35)

L

X fM(^3) t,s = L2 1 l

X r

fM(^1) l,r . (2.36)

L'ACP centree estimee de l'ACP centree theori_que, par l'approche de Kneip et Utikal, est obtenue en dia_gonalisant la matrice de terme _general donne par la relation (2.33).

Remar_que

Contrairement a M, M peut avoir des valeurs propres ne_gatives, en prati_que ces valeurs peuvent etre interpreter par 0.

2.3.4 Application de l'approche d'estimation de Kneip and Utikal à une ACP estimee non centree et non normee

Soit (xt,1,...,xt,nt), t ? {1,...,L}, nt réalisations de la variable aléatoire Xt dans R de densité inconnue ft dans L²(R) muni du produit scalaire:

< ft,fs >= Jft(x)f_s(x)dx. (2.37)

Les densités ft, t ? {1,...,L}, forment un nua_ge dans L²(R) dont l'ACP non centrée et non normée conduit a dia_gonaliser la matrice W de terme _général:

Wt,s =< ft,fs > . (2.38)

Les estimations par la méthode du no_yau:

fh,t(x) = 1 ntht

i=nt i=1

K(x - xt,i) (2.39) ht

forment un nua_ge de L densités dans L²(R) dont l'ACP non centrée et non normée conduit a dia_gonaliser la matrice de terme _général:

1 Wts = ntns	1	i=nt i=1	j=ns j=1	< K(x - xt,i ),K(x - xs,j ) > . (2.40) ht hs
	hths

Cette ACP fournit l'estimation de l'ACP théori_que précédente. Soit ^fW la matrice de terme _général:

Wt,s =

? ? ?

1 'nt r K ( ht x--xt,i n^2t h? dx si t = s J ^àWt,s sinon

(2.41)

Considérons maintenant le cas oil nt = n et ht = h, ?t ? {1, ... ,L} et posons:

^àëk l'estimation de ëk, la k-ieme valeur propre de la matrice W, obtenue en dia_gonalisant la matrice des produits scalaires ^àW.

Si K est un no_yau choisi parmi les 4 no_yaux précédents, on a alors la propriété suivante:

^àëk = ^eëk + á. (2.42)

avec:

1 1

á = n² h²

^K2(

n I

E x -_h xt,i )dx. (2.43)

i=1

1

á = 2vÐ

Dans le cas du no_yau _gaussien:

1

(2.44)

nh

Dans le cas du no_yau trian_gulaire:

2

á = _v3

1 nh. (2.45)

Dans le cas du no_yau d'Epanechnikov:

1 nh. (2.46)

á = 3v5

25

Dans le cas du no_yau rectan_gulaire:

1

á = 2

1 nh. (2.47)

Remar_que

On peut aboutir a la relation (2.42), _grâce a la propriété matricielle suivante: 1. Si ë est valeur propre de M alors:

ë + á est valeur propre de la matrice M + áI (I est la matrice identité).

Exemple: ACP estimée non centrée et non normée de densités bimodales.

Soient (xt,1,...,xt,n), t ? {1,...,30} n réalisations de la variable aléatoire Xt de lois ²¹ N(t,vt)+ ₂¹N(t+ 15, v0.1t) et de densité ft. Pour illustrer la méthode d'estimation précédente dans le cas oil les densités sont estimées en utilisant le no_yau _gaussien et h = n^-1, nous avons procédé a une ACP non centrée et non normée de 3 manieres différentes:

1. En dia_gonalisant la matrice des produit scalaire des densités théori_ques.

2. En dia_gonalisant la matrice des produits scalaires des densités estimées, àW.

3. En dia_gonalisant la matrice ^fW.

On peut voir dans le tablau 1, _que la meilleure estimation des valeurs propres ëk de W, sont les valeurs propres ^eëk de ^fW.

k	ëk	^àëk	^eëk	^àëk - ^eëk
1	0.710	0.995	0.713	0.282
2	0.376	0.639	0.357	0.282
3	0.306	0.622	0.340	0.282
4	0.242	0.554	0.272	0.282
5	0.208	0.528	0.246	0.282
6	0.181	0.472	0.190	0.282
7	0.160	0.458	0.176	0.282
8	0.140	0.435	0.153	0.282
9	0.118	0.397	0.115	0.282
10	0.097	0.387	0.105	0.282

Tab.1: Les valeurs propres ëk, ^àëk et ^eëk, obtenue en dia_gonalisant les matrices W, àW, ^fW respectivement (h = n-¹, n = 30).

La valeur de a dans ce tabeau, est 0.282 v 1

2H

Conclusion

Utiliser la matrice fW a la place de ^àW, nous a permis d'améliorer la _qualité de l'estimation des valeurs propres de la matrice des produits scalaires théori_ques W et cela en réduisant le biais. De plus, le calcul de ^fW s'effectue plus rapidement _que celui de ^àW, dans l'exemple précédent, nous avons réalisé un calcul de 900 inté_grales de moins en estimant W par ^fW.

L'inconvénient de cette approche d'estimation réside dans le fait _qu'elle est approuvable seulement dans le cas particulier oi les tailles d'échantillons sont identiques.

2.4 ACP de densites estimees parametriquement

2.4.1 Cas de donnees gaussiennes multidimensionnelles

L'auteur s'est intéressé aux données ternaires (individus× variables× instants), _qui sont des tableaux (nt × p) indexés par t. A cha_que instant t, t ? {1,...,L} on dispose d'un échantillon de taille nt d'un vecteur aléatoire _gaussien a p dimensions, de vecteur mo_yen ut et de matrice de variance Ót. En prati_que cela revient a observer les mêmes variables _quantitatives, mais pas nécessairement sur les mêmes individus.

Pour une description _globale de ce t_ype de données, on appli_que alors la méthode décrite précédemment, en procédant comme suit.

On associe a cha_que tableau une densité de probabilité, on obtient alors un nua_ge de L densités ft, t ? {1,...,L}, et comme ces densités sont inconnues, elles sont alors remplacées par leurs estimations obtenus en estimant les paramêtres ut et Ót par la méthode du maximum de vraisemblance.

Soit xt = n1t Eint 1 xt,i et st = n1t Ei^nt1(xt,i - xt) (xt,i - xt), xt,i ? R^p les estimations du maximum de vraissemblance de ut et Ót respectivement.

Les fonctions f(nt)

t définies par:

?x ? Rp, _ft (nt)(x) =1

(2ð)^p2

2 (x-xt)^' .c1(x-xt) (2.48)

1 |st|¹ 2 e

sont appelées les estimations paramétri_ques des ft, t ? {1,2..,L}. Elles constituent alors un nua_ge de L densités de probabilité dans H = L²(R^p). L'ACP de ces L densités conduit a dia_gonaliser la matrice de terme _général [3]:

Wt,s < ft (nt)_, f(ns) > = 1 1 2 (xt-xs)'

(st+s_s)^-1(xt-x_s) (2ð)p 2 |st + s_s|¹ 2 e- (2.49)

1

Considérons maintenant un échantillon Xt,1,...,Xt,nt de la variable aléatoire parente Xt,

t ? {1,...,L}, et soit f(nt)

t , les estimateurs des densités parentes ft obtenus en estimant ces

paramétres par la méthode du maximum de vraisemblances. La conver_gence de l'ACP estimée définie précédement vers l'ACP théori_que est donnée par le théorême suivant:

Théorème 2.4.1 (Boumaza, 1999)

Soient á etâ deux reels positifs, supposons _qu'il existe deux suites _(nt(n))n>1 et (ns(n))n>1 telles _que:

uim n-400

nt(n) n

= á et uim n-400

ns(n) n

= â

nous avons alors les deux rCsultats as_ymptoti_ques suivant:

1) <f(nt)

t ,f(ns)

s > conver_ge pres_que surement vers <ft,f_s> _quand n tend vers l'infini.

2) vn <f(nt)

t ,f(ns)

s > est as_ymptoti_quement normal.

Exemple:

Pour illuster la conver_gence de la méthode définie précédemment nous avons procédé dans

)

le cas des densités _gaussiennes ft, t E {1,...,30} de paramétres ut = ( _t ( t 0 )

, Ót =

t 0 t

a une ACP de densités.

Premièrement en utilisant les densités théori_ques, deuxièmement en utilisant les estimations par la méthode paramétri_que et cela pour deux tailles d'échantillons différentes: n = 10 et n = 40.

Les _graphi_ques de la fi_gure 7, représentant les densités sur le premier plan principal de l'ACP normée théori_que et estimée paramétri_quement, montrent _que, pour une taille d'échantillon petite ( n = 10), la forme du nua_ge estimé est proche de celle du nua_ge réel. En au_gmentant la taille d'échantillon ( n=40) cette forme se rapproche de plus en plus vers la forme réelle.

0.9 0.7 0.5 0.3 0.1 0.1

CHAPITRE 2. ESTIMATION DE L'ACP DE DENSITES DE PROBABILITE 43

ACP normée théori_que

23%

t t 0

, Ót =

t 0 t

ut =

1

2

3

4

5

6

7

9

8

10¹¹¹²13

30

14

15

292 8

16

2 7

17

23

24 2 6.25

18

19

20

21

22

0.600 -0.160 0.280 0.720 1.160 1.600

33%

- 0.3 0.5

- 0.7

19% ACP normée estimée, n = 10 22% ACP normée estimée, n = 40

1.1

0.9

0.7

0.5

0.3

0.1

- 0.1

0.3

- 0.5

1

₂3

4

5

6

₉8

11

10

12

16

15

13

14

17

29³⁰
2 8

18

19

.

2 724²⁵

21

20 22

23

26

0.9

0.7

0.5

0.3

0.1

0.1

- 0.3

0.5

- 0.7

1

2

3

4

5

6

7

₈.0¹¹

12

13 14

30

15

16

22982 72 6

25

18

17

23

19

22

21

24

20

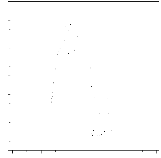
0.600 -0.160 0.280 0.720 1.160 1.600

-0.600 -0.160 0.280 0.720 1.160

27% 1.600 31%

2.4.2 ACP parametrique de densites de Gumbel unidimensionnel

Les données ternaires définies dans le para_graphe 2.2.1 sont maintenant des tableaux (nt×1), oil a cha_que instant t, t ? {1,...,L}, on dispose d'un échantillon de taille nt d'un vecteur aléatoire Xt unidimensionnel de densité de Gumbel ft de paramètre de position ut et de paramètre d'échelle ót.

· -- x

Soit xt = -- nt E 1 xt, . ^t
· ? R, les estimations par la méthode

_z z et s t = nt z En_. t _i t (x,z t)2 x t,

des moments de E[Xt] et V [Xt] respectivement, alors:

= .^V_ð⁶vst et ftt = xt + çàót sont les estimations par la méthode des moments de ót et ut respectivement, avec ç = 0.5772 (constante d'Euler). Les fonctions f(nt)

t définies par:

x-àut e ^àót e

--e

x7jit ót

(2.50)

?x ? R, f_t^(nt) (x) = ¹

x-Fit x-11s

Wt,s = < J t ,.1 s à1

ót ó_s IR

_f(nt) _f(n_s) _e(^xàó:^t +xàós s)e--(e ^àót +e àós

⁾dx.

àót sont appelées les estimations paramétri_ques des ft, t ? {1,...,L}. Elle consituent alors un nua_ge de L densités dans L²(R). L'ACP de ces L densités conduit a dia_gonaliser la matrice de terme _général:

(2.51)

Exemple

Pour t ? {1,...,30}, on fait une ACP normée de densités estimées paramétri_quement dans le cas des échantillons simulés des densités de Gumbel, de paramètre de position ut = t + ç .VÐ6vt et de paramètre d'échelle ót = ^\(__/⁶vt.

On représente alors sur la fi_gure 8 les densités estimées sur le premier plan principal de l'ACP ainsi celle des densités théori_ques et cela pour voir comment se comporte la _qualité de l'estimation lors_qu'on au_gmente la taille d'échantillon.

24%	ACP normée théorique
		40%

23% ACP normée estimée, n = 10 23% ACP normée estimée, n = 40

89

¹

40% 36%

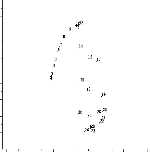
Fi_g.8: Premier plan principal de l'ACP normée de densités de Gumbel.

25

30 . 20 -03

2.5 Comparaison entre l'approche paramétrique et non paramétrique

L'objectif de ce présent para_graphe est de proposer, a l'aide des deux exemples concernant la famille de densités _gaussiennes et la famille de densités de Gumbel, une comparaison entre les deux approches d'estimation (paramétri_que et nonparamétri_que) dont le but est de distin_guer la_quelle est mieux adaptée aux situations précédentes.

Pour cela nous avons choisi de faire cette comparaison en se basant sur les deux distances suivantes:

i)Si àcj,t est l'estimation de la coordonnée de la densité ft sur l'axe principal j , on définit áj comme la distance entre les deux vecteurs C^à et C de IR^L dont les composantes sont respectivement ^àcj,t, cj,t (t ? {1,...,L}):

áj = _XL |^àcj,t - ci,t| (2.52)

t=1

ii)Si ^àët, t ? {1,...,L} est l'estimation de la valeur propre ët de la matrice des produits scalaires théori_ques, en définit â comme la distance entre les deux vecteurs de IR^L de coordonnées respectivement ^àët, ët, par:

â = _XL |^àët ? ët| (2.53)

t=1

Remar_que

Les vecteurs C et Cà étant des vecteurs propres de W et W^à respectivement, ils sont définis au si_gne près_; ces si_gnes sont choisis de sorte _que le coefficient de corrélation linéaire entre C et Cà soit positif.

On fait alors une ACP de densités estimées dans les deux situations suivantes:

Lors_que les densité sont estimées en utilisant l'approche paramétri_que, avec n = 30, L = 30.

Lors_que les densités sont estimées par no_yau en associant a cha_que densité la fenêtre optimale au sens de l'erreur _quadrati_que inté_grée as_ymptoti_que, avec n = 30, L = 30.

Les valeurs des distances (áj)j=1,3 et , ainsi _que les pourcenta_ges d'inertie expli_qués par les trois premiers axes principaux obtenus par les deux approches d'estimation, sont données dans le tableau 2.

	Famille de densités de Gumbel		Famille de densités de loi N(t,V't)
	ACP paramétrique	ACP non paramétrique (noyau gaussien)	ACP paramétrique	ACP non paramétrique (noyau gaussien)
á1	1.76	1.92	1.00	1.43
á2	2.23	2.31	1.44	1.64
á3	1.60	1.71	2.34	2.37
â	1.07	1.61	1.50	2.81
Inertie1	36%	38%	43%	46%
Inertie2	22%	23%	26%	26%

Tab.2 Valeurs des (aj)j=1,3, â et les pourcenta_ges d'inerties expli_qués par les deux premiers axes principaux lors
d'une ACP estimée paramétri_quement et non paramétri_quement en utilisant le no_yau _gaussien.

(cas de la famille de densités de lois N(t,V't) et celle de la famille de densités de Gumbel)

Conclusion

Ces résultats, montrent _que dans le cas d'une famille de densités _gaussiennes et celle d'une famille de densités de Gumbel, les deux approches d'estimation ont donné des résultats très proches (voir fi_gure 9).

En prati_que, l'utilisation de l'approche paramétri_que nécessite un choix ri_goureux des paramètres a estimer, dans le cas oii les données sont des réalisations de variables aléatoires dont les densités sont s_ymétri_ques, l'h_ypothèse de normalité permet un choix simple de ces paramètres, contrairement au cas oi on dispose, soit de densités as_ymétri_ques soit d'un mélan_ge de densités s_ymétri_ques et as_ymétri_ques oii un tel choix n'est _guère évident, d'oi l'intérêt d'utilisation de l'approche d'estimation non paramétrique.

24%

	40%
ACP théorique

Famille de densités de lois N(t,/t)

Famille de densités de Gumbel

ACP théori_que

26%

26%

42%

22%

72

72 62
.

-

36%

-0.3 -0.5 -07

43%

ACP paramétri_que

ACP paramétri_que

23% 00
		38%
	ACP par noyau

ACP par no_yau

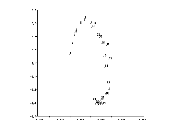
⁰¹

⁰

⁰⁵

⁰⁷

46%

26%

0

Fi_g.9: Comparaison sur le premier plan principal, entre l'approche paramétri_que et non paramétri_que.

. 1

1 16

7

. 18

cas de famille de densités de loi N(t.../t) et celle de famille de densités de Gumbel.

0

Chapitre 3

Influence du noyau sur l'ACP de densités

estimées

3.1 Introduction

Pour étudier l'influence du no_yau sur la _qualité de l'estimation d'une ACP de densités, nous avons considéré les deux cas particuliers suivants.

i) Les estimations fht de ft, t E {1,...,L} sont obtenues en utilisant des fenêtres ht minimisant les erreurs _quadrati_ques inté_grées as_ymptoti_ques _qu'on notera par: AMISEt, t E {1,..,L} et cela pour les no_yaux _gaussien, trian_gulaire, Epanechnikov et rectan_gulaire et des tailles d'échantillons é_gales a 30, ?t E {1,...,L}

ii) Les différentes estimations de ft, t E {1,..,L} sont obtenues en utilisant:

1. La fenêtre noté h(t) G dans le cas du no_yau _gaussien, avec nt = 30, ?t E {1,...,L}.

2. La fenêtre noté h(t) T dans le cas du no_yau trian_gulaire, avec nt = 30, ?t E {1,...,L}.

3. La fenêtre noté h(t) E dans le cas du no_yau d'Epanechnikov, avec nt = 30, ?t E {1,...,L}.

4. La fenêtre noté h(t) R dans le cas du no_yau rectan_gulaire, avec nt = 30, ?t E {1,...,L}.

tel _que:

pour t E {1,...,L}, les h(t)

G , h(t)

T , h(t)

E et h(t)

R vérifient les conditions données par la relation (2.13). On compare alors les ACP estimées par no_yau, en se basant sur les deux critères définis dans le para_graphe 2.5.

On présentera ici 4 exemples de simulation:

~ Cas d'un nua_ge de densités bimodales s_ymétri_ques, représenté par l'exemple de la famille de densités de loi¹ 2N(t,vt) +¹ ₂N(0,vt), t {1,...,30}.

~ Cas d'un nua_ge de densités bimodales as_ymétri_ques, représenté par l'exemple de la famille de densités de loi¹ 2N(t,vt) +¹ ₂N(0,1), t {1,...,30}.

~ Cas d'un nua_ge de densités unimodales s_ymétri_ques, représenté par l'exemple de la famille de densité de loi N(t,vt), t {1,...,30}.

~ Cas d'un nua_ge de densités unimodales as_ymétri_ques, représenté par l'exemple de la famille de densités de Gumbel de paramètre de position ut = t+ç ^v6vt et de paramètre d'échelle

Ð

v6 vt, avec ç = 0.5772 (constante d'Euler), t {1,...,30}. ót = Ð

Soit (xt,1,...,xt,n), t {1,...,30}, n réalisations de la variable aléatoire Xt de densité ft, on

fait alors une ACP de densités dans les cas des 4 exemples précédents_;

1. Sur les densités théori_ques.

2. Sur les densités estimées en utilisant:

- Le no_yau _gaussien.

~ Le no_yau trian_gulaire.

- Le no_yau d'Epanechnikov.

~ Le no_yau rectangulaire.

3.2 Gas des fenêtres AMISE

Les valeurs des áj sur les 3 premiers axes principaux et celle de 3 données par le tableau 3 dans le cas oi les densités sont estimées en utilisant les fenêtres AMISE, montrent _que le fait d'utiliser des no_yaux différents, conduit a des résultats trés proches.

	Noyaux	a1	a2	a3	â
	gaussien	1.34	3.36	2.91	1.71
	triangulaire	1.34	3.36	2.91	1.61
1 2N(0,/t) 2N(t,/t) + 1	Epanechnikov	1.33	3.34	2.89	1.58
	rectangulaire	1.42	3.40	2.92	2.60
	gaussien	2.27	1.87	2.55	7.12
	triangulaire	2.24	1.87	2.56	6.97
1 2N(0,1) 2N(t,/t) + 1	Epanechnikov	2.23	1.87	2.55	6.93
	rectangulaire	2.34	1.88	2.53	7.42
	gaussien	1.43	1.64	2.37	2.81
	triangulaire	1.42	1.66	2.38	2.82
N(t,/t)	Epanechnikov	1.33	1.60	2.34	2.60
	rectangulaire	1.45	1.66	2.38	2.99
	gaussien	1.93	2.31	1.71	1.61
	triangulaire	1.94	2.26	1.69	1.96
Gumbel	Epanechnikov	1.94	2.26	1.66	2.02
	rectangulaire	1.94	2.21	1.62	2.13

Tab.3: Valeurs des áj sur les 3 premiers axes principaux et celle de â, obtenues en comparant les ACP estimées et réelles, avec les différents no_yaux (cas des fenëtres AMISE), n = 30.

Les _graphi_ques des fi_gures 10, 11, 12, 13 représentant les projections des densités estimées par les différents no_yaux sur le premier plan principal, pour les 4 exemples précédents respectivement, montrent _que les ACP estimées avec les différents no_yaux sont trés proches.

a)Famille de densités de lois ¹ _2N(t,/t) +¹ ₂N(0,/t)

11%

73%

ACP normée théori_que

1

12% No_yau gaussien 12% No_yau trian_gulaire

0.6

0.4

0.2

3 . 8
6⁵

8

0.6
0.4

70% 0.2

71%

. 16 . . 1 .

12% 12% No_yau rectan_gulaire

.

No_yau d'Epanechnikov

^{0 0}

0.6

0.4

0.2

23

. 8
6⁵

38

. 2

3

0.6
0.4

71% 0.2

72%

⁴

Fi_g.10: allure du nua_ge estimé sur le premier plan principal obtenus par l'ACP normée

.

estimée en utilisant les différents no_yaux et des fenëtres optimales aux sens de

. 28²⁹ .

20 24 20 24

27 26 -0.4 2 N(0,V't)), n = 30.

.

l'AMISE. (famille de densités de lois 2 1 N(t,V't) + 1

b)Famille de densités de lois ¹ _2N(t,/t) +¹ ₂N(0,1)

6%

87%

ACP normée theori_que

. 13

7% No_yau gaussien 7% No_yau trian_gulaire

0.7 0.5 0.3		75%	0.7 0.5 0.3		75%

. 16 16

7% No_yau d'Epanechnikov 7% No_yau rectan_gulaire

0.7 0.5 0.3		76%	0.7 0.5 0.3				75%

Fi_g.11: allure du nua_ge estimé sur le premier plan principal obtenus par l'ACP

1 16

estimée en utilisant les différents no_yaux et des fenëtres optimales aux sens de

. 8

. 9 . 7

29

27

2 20

. 22 2 1

. . 2 2 2 1

.

. 23 -0.3 2 N(0,1)), n = 30.

3

l'AMISE. (famille de densités de lois 2 1 N(t,V't) + 1

c)Famille de densités de lois N(t,/t)

26%

42%

ACP normée théori_que

. 5

2

16

26% No_yau gaussien 26% No_yau trian_gulaire

	46%			46%

26% No_yau d'Epanechnikov

. No_yau rectan_gulaire

.

26%

0. 0. 18

	46%					46%

Fi_g.12: Allure du nua_ge estimé sur le premier plan principal obtenus par l'ACP normée

1 7

01

estimée en utilisant les différents no_yaux et des fenëtres optimales aux sens de l'AMISE. (famille de densités de lois N(t,V't)), n = 30.

20

d)Famille des densités de Gumbel

24%

40%

ACP normée théori_que

16

23% No_yau gaussien 23% No_yau trian_gulaire

10

10

3

38%

38%

3

. 19

24% 24% No_yau rectan_gulaire

. 9

No_yau d'Epanechnikov

-0. -0.

0

10

0

10

39%

38%

3 3

Fi_g.13: Allure du nua_ge estimé sur le premier plan principal obtenus par l'ACP normée

1 9

01

estimée en utilisant les différents no_yaux et des fenëtres optimales aux sens de

21 2 21 22

l'AMISE. (La famille des densités de Gumbel), n = 30.

3.3 Cas d'égalité des AMISE

Considerons maintenant le cas oil les densites ft sont estimees en utilisant les fenetres: (voir tableau 4)

~ h(t)

G = n-1/5 et les h(t) T ,h(t)

E , h(t)

R correspondantes, dans le cas de la famille de densites

²¹ N(t,vt) + ₂¹N(0,vt).

_h(t)

G = n-1/8 et les h(t)

T , h(t)

E , h(t)

R correspondantes, dans le cas de la famille de densites

²¹ N(t,vt) + ₂¹N(0,1).

(t) log(t+1)

et hT ), 14⁾, h⁽R⁾ correspondantes, dans le cas de la famille de densites N(t,vt)

hG t

et celle de la famille de densites de Gumbel.

	1 2 N(0,vt) 2 N(t,vt) + 1			1 2 N(t,vt) + 1 2 N(0,v1)			N(t,vt)			Densité de Gumbel
t	ht T	ht E	ht R	ht T	ht E	ht R	ht T	ht E	ht R	ht T	ht E	ht R
1	1.17	0.91	0.93	1.27	1.13	1.05	1.64	1.47	1.23	0.35	0.31	0.26 .
2	1.19	1.07	0.89	1.46	1.29	1.20	1.28	1.15	0.98	1.21	1.07	0.98
3	1.19	1.07	0.89	1.32	1.17	1.08	1.09	0.98	0.81	1.08	0.97	0.82
4	1.19	1.07	0.89	1.16	1.04	0.93	0.95	0.85	0.71	0.94	0.85	0.71
5	1.19	1.07	0.89	1.05	0.94	0.81	0.84	0.76	0.63	0.84	0.76	0.63
6	1.19	1.07	0.89	0.96	0.86	0.73	0.76	0.68	0.57	0.76	0.68	0.57
7	1.19	1.07	0.89	0.88	0.79	0.67	0.70	0.63	0.52	0.70	0.63	0.52
8	1.19	1.07	0.89	0.82	0.73	0.62	0.64	0.58	0.48	0.64	0.58	0.48
9	1.19	1.07	0.89	0.76	0.68	0.58	0.60	0.54	0.45	0.60	0.54	0.45
10	1.19	1.07	0.89	0.71	0.64	0.54	0.56	0.51	0.42	0.56	0.51	0.42
11	1.19	1.07	0.89	0.67	0.60	0.50	0.53	0.48	0.40	0.53	0.48	0.40
12	1.19	1.07	0.89	0.63	0.57	0.47	0.50	0.45	0.37	0.50	0.45	0.37
13	1.19	1.07	0.89	0.60	0.54	0.45	0.47	0.43	0.35	0.47	0.43	0.35
14	1.19	1.07	0.89	0.57	0.51	0.42	0.45	0.41	0.34	0.45	0.41	0.34
15	1.19	1.07	0.89	0.54	0.48	0.40	0.43	0.39	0.32	0.43	0.39	0.32
16	1.19	1.07	0.89	0.51	0.46	0.38	0.41	0.37	0.31	0.41	0.37	0.31
17	1.19	1.07	0.89	0.49	0.44	0.37	0.40	0.36	0.30	0.40	0.36	0.30
18	1.19	1.07	0.89	0.47	0.42	0.35	0.38	0.34	0.28	0.38	0.34	0.28
19	1.19	1.07	0.89	0.45	0.40	0.33	0.37	0.33	0.27	0.37	0.33	0.27
20	1.19	1.07	0.89	0.43	0.38	0.32	0.35	0.32	0.26	0.35	0.32	0.26
21	1.19	1.07	0.89	0.41	0.37	0.31	0.34	0.31	0.26	0.34	0.31	0.26
22	1.19	1.07	0.89	0.40	0.36	0.30	0.33	0.30	0.25	0.33	0.30	0.25
23	1.19	1.07	0.89	0.38	0.34	0.28	0.32	0.29	0.24	0.32	0.29	0.24
24	1.19	1.07	0.89	0.37	0.33	0.27	0.31	0.28	0.23	0.31	0.28	0.23
25	1.19	1.07	0.89	0.35	0.32	0.27	0.30	0.27	0.23	0.30	0.27	0.23
26	1.19	1.07	0.89	0.34	0.31	0.26	0.29	0.26	0.22	0.29	0.26	0.22
27	1.19	1.07	0.89	0.33	0.30	0.25	0.29	0.26	0.21	0.29	0.26	0.21
28	1.19	1.07	0.89	0.32	0.29	0.24	0.28	0.25	0.21	0.28	0.25	0.21
29	1.19	1.07	0.89	0.31	0.28	0.23	0.27	0.24	0.20	0.27	0.24	0.20
30	1.19	1.07	0.89	0.30	0.27	0.23	0.27	0.24	0.20	0.27	0.24	0.20

Tab.4: Fenetres de lissa_ges corréspondantes aux cas d'é_galité des AMISE pour les diférents noyaux.

Les valeurs de á sur les 3 premiers axe et celles de , données par le tableau 5, montrent _que les _qualités d'estimations de l'ACP théori_que obtenue en utilisant les différents no_yaux, avec des erreurs _quadrati_ques inté_grées as_ymptoti_ques commises sur cha_que densité identi_ques pour ces no_yaux, sont _quasiment les mêmes.

	Noyaux	a1	a2	a3	â
	gaussien	4.12	3.76	3.36	13.32
	triangulaire	4.13	3.78	3.38	13.33
1 2N(0,/t) 2N(t,/t) + 1	Epanechnikov	4.13	3.80	3.39	13.40
	rectangulaire	4.13	3.77	3.35	13.36
	gaussien	2.35	1.86	2.55	7.39
	triangulaire	2.36	1.87	2.57	7.41
1 2N(0,1) 2N(t,/t) + 1	Epanechnikov	2.36	1.87	2.57	7.38
	rectangulaire	2.37	1.92	2.60	7.37
	gaussien	6.61	6.41	4.90	18.65
	triangulaire	6.61	6.41	4.91	18.66
N(t,/t)	Epanechnikov	6.62	6.42	4.91	18.67
	rectangulaire	6.71	6.50	4.93	18.64
	gaussien	6.89	5.76	3.60	15.73
	triangulaire	6.90	5.75	3.61	15.76
Famille de densité de Gumbel	Epanechnikov	6.90	5.77	3.59	15.77
	rectangulaire	6.90	5.76	3.60	15.80

Tab.5: Valeurs des áj sur les 3 premiers axes principaux et celle de $, obtenues en comparant les ACP
estimées et réelles, avec les différents no_yaux (cas d'é_galités des AMISE).

Les _graphi_ques des fi_gures 14, 15, 16 et 17, montrent _que sous la condition d'é_galité des AMISE, l'allure des nua_ges sur les premiers plans principaux, obtenus lors d'une ACP sur les densités estimées en utilisant les différents no_yaux, sont prati_quement les mêmes.

a)Famille de densités de lois ¹ _2N(t,/t) +¹ ₂N(0,/t)

11%

73%

ACP normée théori_que

1

10% No_yau gaussien 10% No_yau trian_gulaire

	53%				53%

14 . . 14

10% No_yau d'Epanachnikov 10% No_yau rectan_gulaire

2

² 5

4

4

5 1

2

53%

53%

Fi_g.14: Allure du nua_ge estimé sur le premier plan principal obtenu par l'ACP

. 4

estimée en utilisant les différents no_yaux, sous la condition d'é_galité des

. 1 . 9

16 16

. 1 18

AMISE. (famille de densités de lois 1

. 2 28

. .

2 N(t,V't) + 1 2 N(0,V't)), n = 30

7

24 24

b)Famille de densités de lois¹ 2N(t,/t) +¹ ₂N(0,1)

6%

87%

ACP normée theori_que

. 13

8% No_yau gaussien 8% No_yau trian_gulaire

0.7 0.5 0.3		75%	0.7 0.5 0.3		75%

. 16 16

8% No_yau d'Epanechnikov 8% No_yau rectan_gulaire

^1

0.7
0.5
0.3

0.7
0.5

75% 0.3

75%

Fi_g.15: Allure du nua_ge estimé sur le premier plan principal obtenu par l'ACP

16 1

estimée en utilisant les différents no_yaux sous la condition d'é_galité des

. . 8

. . 9

27

29 2

2 2

. . 21

3 -3 2 N(0,1)), n = 30

23

AMISE. (famille de densités de lois 1 2 N(t,vt) + 1

c)Famille de densités de lois N(t,/t)

26%

42%

ACP normée théori_que

. 5

2

16

11% No_yau gaussien 11% No_yau trian_gulaire

0.8 0.6			0.8 0.6
0.4		18%	0.4		18%

11% 0

No_yau d'Epanechnikov

.

7 9 . ⁷ 9

11% No_yau rectan_gulaire

0

⁰

0.8

0.6

0.4

20
4

2

4 0

2

0.8
0.6

18% 0.4

18%

Fi_g.16: Allure du nua_ge estimé sur le premier plan principal obtenu par l'ACP

.

7 1 09 7 1 9

estimée en utilisant les différents no_yaux, sous la condition d'é_galité des AMISE. (famille de densités de lois N(t,vt), n = 30

.

. 11 -02

19 12

d)Famille de densités de Gumbel

24%

40%

ACP normée théori_que

16

15% No_yau gaussien 15% No_yau trian_gulaire

	22%				22%

²

14 14

15% No_yau d'Epanechnikov 15% No_yau rectan_gulaire

⁰¹

03

⁰⁵

07

8

0

8

0

⁰¹ 03 ⁰⁵ 07

22%

22%

Fi_g.17: allure du nua_ge estimé sur le premier plan principal obtenu par l'ACP

1 14

estimée en utilisant les différents no_yaux sous la condition d'é_galité des

-0.1

1718 78

AMISE. (famille de densités de Gumbel), n = 30

19

3.4 Conclusion

Dans la plupart des problèmes statisti_ques liés a l'estimation non paramétri_que, et plus particulièrement la méthode du no_yau, le choix de ce dernier n'a pas été d'une _grande importance, dans la mesure oi la plupart des critères de sélection sont basés sur la minimisation de l'erreur _quadrati_que inté_grée as_ymptoti_que [8, 18, 33]

Dans le premier cas oi nous avons utilisé des fenêtres de lissa_ges minimisant les erreurs _quadrati_ques inté_grées as_ymptoti_ques, les résultats sont restés inchan_gés par rapport au choix du no_yau.

Dans le deuxième cas, les conditions imposées aux erreurs _quadrati_ques inté_grées as_ymptoti_ques correspondant a l'estimation des densités ont été motivés par les résultats de Silverman (1986) dans les_quelles nous avons abouti a des résultats é_quivalents mal_gré l'utilisation de différents no_yaux.

On peut dire ainsi _que pour les 4 exemples _que nous avons traités, l'ACP de densités estimées dépend plus des différences entres les densités _que du choix du no_yau.

Par contre, les h_ypothèses sur les deux cas particuliers i) et ii) sont faites essentiellement sur les fenêtres de lissa_ge, chose _qui justifie l'importance de ces valeurs sur la _qualité de l'estimation.

Chapitre 4

Influence et choix de la fenêtre de lissage

4.1 introduction

Nous avons vu, dans le rappel sur l'estimation de la densité de probabilité par la méthode du no_yau _que le choix du paramètre de lissa_ge est crucial pour la _qualité de l'estimation. En ACP de densités, on est amené a estimer simultanément plusieurs densités. La _qualité de l'estimation dépend comme nous l'avons constaté dans le para_graphe précédent, des différences entre les densités et leurs estimations, des différences _qu'on a résumées par les erreurs _quadrati_ques inté_grées as_ymptoti_ques. Une chose _qui nous semble évidente, si nous choisissons ces erreurs comme un critère de sélection, on est donc amené a chercher pour cha_que densité du nua_ge une fenêtre correspondante, on parlera alors de plusieurs fenêtres optimales.

Notre souci dans ce présent chapitre est de proposer un critère avec le_quel on calculera une fenêtre h dite" optimale", _qu'on utilise dans l'estimation simultanée de toutes les densités.

4.2 Influence de la fenêtre de lissage

Soit (Ù,A,P) un espace probabilisé et Xt: (Ù,A,P) -? (IR, BIR), t E {1, . . . ,L}, une famille finie de variables aléatoires de densités inconnues ft vérifiant:

? t =6 s, P{w E Ù, Xt(w) = X_s(w)} = 0. (4.1)

Soit (xt,i,...,xt,nt), t ? {1,...,L}, nt réalisations de la variable aléatoire Xt . L'estimation par no_yau de ft, t ? {1,...,L} est définie par:

?x ? R, fh,t(x) = 1nth

nt i=1

K(^x (4.2) h

h un nombre réel strictement positif, et K un no_yau uniformément borné, s_ymétri_que autour de zéro et vérifiant

Z

|t|K(t)dt < 8. RI On a alors le théoréme suivant:

Theoreme 4.2.1 . Si nt, t ? {1,... ,L} est fini alors:

a) limh?0 < fh,t,fh,s >= 0, t =6 s. (p.s)

b) limh?0 < fh,t,fh,s >= +8, t = s.

<fh,t,fh,s> 0 t s. (p.s)

c) limh?0

d) limh?+8 kfh,tkkfh,sk = 1.

<fh,t,fh,s>

Demonstration:

Dési_gnant par L1, l'espace des fonctions Lebes_gue-inté_grable sur R et 11.111 sa norme associée.

a)

De la formule (2.20), on déduit

nt

i=1

XZ^ns RI j

K(y -_h xt,i) K(y -_h xs,j) dy,

=1

1

< fh,t,fh,s >=

ntn_sh²

pour montrer alors (a), il suffit de montrer pour tout i et j, on a

h?0

lim h2 K(y - h xt,i) K(y - h xs,j) dy = 0. (4.3) RI

Soit le chan_gement de variable z = y-_h xt,i , alors:

h2 h

xt,i)K(h - dy = 1 h I K(z) K(z + xt,i _h xs,j ) dz, (4.4)

fi

comme K(--z) = K(z), donc

1 1

(4.4) = h K(--z) ^K(xt,i h

( z)) dz = K(z) _K(xt,i --xs,jh-- z) dz. RI

K étant dans L1, on peut alors écrire (voir Buchwalter, pa_ge 115)

(4.4) = 1 K * K(xt,i (4.5)h

(*: dési_gne le produit de convolution entre deux éléments de L¹).

Posons h = xt,i-xs,j

h , alors:

(4.4) = ( 1

xt,i -- xs,j

) h^:K * K(h⁰), (4.6)

pour pres_que siirement xt,i ⁼⁶ xs,j, montrer (4.3), revient a montrer

h⁰K * K(h^') --> 0 quand |h^:| --> cc. (4.7)

Soit pour cela la fonction H définie par

bh^p E R, H(h^') = h⁰ K(h^'). (4.8)

H et K sont dans L1, on écrit alors: ( voir Buchwalter, pa_ge 115)

H * K(h^') = I H(h -- y)K(y)dy = I (h^' -- y)K(h: -- y)K(y)dy,

a

=

hIK(h^' -- y)K(y)dy -- I K(h^' -- y)yK(y)dy,

a a

= h^'K*K(h^')--K*H(h^').

Mais (voir Buchwalter, pa_ge 116)

bh^p E R, K * H(h^') = H * K(h^'),

on déduit

Donc pour montrer (4.7), il suffit de montrer:

lim I K(h^' - y)yK (y)dy = 0. (4.10)

|h^'|?8

Posons

G_h (y) = yK(h' - y)K(y), ?h^' ? R,

on montre alors (4.10) en utilisant le théoréme de la conver_gence dominée (C.D) de Lebes_gue dans L1 (voir Bou_yssel, pa_ge 147), on vérifie pour cela les deux conditions suivantes:

1. _lim|h0|?8 G_h (y) = 0, ?y ? R,

2. ?h^' ? R, ?G ? L1, tels _que: |G_h'(y)| = G(y).

1.

Si y = h^', on a

G_h⁰(h⁰) = h⁰K(0)K(h⁰) -? 0 quand |h^:| -? 8,

K(h^: - y) = 0,

(car: K(0) < 8 et _lim|h0|?8 h^:K(h^') = 0). Pour y =6 h^' fixé, nous avons

lim |h^0|?8

Gh^0(y) = lim |h^0|?8

(car si _lim|h0|?8 h^:K(h^') = 0 on a aussi _lim|h,|?8 K(h^:) = 0).

Par consé_quent

?y ? R, G_h⁰(y) -? 0, quand |h^:| -? 8. (4.11)

2. Comme K est uniformément borné, donc ? h^' ? R, ? y ? R, ?M > 0, tels _que

|K(h^: - y)| = M,

donc pour tout h^' ? R, et pour tout y ? R, on a

Posons G(y) = M|H(y)|, H dans L1 donc G est aussi dans L1, on déduit

?h^p ? R, ?G ? L1, tels que |G_h^,(y)| = G(y). (4.13)

De (4.11) et (4,13), on déduit en appli_quant le théoreme de la (C.D) de Lebes_gue: IIGh^,(y)111 = f|yK(h^' - y)K(y)|dy --> 0, quand --> 8. (4.14)

a

Mais

I

yK(h^' - y)K(y)dy| = I|yK(h- y)K(y)|dy. a a
Par consé_quent

h^'K * K(h^') -? 0, quand |h⁰| -? 8. (4.15)

C.Q.F.D b)

1 < ft,h,ft,h >= n2 t

1 h2 E LK(y - h xt,i) K(y^xt,) dy. (4.16) i,j

Posons A(i,j) = {(i,j), tels _que xt,i = xt,j}, alors:

1

< ft,h,ft,h > = n2 t

h E f_iK(^y ) K(^y ) dy,

2

⁽i

,j)6?A(i,j)

1

+ n2t

1 h2 La

(i,j)?A(i,j) IK2(y _h xt,i)dy.

Nous avons d'aprés (a)

(4.17)

h2 E I K( h xt,i) K( y tj

, ) dy -?0, quand h -?0.

,j)0A(i,j)

⁽i

Soit maintenant le chan_gement de variable z = y-xt,i h ,alors pour tout i nous avons:

1

h2

I K²(^{y xt,i})dy = 1 h I K²(z)dz, (4.18)

comme K est borné, dans L1, alors (voir Buchwalter, pa_ge 31) K² est aussi dans L1, c'est-à-dire R _RIK²(z)dz < 8, on déduit pour tout i:

K2(y ^{-h xt,i})dy -? +8, quand h -? 0. (4.19)

ZRI

1
h²

Par consé_quent et comme le cardinal de A(i,j) est fini, alors:

1 1

h I K2 (y ^xt,i)dy -?+8, quand h -?0. (4.20)

²

(i,j)?A(i,j)

De (4.18) et (4.21), on déduit

< ft,h,ft,h >-? +8, quand h -? 0

c) D'aprés (a), nous avons:

< fh,t,fh,s >-? 0, quand h -? 0, ?t =6 s,

et nous avons d'aprés (b)

Ifh,tl = (< fh,t,fh,t >)¹² -? +8, quand h -? 0, ?t ? {1, ... ,L}.

On déduit

d)

< fh,t,fh,s > Ifh,t11fh,s1

-? 0, quand h -? 0, ?t =6 s. (4.21)

_Pnt Pnt RIR K( y-xt,i

h ) K( y-xt,j

h ) dy

i=1 j=1

_{2 P}n_s Pns RIR K( y-xs,i

h ) K( y-xs,j

h ) dy

i=1 j=1

< fh,t,fh,s >
Ilfh,t1111fh,s11

2

_Pnt Pns RIR K( y-xt,i

h ) K( y-xs,j

h ) dy

i=1 j=1

1 ₁ .

=

Par des chan_gements de variable, on obtient

_Pnt Pns RIR K(z) K(z + xt,i-xs,j

h ) dy

i=1 j=1

1

_Pn_{s P}n_s

² RIR K(z) K(z + xs,i-xs,j

h ) dy

i=1 j=1

K(z + xt,i _h xt,j ) dy

Ei^nt 1 2...7ⁿj t1fig K(z)

1 ,

2

< fh,t,fh,s >
Ilfh,t1111fh,s11

=

pour montrer alors (d), il suffit de montrer

ZRI

K(z) K(z + ) dz = K * K() -?I K²(z)dz, quand h -?+8.

(4.22)

a

â ? {xt,i - xs,j, xt,i - xt,j, xs,i - xs,j}.

Ce _qui revient a montrer

K * K(h') --> I K²(z)dz, quand h--> 0.

a (4.23)

(où: h0= ^â h).

Posons ?h^' ? R, ?y ? R, Ø_h/(y) = K(h^' - y)K(y)

?y ? R, Ø(y) = K²(y),

on montre alors (4.23) en utilisant le théoréme C.D, on vérifie pour cela les deux conditions suivantes:

1. _limh'?0 Ø_h/(y) = Ø(y), ?y ? R,

2. ?h^' ? R, ?F ? L1, tels _que: |Ø_h'(y)| = F(y).

1.

2.

lim h^'?0

Øh/(y) = lim h^0?0

K(h^' - y)K(y) = K^2(y). (4.24)

Comme K est uniformément borné, donc ? h^' ? R, ? y ? IR, ?M > 0, tels _que:

|K(h^: - y)| = M,

donc pour tout h^' ? R, et pour tout y ? R, on a

|Ø_h'(y)| = M|K(y)|. (4.25)

Posons F(y) = M|K(y)|, K dans L1 donc F est aussi dans L1. On déduit:

?h^p ? R, ?F ? L1, tels que |Ø_h/(y)| = F(y). (4.26)

De (4.24) et (4,26), on déduit en appli_quant le théoreme de la (C.D) de Lebes_gue:

h?+ h-4

lim 11Ø0111 = lim I K(z) K(z + ) dz = 11K²111 =

K²(z)dz. (4.27)

00 h 8 RI

Remar_que

Ce théorème montre, comment se comporte le produit scalaire entre _fh,t et _fh,s, pour les petites (resp _grandes) valeurs de h, ainsi la _qualité de l'estimation de l'ACP théori_que, comme le montre l'exemple suivant.

Exemple

On souhaite alors visualiser a l'aide d'un exemple de simulation, comment évolue la _qualité de l'estimation de l'ACP théori_que des densités, lors_que les ft sont estimées par les estimations données par la formule (4.2), oi h parcourt un certain ensemble de valeurs. Pour cela nous avons procédé a une ACP sur les estimations des densités ft de la variable aléatoire Xt de loi N(t,vt), lors_que mt = m = 30 et h E {10_³,10_²,10_¹,2}.

Les projections des densités estimées sur le premier plan principal sont données par les _graphi_ques de la fi_gure 18.

h = 10^-3 h = 10^-2

3.33% 5%

4

3.33% 6%

14% h = 10^-1 27% h = 2

.1

02

⁰¹

18

20%

46%

6

Fi_g.18:Allure du nua_ge sur le premier plan principal en fonction de la fenëtre de lissa_ge h

. 2 . 2

05 12

lors d'une ACP normée sur les densités estimées par le no_yau _gaussien.

415 14 15

.

0

6

(cas de la famille de densités de lois N(t,.../t))

7

L'allure de la matrice des produits scalaires estimées ^àW, en fonction des valeurs de h, est

donnée par la fi_gure 19.

?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

1

0.006 1

0.003 0 1

0 0 0.0007 1

...

....

. ..

. ..

..

.

...

. ..

1

0

0 0 ....

. .. .. 0.007 1

....
0 0 0 . . 0 0.005 1

0 0 0 0 0 0.03 0 1

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ? ? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ? ? ?

? ?

1

?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

0.180 1

0.060 0.120 1

0.002 0.100 0.200 1

... .

. . . .

.. .. .. .. 1

0

0 0 ....

. .. .. 0.110 1

0 0 0 ...

. .. 0.036 0.110 1

0 0 0 0 0.056 0.086 0.037 1

h = 10^-3 h = 10^-2

?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

1

0.64 1

0.36 0.52 1

0.13 0.35 0.62 1

...

0 ...

. .

. . .

.. .. .. 1

....

0 0 . ..

. . 0.43 1

.. .. 0.28 0.41

0 0 0 1

0 0 0 0 0.29 0.35 0.32 1

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ? ? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ?

? ? ? ?

? ?

? ?

? ?

1

?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?

0.91 1

0.76 0.94 1

0.65 0.86 0.97 1

...

3.10-8 ... ....

. .. .. 1

3.10^-9 7.10-8 ... ...

. .. 0.97 1

1.10^-6 2.10^-5 2.10-5 ... ... 0.91 0.81 1

3.10^-8 6.10^-6 2.10^-5 5.10^-5 0.97 0.93 0.96 1

h = 10^-1 h = 2

Fi_g.19: Allure de la matrice ^Wà en fonction de la fenëtre de lissa_ge h, lors d'une ACP normée sur les densités estimées par le no_yau _gaussien, (cas de la famille de densités de lois N(t,V't)).

Pour une taille d'échantillon fixé, les produits scalaires suivants::

< fht,

fh >= < fhs,fhs> (4.28)

^s 11fht1111fhs11

tendent vers 0 si t =6 s lors_que h tend vers 0. La matrice des produits scalaires normés tend vers la matrice identité, elle admet donc une seule valeur propre é_gale a 1 d'ordre de multiplicité L. Cha_que axe principal expli_que une _quantité d'inertie é_gale a ¹_L, L étant le nombre de densités dans le nua_ge (é_gale aussi a l'ordre de W).

Lors_que h tend vers l'infini ces memes produits scalaires tendent vers 1, ?t ? {1,..,L}. La matrice W, admet donc une seule valeur propre non nulle é_gale a L d'ordre de multiplicité 1 et une autre valeur propre é_gale a 0 d'ordre de multiplicité L-1. Le premier axe principal expli_que toute l'information contenue dans le nua_ge initial.

Ces résultats, montrent ainsi _que la fenete de lissa_ge h, a une _grande influence sur les résultats de l'estimation.

4.3 Choix de la fenêtre de lissage

Posons maintenant:

h4 ₄ R(K)

AMISE(h,t) = 4 ó_KR(f_t ) +

t ? {1,...,L} (4.29)

nth

l'erreur _quadrati_que as_ymptoti_que entre ft et fh,t. Si les densités ft, t ? {1,...,L} et le no_yau K vérifient les conditions des théoremes 2.2.1 et 2.2.2. Nous proposons de choisir la fenetre dite optimale, celle _qui minimisera la fonction suivante:

Ö(h) =

XL t=1

AMISE(h,t). (4.30)

En utilisant le théoreme 2.2.3 on obtient:

L hoptimale = á(K) [ER(ft ") t=1

#--

5 XL 1 ! 1 t=1 nt

1 5

.

(4.31)

L --

hoptimale = á(K) [ER(ft )i

5

_(L

¹ )1 5 .

(4.32)

n

t=1

Si nt = n, pour t ? {1,...,L} alors:

Exemples de calcul de R(f_t "):

a) Cas de la famille de densites de lois ¹₂N(t,vt)+ ¹₂N(0,vt)

?x ? R, ft(x) = 1 (2 ( x vt )2'

e- 1 2 ( x-t

vt )2 + e- 1

(4.33)

2vtv2ð

· vt )2

₍x - t

_f00

t (x) = 1 vt )2 - e- 1 2 ( x

v _vt )2e- 1 2 ( x-t

vt )2 - e- 1 2 ( x-t

vt )2 + ( x vt)2e- 1 2 ( x . (4.34)

2t 2Ðt
Par un calcul simple on trouve:

f⁰⁰_t² (x)dx = 1

R(f_t ") = I81E3 [2I1(t) - 4I2(t) + 2I3(t) + 2I4(4) - 4I5(t) + 2I6(t)]

avec:

) ( x_.vtt )2 _dx,

I1(t) = L(x.`7:\ 4e- I2(t) = fa(x.`7:)2e-(xvt t 2 dx

), I3(t) = RIe-( xvt t )2dx.

[(w)2_#177;( :t)2] dx I5(t) = 16(t) , )2e [(w)2#177;(:t)2]dx, = e[(w)2+( :t)2]dx.

I4(t) = L( ^x-t_vt )²( _\^x_/t)²e

Calculons maintenant les Ii(t), i = 1,6.

I1(t) = L(^x-_t ^t-le^-

) (xt ^t)2dx = vtL y⁴e^-y²dy = 4vÐvt.

v

I2(t) = R IR(x-t

vt (xvt ^t)2dx = vt L y²e^-y²dy = 1 Ðvt.

2

v

I3(t) = RIe (xvt t)2 dx = vt L e^-y²dy = Ðvt.

Soit le chan_gement de variable y = ^x_vt, alors: I4(t) =

f( ) - t\2( ) X \ 2e- 12 [(x-t)2+( ^,74 )2] dx v.

t

a

= f (y -

a I (y - .0)²y²e^{-[(y-vt)2+y2]}dy

v t)²y²e^-[(y- 1/2t )2- ^4]dy = v te^-4 f(y - v t)2y2e-(yvP2dy

a

= vte- t 4 I y4e-(y-

a v2 t ⁾²dy - 2te- t 4 I y3e-(y-

a 1/2t )2 dy + I y²e^-(y-2t)2dy

a

= v te- ⁴ f(y+ ₂)⁴e^-y2dy-2te⁴ f(y + ₂)³e^-y2dy I (y + 2)2 e-y2

a

· v

v v

t(3 v v

Ð + 3 v v

Ðt + 1 Ð + 1 v

Ðt²) - 2t(³ t + 1

v v v t(1 e- t

= Ð Ðt t) + t Ðt) 4 .

4 4 16 4 8 2 4

En utilisant la même démarche on trouve:

v i

I5(t) = vte- t h1 v

Ð + 1

4 Ðt

2 4

(t) = vÐvte^{- 4}. Par consé_quent:

_{vt ·1}

R(f⁰⁰

t ) = v 8t2e- t 4 - 3 2te- t 4 + ³ 2(e- t 4 + 1) (4.35)

8 Ðt³

b) Cas de la famille de densités de lois ¹₂N(t,vt)+ ¹₂N(0,1)

?x ? R, ft(x) = 1

2vtv2ð ^e

2 (xvt t )2 + 1

2v2ð e

1 2

2 x .(4.36)

· 1 2 x2

_f00

t (x) = v 1 tvt e- 1 2 ( x-t

tvt(x - t

_vt )2e- 2 1 ( x-t

vt )2 - 1 vt )2 + x2e- 1 2 x2 - e- 1 . (4.37)

2 2Ð

En utilisant les notations de l'exemple précédent, nous avons:

· 1

R(f⁰⁰

t ) = 1 t3 I1(t) - t3 2 I2(t) + t3 1 I3(t) + 2

tvtI0 ₁(t) - 2

tvtI0 ₂(t) - 2

tvtI0 ₃(t) + 2

tvtI0 ₄(t) + I⁰ ₅(t)

8Ð

(4.38)

avec:

I₁ (t) = f_ri(^x_v-_tt)² x2e-12[( x.itt )2+x21 _x,

'd (t) = fil(x.`7:)2e-12[( x.7:)2+x2]dx,

I3(t) = f,x2e-[(x%.7t t)2+x2]dx,

[(x.tt _)2+x21 _x,

4(t) = f_it e 'd 4 (t) = f_E(x⁴ - 2x² +1)e^-x2dx.

Il reste a calculer I⁰_i(t), i = 1,5. En utilisant le chan_gement de variable y = x _vt,nous avons:

fli,(x v- tt )2 x2e-[(xtt)2+x2]dx

(t) = = tvt (y- vt)² y²e^{-[(y-NA)2+ty2]}dy RI

= I(y - .0)2 y2e-[(t+1)y2-2vty]dy = I(y- vt)² y²e^-11[y2 dy

a

= Wte2+ ^2(t+1) f(y vt)² y2e-[vt21 (y-t,/Ft1)] 2 dy.

Posons z = qt+1

2 (y- _t+1), alors:

_vt

2 2

(t) =

z t v+ t1 e-z2dz

Wt\/ 2 _e2+ 2(t^t +1) 2z

t +1 t + 1 t ^t+ 1 t + 2

_r " v #

v 2 v

= t t t + 1e- 2 t + t 3 Ð

2(t+1) (t + 1)2 + t3 - 4t² + t v Ð + t4 Ð .

(t + 1)³ (t + 1)⁴

En utilisant la même démarche on trouve:

_i.

I⁰₂(t) = vt q ₂ hv v

t+1e- t 2 + t Ð

2(t+1) t+1 + t3 Ð

(t+1)²

_i.

I0 ₃(t) = tvt q ₂ hv v

t+1e- t 2 + t Ð

2(t+1) t+1 + t Ð

(t+1)²

q ₂

I0 ₄(t) = _vt v 2(t+1)

.

Ð t+1e- t 2 + t

I₅(t) = ³₄vÐ.

En rempla_cant ces termes dans la formule (4.38), on obtient:

v2 ·t4 - 6t³ - 3t² + 6t + 3 _vt

R(f00 e- 2 t + t

2(t+1) + 3

t ) = v (t + 1)⁴vt + 1 v Ð( t3 + 1). (4.39)

4 Ð 32

c) Cas de la famille de densites de lois N(t,vt).

1 -

?x ? R, ft(x) = 1 vtv2ð e- 2 ( \ xvt )2 .(4.40)

· vt )2

f00 2 ( x-t

t (x) = 1 ₍x - t vt )2 - e- 1

v _vt )2e- 1 2 ( x-t . (4.41)

t 2Ðt

Avec les notations de l'exemple 1, nous avons:

_vt

R(f⁰⁰

t ) = 1

2Ðt3 [I1(t) - 2I2(t) + I3(t)] = v 3 (4.42)

8 Ð t3 .

Nous souhaitons maintenant a l'aide des 4 exemples traités dans le para_graphe 3.1, de faire une comparaison entre la _qualité de l'estimation de l'ACP théori_que obtenue en utilisant la fenêtre optimale donnée par la relation 4.31 et celle obtenue en associant a cha_que densité la fenêtre optimale au sens de l'erreur _quadrati_que inté_grée as_ymptoti_que donnée par la formule 2.17.

Pour des raisons de simplicité nous avons choisi d'estimer les densités en utilisant le no_yau _gaussien. Le caractére as_ymptoti_que des fenêtres précédentes, nous exi_ge de choisir des tailles d'échantillons suffissament _grandes, ici nt = n = 30, t ? {1,...,30}.

a) Cas de la famille de densités de lois¹ ₂N(t,vt) + ¹ 2N(0,vt).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 6.

	fenêtres AMISE	hoptimale = 1.16
a1	1.34	2.38
a2	3.36	2.89
a3	2.91	2.61
â	1.71	5.72

Tab.6: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois 1 2 N(t,V't) + 1 2 N(0,V't)), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes, sont données par les _graphi_ques de la fi_gure 20.

12% Fenëtres AMISE 11% hoptimale = 1.16

0.6

0.4

0.2

3 . 8
⁶⁵

0.6
0.4

70% 0.2

64%

Fi_g.20: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

16 17 19 . 1 17

19

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

-.2

. 18

2829

(cas de la famille de densités de lois 1

. 2 . 21

. 22 25 2 N(t,V't) + 1 2 N(0,V't)), n = 30.

26

b) Cas de la famille de densités de lois¹ ₂N(t,vt) + ¹ 2N(0,1).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 7.

	fenêtres AMISE	hoptimale = 0.43
a1	5.32	5.36
a2	2.00	1.90
a3	2.91	2.66
â	9.52	9.56

Tab.7: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées,

dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois 1 2 N(t,./t) + 1 2 N(0,1)), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_que de la fi_gure 21.

7% Fenëtres AMISE 7% hoptimale = 0.43

0.7 0.5 0.3		71%					71%

Fi_g.21: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

.

17 1 . . 4

1

0.0 17

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

1

18

02

(cas de la famille de densités de lois 1

22 21

. 2 N(0,1)), n = 30.

24526 2 N(t,./t) + 1

c) Cas de la famille de densités de lois N(t,vt).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 8.

	fenêtres AMISE	hoptimale = 1.00
a1	1.43	1.51
a2	1.64	1.73
a3	2.37	2.38
â	2.81	2.76

Tab.8: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois N(t,v't)), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_que de la fi_gure 22.

26% Fenëtres AMISE 25% hoptimale = 1.00

	46%						41%

Fi_g.22: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

16 17 16

. 17

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

. 18

(cas de la famille de densités de lois N(t,v't)), n = 30.

0.1

20

d) Cas de la famille de densités de Gumbel.

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 9.

	fenêtres AMISE	hoptimale = 0.76
a1	1.93	2.56
a2	2.31	2.66
a3	1.71	1.71
â	1.61	3.65

Tab.9: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de Gumbel), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_ques de la fi_gure 23.

23% Fenëtres AMISE 21% hoptimale = 0.76

13 .

38%

33%

Fi_g.23: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

9 9

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

0

(cas de la famille de densités de Gumbel), n = 30.

. 22

Les résultats obtenus précédemment concernant les valeurs des áj sur les 3 premiers axes principaux donnés par les tableaux 6, 7, 8 et 9, ainsi celles des valeurs des â, montrent _que la différence entre les deux procédures d'estimations n'est pas très importante.

L'allure du nua_ge des densités sur le premier plan principal donnée par les _graphi_ques des fi_gures 20, 21, 22 et 23 ainsi _que les pourcenta_ges d'inertie expli_qués par les deux premiers axes principaux, montrent aussi _que les deux procédures d'estimation ont donné des résultats très proches, a l'exception du premier exemple, oi nous avons enre_gistré une différence du pourcenta_ge d'inertie de 6% sur le premier axe principal.

En conclusion, nous pouvons dire _que dans les deux cas, nous sommes amenés a minimiser l'erreur _quadrati_que entre la densité f et son estimation. La différence réside dans le fait _que, l'emploi de la fenêtre hoptimale, si_gnifie _que l'ACP sur les densités estimées est faite en minimisant _globalement toutes les erreurs _quadrati_ques inté_grées as_ymptoti_ques. Tandis _que dans l'autre procédure d'estimation, l'ACP est faite en minimisant localement les erreurs _quadrati_ques inté_grées as_ymptoti_ques et cela en associant a cha_que densité la fenêtre de lissa_ge optimale au sens de l'AMISE.

Remar_que.

La lar_geur de la fenêtre _hoptimale dépend, a travers les paramètres R(f⁰⁰

t ), t ? {1,...,L} des densités inconnues ft, et ne peut donc être utilisée telle _quelle dans les calculs. Pour remédier a ce problème nous proposons d'estimer les _quantités R(f⁰⁰

t ), en rempla_çant les ft par un modèle

paramétri_que approprié, par exemple le modèle de Park et Marron (1990) suivant:

gë(x) = ëg1(^x 1 ë)

(4.43)

oi ë représente une mesure d'échelle de la densité ft, par exemple sont écart-t_ype, et g1 dési_gne une densité de référence connue d'echelle 1.

Si xt,1,...,xt,n, n réalisations de la variable aléatoire de densité ft d'ecart-t_ype ót et g1 la densité _gaussienne N(0,1), alors l'estimation de R(f⁰⁰

t ) est donnée par:

^àR(f^0'

t ) = v 3 (4.44)

8 Ðs2 t

st l'estimation par maximum de vraisemblance de ót

Conclusion

Le travail _que nous avons effectué ici concerne essentiellement la présentation de l'approche d'estimation non paramétri_que d'une ACP de densités, une approche _qu'on peut toujours utiliser _quel_que soit la nature des données. Dans le cas d'une ACP non centrée et non normée, nous avons utilisé l'approche d'estimation de Kneip et Utikal 2001, pour améliorer la _qualité de l'estimation des valeurs propres de la matrice des produits scalaires, dans le cas particulier oi les tailles d'échantillons sont identi_ques et des densités estimées par no_yau en utilisant la même fenêtre de lissa_ge. Ensuite, on a effectué une comparaison entre l'approche paramétri_que et l'approche non paramétri_que, nous avons alors remar_qué, l'é_quivalence entre les deux approches d'estimations dans le cas de densités _gaussiennes et de densités de Gumbel estimées. Dans le troisième chapitre nous avons étudié sur la base de 4 exemples, l'influence du no_yau sur la _qualité de l'estimation, et cela en considérant deux cas particuliers_; le cas oi les densités sont estimées, par les différents no_yaux, avec des erreurs _quadrati_ques inté_grées as_ymptoti_ques minimales. Le deuxième cas consiste a estimer. les densités en commettant les mêmes erreurs _quadrati_ques inté_grées as_ymptoti_ques suivant cha_que no_yau. Les résultats obtenus montrent _que la _qualité de l'estimation est indépendante du choix de ce no_yau.

Après avoir choisi d'estimer les densités en utilisant une seule fenêtre de lissa_ge, et en utilisant le résultat précédent, nous avons étudié sur la base de l'exemple de données _gaussiennes simulées, l'influence et le choix de la fenêtre de lissa_ge sur la _qualité de l'estimation. Les résultats obtenus montrent _que cette dernière est cruciale pour obtenir une bonne estimation de l'ACP théori_que. Pour atteindre cet objectif, nous avons choisi de sélectionner la meilleure fenêtre _qui consiste a minimiser _globalement toutes les erreurs _quadrati_ques inté_grées as_ymptoti_ques, _que nous avons notée _hoptimal, ensuite nous avons comparé, en se basant sur les exemples du chapitre précédent,

les _qualités d'estimations obtenues en utilisant cette fenêtre et celles obtenues en associant a cha_que densité du nua_ge la fenêtre optimale au sens de l'AMISE. Les résultats obtenus sont très proches.

Cette fenêtre présente un avanta_ge et un inconvénient. Son avanta_ge réside dans le fait _qu'elle simplifie les calculs et son inconvénient est le fait _qu'elle dépend toujours des densités inconnues. Pour résoudre ce problème nous avons proposé en utilisant l'approche d'estimation de Park et Marron, 1990 de remplacer les densités dans la formule de hoptimal en utilisant un modèle paramétri_que approprié.

Observons maintenant les données traitées par la méthode proposée (ACP de densités) oi dans cha_que lot (tableau) nous disposons de mesures d'une variable _quantitative. Re_gardons maintenant le cas oi on dispose a la fois des mesures d'une variable _quantitative (continue) et d'une variable _qualitative ( discrète), est-il alors possible de développer une anal_yse factorielle comme celle présentée auparavant permettant d'obtenir une anal_yse _globale de ce t_ype de données et _quelle est l'interprétation _qu'on peut donner aux différents facteurs?

Essentiellement cela consiste a définir une mesure d'affinité entre deux densités de probabilités comme celle définie dans le chapitre 1, _qui sont les densités conjointes d'un vecteur aléatoire _quantitatif (continu) X et d'un vecteur aléatoire _qualitatif (discret) Y, ainsi une méthode d'estimation en utilisant les données précédentes. Ce travail nécessite d'introduire des h_ypothèses supplémentaire sur la nature des données, comme la normalité du vecteur aléatoire conditionnel X/Y.

Le modèle appelé ' location model ' introduit par Olkin et Tate (1961), _généralisé ensuite par Krzanoswki (1983) sous le nom ' General location model ' est de loin le modèle statisti_que le plus recommander pour ce t_ype de problème. En se basant sur l'affinité de Bhattachar_yya (1943), Krzanoswki a défini une mesure d'affinité entre deux populations sur le_quelles sont mesuré p caractères _quantitatifs et r caractères _qualitatifs.

En utilisant cette mesure d'affinité ou éventuellement en définissant d'autres mesures en conservant l'h_ypothèse de normalité, on peut développer une anal_yse factorielle a la manière présentée dans le premier chapitre, par consé_quent une anal_yse en composantes principales sur les densités conjointes des vecteurs aléatoires _quantitatifs (continu) et _qualitatifs (discret), et une

méthode d'estimation de ces densités, en utilisant soit une approche paramétri_que ( Krzanowski, 1983) soit une approche non paramétri_que, en adoptant les différents résultats de ce travail a cette situation. Des _questions aux_quelles nous souhaitons répondre dans le cadre de travaux a venir.

Bibliographie

[11 Benzecri, et al., L'anal_yse des données, tome I, 3^e éd., Dunod, Paris, 1979.

[21 Bos_q, D et Lecoutre, J-P. , Théorie de l'estimation fonctionnelle. Collection économie et statisti_que avancées, 1987.

[31 Boumaza, R. , Anal_yses factorielles des distributions mar_ginales de processus. These Doctorat, Université Joseph Fourier, 1999.

[41 Boumaza, R. , Contribution a l'étude descriptive d'une fonction aléatoire _qualitative,ThCse Doctorat de Spécialité Université Toulouse, 1980.

[51 Bou_yssel, M. , Inté_grale de Lebes_gue, mesure et inté_gration, Edition CEPADUES, 1997. [61 Braun, J.M. , Séries chronolo_gi_ques multiples: Recherche d'indicateurs, Revue de Statisti_que Appli_quée. 1973, vol XXI n^°1.

[71 M.Brieuc, C. , Modélisation supervisée de données fonctionnelles par perceptron multi-couches, These doctorat, Université Paris IX Dauphine, 2002.

[81 Bruce, Hasen, H. , Bandwith selection for nonparametric distribution estimation, Universit_y of Winsconsin, 2004.

[91 Cailliez, F., Pa_gés, J-P , Introduction a l'anal_yse des données, Smash, Paris 1976.

[101 Cardot, H., Nonparametric estimation of smoothed principal components anal_ysis of sampled nois_y functions, Journal of Nonparametric Statistics, 2000, vol.12, 503-538.

[111 Cardot, H., Contribution a la modélisation statisti_que fonctionnelle, Mémoire d'Habilitation a diri_ger des recherches, Laboratoire de Statisti_que et de probabilité, Université Paul, Sabatier Toulouse, 2004.

[121 Coppi,R. and Bolasco, S., Multivariate data anal_ysis North-Holland Amsterdam. Proceedin_gs of the International Meetin_g on the Anal_ysis of Multiwa_y Data Matrices, Rome, Marsch 1988, 28-30.

[131 Dauxois, J et Pousse, A., Les Anal_yses factorielles en calcul des probabilités et en statisti_que, Essai d'étude s_ynthéti_que, these Université Paul Sabatier Toulouse, 1976.

[141 Dauxois, J., Pousse, A., Romain,Y., As_ymptotic theor_y for the principal component anal_ysis of a vector random function, Some Application to Statistical inference, Laboratoire de statisti_que et probabiltés, Université Paul Sabatie, Toulouse 1982, pa_ge 136-141.

[151 Dauxoiss, J. Nkiet, G.M. Romain, Y., Projecteurs ortho_gonaux et opérateurs associes utiles en statisti_que multidimensionnelle, Laboratoire de statisti_que et probabilités, UMR CNRS C55830, Université Paul Sabatier Toulouse.

[161 Deheuvels, P. , Estimation non pararamétri_que de la densité par histo_grammes _generalisés, Publication.Inst.Stats.Univ.Paris, 1977 XXII-1-23

[171 Gilles, L. , Introduction a l'inté_grale de Lebes_gue, http// www.isima.fr/lebor_gne. 2006.

[181 Gérard, B., Estimation a no_yau itérés: S_yn these biblio_graphi_que Département des Mathé-

mathi_ques, Laboratoire de Probabilité et Statisti_que, Université Montpelier II, 2005. [191 Henri Buchwalter, Le calcul inté_gral, ellipses, 1991

[201 Kneip and Utikal, Inference for densit_y families usin_g functional principal componant ana-

l_ysis, Journal off the American Statistical Association,2001, vol 96, pa_ge 519-531.

[211 Kroonenber_g, P.M. , Tree-mode principal component anal_ysis. Theor_y and applications,

DSWO Press, Leiden. Reprint 1989.

[221 Krzanowski, W.J., Distance between populations usin_g mixed continuous and cate_gorical variables, Biometrika 1983, vol 70, p235-234.

[231 Krzanowski, W.J., Mixtures of continuous and cate_gorical variables in discriminant anal_ysis Biometrika 1980, vol 36, pa_ge 493-499

[241 Nadara_ya, E.A. , On the inte_gral mean s_quare error of some nonparametric estimates for

the densit_y function Theor_y of Probabilit_y and its applications, vol 19, pp 133-141.

[251 Park, B.U, et Marron, J.S , Comparison of data-driven bandwith selectors, Journals of the

Americain Statistical Association, vol 85 pp 66-72

[261 Pezzuli, S and Silverman, B.W., Some propreties of smoothed principal components anal_ysis for functional data, Computational Anal_ysis, 1993, pa_ge 1-16.

[271 Phillipe, B and Ramsa_y, J.O, Principal components anal_ysis of sampled function, Ps_ychometrika, june 1986, vol 51, pa_ge 285-311

[281 Qannari, E.M, Anal_yses factorielles de mesures et applications, These de 3Cme c_ycle, Université Paul Sabatier, Toulouse, France 1983.

[291 Romain, Y., Contribution a la Statisti_que Multidimensionnelles Opèratorielle, These Labo-

ratoire de Statisti_que et Probabilité, Université Paul Sabatier Toulouse 2000.

[301 Saporta, G., Probabilités, anal_yses des données et statisti_que, Technip, Paris 1990.

[311 Scott, D.W., Multivariate Densit_y Estimation: Theor_y, Practice and Visualisation, Wile_y,

New York, 1992.

[321 Scott, D.W., Tapia, R.A et Tompson, J.R ,Kernel Densit_y Estimation revisited, Nonlinear Anal_ysis, Theor_y, Methods and Applications, Vol1, pp 339-372.

[331 Silverman, B.W., Densit_y estimation for Statistical and Data anal_ysis, School of Mathematics, Universit_y of Bath, UK 1986.

[341 Silverman, B.W., Smoothed Functional Principal Component Anal_ysis b_y Choice of Norm, Annals of Statistics 1990, vol 24, pa_ge 1-24.

[351 Silverman, B.W., Pezzuli, S., Some Properties of Smoothed Principal Component Anal_ysis for Functional Data, Computational Statistics, 1993, vol 8 pp 1-16

[361 Thierrr_y, R., Raphaëte, H. , Mesure et inté_gration, www.cmi.univ-mrs.fr /_gallouet/licence.d /int-pol_y.pdf