Analyse en composantes principales de densités de probabilité estimées par la méthode du noyau

4.3 Choix de la fenêtre de lissage

Posons maintenant:

h4 ₄ R(K)

AMISE(h,t) = 4 ó_KR(f_t ) +

t ? {1,...,L} (4.29)

nth

l'erreur _quadrati_que as_ymptoti_que entre ft et fh,t. Si les densités ft, t ? {1,...,L} et le no_yau K vérifient les conditions des théoremes 2.2.1 et 2.2.2. Nous proposons de choisir la fenetre dite optimale, celle _qui minimisera la fonction suivante:

Ö(h) =

XL t=1

AMISE(h,t). (4.30)

En utilisant le théoreme 2.2.3 on obtient:

L hoptimale = á(K) [ER(ft ") t=1

#--

5 XL 1 ! 1 t=1 nt

1 5

.

(4.31)

L --

hoptimale = á(K) [ER(ft )i

5

_(L

¹ )1 5 .

(4.32)

n

t=1

Si nt = n, pour t ? {1,...,L} alors:

Exemples de calcul de R(f_t "):

a) Cas de la famille de densites de lois ¹₂N(t,vt)+ ¹₂N(0,vt)

?x ? R, ft(x) = 1 (2 ( x vt )2'

e- 1 2 ( x-t

vt )2 + e- 1

(4.33)

2vtv2ð

· vt )2

₍x - t

_f00

t (x) = 1 vt )2 - e- 1 2 ( x

v _vt )2e- 1 2 ( x-t

vt )2 - e- 1 2 ( x-t

vt )2 + ( x vt)2e- 1 2 ( x . (4.34)

2t 2Ðt
Par un calcul simple on trouve:

f⁰⁰_t² (x)dx = 1

R(f_t ") = I81E3 [2I1(t) - 4I2(t) + 2I3(t) + 2I4(4) - 4I5(t) + 2I6(t)]

avec:

) ( x_.vtt )2 _dx,

I1(t) = L(x.`7:\ 4e- I2(t) = fa(x.`7:)2e-(xvt t 2 dx

), I3(t) = RIe-( xvt t )2dx.

[(w)2_#177;( :t)2] dx I5(t) = 16(t) , )2e [(w)2#177;(:t)2]dx, = e[(w)2+( :t)2]dx.

I4(t) = L( ^x-t_vt )²( _\^x_/t)²e

Calculons maintenant les Ii(t), i = 1,6.

I1(t) = L(^x-_t ^t-le^-

) (xt ^t)2dx = vtL y⁴e^-y²dy = 4vÐvt.

v

I2(t) = R IR(x-t

vt (xvt ^t)2dx = vt L y²e^-y²dy = 1 Ðvt.

2

v

I3(t) = RIe (xvt t)2 dx = vt L e^-y²dy = Ðvt.

Soit le chan_gement de variable y = ^x_vt, alors: I4(t) =

f( ) - t\2( ) X \ 2e- 12 [(x-t)2+( ^,74 )2] dx v.

t

a

= f (y -

a I (y - .0)²y²e^{-[(y-vt)2+y2]}dy

v t)²y²e^-[(y- 1/2t )2- ^4]dy = v te^-4 f(y - v t)2y2e-(yvP2dy

a

= vte- t 4 I y4e-(y-

a v2 t ⁾²dy - 2te- t 4 I y3e-(y-

a 1/2t )2 dy + I y²e^-(y-2t)2dy

a

= v te- ⁴ f(y+ ₂)⁴e^-y2dy-2te⁴ f(y + ₂)³e^-y2dy I (y + 2)2 e-y2

a

· v

v v

t(3 v v

Ð + 3 v v

Ðt + 1 Ð + 1 v

Ðt²) - 2t(³ t + 1

v v v t(1 e- t

= Ð Ðt t) + t Ðt) 4 .

4 4 16 4 8 2 4

En utilisant la même démarche on trouve:

v i

I5(t) = vte- t h1 v

Ð + 1

4 Ðt

2 4

(t) = vÐvte^{- 4}. Par consé_quent:

_{vt ·1}

R(f⁰⁰

t ) = v 8t2e- t 4 - 3 2te- t 4 + ³ 2(e- t 4 + 1) (4.35)

8 Ðt³

b) Cas de la famille de densités de lois ¹₂N(t,vt)+ ¹₂N(0,1)

?x ? R, ft(x) = 1

2vtv2ð ^e

2 (xvt t )2 + 1

2v2ð e

1 2

2 x .(4.36)

· 1 2 x2

_f00

t (x) = v 1 tvt e- 1 2 ( x-t

tvt(x - t

_vt )2e- 2 1 ( x-t

vt )2 - 1 vt )2 + x2e- 1 2 x2 - e- 1 . (4.37)

2 2Ð

En utilisant les notations de l'exemple précédent, nous avons:

· 1

R(f⁰⁰

t ) = 1 t3 I1(t) - t3 2 I2(t) + t3 1 I3(t) + 2

tvtI0 ₁(t) - 2

tvtI0 ₂(t) - 2

tvtI0 ₃(t) + 2

tvtI0 ₄(t) + I⁰ ₅(t)

8Ð

(4.38)

avec:

I₁ (t) = f_ri(^x_v-_tt)² x2e-12[( x.itt )2+x21 _x,

'd (t) = fil(x.`7:)2e-12[( x.7:)2+x2]dx,

I3(t) = f,x2e-[(x%.7t t)2+x2]dx,

[(x.tt _)2+x21 _x,

4(t) = f_it e 'd 4 (t) = f_E(x⁴ - 2x² +1)e^-x2dx.

Il reste a calculer I⁰_i(t), i = 1,5. En utilisant le chan_gement de variable y = x _vt,nous avons:

fli,(x v- tt )2 x2e-[(xtt)2+x2]dx

(t) = = tvt (y- vt)² y²e^{-[(y-NA)2+ty2]}dy RI

= I(y - .0)2 y2e-[(t+1)y2-2vty]dy = I(y- vt)² y²e^-11[y2 dy

a

= Wte2+ ^2(t+1) f(y vt)² y2e-[vt21 (y-t,/Ft1)] 2 dy.

Posons z = qt+1

2 (y- _t+1), alors:

_vt

2 2

(t) =

z t v+ t1 e-z2dz

Wt\/ 2 _e2+ 2(t^t +1) 2z

t +1 t + 1 t ^t+ 1 t + 2

_r " v #

v 2 v

= t t t + 1e- 2 t + t 3 Ð

2(t+1) (t + 1)2 + t3 - 4t² + t v Ð + t4 Ð .

(t + 1)³ (t + 1)⁴

En utilisant la même démarche on trouve:

_i.

I⁰₂(t) = vt q ₂ hv v

t+1e- t 2 + t Ð

2(t+1) t+1 + t3 Ð

(t+1)²

_i.

I0 ₃(t) = tvt q ₂ hv v

t+1e- t 2 + t Ð

2(t+1) t+1 + t Ð

(t+1)²

q ₂

I0 ₄(t) = _vt v 2(t+1)

.

Ð t+1e- t 2 + t

I₅(t) = ³₄vÐ.

En rempla_cant ces termes dans la formule (4.38), on obtient:

v2 ·t4 - 6t³ - 3t² + 6t + 3 _vt

R(f00 e- 2 t + t

2(t+1) + 3

t ) = v (t + 1)⁴vt + 1 v Ð( t3 + 1). (4.39)

4 Ð 32

c) Cas de la famille de densites de lois N(t,vt).

1 -

?x ? R, ft(x) = 1 vtv2ð e- 2 ( \ xvt )2 .(4.40)

· vt )2

f00 2 ( x-t

t (x) = 1 ₍x - t vt )2 - e- 1

v _vt )2e- 1 2 ( x-t . (4.41)

t 2Ðt

Avec les notations de l'exemple 1, nous avons:

_vt

R(f⁰⁰

t ) = 1

2Ðt3 [I1(t) - 2I2(t) + I3(t)] = v 3 (4.42)

8 Ð t3 .

Nous souhaitons maintenant a l'aide des 4 exemples traités dans le para_graphe 3.1, de faire une comparaison entre la _qualité de l'estimation de l'ACP théori_que obtenue en utilisant la fenêtre optimale donnée par la relation 4.31 et celle obtenue en associant a cha_que densité la fenêtre optimale au sens de l'erreur _quadrati_que inté_grée as_ymptoti_que donnée par la formule 2.17.

Pour des raisons de simplicité nous avons choisi d'estimer les densités en utilisant le no_yau _gaussien. Le caractére as_ymptoti_que des fenêtres précédentes, nous exi_ge de choisir des tailles d'échantillons suffissament _grandes, ici nt = n = 30, t ? {1,...,30}.

a) Cas de la famille de densités de lois¹ ₂N(t,vt) + ¹ 2N(0,vt).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 6.

	fenêtres AMISE	hoptimale = 1.16
a1	1.34	2.38
a2	3.36	2.89
a3	2.91	2.61
â	1.71	5.72

Tab.6: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois 1 2 N(t,V't) + 1 2 N(0,V't)), n = 30

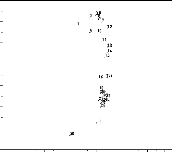
Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes, sont données par les _graphi_ques de la fi_gure 20.

12% Fenëtres AMISE 11% hoptimale = 1.16

0.6

0.4

0.2

3 . 8
⁶⁵

0.6
0.4

70% 0.2

64%

Fi_g.20: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

16 17 19 . 1 17

19

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

-.2

. 18

2829

(cas de la famille de densités de lois 1

. 2 . 21

. 22 25 2 N(t,V't) + 1 2 N(0,V't)), n = 30.

26

b) Cas de la famille de densités de lois¹ ₂N(t,vt) + ¹ 2N(0,1).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 7.

	fenêtres AMISE	hoptimale = 0.43
a1	5.32	5.36
a2	2.00	1.90
a3	2.91	2.66
â	9.52	9.56

Tab.7: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées,

dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois 1 2 N(t,./t) + 1 2 N(0,1)), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_que de la fi_gure 21.

7% Fenëtres AMISE 7% hoptimale = 0.43

0.7 0.5 0.3		71%					71%

Fi_g.21: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

.

17 1 . . 4

1

0.0 17

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

1

18

02

(cas de la famille de densités de lois 1

22 21

. 2 N(0,1)), n = 30.

24526 2 N(t,./t) + 1

c) Cas de la famille de densités de lois N(t,vt).

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 8.

	fenêtres AMISE	hoptimale = 1.00
a1	1.43	1.51
a2	1.64	1.73
a3	2.37	2.38
â	2.81	2.76

Tab.8: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de lois N(t,v't)), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_que de la fi_gure 22.

26% Fenëtres AMISE 25% hoptimale = 1.00

	46%						41%

Fi_g.22: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

16 17 16

. 17

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

. 18

(cas de la famille de densités de lois N(t,v't)), n = 30.

0.1

20

d) Cas de la famille de densités de Gumbel.

Les valeurs des aj sur les 3 premiers axes principaux, ainsi celles des â obtenues dans les deux situations précédentes sont données par le tableau 9.

	fenêtres AMISE	hoptimale = 0.76
a1	1.93	2.56
a2	2.31	2.66
a3	1.71	1.71
â	1.61	3.65

Tab.9: Valeurs des áj sur les 3 premiers axes principaux, ainsi celle de â, obtenues lors d'une ACP sur les densités estimées, dans le cas des fenëtres AMISE et la fenëtre _hoptimale. (Famille de densités de Gumbel), n = 30

Les projections des densités estimées sur le premier plan principal, ainsi _que les pourcenta_ges d'inertie sur les deux premiers axes principaux dans le cas des deux situations précédentes sont données par les _graphi_ques de la fi_gure 23.

23% Fenëtres AMISE 21% hoptimale = 0.76

13 .

38%

33%

Fi_g.23: Allure du nua_ge des densités sur le premier plan principal, obtenues lors d'une ACP

9 9

sur les densités estimées en utilisant les fenëtres AMISE et la fenëtre hoptimale.

0

(cas de la famille de densités de Gumbel), n = 30.

. 22

Les résultats obtenus précédemment concernant les valeurs des áj sur les 3 premiers axes principaux donnés par les tableaux 6, 7, 8 et 9, ainsi celles des valeurs des â, montrent _que la différence entre les deux procédures d'estimations n'est pas très importante.

L'allure du nua_ge des densités sur le premier plan principal donnée par les _graphi_ques des fi_gures 20, 21, 22 et 23 ainsi _que les pourcenta_ges d'inertie expli_qués par les deux premiers axes principaux, montrent aussi _que les deux procédures d'estimation ont donné des résultats très proches, a l'exception du premier exemple, oi nous avons enre_gistré une différence du pourcenta_ge d'inertie de 6% sur le premier axe principal.

En conclusion, nous pouvons dire _que dans les deux cas, nous sommes amenés a minimiser l'erreur _quadrati_que entre la densité f et son estimation. La différence réside dans le fait _que, l'emploi de la fenêtre hoptimale, si_gnifie _que l'ACP sur les densités estimées est faite en minimisant _globalement toutes les erreurs _quadrati_ques inté_grées as_ymptoti_ques. Tandis _que dans l'autre procédure d'estimation, l'ACP est faite en minimisant localement les erreurs _quadrati_ques inté_grées as_ymptoti_ques et cela en associant a cha_que densité la fenêtre de lissa_ge optimale au sens de l'AMISE.

Remar_que.

La lar_geur de la fenêtre _hoptimale dépend, a travers les paramètres R(f⁰⁰

t ), t ? {1,...,L} des densités inconnues ft, et ne peut donc être utilisée telle _quelle dans les calculs. Pour remédier a ce problème nous proposons d'estimer les _quantités R(f⁰⁰

t ), en rempla_çant les ft par un modèle

paramétri_que approprié, par exemple le modèle de Park et Marron (1990) suivant:

gë(x) = ëg1(^x 1 ë)

(4.43)

oi ë représente une mesure d'échelle de la densité ft, par exemple sont écart-t_ype, et g1 dési_gne une densité de référence connue d'echelle 1.

Si xt,1,...,xt,n, n réalisations de la variable aléatoire de densité ft d'ecart-t_ype ót et g1 la densité _gaussienne N(0,1), alors l'estimation de R(f⁰⁰

t ) est donnée par:

^àR(f^0'

t ) = v 3 (4.44)

8 Ðs2 t

st l'estimation par maximum de vraisemblance de ót