Analyse en composantes principales de densités de probabilité estimées par la méthode du noyau

2.2 Rappel sur l'estimation d'une densité par la méthode du noyau

" Il s'a_git d'un problème fondamental de la statisti_que non paramétri_que _qui a connu, durant ces _quarante dernières années, des développements théori_ques et prati_ques a la fois rapides et nombreux "[181.

Soit (X1,...X_n) un échantillon de densité mar_ginale inconnue f. L'idée la plus naturelle consiste a évaluer la densité f au point x en comptant le nombre d'observations "tombées" dans un certain voisina_ge de x. Sur IR^p (p = 1), on peut par exemple choisir un voisina_ge cubi_que de x = (x1,...,x_p) de la forme [x1 - h 2,x1 + h ₂] x ... x [x_p - h 2,xp + h ₂] _qu'on note [x - h ₂,x + h ₂] oi h est un nombre réel strictement positif dépendant de n, ce _qui conduit a l'estimateur [181

Cette dernière expression peut encore s'écrire:

1 fh(x) = mhp

Xn i=1

(x _ Xi 1[_ 1 . (2.2) 2 , 1 2 ]p h

oi la fonction 1[_ 1 ₂]p.

2 , 1 2 ]p est la densité de probabilité uniforme sur [_¹ ₂,¹

En s'inspirant alors de la dernière formule, et en définissant K comme étant une fonction réelle, bornée d'inté_grale 1 sur IR^p, on définit l'estimateur fh associé au no_yau K par:

1 fh(x) = mhp

Xn i=1

K(x _ Xi h ) (2.3)

Lors_que le no_yau K est choisi positif, l'estimation fh est une densité de probabilité et on parle alors parfois de la densité de probabilité empiri_que de no_yau K. Parmi les multiples estimateurs non paramétri_ques de la densité aujourd'hui a la disposition des utilisateurs, l'estimateur a no_yau, est de loin le plus populaire (Akaike, Rosenblatt, 1956, Parzen, 1962, Silverman, 1986, Bos_q et Lecoutre, 1987 ...). Ce succès peut essentiellement s'expli_quer en trois points:

1. L'expression théori_que de fh(x) est simple, puis_que il s'écrit comme une somme de m variables aléatoires i.i.d..

2. fh conver_ge vers f en de nombreux sens, et en particulier au sens L1 pour toute densité f dès que1 _h et mhp tendent tous les deux vers l'infini. D'autre part si l'estimateur est conver_gent, il est conver_gent dans tous les modes, i.e. en probabilité, en mo_yenne, pres_que sürement et pres_que complètement [21.

3. Enfin, cet estimateur est flexible, dans la mesure oi il laisse a l'utilisateur une _grande latitude non seulement dans le choix du no_yau, mais encore dans le choix du paramètre réel h.

" Lors_qu'on se limite aux no_yaux K positifs, les vitesses de conver_gences varient peu en fonction de K et les critères essentiels du choix du no_yau sont alors la simplicité et la vitesse de calcul d'une part, la ré_gularité de la courbe a obtenir d'autre part "[181. En revanche, le choix du paramètre de lissa_ge h se révèle crucial aussi bien pour la précision locale _que pour la pécision _globale de l'estimateur fh, c'est l'objet du para_graphe suivant.

2.2.1 Choix du noyau et de la fenêtre de lissage

" La décision d'un choix optimal pour le no_yau K et la constante de lissa_ge h, suppose la spécification d'un critère d'erreur _qui puisse etre éventuellement optimisé. Bien slir, l'optimalité n'est pas un concept absolu: elle est intimement liée au choix du critère, _qui peut faire intervenir a la fois la densité inconnue f et l'estimateur fh donc h et le no_yau K " [181. Dans le cas _qui nous intéresse, on cherche a minimiser l'erreur _quadrati_que inté_grée mo_yenne, _que nous noterons par MISE (mean inte_grated s_quare error), _qui est définie par:

_{Z Z}

MISE(h) = E IR'[fh(x) -- f(x)]² = IR' E[fh(x) -- f(x)]² (2.4)

Cette écriture si_gnifie _que l'erreur _quadrati_que inté_grée mo_yenne est a la fois une mesure de l'erreur _globale mo_yenne et une mesure de l'erreur mo_yenne ponctuelle accumulée.

On s'intéressera dans la suite de cette partie au cas particulier oi p = 1. On a alors le théorème suivant.

Théorème 2.2.1 (Rosenblatt, 1956)

Si f a une dérivée seconde absolument continue, et si K et f⁰⁰ E L2, oTi K est une densité continue, s_ymétri_que de variance u² _K, alors, sous les conditions h --* 0 et nh --* 00, on a le développement as_ymptoti_que:

¹ (2.5)

n

(

_h4

MISE(h) = 4 u4 _KR(f⁰⁰) + R(K)

nh + O h⁵ +

et l'erreur _quadrati_que inté_grée as_ymptoti_que associée noté AMISE est définie par:

h4 AMISE = 4

u4 KR(f^00) + R(K) nh

.

(2.6)

oi R(K) = f K2(x)dx

Choix du no_yau

Le choix du no_yau optimal K selon le critère de l'erreur _quadrati_que inté_grée as_ympthoti_que pour estimer une densité de probabilité _qu'on choisira parmi la classe de tous les no_yaux s_ymétri_ques, vérifiant de plus ^f t²K(t) =6 0, et donné par le théorème suivant:

Théorème 2.2.2 (Epanechnikov, 1969)

Si f a une dérivée seconde absolument continue dans L2.

Si de plus h ? 0, nh ? +8 et f_IR(f⁰⁰)² =6 0, alors le no_yau d'Epanachnikov d'ordre 1, KE défini par:

KE(x) = ( 3 x

_4v5)(1 - 5)ll[-v5,v5](x), (2.7)

est d'erreur _quadrati_que inté_grée as_ymptoti_que minimum.

Silverman (1986) a défini le coefficient d'efficacité des no_yaux appartennant a cette classe, en les comparant au no_yau optimal précédent, il est donné par la formule suivante.

_(J )

3

eff(K) = v5 t² K(t)dt

1 )-1

K(t)²dt , (2.8)

₂ (J

alors pour un no_yau de cette classe, il montre _que ce coefficient est très proche de 1, si_gnifiant ainsi _que le choix de ce dernier influe peu sur l'AMISE.

1)No_yau Gaussian:

Il est défini pour tous x ? RI par:

1 1

KG(x) = v 2

On présentera ici _quel_ques exemples de no_yaux appartenant a la classe pécédente _qu'on utilisera ensuite dans l'étude de l'influence du no_yau sur l'ACP de densités estimées non paramétri_quement.

exp(- x²) (2.9)

2ð

2) No_yau rectan_gulaire:

KR(x) =		? ? ?		1/2 si |x| = 1 0 sinon	(2.10)
KE(x) =	? ? ?		(3/4)(1 - 1 5x2) 1 ,5 si |x| < v5 0 sinon			(2.11)

3)No_yau d'Epanechnikov:

4)No_yau trian_gulaire:

KT(x) =

1 - |x| si |x| = 1 0 simom

(2.12)

On souhaite alors utiliser le résultat précédent de Silverman pour visualiser a l'aide d'un exemple de simulation, l'influence du choix du no_yau K parmi les 4 no_yaux définis précédemment, sur la courbe associée a l'estimation de la densité de probabilité f.

Soit (x1,...,x_n), m réalisations de la variable aléatoire X de densité f de loi N(4,2). Posons:

~ AMISEG l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau _gaussien et la fenêtre de lissa_ge noté hG.

~ AMISET l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau trian_gulaire et la fenêtre de lissa_ge noté hT.

~ AMISEE l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau d'Epanechnikov et la fenêtre de lissa_ge noté hE.

~ AMISEG l'erreur _quadrati_que inté_grée as_ymptoti_que entre f et son estimation en utilisant le no_yau rectan_gulaire et la fenêtre de lissa_ge noté hR.

tel _que:

AMISEG = AMISET = AMISEE = AMISER. (2.13)

Remar_que

La relation (2.13), va nous permettre de calculer les fenêtres précédentes, et cela en procédant comme suit:

Premièrement on fixe une fenêtre parmi hG, hT, hE, hR, par exemple_; hG = 0.40. Les 3 dernières sont respectivement les solutions réelles positives des 3 é_quations suivantes:

ó⁴KT

4

h5 - (AMISEG) h + ¹R(KT) = 0 (2.14)

m

ó4 KR

4 h5 - (AMISEG) h + ¹ _mR(KR) = 0 (2.16)

pour m = 30 on obtient: hT = 0.95, hE = 0.85, hR = 0.71. L'erreur _quadrati_que inté_grée as_ymptoti_que correspondante est é_gale a 0.023.

Avec ces fenêtres on trace les courbes associées a l'estimation de f en utilisant les différents no_yaux. Les _graphi_ques de la fi_gure 2 montrent _que sous la condition d'é_galité des AMISE, les courbes estimées par les différents no_yaux ont pres_que la même allure.

hG = 0.40 hT = 0.95

Cas du no_yau _gaussien Cas du no_yau trian_gulaire

hE = 0.85 hR = 0.71

Cas du no_yau d'Epanechnikov Cas du no_yau rectan_gulaire

Fi_g.2: Influence du no_yau sur la _qualité de l'estimation d'une densité de probabilité _gaussienne

12

de loi N(4,2) sous la condition d'é_galité des AMISE, n = 30.

Choix de la fenêtre de lissa_ge

Le premier terme du développement de MISE est un terme de biais, alors _que le second un terme de variance. On peut remar_quer _qu'ils varient en sens inverse par rapport a h: une lar_geur de fenêtre trop importante entraInera une au_gmentation du biais et une diminution de la variance (phénomène de sur-lissa_ge), alors _qu'une lar_geur de fenêtre trop faible provo_quera une inflation de la variance et une diminution du biais (phénomène de sous-lissa_ge).

Sous les conditions des théorème 2.2.1 et 2.2.2, la fenêtre h notée hAMISE, _qui minimise l'erreur _quadrati_que as_ymptoti_que est donnée par le théorème suivant.

Théorème 2.2.3 (Rosenblatt, 1956)

hAMISE = á(K)â(f)n- 1 5 (2.17)

]

ou á(K) = [R(K)

_ó4

K

[ ₁ ]

⁵ et â(f) = R(f00)

1

1
5

.

Remar_que

La lar_geur de fenêtre optimale hAMISE dépend de la densité inconnue f au travers du paramètre R(f⁰⁰) et ne peut donc être utilisée telle _quelle dans les calculs. Une fa_çon classi_que d'_y remédier consiste a remplacer la _quantité R(f⁰⁰) par un estimateur approprié. Cette approche conduit a un ensemble de méthodes _que l'on a coutume de re_grouper sous le vocabulaire _général de méthodes plu_g-in, et _qui font l'objet d'une recherche active (pour des références, on peut par exemple voir[16, 18, 24, 25, 311).

Exemples

Pour visualiser l'influence de la fenêtre de lissa_ge h sur la _qualité de l'estimation d'une densité f, nous avons choisi de présenter ici deux exemples oi f est estimée par f_n en utilisant le no_yau _gaussien:

Xn 1 1 1 ?y E RI fn(y) = e- 2 ( y-xi h )2 v2ð nhj=1

.

(2.18)

(xj)j=1,n n réalisations de la variable aléatoire parente X de densité f.

Le premier exemple concerne la densité de la loi N(0,1), oi pour h E {0.1, 0.3, 0.6, 1} on trace les courbes associées a l'estimation de f pour cha_que valeur de h.

Les _graphi_ques de la fi_gure 3 montrent _que la meilleure fenêtre est h = 0.6, et en peut voir, lors_que h = 0.1 l'estimation est très mauvaise, chose _qu'en peut expli_quer par le nombre de pi_ques _qu'elle présente_; de même pour h = 1, l'estimation est beaucoup plus aplatie, ce _qui fait une différence importante de dispersion.

h = 0.1 h = 0.3

h = 0.6 h = 1

(...) courbe estimée + + (-) courbe réelle +

0 +

Fi_g.3: Influence de la fenëtre de lissa_ge sur l'estimation par no_yau _gaussien de la densité f de loi N(0,1), n = 30

+ + + +

+ + +

+ + +

Le deuxième exemple est celui de la densité bimodale ø suivante:

1

ø(x) = ₂(f(x) + g(x)) (2.19)

avec f = N(0,1) et g = N(4,1).

Les _graphi_ques de la fi_gure 4 montrent _que pour h = 0.2 on a une mauvaise _qualité d'estimation. En lissant plus les densité en arrive a améliorer la _qualité de l'estimation , ici la meilleur fenêtre est h = 0.6. Pour h = 1, l'estimation devient moin bonne ce _qui est caractérisé par la diminution de nombre de modes.

h = 0.2 h = 0.4

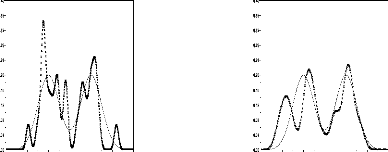
× h = 0.6 h = 1

(...) courbe estimée (-) courbe réelle

× × × × ×

Fi_g.4: Influence de la fenëtre de lissa_ge sur l'estimation par no_yau _gaussien d'une densité bimodale, n = 30

× ×

× × × × × × × × × × × × × × × × × × × × ×