Diagnostic thermique au laser lors d'une opération d'usinage

République Algérienne Démocratique et Populaire

MINISTERE DE L'ENSEIGNEMENT SUPERIEUR
DE LA RECHERCHE SCIENTIFIQUE

UNIVERSITÉ DU 20 AOÛT 1955 - SKIKDA
FACULTÉ DES SCIENCES DE L'INGÉNIEUR
DÉPARTEMENT ELÉCTROMÉCANIQUE

MEMOIRE DE MAGISTER

Spécialité : Électromécanique
Option : Mécatronique

Thème

DIAGNOSTIC THERMIQUE AU LASER LORS

D'UNE OPERATION D'USINAGE

Présenté par : TABET ZOHIR

Soutenu publiquement devant le jury :

Président : Prof. DAOUD El-Aloussi Université de Skikda

Rapporteur : Prof. MZAD Hocine Université de Annaba

Examinateur : Prof. HAIAHEM Ammar Université de Annaba

Examinateur : Dr KHOCHEMANE Lakhdar Université de Skikda

Promotion : 2011

g4ril,eAr.e.-

Mes vifs et profonds remerciements a mon encadreur Monsieur MZAD

Hocine, Docteur d'Etat en Genie mecanique et Maitre de Conferences a

l 'Universite Badji Mokhtar de Annaba pour le present theme qu'il a propose

et pour avoir accepte de me prendre en charge.

Je remercie Monsieur ELGUERRI Mohamed Enseignant en genie

mecanique a l'Universite Ibn Khaldoun de Tiaret qui m'a aide a rediger ce

memoire.

Mes chaleureux remerciements a Monsieur KHOCHMAN Lakhdar au

departement de Genie mecanique a l 'Universite de Skikda,

Je n'oublierais pas de remercier Monsieur HAIAHEM Ammar

Professeur et Directeur du Laboratoire LMI a l 'Universite Badji Mokhtar

de Annaba.

Je tiens a exprimer toute ma reconnaissance et mes remerciements a

Monsieur le president du Jury : DAOUD Souleymane pour avoir accepte de

presider ce Jury.

Je tiens egalement a remercier Messieurs les membres du Jury :

KHOCHMAN Lakhdar.

HAIAHEM Ammar

TABET ZOHIR

~~~~~~~~~

Je dédie ce modeste travail

A

Mon père pour ces encouragement et sacrifices

A

M a mère pour s a tendresse et ces prières qu'il sont l a source

de m a volonté et DJEDA * CHERIFA *

A

M a femme N assim a

A

Mon fils Abd-Elh aye Ch arffe-Eddine

A

Mes frères : Mohamed et s a femme Fouzi a, Salim et s a

Femme S amir a, Karim et s a femme Nejoi a

Adel, Ch aker et m a seur Ibtisseme,

Et les enfants * Ala eddine, Adem, Ahmed, Abde

El-moumen et Imene *

A

Mes amis : N abil, S am ad, moh amed, fou ad, mour ad, adel,

fouzzi, s al ah, amm ar, ali, roudoi ane, rid a, et me cousin

Fethi, Y acin, Y acin.m

TABET ZOHIR

3

Sommaire

NOMENCLATURE
LISTE DES FIGURES
LISTE DES TABLEAUX

INTRODUCTION GENERALE . 11

Chapitre I : GENERALITES SUR L'USINAGE

I-1. GÉNÉRALITÉS

I-2. HISTORIQUE

I-3. PROCEDE D'USINAGE

I-3-1. Procédés de coupe .

I-3-2. Procédés par abrasion

I-3-3. Procédés physico-chimiques

I-4. PRINCIPE DU PHENOMENE DE COUPE

I-4-1. Représentation

I-4-2. Zone de cisaillement primaire

I-4-3. Zone de cisaillement secondaire

I-4-4. Zone en dépouille

I-4-5. Zone morte

I-5. CRITERES SPECIFIQUES DU PROCEDE D'USINAGE

I-5-1. Copeau

I-5-2. Usinabilité .

I-5-2-1. Domaine d'usinabilité

I-5-2-2. Les additions

I-5-3. Dureté

I-5-4. Lubrifiants .

I-5-5. Imperfections .

I-6. FORMATION DU COPEAU .

I-7. PARAMETRES DE COUPE

I-7-1. Echelle macroscopique .

I-7-2. Echelle microscopique

I-7-2-1. Copeau continu

I-7-2-2. Copeau avec arête rapportée .

I-7-2-3. Copeau discontinu .

I-8. CARACTERISTIQUES DES SURFACES USINEES

I-8-1. Rugosité .

I-8-2. Ligne moyenne

15

16

17

17

17

18

18

18

19

20

21
22
22

24

25
25

26
28
28

28

29

30
33

33

34

35
35

36

38

39

I-9. ENDOMMAGEMENT DES OUTILS

I-9-1. Contacts pièce-outil-copeau .

I-9-2. Mécanismes d'endommageant des outils de coupe

I-9-2-1. Endommagement issu des dépôts .

I-9-2-2. Endommagement induit par les dépôts microscopiques

I-9-2-3. Endommagement induit par les débris

I-9-2-4. L'abrasion .

39
39
41

41

42
45
45

Chapitre II : PHENOMENES THERMOMECANIQUE DE L'USINAGE

II-1. INTRODUCTION

II-2. HISTORIQUE DE LA MODELISATION

II-3. MODELES MECANIQUES .

II-3-1. Modèle de Merchant

II-3-2. Modèle des lignes de glissement .

II-4. MODELES THERMOMECANIQUES

II-4-1. Modèle d'Albrecht

II-4-2. Modèle de Boothroyd

II-4-3. Modèle d'Oxley

II-4-4. Modèle de Gilormini et al.

II-3-5. Autres modèles de coupe

II-5. ANALYSE THERMIQUE DU PROBLEME DE COUPE

II-6. MESURE DE LA TEMPERATURE DE COUPE

II-6-1. Mesures indirectes de température .

II-6-2. Mesures directes

II-6-2-1. Mesures par un thermocouple

II-6-2-2. Mesures par la méthode optique

II-7. NOUVELLES APPROCHES DE LA COUPE DES METAUX

48

49
50
50
52

54

54

55

55
57
57

59

60

60

61

61
61

62

Chapitre III : DIAGNOSTIC EXPERIMENTAL DE L'EFFET THERMIQUE EN USINAGE

III-1. INTRODUCTION .

III-2. MATERIEL UTILISE

III-3. CARACTERISTIQUES DE L'APPAREIL DE MESURE .

III-4. PROTOCOLE D'ESSAIS .

III-5. ESSAIS SUR L'ACIER DOUX .

III-6. ESSAIS SUR LE BRONZE

III-7. ESSAIS SUR L'ALUMINIUM

III-8. DETERMINATION DE LA DENSITE DE FLUX DE CHALEUR

III-9. RESULTATS ET DISCUSSION

66
66

68

69 69 74 78 82 85

CONCLUSION GENERALE
BIBLIOGRAPHIE
RESUME

Nomenclature

Symbole Signification

K
P

D f0

f

râ

F_c

Ff

ã
â

a_p,w f ,s V_c Vf R_a

L

A, B F_n

Ft

F
ë,

?

Y

l

m

n C Ve l

á

: effort spécifique de coupe

: puissance

: volume de débit de copeau

: effet de taille

: avance ou épaisseur usinée

: arrondi de la pointe de l'outil

: angle de dépouille

: force de coupe

: force d'avance

: angle de coupe

: angle complémentaire de

: profondeur de passe (mm) ;

: avance par tour (mm)

: vitesse de coupe (m/min).

: vitesse d'avance (mm/min)

: écart arithmétique moyen (.im)

: longueur de l'échantillon de l'état de surface : aires des surfaces à la ligne moyenne

: effort normale

: effort tangentiel

: effort appliqué à l'outil

: angle de frottement

: angle qui minimise la puissance : longueur de contact

: épaisseur du copeau

: coefficient de frottement de Tresca

: indice d'écrouissage de la loi de comportement

: constante empirique issue de l'expression de la vitesse de déformation : est la vitesse d'écoulement du copeau

: est la longueur du plan de cisaillement primaire

ó

w h

T1

T2 T_w

â
ø

ÄTM

óeq

åeq

åeq ^ÿå⁰eq

T Tf

Tseii_A

B n m

C L T X t

d,b,c,d q

È

ë

ñ

w

c

t1

: largeur de coupe

: profondeur de passe

: contrainte de cisaillement

: largeur de coupe

: longueur de contact outil-copeau

: température moyenne dans le plan de cisaillement primaire

: température à l'interface outil-copeau

: température initiale dans le modèle

: proportion de chaleur transmise à la pièce

: coefficient permettant à la température interne d'être une valeur moyenne : variation maximale de la température dans le copeau.

: contrainte d'écoulement [MPa]

: déformation plastique généralisée ;

: vitesse de déformation généralisée [s^-1]

: vitesse de déformation plastique équivalente de référence [s^-1]

: température de référence [K]

: température de fusion du matériau [K]

: température du matériau [K]

: limite d'élasticité statique [MPa]

: facteur d'écrouissage statique [MPa]

: coefficient d'écrouissage statique

: coefficient de sensibilité à la température

: sensibilité à la vitesse de déformation plastique.

: longueur de pièce d'essai

: température de l'environnement de travail

: Longueur usinée : temps d'usinage : coefficients du polynôme

: densité du flux de chaleur

: variable intégrale de la température

: conductivité thermique

: chaleur spécifique : masse volumique

Liste des figures

Référence : ^Intitulé

Figure I-1
Figure I-2

Figure I-3

Figure I-4

Figure I-5
Figure I-6
Figure I-7

Figure I-8

Figure I-9 Figure I-10

Figure I-11

Figure I-12 Figure I-13 Figure I-14 Figure I-15 Figure I-16 Figure I-17

: Représentation des différentes zones de la coupe

: Zone de cisaillement primaire et sa représentation

a) formation du copeau b) schématisation

: Cisaillement secondaire

a) champ des vitesses, Laheurte (2004) b) schématisation

: Zone en dépouille

a) zone en dépouille sur une arête b) schématisation

rapportée, Venkatesh (1996)

: Interactions entre la machine-outil et les aspects technologiques de la coupe : Principe et caractéristiques fondamentales des procédés de coupe

: Diagramme d'usinabilité d'un acier à 0,4 % C (HV 200) [2]

a) outil en carbure WC + 0,6% Co b) outil en carbure Wimet XL 3
: Évolution de l'angle de coupe avec les caractéristiques du matériau d'outil

râ : arrondi de la pointe de l'outil, f : avance, á : angle de dépouille

Fc : force de coupe - Ff : force d'avance - ã : angle de coupe (â = 90°+ã)

: Diagramme d'usinabilité avec outil carbure d'un acier doux à usinabilité améliorée : Influence de la dureté de l'acier usiné sur les avances et vitesse initiant une

déformation plastique d'un outil carbure

: Observation de la formation du copeau par

(a) Tresca et (b) Mallock [5]

: Paramètre de coupe en tournage

: Zones de déformation lors de la formation d'un copeau en coupe orthogonale

: Formes macrographiques de copeaux classées selon la norme ISO DIS 3685[5,7] : Copeau continu (Vc = 100m/min, f = 0,2 mm/tr) Le Calvez (1995)

: Copeau avec arête rapportée [Trent 1991]

: Copeau discontinu

a) cas d'un acier austénitique inoxydable usiné avec un outil carbure (Vc = 130m/min, f = 0,1mm/tr)

b) cas d'un acier à roulement 100Cr6 à 62HRc usiné avec un outil en céramique renforcé SIC

Figure I-18

Figure I-19 Figure I-20 Figure I-21 Figure I-22 Figure I-23 Figure I-24

: Copeau d'acier inoxydable de géométrie continue (Outil cermet, Vc = 300 m/min, f = 0,05 mm/tr)

: Paramètres de l'état de surface d'un corps solide

: Composition et aspect du corps : Composition et aspect du corps : Composition et aspect d'un corps cylindrique

: Formation du copeau (a) et usure de l'outil (b) [15]

: Composition et aspect du corps 3 déposé sur l'outil [17]

Figure II-1 Figure II-2 Figure II-3 Figure II-4 Figure II-5 Figure II-6 Figure II-7 Figure II-8 Figure II-9

Figure II-10
Figure II-11

: Chronogramme sur la modélisation de la coupe

: Modèle de Merchant : géométrie et notations

: Diagramme des efforts

: Réseaux de lignes de glissement [21]

: Efforts de coupe selon Albrecht

: Zones de cisaillements

: Modélisation de Gilormini et al. des zones de cisaillement

: Distribution des flux de chaleur générés par en coupe orthogonale [7] : Modèle plan à cisaillement simple (a)

et trois diagrammes de vitesse connus (b, c et d)

: Trois étapes distinctes dans un cycle de formation de copeau

: Modèle pour la coupe orthogonale :

(a) modèle de la zone de cisaillement avec des frontières parallèles

(b) diagramme de vitesse à la seconde étape l'angle de coupe de l'outil est positif

(c) diagramme de vitesse à la seconde étape l'angle de coupe de l'outil est négatif

(d) diagramme de vitesse à la troisième étape l'angle de coupe de l'outil est positif

(e) diagramme de vitesse à la troisième étape l'angle de coupe d'outil est négatif

Figure III-1 Figure III-2 Figure III-3 Figure III-4 Figure III-5 Figure III-6 Figure III-7

: Vue de face de l'appareil

: Vue de profil de l'appareil

: Vue d'arrière de l'appareil

: Caractéristiques de l'appareil

: Acier doux : n= 400tr/min et ö=34 mm : Acier doux, n= 800tr/min et ö=32 mm : Acier doux, n= 1260tr/min et ö=30 mm

Figure III-8 Figure III-9 Figure III-10 Figure III-11 Figure III-12 Figure III-13 Figure III-14 Figure III-15 Figure III-16 Figure III-17 Figure III-18 Figure III-19 Figure III-20 Figure III-21 Figure III-22

: Acier doux, n= 2000tr/min et ö=28 mm : Bronze, n = 400 tr/min et ö = 42 mm

: Bronze, n = 800 tr/min et ö = 40 mm

: Bronze, n = 1260 tr/min et ö = 38 mm : Bronze, n = 2000 tr/min et ö = 36 mm

: Aluminium, n= 500 tr/min et e=60 mm

: Aluminium, n= 1000 tr/min et e=58 mm : Aluminium, n= 1500 tr/min et e=56 mm : Aluminium, n= 2000 tr/min et e=54 mm

: Interpolation des relevés de température (Data) : Densité de flux de chaleur pour l'acier doux

: Densité de flux de chaleur pour le bronze

: Densité de flux de chaleur pour l'aluminium

: Densité de flux de chaleur en chariotage de l'acier doux et le bronze à 400 tr/min

: Densité de flux de chaleur en chariotage de l'acier doux et le bronze à 2000 tr/min

Liste des tableaux

Référence : ^Intitulé

Tableau III-1 Tableau III-2 Tableau III-3 Tableau III-4 Tableau III-5 Tableau III-6 Tableau III-7 Tableau III-8 Tableau III-9 Tableau III-10 Tableau III-11 Tableau III-12

: Acier doux, n = 400 tr/min ; Ø = 34 mm : Acier doux, n = 800 tr/min ; Ø = 32 mm

: Acier doux, n = 1260 tr/min ; Ø = 30 mm : Acier doux, n = 2000 tr/min ; Ø = 28 mm : Bronze, n = 400 tr/min ; Ø = 42 mm

: Bronze, n = 800 tr/min ; Ø = 40 mm

: Bronze, n = 1260 tr/min ; Ø = 38 mm : Bronze, n = 2000 tr/min ; Ø = 36 mm

: Aluminium, n = 500 tr/min ; e = 60 mm

: Aluminium, n = 1000 tr/min ; e = 58 mm : Aluminium, n = 1400 tr/min ; e = 56 mm : Aluminium, n = 2000 tr/min ; e = 54 mm

INTRODUCTION GENERALE

L'objectif de ce travail est de calculer la puissance thermique mise en jeu lors des opérations d'usinage. Pour cela, il faut connaître l'état de contraintes au sein du matériau, qui est aussi lié au champ de températures et à l'écoulement du métal. Tout d'abord, il faudrait disposer de renseignements concrets sur les échauffements mis en jeu lors de la coupe des métaux, c'est à dire la distribution de température au niveau du copeau et l'interface copeau - outil.

L'aspect thermique joue donc un rôle important à l'interface outil-copeau. En effet, dès qu'on contrôle la carte thermique des composants de la coupe, on peut s'intéresser à l'influence de celle-ci sur les caractéristiques de la pièce et notamment sur les mécanismes d'usure des outils, puisque ce problème était directement lié à la durée de vie des outils que l'on cherchait à augmenter en optimisant les conditions de coupe.

L'interface outil-copeau qui est générée lors d'un processus d'usinage par enlèvement de matière est un lieu d'interactions complexes entre phénomènes mécaniques, thermiques et physico-chimiques. La surface de l'outil en contact avec le copeau subit diverses formes d'usure qui sont le résultat de mécanismes telles que l'adhésion, l'abrasion et la diffusion. La qualité de la surface usinée ainsi que la durée de vie des outils dépendent largement des conditions dans lesquelles s'effectue la coupe. En particulier, l'emploi de fluides de coupe est un paramètre important puisqu'il permet de limiter l'élévation de la température dans les zones de coupe et d'établir la présence d'un film fluide entre les différentes surfaces, atténuant ainsi les effets du frottement. Cependant, dans le souci de protection de l'environnement et de la santé des opérateurs, la tendance actuelle est de limiter, et même de supprimer, l'emploi des lubrifiants.

Dans le cas de l'usinage des structures en alliage d'aluminium, la suppression des fluides de coupe est très néfaste car l'outil voit sa géométrie modifiée par la présence de dépôts d'aluminium sur la face de coupe. Le transfert de matière qui se fait du copeau vers l'outil prend la forme d'une arête rapportée ou d'une couche adhérente et affecte de façon importante la qualité de l'usinage. L'usinage à sec des alliages d'aluminium doit alors passer par le développement de géométries d'outils optimisées, la recherche de conditions de coupe optimales et/ou la réalisation de nouveaux revêtements d'outils. Dans l'industrie, les méthodes d'optimisation sont encore largement basées sur les connaissances acquises au cours des années et sur des essais longs et coûteux. Mais avant de mettre en place des solutions ou de développer des modèles, il est nécessaire de caractériser de manière précise les différents modes d'endommagement et de maîtriser tous les facteurs qui conduisent à l'usure des outils. C'est dans cette optique que s'inscrit le travail de thèse. Il s'applique en particulier à l'usinage à sec de l'alliage d'aluminium aéronautique AA2024 T351 avec des outils carbure WC-Co non revêtu.

L'étude se propose de fournir les éléments nécessaires à la compréhension des mécanismes d'endommagement et se présente comme un travail préparatoire aux méthodes d'optimisation. Les mécanismes de dégradation de surface étant très sensibles aux conditions de sollicitations, une large part de l'étude est consacrée à la caractérisation des paramètres tribologiques à l'interface outil - copeau (température, pression de contact, glissement du copeau). Compte tenu des moyens d'observation limités dans ce domaine, l'utilisation des modèles analytiques et numériques a été privilégiée. Les analyses seront effectuées à partir de la configuration simple de la coupe orthogonale qui a l'avantage de réduire le nombre de paramètres intervenant dans la formation du copeau. Par ailleurs, seule la coupe orthogonale a fait l'objet de travaux aboutis dans le domaine de l'expérimentation et de la modélisation.

Après un bref historique, le premier chapitre fourni des généralités indispensables sur l'usinage des métaux en présentant les différents procédés existant dans l'industrie manufacturière et en décrivant explicitement le procédé d'usinage. Ensuite il expose en détail le principe du phénomène de coupe avec ces différentes zones en passant aux critères spécifiques du procédé d'usinage ainsi que la formation du copeau et les paramètres de coupe. A la fin du chapitre on explique les caractéristiques des surfaces usinées en terminant par fournir les différents modes d'endommagement des outils de coupe.

Réservé à l'étude du phénomène thermomécanique de la coupe des métaux, le chapitre deux commence par une chronologie du développement du processus de modélisation de la coupe des métaux en passant des modèles mécaniques aux modèles thermomécaniques. Une analyse thermique du problème de coupe des métaux a été fournie suivie des différents modes de mesure de la température de coupe vue son importance capitale. Le chapitre est clôturé par un exposé d'une nouvelle approche de la théorie de la coupe orthogonale présentée par Astakhov et al.

Le troisième chapitre est consacré à notre étude expérimentale qui comporte une introduction permettant d'expliquer le but de notre investigation qui est basé sur un diagnostic thermique a laser lors d'une opération de chariotage dans le but de déterminer la densité du flux thermique dans un matériau dans des conditions de coupe données. Après exposition du matériel utilisé et explication du protocole d'essais on a présenté nos résultat expérimentaux par série de tests ensuite nous avons présenté la méthode numérique dont nous nous somme basé pour déterminer la densité de flux de chaleur. Finalement, on a exposé nos résultats avec un leur discussion.

Nous clôturons ce mémoire par une conclusion générale sur le travail qu'on a effectué pour fournir à une petite contribution aux travaux effectués afin de comprendre le phénomène thermique en coupe des métaux.

14

I-1. GÉNÉRALITÉS

L'usinage est un procédé très ancien qui se base sur la coupe de métaux qui a connue une large expansion avec le développement et la modernisation des ateliers de fabrication. L'usinage est une opération de mise en forme par enlèvement de matière destinée à conférer à une pièce des dimensions et un état de surface (écart de forme et rugosité) situés dans une fourchette de tolérance donnée. Il concerne en premier lieu les matériaux métalliques et la plupart des objets métalliques d'utilisation courante qui ont subi une ou plusieurs opérations d'usinage. Ces opérations s'insèrent dans la succession des opérations de mise en forme à deux niveaux principalement : soit comme opérations de découpe d'une ébauche destinée à être laminée, forgée, filée, emboutie, etc. ; soit comme opérations de mise à la cote de pièces préalablement moulées, frittées, filées, embouties, forgées ou assemblées par soudage ; elles peuvent alors précéder ou suivre des traitements thermiques et/ou de surface.

La mise en forme par usinage concerne également, mais de manière moins conséquente en général, toutes les autres classes de matériaux (céramiques, polymères, bois et matériaux dérivés, matériaux composites, verres, semi-conducteurs...), selon des modalités spécifiques, dépendant des caractéristiques du procédé et du matériau.

Au cours des dernières décennies de nouvelles techniques sont apparues et des progrès importants ont été atteints dans ce domaine qui en réalité reste à l'heure actuelle l'un des procédés les plus largement utilisés dans le domaine industriel pour répondre aux exigences économiques. La principale préoccupation à ce stade est la recherche de la meilleure productivité dans le procédé d'usinage qui puisse optimiser différents processus pour le rendre le plus économiquement profitable. Le succès dans ces conditions ne peuvent être réalisable qu'à partir d'études approfondies qui reposent, plus ou moins directement sur la parfaite connaissance des mécanismes physiques et des lois gouvernant le procédé de coupe des métaux qui reste donc l'objectif essentiel malgré le développement de nouveaux moyens d'usinage ou de nouvelles techniques de commande et de programmation qui participent de manière très importante au développement de la fabrication mécanique et l'apparition de nouveaux procédés dérivés tels que l'usinage à grande vitesse ou le tournage dur, etc.

La connaissance approfondie du processus de coupe et la maîtrise des paramètres qui le contrôlent repose sur une mise en oeuvre rationnelle de ces techniques.

I-2. HISTORIQUE

En dépit de son importance économique et technique évidente, l'usinage reste l'une des opérations de fabrication les moins comprises dues à la capacité prédictive inférieure des modèles d'usinage car les spécialistes et les praticiens emploient toujours le modèle à cisaillement-simple plan qui est considérablement inférieur.

Astakhov [1] a spécialement présenté une large note d'historique sur le développement de l'usinage à partie du 19è siècles jusqu'à aujourd'hui, et selon lui, bien que beaucoup d'examens des meilleures publications sur l'usinage discutent des développements dans l'ordre chronologique indiquant et estimant les publications qui supportent le point du critique (Komanduri, 1993 ; Merchant, 2003), les meilleurs examens du développement de l'usinage précisent toujours les problèmes majeurs et/ou sont fixé les buts pour des développements ultérieurs (Byrne et al., 1993 ; Chisholm, 1958 ; Finnie, 1956 ; Jawahir et Van Luttervelt, 1993 ; Kobayashi et Thomson, 1962 ; Kobayashi et al., 1960 ; Usui, 1988 ; Van Luttervelt et autres, 1998 ; Zorev, 1958). Analysant le développement de la coupe des métaux pendant les 100 dernières années, Finnie (1956) a précisé que les rapports fondamentaux entre beaucoup de variables dans la coupe des métaux manquent toujours des solutions. Comparant les résultats de divers modèles de coupe des métaux, Chisholm (1958) a conclu qu'aucun d'eux n'est adéquat aux résultats expérimentaux. Évaluant les résultats de l'essai d'usinage multiple, Zorev (1958) a conclu qu'aucun modèle connu n'est adéquat. Usui (1988) a argumenté que quoique notre compréhension de la coupe des métaux ait été approfondie à bien des égards, les seules théories descriptives de capacité de prévision inférieure ont été développées. Discutant la prédiction contre la compréhension des modèles de coupe des métaux, Shaw (1984) a conclu qu'il est impossible de prévoir le rendement de coupe des métaux. Armarego (1996) a précisé qu'une récente enquête par un principal constructeur d'outil indique qu'aux Etats-Unis l'outil de coupe correct est sélectionné à moins de 50% du temps, l'outil est employé seulement à la vitesse de coupe évaluée 58% du temps et seulement 38% des outils sont utilisés jusqu'à leur pleine capacité. L'étude précise que l'une des raisons de cette mauvaise prestation est le manque des modèles prédictifs pour l'usinage.

I-3. PROCÉDÉ D'USINAGE

L'usinage des métaux intervient dans un ensemble de procédés d'élaboration de pièces, par enlèvement de matière en quantités pouvant représenter une proportion notable par rapport au matériau brut. Cet enlèvement de matière est réalisé par l'action d'un outil possédant un ou plusieurs arrêtes tranchantes de section appropriée animé d'un mouvement relatif par rapport à la pièce. On utilise dans ces conditions une machine outil qui fournit à la fois la puissance mécanique nécessaire et qui réalise le contrôle du mouvement relatif, en considérant plusieurs points de vue, cinématique, dynamique, commande, etc. Le processus de coupe peut être utilisé à l'état simple, ou bien avec une assistance techniques auxiliaires comme des excitations vibratoires, des effets thermiques, etc. pour améliorer certaines performances.

E. Felder [2] a classé les procédés d'usinage qui sont extrêmement variés en procédés mécaniques traditionnels et procédés d'usinage non traditionnels qu'on peut classer selon les phénomènes physiques correspondants, en trois catégories principales :

I-3-1. Procédés de coupe

Action mécanique d'un outil coupant mène à l'enlèvement de matière ; la force appliquée induit la formation, à échelle macroscopique, d'un ou plusieurs copeaux. Il existe un grand nombre de procédés, dont les principaux sont : les procédés à forte vitesse ( » 15 m/min) et grand débit de matière (fraisage, tournage, perçage) ; les procédés de vitesse plus faible (sciage, rabotage, mortaisage, brochage, taraudage et alésage...).

I-3-2. Procédés par abrasion

L'enlèvement de matière est dû à l'action mécanique d'un grand nombre de grains d'abrasifs de petite taille et de haute dureté. Deux modalités différentes d'action des grains sont notés, soit liés à un support solide (rectification, meulage), soit transportés par un milieu fluide (rodage et polissage à la pâte abrasive), usinage par ultrason, par un jet de fluide abrasif.

I-3-3. Procédés physico-chimiques

Ils sont tous qualifiés de non traditionnels et l'enlèvement de matière est réalisé (à l'exception de l'impact d'un jet d'eau) par des actions non mécaniques : action thermoélectrique d'un arc électrique (électroérosion), d'un plasma ou d'un faisceau de lumière cohérente (laser) ou d'électrons ; action thermochimique de la flamme d'un chalumeau (oxycoupage) ; réaction électrochimique dans un électrolyte (usinage électrochimique) ; réaction chimique avec un liquide (usinage chimique).

I-4. Principe du phénomène de coupe

I-4-1. Représentation.

On représente généralement les différentes zones de sollicitation lors de la formation du copeau dans le plan orthogonal à l'arête de l'outil étudié (Figure I-1). Le phénomène de formation du copeau s'identifie en quatre zones Rech [3,4,5] :

1) Zone morte.

2) Zone de cisaillement primaire.

3) Zone de cisaillement secondaire.

4) Zone de cisaillement tertiaire ou de dépouille.

Figure I-1 : Représentation des différentes zones de la coupe Chapitre I - Généralités sur l'usinage

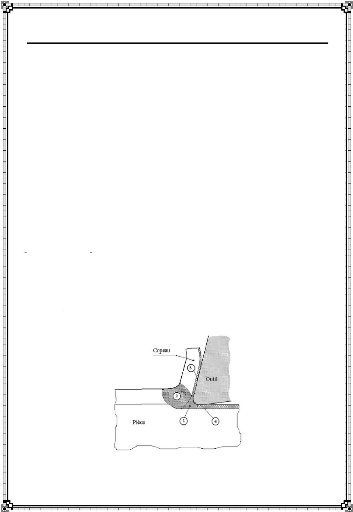
La plupart des modèles de coupe se basent sur cette description et cherchent à représenter les phénomènes présents dans les différentes zones et chacune de ces zones a une influence sur la formation du copeau et elles sont généralement modélisées séparément, puis assemblées pour le calcule les actions de coupe.

I-4-2. Zone de cisaillement primaire

C'est dans cette zone que se forme le copeau. Sous l'action de l'outil, une partie de la matière change brutalement de direction, elle est alors détachée du reste de la pièce et forme le copeau. Ce changement de direction provoque de fortes déformations de la matière aux grandes vitesses. Ce phénomène brutal est à l'origine d'une puissance mécanique importante, qui est évacuée sous forme de chaleur dans un espace très réduit, provoquant une augmentation importante de la température de la matière.

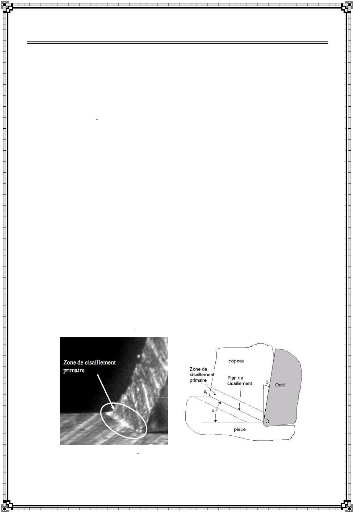
A l'observation de la formation du copeau, grâce à des essais de coupe interrompue ou des images issues de films à haute vitesse (Figure I-2a), il a été remarqué que le copeau se forme parallèlement au plan de cisaillement primaire [Merchant, 1945] (Figure I-2b), incliné d'un angle de cisaillement par rapport à la vitesse de coupe, noté ö (Figure I-2b).

A la sortie de la zone de cisaillement primaire, le copeau n'est pratiquement plus sollicité, en dehors d'une zone située à l'interface outil-copeau : la zone de cisaillement secondaire.

a - Formation du copeau b - Schématisation

Figure I-2 : Zone de cisaillement primaire et sa représentation

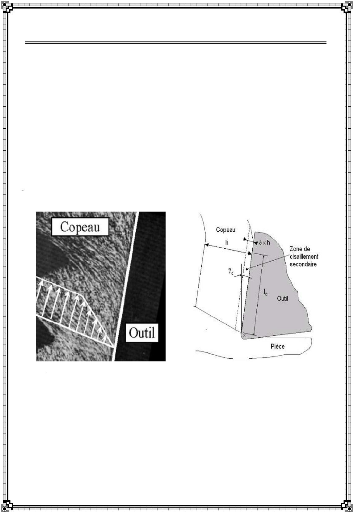
I-4-3. Zone de cisailement secondaire

A l'interface outil-copeau et sous l'effet des frottements à de fortes pressions températures, se crée une zone de déformation locale appelée zone de cisaillement secondaire (Figure I-3). A cet endroit, il existe sur une faible épaisseur du copeau, un gradient de vitesse. La vitesse d'un point du copeau augmente en s'éloignant de l'interface jusqu'à atteindre la vitesse du copeau. Le gradient de vitesse à l'intérieur de la zone de cisaillement secondaire entraîne des déformations dans cette zone du copeau, visibles sur la Figure I-3a. La détermination des actions de la matière sur l'outil est issue de l'intégration des pressions à l'interface outil/copeau. Cependant, dans la zone en dépouille, il y a également contact entre l'outil et la matière.

a - Champ des vitesses [Laheurte, 2004]. b - Schématisation

Figure I-3 : Cisaillement secondaire

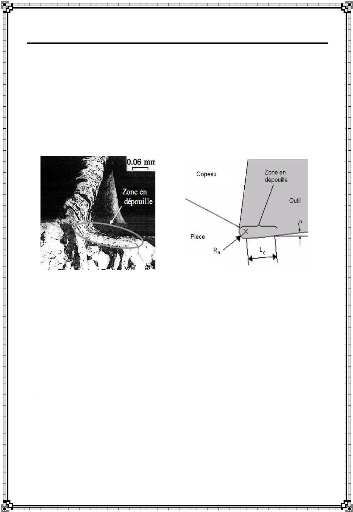
I-4-4. Zone en dépouille

Le raccordement entre la face de coupe et la face en dépouille n'étant pas parfait, il existe un rayon, nommé rayon d'acuité (Ra, Figure I-4b) entre ces deux surfaces. Du fait de cette acuité non parfaite de l'outil, une partie de la matière arrivant au contact avec l'outil ne va pas passer dans le copeau mais sous l'outil (Figure I-4a) et subit une importante déformation.

a - zone en dépouille sur une arête b - schématisation

rapportée [Venkatesh, 1996]

Figure I-4 : Zone en dépouille

Après le passage de l'acuité d'arête, l'élasticité du matériau génère une zone de contact entre l'outil et le matériau sur la face en dépouille. Les déformations élastoplastiques subies par la matière dans la zone en dépouille (acuité et face en dépouille) seront à l'origine d'un effort sur l'outil et des contraintes résiduelles, d'origines mécanique et thermique, présentes en surface de la pièce après usinage

I-4-5. Zone morte

En avant de l'arête de l'outil, existe une zone dans laquelle la matière coupée stagne (zone 1, Figure I-1). En fonction des conditions de coupe et du matériau, les dimensions de la zone morte peuvent varier et engendrer la formation d'une arête rapportée à la pointe de l'outil. Cette arête rapportée occasionne une modification des conditions de coupe ainsi qu'un déplacement de la partie coupante et est instable. L'arête rapportée va s'évacuer soit en passant du côté du copeau, soit en passant du côté de la pièce, avec pour conséquence une détérioration de la qualité de la surface réalisée.

Pour le cas des différentes modélisations de la coupe qui seront présentées, l'influence de la zone morte sur la coupe est négligée, par hypothèse.

I-5. CRITERES SPECIFIQUES DU PROCEDE D'USINAGE

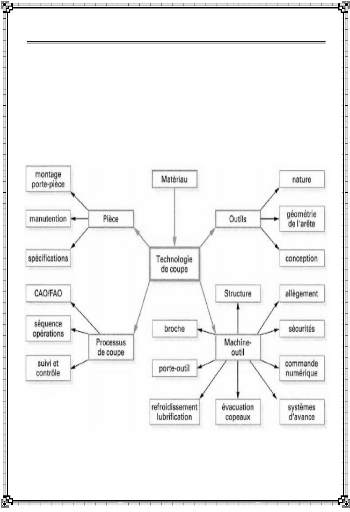
L'opération de coupe consiste à transformer une ébauche, constituée d'un certain matériau, en une pièce par l'action d'outils animés d'un mouvement relatif par rapport à la pièce par la machineoutil. E. Felder [2] décrit de manière synthétique ce processus et ses caractéristiques principales dans la figure I-5.

Le processus de formation du ou des copeaux absorbe de l'énergie sous forme de puissance P pour produire un débit volumique de copeaux D sous l'effet d'un l'effort spécifique de coupe K ; qui est, en première approximation, proportionnel à la dureté Vickers HV du matériau usiné ; il est aussi fonction de l'épaisseur usinée ou de l'avance f (figure I-6a) et est donné par [2] :

K = P / D ( 0 , 2 à 0,7)HV(f 0/f) n (1)

où f0 = 1 mm et n 0,4 traduit un effet de taille et pour être exploitable, ce coefficient doit être associé à un ensemble de paramètres (technologie, matériaux usiné et usinant, type d'outil utilisé, vitesse...). Des banques de données, informatisées ou non, permettent son évaluation.

Chapitre I - Généralités sur l'usinage

Même si leur mise en oeuvre a fortement évolué, les phénomènes physiques présents dans les procédés de coupe demeurent dans une large part inchangés, mais ne sont pas toujours clairement perçus. C'est pourquoi il faut les présenter succinctement, ainsi que leurs conséquences sur le choix des conditions de coupe. L'usinage avec formation de copeaux présente un paradoxe qu'illustre bien

-

l'expression de l'effort spécifique [éq. I 1] : la simplicité de son principe et la complexité des phénomènes physiques impliqués.

Figure I-5 : Interactions entre la machine-outil et les aspects technologiques de la coupe

23

I-5-1. Copeau

La coupe consiste, en effet, à séparer de la pièce un

copeau à l'aide de l'arête tranchante d'un outil à l'instar d'une palette soulevant un paquet de cartes et les faisant glisser les unes sur les autres (figure I-

6a). Toutefois, pour les alliages métalliques, la matière donne naissance au copeau par passage dans la zone de cisaillement primaire (figure I-

6b) où elle subit en un temps très bref une déformation plastique et un échauffement considérables. En outre, le frottement quasi sec du copeau sur l'outil crée, au voisinage de l'interface à basse vitesse de coupe, une arête rapportée (figure I-6b).

Figure I-6 : Principe et caractéristiques fondamentales des procédés de coupe

La rugosité totale Rt de la pièce usinée augmente avec les dimensions de l'arête rapportée et devient inacceptable pour une grande arête rapportée dont les dimensions (épaisseur, longueur) sont du même ordre de grandeur que l'avance. À grande vitesse, cette arête rapportée est remplacée par une zone de cisaillement secondai

re qui élève très fortement la température de l'outil et conditionne directement sa dégradation (par abrasion, déformation plastique, réaction chimique, diffusion...) et sa

de déformation

durée de vie. Le comportement des alliages métalliques dans ces conditions extrêmes

plastique, de vitesse de déformation et de température est encore l'objet de multiples travaux scientifiques depuis ceux de Merchant (1994). Néanmoins, le praticien doit choisir au mieux ses paramètres de coupe dont les principaux sont l'avance f et la vitesse de coupe V (figure I-6a).

Chapitre I - Généralités sur l'usinage

I-5-2. ^Usinabilité

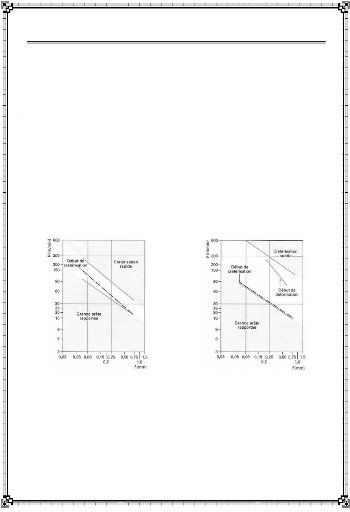
Etablis à l'aide d'essais de coupe, ils illustrent bien les conséquences pratiques de ces phénomènes et peuvent servir de guide.

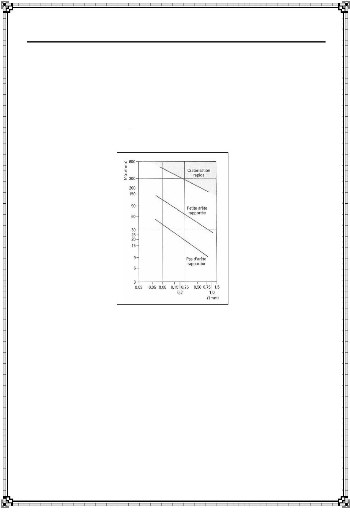
I-5-2- 1. Domaine d'usinabilité

Le domaine d'un acier mi-

dur usiné avec un outil carbure (de tungstène lié cobalt) se situe entre le domaine de formation d'une arête rapportée qui dégrade l'état de surface de la pièce, pour des avances et vitesses faibles, et le domaine de creusement par cratérisation de la face de travail de l'outil qui conduit à une ruine prématurée, pour des avances et vitesses élevées (figure I-

7a) ; toutefois, l'optimisation de la nuance de carbure permet d'élargir notablem ent ce domaine (figure I-7b).

a) outil en carbure WC + 0,6% Co b) outil en carbure Wimet XL 3

Figure I-7 : Diagramme d'usinabilité d'un acier à 0,4 % C (H V 200) [2]

L'augmentation régulière des vitesses de coupe a ainsi été rendue possible par l'utilisation de matériaux d'outil de plus en plus durs [aciers rapides, carbures, céramiques, matériaux ultra-durs (carbure de bore et diamant polycristallins)], mais de fragilité croissante.

25

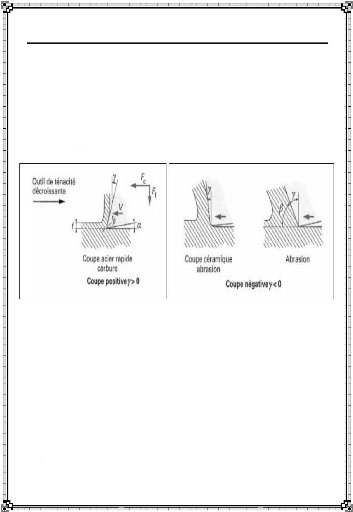
Parallèlement, on a diminué l'angle de coupe ã (figure I-

8) jusqu'à des valeurs d'un matériau très fortement négatives, seules compatibles avec une tenue correcte de l'arête

dur et fragile. Une solution particulièrement intéressante et très employée consiste à utiliser des outils revêtus de films minces (épaisseur de quelques micromètres) pour concilier, tout en conservant un coût raisonnable, les impératifsde ténacité en volume élevée et de forte résistance superficielle à l'abrasion, corrosion, diffusion...

Figure I-8 : Évolution de l'angle de coupe avec les caractéristiques du matériau d'outil
râ : arrondi de la pointe de l'outil - f : avance, á : angle de dépouille

- Ff : force d'avance - ã : angle de coupe (â

Fc : force de coupe = 90°+ã)

I-5-2-2. Les additions

Au cours d'élaboration d'alliages métalliques des éléments d'addition sont ajoutés tels que le plomb dans

les alliages cuivreux, le soufre et le manganèse dans les aciers, ce qui permet d'élargir le domaine d'usinabilité vers les basses avances en réduisant la taille des arêtes rapportées (figure I-

9) [2] ; il importe néanmoins de vérifier que l'incorporation de tels additifs d'usinabilité est compatible avec les autres phases de la mise en forme de la pièce et ses propriétés en service.

27

Chapitre I - Généralités sur l'usinage

Même les matériaux (céramiques) et les métaux durs ont actuellement leurs théories et critères et sont usinables le plus normalement avec l'utilisation de désignations spécifiques des matériaux usiné et usinant présentés par Poulachon [8] comme les superalliages et les

-

matériaux à revêtement dur pour les pièces et le c BN pour les outils qui permet de quadrupler les vitesses normalement adoptées avec les outils en carbures.

Figure I-9 :

Diagramme d'usinabilité avec outil carbure d'un acier doux à usinabilité améliorée

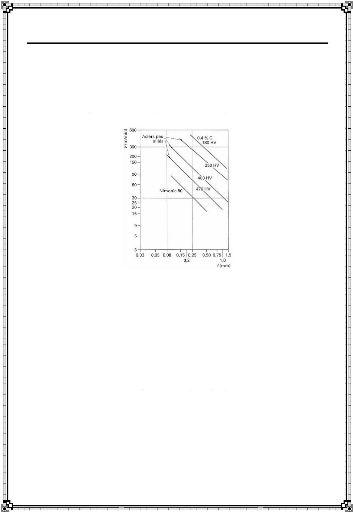
I-5-3. Dureté

La figure I-

10 montre que l'augmentation de dureté de l'alliage usiné réduit considérablement intuitive de l'équation I-1.

les avances et vitesses praticables une conséquence

Figure I-10

: Influence de la dureté de l'acier usiné sur les avances et vitesse initiant une déformation plastique d'un outil carbure

I-5-4. Lubrifiants

Le lubrifiant joue un rôle important dans les opérations de

coupe. A grandes vitesses d'usinage,

sur l'outil et sa

il assure le refroidissement de l'arête de coupe et réduit les arêtes rapportées résiduelles

vitesse de dégradation ; aux vitesses de coupe plus modérées, il diminue le frottement du copeau sur l'outil

et facilite son extraction dans des procédés comme le perçage, le brochage ou le taraudage. Mais la formulation du lubrifiant reste encore pour une large part empirique.

I-5-5. Imperfections

La coupe modifie les propriétés mécaniques, chimiques et

métallurgiques de la pièce sur une

profondeur non négligeable et laisse subsister des bavures qu'il importe de réduire et d'éliminer.

I-6. FORMATION DU COPEAU

Pratiquement beaucoup de chercheurs abordant le problème d'usinage en thèses touchent au problème de formation du copeau comme par exemple Remadna [6], Habak [7], d'autres consacrent des publications spécialement dédiés à ce sujet, Himed [5], Poulachon [8], Astakhov & al. [10,11,12], Zemzemi [13], List [14] et Soldani [15].

La compréhension des différents phénomènes qui interviennent lors du tournage est complexe et pas encore maîtrisée. L'enlèvement de matière se fait par action mécanique d'un outil coupant (Figure I-11). Dans le cas de la coupe orthogonale en régime stationnaire, la force exercée par l'outil lors de son engagement dans la matière provoque, à l'échelle mésoscopique, une forte compression de la matière (une déformation plastique et un échauffement considérable) et engendre une zone de cisaillement intense entre la pointe de l'outil et la surface externe du copeau. Cette zone est appelée zone de cisaillement primaire (ZI) et c'est aussi la zone de formation de copeau Merchant (1945). En outre, le copeau formé s'écoule et frotte sur la face de coupe de l'outil. Ce frottement intense génère la zone de cisaillement secondaire (ZII) Pomey (1971). Cette dernière est constituée d'une fine bande de frottement intense entre le copeau et l'outil et d'une autre bande d'influence du frottement du copeau sur l'outil (cisaillement secondaire) Gilormini (1995) et Puigsegur (2002). De plus, pendant l'avance de l'outil, la face en dépouille de ce dernier frotte sur la nouvelle surface et produit une troisième zone de cisaillement nommée zone de cisaillement tertiaire (ZIII).

a) b)

Figure I-11 : Observation de la formation du copeau par
Tresca (a) et Mallock (b) [5]

I-7. PARAMETRES DE COUPE

De nombreux paramètres influencent la formation du copeau et son écoulement le long de la face de coupe : la vitesse de coupe, l'avance, les angles de coupe, le comportement intrinsèque du matériau usiné, le frottement à l'interface outil-copeau, la lubrification, etc. Soldani [15] a critiqué et présenté quelques uns de ces paramètres en citant :

- La vitesse de coupe, indique le mode d'usinage : usinage conventionnel ou à grande vitesse.

Des études ont montré qu'une augmentation de la plage des vitesses conventionnellement utilisées permet de réduire les efforts de coupe, de limiter la longueur de contact outil-copeau (en segmentant le copeau) ou encore d'accroître la qualité des surfaces finales obtenues. Par contre, en augmentant la vitesse de coupe, on observe une élévation de la température à l'interface outil-copeau et par la même occasion, une usure prématurée des outils.

- L'avance, est la longueur de déplacement de l'outil pendant un tour de la pièce à usiner. Sa

valeur peut alors varier de quelques microns, pour une opération de finition, à quelques dixièmes de millimètres pour des opérations d'ébauche.

- L'angle de coupe á, mesuré dans le plan normal à l'arête de coupe, est l'angle entre la face de

coupe de l'outil et la perpendiculaire à la direction de coupe. Sa valeur est directement liée au niveau de déformation dans le copeau. Les angles de coupe négatifs ou nuls induisent des déformations plus importantes que les angles positifs.

- Le comportement du matériau, à savoir sa capacité à se déformer dans les conditions

particulières apparaissants en usinage est un autre paramètre important lié à la formation du copeau. En effet, le processus d'usinage à grande vitesse se fait sous des conditions extrêmes de déformations, de températures et de vitesses de déformation. Les premiers modèles analytiques (Merchant, 1945 - Lee et Schaffer, 1951) supposaient, comme première approximation, le matériau parfaitement plastique. Par la suite, Gilormini (1982), Oxley (1989) ou Molinari et al, (1992) ont pris en compte dans leur modèle respectif, les effets dynamiques et thermiques sur le matériau au travers de lois de comportement thermo/viscoplastiques.

- Le frottement à l'interface outil-copeau est la conséquence à la fois des paramètres de coupe

cités précédemment et des affinités chimiques entre l'outil et le matériau usiné. C'est une donnée primordiale dans la détermination du champ de température le long de la face de coupe, ainsi que des efforts lors de l'usinage. Dans la plupart des modèles analytiques et numériques, il est supposé être constant sur toute la face de coupe et décrit par une loi le Coulomb.

Les techniques d'usinage n'ont pu se développer que grâce à l'augmentation des performances des matériaux pour outils de coupe, à l'amélioration de la rigidité des machines-outils et à la détermination des conditions de coupe optimales sur la base des paramètres caractéristiques des couples outil-matière mis en oeuvre.

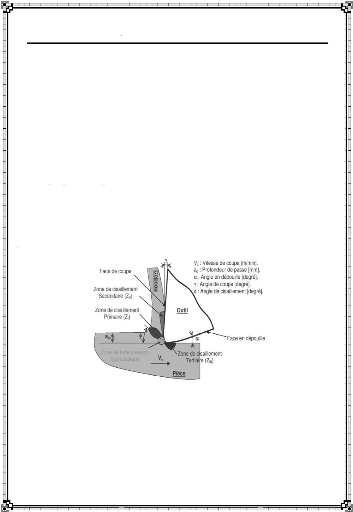
L'opération d'usinage par enlèvement de matière met en présence un outil et la pièce à usiner. La figure I-12 représente le couple outil/matière dans le cas de l'opération de tournage qui est considérée comme référence avec les principaux paramètres de coupe. La productivité dans l'opération d'usinage est liée au taux d'enlèvement de matière défini dans le cas du tournage par:

a

p .f.Vc

(2)

a_p : profondeur de passe (mm) ; f : avance par tour (mm) ; V_c : vitesse de coupe (m/min).

Un outil est constitué d'une partie active et d'un corps qui supporte l'arête de coupe. Son aptitude à l'emploi dépend de sa conception, de la géométrie de la partie F. 1 - Paramètres de coupe en tournage.

a_p : profondeur de passe (mm) ; f : avance par tour (mm) ; Vf : vitesse d'avance (mm/min), soit f × n ; Vc : vitesse de coupe (m/min) active et de la nature du matériau constituant cette partie active.

Figure I-12 : Paramètre de coupe en tournage

Yallese &

al. [18] ont présenté les résultats théoriques et expérimentaux d'une étude qui concerne la mesure des efforts de coupe générés lors de l'usinage de l'acier trempé 100Cr6 à

mise en évidence

roulements avec un outil en nitrure de bore cubique CBN 7020. L'étude a permis la

de l'influence des conditions de coupe (vitesse de coupe, avance et profondeur de passe) sur les composantes de l'effort de coupe. Le traitement des résultats obtenus a permis la détermination des différents modèles qui expriment la relation entre les paramètres d'usinage étudiés et les composantes de l'effort de coupe. L'influence de l'usure en dépouille de la partie active de l'outil sur l'évolution des

l'effort de coupe

efforts de coupe permettant à conduit à la proposition d'une relation puissance entre

et l'usure puisque ces deux paramètres s'influencent mutuellement.

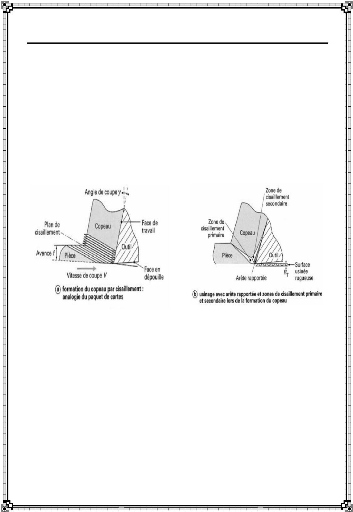
Comme le montre la figure I-

13 [7], la formation du copeau peut être décrite en définissant

e, une zone de forte

différentes zones d'absorption de l'énergie mécanique apportée lors de la coup

pression hydrostatique au niveau de la pointe de l'outil et les trois zones de cisaillement citées précédemment.

Figure I-13 :

Zones de déformation lors de la formation d'un copeau en coupe orthogonale

En plus des paramètres cité précédemment, le phénomène complexe de formation de copeau dépend aussi fortement de :

- La rhéologie du matériau usiné (matériau dur, matériau à usinabilité amélioré, etc.) ; - Les propriétés thermo-physiques du matériau usiné et usinant ;

- La nature et la géométrie de l'outil ;

- La nature du contact outil-copeau ;

- La nature de l'opération effectuée (coupe orthogonale, chariotage, etc.) ;

- Procédé d'usinage utilisé (usinage dur, usinage avec assistance etc.).

I-7-1. Echelle macroscopique

La forme des copeaux varie d'un point de vue macrographique et dépend des conditions d'usinage et du couple outil/matière. La Figure I-14 présente les différentes formes macrographiques de copeaux obtenus en usinage, classées selon la norme ISO DIS 3685.

I-7-2. Echelle microscopique

Plusieurs auteurs Trent (1991), MSaoubi (1998) et Poulachon (1999) ont eu recours à des essais de coupe interrompue pour mieux comprendre les mécanismes de génération de copeaux. Ce type de test permet à la fin de l'essai de conserver la racine du copeau attaché à la pièce, et de donner ainsi des informations sur le mécanisme mis en jeu lors de la génération du copeau.

Les mécanismes de génération de copeaux et les phénomènes thermomécaniques intervenant conduisent, à l'échelle micrographique, à la formation de copeaux de natures et de morphologies très différentes. Les copeaux peuvent être classifiés suivant trois grands groupes : copeau continu, copeau avec arête rapportée, copeau discontinu.

Figure I-14 : Formes macrographiques de copeaux classées selon la norme ISO DIS 3685[5,7]

I-7-2-1. Copeau continu

Généralement, le copeau continu est obtenu pour de faibles

vitesses de coupe et/ou

-

d'avance (MSaoubi 1998). La figure I 15 donne un exemple de copeau continu obtenu par Le Calvez (1995) pendant l'usinage d'un acier. Lors de la génération d'un copeau continu, la valeur de la contrainte de cisaillement que subit la matière à la traversée de la zone primaire n'atteint pas la limite de rupture du métal et ce dernier s'écoule de manière continue le long de l'outil.

Figure I-15 :

Copeau continu (Vc = 100m/min, f = 0,2 mm/tr) Le Calvez (1995)

I-7-2- 2. Copeau avec arête rapportée

Pendant la coupe et pour de faibles vitesses de coupe, une arête rapportée peut se former

lle arête,

par accumulation de la matière à la pointe de l'outil de coupe générant ainsi une nouve qui déplacera le contact outil-copeau (figure I-

17) Trent (1991). Les dimensions de l'arête rapportée, conditionnent la rugosité totale de la surface usinée et sont d'autant plus grandes que les dimensions sont élevées, Felder (1997).

Figure I-16 : Copeau avec arête rapportée [Trent 1991]

I-7-2-3. Copeau discontinu

Dans ce cas, la contrainte de cisaillement dans la zone primaire atteint la limite de

du matériau.

rupture du métal usiné et le copeau se casse sous l'effet de cette rupture finale

Cette morphologie est souvent observée dans l'usinage des aciers inoxydables austénitiques (Figure I- 17a), des aciers durs (Figure I-17b) et des aciers fragiles.

a) cas d'un acier austénitique inoxydable usiné b) cas d'un acier à roulement 100Cr6 à 62HRc

f = 0,1mm/tr)

avec un outil carbure (Vc = 130m/min, usiné avec un outil en céramique renforcé SIC

Figure I-17 : Copeau discontinu

Les différentes morphologies présentées ci-

dessus, représentent les trois grandes familles

de formes de copeaux obtenus en coupe. Il existe le copeau de transition qui est l'intermédiaire

es beaucoup plus

entre un copeau continu et un copeau discontinu et d'autres géométri

-

complexes, à titre d'exemple celle présentée dans la Figure I 18. D'après Changeux (2001), cette géométrie est le résultat des vibrations, observées pour de faibles avances, qui se superposent à la segmentation spontanée des copeaux.

Figure I-1 8 : Copeau d'acier inoxydable de géométrie continue
(Outil cermet, Vc = 300 m/min, f = 0,05 mm/tr)

I- 8. CARACTERISTIQUES DES SURFACES USINEES

L'état de surface d'une pièce usinée inclut d'une part, l'état géométrique de la surface : écarts géométriques d'une pièce réalisée en fabrication par rapport à celle géométriquement idéale et d'autre part, l'état physico-

chimique de la surface : nature de la couche superficielle de la pièce. Les paramètres d'état de surface sont des paramètres importants pour le fabricant. Il doit en connaître la signification pour pouvoir choisir les moyens de fabrication adéquats.

Marin & al. [16] proposent des modèles analytiques et géométriques pour des calculs thermiques et mécaniques et démontrent que la microstructure extérieure obtenue par tournage a un rôle important dans l'évaluation des performances tribologique après processus et comportement en fatigue.

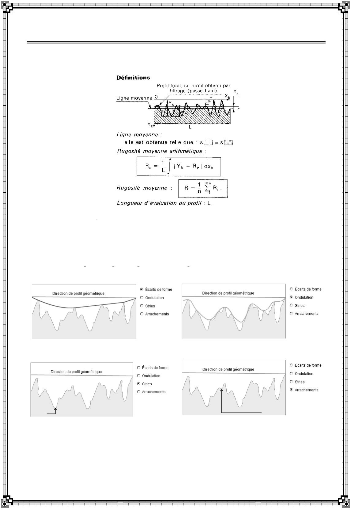
Chapitre I - Généralités sur l'usinage

Figure I-19 : Paramètres de l'état de surface d'un corps solide

Si l'on coupe normalement une surface par un plan, on obtient une courbe appelée profil de la surface. On classe les défauts géométriques en quatre ordres de grandeur :

Figure I-20 : Composition et aspect du corps

37

I-8-1. Rugosité

Parmi l'ensemble des critères d'état de surface, Ra et Rt (exprimés en um) sont souvent utilisés pour caractériser la rugosité des surfaces usinées [6] :

-

Rt : rugosité totale (profondeur ou amplitude maximale de la rugosité),

-

Ra : rugosité arithmétique (écart arithmétique moyen).

Ó + Ó

A ahe B

ahe

R =

a

L

(I-2)

Figure I-21 : Composition et aspect du corps

Figure I-22 : Composition et aspect d'un corps cylindrique

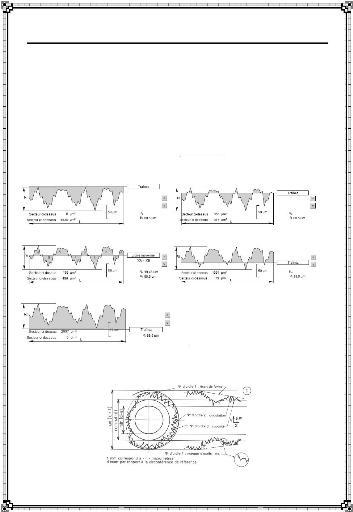
I-8-2. Ligne moyenne

Óahe A = ÓaheB (I-3)

L'état de surface est déterminé par plusieurs facteurs :

- les paramètres de coupe (vitesse de coupe, avance) ;

- la géométrie de l'outil (angle, acuité d'arête, rayon de bec...) ;

- le matériau de l'outil coupant ;

- la rigidité du montage et de la machine, la formation des copeaux, les efforts, etc.

I-9. ENDOMMAGEMENT DES OUTILS

La géométrie des outils de coupe est généralement complexe obtenue de mises au point d'atelier purement empiriques, quelquefois d'études plus analytiques à partir de divers critères (résistance à l'endommagement ou qualité de la surface générée), rarement d'une véritable optimisation qui nécessiterait une modélisation de l'écoulement du ou des copeaux, Leroy [17].

I-9-1. Contacts pièce-outil-copeau

La géométrie des outils quelle que soit la technique d'usinage employée comprend :

1) zone (s) tranchante (s) : que l'on peut décrire comme des dièdres élémentaires (figure I-23) définis par des faces A_a et A_y et une arête d'intersection. La face A_a est appelée face de dépouille et la face A_y face de coupe. La géométrie des zones tranchantes est souvent plus complexe que celle d'un dièdre simple. Notons, enfin, qu'en règle générale l'outil est en contact avec la pièce sur la face de dépouille principale A_a, sur la face de dépouille secondaire A_a et sur la partie arrondie intermédiaire appelée bec ;

2) zones de guidage du copeau : soit pour faciliter son évacuation, soit pour le stocker provisoirement ;

3) zones de résistance mécanique de l'outil : l'angle á (quelques degrés) conditionne le choix du matériau usiné, tandis les critères de résistance déterminé l'angle â entre les faces A_a et A_y et voisin de 90°.

L'angle de coupe défini par :

ã = 90° - á - â

Si ã est positif, on parle de coupe positive ; dans le cas contraire, l'outil a une coupe négative. Un angle de coupe positif assure l'action tranchante la plus efficace. Il est généralement compris entre 0 et 10° pour les matériaux ferreux. On peut travailler avec un angle ã allant jusqu'à 20° si le matériau usiné est mou, collant (aluminium par exemple) et si le matériau usinant résiste bien aux chocs. Le principal avantage d'une géométrie d'outil avec angle de coupe négatif est la robustesse de l'arête.

Figure I-23 : Formation du copeau (a) et usure de l'outil (b) [15]

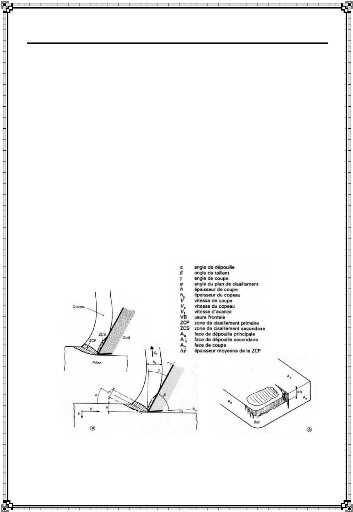
Zemzemi & al. [19] ont conçu un nouveau tribomètre dans le but de simuler le contact aux interfaces pièce-outil-copeau lors d'une opération d'usinage, ce qui a permis de caractériser des frottements dans des conditions très sévères. Leu objectif est de présenter une approche numérique utilisée pour dissocier les grandeurs liées à la déformation de la pièce et celles liées à l'adhésion en vue d'identifier une loi de frottement. Cette démarche est appliquée au cas de l'usinage de l'acier 42CrMo4 traité par un outil de coupe en carbure revêtu TiN. Cette étude a montré que le coefficient de labourage dans le cas de rayage de l'acier 42CrMo4 par une sphère ne dépasse pas le 10% du coefficient apparent. Elle nous a également permis de déterminer les températures moyennes de contact pour chaque condition. Une loi de frottement reliant le coefficient de frottement, la température et la pression de contact a été développée.

I-9-2. Mécanismes d'endommageant des outils de coupe

Il existe une très grande gamme des vitesses de coupe, de la géométrie des copeaux et de leurs conditions d'évacuation, de la rigidité du contact pièce/outil, de la nature et de la géométrie des outils. Dans une telle variété de configurations de coupe, il n'est pas surprenant d'observer une grande variété de faciès de dégradation qui font que les mécanismes d'endommagement soient maintenant bien connus, notamment :

I-9-2-1. Endommagement issu des dépôts

Lors de l'usinage la surface interne du copeau frotte sur l'outil sans corps étranger. La surface de l'outil est systématiquement nettoyée par le copeau. Il peut donc se produire des soudures par friction après écrasement des aspérités des deux antagonistes, à moins qu'un film lubrifiant ne vienne s'interposer. Trois cas peuvent se produire :

1) Effet nul d'endommagement : la plupart des soudures qui se sont constituées n'ont

aucune résistance mécanique ; il en est notamment ainsi si une pollution autogénérée est réalisée. Des matériaux tels que les laitons, les aciers, etc. peuvent être élaborés de telle manière qu'ils contiennent des particules métalliques de métaux à bas point de fusion (plomb, bismuth, etc.) qui jouent le rôle de poisons des soudures de contact ; les sulfures peuvent avoir une efficacité équivalente.

2) Résistance : les soudures constituées résistent plus que les aspérités des deux

antagonistes. La rupture des jonctions conduit à déposer des fragments du matériau le plus doux sur le plus dur. Il y a transfert de l'un sur l'autre. Compte tenu de la nature des corps 1 et 2, c'est pratiquement toujours sur l'outil que se dépose le corps 3, constitué du corps 1 très écroui. Quand la zone de contact C - O est recouverte, des particules du matériau usiné peuvent continuer à se déposer sur lui-même : un dépôt macroscopique se constitue. La géométrie de la zone de coupe évolue (perte d'acuité de l'arête) et un effort plus important doit être appliqué à l'outil pour poursuivre la coupe. Le dépôt atteint une épaisseur et une forme qui dépendent de la rigidité de la liaison outil - pièce et de la résistance au cisaillement du matériau déposé.

La géométrie des dépôts macroscopiques dépend :

· de la dureté, du polyphasage et de l'écrouissabilité à chaud du matériau usiné ;

· de la température dans la ZCS et par conséquent de la vitesse de coupe.

Un régime vibratoire peut être, très souvent, la conséquence des morceaux des dépôts macroscopiques qui sont évacués : l'outil se courbe, puis se relâche, ce qui peut altérer la qualité des surfaces usinées et endommager l'outil soumis à des surcharges importantes.

3) Evacuation de dépôt macroscopique : le dépôt se réalise par arrachement d'une partie de la couche superficielle de l'outil (en particulier une arête rapportée très instable en régime vibratoire).

I-9-2-2. Endommagement induit par les dépôts microscopiques

Dans les conditions d'usinage à vitesses de coupe élevées (et par conséquent températures élevées dans la ZCS), un dépôt du matériau usiné qui se formerait ne serait pas écroui et n'atteindrait pas une taille capable de modifier les efforts de coupe.

Seuls peuvent être obtenus :

1) soit des dépôts (corps 3 d'un frottement sec) du matériau usiné ou d'éléments inclus

dans le matériau usiné, dont l'ordre de grandeur d'épaisseur est celui de la micro géométrie de l'outil ;

2) soit des dépôts un peu plus épais du matériau usiné ou d'éléments inclus dans le

matériau usiné, dont la rhéologie à la température du contact copeau-outil rend possible une lubrification hydrodynamique.

Dans un cas ou dans l'autre de ces deux types de dépôts qui ne font pas croître les efforts de coupe (et par conséquent ne génèrent pas un endommagement mécanique), deux situations peuvent être rencontrées :

· ou bien ces dépôts sont réactifs avec le matériau de l'outil : ils contribuent alors à un endommagement chimique ;

· ou bien ces dépôts ne sont pas réactifs avec le matériau de l'outil et leurs effets endommageants sont assez modestes : étant non durcis, ils ne sont pas abrasifs. Leur évacuation peut toutefois donner lieu à des arrachements de particules de l'outil.

Les phénomènes de réactivité chimique sont très fréquents et multiformes. Chaque couple outil-matière usinée est un cas particulier.

La figure I-24, due à G. Bittes, illustre le rôle de la stabilité des divers corps 3 possibles sur l'endommagement chimique au cours de l'usinage d'aciers de construction mécanique avec des outils en carbure de tungstène.

Si l'on examine après usinage la face de coupe d'outils ayant usiné à des vitesses V de 100 à 200 m/min un acier 42CD4 standard, on observe la présence d'un dépôt de fer sur toute la surface du cratère. Un examen plus approfondi en coupe permet de voir que ce fer porté à haute température diffuse aux joints des carbures et altère la résistance à l'abrasion de l'outil.

Figure I-24 : Composition et aspect du corps 3 déposé sur l'outil [17]

Si l'on usine un acier resulfuré, on observe un double dépôt de fer et de sulfures.

Si l'on usine un acier contenant des sulfures moins fluides à chaud que le sulfure de manganèse, on observe un dépôt de sulfures qui interdit tout dépôt de fer et, par conséquent, empêche un endommagement chimique de l'outil.

Il n'y a pas de réactivité chimique directe entre les outils en céramique et le fer des aciers. Leur usure chimique, mise en évidence par Le Maitre, peut résulter de l'oxydation du dépôt microscopique de fer et de la réactivité de cet oxyde avec la céramique de l'outil.

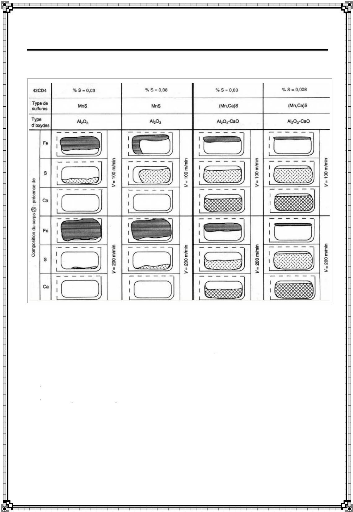
I-9-2-3. Endommagement induit par les débris

L'usure abrasive des outils de coupe (deuxième corps) résulte de l'arrachement de petits morceaux par l'impact sur leur surface de particules ayant une dureté équivalente ou supérieure à la leur. Ces débris peuvent provenir du matériau usiné, de grains de l'outil arrachés par rupture de microsoudures, de morceaux d'arêtes rapportées évacués, de morceaux de l'outil arrachés au moment de l'évacuation de parties de dépôts (phénomène d'attrition, de morceaux de l'outil abrasés par l'impact des autres débris, etc).

I-9-2-4. L'abrasion

L'abrasion donne lieu à de nombreuses études, notamment consacrées à l'usinage par meulage (rectification, affûtage, etc.).

· La nature de l'abrasif est le premier paramètre à prendre en compte. Si l'on se place du côté de l'outil, l'échelle de résistance à l'abrasion est sensiblement celle de sa dureté à chaud, soit dans l'ordre croissant : carbure de tungstène ; cermet ; carbure de titane ; alumine ; nitrure de bore cubique ; diamant. Cette échelle des matériaux de coupe n'est pas nécessairement le critère essentiel pour sélectionner un outil. En général, plus une nuance a une grande dureté, plus sa ténacité est faible et plus le coût de fabrication de l'outil est élevé. La dureté à chaud des phases écrouies du matériau usiné détermine, de manière très symétrique, la vitesse d'usure par abrasion des outils. La nature des débris réfractaires inclus dans le matériau usiné peut parfois être contrôlée.

· La taille des particules abrasives, qu'elles proviennent des outils ou des matériaux usinés, est le deuxième paramètre dont dépend la vitesse d'abrasion : celle-ci est d'autant plus faible que les particules abrasives sont plus petites. Le contrôle de la taille des inclusions dures d'un matériau usiné est souvent très déterminant. Il en est en particulier ainsi dans le cas d'usinage de matériaux moulés alliés riches en éléments carburigènes.

· D'autres paramètres peuvent modifier l'endommagement par abrasion. La possibilité d'enrober des inclusions dures dans le matériau usiné par d'autres particules plus molles est utilisée par des aciéristes dans le cas de la fabrication d'aciers resulfurés : la maîtrise du processus d'élaboration peut permettre d'enrober les oxydes par des sulfures et par conséquent de réduire l'efficacité abrasive des oxydes. La quantité de phases dures est également importante, mais ce paramètre est moins discriminant que leur nature et leur taille. Ainsi, il ne serait pas pertinent d'utiliser la teneur en oxygène d'une coulée d'acier pour juger de son usinabilité en condition d'usure abrasive

47

II-1. INTRODUCTION

La prédiction de l'intensité de la distribution de la chaleur mise en jeu lors d'une opération d'usinage est très difficile à cause de la complexité des phénomènes physiques des effets mécaniques et thermiques extrêmement couplés générant de fortes non linéarités induites du processus. Du point de vue mécanique, cette complexité est relative aux grandes déformations et vitesses de déformation et à la nature des contacts aux interfaces outil-copeau et outil-pièce. À ces effets mécaniques viennent s'ajouter la génération locale de chaleur et le fort gradient de température dus à la conversion d'énergies de déformation plastique et de frottement.

Lors du processus d'usinage il y a création et évacuation d'un copeau faisant intervenir deux mécanismes physiques de base, une déformation plastique au sein du copeau et un contact de ce dernier avec l'outil. La modélisation de la formation du copeau repose essentiellement sur la compréhension de ces deux mécanismes et a pour objet la prévision de la géométrie du copeau, des efforts de coupe et des échauffements de la pièce et de l'outil à partir des conditions de coupe et des propriétés thermomécaniques du matériau usiné et de l'outil. Elle devrait donc apporter une aide à la gestion rationnelle des banques de données sur la coupe et fournir des éléments d'appréciation de divers problèmes pratiques :

- déformation élastique de l'ensemble outil - porte-outil - machine-outil ;

- interprétation des modes d'usure et d'endommagement des outils ;

- qualité de surface de la pièce usinée (rugosité, écrouissage, structure métallurgique, contraintes résiduelles).

Un objectif simple que la modélisation peut être fixé, qui consiste à utiliser un certain nombre de grandeurs relativement faciles à observer, par exemple l'épaisseur du copeau, les efforts de coupe, pour en déduire des quantités plus difficiles d'accès comme les échauffements.

Partant de la présentation des analyses purement mécaniques pour arriver aux approches thermomécaniques décrivant les phénomènes physiques réaliste mis en jeu dans la formation du copeau.

En général, les modélisations d'une opération d'usinage nécessitent d'après Al-

Ahmad [20] dans un premier temps de définir l'échelle à laquelle l'étude est envisagée. Ces modèles traduisent un certain nombre de comportements comme :

- ceux des matériaux usinés (contraintes résiduelles, efforts de coupe...)

- ou usinant (usure) en fonction des phénomènes mécaniques, physico-chimiques en jeux; - de la géométrie voire de la topographie des surfaces usinées ;

- des trajets et stratégies d'usinage (génération de processus d'usinage) ; - le respect des cadences et productivité (durée de vie).

Cependant, les modèles en usinage qui sont prédominants, sont encore aujourd'hui essentiellement issus de l'expérimentation. Néanmoins, la problématique d'industrialisation (procédé et processus), selon Le Calvez (2005) est de prédire le comportement à la fois dimensionnel, géométrique, ainsi que les propriétés mécaniques de la pièce.

II-2. HISTORIQUE DE LA MODELISATION

Laheurte (2004) [20] présente l'état de l'art sur la modélisation de la coupe. Le chronogramme fait par cet auteur est présenté en Figure II-1. Il résume les différents modèles analytiques et numériques et phénoménologiques de la coupe tout en mettant l'accent sur les différentes améliorations apportées par chaque auteur. Le premier modèle réaliste développé le fut par Taylor au début du 20ème siècle.

Chapitre

II - Phénomène thermomécanique de l'usinage

Figure II-1 : Chronogramme sur la modélisation de la coupe

II-3. MODELES MECANIQUES

Les modélisations purement mécaniques sont à l'origine de la

théorie de coupe des métaux où

on néglige les effets thermiques.

Gilormini [21] précise qu'en général le comportement mécanique

lors de l'usinage est supposé plastique sans écrouissage c'est-à-

dire non élastique caractérisé par une

donnée unique qui est la contrainte maximale de cisaillement admissible du matériau.

II-3-1. Modèle de Merchant

Merchant (1945) a été l'auteur de la première modélisation en coupe orthogonale permettant de prévoir les efforts de coupe en considérant que la formation du copeau s'effectue par un simple OA

cisaillement le long d'une ligne droite partant de la pointe de l'outil et inclinée d'un angle ? appelé

-2). La résultante F

angle de cisaillement primaire (figure II des efforts appliqués par l'outil à la pièce

peut se décomp

oser en effort de coupe F_c et effort d'avance F_a

. À noter que l'effort spécifique de coupe, grandeur fondamentale des banques de données d'usinage, est :

F_s = F_c / w.s

(1)

avec w profondeur de passe et s

l'avance.

50

En supposant que les composantes : normale F_n et tangentielle Ft de l'effort - F appliqué à l'outil sont reliées par une loi de Coulomb caractérisée par un angle de frottement ë, l'effort de coupe s'écrit :

F_c = F.cos(ë - ã) (2)

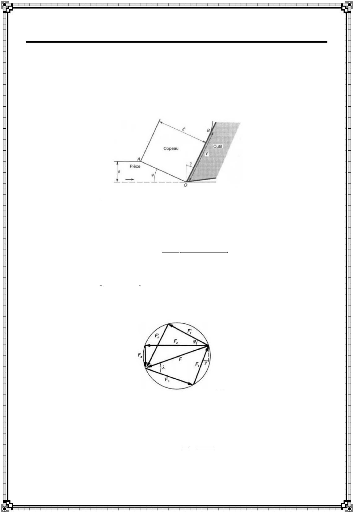
Figure II-2 : Modèle de Merchant : géométrie et notations

l'effort de coupe :

k.s .w cos( )

ë ã
-

F_c = (3)

sin ? cos( ? ë ã

+ - )

L'effort d'avance déduit à partir du diagramme des efforts :

F_a = F_c.tan(ë - ã) (4)

F orts

Le modèle de Merchant suppose que l'angle ? est tel qu'il minimise la puissance fournie au système, ce qui revient à minimiser l'effort de coupe et aboutit finalement à :

ð -

? = - (5)

4 2

ë ã

donc :

ð ë - ã

F_c k.s.w. tan (

= 2 - ) (6)

4 2

L'épaisseur du copeau est liée à l'avance s selon le modèle de Merchant :

l

s. cos( / ( / ))

ð 4 - +

ë ã 2

= (7)

sin( / ( / ))

ð 4 - -

ë ã 2

La longueur de contact Y entre le copeau et l'outil :

s ð ë ã

-

Y = î tan( + ) (8)

cosë 4 2

Si l'interface copeau-outil est le siège d'un frottement de Tresca et non pas de Coulomb, l'angle de frottement de Coulomb ë et le coefficient de frottement m de Tresca sont liés par :

m

=

cos(

sin

ë

2 ë (9)

-

ã

)

II-3-2. Modèle des lignes de glissement

Méthode appliquée au problème de la formation du copeau par plusieurs auteurs dont nous ne citons que le modèle le plus simple, celui de Lee et Shaffer représenté par la figure II-4 a montre l'allure du réseau de lignes de glissement considéré. Composé de segments de droites et déterminé par les deux angles ? et ç et associé à un état de contrainte uniforme et ses trois composantes sont aisément déduites des conditions aux limites du réseau : contrainte de cisaillement égale à k le long de OA (cisaillement primaire) et soit égale à (frottement de Tresca), soit liée à la composante normale par l'angle ë (frottement de Coulomb) le long de OB, et enfin vecteur contrainte nul le long de AB, le copeau étant libre au-delà. Ces trois conditions sont exprimées dans un cercle de Mohr. On établit ainsi la correspondance entre les conditions de frottement de Tresca et de Coulomb menant à des résultats identiques :

m = sin2ë (10)

F_c

1

- ë -

tan(

2 k.s.w (11)

ã

)

l

sin( /

ð

s. cos((ð

4 - -

( ))

ë ã

/ ) )

4 - ë (12)

La longueur de contact Y entre le copeau et l'outil :

s

Y = (13)

2 cos sin(( / )

ë ð - ë + ã

4 )

Les figures II-4 b et c présentent l'allure du réseau de lignes de glissement considéré dans d'autres modèles par lignes de glissement, plus complexes, proposés par Kudo et Dewhurst [21].

Figure II-4 : Réseaux de lignes de glissement [21]

II-4. MODELES THERMOMECANIQUES

Les approches thermomécaniques de la formation du copeau sont apparues plus récemment, car leur complexité exige le recours au calcul par ordinateur. Elles prennent en compte plus de phénomènes physiques mis en jeu dans la coupe que les approches antérieures, comme les échauffements et les grandes vitesses de déformation. Basées sur des observations expérimentales, elles entrent encore dans le cadre de modèles simplifiés, car elles mettent en jeu peu d'inconnues, contrairement à ce que serait une méthode utilisant une discrétisation par éléments finis ou par différences finies, par exemple.

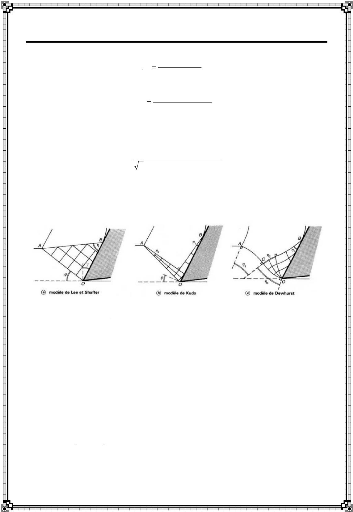
Les composantes d'un modèle thermomécanique de la formation du copeau sont, d'une part, une cinématique simplifiée mais réaliste, dépendant de peu de paramètres et jouant un rôle central et,d'autre part, une analyse thermique approchée associée à cette cinématique et, enfin, un ensemble de données assez étendu pour pouvoir décrire convenablement le comportement thermomécanique du matériau dans les gammes de température, déformation et vitesse de déformation mises en jeu.

II-4-1. Modèle d'Albrecht

Dans son approche, Albrecht (1960) s'est inspiré du modèle de Merchant, sans pour autant prendre en compte un outil de coupe parfaitement aigu. Il considère un outil avec un rayon de courbure au niveau du raccordement entre sa face de dépouille et sa face de coupe (Figure 17). Ce rayon pourrait provenir soit de la géométrie, soit de l'usure de l'outil. Dans ce dernier cas, Il distingue alors deux zones différentes suivant le contact outil/matériau. Une zone (AB) à laquelle il associe une résultante des efforts Q, située au milieu de l'arc (AB), et une deuxième zone (BC) composée de deux portions (BE) et (EC) avec une résultante des efforts P, située, elle aussi, au milieu de l'arc (BC), en supposant que la répartition des efforts le long de cet arc est uniforme. Chacune de ces zones a son propre coefficient de frottement, les différences étant accentuées s'il y a un copeau adhérant au cours de la coupe.

A travers cette présentation, il est possible de calculer séparément P en faisant varier l'avance et le rayon d'acuité et Q en variant l'avance et l'angle de coupe. Grâce à cette présentation des efforts, Albrecht (1960) prouve que la composante de l'effort P n'est pas négligeable comme dans la modélisation de Merchant (1945 a et b).

Figure -II-5 : Efforts de coupe selon Albrecht

II-4-2. Modèle de Boothroyd

Durant les années 50, Lee et Schaffer (1951) basent leur modélisation sur la théorie des lignes de glissements tout en gardant un comportement du matériau parfaitement plastique. Quelques années plus tard, Boothroyd (1963) a mis en place le premier modèle thermomécanique permettant d'évaluer la forme de la source de chaleur dans le copeau et ce dans le cas de la coupe orthogonale. Dans son modèle, Boothroyd considère que toute la puissance mécanique nécessaire au cisaillement est transformée en puissance calorifique et est dissipée par la coupe. Ainsi, il met en évidence la présence de deux sources planes de chaleur uniformes, une au niveau de la zone de cisaillement primaire et la deuxième au niveau de la zone de cisaillement secondaire.

II-4-3. Modèle d'Oxley

Oxley (1989) modélise la formation du copeau en utilisant un modèle thermomécanique. L'auteur prend en compte la vitesse de déformation et la température générée par la coupe. Dans le modèle de Merchant (1945b), le cisaillement se fait suivant un plan et il est calculé d'une façon géométrique. Par contre, dans l'approche d'Oxley, le cisaillement primaire se fait dans un volume et dépend de la géométrie d'écoulement du copeau. De plus, cette approche prend en compte la présence d'une zone de cisaillement secondaire générée par le frottement outil-copeau. En tenant compte du comportement du matériau et de l'équilibre des moments, l'angle de cisaillement 0 s'exprime alors par l'équation I-5.

ð

tan( ö ë ã

+ - = +

) 1 2 - ö - nC (14)

4

n : indice d'écrouissage de la loi de comportement n

ó = ó ₀ .å ; C : constante empirique issue de l'expression de la vitesse de déformation dans le plan de cisaillement primaire ; dã / dt = C.V e / l ("Ve" est la vitesse d'écoulement du copeau par rapport à la pièce et "l" est la longueur du plan de cisaillement primaire).

Les expressions des efforts de coupe F_c et d'avance F_a sont ainsi exprimées par les éqs. 16 et 17.

F_c

3 . sin . cos(

ö ë - ã +ö

t₁ .w. ó.

(15)

cos( ë-ã)

)

F_a

3.sin ö .cos(ë- ã +ö

t₁ .w.6.

(16)

sin ( ë-ã)

)

w : largeur de coupe ; t1 : profondeur de passe ; ó : contrainte de cisaillement.

Pour la longueur de contact outil-copeau (h) il fait intervenir des paramètres (C et n) liés au comportement du matériau et il l'exprime par l'équation 8.

cos

2
·

sinö

h = 1. [1+ 2( j- 2 1

nC

1 (17)

tcos(ö +ë-ã)

4 3

En plus, ce modèle a permis de déterminer la température moyenne dans le plan de cisaillement primaire (T1) et la température à l'interface outil-copeau (T2) dont les formules correspondantes sont données par les équations 18 et 19.

T T

= + .

1 w

t ₁ cos(ö-ã

ñ_p.C _p .w.

( 1 -â) F .cosã

s

(18)

)

T₂ = T₁ +ø .ÄT_M (19)

T_w : température initiale dans le modèle ; â : proportion de chaleur transmise à la pièce ; ø : coefficient permettant à la température interne d'être une valeur moyenne ; ÄTM : variation maximale de la température dans le copeau.

Figure II-6 : Zones de cisaillements

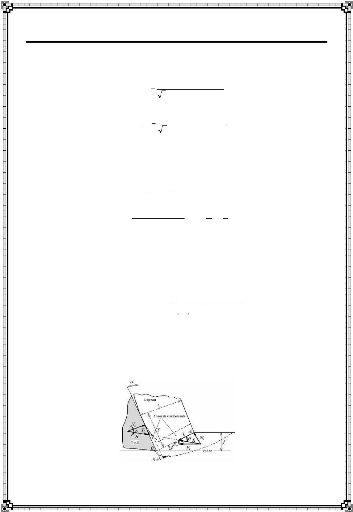
II-4-4. Modèle de Giormini et al.

Dans son étude, Gilormini (1982) [4] modélise la zone commune entre le cisaillement primaire et secondaire. Grâce à un profil des vitesses original, il calcule la puissance dissipée sur le segment AOB et montre que l'influence de la zone commune (OB, Figure II-) est négligeable (inférieure à 2%) si l'épaisseur du cisaillement secondaire est faible devant celle du copeau. Il calcule la contrainte d'écoulement plastique pour le cisaillement primaire en tenant compte de la température. Le champ des températures en amont de la zone de cisaillement primaire et dans le copeau est déterminé à partir de résultats théoriques sur la quantité de chaleur passant de chaque coté d'une source plane en déplacement. Dans ce modèle, la température est implicitement fonction d'elle-même puisque dans le cas d'un couplage, la contrainte d'écoulement est aussi fonction de la température.

Figure II-7 : Modélisation de Gilormini et al. des zones de cisaillement

II-4-5. Autres modèles de coupe

Différentes modélisations et méthodes de mesure ont été développées pour caractériser les transferts thermiques dans la zone de coupe Hahn (1951), Trigger et al. (1951), Loewen et al. (1954), Chao et al. (1995), Molinari et al. (1992) et Dudzinski et Molinari (1997) ont modélisé le processus de formation du copeau continu en coupe orthogonale en régime stationnaire. Le cisaillement stationnaire est décrit par une loi thermo-visco-plastique. Ce modèle focalise l'étude sur l'écoulement dans la zone de cisaillement primaire supposée être une bande avec une épaisseur constante et uniforme. Il prédit une diminution de la largeur de contact outil-copeau et de l'effort de coupe avec une élévation de la vitesse de coupe. Ce modèle a été généralisé au cas de la coupe oblique (la direction d'écoulement du copeau déterminée pour un couple outil-matière donnée) en utilisant une loi dépendante de la

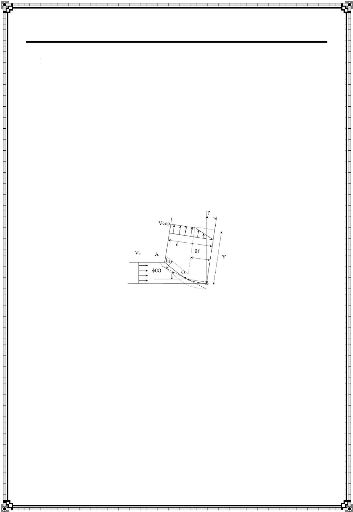
température pour définir le frottement généré par le contact outil-copeau Moufki (1998,2000), (Komanduri et al. (2001) [24,25,26], Puigsegur (2002) et Karpat et al. (2006).

Tous les modèles analytiques présentés ci-dessus ne sont valables que pour des copeaux continus. Il existe d'autres modèles analytiques et numériques permettant de modéliser la coupe orthogonale. En coupe, l'identification des lois est très difficile car elle doit être représentative du comportement du matériau, en grande déformation et en grande vitesse de déformation avec des températures élevées. Pour résoudre ce problème une méthode plus ou moins souple est mise en place par Changeux (2001). Ce dernier identifie la loi Johnson-Cook dans des conditions proches de celle de la coupe par des essais de cisaillements dynamiques réalisés sur un banc de Hopkinson avec des éprouvettes de géométrie particulière permettant de développer une zone de cisaillement.

å ~ T T

- seuil

ó = +

[ ]

A B . 1 C. ln ₀ . 1

å n eq

+ -

eq ^eq å ~ T T

f seuil

-

eq

m

(20)

óeq : contrainte d'écoulement [MPa] ; åeq : déformation plastique généralisée ; ^ÿåeq : vitesse de déformation généralisée [s^-1] ; ^ÿå⁰eq : vitesse de déformation plastique équivalente de référence [s^-1] souvent fixée à 1 ; T : température de référence [K] ; T : température de fusion du matériau [K] ; T : température du matériau [K] ; A limite d'élasticité statique [MPa] ; B : facteur d'écrouissage statique [MPa] ; n : coefficient d'écrouissage statique ; m : coefficient de sensibilité à la température ; C : sensibilité à la vitesse de déformation plastique.

Cette loi a fait l'objet de plusieurs études. Des modifications peuvent être apportées. Joyot (1993) supprime l'influence de la température. Il considère que la déformation engendrée lors du passage de la matière dans la zone de cisaillement primaire s'effectue en un temps très court et ceci ne permet pas à la matière de subir les effets de l'élévation de la température consécutive dans ce cas. Dans son étude, après avoir montré que la dureté a un effet non négligeable sur le comportement du matériau, Umbrello (2004) apporte des modifications à cette loi en ajoutant un autre terme qui fait intervenir la dureté du matériau étudié.

Il existe bien d'autres modèles telles que celui de Toulouse Laheurte et al. Et bien d'autres.

II- 5. ANALYSE THERMIQUE DU PROBLEME DE COUPE

Il est supposé durant le processus d'usinage qu'une grande partie de la puissance mécanique développée

se transforme en effet thermique. Les zones de cisaillement (primaire, secondaire, et tertiaire) générées par la coupe sont le lieu de production de chaleur. Les flux de chaleur produit dans ces zones sources sont dissipés, d'une façon non équivalente, dans la pièce, l'outil de coupe, le copeau,

-8).

et une infime partie est évacuée à l'air (figure II

Figure II-8 : Distribution des flux de chaleur générés par en coupe orthogonale [7]

Pendant le processus de coupe, des phénomènes thermiques induits

doivent être définis pour la compréhension du phénomène de coupe et pour améliorer l'usinabilité de certains matériaux. Les effets thermiques influent systématiquement sur le produit final (contraintes résiduelles, états de surfaces, tolérances géométrique

s ...). En l'occurrence, il est indispensable de présenter l'importance d'une analyse thermique du processus ainsi que les différents modèles thermomécaniques

- mécanique

précédemment établis pour expliquer le problème de l'influence du couplage thermique sur le processus.

L'analyse de température dans la zone de coupe est très complexe et difficile puisque les échauffements sont très liés à la durée de vie des outils, la nature du contact entre les premières analyses thermiques de la formation du copeau sontapparues dès que l'on a disposé de modèles mécaniques permettant d'estimer efforts et vitesses. Nous ne ferons ici que rappeler les faits observés et esquisser les raisonnements menant aux analyses thermiques simplifiées du processus, avec pour objectif l

'évaluation des températures dans les zones de déformation (afin d'y estimer l'adoucissement

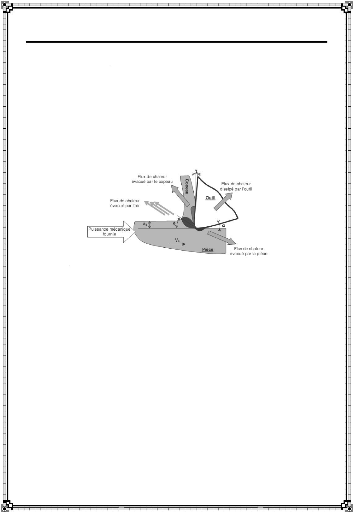
de la contrainte d'écoulement plastique) et à la surface de l'outil (en liaison avec l'usure de celui-ci). Les méthodes expérimentales qui ont été mises en oeuvre pour obtenir la température moyenne à l'interface copeau-outil, son profil le long de cette interface, voire sa distribution au sein du copeau, sont diverses : effet de couple thermoélectrique direct entre l'outil et le copeau, insertion de couples dans le porte-outil et extrapolation au niveau de l'interface copeau-outil à l'aide d'une méthode numérique, insertion de petits couples ou de pyromètres optiques directement dans l'outil, observation de transformations structurales dans l'outil, photographie en infrarouge. Ces mesures ont montré les très forts échauffements atteints au niveau du contact, qui vont croissant avec la vitesse de coupe et avec l'avance. Lorsqu'elles ont pu déterminer le profil de température à la surface de l'outil, les mesures ont de plus montré que le maximum ne se situait pas à la pointe de l'outil, mais plus en aval dans la zone de contact copeau-outil.

II-6. MESURE DE LA TEMPERATURE DE COUPE

II-6-1. Mesures indirectes de température

En 1971, Rosseto et al. [7] ont mesuré la température de coupe à l'aide d'un vernis thermosensible. Ce dernier est déposé sur l'outil et change de couleur à partir d'une valeur de température bien définie. La frontière entre deux couleurs présente l'isotherme. Lo Casto (1989) a utilisé une méthode inspirée de celle mise en place par Rosseto et al. qui consiste à introduire une poudre, dont on connaît le point de fusion, entre deux parties d'une plaquette. Lorsque la température de fusion de la poudre est atteinte, l'essai est arrêté. Les points où la poudre a atteint son point de fusion matérialisent l'isotherme.

Dans le cas des aciers rapides, la cartographie de la température de l'outil peut être décrite par la mesure des microduretés dans le matériau. Après une calibration préalable duretés/températures, cette méthode propose de remonter à la distribution de la température dans l'outil par les mesures de microduretés à la fin des essais Wright (1978). Dans la même logique que cette dernière, Trent (1981) propose de relier l'apparition de phases caractéristiques en fonction de la température sur le copeau et l'outil.

II-6-2. Mesures directes

II-6-2-1. Mesures par un thermocouple

La mesure de la température peut se faire par un thermocouple se base sur le principe suivant : si deux métaux sont soudés à leurs extrémités et si une de ces soudures est portée à une température bien déterminée, l'autre étant maintenue à une température différente, on observera alors une force électromotrice entre les deux jonctions. L'évaluation de cette force, qui dépend des matériaux utilisés, symbolise la température mesurée. L'avantage des thermocouples est la simplicité et la flexibilité de réalisation et d'utilisation pour de simple acquisition et ce à moindre coût. Il existe plusieurs types de thermocouples, les plus répandus sont les thermocouples standard et dynamique.

Les thermocouples dynamiques sont généralement utilisés en tribologie. Les thermocouples incorporés (standards) les plus utilisés pour l'évaluation de la température. Leur utilisation en usinage, nécessite des perçages de trous dans lesquels les thermocouples sont insérés. Pour estimer la température dans la zone de coupe et d'établir la cartographie thermique dans l'outil.

II-6-2-2. Mesures par la méthode optique

L'utilisation thermocouples est une technique très couteuse en plus elle ne permet pas d'effectuer des mesures de la température à l'interface outil-copeau en plus du problème d'usure de l'usure de l'outil. Il est donc nécessaire d'utiliser d'autres systèmes de mesure de température directes qui permettent une acquisition locale et au cours du temps au niveau de la zone de coupe (outil/pièce/copeau), voir même au niveau des zones de cisaillement ZI, ZII, ZIII). Les seules méthodes permettant de faire des relevés de températures de la zone de coupe sur lesquelles l'évolution du contact pièce-outil-copeau n'influe pas, sont celles basées sur l'émission d'onde électromagnétique d'un corps lorsqu' il est chauffé. Les techniques les plus répandues sont le pyromètre optique, la caméra infrarouge et la caméra proche infrarouge.

Le pyromètre est une technique basée sur l'émission d'onde électromagnétique, son principe consiste à comparer deux énergies (dans la même bande de longueur d'onde): celle émise par le corps chauffé à celle émise par une source étalon. Il existe plusieurs types de pyromètres tels que les pyromètres mono et bi chromatique.

II-7. NOUVELLES APPROCHES DANS LA COUPE DES METAUX

Astakhov & al. [30] ont réalisé une étude se basant sur une nouvelle approche qui a permis la réévaluation des mécanismes fondamentaux de la coupe orthogonale des métaux reposant sur le diagramme de vitesses, l'équation du travail virtuel et le théorème de la limite supérieure. Bien que les relations de vitesse connues dans la coupe orthogonale constituent le coeur même de la théorie de coupe des métaux, elles sont en contradictions évidentes avec les résultats des simples observations et des principes de déformation. Ceci peut être l'une des causes principales de l'irrégularité grave entre les résultats théoriques et expérimentaux.

L'approche système pour l'étude de la coupe des métaux proposée auparavant a été étendue pour étudier les rapports de vitesse dans la coupe orthogonale des métaux. Le processus de formation de copeau est considéré comme ayant une nature cyclique. Chaque cycle se compose de trois étapes distinctes (figure II-9).

Figure II-9 : Modèle plan à cisaillement simple (a)
et trois diagrammes de vitesse connus (b, c et d)

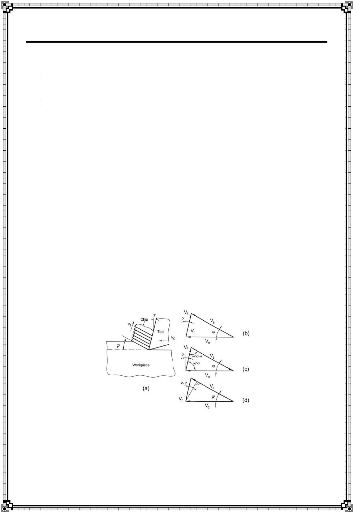
Il est argumenté que les rapports de vitesse, exprimés d'habitude sous forme de diagramme de vitesse, semblent raisonnables seulement aux deuxièmes et troisième étapes. De nouveaux diagrammes de vitesse sont proposés pour ces étapes (figure II-10). De nouveaux diagrammes de vitesse sont proposés pour ces étapes.

Figure II-10 : Trois étapes distinctes dans un cycle de formation de copeau

Il est démontré que la discontinuité de la vitesse tangentielle a lieu dans la zone de déformation et il est expliqué pourquoi le tau de contrainte n'est pas infini même avec un plan de glissement simple. En soi, cette zone peut être considérée comme divisé en deux régions. La première partie peut s'appeler la région large, où la déformation en plastique a lieu à un à bas taux. La seconde est la région étroite, où cette déformation a lieu à un tau élevé.

Figure II-11 : Modèle pour la coupe orthogonale :

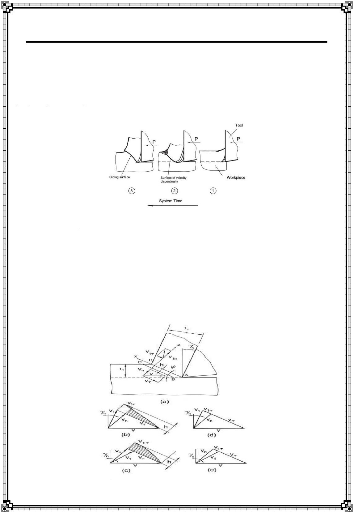
(a) modèle de la zone de cisaillement avec des frontières parallèles;

(b) diagramme de vitesse à la seconde étape quand l'angle de coupe de l'outil est positif;

(c) diagramme de vitesse à la seconde étape quand l'angle de coupe de l'outil est négatif;

(d) diagramme de vitesse à la troisième étape quand l'angle de coupe de l'outil est positif;

(e) diagramme de vitesse à la troisième étape quand l'angle de coupe d'outil est négatif.

Puisque le procédé de formation de copeau est considéré comme cyclique, la fréquence de formation de copeau a été étudiée et avérée dépendant de la vitesse de coupe et du matériau de pièce. Il est montré expérimentalement que quand les expériences sont entreprises correctement, c.-à-d., quand le bruit dû à de diverses inexactitudes dans le système d'usinage est éliminé de la réponse du système et ainsi du signal de mesure, et quand ce signal alors est correctement traité, l'amplitude de la crête à la fréquence de la formation de copeau est la plus grande dans les auto spectres correspondants (figure II-11).

Utilisant les résultats obtenus, Astakhov & al. présentent de nouvelles expressions du théorème pour le cycle entier de formation de copeau et pour l'équation de travail virtuel.

65

III-1. INTRODUCTION

Le but des essais est d'effectuer un diagnostic thermique a laser lors d une opération de chariotage dans le but de déterminer la densité du flux thermique pour un matériau dans des conditions de coupe données. A cet effet, nous avons utilisé trois matériaux différents, l'acier doux, le bronze et l'aluminium, avec deux procédés d'usinage conventionnels, le tournage et le fraisage. Pour le tournage on a procédé à de simples opérations de chariotage avec un outil conventionnel et pour le fraisage on a utilisé une fraise ordinaire.

III-2. MATERIEL UTILISE

Le Matériel utilisé durant ces essais est composé de :

- un pied à coulisse,

- une règle métallique,

- un chronomètre,

- machines à usiner (un tour conventionnel et une fraiseuse),

- outillage de fixation, démontage et contrôle,

- un appareil de mesure de la température au laser présenté par les images des figures III-1, III-2 et III-3 permettant d'avoir les différentes vues de l'appareil.

Figure III-1 : Vue de face de l'appareil

67

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

Figure III-2 : Vue de profil de l'appareil

Figure III-3 : Vue d'arrière de l'appareil

Figure III-4 : Caractéristiques de l'appareil

III-3. CARACTERISTIQUES DE L'APPAREIL DE MESURE

Cet appareil est un outil idéal pour diagnostiquer, inspecter et vérifier n'importe quelle température, avec l'avantage de mesurer sans contact. Il est ainsi possible de mesurer en toute sécurité et sans risque de contamination, les températures de surfaces d'objets brûlants, dangereux ou difficiles d'accès.

C'est un thermomètre portable à infrarouge avec visée laser. Seul, il permet de mesurer des objets aussi petits que 1 mm et de traiter les applications de maintenance les plus diverses sur des distances évaluées en mètres. Il permet donc une prise de mesure facile et précise de petites cibles éloignées. Son étendue de mesure -35 à 900 °C, il permet une utilisation aussi bien dans les contrôles et les mises au point de procédés qu'en recherche ou en analyse de pannes de composants. Le concept authentifié de la visée laser permet une définition très exacte de la taille du spot mesuré. Les performances et les qualités de l'ensemble système optique / visée laser apportent le confort et surtout la certitude à l'utilisateur.

Laser Class II : standard focus - Laser crosshair breveté (taille du crosshair = taille du spot IR quelque soit la distance) close focus: Double pointage laser convergent (à la convergence = le spot IR à distance focale, soit 1 mm à 62 mm).

Les avantages de l'appareil sont :

- 1 seul appareil, 2 types de mesures : Spot de 13 à 200 mm, éloignées rapport optique 75/1 - Visée laser crossX pour définition exacte du spot mesuré

- Entrée thermocouple

- Interface USB et logiciel graphique / 20 acquisitions par seconde

- Afficheur à basculement automatique en fonction de la position

- Précision du système : #177; 0,75 % de la lecture ou #177; 0,75 °C

III-4. PROTOCOLE D'ESSAIS

Après avoir pris toutes les mesures (longueur, diamètre ou épaisseur, température) de l'échantillon préparé pour l'opération d'usinage on le fixe sur le mandrin du tour qui est préalablement réglé à une fréquence de rotation et une vitesse d'avance (profondeur de passe) données, ensuite on remet le chrono à zéro et on démarre la machine et on commence l'opération de chariotage en même temps en déclanchant le chronomètre.

On laisse l'opération s'effectuer jusqu'à la longueur prévue et on arrête le comptage du temps simultanément avec l'arrêt de l'opération. En ce moment là, on mesure la température qui correspond à un temps et une longueur d'usinage.

Tous de suite après, on remet la machine en marche et on reprend la même opération (sans remettre le compteur du chrono à zéro) jusqu'à ce qu'on termine la longueur de la pièce.

Et pour remplir les trois autres tableaux on prend la même pièce après refroidissement et on enregistre son nouveau diamètre (ou épaisseur) puis on change la vitesse de la machine.

Remarque : Le même travail est effectué pour chaque matière. III-5. ESSAIS SUR L'ACIER DOUX

Des essais ont été effectués au laboratoire de mécanique industrielle (LMI) au département de génie mécanique de la faculté des sciences de l'ingénieur de l'université Badji Mokhtar Annaba, en date du 25 janvier 2009 à 10 heure.

Le matériau utilisé lors d'une opération de chariotage est l'acier doux (S235),constituant la pièce de travail de caractéristiques géométriques : L = 165 mm ; Ø = 34 mm , la vitesse d'avance choisie est 0,6 mm/s et la profondeur de passe est de 2 mm. La température de l'environnement de travail est à T = 13 °C.

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

En effectuant plusieurs essais on a pu obtenir les résultats suivants :

X [mm]	0	5	15	25	35	45	55	65	75	85	95
Temps [s]	0	20	40	60	80	100	120	140	160	180	200
Température [°C]	16	19	19.2	19.8	20	21	21.4	21.6	22	22.8	22.6

Tableau III-1 : Acier doux, n = 400 tr/min ; Ø = 34 mm

X [mm]	0	5	15	25	35	45	55	65	75	85	95
Temps [s]	0	10	20	30	40	50	60	70	80	90	100
Température [°C]	17,0	19,6	19,8	20,4	20,6	21,6	21,4	22,0	22,4	22,8	22,6

Tableau III-2 : Acier doux, n = 800 tr/min ; Ø = 32 mm

X [mm]	0	5	15	25	35	45	55	65	75	85	95
Temps [s]	0	7	14	21	28	35	42	49	56	63	70
Température [°C]	17,0	20,0	20,8	21,4	21,6	22,0	22,4	22,6	22,8	23,0	22,8

Tableau III-3 : Acier doux, n = 1260 tr/min ; Ø = 30 mm

X [mm]	0	5	15	25	35	45	55	65	75	85	95
Temps [s]	0	4	8	12	16	20	24	28	32	36	40
Température [°C]	17,0	20.4	21.6	22.8	24,0	25.6	26.2	27.4	28.2	29.4	30,0

Tableau III-4 : Acier doux, n = 2000 tr/min ; Ø = 28 mm

70

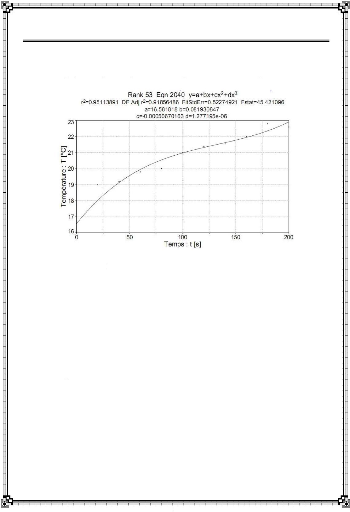
Après les relevés expérimentaux on traçe le graphe de la variation de la température en fonction du temps pour chaque essai par le biais du logiciel TableCurve2D, ce permettra d'obtenir :

Figure III-5 : Acier doux : n= 400tr/min et ö=34 mm

Comme c'est indiqué sur la figure la distribution de la température (T) est une fonction du temps (t) exprimés par une fonction polynomiale d'ordre 3 de la forme :

T = a + b.t + c.t² + d.t³ (1)

En utilisant les coefficient de l'interpollation obtenue par le logiciel TableCurve2D on obtien la fonction de température suivante :

TAcier(34,400) = 16,582 + 0,082.t - 5,067.10^-4.t² + 1,277.10^-6.t³

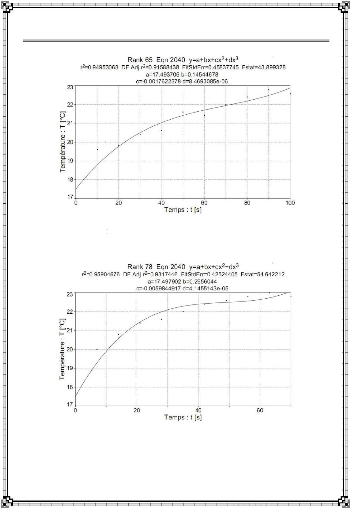
72

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

Figure III-6 : Acier doux, n= 800tr/min et ö=32 mm

Figure III-7 : Acier doux, n= 1260tr/min et ö=30 mm

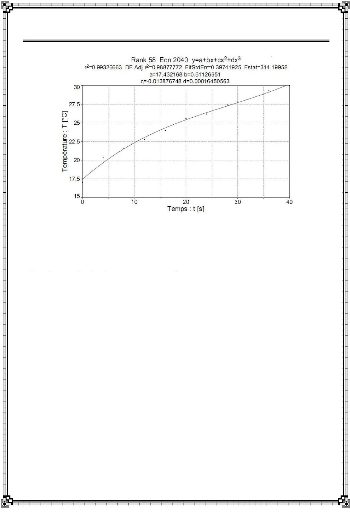
Figure III-8 : Acier doux, n= 2000tr/min et ö=28 mm

De la même manière, on peut déterminer la température comme fonction polynomiale interpolée pour chaque groupe de conditions de coupe :

TAcier(32,800) = 17,494 + 0,146.t - 1,762.10^-3.t² + 8,470.10^-6.t³
TAcier(30,1260) = 17,498 + 0,296.t - 5,985.10^-3.t² + 4,146.10^-5.t³
TAcier(28,2000) = 17,432 + 0,611.t - 1,388.10^-2.t² + 1,645.10^-4.t³

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

III-6. ESSAIS SUR LE BRONZE

Cette série a été aussi effectuée au laboratoire LMI précédemment cité, à la même date.

Diagnostique thermique au laser lors d'une opération de chariotage pour un matériau en bronze (95Cu5Al) de caractéristiques géométriques : L = 95 mm ; Ø = 42 mm ; à une vitesse d'avance 0,6 mm/s, une profondeur de passe 2 mm et température extérieure T= 13 °C.

Plusieurs essais ont permis d'établir les tableaux suivants pour différents paramètres indiqués

X [mm]	0	5	15	25	35	45	55	65	75
Temps [s]	0	20	40	60	80	100	120	140	160
Température [°C]	17,0	20,8	23,4	23,6	25,0	25,4	26,0	26,6	27,2

Tableau III-5 : Bronze, n = 400 tr/min ; Ø = 42 mm

X [mm]	0	5	15	25	35	45	55	65	75
Temps [s]	0	10	20	30	40	50	60	70	80
Température [°C]	17,2	22,4	23,8	24,4	25,2	26,4	27,8	28,8	29,4

Tableau III-6 : Bronze, n = 800 tr/min ; Ø = 40 mm

X [mm]	0	5	15	25	35	45	55	65	75
Temps [s]	0	7	14	21	28	35	42	49	56
Température [°C]	17,6	23,0	25,4	25,8	28,0	28,4	29,0	30,0	30,2

Tableau III-7 : Bronze, n = 1260 tr/min ; Ø = 38 mm

74

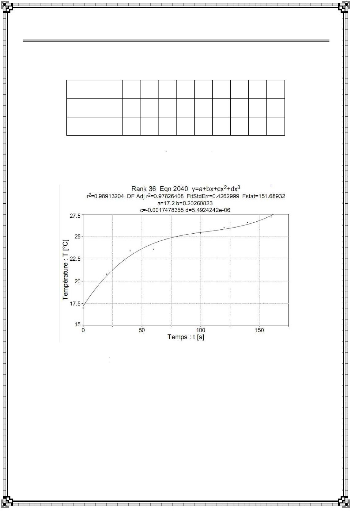
X [mm]	0	5	15	25	35	45	55	65	75
Temps [s]	0	4	8	12	16	20	24	28	32
Température [°C]	17,8	23,4	25,8	26,4	28,8	29,6	30,2	31,0	31,6

Tableau III-8 : Bronze, n = 2000 tr/min ; Ø = 36 mm

Figure III-9 : Bronze, n = 400 tr/min et ö = 42 mm

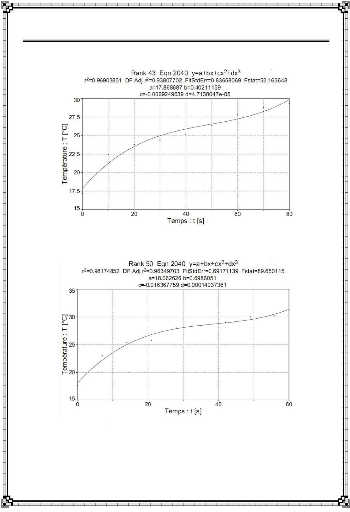
76

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

Figure III-10 : Bronze, n = 800 tr/min et ö = 40 mm

Figure III-11 : Bronze, n = 1260 tr/min et ö = 38 mm

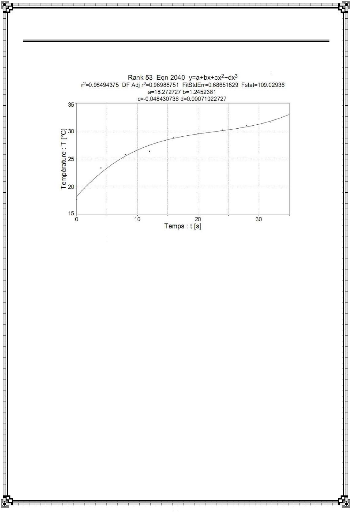
Figure III-12 : Bronze, n = 2000 tr/min et ö = 36 mm

Comme pour l'acier, on déterminer la fonction polynomiale interpolée de la température pour chaque groupe de conditions de coupe :

TBronze(42,400) = 17,2 + 0,203.t - 1,748.10^-3.t² + 5,492.10^-6.t³ TBronze(40,800) = 17,869 + 0,402.t - 6,925.10^-3.t² + 4,714.10^-5.t³ TBronze(38,1260) = 18,063 + 0,697.t - 1,637.10^-2.t² + 1,404.10^-4.t³ TBronze(36,2000) = 18,273 + 1,245.t - 4,843.10^-2.t² + 7,102.10^-4.t³

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

III-7. ESSAIS SUR L'ALUMINIUM

Dans ce cas les essais a été réalisée dans l'atelier de technologie de l'Université 20 Août 1955 de Skikda, en date du 9 février 2009.

Le diagnostique thermique au laser lors d une opération de fraisage utilisant l'aluminium (96Al4Cu) de caractéristiques géométriques : longueur L = 175 mm ; épaisseur e = 60 mm, de vitesse d'avance 160 mm/s et une profondeur de passe 2 mm. La température environnante est T = 14 °C.

X [mm]	0	10	20	30	40	50	60	70	80	90	100
Temps [s]	0	3	6	9	12	15	18	21	24	27	30
Température [°C]	17,0	45,6	56,0	56,8	58,2	59,2	59,0	58,6	59,2	59,0	58,8

Tableau III-9 : Aluminium, n = 500 tr/min ; e = 60 mm

X [mm]	0	10	20	30	40	50	60	70	80	90	100
Temps [s]	0	3	6	9	12	15	18	21	24	27	30
Température [°C]	18,0	56,2	64,4	66,0	67,8	69,2	69,8	69,8	70,2	70,0	70,2

Tableau III-10 : Aluminium, n = 1000 tr/min ; e = 58 mm

X [mm]	0	10	20	30	40	50	60	70	80	90	100
Temps [s]	0	3	6	9	12	15	18	21	24	27	30
Température [°C]	18,0	57,0	65,4	69,8	71,6	71,8	72,2	72,0	72,4	72,2	72,2

Tableau III-11 : Aluminium, n = 1400 tr/min ; e = 56 mm

78

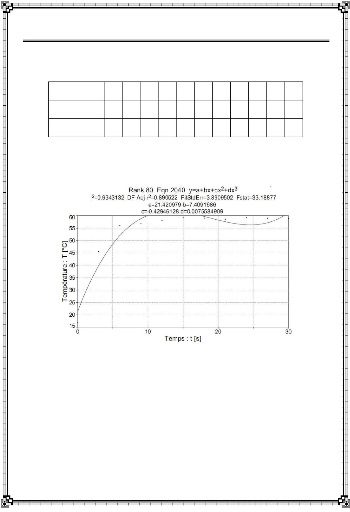
X [mm]	0	10	20	30	40	50	60	70	80	90	100
Temps [s]	0	3	6	9	12	15	18	21	24	27	30
Température [°C]	18,0	58,2	67,6	70,2	71,2	72,6	73,4	73,8	74,0	74,4	74,8

Tableau III-12 : Aluminium, n = 2000 tr/min ; e = 54 mm

Figure III-13 : Aluminium, n= 500 tr/min et e=60 mm

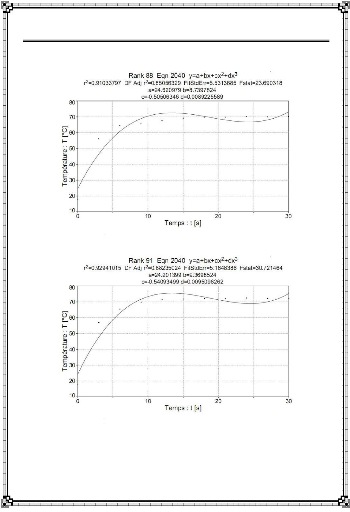
80

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

Figure III-14 : Aluminium, n= 1000 tr/min et e=58 mm

Figure III-15 : Aluminium, n= 1500 tr/min et e=56 mm

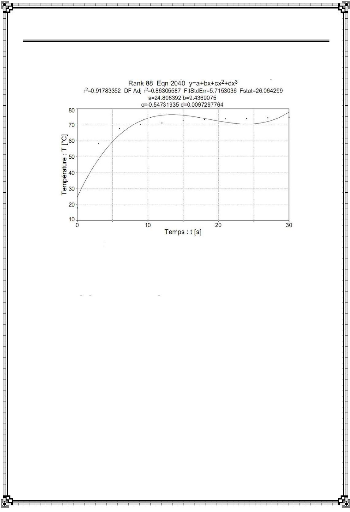
Figure III-16 : Aluminium, n= 2000 tr/min et e=54 mm

Pour le fraisage, les fonctions polynomiales interpolées de la température dans chaque groupe de conditions de coupe peuvent être obtenues par :

TAluminium(60,500) = 21,421 + 7,409.t - 0,43.t² + 7,56.10^-3.t³ TAluminium(58,1000) = 24,621 + 8,74.t - 0,505.t² + 8,923.10^-3.t³ TAluminium(56,1500) = 24,201 + 9,37.t - 0,541.t² + 9,51.10^-3.t³ TAluminium(54,2000) = 24,808 + 9,437.t - 0,547.t² + 9,73.10^-3.t³

III-8. DETERMINATION DE LA DENSITE DE FLUX DE CHALEUR

On se propose de déduire l'expression de la densité de flux de chaleur q(t) sur la surface de l'espace, conducteur de chaleur, semi infini. La température de surface, au cours du temps, mesurée sur cet espace (data) peut être estimée approximativement par un polynôme de degré m [35]. Supposons l'évolution de la température de surface f(ti), i = 1,2, ..., N rapportée au polynôme

y( t) A A t A t A t , m N

m

= + + + + = - 1 (2)

0 1 2 m

Les coefficients de ce polynôme peuvent être déterminés par la méthode des moindres carrés

N

[ y(t _i ) f i

-

]2 =min

(3)

i=1

Où fi est la mesure de température de surface du point i du semi-conducteur dans le temps ti. Pour la détermination des coefficients Aj, j = 0, ..., m on utilisera le programme commercial TableCurve.

L'évolution temporelle de la température de surface mesurée sur l'espace semi infini est obtenue par interpolation en utilisant des segments brisés. La densité de flux de chaleur q(t) à la surface d'un espace semi infini est déterminée par l'expression suivante [36] :

t

ëcñ df ( )

È 1

q( t)

~ = d È (4)

ð d È t-È

0

f (t) étant la température de surface mesurée au cours du temps (figure).

f(È)

fi+1

fi

Ati

1 2 i M

t1 t2

ti ti+1

tM tM+1

Figure III-17 : Interpolation des relevés de température (Data)

Les approches des températures de surface mesurées dans les espaces délimités par les polygones, sont calculées par les intégrales dans l'expression ci-dessous

qYt_M

+

1

)

M t i + 1

ë c ñ df( )

È 1

ð t i dÈ t_M

+

1

È

dÈ

(⁵)

La dérivée dans le temps df (È)/dÈ peut être exprimée par le rapport suivant

df( È)

f f

-

+ 1

i i

=

dÈ t i+1 - t_i

(6)

Compte tenu de l'équation (2), l'expression de la densité de flux de chaleur à la surface (Eq. 4) s'écrit comme suit

4( t) =

t

ëcñ _r dy(È ) 1

dÈ t -ÈdÈ (7)

0

Soit après substitution

t

q( t) = ëcñ

( A ₁+2 A₂È + ...+ mApm- ¹⁾ 1 (8)

0

p t - È

En posant z² = t - È et en utilisant le modèle binomial usuel de l'algèbre, à savoir

( )

a b

+ =

n

j= 0

n n! a b

, n , , ...

n j j

- = 1 2

j! (n j) !

-

(⁹)

L'équation (8) est obtenue après transformation de l'équation suivante [38] :

ëcñm 2i-1

4( t)= 2 A1 t + LiAit 2 × 1+(i -1)!E

ð i i=2 k=1 (2 k + 1)k! (i -1-k) !

i

1

(-1)

k

(10)

Dans le cas particulier où m = 7, il résulte, de l'équation (10), l'expression suivante pour la densité de flux thermique q(t)

4(

t)

=

2

ëcñ

ð

A₁ t

+

4

3

A2

t ³ + ⁸ A₃ t ⁵ +

5

64

35

At

4

128

⁷ + A₅ t ⁹⁺

63

(11)

512

+ At ¹¹⁺

6

231

1024

429

A₇ t

13

Ce modèle (Eq. 11) peut également être utilisé pour un polynôme de degré inférieur. Par exemple pour m = 3, il suffit de poser A4 = A5 = A6 = A7 = 0.

Dans le cas d'un polynôme de degré élevé (m > 5) l'attention devrait être accordée à la possibilité de l'apparition d'oscillations.

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

III-9. RESULTATS ET DISCUSSION

Dans notre cas m=3 donc la densité de flux thermique ÿq(t) devient :

t4( t) = 2 (A₁ + 3 Acp 4 A2 3 +8 A₃ t ⁵⁾

(12)

ð 5

En considérant le cas de l'acier de la fonction de la figure III-6 on peut déterminer la densité du flux de chaleur pour ce matériaux dans ces conditions :

TAcier doux(34,400) = 16,582 + 0,082.t - 5,067.10^-4.t² + 1,277.10^-6.t³

(0, 082 t - 6, 756. 10^-4 . t ³ + 2, 043.10-6 t5

ð

qacier douxt) = 2

ëcñ

Les densités de flux de chaleur pendant l'opération de chariotage de l'acier doux de propriétés thermo-physiques suivantes :

- conductivité thermique ë = 54 W/m.K, - chaleur spécifique c = 465 J/kg.K

- masse volumique ñ = 7830 kg/m³ - à température normale de 20°C

en considérant les conditions de coupe données, sont déterminée après calculs comme suit :

4Acier doux(

34 , 400 , t) = 1297, 398 t - 10, 689. t ³ + 0,032 t5

4Acier doux(

32 800 2310 0 37 166 ³ 0 214 ⁵

, , t) = , . t , . t , . t

- +

4Acier _d(30 , 126Q t) = 4683,29 . t - 126,26. t ³ +1,0 5 . t5

4Acier doux(

28 2000 9667 196 300 617 ³ 4 164 ⁵

, , t) = , . t - , . t , . t

+

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

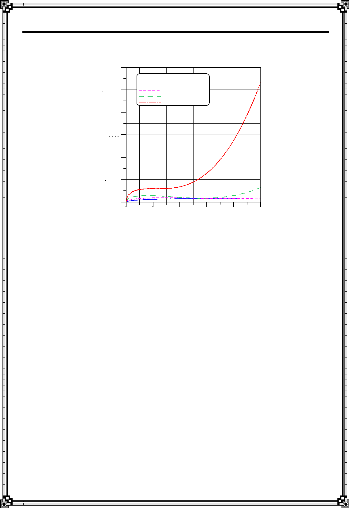
240000

200000

Chariotage de l'acier doux

ö = 34 mm, n = 400 tr/min

ö = 32 mm, n = 800 tr/min ö = 30 mm, n = 1260 tr/min ö = 28 mm, n = 2000 tr/min

160000

gooier doux (Wm-2J

120000

80000

40000

0

0 20 40 60 80 100

t [s]

Figure III-18 : Densité de flux de chaleur pour l'acier doux

On remarque pour le chariotage de l'acier doux, la densité de flux de chaleur prend des valeurs stables entre 5,5 et 7,5 kW/m² pour les régimes d'usinage 400 et 800 tr/min et commence à être instable pour 1260 tr/min (6,5 et 11,5 kW/m²) et diverge complètement pour 2000 tr/min en notant à 40 secondes 27 kW/m² et augmente rapidement pour dépasser 225 kW/m² à 100s. L'instabilité et divergence sont à l'origine de la solution adoptée pour le degré du polynôme choisit qui est dans notre cas d'ordre 3.

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

86

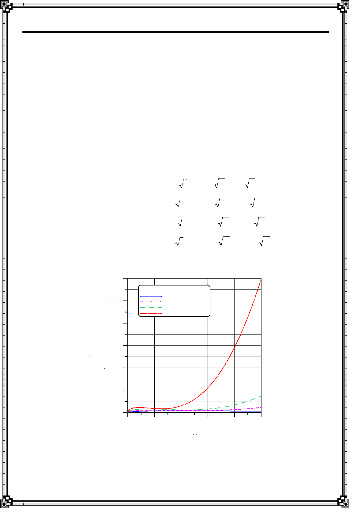
Les densités de flux de chaleur pendant l'opération de chariotage du bronze pour lequel, les propriétés thermo-physiques sont :

- conductivité thermique ë = 83 W/m.K, - chaleur spécifique c = 410 J/kg.K,

- masse volumique ñ = 8666 kg/m³ - à température normale de 20°C

En tenant compte des conditions de coupe, sont calculées ainsi :

qBronze ( , , t) , . t , . t , . t

~ 42 400 3933 611 45 162 ³ 0 1 7

= - +

5

qBronze ( , , t)

~ 40 800 7789 712 178 918 ³ 1 462

= , . t - , . t , . t

+

5

qBronze( ~

38 1260 13506 044 422 944 ³ 4 353 ⁵

, , t) = , . t - , . t , . t

+

qBronze ( ~

36 2000 24124 856 1251 126 ³ 22 019 ⁵

, , t) = , . t - , . t + , . t

1200000

1000000

Chariotage du bronze

ö = 42 mm, n = 400 tr/min ö = 40 mm, n = 800 tr/min ö = 38 mm, n = 1260 tr/min ö = 36 mm, n = 2000 tr/min

800000

qbronze I"W M-2.1

600000

400000

200000

0

0 20 40 60 80 100

t [s]

Figure III-19 : Densité de flux de chaleur pour le bronze

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

Le chariotage du bronze donne des valeurs instables des densités de flux de chaleur aux trois grands régimes d'usinage, à 800 tr/min on relève une oscillation entre 17,5 et 22 kW/m²qui est entre 20 et 80s pour diverger aussitôt à plus de 45 kW/m² à 100s. Pour 1260 tr/min la densités de flux de chaleur oscille également entre 10 et 60s à des valeurs entre 22,5 et 32 kW/m² et monte rapidement à 145 kW/m² à 100s mais à 2000 tr/min on voie clairement une divergence à partir de 35s pour sauter à environ 1200 kW/m² à 100s, par contre pour le bas régime de 400 tr/min on obtient une valeur stable autour de 13 kW/m².

De la même manière que pour le tournage on peut déterminer les densités de flux de chaleur durant le fraisage de l'aluminium qui possède les propriétés thermo-physiques suivante :

- conductivité thermique ë = 169 W/m.K, - chaleur spécifique c = 881 J/kg.K,

- masse volumique ñ = 2790 kg/m³, - à température normale de 20°C,

en tenant compte des conditions de coupe, sont calculées ainsi :

q Alu min ium ( , , t)

~ 60 500 170391 552 13185 471 ³ 278 183 ⁵

= , . t - , . t + , t

qAluminium( ~

58 1000 201001 777 15485 263 ³ 328 337 ⁵

, , t) = , . t - , . t + , . t

qAluminium( ~

56 1500 215490 464 16589 163 ³ 349 936 ⁵

, , t) = , . t - , . t + , . t

q Alu min ium ( , , t)

~ 54 2000 271031 324 16773 146 ³ 358 032 ⁵

= , . t - , . t + , . t

Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

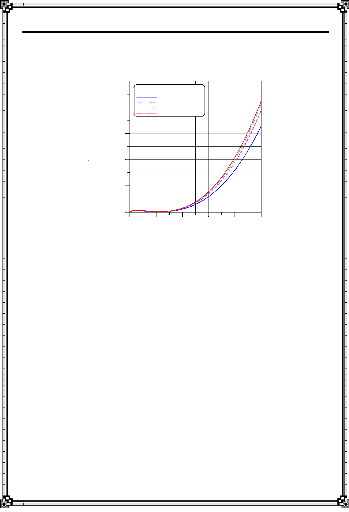
25000000

Fraisage de l'aluminium

20000000

e = 60 mm, n = 500 tr/min e = 58 mm, n = 1000 tr/min e = 56 mm, n = 1500 tr/min e = 54 mm, n = 2000 tr/min

qauminium (w nr1

15000000

10000000

5000000

0

0 20 40 60 80 100

t [s]

Figure III-20 : Densité de flux de chaleur pour l'aluminium

Pour le fraisage de l'aluminium on constate pleinement la divergence à partir de 35s. Les valeurs des densités de flux de chaleur pour tous les régimes de fraisage oscillent entre 60 et 320 kW/m² pour diverger à partir de 40s avec un énorme saut allant de 16000 à 21500 kW/m² à 100s.

89

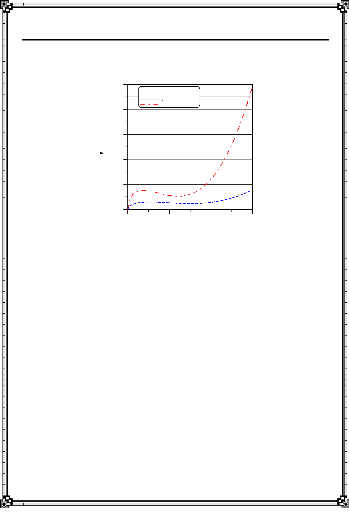
Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

100000

n = 400 tr/min

Acier doux : ö = 34 mm Bronze : ö = 42 mm

80000

60000

_[w ,7,2]

40000

20000

0

0 100 200 300

t [s]

Figure III-21 : Densité de flux de chaleur pour le chariotage de l'acier doux et le bronze à 400 tr/min

Sur la figure III-21 on peut noter que pour le même type d'opération d'usinage et à même régime les densités de flux de chaleur sont différentes en fonction du matériau (5 kW/m² pour l'acier doux et autour de 13 kW/m² pour le bronze) cela est dû d'une part aux propriétés thermo-physiques du matériau et d'autre part aux conditions de coupe.

La densité de flux de chaleur présente une stabilité pour l'acier jusqu'à un peu plus de 200s avec une légère oscillation entre 4,7 et 5,9 kW/m² et un peu moins pour le bronze à environ 170s oscillant entre 10,5 et 15,2 kW/m². Et malgré la stabilité des valeurs obtenue, même à 100s, il serait plus intéressant de voir d'autres paramètres de coupe fixé pour suivre leurs évolutions et influences sur la densité de flux de chaleur.

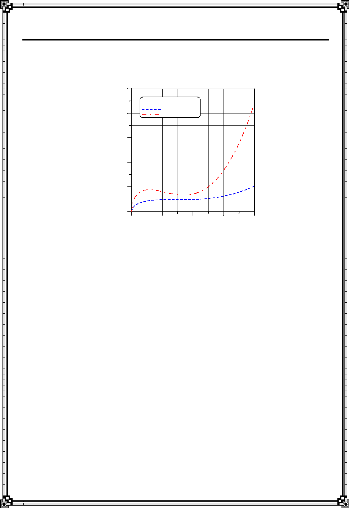
Chapitre III - Diagnostic expérimental de l'effet thermique en usinage

250000

n = 2000 tr/min

200000

Acier doux : ö = 28 mm Bronze : ö = 36 mm

150000

i Iwnr2.1

100000

50000

0

0 15 30 45 60

t [s]

Figure III-22 : Densité de flux de chaleur pour le chariotage de l'acier doux et le bronze à 2000 tr/min

La figure III- 22 montre que pour le même type d'opération d'usinage et à même régime mais élevé, la densité de flux de chaleur n'a pas bien sûr la même valeur et présente des intervalles de temps plus courts, n'arrivant même pas à 25 pour l'acier et 35s pour le bronze après quoi les fonctions de cette densité manifestent des divergences notables. La valeur moyenne qu'elle peut atteindre est de l'ordre de 23,8 kW/m² pour l'acier doux et entre 33 et 44 kW/m² pour le bronze.

Il serait plus intéressant de jouer sur d'autres paramètres de coupe d'un côté et de l'autre côté voir l'ordre du polynôme pour pouvoir définir des solutions stables et appréciables de la densité de flux de chaleur en fraisage.

91