|
ACADÉMIE D'AIX-MARSEILLE
UNIVERSITÉ D'AVIGNON ET DES PAYS DE VAUCLUSE
|
THÈSE
présentée à l'Université d'Avignon
et des Pays de Vaucluse
pour obtenir le diplôme de DOCTORAT
SPÉCIALITÉ :
Informatique
École Doctorale 166 <<Information,
Structures, Systèmes»
Laboratoire d'Informatique (EA 4128)
Techniques hybrides de recherche exacte et
approchée : application à des
problèmes de transport
par
|
Boris BONTOUX
Soutenue publiquement le 08 décembre 2008 devant
un jury composé de :
|
|
|
M.
|
Marc SEVAUX
|
Professeur, Université de Bretagne-Sud, Lorient
|
Rapporteur
|
|
M.
|
Emmanuel NERON
|
Professeur, Université de Tours, Tours
|
Rapporteur
|
|
Mme
|
Françoise DAUMAS
|
Ingénieur, D2A, Aix-en-Provence
|
Examinatrice
|
|
M.
|
Frederic SEMET
|
Professeur, LAGIS, Ecole Centrale Lille
|
Examinateur
|
|
M.
|
Eric BOURREAU
|
Maître de Conférences, LIRMM, Montpellier
|
Examinateur
|
|
M.
|
Philippe MICHELON
|
Professeur, LIA, Avignon
|
Examinateur
|
|
M.
|
Christian ARTIGUES
|
Chargé de Recherches, LAAS-CNRS, Toulouse
|
Directeur de thèse
|
|
M.
|
Dominique FEILLET
|
Professeur, Ecole des Mines de Saint-Etienne, Gardanne
|
Directeur de thèse
|
Laboratoire d'Informatique d'Avignon École Doctorale
166

Laboratoire d'Informatique
<<Information, Structures, Systèmes»
Université d'Av gnon
À Angélique et Nathanael, mes amours
Remerciements
Je tiens tout d'abord à remercier la Region
Provence-Aples-Côte d'Azur, pour le financement de cette thèse,
ainsi que la societe Daumas Autheman et Associes, qui m'ont permis d'obtenir ce
financement.
Ensuite, je souhaite remercier Renato De Mori et Marc
El-Bèze qui en tant que directeurs du Laboratoire m'ont accueilli au
sein du Laboratoire Informatique d'Avignon, ainsi que tous les membres du LIA
avec qui j'ai passe de très bons moments et de très bonnes
soirees.
Je tiens aussi à remercier tous les membres passes et
presents de l'equipe de Recherche Operationnelle que j'ai pu rencontrer :
Audrey et sa petite merveille Lisa, Andrea et son accent si chantant et si
depaysant, Mireille et sa vie si trepidante, Diego, Rodrigo, Philippe,
Dominique Quadri et la dernière arrivee, Claire. . .
Je voudrais egalement saluer l'ensemble des membres du jury et
en particulier, Emmanuel Neron et Marc Sevaux, rapporteurs de cette
thèse, pour avoir eu la patience de lire ce memoire.
Un grand merci à Christian Artigues, pour m'avoir
attire à l'IUP, puis m'avoir fait decouvrir la Recherche Operationnelle.
Sans lui, je n'aurais jamais eu l'envie de faire un doctorat. Son encadrement
m'a beaucoup apporte. . .
Un grand merci à Dominique Feillet, co-encadrant de
cette thèse, qui m'a pousse dans la recherche. Ses conseils ont ete
d'une valeur inestimable, il m'a permis d'avoir le courage de finir ce
doctorat. Je tiens en particulier à souligner la qualite de son
encadrement, ainsi que ses qualites humaines.
Je remercie egalement Eric Bourreau pour son aide precieuse
pour un sujet que je maîtrisais peu, Philippe Refalo pour son aide pour
l'utilisation d'Ilog, Thierry Garaix « Titi » dont la thèse et
les discussions m'ont beaucoup inspire, Jeremie Osmont « Jey » pour
son aide miraculeuse en temps de crise (ce qui arriva très souvent) et
Olivier Liess « Kaoru » pour ses competences inegalees en
programmation.
Je remercie mes nombreux collègues de bureau de m'avoir
si bien supporte et en particulier Cedric « Krusty » pour ses petites
attentions (merci encore pour ces croissants le matin!) et sa mauvaise humeur
si drôle.
Je remercie mes parents, Gilles et Bab, pour leur soutien, leurs
encouragements et
leurs relectures.
Enfin, je ne pouvais pas finir ces remerciements sans
remercier ma femme, Angélique, et mon fils, Nathanaël, mes amours
de tous les jours. Vous m'avez été tous deux d'une grande aide
tout au long de cette thèse. Vous retrouver tous les soirs était
mon rayon de soleil et un des mes vrais bonheurs. Je suis désolé
de vous avoir un peu délaissés en fin de doctorat. Ce
mémoire vous est donc dédié.
Résumé
Nous nous intéressons dans cette thèse aux
possibilités d'hybridation entre les méthodes exactes et les
méthodes heuristiques afin de pouvoir tirer avantage de chacune des deux
approches : optimalité de la résolution exacte, caractère
moins déterministe et rapidité de la composante heuristique. Dans
l'objectif de résoudre des problèmes NPdifficiles de taille
relativement importante tels que les problèmes de transports, nous nous
intéressons dans les deux dernières parties de ce mémoire
à la conception de méthodes incomplètes basées sur
ces hybridations.
Dans la première partie, nous allons nous
intéresser aux méthodes de résolution par recherche
arborescente. Nous introduisons une nouvelle approche pour la gestion des
décisions de branchement, que nous appelons Dynamic Learning Search
(DLS). Cette méthode définit de manière dynamique des
règles de priorité pour la sélection des variables
à chaque noeud et l'ordre des valeurs sur lesquelles brancher. Ces
règles sont conçues dans une optique de
généricité, de manière à pouvoir utiliser la
méthode indépendamment du problème traité. Le
principe général est de tenir compte par une technique
d'apprentissage de l'impact qu'ont eu les décisions de branchement dans
les parties déjà explorées de l'arbre. Nous
évaluons l'efficacité de la méthode proposée sur
deux problèmes classiques : un problème d'optimisation
combinatoire et un problème à satisfaction de contraintes.
La deuxième partie de ce mémoire traite des
recherches à grand voisinage. Nous présentons un nouvel
opérateur de voisinage, qui détermine par un algorithme de
programmation dynamique la sous-séquence optimale d'un chemin dans un
graphe. Nous montrons que cet opérateur est tout particulièrement
destiné à des problèmes de tournées pour lesquels
tous les noeuds ne nécessitent pas d'être visités. Nous
appelons cette classe de problème les Problèmes de
Tournées avec Couverture Partielle et présentons quelques
problèmes faisant partie de cette classe. Les chapitres 3 et 4 montrent,
à travers des tests expérimentaux conséquents,
l'efficacité de l'opérateur que nous proposons en appliquant
cette recherche à voisinage large sur deux problèmes,
respectivement le Problème de l'Acheteur Itinérant (TPP) et le
Problème de Voyageur de Commerce Généralisé (GTSP).
Nous montrons alors que cet opérateur peut être combiné de
manière efficace avec des métaheuristiques classiques, telles que
des algorithmes génétiques ou des algorithmes d'Optimisation par
Colonies de Fourmis.
Enfin, la troisième partie présente des
méthodes heuristiques basées sur un algorithme de
Génération de Colonnes. Ces méthodes sont
appliquées sur un problème
complexe : le problème de Tournées de
Véhicules avec Contraintes de Chargement à Deux Dimensions
(2L-VRP). Nous montrons une partie des possibilités qu'il existe afin de
modifier une méthode a priori exacte en une méthode
heuristique et nous évaluons ces possibilités à l'aide de
tests expérimentaux.
Table des matières
Introduction Générale 10
I Favoriser l'obtention rapide de solutions dans les
méthodes de recherche arborescente 15
1 Dynamic Learning Search : une méthode par
apprentissage 19
1.1 Introduction 19
1.2 État de l'art des recherches arborescentes 20
1.2.1 Méthode de parcours de l'arbre de recherche 21
1.2.2 Méthode de structuration de l'arbre de recherche
22
1.2.3 Parcours réduit de l'arbre 22
1.2.4 Ordre dynamique 24
1.2.5 Apprentissage : look-back 26
1.2.6 Métaheuristiques combinées à la
recherche arborescente 27
1.3 Dynamic Learning Search : une méthode par
apprentissage 28
1.4 Learning : une méthode basée sur un
apprentissage 29
1.4.1 Sondage 29
1.4.2 Apprentissage 30
1.4.3 Prévision 32
1.4.4 Remise en question 32
1.5 Dynamic : un ordre dynamique de choix des variables et de
sélection des
valeurs 33
1.6 Search: un schéma de recherche adapté à
la méthode 34
1.7 Algorithme général de la méthode 34
1.8 Méthode Dynamic Learning Search : critères de
sélection 34
1.8.1 Problèmes de Satisfaction des Contraintes 35
1.8.2 Problèmes d'Optimisation Combinatoire 38
1.8.3 Méthode commune aux deux types de problèmes
39
1.9 Résultats expérimentaux 40
1.9.1 Application au problème du Voyageur de Commerce
40
1.9.2 Application au problème d'Emploi du Temps de Garde
d'Infir-
mières 41
1.9.3 Application à des
problèmes de Satisfaction de Contraintes aca-
démiques 43
|
1.10 Conclusion et perspectives
II Utiliser des méthodes exactes au sein des
métaheuristiques : méthodes
de grands voisinages
2 La recherche à grand voisinage : un nouvel
opérateur
|
47
49
53
|
|
2.1
|
Introduction à la recherche locale
|
53
|
|
|
2.1.1 Bases de la recherche locale
|
53
|
|
|
2.1.2 Principales classes de recherches locales
|
54
|
|
|
2.1.3 Recherche locale à voisinage variable
|
55
|
|
|
2.1.4 Algorithmes utiisant de la recherche locale
|
55
|
|
2.2
|
Recherche à grand voisinage
|
57
|
|
|
2.2.1 Notations et définitions de la recherche à
grand voisinage . . . .
|
58
|
|
2.3
|
Classe des problèmes considérés :
Problèmes de Tournées avec Couver-
|
|
|
|
ture Partielle
|
59
|
|
|
2.3.1 Problèmes de Tournées avec Gains
|
60
|
|
|
2.3.2 Autres variantes de Problèmes de Tournées
à Couverture Partielle
|
61
|
|
|
2.3.3 Complexité des Problèmes de Tournées
avec Couverture Partielle
|
62
|
|
|
2.3.4 Quelques opérateurs de recherche locale pour les
Problèmes de
|
|
|
|
Tournées avec Couverture Partielle
|
62
|
|
2.4
|
Dropstar : une nouvelle structure de grand voisinage
|
64
|
|
|
2.4.1 Des opérateurs existants : drop,
l-ConsecutiveDrop
|
64
|
|
|
2.4.2 L'opérateur de grand voisinage : Dropstar
|
69
|
|
|
2.4.3 Plus court chemin avec contraintes de ressources (SPPRC) .
. . .
|
71
|
|
|
2.4.4 Résolution par un algorithme de programmation
dynamique . .
|
71
|
|
2.5
|
Perspectives : variantes possibles de la procédure
Dropstar
|
74
|
|
3
|
Application au Problème de l'Acheteur
Itinérant
|
77
|
|
3.1
|
Introduction au problème de l'Acheteur Itinérant
|
78
|
|
3.2
|
Notre algorithme : le DMD-ATA
|
81
|
|
|
3.2.1 Fourmis Parallèles
|
81
|
|
|
3.2.2 Fourmis Anamorphiques
|
82
|
|
|
3.2.3 Plans Multi-Dimensionnels
|
83
|
|
|
3.2.4 Dynamique
|
83
|
|
3.3
|
Opérateurs de recherche locale
|
84
|
|
|
3.3.1 Procédures de recherches locales basiques
|
85
|
|
|
3.3.2 Application de l'opérateur Dropstar
|
85
|
|
|
3.3.3 Intégration de la recherche locale dans l'algorithme
DMD-ATA .
|
89
|
|
3.4
|
Résultats expérimentaux
|
89
|
|
3.5
|
Conclusion
|
93
|
|
4
|
Application au Problème du Voyageur de Commerce
Généralisé
|
95
|
|
4.1
|
Introduction au Problème du Voyageur de Commerce
Généralisé . . . .
|
96
|
|
4.2
|
État de l'art
|
96
|
|
4.3
|
Algorithme mémétique
|
98
|
4.3.1 Composants basiques de l'algorithme 98
4.3.2 Croisement 100
4.3.3 Implémentation détaillée de
l'opérateur de croisement 103
4.3.4 Heuristiques de recherche locale 106
4.4 Résultats expérimentaux 108
4.5 Conclusion et perspectives 112
III Tronquer les méthodes exactes : méthode
de Branch & Price heuristique 121
5 Application au problème de Tournées de
Véhicules avec Contraintes de Chargement 125
5.1 Préambule : Intérêt du problème
126
5.2 Problèmes de calcul de tournées de
véhicules 127
5.2.1 Du problème du Voyageur de Commerce au
problème de Tour-
nées de Véhicules 127
5.2.2 Le 2L-VRP parmi les problèmes de Tournées de
Véhicules . . . 128
5.3 État de l'art 128
5.3.1 Résolution du 2L-VRP 128
5.3.2 Algorithmes de chargement 131
5.4 Modèle classique du problème du 2|RO|L-VRP
132
5.5 Génération de colonnes 134
5.5.1 Modélisation d'un ESPPRC 138
5.5.2 Résolution par programmation dynamique 139
5.6 Notre approche : un schéma de Branch & Price
141
5.6.1 Méthode de séparation 142
5.6.2 Initialisation de 1 pour la génération de
colonnes 143
5.6.3 Remontées de colonnes 143
5.6.4 Problème esclave : ESPPRC 144
5.6.5 Problème de chargement séquentiel à
deux dimensions 147
5.7 Deux approches différentes pour la
réalisabilité du chargement 153
5.7.1 Vérification de la réalisabilité a
posteriori 153
5.7.2 Construction de routes réalisables dans le
sous-problème 155
5.8 Branch & Price heuristique 159
5.8.1 Problème esclave heuristique 159
5.8.2 Gestion des colonnes 160
5.8.3 Méthode de séparation 160
5.9 Résultats expérimentaux 161
5.9.1 Paramètres retenus 161
5.9.2 Classes d'instances 161
5.9.3 Analyses des résultats 162
5.10 Conclusions et perspectives 165
Conclusion et perspectives 171
Liste des illustrations 175
Liste des tableaux 177
Bibliographie 179
Introduction Générale
La recherche opérationnelle s'attache à
étudier des problèmes d'optimisation combinatoire dont la
résolution constitue un véritable challenge. Il s'agit de trouver
une affectation de valeurs à un certain nombre de variables tout en
respectant un ensemble de contraintes donné. Parmi les paradigmes de
résolution, la programmation par contraintes est particulièrement
adaptée pour étudier la réalisabilité d'un
problème de satisfaction de contraintes, tandis que la programmation
linéaire en nombres entiers s'inscrit davantage dans le cadre de la
recherche d'un extremum d'une fonction linéaire. Cependant, ces
approches partagent une procédure de résolution commune qui
consiste en l'énumération implicite de l'ensemble des solutions
du problème. Il s'agit alors de parcourir l'espace de recherche et d'en
extraire une solution admissible (problèmes de satisfaction de
contraintes) ou optimale (problèmes d'optimisation combinatoire) ou de
prouver qu'il n'en existe pas. Le schéma classique consiste en une
recherche arborescente qui évalue à chaque noeud la solution
partielle courante et l'étend si possible en affectant une valeur
à une variable non encore instanciée.
Les problèmes combinatoires difficiles ont depuis
longtemps attiré l'attention des chercheurs. On peut citer Garey et
Johnson (1979) qui ont approfondi les bases des concepts de problèmes
NP-difficiles et ont montré que de nombreux problèmes n'avaient
que peu de possibilités d'être résolus efficacement par des
méthodes exactes. Ces méthodes exactes permettent d'obtenir une
ou plusieurs solutions dont l'optimalité est garantie. Cependant, dans
certaines situations, il est nécessaire de disposer d'une solution de
bonne qualité (c'est-à-dire assez proche de l'optimale) dans un
contexte de ressources (temps de calcul et/ou mémoire) limitées.
Dans ce cas, l'optimalité de la solution n'est pas garantie, ni
même l'écart avec la valeur optimale. Néanmoins, le temps
nécessaire pour obtenir cette solution est beaucoup plus faible que dans
le cas d'une méthode exacte. Ce type de méthodes, dites
heuristiques, est particulièrement utile pour les problèmes
nécessitant une solution en temps limité ou pour résoudre
des problèmes difficiles.
Ces méthodes approchées peuvent se classer en
différentes catégories:
- Constructives (algorithmes gloutons),
- Recherche locale (algorithmes de descente, recherche à
grand voisinage, ...), - Métaheuristiques (recuit simulé,
recherche Tabou,...),
- Évolutionnaires (algorithmes génétiques,
algorithmes d'optimisation par colonies de fourmis, algorithmes
mémétiques,...).
L'intuition qui est à la base des travaux menés
sur la plupart des méthodes heuristiques réside dans le fait que
dans la majorité des problèmes d'optimisation combinatoire, les
bonnes solutions sembleraient partager des « structures» communes, ou
du moins, se trouver dans de mêmes régions de l'espace de
recherche. Ainsi, l'idée de la recherche locale est d'atteindre les
solutions optimales d'un problème en modifiant itérativement les
bonnes solutions, trouvées par exemple par des méthodes
gloutonnes.
Dans cette thèse, nous nous intéressons aux
possibilités d'hybridation entre les méthodes exactes et les
méthodes heuristiques afin de pouvoir tirer avantage de chacune des deux
approches : systématicité et optimalité de la
résolution exacte, caractère moins déterministe et
rapidité de la composante heuristique. Dans l'objectif de
résoudre des problèmes NP-difficiles de taille relativement
importante tels que les problèmes de transports, nous nous
intéressons dans les deux dernières parties de ce mémoire
à la conception de méthodes incomplètes basées sur
ces hybridations. Ce mémoire se situe dans la lignée des travaux
de recherche menés précédemment au sein de l'équipe
de Recherche Opérationnelle du Laboratoire Informatique d'Avignon sur
l'hybridation entre recherche exacte et recherche heuristique (Demassey, 2003;
Oliva, 2004; Palpant, 2005).
Ce mémoire est composé de trois parties, qui
soulèvent les questions suivantes :
- Comment favoriser l'obtention rapide de solutions dans les
méthodes de recherche arborescente sans perdre la complétude de
la recherche?
- Comment utiliser des méthodes exactes au
détriment de la propriété de complétude au sein des
métaheuristiques?
- Comment obtenir de bonnes solutions à partir des
méthodes exactes?
Dans la première partie de ce mémoire, nous nous
intéressons aux méthodes de résolution par recherche
arborescente. Nous introduisons une nouvelle approche pour la gestion des
décisions de branchement, appelée Dynamic Learning Search
(DLS). Cette méthode définit de manière dynamique des
règles de priorité pour la sélection des variables
à chaque noeud et l'ordre des valeurs sur lesquelles brancher. Nous
mettons en particulier l'accent sur le caractère générique
de la méthode, c'est-à-dire sa capacité à
s'appliquer à tout type de problème, sans information
extérieure sur la structure du problème. Le principe
général de la méthode est de tenir compte par une
technique d'apprentissage de l'impact qu'ont eu les décisions de
branchement dans les parties déjà explorées de l'arbre. Le
but est de favoriser l'obtention rapide de solutions dans les méthodes
de recherche arborescente. Nos travaux s'appuient en partie sur les travaux de
plusieurs autres chercheurs (Harvey et Ginsberg, 1995; Hooker, 2000; Fischetti
et Lodi, 2003; Refalo, 2004). Nous évaluons l'efficacité de la
méthode proposée sur plusieurs problèmes classiques
comprenant des problèmes d'optimisation combinatoire et des
problèmes de satisfaction de contraintes. Nous montrons que notre
méthode propose des résultats en moyenne meilleurs que les
méthodes par défaut d'un solver commercial.
Dans la deuxième partie de ce mémoire, nous
proposons d'utiliser des méthodes exactes au sein de
métaheuristiques. Pour cela, nous nous intéressons à une
classe des problèmes de tournées de véhicules. Ces
problèmes constituent l'une des classes les
plus étudiées de la recherche
opérationnelle, en particulier puisqu'elle comprend le fameux
Problème du Voyageur de Commerce. Le Problème du Voyageur de
Commerce (Traveling Salesman Problem ou TSP) a été
étudié dès le 19ème siècle par les
mathématiciens Hamilton et Kirkman. En 1972, Karp (1972) a montré
que le problème du voyageur de commerce, entre autres, est
NP-complet. Nos recherches nous ont amenés à nous
focaliser sur une sous catégorie de problèmes de tournées
de véhicules que nous nommons Problèmes de Tournées avec
Couverture Partielle, pour lesquels la visite de l'ensemble des sommets du
graphe n'est pas obligatoire. Après une présentation
d'opérateurs de voisinage classiques adaptés à cette
famille de problèmes, nous présentons un nouvel opérateur
de voisinage, Dropstar, qui détermine par un algorithme de
programmation dynamique, la sous-séquence optimale d'un chemin dans un
graphe. Nous montrons que cet opérateur est tout particulièrement
destiné à des problèmes de tournées pour lesquels
tous les noeuds ne nécessitent pas d'être visités. Les
chapitres 3 et 4 montrent, à travers des tests expérimentaux
conséquents, l'efficacité de l'opérateur que nous
proposons sur deux problèmes, respectivement le Problème de
l'Acheteur Itinérant (TPP) et le Problème de Voyageur de Commerce
Généralisé (GTSP). Nous montrons alors que cet
opérateur de grand voisinage basé sur une méthode exacte
peut être combiné de manière efficace avec des
métaheuristiques classiques, telles que des algorithmes
génétiques ou des algorithmes d'Optimisation par Colonies de
Fourmis.
Dans la troisième partie du mémoire, nous nous
intéressons aux méthodes de résolution exactes
tronquées. Nous appliquons la méthode que nous proposons sur le
problème de Tournées de Véhicules avec Contraintes de
Chargement en Deux Dimensions (Vehicule Routing Problem with
Two-Dimensional Loading Constrains ou 2L-VRP). Nous proposons de
résoudre ce problème à l'aide d'une procédure de
type Branch & Price, c'est-à-dire une procédure de
résolution de type Branch & Bound utilisant une méthode de
génération de colonnes pour le calcul de bornes. Nous
présentons dans un premier temps un schéma classique de
résolution par Branch & Price. De par la complexité des
contraintes de chargement, le problème esclave de la
génération de colonnes n'est pas résolu de manière
exacte. Notre travail s'est donc porté sur les moyens dont nous
disposions afin d'accélérer la résolution. Nous montrons
ainsi dans ce chapitre une partie des possibilités qu'il existe afin de
tronquer une méthode a priori exacte pour la rendre
heuristique. Enfin, nous évaluons ces possibilités à
l'aide de tests expérimentaux. Nous montrons que les méthodes que
nous proposons, sans être de mauvaises qualités, ne
dépassent pas les résultats des meilleurs algorithmes.
Pour chacune des parties, une validation expérimentale
a été réalisée sur divers problèmes
académiques ou applicatifs. Les résultats obtenus montrent
l'intérêt des méthodes proposées et laissent
entrevoir les nombreuses perspectives ouvertes par ce type d'hybridation.
Les travaux présentés sont issus de la
collaboration entre le Laboratoire Informatique d'Avignon et la
société Daumas Autheman et Associés 1. Daumas
Autheman et Associés est une société de service et
d'ingénierie informatique créée en 1988,
spécialisée dans l'informatique avancée, en particulier
dans l'optimisation de ressources et
1. http ://
www.daumas-autheman.com
gestion de l'expertise métier. Le problème
d'Emploi du Temps de Garde d'Infirmières du chapitre 1, ainsi que le
problèmes de Tournées de Véhicules avec Contraintes de
Chargement du chapitre 5 sont des problèmes issus de la collaboration
avec cette société. Les travaux de recherche ont
été financés conjointement par Daumas Autheman et
Associés et par le Conseil Régional de Provence-Alpes-Côte
d'Azur.
Les travaux présentés dans ce mémoire ont
fait l'objet des publications suivantes :
B. Bontoux et D. Feillet, 2006. Résolution heuristique
du problème de l'acheteur itinérant. Dans les actes de
7ème congrès de la société Française de
Recherche Opérationnelle et d'Aide à la Décision (ROADEF
2006). CDROM.
B. Bontoux, D. Feillet, et C. Artigues, 2007a. Une
méthode dynamique de parcours
d'arbre de recherche : Dynamic
Coperative Search. Dans les actes de 8ème congrès de
la
société Française de Recherche Opérationnelle
et d'Aide à la Décision (ROADEF 2007), 99-100.
B. Bontoux, D. Feillet, et C. Artigues, 2007b. Large
neighborhood search for variants of TSP. Dans les actes de The Seventh
Metaheuristics International Conference (MIC 2007), Montréal,
Canada. CDROM.
B. Bontoux, D. Feillet, C. Artigues, et E. Bourreau, 2007c.
Dynamic cooperative search for constraint satisfaction and combinatorial
optimization: application to a rostering problem. Dans P. Baptiste, G. Kendall,
A. Munier-Kordon, et F. Sourd (Eds.), 3rd Multidisciplinary International
Conference on Scheduling: Theory and Application (MISTA 2007), Paris,
France, 557-560.
B. Bontoux et D. Feillet, 2008. Ant colony optimization for the
traveling purchaser problem. Computers & Operations Research 35,
628-637.
B. Bontoux, C. Artigues, et D. Feillet, 2008a. Algorithme
mémétique avec un opérateur de croisement à
voisinage large pour le problème du voyageur de commerce
généralisé. Dans les actes de 9ème
congrès de la société Française de Recherche
Opérationnelle et d'Aide à la Décision (ROADEF 2008),
Clermont-Ferrand, 79-80.
B. Bontoux, C. Artigues, et D. Feillet, 2008b. A memetic
algorithm with a large neighborhood crossover operator for the Generalized
Traveling Salesman Problem. Meta-heuristics for Logistics and Vehicle
Routing, EU/ME, the European Chapter on Metaheuristics, Université
de Technologie de Troyes, France.
B. Bontoux, C. Artigues, et D. Feillet, February 2008c. Memetic
algorithm with a large neighborhood crossover operator for the Generalized
Traveling Salesman Problem. LAAS report, Université de
Toulouse, LAAS-CNRS, Toulouse, France.
Première partie
Favoriser l'obtention rapide de
solutions dans les méthodes de
recherche arborescente
1 Dynamic Learning Search : une méthode par
apprentissage 19
1.1 Introduction 19
1.2 État de l'art des recherches arborescentes 20
1.2.1 Méthode de parcours de l'arbre de recherche 21
1.2.2 Méthode de structuration de l'arbre de recherche
22
1.2.3 Parcours réduit de l'arbre 22
1.2.4 Ordre dynamique 24
1.2.5 Apprentissage : look-back 26
1.2.6 Métaheuristiques combinées à la
recherche arborescente 27
1.3 Dynamic Learning Search : une méthode par
apprentissage 28
1.4 Learning : une méthode basée sur un
apprentissage 29
1.4.1 Sondage 29
1.4.2 Apprentissage 30
1.4.3 Prévision 32
1.4.4 Remise en question 32
1.5 Dynamic : un ordre dynamique de choix des variables et de
sélection des
valeurs 33
1.6 Search: un schéma de recherche adapté à
la méthode 34
1.7 Algorithme général de la méthode 34
1.8 Méthode Dynamic Learning Search : critères de
sélection 34
1.8.1 Problèmes de Satisfaction des Contraintes 35
1.8.2 Problèmes d'Optimisation Combinatoire 38
1.8.3 Méthode commune aux deux types de problèmes
39
1.9 Résultats expérimentaux 40
1.9.1 Application au problème du Voyageur de Commerce
40
1.9.2 Application au problème d'Emploi du Temps de Garde
d'Infirmières 41
1.9.3 Application à des problèmes de
Satisfaction de Contraintes aca-
démiques 43
1.10 Conclusion et perspectives 47
Chapitre 1
Dynamic Learning Search: une
méthode par apprentissage
1.1 Introduction
La plupart des méthodes de résolution exacte
utilisées en optimisation combinatoire s'appuient sur une
énumération intelligente des solutions (Branch & Bound,
Programmation par contraintes, Programmation dynamique ...). Cette
énumération consiste en règle générale en la
construction d'un arbre de recherche, au cours de laquelle la création
d'un fils pour un noeud correspond à une prise de décision:
typiquement fixer une valeur à une variable. L'exploration
complète d'un tel arbre peut s'avérer très coûteuse
en temps. Il est donc classique de fixer une limite de temps, rendant ainsi
l'exploration incomplète. Si cette limite de temps est atteinte avant la
fin de l'exploration complète de l'arbre de recherche, on retourne la
meilleure solution trouvée (dans le cas où une ou plusieurs
solutions ont été trouvées). Un défaut connu de
cette approche est que l'exploration peut se faire dans un premier temps sur un
sous-arbre qui ne contient pas ou peu de solution intéressante et ainsi
utiliser tout le temps alloué à n'explorer que ce sous-arbre.
Cette situation conduit à retourner une mauvaise solution (ou aucune
solution). On a donc tout intérêt à mettre en place des
techniques favorisant l'exploration en priorité de parties de l'espace
de recherche contenant de bonnes solutions. Il s'agit de gérer au mieux
la prise de décision à la fois en ce qui concerne la construction
de l'arbre et le parcours des noeuds créés, et ce dès le
début de l'arbre. La méthode que nous proposons, Dynamic
Learning Search a été conçue dans le but de diriger
l'exploration de l'arbre de recherche vers les parties de l'espace des
solutions contenant les meilleures solutions. Notre objectif est de proposer
une méthode générique, de manière à pouvoir
l'utiliser indépendamment du type de problème traité :
problèmes d'optimisation combinatoire ou problèmes de
satisfaction de contraintes. La méthode DLS définit de
manière dynamique à chaque noeud de l'arbre des règles de
priorité pour la sélection de la variable sur laquelle brancher
et de l'ordre dans lequel les différentes valeurs pour chaque variable
sont explorées. Ces ordres sont déduits des
caractéristiques des sous-arbres obtenus jusqu'ici lors de branchements
concernant la même variable.
1.2 État de l'art des recherches
arborescentes
Les performances d'une recherche arborescente varient de
façon significative selon les stratégies de branchement retenues,
c'est-à-dire l'ordre selon lequel les variables seront choisies, ainsi
que l'ordre dans lequel les valeurs pour cette variable seront
instanciées. On peut noter que ces stratégie dépendent en
partie de la nature du problème et de l'espace des solutions : dans le
cas où le problème n'a qu'une solution ou très peu de
solutions, on cherche généralement à trouver une de ces
solutions le plus rapidement possible; dans le cas où le problème
n'est pas résoluble, on cherche à ce que l'arbre de recherche
soit le plus petit possible afin de prouver l'absence de solution de
manière relativement rapide; enfin, dans le cas pour lequel le
problème possède un nombre de solutions très important, on
cherche généralement la meilleure de ces solutions (selon un
objectif donné). On voit donc qu'une méthode efficace pour un
type de problème peut être inefficace pour un autre type de
problème.
Puisque toutes les variables d'un problème doivent
être instanciées pour obtenir une solution, une réduction
de la taille de l'arbre de recherche peut être obtenue en choisissant en
premier la variable qui contraint le plus l'espace de recherche. Ce choix est
souvent implémenté en choisissant en premier la variable ayant le
plus petit domaine (dom). Pour départager les variables
jugées équivalentes par l'heuristique du plus petit domaine, on
choisit la variable qui appartient au plus grand nombre de contraintes (on
définit le degré d'une variable comme le nombre de contraintes
dans lesquelles apparaît une variable). On peut aussi appliquer une
combinaison de ces deux critères (dom/deg, (Smith et Grant,
1998)) (plus petit domaine divisé par le degré de la variable).
Il a été montré par Haralick et Elliot (1980) que le fait
de calculer des mises à jour des domaines et du degré des
variables à chaque noeud permet de prendre de meilleures
décisions lors de l'exploration (dom/ddeg). En suivant cette
politique, on essaie de contraindre au maximum les variables et ainsi limiter
la taille de l'arbre. Concernant le choix de l'ordre dans lequel les valeurs
sont instanciées, ce choix ne semble pas important dans le cas où
le problème ne possède pas de solution. Cependant, dans le cas
contraire, on pourra atteindre plus rapidement une solution si l'on choisit la
valeur qui tend à maximiser le nombre de possibilités pour les
choix futurs. Enfin, il est facile de se rendre compte que le choix des
variables qui sont au sommet de l'arbre est prépondérant. On a
donc intérêt à choisir les premières variables sur
lesquelles brancher avec précaution.
L'idée d'accélérer l'exploration de
l'arbre de recherche n'est pas nouvelle. Plusieurs techniques ont
été proposées ces dernières années; ces
techniques peuvent être basées sur :
- un parcours réduit de l'arbre de recherche,
- une politique de branchement sur l'ordre des valeurs, - une
politique de branchement sur l'ordre des variables, - une combinaison des
techniques précédentes.
Les paragraphes qui suivent offrent une présentation de
certaines de ces techniques.
1.2.1 Méthode de parcours de l'arbre de
recherche
La plupart des méthodes de parcours d'un arbre de
recherche sont connues depuis déjà plusieurs années. La
différence entre deux stratégies de recherche réside
principalement dans la taille de l'arbre de recherche
généré et donc dans le temps de résolution du
problème traité. Les stratégies appliquées sont la
plupart du temps différentes selon la nature du problème. On
distingue les problèmes d'optimisation combinatoire avec une fonction
objectif et un nombre généralement important de solutions et les
problèmes de satisfaction de contraintes pour lesquels on ne cherche la
plupart du temps qu'une seule solution.
On peut citer différentes stratégies de
recherche (pour plus de détails, voir (Hooker, 2000)). Pour les
méthodes de parcours de l'arbre de recherche, on peut citer, entre
autres, les politiques suivantes :
Depth-first: la méthode
depth-first search est une méthode couramment utilisée.
Elle consiste en une exploration en profondeur de l'arbre de recherche. Les
variables sont fixées une à une itérativement,
jusqu'à obtenir une solution ou jusqu'à ce qu'une variable ait un
domaine vide. Lorsque c'est le cas, on revient sur la dernière
décision qui a été prise et on prend une autre
décision, si cela est possible. Dans le cas contraire, on remonte plus
haut dans les décisions prises. Cette technique est appelée
Backtrack. Lorsque le nombre de solutions est important, cette
méthode permet de trouver très rapidement une solution. Cette
méthode est très classique dans l'implémentation d'un
Branch and Bound. En terme d'occupation mémoire, cette méthode
est la plus intéressante.
Best bound first: on choisit parmi les noeuds
restant à traiter celui qui a la plus petite borne inférieure.
Cette borne peut être calculée par exemple, par relaxation de
contraintes, par une méthode heuristique, ... Ce choix est efficace
lorsque les bornes calculées sont de bonne qualité. Elle
présente par contre l'inconvénient de traiter des noeuds
successifs très différents (valeurs et variables
différentes) et donc de ne présenter que peu
d'incrémentalité dans les calculs, notamment les calculs de
bornes inférieures. De plus, cette méthode n'est applicable que
lorsqu'une borne est calculable, ce qui peut ne pas être le cas pour
certains problèmes de satisfaction de contraintes, dans lesquels il n'y
a pas de fonction objectif.
Breadth-first: cette méthode est la
méthode opposée à la méthode depth-first search.
Elle consiste à explorer l'arbre en largeur. Le parcours en largeur
correspond à un parcours par niveau de noeuds de l'arbre. Un niveau est
un ensemble de noeuds ou de feuilles situés à la même
distance du noeud racine. Ce type de parcours est rarement utilisé, du
fait de l'occupation mémoire trop importante.
Les méthodes présentées ci-dessus
décrivent des politiques d'exploration de l'arbre de recherche. Une fois
l'arbre créé, elles permettent d'ordonner une liste de noeuds
à traiter. Elles ne modifient en aucun cas la structure propre de
l'arbre. Néanmoins, deux politiques de parcours d'arbre de recherche
peuvent donner des résultats différents en terme de
rapidité d'exécution et en terme d'occupation mémoire. En
effet, on peut associer à ces méthodes des calculs de bornes qui
pourront amener à la troncature de sous-espaces de l'arbre de recherche
(par exemple, lorsque la borne inférieure calculée
à un noeud est supérieure à la borne
supérieure). Ainsi, si la structure de l'arbre n'est pas
modifiée, les espaces explorés de l'arbre peuvent être
modifiés par les schémas d'exploration.
1.2.2 Méthode de structuration de l'arbre de
recherche
Lorsqu'on construit un arbre de recherche, la structure
proprement dite de celui-ci sera en grande partie déterminée par
les choix concernant les politiques de séparation. Une fois que la
variable sur laquelle on veut brancher a été
déterminée, on doit choisir la politique en ce qui concerne la
séparation du domaine de cette variable. Classiquement, on choisit de
créer un noeud par valeur possible du domaine de la variable. Cela
conduit à des arbres de recherche dont la structure est assez large. On
peut aussi appliquer une politique de séparation binaire : on
crée d'un côté un noeud pour lequel la variable est
fixée à une valeur, de l'autre côté, un noeud pour
lequel la variable est différente de cette valeur. Éxcepté
pour le cas des problèmes à variables binaires, le
problème d'une telle politique réside dans la création
d'un arbre fortement déséquilibré (l'affectation d'une
variable à une valeur a beaucoup plus de conséquences que
l'interdiction de cette valeur). La stratégie equal split
consiste quant à elle à séparer les domaines des
variables en deux sous-domaines de taille égale. L'intérêt
de cette méthode est principalement de créer un arbre
équilibré. Quelle que soit la politique de séparation du
domaine des variables, une fois les noeuds créés, la politique de
choix de l'ordre de traitement des noeuds ainsi créés reste
elle-aussi à déterminer.
1.2.3 Parcours réduit de l'arbre
Dans le cadre de la résolution d'un problème
d'optimisation combinatoire par une méthode exacte, on peut chercher
à obtenir rapidement de bonnes solutions dans un temps limité. Un
des moyens pour y arriver est de transformer la méthode exacte en une
méthode heuristique. Cela passe la plupart du temps par une exploration
incomplète de l'arbre de recherche. Un des moyens les plus simples est
de ne pas traiter l'ensemble des noeuds en attente. Un ordre de priorité
pour le traitement des noeuds en attente est appliqué et on choisit de
ne traiter qu'un certain nombre de noeuds parmi l'ensemble des noeuds. On
restreint donc la recherche à un sous-espace de l'espace original, par
exemple en ne choisissant que les valeurs les plus prometteuses pour chaque
variable lors de l'exploration. Fondamentalement, dans ces méthodes, on
peut considérer que les noeuds non traités sont des noeuds
restant en attente en fin de résolution. Idéalement, on pourrait
donc conserver l'exactitude de la méthode en continuant le traitement
des noeuds jusqu'au bout (au prix de temps de résolution beaucoup plus
important).
Beam Search (Ow et Morton, 1988) est sûrement
l'alternative la plus connue pour tronquer une exploration. Cette approche est
basée sur une exploration en largeur de l'arbre de recherche. On utilise
une fonction heuristique pour estimer l'intérêt de chaque noeud
examiné. A chaque niveau de l'arbre, on garde seulement les w
noeuds les plus prometteurs dans l'ensemble des noeuds ouverts, qui est
l'ensemble de noeuds à
partir desquels la recherche peut continuer. Le terme w
est appelé la profondeur Beam. On voit facilement que plus w
est grand, plus le nombre de noeuds explorés sera important. Ainsi,
lorsqu'on augmente w, on s'approche de la solution qui aurait
été trouvée par une exploration exacte. En règle
générale, l'efficacité de cette approche dépend de
la qualité des bornes inférieures et supérieures. De plus,
tant que w est petit, cette méthode n'est pas
complète.
Limited Discrepancy Search ou LDS , méthode
proposée par Harvey et Ginsberg (1995), dérive d'une recherche en
profondeur classique, mais peut être combinée avec des
règles de sélection de variables et de valeurs. L'idée
principale de cette méthode est de limiter la recherche aux branches qui
ont au plus z déviations (discrepancies). Une
déviation est définie comme une décision contraire par
rapport à une heuristique qui indique le meilleur noeud fils pour chaque
noeud. Une déviation apparaît à chaque fois que le noeud
fils choisi dans une branche n'est pas le meilleur noeud. Par exemple, si l'on
considère les branches avec z = 0 déviation, l'arbre ne
comportera qu'une seule branche : à chaque étape, la recherche
doit suivre la branche qui mène au meilleur noeud. Plus on augmente
z, plus la méthode s'approche d'une résolution exacte.
Néanmoins, cette méthode est par définition assez
dépendante de la qualité de l'heuristique choisie, qui
détermine à chaque noeud la direction à prendre.
La méthode Branch & Greed a
été présentée par Sourd et Chretienne (1999) (voir
par exemple (Néron et al., 2008) pour un article récent
sur cette méthode). Cette méthode consiste à guider un
arbre de recherche incomplet à l'aide d'un algorithme glouton. Comme
pour Beam Search ou pour LDS, on peut paramétrer
l'algorithme grâce à une valeur, notée ici k, afin
que plus ou moins de feuilles soient visitées. L'algorithme parcourt
alors l'arbre de recherche en partant du noeud racine et suit une branche
jusqu'à trouver une feuille. Considérons une itération de
l'algorithme. A l'étape l, la profondeur du noeud courant
noté N, est égale à l. Pour
déterminer le noeud fils de la prochaine étape, l'algorithme
considère l'ensemble des noeuds fils de N dont la profondeur
est égale à l + k. Chacun de ces noeuds
correspond à une solution partielle et, pour chaque solution partielle,
on construit une solution réalisable en utilisant l'algorithme glouton
suivant : on choisit le meilleur noeud fils jusqu'à ce qu'on arrive
à une feuille. Cet algorithme glouton correspond à suivre la
branche qui ne comporte aucune déviation. Notons
Nbest la meilleure solution trouvée durant cette
étape. Le noeud successeur de N dans l'algorithme de Branch
& Greed est le noeud qui permet d'atteindre le noeud Nbest.
La profondeur de ce noeud est donc l + 1 et la procédure de
Branch and Greed continue avec ce noeud. La qualité de l'algorithme
glouton et l'heuristique choisie pour mesurer les déviations
déterminent en grande partie l'efficacité de la
méthode.
Les méthodes décrites ci-dessus
présentent toutes l'intérêt de dépendre d'un seul
paramètre, qui détermine le niveau de complétude de la
résolution. En effet, si ce paramètre est fixé à
une grande valeur, les résolutions seront de type exactes. Ces
méthodes, bien que pouvant s'avérer très efficaces,
présentent néanmoins un défaut principal : leur
réussite est fortement dépendante de l'efficacité des
heuristiques retenues. Dans le cas d'une heuristique peu efficace, les
déviations ne sont pas significatives. On remarque donc que ces
méthodes doivent être adaptées au problème
traité, pour se montrer le plus efficace possible.
1.2.4 Ordre dynamique
Plusieurs travaux ont déjà
développé l'idée d'utiliser un ordre dynamique dans le
choix des variables ou des valeurs. La plupart de ces méthodes
intègrent un processus de mémorisation, appelé look
back.
Frost et Dechter (1994) ont présenté une
nouvelle heuristique d'ordre de choix de valeurs pour les variables,
appelée sticking value. L'idée principale est de garder
en mémoire la valeur assignée à une variable durant la
phase de remontée dans l'arbre, et de sélectionner cette valeur,
si elle est consistante, la prochaine fois que cette variable devra être
instanciée durant une phase de remontée. Leur intuition est que
si cette valeur a été un succès à un moment
donné, cela peut être utile de la choisir plus tard dans la
recherche, afin d'accélérer la résolution. Les
résultats obtenus montrent que cet algorithme offre de bonnes
améliorations des performances, en réduisant de manière
significative les temps d'utilisation du CPU, surtout lorsque les domaines des
variables sont de tailles réduites.
YIELDS (A yet improved limited discrepancy
search) (Karoui et al., 2007) est une méthode exact qui
résout des problèmes de satisfaction de contraintes. YIELDS
est une version améliorée de Limited Discrepancy Search
qui intègre de la propagation de contraintes et de l'apprentissage
d'ordre de variables. Le schéma d'apprentissage, qui est la contribution
principale de cette méthode, est basé sur les échecs
rencontrés durant la recherche, dans le but d'augmenter
l'efficacité de l'heuristique de sélection des variables. Un des
objectifs de YIELDS est de trouver une amélioration au
principal défaut de LDS, celui d'être un algorithme redondant,
c'est-à-dire que des mêmes parcours peuvent être faits un
nombre important de fois. Avec la méthode LDS, l'ordre de
traitement des variables n'est déterminé que par une heuristique
et n'est pas modifié par la méthode. Cela signifie que lorsque
LDS est relancé en augmentant le nombre de déviations
autorisées, on doit instancier plusieurs fois la même variable
initiale. Or, si on suppose que cette variable est la cause d'échecs, il
n'est pas nécessaire de développer sa branche à nouveau.
Pour éviter ce genre de situation, un poids est associé à
chaque variable. Ce poids est fixé initialement à 0. Durant la
résolution de l'algorithme, le poids associé à la variable
est incrémenté à chaque fois que la variable en question
est en échec à cause de la limite sur le nombre de
déviations autorisées : même si le domaine de cette
variable est non vide, on ne peut choisir aucune de ses valeurs sans augmenter
le nombre de déviations. Dans les itérations suivantes, cette
variable sera privilégiée et placée en priorité
dans la branche. Cette technique permet d'éviter la situation
d'inconsistances causées par cette variable. En introduisant la notion
de poids, le but est de corriger l'heuristique de choix dans les variables afin
de guider ce choix vers les variables très contraintes. En effet, ce
sont ces variables en particulier qui influent sur la qualité de la
recherche de solutions. Afin d'accélérer le processus, les
sous-problèmes difficiles et/ou inconsistants sont placés en haut
de l'arbre de recherche. Cette méthode s'applique surtout aux
problèmes de satisfaction de contraintes.
Refalo (2004) a proposé une stratégie de
recherche générale appliquée à de la programmation
par contraintes, basée sur les impacts. L'impact de l'affection de la
variable xi à la valeur a est défini de la
manière suivante : I(xi = a) = 1 -
Paprès/Pavant où P
est défini comme une estimation de la taille de l'arbre
de recherche. L'estimation retenue dans l'article est le produit
cartésien des domaines de l'ensemble des variables. Plusieurs
stratégies de choix de variables sont proposées. Afin de
réduire l'arbre de recherche, la variable ayant l'impact le plus
important est choisie en premier. Le branchement se fera alors sur la valeur de
la variable ayant le plus petit impact. Afin que les décisions prises au
début de l'arbre de recherche soient les plus judicieuses possibles, la
méthode propose une initialisation des impacts en calculant une
approximation des impacts. Celle-ci sera remplacée par la suite par les
impacts effectifs. Des stratégies de redémarrage sont ensuite
appliquées en cours de résolution, lorsque les impacts deviennent
de plus en plus précis.
Levasseur etal. (2007) proposent une extension de
cette méthode pour les problèmes de Weighted Contraint
Satisfaction. L'impact est alors défini comme étant une
estimation de la capacité de l'affectation de la variable a
à la valeur i à être présente dans des
solutions optimales. Des méthodes de descentes gloutonnes permettent
d'augmenter le nombre de solutions rapidement, afin de rendre les impacts plus
précis. La sélection des variables est dans un premier temps
basée sur une heuristique qui choisit la variable ayant le plus petit
rapport de la taille du domaine sur le degré futur, celui-ci
étant défini comme le nombre de contraintes portant sur la
variable qui ont au moins une variable non affectée.
Zanarini et Pesant (2007) proposent une heuristique
centrée sur les contraintes qui guide l'exploration de l'espace de
recherche vers les sous-espaces qui semblent contenir un grand nombre de
solutions. Ils proposent de nouvelles heuristiques de recherche basées
sur le dénombrement de solutions pour chaque contrainte. De plus, ils
proposent des algorithmes pour évaluer le nombre de solutions pour deux
familles de contraintes : les contraintes de dénombrement d'occurrence
et les contraintes d'ordonnancement. Leur intuition est qu'une contrainte avec
peu de solutions correspond à un sous-espace critique du
problème.
Boussemart et al. (2004) présentent une
heuristique d'ordre dynamique sur les variables, appelée
dom/wdeg, qui guide la recherche vers des espaces inconsistants des
problèmes de Satisfaction de Contraintes. Cette heuristique
générique exploite les informations sur des états
précédents de la recherche. Un poids est associé à
chaque contrainte. Ce poids est incrémenté dès que la
contrainte associée est violée durant la recherche.
Récemment, Balafoutis et Stergiou (2008) ont
proposé une méthode qui utilise l'information des poids des
contraintes pour d'une part, établir un ordre de traitement sur les
variables, et d'autre part, trier efficacement la liste de révision des
méthodes basées sur l'arc-consistance. Ils montrent que les
heuristiques proposées, quand elles sont utilisées en même
temps qu'une heuristique de sélection de variable qui suit la politique
«first fail », se montrent très efficaces en réduisant
la taille de l'arbre de recherche par une recherche centrée sur les
variables les plus significatives.
Les méthodes existantes peuvent soulever certaines
difficultés. Certaines sont plus génériques que d'autres
et nécessitent une adaptation au problème pour se montrer les
plus efficaces. Elles sont pour la plupart dépendantes de la nature du
problème; elles sont soit adaptées à des problèmes
d'optimisation combinatoire, soit à des problèmes
de satisfaction de contraintes.
1.2.5 Apprentissage : look-back
Dans le cadre des problèmes de satisfaction de
contraintes classiques, le Backtracking (voir la section 1.2.1 pour
une définition) souffre fréquemment d'un phénomène
de « trashing >>, qui se traduit par le fait de redécouvrir
de manière répétitive les mêmes échecs et les
mêmes instanciations partielles durant la recherche.
Les procédures dynamiques d'amélioration de
parcours de l'arbre sont les schémas du type « look-ahead>>
(sélection de variables et de valeurs) et « look-back>>
(Backjumping, apprentissage, Nogood Recording). Le
raisonnement du Backtrack conclut au rejet d'un certain nombre de
choix combinatoires; le Nogood Recording (Schiex et Verfaillie, 1994)
consiste à mémoriser ces choix afin de ne plus les reproduire.
Ainsi, plusieurs techniques d'apprentissage des échecs ont
été proposées.
Le Backjumping a été proposé par
Gaschnig (1979). Supposons qu'un échec est rencontré sur la
variable xi. La technique de Backtrack classique revient sur
la dernière variable instanciée xi_1. Si une
autre valeur est possible pour xi_1 mais qu'aucune
contrainte ne porte sur les variables xi et xi_1,
alors la variable xi_1 ne peut être la source de
l'échec rencontré sur xi. Ainsi, on retrouve
nécessairement un échec sur la variable xi pour chaque
valeur instanciée de xi_1. Gaschnig (1979) propose
d'améliorer ce processus en identifiant la variable coupable de
l'échec et en effectuant le retour dans l'arbre sur cette variable.
L'identification est basée sur la notion d'ensemble en conflit. Un
ensemble en conflit est une instanciation d'un sous-ensemble de variables ne
laissant aucune possibilité pour une certaine variable non encore
instanciée. Une instanciation partielle qui n'apparaît dans aucune
solution est un « NoGood >> (Doyle, 1979).
Ginsberg (1993) a proposé un nouvel algorithme pour
résoudre les problèmes de satisfaction de contraintes. Cet
algorithme, appelé Dynamic Backtracking peut être vu
comme une amélioration du principe de Backjumping, de Graph
Based Backjumping (Dechter, 1990) et de la méthode Conflict
Directed Backjumping algorithms (Prosser, 1993) . La méthode
Conflict Directed Backjumping enregistre à chaque étape
de la recherche et pour chaque variable xi, l'ensemble des variables
assignées qui a conduit à une réduction de domaine de
xi. De tels ensembles sont appelés des ensembles de conflits.
Dynamic Backtracking enregistre le même type d'informations,
mais à un niveau plus fin. À chaque étape de la recherche,
pour chaque variable xi et pour chaque valeur j qui a
été supprimée du domaine courant de xi,
l'algorithme enregistre l'ensemble des variables assignées
précédemment qui sont responsables de cette élimination.
Ces ensembles sont appelés des explications
d'élimination. L'ensemble en conflit d'une variable est alors
défini comme l'union des explications d'élimination des
valeurs de cette variable.
Chvátal (1997) a présenté une
méthode exhaustive pour la résolution de problèmes
linéaires en variables binaires, Resolution Search. Cette
méthode se démarque des procédures arborescentes
classiques par une exploration originale de l'espace de recherche,
censée permettre de rendre la résolution du problème moins
largement dépendante de
la stratégie de branchement invoquée. Celle-ci,
à l'instar des procédés de backtracking intelligents, est
basée sur le principe d'apprentissage qui consiste à identifier
et mémoriser les raisons des échecs qui surviennent tout au long
de la recherche. Lorsqu'un échec est détecté au cours de
l'exploration de l'espace de recherche, l'ensemble des variables, dont
l'instanciation est responsable de l'échec, est déterminé
à partir de la configuration partielle courante. Interdire pour la suite
de la recherche cette instanciation partielle revient à
générer une contrainte additionnelle au problème,
appelée Nogood, afin de couper la recherche en amont du noeud
considéré. Resolution Search propose un schéma
original de gestion de ces nogoods. Celui-ci permet de limiter
l'espace mémoire et le temps de traitement des nogoods. De
plus, il permet d'indiquer rapidement comment poursuivre la recherche à
la suite d'un échec, tout en assurant la convergence de l'algorithme.
Demassey (2003) a appliqué cette méthode sur le problème
d'Ordonnancement de Projet à Contraintes de Ressources (RCPSP). Palpant
(2005) a proposé une utilisation de cette approche pour la
résolution du problème des
Queens_n2.
1.2.6 Métaheuristiques combinées à la
recherche arborescente
Frenc et al. (2001) proposent une méthode
hybride qui combine un algorithme génétique et un Branch
& Bound pour un problème de MAX-SAT. Les algorithmes
génétiques appartiennent à la famille des
métaheuristiques; ils utilisent la notion de sélection naturelle
et l'appliquent à une population de solutions potentielles au
problème donné. Il y a trois aspects dans les algorithmes
génétiques : la sélection, le croisement et la mutation
(voir le chapitre 4 pour plus de détails sur les algorithmes
génétiques). Dans cette configuration, chaque
élément de chromosome correspond à une variable binaire de
l'instance du problème. L'hybridation proposée dans cet article
montre de meilleurs résultats que l'utilisation seule d'un Branch and
Bound ou d'un algorithme génétique.
Pessan et al. (2007) présentent une
méthode d'hybridation entre une approche de Branch & Bound et un
algorithme génétique. Leur idée est d'utiliser
l'algorithme génétique pour améliorer la borne
supérieure et ainsi accélérer la résolution par
Branch & Bound, tandis que l'algorithme génétique utilise les
noeuds non instanciés de la méthode de Branch & Bound afin de
réduire l'espace de recherche. Les deux méthodes sont
utilisées en parallèle et collaborent ensemble.
D'autres métaheuristiques sont basées sur la
coopération. On peut citer notamment les algorithmes d'Optimisation par
Colonie de Fourmis (Dorigo et al., 1991) dans lesquels des fourmis
construisent des solutions et déposent des quantités de
phéromone dépendant de la qualité des solutions
trouvées (voir le chapitre 3 pour plus de détails sur les
algorithmes d'Optimisation par Colonie de Fourmis). Cette phéromone est
ensuite utilisée par les fourmis afin de les diriger vers un espace de
recherche. Un processus d'évaporation permet de ne garder qu'un ensemble
de solutions jugées intéressantes. Khichane et al.
(2008) proposent une méthode qui utilise un langage de
programmation par contraintes pour décrire un problème et
remplace la procédure de recherche arborescente par une recherche par
Optimisation par Colonie de Fourmis. Chaque fourmi construit une affection ne
violant aucune contrainte, cette affectation
pouvant être partielle. La qualité des affectations
construites dépend du nombre de variables affectées.
La plupart des métaheuristiques sont utilisées
davantage pour des problèmes d'optimisation combinatoire pour lesquels
le nombre de solutions est important. En effet, ces métaheuristiques
étant pour certaines basées sur la coopération entre les
solutions, le nombre de solutions détermine en partie
l'efficacité de la méthode.
1.3 Dynamic Learning Search: une méthode par
apprentissage
La plupart des méthodes de résolution exactes
utilisées en optimisation combinatoire s'appuient sur une
énumération intelligente des solutions (Branch and Bound,
Programmation par contraintes, Programmation dynamique, ...). Cette
énumération revient généralement à
construire un arbre de recherche, pour lequel un certain nombre de
décisions sont prises à chaque noeud.
La construction d'un arbre dépend de trois niveaux de
décisions:
Le schéma d'exploration : ce
schéma détermine la manière dont va se dérouler
l'exploration de l'arbre (on peut citer par exemple Depth First
Search, Breadth First Search, Back Jumping, ...). Ces
schémas ne modifient pas la structure principale de l'arbre. Par contre,
par des mécanismes de coupes (Branch & Bound, Branch & Cut)
et/ou de calculs de bornes, l'exploration de certaines parties de l'arbre peut
être tronquée, ces parties étant différentes selon
les schémas d'exploration retenus.
Le schéma de recherche: L'arbre est
structuré par les schémas de recherche. Cette structure est
déterminée par la politique de choix des variables, ainsi que par
la politique de séparation du domaine des variables (arbre binaire, un
noeud-fils par valeur possible, equal-split, ...). Ces schémas de
structure ont un impact important sur les performances du parcours de l'arbre
de recherche (en terme de rapidité de temps de calcul et d'occupation
mémoire). Les schémas les plus connus pour les politiques de
choix de variables sont l'ordre lexicographique, MinDom, ou encore
Dom/DDeg.
Le schéma de complétude :
à partir de ce schéma, on détermine la
complétude de l'algorithme, c'est-à-dire le fait de choisir entre
une exploration complète (et donc une résolution exacte) et une
exploration tronquée (et une résolution approchée). Dans
le cas où l'on souhaite une résolution approchée, on peut
par exemple choisir de ne pas tester toutes les valeurs d'une variable, les
valeurs à tester pouvant être déterminées par des
heuristiques (politique de type Limited Discrepancy Search).
La méthode Dynamic Learning Search
détermine un schéma structurel de l'arbre de recherche, mais
aussi un schéma d'exploration de cet arbre. De plus, cette
méthode est facilement adaptable dans le cas où l'on voudrait une
méthode exacte ou heuristique.
La méthode Dynamic Learning Search (DLS) est
conçue dans l'objectif de diriger la recherche vers les parties de
l'espace des solutions contenant les meilleures solutions. Cette méthode
se veut générique, de manière à pouvoir être
utilisée indépendamment du problème traité. La
méthode DLS se greffe sur un parcours en profondeur et définit de
manière dynamique à chaque noeud de l'arbre des règles de
priorité pour la sélection de la variable sur laquelle brancher
et pour l'ordre dans lequel les différentes valeurs possibles pour
chaque variable sont explorées. Ces ordres sont déduits des
caractéristiques des sous-arbres obtenus jusque là lors de
branchements concernant la même variable. Ainsi, lors de l'exploration,
à chaque fermeture de sous-arbre (c'est-à-dire lorsque la branche
issue de la dernière valeur d'une variable vient d'être
explorée), le poids associé à la variable et l'ordre des
valeurs à instancier pour cette variable sont mis à jour. Ces
mises à jour peuvent dépendre de différents
critères : qualité de la meilleure solution trouvée dans
le sous-arbre considéré, nombre de coupes effectuées (dans
le cas d'un Branch and Bound), moyenne des solutions... En pratique, les
critères retenus dépendent principalement de la nature du
problème : optimisation combinatoire ou satisfaction de contraintes.
Le fonctionnement d'une recherche arborescente semble le
même que ce soit pour un problème d'optimisation combinatoire ou
pour un problème de satisfaction de contraintes. A chaque noeud de
l'arbre de recherche, des décisions sont prises. Ces décisions
concernent la plupart du temps la diminution du domaine d'une variable. La
méthode DLS est donc conçue dans l'optique de pouvoir s'appliquer
assez aisément sur ces deux types de problèmes, avec toutefois
une adaptation de la fonction d'évaluation qui permet de
déterminer les règles de priorité pour la sélection
des variables et l'ordre dans lequel les différentes valeurs possibles
pour la variable sont explorées.
Les sections suivantes vont détailler les trois aspects
de la méthode DLS : Dynamic, Learning et Search.
1.4 Learning : une méthode basée sur un
apprentissage
La phase de Learning se décompose en plusieurs
sous-parties : le sondage, l'apprentissage, la prévision et la remise en
question.
1.4.1 Sondage
Le sondage représente la phase de démarrage de
notre méthode. On sait que les décisions prises au sommet de
l'arbre de recherche sont primordiales pour l'efficacité de la
résolution. Il existe donc des méthodes génériques
afin de choisir le plus judicieusement possible les variables. Ces
méthodes sont basées sur l'idée que les variables les plus
intéressantes à choisir au début de la résolution
sont les variables les plus contraintes et les plus contraignantes. On peut
donc choisir les variables ayant le plus petit domaine, le plus fort
degré de connexité ou une combinaison des deux
précédents critères. Mais, il existe des
problèmes oü ces critères ne suffisent pas à
déterminer quelles variables choisir, par exemple, lorsque toutes les
variables ont le même domaine. Un choix pertinent de variables est alors
complexe.
Dans un souci de généricité, notre
méthode se base sur une phase de sondage. Le sondage permet de prendre
connaissance rapidement de l'arbre de recherche, il consiste en un
apprentissage rapide et non exhaustif. Le sondage peut être totalement
aléatoire ou dirigé vers un espace de recherche précis,
notamment en fixant certaines variables à des valeurs. Une des
principales difficultés est de déterminer le temps à
passer dans cette phase. En effet, le fait de passer beaucoup de temps dans la
phase de sondage comporte deux risques principaux. Premièrement, si le
problème est facilement résoluble, la phase de sondage peut
s'avérer plus longue que la résolution proprement dite.
Deuxièmement, on peut risquer d'accorder une confiance trop importante
au sondage et de ne pas remettre en question par la suite les informations
apportées lors du sondage. Le temps accordé à la phase de
sondage est donc un paramètre important. Une fois la phase de sondage
terminée, les fonctions d'évaluation permettent d'attribuer des
poids initiaux aux variables, ainsi qu'aux valeurs appartenant aux domaines des
variables. Ces poids serviront dans la suite de la résolution afin de
déterminer des ordres de branchement.
Un cas pratique de sondage est le suivant. Pour un
problème de satisfaction de contraintes, une variable est choisie
aléatoirement, puis une valeur du domaine de cette variable est choisie
aléatoirement. Un algorithme de filtrage est appliqué. On
réitère ce procédé jusqu'à obtenir un
conflit (une variable dont le domaine a été réduit au
domaine nul). On évalue alors les sous-arbres fermés et on
relance la résolution. Dans le cas d'un sondage dirigé, lorsque
la fonction d'évaluation semble nous indiquer qu'un espace de l'arbre de
recherche est intéressant, on peut alors intensifier le sondage aux
abords de cet espace de l'arbre de recherche.
1.4.2 Apprentissage
Dans un schéma d'exploration classique d'un arbre de
recherche, lorsqu'on arrive à une feuille qui n'est pas une solution
(c'est-à-dire lorsque des variables ont leur domaine vide ou lorsqu'un
calcul de borne inférieure permet d'arrêter l'exploration), on
effectue un Backtrack qui consiste à remettre en cause la
dernière décision prise. On prend alors une nouvelle
décision, si cela est possible. Dans le cas contraire, on remonte dans
la liste des décisions prises. Un des gros inconvénients de cette
méthode est d'oublier tout ce qui a été appris lors de
l'exploration qui a mené à un échec, et ne garder en
mémoire que le fait que les décisions n'étaient pas
bonnes. En effet, lors d'un Backtrack, lorsqu'une valeur d'une variable a
mené à un échec (ou à une solution dans le cas d'un
problème d'optimisation combinatoire), on choisit la plupart du temps
une autre valeur pour cette même variable. Or, parmi toutes les
décisions prises qui mènent à des échecs, certaines
ont pu être mauvaises et d'autres très mauvaises.
A travers la phase d'apprentissage, la méthode Dynamic
Learning Search tente de tirer des enseignements des erreurs passées,
afin de diriger la recherche vers un es-
pace qui soit le plus prometteur possible (voir la section
1.2.5 pour plus de détails sur d'autres techniques basées sur
l'apprentissage). Les techniques existantes se basent en général
sur les « NoGood ». Elles mémorisent ainsi les causes
d'échec et tentent de ne plus commettre les mêmes échecs.
La méthode DLS tente quant à elle de retenir les bonnes
décisions et de les reproduire.
La phase d'apprentissage est donc une des phases les plus
importantes de notre méthode. Durant cette phase, on va évaluer
la qualité d'un sous-arbre, c'est-à-dire d'un es-pace de
solution. De cette évaluation découlera une affectation de poids
aux variables, ainsi qu'aux valeurs appartenant aux domaines des variables. Ces
affectations permettront un ordonnancement parmi les variables non
fixées sur lesquelles brancher, ainsi que l'ordre dans lequel leurs
valeurs seront explorées.
La qualité d'un sous-arbre dépend de plusieurs
paramètres. En particulier, on peut facilement se rendre compte que la
fonction d'évaluation pour un problème de satisfaction de
contraintes n'est pas la même que pour un problème d'optimisation
combinatoire. Dans le cas d'un problème de satisfaction de contraintes,
on cherche à obtenir une seule solution complète,
c'est-à-dire que l'ensemble des variables du problème soient
instanciées. On peut donc estimer que, plus le nombre de variables
instanciées dans un espace de solution est important, plus les
décisions prises correspondantes semblent prometteuses. La profondeur
d'un sous-arbre (déterminée par le cardinal des variables
instanciées) semble une fonction d`évaluation pertinente pour un
problème de satisfaction de contraintes (voir la section 1.8.1 pour plus
de détails). Dans le cas d'un problème d'optimisation
combinatoire, la meilleure solution en terme d'objectif contenue dans le
sous-arbre semble être une fonction d'évaluation judicieuse (voir
la section 1.8.2 pour plus de détails). En effet, si dans un sous-arbre,
il existe une solution de très bonne qualité, on peut supposer
que la solution optimale sera proche en terme d'assignation valeur/variable de
cette solution (on retrouve ce principe dans certains opérateurs de
recherche locale). On peut aussi considérer comme des critères
pertinents, des critères prenant en compte la diminution des domaines
par les algorithmes de filtrage, ou encore le nombre de coupes
effectuées dans un sous-arbre. En effet, on peut avoir
intérêt à retenir les affections de valeurs à des
variables qui ont permis de couper de manière importante l'arbre de
recherche.
On peut remarquer néanmoins que ces critères
sont des critères uniquement « positifs ». En effet, dans le
cas d'un problème à satisfaction de contraintes, on peut obtenir
deux sous-arbres dont les profondeurs maximales sont égales et pouvant
pourtant présenter un intérêt différent. On peut
imaginer qu'un des deux sous-arbres soit beaucoup moins large que l'autre
(à cause par exemple des algorithmes de filtrage). Le temps passé
à explorer ce sous-arbre aura donc été beaucoup plus
court. On aura tout intérêt à mémoriser des
critères « négatifs » afin de départager des
éventuelles égalités entre deux sous-arbres.
Les fonctions d'évaluation proposées
précédemment ne concernaient qu'un critère maximum
(profondeur maximale, meilleure solution, ...). On pourra chercher aussi
à mémoriser la qualité globale d'un sous-arbre en
observant d'autres critères : moyenne du critère sur l'ensemble
du sous-arbre, médiane, écart-type, etc. Le critère retenu
ici
est un critère maximum.
Le besoin d'adapter la méthode à la
spécificité du problème (problème de satisfaction
de contraintes ou d'optimisation combinatoire) n'apparaît que dans la
fonction d'évaluation. On peut néanmoins imaginer avoir un panel
de fonctions d'évaluations à appliquer et ainsi pouvoir
déterminer le type de problèmes en fonction de quelles
évaluations ont été les plus efficaces. Par ce biais, il
n'est plus indispensable de connaître dans quelle catégorie de
problèmes la méthode est appliquée.
1.4.3 Prévision
L'apprentissage, par la fonction d'évaluation, permet
de diriger la recherche vers des sous-espaces qui semblent prometteurs.
Lorsqu'on branche sur une variable et sur une valeur, les pondérations
associées à cette valeur et à cette variable nous donnent
une prévision de la qualité espérée du sous-arbre
qui va être parcouru.
L'apprentissage peut être un apprentissage
supervisé. Un des moyens pour cela est de comparer la qualité
d'un sous-arbre déterminée par la fonction d'évaluation et
la qualité de ce même sous-arbre prévue par les
pondérations lors de la phase d'apprentissage. Dans le cas où ces
valeurs seraient trop éloignées, cela pourrait
éventuellement indiquer que la fonction d'évaluation est
inadaptée. Il peut être alors intéressant d'envisager une
mise à jour des informations qui prenne en compte les différences
entre ce qui était prévu et ce qui est avéré.
1.4.4 Remise en question
La phase de sondage permet de diriger la recherche au sommet
de l'arbre. Cependant, il semble intéressant de ne pas se fier durant
toute l'exploration aux informations récupérées uniquement
lors de la phase de sondage. Pour cela, on peut mettre en place un
phénomène d'évaporation de l'information. Au fur et
à mesure de l'exploration de l'arbre de recherche, les informations
apportées par la phase de sondage risquent de s'avérer de moins
en moins pertinentes, le phénomène d'évaporation
permettrait alors d'oublier ces informations.
Concrètement, cela se traduit par une
décrémentation de l'ensemble des pondérations
associées aux variables et aux valeurs, après chaque branchement.
La phase d'apprentissage prend alors plus d'importance au fur et à
mesure de l'exploration par rapport à la phase de sondage. Un autre
moyen de remettre en question les différents apprentissages est
d'appliquer des processus de redémarrage. On peut imaginer re-passer par
une phase de sondage, avec certaines décisions fixées et donc
accentuer le sondage dans un espace de recherche qui semble prometteur.
L'aspect Learning de la méthode permet donc, lorsqu'un
sous-arbre est complété de déterminer la qualité de
ce sous-arbre par le biais d'une fonction d'évaluation. La section
suivante présente la façon dont sont utilisées les
pondérations associées aux variables et aux valeurs
déterminées par la fonction d'évaluation.
1.5. Dynamic : un ordre dynamique de choix des variables et de
sélection des valeurs
1.5 Dynamic : un ordre dynamique de choix des variables
et de sélection des valeurs
La phase d'apprentissage permet de déterminer la
qualité d'un sous-arbre : une fonction d'évaluation renvoie une
valeur (ou plusieurs valeurs) quant a la qualité estimée de ce
sous-arbre. Ainsi, une pondération va être associée a
chaque décision qui correspond a l'obtention de ce sous-arbre. La mise a
jour des pondérations se passe de la manière suivante : lorsqu'un
sous-arbre est complété, on regarde toutes les décisions
qui ont été prises pour amener a ce sous-arbre et la
pondération associée a ce sousarbre va remplacer les
pondérations précédentes, dans le cas où elle est
de meilleure qualité. Prenons un exemple concret : lors de l'exploration
de l'arbre de recherche, une pondération de valeur n avait
été associée a la variable xi. Si par la suite,
la fonction d'évaluation renvoie une pondération égale a
m (avec m < n), alors la pondération
associée a la variable xi sera dorénavant m.
D'autres choix de mises a jour sont envisageables, tels que la moyenne de
l'ancienne pondération et de la nouvelle, ou encore la somme.
Ces pondérations permettent d'ordonner le choix de
sélection des variables. Lors de l'exploration, quand le choix
concernant la prochaine variable se pose, la méthode DLS choisit la
variable non-instanciée possédant la plus faible
pondération. Puis, la valeur sur laquelle brancher est ensuite choisie
en fonction des pondérations de l'ensemble des valeurs du domaine de la
variable. La phase d'apprentissage a indiqué que cette valeur pour cette
variable semblait conduire vers des espaces de recherches intéressants.
Donc, la recherche est intensifiée dans les sous-arbres correspondant a
ce couple variablevaleur.
Une fois que le sous-arbre a été exploré
et que les algorithmes de filtrage ont été appliqués, les
pondérations sont de nouveau mises a jour a l'aide de la fonction
d'évaluation.
Les fonctions d'évaluation présentées
proposent une pondération pour un couple valeur-variable. A partir de
ces pondérations, il faut déterminer une pondération
associée a une variable. Pour cela, il est possible de faire la moyenne
des pondérations associées aux valeurs du domaine de la variable.
On branchera sur la variable ayant la plus petite moyenne en priorité,
afin de limiter la taille de l'arbre de recherche. D'autres pondérations
sont néanmoins envisageables.
La phase d'apprentissage permet de déterminer des
pondérations qui servent a déterminer un ordre pour les
variables, ainsi que pour chaque variable, l'ordre dans lequel ses valeurs vont
être sélectionnées. Une question importante est de savoir
quand a lieu la mise a jour des pondérations.
1.6 Search: un schéma de recherche adapté
à la méthode
La méthode DLS se base sur une recherche en profondeur.
Une fois qu'une variable a été choisie, on choisit une valeur
(selon les règles déterminées par les
pondérations), puis on applique des algorithmes de filtrage (propagation
de contraintes ou calcul de bornes inférieures). S'il reste des
variables non instanciées, on réitère le processus.
Lorsque l'exploration d'un sous-arbre est complète,
c'est-à-dire que toutes les valeurs d'une variable ont été
instanciées, la fonction d'évaluation est appelée, afin
d'obtenir des pondérations pour les valeurs instanciées, ainsi
que pour la variable instanciée. Le fait de mettre les
pondérations à jour uniquement lorsque le sous-arbre est
complété permet d'assurer d'une part la complétude de la
méthode, d'autre part la non-répétition de solutions.
Néanmoins, on peut imaginer ne pas visiter le
sous-arbre dans son intégralité. Une phase de sondage pour chaque
sous-arbre avec des informations de plus en plus complètes au fur et
à mesure de la descente dans l'arbre de recherche permettrait
d'envisager une méthode efficace applicable dans des temps
limités.
De même, on peut appliquer une méthode de type
Limited Discrepancy Search afin de limiter le nombre de valeurs
instanciées pour chaque variable.
Enfin, lorsqu'il faut choisir la prochaine variable à
instancier, on peut limiter le choix aux variables appartenant au voisinage des
variables déjà instanciées (le voisinage d'une variable
xi étant défini comme l'ensemble des variables qui
partagent une contrainte avec xi). Cela permet une certaine
continuité dans le parcours de l'arbre de recherche.
1.7 Algorithme général de la
méthode
Par la suite, nous utiliserons les notations suivantes : Soit
la variable i pour i allant de 1 à n. On note
Di le domaine de la variable i. Soit
pi,j la valeur de la pondération
associée à la jeme valeur de la variable
i, mini (respectivement maxi) la valeur minimum
(respectivement maximum) des pondérations des valeurs de la variable
i.
L'algorithme de la méthode DLS est le suivant :
1.8 Méthode Dynamic Learning Search:
critères de sélection
La plupart des méthodes existantes consistent à
définir des priorités de branchement sur les variables ou sur les
valeurs. La méthode que nous proposons consiste, quant à elle,
à définir dynamiquement des politiques de priorités de
branchement sur les variables, ainsi que sur les valeurs que peuvent prendre
les variables. N'étant pas basée sur des critères
heuristiques, cette méthode se veut surtout générique. En
effet, dans
Algorithme 1 : Algorithme général
de DLS
1 Phase Sondage;
2 tant que critère d'arrêt non
atteint faire
Construction d'arbres aléatoires : choix aléatoire
d'une variable, choix aléatoire d'une valeur dans son domaine;
4 Mises à jour des pondérations en
fonction des arbres aléatoires obtenus par le biais de la fonction
d'évaluation;
5 tant que critère d'arrêt non
atteint faire
6 Sélectionner la variable k
selon les pondérations;
7
8
9
10
Trier les valeurs j avec j ? Dk selon
les pondérations;
Branchement et propagation des contraintes et/ou calcul d'une
borne inférieure;
Mise à jour des pondérations sur les valeurs et sur
les variables au cours de la recherche dès qu'un sous-arbre est
complété (ou une partie du sous-arbre visitée dans le cas
d'une méthode non complète);
Phase d'évaporation;
un premier temps, sa seule dépendance au problème
est la nécessité de différencier les problèmes
d'optimisation combinatoires aux problèmes de satisfaction de
contraintes.
En s'inspirant des principes énoncés
précédemment, notre méthode propose des politiques de
branchement pour les valeurs et pour les variables.
1.8.1 Problèmes de Satisfaction des Contraintes
Dans le cadre de l'application de la méthode DLS aux
problèmes de Satisfaction de Contraintes, plusieurs possibilités
se sont présentées à nous pour les choix des valeurs,
ainsi que pour le choix des variables.
Choix de sélection des valeurs
Dans un problème de Satisfaction de Contraintes, la
réponse classique au problème est de type « oui >> ou
« non >> (existence ou non d'une solution). Le cas où on
recherche l'ensemble des solutions n'est pas abordé ici. La
qualité des solutions trouvées ne peut donc pas être un
critère pour le calcul des pondérations liées aux valeurs
ou aux variables.
Lorsque l'on cherche à résoudre un
problème de satisfaction de contraintes, une solution correspond
à l'instanciation de l'ensemble des variables. La feuille dans l'arbre
de recherche qui correspond à cette solution a donc une profondeur
égale au nombre de variables du problème. On comprend alors que
lorsqu'une solution existe, la feuille correspondante se situera dans un
sous-arbre de profondeur importante. On va donc
chercher à se diriger dans de tels sous-arbres. Le
critère de pondérations pour la politique de branchement sur les
valeurs est donc le suivant : pour chaque valeur de chaque variable, on garde
en mémoire le maximum des profondeurs maximales des sous-arbres
engendrés. La profondeur correspond dans notre cas au nombre de
variables instanciées. On ne différenciera pas le cas des
variables instanciées lors de la phase de propagation des contraintes,
des variables instanciées lors de la séparation. La
pondération associée au choix de cette valeur est donc mise
à jour chaque fois que le choix de cette valeur engendre un sous-arbre
d'une profondeur plus importante que tous les sous-arbres engendrés
précédemment dans l'arbre par cette valeur.
Comme on cherche à se diriger vers les sous-arbres de
plus grande profondeur, on va donc choisir pour chaque variable la valeur ayant
la pondération la plus importante.
La moyenne de la profondeur du sous-arbre engendré ne
nous a pas semblé être un bon critère de sélection.
En effet, une valeur qui amènerait à un sous-arbre ayant un
chemin de grande profondeur et un grand nombre de chemins de petites
profondeurs aurait une moyenne de profondeur de sous-arbre assez faible et
serait donc pénalisée alors que cette valeur peut s'avérer
très intéressante, puisqu'elle a amené à un chemin
de grande profondeur.
Choix de sélection des variables
On a vu que le choix des variables était primordial
pour la taille de l'arbre de recherche. Plusieurs choix sur l'ordre de
sélection des variables sont possibles, certains tirent parti des
pondérations calculées pour le choix des valeurs, d'autres sont
plus génériques et utilisés de façon assez
répandue. Les choix suivants sont des choix classiques de la
littérature.
- Première variable non instanciée : on choisit
parmi les variables non instanciées la première variable dans un
ordre lexicographique.
- Plus petit domaine : on choisit en priorité parmi les
variables non instanciées la variable qui possède le plus petit
domaine. Ce domaine peut être calculé en phase initiale de la
résolution du problème ou de manière dynamique à
chaque noeud.
- Plus petit regret minimum : ce choix renvoie la variable
avec la plus petite différence entre la plus petite valeur possible et
la prochaine plus petite valeur possible. Ce choix est basé sur le
principe de regret. Le regret est défini comme la différence
entre ce qu'aurait été la meilleure décision possible dans
un scénario et la décision actuelle. Dans un problème des
satisfaction de contraintes, on peut définir le regret minimum comme la
différence entre les deux plus petites valeurs du domaine d'une
variable.
- Plus petit regret maximum: ce choix renvoie la variable avec
la plus petite différence entre la plus grande valeur possible et la
prochaine plus grande valeur possible.
- Plus fort degré : on choisit la variable ayant le
degré futur le plus important, le degré étant
défini pour une variable comme le nombre de contraintes portant sur
celle-ci et ayant au moins une variable non affectée.
- Plus petit domaine divisé par le plus fort
degré (MinDom/Deg) : on choisit la variable ayant le plus petit rapport
entre la taille de son domaine et le degré de cette variable.
Pour les choix des variables qui utilisent les
pondérations sur les variables, nous avons proposé les ordres
suivants :
- Profondeur maximale : on choisit parmi les variables non
instanciées la variable qui a parmi ses valeurs celle qui a amené
au sous-arbre le plus profond. Ce choix ne nous semble pas cohérent. En
effet, lors de la fermeture d'un sous-arbre de profondeur n (où
n est maximal), toutes les variables instanciées ont une de
leurs valeurs qui a une pondération égale à n.
Selon le critère « Profondeur maximale » pour le choix de la
variable, toutes les variables auraient la même pondération et il
faudrait donc choisir parmi toutes ces variables. Ce choix pourrait alors se
faire de manière aléatoire ou lexicographique, mais ne
profiterait pas des informations apportées par les pondérations
sur les valeurs.
- Moyenne maximale : ce critère propose de choisir la
variable ayant la moyenne de pondération de ses valeurs la plus
importante. Par ce principe, on cherche à brancher en priorité
sur les variables qui ont amené à des sous-arbres de taille
importante. Ce critère est en opposition avec certains principes
proposés auparavant (Haralick et Elliot, 1980).
- Moyenne minimale : ce critère propose de choisir la
variable ayant la moyenne de pondération de ses valeurs la moins
importante. On dirige donc la recherche vers les variables les plus
contraintes. Ce critère est proche de la philosophie de la
méthode First Fail.
- Plus petit écart aux extrêmes : ce
critère part du principe que les variables les plus intéressantes
sont les variables dont les valeurs ont amené à des sous-arbres
soit de toute petite profondeur (ces variables réduisent la taille de
l'arbre de recherche) soit de grande profondeur. On cherche donc à
choisir en priorité les variables dont les pondérations sur les
valeurs sont le plus proches possibles des extrêmes. On branchera donc
sur la variable qui minimise l'équation (1.1).
1
|Di| ? minimum(n -
pi,j, pi,j) (1.1)
j?Di
où n représente le nombre de variables (et
donc une borne supérieure de la profondeur maximale de l'arbre de
recherche).
Pour ne pas privilégier les variables dont le domaine
initial est restreint, cette somme est divisée par le nombre de valeurs
du domaine (|Di|).
On peut remarquer que si l'on enlève le premier terme du
minimum, on cherche alors la variable qui minimise
1
|Di| ? (n - pi,j) (1.2)
j?Di
ce qui est équivalent à rechercher la variable qui
maximise
1
|Di| ? (pi,j) (1.3)
j?Di
Ce critère correspond alors à une constante
prêt au critère de choix de Moyenne maximale. De manière
équivalente, si l'on enlève le deuxième terme, on cherche
alors la variable qui minimise
1
|Di| ? (pi,j) (1.4)
j?Di
ce qui correspond au critère de choix de Moyenne
minimale.
Les critères de pondérations retenus pour les
choix des valeurs (et donc certains des critères de choix des variables
qui dépendent des pondérations) ne sont pas adaptés pour
les problèmes d'optimisation combinatoire.
1.8.2 Problèmes d'Optimisation Combinatoire
Dans le cadre de problèmes d'optimisation combinatoire,
plusieurs possibilités se sont présentées à nous
pour les choix des valeurs, ainsi que pour le choix des variables.
Choix des Valeurs
Dans un problème d'optimisation combinatoire, on
cherche à minimiser (ou maxi-miser) un objectif. Par la suite, nous
considérerons uniquement le cas où l'on cherche à
minimiser un objectif.
La qualité des solutions trouvées peut donc
être un critère pertinent pour le calcul des pondérations
liées aux valeurs ou aux variables. Pour chaque valeur de chaque
variable, on garde en mémoire le coût de la meilleur solution
trouvée par cette affectation variable - valeur.
De manière équivalente aux problèmes de
satisfaction de contraintes, la moyenne des coûts des solutions ne nous a
pas semblé être un bon critère de sélection. En
effet, une valeur qui amènerait à un sous-arbre très
déséquilibré (de très bonne qualité d'un
côté et de très mauvaise qualité d'un autre
côté) aurait une moyenne de coût des solutions de sous-arbre
assez élevée, alors que cette valeur peut s'avérer
très intéressante.
Comme on cherche à se diriger vers les sous-arbres
contenant les feuilles de coûts les plus faibles, on va donc choisir pour
chaque variable, la valeur ayant la pondération la moins importante.
Choix des variables
On a vu que le choix des variables était primordial
pour la taille de l'arbre de recherche. Comme pour les problèmes de
satisfaction de contraintes, un certain nombre de choix sur les variables sont
possibles :
- Plus petit domaine,
- Plus petit regret minimum (le regret est calculé
généralement par rapport à la valeur de la fonction
objectif),
- Plus petit regret maximum,
- Plus fort degré,
Pour les choix des variables qui utilisent les
pondérations sur les variables, nous avons proposé les
possibilités suivantes (pour plus de détails, voir la section
1.8.1) :
- Moyenne maximale,
- Moyenne minimale,
- Plus petit écart aux extrêmes.
On remarque que les heuristiques de critères de choix sur
les valeurs doivent être adaptées en fonction du type de
problème sur lequel on veut appliquer notre méthode.
Néanmoins, on retrouve, pour l'heuristique de choix sur
les valeurs à brancher, de grandes ressemblances entre les
problèmes de satisfaction de contraintes et les problèmes
d'optimisation combinatoire.
La question que nous nous sommes posé est de savoir si une
heuristique de choix sur les valeurs peut être identique pour les deux
types de problèmes.
1.8.3 Méthode commune aux deux types de
problèmes
On constate que les heuristiques proposées, en ce qui
concerne les choix des valeurs sur lesquelles brancher, sont fortement
dépendantes du type de problème. Dans la section suivante, nous
proposons une heuristique de choix de valeur qui ne dépend pas du type
de problème étudié.
Choix des valeurs
Rappelons le principe général de fonctionnement
d'un Branch & Bound dans le cas d'un problème d'optimisation
combinatoire. On choisit une variable parmi les variables non
instanciées. On crée autant de noeuds fils que le nombre de
valeurs de la variable. Pour chaque valeur, on calcule une borne
inférieure (par résolution d'une relaxation spécifique, de
programmation linéaire, etc.). Si cette borne inférieure est
supérieure à la plus petite borne supérieure connue, on
arrête l'exploration du sous-arbre engendré par cette valeur et on
passe à une autre valeur. Dans le cas contraire, il existe deux
possibilités : soit on est à une feuille et dans ce cas, on met
à jour la borne supérieure, soit on continue l'exploration de
l'arbre de recherche. On peut remarquer que cette méthode est fortement
dépendante de l'efficacité du calcul de la borne
inférieure.
On peut remarquer une analogie entre la coupe effectuée
dans l'arbre lorsque la borne inférieure est supérieure à
la borne supérieure avec les retraits des valeurs d'un domaine d'une
variable suite à une propagation de contraintes dans un problème
de satisfaction de contraintes. En effet, lorsqu'une valeur est
supprimée d'un domaine, cela revient à dire que l'instanciation
de cette valeur est impossible, puisqu'elle violerait un certain nombre de
contraintes. Lorsqu'un sous-arbre est fermé pour une valeur dans
un Branch & Bound, cela revient à dire que cette
valeur viole la contrainte qui assure que les bornes inférieures doivent
être inférieures à la plus petite borne
supérieure.
Une heuristique de critère de choix pour les valeurs
est donc la suivante. Pour chaque valeur, on garde en mémoire le nombre
de fois où l'arbre est coupé (ou que la valeur est
supprimée du domaine de la variable dans le cas du problème de
satisfaction de contraintes). On triera les pondérations sur les valeurs
par ordre croissant afin de diriger la recherche dans l'arbre vers les
meilleures solutions (ou vers les espaces de recherche étant
supposés contenir une solution). Néanmoins, on se rend compte que
ce critère n'est pas assez précis. En effet, ce critère ne
tient pas compte du nombre de fois où la valeur en question a
été choisie. Le critère retenu est donc le suivant. On
cherche la valeur qui minimise:
nombre de fois où la valeur a mené à un
échec (1.5)
nombre de fois où la valeur a été
choisie
Ce critère est adapté aux deux types de
problèmes et permet dans un cas comme dans l'autre de diriger la
recherche vers un espace de solutions de qualité.
Choix des variables
L'ensemble des heuristiques proposées pour le choix
concernant les variables dans le cas de problèmes d'optimisation
combinatoire ou de problèmes de satisfaction de contraintes sont
adaptées à l'heuristique de critère de choix pour les
valeurs que nous avons proposée ci-dessus.
1.9 Résultats expérimentaux
Les sections suivantes présentent l'application de
notre méthode sur plusieurs problèmes : un problème
d'optimisation combinatoire (le problème du Voyageur de Commerce), un
problème de satisfaction de contraintes pratique (le problème
d'Emploi du Temps de Garde d'Infirmières) et plusieurs problèmes
de satisfaction de contraintes (le problème du Sac-à-dos
Multidimensionnel, le problème du Carré Magique et le
problème de Coloration de Graphes).
1.9.1 Application au problème du Voyageur de
Commerce
La première application de notre méthode se fait
dans le cadre d'un problème d'optimisation combinatoire. Le
problème choisi est le problème du Voyageur de Commerce. Ce
problème présente l'avantage de fournir rapidement un nombre
important de solutions. Le but du problème est de trouver un circuit de
longueur minimal passant par n villes. Chaque ville doit être
visitée une et une seule fois.
Nous utilisons un schéma de branchement naïf dans
lequel chaque noeud est associé à une ville i et chaque
noeud fils correspond à la ville j visitée
immédiatement après i. Nous associons alors un poids
wij à chaque arc (i, j)
égal à la valeur de la meilleure solution trouvée dans
l'ensemble des sous-arbres explorés. Ce poids est mis à jour
à chaque fois qu'une solution de coût inférieur est
trouvée pour le même arc (i, j). Le
schéma de branchement consiste à choisir les arcs candidats dans
l'ordre croissant des poids. Le schéma ainsi présenté
décrit une politique de branchement fixe sur les variables (chaque noeud
du niveau k correspond à fixer une valeur à la variable
xk indiquant quel arc est emprunté à la position
k) tandis que l'ordre des valeurs est déterminé par la
méthode DLS. Les poids associés aux arcs sont initialisés
par une phase d'apprentissage. Cette phase consiste en une
génération aléatoire de chemins dans l'arbre de recherche.
Le nombre de chemins aléatoires est fixé à
n2, où n est le nombre de ville. Les
résultats montrent une réduction importante de la taille de
l'arbre de recherche, ainsi que du temps d'exécution, comparé
à une méthode de Profondeur en Premier (Depth First
Search).
Le tableau 1.1 présente nos résultats sur un
ensemble de 60 instances de problème de Voyageur de Commerce. Les
instances utilisées sont des instances générées
aléatoirement avec un nombre de villes allant de 10 à 22. Les
villes sont situées aléatoirement dans un carré de 100 par
100. 5 instances sont générées par nombre de villes. Les
instances de Problème de Voyageur de Commerce sur lesquelles notre
méthode est appliquée sont des instances de très petites
tailles par rapport à l'état de l'art (les dernières
méthodes par séparation et génération de coupes
sont capables de résoudre des instances de très grandes tailles,
comme une instance comprenant les 24978 villes de Suède), mais
permettent d'évaluer notre méthode. Les résultats
présentent le temps d'exécution moyen (en secondes) et le nombre
de noeuds, sur l'ensemble des instances.
|
Depth First Search
|
DLS
|
DLS avec apprentissage
|
|
Nombre de noeuds Temps exécution (in sec)
|
6,089,428
57
|
4,790,007
45
|
3,258,450
30
|
TABLE 1.1 - Résultats
expérimentaux pour plusieurs méthodes appliquées au
problème du Voyageur de Commerce
1.9.2 Application au problème d'Emploi du Temps de
Garde d'Infirmières
Notre méthode a été ensuite
appliquée à un problème issu d'une application pratique.
Ce problème est un problème de rotation de personnel avec
contraintes, connu sous le nom de problème d'emploi du temps pour les
gardes d'infirmières ou Nurse Rostering Problem (voir (Cheang
et al., 2003) pour plus de détails sur ces problèmes).
Ce problème est un problème de satisfaction de contraintes dont
le but est de satisfaire les contraintes de compétences tout en assurant
que les employés ayant plusieurs compétences soient
employés pour chacune de leurs compétences d'une manière
équilibrée. Le problème d'emploi du temps pour les gardes
d'infirmières est un problème NPdifficile (Osogami et Imai,
2000). Le problème étudié est un problème concret,
proposé
dans le cadre d'un partenariat avec Daumas Autheman et
Associés, qui concerne une rotation de personnel dans une entreprise de
déchargement de ferries.
Soit n le nombre d'employés.
Xijk est l'activité de l'employé i,
le jour j et semaine k, avec i = 1, . . . ,
n, j = 1, . . . , 7, k = 1, . . . , l.
Xijk est égal à 0 quand l'employé ne
travaille pas. S = 1, . . . , t est l'ensemble des
activités considérées. Soit Ci c S pour
i = 1, . . . , n, l'ensemble des activités que
l'employé i est capable d'exécuter.
Emjk est le nombre d'employés requis pour
l'activité m au jour j et semaine k. Les
contraintes sont les suivantes :
|{Xijk|Xijk = m}| = Emjk j =
1, .. . ,7 k = 1, ... , l m = 1, .. . , t (1.6)
|{Xijk|Xijk = 0}| = 2 i = 1, . . . ,
n k = 1, . . . , l (1.7)
|{Xi6k|Xi6k = 0}| = r i
= 1, .. . , n k = 1, .. . , l (1.8)
|{Xi7k|Xi7k = 0}| = r i
= 1, .. . , n k = 1, .. . , l (1.9)
b 5
|Ci|c = |{Xijk|Xijk = m}| = [
5
|Ci|1 m E Ci i = 1, .. . , n k
= 1, .. . , l (1.10)
Xijk E Ci i = 1, ... , n j = 1, ...
,7 k = 1, ... , l (1.11)
Les contraintes (1.6) assurent que, pour chaque période
de temps, le nombre d'employés assignés à
l'activité m est égal au nombre requis
d'employés. Les contraintes (1.7) assurent que chaque employé est
en repos au moins deux jours par semaine. Les contraintes (1.8) et (1.9)
assurent que le nombre de samedis et dimanches vaqués est
supérieur à r (où r est une
donnée du problème). Enfin, la contrainte (1.10) indique que si
un employé possède plusieurs compétences, il doit
être employé pour chacune de ses compétences (5
étant le nombre moyen de jours travaillés par semaine).
Nous avons implémenté une version
préliminaire de la méthode DLS telle que décrite dans la
section 1.3 et nous avons comparé notre méthode avec des
politiques (goals) proposées par le solver commercial ILOG
Solver.
Le tableau 1.2 montre nos résultats sur un ensemble de
25 instances générées aléatoirement sur un horizon
de temps allant de 4 à 75 semaines et un nombre d'employés
égal à 5. Les résultats présentent la moyenne des
temps d'exécution (en secondes) pour obtenir une solution. La limite de
temps est fixée à 600 secondes. Notre méthode est
comparée avec deux politiques par défaut dans ILOG Solver. Les
colonnes ILOG Solver et DLS correspondent à la
politique de choix des valeurs : plus petite valeur possible pour la colonne
ILOG Solver et plus grande pondération pour la méthode DLS. Les
lignes correspondent à la politique de choix des variables :
Première Variable Non Bornée ou First Unbound qui
choisit en premier la première variable non bornée, Plus Petit
Domaine ou dom qui choisit en premier la variable non bornée
avec le plus petit domaine) (ces deux méthodes sont des politiques par
défaut dans ILOG Solver), puis les politiques présentées
dans la section 1.8.1), Moyenne maximale, Moyenne minimale, Plus petit
écart aux extrêmes.
La lecture des résultats nous permet de comparer
l'efficacité des choix dans les variables. Il semble évident que
la politique de choix de variable ayant la plus grande
|
Ilog Solver
|
DLS
|
|
First unbound
|
94 s
|
117 s
|
|
Plus petit domaine
|
52 s
|
24,34 s
|
|
Moyenne minimale
|
|
0,75 s
|
|
Moyenne maximale
|
|
130,28 s
|
|
Écart aux extrêmes
|
|
3,98 s
|
TABLE 1.2 - Résultats
expérimentaux pour plusieurs méthodes appliquées au
problème d'emploi du temps pour les gardes d'infirmières
moyenne des pondérations n'est pas une politique
efficace ici. En appliquant cette politique, les résultats sont plus
mauvais que dans les politiques par défaut d'ILOG Solver. On peut
remarquer que cette politique va a l'encontre de la politique de « First
Fail >>. En choisissant la variable qui a la plus petite moyenne des
pondérations, les variables instanciées ont tendance à
couper rapidement l'arbre de recherche. Ces résultats montrent ainsi que
la politique de « First Fail>> semble la plus efficace. En
conclusion, les résultats montrent que la méthode DLS est
jusqu'à 50 fois plus rapide que les politiques par défaut d'ILOG
Solver.
1.9.3 Application à des problèmes de
Satisfaction de Contraintes académiques
Pour mesurer l'efficacité de notre méthode, nous
l'évaluons sur trois jeux de problèmes académiques. Le
premier est un ensemble d'instances du problème de sac-àdos
multidimensionnel (Multiknapsack Problem, voir (Kellerer et
al., 2004) pour plus de détails). Généralement,
l'objectif du Multiknapsack Problem est de maximiser la valeur des
objets emportés. Dans les instances choisies, le problème est
transformé en un problème de satisfaction de contraintes, pour
lequel une seule solution doit être trouvée. Pour cela, une
contrainte est ajoutée : la valeur de l'objectif doit être
supérieure à une valeur donnée. Le problème est
modélisé par un ensemble de contraintes linéaires portant
sur des variables binaires. Ces problèmes sont
généralement complexes pour des solvers basés sur de la
propagation de contraintes. 6 problèmes sont issus d'une
bibliothèque d'instances de Recherche Opérationnelle1
pour lesquels la fonction objectif est contrainte à prendre la valeur
optimale. Ces problèmes ont entre 6 et 11 contraintes et le nombre de
variables est compris entre 15 et 50.
Le second jeu de problèmes est le problème du
Carré Magique (voir le livre de Descombes (2000) pour une vision
historique de ce problème). Le problème consiste à remplir
une matrice de taille n par n de telle sorte que toutes les
cases contiennent une valeur différente et que les sommes sur chaque
ligne, sur chaque colonne et sur les deux diagonales soient les mêmes.
Enfin, le troisième jeu de problèmes est le
problème de Coloration de Graphes (voir le livre de Jensen et Toft
(1995) pour plus de détails sur ce problème). Les instances
1. Les instances sont disponibles sur le site http ://
mscmga.ms.ic.ac.uk/jeb/orlib/mdmkpinfo.html
sont issues d'une bibliothèque d'instances2.
Afin de mesurer plus efficacement notre méthode dans le temps imparti,
nous limitons la taille des instances à k. Pour cela, nous ne
prenons en considération que les k premiers noeuds du graphe.
Ainsi, nous réduisons le temps de calcul, ce qui nous permet de comparer
notre méthode avec les méthodes du solver ILOG Solver. On peut
noter que les instances ainsi construites sont de petites tailles. De plus, les
méthodes que nous proposons ne sont pas comparables en terme de
qualité et de temps d'exécution aux méthodes
dédiées à ce problème.
Toutes les expérimentations ont été
faites sur un AMD 64 X2 3800, 1 Go de RAM, en utilisant ILOG Solver 6.0. Les
tableaux 1.3, 1.4 et 1.5 présentent les temps d'exécution en
secondes et le temps a été limité à 1500 secondes.
Le nombre de points de choix est présenté afin de montrer une
mesure de la taille de l'arbre de recherche.
Pour tous les problèmes qui suivent, le critère
d'évaluation du sous-arbre qui a été retenu est la
profondeur maximale du sous-arbre. La mise à jour des
pondérations suit le principe du maximum. Ainsi, une pondération
associée à un couple variable-valeur est mise à jour
dès qu'une profondeur de taille plus importante est trouvée dans
un sous-arbre issu du même couple variable-valeur. La mise à jour
consiste en un remplacement de l'ancienne pondération par la nouvelle
pondération. Pour chaque variable, la valeur choisie en premier est
celle ayant la pondération la plus important. Enfin, la phase de sondage
consiste la construction de K chemins aléatoires, où
K est égal à la somme de la cardinalité des
domaines des variables. Ce choix permet de ne pas passer un temps trop
important dans la phase de sondage.
Le tableau 1.3 présente les résultats sur les
instances du problème de sac-à-dos multidimensionnel. Nous
comparons plusieurs méthodes : la méthode « Aléatoire
» choisit aléatoirement la variable à instancier parmi les
variables non instanciées ainsi que la valeur à instancier, la
méthode « MinDomainSize » choisit en premier la variable de
plus petit domaine et la plus petite valeur du domaine, la méthode DLS
est la méthode telle que présentée
précédemment et la méthode DLS avec sondage est la
méthode présentée précédemment,
initialisée par la phase de sondage. Pour les deux dernières
méthodes, le choix de la valeur pour chaque variable est la valeur ayant
la plus grande pondération.
Les en-têtes des colonnes sont les suivants :
- Problemes : numéro de l'instance,
- Random : temps d'exécution en secondes (CPU) et nombre
de points de choix (Pts Ch.) pour la méthode « Aléatoire
»,
- MinDomainSize : temps d'exécution en secondes (CPU) et
nombre de points de
choix (Pts Ch.) pour la méthode de choix de la variable
ayant le plus domaine,
- DLS : temps d'exécution en secondes (CPU) et
nombre de points de choix (Pts
Ch.) pour la méthode DLS,
- DLS et sondage : temps d'exécution en secondes (CPU) et
nombre de points de choix (Pts Ch.) pour la méthode DLS, combiné
avec la phase de sondage.
Les résultats présentés dans le tableau 1.3
montrent l'intérêt de notre méthode cou-
2. Les instances sont disponibles sur le site http ://
mat.gsia.cmu.edu/COLOR/instances.html
|
Problemes
|
Random CPU Pts Ch.
|
Min domain Size CPU Pts Ch.
|
DLS
CPU Pts Ch.
|
DLS et sondage
CPU Pts Ch.
|
|
Mknap1-0
|
0.02
|
2
|
0.01
|
2
|
0.02
|
2
|
0.03
|
2
|
|
Mknap1-2
|
0.02
|
10
|
0.02
|
37
|
0.05
|
15
|
0.06
|
26
|
|
Mknap1-3
|
0.03
|
408
|
0.03
|
384
|
0.06
|
344
|
0.07
|
186
|
|
Mknap1-4
|
0.55
|
11485
|
0.66
|
16946
|
0.44
|
8781
|
0.18
|
411
|
|
mknap1-5
|
48.91
|
1031516
|
3.33
|
99002
|
1.7
|
36951
|
0.74
|
6251
|
|
mknap1-6
|
>1500
|
|
340.53
|
21532775
|
328.21
|
21532762
|
50.46
|
1021984
|
TABLE 1.3 - Résultats
expérimentaux, instances de Sac-à-dos Multidimensionnel
plée avec une phase d'initialisation par sondage. La
méthode « Aléatoire » ne permet pas de résoudre
l'instance mknap1-6 dans le temps imparti. La stratégie du plus
petit domaine est ici peu efficace, puisque toutes les variables ont le
même domaine. On re-marque que la méthode DLS sans phase de
sondage est légèrement plus rapide que la méthode du plus
petit domaine. Par contre, couplée avec la phase de sondage, la
méthode DLS est plus rapide que les autres méthodes, montrant
ainsi clairement l'intérêt d'une phase de sondage.
Le tableau 1.4 présente les résultats sur les
instances du problème de sac-à-dos multidimensionnel. Les
méthodes comparées sont les mêmes que pour le
problème du sacà-dos multidimensionnel. Les en-têtes des
colonnes sont les suivants :
- Taille : taille du carré,
- Random : temps d'exécution en secondes (CPU) et nombre
de points de choix (Pts Ch.) pour la méthode « Aléatoire
»,
- MinDomainSize : temps d'exécution en secondes (CPU) et
nombre de points de
choix (Pts Ch.) pour la méthode de choix de la variable
ayant le plus domaine,
- DLS : temps d'exécution en secondes (CPU) et
nombre de points de choix (Pts
Ch.) pour la méthode DLS,
- DLS et sondage : temps d'exécution en secondes (CPU) et
nombre de points de choix (Pts Ch.) pour la méthode DLS, combiné
avec la phase de sondage.
|
Taille
|
Random CPU Pts Ch.
|
Min domain Size CPU Pts Ch.
|
DLS
CPU Pts Ch.
|
DLS et sondage
CPU Pts Ch.
|
|
5
6
7
8
9
10
|
0.08
12.2 301.17 >1500 >1500 >1500
|
291 348174 7283952
|
0.03
1.52 >1500 >1500 >1500 >1500
|
895
143726
|
0.05
34.27
2.3
48.68
>1500
>1500
|
148 951426 40310 748758
|
0.13 0.16 0.11 9.7 11.47 25.14
|
4286
9178
8261
148233
225244
484541
|
TABLE 1.4 - Résultats
expérimentaux, instances de Carré Magique
Les conclusions que l'on peut tirer à la lecture des
résultats présentés dans le tableau 1.3 sont similaires
à celles pour le problème de sac-à-dos multidimensionnel.
Pour les instances de taille supérieure à 7, la méthode
« Aléatoire » et la méthode de choix du
plus petit domaine ne trouvent aucune solution dans le temps
imparti. La méthode DLS sans phase de sondage est un peu plus rapide et
efficace que la méthode de choix du plus petit domaine, mais ne permet
pas de résoudre l'ensemble des instances. En ce qui concerne la
méthode DLS avec phase de sondage, on peut remarquer que les temps
d'exécution sont légèrement plus longs pour les instances
de petite taille. Cela est dû au temps requis par la phase de sondage.
Néanmoins, la phase de sondage semble important dans la méthode
DLS car elle permet à la méthode de résoudre l'ensemble
des instances dans le temps imparti.
Le tableau 1.5 présente les résultats sur le
problème de Coloration de Graphes. Ce problème est un
problème particulier. L'objectif étant de minimiser le nombre
chromatique (c'est-à-dire le nombre de couleurs différentes
utilisées), on peut voir ce problème comme un problème
d'optimisation combinatoire. Cependant, on peut le voir comme un
problème de satisfaction de contraintes : existe-t-il une solution
à ce problème telle que le nombre chromatique soit
inférieur à C ? Ainsi, les pondérations qui
déterminent les priorités de branchement ne sont pas
calculées pour la variable à minimiser, représentant le
nombre chromatique. Nous comparons dans ce tableau plusieurs méthodes :
la méthode « Aléatoire », la méthode «
MinDomainSize », la méthode DLS avec plusieurs critères de
choix pour les variables (moyenne des pondérations mini-male, moyenne
des pondérations maximales et écarts aux extrêmes,
présentées dans la section 1.8.1). Pour ce problème, la
méthode DLS est toujours couplée avec la phase de sondage.
Les en-têtes des colonnes sont les suivants :
- Problèmes : nom de l'instance,
- k : limite fixée à la taille de l'instance,
- Random : temps d'exécution en secondes (CPU) pour la
méthode « Aléatoire », - MinDomainSize : temps
d'exécution en secondes (CPU) pour la méthode de choix de la
variable ayant le plus domaine,
- Moy Min. : temps d'exécution en secondes (CPU) pour la
méthode DLS avec le
critère de plus petite moyenne des
pondérations pour sélectionner les variables,
- Moy Max. : temps d'exécution en secondes (CPU) pour la
méthode DLS avec le critère de plus grande moyenne des
pondérations pour sélectionner les variables,
- Ecart Min : temps d'exécution en secondes (CPU) pour
la méthode DLS avec le critère de plus petit écart des
pondérations aux extrêmes pour sélectionner les
variables,
Les résultats présentés dans le tableau
1.5 montrent l'efficacité de la plus petite moyenne des
pondérations comme critère de choix pour les variables. Ce
critère, qui suit la politique de « First Fail », est le plus
efficace pour les instances choisies. La méthode « Aléatoire
» et la méthode de choix de la variable ayant le plus domaine ne
permettent pas de résoudre l'ensemble des instances. La méthode
DLS avec le critère de plus petit écart des pondérations
aux extrêmes propose des solutions de bonnes qualités, comparables
à la méthode par défaut d'ILOG Solver, sans toutefois la
surpasser.
1.10. Conclusion et perspectives
|
Problèmes
|
k
|
Random
CPU
|
MinDomain
CPU
|
Moy. Min
CPU
|
Moy. Max
CPU
|
Ecart Min.
CPU
|
|
fpsol2.i.2.col
|
12
|
171.41
|
245.33
|
32.18
|
513.65
|
87.51
|
|
fpsol2.i.2.col
|
13
|
>1500
|
>1500
|
412.46
|
>1500
|
748.09
|
|
fpsol2.i.3.col
|
11
|
14.94
|
19.16
|
8.76
|
32.47
|
13.68
|
|
fpsol2.i.3.col
|
12
|
169.94
|
184.21
|
39.57
|
247.74
|
121.17
|
|
fpsol2.i.3.col
|
13
|
>1500
|
>1500
|
284.15
|
>1500
|
687.25
|
|
le450-25b.col
|
41
|
612.05
|
568.94
|
121.67
|
>1500
|
435.62
|
|
zeroin.i.2.col
|
12
|
171.68
|
144.28
|
61.32
|
784.36
|
135.24
|
|
zeroin.i.2.col
|
13
|
>1500
|
>1500
|
841.27
|
>1500
|
>1500
|
|
inithx.i.1.col
|
12
|
174.69
|
237.2
|
47.52
|
894.25
|
216.58
|
|
inithx.i.2.col
|
12
|
177.04
|
254.91
|
89.16
|
876.14
|
237.81
|
|
inithx.i.3.col
|
12
|
173.29
|
246.24
|
35.41
|
854.62
|
241.83
|
|
inithx.i.3.col
|
13
|
>1500
|
>1500
|
212.59
|
>1500
|
984.21
|
|
jean.col
|
37
|
179.6
|
249.73
|
94.52
|
676.59
|
254.73
|
TABLE 1.5 - Résultats
expérimentaux, instances de Coloration de Graphes
1.10 Conclusion et perspectives
Dans cette première partie, nous nous avons introduit
une nouvelle approche pour la gestion des décisions de branchement, que
nous avons appelée Dynamic Learning Search. Cette approche, basée
sur des techniques d'apprentissage, présente l'intérêt de
chercher à diriger la recherche vers des sous-espaces prometteurs en
définissant dynamiquement des politiques de priorités de
branchement sur les variables, ainsi que sur les valeurs que peuvent prendre
les variables. Nous avons montré qu'une phase de sondage, permettant
d'avoir un aperçu de l'arbre de recherche, pouvait s'avérer
intéressante afin d'initialiser la recherche. Enfin, nous avons
montré qu'il était possible d'appliquer cette approche aussi bien
sur des problèmes de satisfaction de contraintes que sur des
problèmes d'optimisation combinatoire. Les tests expérimentaux
ont montré que notre méthode était plus efficace que les
méthodes génériques par défaut du solver commercial
ILOG. La méthode que nous proposons est évidemment moins efficace
que les heuristiques dédiées aux problèmes d'optimisation
combinatoire ou aux problèmes de satisfaction de contraintes.
Néanmoins, dans l'optique d'une approche générique, la
méthode que nous proposons semble prometteuse.
Nous pensons cependant que d'autres critères permettant
de définir la qualité d'un sous-arbre d'une recherche
arborescente peuvent être proposés. Ces critères devront
être génériques pour permettre une application aussi bien
dans le cas de problèmes de satisfaction de contraintes que dans celui
de problèmes d'optimisation combinatoire.
Deuxième partie
Utiliser des méthodes exactes au
sein des métaheuristiques :
méthodes de grands voisinages
|
2
|
La recherche à grand voisinage : un nouvel
opérateur
|
53
|
|
2.1
|
Introduction à la recherche locale
|
53
|
|
|
2.1.1 Bases de la recherche locale
|
53
|
|
|
2.1.2 Principales classes de recherches locales
|
54
|
|
|
2.1.3 Recherche locale à voisinage variable
|
55
|
|
|
2.1.4 Algorithmes utiisant de la recherche locale
|
55
|
|
2.2
|
Recherche à grand voisinage
|
57
|
|
|
2.2.1 Notations et définitions de la recherche à
grand voisinage . . . .
|
58
|
|
2.3
|
Classe des problèmes considérés :
Problèmes de Tournées avec Couver-
|
|
|
|
ture Partielle
|
59
|
|
|
2.3.1 Problèmes de Tournées avec Gains
|
60
|
|
|
2.3.2 Autres variantes de Problèmes de Tournées
à Couverture Partielle
|
61
|
|
|
2.3.3 Complexité des Problèmes de Tournées
avec Couverture Partielle
|
62
|
|
|
2.3.4 Quelques opérateurs de recherche locale pour les
Problèmes de
|
|
|
|
Tournées avec Couverture Partielle
|
62
|
|
2.4
|
Dropstar : une nouvelle structure de grand voisinage
|
64
|
|
|
2.4.1 Des opérateurs existants : drop,
l-ConsecutiveDrop
|
64
|
|
|
2.4.2 L'opérateur de grand voisinage : Dropstar
|
69
|
|
|
2.4.3 Plus court chemin avec contraintes de ressources (SPPRC) .
. . .
|
71
|
|
|
2.4.4 Résolution par un algorithme de programmation
dynamique . .
|
71
|
|
2.5
|
Perspectives : variantes possibles de la procédure
Dropstar
|
74
|
|
3
|
Application au Problème de l'Acheteur
Itinérant
|
77
|
|
3.1
|
Introduction au problème de l'Acheteur Itinérant
|
78
|
|
3.2
|
Notre algorithme : le DMD-ATA
|
81
|
|
|
3.2.1 Fourmis Parallèles
|
81
|
|
|
3.2.2 Fourmis Anamorphiques
|
82
|
|
|
3.2.3 Plans Multi-Dimensionnels
|
83
|
|
|
3.2.4 Dynamique
|
83
|
|
3.3
|
Opérateurs de recherche locale
|
84
|
|
|
3.3.1 Procédures de recherches locales basiques
3.3.2 Application de l'opérateur Dropstar
3.3.3 Intégration de la recherche locale dans
l'algorithme DMD-ATA
|
85
85
89
|
|
3.4
|
Résultats expérimentaux
|
89
|
|
3.5
|
Conclusion
|
93
|
|
4
|
Application au Problème du Voyageur de Commerce
Généralisé
|
95
|
|
4.1
|
Introduction au Problème du Voyageur de Commerce
Généralisé . . . .
|
96
|
|
4.2
|
État de l'art
|
96
|
|
4.3
|
Algorithme mémétique
|
98
|
|
|
4.3.1 Composants basiques de l'algorithme
|
98
|
|
|
4.3.2 Croisement
|
100
|
|
|
4.3.3 Implémentation détaillée de
l'opérateur de croisement
|
103
|
|
|
4.3.4 Heuristiques de recherche locale
|
106
|
|
4.4
|
Résultats expérimentaux
|
108
|
|
4.5
|
Conclusion et perspectives
|
112
|
Chapitre 2
La recherche à grand voisinage : un
nouvel opérateur
2.1 Introduction à la recherche locale
Un nombre important de problèmes d'optimisation
d'intérêts pratiquessont difficilement résolus de
manière exacte dans des temps de calcul raisonnables. Ainsi, une
approche pratique pour résoudre de tels problèmes est d'employer
des algorithmes heuristiques (ou d'approximation) qui peuvent être
capables de trouver des solutions quasi optimales dans des temps de calcul
raisonnables. La littérature dédiée aux algorithmes
heuristiques distingue fréquemment deux classes d'algorithmes : les
algorithmes constructifs et les algorithmes d'amélioration. Un
algorithme de construction construit une solution à partir de rien en
assignant des valeurs à une ou plusieurs variables de décisions
itérativement. Un algorithme d'amélioration démarre
généralement à partir d'une solution réalisable et
essaie itérativement d'obtenir de meilleures solutions. Les algorithmes
de recherche à voisinage (appelés aussi algorithmes de recherche
locale) sont une vaste classe d'algorithmes d'amélioration pour lesquels
à chaque itération une meilleure solution est trouvée en
explorant le voisinage de la solution courante.
2.1.1 Bases de la recherche locale
Le principe de la recherche locale est le suivant :
l'algorithme débute avec une solution initiale réalisable. Sur
cette solution initiale, on applique une série de modifications locales
(définissant un voisinage de la solution courante), tant que celles-ci
améliorent la qualité de l'objectif. Malheureusement, en
appliquant ce principe, rien ne garantit d'atteindre la ou les solutions
optimales. La recherche peut se retrouver bloquée dans un optimum local
relativement au voisinage considéré et s'arrêter, faute
d'amélioration possible. On voit donc que la qualité des
solutions finales dépend en grande partie de
la complexité et de la diversité des
transformations permises par les opérateurs de recherche locale. Un des
principaux problèmes est donc de faire un compromis entre le temps de
calcul nécessaire pour explorer l'intégralité d'un espace
de recherche défini par le voisinage et sa taille.
On définit l'espace de recherche comme l'espace dans
lequel la recherche locale s'effectue. Cet espace peut correspondre à
l'espace des solutions réalisables du problème
étudié. Chaque point de l'espace correspond ainsi à une
solution satisfaisant l'ensemble des contraintes associées au
problème.
À chaque itération, l'ensemble des modifications
que l'on se permet d'effectuer sur la solution courante S
définit un nouvel ensemble de solutions. Ce nouvel ensemble de
solutions est appelé le voisinage de S ou
N(S). Pour un même problème, il existe un grand
nombre d'opérateurs de voisinages possibles et intéressants.
Les bases de la recherche locale peuvent être
définies ainsi. Soient : - f() la fonction qu'on l'on souhaite
maximiser,
- S la solution courante,
- S* la meilleure solution connue,
- f* la valeur de la meilleure solution
connue,
- N(S) le voisinage de S.
La procédure de recherche locale est la suivante :
7
8
9
Algorithme 2 : Algorithme d'une recherche locale
simple de plus grande pente
1 Initialisation: Construire une solution de
départ S0;
2 S* = S0;
3 S = S0;
4 f* =
f(S0);
5 tant que l'optimum local n'a pas
été atteint faire
6 S =
argmaxSI?N(S)(f(S0));
si f(S) >
f* alors
f* = f(S); S* =
S;
2.1.2 Principales classes de recherches locales Recherche
locale simple ou méthode de descente
La plus simple de toutes les approches de recherches locales
consiste à construire une unique solution initiale et à
l'améliorer en utilisant une unique structure de voisinage
jusqu'à ce qu'un optimum local soit atteint, arrêtant ainsi la
recherche. Il y a cependant deux variantes de cette approche :
- meilleure amélioration : on parcourt
l'intégralité de l'espace de recherche défini
par la
structure de voisinage et on choisit S* tel que
S* =
argmaxSl?N(S)(f(S')),
2.1. Introduction à la recherche locale
- première amélioration: on parcourt l'espace de
recherche et on met à jour la solu-
tion courante dès qu'une solution S' est
trouvée, définie telle que f(S') >
f(S).
Hansen et Mladenovi'c (2006) ont étudié l'impact
de ces variantes pour le problème de Voyageur de Commerce. Ils ont
montré que l'efficacité de ces différentes versions
dépendait en grande partie du choix dans les solutions initiales. La
version de la meilleure amélioration, qui semble la plus attirante car
plus prometteuse dans l'amélioration des solutions, donnait dans leurs
résultats expérimentaux des résultats significativement
plus mauvais que la version de la première amélioration.
Recherche locale à départs
multiples
La recherche locale à départs multiples est une
simple extension du schéma de la recherche locale simple. Plusieurs
solutions générées (par exemple aléatoirement) sont
utilisées comme solutions initiales de la recherche locale.
L'exploration des voisinages à partir de ces solutions initiales permet
d'obtenir plusieurs optima locaux. Parmi ces optima locaux, le meilleur est
sélectionné puis retenu comme solution de la résolution
heuristique.
2.1.3 Recherche locale à voisinage variable
La recherche à voisinage variable a été
introduite par Mladenovi'c et Hansen (1997). Cette recherche utilise à
la place d'une seule structure de voisinage, plusieurs structures
appliquées dans un ordre prédéfini. Depuis son
introduction, la recherche à voisinage variable a vu le
développement d'un nombre important de variantes de diverses
complexités. La plus simple d'entre elles, la descente à
voisinage variable (Variable Neighborhood Descent) (voir Hansen et
al. (2006b) pour plus de détails), est la version multivoisinage de
la recherche locale simple. La procédure de la descente à
voisinage variable est la suivante : on applique sur une solution initiale un
opérateur de recherche locale en utilisant la première structure
de voisinage, jusqu'à ce qu'un optimum local soit atteint; la recherche
locale continue alors, en utilisant une deuxième structure de voisinage
jusqu'à ce qu'un optimum local (par rapport à cette structure)
soit atteint. Une fois que cet optimum local est atteint, on utilise une autre
structure de voisinage, et ainsi de suite, de manière
répétitive. Au bout d'un certain nombre d'itérations, la
descente à voisinage variable s'arrête, une fois qu'elle a atteint
une solution qui est un optimum local pour chacune des structures de voisinages
considérées. On peut cependant remarquer que l'ordre dans lequel
sont appliquées les structures de voisinage peut avoir un impact sur la
qualité de la solution finale.
2.1.4 Algorithmes utilisant de la recherche locale
L'utilisation de la recherche locale en conjonction avec
d'autres méthodes est une procédure très efficace. On peut
citer un certain nombre d'hybridations de méthodes avec de la recherche
locale.
Algorithmes de branchement et
séparation
La recherche locale peut être couplée avec une
procédure de branchement et séparation (Toth et Vigo, 2001;
Haouari et Ladhari, 2003; Danna, 2003; Prescott-Gagnon et al., 2007;
Baptiste et al., 2008). Danna (2003) utilise la recherche locale dans
une procédure de résolution par génération de
colonnes. Lorsqu'une solution entière est trouvée, la recherche
locale est utilisée pour améliorer la solution et ainsi
générer de nouvelles colonnes. Danna et al. (2005)
proposent aussi une méthode appelée RINS (Relaxation
Induced Neighborhood Search), qui utilise la recherche locale pour explorer un
sousespace qui est à la fois le voisinage de la solution entière
et le voisinage de la solution de la relaxation continue. Toth et Vigo (2001)
utilisent la recherche locale pour le calcul de bornes inférieures, en
résolvant de manière heuristique le dual de la relaxation
linaire. Baptiste et al. (2008) utilisent une procédure de
recherche locale afin d'améliorer la borne supérieure.
Prescott-Gagnon et al. (2007) proposent une méthode hybride
entre recherche locale et résolution par génération de
colonnes, dans laquelle une version heuristique de génération de
colonnes est utilisée pour la résolution du problème
restreint.
Métaheuristiques
La recherche tabou (Tabu Search ou TS) est une
métaheuristique présentée par Glover (1989). L'idée
de la recherche tabou consiste à explorer le voisinage d'une solution
par un opérateur de recherche locale et à choisir la solution
dans ce voisinage qui minimise la fonction objectif (dans le cas d'un
problème de minimisation). On autorise cependant à choisir une
solution qui augmente la valeur de la fonction objectif afin de sortir d'un
minimum local. Pour ne pas retomber dans ce minimum local, on garde en
mémoire dans une liste tabou les dernières positions
explorées dont on interdit la visite. Pour plus de détails sur la
recherche tabou, nous conseillons au lecteur l'ouvrage de Glover et Laguna
(1997).
Le recuit simulé (simulated annealing ou SA)
est une métaheuristique probabiliste, inspirée d'un processus
utilisé en métallurgie, proposée par Kirkpatrick et
al. (1983). Par analogie avec le processus physique, la fonction à
minimiser est l'énergie du système. On introduit également
un paramètre fictif, la température du système. À
chaque itération de l'algorithme, on applique un opérateur de
recherche locale sur une solution. Cette modification entraîne une
variation de l'énergie du système. Si cette variation fait
baisser l'énergie du système, elle est appliquée à
la solution courante. Sinon, elle est acceptée avec une certaine
probabilité dépendant de la température. En diminuant
progressivement la température (et ainsi la probabilité
d'accepter des solutions détériorantes), on tend à
minimiser l'énergie du système.
2.2. Recherche à grand voisinage
Algorithmes évolutionnaires
Les métaheuristiques basées sur des algorithmes
évolutionnaires sont souvent couplées avec de la recherche
locale. Pour les algorithmes génétiques (voir le chapitre 4 pour
plus de détails), la recherche locale est souvent utilisée pour
l'amélioration des solutions et l'intensification de la recherche (Tsai
et al., 2004; Snyder et Daskin, 2006; Hart et al., 2005;
Silberholz et Golden, 2007). On trouve aussi de nombreux algorithmes couplant
des algorithmes d'optimisation par Colonie de Fourmis (voir le chapitre 3 pour
plus de détails) et de la recherche locale (Dorigo et al.,
1996; Dorigo et Stutzle, 2004; Bell et McMullen, 2004; Bontoux et Feillet,
2008; Donati et al., 2008). La recherche locale est alors
utilisée pour améliorer les solutions trouvées par les
fourmis. Les algorithmes mémétiques ont été
proposés par Moscato et Norman (1992) et (Moscato et Cotta, 2005) et
peuvent être décrits comme une stratégie de recherche dans
laquelle une population d'agents coopèrent, couplée avec de la
recherche locale (voir la section 4.3 pour plus de détails sur ces
algorithmes).
Algorithmes basés sur de la programmation par
contraintes
Plusieurs méthodes proposent une coopération
entre la programmation par contraintes et la recherche locale (Prestwich, 2008;
Pisinger et Ropke, 2007; Benoist et al., 2007; Hansen et al.,
2006a; Shaw, 1998). Shaw (1998) propose une technique, appelée LNS
(Large Neighborhood Search) qui emploie des opérateurs de recherche
locale et utilise une recherche arborescente à base de propagation de
contraintes afin d'évaluer le coût et la
réalisabilité des mouvements des opérateurs de recherches
locales. Prestwich (2008) utilise le même principe en proposant la
méthode FCNS (Forward checking Colouration Neihbourhood Search)
pour un problème de coloration de graphes. Benoist et al.
(2007) propose une méthode, appelée Branch & Move
qui applique de la recherche locale sur des contraintes maîtresses
d'un problème.
Actuellement, l'hybridation de la recherche locale avec d'autres
méthodes semble proposer les algorithmes les plus performants pour de
nombreux problèmes.
2.2 Recherche à grand voisinage
Dans ce chapitre, on s'intéresse plus
particulièrement aux algorithmes de recherche à voisinage pour
lesquels la taille du voisinage est très importante par rapport à
la taille de l'instance du problème considéré. Pour des
instances de très grandes tailles, il est impossible, dans des temps de
calcul raisonnables, de parcourir énumérativement l'ensemble des
solutions définies par de tels voisinages, et il faut soit explorer un
sous-ensemble du voisinage, soit développer un algorithme efficace pour
l'exploration du voisinage.
Une des principales difficultés dans la création
d'une approche par recherche locale est le choix de la structure de voisinage,
c'est-à-dire la façon dont le voisinage est
défini. Ce choix détermine de façon
très importante si la recherche locale donnera des solutions de
très bonne qualité ou des solutions qui représentent des
optima locaux de mauvaise qualité. Il est évident que plus le
voisinage est de taille importante, plus les solutions renvoyées par la
recherche locale seront de bonne qualité et la solution finale proche de
l'optimum. Malheureusement, en augmentant la taille du voisinage, on augmente
aussi le temps de calcul nécessaire pour explorer ce voisinage. Comme la
recherche locale est généralement appliquée à
partir de plusieurs solutions initiales, de longs temps d'exécutions par
itération restreignent le nombre d'appels à la recherche locale
par unité de temps. Pour cette raison, un voisinage de taille importante
n'amène pas nécessairement à une heuristique efficace,
sauf s'il est possible d'explorer ce voisinage de manière
particulièrement efficace.
Certaines méthodes largement utilisées en
recherche opérationnelle peuvent être vues comme des techniques de
recherche à grand voisinage. Par exemple, si l'algorithme du simplexe
utilisé pour résoudre les programmes linéaires peut
être vu comme un algorithme de recherche locale, alors la
génération de colonnes peut être vue comme une
méthode de recherche à grand voisinage. De manière
équivalente, les techniques d'augmentation utilisées pour la
résolution de nombreux problèmes de flots dans les réseaux
peuvent être classées parmi les méthodes de recherche
à grand voisinage.
Ahuja et al. (2002) ont classé les
méthodes de recherche à grand voisinage dans trois classes
non-exclusives. La première catégorie des algorithmes de
recherche locale représente les méthodes à profondeur
variable. Ces algorithmes se concentrent sur des voisinages de taille
exponentielle et effectuent une exploration partielle de ces voisinages, en
utilisant des heuristiques. La deuxième catégorie est
composée des algorithmes d'améliorations de flots dans les
réseaux. Ces méthodes de recherche à voisinage utilisent
les techniques de flots dans les réseaux pour trouver des solutions
voisines améliorantes. Enfin, la troisième catégorie se
compose de structures de voisinages pour problèmes NP-difficiles dont
certaines sous-classes peuvent être résolues en temps polynomial.
Selon cette classification, l'opérateur de voisinage que nous proposons
appartient à la catégorie des algorithmes d'améliorations
de flots dans les réseaux, basés sur des calculs de plus courts
chemins.
2.2.1 Notations et définitions de la recherche
à grand voisinage
Nous allons maintenant introduire de manière plus
formelle les concepts de problème d'optimisation combinatoire et de
voisinage. Soit E = 1,2, . . . , m un ensemble fini. On note
|S| la cardinalité d'un ensemble S. Soit F
ç 2E, où 2E
représente l'ensemble des sous-ensembles de E. Les
éléments de F sont appelés des solutions
réalisables. Soit f la fonction appelée fonction
objectif. Une instance d'un problème d'optimisation combinatoire est
représentée ainsi :
Minimiserf(S) : S E F
Une structure de voisinage est définie par la fonction
N : F 2E. Pour chaque S F
est associé un sous-ensemble N(S) de
E. Cet ensemble N(S) est appelé le voisinage
de
la solution S, et on pose que S ?
N(S). Une solution S* ? F est
appelée optimum local relativement à la fonction de voisinage
N si f(S*) < f(S)
quel que soit S ? N(S). Le voisinage défini
par N(S) est dit de taille exponentielle si
|N(s)| augmente exponentiellement lorsque m
augmente.
Les techniques faisant appel à de tels voisinages sont
appelées des algorithmes de recherche à grand voisinage. Pour
deux solutions S et T, on appelle S - T
l'ensemble des éléments qui apparaissent dans S,
mais qui n'apparaissent pas dans T. On peut alors définir la
distance d(S, T) égale à |S -
T| + |T - S|, qui représente le nombre
d'éléments de E qui apparaissent dans S ou dans
T mais qui n'apparaissent pas dans les deux solutions (de nombreuses
autres distances, permettant de mesurer la différence entre une paire de
solutions pour des algorithmes génétiques, ont été
présentées par Sevaux et Sörensen (2005)).
On peut donc définir un voisinage de distance k
de la manière suivante : Nk(S) = T ?
F : d(S; T) = k. On peut
facilement remarquer que Nm(S) = F et
donc, se rendre compte qu'explorer un voisinage de distance k peut
être difficile lorsque k augmente. Cela est typiquement la
situation lorsque k n'est pas fixé. Dans ce cas, trouver la
meilleure solution (ou une solution meilleure que la solution actuelle) dans un
tel voisinage est NP-difficile, si le problème original est
NP-difficile.
2.3 Classe des problèmes
considérés : Problèmes de Tournées avec Couverture
Partielle
Le Problème du Voyageur de Commerce, ou Traveling
Salesman Problem (TSP), est un problème qui est largement
étudié depuis le 20ème siècle. L'objectif de ce
problème est de visiter un ensemble donné de villes, en
minimisant la distance totale parcourue. La première publication sur la
résolution du TSP est attribuée à Menger (1932), dans
laquelle il considère une variation appelée das Botenproblem
ou the Messenger Problem. La résolution de ce
problème sous sa forme originale est aujourd'hui encore un challenge
très concurrentiel en optimisation combinatoire. David Applegate, Robert
Bixby, Vasek Chvátal et William Cook ont développé dans
les années 1990 la méthode Concorde 1, basée sur une
méthode de séparation et de coupes (séparation et
génération de coupes) qui permet de résoudre optimalement
des instances de très grande taille (plusieurs milliers de villes). Cet
intérêt pour ce problème a poussé la
communauté scientifique à proposer un grand nombre d'extensions
ou de variantes du TSP. Un ouvrage récent est consacré au
problème du Voyageur de Commerce et à ses variations (Gutin et
Punnen, 2002).
Les premières extensions du TSP portent sur la
considération de transport de marchandises récoltées
durant la tournée, puis ramenées à un dépôt.
À ce problème initial furent ajoutées des contraintes de
temps durant lesquels la récupération des marchandises pouvait
avoir lieu (Problème du Voyageur de Commerce avec Fenêtre de Temps
ou Traveling Salesman with Time Windows), des contraintes de
capacités (Problème du
1. http ://
www-neos.mcs.anl.gov
Voyageur de Commerce avec Contraintes de Capacité ou
Capacitated Traveling Salesman Problem). À tous ces
problèmes fut ajoutée la possibilité d'utiliser plusieurs
véhicules. Ces problèmes sont connus sous le nom de
problèmes de calcul de tournées de véhicules ou Vehicle
Routing Problem (VRP). Pour plus de détails sur les problèmes de
tournées de véhicules, nous conseillons au lecteur le livre de
Toth et Vigo (2002).
Le voisinage que nous présentons à travers deux
exemples dans les chapitres suivants peut s'appliquer à des variantes du
TSP pour lesquelles la visite de l'ensemble des sommets du graphe n'est pas
obligatoire. La classe de problèmes la plus étudiée parmi
les problèmes présentant cette caractéristique est la
classe des Problèmes de Tournées avec Gains (voir (Feillet et
al., 2005) pour plus de détails sur cette classe de
problèmes). Nous nommons par souci de simplicité cette classe de
problèmes les Problèmes de Tournées avec Couverture
Partielle (Partial Covering Routing Problems). Ces problèmes sont
définis comme des problèmes dont les solutions ne visitent pas
nécessairement l'ensemble des noeuds.
L'ensemble de ces problèmes présente une
particularité dans sa structure : l'ensemble des noeuds du graphe ne
doit pas être nécessairement visité. Cette
différence avec un certain nombre d'extensions du problème du
Voyageur de Commerce implique d'avoir des solutions de taille variable. De
plus, on peut remarquer une difficulté supplémentaire dans la
résolution du problème : une fois que les villes à visiter
sont choisies, il reste à déterminer l'ordre dans lequel elles
seront visitées, ce qui se ramène dans la plupart des cas
à un TSP de taille réduite.
2.3.1 Problèmes de Tournées avec Gains
La classe des problèmes de Tournées avec Gains
est une extension bien connue du problème du Voyageur de Commerce. Ces
problèmes sont généralement définis de la
façon suivante. Soit G = (V, A) un graphe
orienté avec V = {v1, . . . , vn}
un ensemble de sommets pour lequel v1 est le dépôt. On
note cij le coût de l'arc (vi, vj).
On associe à chaque sommet vi un gain supposé
positif.
On peut voir cette classe de problèmes comme un
Problème de Voyageur de Commerce bicritère avec deux objectifs
contraires : d'une part, minimiser la distance parcourue (avec le droit de ne
pas visiter l'ensemble des sommets) et d'autre part, maximiser la somme des
gains collectés auprès des sommets desservis.
Dans le cas du problème du Voyageur de Commerce avec
Gains, on trouve trois variantes dont l'objectif ne comporte qu'un
critère :
- Orienteering Problem (Golden et al., 1987) :
l'objectif consiste à maximiser le gain
sous la contrainte que la distance soit inférieure
à une longueur maximale,
- Prize-collecting Traveling Salesman Problem (Balas,
1989) : l'objectif consiste à mini-
miser la distance parcourue sous la contrainte que le gain
récolté soit supérieur à
un montant minimal,
- Profitable Tour Problem (Dell'Amico et al.,
1995) : l'objectif est de minimiser la différence entre la somme des
distances parcourues et la somme des gains récoltés.
Le problème du Voyageur de Commerce avec Gains a
été étudié dans quelques cas sous sa forme
bicritère : Keller (1985) , Bérubé et al.
(2008).
On retrouve ces problèmes sous d'autres noms :
- Selective TSP (Laporte et Martello, 1990; Gendreau et
al., 1998),
- Maximum Collection Problem (Kataoka et Morito, 1988),
- Traveling Salesman Subtour Problem (Gensch, 1978),
- Traveling Salesman Subset-Tour Problem with One additional
Constraint (Mittenthal et Noon, 1992),
- Cardinality Constrained Circuit Problem (Bauer et al.,
1998),
- Score Orienteering Problem (Kataoka et al., 1998),
- Multiobjective Vending Vroblem (Keller et Goodchild, 1988),
- Resource Constrained Traveling Salesman Problem (Pekny et
Miller, 1990), - . . .
Dans le cas où l'utilisation de plusieurs véhicules
est autorisée, on trouve aussi trois variantes mono-critères:
- Team Orienteering Problem (Chao et al., 1996) :
l'objectif est de maximiser les gains collectés sous contrainte de ne
pas dépasser une longueur maximale de distance pour chaque route,
- Prize-collecting VRP (Tang et Wang, 2006) : l'objectif est
de minimiser la distance totale parcourue sous contrainte que le gain total
récolté soit supérieur à un montant minimum et en
respectant des contraintes de capacités sur les véhicules,
- Profitable VRP (Archetti et al., 2007) : l'objectif
est de minimiser la différence entre la somme des distances parcourues
et la somme des gains récoltés sous contrainte de capacité
des véhicules.
2.3.2 Autres variantes de Problèmes de
Tournées à Couverture Partielle
On trouve d'autres variantes du problème du Voyageur de
Commerce relativement proches des problèmes présentés :
- Traveling Purchaser Problem (Ramesh, 1981) : dans ce
problème, les villes sont remplacées par des marchés.
Chaque marché fournit un sous-ensemble de produits. Le prix de vente de
chaque produit est connu et les prix des produits sont dépendants du
marché à partir duquel ils sont achetés. L'objectif
consiste à trouver un tour qui part d'un dépôt, connectant
un sous-ensemble de marchés, de telle sorte que l'ensemble des produits
soit acheté et que la somme des coûts de transport et des
coûts d'achat des produits soit minimisée (voir le chapitre 3 pour
plus de détails sur ce problème).
- Covering Tour Problem (Gendreau et al., 1997) :
dans ce problème, un ensemble T de sommets doit être
visité et un ensemble W de sommets doit être couvert.
L'objectif est de trouver un cycle hamiltonien de longueur minimale qui visite
l'ensemble des sommets de T de telle sorte que chaque sommet de W
ait une distance inférieure à une longueur
prédéterminée avec au moins un sommet du cycle.
- Generalized Traveling Salesman Problem (Henry-Labordere,
1969) : dans ce problème, les sommets appartiennent à des
groupes. L'objectif est de construire un tour qui visite exactement une fois
chaque groupe tout en minimisant les coûts de transport (voir le chapitre
4 pour plus de détails sur ce problème).
2.3.3 Complexité des Problèmes de
Tournées avec Couverture Partielle
L'ensemble des problèmes présentés, aussi
bien dans leurs versions mono-véhicule que dans les versions avec une
flotte de véhicules, sont NP-difficiles. Ceci est
généralement facile à prouver : dans la plupart des cas,
on peut se ramener à un problème de type Voyageur de Commerce qui
est NP-difficile au sens fort.
2.3.4 Quelques opérateurs de recherche locale pour
les Problèmes de Tournées avec Couverture Partielle
Il existe un certain nombre d'opérateurs de recherche
locale, utilisés entre autres pour les problèmes de
Tournées avec Gains. On peut classer les opérateurs de recherche
locale en deux sous catégories:
- sans changement des sommets visités : ces
opérateurs modifient l'ordre de visite des sommets dans un tour dans le
cas où un seul véhicule est disponible (2-opt (Croes, 1958),
heuristique de Lin et Kernighan (1973), ...) ou changent l'affection des
sommets entre les tournées (croisement (Montané et Galvão,
2006), échange (Tan et al., 2001), repositionnement
(Montané et Galvão, 2006), ...);
- avec changement des sommets visités : ces
opérateurs tirent partie du fait que l'ensemble des sommets n'est pas
visité (insertion d'un sommet -ou d'une chaîne de sommets- dans la
tournée (Riera-Ledesma et Salazar-González, 2005), suppression
d'un sommet (Pisinger et Ropke, 2007) ou d'une chaîne de sommets
(RieraLedesma et Salazar-González, 2005)).
Nous nous sommes intéressés plus
particulièrement à cette dernière catégorie de
voisinages. Les quelques exemples qui suivent (figures 2.1-2.5)
présentent un aperçu d'opérateurs connus.
9
6
8
5
2
10
3
7
0 4 1
2
1
3
0
4
5
6
FIGURE 2.1 - Exemple de solution
initiale
FIGURE 2.2 - Application d'un
échange entre les sommets 2 et 6

1
2
3
0
4
5
6
FIGURE 2.3 - Application de
l'opérateur insertion
Chapitre 2. La recherche à grand voisinage : un nouvel
opérateur
2
3
0
4
5

1
6

6
1
2
3
0
4
5
FIGURE 2.4 - Application de
l'opérateur suppression
FIGURE 2.5 - Application d'un
2-opt entre les sommets 2 et 5 : le chemin entre ces
sommets est inversé
2.4 Dropstar : une nouvelle structure de grand
voisinage
2.4.1 Des opérateurs existants : drop,
l-ConsecutiveDrop
Afin de présenter l'intérêt du nouvel
opérateur de voisinage que nous proposons, nous nous appuierons sur un
exemple simpliste du problème de Tour avec Profits (Profitable Tour
Problem ou PTP). On définit le Profitable Tour Problem de la
manière suivante. Soit G = (V, E) un graphe
non orienté avec V = {v1, . . . ,
vn} un ensemble de sommets pour lequel v1 est le
dépôt. On note cij le coût de l'arc
(vi, vj). On associe à chaque sommet vi un
gain supposé positif. L'objectif est de minimiser la différence
entre la somme des distances parcourues et la somme des gains
récoltés. Les chiffres situés sur les sommets de la figure
2.6 représentent le gain associé à chaque sommet et les
chiffres situés sur les arcs, la distance entre deux sommets. Dans le
cas où toutes les villes ne doivent pas être visitées,
comme c'est le cas ici, on peut appliquer la procédure DROP
utilisée par de nombreux chercheurs sur ces classes de problèmes
(Ramesh et Brown, 1991; Mittenthal et Noon, 1992; Voß, 1996). Cet
opérateur retire un sommet d'une solution initiale dans le cas où
ce retrait permettrait de diminuer le coût de la fonction objectif.
Posons la solution initiale (Fig. 2.7), de coût
égal à --1. Lorsqu'on applique la procédure DROP, la seule
suppression qui permet de diminuer le coût de la fonction objectif est la
suppression du sommet 4. On a alors la solution 0 1 2 3 0 de coût
égal à --2, présentée dans la figure 2.8. Le but
étant de minimiser la fonction objectif, on se rend compte que cette
solution est un optimum local relativement à la procédure DROP.
En effet, si l'on se limite à la suppression d'une seule ville de cette
solution, on ne peut améliorer la solution courante.
Devant la limitation de la taille de l'espace de recherche
défini par ce voisinage, Riera-Ledesma et Salazar-González (2005)
ont proposé une extension de ce voisinage qu'ils ont appliquée au
problème de l'Acheteur Itinérant. Ils ont nommé ce nouveau
voisinage : l-ConsecutiveDrop. Ce voisinage peut se retrouver sous des
formes similaires pour ces classes de problèmes (Keller, 1989; Renaud et
Boctor, 1998b; Hachicha et al., 2000; Dell'Amico et al.,
1998). Ce voisinage essaie de réduire la longueur d'un cycle initial en
supprimant l sommets consécutifs. Si on applique cette
procédure à la solution présentée dans la figure
2.8, en choisissant l = 2, on améliore la solution courante en
obtenant la solution présentée dans la figure 2.9, de coût
égal à --4. Cette solution aurait aussi pu être obtenue en
supprimant dans un premier temps les sommets 1 et 2 de la solution initiale (la
solution ainsi obtenue serait 0 3 4 0 de coût égal à -3),
puis en supprimant de cette solution le sommet 4.
Néanmoins, cette procédure présente des
limitations. Considérons l'exemple présenté dans la figure
2.10. Nous posons alors la solution initiale 0 1 2 3 4 5 0 de coût
égal à --1 présentée dans la figure 2.11. Si on
applique la procédure l-ConsecutiveDrop, on peut voir que cette
solution initiale est un optimum local pour l fixé à
4.
En diminuant la valeur de l (l est alors
égal à 3), on améliore la solution courante en obtenant la
solution 0 4 5 0 de coût égal à --2 présentée
dans la figure 2.12. Cette solution est de plus un optimum local relativement
à la procédure l-ConsecutiveDrop. Cependant, on peut
remarquer qu'en appliquant en premier lieu une procédure 2-
ConsecutiveDrop, on aurait obtenu la solution optimale 0 3 4 5 0 de coût
égal à --19, présentée dans la figure 2.13. On se
rend compte ainsi que la valeur de l est déterminante dans
l'efficacité de la procédure et que la limitation à la
suppression de sommets consécutifs peut être un frein à
l'efficacité de cette procédure.
10
10
10
24
10
10
13
FIGURE 2.6 - Exemple de
Profitable Tour Problem
10
10
10
24
10
13
FIGURE 2.7 - Exemple de
Profitable Tour Problem : Solution initiale
10
10
10
0
24
10
4
13
FIGURE 2.8 - Exemple de
Profitable Tour Problem : Solution après un Drop
9

1
9

2
10

3 24
0
10
4

13
FIGURE 2.9 - Exemple de Profitable
Tour Problem : Solution après un 2-ConsecutiveDrop
10
10
10
10
18
18
10
23
10
10
5
4
FIGURE 2.10 - Autre exemple de
Profitable Tour Problem
10


10
10
23


10
10
10
4
18

18

5
FIGURE 2.11 - Autre exemple
Profitable Tour Problem : Solution initiale
1

1
1

2
18
18
3 23
0
10
5
4
10
FIGURE 2.12 - Exemple de Profitable
Tour Problem : Solution après un 3-ConsecutiveDrop
1

1
1

2
10


10

10
FIGURE 2.13 - Exemple de
Profitable Tour Problem: Solution optimale
2.4.2 L'opérateur de grand voisinage : Dropstar
La procédure Dropstar définit un
opérateur de grand voisinage. Il est basé sur le
sous-problème suivant : trouver une sous-séquence optimale
à partir d'une séquence initiale donnée. Cet
opérateur détermine ainsi l'ensemble optimal des sommets
(consécutifs ou non) à supprimer d'une séquence.
On peut penser que la calcul de la sous-séquence
optimale est coûteux. En effet, la recherche d'une sous-séquence
optimale peut être un problème NP-difficile, comme
nous le verrons par exemple dans le chapitre 3. Cette recherche
est ici effectuée par le biais d'un algorithme de programmation
dynamique récursif.
On construit un graphe selon la procédure suivante.
Comme exemple de solution initiale, nous reprenons la solution
présentée dans la figure 2.8. Un sommet est créé
pour chaque ville de la séquence, le premier sommet de la
séquence est dupliqué et placé en fin de séquence.
Des arcs sont ensuite ajoutés entre chaque sommet et les sommets qui le
suivent dans la séquence initiale (cf. Fig. 2.14). La procédure
dropstar consiste alors à trouver le plus court chemin dans le
graphe entre le premier sommet et le dernier sommet, en respectant certaines
contraintes de ressources. Le coût du chemin est alors égal
à la somme des coûts des distances, à laquelle on peut
avoir à ajouter le coût des ressources (par exemple, les
coûts d'achat des produits dans le cas du problème de l'Acheteur
Itinérant).
0 1 2 3 0
9 9 24
10
14
10
10
10
0
10
10
10
10
FIGURE 2.14 - Graphe
résultant de la procédure Dropstar, appliqué sur la
solution de la figure 2.8
La complexité de la recherche d'une
sous-séquence optimale dépend en partie de la présence ou
non de ressources. Dans le cas par exemple du Problème de Tour avec
Profits, en l'absence de ressource, la recherche d'une sous-séquence
optimale et donc d'un plus court chemin est polynomiale. Par contre, la
consommation en cours de chemin des ressources disponibles en quantités
limitées peut rendre le problème NP-difficile (voir par exemple
le chapitre 3 pour plus de détails).
L'algorithme de programmation dynamique que nous utilisons
pour trouver le plus court chemin dans le graphe est inspiré de
l'algorithme développé par Feillet et al. (2004) pour le
Problème du Plus Court Chemin Élémentaire avec Contraires
de Res-sources. Cet algorithme est une extension du célèbre
algorithme de Bellman (1957).
Un important travail est à effectuer afin
d'accélérer cette procédure pour la rendre applicable pour
les instances de taille importante. Ce travail porte essentiellement sur les
conditions de dominances et sur l'analyse des solutions initiales, afin
d'essayer de réduire la taille du graphe sur lequel appliquer la
procédure Dropstar.
2.4.3 Plus court chemin avec contraintes de ressources
(SPPRC)
Le problème de Plus Court Chemin entre deux sommets
dans des graphes est connu depuis longtemps. Dijkstra (1971) a proposé
un algorithme qui s'applique pour le cas de graphes pondérés avec
des poids positifs, Bellman (1957) pour le cas généralisé.
Les algorithmes proposés sont dans les deux cas des algorithmes
polynomiaux. Le fait de rajouter des contraintes de ressources (Shortest Path
Problem with Resource Constraints) rend le problème NP-difficile.
L'ajout de la contrainte d'élémentarité (Elementary
Shortest Path Problem with Resource Constraints) rend le problème
NP-difficile au sens fort. En effet, ce problème est alors une
réduction du problème de Sequencing Within Intervals
(Dror, 1994).
2.4.4 Résolution par un algorithme de programmation
dynamique
L'algorithme 3 part du premier sommet du graphe et construit
itérativement des chemins vers le dernier sommet du graphe. La
construction se fait par extension de chemins partiels. Un chemin partiel a
pour origine le premier sommet du graphe et pour destination terminale un
sommet quelconque de la séquence. L'extension d'un chemin partiel cp
se fait par l'ajout d'un arc sortant de l'extrémité
terminale de cp et la consommation de ressources. Dans le cas
où un nouveau chemin partiel viole une contrainte de ressource, il est
rejeté. Dans le cas contraire, on compare le chemin partiel avec la
liste de chemins partiels mémorisés pour cette
extrémité. Si des chemins partiels sont dominés, ils sont
rejetés. On note ch(w) la consommation de la ressource
w par le chemin partiel ch.
Les figures 2.15, 2.16, 2.17 et 2.18 présentent le
déroulement de la programmation dynamique appliquée au graphe de
la figure 2.14. Les chiffres sur les arcs représentent le coût des
arcs, les chiffres à côté des sommets représentent
le gain associé à chaque sommet. Enfin, entre crochets, se
trouvent les coûts des chemins partiels (on rappelle que le coût
d'une solution est égal à la différence entre la somme des
coûts des distances parcourues et la somme des gains
récupérés). Si le chiffre est barré, cela veut dire
que le chemin partiel est dominé.
stop;
fin
fin
fin
fin
fin
fin
Algorithme 3 : Algorithme de programmation
dynamique
Données : G : un graphe;
W : le nombre de ressources; CH : une liste de chemins partiels non
traités; chi : la liste des chemins partiels
d'extrémité terminale i
1 Initialisation: CH ? chemin partiel
réduit à {0} ;
2 tant que CH =6 0 faire
3 prendre ch E CH;
etch := extrémité de ch;
domine := faux;
pour chaque chemin partiel ch' E
chetch faire
si ch(w) =
ch'(w), ?w = 0, . . . ,W
alors
chetch := chetch \
{ch'};
sinon
si ch'(w) =
ch(w), ?w = 0, ... ,W alors
domine := vrai;
si domine = faux
alors
chetch := chetch U
{ch};
pour chaque arc
(etch, i) faire
ch' := l'extension de ch par
(vetch, vi); si ch'
est valide alors
CH := CH U {ch'};

4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 fin
0
10
14
0 10 1 2 3 0
9 9 24
[1] (0, 1) [5] (0, 2) [-14] (0, 3) [0] (0, 0)
FIGURE 2.15 - Extension depuis le
sommet 0
Règle de dominance
On note la relation de dominance entre les chemins
ch1 et ch2, ch1
< ch2 pour signifier que ch1 domine
ch2. Une règle de dominance doit permettre
d'éliminer le chemin
10
14
0 1 10 2 3 0
9 9 24
[1] (0, 1) [5](0, 2) [-14](0, 3) [0](0, 1)
[2](0, 1, 2) [ 8](0, 1, 3) [11](0, 1, 0)
FIGURE 2.16 - Extension depuis le
sommet 1
14
0 1 2 10 3 0
9 9 24
[0](0, 0)
[16](0, 1, 2, 3)
[1](0, 1) [2](0, 1, 2) [-14](0, 3)
[ 11](0, 1, 2, 3)
FIGURE 2.17 - Extension depuis le
sommet 2
0 1 2 3 10 0
9 9 24
[1](0, 1) [2](0, 1, 2) [-14](0, 3) [0](0, 0)
[-4] (0,3,0)
FIGURE 2.18 - Extension depuis le
sommet 3
dominé en étant certain de pouvoir toujours
atteindre la solution optimale. La relation de dominance est basée sur
deux règles suivantes :
- Un chemin réalisable, qui respecte les contraintes de
ressources, atteignant le sommet final de la séquence, domine tous les
chemins partiels atteignant le sommet final avec un coût
supérieur,
- Un chemin ch1 domine un chemin
ch2 s'il existe une extension de ch1
dominant extension(ch2) pour toute extension
extension(ch2) de ch2.
La relation de dominance est transitive. La
propriété de transitivité permet de limiter le nombre de
chemins partiels mémorisés. Sans règle de dominance,
l'algorithme de programmation dynamique construit toutes les solutions
réalisables. On a donc tout intérêt à utiliser des
règles de dominances fortes, permettant de limiter le nombre de
solutions explorées. Il faut par contre éviter des
procédures trop coûteuses en temps de calcul, ces
procédures étant appelées un nombre exponentiel de
fois.
Taille du voisinage
Le voisinage défini par la procédure Dropstar
est de très grande taille. En effet, si la solution sur laquelle est
appliquée la procédure est de longueur ñ
(ñ est le nombre de sommets visités), alors la
taille du voisinage est égale à 2ñ, puisqu'on
cherche la sousséquence optimale de cette séquence et que par
conséquent, chaque élément présent dans la
séquence peut appartenir ou ne pas appartenir à la
sous-séquence optimale.
Complexité de la procédure
La procédure Dropstar peut être une
procédure très coûteuse en temps. Pour chaque sommet de la
séquence, on mémorise une liste de labels, correspondant à
des chemins partiels. La taille maximum de cette liste est égale
à 2m, où m est le nombre de
ressources binaires. Chaque ressource peut être consommée ou non,
ce qui mène à 2m états
différents. Le nombre de sommets de la séquence est égal
à ñ (avec ñ n). Le nombre maximum de
chemins partiels durant la procédure dropstar est donc
égal à ñ * 2m.
Chaque chemin partiel est étendu vers ñ
villes. Ce nouveau chemin partiel est inséré dans la liste
des chemins partiels associée à la ville vers lequel le chemin
partiel est étendu (le nombre maximum de chemins partiels dans cette
liste est de 2m). L'insertion consiste à comparer le
nouveau chemin partiel avec ceux déjà présents dans la
liste. La complexité de chaque comparaison est en
O(m). Le coût d'insertion d'un nouveau chemin partiel
dans une liste est donc O(m2m) et le
coût d'extension d'un chemin partiel
O(ñm2m). La procédure
Dropstar a donc une complexité en
O(ñ2m22m). De
manière évidente, cette complexité peut être
réduite significativement en appliquant des règles de dominances
efficaces.
2.5 Perspectives : variantes possibles de la
procédure Dropstar
La procédure Dropstar est une procédure
exacte qui détermine la sous-séquence optimale à partir
d'une séquence initiale. Cette procédure peut donc s'appliquer
à l'ensemble des problèmes de type Tournées de
Véhicules ou Problème de Voyageur de Commerce, pour lesquels la
visite de l'ensemble des sommets du graphe n'est pas obligatoire. Nous avons
nommé cette classe de problèmes les Problèmes de
Tournées avec Couverture Partielle.
La procédure Dropstar est une procédure
exacte. Cette exactitude est coûteuse en temps de calcul de par sa
complexité. Il est néanmoins possible de rendre cette
méthode heuristique, en résolvant de manière
approchée le sous-problème de Plus Court Chemin avec Contraintes
de Ressources. Cela peut se faire par exemple en limitant la taille des chemins
partiels mémorisés pour chaque sommet de la séquence.
Une des limites de cette procédure réside dans
le fait que l'ordre initial est respecté; une ville située avant
une autre ville dans la séquence initiale, sera encore située
avant
2.5. Perspectives : variantes possibles de la procédure
Dropstar
dans la sous-séquence, si aucune des deux villes n'est
supprimée par la procédure. On peut cependant étendre
cette procédure à l'insertion d'un ou de plusieurs sommets et
ainsi passer outre cette limitation. La méthode de Meilleure
Insertion de groupes présentée dans la section 4.3.4 permet
par exemple de déterminer la meilleure position d'un groupe dans une
séquence. On pourrait de la même façon trouver la meilleure
position d'insertion de sommets non visités.
Les deux chapitres qui suivent présentent l'application
de la procédure Dropstar pour deux problèmes : le problème
de l'Acheteur Itinérant (Traveling Purchaser Problem ou TPP)
pour lequel l'opérateur est utilisé pour améliorer les
solutions trouvées par un algorithme d'optimisation par Colonie de
Fourmis et le problème du Voyageur de Commerce
Généralisé (Generalized Traveling Salesman Problem
ou GTSP) pour lequel la procédure Dropstar est utilisé comme
élément clé d'un algorithme mémétique.
Chapitre 3
Application au Problème de
8
3
7
1
4
6
7
8 3
5 7 9
7
9
8
0
6
3
9
4
10
4
3
2
7
5
2
1
l'Acheteur Itinérant
3.1 Introduction au problème de l'Acheteur
Itinérant
Le problème de l'Acheteur Itinérant
(Traveling Purchaser Problem ou TPP) est une
généralisation du problème du Voyageur de Commerce,
introduite pour la première fois par Ramesh (1981). Dans le
problème du Voyageur de Commerce, l'objectif est de trouver le tour de
longueur minimale qui passe par m villes données. Chaque ville
doit être visitée une et une seule fois. Dans le problème
de l'Acheteur Itinérant, les villes représentent des
marchés. Chaque marché fournit un sous-ensemble de produits. Le
prix de vente de chaque produit est connu et les prix des produits
dépendent du marché à partir duquel ils sont
achetés. Le problème de l'Acheteur Itinérant consiste
à trouver un tour qui part d'un dépôt, connectant un
sous-ensemble de marchés, de telle sorte que l'ensemble des produits
soit acheté et que la somme des coûts de transport et des
coûts d'achats des produits soit minimisée.
Ce problème apparaît dans plusieurs contextes
industriels, comme par exemple, dans l'achat de parties de matériels
pour des usines (Pearn et Chien, 1998). L'ordonnancement de n
tâches sur une machine à m états peut aussi
se modéliser comme un TPP, comme cela a été proposé
par Ong (1982). Les marchés, produits, coûts de transport et
coûts d'achats, représentent respectivement les états des
machines, les tâches, les temps de préparation et les temps
d'utilisation.
Le TPP peut être décrit de la façon
suivante (Singh et Oudheusden, 1997). Posons G = (V,
A) un graphe complet. Considérons V = {v0, .
. . , vm} où v0 est le dépôt
et v1, . . . , vm sont les marchés. P
= {p1, .. . , pn} est l'ensemble des
produits. Chaque produit pk E P est disponible dans un
ensemble de marchés Vk C V. Les coûts de
transport sont notés cij > 0 quels que soient (vi,
vj) E A. Les coûts d'achats des produits sont
notés ski = 0 quels que soient pk E P et
vi E Vk. Un tour réalisable est un tour comprenant le
dépôt et un sous-ensemble des marchés, vérifiant la
contrainte que tous les produits sont achetés. Les produits sont
achetés au plus petit coût disponible parmi les marchés
visités. L'objectif est de trouver un tour réalisable qui
minimise la somme des coûts de transport et des coûts d'achats des
produits.
Le TPP est NP-difficile, puisque le cas particulier pour
lequel chaque marché ne vend qu'un produit ne pouvant être
acheté dans aucun autre marché est un problème de Voyageur
de Commerce. Dans ce cas, chaque marché doit être visité et
le problème revient à trouver le tour hamiltonien qui minimise
les coûts de transport.
Dans un souci de simplicité, on suppose que les
coûts de transport sont symétriques (cij = cji
quels que soient (vi, vj) E A) et que les
inégalités triangulaires sont respectées.
Soit Xik = 1 si le produit pk est
acheté à partir du marché vi et Xik = 0
dans le cas contraire. Soit Yij = 1 si le marché vj
suit immédiatement le marché vi dans le tour et
Yij = 0 dans le cas contraire. Le problème de l'Acheteur
Itinérant peut être modélisé de la manière
suivante :
3.1. Introduction au problème de l'Acheteur
Itinérant
minimiser ? ? skiXik + ? ? cijYij (3.1)
pkEP viEVk viEV
vjEV
sujet à
? Xik = 1 (pk E P), (3.2)
viEVk
Xik ? Yij (pk E P, vi
E Vk), (3.3)
vjEV
Xik ? Yji (pk E P, vi
E Vk), (3.4)
vjEV
G.S.E.C. (3.5)
Xik E {0,1} (pk E P, vi E
Vk),
Yij E {0,1} (vi, vj E V)
La fonction objectif 3.1 représente la somme des
coûts de transport et des coûts d'achats des produits. La
contrainte 3.2 oblige à ce que l'ensemble des produits soit
acheté. Les contraintes 3.3 et 3.4 assurent que seuls les marchés
présents dans la solution sont considérés pour l'achat des
produits. Les contraintes 3.5 représentent les contraintes sur les
sous-tours (Generalized Subtour Elimination Constraints),
présentés notamment par Fischetti et al. (1995, 1997).
Elles assurent que les marchés sélectionnés sont
connectés avec le dépôt dans un tour unique.
Les premiers travaux concernant la résolution du TPP
ont été proposés par Ramesh (1981), qui a
présenté un algorithme basé sur une procédure de
recherche lexicographique, qui pouvait être déclinée en
résolution exacte ou heuristique. La plupart des travaux sur la
résolution du TPP proposent des solutions du problème avec des
méthodes heuristiques. On peut mentionner les travaux de Golden et
al. (1981) qui ont basé leur heuristique sur une stratégie
d'économie : Generalized Saving Heuristic (GSH). Leur
heuristique a été modifiée par Ong (1982) qui a
proposé un Tour Reduction Heuristic basé sur la
suppression de marchés à partir d'un tour complet, visitant
l'ensemble des marchés. Pearn et Chien (1998) ont suggéré
quelques améliorations pour ces heuristiques et ont proposé une
autre heuristique, Commodity Adding Heuristic, qui part du principe
que l'ensemble des produits est disponible dans chaque marché.
Récemment, Teeninga et Volgenant (2004) ont décrit des
procédures de pré-traitement des données qui peuvent
être ajoutées à des heuristiques déjà
existantes. Les résultats expérimentaux ont montré
l'efficacité de leurs procédures sur la plupart des heuristiques
citées auparavant, en permettant des diminutions dans les temps de
calcul pour la résolution du problème.
Depuis une dizaine d'années, des heuristiques plus
évoluées et des approches par métaheuristiques ont
été proposées. Voß (1996) a présenté
une approche métaheuristique basée sur de la recherche tabou
dynamique et recuit simulé. Il proposa deux stratégies dynamiques
pour la gestion de la liste tabou : Reverse Elimination Method et
Cancellation Sequence Method. Boctor et al. (2003) ont aussi
proposé plusieurs algorithmes
efficaces basés sur de la recherche tabou. Ces
heuristiques sont comparées avec des méthodes de
résolution exacte sur des instances avec un nombre de marchés
allant jusqu'à 200 et un nombre de produits allant jusqu'à 200.
Riera-Ledesma et Salazar-González (2005) ont obtenu les meilleurs
résultats à ce jour, avec une stratégie heuristique
consistant en un échange de k marchés au lieu d'un
échange classique d'un seul marché.
En plus de ces recherches pour résoudre le TPP de
manière heuristique, des méthodes exactes ont été
développées par Ramesh (1981), Singh et Oudheusden (1997) et
Laporte et al. (2003). Ces derniers ont proposé une
méthode de résolution par séparation et
génération de coupes qui a permis de résoudre de
manière exacte des problèmes contenant jusqu'à 250
marchés et 200 produits, avec des solutions dont le nombre de
marchés visités reste réduit. Pour les instances de
tailles plus importantes, les temps de calcul nécessaires
s'avèrent trop long.
Nous proposons de résoudre le TPP avec une optimisation
par Colonie de Fourmis (Ant Colony Optimization ou ACO), introduite
par Dorigo et al. (1991) (voir aussi (Dorigo et al., 1996)).
Inspirée par le comportement des fourmis pour la recherche de nourriture
dans la nature, l'optimisation par Colonie de Fourmis est un algorithme de
recherche basé sur des agents coopératifs. Les fourmis
communiquent en utilisant une substance chimique appelée
phéromone. Quand une fourmi se déplace, elle dépose une
quantité de phéromone que les autres fourmis peuvent suivre.
Quand une fourmi trouve une trace de phéromone, elle peut décider
de la suivre ou de l'ignorer. Si elle suit cette trace, sa propre
phéromone renforce la trace existante, et l'augmentation de
phéromone augmente la probabilité que la prochaine fourmi suive
cette trace. Ainsi, l'attractivité du chemin augmente avec le nombre de
fourmis qui l'empruntent. De plus, une fourmi qui emprunte une route courte
pour aller à la source de nourriture, reviendra au nid rapidement et
donc, déposera deux fois de la phéromone sur son chemin. Au fur
et à mesure que le nombre de fourmis empruntant les routes courtes
augmente, la phéromone s'accumule davantage sur les chemins courts et
les chemins longs sont délaissés. L'évaporation de la
phéromone dans l'air accentue ce phénomène en diminuant
l'utilisation de chemins longs.
L'optimisation par Colonie de Fourmis a été
utilisée avec succès pour un nombre important de problèmes
d'optimisation combinatoire : problème du Voyageur de Commerce ou
Traveling Salesman Problem (Dorigo et al., 1991),
problème de Tournées de Véhicules ou Vehicle Routing
Problem (Bell et McMullen, 2004), problème de Couverture d'Ensemble
ou Set Covering Problem (Lessing et al., 2004) ou encore
problème de Coloration de Graphe ou Graph Coloring Problem
(Costa et Hertz, 1997). Pourtant, à notre connaissance, cette
métaheuristique n'a jamais été utilisée pour
résoudre le TPP. Une étude complète sur l'optimisation par
Colonie de Fourmis a été développée dans le livre
de Dorigo et Stutzle (2004).
Faisant partie des métaheuristiques, l'optimisation par
Colonie de Fourmis fournit un schéma de solution
générique. Néanmoins, ce schéma a besoin
d'être adapté au cas spécifique de chaque problème
afin d'accroître son efficacité. Le schéma de notre
algorithme s'appuie sur une implémentation efficace de l'optimisation
par Colonie de Fourmis. Dans le but de préserver la diversité des
solutions, les opérateurs de recherche
locale sont utilisés pour intensifier la recherche. Ce
schéma est appelé l'algorithme de Fourmis Anamorphiques
Parallèles sur Plans Multi-Dimensionnels Dynamiques (Dynamic
Multi-Dimensional Anamorphic Traveling Ants, ou plus simplement
l'algorithme DMD-ATA.
Le schéma du DMD-ATA est décrit dans la section
3.2. La section 3.3 présente en-suite les opérateurs de recherche
locale utilisés. L'efficacité de notre algorithme est
évaluée dans la section 3.4. Nous comparons notre algorithme avec
la procédure de recherche locale (Local Search algorithm ou LS)
de Riera-Ledesma et Salazar-González (2005). Les résultats
montrent l'efficacité de notre algorithme, qui a permis de trouver un
ensemble de nouvelles meilleures solutions connues.
3.2 Notre algorithme : le DMD-ATA
L'algorithme DMD-ATA propose une
implémentation originale de l'algorithme d'optimisation par Colonie de
Fourmis. Il reprend entre autres des améliorations proposées
précédemment dans la littérature pour l'optimisation par
Colonie de Fourmis.
Dans nos travaux, une fourmi est un agent qui se
déplace de marché en marché sur un graphe de TPP. Les
fourmis ont tendance à préférer les marchés
connectés par des arcs sur lesquels il y a une grosse quantité de
phéromone et qui sont aussi prometteurs selon un critère
heuristique. Quand une fourmi a acheté tous les produits, elle ne
retourne pas au dépôt immédiatement. Elle a la
possibilité de visiter quelques marchés supplémentaires
tandis que la probabilité de retourner au dépôt augmente.
Quand une fourmi a fini son tour, elle dépose sur les arcs faisant
partie de son tour une quantité de phéromone proportionnelle
à la qualité du tour. De plus, si une fourmi a
amélioré la meilleure solution trouvée jusqu'ici, la
solution correspondante est stockée. L'évaporation de la
phéromone est implémentée en introduisant un coefficient
d'évaporation : à chaque itération, la quantité de
phéromone présente sur chaque arc est réduite de 0.1%.
Les prochaines sections décrivent respectivement les
différents composants de l'algorithme DMD-ATA : TA (Fourmis
Parallèlles ou Traveling Ants), A (Anamorphiques), MD (plans
Multi-Dimensionnels) et D (Dynamiques).
3.2.1 Fourmis Parallèles
Dans l'implémentation originale de l'algorithme
d'optimisation par Colonie de Fourmis, chaque fois qu'une fourmi rentre au
dépôt, une nouvelle fourmi en part. Pour résumer, le
Traveling Ants correspond au fait que les fourmis travaillent en
parallèle. L'idée est d'avoir un ensemble de fourmis, cherchant
en parallèle de bonnes solutions pour le TPP et communiquant par le
biais de la phéromone. Chaque fourmi construit une solution du TPP de
manière itérative : on ajoute un nouveau marché à
sa solution partielle en exploitant les informations acquises par les
expériences et un critère heuristique. L'expérience est
modélisée sous la forme de la phéromone
déposée par les fourmis sur les arcs du TPP.
Quand une fourmi rentre au dépôt, une
quantité de phéromone est déposée sur les arcs qui
ont été visités par la fourmi. La quantité de
phéromone déposée dépend de la qualité de la
solution trouvée par la fourmi. Ce dépôt a posteriori de
phéromone permet d'éviter le dépôt de
phéromone sur des arcs appartenant à des tours de mauvaise
qualité, puisque la phéromone n'est déposée que
lorsque la fourmi rentre au dépôt, et donc que la qualité
de la solution est connue. Au stade initial de la résolution, la
quantité de phéromone est la même pour tous les arcs.
Une fois que la fourmi rentre au dépôt, elle
commence un nouveau tour. Comme les chemins qu'elles empruntent ont des
longueurs différentes (en terme de nombre de marchés), les
fourmis ne sont pas synchronisées. Ce traitement permet un meilleur
contrôle sur les fourmis et des mises à jour des phéromones
plus précises.
3.2.2 Fourmis Anamorphiques
La composante Anamorphique correspond à
l'utilisation de fourmis différentes les unes des autres. Chaque fourmi
est définie par un ensemble de paramètres.
- Indépendance (d) : ce paramètre indique
la possibilité de la fourmi à suivre son
propre chemin, c'est-à-dire être moins guidée
par la phéromone.
- Affinité (a) : ce paramètre indique
l'attraction de la fourmi vers la phéromone
- Paresse (s) : ce paramètre accentue la
minimisation des distances plutôt que des coûts d'achats.
- Avidité (v) : ce paramètre accentue la
minimisation des coûts d'achats plutôt que des distances.
Chaque fourmi est initialement définie avec des valeurs
aléatoires pour les paramètres d, a,
s, v. Ces paramètres agissent dans le calcul de la
probabilité pij d'atteindre un marché vj
à partir d'un marché vi :
~~ 1 ~s( 1
)v)d
fiij = (ôij)a j
E Ni
cij Aj
fiij
pij =
?
vkENi
fiik
où ôij est la quantité de
phéromone entre les marchés vi et vj et Aj
est le coût actualisé de produits pour le marché
vj. Le coût Aj correspond à la somme des
coûts d'achats des produits pour le marché vj pour les
produits qui n'ont pas été encore achetés dans le tour,
moins l'économie réalisée en achetant des produits dans le
marché vj à un prix plus faible que le prix payé.
Initialement, à cette somme était ajouté le coût
maximum pour chaque produit non disponible dans le marché vj et
indisponible dans le tour partiel. Ce calcul était un bon moyen pour
comparer l'intérêt de chaque marché. Cependant, la somme
des coûts maximum pour les produits indisponibles dans le marché
vj et indisponibles dans le tour partiel avait tendance à
minimiser l'impact de l'économie réalisée en achetant
à un prix inférieur des produits déjà
achetés. Ainsi, cette somme a
été supprimée de la formule. Cette
formule permet d'utiliser deux informations : l'intérêt du
marché vj selon la distance entre vi et vj et
l'intérêt du marché vj selon les prix des produits
qui y sont vendus. Ni représente l'ensemble des marchés
possibles à partir de vi, c'est-à-dire l'ensemble des
marchés non visités dans le tour partiel. Le critère
heuristique présenté est le résultat
d'expérimentations.
3.2.3 Plans Multi-Dimensionnels
Un inconvénient bien connu pour les algorithmes
d'optimisation à Colonie de Fourmis (Dorigo et al., 1996) est
le risque que la phéromone se concentre en grande quantité sur
seulement quelques arcs, allant jusqu'à interdire de nombreux arcs qui
pourraient appartenir à des solutions optimales ou presque optimales.
Afin d'éviter ce phénomène, une composante
Multi-Dimensional a été ajoutée : 30
étages de phéromone sont exploités en parallèle.
Chaque fourmi est influencée par un seul étage de
phéromone, sur lequel elle dépose sa phéromone. Le nombre
de fourmis par étage reste constant tout au long de la
résolution. Néanmoins, la composante dynamique décrite
ci-dessous joue sur le nombre d'étages et permet la fusion entre
plusieurs étages.
3.2.4 Dynamique
Dans le but d'utiliser efficacement les composantes
précédentes, des paramètres dynamiques ont
été inclus. Premièrement, les caractéristiques
d'une fourmi peuvent évoluer tout au long de la résolution du
problème. Quand le coût de la solution d'une fourmi dépasse
la valeur de la meilleure solution trouvée d'un coefficient fixé,
la fourmi est supprimée, avant même son retour au
dépôt. Ce coefficient est donné par 1.5 + (nombre de
produits + nombre de marchés)/100. Cette formule propose un bon
compromis entre la suppression de fourmis qui ont tendance à trouver de
mauvaises solutions et la préservation de la diversité quand les
instances sont importantes. Quand une fourmi est supprimée, elle perd un
point et repart du dépôt. Chaque fourmi reçoit initialement
10 points. Quand une fourmi a épuisé son stock de points, elle
est définitivement supprimée et une nouvelle fourmi est
créée. Cette nouvelle fourmi est définie comme un clone de
la fourmi ayant trouvé la meilleure solution connue, avec de
légères variations dans ses paramètres (d, a, s, v), afin
d'éviter une convergence trop rapide vers un ensemble de fourmis
identiques. Le nombre de points est augmenté de 50 quand une fourmi
améliore la meilleure solution connue. De cette façon, les
meilleures fourmis sont préservées, et les fourmis visitant des
espaces de recherche peu intéressants sont supprimées.
Deuxièmement, une amélioration pour l'aspect
Multi-Dimensional est d'avoir un nombre variable d'étages. Chaque fois
qu'une fourmi est supprimée, l'étage où elle se trouve
perd un point. Le stock de points est ramené à sa valeur
initiale, 100, quand une fourmi de cet étage améliore la
meilleure solution connue. Quand un étage de phéromone a
épuisé son stock de points, cet étage est supprimé.
Cela permet de concentrer l'effort de recherche sur les étages les plus
prometteurs. Néanmoins, le processus
de suppression des étages est arrêté
lorsque le nombre d'étages est égal à 10, afin de
préserver une diversité dans les solutions. À ce
moment-là, au lieu d'être supprimés, les étages sont
fusionnés avec l'étage de phéromone sur lequel la
meilleure solution connue a été trouvée. La fusion
consiste en l'addition des quantités de phéromones pour chaque
arc. On peut noter que lorsqu'un étage est supprimé, les fourmis
évoluant sur cet étage sont aussi supprimées. La figure 4
présente l'algorithme de la procédure DMD-ATA.
Algorithme 4 : Algorithme DMD-ATA
1 Initialisation: Calculer une première
solution réalisable et en mémoriser le coût;
2 tant que la limite de temps n'est pas
dépassée faire
3 pour chaque étage de
phéromone k faire
pour chaque chaque fourmi j sur chaque
étage k faire
Déplacer j vers le prochain marché;
si j retourne au dépôt
alors
Ajouter de la phéromone sur la route de j selon
la qualité de la solution trouvée;

si j a trouvé une meilleure solution
que la meilleure solution connue alors Mémoriser
j;
Relancer j; sinon
si j n'est pas efficace
alors
Supprimer j;
Enlever un point de j;
si j a épuisé son stock de
points alors

Supprimer j et cloner la meilleure fourmi actuelle;
Relancer j;
Évaporer la phéromone sur l'étage
k;
si l'étage k a épuisé
son stock de points alors
si il y a plus de 10 étages de
phéromone alors Supprimer k;
sinon
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

|
Fusionner k avec le meilleur étage;
|
3.3 Opérateurs de recherche locale
L'optimisation par Colonie de Fourmis a besoin de
coopérer avec une recherche locale afin d'être efficace. Nous
explorons le voisinage de solutions avec plusieurs procédures de
recherche locale. Nous décrivons dans un premier temps ces
procédures, avant de détailler la manière dont elles sont
combinées.
3.3.1 Procédures de recherches locales basiques
2-opt
Cette procédure est bien connue dans le contexte du TSP
(Lin, 1965). Cette procédure consiste à choisir deux
marchés dans le tour et à permuter la circulation entre ces deux
marchés si cela améliore la solution. La complexité de
cette procédure est O(m2). Pour le TPP, la
procédure réoptimise la séquence de marchés
visités, sans modifier l'ensemble des marchés non
visités.
Simplification
Durant la construction du tour, certains produits peuvent
être achetés dans un premier temps dans un marché
vi, puis finalement être achetés dans un marché
visité par la suite, si ces produits sont disponibles à un plus
faible coût. Quand le tour est terminé, certains marchés
peuvent être toujours présents dans le tour, alors qu'aucun
produit n'y est acheté. La procédure simplification
supprime ces marchés du tour.
Insertion
La procédure insertion (voir (Riera-Ledesma et
Salazar-González, 2005) pour plus de détails) tente
d'insérer des marchés non visités dans le tour. Une
insertion est effectuée chaque fois que l'économie
réalisée sur les coûts d'achats des produits dépasse
l'augmentation de coûts de transport. La complexité de cette
procédure est O(m2 × n).
Suppression
La procédure suppression (voir la
procédure drop proposée par (Riera-Ledesma et
Salazar-González, 2005)) est la procédure symétrique de
l'insertion. Un marché est supprimé du tour, à
partir du moment où la diminution des coûts de transport
dépasse l'augmentation des coûts d'achats des produits. La
complexité de cette procédure est
O(m2 × n).
3.3.2 Application de l'opérateur Dropstar
La procédure dropstar, présentée
plus en détail dans le chapitre 2, est une sorte d'extension de la
procédure k-drop proposée par Riera-Ledesma et
Salazar-González (2005). Dans cette procédure, k
marchés consécutifs sont supprimés du tour. Avec la
procédure dropstar, nous proposons de déterminer
l'ensemble optimal de marchés, consécutifs ou non, qui doivent
être supprimés d'une solution. Ainsi, en gardant l'ordre original
du tour, la procédure dropstar en extrait la
sous-séquence optimale (voir la section 2.4.2 pour une vision plus
générale de la procédure Dropstar).
Cette extension permet d'agrandir considerablement la taille
du voisinage. Cependant, trouver la meilleure solution voisine est un
problème NP-difficile comme cela est montre ci-dessous.
Nous definissons maintenant le concept de sous-sequence.
Soit S = (i1, . . . , ik) une sequence, solution
realisable du problème de l'Acheteur Itinerant et S' =
(i'1, ... , i'l) une autre sequence, solution
realisable du problème de l'Acheteur Itinerant. On considère
que S' est une sous-sequence de la sequence S si S'
? S et que quel que soit i' m et
i' n appartenant à S' tel que i'
m precède in', alors i'
m precède i' n dans
S.
Propriete 1 Trouver la meilleure
sous-séquence S' d'une séquence S est un problème
NPdifficile.
Demonstration. Pour montrer que le
problème de recherche d'une sous-sequence optimale (ou PRSS) est
NP-difficile, montrons que le problème decisionnel de recherche d'une
sous-sequence (ou PRSS-dec) est NP-complet. Par rapport au PRSS, le PRSS-dec
cherche une solution de valeur inferieure à un objectif donne,
plutôt qu'une solution de coût optimal. Il est possible de verifier
en temps polynomial si une solution du problème decisionnel est
realisable et si le coût de cette solution est inferieur à un
objectif donne. Le PRSS-dec appartient donc à la classe NP. Pour montrer
que ce problème est NP-complet, nous proposons une reduction du
problème decisionnel de Couverture d'Ensemble (ou PCE-dec) vers le
PRSS-dec.
Considerons une instance du PCE-dec. Soit X un ensemble.
Soit F une famille de sous-ensembles de X, avec ?f?F
f = X. L'objectif du PCE-dec est de trouver un sous-ensemble F'
de F (F' ? F) tel que ?f?F'
f = X et |F'| = Q.
Construisons une instance du problème de l'Acheteur
Itinerant : on definit G = (V, A) un graphe
complet. On note V = {v0, ... , vm}
où v0 est le depôt et v1, . . . ,
vm sont les marches. À chaque f ? F,
on associe une ville vi. Les coûts de transport sont notes
cij = 1 quels que soient vi, vj ?
V\{v0} et civ0 = 0 pour tout vi ?
V\{v0}. P = {p1, . . . ,
pn} est l'ensemble des produits. Chaque
produit pk est un element de X. Chaque produit pk ?
P est disponible dans un ensemble de marches Vk ? V et
les coûts d'achats des produits sk,i est
egal à 0 quels que soient pk ? X et vi ?
Vk.
Construisons la solution realisable S du problème
de l'Acheteur Itinerant qui visite l'ensemble des sommets.
Montrons que resoudre une instance du PCE-dec où le
nombre d'ensembles doit être inferieur à Q revient alors
à savoir s'il existe une sous-sequence S' de S, telle
que le coût de S' soit inferieur à Q.
Supposons qu'il existe une sous-sequence realisable
S' de coût inferieur à Q. Le coût des produits
etant nul, le nombre de marches de S' est donc inferieur ou egal
à Q. On peut donc en deduire qu'il existe une solution
F' au PCE-dec, telle que chaque sous-ensemble f de F'
correspond à un marche de S'. Le nombre de sous-ensemble
f est donc inferieur à Q.
Supposons maintenant qu'il existe une solution F' au
PCE-dec. La solution S' où chaque
marche de S est
un element f de F' est une solution du PRSS-dec
correspondant. La
réponse aux deux problèmes de décision est
donc identique.
Précisons que la réduction se fait en temps
polynomial et rappelons que le problème décisionnel de Couverture
Minimale est NP-complet (Garey et Johnson, 1979). Finalement, ceci permet de
conclure que la recherche d'une sous-séquence optimale appartient
à la classe des problèmes NP-difficiles. ~
Nous calculons la sous-séquence optimale à
l'aide d'un algorithme de programmation dynamique (voir la section 2.4.4 pour
plus de détails sur cet algorithme) appliqué sur un graphe obtenu
à partir du tour original. Ce graphe est construit de la façon
suivante. Un noeud est ajouté pour chaque marché visité
dans le tour. Deux noeuds sont ajoutés, afin de dupliquer le
dépôt en début et en fin de tour. Des arcs sont ensuite
construits entre chaque marché et les marchés situés
à la suite dans le tour. (cf. Fig. 3.1). La procédure
consiste alors à trouver le plus court chemin dans le graphe entre les
deux copies du dépôt, avec la contrainte que tous les produits
soient achetés. Le coût du chemin est égal à la
somme des coûts de transport et des coûts d'achats des produits.
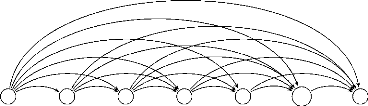
0 4 2 7 3 10 0
FIGURE 3.1 - Exemple d'un tour et
du graphe résultant utilisé par la procédure
dropstar
Dans l'objectif d'accélérer la résolution
de la procédure dropstar, la construction du graphe est
légèrement modifiée. Quand un marché vi
présent dans le tour est le seul marché à proposer un
certain produit parmi les marchés du tour, ce marché doit
être dans toute sous-séquence valide. Ainsi, les arcs entre deux
noeuds situés de part et d'autre de vi ne peuvent être
empruntés. De tels arcs sont alors supprimés du graphe (cf.
Fig. 3.2).
L'algorithme de programmation dynamique que nous avons
utilisé pour trouver le plus court chemin dans le graphe est
inspiré de l'algorithme développé par Feillet et al.
(2004) pour le Problème du Plus Court Chemin
Élémentaire avec Contraintes de Ressources et est
présenté plus en détails dans la section 2.4.4 dans le
chapitre 2. Dans ce problème, des labels correspondent à des
chemins partiels. Afin de limiter le nombre de labels, nous proposons
d'appliquer des règles de dominance.
Dans ce qui suit, nous notons L = (C,
P1, . . . , Pn) un label correspondant à un
chemin partiel, pour lequel C représente le coût du
chemin partiel, comprenant les coûts de transport et les coûts
d'achats des produits, Pj le coût d'achat du produit
pj. Pj est

0 4 2 7 3 10 0
FIGURE 3.2 - Exemple d'un tour et
du graphe résultant pour lequel le marché 7 doit
appartenir au tour
fixé à zéro quand le produit p1
n'a pas été encore acheté dans le chemin partiel. Un
label L1 domine un label L2, ce qui est
noté L1 < L2, quand les deux
chemins partiels représentés par ces labels mènent au
même noeud et que l'on peut être certain que n'importe quelle
extension de L1 serait de coût plus faible que
l'extension identique pour L2. Dans ce cas, le label
L2 peut être alors supprimé.
Un point important à prendre en considération
lorsque deux labels sont comparés est qu'ils n'ont pas
nécessairement acheté les produits au même prix. Ainsi, les
économies potentielles sur les coûts d'achats qui peuvent
être obtenues en étendant les labels sont différentes pour
les deux labels comparés. Nous limitons la comparaison de labels dans le
cas pour lequel les deux labels L1 et
L2 mènent au même marché et que tous
les produits achetés par le label L2 sont aussi
achetés par le label L1. Nous appelons alors
S1 l'ensemble de produits achetés par le label L1 et
S C S1 l'ensemble de produits achetés par le label
L2. Dans ce cas, pour chaque produit p1 E
S, une simple borne supérieure sur le montant additionnel
d'économies sur le coût d'achat de p1 qui peut être
attendu par le label L2 comparé au label
L1 est égal à max(0, P2
1 -- P11 ). Une condition suffisante
pour obtenir la dominance L1 <
L2 est alors
C2 -- ? max(0, P2 1 --
P1 1 ) = C1
p1ES
En effet, cette condition assure que les économies
potentielles sur les coûts d'achats des produits pour le label
L2 ne peuvent pas contrebalancer la différence
actuelle des coûts.
Cette condition peut être renforcée en prenant en
considération les coûts d'achats des produits qui ont
été achetés seulement par le label L1.
Dans cette optique, nous introduisons le coût potentiel c0
ik d'un produit pk dans le marché vi. Ce
coût est égal au coût d'achat minimum du produit pk
dans les marchés situés à la suite du marché
vi dans le tour courant. Avec cette notation, une condition de
dominance renforcée peut être établie telle que :
L1 < L2 si
C2 -- ? max(0, P2 1 --
P11 ) + ? max(c0 i1,
P11 ) = C1
p1ES p1ES1\S
Le nouveau terme de cette condition représente le
coût d'achat minimal pour le label L2 des produits
qui ne sont actuellement achetés que par le label
L1.
3.3.3 Intégration de la recherche locale dans
l'algorithme DMD-ATA
Au vu de la complexité de certaines des
procédures de recherches locales présentées, nous ne
pouvons pas toutes les appliquer à chaque fois qu'une fourmi revient au
dépôt. Par conséquent, seules les procédures
2-opt, insertion, simplification et suppression
sont appliquées, dans cet ordre, lors du retour au
dépôt de chaque fourmi. Chaque procédure, ainsi que la
séquence dans son intégralité, est
répétée tant que des améliorations sur le
coût de la solution sont obtenues.
La procédure dropstar est appliquée
uniquement lorsque la différence entre le coût de la solution
courante et la meilleure solution connue est inférieure à 10% et
que ces deux solutions ont un degré de différence assez
important. Cette différence est évaluée à l'aide de
la mesure suivante :
diff(S, S*) = |(S ?
S*)\(S n S*)|
|S ? S*|
pour laquelle S et S* sont
respectivement l'ensemble des marchés visités par la
solution
courante et par la meilleure solution connue. On considère
que les deux solutions ont
un degré de différence assez important lorsque
diff = 2 3, ce qui signifie que les deux solutions ont moins de la
moitié de leurs marchés en commun.
Par cette condition supplémentaire, nous accentuons
l'exploration du voisinage de bonnes solutions qui diffèrent de
manière significative de la meilleure solution connue. Ceci permet
d'éviter la répétition d'une intensification excessive
dans la même région de l'espace de solutions.
3.4 Résultats expérimentaux
Cette section évalue les performances de notre
algorithme. Nous utilisons les instances symétriques euclidiennes sans
capacité proposées par Riera-Ledesma et SalazarGonzález
(2005). Ces instances vont de m = 50 à 350 marchés et de
n = 50 à 200 produits. Cinq instances sont
générées pour chaque combinaison du nombre de
marchés et du nombre de produits, ce qui amène à un
ensemble de 140 instances. Les solutions optimales sont connues pour 89
instances, par l'approche par séparation et génération de
coupes proposée par Laporte et al. (Laporte et al.,
2003). En ce qui concerne les 51 instances restantes, la valeur de la meilleure
solution connue est fournie par l'algorithme LS de Riera-Ledesma et
Salazar-González (2005). Les expérimentations sont
exécutées en C++ sur un PC Pentium IV 2 Ghz et 1 Go de
mémoire vive sous Linux/Debian.
Tous les paramètres présentés dans ce
chapitre (par exemple, le nombre de niveaux de phéromone) ont
été sélectionnés par des expériences
préliminaires.
Nous comparons plusieurs variantes de notre algorithme avec
l'algorithme de recherche locale (Local Search (LS)) proposé
par Riera-Ledesma et Salazar-González (2005) lorsque les solutions
optimales ne sont pas connues et avec l'approche par séparation et
génération de coupes proposée par Laporte
et al. (2003) lorsque leur algorithme fournit les solutions optimales.
Les résultats sont présentés dans les tableaux 3.1 et 3.2,
respectivement pour les instances pour lesquelles la solution optimale est
connue et celles où la solution optimale n'est pas connue. Les
algorithmes sont :
- LS : algorithme Local Search proposé par
Riera-Ledesma et Salazar-González (2005).
- IN (Improved Neighborhood) : une approche par construction
stochastique simple, améliorée par nos opérateurs de
recherche locale. La construction consiste à choisir
aléatoirement un marché pour lequel au moins un nouveau produit
peut être acheté, puis l'insérer dans le tour courant avec
une approche de plus faible insertion, jusqu'à ce que tous les produits
soient achetés, et ainsi obtenir une solution réalisable. Des
marchés choisis aléatoirement sont ensuite ajoutés
à la solution. Le nombre de marchés à ajouter est un
nombre aléatoire compris entre 0 et 4. La procédure se termine
avec des séquences d'insertion, suppression, dropstar et 2-opt,
jusqu'à ce qu'aucune amélioration ne puisse être obtenue.
Une nouvelle solution est alors générée. L'algorithme
s'arrête lorsqu'il a atteint une limite de temps fixée à
300 secondes.
- DMD-ATA-LS : notre algorithme sans la procédure
Dropstar, avec une limite de temps fixée à 300 secondes.
- DMD-ATA-300 : notre algorithme, avec une limite de temps
fixée à 300 secondes. - DMD-ATA : les résultats moyens de
notre algorithme pour cinq essais, avec une limite de temps fixée
à 3600 secondes.
Les en-têtes de colonnes et des lignes sont les suivants
:
- m : nombre de marchés dans les instances,
- n : nombre de produits dans les instances,
- %gap : écart exprimé en pourcentage entre la
solution optimale (Table 3.1) ou la meilleure solution connue (Tableau 3.2) et
la solution renvoyée par l'algorithme DMD-ATA,
- CPU : Temps en secondes pour finir l'algorithme (LS) ou pour
trouver la meilleure solution,
- #best : nombre d'instances sur 89 pour lesquelles la solution
optimale connue a été trouvée (Tableau 3.1),
- #improved : nombre d'instances sur 51 pour lesquelles la
meilleure solution connue a été atteinte ou
améliorée (Tableau 3.2).
Dans le tableau 3.2, le temps CPU pour l'algorithme LS n'est pas
disponible.
Les tableaux 3.3 et 3.4 présentent les instances pour
lesquelles la meilleure solution connue (fournie par Riera-Ledesma et
Salazar-González (2005)) a été améliorée par
l'algorithme DMD-ATA (avec 5 essais). La première colonne des tableaux
est le nom de l'instance.
La première conclusion qui peut être tirée
à la lecture de ces tableaux est que l'algorithme DMD-ATA est
compétitif lorsqu'on le compare avec les meilleures méthodes
connues, notamment la méthode LS de Riera-Ledesma et
Salazar-González (2005). Sur de petites instances, l'algorithme DMD-ATA
est parfois moins performant que la méthode LS. Sur les instances de
tailles plus importantes, notre algorithme se montre plus efficace en terme de
qualité de la solution que la méthode LS et améliore 48
instances
m n
Methodes #best
50 100 150 200 250 50 100 150 200
%Gap 0.07 0.14 0.03 0.32 0.06 0.07 0.24 0.10 0.08 82/89
LS CPU 3 10 14 19 25 5 13 20 21
%Gap 0.00 0.08 5.4 2.13 2.1 0.15 0.3 3.51 4.13 62/89
IN CPU 5 30 93 71 76 12 44 73 90
DMD-ATA-LS %Gap 0.00 0.00 0.21 0.36 0.51 0.05 0.03 0.34 0.35
75/89
CPU 4 22 60 97 123 36 73 60 51
DMD-ATA-300%Gap 0.00 0.01 0.13 0.03 0.39 0.05 0.15 0.00 0.12
79/89
CPU 5 6 75 66 97 20 53 31 81
DMD-ATA %Gap 0.00 0.00 0.08 0.02 0.01 0.00 0.05 0.00 0.03
86.50/89
CPU 2 20 172 232 154 37 154 96 165
TABLE 3.1 - Résultats
expérimentaux, instances fermées
m n
Methodes 50 100 150 200 #improved
200 250 300 350
%Gap 2.05 6.00 6.66 10.99 0.78 5.43 8.77 8.04 14/51
IN CPU 9 100 88 111 104 85 98 59
DMD-ATA-LS %Gap 0.88 1.61 1.30 1.22 -0.29 1.00 1.49 1.37
32/51
CPU 53 88 165 125 80 124 127 105
DMD-ATA-300%Gap 0.56 1.30 2.08 1.25 -1.16 0.23 1.77 2.46
34/51
CPU 105 83 134 160 61 106 172 105
DMD-ATA %Gap -0.30 -0.33 -0.38 -0.75 -1.27 -0.49 -0.31 -0.09
48/51
CPU 973 470 834 651 133 394 515 909
TABLE 3.2 - Résultats
expérimentaux, instances ouvertes
sur 51 pour lesquelles les solutions optimales ne sont
toujours pas connues. Cependant, on peut noter que notre algorithme se montre
plus coûteux en temps de calcul que LS. En effet celui-ci est basé
sur une descente stratégique et converge donc rapidement vers un optimum
local.
La comparaison entre la méthode DMD-ATA-300 et la
méthode DMD-ATA est intéressante pour un point en particulier.
Sur les instances de grandes tailles, la méthode DMD-ATA s'avère
beaucoup plus efficace en un heure qu'en 300 secondes. La raison pour cela
semble être qu'une partie importante du temps de calcul est
consommée par les opérateurs de recherche locale et donc que la
limite de 300 secondes ne semble pas être un temps assez
conséquent pour tirer entièrement avantage du composant
d'optimisation par Colonies de Fourmis.
Les résultats présentés dans le tableau
3.1 et les tableaux 3.3 et 3.4 sont les moyennes des résultats sur cinq
essais, afin de montrer l'efficacité et la robustesse de l'algorithme.
Les résultats sont très proches d'un essai à l'autre.
D'autres conclusions peuvent être déduites
à partir des comparaisons entre l'algorithme DMD-ATA et l'algorithme
Improved Neighborhood. Les résultats montrent que
|
Instance
|
DMD-ATA
|
LS
|
CPU
|
%gap
|
|
EEuclideo.200.150.4
|
2419
|
2426
|
1216,92
|
-0,29
|
|
EEuclideo.200.200.4
|
2344
|
2353
|
527,03
|
-0,38
|
|
EEuclideo.250.100.1
|
1301
|
1309
|
33,84
|
-0,61
|
|
EEuclideo.250.100.4
|
1673
|
1677
|
10,23
|
-0,24
|
|
EEuclideo.250.100.5
|
1641
|
1648
|
550,24
|
-0,42
|
|
EEuclideo.250.150.4
|
1836
|
1840
|
45,24
|
-0,22
|
|
EEuclideo.250.150.5
|
1531
|
1539
|
21,1
|
-0,52
|
|
EEuclideo.250.200.2
|
2785
|
2787
|
1137,65
|
-0,07
|
|
EEuclideo.250.200.3
|
1924
|
1934
|
281,88
|
-0,52
|
|
EEuclideo.250.200.4
|
2116
|
2128
|
83,83
|
-0,56
|
|
EEuclideo.250.200.5
|
1797
|
1807
|
930,03
|
-0,55
|
|
EEuclideo.300.50.1
|
1477
|
1483
|
160,00
|
-0,40
|
|
EEuclideo.300.50.2
|
813
|
816
|
116,01
|
-0,37
|
|
EEuclideo.300.50.3
|
1117
|
1123
|
20,00
|
-0,53
|
|
EEuclideo.300.50.4
|
1176
|
1183
|
2,11
|
-0,59
|
|
EEuclideo.300.50.5
|
1257
|
1262
|
276,00
|
-0,40
|
|
EEuclideo.300.100.1
|
1035
|
1040
|
55,54
|
-0,48
|
|
EEuclideo.300.100.2
|
1179
|
1184
|
617,22
|
-0,42
|
|
EEuclideo.300.100.3
|
1498
|
1507
|
103,42
|
-0,60
|
|
EEuclideo.300.100.4
|
1749
|
1759
|
312,16
|
-0,57
|
|
EEuclideo.300.100.5
|
1774
|
1781
|
2,74
|
-0,39
|
|
EEuclideo.300.150.1
|
1457
|
1459
|
756,71
|
-0,14
|
|
EEuclideo.300.150.2
|
1656
|
1667
|
483,32
|
-0,66
|
|
EEuclideo.300.150.3
|
2485
|
2492
|
663,24
|
-0,28
|
TABLE 3.3 - Résultats
expérimentaux, instances ouvertes améliorées (1)
les opérateurs de recherche locale que nous proposons
sont assez performants tant que les instances sont de tailles
modérées. Néanmoins, l'intérêt de coupler de
l'optimisation par Colonie de Fourmis avec de la recherche locale est
évident pour les instances de plus grandes tailles. Cela démontre
que le schéma d'optimisation par Colonies de Fourmis permet de diriger
la recherche vers de bonnes régions de l'espace de solutions.
Enfin, la comparaison entre l'algorithme DMD-ATA-300 et
l'algorithme DMD-ATALS montre que la procédure Dropstar apporte
un avantage considérable à notre méthode. Elle permet de
résoudre 4 instances à l'optimum qui n'étaient pas
résolubles sans cette procédure. De plus, la procédure
permet d'améliorer les meilleures solutions connues de 34 instances,
alors que la méthode DMD-ATA-LS (sans la procédure
Drops-tar) n'en améliorait que 32 dans le même temps
imparti. Comme on peut le constater à la lecture des temps de calcul, la
procédure Dropstar nécessite un temps de calcul
raisonnable et fournit une exploration intensive d'une nouvelle
définition de voisinage, qui n'était pas exploré par les
autres procédures de recherche locale.
|
|
|
|
3.5. Conclusion
|
|
|
|
|
|
|
Instance
|
DMD-ATA
|
LS
|
CPU
|
%gap
|
|
EEuclideo.300.150.4
|
1801
|
1809
|
95,93
|
-0,44
|
|
EEuclideo.300.150.5
|
1816
|
1825
|
309,25
|
-0,49
|
|
EEuclideo.300.200.2
|
1791
|
1798
|
1918,52
|
-0,39
|
|
EEuclideo.300.200.3
|
2442
|
2450
|
2852,05
|
-0,33
|
|
EEuclideo.300.200.4
|
1815
|
1829
|
2946,79
|
-0,77
|
|
EEuclideo.350.50.1
|
723
|
727
|
46,04
|
-0,55
|
|
EEuclideo.350.50.2
|
736
|
739
|
25,71
|
-0,41
|
|
EEuclideo.350.50.3
|
942
|
946
|
6,00
|
-0,42
|
|
EEuclideo.350.50.4
|
805
|
809
|
379,39
|
-0,49
|
|
EEuclideo.350.50.5
|
1125
|
1230
|
26,35
|
-8,54
|
|
EEuclideo.350.100.1
|
1317
|
1321
|
1698,48
|
-0,30
|
|
EEuclideo.350.100.2
|
962
|
965
|
155,48
|
-0,31
|
|
EEuclideo.350.100.3
|
796
|
804
|
839,65
|
-1,00
|
|
EEuclideo.350.100.4
|
1059
|
1065
|
13,94
|
-0,56
|
|
EEuclideo.350.100.5
|
1566
|
1576
|
464,86
|
-0,63
|
|
EEuclideo.350.150.1
|
1457
|
1459
|
1986,42
|
-0,14
|
|
EEuclideo.350.150.2
|
1315
|
1322
|
159,12
|
-0,53
|
|
EEuclideo.350.150.3
|
2553
|
2566
|
257,69
|
-0,51
|
|
EEuclideo.350.150.4
|
1239
|
1248
|
595,85
|
-0,72
|
|
EEuclideo.350.150.5
|
2288
|
2297
|
8,93
|
-0,39
|
|
EEuclideo.350.200.1
|
1503
|
1505
|
1033,39
|
-0,13
|
|
EEuclideo.350.200.2
|
1374
|
1377
|
3085,09
|
-0,22
|
|
EEuclideo.350.200.3
|
1873
|
1889
|
368,66
|
-0,85
|
|
EEuclideo.350.200.5
|
2336
|
2347
|
2385,65
|
-0,47
|
TABLE 3.4 - Résultats
expérimentaux, instances ouvertes améliorées (2)
3.5 Conclusion
Nous avons proposé un nouvel algorithme pour la
solution du problème de l'Acheteur Itinérant. Cet algorithme
consiste en l'hybridation d'une méthode d'optimisation à Colonie
de Fourmis avec des procédures de recherche locale. Notre approche a
été la suivante. L'algorithme d'optimisation par Colonie de
Fourmis est essentiellement dédié à mener la recherche
vers des régions intéressantes de l'espace de solutions. La
recherche locale est alors utilisée pour explorer intensivement ces
régions. Ainsi, l'algorithme d'optimisation par Colonie de Fourmis est
modifié de façon à garantir un important degré de
diversité. Nous appelons Fourmis Anamorphiques Parallèles sur
Plans Multi-Dimensionnels Dynamiques (Dynamic Multi-Dimensional
Anamorphic Traveling Ants ou DMD-ATA) l'algorithme résultant de
cette hybridation. En ce qui concerne les opérateurs de recherche
locale, nous utilisons l'opérateur de grand voisinage Dropstar,
introduit dans le chapitre 2. À notre connaissance, un tel
opérateur n'a jamais été proposé pour le
problème de l'Acheteur Itinérant, ni pour d'autres
problèmes de Tournées de Véhicules. L'utilisation
couplée de l'optimisation par Colonie de Fourmis et d'un
opérateur de recherche à grand voisinage semble efficace,
puisqu'elle permet d'améliorer
les meilleures solutions connues pour un nombre important
d'instances.
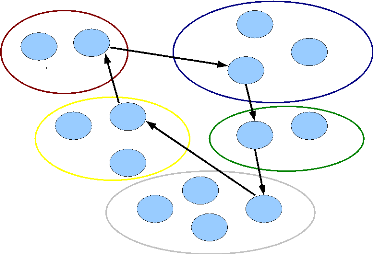
10
Groupe 0 8 Groupe 3
Groupe 2 Groupe 1
3
0
6
7
2
1
13
Groupe 4
9
4
5
12
11
Chapitre 4
Application au Problème du
Voyageur de Commerce
Généralisé
4.1 Introduction au Problème du Voyageur de
Commerce Généralisé
Nous proposons une solution pour le problème du
Voyageur de Commerce Généralisé (Generalized Traveling
Salesman Problem ou GTSP) basée sur un algorithme
mémétique (dans notre cas, un algorithme génétique
combiné avec de la recherche locale, voir (Hart et al., 2005)
ou (Moscato et Cotta, 2005) pour plus de détails). Le problème du
Voyageur de Commerce Généralisé est une
généralisation du classique problème du Voyageur de
Commerce (Traveling Salesman Problem ou TSP). Ma principale
contribution réside dans l'opérateur de croisement basé
sur l'exploration d'un voisinage étendu autour de l'individu père
et de l'individu mère.
Le GTSP peut être décrit de la façon
suivante. Soit G = (V, E) un graphe complet non
orienté, V = {v1, . . . , vn} un
ensemble de villes, W = {W1, . . . , Wm}
un ensemble de groupes, avec 0 < m = n. Chaque ville
vi E V appartient à un et un seul groupe (les groupes
sont disjoints deux à deux, i.e. pour i =6 j, Wi
fl Wj = 0 et W1 U ... U Wm =
V). Les coûts de transports sont notés
cij pour (vi, vj) E V.
L'objectif est de construire un tour qui visite exactement une fois chaque
groupe tout en minimisant la somme des coûts de transport. Dans notre
travail, nous n'avons considéré que le cas pour lequel les
matrices de coûts sont symétriques (cij = cji),
mais l'algorithme peut être facilement généralisé
pour les cas asymétriques. En particulier, l'opérateur de
croisement peut être aussi bien appliqué pour les cas
symétriques que pour les cas asymétriques.
Le GTSP est un problème NP-difficile au sens fort,
puisque ce problème est une généralisation du TSP. En
effet, le cas spécial dans lequel m = n (une ville par
groupe) est un problème de Voyageur de Commerce : le problème est
de trouver un tour qui visite chaque ville en minimisant les coûts de
transports.
Dans la section 4.2, nous présentons un état de
l'art sur le GTSP. La section 4.3 présente un nouvel algorithme
mémétique développé pour la résolution du
GTSP. La principale caractéristique de cet algorithme réside dans
la procédure de croisement basée sur une recherche à grand
voisinage (voir (Ahuja et al., 2002) pour un travail récent sur
les recherches à grand voisinage). La section 4.4 évalue
expérimentalement notre algorithme à l'aide de benchmarks issus
de la librairie GTSPLIB (Reinelt, 1991).
4.2 État de l'art
Le GTSP fut introduit en premier par Srivastava et al.
(1969) et Henry-Labordere (1969), qui ont proposé chacun une
résolution par un algorithme de programmation dynamique. Laporte et
Nobert (1984) et Laporte et al. (1984) ont proposé une approche
par programmation en nombres entiers afin de résoudre le GTSP de
manière exacte. Plus récemment, Fischetti et al. (1997)
ont proposé une résolution efficace basée sur une
procédure de séparation et génération de coupes,
qui a permis de fournir des résultats optimaux pour des instances
contenant jusqu'à 442 noeuds.
4.2. État de l'art
Plusieurs travaux ont été menés pour
transformer le GTSP en TSP (Lien et al., 1993; Noon et Bean, 1993;
Dimitrijevic et Saric, 1997; Laporte et Semet, 1999; Ben-Arieh et al.,
2003). Certaines des instances de TSP issues de ces transformations ont un
nombre similaire de noeuds comparé au nombre de noeuds de l'instance de
GTSP initiale. De plus, certaines transformations de GTSP en TSP (Noon et Bean,
1993) ont une propriété importante : une solution optimale du TSP
créé peut être transformée en une solution optimale
du GTSP. Malheureusement, une solution réalisable non optimale pour le
TSP créé peut ne pas être réalisable pour le GTSP.
De plus, certaines heuristiques très efficaces pour le TSP ont eu des
résultats peu convaincants pour le GTSP (Slavík, 1997; Dror et
Haouari, 2000)
Deux algorithmes d'approximations ont été
proposés pour le GTSP. Slavík (1997) a présenté une
approximation en 3p/2, pour laquelle p est le nombre de
villes dans le plus grand groupe (p = max (|Vm|)).
Cependant, la borne dans le pire cas peut être de
i=1,...,m
piètre qualité, la borne supérieure de
p étant égale au nombre de noeuds. Garg et Konjevod
(2000) ont proposé un algorithme d'approximation pour le problème
d'arbre de Steiner, amenant à un algorithme d'approximation en
O(log2(|V|) log log(|V|))
log(m)) pour le GTSP. Dans les deux cas, les inégalités
triangulaires doivent être respectées.
Noon et Bean (1991) ont proposé plusieurs heuristiques,
en particulier une adaptation de l'heuristique du plus proche voisin
utilisée pour le TSP. Des adaptations similaires ont été
proposées par Fischetti et al. (1997), telles que la plus
lointaine insertion, la plus proche insertion ou encore l'insertion à
plus faible coût. Plus récemment, Renaud et Boctor (1998a) ont
proposé l'heuristique GI3 (Generalized Initialization,
Insertion and Improvement), qui est une généralisation de
l'heuristique I3, présentée dans (Renaud et
al., 1996). Cette heuristique se déroule en trois phases : une
phase d'initialisation du-rant laquelle on construit un tour qui peut ne pas
être valide, une phase d'insertion qui complète les tours
incomplets en insérant au plus faible coût les villes provenant de
groupes non visités et une phase d'amélioration qui utilise des
modifications de voisinages de type 2-opt et 3-opt, appelées ici G2-opt
et G3-opt. Cet article présente aussi l'algorithme ST (pour Shortest
Tour). Cet algorithme détermine la séquence de villes de plus
petit coût qui visite les groupes dans un ordre fixé. Ils montrent
que ce problème peut être résolu en un temps polynomial.
Snyder et Daskin (2006) ont proposé récemment
une résolution par un algorithme génétique utilisant un
encodage par clé aléatoire, encodage qui assure que les solutions
construites par croisement ou mutation sont des solutions valides. Cet
algorithme génétique est couplé avec des
améliorations par recherche locale, définissant un algorithme
mémétique, une procédure d'échange et un voisinage
de type 2-opt (voir (Moscato et Cotta, 2005) pour plus de détails sur
les algorithmes mémétiques). Leurs résultats
expérimentaux montrent que leur algorithme est performant, que ce soit
en terme de qualité de solution ou de temps de calcul. Un algorithme
basé sur l'optimisation par essaims particulaires a été
récemment présenté par Shi et al. (2007). Une
procédure pour supprimer les croisements dans les tours a
été utilisée pour accélérer la vitesse de
convergence, appuyée par deux techniques de recherche locale.
Malgré cela, les résultats présentés ne parviennent
pas à dépasser les meilleures heuristiques connues.
Enfin, Silberholz et Golden (2007) ont proposé un
algorithme génétique avec plusieurs nouvelles techniques, entre
autres, des populations initiales isolées, ainsi qu'une nouvelle
procédure de reproduction, basé sur l'opérateur de
croisement ordonné pour le TSP. Cette nouvelle procédure est
appelée mrOX, pour croisement ordonné de rotation
modifié (modified rotational ordered crossover). Les
procédures d'améliorations locales associées à cet
opérateur de croisement, définissant un algorithme
mémétique, ont permis d'obtenir de très bons
résultats sur de nouvelles instances de taille importante et de
dépasser les autres solutions heuristiques en ce qui concerne la
qualité des solutions obtenues. L'algorithme proposé par
Silberholz et Golden (2007) peut être considéré comme
l'algorithme le plus compétitif publié à ce jour.
4.3 Algorithme mémétique
Un algorithme génétique (Genetic Algorithm
ou GA) est une technique de recherche utilisée pour trouver des
solutions approchées à différents types de
problèmes d'optimisation (voir par exemple (Winter et al.,
1995; Vose, 1998; Man et al., 1999) pour plus de détails). Les
algorithmes génétiques font partie des métaheuristiques et
sont une classe particulière des algorithmes évolutionnaires, qui
utilisent des techniques inspirées de la biologie telles que la
mutation, les croisements ou la sélection naturelle. Les algorithmes
génétiques maintiennent un nombre important de solutions tout au
long de la résolution du problème. L'ensemble des solutions
mémorisées est appelé la population. Chaque
solution est appelé un individu ou un chromosome. Un
individu représente donc une version encodée d'une solution.
À chaque itération d'un algorithme génétique, une
nouvelle population est générée en utilisant un certain
nombre d'opérateurs : la reproduction, la sélection et la
mutation.
Les algorithmes génétiques couplés avec
des techniques de recherche locale sont classés comme des algorithmes
mémétiques, tels qu'ils ont été
présentés par Moscato et Norman (1992) et (Moscato et Cotta,
2005) (voir par exemple (Hart et al., 2005; Sörensen et Sevaux,
2006) pour plus de détails sur des les algorithmes
mémétiques). Dans cette section, nous présentons un
algorithme mémétique. Nous insistons en particulier sur
l'opérateur de croisement, qui est notre principale contribution. Afin
d'évaluer plus facilement l'impact de cet opérateur, nous avons
volontairement développé une implémentation standard pour
le reste de l'algorithme mémétique.
4.3.1 Composants basiques de l'algorithme Individus
Chaque individu (une solution du problème) est
représenté par une liste ordonnée de groupes, dans
laquelle le premier et le dernier groupe sont identiques. À partir de
cette liste, on peut déterminer un tour des villes optimal,
correspondant à cet ordre de visite des groupes. Le coût de
l'individu est le coût du tour des villes. Ce coût est obtenu en
utilisant l'algorithme ST (Shortest Tour) développé par
Renaud et Boctor (1998a).
Le principe de l'algorithme Shortest Tour est le suivant. Une
succession de groupes définit une séquence d'ensembles de villes,
dans laquelle les villes d'un groupe ne peuvent être atteintes que par
des villes appartenant à un groupe précédent. En
représentant les villes par des noeuds, nous obtenons un graphe
orienté acyclique. L'ensemble des chemins du graphe ainsi construit et
dont le sommet de départ est confondu avec le sommet d'arrivée,
correspond alors à l'ensemble des solutions respectant l'ordre
défini par la séquence de groupes. La meilleure de ces solutions
est le plus court chemin du graphe. Le calcul d'un plus court chemin dans un
graphe acyclique peut être effectué en un temps polynomial
à l'aide d'une simple récurrence. Dans le cas du GTSP, le plus
court chemin doit être calculé pour chaque ville du groupe de
départ en ajoutant la contrainte que le chemin commence et finit par la
ville considérée. Le tour des villes optimal est le meilleur tour
parmi ces solutions. Cette procédure n'est pas très
coûteuse en temps de calcul, ce qui nous permet de l'appeler
régulièrement (la complexité de cet algorithme est en
O(n3/m3), voir (Renaud et
Boctor, 1998a) pour plus de détails).
Population initiale
La population initiale contient N individus. Les
individus sont générés à l'aide de listes de
groupes construites aléatoirement. L'algorithme ST est appliqué
afin de déterminer le tour des villes optimal, ainsi que le coût
de chaque individu. Afin de limiter les symétries, le groupe de
départ (et d'arrivée) est fixé pour tous les individus.
Dans le but de réduire le temps de calcul requis par la procédure
ST, le groupe qui contient le moins de villes est choisi pour être le
premier et le dernier groupe de la liste pour chacun des individus.
Renouvellement de la population
À chaque génération, deux individus sont
choisis aléatoirement par sélection proportionnelle à
l'adaptation (Roulette Wheel selection) et appairés à
l'aide de l'opérateur de croisement. Ces deux parents donnent naissance
à deux enfants. Cette opération est répétée
k fois. Les 2 * k nouveaux individus sont alors
ajoutés à la population et seuls les N meilleurs
individus sont gardés. Ainsi, la taille de la population reste constante
dans le temps.
Mutation
Une procédure de mutation est appliquée afin de
diversifier la population. Chaque individu de la population a une
probabilité u d'être sélectionné pour la
procédure de mutation. Dans nos expérimentations, nous avons
fixé u = 0.05 (ce pourcentage arbitraire a été
choisi car il est utilisé dans plusieurs articles, par exemple dans
(Silberholz et Golden, 2007)). La mutation consiste à échanger la
place de deux groupes choisis aléatoirement puis d'appliquer
l'algorithme Shortest Tour pour calculer le tour optimal de villes, ainsi que
le nouveau coût de l'individu.
Critère d'arrêt
L'algorithme s'arrête lorsque N1
générations ont été calculées ou
lorsqu'aucune amélioration n'a eu lieu durant N2
générations.
Algorithme Mémétique
La figure 5 présente une vue synthétique de notre
algorithme.
Algorithme 5 : Algorithme de l'algorithme
mémétique
1 Initialisation: Construire
aléatoirement une population initiale de N individus;
2 tant que le nombre d'itérations est
plus petit que N1 et qu'il y a eu une amélioration depuis moins
de N2 itérations faire
3 pour chaque i = 0 à k
faire
4
5
6
7
8
9
Choisir deux individus aléatoirement;
Construire deux nouveaux individus par croisement;
Appliquer de la recherche locale sur les deux individus;
Ajouter les 2 * k nouveaux individus à la
population; Garder les N meilleurs individus dans la population;
Appliquer une mutation avec une probabilité u
à chaque individu de la population;
4.3.2 Croisement
Le croisement est une procédure importante dans un
algorithme génétique ou dans un algorithme
mémétique. Cet opérateur permet de construire de nouvelles
solutions à partir de solutions existantes et joue un rôle
important pour la diversification des solutions.
Le croisement (appelé aussi la reproduction) est
l'équivalent de la rencontre de deux parents, produisant deux enfants.
Ces enfants portent une ressemblance à chacun de leurs parents. De
nombreux opérateurs de croisement ont été proposés
: croisement de préservation maximale (maximal preservative
crossover ou MPX) proposé par Mühlenbein et al.
(1988), croisement ordonné de rotation modifié (modified
rotational ordered crossover ou mrOX) proposé par Silberholz et
Golden (2007). Une comparaison de différents opérateurs de
croisements utilisés pour le problème du Voyageur de Commerce a
été présentée par Tsai et al. (2004).
La procédure de croisement que nous proposons ici est
une application de la procédure dropstar,
présentée dans le chapitre 2. On peut aussi noter que cet
opérateur a été inspiré d'un algorithme
proposé par Prins (2004), appliqué à un problème de
Tournées de Véhicules.
Soient Wi 1, .. . , Wi
m et vi1, . . . , vim
respectivement le tour des groupes et le tour des villes d'un individu,
appelé le père. Soient Wj 1, . . . ,
Wj m et vj1, . . . ,
vjm respectivement le tour des groupes et le tour des
villes d'un autre individu de la population, appelé la mère. Un
nouvel individu - un enfant - est construit de la manière décrite
ci-dessous. On peut noter qu'une fois qu'un individu fils a été
construit, le rôle des deux parents est inversé et qu'un
deuxième enfant est obtenu en utilisant le même
procédé.
Chaque ville de la mère est insérée
itérativement dans la séquence de villes du père. L'ordre
dans lequel les villes sont insérées est l'ordre
déterminé par le tour des villes de la mère,
c'est-à-dire que la première ville insérée est la
première ville dans le tour des villes de la mère. Nous
déterminons la position d'insertion d'une ville vjk
de la façon suivante : nous considérons chaque position
d'insertion de vjk entre les villes vil
et vil+1 du père de telle sorte que Wi l =6
Wj k et Wi l+1 =6
Wj k (évitant ainsi que deux groupes identiques ne
se suivent); parmi ces possibilités, on choisit celle minimisant le
coût d'insertion ciljk + cjkil+1 -
cilil+1.
Une fois que chaque ville de la mère est
insérée, nous en déduisons un tour des groupes dans lequel
chaque groupe apparaît deux fois. Nous appelons cette séquence la
séquence maître. Dans (Dauzère-Pérès et
Sevaux, 2004), une séquence maître d'un problème
d'ordonnancement est définie comme une séquence contenant au
moins une séquence optimale. Nous cherchons alors la
sous-séquence optimale réalisable, c'est-àdire pour
laquelle chaque groupe est visité une et une seule fois.
Cette recherche est effectuée par le biais d'un
algorithme de programmation dynamique récursif (voir le chapitre 2 pour
plus de détails), appliqué à un graphe obtenu à
partir du tour contenant chaque groupe en double. Ce graphe est construit selon
la procédure suivante. Un sommet est créé pour chaque
ville de chaque groupe, pour chaque apparition du groupe. Un arc est
ajouté pour chaque paire de noeuds issus de groupe de différentes
positions dans la séquence, dans la direction de la séquence (cf.
Fig. 4.1 pour une vision agrégée du graphe et Fig. 4.2 pour un
extrait du graphe complet). Nous définissons par la suite plusieurs
réductions de graphe (voir section 4.3.3). L'objectif est de trouver le
plus court chemin dans le graphe entre les groupes situés aux deux
extrémités, avec la contrainte que tous les groupes doivent
être visités exactement une fois et que la solution doit
être un cycle.
Avant d'expliquer plus en détails l'algorithme de
programmation dynamique, illustrons le comportement de cet opérateur de
croisement sur un exemple simple. Considérons un ensemble de groupe
W = {W1, . . . , W5}. Les tours de groupes du
père et de la mère sont :
père : W4 W3 W1 W5
W2 W4
mère : W4 W1 W3
W5 W2 W4
La procédure d'insertion définit une
séquence maître de groupes de la forme:
enfant: W4 W1 W3 W1
W5 W2 W3 W2 W5 W4
dans laquelle les groupes issus du père sont
soulignés et les positions d'insertion sont définies en utilisant
les tours des villes des individus.
Le graphe représenté par les figures 4.1 et 4.2
est alors défini implicitement. À partir de ce graphe,
l'algorithme de programmation dynamique détermine un tour des villes
optimal, à partir duquel on déduit une séquence de
groupes, définissant ainsi un nouvel individu. L'implémentation
de cet algorithme est détaillé dans la section 4.3.3.
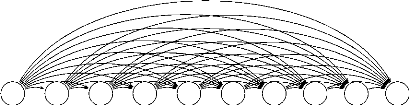
W4 W1 W3 W1 W5 W2 W3 W2 W5 W4
FIGURE 4.1 - Exemple d'un
croisement et du graphe résultant utilisé par la procédure
dropstar : vue avec agrégation des sommets en groupes
groupe W1
V12
V5
groupe W3
V11
V8
V9
groupe W1
V12
V5
FIGURE 4.2 - Exemple d'un
croisement et du graphe résultant utilisé par la procédure
dropstar : vue détaillée
Le principal avantage de cet opérateur est de
s'étendre sur un très grand espace de solutions. En effet, le
nombre de sous-séquences de groupes de la séquence maître
est égal à 2m oü m est le
nombre de groupes. De plus, pour une sous-séquence donnée, le
nombre de tours de villes est en
O((n/m)m) (on peut facilement se
rendre compte que l'espace le plus large est obtenu lorsque chaque groupe a la
même taille (le même nombre de villes) n/m).
Ainsi, la solution définie par cet opérateur de croisement est la
meilleure parmi O(2m *
(n/m)m). Selon nous, cela permet une
diversification importante et des populations de bonne qualité.
Cependant, le prix à payer est un important coût de
complexité comparé aux opérateurs de croisement
classiques. L'objectif de ce travail est d'évaluer si ce prix est digne
d'intérêt.
Devant la complexité de la procédure de
croisement, un important travail a été effectué afin
d'accélérer cette procédure pour la rendre applicable dans
le cas d'instances de taille importante.
4.3.3 Implémentation détaillée de
l'opérateur de croisement
Algorithme de programmation dynamique
L'algorithme de programmation dynamique utilisé pour
trouver le plus court chemin dans le graphe est celui présenté
dans le chapitre 2. L'algorithme commence avec des chemins partiels initiaux
associés à chaque noeud du premier groupe. Les chemins partiels
sont ensuite étendus itérativement avec la contrainte que chaque
groupe doit être visité exactement une fois. Cette contrainte est
traitée comme la contrainte d'élémentarité du
chemin, présentée par Feillet et al. (2004). Le graphe
étant acyclique, l'extension des chemins partiels dans l'ordre
topologique des noeuds fournit le chemin optimal.
Dans ce qui suit, nous notons L = (C,
ä1, .. . , äm) un label correspondant
à un chemin partiel, pour lequel C représente le
coût de transport du chemin partiel et äi E {0, 1} indique
si le groupe Wi est présent dans le chemin ou non. L'extension
d'un label à travers un arc est réalisable quand äi
= 0 pour le groupe Wi de la ville de destination, excepté
lorsque ce groupe est le dernier groupe de la séquence. Dans ce cas, les
conditions de réalisabilité sont que la ville de destination est
la première ville du label et que äi = 1 pour 1 i
m.
Un label L1 domine un label
L2, ce qui est noté L1 <
L2, lorsque ces deux labels mènent au même
noeud et que l'on peut être sûr que n'importe quelle extension de
L1 est de coût moindre que l'extension identique pour
L2. Ici, L1 < L2
quand C1 C2,
ä1 i ä2 i pour 1 i m
et que les premières et dernières villes de deux labels
sont
identiques. Dans ce cas, L2 peut être
supprimé.
Bornes inférieures
À chaque fois qu'un label L = (C,
51, . . . , 5m) est étendu vers une ville,
on calcule une borne inférieure sur le coût de n'importe quel
chemin pouvant être obtenu à partir de ce label. Cette borne
inférieure est comparée avec une borne supérieure
initialement définie par le coût de l'individu père. Cette
borne supérieure est valide, puisque le tour des villes du père
existe dans le graphe. La borne supérieure est mise à jour
à chaque fois qu'une nouvelle meilleure solution est trouvée par
l'algorithme. Lorsque la borne inférieure n'est pas inférieure
à la borne supérieure, le label L est
supprimé.
La borne inférieure LB(L) est
donnée par la formule suivante :
LB(L)=C+ ? Clj
{1=j=m,5j=0}
pour laquelle l est la position dans la séquence
maître du groupe vers lequel L vient d'être étendu
et Clj est le coût minimal induit pour la visite
future du groupe Wj.
Clj est calculé comme le coût minimum de
l'arc parmi les arcs dont :
1. la destination est une des villes de la dernière
occurrence du groupe Wj dans la séquence maître,
2. l'origine est une des villes situés entre le groupe en
position l (incluse) et la dernière occurrence du groupe Wj
dans la séquence maître.
Les valeurs Clj sont calculées dans
une phase de prétraitement, dès que la séquence
maître est fixée, pour chaque position l de la
séquence et pour chaque groupe Wj. La complexité de ce
calcul est en O(nm).
On peut noter qu'il peut arriver que la dernière
occurrence de Wj précède la position l. Dans ce
cas, Clj est fixé à une grande valeur et le
label est automatiquement supprimé si 5j = 0, puisque le groupe
Wj est inaccessible.
Réduction du graphe
Le graphe construit à partir de la séquence
maître peut être réduit. Puisque chaque groupe doit
être visité, aucun arc n'est autorisé à passer
au-dessus de toutes les occurrences d'un groupe. De plus, deux occurrences d'un
même groupe n'ont pas à être connectées. Enfin, un
groupe situé à la position j dans la séquence
maître ne doit être connecté qu'avec la première
occurrence de chaque groupe, dans le cas où les deux occurrences
seraient situées après la position j. En effet, dans ce
cas, toute extension possible à partir de la deuxième occurrence
du groupe est aussi possible à partir de la première occurrence
du groupe. La figure 4.3 présente le graphe obtenu à partir de
l'exemple présenté par la figure 4.1 une fois ces règles
appliquées.
W4 W1 W3 W1 W5 W2 W3 W2 W5 W4
FIGURE 4.3 - Exemple d'un
croisement et du graphe résultant réduit utilisé par la
procédure dropstar : vue avec agrégation des sommets en
groupes
Accélérations heuristiques
La procédure de croisement peut être une
procédure très coûteuse en temps. Dans le but
d'accélérer sa résolution, nous proposons deux
accélérations heuristiques.
Limitation de la taille des listes de chemins partiels
Pendant la déroulement de l'algorithme de programmation
dynamique, une liste de chemins partiels est associée à chaque
ville. Malgré les règles de dominances, ces listes peuvent
être de taille relativement importante. Le but ici est de limiter leur
taille. Une limite unique est fixée (100 dans nos
expérimentations). Un règle d'évaluation est
définie afin de déterminer quels chemins partiels doivent
être supprimés lorsque la taille de la liste dépasse la
limite. L'évaluation eval(L) d'un label L =
(C, ö1, . . . , öm) est :
?{1=j=m} C1j ?
Clj
{1=j=m,öj=0}
pour laquelle UB0 est le coût de l'individu
père et l est la position du chemin partiel dans la
séquence maître. Cette formule cherche à équilibrer
le coût actuel d'un chemin partiel et une évaluation du coût
d'extension (tel que proposée dans la section 4.3.3). Les deux termes
sont normalisés afin que l'évaluation d'un chemin partiel initial
et du chemin partiel correspondant au tour des villes de l'individu père
aient une valeur identique UB0.
UB0
eval(L) = C +
Réduction des groupes Le but ici est
de limiter la taille du graphe, en supprimant des villes de différents
groupes. Une mesure est définie afin d'évaluer l'attrait d'une
ville. Les villes les moins attractives sont supprimées de chaque groupe
de la séquence maître. La mesure quantifiant
l'intérêt de la ville vk du groupe à la position
l de la séquence est :
|
eval(k, l) = ?
vi?-(l) ?
vj?+(l)
|
cik + ckj - cij
|
où -(l) (respectivement,
+(l)) est l'ensemble des villes appartenant aux deux
groupes précédant (respectivement suivant) la position l
dans la séquence maître. Cette mesure indique une tendance du
coût d'insertion de la ville vk dans une solution. En se basant
sur cette mesure, la taille maximale d'un groupe Wi est fixée )
[|Wi|p1, où p est
un paramètre (0.8 dans nos expérimentations). On
peut noter qu'avec cette formule, le pourcentage de villes supprimées
d'un groupe augmente avec la taille du groupe.
Complexité de la procédure de
croisement
Il est intéressant de noter que l'algorithme n'atteint
pas une complexité en temps polynomiale. L'objectif de cette section est
d'apporter plus de précisions quant à la complexité. Dans
cette analyse, nous ne prenons pas en compte les deux
accélérations heuristiques décrites ci-dessus.
Un état est défini pour chaque noeud du graphe
et pour chaque valeur des ressources {ä1, . . . ,
äm}. Le graphe contient 2n villes. Les
ressources äi sont binaires. Ainsi, le nombre d'état est
O(n2m). Le label associé à
un état est étendu vers un maximum de n autres
états. Chaque nouveau label est inséré dans une liste de
labels de taille maxi-male 2m. L'insertion consiste en une
comparaison avec chaque autre label de la liste. Chaque comparaison a une
complexité en O(m). Le coût de l'insertion d'un
nouveau label dans une liste est donc
O(m2m) et le coût d'extension d'un
label O(nm2m).
On peut donc en déduire que la complexité dans
le pire cas de notre algorithme est
O(n2m22m).
Évidemment, on peut espérer que le nombre d'opérations
soit réduit de manière significative en pratique. On peut aussi
noter qu'en limitant la taille des listes des labels, la complexité
devient O(n2m).
4.3.4 Heuristiques de recherche locale
Un appel de chacune des procédures
d'amélioration classiques présentées ci-après nous
permet d'obtenir un tour de coût inférieur ou égal au tour
auquel on applique la procédure. Lorsqu'un nouvel individu est
généré, chaque heuristique de recherche locale est
appelée itérativement tant que le coût de la solution est
amélioré.
2-opt
Cette procédure est classique lorsqu'on étudie
le TSP (voir (Lin, 1965) pour plus de détails). Elle consiste à
choisir deux villes du tour et à permuter la circulation entre ces deux
villes en vue d'améliorer la solution. La complexité de cette
procédure est O(m2) où m
est le nombre de groupes. La procédure 2-opt est
répétée tant que des améliorations sont obtenues.
Ensuite, la séquence de groupe correspondant au tour des villes courant
est extraite et l'algorithme ST est appliqué.
3-opt
De manière similaire au 2-opt, le 3-opt
(présenté aussi dans (Lin, 1965)) choisit trois villes au
lieu de deux, et modifie le chemin entre ces trois villes. La complexité
de la pro-
cédure est O(m3). Une fois
encore, la procédure est répétée tant que des
améliorations sont obtenues et le calcul est terminé par l'appel
de l'algorithme ST.
Lin-Kernighan
Nous utilisons de plus l'heuristique proposée par Lin
et Kernighan (1973), disponible sur le site de Concorde1.
L'algorithme Lin-Kernighan est une des meilleures heuristiques disponibles pour
le problème du Voyageur de Commerce. Il est basé entre autres sur
une généralisation des procédures 2-opt et
3-opt. Cette procédure est appliquée chaque fois qu'une
nouvelle meilleure solution est trouvée et lors de la
génération de nouveaux individus, avec une probabilité
égale à 0.50.
Meilleure insertion de groupe
L'opérateur de Meilleure Insertion de groupe (ou
Move) considère la séquence de groupe d'un individu,
sélectionne un groupe et détermine la meilleure position de ce
groupe dans la séquence. L'opérateur de Meilleure Insertion de
groupe est appliqué une fois pour chaque groupe. Afin de
déterminer la meilleure position pour un groupe donnée
Wi, une séquence maître est créée, pour
laquelle Wi est dans un premier temps supprimé, puis
inséré à nouveau entre chaque paire de groupes.
L'algorithme de programmation dynamique présenté dans les
sections 4.3.2 et 4.3.3 est ensuite appliqué afin de trouver le meilleur
tour des villes réalisable.
L'opérateur de Meilleur Insertion de groupe peut
être illustré avec l'exemple suivant. Soit W4 W3
W1 W5 W2 W4 le tour des groupes d'un
individu. En appliquant l'opérateur sur le groupe W1, on
obtient la séquence maître W4 W1 W3
W1 W5 W1 W2 W1 W4. Le
meilleur tour des villes est ensuite calculé sur le graphe correspondant
(cf. Fig. 4.4).

W4 W1 W3 W1 W5
W1 W2 W1 W4
FIGURE 4.4 - Exemple de
l'opérateur Move et du graphe réduit correspondant : vue
agrégée en terme de groupes
Le voisinage défini par l'opérateur de Meilleure
Insertion de groupe a une taille en
O(m(n/m)m) (cette
taille est calculée de manière similaire aux calculs
présentés dans la section 4.3.2 pour l'opérateur de
croisement). Dans l'algorithme de programmation dynamique, un label L
est défini par une paire (C, 5i). Le nombre
d'états est ainsi O(n) et la complexité de la
procédure est O(nm).
1. http ://
www.tsp.gatech.edu/concorde/DOC/index.html
Contrôle des opérateurs de recherche
locale
L'appel des opérateurs présentés
précédemment est contrôlé de la manière
suivante. Quand un nouvel individu est introduit dans la population pendant la
phase initiale, les opérateurs 2-opt, 3-opt et
Lin-Kernighan sont appliqués successivement, dans cet ordre.
Quand un nouvel individu enfant est calculé avec
l'opérateur de croisement, un des deux schémas de recherche local
suivants est appliqué, avec une probabilité égale à
0.5 : - application de 2-opt, 3-opt et Move, dans
cet ordre,
- application de Lin-Kernighan.
4.4 Résultats expérimentaux
L'algorithme a été codé en C++ et
exécuté sur un Pentium IV 2.00 Ghz. Les instances
utilisées proviennent de la librairie GTSPLIB2 qui propose un
ensemble de 65 instances. Parmi ces instances, nous avons
sélectionné 54 instances utilisées dans plusieurs articles
(Fischetti et al., 1997; Renaud et Boctor, 1998a; Snyder et Daskin,
2006; Silberholz et Golden, 2007) afin de pouvoir nous comparer à
d'autres algorithmes.
Fischetti et al. (1997) ont proposé un
algorithme de séparation et génération de coupes pour
résoudre le GTSP. Dans leur article, ils ont créé des
instances pour le GTSP en appliquant un partitionnement déterministe
à 65 instances de TSP issues de la libraire TSPLIB. Pour une instance
donnée, le nombre de groupes est fixé à m =
[n/5i. Ensuite, m centres sont déterminés en
considérant les m noeuds les plus éloignés les
uns des autres. Les groupes sont finalement obtenus en affectant chaque noeud
à son centre le plus proche. La méthode qu'ils ont
développée a permis d'obtenir les valeurs des solutions optimales
pour ces instances, avec 10 < m < 89, où m est
le nombre de groupes.
La solution optimale est toujours connue (fournis par
l'algorithme de séparation et de génération de coupes de
Fischetti et al. (1997)) pour les instances
sélectionnées avec 10 < m < 89. Pour les instances
restantes (99 < m < 217), Silberholz et Golden (2007)
fournissent les meilleurs résultats connus, qui sont en fait les
moyennes des résultats pour 5 essais de leur algorithme et de
l'algorithme de Snyder et Daskin (2006). Il est important de noter que la
valeur de la meilleure solution trouvée par ces algorithmes pour ces
instances n'est pas disponible.
Pour tous les résultats expérimentaux, nous
avons fixé le nombre d'individus par population (N) à 50
(ce qui est un nombre retenu dans plusieurs articles, par exemple dans
(Silberholz et Golden, 2007)), le nombre de croisements (2 * k) est
égal à 30, le nombre maximum d'itérations (N1)
à 100 et le nombre maximum d'itérations pendant lesquelles la
meilleure solution peut rester inchangée (N2) égal
à 10 (ce nombre est assez bas, mais suffisant vu la taille des
voisinages définis par les opérateurs de recherches
2. GTSPLIB est disponible à l'adresse http ://
www.cs.rhul.ac.uk/home/zvero/GTSPLIB/
locales appliqués à chaque itération). Les
résultats fournis sont les résultats moyens obtenus avec 5 essais
par instance.
Les résultats présentés dans les tableaux
4.1 et 4.2 montrent les performances de notre algorithme en terme
d'écart avec les solutions optimales fournies par le Branch & Cut de
Fischetti et al. (1997) (tableau 4.1). Pour les instances restantes
(pour 99 m
217), nous présentons nos résultats dans
le tableau 4.2, comparés avec les meilleurs résultats fournis par
Silberholz et Golden (2007).
Les en-têtes des colonnes sont les suivants :
- instance : le nom de l'instance testée; le premier
nombre dans le nom indique le nombre de groupes, le deuxième donne le
nombre de villes.
- opt : la valeur de la solution optimale ou la meilleure
solution moyenne connue. - ]best : le nombre de fois où la meilleure
solution (lorsqu'elle est connue) a été atteinte sur 5 essais.
- mean gap : l'écart moyen de notre algorithme à
l'optimal ou la meilleure solution moyenne connue (pourcentage).
- min gap : l'écart minimal de notre algorithme à
l'optimal ou la meilleure solution moyenne connue (pourcentage).
- max gap : l'écart maximal de notre algorithme à
l'optimal ou la meilleure solution moyenne connue (pourcentage).
- CPU time : le temps d'exécution moyen en secondes.
Les chiffres écrits en gras représentent les cas
où la solution trouvée est égale à la solution
optimale, ou meilleure que la meilleure solution connue.
Le tableau 4.1 montre que, avec 5 essais, toutes les solutions
obtenues sur les 41 instances sont égales aux solutions optimales et que
pour 37 instances sur 41, les solutions sont égales aux solutions
optimales pour chaque essai. L'écart entre le meilleur et le moins bon
résultat trouvé sur les 5 tests pour chaque instance est toujours
relativement limité, ce qui tend à montrer que l'algorithme est
robuste. Enfin, dans le pire des cas, le pourcentage d'écart ne
dépasse jamais 0,75 % pour les instances les plus importantes.
Pour les instances de grandes tailles (tableau 4.2), pour
lesquelles les solutions optimales ne sont pas connues, les résultats
montrent que pour certaines instances, nos pires résultats parmi les
cinq essais sont meilleurs que la moyenne des solutions produites par la
méthode proposée par Silberholz et Golden (2007) (par exemple,
l'instance 207si1032 qui contient 1032 noeuds). Dans le pire cas, les
solutions produites par notre algorithme ne dépassent jamais un
écart de plus de 0,66 % par rapport au meilleur résultat moyen
entre l'algorithme de Silberholz et Golden et l'algorithme de Snyder et Daskin.
Enfin, la moyenne de nos solutions est de plus mauvaise qualité que
celles proposées par les algorithmes cités
précédemment pour seulement 3 instances.
Le tableau 4.3 présente nos meilleurs résultats
parmi cinq essais pour douze instances ouvertes pour lesquelles la solution
optimale n'est pas connue. Les résultats présentés sont
les solutions produites par notre algorithme et les meilleures moyennes des
solutions sur cinq essais entre l'algorithme de Silberholz et Golden et
l'algorithme de Snyder et Daskin.
Afin de mesurer plus précisément
l'efficacité de l'opérateur de croisement que nous proposons,
nous avons aussi implémenté un opérateur de croisement
plus simple, connu sous le nom de croisement à un point (One-point
crossover, (Goldberg, 1989)). Les paramètres sont les mêmes pour
les deux opérateurs de croisement. Les tableaux 4.4 et 4.5 donnent des
informations sur les différences en terme de qualité des
solutions et de rapidité d'exécution entre l'opérateur de
croisement dropstar et l'opérateur de croisement One-Point pour
les instances fermées 4.4 et les instances ouvertes 4.5. Les
en-têtes des colonnes sont les suivants :
- instance : le nom de l'instance testée; le premier
nombre dans le nom indique le nombre de groupes, le deuxième donne le
nombre de villes.
- opt : la valeur de la solution optimale pour l'instance ou la
meilleure solution moyenne connue.
- mean gap : l'écart moyen de notre algorithme à
l'optimal ou la meilleure solution moyenne connue (pourcentage).
- CPU time : le temps d'exécution moyen en secondes.
Des expérimentations ont été conduites
afin de déterminer les avantages de l'opérateur de croisement
dropstar comparé à l'opérateur de croisement
One-Point. L'opérateur de croisement dropstar se montre
nettement plus efficace en ce qui concerne la qualité des solutions.
Pour les instances de petites tailles (pour lesquelles la solution optimale est
connue, tableau 4.4), l'écart moyen sur l'ensemble des instances pour
l'opérateur de croisement One-Point est égal à 0,26% alors
que l'écart moyen est réduit à 0,02 % avec
l'opérateur de croisement dropstar. Les temps
d'exécution pour l'opérateur de croisement Dropstar sont
néanmoins beaucoup plus importants, l'opérateur de croisement
One-Point étant en moyenne six fois plus rapide.
Pour les instances de grandes tailles présentées
dans le tableau 4.5, l'opérateur de croisement Dropstar produit
de biens meilleures solutions que l'opérateur de croisement One-Point,
tout en conservant un même ordre de grandeur de différence pour
les temps de calcul.
Le tableau 4.6 présente une comparaison entre
l'algorithme génétique mrOX proposé par
Silberholz et Golden (2007), l'algorithme génétique de Snyder et
Daskin (2006), le GI3 de Renaud et Boctor (1998a) et enfin, l'
algorithme de Branch & Cut de de Fischetti et al. (1997).
Les résultats des différents algorithmes
présentés ont été obtenus sur les machines
suivantes :
- mrOX et Snyder et Daskin : Pentium IV 3.0 GHz et 1 Go de
RAM.
- GI3 : Sun Sparc Station LX.
- B& C. : HP 9000/720.
Pour chaque algorithme, deux colonnes sont
présentées:
- Gap : l'écart moyen de l'algorithme à l'optimal
(pourcentage).
- CPU : le temps mis par l'algorithme en secondes.
La colonne B&C ne présente pas d'écart, puisque
cet algorithme est un algorithme exact, qui propose des solutions optimales.
Les résultats présentés dans le tableau
4.6 montrent que notre algorithme est plus performant que les autres
algorithmes heuristiques. Pour l'ensemble des solutions pour lesquelles les
solutions optimales sont connues, notre algorithme retourne en moyenne un taux
d'erreur égal à 0,02 %. De plus, les solutions renvoyées
peuvent être très proches des solutions optimales et ce,
même pour les instances de grandes tailles.
On peut remarquer par ailleurs que les instances de petites
tailles sont résolues à l'optimum très rapidement par
l'ensemble des algorithmes.
Les comparaisons de temps de calcul avec les autres
algorithmes heuristiques sont complexes car différentes machines ont
été utilisées pour tester les algorithmes. Les
expérimentations montrent tout de même que notre algorithme est
plus lent que l'algorithme mrOX ou l'algorithme de Snyder et Daskin.
Cependant, le but de notre algorithme était d'obtenir les meilleurs
résultats possibles en terme d'écart avec les solutions
optimales. On peut cependant noter que notre algorithme peut proposer des
solutions de bonne qualité en des temps relativement courts.
Nous proposons aussi nos propres instances, basées sur
les instances classiques du problème du Voyageur de Commerce,
tirées de la librairie TSPLIB3. Pour une instance
donnée, le nombre de groupes est fixé à m =
[n/51. Les groupes sont numérotés de 0 à m
- 1. Chaque ville vi est associée au groupe Wj
pour lequel j est égal à i mod m.
Puisque les instances du problème du Voyageur de Commerce
proposées par la librairie TSPLIB sont construites de telle façon
que les villes sont placées aléatoirement, le partitionnement que
nous proposons ne simule pas de régions géographiques. Dans ce
partitionnement de villes, un groupe de villes peut représenter un
ensemble de villes dans lequel chaque ville propose un service identique ou un
même produit. L'objectif du problème du Voyageur de Commerce
Généralisé est alors de trouver un tour qui minimise la
somme des distances, tout en respectant la contraintes d'obtenir une fois
chaque service ou chaque produit. Le partitionnement que nous proposons est
déterministe, il peut donc être facilement reproduit.
Les tableaux 4.7 et 4.8 donnent des informations sur les
différences en terme de qualité des solutions et de
rapidité d'exécution entre l'opérateur de croisement
dropstar et l'opérateur de croisement One-Point pour les
instances que nous proposons. Les entêtes des colonnes sont les suivants
:
- instance : le nom de l'instance testée; le premier
nombre dans le nom indique le nombre de groupes, le deuxième donne le
nombre de villes.
- min : la valeur minimale trouvée par l'algorithme.
- mean : la moyenne des valeurs trouvées par
l'algorithme.
- CPU time : le temps d'exécution moyen en secondes.
Les conclusions tirées à la lecture des tableaux
4.7 et 4.8 sont similaires à celles énoncées pour les
tableaux 4.4 et 4.5. L'opérateur de croisement dropstar se
montre nettement plus efficace en ce qui concerne la qualité des
solutions. Pour les instances de petites tailles, les meilleures solutions pour
l'opérateur de croisement One-Point sont à peine
supérieures à celles trouvées avec l'opérateur de
croisement dropstar. Les temps d'exécution pour
l'opérateur de croisement Dropstar sont néanmoins
beaucoup plus impor-
3. http ://
www.iwr.uni-heidelberg.de/groups/comopt/software/TSPLIB95/
tants, l'opérateur de croisement One-Point étant
en moyenne onze fois plus rapide. Par contre, pour les instances de grandes
tailles, l'écart se creuse, mais les temps de calcul nécessaires
pour l'opérateur de croisement Dropstar sont beaucoup plus
importants. On remarque néanmoins que les instances que nous proposons
semblent plus difficiles à résoudre, même pour
l'opérateur de croisement One-Point. On peut donc en déduire que
les opérateurs de recherche locale semblent être plus efficaces
avec le partitionnement proposé par Fischetti et al. (1997).
4.5 Conclusion et perspectives
Nous étudions la résolution du GTSP par un
algorithme mémétique dans lequel l'opérateur de croisement
se base sur une recherche à grand voisinage dont l'opérateur,
appelé Dropstar, a été présenté
dans le chapitre 2. Notre principale contribution est l'originalité de
notre opérateur de croisement. Nous montrons par les résultats
expérimentaux que notre algorithme est robuste et offre un bon compromis
entre temps de calcul et qualité des solutions. Il résout 41
instances sur 41 à l'optimal et les solutions renvoyées ne sont
jamais à plus de 0,75 % de pourcentage d'erreur par rapport aux
solutions optimales. Nous montrons donc que l'hybridation entre un
opérateur de recherche locale à grand voisinage et un algorithme
génétique (l'ensemble définissant un algorithme
mémétique) est une méthode qui semble efficace.
|
instance
|
opt
|
best
|
mean gap
|
min gap
|
max gap
|
CPU time
|
|
10att48.gtsp
|
5394
|
5
|
0.00
|
0.00
|
0.00
|
0.76
|
|
10gr48.gtsp
|
1834
|
5
|
0.00
|
0.00
|
0.00
|
0.79
|
|
10hk48.gtsp
|
6386
|
5
|
0.00
|
0.00
|
0.00
|
0.50
|
|
11eil51.gtsp
|
174
|
5
|
0.00
|
0.00
|
0.00
|
0.81
|
|
12brazil58.gtsp
|
15332
|
5
|
0.00
|
0.00
|
0.00
|
0.65
|
|
14st70.gtsp
|
316
|
5
|
0.00
|
0.00
|
0.00
|
0.93
|
|
16eil76.gtsp
|
209
|
5
|
0.00
|
0.00
|
0.00
|
1.00
|
|
16pr76.gtsp
|
64925
|
5
|
0.00
|
0.00
|
0.00
|
1.17
|
|
20kroA100.gtsp
|
9711
|
5
|
0.00
|
0.00
|
0.00
|
1.81
|
|
20kroB100.gtsp
|
10328
|
5
|
0.00
|
0.00
|
0.00
|
2.17
|
|
20kroC100.gtsp
|
9554
|
5
|
0.00
|
0.00
|
0.00
|
1.85
|
|
20kroD100.gtsp
|
9450
|
5
|
0.00
|
0.00
|
0.00
|
2.77
|
|
20kroE100.gtsp
|
9523
|
5
|
0.00
|
0.00
|
0.00
|
1.81
|
|
20rat99.gtsp
|
497
|
5
|
0.00
|
0.00
|
0.00
|
3.89
|
|
20rd100.gtsp
|
3650
|
5
|
0.00
|
0.00
|
0.00
|
2.91
|
|
21eil101.gtsp
|
249
|
5
|
0.00
|
0.00
|
0.00
|
2.09
|
|
21lin105.gtsp
|
8213
|
5
|
0.00
|
0.00
|
0.00
|
3.18
|
|
22pr107.gtsp
|
27898
|
5
|
0.00
|
0.00
|
0.00
|
4.78
|
|
24gr120.gtsp
|
2769
|
5
|
0.00
|
0.00
|
0.00
|
2.34
|
|
25pr124.gtsp
|
36605
|
5
|
0.00
|
0.00
|
0.00
|
2.84
|
|
26bier127.gtsp
|
72418
|
5
|
0.00
|
0.00
|
0.00
|
3.35
|
|
28pr136.gtsp
|
42570
|
5
|
0.00
|
0.00
|
0.00
|
4.23
|
|
29pr144.gtsp
|
45886
|
5
|
0.00
|
0.00
|
0.00
|
5.42
|
|
30kroA150.gtsp
|
11018
|
5
|
0.00
|
0.00
|
0.00
|
5.95
|
|
30kroB150.gtsp
|
12196
|
5
|
0.00
|
0.00
|
0.00
|
5.02
|
|
31pr152.gtsp
|
51576
|
5
|
0.00
|
0.00
|
0.00
|
5.24
|
|
32u159.gtsp
|
22664
|
5
|
0.00
|
0.00
|
0.00
|
5.58
|
|
39rat195.gtsp
|
854
|
5
|
0.00
|
0.00
|
0.00
|
11.01
|
|
40d198.gtsp
|
10557
|
5
|
0.00
|
0.00
|
0.00
|
10.15
|
|
40kroA200.gtsp
|
13406
|
5
|
0.00
|
0.00
|
0.00
|
10.41
|
|
40kroB200.gtsp
|
13111
|
5
|
0.00
|
0.00
|
0.00
|
10.81
|
|
45ts225.gtsp
|
68340
|
3
|
0.04
|
0.00
|
0.09
|
31.45
|
|
46pr226.gtsp
|
64007
|
5
|
0.00
|
0.00
|
0.00
|
8.25
|
|
53gil262.gtsp
|
1013
|
2
|
0.14
|
0.00
|
0.3
|
24.34
|
|
53pr264.gtsp
|
29549
|
5
|
0.00
|
0.00
|
0.00
|
18.27
|
|
60pr299.gtsp
|
22615
|
5
|
0.00
|
0.00
|
0.00
|
21.25
|
|
64lin318.gtsp
|
20765
|
5
|
0.00
|
0.00
|
0.00
|
26.33
|
|
80rd400.gtsp
|
6361
|
1
|
0.42
|
0.00
|
0.75
|
32.21
|
|
84fl417.gtsp
|
9651
|
5
|
0.00
|
0.00
|
0.00
|
31.63
|
|
88pr439.gtsp
|
60099
|
5
|
0.00
|
0.00
|
0.00
|
42.55
|
|
89pcb442.gtsp
|
21657
|
1
|
0.19
|
0.00
|
0.38
|
62.53
|
TABLE 4.1 - Résultats
expérimentaux : qualité des solutions sur instances
fermées
|
instance
|
best
|
mean gap
|
min gap
|
max gap
|
CPU time
|
|
99d493.gtsp
|
20117.2
|
-0.03
|
-0.28
|
0.23
|
166.11
|
|
107att532.gtsp
|
13510.8
|
-0.30
|
-0.34
|
-0.17
|
137.54
|
|
107si535.gtsp
|
13513.2
|
-0.01
|
-0.05
|
0.06
|
90.98
|
|
113pa561.gtsp
|
1051.2
|
-0.84
|
-1.26
|
-0.21
|
149.43
|
|
115rat575.gtsp
|
2414.8
|
0.04
|
-0.45
|
0.09
|
157.01
|
|
131p654.gtsp
|
27439
|
-0.03
|
-0.04
|
0.00
|
144.95
|
|
132d657.gtsp
|
22599
|
-0.15
|
-0.43
|
0.28
|
259.11
|
|
145u724.gtsp
|
21657
|
0.45
|
0.24
|
0.66
|
218.66
|
|
157rat783.gtsp
|
3300.2
|
-0.07
|
-0.58
|
0.12
|
391.79
|
|
201pr1002.gtsp
|
114582.2
|
0.03
|
-0.18
|
0.16
|
513.48
|
|
207si1032.gtsp
|
22388.8
|
-0.26
|
-0.33
|
-0.17
|
616.28
|
|
212u1060.gtsp
|
108390.4
|
-0.92
|
-1.58
|
0.19
|
762.86
|
|
217vm1084.gtsp
|
131884.6
|
-0.26
|
-0.65
|
0.09
|
583.44
|
TABLE 4.2 - Résultats
expérimentaux : qualité des solutions sur instances
ouvertes
|
instance
|
mrOX
|
Bontoux
|
|
99d493.gtsp
|
20117.2
|
20061
|
|
107att532.gtsp
|
13510.8
|
13464
|
|
107si535.gtsp
|
13513.2
|
13506
|
|
113pa561.gtsp
|
1051.2
|
1038
|
|
115rat575.gtsp
|
2414.8
|
2404
|
|
131p654.gtsp
|
27439
|
27428
|
|
132d657.gtsp
|
22599
|
22502
|
|
157rat783.gtsp
|
3300.2
|
3281
|
|
201pr1002.gtsp
|
114582.2
|
114374
|
|
207si1032.gtsp
|
22388.8
|
22315
|
|
212u1060.gtsp
|
108390.4
|
106677
|
|
217vm1084.gtsp
|
131884.6
|
131028
|
TABLE 4.3 - Résultats
expérimentaux : meilleures solutions connues
|
name
|
opt
|
Dropstar
Gap CPU
|
One-Point
Gap CPU
|
|
10att48.gtsp
|
5394
|
0.00
|
0.76
|
0.00
|
0.15
|
|
10gr48.gtsp
|
1834
|
0.00
|
0.79
|
0.00
|
0.14
|
|
10hk48.gtsp
|
6386
|
0.00
|
0.50
|
0.00
|
0.17
|
|
11eil51.gtsp
|
174
|
0.00
|
0.81
|
0.00
|
0.15
|
|
12brazil58.gtsp
|
15332
|
0.00
|
0.65
|
0.00
|
0.24
|
|
14st70.gtsp
|
316
|
0.00
|
0.93
|
0.00
|
0.20
|
|
16eil76.gtsp
|
209
|
0.00
|
1.00
|
0.00
|
0.17
|
|
16pr76.gtsp
|
64925
|
0.00
|
1.17
|
0.00
|
0.25
|
|
20kroA100.gtsp
|
9711
|
0.00
|
1.81
|
0.00
|
0.27
|
|
20kroB100.gtsp
|
10328
|
0.00
|
2.17
|
0.00
|
0.27
|
|
20kroC100.gtsp
|
9554
|
0.00
|
1.85
|
0.00
|
0.27
|
|
20kroD100.gtsp
|
9450
|
0.00
|
2.77
|
0.00
|
0.27
|
|
20kroE100.gtsp
|
9523
|
0.00
|
1.81
|
0.00
|
0.53
|
|
20rat99.gtsp
|
497
|
0.00
|
3.89
|
0.00
|
0.44
|
|
20rd100.gtsp
|
3650
|
0.00
|
2.91
|
0.36
|
0.40
|
|
21eil101.gtsp
|
249
|
0.00
|
2.09
|
0.56
|
0.61
|
|
21lin105.gtsp
|
8213
|
0.00
|
3.18
|
0.00
|
0.36
|
|
22pr107.gtsp
|
27898
|
0.00
|
4.78
|
0.08
|
0.33
|
|
24gr120.gtsp
|
2769
|
0.00
|
2.34
|
0.62
|
0.07
|
|
25pr124.gtsp
|
36605
|
0.00
|
2.84
|
0.00
|
0.44
|
|
26bier127.gtsp
|
72418
|
0.00
|
3.35
|
0.00
|
0.42
|
|
28pr136.gtsp
|
42570
|
0.00
|
4.23
|
0.72
|
0.86
|
|
29pr144.gtsp
|
45886
|
0.00
|
5.42
|
0.00
|
0.54
|
|
30kroA150.gtsp
|
11018
|
0.00
|
5.95
|
0.01
|
1.14
|
|
30kroB150.gtsp
|
12196
|
0.00
|
5.02
|
0.33
|
1.45
|
|
31pr152.gtsp
|
51576
|
0.00
|
5.24
|
0.00
|
0.68
|
|
32u159.gtsp
|
22664
|
0.00
|
5.58
|
0.43
|
0.83
|
|
39rat195.gtsp
|
854
|
0.00
|
11.01
|
1.05
|
1.63
|
|
40d198.gtsp
|
10557
|
0.00
|
10.15
|
0.07
|
1.41
|
|
40kroA200.gtsp
|
13406
|
0.00
|
10.41
|
0.21
|
1.65
|
|
40kroB200.gtsp
|
13111
|
0.00
|
10.81
|
0.15
|
2.09
|
|
45ts225.gtsp
|
68340
|
0.04
|
31.45
|
0.29
|
1.91
|
|
46pr226.gtsp
|
64007
|
0.00
|
8.25
|
0.00
|
1.03
|
|
53gil262.gtsp
|
1013
|
0.14
|
26.34
|
1.8
|
2.35
|
|
53pr264.gtsp
|
29549
|
0.00
|
18.27
|
0.46
|
2.43
|
|
60pr299.gtsp
|
22615
|
0.00
|
21.25
|
0.20
|
5.79
|
|
64lin318.gtsp
|
20765
|
0.00
|
26.33
|
0.59
|
4.67
|
|
80rd400.gtsp
|
6361
|
0.42
|
32.21
|
1.45
|
10.12
|
|
84fl417.gtsp
|
9651
|
0.00
|
31.63
|
0.00
|
3.41
|
|
88pr439.gtsp
|
60099
|
0.00
|
42.65
|
0.09
|
10.56
|
|
89pcb442.gtsp
|
21657
|
0.19
|
62.53
|
1.26
|
11.22
|
TABLE 4.4 - Résultats
expérimentaux : comparaisons des opérateurs de croisement sur
instances fermées
|
name
|
best
|
Dropstar
Gap CPU
|
One-Point Gap CPU
|
|
99d493.gtsp
|
20117.2
|
-0.03
|
166.11
|
0.03
|
12.1
|
|
107att532.gtsp
|
13510.8
|
-0.30
|
121.54
|
0.21
|
18.73
|
|
107si535.gtsp
|
13513.2
|
-0.01
|
90.98
|
0.01
|
10.58
|
|
113pa561.gtsp
|
1051.2
|
-0.84
|
149.43
|
1.58
|
11.66
|
|
115rat575.gtsp
|
2414.8
|
0.04
|
157.01
|
5.01
|
17.99
|
|
131p654.gtsp
|
27439
|
-0.03
|
144.95
|
-0.01
|
10.95
|
|
132d657.gtsp
|
22599
|
-0.15
|
259.11
|
1.15
|
27.2
|
|
145u724.gtsp
|
17370
|
0.45
|
218.66
|
2.76
|
45.31
|
|
157rat783.gtsp
|
3300.2
|
-0.07
|
391.79
|
3.68
|
42.76
|
|
201pr1002.gtsp
|
114582.2
|
0.03
|
513.48
|
1.49
|
76.54
|
|
207si1032.gtsp
|
22388.8
|
-0.26
|
616.28
|
0.33
|
75
|
|
212u1060.gtsp
|
108390.4
|
-0.92
|
762.86
|
-0.28
|
88.6
|
|
217vm1084.gtsp
|
131884.6
|
-0.26
|
583.44
|
0.3
|
89.87
|
TABLE 4.5 - Résultats
expérimentaux : comparaisons des opérateurs de croisement sur
instances ouvertes
|
instance
|
Bontoux
Gap CPU
|
mrOX
Gap CPU
|
Snyder
Gap CPU
|
GI
Gap CPU
|
BC CPU
|
|
10att48
|
0
|
0.76
|
0
|
0.36
|
0
|
0.18
|
*
|
*
|
2.1
|
|
10gr48
|
0
|
0.79
|
0
|
0.32
|
0
|
0.08
|
*
|
*
|
1.9
|
|
10hk48
|
0
|
0.5
|
0
|
0.31
|
0
|
0.08
|
*
|
*
|
3.8
|
|
11eil51
|
0
|
0.81
|
0
|
0.26
|
0
|
0.08
|
0
|
0.3
|
2.9
|
|
12brazil58
|
0
|
0.65
|
0
|
0.78
|
0
|
0.1
|
*
|
*
|
3
|
|
14st70
|
0
|
0.93
|
0
|
0.35
|
0
|
0.07
|
0
|
1.7
|
7.3
|
|
16eil76
|
0
|
1
|
0
|
0.37
|
0
|
0.11
|
0
|
2.2
|
9.4
|
|
16pr76
|
0
|
1.17
|
0
|
0.45
|
0
|
0.16
|
0
|
2.5
|
12.9
|
|
20kroA100
|
0
|
1.81
|
0
|
0.5
|
0
|
0.24
|
0
|
5
|
51.5
|
|
20kroB100
|
0
|
2.17
|
0
|
0.63
|
0
|
0.25
|
0
|
6.8
|
18.4
|
|
20kroC100
|
0
|
1.85
|
0
|
0.6
|
0
|
0.22
|
0
|
6.4
|
22.2
|
|
20kroD100
|
0
|
2.77
|
0
|
0.62
|
0
|
0.23
|
0
|
6.5
|
14.4
|
|
20kroE100
|
0
|
1.81
|
0
|
0.67
|
0
|
0.43
|
0
|
8.6
|
14.3
|
|
20rat99
|
0
|
3.89
|
0
|
0.58
|
0
|
0.15
|
0
|
6.7
|
13
|
|
20rd100
|
0
|
2.91
|
0
|
0.51
|
0
|
0.29
|
0.08
|
7.3
|
16.6
|
|
21eil101
|
0
|
2.09
|
0
|
0.48
|
0
|
0.18
|
0.4
|
5.2
|
25.6
|
|
21lin105
|
0
|
3.18
|
0
|
0.6
|
0
|
0.33
|
0
|
14.4
|
16.4
|
|
22pr107
|
0
|
4.78
|
0
|
0.53
|
0
|
0.2
|
0
|
8.7
|
7.4
|
|
24gr120
|
0
|
2.34
|
0
|
0.66
|
0
|
0.32
|
*
|
*
|
41.9
|
|
25pr124
|
0
|
2.84
|
0
|
0.68
|
0
|
0.26
|
0.43
|
12.2
|
25.9
|
|
26bier127
|
0
|
3.35
|
0
|
0.78
|
0
|
0.28
|
5.55
|
36.1
|
23.6
|
|
28pr136
|
0
|
4.23
|
0
|
0.79
|
0.16
|
0.36
|
1.28
|
12.5
|
43
|
|
29pr144
|
0
|
5.42
|
0
|
1
|
0
|
0.44
|
0
|
16.3
|
8.2
|
|
30kroA150
|
0
|
5.95
|
0
|
0.98
|
0
|
0.32
|
0
|
17.8
|
100.3
|
|
30kroB150
|
0
|
5.02
|
0
|
0.98
|
0
|
0.71
|
0
|
14.2
|
60.6
|
|
31pr152
|
0
|
5.24
|
0
|
0.97
|
0
|
0.38
|
0.47
|
17.6
|
94.8
|
|
32u159
|
0
|
5.58
|
0
|
0.98
|
0
|
0.55
|
2.6
|
18.5
|
146.4
|
|
39rat195
|
0
|
11.01
|
0
|
1.37
|
0
|
1.33
|
0
|
37.2
|
245.9
|
|
40d198
|
0
|
10.15
|
0
|
1.63
|
0.07
|
1.47
|
0.6
|
60.4
|
763.1
|
|
40kroA200
|
0
|
10.41
|
0
|
1.66
|
0
|
0.95
|
0
|
29.7
|
187.4
|
|
40kroB200
|
0
|
10.81
|
0.05
|
1.63
|
0.01
|
1.29
|
0
|
35.8
|
268.5
|
|
45ts225
|
0.04
|
31.45
|
0.14
|
1.71
|
0.28
|
1.09
|
0.61
|
89
|
37875.9
|
|
46pr226
|
0
|
8.25
|
0
|
1.54
|
0
|
1.09
|
0
|
25.5
|
106.9
|
|
53gil262
|
0.14
|
24.34
|
0.45
|
3.64
|
0.55
|
3.05
|
5.03
|
115.4
|
6624.1
|
|
53pr264
|
0
|
18.27
|
0
|
2.36
|
0.09
|
2.72
|
0.36
|
64.4
|
337
|
|
60pr299
|
0
|
21.25
|
0.05
|
4.59
|
0.16
|
4.08
|
2.23
|
90.3
|
812.8
|
|
64lin318
|
0
|
26.33
|
0
|
8.08
|
0.54
|
5.39
|
4.59
|
206.8
|
1671.9
|
|
80rd400
|
0.42
|
32.21
|
0.58
|
14.58
|
0.72
|
10.27
|
1.23
|
403.5
|
7021.4
|
|
84fl417
|
0
|
31.63
|
0.04
|
8.15
|
0.06
|
6.18
|
0.48
|
427.1
|
16719.4
|
|
88pr439
|
0
|
42.55
|
0
|
19.06
|
0.83
|
15.09
|
3.52
|
611
|
5422.8
|
|
89pcb442
|
0.19
|
62.53
|
0.01
|
23.43
|
1.23
|
11.74
|
5.91
|
567.7
|
58770.5
|
|
Averages
|
0.02
|
10.12
|
0.03
|
2.69
|
0.11
|
1.77
|
0.98
|
83.09
|
3356.47
|
|
Essais
|
5
|
|
5
|
|
5
|
|
1
|
|
1
|
TABLE 4.6 - Résultats
expérimentaux : comparatifs entre plusieurs algorithmes
|
instance
|
Min
|
Dropstar
Mean CPU Time
|
Min
|
One-Point
Mean CPU Time
|
|
baf10att48.gtsp
|
1774
|
1774
|
0.68
|
1774
|
1774
|
0.15
|
|
baf10gr48.gtsp
|
1182
|
1182
|
1.33
|
1182
|
1182
|
0.16
|
|
baf10hk48.gtsp
|
2112
|
2112
|
0.77
|
2112
|
2112
|
0.17
|
|
baf11eil51.gtsp
|
86
|
86
|
1.52
|
86
|
86
|
0.15
|
|
baf12brazil58.gtsp
|
3378
|
3378
|
2.16
|
3378
|
3378
|
0.23
|
|
baf14st70.gtsp
|
141
|
141
|
4.32
|
141
|
141
|
0.26
|
|
baf16eil76.gtsp
|
107
|
107.2
|
4.79
|
107
|
110.2
|
0.47
|
|
baf16pr76.gtsp
|
18349
|
18349
|
5.06
|
18349
|
18481
|
0.45
|
|
baf20kroA100.gtsp
|
5044
|
5076.2
|
22
|
5117
|
5254.4
|
0.6
|
|
baf20kroB100.gtsp
|
5395
|
5395
|
12.64
|
5413
|
5793.8
|
0.58
|
|
baf20kroC100.gtsp
|
5799
|
5804.8
|
25.09
|
5799
|
5849.6
|
0.61
|
|
baf20kroD100.gtsp
|
5266
|
5298.2
|
23.31
|
5266
|
5360
|
0.62
|
|
baf20kroE100.gtsp
|
5449
|
5449
|
6.98
|
5449
|
5449.4
|
0.41
|
|
baf20rat99.gtsp
|
230
|
231.6
|
13.91
|
230
|
235.8
|
0.41
|
|
baf20rd100.gtsp
|
1747
|
1747.4
|
7.9
|
1747
|
1793.8
|
0.7
|
|
baf21eil101.gtsp
|
105
|
105
|
4.8
|
105
|
105
|
0.32
|
|
baf21lin105.gtsp
|
2758
|
2758
|
14.05
|
2758
|
2764.4
|
0.37
|
|
baf22pr107.gtsp
|
6849
|
6879.6
|
4.97
|
6849
|
6889.8
|
0.39
|
|
baf24gr120.gtsp
|
1412
|
1434
|
18.03
|
1414
|
1440.8
|
0.9
|
|
baf25pr124.gtsp
|
10745
|
10745
|
8.3
|
10745
|
10745
|
0.38
|
|
baf26bier127.gtsp
|
11740
|
11973.2
|
5.92
|
12164
|
12258.8
|
0.59
|
|
baf28pr136.gtsp
|
17824
|
17857.8
|
22.88
|
17824
|
17959.2
|
0.55
|
|
baf29pr144.gtsp
|
14070
|
14071
|
26.55
|
14070
|
14269
|
0.8
|
|
baf30kroA150.gtsp
|
7076
|
7316.4
|
52.39
|
7248
|
7319
|
2.18
|
|
baf30kroB150.gtsp
|
5855
|
5992.6
|
31.27
|
6055
|
6147
|
1.63
|
|
baf31pr152.gtsp
|
13002
|
13154.6
|
29.09
|
13002
|
13223.8
|
1.09
|
|
baf32u159.gtsp
|
7301
|
7309.2
|
27.89
|
7326
|
7595.8
|
0.78
|
|
baf39rat195.gtsp
|
477
|
477.4
|
144.94
|
477
|
480
|
1.09
|
TABLE 4.7 - Résultats
expérimentaux : comparatifs des opérateurs de croisement sur de
nouvelles instances (1)
|
instance
|
Min
|
Dropstar
Mean CPU Time
|
Min
|
One-Point
Mean CPU Time
|
|
baf40d198.gtsp
|
1500
|
1555.4
|
18.71
|
1514
|
1555.6
|
1.54
|
|
baf40kroA200.gtsp
|
7126
|
7416.8
|
82.2
|
7316
|
7537.2
|
2.82
|
|
baf40kroB200.gtsp
|
7375
|
7544.6
|
152.83
|
7420
|
7732.4
|
2.99
|
|
baf41gr202.gtsp
|
3656
|
3656
|
16.57
|
3656
|
3656
|
1.32
|
|
baf45ts225.gtsp
|
26059
|
26359.6
|
113.32
|
26076
|
26369.2
|
1.79
|
|
baf46pr226.gtsp
|
13555
|
13555
|
86.31
|
13555
|
13555
|
0.95
|
|
baf53gil262.gtsp
|
591
|
624.8
|
223.63
|
642
|
659.2
|
3.06
|
|
baf53pr264.gtsp
|
7716
|
7748
|
40.56
|
7772
|
7821.6
|
2.06
|
|
baf60pr299.gtsp
|
10137
|
10795.4
|
265.09
|
10933
|
11771.8
|
6.11
|
|
baf64lin318.gtsp
|
7762
|
8113
|
259.89
|
8054
|
8216.6
|
5.74
|
|
baf80rd400.gtsp
|
3725
|
3899.2
|
635.63
|
3782
|
3919.6
|
12.34
|
|
baf84fl417.gtsp
|
2267
|
2335.2
|
422.72
|
2296
|
2572.6
|
7.93
|
|
baf87gr431.gtsp
|
10787
|
10861.4
|
105.07
|
10825
|
10917.8
|
7.69
|
|
baf88pr439.gtsp
|
14292
|
15280.2
|
325.86
|
15334
|
16579
|
8.99
|
|
baf89pcb442.gtsp
|
10266
|
10707.8
|
464.16
|
11716
|
12855
|
17.63
|
|
baf99d493.gtsp
|
3156
|
3232.4
|
217.08
|
3273
|
3321.6
|
16.16
|
|
baf107att532.gtsp
|
4392
|
4529.6
|
508.4
|
4530
|
4705
|
16.4
|
|
baf107si535.gtsp
|
9059
|
9129.8
|
444.81
|
9258
|
9741
|
22.35
|
|
baf113pa561.gtsp
|
460
|
470.4
|
817.12
|
478
|
512.4
|
12.22
|
|
baf115rat575.gtsp
|
1366
|
1376
|
382.36
|
1419
|
1477.6
|
11.92
|
|
baf131p654.gtsp
|
5956
|
6033.6
|
833.75
|
6130
|
6225.2
|
18.3
|
|
baf132d657.gtsp
|
8821
|
9377.6
|
421.54
|
8870
|
11216.8
|
21.75
|
|
baf145u724.gtsp
|
10165
|
10253.6
|
877.34
|
13794
|
15031.6
|
45.79
|
|
baf157rat783.gtsp
|
1931
|
2131.4
|
439.91
|
2878
|
2983.6
|
39.77
|
|
baf201pr1002.gtsp
|
50225
|
52626.8
|
754.24
|
56844
|
60121
|
82.89
|
|
baf207si1032.gtsp
|
19108
|
19228.6
|
653.14
|
20066
|
20306.6
|
82.26
|
|
baf212u1060.gtsp
|
44684
|
46058.6
|
731.6
|
52151
|
65714.8
|
97.58
|
|
baf217vm1084.gtsp
|
61595
|
64708.8
|
976.06
|
102578
|
105324
|
114.43
|
TABLE 4.8 - Résultats
expérimentaux : comparatifs des opérateurs de croisement sur de
nouvelles instances (2)
Troisième partie
Tronquer les méthodes exactes :
méthode de Branch & Price
heuristique
5 Application au problème de Tournées de
Véhicules avec Contraintes de Chargement 125
5.1 Préambule : Intérêt du problème
126
5.2 Problèmes de calcul de tournées de
véhicules 127
5.2.1 Du problème du Voyageur de Commerce au
problème de Tour-
nées de Véhicules 127
5.2.2 Le 2L-VRP parmi les problèmes de Tournées de
Véhicules . . . 128
5.3 État de l'art 128
5.3.1 Résolution du 2L-VRP 128
5.3.2 Algorithmes de chargement 131
5.4 Modèle classique du problème du 2|RO|L-VRP
132
5.5 Génération de colonnes 134
5.5.1 Modélisation d'un ESPPRC 138
5.5.2 Résolution par programmation dynamique 139
5.6 Notre approche : un schéma de Branch & Price
141
5.6.1 Méthode de séparation 142
5.6.2 Initialisation de 1 pour la génération de
colonnes 143
5.6.3 Remontées de colonnes 143
5.6.4 Problème esclave : ESPPRC 144
5.6.5 Problème de chargement séquentiel à
deux dimensions 147
5.7 Deux approches différentes pour la
réalisabilité du chargement 153
5.7.1 Vérification de la réalisabilité a
posteriori 153
5.7.2 Construction de routes réalisables dans le
sous-problème 155
5.8 Branch & Price heuristique 159
5.8.1 Problème esclave heuristique 159
5.8.2 Gestion des colonnes 160
5.8.3 Méthode de séparation 160
5.9 Résultats expérimentaux 161
5.9.1 Paramètres retenus 161
5.9.2 Classes d'instances 161
5.9.3 Analyses des résultats 162
5.10 Conclusions et perspectives 165
Chapitre 5
Application au problème de
Tournées de Véhicules avec
Contraintes de Chargement
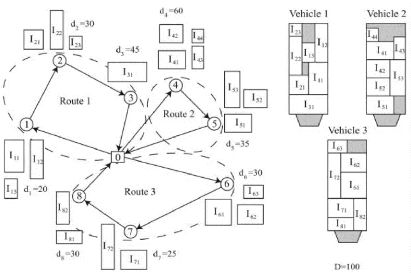
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
5.1 Préambule : Intérêt du
problème
Le problème tel qu'il nous a été
présenté par l'entreprise Daumas, Autheman et Associés,
est le suivant. Un service de traiteur avec livraisons de repas à
domicile, situé en région parisienne, a fait une étude de
marché afin d'optimiser les trajets des livraisons, ainsi que
l'agencement du chargement des livraisons.
La problèmatique se compose de plusieurs
problèmes. Le premier est un problème de chargement. Les
commandes de repas et de matériel à livrer sont
préparées dans des entrepôts. Pour le chargement de ce
matériel, les livreurs doivent remplir les surfaces de livraison des
véhicules sans plan de chargement. Un temps important est donc perdu
dans l'essai de configurations afin de remplir les surfaces de livraison. Le
nombre d'objets à charger est, de plus, calculé au plus juste par
rapport à la capacité de la surface de livraison. Les repas
à livrer sont posés sur des chariots dont les dimensions sont
connues. Les objets à livrer sont des produits fragiles. Ainsi, dans la
plupart des cas, il n'y a pas d'empilage possible, les plats étant trop
fragiles pour pouvoir résister aux poids d'autres objets posés
au-dessus. Pour chaque véhicule, la taille de la surface de chargement
est connue et cette taille est identique pour tous les véhicules. Les
déchargements des livraisons ne peuvent se faire que par les portes
arrières. Pour accélérer le temps de livraison, il est
préférable de pouvoir facilement décharger les produits
à livrer, lors de la livraison pour chaque client.
Le deuxième problème concerne l'optimisation des
livraisons. Tous les départs des livraisons se font à partir d'un
dépôt central. Les distances entre les différents points de
livraisons sont connues, ainsi que les distances entre les points de livraisons
et le dépôt central. L'entreprise dispose d'une flotte fixe de
véhicules homogènes.
Ce problème, dans une version simplifiée, est
similaire à un problème connu dans la littérature sous le
nom de problème de Tournées de Véhicules avec Contraintes
de Chargement en Deux Dimensions (Vehicule Routing Problem with
Two-Dimensional Loading Constrains ou 2L-VRP).
La section 5.2 expose un bref historique des problèmes
de Tournées de Véhicules. La section 5.3 présente un
état de l'art sur le problème de Tournées de
Véhicules avec Contraintes de Chargement. Un modèle classique du
2L-VRP est décrit dans la section 5.4, puis nous présentons le
fonctionnement de la méthode de résolution par
génération de colonnes dans la section 5.5. Les
différentes méthodes de résolution que nous proposons sont
introduites dans les sections 5.6, 5.7 et 5.8. Enfin, l'efficacité de
nos méthodes est évaluée à travers des
résultats expérimentaux proposés dans la section 5.9.
5.2. Problèmes de calcul de tournées de
véhicules
5.2 Problèmes de calcul de tournées de
véhicules
5.2.1 Du problème du Voyageur de Commerce au
problème de Tournées de Véhicules
Le célèbre Problème du Voyageur de
Commerce, ou Traveling Salesman Problem, est un des
problèmes d'optimisation combinatoire les plus connus (voir le chapitre
2 pour plus de détails sur ce problème).
Au cours des années, au vu des progrès
effectués en terme de résolution, ainsi qu'en raison de la
variété des applications aux systèmes de transports, les
chercheurs ont été amenés à proposer de nombreuses
extensions ou variantes du problème du Voyageur de Commerce.
Le problème du Voyageur de Commerce a été
étendu au cas où m voyageurs de commerce doivent visiter
n villes, défini comme le Problème de Voyageurs de
Commerce Multiples ou Multiple Traveling Salesman Problem (mTSP). Ce
problème est très proche du problème de Tournées de
Véhicules ou Vehicle Routing Problem (VRP) pour lequel une
flotte de véhicules est disponible, et chaque véhicule est
limité par les distances qu'il peut parcourir.
Une des extensions les plus étudiées fut ensuite
de considérer les transports de marchandises. Ces marchandises sont
récoltées chez des clients au cours du trajet et ramenées
à un dépôt unique. De plus, les objets ramassés
possèdent un poids et une capacité maximale à ne pas
dépasser est associée à chaque véhicule. L'objectif
est donc d'assigner des clients à des véhicules. Cette extension
est connue sous le nom de problème de Tournées de
Véhicules avec Contraintes de Capacités (Capacited Vehicle
Routing Problem ou CVRP).
À cette extension se rajoutent un certain nombre de
contraintes :
- Contraintes temporelles : la visite des clients peut avoir
lieu uniquement pendant
des fenêtres de temps (Vehicle Routing
Problem with Time Windows ou VRPTW),
- Contraintes de précédence : les marchandises
doivent être transportées d'un lieu vers un autre au lieu
d'être ramenées au dépôt (Pick Up & Delivery
Problem ou PDP),
- Contraintes de chargement : plusieurs objets doivent
être livrés à des clients, en
respectant des contraintes de poids et de surface (ou de volume)
de chargement
du véhicule (Vehicle Routing Problem with Loading
Constraints ou VRPLC).
On peut relever d'autres extensions du TSP dans la
littérature, comme les problèmes avec fractionnement de la
livraison. Dans la version la plus simple connue sous le nom de Split &
Delivery Problem, une visite à un sommet peut ne donner lieu
qu'à une livraison partielle.
Pour chacun de ces problèmes, on distingue
généralement le cas à un seul véhicule, souvent
plus facile et rencontré comme sous-problème du cas à
plusieurs véhicules.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
En plus de ces contraintes, une classification peut être
faite en se basant sur la distinction entre la nature des données :
- problèmes statiques, pour lesquels l'ensemble des
données est connu avant la résolution du problème,
- problèmes stochastiques, pour lesquels les
données sont définies par une fonction de probabilité,
- problèmes dynamiques, pour lesquels de nouvelles
données apparaissent au cours du temps.
5.2.2 Le 2L-VRP parmi les problèmes de
Tournées de Véhicules
Le problème de Tournées de Véhicules avec
Contraintes de Chargement à Deux Dimensions ou Vehicle Routing
Problem with Two-Dimensional Loading Constraints (2LVRP) est une extension
du classique Capacited Vehicle Routing Problem auquel ont
été ajoutées des contraintes de chargement. Le
problème combine ainsi le chargement des marchandises dans les
véhicules et la construction de tournées de véhicules sur
un réseau de routes, de telle sorte que les demandes des clients soient
satisfaites.
Le problème 2L-VRP apparaît donc comme une suite
d'extensions de problèmes de transports, dont nous présentons les
caractéristiques dans le tableau 5.1.
Problème dépôt multiples véhicules
capacité fenêtres de temps autres TSP
VRP x x
mTSP x x
CVRP x x x
VRPTW x x x x
2L-CVRP x x x x
TABLE 5.1 - Récapitulatif
des caractéristiques de quelques problèmes classiques
5.3 État de l'art
5.3.1 Résolution du 2L-VRP
Le problème de Tournées de Véhicules avec
Contraintes de Capacité ou Capacited Vehicle Routing Problem
(CVRP) est un des problèmes d'optimisation combinatoire les plus
fréquemment étudiés. L'objectif est de minimiser la
distance totale parcourue par une flotte de véhicules d'une
capacité limitée, sous la contrainte de satisfaire l'ensemble des
demandes de livraisons des clients. L'application de ce modèle à
des cas pratiques est limitée par la présence d'une multitude de
contraintes additionnelles. En particulier, dans le CVRP, les demandes des
clients sont exprimées par des valeurs entières,
résumant le poids total ou le volume total des objets
devant être livrés. Pour des applications pratiques, les demandes
consistent en un ensemble d'objets, caractérisés par un poids et
une forme.
Dans le domaine des transports, il est souvent
nécessaire de manipuler des objets de formes rectangulaires. Dans
certains cas, ces objets ne peuvent être empilés les uns au-dessus
des autres (par exemple, pour cause de fragilité). Dans ce cas, on peut
se limiter à caractériser les objets à livrer en deux
dimensions : largeur et hauteur. On part alors du principe que la hauteur de
chacun des objets est inférieure à la hauteur de la surface de
chargement des véhicules (de même que la largeur). De plus, chaque
client peut avoir une demande représentée par plusieurs objets.
On parle alors de problème de Tournées de Véhicules avec
Contraintes de Chargement à Deux Dimensions.
Le problème de Tournées de Véhicules avec
Contraintes de Chargement Tri-Dimensionnelles ou three-dimensional loading
capacitated vehicle routing problem (3L-CVRP) a été
étudié par Gendreau et al. (2006). L'algorithme
proposé est une généralisation au cas à trois
dimensions de la méthode par recherche tabou publiée
postérieurement (Gendreau et al., 2008). Dans le
problème tel qu'il est présenté, la demande des clients
est représentée par des objets en trois dimensions avec un poids.
Ce problème a été moins étudié que la
version à deux dimensions.
Dans le domaine de l'optimisation combinatoire, le chargement
d'objets et les problèmes de Tournées de Véhicules ont
été intensément étudiés, mais dans la
plupart des cas, de manières séparées. Ce n'est que
récemment que les chercheurs se sont penchés sur la
résolution de problèmes combinant les deux aspects.
Le 2L-VRP a une décomposition naturelle en trois
sous-problèmes:
1. Un problème d'affectation, qui consiste à
déterminer par quel véhicule les clients sont servis,
2. Un problème de Tournées, qui consiste à
déterminer l'ordre dans lequel les clients sont visités,
3. Un problème de chargement qui consiste à
vérifier si les tournées sont réalisables vis-à-vis
des contraintes de séquentialité, de capacité et de
surface.
Ces trois problèmes peuvent être traités de
manière globale, par coopération d'algorithmes ou par une
succession d'algorithmes.
Le problème 2L-VRP consiste donc à proposer des
routes avec des chargements réalisables. Nous allons maintenant
détailler le concept de réalisabilité pour une route. Dans
le problème 2L-VRP, le chargement est restreint à être
orthogonal, c'est-à-dire que chaque objet doit être chargé
avec ses côtés parallèles aux cotés du
véhicule dans lequel il est chargé. Pour chaque véhicule,
tous les objets transportés doivent être entièrement
compris dans la surface de livraison et ne peuvent se chevaucher. De plus, la
somme totale des poids des objets ne peut dépasser la capacité en
poids des véhicules.
Une contrainte d'ordre pratique assez courante est la suivante
: lorsqu'un client est visité, tous les objets devant lui être
livrés doivent être déchargés à l'aide d'un
chariot élévateur, sans avoir à déplacer les objets
qui seront livrés aux prochains clients sur la
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
tournée du véhicule. Cela implique donc que la
portion de surface de chargement située entre chaque objet du client qui
est en train d'être servi et l'arrière du véhicule doit
être vide (ou utilisée par d'autres objets du même client,
qui seront déchargés en premier). Cette contrainte est
notée dans la littérature comme un chargement séquentiel,
ou une contrainte de chargement arrière (rear loading
constraint, (Iori et al., 2007)). Le terme de chargement libre ou
unrestricted loading (voir (Gendreau et al., 2008) pour plus
de détails) est utilisé lorsque des arrangements du chargement
d'objets dans le véhicule sont autorisés à chaque
livraison.
Enfin, dans certains cas, les objets peuvent être
tournés de 90°. Il existe néanmoins des cas pratiques pour
lesquels cette rotation n'est pas autorisée. Ce cas est appelé un
chargement orienté (oriented loading). Il peut avoir lieu, par
exemple, lorsque les objets sont placés sur des palettes d'ancienne
génération qui ne sont accessibles pour les chariots
élévateurs que depuis une seule direction, ou encore, lorsque le
poids de l'objet est mal réparti sur les palettes. Dans la plupart des
cas de la littérature, le problème du 2L-VRP a été
étudié dans le cas où les objets ne peuvent être
tournés et dont l'orientation est fixe. Le chargement pour lequel on
autorise la rotation des objets est appelé non-orienté.
En se référant aux classifications
présentées ci-dessus concernant les configurations de chargement,
on peut distinguer quatre cas :
- 2|RO|L : chargement par l'arrière orienté
à deux dimensions (two-dimensional rear oriented loading);
- 2|UO|L : chargement par l'arrière non-orienté
à deux dimensions (two-dimensional unrestricted oriented
loading);
- 2|RN|L : chargement libre orienté à deux
dimensions (two-dimensional rear non-oriented loading);
- 2|UN|L : chargement libre non-orienté à deux
dimensions (two-dimensional unrestricted non-oriented loading).
Iori et al. (2007) ont résolu le
problème du 2|RO|L-VRP de manière exacte, à l'aide d'une
procédure de séparation et coupe (Branch & Cut). Leur
algorithme est basé sur une formulation de type problème de flot,
avec une procédure de séparation additionnelle, afin de
vérifier la réalisabilité des routes par rapport aux
contraintes de chargement. Cette vérification de chargement est
réalisée à l'aide de calculs de bornes inférieures,
une heuristique de placement des objets, ainsi qu'un algorithme de type Branch
& Bound, dans lequel l'arbre de recherche suit les principes
proposés par Martello et Vigo (1998) et Martello et al. (2000).
L'approche qu'ils ont proposée a permis de résoudre optimalement
toutes les instances du 2|RO|L-VRP, avec un nombre de clients allant
jusqu'à 25 et un nombre d'objets allant jusqu'à 91 (chaque client
pouvant avoir plusieurs objets), en limitant les temps de calcul à une
journée par instance.
Gendreau et al. (2008) ont proposé un
algorithme permettant de résoudre aussi bien le cas 2|RO|L que le cas
2|UO|L, basé sur une recherche tabou, qui est une adaptation de
l'algorithme Taburoute (voir (Gendreau et al., 1994) pour plus de
détails sur cet algorithme). Dans leur algorithme, les routes
irréalisables, que ce soit à cause d'un dépassement de
capacité ou d'un chargement trop important en terme de surface, sont
acceptées mais avec une pénalité ajoutée dans la
fonction objectif. Le voisinage utilisé
par la recherche tabou consiste à enlever un client
d'une tournée et à l'insérer dans une tournée d'un
autre véhicule, en optimisant les deux routes concernées par le
mouvement. La vérification de réalisabilité du chargement
a lieu au moyen de bornes inférieures, d'algorithmes heuristiques,
d'opérateurs de recherche locale et d'une recherche arborescente
tronquée. La méthode proposée a été
testée sur des instances comprenant jusqu'à 255 clients et 768
objets.
Fuellerer et al. (2008) ont proposé une
méthode heuristique efficace basée sur un algorithme
d'optimisation par Colonie de Fourmis. Leur point de départ est
l'algorithme Saving based ACO développé pour le CVRP
(voir (Reimann et al., 2004) pour plus de détails sur cet
algorithme). Cet algorithme est modifié et étendu afin
d'intégrer les heuristiques de chargement. L'algorithme cherche dans
l'espace des solutions de tournées, tout en vérifiant la
réalisabilité du chargement en deux dimensions de chaque route au
moyen de calculs de bornes inférieures, d'algorithmes heuristiques et de
recherches arborescentes tronquées. Leur but était de fournir de
bonnes solutions pour des instances de grandes tailles.
La littérature portant sur les problèmes de
tournées de véhicule et les problèmes de chargement pris
séparement est conséquente. En ce qui concerne le Capacited
Vehicle Routing Problem, le lecteur intéressé peut lire l'ouvrage
récent consacré à ce sujet par Toth et Vigo (2002), ainsi
que les travaux de Cordeau et Laporte (2004) et Cordeau et al.
(2005).
Pour le cas du chargement multi-dimensionnel, nous conseillons au
lecteur de lire les récents travaux de Wäscher et al.
(2007).
5.3.2 Algorithmes de chargement
Le problème de chargement d'objets à deux
dimensions est très proche de plusieurs
problèmes de rangement. On peut détailler deux
problèmes en particulier :
- Le problème de Bin Packing à deux
dimensions ou Two Dimensional Bin Packing Problem (2BPP) : l'objectif
est de ranger un ensemble d'objets rectangulaires dans un nombre minimal de
boites rectangulaires identiques. Les approches exactes pour le 2BPP sont
généralement basées sur des techniques de recherches
arborescentes et permettent de résoudre des instances contenant
jusqu'à une centaine d'objets. Cependant, certaines instances avec
seulement 20 objets restent non résolues. Des algorithmes exacts et des
calculs de bornes inférieures ont été proposés par
Martello et Vigo (1998), Boschetti et Mingozzi (2003a,b) et Pisinger et Sigurd
(2007).
- Le problème de Strip Packing à deux
dimensions ou Two Dimensional Strip Packing Problem (2SP) : l'objectif
est de ranger un ensemble d'objets rectangulaires dans une bande de largeur
définie et de hauteur infinie de façon à minimiser la
hauteur totale occupée par le rangement. Un algorithme exact a
été proposé par Martello et al. (2003) et peut
résoudre des instances contenant jusqu'à 200 objets.
Néanmoins, encore une fois, certaines instances de petites tailles ne
sont pas résolues optimalement.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Du point de vue de la complexité algorithmique, le
problème de Tournées de Véhicules avec Contraintes de
Capacités et le problème de Bin Packing à deux dimensions
sont tous les deux NP-difficiles et en pratique se montrent
séparément difficiles à résoudre. De manière
évidente, ces remarques sont également valables pour le
2|RO|LVRP. À notre connaissance, la seule méthode exacte
disponible à ce jour pour le 2|RO|LVRP est l'approche
développée par Iori et al. (2003) et (Iori et
al., 2007).
5.4 Modèle classique du problème du
2|RO|L-VRP
Dans cette section, nous présentons le modèle du
2|RO|L-VRP. Soit G = (V, E) un graphe complet
non-orienté pour lequel V est un ensemble de n + 1
noeuds, correspondant au dépôt (noeud v0) et aux clients
({v1, . . . , vn}). E est l'ensemble des
arêtes (vi, vj) entre chaque paire de noeuds et
cij est le coût associé pour (vi,
vj) E V.
Un ensemble de K véhicules identiques est
disponible depuis le dépôt. Chaque véhicule a une limite de
capacité en poids D et une surface de chargement rectangulaire
dont les dimensions sont caractérisées par une hauteur H
et une largeur W. Chaque véhicule possède une seule
ouverture pour le chargement et le déchargement des objets. On note
A = W x H la surface totale de chargement.
À chaque client i (i = v1, .
. . , vn), on associe un ensemble de mi objets
rectangulaires, dont la somme des poids est égal à di.
Chaque objet a une largeur et une hauteur spécifique, notées
respectivement wil et hil
avec l = {1, . . . , mi}. Chaque objet est
désigné
mi
par une paire d'indices (i, l). On note ai
=
? wil x hil l'aire totale des objets
du client i.
l=1
n
Enfin, soit M = ? mi le nombre total
d'objets.
i=1
Nous partons du principe que l'ensemble des objets d'un client
peut être chargé dans un véhicule. Ainsi, pour chaque
client, on suppose que di = D et qu'il existe un chargement
à deux dimensions réalisable pour les mi objets dans la
surface de chargement d'un seul véhicule. On suppose aussi que la
demande de l'ensemble des clients peut être satisfaite en utilisant au
maximum K véhicules. La livraison partagée n'est pas
autorisée, c'est-à-dire que chaque client n'est servi qu'en une
seule fois.
Les objets ont une orientation fixe et doivent être
chargés parallèlement aux côtés de la surface de
chargement. De plus, le déchargement des objets ne peut se faire que par
un côté du véhicule (rear unloading). Dans notre
notation, le déchargement se fait par le côté situé
le plus en haut. Enfin, le chargement est dit séquentiel : lors du
déchargement des objets d'un client, aucun objet appartenant à un
client situé sur la suite de la tournée ne doit bloquer le
déchargement des objets du client actuel. La figure 5.1 illustre la
surface de chargement, ainsi que la zone de déchargement.
Nous donnons maintenant une définition plus formelle de
la réalisabilité d'une route dans le problème de
tournées de véhicules. On associe à une route
réalisable un sous-ensemble S de clients et un ordre
noté ó. ó(i) est l'ordre dans
lequel chaque client
~~~~
~~~~
~~~~
~~ ~~ ~~~~ ~~~~ ~~~~ ~~~~
(0,0)
H
5.4. Modèle classique du problème du 2|RO|L-VRP


W
FIGURE 5.1 - Surface de
chargement
i ? S est visité lors de la
tournée. La condition 5.1 porte sur la contrainte de capacité des
véhicules :
? di = D (5.1)
i?S
Les conditions qui suivent portent sur le chargement. Dans un
souci pratique, on représente la surface de chargement selon des
coordonnées cartésiennes. Le point (0,0) représente le
coin situé en bas à gauche. L'axe des abscisses et l'axe des
ordonnées correspondent respectivement au côté bas et au
côté gauche. Le côté par lequel se fait le
déchargement correspond au côté allant du point (0,
H) au point (W, H). La position d'un objet
(i, l) dans la surface de chargement peut être
définie par deux variables xil et yil. Ces
deux variables représentent les coordonnées du coin de l'objet
situé en bas à gauche. Nous avons donc les conditions suivantes
:
0 = xil = W - wil et 0 = yil
= H - hil ?i ? S l ? {1, . . . ,
mi} (5.2)
Les objets ne doivent pas se chevaucher. On a donc les
contraintes suivantes :
xil + wil = xjli
ou xjl0 + wjli = xil
ou yil + hil = yjl'
ou yjl' + hjl0 = yil
(5.3) ?i, j ? S, l ? {1, . . . ,
mi}, l' ? {1, . . . , mj} et (i,
l) =6 (l, l')
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Enfin, il existe des contraintes concernant le chargement
séquentiel :
yil = yjl' + hjl
ou xil + wjl = xjl0
ou xjl0 + wjl0 = xil
(5.4)
?i, j ? S :
ó(i) < ó(j), l ?
{1, . . . , mi}, l' ? {1, . . . , mj}
En effet, tout objet appartenant à un client i
doit être soit situé au-dessus, soit à droite, soit
à gauche de l'ensemble objets des clients j visités
après i.
Étant donné un sous-ensemble de clients
S, on note ä(S) l'ensemble des arcs dont une
extrémité appartient à S et l'autre
extrémité appartient à V\S.
ä(i) est utilisé au lieu de
ä({i}). De plus, on note E(S,
ó) l'ensemble des arcs empruntés par la route
définie par le couple (S, ó). Enfin,
étant donné un sous-ensemble de clients S, on note
Ë(S) l'ensemble des séquences ó telles que
(S, ó) est une route réalisable.
Posons ze une variable binaire pour chaque
e ? E qui prend la valeur 1 si un véhicule emprunte
l'arête e. Iori et al. (2007) proposent le
modèle suivant du 2|RO|L-VRP:
min? ceze (5.5)
e?E
s.c.q.
? ze = 2 ?i ?
V\{v0} (5.6)
e?ä(i)
? ze = 2 × K (5.7)
e?ä(0)
? ze = 2 × r(S)
?S ? V\{v0}, S =6 Ø (5.8)
e?ä(S)
? ze = |S| - 1 ?S ?
V\{v0} ?(S, ó) tel que ó
?/ Ë(S) (5.9)
e?E(S,ó)
ze ? {0,1} ?e ?
E\ä(v0) (5.10)
ze ? {0,1,2} ?e ?
ä(v0) (5.11)
Les contraintes 5.6 et 5.7 imposent la visite des sommets et
les départs du dépôt. Les contraintes 5.8 imposent la
réalisabilité du chargement (r(S) est le nombre
minimum de véhicules nécessaires pour servir les clients dans
l'ensemble S). Les contraintes 5.9 imposent une
réalisabilité relativement au chargement séquentiel.
Enfin, les contraintes 5.10 imposent aux variables associées aux arcs
connectant deux clients d'être binaires. Les variables associées
aux arcs connectant les clients au dépôt peuvent prendre la valeur
2 (dans le cas d'une route à client unique) 5.11.
5.5 Génération de colonnes
Dans cette section, nous présentons les principes de la
méthode de résolution par génération de colonnes.
Cette méthode est classique pour les problèmes de tournées
de
véhicules; c'est avant tout une méthode exacte
mais elle peut aussi bien être utilisée en méthode
heuristique. Le lecteur intéressé par la génération
de colonnes et par ses applications pour les problèmes de transport peut
consulter les articles de Lübbecke et Desrosiers (2005) ou Barnhart et
al. (1998), ainsi que le récent livre de Desaulniers et al.
(2005).
La méthode de résolution par
génération de colonnes permet de résoudre des programmes
linéaires de grandes tailles. Dans cette formulation, les variables du
modèle sont appelées des colonnes. On parle de Branch &
Price lorsque la génération de colonnes est
intégrée dans une recherche arborescente (notamment pour la
résolution de programmes linéaires en nombres entiers). Une
résolution par génération de colonnes est une
méthode itérative. De nouvelles colonnes enrichissent un
problème restreint à chaque itération. Le problème
initial à résoudre est appelé problème maître
ou problème principal, tandis que l'algorithme qui génère
de nouvelles colonnes est appelé problème esclave ou
sous-problème.
Le problème du 2|RO|L-VRP se prête a priori bien
à une résolution par génération de colonnes. C'est
l'approche que nous explorons dans ce chapitre. Pour cela, nous
présentons un modèle de type couverture. Posons Ù =
{r1, . . . , r|Ù|}, l'ensemble des routes
réalisables. On associe à une route rk un coût
ck égal à la somme des distances des arcs
empruntés par cette route. aik est égal
à 1 si la route rk visite le client vi et est
égal à 0 dans le cas contraire.
Les variables sont notées èk.
èk est égale à 1 si la route rk est
sélectionnée et égale à 0 dans le cas contraire.
(P )
min? ckèk (5.12)
rkEÙ
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.13)
rkEÙ
? èk K (5.14)
rkEÙ
èk E {0,1} (rk E Ù) (5.15)
Considérons la relaxation linéaire du modèle
5.12, appelée problème maître (MP) : (MP )
min? ckèk (5.16)
rkEÙ
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.17)
rkEÙ
? èk K (5.18)
rkEÙ
èk E [0,1] (rk E Ù) (5.19)
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
À l'itération it de la
résolution par génération de colonnes, on résout de
manière exacte le problème maître restreint à
Ùit c Ù, défini ci-dessous. On choisit
une méthode de résolution de telle sorte que celle-ci fournisse
aussi une solution optimale au dual du programme linéaire.
(PMR )
min ? ckèk (5.20)
rkEÙit
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.21)
rkEÙit
? èk = K (5.22)
rkEÙit
èk = 0 (rk E
Ùit) (5.23)
Notons ëi la variable duale associée
à la iième contrainte (5.21). Toute colonne
ù E Ù \ Ùit susceptible de
diminuer la valeur de la fonction objectif si on l'ajoute au problème
maître restreint, a un coût réduit négatif (ce
coût est défini par l'équation 5.24). Le problème
esclave consiste donc à trouver de telles colonnes. Si aucune colonne de
coût réduit négatif n'existe, on déduit alors
l'optimalité pour MP de la solution obtenue à l'itération
it.
ck - ? aikëi - ë0 (5.24)
viEV\{v0}
Le problème qui consiste à chercher dans
Ù une variable de coût négatif est appelé le
sous-problème (connu aussi sous le nom de problème
esclave, oracle ou problème de pricing).
Le schéma de la figure 5.2 illustre le déroulement
de l'algorithme de génération de colonnes.
La génération de colonnes augmente donc
progressivement la taille du problème à résoudre, ce qui
est particulièrement adapté à la résolution de
problèmes possédant un grand nombre de colonnes. Le but
recherché est par conséquent d'obtenir une solution optimale sans
avoir à générer l'ensemble des colonnes.
Néanmoins, la solution optimale retournée par la
génération de colonnes est la solution du problème (MP),
qui est la relaxation linéaire du problème initial (P). Une
méthode de résolution efficace pour les programmes
linéaires en nombres entiers est basée sur la combinaison de la
résolution de la relaxation linéaire du problème et de la
méthode classique de séparation et évaluation progressive
(Branch & Bound). À chaque noeud de l'arbre de recherche,
on résout un programme linéaire donnant, dans le cas d'une
minimisation, une borne inférieure au problème. Lorsque cette
résolution se fait par génération de colonnes, on parle de
Branch & Price.

Résolution
Problème
Maître
Restreint
sur Ù1
Existence de
variables
améliorantes
Oui : ajouter à Ùit
Fin
Non
Ensemble initial
de colonnes Ù1

Chercher dans Ùit
une variable de coût
négatif
(Sousproblème)
FIGURE 5.2 - Méthode de
génération de colonnes Résolution du
problème esclave
Le sous-problème cherche un élément de 1)
tel que :
ck - E aikAi - A0 < 0 (5.25)
vi?V\{v0}
Posons bkij égal à 1 si la
route rk utilise l'arc (vi, vj) et égal
à 0 dans le cas contraire. L'équation 5.25 devient alors :
ck - E bk ij(cij - Ai) < 0
(5.26)
vi?V
On cherche alors l'élément de 1) minimisant
cette valeur. Cette recherche est un problème d'optimisation
combinatoire qui revient à trouver le chemin de v0 à
v0, passant au plus une fois par chaque sommet et tout en étant
une route réalisable (dans le cas du 2|RO|L-VRP cela équivaut au
respect des contraintes de capacité, des contraintes de surface, des
contraintes de chargement, etc.). Il s'agit d'un Problème de Plus Court
Chemin Élementaire avec Contraintes Additionnelles pour lequel le
coût des arcs (vi, vj) est égal à
cij - Ai. Comme nous allons le voir, la plupart
des contraintes additionnelles
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
se modélisent comme des contraintes de ressources
classiques, mais les contraintes de chargement sont plus complexes à
gérer. Ainsi, le problème esclave pour le problème du
2|RO|L-VRP est plus complexe que la résolution d'un problème de
Plus Court Chemin Élémentaire avec Contraintes de Ressources
(voir la section 2.4.3 pour plus de détails sur le problème de
Plus Court Chemin avec Contraintes de Ressources).
La figure 5.3 représente un problème de plus
court chemin avec contraintes de ressources entre le noeud v0 et le
noeud v3. Une seule ressource est présente, la consommation
cumulée de celle-ci est contrainte en chaque sommet (la valeur limite
à ne pas dépasser est indiquée à côté
de chaque sommet).
cout, consommation
^ contrainte de ressource
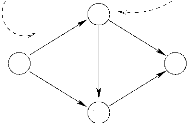
3,1
1,1
v 1
1
1,1
2,1
0 v 1,1 v3 2
0
1
v2
FIGURE 5.3 - Un SPPRC a une
ressource
Dans la section 5.5.1, nous définissons formellement le
problème. Une présentation d'un algorithme standard basé
sur de la programmation dynamique est détaillée dans la section
5.5.2. Ce principe de programmation dynamique est le même que celui
présenté dans les chapitres 2, 3 et 4.
5.5.1 Modélisation d'un ESPPRC
Nous présentons maintenant la modélisation d'un
problème classique de Plus Court Chemin Élémentaire avec
Contraintes de Ressources. Soit G = (V, E,
W) un graphe complet pour lequel V est un ensemble de n
+ 1 noeuds, correspondant à la source (noeud v0), le puits
(noeud vn) et aux clients vi (i = 1, . .
. , n - 1}). Chaque arc (vi, vj) a une consommation
cij(w) de ressource w (w = 0, . . . ,
W). On définit la ressource 0 comme le coût de l'arc. Une
contrainte sur chaque ressource est associée à chaque sommet. La
consommation cumulée au long du chemin jusqu'au sommet vi est
notée ci(w). Cette consommation est limitée par
Biw.
L'objectif du problème (équation (5.27)) est de
trouver le plus court chemin de v0 à vn
parmi les chemins réalisables sur l'ensemble des ressources. La variable
de décision äij est fixée à 1 si l'arc
(vi, vj) appartient à une solution et 0 sinon.
(EP)
min? cij(0)äij (5.27)
(vi,vj)?E
s.c.q.
E äij - E äji = 0 Vj = 1,
... , n - 1, (5.28)
(vi,vj)EE
(vj,vi)EE
E äij < 1 Vi = 0, . . . , n,
(5.29)
(vi,vj)EE
E ä0j = 1, (5.30)
(v0,vj)EE
ci(w) < Biw
Vi = 0, . . . ,V; Vw = 1, . . . ,W,
(5.31)
äij(ci(w) +
cij(w) - cj(w)) < 0 V(vi,
vj) E A; Vw = 1, .. . ,W, (5.32)
äij E {0,1} V(vi, vj) E A.
(5.33)
Les inégalités (5.28) représentent les
contraintes de flots assurant la continuité du chemin. Les contraintes
(5.29) assurent l'élémentarité du chemin. La contrainte
(5.30) impose qu'un unique chemin parte de la source. Les contraintes (5.31)
contrôlent la consommation cumulée sur chaque ressource et les
contraintes (5.32) la continuité du flot de consommation des ressources.
On admet que toutes les ressources se cumulent par incrémentation du
poids de l'arc associé à la ressource dans la limite du seuil
autorisé.
5.5.2 Résolution par programmation dynamique
L'algorithme 6 construit un chemin qui part de la source et
construit itérativement des chemins vers la destination. La construction
se fait par extension de chemins partiels (appelés aussi labels
ou étiquettes). Un chemin partiel est un chemin qui a pour
origine la source et pour extrémité terminale un sommet du
graphe. L'extension d'un chemin partiel L se fait au travers du calcul
de nouveaux chemins partiels, correspondant à L augmenté
d'un arc sortant par l'extrémité terminale de L. Dans le
cas où l'extension d'un chemin partiel vers un nouveau sommet viole une
contrainte, le chemin partiel correspondant est supprimé. On
vérifie aussi la faisabilité de chaque extension. Chaque chemin
partiel ainsi construit est comparé avec les autres chemins partiels
possédant la même extrémité terminale. On dit qu'un
chemin partiel L1 domine un chemin partiel
L2, ce qui est noté L1 <
L2, lorsque les deux chemins partiels ont la même
extrémité terminale et que l'on peut être sûr que
n'importe quelle extension de L1 sera de coût moindre
que l'extension identique pour le chemin partiel L2. Les
chemins partiels dominés sont éliminés de la liste des
chemins partiels associés au sommet. La consommation d'un chemin partiel
L sur une ressource w est notée
cL(w).
On peut voir que la complexité de cet algorithme
dépend donc des ressources considérées.
La figure 5.4 illustre le déroulement de l'algorithme
sur un graphe à quatre sommets et deux ressources dont le coût. Un
chemin partiel est identifié par son nom et son niveau de consommation
des ressources entre accolades, sur le modèle
Li {coût, autre ressource} .
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Algorithme 6 : Algorithme de programmation
dynamique
Données : G : un graphe sur
W ressources; L : une liste de chemins partiels non traités;
Li : la liste des chemins partiels d'extrémité terminale
i Résultat : LV
1 Initialisation: L ? chemin partiel
réduit à {0} ;
|
2
3
4
|
tant que L =6 0
faire
prendre L E L;
etL := extrémité de L;
|
|
5
|
domine := faux;
|
|
6
|
pour chaque chemin partiel L' E
LetL faire
|
|
7
|
|
si cL(w) =
cL'(w), ?w = 0, ... ,W
alors
|
|
8
|
|
LetL := LetL \ {L'};
|
|
9
|
|
sinon
|
|
10
|
|
|
si cL'(w) =
cL(w), ?w = 0, . . . ,W
alors
|
|
11
|
|
|
|
domine := vrai;
|
|
12
|
|
|
|
stop;
|
|
13
|
|
|
fin
|
|
14
|
|
fin
|
|
15
|
fin
|
|
16
|
si domine = faux
alors
|
|
17
|
|
LetL := LetL U {L};
|
|
18
|
|
pour chaque arc (etL,
i) faire
|
|
19
|
|
|
L' := l'extension de L par (vetL,
vi);
|
|
20
|
|
|
si L' est valide
alors
|
|
21
|
|
|
L := L U {L'};
|
|
22
|
|
|
fin
|
|
23
|
|
fin
|
|
24
|
fin
|
25 fin
L'objectif est de minimiser le coût des chemins partant
de v0 en respectant les contraintes de consommation de ressource en
chaque sommet, indiquées entre crochets sur la figure 5.4. À
chaque itération, on étend le chemin partiel marqué par
une étoile dans L. Le chemin partiel L3 issu de
L1 est supprimé car il consomme 2 unités sur
la ressource qui est limitée à 1 au sommet v2. Le chemin
partiel L5 est quant à lui supprimé car il
est dominé par L4.
Les sections 5.6, 5.7 et 5.8 présentent de manière
détaillée les méthodes que nous proposons pour la
résolution du problème du 2|RO|L-VRP.
|
L : L0
|
v [1]
1
|
|
|
L : L0, L1, L2
*
|
L1{1,1}
v [1]
1
|
|
|
|
1,1
|
|
|
2,1
|
|
1,1
|
|
|
2,1
|
|
|
L0{0,0}
|
|
|
|
|
L0{0,0}
|
|
|
|
|
|
[0] v 0
|
1,1
|
|
v3
|
2
|
[0] v 0
|
1,1
|
|
|
v3 [2]
|
|
3,1
|
|
|
1,1
|
|
3,1
|
|
|
1,1
|
|
|
v2 [1]
|
|
|
|
v2 [1]
|
|
|
|
initialisation
|
|
|
|
itération 1
|
L2{3,1}
|
|
|
|
L : L1, L2, L3,
L4 *
|
|
|
L : L2, L4, L5
*
|
|
|
|
|
L1{1,1}
|
|
|
|
L1{1,1}
|
|
|
|
v [1]
1
|
|
|
|
v 1
1
|
|
|
|
1,1
|
|
|
2,1
|
1,1
|
|
|
2,1
|
|
|
L0{0,0}
|
|
|
L4{3,2}
|
L0{0,0}
|
|
|
|
L4{3,2}
|
|
[0] v 0
|
1,1
|
|
v3
|
[2]
|
[0] v 0
|
1,1
|
|
|
v3 [2]
|
|
|
|
|
|
|
|
|
|
L5{4,2}
|
|
3,1
|
|
1,1
|
|
3,1
|
|
1,1
|
dominé
|
|
v2 [1]
|
|
|
|
v2 [1]
|
|
|
|
itération 2
|
L2{3,1}
L3{2,2}
|
violation de contrainte
|
|
itération 3
|
L2{3,1}
|
|
|
FIGURE 5.4 - Trace de
l'algorithme de programmation dynamique
5.6 Notre approche : un schéma de Branch &
Price
La méthode de génération de colonnes
couplée avec une méthode de séparation (Branch &
Price) est, dans la plupart des cas, utilisée pour une
résolution exacte des problèmes sur lesquels elle est
appliquée. Pour le problème 2|RO|L-VRP, de par la
complexité du problème de chargement en deux dimensions, ces
contraintes ne pouvant être modélisées sous forme de
ressources dans le sous-problème, le sous-problème n'est pas
résolu de manière exacte. Dans cette section, nous
décrivons un schéma de Branch & Price, tel qu'il
faudrait l'appliquer dans le cas où l'on voudrait une résolution
exacte (pour cela, le sous-problème doit être lui aussi
résolu de manière exacte). Nous présentons dans les
sections 5.7 et 5.8 notre approche, qui s'inscrit dans une recherche des moyens
pour rendre heuristique une méthode a priori exacte.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Cette section présente dans un premier temps les
spécificités de notre algorithme pour la méthode de
séparation, puis pour la résolution du problème esclave.
Les heuristiques de chargement utilisées seront présentées
par la suite et nous montrerons les différentes mises en oeuvre
possibles de ces algorithmes dans notre schéma de résolution.
5.6.1 Méthode de séparation
Une fois que la génération de colonnes est
terminée, c'est-à-dire que le problème esclave n'a pas
réussi à trouver de chemins de coûts négatifs, nous
obtenons une borne inférieure au problème. En effet, le
problème considéré ne possède pas de contraintes
d'intégralité sur les variables
èù. Si toutes les variables
sélectionnées sont entières (représentant ainsi des
routes complètes), la solution est réalisable. Dans le cas
contraire, afin de rendre cette solution réalisable, une méthode
de séparation est appliquée. On est donc confronté au
choix de politique de séparation. Une approche simple est de brancher
sur la valeur des variables èù. On
crée alors un noeud fils pour lequel on fixe une variable fractionnaire
èù à 1 et un autre noeud pour lequel
la variable est fixée à 0. On obtient donc un
sous-problème dans lequel la route correspondant à la variable
èù est obligatoire et un sous-problème
où cette route est interdite.
Une telle stratégie est dans la plupart des cas
mauvaise : en effet, elle a pour conséquence la création d'un
arbre fortement déséquilibré. De plus, le fait d'interdire
une route n'a que peu de répercussions dans le problème esclave
et peut être difficile à intégrer.
Il est donc commun de brancher sur les variables de la
formulation initiale. Si la solution est fractionnaire, alors il existe un arc
xij traversé par un flot fractionnaire.
xij = ? bk ijèk (5.34)
rk?Ù
On choisit le premier arc fractionnaire. On définit
alors deux fils : un fils pour lequel xij = 0 et un fils pour lequel
xij = 1. Dans le premier cas, cela implique de sup-primer toutes les
routes empruntant cet arc dans le problème maître et de supprimer
l'arc (vi, vj) dans le sous-problème. Dans le cas
où l'arc est fixé à 1, on supprime dans le problème
maître toutes les routes traversant un arc ayant pour
extrémité initiale vi (autre que (vi,
vj)) et toutes les routes traversant un arc ayant pour
extrémité terminale vj (autre que (vi,
vj)). Dans le sous-problème, on supprime alors tout arc
(vi, vk) avec vk =6 vj et (vk,
vj) avec vk =6 vi. Cette règle de branchement
assure la convergence.
Une fois qu'un noeud est créé, on résout par
génération de colonnes, la relaxation linéaire du
problème correspondant aux branchements choisis.
Les noeuds sont traités dans l'ordre respectant la
valeur croissante de leur borne inférieure (méthode connue sous
le nom de Best Bound First). La borne inférieure est
égale à la valeur de la relaxation linéaire.
Lorsqu'on obtient une solution entière, cette solution
est réalisable et le coût de cette solution devient par
conséquent une borne supérieure au problème. Cette borne
est utilisée afin de ne pas explorer les noeuds dont la borne
inférieure est supérieure à la plus petite borne
supérieure.
5.6.2 Initialisation de Ù pour la
génération de colonnes
Pour initialiser Ù, on construit une route non
réalisable complète qui passe par l'ensemble des sommets. On
associe à cette route un coût très élevé.
Cette méthode est appelée BigM. Cette route ne sera
ainsi plus sélectionnée dans la suite de la résolution,
dès qu'une solution utilisant uniquement des routes réalisables
existe.
5.6.3 Remontées de colonnes
Le but du problème esclave est de trouver des routes
ayant des coûts réduits négatifs. S'il en existe plusieurs,
ce qui est généralement le cas dans les premières
itérations de la résolution, on peut décider du nombre de
routes et donc du nombre de colonnes à insérer dans l'ensemble
Ù. Pour cela, on peut limiter la taille du nombre de chemins partiels
associés au puits v0 (qui est une copie du sommet
dépôt v0). Une fois que la limite fixée sur le
nombre de chemins partiels est atteinte, la résolution du
sous-problème est arrêtée et les colonnes correspondant aux
chemins partiels associés au puits (qui sont des routes
complètes) sont ajoutées à l'ensemble Ù.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
5.6.4 Problème esclave : ESPPRC
Nous présentons dans cette section les
spécificités du problème esclave pour la résolution
heuristique du problème du 2|RO|L-VRP. Le problème esclave est
résolu par la résolution d'un problème de Plus Court
Chemin Élémentaire avec Contraintes Additionnelles. Les
contraintes additionnelles peuvent être vues pour certaines comme des
contraintes de ressources. La résolution de ce problème se base
donc sur la résolution de l'ESPPRC, telle que présentée
dans la section 5.5.2. Nous définissons dans les sections suivantes les
règles d'extensions de chemins partiels, puis les règles de
dominance entre deux chemins partiels.
Extension d'un chemin partiel
Lors de la résolution du problème de plus court
chemin avec contraintes de ressources, les chemins partiels sont étendus
vers de nouveaux sommets. Les ressources prises en considération ici
sont : la capacité, une borne inférieure sur l'aire
occupée (définie comme la somme des aires des objets
transportés) et le coût (défini comme la somme des
coûts des arcs composant le chemin partiel, les coûts étant
égaux à cij - )ti pour tout arc
(vi, vj)). Lorsque le chemin partiel L dont
l'extrémité terminale est vi, est étendu vers le
sommet vj, le poids est augmenté de dj (où
dj est le poids total des objets du sommet vj). Le coût
est augmenté de cij - )ti. L'aire
occupée est augmentée de
mj
aj = ? wjl × hjl,
définie comme l'aire totale des objets du client j. Une
extension vers le
l=1
sommet vj est donc considérée
uniquement dans le cas où, une fois le sommet vj ajouté,
le poids associé au chemin partiel ne dépasse pas la
capacité totale du véhicule et la borne inférieure sur
l'aire occupée n'est pas strictement supérieure à la
surface de chargement. Dans le cas où ces contraintes sont
vérifiées, le chemin partiel est étendu vers le sommet
vj et le sommet vj est ajouté à la liste des
sommets non atteignables pour ce chemin partiel, afin de s'assurer de
l'élémentarité du chemin.
À l'état initial, le chemin partiel associé
au dépôt est caractérisé par un poids nul, une liste
de sommets non atteignables vide et une aire occupée nulle.
Dominance de deux chemins partiels
Afin de dominer le chemin partiel L2, le
chemin partiel L1 doit être contenu dans au moins un
chemin complet (de dépôt à dépôt) dominant
tous ceux contenant L2. Ceci peut se contrôler en
s'assurant de la réalisabilité d'extensions dominantes pour
L1 à chaque extension réalisable de
L2. Nous comparons donc des chemins qui ont la même
extrémité terminale. Les règles de dominances sont
importantes afin d'éliminer un grand nombre de chemins partiels.
Néanmoins, la vérification de la dominance ou de la non-dominance
peut rapidement s'avérer coûteuse en temps de calcul. Il faut donc
trouver un compromis entre l'efficacité et la complexité. Une
première règle est de s'assurer que toute extension de
L2 est réalisable à partir de
L1. Il suffit alors que L1 soit
5.6. Notre approche : un schéma de Branch & Price
de moindre coût pour être dominant. Une telle
règle est contraignante mais présente l'avantage d'être
robuste car toujours valide. Dans le cas du 2|RO|L-VRP, il faut donc s'assurer
que le coût et la capacité associés au chemin partiel
L1 soient inférieurs à ceux associés
au chemin partiel L2. La gestion de la ressource
correspondante à l'aire occupée est un cas particulier, qui est
précisée dans les sections 5.7.1 et 5.7.2. Afin d'avoir une
dominance sur l'aire occupée valide, la condition suivante doit
être ajoutée : quels que soient les objets futurs à
insérer dans un chargement, s'il existe un chargement réalisable
pour L2, alors il doit exister un chargement possible pour
L1. Du fait de la complexité d'une telle condition,
nous utilisons une règle de dominance heuristique.
Les règles de dominance peuvent néanmoins
être affinées. On peut dire qu'il y a dominance de
L1 sur L2, lorsque l'ensemble des
objets pris séparément de L1 peuvent
être contenus dans les objets de L2. La figure 5.5
illustre une telle dominance. Le label L1 est représenté
par le chargement contenant les objets hachurés. Le label L2
est représenté à droite du label L1. La
troisième figure montre que l'ensemble des objets de L1 peut
être contenu dans les objets de L2, ce qui permet de conclure
que L1 domine L2.
~
~~
~ ~~~
~ ~~~
~ ~~~ ~
~ ~~~
~ ~~ ~ ~~~ ~~
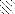

~
~~
~ ~~~
~ ~~~
~ ~~~ ~
~ ~~~
~ ~~ ~ ~~~ ~~
FIGURE 5.5 - Règle de
dominance affinée
Recherche à limitation d'écarts
(LDS)
Lorsqu'on étend un chemin partiel vers tous les
successeurs, le nombre de chemins partiels peut rapidement exploser,
malgré les règles de dominance. Afin de pallier ce
problème, nous utilisons une méthode qui permet de limiter le
nombre de successeurs vers lesquels l'extension des chemins est
réalisée. Cette méthode, appelée recherche à
limitation d'écarts (Limited Discrepancy Search ou LDS), a
été proposée par Harvey et Ginsberg (1995). Le principe de
cette méthode est le suivant. Lorsqu'une heuristique de recherche ne
permet pas de trouver une solution, on peut supposer que le nombre de retours
en arrière correspondant à de « mauvais » choix est
assez faible. Ce procédé a déjà été
utilisé pour un problème de Tournées de Véhicules
par Rousseau et al. (2004), pour le VRPTW.
Dans le cas du 2|RO|L-VRP, cela revient à penser qu'une
bonne tournée est composée de clients proches les uns des autres.
Nous définissons donc un critère permettant de
sélectionner des successeurs prometteurs pour chaque client. Le
critère retenu est
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
le plus proche voisin. Ainsi, un successeur est
considéré comme bon s'il est le plus proche voisin du client
depuis lequel il est étendu. Nous définissons aussi le nombre
maximal de mauvaises liaisons que peut contenir une tournée (une
mauvaise liaison étant définie comme un arc dont le client
correspondant à l'extrémité terminale ne fait pas partie
des successeurs prometteurs du client correspondant à
l'extrémité initiale de l'arc). L'extension d'un chemin partiel
se fait alors vers tous les bons successeurs et vers tous les autres si le
nombre maximum de mauvais successeurs n'est pas atteint par ce chemin
partiel.
Le fait de limiter le nombre de mauvais successeurs peut
soulever certains problèmes. Lorsqu'on cherche une route de coût
négatif, si le problème esclave n'est pas capable de trouver une
telle route, on conclut que le problème maître
relâché est optimal à l'itération courante. Or, sans
limitation sur le nombre de mauvais successeurs, une telle route peut exister.
Ainsi, si à la fin de l'algorithme, aucune colonne de coût
négatif n'est trouvée, l'algorithme est relancé avec un
nombre maximum d'écarts possible augmenté. La recherche à
limitation d'écarts fournit ainsi une méthode exacte combinant
à chaque itération les effets d'une réduction du graphe
avec ceux d'une limitation du nombre de chemins partiels
étudiés.
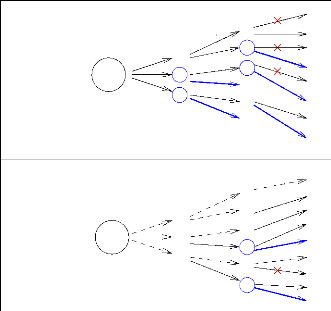
Première itération : limite d'écarts
à 2
Chemins limités : (y) ; (z) ; (x,z) ;
(y,x)
Chemins : (x,y,z) ; (z,x,y)
Deuxième itération : limite d'écarts
à 3
x
2 2
Chemins limités : (y,z) ; (z,y) y
Chemins : (x,z,y) ; (y,x,z) ; (y,z,x) ;
(z,y,x)
depot
depot
0
1
1
x
y
z
x
y
z
0
2
2
2
1
1
1
y 1
1
z
x 1
z 2
x
y
y
z
x
z
2
0
2
2
2
2
3
2
3
1
z
x
y
y
z
y
z
y
z
x
y
y
x
z
z
x
z
FIGURE 5.6 - Recherche de chemins
élémentaires par un LDS paramétré à 1
bon voisin
L'application de LDS à la recherche de chemins
élémentaires de longueur 3 est illustrée par la figure 5.6
qui retrace les deux premières itérations de l'algorithme. Le
bon
voisin de x est le sommet y, le bon voisin
de y est le sommet x et le bon voisin de z est le
sommet x. Au dessus de chaque arc, est indiqué le nombre
d'écarts du chemin partiel. Lors de la première itération,
cinq extensions (dont l'avant dernier sommet est entouré et dont l'arc
terminal est en gras) sont ignorées car elles atteignent la limite
d'écarts de 2. Ces extensions sont effectuées lors de
l'itération suivante, et ce sont les extensions atteignant la limite
d'écart de 3 qui sont alors ignorées. Dans cet exemple,
lorsqu'une extension vers un bon voisin est impossible, à cause de la
contrainte d'élémentarité par exemple, on considère
toujours la destination de cette extension comme un bon voisin. Les arcs
marqués d'une croix représentent des extensions violant la
contrainte d'élémentarité.
5.6.5 Problème de chargement séquentiel
à deux dimensions
Le problème de chargement à deux dimensions est
un problème que l'on retrouve fréquemment dans la
littérature. Les méthodes que nous décrivons par la suite
sont des méthodes classiques et qui ont montré leur
efficacité.
Méthodes de calcul de bornes
inférieures
Nous avons appliqué deux calculs de bornes
inférieures sur la hauteur totale d'un chargement à deux
dimensions. Ces bornes ont été définies dans un contexte
dans lequel l'aspect séquentiel n'était pas présent. Elles
restent cependant valides, bien que de qualité inférieures.
À notre connaissance, il n'existe pas de borne inférieure prenant
en compte les contraintes séquentielles.
La première borne est dérivée d'une borne
proposée par Martello et Toth (1990) pour le Two-Dimensional Bin
Packing. Cette borne inférieure se base sur un partitionnement des
objets. Étant donnée une valeur entière q telle
que 1 = q = 1 2W où W est la
largeur de la surface de chargement des véhicules et étant
donné J l'ensemble des objets du chargement, on pose:
K1 = {j ? J : wj > W
- q} (5.35)
1
K2 = {j ? J : W - q
= wj > 2W} (5.36)
1
K3 = {j ? J : 2W
= wj = q} (5.37)
On remarque que deux objets appartenant à K1 ou
K2 ne peuvent être chargés côte à côte
sur la surface de chargement.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
On définit pour tout entier q tel que 1 =
q = 12W la borne suivante :
B(q) = ? hj + max (0, [{ ? wjhj
- ? (W - wj)hj )}\W1) (5.38)
j?K1?K2 j?K3
j?K2
On obtient donc une borne inférieure définie par
:
LS 1= 1=q max=
{B(q)} (5.39)
/2
La complexité de cette borne est en O(n
log n). En effet, Martello et Toth (1990) ont montré qu'on
pouvait limiter les valeurs de q aux différentes valeurs prises
par wj telles
1
que 1 =wj= 2W.
Une autre borne a été proposée par
Martello et al. (2000) pour le problème du Strip
Packing. En considérant que les objets sont rangés par ordre
décroissant de hauteurs,
|
on définit k = max{i :
|
i
?
j=1
|
wj = W} et soit i(l) la
valeur minimale d'index telle que
|
|
wl +
|
i(l)
?
j=1
|
wj > W quel que soit l >
k vérifiant wl +
|
k
?
j=1
|
wj > W. Une borne inférieure est
|
donnée par :
|
LS2= max{hl +
hi(l) : l > k et wl + ?
j=1
|
wj > W} (5.40)
|
La complexité de cette borne est en O(n
log n). Il a été montré qu'il n'existe pas de
relation de dominance entre LS1 et
LS2.
Remplissage heuristique
Nous décrivons maintenant les différents
algorithmes heuristiques que nous avons utilisés pour déterminer
si un chargement est réalisable ou non. Tous ces algorithmes prennent en
entrée une liste d'objets à insérer. Les différents
tris possibles sur cette liste ont des conséquences sur les
résultats des algorithmes. En règle générale, on
considère que la liste est triée selon l'ordre de visite des
clients (pour satisfaire les contraintes de séquentialité des
chargements), puis par ordre décroissant soit sur la largeur des objets,
soit sur la hauteur des objets.
Une première famille d'algorithmes heuristiques sont
les algorithmes par niveau ou par étage. Le chargement est obtenu en
plaçant les objets de gauche à droite, sur des lignes formant
ainsi des niveaux ou des étages. Le premier niveau est le fond de la
surface de chargement (la largeur de la surface). Les niveaux suivants sont
formés
par une ligne horizontale coïncidant avec le haut du plus
grand objet placé au niveau inférieur. On retrouve dans la
littérature trois stratégies classiques pour le chargement
à deux dimensions. Ces stratégies ont été
adaptées à partir d'algorithmes prévus pour le cas
à une dimension. Dans chaque cas, les objets sont triés par ordre
de passage des clients à qui ils appartiennent, puis par ordre
décroissant de hauteur. Soit j l'objet courant et s le
dernier niveau créé :
Next-Fit Decreasing Height (NFDH) : L'objet
j est inséré le plus à gauche possible sur le
niveau s, s'il rentre. Si ce n'est pas le cas, on crée un
nouveau niveau (s := s + 1), et j y est
inséré le plus à gauche possible (voir la figure 5.7).
First-Fit Decreasing Height (FFDH) : L'objet
j est inséré le plus à gauche possible sur le
premier niveau dans lequel il rentre. Si aucun niveau ne peut contenir
j, un nouveau niveau est créé de manière
similaire à l'heuristique NFDH (voir la figure 5.8). Pour satisfaire la
contrainte de séquentialité du chargement, on fixe le premier
niveau dans lequel on peut insérer un objet, égal au dernier
niveau créé pour le client précédent. Cet
algorithme présente un intérêt lorsque les clients
proposent un nombre important d'objets. Dans le cas contraire, le chargement
est très proche de celui renvoyé par l'algorithme NFDH.
Best-Fit Decreasing Height (BFDH) : L'objet
j est inséré le plus à gauche possible sur le
niveau, parmi ceux sur lesquels il rentre, pour lequel l'espace horizontal
perdu est le plus faible. Si aucun niveau ne convient, un nouveau niveau est
créé tel que décrit précédemment (voir la
figure 5.9). Pour satisfaire la contrainte de séquentialité du
chargement, on fixe le premier niveau dans lequel on peut insérer un
objet, égal au dernier niveau créé pour le client
précédent. Cet algorithme présente un intérêt
lorsque les clients proposent un nombre important d'objets. Dans le cas
contraire, le chargement est très proche de celui renvoyé par
l'algorithme NFDH.
Coffman et al. (1980) ont analysé les
algorithmes heuristiques NFDH et FFDH pour la résolution du
problème de Strip Packing à deux dimensions, pour lequel tous les
objets sont insérés dans une boîte unique dont on cherche
à minimiser la hauteur. Étant donné un problème de
minimisation P et un algorithme heuristique A, on note
A(I) et Opt(I) la valeur renvoyée
par l'algorithme A et la valeur de la solution optimale, pour une
instance I du problème P. Coffman et al. ont
prouvé que, si les hauteurs des objets sont normalisées de telle
sorte que maxj{hj} = 1, alors :
NFDH(I) = 2 x Opt(I) + 1
(5.41)
FFDH(I) = 17
10 x Opt(I) + 1 (5.42)
Les deux bornes sont les plus restrictives, c'est-à-dire
que les facteurs multiplicatifs sont les plus petits possibles.
Nous présentons maintenant plusieurs heuristiques de
chargement dont la plupart dérivent de l'heuristique Bottom Left
proposée initialement par Baker et al. (1980).
Ces algorithmes suivent tous le même principe. Étant
donnée une liste d'objets à insérer, les objets sont
sélectionnés successivement pour être insérés
dans la surface de
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
1
5
3
2
6
4
FIGURE 5.7 - Next Fit Decreasing
Height
chargement. Tout au long de la résolution des
algorithmes, on garde en mémoire une liste ordonnée de positions
de chargements disponibles pour de nouveaux objets. À l'initialisation,
il n'y a qu'une position, la position en bas à gauche (d'où le
nom de Bottom Left). Chaque fois qu'un objet est inséré,
la position à laquelle il est inséré est modifiée
et on ajoute au plus une nouvelle position. Ainsi, la taille de la liste de
positions de chargements disponibles est bornée par le nombre d'objets
insérés, augmenté d' une unité. Les figures 5.10 et
5.11 représentent la gestion de la liste de positions avant et
après insertion d'un objet.
La position pour le placement d'un objet est
sélectionnée à partir d'une liste de positions
disponibles. Ce placement ne doit pas violer les contraintes de chargement
(l'objet ne doit pas dépasser des limites de la surface de chargement,
il ne doit pas chevaucher un autre objet, et enfin, son placement ne doit pas
empêcher le déchargement d'objets situés sur la suite du
parcours). La position choisie va dépendre de l'algorithme de
chargement. Si tous les objets sont placés dans la surface de
chargement, la route est considérée comme réalisable. Dans
le cas contraire, la liste des positions disponibles est ramenée
à la position initiale, et un autre algorithme de chargement est
appelé afin de proposer un chargement de l'ensemble des objets.
La gestion de la liste des positions est
représentée par les figures 5.10 et 5.11. Pour chaque position,
on ne conserve que deux informations : la hauteur de la position et la longueur
du segment jusqu'à la prochaine position (qui correspond à un
changement
5.6. Notre approche : un schéma de Branch & Price
1
3
2
4
5
6
FIGURE 5.8 - First Fit Decreasing
Height
de hauteur). Pour la position la plus à droite, la
deuxième information est la distance jusqu'au côté droit de
la surface de chargement. On peut remarquer sur la même figure qu'on ne
garde pas en mémoire les positions correspondant à des «
trous ». Étant données les contraintes de
séquentialité, le cas d'un objet pouvant se placer sous un autre
ne peut arriver que pour deux objets du même client. En partant du
principe qu'en cas de chargement non-réalisable, plusieurs ordres de
tris sur les objets seront appliqués, les configurations de trous ont
peu de chance d'empêcher un chargement.
La figure 5.10 représente un chargement pour lequel la
liste de positions disponibles est :
(4,4); (3,2); (2,2); (0,2)
Après insertion d'un objet de largeur 5 et de hauteur 2
telle que présentée dans la figure 5.11, la liste des positions
disponibles devient :
(7,5); (3,1); (2,2); (2,0)
Les figures 5.12 et 5.13 présentent à partir
d'un autre exemple de configuration de chargement les différentes mises
à jour possibles sur la liste des positions possibles après
l'insertion d'un objet.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
1
3
2
4
5
6
FIGURE 5.9 - Best Fit Decreasing
Height
Les heuristiques que nous avons utiisées sont les
suivantes :
Bottom-Left: Proposé par Chazelle
(1983), la position choisie pour chaque objet à in-
sérer est
la position la plus en bas, puis la plus à gauche (voir la figure
5.14).
Improved Bottom-Left: Liu et Teng (1999) ont
développé un algorithme amélioré du Bottom-Left, en
donnant la priorité aux mouvements vers le bas de telle sorte que
l'objet soit déplacé vers la gauche uniquement si aucun mouvement
vers le bas n'est possible (voir la figure 5.15).
Max Touching Perimeter: Cet algorithme a
été proposé par Lodi et al. (1999). Pour chaque
position, on calcule le périmètre des zones de contact entre
l'objet à insérer et les objets déjà
insérés. On choisit alors la position qui maximise ce
périmètre (voir la figure 5.16, appliquée sur le
même exemple que celui présenté par la figure 5.11). Une
variante a été proposée (Max Touching Perimeter No
Wall) qui ne prend pas en considération dans le calcul du
périmètre la zone de contact entre l'objet et les parois de la
surface de chargement.
Ces algorithmes heuristiques offrent un panel de solutions de
chargement. La complexité de ces algorithmes est de l'ordre de
O(n2) (pour chaque objet, on vérifie les
n positions possibles).
(4,4)
4
4
(3,2)
2
3
(2,2)
2
2
(0,2)
FIGURE 5.10 - Représentation
des coordonnées des objets
5.7 Deux approches différentes pour la
réalisabilité du chargement
Nous avons développé deux approches
résolument différentes : dans la première, le
problème esclave de recherche de plus court chemin renvoie des routes
réalisables du point de vue de la contrainte de capacité, mais,
dont la réalisabilité en ce qui concerne le chargement à
deux dimensions n'est pas assurée. Cette réalisabilité est
vérifiée a posteriori. La seconde approche, quant
à elle, construit des routes entièrement réalisables
(capacité et chargement séquentiel en deux dimensions) pendant la
résolution du sousproblème.
5.7.1 Vérification de la
réalisabilité a posteriori
Dans la méthode telle que nous l'avons
présentée, le problème esclave trouve des routes de
coûts réduits négatifs et insère les colonnes
correspondant à ces routes dans 1). Par contre, on a montré que,
si les routes renvoyées par le problème esclave respectent les
contraintes de capacités, elles ne respectent pas nécessairement
les contraintes de chargement. Il est donc nécessaire de vérifier
ces contraintes avant d'insérer les colonnes dans 1). Dans cette
méthode, l'aire occupée par le chargement n'est pas prise en
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
(7,5)
5
(3,1)
4
(2,2)
2
4
2
3
2
(0,2)
~~~~~~~~~~
~~~~~~~~~~
~~~~~~~~~~
~~~~~~~~~~ 3
~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~
FIGURE 5.11 -
Représentation des coordonnées des objets
après insertion
considération pour les règles de dominances,
puisque le chargement n'est déterminé qu'a posteriori. La borne
inférieure sur l'aire occupée (définie comme la somme des
aires des objets chargés) est néanmoins utilisée pour
vérifier la réalisabilité de l'extension d'un chemin
partiel vers un client.
Si le calcul des bornes inférieures montre que le
chargement n'est pas réalisable, la route est ajoutée dans
l'annuaire de routes non-réalisables. Dans le cas contraire, nous
appliquons les algorithmes dans l'ordre dans lequel ils ont été
présentés dans la section 5.6.5. Les heuristiques de chargement
sont appelées, avec des listes d'objets triées selon des ordres
différents (ordre décroissant sur la largeur, ordre
décroissant sur la hauteur, ordre croissant sur la largeur et ordre
croissant sur la hauteur). Dès qu'un algorithme indique que le
chargement est réalisable, la route est ajoutée. Si aucun
algorithme ne trouve un chargement réalisable, la route est
ajoutée à l'annuaire des routes non-réalisables. Enfin,
dans le cas où le sous-problème ne trouve aucune route de
coût réduit négatif respectant les contraintes de
chargement, la résolution du problème esclave est
arrêtée et la relaxation linéaire du problème
maître restreint est alors résolue.
(5,4)
4
5
(3,2)
2
3
(2,2)
2
2
(4,2)
4
2
FIGURE 5.12 - Représentation
des coordonnées des objets sur un autre exemple
Gestion efficace des chargements
Nous avons ajouté une gestion efficace des routes non
réalisables. Le calcul de réalisabilité d'une route est un
calcul complexe, nécessitant d'être appelé un nombre
important de fois. Ainsi, dès qu'une route est désignée
comme non-réalisable par les méthodes de calculs de bornes
inférieures, cette route est stockée dans un annuaire de routes.
Cet annuaire a une structure d'arbre n-aire classé, pour lequel
l'insertion d'une route et la vérification de la présence d'une
route sont des méthodes rapides et peu complexes. L'annuaire a la
structure décrite par la figure 5.17.
Dans cet annuaire, nous ne stockons que les routes non
réalisables. En effet, les routes réalisables ne sont
vérifiées qu'une seule fois, puisqu'elle sont ensuite
ajoutées dans 1) et qu'elles ne sont jamais supprimées de cet
ensemble. On ne vérifie donc jamais deux fois la même route, si
celle-ci est réalisable.
5.7.2 Construction de routes réalisables dans le
sous-problème
Nous proposons dans cette méthode de construire dans le
problème esclave des routes réalisables, respectant donc les
contraintes de chargement séquentiel. Pour cela, nous modifions les
données sauvegardées pour chaque chemin partiel. Tel que
présenté précédemment, sont associés
à un chemin partiel un coût, un poids, une aire restante et
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement

(5,4)
(4,6)
4
2
2
5
4
2
2
3
~~~~~~~~ ~~~~~~~~ ~~~~~~~~ ~~~~~~~~
FIGURE 5.13 - Mise à jour
des coordonnées des objets après insertion sur un autre
exemple
FIGURE 5.14 - Bottom
Left
FIGURE 5.15 - Improved Bottom
Left
une liste de sommets non accessibles. À cela, nous
ajoutons une liste des positions possibles telle que présentée
dans les figures 5.10 et 5.11. Chaque fois qu'un chemin partiel est
étendu vers un sommet, la liste des objets proposés par le sommet
est crée. On essaie alors d'ajouter les objets dans le chargement
existant, ce chargement étant représenté par la liste des
positions possibles. Pour cela, nous faisons appel aux algorithmes heu-
(7,5)
4
5
4
(3,1)
3
2
~
~
~
~~
~~
~~
~~
~~
~~
~~
~
~~
~
3
(2,2)
2
2
(0,2)
FIGURE 5.16 - Max Touching
Perimeter
5
1
0
6
7 8
2
FIGURE 5.17 - Structure d'un
annuaire
ristiques présentés dans la section 5.6.5. Ainsi,
toutes les routes de coût négatif trouvées
157
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
par le problème esclave sont nécessairement des
routes réalisables. Cependant, dans le cas où l'heuristique
utilisée ne trouve pas de chargement réalisable, la route est
éliminée, bien qu'un chargement réalisable puisse exister.
La méthode proposée est donc une méthode heuristique.
Chaque heuristique peut calculer l'aire restante à
partir de la liste des positions disponibles. Soit wni
et hni la largeur et la hauteur correspondant aux
point ni de la liste des points disponibles et H la hauteur
de la surface de chargement. Soit T la taille de la liste des points
possibles. L'aire restante est égale à :
T
airerestante = ? wni × (H - hni)
(5.43)
i=0
La figure 5.18 présente le calcul de l'aire restante
appliquée sur l'exemple présenté par la figure 5.11.
2
~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~
~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~ ~~~~~~~~~~
~~~~~~~~~~ ~~~~~~~~~~
|
(7,5)
~~~~~~~~~~
|
~ (3,1)
|
~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~ ~~~~~ ~
~~~~~ ~ ~~~~~ ~~~~~ ~
~~~~~ ~~~~ ~~~~ ~~~~~
|
~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~
~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~ ~~~~~
(2,2) ~~~~~
~~~~
(0,2)
~~~~
~~~
~~~~~
|
|
~~~~~~~~~~
3
|
|
4
4
|
|
|
2
3
|
|
2
|
FIGURE 5.18 - Calcul de l'aire
restante d'un chargement
Cette aire peut être utilisée pour
vérifier en prétraitrement si les objets du sommet j
peuvent être ajoutés. Lorsque les routes sont construites
dans le sous-problème, l'heuristique de chargement reste tout le temps
la même. Ainsi, l'aire occupée peut être utilisée de
manière heuristique afin de renforcer les règles de dominance.
Néanmoins, il faut garder en mémoire que dans ce cas, les
régles de dominance sont trop fortes et risquent donc de supprimer des
chemins partiels non véritablement dominés.
5.8. Branch & Price heuristique
Cette méthode présente l'intérêt de
laisser tout le calcul de réalisabilité des routes dans le
problème esclave. On peut donc garantir l'optimalité de la
méthode, sous réserve d'avoir défini une règle de
chargement exacte.
5.8 Branch & Price heuristique
Nous avons présenté dans la section
précédente un schéma classique de résolution par
Branch & Price. De par la complexité des contraintes de chargement,
le sousproblème n'est pas résolu de manière exacte. Notre
travail s'est donc porté sur les méthodes
d'accélération de résolution. Dans cette section, nous
montrons tous les moyens dont nous disposons pour rendre la méthode
heuristique, que ce soit au niveau du problème esclave, de la
méthode de séparation, ou de la résolution du
problème maître restreint. La plupart des changements que nous
proposons présentent l'intérêt de dépendre de
paramètres. Ainsi, nous pouvons rendre à nouveau la
méthode exacte (du moins pour la méthode de séparation et
la gestion des colonnes) en ne modifiant que certains paramètres.
5.8.1 Problème esclave heuristique
On peut rendre heuristique le problème esclave de
plusieurs manières différentes.
Gestion de la taille de la liste des chemins
partiels
La première technique, et l'une des plus
intéressantes afin d'accélérer la résolution du
problème esclave, est de limiter le nombre de chemins partiels pour
chaque sommet. On l'a vu précédemment, le nombre de chemins
partiels pour chaque sommet peut rapidement exploser. Afin de limiter ce
nombre, on peut ne garder en mémoire que les nblabels premiers
chemins partiels de la liste triée de chemins partiels qui nous semblent
les plus prometteurs. Le tri de cette liste est effectué selon le
coût du chemin partiel. On peut aussi par ailleurs renforcer les
règles de dominances entre deux chemins partiels en créant des
règles de dominances « trop fortes >>. Ces règles
risquent de supprimer des chemins partiels non dominés, mais permettent
d'accélerer la résolution du sousproblème.
Gestion des successeurs
Cette technique est proche de la technique de Recherche
à Limitation d'Écarts. En limitant le nombre de successeurs pour
chaque sommet, on oblige les chemins partiels à être
étendus uniquement vers de « bons>> voisins. On peut donc
modifier le nombre de sommets considérés comme « bons
>>. Cette méthode est plus restrictive que la méthode de
Recherche à Limitation d'Écarts puisqu'elle n'autorise aucun
écart.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
5.8.2 Gestion des colonnes
Lors de la résolution de la relaxation linéaire
du problème maître restreint par le solveur, celui-ci va fixer au
bout d'un certain nombre d'itérations des colonnes. Les variables seront
alors égales à 1. Afin d'accélérer la
résolution, il peut être intéressant de fixer de telles
variables pour toute la suite de la résolution. Il faut cependant
attendre qu'un nombre suffisant de colonnes ait été
générées, afin de ne pas fixer à 1 une colonne
inintéressante. Lorsque l'on choisit de fixer une colonne 0k
à 1, cela revient à ajouter dans le noeud courant les
contraintes qui fixent à 1 l'ensemble des arcs empruntés par la
colonne considérée. On peut remarquer que le fait d'imposer une
route interdit toutes les routes partageant les mêmes sommets (les
sommets étant déjà visités). Cela revient donc
à travailler sur un problème de taille réduite, pour
lequel on retire les sommets appartenant à la route 0k. Cette
méthode est différente d'une méthode de séparation
car la colonne est fixée à 1 pour toute la suite de la
résolution.
5.8.3 Méthode de séparation
Dans une méthode classique de Branch & Price, telle
que présentée précédemment, une fois que le
problème maître restreint est résolu à l'optimum,
dans le cas où il existe des variables fractionnaires, on applique une
méthode de séparation. On crée donc un certain nombre de
noeuds (généralement deux voire trois). Ces noeuds consistent
à rajouter une contrainte sur une variable ou un ensemble de variables
(contrainte d'intégralité, borne inférieure ou
supérieure,...). La génération de colonnes est ensuite
appelée à nouveau par le biais du problème esclave, qui
intègre les contraintes rajoutées par le noeud courant. Le
problème esclave va donc rajouter un certain nombre de colonnes dans
l'ensemble 1. Lorsqu'aucun chemin de coût négatif ne sera
trouvé, la méthode de séparation sera rappelée.
Un des moyens de rendre un Branch & Price heuristique est
de supprimer l'aspect « Pricing ». Pour cela, il suffit de ne pas
générer de nouvelles colonnes une fois qu'un noeud est
créé, en dehors du noeud racine. Les contraintes contenues dans
le noeud sont rajoutées dans le problème maître restreint.
La résolution de la relaxation linéaire du problème
correspondant permet d'avoir une borne inférieure sur le coût du
noeud. On se retrouve donc dans la configuration d'un Branch & Bound
classique pour lequel la borne inférieure est calculée par la
relaxation linéaire du problème maître restreint, la borne
supérieure étant la meilleure solution entière connue.
Cette méthode peut s'avérer efficace si un grand nombre de
colonnes est rajouté au noeud racine, étant donné
qu'aucune nouvelle colonne ne sera ajoutée lors des itérations
suivantes. Cette transformation d'un Branch & Price en un Branch &
Bound est possible pour l'arbre complet ou pour n'importe quel sous-arbre.
5.9 Résultats expérimentaux
Nous présentons dans cette section les instances que
nous avons utilisées pour me-surer les performances et nous comparons
nos résultats avec plusieurs algorithmes de la littérature.
5.9.1 Paramètres retenus
Dans les méthodes de résolution, nous avons
fixé une limite de temps à 3600 secondes. Lorsque cette limite de
temps est atteinte, la résolution est arrêtée et la
meilleure solution entière est renvoyée. La taille de la liste
des chemins partiels (définie dans la section 5.8.1 a été
limitée à 500. Le nombre de bons voisins pour chaque sommet dans
la résolution du problème esclave (définie dans la section
5.8.1 est fixé à n/2 où n est le nombre
de clients. Lorsque 95% du temps alloué a été
utilisé par la résolution, l'aspect « Pricing» est
supprimé. Aucune nouvelle colonne n'est alors
générée.
L'heuristique retenue pour la génération de
routes réalisables (présentée à la section 5.7.2)
est l'heuristique Improved Bottom Left avec un tri des objets par
ordre décroissant de largeur pour les objets appartenant à un
même client. Cette heuristique est celle qui a donné les meilleurs
résultats parmi les heuristiques présentées. Cependant,
l'analyse des résultats expérimentaux montrent que l'heuristique
choisie n'est pas de qualité suffisante pour obtenir de bons
résultats.
Tous les paramètres ont été
sélectionnés par des expériences préliminaires.
5.9.2 Classes d'instances
Afin de tester les performances de notre algorithme, nous
avons utilisé un ensemble de 180 instances du problème
2|RO|L-VRP, introduites par Iori et al. (2007) et Gendreau et al.
(2008). Ces instances proviennent de 36 instances du problème de
Capacited Vehicle Routing Problem, décrites par Toth et Vigo (2002), en
caractérisant la demande des clients comme un ensemble d'objets de forme
rectangulaire à deux dimensions auxquels est associé un poids.
À partir des instances du CVRP, 5 classes d'instances ont
été introduites par Iori et al. (2007).
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Classe 1 On associe à chaque client un
seul objet de taille nulle. Ainsi, les problèmes de la classe 1 sont des
problèmes classiques de CVRP, puisqu'il n'y a pas de contraintes de
chargement (à part les contraintes de capacité). Ces instances
permettent de mesurer l'efficacité des algorithmes en ce qui concerne
les aspects de tournées.
Classe 2 - 5 On associe à chaque
client i un ensemble de mi objets. mi est
distribué uniformément dans un intervalle donné. Chaque
objet est classé parmi une des trois catégories de formes
(verticale, homogène, ou horizontale) de manière
aléatoire, avec la même probabilité pour chaque
catégorie de forme. Les dimensions de chaque objet sont
uniformément distribuées dans un intervalle,
déterminé par la catégorie de la forme de l'objet. Le
nombre d'objets mi et les intervalles des dimensions sont fournis dans
le tableau 5.2. La hauteur et la largeur de la surface de chargement sont
égales respectivement à 40 et 20. Les coûts des arcs sont
égaux aux distances euclidiennes entre les paires de noeuds. Le tableau
5.3 résume les caractéristiques des 36 instances pour les classes
2 à 5. Pour chacune des 36 instances du CVRP, 5 instances sont
créées selon les 5 classes présentées ci-desssus.
On obtient alors un total de 180 instances. Afin d'assurer la
réalisabilité des instances, la taille de la flotte de
véhicules vh est déterminée par une heuristique
de rangement.
|
Classe mi
|
Verticale
Hauteur Largeur
|
Homogène
Hauteur Largeur
|
Horizontale Hauteur Largeur
|
|
2
|
[1,
|
2]
|
[0.4H,
|
0.9H][0.1W,
|
0.2W]
|
[0.2H,
|
0.5H][0.2W,
|
0.5W]
|
[0.1H,
|
0.2H][0.4W,
|
0.9W]
|
|
3
|
[1,
|
3]
|
[0.3H,
|
0.8H][0.1W,
|
0.2W]
|
[0.2H,
|
0.4H][0.2W,
|
0.4W]
|
[0.1H,
|
0.2H][0.3W,
|
0.8W]
|
|
4
|
[1,
|
4]
|
[0.2H,
|
0.7H][0.1W,
|
0.2W]
|
[0.1H,
|
0.4H][0.1W,
|
0.4W]
|
[0.1H,
|
0.2H][0.2W,
|
0.7W]
|
|
5
|
[1,
|
5]
|
[0.1H,
|
0.6H][0.1W,
|
0.2W]
|
[0.1H,
|
0.3H][0.1W,
|
0.3W]
|
[0.1H,
|
0.2H][0.1W,
|
0.6W]
|
TABLE 5.2 - Caractéristiques
des classes d'instances
5.9.3 Analyses des résultats
Les algorithmes présentés ont été
codés en C++ et exécutés sur un processeur AMD X2 3800+
cadencé à 2 Ghz avec 1 Go de mémoire vive. Les 17
premières séries d'instances contiennent jusqu'à 40
clients et 127 objets. Chaque série contient 5 instances. Ces instances
ont été résolues de manière exacte par une
méthode de séparation et génération de coupe (Iori
et al., 2007). Par rapport aux instances originales du CVRP, les arcs
sont arrondis à la prochaine valeur entière. Dans la plupart des
cas, les solutions optimales sont connues.
Le tableau 5.4 présente les résultats
agrégés par série d'instances obtenus sur les 85 instances
de taille moyenne. Nos résultats (HBP) sont comparés avec la
méthode Branch & Cut proposée par Iori et al.
(2007), la recherche Tabou proposée par Gendreau et al.
(2008) et l'algorithme d'optimisation par Colonie de Fourmis de Fuellerer
et al. (2008).
|
Inst
|
client
|
Class 2
obj. vh r%
|
Class 3
obj. vh r%
|
Class 4 obj. vh
|
r%
|
Class 5
obj. vh r%
|
|
1
|
15
|
24
|
3
|
78
|
31
|
3
|
82
|
37
|
4
|
70
|
45
|
4
|
61
|
|
2
|
15
|
25
|
5
|
52
|
31
|
5
|
59
|
40
|
5
|
53
|
48
|
5
|
39
|
|
3
|
20
|
29
|
5
|
68
|
46
|
5
|
77
|
44
|
5
|
62
|
49
|
5
|
54
|
|
4
|
20
|
32
|
6
|
58
|
43
|
6
|
58
|
50
|
6
|
63
|
62
|
6
|
47
|
|
5
|
21
|
31
|
4
|
72
|
37
|
4
|
75
|
41
|
4
|
76
|
57
|
5
|
53
|
|
6
|
21
|
33
|
6
|
54
|
40
|
6
|
63
|
57
|
6
|
72
|
56
|
6
|
46
|
|
7
|
22
|
32
|
5
|
71
|
41
|
5
|
66
|
51
|
5
|
67
|
55
|
6
|
49
|
|
8
|
22
|
29
|
5
|
63
|
42
|
5
|
71
|
48
|
5
|
68
|
52
|
6
|
38
|
|
9
|
25
|
40
|
8
|
57
|
61
|
8
|
61
|
63
|
8
|
60
|
91
|
8
|
53
|
|
10
|
29
|
43
|
6
|
74
|
49
|
6
|
66
|
72
|
7
|
73
|
86
|
7
|
63
|
|
11
|
29
|
43
|
6
|
77
|
62
|
7
|
74
|
74
|
7
|
83
|
91
|
7
|
63
|
|
12
|
30
|
50
|
9
|
62
|
56
|
9
|
52
|
82
|
9
|
66
|
101
|
9
|
58
|
|
13
|
32
|
44
|
7
|
69
|
56
|
7
|
68
|
78
|
7
|
77
|
102
|
8
|
59
|
|
14
|
32
|
47
|
7
|
65
|
57
|
7
|
65
|
65
|
7
|
61
|
87
|
8
|
49
|
|
15
|
32
|
48
|
6
|
76
|
59
|
6
|
84
|
84
|
8
|
72
|
114
|
8
|
72
|
|
16
|
35
|
56
|
11
|
55
|
74
|
11
|
57
|
93
|
11
|
64
|
114
|
11
|
49
|
|
17
|
40
|
60
|
14
|
46
|
73
|
14
|
42
|
96
|
14
|
51
|
127
|
14
|
40
|
|
18
|
44
|
66
|
9
|
72
|
87
|
10
|
75
|
112
|
10
|
77
|
122
|
10
|
58
|
|
19
|
50
|
82
|
11
|
77
|
103
|
11
|
83
|
134
|
12
|
79
|
157
|
12
|
61
|
|
20
|
71
|
104
|
14
|
84
|
151
|
15
|
83
|
178
|
16
|
81
|
226
|
16
|
69
|
|
21
|
75
|
114
|
14
|
84
|
164
|
17
|
82
|
168
|
17
|
70
|
202
|
17
|
61
|
|
22
|
75
|
112
|
15
|
82
|
154
|
16
|
81
|
198
|
17
|
82
|
236
|
17
|
66
|
|
23
|
75
|
112
|
14
|
86
|
155
|
16
|
83
|
179
|
16
|
83
|
225
|
16
|
72
|
|
24
|
75
|
124
|
17
|
81
|
152
|
17
|
77
|
195
|
17
|
82
|
215
|
17
|
66
|
|
25
|
100
|
157
|
21
|
83
|
212
|
21
|
85
|
254
|
22
|
83
|
311
|
22
|
65
|
|
26
|
100
|
147
|
19
|
84
|
198
|
20
|
82
|
247
|
20
|
87
|
310
|
20
|
75
|
|
27
|
100
|
152
|
19
|
84
|
211
|
22
|
82
|
245
|
22
|
78
|
320
|
22
|
71
|
|
28
|
120
|
183
|
23
|
83
|
242
|
25
|
83
|
299
|
25
|
84
|
384
|
25
|
72
|
|
29
|
134
|
197
|
24
|
85
|
262
|
26
|
83
|
342
|
28
|
85
|
422
|
28
|
74
|
|
30
|
150
|
225
|
29
|
83
|
298
|
30
|
87
|
366
|
30
|
86
|
433
|
30
|
70
|
|
31
|
199
|
307
|
38
|
84
|
402
|
40
|
85
|
513
|
42
|
86
|
602
|
42
|
70
|
|
32
|
199
|
299
|
38
|
84
|
404
|
39
|
85
|
497
|
39
|
86
|
589
|
39
|
73
|
|
33
|
199
|
301
|
37
|
85
|
407
|
41
|
84
|
499
|
41
|
87
|
577
|
41
|
71
|
|
34
|
240
|
370
|
46
|
85
|
490
|
49
|
86
|
604
|
50
|
86
|
720
|
50
|
72
|
|
35
|
252
|
367
|
45
|
85
|
507
|
50
|
85
|
634
|
50
|
90
|
762
|
50
|
74
|
|
36
|
255
|
387
|
47
|
86
|
511
|
51
|
86
|
606
|
51
|
83
|
786
|
51
|
74
|
TABLE 5.3 -
Caractéristiques des classes d'instances
Les en-têtes sont les suivants :
- I : numéro de l'instance,
- n : nombre de clients,
- Branch & Cut : valeur des solutions (z) et temps
d'exécution en secondes (CPU),
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
- Tabu Search : valeur des solutions (z), temps
d'exécution en secondes (CPU) et différence avec les solutions
proposées par Iori et al. (2007),
- ACO : valeur moyenne des solutions (z) sur 5 essais, temps
d'exécution en se-
condes (CPU) et différence avec les solutions
proposées par Iori et al. (2007),
- HBP : valeur des solutions (z), temps d'exécution en
secondes (CPU) et différence
avec les solutions proposées par Iori et al.
(2007).
La lecture des résultats nous permet de dire que notre
méthode semble intéressante. Elle est en moyenne moins efficace
que la méthode ACO proposée par Fuellerer et al. (2008),
mais permet d'obtenir de bons résultats en des temps d'exécutions
raisonnables. En limitant le temps à une heure (limite de temps qui
n'est jamais atteinte pour ces instances), elle permet d'améliorer
certaines instances non résolues à l'optimum dans la limite de
temps de 24 heures par la méthode de Branch & Bound de Iori et
al. (2007) (ce qui explique que dans certains cas le pourcentage de
différence avec les solutions optimales soit négatif). Les temps
d'exécution sont similaires au temps des autres méthodes.
Néanmoins, il semble que les heuristiques de chargement utilisées
ne permettent pas de retrouver toutes les routes réalisables
relativement aux contraintes de chargement, ce qui explique des
résultats inférieurs aux méthodes les plus
performantes.
|
I
|
n
|
Branch & Cut
z CPU
|
Tabu search z CPU
|
Gap
|
ACO z CPU
|
gap
|
z
|
HBP CPU
|
gap
|
|
1
|
15
|
281
|
29.9
|
281.4
|
7.6
|
0.14
|
286.4
|
8.9
|
1.92
|
285
|
12.1
|
1.42
|
|
2
|
15
|
336.6
|
14.7
|
337.2
|
3.9
|
0.18
|
337.4
|
0.7
|
0.24
|
337.8
|
4.5
|
0.36
|
|
3
|
20
|
375.4
|
25.4
|
377.6
|
18
|
0.59
|
376.6
|
7
|
0.32
|
378.2
|
15.6
|
0.75
|
|
4
|
20
|
430
|
17
|
433.8
|
14
|
0.88
|
431
|
4.1
|
0.23
|
433.6
|
15.1
|
0.84
|
|
5
|
21
|
377.2
|
597.8
|
387
|
28.8
|
2.6
|
378
|
19.5
|
0.21
|
385
|
27.3
|
2.07
|
|
6
|
21
|
490.4
|
67.4
|
494.6
|
23.1
|
0.86
|
491.7
|
5.6
|
0.27
|
495.2
|
22.4
|
0.98
|
|
7
|
22
|
687.2
|
676.3
|
699.8
|
39.2
|
1.83
|
690
|
11.9
|
0.41
|
698.6
|
31.5
|
1.66
|
|
8
|
22
|
705.8
|
261.6
|
717.4
|
45
|
1.64
|
713.1
|
16.6
|
1.03
|
718.6
|
38.7
|
1.81
|
|
9
|
25
|
614.2
|
469.9
|
616.6
|
38.2
|
0.39
|
616
|
8.3
|
0.29
|
616.6
|
32.8
|
0.39
|
|
10
|
29
|
676
|
51791.2
|
684
|
150.8
|
1.18
|
666.9
|
48.6
|
-1.35
|
678
|
72.9
|
0.3
|
|
11
|
29
|
725.6
|
69120.4
|
718.4
|
175.7
|
-0.99
|
691.7
|
134
|
-4.67
|
724.2
|
183.5
|
-0.19
|
|
12
|
30
|
609.4
|
86400.4
|
612
|
87.3
|
0.43
|
602.3
|
12.9
|
-1.17
|
610.4
|
74.2
|
0.16
|
|
13
|
32
|
2713.6
|
58268
|
2588.4
|
296.2
|
-4.61
|
2540.7
|
59
|
-6.37
|
2653.6
|
259.4
|
-2.21
|
|
14
|
32
|
1233.4
|
74228.8
|
1157.8
|
343.3
|
-6.13
|
1146
|
131.9
|
-7.09
|
1181.4
|
354.8
|
-4.22
|
|
15
|
32
|
1252.6
|
69124.2
|
1191.6
|
308
|
-4.87
|
1182.4
|
235.2
|
-5.6
|
1201.6
|
291.8
|
-4.07
|
|
16
|
35
|
683.8
|
10098.1
|
686.4
|
161.8
|
0.38
|
684.9
|
11.1
|
0.16
|
687.4
|
212.5
|
0.53
|
|
17
|
40
|
854.6
|
86400.3
|
844.4
|
234.7
|
-1.19
|
846.2
|
9.4
|
-0.98
|
848.8
|
176.3
|
-0.68
|
|
Moyenne
|
767.46
|
29858.32
|
754.61
|
116.21
|
-0.39
|
745.96
|
42.63
|
-1.3
|
760.82
|
107.38
|
-0.01
|
TABLE 5.4 - Résultats
expérimentaux : qualité des solutions sur instances
moyennes
Le tableau 5.5 présente les résultats
agrégés par série d'instances obtenus sur les 180
instances de grande taille. Dans ces instances, les distances ne sont pas
arrondies à la prochaine valeur entière. Les en-têtes des
colonnes sont les mêmes que les en-têtes
du tableau précédent, à la
différence que la qualité des solutions est calculée
relativement aux solutions fournies par la recherche Tabou de Gendreau et
al. (2008). À ce jour, aucune méthode de résolution
exacte n'a été proposée.
Les résultats présentés dans le tableau
5.5 sont similaires aux résultats des solutions sur les instances de
taille moyenne. Notre méthode est moins performante que la
méthode d'Optimisation par Colonie de Fourmis de Fuellerer et al.
(2008), que ce soit en terme de qualité des solutions ou de temps
d'éxécution. Cependant, les résultats obtenus par notre
méthode sont comparables en terme de qualité et de temps avec la
méthode de Recherche Tabou de Gendreau et al. (2008).
Enfin, le tableau 5.6 présente les résultats
agrégés sur les 180 instances pour nos deux méthodes
heuristiques. La différente de qualité de solution de la
méthode de génération de routes réalisables est
calculée relativement aux valeurs de solutions de la méthode de
Branch & Price heuristique.
Très clairement, la méthode de
génération de routes réalisables (HCG) est de moins bonne
qualité que la méthode de Branch & Price heuristique(HBP)
avec en moyenne un pourcentage de différence proche de 20%. Cela
s'explique par le fait que la méthode de génération de
routes réalisables ne fait appel qu'à une seule heuristique de
chargement. De plus, une fois que les objets sont insérés, le
chargement de ceux-ci n'est jamais remis en question. Ainsi, un nombre
important de routes réalisables ne sont pas ajoutées. On peut
cependant noter que cette méthode est plus rapide que la méthode
de Branch & Price heuristique, ce qui s'explique encore une fois par
l'utilisation limitée des heuristiques de chargement.
5.10 Conclusions et perspectives
Dans ce chapitre, nous avons proposé une
résolution heuristique du problème de Tournées de
Véhicules avec Contraintes de Chargement. De par la complexité
des contraintes de chargement, ce problème n'est pas résolu par
une approche exacte. Nous avons montré un aperçu des
possibilités qu'il existait pour tronquer la méthode de Branch
& Price, qui est une méthode a priori exacte. Les approches
heuristiques que nous proposons permettent d'accélérer la
résolution. Il est cependant clair que la qualité des
heuristiques de chargement est déterminante dans la qualité des
solutions. Malgré une utilisation de plusieurs heuristiques de
chargement, les résultats que nous proposons ne permettent pas de
dépasser les meilleurs résultats connus. Cependant, que ce soit
en terme de qualité de solution ou en temps d'éxécution,
nos résultats restent dans une moyenne des méthodes
publiées à ce jour.
Les perspectives de recherche sur ce chapitre sont nombreuses.
Les résultats que nous présentons pourraient être
améliorés par l'utilisation d'heuristiques de chargement plus
efficaces. Enfin, les résultats de la méthode de
génération de routes réalisables ne sont pas à la
hauteur de nos espérances. Cependant, on peut noter que cette
méthode peut être une base de futurs travaux de recherche, dans le
but de proposer une
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
|
I
|
n
|
Tabu Search
z CPU
|
z
|
ACO
CPU
|
Gap
|
z
|
HBP
CPU
|
Gap
|
|
1
|
15
|
295.01
|
9.2
|
291.83
|
7.2
|
-1.08
|
294.21
|
11.6
|
-0.27
|
|
2
|
15
|
343.18
|
3.5
|
343.22
|
0.6
|
0.01
|
343.2
|
4.4
|
0.01
|
|
3
|
20
|
380.19
|
18.9
|
378.18
|
3.1
|
-0.51
|
382.56
|
15.2
|
0.62
|
|
4
|
20
|
440.91
|
17
|
439.07
|
3
|
-0.41
|
440.51
|
18.7
|
-0.09
|
|
5
|
21
|
382.3
|
27.6
|
381.63
|
12.8
|
-0.17
|
382.68
|
27.5
|
0.1
|
|
6
|
21
|
501.4
|
19.5
|
499.77
|
4.3
|
-0.32
|
502.56
|
21.8
|
0.23
|
|
7
|
22
|
691.23
|
53
|
678.22
|
11.7
|
-1.79
|
690.11
|
31.3
|
-0.16
|
|
8
|
22
|
691.89
|
83.7
|
684.37
|
16.1
|
-1.02
|
690.85
|
37.2
|
-0.15
|
|
9
|
25
|
620.77
|
40
|
614.88
|
4.9
|
-0.93
|
618.65
|
31.8
|
-0.34
|
|
10
|
29
|
679.68
|
179.6
|
668.48
|
50.1
|
-1.64
|
680.56
|
73.5
|
0.13
|
|
11
|
29
|
719.76
|
199.4
|
690.22
|
57.8
|
-3.51
|
716.84
|
201.2
|
-0.41
|
|
12
|
30
|
627.59
|
99.5
|
615.9
|
7.4
|
-1.77
|
631.51
|
76.8
|
0.62
|
|
13
|
32
|
2550.89
|
312.8
|
2480.04
|
61.8
|
-2.6
|
2560.22
|
282.6
|
0.37
|
|
14
|
32
|
1048.72
|
439.5
|
1007.92
|
163.1
|
-3.69
|
1043.16
|
392.3
|
-0.53
|
|
15
|
32
|
1160.25
|
313.4
|
1145.96
|
138.8
|
-1.17
|
1161.65
|
315.2
|
0.12
|
|
16
|
35
|
703.6
|
157.2
|
701.09
|
8.3
|
-0.35
|
702.69
|
191.7
|
-0.13
|
|
17
|
40
|
865.72
|
226.2
|
864.92
|
7.2
|
-0.09
|
864.39
|
190.8
|
-0.15
|
|
18
|
44
|
1037.65
|
1167.8
|
1003.84
|
292.6
|
-3.03
|
1026.18
|
1745.8
|
-1.11
|
|
19
|
50
|
746.91
|
1521.5
|
728.89
|
122.1
|
-2.15
|
759.37
|
1429.1
|
1.67
|
|
20
|
71
|
513.84
|
3370.3
|
484.23
|
1073.8
|
-4.95
|
517.48
|
3251.2
|
0.71
|
|
21
|
75
|
1025.79
|
3561.2
|
987.54
|
1037.3
|
-3.4
|
1023.93
|
3600.1
|
-0.18
|
|
22
|
75
|
1052.39
|
3461.8
|
1018.76
|
738.9
|
-2.89
|
1053.1
|
3600
|
0.07
|
|
23
|
75
|
1121.18
|
3600
|
1051.16
|
1206.5
|
-5.71
|
1119.74
|
3600.2
|
-0.13
|
|
24
|
75
|
1208.52
|
3324.6
|
1134.9
|
323.4
|
-5.62
|
1211.34
|
3600.2
|
0.23
|
|
25
|
100
|
1350.56
|
3600.1
|
1309.98
|
2454.9
|
-2.74
|
1346.13
|
3600.5
|
-0.33
|
|
26
|
100
|
1341.3
|
3600.3
|
1306.24
|
3558.1
|
-2.52
|
1337.84
|
3600.5
|
-0.26
|
|
27
|
100
|
1439.37
|
3600
|
1341.25
|
1570.3
|
-6.3
|
1431.29
|
3600.4
|
-0.56
|
|
28
|
120
|
2502.48
|
3600.1
|
2417.89
|
8714.5
|
-2.16
|
2494.36
|
3600.5
|
-0.32
|
|
29
|
134
|
2296.03
|
3600.2
|
2131.54
|
8837.5
|
-6.02
|
2279.63
|
3600.5
|
-0.71
|
|
30
|
150
|
1873.27
|
3600.2
|
1734.46
|
8720.3
|
-6.9
|
1871.62
|
3600.2
|
-0.09
|
|
31
|
199
|
2366.54
|
3600.5
|
2219.34
|
8747.4
|
-6.27
|
2354.68
|
3600.9
|
-0.5
|
|
32
|
199
|
2354.6
|
3600.6
|
2191.97
|
8745.8
|
-6.21
|
2353.78
|
3600.4
|
-0.03
|
|
33
|
199
|
2360.74
|
3600.6
|
2245.46
|
8742.7
|
-4.45
|
2354.8
|
3600.5
|
-0.25
|
|
34
|
240
|
1408.64
|
3601
|
1160.98
|
8771.6
|
-17.51
|
1421.21
|
3600.8
|
0.89
|
|
35
|
252
|
1786.93
|
3600.2
|
1465.85
|
8942.2
|
-16
|
1798.55
|
3602
|
0.65
|
|
36
|
255
|
1693.1
|
3600.9
|
1603.86
|
9011.7
|
-5.46
|
1694.2
|
3600.8
|
0.06
|
|
moyenne
|
1171.75
|
1817
|
1111.77
|
2560.27
|
-3.65
|
1170.99
|
1832.17
|
-0.01
|
TABLE 5.5 - Résultats
expérimentaux : qualité des solutions sur l'ensemble des
instances
résolution exacte du problème de Tournées
de Véhicules avec Contraintes de Charge-
ment. Nous avons
montré que dans le cas d'une résolution exacte du
sous-problème,
cette méthode peut proposer une
résolution exacte. Cela pourrait permettre de trouver
|
I
|
n
|
HBP
z CPU
|
z
|
HCG
CPU
|
Gap
|
|
1
|
15
|
294.21
|
11.6
|
296.56
|
5.6
|
0.8
|
|
2
|
15
|
343.2
|
4.4
|
369.2
|
3.1
|
7.58
|
|
3
|
20
|
382.56
|
15.2
|
391.26
|
10.2
|
2.27
|
|
4
|
20
|
440.51
|
18.7
|
469.2
|
9.7
|
6.51
|
|
5
|
21
|
382.68
|
27.5
|
402.18
|
12.1
|
5.1
|
|
6
|
21
|
502.56
|
21.8
|
612.53
|
10.5
|
21.88
|
|
7
|
22
|
690.11
|
31.3
|
746.28
|
11.4
|
8.14
|
|
8
|
22
|
690.85
|
37.2
|
762.59
|
12.8
|
10.38
|
|
9
|
25
|
618.65
|
31.8
|
689.14
|
11.6
|
11.39
|
|
10
|
29
|
680.56
|
73.5
|
749.51
|
21.8
|
10.13
|
|
11
|
29
|
716.84
|
201.2
|
827.64
|
58.5
|
15.46
|
|
12
|
30
|
631.51
|
76.8
|
784.52
|
26.7
|
24.23
|
|
13
|
32
|
2560.22
|
282.6
|
2735.12
|
121.5
|
6.83
|
|
14
|
32
|
1043.16
|
392.3
|
1373.37
|
142.3
|
31.65
|
|
15
|
32
|
1161.65
|
315.2
|
1283.42
|
159.9
|
10.48
|
|
16
|
35
|
702.69
|
191.7
|
845.1
|
62.3
|
20.27
|
|
17
|
40
|
864.39
|
190.8
|
979.38
|
55.2
|
13.3
|
|
18
|
44
|
1026.18
|
1745.8
|
1592.17
|
458.9
|
55.16
|
|
19
|
50
|
759.37
|
1429.1
|
827.49
|
324.8
|
8.97
|
|
20
|
71
|
517.48
|
3251.2
|
742.54
|
1526.1
|
43.49
|
|
21
|
75
|
1023.93
|
3600.1
|
1217.26
|
1216.1
|
18.88
|
|
22
|
75
|
1053.1
|
3600.7
|
1239.37
|
1843.5
|
17.69
|
|
23
|
75
|
1119.74
|
3600.2
|
1296.41
|
1495.6
|
15.78
|
|
24
|
75
|
1211.34
|
3600.2
|
1427.49
|
2134.5
|
17.84
|
|
25
|
100
|
1346.13
|
3600.5
|
1489.81
|
2948.9
|
10.67
|
|
26
|
100
|
1337.84
|
3600.5
|
1502.24
|
2198.7
|
12.29
|
|
27
|
100
|
1431.29
|
3600.4
|
1678.52
|
1982.4
|
17.27
|
|
28
|
120
|
2494.36
|
3600.5
|
2845.12
|
1584.3
|
14.06
|
|
29
|
134
|
2279.63
|
3600.5
|
2589.41
|
1264.9
|
13.59
|
|
30
|
150
|
1871.62
|
3600.2
|
2413.27
|
1863.4
|
28.94
|
|
31
|
199
|
2354.68
|
3600.9
|
2938.71
|
1865.2
|
24.8
|
|
32
|
199
|
2353.78
|
3600.4
|
2947.99
|
1736.3
|
25.24
|
|
33
|
199
|
2354.8
|
3600.5
|
2981.26
|
3600.1
|
26.6
|
|
34
|
240
|
1421.21
|
3600.8
|
1784.51
|
3601.5
|
25.56
|
|
35
|
252
|
1798.55
|
3602
|
2251.47
|
3600.5
|
25.18
|
|
36
|
255
|
1694.2
|
3600.8
|
2145.21
|
3600.2
|
26.62
|
|
Moyenne
|
1170.99
|
1832.19
|
1395.2
|
1099.48
|
17.64
|
TABLE 5.6 - CRésultats
expérimentaux : comparaisons des deux heuristiques
les solutions optimales de certaines instances.
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
Conclusion et perspectives
Dans ce mémoire, nous nous sommes
intéressés aux possibilités d'hybridation entre des
méthodes exactes et des méthodes heuristiques. Ces
méthodes hybrides permettent de tirer avantage de chacune de deux
approches : systématicité et optimalité de la
résolution exacte, caractère moins déterministe et
rapidité de la composante heuristique. Nous nous sommes ainsi
focalisés dans les deux dernières parties de ce mémoire
sur la mise au point de procédures intégrant ces deux approches
au sein d'un processus incomplet unique.
Nous commençons par faire la synthèse des
différents aspects sur lesquels portent nos contributions, puis nous
évoquerons les perspectives de recherches.
Dans la première partie du mémoire, nous nous
sommes intéressés aux méthodes de résolution par
recherche arborescente. Nous avons introduit une nouvelle approche pour la
gestion des décisions de branchement, que nous avons appelée
Dynamic Learning Search. Cette approche, basée sur des techniques
d'apprentissage, présente l'intérêt de chercher à
diriger la recherche vers des sous-espaces prometteurs en définissant
dynamiquement des politiques de priorités de branchement sur les
variables, ainsi que sur les valeurs que peuvent prendre les variables. Cette
politique d'apprentissage est plutôt contraire aux techniques
d'apprentissage basées sur la notion de « NoGood », qui
cherchent quant à elles, à mémoriser les configurations
qui mènent à des échecs et à ne pas reproduire ces
échecs. Nous avons de plus montré qu'une phase de sondage,
permettant d'avoir un aperçu de l'arbre de recherche, pouvait
s'avérer intéressante afin d'initialiser la recherche. Enfin,
nous avons montré qu'il était possible d'appliquer cette approche
aussi bien sur des problèmes de satisfaction de contraintes que sur des
problèmes d'optimisation combinatoire. Pour cela, il suffit d'adapter
les critères d'apprentissage. Nous avons pu illustrer
l'intérêt de mettre en place des stratégies de branchement
sur les variables, ainsi que sur les valeurs, dans le but
d'accélérer la résolution d'un problème par
recherche arborescente.
Dans la deuxième partie de ce mémoire, nous nous
sommes intéressés à une classe de problèmes de
tournées de véhicules, que nous avons nommée
Problèmes de Tournées avec Couverture Partielle. Ces
problèmes sont caractérisés par le fait que la visite de
l'ensemble des sommets du graphe n'est pas obligatoire. Les problèmes
appartenant à cette classe sont NP-difficiles. Nous avons introduit un
nouvel opérateur de voisinage large, nommé Dropstar, qui
détermine par un algorithme de programmation dynamique la
sous-séquence optimale d'un chemin dans un graphe. Nous avons
montré
que la recherche d'une sous-séquence optimale pouvait
être un problème NP-difficile, sous certaines conditions. Nous
avons montré sur des exemples simples que l'opérateur que nous
présentons définit un voisinage de très grande taille. En
intégrant cet opérateur dans des algorithme basés des
métaheuristiques (algorithmes mémétiques et algorithmes
d'optimisation par colonies de fourmis), nous avons globalement obtenu de
meilleurs résultats que les résultats publiés à ce
jour. Nous avons enfin montré les moyens que nous avions à notre
disposition pour accélérer la résolution du
problème de recherche d'une sous-séquence optimale. Cette partie
illustre donc l'efficacité d'utiliser une approche d'hybridation entre
des méthodes heuristiques et un opérateur de grand voisinage,
basé sur une méthode exacte.
Dans la troisième partie du mémoire, nous avons
proposé une résolution par génération de colonnes
tronquée pour un problème complexe de transport. Il s'agit du
problème de Tournées de Véhicules avec Contraintes de
Chargement en Deux Dimensions, problème qui se retrouve
fréquemment en entreprise. La principale difficulté de ce
problème réside dans les contraintes de chargement. En effet, ce
sous-problème est un problème NP-difficile. Devant la
complexité de ce sous-problème qui intervient dans le
problème esclave du Branch & Price, ce problème
n'est pas résolu par une approche exacte. Nous avons alors montré
un aperçu des possibilités qu'il existait pour tronquer la
méthode de Branch & Price, qui est une méthode a priori
exacte. Les approches heuristiques que nous proposons ont permis
d'accélérer la résolution. Les résultats que nous
avons présenté sont comparables en terme de qualité et en
terme de temps d'exécution aux algorithmes publiés à ce
jour. Cependant, les heuristiques de chargement retenues ne permettent pas de
dépasser les meilleurs solutions connues.
Les résultats obtenus montrent l'intérêt
des méthodes proposées et laissent entrevoir les nombreuses
perspectives ouvertes par ce type d'hybridation. En ce qui concerne la
première partie, nous aimerions consacrer du temps à la recherche
de critères permettant de définir la qualité d'un
sous-arbre d'une recherche arborescente. Ces critères devront de plus
être génériques pour permettre une application aussi bien
dans le cas de problèmes de satisfaction de contraintes que dans celui
de problèmes d'optimisation combinatoire.
En ce qui concerne la deuxième partie, une
première perspective est de définir avec plus de
précisions la classe des problèmes de Tournées avec
Couverture Partielle. En particulier, les recherches pourront porter sur la
détermination de la complexité de la recherche d'une
sous-séquence optimale en fonction des ressources. Nous avons vu en
effet que la recherche d'une sous-séquence optimale pouvait aussi bien
être un problème NP-difficile que polynomial, ceci en fonction des
ressources. Enfin, nous aimerions travailler sur d'autres problèmes de
cette classe, dans l'objectif de mesurer l'efficacité de
l'opérateur de grand voisinage que nous avons proposé sur un plus
grand nombre de problèmes. La deuxième perspective de cette
partie concerne une extension de l'opérateur que nous avons
proposé. Nous pensons qu'il est possible de proposer un opérateur
d'insertion de sommets non visités, basé sur les mêmes
principes que l'opérateur Dropstar. Ainsi, une méthode
couplant les deux opérateurs pourrait explorer un voisinage de
très grande taille.
Enfin, en ce qui concerne la troisième partie,
l'application industrielle des travaux n'est pas encore
concrétisée. Nous aimerions cependant travailler sur une
résolution exacte du sous-problème de chargement, cela dans
l'objectif de proposer une résolution exacte du problème de
Tournées de Véhicules avec Contraintes de Chargement par
génération de colonnes.
Nous nous sommes efforcés dans ce mémoire
d'apporter des éléments de réponses
aux trois questions suivantes, en particulier pour une classe de
problèmes de transport: - Comment favoriser l'obtention rapide de
solutions dans les méthodes de recherche
arborescente?
- Comment utiliser des méthodes exactes au sein des
métaheuristiques? - Comment tronquer des méthodes exactes?
Une des perspectives les plus intéressantes et les plus
complexes serait de proposer des réponses à la question suivante
: Comment rendre exact un schéma de résolution heuristique pour
obtenir une garantie d'optimalité (ou de performance) des solutions
trouvées?
Liste des illustrations
2.1 LNS : Exemple de solution initiale 63
2.2 LNS : Application d'un échange entre les
sommets 2 et 6 63
2.3 LNS : Application de l'opérateur insertion
63
2.4 LNS : Application de l'opérateur suppression
64
2.5 LNS : Application d'un 2-opt entre les sommets 2 et
5 64
2.6 LNS : Exemple de Profitable Tour Problem 66
2.7 LNS : Exemple de Profitable Tour Problem: Solution initiale
66
2.8 LNS : Profitable Tour Problem : après un Drop 67
2.9 LNS : Profitable Tour Problem : après un
2-ConsecutiveDrop 67
2.10 LNS : Autre exemple de Profitable Tour Problem 68
2.11 LNS : Autre exemple de Profitable Tour Problem: Solution
initiale . . . 68
2.12 LNS : Profitable Tour Problem : après un
3-ConsecutiveDrop 69
2.13 LNS : Profitable Tour Problem : Solution ptimale 69
2.14 LNS : Graphe résultant de la procédure
Dropstar 70
2.15 LNS : Extension depuis le sommet 0 72
2.16 LNS : Extension depuis le sommet 1 73
2.17 LNS : Extension depuis le sommet 2 73
2.18 LNS : Extension depuis le sommet 3 73
3.1 TPP : graphe complet utilisé par la procédure
dropstar 87
3.2 TPP : graphe réduit utilisé par la
procédure dropstar 88
4.1 GTSP : croisement et graphe résultant utilisé
par dropstar : vue agrégée 102
4.2 GTSP : croisement et graphe résultant utilisé
par dropstar : vue détaillée 102
4.3 GTSP : croisement et graphe résultant réduit
utilisé par dropstar : vue
agrégée 105
4.4 GTSP : opérateur
Move et graphe réduit correspondant : vue agrégée
en
terme de groupes 107
5.1 2L-VRP: Surface de chargement 133
5.2 2L-VRP : Méthode de génération de
colonnes 137
5.3 2L-VRP : Un SPRC à une ressource 138
5.4 2L-VRP : Trace de l'algorithme de programmation dynamique
141
5.5 2L-VRP: Règle de dominance affinée 145
Liste des illustrations
5.6 2L-VRP : Recherche de chemins élémentaires par
un LDS paramétré à 1
bon voisin 146
5.7 2L-VRP : Next Fit Decreasing Height 150
5.8 2L-VRP: First Fit Decreasing Height 151
5.9 2L-VRP: Best Fit Decreasing Height 152
5.10 2L-VRP: Représentation des coordonnées des
objets 153
5.11 2L-VRP: Représentation des coordonnées des
objets après insertion. . 154
5.12 2L-VRP: Représentation des coordonnées des
objets sur un autre exemple 155 5.13 2L-VRP : Mise à jour des
coordonnées des objets après insertionsur un
autre exemple 156
5.14 2L-VRP: Bottom Left 156
5.15 2L-VRP: Improved Bottom Left 156
5.16 2L-VRP : Max Touching Perimeter 157
5.17 2L-VRP: Structure d'un annuaire 157
5.18 2L-VRP: Calcul de l'aire restante d'un chargement 158
Liste des tableaux
1.1 Résultats expérimentaux pour plusieurs
méthodes appliquées au pro-
blème du Voyageur de Commerce 41
1.2 Résultats
expérimentaux pour plusieurs méthodes appliquées au
pro-
blème d'emploi du temps pour les gardes
d'infirmières 43
1.3 DLS : Résultats expérimentaux,
instances de Sac-à-dos Multidimensionnel 45
1.4 DLS : Résultats expérimentaux, instances de
Carré Magique 45
1.5 DLS : Résultats expérimentaux, instances de
Coloration de Graphes . . 47
3.1 TPP : Résultats expérimentaux, instances
fermées 91
3.2 TPP : Résultats expérimentaux, instances
ouvertes 91
3.3 TPP : Résultats expérimentaux, instances
ouvertes améliorées (1) . . . 92
3.4 TPP : Résultats expérimentaux, instances
ouvertes améliorées (2) . . . 93
4.1 GTSP : Résultats expérimentaux : qualité
des solutions sur instances fer-
mées 113
4.2 GTSP : Résultats
expérimentaux : qualité des solutions sur instances ou-
vertes 114
4.3 GTSP : Résultats expérimentaux : meilleures
solutions connues 114
4.4 GTSP : Résultats expérimentaux : comparaisons
des opérateurs de croi-
sement sur instances fermées 115
4.5 GTSP :
Résultats expérimentaux : comparaisons des opérateurs de
croi-
sement sur instances ouvertes 116 4.6 GTSP :
Résultats expérimentaux : comparatifs entre plusieurs algorithmes
117 4.7 GTSP : Résultats expérimentaux : comparatif des
opérateurs de croise-
ment sur de nouvelles instances (1) 118
4.8 GTSP :
Résultats expérimentaux : comparatif des opérateurs de
croise-
ment sur de nouvelles instances (2) 119
5.1 2L-VRP: Récapitulatif de quelques problèmes
classiques 128
5.2 2L-VRP: Caractéristiques des objets des classes
d'instances 162
5.3 2L-VRP: Caractéristiques des objets des classes
d'instances 163
5.4 2L-VRP : Résultats expérimentaux :
qualité des solutions sur instances
moyennes 164
5.5 2L-VRP : Résultats
expérimentaux : qualité des solutions sur l'ensemble
des instances 166
Liste des tableaux
5.6 2L-VRP: Résultats expérimentaux : comparaisons
des deux heuristiques 167
Bibliographie
(Ahuja et al., 2002) R. K. Ahuja, O. Ergun, J. B.
Orlin, et A. Punnen, 2002. A survey of very large-scale neighborhood search
techniques. Discrete Applied Mathematics 123, 75-102.
(Archetti et al., 2007) C. Archetti, D. Feillet, A.
Hertz, et G. Speranza, 2007. The Capacitated Team Orienteering and Profitable
Tour Problems. Journal of the Operational Research Society. à
paraître.
(Baker et al., 1980) B. S. Baker, E. G. Coffman, et R.
L. Rivest, 1980. Orthogonal packings in two dimensions. SIAM Journal on
Computing 9(4), 846-855. SIAM.
(Balafoutis et Stergiou, 2008) T. Balafoutis et K. Stergiou,
2008. Exploiting Constraint Weights for Revision Ordering in Arc Consistency
Algorithms. Dans les actes de ECAI-2008 workshop on Modeling and Solving
Problems with Constraints.
(Balas, 1989) E. Balas, 1989. The Prize collecting traveling
salesman problem. Networks 19(6), 621-636.
(Baptiste et al., 2008) P. Baptiste, M. Flamini, et F.
Sourd, 2008. Lagrangian bounds for
just-in-time job-shop scheduling.
Computers & Operations Research 35(3), 906-915.
(Barnhart et al., 1998) C. Barnhart, L. J. Ellis, G.
L. Nemhauser, M. W. P. Savelsbergh, et P. H. Vance, 1998. Branch-and-Price :
Column Generation for Solving Huge Integer Programs. Operations Research
46(3), 316-329.
(Bauer et al., 1998) P. Bauer, J. T. Linderoth, et M.
W. P. Savelsbergh, 1998. A branch and cut approach to the cardinality
constrained circuit problem. Rapport technique, School of Industrial and
Systems Engineering, Georgia Institute of Technology, Atlanta, GA.
(Bell et McMullen, 2004) J. E. Bell et P. R. McMullen, 2004.
Ant colony optimization techniques for the vehicle routing problem.
Advanced Engineering Informatics 18(1), 41-48.
(Bellman, 1957) R. Bellman, 1957. Dynamic programming.
Princeton, New Jersey : Princeton University Press. XXV.
(Ben-Arieh et al., 2003) D. Ben-Arieh, G. Gutin, M.
Penn, A. Yeo, et A. Zverovitch, 2003. Transformations of generalized ATSP into
ATSP. Operations Research Letters 31, 357-365.
(Benoist et al., 2007) T. Benoist, E. Bourreau, et B.
Rottembourg, 2007. The TV-Break Packing Problem. European Journal of
Operational Research 176(3), 1371-1386.
(Boctor et al., 2003) F. F. Boctor, G. Laporte, et J.
Renaud, 2003. Heuristics for the Traveling Purchaser Problem. Computers
& Operations Research 30, 491-504.
(Bontoux, 2005) B. Bontoux, 2005. Méthode
métaheuristique basée sur l'optimisation à Colonie de
Fourmis appliquée au Traveling Purchaser Problem. Mémoire de
Master, Laboratoire Informatique d'Avignon.
(Bontoux et al., 2008a) B. Bontoux, C. Artigues, et
D. Feillet, 2008a. A Memetic Algorithm with a Large Neighborhood Crossover
Operator for the Generalized Traveling Salesman Problem. University of
Technology of Troyes, France. Metaheuristics for Logistics and Vehicle Routing,
EU/ME, the European Chapter on Metaheuristics.
(Bontoux et al., 2008b) B. Bontoux, C. Artigues, et
D. Feillet, 2008b. Algorithme mémétique avec un opérateur
de croisement à voisinage large pour le problème du voyageur de
commerce généralisé. Dans les actes de 9ème
congrès de la société Française de Recherche
Opérationnelle et d'Aide à la Décision (ROADEF 2008),
Clermont-Ferrand, 79-80.
(Bontoux et al., 2008c) B. Bontoux, C. Artigues, et
D. Feillet, February 2008c. Memetic Algorithm with a Large Neighborhood
Crossover Operator for the Generalized Traveling Salesman Problem. LAAS report,
Université de Toulouse, LAAS-CNRS, France. 21 p.
(Bontoux et Feillet, 2008) B. Bontoux et D. Feillet, 2008. Ant
Colony Optimization for the Traveling Purchaser Problem. Computers &
Operations Research 35, 628-637.
(Bontoux et al., 2007a) B. Bontoux, D. Feillet, et C.
Artigues, 2007a. Large Neighborhood Search for Variants of TSP. Dans les actes
de The Seventh Metaheuristics International Conference (MIC 2007),
Montréal, Canada. CDROM.
(Bontoux et al., 2007b) B. Bontoux, D. Feillet, et C.
Artigues, 2007b. Une méthode dynamique de parcours d'arbre de recherche
: Dynamic Cooperative Search. Dans les actes de 8ème congrès
de la société Française de Recherche Opérationnelle
et d'Aide à la Décision (ROADEF 2007), 99-100.
(Bontoux et al., 2007c) B. Bontoux, D. Feillet, C.
Artigues, et E. Bourreau, 2007c. Dynamic Cooperative Search for constraint
satisfaction and combinatorial optimization: application to a rostering
problem. Dans P. Baptiste, G. Kendall, A. Munier-Kordon, et F. Sourd (Eds.),
3rd Multidisciplinary International Conference on Scheduling: Theory and
Application (MISTA 2007), Paris, France, 557-560.
(Boschetti et Mingozzi, 2003a) M. A. Boschetti et A. Mingozzi,
2003a. The two-dimensional finite bin packing problem, Part I : New lower
bounds for the oriented case. 4OR : A Quarterly Journal of Operations
Research 1, 27-42.
(Boschetti et Mingozzi, 2003b) M. A. Boschetti et A. Mingozzi,
2003b. The two-dimensional finite bin packing problem, Part II : New lower
bounds and upper bounds. 4OR : A Quarterly Journal of Operations Research
1, 135-147.
(Boussemart et al., 2004) F. Boussemart, F. Hemery, C.
Lecoutre, et L. Sais, 2004. Boos-
ting systematic search by weighting
constraints. 146-150. Proceedings of ECAI'04.
(Bérubé et al., 2008) J.-F.
Bérubé, M. Gendreau, et J.-Y. Potvin, 2008. An exact
e-constraint method for bi-objective combinatorial optimization
problems : Application to the Traveling Salesman Problem with Profits.
European Journal of Operational Research. à paraître.
(Chao et al., 1996) I.-M. Chao, B. L. Golden, et E. A.
Wasil, 1996. The team orienteering problem. European Journal of Operational
Research 88(3), 464-474.
(Chazelle, 1983) B. Chazelle, 1983. The Bottom-Left Bin-Packing
Heuristic : An Efficient Implementation. IEEE Trans. Computers 32(8),
697-707.
(Cheang et al., 2003) B. Cheang, H. Li, A. Lim, et B.
Rodrigues, 2003. Nurse rostering problems - A bibliographic survey.
European Journal of Operational Research 151, 447- 460.
(Chvátal, 1997) V. Chvátal, 1997. Resolution
Search. Discrete Applied Mathematics 73(1), 81-99.
(Coffman et al., 1980) E. G. Coffman, M. R. Garey, D.
S. Johnson, et R. E. Tarjan, 1980. Performance Bounds for Level-Oriented
Two-Dimensional Packing Algorithms. SIAM Journal on Computing 9(4),
808-826. SIAM.
(Cordeau et al., 2005) J. F. Cordeau, M. Gendreau, A.
Hertz, G. Laporte, et J. S. Sormany, 2005. New heuristics for the vehicle
routing problem. Dans les actes de Logistics Systems : Design and
Optimization, 279-297. Public Health Service.
(Cordeau et Laporte, 2004) J. F. Cordeau et G. Laporte, 2004.
Metaheuristic Optimization via Memory and Evolution : Tabu Search and
Scatter Search, Chapter Tabu Search Heuristics for the Vehicle Routing
Problem, 145-163. Kluwer, Boston.
(Costa et Hertz, 1997) D. Costa et A. Hertz, 1997. Ants Can
Colour Graphs. Journal of the Operational Research Society 48,
295-305.
(Croes, 1958) G. A. Croes, 1958. A method for solving
traveling-salesman problems. Operational Research 6, 791-812.
(Danna, 2003) E. Danna, 2003. Accelerating Column Generation
with Local Search: A Case Study on the Vehicle Routing Problem with Time
Windows. Skodsborg, Denmark. ROUTE 2003 - International Workshop on Vehicle
Routing.
(Danna et al., 2005) E. Danna, E. Rothberg, et C. L.
Pape, 2005. Exploring relaxation induced neighborhoods to improve MIP
solutions. Mathematical Programming 102(1), 71-90.
(Dauzère-Pérès et Sevaux, 2004) S.
Dauzère-Pérès et M. Sevaux, 2004. An exact method to
minimize the number of tardy jobs in single machine scheduling. Journal of
Scheduling 7, 405-420.
(Dechter, 1990) R. Dechter, 1990. Enhancement schemes for
constraint processing : backjumping, learning, and cutset decomposition.
Artifical Intelligence 41(3), 273- 312. Essex, UK. Elsevier Science
Publishers Ltd.
(Dell'Amico et al., 1998) M. Dell'Amico, F. Maffioli,
et A. Sciomachen, 1998. A Lagrangian heuristic for the prize-collecting
travelling salesman problem. Annals of Operations Research 81,
289-305.
(Dell'Amico et al., 1995) M. Dell'Amico, F. Maffioli,
et P. Värbrand, 1995. On prize-collecting tours and the asymmetric
travelling salesman problem. International Transportaion Operations
Research 2(3), 297-308.
(Demassey, 2003) S. Demassey, 2003. Méthodes
hybrides de programmation par contraintes et programmation linéaire pour
le problème d'ordonnancement de projet à contraintes de
ressources. Thèse de Doctorat, Université d'Avignon.
(Desaulniers et al., 2005) Desaulniers, G., J.
Desrosiers, et M. M. Solomon (Eds.), 2005. Column Generation.
Springer.
(Descombes, 2000) R. Descombes, 2000. Les Carrés
Magiques : Histoire, théorie et technique du carré magique,de
l'Antiquité aux recherches actuelles. Editions Vuibert.
(Dijkstra, 1971) E. W. Dijkstra, 1971. A short introduction to
the art of programming. Department of Mathematics EWD-316, Technische
Hogeschool, Eindhoven.
(Dimitrijevic et Saric, 1997) V. Dimitrijevic et Z. Saric,
1997. An Efficient Transformation of the Generalized Traveling Salesman Problem
into the Traveling Salesman Problem on Digraphs. Information Sciences
102, 105-110.
(Donati et al., 2008) A. V. Donati, R. Montemanni, N.
Casagrande, A. E. Rizzoli, et L. M. Gambardella, 2008. Time dependent vehicle
routing problem with a multi ant colony system. European Journal of
Operational Research 185(3), 1174-1191.
(Dorigo et al., 1991) M. Dorigo, V. Maniezzo, et A.
Colorni, 1991. Positive feedback as a search strategy. Technical report 91-016,
Dipartimento di Elettronica Politecnico di Milano, Italy.
(Dorigo et al., 1996) M. Dorigo, V. Maniezzo, et A.
Colorni, 1996. The Ant System: Optimization by a colony of cooperating agents.
IEEE Transactions on Systems, Man, and Cybernetics-Part B 26(1),
29-41.
(Dorigo et Stutzle, 2004) M. Dorigo et T. Stutzle, 2004. Ant
Colony Optimization. Cambridge, MA : MIT Press Bradford Books.
(Doyle, 1979) J. Doyle, 1979. A Truth Maintenance System.
Artificial Intelligence 12, 231-272.
(Dror, 1994) M. Dror, 1994. Note on the Complexity of the
Shortest Path Models for Column Generation in VRPTW. Operations Research
42(5), 977-978.
(Dror et Haouari, 2000) M. Dror et M. Haouari, 2000. Generalized
Steiner Problems and Other Variants. Journal of Combinatorial Optimization
4(4), 415-436.
(Feillet et al., 2005) D. Feillet, P. Dejax, et M.
Gendreau, 2005. Traveling Salesman Problems with Profits. Transportation
Science 39(2), 188-205.
(Feillet et al., 2004) D. Feillet, P. Dejax, M.
Gendreau, et C. Gueguen, 2004. An exact algorithm for the Elementary Shortest
Path Problem with Resource Constraints : application to some vehicle routing
problems. Networks 44, 216-229.
(Fischetti et Lodi, 2003) M. Fischetti et A. Lodi, 2003. Local
branching. Mathematical Programming 98(1), 23-47.
(Fischetti et al., 1995) M. Fischetti, J. J.
Salazar-González, et P. Toth, 1995. The Symmetric Generalized Traveling
Salesman Polytope. Networks 26(2), 113-123.
(Fischetti et al., 1997) M. Fischetti, J. J.
Salazar-González, et P. Toth, 1997. A Branch-andCut algorithm for the
Symmetric Generalized Traveling Salesman Problem. Operations Research
45(3), 378-394.
(Frenc et al., 2001) A. P. Frenc, A. C. Robinson, et
J. M. Wilson, 2001. Using a Hybrid Genetic-Algorithm/Branch and Bound Approach
to Solve Feasibility and Optimization Integer Programming Problems. Journal
of Heuristics 7, 551-564.
(Frost et Dechter, 1994) D. Frost et R. Dechter, 1994. In
Search of the Best Constraint Satisfaction Search. Dans les actes de
Proceedings of the National Conference on Artificial Intelligence,
Seattle, 301-306.
(Fuellerer et al., 2008) G. Fuellerer, K. F. Doerner,
R. F. Hartl, et M. Iori, 2008. Ant colony optimization for the two-dimensional
loading vehicle routing problem. Computers & Operations Research.
à paraître.
(Garey et Johnson, 1979) M. R. Garey et D. S. Johnson, 1979.
Computers and Intractibility; A Guide to the Theory of
NP-Completeness. Freeman and Company.
(Garg et Konjevod, 2000) N. Garg et G. Konjevod, 2000. A
Polylogarithmic Approximation Algorithm for the Group Steiner Tree Problem.
Journal of Algorithms 37, 66-84.
(Gaschnig, 1979) J. G. Gaschnig, 1979. Performance
measurement and analysis of certain search algorithms. Thèse de
Doctorat, Pittsburgh, USA.
(Gendreau et al., 1994) M. Gendreau, A. Hertz, et G.
Laporte, 1994. A tabu search
heuristic for the vehicle routing problem.
Management Science 40(10), 1276-1290.
(Gendreau et al., 2006) M. Gendreau, M. Iori, G.
Laporte, et S. Martello, 2006. A Tabu Search Algorithm for a Routing and
Container Loading Problem. Transportation Science 40(3), 342-350.
(Gendreau et al., 2008) M. Gendreau, M. Iori, G.
Laporte, et S. Martello, 2008. A Tabu search heuristic for the vehicle routing
problem with two-dimensional loading constraints. Networks 51(1),
4-18.
(Gendreau et al., 1997) M. Gendreau, G. Laporte, et F.
Semet, 1997. The covering tour problem. Operations Research 45,
568-576.
(Gendreau et al., 1998) M. Gendreau, G. Laporte, et F.
Semet, 1998. The Selective Traveling Salesman Problem. Networks 32,
263-273.
(Gensch, 1978) D. H. Gensch, 1978. An industrial application of
the traveling salesman subtour problem. AIIE Trans. 10(4), 362-370.
(Ginsberg, 1993) M. L. Ginsberg, 1993. Dynamic backtracking.
Journal of Artificial Intelligence Research 1, 25-46.
(Glover, 1989) F. Glover, 1989. Tabu Search - Part I. ORSA
Journal on Computing 1(3), 190-206.
(Glover et Laguna, 1997) F. Glover et M. Laguna, 1997. Tabu
Search. Kluwer Academic Publishers.
(Goldberg, 1989) D. E. Goldberg, 1989. Genetic Algorithms in
Search, Optimization and Machine Learning. Addison-Wesley Longman
Publishing Co., Inc.
(Golden et al., 1981) B. L. Golden, L. Levy, et R. Dahl,
1981. Two Generalizations of the Traveling Salesman Problem. Omega 9,
439-445.
(Golden et al., 1987) B. L. Golden, L. Levy, et R.
Vohra, 1987. The Orienteering Problem. Naval research logistics 34(3),
307-318.
(Gutin et Punnen, 2002) G. Gutin et A. Punnen, 2002. The
Traveling Salesman Problem and its variations. Dordrecht: Kluwer Academic
Publishers.
(Hachicha et al., 2000) M. Hachicha, M. J. Hodgson,
G. Laporte, et F. Semet, 2000. Heuristics for the multi-vehicle covering tour
problem. Computers & Operations Research 27(1), 29-42.
(Hansen et Mladenovi'c, 2006) P. Hansen et N. Mladenovi'c, 2006.
First vs. best improvement : An empirical study. Discrete Applied
Mathematics 154(5), 802-817.
(Hansen et al., 2006a) P. Hansen, N. Mladenovi'c, et
D. Urosevi'c, 2006a. Variable neighborhood search and local branching.
Computers & Operations Research 33(10), 3034- 3045.
(Hansen et al., 2006b) P. Hansen, N. Mladenovi'c, et
D. Uroevi'c, 2006b. Variable neighborhood search and local branching.
Computers & Operations Research 33(10), 3034- 3045.
(Haouari et Ladhari, 2003) M. Haouari et T. Ladhari, 2003. A
branch-and-bound-based local search method for the flow shop problem. The
Journal of the Operational Research Society 54(10), 1076-1084.
(Haralick et Elliot, 1980) R. Haralick et G. Elliot, 1980.
Increasing tree search efficiency for constraint satisfaction problems.
Artificial Intelligence 14, 263-313.
(Hart et al., 2005) W. E. Hart, N. Krasnogor, et J. E.
Smith, 2005. Recent Advances in Memetic Algorithms. Springer.
(Harvey et Ginsberg, 1995) W. Harvey et M. Ginsberg, 1995.
Limited discrepancy search. Dans les actes de In Proceedings of
IJCAI95, 607-613.
(Henry-Labordere, 1969) A. L. Henry-Labordere, 1969. The
record balancing problem : A dynamic programming solution of a generalized
traveling salesman problem. RAIRO B2, 43-49.
(Hooker, 2000) J. Hooker, 2000. Logic-Based Methods for
Optimization - Combining Optimization and Constraint Satisfaction.
Wiley-Interscience series in discrete mathematics and optimization. John Wiley
and Sons.
(Iori et al., 2003) M. Iori, J. J. S.
González, et D. Vigo, 2003. An exact approach for the symmetric
capacitated vehicle routing problem with two dimensional loading constraints.
Rapport technique, University of Bologna, Italy.
(Iori et al., 2007) M. Iori, J. S. Gonzàlez,
et D. Vigo, 2007. An exact approach for the vehicle routing problem with
two-dimensional loading constraints. Transportation Science 41(2),
253-264.
(Jensen et Toft, 1995) T. R. Jensen et B. Toft, 1995. Graph
Coloring Problems. Wiley.
(Karoui et al., 2007) W. Karoui, M. Huguet, P. Lopez,
et W.Naanaa, 2007. YIELDS : A yet improved limited discrepancy search for CSPs.
Dans les actes de 4th International Conference, CPAIOR 2007,
Bruxelles, Belgique, 99-111.
(Karp, 1972) R. M. Karp, 1972. Reducibility Among Combinatorial
Problems. Complexity of Computer Computations, 85-103.
(Kataoka et Morito, 1988) S. Kataoka et S. Morito, 1988. An
Algorithm for the Single Constraint Maximum Collection Problem. Journal of
Operations Research Society of Japan 31, 515-530.
(Kataoka et al., 1998) S. Kataoka, T. Yamada, et S.
Morito, 1998. Minimum directed 1-subtree relaxation for score orienteering
problem. European Journal of Operational Research 104, 139-153.
(Keller, 1985) C. P. Keller, 1985. Multiobjective routing
through space and time : The MVP and TDVP problems. Unpublished doctoral
dissertation, The University of Western Ontario, Canada.
(Keller, 1989) C. P. Keller, 1989. Algorithms to solve the
orienteering problem : A comparison. European Journal of Operational
Research 41, 224-231.
(Keller et Goodchild, 1988) C. P. Keller et M. Goodchild,
1988. The multiobjective vending problem : A generalization of the traveling
salesman problem. Environ. Planning B : Planning Design 15,
447-460.
(Kellerer et al., 2004) H. Kellerer, U. Pferschy, et D.
Pisinger, 2004. Knapsack Problems. Springer, Berlin, Germany.
(Khichane et al., 2008) M. Khichane, P. Albert, et C.
Solnon, 2008. Programmation par contraintes avec des fourmis. Journées
Francophones de Programmation par Contraintes.
(Kirkpatrick et al., 1983) S. Kirkpatrick, C. D. Gelatt,
et M. P. Vecchi, 1983. Optimization by simulated annealing. Science
220, 671-680.
(Laporte et Martello, 1990) G. Laporte et S. Martello, 1990. The
Selective Traveling Salesman Problem. Discrete Applied Mathematic 26,
193-207.
(Laporte et al., 1984) G. Laporte, H. Mercure, et Y.
Nobert, 1984. Generalized Travelling Salesman Problem through n Sets of Nodes :
the Asymmetrical Case. Discrete Applied Mathematics 18, 185-197.
(Laporte et Nobert, 1984) G. Laporte et Y. Nobert, 1984.
Generalized Travelling Salesman Problem through n Sets of Nodes : An integer
programming approach. IN-FOR 31, 61-75.
(Laporte et al., 2003) G. Laporte, J. Riera-Ledesma,
et J. J. Salazar-Gonzáles, 2003. A branch-and-cut algorithm for the
Undirected Traveling Purchaser Problem. Operations Research 51,
940-951.
(Laporte et Semet, 1999) G. Laporte et F. Semet, 1999.
Computational evaluation of a transformation procedure for the symmetric
generalized traveling salesman problem. INFOR 37, 114-120.
(Lessing et al., 2004) L. Lessing, I. Dumitrescu, et T.
Stutzle, 2004. A Comparison Between ACO Algorithms for the Set Covering
Problem. 1-12.
(Levasseur et al., 2007) N. Levasseur, P. Boizumault, et
S. Loudni, 2007. Une heuristique de sélection de valeur dirigée
par l'impact pour les WCSP. Rapport technique.
(Lien et al., 1993) Y.-N. Lien, E. Ma, et B. Wah,
1993. Transformation of the Generalized Traveling-Salesman Problem into the
Standard Traveling-Salesman Problem. Information Sciences 74,
177-189.
(Lin, 1965) S. Lin, 1965. Computer solutions of the traveling
salesman problem. 44, 2245-2269.
(Lin et Kernighan, 1973) S. Lin et B. W. Kernighan, 1973. An
Effective Heuristic Algorithm for the Traveling-Salesman Problem.
Operations Research 21, 498-516.
(Liu et Teng, 1999) D. Liu et H. Teng, 1999. An improved
BL-algorithm for genetic algorithm of the orthogonal packing of rectangles.
European Journal of Operational Research 112(2), 413-420.
(Lodi et al., 1999) A. Lodi, S. Martello, et D. Vigo,
1999. Heuristic and Metaheuristic Approaches for a Class of Two-Dimensional Bin
Packing Problems. INFORMS J. on Computing 11(4), 345-357.
(Lübbecke et Desrosiers, 2005) M. E. Lübbecke et J.
Desrosiers, 2005. Selected topics in column generation. Operations Research
53(6), 1007-1023.
(Man et al., 1999) K. F. Man, K. S. Tang, et S. Kwong,
1999. Genetic Algorithms : Concepts and Designs. Springer.
(Martello et al., 2000) S. Martello, M. Monaci, et D.
Vigo, 2000. An exact approach to the strip packing problem. Rapport technique,
University of Bologna, Italy.
(Martello et al., 2003) S. Martello, M. Monaci, et D.
Vigo, 2003. An Exact Approach to the Strip-Packing Problem. INFORMS J. on
Computing 15(3), 310-319.
(Martello et al., 2000) S. Martello, D. Pisinger, et D.
Vigo, 2000. The Three-Dimensional Bin Packing Problem. Operational Research
48(2), 256-267.
(Martello et Toth, 1990) Martello, S. et P. Toth (Eds.), 1990.
Knapsack Problems : Algorithms and Computer Implementations. Wiley,
Chichester.
(Martello et Vigo, 1998) S. Martello et D. Vigo, 1998. Exact
Solution of the Two-Dimensional Finite Bin Packing Problem. Management
Science 44(3), 388-399.
(Menger, 1932) K. Menger, 1932. Das botenproblem. Ergebnisse
eines mathematischen kolloquiums 2, 11-12.
(Mittenthal et Noon, 1992) J. Mittenthal et C. E. Noon, 1992.
Insert/delete heuristic for the travelling salesman subset-tour problem with
one additional constraint. Operations Research 43(3), 277-283.
(Mladenovi'c et Hansen, 1997) N. Mladenovi'c et P. Hansen, 1997.
Variable neighborhood search. Computers and Operations Research
24(11), 1097-1100.
(Montané et Galvão, 2006) F. A. T.
Montané et R. D. Galvão, 2006. A tabu search algorithm for the
vehicle routing problem with simultaneous pick-up and delivery service.
Computers & Operations Research 33(3), 595-619.
(Moscato et Cotta, 2005) P. Moscato et C. Cotta, 2005. A Gentle
Introduction to Memetic Algorithms. Operations Research & Management
Science 57(2), 105-144.
(Moscato et Norman, 1992) P. Moscato et M. G. Norman, 1992. A
Memtic approach for the traveling salesman problem implementation of a
computational ecology for combinatorial optimization on message-passing
systems. Dans les actes de Parallel Computing and Transputer
Applications, Amsterdam, 177-186. IOS Press.
(Mühlenbein et al., 1988) H. Mühlenbein, M.
Gorges-Schleuter, et O. Krämer, 1988.
Evolution algorithms in
combinatorial optimization. Parallel Computing 7, 65-85.
(Néron et al., 2008) E. Néron, F.
Tercinet, et F. Sourd, 2008. Search tree based approaches for parallel machine
scheduling. Computuers & Operations Research 35(4), 1127-1137.
(Noon et Bean, 1991) C. E. Noon et J. C. Bean, 1991. A
Lagrangian Based Approach for the Asymmetric Generalized Traveling Salesman
Problem. Operations Research 39, 623-632.
(Noon et Bean, 1993) C. E. Noon et J. C. Bean, 1993. An Efficient
Transformation of the Generalized Traveling Salesman Problem. INFOR
31, 39-44.
(Oliva, 2004) C. Oliva, 2004. Techniques hybrides de
Propagation de Contraintes et de Programmation Mathématique.
Thèse de Doctorat, Université d'Avignon.
(Ong, 1982) H. L. Ong, 1982. Approximate Algorithms for the
Traveling Purchaser Problem. Operations Research Letters, 201-205.
(Osogami et Imai, 2000) T. Osogami et H. Imai, 2000.
Classification of Various Neighborhood Operations for the Nurse Scheduling
Problem. Dans les actes de ISAAC '00 : Proceedings of the 11th
International Conference on Algorithms and Computation, London, UK, 72-83.
Springer-Verlag.
(Ow et Morton, 1988) P. S. Ow et T. E. Morton, 1988. Filtered
beam search in scheduling. International Journal of Production Research
26, 35-62.
(Palpant, 2005) M. Palpant, 2005. Recherche exacte et
approchée en optimisation combina-
toire : schémas
d'intégration et applications. Thèse de Doctorat,
Université d'Avignon.
(Pearn et Chien, 1998) W. L. Pearn et R. C. Chien, 1998. Improved
Solutions for the Traveling Purchaser Problem. Computers & Operations
Research 25, 879-885.
(Pekny et Miller, 1990) J. F. Pekny et D. L. Miller, 1990. An
exact parallel algorithm for the resource constrained travelling salesman
problem with application to scheduling with an aggregate deadline. Dans A.
Press (Ed.), ACM 18th Annual Comput. Sci. Conf., 208-214.
(Pessan et al., 2007) C. Pessan, J.-L. Bouquard, et E.
Néron, 2007. Genetic Branch-andBound or Exact Genetic Algorithm?
Artificial Evolution, 136-147.
(Pisinger et Ropke, 2007) D. Pisinger et S. Ropke, 2007. A
general heuristic for vehicle routing problems. Computers & Operations
Research 34(8), 2403-2435.
(Pisinger et Sigurd, 2007) D. Pisinger et M. Sigurd, 2007.
Using Decomposition Techniques and Constraint Programming for Solving the
Two-Dimensional Bin-Packing Problem. INFORMS J. on Computing 19(1),
36-51. Institute for Operations Research and the Management Sciences (INFORMS),
Linthicum, Maryland, USA. INFORMS.
(Prescott-Gagnon et al., 2007) E. Prescott-Gagnon, G.
Desaulniers, et L.-M. Rousseau, 2007. A Large Neighborhood Search Algorithm for
the Vehicle Routing Problem with Time Windows. Montreal, Canada. Optimization
Days.
(Prestwich, 2008) S. Prestwich, 2008. Generalised graph
colouring by a hybrid of local
search and constraint programming.
Discrete Applied Mathematics 156(2), 148-158.
(Prins, 2004) C. Prins, 2004. A simple and effective evolutionary
algorithm for the VRP. Computers & Operations Research 31,
1985-2002.
(Prosser, 1993) P. Prosser, 1993. Hybrid Algorithms for the
Constraint Satisfaction Problem. Computational Intelligence 9(3),
268-299.
(Ramesh et Brown, 1991) R. Ramesh et Brown, 1991. An efficient
four-phase heuristic for the generalized orienteering problem. Computers
& Operations Research 18(2), 151-165.
(Ramesh, 1981) T. Ramesh, 1981. Traveling Purchaser Problem.
Opsearch 18, 78-91.
(Refalo, 2004) P. Refalo, 2004. Principles and Practice of
Constraint Programming - CP 2004, Volume 3258 de Lecture Notes in
Computer Science, Chapter Impact-Based Search Strategies for Constraint
Programming, 557-571. Springer Berlin / Heidelberg.
(Reimann et al., 2004) M. Reimann, K. Doerner, et R.
F. Hartl, 2004. D-ants : savings based ants divide and conquer the vehicle
routing problem. Computers & Operations Research 31(4),
563-591.
(Reinelt, 1991) G. Reinelt, 1991. TSPLIB - A Traveling Salesman
Problem Library. ORSA Journal on Computing 3, 376-384.
(Renaud et Boctor, 1998a) J. Renaud et F. F. Boctor, 1998a. An
Efficient Composite Heuristic for the Symmetric Generalized Traveling Salesman
Problem. European Journal of Operational Research 108, 571-584.
(Renaud et Boctor, 1998b) J. Renaud et F. F. Boctor, 1998b.
Improved Heuristics for the
Traveling Purchaser Problem. European
Journal of Operational Research 108, 571-584.
(Renaud et al., 1996) J. Renaud, F. F. Boctor, et G.
Laporte, 1996. A fast composite heuristic for the symmetric traveling salesman
problem. INFORMS Journal on Computing 8, 134-143.
(Riera-Ledesma et Salazar-González, 2005) J.
Riera-Ledesma et J. J. Salazar-González, 2005. A Heuristic approach for
the Traveling Purchaser Problem. European Journal of Operational Research
162, 142-152.
(Rousseau et al., 2004) L. M. Rousseau, D. Feillet,
et M. Gendreau, 2004. New refinements for the solution of vehicle routing
problems with column generation. Le Gosier, Guadeloupe (France). TRISTAN 5.
(Schiex et Verfaillie, 1994) T. Schiex et G. Verfaillie, 1994.
Nogood recording for static and dynamic constraint satisfaction problems.
International Journal of Artificial Intelligence Tools 3, 48-55.
(Sevaux et Sörensen, 2005) M. Sevaux et K. Sörensen,
2005. Permutation distance measures for memetic algorithms with population
management. Dans les actes de Proceedings of 6th Metaheuristics
International Conference, MIC 2005, Vienna, Austria, 832-838.
(Shaw, 1998) P. Shaw, 1998. Using constraint programming and
local search methods to solve vehicle routing problems. Dans les actes de
CP-98, Fourth international conference on principles and practice of
constraint programming, Volume 1520, 417-431.
(Shi et al., 2007) X. H. Shi, Y. C. Liang, H. P. Lee,
C. Lu, et Q. X. Wang, 2007. Particle swarm optimization-based algorithms for
TSP and generalized TSP. Information Processing Letters 103,
169-176.
(Silberholz et Golden, 2007) J. Silberholz et B. Golden, 2007.
The Generalized Traveling Salesman Problem : A New Genetic Algorithm Approach.
165-181.
(Singh et Oudheusden, 1997) K. N. Singh et D. L. V.
Oudheusden, 1997. A Branch and Bound Algorithm for the Traveling Purchaser
Problem. European Journal of Operational Research 97, 571-579.
(Slavík, 1997) P. Slavík, 1997. On the
approximation of the generalized traveling salesman problem. Rapport technique,
Department of Computer Science, SUNY-Buffalo.
(Smith et Grant, 1998) B. M. Smith et S. A. Grant, 1998. Trying
Harder to Fail First. European Conference on Artificial Intelligence,
249-253.
(Snyder et Daskin, 2006) L. V. Snyder et M. S. Daskin, 2006. A
Random-Key Genetic Algorithm for the Generalized Traveling Salesman Problem.
European Journal of Operational Research 174, 38-53.
(Sörensen et Sevaux, 2006) K. Sörensen et M. Sevaux,
2006. MA|PM : memetic algorithms with population management. Computers
& Operations Research 33(5), 1214- 1225.
(Sourd et Chretienne, 1999) F. Sourd et P. Chretienne, 1999.
Fiber-to-Object Assignment Heuristics. European Journal of Operational
Research 117(1), 1-14.
(Srivastava et al., 1969) S. S. S. Srivastava, R. C. G.
Kumar, et P. Sen, 1969. Generalized Traveling Salesman Problem through n
sets of nodes. CORS Journal 7, 97-101.
(Tan et al., 2001) K. C. Tan, L. H. Leeb, Q. L. Zhua,
et K. Oua, 2001. Heuristic methods for vehicle routing problem with time
windows. Artificial Intelligence in Engineering 15(3), 281-295.
(Tang et Wang, 2006) L. Tang et X. Wang, 2006. Iterated local
search algorithm based on very large-scale neighborhood for prize-collecting
vehicle routing problem. The International Journal of Advanced
Manufacturing Technology 29(11), 1246-1258.
(Teeninga et Volgenant, 2004) A. Teeninga et A. Volgenant,
2004. Improved Heuristics
for the Traveling Purchaser Problem. Computers
& Operations Research 31, 139-150.
(Toth et Vigo, 2001) P. Toth et D. Vigo, 2001.
Branch-and-bound algorithms for the capacitated VRP. 29-51. Philadelphia, PA,
USA. Society for Industrial and Applied Mathematics.
(Toth et Vigo, 2002) P. Toth et D. Vigo, 2002. The vehicle
routing problem. Philadelphia, PA, USA : Society for industrial and
Applied Mathematics.
(Tsai et al., 2004) H. K. Tsai, J. M. Yang, Y. F.
Tsai, et C. Y. Kao, 2004. Some issues of designing genetic algorithms for
traveling salesman problems. Soft Computing 8, 689-697.
(Vose, 1998) M. D. Vose, 1998. The Simple Genetic Algorithm :
Foundations and Theory. MIT Press.
(Voß, 1996) S. Voß, 1996. Dynamic Tabu Search
Strategies for the Traveling Purchaser Problem. Annals of Operational
Research 63, 253-275.
(Wäscher et al., 2007) G. Wäscher, H.
Haussner, et H. Schumann, 2007. An improved typology of cutting and packing
problems. European Journal of Operational Research 103, 1109-1130.
(Winter et al., 1995) G. Winter, J. Périaux, M.
Galaán, et P. Cuesta, 1995. Genetic Algorithms in Engineering and
Computer Science. Wiley.
(Zanarini et Pesant, 2007) A. Zanarini et G. Pesant, 2007.
Solution Counting Algorithms for Constraint-Centered Search Heuristics. Dans
les actes de Principles and Practice of Constraint Programming - CP
2007, 743-757.



