2.4.3 Plus court chemin avec contraintes de ressources
(SPPRC)
Le problème de Plus Court Chemin entre deux sommets
dans des graphes est connu depuis longtemps. Dijkstra (1971) a proposé
un algorithme qui s'applique pour le cas de graphes pondérés avec
des poids positifs, Bellman (1957) pour le cas généralisé.
Les algorithmes proposés sont dans les deux cas des algorithmes
polynomiaux. Le fait de rajouter des contraintes de ressources (Shortest Path
Problem with Resource Constraints) rend le problème NP-difficile.
L'ajout de la contrainte d'élémentarité (Elementary
Shortest Path Problem with Resource Constraints) rend le problème
NP-difficile au sens fort. En effet, ce problème est alors une
réduction du problème de Sequencing Within Intervals
(Dror, 1994).
2.4.4 Résolution par un algorithme de programmation
dynamique
L'algorithme 3 part du premier sommet du graphe et construit
itérativement des chemins vers le dernier sommet du graphe. La
construction se fait par extension de chemins partiels. Un chemin partiel a
pour origine le premier sommet du graphe et pour destination terminale un
sommet quelconque de la séquence. L'extension d'un chemin partiel cp
se fait par l'ajout d'un arc sortant de l'extrémité
terminale de cp et la consommation de ressources. Dans le cas
où un nouveau chemin partiel viole une contrainte de ressource, il est
rejeté. Dans le cas contraire, on compare le chemin partiel avec la
liste de chemins partiels mémorisés pour cette
extrémité. Si des chemins partiels sont dominés, ils sont
rejetés. On note ch(w) la consommation de la ressource
w par le chemin partiel ch.
Les figures 2.15, 2.16, 2.17 et 2.18 présentent le
déroulement de la programmation dynamique appliquée au graphe de
la figure 2.14. Les chiffres sur les arcs représentent le coût des
arcs, les chiffres à côté des sommets représentent
le gain associé à chaque sommet. Enfin, entre crochets, se
trouvent les coûts des chemins partiels (on rappelle que le coût
d'une solution est égal à la différence entre la somme des
coûts des distances parcourues et la somme des gains
récupérés). Si le chiffre est barré, cela veut dire
que le chemin partiel est dominé.
stop;
fin
fin
fin
fin
fin
fin
Algorithme 3 : Algorithme de programmation
dynamique
Données : G : un graphe;
W : le nombre de ressources; CH : une liste de chemins partiels non
traités; chi : la liste des chemins partiels
d'extrémité terminale i
1 Initialisation: CH ? chemin partiel
réduit à {0} ;
2 tant que CH =6 0 faire
3 prendre ch E CH;
etch := extrémité de ch;
domine := faux;
pour chaque chemin partiel ch' E
chetch faire
si ch(w) =
ch'(w), ?w = 0, . . . ,W
alors
chetch := chetch \
{ch'};
sinon
si ch'(w) =
ch(w), ?w = 0, ... ,W alors
domine := vrai;
si domine = faux
alors
chetch := chetch U
{ch};
pour chaque arc
(etch, i) faire
ch' := l'extension de ch par
(vetch, vi); si ch'
est valide alors
CH := CH U {ch'};

4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25 fin
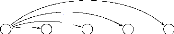
0
10
14
0 10 1 2 3 0
9 9 24
[1] (0, 1) [5] (0, 2) [-14] (0, 3) [0] (0, 0)
FIGURE 2.15 - Extension depuis le
sommet 0
Règle de dominance
On note la relation de dominance entre les chemins
ch1 et ch2, ch1
< ch2 pour signifier que ch1 domine
ch2. Une règle de dominance doit permettre
d'éliminer le chemin
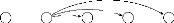
10
14
0 1 10 2 3 0
9 9 24
[1] (0, 1) [5](0, 2) [-14](0, 3) [0](0, 1)
[2](0, 1, 2) [ 8](0, 1, 3) [11](0, 1, 0)
FIGURE 2.16 - Extension depuis le
sommet 1
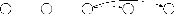
14
0 1 2 10 3 0
9 9 24
[0](0, 0)
[16](0, 1, 2, 3)
[1](0, 1) [2](0, 1, 2) [-14](0, 3)
[ 11](0, 1, 2, 3)
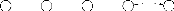
FIGURE 2.17 - Extension depuis le
sommet 2
0 1 2 3 10 0
9 9 24
[1](0, 1) [2](0, 1, 2) [-14](0, 3) [0](0, 0)
[-4] (0,3,0)
FIGURE 2.18 - Extension depuis le
sommet 3
dominé en étant certain de pouvoir toujours
atteindre la solution optimale. La relation de dominance est basée sur
deux règles suivantes :
- Un chemin réalisable, qui respecte les contraintes de
ressources, atteignant le sommet final de la séquence, domine tous les
chemins partiels atteignant le sommet final avec un coût
supérieur,
- Un chemin ch1 domine un chemin
ch2 s'il existe une extension de ch1
dominant extension(ch2) pour toute extension
extension(ch2) de ch2.
La relation de dominance est transitive. La
propriété de transitivité permet de limiter le nombre de
chemins partiels mémorisés. Sans règle de dominance,
l'algorithme de programmation dynamique construit toutes les solutions
réalisables. On a donc tout intérêt à utiliser des
règles de dominances fortes, permettant de limiter le nombre de
solutions explorées. Il faut par contre éviter des
procédures trop coûteuses en temps de calcul, ces
procédures étant appelées un nombre exponentiel de
fois.
Taille du voisinage
Le voisinage défini par la procédure Dropstar
est de très grande taille. En effet, si la solution sur laquelle est
appliquée la procédure est de longueur ñ
(ñ est le nombre de sommets visités), alors la
taille du voisinage est égale à 2ñ, puisqu'on
cherche la sousséquence optimale de cette séquence et que par
conséquent, chaque élément présent dans la
séquence peut appartenir ou ne pas appartenir à la
sous-séquence optimale.
Complexité de la procédure
La procédure Dropstar peut être une
procédure très coûteuse en temps. Pour chaque sommet de la
séquence, on mémorise une liste de labels, correspondant à
des chemins partiels. La taille maximum de cette liste est égale
à 2m, où m est le nombre de
ressources binaires. Chaque ressource peut être consommée ou non,
ce qui mène à 2m états
différents. Le nombre de sommets de la séquence est égal
à ñ (avec ñ n). Le nombre maximum de
chemins partiels durant la procédure dropstar est donc
égal à ñ * 2m.
Chaque chemin partiel est étendu vers ñ
villes. Ce nouveau chemin partiel est inséré dans la liste
des chemins partiels associée à la ville vers lequel le chemin
partiel est étendu (le nombre maximum de chemins partiels dans cette
liste est de 2m). L'insertion consiste à comparer le
nouveau chemin partiel avec ceux déjà présents dans la
liste. La complexité de chaque comparaison est en
O(m). Le coût d'insertion d'un nouveau chemin partiel
dans une liste est donc O(m2m) et le
coût d'extension d'un chemin partiel
O(ñm2m). La procédure
Dropstar a donc une complexité en
O(ñ2m22m). De
manière évidente, cette complexité peut être
réduite significativement en appliquant des règles de dominances
efficaces.
| 


