Techniques hybrides de recherche exacte et approchée: application à des problèmes de transport

3.3 Opérateurs de recherche locale

L'optimisation par Colonie de Fourmis a besoin de coopérer avec une recherche locale afin d'être efficace. Nous explorons le voisinage de solutions avec plusieurs procédures de recherche locale. Nous décrivons dans un premier temps ces procédures, avant de détailler la manière dont elles sont combinées.

3.3.1 Procédures de recherches locales basiques 2-opt

Cette procédure est bien connue dans le contexte du TSP (Lin, 1965). Cette procédure consiste à choisir deux marchés dans le tour et à permuter la circulation entre ces deux marchés si cela améliore la solution. La complexité de cette procédure est O(m²). Pour le TPP, la procédure réoptimise la séquence de marchés visités, sans modifier l'ensemble des marchés non visités.

Simplification

Durant la construction du tour, certains produits peuvent être achetés dans un premier temps dans un marché vi, puis finalement être achetés dans un marché visité par la suite, si ces produits sont disponibles à un plus faible coût. Quand le tour est terminé, certains marchés peuvent être toujours présents dans le tour, alors qu'aucun produit n'y est acheté. La procédure simplification supprime ces marchés du tour.

Insertion

La procédure insertion (voir (Riera-Ledesma et Salazar-González, 2005) pour plus de détails) tente d'insérer des marchés non visités dans le tour. Une insertion est effectuée chaque fois que l'économie réalisée sur les coûts d'achats des produits dépasse l'augmentation de coûts de transport. La complexité de cette procédure est O(m² × n).

Suppression

La procédure suppression (voir la procédure drop proposée par (Riera-Ledesma et Salazar-González, 2005)) est la procédure symétrique de l'insertion. Un marché est supprimé du tour, à partir du moment où la diminution des coûts de transport dépasse l'augmentation des coûts d'achats des produits. La complexité de cette procédure est

O(m² × n).

3.3.2 Application de l'opérateur Dropstar

La procédure dropstar, présentée plus en détail dans le chapitre 2, est une sorte d'extension de la procédure k-drop proposée par Riera-Ledesma et Salazar-González (2005). Dans cette procédure, k marchés consécutifs sont supprimés du tour. Avec la procédure dropstar, nous proposons de déterminer l'ensemble optimal de marchés, consécutifs ou non, qui doivent être supprimés d'une solution. Ainsi, en gardant l'ordre original du tour, la procédure dropstar en extrait la sous-séquence optimale (voir la section 2.4.2 pour une vision plus générale de la procédure Dropstar).

Cette extension permet d'agrandir considerablement la taille du voisinage. Cependant, trouver la meilleure solution voisine est un problème NP-difficile comme cela est montre ci-dessous.

Nous definissons maintenant le concept de sous-sequence. Soit S = (i1, . . . , ik) une sequence, solution realisable du problème de l'Acheteur Itinerant et S' = (i'1, ... , i'l) une autre sequence, solution realisable du problème de l'Acheteur Itinerant. On considère que S' est une sous-sequence de la sequence S si S' ? S et que quel que soit i' _m et i' n appartenant à S' tel que i' _m precède i_n', alors i' _m precède i' _n dans S.

Propriete 1 Trouver la meilleure sous-séquence S' d'une séquence S est un problème NPdifficile.

Demonstration. Pour montrer que le problème de recherche d'une sous-sequence optimale (ou PRSS) est NP-difficile, montrons que le problème decisionnel de recherche d'une sous-sequence (ou PRSS-dec) est NP-complet. Par rapport au PRSS, le PRSS-dec cherche une solution de valeur inferieure à un objectif donne, plutôt qu'une solution de coût optimal. Il est possible de verifier en temps polynomial si une solution du problème decisionnel est realisable et si le coût de cette solution est inferieur à un objectif donne. Le PRSS-dec appartient donc à la classe NP. Pour montrer que ce problème est NP-complet, nous proposons une reduction du problème decisionnel de Couverture d'Ensemble (ou PCE-dec) vers le PRSS-dec.

Considerons une instance du PCE-dec. Soit X un ensemble. Soit F une famille de sous-ensembles de X, avec ?f?F f = X. L'objectif du PCE-dec est de trouver un sous-ensemble F' de F (F' ? F) tel que ?f?F' f = X et |F'| = Q.

Construisons une instance du problème de l'Acheteur Itinerant : on definit G = (V, A) un graphe complet. On note V = {v0, ... , v_m} où v0 est le depôt et v1, . . . , v_m sont les marches. À chaque f ? F, on associe une ville vi. Les coûts de transport sont notes cij = 1 quels que soient vi, vj ? V\{v0} et civ0 = 0 pour tout vi ? V\{v0}. P = {p1, . . . , p_n} est l'ensemble des produits. Chaque produit pk est un element de X. Chaque produit pk ? P est disponible dans un ensemble de marches Vk ? V et les coûts d'achats des produits _sk,i est egal à 0 quels que soient pk ? X et vi ? Vk.

Construisons la solution realisable S du problème de l'Acheteur Itinerant qui visite l'ensemble des sommets.

Montrons que resoudre une instance du PCE-dec où le nombre d'ensembles doit être inferieur à Q revient alors à savoir s'il existe une sous-sequence S' de S, telle que le coût de S' soit inferieur à Q.

Supposons qu'il existe une sous-sequence realisable S' de coût inferieur à Q. Le coût des produits etant nul, le nombre de marches de S' est donc inferieur ou egal à Q. On peut donc en deduire qu'il existe une solution F' au PCE-dec, telle que chaque sous-ensemble f de F' correspond à un marche de S'. Le nombre de sous-ensemble f est donc inferieur à Q.

Supposons maintenant qu'il existe une solution F' au PCE-dec. La solution S' où chaque
marche de S est un element f de F' est une solution du PRSS-dec correspondant. La

réponse aux deux problèmes de décision est donc identique.

Précisons que la réduction se fait en temps polynomial et rappelons que le problème décisionnel de Couverture Minimale est NP-complet (Garey et Johnson, 1979). Finalement, ceci permet de conclure que la recherche d'une sous-séquence optimale appartient à la classe des problèmes NP-difficiles. ~

Nous calculons la sous-séquence optimale à l'aide d'un algorithme de programmation dynamique (voir la section 2.4.4 pour plus de détails sur cet algorithme) appliqué sur un graphe obtenu à partir du tour original. Ce graphe est construit de la façon suivante. Un noeud est ajouté pour chaque marché visité dans le tour. Deux noeuds sont ajoutés, afin de dupliquer le dépôt en début et en fin de tour. Des arcs sont ensuite construits entre chaque marché et les marchés situés à la suite dans le tour. (cf. Fig. 3.1). La procédure consiste alors à trouver le plus court chemin dans le graphe entre les deux copies du dépôt, avec la contrainte que tous les produits soient achetés. Le coût du chemin est égal à la somme des coûts de transport et des coûts d'achats des produits.

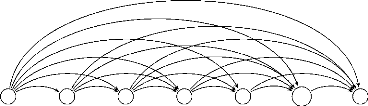
0 4 2 7 3 10 0

FIGURE 3.1 - Exemple d'un tour et du graphe résultant utilisé par la procédure dropstar

Dans l'objectif d'accélérer la résolution de la procédure dropstar, la construction du graphe est légèrement modifiée. Quand un marché vi présent dans le tour est le seul marché à proposer un certain produit parmi les marchés du tour, ce marché doit être dans toute sous-séquence valide. Ainsi, les arcs entre deux noeuds situés de part et d'autre de vi ne peuvent être empruntés. De tels arcs sont alors supprimés du graphe (cf. Fig. 3.2).

L'algorithme de programmation dynamique que nous avons utilisé pour trouver le plus court chemin dans le graphe est inspiré de l'algorithme développé par Feillet et al. (2004) pour le Problème du Plus Court Chemin Élémentaire avec Contraintes de Ressources et est présenté plus en détails dans la section 2.4.4 dans le chapitre 2. Dans ce problème, des labels correspondent à des chemins partiels. Afin de limiter le nombre de labels, nous proposons d'appliquer des règles de dominance.

Dans ce qui suit, nous notons L = (C, P1, . . . , P_n) un label correspondant à un chemin partiel, pour lequel C représente le coût du chemin partiel, comprenant les coûts de transport et les coûts d'achats des produits, Pj le coût d'achat du produit pj. Pj est

0 4 2 7 3 10 0

FIGURE 3.2 - Exemple d'un tour et du graphe résultant pour lequel le marché 7 doit appartenir au tour

fixé à zéro quand le produit p1 n'a pas été encore acheté dans le chemin partiel. Un label L1 domine un label L², ce qui est noté L¹ < L², quand les deux chemins partiels représentés par ces labels mènent au même noeud et que l'on peut être certain que n'importe quelle extension de L¹ serait de coût plus faible que l'extension identique pour L². Dans ce cas, le label L² peut être alors supprimé.

Un point important à prendre en considération lorsque deux labels sont comparés est qu'ils n'ont pas nécessairement acheté les produits au même prix. Ainsi, les économies potentielles sur les coûts d'achats qui peuvent être obtenues en étendant les labels sont différentes pour les deux labels comparés. Nous limitons la comparaison de labels dans le cas pour lequel les deux labels L¹ et L² mènent au même marché et que tous les produits achetés par le label L² sont aussi achetés par le label L¹. Nous appelons alors S1 l'ensemble de produits achetés par le label L1 et S C S1 l'ensemble de produits achetés par le label L². Dans ce cas, pour chaque produit p1 E S, une simple borne supérieure sur le montant additionnel d'économies sur le coût d'achat de p1 qui peut être attendu par le label L² comparé au label L¹ est égal à max(0, P2 1 -- P¹1 ). Une condition suffisante

pour obtenir la dominance L¹ < L² est alors

C2 -- ? max(0, P2 1 -- P1 1 ) = C1

p1ES

En effet, cette condition assure que les économies potentielles sur les coûts d'achats des produits pour le label L² ne peuvent pas contrebalancer la différence actuelle des coûts.

Cette condition peut être renforcée en prenant en considération les coûts d'achats des produits qui ont été achetés seulement par le label L¹. Dans cette optique, nous introduisons le coût potentiel c0 ik d'un produit pk dans le marché vi. Ce coût est égal au coût d'achat minimum du produit pk dans les marchés situés à la suite du marché vi dans le tour courant. Avec cette notation, une condition de dominance renforcée peut être établie telle que : L¹ < L² si

C2 -- ? max(0, P2 1 -- P¹1 ) + ? max(c0 i1, P¹1 ) = C1

p1ES p1ES1\S

Le nouveau terme de cette condition représente le coût d'achat minimal pour le label L² des produits qui ne sont actuellement achetés que par le label L¹.