5.5 Génération de colonnes
Dans cette section, nous présentons les principes de la
méthode de résolution par génération de colonnes.
Cette méthode est classique pour les problèmes de tournées
de
véhicules; c'est avant tout une méthode exacte
mais elle peut aussi bien être utilisée en méthode
heuristique. Le lecteur intéressé par la génération
de colonnes et par ses applications pour les problèmes de transport peut
consulter les articles de Lübbecke et Desrosiers (2005) ou Barnhart et
al. (1998), ainsi que le récent livre de Desaulniers et al.
(2005).
La méthode de résolution par
génération de colonnes permet de résoudre des programmes
linéaires de grandes tailles. Dans cette formulation, les variables du
modèle sont appelées des colonnes. On parle de Branch &
Price lorsque la génération de colonnes est
intégrée dans une recherche arborescente (notamment pour la
résolution de programmes linéaires en nombres entiers). Une
résolution par génération de colonnes est une
méthode itérative. De nouvelles colonnes enrichissent un
problème restreint à chaque itération. Le problème
initial à résoudre est appelé problème maître
ou problème principal, tandis que l'algorithme qui génère
de nouvelles colonnes est appelé problème esclave ou
sous-problème.
Le problème du 2|RO|L-VRP se prête a priori bien
à une résolution par génération de colonnes. C'est
l'approche que nous explorons dans ce chapitre. Pour cela, nous
présentons un modèle de type couverture. Posons Ù =
{r1, . . . , r|Ù|}, l'ensemble des routes
réalisables. On associe à une route rk un coût
ck égal à la somme des distances des arcs
empruntés par cette route. aik est égal
à 1 si la route rk visite le client vi et est
égal à 0 dans le cas contraire.
Les variables sont notées èk.
èk est égale à 1 si la route rk est
sélectionnée et égale à 0 dans le cas contraire.
(P )
min? ckèk (5.12)
rkEÙ
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.13)
rkEÙ
? èk K (5.14)
rkEÙ
èk E {0,1} (rk E Ù) (5.15)
Considérons la relaxation linéaire du modèle
5.12, appelée problème maître (MP) : (MP )
min? ckèk (5.16)
rkEÙ
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.17)
rkEÙ
? èk K (5.18)
rkEÙ
èk E [0,1] (rk E Ù) (5.19)
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
À l'itération it de la
résolution par génération de colonnes, on résout de
manière exacte le problème maître restreint à
Ùit c Ù, défini ci-dessous. On choisit
une méthode de résolution de telle sorte que celle-ci fournisse
aussi une solution optimale au dual du programme linéaire.
(PMR )
min ? ckèk (5.20)
rkEÙit
s.c.q.
? aikèk = 1 Vvi E
V\{v0} (5.21)
rkEÙit
? èk = K (5.22)
rkEÙit
èk = 0 (rk E
Ùit) (5.23)
Notons ëi la variable duale associée
à la iième contrainte (5.21). Toute colonne
ù E Ù \ Ùit susceptible de
diminuer la valeur de la fonction objectif si on l'ajoute au problème
maître restreint, a un coût réduit négatif (ce
coût est défini par l'équation 5.24). Le problème
esclave consiste donc à trouver de telles colonnes. Si aucune colonne de
coût réduit négatif n'existe, on déduit alors
l'optimalité pour MP de la solution obtenue à l'itération
it.
ck - ? aikëi - ë0 (5.24)
viEV\{v0}
Le problème qui consiste à chercher dans
Ù une variable de coût négatif est appelé le
sous-problème (connu aussi sous le nom de problème
esclave, oracle ou problème de pricing).
Le schéma de la figure 5.2 illustre le déroulement
de l'algorithme de génération de colonnes.
La génération de colonnes augmente donc
progressivement la taille du problème à résoudre, ce qui
est particulièrement adapté à la résolution de
problèmes possédant un grand nombre de colonnes. Le but
recherché est par conséquent d'obtenir une solution optimale sans
avoir à générer l'ensemble des colonnes.
Néanmoins, la solution optimale retournée par la
génération de colonnes est la solution du problème (MP),
qui est la relaxation linéaire du problème initial (P). Une
méthode de résolution efficace pour les programmes
linéaires en nombres entiers est basée sur la combinaison de la
résolution de la relaxation linéaire du problème et de la
méthode classique de séparation et évaluation progressive
(Branch & Bound). À chaque noeud de l'arbre de recherche,
on résout un programme linéaire donnant, dans le cas d'une
minimisation, une borne inférieure au problème. Lorsque cette
résolution se fait par génération de colonnes, on parle de
Branch & Price.

Résolution
Problème
Maître
Restreint
sur Ù1
Existence de
variables
améliorantes
Oui : ajouter à Ùit
Fin
Non
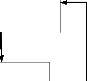
Ensemble initial
de colonnes Ù1

Chercher dans Ùit
une variable de coût
négatif
(Sousproblème)
FIGURE 5.2 - Méthode de
génération de colonnes Résolution du
problème esclave
Le sous-problème cherche un élément de 1)
tel que :
ck - E aikAi - A0 < 0 (5.25)
vi?V\{v0}
Posons bkij égal à 1 si la
route rk utilise l'arc (vi, vj) et égal
à 0 dans le cas contraire. L'équation 5.25 devient alors :
ck - E bk ij(cij - Ai) < 0
(5.26)
vi?V
On cherche alors l'élément de 1) minimisant
cette valeur. Cette recherche est un problème d'optimisation
combinatoire qui revient à trouver le chemin de v0 à
v0, passant au plus une fois par chaque sommet et tout en étant
une route réalisable (dans le cas du 2|RO|L-VRP cela équivaut au
respect des contraintes de capacité, des contraintes de surface, des
contraintes de chargement, etc.). Il s'agit d'un Problème de Plus Court
Chemin Élementaire avec Contraintes Additionnelles pour lequel le
coût des arcs (vi, vj) est égal à
cij - Ai. Comme nous allons le voir, la plupart
des contraintes additionnelles
Chapitre 5. Application au problème de Tournées de
Véhicules avec Contraintes de Chargement
se modélisent comme des contraintes de ressources
classiques, mais les contraintes de chargement sont plus complexes à
gérer. Ainsi, le problème esclave pour le problème du
2|RO|L-VRP est plus complexe que la résolution d'un problème de
Plus Court Chemin Élémentaire avec Contraintes de Ressources
(voir la section 2.4.3 pour plus de détails sur le problème de
Plus Court Chemin avec Contraintes de Ressources).
La figure 5.3 représente un problème de plus
court chemin avec contraintes de ressources entre le noeud v0 et le
noeud v3. Une seule ressource est présente, la consommation
cumulée de celle-ci est contrainte en chaque sommet (la valeur limite
à ne pas dépasser est indiquée à côté
de chaque sommet).
cout, consommation
^ contrainte de ressource
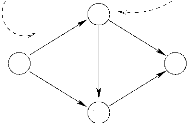
3,1
1,1
v 1
1
1,1
2,1
0 v 1,1 v3 2
0
1
v2
FIGURE 5.3 - Un SPPRC a une
ressource
Dans la section 5.5.1, nous définissons formellement le
problème. Une présentation d'un algorithme standard basé
sur de la programmation dynamique est détaillée dans la section
5.5.2. Ce principe de programmation dynamique est le même que celui
présenté dans les chapitres 2, 3 et 4.
5.5.1 Modélisation d'un ESPPRC
Nous présentons maintenant la modélisation d'un
problème classique de Plus Court Chemin Élémentaire avec
Contraintes de Ressources. Soit G = (V, E,
W) un graphe complet pour lequel V est un ensemble de n
+ 1 noeuds, correspondant à la source (noeud v0), le puits
(noeud vn) et aux clients vi (i = 1, . .
. , n - 1}). Chaque arc (vi, vj) a une consommation
cij(w) de ressource w (w = 0, . . . ,
W). On définit la ressource 0 comme le coût de l'arc. Une
contrainte sur chaque ressource est associée à chaque sommet. La
consommation cumulée au long du chemin jusqu'au sommet vi est
notée ci(w). Cette consommation est limitée par
Biw.
L'objectif du problème (équation (5.27)) est de
trouver le plus court chemin de v0 à vn
parmi les chemins réalisables sur l'ensemble des ressources. La variable
de décision äij est fixée à 1 si l'arc
(vi, vj) appartient à une solution et 0 sinon.
(EP)
min? cij(0)äij (5.27)
(vi,vj)?E
s.c.q.
E äij - E äji = 0 Vj = 1,
... , n - 1, (5.28)
(vi,vj)EE
(vj,vi)EE
E äij < 1 Vi = 0, . . . , n,
(5.29)
(vi,vj)EE
E ä0j = 1, (5.30)
(v0,vj)EE
ci(w) < Biw
Vi = 0, . . . ,V; Vw = 1, . . . ,W,
(5.31)
äij(ci(w) +
cij(w) - cj(w)) < 0 V(vi,
vj) E A; Vw = 1, .. . ,W, (5.32)
äij E {0,1} V(vi, vj) E A.
(5.33)
Les inégalités (5.28) représentent les
contraintes de flots assurant la continuité du chemin. Les contraintes
(5.29) assurent l'élémentarité du chemin. La contrainte
(5.30) impose qu'un unique chemin parte de la source. Les contraintes (5.31)
contrôlent la consommation cumulée sur chaque ressource et les
contraintes (5.32) la continuité du flot de consommation des ressources.
On admet que toutes les ressources se cumulent par incrémentation du
poids de l'arc associé à la ressource dans la limite du seuil
autorisé.
| 


