Intégration financière et diversification internationale

2.6.2 Modèles contraints

Il ne s'agit pas de lister de manière exhaustive toutes les modélisations multivariées incluant des contraintes, mais nous essayons de présenter brièvement les modèles les plus connus qui nous permettent de mieux cerner notre étude.

2.6.3 Moo:Me Diagonal

C'est aux travaux de Bollerslev, Engle et Wooldridge (1988) que remonte l'un des plus anciens modèles contraints connu sous le nom de GARCH diagonal. Il s'agit concrètement d'une même représentation que le modèle contraint vu précédemment sauf que les éléments hors diagonale des matrices A et B sont nuls c'est-à-dire :

a 110 0

0 0a

A = 0 a 22 0?,B= 0

0 0 ?

?

0 ? .

?

b33 ?

b22

0

b11

33

Ceci conduit à :

h = c +a å ² +b h

^{1 1}

, t

11 11 1,

t

- 1

¹¹

1 1, t-1

h 2 1 , t = c21 + a22å 1, tå 2, t- 1 + b22h 1 2,t-

1

;

(2.32)

h 22 ,t = c₂₂ + a33å

2, t- 1

b33 h 22, t-1 .

Cette technique permet de contourner le problème du nombre de paramètres à estimer, que nous avons soulevé auparavant. Cependant comme le note Gourieroux (1994) seule une dépendance des termes avec leurs propres valeurs passées est possible. De plus la condition que la matrice variance - covariance soit positive définie n'est pas garantie et encore cette modélisation n'est pas stable par composition de portefeuille.

2.6.4 Le Modèle BEKK-GARCH

Engle et Kroner (1995) ont proposé la spécification suivante désignée sous le nom BEKK. Cette modélisation élimine l'handicap du modèle diagonal en garantissant une variance positive dans un cadre relativement moins contraignant :

'

H C C A

= ' + ' å - 1 å - 1 + ' - , ( 2.33)

A B H B

t t t t ¹

où C est une matrice ( N x N) symétrique, A et B sont deux matrices (N x N) de paramètres constants. Si on se limite à la variante bivariée on aura :

? ?

?

?h h ? ? å ² å å ?

1 1 , t 1 2 , t 1 , 1

t - 1 , 1 2 . 1

t - t -

? ? = C C A

' + ' ?? ?? A B

+ '

2

? h h

t t ? ? å å

22 , å

2 1 , 2 , 1 1 , 1

t - t - 2 , 1

t - ?

h h

, (2.34)

?

? B

?

1 1 , 1

t - 1 2 , 1

t -

1

h h

2 1 . 1

t - 22 , t -

avec : ? c 11 0 ? ? a a ? 11 C = ? , ? 12 ? A = ? , ? c c 21 22 ? a a ? 21 22 ?

? b b ? 11 12 B = ? ? . ? b b 21 22 ?

2 2 2

å a a å å b h

2

h c c a ²

= + +

2 2 ² + 2 + a + + 2 b b h b h

+

1 1 , 11 21 11 1 , 1

- 11 21 1 , 1 2 , 1

- - ₂₁ å 2 , 1

- 11 1 1 , 1

- 11 2 1 , 1 2 1 , 1

- - 21 22 , 1 ,

t t t t t t t t t -

2

h c c a a

= + å ² + ( a a a a ) å å + b b h ( )

2 1, 21 22 11 21 1 , 1

- 21 21 + a a

11 22 1, 1 2 , 1

- - 21 22 2, 1

å +

- 11 12 1 1, 1 + b b b b h

- 21 12 +

t t t t t t 11 22 2 1, 1

t -

+ b21

b 22h 22, 1 t -

,

2 2 2 2 2

h = + å 2 å ²

c a

² + +

a a a + b h + 2 b b h + b h

22 , 22 12 1 , 1

- 12 22 1 , 1 2 , 1

å å

- - 22 2 . 1

- 12 1 1 , 1

- 12 22 2 1 , 1

- 22 22 , 1 ,

t t t t t t t t -

h 2 1, t est identique que h 1 2 , t puisque la matrice variance - covariance est symétrique.

La spécification diagonale symétrique du modèle oblige l'observation des contraintes suivante : a_{1 2} = a_{2 1} = 0 et b_{1 2} = b2 1 = 0 et par conséquent on aura :

h 1 1 , t = c 2 11 +c 2 21 +a1² 1å1² t- 1 b1²1h 1 1 , t-1

h = c c a a å å + + b b h , 2 1 , t 21 22 11 22 1 , 1 2 , 1 t - t - 11 22 2 1 , 1 t - 2 et h 22 , t = c22 a2^2 2å 2^2, t- 1 b^2 h 22 22, t-1 .

(2.35)

Quant à la spécification diagonale asymétrique :

22

( )

² å ² î ²

= + + s ²

c c a

2 2

h + + t

1 1 , 11 12 11 1 , 1

- 11 1 , 1

- 11 ç ,

t t t 1 , 1

t -

î _it = å _{itÉ it} ou I_îit = 1 si å_it = 0 et 0 sinon , (2.36)

2 2

s ²

h b h

2

å ²

c a ²

= + +

+

22 , 22 22 2 , 1

- 22 22 , 1

- 22 î ,

t t t 2 , t-1

h 1 2 , t = c₁₂ c 22 a11a22å 1, t- 1 å 2 , t- 1 b11b 22h 1 2, t- 1 s11s 221, t- 1 2 , t - 1 2 , t-1 .

Enfin la spécification asymétrique avec effet de taille :

2 2 2 2

= +

( ) î ²

c c a

2 2 2

h b h

2

+ + s + t ,

1 1 , t 11 22 11 å +

1 , 1

t - 11 1 1 , 1

t - 11 1 , 1

t - 11ç 1, t-1

çit = åitÉçit oil É çit = 1 si å_it = hiit et 0 sinon ;

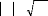
(2.37)

2 2 2 2 h c a = + 2 ^2 å b h 2 + + s î + t 22 22 22 2 , 1 - 22 22 , 1 - 22 2 , 1 22 ç t t t t -

, 2, t-1

h 1

= c c a a

+ å å + b b h + s s t t

2 , 12 22 11 22 1 , 1 2 , 1

- - 11 22 1 2 , 1

- 11 22 1 , 1 2 , 1

î î +

- - 11 22 1 , 1 2 , 1

.

ç ç

t t t t t t t - t -

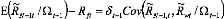
mt? 1) ? R ft =ä t? 1Cov( 1`? 1,t , 14wt / Ù t?1)