Conception d'une application pour le calcul et la simulation des efforts sur les pylônes

3-4 Elément fini barre

3-4-1 Définition

Géométriquement, une barre correspond à un solide orienté dans la direction x (repère local). Les dimensions dans le plan (y--z) normal à x sont relativement petites par rapport à la

dimension longitudinale (figure 3-2). Un élément fini barre (figure 3-3) schématise un composant d'une structure qui travaille uniquement en traction ou compression. C'est généralement un élément à 2 noeuds, qui comporte 3 inconnues ou degrés de liberté (d.d.l.) par noeud représentant les composantes de son déplacement dans l'espace.

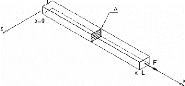
Figure 3-2 : géométrie d'un élément barre

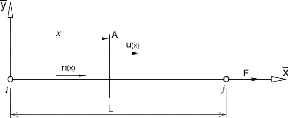
Figure 3-3 : modélisation d'un élément barre

Les principales hypothèses pour un élément barre rectiligne qui ne travaille qu'en traction ou compression sont :

- Petits déplacements

, U

, (M, t) = u

(x, t) x

( 3-7)

- Déformations en petits déplacements :

s =

Ou Ox

(3-8)

- Loi de Hooke dans un milieu isotrope homogène élastique :

a = E E

( 3-9)

avec a, la contrainte dans la barre et E est le module de Young du matériau. En intégrant les contraintes sur la section A, nous obtenons la loi de comportement intégrée des barres:

n(x) = E A E (3-1 0)

Où n(x) est l'effort normal dans la barre dû à la force nodale F.

3-4-2 Formulation de l'élément barre dans le plan

3-4-2-1 Identification du problème

Considérons un élément barre dans le plan défini par deux noeuds i et j, de longueur L et de section uniforme A (figure 3-4).

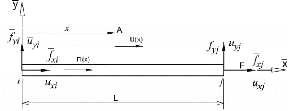
Figure 3-4 : élément barre dans le plan (i ,x,y)

Dans le repère local (i,.,~ y), on note par u_xi et 1~xj les déplacements aux noeuds i et j, et

~	~
par f xi et f		xj les forces aux noeuds i et j. Le vecteur force relatif à l'élément e est donné par :

xj f^~yj] (3-11)

~

~

~

F^e= [ f

xi fyi f

Le vecteur déplacement est donné par:

U^~e= [U_xi U_yi U_xj U_yj] (3-12)

~ ~

Dans le cas qui nous occupe, f_yi fyj, U_yj et U_yj sont nuls puisque l'élément barre ne travaille qu'en traction ou compression.

3-4-2-2 Fonction d'interpolation

Pour un problème statique, lorsque l'élément est chargé au niveau de ses noeuds, l'effort normal est uniforme. Compte tenu des relations (3.8) et (3.10), la solution u(x) sera linéaire. Pour chercher cette solution, nous allons utiliser une approximation polynomiale linéaire de la forme :

u(x) = N1 fixi + N2 fixj (3-13)
où N1 et N2 sont les coordonnées naturelles.

Nous identifions aux noeuds i (x=0) et j (x=L) la valeur de l'approximation des déplacements axiaux. Nous en déduisons :

N1= 1- ^x_i et N2= ^x_i (3-14)

Sous forme matricielle nous écrivons :

U(x)=Nt U^e = [1- A _B A B]C9A~

9A~D (3-15)

La matrice N d'interpolation reliant les déplacements d'un point intérieur de l'élément aux déplacements nodaux est donc :

_{N= [1-} x x]t (3-16)

/ /