Estimation de la demande régionale d'eau résidentielle en présence d'une tarification progressive et non linéaire en Tunisie. Une approche par cointégration sur données de panel

UNIVERSITE TUNIS EL MANAR

Faculté des Sciences Economiques et de Gestion

Mémoire de mastère en Economie Mathématique et
Econométrie

Estimation de la demande régionale d'eau résidentielle

en présence d'une tarification progressive et non

linéaire : Une approche par cointégration sur données

de panel

Encadré par : professeur Matoussi Mohamed Salah

Etudiant : Ben zaied younes

Année Universitaire : 2008-2009

Dédicaces

Je dédie ce travail

A ma famile pour l'aide moral et financier

A tous mes professeurs en première année de mastère
A tous qui ont participé de prés ou de loin à l'accomplissement de ce travail

Remerciements

Au terme de ce travail, je tiens à exprimer mes vifs remerciements à Monsieur le professeur MATOUSSI MOHAMED SALAH, directeur de LAREQUAD, qui a accepté de diriger ce travail, pour la confiance qu'il m'a témoigné, pour ces nombreux conseils et pour son effort qu'il m'a personnellement fourni.

A Monsieur BACCOUCH RAFIK, professeur à la faculté des sciences économiques et de gestion de TUNIS, mes vifs remerciements pour son aide en particulier analytique et constructif, sans quoi le présent travail pourrait ne pas être réalisé dans les meilleurs conditions.

A Monsieur RZIGUI LOTFI, chercheur à FSEG Sfax, pour ces encouragements et conseils ainsi qu'à mon ami BELHAJ HMID YASSINE, chercheur en réseau d'accès à ENIT.

J'adresse aussi mes remerciements à Mon frère MOHAMED BEN ZAIED, pour son encouragement régulier et ses commentaires ainsi qu'à tous mes amis pour tous les bons moments qu'on a eu durant ces deux années de mastère à TUNIS.

Enfin, que les membres de jury trouvent l'expression de mon profond respect et pour la gentillesse d'avoir accepté d'évaluer ce travail de recherche.

Tables des Matières

1 2 3

introduction Revue de la littérature 2.1 Les études portant sur des données d'enquête 2.2 Les études portant sur des données temporelles: 2.3 Les études portant sur des données de panel: 2.4 Les études portant sur des données de panel non stationnaire: . . . Non stationnarité et données de panel 3.1 Les tests de racine unitaire sur données de panel 3.1.1 Test de racine unitaire de Levin, Lin et chu [2002] 3.1.2 Test de racine unitaire d'Im, Pesaran et Shin [2003]: 3.1.3 Test de racine unitaire de Maddala et Wu [1999]: (approche non paramétrique) 3.1.4 Test de stationnarité de Hadri [2000]:(hypothèse nulle de sta- tionnarité) 3.2 Notions de cointégration en panel 3.2.1 Relations de cointégration intra-individuelles 3.2.2 Relations de cointégration inter-individuelles 3.3 Les tests de cointégration sur données de panel

2 4 5 6 7 12 15 16 16 20 23 24 27 27 28 28

3.3.1 Le test de cointégration sur données de panel de larsson et al

[2001] 28

3.3.2 Le Test de cointégration sur données de panel de Pedroni

[1999,2004]: 31

3.4 Estimation 34

		3.4.1 La méthode FM-OLS (fully modified ordinary least squares) 35 3.4.2 La méthode DOLS (Dynamic Ordinary Least Squares) . . . 36
4	Analyse des données et présentation du modèle théorique		38
	4.1	Présentation des données:	38
		4.1.1 Découpage de la Tunisie en six régions homogènes:	39
		4.1.2 Evolution des variables clés:	40
		4.1.3 Les explications préliminaires:	44
		4.1.4 Les statistiques descriptives:	45
	4.2	Le modèle :	46
		4.2.1 Les déterminants de la demande d'eau - aspects théoriques .	46
		4.2.2 Le glissement de consommateur d'un bloc à un autre:	48
	4.3	SpéciÞcation économétrique du modèle:	48
5	Résultats empiriques et intérpretations		51
	5.1	Introduction	51
	5.2	Résultats des tests de racine unitaire :	52
	5.3	Résultats des tests de cointégration :	55
	5.4	Résultats des estimations	57
		5.4.1 Résultats des estimations sur la période 1980-1996	57
		5.4.2 Les points de divergence par rapport à l'étude de Ayadi et al
		[2002]	63
		5.4.3 Résultats des estimations sur toute la période (1980-2007) .	64
	5.5	Conclusion	69

6 Conclusion générale 70

7 Annexes 77

Introduction

La Tunisie est un pays à climat semi-aride caractérisé par une rareté des ressources en eau. Cette rareté naturelle est accentue par une croissance rapide de la demande suite au développement économique, urbain et démographique qui connait la Tunisie depuis l'indépendance.

L'autorité de l'eau, qui s'engage à promouvoir l'offre afin de satisfaire la demande, se trouve devant une contrainte naturelle qui se traduit par la limite des ressources conventionnelles. Un tel probléme pousse l'autorité à penser à mobiliser d'autre ressources non-conventionnelles, tel que le dessalement de l'eau de mer et l'épuration des eaux déja utilisées. Notons que ces ressources non-conventionnelles se caractérisent par un coût de mobilisation plus élevés que les ressources naturelles. L'économie Tunisienne qui est encore émergente pourrait être handicapée par les conséquences négatives qui découlent de cet accroissement brutal du coût. La seule alternative résiderait dans la maîtrise de la demande afin d'alléger ces conséquences négatives susceptibles de ralentir le rythme de la croissance économique déja remarquable.

L'agriculture, qui accapare plus de 80% des ressources disponibles, est au centre de l'intéret dans toute politique de gestion de la ressource en eau. Sachant que les responsables de la gestion des ressources en eau dans le secteur résidentiel sont convencus de l'inélasticité de la demande en eau à son prix, le recours à la conservation de la ressource, grâce à une tarification appropriée, est malheureusement négligé au profit de la mobilisation de l'offre.

Si la demande d'eau résidentielle paraît beaucoup moins importante que la demande agricole en terme absolu, sa maîtrise est cependant primordiale pour des raisons absolument évidentes. En effet, cette composante se distingue par au

moins deux caractéristiques intrinsèques qui justifient amplement qu'on lui prête le maximum d'attention. Premièrement, l'usage résidentiel est considéré comme le plus vital, parce qu'il touche un domaine hautement sensible lié à la satisfication des besoins perçus comme indispensable à la survie de toute société humaine. Deuxièmement, la demande en eau résidentielle accapare les meilleures ressources du pays. En effet les eaux réellement douces, d'accès facile et surtout les plus régulières et caractérisées par des niveaux de fiabilités minimales sont allouées en priorité à ce secteur.

Afin d'aider les preneurs des décisions en matiére de gestion de la ressource, plusieurs chercheurs ont produit des travaux d'analyse économétriques de la demande d'eau résidentielle en Tunisie durant les dernières decenies. Ces études ont réellement contribués à clarifier le problème et surtout à montrer que la demande n'est pas, comme prétendu, inélastique au prix. Notre travail s'inscrit dans cette perspectives en mettant surtout un accent particulier sur le recours aux techniques économétriques les plus récentes afin d'améliorer la qualité de l'estimation de la demande d'eau résidentielle. En effet, la base des données utilisée dans ces études est souvent considérée stationnaire. Nous nous intéressons dans ce travail à l'application d'une technique économétrique récente qui évoque le probléme de la stationnarité en panel. Nous actualisons la base des données utilisée par Ayadi et al (2002) et nous posons la question sur la situation d'équilibre de long terme entre la consommation moyenne d'eau résidentielle et ses déterminants pour le cas de la Tunisie. Notre base des données commencent avec la disponibilité des données désagrégés jusqu'à nos jours (1980-2007). Nous adoptons le découpage retenu par le travail de Ayadi et al (2002).

Notre travail est organisé en quatre chapitre. Le premier est consacré à une présentation synthétique de la littérature économétrique qui nous utilise dans notre partie empirique. Nous avons mis un accent particulier dans le chapitre deux sur les tests de stationnarité en panel, de cointégration en panel et les méthodes d'estimation des relations de cointégration en panel. L'analyse des données forme le chapitre trois et Enfin, le dernier chapitre résume les résultats obtenus ainsi que leur intérpretation économique.

Chapitre 1

Revue de la littérature

L'économétrie appliquée est un mode d'investigation économique qui utilise le calcul mathématique et statistique, l'informatique et les lois économiques pour faire des estimations permettant d'éclaircir la réalité compliquée. Cette complexité nous incite à chercher un principe qui facilite la mission des responsables à la prise des bonnes décisions. Le probléme d'estimation de la demande d'eau résidentielle s'inscrit dans la liste des problémes auxquels sont confrontés bon nombre d'économétres. Toutefois, La résolution d'un tel probléme nécessite, pour un économètre appliqué, l'observation de la réalité, la formulation, l'estimation et la validation des résultats. Cette démarche a été entreprise dans plusieurs pays en utilisant diverses techniques économétriques. C'est en fait l'objectif du présent chapitre consacré à une revue de la littérature plus ou moins exhaustive, qui nous ramènera à la bonne spéciÞcation d'une formule standard innovatrice à appliquer dans notre travail. Ainsi, la revue est présentée en prenant en considération l'aspect économétrique à travers la synthése des travaux sur données d'enquête, les travaux utilisant des données temporelles et, dans une dernière section, ceux portant sur des données de panel.

La demande d'eau résidentielle a été étudiée depuis la Þn des années soixante. Plusieurs estimations ont été entreprises pour le cas des Etats-Unis tels que les travaux de Howe et Lineaweaver [1967][20], Foster et Beattie [1979][17], Chicoine et Ramamurthy [1986][11],Nieswiadomy et Molina [1989][38] et Hewitt et Hanemann [1995][21]. Alors que l'émergence des études portant sur des pays européens date des années quatre vingt dix à travers les travaux de Hansen [1996][23], Höglund [1997][22], CREDOC [1997][13], et Très récemment le travail de Nauges C et A Thomas [2003][40] a traité le cas de la France.

Pour le cas de la Tunisie, la plupart des études ont été entreprises sur la base des données agrégées. Ainsi, les mémoires de Ben Naceur [1984][5] et Tlili [1993], les études de Rodriguez [1991][48], Lahoual et al [1994][34], Ayadi et al [2002][1] ont utilisé respectivement des données annuelles, trimestrielles et en double indice pour estimer des fonctions de demande nationale d'eau résidentielle. Notant au passage que notre étude sera la nouvelle version de celle de Ayadi et al [2002][1].

Nous allons présenter l'état de l'art selon la technique économétrique utilisée pour estimer la demande d'eau résidentielle. Ainsi, Les études portant sur des données d'enquête seront synthétisées dans une première section, les études basées sur des séries temporelles et ceux sur données de panel le seront dans une dernière section.

2.1 Les études portant sur des données d'enquête

Malgré la faiblesse statistique des estimations sur des données individuelles, plusieurs travaux en économétrie appliquée et notamment en économétrie de la demande ont été établis. Le premier travail qui tente à estimer la demande d'eau résidentielle sur la base des données individuelles ( cross section ou en coupe transversal) a été mené par Vaillancourt F et Mireille C [1978][54]. Cette application tente à estimer la demande d'eau résidentielle pour un échantillon de 560 ménages d'une ville Québécoise appelée Saint-Laurent. Les auteurs ont déterminé les variables principales susceptibles d'affecter la demande d'eau résidentielle à travers l'estimation d'une simple régression linéaire de la consommation d'eau sur le prix par unité, le revenu par ménage, le nombre des membres du ménage, les conditions climatiques sèches et la présence d'équipements consommateurs d'eau. Pour le cas du Québec, le prix est Þxe pour les ménages dont la consommation ne dépasse pas 68,000 gallons par an. Les auteurs ont procédé à un échantillonnage par la méthode du hasard systématique; ils ont trouvé que 87% parmi les 560 ménages ne dépassent pas 68,000 gallons par an, parsuite, ils ont écarté la variable prix de la régression. Conformément à l'intuition économique et compte tenu que l'eau est un bien normal, les résultats ont ressorti que le revenu affecte positivement la consommation d'eau. Le nombre des membres du ménage et la présence d'équipements consommateurs d'eau vinent à augmenter la consommation d'eau pour les ménages de l'échantillon. Notons que les auteurs ont estimé l'équation de la consommation à travers la linéarisation en forme logarithmique et ces résultats ont été similaires à ceux des études américaines et à ceux obtenus pour la même ville en 1977 pour un échantillon de 108 ménages.

2.2 Les études portant sur des données temporelles:

L'économétrie des séries temporelles est souvent la plus utilisée dans les travaux de recherche en économétrie appliquée, grâce à l'accès facile aux bases des données temporelles d'une part, et à la puissance statistique des résultats d'autre part. En effet, beaucoup de travaux tentent d'estimer la demande d'eau résidentielle, en utilisant des données chronologiques. Nous citons à titre d'exemple les mémoires de Ben Naceur [1984][5] et de Tlili [1993] et les études de Rodriguez [1991][48] et de Lahouel et al [1994][34] qui ont utilisé respectivement des données annuelles et trimestrielles. D'autre part, l'étude de R Martinez Espenira [2007][49] a été la première à utiliser la technique de cointégration et ECM pour estimer les élasticités de court et de long terme.

R.Martnez Espenira a utilisé des données relatives à Seville en Espagne. L'objectif de cette étude a été l'évaluation de l'utilité de la technique de cointégration et d'ECM à estimer la demande d'eau résidentielle et l'estimation des élasticités prix de court et de long terme à travers des données mensuelles¹.

L'estimation d'une équation de la demande d'eau a montré que la réaction des ménages face à la politique tarifaire est plus importante à long terme qu'à court terme. En effet, l'élasticité de court terme est autour de (-0, 1) alors que celle de long terme est autour de (-0, 5).

Le modèle que R Martinez Espenira [2006] a utilisé est le suivant;
Qt = a + Pt + P2 t + RESt + V It + BANt + SUMt + ut

Là où Q, P, RES, V I, BAN et SUM sont respectivement: la consommation moyenne par abonné, le Prix marginal de l'eau basé sur les spéciÞcations de Taylor-Nordin (Taylor 1975) et Nordin (1976)[39], Les heures quotidiennes des restrictions d'ap-provisionnement sont appliquées pendant la sécheresse, Revenu virtuel (différence entre les salaires moyens une approximation pour le revenu, et le D, l'instrument pour les équivalents variable de Nordin-différence (Nordin 1976)), la variable binaire appliquée pendant la sécheresse et la variable binaire (qui prend 1 durant les mois de Mai, Juin, juillet et Aout). le terme d'erreur est u supposé IID.

¹La base des données couvre la période 1991-1999, des observations mensuelles.

Sur la base de cette spécification les paramètres ont été significatifs, le revenu affecte positivement la consommation de l'eau alors que l'effet des variables climatiques est négatif pendant les sessions froides, et positif durant les sessions sèches conformément à l'intuition.

2.3 Les études portant sur des données de panel:

L'économétrie des données de panel est l'approche la plus pertinente en termes de significativité statistique et/ou en terme d'interprétation économique. Les données de panel ont deux avantages qu'on ne trouve pas en travaillant avec des données temporelles ou individuelles, à savoir l'augmentation de la base des données, et la prise en compte de l'hétérogénéité inter-individuelle. Les travaux en économétrie appliquée qui utilisent les modèles à double indice sont nombreux, et ceux qui ten-tent à étudier la demande d'eau résidentielle ne font pas l'exception. Ainsi, nous avons constaté durant la dernière décennie une progression des travaux étudiant la demande d'eau résidentielle en utilisant le modèle à double indice à savoir Ayadi et al [2002][1], Nauges C et A Thomas [2003][40] et R Martinez Espenira [2003][50]. Dans cette section, nous essayons à synthétiser les principaux apports théoriques et empiriques de ces études, ainsi que leurs limites réciproques, en précisant enfin l'intérêt de notre travail par rapport aux autres travaux, et son caractére innovant.

Le travail de Nauges C et A Thomas [2003][40] est une nouvelle approche microéconométrique qui vise à combiner l'utilisation de la programmation à plusieurs objectifs et l'économétrie de données de panel. Ainsi, les auteurs ont dérivé le modèle de la demande d'eau résidentielle, pour un échantillon de 116 municipalités observées sur six ans (1988-1993), à partir d'un programme d'optimisation dynamique qui traduit le comportement de la municipalité² en utilisant le prix de l'eau comme étant la variable de contrôle. Sous l'hypothèse que la communauté a un double objectif, la maximisation de l'utilité indirecte des consommateurs locaux, et la réduction de sa dette chez la sociéte privée. Céline N et Alban T [2003][40] formulent le programme intertemporel suivant:

²En france la municipalité à le choix entre distribuer l'eau par elle même ou donner la mission à une sociéte privé.

_X8
t=0

max

{Pt}

(1 + ñ)^-t[v(Pt, Mt) - Dt]

? ?

?

S/c

Dt+1 = Dt(1 + r) - kPtCt D0 = D P0 = P	? ? ?
Pm avec Ct = BP^â1 t Mâ2 t ; B = Câ0 j=3		Zâj j (j = 3 m), v(Pt, Mt) est l'utilité indirecte,

Dt est la dette de la municipalité et Mt est le prix d'un m3

La résolution de ce programme intertemporel, à travers l'équation de BELL-MAN, puis les conditions de premier ordre, donne lieu à la spécification d'un modèle dynamique à erreur composé avec un effet fixe individuel qui tient compte de l'existence d'une éventuelle hétérogénéité interindividuelle observable et inobservable. Le biais d'endogeneité augmente grâce à la présence de la variable endogène retardée et l'effet individuel. En outre, la corrélation entre les autres régresseurs et l'effet individuel est une autre source d'inconsistance de l'estimateur MCO. La solution souvent adoptée est la différence première, pour éliminer l'effet fixe individuel, et la quasi-différence pour éliminer le temps-variable effet fixe aléatoire. Ainsi, les auteurs proposent une double transformation du modèle en utilisant à la fois les deux types de transformations pour éliminer les deux effets individuels. Ils l'ont appelé "GMM on double-differenced data" qui est consistent et qui donne des résultats meilleurs que l'estimateur GMM FD et QD. Le modèle dérivé de la résolution de programme intertemporel est un modèle non linéaire tel que ;

!

u Cit

u1 + ñ u Pit k(1 + â₁)M^â2

it

log = - log + â₁ log + log + 1 + _uit ,

Ci,t-1 1 + r Pi,t-1 1 + r

Avec i = 1...N et t = 1...T

Sur une base de données composée de 696 observations, l'estimation de ce modèle fait apparaitre une élasticité prix (â₁ = -0.2646) significative et une élasticité revenu (â₂ = -0.3366) non significative.

Le modèle linéaire en logarithme est ;

Cit = äCi,t-1 + _â1Pit + _â2Mit + ái + _ètíi + åit

L'estimation de ce modèle par la méthode "GMM on double-differenced data" donne une élasticité prix (â₁ = -0.3186) et une élasticité revenu (â₂ = 0.4080) qui sont très significatives.

L'application de test Rivers-Vuong d'équivalence asymptotique entre les deux modèles montre qu'on ne peut pas rejeter l'hypothèse nulle d'équivalence à 5% risque de premier espèce.

Le papier de Céline et Alban [2003] est intitulé "Long run study of residential water consumption", alors que l'investigation d'une méthode économétrique susceptible d'estimer un effet de long terme sur données de panel n'a pas été utilisée. L'estimation d'une éventuelle relation de long terme sur un panel non stationnaire fait recours à la littérature économétrique relative à l'estimation d'une relation de cointégration sur données de panel à savoir l'application de différents tests de stationnarité sur panel, puis les tests de cointégration sur données de panel, et par la suite l'estimation d'une relation de cointégration, si elle existe, qui relie les variables du modèle en double indice par la méthode appropriée (FMOLS et/ou DOLS). Les paramètres estimés par l'une de ces méthodes seront interprétés comme étant les élasticités de long terme. L'estimation d'un VECM en panel donne les élasticités de court terme. En revanche, les auteurs ont procédé à une estimation qui ne tient pas compte du paramètre de nuisance (variance de long terme) et ils interprètent l'estimateur GMM comme étant l'effet de long terme.

La non prise en compte d'une variable, dans le modèle, susceptible de capter l'effet pluviométrie, est une limite. En effet, les études de la demande d'eau résidentielle montrent la contribution de cette variable à expliquer une partie de la consommation de l'eau, Ayadi et al [2002][1],R Martinez Espenira [2003][50], R Martinez Espenira [2007][49], l'omission d'une telle variable peut avoir comme conséquence la non robustesse des résultats, une approche qui n'a pas été testée dans ce travail.

Une des issues les plus controversées concernant la littérature de la demande d'eau, est l'analyse des tarifs non linéaires par blocs. L'étude de R Martinez Espenira [2003][50] est la plus récente qui utilise cette approche sur données de panel, et qui permet de mieux comprendre l'intérêt d'une telle spécification de prix dans un systéme de tarification non linéaire. L'analyse représente une modification de celle entreprise par Corral et al.[1998][12], les seuls auteurs connus qui ont employés le prix marginal (weighted-mean) avec de vraies données. Leur modèle est inspiré de celui de Moffitt [1986][?] et Hewitt et Hanemann [1995][21]. La divergence principale de Corral et al [1998][12] est que chez R Martinez Espineira [2003][50], la variable de différence est définie avec précision comme en Nordin

[1976][39] et Schefter et David [1985][51], Notons que la variable différence sera intérpretée comme étant l'indicateur de niveau de vie.

Les spéciÞcations des prix suggérées par Nordin [1976][39] pour l'analyse de la demande sous des tarifs de bloc sont appliquées pour estimer des fonctions de demande de l'eau, en utilisant des données agrégées du nord-ouest de l'Espagne, La disponibilité des données sur la proportion d'utilisateurs par bloc, permet également de modéliser explicitement le choix du bloc. Les résultats prouvent que, dans l'échantillon analysé, les valeurs de l'élasticité des prix sous les spéciÞcations traditionnelles et ceux modernes ne sont pas sensiblement différent. Notons que l'estimation a été conduite sur un panel non cylindré. Les élasticités prix, en introduisant la proportion de nombre d'abonnés par bloc, ont été de l'ordre de (-0.662) par MCO et (-0.475) par 2-step GLS.

La limite de ce travail se traduit par le faite que les séries de données peuvent être non stationnaires, et que l'estimation à tort d'une telle régression conduit à l'interprétation des résultats qui n'ont pas un sens économique (Granger et Newbold [1974])[18] et augmente le risque de faire face à des régressions fallacieuses.

Au niveau national, l'utilisation des données de panel pour estimer la demande d'eau résidentielle, a constitué l'innovation apportée par le travail de Ayadi et al [2002][1]. L'objectif de cette étude a été l'évaluation de la politique tarifaire pratiquée par la SONEDE³, un tel objectif ne pourra être concrétisé que lorsque la Tunisie sera classée parmi les pays les plus pauvres en eau et qu'elle connaîtra un déÞcit entre les ressources mobilisables et les besoins potentiels à l'horizon 2010. En revanche, cette étude a été motivée par l'inclusion de plusieurs innovations, à savoir la subdivision de la Tunisie en six régions, la construction de deux blocs de consommation permettant de mieux capter l'effet prix et l'introduction de l'effet de l'extension du réseau de distribution propre à tout pays en développement.

Pour répondre à cet objectif, les auteurs ont estimé en premier lieu une équation de la demande d'eau pour les deux blocs;

LogC^(j)

it = á(j)

0i + á(j)

1i LogRit + á(j)

2i LogPit + á(j)

3i LogNit + á(j)

4i LogRLit

X + s=1,2,4

á4siQDsit + å(j) (j) 1it

Avec i = 1...6, t = 1...68 et j = 1, 2 (1:bloc supérieur et 2:bloc inférieur)

³SONEDE est la sociéte nationale d'exploitation et de distribution de l'eau en Tunisie, C'est l'autorité responsable de ce secteur.

Là oft C, R et P sont respectivement la consommation moyenne de l'eau par ménage, le revenu moyen des ménages et le prix payé par les consommateurs dans le bloc considéré, N représente la taille de réseau actuelle pour capturer l'effet de l'extension du réseau, RL est un indicateur des précipitations,

QDs est un dummy trimestriel pour le trimestre s et å(j)

1it est un terme

d'erreur aléatoire.

Pour tenir compte de l'aspect non linéaire du tarif, les auteurs estiment une deuxième équation du modèle, la proportion de ménages dans chaque bloc j (pour la région i et la période t) est exprimé en fonction des mêmes variables explicatives que celles de la consommation moyenne excepté le revenu.

1/2NB 3/4(j)

Log N it

_X

= á_0i +á^(j)

(j) 1i LogPit+á(j)

2i LogNit+á(j)

3i LogRLit+ á(j)

4_siQDsit+å^(j)

2it

s=1,2,4

oft N dénote le nombre des consommateurs dans le bloc j .

Les résultats de Ayadi et al [2002][1] ont été conformes aux intuitions i.e. L'effet prix a été négatif pour le bloc supérieur, ce qui traduit le glissement des consommateurs de bloc supérieur vers le bloc inférieur grâce à la tarification rigoureuse qui a comme objectif l'incitation des ménages qui consomment beaucoup de l'eau à le conserver. L'effet prix positif pour le bloc inférieur signifie que la demande de l'eau est relativement inélastique pour les consommateurs de ce bloc.

Les élasticités prix ont été autour de (-0,1) pour le bloc inférieur et autour de (-0,40) pour le bloc supérieur. Les constantes sont toutes positives et varient entre les régions (implique une consommation minimale positive).

L'effet d'extension de réseau est fortement significatif pour les deux blocs, mais du signe opposé pour toutes les méthodes. La consommation moyenne des nouveaux débutants semble être légèrement plus haute, puisque des consommateurs inférieurs existent, de ce fait les coefficients de l'effet de réseau sur le bloc inférieur ont été positifs. Cependant les nouveaux arrivants ne consomment pas autant que le consommateur moyen du bloc supérieur ayant pour résultat un impact négatif sur la consommation moyenne de ce bloc.

Les précipitations ont un impact significatif sur la consommation pour les deux blocs. Son coefficient est négatif comme prévu. L'effet des variables binaires saisonnières a été comme prévu, la consommation augmente pendant les sessions sèches et diminue pendant l'hiver.

Cette étude a été entreprise sans tenir compte du problème de stationnarité des séries en double indice. En revanche, l'utilisation des méthodes habituelle pour estimer une régression linéaire en panel n'a de sens que lorsque les variables sont stationnaires. Ainsi, l'hypothèse de stationnarité si elle impose d'une manière adhoc, aura comme conséquence l'estimation d'une régression fallacieuse.

Notre travail sera la nouvelle version de l'étude de Ayadi et al [2002][1] en évoquant le problème de la non stationnarité et les données de panel. Nous conduisons l'estimation du même modèle toute en utilisant les méthodes susceptibles d'estimer une relation de long terme entre les variables non stationnaires. Par conséquence, notre objectif sera l'évaluation de la politique tarifaire pratiquée par la SONEDE⁴ depuis son existence jusqu'à nos jours, il sera aussi très intéressant d'avoir l'utilité de la technique de cointégration sur données de panel à estimer la demande de l'eau résidentielle. Cette technique économétrique a été beaucoup utilisée pour estimer la demande d'autres types des ressources naturelles mais elle n'était pas utilisée auparavant pour estimer la demande d'eau résidentielle, c'est en faite cette motivation qui nous pousse à conduire ce travail d'économétrie appliquée.

2.4 Les études portant sur des données de panel non stationnaire:

Au début des années quatre vingt dix, La recherche en économétrie théorique a développé une nouvelle littérature qui consiste à appliquer les méthodes des séries temporelle sur la base des données à double dimension, à savoir: les données de panel. L'économétrie appliquée dans cette voie de recherche est actuellement en plein développement et la plupart des économètres appliqués tels que Baltagi H, Pesaren H, Pedroni P, Krichen N ont appliqué cette littérature pour mettre en évidence des relations de long terme en économie internationale aussi bien qu'en économie de développement. Nous synthétisons dans cette section trois études portant sur la relation entre le marché noir et le taux de change, la validation de PPA et la relation entre PIB et la demande de l'énergie.

Pour établir la relation de long terme entre le taux de change sur le marché noir et le taux de change officiel, une méthodologie appropriée serait la technique de cointégration. Cependant, puisque la technique de cointégration exige des données

⁴La base des données couvre la période 1980-2007, des données trimestrielles par governorat;

de série chronologique sur une longue période, il y a seulement un nombre limité d'études dans ce domaine. Booth et Mustafa [1991] [6] et Baghestani et Noer [1993] [4] ont fait deux études qui ont étudiées la relation entre le taux de change sur le marché noir et celui officiel, respectivement pour le cas de la Turquie et l'Inde, ils ont constaté que les deux taux dans les deux pays sont cointégrés et donc l'existence d'un rapport de long terme. Le but de Bahmani-Oskooee M et al [2002][2] est de dépasser le problème de la non existence des séries chronologiques de longue période en empilant les séries temporelles relatives à 49 pays pour appliquer la technique de cointégration sur données de panel et la mise en place d'un rapport de long terme homogène entre les deux taux pour les 49 pays.

Bahmani-Oskooee M et al [2002][2] appliquent les tests de stationnarité inspirés de la logique ADF et le test de cointégration en panel de Pedroni [1999][43] à la Engele et Granger [1987][16]. Le test de cointégration de Pedroni montre que l'hypothèse nulle de stationnarité des résidus est acceptée, les deux taux sont cointégrés.

BEXit = ai + â_it + _ã1iOEXit + _åit ,i = 1....49 et t = 1 18

L'application de test de cointégration sur les résidus de cette régression montre l'existence d'une relation de long terme entre BEX (le taux de change sur le marché noir) et OEX(le taux de change officiel). L'estimation d'une telle relation a été faite par la méthode GLS. Les résultats montrent que le coefficient de long terme est très proche de l'unité. Ainsi, dans le long terme le taux de change officiel sera proche de celui sur le marché noir.

Bien que l'étude de Bahmani-Oskooee M et al [2002][2] était la première à utiliser une base de données relatives à plus que deux pays, La contradiction vient du fait que l'estimation de la relation de long terme n'était pas par une méthode susceptible d'introduire les paramètres de nuisance de long terme, et donc l'application de la méthode FMOLSet/ou DOLS.

Le travail de Chien-Chiang Lee [2005][10] est une étude d'économétrie appliquée sur l'économie de développement portant sur la relation de long terme entre le PIB et la consommation de l'énergie pour un panel de 18 pays développés durant la période 1975-2001.

L'objectif de ce travail est d'estimer la relation de long terme entre le PIB, la consommation de l'énergie et le stock de capital pour les 18 pays du panel, et de déterminer aussi les élasticités de court et de long terme. Ainsi, la relation à estimer est :

GDPit = ái + äit + _âiECit + _ciKit + åit

Là où GDP indique le produit intérieur brut, EC indique la consommation d'énergie et K le stock de capital.

L'implémentation des trois tests de racine unitaire sur panel (LLC, IPS et HADRI) et puis le test de cointégration de Pedroni pour les trois variables montre le rejet de l'hypothèse nulle du non cointégration.

L'estimation de la relation de cointégration par la méthode FMOLS a donné de bons résultats pour les estimateurs individuels, aussi bien que pour les estimateurs Between. En effet, l'étude de Chien-Chiang Lee [2005][10] suggère qu'EC et K promouvoir la croissance économique pour 14 pays de panel (les 14 pays où les estimateurs sont signiÞcatives). Ainsi, les résultats suggèrent qu'il y ait un long-run steady-state entre la consommation d'énergie et le PIB pour un panel des 18 pays après avoir tenu compte d'un effet pays-spéciÞque.

La causalité de long terme et de court terme est uni-directionnelle de EC vers PIB, Ceci implique que la consommation d'énergie soutient le fardeau des ajustements à court terme pour rétablir l'équilibre de long terme entre l'EC et le PIB.

Pour tester l'hypothèse forte de PPA, Pedroni [2001][44] a employé les techniques récentes de cointégration sur données de panel. Cela revient à estimer la relation de long terme pour un panel des pays entre ratio de prix et le taux de change nominal. En utilisant l'estimateur between de la méthode FMOLS et celui de la méthode DOLS, Pedroni [2001][44] montre la valididité de la version forte du PPA pour un panel de post Bretton Woods data.

Dans ce qui suit nous présentons une synthèse des tests de stationnarité et de cointégration sur données de panel, ainsi que les méthodes d'estimation que nous employons pour estimer la situation de long terme de la demande d'eau résidentielle en Tunisie.

Chapitre 2

Non stationnarité et données de

panel

Depuis les travaux de simulations par la méthode de Monte Carlo, menés par Granger et Newbold [1974][18], les études des séries temporelles non stationnaires sont devenue aujourd'hui incontournables dans la pratique économétrique courante. Les travaux en économétrie appliquée doivent débuter par une analyse de la stationnarité des séries temporelles considérées, par l'application de divers tests de racine unitaire en premier lieu, et par l'application de tests de cointégration par la suite, pour mettre en évidence des relations d'équilibre de long terme entre les variables intégrés d'ordre un. En revanche, l'analyse de panel non stationnaire ne s'est développée qu'après les travaux fondateurs de Levine et Lin [2002][35]. Elle s'est en particulier développée avec l'utilisation des bases de données macroéconomiques présentant une dimension temporelle suffisante⁵. Les études portant sur les tests de racine unitaire en panel couvrent aujourd'hui l'étude de PPA Pedroni [2001][44],Oh [1996] et Kao et al [1999][31], les activités de R&D au niveau international, etc....

L'ampleur de tester la stationnarité en panel vient du fait que l'ajout de la dimension individuelle à la dimension temporelle augmente la puissance du test et permet de tenir compte de l'hétérogénéité des propriétés dynamique, de la variable considérée. Ces avantages ne sont plus disponibles lorsqu'on travaille avec des séries chronologiques, et même si on tente d'étendre la période d'étude pour augmenter la puissance du test en séries temporelles, on y risque de faire face à des ruptures

⁵pour que la problématique présente un intéret,la dimension temporelle doit dépasser vingt ans.Voir Hurlin et Mingion [2005] pour plus de discussion.

structurelles⁶.

La différence entre les tests de racine unitaire en séries temporelles et en panel est au niveau des distributions asymptotiques. En effet, dans le cas des séries temporelles, les statistiques des tests usuels ont des distributions asymptotiques non standards et varient selon la spécification du modèle avec ou sans constante et tendance déterministe, alors qu'en panel les tests de racine unitaire (à l'exception de test du fisher) sont normalement distribués asymptotiquement. Notons au passage que la convergence qu'on admet est de type séquentielle⁷.

L'objectif de ce chapitre est de rendre compte des développements théoriques sophistiqués relatifs aux tests de stationnarité et de cointégration sur données de panel.

3.1 Les tests de racine unitaire sur données de panel

3.1.1 Test de racine unitaire de Levin, Lin et chu [2002]

1.1.1.1 objet du test

Andrew Levin,Chien-Fu Lin et Chu [1992,1993,2002][35] ont proposé le premier test de racine unitaire en panel. Ce test est inspiré de celui de DF [1979] et ADF [1981] en séries temporelles.

L'objectif du recours aux données de panel est d'augmenter la puissance du test. La procédure utilisée ici consiste à admettre sous l'hypothèse nulle que chaque individu de panel possède une série chronologique intégrée d'ordre un (I(1)), contre l'alternative selon laquelle la chronique est globalement stationnaire⁸. Tout en précisant l'avantage de ce test par rapport aux tests DF et ADF [1981][15] en terme de puissance, les auteurs montrent que la statistique de ce test est distribuée

⁶Des recherches en économétrie théorique sont aujourd'huit en pleine développement à fin de produire des tests de racine unitaire en panel incluant la possibilité de ruptures structurelles. Parmi ces tentatives, nous citons Im, Lee et Tieslau (2002), reprenant les développements de Im et Lee (2001). Ce test, constituant une extension du test de Schmidt et Phillips (1992) et Amsler et Lee (1995) basé sur le principe du multiplicateur de Lagrange.

⁷la convergence séquentielle signifie qu'on raisonne dans un premier temps à N fixe (ou T) et l'on fait tendre T (ou N) vers l'infini, puis l'on fait tendre N (ou T) vers l'infini.

⁸c'est en faite le défaut majeur de ce test est qu'il impose l'homogénéité de la racine autorégressive sous l'hypothèse alternative.

asymptotiquement selon une loi normale centrée réduite à l'inverse de statistique des tests DF et ADF qui ne rêvent pas d'une loi usuelle et qui varie selon la spécification du modèle (avec ou sans constante et tendance déterministe).

1.1.1.2 Procédure de test

Supposons que la variable {yit} est génerée par l'un des trois modèles suivants

:

Modéle 1: Ayit = ä yi,t-1 + åit

Modéle 2: ?yit = á0i + äyi,t-1 + åit Modéle 3: ?yit = á0i + á1it + äyi,t-1 + åit

oil --2 ? ä 1 0 pour i = 1 N et pour t = 1 T

Le processus _åit est indépendament distribué entre les individus selon MA

(00) inversible: åit =

P8 j=1

èij åi,t-j + uit

pour tout i = 1 N et t = 1 T

E( å^4it) < 00 ; E(u^2it) ° Bu > 0 et E( å2 it) +2

P8 j=1

E(åit åi,t-j) < Bå < 00

Dans le modèle 1 la procédure de test de racine unitaire sur panel examine l'hypothèse nulle H0 : ä = 0 contre l'alternative H_a : ä < 0 Dans le modéle 2, la série {yit} a une constante spécifique individuelle mais sans tendance temporelle et dans ce cas la procédure de test de racine unitaire sur panel examine l'hypothèse nulle H0: ä = 0 et á0i = 0 Vi contre H_a : ä < 0 et á0i E R. Finalement pour le modéle 3 la série {yit} a une constante et tendance temporelle, dans ce cas, la procédure de test examineH0: ä = 0 et á1i = 0 Vi contre H_a : ä < 0 et á1i E R

Comme dans le cas de série temporelle si la série présente une constante et /ou tendance mais non inclut dans la spécification, céla réduit la puissance statistique de test, pour simplifier la notation, dmt et ámi sont utilisés pour indiquer le vecteur des variables déterministes et celui de coefficients associées.

avec m = 1, 2, 3

2 óui

=

1 T -pi-1

T t=pi+2

(àeit -- ^àäiàvi,t-1)^2

L'écriture ADF des modéles 1,2 et 3 est la suivante:

Pi

?yit = äyi,t-1 + èil?yi,t-L + ámidmt + uit (3.1)

L=1

oil d1t = o, d2t = {1} et d3t = {1,t}.

Les auteurs proposent une procédure en trois étapes à fin d'implimenter leurs test.

Étape 1: régression ADF et résidus orthogonalisés Pour chaque indi-

vidu, la régression ADF est appliquée,

Pi

?yit = äiyi,t-1 + èil?yi,t-L + ámidmt + uit o`u m = 1, 2, 3 (3.2)

L=1

Il est permis à Pide varier entre les individus. Les auteurs ont adopté la méthode P_max proposée par HALL [1990]. Il s'agit de tester la signiÞcativité statistique du dernier ^àèil pour séléctionner le nombre de retard optimal.

une fois le retard Pi est sélectionné pour chaque individu,on régresse ?yit et _yi,t-1 sur _?yi,t-L (L = 1 Pi) et on récupère les résidus de ces régressions :

Pi

àeit = ?yi t -- àðiL?yi,t-L àámidmt

L=1

Pi

ikt-1 = yi,t-1 E ðiL?yi,t-L ámidmt L=1

Pour contrôler l'hétérogéneité entre les individus, on normalise ces deux résidus par rapport à l'écart type de résidus de l'équation (1.2) , soit àóui

àeit àóui

eit =

et 'bi,t-1 = oil _àóui peut être calculée à partir de la régression de

"^dui

àeit sur àvi,t-1.

Étape 2: Estimation de la ratio de la variance: Sous l'hypothèse nulle

(H0) de racine unitaire la variance de long terme pour le modèle (1.2) peut s'estimer comme suit:

àó 2 = 1 yi T-1

PT t=1

?2yi t + 2.

PK L=1

w [ 1 KL LT-1

PT t=2+L

?yi t?yi,t-L]

Pour le modèle (2) on remplace ?yi t par (?yi t - ^E?yi t ). Si la série inclut une tendance temporelle (m = 3) alors, la série doit être corrigée de la tendance avant l'estimation de la variance de long terme. Les auteurs appliquent la procédure d'Andrews[1991] pour déterminer K.La pondération w _KL depend du choix de K ainsi w = 1 L

K L k+1

Maintenant pour chaque individu i le ratio de la variance de long terme par rapport au variance des innovations est;

si = yi qu'on l'estime par: = åi åi Le moyen de la ratio de variance est: SN = N 1			PN i=1	si et qu'on l'estime par
1 N = N	PN i=1	àsi.

Cette spéciÞcation sera utilisée dans l'étape 3,notammant dans l'équation (1.3) pour ajuster l'ésperance de la t-statistique.

Étape 3: Calcul de statistique de test sur panel; On empile toutes les

observations relatives aux individus pour estimer:

eit = ä vi,t-1 + uit

3 N × Test le nombre totale de données oil T = T - pE -1 et pE= 1 P pi

N

i=1

.

La statistique conventionnelle pour tester ä = 0 est donnée par ;

äà

tä = àóàä

_PT
t=2+pi

_PN
i=1

äà =

T

X (eit - ^àävi,t-1)²

vi,t-1eit

i=1 _PN

1

2

t=2+pi

_PT vz,t-1

2


·

àóàä =



" N T_XXàóå v2 i,t-1

i=1

t=2+pi

N

óå

=
2 N x 1 T i=1 t=2+pi

Sous H0 : ä = 0 .Les auteurs montrent que la t-statistique (tä) a une distribution asymptotique normale centrée réduite pour le modèle 1, mais diverge vers moins l'inÞni en ce qui concerne les modéles 2 et 3. Toutefois pour corriger cette divergence il convient de calculer la t-statistique ajustée de la manière suivante:

t* ä=	tä - N x T x^àSN x o-i^2 x std(ä) x u*mT	T , N -?8N(0; 1)avec v T ? 0
	ó* m T

(3.3)

u* mT et ó*m _T servent à ajuster respectivement la moyenne et l'écart type de tä .Leurs valeurs ont été simulées par les auteurs et reportées au tableau 2 de leur papier (voir Levine, lin et chu [2002][35]).

L'hypothèse nulle est rejetée pour une réalisation de la statistique corrigée t^*ä inférieure au seuil de la loi normale centre réduite (-1, 64) pour un test non symétrique à 5% risque de prmière espèce), ainsi l'hypothèse de racine unitaire est rejetée pour l'ensemble des individus de panel. C'est en fait la limite principale de test LLC [2002].

3.1.2 Test de racine unitaire d'Im, Pesaran et Shin [2003]:

-

Le défaut majeur de test LLC [2002] est qu'il impose l'homogénéité de la racine autorégressive sous l'hypothèse alternative. Le test d'Im,Pesaran et Shin [2003][28]

que nous venons à présenter permet de répondre à cette critique puisqu'il permet une certaine hétérogénéité de la racine autorégressive sous H_a pour un groupe d'individu N1 E ]0; N[, telque limN?8(N1/N) = ä o 0 - ä -< 1. Si N1 = 0, on retrouve l'hypothèse nulle.IPS sont les premiers à développer un test qui permet non seulement une hétérogénéité de racine autorégressive sous H_a (ñi =6 ñj), mais aussi une hétérogénéité quant à la présence d'une racine unitaire dans le panel.

La méthode d'IPS peut être décriter de cette maniére :

Premièrement,IPS considérent un modèle de type ADF pour chaque individu i = 1 N du panel.

Modéle IPS:

?yit = ái + _ñiyi,t?1 + _XPi âij?yi,t-j + _åit , V i = 1 N; Vt = 1 T (3.4)

J=1

O l'effet individuel ái est déÞni par ái = --ñiãi avec ã_i E J1 et o _åit est N.i.d(0, ó2 i ).

IPS autorisent la présence d'une autocorrélation des résidus d'ordre différent pour chaque individu du panel. Le nombre de termes ADF diffère à priori entre les individus pi =6 pj comme dans le test de Levine et al [2002][35].

L'hypothèse qui fait l'objet de ce test est formulée comme suit: H0 : ñ_i = 0 V i = 1 N

H_a : ñ_i -0Vi=1 N1

ñi=0?i= N1+1,N1+2, N

Pour tester cette hypothèse IPS proposent d'utiliser la moyenne des statistiques individuelles ADF:

1

tiT(pi, âi)

N

tNT =

_XN
i=1

o _tiT (pi, âi) correspond à la statistique individuelle de student associée à l'hypothèse nulle H0,i : ñi = 0 dans le modèle d'IPS pour un nombre de retards pi et un vecteur de paramétres ADF â_i = (âi,1 âi,pi)⁰.

Le choix du retard optimal pi permet de purger l'auto corrélation des résidus. La méthode de sélection du retard peut être choisie de la même façon que dans le cas des tests de Levin et al [2002][35].

En utilisant les N statistiques ADF individuelles _tiT(pi, â_i), on construit la statistique standardisée:

"v #

N(tNT - E(tiT))

_p

V ar(tiT)

Ztb_ar(p,â) =

l -'- N(0,1)siT - 6 (3.5)

N ? 8

E(tiT) et V ar(tiT) sont l'espérance et la variance de la distribution asymptotique (quand T ? 8) d'une statistique ADF sous l'hypothèse nulle de racine unitaire (ñ_i = 0) dans un modèle avec constante. Ces moments sont respectivement égaux à -1, 533 et 0, 706.

Ainsi,nous pouvons montrer facilement que la statistiqueZtb_ar(p, â) converge séquentiellement vers une loi normale centrée réduite lorsqueT puis N tendent

vers l'infini.

"v # N(tNT - E(tiT )) Ztbar(p, â) = p V ar(tiT)

T,N ? 8 -'- N(0,1)

Cette approche est fondée sur la distribution asymptotique, ce qui peut poser problème dans des échantillions de dimension temporel finie. IPS proposent une autre statistique _Wtbar(p, â) qui a la même distribution que _Ztbar mais qui est plus puissante à distance finie. C'est la plus génerale puisqu'elle tient compte de l'autocorrelation des résidus. Cette statistique est définie de la même façon que _Ztbar(p, â) à la différence prés que l'on centre et l'on réduit à partir des moments de la statistique ADF obtenue sous l'hypothèse nulle de racine unitaire et sous l'hypothèse que âi sont des termes ADF, ces moments sont respectivement E(tiT(pi, 0)/ñi = 0) et V _(tiT(pi, 0)/ñi = 0) et qu'ils tiennent compte de l'information contenue dans le nombre de retard pi.

Wt(p,â) =

? ? ? ? ? ?

· ? v PN N tNT - N-1 E(tiT (pi, 0)/ñi = 0) ?? i=1 s ? T, N ? 8 -'- N(0, 1) ? PN ? N-1 V (tiT (pi, 0)/ñi = 0) i=1

Ces moments sont tabulées pour différentes ordre des retards pi et pour différentes tailles temporelles T.

L'hypothèse nulle est rejetée lorsque la réalisation de la statistique Wt(p, â) est inférieure au seuil de la loi normale centrée réduite .

3.1.3 Test de racine unitaire de Maddala et Wu [1999]: (approche non paramétrique)

Les deux tests précedents sont deux tests paramétriques.Le test de Maddala etWu [1999][36] est une approche non paramétrique de Fisher [1932] pour tester la présence d'une racine unitaire en panel. Cette approche se base sur la combinaison des différents niveaux de signiÞcativité (p-value) des N tests individuels de racine unitaire indépendants.

Soit æi la statistique de test de racine unitaire pour l'individu i dans le modèle suivant:

?yit = ái + _ñiyi,t?1 + _XPi âij?yi,t-j + _åit , ? i = 1 N; ? t = 1 T (3.6)

J=1

Soit pi = -FTi( æi) la p-value associée à une statistique de test æi de l'hypothèse nulle de racine unitaire pour un individu i donné oft -FT_i(.) désigne la fonction de répartition associée à la statistique individuelle æi pour un échantillon de taille Ti . La statistique de test æ_i peut être choisie comme la t-statistique d'un test ADF ou la statistique de n'importe quel autre test de l'hypothèse nulle de racine unitaire ( Phillips et Perron [1988][46], KPSS, etc...).

Ce test est directement comparable au test IPS et lui est trés similaire.

Maddala et Wu [1999][36] ont proposé la statistique suivante pour combiner les différents niveaux de signiÞcativité.

PMW = -2 _XN ln(pi) (3.7)

i=1

L'avantage de ce test par rapport à celui de IPS est qu'il n'exige pas que le panel soit cylindré.

Si les statistiques individuelles du test sont continues, les p-value sont distribuées selon un ÷²(1) alors,

N

PMW = -2 i=1 ln(pi) ÷²(2N)

Pour une dimension individuelle très élevée, Choi [2001][14] propose la statistique standardisée suivante;



v

N [PMW - E(-2ln(pi)]

1

_XN
i=1

=

2vN

(-2ln(pi) - 2) (3.8)

ZMW =

_p

V ar(-2 ln(pi))

Or ln(pi) -? 1, donc E(-2 ln(pi) = 2 et V ar(-2 ln(pi)) = 4.La statistique de Choi correspond tout simplement à une statistique moyenne de type NW centrée et réduite, ainsi sous l'hypothèse nulle, si on suppose que les p-value sont i.i.d, la théoreme centrale limite permet de juger que ZMW --+ N(0, 1) lorsque N-? 8.

En ce qui concerne la décision de stationnarité, l'hypothèse nulle est rejeté tant que la réalisation de _PMW est supérieure au seuil de la loi de chideux.

3.1.4 Test de stationnarité de Hadri [2000]:(hypothèse nulle de stationnarité)

Hadri K [2000][25] a dérivé un test basé sur le multiplicateur de lagrange de résidus. A l'inverse des autres tests, Hadri [2000] est un test de l'hypothèse nulle de stationnarité contre l'alternative de racine unitaire dans le panel considéré. Il est basé sur les résidus de la régression MCO de yit sur une constante et une tendance, en particulier Hadri [2000] considére les deux modéles suivants:

yit = rit + åit, ? i = 1 N et ? t = 1 T (3.9)

yit = rit + âit + åit ,? i = 1 N et ? t = 1 T (3.10)

avec rit = ri,t-1 + uit est une marche aléatoire, _åit IIN(0, ó²_å) et uit

IIN(0, ó²_u)

cov(åit, uit) = 0 V i, t.

Par une substitution de rit dans yit on aura:

yit = ri0 + âit +

Xt s=1

uis + åit = ri0 + âit + vit (3.11)

t

o`u vit = uis + åit

s=1

ri0 étant des valeurs intiales jouant le rôle de constante hétérogénes. Si ó2 _u = 0 alors vit = åit est stationnaire (rit est une constante).

Si ó²_u =6 0 alors ,vit est non stationnaire (rit est une marche aléatoire ).

Hadri [2000] test l'hypothèse nulle ë = 0 contre l'hypothèse alternative ë 0 o`u

_ó2

ë = u

ó2 _å

i.e; H0 : ë = 0

Ha : ë 0

En notant _àvit les résidus estimés de (yit = ri0 +vit) ou (yit = ri0 + â_it +vit), La statistique LM est donnée par:

1 LM = àó2 å

1 NT2 (

XN i=1

XT t=1

S2 it)(3.12)

Avec Sit désigne la somme partielle des résidus.

t

Sit = vis et àó²_å est un estimateur convergent de ó² _å.

s=1

Sous H0 de stationnarité en niveau, la statistique de test est;

Zu =

N^h LM - E hR 0 1 v(r)2drii rV hR 0 1 v(r)2dri

--+ N(0,1) (3.13)

v(r) est un pont brownien standard, pour T ? 8 suivi de N ? 8, les cumulants de la fonction caractéristique de ^R01 v(r)² donnent respectivement la moyenne et la variance de ^R01 v(r)² intervenant dans Z_u :¹₆(cumulant d'ordre 1) pour l'espérance et ₄¹₅ (cumulant d'ordre 2) pour la variance (voir K.Hadri [2000] pour les détails).

Sous H0 de stationnarité autour d'une tendance déterministe (modéle yit = rit + â_it + _åit) la statistique de test est:

Zô =	N^h LM - EhR 0 1 v2 (r )^2dri		--+ N(0, 1) (3.14)
	rV hR 0 1 v2(r)2dri

Où v2(r) = w_r + (2r - 3r²) x w(1) + 6r(r - 1) R₀¹w(s)ds (Voir Kwiatkowski et al [1992][32]).

Z 1

La moyenne et la variance de v2(r)²dr sont données par les deux pre-

0

miers cumulants soit,respectivement,¹₅ et ₆₃¹₀¹₀.

Afin d'étudier la performance de son test, Hadri (2000) a mené des simulations de monte carlo, celles-ci ont ressorti que la taille de Z_u est proche de la taille théorique de 5% pour T > 10 et la taille de test Z_ô est correcte pour T > 25. La puissance de test augmente avec la valeur ë pour tout T et N.

La décision de test sera prise en comparant la réalisation de la statistique Z_u et/ou Z_ô à la quantile de table de la loi normale centré réduite, la différence par rapport aux autres tests est que le rejet de l'hypothèse H0 signifie la non stationnarité.

Une fois la stationnarité de panel est testée, l'estimation par les méthodes classiques n'a plus de sens et une tentative d'estimation doit passer par un test de cointégration sur données de panel. L'estimation d'une éventuelle relation de long terme en panel sera à travers d'autres méthodes plus sophistiquées telleque la

méthode FMOLS (fully modiÞed ordinary least squares) et/ou DOLS (dynamic ordinary least squares).

3.2 Notions de cointégration en panel

L'économétrie de données de panel non stationnaire est l'utilisation des différentes méthodes des séries temporelles en tenant compte de dépendances interindividuelles, cette dépendance est une concept spéciÞque à l'utilisation des données de panel. L'économétrie de panel non stationnaire appliquée sur la macroéconomie ne doit pas ignorer une telle dépendance interindividuelle parce qu'il est rare que les pays se comportent de la même manière à long terme. Ainsi, nous pouvons envisager l'existence des deux types de relations de cointégration, des relations intra-individuelles, et d'autres inter-individuelles.

3.2.1 Relations de cointégration intra-individuelles

Nous évoquons à présent la dimension spéciÞque à l'économétrie de données de panel à savoir la distinction entre l'inter et l'intra-individuelles. L'existence de relations de cointégration intra-individuelles signiÞe la présence d'une ou de plusieurs combinaisons linéaires des variables y(j)

it ~ I(1) qui soient stationnaires. i.e, pour l'individu i, il existe ri relations de cointégration intra-individuelles parmi les j variables non stationnaires si et seulement si:

â0 iyit = uit ~ I(0)

âi de dimension (ki, ri) désigne la matrice contenant les vecteurs de cointégration pour l'individu i. Ces relations de cointégration ne font intervenir que des variables propres à l'individu i.Par exemple, pour notre application l'existence d'une relation de cointégration entre la consommation d'eau résidentielle et le prix moyen implique que pour une région donnée, il existe une combinaison linéaire de la consommation d'eau résidentielle et de prix moyen qui soit stationnaire. C'est ce qu'on qualiÞe de relations de long terme hétérogènes. Alors que le cas contraire sera qualiÞé de relations de long terme homogènes ou inter-individuelle (cross unit cointegration).

3.2.2 Relations de cointégration inter-individuelles

On parle de relations de cointégration inter-individuelles si l'on souhaite tester ou estimer des variables observées sur plusieurs individus. Ainsi, nous considérons le vecteur empilé des variables individuelles yt et pour simpliÞer nous supposons le même nombre de variables endogènes pour tous les individus, i.e.ki = k ,on dit qu'il existe r relations de cointégration inter-individuelles si et seulement si :

âyt = ut ~ I(0)

â de dimension (Nk, r) désigne la matrice contenant les vecteurs de cointégration communs pour tous les individus de panel.

3.3 Les tests de cointégration sur données de panel

Dans cette section nous abordons une présentation détaillée des tests de cointégration sur données de panel non stationnaire. L'esprit de cette littérature ne se diffère pas de celle des tests de racine unitaire en panel. Ainsi que le notent Baltagi et Kao [2000][7], L'économétrie des données de panel non stationnaire vise à combiner le "meilleur des deux mondes": le traitement des séries non stationnaires à l'aide des méthodes des séries temporelles, et l'augmentation du nombre des données et de la puissance des tests avec le recours à la dimension individuelle.

Les sept tests de Pedroni [1999][43] se basent sur l'hypothèse nulle d'absence de relation de cointégration. Ces sont des tests résiduels analogues aux tests proposés par Engel et Granger [1987][16] dans le cadre des séries temporelles.

Larsson et al [2001][33] est un test inspiré des travaux de Johansen [1991][29] basé sur les méthodes algébriques. C'est le test de cointégration multiple qu'on l'applique dans ce modeste travail.

3.3.1 Le test de cointégration sur données de panel de larsson et al [2001]

Larsson R, Lyhagen J et Löthgren M [2001][33] ont proposé un test de cointégration analogue au test de johansen [1991][29] en série temporelle. La procédure de

test consiste à tester la présence de r relations de cointégration entre les p variables I(1), (p - 1) sont supposées des variables explicatives. Le problème d'endogénéité n'est plus posé puisque la spéciÞcation initiale est un VAR(Ki) sur panel⁹.

Yit = _XKi Ðik(Yi,t-k) + åit ? i = 1 N, Ki denote l'ordre du processus VAR

k=1

Yit = (y⁽¹⁾

it , , _y(P )

it ) _,åit iidN(0, ?i)

Parmi les P variables (P - 1) sont des régresseurs.

Sous cette représentation, une représentation à correction d'erreur existe (Voir Engel et Granger [1987][16]). Le modèle vectoriel à correction d'erreur ( V ECM) hétérogène est:

?Yit = ÐiYi,t-1 + Ki-1_X ik?Yi,t-k + åit ? i = 1 N, ? t = 2 T (3.15)

k=1

on montre que Ði = áiâ0 _i oft ái de dimension (p x ri) est la matrice qui capte les forces de rappels individuelles à l'équilibre de long terme. â0 i de dimension (ri x p) est la matrice des coefficients de cointégration.

L'idée de test consiste à examiner le rang de la matrice Ði de dimension

(p x p).

H(r) : rang(Ð) = r H(p) : rang(Ð) = p

Le ratio de vraisemblance applé aussi statistique trace est:

-2 ln QT {H(r)\H(p)} = -T		XP j=r+1	ln(1 - ^àëj) (3.16)

⁹la spéciÞcation VAR est une forme de modélisation en boite noire et on ignore la distinction entre variable exogène et variable endogène.

oft ëj est la ^ji'eme valeur propre de la matrice Ði .

Johansen [1995] a étudié la distribution asymptotique de statistique trace comme suit:

1/2Z ₁ Z 1 Z 1 3/4

-2 ln QT {H(r)\H(p)} ?- w Zk = tr (dw)w⁰( ww⁰)^-1 w(dw)⁰

0 0 0

Avec w un mouvement Brownien de dimension K = p - r.

Nous nous intéressons à tester l'hypothèse nulle (H0) que chaque individu de panel possède au plus r relations de cointégration entre les P variables supposéesI(1). Formellement, Cela revient à tester;

H0 : rang(Ði) = ri = r ? i = 1 N

H_a : rang(Ði) = P ? i = 1 N

La statistique trace susceptible de tester le rang de cointégration pour chaque individu de panel est;

LRit {H(r)\H(P)} = -2 ln _QiT {H(r)\H(P)}

La statistique trace moyenne est; XN 1 LRNT {H(r)\H(P)} = N i=1

LRiT {H(r)\H(P)}



EnÞn, Larsson et al [2001] ont proposé la statistique trace standardisée pour tester le rang de cointégration du panel déÞnie par;

v

N(LRNT {H(r)\H(P)} - E(Zk))

ÕLR {H(r)\H(P)} = _p N(0, 1) (3.17)

V ar(Zk)

E(Zk) et V ar(Zk) sont les moments de la variable aléatoire Brownienne, qui ont été simulés par Larsson et al [2001].

Les auteurs ont prouvé que ces moments existent et sont Þnis (Voir papier LLL[2001] pour plus de discussion).

Notons que ce test est unilatéral, pour un risque de premier espéce á, H0 : rangÐi = ri = r est rejetée si Õ_LR {H(r)\H(P)} Â _z1?á ^oft _(z1?á est la quantile standard de la loi normale).

La procédure de test est celle de Johansen [1988], C'est une procédure séquentielle.

3.3.2 Le Test de cointégration sur données de panel de Pedroni [1999,2004]:

Dans une série de contribution Pedroni Peter a proposé des tests de cointégration à la Engel et Granger [1987][16] d'hypothèse nulle d'absence de relation de long terme oft le rang de cointégration est à priori connu. Le test de pedroni [1999][43] est une extension au cas oft la relation de cointégration comprend au plus deux variables. Tout comme les tests de racine unitaire d'IPS, Il est permis à la racine autorégressive de varier entre les individus sous l'hypothèse alternative. Ainsi, la relation de cointégration, si elle existe sous l'hypothèse alternative, est hétérogène.

La prise en compte d'une telle hétérogénéité est un avantage puisqu'en pratique, il est rare que les individus se comportent de la même manière. Dans ces conditions, imposer de manière erronnée une homogénénité conduit au non rejet de l'hypothèse nulle, même si les variables sont cointégrées.

yit = ái + äit + _â1ix1,it + _â2ix2,it + + _âMixM,it + åit (3.18)

oft i = 1,....,N,t=1,...,Tetm=1,...,M (3.19)

Sur les sept tests proposés par Pedroni, quatre sont basés sur la dimension within (intra) et trois sur la dimension between (inter). Les deux catégories de tests reposent sur l'hypothèse nulle d'absence de cointégration: ñi = 1 ? i ,ñi désignant le terme autorégressif des résidus estimés sous l'hypothèse alternative tels que;

àåit = ñiàåi,t-1 + uit (3.20)

Les Tests basés sur la dimension Within (intra) {panel cointegration statistics}

Les quatres tests basés sur la dimension intra sont critiqués du fait que l'alternative, si on l'accepte, est commune à tous les individus.

Test non paramètrique de type rapport de vraisemblance (panel õ - statistic):

XXL-2:àå

(3.21)

N T -1

T2 N ZàvN,T T2 .10 11i i,t-1



i=1t=1

Test non paramètrique du type de la statistique rho de Phillips-Perron (Panel ñ - statistic) :

N T 1 N T

TNZàñN,T-1 XX

àL-1gt-1! × XX ^àL11²i(àåi,t-1?'eit - aki

i=1 t=1 z=1 t=1

Test non paramètrique du type de la statistique t de Phillips-Perron ( Panel t - statistic):

N T -1/2 N T

6-N,T XX àL11ig.

ZtN,T

i,t-1 XX^àL^-11²i(àåi,t-1?'eit - aki)

i=1 t=1 i=1 t=1

Test paramètrique du type de la statistique t de Dickey-Fuller Augmenté (panel t - statistic) :

N T -1/2 N T

ZtN,T 4,T XX

_XX

i=1 t=1 11i i,t-1 i=1 t=1

Avec :

T

^àL²11i = T1 P

t=1

(1)

+1

T

t=s+1 ^àçit^àçi,t-s ;

^àëi = T-1

(1)

+1

t=s+1 _PT àuitàui,t-s

_Pki

s=1

à2+2T -1

çit

ki

s=1

s^*2 = ikr-1 .L Y	N i=1		à*2 si
T -1 si =		PT t=1		,,à *2 , Pit ,	ó2 N,T = N-1	PN i=1	T -2 à 2 ; à2 à2 ói = si + 2 ati ; às2i T-1 P t=1		àu2 it

ki

et ; ^àuit = àåit - àñiåi,t-1 ,àu^*_it = àåit - àñiåi,t-1 - àñik?àåi,t-k ,^àçit =

k=1

1

?yit - _PM ^àbmi?xmi,t .

m=1

Les Tests basés sur la dimension between (group mean panel cointegration statistics):

Test non paramètrique du type de la statistique rho de Phillips-Perron ( group ñ - statistic):

i=1 t=1 t=1

\

XX4N _T -1 ,t-1) × E(àåi,t-1^,wit - ëi

TN¹²ZàñN,T-¹ = TN¹²



Test non paramètrique du type de la statistique t de Phillips-Perron ( group t - statistic) :

N-1/2ZtN,T = N-1/2

N T ! -1/2 T eri2 X X(àåi,t-1?:àåit - i=1 t=1 t=1

Test paramètrique du type de la statistique t de Dickey-Fuller Augmenté ( group t - statistic) :



_{N T} ! -1/2 T

s_i åit-1

åit?1?åit

i=1

t=1 t=

XX

N-1/2 Z*tN,T = N-1/2

Pour mettre en oeuvre ces sept tests, Pedroni [1999][43] a procédé en cinq

étapes :

1. L'estimation de l'équation (1.19) et la récupération des résidus àåit.

2. Le calcul des résidus issus de la régression; ? yit = b1i?x1,it + b1i?x2,it + ... + b1i?xM,it + çit

3. L'estimation de la variance de long terme àL2 11i de ^àçit.

4. L'utilisation de _àåit pour choisir la régression appropriée, L'estimation de (1.20) pour les tests non paramètriques et puis le calcul de la variance de long terme de _àuit (àó2 _i ) et L'estimation de (1.20) augmentée du retard pour les tests paramètriques, puis le calcul de às^*2

i la variance de àu* _it .

5. à partir des calculs réalisés dans les étapes précédentes, on construit n'importe quel statistique parmi les sept proposées par Pedroni.

v

£N,T - u N

_võ N(0, 1) (3.22)

£N,T désigne l'une des sept statistiques proposées, par Pedroni, les deux moments u et õ ont été tabulés par l'auteur en fonction du nombre de régresseurs et de la présence ou non d'une composante déterministe dans les relations de long terme. Ils sont nécessaires à la normalisation. Ainsi, le calcul des valeurs critiques relatives à chaque test devient possible (Voir pedroni [1999][43], tableau 2).

3.4 Estimation

Bien que l'estimateur de moindre carrée ordinaire MCO est le plus efficace dans la famille des estimateurs linéaires depuis son existence, on le note souvent BLUE (best linear unbased estimateur), sa distribution est asymptotiquement biaisée, et dépend des paramétres de nuisance associés à la présence de corrélation sérielle dans les données ( Voir Hurlin et Mignon (2006))[27], Un tel problème est posé également pour les données de panel.

Pour estimer une relation de cointégration sur un panel non stationnaire, il est nécessaire d'utiliser une méthode d'estimation efficace. Deux techniques existent à savoir la méthode FMOLS (Fully ModiÞed Ordinary Least Squares) proposée par Phillips et Hansen [1990][45], étudiée par Pedroni [1996][42] et la méthode DOLS ( (Dynamic Ordinary Least Squares) de Saikkonen [1991][52] et Stock et Watson [1993][53].

Dans le cas des données de panel, Kao et Chiang [2000][30] ont montré que ces deux techniques conduisaient à des estimateurs asymptotiquement distribués selon une loi normale de moyenne nulle. Des résultats similaires sont obtenus par Pedroni [1996][42] et Phillips et Moon [1999][47] pour la méthode FM-OLS.

3.4.1 La méthode FM-OLS (fully modified ordinary least squares)

Cette procédure, étudiée notamment par Pedroni [1996][42], permet de tenir compte des problèmes d'endogénéité du second ordre des régresseurs (engendrée par la corrélation entre le résidu de cointégration et les innovations des variables I(1) présentes dans la relation de cointégration)¹⁰ et des propriétés d'autocorrélation et d'hétéroscédasticité des résidus.

Soit le modèle de régression entre deux variables avec un terme constant :

yit = ái + _âxit + u1,it (3.23)

Avec :

xit = xi,t-1 + u2,it

Soit wit = (u1,it ; u2,it)^' un vecteur stationnaire de matrice de variance covaraince asymptotique ?i? i = 1, ..., N.que l'on peut décomposer d'une maniére usuelle en une covaraince contemporaine ?0 i et une somme pondérée d'autocovariance i. Formellement,

?i = ?0 i + i + ' i

oft ?0 i désigne la covariance contemporaine et i désigne la somme pondérée d'autocovariances. â est le vecteur de cointégration:

L'estimateur FMOLS de â est donné par Pedroni P [1996][42]:

XN !-1 XN XT !

_XT

àâF MOLS = àL-2 (xit - xi)2 àL-1

11i àL-1 (xit - xi)y* it - T àãi

22i 22i

i=1 t=1 i=1 t=1

(3.24)

oft:

y* it = (yit - yi)	^àL21i ^àL22i	?xit +	^àL11i - àL22i â(xit - xi) (3.25) ^àL22i

¹⁰Nous considérons que xi est univariée alors que dans le cas générale xi peut inclure M régresseurs qui ne sont pas cointégrées entre eux.

^àLi est la décomposition triangulaire inférieure de l'estimateur ^à?i de la ma-trice de variance covariance asymptotique ?i, ^àLi étant normalisé de telle sorte que

^àL22i = à?-1/2

22i , et le paramètre d'ajustement pour la corrélation sérielle àãi s'écrit :

àãi = ^à21i +	à?^0 21i	à21i ( à22i +	à?022i)
		à 22i

comme nous l'avons précédemment mentionné, les distributions asymptotiques des estimateurs basés sur la méthode FM - OLS sont non biaisés et ne dépendent pas des paramètres de nuisance.(Voir Phillips et Moon [1999][47])

En passant aux données groupées et suivant l'approche Between, l'estimateur FMOLS appliqué aux données de panel se calcule comme la moyenne des ^àâFMOLS individuels.

Panel Group FMOLS : ^àâFMOLSG = N-1 _XN ^àâFMOLS (3.26)

i=1

3.4.2 La méthode DOLS (Dynamic Ordinary Least Squares)

Cette procédure a été proposée initialement par Saikkonen [1991][52] dans le cas de série temporelle puis par Kao, Chiang [2000][30] et Mark , Sul [2003][37] en cas de données de panel. La méthode DOLS permet d'estimer une relation de cointégration homogène, une telle hétérogénéité entre les individus est prise en compte à travers l'inclusion de l'effet Þxe individuel.

L'estimateur between de la méthode DOLS peut être formulé comme suit:

le modèle : yit = ái + _âixit + _XKi ãik?xit-k + uit (3.27)

k=-Ki

On obtient l'estimateur de données de panel par la méthode DOLS:

? ? ?

_!-1 XT !?

XT

_XN ? ?

^àâGD = ?N-1 zitz⁰ zityit ? (3.28)

it

? ?

i=1 t=1 t=1 1

Avec zit est un vecteur de régresseur de dimension 2(K + 1) x 1 telque zit = (xit -- xi , _?xit-k, , ?xit+k), yit = yit -- yi et l'indice 1 signifie qu'on s'intéresse seulement à l'estimation de la pente groupée.

_PN
i=1

_N-1

L'estimateur between de la méthode DOLS n'est autre que la moyenne des N estimateurs conventionnels DOLS en série temporelle. Autrement, ^àâGD =

·

_PT

^àâD,i et si on note ó2 i = limT ?8 E (T^-1 àuit)² la variance de long terme

t=1

de résidus de l'équation (1.26)⁷. La statistique de significativité de l'estimateur between est :

XN æ^àâGD = N-1/2 i=1

æàâi,D (3.29)

Où la statistique de significativité individuelle est :

1/2

D,i - â0) 6-I2 X(xit

â

(3.30)

i=1

æ^àâi,D = (



Sachant que â₀ est le paramètre de la restriction qu'on teste (que les six régions se comportent de la même manière à long terme vis à vis l'augmentation de prix de l'eau en Tunisie ou le contraire)

Notons enfin que la méthode DOLS n'est appliquée que pour le cas d'un panel cylindré.

⁷l'estimation de ces résidus peut être par la méthode HAC standard.(Voir Pedroni [2000]).

Chapitre 3

Analyse des données et

présentation du modèle théorique

Dans ce que suit, nous nous intéressons aux diffèrents aspects empiriques qui peuvent évaluer la politique tarifaire pratiquée par la SONEDE⁸ durant la période entre 1980 et 2007. Une telle tarife non linéaire progressive est sensée inciter les ménages tunisiens à diminuer leur consommation d'eau. Nous présentons la base des données puis nous abordons une analyse préalable susceptible de guider la modélisation économétrique du problème.

4.1 Présentation des données:

Les données sont collectées par la SONEDE par tranches de consommation, par trimestre et par district. La SONEDE n'a commencé à individualiser la consommation en eau potable "domestique branché" qu'à partir de 1980. Nous conduirons notre estimation sur la base des données trimestrielles par région qui s'étendra du premier trimestre 1980 au ^4i`eme trimestre 2007. Nous avons bénéficiés d'un financement auprés du laboratoire LAREQUAD⁹ pour avoir la pluviométrie mensuelle par station durant la période considèrée.

⁸La sociéte nationale d'exploitation et de distribution de l'eau en Tunisie.

⁹Laboratoire de recherche en economie quantitative de développement. Nous avons béneficier d'un fiancement de 2112 dinars pour avoir les données de la pluviométrie mensuelle concernant les 8 gouvernorats; TUNIS, NABEUL, ELKEF, MAHDIA, SIDIBOUZID, MEDNINE, BEJA ET TATAOUINE.

Les statistiques de la SONEDE regroupent des données très détaillées en 13 tranches de consommation très Þnes. Nous avons construit, à partir de ce découpage semi désagrégé, cinq tranches de consommation à la lumière des cinq tranches tarifaires:

1i`ere tranche: 0 à 20 m<sup>3</sup> par abonné et par trimestre. 2i`eme tranche: 21 à 40 m³ par abonné et par trimestre. 3i`eme tranche: 41 à 70 m<sup>3</sup> par abonné et par trimestre. 4i`eme tranche: 71 à 150 m³ par abonné et par trimestre.

5i`eme tranche: plus que 150 m³ par abonné et par trimestre.

Le point critique de notre travail est au niveau de la construction de la variable revenu. En effet, nous utilisons la dépense totale du ménage tunisien par région fournit par l'INS¹⁰ dans ces enquêtes comme un indicateur du revenu. La dépense est le seul indicateur régional de l'INS qui peut approximer le revenu.

4.1.1 Découpage de la Tunisie en six régions homogènes:

Nous adoptons le découpage de la Tunisie en six régions homogènes telqu'il est présentée dans l'étude de Ayadi et al [2002][1] aÞn de rendre possible l'application de l'économetrie des données de panel, dont l'avantage est de rendre possible l'estimation des effets prix, revenu, pluviométrie et extension réseau SONEDE au niveau régional.

Un découpage naturel (Nord, Centre et Sud) ne permet pas d'affiner l'analyse de la demande d'eau résidentielle. Nous ajoutons un découpage qui s'appuie sur les caractéristiques économiques. La Tunisie est plutôt formée du Grand Tunis et de deux ensembles homogènes à savoir le littoral et l'intérieur.

La grande agglomération de Tunis qui abrite à peu près le quart de la population totale se distingue par une spéciÞcité propre. En effet, ce qu'on appelle communément le Grand Tunis, étant donné ses dimensions économique, politique, administrative, sociale et historique, mérite d'être individualisé.

La Tunisie Littorale (Bizerte, le Cap-Bon, le Sahel, Sfax et Gabès) connaît, surtout depuis l'indépendance, un essor économique et social substantiel. Cette frange côtière qui s'étend du nord au sud de la Tunisie abrite avec le Grand Tunis l'essentiel de l'activité touristique, indistrielle et urbaine du pays.

¹⁰L'institut national de statistique

La Tunisie Intérieure y compris le sud, c'est à dire le reste du pays connaît, malgré un certain progrès, des problèmes d'ordre économique et social relativement aigus. Nous pouvons même affirmer qu'un déséquilibre régional "Intérieur-Littoral" est la caractéristique fondamentale de la Tunisie actuelle.

Si nous prenons le critère de la dépense par tête durant l'année 1990, nous avons 1008 DT pour le Grand Tunis, 749 DT pour le littoral et 505 DT pour l'Intérieure. Ces chiffres nous montrent les différences substantielles qui existent entre les trois ensembles. En effet, la dépense moyenne par tête à Tunis est de 1,4 celle du ménage du littoral et atteint le double de celle du ménage de l'intérieur. Si nous considérons la dépense du ménage résidant dans la zone littorale nous réalisons tout de suite qu'elle arrive à 1,5 celle du ménage de l'intérieur.

La combinaison des deux dimensions climatique et économique nous autorisent à construire les six régions homogènes suivantes: Le Grand Tunis, le Nord Est, Le Centre Est, Le Nord Ouest, Le Centre Ouest et le Sud.

4.1.2 Evolution des variables clés:

La consommation par région:

AÞn de mettre en ouevre une modèlisation claire de comportement du consommateur tunisien en eau potable, nous observons les graphiques relatifs aux variables clés sans effets saisonniers. La consommation totale annuelle moyenne (Figure 1) se caractérise par une tendance à la baisse pour toutes les régions. Cette tendance est plus importante pour la région Grand Tunis oft la consommation d'eau résidentielle est trés importante. Cette baisse est due soit à une extension du réseau SONEDE soit à une incitation causée par la politique tarifaire à conserver de l'eau, soit à une combinaison des deux facteurs. Nous sommes préinformés selon cette évolution de la consommation annuelle que les variables prix et extension réseau auront des élasticités de long terme négatives importantes en valeur absolut pour la région Grand Tunis.



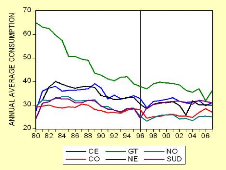
Figure1: Consommation annuelle totale par région

La consommation annuelle par tranches:

Les piques annuelles peuvent être dus à des périodes de séchersse. Ces piques sont plus prononcés lorsque nous désagrégeons la consommation annuelle totale par tranches de consommation. En effet, l'année 2001 était une année séche, à contrario, l'année 1997 était une année pluvieuse ce que conÞrme les positions des piques inférieurs et supérieurs de la Þgure ci-dessous.



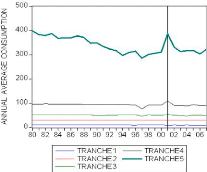
Figure 2: Consommation annuelle par tranche

Lorsque nous désagrégeons la consommation annuelle totale pour ces cinq tranches, nous distinguons deux types de comportement en terme de consommation

d'eau potable pour les ménages tunisiens. La consommation moyenne totale se stabilise dans le temps pour les deux premières tranches alors qu'elle diminue pour la quateriéme et la cinquième (cette baisse est peu prononcée pour la quaterième tranche). La troisième tranche se caractérise par une ßuctuation non standard, elle augmente pendant la sécheresse et diminue durant les périodes humides.

Par conséquent, l'estimation de l'équation de la demande d'eau sur la base des données en cinq tranches ne pas la partition idéale, nous faisons la distinction entre deux blocs. Un bloc inférieur qui regroupe les deux premières tranches et un bloc supérieur qui regroupe les deux dernières, c'est en fait l'estimation du même modèle pour les deux blocs.



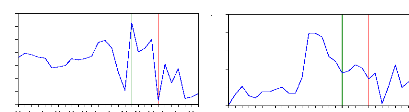
T RAN C H E 1

8 0 8 2 8 4 8 6 8 8 9 0 9 2 9 4 9 6 9 8 0 0 0 2 0 4 0 6

T RANCH E 2

8 0 8 2 8 4 8 6 8 8 9 0 9 2 9 4 9 6 9 8 0 0 0 2 0 4 0 6

1 0 . 8

1 0 . 6

1 0 . 4

1 0 . 2

1 0 . 0

9 .8

9 .6

9 .4

3 1 .2

3 0 .8

3 0 .4

3 0 .0

2 9 .6

2 9 .2

Figure 3: la consommation totale annuelle moyenne



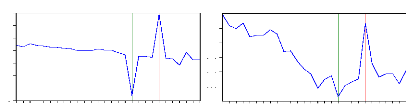
T RAN C H E 4

8 0 8 2 8 4 8 6 8 8 9 0 9 2 9 4 9 6 9 8 0 0 0 2 0 4 0 6

T RAN C H E 5

8 0 8 2 8 4 8 6 8 8 9 0 9 2 9 4 9 6 9 8 0 0 0 2 0 4 0 6

1 1 0

1 0 5

1 0 0

9 5

9 0

8 5

8 0

7 5

4 0 0

3 8 0

3 6 0

3 4 0

3 2 0

3 0 0

2 8 0

Figure 4: consommation annuelle moyenne totale

Les graphiques ci-dessus montrent la non stabilité temporelle de la consommation moyenne au sein de chaque tranche. Il est claire que les piques supérieurs des deux premières tranches en 1997 correspondent à des piques inférieurs dans les deux dernières pour la même année, alors que les deux piques inférieurs durant l'année 2001 correspondent à des piques supérieurs dans les deux derniers tranches. Nous pensons qu'il sera utiler d'estimer une équation qui capte l'effet glissement

des consommateurs d'un bloc à un autre, une telle équation doit tenir compte de la structure non linéaire de tarife.

Le nombre de consommateurs:

Nous supposons que le consommateur est représentatif, La consommation moyenne est le rapport entre la consommation globale et le nombre d'abonnés. Les deux graphiques ci-dessous montrent l'évolution de taux de branchement ( rapport entre

le nombre d'abonné dans le bloc et le nombre total).



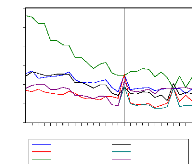
80 82 84 86 88 90 92 94 96 98 00 02 04 06

24

20

16

12

8

4

0

POURCENTAGE DE NOMBRE D'ABONNES

UPPERBLOCCE
UPPERBLOCCO
UPPERBLOCGT

UPPERBLOCNE
UPPERBLOCNO
UPPERBLOCSD

Figure 5: taux de branchement du bloc supérieur



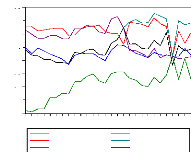
80 82 84 86 88 90 92 94 96 98 00 02 04 06

POURCENTAGE DE NOMBRE D'ABONNES

88

84

80

76

72

68

64

60

56

LOWERBLOCCE
LOWERBLOCCO
LOWERBLOCGT

LOWERBLOCNE
LOWERBLOCNO
LOWERBLOCSD

Figure 6: Taux de branchement du bloc inférieur

Le nombre d'abonnés dans le bloc inférieur se caractérise par une tendance à la hausse, cela peut être dû à un effet prix qui incite le consommateur à conserver de

l'eau, donc au glissement vers le bloc inférieur. Au contraire, le taux branchement du bloc supérieur ne cesse de diminuer sur toute la période quelque soit la région retenue.

4.1.3 Les explications préliminaires:

A ce niveau d'analyse préalable des données nous pouvons dégager quelques explications de l'évolution inattendus des variables clés :

La tendance à la baisse, qui caractérise la consommation annuelle totale moyenne pour la cinquième tranche, est dûe à la traification rigoureuse pratiquée par la SONEDE pour ces consommateurs. A contrario, la stabilité relative qui caractérise la consommation moyenne dans les deux tranches inférieures est expliquée soit par un glissement des consommateurs du bloc supérieur vers le bloc inférieur soit par les nouveaux branchés qui sont géneralement les ménages de faible revenu et qui doivent apparttenir par défaut au bloc inférieur. Cela va augmenter le nombre d'abonnés dans ce bloc et par conséquence la stabilité de la consommation moyenne. Ce phénomène de glissement d'un bolc à un autre justifie les piques opposés de 1997 et 2001.

La consommation annuelle moyenne totale pour chaque régions ne cesse de diminuer sur toute la période (1980-2007). Cela est expliqué par l'action de systéme tarifaire qui a comme objectif principal l'incitation des ménages à conserver l'eau. Notre discussion portera sur l'évaluation de la politique tarifaire de la SONEDE dés qu'elle commence à individualiser la consommation par districte en 1980 jusqu'à 2007.

Comme nous voyons dans les figures 2, 3 et 4 l'évolution est plutôt semblable pour les trois premières tranches oft la consommation moyenne est stable (ou très légèrement croissante). De la même manière, il y a une diminution uniforme de la consommation moyenne pour la cinquième tranche et une diminution légère pour la quaterième tranche. Ainsi, il est judicieux de regrouper les cinq tranches dans deux blocs en remontant les tranches 1, 2 (et 3) dans un bloc inférieur et les tranches 4 et 5 dans un bloc supérieur Ayadi et al [2002]. Après quelques épreuves avec et sans la troisième tranche dans le bloc inférieur, nous avons choisi de ne pas le maintenir dans ce bloc afin d'améliorer la qualité de notre estimation.

Sur la base de ce regroupement, le bloc inférieur représente entre 70% et 85% des abonnés et entre 40% et 65% de la consommation globale alors que le bloc supérieur représente entre 4% et 10% des abonnés et entre 18% et 30% de la consommation globale sur toute la période et pour les six régions.

4.1.4 Les statistiques descriptives:

Dans notre étude, nous utilisons le taux de branchement ( rapport de nombre d'abonnés dans le bloc considèré sur le nombre d'abonnés totale) pour estimer les effets glissement de consommateur moyen entre les deux blocs en considèrant la nonlinéarité du tarif.

Le tableau ci-dessous reprèsente les statistiques relatives aux diffèrentes variables calculées sous Winrats6.

Le minimum de le consommation pour le bloc inférieur se situe au niveau de la région Nord ouest pendant le premier trimestre 2004, tandis que le maximum se situe au grand tunis pendant le deuxième trimestre 1997 avec un écart type de 2,19. Cela nous donne l'intuition que la consommation moyenne dans ce bloc sera élastique sur toute la période au changement de prix aussi bien qu' à l'extension réseau.

Ces intuitions se conforment lorsque nous voyons que le maximum de la consommation moyenne du bloc supérieur se situe dans la région la plus pauvre (le centre ouest), durant la même année de max que le bloc inférieur, oft l'extension réseau et moins développée jusqu'à nos jours dans cette région.

Le maximum de la pluviométrie est au niveau de la région grand tunis, nous pensons que la consommation sera moins élastique au prix par rapport au pluviométrie.

Statistiques descritives sur le panel ( N=6 , T=112 )

Variable	descriptif	moyenne	Min	Max	écart type
Ci	cons.inf	18.16	12.46 at 4//2004:01	25.73 at 6//1997:02	2.19
Cs	cons.sup	141.61	137.98 at 4//2004:04	398.12 at 1//1997:01	35.52
PMi	px moy.inf	448.56	165.72 at 1//1982:02	877.24 at 1//2005:01	189.49
PMs	px moy.sup	826.16	214.95 at 5//1980:01	1404.41 at 1//2005:01	419.86
PMGi	px marg.inf	158.36	79.79 at 1//1980:01	566.81 at 6//1994:02	48.86
PMGs	px marg.sup	914.33	221.0 at 2//1980:01	1479.8 at 1//2005:01	439.61
Ri	revenu.inf	310.77	154 at 1//1980:01	724 at 2//2004:04	120.87
Rs	revenu.sup	1434.06	959 at 1//1980:01	2195 at 2//2004:04	334.76
PL	pluvi	172.02	0.13 at 5//2004:03	3418 at 6//1988:01	431.64
NAi	nbr ab.inf	138284.58	15905 at 1//1980:03	1444541 at 6//2006:01	119847.43
NAs	nbr ab. sup	15335.63	869 at 1//1981:01	121072 at 2//2006:03	15899.26
TXi	tx branch.inf	0.88	0.55 at 6//1999:03	0.99 at 1//1996:01	0.12
TXs	tx branch.sup	0.10	0.01 at 4//2003:01	0.66 at 6//1982:03	0.08
N	exten.réseau	168659.04	17233.66 at 1//1980:03	1780970 at 6//2006:01	163776

1//, 2, 3, 4, 5 et 6 désignent respectivement CO, CE, NE, NO, SUD et GT

4.2 Le modèle :

4.2.1 Les déterminants de la demande d'eau - aspects théoriques

Dans notre étude, nous adoptons la spéciÞcation de Ayadi et al [2002][2]. Une telle spéciÞcation d'un modèle de demande d'eau résidentielle est justiÞée par la théorie économique classique de la demande, le contexte de l'étude et les caractéristiques climatiques.

La théorie économique de la demande suggére que le revenu et le prix sont les deux variables principales qu'on ne peut ignorer en modèlisant la demande du consommateur. En effet, Le ménage emploi une partie de sa consommation en eau pour l'usage essentiel ( boisson, cuisine, nettoyage,...) qui est inélastique au changement de prix et de revenu. Cependant, le ménage de haut revenu emploi une partie de sa consommation pour un usage supplementaire ( arrosage, piscine, nettoyage de voiture, ...) supposé de luxe, et qui doit être trés élastique au changement de prix et de revenu dans un système tarifaire progressif.

La consommation moyenne que nous essayons d'expliquer dans notre travail diminue chaque fois qu'il y a de nouveaux branchés. Pour tenir compte d'une

telle fluctuation, nous introduisons la taille du réseau comme facteur explicatif de l'extension réseau. Cette variable est spécifique pour un pays qui n'arrive pas à réaliser un taux de branchement de 100%, nous pensons que l'effet de cette variable sera négatif et que les nouveaux branchés viennent à diminuer la moyenne et à maintenir la consommation stable ou légèremet croissante dans le bloc inférieur.

Les variables climatiques, notamment la pluviométrie et la température sont le premier élément qui vient à l'ésprit lorsqu'on cherche les déterminants de la consommation d'eau. Ces variables sont proposées dans la littérature (Bient M E et al (2006)[8],Foster & Beattie (1979, 1981)[17], Martinez-Espineira (2003, 2007)). La Tunisie se caractérise par un climat disparate ( une variabilité pluviométrique importante entre régions) qui doit nécessairement agir sur le comportement du consommateur, le signe escompté d'une telle variable est négatif. On s'attend à ce que cette variable contribue à l'explication de la différence inter-régionale en Tunisie en terme de consommmation d'eau.

Le problème est au niveau de la tarification qui est non linéaire et progressive. Cette dernière est constituée d'une part fixe et d'une part variable par tranche et avec le prix du m³ par tranches _(p1,p2,p3,p4 et p5) qui sont croissants avec la consommation. Le consommateur est sensible à deux types de prix. Le premier est le prix moyen, qui est le rapport entre le montant de la facture et le volume consommé (Wong (1972)[55], Foster and Beattie (1980))[17]. Au niveau régional cette variable est la somme des factures payées par tous les ménages dans le bloc divisée par le volume total en m³ par ces derniers. Le consommateur est ainsi sensible au montant de la facture d'eau qu'il paye chaque trimestre. L'autre variable est le prix de dernier m³ consommé qu'on l'appele le prix marginal (Howe & Linaweaver (1967)), dans notre cas c'est le prix du m³ dans chaque tranche. Selon Bient M E et al [2006][8], l'utilisation de cette variable doit inclure le D de Nordin [1976] qui estime l'effet remboursement vertuel. Le tableau ci-dessous présente le D de Nordin [1976].

Tableau 2 : le D de Nordin

Tranche	prix marginal	D de Nordin
1	P1	0
2	P2	(P2--P1) x Q1
3	P3	(P3--P1) x Q1+(P3--P2) x Q2
4	P4	(P4--P1) x Q1+(P4--P2) x Q2+(P4--P3) x Q3
5	P5	(P5--P1) x Q1+(P5--P2) x Q2+(P5--P3) x Q3+(P5--P4) x Q4

Où Qi est le volume total qui distingue chaque tranche tarifaire ( i.e: Q1 = 20 m³)

4.2.2 Le glissement de consommateur d'un bloc à un autre:

D'aprés les graphiques 5 et 6, la non stabilité du taux de branchement dans les deux blocs est sans doute dûe à la non linéarité du tarif. Cela nous pousse à estimer une équation qui explique le taux de branchement en fonction de prix, pluviométrie, l'extension réseau et la variable saisonnière.

Le signe escompté de la variable prix pour le bloc supérieur est négatif et trés singniÞcatif du faite que la variable prix est la seule moyenne qui peut inciter les ménages à conserver l'eau et donc de glisser de boc supérieur vers le bloc inférieur. Pour le bloc inférieur les effets sont inattendus par le fait que le prix dans ce bloc est faible et que la consommation d'eau est employée pour satisfaire des besoins nécessaires, donc incompressible.

4.3 SpéciÞcation économétrique du modèle:

Notre modèle est constituée de deux équations, la première explique la consommation moyenne dans chaque bloc, la seconde explique le taux de branchement dans chaque bloc en fonction des même variables, excépté le revenu, pour tenir compte de l'effet glissement de consommateur moyen entre les deux blocs. Le modèle est spéciÞé au niveau régional pour la période entre 1980 et 2007. Le comportement qu'on essaye d'expliquer est celui de consommateur moyen supposé représentatif de chaque région.

Pour la région i et durant la période t ( trimestre), la demande d'eau moyenne dans le bloc j s'écrit ;

Avec i = 1...6, t = 1...112 et j = 1,2 (1:bloc supérieur et 2:bloc inférieur)

oil C, R, P , N, Q et PL sont réspectivement la consommation, le revenu, l'extension réseau, les dummies trimestriels et la pluviométrie dans chaque bloc.å est le terme d'erreur qui regroupe les aléas non spéciÞés.

Dans la deuxième équation, le taux de branchement (^NB_N ) est expliqué par les même variables explicatives de l'équation de la demande excépté le revenu. L'estimation d'une telle relation a pour objectif l'estimation des effets prix , pluviométrie et extension réseau sur le glissement de consommateur d'un bloc à un autre.

NB} ^(j)

Log

JJJ it .s=1,3,4 =

+ á(1ji ) Log _Pit + á&ji ) Log _Nit + Log P _Lit +

E á(12Qsit + ji)t

Avec i = 1...6, t = 1...112 et j = 1, 2 (1:bloc supérieur et 2:bloc inférieur)

Le changement de la variable prix dans le bloc supérieur agit négativement sur le taux de branchement de telle façon que la tarification rigoureuse dans ce bloc incite les ménages à glisser vers le bloc inférieur et le même effet attendu pour la pluviométrie.

Nous évoquons le problème de la non stationnarité en panel pour ses diffèrentes variables, une telle approche rend les techniques économétrique classiques (MCO, MCG, DMC...) inapplicables. Notre investigation consiste à estimer des relations de cointégration sur données de panel par les méthodes FMOLS et DOLS.

L'avantage de notre investigation par rapport à la littérature est qu'on dépasse le problème d'endogénéité causé par la corrélation entre le prix et la consommation. En effet, dans la théorie de cointégration il n'y a pas une distinction entre l'exogénéité et l'endogénéité des variables. L'estimation de modèle déÞnit cidessus revint à l'estimation d'une relation de long terme sur données de panel entre les variables d'intérêt, les coefficients estimés de cette relation seront les élasticités de long terme, c'est à dire la réaction du consommateur moyen sur toute la période d'étude vis à vis du changement des variables du modèle.

Peu de travaux publiés qui tente à estimer la demande d'eau et qui applique les diffèrantes méthodes de l'économétrie des données de panel non stationnaire. C'est en faite la motivation qui nous a améné à conduire cette étude, l'objectif sera d'évaluer la politique tarifaire de la SONEDE sur toute la période et d'avoir l'utilité des méthodes des séries temporelles appliqués sur panel pour estimer la demande de l'eau résidentielle.

Chapitre 4

Résultats empiriques et

intérpretations

5.1 Introduction

Notre échantillon est constitué de six régions qui couvrent toute la Tunisie. Ces régions sont : le centre ouest, le centre east, le nord east, le nord ouest, le sud et le grand tunis. Les données receuillies sont trimestrielles et s'inscrivent dans la période allant du premier trimestre de l'année 1980 au quatérième trimestre de l'année 2007. En conséquence, les variables ont pour indice (it) oft i = 1,2,...,6 dénote la région et t =1,2,...,112 exprime le trimestre concerné. Les données ont été fournies par la SONEDE, l'INM¹¹, l'INS et l'ONAS¹². Il convient de souligner en outre qu'il a fallu procéder à une construction mathématique pour obtenir le taux de branchement et le prix moyen. La non disponibilité d'un revenu régional en Tunisie auprés de l'INS nous a améné à utiliser les enquêtes consommations de L'INS pour approximer le revenu.

Nous estimons les deux équations pour les deux blocs sur la base des données entre 1980 et 1996 aÞn de comparer nos résultats avec ceux de l'étude de Ayadi et al [2002][1] sur la même base qui ne tient pas compte de la non stationnarité en panel puis nous conduisons la même estimation sur toute la période (1980 et 2007).

¹¹L'instutit national de méterologie ¹²L'office natinal d'assainissement

5.2 Résultats des tests de racine unitaire :

Avant de déterminer l'existence ou l'absence de liens dynamiques entre les variables qui composent nos deux modèles, il est indispensable de déterminer l'ordre de l'intégration de chaque série. C'est pour cette raison que nous employons les tests de racine unitaire appliqués à un panel, selon les approches de Levine et al [2002], IPS[2003], MW [1999] et Hadri [2000]. Le tableau 3 présente les résultats des tests de RU pour les deux périodes d'estimation ( 1980 à 1996 et 1980 à 2007).

Le tableau ci-dessous présente les résultats des 4 tests que l'on appliquent pour juger l'ordre d'intégration des séries par lesquelles nous procédons aux diffèrents tests de cointégration qui sont applicables à des séries I(1).

Les valeurs de la statistique corrigée de Levin et al ainsi que la statistique d'IPS et de Hadri [2000] sont distribuées suivant la loi normale centrée réduite alors que le test de MW suit la loi de ÷²(12). Tous les tests sont unilatéraux, si bien que les valeurs critiques largement positives de la statistique de MW devraient conduire au rejet de l'hypothèse nulle de racine unitaire ; à contrario, pour tous les autres tests, les valeurs largement négatives de leurs statistiques nous amèneraient à rejeter la même hypothèse exception faite du test de Hadri[2000] oft les valeurs largement négatives conduisent à accepter la stationnarité. Les résultats des tests sur toutes les séries en niveau et en diffèrence première sont rapportés par le Tableau 3.

En se basant sur ces régles des décisions, il est claire que toutes les séries sont intégrées d'ordre un [ I(1)] durant les deux périodes ((1980-1996) et (1980- 2007)) exception faite du revenu du bloc supérieur (Rs) en logarithme, le nombre d'abonnés dans le bloc inférieur (NAi) et le taux de branchement de ce même bloc (TXi) en logarithme, qui sont intégrés d'ordre deux [I(2)]. La non stationnarité de ces séries en diffèrence primère est due à la non Þabilité des données sur le revenu d'une part, du faite qu'on lisse les enquêtes INS de consommation qui s'observe chaque cinq ans sur toute la période, et au mouvement des abonnés entre les deux blocs ( les abonnés dont le revenu augmente glissent vers le bloc supérieur et les autres qui pratique des politiques économes d'eau glissent vers le bloc inférieur via la tariÞcation rigoureuse dans le bloc supérieur). Le test IPS nous conduirait à rejeter l'hypothèse nulle de la non stationnarité pour la variable PL en logarithme durant la prémière période d'estimation (1980_1996), c'est une contradiction avec la décision du test LLC. Sous l'hypothèse alternative de ce test, la série peut être stationnaire pour un nombre d'individu N1 et non stationnaire pour N -N1.Ce qui rend ces résultats acceptables.

La décision du test de MW est de réjeter l'hypothèse nulle pour la plupart des séries et durant les deux périodes d'estimation. Cela est contradictoire avec

les décisions des autres tests, mais l'approche de MW est non paramètrique et la puissance de ce test augmente avec la dimension temporelle.

Notons enÞn que l'application de ces quatre tests nous a aménée à juger les séries non stationnaires pour les deux périodes d'estimation. Toutes les variables sont intégrées d'ordre un (I(1)) exception faite du revenu du bloc supérieur et du nombre d'abonnés pour la première période d'estimation (1980_1996).

Tableau 3: Test de racine unitaire pour les deux périodes

	t* ä(1)	t^* ä(2)	Wt(1)	Wt(2)	Zô(1)	Zô(2)	PMW(1)	PMW(2)
LCi	-0.82	-2.90	-1.55	-4.09	4.97	4.87	23.82	43.98
LCs	1.90	-1.54	2.09	-2.34	4.54	3.57	93.93	39.69
LNAi	2.66	0.36	3.16	0.012	5.20	6.89	54.62	31.80
LNAs	1.70	0.13	-0.98	-0.66	7.01	2.80	17.65	43.81
LRi	1.21	0.94	1.53	1.04	5.85	7.07	10.06	12.33
LRs	0.87	0.59	1.17	0.71	5.99	9.78	6.85	11.79
LPL	-1.56	-1.18	-2.43	-1.91	9.61	4.55	18.43	12.53
LPMi	2.22	0.37	2.96	0.49	6.79	10.51	49.75	0.88
LPMs	1.70	-0.49	2.25	-.67	6.15	11.36	11.73	0.49
LPMGi	2.33	-1.04	2.87	-1.58	0.36	12.45	105.52	3.39
LPMGs	0.92	-1.21	1.19	-1.64	8.01	11.85	7.12	2.29
LTXi	0.62	1.99	0.35	2.65	6.75	6.69	49.58	13.27
LTXs	3.44	1.04	4.67	1.16	3.26	4.15	55.23	17.59
LN	2.75	1.02	3.27	0.96	-	-	-	-
?LCi	-5.38	-20.87	-5.83	-27.68	1.85	-1.13	146.31	141.75
?LN	-5.13	-17.53	-7.52	-17.73	-	-	-	-
?LCs	-11.75	-18.63	-18.89	-24.83	1.79	-3.086	130.04	218.61
?LPMi	-10.57	-15.86	-14.09	-21.04	5.33	-1.73	216.56	166.12
?LPMs	-8.28	-14.03	-11.58	-18.10	1.52	-1.24	140.24	110.22
?LPMGi	-11.75	-14.60	-16.41	-20.06	4.87	-1.25	208.63	133.70
?LPMGs	-8.48	-11.32	-11.80	-14.85	0.33	-1.37	121.07	126.28
?LRi	-2.68	-6.67	-4.56	-9.56	-0.38	-1.11	77.40	91.47
?LRs	0.53	-1.58	-1.35	-4.84	-0.45	-1.62	77.85	93.99
?LNAi	-0.59	-17.46	8.49258e-05	-19.03	7.71	-1.60	144.3	93.85
?LNAs	-13.79	-19.55	-18.42	-21.61	9.04	-1.33	140.49	89.19
?LTXi	1.29	-8.32	1.78	-8.97	3.19	1.68	162.17	96.80
?LTXs	-21.80	-30.09	-28.18	-36.28	16.29	-1.60	124.19	103.92
?LPL	-13.73	-21.43	-18.59	-28.81	5.50	-1.32	177.95	145.08
?^2LRS	2.10	-4.92	1.86	-10.92	25.40	25.40	195.61	223.93
?^2LTXi	4.28	-	5.44	-	3.32	-	179.25	-
?^2LNAi	-3.95	-	-5.66	-	5.08	-	141.95	-

1, 2 indique respectivement les périodes (1980_1996) et (1980_2007)

t* ä:Levin,lin et chu ADF statistic, Wt;IPS, Z_ô; HADRI

5.3 Résultats des tests de cointégration :

Les résultats des tests de racine unitaire en panel nous confirme l'argumentation du choix de l'économétrie des données de panel non stationnaire. En effet, toutes les séries qui composent nos équations de la demande et du taux de branchement pour les deux bloc sont I(1)¹³. Nous conduisons les tests de cointégrations selon les approches de Pedroni [2004] et Larson et al [2001] pour s'assurer que nos modèles constituent effectivement des systèmes cointégrés, bien évidement la non existence des relations de long terme entre les variables conduit à l'estimation d'une régression fallacieuse (Granger et Newbold [1974] )[18]. Pour effectuer ces tests nous spécifions pour les deux blocs la relation suivants:

yit = ái + äit + _â1ix1,it + _â2ix2,it + + _âMixM,it + åit

où i = 1,....,6,t=1,...,112etm=1,...,5ou4

Nous introduisons la tendance temporelle et l'effet spécifique individuel lors de l'implèmentation de ces tests, du faite que nous pensons que les comporte-

ments tendanciels des variables sont déterministes.

Ainsi, même si la prépondérance est donnée à la tendance stochastique, il n'en reste pas moins que la tendance déterministe puisse tenir un rôle non négligeable dans la relation de cointégration, car les tests de racine unitaire en panel ont révélé que les variables possèdent une tendance significative. Le tableau suivant synthètise les diffèrentes statistiques des tests de cointégration appliqués à notre panel. La partie supérieure récapitule les résultats qui se rapportent aux tests de Pedroni que l'on manipule sous Rats 6.0 alors que la partie inférieure récapitule les résultats relatives au test "Fisher combined Johansen" que l'on manipule sous le logiciel Eviews 6.0.

Les tests de cointégration peuvent être mener en faisant appel aux tests IPS ou LLC, par l'application de ces derniers sur les résidus estimés de la relation de cointégration.

¹³Les deux séries qui sont I(2), le revenu de bloc sup, le nombre d'abonnes et le taux de branchement dans le bloc inf ne sont pas utilisées lors de l'établissement des ces relations.

Tableau 4: Tests de cointégration pour les deux périodes 1 et 2

yit= ái+äit + _{â1ix1,it+â2ix2,it+...} + âMixM,it+åit

dep. var	lci		lcs			ltxi	ltxs
période	1	2	1	2	1	2	1	2
		Tests de Pedroni (1999, 2004)
Panel v	0.80*	2.29*	1.08**	4.62*	0.02	2.33*	1.00**	3.96*
Panel ñ	-5.78*	-11.12*	-7.45*	-20.03*	-2.56**	-10.55*	-4.43*	-11.28*
Panel t	-0.31	-4.15*	-8.59*	-16.70*	-2.22**	2.22	0.47	-3.19*
Panel t (P)	-7.83*	-12.11*	-10.06*	-22.19*	-3.84*	-9.42*	-4.59*	-10.19*
Group ñ	-5.59*	-12.00*	-7.53*	-21.11*	-2.68**	-11.11*	-3.77*	-12.24*
Group t	1.54	-2.42**	-8.06*	-19.00*	-2.03**	3.32	1.97	-2.98**
Group t (P)	-8.85*	-14.58*	-11.70*	-26.09*	-4.54*	-11.15*	-4.55*	-12.04*
		Fisher combined Johansen [1991]
Nbre de relation/(H0)	LR	LR	LR	LR	LR	LR	LR	LR
Au plus 0	369.4 (0.00)	407.6 (0.00)	323.8 (0.00)	323.7 (0.00)	169.8 (0.00)	312.2 (0.00)	304.6 (0.000)	223.3 (0.00)
Au plus 1	82.40 (0.00)	87.71 (0.00)	75.24 (0.00)	84.24 (0.00)	55.61 (0.00)	92.25 (0.00)	83.52 (0.000)	98.68 (0.00)
Au plus 2	17.80 (0.121)	16.16 (0.184)	12.72 0.389	13.48 (0.335)	26.66 (0.008)	32.16 (0.0013)	9.812 (0.632)	16.28 (0.178)

les p-values du statistique trace sont reportés entre paranthèse

une et deux étoiles désignent respectivement la signiÞcativité à 1%, 5%

Tous les tests présentés ci-dessus sont distribués selon la loi normale centrée réduite. Ce sont des tests unilatéraux dont les réalisations largement négatives conduisent au rejet de l'hypothèse nulle d'absence d'une relation de cointégration entre les variables. A l'exception du test Panel-v que selon Pedroni [1999][43], ce test diverge (vers plus l'inÞnie), par conséquence la réalisation largement positive conduit au rejet de l'hypothèse nulle.

Les statistiques des tests de Pedroni P nous aménées à s'assurer que nos équations forment des relations de long terme. Cela permet de parfaire notre critique adressée à l'étude de Ayadi et al[2002][1] qui estime les même modèles sur la même base des données en utilisant les méthodes économétriques de panel statique.

La statistique trace du test algebrique va au-déla de ce que nous fournissent les précédents, car en sus de sa faculté à détecter l'existence de la relation de cointégration pour un modéle, il informe que certaines variables qui composent le modèle pourraient être combinées entre elles pour forme d'autres équilibres de

long terme. Autrement dit, il met en évidence, pour chaque modèle, le nombre maximal de relations de cointégration susceptibles d'être interprétées d'un point de vue économique. L'inconvénient de ce test est qu'il permet uniquement de compter le nombre de relations de long terme sans pour autant permettre l'établissement de ces relations. L'écriture mathématique des relations est un point obscur que le test est incapable de résoudre.

Compte tenu que la statistique trace suit la loi de chideux, le test admettent l'existance de deux relations de long terme au seuil de 10% pour les deux équations et durant les deux périodes d'estimation.

5.4 Résultats des estimations

5.4.1 Résultats des estimations sur la période 1980-1996

Comme indiqué précedament, les deux équations du modèle constituent un système cointégré sur la période entre 1980 et 1996. Nous procédons à une estimation de ces deux équations afin de juger la pertinance de la technique de cointégration sur panel pour estimer la demande d'eau résidentielle. Nous essayons, à chaque fois, de comparer ces résultats avec ceux de l'étude de Ayadi et al[2002] afin d'avancer l'avantage de la technique économétrique que l'on applique par rapport aux autres techniques des données de panel qui ignorent la stationnarité du panel.

Estimation de la consommation et du taux de branchement pour le bloc inférieur :

L'examen du tableau 5 présenté ci-dessous confirme notre choix de regroupement des consommateurs en deux blocs. En effet, les élasticités prix de long terme sur toute la période ( 1980 à 1996) sont positives, ce qui nous a améné à juger la demande d'eau résidentielle inélastique au changement de prix pour le consommateur moyen dans ce bloc. Cela est acceptable, de faite que la consommation du ménage appartenant à ce bloc est de type incompressible. L'effet de long terme de revenu est non significatif pour toute les régions.

L'effet pluviométrie de long terme varie entre les régions et diminue la consommation sur toute la période. Ce dernier est trés important en valeur absolut pour la région grand tunis, qui se caracterise par un climat humide durant toute l'année.

L'extension réseau SONEDE a un effet négatif significatif, ce qui est du au fait que la consommation d'un nouvel abonné est inférieure à la moyenne. En ce qui concerne les dummies trimestriels, les effets sont négatifs significatifs pour les six régions.

L'estimation du taux de branchement, présentée dans le tableau 6, fournit les résultats suivants:

L'effet prix de long terme sur le glissement de consommateur du bloc inférieur vers le bloc supérieur est négatif significatif pour les régions NE et CE, alors qu'il est positif pour la région CO, caractérisée par un faible revenu. Cependant, l'effet commun est positif faible ( 0.002), nous pouvons juger le taux de branchement globalement inélastique au changement de prix au sein du bloc inférieur. Cela confirme nos intuitions que le consommateur moyen ne quitte le bloc inférieur que lorsque son revenu augmente et que la plupart des abonnés dans ce bloc sont des nouveaux branchés.

L'effet pluviométrie est négatif trés significatif aussi bien que les dummies trimestriels. Cela est tout à fait naturel, durant les périodes pluvieuses la consommation d'eau potable diminue, un tel principe a été prouvé dans la plupart des études d'économétrie appliquée sur la demande d'eau résidentielle.

L'estimateur between dols s'inscrit dans le moix perspective que FMOLS sauf que l'effet prix de long terme est non significative.

Tableau 5: Estimation de la consommation pour le bloc inférieur

dep.vari LCi

- lpmi lpl ln lri Q1 Q2 Q4

Fmols within estimator

CO 0.10 -0.015 -0.012 0.017 -0.28 -0.06 -0.22

(2.81) (-1.62) (-1.04) (0.32) (-22.9) (-4.9) (-17.9)

CE -0.035 -0.006 0.101 -0.011 -0.25 -0.07 -0.21

(-0.51) (-1.19) (1.53) (-0.2) (-11..79) (-4.68) (-9.75)

NE 0.049 0.003 -0.05 0.1 -0.2 -0.04 -0.17

(0.7) (0.05) (-0.66) (1.04) (-9.25) (-2.6) (-7.22)

NO 0.12 -0.001 0.02 -0.20 -0.31 -0.055 -0.28

(2.2) (-0.012) (0,33) (-2.74) (-17.3) (-3.54) (-14.45)

SUD 0.11 -0.01 -0.055 -0.14 -0.26 -0.04 -0.22

(1.11) (-1.47) (-0.53) (-0.81) (-9.53) (-2.01) (-7.65)

GT 0.047 -0.016 0.017 -0.05 -0.13 -0.04 -0.08

(0.83) (-2.86) (0.32) (-0.97) (-6.13) (-2.68) (-3.94)

Fmols between estimator

0.066 -0.008 0.0037 -0.05 -0.24 -0.05 -0.2

(2.91) (-2.9) (-0.018) (-1.37) (-31.39) (-8.35) (-24.88)

DOLS between estimator

0.14 0.022 0.074 0.22 -0.24 -0.04 -0.203

(1.3) (0.94) (0.69) (1.09) (-2.76) (-0.49) (-2.28)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 68 , no. regressors = 7

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Tableau 6: Estimation du taux de branchement pour le bloc inférieur

dep.vari LTXi

- lpmi lpl ln Q1 Q3 Q4

Fmols within estimator

CO 0.016 -0.004 0.017 0.0004 -0.001 0.0017

(5.94) (-3.23) (10.47) (0.27) (-0.95) (1.06)

CE -0.002 0.0006 0.008 0.0009 -0.0008 0.001

(-1.16) (0.28) (4.15) (1.48) (-1.48) (1.7)

NE -0.004 -0.0015 0.023 -0.0005 -0.001 -0.0006

(-1.41) (-5.52) (6.7) (-0.56) (-1.25) (-0.62)

NO 0.006 -0.003 0.02 0.0001 -0.0005 0.0007

(1.14) (-3.9) (3.62) (0.1) (-0.31) (0.43)

SUD 0.004 -0.002 0.024 -0.0001 -0.0006 0.0002

(1.01) (-5.4) (7.014) (-013) (-0.662) (0.17)

GT -0.006 -0.003 0.026 -0.0036 -0.0005 -0.0023

(-0.71) (-3.5) (4.9) (-1.31) (-0.22) (-0.88)

Fmols between estimator

0.002 -0.002 0.02 -0.0004 -0.0008 0.0001

(1.9) (-8.68) (15.05) (-0.07) (-1.99) (0.75)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 68 , no. regressors = 6

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Estimation de la consommation et du taux de branchement pour le bloc supérieur:

Nous conduisons la même estimation pour le bloc supérieur, aÞn de dégager les effets prix, pluviométrie, extension réseau et revenu de long terme sur la consommation moyenne.

Tableau 7: Estimation de la consommation pour le bloc supérieur

dep.vari LCs

- lpms lpl ln lrs Q1 Q2 Q4

Fmols within estimator

CO -0.22 -0.03 -0.013 0.25 0.25 0.04 0.21

(-2.77) (-1.41) (-0.41) (1.19) (9.3) (1.45) (7.8)

CE 0.13 -0.017 -0.5 -0.12 0.28 0.06 0.3

(1.08) (-1.72) (-2.82) (-1.04) (5.25) (2.10) (5.65)

NE -0.23 0.003 -0.2 0.3 0.26 0.06 0.25

(-2.58) (0.35) (-1.61) (1.18) (6.85) (2.4) (5.89)

NO 0.027 -0.05 -0.4 0.18 0.32 0.03 0.332

(0.24) (-3.41) (-2.5) (0.84) (8.23) (1.13) (8.1)

SUD -0.3 -0.016 0.11 0.58 0.216 0.03 0.207

(-4.6) (-2.3) (1.12) (1.02) (9.15) (2) (8.36)

GT -0.1 0.01 -0.334 0.313 0.124 0.06 0.13

-1.88 2.11 (-4.33) (3.25) (4.32) (3.86) (4.56)

Fmols between estimator

-0.11 -0.017 -0.22 0.23 0.24 0.047 0.237

(-4.3) (-2.61) (-4.31) (2.63) (17.6) (5.38) (16.52)

DOLS between estimator

-0.196 -0.014 -0.31 1.34 0.25 0.06 0.27

(-1.76) (-0.45) (-2.76) (8.21) (2.25) (0.52) (2.37)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 68 , no. regressors = 7

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Les résultats présentés ci-dessus sont compatibles avec les intuitions basées sur l'observation de Figure 2. En effet, Lorsque nous avons désagrègé la consommation annuelle totale pour les cinq tranches, nous étions informés que les effets de long terme serons trés importants selon le poid de la régions en terme de consommation d'eau. Une telle intuition se trouve validée comme le montre le tableau ci-dessus.

L'élasticité prix de long terme se caractérise par une variabilité spatiale entre -0.1 et -0.3 selon les estimatons "fmols within", sa valeur absolut maximal est au niveau de la région sud ( -0.3). Cela prouve bien que l'eau est un bien élastique au changement de prix et que la partie de consommation nommée de luxe est la plus élastique compte tenu des résultats trouvés lors de l'estimation pour le bloc inférieur. L'élasticité prix basée sur l'estimateur "Fmols between" est de

(-0,1). Une faible élasticité basée sur ce dernier ne change pas notre jugement sur la nature du bien eau, du faite que l'estimateur between est la moyenne des estimateurs individuels.

Le revenu affecte positivement la consommation sur le long terme, cet effet varie selon la situation économique de la région. La consommation moyenne diminue durant les sessions hmides et augmente pendant les saisons séches, les élasticités de long terme de la pluviométrie et des variables saisonnières montrent bien cet effet. L'extension réseau tend à diminuer la consommation moyenne quelque soit la région.

Selon l'estimateur DOLS, la demande d'eau résidentielle est globalement élastique au changement de prix. Cela performe notre jugement que la maîtrise de la demande passe par le prix. Les autres coefficients sont presque similaires à ceux obtenus par FMOLS.

Tableau 8: Estimation du taux de branchement pour le bloc supérieur

dep.vari LTXs

- lpms lpl ln Q1 Q3 Q4

Fmols within estimator

CO -0.27 -0.06 0.08 -0.98 0.32 -0.8

(-3.29) (-1.38) (1.24) (-16.57) (5.6) (-13.37)

CE 0.43 -0.02 -0.94 -0.8 0.3 -0.62

(1.3) (-0.81) (-1.88) (-6.81) (3.49) (-5.58)

NE 0.48 -0.027 -1.25 -0.83 0.18 -0.7

(2.23) (-1.08) (-3.958) (-9.43) (2.87) (-7.22)

NO 0.79 -0.06 -1.62 -0.84 0.11 -0.7

(2.66) (-1.42) (-4.24) (-8.99) (1.53) (-7.33)

SUD 0.76 -0.04 -1.58 -0.84 0.12 -0.7

(2.13) (-1.45) (-3.51) (-7.97) (1.48) (-6.52)

GT 0.22 0.007 -1.03 -0.505 0.13 -0.46

(1.21) (0.46) (-5.12) (-7.56) (2.49) (-7.38)

Fmols between estimator

0.4 -0.03 -1.06 -0.8 0.19 -0.66

(2.52) (-2.31) (-7.14) (-23.41) (7.13) (-19.36)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 68 , no. regressors = 6

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

L'estimation du taux de branchement, ci-dessus, présente des résultats qui sont à première vue paradoxaux. L'effet prix de long terme, qui devrait être négatif,

est positif pour toutes les régions excepté celle du centre ouest. Si nous rélions ce résultat avec le revenu, nous constatons que le centre ouest est la région la plus pauvre. Un changement de prix aura comme conséquence direct le glissemnt de l'abonné vers le bloc inférieur. Cependant, les abonnés des autres régions, qui appartiennent au bloc supérieur, ne répondent au changement rigoureux de tarif qu'aprés une longue période, car leurs revenu est relativement fort. Une telle explication sera validée lors de l'estimation de la même équation sur 28 ans. C'est en faite l'avantage de l'estimation des relations d'équilibre de long terme par rapport aux estimations par les méthodes statiques.

Les effets de long terme des autres variables sont compatibles avec ceux du bloc inférieur. En effet, les coefficients positifs des dummies trimestriels réfletent bien le phénomène glissement des consommateurs vers le bloc inférieur.

5.4.2 Les points de divergence par rapport à l'étude de Ayadi et al [2002]

Les résultats de l'étude de Ayadi et al [2002] sur la même base des données appliquant les méthodes des données de panel stationnaires ( MCO, GLS, IV, GMM...) se résument dans les trois principes suivants:

1. La demande d'eau résidentielle est élastique au changement de prix dans les deux blocs ( élasticité prix de -0.1 pour le bloc inf et -0.4 pour le bloc sup) et plus élastique dans le bloc supérieur.

2. La pluviométrie et l'extension réseau ont un effet négatif sur la consommation moyenne dans les deux blocs.

3. Les effets prix sur le taux de branchement sont positifs dans le bloc inférieur et négatifs trés significatifs dans le bloc supérieur; le mouvement des abonnés est plutôt du bloc supérieur vers le bloc inférieur.

Nous avons conduit une estimation sur la même base des données que celle qu'utilise Ayadi et al[2002], afin de comparer nos résultats. Les deux points de divergence sont au niveau du premier et du troisième principe cités plus haut. En effet, nous démontrons empiriquement que la demande d'eau résidentielle dans sa partie essentielle ( i.e la consommation du bloc inférieur) est un point obscur de faite que leur effet prix de long terme est indéterminé ( sa coefficient est non significative en estimant par DOLS). Sur une période de 17 ans, le consommateur moyen du bloc supérieur ne répond pas rapidement au changement de prix par un glissement vers le bloc inférieur. Cela s'éclaircit lorsque nous actualisons la base des données.

5.4.3 Résultats des estimations sur toute la période (1980- 2007)

Durant cette période, la Tunisie a connu un développement remarquable, certains parlent d'un miracle tunisien. Cet essort économique et social a donné lieu à un niveau de vie du ménage tunisien légerement confortable, et comme la consommation, y compris l'eau, est l'indicateur "d'une vie en rose" elle ne cesse d'augmenter sur toute la période. L'objectif principal de la SONEDE est d'inciter les ménages à conserver l'eau plutôt que de récupérere le coût de distribution. Nous présentons dans ce qui suit une évaluation, basée sur des estimations économétrique trouvant leur base théorique dans la littérature, de cette politique pratiquée par la SONEDE durant ce 28 ans.

Estimation de la consommation et du taux de branchement pour le bolc inférieur:

Tableau 9: Estimation de la consommation pour le bloc inférieur

dep.vari LCi

- lpmi lpl ln lri Q1 Q2 Q4

Fmols within estimator

CO 0.06 0.002 -0.006 -0.006 -0.26 -0.058 -0.201

(1.316) (-0.34) (-0.32) (-0.082) (-15.95) (-3.7) (-12.67)

CE 0.004 -0.01 -0.027 0.08 -0.19 -0.06 -0.16

(0.13) (-2.49) (-1.56) (2.33) (-17.38) (-5.3) (-14.14)

NE 0.1 -0.003 -0.09 0.072 -0.18 -0.039 -0.15

(2.09) (-0.68) (-2.81) (0.92) (-12.6) (-2.44) (-10.3)

NO 0.17 -0.003 -0.12 -0.05 -0.28 -0.058 -0.22

(2.7) (-0.29) (-1.91) (-0.51) (-13.88) (-3.11) (-10.69)

SUD -0.01 -0.008 0.068 -0.1 -0.22 -0.037 -0.18

(-0.33) (-1.24) (1.52) (-0.77) (-11.97) (-2.16) (-9.94)

GT 0.10 -0.01 -0.07 0.014 -0.11 -0.03 -0.07

(2.6) (-4.44) (-2.51) (0.31) (-7.07) (-2.43) (-4.62)

Fmols between estimator

0.07 -0.006 -0.04 0.002 -0.2 -0.04 -0.16

(3.48) (-3.58) (-3.1) (0.9) (-32.16) (-7.82) (-25.44)

DOLS between estimator

0.1 0.05 0.01 0.34 -0.14 -0.09 -0.12

(1.221) (2.85) (0.207) (2.45) (-2.13) (1.28) (1.687)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 112 , no. regressors = 7

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Les résultats des estimations présentés dans le tableau ci-dessus montrent que la consommation d'eau essentielle ( cuisine, nettoyage, boisson...) du ménage a un effet de long terme non signiÞcative. Elle est inélastique au changement du revenu et du climat, alors qu'elle est légerement élastique à l'extension réseau. En effet, sur 28 ans le ménage du bloc inférieur n'a pas réagit au changement de tarif pratiqué par l'autorité comme le montre les effets de long terme estimés pour le bloc inférieur. Cela est structurel du fait que les frais variables des deux premières tranches sont incomparables avec ceux du tarif chargés par la SONEDE pour les abonnés des deux dernières tranches. Il est claire donc que l'objectif de l'autorité

responsable de secteur est d'inciter l'abonnés à bien gérer leur consommation supplémentaire. Mais compte tenu que la moyenne de consommation du bloc inférieur est de 18,16 m³, La SONEDE doit agir sur les consommateurs de ce bloc, soit en augmentant les prix des deux premières tranches soit en diminuant l'altitude de première tranche tarifaire. Une telle action va donner lieu à des habitudes de consommation économes au sein du bloc inférieur.

Les variables saisonnières ont des effets négatifs signiÞcatifs pour toutes les

régions.

Le tableau 10 regroupe le résultat de l'estimation du taux de branchement pour le bloc inférieur en fonction du prix, de la pluviométrie et de l'extension réseau. Le prix ne contribue pas au glissement des abonnés de bloc inférieur vers le bloc supérieur pour toutes les régions excépté le centre east. L'extension réseau agit négativement sur le taux de branchement, le même signe est retrouvé pour l'effet de long terme de la troisième trimestre, cela justiÞe le glissement de consommateur pendant l'été vers le bloc supérieur.

Tableau 10: Estimation du taux de branchement pour le bloc inférieur

dep.vari LTXi

- lpmi lpl ln Q1 Q3 Q4

Fmols within estimator

CO -0.03 0.07 0.023 0.08 -0.012 0.064

(-0.6) (5.75) (-0.78) (3.15) (-0.47) (2.54)

CE -0.12 0.04 -0.09 0.07 -0.03 0.05

(-1.62) (3.14) (-1.82) (1.96) (-1.05) (1.48)

NE 0.35 0.034 -0.46 0.10 -0.013 0.11

(4.92) (3.59) (-7.58) (4.018) (-0.52) (4.24)

NO 0.23 0.024 -0.304 0.068 -0.014 0.07

(2.49) (1.46) (-3.55) (2.37) (-0.506) (2.37)

SUD 0.39 0.02 -0.37 0.08 -0.014 0.01

(7.95) (3.08) (-11.9) (4.79) (-0.77) (5.33)

GT -0.23 -0.03 -0.14 0.10 -0.04 0.09

(-1.59) (-2.65) (-1.6) (1.86) (-0.78) (1.73)

Fmols between estimator

0.1 0.026 -0.23 0.086 -0.022 0.082

(4.71) (5.87) (-11.12) (7.42) (-1.68) (7.22)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 112 , no. regressors = 6

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Estimation de la consommation et du taux de branchement pour le bolc supérieur :

Nous conduisons l'estimation de la consommation et du taux de branchement pour le bloc supérieur aÞn de dégager les effets de long terme des diffèrentes variables. Nous pensons que les résultats seront compatibles avec nos intuitions du fait que la consommation au sein de ce bloc comprend une partie de luxe qui sera trés sensible au changement de prix.

Tableau 11: Estimation de la consommation pour le bloc supérieur

dep.vari LCs

- lpms lpl ln lrs Q1 Q2 Q4

Fmols within estimator

CO -0.132 0.031 -0.05 -0.11 0.19 0.013 0.12

(-1.15) (1.62) (-1.03) (-0.38) (5.12) (0.35) (3.358)

CE -0.13 -0.028 -0.064 -0.207 0.15 0.048 0.165

(-2.003) (-2.55) (-1.43) (-1.48) (4.85) (1.52) (5.05)

NE -0.203 -0.013 -0.034 -0.3 0.19 0.027 0.132

(-2.26) (-1.28) (-0.523) (-0.97) (6.73) (1.003) (4.37)

NO 0.2 -0.13 -0.58 -0.033 0.32 0.08 0.31

(0.77) (-2.07) (-1.57) (-0.07) (3.8) (1.07) (3.36)

SUD 0.003 -0.03 -0.25 0.428 0.24 0.08 0.24

(0.03) (-2.26) (-3.6) (0.44) (6.37) (2.16) (6.23)

GT -0.13 0.026 -0.0007 -0.405 0.026 0.021 -0.007

(-1.46) (3.25) (-0.012) (-2.31) (0.72) (0.66) (-0.22)

Fmols between estimator

-0.06 -0.02 -0.16 -0.1 0.21 0.045 0.162

(-2.48) (-1.36) (-3.34) (-1.95) (11.24) (2.77) (9.04)

DOLS between estimateur

-0.22 -0.01 -0.23 1.25 0.16 0.02 0.14

(-3.34) (-0.41) (-4.066) (15.44) (2.36) (-0.37) (2.036)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 112 , no. regressors = 7

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

L'estimation de la relation de long terme entre la consommation et ses déterminants montre bien l'effet prix négatif. Les élasticités prix de long terme négatives pour toutes les régions nous informent sur la réaction de longue durée du

ménage tunisien vis à vis la politique tarifaire rigoureuse pratiquée par la SONEDE durant les derniers 28 ans. Une telle réaction consiste pour un consommateur moyen du bloc supérieur de pratiquer avec le temps des habitudes économes d'eau. La variabilité inter-régionale de ces élasticités est due à un niveau de vie disparate.

La pluviométrie affecte négativement la consommation moyenne. Aussi, les variables saisonnières et l'extension réseau ont des effets de long terme négatifs.

La discussion porte alors sur l'effet revenu négatif, qui parait un peu paradoxal. Mais lorsque nous rélions ces résultats avec la Þabilité des données sur les enquêtes consommations et leur capacité d'approximer le revenu, nous pouvons juger nos résultats acceptables.

L'estimateur "FMOLS between" s'inscrit dans le même voix d'intérpretation cité ci-dessus, sauf qu'il cache la variabilité inter-régionale des effets de long terme.

L'estimation par DOLS donne des effets montrant la forte élasticité de la demande pour les gros consommateurs au changement de prix.

Tableau 12: Estimation du taux de branchement pour le bloc supérieur

dep.vari LTXs

- lpms lpl ln Q1 Q3 Q4

Fmols within estimator

CO -0.41 0.17 0.08 -0.91 0.34 -0.75

(-3.014) (1.96) (0.79) (-10.53) (4.04) (-8.68)

CE -0.068 0.017 -0.37 -0.79 0.34 -0.65

(-0.73) (0.76) (-4.07) (-12.25) (5.28) (-10.06)

NE 0.031 -0.017 -0.65 -0.86 0.22 -0.76

(0.2) (-0.67) (-4.06) (-11.93) (2.73) (-10.21)

NO 0.08 -0.026 -0.85 -0.94 0.2 -0.78

(0.257) (-0.42) (-2.27) (-8.78) (1.92) (-6.99)

SUD -0.67 -0.05 0.337 -0.96 0.19 -0.875

(-4.27) (-1.84) (2.63) (-12.5) (2.69) (-11.26)

GT -0.24 0.001 -0.55 -0.62 0.17 -0.52

(-2.41) (0.11) (-6.37) (-11.91) (3.68) (-10.83)

Fmols between estimator

-0.21 0.002 -0.33 -0.84 0.24 -0.72

(-4.07) (-0.03) (-5.45) (-27.72) (8.27) (-23.7)

( ): la statistique de signiÞcativité

Nsecs = 6 , Tperiods = 112 , no. regressors = 6

CO, CE, NE, NO, SUD et GT; centre ouest, centre east, nord east, nord ouest, sud et grand tunis

Les effets de long terme présentés ci-dessus montrent la pertinance de la tarification progressive rigoureuse pour les consommateurs du bloc supérieur. Cela incite le ménage de ce bloc à conserver l'eau et de glisser ainsi vers le bloc inférieur. Par conséquant, le prix est le seul moyen capable de réduire le gaspillage des ressources provoqué par l'irresponsabilité du consommateur.

L'effet pluviométrie sur le taux de branchement est non significatif pour les deux types des estimateurs. L'extension réseau affecte négativement le taux de branchement dans le bloc supérieur. Le troisième trimestre a un effet positif et significatif, cela montre que le consommateur garde sa consommation élévée pendant l'été et la réduit pendant les autres sessions comme l'indique les effets négatifs des autres coefficients ( Q1 et Q4).

5.5 Conclusion

L'application de la technique relative à la cointégration sur données de panel parait utile en estimant l'équilibre de long terme entre la consommation d'eau résidentielle et ses déterminants pour le cas de la Tunisie durant une période de 28 ans. En effet, nos résultats montrent que la consommation moyenne s'ajuste au prix, au revenu, au climat et à l'extension réseau. Malgré que l'eau est un bien de première nécessité dont la consommation ne dépend pas du prix comme prétend la plupart, nous montrons via cette étude économétrique que l'eau est un bien élastique au prix.

La consommation d'eau d'un ménage, qui se caractérise par un niveau de vie relativement confortable, est constituée par une partie essentielle et une autre de luxe. C'est cette dernière qui est élastique au prix.

L'action de la tarification sur le glissement de consommateur, du bloc supérieur vers le bloc inférieur, est visible à travers l'effet de long terme négatif du prix sur le taux de branchement au sein du bloc supérieur.

Conclusion générale

L'application de l'économétrie des données de panel non stationnaire, nous a améné à des résultats intuitifs qui peuvent servir comme un aide à la décision pour les responsables du secteur d'eau en Tunisie. Nous avons eu la chance d'appliquer une nouvelle approche économétrique gràce à la non stationnarité des données en double indice sur la consommation d'eau et ses déterminants pour le cas de la Tunisie durant la période (1980-2007).

La demande d'eau résidentielle en Tunisie est relativement sensible aux prix pour les gros consommateurs situés dans les régions caractérisées par un certain dynamisme économique et qui bénéficient de sources d'approvisionnement alternatives (nappes souterraines facilement accessibles). En effet les élasticités prix de long terme relatives au bloc supérieur dans le SUd et le Nord East sont partout autour de -0.3. Ce résultat nous autorsie à énoncer que toute politique de conservation de la ressource par des mécanismes économiques décentralisés serait possible. En effet, une tarification appropriée et centrée essentiellement sur le bloc supérieur pourrait résulter par un infléchissement de la croissance de la demande dans ce secteur avec tous les effets bénéfiques sur la balance globale des ressources en eau. Notons au passage qu'actuellement les gros consommateurs découragés par la politique de la SONEDE recourent au pompage de la nappe phréatique déjà sur exploitée. Afin de contraindre ces usagers à conserver la ressource, il est indispensable d'associer à la tarification une politique appropriée de préservation des nappes caractérisées malheureusement par ce qu'on appelle communément "open access".

L'élasticité prix de long terme du bloc inférieur, formé essentiellement de petits consommateurs ayant des revenus plutôt modestes, est presque négligeable et non significative pour la plupart des régions. Ce résultat expliquerait la croyance presque générale que la demande d'eau résidentielle est inélastique. Il est

donc important de noter que tout relévement des prix qui touche le bloc inférieur, caractérisé par une inélasticité presque certaine de la demande, conduirait nécessairement à des effets néfastes sur le bien-être des consommateurs concernés sans pour autant permettre de conserver la ressource. En effet, toute augmentation des prix étant donné l'absence de sources alternatives Þables et vu l'importance vitale de cette ressource, mène inéluctablement à réduire le pouvoir d'achat des consommateurs touchés. Les raisons fondamentales que nous venons d'évoquer expliquent la politique des responsables du secteur de pratique des prix largement inférieurs aux coûts de mobilisation pour ces couches défavorisées.

Finalement, nous constatons que la politique des prix conduite par la SONEDE durant la période passée s'est soldée par un succés certain. En effet suite à une tariÞcation appropriée, les gros consommateurs, dont l'impact sur la ressource est net, ont répondu positivement par une baisse sensible de leur demande. Nos résultats indiquent qu'il faudra continuer à agir dans ce sens. Il est conseillée d'augmenter le prix des tranches inférieures ou de réduire l'altitude de première tranche.

Nous avons procédé à une estimation de la relation d'équilibre de long terme entre la consommation et ses déterminants d'une part et celle entre le taux de branchement et les même variables explicatives excepté de revenu d'autre part. Nous n'avons pas posé la question sur l'ajustement de court terme, les forces de rappelles, dans ce tarvail, cela va faire l'objet d'un tarvail ultérieur. L'introduction d'autre variable comme la témperature peut améliorer les résultats. Nous pensons aussi que le découpage de la Tunisie en des régions basé sur des régles scientiÞques, comme l'analyse en composante principale, peut améliorer la qualité de tarvail.

Réferences Bibliographiques

[1] Ayadi, M., J. Krishnakumar and M. S. Matoussi (2002), A Panel data analysis of residential water demand in presence of nonlinear progressive tariffs", cahiers du département d'économétrie, Université de Genève , No 2002.06.

[2] Bahmani-Oskooee. M, Mitezab. I, Nasir. A. B. M (2002), The long run relation between black market and official exchange rates: evidence from panel cointegration, Economics Letters ,76, 397--404.

[3] Baltagi, B. H. (1995), Econometric Analysis of Panel Data, John Wiley and Sons.

[4] Baghestani, H., Noer. J (1993), Cointegration analysis of the black market and official exchange rates in India. Journal of Macroeconomics 15, 709--721.

[5] Ben Naceur H (1984), Estimation de la demande d'eau résidentielle: cas de la Tunisie, Mémoire de DEA, Faculté des sciences Economiques et de Gestion de Tunis.

[6] Booth, G.G., Mustafa, C., (1991), Long-run dynamics of black and official exchange rates, Journal of International Money and Finance,10, 392--405.

[7] Baltagi, B.H. et Kao, C. (2000), «Nonstationary panels, cointegration in panels and dynamic panels : a survey», in Advances in Econometrics, 15, edited by B. Baltagi et C. Kao, pp. 7-51, Elsevier Science.

[8] Bient, M, E. Carlevaro, F. DURAND, S et PAUL, M, (2006), La demande d'eau potable à La Réunion estimation à partir de données d'enquête, working paper, université de la réunion.

[9] Billings, B.R. and D.E. Agthe (1980) «Price Elasticities for Water: A Case Study of Increasing Block Rates», Land Economics, Vol. 56, No.1, pp. 73-84.

[10] Chien-Chiang, L. (2005), Energy consumption and GDP in developing countries: A cointegrated panel analysis, Energy Economics, 27, 415-- 427.

[11] Chicoine, D.L., S.C. Deller and G. Ramamurthy (1986) «Water Demand Estimation Under Block Rate Pricing: A Simultaneous Equation Approach», Water Resources Research, Vol.22, No.6, pp. 859-863.

[12] Corral, L., A. C. Fisher and N. Hatch (1998), `Price and Non-Price Inßuences onWater Conservation: An Econometric Model of Aggregate Demand under Non-linear Budget Constraint'. Working Paper No. 881, Department Of Agricultural and Resource Economics and Policy, University of California at Berkeley.

[13] Credoc (1997), L'Eau et les Usages Domestiques. Comportements de consommation de l'eau dans les ménages, Cahier de Recherche numéro 104.

[14] Choi, I. (2001), «Unit Root Tests for Panel Data», Journal of International Money and Finance, 20, 249-272.

[15] Dickey, D.A. et Fuller, W.A. (1981), «Likelihood Ratio Statistics for AutoRegressive Time Series with a Unit Root», Econometrica, 49, 1057-1072.

[16] Engle, R.F. et Granger, C.W.J. (1987), «Cointegration and error-correction : representation, estimation and testing», Econometrica, 64, pp. 813-836.

[17] Foster, H.S. and B.R. Beattie (1981) «On the SpeciÞcation of Price in Studies of Consumer Demand Under Block Price Rescheduling», Land Economics, Vol. 57, No.4, pp. 624-629.

[18] Granger, C.W.J. et Newbold, P. (1974), «Spurious regressions in econometrics», Journal of Econometrics, 2, 111-120.

[19] Groen, J.J.J. et Kleibergen, F. (2003), «Likelihood-based cointegration analysis in panels of vector error correction models», Journal of Busines and Economic Statistics, 21(2), 295-318.

[20] Howe, C.W. and F.P. Linaweaver (1967) «The Impact of Price on Residential Water Demand and its Relation to System Design and Price Structure», Water Resources Bulletin, 3 (1), 13-32.

[21] Hewitt, J. and W. Hanemann (1995), A Discrete/Continuous Choice Approach to Residential Water Demand under Block Rate Pricing, Land Economics, 71(2), 173--192.

[22] Höglund, L. (1997), Estimation of Household Demand for Water in Sweden and its Implications for a Potential Tax on Water Use, miméo, University of Göteborg.

[23] Hansen, L. (1996), Water and Energy Price Impacts on Residential Water Demand in Copenhagen, Land Economics 72(1), 66--79.

[24] Hamilton, J.D. (1994), Time Series Analysis, Princeton.

[25] Hadri, K. (2000), «Testing for Unit Roots in Heterogeneous Panel Data», Econometrics Journal, 3, 148-161.

[26] Hurlin, C. et Mignon, V. (2005), «Une synthèse des tests de racine unitaire sur données de panel», Economie et Prévision, 169-170-171, 253-294.

[27] Hurlin, C. et Mignon, V. (2006), «Une synthèse des tests de cointégration sur données de panel», Economie et Prévision,.

[28] Im, K.S., Pesaran, M.H. et Shin, Y. (2003), «Testing for Unit Roots in Heterogeneous Panels», Journal of Econometrics, 115, 1, 53-74.

[29] Johansen, S. (1991), «Estimation and hypothesis testing of cointegration vectors in Gaussian vector autoregressive models», Econometrica, 59, 1551- 1580.

[30] Kao, C. et Chiang, M.H. (2000), «On the estimation and inference of a cointegrated regression in panel data», Advances in Econometrics, 15, edited by B. Baltagi et C. Kao, 179-222, Elsevier Science.

[31] Kao, C., Chiang, M.H. et Chen, B. (1999), «International R&D spillovers : an application of estimation and inference in panel cointegration», Oxford Bulletin of Economics and Statistics, 61, 691-709.

[32] Kwiatkowski, D., Phillips, P.C.B., Schmidt, P. et Shin, Y. (1992), «Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root», Journal of Econometrics, 54, 91-115.

[33] Larsson, R., Lyhagen, J. et Löthgren, M. (2001), «Likelihood-based cointegration tests in heterogenous panels», Econometrics Journal, 4, 109-142.

[34] Lahouel M.H., M.S. Rejeb, C. Mamoghli and M. Daoues (1994) «Etude économique sur l'eau potable en Tunisie », SONEDE, Tunisia.

[35] Levin A., Lin, C.F. et Chu, J. (2002), «Unit root tests in panel data : Asymptotic and Þnite sample properties», Journal of Econometrics, 108, 1-24.

[36] Maddala, G.S. et Wu, S. (1999), «A Comparative Study of Unit Root Tests with Panel Data and a New Simple Test», Oxford Bulletin of Economics and Statistics, special issue, 631-652.

[37] Mark, N.C. et Sul, D. (2003), «Cointegration vector estimation by panel DOLS and long-run money demand», Oxford Bulletin of Economics and Statistics, 65, 655-680.

[38] Nieswiadomy, M.L. and D.J. Molina (1989) «Comparing Residential Water Demand Estimates under Decreasing and Increasing Block Rates», Land Economics, 65, No.3, 280-289.

[39] Nordin, J.A. (1976) «A Proposed ModiÞcation of Taylor's Demand Analysis: Comment», Bell Journal of Economics, 6, No.1, 719-721.

[40] Nauges, C. and A. Thomas (2003), Long-run Study of ResidentialWater Consumption, Environmental and Resource Economics, 26, 25--43.

[41] Oh, K. (1996), «Purchasing power parity and unit root tests using panel data», Journal of International Money and Finance, 15, 405-418.

[42] Pedroni, P. (1996), «Fully modiÞed OLS for heterogeneous cointegrated panels and the case of purchasing power parity», Working Paper in Economics, Indiana University.

[43] Pedroni, P. (1999), «Critical values for cointegration tests in heterogenous panels with multiple regressors», Oxford Bulletin of Economics and Statistics, S1, 61, 653-670.

[44] Pedroni, P. (2001), «Purchasing power parity tests in cointegrated panels», The Review of Economics and Statistics, November 2001, 83(4): 727--731.

[45] Phillips, P.C.B. et Hansen, B.E. (1990), «Statistical inference in instrumental variables regression with I(1) processes», Review of Economic Studies, 57, 99-125.

[46] Phillips, P.C.B. et Moon, H.R. (1999), «Linear regression limit theory for nonstationary panel data», Econometrica, 67, 1057-1111.

[47] Phillips, P.C.B. et Perron, P. (1988), «Testing for a Unit Root in Time Series Regression», Biometrika, 75, 335-346.

[48] Rodriguez F. and E. Betteta (1991) « Economics of Urban Water Supply : Theory and Case Study », E.D.I. Washington D.C.

[49] R Martínez-Espiñeira (2007), «An estimation of residential water demand using cointegrationand error correction techniques», Journal of Applied Economics. Vol X, No.1, 161-184

[50] R Martínez-Espiñeira (2003), Estimating Water Demand under Increasing-Block Tariffs Using Aggregate Data and Proportions of Users per Block, Environmental and Resource Economics, 26: 5--23.

[51] Schefter, J.E. et E.L. David (1985) «Estimating Residential Water Demand Under Multi-Part Tariffs Using Aggregate Data», Land Economics, 61, No.3, 352-359.

[52] Saikkonen, P. (1991), «Asymptotically efficient estimation of cointegrating regressions», Econometric Theory, 58, 1-21.

[53] Stock, J. et Watson, M. (1993), «A simple estimator of cointegrating vectors in higher order integrated systems», Econometrica, 61, 783-820.

[54] Vaillancourt F et Mireille C (1984), La demande résidentielle d'eau ; ville de saint-Laurent 1978, cahier 8406, Université de Montéral, ISSN 0709-9231.

[55] Wong, S.T. (1972), «A Model of Municipal Water Demand: A Case Study Northeastern Illinois», Land Economics, 48, No.1, 34-44.

Annexes

ESTIMATION POUR la période 1980-1996

************test de racine unitaire lntot**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -31.93797

Levin-Lin t-rho-stat = -19.96045

Levin-Lin ADF-stat = -5.13155

IPS ADF-stat = -7.52747

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LCI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -33.42969

Levin-Lin t-rho-stat = -14.19060

Levin-Lin ADF-stat = -0.82937

IPS ADF-stat = -1.55815

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LCS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -6.54261

Levin-Lin t-rho-stat = -2.64101

Levin-Lin ADF-stat = 1.90215

IPS ADF-stat = 2.09345

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LPMI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 1.01628

Levin-Lin t-rho-stat = 1.46122

Levin-Lin ADF-stat = 2.22748

IPS ADF-stat = 2.96071

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LPMS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 1.50365

Levin-Lin t-rho-stat = 1.63521

Levin-Lin ADF-stat = 1.70102

IPS ADF-stat = 2.25136

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LRI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.84836

Levin-Lin t-rho-stat = 1.16145

Levin-Lin ADF-stat = 1.21776

IPS ADF-stat = 1.53265

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LRS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.65128

Levin-Lin t-rho-stat = 0.82636

Levin-Lin ADF-stat = 0.87435

IPS ADF-stat = 1.17932

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LTXi**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -1.57752

Levin-Lin t-rho-stat = -0.50299

Levin-Lin ADF-stat = 0.62222

IPS ADF-stat = 0.35047

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LTXs**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -33.64354

Levin-Lin t-rho-stat = -12.33282

Levin-Lin ADF-stat = 3.44606

IPS ADF-stat = 4.67315

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLRI**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -49.97680

Levin-Lin t-rho-stat = -2.82419

Levin-Lin ADF-stat = -2.68955

IPS ADF-stat = -4.56996

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLRS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

********************************************
-raw panel unit root test results-

Levin-Lin rho-stat = -49.68859

Levin-Lin t-rho-stat = 0.33849

Levin-Lin ADF-stat = 0.53898

IPS ADF-stat = -1.35556

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPMS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -46.66672

Levin-Lin t-rho-stat = -7.80998

Levin-Lin ADF-stat = -8.28039

IPS ADF-stat = -11.58397

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLCI**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -26.55728

Levin-Lin t-rho-stat = -6.20553

Levin-Lin ADF-stat = -5.38701

IPS ADF-stat = -5.83379

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLCS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -40.53423

Levin-Lin t-rho-stat = -12.71387

Levin-Lin ADF-stat = -11.75258

IPS ADF-stat = -18.89916

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPMI**********

Currently computing panel statistics. Please wait.

offset = 2
offset = 2

offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -55.38040

Levin-Lin t-rho-stat = -16.81704

Levin-Lin ADF-stat = -10.57342

IPS ADF-stat = -14.09150

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLTXi**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -184.00791

Levin-Lin t-rho-stat = 0.74483

Levin-Lin ADF-stat = 1.29601

IPS ADF-stat = 1.78070

(using large sample adjustment values)
Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLTXs**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************
-raw panel unit root test results-

Levin-Lin rho-stat = -28.34786

Levin-Lin t-rho-stat = -15.28633

Levin-Lin ADF-stat = -21.80867

IPS ADF-stat = -28.18459

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPL**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -61.45548

Levin-Lin t-rho-stat = -30.15130

Levin-Lin ADF-stat = -13.73420

IPS ADF-stat = -18.59758

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDLRS**********

Currently computing panel statistics. Please wait.

offset = 3
offset = 3
offset = 3

offset = 3
offset = 3
offset = 3

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -62.69054

Levin-Lin t-rho-stat = 2.31640

Levin-Lin ADF-stat = 2.10612

IPS ADF-stat = 1.86334

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour Lpl**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -22.33080

Levin-Lin t-rho-stat = -6.72293

Levin-Lin ADF-stat = -1.56276

IPS ADF-stat = -2.43367

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDLTXI**********

Currently computing panel statistics. Please wait.

offset = 3 offset = 3 offset = 3 offset = 3 offset = 3 offset = 3

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -123.97512

Levin-Lin t-rho-stat = 1.94249

Levin-Lin ADF-stat = 1.40190

IPS ADF-stat = 1.84023

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDDLTXI**********

Currently computing panel statistics. Please wait.

offset = 4 offset = 4 offset = 4 offset = 4 offset = 4 offset = 4

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -54.99975

Levin-Lin t-rho-stat = -41.29335

Levin-Lin ADF-stat = -31.62455

IPS ADF-stat = -41.99411

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDDLRS**********

Currently computing panel statistics. Please wait.

offset = 4 offset = 4 offset = 4 offset = 4 offset = 4 offset = 4

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -72.65484

Levin-Lin t-rho-stat = -74.86985

Levin-Lin ADF-stat = -15.30262

IPS ADF-stat = -20.27540

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 68 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

********************************************

*******test de cointegration pedroni.P[2004](lower bloc)(1980-1996)******

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

panel v-stat = 0.82298

panel rho-stat = -5.87899

panel pp-stat = -7.93154

panel adf-stat = -0.35383

group rho-stat = -5.66646

group pp-stat = -8.95441

group adf-stat = 1.49618

Nsecs = 6 , Tperiods = 68 , no. regressors = 5

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

********************************************

********estimation de la relation de cointegration (lower bloc)*****

Currently computing panel statistics. Please wait.

Dependent Variable : LCI

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

	Member ***********		Variable *************		Coefficient **************		t-statistic **************
	No.1		LPMI		0.10143		( 2.81181 )
	No.1		LPL		-0.01571		( -1.62211 )
	No.1		LRI		0.01737		( 0.32588 )
	No.1		LNTOT		-0.01289		( -1.04068 )
	No.1		Q1		-0.22841		( -17.99344
)
	No.1		Q3		0.06050		( 4.92334 )
	No.1		Q4		-0.16103		( -12.86011
)
	No.2		LPMI		-0.03531		( -0.51691 )
	No.2		LPL		-0.00670		( -1.19025 )
	No.2		LRI		-0.01188		( -0.19944 )
	No.2		LNTOT		0.10186		( 1.53789 )
	No.2		Q1		-0.18346		( -9.78723 )
	No.2		Q3		0.07458		( 4.68018 )
	No.2		Q4		-0.14320		( -7.60647 )
	No.3		LPMI		0.04892		( 0.69387 )
	No.3		LPL		0.00037		( 0.05557 )
	No.3		LRI		0.09909		( 1.04423 )
	No.3		LNTOT		-0.05160		( -0.66441 )
	No.3		Q1		-0.16240		( -7.53520 )
	No.3		Q3		0.04171		( 2.60261 )
	No.3		Q4		-0.13282		( -5.63442 )
	No.4		LPMI		0.12589		( 2.20072 )
	No.4		LPL		-0.00011		( -0.01293 )
	No.4		LRI		-0.20382		( -2.74886 )
	No.4		LNTOT		0.02271		( 0.33459 )
	No.4		Q1		-0.26206		( -14.44251
)
	No.4		Q3		0.05525		( 3.54747 )
	No.4		Q4		-0.22409		( -11.76857
)
	No.5		LPMI		0.11121		( 1.11128 )
	No.5		LPL		-0.01425		( -1.47485 )
	No.5		LRI		-0.14264		( -0.81904 )
	No.5		LNTOT		-0.05522		( -0.53919 )
	No.5		Q1		-0.21685		( -7.71503 )
	No.5		Q3		0.04753		( 2.01156 )
	No.5		Q4		-0.17722		( -5.95474 )
No.6		LPMI		0.04756		( 0.83085 )
No.6		LPL		-0.01677		( -2.86445 )
No.6		LRI		-0.05234		( -0.97070 )
No.6		LNTOT		0.01729		( 0.32623 )
No.6		Q1		-0.09625		( -4.90428 )
No.6		Q3		0.04012		( 2.68747 )
No.6		Q4		-0.04598		( -2.39623 )

*********** ************* ************** **************

	PANEL GROUP FMOLS Coefficient	RESULTS t-statistic
LPMI	0.06661	(	2.91147 )
LPL	-0.00886	(	-2.90225 )
LRI	-0.04904	(	-1.37495 )
LNTOT	0.00369	(	-0.01861 )
Q1	-0.19157	(	-25.46559 )
Q3	0.05328	(	8.34975 )
Q4	-0.14739	(	-18.86945 )

Nsecs = 6 , Tperiods = 68 , no. regressors = 7
********************************************

******test de cointegration pedroni.P[2004](upper bloc)(1980-1996)******

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

panel	v-stat	=	2.26166
panel	rho-stat	=	-8.05653
panel	pp-stat	=	-8.97103
panel	adf-stat	=	-4.07297
group	rho-stat	=	-7.97861
group	pp-stat	=	-10.90046
group	adf-stat	=	-2.48021

Nsecs = 6 , Tperiods = 68 , no. regressors = 4

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances (see OBES reference for details)

********************************************

******estimation de la relation de cointegration(upper bloc)******

Currently computing panel statistics. Please wait. Dependent Variable : LCS

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

No.1	LPMS	-0.22101	( -2.77162 )
No.1	LPL	-0.03075	( -1.40944 )
No.1	LNTOT	-0.01288	( -0.41101 )
No.1	LRS	0.24998	( 1.18980 )
No.1	Q1	0.25529	( 9.31835 )
No.1	Q2	0.03943	( 1.45458 )
No.1	Q4	0.21205	( 7.79263 )
No.2	LPMS	0.12924	( 1.08297 )
No.2	LPL	-0.01751	( -1.72468 )
No.2	LNTOT	-0.49038	( -2.82472 )
No.2	LRS	-0.12604	( -1.04054 )
No.2	Q1	0.28197	( 5.24966 )
No.2	Q2	0.06339	( 2.10847 )
No.2	Q4	0.29688	( 5.65829 )
No.3	LPMS	-0.22934	( -2.57979 )
No.3	LPL	0.00356	( 0.35626 )
No.3	LNTOT	-0.20478	( -1.61353 )
No.3	LRS	0.30719	( 1.18039 )
No.3	Q1	0.26238	( 6.85145 )
No.3	Q2	0.06025	( 2.40913 )
No.3	Q4	0.24918	( 5.89653 )
No.4	LPMS	0.02743	( 0.24651 )
No.4	LPL	-0.05110	( -3.41378 )
No.4	LNTOT	-0.40015	( -2.49317 )
No.4	LRS	0.18381	( 0.84708 )
No.4	Q1	0.32192	( 8.23446 )
No.4	Q2	0.03102	( 1.13868 )
No.4	Q4	0.33190	( 8.10084 )
No.5	LPMS	-0.30664	( -4.60692 )
No.5	LPL	-0.01624	( -2.31443 )
No.5	LNTOT	0.11475	( 1.12216 )
No.5	LRS	0.49857	( 1.02448 )
No.5	Q1	0.21651	( 9.14977 )
No.5	Q2	0.03082	( 2.00106 )
No.5	Q4	0.20740	( 8.36126 )
No.6	LPMS	-0.10001	( -1.88617 )
No.6	LPL	0.01069	( 2.10802 )
No.6	LNTOT	-0.33892	( -4.33586 )
No.6	LRS	0.31311	( 3.25363 )
No.6	Q1	0.12410	( 4.32674 )
No.6	Q2	0.05922	( 3.86756 )
No.6	Q4	0.12813	( 4.56400 )

*********** ************* ************** **************

PANEL GROUP FMOLS RESULTS

	Coefficient	t-statistic
LPMS	-0.11672	(	-4.29274 )
LPL	-0.01689	(	-2.61200 )
LNTOT	-0.22206	(	-4.30952 )
LRS	0.23777	(	2.63518 )
Q1	0.24369	(	17.60793 )
Q2	0.04735	(	5.29884 )
Q4	0.23759	(	16.48243 )

Nsecs = 6 , Tperiods = 68 , no. regressors = 7
********************************************

******test de cointegration de pedroni( taux de branchement)bloc inf****

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

panel	v-stat	=	0.53158
panel	rho-stat	=	-4.01311
panel	pp-stat	=	-4.61527
panel	adf-stat	=	-0.45646
group	rho-stat	=	-4.41823
group	pp-stat	=	-5.74204
group	adf-stat	=	-0.48969

Nsecs = 6 , Tperiods = 68 , no. regressors = 3

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ******estimation de la relation******

Currently computing panel statistics. Please wait. Dependent Variable : LTXI

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

Member ***********	Variable *************		Coefficient **************		t-statistic **************
No.1	LPMI		0.01665		( 5.94875 )
No.1	LPL		-0.00405		( -3.23621 )
No.1	LNTOT		0.01680		( 10.47089 )
No.1	Q1		0.00045		( 0.27328 )
No.1	Q3		-0.00151		( -0.95029 )
No.1	Q4		0.00171		( 1.05939 )
No.2	LPMI		-0.00263		( -1.16484 )
No.2	LPL		0.00006		( 0.28644 )
No.2	LNTOT		0.00844		( 4.15195 )
No.2	Q1		0.00094		( 1.48155 )
No.2	Q3		-0.00082		( -1.48878 )
No.2	Q4		0.00106		( 1.69344 )
No.3	LPMI		-0.00442		( -1.41286 )
No.3	LPL		-0.00154		( -5.52819 )
No.3	LNTOT		0.02299		( 6.68249 )
No.3	Q1		-0.00055		( -0.56775 )
No.3	Q3		-0.00093		( -1.25468 )
No.3	Q4		-0.00066		( -0.62680 )
No.4	LPMI		0.00652		( 1.14645 )
No.4	LPL		-0.00331		( -3.89220 )
No.4	LNTOT		0.01972		( 3.62069 )
No.4	Q1		0.00016		( 0.09209 )
No.4	Q3		-0.00049		( -0.31437 )
No.4	Q4		0.00075		( 0.43067 )
No.5	LPMI		0.00388		( 1.01512 )
No.5	LPL		-0.00195		( -5.39748 )
No.5	LNTOT		0.02489		( 7.01429 )
No.5	Q1		-0.00013		( -0.12934 )
No.5	Q3		-0.00060		( -0.66200 )
No.5	Q4		0.00019		( 0.17172 )
No.6	LPMI		-0.00610		( -0.71813 )
No.6		LPL		-0.00301		( -3.50686 )
No.6		LNTOT		0.02673		( 4.93709 )
No.6		Q1		-0.00363		( -1.31978 )
No.6		Q3		-0.00053		( -0.22804 )
No.6		Q4		-0.00232		( -0.88017 )

*********** ************* ************** **************

PANEL GROUP FMOLS RESULTS

	Coefficient	t-statistic
LPMI	0.00232	(	1.96550 )
LPL	-0.00230	(	-8.68528 )
LNTOT	0.01993	(	15.05513 )
Q1	-0.00046	(	-0.06938 )
Q3	-0.00081	(	-1.99966 )
Q4	0.00012	(	0.75454 )

Nsecs = 6 , Tperiods = 68 , no. regressors = 6

******************************************** ****test de cointegration de pedroni (bloc sup)*****

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

panel	v-stat	=	2.20086
panel	rho-stat	=	-5.10796
panel	pp-stat	=	-4.96712
panel	adf-stat	=	-1.03185
group	rho-stat	=	-4.55337
group	pp-stat	=	-5.25190
group	adf-stat	=	-0.01764

Nsecs = 6 , Tperiods = 68 , no. regressors = 3

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** *******estimation de la relation*****

Currently computing panel statistics. Please wait. Dependent Variable : LTXS

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

Member Variable Coefficient t-statistic

***********		*************		**************		**************
No.1		LPMS		-0.27075		( -3.28816 )
No.1		LPL		-0.06361		( -1.38213 )
No.1		LNTOT		0.07817		( 1.24222 )
	No.1		Q1		-0.98452		( -16.57385
)
	No.1		Q3		0.31992		( 5.59320 )
	No.1		Q4		-0.78575		( -13.37674
)
	No.2		LPMS		0.43478		( 1.29447 )
	No.2		LPL		-0.02148		( -0.79135 )
	No.2		LNTOT		-0.94848		( -1.88899 )
	No.2		Q1		-0.79004		( -6.81206 )
	No.2		Q3		0.30754		( 3.49750 )
	No.2		Q4		-0.62467		( -5.58770 )
	No.3		LPMS		0.48198		( 2.23577 )
	No.3		LPL		-0.02756		( -1.08751 )
	No.3		LNTOT		-1.25480		( -3.95810 )
	No.3		Q1		-0.83329		( -9.43512 )
	No.3		Q3		0.18606		( 2.87311 )
	No.3		Q4		-0.70439		( -7.22116 )
	No.4		LPMS		0.79404		( 2.59619 )
	No.4		LPL		-0.06027		( -1.42018 )
	No.4		LNTOT		-1.62587		( -4.24747 )
	No.4		Q1		-0.84921		( -8.99437 )
	No.4		Q3		0.11983		( 1.53634 )
	No.4		Q4		-0.70545		( -7.33079 )
	No.5		LPMS		0.76526		( 2.13725 )
	No.5		LPL		-0.04839		( -1.45358 )
	No.5		LNTOT		-1.57978		( -3.51167 )
	No.5		Q1		-0.84230		( -7.97227 )
	No.5		Q3		0.12278		( 1.47941 )
	No.5		Q4		-0.70265		( -6.52156 )
	No.6		LPMS		0.22431		( 1.21161 )
	No.6		LPL		0.00775		( 0.46429 )
	No.6		LNTOT		-1.03504		( -5.12575 )
	No.6		Q1		-0.50528		( -7.56657 )
	No.6		Q3		0.12906		( 2.49424 )
	No.6		Q4		-0.46476		( -7.38629 )

*********** ************* ************** **************

PANEL GROUP FMOLS RESULTS

Coefficient t-statistic

LPMS 0.40494 ( 2.52588 )

LPL -0.03559 ( -2.31495 )

LNTOT -1.06097 ( -7.14017 )

Q1 -0.80077 ( -23.41477 )

Q3 0.19753 ( 7.13365 )

Q4 -0.66461 ( -19.36086 )

Nsecs = 6 , Tperiods = 68 , no. regressors = 6

******************************************** *************estimation dols*****

Linear Regression - Estimation by Least Squares Dependent Variable LCI

Panel(68) of Undated Data From 1//01 To 6//68

Usable Observations 408 Degrees of Freedom 401

Centered R**2 0.040730 R Bar **2 0.026376

Uncentered R**2 0.998109 T x R**2 407.228

Mean of Dependent Variable 2.8809887087
Std Error of Dependent Variable 0.1281950278

Standard Error of Estimate 0.1264930668

Sum of Squared Residuals 6.4161988789

Log Likelihood 268.17111

Durbin-Watson Statistic 0.276504

Variable Coeff Std Error T-Stat Signif

*******************************************************************************

1. LPMI 0.145543947 0.023090861 6.30310 0.00000000

2. LPL 0.022121537 0.004869037 4.54331 0.00000734

3.	LRI		0.223498202			0.042480590	5.26118	0.00000023
4.	LNTOT		0.074196640			0.022034520	3.36729	0.00083247
5.	Q1		-0.242331877			0.018204112	-13.31193	0.00000000
6.	Q2		-0.041925969			0.017759939	-2.36070	0.01871805
7.	Q4		-0.203089269			0.018478801	-10.99039	0.00000000
Nobs = 396 JB test Standard Errors are Var.# Coeff.				= 1.58648 ( 0.4523771 ) adjusted for long-run variance. S.E. t-statistic
1		0.14554		0.11135	1.307
2		0.02212		0.02348	0.942
3		0.22350		0.20486	1.091
4		0.07420		0.10626	0.698
5		-0.24233		0.08779	-2.760
6		-0.04193		0.08565	-0.490
7		-0.20309		0.08911	-2.279

*************estimation dols*****

Linear Regression - Estimation by Least Squares Dependent Variable LCS

Panel(68) of Undated Data From 1//01 To 6//68

Usable Observations 408 Degrees of Freedom 401

Centered R**2 -0.304230 R Bar **2 -0.323745

Uncentered R**2 0.998733 T x R**2 407.483

Mean of Dependent Variable 5.0202845011
Std Error of Dependent Variable 0.1567548440

Standard Error of Estimate 0.1803528940

Sum of Squared Residuals 13.043393718

Log Likelihood 123.44210

Durbin-Watson Statistic 0.344165

Variable Coeff Std Error T-Stat Signif

*******************************************************************************

1.	LPMS		-0.196799571			0.025099605	-7.84074	0.00000000
2.	LPL		-0.014377846			0.007107888	-2.02280	0.04375676
3.	LRS		1.347813574			0.036881583	36.54435	0.00000000
4.	LNTOT		-0.310948023			0.025239699	-12.31980	0.00000000
5.	Q1		0.257292758			0.025634044	10.03715	0.00000000
6.	Q2		0.058608190			0.025268795	2.31939	0.02087554
7.	Q4		0.272553340			0.025813411	10.55859	0.00000000
Nobs = 396 JB test Standard Errors are Var.# Coeff.				= 93.69797 ( 0.0000000 ) adjusted for long-run variance. S.E. t-statistic
1		-0.19680		0.11173	-1.761
2		-0.01438		0.03164	-0.454
3		1.34781		0.16418	8.209
4		-0.31095		0.11236	-2.767
5		0.25729		0.11411	2.255
6		0.05861		0.11249	0.521
7		0.27255		0.11491	2.372

Johansen Fisher
Panel
Cointegration
Test

Series: LCI LPMI LRI LPL LNTOT

Date: 05/28/09 Time: 23:31

Sample: 1980Q1 1996Q2

Included observations: 396

Trend assumption: Linear deterministic trend (restricted)

Lags interval (in first differences): 1 1

Unrestricted Cointegration Rank Test (Trace and Maximum Eigenvalue)

No. of CE(s)	(from trace test)	Prob.	(from max-eigen test)	Prob.
None	369.4	0.0000	126.2	0.0000
At most 1	82.40	0.0000	281.8	0.0000
At most 2	17.80	0.1218	13.94	0.3043
At most 3	9.766	0.6365	7.929	0.7906
At most 4	8.263	0.7643	8.263	0.7643
* Probabilities are computed using asymptotic Chi- square distribution.

Individual cross section results

Cross Section	Trace Test Statistics	Prob.**	Max-Eign Test Statistics	Prob.**
Hypothesis of no cointegration
1	299.3965	0.0000	233.5533	0.0001
2	452.6606	0.0001	224.9686	0.0001
3	244.0600	0.0000	167.8062	0.0000
4	270.9142	0.0000	215.4557	0.0001
5	264.9514	0.0000	213.2474	0.0001
6	199.8923	0.0000	151.3339	0.0000
Hypothesis of at most 1 cointegration relationship
1	65.8433	0.0339	32.6746	0.0427
2	227.6919	0.0000	187.5269	0.0000
3	76.2538	0.0032	29.2632	0.1073
4	55.4585	0.2081	23.7639	0.3645
5	51.7040	0.3413	24.1532	0.3386
6	48.5584	0.4795	27.1015	0.1813
Hypothesis of at most 2 cointegration relationship
1	33.1686	0.3280	20.9481	0.1933
2	40.1650	0.0918	18.6734	0.3278
3	46.9905	0.0185	26.7872	0.0372
4	31.6946	0.4051	14.3552	0.6917
5	27.5508	0.6488	14.6110	0.6692
6	21.4569	0.9279	12.2209	0.8588
Hypothesis of at most 3 cointegration relationship
1	12.2205	0.7965	9.5776	0.6639
2	21.4916	0.1595	12.0156	0.4137
3	20.2034	0.2158	15.2964	0.1781
4	17.3394	0.3900	11.6418	0.4492
5	12.9398	0.7429	7.2788	0.8809
6	9.2360	0.9534	5.2592	0.9803
Hypothesis of at most 4 cointegration relationship
1	2.6430	0.9160	2.6430	0.9160
2	9.4760	0.1530	9.4760	0.1530
3	4.9069	0.6098	4.9069	0.6098
4	5.6976	0.4996	5.6976	0.4996
5	5.6610	0.5045	5.6610	0.5045
6	3.9768	0.7455	3.9768	0.7455

**MacKinnon-Haug-Michelis (1999) p-values

Johansen Fisher
Panel
Cointegration
Test

Series: LCS LPMS LRS LNTOT LPL

Date: 05/28/09 Time: 23:30

Sample: 1980Q1 1996Q2

Included observations: 396

Trend assumption: Linear deterministic trend (restricted)

Lags interval (in first differences): 1 1

Unrestricted Cointegration Rank Test (Trace and Maximum Eigenvalue)

Hypothesized No. of CE(s)	Fisher Stat.* (from trace test)	Prob.	Fisher Stat.* (from max-eigen test)	Prob.
None	323.8	0.0000	219.4	0.0000
At most 1	75.24	0.0000	280.2	0.0000
At most 2	12.72	0.3896	10.54	0.5689
At most 3	6.818	0.8694	5.934	0.9194
At most 4	5.882	0.9219	5.882	0.9219
* Probabilities are computed using asymptotic Chi- square distribution.

Individual cross section results

Cross Section		Trace Test Statistics		Prob.**	Max-Eign Test Statistics			Prob.**
Hypothesis of no cointegration
1		178.1101		0.0000	121.4457			0.0000
2		343.4654		0.0000	180.1517			0.0001
3		179.7027		0.0000	111.8097			0.0000
4		172.0963		0.0000	132.3268			0.0000
5		198.3617		0.0000	142.8418			0.0000
6		198.8559		0.0000	144.7367			0.0000
Hypothesis of at most 1 cointegration relationship
1		56.6644		0.1741	33.6725			0.0320
2		163.3137		0.0000	123.5143			0.0000
3		67.8930		0.0221	27.8048			0.1538
4		39.7695		0.8560	14.8907			0.9513
5		55.5199		0.2062	22.4636			0.4579
6		54.1192		0.2509	29.3684			0.1045
Hypothesis of at most 2 cointegration relationship
1 22.9919 0.8782					11.1508			0.9193
2	39.7993		0.0991			22.5932	0.1262
3	40.0882		0.0933			20.9026	0.1955
4	24.8788		0.7958			12.1924	0.8606
5	33.0564		0.3336			17.3855	0.4258
6	24.7508		0.8021			15.1647	0.6196
Hypothesis of at most 3 cointegration relationship
1	11.8411		0.8229			9.2030	0.7034
2	17.2061		0.3997			12.3990	0.3789
3	19.1856		0.2699			11.4591	0.4671
4	12.6864		0.7623			8.0913	0.8133
5	15.6709		0.5192			10.7359	0.5407
6	9.5861		0.9414			6.3442	0.9398
Hypothesis of at most 4 cointegration relationship
1	2.6381		0.9165			2.6381	0.9165
2	4.8071		0.6242			4.8071	0.6242
3	7.7266		0.2748			7.7266	0.2748
4	4.5951		0.6551			4.5951	0.6551
5	4.9350		0.6057			4.9350	0.6057
6	3.2419		0.8466			3.2419	0.8466

**MacKinnon-Haug-Michelis (1999) p-values

Résultats des estimations pour la période 1980-2007:

************test de racine unitaire lntot********** Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -62.47497

Levin-Lin t-rho-stat = -26.57930

Levin-Lin ADF-stat = -17.53012

IPS ADF-stat = -17.73521

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LCI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -57.29466

Levin-Lin t-rho-stat = -18.17733

Levin-Lin ADF-stat = -2.90258

IPS ADF-stat = -4.09191

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LCS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1

offset = 1
offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -31.46655

Levin-Lin t-rho-stat = -8.24580

Levin-Lin ADF-stat = -0.51805

IPS ADF-stat = -0.81176

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LPMI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.69037

Levin-Lin t-rho-stat = 0.49136

Levin-Lin ADF-stat = 0.37458

IPS ADF-stat = 0.49380

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LPMS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.90816

Levin-Lin t-rho-stat = -0.46058

Levin-Lin ADF-stat = -0.49439

IPS ADF-stat = -0.67031

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LRI**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.92693

Levin-Lin t-rho-stat = 0.92373

Levin-Lin ADF-stat = 0.94385

IPS ADF-stat = 1.04892

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LRS**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = 0.68289

Levin-Lin t-rho-stat = 0.58391

Levin-Lin ADF-stat = 0.59964

IPS ADF-stat = 0.71208

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LTXi**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -10.24705

Levin-Lin t-rho-stat = -3.40094

Levin-Lin ADF-stat = 1.99807

IPS ADF-stat = 2.65745

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour LTXs**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -50.63625

Levin-Lin t-rho-stat = -12.93844

Levin-Lin ADF-stat = 1.04933

IPS ADF-stat = 1.16388

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLRI**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -83.55340

Levin-Lin t-rho-stat = -6.69959

Levin-Lin ADF-stat = -6.67989

IPS ADF-stat = -9.56023

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLRS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -83.77476

Levin-Lin t-rho-stat = -1.75979

Levin-Lin ADF-stat = -1.58560

IPS ADF-stat = -4.84274

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPMS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -96.93893

Levin-Lin t-rho-stat = -16.23782

Levin-Lin ADF-stat = -14.03807

IPS ADF-stat = -18.10985

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLCI**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -50.60288

Levin-Lin t-rho-stat = -13.86359

Levin-Lin ADF-stat = -20.87066

IPS ADF-stat = -27.68438

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLCS**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -90.16863

Levin-Lin t-rho-stat = -34.18184

Levin-Lin ADF-stat = -16.98361

IPS ADF-stat = -23.26185

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPMI**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

********************************************
-raw panel unit root test results-

Levin-Lin rho-stat = -99.60124

Levin-Lin t-rho-stat = -29.65520

Levin-Lin ADF-stat = -15.86289

IPS ADF-stat = -21.04360

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLTXi**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -65.19546

Levin-Lin t-rho-stat = -21.82314

Levin-Lin ADF-stat = -8.32385

IPS ADF-stat = -8.97915

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLTXs**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -51.07769

Levin-Lin t-rho-stat = -23.85272

Levin-Lin ADF-stat = -30.09654

IPS ADF-stat = -36.28432

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DLPL**********

Currently computing panel statistics. Please wait.

offset = 2 offset = 2 offset = 2 offset = 2 offset = 2 offset = 2

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -90.20229

Levin-Lin t-rho-stat = -35.55282

Levin-Lin ADF-stat = -21.43623

IPS ADF-stat = -28.82197

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances (see OBES reference for details)

******************************************** ************test de racine unitaire pour DDLRS**********

Currently computing panel statistics. Please wait.

offset = 3 offset = 3 offset = 3 offset = 3 offset = 3 offset = 3

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -104.87718

Levin-Lin t-rho-stat = 1.71759

Levin-Lin ADF-stat = 1.38870

IPS ADF-stat = 0.68106

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour Lpl**********

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -27.66841

Levin-Lin t-rho-stat = -7.60820

Levin-Lin ADF-stat = -1.18345

IPS ADF-stat = -1.91718

(using large sample adjustment values)
Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDLTXI**********

Currently computing panel statistics. Please wait.

offset = 3 offset = 3 offset = 3 offset = 3 offset = 3 offset = 3

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -70.59447

Levin-Lin t-rho-stat = -18.60891

Levin-Lin ADF-stat = -26.08274

IPS ADF-stat = -35.41405

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDDLTXI**********

Currently computing panel statistics. Please wait.

offset = 4 offset = 4 offset = 4 offset = 4 offset = 4 offset = 4

RESULTS:

********************************************

-raw panel unit root test results-

Levin-Lin rho-stat = -72.30862

Levin-Lin t-rho-stat = -30.75060

Levin-Lin ADF-stat = -19.49161

IPS ADF-stat = -24.93524

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ************test de racine unitaire pour DDDLRS**********

Currently computing panel statistics. Please wait.

offset = 4 offset = 4 offset = 4 offset = 4 offset = 4

offset = 4

RESULTS:

********************************************
-raw panel unit root test results-

Levin-Lin rho-stat = -121.27915

Levin-Lin t-rho-stat = -46.94658

Levin-Lin ADF-stat = -14.54680

IPS ADF-stat = -21.38631

(using large sample adjustment values)

Nsecs = 6 , Tperiods = 112 , no. regressors = 0

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

********************************************

*******test de cointegration pedroni.P[2004](lower bloc)(1980-1996)******

Currently computing panel statistics. Please wait.

offset = 1 offset = 1 offset = 1 offset = 1 offset = 1 offset = 1

RESULTS:

********************************************

panel	v-stat	=	3.44542
panel	rho-stat	=	-13.12683
panel	pp-stat	=	-14.13123
panel	adf-stat	=	0.52636
group	rho-stat	=	-13.52092
group	pp-stat	=	-16.55490
group	adf-stat	=	1.58620

Nsecs = 6 , Tperiods = 112 , no. regressors = 5

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

********************************************

********estimation de la relation de cointegration (lower bloc)*****

Currently computing panel statistics. Please wait. Dependent Variable : LCI

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

)

Member
***********

	Variable *************		Coefficient **************		t-statistic **************
No.1	LPMI		0.06403		( 1.31689 )
No.1	LPL		0.00236		( 0.29495 )
No.1	LRI		-0.00611		( -0.08286 )
No.1	LNTOT		-0.00606		( -0.32262 )
No.1	Q1		-0.19982		( -12.44427
No.1	Q3		0.05876		( 3.70259 )
No.1	Q4		-0.14292		( -8.99465 )
No.2		LPMI		0.00465		(	0.13770 )
No.2		LPL		-0.00962		(	-2.39945 )
No.2		LRI		0.08483		(	2.33918 )
No.2		LNTOT		-0.02728		(	-1.55907 )
No.2		Q1		-0.13926		(	-12.41772 )
No.2		Q3		0.05888		(	5.30299 )
No.2		Q4		-0.10450		(	-9.29807 )
No.3		LPMI		0.09230		(	2.09644 )
No.3		LPL		-0.00360		(	-0.68465 )
No.3		LRI		0.07271		(	0.92306 )
No.3		LNTOT		-0.09755		(	-2.81260 )
No.3		Q1		-0.14814		(	-10.40225 )
No.3		Q3		0.03389		(	2.44420 )
No.3		Q4		-0.11950		(	-8.16263 )
No.4		LPMI		0.17054		(	2.70948 )
No.4		LPL		-0.00335		(	-0.29348 )
No.4		LRI		-0.04971		(	-0.51496 )
No.4		LNTOT		-0.12263		(	-1.91288 )
No.4		Q1		-0.21960		(	-11.41798 )
No.4		Q3		0.05849		(	3.11971 )
No.4		Q4		-0.16740		(	-8.31264 )
No.5		LPMI		-0.01600		(	-0.33680 )
No.5		LPL		-0.00801		(	-1.24747 )
No.5		LRI		-0.10016		(	-0.77026 )
No.5		LNTOT		0.06857		(	1.52265 )
No.5		Q1		-0.18599		(	-10.29192 )
No.5		Q3		0.03761		(	2.16681 )
No.5		Q4		-0.15126		(	-8.17741 )
No.6		LPMI		0.10496		(	2.60306 )
No.6		LPL		-0.01628		(	-4.44327 )
No.6		LRI		0.01451		(	0.31613 )
No.6		LNTOT		-0.07057		(	-2.51110 )
No.6		Q1		-0.07709		(	-4.90744 )
No.6		Q3		0.03568		(	2.43518 )
No.6		Q4		-0.03684		(	-2.38499 )

*********** ************* ************** **************

LPMI LPL LRI LNTOT Q1 Q3 Q4 Nsecs =

6

PANEL GROUP Coefficient 0.07008 -0.00642 0.00268 -0.04259 -0.16165 0.04722 -0.12040 , Tperiods =

FMOLS 112 ,

RESULTS t-statistic ( 3.48104 ) ( -3.58172 ) ( 0.90235 ) ( -3.10089 ) ( -25.26305 ) ( 7.82672 ) ( -18.50606 ) no. regressors = 7

********************************************

******test de cointegration pedroni.P[2004](upper bloc)(1980-1996)****** Currently computing panel statistics. Please wait.
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
		RESULTS:
		********************************************
panel			v-stat	=	6.98715
panel			rho-stat	=	-21.51332
panel			pp-stat	=	-18.87245
panel			adf-stat	=	-6.34237
group			rho-stat	=	-22.60687

group pp-stat = -22.81424

group adf-stat = -5.67944

Nsecs = 6 , Tperiods = 112 , no. regressors = 4

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances (see OBES reference for details)

********************************************

******estimation de la relation de cointegration(upper bloc)******

Currently computing panel statistics. Please wait. Dependent Variable : LCS

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000 0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

Member ***********	Variable *************	Coefficient **************	t-statistic **************
No.1	LPMS	-0.13237	( -1.15559 )
No.1	LPL	0.03092	( 1.59263 )
No.1	LNTOT	-0.05032	( -1.03030 )
No.1	LRS	-0.11675	( -0.38029 )
No.1	Q1	0.19319	( 5.12159 )
No.1	Q2	0.01338	( 0.35677 )
No.1	Q4	0.12619	( 3.35825 )
No.2	LPMS	-0.13065	( -2.00292 )
No.2	LPL	-0.02877	( -2.55109 )
No.2	LNTOT	-0.06437	( -1.43408 )
No.2	LRS	-0.20756	( -1.48153 )
No.2	Q1	0.15748	( 4.85536 )
No.2	Q2	0.04812	( 1.52447 )
No.2	Q4	0.16494	( 5.05259 )
No.3	LPMS	-0.20311	( -2.26275 )
No.3	LPL	-0.01356	( -1.28388 )
No.3	LNTOT	-0.03435	( -0.52298 )
No.3	LRS	-0.30336	( -0.97442 )
No.3	Q1	0.19559	( 6.73274 )
No.3	Q2	0.02780	( 1.00395 )
No.3	Q4	0.13225	( 4.37942 )
No.4	LPMS	0.20256	( 0.77614 )
No.4	LPL	-0.09293	( -2.07451 )
No.4	LNTOT	-0.58688	( -1.57620 )
No.4	LRS	-0.03377	( -0.07531 )
No.4	Q1	0.32689	( 3.80559 )
No.4	Q2	0.08090	( 1.07857 )
No.4	Q4	0.30933	( 3.36643 )
No.5	LPMS	0.00283	( 0.03060 )
No.5	LPL	-0.03039	( -2.26793 )
No.5	LNTOT	-0.25759	( -3.60737 )
No.5	LRS	0.42792	( 0.43901 )
No.5	Q1	0.24639	( 6.29782 )
No.5	Q2	0.07981	( 2.16684 )
No.5	Q4	0.24706	( 6.23092 )
No.6	LPMS	-0.11992	( -1.46365 )
No.6	LPL	0.02671	( 3.25331 )
No.6	LNTOT	-0.00075	( -0.01227 )
No.6	LRS	-0.40520	( -2.31845 )
No.6	Q1	0.02622	( 0.72264 )

No.6 Q2 0.02186 ( 0.66210 )

No.6 Q4 -0.00784 ( -0.22273 )

*********** ************* ************** **************

PANEL GROUP FMOLS RESULTS

LPMS LPL LNTOT LRS Q1 Q2 Q4 Nsecs =

6

Coefficient -0.06344 -0.01800 -0.16571 -0.10645 0.19096 0.04531 0.16199 , Tperiods =

112 ,

no.

t-statistic ( -2.48140 ) ( -1.36007 ) ( -3.34078 ) ( -1.95591 ) ( 11.24142 ) ( 2.77311 ) ( 9.04877 ) regressors = 7

********************************************

******test de cointegration de pedroni( taux de branchement)bloc inf****

	Currently computing panel statistics. Please wait.
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
		RESULTS:
		********************************************
panel			v-stat	=	3.27929
panel			rho-stat	=	-14.68195
panel			pp-stat	=	-11.35698
panel			adf-stat	=	1.18731
group			rho-stat	=	-15.58116
group			pp-stat	=	-13.71275
group			adf-stat	=	2.00289

Nsecs = 6 , Tperiods = 112 , no. regressors = 3

All reported values are distributed N(0,1) under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** ******estimation de la relation******

Currently computing panel statistics. Please wait.

Dependent Variable : LTXI

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

Member ***********	Variable *************		Coefficient **************		t-statistic **************
No.1	LPMI		-0.02838		( -0.59990 )
No.1	LPL		0.07300		( 5.75388 )
No.1	LNTOT		-0.02347		( -0.78283 )
No.1	Q1		0.08012		( 3.15071 )
No.1	Q3		-0.01210		( -0.47704 )
No.1	Q4		0.06444		( 2.54532 )

)

No.2

	LPMI	-0.12307	( -1.62122 )
No.2	LPL	0.03964	( 3.14130 )
No.2	LNTOT	-0.09697	( -1.82164 )
No.2	Q1	0.07034	( 1.96940 )
No.2	Q3	-0.03708	( -1.05080 )
No.2	Q4	0.05304	( 1.48206 )
No.3	LPMI	0.35029	( 4.92270 )
No.3	LPL	0.03399	( 3.59081 )
No.3	LNTOT	-0.45962	( -7.58621 )
No.3	Q1	0.10292	( 4.01893 )
No.3	Q3	-0.01320	( -0.52798 )
No.3	Q4	0.11206	( 4.24312 )
No.4	LPMI	0.23887	( 2.49200 )
No.4	LPL	0.02474	( 1.46380 )
No.4	LNTOT	-0.30433	( -3.55523 )
No.4	Q1	0.06872	( 2.37630 )
No.4	Q3	-0.01449	( -0.50623 )
No.4	Q4	0.07088	( 2.37282 )
No.5	LPMI	0.39674	( 7.95779 )
No.5	LPL	0.02025	( 3.08821 )
No.5	LNTOT	-0.37489	( -11.90256
No.5	Q1	0.08894	( 4.79935 )
No.5	Q3	-0.01412	( -0.77520 )
No.5	Q4	0.09972	( 5.33038 )
No.6	LPMI	-0.23367	( -1.59605 )
No.6	LPL	-0.03457	( -2.65659 )
No.6	LNTOT	-0.14383	( -1.60829 )
No.6	Q1	0.10543	( 1.86884 )
No.6	Q3	-0.04177	( -0.78529 )
No.6	Q4	0.09623	( 1.73475 )

*********** ************* ************** **************

LPMI LPL LNTOT Q1 Q3 Q4 Nsecs =

6

PANEL GROUP Coefficient 0.10013 0.02617 -0.23385 0.08608 -0.02213 0.08273 , Tperiods =

FMOLS 112 ,

RESULTS t-statistic ( 4.71744 ) ( 5.87118 ) ( -11.12753 ) ( 7.42339 ) ( -1.68302 ) ( 7.22944 ) no. regressors = 6

******************************************** ****test de cointegration de pedroni (bloc sup)*****

	Currently computing panel statistics. Please wait.
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
offset	=	1
		RESULTS:
		********************************************
panel			v-stat	=	1.71843
panel			rho-stat	=	-7.37342
panel			pp-stat	=	-6.17932
panel			adf-stat	=	2.97039
group			rho-stat	=	-8.36935
group			pp-stat	=	-7.64256
group			adf-stat	=	3.46926

Nsecs = 6 , Tperiods = 112 , no. regressors = 3 All reported values are distributed N(0,1)

under null of unit root or no cointegration

Panel stats are weighted by long run variances

(see OBES reference for details)

******************************************** *******estimation de la relation*****

Currently computing panel statistics. Please wait. Dependent Variable : LTXS

common time dummies NOT included

Null vector for t-stats is:

0.0000 0.0000 0.0000 0.0000 0.0000

0.0000

INDIVIDUAL FMOLS RESULTS
(t-stats in parentheses)

Member ***********	Variable *************	Coefficient **************	t-statistic **************
No.1	LPMS	-0.40822	(	-3.01401 )
No.1	LPL	0.08713	(	1.96361 )
No.1	LNTOT	0.08703	(	0.79134 )
No.1	Q1	-0.91575	(	-10.53822 )
No.1	Q3	0.34680	(	4.04409 )
No.1	Q4	-0.75032	(	-8.68515 )
No.2	LPMS	-0.06865	(	-0.73210 )
No.2	LPL	0.01760	(	0.76853 )
No.2	LNTOT	-0.37085	(	-4.07285 )
No.2	Q1	-0.79568	(	-12.25393 )
No.2	Q3	0.33927	(	5.28784 )
No.2	Q4	-0.65320	(	-10.06632 )
No.3	LPMS	0.03149	(	0.20764 )
No.3	LPL	-0.01793	(	-0.67046 )
No.3	LNTOT	-0.65652	(	-4.05912 )
No.3	Q1	-0.86600	(	-11.93396 )
No.3	Q3	0.19299	(	2.73803 )
No.3	Q4	-0.76029	(	-10.21446 )
No.4	LPMS	0.08502	(	0.25759 )
No.4	LPL	-0.02634	(	-0.42492 )
No.4	LNTOT	-0.85267	(	-2.27227 )
No.4	Q1	-0.94862	(	-8.78792 )
No.4	Q3	0.20144	(	1.92255 )
No.4	Q4	-0.78114	(	-6.99346 )
No.5	LPMS	-0.67843	(	-4.27393 )
No.5	LPL	-0.05073	(	-1.83946 )
No.5	LNTOT	0.33768	(	2.63488 )
No.5	Q1	-0.96865	(	-12.49053 )
No.5	Q3	0.19744	(	2.59957 )
No.5	Q4	-0.87519	(	-11.26532 )
No.6	LPMS	-0.24441	(	-2.41459 )
No.6	LPL	0.00130	(	0.11186 )
No.6	LNTOT	-0.55599	(	-6.37570 )
No.6	Q1	-0.59220	(	-11.89158 )
No.6	Q3	0.17330	(	3.68248 )
No.6	Q4	-0.52714	(	-10.83155 )

*********** ************* ************** **************

PANEL GROUP FMOLS RESULTS

	Coefficient		t-statistic
LPMS	-0.21387		(		-4.07000 )
LPL	0.00184		(		-0.03709 )
LNTOT		-0.33522		(	-5.45163 )
Q1		-0.84782		(	-27.71848 )
Q3		0.24187		(	8.27706 )
Q4		-0.72455		(	-23.70137 )

Nsecs = 6 , Tperiods = 112 , no. regressors = 6

******************************************** *************estimation dols*****

Linear Regression - Estimation by Least Squares Dependent Variable LCI

Panel(112) of Undated Data From 1//001 To 6//112

Usable Observations 672 Degrees of Freedom 665

Centered R**2 -0.444666 R Bar **2 -0.457701

Uncentered R**2 0.997397 T x R**2 670.251

Mean of Dependent Variable 2.8918446211
Std Error of Dependent Variable 0.1229549689

Standard Error of Estimate 0.1484500178

Sum of Squared Residuals 14.654876170

Log Likelihood 331.83634

Durbin-Watson Statistic 0.328281

Variable Coeff Std Error T-Stat Signif

*******************************************************************************

1.	LPMI		0.101736877			0.019130615	5.31801	0.00000014
2.	LPL		0.050834203			0.004137919	12.28497	0.00000000
3.	LRI		0.356026985			0.032222910	11.04888	0.00000000
4.	LNTOT		0.013672058			0.017472542	0.78249	0.43420626
5.	Q1		-0.210013363			0.016399393	-12.80617	0.00000000
6.	Q2		-0.032207720			0.016226871	-1.98484	0.04757291
7.	Q4		-0.179662755			0.016546396	-10.85812	0.00000000
Nobs = 660 JB test Standard Errors are Var.# Coeff.				= 14.18296 ( 0.0008322 ) adjusted for long-run variance. S.E. t-statistic
1		0.10174		0.08534	1.192
2		0.05083		0.01846	2.754
3		0.35603		0.14375	2.477
4		0.01367		0.07795	0.175
5		-0.21001		0.07316	-2.871
6		-0.03221		0.07239	-0.445
7		-0.17966		0.07381	-2.434

*************estimation dols*****

Linear Regression - Estimation by Least Squares Dependent Variable LCS

Panel(112) of Undated Data From 1//001 To 6//112

Usable Observations 672 Degrees of Freedom 665

Centered R**2 -0.079400 R Bar **2 -0.089139

Uncentered R**2 0.997702 T x R**2 670.455

Mean of Dependent Variable 4.9120750403
Std Error of Dependent Variable 0.2270780530

Standard Error of Estimate 0.2369827961

Sum of Squared Residuals 37.346962358

Log Likelihood 17.51558

Durbin-Watson Statistic 0.823137

Variable Coeff Std Error T-Stat Signif

*******************************************************************************

1.	LPMS			-0.226665518				0.024493437		-9.25413	0.00000000
2.	LPL			-0.009052927				0.007410797		-1.22159	0.22229709
3.	LRS			1.243236418				0.029125312		42.68577	0.00000000
4.	LNTOT			-0.230266576				0.020577357		-11.19029	0.00000000
5.	Q1			0.213807271				0.026034121		8.21258	0.00000000
6.	Q2			0.063771204				0.025873240		2.46476	0.01396236
7.	Q4			0.191460857				0.026242147		7.29593	0.00000000
Nobs = 660 JB test Standard Errors are Var.# Coeff.					= 2981.85146 ( 0.0000000 ) adjusted for long-run variance. S.E. t-statistic
1		-0.22667			0.06691		-3.387
2		-0.00905			0.02025		-0.447
3		1.24324			0.07957		15.625
4		-0.23027			0.05622		-4.096
5		0.21381			0.07112		3.006
6			0.06377			0.07068			0.902
7			0.19146			0.07169			2.671

Johansen Fisher
Panel
Cointegration
Test

Series: LCI LPMI LRI LPL LNTOT

Date: 05/28/09 Time: 23:33

Sample: 1980Q1 2007Q4

Included observations: 672

Trend assumption: Linear deterministic trend (restricted)

Lags interval (in first differences): 1 1

Unrestricted Cointegration Rank Test (Trace and Maximum Eigenvalue)

Hypothesized No. of CE(s)	Fisher Stat.* (from trace test)	Prob.	Fisher Stat.* (from max-eigen test)	Prob.
None	407.6	0.0000	136.0	0.0000
At most 1	87.71	0.0000	124.0	0.0000
At most 2	16.16	0.1840	14.87	0.2486
At most 3	7.126	0.8492	7.983	0.7865
At most 4	4.645	0.9688	4.645	0.9688
* Probabilities are computed using asymptotic Chi- square distribution.

Individual cross section results

Cross Section	Trace Test Statistics	Prob.**	Max-Eign Test Statistics	Prob.**
Hypothesis of no cointegration
1	282.7903	0.0000	213.9653	0.0001
2	288.9604	0.0000	221.8639	0.0001
3	265.1918	0.0000	168.9276	0.0000
4	331.5599	0.0000	215.9903	0.0001
5	270.8898	0.0000	205.2221	0.0001
6	198.4187	0.0000	128.1361	0.0000
Hypothesis of at most 1 cointegration relationship
1	68.8250	0.0181	36.3778	0.0141
2	67.0965	0.0261	26.2980	0.2173
3	96.2642	0.0000	62.9252	0.0000
4	115.5696	0.0000	75.9388	0.0000
5	65.6678	0.0351	33.2917	0.0358
6	70.2826	0.0131	47.2436	0.0004
Hypothesis of at most 2 cointegration relationship
1 32.4472 0.3646			16.6692	0.4859

2 40.7985 0.0802 23.1383 0.1088

3 33.3390 0.3197 19.5304 0.2711

4 39.6308 0.1026 22.7780 0.1200

5 32.3760 0.3684 17.9044 0.3846

6 23.0390 0.8764 11.6576 0.8930

Hypothesis of at most 3 cointegration relationship

1 15.7780 0.5105 10.9492 0.5186

2 17.6602 0.3672 13.1700 0.3145

3 13.8086 0.6734 9.2709 0.6963

4 16.8528 0.4260 13.8119 0.2670

5 14.4717 0.6185 9.4749 0.6748

6 11.3814 0.8526 6.9699 0.9028

Hypothesis of at most 4 cointegration relationship

1 4.8288 0.6211 4.8288 0.6211

2 4.4902 0.6705 4.4902 0.6705

3 4.5377 0.6635 4.5377 0.6635

4 3.0408 0.8717 3.0408 0.8717

5 4.9967 0.5969 4.9967 0.5969

6 4.4115 0.6820 4.4115 0.6820

**MacKinnon-Haug-Michelis (1999) p-values

Johansen Fisher
Panel
Cointegration
Test

Series: LCS LPMS LRS LPL LNTOT Date: 05/28/09 Time: 23:34

Sample: 1980Q1 2007Q4

Included observations: 672

Trend assumption: Linear deterministic trend (restricted)

Lags interval (in first differences): 1 1

Unrestricted Cointegration Rank Test (Trace and Maximum Eigenvalue)

Hypothesized Fisher Stat.* Fisher Stat.*

No. of CE(s) (from trace test) Prob. (from max-eigen test) Prob.

None 323.7 0.0000 244.8 0.0000

At most 1 84.24 0.0000 107.2 0.0000

At most 2 13.48 0.3355 12.11 0.4371

At most 3 7.408 0.8295 7.904 0.7926

At most 4 4.701 0.9672 4.701 0.9672

* Probabilities are
computed using
asymptotic Chi-
square
distribution.

Individual cross section results

Hypothesis of no cointegration

1	161.0538	0.0000	97.5388	0.0000
2	169.9608	0.0000	106.1523	0.0000
3	220.2138	0.0000	114.8512	0.0000
4	239.0623	0.0000	143.2477	0.0000
5	170.9629	0.0000	96.0229	0.0000
6	166.3293	0.0000	90.8615	0.0000
Hypothesis of at most 1 cointegration relationship
1	63.5150	0.0536	34.5886	0.0244
2	63.8085	0.0507	27.3428	0.1715
3	105.3626	0.0000	67.9058	0.0000
4	95.8146	0.0000	61.3292	0.0000
5	74.9400	0.0044	43.6424	0.0013
6	75.4678	0.0039	47.3077	0.0004
Hypothesis of at most 2 cointegration relationship
1	28.9264	0.5664	13.2228	0.7864
2	36.4657	0.1898	22.5566	0.1274
3	37.4568	0.1580	22.6257	0.1251
4	34.4854	0.2668	18.0682	0.3720
5	31.2976	0.4271	15.1772	0.6185
6	28.1600	0.6125	12.8499	0.8149
Hypothesis of at most 3 cointegration relationship
1	15.7036	0.5165	11.3906	0.4739
2	13.9091	0.6651	9.9398	0.6253
3	14.8312	0.5886	10.5067	0.5648
4	16.4172	0.4595	11.4901	0.4640
5	16.1204	0.4829	11.4743	0.4656
6	15.3101	0.5488	10.8253	0.5314
Hypothesis of at most 4 cointegration relationship
1	4.3130	0.6965	4.3130	0.6965
2	3.9694	0.7466	3.9694	0.7466
3	4.3244	0.6948	4.3244	0.6948
4	4.9271	0.6069	4.9271	0.6069
5	4.6461	0.6477	4.6461	0.6477
6	4.4848	0.6713	4.4848	0.6713

**MacKinnon-Haug-Michelis (1999) p-values