
 |
Contribution à la caractérisation mécanique des critères de qualités du départ de la course vitesse sur 100 m( Télécharger le fichier original )par Khalil Ben Mansour Université de Poitiers - Doctorat 2008 |
3-Retour sur les conditions experimentales en dynamometrie
4-A propos de la quadrupedie du depart de course
Ces positions ne présentent pas des attitudes naturelles, et l'adoption de l'une parmi les deux autres, suppose l'acquisition d'une musculature et d'une coordination segmentaire spécifiques. Une des premières études qui compare ces trois positions en termes de forces maximales exercées sur chaque bloc de départ suivant l'axe horizontal est réalisée par Kistler en 1934 (citée dans Henry 1952) [Henr 52]. Il montre que la somme des forces maximales exercées au niveau des deux pieds augmente d'une manière proportionnelle en fonction de l'écart antéropostérieur entre les deux pieds. Cette augmentation est principalement liée à l'accroissement de la force exercée par le pied arrière (tab.2). Payne (1971) précise qu'une grande force exercée au niveau du pied arrière caractérise un bon départ [Payn 71]. Tableau 2 Forces exercées sur les blocs en
fonction de leurs écartements respectifs
D'après ces résultats, la position de départ qui permet de générer la plus grande force est celle où l'écart entre les deux pieds est le plus important. Cependant, il n'est pas possible d'évaluer l'efficacité des différentes positions puisque le temps de l'action de l'athlète dans les blocs n'est pas estimé. Dickinson (1934) étudie l'influence de l'écart antéropostérieur des pieds sur le temps de sortie des blocs [Dick 34]. Il remarque que la position groupée permet aux athlètes de s'éjecter plus rapidement des blocs par rapport aux autres positions (tab.3). Tableau 3 Durée de l'action de l'athlète
dans les blocs en fonction de l'écartement, Technique de départ Durée de l'action [ms] Groupé 244 Moyen 326 Allongé 387 À la suite de ces deux études préliminaires, plusieurs recherches portant sur la comparaison de ces différentes techniques de départ sont apparues [Henr 52 ; Sige 62 ; Baum 76 ; Salo 04]. Elles se rejoignent toutes sur le fait que le départ groupé permet une éjection plus rapide, alors que le départ allongé permet de générer une force plus grande. Suite à ces investigations, une étude de référence réalisée par Henry en 1952 [Henr 52] préconise le départ moyen puisqu'il permet de réaliser une grande force dans un court délai. Il précise aussi que le départ groupé permet effectivement de s'éjecter très rapidement mais avec une faible vitesse tandis que le départ allongé permet de s'éjecter avec une grande vitesse mais après un temps d'action très important. Ces résultats sont confirmés par d'autres études [Sige 62 ; Salo 04]. Elles précisent que cette position permet d'effectuer une meilleure performance sur 10, 20, 30, 40 et 50 m. Influence de l'inclinaison des blocs de depart L'acquisition d'une importante vitesse d'éjection est non seulement liée à la distance qui sépare les blocs mais également à l'inclinaison des blocs par rapport au plan de la piste. Lorsque l'angle du bloc avant se réduit de 70° à 30°, l'activité électromyographique des jumeaux devient plus importante [Duch 86]. L'augmentation de la force de contraction de ce groupe musculaire est due à l'allongement du triceps sural qui est provoqué par la diminution de l'angle du bloc avant. Ces résultats sont en accord avec ceux de Guissard (1992) qui précise que la diminution de l'inclinaison du bloc avant favorise l'augmentation de la vitesse d'éjection de l'athlète sans prolonger le temps de son action dans les blocs [Guis 92]. Toutefois, la modification de l'inclinaison du block arrière ne montre pas de variation significative. En définitive, ces études démontrent l'intérêt de diminuer l'inclinaison du bloc avant. Cependant, l'influence de ce réglage sur la direction de la vitesse d'éjection n'est pas précisée. Influence de la posture Des analyses cinématiques précédentes [Baum 76 ; Harl 97 ; Natt97 ; Natt98 ; Scho 92] montrent que l'augmentation de l'écart antéropostérieur (PG) entre le centre de gravité et le centre de pression des forces résultantes exercées au niveau des pieds favorise le développement d'une force plus importante dans un délai plus court ce qui n'est pas nécessairement synonyme de meilleure performance.
Figure 19 Ecart antéropostérieur entre le
centre de gravité (C.G.) En gardant la même distance entre les deux pieds, et le même écart entre le pied avant et les mains, l'athlète peut adopter différentes postures tout en gardant une position quadrupédique. De nombreuses études [Natt 97 ; Natt 98] ont étudié l'effet de différentes position de départ (positions : habituelle de l'athlète, limite vers l'avant et plus assise) sur la de la qualité du départ. Ces études montrent que la « position quadrupédique limite vers l'avant » permet de traduire le déséquilibre initial de l'athlète en favorisant un pic de force plus grand ainsi qu'un temps plus court pour accomplir la première enjambée. D'autres investigations inter et intra groupe(s) visant à étudier cette synergie segmentaire ont permis de mettre au jour l'importance de l'ajustement des conditions externes (écartement et inclinaison des blocs) par rapport aux caractéristiques morphologiques de chaque athlète. En effet, la position la plus efficace varie d'un sujet à un autre [Delh 80]. Chaque position se caractérise par l'unicité des ajustements des angles articulaires. Les analyses dynamométriques ont montré que le « départ moyen » permet d'établir une bonne performance. Afin, d'adapter cette technique à des athlètes présentant des caractéristiques anthropométriques différentes, l'écart entre les deux blocs est exprimé en fonction de la longueur du tibia de l'athlète [Scho 92] soit 45% de la longueur totale du membre inférieur (du grand trochanter jusqu'à la malléole latérale). D'autres études [Capp 89 ; Coh 98 ; Natt 06] ajoutent qu'il faut tenir compte de l'angle inter segmentaire relatif jambe/cuisse (angle du genou). Cet angle doit être aux alentours de 110 #177;10° au niveau du genou arrière et 90 #177;10° au niveau du genou avant. Ces ajustements posturaux ont pour objectif d'optimiser les longueurs initiales des différents groupes musculaires afin d'obtenir l'activité contractile la plus importante. Ainsi le moment articulaire résultant sera augmenté. Toutefois, la relation force-longueur présente une grande variabilité entre les groupes musculaires [Goub 98]. Cette variabilité est attribuée à la longueur des fibres musculaires ainsi que leurs orientations par rapport à l'axe longitudinal du muscle (angle de pennation) [Ardl 01]. 5-ConclusionEn identifiant les variables qui permettent d'influencer la qualité d'un départ, les études antérieures (§-II.tab.1) tentent de donner des indices pour orienter l'entraîneur dans ses prises de décision lors des séances d'entraînements. Différentes stratégies de départ sont étudiées afin d'identifier leur influence sur la performance. La qualité du départ de course vitesse est considérée principalement à partir de l'évaluation de la vitesse d'éjection. Pour ces auteurs, l'intensité antéropostérieure de cette grandeur est signe d'un bon départ. En adoptant ce constat, les études précédentes présentent des divergences quand à la définition de la position de départ la plus efficace. Cette divergence démontre sans doute la nécessité de redéfinir les critères de réussite du départ de course de vitesse. Ainsi, au cours du quatrième chapitre une analyse en composante principale est effectuée afin de tester la possibilité de définir une nouvelle variable synthétique permettant d'estimer la qualité d'un départ de sprint d'une manière plus globale (§-IV.4). Il importe de souligner que les grandeurs qui caractérisent le départ ne sont pas toutes exprimées en temps (ex : module et direction de la vitesse d'éjection). Il est donc nécessaire de pouvoir « traduire » ces grandeurs en temps. Un modèle cinématique de la course est donc développé au cours du cinquième chapitre afin d'estimer, à une distance donnée du départ, la pénalité ou le gain en temps induit par ces grandeurs (§-V). Il ressort des investigations antérieures (§-II.tab.1) que la variation de la posture initiale de départ possède une influence directe sur l'intensité des forces maximales exercées sur les blocs lors du départ. Cette analyse est de notre point de vue restrictive car elle ne prend pas en compte la durée pendant laquelle cette force est exercée, notée durée d'impulsion. En effet, la vitesse d'éjection dépend à la fois de la force et du temps. Une intensité de force moindre peut être compensée par une durée d'impulsion plus grande, au risque d'être pénalisé, pour autant, Mero et al. (1983) considèrent que la vitesse horizontale est un critère plus important que la durée de l'impulsion [Mero 83]. Aussi, pour une position de départ donnée l'accroissement de la vitesse d'éjection est dû en grande partie à l'augmentation de la durée de l'impulsion plutôt qu'à l'augmentation de l'intensité des forces résultantes puisque les caractéristiques mécaniques articulaires et les propriétés physiologiques musculaires humaines limitent le développement d'efforts articulaires internes [Jaco 92]. Ces variables articulaires sont quantifiées en 3D au cours du huitième chapitre de ce manuscrit (§-VIII). Deuxième partieEtude dynamometriquedu depart de course de vitesseExperimentation et résultats
Deuxième partieLes études dynamométriques (§-II.5) qui s'intéressent à la caractérisation du départ de course vitesse sur 100 m, considère la vitesse d'éjection comme étant le critère principal d'un bon départ. Ces études analysent l'effet de différentes positions de départ en adoptant deux approches : la première consiste à prendre en compte les forces exercées distinctement au niveau de chaque pied en négligeant les forces exercées au niveau des mains, et la deuxième consiste à mesurer directement la force résultante qu'exerce l'athlète sur son environnement. Contrairement à ces approches, la présente étude prend en compte les efforts exercés distinctement au niveau de chaque appui afin d'effectuer une analyse complète. Le but est de revoir et redéfinir les critères de performance d'un départ de course vitesse. Ainsi, le premier chapitre de cette partie (§-III) décrit les outils et méthodes utilisées lors de l'analyse dynamométrique du départ de course vitesse. Ainsi, suite à la description du protocole expérimental les différentes étapes de traitements de données sont décrites. Enfin l'étude de l'état du centre de gravité de l'athlète lors des différentes phases du départ est réalisée en appliquant les principes et lois de la mécanique du point matériel. Suite à ces analyses théoriques, le deuxième chapitre de cette partie (§-V) expose et discute les résultats issus du traitement des données dynamométrique. L'accent est mis en premier temps sur la précision de la méthode adoptée par l'IAAF pour la détection des faux départs. Ainsi, une analyse comparative est effectuée afin d'étudier l'influence relative de différentes approches, dont celle de l'IAAF, pour estimer l'instant de la mise en action et de ce fait apprécier les faux départs. Enfin, après avoir analysé les grandeurs dynamiques et cinématiques accessibles par dynamométrie, des analyses en composantes principales sont effectuées dans le but de redéfinir les critères de performance permettant une qualification juste et reproductible du départ de sprint. Plus exactement, ce type d'analyse offre la possibilité de créer de nouvelles variables synthétiques, en nombre réduit, à partir d'une grande quantité de grandeurs (cinématiques, dynamiques, temporelles ...). ChapitreMatériels et méthodesEn mécanique, le point matériel est un élément sans dimension et possédant une masse qui peut prendre toutes valeurs arbitraires. La modélisation de l'athlète par un point matériel de masse conservative revient à réduire l'athlète à son centre de gravité, appelé aussi centre de masse ou centre d'inertie. La notion de centre de gravité est souvent utilisée d'une manière inconsciente par les entraîneurs et les athlètes lorsqu'ils disent qu'un athlète est rapide. L'athlète, pris comme un tout, est en soi une simplification qui se rapproche du concept de centre de gravité. 1-Protocole experimental1.1-Population etudieeQuarante six athlètes ont participé à cette étude. Il s'agit d'étudiants de la Faculté des Sciences du Sport de l'Université de Poitiers (Tableau 4). Soixante seize pourcent d'entre eux se positionnent pied gauche en avant dans les blocs de départ. Les expérimentations se sont déroulées au cours de trois périodes distinctes au CREPS17 Poitou Charentes. Toutefois, un seul et même protocole a été utilisé au cours de ces tests. Au début de chaque période d'essais, les athlètes bénéficient d'une présentation des différentes parties de la station de mesure. Elle 17 CREPS : Centre Régional d'Éducation Populaire et de Sports (www.creps-poitou-charentesjeunesse-sports.gouvir) est suivie par une démonstration des différents réglages possibles des blocs de départ et des appuis mains (figure 1). Tableau 4 Principales caractéristiques des athlètes ayant participé à cette étude
Après une période d'échauffement spécifique, chaque athlète exécute successivement deux départs afin de parcourir le plus rapidement possible une distance de dix mètres. Les essais se déroulent dans une salle d'expérimentation. Pour chaque départ, l'athlète reçoit les commandes suivantes :
1.2-Definition de l'espace geometrique
La précision de la mesure des forces exercées par le coureur est de l'ordre de 1%. Les deux termes correctifs sont donc négligeables devant la précision de la mesure. La terre peut donc être raisonnablement considérée comme un repère galiléen, d'autant que le départ de sprint s'effectue dans un laps de temps très court (< 0,5 s). Le repère galiléen de référence de notre étude est un repère terrestre (figure 21) Ro0(O|X0,Y0,Z0) défini par trois axes (OX0), (OY0) et (OZ0) non coplanaires concourant en O0 point particulier de l'espace géométrique représentant l'origine du repère. Usuellement, les trois axes de Ro0 sont choisis orthogonaux, et leur orientation est définie par une base
Figure 21 Situation de l'athlète en position Prêt par rapport à Ro0 La définition de ce repère Ro0 permet de décrire l'orientation et l'intensité des actions mécaniques exercées sur l'athlète et ainsi de prédire son état. 1.3-InstrumentationLes dynamomètres utilisés au cours de ces tests (figure 22) sont deux plateformes de forces (PFF) piézoélectriques de marque Kistler18 et deux dynamomètres composites de marque Médicapteur19 (Annexe 3.2) évaluant les efforts de contact suivant les trois directions de l'espace dans leurs repères respectifs. Les blocs de départ utilisés sont des blocs standards présentant des possibilités de réglages d'inclinaison et d'écartement suivant l'axe de déplacement de l'athlète. La variation de la position antéropostérieure d'un bloc sur une PFF est assurée par une interface en tôle d'acier de 3 mm d'épaisseur qui permet la fixation du bloc à différents niveaux. Le poids additionnel que représente ce dispositif (bloc de départ et interface) sur la PFF est éliminé par une correction du zéro électrique.
Figure 22 Station expérimentale pour l'évaluation de la dynamique du départ de sprint Les deux PFF sont solidement fixées au sol l'une à coté de l'autre de telle sorte que l'orientation de leurs repères aPd et aPg soient identiques (figure 23) et que leurs centres respectifs soient à la même distance de la ligne de départ. Ce positionnement offre la possibilité de réglage de l'écartement antéropostérieur entre les deux blocs ce qui permet l'adoption des différentes techniques de départ (§-II.2.1) réalisées par les athlètes. Les appuis mains sont instrumentés par deux capteurs composites de la société Médicapteur mesurant les efforts suivant les trois directions de l'espace. Le fonctionnement de ces capteurs repose sur le principe d'extensométrie qui est décrit en annexe (Annexe 3.1). 18 PFF Kistler : type 9287B pour la grande (figure 3) et 5233A pour la petite (figure 3) ( www.kistler.com) 19 Capteurs six composantes de la société Médicapteur : modèle EX 114.45-200 La base de chaque appui main est dotée d'une liaison glissière qui permet l'ajustement de l'écart médiolatéral entre les deux dynamomètres composites (figure 22) tout en gardant la même orientation de leurs repères de références gMd et gMg par rapport à ceux des PFF (gPd et ~Pg) (figure 23).
Figure 23 Vue de profil de la station
expérimentale. Orientation des repères PFF droite gPd Au cours des tests, le signal déclenchant le départ est émis par un BUZZER délivrant simultanément un signal sonore et une impulsion électrique de 9 V permettant d'une part de marquer cet instant par rapport à l'évolution des forces, et d'autre part, de synchroniser les enregistrements des forces mesurées par les 4 capteurs. L'acquisition se fait à une fréquence de 1000 Hz. L'acquisition et la conversion des tensions électriques délivrées par les 29 voies analogiques est assurée via une carte analogique-numérique20 :
2-Traitement des donnees numeriques
2.1-Conversion des tensions electriques
2.2-Evaluation de la precision des mesures dynamometriques
2.3-L'etude des actions mecaniques
2.4-Determination du torseur dynamique
v, 0, v, respectivement autour des axes Z0, X0, Z0 noté : ~ ????? ~ ' ????? ~ '
????? p 1 0 2 0 3 0 0 0 0
~ ????? ~ ' ????? ~ '
????? p 1 0 1 2 0 2 3 0 ? 3 0 0 0 La définition de ces matrices de passages repose sur le principe de la transformation simple qui permet de déduire une base à partir d'une autre par une seule rotation (sans tenir compte de la translation) d'angle 0 autour de l'axe OX0 ou OY0 ou OZ0. De ce fait, les angles d'Euler et les angles de Cardan sont définis par une succession de transformations simples. Trois matrices décrivant chacune une transformation simple d'un angle 0 autours d'un seul axe à la fois peuvent être décrites :
Cè -Sè 0 rot(Z 0 , )= è Sè Cè 0 0 0 1 avec C désigne la fonction cosinus et S la fonction sinus. Ainsi, dans le cas de cette étude, les éléments de la matrice de passage R 0 peuvent p être déterminés suite à la
succession de deux transformations simples. La première comporte 0 = - 2 autour de l'axe OZ0 ~ ?????~ ' ????? p rot Y á 1 0 ( , ) rot Z è 2 ( 0 , ) 0 0 Compte tenu de la définition d'une matrice de passage, il est possible d'écrire : [ CèCá -Sè CèSá 0 -1 0 R 0 rot 1 ( Y 0 , ) rot 2 ( Z 0 , ) p = á · è SèCá Cè SèCá -1 0 0 = = -Sá 0 Cá j 0 0 -1
l'athlète décrit initialement par rapport au repère Rp, permet de l'exprimer par rapport au repère absolu g0 :
De même, le calcul suivant est effectué afin d'exprimer les moments initialement décrient en Oi de Rp dans R0: ~~~ ~~~ DX(Oi,iii)/gt0 = Éq.III.4 Les moments de force calculés en Oi (origine d'un repère dynamomètre) et exprimés par rapport à J0 présentent peu d'intérêt. Par contre, un moment calculé en un centre articulaire d'une articulation ou au centre de gravité est beaucoup plus intéressant. La détermination de la position du centre de gravité (G) par dynamométrie lors de la position Prêt est décrite par la suite dans ce même chapitre (§-III.4). Il existe la relation suivante entre deux vecteurs-moments en deux points Oi et G du même référentiel (relation de transport des moments) : ~~~ ~~~ ~~~ ~~~~~ Olt( G x) / a0 = ®1( Oi,k)/ gt0 + Ri / 91,0 ? OiG/910 Éq.III.5 La détermination des torseurs ( g ) au niveau des quatre appuis : main droite (Md), main gauche (Mg), pied droit (Pd) et pied gauche (Pg) par rapport à g0 et leur addition, permet de définir le torseur des actions mécaniques externes ( gG ) exercées au centre de gravité de l'athlète. 5G/ 90 = 'Md /910 + 'Mg / 910 + 'Pd / 90 +5Pg /t0 Éq.III.6 Le champ des moments dynamiques du centre de gravité G par rapport à g0 est un torseur dynamique dont la quantité d'accélération est la résultante. G étant le centre de gravité de l'athlète de masse m dans g0 et O un point quelconque. Les éléments de réduction en O du torseur gG à tout instant sont :
3-Description de l'etat du centre de gravite de l'athlete lors de la phase du depart
et opposées (sur la ligne d'action S1S2) : F 1 2 = - F2 1 (principe de réciprocité également dénommé principe d'action-réaction). Lors de la phase Pret Au cours de cette phase, le point matériel (athlète réduit à son centre de gravité) est considéré en équilibre (état de repos). Cela signifie que sa position est fixe par rapport à ~~~~ ( OG = cte ). Étant initialement immobile dans 0, la somme des forces externes qui lui sont appliquées est nulle : ~~ ~~ ~~ ~~ ~~ ~ F Md Ro +F Mg Ro +F Pd Ro +F Pg Ro + 9G Ro=0 Éq.III.10 La mesure dynamométrique de ces actions mécaniques permet de déterminer la position du centre de gravité (figure 27) du coureur par rapport à M et P respectivement points ~~ d'applications des résultantes des forces exercées au niveau des deux mains ( RM) et des deux ~~ pieds ( RP ). Il est possible de représenter par des vecteurs les actions mécaniques qui s'exercent sur l'athlète assimilé à un solide rigide (S) de masse (m) (figure 27). Dans un souci de simplification de la représentation figurant ci-dessous, les directions ~~ ~~ des vecteurs RP et RM sont choisies identiques au poids. Deuxième partie Chapitre III
9 9 Figure 27 Évaluation de la position du centre de
gravité (G) de l'athlète au repos suite à L'application du principe fondamental de la statique au solide (S) permet d'écrire : 5G/ 90 = 0 RG/910 ~~~ d'où /910 ~ ~~ ( ) G,R ~~ ~ 0 MP. La connaissance de la distance représentant l'écart antéropostérieur entre M et P (figure 27) ainsi que l'application de la seconde condition d'équilibre permet de déterminer la position horizontale du centre de gravité de S suivant l'axe antéropostérieur OX0 comme suit : ~~~ ~~~ ~~~ ~ DIE( MjiM ) /91,, + OTC( MiP ) /91., + DIE( AOG )/91,, = 0 ~ ~~~~ ~~ ~~~~~ ~~ ~ 0 + MP ? R P + MG ? = Sachant que MPy = 0 , MPz = 0 et Ry = 0 il devient : 0 1 0 1 0 - · R MP + - · mg MG = 0 Pz x z x 0 J 0 J 0 - R · MP d'oùMGx= Éq III.11 mg et PGx = MPx - MGx Éq.III.12 La position horizontale du centre de gravité Gx correspond à la position du point d'application de la résultante des forces qui s'exercent sur l'athlète. C'est le barycentre des actions mécaniques de contact de l'athlète avec le milieu extérieur. Lors de l'impulsion Lors de l'impulsion, la variation de la quantité de mouvement du centre de gravité de l'athlète est d'autant plus grande que les actions mécaniques mesurées sont importantes. Cette phase débute à l'instant (ta) et prend fin à l'instant d'éjection (te). L'application du principe fondamental de la dynamique permet d'exprimer la variation élémentaire de la quantité de ~~ mouvement du centre de gravité ( mdVG ) suivant un axe donné en fonction de la composante de l'impulsion élémentaire des forces extérieures suivant le même axe. Cette relation est exprimée par l'équation suivante : mg z F F F Éq.III.13 m · [dV Gy = 0 + [F M d x + [F A IMgy gx }+ F Pdx + [P g x F Mdy Pdx d V Gz Pgy Mdz Mgz Pdz Pgz · dt d V Gx 0 F F F Pour évaluer la vitesse du centre de gravité de l'athlète, il faut calculer les variations
ÄVG ~~ entre l'instant initiale ti et un instant quelconque t est égale à la somme discrète des d V G élémentaires suivant la relation suivante :
ti Ä V G =V Gt Gt 1 = f R Gdt V m Éq III.14 En posant ti comme étant un instant de la phase Prêt, il devient possible de déterminer directement la vitesse du centre de gravité de l'athlète à n'importe quel instant t. Cela est due au fait que la vitesse du centre de gravité au cours de cette phase est considérée nulle ~~ ~ ( VGti = 0 ) ; ce qui permet d'écrire : Fx ( t ) VGxt 1 V Gyt = · Nt) · dt
Gz t Éq.III.15 t ( + F z( t )) ti D'après l'équation III.15, l'intensité de la vitesse du centre de gravité de l'athlète à l'instant t est proportionnelle à la grandeur de la somme des forces qui s'exercent sur l'athlète suivant le même axe. Toutefois, l'athlète est contraint de générer la plus grande force dans la plus courte durée (dt). Possédant la variation de la résultante des forces qui s'exercent sur l'athlète au cours de la phase d'action, le calcul de la vitesse instantanée de son centre de gravité est réalisé par un procédé d'intégration numérique pas à pas suivant une méthode d'intégration approchée, dite méthode des trapèzes. Cette méthode consiste à remplacer un arc de la courbe par un segment. Il s'agit donc d'une interpolation linéaire. Les mesures des actions mécaniques sont échantillonnées à une fréquence de 1000 Hz, ainsi les intervalles de temps sont relativement petits. Cela assure une exploitation plus précise des données numériques de forces. L'aire totale sous la courbe est ainsi divisée sur des intervalles réguliers représentés par des trapèzes. Ainsi, la somme des aires représente une approximation de l'intégrale de la force en question. Cette méthode est également utilisée pour estimer la variation de la position du centre
Lors de la phase aerienne Le début de la phase aérienne est déterminé par l'instant d'éjection (te) qui correspond au décollage du pied avant de l'athlète. Dès cet instant, toutes les actions de contacts s'annulent jusqu'à la réception du pied arrière au sol. Seule l'action de la gravitation terrestre appliquée au centre de gravité de l'athlète suivant la verticale descendante (OZ0) continue à être exercée tout au long de cette phase. D'après la première loi de Newton, au cours de cette phase, le mouvement du centre de gravité de l'athlète dans g0 suivant l'horizontale OX0 et OY0, est un mouvement rectiligne uniforme (la résistance de l'air est négligée). L'application des lois du mouvement rectiligne uniforme permet d'écrire : x( t ) = xi + Vxt Vx ( t ) = V = Vi ax ( t ) = 0 avec x( t) chemin parcouru, xi position initiale (à t = Prêt), Vx ( t ) vitesse uniforme, (t) temps écoulé, vi vitesse initiale et ax accélération. Suivant la verticale (OZ0), le centre de gravité possède un mouvement accéléré d'intensité 2 gz 9 , 81 ms - = - . L'application des lois du mouvement rectiligne uniformément accéléré évalue le déplacement, la vitesse et l'accélération du centre de gravité du coureur comme suit : ( ) 2 1 z t = at +V t+ z V z ( t ) = at+V i az ( t ) = g i i 2 La connaissance de l'intensité des composantes de la vitesse du centre de gravité à te
défini comme étant le degré d'élévation de la norme de la vitesse d'éjection ) par rapport au plan horizontal. La non prise en compte de
( V éject Vé ject+ V éject + V éject 2 2 2 x y z = la faible vitesse médio latérale ( Vy ) dans le calcul de l'angle d'éjection, et l'utilisation de la
fonction cosinus fournit un résultat de 8° au lieu
de 6° (soit une erreur relative de 20%) pour un résultat fiable indépendamment du nombre de composante mesurée. L'estimation de l'angle d'éjection sera obtenue à partir de cette seconde méthode. Chapitre I3Resultats et analyses1-Chronologie de la phase de departLe traitement et l'analyse des données expérimentales ont nécessité de définir, avec précision, certains instants remarquables de la phase de départ de la course de vitesse. Dans toutes les figures de cette étude, l'instant d'émission du signal de départ correspond à l'origine des temps (figure 28). Toutes les variables sont exprimées par rapport au référentiel galiléen g0 (§-III.2.1). Un rééchantillonnage à 250 Hz des données numériques est effectué afin de faciliter la lecture des courbes.
Figure 28 Variation typique de la norme de la somme des forces externes lors d'un départ de sprint La détermination des instants tels que ta (mise en action) ou te (éjection) repose sur l'analyse des variations de la norme des forces qui s'exercent au niveau de chaque appui (figure 29). Les différents instants de la phase de départ sont notés comme suit :
mouvement de son centre de gravité)
1.1-Les instants de mise en action :
Approches A1 A2 A3 A4 A5 A6 A7 A8 A9 A10 [Newton] 20 30 40 200 270 300 3 x sd 4 x sd 5 x sd Inter
pas de marche [Mick 00, Tiro 03].
1.2-Les instants de d~collage :
1.3-Les séquences du départ
2-Etudes des actions mecaniques lors du depart
3-Cinematique du centre de gravite
4-Caracterisation de la performance lors d'un depart de course vitesse
4.1-Analyse en composantes principales
4.2-Interpretation de 1'ACPN
4.3-Analyse des relations intervariables
5-Conclusions
Troisieme partieDeveloppement d'outils de diagnosticde la performance
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||
E 1 104 438 33 0.61 2.90 10
E 2 110.5 365 27 0.54 3.2 11
E 3 106 442 14 0.53 2.84 5
E 4 128.5 492.5 64 0.75 3.03 8
E 5 108 406 24 0.68 3.37 3
E 6 125 449 32 0.61 2.83 0
Ce tableau (tableau 1) montre que le sujet ayant la plus grande vitesse d'éjection est toutefois pénalisé lorsque l'on considère les autres paramètres de départ.
La meilleure performance de départ serait celle qui comprend non seulement la plus
V éj ect
grande norme de vitesse à l'éjection
, mais aussi le temps de réaction ( Ätréaction ) et le
délai d'impulsion ( Ätimpulsion ) les plus courts, les positions initiale OGta et finale OGte du centre
de gravité les plus lointaines et l'angle d'éjection le plus faible lui permettant ainsi de poursuivre sa course dans de bonnes conditions. La valeur minimale de l'angle d'éjection du centre de gravité avancée dans le tableau 1 doit donc être redéfinie en tenant compte des paramètres mécaniques dès les premières foulées de course.
Au cours du premier chapitre de ce manuscrit, la notion de performance sur 100 m a été définie. Tenant compte de cette définition, une conversion en temps de ces paramètres s'impose. Un modèle cinématique de la course est développé afin de permettre, à une distance donnée du départ, d'estimer la pénalité (ou le gain) en temps induit par ces grandeurs.
Les positions initiale (OGta) et finale (OGte) du centre de gravité de l'athlète par rapport à la ligne de départ sont deux grandeurs exprimées en mètre. Elles peuvent être converties en seconde en considérant que la perte (ou le gain) de temps est égale à :
O Gt
Ä t position = Éq.V .1
V
lim
où Vlim est la vitesse maximale limite de la course, soit environ 10 à 12 m/s (§-I.1.3).
Le temps de réaction (§-I.3.1) qui comprend le délai que met le signal de départ pour parvenir à l'athlète et le délai que met ce dernier pour y répondre peut être directement calculé par la soustraction de l'instant de début de l'action de l'athlète dans les blocs G à l'instant du signal du départ G.
Ä tréaction = ta - ts Éq.V.2
La durée de l'impulsion correspond à la différence en temps entre l'instant d'éjection te et l'instant de début de l'action de l'athlète dans les blocs ta.
Ä timpulsion = te - ta Éq.V.3
Ces différences (Éq.V.4 et 3), exprimées en temps, estiment directement la pénalité ou l'avantage qui peut être attribué à l'athlète. Les méthodes d'estimation des instants ta, ts et te sont décrites dans le quatrième chapitre de ce manuscrit (§-IV.1).
Vu la complexité du paramètre vitesse, l'appréciation de son influence sur la performance au 100 m est estimée à partir d'un modèle de variation de la vitesse du centre de gravité du coureur en fonction de la distance parcourue (§-I.1.figure 1). L'étude de la variation de cette quantité permet d'émettre l'hypothèse que la vitesse de l'athlète suit une loi exponentielle. Ce modèle introduit deux nouveaux paramètres D et Vlim qui caractérisent « l'état » du coureur.
V = ( V lim - V éject ) × ( 1 - e K+Véject Éq.V .5
avec K = -ln2× ( d - déject) / D
V : vitesse instantanée du CG du coureur suivant l'axe antéropostérieur OX0
Vlim : vitesse maximale de course du CG du coureur atteinte au cours du 100 m Véject : vitesse du CG du coureur au moment de l'éjection des blocs de départ (te) d : distance parcourue par le CG du coureur depuis la ligne de départ
déject : distance du CG à la ligne de départ à te
D : période spatiale de la variation de vitesse. Elle correspond à la distance où la variable varie d'un facteur 2 (figure 55).
Figure 55 Variation de la vitesse (exprimée en pourcentage de la vitesse limite Vlim) en fonction
de la distance parcourue pour une période spatiale D = 10 mPour connaître la loi de variation en fonction de la distance parcourue, il faut considérer quatre constantes Vlim, Véject, D et déject. Les grandeurs à l'éjection (Véject et déject) sont directement accessibles suite à des mesures dynamométriques. Les deux autres (Vlim et D) peuvent être évaluées par effet photoélectrique (OptoJump31)et/ou par effet doppler (radar).
Le paramètre déject n'influence pas sensiblement les résultats finaux. En effet, pour une variation grossière de 100% de déject (soit une variation de 0 à 0,5 m), tout en maintenant constant les autres paramètres (D = 7 m, Véject =3,5 m/s et Vlim= 11,5 m/s), la performance sur 100 m ne varie que de 1,4%, soit environ 0,1 s. De ce fait, en se référant à l'équation 5 (Éq.V.6), le terme K s'écrit :
K = -ln2×d/ D
La période spatiale D et la vitesse limite Vlim dépendent, quant à elles, du niveau d'entraînement de l'athlète et de son « état de forme ».
Pour déterminer la pénalité induite par Véject, il importe d'estimer les paramètres Vlim et D en fonction du niveau d'entraînement du coureur (régional, national, international). Actuellement, l'ajustement des paramètres est effectué à partir de données obtenues par des mesures dynamométriques (plateforme de force) et photoélectriques (OptoJump). Le premier outil permet l'évaluation des différents paramètres mécaniques à l'éjection tandis que le
31 www.microgate.it (voir dans : Home > Timing & Sport > Produits > OptoJump)
* Concernant la loi exponentielle, les théoriciens utilisent souvent une écriture de la forme ( - d )
e ë· ou ( -d )
e ô .
Les constantes A ou z ont cependant une signification peu pratique de point de vue des expérimentateurs. correspond à la distance où la variable varie du rapport 1/e. Ici, l'écriture de la forme ( -ln2d D )
e est adoptée.
second, positionné sur 20 m, permet l'estimation de la vitesse du coureur32 en fonction de la distance parcourue.
Ces mesures non synchrones ne peuvent donner que des tendances. L'OptoJump mesure les instants de contact des pieds avec le sol. Considérant la course comme un mouvement cyclique, il devient légitime d'estimer la vitesse de déplacement du centre de gravité du coureur. La distance entre le centre de gravité et le pied au moment du contact est sensiblement constante [Leha 05]. Malgré ces limitations, les premiers essais de détermination de Vlim et D donnent des résultats plutôt satisfaisants (figure 56).
Figure 56 Vitesse expérimentale (Vitesse Exp) d'un coureur et modèle de la variation de la vitesse en
fonction de la distance parcourue (D = 6 m et Vlim = 10 m)L'étude de corrélation entre les valeurs expérimentales de la variation de la vitesse expérimentale et le modèle d'estimation de la même grandeur présente un résultat positif avec un coefficient de détermination R2= 0,99 et une équation de régression linéaire de la forme :
y = 1,05x - 0,36.
La validation du modèle de vitesse est effectuée en utilisant ces outils de mesures :
§ une caméra HDV dont l'axe optique est horizontal et perpendiculaire au plan du mouvement
§ un OptoJump de 10 m
? un radar dont l'axe est confondu avec celui de la piste
32 Le coureur participant à cette expérimentation est de niveau national ; âge = 20 ans ; taille = 1,8 m et masse = 78 kg.
Suite à la calibration du champ de course, le dé-tramage du film en une séquence d'images et la détermination de points remarquables définies par des marqueurs fixés au préalable sur l'athlète, la vitesse d'éjection de l'athlète33 a pu être estimé à 3,3 m/s avec une incertitude de #177;0,2 m/s. Les données de l'OptoJump et du radar permettent quant à elles d'estimer la variation de la vitesse du coureur (figure 57). Ce dernier doit parcourir le plus rapidement possible la distance de 30 m à partir d'un départ en quadrupédie dans les blocs de départ.
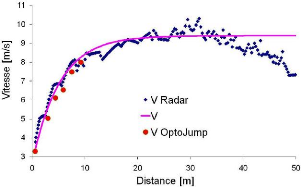
Modèle
Figure 57 Variation de la vitesse horizontale d'un
coureur en fonction de la distance parcourue. Les
critères de
simulation sont définis comme suit : Vli, = 9,4 m/s,
Véj, = 3,28 m/s, D =3,6 m et d4, = 0,52
m
La période spatiale D de ce coureur est plus courte en comparaison à celles des coureurs de niveaux moins élevés. Il convient d'être prudent sur la valeur de la vitesse limite mesurée par le radar du fait que le coureur a commencé à ralentir à 30 m.
Pour caractériser « la montée en vitesse » du coureur, la période spatiale de la variation de vitesse est en concurrence avec l'accélération du coureur qui est caractérisée par son intensité maximale et par sa durée. La période spatiale rend compte de ces deux paramètres. Elle représente une variable de synthèse qui ne subit pas l'amplification du bruit lors du calcul de l'accélération du coureur à partir de sa vitesse (figure 58).
Rappelons que l'utilisation des outils OptoJump et radar, dans le cadre de notre étude, se justifie par une nécessité d'approcher l'évolution de la vitesse du coureur après son éjection des blocs de départ.
33 L'
·
athlete participant à cette expérimentation est de niveau national ; âge = 20 ans ; taille = 1,75 m
et masse = 76 Kg.
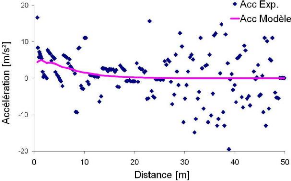
Figure 58 Variation de l'accélération
(Acc) du coureur en fonction de la distance parcourue.
Ces résultats
sont obtenus à partir de ceux de la figure 57 (Modèle et
Radar)
Les résultats obtenus avec un seul coureur semblent être satisfaisants et méritent d'être confirmés. Toutefois, il convient de disposer, pour des groupes de niveaux, de différentes mesures de la variation de la vitesse afin d'établir un modèle prédictif de la pénalité par la seule connaissance de Véject.
La détermination de la variabilité des critères de simulation D et Vlim en fonction du niveau d'entraînement de l'athlète fournit des informations utiles aux entraîneurs qui cherchent à caractériser l'évolution de leurs coureurs pour établir un suivi longitudinal. Afin de se rendre compte de l'importance de ces critères, leur impact sur la performance est étudié.
L'étude de l'influence de la variation des critères de simulation (D et Vlim) sur l'estimation de la performance de course de vitesse au 100 m est effectuée en faisant varier :
§ la vitesse d'éjection de 2 à 4,5 m/s
§ la période spatiale de 5 à 9 m
§ la vitesse limite de 10 à 12 m/s
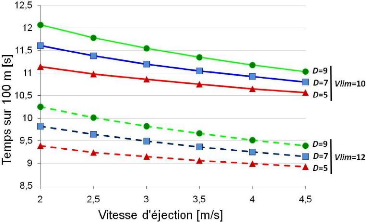
Figure 59 Simulation de la performance sur 100 m en
fonction de la vitesse d'éjection,
de la vitesse limite
(Vlim) et de la période spatiale (D)
Les courbes ci-dessus (figure 59) sont des exponentielles. Cependant compte tenu de la faible variabilité des paramètres (Véject, Vlim , D), il est possible de considérer que la performance varie linéairement avec les paramètres. Il vient alors :
? APerformance (s) - 0,85 s par m/s de la vitesse limite
? APerformance (s) - 0,32 s par m/s de la vitesse d'éjection
? APerformance (s) 0,17 s par m de la période spatiale
Expérimentalement, pour obtenir une estimation de la performance à 1%o près (c'est-àdire à 0,01 s), il faut avoir une précision sur ces paramètres de :
? 1%o pour la vitesse limite
? 1% pour la vitesse d'éjection
? 1 % pour la période spatiale
La précision sur la vitesse d'éjection est accessible par mesure dynamométrique. L'évaluation de la période spatiale et surtout de la vitesse limite avec de telles précisions nécessite l'emploi d'un lourd dispositif expérimental utilisant des outils sophistiqués.
à
~~
La forte corrélation entre la vitesse antéropostérieure x
Véject et sa norme
V
l'éjection (§-IV.figure 51) est, pour l'essentiel, due au fait que l'angle d'éjection est faible
d'où x
Véject
). Afin d'acquérir une grande x
Véject il importe de
~~
V
é
V éject
(
cos ( è)
x =
ject
~~
V éject
s'éjecter avec le plus petit angle.
Afin d'estimer l'angle d'éjection optimum, il importe de connaître la distance parcourue par le centre de gravité du coureur au cours de sa première phase aérienne.
Pour des coureurs de haut niveau, lors de la première phase aérienne qui dure de 60 à 70 ms [Harl 97], le centre de gravité parcours horizontalement 0.30 m [Natt 06]. En émettant l'hypothèse que le centre de gravité de l'athlète est à la même hauteur à l'éjection et à la réception, les équations paramétriques du centre de gravité du coureur pendant la phase aérienne s'écrivent comme suit :
|
|
|
||
~~
V éject
2
et ( )
z t
= 1 gt 2 +
cos ( è)t
soit ( ) ( ) ( )
x t g
cos sin
~~
2
è è =
2
V éject
AN : ( ) ( ) 2
0 3 9 81 016 , ,
×
cos è sin è = = ,
2 3
×
Finalement 0 = 9°
Il n'a pas été possible dans cette étude d'établir une relation entre la variabilité de l'angle d'éjection et la performance. C'est pour cela qu'il est apparu souhaitable d'introduire la phase d'accélération qui peut être caractérisée en terme de performance. La qualité de la phase d'accélération dépend, sans aucun doute, de la réception du coureur à la fin de sa première phase aérienne qui dépend pour une part de l'angle d'éjection.
Pour des raisons de clarté ce modèle ne comprend que 3 phases : le départ, l'accélération et la vitesse stabilisée (§-I.1). Les phases de décélération et d'arrivée ne sont pas prises en compte. L'hypothèse simplificatrice est donc d'admettre qu'il n'y a pas de corrélation forte entre la gestion du départ et l'effet de fatigue en fin de course (phase de décélération) d'une part, et la gestion de l'arrivée, d'autre part. Cette hypothèse qui semble « raisonnable » peut, pour les esprits qui considèrent que « tout est dans tout », être contournée en limitant, dans le modèle cinématique de la course, l'influence des grandeurs caractéristiques du départ à une distance de l'ordre de 70 à 80 mètres.
Offrant des indications directes concernant le gain ou la perte du temps cet outil théorique de diagnostic de la performance de course vitesse au 100 m ne nécessite aucun traitement préalable. Cela présente un gain de temps important lors des séances d'entraînement. Toutefois, afin d'être opérationnel il importe de disposer de données d'entrée. Dans le chapitre qui suit (§-VI) sont décrite les différentes étapes de développement d'un outil de terrain permettant de quantifier le geste du départ de course vitesse et fournir des informations en temps quasi instantanée.
|
||||
Conception et developpement d'un outil de terrain
pour l'evaluation du depart de course vitesse
La caractérisation de la performance de départ, particulièrement celle des athlètes de haut niveau, est sensible aux outils d'évaluation utilisés. La miniaturisation des composants électroniques conjuguée à l'augmentation des capacités de l'outil informatique sont deux facteurs prépondérants au développement de tels outils. Cependant la démarche reste complexe dans le sens où ces outils doivent être à la fois robustes et simples de mise en oeuvre car utilisés en milieu sévère et d'un coût modeste afin d'en assurer une large diffusion. De plus, pour être attractifs, ils doivent offrir un traitement des données en temps (quasi) réel conduisant à une analyse et une interprétation fines afin de différencier des performances souvent très voisines.
Les études basées sur le principe de la cinématographie présentent l'inconvénient de ne donner des résultats qu'en temps différé. Ces analyses, si elles restent indispensables à la compréhension de la coordination segmentaire du geste, ne répondent pas aux attentes immédiates de l'entraîneur. Dans ce sens, les travaux de Howell (1956) ainsi que ceux de Fortier et al. (2005), démontrent tout l'intérêt d'avoir un feedback immédiat dans l'apprentissage et la progression rapide des athlètes [Fort 05 ; Howe 56]. Il est donc nécessaire de trouver des solutions qui offrent un retour d'information quasi instantané afin d'orienter les prises de décision de l'entraîneur et d'objectiver ses consignes.
Utilisé surtout en laboratoire, la dynamométrie constitue depuis l'apparition des blocs de départ en 1934 la solution de mesure la plus exploitée lorsqu'on s'intéresse à la dynamique du départ de course vitesse (§-II.tableau 1). Les avantages et les limites de ce type d'instrumentation sont décrits dans le deuxième chapitre de ce manuscrit (§-II.1.1).
La première instrumentation visant à évaluer les actions mécaniques de contacts des pieds sur les blocs lors d'un départ de course vitesse est effectuée par Kistler dès l'apparition des blocs de départ en 1934 (cité dans [Henr 52]). Kistler a encastré deux balances à plateaux dans la piste d'athlétisme sur lesquelles il a monté les blocs de départ afin d'évaluer la force horizontale maximale exercée distinctement au niveau de chaque pied. En 1952, Henry utilise un arrangement entre une crémaillère et un pignon pour évaluer la somme des forces horizontales exercées par les deux pieds sur les blocs [Henr 52]. Payne et Blader (1971) ont utilisé des capteurs semi circulaires instrumentés par des jauges de déformation reliées dans un pont de Wheatstone (Annexe 3.2.2). Ce dispositif permet de mesurer, en laboratoire, la force normale et tangentielle au cale pied34. Par la suite, et avec le développement des moyens instrumentaux, la plateforme de force a fait l'objet de plusieurs études considérant la somme des forces externes qui s'exercent à l'athlète lors du départ de course de vitesse. D'autres études [Davi 06 ; Gagn 78 ; Mero 83 ; Vign 97 ] utilisent encore cette approche de laboratoire pour caractériser la dynamique et la cinématique du départ.
L'une des premières études qui développe une instrumentation destinée à être utilisée sur le terrain est celle de Barry et al. (1983). Leur objectif était de développer un outil d'apprentissage et d'entraînement qui offre des informations instantanées aux athlètes. Toutefois, les blocs développés ne sont pas réglables en inclinaison, et les forces sont mesurées suivant un seul axe : la normale au cale pied. Lemaire et Robertson (1990) ont conçu des blocs instrumentés (figure 60) pour l'évaluation des forces horizontales exercées lors d'un départ de course vitesse. Afin de valider leur instrumentation, ils ont testés sa linéarité, son hystérésis et sa réponse fréquentielle [Lema 90].
34 Le terme « cale pied » désigne ici la plaque inclinable du bloc de départ sur laquelle repose directement le pied de l'athlète.
Figure 60 Mise en place des jauges sur la barre du bloc de départ [Lema 90]
Ce n'est qu'en 1991 que l'un des premiers outils de terrain permettant à la fois l'évaluation instantanée de la dynamique et la cinématique du départ est développé. Il s'agit de l'instrumentation conçu par Sanderson et al. de l'université Saskatchewan (Canada) [Sand 91]. Leur instrumentation comporte un radar et des blocs de départ instrumentés chacun par un capteur relié à un ordinateur. L'auteur précise que le dispositif permet d'évaluer les forces exercées sur les blocs lors du départ suivant les trois dimensions de l'espace ainsi que la vitesse instantanée de l'athlète jusqu'à 25 mètres avec une précision estimée à 2%.
À notre connaissance, aucune instrumentation de terrain n'est, à ce jour, disponible en France pour étudier conjointement et instantanément les paramètres dynamiques et cinématiques du départ en 3D tout en dissociant les actions mécaniques de contacts. Natta et Réga (2001), de l'INSEP35, ont conçu un starting blocs muni de capteurs de forces sensibles aux forces horizontales afin de recueillir les poussées horizontales exercées par l'athlète sur les blocs arrière et avant [Natt 01]. Ces mesures sont couplées à des analyses cinématographiques afin d'étudier la cinématique de l'athlète en deux dimensions.
La démarche de développement et de conception d'un outil de terrain permettant la caractérisation mécanique de la performance de départ de course de vitesse en situation réelle de pratique a vue le jour suite à une collaboration entre notre équipe (Mécanique du Geste Sportif du Laboratoire de Mécanique des Solides de l'Université de Poitiers) et la FFA36.Cette collaboration est effectuée dans le cadre d'un projet financé par le MSJSVA.37
35 INSEP : Institut Nationale du Sport et de l'Éducation Physique - France ( www.insep.fr)
36 FFA : Fédération Française d'Athlétisme ( www.athle.org)
37 MSJSVA : Ministère de la Santé de la Jeunesse, des Sports et de la Vie Associative ( www.sante-jeunessesports.gouv.fr)
La suite de ce chapitre expose les étapes de construction et de validation des blocs de départ instrumentés chacun par un dynamomètre. Le développement de cet outil de terrain s'appuie sur une analyse standardisée effectuée au préalable en laboratoire et décrite dans le troisième chapitre de ce manuscrit (§-III.1.2). De cette manière, les caractéristiques techniques de l'outil sont minutieusement choisies. L'influence de la mesure de la somme des forces externes sur l'évaluation des paramètres du départ de course de vitesse est étudiée. Une description de différentes solutions de l'estimation des actions de contacts des mains est effectuée. Les résultats obtenus sont utilisés pour limiter au mieux l'investissement en matériel de mesure des forces de contacts tout en ayant une estimation fine des différents paramètres de départ. Le système final associé à une interface graphique fourni un feedback quasi instantané exposant :
? le temps de réaction
? la durée de l'impulsion
? l'instant de l'éjection
? la variation des actions mécaniques de contact exercées au niveau des appuis (pied droit, pied gauche et les deux mains)
? la variation de la vitesse du centre de gravité et son intensité à l'éjection
? la direction de la vitesse à l'éjection
? le déplacement du centre de gravite
La détermination des efforts de contact des pieds sur les blocs et des mains sur le sol lors d'un départ de course de vitesse est une approche indispensable qui permet de définir les caractéristiques du dynamomètre : type, dimensions, étendu de mesure, sensibilité...
L'outil utilisé est un capteur composite. Le choix de ce type de dynamomètre se justifie par un coût relativement faible et une facilité de contrôle et de production. Les étapes de mise au point de cet instrument sont détaillées en annexe (Annexe 2).
Les études antérieures (§-II.tableau 1) qui s'intéressent à l'appréciation de la performance du départ de course de vitesse considère rarement les forces s'exerçant sur l'athlète suivant les trois directions de l'espace. Il s'agit le plus souvent de mesures effectuées suivant l'axe antéropostérieur ou normal aux cales pieds. Quant aux actions de contact des mains, à notre connaissance, les études sont inexistantes.
Ainsi, la caractérisation des dynamomètres instrumentant les blocs de départ et les appuis mains, s'est appuyée sur les données numériques issues de 92 mesures de départ de course dissociant les efforts de contact exercée distinctement au niveau de chaque appui de l'athlète (§-IV.2)
L'utilisation de deux plates formes de forces comme moyen permettant de quantifier l'intensité des efforts de contact de chaque pied avec le bloc correspondant est décrite dans le troisième chapitre de ce document (§-III.1.2).
Pour définir l'étendu de mesure du dynamomètre en termes de moments de forces, il importe de connaître l'intensité de la résultante des forces ainsi que son point d'application. Cependant, cette dernière information n'est pas directement accessible. La procédure de calcul du centre de pression38 fournie par le constructeur (Kistler) ne prend en compte que la seule géométrie de la plateforme de force. La modification du dimensionnement de cette géométrie par l'ajout d'un dispositif, tel que celui des blocs de départ, fourni un résultat erroné concernant le centre de pression. La position de ce dernier est estimée en dehors des dimensions de la plateforme de force.
L'évaluation de la position du centre de pression dépend de la matrice d'étalonnage de la plateforme de force qui est définie par rapport à sa géométrie initiale fixée par le constructeur. La fixation d'un bloc de départ sur la plateforme représente une liaison d'encastrement. Ce type de liaison ne permet pas de définir un point quelconque où le moment du torseur est nul. Le torseur n'étant pas un glisseur, il n'est donc pas possible de déduire le centre de pression. Cela explique les résultats biaisés trouvés lors de l'utilisation de la matrice d'étalonnage de la plateforme de force pour le calcul du centre de pression au niveau du pied.
Contrairement, l'estimation de l'intensité du moment de force engendré par rapport au centre du dynamomètre est possible suite à la connaissance des dimensions du cale pied et des forces qui s'y appliquent. L'éloignement du point d'application de la force par rapport au centre du capteur engendre un moment qui est d'autant plus grand que la distance entre les deux points est importante.
38 Centre de pression : point d'application ou barycentre des forces de réaction.
Le dynamomètre est centré par rapport au cale pied. Ce dernier possède une longueur standard L = 0,160 m. Afin d'évaluer l'intensité des moments de force en un point dont la position ne dépasse pas d = L / 2 = 0,08 m par rapport au centre du dynamomètre, une force d'intensité constante égale à 1200 N est appliquée à différents points situés sur l'axe longitudinal du cale pied. Au niveau de chaque point d'application, l'angle du vecteur force varie de 0 à 90° par rapport au cale pied (figure 61).
Cale pied
Figure 61 Points d'application et orientation de la force simulée sur le cale pied
~~~ ~~~~Le moment de force ( NO, P.) / 910 = OPi ? Pext ? O) est ensuite calculé en chaque
point en fonction de la variation de l'angle (figure 62).
Figure 62 Variation du moment de force en fonction de l'angle et de la position
du centre de pression par rapport au centre du dynamomètre pour une force de 1200 NCette simulation permet de prédire les moments de force qui peuvent être appliqués au dynamomètre suivant des conditions prédéfinies. Connaissant par mesure dynamométrique (plateforme de force) la grandeur des forces de contact exercées au niveau des pieds, il devient possible de décrire les propriétés finales des dynamomètres destinés à instrumenter les
blocs de départ. Le torseur le plus contraignant a été défini à partir des informations suivantes :
? une résultante maximale de 1200 N
? une colatitude maximale du vecteur force de 30°
? une distance maximale du centre de pression de 65 mm par rapport au centre géométrique du capteur
La procédure de dimensionnement du dynamomètre se base sur l'hypothèse suivante ...connaissant l'ensemble des actions mécaniques pouvant être appliquées sur le capteur, quelle doit être la géométrie de ce dernier et la capacité de mesure des poutres... [Bouc 05]. Ce travail a fait l'objet de la thèse de doctorat de Boucher [Bouc 05] effectuée au sein de notre laboratoire. L'encombrement du capteur est défini par rapport à la géométrie d'un bloc de départ standard. Ainsi son diamètre ne doit pas dépasser 80 mm. Ces éléments ont permis de définir les caractéristiques du dynamomètre destiné à équiper le bloc de départ :
? Diamètre externe : 79 mm
? Hauteur : 40 mm
? Étendue de mesure par composantes :
- Fx = 3500 N ; Fy = 3300 N ;Fz = 11000 N
- Mx = 190 Nm ; My = 220 Nm ; Mz = 230 Nm
? Étendue de mesure en application simultanée des composantes : - Fx = Fy = Fz = 870 N
- Mx = My = 60 Nm ; Mz = 85 Nm
Une fois la détermination des propriétés du dynamomètre achevée, sa construction est lancée. En parallèle, la conception et le développement des blocs de départ adaptés sont assurés. Ce développement est détaillé plus loin dans ce même chapitre (§-VI.4).
Suite à des recherches bibliographiques, aucune étude scientifique ne fait référence aux efforts exercés au niveau des mains lors d'un départ de course de vitesse. Les expérimentations précédentes (§-III.1.2) permettent d'évaluer les efforts de contact exercés au
niveau des mains suivant les trois dimensions de l'espace. Cependant, l'utilisation sur le terrain d'un tel dispositif présente un coût élevé.
Dans le paragraphe qui suit, différentes solutions sont étudiées afin de déterminer l'influence de l'estimation des forces verticales et tangentielles sur l'évaluation des paramètres caractéristiques du départ de course de vitesse.
Dans ce qui suit, la précision des paramètres du départ de course de vitesse est estimée dans les cas où l'étude repose sur l'exploitation totale ou partielle des composantes de forces de contact de l'athlète avec le sol (i.e. pieds, mains).
Nous désignions par :
§ méthode de référence : les analyses effectuées à partir de la mesure synchrone des
forces exercées au niveau des mains et des pieds de l'athlète lors du départ (§-III.1).
§ méthode partielle : les analyses effectuées en ne prenant en compte que les forces
exercées au niveau des pieds.
§ méthode approchée : les analyses effectuées en mesurant les efforts de contact des
pieds et en simulant les efforts de contacts des mains.
Ces deux dernières méthodes (partielle et approchée) sont comparées à la méthode de référence afin d'évaluer les erreurs relatives concernant la vitesse et l'angle à l'éjection. Les résultats obtenus sont utilisés pour limiter au mieux l'investissement du matériel de mesure des composantes des forces de contact.
La non prise en compte des efforts exercés au niveau des mains a pour effet de rompre l'équilibre du système dès les premiers instants.
Suivant la verticale, le poids du corps n'est plus contrebalancé par la somme des forces exercées au niveau des mains et des pieds. La même intensité de la force des pieds à elle seule ne peut pas maintenir le centre de gravité au repos. Ce dernier se trouve donc soumis à une force égale à la différence entre le poids et la force des pieds. Le centre de gravité est donc « tiré » dans la direction du poids avec une accélération d'autant plus grande que les forces exercées au niveau des pieds sont de faibles intensités (figure 63).
Suivant l'axe antéropostérieur, les forces exercées au niveau des pieds ne sont plus contrebalancées par celles des mains ce qui provoque l'apparition d'une vitesse antéropostérieure proportionnelle à l'intensité des forces exercées à chaque instant au niveau des pieds alors que le sujet est immobile lors de la position Prêt (figure 63). Rappelons aussi que l'axe des ordonnées coupe celui des abscisses à l'instant zéro correspondant à l'instant du signal de départ (ts = 0s).
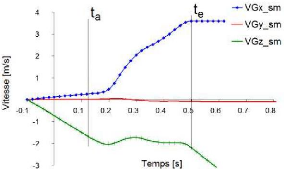
Figure 63 Variation de la vitesse du centre de
gravité lors du départ
calculée à partir des
seules forces exercées au niveau des pieds sans les mains (VG_sm)
(t
= 0 correspond à l'instant du signal de départ)
Lorsque les forces exercées au niveau des mains ne sont pas prises en compte, l'application du principe fondamental de la dynamique au système athlète ne permet pas de déduire les variations réelles de la vitesse du centre de gravité (figure 63). La vitesse d'éjection antéropostérieure est surestimée de 12%.
Suivant l'axe vertical, l'erreur est très importante (>100%) et présente une vitesse d'éjection négative. La vitesse médiolatérale, quant à elle, reste insensible à la non prise en compte des forces exercées latéralement au niveau des mains. Ces résultats évaluent la norme de la vitesse du centre de gravité à 38% lors de l'éjection et fournissent un angle d'éjection biaisé (>100%).
L'amplitude de ces erreurs relatives démontre toute l'importance d'intégrer les efforts de contacts des mains lorsqu'on cherche à étudier la cinématique du centre de gravité de l'athlète.
|
x |
ts |
Cependant, la prise en compte de ces efforts nécessite l'emploi d'un dynamomètre 3D supplémentaire ce qui augmente le coût. Une des solutions consiste à coupler les mesures de forces exercées au niveau des blocs avec une solution d'estimation des forces exercées au niveau des mains. De ce fait, la possibilité de simuler les forces exercées au niveau des mains est étudiée afin d'en déterminer les limites.
Dans l'optique d'approcher au mieux les forces exercées au niveau des mains, plusieurs méthodes de simulation sont développées afin d'évaluer la qualité du départ de course de vitesse. Ces approches reposent sur la connaissance des forces exercées au niveau des pieds (forces de référence) et de l'instant de décollage des mains (teM). Cet instant peut être défini par la mise en place d'un « contacteur » au niveau de la surface de contact des mains avec la piste. Les vitesses et les angles d'éjection issus de chaque simulation sont confrontées aux valeurs de référence afin de définir l'erreur relative de chaque approche. Les instants de mise en action (taP) et d'éjection (te) sont définis à partir de la mesure des forces exercées au niveau des pieds.
Suivant l'axe antéropostérieur : deux approches sont développées en se basant sur l'hypothèse de l'équilibre statique de l'athlète jusqu'à l'instant taP.
-La première approche consiste à supposer que l'intensité des actions exercées au niveau des mains ( x
FM ) suivant cet axe est constante jusqu'à l'instant teM là où elle s'annule (figure 64). x
FM possède une intensité égale à celle des actions
exercées au niveau des pieds mais de sens opposé
jusqu'à l'instant du signal de départ.
Ainsi à partir
de l'instant initial ts correspondant au signal de
départ jusqu'à l'instant
teM -1 :

Fx
P
gt o
F

M gtt s - ti
avec ti un instant quelconque où l'athlète est considéré en position quadrupédique statique avant le signal de départ, c'est-à-dire lors de la position « Prêt ». Dans le cas de cette étude, l'échantillonnage est réalisé à 1000 Hz et ti = ts - 100.
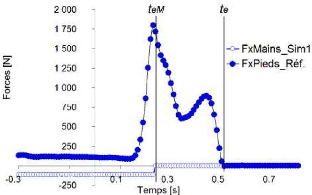
Figure 64 Illustration de la 1ère
approche de simulation des forces antéropostérieures
exercées au niveau
des mains (FxMains_Sim1) et des forces
mesurées exercées au niveau des pieds suivant le même
axe
Cette première approche simule FM gt suite a la seule connaissance de la
o
valeur moyenne de cette grandeur lors de la position «
Prêt ». Testée pour tous les
essais de départ de la
population de cette étude, cette approche réduit l'erreur
relative
par rapport à la méthode partielle et
d'évaluer la vitesse d'éjection
antéropostérieure
(Vé;ect gto ) à 4,5 #177;3%.
- La deuxième approche repose sur l'application du principe de la statique à
chaque instant jusqu'à l'instant taP correspondant à la mise en action des pieds. Cela
permet la déduction de la variation de FM o à partir de la mesure instantanée des forces exercées au niveau des pieds F; o suivant le même axe (figure 65). De ce fait, à chaque instant et jusqu'à taP -1, on suppose que :
F:1 = - FxP


Ro

À partir de taP, l'intensité de FM ~odiminue linéairement pour s'annuler à l'instant d'éjection des mains (teM).
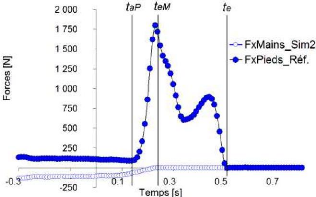
Figure 65 Illustration de la 2ème
approche de simulation des forces horizontales exercées au niveau
des
mains (FxMains_Sim2) et des forces mesurées au niveau des pieds
suivant le même axe

L'adoption de cette approche améliore l'appréciation de V é;ect o par rapport à son intensité de référence en réduisant l'erreur relative à 2,5 #177;1,5%.
Suivant l'axe vertical, deux méthodes de simulations sont testées afin d'approcher les forces verticales FL o exercées au niveau des mains.
-La première approche consiste à déduire l'intensité de FM ao par la soustraction au poids (9G ~ o) à chaque instant, de la force exercée au niveau des pieds suivant le même axe. Cette procédure est réalisée jusqu'à l'instant taP.
FM €o = gG -FPS
Dès l'instant taP+1, l'intensité de FL o décroit linéairement pour s'annuler à l'instant de décollage des mains (teM) (figure 66).
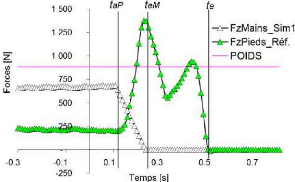
Figure 66 Illustration de la 1ère
approche de simulation des forces verticales exercées au niveau des
mains
(FzMains_Sim1) et des forces mesurées au niveau des pieds
suivant le même axe
L'adoption de cette méthode réduit l'erreur relative de l'évaluation de la vitesse d'éjection verticale à 75%. Toutefois, cette réduction n'est pas encore satisfaisante en termes de précision.
- La deuxième approche consiste à prendre en compte l'effet de « pompage »
effectué par le sujet dès sa mise en action. L'intensité de la force maximale étant différente d'un sujet à un autre et pour un même sujet d'un essai à un autre, cela nécessite l'adoption d'un moyen permettant d'approcher au maximum l'intensité de référence.
Selon les études de corrélations menées au cours du quatrième chapitre (§-
IV.4.3.figure 47), il existe une relation affine entre l'intensité de FL o exercée lors de
la position Prêt et son intensité maximale atteinte plus tard lors de la mise en action (R2 = 0,77).
En utilisant l'équation de la droite de régression linéaire (y = 1,42x - 11,65) et en approchant la variation de référence par la courbe issue d'une fonction sinus, il est
possible de simuler la variation de FL o à partir de l'instant taP jusqu'à l'instant teM (figure 67) suite à la connaissance de sa grandeur lors de la position Prêt.

Cette approche estime l'amplitude maximale atteinte par FL o avec une erreur relative de l'ordre de 8 #177;6%.
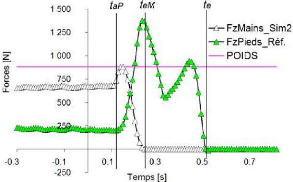
Figure 67 Illustration de la 2ème
approche de simulation des forces verticales exercées au niveau des
mains
(FzMains_Sim2) et des forces mesurées au niveau des pieds
suivant le même axe
L'application de cette approche réduit l'erreur d'estimation de la vitesse d'éjection à 42%, cependant cela reste toujours insuffisant.
Suivant l'axe médiolatéral, les forces mesurées qui s'exercent au niveau des pieds sont nulles jusqu'à l'instant teM. Les forces mesurées exercées au niveau de la main droite
( y


FMd 9to ) et la main gauche ( y
FMg ~o) sont de même intensité mais de sens opposé :
y
Mg gto


et de l'angle (èéject) à
La somme des forces exercées au niveau des mains suivant l'axe médiolatéral peut être négligée sans conséquence sur la précision des grandeurs d'éjections estimées.


Lors d'un départ de course de vitesse, la qualité d'estimation de F ao et de F ao

V éj e ct
détermine la précision d'évaluation de la norme de la vitesse l'éjection.
L'objectif de cette partie est de déterminer le matériel de mesure dynamométrique

V éj ect
nécessaire (à minima) pour une estimation fine de
et de èéject. Suite aux différentes
approches réalisées, la deuxième simulation des forces suivant l'axe antéropostérieur ainsi que la deuxième simulation suivant l'axe vertical réduisent considérablement l'erreur relative.
La bonne corrélation qui existe entre V é;ect de référence et sa norme (R2 = 0.99) est
biaisée lorsque cette dernière est estimée sans prendre en compte les forces exercées au niveau des mains (étude partielle, R2 = 0,74) (figure 68). Lorsque la norme est estimée par l'intermédiaire de la deuxième approche de simulation, la corrélation est rétablie (R2 = 0,92).
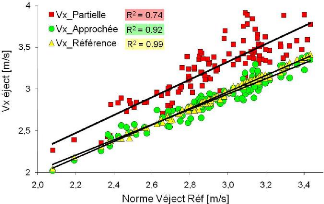
Figure 68 Corrélation entre la norme de la
vitesse de référence à l'éjection et la vitesse
antéropostérieure
au même instant (Vx éject)
estimée par trois études différentes : de
référence, approchée et partielle
Ces résultats montrent que la norme peut être estimée en mesurant les forces des pieds et les seules forces antéropostérieures exercées au niveau des mains. Quant à l'angle d'éjection, il est dépendant de la grandeur de la vitesse verticale d'éjection. Étant de faible intensité, la vitesse verticale semble ne pas contribuer fortement dans la définition de l'intensité de la norme, toutefois la qualité de son estimation influe directement et considérablement la valeur de l'angle d'éjection.
Dans la figure qui suit (figure 69), les erreurs relatives à la norme de la vitesse d'éjection et sa direction sont définies en combinant différentes possibilités de mesures ou de simulations d'une ou des deux composantes de forces exercées au niveau des mains.
Erreur sur
Méthode
référence
38%
Erreur sur èéject
Méthode
référence
>100%
F z mesurée
Mai ns
F Mains et z
x F Mains
Sim2
F Mains mesurée
x
F Sim2
Mains
28,5%
12%
2,5%
0,5%
>100%
4%
43%
42,5%
Pas de mesure
F Sim2
Mains
F Mains mesurée
z
2,5%
2%
F Mains et z
x F Mains
mesurées
V éj ect
x
F Pieds
mesurée
FPzieds
mesurée
F x mesurée
Mai ns
Figure 69 Influence de la mesure et/ou de la simulation
des forces antéropostérieures et verticales exercées
au
niveau des mains sur l'estimation de la norme de la vitesse et l'angle
d'éjection
La simulation des forces exercées au niveau des mains suivant l'axe vertical ne permet pas d'avoir une estimation précise des paramètres cinématiques (vitesse et angle d'éjection). Cela est dû au fait que les efforts exercés au niveau de ces segments ne présentent pas de variations régulières permettant de prédire avec précision leur intensité maximale. Une étude complémentaire devrait dresser une approche de simulation plus spécifique selon le niveau des athlètes.
Enfin, ces résultats montrent qu'un dispositif comprenant la mesure des actions de contact X
Fpieds , Z
Fpieds , Z
Fmains et X
Fmains étant simulée, est un compromis satisfaisant en termes de précision du résultat obtenu, de coût et de facilité d'utilisation.
Il vient d'être démontré que pour une bonne estimation de la norme et de la direction de la vitesse d'éjection du centre de gravité d'un coureur lors d'un départ de course de vitesse, il est indispensable d'associer aux forces exercées au niveau des pieds, les forces verticales
exercées au niveau des mains. Une plate forme est donc développée à fin de mesurer sélectivement ces forces. Elle comporte trois pieds instrumentés chacun par un pont de jauges sensible aux forces verticales (figure 70).
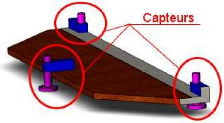
Figure 70 Plate forme dynamométrique pour la
mesure des forces verticales exercées
au niveau des mains
(CAO39)
Concernant l'instrumentation des blocs de départ, il est important de conserver leurs propriétés de réglage tout en permettant au dynamomètre de réagir aux seules forces qui sont exercées par le pied de l'athlète. Toutefois, pour un dynamomètre de hauteur h positionné sur un bloc de départ standard, la variation de l'angle 0 du bloc dans un sens ou dans un autre implique soit la butée de la plaque fixée sur le dynamomètre au niveau du sol soit son décollage (figure 71).
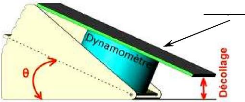
Cale pied
Figure 71 Éloignement du cale pied par rapport
au sol lors de la variation
de l'angle d'inclinaison 0 du bloc de
départ.
Dans le paragraphe suivant, une solution de conception est présentée afin d'instrumenter le bloc tout en respectant ses propriétés d'inclinaisons.
39 Conception Assisté par Ordinateur
Une première solution consiste à doter le cale pied d'une liaison glissière avec la surface supérieure du dynamomètre. Cela permet d'ajuster le cale pied en le glissant pour le remettre au même niveau par rapport au sol. Toutefois, cette solution nécessite un réglage supplémentaire et engendre un décalage important du centre du dynamomètre par rapport à la zone de pression du pied. Or, l'application d'une force en dehors de la surface du dynamomètre produit un moment d'autant plus grand que son point d'application est écarté du centre du capteur. Lorsqu'une grandeur dépasse l'étendu de mesure du dynamomètre, elle peut engendrer des effets irréversibles [Cou 00].
Plusieurs solutions adoptant différents types de liaison entre les éléments du bloc sont alors étudiées. Il en ressort qu'une liaison linéaire rectiligne permet un meilleur fonctionnement de ce dispositif. Ce type d'attache est une liaison parfaite à quatre degré de liberté entre deux solides S1 et S2 qui doivent remplir la condition suivante au cours de leurs mouvements : une droite D2 de S2 doit rester dans un plan P1 de S1 (figure 72.a).
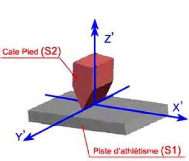
(a)
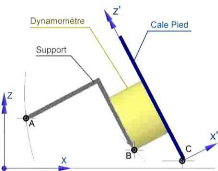
(b)
Figure 72 Liaison linéaire rectiligne du cale pied avec la piste d'athlétisme
En adaptant ce principe, le cale pied se trouve doté d'une liaison linéaire rectiligne contrainte à deux degrés de liberté. En comparaison au solide S2, le cale pied n'effectuera qu'une rotation autours de Y et une translation suivant X par rapport à la piste d'athlétisme (figure 72.b). Ainsi, en fonction de la variation de l'inclinaison du cale pied, l'extrémité inférieure C (figure 72.b) se trouve dotée d'un mouvement de translation suivant l'axe X. Afin de pouvoir fixer le cale pied à différentes inclinaisons, les positions des points A et B du support sont définies pour toutes les inclinaisons du cale pied (de 30° à 80°).
Un bloc de départ adéquat est ensuite conçu pour permettre le réglage de l'inclinaison du cale pied à partir de la variation des points de fixation (A et B) (figure 73). Cette conception est effectuée avec un logiciel de CAO.
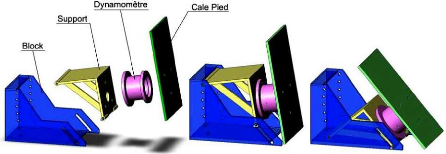
Figure 73 Bloc de départ instrumenté par un dynamomètre (CAO)
La production d'un premier prototype en acier est effectuée au sein de l'atelier du LMS. Cette conception a validé la procédure de dimensionnement des blocs. La qualité de réponse de l'engin, suite aux sollicitations extérieures, est vérifiée par un étalonnage. Cette procédure est décrite dans le paragraphe qui suit.
L'étalonnage est une procédure délicate qui permet de quantifier les efforts qui sont appliqués au dynamomètre. Cette opération doit prendre en compte le domaine d'utilisation du dynamomètre prédéfinit suite à la procédure de dimensionnement du corps d'épreuve.
Cette procédure comprend des opérations qui permettent d'exprimer sous formes graphique et algébrique les relations entre l'intensité des efforts et les tensions recueillies à la sortie du conditionneur. Elle consiste à trouver le coefficient de proportionnalité entre la valeur imposée et la valeur affichée en réponse à la sollicitation du dynamomètre. Elle permet aussi de vérifier d'une part, les hypothèses sur lesquelles reposent la procédure de dimensionnement du corps d'épreuve (épaisseur, longueur et inclinaison des poutres...) et d'autre part, le bon fonctionnement des ponts de jauges (collage, câblage, hypothèse d'élasticité linéaire...).
Il est possible de distinguer deux procédures d'étalonnage. La première procédure est dite directe ou absolu. Il s'agit d'appliquer au dynamomètre des forces bien définies dans les directions X, Y, Z, sur le centre de réduction des forces, puis des couples connus suivant X, Y, Z. À propos de la précision des forces appliquées au dynamomètre, il est recommandé d'utiliser des masses étalons dont la valeur est connue avec une précision qui dépasse cent fois celle recherchée pour le capteur [Asch 99]. Cette procédure d'étalonnage est utilisée pour la vérification de la linéarité de la réponse de la plateforme de force Kistler (type 9287B) suivant son axe vertical (§-III.2.2). Suite à cette procédure, il devient possible d'utiliser la plateforme de force pour l'étalonnage indirect du dynamomètre. Il s'agit ici de la deuxième procédure d'étalonnage. En effet, il est admis d'utiliser un capteur de référence dont on possède la courbe d'étalonnage et dont on est assuré de la stabilité pour l'étalonnage indirecte du dynamomètre [Ash 99]. Le dynamomètre à étalonner est fixé sur la plateforme de force par l'intermédiaire d'une interface permettant de conserver les mêmes contraintes qui s'exercent sur le dynamomètre lorsqu'il est dans son milieu de mesure (figure 74).

Figure 74 Position du dynamomètre dans
l'interface d'étalonnage fixée sur la plate forme
lors de la
procédure d'étalonnage indirecte
Une interface est développée pour assurer l'étalonnage du dynamomètre tout en étant fixé entre les deux éléments du bloc de départ (figure 74). Les deux capteurs, la plateforme de force et le dynamomètre instrumentant le bloc, se trouvent donc soumis dans les mêmes conditions, simultanément, à l'action du mesurande identique dont le capteur de référence permet de connaître les valeurs.
Rappelons que le développement de cet outil d'analyse est effectué dans le cadre d'un projet de recherche financé par le MSJSVA40 en partenariat avec la FFA41. Cette dernière souhaite disposer d'un outil de terrain permettant de discriminer mécaniquement les
40 MSJSVA : Ministère de la Santé de la Jeunesse, des Sports et de la Vie associative ( www.sante-jeunessesports.gouv.fr)
41 FFA : Fédération Française d'Athlétisme ( www.athle.org)
performances d'athlètes lors d'un départ de course de vitesse en situation réelle de pratique. La conception d'un premier prototype en acier à vu le jour dans les ateliers du LMS. Cette première démarche à permis de valider le dimensionnement des blocs qui sont désormais fabriqués en fibres de carbone tout comme l'appui mains instrumenté (figure 75).

Blocs instrumentés
Appui mains instrumenté
Figure 75 Station dynamométrique pour
l'évaluation du départ de course de vitesse
en situation
réelle de pratique
La simplification de la mesure des forces exercées au niveau des mains (mesure des seules forces verticales et simulation des forces antéropostérieures), permet d'estimer la vitesse du centre de gravité à l'éjection avec une précision de 2,5 #177;1,5% selon les sujets (figure 69). Puisque la norme de la vitesse d'éjection est fortement dépendante de la vitesse antéropostérieure, elle est affectée de la même manière (2,5 #177;1,5%). Quand à l'angle d'éjection qui dépend principalement de la grandeur de la vitesse verticale à l'éjection, il est évalué avec une précision de 2 #177;1%.
N'offrant que des renseignements concernant la dynamique et la cinématique du centre de gravité jusqu'à l'instant de l'éjection, la possibilité de synchroniser une caméra vidéo est proposée grâce à une interface électronique. Ce couplage d'outils dynamométrique et cinématographique permet d'étudier la variation des données dynamométriques et de visualiser l'image correspondante à chaque instant (chronophotographie).
Offrant des renseignements précieux susceptibles d'orienter objectivement les décisions de l'entraîneur, un tel dispositif n'accorde cependant que la possibilité d'étudier le geste d'une manière globale. Il ne fournit en aucun cas des données concernant la cinématique segmentaire et/ou la dynamique articulaire de l'athlète lors du départ.

Quatrième partie
L'objectif de cette partie est de proposer un protocole adapté à l'analyse de la gestuelle du départ de sprint. Il est certain que le système dynamométrique développé au cours de cette étude (§-6) offre des indications précieuses concernant la dynamique du départ de sprint. L'étude de la gestuelle permet l'analyse des différentes quantités d'accélérations segmentaires responsables de la mise en mouvement du corps de l'athlète. Ainsi, avant toute analyse, il importe de résoudre les problèmes liés aux traitements de données cinématographiques et à la modélisation du corps humain.
En effet, étant au carrefour de plusieurs secteurs de recherches scientifiques, la biomécanique, et plus exactement la mécanique du geste sportif, se sert d'un large panel d'outils, de modèles, de méthodes d'analyse et de traitement de données qui exigent une attention particulière. Dans une approche directe ou indirecte42, l'expérimentateur doit accomplir plusieurs étapes avant l'étude du geste et avant même son enregistrement. Ces étapes préliminaires ont pour objectif de réduire les incertitudes liées aux systèmes utilisés d'une part, et celle de la modélisation de la chaîne cinématique, d'autre part. Toutefois, l'opérateur se trouve confronté à l'abondance et à la divergence de la littérature scientifique ainsi qu'à la multiplication des boîtes à outils informatiques de traitement de données mises à sa disposition.
Cette partie comporte deux chapitres. Le premier (§-VII), présente les méthodes adoptées pour le traitement des données cinématographiques et la modélisation de l'athlète dans un espace tridimensionnel (définition de la position et l'orientation des segments, approximation des centres fonctionnels de rotation et estimation des repères anatomiques). L'accent est mis sur le problème irrésolu de la non rigidité des segments du corps humain. De ce fait, les issues proposées dans la littérature scientifique sont discutées afin de montrer leurs limites dans l'application rigoureuse des principes de la mécanique des solides.
42 L'approche directe consiste en l'enregistrement de déplacement à l'aide d'outils tels que les potentiomètres, les goniomètres, et l'enregistrement des accélérations par des accéléromètres. À l'inverse, l'approche indirecte consiste en l'enregistrement d'images du mouvement sur un support donné. Colloud (2003), expose et discute ces deux approches [Coll 03].
Quatrième partie
Le deuxième chapitre (§-VIII), présente une nouvelle procédure de minimisation des artéfacts dus aux mouvements de la peau. Cette procédure se base sur un raisonnement par récurrence à partir de données contenues dans les matrices de roto-translations segmentaires. Afin de tester son efficacité, une confrontation est effectuée avec une procédure d'optimisation globale [Lu 99]. Ainsi, la dernière section de ce chapitre étudie l'effet de ces deux procédures de solidification sur la définition de la configuration du système polyarticulé, puis sur la cinématique segmentaire et enfin sur la dynamique articulaire.
L'objectif de ce chapitre est de déterminer la configuration segmentaire la plus précise de l'athlète, à chaque instant, lors d'un départ de sprint. Le repérage de chaque segment dépend directement des méthodes de traitement et d'analyse de données cinématographiques adoptées. Un déroulement rigoureux de ces étapes permet la modélisation des différents segments du corps de l'athlète par des solides indéformables reliés entre eux par des liaisons parfaites. On parle alors de système poly-articulé de solides rigides. L'hypothèse de la rigidité des segments étant primordiale à l'application des principes de la mécanique classique, elle contraint l'expérimentateur à trouver des solutions au problème que pose le mouvement relatif des marqueurs définissant un segment donné.
En effet, en se basant sur le suivi de marqueurs collés sur la peau, l'étude de la gestuelle doit tenir compte, d'une part, des perturbations provoquées par l'élasticité de ce tissu biologique, et d'autre part, de la présence de masses molles. Ces perturbations n'ont pas seulement pour effet de faire varier la longueur des segments mais aussi de modifier la position des marqueurs par rapport à la structure osseuse sous jacente (saillies osseux), ce qui biaise l'estimation des centres articulaires, des axes anatomiques segmentaires et toutes les grandeurs calculées qui en dépendent. Dans ce qui suit seront donc présentées les différentes
étapes de traitement de données cinématographiques afin de garantir une application rigoureuse des différents principes permettant l'étude mécanique de la gestuelle du départ de course vitesse.
L'une des étapes les plus importantes est la mise en place du système d'acquisition destiné à capturer la gestuelle d'un athlète qui effectue un départ de course vitesse à partir d'une position en quadrupédie. Dans ses travaux, Boucher (2005) discute les problèmes liés au placement des caméras ainsi qu'à la calibration du volume d'étude. Il aboutit à un protocole d'évaluation de la précision des coordonnées des marqueurs [Bouc 05]. Ces recommandations sont prises en compte lors de la capture du mouvement du départ de sprint.
L'outil de capture d'image utilisé est un système optoélectronique Motion Analysis43 comportant six caméras équipées chacune d'un projecteur émettant une lumière rouge à fréquence réglable (200 Hz dans le cas de cette étude). Ce système est piloté par une interface EVaRT permettant, outre la capture et la reconstruction tridimensionnelle des données, leur traitement par des procédures de filtrage. Les marqueurs utilisés sont dits marqueurs passifs. Ils renvoient la lumière (émise par les projecteurs) dans la direction du rayon incident grâce à leurs propriétés rétrofléchissantes (Scotch Light). Suite à la définition d'un référentiel galiléen, la calibration du champ d'étude et l'acquisition simultanée des coordonnées 2D des marqueurs par au moins deux caméras, puis le calcul des coordonnées 3D de chaque marqueurs par des procédures d'optimisation (Annexe-4), il devient possible de définir la situation complète (position et orientation) d'un segment dans l'espace 3D (§-VII-2).
Les acquisitions cinématographiques sont couplées aux mesures des forces instantanées exercées distinctement au niveau de chaque appui (main droite, main gauche, pied droit et pied gauche). L'échantillonnage des 40 voies analogiques issues des six dynamomètres se fait à une fréquence de 1000 Hz. La répartition des voies est la suivante :
m 6 × 2 voies pour les deux blocs de départ instrumentés (Sensix) ;
m 6 × 2 voies pour les deux appuis mains instrumentés (Médicapteurs) ;
m 8 × 2 pour les deux plates formes de force (PFF) (Kistler).
43Le système Motion Analysis ( www.motionanalysis.com) utilisé lors de cette étude nous a été prêté par le Professeur Laurence Chèze - Université Claude Bernard Lyon1
Les PFF sont placées sous les blocs de départ instrumentés. Elles sont utilisées de façon simultanée avec les blocs de départ pour trois raisons : la première est que les blocs de départ instrumentés permettent l'estimation du centre de pression des forces exercées au niveau des pieds (§-VI.2.1). La deuxième consiste à contrôler l'angle d'inclinaison des cales pieds, en considérant les forces recueillies et exprimées dans les référentiels respectifs des PFF et blocs instrumentés. La troisième est d'ordre pratique, elle permet aux blocs de départ, une fois fixés sur les PFF, d'être à la même hauteur que les appuis mains instrumentés.
Un BUZZER délivrant simultanément un bip sonore et une impulsion électrique de +9 V permet de marquer l'instant du signal de départ.
Toutes les grandeurs cinématographiques et dynamométriques enregistrées sont exprimées dans le référentiel galiléen R0 représenté à la figure ci-dessous (figure 76).
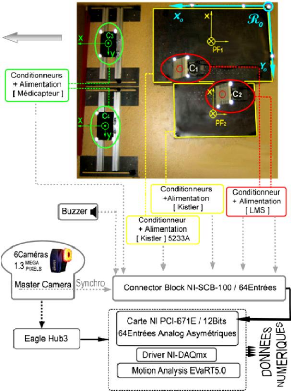
Sens du
déplacement
Orientation de g0 = ( O| X 0 ,Y0 ,Z0)
a X0 : horizontal positif dans le sens du déplacement
a
Y0: horizontal positif vers la gauche du coureur
. Z0 : vertical positif vers le haut
n C1 et C2 :
Blocs de départ instrumentés
n C3 et C4 :
Appuis mains instrumentés
n PFF1 et PFF2 : Plates formes de force
Figure 76 Chaîne de mesure cinématographique et dynamométrique
L'estimation des forces exercées sur l'athlète constitue d'une part un point de contrôle pour retrouver l'accélération du centre de gravité égale à la somme des accélérations linéaires
segmentaires définies par cinématographie ( a
G = E aGi), et d'autre part, elles
représentent le
point de départ du raisonnement par
récurrence permettant le calcul des efforts intersegmentaires suite
à l'application du modèle dynamique inverse (§-VIII).
Le sujet participant à cette étude est un athlète de niveau régional, ayant une masse de 85 kg, une taille 1,80 m. Sa meilleure performance sur 100 m est de 10,74 s.
L'orientation d'un corps dans l'espace tridimensionnel 0 nécessite son repérage par au moins trois marqueurs non colinéaires.
Au cours des enregistrements dynamiques (§-.2.1) du geste de départ, le coureur est équipé de 41 marqueurs. Ces marqueurs sont dits techniques. Ils assurent la modélisation de l'athlète par 15 corps poly-articulés (figure 77.a).
À ces marqueurs, s'ajoutent 12 autres marqueurs pour définir la situation des quatre dynamomètres (figure 77.b) répartis au niveau des appuis de l'athlète lors de la position Prêt.
(a) (b) (c)
g0
Figure 77 Modèles filaires définis suite
à l'emplacement de 41 marqueurs techniques (a), et 13
marqueurs
anatomiques positionnés sur l'athlète (c), ainsi que
12 marqueurs positionnés
sur les quatre dynamomètres
(b)
Afin de déterminer les positions des centres articulaires et construire des repères segmentaires suivant les recommandations de l'ISB44 [Wu 02, Wu 05], des enregistrements statiques (§-VII.2.1) sont effectués après avoir ajouté à l'ensemble des 53 marqueurs, déjà présents, 13 autres marqueurs dits anatomiques (figure 77.c).
Le positionnement des marqueurs sur l'athlète est soigneusement défini afin de d'estimer précisément les repères anatomiques segmentaires. Les positions des marqueurs par rapport aux repères anatomiques d'un segment Si sont définies dans le paragraphe qui suit.
Positions des 41 marqueurs techniques sur le corps de l&athlete (figure 77.a)
Tête (1) oreille droite, (2) oreille gauche et (3) os frontal
Tronc (4) processus épineux de la 7ème cervicale [C7], (5) bord proximal du
manubrium sternal, (6) apophyse épineuse de la 10ème vertèbre thoracique [T10], (7) apophyse épineuse de la 5ème lombaire [L5]
Bras
Bras droit (8) pointe antérosupérieure de l'acromion de la scapula droite [Acro D], (9)
biceps brachial droit [Biceps D] et (10) épicondyle latéral de l'humérus droit [EpicLat D]
Bras gauche (14) [Acro G], (15) [Biceps G], (16) [EpicLat G]
Avant-bras
Av. bras droit (11) bord latéral du radius droit [BLR D], (12) processus styloïde ulnaire droit [PSU D]
Av. bras gauche (17) [BLR G], (18) [PSU G]
Mains
Main droite (13) partie distale du 5ème métacarpien droit [MétaCarp5 D]
Main gauche (19) [MétaCarp5 G]
Pelvis (20) épine iliaque postérosupérieure droite [EIPS D], (21) épine iliaque
postérosupérieure gauche [EIPS G], (23) épine iliaque antérosupérieure droite [EIAS D] et (24) épine iliaque antérosupérieure gauche [EIAS G]
44 ISB : International Society of Biomechanics ( http://isbweb.org/)
Cuisses
Cuisse droite (24) grand trochanter [GT D], (25) quadriceps fémoral [Quad D] et (26) condyle latéral [CondLat D]
Cuisse gauche (33) [GT G], (34) [Quad G], (35) [CondLat G]
Jambes
Jambe droite (27) tubérosité tibiale antérieure [TTA D], (28) crête tibiale inférieur [CTI D]
(29) triceps sural droit [TS D]
Jambe gauche (36) [TTA G], (37) [CTI G], (38) [TS G]
Pieds
Pied droit (30) malléole externe du péroné droit [ME D], (31) tubérosité calcanéenne
droite [TC D], (32) 5ème orteil droit [Ort D]
Pied gauche (39) [ME G], (40) [TC G], (41) [Ort G]
Positions des 12 marqueurs sur les dynamometres (figure 77.b)
Les faces supérieures des deux blocs de départ instrumentés et des deux appuis mains instrumentés sont équipées chacune de trois marqueurs : (44-43-44) appui main droit, (45-46-47) appui main gauche, (48-49-50) cale pied droit, (51-52-53) cale pied gauche (figure 77.b). Ces marqueurs sont conservés tout le long des enregistrements dynamiques. Leurs coordonnées définissent les positions relatives des dynamomètres, d'une part, et permettent de contrôler la précision des mesures en mode statique lors des différents types d'acquisitions, d'autre part.
Position des 13 marqueurs anatomiques sur le corps de l&athlete (figure 77.c)
Thorax (55) Appendice xiphoïde
Bras (62), (63) épicondyle médiale de l'humérus droit [EpicMed D] et gauche
[EpicMed G]
Avant-bras (64), (65) processus styloïde du radius droit [PSRad D] et gauche [PSRad G]
Cuisse (66), (67) condyle médial droit [CondMed D] et gauche [CondMed G]
Jambe (58), (59) malléole médiale droite [MalMed D] et gauche [MalMed G]
(56), (67) base de la patella droite [Pat D] et gauche [Pat G]
Pieds (60), (61) premier orteil du pied droit [Ort1 D] et gauche [Ort1 G]
La définition de la position et de l'orientation d'un segment distal par rapport à un segment proximal adjacent ne peut se faire que suite à la construction des repères locaux relatifs à chaque segment.
La construction de ces repères est effectuée en accord avec les recommandations de l'ISB [Wu 02, Wu 05]. Cependant, avec un axe Z horizontal, ces recommandations sont contraires aux conventions internationales (mécanique, physique, mathématiques appliquées) ce qui crée des conflits au sein même des biomécaniciens. Cette normalisation vient suite aux travaux de Grood et Suntay (1983) qui définissent la séquence des rotations élémentaires de référence [Groo 83]. Cette référence est reprise dans les articles de recommandation de l'ISB.
Ainsi, la désignation des axes de rotations articulaires se fait par rapport à un repère anatomique dont la définition est la suivante :
§ Oi est l'origine du repère, ce point coïncide avec le centre fonctionnel de l'articulation,
§ Xi est l'axe antéropostérieur suivant lequel se font les mouvements d'abduction et d'adduction, il est orienté en sens opposé pour les deux cotés du corps
§ Yi est l'axe proximodistal (orienté vers le haut) suivant lequel se font les mouvements
de rotation médiale et latérale
§ Zi est l'axe médiolatéral orienté en sens opposé pour les deux cotés du corps. Les
mouvements de flexion et d'extension se font suivant cet axe.
0
0
a0
Definition des Ei :
0
Definition des oriaines des
A, A' : Pieds droit et gauche
B, B' : Jambes droite et gauche
C, C' : Cuisses droite et gauche
D, D' : Pelvis droit et gauche
E : Abdomen
F : Thorax
Figure 78 Positions et orientations des axes de rotations articulaires
Aussi, afin d'uniformiser les méthodes de calculs et conduire une analyse comparative des différentes études, l'ISB recommande l'utilisation des opérateurs homogènes (matrices de roto-translation).
La description de la position et de l'orientation d'un segment Si par rapport au repère galiléen de référence R0 se fait donc suite à la détermination des éléments de la matrice de roto-translation i
T0 . Il s'agit d'une matrice 4 x 4 qui contient un vecteur colonne de translation de l'origine Oi et une matrice de rotation R0i des axes unitaires.

xi
Ri 0 yi
z i
0 0 0 1
T i
0
~ 0
Éq.VII.1
Afin de déterminer l'orientation d'un repère segment distal gtsd par rapport à un repère segment proximal ~sp, il faut définir la matrice sd
Rsp en fonction de sp
R0 et R0sd qui
représentent respectivement les orientations de asp et gtsd par rapport à g0. La matrice de passage du segment proximal au segment distal est telle que :
Dsd = R0 sp0 Rsd
Éq.VII.2
'sp
dont Rsp0 est la matrice transposée de sp
R0 .
Afin de contourner le problème d'occlusion de marqueurs, la construction d'un repère
segmentaire dit repère dynamique / anatomique et de son opérateur homogène noté Dyn / Anat
T0
est réalisée suite à une procédure combinant deux types d'enregistrements :
§ enregistrements statiques : l'athlète est immobile en position anatomique de référence.
Il est équipé des marqueurs techniques et anatomiques.
§ enregistrements dynamiques : seuls les marqueurs techniques sont conservés collés sur
le coureur.
Approximation des reperes lors des enregistrements statiques
La position statique de l'athlète debout bras écartés évite les problèmes d'occlusion des marqueurs. Au cours de cette phase, l'athlète est équipé à la fois de marqueurs techniques et anatomiques.
Les coordonnées de trois marqueurs non colinéaires (A, B et C) d'un même segment permettent d'approcher à la fois l'origine du repère anatomique segmentaire et la direction de
ces axes Xi, Yi, Zi. Un tel repère est noté R.i Stat/ Anat = ( Oi | Xi ,Yi ,Z i) .
La figure 79 illustre les étapes de construction du repère statique/anatomique de la
jambe droite R.jd Stat/ Anat à partir de la position de deux marqueurs anatomique A et C, et deux
marqueurs techniques B et D.
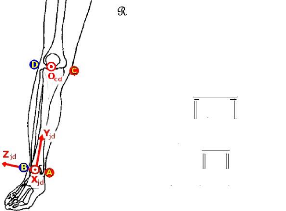
~~~ ~~ ~~
Ojd milieu de [ AB ]
Ocd milieu de[ CD ]
~~~~~~~~
O jd Ocd
O jd Ocd
~~~~
AB
= ~~~~~~
AB
~~~ ~~ ~~
X jd = Y jd ? Zjd
jd Stat/ Anat
= (O jd| X jd ,Yjd ,Zjd)
~~
=
Yjd
~~
Z jd
Figure 79 Exemple d'approximation du repère anatomique de la jambe droite (vue antérieure)
Ainsi,
i Stat / Anat
T0
définit l'opérateur homogène associé à un segment i dont la position
et l'orientation sont définies dans R.0
suite aux enregistrements statiques des marqueurs
anatomiques. Au cours de
ces mêmes enregistrements, la construction d'un deuxième type
de
repère segmentaire appelé repères
statique/technique noté R.i
Stat/Tech est assurée à partir des
seuls marqueurs techniques. L'opérateur homogène qui y est associé est noté i Stat /Tech
T0 .
Approximation des reperes lors des enregistrements dynamiques
Rappelons que lors des enregistrements dynamiques, seuls les marqueurs techniques sont gardés collés sur l'athlète. La position de ces marqueurs dans 0 permet la construction
d'un repère dynamique/technique ~ iDyn/Tech et sa matrice de roto-translation notéT0 i Dyn/Tech .
i Stat/ Anat
et Ti Stat/Tech lors des
Ayant déjà défini les opérateurs homogènes 7; 0
enregistrements statiques, il est possible de déterminer la matrice i Anat
TTech décrivant la situation
du repère anatomique par rapport au repère technique d'un segment Si comme suit :
,ri Anat T0 T i Stat/ Anat
1Tech =i Stat /Tech· 0 Éq.VII.3
tel que = ( ) -1
T i Stat /Tech T 0
0 i Stat /Tech
La matrice de passage i Anat
TTech
présente l'expression du repère statique/anatomique
dans le repère statique/technique. Cette
matrice est considérée invariable au cours du temps.
Elle
estime la position et l'orientation du repère anatomique lors
des enregistrements
dynamiques (T0 i Dyn/ Anat) à partir de la connaissance de la position et de l'orientation du repère dynamique/technique ( i Dyn / Tech
T0 ). Le calcul se fait comme suit :
T i Dyn/ Anat Tio.
i Dyn/Tech Ti Anat É
0 · 1Tech VII.4
Ainsi, lors des enregistrements dynamiques du geste de départ, la position et l'orientation de chaque repère anatomique segmentaire sont définies à chaque instant dans
par l'opérateur homogène 70 i Dyn/ Anat .
Il est important de souligner que la position de l'origine du repère anatomique correspond au centre fonctionnel de l'articulation en question. Vu l'éloignement de ces points des points anatomiques palpables (tubérosités), leurs approximation in vivo est une étape importante qui permet de minimiser l'incertitude sur les quantités cinématiques et dynamiques calculées [Crea 07 ; Hold 98 ; Stag 00].
Le mouvement de départ du sprint sollicite à la fois les membres inférieurs et supérieurs. Vu la grande amplitude des efforts exercés au niveau de ces segments (§-4.2), la précision des couples articulaires calculés est dépendante de la précision avec laquelle les centres articulaires sont localisés. Les études qui traitent de ce problème sont nombreuses et il est possible de les distinguer selon deux grandes approches.
La première approche est dite prédictive : elle estime la position du centre articulaire à partir de régressions linéaires faisant intervenir les dimensions et la géométrie du segment. La position du centre articulaire est donc exprimée dans un repère local défini par un emplacement précis de marqueurs cutanés. Suite à la comparaison de trois approches prédictives, Kirwood et al. (1999) démontrent que la détermination du centre articulaire de la hanche peut se faire en calculant le milieu de la distance entre l'épine iliaque antérosupérieure et la symphyse pubienne pour ensuite descendre de 2 cm. Les erreurs d'approximation sont de l'ordre de 0,7 cm suivant l'axe médiolatéral (OiZi) et 0,8 cm suivant la verticale (OiYi). L'auteur considère cette méthode valable pour l'analyse de la marche puisqu'elle permet l'estimation des moments articulaires avec une précision de 95% [Kirw 99].
Dans le cas de l'étude du départ de sprint, l'approche prédictive est adoptée pour les articulations du poignet, du coude, du genou et de la cheville. Le centre fonctionnel de ces articulations est donc défini au milieu des deux marqueurs techniques et anatomiques situés respectivement sur la partie latérale et médiale de l'articulation concernée, telles que les malléoles latérale et médiale dans le cas de la cheville (figure 79).
La seconde approche est dite fonctionnelle : elle se base sur la réalisation de mouvements simples de flexion-extension, d'abduction-adduction et de circumduction. L'ISB recommande l'utilisation de la méthode des axes hélicoïdaux [Wu 05]. Toutefois, cette méthode est sensible à l'amplitude et à la vitesse du mouvement [Camo 06, Ehri 06].
Plusieurs études se sont intéressées à la comparaison des différentes méthodes fonctionnelles. Dans ce sens, Begon et al. (2007) démontrent que le type de mouvement, son amplitude et le nombre de répétitions possèdent un effet significatif sur la détermination du centre articulaire de la hanche. Ces auteurs recommandent d'effectuer 10 répétitions avec des amplitudes limitées tout en associant des mouvements de flexion-extension, d'abductionadduction et de circumduction [Bego 07]. L'étude de Monnet et al. (2007) confirme ces recommandations, et démontre la validité de la méthode SCoRE (pour Symmetrical Centre of
Rotation Estimation) lorsque les mouvements sont réalisés à faible vitesse. La méthode SCoRE a été développée par Ehrig et al. (2006) pour la détermination du centre fonctionnel de l'épaule (articulation scapulo-humérale).
Prenant en compte ces recommandations, des pré-tests sont effectués en utilisant les coordonnées de marqueurs techniques et anatomiques afin d'estimer les positions des centres articulaires de la hanche et de l'épaule dans un repère proximal et/ou distal (figure 80) tout en utilisant la méthode SCoRE.
Ainsi, connaissant la position de chaque marqueur dans R0, il devient possible de construire un repère distal gtd d'origine d et un repère proximal gP d'origine P. La position du point I correspondante au centre fonctionnel de l'articulation est supposée invariable en fonction du temps dans Rd et ap. Cette hypothèse est simplificatrice car les articulations possèdent des centres instantanés de rotation du fait de la complexité de la géométrie des surfaces osseuses en contact. Toutefois, malgré cette hypothèse, la méthode SCoRE permet une approximation des centres articulaires avec une incertitude de 1,2 mm [Ehri06].
|
Pour la hanche A : [EIPS D]
F : [CondMed D]
|
||||
|
g0 |
||||
Figure 80 Positions des marqueurs pour la
définition des centres articulaires
de la hanche droite et de
l'épaule droite (Vue antérieure)
La position du point I (figure 80) peut être définie dans R.0 comme suit :
~~~ ~~~~ ~~~
OI oto = Odoto + R 0d dI ad Éq.VII. 5
tel que R0d est la matrice rotation de Rd dans le repère fixe R.0
aussi Oho = OP go+ R0P PI aP Éq.VII. 6
tel que Rf est la matrice rotation de RP dans le repère fixe R.0 ~~~~ ~~~ ~~~~ ~~~
d'où Odgo+ R 0 d dI = OPgo +R o PIgtP Éq.VII. 7
~~~
Dans cette dernière équation, seuls les vecteurs positions du centre articulaires (dI ad
|
~~~ et PI aP |
) sont inconnus. Cette relation peut s'écrire en regroupant les deux grandeurs |
inconnues dans un seul vecteur :
dI~~~~ ~~~~ ~ d ~~~ = OP Od
~ - ~
~ ~
PI ~ P
~~~
Éq.VII.8
R d
0 R0

3 x 6 6 x 1 3 x 3
L'écriture de l'équation (Éq.VII.8) sous cette forme présente un système linéaire composée de six inconnues pour trois équations. Ainsi, suite à l'enregistrement de la position des marqueurs techniques et anatomiques de l'instant ti à l'instant tf lors des mouvements de flexion-extension, d'abduction-adduction et de circumduction de l'épaule et de la hanche répétés 10 fois à faible vitesse, il devient possible de former le système linéaire suivant :
|
~~~~ ~~~~ R d ( ) ( ) t -R P t ~~~ OP Od ( ) ( ) t - t 0 i 0 i i i dI ~ d ? ? ~~~ = ? PI ~~~~ ~~~~ d ~ P ( ) ( ) t -R P R t OP ( ) ( ) t - Od t 0 f 0 f f f |
~ ~ |
Éq.VII. 9 |
Étant exprimée dans les repères locaux ad et RP, la position instantanée du centre articulaire I est donc invariable tout au long de l'enregistrement.
Le système obtenu (Éq.VII.9) est de la forme ax = b . La résolution d'un tel système linéaire se fait en introduisant la pseudo inverse a+ tel que a+b donne la solution des moindres
carrées x qui minimise
ax - b 2 tel que a + = ( a T a )-1 aT avec aT et a-1 respectivement

transposé et inverse de a .
Ainsi, suite à l'adoption de la méthode SCoRE, la position du centre articulaire de la hanche et de l'épaule dans Ed et aP sont estimées par l'équation suivante :
|
~~~ dI ad RaP |
( a T a ) -1a T b |
Éq.VII. 10 |
Les résultats issus de ces calculs d'approximation des centres articulaires comme ceux issus de l'approximation des axes anatomiques dépendent fortement des positions des marqueurs cutanés placés sur l'athlète. À ce sujet, une série d'études portant sur l'analyse du mouvement en biomécanique, démontre que l'incertitude associée à la position des marqueurs est importante [Capp 05 ; Chia 05 ; Croc 05 ; Lear 05]. Cette imprécision provient des tissus mous et de leurs mouvements qui reste l'un des problèmes irrésolus de l'analyse du mouvement in vivo.
Le problème de la rigidité des segments lié aux mouvements de la peau par rapport à la structure osseuse sous jacente est bien connu. Les erreurs engendrées diffèrent d'un sujet à un autre et pour un même sujet d'un segment à un autre. Ainsi, lors d'un geste ordinaire tel que la marche, le pédalage ou la flexion extension d'un membre, les artefacts dus aux mouvements de la peau peuvent entraîner des erreurs de positions pouvant atteindre 50 mm [Capp 96]. Dans le cas de la présente étude, afin de cerner l'amplitude de cette erreur, les longueurs segmentaires relevées suite aux enregistrements statiques et dynamiques (§- VII.2.1) sont confrontées afin d'estimer la variation maximale et, de ce fait, l'erreur relative maximale due aux mouvements de la peau (tableau 1).
Tableau 8 Variations maximales des longueurs segmentaires et erreurs relatives
|
Segment |
Longueur stat. [mm] Droit Gauche |
Variation max.[mm] Droit Gauche |
Erreur relative [%] Droit Gauche |
||||||
|
Pied |
132 |
136 |
25 |
23 |
19 |
17 |
|||
|
Jambe |
434 |
408 |
46 |
62 |
11 |
15 |
|||
|
Cuisse |
414 |
419 |
45 |
40 |
11 |
10 |
|||
|
Pelvis |
198 |
181 |
12 |
18 |
6 |
10 |
|||
|
Abdo. + Thorax |
517 |
26 |
5 |
||||||
|
Tête + Cou |
271 |
12 |
4 |
||||||
|
Bras |
325 |
300 |
22 |
20 |
7 |
7 |
|||
|
Avant bras |
285 |
279 |
29 |
17 |
10 |
6 |
|||
|
Main |
79 |
87 |
11 |
13 |
14 |
15 |
|||
|
Cale pied |
201 |
208 |
3 |
3 |
1 |
1 |
|||
Cette confrontation des longueurs (tableau 1) permet de distinguer deux types d'erreurs :
m la première est systématique, elle témoigne de l'imprécision du positionnement des marqueurs entre segments droits et gauches lors des enregistrements statiques.
m la deuxième est due aux mouvements relatifs des marqueurs cutanés d'un même segment lors de l'exécution du geste de départ.
Ces erreurs ont pour conséquence de biaiser le calcul de la position et l'orientation des segments, ainsi que les paramètres cinématiques et dynamiques qui en découlent. À ce titre, en étudiant les amplitudes articulaires du genou lors de la course, Reinschmidt et al. (1997) précisent que le mouvement de la peau entraîne des erreurs d'estimation de l'ordre de 21% pour la flexion/extension, 63% pour la rotation interne/externe et 70% pour l'abduction/adduction [Rein 97]. De même, l'étude de Karlsson et al. (1994) montre une différence de 30° lors de l'estimation de la rotation médiolatéral de la cuisse (50° contre 20°) à partir de la position de marqueurs cutanés versus marqueurs fixés dans l'os (pins) [Karl 94].
Concernant l'effet des artéfacts dus aux mouvements de la peau (ADMP) sur la dynamique articulaire, Holden et al. (1997) montrent que pour différentes cadences de marche, la force et le couple articulaire estimés au niveau du genou suivant l'axe de flexion, présentent des erreurs pouvant atteindre respectivement 39 N et 9 Nm [Hold 97].
La peau étant un tissu mou qui se déforme selon la posture du sujet, la variation de position d'un marqueur ne définit pas seulement le mouvement du segment mais aussi celui de la peau par rapport à l'os. Ainsi, suite à une contraction musculaire, il peut y avoir une variation de la position d'un marqueur sans qu'il y ait mouvement réel du segment osseux. De plus, à la différence des mouvements cycliques, la gestuelle de départ du sprint ne présente pas de déformations segmentaires systématiques.
Le bruit provoqué par les ADMP représente donc une source d'erreur qui n'est ni constante ni aléatoire. De ce fait, puisqu'elle n'est pas constante et dépend de la nature du mouvement, l'application des procédures d'offset ne permet pas de résoudre le problème. Et, puisqu'elle n'est pas aléatoire et que sa fréquence est approximativement celle du mouvement analysé, il devient inadéquat d'adopter des techniques de traitement de données telles que le
lissage45 ou le filtrage46. Ces deux méthodes de traitement de données sont détaillées dans une revue de bibliographie exposée par Leboeuf (2004) [Lebo 04].
Pour résoudre ce problème, et permettre une application rigoureuse des principes de la mécanique des solides rigides, il importe d'adopter la solution adéquate pour la minimisation des ADMP. La littérature scientifique offre plusieurs issues telles que l'utilisation de pins fixés directement dans l'os. Néanmoins, étant invasive, son utilisation est très limitée. Une alternative à cette méthode est le cluster rigide sur lequel sont fixés les marqueurs et qui se fixe à son tour sur la peau. Cette méthode permet de réduire les ADMP, toutefois, tous les marqueurs se trouvent entachés de la même erreur inconnue ce qui ne permet pas de résoudre le problème. Alexander (2001) propose d'augmenter le nombre de marqueurs collés sur un segment et de considérer que la trajectoire de chacun ; par rapport à l'os sous-jacent ; est entachée d'un bruit propre prédéfini suite à un pré-test qui prend en compte la cinématique du geste effectué [Alex 01]. Cette dernière méthode est prédestinée aux gestes cycliques vu que les déformations segmentaires sont considérées comme systématiques. Cela exclut son utilisation dans le cas de l'étude de départ du sprint. De plus, vu la position initiale de l'athlète, l'augmentation du nombre de marqueurs se confronte à un autre type de problème : celui des occlusions de marqueurs.
Methodes de minimisation des ADMP par optimisation
Dans une optique de minimisation des ADMP par optimisation, Chèze (1995) propose une méthode appelée solidification [Chèz 95]. Cette méthode consiste à conserver un triplet de marqueurs positionnés sur chaque segment (§-VII.1.1) afin de le représenter par un triangle. La description de la position et de l'orientation de ce triangle se fait suite à la définition des matrices de roto-translation (§-VII.2). Les triangles de référence sont définis en calculant les moyennes des triangles les moins bruités déterminés suite à une procédure itérative d'élimination. Finalement, un ajustement par la méthode des moindres carrés est effectué pour substituer à chaque instant un triangle rigide au triangle déformé.
45 Le lissage est une technique de traitement de données basée sur l'interpolation. Elle consiste à remplacer une valeur numérique par celle qui apparaît le plus fréquemment dans le voisinage.
46 Le filtrage est une technique de traitement de données basée sur la notion de tri. Elle permet d'éliminer les valeurs à hautes fréquence et de garder les autres et inversement.
L'emploi de cette procédure d'optimisation par moindres carrés permet de définir la matrice de rotation R et le vecteur de translation t qui minimisent l'écart entre les positions a et b des marqueurs i entre deux instants voisins tel que :
n
min f = E R a i + t -bi 2 Éq.VII. 11


i =1
dont n est le nombre de marqueurs (n = 3) et R est contraint tel que R TR = I et det ( R) = 1
pour assurer l'orthogonalité de la matrice de rotation et donc un déplacement qui correspond à celui d'un corps rigide. Néanmoins, vu l'absence de contraintes articulaires entre les segments, ces derniers peuvent présenter des amplitudes articulaires inattendues voire même des ruptures de liaisons entre les segments voisins.
En effet, suite à l'application de cette procédure de solidification aux données de départ du sprint, des dislocations sont remarquées au niveau des articulations constituant la chaîne cinématique. L'écart le plus important est noté au niveau du genou droit (figure 81).
Un éloignement de 3,6 cm de l'origine du repère fémur aFémur par rapport à l'axe
proximodistal du tibia est noté. Cette amplitude est comparable à celle avancée dans Lu et O'Connor (1999) [Lu 99].
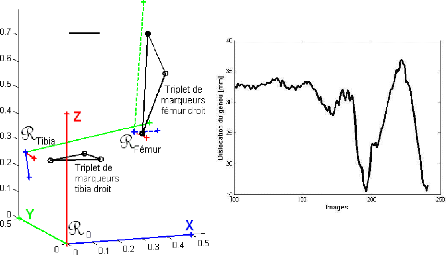
Vue 3D
Figure 81 Écartement de la position de l'origine
du repère fémur gFémur par rapport à
l'axe
proximodistal du tibia suite à l'application de la
procédure de solidification
proposée par Chèze 1995 aux
données du départ du sprint
Cette dislocation articulaire (figure 81) est due principalement au traitement séparé des segments. Si cette méthode a démontré l'efficacité de minimiser les ADMP lors de gestes tels que la marche, il n'en est pas de même pour le traitement d'un geste « explosif » tel que le départ de sprint. De nombreuses études ont souligné l'effet indésirable de cette méthode dans l'estimation des grandeurs mécaniques. C'est pourquoi Lu et O'Connor (1999) ont introduit les contraintes articulaires pour rechercher, à chaque image, la configuration optimale de la chaîne cinématique. La solution recherchée est celle qui minimise, à un instant donné, la différence entre les coordonnées des marqueurs issues de la mesure et celles redéfinies par le modèle rigide (figure 82). Le problème d'optimisation s'écrit :
min f( q )= [P - P( q) T W - ' (
P P q ) Éq.VII. 12
où q désigne les variables articulaires décrivant la configuration de la chaîne cinématique, P les coordonnées des marqueurs mesurés à une image donnée et P' ( q ) les coordonnées du
modèle rigide à la même image. W désigne la matrice de pondération. Cette matrice est définie afin que le rôle de chaque marqueur soit identique ou afin que certains marqueurs aient plus d'impact que d'autres [Lu 99].
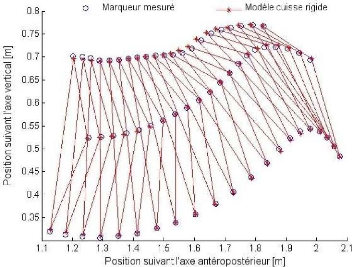
Figure 82 Ajustement du modèle rigide de la
cuisse droite aux positions mesurées des marqueurs du
même
segment aux mêmes instants. (Vue sagittale du coté
droit, représentation d'une image sur deux).
Application de la
procédure de solidification globale proposée dans Lu et O'Connor
(1999)
La figure 82 expose une partie de la chaîne cinématique afin de montrer l'ajustement du modèle rigide de la cuisse aux marqueurs mesurés suite à l'adoption de la procédure de solidification globale.
L'ajustement du modèle rigide aux positions mesurées de marqueurs permet de solidifier les segments de la chaîne cinématique. Néanmoins, l'application de cette procédure de solidification globale [Lu 99] modifie l'orientation des segments et de ce fait la configuration de la chaîne. C'est ce que démontre le paragraphe qui suit.
Les angles relatifs appelés aussi angles articulaires sont les angles qui permettent de définir l'orientation d'un repère gt.i+1 par rapport à un repère gt.i . La figure 83 ci-dessous illustre les angles relatifs segmentaires du notre modèle projeté sur le plan sagittal.
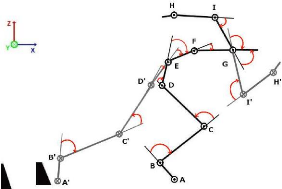
gt.0
0
0
0
Figure 83 Configuration de la chaîne
cinématique plane, arborescente du départ du
sprint.
Illustration des angles relatifs du modèle
étudié
Effectuant l'analyse dans un espace 3D, l'orientation globale d'un repère gt.i+1 par
rapport à un repère gt.i se définie par trois rotations (séquences) élémentaires. L'ordre de séquences choisi influe l'amplitude des angles relatifs calculés.
Afin de normaliser les procédures de calcul et éviter l'indétermination des amplitudes articulaires, l'ISB [Wu 02] recommande l'adoption de la séquence de rotation (rot) suivante proposée initialement par Grood (1983) pour l'articulation du genou (§-VII.2) :
rot1 ( Z i ø, ) - Flexion/Extension autour de l'axe Zi d'un angle ø
rot2 ( X i,è ) 4 Abduction/Adduction autour de l'axe Xi d'un angle è
rot3 ( Yi,? ) - Rotation Interne/Externe autour de l'axe Yi d'un angle ö
La matrice de rotation i+1
Ri qui permet le passage de gLi à gi+1 est définie en
utilisant les matrices de transformation simple (§-III.3.4) pour décrire les trois rotations élémentaires :
C C S S S S C C S S S C
- +
ø ö ø è ö ø è ø ö ø è ö
i i i i i i i i i i i i
[
Ri+1 = rot1 · rot2 · rot3 = S ø C öi + C cfri S e S so C cfri C o S S ö- C i SèC öi Éq.VII. 13
i

- CS ö i S C è i Cö i
avec C désigne la fonction cosinus et S la fonction sinus.
Traduisant le passage de gi à i+1 , la matrice i+1
Ri se définit comme étant la matrice dont les colonnes sont les composantes des vecteurs unitaires de Ri+1 exprimées dans gi . De ce fait, la matrice i+1
Ri peut aussi s'écrire comme suit :
|
X X Y X Z X i+1 i i+1 i i+1 i R i+1 = X Y Y Y Z Y i i+1 i i+1 i i+1 i XZ i Y i+1 Z Z i+1 Z i |
Éq.VII. 14 |
dont Xi+1 , Y i+1 , Zi+1 et Xi , Yi , Zi sont respectivement les vecteurs unitaires de gi+1 et gi .
La définition des angles relatifs se fait donc par correspondance entre les termes de la première (Éq.VII.13) et de la deuxième forme (Éq.VII.14) de la matrice i+1
Ri .
La détermination des amplitudes articulaires se fait donc comme suit :
pour la flexion/extension : S ø iCè i = Y i+1Xi et Cø i Cè i = Y i+1Yi d'où
Y i+1 X i Y i+1 Yi
ø = atan2
i

Éq.VII. 135
,
Cè i Cèi
pour l'abduction/adduction : Sèi = Y i+1Zi d'où
èi = asin ( Yi+1Zi)ou èi = ð - asin ( Yi+1Zi) Éq.VII. 14
pour la rotation interne/externe : -C èi S ö i= X i+1 Zi et = Z Z
C è i C ö i i+1 i d'où
atan2 X Z Z Z
i+1 i i+1 ,i -CèCèi i


Éq.VII. 15
Vu le paramétrage de la chaîne cinématique (§-VII.2), il importe de souligner que, pour un segment donné, l'interprétation des angles diffère selon qu'ils soient du côté droit ou gauche de l'athlète. En effet, en prenant l'exemple de la cuisse droite, une rotation positive autour de l'axe segmentaire Z traduit une flexion alors qu'elle traduit une extension dans le cas de la cuisse gauche. Cette opposition concerne aussi les mouvements d'abduction/adduction. Seule la rotation interne/externe peut être interprétée de la même manière pour les deux côtés du corps.
La figure 84 illustre le résultat de la confrontation des angles relatifs calculés suite à l'application de la procédure d'optimisation globale [Lu 99] aux angles relatifs bruts issus directement des mesures cinématographiques (sans traitement préalable).
Il apparaît que l'écart entre les angles optimisés et les angles mesurés est conséquent dès le début du mouvement47 (figure 84). En d'autres termes, la méthode d'optimisation globale modifie l'orientation des segments. En prenant l'exemple d'un segment Si, on remarque que l'erreur d'estimation des angles articulaires n'est pas systématique. De plus, l'erreur d'estimation des angles relatifs dépend de l'amplitude articulaire, les segments droits et gauches n'étant pas affectés de la même façon. Cette erreur n'est donc pas aléatoire.
47 Le début du mouvement de l'athlète est défini par la variation des amplitudes articulaires.
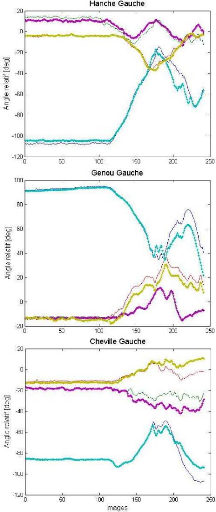
|
Angles relatifs optimisés |
Angles relatifs bruts |
Figure 84 Confrontation des angles relatifs issus des
mesures directes et suite à l'adoption d'une
procédure
d'optimisation globale par moindres carrés proposée dans [Lu 95].
Exemple des angles de
flexion/extension (Flex), abduction/adduction (Abd) et
Rotation interne/externe (Rot) pour
les articulations du membre
inférieur gauche (cheville, genou et hanche)
Les écarts relatifs aux mouvements de flexion/extension, Abduction/Adduction et Rotation externe/Externe sont exprimées dans le tableau 2 ci-dessous afin d'avoir un ordre de grandeur concernant la différence entre les angles relatifs mesurés et les angles optimisés (procédure d'optimisation globale).
Tableau 9 Écarts relatifs entre les angles
optimisés versus les angles bruts pour les mouvements
de
Flexion/Extension, Abduction/Adduction et Rotation
Interne/Externe
|
Articulation |
moy |
Flex./Ext. [%] |
min |
Abd./Add. [%] moy max |
min |
Rotation Int./Ext. [%] |
||||
|
Cheville |
3 |
10 |
0 |
16 |
84 |
0 |
8 |
>100 |
0 |
|
|
Côté |
Genou |
10 |
>100 |
0 |
80 |
>100 |
0 |
18 |
>100 |
0 |
|
droit |
Hanche |
4 |
13 |
0 |
>100 |
>100 |
28 |
>100 |
>100 |
0 |
|
Coude |
4 |
30 |
0 |
2 |
16 |
0 |
5 |
24 |
0 |
|
|
Cheville |
4 |
17 |
0 |
12 |
40 |
0 |
78 |
>100 |
3 |
|
|
Côté |
Genou |
8 |
87 |
0 |
13 |
>100 |
0 |
10 |
>100 |
0 |
|
gauche |
Hanche |
7 |
38 |
0 |
>100 |
>100 |
0 |
13 |
>100 |
0 |
|
Coude |
6 |
20 |
0 |
63 |
>100 |
0 |
17 |
>100 |
0 |
|
|
T12/L1* |
3 |
17 |
0 |
>100 |
>100 |
1 |
>100 |
>100 |
0 |
|
|
Tronc |
C7/T1* |
10 |
33 |
0 |
>100 |
>100 |
0 |
32 |
>100 |
2 |
*T12/L1 : articulation de la 12ème vertèbre thoracique et de la 1ère lombaire *C7/T1 : articulation de la 7ème vertèbre cervicale et de la 1ère thoracique
L'analyse des écarts relatifs montre que la méthode d'optimisation globale estime les angles articulaires à 10% pour les mouvements de flexion/extension. Concernant les autres mouvements : Abduction/Adduction et Rotation Interne/Externe, les écarts peuvent atteindre des valeurs très importantes dépassant les 100% ce qui traduit des orientations segmentaires fort différentes de celles mesurées.
À la lecture de ces résultats, on remarque que l'adoption de cette méthode dans le but de pouvoir appliquer les principes de la mécanique des solides rigides au corps humain possède un effet inconnu sur l'orientation réelle des segments.
Cette procédure de solidification par optimisation modifie l'orientation du segment sans toutefois fournir d'intervalles d'incertitudes. De ce fait, suite à son application, l'opérateur est dans l'incapacité de savoir directement si le mouvement optimisé s'est rapproché de la réalité ou s'il s'en est éloigné d'avantage.
Afin de résoudre le problème de dislocation articulaire survenue suite à l'application de la procédure de solidification proposée par Chèze (1995) (§-VII.3.1), Lu et O'Connor (1999) résolvent le problème de déformation des segments provoqué par les ADMP en appliquant une procédure d'optimisation globale se basant sur le principe des moindres carrées (§-VII.3.1). Toutefois, l'application de ce principe suppose que les erreurs de positionnement des marqueurs par rapport aux points anatomiques suivent une distribution normale symétrique (Loi de Gauss). Or, le mouvement de la peau dépend de l'orientation relative des segments ce qui ne permet pas de le considérer comme aléatoire (§-VII.4.2). De plus, cette méthode ayant pour objectif final de rigidifier les segments poly-articulés provoque un changement dans l'orientation des segments (§-VII.4.2).
Ainsi, suite à l'adoption de la procédure d'optimisation globale le résultat final comprend une erreur supplémentaire ås qui traduit l'écart entre l'orientation du segment
mesuré (brut) et optimisé. Cette erreur (ås) vient s'additionner à åd qui correspond à la
différence entre l'orientation réelle du segment et celle mesurée.
Le seul moyen connu à ce jour permettant l'estimation de åd est l'utilisation de pins fixés directement dans l'os. L'adoption de cette méthode invasive dans le milieu sportif est très limitée voir même exclue. Toutefois, comme il a été décrit précédemment (§-VII.3), quelques études l'ont adopté afin de quantifier l'effet de l'erreur åd lors de l'estimation de différents paramètres mécaniques tels que les orientations relatives des segments, les forces et couples articulaires [Rein 97, Karl 94, Hold 97].
Il importe de rappeler que l'adoption d'une méthode de solidification est justifiée par le fait que les procédures de filtrage et de lissage ne sont pas adaptées pour des erreurs systématiques comme celles engendrées par le mouvement de la peau. Le seul intérêt de ces méthodes comme le souligne Cappozo (2005) réside dans la possibilité d'appliquer les principes de la mécanique des solides rigides.
Le chapitre qui suit (§-VIII), présente une nouvelle méthode exploitant les matrices de transformation homogène et un raisonnement par récurrence afin de rigidifier la chaîne cinématique tout en respectant les degrés de liberté de chaque segment et cela sans accumulation d'erreurs (åd + ås). Cette méthode est confrontée à celle de Lu et O'Connor (1999) pour étudier leurs effets sur les grandeurs cinématiques et dynamiques.
Chapitre |
||
Afin de minimiser les artéfacts dus aux mouvements de la peau (ADMP) tout en conservant les contraintes de liaison propres à chaque articulation et sans modifier l'orientation mesurée des segments (§-VII.5), il est possible de procéder comme suit.
Etape 1 : Determination des positions et orientations relatives des segments
Suite à l'approximation des centres articulaires (§-VII.2.2), l'attribution d'un repère
dynamique/technique ~ iDyn/Tech à chaque segment et la définition de l'opérateur homogène
i Dyn / Anat
T (§-VII.2.1), la matrice i+1
T i Dyn / Anat décrivant la position et l'orientation relative d'un
0
segment Si+1 par rapport à un segment Si est définie par :
Ti iD+yn1 / Anat = Ti0 Dyn/ Anat · T i+1Dyn/ Anat Éq.VIII. 16 0
tel que ( ) - 1
T i Dyn / Anat T 0 Dyn / Anat
0 i
? Etape 2 : Définition des longueurs segmentaires
La position de l'origine d'un repère Ri Dyn/ Anat d'un segment Si est coïncidente avec le
centre articulaire de ce segment (§-VII.2.2). La distance entre un repère proximal
|
ai+1 Dyn/ Anat et un repère distal a.i Dyn/ Anat correspond donc à la longueur |
~~ Li |
de Si. Cette |
||
|
relation se formule de la manière suivante : |
||||
~ ~ ~
= ( O - O ) i + ( O - O ) j + ( O - O ) k
2 2 2
i+1 i i+1 i i+1 i
Éq.VIII. 2

~~
L i
~ - -
dont Oi et ( i, j, k) correspondent respectivement à l'origine et à la base orthonormée
directe de ai Dyn/ Anat . Oi+1 est l'origine de ai+1 Dyn/ Anat .
§ Etape 3 : Expression de la longueur dans le repere segmentaire correspondant L'axe Y est l'axe proximodistal de ai Dyn/ Anat passant par Oi et Oi+1 (§-VII.2). Ce
~~
dernier point permet de définir directement les composantes de Li dans ~i Dyn/ Anat .
~~ ~ ~ ~
L = 0 i + l j + 0 k i Éq.VIII. 3
tel que l est la longueur du segment définit suite aux relevés des mesures anthropométriques.
§ Etape 4 : Solidifier les segments de la cha'ine cinématique
La matrice de transformation homogène i+1
T i Dyn / Anat dont les colonnes sont les
composantes des vecteurs de ai+1 Dyn/ Anat dans ai Dyn/ Anat se définit comme suit :
T
i +1
i Dyn/ Anat
Éq.VIII. 4
( O i O i+1) iR ( O i O i+1)( O i O i+1)k0 0 0 1i+1
Tenant compte des trois premières étapes, il est possible de définir les termes du vecteur translation de cette matrice.
En effet, étant à l'origine de la construction de l'axe proximodistal Y de chaque segment, les coordonnées des centres articulaires doivent être nuls suivants les axes segmentaires antéropostérieur X et médiolatéral Z. De plus, la distance entre les deux centres fonctionnels doit être constante en fonction du temps. Ainsi, à tout instant, la matrice de
passage homogène de ai Dyn/ Anat à ai+1 Dyn/ Anat s'écrit :

0
T i +1
i Dyn/ Anat
Ri+1 l
i i
0
0 0 0 1
La mise en place d'une contrainte de position au niveau du vecteur translation de
l'opérateur homogène i+1
T i Dyn / Anat permet de fixer la position d'un repère ai+1 Dyn/ Anat par
rapport à son homologue ai Dyn/ Anat .

Li
De ce fait la distance
entre deux centres articulaires proximal et distal d'un
même segment reste constante tout en conservant l'orientation originelle du repère segmentaire. Un raisonnement par récurrence permet alors de solidifier les autres segments de la chaîne cinématique.
Dans le cas de cette étude, vue l'orientation des repères segmentaires déjà définie (§- VII.2), le raisonnement par récurrence suit l'arborescence suivante (figure 85) :
Bras
Segments droits ?
T Pied T Jambe T Cuisse
Jambe Cuisse Pelvis
? T Bras T Av.bras
Tête ??
Tronc T Pelvis
Abdomen ? T Abdomen T Thorax
Thorax Tête
?Bras
Segments gauches ?
T Pied T Jambe T Cuisse
Jambe Cuisse Pelvis
? T Bras T Av.bras
Tête ??
Figure 85 Arborescence de la chaîne cinématique
La figure 86 illustre l'exemple de la variation instantanée de l'intensité du vecteur
LCuisse
dans aCuisse Dyn/ Anat avant et après l'application des contraintes sur les positions des
centres articulaires.
Avant Après
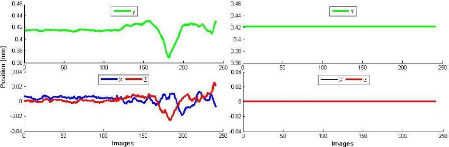
Figure 86 Position du repère pelvis droit par
rapport au repère cuisse droite avant et après
l'application
des contraintes de position suivant les trois dimensions de
l'espace
Etape 5 : Definition des positions et orientations absolues des segrnents rigidifies Suite à la redéfinition de toutes les matrices i+1
T i Dyn
/ Anat , une dernière transformation est
effectuée afin d'exprimer la position et l'orientation des repères segmentaires ai+1 Dyn/ Anat
dans g0. L'équation de cette transformation s'écrit :
T i +1 Dyn/ Anat T i Dyn/ Anat Ti+1
·i Dyn/ Anat Éq.VIII. 5 0 0
Suite à l'application de la procédure de solidification par récurrence (PSR) et l'expression de la chaîne cinématique des segments rigides poly-articulés dans R0, il importe de déterminer son effet sur la définition de la position des repères segmentaires.
Rappelons que l'orientation mesurée (originale, brute) des repères segmentaires est conservée suite à l'application de la PSR.
Dans les figures qui suivent (figures 87, 88 et 89) est exposée la différence entre les positions des centres articulaires48 mesurées et recalculées suite à l'application de la PSR.
48 La position d'un centre articulaire d'une articulation coïncide, par définition, avec l'origine du repère segmentaire amont. Exemple : le centre articulaire du genou coïncide avec l'origine du repère cuisse (fémur).
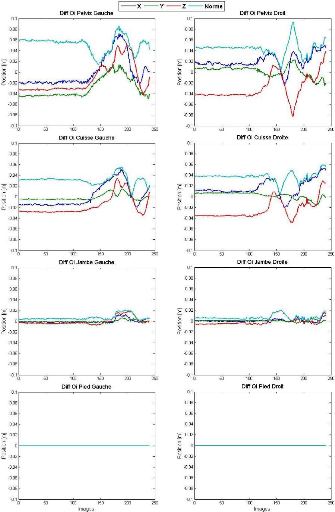
Figure 87 Différences entre les positions
mesurées (brutes) et recalculées
des centres articulaires
Oi des membres inférieurs
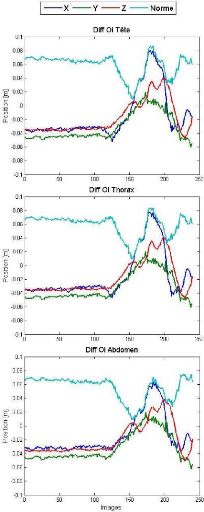
Figure 88 Différences entre les positions
mesurées (brutes) et recalculées
des centres articulaires
Oi de la tête, du thorax et de l'abdomen
Figure 89 Différences entre les positions
mesurées (brutes) et recalculées
des centres articulaires
Oi des membres supérieurs
L'écart moyen le plus important entre les positions mesurées (brutes) et recalculées des centres articulaires (Oi) est de 5 #177;1 cm atteint au niveau de Oi tête (figure 88). Suite à l'adoption des recommandations de l'ISB [Wu 02, Wu 05] (§-VII.2), les origines des repères segmentaires des bras et des pieds représentent les points de départ du raisonnement par récurrence (figure 85). Les écarts entre les positions de Oi mesurées et recalculées de ces segments sont donc quasi nuls (figures 87 et 89).
Il importe de rappeler ici que l'objectif attendu, suite à l'adoption d'une procédure de minimisation des artéfacts, est de pouvoir appliquer les principes de la mécanique des solides rigides [Capp 05]. La méthode adoptée doit donc fixer les longueurs segmentaires tout au long du geste enregistré.
Contrairement aux procédures d'optimisation par moindres carrés, la PSR :
§ n'entraîne pas de dislocations articulaires (§-VII.5), puisqu'elle met des contraintes de
positions au niveau des centre articulaires (§-VIII.1. Étape 2 et 3) ;
§ ne modifie pas l'orientation des segments et de ce fait n'entraîne pas l'accumulation
d'incertitude de mesure (§-VII.5), puisqu'elle ne modifie que la position du segment en conservant ses orientations (§-VIII.1. Étape 4 et 5) ;
§ nécessite un temps de calcul vingt cinq fois plus court (6 s contre environ 150 s).
Dans ce qui suit, l'estimation des grandeurs cinématiques segmentaires et dynamiques articulaires est réalisée suite à l'adoption de la PSR et la procédure de solidification globale (PSG) proposée par Lu et O'Connor (1999). Les grandeurs calculées en appliquant ces deux procédures (PSR et PSG) sont confrontées afin d'estimer les éventuelles différences.
L'objet de ce paragraphe est de présenter la démarche adoptée pour l'évaluation des paramètres cinématiques segmentaires. Cette démarche se base sur le concept des opérateurs homogènes développée par Legnani et al. (1996)Contrairement à l'écriture vectorielle introduite par Newton-Euler, la formulation matricielle (4x4) proposée par Legnani et al. (1996) ne nécessite aucune hypothèse sur la cinématique articulaire [Legn 96].
Cette formulation matricielle présente un avantage d'ordre pratique. Elle combine dans une même écriture les grandeurs angulaires et linéaires pour l'estimation des paramètres cinématiques et dynamiques.
L'application de ce concept dans le domaine de la biomécanique a été récemment réalisée, par Doriot et col. (2001), pour l'analyse tridimensionnelle du membre inférieur durant la phase d'appui de la marche [Dori 01]. Par la suite Colloud (2003) l'adopte pour la modélisation dynamique du rameur lors d'exercices réalisés sur ergomètres [Coll 03].
Suite à la détermination des opérateurs homogènes 70i Djai/ Anat décrivant la position et l'orientation d'un segment Si dans R.0 (§-7.2), l'estimation des vitesses linéaires et angulaires segmentaires se fait en déterminant la matrice Wi /comme suit :
0
c0 oz -ù0 z -ù ùy x vvy x
Éq.VII. 6
-1
|
|
||
Q i Ili
= =
-ù ù 0 v
y x z
0 0 0 0 I 0 0 0 0
90 R0
i Dyn / Anat
( T0 ) -1
i et T0 ? i représentent respectivement l'inverse et la dérivée première de T0
La sous-matrice Qi/% de W/ est une matrice antisymétrique 3x3 qui renferme les igto
~~
composantes du vecteur vitesse angulaire Ùi/ 0 du segment Si par rapport à g0 tel que :
ù y
x
Éq.VII. 7
g0
~~
Ù i/ gt0 =
|
|
||
Une seconde dérivation de 70i Dyn/ Anat définie la matrice Hi/,t0 décrivant lesaccélérations linéaires et angulaires comme suit :
Hi/ R0
??
=· T i 0
~
-1 A i ai
( T0i
0 0 0 0
g0
Éq.VII. 8
avec T0
? ? i est la dérivée seconde de T0i ,
Ai/gt0 est la sous-matrice accélération angulaire correspond à la somme Ù+
~
ai / ~ 0 est le vecteur accélération linéaire de l'origine Oi de ai par rapport à R0 Procedure d'estimation de la cinematique globale
La cinématique globale est le reflet de la cinématique segmentaire, on parle dans ce cas de la synergie segmentaire. À chaque instant, la position du centre de gravité G d'un système poly-articulé de masse M se définie comme étant le barycentre des centres de gravités segmentaires Gi affectés des coefficients mi.
Définit dans R.0 = ( O| X0 ,Y0 ,Z0) , l'équation s'écrit comme suit :
n
~~~~ ~~~~
~
90
m i OG i 91 = MOG 0
Éq.VIII. 9
i=1
La détermination des positions instantanées des centres de gravités Gi segmentaires s'est basée sur les équations de régression établies par Zatsiorsky (1985) ainsi que les mesures anthropométriques effectuées sur le sujet de l'étude [Zats 85]. Le choix de ce modèle se justifie par sa précision à estimer les paramètres inertiels segmentaires (masses, positions des centres de masses, matrices d'inerties) [Coll 02 ; Rao 06].
Étant positionnée sur l'axe proximodistal OiYi de ~i, la matrice homogène G
T i
i
décrivant la position de Gi par rapport au repère segmentaire gti s'écrit comme suit :
1 0 0 0
m 0 1 0
m 0 0 1
m 1 0 O i Gi
i =
i
Éq.VIII. 10
La sous matrice rotation de G
T i
i est une matrice identité. De ce fait, le nouveau repère
ayant pour origine Gi, noté Gi
~ , possède la même base que Ri. En d'autres termes, cela
revient à effectuer une simple translation du repère gti suivant OiYi pour le positionner en Gi. Connaissant la matrice T0i décrivant la situation de gti dans g0, et la matrice G
T i
i
décrivant la situation de Gi
~ dans ERi, la situation de Gi
~ dans g0 se définie comme suit :
T 0G i = T o·TiG i Éq.VIII. 117
Enfin, suite à la description de la position de l'ensemble des Gi dans g0 le calcul du centre de gravité global se fait en appliquant l'équation VIII.11. L'estimation des paramètres linéaires et angulaires de la vitesse WG / ,0 et de l' accélération HG/ ,0 du centre de gravité global est calculée d'après les équations VIII. 6 et VIII.8.
Les variations de la position du centre de gravité (OG) estimées suite à l'application de la procédure de la solidification par récurrence (PSR) et la procédure de solidification globale (PSG) sont confrontées à la même grandeur évaluée par dynamométrie (fig15).
Differences de positions du centre de gravite
? OG (PFF - PSR) ? OG (PFF - PSG)
Figure 90 Différences de variation de la position du centre de gravité (? OG) estimée par dynamométrie
(PFF) et suite à l'application de la PSR et de la PSG (ts : signal de départ, ta : début de l'impulsion,
tem : éjection des mains, tePr : éjection du pied arrière, te : éjection du pied avant)Il importe de rappeler, que contrairement au données cinématographiques qui s'achèvent à la pose du premier appui au sol, l'interprétation des données dynamométriques prend fin à l'instant de l'éjection te de l'athlète. Ainsi, au delà de l'instant te (figure 90), l'étude de la différence entre les données cinématographiques et dynamométriques n'a plus de sens.
Les figures 90 et 91 montrent que les deux procédures de solidification (PSR et PSG) estiment la position 3D du centre de gravité et sa norme avec la même précision jusqu'à l'instant de l'éjection des mains tem.
À partir de tem jusqu'à te, l'application de la PSR, contrairement à la PSG, estime la variation de la position du centre de gravité suivant l'axe antéropostérieur (OX) avec une bonne précision (1% contre 8% à te). Cependant, suivant les axes médiolatéral (OY) et vertical (OZ), la PSG fournit une meilleure précision (56% et 5% contre >100% et 7% à te).
Contrairement à l'axe antéropostérieur, le déplacement du centre de gravité suivant les axes médiolatéral (OY) et vertical (OZ) est très faible (§-IV.3.figures 40 et 43). De ce fait, la qualité des données suivant OY et OZ n'affecte pas ou peu l'estimation de la norme du déplacement du centre de gravité (figure 91). En d'autres termes, la précision de la norme du déplacement du centre de gravité dépend fortement de la précision des données suivant OX.
|
|||
Figure 91 Différences de la norme de la variation de position du centre de gravité estimée par
dynamométrie (PFF) et suite à l'application de la PSR et de la PSGAinsi, malgré les faibles précisions de la position du centre de gravité suivant l'axe OY et OZ la PSR permet une estimation plus précise de la norme de cette grandeur. Elle estime la norme à te à 1% tandis que la PSG l'estime à 7%.
De même, contrairement à la PSG qui estime la vitesse d'éjection antéropostérieure à 12%, la PSR l'estime à 1%. Vu la forte corrélation qui existe entre la vitesse antéropostérieure et sa norme à l'éjection décrite au quatrième chapitre (§-IV.4.3.figure 51), la précision de l'une dépend fortement de la précision de l'autre.
La modélisation du corps de l'athlète par un système poly-articulé de solides rigides constitue l'une des étapes préliminaires nécessaire à l'étude mécanique des forces intersegmentaires et moments articulaires. En effet, afin de pouvoir appliquer les lois de la mécanique des solides rigides pour chacun des n corps rigides qui constituent la chaîne il importe de considérer :
§ que la répartition des masses de chaque segment reste constante à chaque instant. Cela
revient à supposer que la forme des muscles est invariante lors de la contraction ;
§ que les frottements et glissements entre les surfaces articulaires sont négligés.
L'adoption de ces hypothèses simplificatrices introduit des erreurs dans le calcul de dynamique inverse. Ainsi, il est recommandé de ne pas prendre en compte plus de trois segments afin de limiter la multiplication des incertitudes de mesures d'un segment à l'autre. De ce fait, pour l'analyse du mouvement du rameur [Coll 03], de la marche [Fros 98], de soulevé de charge [Moua 01], ou de pédalage [Bouc 05] la plupart des calculs s'arrêtent au niveau de la hanche.
Dans le cas de l'analyse du départ de course vitesse, les forces calculées au niveau de la cinquième vertèbre lombaire obtenues à partir de deux stratégies (descendante et ascendante) sont comparées pour valider le modèle.
Dans la même logique que l'analyse cinématique (§-VIII2.1), l'écriture des équations de la dynamique adoptée correspond au formalisme introduit par Legnani et al. (1996). Il s'agit, rappelons-le, d'une formulation très synthétique des théorèmes de Newton-Euler qui emploie les matrices de roto-translation pour la modélisation dynamique d'un système polyarticulé.
La mise en équation de la dynamique articulaire nécessite un bilan des torseurs des actions mécaniques qui s'exercent sur chaque segment de la chaîne articulée. La figure 92
présente un exemple d'une chaîne composée de trois solides rigides (Sol, S1 et S2) en liaisons
ponctuelles (O1 et O2).
- Si : Solide i
-
Y0
X0
S2
Ö( Sol /S1 )
O1
O2
Ö( S2 / S1 )
Ö (pesanteur/ S1 )
Sol
Z0
g0
S1
G1 : centre de gravité de S1
- O1 : point d'application de R1
- O2 : point d'application de R2
- Ö ( Sol / S 1 ) : TAM exercée par le Sol sur S1
- Ö ( S 2 / S 1 )
: TAM exercée par S2 sur S1
- Ö(
pesanteur/
S1 ) : TAM de la pesanteur sur S1
Figure 92 Représentation des torseurs des actions mécaniques (TAM) qui s'exercent sur le solide S1
La détermination du bilan des torseurs des actions mécaniques qui s'exercent sur le solide S1 (figure 17) permet d'écrire, à chaque instant, l'équation de l'équilibre dynamique de ce segment dans g0 en appliquant le principe fondamental de la dynamique (§-III.3) :
N
Ö( SoilS 1 Yet0 + Ö ( S 2 / S 1 Va0 ( pesanteur/ S1 ) / gt0 = AS1 / Éq.VIII. 12RD
Ö( Sol /S1 ) / ~ 0 : torseur des actions mécaniques exercées par le Sol sur S1 dans 0 en O1
: torseur des actions mécaniques exercées par S2 sur S1 dans gt0 en O1
Ö( S2 /S1) /a0
Ö( pesanteur/S1 ) / 910 : torseur d'action de la pesanteur exercée sur S1 dans R.0 en O1 AS1 / 90 : torseur dynamique associé au mouvement de S1 dans R.0 en O1
Ayant déjà défini le torseur Ö(Sol/S1)/~0 par mesure dynamométrique, il devient possible d'estimer le torseur Ö ( S 2 / S 1 ) / ~ 0 comme suit :
Ö( S 2 / S 1 Vet0 = A S1 /91.0 - Ö( SollS 1 )/ a0 - Ö( pesanteur/ S1 )/9t0Éq.VIII. 13 Finalement, afin d'estimer le torseur des actions mécaniques exercées par un solide
Si+1 sur Si dans g0, il importe de définir deux constantes :
§ l'opérateur du champ de pesanteur Hi/ 0 nécessaire à la définition du torseur d'action de la pesanteur Ö (
Pesanteur / i )/910 .
§ la pseudo matrice d'inertie J iei d'un segment Si nécessaire au calcul du torseur dynamique Ai/ ~ 0 et du torseur d'action de la pesanteur Ö(
Pesanteur/ i ) / e0 .
Definition de l'opérateur du champ de pesanteur
Par analogie avec la matrice Hi/ ~ 0 , l'opérateur du champ de pesanteur possède la forme matricielle suivante :
~~
H
g
g/=
0
0 0 0 0
0
~~
où g= 0
-9,81
~
[ 0]

Éq.VIII. 14
~~
avec g accélération gravitationnelle
Definition de la pseudo-matrice d'inertie
Définie en Gi suite à l'application des équations de régression proposées par Zatsiorsky (1985), la matrice d'inertie de Si est d'abord transférée à l'origine Oi de ~i en appliquant le théorème de Huygens :
I( Oi )91.i = I( Gi )91.i + I91. Éq.VIII. 15
Où I ~i représente la matrice d'inertie en Oi du point Gi affecté de la masse mi de Si.
L'expression de I ( O i ) . est la suivante :
I ( Oi )a = [-F B -D i
[
O i G i = Yi
Zi ai
A -F -E
-E -D C
X
i
~~~~~~
Éq.VIII. 16
et
9Li
En adoptant cette notation (Éq.VIII.), la pseudo-matrice d'inertie défini en Oi de ~i
s'écrit :

S 2- A F E m i Xi
F S 2- B D m i Yi
E D S 2- C m i Zi


Éq.VIII. 17
9Li
avec S = A + B + C
m i X i m i Y i m i Z i mi 9Li
Architecture de la chaine cinematique lors d'un depart de course vitesse
Lors d'un départ de course vitesse, l'étude de l'architecture de la chaîne cinématique permet de distinguer trois types de configurations (figure 93).
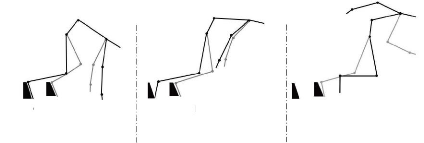
Bipédie Unipodale
Quadrupédie
CC fermée
(Membres inférieurs et
supérieurs)
CC ouverte membres supérieurs
CC fermée
membres inférieurs
CC ouverte
(Membres inférieurs et
supérieurs)
Figure 93 Chaînes cinématiques (CC) lors d'un départ de course vitesse
La disposition d'un dynamomètre au niveau de chaque appui (C1 : pied avant, C2 : pied arrière, C3 : main droite, C4 : main gauche) (figure 76) estime le torseur des actions mécaniques externes qui s'y exercent.
Les quatre torseurs exprimant la résultante et le moment des actions mécaniques réduit à l'origine du repère R.0 sont écrit sous forme matricielle 4x4. L'expression d'un torseur
décrivant les actions mécaniques d'un segment Si sur un capteur Ci dans R.0 est de la forme
suivante :
0 - M M F
z y x
Ö S i C i ~
( )
/ / 0
0 - M F
z x y
M M 0 F
z z z
M
=
-
-
Éq.VIII. 18
F - F -F
x y z
0
9t0
Mx Fx
~~~ ~~
avec M( O , PSvCi)/ gt0 = I My
Mz
et ( ) 0
F S i C i ~
/ /
910
= Fy
Fz

910
Il importe de signaler que l'introduction de ces torseurs dans l'écriture de l'équation de l'équilibre dynamique doit tenir compte de la définition de la configuration de la chaîne cinématique et la détermination des instants de décollage de chaque segment (§-IV.1.2). Le bilan des torseurs des actions mécaniques qui s'exercent sur l'athlète lors des différentes configurations figure dans le tableau 3.
-1
( )
T 0 i
Tableau 10 Bilan des torseurs décrivant les
actions mécaniques exercée par l'athlète
sur son milieu
extérieure lors de différentes configurations
|
Configurations |
Pied Avant [Pv] |
Pied arrière [Pr] |
Main droite [md] |
Main gauche [Mg] |
|
Quadrupédie |
Ö( Pv /C1 ) / g0 |
Ö ( Pr /C2 ) /a0 |
Ö( Md/C3 ) /R0 |
Ö ( Mg/C4)/91.0 |
|
Bipédie |
Ö( Pv /C1) / 90 |
Ö( Pr /C2 ) /g0 |
Torseur nul |
Torseur nul |
|
Unipodale |
Ö( Pv /C1 ) / g0 |
Torseur nul |
Torseur nul |
Torseur nul |
Au cours de cette étude la masse des mains est négligée, les torseurs mesurés au niveau de ces appuis sont donc directement rapportés au centre fonctionnel du poignet.
Structure de l'algorithme de calcul
Pour t = temps Pour i = segment
Calcul des matrices vitesses du segment Si dans g0

W = T 0 ·
i
i / ~ 0
Calcul des matrices accélérations du segment Si dans gt0
·

-1
Hi
·T= i
/e0
( T0i )
J = T · J ·
i
i ~ 0 i ~
0 i
( T0i )


Calcul de la pseudo-matrice d'inertie dans g0
À chaque itération (i) l'algorithme fournit la matrice Ö (i+1/ i ) /ai+1 décrivant le torseur
des efforts inter-segmentaires entre les segments Si+1 et Si. Ce torseur est par convention symétrique et il est exprimé dans le repère du segment Si+1. Son centre de réduction est par hypothèse confondu avec le centre articulaire Oi+1 de gi+1. Par analogie avec le torseur des actions mécaniques externes, le torseur des actions mécaniques internes de Si+1 sur Si s'écrit :
|
Ö ( ) i+1 i / |
/ |
~ i+1 |
[ 0 - N M X i i i N 0 - L Y i i i
|
~ i+1 |
Éq.VIII. 19 |
L i
~ = M
i+1 i
N i
X i
et /
F Y
i+1 i = i
~ i+1 Z i ~ i+1

avec (
M O , i+1 i
/ ) /
i
Le choix du centre de réduction au centre fonctionnel de l'articulation trouve origine dans une hypothèse classique : la distance entre la droite d'action de la force de contact et le centre articulaire est négligée. Les forces ligamentaires sont également négligées au regard des forces musculaires [Coll 03]. Ainsi, le moment calculé représente, au signe près, les actions musculaires croisant l'articulation.
Validation du modele dynamique inverse
Afin d'éliminer l'effet des méthodes de traitement et de calculs et permettre la comparaison des deux procédures de solidification, les matrices issues de la PSR et de la PSG sont injectées dans le même algorithme de calcul. La validation du modèle dynamique inverse est effectué en calculant le torseur des actions inter segmentaires au niveau de la cinquième vertèbre lombaire en adoptant deux stratégies de dynamique inverse :
descendante : Ö ( ) 0
/ ~ = A ~ + Pelv/ Cuisse / - pesanteur / Pelvis /
0 Ö ( Ö
Abdomen/ Pelvis Pelvis / ) ~ ( ) ~
0 0
~ascendante : Ö ( ~ = A ~ + Abdomen/Thorax / - pesanteur / Abdomen /
Ö Ö
Pelvis / Abdomen ) Abdomen/
/ 0 ( ) ~ ( ) ~
0 0 0
En appliquant le principe de réciprocité (§-III.3) aux segments abdomen et pelvis (figure 94), nous vérifions que Ö( Abdomen/Pelvis ) /g0 et Ö( Pelvis/Abdomen ) /a0 sont équivalents au signe prêt.
Force exercees par ('abdomen sur le pelvis exprimees dans ao [N]
Figure 94 Forces exercées par l'abdomen sur le
pelvis suivant les trois dimensions de l'espace
to.
Données issues de la PSR et PSG en adoptant deux
stratégies : ascendante (Asc) et descendante (Desc)
La figure 94 montre, jusqu'à l'instant ta, une bonne concordance entre les données issues des deux stratégies de dynamique inverse (ascendante et descendante). Cela permet, d'une part, de valider notre processus de dynamique inverse basé sur le formalisme matriciel de Legnani et al. (1996) et, nous autorise, d'autre part, à étudier l'effet des deux procédures de solidification sur l'estimation de la dynamique articulaire.
À partir de l'instant ta, la concordance entre les deux stratégies de dynamique inverse est perturbée. Cette perturbation est due à :
§ l'amplification des incertitudes provoquée par la double dérivation des données
cinématographiques lors du calcul des accélérations ;
§ l'accumulation de ces incertitudes suite à l'application de la procédure itérative de
dynamique inverse.
Il importe de souligner que ces perturbations n'entravent pas l'étude comparative des torseurs d'actions inter segmentaires issus de la PSR et de la PSG. Ayant subie exactement la même procédure de calcul de dynamique inverse, une éventuelle différence dans les résultats serait fortement due à l'application de la PSR versus la PSG.
Elements permettant l&interpretation des resultats
Suite au calcul itératif, les torseurs des actions mécaniques inter segmentaires entre les
segments Si+1 et Si exprimées dans Si+1 sont quantifiés. Tenant compte de l'arborescence de la
chaîne cinématique (§-VII.2.figure 78) les vecteurs forces et moments inter segmentaires au niveau d'une articulation donnée caractérisent l'action d'un segment amont sur le segment aval pour les membres inférieurs et supérieurs et d'un segment aval sur un segment amont pour le tronc et la tête. Ces éléments sont décrits dans le tableau 11 ci-dessous.
Tableau 11 Définition des actions mécaniques inter segmentaires au niveau des articulations
|
Articulations |
Si+1 / Si |
Articulations |
Si+1 / Si |
|
Cheville |
Jambe / Pied |
C7 |
Thorax / Tête |
|
Genou |
Cuisse / Jambe |
T12 |
Abdomen / Thorax |
|
Hanche |
Pelvis / Cuisse |
L5 |
Pelvis / Abdomen |
|
Coude |
Bras / Av. bras |
Épaule |
Thorax / Bras |
L'interprétation des forces et des moments doit tenir compte de l'orientation des repères segmentaires qui possèdent des bases différentes selon le coté gauche ou droit. L'orientation de ces repères est détaillée dans le précédent chapitre (§-VII.2.figure 78).
Dans le plan sagittal, les articulations du tronc (C7, T12 et L5) ainsi que celles du côté droit du corps : cheville, hanche, coude et épaule, présentent une valeur positive du moment lors de la flexion49. Quant au genou droit, c'est une valeur négative du moment qui traduit sa flexion (Voir orientation des axes §-VII.2.figure 78). Mis à part le genou gauche qui présente un moment positif lors de sa flexion, les articulations du coté gauche du corps (cheville, hanche, coude et épaule) présentent un moment négatif lors de leur flexion.
Dans le plan frontal, une valeur positive du moment, au niveau d'une articulation du coté droit du corps traduit une adduction d'un segment droit. Contrairement elle traduit une abduction dans le cas d'une articulation du coté gauche. Concernant les articulations du tronc, un moment positif signifie une inclinaison latérale sur le coté droit.
Dans le plan horizontal, une valeur positive du moment articulaire traduit invariablement une rotation médiale (interne) du segment.
Dans le paragraphe qui suit, les forces inter segmentaires, puis les moments articulaires, sont exposés afin de quantifier l'effet des deux méthodes de solidification (PSR vs PSG) sur leur quantification.
De manière visuelle, la similitude des résultats issues de la PSR et de la PSG semble être très forte (figure 95, 96, 97 et 98). Nous pouvons cependant quantifier cette comparaison par le calcul de l'écart moyen quadratique normalisé (EQMN) qui consiste à mesurer la dispersion des n données issues des deux procédures pour enfin les normaliser en prenant en compte les amplitudes maximales et minimales des deux courbes (correspond en Anglais à Normalized Root Mean Square errors NRMSe [Caho 02]) tel que :
1 2
Éq.VIII.20
n ( ( ) ( ) ) 2
PSG PSR
0
1 n F t - F t
NRMSe = ×100
( ( ( ( ) ) ( ( ) ) ) )
PSR Max F t - Min F t
i=PSG 0<t<T i 0<t<T i
49 Il s'agit de la flexion dorsale pour l'articulation de la cheville.
Genou [N]
Hanche [N]
Quatrieme partie Chapitre VIII
Fx
Fx Fy Fz
Fy
Fz

600
400
200
0
-200
m 0,1 0,2 0.6 0,4 0,5 0,6 0,7 0,8 0,9
0
-500
-1000
-1500
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
150
100
50
0
-50
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Cheville [N]
NRMSe = 2%
te
NRMSe = 0%
te
NRMSe = 6%
te
200 100 0 -100 -200
NRMSe = 2%
1000
500
0 -500 -1000
500
0 -500 -1000
500
0
-500
-1000
m
1000
500
0 -500 -1000
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
m
NRMSe = 5%
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
NRMSe = 1%
PSG PSR
NRMSe = 4%
-100
-200
100
0
NRMSe = 7%
200
Temps [s]
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
NRMSe = 3%
Temps [s]
Cheville [N]
Genou [N]
Figure 95 Force inter segmentaires au niveau de la cheville droite, genou droit et hanche droite
exprimées respectivement dans atibia , afémur et apelvis (membre inférieur droit)
Les deux procédures de solidification (PSR et PSG) estiment les forces inter segmentaires de la cheville droite et gauche et du genou droit et gauche de la même manière suivant les trois dimensions de l'espace (figure 95 et 96). L'écart NRMSe ne dépasse pas les 6%. Contrairement au niveau de la hanche les deux procédures divergent. Cette différence est plus accentuée au niveau de l'articulation de la hanche gauche (figure 96).
Fx
Fx Fy Fz
Fy
Fz
200
0
te
0
100
-200
-400
-600
NRMSe = 2%
-500
0
NRMSe = 0%
te
te
NRMSe = 2%
-1000
m
500
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-100
m
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
500
200
PSG PSR
0
0
-500
0
NRMSe = 1%
NRMSe = 1%
-200
NRMSe = 1%
-1000
-500
NRMSe = 27%
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
500
400
200
0
0
-500
NRMSe = 11%
-200
Hanche [N]
NRMSe =20%
200 0 -200 -400
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
-1000
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
-400
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
Figure 96 Forces inter-segmentaires au niveau de la cheville gauche, genou gauche et hanche gauche
exprimées respectivement dans atibia , afémur et apelvis (membre inférieur gauche)
178
Cheville [Nm]
Genou [Nm]
Hanche [Nm]
Quatrieme partie Chapitre VIII
Mx My Mz
Mx
My
Mz
NRMSe = 1%
300
200
250
150
te
t e
200
te
400
150
NRMSe = 0%
NRMSe = 2%
100 NRMSe = 2%
300
200
100
0
100
50
50
0
0
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-50
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-50
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
700
600
500
100
800
0
600
NRMSe = 8%
-100
400
-200
NRMSe = 1%
200
-300
0
PSGP PSR
-200
600 400 200 0
-400
-400
-2000 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-500
m m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9

300
200
500
NRMSe = 0%
100
NRMSe = 9%
NRMSe = 10%
0
0
-100
-500
-200
600
400
200
0
m
Cheville [Nm]
Genou [Nm]

0
100 0 -100 -200 -300
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 O 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 O 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
Temps [s] Temps [s] Temps [s]
Temps [s]
Temps [s]
Figure 97 Moments articulaires au niveau de la cheville droite, genou droit et hanche droite exprimées
Figure 97 Moments articulaires au niveau de la cheville droite, genou droit et hanche droite expriméesrespectivement dans atibia , afémur et apelvis (membre inférieur droit)
respectivement dans atibia , afémur et apelvis (membre inférieur droit)L'estimation des moments articulaires par la PSG et la PSR ne montre pas de différence suivant les trois dimensions de l'espace au niveau des articulations droites et gauches de la cheville et du genou (figure 97 et 98). Toutefois, les moments nets quantifiés au niveau de l'articulation de la hanche (droite et gauche) montre une divergence plus accentuée du coté gauche par rapport au coté droit (figure 97 et 98).
Mx My Mz
100
400
0
0
-100
300
te
-200
-200
-300
-400
200
-400
-600
100
te
te
-500
NRMSe = 3%
NRMSe = 0%
NRMSe = 3%
-600
-800
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
00 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
500
PSG PSR
200
0
-200
-400
-600
-800
NRMSe = 4%
NRMSe = 10%
0
-200
-500
NRMSe = 5%
NRMSe = 3%
-400
-1000
-600
-1500
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
400
300
0
200
100
NRMSe = 18%
0
-200
NRMSe = 14%
-400
Hanche [Nm]
-100
-600
-200

-1000
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-300
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-800
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
Temps [s] Temps [s] Temps [s]
Temps [s]
Temps [s]
Figure 98 Moments articulaires au niveau de la cheville
gauche, genou gauche et hanche gauche exprimés
Figure 98 Moments
articulaires au niveau de la cheville gauche, genou gauche et hanche gauche
exprimés
respectivement dans atibia ,
afémur et apelvis (membre inférieur
gauche)
respectivement dans atibia , afémur et
apelvis (membre inférieur gauche)
179
Le tableau 12 ci-dessous illustre les écarts NRMSe entre les éléments du torseur d'actions inter-segmentaires estimés suite à l'adoption de la PSG et la PSR. Les figures confrontant les courbes des données des membres supérieurs et du tronc sont exposées en annexe (Annexe 4.2).
Tableau 12 Écarts entres la PSG et la PSR lors
de l'estimation des force inter segmentaires (Fi)
et des moments
articulaires (Mi) suivants les trois directions de l'espace
NRMSe [%]
Articulations
Fix Fiy Fiz Mix Miy Miz
Cheville D 2 0 5 0 2 2
G 2 0 2 3 0 3

Genou D 2 1 3 1 1 8
G 1 1 0 4 3 5

Hanche D 5 4 7 0 9 10
G 27 11 20 10 18 14

C7 39 50 22 25 1 16

T12 3 22 47 21 1 28

L5 25 66 19 30 5 39

Coude D 1 6 10 11 7 1
G 3 3 1 10 5 1

Épaule D 2 0 2 1 6 4
G 10 3 5 1 2 9
À notre connaissance, aucune étude n'a quantifié les forces inter segmentaires et moments articulaires dans les trois dimensions de l'espace lors d'un départ de course vitesse.
La rigidité des segments constitue un critère primordial lors de l'application des principes de la mécanique des systèmes poly-articulés au corps humain. La procédure de solidification par récurrence (PSR) proposée au cours de cette étude satisfait cette condition. Toutefois, son effet sur l'estimation de la cinématique segmentaire et la dynamique articulaire doit être étudié.
Suite à l'adoption de la formulation matricielle des opérateurs homogènes proposée par Legnani et al. (1996), nous avons approché les quantités cinématiques, cinétiques et dynamiques avec une formulation très synthétique en s'appuyant sur les théorèmes de Newton-Euler. Cette formulation matricielle possède l'avantage de présenter dans la même écriture des grandeurs linéaires et angulaires, de plus sa transcription sous la forme d'un algorithme s'avère très performante par son adéquation avec les langages informatiques actuels.
La quantification de la cinématique segmentaire et la dynamique articulaire est ainsi effectuée en intégrant les données issues de la PSR et de la PSG50 Afin, de valider le modèle de dynamique inverse, le torseur d'actions inter-segmentaires au niveau de l'articulation sacro-lombaire (L5) est évalué en adoptant deux stratégies de dynamique inverse (ascendante et descendante).
Suite à la confrontation des grandeurs cinématiques, il est apparu que la PSR offre une estimation plus précise concernant la vitesse du centre de gravité à l'éjection suivant l'axe antéropostérieur. Cela permet d'approcher la norme avec une bonne précision vu la forte corrélation entre ces deux grandeurs.
La comparaison des forces inter-segmentaires et des moments articulaires nets, montre une grande similitude des courbes provenant des deux procédures (PSR et PSG). Toutefois, suite au calcul de la NRMSe il est apparu une divergence entre les données issues des procédures. Cette divergence croît dans le sens ascendant des itérations. Ainsi, les écarts les plus importants sont notés au niveau des articulations : sacro-lombaire (L5), lombo-thoracique (T12) et thoraco-cervicale (C7).
Cette différence peut être due au principe de fonctionnement de la PSR qui se base sur une méthode récurrente ascendante. Cependant, cette méthode se base sur le relevé des données anthropométriques pour reconstituer la situation des segments. Contrairement, la PSG se base sur les longueurs mesurées. Ainsi, la différence observée lors de l'étude de l'effet de la PSR sur la configuration du système poly-articulé peut expliquer cette divergence.
50 PSG : Procédure de Solidification Globale proposée par Lu et O'Connor (1999). Cette procédure est détaillée dans le précédent chapitre (§-VII.3.1)

La démarche initiale qui a guidé ce travail visait à caractériser mécaniquement les critères de qualités du départ de la course vitesse sur 100 m afin d'orienter le choix de l'entraîneur lors de ces prises de décisions en situation réelle de pratique. Pour atteindre cet objectif, il a été nécessaire d'acquérir une meilleure connaissance des déterminants mécaniques de la performance de l'athlète, mais aussi de tenir compte de la précision des méthodes et moyens utilisés pour l'acquisition de ces paramètres.
En analysant la réglementation de l'IAAF pour les épreuves de course, nous avons montré la faible précision des méthodes employées pour la quantification de la performance finale de course et la détection des faux départs. La méthode de détection de l'instant de mise en action adoptée par l'IAAF a fait l'objet d'une étude comparative. Nous montrons l'inefficacité de cette méthode pour mesurer réellement et avec précision, le temps de réaction de l'athlète. En effet, outre le fait d'utiliser un seuil élevé (entre 200 et 300 N) pour détecter l'instant de la mise en action, la mesure du temps de réaction se fait uniquement par des mesures relevées au niveau des pieds. Or, suite à nos expérimentations, il apparaît que la réponse au niveau des mains devance celle des pieds de 0,05 s. Ce résultat est important au regard des dernières évolutions de la réglementation de l'IAAF qui aboutissent à éliminer l'athlète responsable du deuxième « faux départ ». Notre travail propose des critères d'évaluation du faux départ plus équitables car fondés sur une démarche rigoureuse.
La littérature scientifique qui porte sur la performance de départ de course de vitesse, exprime que la performance du départ est essentiellement qualifiée par l'intensité de la composante antéropostérieure de la vitesse d'éjection. Nos résultats montrent que la prise en compte de ce seul critère ne suffit pas à différencier la performance du départ. L'analyse comparative fine, intra et inter sujets, n'est pas possible avec ce seul critère. En d'autres termes, l'entraîneur ne peut pas différencier objectivement et avec précision deux performances, en ne tenant compte que du seul critère : vitesse d'éjection. De ce fait, à partir d'une analyse multidimensionnelles par composantes principales portant sur un nombre
important de variables mécaniques estimées par dynamométries, nous avons tenté de créer un (des) critère(s) synthétique(s) de la performance du départ. Cette démarche n'a pas abouti au résultat escompté. Toutefois, elle a mis en évidence le caractère indépendant des variables étudiées.
Afin de ne pas submerger l'observateur par une grande quantité d'information, six paramètres mécaniques principaux caractérisant le départ de course de vitesse ont pu être identifié : temps de réaction, durée de l'impulsion, positions initiale et finale du centre de gravité, la norme de la vitesse à l'éjection et sa direction. Cinq de ces paramètres directement accessibles par dynamométrie sont « convertis », à l'aide d'un modèle ou directement, en seconde pour offrir à l'entraîneur des indications concernant la perte ou le gain en temps sur 100 m. Le sixième paramètre (direction de la vitesse d'éjection) n'a pas pu être caractérisé en « temps ». Son influence est intégrée dans la phase d'accélération. Enfin, le développement d'une station de mesure de terrain est minutieusement étudiée afin de permettre une quantification juste et fidèle, en temps quasi réel, accordant un suivi longitudinal de la performance des athlètes lors du départ de course vitesse. Dans le cadre d'une collaboration avec le Ministère de la Santé de la Jeunesse, des Sports et de la Vie associative et la Fédération Française d'Athlétisme, nous avons transféré nos connaissances et nos résultats au Centre Régional d'Éducation Populaire et Sportive Poitou-Charentes qui disposera prochainement de la première station dynamométrique 3D en France permettant une quantification fine et rapide de la performance de départ en situation réelle de pratique.
Suite au couplage de mesures cinématographiques et dynamométriques du départ de course de vitesse, il est apparu nécessaire de trouver des solutions adaptées aux problèmes induits par le mouvement de la peau par rapport aux structures osseuses sous-jacentes. Étant l'un des critères primordial à l'application des principes de la mécanique au corps humain, la rigidité des segments nécessite l'adoption de procédures de solidifications par optimisation. Adoptées généralement pour l'analyse de la marche humaine, leurs applications au geste de départ de course de vitesse ont mis au jour des effets indésirables. Elles provoquent des dislocations articulaires ou des changements des orientations segmentaires. La méthode de solidification que nous proposons, résout ces deux problèmes et surtout permet l'application des principes de la mécanique pour l'étude du geste de départ de course vitesse. L'effet de cette nouvelle procédure de solidification sur l'analyse de la cinématique segmentaire et la dynamique articulaire a démontré son efficacité. Cette nouvelle procédure fournit des résultats qui nous permettent d'envisager des perspectives de développement prometteuses. Un autre
résultat important prometteur est la quantification des efforts inter segmentaires et les moments articulaires tridimensionnels. Ces résultats, absents dans la littérature scientifique, sont évalués par dynamique inverse en adoptant une écriture matricielle originale initialement développée dans le domaine de l'ingénierie mécanique et adoptée récemment dans le domaine de la biomécanique pour l'analyse de la marche humaine. La quantification de la dynamique articulaire constitue une étape essentielle pour l'optimisation du geste de départ par simulation numérique.
En tout état de cause, il sera opportun d'approfondir l'ensemble de ce travail en analysant un plus grand nombre de performances d'athlètes de haut niveau afin de conforter les résultats avancés dans cette étude, d'une part, et de mieux appréhender la variabilité des critères de performance en fonction du niveau des athlètes, d'autre part.
Les travaux à venir sur la cinématique du sujet devront, sans aucun doute, intégrer des paramètres posturaux, particulièrement lorsque le coureur s'éjecte des blocs de départ.
Si le départ présente par sa variabilité temporelle, un élément de la performance, la phase d'accélération et la phase de vitesse stabilisée constituent les éléments majeurs de la variabilité de la performance. Dans un futur proche, leurs variabilités induites par l'évolution de la morphologie humaine et des qualités des matériaux lors des phases de contacts seront encore, probablement, la source d'amélioration de la performance.

[Ae 92] Ae M., Ito A., Suzuki M. The men's 100 meters. New Studies in Athletics, IAAF,
1992, 7(1):47-52
[Alex 01] Alexander E.J., Andriacchi T.P. Correcting for deformation in skin-based marker systems. Journal of Biomechanics, 2001, 34:355-361
[Alla 95] Allard P., Stokes L.A.F., Blanchi J.P. Three-dimensional analysis of human
movement. Humain Kinetics, England, 1995, 19-40;
[Alla 00] Allard P., Blanchi J. P. Analyse du mouvement humain par la biomécanique. 2ème
edition, Décarie, Canada, 2000
[Ardl 01] McArdle M., Katch F., Katch V. P hysiologie de l'activité physique, énergie, nutrition et performance. 4ème éd., Maloine, Paris, 2001
[Asch 99] Asch G. Les capteurs en instrumentations industrielle, 5ème éd., Dunod, Paris, 1999 [Barr 83] Barry B., Woodman L. Sprint starting block teaching aid. Pelops, 1983, 4:7-10
[Baum 76] Baumann W. Kinetic and dynamic characteristics of the sprint start. In: Komi PV, editor. Biomechanics V-B Baltimore: University Park Press, 1976, 194-199
[Bego 07] Begon M., Monnet T., Lacouture P. Effects of movement for estimating the hip joint centre. Gait and Posture, 2007, 25:353-359
[Bend 34] Bender W. R. G. Factors contributing to speed in start of race and characteristics of trained sprinters: A summary of experimental investigations. Research Quarterly, 1934, 5(1):72-78
[Bill 98] Billat V. Physiologie et méthodologie de l'entraînement, de la théorie à la pratique.
De Boek Université, Paris, Bruxelles, 1998
[Bren 86] Brenière Y., Do M.C. Mouvements et
ajustements posturaux anticipateurs de la
marche. Journal de
Biophysique et de Biomécanique, 1986, 10(1):39-40
[Bouc 05] Boucher M., Limites et précisions d'une analyse mécanique de la performance sur ergocycle. Thèse Université de Poitiers, 2005
[Bren 87] Brenière Y., Do M.C. Modification posturales associées au lever du talon dans l'initiation du pas de la marche normale. Journal de biophysique et de biomécanique, 1987, 11(4): 161-167
[Broo 94] Brooks G.A., Mercier J. Balance of carbohydrate and lipid utilization during exercise: «the cross-over» concept. Journal Applied Physiology, 1994, 76:2253- 2261
[Caho 02] Cahouët V., Martin L., Amarantini D. Static optimal estimation of joint accelerations for inverse dynamics problem solution. Journal of Biomechanics, 2002, 35:1507-1513
[Camo 06] Camomilla, V., Cereatti, A., Vannozzi, G., Cappozzo. An optimized protocol for hip joint centre determination using the functional method. Journal of Biomechanics, 2006, 39:1096-1106
[Capp 89] Cappozzo A., De Vito G., Gazzani F., Massacesi R. Analisi biomeccanica della partenza dai blocchi. Atleticastudi, 1989, 5:347-375
[Capp 96] Cappozzo A., Catani F., Leardini A., Benedetti M., Della Croce U. Position and orientation in space of bones during movement : experimental artefacts. Clinial Biomechanics,1996, 11:90-100
[Capp 05] Cappozo A., Della Croce U., Leardini A., Chiari L. Human movement analysis using stereophotogrammetry. Part 1: theoretical background. Gait and Posture, 2005, 21:186-196
[Chèz 95] Chèze L., Fregley B. J., Dimnet J. A solidification procedure to facilitate kinematic analyses based on video system data. Journal of Biomechanics, 1995, 28(7):879-884
[Chia 05] Chiari L., Della Croce U., Leardini A., Cappozzo A. Human movement analysis using stereophotogrammetry. Part 2: Instrumental errors. Gait and Posture, 2005, 21:197-211
[Coh 98] Coh M., Jost B., Skof B., Tomazin K, Dolenec A. Kinematic and kinetic parameters
of the sprint start acceleration model of top sprinters. Gymnica, 1998, 28:33-42
[Coh 02] Coh M. Application of biomechanics in track and field. Institue of Kinesiologie,
Faculty of sport, University of Ljubljana, 2002
[Coll 03] Colloud F., Modélisation dynamique du rameur lors d'exercices réalisés sur
ergomètres d'aviron. Implication pour l'entraînement. Thèse Universités Claude Bernard - Lyon, 2003
[Copp 89] Coppenolle V. H., Delecluse C., Goris M., Diels R., Seagrave L., Kreeyenhof H. An evaluation of the starting action of world class female sprinters. Track Technique, 1990, 112:3581-3582
[Cous 04] Cousins S., Dyson R. Forces at the front and rear blocs during the sprint start. 22 International Symposium on Biomechanics in Sport, 2004, 198-201
[Cout 00] Coutard Y. Caractérisation et étalonnage des dynamometers a six composantes pour torseur associé à un système de force. Thèse Université de Bordeaux 1, 2000
[Crea 07] Cereatti A., Camomilla V., Vannozzi G, CappozzoA. Propagation of the hip joint centre location error to the estimate of femur vs pelvis orientation using a constrained or an unconstrained approach. Journal of Biomechanics, 2007, 40:1228-1234
[Croc 05] Della Croce U., Leardini A., Chiari L., Cappozzo A. Human movement analysis using stereophotogrammetry. Part 4: assessment of anatomical landmark misplacement. Gait and Posture, 2005, 21:226-237
[Davi 06] Davila M.G., Dapena J., Campos J. The effect of muscular pre-tensing on the sprint start. Journal of Biomechanics, 2006, 22:194-201
[Delh 80] Delhez L., Loverius, Timmermans, J.M. Dynamique du mouvement horizontal lors du départ du sprint. Revue Sport 23, 1980, 2(90):81-90
[Dick 89] Dick F. W. Developing and maintaining maximum speed in sprints over one year. Athletics Coach 23(1): 3-8, 1989
[Dick 34] Dickinson A. D. The effect of foot spacing on the starting time and speed in sprinting and the relation of physical measurements to foot spacing. Research Quarterly, 1934, 5(1):12-19
[Diu 05] Diu B., Leclercq B. La physique mot à mot. Odile Jacob science, 2005
[Duch 86] Duchateau J. Guissard N., Hainaut K. Electromyographie du départ en starting blocs en athlétisme. Journal de Biophysique et de biomécanique, 1986, 10(1):77-78
[Dori 01] Doriot N., Cheze L. Analyse tridimensionnelle du membre inférieur durant la phase d'appui de la marche. ITBM-RBM,2001, 22(3):178-184
[Ehar 95] Ehara Y., Fujimoto H., Miyazaki S., Tanaka S.,
Yamamoto S. Comparison of the
performance of 3D camera systems.
Gait and Posture, 1995, 3:166-169
[Ehar 97] Ehara Y., Fujimoto H., Miyazaki S., Mochimaru M., Tanaka S., YamamotoS., Comparison of the performance of 3D camera systems II. Gait and Posture, 1997, 5:251-255
[Ehri 06] Ehrig R. M., Taylor W. R., Duda G. N. et Heller M. O. A survey of formal methods for determining the centre of rotation of ball joints. Journal of Biomechanics, 2006, 39(5): 2798-2809
[Esco 98] Escofier B., Pagès J. Analyses factorielles simples et multiples. Objectifs, méthodes et interprétation. 3ème éd., Dunod, Paris, 1998
[Faiv 04] Faivre A., Dahan M., Monnier B., Instrumented shoes for pathological gait assessment. Mechanics research communications, 2004, 31:627-632
[Fort 05] Fortier S., Basset F. A., Mbourou G. A., Favérial J. Starting Block performance in
sprinters: A statistical method for identifying discriminative parameters of the performance and an analysis of the effect of providing feedback over a 6 week period. Journal of sport Sciences and Medicine, 2005, 4:134-143
[Fros 98] Frossard L. Étudedes limites de l'analyse mécanique de la marche d'un amputé comparé à celle d'un sujet sain. Thèse Université de Poitiers, 1998
[Gail 83] GailletA., Reboulet C. A isostatic six component force and torque sensors. In
Proceeding of th 13th International Symposium on Industrial Robots, 1983; 102-111
[Gagn 78] Gagnon M. A kinematic analysis of the kneeling and the starting starts in female sprinters of different ability. Biomechanics VI-B, Baltimore university park press, Copenhagen, Denmark, 6th, International Congress of Biomechanics, 1978, 46-50
[Gerb 99] Gerbeaux M., Berthon S. Aptitude et pratique aérobie chez l'enfant et l'adolescent, la préparation physique à l'horizon 2000. 1ère éd., Puf, Paris, 1999
[Goub 98] Goubel F., Lensel-Corbeil G. Biomécanique : élements de la mécanique musculaire. Masson, Paris, 1998
[Groo 83] Grood E., Suntay W. A joint coordinate system for the clinical description of three dimensional motions : application to the knee. Journal of Biomechanical Engineering, 1983, 32:1221-1227
[Guis 92] Guissard N., Duchateau J. EMG and mechanical changes during sprint start at different block obliquities. Medicine and science in sport and exercise, 1992, 24(11):1257-1263
[Hafe 85] Hafez A.M.A., Roberts E.M., Seireg A.A. Force and velocity during front foot contact in the sprint start. International Series On Biomechanics, 1985, 5B:350-355
[Harl 97] Harland M.J., Steele J.R. Biomechanics of the Sprint Start. Sport Medicine,
1997, 23(1):11-20
[Henr 52] Henry F.M., Force time characteristics of the sprint start. Research Quarterly, 1952, 5(1):27-32
[Hold 97] Holden J.P., Orsini J.A., Siegel K.L., Kepple T.M., Gerber L.H., Stanhope S.J. Surface movement errors in shank kinematics and knee kinetics during gait. Gait and Posture, 5:217-227
[Hold 98] Holden J. P., Stanhope S. J. The effect of variation in knee center location estimates on net knee joint moments. Gait and posture, 1998, 7:1-6
[Houe 04] Houel N., Intérêts et limites de l'analyse cinématique par imagerie. Contribution a la réalisation de modèles cinématiques et dynamiques du mouvement. Application au ski de fond et au saut à ski. Thèse Université de Poitiers, 2004
[Howe 56] Howell M.L. Use of force-time graphs for performance analysis in facilitating motor learning. Research and Quarterley, 27:12-22
[Jaco 92] Jacob R. Van Ingen Schenau G.J. Intermuscular coordination in a sprint push-off. Journal of Biomechanics, 1992, 25(9):953-965
[Karl 94] Karlsson, D., Lundberg, A.. Accuracy estimation of kinematic data derived from bone anchored external markers. In: Proceedings of the 3rd International Symposium on 3-D Analysis of Human Motion, 1994
[Kirk 99] Kirkwood R. N., Culham E.G., Costigan P. Radiographic and non-invasive determination of the hip joint center location: effect on hip joint moments. Clinical Biomechanics, 1999, 14:227-235
[Kraa 01] Kraan G.A., Veen J.V., Snijders C.J., Storm C.J. Starting from standing; why step backwards? Journal of Biomechanics, 2001, 34:211-215
[Lear 05] Leardini A., Chiarib L., Della Crocec U., Cappozzo A. Human movement analysis using stereophotogrammetry. Part 3. Soft tissue artifact assessment and compensation. Gait and Posture,2005, 21:212-225
[Leba 00] Lebart L., Piron M., Mrineau A. Statistique exploratoire multidimensionnelle. 3ème éd., Dunod, Paris, 2000
[Lebo 04] Leboeuf F. Contribution à l'analyse et à la synthèse dynamique du mouvement humain. Thèse Université de Poitiers, 2004
[Legn 96] Legnani G., Casalo F., Righettini P., Zappa B. A Homogeneous matrix approach to 3D kinematics and dynamics. Part I : theory. Mechanism and Machine Theory, 1996, 31(5):589-605
[Legn 96] Legnani G., Casalo F., Righettini P., Zappa B. A Homogeneous matrix approach to 3D kinematics and dynamics. Part II : Applications to chains of rigid bodies and serial manipulators. Mechanism and Machine Theory, 1996, 31(5):589-605
[Leha 05] Lehance C., Croisier J.L., Bury T. Validation du système Optojump en tant qu'outil d'évaluation de la force-vitesse (puissance) des membres inférieurs. Science et Sports, 2005, 20 :131-135
[Lema 90] Lemaire E.D., Robertson D.G.E. Force-time data acquisition system for sprint starting. Canadian Journal of Sport Sciences, 1990, 15(2):149-152
[Lu 99] Lu T. W., O'Connor J. J. Bone position estimation from marker co-ordinates using
global optimization with constraints. Journal of Biomechanics, 1999, 32:129-134
[Mare 85] Marey E.J., Demeny G. Compte rendus de l'Académie des Sciences. 24 août 1885
[Mend 93] Mendoza L., Scöllhorn Wolfgang. Training of the sprint start technique with biomechanical feedback. Journal of Sports Sciences, 1993, 11,25-29
[Mero 83] Mero A., Luhtanen P., Komi P. V. A biomechanical study of the sprint start. Scandinavian Journal of Sport Sciences, 1983, 5(1):20-28.
[Mero 88] Mero A. Force time characteristics and running velocity of male sprinters during the acceleration phase of sprint. Research Quarterly for Exercise and Sport, 1988, 94(2):94-98
[Mero 90] Mero A., Komi P. V. Reaction time and electromyographic activity during a sprint start. European Journal of Applied Physiology, 1990, 61:73-80
[Mero 92] Mero A., Komi P.V., GRegor R.J. Biomechanics of Sprint Running. Sports Medicine, 1992, 13(6):376-392
[Mero 06] Mero A., Kuittunen S., Harland M., Kyröläinen H., Komi P.V. Effect of muscle tendon length on joint moment and power during sprint starts. Journal of Sport Sciences, 2006, 24(2):165-173
[Mick 00] Mickelborough J., van der Linden M.L., Richards J., Ennos A.R. Validity and reliability of kinematic protocol for determining foot contact event. Gait And Posture, 2000, 11:32-37
[Monn 07] Monnet T., Desailly E., Begon M., Valle C., Lacouture P., Comparison of the SCoRE and HA methods for locating in vivo the glenohumeral joint centre. Journal of Biomechanics, 2007, 40:3487-3492
[Mono 97] Monod R., Flandrois H. Physiologie de l'activité physique, énergie, nutrition et performance. 2ème éd., Vigot, Paris, 1997
[Mora 88] Moravec P., Ruzicka J., Susanka P., Dostal E., Kodejs M. Nosek M. The 1987
International Athletic Foundation / IAAF scientific project report: time analysis of
the 100 metres events at the II Worlds Championships in athletics. IAAF Quarterly,
1988, 3:61-96
[Moua 01] Mouahid El K. Les tests d'évaluation de « l'explosivité » des athlètes revisités ; contribution à l'analyse mécanique de manipulations de charges à des fins d'entraînement. Thèse, Université de Poitiers. 2001
[Müll 97] Müller H., Hommel H. Biomechanical research project at the Vth Championships in athletics, Athens 1997: preliminary report. New studies in athletics IAAF, 1997, 12:2-3, 43-73
[Natt 97] Natta F., Breniere Y. Effets de la posture initiale dans le départ du sprint chez les
athlètes féminines de haut niveau. Science et Sport, 1997, 12(1):27s
[Natt 98] Natta F., Breniere Y. Influence de la posture initiale sur la dynamique du départ de
sprint en starting blocs. Science et motricité, 1998, 34:44-51
[Natt 01] Natta F., Réga C. Analyse cinétique et cinématique : du départ en starting blocs, de
la foulée de course a vitesse maximale. Rapport de recherche, Département des Sciences du Sport, INSEP, 2001
[Natt 06] Natta F., Decker L., Boisnoir A. Caractérisation des comportements posturo-
cinétiques en sprint. Rapport du projet de recherche MJSVA N°03-006, Département des Sciences du Sport, Laboratoire Mouvement, Action et Performance-INSEP. Décembre 2006
[Payn 71] Payne A.H., Blader F.B. The mechanics of the sprint start. Medicine and Sport, Biomechanics II, 1971, 6:225-231
[Pias 94] Piasenta J. Apprendre à observer. Plaidoyer pour une formation à l'observation du
comportement du sportif. INSEP-Publications, 1994
[Prov 01] Provost P. La mécanique présentée autrement. L'Harmattan, 2001
[Pont 90] Pontier J., Dufour A.B., Normand M. Le modèle euclidien en analyse des données. Editions de l'Université de Bruxelles, éd. Ellipses, 1990
[Rao 06] Rao G., Amarantini D., Berton E., Favier D. Influence of body segment's
parameters estimation models on inverse dynamics during gait. Journal of Biomechanics, 2006, 39:1531-1536
[Rein 97] Reinschmidt, C., Bogert, A., Nigg, B., Lundberg, A., Murphy, N. Effect of skin movement on the analysis of skeletal knee joint motion during running. Journal of Biomechanics, 1997, 30(7):729-732
[Rich 99] Richards J.G. The measurement of human motion: A comparison of commercially available systems. Human Movement Science, 1999, 18:589-602
[Robe 04] Robert P. Des jauges, des ponts ... et une solution de câblage pour chaque cas. Mesures, Septembre 2004, 767:57-60
[Sand 91] Sanderson L.K., McClements J.D., Robert E.G. Development of apparatus to provide immediate feedback to sprinters in the normal training environment. New Studies in Athletics, by IAAF, 1991, 6(2):33-41
[Salo 04] Salo A., Bezodis I., Wich starting style is faster in sprint running, a standing or
crouching start?, Sport Biomechanics, 2004, 3(1):43-54
[Sapo 90] Saporta G. Probabilités, analyse des données et statistique. Editions Technip, Paris, 1990
[Scho 92] Schot P.K., Knutzen M., K., Philip K. A
biomechanical analysis of four sprint start
positions. Research
Quarterly for Exercise and Sport, 1992, 63(2):137-147
[Sige 62] Sigerseth P. O., Grinaker V. F. Effect of foot spacing on velocity in sprints. Research
Quarterly, 1962, 33(4):599-606
[Stag 00] Stagni R., Leardini A, Cappozzo A, Benedetti M.G. Effects of hip joint centre
mislocation on gait analysis results. Journal of Biomechanics, 2000, 33:1479-1487
[Tayl 00] Taylor J. Incertitudes et analyse des erreurs dans les mesures physiques. Dunod, Paris, 2000
[Tiro 03] Tirosh O., Sparrow W. A. T. Identifying heel contact and toe-off using force plate
thresholds with a range of digital-filter cut-off frequencies. Journal of Applied Biomechanics, 2003, 19:178-184
[Vign 95] Vignerot V. Analyse mécanique des conditions optimales de départ en sprint - Application aux modalités d'apprentissage du déséquilibre. Thèse Université de Poitiers, 1995
[Vign 97] Vignerot V., Duboy J., Lacouture P. Mise au point d'une analyse mécanique en translation des différentes modalités de départ de sprint. Science et motricité, 1997, 34:26-36
[Wint 90] Winter D.A. Biomechanics and motor control of human movement. Second Edition University of Waterloo, Ontario, Canada, 1990
[Wu 02] Wu G. et al. ISB recommendation on definitions of joint coordinate systems of
various joints for reporting of human joint motion-part I: ankle, hip, and spine. Journal of Biomechanics, 2002, 35:543-548
[Wu 05] Wu G. et al. ISB recommendation on definitions of joint coordinate systems of
various joints for reporting of human joint motion-part II: shoulder, elbow and hand. Journal of Biomechanics, 2005, 38:981-992
[Zats 85] Zatsiorsky V., Seluyanov V. Estimation of the mass and inertia characteristics of
the human body by means of the best predictive regressions equations. In Biomechanics IX-B, 1985, 233-239

1
Annexe
Analyse en composantes principales
Le tableau 1 ci-dessous présente les variables (p = 91) déterminées suites aux mesures dynamométriques réalisées lors de 92 essais de départ de sprint. Ces variables sont utilisées dans l'analyse en composantes principales.
Tableau 1 Description des indices attribués aux variables issues des mesures dynamométriques Natures N° Indice Description
Poids [N] 1 'Poids' Poids du sujet
Temps [ms]
2 'dtLat' délai de latence
3 'dtImpul' durée d'impulsion
4 'tacMd' instants de la mise en action Mains droite
5 'tacMg' instants de la mise en action Mains gauche
6 'tac2M' instants de la mise en action les 2Mains
7 'tac2P' instants de la mise en action les 2Pieds
8 'tacPar' instants de la mise en action Pied arrière
9 'tacPav' instants de la mise en action Pied avant
10 'tFmaxMdX' instants de la Fx max Mains droite
11 'tFmaxMdZ' instants de la Fz max Mains droite
12 'tFmaxMgX' instants de la Fx max Mains gauche
13 'tFmaxMgZ' instants de la Fz max Mains gauche
14 'tFmax2Mx' instants de la Fx max 2Mains
15 'tFmax2Mz' instants de la Fz max 2Mains
16 'tFmaxParX' instants de la Fx max Pied arrière
17 'tFmaxParZ' instants de la Fz max Pied arrière
18 'tFmax2PX' instants de la Fx max 2Pieds
19 'tFmax2PZ' instants de la Fz max 2Pieds
20 'tFmaxPavX' instants de la Fx max Pied avant
21 'tFmaxPavZ' instants de la Fz max Pied avant
22 'tFmax4segX' instants de la Fx max 4segments
23 'tFmax4segZ' instants de la Fz max 4segments
24 'teMd' instants d'éjection Mains droite
25 'teMg' instants d'éjection Mains gauche
26 'te2M' instants d'éjection 2Mains
27 'tePar' instants d'éjection Pied arrière
28 'tePav' instants d'éjection Pied avant
Forces [N]
29 '2M_statX' Force 2Mains statique suivant Ox
30 '2M_statZ' Force 2Mains statique suivant Oz
31 'Md_statX' Force Main droite statique suivant Ox
32 'Md_statZ' Force Main droite statique suivant Oz
33 'Mg_statX' Force Main gauche statique suivant Ox
34 'Mg_statZ' Force Main gauche statique suivant Oz
35 '2P_statX' Force 2Pieds statique suivant Ox
36 '2P_statZ' Force 2Pieds statique suivant Oz
37 'Par_statX' Force Pied arrière statique suivant Ox
38 'Par_statZ' Force Pied arrière statique suivant Oz
39 'Pav_statX' Force Pied avant statique suivant Ox
40 'Pav_statZ' Force Pied avant statique suivant Oz
41 '2M_maxX' Force 2Mains maximale suivant Ox
42 '2M_maxZ' Force 2Mains maximale suivant Oz
43 'Md_maxX' Force Main droite maximale suivant Ox
44 'Md_maxZ' Force Main droite maximale suivant Oz
45 'Mg_maxX' Force Main gauche maximale suivant Ox
46 'Mg_maxZ' Force Main gauche maximale suivant Oz
47 '2PmaxX' Force 2Pieds maximale suivant Ox
48 '2PmaxZ' Force 2Pieds maximale suivant Oz
49 'Par_maxX' Force Pied arrière maximale suivant Ox
50 'Par_maxZ' Force 2Pied arrière maximale suivant Oz
51 'Pav_maxX' Force Pied avant maximale suivant Ox
52 'Pav_maxZ' Force 2Pied avant maximale suivant Oz
53 'SFR_maxX' Somme des Forces de réaction 2Mains maximale suivant Ox
54 'SFR_maxy' Somme des Forces de réaction 2Mains maximale suivant Oy
55 'SFR_maxZ' Somme des Forces de réaction 2Mains maximale suivant Oz
56 Fx2P_te2M' Force 2Pieds suivant Ox à (te2M)
57 Fz2P_te2M' Force 2Pieds suivant Oz à (te2M)
58 'Fxpav_tepar' Force Pied av suivant Ox à (tepar)
59 'Fzpav_tepar' Force Pied av suivant Oz à (tepar)
Vitesses [m/s]
60 Vxte2M' vitesse suivant Ox à (te2M) instant d'éjection des 2Mains
61 'Vxtepar' vitesse suivant Ox à (tepar) instant d'éjection du pied arrière
62 'Vxtepav' vitesse suivant Ox à (tepav) instant d'éjection du pied avant
63 Vyte2M' vitesse suivant Oy à (te2M) instant d'éjection des 2Mains
64 'Vytepar' vitesse suivant Oy à (tepar) instant d'éjection du pied arrière
65 'Vytepav' vitesse suivant Oy à (tepav) instant d'éjection du pied avant
66 Vzte2M' vitesse suivant Oz à (te2Mm) instant d'éjection des 2Mains
67 'Vztepar' vitesse suivant Oz à (tepar) instant d'éjection du pied arrière
68 'Vztepav' vitesse suivant Oz à (tepav) instant d'éjection du pied avant
69 NVte2M' Norme de V à (te2M) instant d'éjection des 2Mains
70 'NVtepar' Norme de V à (tepar) instant d'éjection du pied arrière
71 'NVtepav' Norme de V à (tepav) instant d'éjection du pied avant
72 'VxtFmax2P' Vitesse suivant Ox à (tFmax2P) instant de Fmax des 2Pieds
Positions [m]
73 Oxte2M' déplacement suivant Ox à (te2M) instant d'éjection des 2Mains
74 'Oxtepar' déplacement suivant Ox à (tepar) instant d'éjection du pied arrière
75 'Oxtepav' déplacement suivant Ox à (tepav) instant d'éjection du pied avant
76 Oyte2M' déplacementsuivant Oy à (te2M) instant d'éjection des 2Mains
77 'Oytepar' déplacement suivant Oy à (tepar) instant d'éjection du pied arrière
78 'Oytepav' déplacement suivant Oy à (tepav) instant d'éjection du pied avant
79 Ozte2M' déplacement suivant Oz à (te2M) instant d'éjection des 2Mains
80 'Oztepar' déplacement suivant Oz à (tepar) instant d'éjection du pied arrière
81 'Oztepav' déplacement suivant Oz à (tepav) instant d'éjection du pied avant
82 NOCG_te2M' Norme du déplacement à (te2M) instant d'éjection des 2Mains
83 'NOCG_tepar' Norme du déplacement V à (tepar) instant d'éjection du pied arr.
84 'NOCG_tepav' Norme du déplacement à (tepav) instant d'éjection du pied avant
Angles [deg]
85 ieta_te2M' angle à (te2M) instant d'éjection des deux mains
86 ieta_tFmax2PX' angle à (tFmax2PX) instant de Fx max des deux pieds
87 ieta_tFmax2PZ' angle à (tFmax2PZ) instant de Fz max des deux pieds
88 ieta_tePar' angle à (tePar) instant d'éjection du pied arrière
89 ieta_tFmaxPavX' angle à (tFmaxPavX) instant de Fx max Pied avant
90 ieta_tFmaxPavZ' angle à (tFmaxPavZ) instant de Fz max Pied avant
91 ieta_tePav' angle à (tePav) instant d'éjecton
Tableau 2 Paramètres descriptifs des variables
issues de 92 mesures dynamométriques
du départ de
sprint
Natures
Dans le tableau 2, les paramètres statistiques descriptifs sont calculés en prenant en compte l'ensemble des essais (m = 92) de départ de sprint. Les temps sont référencés par rapport à l'instant de mise en action déterminés suite à la mesure de la somme des forces.
Poids [N]

Les Temps [ms]
Les Forces [% Folds]
N°
|
Variables |
Moyenne |
Ecart type |
Minimum |
Maximum |
|||||||
|
1 |
'Poids' |
684 |
101 |
469 |
938 |
||||||
|
2 |
'dtLat' |
146 |
32 |
101 |
263 |
||||||
|
3 |
'dtImpul' |
450 |
46 |
365 |
616 |
||||||
|
4 |
'tacMd' |
39 |
40 |
-29 |
148 |
||||||
|
5 |
'tacMg' |
20 |
35 |
-47 |
133 |
||||||
|
6 |
'tac2M' |
5 |
29 |
-98 |
85 |
||||||
|
7 |
'tac2P' |
4 |
30 |
-112 |
71 |
||||||
|
8 |
'tacPar' |
16 |
24 |
-94 |
64 |
||||||
|
9 |
'tacPav' |
28 |
34 |
-43 |
154 |
||||||
|
10 |
'tFmaxMdX' |
136 |
53 |
-79 |
498 |
||||||
|
11 |
'tFmaxMdZ' |
37 |
63 |
-134 |
201 |
||||||
|
12 |
'tFmaxMgX' |
153 |
73 |
73 |
636 |
||||||
|
13 |
'tFmaxMgZ' |
44 |
59 |
-178 |
189 |
||||||
|
14 |
'tFmax2Mx' |
12 |
75 |
-178 |
221 |
||||||
|
15 |
'tFmax2Mz' |
46 |
55 |
-172 |
197 |
||||||
|
16 |
'tFmaxParX' |
125 |
34 |
62 |
268 |
||||||
|
17 |
'tFmaxParZ' |
122 |
31 |
56 |
263 |
||||||
|
18 |
'tFmax2PX' |
142 |
44 |
73 |
392 |
||||||
|
19 |
'tFmax2PZ' |
137 |
42 |
71 |
311 |
||||||
|
20 |
'tFmaxPavX' |
364 |
45 |
285 |
522 |
||||||
|
21 |
'tFmaxPavZ' |
363 |
43 |
282 |
525 |
||||||
|
22 |
'tFmax4segX' |
175 |
91 |
80 |
493 |
||||||
|
23 |
'tFmax4segZ' |
107 |
40 |
50 |
351 |
||||||
|
24 |
'teMd' |
167 |
32 |
113 |
257 |
||||||
|
25 |
'teMg' |
171 |
38 |
115 |
304 |
||||||
|
26 |
'te2M' |
180 |
36 |
128 |
303 |
||||||
|
27 |
'tePar' |
223 |
40 |
108 |
357 |
||||||
|
28 |
'tePav' |
450 |
46 |
365 |
616 |
||||||
|
29 |
'2M_statX' |
-11 |
4 |
-19 |
0 |
||||||
|
30 |
'2M_statZ' |
66 |
11 |
36 |
86 |
||||||
|
31 |
'Md_statX' |
-5 |
2 |
-9 |
0 |
||||||
|
32 |
'Md_statZ' |
34 |
8 |
12 |
49 |
||||||
|
33 |
'Mg_statX' |
-6 |
2 |
-10 |
0 |
||||||
|
34 |
'Mg_statZ' |
32 |
5 |
17 |
41 |
||||||
|
35 |
'2P_statX' |
11 |
4 |
0 |
18 |
||||||
|
36 |
'2P_statZ' |
34 |
11 |
14 |
64 |
||||||
|
37 |
'Par_statX' |
6 |
3 |
0 |
14 |
||||||
|
38 |
'Par_statZ' |
16 |
5 |
6 |
28 |
||||||
|
39 |
'Pav_statX' |
5 |
2 |
0 |
10 |
||||||
|
40 |
'Pav_statZ' |
18 |
10 |
2 |
48 |
||||||
|
41 |
'2M_maxX' |
13 |
4 |
4 |
21 |
||||||
|
42 |
'2M_maxZ' |
83 |
18 |
38 |
125 |
||||||
|
43 |
'Md_maxX' |
3 |
3 |
0 |
17 |
||||||
|
44 |
'Md_maxZ' |
42 |
13 |
12 |
81 |
||||||
|
45 |
'Mg_maxX' |
2 |
2 |
0 |
8 |
||||||

Les Vitesses [m/s]
Les Positions [m]
Les Angles [deg]
|
Annexe 1 |
|||||
|
46 |
'Mg_maxZ' |
42 |
9 |
18 |
59 |
|
47 |
'2PmaxX' |
108 |
25 |
44 |
207 |
|
48 |
'2PmaxZ' |
127 |
19 |
56 |
162 |
|
49 |
'Par_maxX' |
60 |
21 |
23 |
133 |
|
50 |
'Par_maxZ' |
63 |
19 |
23 |
109 |
|
51 |
'Pav_maxX' |
93 |
13 |
53 |
125 |
|
52 |
'Pav_maxZ' |
123 |
11 |
103 |
150 |
|
53 |
'SFR_maxX' |
114 |
24 |
53 |
209 |
|
54 |
'SFR_maxy' |
11 |
5 |
1 |
20 |
|
55 |
'SFR_maxZ' |
169 |
16 |
131 |
218 |
|
56 |
'Fx2P_teM' |
94 |
24 |
37 |
203 |
|
57 |
'Fz2P_teM' |
107 |
23 |
59 |
161 |
|
58 |
'Fxpav_tepav' |
63 |
14 |
34 |
92 |
|
59 |
'Fzpav_tepar' |
77 |
13 |
52 |
108 |
|
60 |
'Vxtem' |
0,99 |
0,21 |
0,51 |
1,41 |
|
61 |
'Vxtepar' |
1,33 |
0,33 |
0,59 |
2,23 |
|
62 |
'Vxtepav' |
2,87 |
0,25 |
2,19 |
3,42 |
|
63 |
'Vytem' |
0,02 |
0,06 |
-0,15 |
0,15 |
|
64 |
'Vytepar' |
-0,01 |
0,06 |
-0,17 |
0,12 |
|
65 |
'Vytepav' |
-0,06 |
0,17 |
-0,39 |
0,34 |
|
66 |
'Vztem' |
0,62 |
0,14 |
0,18 |
0,90 |
|
67 |
'Vztepar' |
0,60 |
0,13 |
0,17 |
0,84 |
|
68 |
'Vztepav' |
0,34 |
0,18 |
-0,03 |
0,69 |
|
69 |
'NVtem' |
1,18 |
0,19 |
0,66 |
1,52 |
|
70 |
'NVtepar' |
1,47 |
0,33 |
0,69 |
2,38 |
|
71 |
'NVtepav' |
2,90 |
0,25 |
2,19 |
3,43 |
|
72 |
'VxtFmax2P' |
0,61 |
0,22 |
0,14 |
1,32 |
|
73 |
'Oxtem' |
0,05 |
0,03 |
0,00 |
0,14 |
|
74 |
'Oxtepar' |
0,11 |
0,05 |
0,00 |
0,25 |
|
75 |
'Oxtepav' |
0,59 |
0,06 |
0,44 |
0,75 |
|
76 |
'Oytem' |
0,00 |
0,01 |
-0,03 |
0,02 |
|
77 |
'Oytepar' |
0,00 |
0,01 |
-0,03 |
0,03 |
|
78 |
'Oytepav' |
-0,01 |
0,03 |
-0,10 |
0,06 |
|
79 |
'Oztem' |
0,05 |
0,02 |
0,01 |
0,10 |
|
80 |
'Oztepar' |
0,08 |
0,03 |
0,01 |
0,16 |
|
81 |
'Oztepav' |
0,20 |
0,05 |
0,08 |
0,30 |
|
82 |
'NOCG_tem' |
0,08 |
0,03 |
0,03 |
0,15 |
|
83 |
'NOCG_tepar' |
0,14 |
0,05 |
0,03 |
0,30 |
|
84 |
'NOCG tepav' |
0,63 |
0,06 |
0,50 |
0,81 |
|
85 |
ieta_te2M' |
32 |
9 |
9 |
56 |
|
86 |
ieta_tFmax2PX' |
41 |
10 |
11 |
65 |
|
87 |
ieta_tFmax2PZ' |
43 |
11 |
9 |
80 |
|
88 |
ieta_tePar' |
25 |
6 |
10 |
41 |
|
89 |
ieta_tFmaxPavX' |
14 |
4 |
7 |
23 |
|
90 |
ieta_tFmaxPavZ' |
14 |
4 |
6 |
22 |
|
91 |
ieta_tePav' |
7 |
4 |
-1 |
14 |
La confrontation simultanée des 91 variables permet de définir la matrice des corrélations exprimées dans le tableau 3. Dans le triangle inférieur de cette matrice sont exprimés les seuls éléments significatifs (p < 0,05).
Tableau 3 Matrice des corrélations entre toutes les variables présentées en six parties
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
1 1 -0,2 -0,1 -0,1 0,1 0,13 -0 -0,1 0,17 0,02 0,12 0,1 -0 0,12 0,04 -0 -0 -0 -0,1 -0,1 -0,1 -0,1 0,17 0,3 0,1 0,14 0 -0,1 0,04 0,3
2 0 1 0,04 -0,1 -0,3 -0,4 -0,3 -0,1 -0,5 0,07 0 -0,1 -0,3 -0,1 -0,1 0,01 -0 0,02 0,1 0,01 0,01 -0,1 0,13 0,04 -0,1 -0 0,03 0,04 -0 -0,2
3 0 0 1 0,38 0,38 0,27 -0 0,1 0,02 0,28 -0,1 0,25 0,08 0,01 0,05 0,7 0,68 0,8 0,6 0,95 0,96 0,5 0,35 0,5 0,46 0,54 0,7 1 0,17 -0,5
4 0 0 0 1 0,06 0,36 0,09 0,13 0,12 0,28 -0,1 0,04 0,02 0,07 -0 0,26 0,21 0,32 0,21 0,33 0,37 0,33 0,06 0,26 0,48 0,4 0,23 0,38 0,1 -0,2
5 0 0 0 0 1 0,64 0,22 -0,1 0,35 0,19 -0,1 0,23 0,03 -0,2 0,09 0,43 0,43 0,43 0,17 0,4 0,39 0,21 0,26 0,27 0,18 0,26 0,41 0,38 -0,1 -0,4
6 0 0 0 0 0 1 0,37 0,07 0,32 0,14 -0,2 0,13 0,07 -0,1 0,07 0,24 0,19 0,33 0,02 0,29 0,31 0,25 -0 0,13 0,23 0,19 0,21 0,27 0,07 -0,3
7 0 0 0 0 0 0 1 0,57 0,56 0,06 0,25 0,29 -0 0,14 0,05 0,18 0,14 0,07 0,17 -0 -0 0,12 0,03 0,23 0,24 0,25 -0,1 -0 0,08 0,27
8 0 0 0 0 0 0 0 1 0,21 0,07 0,25 0,27 0,13 0,23 0,14 0,24 0,22 0,14 0,3 0,14 0,15 0,16 -0 0,22 0,23 0,25 0,07 0,1 0,31 0,27
9 0 0 0 0 0 0 0 0 1 0,12 0,27 0,23 0,31 0,22 0,32 0,39 0,38 0,21 0,27 0,05 0,05 0,12 0,16 0,33 0,34 0,31 0,19 0,02 -0,1 0,23
10 0 0 0 0 0 0 0 0 0 1 0,13 0,28 0,08 -0,1 0,06 0,31 0,28 0,27 0,24 0,25 0,31 0,12 0,29 0,41 0,41 0,45 0,18 0,28 -0,3 -0,1
11 0 0 0 0 0 0 0 0 0 0 1 0,19 0,29 0,52 0,47 0,14 0,08 -0,1 0,12 -0,1 -0 -0,2 -0,1 0,31 0,15 0,16 -0,1 -0,1 -0,1 0,41
12 0 0 0 0 0 0 0 0 0 0 0 1 0,08 0,1 0,1 0,41 0,31 0,27 0,28 0,25 0,26 0,12 0,2 0,47 0,37 0,47 0,15 0,25 -0,1 -0
13 0 0 0 0 0 0 0 0 0 0 0 0 1 0,47 0,82 0,19 0,12 0,12 0,03 0,13 0,16 0,09 -0,1 0,15 0,11 0,06 0,03 0,08 -0,1 0,2
14 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,48 0,1 0,03 -0,1 0,15 -0 0,02 0,03 -0,1 0,31 0,18 0,17 -0,1 0,01 0,17 0,42
15 0 0 0 0 0 0 0 0 0 0 0 0 0,82 0 1 0,21 0,11 0,07 -0 0,08 0,11 -0,1 -0,3 0,16 0,04 0,02 -0 0,05 -0,1 0,27
16 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,89 0,71 0,7 0,71 0,7 0,24 0,43 0,56 0,55 0,58 0,8 0,7 -0 -0,3
17 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,89 1 0,73 0,75 0,7 0,67 0,29 0,51 0,53 0,5 0,53 0,83 0,68 0,01 -0,3
18 0 0 0,8 0 0 0 0 0 0 0 0 0 0 0 0 0,71 0,73 1 0,64 0,78 0,75 0,48 0,42 0,54 0,47 0,55 0,71 0,8 0,1 -0,5
19 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,7 0,75 0 1 0,54 0,53 0,48 0,54 0,58 0,66 0,69 0,6 0,6 0,2 -0,1
20 0 0 0,95 0 0 0 0 0 0 0 0 0 0 0 0 0,71 0,7 0,78 0 1 0,97 0,43 0,32 0,43 0,37 0,43 0,74 0,95 0,11 -0,6
21 0 0 0,96 0 0 0 0 0 0 0 0 0 0 0 0 0,7 0 0,75 0 0,97 1 0,45 0,32 0,48 0,41 0,49 0,69 0,96 0,1 -0,5
22 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,39 0,39 0,48 0,54 0,13 0,5 0,27 -0,1
23 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,6 0,48 0,58 0,4 0,35 -0 -0,1
24 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,66 0,83 0,36 0,5 -0 0,1
25 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,93 0,31 0,46 0,05 0,05
26 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,83 0,93 1 0,34 0,54 0,04 0,02
27 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,8 0,83 0,71 0 0,74 0 0 0 0 0 0 1 0,7 0,02 -0,6
28 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,8 0 0,95 0,96 0 0 0 0 0 0 1 0,17 -0,5
29 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,17
30 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
31 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,93 0
32 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,91
33 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,93 0
34 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,76
35 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0,9 0
36 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -1
37 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0,7 0
38 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
39 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
40 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0,9
41 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0,9 0
42 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,88
43 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
44 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,72
45 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
|
Annexe 1 |
||||||||||||||||||||||||||||||
|
2ème partie de la matrice des corrélations |
||||||||||||||||||||||||||||||
|
1 2 3 4 5 6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
||||||
|
46 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
47 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
48 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
49 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
50 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
51 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0,7 |
|
52 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
53 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
54 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
55 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
56 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
57 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
58 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
59 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
60 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
61 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
62 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
63 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
64 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
65 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
66 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
67 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
68 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
70 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
71 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
72 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
73 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
74 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
75 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
76 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
77 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
78 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
79 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
80 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
82 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
83 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
84 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
85 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
86 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
87 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
88 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
89 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
90 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
91 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
31 32 33 34 35 36 37 38 39 40 41 42 43 44 45
1 0,13 0,37 -0,1 0,09 0,03 -0,3 0,1 -0,2 -0,1 -0,2 -0,1 0,18 0,46 0,26 0,06
2 -0,1 -0,2 0,05 -0,1 -0,1 0,15 -0,2 0,19 0,15 0,07 0,06 -0,1 -0,1 -0,1 -0,2
3 0,14 -0,5 0,17 -0,4 -0,2 0,54 -0,4 -0 0,22 0,59 -0,1 -0,4 -0,1 -0,3 0,04
4 0,08 -0,2 0,1 -0,1 -0,1 0,21 -0,1 -0 -0 0,22 -0,1 -0,3 -0,3 -0,5 0,15
5 -0 -0,3 -0,1 -0,5 0,09 0,44 -0,1 0,03 0,31 0,46 -0,1 -0,4 0,19 -0,1 -0,2
6 0,12 -0,2 -0 -0,3 0,03 0,27 0 -0,1 0,06 0,34 -0,2 -0,3 -0 -0,2 0,01
7 0,21 0,29 -0,1 0,13 0,04 -0,3 0,21 -0,1 -0,3 -0,2 -0,2 0,26 0,24 0,36 -0,1
8 0,36 0,24 0,22 0,2 -0,2 -0,3 -0,1 -0,2 -0,3 -0,2 -0,3 0,36 0 0,33 -0,1
9 0,01 0,27 -0,3 0,07 0,3 -0,2 0,36 0,03 -0 -0,3 0,07 0,27 0,42 0,33 -0,1
10 -0,2 -0,1 -0,2 -0,2 0,23 0,12 0,14 0,1 0,21 0,08 0,21 -0,1 -0 -0 -0,1
11 -0 0,42 -0,2 0,24 0,21 -0,4 0,31 -0 -0,1 -0,4 0,27 0,6 0,43 0,58 -0,1
12 0,03 0,12 -0,2 -0,2 0,23 -0 0,16 0,01 0,17 -0 0,07 0,08 0,18 0,25 -0,3
13 0,02 0,22 -0,1 0,09 0,15 -0,2 0,15 -0,1 0,04 -0,2 0,2 0,4 0,18 0,26 0,08
14 0,25 0,41 0,06 0,29 -0,1 -0,4 -0 -0,2 -0,2 -0,4 0,09 0,52 0,34 0,38 0,17
15 0,02 0,29 -0,2 0,13 0,14 -0,3 0,19 -0,2 -0 -0,2 0,22 0,5 0,3 0,41 -0
16 0,04 -0,3 -0,1 -0,2 0,03 0,32 -0,1 0,03 0,26 0,33 0,03 -0,1 0,14 -0 -0,1
17 -0 -0,3 0,02 -0,2 -0 0,33 -0,2 -0 0,28 0,35 0,01 -0,1 0,08 -0,1 -0,1
18 0,1 -0,4 0,08 -0,4 -0,1 0,47 -0,2 0,01 0,19 0,49 -0,1 -0,3 0,01 -0,2 -0,1
19 0,2 -0,1 0,17 0,03 -0,2 0,09 -0,2 0 -0 0,1 -0,1 0,01 0,04 -0 0,03
20 0,09 -0,5 0,12 -0,4 -0,1 0,57 -0,3 0,02 0,25 0,6 -0 -0,4 -0,1 -0,3 -0
21 0,09 -0,5 0,1 -0,4 -0,1 0,53 -0,3 0,01 0,23 0,56 -0 -0,4 -0,1 -0,3 -0
22 0,24 -0,1 0,26 -0,1 -0,3 0,11 -0,3 -0,1 -0,1 0,18 -0,3 -0,2 -0,1 -0,2 -0
23 -0,1 -0,1 -0 -0,1 -0 0,12 -0,1 0,17 0,15 0,05 0,04 -0,1 0,19 -0 0,05
24 0,05 0,21 -0,1 -0,1 0,05 -0,1 0,06 0,01 0 -0,1 0,15 0,16 0,44 0,28 -0
25 0,12 0,01 -0 0,11 -0 -0,1 -0 -0 -0 -0 0 0,02 0,07 -0,1 0,14
26 0,11 0,05 -0 -0 -0 -0 -0 0,01 -0 -0 0,02 0,01 0,19 0,05 0,07
27 0 -0,5 0,04 -0,4 -0 0,56 -0,2 0,14 0,34 0,53 0,01 -0,4 -0 -0,3 -0
28 0,14 -0,5 0,17 -0,4 -0,2 0,54 -0,4 -0 0,22 0,59 -0,1 -0,4 -0,1 -0,3 0,04
29 0,93 0,03 0,93 0,32 -0,9 -0,2 -0,7 -0,6 -0,5 0,08 -0,9 0,06 -0,2 -0,1 0,4
30 0,26 0,91 0,05 0,76 -0,1 -1 0,27 -0,4 -0,6 -0,9 -0,1 0,88 0,4 0,72 0,13
31 1 0,14 0,73 0,36 -0,8 -0,3 -0,5 -0,5 -0,6 -0 -0,8 0,18 0,03 0,08 0,3
32 0 1 -0,1 0,43 0,07 -0,9 0,38 -0,3 -0,5 -0,8 0,01 0,82 0,53 0,82 -0
33 0,73 0 1 0,24 -0,9 -0 -0,8 -0,5 -0,5 0,17 -0,8 -0,1 -0,3 -0,2 0,44
34 0 0 0 1 -0,3 -0,8 -0 -0,3 -0,6 -0,6 -0,2 0,65 0,05 0,28 0,31
35 -0,8 0 -0,9 0 1 0,08 0,85 0,55 0,47 -0,2 0,78 0,05 0,21 0,18 -0,4
36 0 -0,9 0 -0,8 0 1 -0,3 0,35 0,61 0,9 0,09 -0,9 -0,4 -0,7 -0,1
37 0 0 -0,8 0 0,85 0 1 0,5 -0,1 -0,5 0,62 0,33 0,27 0,38 -0,3
38 0 0 0 0 0 0 0 1 0,19 -0,1 0,5 -0,3 -0,1 -0,2 -0,1
39 0 0 0 0 0 0 0 0 1 0,56 0,44 -0,5 -0,1 -0,3 -0,4
40 0 -0,8 0 0 0 0,9 0 0 0 1 -0,1 -0,8 -0,4 -0,7 -0,1
41 -0,8 0 -0,8 0 0,78 0 0 0 0 0 1 0,1 0,23 0,12 -0,2
42 0 0,82 0 0 0 -0,9 0 0 0 -0,8 0 1 0,49 0,85 0,03
43 0 0 0 0 0 0 0 0 0 0 0 0 1 0,66 -0,1
44 0 0,82 0 0 0 -0,7 0 0 0 0 0 0,85 0 1 -0,3
45 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1
|
Annexe 1 |
||||||||||||||
|
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
|
-0 |
0,29 |
-0 |
0,32 |
0,1 |
0,1 |
-0,3 |
0,38 |
-0,3 |
0,17 |
0,22 |
-0 |
0,2 |
0,11 |
0,36 |
|
-0,1 |
-0,1 |
0,07 |
-0,1 |
0,01 |
-0,1 |
0,16 |
-0,1 |
-0 |
-0,3 |
-0,1 |
0,13 |
-0,1 |
0,19 |
-0,2 |
|
-0,3 |
-0,5 |
0,1 |
-0,3 |
-0,1 |
-0,6 |
-0,1 |
-0,6 |
-0,2 |
-0,1 |
-0,4 |
0,11 |
-0,6 |
-0,3 |
-0,5 |
|
0 |
-0,5 |
-0,2 |
-0,4 |
-0,2 |
-0,3 |
-0,2 |
-0,4 |
0,1 |
-0,2 |
-0,4 |
-0,1 |
-0,2 |
-0,1 |
-0,1 |
|
-0,6 |
-0 |
0,22 |
0,01 |
0,06 |
-0,2 |
-0,2 |
-0,1 |
-0,2 |
0,03 |
0,03 |
0,12 |
-0,2 |
-0,1 |
0,1 |
|
-0,3 |
-0,2 |
0,02 |
-0,1 |
-0,1 |
-0,2 |
-0,3 |
-0,2 |
-0,1 |
0,1 |
-0,2 |
-0,1 |
-0,2 |
-0,3 |
0,09 |
|
0,01 |
0,01 |
-0,3 |
-0,1 |
-0,2 |
0,31 |
-0,1 |
0,07 |
0,2 |
0,08 |
0,03 |
-0,3 |
0,2 |
-0,2 |
0,19 |
|
0,23 |
-0,1 |
-0,2 |
-0 |
-0,2 |
0,11 |
0,06 |
-0,1 |
0,2 |
0,04 |
-0 |
-0,2 |
-0 |
-0,2 |
-0,1 |
|
0,07 |
0,18 |
-0,2 |
0,05 |
-0,1 |
0,28 |
-0,2 |
0,24 |
0,11 |
0,13 |
0,19 |
-0,2 |
0,25 |
-0,2 |
0,26 |
|
-0,1 |
-0,1 |
-0 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
0,05 |
0,08 |
-0,2 |
-0,1 |
-0 |
-0,1 |
0,08 |
|
0,3 |
0,27 |
-0,2 |
0,13 |
-0,1 |
0,35 |
0,02 |
0,35 |
-0 |
0,32 |
0,24 |
-0,2 |
0,27 |
-0,2 |
0,11 |
|
-0,2 |
-0,1 |
-0,2 |
-0,2 |
-0,2 |
-0 |
-0,3 |
-0,1 |
0,1 |
0,06 |
-0,2 |
-0,3 |
-0 |
-0,3 |
0,24 |
|
0,4 |
0,13 |
-0,1 |
0 |
-0,1 |
0,13 |
0,03 |
0,15 |
0,15 |
0,33 |
0,12 |
-0,2 |
0,04 |
-0,3 |
-0,1 |
|
0,44 |
0,02 |
-0,4 |
-0,1 |
-0,3 |
0,24 |
-0 |
0,13 |
0,12 |
0,21 |
0,06 |
-0,3 |
0,18 |
-0,1 |
-0 |
|
0,36 |
0,17 |
-0,2 |
0,02 |
-0,2 |
0,18 |
-0 |
0,21 |
0,06 |
0,39 |
0,18 |
-0,2 |
0,09 |
-0,3 |
-0,1 |
|
-0,1 |
-0 |
0,16 |
0,02 |
0,06 |
-0,3 |
-0,1 |
-0,1 |
-0,1 |
-0 |
0,08 |
0,16 |
-0,3 |
-0,3 |
-0,2 |
|
-0,2 |
0 |
0,28 |
0,07 |
0,14 |
-0,3 |
-0,1 |
-0,1 |
-0,2 |
-0,1 |
0,11 |
0,28 |
-0,3 |
-0,2 |
-0,3 |
|
-0,3 |
-0,3 |
0,13 |
-0,1 |
0,03 |
-0,5 |
-0,2 |
-0,3 |
-0,1 |
-0,2 |
-0,2 |
0,1 |
-0,4 |
-0,3 |
-0,3 |
|
0,05 |
-0,2 |
-0 |
-0,1 |
-0,1 |
-0,3 |
-0,1 |
-0,2 |
0,06 |
-0,3 |
-0,1 |
0,02 |
-0,2 |
0 |
-0,1 |
|
-0,3 |
-0,4 |
0,22 |
-0,2 |
-0 |
-0,5 |
0 |
-0,5 |
-0,1 |
-0,1 |
-0,2 |
0,19 |
-0,7 |
-0,4 |
-0,5 |
|
-0,3 |
-0,4 |
0,15 |
-0,3 |
-0,1 |
-0,5 |
-0 |
-0,5 |
-0,1 |
-0 |
-0,3 |
0,13 |
-0,6 |
-0,4 |
-0,5 |
|
-0,1 |
-0,5 |
-0,3 |
-0,5 |
-0,4 |
-0,2 |
-0,1 |
-0,5 |
0,13 |
-0,4 |
-0,4 |
-0,2 |
-0,1 |
0,08 |
-0,1 |
|
-0,2 |
-0,1 |
0,05 |
-0 |
0,09 |
-0,1 |
0,09 |
-0 |
-0,1 |
-0,2 |
-0,1 |
0 |
0,07 |
0,14 |
0,14 |
|
-0,1 |
-0,2 |
-0,3 |
-0,2 |
-0,2 |
0,03 |
-0,1 |
-0,1 |
-0,1 |
0,05 |
-0,2 |
-0,4 |
0,12 |
-0,1 |
0,22 |
|
0,14 |
-0,3 |
-0,3 |
-0,3 |
-0,4 |
-0,1 |
-0,4 |
-0,2 |
0,14 |
-0,1 |
-0,3 |
-0,3 |
0,04 |
-0,1 |
0,3 |
|
-0 |
-0,4 |
-0,3 |
-0,4 |
-0,3 |
-0,1 |
-0,3 |
-0,3 |
0,1 |
-0,1 |
-0,4 |
-0,4 |
0,04 |
-0,1 |
0,3 |
|
-0,3 |
0,02 |
0,48 |
0,28 |
0,43 |
-0,5 |
-0 |
-0,1 |
-0,3 |
-0 |
0,17 |
0,48 |
-0,6 |
-0,3 |
-0,3 |
|
-0,3 |
-0,5 |
0,1 |
-0,3 |
-0,1 |
-0,6 |
-0,1 |
-0,6 |
-0,2 |
-0,1 |
-0,4 |
0,11 |
-0,6 |
-0,3 |
-0,5 |
|
0,23 |
-0,3 |
-0,2 |
-0,1 |
-0,2 |
-0,2 |
0,01 |
-0,3 |
-0,1 |
-0,2 |
-0,2 |
-0 |
-0,3 |
0,04 |
-0,2 |
|
0,67 |
0,29 |
-0,5 |
0,06 |
-0,3 |
0,7 |
0,07 |
0,44 |
0,16 |
0,22 |
0,18 |
-0,5 |
0,65 |
0,11 |
0,35 |
|
0,24 |
-0,2 |
-0,4 |
-0,1 |
-0,2 |
-0,1 |
-0,1 |
-0,2 |
-0 |
-0,1 |
-0,2 |
-0,2 |
-0,2 |
-0,1 |
-0 |
|
0,4 |
0,28 |
-0,5 |
0,03 |
-0,3 |
0,72 |
0,02 |
0,45 |
0,1 |
0,24 |
0,18 |
-0,5 |
0,68 |
0,06 |
0,4 |
|
0,18 |
-0,3 |
-0,1 |
-0,1 |
-0,1 |
-0,3 |
0,08 |
-0,4 |
-0,2 |
-0,3 |
-0,3 |
0,08 |
-0,4 |
0,16 |
-0,3 |
|
0,83 |
0,19 |
-0,3 |
0,08 |
-0,2 |
0,41 |
0,13 |
0,25 |
0,2 |
0,1 |
0,12 |
-0,2 |
0,36 |
0,15 |
0,14 |
|
-0,2 |
0,39 |
0,19 |
0,22 |
0,22 |
0,24 |
-0,1 |
0,38 |
0,17 |
0,29 |
0,3 |
-0 |
0,28 |
-0,2 |
0,34 |
|
-0,7 |
-0,3 |
0,51 |
-0 |
0,31 |
-0,7 |
-0,1 |
-0,4 |
-0,2 |
-0,2 |
-0,2 |
0,46 |
-0,7 |
-0,1 |
-0,4 |
|
0,09 |
0,38 |
-0 |
0,19 |
0,11 |
0,44 |
-0 |
0,44 |
0,29 |
0,32 |
0,27 |
-0,2 |
0,42 |
-0,2 |
0,4 |
|
-0,2 |
0,06 |
0,31 |
0,12 |
0,41 |
-0,1 |
0,24 |
0,02 |
0,2 |
-0,1 |
-0 |
0,13 |
-0,1 |
0 |
0,12 |
|
-0,5 |
0,09 |
0,42 |
0,1 |
0,24 |
-0,3 |
-0,1 |
-0 |
-0,2 |
0,02 |
0,11 |
0,31 |
-0,2 |
0 |
-0 |
|
-0,6 |
-0,3 |
0,39 |
-0,1 |
0,13 |
-0,7 |
-0,2 |
-0,5 |
-0,3 |
-0,2 |
-0,2 |
0,43 |
-0,7 |
-0,1 |
-0,4 |
|
-0 |
0,28 |
0,18 |
0,09 |
0,17 |
0,2 |
0,08 |
0,29 |
0,15 |
0,27 |
0,2 |
-0 |
0,28 |
-0,1 |
0,09 |
|
0,69 |
0,45 |
-0,3 |
0,19 |
-0,2 |
0,67 |
0,14 |
0,55 |
0,17 |
0,41 |
0,36 |
-0,4 |
0,55 |
-0,1 |
0,2 |
|
-0 |
0,33 |
-0,2 |
0,17 |
-0,1 |
0,43 |
-0,1 |
0,48 |
-0,1 |
0,32 |
0,32 |
-0,2 |
0,44 |
-0,1 |
0,31 |
|
0,22 |
0,48 |
-0,2 |
0,24 |
-0,1 |
0,66 |
0,11 |
0,58 |
0,04 |
0,39 |
0,41 |
-0,3 |
0,55 |
-0 |
0,3 |
|
0,41 |
-0,2 |
-0,1 |
-0,1 |
0,01 |
-0,1 |
0,05 |
-0,1 |
-0,1 |
0,08 |
-0,2 |
-0,2 |
-0,1 |
-0 |
0,05 |
3ème partie de la matrice des corrélations
4ème partie de la matrice des corrélations
0 0 0 0 0 0 0 0 0 0 0
210
|
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
|||||||||||||||||||||||||||||||||||||
|
46 |
0 |
0 |
0 |
0,83 |
0 |
0 |
0 46 0 0 0 0,83 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
47 |
0 |
0 |
0 |
0 |
0 |
0 |
0 47 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
48 |
0 |
0 |
0 |
0 |
0 |
0 |
0 48 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
49 |
0 |
0 |
0 |
0 |
0 |
0 |
0 49 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
50 |
0 |
0 |
0 |
0 |
0 |
0 |
0 50 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
51 |
0 |
0,72 |
0 |
0 |
0 |
-0,7 |
0 51 0 0,72 0 0 0 -0,7 0 0 0 -0,7 0 0 0 0 0 |
0 |
0 |
-0,7 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
52 |
0 |
0 |
0 |
0 |
0 |
0 |
0 52 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
53 |
0 |
0 |
0 |
0 |
0 |
0 |
0 53 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
54 |
0 |
0 |
0 |
0 |
0 |
0 |
0 54 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
55 |
0 |
0 |
0 |
0 |
0 |
0 |
0 55 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
56 |
0 |
0 |
0 |
0 |
0 |
0 |
0 56 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
57 |
0 |
0 |
0 |
0 |
0 |
0 |
0 57 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
58 |
0 |
0 |
0 |
0 |
0 |
0 |
0 58 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
59 |
0 |
0 |
0 |
0 |
0 |
0 |
0 59 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
60 |
0 |
0 |
0 |
0 |
0 |
0 |
0 60 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
61 |
0 |
0 |
0 |
0 |
0 |
0 |
0 61 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
62 |
0 |
0 |
0 |
0 |
0 |
0 |
0 62 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
63 |
0 |
0 |
0 |
0 |
0 |
0 |
0 63 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
64 |
0 |
0 |
0 |
0 |
0 |
0 |
0 64 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
65 |
0 |
0 |
0 |
0 |
0 |
0 |
0 65 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
66 |
0 |
0 |
0 |
0 |
0 |
0 |
0 66 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
67 |
0 |
0 |
0 |
0 |
0 |
0 |
0 67 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
68 |
0 |
0 |
0 |
0 |
0 |
0 |
0 68 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
69 |
0 |
0 |
0 |
0 |
0 |
0 |
0 69 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
70 |
0 |
0 |
0 |
0 |
0 |
0 |
0 70 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
71 |
0 |
0 |
0 |
0 |
0 |
0 |
0 71 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
72 |
0 |
0 |
0 |
0 |
0 |
0 |
0 72 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
73 |
0 |
0 |
0 |
0 |
0 |
0 |
0 73 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
74 |
0 |
0 |
0 |
0 |
0 |
0 |
0 74 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
75 |
0 |
0 |
0 |
0 |
0 |
0 |
0 75 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
76 |
0 |
0 |
0 |
0 |
0 |
0 |
0 76 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
77 |
0 |
0 |
0 |
0 |
0 |
0 |
0 77 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
78 |
0 |
0 |
0 |
0 |
0 |
0 |
0 78 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
79 |
0 |
0 |
0 |
0 |
0 |
0 |
0 79 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
80 |
0 |
0 |
0 |
0 |
0 |
0 |
0 80 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
81 |
0 |
0 |
0 |
0 |
0 |
0 |
0 81 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
82 |
0 |
0 |
0 |
0 |
0 |
0 |
0 82 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
83 |
0 |
0 |
0 |
0 |
0 |
0 |
0 83 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
84 |
0 |
0 |
0 |
0 |
0 |
0 |
0 84 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
85 |
0 |
0 |
0 |
0 |
0 |
0 |
0 85 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
86 |
0 |
0 |
0 |
0 |
0 |
0 |
0 86 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
87 |
0 |
0 |
0 |
0 |
0 |
0 |
0 87 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
88 |
0 |
0 |
0 |
0 |
0 |
0 |
0 88 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
89 |
0 |
0 |
0 |
0 |
0 |
0 |
0 89 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
90 |
0 |
0 |
0 |
0 |
0 |
0 |
0 90 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
91 |
0 |
0 |
0 |
0 |
0 |
0 |
0 91 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
||||||||||||||||||||||||||||||||||||
|
5ème |
Annexe 1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
partie de la matrice des corrélations |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
||||||||||||||||||||||||||||
|
62 63 64 65 66 67 68 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
61 |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
0,22 |
0,34 |
-0,2 |
-0,2 |
0,2 |
0,06 |
0,11 |
-0,1 |
0,36 |
0,22 |
0,33 |
0,08 |
0,31 |
0,19 |
0,28 |
-0,3 |
-0,3 |
-0 |
0,03 |
-0,1 |
-0 |
0,26 |
0,12 |
0,25 |
-0,2 |
-0,1 |
-0,1 |
-0,1 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
2 |
-0,1 |
-0,2 |
0,25 |
0,11 |
-0,2 |
-0,2 |
-0,1 |
0,1 |
-0,2 |
-0,1 |
-0,2 |
-0,1 |
-0,2 |
-0,2 |
-0,3 |
0,22 |
0,22 |
-0,1 |
-0,2 |
-0,1 |
-0 |
-0,2 |
-0,2 |
-0,3 |
0,04 |
-0 |
-0,1 |
-0 |
0,17 |
0,17 |
0,14 |
||||||||||||||||||||
|
3 |
-0,2 |
-0,5 |
0,23 |
0,2 |
-0,2 |
0,19 |
0,16 |
-0,2 |
-0,3 |
-0,1 |
-0,5 |
0,24 |
-0,2 |
0,01 |
0,2 |
0,29 |
0,29 |
-0,1 |
0,25 |
0,37 |
0,34 |
0,03 |
0,15 |
0,27 |
0,49 |
0,07 |
0,26 |
0,31 |
0,01 |
0,03 |
-0,1 |
||||||||||||||||||||
|
4 |
-0,3 |
-0,4 |
0,05 |
0,1 |
0,23 |
-0,1 |
-0,1 |
-0,2 |
-0,1 |
-0,3 |
-0,4 |
-0 |
0,11 |
-0,1 |
-0,2 |
-0,1 |
0,02 |
0,21 |
0,08 |
-0 |
-0,1 |
0,15 |
-0,1 |
-0,2 |
0,01 |
-0 |
0,12 |
0,15 |
-0,1 |
-0,1 |
-0,2 |
||||||||||||||||||||
|
5 |
0,26 |
0,15 |
-0 |
-0,1 |
-0,2 |
0,27 |
0,25 |
0 |
0,18 |
0,28 |
0,14 |
0,44 |
0,16 |
0,37 |
0,51 |
0,03 |
0 |
-0,2 |
0,16 |
0,3 |
0,26 |
0,18 |
0,38 |
0,52 |
0,09 |
-0,2 |
0 |
-0 |
-0 |
-0 |
-0 |
||||||||||||||||||||
|
6 |
0,06 |
-0 |
-0,1 |
-0,1 |
0,13 |
0,16 |
0,11 |
-0,2 |
0,14 |
0,07 |
-0,1 |
0,35 |
0,3 |
0,28 |
0,33 |
-0,2 |
-0,2 |
0,01 |
0,24 |
0,2 |
0,07 |
0,29 |
0,26 |
0,31 |
0,03 |
-0,1 |
0,09 |
0,06 |
-0,2 |
-0,2 |
-0,2 |
||||||||||||||||||||
|
7 |
-0,1 |
0,14 |
-0,3 |
-0,2 |
0,16 |
-0,1 |
-0,2 |
-0,3 |
0,11 |
-0,1 |
0,12 |
-0 |
0,33 |
-0 |
0,01 |
-0,3 |
-0,4 |
-0 |
0,1 |
-0,2 |
-0,3 |
0,31 |
-0,1 |
-0,1 |
-0,3 |
-0,1 |
-0,1 |
-0,1 |
-0,3 |
-0,3 |
-0,3 |
||||||||||||||||||||
|
8 |
-0,2 |
-0,2 |
-0,1 |
-0 |
-0 |
-0,1 |
-0,1 |
-0,2 |
-0,1 |
-0,2 |
-0,2 |
-0,1 |
0,11 |
-0,1 |
-0,2 |
-0,1 |
-0,1 |
-0,1 |
0,12 |
-0,1 |
-0,2 |
0,17 |
-0,1 |
-0,2 |
0,01 |
0,11 |
0,02 |
0,06 |
-0,1 |
-0,2 |
-0,2 |
||||||||||||||||||||
|
9 |
0,18 |
0,28 |
-0,3 |
-0,2 |
0,15 |
0,06 |
-0 |
-0,2 |
0,24 |
0,16 |
0,25 |
0,19 |
0,36 |
0,21 |
0,2 |
-0,3 |
-0,3 |
-0 |
0,19 |
0,02 |
-0,1 |
0,34 |
0,15 |
0,14 |
-0,2 |
-0 |
-0,1 |
-0,2 |
-0,3 |
-0,3 |
-0,3 |
||||||||||||||||||||
|
10 |
-0,2 |
-0,1 |
-0 |
-0 |
0,16 |
0,08 |
0,02 |
-0,1 |
0,13 |
-0,1 |
-0,1 |
-0 |
0,12 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
0,09 |
0,19 |
-0 |
-0 |
0,21 |
-0,1 |
-0,1 |
0,02 |
0,09 |
0,16 |
0,18 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
11 |
-0 |
0,21 |
-0,2 |
-0,2 |
-0 |
0,14 |
0,04 |
-0,1 |
0,16 |
-0 |
0,2 |
-0,2 |
0,03 |
-0,2 |
-0,1 |
-0,2 |
-0,3 |
-0,1 |
0,18 |
-0,1 |
-0,1 |
0,12 |
-0,1 |
-0,1 |
0,02 |
0,36 |
0,23 |
0,07 |
-0,1 |
-0,1 |
-0,1 |
||||||||||||||||||||
|
12 |
-0,1 |
-0 |
0,06 |
0,05 |
-0 |
0,08 |
-0 |
-0,4 |
0,27 |
-0,1 |
-0 |
0,11 |
0,41 |
-0 |
0,12 |
0,08 |
0,07 |
0 |
0,27 |
-0,1 |
-0,2 |
0,47 |
-0 |
0,07 |
-0,1 |
-0 |
0,03 |
0,08 |
-0,3 |
-0,3 |
-0,4 |
||||||||||||||||||||
|
13 |
-0 |
0,07 |
0,06 |
-0 |
-0,1 |
0,31 |
0,21 |
0,01 |
0,04 |
0 |
0,07 |
0,04 |
-0 |
-0 |
0,02 |
0,03 |
0,08 |
-0 |
0,42 |
0,22 |
0,16 |
0,1 |
0,03 |
0,05 |
0,25 |
0,39 |
0,36 |
0,25 |
-0 |
-0,1 |
0,01 |
||||||||||||||||||||
|
14 |
-0,2 |
0,09 |
0,03 |
0,01 |
0,03 |
0,03 |
0 |
-0,1 |
0 |
-0,1 |
0,09 |
-0,3 |
-0 |
-0,2 |
-0,1 |
0,01 |
0,01 |
0,05 |
0,18 |
-0,1 |
-0 |
0,07 |
-0,2 |
-0,1 |
0,01 |
0,34 |
0,19 |
0,15 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
15 |
-0,1 |
0,1 |
-0 |
-0,1 |
-0,1 |
0,37 |
0,25 |
-0 |
0,01 |
-0 |
0,1 |
-0,1 |
-0,2 |
-0,1 |
-0 |
-0 |
0,01 |
-0,1 |
0,42 |
0,21 |
0,19 |
0,01 |
-0 |
0,03 |
0,32 |
0,52 |
0,49 |
0,33 |
-0 |
-0 |
-0 |
||||||||||||||||||||
|
16 |
0,19 |
-0,1 |
0,15 |
0,06 |
-0,2 |
0,23 |
0,19 |
-0,1 |
-0,1 |
0,2 |
-0,1 |
0,35 |
-0 |
0,28 |
0,24 |
0,16 |
0,16 |
-0,1 |
0,17 |
0,39 |
0,22 |
0,1 |
0,36 |
0,27 |
0,29 |
-0 |
0,06 |
-0 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
17 |
0,21 |
-0,2 |
0,12 |
0,03 |
-0,3 |
0,19 |
0,17 |
-0,1 |
-0,1 |
0,22 |
-0,2 |
0,34 |
-0,1 |
0,26 |
0,16 |
0,18 |
0,15 |
-0,2 |
0,05 |
0,35 |
0,21 |
0 |
0,34 |
0,2 |
0,31 |
-0,1 |
-0 |
-0,1 |
0,04 |
0,06 |
-0 |
||||||||||||||||||||
|
18 |
0,01 |
-0,3 |
0,18 |
0,17 |
-0,1 |
0,16 |
0,1 |
-0,2 |
-0,2 |
0,03 |
-0,4 |
0,61 |
-0 |
0,17 |
0,16 |
0,16 |
0,17 |
-0,1 |
0,22 |
0,32 |
0,2 |
0,13 |
0,25 |
0,19 |
0,32 |
-0,3 |
0,04 |
0,1 |
-0 |
-0 |
-0,2 |
||||||||||||||||||||
|
19 |
-0,1 |
-0,3 |
0,16 |
0,17 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
-0,3 |
0,17 |
0,07 |
-0 |
-0,1 |
0,18 |
0,12 |
-0 |
0,08 |
0,03 |
-0 |
0,16 |
0,03 |
-0,1 |
-0 |
-0,2 |
-0,4 |
-0,1 |
0,03 |
0,05 |
-0,1 |
||||||||||||||||||||
|
20 |
-0,1 |
-0,4 |
0,2 |
0,16 |
-0,2 |
0,26 |
0,21 |
-0,1 |
-0,3 |
-0 |
-0,4 |
0,34 |
-0,2 |
0,14 |
0,28 |
0,23 |
0,25 |
-0,1 |
0,19 |
0,46 |
0,35 |
-0 |
0,28 |
0,35 |
0,54 |
0,04 |
0,27 |
0,23 |
-0,1 |
-0 |
-0,1 |
||||||||||||||||||||
|
21 |
-0,1 |
-0,4 |
0,21 |
0,18 |
-0,1 |
0,28 |
0,22 |
-0,1 |
-0,3 |
-0,1 |
-0,4 |
0,24 |
-0,2 |
0,06 |
0,23 |
0,24 |
0,26 |
-0 |
0,25 |
0,42 |
0,36 |
0,03 |
0,21 |
0,3 |
0,54 |
0,13 |
0,34 |
0,33 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
22 |
-0,4 |
-0,3 |
0,05 |
0,06 |
0,03 |
-0,3 |
-0,3 |
-0,3 |
-0,2 |
-0,5 |
-0,3 |
0,06 |
0,19 |
-0,2 |
-0,1 |
0,09 |
0,07 |
0,03 |
0,13 |
-0,2 |
-0,2 |
0,24 |
-0,2 |
-0,1 |
-0,2 |
-0,2 |
-0,2 |
0,16 |
-0,1 |
-0,1 |
-0,3 |
||||||||||||||||||||
|
23 |
0,01 |
-0 |
0,07 |
0,05 |
-0,1 |
-0,1 |
-0,1 |
0,04 |
0,1 |
-0 |
-0 |
0,11 |
0,17 |
-0 |
0,01 |
0,08 |
0,03 |
-0,1 |
-0,1 |
-0,1 |
-0,1 |
0,17 |
-0 |
-0 |
-0,2 |
-0,3 |
-0,3 |
-0,2 |
0,1 |
0,1 |
0,03 |
||||||||||||||||||||
|
24 |
-0,2 |
-0 |
-0,1 |
-0 |
0 |
0,08 |
-0 |
-0,2 |
0,26 |
-0,2 |
-0 |
-0 |
0,29 |
-0,2 |
-0 |
-0,1 |
-0,1 |
-0,1 |
0,33 |
-0,1 |
-0,1 |
0,44 |
-0,2 |
-0 |
-0,1 |
0,05 |
0,09 |
0,16 |
-0 |
-0,1 |
-0,2 |
||||||||||||||||||||
|
25 |
-0,3 |
-0,2 |
0,02 |
0,05 |
0,21 |
-0,1 |
-0,1 |
-0,4 |
0,27 |
-0,3 |
-0,3 |
-0 |
0,48 |
-0,2 |
-0,1 |
-0,1 |
-0,1 |
0,13 |
0,34 |
-0,2 |
-0,2 |
0,58 |
-0,2 |
-0,2 |
-0,2 |
-0,1 |
-0,1 |
0,15 |
-0,1 |
-0,1 |
-0,3 |
||||||||||||||||||||
|
26 |
-0,3 |
-0,2 |
0,03 |
0,11 |
0,13 |
-0,1 |
-0,2 |
-0,3 |
0,29 |
-0,3 |
-0,2 |
-0 |
0,46 |
-0,2 |
-0,1 |
-0 |
-0 |
0,09 |
0,38 |
-0,2 |
-0,2 |
0,6 |
-0,2 |
-0,2 |
-0,2 |
-0,1 |
-0,1 |
0,17 |
-0,1 |
-0,1 |
-0,3 |
||||||||||||||||||||
|
27 |
0,48 |
-0,2 |
0,22 |
0,17 |
-0,3 |
0,36 |
0,36 |
0,14 |
-0,1 |
0,51 |
-0,2 |
0,5 |
-0,2 |
0,57 |
0,34 |
0,25 |
0,26 |
-0,1 |
0,06 |
0,66 |
0,46 |
-0,1 |
0,68 |
0,42 |
0,47 |
-0,1 |
0,03 |
-0,2 |
0,2 |
0,22 |
0,16 |
||||||||||||||||||||
|
28 |
-0,2 |
-0,5 |
0,23 |
0,2 |
-0,2 |
0,19 |
0,16 |
-0,2 |
-0,3 |
-0,1 |
-0,5 |
0,24 |
-0,2 |
0,01 |
0,2 |
0,29 |
0,29 |
-0,1 |
0,25 |
0,37 |
0,34 |
0,03 |
0,15 |
0,27 |
0,49 |
0,07 |
0,26 |
0,31 |
0,01 |
0,03 |
-0,1 |
||||||||||||||||||||
|
29 |
-0,2 |
-0,3 |
0,08 |
0 |
-0,3 |
-0,3 |
-0,3 |
-0,2 |
-0,3 |
-0,2 |
-0,3 |
0,02 |
0,1 |
-0 |
-0 |
0,14 |
0,07 |
-0,2 |
0,03 |
-0 |
-0,1 |
0,09 |
-0 |
-0 |
-0 |
-0,1 |
-0,2 |
-0 |
-0 |
-0 |
-0,1 |
||||||||||||||||||||
|
30 |
-0,2 |
0,38 |
-0,4 |
-0,3 |
0,19 |
-0,2 |
-0,3 |
-0,1 |
0,25 |
-0,2 |
0,37 |
-0,5 |
0,26 |
-0,4 |
-0,3 |
-0,4 |
-0,5 |
-0,1 |
0,07 |
-0,5 |
-0,4 |
0,23 |
-0,5 |
-0,3 |
-0,4 |
0,24 |
-0,1 |
-0 |
-0,1 |
-0,2 |
-0,1 |
||||||||||||||||||||
|
31 |
-0,1 |
-0,1 |
0,06 |
0,02 |
-0,2 |
-0,2 |
-0,2 |
-0,3 |
-0,1 |
-0,2 |
-0,1 |
0,08 |
0,28 |
0,06 |
0,11 |
0,03 |
-0 |
-0,2 |
0,12 |
-0 |
-0,1 |
0,27 |
0,03 |
0,07 |
-0,1 |
-0,1 |
-0,2 |
-0,1 |
-0,2 |
-0,2 |
-0,3 |
||||||||||||||||||||
|
32 |
-0,2 |
0,43 |
-0,4 |
-0,4 |
0,2 |
-0,2 |
-0,3 |
-0,2 |
0,31 |
-0,2 |
0,42 |
-0,4 |
0,29 |
-0,4 |
-0,2 |
-0,4 |
-0,5 |
-0,1 |
0,07 |
-0,5 |
-0,4 |
0,27 |
-0,4 |
-0,3 |
-0,4 |
0,19 |
-0 |
-0 |
-0,2 |
-0,3 |
-0,2 |
||||||||||||||||||||
|
33 |
-0,2 |
-0,4 |
0,08 |
-0 |
-0,4 |
-0,3 |
-0,2 |
-0 |
-0,4 |
-0,2 |
-0,4 |
-0 |
-0,1 |
-0,1 |
-0,2 |
0,22 |
0,15 |
-0,3 |
-0,1 |
-0 |
-0 |
-0,1 |
-0,1 |
-0,2 |
0,05 |
-0,1 |
-0,2 |
-0 |
0,11 |
0,12 |
0,02 |
||||||||||||||||||||
|
34 |
-0,2 |
0,15 |
-0,2 |
-0,2 |
0,11 |
-0,1 |
-0,2 |
0,04 |
0,07 |
-0,2 |
0,16 |
-0,4 |
0,1 |
-0,3 |
-0,3 |
-0,2 |
-0,3 |
-0 |
0,05 |
-0,3 |
-0,2 |
0,1 |
-0,3 |
-0,3 |
-0,2 |
0,23 |
-0,1 |
-0,1 |
0,06 |
0,04 |
0,04 |
||||||||||||||||||||
|
35 |
0,27 |
0,33 |
-0,1 |
-0 |
0,34 |
0,26 |
0,2 |
-0 |
0,41 |
0,28 |
0,32 |
0,13 |
0,15 |
0,19 |
0,16 |
-0,2 |
-0,2 |
0,25 |
0,01 |
0,04 |
-0 |
0,11 |
0,15 |
0,13 |
-0,1 |
0,03 |
0,13 |
-0,1 |
-0,2 |
-0,2 |
-0 |
||||||||||||||||||||
|
36 |
0,22 |
-0,4 |
0,38 |
0,34 |
-0,2 |
0,19 |
0,29 |
0,12 |
-0,3 |
0,25 |
-0,4 |
0,47 |
-0,3 |
0,39 |
0,28 |
0,42 |
0,48 |
0,06 |
-0,1 |
0,49 |
0,41 |
-0,2 |
0,47 |
0,35 |
0,39 |
-0,2 |
0,06 |
0,04 |
0,15 |
0,18 |
0,15 |
||||||||||||||||||||
|
37 |
0,13 |
0,36 |
-0,3 |
-0,1 |
0,42 |
0,15 |
0,02 |
-0,1 |
0,43 |
0,13 |
0,34 |
-0 |
0,25 |
0,05 |
0,01 |
-0,4 |
-0,4 |
0,23 |
0,04 |
-0,1 |
-0,2 |
0,21 |
-0 |
-0,1 |
-0,2 |
0,09 |
0,1 |
-0,1 |
-0,3 |
-0,3 |
-0,1 |
||||||||||||||||||||
|
38 |
0,18 |
-0,1 |
0,24 |
0,33 |
0,13 |
0,09 |
0,1 |
0,26 |
0,16 |
0,18 |
-0 |
0,09 |
-0 |
0,15 |
-0,1 |
0,17 |
0,24 |
0,3 |
-0,1 |
0,07 |
0,07 |
-0 |
0,15 |
-0,1 |
-0 |
-0,1 |
-0,1 |
-0,1 |
0,16 |
0,16 |
0,27 |
||||||||||||||||||||
|
39 |
0,3 |
0,03 |
0,24 |
0,15 |
-0,1 |
0,25 |
0,35 |
0,13 |
0,06 |
0,33 |
0,04 |
0,26 |
-0,1 |
0,28 |
0,3 |
0,25 |
0,3 |
0,09 |
-0 |
0,3 |
0,28 |
-0,1 |
0,31 |
0,33 |
0,2 |
-0,1 |
0,08 |
-0 |
0,11 |
0,12 |
0,12 |
||||||||||||||||||||
|
40 |
0,15 |
-0,4 |
0,29 |
0,21 |
-0,3 |
0,16 |
0,26 |
0 |
-0,3 |
0,18 |
-0,4 |
0,46 |
-0,3 |
0,34 |
0,33 |
0,36 |
0,4 |
-0,1 |
-0 |
0,49 |
0,4 |
-0,2 |
0,43 |
0,39 |
0,42 |
-0,2 |
0,09 |
0,08 |
0,09 |
0,11 |
0,03 |
||||||||||||||||||||
|
41 |
0,07 |
0,2 |
-0 |
0,05 |
0,23 |
0,27 |
0,25 |
0,19 |
0,19 |
0,1 |
0,21 |
-0,1 |
-0,2 |
-0,1 |
-0,1 |
-0,1 |
-0 |
0,22 |
0,01 |
0,02 |
0,1 |
-0,2 |
-0,1 |
-0 |
0,12 |
0,27 |
0,29 |
0,14 |
0,08 |
0,08 |
0,18 |
||||||||||||||||||||
|
42 |
-0,1 |
0,39 |
-0,3 |
-0,3 |
0,03 |
0,05 |
-0,1 |
-0 |
0,2 |
-0,1 |
0,39 |
-0,4 |
0,08 |
-0,3 |
-0,2 |
-0,3 |
-0,3 |
-0,1 |
0,14 |
-0,2 |
-0,2 |
0,13 |
-0,3 |
-0,2 |
-0,1 |
0,39 |
0,12 |
0,02 |
-0,1 |
-0,1 |
-0,1 |
||||||||||||||||||||
|
43 |
0,14 |
0,55 |
-0,2 |
-0,2 |
0,04 |
0,11 |
0,1 |
-0,1 |
0,32 |
0,15 |
0,53 |
0,01 |
0,17 |
0,01 |
0,27 |
-0,3 |
-0,3 |
-0,1 |
0,11 |
-0,1 |
-0,1 |
0,19 |
-0 |
0,23 |
-0,1 |
0,1 |
0,06 |
-0 |
-0,1 |
-0,1 |
-0,2 |
||||||||||||||||||||
|
44 |
0,04 |
0,51 |
-0,3 |
-0,3 |
-0,1 |
0,09 |
-0 |
-0 |
0,31 |
0,03 |
0,51 |
-0,2 |
0,15 |
-0,1 |
-0 |
-0,3 |
-0,3 |
-0,2 |
0,09 |
-0,2 |
-0,2 |
0,17 |
-0,2 |
-0,1 |
-0,2 |
0,24 |
0,06 |
-0,1 |
-0,1 |
-0,2 |
-0,1 |
||||||||||||||||||||
|
45 |
-0,1 |
-0,1 |
0,02 |
0,05 |
-0,1 |
0,01 |
-0,1 |
0,05 |
0,05 |
-0,1 |
-0,1 |
-0,1 |
0,06 |
-0,1 |
-0,1 |
0,09 |
0,05 |
-0,1 |
0,17 |
-0 |
0,01 |
0,11 |
-0,1 |
-0,1 |
-0 |
0,11 |
0,01 |
0,04 |
0,07 |
0,07 |
0,07 |
||||||||||||||||||||
6ème partie de la matrice des corrélations
61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91
46 -0,2 0 -0,1 -0,1 0,12 -0,1 -0,1 -0 -0 -0,2 0 -0,4 -0 -0,3 -0,4 -0,1 -0,1 0,03 0,15 -0,2 -0,2 0,03 -0,3 -0,4 -0 0,39 0,11 0,11 -0 -0 0,01
47 0,7 0,67 -0,2 -0,3 -0,1 0,24 0,23 0,27 0,31 0,68 0,68 0,15 -0,1 0,44 0,28 -0,2 -0,3 -0,2 -0,2 0,17 0,05 -0,2 0,38 0,26 -0 -0,1 -0,1 -0,5 0,03 0,04 0,19
48 0,62 -0 0,1 -0,1 -0,3 0,47 0,58 0,51 -0 0,67 0,03 0,31 -0,4 0,55 0,24 0,21 0,18 -0,1 -0,2 0,59 0,54 -0,4 0,62 0,35 0,49 -0,1 0,08 -0,1 0,4 0,44 0,52
49 0,85 0,46 -0 -0,1 -0,1 0,28 0,29 0,31 0,25 0,83 0,47 0,32 -0,1 0,69 0,37 -0,1 -0,1 -0,1 -0,3 0,37 0,17 -0,2 0,64 0,37 0,08 -0,2 -0,2 -0,5 0,11 0,12 0,26
50 0,77 0,16 0,14 0,13 -0,1 0,34 0,36 0,47 0,13 0,77 0,18 0,38 -0,2 0,65 0,23 0,11 0,13 0,01 -0,3 0,46 0,31 -0,3 0,66 0,28 0,25 -0,2 -0,1 -0,4 0,3 0,31 0,46
51 0,03 0,76 -0,4 -0,4 0,16 -0,1 -0,3 0,03 0,33 -0 0,75 -0,3 0,16 -0,2 0,01 -0,4 -0,4 -0,1 -0,1 -0,4 -0,4 0,08 -0,3 -0,1 -0,4 0,1 -0 -0,2 -0,3 -0,3 -0,1
52 0,01 0,13 0,12 0,09 -0,2 0,06 -0 0,55 -0,2 0,01 0,17 -0,2 -0,4 -0,1 -0,1 0,15 0,16 -0,1 -0,2 0,03 0,15 -0,4 -0,1 -0,1 0,22 0,17 0,16 -0,1 0,24 0,23 0,54
53 0,63 0,73 -0,3 -0,4 -0,1 0,19 0,17 0,22 0,39 0,61 0,74 0,03 0,02 0,35 0,24 -0,3 -0,3 -0,2 -0,2 0,05 -0 -0,1 0,27 0,2 -0,1 -0 -0,1 -0,4 0,01 0,01 0,13
54 -0,3 -0 0,36 0,49 0,47 -0,3 -0,4 -0,2 -0 -0,3 -0,1 -0,1 0,15 -0,2 -0,2 0,1 0,22 0,6 0,01 -0,3 -0,3 0,14 -0,3 -0,3 -0,3 -0 -0,1 -0 -0,3 -0,3 -0,2
55 0,24 0,34 -0,2 -0,2 0,05 0,68 0,51 0,14 0,43 0,3 0,35 -0,1 0,06 0,17 0,24 -0,2 -0,2 -0 0,33 0,34 0,28 0,17 0,23 0,29 0,37 0,53 0,6 0,23 -0 -0 0,12
56 0,76 0,64 -0,1 -0,3 -0,1 0,25 0,29 0,3 0,13 0,75 0,65 0,19 -0,2 0,54 0,38 -0,2 -0,2 -0,2 -0,3 0,32 0,18 -0,3 0,51 0,38 0,12 -0 -0,1 -0,4 0,08 0,09 0,23
57 0,59 -0 0,28 0,02 -0,2 0,22 0,46 0,5 -0,3 0,62 0 0,28 -0,5 0,55 0,25 0,26 0,25 -0,1 -0,4 0,54 0,52 -0,6 0,61 0,35 0,46 -0,2 -0,1 -0,2 0,45 0,47 0,51
58 -0,1 0,6 -0,4 -0,4 0,16 -0,2 -0,3 0,01 0,4 -0,1 0,6 -0,4 0,21 -0,4 -0,2 -0,4 -0,4 -0,1 -0,1 -0,6 -0,4 0,14 -0,5 -0,3 -0,6 0,01 -0,2 -0,2 -0,1 -0,1 -0,1
59 -0,2 -0,1 -0,1 -0,1 -0 -0,4 -0,2 0,35 -0,1 -0,2 -0,1 -0,3 -0,1 -0,3 -0,4 0,08 -0 -0,1 -0,3 -0,4 -0,1 -0,2 -0,4 -0,4 -0,4 -0,2 -0,4 0 0,48 0,48 0,34
60 0,17 0,49 -0,2 -0 0,27 -0 -0,1 -0,2 0,91 0,13 0,47 0,06 0,82 0,11 0,15 -0,3 -0,3 0,12 0,2 -0,4 -0,4 0,72 -0,1 0,03 -0,7 -0,3 -0,3 -0,3 -0,2 -0,2 -0,2
61 1 0,5 0,04 -0 -0,2 0,39 0,41 0,32 0,3 0,99 0,5 0,55 -0 0,91 0,6 0,01 0,01 -0,1 -0,2 0,58 0,32 -0,1 0,87 0,61 0,14 -0,3 -0,2 -0,6 0,13 0,14 0,25
62 0 1 -0,3 -0,3 0,04 0,14 0,05 0,14 0,49 0,46 1 0,11 0,19 0,3 0,57 -0,3 -0,3 -0,1 -0,1 -0 -0,1 0,08 0,21 0,5 -0,3 -0,1 -0,1 -0,4 -0,2 -0,2 0
63 0 0 1 0,83 -0 0,01 0,03 0,1 -0,1 0,04 -0,3 0,22 -0,1 0,11 0,03 0,78 0,88 0,54 -0 0,16 0,14 -0 0,16 0,05 0,15 -0,1 -0,1 0 0,11 0,11 0,13
64 0 0 0,83 1 0,25 -0 -0,1 -0 -0 -0,1 -0,3 0,2 0,03 0,06 -0,1 0,65 0,77 0,72 0,09 0,09 0,03 0,09 0,09 -0,1 0,03 -0,1 -0,1 -0 0,02 0,02 0,02
65 0 0 0 0 1 -0,2 -0,3 -0,3 0,17 -0,2 0,01 -0,1 0,33 -0,1 -0,1 -0,4 -0,2 0,81 -0,1 -0,3 -0,4 0,25 -0,2 -0,2 -0,3 -0,1 -0,1 0,01 -0,3 -0,3 -0,3
66 0 0 0 0 0 1 0,87 0,41 0,37 0,5 0,17 0,21 -0,1 0,34 0,35 0,13 0,11 -0,1 0,6 0,77 0,77 0,11 0,52 0,51 0,72 0,53 0,66 0,36 0,35 0,36 0,41
67 0 0 0 0 0 0,87 1 0,54 0,2 0,55 0,09 0,15 -0,3 0,36 0,29 0,13 0,1 -0,2 0,45 0,78 0,87 -0,1 0,54 0,48 0,72 0,47 0,54 0,45 0,56 0,56 0,55
68 0 0 0 0 0 0 0 1 -0 0,39 0,22 -0,1 -0,5 0,12 -0 0,24 0,19 -0,1 -0 0,38 0,69 -0,4 0,23 0,13 0,39 0,28 0,19 0,12 0,85 0,85 0,99
69 0 0 0 0 0 0 0 0 1 0,31 0,49 0,13 0,71 0,22 0,27 -0,2 -0,2 0,08 0,42 -0 -0,1 0,73 0,14 0,23 -0,4 -0 -0 -0,1 -0,1 -0,1 -0,1
70 0,99 0 0 0 0 0 0 0 0 1 0,48 0,53 -0 0,9 0,6 0,03 0,03 -0,2 -0,1 0,67 0,44 -0,1 0,89 0,64 0,25 -0,2 -0,1 -0,5 0,22 0,23 0,33
71 0 1 0 0 0 0 0 0 0 0 1 0,09 0,15 0,29 0,56 -0,3 -0,3 -0,1 -0,1 -0 -0 0,05 0,21 0,5 -0,2 -0 -0,1 -0,4 -0,1 -0,1 0,08
72 0 0 0 0 0 0 0 0 0 0 0 1 0,2 0,69 0,56 0,07 0,14 0,03 0,03 0,45 0,14 0,14 0,66 0,53 0,13 -0,6 -0,2 -0,4 -0,2 -0,2 -0,2
73 0 0 0 0 0 0 0 0 0,71 0 0 0 1 0,15 0,21 -0,3 -0,3 0,18 0,28 -0,3 -0,5 0,91 -0 0,07 -0,6 -0,4 -0,4 -0,2 -0,5 -0,5 -0,5
74 0,91 0 0 0 0 0 0 0 0 0,9 0 0 0 1 0,69 0,01 0,05 -0 -0,1 0,64 0,3 0,02 0,96 0,69 0,16 -0,4 -0,2 -0,5 -0 -0 0,08
75 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 -0 -0 -0,1 0,05 0,47 0,28 0,14 0,67 0,97 0,14 -0,2 0 -0,3 -0,3 -0,2 -0,1
76 0 0 0,78 0 0 0 0 0 0 0 0 0 0 0 0 1 0,96 0,21 0,06 0,24 0,31 -0,2 0,11 0,04 0,28 0,04 -0 0,1 0,31 0,32 0,26
77 0 0 0,88 0,77 0 0 0 0 0 0 0 0 0 0 0 0,96 1 0,36 0,05 0,26 0,28 -0,2 0,14 0,05 0,28 0,01 0,02 0,07 0,24 0,24 0,23
78 0 0 0 0,72 0,81 0 0 0 0 0 0 0 0 0 0 0 0 1 -0,1 -0,1 -0,2 0,15 -0,1 -0,1 -0,2 -0,1 -0,1 0,01 -0,2 -0,2 -0,1
79 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,34 0,41 0,62 0,03 0,15 0,28 0,51 0,49 0,57 0,14 0,14 0,01
80 0 0 0 0 0 0,77 0,78 0 0 0 0 0 0 0 0 0 0 0 0 1 0,83 -0,2 0,83 0,63 0,79 0,27 0,43 0,1 0,35 0,37 0,39
81 0 0 0 0 0 0,77 0,87 0 0 0 0 0 0 0 0 0 0 0 0 0,83 1 -0,2 0,52 0,51 0,8 0,45 0,51 0,42 0,72 0,73 0,7
82 0 0 0 0 0 0 0 0 0,73 0 0 0 0,91 0 0 0 0 0 0 0 0 1 -0,1 0,08 -0,4 -0,1 -0,1 0,09 -0,3 -0,3 -0,4
83 0,87 0 0 0 0 0 0 0 0 0,89 0 0 0 0,96 0 0 0 0 0 0,83 0 0 1 0,72 0,41 -0,2 0,01 -0,4 0,12 0,14 0,21
84 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,97 0 0 0 0 0 0 0 0,72 1 0,33 -0,1 0,14 -0,2 -0 -0 0,05
85 0 0 0 0 0 0,72 0,72 0 0 0 0 0 0 0 0 0 0 0 0 0,79 0,8 0 0 0 1 0,54 0,71 0,47 0,39 0,4 0,44
86 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,79 0,64 0,28 0,27 0,31
87 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0,71 0,79 1 0,65 0,16 0,15 0,22
88 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0,32 0,31 0,19
89 0 0 0 0 0 0 0 0,85 0 0 0 0 0 0 0 0 0 0 0 0 0,72 0 0 0 0 0 0 0 1 1 0,88
90 0 0 0 0 0 0 0 0,85 0 0 0 0 0 0 0 0 0 0 0 0 0,73 0 0 0 0 0 0 0 1 1 0,88
91 0 0 0 0 0 0 0 0,99 0 0 0 0 0 0 0 0 0 0 0 0 0,7 0 0 0 0 0 0 0 0,88 0,88 1
1.1-Etude de regression lineaire
Des études de régression linéaire sont effectuées afin de rechercher une éventuelle relation de la forme y = f(x) entre deux variables ( x et y ). La relation recherchée entre x et y est affine ( y = ax + b), elle consiste à rechercher une droite qui s'ajuste le mieux possible à l'ensemble des grandeurs. Cette droite rend minimale la somme des carrées des écarts des grandeurs y à la droite y = ax + b . C'est suite à l'exploitation du principe des moindres carrées, qu'il devient possible de trouver les valeurs de a et b qui minimisent la somme :
n
( yi - (axi + b)) 2
i=0
La qualité de la régression peut être évaluée en calculant le coefficient de détermination (R2) qui est le carré du coefficient de corrélation linéaire (R). Ce dernier est un nombre compris entre 0 et +1, qui vaut +1 si les points du nuage sont exactement alignés sur la droite. Cela traduit l'existence d'une parfaite corrélation entre les grandeurs étudiées.
1.2-Standardisation des donnees : Centrage - Reduction
Avant d'effectuer l'ACP, le tableau de données (n x p) est standardisé ou transformé. Cette transformation comporte deux étapes : le centrage puis la réduction.
Le centrage consiste à soustraire la moyenne de la variable en cause à chaque valeur numérique. Le tableau obtenu est alors de terme général.
Centrage : p i' = pik - pk
Cette transformation n'a aucune incidence sur les définitions de la ressemblance entre individus et de la liaison entre variables. L'ACP peut être réalisée sur des données uniquement centrées. Toutefois, ces résultats sont alors très sensibles au choix des unités de mesures. La façon classique de s'affranchir de l'arbitraire de ces unités est de réduire les données :
1 p
1 (p ik p
-k )
var(x) var(x)
Réduction : i
p ' =
: =
Suite à la standardisation des données, toutes les variables présentent la même variabilité et de ce fait la même influence dans le calcul des distances entre individus.
Tableau 4 Valeurs propres, pourcentage d'inertie et pourcentage cumulé
|
Axes |
Valeurs |
Pourcentage |
Pourcentage |
Axes |
Valeurs |
Pourcentage |
Pourcentage |
|
|
1 |
17,283 |
18,99 |
18,99 |
47 |
0,043 |
0,05 |
99,70 |
|
|
2 |
13,797 |
15,16 |
34,15 |
48 |
0,036 |
0,04 |
99,74 |
|
|
3 |
10,165 |
11,17 |
45,32 |
49 |
0,034 |
0,04 |
99,77 |
|
|
4 |
8,065 |
8,86 |
54,19 |
50 |
0,030 |
0,03 |
99,81 |
|
|
5 |
6,589 |
7,24 |
61,43 |
51 |
0,023 |
0,03 |
99,83 |
|
|
6 |
4,763 |
5,23 |
66,66 |
52 |
0,021 |
0,02 |
99,86 |
|
|
7 |
3,948 |
4,34 |
71,00 |
53 |
0,020 |
0,02 |
99,88 |
|
|
8 |
3,819 |
4,20 |
75,20 |
54 |
0,016 |
0,02 |
99,89 |
|
|
9 |
2,672 |
2,94 |
78,13 |
55 |
0,015 |
0,02 |
99,91 |
|
|
10 |
1,989 |
2,19 |
80,32 |
56 |
0,013 |
0,01 |
99,92 |
|
|
11 |
1,917 |
2,11 |
82,42 |
57 |
0,012 |
0,01 |
99,94 |
|
|
12 |
1,809 |
1,99 |
84,41 |
58 |
0,008 |
0,01 |
99,95 |
|
|
13 |
1,571 |
1,73 |
86,14 |
59 |
0,007 |
0,01 |
99,95 |
|
|
14 |
1,242 |
1,36 |
87,50 |
60 |
0,007 |
0,01 |
99,96 |
|
|
15 |
1,092 |
1,20 |
88,70 |
61 |
0,006 |
0,01 |
99,97 |
|
|
16 |
1,035 |
1,14 |
89,84 |
62 |
0,005 |
0,01 |
99,97 |
|
|
17 |
0,903 |
0,99 |
90,83 |
63 |
0,004 |
0,00 |
99,98 |
|
|
18 |
0,726 |
0,80 |
91,63 |
64 |
0,003 |
0,00 |
99,98 |
|
|
19 |
0,674 |
0,74 |
92,37 |
65 |
0,003 |
0,00 |
99,99 |
|
|
20 |
0,668 |
0,73 |
93,10 |
66 |
0,003 |
0,00 |
99,99 |
|
|
21 |
0,610 |
0,67 |
93,77 |
67 |
0,002 |
0,00 |
99,99 |
|
|
22 |
0,521 |
0,57 |
94,35 |
68 |
0,002 |
0,00 |
99,99 |
|
|
23 24 |
0,496 |
0,55 |
94,89 |
69 70 |
0,001 |
0,00 |
99,99 |
|
|
25 |
0,422 |
0,46 |
95,86 |
71 |
0,001 |
0,00 |
100,00 |
|
|
26 |
0,399 |
0,44 |
96,30 |
72 |
0,001 |
0,00 |
100,00 |
|
|
27 |
0,341 |
0,37 |
96,67 |
73 |
0,001 |
0,00 |
100,00 |
|
|
28 |
0,301 |
0,33 |
97,00 |
74 |
0,000 |
0,00 |
100,00 |
|
|
29 |
0,281 |
0,31 |
97,31 |
75 |
0,000 |
0,00 |
100,00 |
|
|
30 |
0,253 |
0,28 |
97,59 |
76 |
0,000 |
0,00 |
100,00 |
|
|
31 |
0,201 |
0,22 |
97,81 |
77 |
0,000 |
0,00 |
100,00 |
|
|
32 |
0,194 |
0,21 |
98,02 |
78 |
0,000 |
0,00 |
100,00 |
|
|
33 |
0,192 |
0,21 |
98,24 |
79 |
0,000 |
0,00 |
100,00 |
|
|
34 |
0,174 |
0,19 |
98,43 |
80 |
0,000 |
0,00 |
100,00 |
|
|
35 |
0,156 |
0,17 |
98,60 |
81 |
0,000 |
0,00 |
100,00 |
|
|
36 |
0,144 |
0,16 |
98,76 |
82 |
0,000 |
0,00 |
100,00 |
|
|
37 |
0,121 |
0,13 |
98,89 |
83 |
0,000 |
0,00 |
100,00 |
|
|
38 |
0,117 |
0,13 |
99,02 |
84 |
0,000 |
0,00 |
100,00 |
|
|
39 |
0,100 |
0,11 |
99,13 |
85 |
0,000 |
0,00 |
100,00 |
|
|
40 |
0,097 |
0,11 |
99,24 |
86 |
0,000 |
0,00 |
100,00 |
|
|
41 |
0,083 |
0,09 |
99,33 |
87 |
0,000 |
0,00 |
100,00 |
|
|
42 |
0,074 |
0,08 |
99,41 |
88 |
0,000 |
0,00 |
100,00 |
|
|
43 |
0,066 |
0,07 |
99,48 |
89 |
0,000 |
0,00 |
100,00 |
|
|
44 |
0,057 |
0,06 |
99,54 |
90 |
0,000 |
0,00 |
100,00 |
|
|
45 |
0,054 |
0,06 |
99,60 |
91 |
0,000 |
0,00 |
100,00 |
|
|
46 |
0,045 |
0,05 |
99,65 |
Tot. |
91,000 |
- |
- |
|
Tableau 5 Corrélations entre les variables avec
les dix premiers axes principaux (CP).
Les cases grisées
correspondent aux valeurs significatives
|
N° |
Variables |
CP1 |
CP2 |
CP3 |
CP4 |
CP5 |
CP6 |
CP7 |
CP8 |
CP9 |
CP10 |
||||||||||||
|
1 |
'Poids' |
-0,22 |
0,20 |
0,34 |
0,05 |
-0,23 |
-0,01 |
-0,25 |
-0,22 |
0,02 |
-0,07 |
||||||||||||
|
2 |
'dtLat' |
0,12 |
-0,10 |
-0,33 |
0,04 |
0,13 |
0,36 |
0,02 |
0,06 |
0,19 |
-0,45 |
||||||||||||
|
3 |
'dtImpul' |
0,74 |
-0,43 |
0,33 |
-0,23 |
-0,06 |
0,10 |
-0,01 |
0,13 |
0,06 |
0,03 |
||||||||||||
|
4 |
'tacMd' |
0,23 |
-0,50 |
0,14 |
0,02 |
0,10 |
-0,07 |
-0,04 |
0,01 |
-0,41 |
0,19 |
||||||||||||
|
5 |
'tacMg' |
0,43 |
0,10 |
0,51 |
0,14 |
-0,03 |
-0,10 |
-0,32 |
0,00 |
0,22 |
0,26 |
||||||||||||
|
6 |
'tac2M' |
0,26 |
-0,11 |
0,44 |
0,13 |
-0,07 |
-0,43 |
-0,23 |
0,02 |
-0,21 |
0,29 |
||||||||||||
|
7 |
'tac2P' |
-0,29 |
-0,16 |
0,44 |
0,02 |
-0,15 |
-0,01 |
0,01 |
0,17 |
-0,18 |
0,20 |
||||||||||||
|
8 |
'tacPar' |
-0,13 |
-0,28 |
0,21 |
-0,22 |
-0,29 |
0,12 |
0,23 |
0,15 |
-0,22 |
-0,10 |
||||||||||||
|
9 |
'tacPav' |
-0,19 |
0,05 |
0,67 |
-0,04 |
-0,06 |
0,08 |
0,05 |
0,09 |
-0,18 |
0,34 |
||||||||||||
|
10 |
'tFmaxMdX' |
0,12 |
-0,19 |
0,34 |
-0,11 |
0,34 |
0,17 |
-0,16 |
0,01 |
-0,14 |
-0,11 |
||||||||||||
|
11 |
'tFmaxMdZ' |
-0,36 |
0,11 |
0,31 |
-0,44 |
0,00 |
0,19 |
0,14 |
0,17 |
0,02 |
-0,26 |
||||||||||||
|
12 |
'tFmaxMgX' |
0,02 |
-0,22 |
0,57 |
-0,02 |
0,15 |
0,03 |
0,07 |
-0,03 |
0,23 |
-0,37 |
||||||||||||
|
13 |
'tFmaxMgZ' |
-0,07 |
0,05 |
0,27 |
-0,53 |
0,02 |
-0,09 |
0,33 |
0,03 |
0,06 |
0,17 |
||||||||||||
|
14 |
'tFmax2Mx' |
-0,28 |
-0,12 |
0,16 |
-0,47 |
-0,16 |
0,10 |
0,31 |
-0,04 |
0,14 |
0,08 |
||||||||||||
|
15 |
'tFmax2Mz' |
-0,13 |
0,10 |
0,25 |
-0,65 |
0,01 |
-0,12 |
0,26 |
0,16 |
0,12 |
0,06 |
||||||||||||
|
16 |
'tFmaxParX' |
0,52 |
-0,11 |
0,61 |
-0,16 |
-0,11 |
0,37 |
0,13 |
0,12 |
-0,03 |
0,01 |
||||||||||||
|
17 |
'tFmaxParZ' |
0,55 |
-0,09 |
0,51 |
-0,11 |
-0,16 |
0,48 |
0,06 |
0,15 |
-0,08 |
0,01 |
||||||||||||
|
18 |
'tFmax2PX' |
0,63 |
-0,30 |
0,48 |
-0,03 |
-0,09 |
0,21 |
0,01 |
0,08 |
-0,04 |
0,01 |
||||||||||||
|
19 |
'tFmax2PZ' |
0,30 |
-0,39 |
0,39 |
-0,02 |
-0,21 |
0,62 |
0,13 |
-0,06 |
-0,09 |
0,01 |
||||||||||||
|
20 |
'tFmaxPavX' |
0,76 |
-0,29 |
0,36 |
-0,20 |
-0,06 |
0,07 |
0,05 |
0,23 |
0,01 |
0,05 |
||||||||||||
|
21 |
'tFmaxPavZ' |
0,73 |
-0,35 |
0,37 |
-0,27 |
-0,01 |
0,05 |
0,04 |
0,18 |
0,03 |
0,06 |
||||||||||||
|
22 |
'tFmax4segX' |
0,18 |
-0,63 |
0,22 |
0,08 |
-0,10 |
0,13 |
-0,12 |
0,00 |
0,11 |
0,30 |
||||||||||||
|
23 |
'tFmax4segZ' |
0,19 |
-0,18 |
0,33 |
0,15 |
0,00 |
0,62 |
-0,20 |
-0,18 |
0,09 |
0,10 |
||||||||||||
|
24 |
'teMd' |
0,04 |
-0,34 |
0,66 |
-0,26 |
0,05 |
0,42 |
-0,17 |
-0,13 |
0,12 |
-0,04 |
||||||||||||
|
25 |
'teMg' |
0,04 |
-0,54 |
0,58 |
-0,07 |
0,06 |
0,29 |
-0,06 |
-0,27 |
-0,22 |
-0,01 |
||||||||||||
|
26 |
'te2M' |
0,08 |
-0,57 |
0,62 |
-0,09 |
0,09 |
0,36 |
-0,11 |
-0,28 |
-0,04 |
-0,03 |
||||||||||||
|
27 |
'tePar' |
0,77 |
0,13 |
0,39 |
-0,04 |
-0,18 |
0,32 |
0,10 |
0,00 |
-0,16 |
-0,01 |
||||||||||||
|
28 |
'tePav' |
0,74 |
-0,43 |
0,33 |
-0,23 |
-0,06 |
0,10 |
-0,01 |
0,13 |
0,06 |
0,03 |
||||||||||||
|
29 |
'2M_statX' |
0,05 |
-0,42 |
-0,18 |
-0,01 |
-0,84 |
-0,14 |
0,09 |
-0,15 |
0,03 |
-0,04 |
||||||||||||
|
30 |
'2M_statZ' |
-0,88 |
-0,02 |
0,05 |
-0,28 |
-0,26 |
0,10 |
0,07 |
-0,08 |
-0,05 |
0,02 |
||||||||||||
|
31 |
'Md_statX' |
-0,06 |
-0,37 |
0,04 |
-0,01 |
-0,80 |
-0,20 |
0,17 |
-0,17 |
0,07 |
-0,02 |
||||||||||||
|
32 |
'Md_statZ' |
-0,86 |
0,01 |
0,18 |
-0,23 |
-0,13 |
0,07 |
-0,01 |
0,02 |
0,09 |
-0,03 |
||||||||||||
|
33 |
'Mg_statX' |
0,15 |
-0,40 |
-0,38 |
-0,01 |
-0,76 |
-0,05 |
0,00 |
-0,11 |
-0,02 |
-0,04 |
||||||||||||
|
34 |
'Mg_statZ' |
-0,58 |
-0,06 |
-0,16 |
-0,26 |
-0,37 |
0,11 |
0,16 |
-0,19 |
-0,26 |
0,09 |
||||||||||||
|
35 |
'2P_statX' |
-0,14 |
0,45 |
0,37 |
0,09 |
0,74 |
0,01 |
0,04 |
0,15 |
-0,10 |
-0,05 |
||||||||||||
|
36 |
'2P_statZ' |
0,88 |
0,03 |
-0,05 |
0,28 |
0,26 |
-0,09 |
-0,07 |
0,07 |
0,05 |
-0,01 |
||||||||||||
|
37 |
'Par_statX' |
-0,44 |
0,35 |
0,34 |
0,01 |
0,56 |
-0,03 |
0,10 |
0,12 |
-0,26 |
0,00 |
||||||||||||
|
38 |
'Par_statZ' |
0,17 |
0,22 |
-0,02 |
0,18 |
0,61 |
0,24 |
0,15 |
-0,16 |
-0,18 |
0,01 |
||||||||||||
|
39 |
'Pav_statX' |
0,48 |
0,28 |
0,13 |
0,15 |
0,46 |
0,07 |
-0,10 |
0,08 |
0,26 |
-0,09 |
||||||||||||
|
40 |
'Pav_statZ' |
0,86 |
-0,07 |
-0,05 |
0,21 |
-0,01 |
-0,21 |
-0,14 |
0,15 |
0,14 |
-0,02 |
||||||||||||
|
41 |
'2M_maxX' |
-0,07 |
0,34 |
0,13 |
-0,20 |
0,78 |
0,22 |
0,04 |
0,16 |
0,00 |
0,01 |
||||||||||||
|
42 |
'2M_maxZ' |
-0,73 |
0,14 |
0,15 |
-0,49 |
-0,21 |
0,18 |
0,25 |
0,05 |
0,02 |
-0,09 |
||||||||||||
|
43 |
'Md_maxX' |
-0,36 |
0,23 |
0,50 |
-0,19 |
-0,07 |
0,14 |
-0,06 |
0,03 |
0,36 |
0,08 |
||||||||||||
|
44 |
'Md_maxZ' |
-0,63 |
0,24 |
0,32 |
-0,33 |
-0,14 |
0,21 |
0,08 |
0,11 |
0,27 |
-0,12 |
||||||||||||
|
45 |
'Mg_maxX' |
-0,03 |
-0,18 |
-0,16 |
-0,13 |
-0,32 |
-0,14 |
0,03 |
-0,38 |
-0,21 |
0,08 |
||||||||||||
|
Annexe 1 |
|||||||||||||||||||||||
|
CP1 |
CP2 |
CP3 |
CP4 |
CP5 |
CP6 |
CP7 |
CP8 |
CP9 |
CP10 |
||||||||||||||
|
46 |
'Mg_maxZ' |
-0,50 |
-0,12 |
-0,15 |
-0,45 |
-0,21 |
0,08 |
0,36 |
-0,08 |
-0,33 |
0,05 |
||||||||||||
|
47 |
'2PmaxX' |
-0,29 |
0,82 |
0,14 |
0,04 |
-0,14 |
0,24 |
0,09 |
0,11 |
-0,05 |
-0,10 |
||||||||||||
|
48 |
'2PmaxZ' |
0,56 |
0,63 |
-0,14 |
0,04 |
0,01 |
0,15 |
-0,07 |
0,03 |
-0,21 |
-0,15 |
||||||||||||
|
49 |
'Par_maxX' |
0,00 |
0,81 |
0,08 |
0,16 |
-0,28 |
0,18 |
0,19 |
-0,04 |
-0,19 |
-0,15 |
||||||||||||
|
50 |
'Par_maxZ' |
0,32 |
0,71 |
-0,09 |
0,20 |
-0,05 |
0,21 |
0,15 |
-0,12 |
-0,28 |
-0,13 |
||||||||||||
|
51 |
'Pav_maxX' |
-0,80 |
0,28 |
0,13 |
-0,07 |
0,00 |
0,11 |
0,04 |
0,14 |
0,17 |
0,24 |
||||||||||||
|
52 |
'Pav_maxZ' |
-0,01 |
0,19 |
-0,36 |
-0,22 |
-0,01 |
0,27 |
0,19 |
0,08 |
0,09 |
0,30 |
||||||||||||
|
53 |
'SFR_maxX' |
-0,44 |
0,77 |
0,19 |
0,00 |
-0,15 |
0,25 |
0,05 |
0,05 |
-0,02 |
-0,06 |
||||||||||||
|
54 |
'SFR_maxy' |
-0,28 |
-0,28 |
-0,02 |
0,10 |
0,35 |
0,00 |
0,59 |
-0,05 |
-0,05 |
0,29 |
||||||||||||
|
55 |
'SFR_maxZ' |
-0,14 |
0,45 |
0,28 |
-0,49 |
0,06 |
-0,34 |
0,08 |
-0,06 |
-0,09 |
-0,12 |
||||||||||||
|
56 |
'Fx2P_teM' |
-0,13 |
0,82 |
0,12 |
0,01 |
-0,23 |
0,23 |
0,15 |
0,21 |
-0,02 |
0,03 |
||||||||||||
|
57 |
'Fz2P_teM' |
0,56 |
0,52 |
-0,29 |
0,11 |
-0,16 |
0,22 |
0,04 |
0,10 |
-0,13 |
0,05 |
||||||||||||
|
58 |
'Fxpav_tepar' |
-0,81 |
0,14 |
0,09 |
0,02 |
0,16 |
0,25 |
-0,22 |
-0,03 |
0,18 |
0,16 |
||||||||||||
|
59 |
'Fzpav_tepar' |
-0,19 |
-0,06 |
-0,50 |
0,20 |
0,00 |
0,44 |
-0,42 |
-0,21 |
0,09 |
0,10 |
||||||||||||
|
60 |
'Vxtem' |
-0,53 |
0,14 |
0,44 |
0,34 |
0,15 |
-0,05 |
-0,15 |
-0,53 |
0,05 |
-0,11 |
||||||||||||
|
61 |
'Vxtepar' |
0,24 |
0,84 |
0,21 |
0,27 |
-0,24 |
0,07 |
0,12 |
-0,09 |
-0,08 |
-0,04 |
||||||||||||
|
62 |
'Vxtepav' |
-0,46 |
0,63 |
0,32 |
0,12 |
-0,10 |
-0,02 |
-0,04 |
0,03 |
0,33 |
0,27 |
||||||||||||
|
63 |
'Vytem' |
0,42 |
-0,11 |
-0,18 |
0,12 |
0,16 |
0,09 |
0,64 |
-0,34 |
0,30 |
0,01 |
||||||||||||
|
64 |
'Vytepar' |
0,32 |
-0,21 |
-0,12 |
0,19 |
0,29 |
-0,01 |
0,65 |
-0,39 |
0,14 |
0,07 |
||||||||||||
|
65 |
'Vytepav' |
-0,33 |
-0,16 |
0,15 |
0,24 |
0,42 |
-0,17 |
0,19 |
-0,05 |
-0,37 |
0,27 |
||||||||||||
|
66 |
'Vztem' |
0,36 |
0,51 |
0,25 |
-0,57 |
0,10 |
-0,26 |
-0,03 |
-0,24 |
-0,03 |
-0,10 |
||||||||||||
|
67 |
'Vztepar' |
0,45 |
0,55 |
0,07 |
-0,51 |
0,09 |
-0,18 |
-0,17 |
-0,23 |
-0,06 |
-0,06 |
||||||||||||
|
68 |
'Vztepav' |
0,22 |
0,53 |
-0,44 |
-0,33 |
0,04 |
0,29 |
-0,18 |
-0,31 |
0,01 |
0,29 |
||||||||||||
|
69 |
'NVtem' |
-0,34 |
0,31 |
0,51 |
0,09 |
0,18 |
-0,13 |
-0,14 |
-0,60 |
0,02 |
-0,15 |
||||||||||||
|
70 |
'NVtepar' |
0,30 |
0,86 |
0,20 |
0,16 |
-0,21 |
0,03 |
0,08 |
-0,12 |
-0,09 |
-0,04 |
||||||||||||
|
71 |
'NVtepav' |
-0,44 |
0,66 |
0,28 |
0,08 |
-0,10 |
0,00 |
-0,06 |
0,00 |
0,33 |
0,28 |
||||||||||||
|
72 |
'VxtFmax2P' |
0,47 |
0,25 |
0,40 |
0,41 |
-0,16 |
-0,15 |
0,17 |
-0,02 |
0,02 |
0,02 |
||||||||||||
|
73 |
'Oxtem' |
-0,35 |
-0,21 |
0,58 |
0,38 |
-0,03 |
-0,22 |
-0,04 |
-0,45 |
-0,07 |
-0,13 |
||||||||||||
|
74 |
'Oxtepar' |
0,41 |
0,63 |
0,30 |
0,37 |
-0,29 |
-0,14 |
0,16 |
-0,09 |
-0,15 |
-0,02 |
||||||||||||
|
75 |
'Oxtepav' |
0,29 |
0,46 |
0,47 |
0,23 |
-0,23 |
-0,34 |
0,01 |
0,03 |
0,32 |
0,17 |
||||||||||||
|
76 |
'Oytem' |
0,50 |
-0,10 |
-0,30 |
-0,06 |
0,06 |
0,15 |
0,42 |
-0,32 |
0,43 |
-0,07 |
||||||||||||
|
77 |
'Oytepar' |
0,52 |
-0,10 |
-0,29 |
0,00 |
0,16 |
0,07 |
0,52 |
-0,29 |
0,39 |
-0,02 |
||||||||||||
|
78 |
'Oytepav' |
-0,03 |
-0,16 |
-0,02 |
0,24 |
0,48 |
-0,11 |
0,54 |
-0,26 |
-0,14 |
0,23 |
||||||||||||
|
79 |
'Oztem' |
0,08 |
-0,16 |
0,37 |
-0,57 |
0,09 |
-0,35 |
-0,06 |
-0,46 |
0,03 |
-0,06 |
||||||||||||
|
80 |
'Oztepar' |
0,69 |
0,49 |
0,12 |
-0,32 |
-0,15 |
-0,22 |
0,12 |
-0,05 |
-0,11 |
0,00 |
||||||||||||
|
81 |
'Oztepav' |
0,62 |
0,42 |
-0,11 |
-0,53 |
-0,02 |
-0,08 |
-0,15 |
-0,22 |
0,03 |
0,15 |
||||||||||||
|
82 |
'NOCG_tem' |
-0,24 |
-0,28 |
0,63 |
0,06 |
0,03 |
-0,25 |
-0,05 |
-0,56 |
-0,03 |
-0,13 |
||||||||||||
|
83 |
'NOCG_tepar' |
0,56 |
0,63 |
0,26 |
0,16 |
-0,26 |
-0,15 |
0,17 |
-0,08 |
-0,15 |
-0,01 |
||||||||||||
|
84 |
'NOCG_tepav' |
0,41 |
0,51 |
0,40 |
0,06 |
-0,21 |
-0,33 |
-0,04 |
-0,03 |
0,29 |
0,19 |
||||||||||||
|
85 |
'teta_te2M' |
0,63 |
0,24 |
-0,12 |
-0,63 |
-0,02 |
-0,16 |
0,08 |
0,19 |
-0,06 |
-0,04 |
||||||||||||
|
86 |
'teta_tFmax2PX' |
-0,08 |
0,05 |
-0,11 |
-0,88 |
0,17 |
-0,19 |
-0,01 |
0,02 |
0,01 |
-0,04 |
||||||||||||
|
87 |
'teta_tFmax2PZ' |
0,17 |
0,09 |
0,02 |
-0,76 |
0,25 |
-0,38 |
-0,06 |
0,15 |
0,00 |
-0,04 |
||||||||||||
|
88 |
'teta_tePar' |
0,14 |
-0,33 |
-0,12 |
-0,69 |
0,31 |
-0,25 |
-0,25 |
-0,09 |
0,04 |
-0,01 |
||||||||||||
|
89 |
'teta_tFmaxPavX' |
0,31 |
0,26 |
-0,44 |
-0,39 |
0,01 |
0,35 |
-0,29 |
-0,43 |
-0,07 |
0,12 |
||||||||||||
|
90 |
'teta_tFmaxPavZ' |
0,33 |
0,27 |
-0,44 |
-0,38 |
0,01 |
0,35 |
-0,29 |
-0,42 |
-0,07 |
0,12 |
||||||||||||
|
91 |
'teta_tePav' |
0,27 |
0,46 |
-0,49 |
-0,37 |
0,06 |
0,29 |
-0,16 |
-0,32 |
-0,06 |
0,24 |
||||||||||||
|
Variables explicatives |
17,28 |
13,80 |
10,16 |
8,07 |
6,59 |
4,76 |
3,95 |
3,82 |
2,67 |
1,99 |
|||||||||||||
Annexe 2
Cahier des charges des blocs de depart
Sommaire
1-Analyse fonctionnelle
1.1-Contrôle de validité
1.2-Définition des fonctions
2-Caractéristiques des blocs de départ homologués
1-Analyse fonctionnelle
Afin de cerner les propriétés des starting blocs instrumentés une analyse fonctionnelle est réalisée en s'appuyant sur des méthodes simples de gestion de projet. La Bête à cornes (figure 99) est un des outils de représentation permettant d'effectuer une analyse fonctionnelle pour identifier le besoin satisfait par le système en se posant les questions suivantes :
- À qui rendre service ?
- Sur quoi agit le système ?
- Dans quel but ? (fonction d'usage ou besoin)
Sur quoi agit
le système ?
A qui rend service
le système ?
Dans quel but le
système existe-t-il ?
Prise de décision de l'entraîneur
Comprendre et
Améliorer le départ
Dissocier la mesure et l'analyse des
efforts
Figure 99 Bête à cornes
Entraîneur
Consignes
Athlète
Efforts
Feedback
Starting-block
instrumenté
1.1-Controle de validite
Un contrôle de validité du besoin est ensuite effectué en répondant aux trois questions suivantes :
Raison But
Pourquoi existe Incapacité d'apprécier un geste très Dissocier les efforts exercés au
t-il ? rapide niveau de chaque pied
Peut-il Parce que les efforts au niveau des Évaluer les variations de la vitesse et
évoluer ? mains ne sont pas considérés de la position du centre de gravité
|
Peut-il |
Déplacement de l'instrumentation Probable (à long terme) (ex. : chaussure instrumentée,...) |
1.2-Definition des fonctions
Les fonctions des blocs de départ instrumentés sont de deux catégories : principale et secondaire. Le premier objectif du développement de cet instrument est de mesurer sélectivement les efforts qui sont exercés sur les blocs.
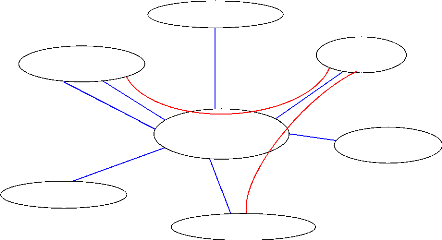
Environnement
FC1
Athlète
Dynamomètre
FP2
FC4
FC6
FC5
Blocs de départ
instrumentés Maintenance
F
FC7
Règlementation
FC3
FP1
Piste d'athlétisme
Figure 100 Détermination des fonctions
principales (FP) et fonctions secondaires (FC)
des blocs de départ
instrumentés
Fonctions Principales :
FP1 : Isoler les efforts du sol
FP2 : Mesurer les efforts de l'athlète et transmettre les données au logiciel Fonctions Secondaires :
FC1 : Isolation et résistance à l'usure
F : Respecter la réglementation de l'IAAF
FC3 : Doit être fixé au sol
FC4 : Être adapté à tous les athlètes
FC5 : Prévoir le passage des fils
FC6 : Alimentation des ponts de jauges
FC7 : Faciliter l'entretient et la réparation
Fonctions Origine But Évolution / Disparition
FP1 Le pied ne doit pas toucher le sol Pour mesurer le torseur réel Que les efforts sur le sol soient
négligeables
|
FP2 L'entraîneur a besoin d'un outil d'aide à la prise de décision |
Pour évaluer les paramètres mécaniques lors du départ |
Que l'analyse du départ ne permet plus d'amélioration |
||
|
FC1 Le Starting-block pourrait être utilisé à l'extérieur |
Pour que le climat n'influx pas les mesures et pour protéger le capteur /// |
|||
|
F L'utilisation des starting blocs doit respecter la réglementation de l' IAAF |
Pour pouvoir être utilisé lors des /// compétitions |
|||
FC3 L'implantation du starting-block est Pour préserver la piste d'athlétisme ///
normalisée
|
FC4 Chaque athlète possède ses propres caractéristiques morphologiques |
Pour que chaque athlète puisse effectuer ses propres réglages (inclinaison et écart entre les blocs) |
/// |
FC5 Les fils doivent être protégés Pour que l'environnement de Infrarouge, ...
l'athlète soit sûr
FC6 Le fonctionnement du capteur en dépend Pour alimenter les ponts de jauges ///
FC7 Le capteur ou d'autres pièces peuvent être Pour améliorer la durée de vie Si rien ne peut tomber en panne
en panne ou cassés
2-Caracteristiques des blocs de depart homologues
D'après la règle 161 instaurée par l'IAAF les blocs de départ doivent être conformes aux caractéristiques générales suivantes :
(a) Ils devront être d'une construction absolument rigide et ne devront procurer aucun avantage inéquitable à l'athlète.
(b) Ils devront être fixés sur la piste par un nombre de clous ou de pointes prévus pour endommager le moins possible la piste.
Cette disposition doit permettre d'enlever rapidement et facilement les blocs. Le nombre, l'épaisseur et la longueur des clous ou des pointes dépendent de la nature de la piste. Les points de fixation ne doivent permettre aucun mouvement au moment du départ proprement dit.
(c) Lorsqu'un athlète emploie ses blocs de départ personnels, ils doivent être conformes aux dispositions des alinéas (a) et (b) ci-dessus. Ils peuvent être de n'importe quelle conception ou construction à condition qu'ils ne causent aucune gêne aux autres athlètes.
(d) Lorsque les blocs de départ sont fournis par le Comité Organisateur, ils doivent être conformes aux dispositions suivantes: ... les blocs de départ doivent être constitués par deux plaques contre lesquelles les pieds des athlètes prennent appui dans la position de départ. Les plaques doivent être montées sur un cadre rigide qui ne pourra, en aucune manière, gêner les pieds des athlètes lorsqu'ils quittent les blocs. Les plaques devront être inclinables pour convenir à la position de départ de l'athlète et pourront être plates ou légèrement concaves. La surface des plaques devra être préparée pour convenir aux pointes des chaussures des athlètes, soit en pratiquant des cannelures sur la plaque, soit en la recouvrant d'un matériau approprié permettant l'usage de chaussures à pointes. Le montage des plaques sur un cadre rigide peut être réglable, mais il ne doit permettre aucun mouvement pendant le départ proprement dit. Dans tous les cas, les plaques doivent être réglables en avant comme en arrière et l'une par rapport à l'autre. Le réglage doit être complété par un système de serrage ou de verrouillage qui pourra être manoeuvré facilement et rapidement par l'athlète.
Annexe 3
Chaine de mesure dynamométrique
Sommaire
1-Principes de la métrologie
2-Mise au point d'un capteur composite
2.1-Propriétés mécaniques du corps d'épreuves 2.2-Principe de jauges de déformation
2.3-Conditionnement et acquisition des signaux
1-Principes de la metrologie
L'évaluation des forces repose sur la mesure de leurs conséquences qui se traduit par le changement de l'état du système c'est-à-dire sa déformation et/ou la variation de sa position. Lors de notre étude, l'évaluation des actions mécaniques au cours du départ de sprint est assurée suite à l'exploitation de deux principes, celui de la piézoélectricité et celui de l'extensométrie.
Principe de piézoélectricité : découvert par Jacques et Pierre Curie en 1880, désigne la propriété qu'ont certain matériaux de développer une charge électrique proportionnelle à la contrainte qui leur est appliquée, et inversement de se déformer en fonction du champ électrique. Le phénomène de piézoélectricité consiste en l'apparition d'une polarisation déjà existante dans certains diélectriques anisotropes naturels ou artificiels. Le quartz est le plus connu, certain matériaux céramiques ferroélectriques génèrent aussi des différences de potentiel lorsqu'ils sont soumis à des contraintes. Les applications de ce principe sont nombreuses et diverses, elles s'étendent jusqu'aux domaines de l'électronique, de
l'électroacoustique et bien entendue de la métrologie. Cette dernière application est à l'origine du fonctionnement des capteurs équipant les plates de formes de forces Kistler (Type 9281B et 9287B) utilisées au cours de nos expérimentations.
Principe d'extensométrie : les capteurs utilisés sont dits passifs, se sont des jauges résistives qui traduisent en variation de résistance leur propre déformation qui est en principe proportionnelle à celle de la structure à l'endroit où elles sont collées. Leur domaine de mesure est basé sur le principe de l'élasticité linéaire qui représente le domaine dans lequel la relation entre force et déformation est linéaire et réversible. C'est une région de la relation entre force et déplacement correspondant à de faibles déformations. La connaissance des déformations sert à calculer les contraintes lorsque les lois qui lient ces grandeurs sont connues. Les capteurs composites (3D) développés reposent sur ce principe.
2-Mise au point d'un capteur composite
La mise au point d'un tel outil métrologique nécessite l'utilisation de moyens sophistiqués tant dans le domaine de l'extensométrie que celui de l'électronique. L'expérience de notre équipe dans le domaine de l'extensométrie ainsi que la proximité d'un atelier d'électronique ont favorisé le développement d'un capteur composite. Le principe de la chaîne de mesure développée est résumé dans la figure ci-dessous (figure 101). Les détails de fonctionnement de cette chaîne sont effectués à la suite.
Figure 101 Schéma du principe d'une chaîne de mesure
2.1-Proprietes mecaniques du corps d'epreuve
La conception du corps d'épreuve destiné à instrumenter les blocs de départ repose sur le principe de la plate forme de Stewart qui représente un mécanisme parallèle à six degrés de liberté très bien connue des roboticiens et des constructeurs d'hexapodes. Ce type de corps d'épreuve a été développé par la première fois en 1983 par Gaillet [Gail 83].
De forme cylindrique, il est composé d'une plate forme (S1), une base (S2), et six poutres en liaison rotule avec S1 et S2 (figure 102).

(a) (b)
Figure 102 (a) Schéma reprenant l'allure la
plate forme de Stewart,
(b) Photo d'un corps d'épreuve de la
société Médicapteur
Ce système se compose donc de huit corps en jeux et de douze liaisons. Cela fait perdre la simplicité de la structure et diminue sa rigidité. C'est ainsi que les données recueillies lors de notre étude ont permit de choisir judicieusement et spécifiquement les matériaux constituant le cops d'épreuve ainsi que la procédure de son dimensionnement. Toutefois, le corps d'épreuve doit être utilisé dans sa limite élastique linéaire afin d'assurer une relation linéaire entre la déformation mesuré et l'effort appliqué.
La pièce mécanique constituant le corps d'épreuve est un solide homogène isotrope51. Lorsque cette structure est soumise à des efforts extérieurs ces poutres subissent des déformations élastiques d'ordre microscopique qui varient linéairement par rapport aux contraintes qui lui sont appliquées (figure 103).

Figure 103 Courbe d'effort/déformation typique
Selon la loi de Hooke, la relation liant le tenseur des contraintes ä à celui des déformations å s'exprime sous la forme ä = Eå où E est un coefficient propre à la matière appelé module de Young ou module d'élasticité.
51 Isotrope : corps qui présente les mêmes propriétés dans toutes les directions.
Grâce à sa propriété élastique linéaire le corps d'épreuve se déforme d'une manière proportionnelle sous l'effet de la contrainte qui lui est appliquée. Les jauges collées à la surface des poutres ont pour rôle la mesure de ces déformations afin de les traduire en signaux électriques. Ce dispositif nous permet ainsi de calculer l'état de contrainte. C'est le principe de l'extensométrie. L'exploitation de la théorie de l'élasticité linéaire a permis de mettre en place le capteur qui traduit la valeur de la contrainte en une grandeur ou une indication exploitable.
2.2-Principe de jauges de deformation
Les jauges de déformation ou jauges d'extensométrie nommées parfois « jauges de contrainte » par abus de langage, sont constituées par un fil résistant très fin (sous forme de spires rapprochées) imprimé ou collé sur un support isolant de petite taille (de quelque millimètre à quelque centimètre de longueur).

Figure 104 Exemple d'une jauge de déformation
Lorsqu'une poutre supportant une jauge d'extensométrie se déforme, le fil qui est collé sur sa surface s'étire. Sa résistance électrique donnée par R = ñL / S ( ñ : résistivité du
conducteur, L : longueur en mètre et S : section en mètre carré) varie proportionnellement avec la variation de sa longueur : ÄR / R = KÄL / L . La constante K est le facteur de jauge, il dépend du matériau qui la compose et caractérise sa sensibilité. Cette relation est à la base de l'extensométrie [Cout 00].
La mise en pratique de cette relation se réalise en montant quatre jauges collées sur un support en pont de Wheatstone, ce qui permet de traduire des déformations de support de jauge ( ÄL / L) atteignant les 10-6mètres. En mesurant la variation de résistance de jauge, on
en déduit alors sa déformation et par conséquent l'amplitude de l'effort exercé sur le corps d'épreuve.
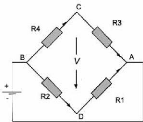
Figure 105 Montage en pont de Wheatstone
Suivant le nombre de jauges constituant le pont, il est possible de distinguer trois types de montage possibles :
- Montage en quart de pont : comporte une jauge active.
- Montage en demi-pont : comporte deux jauges actives.
- Montage en pont complet : comporte quatre jauges actives.
Les jauges manquantes sont remplacées par des résistances fixes ou par des jauges dites jauges de complément.
Dans le cas du capteur développé au cours de cette étude le corps d'épreuve est instrumenté par six ponts complets. Chaque pont comporte ainsi quatre jauges actives collées deux à deux en sens opposé sur la même poutre.
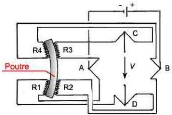
Figure 106 Montage de jauges de déformation en
pont de Wheatstone sur une poutre.
Modifié d'après Asch 1999
[Asch 99]
L'adoption de ce type de montage en pont de Wheatstone complet offre la possibilité de détecter le courant passant par la diagonale du pont (entre les broches C et D) lorsque A et B sont connectés à une source de courant. À l'équilibre, la tension entre les deux points (C et D) situés entre les deux extrémités est nulle.
Si l'une des résistances varie, le pont est déséquilibré et la tension de sortie Vm mesurée est pratiquement proportionnelle aux variations relatives de résistance ÄR / R de chacune des jauges.
Autres particularités de ce montage, deux résistances adjacentes du pont (R1 et R3) agissent en sens opposé, alors que deux résistances opposées (R1 et R2) agissent dans le même sens pour l'équilibre du pont
ÄR1 = - ÄR2 = ÄR4 = - ÄR3 = ÄR
Il est ainsi possible d'éliminer l'influence de certains phénomènes (telle que la température) et d'accroître la sensibilité au profit de la grandeur à mesurer (la force) [Robe 04]. Le pont de jauge est ensuite raccordé à un conditionneur-amplificateur qui alimente le capteur, conditionne et amplifie le signal de quelques millivolts à quelques dizaines de volts.
2.3-Conditionnement et acquisition des signaux
Le rôle du conditionneur dans la chaîne d'acquisition est fondamental. Grâce à ces deux parties distinctes, il permet en premier temps d'alimenter les ponts de Wheatstone en générant une tension très stables de 5 à 10 mv, suivant les valeurs de résistance qui constitue le pont. Dans un second ordre il permet d'amplifier les signaux issus des ponts afin d'obtenir des tensions en sortie de l'ordre du Volt qui pourront ensuite être envoyées sur une carte d'acquisition analogique numérique.
Il existe généralement deux types de conditionneurs, l'un est unipolaire (ou asymétrique référencé), il génère une tension de sortie comprise entre [0 V , 10 V] ; l'autre est bipolaire (ou différentiel) dont la tension de sortie est comprise entre [-5 V , 5 V].
L'électronique de conditionnement constitue le premier maillon de la chaîne d'acquisition des signaux en provenance des ponts de Wheatstone. L'enregistrement des signaux est ensuite assuré via une carte de Conversion Analogique Numérique (CAN) ; de la société National Instrument52 ; reliée à un ordinateur qui stockera l'ensemble des signaux provenant des conditionneurs à une fréquence fixée au préalable par l'expérimentateur.
52 www.ni.com/
Annexe 4
Mesures cinématographiques
Sommaire
1.1- Le calibrage des caméras
1.2-Acquisition des coordonnées 2D
1.3-Calcul des données 3D
1.4-Précision des données vidéo
2-Effets de la PSR vs la PSG sur la dynamique articulaire
1.1-Le calibrage des cameras :
Le calibrage consiste à identifier pour chaque caméra un modèle donnant des relations entre les cordonnées 3D d'un marqueur dans l'espace et les coordonnées 2D de ce même marqueur dans l'espace image des caméras. L'étape de reconstruction 3D requiert l'étalonnage préalable des paramètres intrinsèques des caméras et de leurs situations relatives.
Le système cinématographique utilisé est basé sur la stéréovision passive. Il s'agit du même principe qui gouverne la vision humaine. En effet, l'image d'un objet permet de déterminer sa position horizontale et verticale mais pas sa profondeur. Ainsi, nos deux yeux délivrent deux images légèrement décalées qui nous permettent d'évaluer la profondeur. De ce fait, pour la reconstruction 3D, chaque marqueur doit être vu par au moins deux caméras.
Cette manipulation s'effectue en plaçant dans le champ des caméras un objet de taille connue sur lequel on place un repère précis ; celui ci peut être un cube ou une grille de calibration que l'on déplace dans le volume expérimental.
Au cours du calibrage, une baguette rigide en forme de T contenant un marqueur à chaque extrémité est utilisé. La distance qui sépare les deux marqueurs est de 581,2 mm.
1.2-Acquisition des cordonnees 2D :
Cette étape a pour fonction de déterminer les coordonnées 2D des marqueurs, c'est-àdire leurs coordonnées dans les images de chaque caméra. Ces coordonnées constituent les données de base. Elles sont acquises à une fréquence de 250 HZ par l'intermédiaire de six caméras monochromes synchronisées et associées à des sources infrarouges spécifiques.
1.3-Calcul des donnees 3D :
L'étape de calibrage des caméras est essentielle et très importante car elle va permettre l'application du principe de stéréovision passive sur lequel repose le calcul des coordonnées tridimensionnelles. Ainsi le logiciel peut effectuer un calcul automatique optimisé des coordonnées 3D de chaque marqueur à la suite d'une identification de sa trajectoire en 2D.
Plus précisément, la position d'un marqueur est trouvée en lui attribuant des coordonnés du point M situé sur le milieu du segment H1-H2 qui minimise l'écart entre les deux droites objets D1 et D2 (figure 107).
Figure 107 Détermination des coordonnées 3D d'un marqueur
Ainsi à l'aide d'une méthode des moindres carrés et des équations de D1 et D2, les coordonnées tridimensionnelles de H1 et H2 sont calculées puis utilisées pour trouver celles du point M.
|
X |
xH |
1+ xH2 |
2
|
M |
Y |
yH1 + yH2 |
2
|
Z |
zH |
1+zH2 |
2
Parallèlement au calcul des coordonnées 3D, nous pouvons procéder à une interpolation des trajectoires en 2D. Ceci est particulièrement utile lorsque des marqueurs n'ont pas été détectés pendant un bref instant comme par exemple lorsqu'une partie du corps est masquée par un membre ou encore lors d'une rotation trop importante d'un segment corporel qui empêche la détection des marqueurs.
1.4-Precision des donnees video
Le but des mesures cinématiques est de déterminer le plus précisément possible les positions au cours du temps des marqueurs distaux et proximaux de chaque articulation.
Selon Allard et al. (1994), l'imprécision de mesure est due à l'accumulation d'un certain nombre d'erreurs (figure 108).

Figure 108 Propagation des erreurs de mesure en
fonction des différentes étapes nécessaires
à la
reconstruction des coordonnées 3-D [Alla 95]
Nous pouvons répartir ces erreurs suivant deux catégories :
- celles relatives à la reconstruction tridimensionnelle (équipements, objet de calibration)
- celles dues aux mouvements de la peau sur l'articulation et des marqueurs sur la peau.
De ce fait, il est important d'évaluer la précision avec laquelle le système fournit les deux grandeurs que sont : la distance entre les deux points et l'angle entre deux segments consécutifs par exemple.
Dans le cas de nos mesures, bien que l'erreur systématique de l'instrument annoncée par le constructeur soit de l'ordre du millimètre (< 0,1% du champ de mesure), il est tout de même nécessaire d'effectuer un certain nombre de mesures pour cerner au plus près l'erreur de nos évaluations.
La précision de nos données est testée selon deux modes : le mode statique et le mode dynamique. Dans le cas des tests en mode statique, nous avons positionné dans le champ des caméras la baguette de calibration. Dans le cas des tests en mode dynamique, la baguette de calibration est déplacée dans l'ensemble du champ.
Enfin, nous avons vérifié la distance séparant les deux marqueurs au cours de toute la durée de l'acquisition. Nos erreurs sont de #177;11,6 mm en mode dynamique et #177;0,8 mm en mode statique. Ces résultats sont satisfaisants pour une baguette rappelons le de 581,2 mm de longueur soit respectivement #177;2% et #177;1%.
2-Effets de la methode de solidification globale sur la definition des angles articulaires
La figure 109 illustre le résultat de la confrontation des angles relatifs calculés suite à l'application de la procédure d'optimisation globale [Lu 99] aux angles relatifs bruts issus directement des mesures cinématographiques (sans traitement préalable). La procédure d'optimisation globale est détaillée dans le chapitre VII.
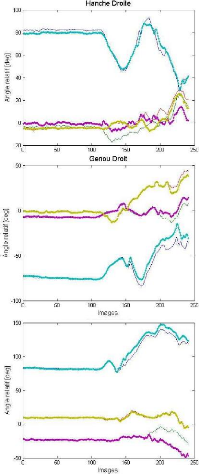
|
Angles relatifs optimisés |
Angles relatifs bruts |
Figure 109 Confrontation des angles relatifs issus des
mesures directes et suite à l'adoption d'une
procédure
d'optimisation globale par moindres carrés proposée dans [Lu 95].
Exemple des angles de
flexion/extension (Flex), abduction/adduction (Abd) et
Rotation interne/externe (Rot) pour
les articulations du membre
inférieur droit (cheville, genou et hanche)
300
200
200
-100
-200
-300
-400
e
-500
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
te
0
-100
100
0
te
-100
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
100
t
200
200
600
0
400
0
-200 PSG PSR
200
-200
-400
0
-400
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
-600
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
-200
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
-800
100
0
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Figure 110 Forces inter-segmentaires au niveau du coude droit et de l'épaule droit exprimées
respectivement dans abras , athorax (membre supérieur droit)
Fx
200
Fy
300
Fz
250
te
-100
200
100
0
200
te
150
100
50
te
0
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-2000 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-50
m 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
PSG PSR
100
0
-100
-200
-300
Epaule [N] Coude [N] Epaule [N] Coude [N]
400
200
0
-200
600
400
200
0
-200
-400
200
0
-200
Temps [s]
Temps [s]
100
20
50
50
0
0
0
-20
-50
-50
te
te
te
-100
-40
-100
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1000
500
0
-500
-1000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
2000
1000
0
-1000
-2000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
1000
0
-1000
-2000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
2000
1000
0
-1000
-2000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
1000
500
0
-500
-1000
-1500
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
2000
1000
0
-1000
-2000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Temps [s]
Figure 112 Force inter-segmentaires au niveau de C7, T12 et L5 exprimées respectivement
dans atête , athorax et aabdomen
PSG PSR
400
200
0
PSG PSR
-200
-2000
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-400
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-
-
Epaule [Nm] Coude [Nm] L5 [N] T12 [N] C7 [N]
Mx
200
0
-200
-400
-600
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
My
400
300
200
100
0
-100
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Mz
150
100
50
0
-50
-100
-150
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
te
te
te
400
200
0
-200
-400
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
Temps [s]
500
0
-500
1000
1500
Figure 113 Moments articulaires au niveau du coude droit et de l'épaule droite exprimés respectivement
dans abras , athorax (membre supérieur droit)
235
236
Temps [s]
Temps [s]
Temps [s]
200
0
-200
-400
-600
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
1500
1000
500
0
-500
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
500
400
300
200
100
0
600
400
200
-200
-400
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
300
200
100
0
-100
1000
500
0
-500
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
0
t e
te
te
-100
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
PSG PSR
-200
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
Figure 114 Moments articulaires au niveau du coude gauche et de l'épaule gauche exprimés
respectivement dans abras , athorax (membre supérieur gauche)
Mx
My
Mz
-1500
-1000
20
50
te
0
0
-20
t e
-50
te
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
-40
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
-100
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
2000
1000
1000
PSG PSR
500
0
0
-500
-1000
-1000
-2000
-1500
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
1500
1000
1000
500
500
0
0
-500
-500
-1000
L5 [Nm] T12 [Nm] C7 [Nm] Epaule [Nm] Coude [Nm]
-1000
-2000
-3000
-2000
-4000
200
100
0
-100
3000
2000
1000
0
4000
2000
0
Achevé d'imprimer en Février 2009
Laboratoire de Mécanique des Solides
UMR
6610
SP2MI - Téléport 2
Boulevard Marie et Pierre
Curie
BP 30179
86962 Futuroscope Chasseneuil Cedex
http://www-lms.univ-poitiers.fr
Contribution a la caracterisation mecanique des
criteres de qualites du
depart de la course vitesse sur 100 m
L'objectif de ce travail est de définir les paramètres mécaniques qui caractérisent le départ de course vitesse sur 100 m.
La première partie, suite à une analyse de la littérature technique, du règlement instauré par l'IAAF et des études scientifique, cerne les problèmes liés à la mesure et au choix des critères de qualification de la performance du départ de course vitesse sur 100m.
La seconde partie met en évidence la nécessité de déterminer avec plus de précision l'instant de mise en action du coureur notamment lors des compétitions internationales. Une analyse en composante principale est réalisée afin de tester la possibilité de créer de nouveaux critères permettant une interprétation objective et fiable de la performance du départ de course vitesse.
Au cours de la troisième partie, l'efficacité d'un départ est approchée en intégrant des paramètres directement accessibles par dynamométrie pour enfin les « traduire » en unités de temps. Une station dynamométrique est validée afin d'offrir à l'entraîneur des indications fines, en temps quasi réel, lors des séances d'entraînement.
La quatrième partie, propose une nouvelle méthode de solidification permettant une application rigoureuse des principes de la mécanique lors de la modélisation tridimensionnelle de l'athlète. Le calcul des torseurs d'action inter segmentaire est réalisé par programmation de l'algorithme de Newton-Euler, en utilisant un formalisme d'opérateurs homogènes.
* * * * * * * * * * * * * * *
Contribution to the mechanical characterization of the
quality criteria of the
sprint start on 100 m running event
The purpose of this work is to define the mechanics parameters which characterize the sprint start on 100 m running event.
The first part of this work analyzes technical writings, IAAF laws and scientific studies to indicate problems concerning measurement and choice of the quality criteria to describe performance on sprint start.
The second part draws attention to the necessity to define the athlete's action time with more accuracy, especially at the international competitions. A principal component analysis is realized to test the eventual possibility to create a new criterion allowing an objective and reliable performance interpretation on sprint start.
In the third part the efficiency of sprinting start is estimated by using kinetic parameters measured by sensor. A dynamometric apparatus is developed to provide immediate and accurate feedback to coaches and sprinters.
The fourth part suggests a new solidification procedure which permits a rigorous application of mechanical laws during the athlete's 3D modeling approach. The 3D inter segmental mechanical actions of the whole body are calculated by using homogeneous matrix developed in field of robotics.

