|
i
Table des matières
Table des matières i
Table des figures iii
Liste des tableaux v
Remerciements vi
Introduction vii
|
1
|
Reconstruction des images binaires
|
1
|
|
1.1
|
Définition
|
1
|
|
1.2
|
Problème de la reconstruction d'une image binaire
|
2
|
|
1.3
|
Problème standard de reconstruction de l'image binaire . .
. .
|
2
|
|
|
1.3.1 Existence d'une solution
|
3
|
|
|
1.3.2 Reconstruction d'une solution
|
3
|
|
|
1.3.3 Unicité et Equivalence entre les solutions
|
4
|
|
1.4
|
Etat de l'art
|
6
|
|
1.5
|
Conclusion
|
6
|
|
2
|
Etat de l'art sur la reconstruction des images
hv-convexes
|
7
|
|
2.1
|
Définition
|
7
|
|
2.2
|
Etat de l'art sur la reconstruction des images hv-convexe . .
.
|
8
|
|
2.3
|
Conclusion
|
16
|
|
3
|
Reconstruction des Images Binaires par recherche
Taboue
|
18
|
|
3.1
|
Paramétrage de l'algorithme Tabou
|
18
|
|
|
3.1.1 Définition du voisinage
|
19
|
|
|
3.1.2 Liste tabou
|
20
|
Abdessalem DAKHLI ii
Table des matières
3.1.3 Condition d'arrêt 20
3.1.4 Fonction d'évaluation 20
3.2 L'application de la recherche taboue pour reconstruire des
images hv-convexe 21
3.2.1 Reconstruction des images
11V-CONVEXES par la re-
cherche taboue sans amélioration 24
3.2.2
Reconstruction des images 11V-CONVEXES par la re-
cherche taboue avec amélioration 30
3.3 Conclusion et interprétations des résultats
33
Conclusion et pérspectives 35
Annexe 36
Bibliographie 49
iii
Table des figures
|
1.1
|
Projection orthogonales (horizontale et verticale) d'une ma-
|
|
|
trice binaire
|
2
|
|
1.2
|
Reconstruction d'une matrice binaire par l'algorithme glouton
|
4
|
|
1.3
|
Illustration d'une bascule
|
5
|
|
1.4
|
Voisinage à l'aide d'une opération Bascule
|
5
|
|
2.1
|
Définition d'une matrice convexe
|
8
|
|
2.2
|
Principe de reconstruction d'une image binaire
|
9
|
|
2.3
|
Opération bascule
|
13
|
|
3.1
|
Modélisation de la mémoire dans la recherche Tabou
|
22
|
|
3.2
|
Principe de reconstruction d'une image binaire
|
23
|
iv
Liste des tableaux
|
2.1
|
Résultat de Reconstruction des images hv-convexe
|
25
|
|
3.1
|
Résultat de Reconstruction des images hv-convexe
|
37
|
|
3.2
|
Résultat de Reconstruction des images70x70 hv-convexe . .
. .
|
38
|
|
3.3
|
Résultat de Reconstruction des images100x100 hv-convexe .
.
|
39
|
|
3.4
|
Résultat de Reconstruction des images 40x40 hv-convexe
en
|
|
|
appliquant le principe d'intensification
|
44
|
|
3.5
|
Résultat de Reconstruction des images 70x70 hv-convexe
en
|
|
|
appliquant le principe d'intensification
|
45
|
|
3.6
|
Résultat de Reconstruction des images 40x40 hv-convexe
en
|
|
|
appliquant le principe de diversification
|
46
|
v
Remerciements
Je tiens tout d'abord à remercier mon encadreur Mr.
Fethi jarray pour sa disponibilité et ses conseils avisés. Mais
aussi pour sa bonne humeur et sa franchise qui ont donné une ambiance de
travail stimulante et productive.
Je remercie bien évidement mes parents, mes grands
parents et ma famille pour m'avoir soutenu, aimé et permis de faire ces
longues études qui je l'espère seront payante. Merci de m'avoir
fait confiance et j'espère avoir pu faire votre fierté.
Je tiens à remercier très sincèrement
l'ensemble des membres du jury qui me font le grand honneur d'avoir
accepté de juger mon travail.
Je tiens également à remercier tous mes amis et
mes enseignants qui ont encouragé dans mes études. Vous l'avez
tous fait à votre manière et je vous en suis extrement
reconnaissant
vi
Introduction
La tomographie discrète ou reconstruction d'images
discrètes à partir de certaines de leurs projections est un sujet
en pleine expansion et souvent on fait une tomographie dès qu'une image
n'est pas comprise ou de mauvaise qualité d'incidence ou de
contraste.
Ses applications industrielles en cristallographie et en
imagerie médicale font de ce sujet une source importante de
problèmes algorithmiques. Cette discipline consiste à
reconstruire un sous-ensemble à partir d'un ensemble de projections. Ces
sous-ensembles reconstruits peuvent correspondre à des images
monochromatiques, des images en couleur, des emplois de temps,.. .
Les problèmes traités peuvent être
formulés comme suit : étant donnés H = (h1,
... , hm) et V = (v1, ... ,
vn) deux vecteurs à coordonnées
entières positives, est-ll possible de reconstruire un matrice
m*n éléments qui respecte les projections
(H, V ) ? Le plus souvent les projections donnent le nombre des
éléments dans chacune des lignes et des colonnes. Ces
éléments se fixent selon la nature de problème.
Notre travail se situe dans le cadre de reconstruction des
images binaires monochromatiques. Le problème qu'on traite est la
reconstruction des images binaires étant données ses projections
orthogonales (H, V ). Pour résoudre ce problème on doit
utiliser la recherche taboue.
Le présent rapport est composé de trois chapitres.
Le premier chapitre traite essentiellement le problème de reconstruction
des images binaires et introduit certaines notions fondamentales en
reconstruction d'images, le deuxième chapitre s'adresse à
l'état de l'art conçernant la reconstruction des images
hv-convexe et le troisième chapitre présente les résultats
pratiques et théoriques informatiques d'algorithme tabou concernant la
reconstruction des images hv-convexe.
1
Chapitre1
Reconstruction des images binaires
L'objet de ce chapitre est de présenter le
problème de reconstruction d'une image binaire et les motivations
à la fois applicatives et théorique qui a poussé la
communité scientifique à se pencher sur ce problème.
1.1 Définition
Une image binaire est une image pour laquelle chaque pixel ne
peut avoir pour valeur que 0 ou 1. La manipulation de telles images regorge
d'outils spécialisés ainsi que de théories
mathématiques pour plusieurs raisons. En effet, les débuts du
traitement des images numériques ne permettaient pas le traitement
d'images complexes (problème de temps de calcul, d'espace mémoire
disponible et qualité des périphériques de sortie). De
plus, les premières applications (reconnaissance de caractères,
analyse de traces laissées dans les chambres à bulles par des
particules) vers 1950 s'adaptaient bien à ce type d'images.
De même les images binaires sont un contexte simple
permettant une formalisation mathématique des problèmes par des
outils tels que la topologie. Dans le domaine de la vision industrielle
(détection de défauts, contrôle qualité, mesure,
...). On considère souvent l'image binaire comme un passage
obligé, suivant en général la phase de segmentation. Deux
catégories d'outils sont alors nécessaires pour d'une part le
codage efficace (et éventuellement la compression) et d'autre part pour
le traitement (analyse et description des formes).
Abdessalem DAKHLI 2
Chapitre 1. Reconstruction des images binaires
1.2 Problème de la reconstruction d'une image
binaire
Le problème de la reconstruction des images binaires
consiste à trouver une image binaire respectant certaines contraintes,
par exemple la projection dans plusieurs directions. Les problèmes
peuvent être classés suivant le nombre de directions et les
propriétés géométriques des objets
(convexité, connexité, périodicité, etc), c'est
à dire selon la projection horizontale et verticale de l'image on
essayera de l'élaborer sa matrice binaire.
Soit A une matrice binaire :A = (
a11...a1n ) avec aii 2
{f; 1} , on définit :
hi = Xn
i=1
am1...amn
aii : la projection horizontale de la lignei;
i = 1; :::; n. Elle donne
le nombre des '1'de chaque ligne.
H = (h1;::: ;
hn) : la projection horizontale de la matrice
binaire A:
vi = Xm
i=1
aii la projection verticale de la colonne j;
j = 1;::::; m; Elle
donne le nombre des '1'de chaque colonne.
V = (v1;::: ;
vm) : la
projection de la matrice binaire A.
Exemple : soient H = (1;
3; 3; 3; 3) et
V = (2;3;
1;4; 3) les projections
horizontale et verticale de la matrice suivante :
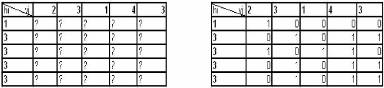
FIG. 1.1 - Projection orthogonales (horizontale et verticale)
d'une matrice binaire
1.3 Problème standard de reconstruction de l'image
binaire
Le problème de reconstruction d'une matrice binaire
à partir des ses projections orthogonales (H; V ),
noté MB(H; V ), consiste à trouver une
matrice binaire A de projection horizontale H et de projection verticale V . On
note
Abdessalem DAKHLI 3
Chapitre 1. Reconstruction des images binaires
par R(H, V ) la classe des matrices binaires m
* n de projection orthogonales (H,V ).
Il est couramment admis que le premier problème de
tomographie discret, étudié par H.Ryser[6] à la fin des
années 50 est la reconstruction d'une matrice. La projection horizontale
d'une matrice binaire est le vecteur H = (h1;... ; hn)
où hi est la somme des éléments de la ligne
j. De façon analogue, la projection verticale est le vecteur :
V = (v1;... ; vm) où les sommes sont
calculées par colonne.
Plusieurs types de problèmes peuvent être
définis : existence, reconstruction et unicité.
1.3.1 Existence d'une solution
Données H = (h1;... ;
hn) et V = (v1;... ; vm)
deux vecteurs à coordonnées entières positives.
Question Existe-il une matrice binaire M
ayant pour projections H et
V ?
Le théorème 1 [6] suivant est fondamental et
donne, sous l'hypothèse de la décroissance de la projection
verticale, des conditions nécessaires et suffisantes pour l'existence
d'une matrice binaire à partir des projections orthogonales sous la
forme de deux vecteurs décroissante. En effet, une vecteur V de
dimension m est décroissante si t1 ~ t2 ~ .....
~ tm.
Theorem 1 (Ryser) :
Si V est décroissante (V est
décroissante si v1 ~ v2 ~ .... =
vm) alors le problème MB(H, V ) a pour
réponse 'oui'si et seulement si :
Xk j=1
hi =
vj et
v j >
Xm
i=1
Xn j=1
Xk j=1
vj ; k = 1,....,n - 1
Avec ...
v j désigne le nombre de projections horizontales
supérieure ou égales à j.
1.3.2 Reconstruction d'une solution
Données : H = (h1;. . . ;
hm) et V = (v1; . .. ; vn)
deux vecteurs à coordonnées entières positives.
Question : Reconstruire une matrice binaire
respectant H et V
Pour reconstruire une matrice binaire il existe plusieurs
algorithmes basés sur le théorème 1 qui permettent de
reconstruire une matrice binaire [6]. Par exemple l'algorithme glouton en
O(mn+max(mlogm,nlogn)). A chaque étape (colonne) j, vj '1'sont
placés à la colonne j et sur les lignes disponibles
les
Abdessalem DAKHLI 4
Chapitre 1. Reconstruction des images binaires
plus prioritaires. Si le nombre de lignes disponibles est
inférieur à v alors l'algorithme s'arrête et il n'y a pas
de solution au problème. La ligne i est dite disponible à
l'étape j lorsque ai > 0. ai étant le nombre
des '1' non encore placés à l'étape j de l'algorithme.
Les lignes les plus prioritaires sont celles qui ont les plus
grandes valeurs
ai.
Pseudo Code de l'algorithme glouton:
1 - ai = hi; i =
1;::::; m;
2 - pour j = 1 à n
Faire
2.1 - s'il n'existe pas v ligne disponible alors
fin;
2.2 - placer v '1' sur les lignes disponibles les plus
priotaires;
2.3 - si un '1' est placé sur la ligne i
alors ai -p i1;
Fin Faire.
i : étant le nombre des '1'non encore
placés à l'étape j de l'algorithme.
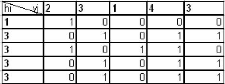
FIG. 1.2 -Reconstruction d'une matrice binaire par l'algorithme
glouton
1.3.3 Unicité et Equivalence entre les solutions
Bascule
Une bascule est un ensemble de quatre cellules (i ;j), (i
;j+k), (i+h ;j) et (i+h ;j+k) tel que les cellules (i ;j) et (i+h ;j+k) sont de
valeur 1 et les cellules (i+h ;j) et (i ;j+k) sont de valeur 0.
L'opération de bascule consiste à
échanger les 1 et 0 pour ces quatre cellules. Les projections
orthogonales d'une matrice binaire demeurent inchangées après les
opérations de bascules.
Ryser [6] a montré que les solutions sont
équivalentes dans le sens où l'on peut passer d'une solution
à une autre par une suite finie de bascules, comme le
théorème 2.
Théorem 2 :
Si A; A' 2 R(H; V ) alors se transforme en A'
à l'aide d'une suite finie d'opérations de bascules.
Chapitre 1. Reconstruction des images binaires
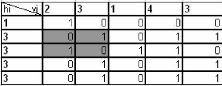
FIG. 1.3 -Illustration d'une bascule
De ce théorème, on déduit que les
éléments de la classe R(H, V ) sont
représentés par un graphe fortement connexe. Les sommets sont
associés aux matrices et les arcs traduisent les opérations de
bascules de passage d'une solution à une autre.
Wang et Zhang [2] ont calculé le nombre de solutions
équivalentes. Par exemple, lorsque les projections orthogonales sont
unitaires (V est unitaire si v = 1, j = 1, : : : in) , il
existe n! matrices équivalentes.
Remarque deux matrice binaires sont voisines
si l'on peut passer de l'une à l'autre avec une transformation
élémentaire ou une opération de bascule.
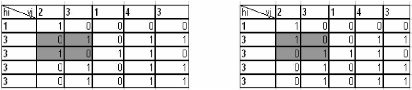
FIG. 1.4 -Voisinage à l'aide d'une
opération Bascule
Unicité de la solution
La solution MB(H, V ) C R(H, V
) est-elle unique?
Existe-il une autre solution MBI(H, V ) C R(H, V
), qui est tomo-graphiquemnt équivalent à MB(H, V )
c'est-à-dire respecte projection orthogonales (H, V ).
D'après le théorème 2, une matrice est invariante
(solution unique) si et seulement si elle n'a pas de bascules. Par
conséquent, tester l'unicité de la matrice, revient à
tester si toutes les cellules sont invariantes. Haber [9] a donné les
conditions nécessaires et
Abdessalem DAKHLI 5
Abdessalem DAKHLI 6
Chapitre 1. Reconstruction des images binaires
suffisantes pour qu'une cellule soit invariante. En effet, Une
cellule (i, j) est invariante si elle est 1- invariante lorsque
A(i, j) = 1 ou 0-invariante si A(i, j) = 0
pour toute A c R(H, V ).
1.4 Etat de l'art
- Gardner et al. [8] ont montré que le problème
de reconstruction d'une matrice binaire est NP-complet pour une dimension du
tableau et un nombre d'axes non parallèles de projection bien
déterminés.
- Woeginger [5] a montré que l'existence,
l'unicité et la reconstruction d'une matrice binaire sont des
problèmes NP-complet et redeviennent polynomial selon le type de convexe
à reconstruire.
- Barcucci et al.[4] ont signalé que l'existence d'une
solution initiale est un problème NP-complet et la reconstruction est un
problème NP-difficile pour de type convexe bien déterminé
et pour d'autre devient un problème polynomial.
- Le problème de reconstruction de matrices binaires
peut être vu comme un problème de reconstruction d'un tableau
monocoloré où toutes les cellules de valeur 1 sont
colorées en noir et toutes les cellules de valeur 0 sont colorées
en blanc. Dans ce contexte, Chrobak et Dflrr [7] ont démontré que
le problème est NP-complet.
- Ryser [6] a signalé que l'existence, l'unicité
et la reconstruction d'une solution sont des problèmes polynomiaux pour
une image de taille réduite. Il a montré aussi que l'existence et
l'unicité deviennent des problèmes NP-complet et la
reconstruction devient un problème NP-difficile concernant l'image de
taille importante.
1.5 Conclusion
On a étudié, dans ce chapitre, le
problème de reconstruction de matrices binaires et on a constaté
que cette reconstruction peut être vue comme un problème de
reconstruction d'un tableau monocoloré où toutes les cellules de
valeur 1 sont colorées en noir et toutes les cellules de valeur 0 sont
colorées en blanc.
Et on a constaté aussi que dans certain cas la
vérification de l'existence et l'unicité est un problème
polynomial et dans d'autre redevient NP-complet selon la taille de la matrice
et le type de convexe à reconstruire.
7
Chapitre2
Etat de l'art sur la reconstruction des
images hv-convexes
Introduction
Ce chapitre expose la définition des images hv-convexe
de même il présente le tour d'horizon de résolution du
problème de reconstruction des images hv-convexe.
2.1 Définition
Dans certains cas la tomographie exige les
propriétés de connexité pour assurer la continuité
de l'objet suivant ces directions surtout dans l'imagerie médicale.
Soit A une matrice binaire, on définit les
propriétés suivantes de A :
- h : A est h-convexe si les cellules de valeur 1 de chaque
ligne constituent un ensemble connexe, c'est-à-dire, les cellules de
valeur 1 ne sont pas séparées par des cellules de valeur 0
(Figure 1.2- a-).
- v : A est v-convexe si les cellules de valeur 1 de chaque
colonne constituent un ensemble connexe (Figure 1.2-b-).
- hv : A est hv-convexe si les cellules de valeur 1 de chaque
ligne et colonne constituent un ensemble connexe, c'est-à-dire A est
h-convexe et v-convexe (Figure 1.2- c-).
Exemple :
La matrice à reconstruire doit respecter les
projections orthogonales et la convexité de l'image. C'est à dire
reconstruction des images binaires sous contraintes de convexité.
Abdessalem DAKHLI 8
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
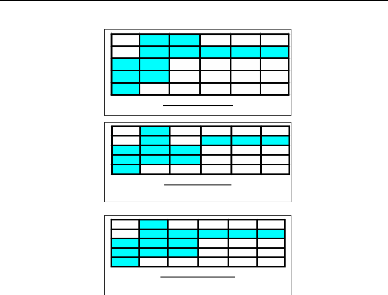
Matrice hconvexe
Marice vconvexe
Matrice hvconvexe
FIG. 2.1 -Définition d'une matrice convexe
2.2 Etat de l'art sur la reconstruction des images
hv-convexe
- E. Barcucci, A. Del Lungo, M. Nivat et R. Pinzani [10] ont
montré que le problème de reconstr uction h-convexe et v-convexe
d'une matrice binaire est NP-complet. Ils ont montré que le
problème de reconstruction d'une matrice devient NP-complet dès
que l'on exige les propriétés (h, v) ou hv. Ils ont
proposé aussi un algorithme qui repose sur trois phases. La
première phase consiste à choisir une configuration initiale sur
les bords du tableau, c'est-à-dire, sur les lignes 1 et n-i et
les colonnes 1 et n. Le nombre de ces configurations est borné
par in2n2 car la solution
cherchée satisfait les propriétés (p, h, v).
Ensuite, pour chaque configuration de départ, une procédure
de propagation de contraintes permet de fixer les valeurs de certaines cellules
pour respecter les propriétés (p, h, v). A l'issue de
cette phase on ne peut pas conclure l'existence d'une solution car il reste
souvent quelques cellules indéterminées. Les valeurs de ces
cellules peuvent s'exprimer par des
Projections (H,V) Matrice Reconstruite Image
Reconstruite
(a) : Reconstruction d'une matrice binaire.
(b) : Passage d'une matrice à une image
binaire

2 1 3 1 V
1
1 (a)
3
2 H
|
1
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
|
0
|
0
|
1
|
1
|
(b)
Abdessalem DAKHLI 9
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
FIG. 2.2 -Principe de reconstruction d'une image
binaire
clauses booléennes à deux variables. En fin,
l'éventuel problème 2-SAT est résolu pour trouver une
solution s'il en existe une. L'algorithme global est de complexité
O(m4m4).
- G. J. Woeginger [11] a montré que la reconstruction
de hv-convexe est NP-complet. Il a montré que le problème reste
toujours NP-complet même si les propriétés (hv, v),
(hv, h), h ou v sont considérées. Toutefois, le
problème redevient polynomial si l'on exige les trois
propriétés (h,v) à la fois.
- Geir dahl et Truls Flatberg [12] ont fournit un algorithme
basé sur une relaxation lagrangienne pour reconstruire une matrice
hv-convexe en respectant les projections prescrites.
- F.Jarray et al. [13] ont proposé un nouvel algorithme
pour reconstruire approximativement une matrice hv-convexe de leurs
projections, cet algorithme exécute une séquence de
reconstruction apparentée, en utilisant une seule projection (HouV
). Il utilise le plus long chemin pour fournir une solution approximative.
Le problème de reconstruction des images hv-convex respectant une seule
projection orthogonal (H ou V).
- F.Jarray et al. [13] ont proposé aussi une
heuristique qui utilise un long chemin et des modèles de réseau
pour fournir une solution approxima-
Abdessalem DAKHLI 10
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
tive respectant les projections orthogonales (H et V). Cette
heuristique est un algorithme du temps polynomial parce que la ressemblance
n'est pas râpe que le nombre maximal de 1 adjacents. Pour le
problème de petite taille l'heuristique donne une image hv-convex
c'est-à-dire presque l'image réelle et pour les autres instances
(problème de grande taille) la solution est approximative avec un nombre
d'adjacent maximal, en respectant les projections orthogonales.
- Gardner et al. [14] ont appliqué un algorithme et il
ont montré que le problème de reconstruction des images
hv-convexe est NP-complet pour d >= 2 et €
>= 3(avec d c'est le dimension du tableau et € c'est le nombre d'axes
non parallèles de projection. € = 2 si l'on considère
seulement les projections orthogonales.
- Ryser [15] a proposé un algorithme pour reconstruire
de polyominos horizontalement et verticalement convexes avec contraintes
tomogra-phiques. Les méthodes utilisées font appel à la
géométrie discrète mais aussi à des
réductions à 2-SAT et il a montré que la reconstruction
est un problème NP-complet et NP-difficile selon la taille de matrice
qui représente l'image.
- S. REBOUL et al.[28] ont utilisé un algorithme de
flot maximum à coût minimum inspiré de la théorie
des graphes et le modèle de l'image à reconstruire. Ils ont
utilisé le deux projections orthogonales de l'image pour faire cette
reconstruction. Les taux de conformités, obtenus entre l'image à
reconstruire et l'image reconstruite, sont supérieurs à 95%.
- R.L.YANG et al.[29] ont proposé deux algorithmes pour
reconstruire une image binaire 3D à partir de deux projections
radiologique orthogonales. Ils ont signalé que cette reconstruction peut
se réduire, en angiographie numérique, à de multiples
reconstructions 2D des matrices de sections. Le premier algorithme
utilisé est basé sur l'existence d'une courbe médiane de
section et le deuxième utilise un modèle pour la première
section à reconstruire et donne des solutions optimales à l'aide
de la méthode dites du flot maximal de coût minimal. Les
résultats obtenus on montré que la reconstruction 3D en
angiographie et à partir de deux projections orthogonales peut donner de
très bon résultats. L'application des ces algorithmes à
des cas cliniques implique néanmoins des précautions
particulières afin d'assurer un mélange aussi homogène que
possible du produit de contraste avec le sang pendant la phase d'acquisition et
qualité minimale d'image.
- Stéphane Chrétien et Franck Corset [30] ont
utilisé l'estimation moindre carrée et l'optimisation valeur
propre pour reconstruire des images binaires hv-convexe. Plus
précisément, ils ont estimé que ce problème
appartient à la classe des problèmes NP-hard. Ils ont
étudié l'estima-
Abdessalem DAKHLI 11
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
tion d'une image corrompue par un bruit. Ils ont
approché le problème par la méthode des moindres
carrés linéaires pénalisés et ils ont introduit une
relaxation de type valeur propre qui transforme le problème original en
un problème approché convexe. Dans la plupart des cas, le
schéma relaxé ne redonne pas une solution binaire. Pour
résoudre ce problème ils ont proposé un algorithme
stochastique qui donne une interprétation géométrique
simple. Enfin, ils ont prouvé que dans le cas d'une image faiblement
bruitée, la relaxation donne la solution optimale.
- S. Brunetti et al [30] ont utilisé une approche de
programmation dynamique, ils ont prouvé qu'une grande
variété de problèmes de reconstruction matriciels de deux
projections peut être résolue dans le temps de polynôme
chaque fois que le nombre des lignes et des colonnes est fixé. Ils ont
limité leurs résultats à quelques problèmes
représentatifs mais leur approche peut être facilement
adaptée à une large classe d'autres problèmes. Ils ont
prouvé aussi quelques résultats de complexité pour
plusieurs problèmes concernant la reconstruction d'une matrice binaire
quand une contrainte de voisinage arrive. Dans le cas où pour chaque 1
il y a exactement un autre 1 dans le quatre voisinage le problème est
plus dur que les trois problèmes de reconstruction matricielle
colorée. Si la contrainte consiste en ce qu'il y a exactement deux autre
1 dans le Quatre voisinage, alors ils ont montré le problème peut
être NP-complete.
- C. Picouleau [31] a étudié la reconstruction
de chacun polyomino convexe quand les projections orthogonales sont
définies comme la longueur de contour de l'objet intercepté par
le rayon. Il a prouvé que ce problème est NP-dur pour plusieurs
classes de polyominoes : Général, h-convex, v-convex. Pour
hv-convex polyominoes il a proposé un algorithme de temps de
polynôme pour le problème de reconstruction.
- K.J. Bateleur [16] a appliqué l'algorithme
génétique pour résoudre le problème de
reconstruction des images convexes. En effet, il a signalé aussi qu'il
existe des algorithmes de reconstruction de temps polynomial [21] concernant
les images qui appartiennent aux classes hautement structurées [16], et
pour d'autre images qui appartiennent à une classe plus
générale c'est à dire de polyominoes hv-convexe
formé par plusieurs polyominoes séparés, le
problème de reconstruction est NP-difficile [17]. Pour reconstruire une
image hv-convexe K.J. Bateleur [16] a définit une fonction
d'évaluation pour chacune des solutions pour assumer les
propriétés spécifiques de la structure d'image. La valeur
de la fonction objective pour une solution optimale, est évaluée
par le nombre de pixel noir voisine d'horizontal ou de verticale [19]. Cette
fonction est maximisée par une re-
Abdessalem DAKHLI 12
Chapitre 2. Etat de l'art sur la reconstruction des
images hv-convexes
construction qui restera également hv-convexe. De
même, il a remarqué que le problème de reconstruction des
images à partir de plusieurs projections, est NP- difficile [22]. Ce
problème a un codage binaire naturel d'ou l'application de l'algorithme
génétique classique [26], en utilisant une représentation
bit string.
Il a appliqué l'algorithme génétique sur
des matrices binaires construites à partir des projections horizontale
et verticale. En effet, une matrice binaire A construite à partir de
deux vecteurs non négatifs V et H.
Avec H = (h1; . . . ; hn) et V = (v1;.
. . ; vm) sont respectivement
la projection horizontale et verticale de la matrice binaire A.
La construction de la matrice A = (aij) doit
satisfaire à la contrainte suivante : il faut que
n
X aij = vi, i = 1, ...m
J=1
Xm aij = hj,j = 1,...m
i=1
Le choix de cette configuration due au tomographie discret qui
est fortement lié au traitement d'image digitale, c'est-à-dire
des matrices binaires comme des images, dont la matrice binaire le noir pour
les valeurs (1) et blanc pour les valeurs (0) on l'appelle aussi les pixel
d'entrées de matrice [18]. La contrainte qu'il faut respecter au cours
de la reconstruction des images binaires selon la projection verticale et
horizontale [27], il faut que :
Xn aij = Xm aij
J=1 i=1
Les principaux problèmes de la tomographie discret, il
faut que les deux vecteurs V et H soient données pour
construire la matrice binaire A E A(V, H). Et pour limiter le
nombre de solutions à élaborer, il faut ajouter des autres
propriétés supplémentaires concernant les solutions
souhaitées.
K.J. Bateleur a ajouté que la fonction objectif
f : A(V, H) --p Z, sera
évalué pour chaque solution A E A(V, H)
élaborée pour prendre la valeur maximale de f.
C'est-à-dire que la fonction f a un domaine d'étude
limité concernant la classe A(V, H).
K.J. Bateleur [16] a signalé aussi que la notion de
bascule joue un rôle très important dans les
caractéristiques de classe A(V, H) de solution
élaborée. Une bascule est un sous matrice qui se trouve dans une
solution A E A(V, H) sous la forme suivante :
L'opération de bascule consiste à
échanger les 1 et 0 pour ces quatre cellules et les
projections orthogonales d'une matrice binaire demeurent in-
Chapitre 2. Etat de l'art sur la reconstruction des
images hv-convexes
Abdessalem DAKHLI 13
FIG. 2.3 -Opération bascule
changées après les opérations de
bascules. Cette opération est élémentaire dans la classe
de solution A(V, H) selon Ryser[15,20].
C'est-à-dire, l'opération d'une bascule joue une
rôle très important pour élaborer une solution
équivalente B 2 A(V, H) avec B =6 A.
Cette solution élaborée a la même projection que la
solution A. Donc l'algorithme génétique doit utiliser
les opérations de bascules d'une façon très importante
pour faire apparaître d'autres solutions (d'autres individus).
K.J. Bateleur a montré que le nombre des matrices (ou
les solutions) est une opération très importante à faire
pour l'algorithme à utiliser. Il a signalé que le traitement de
toutes les opérations de bascules, se trouvant d'une image, est de
O((mm)2) opération, et aussi le nombre des
applications des opérations bascules est
O((mm)2).
K.J. Bateleur a évoqué que l'algorithme
génétique est insatisfaisants pour plusieurs raisons, en premier
lieu, l'opérateur de croisement a habituellement comme
conséquence les solutions de candidat qui deviennent
considérablement des projections prescrites de même lorsque les
deux solutions parents ont plusieurs différences, ce comportement rend
l'opérateur de croisement inefficace. Pour cette raison l'algorithme
recourt à l'opérateur de mutation pour améliorer la
solution. En deuxième lieu l'opérateur de croisement quelque soit
son type ne tient pas compte de la structure spatiale bidimensionnelle des
solutions de candidat [16].
K.J. Bateleur a conçu un algorithme
évolutionnaire [24] spécifique au problème pour surmonter
les inconvénients de l'algorithme génétique classique.
Afin d'exploiter entièrement la puissance de
l'opérateur de crossover, la procédure de hillclimb augmente la
qualité de solution. L'importance des opérateurs de croisement
crossover et de mutation explique la raison de choix de cette approche.
K.J. Bateleur a définit l'opérateur de crossover
comme étant une des parties principales dans cet algorithme, son
entrée se compose de deux images de parent et sa sortie une image enfant
qui a certains dispositifs des deux
Abdessalem DAKHLI 14
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
L'algorithme évolutionnaire
Générer une population initiale P0 de
la taille À composée par des matrices
E A(V,H).
Effectuer une opération de hillclimb
sur chaque matrice dans P0.
t 4--0
TANT QUE (Non condition d'arrêt)
FAIRE
Début
P t ' = ~
Pour ide 1 à Faire // le nombre des
enfants qui sont créés dans chaque
génération.
Début
Générer une matrice C d'enfant par
l'opérateur de crossover ou mutation
Effectuer une opération de hillclimb
sur C
P t '=P t
'u{C}
Fin
Choisir la nouvelle population
P't+4 à partir Pt u
P't
t 4--t + 1
FIN TANT QUE
Produire le meilleur individu trouvé.
Toutes les images dans la population sont des membres de
classe
A(V, H), et chaque image résultante devrait
avoir les projections prescrites, de même il a définit
l'opérateur de Hillclimb, comme étant un opérateur qui
permet d'appliquer une petite modification pour augmenter la fonction objective
jusqu'à l'optimum local et pour conserver l'appartenance de solution
à la classe A(H, V ).
Cette approche exige que l'opération d'une bascule soit
élémentaire comme étape locale. Et le choix
d'opération de bascule se fait d'une façon arbitraire bien
sûr l'opération qui augmente la fonction objective.
L'exécution l'opération de hillclimb offre
plusieurs défis informatiques. En effet, L'opération hillclimb
est très efficace pour améliorer la fonction d'évaluation.
Dans l'algorithme existe des boucles qui permettent de mieux évaluer les
opérations des bascules pour avoir à la fin une fonction
objective maximale.
Contour de la procédure de Hillclimb
TANT QUE (il n'existe pas une
opération de bascule qui permet d'améliorer la fonction
objective) FAIRE
Début
Choisir aléatoirement une telle opération de
bascule.
Abdessalem DAKHLI 15
Chapitre 2. Etat de l'art sur la reconstruction des
images hv-convexes
Appliquer l'opération de bascule.
Fin
L'application de l'algorithme évolutionnaire [25] sur
la première classe de test image concernant les images hv-convexe de
taille 40 * 40, a généré 10 images hv-convexe et chaque
image est constituée par trois ou quatre objets hv-convexe. Dans cette
classe image, la fonction d'évaluation est le nombre de '1'adjacents et
le test d'essai est fait sur 10 images, Les résultats de l'application
de cet algorithme sont illustrés dans la table ci-dessous, La
reconstruction est parfaite lorsqu'il y a reconstruction de la même image
origine. La table visualise aussi le nombre d'exécutions concernant la
reconstruction parfaite, le temps moyen d'exécution des programmes est
exprimé en minutes et le nombre moyen de générations avant
de retrouver la solution optimale c'est à dire la meilleure
reconstruction.
Lorsque l'algorithme qui ne donne pas une reconstruction
parfaite c'est-à-dire très différente à l'image
originale. Cette reconstruction est une solution de mauvaise qualité.
TAB. 2.1 -Résultat de Reconstruction
des images hv-convexe
|
Image
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Parfait
|
9
|
5
|
8
|
8
|
9
|
6
|
6
|
6
|
6
|
6
|
|
Temps exécution
|
25.6
|
16.6
|
15.5
|
8.8
|
8.5
|
10.8
|
17.7
|
17.7
|
8.8
|
15.7
|
|
Moyenne
|
|
|
|
|
|
|
|
|
|
|
|
Nombre moyenne de génération
|
24.6
|
17.3
|
18.5
|
14.8
|
15.8
|
18.5
|
30.2
|
15.0
|
21.0
|
23.6
|
Cet algorithme ne donne pas une solution optimale qui converge
vers un optimum locale. En effet les difficultés dans l'optimisation de
problème est expliqué par exemple par l'existence d'une solution
quelconque et d'une solution obtenu dans un optimum local qui ont les
même projections orthogonales et verticales et qui ont des nombres des
'1'voisin différents. Ce problème est dû à
l'existence d'un grand nombre de blocs de composants de bascules.
Abdessalem DAKHLI 16
Chapitre 2. Etat de l'art sur la reconstruction des
images hv-convexes
2.3 Conclusion
Ce tour d'horizon nous montre bien qu'il y a peu de
résultats dans le domaine de la tomographie discrète. Dans ce
chapitre, on a décrit le problème de reconstruction des images
binaires sous contraintes de convexité. La matrice binaire à
reconstruire doit respecter les projections orthogonales et la convexité
de l'image. On a constaté que le principe de reconstruction est simple
et facile mais la difficulté réside dans la résolution
pratique de problème. D'après ce tour d'horizon on a
constaté aussi que dans certain cas la reconstruction d'une image
hv-convexe est un problème NP-complet et dans d'autre cas redevient
NP-difficile selon la taille de matrice qui représente l'image et selon
le type d'image convexe à reconstruire. Et on a constaté aussi
l'existence des méthodes heuristiques qui sont algorithmes du temps
polynomial qui donnent une image hv-convex parfait c'est-à-dire presque
l'image réelle concernant les images de petites taille et pour les
autres instances (image de grande taille) la solution est approximative avec un
nombre d'adjacent maximal, en respectant les projections orthogonales. Dans ce
chapitre on a signalé aussi les résultats théoriques et
pratiques de l'utilisation de l'algorithme génétique pour
reconstruire des images convexes. Ces résultats démontrent que
l'algorithme est efficace pour plusieurs différentes fonctions
d'évaluation, correspondant à la reconstruction de plusieurs
problèmes. Ils démontrent aussi une caractéristique
principale de cette approche et sa capacité d'incorporer de diverses
formes de l'information à priori dans la fonction d'évaluation.
Pour mieux améliorer la solution il y a utilisation de
l'opérateur de hillclimb. Cet opérateur permet d'améliorer
la complexité. En effet, lorsque l'algorithme est limité à
une image de la taille réduite cette type d'image rend
l'opération de hillclimb moins approfondie a pu avoir comme
conséquence la complexité améliorée de temps de
l'opération.
On a constaté que le traitement de toutes les
opérations de bascules, se trouvant d'une image, est de
O((mm)2) opération, et aussi le nombre des
applications des opérations bascules est
O((mm)2).
Les résultats montrent aussi que les algorithmes
génétiques sont coûteux en temps de calcul, puisqu'ils
manipulent plusieurs solutions simultanément. C'est le calcul de la
fonction de performance qui est le plus pénalisant, et on optimise
généralement l'algorithme de façon à éviter
d'évaluer trop souvent cette fonction.
De même l'ajustement d'un algorithme
génétique est délicat. L'un des problèmes les plus
caractéristiques est celui de la dérive
génétique, qui fait qu'un bon individu se met, en l'espace
de quelques générations, à envahir toute la population. On
parle dans ce cas de convergence prématurée, qui revient à
lancer à une recherche locale autour d'un minimum... qui n'est pas
Abdessalem DAKHLI 17
Chapitre 2. Etat de l'art sur la reconstruction des
images hv-convexes
forcément l'optimum attendu, c'est à dire que
les reconstructions obtenues par cet algorithme ne sont pas totalement
parfaites. Les méthodes de sélection proportionnelle peuvent en
particulier favoriser ce genre de dérive. Un autre problème
surgit lorsque les différents individus se mettent à avoir des
performances similaires : les bons éléments ne sont alors plus
sélectionnés, et l'algorithme ne progresse plus.
Le choix d'une représentation « intelligente
» pour permettre un remplacement générationnel efficace est
un autre aspect de la question, et l'efficacité d'un algorithme
génétique dépend beaucoup de la façon dont on
opère le croisement des individus.
18
Chapitre3
Reconstruction des Images Binaires
par recherche Taboue
Dans ce chapitre nous allons essayer de présenter notre
paramétrage et le principe de l'algorithme Tabou de même nous
allons présenter les résultats de reconstruction des images
hv-convexes en appliquant cet algorithme.
3.1 Paramétrage de l'algorithme Tabou
La recherche taboue est une méthode de recherche locale
avancée qui fait appel à un ensemble de règles et de
mécanismes généraux pour guider la recherche de
manière intelligente.
a - Paramétrage
Pour cette approche on doit fixer le voisinage, la taille des
listes tabous, le Critère d'arrêt et la sélection du voisin
: Best Fit (le meilleur voisin), First Fit (le premier qui satisfait un certain
critère).
b - Améliorations
On peut utiliser une liste de candidats plutôt que
l'ensemble du voisinage et éventuellement un tirage aléatoire du
successeur en fonction de la valeur de la fonction objective.
Pour améliorer la solution on doit fixer des
Stratégies d'intensification et de diversification, revenir sur une zone
intéressante, dégager des propriétés communes de
bonnes solutions, favoriser l'exploration de régions peu ou pas
explorées et on doit indiquer l'aspiration; il arrive qu'un mouvement
mis à l'état tabou soit intéressant(Conduise à une
solution de nombre '1'adja-cents maximale) alors on accepte de
lever l'état tabou, on utilise un critère d'aspiration pour lever
cet état tabou.
Nous définissons maintenant les composantes de notre
recherche taboue.
On part d'une solution initiale (sous forme de matrice
binaire) construite à l'aide de l'algorithme glouton, qui
vérifie les contraintes de projections orthogonales (horizontale et
verticale);
Ensuite, on essaie d'améliorer cette solution afin
d'augmenter les nombres
Abdessalem DAKHLI 19
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
de '1' adjacents en respectant les contraintes de projections
orthogonales (horizontale et verticale), à l'aide d'une recherche
tabou
Algorithme Tabou
Variables
s;s* Configuration courante et
meilleure configuration obtenue jusqu'à pré-
sent
f; f* Fonction d'évaluation et sa
meilleure valeur obtenue jusqu'à présent
début
Initialisation de la liste tabou (liste vide)
Génération d'une configuration initiale s
s* := s
f* := f(s)
Tant que la condition d'arrêt n'est pas
vérifiée Faire
s := un des meilleurs voisins non tabou de
N(s)
si f(s) <=
f* alors
s* := s
f* := f(s)
Sinon si f* n'a pas été
améliorée depuis un certain temps alors
s := s
Vider la liste tabou
Retourner s*
Fin
3.1.1 Définition du voisinage
On associe à chaque configuration s un voisinage
N(s) construit de la manière suivante :
1.2 on recherche une bascule dans la solution initiale
(Matrice binaire)
et on change les 1 et 0 pour les quatre cellules de la
bascule. Une bascule est un ensemble de quatre cellules
(i;j), (i;j + k), (i
+ h;j) et (i + h; j +
k) tel que les cellules (i; j) et
(i + h; j + k) sont de valeur
1 et les cellules (i + h; j) et
(i;j + k) sont de valeur 0.
1.3 Les projections orthogonales de la nouvelle matrice
binaire de-
meurent inchangées après les opérations de
la bascule. On calcule les nombres d'adjacences.
1.4 on choisit les échanges qui ne sont pas dans la
liste tabou et qui
ont les nombres '1'adjacents les plus
élevés.
1.5 on crée le voisinage N(s) de s
correspondant aux échanges choisis
précédemment.
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
3.1.2 Liste tabou
Un élément fondamental de la recherche tabou est
l'utilisation d'une mémoire flexible, à court terme, qui garde
une certaine trace des dernières opérations passées. On
peut y stocker des informations pertinentes à certaines étapes de
la recherche pour en profiter ultérieurement. Cette liste permet
d'empêcher les blocages dans les minima locaux en interdisant de passer
à nouveau sur des configurations de l'espace de recherche
précédemment visitées.
Pour implémenter la liste tabou, on a choisit
d'utiliser une structure liste dont chaque élément correspond
à l'échange des contenus de quatre cellules de chaque bascule. A
chaque itération, on ajoute un échange à la liste
tabou.
Quand aucun échange n'est possible ou après un
certain nombre d'itération, on vide la liste tabou.
3.1.3 Condition d'arrêt
On doit fixer le nombre maximal d'itération.
3.1.4 Fonction d'évaluation
On définit la fonction d'évaluation comme
étant le nombre de '1' adjacents apparents pour
chaque solution (matrice trouvé) dans chaque itération. On essaie
de maximiser cette fonction afin d'obtenir un nombre de '1'adjacents
maximale
Soient Lij et
Cij sont respectivement le nombre de '1'adjacents en ligne et le
nombre de '1'adjacents en colonne.
|
F = Max (
|
Xn i=1
|
m-1X j=1
|
Lij +Cij) ,l'objectif c'est de maximiser
F c'est à
|
vj
hi =
Xm i=1
Xn j=1
Abdessalem DAKHLI 20
dire le nombre de '1'adjacents dans la solution en respectant
les contraintes projections orthogonales :
|
Xm
i=1
|
hi est la projection horizontale de la ligne i, i
= 1, : : : , m. Elle donne
|
le nombre des '1'de chaque ligne.
Xn vj est la projection horizontale de la
ligne i, i = 1, : : : , m. Elle donne
j=1
le nombre des '1'de chaque colonne et vjdésigne
le nombre de projections
horizontales supérieure ou égales à
j.
Abdessalem DAKHLI 21
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
3.2 L'application de la recherche taboue pour reconstruire
des images hv-convexe
Pour réduire la taille de l'espace de recherche de
solutions, deux approches sont envisageables. La première consiste
à augmenter le nombre des projections à satisfaire. Son
inconvénient est que le problème de reconstruction est NP-complet
pour un nombre de projections supérieur à deux. La
deuxième approche consiste à prendre en compte certaines
propriétés connues à priori sur l'objet à
reconstruire (convexité, symétrie, périodicité).
Cette approche nous semble plus pratique que la première parce qu'on
dispose souvent des informations sur la solution. De plus, une solution
donnée par la première approche ne respecterait pas forcement ces
propriétés malgré le nombre élevé des
projections.
La reconstruction d'une matrice hv-convexe à l'aide
d'une métaheuris-tique se fait en trois étapes :
- Etape 1 : Reconstruire une solution en
utilisant une approche du gloutonne.
- Etape 2 : Reconstruire une solution
optimale en utilisant l'approche de la recherche Tabou sans
amélioration
- Etape 3 : Reconstruire une solution
optimale en utilisant l'approche de la recherche Tabou avec amélioration
en utilisant le principe de diversification et
l'intensification.
Dans cette étape on doit favoriser une exploration
efficace de l'espace des solutions S par des règles d'aspiration, de
diversification et d'intensification de la recherche.
L'Aspiration c'est chercher à passer outre le
caractère tabou d'un mouvement dans certains cas plusieurs solutions
pour déclencher le mécanisme d'aspiration, une solution est
proposée par Glover et Laguna [32], cette proposition indique que si t
est tabou mais que (t(X)) < f(X*) alors on autorise t
appliqué à X. Une autre solution indique que si le mouvement t a
été rendu tabou lors du passage de la configuration X à Y
= t--1(X), on lève le statut tabou d'un mouvement s'il conduit à
une solution meilleure que celle qui avait entraînée son
interdiction. Comme dans un autre cas on lève le statut de tabou du plus
«ancien».
Donc l'idée de base de la recherche Tabou est la
modélisation de la mémoire.
Dans une première phase, la méthode de recherche
tabou peut être vue comme une généralisation des
méthodes d'amélioration locales. En effet, l'algorithme Glouton
génère une solution initiale S sous forme d'une matrice,
Abdessalem DAKHLI 22
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
CONFIGURATION INITIALE S
(Élaboration de la solution initiale sous forme
d'une matrice binaire en utilisant
l'approche Glouton)
LISTE TABOU INITIALE VIDE
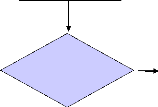
NOUVELLE CONFIGURATION
COURANTE S = t
INSERTION DU
MOUVEMENT
t3?S DANS LA LISTE TABOU circulaire
PERTURBATION DE S SUIVANT
N MOUVEMENTS non
tabous;
EVALUATION DES N VOISINS
SELECTION DU
MEILLEUR VOISIN t
OUI Amélioration
observée récemment?
FIG. 3.1 -Modélisation de la mémoire dans la
recherche Tabou
NON
STOP
en partant de cette solution qui appartient à
l'ensemble de solutions X, on se déplace vers une solution
s(x) située dans le voisinage [S(x)] de S0.
Donc l'algorithme explore itérativement l'espace de solutions
X.
Afin de choisir le meilleur voisin s(x) dans
S(x), l'algorithme évalue la fonction objectif f qui
désigne le nombre de '1' adjacent dans la matrice
trouvée en chaque bascule s(x), et retient le voisin qui
améliore la valeur de la fonction objectif f, ou au pire celui
qui la dégrade le moins.
L'originalité de la méthode de recherche tabou,
par rapport aux méthodes locales, qui s'arrêtent dès qu'il
n'y a plus de voisin s(x) permettant d'améliorer la valeur de
la fonction objectif f, réside dans le fait que l'on retient le
meilleur voisin, même si celui-ci est plus mauvais que la solution
d'où l'on vient. Ce critère autorisant les dégradations de
la fonction objectif évite à l'algorithme d'être
piégé dans un minimum local. Mais il induit un risque de cyclage.
En effet, lorsque l'algorithme a quitté un minimum quelconque par
acceptation de la dégradation de la fonction objectif, il peut revenir
sur ses pas, à l'itération suivante.
Pour régler ce problème, l'algorithme a besoin
d'une mémoire pour conser-
Abdessalem DAKHLI 23
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
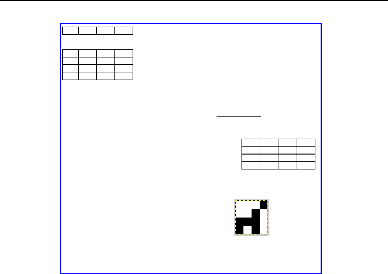
2
1
3
1
Projections (H,V) Matrice initiale
(Approche Tabou) (b)
|
0
|
0
|
0
|
1
|
|
0
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
|
1
|
0
|
1
|
0
|
Image Reconstruite : Image Application GIMP 2
a) : Reconstruction d'une matrice binaire (solution
initiale) en utilisant l'approche
FIG. 3.2 -Principe de reconstruction d'une image binaire
ver pendant un moment la trace des dernières meilleures
solutions déjà visitées. Ces solutions sont
déclarées tabou, d'où le nom de la méthode. Elles
sont stockées dans une liste de longueur L donnée,
appelée liste taboue. Une nouvelle solution n'est
acceptée que si elle n'appartient pas à cette liste taboue. Ce
critère d'acceptation d'une nouvelle solution évite le
cyclage de l'algorithme, durant la visite d'un nombre de solutions au
moins égal à la longueur de la liste tabou, et il dirige
l'exploration de la méthode vers des régions du domaine de
solutions non encore visitées.
La liste taboue est généralement
gérée comme une liste "circulaire" : on élimine
à chaque itération la solution taboue la plus ancienne, en la
remplaçant par la nouvelle solution retenue. Mais le codage d'une telle
liste est encombrant, car il faudrait garder en mémoire tous les
éléments qui définissent une solution. Pour pallier cette
contrainte, on remplace la liste taboue de solutions interdites par une liste
de "transformations interdites", en interdisant la transformation
inverse d'une transformation faite récemment.
Concernant le critère d'aspiration, le remplacement de
la liste tabou des solutions visitées par la liste des transformations
élémentaires {x, s(x)}
Abdessalem DAKHLI 24
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
conduit non seulement à l'interdiction de revenir vers
des solutions
précédentes (on évite le cyclage court),
mais aussi vers un ensemble de solutions dont plusieurs peuvent ne pas avoir
été visitées jusqu'ici. Il est donc primordial de corriger
ce défaut et de trouver un moyen de lever l'interdiction de
l'acceptation d'une transformation élémentaire {x, s(x)}
déjà effectuée (donc appartenant à la liste tabou),
sous un certain critère, appelé critère d'aspiration.
Cette correction permet aussi de revenir à une solution
déjà visitée et de redémarrer la recherche dans une
autre direction. Cette idée est développée dans [1]. On a
fait plusieurs exécutions de l'algorithme, afin de démontrer la
polyvalence de cet algorithme dans la reconstruction des images hv-convexes.
Les résultats expérimentaux sont prévus
pour démontrer la praticabilité et la flexibilité de
l'approche considérée.
Les tests sont exécutés par un pc Pentium IV,
2800 MHz et 512 Mb de mémoire.
3.2.1 Reconstruction des images HV-CONVEXES par la
recherche taboue sans amélioration
L'application de l'algorithme sur la première classe de
test image concernant les images hv-convexe de taille 40 x 40, les images
hv-convexe obtenues est constituée par deux ou plusieurs objets
hv-convexe.
Dans cette classe image, la fonction d'évaluation est
le nombre de '1' adjacents et le test d'essai est fait sur 10 images.
Dans l'algorithme on a utilisé le nombre
d'itération égale 100 et la taille de la liste taboue est
égale à 7 mouvements interdits pour éviter le cyclage
pendant la recherche des solutions.
Les résultats de l'application de cet algorithme sont
illustrés dans la table ci-dessous. La reconstruction est parfaite
lorsque le taux de reconstruction est faible c'est-à-dire la
différence entre l'image reconstruite et image originale est faible. La
table ci-dessous visualise les résultats d'exécution concernant
les images hv-convexe de taille 40*40. Le temps d'exécution des
programmes est exprimé en secondes avant de retrouver la solution
optimale c'est -à-dire la meilleure reconstruction.
Test image :Taille 40x40
Abdessalem DAKHLI 25
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
TAB. 3.1 -Résultat de Reconstruction des
images hv-convexe
|
Image
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Nombre
de '1' ad-
jacents de
l'image originale
|
842
|
560
|
684
|
644
|
364
|
384
|
784
|
1564
|
526
|
296
|
|
Nombre
de '1' ad-
jacents de
l'image obtenue par l'algorithme glouton
|
736
|
458
|
601
|
558
|
257
|
271
|
645
|
1508
|
432
|
191
|
|
Temps
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
|
d'exécu-
tion (en
seconde) concernant
la solution
gloutonne..
|
|
|
|
|
|
|
|
|
|
|
|
Nombre
de '1' ad-
jacents de
l'image Reconstruite par Tabou
|
761
|
477
|
618
|
562
|
275
|
292
|
680
|
1518
|
438
|
200
|
|
Temps
|
10,8
|
4,6
|
8,7
|
6,3
|
2,7
|
3,1
|
8,5
|
3,3
|
4,6
|
1,9
|
|
d'exécu-
tion (en
seconde)
|
|
|
|
|
|
|
|
|
|
|
|
Taux de
|
0,761
|
1,484
|
1,298
|
0,906
|
1,7
|
1,578
|
1,225
|
0,351
|
1,644
|
1,702
|
Reconstruction
Abdessalem DAKHLI 26
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
Cet algorithme donne une solution optimale qui converge vers
un optimum local. En effet les difficultés dans l'optimisation de
problème sont expliquées par exemple par l'existence d'une
solution quelconque et d'une solution obtenue dans un optimum local qui a les
mêmes projections orthogonales et verticales et qui ont des nombres des 1
voisins différents, ces images obtenues sont un peu différentes
à l'exception de l'image origine. Ce problème est dû
à l'existence d'un grand nombre de blocs de composants de bascules.
D'après les résultats obtenus on a
constaté que les taux de reconstructions sont un peu faibles concernant
les 10 types des images hv-convexe qui ont des matrices de taille 40x40.
La solution obtenue par la recherche taboue est très
améliorée devant la solution élaborée par
l'algorithme glouton, c'est-à-dire que la fonction objective augmente
d'une façon très important, malgré que le temps
d'exécution est faible pour glouton.
En effet, l'image originale et l'image reconstruite qui se
trouvent respectivement dans la figure 9.5 et la figure 10.5 sont presque
identiques. Elles ont un taux de différence faible.
L'application de l'algorithme sur la deuxième classe de
test image concernant les images hv-convexe de taille 70 x 70 et taille
100x100, de même on a pris 10 images pour chaque type pour
exécuter l'algorithme. Chaque image générée est
constituée par deux ou plusieurs objets hv-convexe.
Test image :Taille 70x70
Abdessalem DAKHLI 27
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
TAB. 3.2 -Résultat de Reconstruction
des images70x70 hv-convexe
|
Image
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Nombre
de '1' ad-
jacents de
l'image origine
|
2106
|
1044
|
890
|
3026
|
1544
|
1842
|
2318
|
1934
|
1448
|
1326
|
|
Nombre
de '1' ad-
jacents de
l'image obtenue par l'algorithme glouton
|
1801
|
727
|
601
|
2809
|
1329
|
1641
|
2176
|
1727
|
1265
|
1090
|
|
Temps
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
|
d'exécu-
tion (en
seconde) concernant
la solution
gloutonne.
|
|
|
|
|
|
|
|
|
|
|
|
Nombre
de '1' ad-
jacents de
l'image Reconstruite par Tabou
|
1854
|
792
|
642
|
2818
|
1348
|
1666
|
2186
|
1759
|
1286
|
1104
|
|
Temps
|
137,7
|
35,7
|
24,3
|
169,9
|
65,8
|
48,6
|
67,3
|
51,8
|
27,1
|
43,4
|
|
d'exécu-
tion (en
seconde)
|
|
|
|
|
|
|
|
|
|
|
|
Taux de
|
0,804
|
1,671
|
1,730
|
0,747
|
1,399
|
0,823
|
0,770
|
0,949
|
0,992
|
1,476
|
Reconstruction
Abdessalem DAKHLI 28
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
TAB. 3.3 -Résultat de Reconstruction
des images100x100 hv-convexe
|
Image
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Nombre
de '1' ad-
jacents de
l'image origine
|
1796
|
2324
|
2780
|
3044
|
2856
|
2344
|
3910
|
1670
|
1362
|
3166
|
|
Nombre
de '1' ad-
jacents de
l'image Reconstruite par glouton
|
1385
|
1919
|
2470
|
2472
|
2269
|
1970
|
3658
|
1170
|
1044
|
2665
|
|
Temps
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
0,0
|
|
d'exécu-
tion (en
seconde) concernant
la solution
gloutonne.
|
|
|
|
|
|
|
|
|
|
|
|
Nombre
de '1' ad-
jacents de
l'image Reconstruite par Tabou
|
1413
|
1966
|
2489
|
2548
|
2335
|
1990
|
3684
|
1221
|
1078
|
2703
|
|
Temps
|
146,4
|
249,2
|
241,8
|
351,7
|
274,4
|
243,3
|
354,6
|
123,9
|
47,5
|
324,2
|
|
d'exécu-
tion (en
seconde)
|
|
|
|
|
|
|
|
|
|
|
|
Taux de
|
1,878
|
1,355
|
1,694
|
1,524
|
1,685
|
1,420
|
0,830
|
1,739
|
1,554
|
1,628
|
Reconstruction
Abdessalem DAKHLI 29
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
Ces deux types d'images montrent bien que le temps
d'exécution augmente lorsque la taille de matrice carrée
augmente.
La solution obtenue par la recherche taboue a une fonction
objective assez important par rapport à la solution obtenue de
même par rapport au test image de taille 40x40, c'est-à-dire
l'image reconstruite a un nombre de '1'adjacents important. La reconstruction
montre bien l'existence d'un grand nombre de blocs de composants de bascules.
Cette solution a un taux de reconstruction faible par rapport à l'image
originale, malgré le nombre d'objets dans les solutions
élaborées est assez important par rapport à l'image
origine.
On a constaté encore que la solution obtenue par la
recherche taboue, est une amélioration pour la solution gloutonne,
c'est-à-dire amélioration de la fonction objective qui
désigne le nombre de '1'adjacents.
3.2.2 Reconstruction des images HV-CONVEXES par la
recherche taboue avec amélioration
On reconstruit une solution optimale en utilisant l'approche
de la recherche Tabou avec amélioration en utilisant les principes de
diversification et l'intensification.
Intensification
L'intensification consiste à approfondir la recherche
dans certaines régions du domaine, identifiées comme susceptibles
de contenir un optimum global. Cette technique est appliquée
périodiquement, et pour une durée limitée. Pour mieux
intensifier la recherche dans une zone bien localisée, plusieurs
stratégies sont proposées dans la littérature. La plus
simple consiste à retourner à l'une des meilleures solutions
trouvée jusqu'à présent, puis de reprendre la recherche
à partir de cette solution, en réduisant la longueur de la liste
taboue pour un nombre limité d'itérations. Dans ce cas, on adapte
la procédure de recherche taboue, en élargissant le voisinage de
la solution courante (en augmentant la taille de l'échantillon
8(x)), tout en diminuant le pas des transformations. On peut aussi
remplacer simplement l'heuristique taboue par une autre méthode plus
puissante, ou mieux adaptée, pour une recherche locale.
Dans notre contexte on a démarré par la solution
obtenue par tabou sans amélioration et on a diminué la taille de
la liste taboue à 4 au lieu de 7. Les résultats de l'application
de cet algorithme en appliquant le principe d'intensification, sont
illustrés dans la table ci-dessous :
Image
Nombre de '1' adjacents de l'image originale
Nombre de '1' adjacents de la meilleure solution obtenue en
appliquant tabou sans amélioration
Nombre de '1' adjacents de l'image Reconstruite par Tabou avec
amélioration en utilisant le principe d'intensification
Temps d'exécution (en seconde)
Taux de Reconstruc-
tion
|
1
|
2
|
3
|
|
842
|
560
|
684
|
|
761
|
477
|
618
|
|
764
|
481
|
618
|
|
10,8
|
4,6
|
8,7
|
|
0,083
|
1,2
|
1,298
|
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
TAB. 3.4 -Résultat de Reconstruction des
images 40x40 hv-convexe en appliquant le principe d'intensification
Abdessalem DAKHLI 30
Image
Nombre de '1' adjacents de l'image originale
Nombre de '1' adjacents de la meilleure solution obtenue en
appliquant tabou sans amélioration
Nombre de '1' adjacents de l'image Reconstruite par Tabou avec
amélioration en utilisant le principe d'intensification
Temps d'exécution (en seconde)
Taux de Reconstruc-
tion
|
1
|
2
|
3
|
|
2106
|
1044
|
890
|
|
1854
|
792
|
642
|
|
1854
|
793
|
644
|
|
128,3
|
19,7
|
18,3
|
|
0,797
|
1,670
|
1,720
|
Chapitre 3. Reconstruction des Images Binaires par recherche
Taboue
Test image Taille 70x70
TAB. 3.5 -Résultat de Reconstruction des
images 70x70 hv-convexe en appliquant le principe d'intensification
Abdessalem DAKHLI 31
Abdessalem DAKHLI 32
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
Les résultats de l'application montrent bien que la
solution est améliorée en restant dans la même zone
d'espace de recherche, c'est à dire que la recherche est bien
localisée. Cette technique montre bien qu'il peut pénaliser des
solutions éloignées.
Diversification
La diversification permet à l'algorithme de bien
explorer l'espace des solutions, et d'éviter que le processus de
recherche ne soit trop localisé et laisse de grandes régions du
domaine totalement inexplorées.
La plus simple des stratégies de diversification
consiste à interrompre périodiquement l'acheminement normal de la
procédure tabou, et à la faire redémarrer à partir
d'une autre solution, choisie aléatoirement, ou "intelligemment". Une
autre méthode consiste à biaiser la fonction d'évaluation
f, en introduisant un terme qui pénalise les transformations
effectuées fréquemment, afin de favoriser des transformations
nouvelles. Ce type de stratégie de diversification peut être
utilisé de façon continue, sans interrompre la procédure
de recherche taboue.
Dans notre contexte on a utilisé la stratégie de
diversification qui consiste à redémarrer à partir d'une
autre solution et on a augmenté la taille de la liste taboue à 12
au lieu de 7.
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
TAB. 3.6 -Résultat de Reconstruction
des images 40x40 hv-convexe en appliquant le principe de diversification
Image
Nombre de '1' adjacents de l'image originale
Nombre de '1' adjacents d'une solution prise par hasard
obtenue en appliquant tabou sans amélioration
Nombre de '1' adjacents de l'image Reconstruite par Tabou avec
amélioration en utilisant le principe de diversification
Temps d'exécution (en seconde)
Taux de Reconstruc-
tion
|
1
|
2
|
3
|
|
842
|
560
|
684
|
|
740
|
445
|
610
|
|
620
|
447
|
620
|
|
10,8
|
4,6
|
8,7
|
|
0,083
|
1,2
|
1,298
|
Abdessalem DAKHLI 33
Les résultats ont montré que le principe de
diversification a amélioré la solution prise dans certain cas,
c'est-à-dire qu'avec cette technique on peut explorer des autres zones
de recherche. Dans ces zones la fonction objective augmente en rapprochant
à l'optimum global.
En résumé, nous disons que la diversification et
l'intensification sont des concepts complémentaires, qui enrichissent la
méthode de recherche taboue et la rendent plus robuste et plus
efficace.
Les résultats prouvent clairement que la reconstruction
est presque parfaite en appliquant la recherche tabou améliorée
c'est-à-dire l'utilisation de principe diversification et de
d'intensification.
On a constaté que le principe de diversification permet
de bien couvrir l'espace des solutions, explorer de nouvelles régions,
loin de la solution et de même, il pénalise les solutions
très proches contrairement au technique d'intensification qui explore
plus en profondeur la 'région'de la solution courante c'est à
dire permet d'approfondir la recherche, et qui pénalise les solutions se
trouvant dans des zones loin de la solution courante.
Abdessalem DAKHLI 34
Chapitre 3. Reconstruction des Images Binaires par
recherche Taboue
3.3 Conclusion et interprétations des
résultats
D'après ces résultats on a constaté que
la méthode Tabou exige une gestion de la mémoire de plus en plus
lourde à mesurer. Elle exige des stratégies de
mémorisation complexe.
Les résultats expérimentaux démontrent
que l'algorithme est efficace pour résoudre le problème de
reconstruction des images binaires. On a constaté que la fonction
n'incorpore pas de diverses informations contrairement à l'approche
génétique [33] qui a une capacité d'incorporer de diverses
formes de l'information a priori dans la fonction d'évaluation.
Les résultats démontrent aussi que la recherche
taboue est efficace lorsque les méthodes d'améliorations, sont
claires et bien étudiés.
L'application de la recherche taboue présente aussi que
l'augmentation de la fonction objective relative à l'existence des blocs
des composants des bascules. Et on a constaté que le temps
d'exécution est faible pour reconstruire une solution initiale et une
solution finale améliorée. De même on a constaté que
l'algorithme tabou est simple à paramétrer contrairement à
l'algorithme génétique [33] qui exige diverses formes
d'information. Les expériences présentent que l'optimum global de
la fonction d'évaluation est aussi nécessaire pour reconstruire
une image qui ressemble à l'image originale inconnue, qui a
été employée pour produire des données de
projection.
De même les résultats montrent que le taux de
différence entre l'image origine et l'image reconstruite est faible
concernant les images de taille réduite et les images de taille
important. Les divers résultats de reconstruction prouvent aussi
l'importance de la liste taboue pour améliorer la recherche et pour
éviter le cyclage pendant la recherche de la meilleure solution pour
avoir une reconstruction précise de l'image. La taille de la liste Tabou
est également un facteur de réglage : plus la taille de la liste
est petite, plus l'algorithme explore des petites régions. Plus la
taille est grande, plus la recherche est contrainte de s'opérer sur de
plus larges étendues.
On a constaté que les images de taille petite
l'algorithme tabou donne une reconstruction parfaite contrairement aux images
de taille important qui ont une fonction objective très importante.
Enfin dans ce chapitre on a présenté la
reconstruction des images hv-convexe par l'algorithme tabou, les
résultats pratiques et théoriques informatiques de cet algorithme
et aussi on a terminé par une conclusion et une interprétation
des résultats trouvés.
Abdessalem DAKHLI 35
Conclusion
L'objectif de ce mémoire était la reconstruction
d'images binaires monochromatique a partir des coupes (projections)
orthogonales et vérifiant certaines propriétés de
convexité (hv-convex). Cette mémoire montre l'efficacité
de l'approche taboue pour la résolution de problèmes de
reconstruction. Nous avons également tester l'importance
d'intégrer les techniques avancées d'intensification et de
diversification.
Cette mémoire sera poursuivie par la reconstruction
d'autre classes d'images colorées respectant autres contraintes
réelles et à partir de plusieurs projections. Nous
espérons réaliser un Framework général pour la
résolution de problèmes présentés en
discrète tomographies
Abdessalem DAKHLI 36
Annexe
Reconstruction des images HV-CONVEXES par la recherche
taboue sans amélioration
les images hv-convexe de taille 40 * 40
FIG.
4.3 -Image1 origine Taille 40x40
Abdessalem DAKHLI 37
Annexe

|
FIG.
|
4.4 -Image1 Reconstruite par Tabou
|

FIG.
4.5 -Image2 origine 40X40
Abdessalem DAKHLI 38
Annexe

|
FIG.
|
4.6 -Image2 Reconstruite par Tabou
|

FIG.
4.7 -Image3 origine 40x40
Abdessalem DAKHLI 39
Annexe

|
FIG.
|
4.8 -Image3 Reconstruite par Tabou
|

FIG.
4.9 -Image4 origine 40x40
Abdessalem DAKHLI 40
Annexe

|
FIG.
|
4.10 -Image4 Reconstruite par Tabou
|
les images hv-convexe de taille 70 * 70

FIG.
4.11 -Image1 origine 70x70
Abdessalem DAKHLI 41
Annexe

|
FIG.
|
4.12 -Image1 Reconstruite 70x70
|

FIG.
4.13 -Image 2 d'origine 70 x 70
Abdessalem DAKHLI 42
Annexe

|
FIG.
|
4.14 -Image 2 reconstruite 70 x 70
|

FIG.
4.15 -Image 3 d'origine 70 x 70
Abdessalem DAKHLI 43
Annexe
|
FIG.
|
4.16 -Image 3 reconstruite 70 x 70
|

FIG.
4.17 -Image 4 d'origine 70 x 70
Abdessalem DAKHLI 44
Annexe

|
FIG.
|
4.18 -Image 4 reconstruite 70 x 70
|
les images hv-convexe de taille 100 * 100

FIG.
4.19 -Image1 origine 100x100
Abdessalem DAKHLI 45
Annexe

FIG.
4.20 -Image1 Reconstruite 100x100
Abdessalem DAKHLI 46
Annexe

FIG.
4.21 -Image2 origine 100x100
Annexe

FIG.
Abdessalem DAKHLI 47
4.22 -Image2 reconstruite 100x100
Abdessalem DAKHLI 48
Annexe
Reconstruction des images HV-CONVEXES par la recherche
taboue avec amélioration
Test image :Taille 40x40

|
FIG.
|
4.24 -Image1 Reconstruite par tabou en appliquant le principe
d'in-
|
tensification
FIG.
4.23 -Image1 origine 40x40
49
Bibliographie
[1] A. Kuba and G.T. Hermann. Discrete tomography : a historical
overview. In Discrete Tomography: Foundations, Algorithms and Applications,
pages 3-33. Birkhauser, 1999.
[2] B. Wang and F. Zhang. On the precise number of (0,
1)-matrices in u(r, s). Discrete Mathematics, 187 : 211-220, 1998.
[3] C. Picouleau. Reconstruction of domino tiling from its two
orthogonal projections. Theoretical computer science, 255(1) : 437-447,
2001.
[4] E. Barcucci and A. Del Lungo. Reconstructing convex
polyominoes from their horizontal and vertical projections. Theoretical
computer science, 155(1) :321-347, 1996.
[5] G.J.Woeginger. The reconstruction of polyominoes from their
orthogonal projections. Information Processing Letters, 77(5-6) : 225-229,
2001.
[6] H.J. Ryser. Combinatorial properties of matrices of zeros
and ones. Ca-nad. J. Math, 9 :371-377, 1957.
[7] M. Chrobak and C. Durr. Reconstructing hv-convex polyominoes
from orthogonal Projections. Information Processing Letters, 69 : 283-289,
1999.
[8] R.J. Gardner,P. Gritzmann, and D. Prangenberg. On the
computionnal complexity of reconstructing lattice sets from their x-rays.
Discrete Mathematics, 202 : 45-71, 1999
[9] R. M. Haber. Term rank of 0,1 matrices. Rend. Sem. Mat.
Univ. padova, 30 :24-51,1960.
[10] E. Barcucci, A. Del Lungo, M. Nivat and R. Pinzani,
Reconstructing convex polyominoes from their horizontal and vertical
projections, Theoret. Comput. Sci., 155 (1996), 321-347.
[11] G.J.Woeginger.The reconstruction of polyominoes from
their orthogonal projections. Information Processing Letters, 77(5-6) :
225-229, 2001.
Abdessalem DAKHLI 50
Bibliographie
[12] Geir dahl, Truls Flatberg, Optimization and
reconstruction of hv-convex (0, 1)-matrices. (2003), 58-69.
[13] F.Jarray, M.Costa, C. Picouleau. Approximating hv-convex
binary matrices and images from discrete projections.1-10.
[14] R.J. Gardner, P. Gritzmann, and D. Prangenberg. On the
computational complexity of determining polyatomic structures by x-rays.
Theoretical computer science, 233 :91-106, 2000
[15] H.J. Ryser. Combinatorial properties of matrices of
zeros and ones. Ca-nad. J. Math, 9 :371-377, 1957.
[16] K.J. Bateleur. An Evolutionary Algorithm for Discrtee
tomography : Mathemaical Institue, Leinden University, Niels Bohrweg, I, 2333
CA Leinden and CWI.
[17] A. Del Lungo and M. Nivat. Reconstruction of connected
sets from two projections. Chapter 7 of [15], page 163-188, 1999.
[18] D. Gale. A theorem on flows in networks. Pacific journal
of Mathematics, 7 : 1073-1082, 1957.
[19] G. Dahl and T. Flatberg. Optimization and reconstruction
of hv-convex (0, 1)-matrices. In A. Del Lungo. V. Di Gesù and A. Kuba.
Editors, Electronic Notes in Discrete Mathematics. Volume 12. Elsevier,
2003.
[20] H.J. Ryser. Combinatorial Mathematics. The Carus
Mathematical Monographs no. 14, chapter 6. AMS, 1963.
[21] R.J. Gardner, P. Gritzmann, and D. Prangenberg. On the
computational complexity of reconstructing lattice sets from their X-rays.
Discrete Mathematics, 202 : 45-71, 1999.
[22] S. Brunetti, A. Del Lungo, F. Del Ristoro, A. Kuba, and
M. Nivat. Reconstruction of 4-and 8-connected convex discrete sets from row and
column projections. Linear Algebra and its Applications, 339 : 37-57, 2001.
[23] S. Matej, A. Vardi, G.T Herman, and E. Vardi. Binary
tomography using gibbs priors. Chapter 8 of [15], pages 191-212, 1999
[24] Th. Back, D.B. Fogel, and T. Michalewiez, editors.
Evolutionary Computation 1. Institute of Physics Publishing, Bristol and
Philadelphia, 2000.
[25] W. Hochstattler, M. Loebl, and C. Moll. Generating
convex polyominoes at random. Discrete Mathematics, 153 :165-176, 1996.
[26] Z. Michalewiez. Genetic Algorithms + Data Structures=
Evolution Programs; 3rd Revision edition. Springer Verlag, 1996.
[27] A. kuba and G.T. Herman. Discrete tomography: A
historical overview. Chapter 1 of [15], pages 3-34, 1999.
Abdessalem DAKHLI 51
Bibliographie
[28] S. REBOUL et al. Reconstruction of Binary Objects From
Two Orthogonal Projections by an Inspired Technique of the Graph's Theory: the
Research of Maximum Flow with Minimum: Traitement du Signal 1995 -Volume 12 -
n° 5
[29] R.L YANG e al. Reconstruction d'image 3D en angiographie
numérique et à partir de deux projections orthogonales.
Laboratoire "Signaux e Systems " du cnam 292, rue Sain Marin 75141 Paris CDEX
03 : juin 1989.
[30] S. Brunetti, M.C. Costa, A. Frosini, F. Jarray, C.
Picouleau. Reconstruction of binary matrices under adjacency constraints, pages
125{150. Birkhauser Boston, 2007.
[31] C. Picouleau. Reconstruction of convex polyominoes from
orthogonal projections of their contours. Volume 346, Issues 2-3, 28 November
2005, Pages 439-454.
[32] GLOVER F. et LAGUNA M., Tabu Search, Kluwer, 1997.
[33] K.J. Bateleur. An Evolutionary Algorithm for Discrtee
tomography : Mathemaical Institue, Leinden University, Niels Bohrweg, I, 2333
CA Leinden and CWI.
| 


