Chapitre2
Etat de l'art sur la reconstruction des
images hv-convexes
Introduction
Ce chapitre expose la définition des images hv-convexe
de même il présente le tour d'horizon de résolution du
problème de reconstruction des images hv-convexe.
2.1 Définition
Dans certains cas la tomographie exige les
propriétés de connexité pour assurer la continuité
de l'objet suivant ces directions surtout dans l'imagerie médicale.
Soit A une matrice binaire, on définit les
propriétés suivantes de A :
- h : A est h-convexe si les cellules de valeur 1 de chaque
ligne constituent un ensemble connexe, c'est-à-dire, les cellules de
valeur 1 ne sont pas séparées par des cellules de valeur 0
(Figure 1.2- a-).
- v : A est v-convexe si les cellules de valeur 1 de chaque
colonne constituent un ensemble connexe (Figure 1.2-b-).
- hv : A est hv-convexe si les cellules de valeur 1 de chaque
ligne et colonne constituent un ensemble connexe, c'est-à-dire A est
h-convexe et v-convexe (Figure 1.2- c-).
Exemple :
La matrice à reconstruire doit respecter les
projections orthogonales et la convexité de l'image. C'est à dire
reconstruction des images binaires sous contraintes de convexité.
Abdessalem DAKHLI 8
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
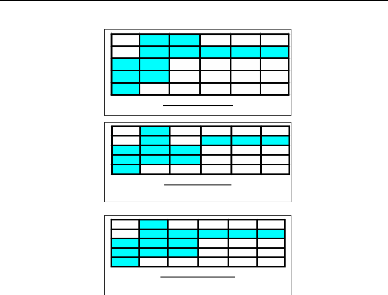
Matrice hconvexe
Marice vconvexe
Matrice hvconvexe
FIG. 2.1 -Définition d'une matrice convexe
2.2 Etat de l'art sur la reconstruction des images
hv-convexe
- E. Barcucci, A. Del Lungo, M. Nivat et R. Pinzani [10] ont
montré que le problème de reconstr uction h-convexe et v-convexe
d'une matrice binaire est NP-complet. Ils ont montré que le
problème de reconstruction d'une matrice devient NP-complet dès
que l'on exige les propriétés (h, v) ou hv. Ils ont
proposé aussi un algorithme qui repose sur trois phases. La
première phase consiste à choisir une configuration initiale sur
les bords du tableau, c'est-à-dire, sur les lignes 1 et n-i et
les colonnes 1 et n. Le nombre de ces configurations est borné
par in2n2 car la solution
cherchée satisfait les propriétés (p, h, v).
Ensuite, pour chaque configuration de départ, une procédure
de propagation de contraintes permet de fixer les valeurs de certaines cellules
pour respecter les propriétés (p, h, v). A l'issue de
cette phase on ne peut pas conclure l'existence d'une solution car il reste
souvent quelques cellules indéterminées. Les valeurs de ces
cellules peuvent s'exprimer par des
Projections (H,V) Matrice Reconstruite Image
Reconstruite
(a) : Reconstruction d'une matrice binaire.
(b) : Passage d'une matrice à une image
binaire

2 1 3 1 V
1
1 (a)
3
2 H
|
1
|
0
|
0
|
0
|
|
0
|
0
|
1
|
0
|
|
1
|
1
|
1
|
0
|
|
0
|
0
|
1
|
1
|
(b)
Abdessalem DAKHLI 9
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
FIG. 2.2 -Principe de reconstruction d'une image
binaire
clauses booléennes à deux variables. En fin,
l'éventuel problème 2-SAT est résolu pour trouver une
solution s'il en existe une. L'algorithme global est de complexité
O(m4m4).
- G. J. Woeginger [11] a montré que la reconstruction
de hv-convexe est NP-complet. Il a montré que le problème reste
toujours NP-complet même si les propriétés (hv, v),
(hv, h), h ou v sont considérées. Toutefois, le
problème redevient polynomial si l'on exige les trois
propriétés (h,v) à la fois.
- Geir dahl et Truls Flatberg [12] ont fournit un algorithme
basé sur une relaxation lagrangienne pour reconstruire une matrice
hv-convexe en respectant les projections prescrites.
- F.Jarray et al. [13] ont proposé un nouvel algorithme
pour reconstruire approximativement une matrice hv-convexe de leurs
projections, cet algorithme exécute une séquence de
reconstruction apparentée, en utilisant une seule projection (HouV
). Il utilise le plus long chemin pour fournir une solution approximative.
Le problème de reconstruction des images hv-convex respectant une seule
projection orthogonal (H ou V).
- F.Jarray et al. [13] ont proposé aussi une
heuristique qui utilise un long chemin et des modèles de réseau
pour fournir une solution approxima-
Abdessalem DAKHLI 10
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
tive respectant les projections orthogonales (H et V). Cette
heuristique est un algorithme du temps polynomial parce que la ressemblance
n'est pas râpe que le nombre maximal de 1 adjacents. Pour le
problème de petite taille l'heuristique donne une image hv-convex
c'est-à-dire presque l'image réelle et pour les autres instances
(problème de grande taille) la solution est approximative avec un nombre
d'adjacent maximal, en respectant les projections orthogonales.
- Gardner et al. [14] ont appliqué un algorithme et il
ont montré que le problème de reconstruction des images
hv-convexe est NP-complet pour d >= 2 et €
>= 3(avec d c'est le dimension du tableau et € c'est le nombre d'axes
non parallèles de projection. € = 2 si l'on considère
seulement les projections orthogonales.
- Ryser [15] a proposé un algorithme pour reconstruire
de polyominos horizontalement et verticalement convexes avec contraintes
tomogra-phiques. Les méthodes utilisées font appel à la
géométrie discrète mais aussi à des
réductions à 2-SAT et il a montré que la reconstruction
est un problème NP-complet et NP-difficile selon la taille de matrice
qui représente l'image.
- S. REBOUL et al.[28] ont utilisé un algorithme de
flot maximum à coût minimum inspiré de la théorie
des graphes et le modèle de l'image à reconstruire. Ils ont
utilisé le deux projections orthogonales de l'image pour faire cette
reconstruction. Les taux de conformités, obtenus entre l'image à
reconstruire et l'image reconstruite, sont supérieurs à 95%.
- R.L.YANG et al.[29] ont proposé deux algorithmes pour
reconstruire une image binaire 3D à partir de deux projections
radiologique orthogonales. Ils ont signalé que cette reconstruction peut
se réduire, en angiographie numérique, à de multiples
reconstructions 2D des matrices de sections. Le premier algorithme
utilisé est basé sur l'existence d'une courbe médiane de
section et le deuxième utilise un modèle pour la première
section à reconstruire et donne des solutions optimales à l'aide
de la méthode dites du flot maximal de coût minimal. Les
résultats obtenus on montré que la reconstruction 3D en
angiographie et à partir de deux projections orthogonales peut donner de
très bon résultats. L'application des ces algorithmes à
des cas cliniques implique néanmoins des précautions
particulières afin d'assurer un mélange aussi homogène que
possible du produit de contraste avec le sang pendant la phase d'acquisition et
qualité minimale d'image.
- Stéphane Chrétien et Franck Corset [30] ont
utilisé l'estimation moindre carrée et l'optimisation valeur
propre pour reconstruire des images binaires hv-convexe. Plus
précisément, ils ont estimé que ce problème
appartient à la classe des problèmes NP-hard. Ils ont
étudié l'estima-
Abdessalem DAKHLI 11
Chapitre 2. Etat de l'art sur la reconstruction des images
hv-convexes
tion d'une image corrompue par un bruit. Ils ont
approché le problème par la méthode des moindres
carrés linéaires pénalisés et ils ont introduit une
relaxation de type valeur propre qui transforme le problème original en
un problème approché convexe. Dans la plupart des cas, le
schéma relaxé ne redonne pas une solution binaire. Pour
résoudre ce problème ils ont proposé un algorithme
stochastique qui donne une interprétation géométrique
simple. Enfin, ils ont prouvé que dans le cas d'une image faiblement
bruitée, la relaxation donne la solution optimale.
- S. Brunetti et al [30] ont utilisé une approche de
programmation dynamique, ils ont prouvé qu'une grande
variété de problèmes de reconstruction matriciels de deux
projections peut être résolue dans le temps de polynôme
chaque fois que le nombre des lignes et des colonnes est fixé. Ils ont
limité leurs résultats à quelques problèmes
représentatifs mais leur approche peut être facilement
adaptée à une large classe d'autres problèmes. Ils ont
prouvé aussi quelques résultats de complexité pour
plusieurs problèmes concernant la reconstruction d'une matrice binaire
quand une contrainte de voisinage arrive. Dans le cas où pour chaque 1
il y a exactement un autre 1 dans le quatre voisinage le problème est
plus dur que les trois problèmes de reconstruction matricielle
colorée. Si la contrainte consiste en ce qu'il y a exactement deux autre
1 dans le Quatre voisinage, alors ils ont montré le problème peut
être NP-complete.
- C. Picouleau [31] a étudié la reconstruction
de chacun polyomino convexe quand les projections orthogonales sont
définies comme la longueur de contour de l'objet intercepté par
le rayon. Il a prouvé que ce problème est NP-dur pour plusieurs
classes de polyominoes : Général, h-convex, v-convex. Pour
hv-convex polyominoes il a proposé un algorithme de temps de
polynôme pour le problème de reconstruction.
- K.J. Bateleur [16] a appliqué l'algorithme
génétique pour résoudre le problème de
reconstruction des images convexes. En effet, il a signalé aussi qu'il
existe des algorithmes de reconstruction de temps polynomial [21] concernant
les images qui appartiennent aux classes hautement structurées [16], et
pour d'autre images qui appartiennent à une classe plus
générale c'est à dire de polyominoes hv-convexe
formé par plusieurs polyominoes séparés, le
problème de reconstruction est NP-difficile [17]. Pour reconstruire une
image hv-convexe K.J. Bateleur [16] a définit une fonction
d'évaluation pour chacune des solutions pour assumer les
propriétés spécifiques de la structure d'image. La valeur
de la fonction objective pour une solution optimale, est évaluée
par le nombre de pixel noir voisine d'horizontal ou de verticale [19]. Cette
fonction est maximisée par une re-
Abdessalem DAKHLI 12
| 


