I.2. La congruence
Définition
Soient   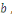 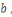 et et   des entiers, alors on dit que des entiers, alors on dit que   est congru à est congru à 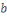 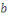 modulo modulo  , ce qui s'écrit , ce qui s'écrit 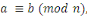 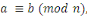 si si 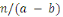 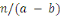 ; ; 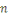 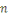 est le module de la congruence. est le module de la congruence.
Propriétés de la congruence
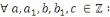 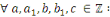
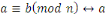 - - 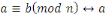 et et 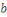 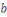 ont le même reste dans la division par ont le même reste dans la division par 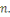 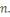
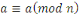 - - 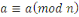 (réflexivité). (réflexivité).
 - -  (symétrie). (symétrie).
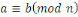 - - 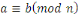 et et 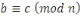 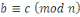 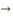 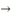 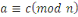 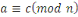 (transitivité). (transitivité).
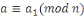 - - 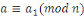 et et 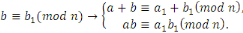 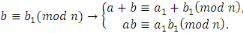
I.3. Classes des
résidus
Soit 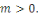 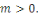 Pour chaque entier Pour chaque entier   on définit on définit 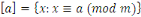 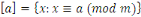 , en d'autres termes , en d'autres termes 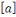 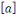 est l'ensemble de tous les entiers qui sont congrus à est l'ensemble de tous les entiers qui sont congrus à 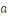 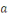 modulo modulo 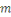 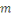 . Les autres auteurs appellent . Les autres auteurs appellent 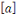 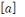 la classe congruence ou la classe d'équivalence de la classe congruence ou la classe d'équivalence de 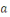 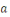 modulo modulo 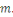 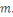
Théorème.
Pour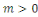 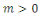 on a : on a : 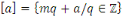 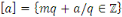 . .
Preuve
Supposons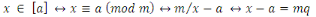 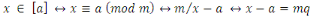
pour tout   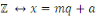 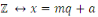 . Notons que . Notons que 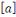 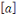 dépends de dépends de 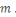 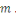
On a deux façons d'écrire l'équation
ci-haut :
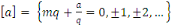 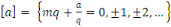 ou ou 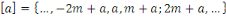 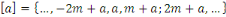
Tout élément 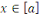 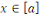 est une représentation de la classe de résidu est une représentation de la classe de résidu 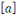 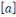 . .
I.4. Ensemble réduit des
résidus
Définition
On défini 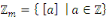 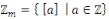 , alors , alors 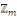 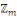 est l'ensemble de toutes les classes modulo est l'ensemble de toutes les classes modulo 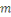 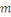 . Nous appelons . Nous appelons 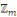 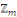 l'anneau des entiers l'anneau des entiers 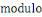 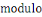 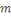 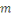 . .
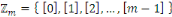 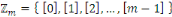
Addition et multiplication dans 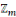 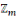
Pour 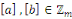 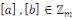 , on a : , on a :
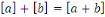 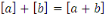 et et 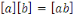 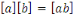
Exemple
Pour 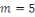 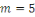
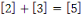 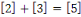 et et 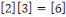 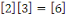
Notons que puisque 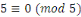 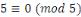 et et 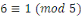 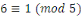 ,nous avons ,nous avons 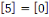 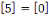 et et 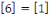 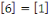 . Nous pouvons aussi écrire . Nous pouvons aussi écrire 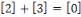 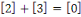 et et 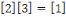 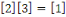
I.5. La fonction d'Euler ou
fonction totient
Définition
Pour 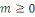 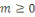 ,soit ,soit 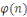 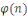 le nombre d'entiers premiers avec le nombre d'entiers premiers avec 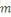 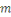 dans l'intervalle dans l'intervalle 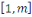 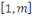 . La fonction . La fonction   est la fonction d'Euler. est la fonction d'Euler.
Exemple
Pour 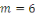 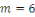 , il y a , il y a   différentes classes de résidu modulo différentes classes de résidu modulo   ; les classes ; les classes 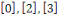 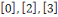 et et 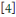 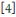 ne sont pas premiers avec ne sont pas premiers avec   ; ainsi seules les classes ; ainsi seules les classes 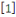 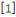 et et 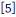 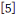 sont premiers avec sont premiers avec   :alors :alors 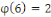 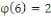 . .
Si   est un premier, toutes les est un premier, toutes les   classes classes 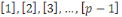 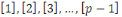 sont premiers avec , alors sont premiers avec , alors 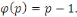 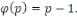
Exemple :
|
2
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
12
|
15
|
|
2
|
2
|
4
|
2
|
6
|
4
|
6
|
4
|
4
|
8
|
Théorème (Euler)
Soit 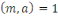 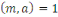 , alors , alors 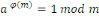 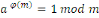
Ceci permet de calculer l'inverse modulaire définit
par :
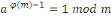 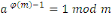
Exemple
Quel est l'inverse de 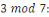 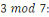 on sait que on sait que 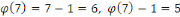 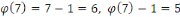
On a 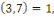 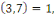 d'où d'où 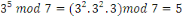 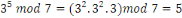
Théorème (Petit théorème
de Fermat)
Soit 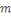 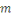 un premier et un premier et   un entier tel que un entier tel que 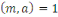 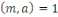 alors alors 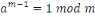 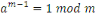
Preuve
Considérons les 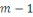 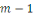 entiers suivants : entiers suivants :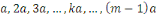 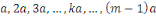 ainsi que leurs restes dans la division euclidienne par ainsi que leurs restes dans la division euclidienne par 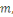 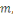 notés : notés :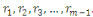 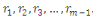 Ces restes sont compris entre Ces restes sont compris entre 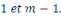 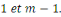
En effet, d'après le même de Gauss, si 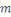 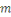 divisait un des ces produits divisait un des ces produits 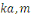 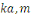 diviserait diviserait 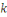 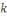 puisque puisque   et et 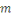 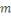 sont premiers entre eux, mais ceci est impossible puisque sont premiers entre eux, mais ceci est impossible puisque 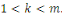 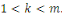 De plus les restes de division de De plus les restes de division de 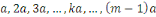 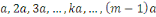 par par 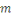 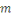 sont tous différents. Si on trouvait des restes identiques pour sont tous différents. Si on trouvait des restes identiques pour
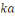 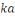 et et 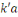 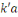 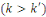 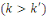 alors le reste de alors le reste de 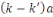 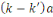 par par 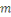 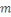 serait nul, ce qui est impossible d'après ce qui
précède. serait nul, ce qui est impossible d'après ce qui
précède.
Notons que ces restes sont donc des entiers compris entre 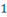 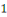 et et 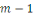 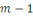 . .
En multipliant membre à membre les
congruences :
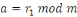 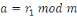 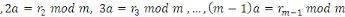 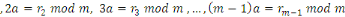
Alors nous obtenons :
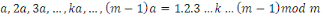 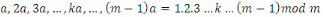
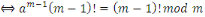 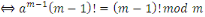
Par définition de la congruence, cette
égalité signifie que 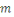 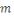 divise divise 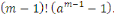 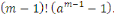 Or Or 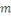 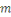 ne divise aucun des entiers ne divise aucun des entiers 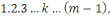 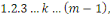 il est également premier avec leur produit il est également premier avec leur produit  
Ainsi d'après le lemme de Gauss 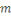 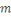 divise divise 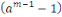 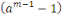 c'est-à-dire c'est-à-dire 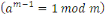 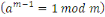 . .
Théorème de Wilson
Si 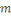 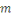 est un premier, alors est un premier, alors 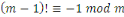 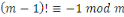
Preuve
Considérons la congruence 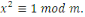 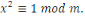 Alors Alors 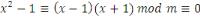 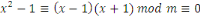 , ainsi les seules solutions sont , ainsi les seules solutions sont   et et 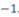 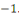 Donc, pour chaque Donc, pour chaque 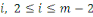 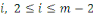 , il existe qu'un inverse unique , il existe qu'un inverse unique 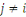 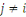 de de 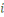 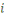 , ,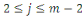 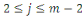 . Ainsi lorsque nous groupons des inverses en pairs, nous
obtenons : . Ainsi lorsque nous groupons des inverses en pairs, nous
obtenons :
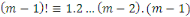 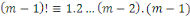
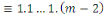 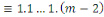
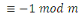 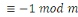
Théorème du reste Chinois
Soit 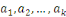 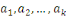 des entiers et des entiers et 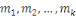 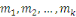 des entiers relativement premiers entre eux, alors le
système des congruences des entiers relativement premiers entre eux, alors le
système des congruences
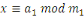 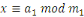 , ,
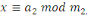



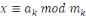
admet une unique solution modulo 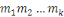 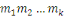
Preuve
Soit 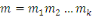 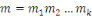 ,et considérons ,et considérons 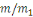 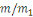 .Ceci est relativement premier à .Ceci est relativement premier à 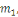 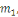 ainsi il existe un entier ainsi il existe un entier 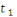 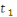 tel que tel que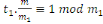 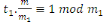 . .
En conséquence, soit 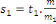 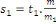 . Alors . Alors 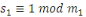 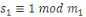 et et 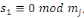 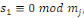 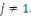 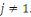 D'une manière similaire, D'une manière similaire, 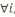 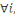 il existe un il existe un 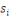 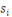 tel que tel que 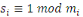 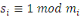 et et 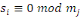 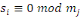 , ,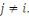 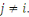 Alors Alors 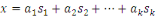 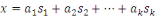 est une solution du système ci-haut. est une solution du système ci-haut.
Soit 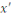 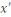 une autre solution, alors une autre solution, alors 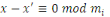 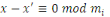
pour tout 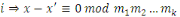 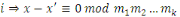
| 


