Dette extérieure et fuite des capitaux au Cameroun.

2.2. Présentation de la méthode économétrique

La présentation de la méthode économétrique ne saurait se faire sans justifier au préalable le choix de cette méthode.

2.2.1. Justification de la méthode économétrique

Il existe plusieurs techniques économétriques pour tester les relations de long terme entre les séries. Les plus utilisées sont la procédure en deux étapes d'Engle et Granger (1987), l'approche de Johansen (1988) et la méthode de Johansen et Juseluis (1990). La condition nécessaire de mise en oeuvre de ces méthodes est que les séries soient toutes intégrées d'ordre 1. Or, dans la plupart des séries macroéconomiques cette condition n'est pas vérifiée (Nelson et Plosser, 1982). Cette exigence suppose alors que l'étude de la stationnarité de ces séries soit effectuée. De plus, l'application des tests de stationnarité sur des échantillons de petite taille conduit à des résultats qui manquent de puissance. Face à cette insuffisance, la méthode ARDL de Pesaran et al. (2001) propose au contraire de ces modèles une nouvelle approche permettant d'obtenir de meilleures estimations. Elle est plus appropriée pour tester l'existence des relations de long terme et de court terme dans des échantillons de petite taille et, contrairement à l'approche de Johansen et Juselius (1990), elle permet de les tester entre des variables dont les ordres d'intégration sont différents (Acikgoz et Merter, 2010).

2.2.2. Le modèle Autorégressif à Décalage Temporel de Pesaran et al. (2001)

Un ARDL est une régression des moindres carrés contenant des retards des variables dépendantes et des variables explicatives. Ces modèles sont généralement notés ainsi : ARDL (p, q₁,...q_k), où p est le nombre de retards de la variable dépendante, q₁ est le nombre de retards de la première variable explicative, et q_k le nombre de retards de la k^ème variable explicative. Un modèle ARDL peut-être écrit ainsi:

p k q_j

y_t = á + ? u_i y_t-i + ? ?â_j,i X_j,t-i + å_t (15)

i=1 j=1 i=1

Certaines variables explicatives, X_j, peuvent avoir des termes non-décalés dans le modèle (q_j=0). Ces variables sont appelées variables explicatives statiques ou fixes. Les variables explicatives avec au moins un terme décalé sont appelées variables explicatives dynamiques. Pour spécifier un modèle ARDL, nous devons déterminer le nombre de décalages de chacune des variables qui doivent être incluses (C'est-à-dire spécifier p et q₁,...,q_k). Puisqu' un modèle ARDL peut-être estimé par la méthode des moindres carrés, les critères d'information standards tels que celui d'Akaike, Schwarz et Hannan-Quinn peuvent-être utilisés pour la sélection du modèle. Alternativement, on pourrait utiliser le R² ajusté des différentes régressions.

Pesaran et al. (2001) ont estimé le modèle ARDL conditionnel suivant les « bounds testing approaches ». Il s'agit d'une méthode plus générale que celle développée par Johansen. En effet, pour effectuer ce test, les variables du modèle n'ont plus l'obligation d'être intégrées du même ordre. On peut donc utiliser des séries qui sont intégrées d'ordre 0 ou 1. Ainsi, Pesaran et al. (2001) ont formulé un modèle à correction d'erreurs qui peut s'estimer en trois étapes suivantes :

Première étape : on estime la version bivariée d'un modèle à correction d'erreur (ECM)

Äy_{t =} á₀ + á₁t + ??y_t-1 + ?x_t-1+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (16)

où ?? et ? sont les multiplicateurs de long terme, les paramètres ?_i,i= 1,..., p-1 et ?_i,j = 1,...,q-1 sont les coefficients dynamiques de court terme, p et q sont les ordres du modèle ARDL sous-jacent (p fait référence à y_t et q fait référence à x_t ), t représente le temps (variable déterministe) et E_t est un bruit blanc non-autocorrélé avec Äxt et avec les valeurs retardées de xt et de yt . La procédure PSS (Pesaran-Shin-Smith) distingue entre cinq cas suivant la présence des composantes déterministes dans le modèle :

Cas 1 (sans constante et sans trend) : le modèle à correction d'erreur (ECM) devient :

Äy_{t =} ??y_t-1 + ?x_t-1+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (17)

Cas 2 (avec une restreinte constante et sans trend): le modèle ECM devient:

Äy_{t =} (y_t-1- ?_oy) + ?(x_t-1- ?_ox)+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (18)

Cas 3 (avec une constante et sans trend): le modèle ECM devient:

Äy_{t =} á₀ + ??y_t-1 + ?x_t-1+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (19)

Cas 4 (avec une constante et avec un restreint trend):

Äy_{t =} á₀+ (y_t-1- á_1yt) + ?(x_t-1- á_1xt)+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (20)

Cas 5 (avec une constante et avec un trend):

Äy_{t =} á₀ + á₁t + ??y_t-1 + ?x_t-1+ ?^p-1?_iÄy_t-i + ?^q-1?_jÄx_t-j + E_t (21)

Deuxième étape : on teste la nullité jointe des multiplicateurs de long terme ?? et ?  utilisant la statistique de Fisher associée au test de Wald dont on considère l'hypothèse nulle suivante:

Ho: 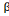= ? = 0 (non cointégration)

En effet, il s'agit d'un test de rapport de vraisemblance standard appliqué à l'hypothèse nulle. L'hypothèse nulle est rejetée pour les valeurs calculées élevées de la statistique de test. Cependant, la distribution asymptotique de ce test varie si les variables sous-jacentes sont I(0) ou I(1). En tout cas, ce n'est pas une distribution de Fisher standard et par suite la valeur calculée de cette statistique doit être comparée aux valeurs critiques fournies par PSS. On dispose de deux ensembles de valeurs critiques appropriées : un ensemble suppose que toutes les variables sont I(1) et un autre suppose qu'elles sont toutes I(0). Cela fournit une bande couvrant toutes les classifications possibles des variables entre I(1) et I(0) ou même fractionnement intégrées.

Troisième étape : les F-Statistiques calculées à la deuxième étape seront comparées aux bornes inférieures (F_lower , F_l) et (F_upper, F_u) supérieures de la bande critique de la procédure PSS aux niveaux de confiance 90, 95 et 99 %. Trois cas se manifestent: Si F > F_u alors on rejette l'hypothèse nulle et on conclut qu'il existe une relation d'équilibre de long terme entre x_t et y_t, en indiquant la présence d'une relation de cointégration. Si F < F_l alors on ne peut pas rejeter l'hypothèse nulle, et dans une telle situation, une relation d'équilibre à long terme ne semble pas exister entre les variables en question. Finalement si F_l < F < F_u alors le test est non conclusif et l'ordre d'intégration des variables sous-jacentes doit être étudié plus profondément.

Ø Tests de Diagnostics et de tests de Stabilité

Afin d'évaluer la robustesse des modèles choisis, nous ferons un ensemble de tests. D'une part, des tests de diagnostic: le test du multiplicateur de Lagrange pour l'autocorrélation des résidus, le test de la forme fonctionnelle de Ramsey (RESET), le test de Jarque-Béra pour la normalité des résidus et le test de White pour l'homoscédasticité. D'autre part, nous ferons les tests du Cusum et du carré du Cusum pour la stabilité des coefficients de long terme et de court terme.