|
ÉCOLE DOCTORALE
de Sciences Économiques et de Gestion
de l'Université de RENNES I
LOCALISATION COMMERCIALE MULTIPLE:
UNE APPLICATION DU TRAITEMENT DU SIGNAL ET DU MODELE P-MEDIAN
AU DEVELOPPEMENT D'UN RESEAU DE MAGASINS DE PRODUITS BIOLOGIQUES
THÈSE DE DOCTORAT DE L'UNIVERSITÉ DE RENNES
I
MENTION SCIENCES DE GESTION
Mention très honorable avec félicitations du
jury.
Présentée et soutenue publiquement par
Jérôme BARAY
le 3 décembre 2002
JURY
Directeur de thèse
Rapporteurs
Suffragants
Gérard CLIQUET
Jacques-Marie AURIFEILLE Alain JOLIBERT
Philippe ROBERT- DEMONTROND
Alexandre STEYER
Professeur à l'Université de Rennes I
Professeur à l'Université de la Réunion
Professeur à l'Université Pierre Mendes- France
de Grenoble
Professeur à l'Université de Rennes I,

Professeur à l'Université de Paris I

Centre de REcherche
Rennais en Economie et en
Gestion
UMR CNRS C6585
IGR-IAE : 11 Rue Jean Macé - CS 70803 - 35708 Rennes
Cédex 7 France : 02 23 23 77 77 Fax : 02 23 23 78 00
LOCALISATION COMMERCIALE MULTIPLE :
UNE APPLICATION DU TRAITEMENT DU SIGNAL ET DU MODELE
P-MEDIAN AU DEVELOPPEMENT D'UN RESEAU DE MAGASINS DE PRODUITS
BIOLOGIQUES
Sommaire
Introduction
générale...........................................................................................................1
Partie I : La localisation commerciale multiple:
enjeux et théories............19
Chapitre 1 : Enjeux et pratiques de la localisation commerciale
.........................................20
Chapitre 2 : Les théories de la localisation
..........................................................................57
Chapitre 3 : L'apport du traitement du signal dans le
modèle p-médian ............................113
Partie II : La localisation d'un réseau
.................................................................193
Chapitre 4 : Analyse d'un réseau de points de vente de
produits biologiques dans l'Ouest parisien
..........................................................................................................194
Chapitre 5 : Mise au point d'un système rapide d'aide
à la décision de localisation ..........240
Chapitre 6 : Comparaison et implications managériales et
stratégiques ............................260
Conclusion générale
.........................................................................................................300
Bibliographie.....................................................................................................................312
Table des matières
............................................................................................................332
Tables des
illustrations.....................................................................................................335
Annexe A : Cartes des clients géocodés par
arrondissement et communes de périphérie ...........339
Annexe B : Répertoire français-anglais des
termes du traitement du signal et de
l'analyse automatique d'image
......................................................................344
Introduction générale
Les regroupements massifs des réseaux de
distribution ces dernières années et la
conjoncture fluctuante et imprévisible ont rappelé
que leur organisation n'était jamais figée et restait soumis
à la loi impitoyable de la concurrence. De 1995 à 2000 surtout,
les opérations
de fusions-acquisition se sont répandues dans
l'ensemble des pays développés en atteignant la dernière
année 1143 milliards de dollars, soit une progression de 49,2
% en 1999 (source
www.Ipsofaxo.com). L'Union
Européenne, à elle seule, a compté pour 64,4 % de
ces réorganisations et les Etats-Unis pour 14,6 %. Les avantages
recherchés sont en général :
1°) l'effet de taille : une entreprise de taille
optimale permettrait d'atteindre une meilleure rentabilité, mais
cette hypothèse est sujette à de nombreuses controverses
(par exemple dans le domaine bancaire, de petits établissements
centrés sur leur clientèle peuvent coexister à
côté de mastodontes) 316;
2°) des économies d'échelle : une
fusion permettrait de réduire les coûts de
fonctionnement même si les coûts humains et
organisationnels, parfois imprévisibles, peuvent perturber le simple
calcul économique des gains escomptés par une telle manoeuvre.
Mais l'avantage le plus immédiat d'une fusion
est d'obtenir une part de marché plus importante sur son secteur
et dans le cas de la distribution de biens ou de services, une bien meilleure
présence et une couverture du marché géographique, un
accès plus aisé aux grands médias et une meilleure
efficience logistique317. Cela dit, certaines entreprises subissent
plutôt
les fusions qu'elles ne les souhaitent réellement, sachant
que celles-ci sont souvent le résultat
de la déréglementation des marchés comme
dans le secteur de la banque ou de l'assurance 318
(réduction des entraves à l'accès aux
services financiers de détail).
316 FILSER M. (1998) Taille critique et
stratégie du distributeur. Analyse théorique et implications
managériales,
Décisions Marketing, Numéro : 15,
p.7-16.
317 CLIQUET G. (1998) Valeur Spatiale des
Réseaux et Stratégies d'Acquisition des Firmes de Distribution,
in
Valeur, Marché et Organisation, Ed. J-P. Brechet,
Presses Académiques de l'Ouest.
318 UNI-Europa Finance (2000) L'impact des Fusions
dans le Secteur de la Banque et de l'Assurance, Rapport
Interne d'Entreprise, janvier 2000.
Les fusions ou tout simplement les difficultés
financières des entreprises ne sont pas les seules responsables des
réorganisations de réseaux de distribution ou de l'appareil
industriel.
Le progrès technique et l'introduction de
nouvelles technologies (Internet, distributeurs automatiques) remettent
périodiquement en question en particulier la pertinence
des localisations commerciales. Par exemple en Belgique, alors
que le nombre d'agences bancaires a diminué de 24 % de 1993
à 1998 (en passant de 17 757 à 13 444 en 5 ans), le nombre de
distributeurs automatiques de billets s'est accru de 150 % (2 636 distributeurs
à
6 323)319. Afin de compenser cette baisse
importante du nombre d'agences, les banques
développent en parallèle les services de banque par
téléphone ou sur Internet moins coûteux
en terme d'exploitation.
Ainsi, des dizaines de grandes entreprises et des centaines de
filiales cherchent à ou se voient contraintes de restructurer leur mode
de production dans les secteurs industriels et leur réseau de
distribution pour celles dont l'activité se situe dans le domaine de la
distribution des biens ou des services. Ces quelques lignes du rapport
d'activité d'une grande entreprise comme France
Télécom sont évocatrices : «
Amorcé en 2000, un programme de relocalisation vise
à implanter les agences dans les meilleures zones de chalandise. A la
fin
2001, près de la moitié des agences auront
été relocalisées »320. Cette
société en proie à des
difficultés financières compte en effet selon
d'autres propos fermer à moyen terme 10 % de
ses agences, agences qui regroupent 35 % des effectifs de
l'entreprise soit près de 130 000
salariés321. De nombreux cas illustrent, de
manière concrète, l'impact énorme d'une fusion sur
les implantations commerciales des sociétés.
La fusion de la banque Lloyds avec le TSB Group en décembre
1995, a propulsé l'ensemble au deuxième rang des groupes
bancaires britanniques, derrière le géant HSBC-Midland. Cela
s'est traduit par un bénéfice avant impôt
de 31 milliards de francs en 1997 en hausse de 26 % et un profit
net de 23 milliards en hausse
319 Source des données : entreprise ABB.
320 FRANCE TELECOM (2001) Rapport
d'Activité de la Société, Mars 2001.
321 LES ECHOS (2001) Les Echos Magazine,
parution du 28 août 2001.
de 48 % par rapport à 1996 : « deux ans
après la fusion, le groupe a déjà réduit ses
coûts de fonctionnement annuels de 2,2 milliards de francs et
prévoit encore de réaliser 4 milliards d'économies
à travers l'intégration des deux réseaux d'ici
1999. L'intégration des réseaux des deux banques devrait se
traduire par la fermeture de 650 agences et 10 000 suppressions
d'emplois (sur un effectif de 82 500 salariés).
» 322
Pour des entreprises comportant plusieurs centaines de
points de vente ou même plusieurs milliers comme dans le cas des
agences de compagnies d'assurance ou de banque, la réorganisation d'un
réseau s'avère être une tâche colossale. Chaque point
de vente ou agence doit être passé à la loupe,
comparé en termes de rentabilité, de chiffre d'affaires et de
zone de chalandise par rapport à ses plus proches voisins dans certains
cas concurrents par le passé et désormais, partenaires d'un
même réseau. Les sacrifices sont très souvent
inévitables pour éviter le double emploi de points de vente et
améliorer la rentabilité du nouvel ensemble. Cet examen en
détail des situations individuelles de chaque
élément du réseau doit être
particulièrement bien mené afin de ne pas supprimer des
points de vente ou des agences stratégiques pour la bonne
rentabilité ou même pour la survie du groupe. Ce constat est tout
aussi valable dans les services publics que privés. Par exemple pour la
Poste Suisse soumis à une prochaine libéralisation du
marché de la distribution du courrier : "dans un délai de
cinq ans, l'entreprise va réduire ce réseau de 140 à 180
unités par année, pour conserver à terme
2500 à 2700 offices de poste. Cette
évolution se déroulera dans des conditions sociales
acceptables, et le service public restera garanti sur l'ensemble du
territoire national. Les syndicats ont donné leur accord à la
procédure envisagée, qui, à terme, permettra à la
Poste d'économiser quelque 100 millions de francs par
année.323" Les bureaux de poste avec leur
hiérarchie (bureau de poste principal ou secondaire)
constituent les éléments d'un réseau dans
322 BEHBAHANI A. et HOZMAN H. (1998) La
Concentration dans le Secteur Bancaire, Mémoire de maîtrise
d'Economie mention Economie Internationale, Monnaie et Finance,
Université des Sciences Sociales de Toulouse.
323 LA POSTE SUISSE (2001) Communiqué de
Presse
, http://www.poste.ch
la distribution du courrier avec les centres de tri en
amont et les facteurs en aval qui acheminent le courrier à
domicile. On conçoit donc aisément que la suppression d'un
bureau
de Poste engendre des conséquences notables
sur l'organisation de tout le réseau de distribution du
courrier. Même chose pour d'autres services publics comme les
réseaux de services hospitaliers qui cherchent dans la majorité
des pays à rationaliser leur fonctionnement.
Parfois, ne s'agit-il pas forcément d'une
suppression pure et simple, mais d'un recentrage de deux
activités ou plus en une relocalisation plus optimale. Mais encore
faut-il que les différentes parties impliquées de
près ou de loin dans le fonctionnement de ces activités
(dirigeants, salariés, clients, fournisseurs ou même hommes
politiques) trouvent leur compte dans ce recentrage. Ainsi en
est-il du cas de figure suivant qui illustre la
réorganisation d'un ensemble de cinq sites hospitaliers dans le canton
de Vaud en Suisse où il s'agissait de choisir entre le statu quo, le
regroupement en deux monosites ou bien la création
d'un monosite entraînant la disparition des centres de soin
initiaux324.
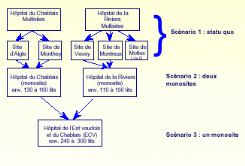
Introduction - Fig. 1: Scénarii de la
réorganisation de sites hospitaliers dans le canton de Vaud
Les critères de sélection entre ces trois
scénarii retenus étaient la taille optimale du bassin de
captation, la flexibilité, l'accessibilité et la proximité
des installations vis-à-vis du public, et la rentabilité ou
l'efficience relative de chaque scénario.
324 CAP GEMINI / ERNST & YOUNG (2000) Etudes de
Divers Scenarii d'Organisation liés aux Hôpitaux du
Chablais et de la Riviera, Rapport Final pour le
Département de la Santé / Service Santé Public,
p.3-16

Introduction - Fig. 2 : Notation des scénarii de la
réorganisation de sites hospitaliers dans le canton de Vaud
Un système de notation pondérée a
bien mis en évidence que le scénario 3 du regroupement
des cinq hôpitaux en un seul était le cas le plus favorable bien
que l'on puisse s'interroger sur la rationalité du système de
notation non-explicité. Mais, les différents acteurs
ont tous eu des vues différentes sur le site
exact d'implantation de cet hôpital unique, les dirigeants des
cinq centres souhaitant chacun agrandir le leur au détriment
des autres, les habitants désirant être au plus proche du futur
site,... d'où un gros problème décisionnel en perspective
qui ne pourra que retarder le projet ou même remettre en cause
le choix du scénario du site hospitalier unique pour la région
! D'autres contraintes dans le processus de réorganisation viennent
alors immédiatement à l'esprit : comment établir un
processus de décision plus rationnel avec une force de
démonstration telle que le scénario en découlant
fasse l'unanimité entre tous les acteurs ?
D'un autre côté, on remarque depuis les
années 60, une profonde mutation dans la distribution des
produits et des services caractérisée par la
réticulation des activités commerciales 325. Bien
que l'apparition des premières chaînes de magasins date de la
seconde moitié du XIXème siècle, le
développement des réseaux d'agences bancaires, de
supermarchés et hypermarchés, de concessionnaires
automobiles, de chaînes d'hôtels s'est
considérablement accéléré. On
évalue qu'à l'heure actuelle, les chaînes de
magasins
325 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
représentent près de la moitié du
commerce du détail aux Etats-Unis 326 327. Les
formes organisationnelles prises par ces groupes sont variées.
L'organisation en succursales même si elle coûte cher, favorise
l'opérateur du réseau en ce qui concerne son pouvoir et le
contrôle
des différentes entités. Le système de
franchise outre son développement à moindre coût,
permet au réseau d'avoir une réactivité plus
élevée sur le marché local, tout comme d'accéder
à une connaissance plus fine du marché et de
responsabiliser les gérants qui possèdent alors
une affaire bien à eux 328 329. Des formes
mixtes associant succursales et franchises permettent dans certains cas, de
tirer profit des avantages de chaque type d'organisation en particulier par
330 331 :
? une plus grande souplesse stratégique : il est
plus facile d'acquérir par exemple des hôtels individuels en
proposant à l'entrepreneur une formule de rachat ou de franchise,
? une implication et une démonstration des
capacités du franchiseur accrues par sa responsabilisation,
? une meilleure efficacité économique : les
franchises stimulent le développement du réseau et les
filiales participent beaucoup à l'amélioration des
résultats financiers 332,
? une plus grande souplesse d'organisation : il est plus
facile à une organisation mixte de répondre aux évolutions
comportementales du client et de l'environnement juridique (loi Raffarin par
exemple). L'innovation s'enrichit par un travail conjoint du franchiseur et
des franchisés tout comme l'information également
de meilleure qualité.
326 BRADACH J.L. (1998) Franchise
Organizations, Harvard Business School Press, Boston, Ma.
327 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
328 BRICKLEY J.A., DARK F.H. (1987) The Choice of
Organizational Form : The Case of Franchising, Journal
of Financial Economics, 18, 401-20.
329 CAVES R.E. , MURPHY II W.F. (1976)
Franchising : Firms, Markets, and Intangible Assets,
Southern
Economic Journal, 42, 572-86.
330 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
331 BRADACH J.L. (1998) Franchise
Organizations, Harvard Business School Press, Boston, Ma
332 BRIEC W., CLIQUET G. (1999) Plural Forms
Versus Franchise and Company-owned Systems : A DEA Approach of Hotel
Chain Performance, 28th EMAC Conference, Berlin, May, 11th-14th
5proceedings on CD-
ROM).
? une stimulation de la dynamique commerciale avec une
concurrence plus constructrice entre les franchisés et les filiales. Au
niveau local, l'animation commerciale est facilitée par l'effet
synergique des efforts mis en commun de toutes les entités du
réseau,
? une maîtrise de la rapidité de
développement du groupe par rapport à l'assimilation du concept :
le développement peut se faire rapidement par la création de
franchises alors que les filiales permettent de mailler le territoire
tout en assimilant graduellement le concept.
Ainsi, qu'il s'agisse de la création pure d'un
réseau ou de sa réorganisation et quel que soit le mode
d'organisation choisi, un choix précis de la localisation de ses
différents points de vente est indispensable tout comme une
certaine rapidité des prises de décision et de leur
application dans ce domaine. Toute organisation commerciale doit en effet avoir
une capacité
de réaction correspondante à la rapidité du
changement afin d'assurer sa survie 333 334, cette
capacité de réaction se décomposant en
temps de perception, temps de prise de décision et temps
d'exécution. Il apparaît clair que la qualité de la
décision concernant les localisations commerciales d'une chaîne
dépendra étroitement de celle de son système d'information
et que
la bonne exécution de la décision sera
influencée par sa maîtrise. Concrètement, quelques
mois de trop de fonctionnement d'un réseau "boiteux" peut aller
jusqu'à représenter des millions ou des dizaines de
millions d'euros de coûts supplémentaires pour un
réseau d'importance moyenne (de quelques dizaines à trois
cents points de vente) qui auraient été
économisés si la procédure avait été
plus rapide. Dans certains cas, un retard dans la restructuration d'un
réseau est susceptible de pénaliser lourdement la
performance d'une entreprise et de faire fléchir
irrémédiablement le cours de ses actions même si ce retard
n'est
pas forcément imputable au processus de
restructuration lui-même. En témoignent les
333 VERAN L. (1991) La prise de Décisions
dans les Organisations : Prise de Décision et Changement, Les
Editions de l'Organisation.
334 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
péripéties de la réorganisation de
Swiss Telecom planifiée dès sa privatisation partielle : "si
Swiss Telecom n'aura pas à supporter une lourde dette, son plan de
restructuration va tout de même engloutir 3 à 4 milliards de
francs. Sans attendre l'issue des débats parlementaires,
l'entreprise prépare déjà la réforme de ses
structures et devrait annoncer sous peu les noms
de ses futurs dirigeants. Plus qu'un affrontement entre la
gauche et la droite, le Parlement redoute le lancement d'un
référendum. A l'origine, la Suisse voulait prendre
l'Europe de vitesse. Au mieux, elle aura quelques mois d'avance. Au pire, en
cas de votation populaire, deux ans de retard. Dans un tel scénario, le
capital de Swiss Telecom serait considérablement dévalué.
Car, en l'an 2000, le marché des télécommunications
sera agité et risqué."335 La
compétitivité d'une grande entreprise comme Swiss Telecom peut
donc être amoindrie d'une manière irréversible si la
réorganisation de son réseau commercial n'est pas
effectuée en temps et en heure. Il s'agit donc non seulement de ne pas
rater le train du changement quel
qu'en soient les motifs, mais aussi de savoir très vite
où l'on veut diriger l'entreprise.
D'où cette problématique gestionnaire qui en
découle : quel outil de réorganisation ou de
déploiement d'un réseau de points de vente sur le plan de la
localisation à la fois rapide, précis
et démonstratif peut-on utiliser dans un tel cas ? Il
s'agit également de ne pas perdre de vue, dans cette réflexion
managériale, le fonds de commerce des points de vente à
savoir, leur clientèle. Les grands distributeurs, les banques, les
assurances possèdent des bases de données très
élaborées sur leur clientèle. Les data
warehouse ou "entrepôts de données" qui rassemblent
l'ensemble des données (marketing, comptables, ressources
humaines, achats, production,...) de l'entreprise, mais aussi son
système d'information décisionnel en sont un
exemple.
335 L'HEBDO (1998) Le "T"qui Vaut 20 Milliards de
Marks, L'Hebdo N°47, 21 novembre 1996
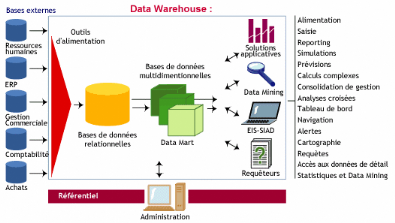
Introduction - Fig. 3 : Schéma d'un data warehouse
classique dans une entreprise336
Adossés au data warehouse, les outils de data mining ou de
"forage des données" ou encore
"d'extraction de la connaissance" font apparaître les
corrélations cachées qui existent au sein
du gisement de données de l'entreprise. Ces
outils sont de trois types : les filtres qui
sélectionnent certaines catégories de données (ex:
les points de vente ayant un chiffre d'affaires inférieur
à moins de 80 % de l'objectif), les outils fondés
sur l'intelligence artificielle qui découvrent des relations
logiques entre les variables, les agents intelligents capables
de naviguer en permanence dans les différentes bases de données
et élaborent ainsi
de nouvelles connaissances même en l'absence de
l'utilisateur.
En particulier, les hypermarchés se sont
constitués des bases de données monumentales à partir des
sorties de caisse qui répertorient le type d'achats effectués par
les clients (nombre d'articles, panier moyen, liste des articles par
client obtenus classiquement grâce au système code barre /
scanner, et également possibilités de suivi des achats de
certains clients identifiés par leurs moyens de paiement ou par leur
carte de fidélité,...). Les magasins d'importance plus modeste,
les hôtels, les restaurants peuvent aussi se constituer ce type de
données toujours grâce à un matériel informatique et
des logiciels spécifiques (Ok-Gestion,
336 Source :
http://www.businessdecision.com
WinCash, Gest-Mag pour les caisses individuelles, Cocktess pour
les restaurants ou bars, SHS
pour les hôtels, Columbus ou Winmaster pour des caisses en
réseau,...).
Les distributeurs automatiques savent également
établir des statistiques très précises
sur leurs clients et peuvent même les suivre à la
trace. Les sociétés de transport public, les
sociétés de gestion des autoroutes ou de parking, les
cinémas ont développé des cartes à puce avec et
sans contact qui permettent au client de franchir péages, portillons de
station de métro, parkings ou salles de cinéma (systèmes
commercialisés par la société Ascom et King Products
Inc.),... De la même façon, les agences bancaires
possèdent un suivi des retraits d'argent à partir de leurs
distributeurs automatiques de billets (ex. logiciel Prognis pour DAB).
Les cabinets d'études de marché et les
organismes spécialisés dans les habitudes de consommation,
eux aussi, ont entre leurs mains des millions d'adresses de clients
potentiels
par secteur, par produit, par segment de marché :
Consodata revendique par exemple le fait de posséder 22 millions de
fiches nominatives sur les citoyens de 4 pays. Une société
comme DoubleClick possède une technologie particulière lui
permettant de connaître les habitudes de navigation de plusieurs
millions d'internautes grâce à l'utilisation de cookies
(fichiers résidents sur le disque dur rassemblant des informations
personnelles du surfeur localisé sur le réseau Internet).
Les "géodonnées" sur les consommateurs ne
manquent donc pas, mais les moyens de les exploiter de manière
concrète font cruellement défaut. Les systèmes
d'information géographique, les fameux SIG, constituent l'outil
classique utilisé par un bon nombre d'entreprises pour analyser
leurs données géomarketing337. Ces systèmes
ne permettent malheureusement en fait que d'établir des
cartographies un peu élaborées. Parmi ces SIG,
citons les principaux :
337 CLIQUET G. (2002) Le Géomarketing :
Méthodes et Stratégies du Marketing Spatial, Hermès,
Paris.
· MapInfo : "Reconnu comme étant l'outil
cartographique le plus puissant et le plus intuitif
en environnement bureautique, MapInfo Professional est
distribué dans 54 pays, en 20 langues."338 Parmi les
seuls outils d'analyse marketing de MapInfo, on trouve un
générateur d'isochrones, d'isodistances ou d'isocoût
à partir d'un centre géographique donné (outil
Chronomap).
· MacMap : "il permet de créer
et d'exploiter des bases de données intégrant une
représentation des éléments géographiques
(points, axes, surfaces...), associées à des données
de format quelconque (numérique, alphabétique, date,
heure...). Il est naturellement possible d'effectuer des requêtes
(géographiques ou non) à partir de cette base de données,
comme par exemple, chercher les points de vente situés le long de la N20
générant plus de 4 % du CA total, et de
générer de nouvelles données et
cartographies grâce à des modules de
calcul."339
Il existe encore de nombreux autres SIG tels
Logicarte-SIG ou Carte & Données qui tous, n'offrent qu'une
solution passive de représentation de données sous forme
symbolique (points, camemberts, rectangles) superposée à une
cartographie (appelée image raster et constituée de pixels)
agrémentée de quelques opérateurs d'analyse
statistique ou de création de requêtes, sans jamais
intégrer une quelconque méthode de recherche de
localisations optimales. L'absence de progrès des SIG dans ce
domaine vient aussi sans doute de la difficulté technique
d'établir une passerelle entre le géocodage et la
représentation d'informations sur une carte et les techniques
classiques de calcul des localisations optimales : au contraire d'une
représentation planaire, ces techniques de localisation, nous le
verrons plus loin, font en général au contraire appel
à une représentation en réseau constitué de points
(les noeuds du réseau) et de liaisons entre ces points. Le
problème surgit donc du fait de l'incompatibilité entre la
représentation en deux dimensions des cartographies d'informations
géocodées et la
338
http://w3.claritas.fr : site Internet de
Claritas France distributeur de MapInfo
339
http://www.macmap.com : site Internet du
distributeur de Macmap
représentation monodimensionnelle des réseaux
(voir plus loin les modèles de localisation-
allocation340).
Nous démontrerons donc qu'il est possible de faire
évoluer les systèmes d'information géographique existants
vers de véritables outils de préconisation dans la
recherche de localisations optimales. Nous établirons ainsi pour cela
une passerelle entre les représentations cartographiques de ces
systèmes et les réseaux utilisés traditionnellement en
recherche de localisations. De plus, toutes les données
très précises de localisation des consommateurs,
réels ou potentiels, doivent pouvoir être prises en compte
dans un nouvel outil de décision capable d'aiguiller le manager
sur les emplacements optimaux des futurs
points de vente de son réseau. Tel est en effet le but de
notre présente démarche : découvrir et
démontrer la faisabilité d'un nouvel
instrument de décision précis, rapide et
également
démonstratif pour sélectionner les meilleurs
emplacements commerciaux dans l'optique d'une
restructuration ou de la création d'un réseau de
points de vente.
Il est un fait que cet outil performant ne connaît
à ce jour pas réellement d'existence, chose confirmée
par la lenteur des réorganisations de réseaux qui
même, sans connaître de problèmes sociaux, peuvent
prendre de nombreuses années. La majorité des responsables que
nous avons interviewés (Chambre Syndicale des Banques Populaires,
AGF, Groupe Etam, CCF, Groupe AXA) nous ont d'ailleurs
généralement fait part d'un déficit de méthodes en
ce
qui concerne l'optimisation de la localisation des agences ou
des boutiques malgré l'énorme quantité de données
disponibles : trop d'informations tue l'information pourrait-on clamer
! Qu'il s'agisse de la création pure ou bien de la
réorganisation d'un réseau, le manager est constamment en
proie à des doutes, à des interrogations sur la
méthodologie à suivre pour localiser de la meilleure
façon ses futurs centres de profit. Il se sent
généralement frustré et
impuissant devant tous ces monceaux de données
géomarketing qu'il n'a pas les moyens
340 WEBER A. (1909) Über den Standort der
Industrien, Tübingen, Traduction Anglaise de Friedrich
(1929)
Theory of the Location of Industries, University of
Chicago Press, Chicago.
d'exploiter ce qui est renforcé par le fait que
son Directeur lui demande de justifier très
précisément tous ses choix de localisation. Cela est sans compter
que les conséquences d'une mauvaise décision d'implantation ne
restent jamais inaperçues et se révèlent très
rapidement dans les résultats financiers désastreux
engendrés. L'investissement souvent onéreux dans les surfaces
commerciales, est lui-même de nature pratiquement
irréversible et des erreurs de localisation risquent d'obérer
à jamais la rentabilité future de l'ensemble du réseau.
Quels sont aujourd'hui brièvement les moyens
à disposition du décideur pour sélectionner la (ou
les) localisation(s) optimale(s) dans la perspective d'une création
intégrale
ou d'une réorganisation de points de vente ? Les
principales méthodes de choix de localisations se fondent sur
les modèles gravitaires ou d'interaction spatiale341
et sur les modèles de localisation-allocation. D'une
manière générale, ces méthodes comparent
plusieurs localisations potentielles en se fondant sur
différents critères. Les modèles gravitaires342
343 344 ou d'interaction spatiale se fondant sur une analogie
avec la loi de la gravitation, considèrent que chaque point de
vente attire à lui d'autant plus de clients que son niveau
d'attractivité est élevé. Cette attractivité est
fonction de la proximité géographique du magasin avec sa
clientèle ou encore d'autres facteurs comme la surface de vente
345. Le
modèle MCI (multiplicative competitive interaction) ou
Modèle Interactif de Concurrence346
est une généralisation des modèles
d'interaction spatiale pouvant intégrer d'autres facteurs
d'attractivité que la distance ou la surface de vente tels que le
service de paiement par carte bancaire, le nombre d'allées du
magasin, le nombre de caisses, l'emplacement à une
341 WILSON (1971) A Family of Spatial
Interaction Models, and Associate Developments, Environment
and
Planning A, vol. 3, 1-32.
342 REILLY W. J. (1931) The Law of Retail
Gravitation, W. Reilly ed, 285 Madison Ave, New York, NY.
343 CONVERSE P.D. (1949) New Laws of Retail
Gravitation, Journal of Marketing 14, p.379-384.
344 GUIDO P. (1971) Vérification
Expérimentale de la Formule de Reilly en Tant que Loi
d'Attraction des
Supermarchés en Italie, Revue Française de
Marketing n°39, p. 101-107.
345 HUFF D. L. (1964) Defining and Estimating a
Trading Area, Journal of Marketing, Vol 28, p. 38.
346 NAKANISHI M. et COOPER L.G. (1974) Parameter
Estimates for Multiplicative Competitive Interaction
Models: Least Square Approach, Journal of Marketing Research
11: 303-311.
intersection347 ou même des facteurs
subjectifs comme l'image du magasin348 349 dans le MCI subjectif
350 351. Ainsi, il s'agit d'abord de calculer les
différents paramètres d'une formule donnant la
probabilité qu'un client fréquente tel ou tel point de
vente en fonction des paramètres précités le plus
souvent par la méthode classique des moindres carrés
352. Mais, les méthodes d'interaction spatiale sont lourdes
à mettre en oeuvre et nécessitent un découpage
géographique du territoire à analyser,
découpage qui, nous le verrons, peut difficilement ainsi être
établi de manière rationnelle.
La seconde catégorie de méthodes de localisation
est constituée d'un autre côté par les modèles de
localisation-allocation et leur résolution353. Ces
modèles (représentés en général sous forme
de réseaux constitués de noeuds et de segments inter-noeuds) et
en particulier le modèle p-médian, sont l'un des moyens les
plus rationnels à disposition pour optimiser la localisation
d'un ensemble de p points de vente par rapport à un ensemble
de n clients354. Mais, malgré des méthodes de
résolution parfois très pointues, la mise en oeuvre de ce
modèle engendre un nombre de calculs si important que des
solutions même approchées sont difficilement atteignables
dès que le nombre de clients atteint quelques milliers compte tenu
du nombre considérable de configurations de magasins
à passer en revue. D'autre part, les
solutions avancées par les hermétiques
modèles de localisation-allocation ne sont ni très
347 JAIN K. et MAHAJAN V. (1979) Evaluating the
Competitive Environment in Retailing Using Multiplicative
Interactive Model, Research in Marketing, Vol. 2,
Jagdish Sheth ed., Greenwich, Conn.: JAI Press.
348 NEVIN J.R. et HOUSTON M.J. (1980) Image as a
Component of Attraction to Intraurban Shopping Areas,
Journal of Retailing, Vol. 56, No. 1, pp.77-93.
349 COOPER L.G. et FINKBEINER C.T. (1983) A
Composite MCI Model for Integrating Attribute and
Importance Information, Advance in Consumer Research,
109-113.
350 STANLEY T.J., SEWALL M.A. (1976) Image Inputs to
a Probabilistic Model: Predicting Retail Potential, Journal of
Marketing, 40 (July), 48-53.
351 CLIQUET G. (1995) Implementing a Subjective
MCI Model: An Application to the Furniture Market,
European Journal of Operational Research 84, 279-291.
352 NAKANISHI M. et COOPER L.G. (1974) Parameter
Estimates for Multiplicative Competitive Interaction
Models: Least Square Approach, Journal of Marketing Research
11: 303-311.
353 WEBER A. (1909) Über den Standort der
Industrien, Tübingen, Traduction Anglaise de Friedrich
(1929)
Theory of the Location of Industries, University of
Chicago Press, Chicago.
354 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc : A Multiple Store Location Decision
Model, Journal of Retailing, 58, 5-24.
démonstratives, ni très convaincantes pour le
décideur qui n'est généralement pas un homme
de l'art en la matière.
Dans la pratique, les professionnels font souvent appel
à des méthodes statistiques plus simples et rapides mais
très peu précises comme la méthode par le
modèle de régression multiple ou la méthode
analogique355 356. En se fondant sur l'expérience,
ces méthodes essayent en général dans un premier
temps d'identifier quels sont les paramètres et critères
socio-économiques qui influencent la performance du point de vente, et
ensuite détectent les zones géographiques répondant
à ces conditions pour y implanter un futur magasin. Les
méthodes statistiques sont intéressantes pour cerner
grossièrement les zones géographiques possédant
globalement un certain potentiel commercial, mais se
révèlent incapables de positionner avec soin le (ou les)
futur(s) point(s) de vente. Elles ne tiennent pas compte de la
localisation exacte des clients potentiels et ignorent en
général la présence d'éventuels concurrents.
Nous pensons en revanche que les méthodes d'analyse
dérivées de celles du traitement
du signal et de l'analyse d'image associés au
modèle p-médian peuvent répondre aux critères
de rapidité, de précision et de
capacité de traitement d'informations en grand nombre pour servir
le géomarketing. En effet, les algorithmes développés pour
traiter les images capturées
en temps réel enregistrent les performances de vitesse les
plus élevées au monde357. Conçus
pour la rapidité, ils sont également capables
d'assimiler d'énormes quantités de données puisque,
à une image dynamique, correspondent au minimum plusieurs
mégabits de données
par seconde. Ainsi, l'apport de notre démarche est
constitué par l'introduction de méthodes
originales de filtrage et de convolution destinées
à accélérer le traitement des données
355 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass.
356 ROGERS D.S. (1980) 5 ways to Evaluate a Store
Location, Store Location, 42-48.
357 CHESNAUD C. (2001) Activité de Simag -
Développement en Recalage, Tracking et Reconstruction 3D,
Aux Frontières de l'Instrumentation et du
Traitement d'Image, Journée Thématique Organisée
par le Pôle
Optique et Photonique Sud, Marseille, 20 mars 2001, p.11.
géomarketing, méthodes ayant déjà
fait leurs preuves dans le domaine des "sciences dures" :
le filtrage permet par une multiplication de la valeur d'un
signal à une ou plusieurs dimensions d'accentuer ou de lisser
certaines parties dudit signal alors que la convolution consistant
à intégrer un signal en utilisant un second signal comme poids
offre la possibilité d'extraire par exemple les
caractéristiques fondamentales d'informations géomarketing
comme le contour des zones de chalandise. Ces moyens d'analyse issus de
l'analyse d'image ou visionique nous serviront à introduire
un nouvel algorithme fondé sur le modèle p-médian,
pour faciliter la recherche de localisations optimales de points de
vente, de points de services ou même
d'entrepôts dans le domaine de la logistique.
Ainsi, nous montrons au chapitre 1 dans la
première partie de notre démarche, les enjeux de
la localisation commerciale et nous présentons les
méthodes actuelles de localisation faisant souvent appel
à la notion de zone de chalandise tout en exposant leurs
inconvénients. Dans le domaine de la localisation, les théories
développées par de nombreux chercheurs, et objets du chapitre
2, ont largement devancé les méthodes utilisées en
pratique, sans toutefois dans leur grande majorité, réussir
à devenir populaire du fait de leur difficulté
de mise en oeuvre ou simplement de leur approche trop
éloignée de la réalité. Ce chapitre nous permet
d'introduire les modèles de localisation-allocation et en particulier le
modèle p-médian dont les méthodes de résolution, on
l'a dit, sont trop peu performantes pour donner lieu à des applications
répondant aux attentes des professionnels. Le chapitre 3 offre
une réponse à ce déficit de méthode en montrant
comment les principes du traitement du signal rappelés à ce
moment, peuvent améliorer considérablement la formulation
d'un problème de localisation multiple : cette approche permet, nous
le verrons, de modéliser un problème de localisation en partant
d'une base de données de clients potentiels, de simplifier l'approche de
la recherche de
localisations et de déterminer ainsi avec précision
et de façon démonstrative les localisations
optimales tout en fournissant en parallèle des
informations commerciales stratégiques comme
les limites de zones de chalandise ou leur importance.
La deuxième partie de notre thèse
fournit l'occasion de mettre en pratique notre méthode combinant
traitement du signal et modèle p-médian pour la recherche
de localisations optimales de magasins distribuant des produits bio
dans l'Ouest Parisien. Le chapitre 4 présente le
marché récent et en plein développement du "bio"
en France ainsi que les principaux réseaux commerciaux. Une base de
données d'adresses de clients potentiels vis-à-
vis des produits biologiques est géocodée et
modélisée sous la forme d'un modèle p-médian
grâce à certaines fonctions du traitement du signal. Le
chapitre 5 est l'occasion de résoudre le modèle
simplifié obtenu pour dégager les localisations optimales
de points de vente de produits biologiques. Enfin, le dernier chapitre
montre la supériorité de notre méthode sur le plan de
la précision, de la rapidité et de la
démonstrativité comparée aux pratiques courantes dans le
domaine de la localisation avec un éclairage particulier sur la
localisation des réseaux
de points de vente. Ce cheminement intellectuel met
naturellement en lumière les nombreux autres avantages du traitement
du signal associé au p-médian dans la gestion du point
de vente. Les perspectives d'un apport du traitement du signal
à d'autres problèmes de
localisation-allocation comme la localisation de services publics
seront alors évoquées
Partie I
La localisation commerciale multiple :
enjeux et théories
Chapitre 1 :
Enjeux et pratiques de la localisation commerciale
Introduction
Quel que soit le type d'activité commerciale
considérée, le choix d'une bonne localisation est sans doute
l'une des décisions les plus importantes qu'un manager
doive prendre. L'emplacement du point de vente est en effet un investissement
fixé sur le long terme et son choix bon ou mauvais se ressentira sur le
niveau des ventes, sur la part de marché et sur la rentabilité
de l'activité d'une manière d'autant plus importante que
le niveau local de concurrence est élevé 358
359. Les prix peuvent être réexaminés, les
services réorientés, les marchandises changées, mais une
mauvaise localisation est une décision pénalisante parfois
irréversible pour l'entreprise.
La sélection d'un site pour l'implantation d'un point
de vente s'accompagne nécessairement, dans la plupart des cas,
d'une mesure quantitative et parfois qualitative du potentiel
commercial au voisinage du ou des emplacements pressentis, non seulement pour
décider en finalité de la localisation la plus
intéressante, mais aussi pour établir des prévisions de
vente et élaborer une politique marketing adéquate.
Nous verrons, dans le présent chapitre,
précisément quels sont les enjeux de la localisation commerciale
et comment déterminer ce potentiel commercial à travers la
circonscription dans l'environnement du point de vente de la part la plus
représentative des clients traditionnellement dénommée
«zone de chalandise». La détermination de la zone de
chalandise est en effet l'étape initiale fondamentale qui va orienter
la recherche d'une localisation optimale de points de vente. Il
est préférable de focaliser sa recherche dans les zones
géographiques les plus porteuses, les plus riches en clients pour ne
pas risquer de trouver une "aiguille dans une botte de
foin" comme le dit le dicton populaire.
358 INGENE C.A. (1984) Structural Determinants of
Market Potential, Journal of Retailing, Vol.60 N°I, p.37.
359 STANLEY T.J., SEWALL M.A. (1976) Image Inputs to
a Probabilistics Model : Predicting Retail Potential,
Journal of Marketing, 40, P.48
Prendre la décision d'ouvrir un point de vente
présente toujours le risque financier de
ne jamais voir l'activité devenir rentable : «
alors qu'une bonne localisation engendrera un chiffre d'affaires et des
profits élevés, une localisation pauvre se transformera en
dettes. »360
Il sera possible cependant après coup de
relocaliser le point de vente, mais au prix d'une charge
financière importante361. De plus, l'échec
d'une implantation peut avoir des conséquences sur l'image
de l'entreprise auprès de la clientèle362.
Au contraire, une localisation optimisée offrant un accès
aisé aux produits ou aux services proposés drainera en
effet un grand nombre de clients et induira une
rentabilité élevée. La localisation d'un unique magasin
se fondera beaucoup sur la sélection et sur la comparaison de
plusieurs sites potentiels. Les chaînes de magasins devront prendre en
considération de nombreux facteurs comme les objectifs de l'entreprise,
ses ressources (financières, managériales et autres), ses
capacités commerciales et logistiques, la concurrence, le marché
potentiel, la démographie, le comportement des consommateurs, les
facteurs environnementaux influençant la tendance économique,
les transports, les lois gouvernementales (impôts et taxes) sans compter
un adroit
timing363. Le niveau à long terme de
l'activité et de la rentabilité d'un tel réseau de
magasins
dépendra alors beaucoup des interactions et des
relations entretenues entre ses différentes localisations et forces
de vente.
Il n'y a pas à proprement parler de recette-miracle ou une
science bien ordonnée pour choisir
au mieux sa ou ses localisations commerciales.
Alors que les décisions de choix d'implantation se fondaient
dans les siècles précédents essentiellement sur un
jugement
360 KIMES S.E. et FITZSIMMONS (1990) Selecting
Profitable Hotel Sites at La Quinta Motors Inn, Interfaces
20, Mars-Avril 12-20.
361 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc : A Multiple Store Location Decision
Model, Journal of Retailing, 58, 5-24.
362 GHOSH A. et McLAFFERTY S. (1987) Location
Strategies for Retail and Service Firms, Lexington Books, p.10.
363 APPLEBAUM W. (1952) Store Location Strategy
Classes, Preface, Addison-Wesley Publishing Co.
subjectif fondé le plus souvent sur des
check-lists de critères à respecter364, les
années d'après-guerre marquées par la croissance des
pôles urbains et l'augmentation des revenus ont conduit à la
nécessité de mieux formaliser le processus de choix à
travers le développement de techniques nouvelles. Cette
évolution s'est faite parallèlement à la
démocratisation de l'automobile et au déploiement de grands
centres commerciaux de périphérie urbaine tout d'abord aux
Etats-Unis puis en Europe. On attendait de ces nouvelles techniques
non seulement la possibilité de pouvoir orienter au mieux le
décideur vers un emplacement sinon optimal du moins optimisé,
mais aussi de prédire avec une certaine exactitude le niveau
d'activité du futur point de vente. Ainsi, les ventes du futur magasin
étant évaluées, on aurait
moins de mal à convaincre et à rassurer les
organismes prêteurs ou les investisseurs potentiels
à participer financièrement au projet d'ouverture.
D'un autre côté, ces chiffres fournissaient la possibilité
de fixer des objectifs réalistes à atteindre dans le centre de
profit géré par tel ou tel manager. En comparant le niveau
prévu avec le niveau effectif des ventes, il devient alors
possible de cerner quels facteurs jouent sur l'activité et sur
la rentabilité en se posant par exemple les questions de base :
« quels facteurs affectent les ventes de différents points
de vente ? » ; « pourquoi les ventes de deux points de vente
sont-elles différentes ? ». L'analyse des différences de
potentiel entre deux magasins met en évidence les facteurs
externes sur lesquels la politique marketing n'a pas de prise et ceux relatifs
à un marketing inefficace365.
Un exemple de facteur externe sur lequel il n'est pas possible
d'agir et mis en évidence dans
un modèle de localisation est l'augmentation du
prix du carburant automobile ou d'une manière
générale l'augmentation du prix des transports qui érodent
le chiffre d'affaires des grands centres commerciaux366. Le manager
peut alors en prenant conscience des paramètres modulant
l'activité de son point de vente, réorienter sa politique
marketing si nécessaire et
364 JALLAIS J., ORSONY J. et FADY A. (1994)
Marketing du Commerce de Détail, Vuibert, Paris.
365 GHOSH A. et McLAFFERTY S. (1987) Location
Strategies for Retail and Service Firms, Lexington Books, p.11.
366 GAUTSCHI D.A. (1981) Specification of Patronage
Models for Retail Center Choice, Journal of Marketing
Research, Vol. XVIII, 162-174.
même connaître l'impact de futures
réorientations stratégiques ou celui de modifications dans
la structure concurrentielle ou économique avoisinante.
Avant de procéder à toute étude de
localisation, il est cependant utile de bien déterminer quelle
va être la clientèle future du point de vente et de la
repérer dans l'espace. La connaissance précise des
caractères des zones concentrant la clientèle
baptisée zones de chalandise s'avère également
nécessaire, si l'on veut prévoir la performance du futur
magasin
en établissant par exemple des prévisions de vente
au niveau du commerce de détail.
1.1 Enjeux d'une bonne connaissance de la zone de
chalandise
Même si cela constitue un défi, définir
et surveiller attentivement les frontières et les
caractéristiques des zones de chalandise est stratégique pour la
survie de magasins existants
ou pour projeter la création de nouveaux points de vente
de détail ou de service. Dans le cas des magasins existants,
l'analyse des caractéristiques de la zone de chalandise est
utile principalement pour adapter continuellement la politique marketing
afin d'attirer autant de clients que possible tout en contrebalançant
l'effort commercial des concurrents s'exerçant en sens opposé.
Dans le cas des nouveaux points de vente, l'évaluation des zones de
chalandise donne l'occasion de juger l'intérêt d'un investissement
à un endroit géographique spécifique aussi bien que
d'établir des prévisions de ventes et de déterminer une
future stratégie de vente.
La délimitation précise des zones denses
de clients potentiels s'insère également dans la
perspective de recherche d'une localisation optimale par une
modélisation de type p-médian (voir plus
particulièrement le paragraphe 1.3, le chapitre III et la
deuxième partie).
On parle assez souvent de la zone de chalandise primaire367
pour désigner la partie de la zone
de chalandise qui contribue le plus fortement au chiffre
d'affaires du magasin, c'est-à-dire à hauteur d'au moins 75 % du
chiffre d'affaires mais sur une période entière et
suffisamment
367 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass.
longue. Il arrive en effet que même des professionnels du
marketing fassent des erreurs sur la période de référence
à prendre en compte pour évaluer la zone de chalandise. Pour
exemple,
ce magasin qui fut surpris de n'assister à aucune
retombée positive de ses mailings et pour cause: il n'avait retenu
comme base de son chiffre d'affaires que les mois de vacances et
n'avait alors considéré pour ses relances postales
que des clients de passage, des consommateurs vraiment très
occasionnels368.
Lorsque la zone de chalandise ou au moins la zone de chalandise
primaire a été définie avec
précision pour un point de vente existant, il est
alors possible de procéder à différentes analyses
fondamentales destinées à évaluer et à
améliorer la performance du point de vente:
A- l'analyse du taux de pénétration du
marché
B- l'analyse démographique
C- l'analyse de performance statistique
D- la recherche de consommateurs cibles
E- les promotions ciblées
A- l'analyse du taux de pénétration du
marché
Il est intéressant suite à la délimitation
de la zone de chalandise et en se procurant les données
de consommation et les données démographiques de
déterminer soit le taux de pénétration ou d'emprise, soit
la part de marché du point de vente. Cette analyse peut être
conduite pour le point de vente dans son ensemble, pour chaque
département ou encore par catégorie de produits ou pour
chaque produit. Dans le cas d'un réseau de points de vente, on comparera
ensuite ces taux avec ceux des autres magasins de manière
à les classer par niveaux de performance.
368
http://visionarymarketing.com/articles/
B- l'analyse démographique
On peut, avant de sélectionner les catégories de
produits à inclure dans l'offre ou même plus
en amont lors du choix de l'implantation d'un
commerce, comparer les caractéristiques démographiques de la
zone de chalandise du point de vente avec celles d'autres zones de
chalandise aux performances connues. L'hypothèse que des
performances identiques s'observeront dans des régions sert de
base à la méthode analogique369 de
délimitation des zones de chalandise, méthode exposée
plus loin au paragraphe 1.3. Par exemple, dans les zones de
chalandise où le niveau d'éducation est plus élevé,
il sera plus facile de vendre des livres mais moins évident de
commercialiser des cigarettes. Une segmentation de la clientèle pourra
aussi être élaborée en comparant ses
spécificités aux caractéristiques générales
de la population résidant au sein de la zone de chalandise
préalablement identifiée.
C- l'analyse de performance statistique
Comme on le verra un peu loin au travers du modèle de
régression, il est possible grâce à une base de
données incluant, par exemple, la part de marché du magasin, les
spécificités de la concurrence et les caractéristiques
socio-économiques, d'identifier les paramètres ayant un lien
positif ou négatif de cause à effets sur la performance du point
de vente370. Néanmoins,
ce type de modèle doit être utilisé avec
prudence car une faible performance peut être due à
des raisons complémentaires à celles
invoquées dans l'analyse.
D- l'identification de consommateurs cibles
Une bonne délimitation de la zone de chalandise permet
aussi d'enquêter dans la zone à l'aide d'entretiens
téléphoniques ou d'interviews, cela afin de spécifier avec
précision le profil des
369 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass.
370 LORD J.D. et OLSEN L.M. (1979) Market Area
Characteristics and Branch Bank Performance, Journal of
Bank Research 10, p. 102-110.
consommateurs. Des informations complémentaires
peuvent être obtenues par des enquêtes répondant
à des interrogations comme371 :
· quels autres concurrents les consommateurs
fréquentent-ils et pourquoi ?
· pour quelles raisons les consommateurs ne
fréquentent-ils pas le point de vente ?
· quelles perceptions les consommateurs ont-ils du magasin
et des magasins concurrents sur
les points stratégiques du type prix, offre et service
?
E- les promotions ciblées
Enfin, une bonne délimitation de la zone de
chalandise permet de cibler efficacement le consommateur par des
courriers personnalisés, des mailings, des contacts
téléphoniques ou
des tracts publicitaires au sein de l'aire
spécifiée372. C'est donc en premier lieu les
clients
potentiels qui seront contactés ce qui aura aussi pour
effet de réduire sensiblement les coûts
de promotion en ayant un meilleur rendement
(meilleur succès de la campagne de communication) et moins de
déchets (contacts sans objet et ratés).
1.2 Définir précisément la zone de
chalandise
De multiples définitions de la zone de chalandise ont
été introduites depuis une cinquantaine d'années prenant
pour fondement des approches variées. Mais que cette aire
géographique s'apprécie par une approche comportementale,
managériale, sociale, financière, commerciale
ou géographique, la zone de chalandise est une
zone de peuplement qui se différencie des aires
géographiques voisines par l'importance de son potentiel de
consommation.
Ainsi, si l'on se réfère à toutes les
définitions avancées, la zone de chalandise est en termes de
pouvoir attractif:
371 DRUMMEY G.L. (1984) Traditional Methods of Sales
Forecasting, in Store Location and Store Assessment
Research, R.L. Davies and D.S. Rogers eds., Wicley,
279-299.
372 DESMET P. (2001) Marketing Direct,
2ème éd., Dunod, Paris.
Î "l'aire géographique locale d'où
proviennent 90 % de la clientèle total du
commerce."373
ou:
Î "l'aire d'influence à partir de laquelle
un centre commercial peut espérer attirer au
moins 85 % de son volume total des ventes " 374.
en termes de chiffre d'affaires:
Î "toute aire susceptible de fournir à un magasin
un chiffre d'affaires minimum annuel
de un dollar" 375 ou au minimum 0,5 % de la part de
marché 376,
en termes d'éloignement:
Î "d'une manière générale... une
grande majorité des clients qui sont prêts à se
déplacer
de 12 à 15 minutes jusqu'à un maximum de
25 minutes pour atteindre un centre commercial régional"
377.
en termes de concurrence:
Î "la véritable zone de chalandise est
entièrement déterminée par les opérations
d'attraction et de résistance des zones de chalandise en
compétition... La zone de
373 ISADORE V.F. (1954) Retail Trade
Analysis, University of Wisconsin, Bureau of Business Research
and
Service, Madison.
374 GRUEN V. et SMITH L. (1960) Shopping
Town USA: The Planning of Shopping Centers, Reinhold
Publishing Co., New York.
375 GREEN H.L. (Avril 1959) Correspondence with
Applebaum W. & Cohen S.B.
376 APPLEBAUM W. et COHEN S.B. (1961) The Dynamics of
Store Trading Areas and Market Equilibrium,
Annals of the Association of American Geographers
n°51/1, reprinted with permission of the original publishers by
Kraus Reprint Ltd Nendeln Lichtenstein in 1967.
377 GRUEN V. et SMITH L. (1960) Shopping
Town USA: The Planning of Shopping Centers, Reinhold
Publishing Co., New York., p.33.
chalandise n'est pas un fait géographique mais est
créée entièrement par la réponse et
le comportement des individus" 378.
Huff 379 a une approche plus statistique en
définissant la zone de chalandise comme "une région
délimitée géographiquement, contenant des clients
potentiels pour lesquels il existe une probabilité plus grande
que zéro qu'ils achètent une classe donnée de
produits ou de services offerts à la vente par une firme
particulière ou par un groupe particulier de firmes".
Selon Ghosh et McLafferty 380 qui ont tenté
d'unifier ces définitions, la zone de chalandise est
tout simplement:
Î "le secteur géographique à partir duquel
le magasin tire la plupart de ses clients et dans lequel son taux de
pénétration du marché est le plus fort".
On remarque aussi que la zone de chalandise soit considère
la clientèle effective d'un magasin
ou d'un service existant (définitions d'Isadore,
de Ghosh et McLafferty), soit s'attache à mesurer une
clientèle potentielle dans l'optique de création d'un nouveau
point de vente ou avec l'objectif de conquérir des parts de
marché en empiétant sur la zone de chalandise effective
d'un concurrent (définitions de Gruen et Smith, d'Applebaum et Cohen, de
Green, de Huff).
1.2.1 Variables façonnant l'étendue et la forme
des zones de chalandise
Un grand nombre de paramètres façonnent la
zone de chalandise d'un magasin ou d'une société de
services. Ces paramètres sont aussi bien des facteurs
intrinsèques marketing liés au magasin comme les prix, la
taille du magasin, le choix des marchandises, que des facteurs
378 NELSON R.L. (1958) The Selection of Retail
Locations, F.W. Dodge Corp, p.153, New York.
379 HUFF D. L. (1964) Defining and Estimating a
Trading Area, Journal of Marketing, Vol 28, p. 38.
380 GHOSH A. et McLAFFERTY S. L. (1987)
Location Strategies for Retail and Service Firms, Lexington
Books, Reading, Mass.
environnementaux tels l'existence de concurrents dans le
voisinage ou l'environnement sociologique et économique.
1.2.1.1 Variables intrinsèques au point de
vente
Une multiplicité de facteurs influence la forme,
l'étendue spatiale et la nature intrinsèque de la zone de
chalandise d'un point de vente parmi lesquels on recense:
· les caractéristiques propres au point de
vente rigidifiées lors de la création du point de
vente:
- la taille,
- les voies d'accès et les facilités de parking.
· des paramètres liés à la politique
marketing:
- la promotion des ventes,
- les prix,
- l'assortiment des marchandises,
- la décoration,
- les services complémentaires offerts.
1.2.1.2 Variables environnementales
Comme on l'a mentionné, des check-lists de
critères ont été établis pour choisir au
mieux l'emplacement de son futur point de vente en examinant les
infrastructures existantes 381 382 383
384 385 386. L'effet recherché est de
réussir à centrer son point de vente dans un bassin
géographique riche en consommateurs potentiels
compte-tenu bien évidemment de la
381 DELOZIER M.W. et LEWISON D.M. (1986)
Retailing, 2nd ed., Merill.
382 CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, p.187-191, Ed. Sirey.
383 NELSON R.L. (1958) The Selection of Retail
Locations, F.W. Dodge Corp, p.153, New York.
384 KANE B.J. (1966) A Systematic Guide to
Supermarket Location Analysis, Fairchild, New York.
385 APPLEBAUM W. (1966) Method for determining Store
Trade Areas, Market Penetration and Potential Sales,
Journal of Marketing Research, 3, 127-141.
386 GRUEN V. et SMITH L. (1960) Shopping
Town USA: The Planning of Shopping Centers, Reinhold
Publishing Co., New York.
concurrence. En se référant à ces
études, on peut s'apercevoir que la forme des zones de
chalandise est en général conditionnée par:
· des paramètres environnementaux
variés387 dont :
- l'accessibilité mesurée par la
qualité et le nombre de voies de circulation automobile et
piétonnière, le niveau et la fluidité du trafic,
ainsi que par les dessertes de transports en commun, l'existence de stations
de taxi,...,
- la qualité et le débit de la circulation
piétonnière et automobile,
- la concurrence et particulièrement son importance
et sa nature, la politique marketing, son éloignement au point de
vente considéré,
- la complémentarité avec d'autres
activités,
- les barrières physiques et psychologiques,
- l'utilisation du foncier
Plus précisément, les facteurs liés
à l'infrastructure jouant sur l'accessibilité et
donc influençant les caractéristiques des zones de chalandise
sont:
- la structure du réseau routier ou
piétonnier (sinuosité et configuration des voies),
- la qualité des infrastructures,
appréhendée par leurs caractéristiques techniques (nombre
et largeur des voies, aménagement des côtés, existence
d'un séparateur central de chaussées, etc...),
- les contraintes topographiques (pente),
- les réglementations en vigueur (code de la route et
particularités locales),
- la congestion qui perturbe le fonctionnement du système
et fait ainsi varier la qualité du service selon les jours de
l'année et les heures de la journée.
387 JALLAIS J., ORSONY J. et FADY A. (1994)
Marketing du Commerce de Détail, Vuibert, Paris.
Egalement, la qualité des transports collectifs
dégrade ou améliore sensiblement l'accessibilité
à un site en particulier concernant:
- le schéma de services en vigueur tenant compte des
règles de sécurité (noeuds desservis, fréquence de
la desserte et horaires de circulation),
- le taux de remplissage du véhicule qui peut en interdire
l'utilisation lorsque la capacité maximale est atteinte.
Selon la clientèle ciblée, d'autres critères
peuvent être examinés : économiques, esthétiques,
paysagers, environnementaux, touristiques,...
Même s'il est bien évident que chaque
activité recherchera plutôt une clientèle-cible
particulière, d'autres études ont dégagé les
paramètres environnementaux cette fois liés à la
population résidente, ayant une influence sur les
caractéristiques de la zone de chalandise parmi lesquels:
· des variables démographiques et
socio-économiques recensées par Ingene 388 et
parfois plus particulièrement étudiées par d'autres
chercheurs:
- le revenu 389 390,
- l'âge de la population 391,
- l'âge du chef de famille,
- le pourcentage d'hommes dans la population,
- l'âge médian des femmes et des hommes,
388 INGENE C.A. (1984) Structural Determinants of
Market Potential, Journal of Retailing, Vol.60 N°I, p.37-64.
389 FERBER R. (1958) Variations in Retail Sales
Between Cities, Journal of Marketing, 22, p.295-303.
390 INGENE C. et LUSCH R. (1980) Market Selection
Decisions for Department Stores, Journal of Retailing,
56, p.21-40.
391 WELLS W. et GUBAR G. (1966) The Life
Cycle Concept in Marketing Research, Journal of Marketing
Research, 3, p.355-363.
- la taille des ménages 392,
- la population ou la densité de population
393,
- la mobilité394 395.
1.2.1.3 La variable temporelle
Les frontières et les caractéristiques
internes des zones de chalandise ne sont pas statiques mais
évoluent dans le temps396, influencées par des
facteurs d'espace-temps comme la concurrence locale, la stratégie
marketing, la saisonnalité ou même la mode.
Une réduction de prix (ou des soldes) réussira par
l'augmentation de son attractivité à attirer
les consommateurs sur une plus grande distance,
hypothèse vérifiée dans la pratique en particulier
sur le marché du meuble397. De même, la taille
de la zone de chalandise peut croître en fonction de la
publicité et des efforts de promotion du point de vente.
1.3 Méthodes traditionnelles de délimitation
des zones de chalandise
Deux classes de méthodes de
délimitation, l'une subjective et l'autre normative, sont
employées pour déterminer les frontières de zones
de chalandise. Alors que la première catégorie de
méthodes reste théorique, les méthodes normatives au
contraire sont caractérisées
par leurs observations du monde réel. Elles sont donc plus
précises et plus commodes à mettre
en oeuvre et peuvent même aller jusqu'à
décrire les variations dynamiques des frontières des
392 INGENE C. et YU (1981) Determinants of
Retail Location in SMSAs, Regional Science and Urban
Economics 11, p.529-547.
393 HALL M. et KNAPP J. et WINSTEN C. (1961)
Distribution in Great Britain and North America, Oxford
University Press, London.
394 INGENE C. et LUSCH R. (1980) Market Selection
Decisions for Department Stores, Journal of Retailing, 56, p.21-40.
395 INGENE C. et YU (1981) Determinants of
Retail Location in SMSAs, Regional Science and Urban
Economics 11, p.529-547.
396 APPLEBAUM W. et COHEN S.B. (mars 1961)
The Dynamics of Store Trading Areas and Market
Equilibrium, Annals of the Association of American
Geographers, N°51/1.
397 CLIQUET G. (1995) Implementing a Subjective
MCI Model: An Application to the Furniture Market,
European Journal of Operational Research 84, pp
279-291.
zones de chalandise. Nous allons d'abord passer en
revue les principales méthodes subjectives.
1.3.1 Approches subjectives : la méthode du temps de
conduite
Cette méthode employée par beaucoup de
professionnels suppose que les clients sont disposés
à fréquenter un magasin seulement selon
des critères de proximité mesurés en termes de
distance ou de temps de conduite. En pratique, on trace des courbes
isochrones autour du point de vente ou de son implantation envisagée.
Les courbes indiquent les temps de trajet en général automobile
qui les séparent du point de vente en tenant compte des voies
de circulation et des obstacles (feux tricolores, croisements et
inter-parties, limitations de vitesse,...). La zone de chalandise
équivaut à la surface géographique intérieure
à l'une de ces courbes en se fixant un temps de conduite limite
au-delà duquel on pense qu'une faible
proportion de consommateurs potentiels sera prête à
se déplacer jusqu'au point de vente 398.
Parmi différents paramètres déterminant les
habitudes des consommateurs comme la densité
de population, le pouvoir d'achat, l'importance des
réseaux de communication, on a montré en effet
numériquement que les temps de conduite requis pour atteindre
un ensemble de magasins a une influence forte sur le choix d'un
centre commercial 399. Certaines études comportementales
avaient montré en leur temps qu'à partir d'un temps de conduite
supérieur à
20 minutes, les consommateurs hésitaient à se
rendre dans un centre commercial 400.
Actuellement, certains clients, particulièrement dans
les zones rurales, n'hésitent pas à parcourir 50
kilomètres pour faire leurs courses dans les hypermarchés qui
remplacent de plus
en plus les petits commerces traditionnels de plus en plus
rares401. Mais, dans les zones de
398 BRUNNER J. A. et MASON J. L. (1968) The Influence
of Driving Time Upon Shopping Center Preference,
Journal of Marketing Vol. 32, p.57.
399 BRUNNER J. A. et MASON J. L. (1968) The Influence
of Driving Time Upon Shopping Center Preference,
Journal of Marketing Vol. 32, p.57.
400 NELSON R.L. (1958) The Selection of Retail
Locations, F.W. Dodge Corp, p.153, New York.
401 BOVET P. (2001) L'hypermarché, le Caddie
et le congélateur, Le Monde Diplomatique, Mars 2001, p.32.
périphérie urbaine où les
services commerciaux sont plus denses, les consommateurs deviennent
plus exigeants quant à la proximité des centres commerciaux. Aux
Etats-Unis, au début des années 90, on était
prêt, selon Madame Yecko, une spécialiste renommée
de la distribution et la présidente du groupe d'immobilier
commercial Capital Realty Group, à parcourir 50 miles pour se
rendre dans un hypermarché Wal-Mart402. De nos jours,
une distance de 20 à 30 miles (30 à 50 kilomètres
environ) semble être la limite que les gens peuvent supporter
pour accéder à un tel centre commercial.
Brunner et Mason ont avancé, quant à eux,
que les limites de zone de chalandise se ramenaient à un temps
de conduite de 15 minutes autour du centre commercial et que ce sont
l'importance de la population, le nombre de ménages et les revenus au
sein de cette zone qui conditionnent les performances du centre. D'autres
auteurs ont énoncé que les consommateurs sont prêts
à parcourir en moyenne une distance correspondant à un temps
moyen de conduite
de 10 minutes403. Même si la méthode ne
prétend pas être parfaite puisqu'elle ne prend pas en
considération la puissance d'attractivité du
magasin, on constate donc qu'il n'y a pas dans la littérature un temps
de conduite bien défini pour mesurer les limites de la zone de
chalandise. Sans doute, l'effort que les consommateurs sont prêts
à fournir pour atteindre un centre commercial dépend-il
d'autres facteurs que le simple temps de conduite ou que des facteurs
d'attractivité. Les conditions météorologiques,
l'âge, le sexe, les quartiers traversés, les
facilités de parking, le pouvoir d'achat plus généralement
peuvent conduire à ce que l'effort fourni ou évalué soit
ressenti comme étant plus ou moins élevé par
l'individu.
402 SCHOOLEY T. (2001) For some retailers,
drive-time is more important than location, Pittsburgh Business
Times, American City Business Journals, march 9, 2001, p.10.
403 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
1.3.2 Approches normatives
L'approche subjective de la méthode du temps de
conduite décrite précédemment est facile à mettre
en application et fournit des données assez fiables mais avec
un degré de précision inconnue. Elle est
préconisée dans le cas où les données marketing sur
la clientèle ne sont pas accessibles ou lorsque cette méthode est
trop longue ou trop coûteuse à mettre en oeuvre. En revanche, les
méthodes normatives prennent en considération l'information
sur la clientèle et/ou les performances passées du point
de vente. Ces données d'observation obtenues par enquêtes
s'avèrent indispensables pour évaluer une zone de
chalandise existante avec une précision accrue par rapport aux
méthodes subjectives qui n'utilisaient que des données
environnementales.
Les méthodes normatives les plus populaires fondées
sur l'expérience passée pour déterminer
les frontières de zone de chalandise sont:
- la méthode analogique
- la méthode par le modèle de régression
- la méthode par les surfaces enveloppantes
- la méthode des nuées dynamiques
Détaillons ces différentes approches dans leurs
principes et leurs inconvénients.
1.3.2.1 La méthode analogique
La méthode analogique sous-tend que la géographie
se répète: si un point de vente est placé à
un emplacement similaire à un autre, ou alors on
s'attend à ce que la performance des deux points de vente soit
identique. Supposons qu'un magasin connaisse les adresses de ses clients.
Celles-ci peuvent alors être représentées sur une carte par
des points dont la densité indique
grâce à un examen visuel, la taille, la
forme et les caractéristiques générales de la zone
de chalandise de ce magasin 404.
La délimitation des zones de chalandise s'apprécie
traditionnellement en prenant des paliers
en matière de niveau de clientèle en progression
linéaire 405. En première approximation, la zone de
chalandise est supposée à frontière circulaire irradiant
à partir du point de vente sur
un rayon r. Ainsi, on considère en
général la zone de chalandise comme le disque dont le
rayon a une dimension telle qu'il concentre au minimum X % de la
clientèle (X=80 % par exemple). Le problème est que la zone de
chalandise est loin d'avoir la géométrie parfaite d'un disque. En
outre, ce mode de procédure s'avère peu précis, car il
présuppose une diminution régulière du taux de
pénétration selon l'éloignement au point de vente ou bien
une certaine homogénéité et une bonne
répartition de la clientèle sur la surface
géographique compacte déterminée par cette
méthode.
Fig 1.1 - Exemple de détermination d'une zone de
chalandise par un logiciel commercial utilisant la méthode analogique
Or, les irrégularités
socio-économiques de la population dans l'espace, les
frontières géographiques, les caractéristiques de la
concurrence et la politique commerciale du magasin
404 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
405 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass.
font que très souvent les zones de chalandise ne sont pas
totalement compactes. Les "trous"
ou discontinuités de la clientèle au sein de
cette surface sont donc négligés dans la méthode
précédente. On ne pense pas également à
considérer la rupture pouvant être assez brusque qui
s'opère entre une zone à forte densité de clients et une
zone à faible densité.
1.3.2.2 La méthode par les modèles de
régression
La méthode par le modèle régression
cherche à mesurer un paramètre de performance en le
corrélant avec diverses variables socio-économiques,
environnementales et marketing. Il suppose ainsi d'avoir pour base un
certain nombre de magasins ou des études commerciales antérieures
à partir desquelles, on mesurera les coefficients d'une droite de
régression du type:
Y = b0 + b1X1 + b2X2 + ... + bnXn
où Y est le paramètre de performance ; X1, X2, ...
, Xn les variables explicatives et b0, b1, b2,
..., bn les coefficients de la droite de régression.
Les modèles de régression sont fondés sur
deux hypothèses: premièrement, la performance du point de vente
est fonction des caractéristiques de localisation de son
emplacement, de l'environnement socio-économique, du niveau de la
concurrence et des caractéristiques du magasin. Deuxièmement,
les facteurs fondamentaux de performance peuvent être isolés
grâce
à une analyse statistique des données.
La méthode est en particulier employée pour
prévoir la performance globale projetée Y d'un magasin qui est
évaluée par cette formule et l'emploi de données locales
406. Mais elle peut également être utilisée pour
estimer la part du marché des zones entourant un nouveau point
de vente et délimiter alors la zone de chalandise.
Il suffit pour cela de parcourir l'espace
entourant le point de vente à la recherche des populations
tendant à accroître le paramètre de
406 LORD J.D. et OLSEN L.M. (1979) Market Area
Characteristics and Branch Bank Performance, Journal of
Bank Research 10, p. 102-110.
performance Y du fait de leurs caractéristiques
démographiques et socio-économiques entrant
en tant que variables dans le modèle de
régression. On pourra considérer qu'au-dessus ou qu'en
dessous d'un certain niveau de contribution à la
performance, les populations considérées appartiendront ou
n'appartiendront pas à la zone de chalandise.
Des difficultés peuvent cependant
apparaître dans l'utilisation de la méthode lorsque
apparaissent des corrélations entre des variables supposées
indépendantes dans le modèle de régression. Un test
simple préalable consiste à mesurer le taux de
corrélation entre les données. Un taux supérieur
à 0,5 ou plus est significatif d'une certaine
multicolinéarité entre des variables redondantes 407
408.
On peut également utiliser le test de Fisher (ou test
d'égalité des variances) qui a pour but de
comparer deux distributions de valeurs X et Y supposées
suivre chacune une loi normale. Si
n1 et (S1)² respectivement la taille et la variance non
biaisée du premier échantillon et n2 et (S2)² sont la
taille et la variance non biaisée du second échantillon (S1 et
S2 sont les écarts- types), alors le calcul de la quantité F
définie par :
F = [ n1 * (S1)² / (n1 - 1) ] / [ n2 * (S2)² / (n2 -
1) ]
(dans le cas où F<1, on inverse le numérateur et
le dénominateur)
permettra de savoir si les distributions sont de
même nature en se fondant sur la règle de décision
suivante : si F est supérieure au quantile d'une loi de Fisher de
paramètres n1 et n2 au risque 0,05, les variances ne sont pas
homogènes et les distributions sont de natures différentes.
Dans le cas contraire, les variances sont
considérées équivalentes et les distributions de
même nature.
Un autre moyen pour détecter la
multicolinéarité est de séparer les données en deux
groupes
et de calculer pour chaque groupe un modèle de
régression. L'absence de multicolinéarité se
révèlera par une certaine similitude des résultats
en ce qui concerne les coefficients de
407 JOHNSTON J. (1972) Econometric Methods,
McGraw-Hill, New York.
408 MALINVAUD E. (1980) Statistical Methods of
Econometrics, North Holland, New York.
régression et la qualité d'ajustement. Dans
le cas contraire, il est souhaitable d'éliminer certaines
variables parmi celles corrélées entre elles soit en examinant
les variables prises 2
par 2, en pratiquant une analyse factorielle, ou
mieux une régression ridge qui considère un estimateur
légèrement biaisé des paramètres pour
améliorer la variance des estimations (coûteux en temps de
calcul) ou une régression pas à pas (stepwise) qui
consiste à introduire
les variables l'une après l'autre dans le modèle
(selon leur contribution partielle) et, à chaque étape, à
vérifier si l'ensemble des variables déjà
introduites sont encore significatives (une variable qui ne le serait plus
serait rejetée).
Un autre problème pouvant surgir dans
l'élaboration d'un modèle de régression est
l'intégration de données difficilement quantifiables comme celles
relatives à la perception du consommateur ou bien concernant
l'évaluation de la concurrence ou bien l'image de marque malgré
que cette difficulté ait été surmontée dans
certains modèles comme le MIC subjectif409
que nous verrons plus tard (§ 2.1.5). L'objectif de
ce modèle est en effet avant tout de se
fonder sur l'expérience d'un site commercial pour
approcher par calcul la performance future d'un nouvel emplacement et
accessoirement d'identifier ce que pourra être sa zone de
chalandise.
1.3.2.3 La méthode par les surfaces
enveloppantes
Les surfaces enveloppantes ont été mises en
application par Peterson 410 dans la continuation
des travaux de Bucklin 411 et de McKay
412. Cette méthode consiste à représenter les
taux de pénétration sur une carte quadrillée en zones de
manière à obtenir un relief. La surface de ce relief
épousant les variations spatiales du taux de pénétration
est approximée par des courbes
409 CLIQUET G. (1995) Implementing a Subjective
MCI Model: An Application to the Furniture Market,
European Journal of Operational Research 84, 279-291.
410 PETERSON R.A. (1974) Trade Area Analysis
Using Trend Surface Mapping, Journal of Marketing
Research, Vol. XI, 338-42.
411 BUCKLIN L.P. (1971) Trade Areas Boundaries:
Some Issues in Theory and Methodology, Journal of
Marketing Research, 30-7.
412 MCKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
ou des plans et en particulier par des équations dont les
coefficients sont déterminés grâce à
un modèle de régression. Ces surfaces peuvent
être modélisées par des séries de Fourier
surtout si elles présentent une certaine périodicité.
Mais, comme cette régularité de l'espace
est plutôt rare dans le monde réel, on
préfère décrire le taux de pénétration
spatiale par des polynômes orthogonaux qui sont plus aptes à
rendre compte de la concurrence et des irrégularités
spatiales telles que les barrières naturelles (rivières,
espaces verts protégés, autoroutes,...).
Il serait théoriquement possible, même si
les auteurs n'effectuent pas la démonstration, de délimiter
la zone de chalandise en déterminant les minima de cette courbe
polynomiale par l'annulation de sa dérivée seconde.
Cependant, la méthode des surfaces enveloppantes comporte des
limitations notamment l'impossibilité de trouver des polynômes
orthogonaux ou d'autres fonctions pas trop élaborées qui puissent
suffisamment bien modéliser le relief des taux de
pénétration. Peterson l'a bien compris dans son étude en
faisant remarquer qu'il y avait une faible corrélation entre
certains paramètres spatiaux du type socio-économique et
les variations de taux de pénétration
modélisé: la raison en était sans doute en
particulier la présence de termes résiduels,
différences entre les courbes du modèle et les taux de
pénétration constatés.
1.3.2.4 La méthode des nuées dynamiques
La méthode de délimitation par les nuées
dynamiques repose sur une famille d'algorithmes
dus à Diday 413. Son principe est de construire
itérativement une classification d'un nuage de points.
- chaque classe étiquetée i est
représentée par son noyau Ni (souvent le barycentre de
la
classe, mais pas nécessairement), calculable en
utilisant une fonction à partir des
413 CELLEUX G. et DIDAY E. (1980) L'analyse
des Données, Bulletin de liaison de la recherche en
informatique et automatique, INRIA.
représentants de la classe.
- on dispose d'une mesure de similarité d entre
un point et un noyau de classe. (d est par exemple la distance
euclidienne au noyau lorsque ce dernier est un point).
L'algorithme est alors le suivant:
i,
· On initialise les noyaux Ni, 1 i k à leur valeur
de départ N
1 i k, la variable
booléenne STABLE à FAUX et le compteur
d'itérations t à 1.
· Tant que (STABLE - FAUX) et
(t < tmax), on effectue :
Î Début
i
· On affecte chacun des points à la classe dont le
noyau N(t) est le plus proche au
sens de la mesure de similarité d.
i
· Pour chacune des classes, on calcule le nouveau noyau
N(t+1)
avec .
· Si l'un des noyaux a été modifié,
alors STABLE vaut FAUX sinon il vaut VRAI.
Î Fin
(les instructions principales de l'algorithme sont en
gras).
Cette méthode consiste donc à incorporer des
zones autour de centres mobiles ou centres de gravité: une
nécessité est de définir au préalable le
nombre k de zones. Puis, k centres de gravité supposés
sont alors tirés au hasard et chaque point géographique
appartenant à l'espace géographique est assigné au plus
proche des k centres de gravité engendrant ainsi k cellules
géographiques. Le vrai centre de gravité de chacune des
k zones est calculé et le processus qui consiste à assigner
chaque point géographique à l'un des nouveaux centres de
gravité recommence. Cet algorithme fonctionne en boucle jusqu'à
ce que les k zones et les k centres de gravité soient invariables. Un
calcul de la variance à l'intérieur de chaque zone peut
être effectué pour vérifier si les moyennes sont
sensiblement différentes d'une classe à une autre et si le
nombre de classes est exact.
La méthode a été employée pour
indiquer les limites de zones de chalandise de centres commerciaux
414 avec l'exécution de fonctions spline qui consiste
à réduire au minimum le
rayon de courbe de la fonction représentant les limites de
la zone de chalandise f(x) pour la
rendre plus régulière (
[f(x)' ' ]² dx
minimisé). Ainsi, lors de l'application de cette
méthode à
la délimitation des zones de chalandise, l'aire
géographique est initialement découpée en
secteurs caractérisés par une plus ou
moins forte fréquentation du point de vente considéré
(l'étude de Roger415 comporte par exemple 50 secteurs). Les
fréquentations obtenues auprès d'un échantillon de
clients sont chacune affectées au secteur géographique de
leur lieu de domicile, l'ensemble desdites fréquentations
étant ensuite moyenné. Ces secteurs sont alors
agglomérés en zones de fréquentation homogènes
(les classes mentionnées précédemment)
par l'algorithme des nuées dynamiques ce qui permettra
ultérieurement de tracer les lignes de niveau de fréquentation
entourant le point de vente considéré grâce en
particulier aux fonctions splines qui joignent harmonieusement les
centres de gravité des secteurs. On constate que la zone de
chalandise est finalement délimitée de façon assez
imprécise puisqu'en général le nombre de secteurs pour
définir sa frontière est faible. Ces secteurs ne correspondent
d'autre part qu'à un découpage artificiel pas forcément
logique le plus souvent
en quartiers ou en arrondissements dans les grandes
villes. De plus, les secteurs peuvent rassembler des populations et des
fréquentations inhomogènes ce qui risque de conduire à des
erreurs puisqu'en considérant une fréquentation moyenne au
sein de ces secteurs, on fait abstraction de cette
hétérogénéité de clientèle. D'autre
part, la transition de fréquentation de la clientèle entre les
secteurs voisins est supposée s'effectuer de manière progressive
ce qui n'est pas forcément le cas. La lourdeur de la méthode et
son manque de côté pratique la rendent très
difficilement accessibles aux professionnels.
414 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
415 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
La méthode des nuées dynamiques est
cependant susceptible en fait de résoudre la
problématique de l'analyse typologique qui vise à chercher les
principales représentants d'un nuage de points. Nous verrons au
paragraphe 2.2.3 que ce type de méthode peut simplifier la recherche de
localisations commerciales en particulier lors de l'utilisation du
modèle p- médian. En bref, le modèle p-médian
(voir § 2.2) pose le problème de positionner et d'allouer
p centres (p points de vente pour l'application
à la localisation commerciale) à chacun des points d'un
nuage de points (les clients) de telle manière que la somme des
distances de ces points au centre correspondant atteigne un minimum, ce
qui permet effectivement de rassembler les points en un certain
nombre de cellules (ou clusters en anglais) de
caractéristiques (souvent le niveau moyen de fréquentation)
homogènes.
1.4 Inconvénients et limitations des méthodes
traditionnelles de délimitation
Comme on l'a vu, les méthodes subjectives
ne prennent pas en considération les caractéristiques
propres du point de vente, ni celles de la clientèle pour
évaluer la zone de chalandise, et s'attachent uniquement
à déterminer les emplacements stratégiquement
intéressants en termes d'accessibilité pour la
majorité des clients potentiels. Ces méthodes rapides mais
sans grande précision s'avèrent utiles principalement dans une
première phase de prospection de la localisation d'un point de vente
à créer. Rien ne saurait en effet remplacer une bonne
connaissance des consommateurs.
Les méthodes de type normatif leur sont donc
préférables si l'on dispose d'informations sur les clients
existants ou potentiels d'un magasin. Il est cependant hasardeux de
réduire une zone de chalandise à un disque rassemblant un
pourcentage élevé de clients comme le fait la méthode
analogique. La réalité est souvent différente et on
peut constater l'existence d'une zone de
chalandise réduite en fragments au lieu d'une zone de
chalandise compacte entourant le point
de vente416. Les caractéristiques de la
population (densité, caractéristiques socio- économiques,
préoccupations), l'environnement (infrastructure des routes,
barrières naturelles), les facteurs commerciaux (concurrence,
stratégies d'entreprise et en particulier différenciation)
changent dans l'espace et, de ce fait, expliquent la répartition des
clients en plusieurs secteurs parfois sans relation. Les limites des
zones de chalandise sont devenues plus floues qu'autrefois également
du fait du comportement plus versatile et de la plus grande
mobilité417 du consommateur, et leur détermination
précise nécessite désormais des analyses plus
poussées : "l'approche d'une zone de chalandise est rendue plus
complexe aujourd'hui
par les nouveaux comportements des consommateurs, plus
mobiles et moins fidèles."418
Les surfaces enveloppantes constituent une approche
intéressante bien qu'à force de vouloir trop modéliser une
réalité fort complexe par des équations
paramétriques, on ne fait que s'en éloigner. Il est en effet
souvent indispensable d'approximer les données discrètes de
clientèle
par des équations suffisamment simples pour ne
pas voir les difficultés de résolutions augmenter de
manière exponentielle. D'où, là encore, la naissance
d'incertitudes dont il est impossible de mesurer l'importance et la
portée sur les résultats de la délimitation.
La méthode par les nuées dynamiques est certes
novatrice, mais aussi coûteuse en temps de calcul puisque chaque point
est examiné et lié à la classe la plus proche et que
l'algorithme tourne en boucle jusqu'à parvenir à une
stabilité des centres de gravité et des zones. Le
problème de ce processus est aussi qu'il faut au départ
pressentir et fixer un nombre de types
de zone pour pouvoir choisir aléatoirement les centres de
gravité puis assigner chaque point
au centre de gravité le plus proche. Un autre point est
que cette méthode n'a été expérimentée que
sur des zones géographiques massives bien qu'assimilées à
des points, en l'occurrence sur
416 CLIQUET G., FADY A., BASSET G. (2002)
Management de la Distribution, Dunod, Paris.
417 MOATI P. (2001) L'avenir de la Grande
Distribution, Ed. Odile Jacob.
418 DOUARD J.P. (2002) Géomarketing et
Localisation des Entreprises Commerciales, Stratégies de
localisation
des Entreprises Commerciales et Industrielles : De
Nouvelles Perspectives, Gérard Cliquet et Jean-Michel
Josselin éditeurs, De Boeck Université, à
paraître p.120
des communes de différentes tailles telles que celles
de la Communauté Urbaine de Lille419, et non sur des
secteurs équidistants, de tailles égales en terme de
superficie et suffisamment petits pour obtenir une précision de
délimitation intéressante.
La majorité de toutes les méthodes
évoquées, peu précises, font appel à un
découpage initial
de l'aire analysée en secteurs géographiques qui
ne peut en règle générale, on l'a dit, que se fonder que
sur l'intuition ou sur des limites administratives ce qui risque
fortement de compromettre la qualité de la délimitation de la
zone de chalandise.
Une bonne connaissance de la zone de chalandise et de
ses limites conditionne pourtant l'analyse et les résutats de
la recherche de localisations commerciales, d'autant que les
méthodes utilisées dans le monde professionnel font
souvent appel à des notions de statistiques prenant pour cible la
zone de chalandise elle-même.
1.5 Les méthodes de localisation actuellement
utilisées
Une étude récente auprès des
décideurs du commerce de détail a démontré que le
choix d'une localisation commerciale était plutôt fondée
sur l'approche intuitive et informelle autant que
sur les approches statistiques rigoureuses des analystes de la
localisation420 421. Les décideurs
rechignent à utiliser les méthodes trop lourdes
développées par les chercheurs, même si ces derniers sont
allés jusqu'à développer des systèmes intelligents
d'aide à la décision (SIAD) qui parviennent assez bien sinon
à déterminer un emplacement optimal, du moins à
prévoir le chiffre d'affaires du futur point de
vente422. Ces derniers décideurs préfèrent
souvent incorporer dans la décision leur propre vision,
intuition ou expérience, rassurante et
419 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
420 CLARKE I., HORITA M. et MACKANESS W.
(2002) Intuition et Evaluation des Sites Commerciaux :
Appréhender la Connaissance des Commerçants, ,
Stratégies de localisation des Entreprises Commerciales et
Industrielles : De Nouvelles Perspectives, p.107,
Gérard Cliquet et Jean-Michel Josselin éditeurs, De Boeck
Université, à paraître.
421 HERNANDEZ J.A. (1998) The Role of
Geographical Information Systems Within Retail Location Decision
Making, PhD Thesis, The Manchester Metropolitan
University Manchester.
422 LAPARRA L. (1995) L'implantation
d'hypermarché : comparaison de deux méthodes
d'évaluation du potentiel, Recherche et Applications en
Marketing, Vol. : 10, Numéro : 1, p. 69-79
explicative. D'un autre coté, ceux-ci rechignent
à utiliser des représentations spatiales alimentées en
d'immenses quantités d'impalpables données et se méfient
souvent des variables adoptées comme critères d'implantation trop
souvent laissées au libre arbitre de l'analyste.
Dans la pratique, les professionnels utilisent des
méthodes statistiques démonstratives en général
assez simples qui ont aussi le bénéfice de la
rapidité. Une autre étude auprès des décideurs
de 226 réseaux de distribution canadiens a montré que
87 % des décideurs utilisaient l'expérience pour orienter
leurs décisions de localisation, mais aussi d'autres
méthodes statistiques simples comme les checklists (46 %), la
méthode analogique (37 %), les méthodes statistiques du type
parts de marché ou marché potentiel (34 %), le
modèle de régression multiple (29 %), les modèles
d'interaction spatiale (13 %), les systèmes experts (8
%). La difficulté de mettre en pratique des
modèles vient souvent du fait de ne pouvoir accéder
à toutes les données dont on aurait besoin. Comment
connaître la performance des points de vente concurrents, mesurer la
valeur de leurs managers, évaluer le pouvoir d'achat
de consommateurs potentiels, déterminer avec exactitude
les limites d'une zone de chalandise
? Rogers423 de la société DSR
Marketing Systems Inc. recense cinq méthodes pratiques
inspirées de la recherche dans le domaine de la localisation et
cependant accessibles à tout manager désireux de créer une
nouvelle implantation commerciale ou d'étendre un réseau de
points de vente. Ces cinq méthodes sont :
- la méthode par les parts de marché et les
surfaces de vente,
- la méthode analogique,
- la méthode par le modèle de régression
multiple,
- l'analyse discriminante,
- la méthode du marché potentiel.
423 ROGERS D.S. (1980) 5 ways to Evaluate a Store
Location, Store Location, 42-48.
1.5.1 La méthode par les parts de marché et les
surfaces de vente
Elle consiste tout d'abord à déterminer
quelle peut être la zone de chalandise au sein de chacune des
aires qui représente une alternative d'implantation, en tenant
compte de la concurrence, de la population et de sa répartition
géographique, de l'infrastructure routière et
piétonnière et des barrières naturelles (ex. lacs,
rivières)424. Il s'agit ensuite, de calculer le nombre
de personnes habitant dans la zone de chalandise, à la fois à
l'instant présent et dans le futur, puis d'estimer le potentiel du
marché par individu pour le produit ou le service qui sera
proposé. La multiplication du potentiel de marché individuel par
le nombre d'habitants de la zone fournira le potentiel
général du marché pour l'activité
considérée. Une règle de trois indiquera alors la part
de ce potentiel que représentera le point de vente à créer
en fonction de
son importance au point de vue de sa surface de vente
prévue, par rapport à celle, globale, représentée
par les concurrents toujours au sein de la zone de chalandise. Il
convient de sélectionner l'emplacement de la zone de chalandise
qui maximise le potentiel calculé en termes de chiffre d'affaires,
de marge ou de rentabilité. Cette méthode ne permet pas de cerner
avec précision un emplacement, mais seulement de
sélectionner les aires intéressantes de localisation. Elle
ne tient compte que des surfaces commerciales en ignorant les autres
facteurs d'attractivité tels que les prix pratiqués par la
concurrence, les efforts de promotion,... Egalement, l'étape initiale de
délimitation de la zone de chalandise qui n'est pas
réputée facile, joue un rôle capital dans la
tangibilité des résultats obtenus.
1.5.2 La méthode analogique
Comme nous l'avons vu au chapitre 1, le modèle
analogique425 426 développé par Applebaum pour les
supermarchés Kroger dans les années 50, prend
l'hypothèse que la géographie se
424 GHOSH A. et McLAFFERTY S.L. (1987)
Location Strategies for Retail and Service Firms, Lexington
Books, Reading, Mass, p.43.
425 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
répète: si un point de vente est placé
à un emplacement similaire à un autre, la performance des deux
points de vente sera identique selon ce modèle. La méthode
revient tout d'abord à établir une cartographie des clients
potentiels représentés spatialement par des points. Il s'agit
ensuite de déterminer la zone de chalandise correspondant à
l'emplacement pressenti pour le point de vente, puis de chercher des
points de vente analogues en termes d'accessibilité et
d'environnement économique et concurrentiel. La performance du futur
magasin s'inspirera de celle d'un magasin analogue en calculant pour ce dernier
le chiffre d'affaires par client et en l'extrapolant à la zone de
chalandise du premier. Le problème est que la notion de similitude
est subjective et dépend de l'appréciation de
l'analyste. D'autre part, cette approche ne tient pas compte des interactions
concurrentielles locales et est assez lourde à mettre en oeuvre dans
le cas où un grand nombre de points de vente seraient
à localiser.
Lorsqu'un distributeur possède un grand nombre de
magasins, une vingtaine voire plus, la méthode analogique offre
une voie intéressante pour réaliser des prévisions
de vente en corrélant le chiffre d'affaires par les
caractéristiques des magasins (surface, nombre de
départements, nombre de caisses), les caractéristiques des
sites commerciaux (facilités de parking et d'accès), les
caractéristiques de la population au sein de la zone de chalandise
(âge, revenu, taille des ménages, niveau d'éducation) et
l'importance de la concurrence (poids des concurrents et niveau de leur chiffre
d'affaires).
1.5.3 La méthode par le modèle de
régression multiple
La méthode par le modèle de
régression multiple s'appuie sur l'analyse de points de vente
existants à travers la détection de facteurs modelant leur
chiffre d'affaires ou d'une manière générale une mesure
de leur performance. Les données analysées par des
traitements
426 APPLEBAUM W. (1968) The Analog Method for
Estimating Potential Store Sales, Guide to Store Location
Research, Addison-Wesley, Reading, Mass. by Kraus
Reprint Ltd Nendeln Lichtenstein in 1967.
statistiques seront en l'occurrence celles qui identifient les
variables les plus en relation avec
les ventes comme :
- les ventes ou les parts de marché estimées de
magasins;
- les ventes prévisionnelles;
- le niveau de concurrence mesuré par exemple par la
surface totale des magasins concurrents
au sein de la zone de chalandise;
- la proportion des ménages ou des individus correspondant
à la cible commerciale recherchée dans la zone de chalandise;
- le revenu moyen des ménages dans cette même
zone.
La méthode par le modèle de régression a
été codifiée de manière précise afin de
donner au monde professionnel des moyens clairs pour évaluer une
localisation, identifier des facteurs
de performance ou établir des prévisions de
vente. La méthode a, en France, été baptisée
méthode EVEC ou méthode d'Evaluation des Emplacements
Commerciaux.
La méthode EVEC427
La méthode EVEC, mise au point par la
société Gallup Poll en Grande-Bretagne en 1968, permet de
tenir compte d'un très grand nombre de données pour
à la fois évaluer la performance d'une chaîne de
points de vente ou de l'un de ses composants ainsi que pour
sélectionner les meilleurs emplacements dans le cadre de la
création d'un nouveau magasin ou d'un établissement. Une
application dérivée consiste également à
détecter les emplacements à fermer.
Les différentes étapes de la méthode EVEC
sont:
- la reconnaissance des facteurs: il s'agit de cerner
quels sont les facteurs qui peuvent avoir une influence sur le chiffre
d'affaires du magasin ramené à sa superficie. Ces
facteurs sont
427 DELENDA J.F. (1970) EVEC : Une Méthode
d'Evaluation des Emplacements Commerciaux, L.S.A. n° 335, sept. 1970,
57-61.
ensuite regroupés si possible en ensembles
homogènes (facteurs de concurrence, de taille, de trafic...). Les
facteurs individuels non regroupables sont dits "composants
spécifiques".
- la mesure des facteurs : les facteurs
préalablement identifiés sont mesurés, soit de
manière objective (ex. nombre de caisses, superficie du magasin),
soit plus rarement de manière subjective (ex. valeur du personnel
dirigeant).
- le rassemblement des données : les
données se regroupent en 3 classes:
É les statistiques internes caractérisant le
point de vente étudié (ex. surface de vente, nombre de
vendeurs, valeur du personnel dirigeant);
É les statistiques démographiques liées
à la zone de chalandise entourant chaque point de vente (ex. population,
structure d'âge, de revenus ou socioprofessionnelle);
É les statistiques externes de l'environnement
qui proviennent d'études de marché (ex. nombre et type de
concurrents, nombre et type de commerces influents, nombre de bureaux,
importance du trafic piétonnier, facilité de parking,
possibilité de transport en commun).
- l'analyse de régression: le chiffre d'affaires
(CA) est alors exprimé en fonction de n facteurs
par une analyse de régression multiple (voir
méthodes d'analyse au chapitre 1) et donné par
l'équation de régression:
CA = ax1 + bx2 + cx3 + ...nxn + K
- l'analyse comparative par magasin :
l'équation de régression sert à calculer le chiffre
d'affaires attendu pour chaque magasin. Ce chiffre est ensuite comparé
au chiffre réel et sa différence, positive ou négative,
indique une performance élevée ou faible. Pour choisir parmi
un échantillon de localisations possibles, un
emplacement pour un ou plusieurs points de vente à créer,
on calcule le chiffre d'affaires théorique pour les
différentes configurations possibles à partir de la
même équation de régression et on sélectionne
celle maximisant le
chiffre d'affaires.
La difficulté dans cette méthode de
régression, comme dans la méthode précédente,
est de définir la zone de chalandise dans laquelle mesurer les
statistiques démographiques ou celles liées aux consommateurs
potentiels du futur magasin. La méthode EVEC définit la zone de
chalandise telle que l'a fait Applebaum, c'est-à-dire l'aire circulaire
qui contiendra au moins
80 % de la clientèle. Cette zone se décompose en
général en un certain nombre d'îlots au sein desquels il
est aisé de se procurer des statistiques démographiques
commercialisées par des organismes étatiques comme l'Insee.
Or, comme on l'a vu au chapitre 1, les zones de chalandise ont
très rarement une forme idéale de cercle mais sont
plutôt constituées d'aires séparées de formes
variables. Ainsi, la méthode EVEC dont la promotion en France
a été assuré par l'Ifop-Etmar, convient plutôt
à une recherche primaire de localisation de point de vente pas trop
exigeante sur la précision des résultats obtenus. Ses promoteurs
reconnaissent eux-mêmes que EVEC n'est pas applicable pour des
chaînes de magasin en nombre réduit (au minimum 20 magasins) ou
pour des points de vente très dissemblables comme pour un
échantillon composé de petites surfaces urbaines et de grandes
surfaces en pleine nature, ou bien des magasins de création
récente en phase de développement et d'autres ayant atteint leur
rythme de croisière. Il est donc nécessaire, pour appliquer une
méthode du type modèle de régression, d'avoir à sa
disposition un échantillon de points de vente suffisamment
homogènes pour obtenir des résultats d'évaluation des
emplacements, fiables et pertinents.
1.5.4 L'analyse discriminante
L'analyse discriminante possède des analogies
méthodologiques avec le modèle de régression, mais ne
débouche pas sur des prévisions de vente pour le nouvel
emplacement. Alors que l'analyse de régression identifie, par une
équation linéaire, les relations qui lient les variations des
ventes entre différents points de vente et des facteurs explicatifs,
l'analyse multidiscriminante sépare les magasins en plusieurs groupes
selon leurs résultats
commerciaux, en l'occurrence les magasins ayant une
performance acceptable et les autres plutôt inacceptables.
L'analyse discriminante ne constitue pas à elle seule une
méthode de localisation, mais aide seulement à cerner
quels sont les magasins performants afin d'implanter plus en
aval, une méthode du type analogique ou de régression
multiple : on recherchera ainsi à créer un nouvel
établissement dans un endroit ayant les caractéristiques d'une
zone où est implanté un magasin performant avec
éventuellement les caractéristiques de
ce type de magasins.
1.5.5 La méthode du marché potentiel
La méthode du marché potentiel découle
directement du principe de gravité du commerce de détail de
Reilly428 (voir § 2.1.2). Cette technique souvent
utilisée par la grande distribution minimise la distance du futur
emplacement aux consommateurs potentiels et la maximise par rapport à
celle des concurrents. Les clients sont censés fréquenter
d'autant plus le magasin qu'ils en sont proches. Les facteurs
d'attraction jouant sur la fréquentation et propres aux magasins
ne sont pas examinés par souci de simplicité ou tout simplement
du fait de l'absence
de données disponibles : les données
de performance des magasins concurrents, les caractéristiques
de leurs surfaces commerciales ou de leurs produits ne sont pas,
dans la majorité des cas, accessibles. Cependant, il est
possible en affectant les consommateurs au point de vente situé
à l'emplacement pressenti, de prévoir la part de
marché du futur commerce par rapport à celle des
concurrents (qui eux aussi se voient affectés les
consommateurs qui leur sont les plus proches).
1.5.6 Le modèle p-médian
Le modèle p-médian est plus simpliste que
les méthodes précédentes dans le sens où il
ne tient compte que des critères de la distance (minimisation de la
somme des distances entre les
428 REILLY W. J. (1931) The Law of Retail
Gravitation, W. Reilly ed, 285 Madison Ave, New York, NY.
clients et les points de vente), de la demande et
éventuellement du coût d'ouverture des points
de vente pour sélectionner les emplacements
adéquats. En revanche, il sait en théorie être plus
précis lorsqu'il calcule la position idéale des points de vente
la plus proche en moyenne des clients car contrairement aux autres
méthodes de localisation, la situation géographique des clients
est examinée individu par individu, même si ensuite on effectue
des regroupements par quartier ou rue dans un souci de simplification.
Dans la pratique, on localise sur le terrain les clients
potentiels par leur adresse ou leur origine géographique en
réalisant des enquêtes de terrain. L'auteur a
lui-même effectué ce type d'enquête pour des compagnies
de transport urbain : dans ce secteur d'activité, les clients sont
interrogés directement dans les bus ou les tramways. On leur demande en
particulier de situer
sur une carte le lieu de départ de leur trajet qui est
ensuite codifié par quartier ou par cellule géographique
urbaine, l'objectif étant dans ce cas d'améliorer la
localisation des arrêts de transport en commun. Dans la
restructuration d'un réseau d'agences bancaires, les adresses des
clients sont connues, de même que dans la grande distribution lorsque la
chaîne de magasins a réussi à populariser parmi ses clients
un système de cartes de fidélité ou d'avantages. Pour
ce
qui est de la création pure et simple d'un point de
vente, c'est alors une base de données de consommateurs potentiels
qu'il s'agit d'élaborer. De nombreux organismes de sondage
constituent de telles bases principalement par enquête
téléphonique. Dans certains pays comme au Japon, les
consommateurs potentiels sont épiés dans leurs faits et
gestes jusque dans la rue : ainsi en est-il de cette grande entreprise de
construction automobile qui, pour créer un nouveau concessionnaire
dans une ville, allait jusqu'à repérer les conducteurs
de
vieilles voitures et à les suivre jusqu'à leur
domicile en repérant leur adresse429.
C'est en effet du domicile que partent, en semaine, 68
% des trajets ayant une destination commerciale. Ce pourcentage
croît même encore plus le week-end (73 % le samedi et 79 % le
429 Interview personnel en 1999 d'un commercial d'une
grande entreprise automobile japonaise.
dimanche)430. De là, naît
l'importance stratégique de réussir à se constituer
une base de données d'adresses de clients potentiels ou réels
pour alimenter un modèle p-médian. Ceci dit,
les pratiques actuelles d'utilisation d'un tel
modèle souffrent d'approximations qui malheureusement font
fléchir son intérêt commercial. Comme nous l'avons
vu dans le chapitre précédent, l'examen de toutes les
configurations des différentes localisations possibles des
points de vente vis-à-vis des clients ne peut être fait compte
tenu de leur nombre exhorbitant. Dans un premier temps, lors de la
construction du modèle, on cherche donc à assigner chaque
client de la base de données d'adresses à un quartier ou à
un secteur urbain de manière à réduire le nombre de
cellules d'analyse. Ainsi, c'est le centre de gravité de chacun
de ces secteurs qui servira de noeud au réseau du
modèle. Le nombre de noeuds qui correspond chacun à un secteur,
est alors considérablement réduit comparé au cas où
l'on aurait créé pour chaque client un nouveau noeud. Le
problème est que ce découpage en secteurs géographiques
correspond plus à une logique administrative qu'à une
logique commerciale. En effet, les secteurs sont le plus souvent des
quartiers, des arrondissements, le découpage Insee (Iris), le
découpage de la société Adde (ZAD) dans le cas de grandes
villes pour lesquelles il est facile
de se procurer les statistiques démographiques mais qui
forment une partition trop grossière
de la zone géographique d'analyse. De plus,
l'affectation des clients à ces secteurs
géographiques non homogènes, de tailles souvent
inégales en population et en superficie, choisis uniquement par
commodité risque de déboucher sur des choix de localisation
erronés.
Il est plutôt rare de constater dans la pratique
que les zones de chalandise épousent exactement les formes de
ce découpage administratif artificiel. Le paragraphe 8.1 dans la
deuxième partie montrera un exemple concret de cette pratique portant
sur un découpage de l'Ouest parisien en arrondissements et communes de
périphérie qui conduit à des solutions de
localisation de points de vente loin de l'optimal.
430 MOATI P. et POUQUET L. (1998)
Stratégies de Localisation de la Grande Distribution et Impact
sur la
Mobilité des Consommateurs, Collection des Rapports
n°194, Crédoc, p.53.
Conclusion
Nous avons vu qu'une localisation optimisée
facilitant l'accès aux produits ou aux services d'un point de
vente aura tendance à attirer un grand nombre de clients et
induira une rentabilité élevée à l'instar d'une
localisation pauvre pouvant aller jusqu'à conduire le point de vente
à la banqueroute. Le choix d'une localisation optimale
doit s'accompagner de l'évaluation des caractéristiques
de sa zone de chalandise, démarche stratégique pour
sélectionner, entre plusieurs localisations, la plus prometteuse
commercialement. L'observation de la zone de chalandise doit être
suivie dans le temps car celle-ci est susceptible d'évoluer
suivant les aléas des modifications du tissu économique
et social. Malheureusement, les méthodes disponibles pour
localiser de manière adéquate ou pour évaluer une
zone de chalandise sont, soit trop simplistes et donc peu
précises, soit trop complexes pour être mis en oeuvre. D'un
autre côté, malgré la masse importante de données
disponibles et souvent organisée dans les entreprises sous forme
de datawarehouses, les systèmes d'informations géographiques
n'ont pas encore réussi à devenir de véritables
instruments de décision dans les problèmes d'optimisation en
dépassant leurs fonctionnalités
de représentation cartographique
améliorée.
Ainsi, nous nous proposons dans le prochain chapitre de
présenter de manière exploratoire les différentes
théories de la localisation dont une au moins, on l'espère,
pourra servir de marche- pied à une véritable méthode
pratique et rapide susceptible de tirer parti des grandes bases de
données constituées par les entreprises concernant leur
clientèle.
Chapitre 2
Les théories de la localisation
Introduction
Le processus d'ouverture d'un ou de plusieurs
commerces de détail se décompose habituellement en quatre
décisions fondamentales431. La société doit
d'abord déterminer sur quel marché elle souhaite s'implanter. Il
est ensuite nécessaire pour elle de spécifier le nombre
de points de vente qu'elle compte ouvrir en fonction de ses
capacités financières et du taux de saturation du marché.
Puis, la société doit examiner les localisations possibles et
retenir après une étude poussée celle qui lui semble la
plus convenable. En dernier lieu, il s'agit de spécifier
la taille du magasin et de ses caractéristiques
(aménagement, décoration, assortiment, merchandising, ...). Les
théories de la localisation s'attachent à résoudre le
troisième point et tentent de modéliser à travers des
concepts mathématiques plus ou moins élaborés
l'espace commercial pour y détecter d'éventuelles
opportunités d'implantation.
Il existe deux grandes familles de modèles de localisation
représentées par :
- les modèles gravitaires et d'interaction spatiale,
- les modèles de localisation-allocation.
Alors que les modèles gravitaires dérivent de
modèles physiques en postulant une interaction réciproque entre
points de vente et clients, les modèles de localisation-allocation
cherchent à optimiser la localisation et éventuellement le
nombre de points de vente en minimisant les coûts de
déplacement des clients. Nous allons examiner, dans le présent
chapitre, en exposant leurs forces et faiblesses, ces modèles
caractérisés le plus souvent par une approche plus ou moins
théorique et simplifiée de la réalité.
Les modèles gravitaires et d'interaction spatiale
comparent plusieurs localisations potentielles
en se fondant sur différents critères objectifs
(éloignement à la clientèle, accessibilité,
surface)
ou subjectifs (enquête d'opinion). Ils se fondent
principalement sur l'analogie avec la
431 KOTLER P. (1971) Marketing Decision Making: A
Model Building Approach, New York: Holt, Rinehart & Winston.
gravitation. Le territoire géographique est
supposé être occupé par des espaces agrégés
ou des zones qui comportent un certain nombre d'activités. Ces
agrégats décrits par des attributs interagissent les uns avec
les autres par l'intermédiaire de flux pouvant être des
déplacements, des migrations ou encore des transports de marchandises.
Les modèles d'interaction spatiale
peuvent s'écrire d'une façon très
générale sous la forme432:
Tij
= K Wi
(1)W j
Cijn
(2)
où :
Tij est une mesure de l'interaction entre deux zones i et j; Wi
(1) : une mesure de masse associée à la zone i;
Wj (2) : une mesure de masse associée à
la zone j;
Cij : une mesure de la distance ou du coût de transport;
n : un paramètre à estimer;
k : une constante de proportionnalité.
D'autre part, il existe les modèles de
localisation-allocation qui cherchent à placer un nombre défini
de points de vente en les rapprochant le plus près possible de la
demande. Ce dernier type de modèles pour lesquels ont été
développés de nombreux algorithmes sur ordinateur, est bien
adapté à la multi-localisation d'activités.
Passons tout d'abord en revue les modèles
d'interaction spatiale, le premier dans l'histoire
ayant été la loi de Hotelling.
432 WILSON (1971) A Family of Spatial
Interaction Models, and Associate Developments, Environment
and
Planning A, vol. 3, 1-32.
2.1 Les modèles d'interaction spatiale
Comme on l'a dit, les modèles d'interaction
spatiale abordent les problèmes de localisation sous l'angle de
l'analogie avec certains principes physiques fondamentaux. Les
principaux modèles de ce type sont :
- la loi de Hotelling,
- la loi de Reilly et la formule du point de rupture,
- la méthode des secteurs proximaux et la théorie
des places centrales de Christaller,
- le modèle de Huff,
- le modèle MCI ou Modèle Interactif de
Concurrence.
Les modèles d'interaction spatiale comportent
certains inconvénients liés justement à leur approche
un peu trop idéaliste de la réalité.
2.1.1 La loi de Hotelling
La loi de Hotelling433 n'est pas à
proprement parler un modèle mais permet de prendre conscience
des interactions concurrentielles. Elle part de la problématique
mathématique suivante : considérons une répartition
homogène de clients le long d'un segment AB. Il s'agit
de déterminer l'emplacement optimal sur ce segment de
deux points de vente de même type gérés individuellement
par deux managers, qui prennent leur décision sans se consulter l'un
l'autre. On part du principe que les clients chercheront à
fréquenter le magasin le plus proche
et que les managers voudront obtenir un profil maximal en ayant
le plus de clients possibles.
Si ces clients avaient la possibilité de choisir
eux-mêmes les deux emplacements ou que les managers puissent se consulter
en ayant à l'esprit de se partager le marché, les deux magasins
seraient placés au tiers et au deux tiers du segment AB et donc à
équidistance l'un de l'autre. Dans ce cas, chaque magasin capterait une
moitié des clients et ils atteindraient tous les deux
433 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, Vol. 39, p 41-57.
un profit identique. Mais, si chaque manager ignore la
décision de son concurrent, ils auront alors la saine réaction
de vouloir en premier s'installer au milieu du segment de manière
à attirer en moyenne le plus de clients possibles. Ainsi,
Hotelling met par là en évidence les
phénomènes possibles d'interactions qui existent entre les
concurrents au sein d'un même marché géographique,
interactions qui conditionnent le choix des localisations commerciales. Mais,
sa théorie appelée aussi principe de différenciation
minimale explique aussi la tendance
de certains magasins à se regrouper. Si l'on
considère à nouveaux les deux sociétés A et B
identiques qui souhaitent maximiser leur profit en vendant des produits
identiques au même prix en présence d'une demande
inélastique et constante, en réduisant, par souci
de simplification, l'éventail des localisations possibles de ces deux
distributeurs à un segment de droite (xy), les entreprises vont chercher
idéalement en premier lieu à se partager le marché en deux
demi-segments sur lesquels elles occuperont des positions centrales
(étape 1 - fig. 1).
Fig. 2.1 - Le principe de différenciation
minimale434
Dans un deuxième temps, l'une d'elles deviendra plus
ambitieuse et s'installera vraisemblablement à proximité de
l'autre de manière à être à la fois proche de son
marché et à capter une part du marché concurrent
(étape 2). Ensuite, l'entreprise B se sentant menacée
jouera à "saute-mouton" pour aller empiéter sur le
marché de l'autre (étape 3) ce qui
434 Source : BROWN S. (1992) Retail Location : A
Micro-scale Perspective, Ashgate, England.
contraindra l'entreprise A à faire de même,... On
s'aperçoit qu'au bout d'un certain temps, les entreprises A et B se
seront toutes les deux regroupées au centre du marché qui
correspond en fait au milieu du segment (XY).
Ainsi, la loi de Hotelling offre essentiellement la
possibilité de comprendre la logique de répartition des
points de vente concurrents dans l'espace sans pouvoir être
utilisée en pratique dans une recherche de localisations optimales
au sein d'un même réseau. Cependant, là encore, les
explications de ces phénomènes restent purement
spéculatives. Les points de vente
ne sont généralement pas si mobiles que
le laisse entendre le principe de différenciation minimale
même si on assiste parfois dans la réalité à ce jeu
de "saute-mouton" que Hotelling a introduit pour expliquer le regroupement des
activités en groupes ou cellules. Les magasins plutôt
qu'être nomades ont tendance à vouloir rentabiliser les
investissements qu'ils ont consacrés à un site et à
rester donc assez longtemps à un emplacement donné.
2.1.2 La loi de Reilly et la formule du point de
rupture
En se fondant sur une analogie avec les
propriétés de pesanteur des corps célestes, la
population intermédiaire I localisée entre deux pôles
urbains A et B sera attirée par chacun de
ces pôles proportionnellement à leur taille et en
proportion inverse de la distance entre la zone
I et les pôles urbains A et B 435:
Va = [Pa ]
[Db ]
Vb Pb Da
Va et Vb: Proportion des ventes
réalisées en A et B auprès des habitants de la
zone
intermédiaire I,
Pa et Pb: population des pôles urbains A et B,
Da et Db: distance entre la zone intermédiaire I et les
pôles urbains A et B,
: coefficient positif mesurant l'importance du facteur population
sur le niveau des ventes,
435 REILLY W. J. (1931) The Law of Retail
Gravitation, W. Reilly ed, 285 Madison Ave, New York, NY.
: coefficient positif mesurant l'impact de la distance entre
clients et point de vente jouant sur
le niveau des ventes.
Comme et sont souvent pris égaux à 1 et à
2 respectivement 436 437, on obtient la formule:
Va Pa
=
Vb Pb
Db²
Da ²
Pour délimiter la frontière de la zone de
chalandise de deux aires de marché éloignées, les
populations des pôles urbains A et B, Va et Vb, sont
remplacées par la surface de vente des deux zones. Le point de rupture
de l'attractivité commerciale issue du pôle urbain A et du
pôle
B est alors indiqué par son abscisse X à partir du
pôle A :
x = distance entre le pôle A et le pôle
B

1+ surface de vente du pôle B
surface de vente du pôle A

Fig. 2.2 - Illustration de la Formule du Point de Rupture
Fig. 2.3 - Estimation d'une Zone de Chalandise par la
Méthode du Point de Rupture
436 CONVERSE P.D. (1949) New Laws of Retail
Gravitation, Journal of Marketing 14, p.379-384.
437 GUIDO P. (1971) Vérification
Expérimentale de la Formule de Reilly en Tant que Loi
d'Attraction des
Supermarchés en Italie, Revue Française de
Marketing n°39, p. 101-107.
De nombreuses études empiriques dont celles de Reilly
lui-même sont venues confirmer la validité de sa loi même
s'il s'avère que l'exposant de la distance n'était pas
forcément le carré. Converse438 a
vérifié la loi de Reilly avec un coefficient
égal à 1 et égal à 2 pour un certain
nombre de centres urbains en Illinois, mais la puissance
prédictive de la formule a semblé diminuer quand les centres
concurrents étaient approximativement de taille égale. Elle
a également servi à localiser des agences
bancaires439. La loi de Reilly, très
théorique,
suppose une isotropie de l'espace, l'absence de
barrières naturelles, un comportement invariable des
consommateurs en tout point de l'espace ce qui n'est pas
forcément le cas. Ainsi, la localisation optimale du magasin selon les
hypothèses de la loi de Reilly se trouve au coeur même du bassin
de population en l'absence de concurrence.
En résumé, prétendre que la forme de la
zone de chalandise ne dépend que de l'importance des populations en
présence et de la seule surface commerciale des points de vente est
assez hasardeux alors même que les magasins ont en
général une attractivité propre vis-à-vis de
consommateurs éventuels qui n'ont pas forcément les mêmes
attentes. Le modèle de Huff à l'approche probabiliste reprend
cependant les mêmes hypothèses approximatives que la loi de Reilly
à savoir que seules la distance entre le point de vente et les clients
potentiels d'une part,
et la surface de vente du point de vente d'autre part
influenceront l'importance de sa fréquentation.
2.1.3 La méthode des secteurs proximaux et la
théorie des places centrales de
Christaller
La théorie des places centrales rend compte de
la taille, de l'espacement et du nombre des villes. On
considère un espace géographique non
différencié, une zone homogène, où la
densité de population est uniforme, où tous les habitants ont le
même revenu à dépenser et où
438 CONVERSE P.D. (1949) New Laws of Retail
Gravitation, Journal of Marketing 14, p.379-384.
439 JOLIBERT A., ALEXANDRE D. (1981) L'utilisation du
modèle gravitaire généralisé dans la localisation
des agences bancaires, Techniques Economiques, 123, 31-44.
les biens sont offerts à des prix identiques,
auxquels s'ajoutent seulement les coûts de transport, lesquels ne
dépendent que de la distance au centre. On fait aussi l'hypothèse
d'un comportement rationnel des individus, qui cherchent à se procurer
les biens et les services au meilleur coût et s'approvisionnent donc au
centre le plus proche.
Selon cette théorie 440, dans cet espace
physique idéal représenté par une distribution
uniforme des consommateurs pouvant se déplacer
uniformément, la localisation des magasins
est régulière et occupe le sommet
d'hexagones. Ces sommets correspondent aux points d'accessibilité
maximale pour les consommateurs potentiels de la zone de chalandise.
Christaller traite, sur une base hiérarchique, les points de vente selon
leur niveau d'importance
et prouve que la localisation d'un point de vente d'un niveau
plus élevé (chiffre d'affaires plus important pour plus de
clients avec une exigence plus élevée) sera optimale au
centre de l'hexagone constitué par six magasins
élémentaires:
Fig. 2.4 - Les hexagones de la théorie des places
centrales
Plus précisément, La disposition des lieux
centraux qui permet de desservir toute la population en couvrant tout
l'espace (pavage du territoire) varie alors selon le point de vue que l'on
privilégie:
440 CHRISTALLER W. (1935) Die Zentralen Orte in
Süddeutschland, G.Fischer, Germany, Jena.
Î le principe de marché: si l'on
veut maximiser le nombre de lieux centraux (meilleure desserte de la
population) tout en assurant un partage équitable de la clientèle
entre
les centres, les villes d'un même niveau
hiérarchique sont disposées au sommet de triangles
équilatéraux. La limite d'influence de chaque ville passe
par le milieu de chaque côté du triangle, ce qui forme
autour de chaque ville une zone d'influence hexagonale. Chaque centre
de niveau inférieur est partagé entre l'influence de
trois centres de niveau supérieur. La superficie de la zone desservie
par un centre est trois fois plus grande que celle que dessert un centre de
niveau immédiatement supérieur (rapport k=3);
Î le principe de transport: si l'on
déforme la configuration des villes précédentes de
façon à en placer plusieurs sur un même axe de transport,
afin de réduire les coûts d'infrastructures de circulation, on
obtient une hiérarchie où la dimension de la zone d'influence
d'un centre supérieur est quatre fois celle d'un centre
de niveau immédiatement inférieur (rapport k=4);
Î le principe administratif: les
fonctions d'encadrement politique et de gestion territoriale ne se
partagent pas entre des centres concurrents, mais s'exercent dans des
circonscriptions aux limites fixées et sans recouvrement. Chaque ville
au centre d'une circonscription hexagonale contrôle six centres de niveau
inférieur, et la superficie de
sa zone d'influence est sept fois celle d'un centre de niveau
inférieur (rapport k=7)441.
La méthode des secteurs proximaux suppose que les
consommateurs choisiront le service le plus proche d'eux selon
l'hypothèse de la théorie des places centrales. Les zones de
chalandise
441 CHAMUSSY H., CHAPELON L.,
DURAND-DASTES F., ELISSALDE B., GRASLAND C., GRATALOUP C., PUMAIN D.,
ROBIC M.C., SANDERS L., SAINT-JULIEN T. (2001)
http://www.cybergeo.presse.fr/
ou secteurs proximaux sont dessinés en
construisant des polygones de Thiessen 442 ou de Dirichlet
443 qui représentent chacun la surface polygonale la
plus proche d'un magasin particulier que de tout autre. Ces
polygones se dessinent en 4 étapes
élémentaires.
Premièrement, on localise les points de vente ou
de services sur une carte, ensuite on lie chaque point les uns aux
autres, troisièmement on trace la médiatrice à partir du
point médian
de chaque segment et enfin, on prolonge les médiatrices
pour former à leurs inter-parties les sommets des polynômes de
Thiessen.
La méthode des secteurs proximaux essentiellement
géométrique permet de repérer les lacunes spatiales
représentant autant d'opportunités d'implantation en
supposant qu'une saturation de l'espace commercial se note par de petits
polygones contrairement à une vaste

zone polygonale dotée d'un fort potentielle.
Fig. 2.5 - Etapes pour la Détermination des Secteurs
Proximaux 444
442 THIESSEN A.H. et ALTER J.C. (1911), Precipitation
Averages for Large Areas, Monthly Weather Review,
39, p. 1082-1084.
443 DIRICHLET, G. L. (1850), Über die Reduktion
der Positiven Quadratischen Formen mit Drei Unbestimmten
Ganzen Zahlen , Journal für die Reine und Angewandte
Mathematik 40, p. 216.
444 GHOSH A. et McLAFFERTY S.L. (1987)
Location Strategies for Retail and Service Firms, Lexington
Books, Reading, Mass.
En accord avec les hypothèses posées par
Christaller, on sous-entend en utilisant cette méthode qu'il n'y a
aucune complémentarité entre les points de vente contrairement
à ce qui
est constaté pour certaines activités qui
ont au contraire tendance à se regrouper pour augmenter leur
pouvoir d'attractivité445 446. Ce phénomène
n'est pas nouveau et a été constaté chez les
confréries et guildes d'artisans et de commerçants au
moyen-âge ou dans les souks
des pays du Maghreb 447.
Fig. 2.6 - Répartition des commerces et de l'artisanat par
métier dans un souk marocain 448
Le problème est qu'un secteur du marché souvent
composé de distributions non-isotropes de consommateurs engendre donc
une distorsion de la forme de la zone de chalandise 449.
Quelques tentatives ont tout de même été
réalisées pour prolonger le modèle de Christaller
grâce à des transformations géographiques permettant
de convertir un environnement non- isotrope en un environnement
isotrope et réciproquement 450. D'autres chercheurs
comme Lösch ont tenté d'expliquer la taille et
l'organisation de certaines villes à partir de ce
modèle451. A peu près à la
même époque que durant les recherches de Christaller,
Reilly
445 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, vol. 39, p. 41-57.
446 DELOZIER M.W. et LEWISON D.M. (1986)
Retailing, 2nd ed., Merill.
447 FOGG W. (1932) The Suq: a study in the human
geography of Morocco, Geography 12, p. 257-258.
448 BROWN S. (1992) Retail Location: A
Micro-Scale Perspective, Edit. Ashgate, Grande-Bretagne.
449 ISARD W. (1956) Location and Space
Economy, p. 254-287, New York.
450 GETIS A. (1961) The Determination of the
Location of Retail Activities with the Use of a Map
Transformation, Economic Geography, p. 12-22.
451 LÖSCH A. (1940) Die Räumlische
Ordnung der Wirtschaft, Fischer, Iena.
allait, lui, introduire un modèle tenant compte de
la répartition des clients et des points de vente ainsi que de
leur interaction réciproque.
2.1.3 Le modèle de Huff
Huff452 a été le premier à
introduire au début des années 60 un modèle d'interaction
spatiale tenant compte de la concurrence. Selon lui, un consommateur n'est pas
rivé irrémédiablement
à un magasin mais est susceptible d'hésiter
entre plusieurs choix de lieux d'achats. Tous les magasins ont donc une
chance d'être fréquentés, cette approche probabiliste
tranchant avec l'approche déterministe qui prévalait
à cette époque. Selon Huff, la surface de vente du
commerce en particulier joue un rôle important dans son
attractivité vis-à-vis des clients tout autant que sa
proximité.
La probabilité qu'un consommateur au point i
fréquente un magasin particulier au point j est
donnée par l'axiome de Luce453:
Pij
= Uij
U ik
k Ni
S
=
avec l'utilité du point de vente Uij
D
j ij
et Sj: la taille du point de vente j
Dij: la distance entre le consommateur en i et le magasin en j
á et â reflètent l'importance
accordée à la taille et à la distance dans la
décision du consommateur de fréquenter tel ou tel magasin. Etant
donné que l'utilité diminue avec
la distance, le paramètre â est négatif.
Plus l'utilité est grande, plus le consommateur aura
tendance à être attiré par le point de vente.
Il est à noter que dans la formule, la taille
Sj du point de vente en j peut être remplacée
par
452 HUFF D. L. (1964) Defining and Estimating a
Trading Area, Journal of Marketing, Vol 28, p. 38.
453 LUCE R. (1959) Individual Choice
Behavior, New York: John Wiley & Sons.
une quelconque autre mesure de l'attractivité du
magasin comme dans le modèle MCI que nous examinerons un peu plus
loin. Le modèle de Huff est approximatif de la même façon
que
la loi de Reilly puisque, comme nous l'avons vu au chapitre 1,
l'étendue et la forme de la zone
de chalandise conditionnant la fréquentation du
point de vente dépendent de nombreux facteurs environnementaux,
socio-économiques et marketing (les caractéristiques propres du
magasin) autres que la distance à la clientèle ou que la surface
commerciale. Le modèle de Huff a cependant, vis-à-vis de la
loi de Reilly, l'avantage de pouvoir comparer entre elles plusieurs
localisations potentielles par le calcul des probabilités de
fréquentation. Il peut constituer une approche rapide et sommaire
pour évaluer très grossièrement la qualité
d'un site par rapport à un autre malgré le fait que les
paramètres de puissance á et â demandent à
être évalués au préalable grâce
éventuellement à l'expérience tirée de points de
vente existants pour lesquels on connaît les surfaces commerciales, les
fréquentations et la distance moyenne des consommateurs au point de
vente.
2.1.5 Le modèle MCI
Le modèle MCI ou Modèle Interactif de Concurrence
(multiplicative competitive interaction)
est en fait une prolongation du modèle de comportement
spatial de Huff avec l'avantage de tenir compte d'autres facteurs que la
distance ou la surface de vente. Dans ce modèle, on a simplement
remplacé la surface Sj dans la formule de Huff donnant la
probabilité de fréquentation du magasin j par le
consommateur i par une mesure plus générale de
l'attractivité du magasin comportant L facteurs d'attraction Alj
à la puissance ál (facteurs
d'attraction pouvant être comme nous l'avons
déjà dit le service de paiement par carte
bancaire, le nombre d'allées du magasin, le nombre
de caisses, l'emplacement à une
intersection 454 ou des paramètres subjectifs
comme l'image du magasin 455 456) :
A
L l
lj
l =
1
)
Cette probabilité devient donc:
L L
Pij
= ( l
A
D
lj
ij
l =1
/
k Ni
l
D
(
)
lk ik
A
l =1
Ni étant le nombre d'alternatives de
points de vente où les consommateurs sont susceptibles
d'effectuer leurs emplettes. Les différents
paramètres du modèle MCI peuvent être
calculés
par la méthode classique des moindres
carrés457. Les consommateurs font effectivement appel
à leurs affections personnelles pour fréquenter
tel ou tel point de vente 458. Ce phénomène a permis
de distinguer MCI objectif qui ne se préoccupe que de
données rationnelles le plus souvent liées au magasin (ex.
surface de vente, prix, nombre de caisses), du MCI subjectif 459
qui prend en compte les perceptions des consommateurs
quant aux attributs les plus déterminants pour le choix du
point de vente. Le modèle MCI subjectif montre des taux
d'explication de la variance dans la régression bien supérieurs
du fait de l'importance de la perception dans le choix du magasin, la
difficulté étant néanmoins de quantifier cette
perception sur une échelle de mesure. Le MCI objectif et le
modèle de Huff sous-entendent un calibrage parfait dans toutes les
cellules du découpage géographique de l'analyse (ou
condition de stationnarité) avec l'incertitude non
levée de savoir si les consommateurs auront
454 JAIN K. et MAHAJAN V. (1979) Evaluating the
Competitive Environment in Retailing Using Multiplicative
Interactive Model, Research in Marketing, Vol. 2,
Jagdish Sheth ed., Greenwich, Conn.: JAI Press.
455 NEVIN J.R. et HOUSTON M.J. (1980) Image as a
Component of Attraction to Intraurban Shopping Areas,
Journal of Retailing, Vol. 56, No. 1, pp.77-93.
456 COOPER L.G. et FINKBEINER C.T. (1983) A
Composite MCI Model for Integrating Attribute and
Importance Information, Advance in Consumer Research,
109-113.
457 NAKANISHI M. et COOPER L.G. (1974) Parameter
Estimates for Multiplicative Competitive Interaction
Models: Least Square Approach, Journal of Marketing Research
11: 303-311.
458 WRIGHT P. et RIPS P.D. (1981) Retrospective
Reports on the Causes of Decisions, Journal of Personality and Social
Psychology 40, 601-614.
459 STANLEY T.J., SEWALL M.A. (1976) Image Inputs to
a Probabilistic Model: Predicting Retail Potential, Journal of
Marketing, 40 (July), 48-53.
ou non des réactions différentes d'une cellule
à l'autre460. Ainsi, certaines personnes résidant dans
les secteurs résidentiels les plus isolés peuvent par exemple
être beaucoup plus sensibles
à la distance que le reste de la population en raison
du manque d'accès aux transports461. Le modèle MCI a
pourtant montré son efficacité en particulier sur le
marché du meuble462 où des variables subjectives
telles que l'influence de la promotion sur les décisions d'achat, la
qualité
des produits et de l'accueil ont été prises en
compte. Le modèle a alors été calibré dans chaque
cellule de découpage géographique pour respecter la
condition de stationnarité463 et des facteurs
subjectifs comme le jugement des consommateurs ont été
introduits en utilisant la transformation mathématique du
zéta-carré 464. Cependant, le traitement et la
détection de la non-stationnarité est difficile même s'il
existe des moyens mathématiques de s'en affranchir comme la
procédure du jackknife popularisée par Tukey465
et donc le modèle MCI reste
difficile à mettre en pratique pour les
problématiques de localisation des professionnels.
Mais, l'approche MCI peut être adoptée, si
on le souhaite, en complément du modèle analogique, pour
localiser un magasin unique ou en complément du modèle de
localisation- allocation dans un processus de localisation
multiple466.
2.1.6 Le modèle MNL
Le modèle MNL ou Multinomial Logit est un modèle
destiné à analyser le processus de choix des consommateurs. Il
prend l'hypothèse que les alternatives de choix sans rapport les unes
460 GHOSH A. (1984) Parameter Nonstationarity in
Retail Choice Models, Journal of Business Research 12,
425-426.
461 GHOSH A. et McLAFFERTY S. (1987) Location
Strategies for Retail and Service Firms, Lexington Books, p.117.
462 CLIQUET G. (1990) La Mise en OEuvre du
Modèle Interactif de Concurrence Spatiale (MICS) Subjectif,
Recherche et Applications en Marketing 5 / 7, 3-18.
463 GHOSH A. (1984) Parameter Nonstationarity in
Retail Choice Models, Journal of Business Research 12,
425-426.
464 COOPER L.G. et NAKANISHI M. (1983) Standardizing
Variables in Multiplicative Choice Models, Journal
of Consumer Research , 10, 96-108.
465 TUKEY (1958) Bias and Confidence in
Not-Quite Large Samples, Annals of Mathematical Statistics 29,
p.614.
466 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc: A Multiple Store Location Decision
Model, Journal of Retailing, 5-24.
avec les autres (IIA : Independence of Irrelevant
Alternatives), liées à un processus aléatoire, sont des
évènements indépendants et que l'introduction d'une
nouvelle alternative de choix influencera la probabilité de choix de
toutes les autres alternatives. La résolution du modèle
s'apparente à l'analyse discriminante multiple. Si la probabilité
de choix d'un magasin au point
j par un consommateur au point i est, selon l'axiome de
Luce467:
Pij
= Uij
U ik
k Ni
alors le modèle MNL considère
l'hypothèse que la part stochastique des fonctions d'utilité
Uik
sont indépendantes et non corrélées . Le
modèle MNL est surtout utilisé dans les transports, pour
prévoir le choix du mode, pour analyser le choix des marques468
ou encore pour choisir l'emplacement de magasins 469. Un
modèle encore plus général, le NMNL ou nested
multinomial logit, suppose que le choix entre deux alternatives
ne dépend pas des caractéristiques d'une quelconque autre
alternative: le consommateur prend d'abord le choix
de fréquenter un point de vente et décide seulement
ensuite lequel470. Le principe du NMNL
est en fait d'établir une hiérarchie de
préférence dans les choix et de prendre l'hypothèse qu'un
individu prendra la décision correspondant à sa
préférence la plus élevée en connaissant tous
les choix de niveaux inférieurs et leurs
caractéristiques471. Ainsi, on prend l'hypothèse dans
ce
modèle qu'un consommateur sélectionnera le
point de vente le meilleur selon ses propres critères parmi tous
les points de vente qu'il connaît suffisamment pour s'en faire une
opinion.
467 LUCE R. (1959) Individual Choice
Behavior, New York: John Wiley & Sons.
468 HRUSCHKA H., FETTES W. et PROBST M. (2001) A
Neural Net-Multinomial Logit (NN-MNL) Model to Analyze Brand Choice. In:
Govaert, G., Janssen, J., Limnios, N. (eds.): Applied Stochastic Models and
Data Analysis, Volume 2. ASMDA, Compiègne 2001, 555-560.
469 FOTHERINGHAM A. S. (1988) Market Share Analysis
Techniques : A review and Illustration of Current
US Practice, in Store Choice, Store Location and Market
Analysis, Neil Wrigley, Routlege, 120-159.
470 GUPTA I. et DASGUPTA P. (2000) Report :
Demand for Curative Health Care in Rural India : Choose between
Private, Public and No Care, Programme on Research Development of
the National Council of
Applied Economic Research sponsored by the United
Nations Development Programme, Dec. 2000.
471 DENG Y., ROSS L.S. et WATCHER S.M.
(1999) Employment Access, Residential Location and
Homeownership, Lusk Center for Real Estate Report, Los
Angeles.
2.2 Les modèles de localisation multiple
Pouvoir gérer en parallèle plusieurs points de
vente, outre l'intérêt économique qu'une telle organisation
commerciale représente, permet de réaliser des
économies d'échelle sur la promotion, la main d'oeuvre et
la distribution. Ce mode de gestion synergique de plusieurs
implantations offrant une meilleure représentation
géographique conduit également à diminuer le
risque lié à l'incertitude de l'environnement
économique qui pèse tant sur un magasin individuel. Ces
avantages ne sont effectifs que si les localisations des
différents points de vente ont été examinées avec
soin, l'impact réciproque d'ouverture d'un magasin sur l'activité
de l'autre étant alors connu.
La problématique de localisation multiple contraint le
décideur à trouver la réponse à quatre
questions472 473dont :
- sur quels marchés faut-il s'implanter ?
- combien de points de vente faut-il créer ?
- comment évaluer les localisations possibles ?
- quelles seront la taille et les caractéristiques des
magasins et des sites retenus ? Parmi les instruments capables de
répondre à ces questions, on trouve :
- les modèles de localisation-allocation474,
- le modèle Multiloc475,
- la méthode d'analyse de portefeuille476.
472 KOTLER Philippe (1971) Marketing
Decision Making : A Model Building Approach, Holt, Rinehart et
Winston, NY.
473 CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, p.187, Ed. Sirey.
474 GHOSH A., RUSHTON G. (1987) Spatial
Analysis and Location-Allocation Models, Van Nostrand, Rheinhold,
1987.
475 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc: A Multiple Store Location Decision
Model, Journal of Retailing, 5-24.
476 MAHAJAN V., SHARMA S. et SRINIVAS D. (1985) An
Application of Portfolio Analysis for Identifying
Attractive Retail Locations, Journal of Retailing,
vol.61, n°5, hiver 1985, 19-34.
2.2.1 les méthodes de localisation-allocation
Pour faciliter la recherche d'implantation,
différents modèles baptisés modèles de
localisation-allocation ont été mis au point. La question
fondamentale soulevée par ces modèles est de savoir
comment approvisionner ou servir au mieux une aire géographique
vaste à partir d'un nombre limité de points de vente. Etant
donné que les entreprises ont toutes des moyens financiers
limités (coûts d'ouverture et d'exploitation), le nombre
maximal de commerces de détail à ouvrir est souvent fixé
au préalable et constitue une donnée de base de
ce type de modèle. Les modèles de
localisation-allocation prennent d'une manière générale
l'hypothèse que la probabilité d'un consommateur de
fréquenter un point de vente ou de service donné est
d'autant plus élevée qu'il en est plus proche, compte-tenu
de son niveau d'attractivité. L'analyse tend ainsi à
réduire la distance moyenne séparant l'ensemble des
consommateurs au point de vente le plus proche de son domicile en maximisant
l'accessibilité des localisations. Les modèles de
localisation-allocation regroupent d'une manière
générale
cinq composants de base dont :
- la fonction objectif : c'est une fonction
qui intègre la notion de distance séparant les consommateurs aux
emplacements potentiels des points d'offre ainsi éventuellement
qu'une mesure de leur attractivité. Elle quantifie donc
l'accessibilité globale des points d'offre vis-à-vis des clients
ou bien encore une mesure de la viabilité économique des
emplacements.
- les points de demande : ils
représentent le niveau de la demande concernant un ensemble de
marchandises ou de services concernant un certain zonage géographique
pouvant être une région, une ville ou
un quartier. Les points de demande
correspondent en général à des cellules
densément peuplées où réside un pouvoir
d'achat intéressant pour l'activité considérée.
- les emplacements potentiels : ce sont les
localisations possibles en termes de disponibilité foncière,
coût, accessibilité.
- la matrice d'éloignement ou de temps
: cette matrice rend compte de la distance géographique
ou temporelle séparant les emplacements potentiels des points de
demande. Plus précisément, ces distances peuvent être
mesurées en pâtés de maison,
en distance kilométrique à vol d'oiseau,
en terme de cheminement piétonnier, en temps de conduite selon
la clientèle considérée et les moyens investis pour
la déterminer.
- la règle d'allocation : cette
règle spécifie de quelle manière les emplacements
potentiels seront alloués aux points de demande. On peut par exemple
considérer dans
le cas le plus simple que chaque client fréquentera le
point de vente le plus proche de son domicile, la règle d'allocation
étant alors la proximité géographique. Il est
possible d'envisager des règles plus complexes à
savoir par exemple que la fréquentation de tel ou tel point de
vente dépendra de la saison et se reportera sur un autre emplacement
à d'autres moments de l'année.
Ainsi, compte tenu de ces cinq facteurs décrivant
entièrement un modèle de localisation- allocation
donné, l'espace commercial peut être apprécié sous
la forme d'un réseau constitué
de noeuds caractérisés par une certaine demande
et/ou pouvant accueillir un point d'offre, les segments liant les noeuds de
ce réseau représentant les éloignements. A ce
réseau doit être néanmoins associé une
fonction objectif qui, exprimé le plus souvent sous
forme mathématique, spécifie la manière selon
laquelle les clients opteront pour tel ou tel
emplacement potentiel.
Dans le cas où n'existerait qu'un seul point d'offre
à localiser, le problème revient à le placer virtuellement
tour à tour à l'un ou à l'autre des emplacements
potentiels puis à choisir celui pour lequel la fonction objectif est la
plus favorable. Tout se complique si l'on doit localiser plusieurs
activités, car le nombre de noeuds étant souvent
élevé, il devient pratiquement impossible physiquement,
même avec des ordinateurs puissants, de calculer la fonction
objectif exhaustivement pour chacune des combinaisons d'emplacements
envisageables. Il a donc été développé pour cela
des solutions approchées par la mise en oeuvre d'heuristiques
qui conduisent, non pas à une série de
localisations optimales mais tout au moins à un niveau satisfaisant de
la fonction objectif.
L'un des premiers modèles de localisation-allocation a
été développé par Alfred Weber avec comme
problématique la réduction du coût total de transport de
matières premières à l'usine
et de l'usine au marché.
Le modèle p-médian
La recherche opérationnelle en matière
de localisations d'activités a été l'une des
préoccupations majeures pour beaucoup de champs d'applications
(logistique, transport, grande distribution, services bancaires,
assurance). En particulier, en ce qui concerne la localisation de
points de vente ou de services ou même d'entrepôts, une
problématique importante est de trouver les localisations pour un
nombre p d'activités devant fournir n clients de telle
manière que la somme de l'ensemble des distances séparant chaque
activité aux clients les plus proches soit minimale. Ce problème
lié à un réseau discrétisé bien
identifié est classiquement connu sous le nom de
p-médian477 478 qui trouve son origine au
début du
477 HAKIMI S.L. (1965) Optimum Distribution of
Switching Centers in a Communication Network and Some
Related Graph Theoretic Problems, Operations Research
13, 462-475.
478 REVELLE C. et SWAIN R. (1970) Central Facilities
Location, Geographical Analysis, 2, 30-40.
XXème siècle dans les réflexions d'Alfred
Weber 479 sur la meilleure manière de placer un centre de
production par rapport aux sources de matières premières. En
pratique, le problème
du p-médian (nommé en abrégé p-MP)
est soulevé dans la plupart des réseaux qu'ils soient routiers,
aériens ou téléphoniques 480 481. Handler et
Mirchandani 482 ont dressé la liste très
variée des applications potentielles du modèle p-médian
comme les décisions de localisation pour les services d'urgence
(police, pompiers, urgences médicales), les réseaux
de communication et informatique (localisation des fichiers informatiques
sur une série de serveurs identifiés), les applications
militaires (centres militaires stratégiques), les activités de
service public ou privé (les magasins, centres commerciaux, postes), les
activités de transport (arrêts de transport en commun,
entrepôts), l'intelligence artificielle et les modèles
statistiques (partition de nuage de points). Mais, les applications vraiment
centrées sur le domaine de la
distribution ont été mises en oeuvre dans
les années 1980 avec comme objectif principal d'optimiser le
nombre de points de vente et leurs emplacements, connaissant la localisation
précise de consommateurs, les coûts de déplacement et
éventuellement la demande 483 484 485.
Le présent exposé même s'il se concentre sur
l'application à la localisation spatiale d'activités,
pourrait très bien être directement transposé
aux autres domaines précédemment cités.
Il existe bien entendu de nombreux autres
modèles dits de localisation-allocation que le p- médian,
plus ou moins bien adaptés selon les cas. On peut citer parmi
eux le modèle p- centré486 qui recherche les
p localisations les plus proches de clients: créer p
activités, en
479 WEBER A. (1909) Über den Standort der
Industrien, Tübingen, Traduction Anglaise de Friedrich
(1929)
Theory of the Location of Industries, University of
Chicago Press, Chicago.
480 DASKIN M.S. (1995) Network and Discrete
Location - Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York..
481 GALVAO R.D. (1993) Use of Lagrangean
Relaxation in the Solution of Uncapacited Facility Location
Problems, Location Science 1, 57-70.
482 HANDLER G.Y. et MIRCHANDANI P.B. (1979)
Locations on Networks, MIT Press, Cambridge, MA.
483 GHOSH A. et CRAIG C.S. (1984) A Location
Allocation Model for Facility Planning in a Competitive
Environment, Geographical Analysis, Vol. 16, n°1,
39-51.
484 McLAFFERTY S.L. et GHOSH A. (1987) Optimal
Location and Allocation with Multipurpose Shopping,
Spatial. Analysis and Location-Allocation Models, ed.
Ghosh Avijit, Rushton Gerard, Van Nostrand Reinhold.
485 CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, p.187-191, Ed. Sirey.
486 KARIV O. et HAKIMI S.L. (1979) An algorithmic
Approach to Location Problems, Part 1: The p-Centers,
SIAM J. Math. 37, 513-538.
assignant chaque client à l'une d'entre elles,
de telle manière que la distance maximale de n'importe quelle
activité à l'ensemble de ses clients soit minimale. Cette
problématique, dénommée également minimax, cadre
bien avec la localisation d'ambulances ou de stations de pompiers qui doivent
être les plus proches possibles des zones d'intervention. Il
existe des modèles plus élaborés et plus
spécifiques à la localisation d'enseignes commerciales tels
que
le MCI487 déjà
évoqué et associé au modèle
Multiloc488, qui intègrent la notion de
concurrence, le coût d'ouverture des points de vente ou
même les attributs des magasins.
Mais, il est vrai que les caractéristiques des
points de vente et des clients ne sont pas une information facile
à obtenir, tâche d'autant plus ardue que le nombre de ces derniers
est élevé. Rassembler des données sur les activités
concurrentes s'avère également souvent particulièrement
difficile pour le manager. C'est l'une des raisons pour laquelle
notre thèse s'est concentrée sur le problème plus simple
mais pas plus simpliste du p-médian. De plus, il
est fondamental dans la plupart des projets d'ouverture de
commerces (ou même d'entrepôts) d'être le plus proche
possible de ses clients potentiels et de se mettre en quête
d'un emplacement commercial en étant guidé par cette logique, au
moins dans un premier temps. A quoi bon tenter en effet de chercher des
informations sur une clientèle trop distante pour être conquise
par le service offert au sens large du terme ! D'une manière
générale, on peut
distinguer deux catégories de
clientèle489: l'une domiciliée dans une zone proche du
point de
vente nommée zone de chalandise, est attirée par
un point de vente jouant le rôle d'un pôle (attraction polaire).
L'autre, ayant un caractère plus aléatoire, est induite
par le flux de clientèle passant à proximité du
point de vente et interceptée par ce dernier (attraction
passagère). Les points de vente eux-mêmes selon le produit ou le
service proposés se rangent
487 NAKANISHI M. et COOPER L.G. (1974)
Parameter Estimate for Multiplicative Competitive Interactive
Model - Least Squares Approach, Journal of Marketing
Research, 11, 303-311.
488 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc: A Multiple Store Location Decision
Model, Journal of Retailing, 5-24.
489 CLIQUET G. (1997) Attraction Commerciale,
Fondement de la Modélisation en Matière de Localisation
Différentielle, Revue Belge de Géographie,
121ème année, p. 62-65.
dans l'une ou l'autre des catégories selon leur
capacité à capter le flux de clients circulant à
proximité (ex.: bureau de poste, agence bancaire, distributeur
automatique) ou à attirer "à distance" les consommateurs
selon un principe similaire à celui de la gravitation étendue au
commerce de détail par Reilly490 (ex.: agence
d'intérim, supermarché, charcuterie,
papeterie)491. Certaines activités
possèdent un caractère mixte et comptent donc les deux types
de clientèle évoqués avec
éventuellement une certaine prépondérance pour l'un ou
pour l'autre
(ex.: bar-café-brasserie, épicerie,
pâtisserie).
Notre recherche visera à considérer la
clientèle de points de vente ou de services jouant plutôt
sur le principe de l'attraction polaire. Nous supposerons la
localisation de cette clientèle au sein de zones de chalandise connue,
par exemple identifiée par les adresses du domicile avec
l'hypothèse que les clients seront d'autant plus fidèles (ou
satisfaits) que le point de vente leur
est proche. Les termes de "points de vente" et de "clients"
peuvent être pris au sens large à savoir que le raisonnement
qui suit s'appliquerait de la même manière à un
service de livraison à partir d'entrepôts (les points de
services) devant acheminer un produit vers des centres de distribution ou
vers des détaillants (ex: services de tri postal et bureaux de poste;
grossistes en boissons et cafés-bars-brasseries).
Bien que le modèle p-médian ne s'appuie
que sur la notion de distance (ou de coût de déplacement)
entre clients et sites potentiels d'activité, compiler
les données sur les localisations de ces différents
acteurs pour trouver une localisation proche de l'optimal demande
beaucoup d'efforts et de temps de calcul ainsi que nous le constaterons plus
loin.
2.2.1.1 Formulation mathématique du p-MP
La résolution du problème p-médian
n'échappe pas à sa nécessaire rationalisation consistant
à l'exprimer en langage mathématique: le p-MP sous-entend
l'existence d'un réseau constitué
490 REILLY W. J. (1931) The Law of Retail
Gravitation, W. Reilly ed, 285 Madison Ave, New York, NY.
491 CLIQUET G. (1997) Attraction Commerciale,
Fondement de la Modélisation en Matière de Localisation
Différentielle, Revue Belge de Géographie,
121ème année, p. 66.
de noeuds ou points et de liens, ces derniers étant
associés à un coût de déplacement
représenté
par la distance di,j (distance du point i au point j).
L'objectif est ainsi de trouver un emplacement optimal pour p
activités au sein des noeuds du réseau en cherchant à
minimiser
la distance totale entre les p activités et les clients
qui leur sont associés (un client est associé
à une activité s'il se trouve plus proche de cette
dernière que de toutes les autres). Les modèles
p-médian pondérés et
non-pondérés se différencient par le fait que les
premiers tiennent compte de la demande ai au point i avec l'objectif de
minimiser la somme totale des distances pondérées par la
demande.
D'une manière générale, la formulation
mathématique du p-MP s'écrit de la façon
suivante492:
Minimiser
i j
ai dij xij représente la fonction objectif,
(1)
avec
i
xij = 1, i, assure que tous les clients sont
assignés à une activité et une seule, (2)
xij yj, i, j empêche d'assigner un client à
une activité si elle n'est pas ouverte, (3)
yj = p, le nombre total d'activités est
p, (4)
j
xij, yj {0,1}, i, j nature binaire des variables xij, yj
(5)
où
ai : la demande au noeud i,
di,j : la distance du noeud i au noeud j,
p : le nombre d'activités à localiser,
xi,j = 1, si le noeud i est assigné à
l'activité j et 0 autrement,
yj = 1, si l'activité j est ouverte et 0 autrement.
492 BEAUMONT J.R. (1987) Location-Allocation
Models and Central Place Theory, Spatial Analysis and
Location-Allocation Models, ed. Ghosh Avijit, Rushton
Gerard, Van Nostrand Reinhold.
Cette formulation suppose que tous les noeuds du
réseau ont la qualité de localisation potentielle pour les
activités et que les p activités seront localisées
en des points distincts. Dans le cas non-pondéré, les
demandes ai sont toutes égales à 1.
Le problème p-MP est réputé appartenir
à la classe des problèmes connus comme étant NP-
complets493: ses solutions issues d'algorithmes
linéaires deviennent insolubles au fur et à mesure que
le nombre des variables (activités et clients) augmente avec
une progression exponentielle de la taille du problème. En effet, selon
une logique d'analyse combinatoire, le nombre de solutions à examiner
est en fonction de n, le nombre de noeuds, et p, le nombre d'activités
à placer:
n!
p! (n -
p)!
ce qui signifie par exemple que si l'on devait simplement
chercher à placer 15 points de vente
au milieu d'un réseau de 100 clients et que l'on
dispose d'un ordinateur capable de réaliser un million
d'opérations par seconde, le temps requis pour parvenir à la
solution optimale serait de huit millénaires494 ! Dans le
cas où l'on voudrait solutionner tous les problèmes
p-médian (p variant de 1 à p activités à placer) si
on ne connaît que le nombre maximum p d'activités à placer,
le nombre de combinaisons à étudier serait alors de:
n n!
-
=2n -1
j = 1 p! (n
j)!
Il existe donc un grand nombre d'heuristiques pour
trouver une solution acceptable au
problème p-Médian malgré le fait que
toutes ces solutions ne convergent que vers des optima locaux et non vers une
solution globale et qu'il ne soit pas possible a priori de connaître le
niveau d'optimalité de cette solution. Dans les algorithmes de
résolution fondamentaux, on trouve l'algorithme flou,
l'algorithme de recherche de voisinage, une heuristique de
493 KARIV O et HAKIMI S.L. (1979) An Algorithmic
Approach to Network Location Problems, Part 2: The p- median", SIAM Journal
of Applied Mathematics 37, 539-560.
494 DASKIN M.S. (1995) Network and Discrete
Location - Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York.
substitution495 et ses variantes496, cette
dernière catégorie étant l'une des plus robustes selon
Densham et Rushton497.
2.2.1.2 Les algorithmes de résolution du p-MP
Mais d'une façon générale, les heuristiques
se rangent en deux classes498: les algorithmes de construction
qui permettent de rechercher des localisations avec un degré
d'optimalité faible
et les algorithmes d'amélioration
destinés comme leur nom l'indique, à améliorer les
résultats fournis par les algorithmes de construction. Alors
que l'algorithme flou est du type construction, l'heuristique de
substitution et l'algorithme de recherche de voisinage ont une approche
d'amélioration. Pour clarifier la signification de ces termes, nous
passerons en revue
le principe de mise en oeuvre de ces heuristiques.
Localisation d'une activité unique dans la
problématique du p-MP : le 1-médian
Examinons tout d'abord la recherche de solutions dans le cas le
plus simple, la localisation d'une activité unique ou problème
1-médian. Dans le cas où, plus de la moitié de la
demande
ai est localisée en un point, une des solutions
optimales consiste à placer l'activité en ce
i
noeud. Et si ce noeud concentre plus de la moitié de la
demande, cette localisation est alors la
localisation optimale unique499.
495 TEITZ M.B. et BART P. (1968) Heuristic
Methods for Estimating the Generalized Vertex Median of a
Weighted Graph, Operations Research 16, 955-961.
496 GOODSCHILD M.F. et NORONHA V. (1983),
Location-Allocation for Small Computers, University of
Iowa, Monograph N°8.
497 DENSHAM P.J. et RUSHTON G. (1992) A More
Efficient Heuristic for Solving Large p-median Problems,
Papers in Regional Science: The Journal of the RSAI
71/3, 307-329.
498 GOLDEN B, BODIN L., DOYLE T. et STEWART Jr.
(1980) Approximate Travelling Salesman Algorithms,
Operations Research, 28, 694-711.
499 DASKIN M.S. (1995) Network and Discrete
Location - Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York.
La résolution du cas le plus
général a été donnée par
Goldman500. Elle consiste à choisir aléatoirement
un noeud d'extrémité de branche sur le réseau et
si au moins la moitié de la demande n'est pas fixée en ce
noeud à le supprimer (ainsi que le lien) et à reporter sa
demande
sur le noeud suivant. Si l'un des noeuds du réseau
concentre plus de la moitié de la demande, alors l'activité est
à localiser en ce point et on peut calculer la distance totale
pondérée par la demande.
Un exemple concret plus explicite selon Daskin501 est
donné par le réseau suivant qui compte
une demande totale de 48 (la demande au point x est
représenté par hx) :
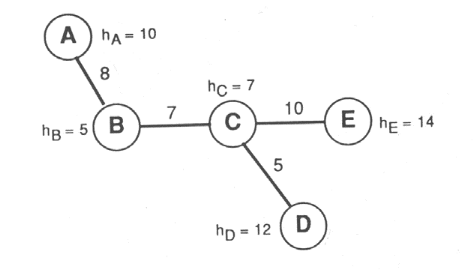
Fig. 2.7 - Méthode de résolution du 1-médian
: étape 1
Aucun des noeuds ne compte plus de la moitié de la
demande. Si l'on considère donc le point
A dont la demande égale à 10 est inférieure
à 48/2 = 24, on reporte cette demande sur le point
B en supprimant le point A, demande qui atteint alors 5 + 10 =
15:
500 GOLDMAN 1J (1971) Optimal Center Location in
Simple Networks; Transportation Science 5, 212-221.
501 DASKIN M.S. (1995) Network and Discrete
Location - Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York.
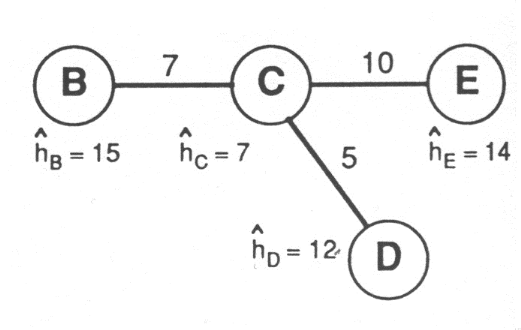
Fig. 2.8 - Méthode de résolution du 1-médian
: étape 2
La demande en B égale à 15 est toujours
inférieure à 24 (comme celle de tous les autres points).
Supprimons alors le point D où la demande, 12, est la plus faible en la
reportant sur le point adjacent C:
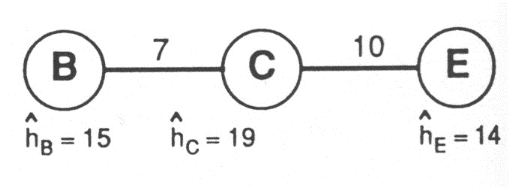
Fig. 2.9 - Méthode de résolution du 1-médian
: étape 3
Comme les demandes de B, C et D sont toujours inférieures
à 24, supprimons E et reportons
sa demande sur C. On s'aperçoit alors que la
demande de C égale à 33 est supérieure à
la
demande totale divisée par deux (24), ce qui signifie que
C est le point optimal sur lequel doit être placée
l'activité:
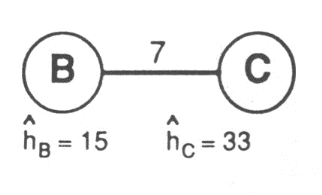
Fig. 2.10 - Méthode de résolution du
1-médian : étape 4
L'algorithme flou
L'algorithme flou consiste tout simplement à localiser
les activités sur le réseau une par une, puis à utiliser
une procédure de voisinage ou de substitution pour optimiser les
localisations. Dans un premier temps, on choisit donc le meilleur emplacement
pour la première activité ce
qui est facile si on calcule la fonction objectif pour chaque
noeud envisagé en retenant le noeud pour lequel cette fonction objectif
est la plus faible. Ensuite, on localise un deuxième point envisageant
chaque noeud (sauf celui déjà occupé) et en assignant
à la localisation précédente,
les noeuds qui lui sont les plus proches comparés au
noeud examiné. La fonction objectif est calculée de la même
manière et on retient toujours comme second emplacement le noeud pour
lequel cette fonction possède la valeur minimale. Ce processus est
réitéré autant de fois qu'il y
a d'activités à localiser.
Ainsi, l'organigramme de cette procédure se résume
à:
Localiser la première
activité en utilisant
l'énumération totale
Avons-nous p
activités ?
Non
Localiser l'activité suivante en utilisant
l'énumération totale et en fixant les autres
localisations
Oui
Algorithme
d'amélioration par substitution ou de voisinage
Fin
Fig. 2.11 - Organigramme de l'algorithme flou
Résolution par les multiplicateurs de
Lagrange502
Une méthode de résolution appartenant aux
algorithmes de construction, plus classique mais moins performante, est
représentée par les contraintes du p-médian
relaxées à l'aide des multiplicateurs de Lagrange. Elle
permet de transformer un problème contraint en un problème
sans contraintes503. Nous la mentionnons pour mémoire.
Appliquée à la relation (2)
de la formulation générale du problème du
p-médian, une relaxation par les multiplicateurs de
Lagrange devient:
502 DE LAGRANGE Louis, mathématicien
français né en 1736, mort en 1813.
503 DASKIN M.S. (1995) Network and Discrete
Location - Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York.
Minimiser
i j
ai dij xij +
i
i [1 -
j
xij ] (1)
=
i j
( ai dij + i ) xij + i
i
avec
i
xij = 1, i, (2)
xij yj, i, j, (3)
yj = p, (4)
j
xij, yj {0,1}, i, j (5)
Les coefficients i considérés comme fixes
sont appelés multiplicateurs de Lagrange et la nouvelle fonction
objectif à minimiser devient (1). En appliquant une relation identique
à la relation (3) de la formulation générale du
p-médian, on démontre que les multiplicateurs de Lagrange
peuvent être calculés à partir d'une formule
récurrente, avec des multiplicateurs
initialisés à une valeur quelconque:
n
in+1 = max { 0, in - tn
(Xij
- Yjn)}
n
avec t n =
(UB -
Ln)
( X
j
n
ij
i j
- Y n )2
où
tn : le pas de la procédure de Lagrange
à la nième itération,
n : une constante généralement prise
égale à 2,
UB : (upper bound) la plus petite limite supérieure de la
fonction objectif,
Ln : la fonction objectif de Lagrange (1)
ci-dessus,
Yjn : la valeur optimale de la variable de
localisation Yj à la nième itération.
La méthode de résolution du p-médian par
les multiplicateurs de Lagrange a été récemment
utilisée dans des travaux de recherche en informatique pour
déterminer sur quels serveurs en réseau il était
préférable d'implanter les informations pour obtenir des
traitements de calcul plus rapides au niveau de l'ensemble504. Le
même algorithme a été utilisé dans le même
esprit
pour améliorer la configuration des réseaux de
communication505.
Une méthode de résolution
générale et (presque) exacte des problèmes de
localisation développée par Homberg, Rönnqvist et Yuan fait
appel à l'algorithme par les multiplicateurs
de Lagrange en parallèle d'une procédure par
séparation et évaluation (Branch and Bound en anglais)
dans le cas où chaque noeud de demande est assigné à une
activité et une seule506. La procédure par
séparation et évaluation est une méthode
d'énumération implicite qui repose sur
le principe de diviser les solutions en paquets. Plus
précisément, on divise l'ensemble des solutions possibles
d'un problème de localisation-allocation (ou plus
généralement d'optimisation combinatoire) en sous-ensembles de
plus en plus petits afin d'isoler dans l'un
de ces sous-ensembles une solution optimale. Le parcours est
représentable par un arbre avec comme racine le problème de
départ et toutes les combinaisons possibles, les branches
représentant les sous-problèmes correspondant à
des sous-ensembles de toutes les combinaisons admissibles.
L'exploration de l'arbre se fait vers des niveaux d'optimalité
des solutions obtenues croissantes et la partition des ensembles de solutions
(destinée à créer des branches) est produite en
allouant un ou plusieurs clients d'une activité à une
autre si l'on considère la solution explorée en cours. Cette
réallocation des clients se fait généralement par
un processus aléatoire. La recherche de Homberg,
Rönnqvist et Yuan montre que l'utilisation
individuelle de la procédure par séparation
et évaluation (grâce à l'algorithme commercial
504 CHURCH R.L. et SORENSEN P.A. (1995) A
Comparison of Strategies for Data Storage Reduction in
Location-Allocation Problems, National Center for Geographic
Information and Analysis, Technical Report
95-4, University of Santa Barbara, California.
505 GUPTA R. (1996) Problems in
Communication Network Design and Location Planning; New Solution
Procedures, PhD, Graduate School of the Ohio State
University.
506 HOLMBERG K., RÖNNQVIST M. et YUAN D. (1999)
An Exact Algorithm for the Capacitated Facility
Location Problems with Single Sourcing, European Journal of
Operational research 113, 544-559.
CPLEX) met jusqu'à 5 heures pour résoudre un
problème de 30 activités à localiser en prenant
en compte la position de 300 clients alors que la
méthode associant cet algorithme avec les multiplicateurs de Lagrange
ne met qu'une heure pour obtenir des solutions
généralement meilleures. On le voit, les meilleurs
algorithmes de résolution même s'ils tournent sur des
ordinateurs puissants (un ordinateur Sun Sparc 20/HS151 pour cette recherche)
n'arrivent à résoudre dans un temps raisonnable que des
problèmes de localisation-allocation de quelques centaines de noeuds.
Dans certains cas (1 cas sur 71 cas étudiés), l'algorithme de
Homberg, Rönnqvist et Yuan ne réussit cependant pas à
trouver une solution optimale et donc cet algorithme ne peut être
qualifié de méthode de résolution exacte.
Résolution par la méthode des algorithmes
génétiques
Les algorithmes génétiques se fondent sur la
théorie générale de l'évolution de Darwin selon
laquelle les espèces vivantes progressent en organisation et en
complexité par la simple sélection naturelle de leurs
caractères génétiques les plus performants lors des
phases de reproduction. Ainsi, ce principe qui optimiserait la
configuration génétique des systèmes vivants face
à un environnement hostile serait tout aussi bien capable de traiter des
problèmes d'optimisation beaucoup plus généraux tels que
la résolution des problèmes d'optimisation ou des modèles
de localisation-allocation. Les premières applications à ces cas
datent des années
70 507 508. De manière analogue pour ces
modèles, un individu ou une solution se caractérise
par son empreinte génétique ou sa
structure de données. Les opérations
génétiques de croisement et de mutation modifient les
données ou chromosomes de chaque individu ce qui permet en
théorie de parcourir tout l'éventail des solutions possibles.
L'algorithme génétique
va donc à chaque nouvelle génération
créer de nouvelles solutions mais aussi en détruire ainsi
507 HOLLAND J.H. (1975) Adaptation in
natural and artificial systems, Ann Arbor: University of
Michigan
Press.
508 GOLDBERG D.E. et LINGLE R. Jr. (1985) Alleles,
loci and the travelling salesman problem, Proceedings of
an International Conference on Genetic Algorithms, J.J.
Grefenstette (Ed.), LEA Pub, p 154-159.
que le décrit la théorie de la
sélection naturelle509. La performance de l'individu ou
l'optimalité de la solution se mesure par le niveau de sa fonction
objectif. Dans un premier temps, l'algorithme génétique va
générer des solutions de manière aléatoire,
puis il va les laisser évoluer jusqu'à obtenir les meilleures
solutions possibles.
Pour utiliser avec succès un algorithme
génétique, il est nécessaire :
- de réussir à coder les solutions en des ensembles
de chromosomes,
- de partir d'une population ou de solutions de base,
- de disposer d'une fonction objectif qui va mesurer le niveau
d'optimalité de chaque solution,
- de décider comment sélectionner les chromosomes
les plus performants,
- de décrire les opérateurs
génétiques ou le mode d'échange des données,
- de spécifier les paramètres de l'algorithme tels
que taille de la population initiale, probabilités de croisement et de
mutation,
- de donner un critère d'arrêt de l'algorithme.
Le codage d'un modèle p-médian est
une succession binaire de 0 et de 1 correspondant à l'absence
ou à la présence d'un point de vente dans la liste des
noeuds du réseau. Les caractéristiques des solutions de
départ et leur nombre (population de départ) peuvent
être tirées au hasard ou bien déterminées par une
autre heuristique du modèle p-médian. Dans ce dernier cas,
l'algorithme génétique constituera une procédure
d'amélioration de la solution.
La fonction objectif du p-médian nous conduisait à
minimiser la quantité :
ai dij xij
i j
L'évaluation la plus simple de la force de
l'individu ou optimalité de la solution consiste à
prendre l'inverse de la fonction objectif que l'on cherchera
à maximiser :
509 HOLLAND J.H. (1992) Les algorithmes
génétiques, revue Pour la Science, No 179, Sept. 1992,
p. 44-51.
1 / ai dij xij
i j
La sélection ou reproduction va déterminer
à partir de quels individus on va construire la
génération suivante. On utilise assez souvent la
roue de Goldberg510 qui consiste à tirer les solutions sur
une roue de loterie sur laquelle les individus sont
représentés sur une surface proportionnelle à leur
force ou optimalité. De cette façon, les individus les plus forts
auront à l'étape ultérieure de croisement et de mutation,
une représentativité plus forte avec un nombre
de copies plus importantes au sein de la population. Le
croisement consiste alors à échanger des paquets de
données (des suites de 0 et de 1 découpées dans la
solution) entre des paires d'individus. La mutation consiste, elle,
à basculer dans notre cas un 0 en 1 ou réciproquement
un 1 en 0 en de très rares occasions selon une
probabilité de mutation fixée à l'avance. Cette
procédure permettrait d'explorer tous les recoins de
l'espace des solutions en évitant d'emprisonner la recherche
dans un maximum local (ou un minimum pour la fonction objectif). En
pratique, les chromosomes sont tirés de façon aléatoire et
sont remplacés par un chromosome d'une autre valeur toujours prise
aléatoirement. Enfin, le nombre maximal de
générations correspond au nombre d'itérations que l'on se
fixe pour stopper la procédure.
Tous les paramètres de l'algorithme
génétique sont généralement fixés
empiriquement. Une population de 20 à 1000 individus qui en
général reste stable au fur et à mesure des
générations, satisfait généralement la
résolution de tous les problèmes. Une taille de
population trop faible ne permettra pas d'explorer tous les champs de solutions
possibles alors qu'une taille très élevée engendrera un
nombre d'opérations importantes qui pourra nuire à la
rapidité d'exécution. Les valeurs de moyennes des
probabilités de croisement oscillent entre
0,65 et 0,9 : une probabilité élevée
favorisera l'examen d'un grand nombre de solutions, mais
une probabilité de croisement excessive risque
d'emprisonner la recherche dans des maxima
510 GOLDBERG D.E. (1991) Genetic Algorithms,
Addison-Wesley, New York.
locaux. Une certaine probabilité de
mutation511 est au contraire nécessaire pour
réussir de temps en temps à générer des individus
hors-normes qui sont susceptibles de constituer des super-solutions au
problème. Ces solutions bien meilleures ne sauraient dans certains cas
être générées par des simples transformations de
croisement. Il reste que la probabilité de mutation doit rester faible,
de 0,001 à 0,2 voire 0,1 à 10 pour ne pas entraver le processus
normal de reproduction et d'empêcher l'algorithme de converger
vers un optimum512. Outre ces paramètres
fixés empiriquement, il n'existe pas à l'heure actuelle
de critère de convergence efficace pour stopper le processus
dès qu'une solution intéressante est atteinte. Il est
donc indispensable de déterminer au départ le nombre de
générations ou d'itérations au bout duquel
on arrête l'algorithme513.
Les algorithmes génétiques sont, d'une
façon générale, particulièrement
recommandés pour
les problèmes pour lesquels n'existe aucune autre
méthode de résolution ou bien pour lesquels
les méthodes de résolution existantes
n'offrent que des solutions approchées comme les modèles de
localisation-allocation514.
Les algorithmes d'amélioration
Dans un second temps, on utilise l'algorithme
d'amélioration de voisinage515 ou celui de
substitution516.
511 GOLDBERG D.E. (1994) Algorithmes
Génétique, Exploration, Optimisation et Apprentissage
Automatique, Editions Addison-Wesley, 1994.
512 AURIFEILLE J.M. (2001) Les
algorithmes génétiques, Conférence
invitée à l'IREIMAR, Institut de
Recherche Européen sur les Institutions et les
Marchés, CNRS, Mars 2001.
513 AURIFEILLE J.M. (2001) Conjoint fuzzy vs
non-fuzzy clustering : some empirical evidence using a genetic algorithm
optimization, Actes du 7ème congrès international SIGEF,
sept. 2001.
514 ROBERT-DEMONTROND P., THIEL D. (2002) Algorithmes
génétiques et stratégies spatiales des firmes de
distribution, in Stratégies de Localisation des
Entreprises Commerciales et Industrielles : De Nouvelles
Perspectives, G. Cliquet et J-M. Josselin éd., De
Boeck Université, Bruxelles.
515 MARANZANA F.E (1964) On the Location of
Supply Points to Minimize Transport Costs, Operational
Research Quarterly, 15, 261-270.
516 TEITZ M.B. et BART P. (1968) Heuristic Methods
for Estimating Generalized Vertex Median of a Weighted
Graph, Operations Research, 16, 955-961.
· L'algorithme de recherche de voisinage
Dans l'algorithme de voisinage, on
considère le voisinage de chaque localisation d'activité,
c'est-à-dire l'ensemble des noeuds qui lui sont le plus proche et on
calcule dans ce voisinage une localisation améliorée par
l'algorithme du 1-médian vu précédemment. L'algorithme
de voisinage peut être utilisé comme algorithme de construction
si l'on démarre la recherche de localisation avec une configuration
aléatoirement choisie.
· L'heuristique de substitution
On procède à l'heuristique de substitution
en supprimant tout à tour chacune des p activités
déterminées dans la procédure initiale de localisation,
ensuite en recherchant le meilleur autre emplacement pour cette
activité supprimée par une simple énumération
et en calculant la fonction objectif correspondante. La recherche d'une
valeur plus faible de la fonction objectif parmi celles calculées en
recherchant une nouvelle localisation pour chaque activité
déjà déterminée donnera éventuellement une
configuration améliorée par rapport à celle obtenue
à l'étape précédente.
Les variantes des algorithmes d'amélioration
La variante très proche de l'algorithme
précédent, donnée par Goodschild et
Noronha517, revient à identifier le noeud
d'activité et le noeud libre dont la substitution offre la
fonction objectif la plus basse. Si la fonction objectif a tendance à
diminuer par rapport à la solution trouvée initialement, alors
ce nouvel emplacement peut être considéré comme un
optimum local.
Une autre variante des algorithmes d'amélioration consiste
à travailler au niveau global, puis
régional518. Considérons l'ensemble des
noeuds occupés par une activité S et celui des noeuds
517 GOODSCHILD M.F. et NORONHA V. (1983),
Location-Allocation for Small Computers, University of
Iowa, Monograph N°8.
518 DENSHAM P.J. et RUSHTON G. (1992) A More
Efficient Heuristic for Solving Large p-median Problems,
Papers in Regional Science: The Journal of the RSAI
71/3, 307-329.
non occupés (V-S) avec V l'ensemble de tous les noeuds.
Si un nouveau noeud est mis dans l'ensemble S, on appelle cette
procédure ADD alors que si on retire un noeud de l'ensemble S, cette
procédure est nommée DROP. Dans la première phase
globale, on réalisera une séquence de DROP et d'ADD
jusqu'à ce que l'on ne trouve plus d'amélioration à la
fonction objectif. Dans la phase locale, on décomposera le réseau
en p problèmes 1-médian que l'on résoudra par l'algorithme
de voisinage explicité précédemment.
Enfin, la procédure "Tabu" (mot anglais signifiant tabou)
mise au point par Rolland, Schilling
et Current519 utilise un temps dit tabou,
mesuré en nombre d'itérations, durant lequel il est
interdit de pratiquer une procédure DROP sur un noeud
incorporé à l'ensemble S par une procédure ADD (le
compteur d'itérations est initialisé dès que ce
noeud est placé dans l'ensemble S). Cette durée "taboue" fixe,
aléatoire ou dynamique durant le fonctionnement de l'algorithme doit
être écoulée pour avoir le droit à nouveau
de supprimer le noeud de l'ensemble S. Ce programme d'amélioration
semble enregistrer de meilleurs résultats que les heuristiques
déjà citées. Les auteurs ne s'attachent cependant
à démontrer l'efficacité de l'algorithme par rapport
aux autres méthodes qu'en se fondant sur un cas particulier.
En tous les cas, l'algorithme flou correspond assez
bien à la logique d'implantation des chaînes de magasins :
celui-ci cherche en effet dans la procédure à localiser
les points de vente les uns après les autres de la même
manière qu'un manager voudra la plupart du temps
en pratique les ouvrir graduellement avec une mise en
puissance progressive et non d'une manière simultanée. De
plus, dans un deuxième temps, l'algorithme d'amélioration
s'identifie
en quelque sorte à la phase de réorganisation des
points de vente déjà créés qui est
marquée
par exemple soit par la suppression d'un point de vente non
rentable (que se passe-t-il si je
519 ROLLAND E., SCHILLING D.A. et CURRENT J.R. (1996)
An Efficient Tabu Procedure for the p-Median
Problem, European Journal of Operational Research,
329-342.
supprime un magasin ? algorithme de substitution), soit
par la redistribution au niveau local des localisations ( algorithme de
voisinage) .
2.2.2 Le modèle Multiloc
Supposons que l'on veuille placer r points de vente
parmi un éventail de n emplacements possibles. Le modèle
Multiloc520 est en fait une extension du modèle MCI qui,
d'une manière générale, considère q attributs
d'attractivité de ces magasins Aijk, attributs susceptibles de
prendre ík valeurs: par exemple, on a pour k=1 un attribut Aij1 qui
peut être la distance (í1 =1); pour k=2, Aij2 peut signifier la
taille du magasin qui peut être petite, moyenne ou grande (í2
=3 et valeurs discrètes),...
Si l'on considère le nombre de combinaisons des
attributs d'attractivité, le nombre de
"designs" ou de configurations possibles que peuvent prendre les
magasins est : L = í1 í2 ...íq
La fonction objectif qui doit maximiser le profit est la
suivante:
m n n L
Max Z = C j Ei
Pij - Fjl X
jl
i =1
j =1
j =1 l =1
avec
Z : le profit
Ei: Le chiffre d'affaires total par groupe i sur le
marché
Fjl: les coûts fixes d'un magasin du plan l au site j
Cj: un coefficient multiplicateur
Xjl = 1 si un magasin avec le design l est implanté sur le
noeud j et égale à 0 sinon
j: la localisation considérée qui varie de 1
à n l: le design considéré qui varie de 1 à L
on a aussi les conditions suivantes sur le nombre r de points de
vente à localiser :
520 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc: A Multiple Store Location Decision
Model, Journal of Retailing, 5-24.
n L
X jl = r
j = 1l = 1
L
et X jl 1
j=1,...,n
l =1
La probabilité qu'un consommateur au point i
fréquente un magasin particulier au point j est
alors:
Pij
L q n
( Akl X jl) /
L q
( Akl X jl)
n + s
q
( Akl )
=
ijkl
ijkl
+
ijkl
l =1 k =1
j =1l =1 k =1
j = n + l
k =1
Comme pour le modèle p-médian ou pour le
modèle MCI, il n'est pas possible de résoudre le
modèle Multiloc par la complète
énumération des combinaisons d'emplacements possibles.
En effet, si l'on doit placer r points de vente au niveau de n
emplacements possibles avec L
configurations de magasin possibles, le nombre de solutions
à examiner est:
W Lr n!
= r! (n
- r)!
De la même manière que pour les
modèles p-médian ou MCI précités ou n'importe
quel
problème d'analyse combinatoire de ce type, l'une
des méthodes les plus réputées pour résoudre
le modèle Multiloc est sans conteste encore l'algorithme de substitution
de Teitz et Bart 521 mis en pratique dans la localisation d'agences
bancaires 522.
Une alternative consiste à employer
l'échantillonnage aléatoire développé par
McRoberts523.
Le nombre de solutions h tirées d'une
manière aléatoire à examiner pour qu'il y ait
une
521 TEITZ M.B. et BART P. (1968) Heuristic
Methods for Estimating the Generalized Vertex Median of a
Weighted Graph, Operations Research 16, 955-961.
522 CORNUEJOLS G., MARSHALL L.F. et NEMHAUSER
G.L. (1977) Location of Bank Accounts to
Optimize Float: An Analytic Study of Exact and Approximate
Algorithms, Management Science, 23 (1pril),
789-810.
523 Mc ROBERTS K.L. (1971) A Search Model for
Evaluating Combinatorially Explosive Problems, Operations
Research, 19, 1331-1349.
probabilité y qu'au moins l'une des p meilleures
configurations possibles soit dans cet
échantillon est de:
1
h = W 1- (1- y)
pW
Ainsi, si l'on veut avoir 99 % de chance de trouver 1
% des meilleures configurations
d'emplacements et de designs possibles dans un échantillon
aléatoire, il faudra un ensemble de
460 combinaisons tirées au hasard. Si l'on a 7 magasins (r
= 7) de 3 designs possibles (L = 3)
à localiser sur 35 localisations potentielles (n =
35), il y a 14,7 milliards d'alternatives. La méthode de
l'échantillonnage aléatoire revient donc si l'on se satisfait de
la probabilité d'avoir
99 % de chance de tomber sur les 1 % des
configurations les plus optimales, à tirer 460 combinaisons
parmi les 105 configurations possibles d'emplacement et de
design (7 emplacements x 3 designs possibles), puis à
sélectionner le meilleur emplacement et le meilleur design
possibles en calculant la fonction objectif qui doit être la
plus importante possible524.
2.2.3 La méthode d'analyse de portefeuille
La méthode d'analyse des portefeuilles issue du monde de
la finance525 puis popularisée par
les consultants de cabinets tels que le Boston Consulting Group
(BCG), Mc Kinsey ou Arthur
D. Little526 a été
adaptée pour cibler les localisations les plus
intéressantes ou comparer plusieurs localisations entre
elles527. En variations verticales, on trouve l'attrait du
secteur (atractiveness en anglais) alors qu'en horizontal, on a la
force concurrentielle du réseau de points de vente (competitive
strenght).
524 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc: A Multiple Store Location Decision
Model, Journal of Retailing, 5-24.
525 MARKOWITZ H. (1952) Portfolio Selection, Journal
of Finance, Vol. 7, mars, p.77-91.
526 KOENIG G. (1990) Management
Stratégique : Visions, Manoeuvres et Tactiques, Nathan.
527 MAHAJAN V., SHARMA S. et SRINIVAS D. (1985) An
Application of Portfolio Analysis for Identifying
Attractive Retail Locations, Journal of Retailing, vol.
61, n°4, hiver 1985, 19-34.
L'attrait du secteur, en l'occurrence le plus souvent de la zone
de chalandise, est quantifiable
en prenant une combinaison de paramètres comme 528
529:
- la taille de la zone de chalandise ;
- son taux de croissance ;
- le taux de profit ;
- l'intensité de la concurrrence au sein de la zone de
chalandise. Et la force concurrentielle est, elle, une combinaison de :
- la part de marché ;
- la qualité des points de vente (équivalents aux
produits) ;
- la réputation des enseignes ;
- l'efficacité promotionnelle.
L'exemple ci-dessous montre l'utilisation de la matrice
des portefeuilles par le groupe Lévi Strauss, fabricant de Jeans,
pour renforcer sa présence dans les pays de distribution où il
est le moins bien implanté.
Fig. 2.12 : La matrice de Portefeuille appliquée à
l'Europe par le groupe Lévis Strauss530
Il n'y a eu cependant aucune étude qui est venue
confirmer la validité et l'efficacité de la méthode
d'analyse de portefeuille531. Certaines études sur les prises
de décision ont montré au
528 THIETARD Raymond-Alain (1988) La
Stratégie d'Entreprise, Mc Graw-Hill.
529 CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, Ed. Sirey., p.193
530 University of Newcastle upon Tyne, Agricultural
Economics & Food Marketing Department (2001) Student
Ressources,
http://www.ncl.ac.uk/aefm/student_resources/aef334/LeviStrauss.pdf
contraire que l'utilisation de cette méthode
aboutissait dans 64 % des cas à la sélection d'un investissement
non-rentable et dans 87 % des cas à l'un des investissements
les moins rentables.
2.2.4 Les autres modèles de
localisation-allocation
Il existe de nombreux autres modèles dont la
fonction objectif est dérivée de celle du p-
médian. Citons les modèles p-centrés et le modèle
de couverture maximale. Alors que le p- médian imposait de minimiser
la somme des distances entre chaque client et son point de vente
assigné, le modèle p-centré cherche la configuration
pour laquelle la distance entre chaque point de vente et le plus
éloigné de ses clients soit minimale. Ce modèle
est particulièrement indiqué pour placer des services d'urgence,
des hôpitaux ou des casernes de
pompiers étant donné une population. Le
modèle de couverture maximale532 vise à
assurer
que la majorité des clients sont à une distance
maximale au moins d'un service donné : si cette condition est bien
vérifiée, on dit alors que l'ensemble des clients est couvert :
les modèles de couverture sont tout indiqués pour placer
des services généraux du type poste, trésorerie,
services de mairie et administrations d'une manière
générale. Les algorithmes de résolutions
de ces autres modèles de localisation-allocation se
calquent sur ceux du p-médian.
2.3 Limitations du modèle p-médian et de ses
méthodes actuelles de résolution
2.3.1 Le modèle p-médian : une
réalité simplifiée
Le modèle p-médian est uniquement
axé, comme nous l'avons précisé, sur les notions
de distance et de demande dans le cas du modèle p-médian
pondéré. Mais, même si le propos n'est pas
fondamentalement de critiquer le modèle lui-même, il
est évident que le
531 ARMSTRONG J.S. et BRODIE R.J. (1994)
Effects of Portfolio Planning Methods on Decision Making : Experimental
Results, International Research Journal in Marketing 11,
North-Holland, 73-84.
532 KOLEN A. et TAMIR A. (1990) Covering Problems,
Discrete Location Theory de Mirchandani & Francis
Chap. 6, Wiley & Sons.
consommateur ne se fondera pas seulement sur le seul
critère de distance pour choisir son point de vente parmi un
éventail de concurrents. Les autres paramètres jouant sur la
décision des clients peuvent être formulés sous forme de
cinq principes qui guideront la sélection des emplacements
commerciaux533 534:
- le principe d'interception: le point de vente a
d'autant plus de chance de capter la clientèle
que le passage de consommateurs à proximité,
mesuré le plus souvent en terme de trafic piétonnier ou
routier, est important.
- le principe d'attraction cumulative: le
regroupement de commerces dans un environnement géographique proche
d'activités similaires crée souvent une synergie
d'attractivité alors supérieure à la somme des
attractivités individuelles des commerces.
- le principe de compatibilité: de même, le
regroupement d'activités complémentaires permet assez souvent de
parvenir à ce même effet synergique des attractivités.
- le principe de suréquipement: une trop grande
concentration de points de vente a tendance à avoir un effet
répulsif sur la clientèle alors soumis à l'inconfort de la
congestion du trafic.
- le principe d'accessibilité:
l'accessibilité au point de vente, c'est-à-dire la
facilité d'entrer, de pénétrer, de traverser et de
sortir du site commercial doit être le plus facile possible.
Une bonne signalisation, la qualité et le nombre de voies
d'accès, les facilités de parking sont autant de
paramètres à privilégier dans le choix d'un emplacement
convenable.
Une solution que nous proposons pour intégrer tous ces
critères seraient d'introduire dans le
problème p-médian un poids évaluant
chaque site potentiel. Rien n'empêche en effet de
mesurer et de quantifier pour chaque emplacement potentiel des
points de vente les différents critères mentionnés tels
que l'ont fait Lewison et Delozier535 et Jallais, Orsony et
Fady 536.
533 DELOZIER M.W. et LEWISON D.M. (1986)
Retailing, 2nd ed., Merill.
534 CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, p.187-191, Ed. Sirey.
535 DELOZIER M.W. et LEWISON D.M. (1986)
Retailing, 2nd ed., Merill.
536 JALLAIS J., ORSONY J. et FADY A. (1994)
Marketing du Commerce de Détail, Vuibert, Paris.
Puis il convient d'attribuer une note globale à
chaque site potentiel, note résultant d'une pondération de
ces critères. A titre d'exemple, il suffirait d'attribuer des notes par
exemple de
0 (emplacement vraiment médiocre) à 100
(emplacement excellent) pour chaque critère, de
les pondérer avec des coefficients positifs de
manière à quantifier leur importance et d'obtenir une note
globale nj. Cette note introduite dans la fonction objectif avec un signe
négatif (ayant tendance à minimiser avantageusement la
fonction) au même niveau que les distances dij servirait de
pondération à chaque site potentiel d'activité. La
distance dij en tant que critère impliquant à la fois le
commerce et le client considéré devrait alors être
normalisée (sur la même échelle de notes) de manière
à obtenir une homogénéité au sein de la fonction
objectif.
La formulation mathématique du p-médian deviendrait
alors:
Minimiser
i j
ai (dij - nj) xij représente la
nouvelle fonction objectif, (1)
avec
i
xij = 1, i, assure que tous les clients sont
assignés à une activité et une seule, (2)
et dij - nj
0, j assure que toute
activité possède un minimum d'attractivité,
(2)'
xij yj, i, j empêche d'assigner un client à
une activité si elle n'est pas ouverte, (3)
yj = p, le nombre total d'activités est p,
(4)
j
xij, yj {0,1}, i, j nature
binaire des variables xij, yj (5)
où
ai : est la demande au noeud i,
nj: la note positive attribuée au site potentiel du noeud
j, di,j : la distance du noeud i au noeud j,
p : le nombre d'activités à localiser,
xi,j = 1, si le noeud i est assigné à
l'activité j et 0 autrement,
yj = 1, si l'activité j est ouverte et 0 autrement.
On observe que logiquement dans la fonction objectif, plus
l'activité au noeud j est attractive
(note nij importante), meilleure est la fonction objectif
(valeur plus faible) et que l'attractivité
est un réducteur de distance, la valeur
(dij - nj) pouvant être qualifiée de "distance
psychologique" qui est la distance ressentie effectivement par les
consommateurs et non plus seulement la distance routière ou
temporelle537 538. Un autre avantage de cette nouvelle
formulation que l'on pourrait qualifier de "modèle p-médian
généralisé" est qu'elle est soluble
par les méthodes traditionnelles de résolution
du p-médian puisque la forme de la fonction objectif est
similaire (forme linéaire).
2.3.2 La complexité des méthodes de
résolution du p-médian
L'autre reproche déjà évoqué
au niveau du modèle p-MP concerne cette fois ses
méthodes existantes de résolution. Celles-ci sont très
lourdes et même souvent impossibles à mettre en oeuvre si l'on
considère un réseau de plusieurs centaines de milliers de noeuds.
Quelle tâche herculéenne que d'imaginer vouloir trouver une
solution plus ou moins optimale à un réseau comprenant l'ensemble
des clients potentiels d'une future grande surface ! Un autre
problème
du même ordre, mais cette fois dans le domaine
de la gestion informatique serait de considérer le réseau de
communication Internet et les différents micro-ordinateurs, serveurs et
réseaux Intranet le composant (soit des millions d'ordinateurs à
travers le monde): sur quels serveurs (les noeuds d'activités) serait-il
préférable de localiser les données pour que celles-ci
soient acheminées le plus rapidement possible à destination des
autres ordinateurs (les clients)
connaissant les probabilités de requête (les
demandes ) ?
537 HUBBARD R. (1978) A Review of Selected Factors
Conditioning Consumer Travel Behavior, Journal of
Consumer Research, vol. 5, june, p.1-21.
538 VOLLE P. (1999) Du Marketing des Points de Vente
à Celui des Sites Marchands : Spécificités,
Opportunités
et Questions de Recherche, Cahier n°276, Centre de
Recherche DMSP, juin 1999.
Le problème classique du p-médian a pourtant fait
couler beaucoup d'encre, en témoigne le

nombre d'articles où ce modèle est cité (en
excluant les auto-citations):
Fig. 2.13 - Nombres d'articles traitant du p-médian par
année - source: The Scientific Literature Digital Library
Les 225 articles cités sur 30 ans ne s'attaquent
cependant qu'à l'affinage de la résolution du p- médian
à savoir essentiellement améliorer l'optimalité des
solutions à travers de nouvelles heuristiques
d'amélioration (et rarement des algorithmes de
résolution). Les autres publications de recherche traitent
principalement des applications du p-MP en adaptant le modèle
à certains cas particuliers comme l'efficacité des moteurs de
recherche539, le coloriage
de graphes à l'aide du p-MP et d'un algorithme
génétique540 ou encore la localisation de
simulateurs de conduite de char de l'armée américaine au plus
près des casernes541.
2.3.3 L'analyse typologique : une approche pour simplifier
la problématique du p-MP Peu d'articles abordent vraiment la
partie fondamentale, mais ô combien stratégique de la
formulation ou de la modélisation même du problème p-MP.
Si elle est mieux établie, elle permettra de simplifier le
problème et de parvenir à une solution plus rapidement ou
à une
meilleure solution en utilisant un algorithme plus lent mais plus
performant capable de traiter
539 CRASWELL N. et BAILEY P. (1999) Is it fair to
evaluate Web systems using TREC ad hoc, Department of
Computer Science - CSIRO, The Australian National University
Pub.
540 RIBEIRO FILHO G. et NOGUEIRA LORENA L.A.
(2000) Improvements On Constructive Genetic
Approaches To Graph Coloring, Sao José Dos
Campos, Spain.
541 MURTY K.G. et DJANG P.A. (2000) The US Army
National Guard's Mobile Training Simulator Location and Routing Problem,
US Army Training and Doctrine Analysis Command, Dept. of IOE,
University of
Michigan.
les modèles intégrant un très grand
nombre de noeuds. Cependant, il est à noter qu'un
problème assez étudié et à la mode est
celui de l'analyse typologique (cluster analysis en anglais).
Déjà évoqué par Aristote, cette dernière
consiste à partitionner un ensemble d'entités
en sous-ensembles bien séparés et homogènes
selon un certain nombre de paramètres. Dans le domaine de
l'identification de classes, on peut recenser dans la littérature deux
approches qui
se sont développées, la première
étant celle de la reconnaissance déterministe et de
décision
par sélection de distance; la seconde est
statistique car elle a pour base des probabilités acquises lors
d'une phase d'apprentissage et une décision par
sélection de pénalisations
encourues. En particulier, la classification
séquentielle utilisée par de nombreux chercheurs
dans les procédures de reconnaissance de forme se rattache
à cette dernière approche542 543 544
545 546 547 548. Il existe également
des méthodes de segmentation fondées sur un algorithme
génétique associé à un modèle de
régression549.
Fig. 2.14 - Un exemple de 3 classes , et identifiées par
les variables x1, x2, x3
542 DUDA R.O. et HART P.E. (1973) Pattern
Classification and Scene Analysis Editions J. Wiley, New York, N.Y.
543 TOU J.T. et GONZALEZ R.C. (1974) Pattern
Recognition Principles, Edition Addison-Wesley, Reading,
Mass.
544 FU K.S. (1968) Sequential Methods in Pattern
Recognition and Machine Learning, Editions Academic Press, New York,
N.Y.
545 PAVLIDIS T. (1977) Structural Pattern
Recognition, Editions Springer-Verlag, New York, N.Y.
546 PATRICK E.A. (1972) Fundamentals of Pattern
Recognition, Edition Prentice-Hall, Englewood Cliffs, N.J.
547 POSTAIRE J.G. (1987) De l'Image à la
Décision, Editions Dunod-Informatique Bordas, Paris.
548 CHEN C.H. (1973) Statistical Pattern
Recognition, Editions Spartan Books, Rochelle Park, N.J.
549 AURIFEILLE J.M. (2000) A Bio-mimetic
Approach to Marketing Segmentation : Principles and
Comparative Analysis, European Journal of Economic and Social
Systems 14 N°1, p. 93-108.
Si l'analyse typologique intéresse principalement le
domaine des mathématiques statistiques, elle recense également
des applications dans le domaine de la localisation et du problème p-
médian550 (voir son utilisation au § 2.4.2.4. dans la
délimitation des zones de chalandise). Un exemple récent est
représenté par la décomposition de la Suisse ou
plutôt des 2863 principales communes suisses en 23 cellules
associées chacune à un centre urbain551 selon
diverses
méthodes comparées: p-médian,
méthode Alt552, algorithme de
décomposition553. Le
problème est en premier lieu d'identifier les 23
centres urbains et d'y affecter ensuite des communes selon le
critère du plus proche voisin en terme de distance à vol
d'oiseau. Selon notre point de vue, cette analyse typologique
géographique peut conduire en quelque sorte à une simplification
du problème p-médian, dans le sens où, plutôt que
prendre comme noeuds
du réseau l'ensemble des 2863 communes au sein
desquelles on rechercherait une ou plusieurs localisations optimales, on
pourrait plus aisément considérer les 23 centres urbains
comme étant les noeuds d'un réseau p-médian
simplifié: l'étape d'analyse typologique constituerait une
étape amont destinée à constituer ce réseau
p-médian simplifié (avec comme noeuds les 23 centres
urbains) préalablement à sa résolution.
Mais, cette manière de simplifier le
problème p-médian comporterait de nombreuses limitations
dont celle en premier lieu de devoir spécifier à l'avance en
combien de classes (et donc de noeuds du futur réseau p-médian
simplifié) il conviendrait de partitionner l'ensemble des
entités de départ: ainsi, dans le problème
précédent, il a été fixé
d'entrée de jeu de partitionner le territoire suisse en un nombre de
23 cellules associées à 23 centres urbains sans
que ce nombre ait été ultérieurement
justifié.
550 ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de Doctorat, Lille.
551 TAILLARD E.D. (1996) Heuristic Methods for Large
Centroid Clustering Problems, Technical Report Idsia
96-96, Idsia.
552 COOPER L.G. (1963) Location-Allocation Problems,
Operations Research 11, 331-341.
553 TAILLARD E.D. (1996) Heuristic Methods for Large
Centroid Clustering Problems, Technical Report Idsia
96-96.
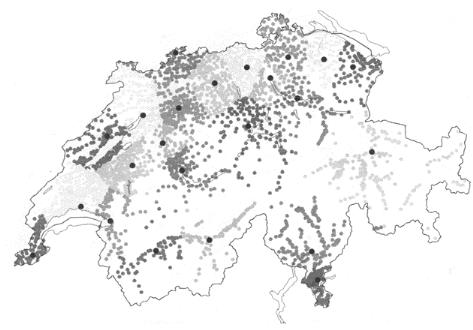
Fig. 2.15- Partition des communes suisses en 23 cellules
représentées chacune par un centre urbain 554
Les exemples personnels suivants illustrent le principe de
l'analyse typologique utilisée dans
le cadre du p-médian et l'erreur dans la recherche
d'une localisation optimale qui peut résulter d'un nombre
prédéfini de partitions. D'abord, un cas où l'approche de
l'analyse typologique fonctionne bien: considérons 76 villes de
même taille réparties sur un territoire, chaque ville étant
représentée par un cercle :
554 TAILLARD E.D. (1996) Heuristic Methods for Large
Centroid Clustering Problems, Technical Report Idsia
96-96, Idsia.
Fig. 2.16 - Les 76 villes représentées chacune par
un cercle
Si l'on décide de partitionner l'espace
géographique en deux par la méthode des k-plus
proches voisins (k=2) par exemple, on aura deux régions A et B avec
leurs centres respectifs,
les noeuds a et b:
Fig. 2.17 - Partition des 76 villes en 2 ensembles
Prenons comme poids des noeuds a et b de ce réseau
pondéré, l'importance de la population représentée
respectivement par le nombre de villes des deux ensembles soit 39 villes
et 37 villes. Alors la localisation optimale d'une activité
unique selon le problème 1-médian sera choisie au noeud a
car il a un coefficient de pondération plus important. Mais, si l'on
choisit un nombre de partitions égal à 4, on obtient alors la
répartition suivante avec chacun des noeuds reliés aux noeuds de
ceux des autres ensembles les plus proches:
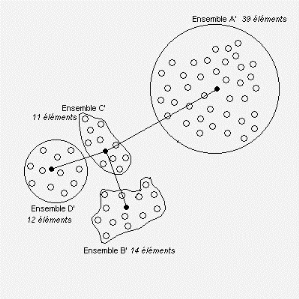
Fig. 2.18 - Partition des 76 villes en 4 ensembles
Le centre optimal est alors situé sur le noeud de
l'ensemble A' qui correspond bien au noeud a
de l'ensemble A précédemment. Si on
considère maintenant le contre-exemple suivant avec 3
partitionsde 17 villes, la droite verticale passant par O
étant la droite médiane du segment ab:
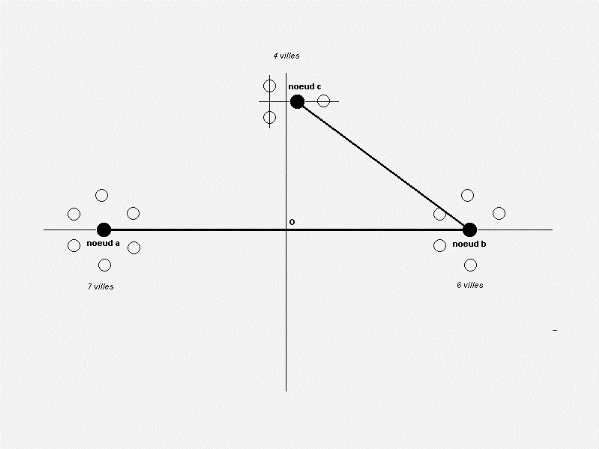
Fig. 2.19 - Partition de 17 villes en 3 ensembles
Selon le modèle 1-médian, le centre optimal est
situé au noeud b. En considérant une partition
en deux ensembles, le centre optimal est cette fois
situé au noeud a puisque que sa partition a
une pondération plus élevée en nombre de
villes (9 villes):
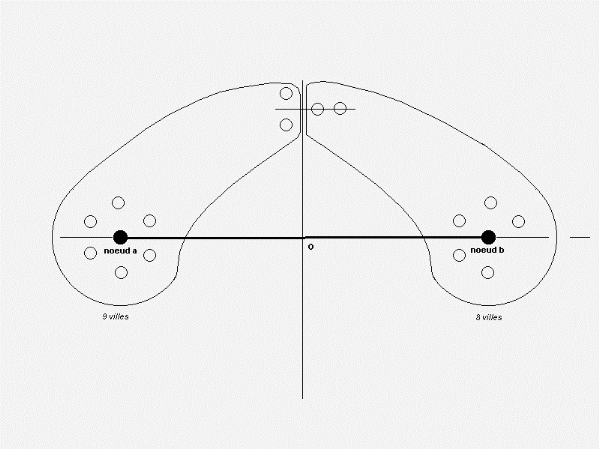
Fig. 2.20 - Partition des 17 villes en 2 ensembles
De plus, on peut se poser la question de savoir si certaines
villes, ou paquets de villes, très éloignées valent ou non
la peine d'être prises en compte dans l'étude de localisation:
quel que soit leur potentiel de clientèle même faible, leur
éloignement a tendance à attirer vers elles le (ou les) site(s)
à implanter sans que cela ne vaille peut-être la peine.
Dans l'exemple précédent, la partition constituée des
quatre villes du noeud c est d'une importance moindre devant les deux autres
partitions des noeuds a (7 villes) et b (6 villes). Si le problème
était de livrer un produit ou un service à partir du noeud a
à un ensemble de clients, faudrait-il intégrer
les clients associés au noeud c qui, compte tenu du
faible potentiel et du coût de déplacement, engendrerait une
faible rentabilité ? La réponse à cette question n'est pas
fournie par l'analyse typologique et ses méthodes de partition qui
traitent le problème d'une manière brute et
mathématique.
Outre le fait de fournir des résultats
rationnels, le développement de méthodes plus
performantes dans la recherche de localisations optimales
doit conduire à notre sens, à
améliorer la capacité du p-médian
à traiter des réseaux de plus en plus importants afin
de modéliser de manière plus précise le monde réel
et pouvoir prendre en compte par exemple l'ensemble des clients d'une grande
surface, le réseau Internet et ses nombreux ordinateurs, la
totalité des entrepôts d'un transporteur,...
Conclusion
Ainsi, les théories de la localisation rassemblent un
certain nombre de modèles dont certains comme le modèle de
Christaller ou la loi de Hotelling, deviennent plutôt des
curiosités intellectuelles en présentant la réalité
sous un jour très idéal, mais permettent néanmoins de
prendre conscience des phénomènes non-aléatoires de
répartition des activités commerciales dans l'espace. D'autres
modèles dérivant de la loi de Reilly comme les modèles MCI
ou MNL
ont permis d'analyser les variations de
fréquentation selon les caractéristiques de
l'environnement ou du point de vente considéré. Leur mise
en oeuvre pour répondre aux problématiques de localisation
reste cependant ardue d'une part par le fait qu'il faille identifier
précisément quels sont les paramètres fondamentaux jouant
sur le choix des consommateurs
de tel ou tel magasin en se fondant sur l'expérience,
et d'autre part, car il est nécessaire de rassembler les données
relatives à ces paramètres avant de lancer l'analyse : rien ne
prouve d'un autre côté que les paramètres identifiés
dans une zone soient transposables dans celle où l'on recherche un ou
plusieurs emplacements commerciaux. Les modèles de localisation
multiple comme le modèle p-médian jouent essentiellement
sur la notion de distance en choisissant les sites les plus proches d'une
clientèle potentielle. D'autres variables comme le coût
d'ouverture des points de vente, les coûts de déplacement
ou même une mesure de
l'attractivité des points de vente avec le modèle
Multiloc555, peuvent être pris en compte dans
ces modèles ce qui est susceptible de les
rendre assez intéressants pour la recherche de localisations
multiples optimales. Mais, les algorithmes approchés permettant de
résoudre ces problèmes élaborés, trop lents, ne
sont pas suffisamment performants pour être utilisés tels
quels. Partant d'une base de données de clients potentiels, le processus
initial de modélisation conduisant à un réseau de
localisation-allocation s'avère souvent être une tâche
difficile.
555 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc : A Multiple Store Location Decision
Model, Journal of Retailing, 58.
Alliés au modèle le plus adapté
à la localisation multiple de points de vente
c'est-à-dire le modèle p-médian, les principes du
traitement du signal introduits dans le chapitre suivant
réussiront à surmonter ces difficultés en facilitant
considérablement à la fois la modélisation d'un
réseau de localisation-allocation et la résolution de ce
modèle. D'autres avantages
complémentaires apparaîtront à la lecture de
l'exposé.
Chapitre 3
L'apport du traitement du signal dans le modèle
p-médian
Introduction
Comme nous l'avons vu au chapitre précédent, la
problématique de recherche de localisations optimales mérite
d'être repensée à la fois sur le plan de la
modélisation et au niveau de la résolution ultérieure
du modèle. Pour cela, il nous est apparu comme pratiquement
logique que les informations concernant la clientèle potentielle des
futurs points de vente devaient être réagencées et si
nécessaire "pré-digérées" au lieu de se
lancer à corps perdu dans la construction d'un modèle
trop complexe à résoudre. Ce pré-traitement peut
être réalisé en faisant appel à une technique de
traitement de l'information assez élaborée et
dénommée dans
le jargon scientifique «traitement du
signal». Le traitement du signal est un domaine d'importance
si l'on s'en réfère aux 50 000 ingénieurs
travaillant sur ce sujet directement à travers le monde et
plusieurs centaines de milliers indirectement. Cette science bien
qu'inconnue il y a cinquante ans, s'est discrètement introduite
dans notre vie quotidienne à travers l'électronique,
l'informatique ou les télécommunications. On pourrait
qualifier le traitement du signal de technique capable de
réaliser des opérations variées sur une
information quantifiable dont la valeur est mesurable sur une certaine
période. Ces opérations peuvent être une simple conversion
(par exemple entre informations analogiques et digitales), une compression de
l'information pour minimiser le nombre de données qui la
caractérise, une correction d'erreur, une amplification destinée
à accroître l'amplitude de cette information,...
Or, malgré la richesse de la recherche en traitement du
signal, sa contribution aux sciences de gestion et en particulier au
géomarketing s'avère pour l'instant très mince. Nous
verrons au cours de ce chapitre que le traitement du signal se combine pourtant
très harmonieusement aux modèles de localisation-allocation
en particulier au modèle p-médian pour faciliter la
recherche de localisations multiples.
3.1 Une nouvelle approche du p-MP par le traitement du
signal : premier aperçu d'un nouvel algorithme rapide de
multilocalisation d'activités
Nous avons abordé le problème de recherche
de localisations optimales par une approche modélisatrice.
L'approche modélisatrice passe par une attention portée à
ce qui est représenté, mais aussi à la symbolisation de ce
qui est représenté, donc aux fondements et aux
propriétés même de la projection556. "Le
système de modélisation est récursif,
s'établissant dans l'interaction entre le système
modélisé (le phénomène perçu comme complexe)
et le système modélisant. [...] Le système de
modélisation (le modélisateur concevant et
interprétant le modèle d'un système complexe) se comprend
comme s'auto-finalisant : il élabore ses projets,
il est projectif "557. Ainsi, le premier
niveau de notre réflexion est global et peut nous conduire
à retenir une méthodologie. Ensuite, les
idées vont se transformer en variables au niveau du système,
"cet ensemble d'unités en interrelations
mutuelles558" qui seront alors analysées et
organisées pour parvenir à des conclusions en effectuant
un retour vers le niveau initial (processus récursif).
Ceci nous a conduit à élaborer un algorithme du
type poupées russes. Son organigramme sera d'ores et déjà
présenté étant donné que certaines de ses
fonctionnalités, comme la délimitation
de zones de chalandise, mériterons d'être
améliorées vis-à-vis de l'état de l'art
existant (cf. chapitre II). La modélisation des données a
été faite par une analyse systémique de la zone de
chalandise composée de la demande 'les clients). Il s'agit de
définir un modèle de données de
la zone de chalandise composée d'objets
c'est-à-dire les aires de la zone de chalandise denses
en clientèle (voir pages suivantes). Cette approche
correspond à l'idée de modélisation
556 MABILLOT V. (2000) Mises en Scène
de l'Interactivité : Représentations des Utilisateurs dans
les
Dispositifs de Médiations Interactives, Thèse
soutenue le 7 janvier 2000, Université de Lyon II, p.6
557 LE MOIGNE J.L. (1990) La modélisation
des Systèmes Complexes, Bordas, Paris, 178p.
558 VON BERTALANFFY L. (1968) Théorie
générale des systèmes, Trad. fr. par J. B. Chabrol.,
Dunod, Paris.
projective avancée par Le Moigne où le
territoire géographique est analysée à
différentes échelles 559.
Rappelons et résumons tout d'abord à nouveau la
problématique à résoudre.
Problématique:
Trouver les localisations optimales pour un ensemble de p
activités destinées chacune à servir
un ensemble de clients, de telle manière que la somme
totale des distances de l'ensemble des activités à ses clients
soit minimale, avec la contrainte que le nombre n de clients est
élevé. Les données disponibles sont au minimum la
localisation spatiale des clients représentée par exemple par
leurs adresses, le nombre p d'activités à localiser et
éventuellement le niveau de demande de chaque client quant aux services
ou aux produits offerts par lesdites activités.
L'algorithme recherchera une solution globale avant de
s'attaquer à la recherche d'une solution locale ce qui permettra de
simplifier le problème. Voici l'organigramme de l'algorithme
proposé :
559 CRAUSAZ P.A., MUSY A., MATTEI A. (1999) GESREAU :
GESREAU: Ein Konzept für ein Integriertes
Management der Fliessgewässer, Rapport de l'Hydram, Suisse,
p.6
Nous proposons dans ce cadre l'algorithme global suivant qui
prendra en compte les données
disponibles pour les traiter dans l'optique de résoudre la
problématique exposée :
Initialisation:
Echelle Globale
Géocodage: Repérer
les
1 clients à l'aide de leurs
coordonnées spatiales.
Délimitation: Délimiter des
zones homogènes de
2 localisation de clients à
l'aide de filtres et/ou d'un
algorithme morphologique.
Identification des centres
3 de gravité: les centres de
gravité constitueront les
noeuds d'un réseau.
Changement d'échelle: Echelle plus fin e,
locale
Résolution du p-MP: les
4 algorithmes du p-médian sont
utilisés pour trouver les
p localisations d'activités.
La résolution est-
elle suffisante ?
Non
Oui
Fin
Fig. 3.1 - Organigramme du nouvel algorithme proposé
Explicitons le fonctionnement de cet algorithme
avant d'étudier plus précisément ses
différentes fonctions: notre procédure de recherche de
localisations optimales comprend donc quatre phases suivies d'une boucle de
rétroaction. Elle fonctionne en quelque sorte par effet
loupe en s'attachant dans un premier temps à
déterminer les meilleurs emplacements au niveau global, par exemple
au niveau national, puis à faire une boucle pour réitérer
le même processus mais au niveau local. Les noeuds du
modèle p-médian sont constitués dans un premier temps
des zones géographiques (zones de chalandise) dans lesquelles la
densité de clients est homogène et plus importante qu'ailleurs.
Les frontières de ces zones de chalandise seront
déterminées, comme nous le verrons plus loin, par les
méthodes classiques utilisées en traitement du signal qui
rassemble en fait un ensemble d'outils mathématiques
destinés à extraire de manière rapide des informations
précises d'une source.
Dans un second temps, on se concentrera sur les p
noeuds calculés par l'algorithme de résolution et on
déterminera au sein de chacun de ces p zones géographiques
à nouveau un certain nombre de noeuds constitués de la
même manière de zones de clientèle homogènes
mais au niveau local cette fois. Le modèle p-médian (ou
un autre modèle incorporant des paramètres de coût, de
concurrence ou des critères socio-économiques) sera
ré-appliqué dans chacune de ces p zones locales de
manière à améliorer la précision de
localisation des activités.
Les dessins suivants résument le fonctionnement de
ce nouvel algorithme fondé sur la délimitation de zones de
chalandise.
1
La phase 1 consiste à codifier les
adresses de clients potentiels ou réels
en termes de coordonnées géographiques, adresses
tirées d'une base de données. On pourra alors obtenir une
représentation cartographique des différentes localisations de
la clientèle, chaque client étant représenté
par un point.
2
La phase 2 correspond à la
délimitation des "paquets" de clients ou aires appartenant
à la zone de chalandise. Nous utiliserons dans cette optique les
techniques de traitement du signal qui font aussi l'originalité
de notre démarche.
3
On calculera dans la phase 3 les
coordonnées des centres de gravité
de chaque aire délimitée dans la phase
précédente de manière à modéliser un
réseau: les noeuds du réseau seront représentés par
les centres de gravité et les segments par les distances
routières ou par un indicateur d'éloignement (temporel,
kilométrique, généralisé...). Des localisations
potentielles supplémentaires pourront d'autre part être
introduites comme noeud même si elles ne comptent pas de
clients. Ce réseau peut être, si nécessaire,
pondéré et dans ce cas, à chaque noeud sera
affecté un poids représentatif de l'importance de
la clientèle ou de son potentiel.
4
Dans la phase 4, le réseau sera
résolu sur la base du modèle p-médian grâce aux
algorithmes classiques de résolution et d'amélioration. On
aboutira donc au choix de certains noeuds comme localisations
optimales.
Rétroaction et changement d'échelle:
après avoir identifié les p noeuds optimaux par
l'algorithme du p-médian, on pourra, si un degré de
précision supplémentaire s'avère nécessaire,
réitérer le processus en se concentrant cette fois au niveau de
chaque noeud. L'examen d'aires de plus en plus petites pour améliorer la
finesse du choix de localisation pourra se faire autant de fois que
souhaité sous réserve de l'existence d'un nombre suffisant
de clients ou d'emplacements potentiels à cette échelle.
Ainsi, la partie centrale et novatrice de cette méthode
est constituée par la délimitation des
aires de chalandise (zones denses de clientèle appartenant
à la zone de chalandise) au niveau
desquelles il sera possible de définir un centre de
gravité caractérisant la localisation spatiale
de ladite aire. Ces centres de gravité
constitueront les noeuds d'un modèle p-médian. Il est donc
fondamental de définir avec précision les contours de
ces aires de chalandise: une évaluation grossière des
frontières induira nécessairement un repérage des centres
de gravité entachés d'erreurs ce qui ne manquera pas de se
répercuter sur le résultat final de localisation des p centres au
niveau global et plus encore au niveau local. La deuxième innovation
découle
du fait que l'on simplifie le problème en
l'appréhendant de manière globale grâce à
l'identification de "paquets" de clients, et qu'ensuite seulement, on
pousse l'analyse dans le détail en recherchant dans les zones
intéressantes des emplacements plus précis toujours en utilisant
la délimitation d'aires de chalandise caractérisées
par leurs centres de gravité et le modèle p-médian.
Cette technique utilise à la fois des principes de la localisation
discrète (à travers le modèle p-médian) et
celles du modèle planaire (à travers le calcul de
centres de gravité).
Le prochain paragraphe donnera tout d'abord
l'occasion de récapituler les techniques existantes de
traitement du signal, puis de montrer leur capacité à
s'intégrer dans une problématique de multilocalisation
d'activités du type p-médian.
3.2 Méthodes de délimitation fondées
sur le traitement du signal et l'analyse d'image
La première étape de l'algorithme introduit
précédemment et destiné à localiser un ensemble
de points de vente avec un bon niveau
d'optimalité consiste à délimiter les zones de
chalandise. Or, comme on l'a vu au chapitre 1, les méthodes
actuelles de délimitations comportent un grand nombre de lacunes et
d'imprécisions.
3.2.1 Introduction au traitement du signal et à
l'analyse d'image
Les limitations précédentes se devaient
d'être surmontées en introduisant une nouvelle approche pour
délimiter les aires composant la zone de chalandise ou même toute
autre zone géographique possédant des
caractéristiques commerciales, économiques, sociologiques
propres. Cette nouvelle solution devait à la fois être rapide,
précise et pouvoir être convertie
en algorithmes de manière à pouvoir être mise
en application sur ordinateur et de préférence sur les
calculateurs les plus courants du marché, c'est-à-dire les
micro-ordinateurs.
Pour répondre à ces exigences, il est un
fait que les algorithmes nécessitant la plus grande vitesse
d'exécution sont ceux fonctionnant en dynamique. Dans ce cas, les
informations issues
de capteurs sont fournies en temps réel au calculateur
qui les traite au même rythme que les données sont
prélevées. Outre les applications purement
électroniques, les domaines qui utilisent ce genre de
traitement d'information ne sont pas légion et se
rassemblent essentiellement autour du traitement du signal. Le traitement du
signal vise à interpréter une information possédant une
certaine continuité soit dans le temps, soit dans l'espace. Il s'agit
ainsi d'arriver à distinguer, dans la masse de données, les
informations non-aléatoires, et de caractériser ces
données atypiques pour éventuellement les reconnaître
à chaque fois qu'elles
se présenteront à nouveau. De nombreuses
applications utilisent les principes du traitement du signal dont la plus
élaborée est la vision artificielle, une technique
complémentaire de la robotique. D'autres disciplines font largement
appel au traitement du signal comme toutes les sciences désireuses de
rendre de façon automatique le résultat de leurs observations.
Ainsi,
ont procédé la cristallographie et la
biologie en microscopie électronique, la médecine en
échographie et radiographie, la géographie et la géologie
pour traiter les images prises d'avion
ou de satellite, l'acoustique pour les signaux sonores, la
climatologie dans l'interprétation des
images radars, la physique pour l'examen des spectrographes,
etc... Les premières études sur
la vision artificielle furent menées à
partir de 1950 par Gibson 560 à Boston puis dans
les années 60 dans le domaine de la recherche spatiale en particulier
pour tout ce qui concerne le traitement des images provenant des sondes et des
satellites. Plus tard, la robotique, avec les travaux de Binford 561
et de Horn 562 563, a pris le relais dans le
développement de ce domaine récent qui allait désormais
s'appeler visionique ou computer vision en anglais.
On observe une grande similitude entre les
données issues de capteurs électroniques ou optiques et les
données géomarketing. Ces données, quelle qu'en soit la
source, sont en effet variables dans l'espace et dans le temps. D'autre part,
les capteurs ou les moyens d'obtention des informations marketing
n'étant pas parfaits, elles comportent toutes des erreurs de mesure soit
aléatoires du type neige, soit de type absences d'information,
soit encore de type perturbations hautes ou basses fréquences
liées à des interférences dans le cas de capteurs
"physiques" ou liées au mode de collecte des données dans le cas
de données géomarketing.
McKay 564, de l'Université d'Indiana, fut le
premier à avoir noté que les données
géomarketing
comportaient un signal de base avec une perturbation,
le bruit, à éliminer par un filtrage approprié. Son
travail s'est malheureusement limité à un filtre médian de
base sans explorer toutes les possibilités qu'offre la science du
signal.
Il y a quatre étapes fondamentales qui se succèdent
d'une façon générale dans le processus d'analyse du signal
et qui sont dans l'ordre:
%o l'acquisition des données par un
capteur, dans le cas du géomarketing, ce capteur prenant la forme
d'une enquête auprès d'une population donnée de clients
effectifs, de
clients potentiels, de non-clients ou de toutes autres
informations commerciales
560 GIBSON J.J. (1950) The Perception of the
Visual World, Editions Houghton-Miffin, Mass., Boston.
561 BINFORD T. (1971) Visual Perception by Computer,
IEEE Systems Science & Cybernetics Conference, FA, Miami.
562 HORN B.K.P. (1975) The Psychology of Computer
Vision, Editeur P.Winston, NY.
563 HORN B.K.P. (1986) Robot Vision,
Editions MIT, Press Mc Graw-Hill, NY.
564 MCKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
quantifiées et liées à une
localisation géographique précise. Dans le cas de
données d'adresses, celles-ci sont géocodées afin
d'obtenir une cartographie représentant l'ensemble des clients
potentiels.
%o le pré-traitement des données
destiné à éliminer les imperfections du capteur
ou de
la source d'information à savoir dans le cas d'une
enquête marketing, les non-réponses
ou l'absence de réponse, les fausses
réponses, les erreurs d'échantillonnage ou les biais,
%o le traitement à proprement parler
qui s'attache dans notre problématique à détecter
par des algorithmes les frontières de la zone de chalandise,
%o l'exploitation des résultats qui
vise à caractériser les informations extraites de la
masse des données, ici, en l'occurrence, il s'agit de donner les
caractères propres à la zone de chalandise,
c'est-à-dire les paramètres géométriques qui
vont nous servir à construire le modèle p-médian tels
que les coordonnées des centres de gravité (noeuds
du réseau) de chaque aire composant la zone de
chalandise ou éventuellement la surface de ces aires (qui pourra
constituer une possibilité de mesure de la demande).
Nous allons maintenant décrire plus
précisément les étapes de pré-traitement
et de délimitation des zones de chalandise sachant que nous supposons
avoir obtenu à ce stade une cartographie des données d'adresses
clients. Les deux étapes suivantes seront illustrées par des
exemples concrets de délimitation de zones de chalandise
théoriques. A noter que la répartition de clients dans
l'espace va être prise en considération à titre d'exemple,
mais on aurait aussi bien pu, en suivant les mêmes
méthodes, s'attacher à la délimitation de zones
d'implantation de commerces ou d'activités de services.
3.2 2 Le géocodage et la représentation des
données géomarketing
La première phase de notre algorithme consiste donc
à repérer les coordonnées géographiques des
clients: leur localisation conditionnera en effet le choix
d'une (ou de plusieurs) localisation(s) d'activités. Supposons
qu'on connaisse la localisation géographique de la
clientèle d'un point de vente. Une base de données
d'adresses peut être construite grâce à l'information
obtenue à partir:
1- des cartes de fidélité (grands magasins,
chaînes) 
2- des modes de paiement comme les chèques (magasins,
banques)

3- des bulletins d'un jeu-concours spécialement
organisé pour l'occasion 

4- d'un repérage des immatriculations des véhicules
sur le parking
s)
5- d'une enquête directe (questionnaire auprès des
client

.
En utilisant en premier lieu, la méthode empirique, on
représente chaque adresse client par un
point sur un graphique correspondant au plan
géographique 2D (géocodage), on obtient un nuage de points
dont la densité varie dans le plan en fonction de la
concentration de la clientèle. Les amas de points figurent les zones
de chalandise à partir desquelles le point de vente tire l'essentiel de
sa clientèle. L'oeil humain réussit assez bien, en visualisant
une telle carte, à délimiter les frontières de ces
amas grâce à ses fonctions performantes d'analyse spectrale.
Ceci dit, la vision humaine n'est pas parfaite et un examen visuel, outre le
fait que
ce mode de procédure, pour délimiter les zones de
chalandise, est long et fastidieux, risque de
conduire à des erreurs d'interprétation.
La délimitation analytique des aires denses
s'avère aussi difficile sur le plan mathématique mais
nécessaire néanmoins si l'on veut non seulement bien
connaître sa clientèle, par exemple pour de futures
opérations promotionnelles (mailing par quartier), mais aussi pour
s'assurer de
la bonne localisation de ses points de vente.

Y
O X
Fig. 3.2 - Exemple de représentation de clients sous forme
de pixels
Si l'on revient au cas précédent,
l'analyse peut porter sur les données d'adresses clients
précédemment évoquées ou bien encore sur les
données de fréquentation du point de vente. A chacun des k
clients C1,...Ck , recensés, on peut associer une fréquentation
du point de vente respectivement f1,...,fk sur une période T qui est
choisie de manière adéquate (une semaine, un mois, un an,...)
selon le type de point de vente considéré.
Les données d'enquête sont de type discret tout
comme les données graphiques numériques,
ce qui facilite leur représentation visuelle (Le
présent exposé mathématique pourrait être
établi sans mise en parallèle avec une quelconque
représentation visuelle, mais cette approche
en facilite la compréhension).
Chaque adresse d'un client Ci correspond à un point
allumé soit un pixel noir de coordonnées
(xi, yi) dans une base orthonormée (OX,OY) : i
variant de 1 à n et j de 1 à m pour un
découpage de la région géographique analysée en n x
m petites zones (xi,yi). Le pixel noir (présence d'au moins un
client) ou blanc (absence de client) correspond dans ce cas à
un élément de l'espace géographique quadrillé sous
forme d'un réseau carré. Ceci dit, le réseau carré
(matriciel), bien que très pratique, n'est pas forcément la
partition la plus adéquate de l'espace géographique, car celle-ci
ne conserve pas les propriétés topologiques du monde
réel,
et en particulier la propriété de connexité
(contrairement au réseau hexagonal).
Pour améliorer la représentativité de
la zone de chalandise, on peut faire correspondre à chaque
pixel un niveau linéaire de gris (ou de couleur) en fonction soit du
nombre de clients dans la zone (xi,yi), soit de la somme f = fij
des fréquentations du point de vente par l'ensemble des clients de
la zone (xi,yi) sur une période T. Ce codage est souhaitable lorsque
le quadrillage de la zone géographique possède une
faible résolution (peu de pixels). D'autres
variables peuvent être bien sûr prises en compte
selon les préoccupations de l'analyse, comme
le chiffre d'affaires (ou la rentabilité)
lié à chaque client sur une période de temps. Si
l'on considère par exemple chaque pixel d'une matrice carrée 512
x 512, formé d'une information codée sur 8 bits, on a alors
256 niveaux de valeurs disponibles pour chaque point pour un
encombrement mémoire sur 256 k octets. Le dessin suivant montre
une possibilité de représentation des points-clients sur une
carte bidimensionnelle.
Y
O  X
X
Fig. 3.3 - Exemple de localisation de clients associés
à leur fréquentation, sous forme d'un nuage de pixels en niveaux
de gris
Il existe cependant de nombreuses possibilités
différentes de représentations graphiques des
données géomarketing que par des points comme :
%o la projection cavalière qui est une
représentation en 3 dimensions des données
géomarketing (exemple: niveau de fréquentation des clients d'un
magasin) dans l'espace géographique:

Fig. 3.4 - Exemple de projection cavalière
%o les lignes de Niveau délimitant les
frontières de zones possédant des valeurs homogènes
(exemple: niveaux d'équi-fréquentation):
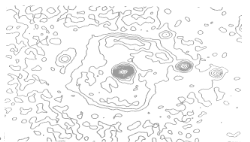
Fig. 3.5 - Exemple de lignes de niveaux
%o le code Ternaire qui est une simplification de
la représentation ponctuelle. Ce code de représentation ne
possède que 3 valeurs possibles avec par exemple, si l'on
considère les différents types de zones d'une ville en termes de
fréquentations d'un point de vente, les zones comptant au moins un
client (point foncé), les zones comptant uniquement des
habitants non-clients (point clair) et les zones urbaines sans
habitants (en blanc):

Fig. 3.6 - Exemple de représentation en code ternaire
Après avoir vu les modes de représentation
possible des données géomarketing et la manière d'obtenir
les adresses, l'étape suivante consiste à délimiter les
aires denses en terme de clients dont le regroupement est appelé
communément "zone de chalandise" (la zone concentrant au mieux le
meilleur du potentiel commercial). Après avoir rappelé les
différentes approches de
ces aires dans la littérature, nous nous proposons
d'introduire de nouvelles méthodes de délimitation pour
pallier le manque de précision et de rapidité des méthodes
actuelles.
3.2.3 Le prétraitement des données par
filtrage
Le prétraitement des données d'enquête
est destiné à faciliter l'analyse des données sans
réduire la qualité de l'information disponible, bien au
contraire. En traitement du signal, la principale méthode
consiste en un filtrage ondulatoire (une image ou une enquête
sur un secteur géographique étant une onde bidimensionnelle). On
cherchera ainsi non seulement à accentuer le crénelage
(accentuation des contours entre les zones de différentes
caractéristiques à peu près homogènes), mais
aussi à s'affranchir de la pollution par des données
atypiques (bruit) dues par exemple à des erreurs
d'enquête (ex. mauvaise administration ou saisie), aux fausses
réponses (ex. fausse adresse) ou tout simplement à des
réponses marginales au sein de la zone de caractéristiques
homogènes.
Comme on l'a déjà vu, McKay est le premier à
avoir utilisé la technique du filtrage sur des
données de localisation spatiale d'un
échantillon de clients 565 en constatant que ces
informations étaient composées d'un signal fondamental de base et
d'un signal perturbateur ou bruit dont il fallait s'affranchir. Mais, cette
imperfection des données n'était pour lui que le fait
de fortes différences comportementales entre des
consommateurs habitant à proximité les uns des autres, alors
que le bruit trouve aussi son origine dans des informations
erronées ou manquantes. Etudiant un échantillon d'une
centaine de clients seulement, le traitement des données
s'était limité à l'utilisation d'un filtre binomial
(filtrage en moyenne pondérée) du
type:
1 / 16
C = [cmn]= 2 / 16
1 / 16
2 / 16
4 / 16
2 / 16
1 / 16
2 / 16
1 / 16
avec, si Zij représente la valeur
mesurée au point de localisation (Xi, Yi), une
nouvelle valeur
Wij modifiée par ce filtre est donnée par :
M N
W ij
=
m = -M n = -N
cmn Z i + m,
j + n
le filtre ayant pour dimension 2M+1 par 2N+1 (c'est-à-dire
M= et N =1 pour le filtre binomial
précédent). Comme on va le voir, le filtre binomial
bien qu'éliminant le bruit lié par exemple à des erreurs
d'enquête n'est pas le plus recommandé pour conserver les
contours.
Le filtrage spatial repose d'une manière
générale sur des opérations ponctuelles appliquées
de manière itérative sur chaque valeur ou agrégat de
valeurs d'une matrice ou d'une image (en quelque sorte des opérations
portant sur les aires géographiques regroupant des clients d'un niveau
moyen de fréquentation homogène). Les filtres spatiaux les plus
courants sont:
565 McKAY D.B. (1973) Spatial Measurement of Retail
Store Demand, Journal of Marketing Research, 10, 4, p.
447-453.
- le filtre en moyenne
- le filtre médian
- le filtre sigma
- le filtre Nagao
Il est également intéressant d'utiliser la
transformation de dilatation lorsque les points
représentant les clients sont assez éloignés les uns des
autres et qu'il n'y alors pas possibilité
de distinguer de forme claire de la zone de chalandise.
Le filtre en moyenne
Ce traitement revient à traiter la matrice de
données en prenant comme nouvelle valeur de chaque point, la
moyenne du point considéré aggloméré avec ses
voisins. Il correspond en fait
au filtre binomial avec des coefficients de pondération
égaux à 1. Dans une matrice, chaque élément
(excepté sur les bords) compte 8 voisins adjacents de
même que sur une image à matrice carrée.

Fig. 3.7- 8 voisins adjacents à un point central
Ainsi, la nouvelle valeur f 'i,j de fi,j est :
f 'i,j = [fi,j + fi+1,j+1
+ fi+1,j + fi,j+1 + fi-1,j-1 +
fi-1,j + fi,j-1 + fi+1,j-1 +
fi-1,j+1] / 9
Ce procédé comme tous les filtres binomiaux en
général a l'inconvénient de lisser les données mais
lisse aussi les transitions (les bords d'objets à fort gradient
d'intensité deviennent souvent
flous). Très simple, rapide, il n'est à utiliser
que lorsque la densité des clients dans les aires de chalandise est
faible afin d'obtenir un effet de lissage fort.
le filtre médian
Le filtrage en moyenne compte tenu de ses inconvénients
peut être avantageusement remplacé
par le filtrage médian, un filtre passe-bas qui a tendance
à accentuer les intensités sans lisser
les bords. La médiane M d'une variable x vérifie
par définition les probabilités suivantes: P(x M) 1/2 et P(M
x) 1/2
Le filtrage médian élimine le bruit de type neige
(erreur dispersée de façon aléatoire) mais au
détriment d'une légère perte de
résolution.
L'exemple suivant représente la même
représentation des localisations de clients virtuels selon leurs niveaux
de fréquentation d'un point de vente (les points foncés
représentent les clients fréquentant assidûment le
magasin, les points plus clairs les clients moins fidèles). Le dessin
à côté montre cette cartographie
traitée par deux filtres médians successifs: les aires de
chalandise à forte fréquentation de clients apparaissent plus
nettement (zones foncées) ce qui facilitera la délimitation des
frontières :
Fig. 3.8 - Adresses clients associées aux
fréquentations Fig. 3.9 - La représentation traitée par 2
filtres médians

Comme vu précédemment (§ 1.4), nous
remarquons que les zones denses de clientèle ne
forment pas un ensemble géographique compact
566, mais se répartissent en différentes aires
de chalandise (nous dirons que la zone de chalandise se compose
en fait de plusieurs aires de chalandise).
le filtre sigma
Le filtre sigma est surtout un filtre de débruitage. A
tout point (i, j) de la zone image active de niveau de fi,j est
affectée la moyenne de ses voisins dont le niveau appartient
à l'intervalle centré en fi,j de demi-largeur 2 sigma,
sigma étant la variance locale dans la fenêtre.
Toutefois, si le nombre de voisins appartenant à cet intervalle est
inférieur ou égal au nombre
de voisins V=2L+1, alors f i,j sera remplacé par la
moyenne de ses huit voisins immédiats.
Ce traitement est bien adapté au filtrage d'un
bruit impulsionnel (erreur très forte, répétée
mais localisée, cas de réponses totalement erronées
mais rares), en choisissant <2 et L=1 (V=2L+1=3, correspondant
à un voisinage 3x3) ce qui peut être le cas si les
données géomarketing présentent des erreurs importantes
mais espacées.
le filtre de Nagao
Un des filtrages spatiaux les plus utilisés et
les plus intéressants de nos jours est celui de Nagao
567. On considère cette fois le voisinage d'un pas
de deux éléments (ou plus généralement de e
éléments) autour du point (i, j) considéré, soit
une sous-matrice de 5 x 5 =
25 éléments. On calcule ensuite pour 9
configurations compactes d'éléments de 3 types
différents (voir dessin suivant), la moyenne et la variance des
valeurs des éléments les
composant.
566 CLIQUET G., FADY A., BASSET G. (2002)
Management de la Distribution, Dunod, Paris.
567 NAGAO M., (1979) Edge Preserving Smoothing,
CGIP, vol. 9, p.394-407.
1 du type (1) + 4 du type (2) + 4 du type (3)
Fig. 3.10 - Les 3 catégories des 9 configurations du
filtrage de Nagao sur lesquelles porte le calcul des moyennes et des
variances
La nouvelle valeur choisie pour le point (i, j) est alors
celle de la moyenne correspondant à la plus faible variance. Ce
traitement est réalisé en considérant tour à tour
tous les points de la matrice des données de fréquentation.
Les contours sont ainsi bien conservés car le
lissage ne se fait que dans sa direction tangentielle
c'est-à-dire dans la direction où la modification est la moins
visible 568. C'est la raison pour laquelle on dit que le filtre de
Nagao est qualifié de lissage avec conservation et même
accentuation des contours. Ce filtrage peut être
réitéré plusieurs fois sur la matrice déjà
traitée. On observe que ce filtre est pratiquement idempotent: au bout
de quelques itérations, l'image (ou la matrice) ne se modifie presque
pas. On arrête alors le processus de traitement. L'exemple suivant montre
la même représentation des localisations de clients virtuels selon
leur niveau de fréquentation d'un point de vente (les points
foncés représentent les clients fréquentant
assidûment le magasin, les points plus clairs les clients moins
fidèles). Le dessin
à côté montre cette cartographie
traitée par deux filtres successifs: on distingue beaucoup plus
nettement les frontières des aires de chalandise à forte
fréquentation de clients (zones foncées
plus homogènes que pour les filtres
précédents):
568 ORSTOM (1998) Image Satellite et Milieux
Terrestre en Régions Arides et Tropicales, Editions de l'Orstom,
Bondy.
Fig. 3.11- Adresses clients associées aux
fréquentations Fig. 3.12 - La représentation traitée par 2
filtres Nagao

Il existe encore de nombreux autres filtres capables
d'améliorer la qualité de l'image cela afin
de faciliter dans l'étape suivante, le processus
de délimitation des contours des aires. En particulier, de la
même façon que sur une photo de mauvaise
qualité, les données géomarketing sont
susceptibles de comporter soit des perturbations basses
fréquences aléatoires et stationnaires (ex: données
manquantes, échantillon d'enquête trop faible ou base
de données d'adresses clients incomplète) qui
influent négativement sur les frontières de zone
de chalandise en les rendant floues. Un deuxième
type d'interférences est constitué par les perturbations
hautes fréquences liées plus spécifiquement au mode de
collecte des données: il peut par exemple arriver dans une
enquête que tous les 100 questionnaires, il y ait une ou
plusieurs réponses fantaisistes (clients donnant une fausse
adresse ou bien surestimant son taux de fréquentation ou d'achat
dans le magasin). Même si les filtres précédents ont
tendance
à lisser ces erreurs, il existe des filtrages de
fréquence spécifiques dont le rôle est d'assurer la
suppression de ces fréquences non désirées. Le premier
type s'atténue avec les filtres passe- haut (laissant passer les hautes
fréquences) alors que le deuxième s'estompe grâce à
des filtres
passe-bas (laissant passer les faibles fréquences).
La transformation de dilatation
Elle consiste en résumé à grossir les
points représentatifs des clients jusqu'à ce que ceux-ci se
touchent et que l'on distingue les formes pleines de la zone de
chalandise. En effet, dans certains cas, les clients d'un point de vente
représentés sur une carte à la suite d'une phase de
géocodage, apparaissent si éloignés les uns des
autres qu'il est impossible de percevoir les formes de la zone de
chalandise, la dilatation permettant alors de résoudre ce
problème. La dilatation tend donc à connecter les parties
disjointes et à lisser les contours. Nous reviendrons plus
précisément sur cette transformation dite "morphologique"
dans le paragraphe suivant
qui montre comment délimiter de cette manière
les zones de chalandise (la dilatation sera également
utilisée dans la deuxième partie pour lisser les zones de
chalandise constituées par
les clients potentiels de l'Ouest parisien
intéressés par les produits biologiques).
3.2.4 La délimitation des zones de chalandise par
traitement du signal
Après avoir lissé les données par
un filtrage approprié pour obtenir une cartographie plus nette
des données géomarketing, on choisit une méthode parmi
celles disponibles, méthodes toujours inspirées du traitement
du signal ou de l'analyse d'image, pour procéder à la
délimitation de la zone de chalandise. Les méthodes de
délimitation possibles sont:
- une méthode empirique (le seuillage d'histogramme),
- la méthode par masquage et convolution: gradient,
laplacien, Sobel, Prewitt,
- la méthode par analyse morphologique.
· Délimitation par seuillage
d'histogramme
La délimitation par seuillage d'histogramme
consiste en premier à comptabiliser chaque valeur discrète
que les éléments de la matrice f'i,j des fréquentations
préalablement obtenues peut prendre puis de les tracer sous la forme
d'un histogramme. On tente alors de déterminer une valeur seuil T qui
permette de séparer le groupe appartenant à l'objet et celui
appartenant
au fond. Ainsi, pour toute valeur de l'image ou de la matrice
f'i,j supérieure ou égale à T, le point correspondant
appartiendra à la zone de chalandise au contraire des valeurs
inférieures à
T.
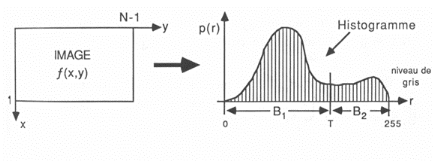
Fig. 3.13 - Exemple de représentation sous forme d'un
histogramme des valeurs f(x,y) des points d'une image
Dans le cas plus général, on peut
réussir à distinguer plusieurs seuils T1,...Ts sur
l'histogramme avec donc plusieurs types de zones de
fréquentation du point de vente considéré par la
clientèle :
si f'i,j < T1, fréquentation quasi nulle
si T1 f'i,j < T2, fréquentation faible
. .
. .
. .
si Ts f'i,j, fréquentation
élevée
Le seuillage T1,...Ts déterminé peut être
soit global (valable pour tout l'espace géographique
analysé), soit local (les valeurs du seuil varie selon les
régions du plan),
Mais, dans beaucoup de cas, l'histogramme ne présente pas
de seuils distinctifs de zones bien nets comme dans l'exemple ci-dessous.
Fig. 3.14 - Détermination d'un seuil de valeurs sur un
histogramme
Une première méthode, empirique, consiste
à tenter de définir un seuil T par tâtonnements successifs
en observant la pertinence de l'image seuillée. Il est
également possible de rechercher un seuil T en considérant que
l'histogramme H(f) est la somme de deux densités de probabilité
:
H(f) = H1 x h1(f) + H2 x h2(f)
h1(f) et h2(f) sont les fonctions de densité de
probabilité et H1 et H2 sont les probabilités d'existence
de 2 groupes de valeurs dans la matrice (ou des 2 types de niveaux de gris dans
l'image).
Fig. 3.15 - Exemples d'un histogramme et de son enveloppe
comportant plusieurs valeurs de seuils
La probabilité de classement par erreur d'un point
à fréquentation faible dans la zone 2 à forte
fréquentation (zone de chalandise) s'exprime par :
T
E1(T) =
h2(f)df
-
Et inversement, la probabilité de classement par erreur
d'un point à fréquentation importante
(appartenant à la zone de chalandise) dans la zone 1
à faible fréquentation s'exprime par :
+
E2(T) =
h1(f)df
T
La probabilité d'erreur totale est donnée par
: E(T) = H2 E1(T) + H1
E2(T)
Celle-ci doit être minimisée et en
conséquence la dérivée de E(T) par rapport à T est
nulle. On
a donc H1 h1(T) = H2 h2(T). Le seuil T qui permet
de départager les deux densités de
probabilité h1(T) et h2(T) correspond ainsi à
la valeur du minimum de l'histogramme
correspondant à la densité h1(T)
c'est-à-dire :
1 2
P1
T = 2 ( + )+ 1 -2 Ln(P2 )
1 2
1 et 2 étant les luminances
des densités de probabilité p1(f) et
p2(f),
1 et 2 étant les écarts-types de ces mêmes
densités de probabilité.
· Délimitation par le gradient
La méthode par le gradient et celle par le
laplacien décrite dans le paragraphe suivant, utilisent les
différences de valeur entre les points proches pour déterminer
les frontières. Le vecteur gradient qui traduit les variations de
fréquentation des clients dans le sens vertical (composante de
l'abscisse sur la cartographie) et dans le sens horizontal (composante
de l'ordonnée sur la cartographie) a pour expression dans l'espace
f'i,j du chapitre précédent :
f
r i
G =
f
j
f
lim f i, j - f i + h,
j
f lim f i, j - f i, j
+ h
avec
i = h0 h
et j = h0 h
r
La norme du vecteur G orienté dans le sens
de la variation maximale correspond au maximum
de variation d'intensité.
r 2
1/ 2
G = (f )2+ f
i j
en approximation dans les algorithmes, on prend :
r ( f - f
)2 ( f - f
)2 1/ 2
G
i, j
i+1, j +
i, j
i, j+1
et surtout :
r
G f i, j-
f i+1, j + f i,
j- f i, j+1
ou bien lorsque les contours sont peu marqués, on
utilise l'approximation de Roberts
(variations du gradient peu importantes)569 570 :
r
G f i, j-
f i+1, j+1 +
f i+1, j- f
i, j+1
r
Pour délimiter les contours par la méthode du
gradient, il faudra en pratique comparer G à
une valeur seuil T positive. Si
r
G 0 , alors le point considéré appartient
au contour (qui peut
comporter une épaisseur de plusieurs pixels) et dans le
cas inverse, le point appartient au fond
ou à l'objet.
0 0 0
Le gradient s'exprime par l'opérateur matriciel : -1 1
0
0 0 0
· Délimitation par le laplacien
L'opérateur laplacien est défini par :
2f
=
+ 2f
i2
j2
soit en première approximation,
= fi+1, j - 2 fi,j + fi-1,j
+ fi,j+1 - 2fi,j + fi,j-1 =
fi+1,j + fi-1,j + fi,j+1 + fi,j-1
- 4fi,j
On définit la norme du vecteur laplacien par :
2
r
2 1/ 2
= 2f + 2f
i2
j2
569 CANNY J. (1986) A Computational Approach to
Edge Detection, IEEE Transactions on Pattern Analysis and Machine
Intelligence, Vol. PAMI-8, No. 6, pp. 679-698.
570 LIM J. S. (1990) Two-Dimensional Signal and
Image Processing, Englewood Cliffs, NJ: Prentice Hall, pp.
478-488.
0 -1
et le laplacien s'exprime par l'opérateur matriciel : -1
4
0 -1
0
-1
0
Le gradient et le laplacien sont en fait des masques
linéaires. Nous examinons dans le
paragraphe suivant la technique de délimitation par
masquage d'une façon générale.
La même représentation des localisations
de clients virtuels selon leurs niveaux de fréquentation
d'un point de vente nous permet d'illustrer le filtre laplacien de
délimitation (dessin de droite) suite à l'application de
deux filtres médians sur la cartographie initiale (dessin de
gauche) conformément à l'étape précédente.
Les contours sont nets mais présentent
des courbes non fermées à ébavurer:
Fig. 3.16 - Adresses clients associées aux Fig. 3.17 - La
représentation traitée par le fréquentations laplacien
après 2 filtres médian

· Délimitation par masquage
Le masquage est un type de filtrage qui généralise
le principe des filtres laplacien et gradient vus précédemment en
faisant appel au produit de convolution de deux fonctions.
Pour rappel, le produit de convolution de deux fonctions f et g :
Z Æ R est une fonction h : Z
Æ R définie par :
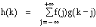
Ses propriétés sont d'être commutatif,
associatif et d'avoir pour élément unité
l'impulsion
unité. On utilise la notation h = f*g. Dans le cas
d'une fonction à 2 variables ou d'une matrice carrée à 2
dimensions telle fi,j (image) convoluée avec une fonction ou une
matrice du même type hi,j , (filtre) on a :
i +k
j +k
gi,j = fi,j * hi,j = f,
hi -, j -
=i -k
= j -k
Fig. 3.18 - L'image fi,j et le filtre
hi,j
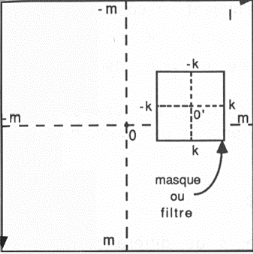
Les dimensions de l'image fi,j et du filtre hi,j sont
respectivement de 2m+1 et de 2k+1 et celle
du produit de convolution de 2(m+k)+1. Si la dimension du filtre
est très petite devant celle
de l'image, ce filtre constitue une fenêtre. Il est
à noter que les bords extérieurs de la nouvelle image issue du
produit de convolution sont entachés d'erreurs.
On a plus spécifiquement pour le produit scalaire
matriciel de 2 matrices A , l'image et M ,
le masque, la notation :
A M
. La matrice résultante
A M
possède les mêmes
dimensions que la matrice image A . Pour une matrice
masque M , 3x3, et le produit scalaire
matriciel est défini par :
3 3
A M
= ai, j mi, j
i = 1 j = 1
avec : 
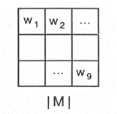
r r
Le produit scalaire Ps s'écrit : Ps =
A. M = a1w1 +
a2w2 + ...+ a9w9
r r
Les coefficients ai et wi
respectivement de A et de M étant rangés dans les vecteurs
A et M .
Le contour s'apprécie en comparant la valeur Ts à
une valeur seuil T. Dans le cas où Ps>T, le pixel transformé
par la convolution est rangé dans la nouvelle matrice de
délimitation.
Voici différents types de masques possibles :
Les masques linéaires
Les masques linéaires les plus connus sont le
gradient et le laplacien déjà évoqués au
paragraphe précédent :
-le Gradient
0 0 0
0 0 0
0 0 0
0 1 0
- 1 1
0 ou
- 1 0
1 ;
0 1
0 ou
0 0 0
0 0 0
0 0 0
0 - 1 0
0 - 1 0
Matrices de détection horizontale ; et matrices de
détection verticale
-Le laplacien
0 0 0
0 0 0
0 0 0
0 1 0
- 1 1
0 ou
- 1 0
1 ;
0 1
0 ou
0 0 0
0 0 0
0 0 0
0 - 1 0
0 - 1 0
Matrices de détection horizontale ; et matrices de
détection verticale
On a en parallèle des masques linéaires pouvant
faire apparaître par convolution uniquement
les frontières d'objet orientés dans une certaine
direction avec par exemple:
- un masque pour la détection des
droites horizontales
- 1
- 1 - 1
2 2 2
- 1
- 1 - 1
- un masque pour la détection des
droites à 45°
- 1 - 1 2
- 1 2
- 1
2 - 1
- 1
Il existe aussi des matrices 3x3 dont les termes sont des
facteurs de corrélation de Markov
(voir chapitre sur le filtre spatial) ou bien des composantes
issues de fonctions gaussiennes. Voici d'autres masques parmi les plus courants
avec dans les masques non-linéaires :
- les masques de Sobel
Ils sont représentés par les deux matrices:
0 0 0
0 1 0
Sx = - 1 1 0
; Sy = 0 0 0
0 0 0
0 - 1 0
Matrice de détection horizontale ; et matrice de
détection verticale
Le "pseudo-gradient" G de Sobel (une approximation du
gradient vu précédemment) est donné par :
G = Gx2 +
Gy
2 1 / 2 ou
G = Gx
+ Gy
(formule encore plus approchée)
avec Gx = (w7 + 2w8 +
w9) - (w1 + 2w2 + w3)
Gy = (w3 + 2w6 + w9) - (w1 + 2w4 + w7)
La direction du pseudo-gradient est alors = tg -1
(Gy / Gx)
Fig. 3.20 - La représentation traitée par
filtres Fig. 3.19- Adresses clients Sobel après 2 filtres médian
(les contours sont associées aux fréquentations superposés
à l'image filtrée par les 2 Nagao)


On remarque que le filtre Sobel possède grâce
à sa fonction de détection des sauts de valeurs
(de fréquentation) la propriété de
fragmenter l'espace à la manière d'un puzzle en séparant
les régions pleines et celles vides de clients. Une suggestion
d'application est que ce filtre pourrait servir à découper de
manière très fine une zone géographique en un certain
nombre
de cellules juxtaposées pour effectuer une
étude sur la proximité spatiale des activités
commerciales ou non, en utilisant le principe de l'analyse quadratique571
572. Cette technique visant à mesurer la dispersion spatiale
des activités repérées par la position du centre
de gravité de ces cellules par rapport à une distribution
aléatoire ou la méthode voisine des plus proches voisins573
ont déjà été utilisées dans de
nombreuses études sur la proximité spatiale
dans des comme le Canada574 575, la
Grande-Bretagne576 577, l'Irlande578 579, la
Suède580, la
571 ROGERS A. (1969) Quadrat Analysis of Urban
Dispersion : 2. case studies of urban retail systems,
Environment and Planning, 1, p. 155-171.
572 BROWN S. (1992) Retail Location : A
Micro-scale Perspective, Ashgate, England.
573 PINDER D.A. & WITHERICK M.E. (1972)
The Principles, Practice and Pitfalls of Nearest-neighbour
Analysis in Linear Situations, Geography, 57,
p.277-288.
574 BOUCHARD D.C. (1973) Location Patterns of
Selected Retail Activities in the Urban Environment : Montreal,
1950-1970, Revue Géographie Montréal, 27, p. 319-327.
575 SMITH S.L.J. (1985) Location Pattern of Urban
Restaurants, Annals of Tourism Research, 12, p. 581-602.
576 SORENSON A.D. (1970) A Comparative
Study of the Changing Patterns of Distribution of Service
Industries on Tyneside, Wearside and Teeside,
unpublished Ph.D. thesis, University of Newcastle-upon-Tyne.
Yougoslavie581, Israël582,
Singapour583, l'Australie584, Hong Kong585 ou
le Japon586. L'analyse quadratique difficile à mettre en
oeuvre, compare donc la distribution des localisations par rapport
à celle qui aurait été générée
aléatoirement : les résultats de cette technique risquée
sont malheureusement sujets à variation en fonction du
découpage géographique retenu de l'aire d'analyse. La
méthode des plus proches voisins consiste, quant à elle, en une
mesure de l'écart d'une configuration spatiale de points par
rapport à une répartition aléatoire : le
problème est que, selon l'étendue de la zone d'analyse,
les mêmes distributions de points peuvent engendrer des mesures
différentes de proximité spatiale et que la méthode est,
d'une manière générale, très sensible aux effets de
bord 587 588 589. La majorité de ces études
ont cependant remarqué que les commerces de détail avaient
tendance à se regrouper comme le prévoit la loi de Hotelling
590 (voir § 2.1.1), au niveau des zones urbaines surtout en ce
qui concerne la distribution de biens élaborés comme les
grands magasins, le prêt-à-porter
féminin, à l'inverse des stations-service ou de
certaines activités de services basiques. Le filtre
577 SIBLEY D. (1975) A Temporal Analysis of the
Distribution of the Distribution of Shops in British Cities, unpublished
Ph.D. thesis, University of Cambridge.
578 PARKER A.J. (1973) The Structure and Distribution
of Grocery Shops in Dublin, Irish Geography, 5, p. 625-
630.
579 BRADY J.E.M. (1977) The Pattern of
Retailing in Central Dublin, unpublished M.A. thesis, University
College Dublin.
580 ARTLE A. (1959) Study in the Structure of the
Stockholm Economy : Towards a Framework for Projecting
Metropolitan Community Development, Business
Research Institute, Stockholm School Economics, Stockholm.
581 ROGERS A. (1974) Statistical Analysis of
Spatial Dispersion, Pion, London.
582 SHACHAR A. (1967) Some Application of
Geo-statistical Methods in Urban Research, Papers of the
Regional Science Association, 18, p.85-92.
583 WING H.C. & LEE S.L. (1980) The
Characteristics and Locational Patterns of Wholesale and Service
Trades in the Central Area of Singapore, Singapore
Journal Geography, 1, p.23-36.
584 JOHNSTON R.J. (1967) Land Use Changes in the
Melbourne CBD : 1857-1972, Troy, P.N., (ed), Urban
Redevelopment in Australia, Research School of Social
Sciences, Urban Research Unit, Australian National
University, Canberra, p. 77-201.
585 LEE Y. (1979) A Nearest-neighbour Spatial
Association Measure for the Analysis of Firm Interdependence,
Environment and Planning A, 1, p. 169-176.
586 OKABE A., ASAMI Y. & MIKI F. (1985)
Statistical Analysis of the Spatial Association of Convenience- good Stores by
Use of a Random Clumping Model, Journal of Regional Science, 25, p.
11-28.
587 PINDER D.A. & WITHERICK M.E. (1972)
The Principles, Practice and Pitfalls of Nearest-neighbour
Analysis in Linear Situations, Geography, 57,
p.277-288.
588 DE VOS (1973) The Use of Nearest-neighbour
Methods, Tijdschrift voor Economische en Sociale Geografie,
64, p. 307-319.
589 RODER W. (1975) A Procedure for Assessing
Point Patterns without Reference to Area or Density,
Professional Geographer, 27, p. 432-440.
590 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, Vol. 39, p 41-57.
Sobel pourrait donc avantageusement servir à construire
de manière précise et harmonieuse le découpage
géographique introduit dans ce type d'études qui deviendrait
ainsi plus fiable (les découpages retenus dans la plupart des cas
étaient les limites administratives pas forcément très
logiques).
D'autres masques sont pratiquement équivalents au
masque Sobel comme les masques de
Kirch ou de Prewitt:
7
- le masque de Kirch
Le pseudo-gradient est cette fois donné par l'expression
:
G = max
1, max[ 5Si - 3Ti ]
i = 0
avec : Si = wi + wi+1 +
wi+2 et Ti = wi+3 + wi+4 +
wi+5 + wi+6 + wi+7
- le masque de Prewitt
Le masque de Prewitt 591 est l'un des filtres du type
dérivatif le plus simple.
- 1 - 1
- 1
- 1
0 1
Px = 0
1
0 0
1 1
; Py = - 1
- 1
0 1
0 1
Détection Horizontale Détection Verticale
Il existe aussi de nombreux masques commerciaux
proposés par diverses sociétés comme
Robotronics, ITMI, Visiomat, FTR proposent d'autres types de
détermination de contour par
le procédé de masquage. Vicom, par exemple
propose l'extracteur de contour (passe-haut)
suivant:
591 PREWITT J.M.S. (1970) Picture Processing and
Psychopictories, Academic Press, p.75.
1 - b 1
( 1 )2 - b b²
- b
b + 2
1
- b 1
suivi par un atténuateur (filtre passe-bas pour supprimer
les aires de clientèle bien identifiées
mais trop petites pour être intéressantes dans
l'analyse):
1 b 1
b
( 1 )2 b² b
b + 2
1 b 1
b pouvant adopter selon les cas une valeur comprise entre 0 et
9.
Voici un algorithme général qui sera capable
de mettre en oeuvre tous ces processus de masquage:
FONCTION MASQUE;
DEBUT
DE i=1 A largeur
DE j=1 A hauteur
DE x=1 A 3
DE y=1 A 3
ImageTransformée(i, j) = ImageTransformée(i, j) +
Masque (x, y) x
ImageOriginale(i+x-1, j+y-1);
FIN FIN
FIN FIN
(les instructions de programmation sont en caractères
gras).
· Délimitation par transformation
morphologique
L'application de la théorie du morphisme
mathématique à la science de la localisation vise à
pallier ces manques en rationalisant le concept de zone de
chalandise. Le morphisme mathématique qui s'inspire de notions de
topologie, de traitement du signal, de probabilités et
de théorie des graphes comporte un grand nombre
d'applications qui toutes relèvent du monde réel. Les domaines
intéressés par cette technique sont très variés et
l'on trouve par exemple la science des matériaux, la géologie, la
biologie, la géographie, la robotique. Le point commun des champs
d'applications possibles est que les données traitées sont
variables dans un espace d'observation assez souvent supérieur ou
égal à deux dimensions.
Le morphisme mathématique s'attache à analyser
les informations dans leur globalité. Voilà pourquoi, cette
science a beaucoup apporté, comme son nom l'indique, à la
reconnaissance des formes (empreinte digitale; voix, écriture;
structure des matériaux; structure géologique, cytologique ou
génétique; circuit électronique) et donc au traitement des
images provenant de diverses sources: enregistrement sonore, photographie,
microscopie électronique ou optique, images satellites, images radar ou
sonar, radiographie, échographie.
Or, pourquoi ne pas utiliser les méthodes du
morphisme, en s'appuyant sur le principe d'universalité des
mathématiques, sur d'autres données que celles acquises
par vision ou enregistrement direct du monde réel ? Le morphisme est
en effet tout aussi apte à traiter des informations qui sont issues
de capteurs humains (ex. enquêtes marketing quantitatives ou
qualitatives) que de capteurs électroniques ou optiques ainsi que de
bases de données mixtes. Cette nouvelle méthode fondée
sur le morphisme mathématique peut être décrite par
une succession de plusieurs étapes:
· Segmentation des données
· Amincissement et régularisation de la
frontière de la zone de chalandise
Segmentation des données
Avant de poursuivre la description du traitement sur la matrice,
nous allons évoquer certaines notions utiles sur les transformations
morphologiques de base.
Transformations Morphologiques de Base: dilatation -
érosion - fermeture - ouverture - chapeau "haut-de-forme"
Les premiers filtres morphologiques sur des données
discrètes ou continues datent de la fin
des années 1970 592 593, mais c'est entre 1982
et 1986 que les Français Matheron et Serra ont établi une
théorie de la morphologie mathématique possédant une
véritable unité 594 595.
Voici les principes fondamentaux de cette théorie
d'analyse des formes :
Soit X un ensemble connexe de données binaires d'une
matrice (0 ou 1, point allumé ou éteint dans un espace 2D),
une première transformation de base possible de cet ensemble
est la dilatation binaire 596 qui a pour effet d'augmenter
la surface totale de cet ensemble. Elle tend à
connecter les parties disjointes et à lisser les
contours.
592 MEYER F. (1978) IIème Symposium
Européen d'Analyse d'Images en Sciences des Matériaux, Biologie
et
Médecine, 4-7 oct. 1977. Pract. Met., S8, p. 374,
Caen, France.
593 STERNBERG (1979) Proc. 3rd Int. IEEE
Comprac, Chicago 1979.
594 SERRA J. (1982) Image Analysis and
Mathematical Morphology, Academic Press.
595 MATHERON G. (1982) Les Applications
Idempotentes, Rapport du Centre de Géostatistique et
de
Morphologie Mathématique n°743, Ecole des
Mines, Fontainebleau.
596 MINKOWSKI H. (1903) Mathematics Annals,
Vol. 57, p.447.
Fig. 3.21 - Exemple d'une dilatation:

en hachures, la forme originale
Une autre transformation morphologique de base est
l'érosion binaire 597 qui lisse aussi la
surface mais à l'inverse la réduit.
Fig. 3.22- Exemple d'une érosion:
en hachures, la forme originale
Pour obtenir des contours plus réguliers, il est
possible de réaliser une succession d'érosion- dilatation
c'est-à-dire qu'en partant de l'image initiale, on élimine tous
les points de la forme considérée en contact en bas, en
haut, à droite ou à gauche avec au moins un point
n'appartenant pas à la dite forme (érosion). Seule, donc,
restent les points de sa partie intérieure. Puis, on entoure
chaque point frontière de la forme érodée de nouveaux
points, à
597 HADWIGER H. (1957) Vorlesung Über
Inhalt, Oberfläche und Isoperimetrie, Springer Verlag, Berlin.
droite, à gauche, en haut, en bas (dilatation).
Fig. 3.23 - Image Initale, érosion, puis dilatation.
Si on considère au lieu de données binaires, des
données réelles comme les fréquentations fi, j
préalablement définies, alors on a un relief qui
varie en tout point défini par ses coordonnées
(i, j) selon la valeur fi, j , (ensemble de valeurs
représentées par la matrice [ f i, j ]).
La dilatation ou l'érosion binaire peut être
généralisée aux paramètres évoluant sur un
éventail
de données 598 comme les
fréquentations fi, j : dans la transformation d'érosion, la
valeur de chaque point est remplacée par la valeur la plus
basse l'entourant à moins qu'elle n'ait la valeur la plus
élevée parmi tous ses voisins. La dilatation est
définie de la même manière, suivant le principe
qu'une dilatation d'une forme est l'érosion de son
complémentaire. Appliquée à de telles données, la
dilatation a tendance à élargir les vallées et à
abaisser les pics.
Fig. 3.24 - En Noir: La Courbe Originale / En Gris: a courbe
transformée par dilatation

598 CHERMANT J.L. et COSTER M. (1989)
Précis d'Analyse d'Images, Presses du CNRS.
Fig. 3.25 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par dilatation

Les régions à valeurs maximales ont tendance
à élargir leur surface et les régions à valeurs
minimales décroissent. Dans le cas de l'érosion, les
vallées sont élargies et les pics sont abaissés:
Fig. 3.26 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par érosion
Les régions à valeurs minimales ont tendance
à élargir leur surface et les régions à valeurs
maximales décroissent.
La transformation morphologique de fermeture combine la
dilatation et l'érosion (remplit les
vallées sans transformer les pics).
Fig. 3.27 - En Noir: la courbe originale / En Gris: la courbe
transformée par fermeture
On peut citer aussi la transformation morphologique
d'ouverture qui est la succession, dans
cet ordre, d'une érosion et d'une
dilatation de même taille. Enfin, la transformation
morphologique du "chapeau haut-de-forme" est la soustraction des
données de la matrice initiale [f i, j] aux
données de la matrice fermée [f T i,
j]. Elle constitue un filtre morphologique
qui met donc en évidence les contours. Un exemple
à la fin de ce paragraphe montre son
utilisation pour délimiter les frontières d'une
zone de chalandise.
Fig. 3.28 - En Noir: la courbe originale / En Gris: la courbe
transformée par chapeau haut-de-Forme
La matrice résultat est faite de données binaires
correspondant à une valeur de 1 si l'élément
de matrice appartient à la frontière, et
inversement à une valeur nulle.
· Amincissement et régularisation de la
frontière de la zone de chalandise
Les éléments binaires appartenant à la
frontière de la zone de chalandise sont amincis. Ceci signifie que
pour un ensemble d'éléments caractérisant la
frontière, seul l'élément moyen représentatif de
cette frontière est maintenu dans la matrice tandis que les autres
éléments sont mis à 0.
Les points qui ont été calculés lors de
la dernière étape sont liés par les courbes
régulières de Bézier: considérons une suite de n+1
points du plan: {Pi = (xi ,yi) } / i = 0 to n}, qui définit un polygone
à n côtés appelés polygone de commande. On appelle
approximation de Bernstein-

Bézier de cet ensemble de points 599, la courbe
paramétrée par:
Nous avons pris n = 3 et obtenu des courbes dites cubiques: les
courbes cubiques sont définies
en utilisant quatre points, deux points situés aux
deux extrémités de la courbe, et les deux autres sur les
deux tangentes exerçant dans une certaine mesure une attraction sur la
courbe.
Fig. 3.29 - Les 2 points et les 2 tangentes définissant
une courbe de Bézier cubique
Soient t un nombre entre 0 et 1, et p(t) un point non
spécifié de la courbe. Lorsque t varie de 0
à 1, on obtient l'ensemble des points qui
constituent la courbe. Voici les équations qui permettent de
définir la courbe:
Le polynôme p(t) = ap t 3 + bp t ² + cp t +
p0
599 LANE J.M. et RIESENFELF R.F. (janvier 1980) A
Theoretical Development for the Computer Generation and display of Piecewise
Polynomial Surfaces, IEEE Trans. on PAMI, Vol. PAMI-2, No 1, p.
35-46.
où t [0, 1]
et ses coefficients:
p1 = p0 + cp / 3
p2 = p1 + (cp + bp) / 3
p3 = p0 + cp + bp + ap
L'exemple concret suivant de délimitation
morphologique reprend le cas de clients virtuels abordé au
chapitre précédent avec en premier lieu une cartographie des
clients associés à leurs fréquentations d'un point de
vente suivi de deux filtres Nagao (voir paragraphe 2.6.2.1).
Fig. 3.30 - Adresses clients associées aux
fréquentations Fig. 3.31 - suivies de deux filtres Nagao,

Fig. 3.32 - puis une dilatation, Fig. 3.33 - ensuite une
érosion
(transformation de fermeture),


Fig. 3.34 - Une soustraction par rapport Fig. 3.35 - Enfin un
amincissement
à l'image filtrée du début (transformation
et une régularisation, des contours chapeau haut-de-forme) (grâce
aux courbes de Bézier)

A la suite de ces délimitations de zones de chalandise, il
convient de construire le modèle p-
médian avant de le résoudre ce qui signifie au
minimum, définir les noeuds du réseau (noeuds constitués
par les centres de gravité de chacune des aires formant la zone de
chalandise) et quantifier la demande associée à chaque noeud. La
construction de ce réseau est ainsi l'objet
de notre prochain paragraphe.
3.3 La construction du modèle p-médian :
détermination des centres de gravité, distances et
pondérations du modèle p-médian
La délimitation de la zone de chalandise a mis en
évidence les diverses régions de l'espace concentrant un grand
nombre de clients. Pour déterminer les coordonnées des
centres de gravité de ces régions (futurs noeuds du
modèle) et procéder à une analyse en profondeur des
caractéristiques de la clientèle (demandes du
modèle), il s'agit auparavant de définir analytiquement
ces régions, c'est-à-dire de préférence par les
coordonnées de leurs contours. Connaître d'une manière
rationnelle les frontières des régions formant la zone de
chalandise nous permettra de calculer la position de leurs centres de
gravité, futurs noeuds du modèle p- médian. L'autre
intérêt est de déterminer l'étendue de ces
régions dans lesquelles la densité de
clients est forte et de même niveau, afin d'évaluer
le niveau de la demande dans chacune de
ces aires (demande associée à chaque noeud du futur
modèle p-médian).
Plus précisément, les frontières des
régions géographiques peuvent être définies par
différents types de coordonnées comme la succession des
coordonnées, le code de Freeman, le code hexagonal ou
les points essentiels.
· la succession des coordonnées
La succession des coordonnées (i, j ) des points de
la frontière linéique s'obtient en parcourant
la frontière dans un sens ou dans l'autre. Ce codage a
l'inconvénient de nécessiter un grand nombre de données (2
x Nf, où Nf est le nombre de points de la frontière).
· le code de Freeman 600
On décrit en partant d'un point de la frontière et
en la parcourant dans un sens de convention,
les différentes orientations prises par la courbe
(vecteurs successifs), soit en général 8 orientations :
N(nord), NE (nord-est), NO (nord-ouest), O (ouest), SO (sud-ouest), S (sud), SE
(sud-est), E (est) ou bien avec moins de précision seulement 4 : N
(nord), O (ouest), S (sud), E (est). Ce type de codage ne nécessite que
Nf + 2 données distinctes (incluant les coordonnées
du point de départ, chaque élément
directionnel du codage n'étant représenté que par
un nombre restreint de bits, 4 ou 8).
· le code hexagonal (dans le cas d'une matrice [de
points images] hexagonale)
Le contour est décrit par le point de départ et 3
directions (comme pour le code de Freeman)
mais on simplifie en n'indiquant que la direction d'orientation
du segment courant par rapport
au précédent en parcourant la courbe selon
un sens de convention. Le nombre de bits nécessaire au codage
descend à 2 et nécessite le même nombre de données
distinctes que le code de Freeman.
Fig. 3.36 - Exemple de Codage Hexagonal
600 FREEMAN H. (1970) Boundary Encoding and
Processing in Picture and Processing and Psychopictrorics, Lipkin B.S. and
Rosenfeld A., Academic Press, New York, p. 241-266.
G=direction gauche et D=direction droite par rapport au segment
précédent
· les points essentiels
On cherche alors à minimiser le nombre de points de
description en approximant le contour
par une courbe enveloppante continue et dérivable
(familles de fonctions B-splines). Ce principe est surtout utilisé
dans les logiciels de CAO.
Comment connaître les coordonnées des
points formant les frontières de la zone de chalandise par
l'algorithme de description ?
La procédure de segmentation
précédente a, comme on l'a souligné, permis
d'identifier des points P(i, j) connexes formant des zones
d'équi-fréquence. La réunion de ces
différentes zones constitue l'ensemble de la zone de chalandise.
Un algorithme de description simple permet d'extraire les
coordonnées de la frontière de la zone de chalandise
à partir de la fonction caractéristique à
l'étape précédente de délimitation. En effet, pour
chaque zone de chalandise Z, on peut définir une fonction
caractéristique fZ (i, j) telle que:
P(i, j) Z , fZ (i, j) = 1 et P(i, j) Z ,
fZ (i, j) = 0
Cette fonction permet de toujours savoir si on est à
l'intérieur ou à l'extérieur de la zone. On applique
maintenant l'algorithme de suivi de contour:
1) On balaye la matrice fZ (i, j) de la fonction
caractéristique ligne par ligne jusqu'à atteindre
le point P'(i', j'), le plus haut de la zone Z :
Fig. 3.37 - Exemple de parcours d'une forme à l'aide de
l'algorithme
destiné à extraire les coordonnées du
contour
2) Si on est en un point situé à
l'intérieur de la zone Z, [fZ (i, j) = 1] , tourner
à droite puis
avancer d'un cran dans cette direction (d'une colonne ou d'une
ligne).
3) Si on se trouve en un point situé à
l'extérieur de la zone Z, [fZ (i, j) = 0] , tourner à gauche
puis avancer d'un cran dans cette direction (d'une colonne ou d'une ligne).
4) Interrompre l'algorithme dès que l'on atteint à
nouveau le point de départ.
Fig. 3.38 - Exemple de parcours de frontière de zone de
chalandise à l'aide de l'algorithme
On enregistre ainsi les directions successives prises par
l'algorithme de suivi ce qui donne une description du contour sous la forme
d'une chaîne ascii en codes de Freeman :
[
E,S,E,S,O,S,O,S,E,S,E,N,E,N,E,S,E,N,E,S,E,N,O,N,E,N,O,S,O,N,E,N,O,S,O,N,O,S,O,N,E,N,O,S,O
]
Ce codage a aussi le grand avantage de pouvoir tout de suite
déterminer très simplement la surface géographique Sg de
la zone de chalandise par l'algorithme suivant en supposant que la chaîne
en code de Freeman s'écrive [a1, a2,...ai,...,an] :
1) Au départ; u = 0 et t =0
2) De i = 1 à n Faire
A) Si ai = Nord Alors
t = t + 1 Sinon Aller en B)
|
B) Si ai = Sud
|
Alors
|
u =
|
u + t
|
Sinon Aller en C)
|
|
C) Si ai = Ouest
|
Alors
|
t =
|
t - 1
|
Sinon Aller en D)
|
D) Si ai = Est Alors
u = u - t
3) Sg = u x S
où la valeur du paramètre u à la
fin de la procédure est le nombre de points contenus dans la zone de
chalandise considérée, t un paramètre de comptage et S la
superficie géographique unitaire d'un point.
Comment calculer les coordonnées des centres de
gravité des aires de chalandise ?
Les coordonnées des contours des aires
délimitées vont nous permettre d'accéder simplement aux
coordonnées des centres de gravité des différentes
aires constitutives de la zone de chalandise globale. Le repérage
de ces centres de gravité correspondant aux futurs noeuds du
modèle p-médian dans notre algorithme, donnera aussi par un
simple calcul de longueur, les distances de chaque segment du réseau (de
plus, si la zone de chalandise est très fragmentée et pas du
tout rassemblée, la moyenne des distances entre les centres de
gravité fournira une mesure de l'éloignement des noeuds). Une
question basique que l'on peut se poser est de savoir pourquoi, dans la
recherche d'une localisation optimale unique à partir de l'adresses de
clients,
on ne procèderait pas directement au calcul du centre
de gravité (localisation moyenne) par rapport à ces
mêmes clients pour choisir un emplacement bien centré de
son futur site. Considérons la cartographie suivante qui montre un
ensemble de clients potentiels représentés
par des points (voir figure 3.39). Le centre de gravité de
la totalité des clients est au point J, en pleine campagne. On remarque
que J est très éloigné de l'ensemble majoritaire des
clients de
l'agglomération rassemblés dans le cercle et donc
du potentiel commercial le plus intéressant.
Fig. 3.39 - Ensemble de clients potentiels
représentés par des points

Le fait de pratiquer un filtrage, par exemple
médian, et de délimiter la zone de chalandise (zone dense
de clients) permet de ne prendre en compte que les régions ayant
un potentiel commercial suffisant. L'analyse de localisation fait donc
abstraction de tous les clients "saupoudrés" dans l'espace et dont
la prise en compte risque de perturber les calculs. On voit
sur la cartographie suivante la zone de chalandise principale
délimitée par filtrage: le centre
de gravité est bien centré sur cette zone à
potentiel et non plus décalé en pleine campagne
(voir figure 3.40).

Fig. 3.40 - Centre de gravité d'une zone de chalandise
délimitée
Le centre de gravité convient donc bien pour
représenter la position moyenne d'une entité dans l'espace
en l'occurrence ici la position de l'agglomération (centre d'un futur
noeud du p- médian), mais celui-ci n'est pas compatible avec les
contraintes du modèle p-médian pour déterminer une
localisation optimale. D'autre part, au niveau régional ou national, il
est plus significatif de comparer entre eux les centres de
gravité des aires mises en évidence par le processus de
délimitation que les centres de gravité calculés
sur l'ensemble des points appartenant aux aires (localisation moyenne des
clients). Le centre de gravité d'une aire est en effet
théoriquement le point à partir duquel on parcourt la distance la
plus courte en moyenne
pour l'atteindre à partir de tous les autres points de
l'aire (point le plus accessible). L'aire est,
on le rappelle, constituée d'une masse de
clients de densité homogène obtenue par lissage (filtrage).
Le centre de gravité de l'aire qui circonscrit l'esnsemble des clients
ne correspond pas forcément à la moyenne des localisations des
clients (voir figure 3.41). Prendre un tel centre de gravité des
adresses des clients au lieu de celui de la surface de l'aire totale revient
aussi à ne pas tenir compte de ce lissage destiné à
éliminer une partie des erreurs d'enquête (adresses manquantes ou
fausses adresses, clients ayant déménagé).
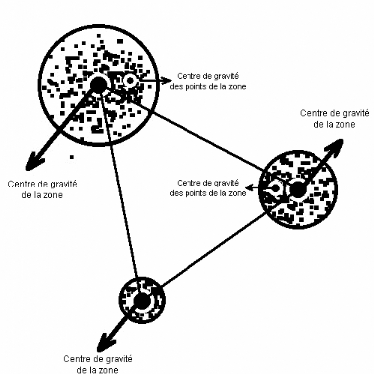
Fig. 3.41 - Les centres des aires et ceux des points appartenant
à ces mêmes aires
Le centre de gravité des aires est également
très intéressant dans le cas de desserte de transport
interurbaine qu'il s'agisse de transport de voyageurs (gare Sncf ou gare
routière) ou
de transport de marchandises (entrepôt) : on cherche en
effet le point le plus central possible
au sein d'une aire pour implanter un entrepôt
destiné à recevoir des marchandises de gros, entrepôt
à partir duquel on effectuera des livraisons au détail
vers des clients situés en périphérie de ce centre
local de distribution.
Le repérage du centre de gravité au
niveau global sur un ensemble d'adresses clients ne permet d'obtenir
qu'une position moyenne pour une localisation sans tenir compte des
barrières naturelles ou des sites géographiquement inaccessibles.
En outre, cette méthode est complètement inadaptée
à la recherche de localisations multiples.
Ayant déterminé précédemment les
coordonnées des points décrivant la frontière de la
zone
de chalandise, les coordonnées de son centre de
gravité seront tout simplement la moyenne
des coordonnées de ces points de contour.
Cependant, d'une manière plus générale, le
centre de gravité G d'une zone Z composée de n points clients P1,
..., Pn auxquels sont affectées des fréquentations (ou une
demande) f1, ..., fn
est tel que :
n
[ fu GPu] = 0
u=1
Considérons la fonction caractéristique
fZ (i, j) de la zone de chalandise Z,
préalablement
définie par:
P(i, j) Z , fZ (i, j) = 1 et P(i, j) Z , fZ (i, j) = 0
Pour déterminer G le plus simplement possible sur un
espace de valeurs discrètes, l'expression
de la fréquentation étant alors sous la forme f(i,
j) pour un point P de coordonnées P(i, j), on utilisera la relation:
m p
[fz(i, j) f(i, j) GPij] = 0
i =1
j =1
Avec m, le nombre de lignes de la matrice des
fréquentations associées à l'espace
géographique 2D considéré et p son nombre de
colonnes.
A noter que comme dans chaque aire, la
fréquentation est environ la même (f(i, j) =
constante), l'équation précédente se
réduit à:
p
m [fz(i, j)
GPij ] = 0
i = 1 j = 1
Comment déterminer les distances entre les noeuds du
modèle p-médian ?
Les distances des segments du modèle p-médian
reliant noeuds ou centres de gravité des zones sont calculées
soit en utilisant la distance euclidienne classique, soit en
déterminant les distances routières ou temps de
parcours (par exemple à l'aide d'un logiciel comme
AutorouteExpress de Microsoft), soit encore en utilisant la notion de distance
psychologique
(dij - nj) introduite dans un modèle p-médian
"généralisé" (voir § 2.3.1).
Comment déterminer le niveau de la demande
associé à chaque noeud ?
Cette même fonction caractéristique permet en
outre de fournir les propriétés marketing ou
socio-économiques liées aux zones et donc d'obtenir le niveau de
demande dans chaque zone (demandes dans le modèle p-médian
pondéré): soit V une variable dont la valeur évolue dans
l'espace total de la zone de chalandise. V est donc fonction du
point P(i,j) de l'espace géographique et s'écrit V(i,j).
La variable V peut être simplement le chiffre d'affaires
escompté dans la zone pour un produit ou un service spécifique
(niveau de la demande), une variable socio-économique (taux de
possession d'un véhicule, PCS, pouvoir d'achat moyen), une mesure de la
contribution locale à la performance (fréquentation comme dans
l'exemple
qui suit, chiffre d'affaires ou bénéfices
perçus par des clients en P(i,j)), un paramètre
environnemental (densité de la concurrence en P, places de parking,
circulation automobile),... Pour connaître la valeur de V à
l'intérieur d'une zone soit en somme, soit en moyenne, on
utilise encore la fonction caractéristique fZ(i, j). Pour une variable
V(i, j) à sommer comme
par exemple le nombre de places de parking dans la zone Z ou le
chiffre d'affaires tiré de la
zone Z, on aura Vz, la somme des V(i, j) sur l'ensemble de la
zone Z comme étant:
m p
Vz =
[f z (i, j)
i = 1 j = 1
V(i, j) ]
Pour une variable V(i, j) à étudier en valeur
moyenne comme par exemple le pouvoir d'achat
moyen dans la zone Z, on aura pour expression de Vz, la moyenne
des V(i, j) sur l'ensemble
de la zone Z:
m p
[f Z (i, j)
i =1 j =1
V(i, j) ]
VZ = m p
[f z (i, j) ]
i =1 j =1
Considérons la variable N(i, j) représentant le
nombre de clients en chaque point P(i,j). Alors
le pourcentage de clients contenu dans la zone de chalandise
à forte densité de clientèle par rapport au nombre de
clients total, est donné par:
p
Z
m [f
(i, j) N(i, j) ]
i =1 j =1
m
p
[N(i, j) ]
100
i =1 j =1
Si la zone de chalandise Z est morcelée en plusieurs
aires Z1,...Zh, il suffit de faire le calcul
sur chaque région et de sommer pour avoir le
pourcentage total, une alternative étant de définir la
fonction caractéristique réunissant toutes ces régions.
3.4 Approches stratégiques de la localisation
Les techniques de localisation peuvent être introduites
pour élaborer de véritables stratégies
de développement au niveau de réseaux de
magasins. Dans un contexte favorable et avec à l'esprit une
stratégie spatiale bien définie, un réseau de distribution
en croissance cherchera à s'étendre par addition de nouveaux
points de vente 601. La recherche de croissance par simple
accroissement de la surface commerciale de magasins existants est en effet bien
vite limitée et
601 MERCURIO J. (1984) Store Location Strategies,
dans Store Location and Store Assessment Research cité par
CLIQUET G. dans Valeur Spatiale des Réseaux et
Stratégies d'Acquisition des Firmes de Distribution, in
Valeur, Marché et Organisation, Ed. J-P. Brechet,
Presses Académiques de l'Ouest.
modifie d'autre part le concept initial et
éventuellement porteur du magasin dont la taille est l'un des
éléments. Outre un pouvoir de négociation accru
vis-à-vis des producteurs, une extension d'un réseau de
points de vente apporte une meilleure couverture géographique.
Cette couverture géographique est en effet importante car,
agissant comme un phare, elle permet aux consommateurs de
repérer leur enseigne en tous points du territoire et les
producteurs de voir en elle un moyen d'écouler en plus grandes
quantités leurs produits et de réaliser des
bénéfices accrus. Cliquet a effectué un état
de l'art des différents types de
stratégies spatiales et de leur
classification602. Six stratégies principales sont
offertes aux
distributeurs pour croître, dont les trois
premières seulement mettent en scène la
problématique de localisation spatiale 603:
1) Conquérir de nouvelles aires de marché par
ouvertures de nouveaux points de vente, mais
en conservant l'assortiment existant. Ce scénario augmente
la couverture spatiale du réseau,
2) Etendre son réseau dans des aires de
marché déjà occupées toujours en conservant
son choix de marchandises,
3) Conquérir de nouvelles aires de marché en
ouvrant et en diversifiant ses nouveaux points
de vente avec un nouvel assortiment,
4) Ouvrir de nouveaux points de vente avec de nouvelles
marchandises, mais sur des aires de marché déjà
conquises,
5) Augmenter sa part de marché avec les mêmes points
de vente et le même assortiment,
6) Diversification en améliorant l'assortiment dans des
points de vente existants.
La conquête de nouvelles aires est susceptible de se
réaliser par contagion, les points de vente s'implantent alors sur un
large front ou bien par diffusion hiérarchique ou par stratégie
de tête
602 CLIQUET G. (1998) Valeur Spatiale des
Réseaux et Stratégies d'Acquisition des Firmes de Distribution,
in
Valeur, Marché et Organisation, Ed. J-P. Brechet,
Presses Académiques de l'Ouest.
603 GHOSH A. et McLAFFERTY S. (1987) Location
Strategies for Retail and Service Firms, Lexington Books, p.10.
de pont604. Les points de vente s'implantent
alors dans les villes principales puis dans les villes de moindre
importance comme le décrit la théorie des places
centrales605. Par analogie avec le monde animal, un autre classement
des types de stratégies distingue l'évitement dans
l'esprit du principe de différenciation minimale de
Hotelling (voir § 2.1.4) qui consiste à s'installer loin des
concurrents, la recherche de concurrents et en particulier la
prédation qui
au contraire recherche l'affrontement souvent par une guerre des
prix en visant la proximité
des compétiteurs 606. Davidson, Sweeney et
Stampfl utilisent la méthode d'analyse de portefeuille
(décriée par certains auteurs - voir § 2.2.3) en croisant
les décisions sur les points
de vente, sur les aires de marché et sur les
segments de consommateurs à privilégier et dégagent
trois grandes catégories de stratégies 607 :
1) la stratégie d'expansion de
marché, par contagion, établissement de têtes de
ponts, constitution de grappes et recyclage de sites et l'acquisition de sites
concurrents ;
2) la stratégie de remplissage : on conforte
les positions acquises en agrandissant les points
de vente, en conquérant des marchés
secondaires et également comme précédemment, en
prenant le contrôle de sites concurrents ;
3) le downsizing : les performances sont
améliorées en réorganisant le réseau par la
fermeture des points de vente à la traîne et en en relocalisant
d'autres ainsi qu'en revoyant le mix produit.
Le choix d'une stratégie spatiale particulière est
dicté par le niveau d'ambition du réseau qui,
si elle est internationale ou même nationale,
nécessite l'établissement de têtes de pont avec
éventuellement des hiérarchies d'implantation à respecter.
Un niveau d'ambition modeste avec une volonté régionale
uniquement ne nécessitera qu'une stratégie de diffusion par
contagion. D'une manière générale, les
stratégies spatiales se découpent simplement en deux
grandes
604 LAULAJAINEN R. (1987) Spatial Strategies in
Retailing, Dordrecht, Holland, Reidel.
605 CHRISTALLER W. (1935) Die Zentralen Orte in
Süddeutschland, G.Fischer, Germany, Jena.
606 BROWN S. (1992) Retail Location : A
Micro-Scale Perpective, Aldershot : Avebury, p.170-171
607 DAVIDSON W.R., SWEENEY D.J. et STAMPFL R.W.
(1988) Retailing Management, 6th Ed., New York : Wiley, cité
par Cliquet G. dans Valeur Spatiale des Réseaux et
Stratégies d'Acquisition des Firmes de
Distribution, in Valeur, Marché et Organisation,
Ed. J-P. Brechet, Presses Académiques de l'Ouest, p.234.
catégories, les stratégies de
développement externe où le développement passe
par l'absorption d'autres chaînes ou par la coopération
avec les concurrents pour l'ouverture de centrales d'achat ou de
référencements communs et d'un autre côté, les
stratégies de développement interne608.
Cette variété de stratégies peut
s'observer effectivement sur le terrain. Le centre d'étude de
l'activité commerciale (Centre for the Study of
Commercial Activity) au Canada a réalisé une étude
à l'été 2000 sur les orientations stratégiques
pressenties auprès d'un échantillon de 475 décideurs, en
majorité présidents et directeurs généraux
appartenant à 226 réseaux de distribution canadien 609
représentant 32000 points de vente de l'alimentation,
l'habillement,
de l'équipement ménager et de grands magasins
plus généralement (voir figure ci-dessous).
Arrivent en tête des décisions que ces responsables
envisagent pour environ 80 % d'entre eux,
la modernisation et la rénovation des points de
vente (refurnishment), la relocalisation (relocation) puis
l'extension des réseaux de distribution et de façon moindre le
changement d'enseigne. L'extension du réseau de points de vente est
envisagée en majorité par l'ouverture
de nouvelles surfaces pour 74 % des décideurs (opening an
established format) ou de façon accessoire par l'acquisition d'un groupe
de points de vente appartenant à un autre réseau pour
35 % d'entre eux. Enfin, 10 % des décideurs pensent
à fermer des points de vente.
608 CLIQUET G. (1998) Valeur Spatiale des
Réseaux et Stratégies d'Acquisition des Firmes de Distribution,
in
Valeur, Marché et Organisation, Ed. J-P. Brechet,
Presses Académiques de l'Ouest.
609 HERNADEZ T., BIASIOTTO M. (2001) The Survey of
Corporate Planning : Summary Findings, Research
Letter 2001-2, Centre for the Study of Commercial Activity,
p.1-8.
Fig. 3.42 - Type de Décisions prise par les
décideurs dans un avenir proche pour leur réseau de
distribution610
Cette enquête a montré également que 40
décisions impliquant la notion de localisation étaient
prises par an dans chaque réseau comptant en moyenne 437 magasins.
Les décisions impliquant la localisation des points de
vente tournent d'une manière générale autour de:
- la création pure d'un réseau de points de vente
;
- l'extension d'un réseau par création de nouveaux
points de vente ;
- l'extension d'un réseau par acquisition de points de
vente concurrents ;
- la relocalisation de points de vente ;
- la suppression de points de vente.
Ces décisions ne sont pas, comme on l'a vu,
forcément contradictoires entre elles. On peut par exemple envisager
l'extension d'un réseau tout en supprimant certains points de vente et
en relocalisant d'autres. D'autre part, nous avons vu en introduction
que les réseaux peuvent adopter une organisation différente,
en franchises pour bénéficier d'une réactivité plus
élevée
610 HERNADEZ T., BIASIOTTO M. (2001) The Survey of
Corporate Planning : Summary Findings, Research
Letter 2001-2, Centre for the Study of Commercial Activity,
p.2.
et une connaissance du marché plus fine au niveau local
611 612, en succursales pour asseoir le contrôle du
franchiseur sur son réseau ou bien sous forme mixte associant
les deux types d'établissements. Cette dernière forme
d'organisation présente un intérêt indéniable
pour accroître la souplesse stratégique de l'ensemble pour
faciliter l'acquisition de nouveaux points
de vente en proposant aux propriétaires
différentes formules de rachat ou de franchise ainsi que pour animer le
réseau en bénéficiant des efforts d'innovation et de
promotion des deux catégories d'établissements commerciaux
613. Le point important qui nous concerne est surtout que
cette organisation mixte permet de trouver un compromis entre le
développement
du réseau et l'assimilation du concept du groupe.
Ainsi, le développement du réseau peut se faire assez rapidement
et à moindre prix par la création de franchises alors que les
filiales plus sous contrôle permettent de mailler le territoire tout en
assimilant graduellement le concept.
Le choix de tel ou tel type d'organisation dépend plus
des vues stratégiques du manager et de l'activité commerciale
considérée. La méthode associant modèle
p-médian et traitement du signal pourra, après avoir
délimité la zone de chalandise, spécifier la localisation
idéale des points de vente et hiérarchiser l'intérêt
des différents sites. Mais, ce n'est qu'au cas par cas et selon les
moyens financiers du groupe que l'on pourra décider de la
configuration en succursalisme, franchise ou de bâtir un réseau
mixte. Sans doute, les sites sans trop de risques liés à la
concurrence ou à l'environnement, établis depuis longue
date et qui peuvent ainsi contribuer majoritairement à
l'amélioration des résultats financiers tout en structurant
le réseau, bénéficieront plus facilement de la
structure en succursales ce qui leur permettra d'assimiler plus
aisément l'identité du groupe. Une identité commune
au réseau facilite et
fluidifie en effet les efforts de promotion et de communication
vis-à-vis de l'extérieur. Elle
611 BRICKLEY J.A., DARK F.H. (1987) The Choice of
Organizational Form : The Case of Franchising, Journal
of Financial Economics, 18, 401-20.
612 CAVES R.E. , MURPHY II W.F. (1976)
Franchising : Firms, Markets, and Intangible Assets,
Southern
Economic Journal, 42, 572-86.
613 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
constitue en quelque sorte un signe de ralliement pour
une masse de clients fidèles ou potentiels qui chercheront alors
à fréquenter les points de vente du réseau où
qu'ils soient. La structure en franchise conviendrait sans doute mieux
à des implantations récentes, plus risquées où
il s'agit d'avoir une grande capacité d'innovation pour s'adapter au
marché local. Les managers des franchises à l'esprit
entrepreneurial, sans doute plus motivés car plus responsables de
leur affaire, défricheront en pionniers les territoires non
encore conquis et plus en proie à la concurrence. Une plus grande
marge de manoeuvre dans le marketing et la gestion souple quotidienne du point
de vente leur sera nécessaire pour conforter la position du groupe dans
ces régions. A plus long terme, ces franchises pourront
éventuellement être converties en succursales de manière
à renforcer globalement le concept du groupe et pour transformer une
simple chaîne de points de vente en "un dispositif de forme
éclatée permettant de mettre en oeuvre simultanément
en plusieurs endroits un ensemble d'actions
avec une adaptation souple sur le
terrain"614.
L'ouverture ou la réorganisation d'une chaîne de
points de vente est un art difficile qui consiste, comme on l'a vu, à
choisir au mieux le nombre et la localisation des magasins ainsi que leur
type d'organisation (en succursales, en franchises ou mixte). Mais une
stratégie d'implantation peut être beaucoup plus
élaborée, sans se limiter à ces deux paramètres.
Ainsi, faut-il par exemple ouvrir tous les points de vente en même temps
ou bien adopter un ordre séquentiel de création judicieusement
conçu ? Nous avons d'autre part sous-entendu lors de la construction du
modèle p-médian précédent, que les points de vente
devaient se situer au plus proche des clients, d'autres paramètres
liés à la notion de distance méritent d'être
examinés. Certes le modèle p-médian peut incorporer
un coût d'ouverture des activités en chacun des
différents noeuds du réseau correspondant. Mais d'un autre
côté, les modèles de localisation- allocation prennent
d'une manière générale l'hypothèse, on l'a dit au
début de cet exposé, que
614 BOULANGER P., PERELMAN G. (1990) Le
réseau et l'Infini, Nathan, Paris, Cité par Cliquet G.
dans
CLIQUET G. (2000) Plural Form in Store Networks : A
Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
le futur site du point de vente que l'on cherche
à implanter devra se situer au plus près de clients
potentiels. Une manière d'aborder le problème consiste à
localiser ses points de vente non seulement par rapport aux clients, mais aussi
par rapport à la concurrence. La stratégie d'évitement
615 décrite précédemment
privilégiera dans les choix de localisation les zones encore peu
exploitées par la concurrence. Sur le plan stratégique,
on se situe alors dans la première étape du principe de
différenciation minimale correspondant à la phase
primaire
d'implantation d'une activité dans un territoire
vierge de concurrence (voir §2.1.4). Notre méthode
est tout à fait apte à cerner de telles régions qui, si
elles s'avèrent comporter un fort potentiel de clients, constituent des
mines d'or sur le plan commercial. S'installer en un lieu à
la fois riche en clientèle et dépourvu de
concurrence est un avantage stratégique indéniable que les
compétiteurs surmonteront sans doute (phase 2 du principe de
différenciation minimale616), mais au bout seulement
d'un certain temps. Nous nous proposons de décrire dans le
prochain paragraphe comment développer cette stratégie
d'évitement à partir de la méthode associant
traitement du signal et modèle p-médian.
3.4.1 La stratégie d'évitement ou
rechercher les zones non exploitées par la
concurrence
Considérons l'exemple où la première carte
représente cette fois l'ensemble de ces magasins associés
à leur chiffre d'affaires sur un territoire vaste
(région, pays) et que la deuxième
représente la même cartographie mais filtrée
par deux filtres Nagao :
615 BROWN S. (1992) Retail Location : A
Micro-Scale Perpective, Aldershot : Avebury, p.170-171
616 Source : BROWN S. (1992) Retail Location : A
Micro-scale Perspective, Ashgate, England.
Fig. 3.43- Adresses de magasins associées à leur
chiffre d'affaires, Fig. 3.44 - suivies de deux filtres Nagao

Dans ce cas, pour trouver la localisation la plus
éloignée et remplir les trous ou interstices de zones non
encore exploitées, il suffira de considérer la
cartographie "inverse" (c'est-à-dire celle obtenue en prenant pour
nouvelle valeur en chaque point la valeur maximale représentée
retranchée de la valeur actuelle du point: Vmax - Vactuelle =
Vnouvelle valeur). On obtient alors en reprenant l'exemple
précédent les figures 3.45 et 3.46 :
Fig. 3.45 - Cartographie inverse, Fig. 3.46 - Cartographie
inverse filtrée par deux filtres Nagao

En procédant à une délimitation par
transformation morphologique, on obtient la figure 3.47 :
Fig. 3.47 - Délimitation des zones vides de concurrence
Les zones vides où la concurrence est rare sont
bien délimitées. Il faut néanmoins prendre garde aux
effets de bords: la cartographie, mal ajustée, a ici coupé des
zones vides en limite
de représentation ce qui fait que celles-ci sont
limitées par des segments rectilignes (voir dessin ci-dessus).
D'autre part, certaines zones vides d'activités (ou
à faible nombre d'activités) ne correspondent peut-être
pas à des zones d'implantation possibles pour un point
de vente mais à des barrières naturelles
(bois, lac, rivière, aéroport) qu'il s'agit d'identifier.
Cette dernière approche reprend en fait la théorie des secteurs
proximaux (voir § 2.1.1) qui cherchait à cibler les lacunes
spatiales au niveau desquelles résident des opportunités
d'implantation (zones dépourvues de concurrence). Dans cette
perspective, il est intéressant de comparer les deux approches à
savoir la délimitation des zones de chalandise (à forte
densité
de clients) et la délimitation de zones vides (à
faible densité de concurrents) pour sélectionner
les régions cumulant les deux avantages.
3.4.2 La recherche de concurrents ou la
prédation
Certaines activités ont cependant au contraire
tendance à se regrouper pour augmenter leur pouvoir
d'attractivité dans une stratégie de recherche de concurrents ou
pour se lancer dans un affrontement direct par exemple à travers une
guerre des prix dans l'optique d'une stratégie de prédation
617 618 619. Il sera alors intéressant de délimiter
les zones de chalandise de clients potentiels pour rechercher les emplacements
qui leur sont les plus proches et en parallèle, de délimiter les
zones d'implantations de concurrents pour également
détecter les régions géographiques où ceux-ci ont
tendance à se concentrer pour également s'en rapprocher le plus
possible. La démarche cherchera alors à être
à la fois proche des clients et proche des concurrents en
procédant à une délimitation à la fois des
zones de chalandise et des zones
commerciales du secteur. Dans la pratique cependant, au niveau
local, les concurrents ne sont
617 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, vol. 39, p. 41-57.
618 DELOZIER M.W. et LEWISON D.M. (1986)
Retailing, 2nd ed., Merill.
619 BROWN S. (1992) Retail Location : A Micro-Scale
Perpective, Aldershot : Avebury, p.170-171
pas en général suffisamment nombreux pour
pouvoir clairement définir par traitement du signal les zones de
leur implantation. On cherchera, dans ce cas, à
sélectionner par simple examen les emplacements de
préférence à proximité des regroupements de
concurrents. L'identification des zones de concurrence peut être
intéressante dans le cadre d'une stratégie
de recherche de concurrents parfois aussi car ces zones
d'implantation sont révélatrices d'une activité
florissante du secteur et sont donc porteuses commercialement. C'est en
particulier le
cas dans la filière du tourisme (hébergement,
restauration, centres de loisirs). Par exemple, un terrain de camping
souhaitant accueillir une clientèle de touristes n'aura pas
intérêt à s'installer dans les régions à
fortes populations puisque durant les saisons touristiques, celles-ci migrent
vers d'autres lieux. Géocoder les implantations de campings et
délimiter leurs régions d'installation comme nous l'avons
fait ci-dessous, paraît dans ce cas assez intéressant. La
même procédure s'appliquerait pour une stratégie de
prédation.
Fig. 3.48 - Représentation des campings sur le
territoire national par des points Source des données : CD
Stratégie & Localisation de J.Baray et Société
Articque Géocodage par Logiciel Carte & Données
d'Articque
Fig. 3.49 - Délimitation des zones d'implantation de
campings par filtre Sobel
Fig. 3.50 - Numérotation des zones d'implantation de
campings
Après avoir délimité les zones
d'activité par traitement du signal (filtre Sobel), nous avons
identifié 16 zones d'implantation principale de campings qui
correspondent chacune à des zones touristiques comme la logique
le veut, souvent à proximité du bord de mer: Côte
d'Azur, côte vendéenne, Bretagne, Bouches du Rhône,
Pyrénées Orientales,... Il convient donc
de rechercher pour un camping touristique une
implantation au sein même de l'une de ces zones denses en
concurrents en évitant tout de même les régions
saturées en offre. Une approche encore meilleure serait
d'établir ce même type de carte sur plusieurs années et de
cibler les zones d'implantation de camping en
développement (ayant un nombre de concurrents en croissance ou
s'étendant) et d'éviter celles ayant tendance à
régresser.
3.4.3 Stratégie d'ouverture des points de
vente
Un réseau de points de vente peut adopter
différentes stratégies d'ouverture, en se déployant
rapidement sur un territoire ou bien en créant ses magasins, tour
à tour, selon un ordre bien déterminé. Les modèles
de localisation multiple de points de vente ont longtemps passé sous
silence les effets des délais d'ouverture. Il est rare qu'une
société décide l'ouverture simultanée
de plusieurs magasins que ce soit pour des raisons de budget
ou même par souci de prudence afin de mesurer le succès des
premières créations initiales sur un marché
donné et de se conforter dans l'idée dans lancer d'autres
ultérieurement. Ceci dit, dans le choix même des
localisations, il est possible soit de sélectionner les
meilleures localisations de manière itérative, soit de
chercher à implanter un réseau de manière globale. Dans le
premier cas, le décideur identifiera une première
localisation optimale en essayant de maximiser le chiffre d'affaires du
magasin, puis un peu plus tard va ouvrir de la même façon un
certain nombre
d'autres sites en tenant compte des magasins existants et de la
concurrence 620. Ce processus
se poursuivra jusqu'à ce que le marché ait atteint
son point de saturation en terme d'offre. Le
620 KAUFMANN P.J., DONTHU N. et CHARLES M.B.
(2000) Multi-unit Retail Site Selection Processes : Incorporating Opening
Delays and Unidentified Competition, Journal of Retailing, Vol.76(1),
p. 113-127
problème est qu'en suivant cette procédure, le
fait de placer au départ un point de vente entre deux localisations
potentiellement très intéressantes va condamner ces
opportunités à moyen terme621. Il est en effet
impensable pour des raisons de coût, d'ouvrir ultérieurement ces
deux nouvelles surfaces commerciales après avoir fermé le magasin
existant devenu inutile et sans doute non-rentable, sans avoir au minimum
rentabilisé l'investissement souvent onéreux de la
création de ce dernier.
Il est donc presque indispensable de choisir les sites optimaux
en une étape unique 622 623 624
ce qui permet en outre d'avoir ultérieurement une
meilleure couverture du marché 625. Même
s'il existe un délai d'ouverture entre les points de vente
sélectionnés de cette manière globale,
le chiffre d'affaires de ces différentes entités
sera en général plus équilibré et meilleur à
long terme que ne le seraient des localisations déterminées
séquentiellement. Dans ce dernier cas,
le premier magasin avec sa localisation très centrale
par rapport au potentiel du marché aura tendance à avoir un
revenu excellent alors que les magasins suivants devront se contenter des
restes et seront moins performants 626. Mais si, pour
différentes raisons, les délais d'ouverture entre les premiers
magasins à ouvrir et les suivants doivent être longs, il
est préférable d'adopter le processus séquentiel de
décision afin d'amasser durant cette période les profits sur
ces premiers magasins possédant un potentiel commercial
plus intéressant. Cette stratégie est également
confortée par le fait que plus le délai d'ouverture est long,
plus le risque que les
meilleurs emplacements soient préemptés par un
concurrent est élevé 627. Kaufmann, Donthu
621 KAUFMANN P.J., DONTHU N. et CHARLES M.B.
(2000) Multi-unit Retail Site Selection Processes : Incorporating Opening
Delays and Unidentified Competition, Journal of Retailing, Vol.76(1),
p. 113-127
622 GHOSH A., CRAIG S. (1991) Fransys : A
Franchise Distribution System Location Model, Journal of
Retailing, 67, p. 466-495.
623 GOODSCHILD M.F. (1984) Ilacs : A
Location-Allocation Model for Retail Site Selection, Journal
of
Retailing, 60, p. 84-100.
624 ACHABAL D.D., GORR W.L. et MAHAJAN V.
(1982) Multiloc : A Multiple Store Location Decision
Model, Journal of Retailing, 58, 5-24.
625 SCOTT A.J. (1971) Combinatorial
Programming, Spatial Analysis and Planning, London: Methuen and
Company Limited.
626 GHOSH A., TIBREWALA (1992) Optimal Timing
and Location in Competitive Markets, Geographical
Analysis, 24 (4): 317-334.
627 GHOSH A., CRAIG S. (1983) Formulating Retail
Location Strategy in a Changing Environment, Journal of
Marketing, 47, p. 56-68.
et Brooks ont vérifié toutes ces hypothèses
assez logiques en simulant l'implantation de deux réseaux de magasins
à travers un modèle MCI 628.
3.5 Un exemple de construction d'un modèle
p-médian par traitement du signal
Reprenons l'exemple du magasin avec les clients virtuels
associés à leurs fréquentations du chapitre
précédent :
Fig. 3.51 - Adresses clients associées aux
fréquentations Fig. 3.52 - La délimitation des zones par filtres
médian et Sobel


En calculant les coordonnées (X,Y) du
centre de gravité et la valeur moyenne des
fréquentations (ainsi que divers paramètres
géométriques) de chaque aire selon les méthodes
décrites ci-dessus, on obtient la cartographie avec chaque aire
numérotée et les deux tableaux
de valeurs suivants (3.1 et 3.2).
628 KAUFMANN P.J., DONTHU N. et CHARLES M.B.
(2000) Multi-unit Retail Site Selection Processes : Incorporating Opening
Delays and Unidentified Competition, Journal of Retailing, Vol.76(1),
p. 113-127
Fig. 3.53 - Numérotation des aires de chalandise
Tableau 3.1 - Paramètres géométriques des 12
aires de la zone de chalandise obtenus après délimitation
|
Aire
|
Superficie
|
X
|
Y
|
Périmètre
|
Diamètre Ds
|
Epaisseur De
|
Angle
|
|
1
|
346
|
87
|
9
|
142
|
24
|
20
|
138
|
|
2
|
110
|
165
|
6
|
60
|
13
|
10
|
49
|
|
3
|
156
|
239
|
4
|
59
|
18
|
10
|
175
|
|
4
|
194
|
134
|
37
|
88
|
19
|
12
|
129
|
|
5
|
124
|
55
|
41
|
64
|
13
|
11
|
53
|
|
6
|
143
|
182
|
45
|
89
|
17
|
10
|
31
|
|
7
|
1048
|
105
|
74
|
236
|
52
|
25
|
152
|
|
8
|
322
|
32
|
90
|
148
|
28
|
14
|
134
|
|
9
|
467
|
235
|
122
|
147
|
45
|
13
|
102
|
|
10
|
7594
|
70
|
152
|
1139
|
134
|
77
|
34
|
|
11
|
467
|
180
|
137
|
213
|
28
|
21
|
144
|
|
12
|
689
|
183
|
167
|
233
|
45
|
19
|
1
|
Tableau 3.2 - Paramètres marketing des 12 régions
de la zone de chalandise obtenus après délimitation
|
Aire
|
Fréquentation
Moyenne
|
Valeur
Modale
|
Maximum des
Fréquentations
|
|
1
|
143
|
128
|
192
|
|
2
|
134
|
128
|
173
|
|
3
|
145
|
128
|
190
|
|
4
|
135
|
128
|
173
|
|
5
|
136
|
128
|
173
|
|
6
|
136
|
128
|
173
|
|
7
|
164
|
192
|
192
|
|
8
|
133
|
128
|
173
|
|
9
|
157
|
128
|
192
|
|
10
|
161
|
173
|
192
|
|
11
|
134
|
128
|
173
|
|
12
|
147
|
128
|
192
|
Les valeurs de X et de Y nous donnent les coordonnées des
centres de gravité de chaque aire
de chalandise et donc les noeuds du réseau
p-médian. La demande en chaque noeud peut être
caractérisée soit par la fréquentation, soit par la
demande globale dans l'aire égale à la
fréquentation moyenne par la superficie (les fréquentations
moyennes représentent les valeurs
de la fréquentation au sein des aires qui
possède, par notre définition, le caractère d'avoir un
niveau homogène). L'intérêt de prendre la demande globale
dans l'aire comme valeur de la demande en chacun des noeuds est que celle-ci
est révélatrice à la fois du niveau moyen de
fréquentation dans l'aire considérée et de
l'étendue de cette aire, et constitue ainsi une mesure
intéressante du potentiel commercial au voisinage du centre de
gravité. Il est à noter que ces fréquentations
associées aux adresses des clients peuvent être les
fréquentations effectives d'un point de vente ou d'un ensemble de
points de vente existants dans le cas où l'on voudrait
réorganiser un réseau de magasin en tirant parti de
l'expérience commerciale acquise. Mais,
ces fréquentations tout aussi bien susceptibles
d'être tirées d'une enquête marketing en demandant
à un échantillon de clients potentiels répartis dans
l'espace s'ils comptent acheter
tel ou tel produit ou service et à quel rythme. Pour
caractériser la demande, nous aurions aussi
bien pu prendre en compte d'autres paramètres que
les fréquentations comme le volume d'affaires ou même les
bénéfices.
La dernière étape avant d'obtenir le réseau
p-médian complet est de lier les noeuds en fonction
du réseau de routes existant et d'évaluer les
distances kilométriques (ou de mesurer les temps
de parcours) pour évaluer les "coûts" de
déplacement.
Fig. 3.54 - Le p-médian modélisé
après délimitation de la zone de chalandise et calcul des
centres de gravité et fréquentations moyennes. La valeur de
fréquentation au sein des aires est ici prise comme valeur de la
demande aux noeuds.
Ensuite, peut alors s'effectuer la résolution du
modèle p-médian (simplifié) selon les méthodes
existantes. En utilisant par exemple la méthode de
Goldman629 (voir chapitre I) pour la recherche d'une
localisation proche de l'optimale, on trouve que l'aire 7 avec sa
fréquentation
de 164 est un site convenable pour l'implantation d'un
magasin. En admettant que nous ne soyons pas encore satisfaits de la
précision du lieu d'implantation (dans l'aire 7), notre nouvel
algorithme associant le p-médian et le traitement du signal
(exposé au paragraphe 4.2.1) nous
demande alors d'effectuer la même démarche au sein
de cette aire 7, à savoir une délimitation
629 GOLDMAN J.L. (1971) Optimal Center Location in
Simple Networks; Transportation Science 5, 212-221.
par filtrage et une analyse des intra-aires de chalandise pour
constituer un nouveau réseau p-
médian plus petit occupant l'aire :

Fig. 3.55 - L'aire 7 agrandie

puis un filtrage médian (les fréquences sont
très semblables):
Fig. 3.56 - L'aire 7 filtrée par un filtre
médian

une délimitation par filtrage Sobel:
Fig. 3.57 - L'aire 7 délimitée par un filtre
Sobel
puis un nouveau calcul de centres de gravité et une
évaluation des fréquentations intra-aires:


Fig. 3.58 - Les éléments de l'aire 7
numérotés après délimitation
pour constituer le nouveau réseau p-médian:
Fig. 3.59 - Le réseau p-médian correspondant
à l'aire 7
Sa résolution montre que le site commercial doit non
seulement se situer dans l'aire 7 mais aussi plutôt dans la sous-aire
7.2.
3.6 Utiliser toutes les sources d'informations commerciales
disponibles
L'intérêt du traitement du signal associé
à un modèle de localisation-allocation tel que le p-
médian réside aussi pour le manager dans les nouvelles
perspectives offertes pour manipuler
de façon souple des informations de sources
d'extraction variées. Les bases de données d'adresses de
consommateurs potentiels construites par enquête ou déduites
des modes de paiement servent comme on l'a vu, à alimenter le
modèle après une phase de géocodage et de
délimitation. Mais rien n'empêche non plus d'introduire des
informations déjà mises en forme comme des cartes de
données statistiques en format électronique ou même
sur support imprimé. L'exemple suivant nous montrera qu'il
est possible d'effectuer une étude d'implantation sans
même passer par la fastidieuse étape de géocodage
d'adresses, mais
simplement en reprenant des documents glanés au fil de ses
lectures.
Exemple de l'implantation d'activités commerciales au
niveau national
Le traitement du signal peut aussi s'attaquer à
traiter des informations issues de sources variées comme par
exemple des cartographies sur support papier, qui seront directement
intégrées dans un modèle p-médian. En
témoigne l'exemple de cette carte représentant des
densités de population en 2000, carte publiée dans le
supplément "l'atlas des régions"630 du magazine les
Echos.
Une première phase consiste à acquérir
l'information, c'est-à-dire à scanner le document de la
même manière que précédemment. Les données
d'enquête ont été saisies pour constituer une base de
données, puis ont été géocodées. Le
procédé consiste alors à appliquer à ces
données scannées le même traitement de filtrage et de
convolution par un filtre Sobel pour en extraire
les contours les plus marquants, en l'occurrence ceux des
bassins de population. Cet exemple illustre bien la souplesse et la
rapidité du traitement du signal qui permet d'intégrer n'importe
quel document dans une logique p-médian (ou autre modèle de
localisation-allocation) sans
même ici perdre de temps ou d'énergie à
saisir les données !
630 LES ECHOS (2000) L'atlas des Régions
Tome 1, Les Echos, réalisé en collaboration avec l'Insee.
Fig. 3.60 - Carte de France des densités de population en
2000 631

Fig. 3.61 - La carte traitée par un filtre médian,
Fig. 3.62 - puis délinée par filtre Sobel
631 LES ECHOS (2000) L'atlas des Régions
Tome 1, Les Echos, réalisé en collaboration avec l'Insee.


Fig. 3.63 - Les zones numérotées et
analysées
Nous obtenons tout de suite les caractéristiques de
bassins de population en terme de
localisation de leur centre d'inertie et de leur
étendue (voir tableau 3.3). Il est à noter que nous avons pris
comme exemple une carte de densité de population, mais que
n'importe quelle autre carte issue d'une quelconque source électronique
ou papier aurait pu convenir, cela en fonction des besoins de l'analyse.
Supposons que la France ne compte pas encore
d'hypermarchés et qu'un grand groupe décide
d'y créer 10 magasins. Où faudrait-il les installer
compte tenu des bassins de population ? Le
p-médian (ou plutôt 10-médian) va nous
donner ici encore une fois rapidement la réponse
grâce à l'étape précédente
de délimitation des zones par traitement du signal. La résolution
du modèle avec les paramètres X, Y et la superficie,
pour une distance limite raisonnable de parcours pour les consommateurs
de 50 miles, nous apprend très rapidement que les meilleures
implantations sont en : 1 (Lille-Roubaix), 6 (Paris et Région
Parisienne), 9 (Strasbourg), 18 (Tours), 24 (Lyon), 33 (Bordeaux), 35 (Nice),
36 (Montpellier et la côte), 37 (Marseille et Région) et 38 (la
distance maximale à parcourir est alors en théorie 645 pour une
fonction objective de 10 253 440). Dans le cas où un nouvel
hypermarché viendrait à s'installer, il lui faudrait se placer
en 5. Les premiers hypermarchés ont en effet été
créés dans
ces régions fortement peuplées à partir des
années 60.









































































Tableau 3.3 : Les caractéristiques des 43 aires de
population détectées par traitement du signal
|
ZONE
|
Superficie
|
X
|
Y
|
Longueur
|
Majeur
|
Mineur
|
Angle
|
|
1
|
13272
|
1237
|
168
|
1050
|
177
|
98
|
155
|
|
2
|
740
|
1373
|
213
|
163
|
50
|
19
|
29
|
|
3
|
2443
|
952
|
420
|
371
|
69
|
45
|
96
|
|
4
|
870
|
1211
|
409
|
198
|
58
|
19
|
63
|
|
5
|
2680
|
1706
|
433
|
308
|
89
|
38
|
91
|
|
6
|
18179
|
1135
|
531
|
1324
|
165
|
145
|
102
|
|
7
|
1256
|
733
|
454
|
245
|
45
|
35
|
70
|
|
8
|
1435
|
1815
|
448
|
290
|
68
|
27
|
174
|
|
9
|
4594
|
1951
|
557
|
528
|
116
|
51
|
59
|
|
10
|
1356
|
1721
|
556
|
230
|
51
|
34
|
133
|
|
11
|
753
|
97
|
599
|
132
|
49
|
20
|
13
|
|
12
|
875
|
1908
|
680
|
142
|
45
|
25
|
42
|
|
13
|
1803
|
518
|
696
|
225
|
54
|
42
|
162
|
|
14
|
850
|
810
|
731
|
143
|
41
|
27
|
106
|
|
15
|
2021
|
1900
|
749
|
263
|
65
|
41
|
126
|
|
16
|
922
|
1076
|
753
|
134
|
41
|
29
|
4
|
|
17
|
1389
|
1837
|
811
|
307
|
55
|
32
|
89
|
|
18
|
1132
|
693
|
845
|
155
|
39
|
37
|
68
|
|
19
|
1495
|
885
|
874
|
198
|
44
|
43
|
12
|
|
20
|
805
|
1710
|
883
|
165
|
48
|
21
|
37
|
|
21
|
2452
|
532
|
896
|
253
|
61
|
51
|
159
|
|
22
|
831
|
827
|
1041
|
159
|
42
|
25
|
104
|
|
23
|
1065
|
1780
|
1108
|
301
|
55
|
24
|
63
|
|
24
|
7045
|
1553
|
1230
|
606
|
114
|
79
|
135
|
|
25
|
870
|
1746
|
1186
|
140
|
43
|
26
|
117
|
|
26
|
1770
|
1273
|
1229
|
239
|
69
|
33
|
107
|
|
27
|
1046
|
971
|
1218
|
161
|
43
|
31
|
38
|
|
28
|
827
|
1717
|
1249
|
160
|
51
|
21
|
100
|
|
29
|
706
|
792
|
1259
|
114
|
37
|
25
|
27
|
|
30
|
2390
|
1475
|
1293
|
339
|
64
|
48
|
20
|
|
31
|
2627
|
1690
|
1339
|
443
|
60
|
56
|
116
|
|
32
|
1046
|
1560
|
1410
|
201
|
54
|
25
|
112
|
|
33
|
3138
|
669
|
1436
|
300
|
76
|
53
|
180
|
|
34
|
2633
|
1579
|
1635
|
334
|
59
|
57
|
66
|
|
35
|
4155
|
1930
|
1690
|
522
|
149
|
36
|
41
|
|
36
|
4911
|
1434
|
1705
|
626
|
168
|
37
|
36
|
|
37
|
8558
|
1685
|
1766
|
870
|
162
|
67
|
148
|
|
38
|
3642
|
990
|
1731
|
303
|
77
|
60
|
58
|
|
39
|
1524
|
1594
|
1725
|
274
|
61
|
32
|
71
|
|
40
|
1547
|
1315
|
1782
|
306
|
68
|
29
|
8
|
|
41
|
893
|
696
|
1788
|
165
|
37
|
31
|
146
|
|
42
|
906
|
1266
|
1819
|
189
|
41
|
29
|
33
|
|
43
|
1992
|
1247
|
1936
|
254
|
53
|
48
|
111
|













Fig. 3.64- Pour 10 localisations: zones de potentiel commercial
associées aux points de vente en gras
(en ignorant la distance limite de parcours des 50 miles)
Il est à noter cependant qu'avec 10
hypermarchés, seulement 40,6 % de la demande est couverte.
D'autre part, on s'aperçoit que, compte-tenu d'une distance limite de 50
miles que les consommateurs seraient prêts à parcourir, les
hypermarchés ne couvrent en terme d'offre que leur propre aire
d'implantation soit 10 aires sur 43, ces aires étant en France parmi les
plus peuplées. Si cette logique d'implantation
préoccupait une activité pour laquelle les
consommateurs sont prêts à parcourir une plus grande distance
comme par exemple celle des parcs d'attraction qui doivent aussi se placer au
plus près de leurs clients, nous aurions obtenu
les mêmes résultats mais avec un taux de couverture
de 100 % (en supposant que les clients soient prêts à parcourir
deux cents ou trois cents kilomètres) : les zones de population sont
en
effet éloignées les unes des autres ce qui ne les
met pas en concurrence.
Fig. 3.65 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts
(en ignorant la distance limite de parcours des 50 miles)
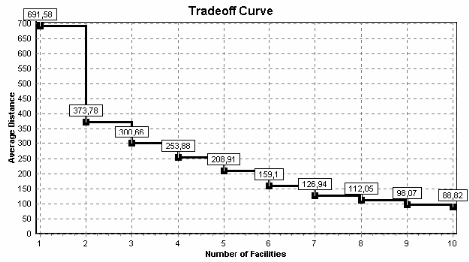
Conclusion
Nous avons vu dans ce chapitre que les principes du
traitement du signal pouvaient être introduits dans une
problématique de gestion et en particulier la recherche de
localisations commerciales optimales. Dans ce cadre, nous avons
présenté un nouvel algorithme composé
de quatre étapes en l'occurrence :
- une phase d'acquisition des données
constituées par les adresses des clients qui seront
géocodées afin d'obtenir une cartographie représentant
l'ensemble des clients potentiels.
- un pré-traitement des données
destiné à éliminer par un filtrage les imperfections
de la base
de données d'adresses entraînées par
exemple par des adresses incomplètes, de mauvaises saisies, des
erreurs d'échantillonnage,.... Cette étape comprend en
deuxième lieu la phase de traitement ou la mise en forme des
données à proprement parler qui s'attache dans notre
problématique à détecter par une convolution avec
un filtre du type Sobel et un sous- algorithme, les frontières de
la zone de chalandise,
- l'exploitation des résultats
qui permet de spécifier les caractéristiques propres de la
zone de chalandise, c'est-à-dire les paramètres
géométriques qui vont nous servir à construire le
modèle p-médian (coordonnées des centres de gravité
de chaque aire composant la zone de chalandise correspondant aux noeuds du
réseau et la surface de ces aires mesurant la demande).
- la résolution du modèle ainsi
élaboré par les heuristiques bien connues de résolution du
p- médian.
Nous avons déjà laissé entrevoir à
travers quelques exemples, les avantages d'un tel mode de recherche de
localisations optimales à savoir la rapidité, la souplesse
d'utilisation et la démonstrativité. La deuxième partie
nous donnera l'occasion de vérifier ces avantages sur des exemples
concrets portant sur la filière de distribution des produits
biologiques, et en
particulier l'exactitude de la méthode, sa
rapidité, sa précision et sa capacité à traiter de
larges
bases de données d'adresses clients pour la
recherche de localisations proches de l'optimal. Pour introduire ces
exemples, nous allons dans un premier temps établir un bilan du
marché des produits bio en France et dans le monde, puis
présenter les différents modes de distribution de ces
produits pour illustrer enfin le fonctionnement de notre algorithme avec le
cas particulier de la localisation de points de vente de
produits biologiques dans l'Ouest
parisien.
Partie II :
La localisation d'un réseau
Chapitre 4 :
Analyse d'un réseau de points de vente
de produits biologiques dans l'Ouest parisien
Introduction
Les produits bio sont un secteur qui en France comme
en Europe ou aux Etats-Unis connaissent une forte croissance d'abord
car les consommateurs échaudés par les scandales
alimentaires souhaitent de plus en plus acheter des produits à la fois
sûrs, sains et savoureux. D'autre part, les politiques
françaises et européennes favorisent très largement
l'agriculture biologique en octroyant aux surfaces agricoles
dédiées à ce mode de production des subventions non
négligeables. Enfin, les grands distributeurs voient dans ce type de
produits
un moyen d'améliorer leur image de marque et leur
rentabilité. La distribution des produits biologiques constitue un
champ intéressant d'étude dans le cadre d'une
problématique d'implantation commerciale étant donné que
les magasins "bio" sont actuellement en pleine phase d'expansion, les
premières créations datant d'une dizaine d'années.
Ainsi, il reste en France encore de nombreuses opportunités pour
créer son point de vente de produits biologiques en particulier
dans les villes de taille moyenne. Nous nous proposons donc
d'appliquer la nouvelle méthode explicitée au chapitre
précédent à la localisation d'un réseau
de points de vente de produits biologiques dans l'Ouest Parisien.
Ce choix géographique n'est pas anodin car l'Ouest Parisien à
fort pouvoir d'achat et très hétéroclite est
constitué de zones
où les magasins "bio" sont bien implantés (en
particulier certains arrondissements de Paris) et d'autres zones apparemment
encore libres de toute offre dans ce secteur. Notre démarche dans
ce chapitre constituera à partir d'une base de
données d'adresses de clients potentiels habitant cette région
et dans l'optique d'une recherche de localisations optimales pour des
points de vente de produits biologiques, à construire le
modèle p-médian correspondant grâce aux
principes du traitement du signal vus
précédemment.
4.1 Le marché et la distribution des produits
biologiques
4.1.1 Les produits biologiques : définition et
importance du marché
Dopés par les nombreux scandales alimentaires (vache
folle, poulet aux hormones, dioxine, fièvre aphteuse...), les produits
biologiques sont un secteur dynamique et en pleine expansion bien que le
commerce "bio" reste pour l'instant un micro-marché qui
n'implique à l'heure actuelle que 1 % de la production
agroalimentaire française et moins de 1 % du chiffre d'affaires
du commerce de détail. Les qualités hygiéniques ou
gustatives de ces produits très souvent au moins 10 % plus chers
que les aliments industriels, n'apparaissent pas encore évidentes
aux yeux des consommateurs : cependant, malgré leur
chèreté, la vente de produits biologiques progresse en France et
aux Etats-Unis au rythme de 20 % par an et les experts
tablent qu'à moyen terme, 5 % des dépenses des
Français seront consacrées au "bio" 632 (soit
encore une marge de progression de 400 %).
En termes de statistiques, l'agriculture biologique concerne en
France :
? 7500 exploitations agricoles sur 270 000 ha soit
seulement encore 0,9 % de la surface agricole ; à titre de
comparaison, l'agriculture biologique en Europe représente 2,1 % de la
surface agricole ;
? un marché actuel de 4,5 milliards de francs et 1000
entreprises de transformation633.
L'engouement pour le "bio" se remarque dans la
plupart des pays développés et particulièrement
aux Etats-Unis où ce secteur pèse déjà 4 milliards
de dollars634.
632 SYLVANDER B. (1999) Les Tendances de
Consommation de Produits Biologiques en France et en Europe :
Conséquences sur les Perspectives d'Evolution du Secteur.
Colloque l'Agriculture Biologique Face à Son
Développement, Les enjeux Futurs, 6-8 déc. 1999, Lyon.
633 INRA (1999) L'agriculture Biologique en
France, Document du Groupe de Travail de l'Inra sur le Secteur
Biologique, Présidé par Guy Riba.
634 FOSTER C. et LAMPKIN N. (1999) European
Organic Production Statistic 1993-96, Stuttgart, Hohenheim
University.
Mais que sont exactement les produits biologiques ?
L'appellation "biologique" est réglementée et
strictement contrôlée par la loi.
Le logo "AB" (Agriculture Biologique) accordé par le
ministère de l'agriculture sur un produit garantit en
résumé635 :



o la conformité du produit avec la
réglementation européenne en ce qui concerne les aliments
d'origine végétale (interdiction d'utiliser des organismes
génétiquement modifiés) ;
o la conformité au cahier des charges
fixé par les pouvoirs publics français et
européens pour tous les produits ayant des ingrédients
d'origine animale ou destinés à la production animale ;
o que l'aliment a été obtenu par une
production respectant à la fois la nature et l'homme par
exemple par l'utilisation exclusive d'engrais ou de traitements
écologiques et naturels ;
o que l'aliment incorpore au minimum 95 %
d'ingrédients issus de la production
biologique.
Ecocert est l'organisme privé (mais
néanmoins dépendant du ministère de l'agriculture)
chargé
de s'assurer du contrôle annuel des productions
classées comme biologiques. La certification "bio" est accordée
par les organismes accrédités : Ecocert, Qualité
France ou Socotec. Les entreprises souhaitant être
agréées "biologiques" doivent de plus acquitter un
droit d'utilisation du logo AB et être inscrites à la
Direction Régionale de l'Agriculture. Une accréditation
encore plus sévère pour les produits issus de
l'agriculture biodynamique est accordée par l'organisme
Demeter.
En outre, les exploitations agricoles ont la possibilité
de s'engager avec l'Etat français dans un
contrat territorial d'exploitation (le label est encore
inexistant). Ce contrat "écologique" oblige
635 BARAY J. (2002) Le Guide des Produits
Bio, Editions Grancher, Paris.
alors l'exploitation qui l'adopte à respecter la flore
et la faune, le paysage rural, à utiliser des matériaux
traditionnels,... Au niveau des entreprises industrielles, on a
prévu, à l'échelon international, la norme Iso 14000 de
management de l'environnement qui vise également à ce que les
activités humaines s'insèrent au mieux dans l'environnement sans
trop lui nuire.
Les produits non-alimentaires tels qu'ampoule
électrique, aspirateur traîneau, chaussures, colle pour
revêtement de sols, congélateur, détergent pour
textiles, filtre à café, lave-linge, linge, matelas,
mobilier de bureau, mobilier scolaire, ordinateur personnel, papier
à copier, papier absorbant, peinture,
réfrigérateur, sac-poubelle, tee-shirt, textiles, vernis
sont susceptibles de comporter le logo NF (Norme Française) de
l'AFNOR ou l'Eco-label au niveau européen.
Les produits susceptibles d'être commercialisés
dans une épicerie ou dans un supermarché dits "bio",
correspondent donc à ceux que l'on pourrait trouver dans
une grande surface traditionnelle avec en plus la contrainte de comporter
des articles alimentaires incorporant au moins 95 % d'ingrédients issus
de l'agriculture biologique. Les produits sont alors étiquetés
avec les mentions obligatoires :
? "Agriculture Biologique"
É ou "Produit de l'Agriculture Biologique"
É ou "Produit issu de l'Agriculture Biologique"
É ou "X % des ingrédients d'origine agricole ont
été obtenus selon les règles de
la production biologique (la mention 100% "bio" n'est pas
autorisée)";
? nom de l'organisme certificateur (ex : Ecocert);
et peuvent comporter les mentions facultatives :
? "Système de contrôle CEE";
? le logo AB.
Dans les produits alimentaires, un cas particulier est
représenté par le vin : il n'existe en effet à
ce jour aucun cahier des charges au niveau européen
concernant sa fabrication. Les mentions pouvant figurer sur les
étiquettes de vin sont seulement : "vin issu de raisins de l'Agriculture
Biologique" avec le nom de l'organisme certificateur. Le logo AB n'est pas
autorisé.
Rien n'empêche ces commerces de distribuer des produits
n'ayant pas la qualité "bio" sinon le risque d'être
attaqués pour publicité mensongère. On trouve
pourtant rarement des produits alimentaires non-bio dans ce type de
magasin. Dans le cas où des aliments contiendraient seulement de
70 % à 95 % d'ingrédients "bio", leur étiquette
peut comporter les mentions suivantes :
? "X % des ingrédients d'origine agricole ont
été obtenus selon les règles de la production
biologique";
? le nom de l'organisme certificateur;
? la liste des ingrédients par ordre décroissant
avec référence au mode de production biologique.
4.1.2 Le commerce de détail des produits biologiques
en France
On recense en France à ce jour un peu
plus de 2200 points de vente distribuant indistinctement des
produits biologiques, naturels ou diététiques sans pouvoir
parfois les classer dans une catégorie particulière. Ces
activités se concentrent dans les régions très
urbaines à pouvoir d'achat plutôt élevé, avec
une prépondérance pour les départements comportant
d'importants pôles urbains, souvent frontaliers ou côtiers
avec en particulier : Paris et région parisienne, région
lilloise, Strasbourg et Bas-Rhin, Lyon et Région Rhône-
Alpes, Haute-Savoie, Bouches du Rhône, Côte d'Azur,
Gironde (Bordeaux), Hérault (Montpellier), Haute-Garonne
(Toulouse).
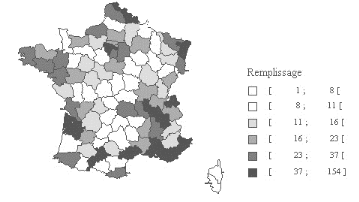
Fig. 4.1 - Les magasins "bio" et boutiques de produits
diététiques en France par département en nombre
Source : CD Stratégie & Localisation -
Jérôme Baray / société Articque
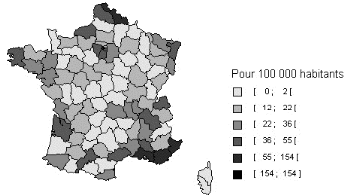
Fig. 4.2 - Les magasins "bio" et boutiques de produits
diététiques
en France par département en densités par
habitant
Source : CD Stratégie & Localisation -
Jérôme Baray / société Articque
En région parisienne, les secteurs de la
distribution de produits naturels, biologiques et
diététiques se sont implantés dans les départements
à revenus élevés (Ouest parisien et Hauts
de Seine surtout).
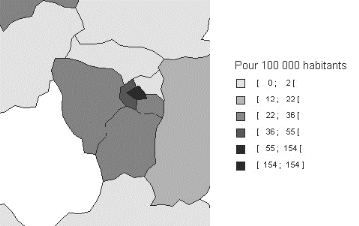
Fig. 4.3 - Les magasins "bio" et boutiques de produits
diététiques et naturels en Ile-de-France en densité par
habitant
Source : CD Stratégie & Localisation -
Jérôme Baray / société Articque
Très peu de magasins de produits naturels (biologiques
pour certains) peuvent se comparer aux commerces de détail
traditionnels. En effet, la majorité des commerces recensés dans
les statistiques ci-dessus, sont surtout spécialisés dans les
produits non-alimentaires, par exemple dans la vente de suppléments
diététiques ou naturels tels le groupe La Vie Claire ou encore
dans les remèdes naturels, la phytothérapie, les huiles
essentielles, les encens et plus généralement dans les
articles proches de la philosophie spiritualiste dite du "New Age" qui
prône sérénité, décontraction, partage des
cultures et paix universelle.
Echappant à ce mouvement, seuls quelques acteurs du
"bio" proposent un assortiment complet rivalisant avec le commerce de
détail classique, allant de l'alimentaire (produits frais, fruits,
légumes, viande, pain, céréales, vins certifiés
biologiques) aux produits d'hygiène (dentifrice naturel dépourvu
de fluor, savon végétal, lessive sans phosphate) en
passant par quelques remèdes (aspirine naturelle, vitamines
végétales) ou même par l'habillement (vêtement
en coton "bio"). Seuls en France, deux groupes se sont pour l'instant
structurés en réseau de points de vente qui n'ont rien
à envier au supermarché ou au commerce de
proximité
classique.
La première chaîne de distribution de produits
"bio" en France est représentée par le réseau de franchise
BioCoop avec 170 points de vente répartis sur tout le territoire. Sa
centrale d'achats exclusive aux BioCoops propose près de 4000
références de produits biologiques, secs et frais
et d'éco-produits sélectionnés par les
BioCoops. Selon les responsables du groupe, adhérer au réseau
BioCoop créé en 1987 signifie636 :
· "promouvoir l'agriculture biologique, seule
agriculture durable certifiée, respectueuse
de l'environnement et de la santé des hommes qui la
cultivent et la consomment.
· entreprendre autrement en construisant, avec les
BioCoops et leurs partenaires de la filière, un commerce
équitable et transparent.
· bénéficier des services d'un
réseau unique en France regroupant les pionniers de la distribution
moderne des produits biologiques et écologiques, le premier du secteur
en France, et proposer aux consommateurs des produits rigoureusement
sélectionnés à des prix justes."
Le chiffre d'affaires des points de vente BioCoop varie de 1,5
million de francs dans les points
de vente de province à 7 ou 8 millions concernant ses
implantations parisiennes dont certaines atteignent la taille d'un
supermarché (ex. Canal "bio" dans le 19ème
arrondissement de Paris).
Les adresses des implantations de BioCoop sont :
É O'racines 28 Rue Petrelle 75009 Paris
É Canal "bio" 300 Rue de Charenton 75012
Paris
É BioCoop Paris "Glacière" 55 Rue de la
Glacière 75013 Paris
É Canal "bio" 46 Bis Quai de la Loire 75019
Paris
É BioCoop Grenelle 44 Bd de Grenelle 75015
Paris
É BioCoop Paris 17ème 153 Rue Legendre 75017
Paris
É Les Nouveaux Robinsons 127 Avenue Jean-Baptiste
Clément 92100 Boulogne-Billancourt
É Les Nouveaux Robinsons 14 Rue des Graviers 92200
Neuilly Sur Seine
Il est à noter que ces implantations sont loin
d'être toutes sous l'enseigne commune BioCoop.
Le réseau de points de vente ne bénéficie
donc pas de la notoriété dont il aurait pu tirer profit
auprès de ses clients. Sans doute, cet état de fait vient de
l'histoire de ce groupe créé lors de la
636 Site du groupe Biocoop :
www.biocoop.fr
fédération en novembre 1986, d'une quarantaine
de coops aux noms évocateurs, dont Germinal, Sonneblüm,
Regain, Soleil Levain, Aquarius, Kerbio, Scarabée, Floréal,
Nature et Vie, Bigorre etc.. qui se sont aperçus qu'elles avaient le
même souci de développer le "bio". Naturalia est le
deuxième réseau de 16 points de vente pesant un chiffre
d'affaires de 63 millions de francs (en 1999) et distribuant des
produits biologiques alimentaires en étant
implanté majoritairement à Paris637.
Les implantations de Naturalia :
É 11-13 rue Montorgueil 75001 Paris
É 52 rue Saint Antoine 75004 Paris
É 36 rue Monge 75005 Paris
É 126 bd Raspail 75006 Paris
É 38 av de la Motte Picquet 75007 Paris
É 121 bd Magenta 75010 Paris
É 33 rue de la Roquette 75011 Paris
É 44 av d'Italie 75013 Paris
É 16 av du général Leclerc 75014
Paris
É 86 rue de Cambronne 75015 Paris
É 25 rue des Sablons 75016 Paris
É 26 rue Poncelet 75017 Paris
É 16 rue de Levis 75017 Paris
É 107 rue de Caulaincourt 75018 Paris
É 37 rue du Poteau 75018 Paris
É 188 rue de Fontenay 94300 Vincennes
A noter que le chiffre d'affaires de Naturalia suit bien la
tendance du secteur en connaissant une hausse de 23 % en 1997, de 18 % en 1998
et de 15 % en 1999.
Hormis BioCoop et Naturalia, il existe quelques rares
commerces individuels distribuant des produits biologiques, alimentaires et
autres. Ce serait le seul cas en région parisienne du
supermarché Espace "bio" St. Charles situé dans le
15ème arrondissement de Paris. Ce magasin
est selon ses dirigeants, la plus grande surface consacrée
au "bio" en France. Avec plus de
6000 références et environ 10 millions de
chiffre d'affaires sur 500 m² environ, il accueille quotidiennement 400
clients et compte environ 4000 consommateurs réguliers au total,
certains n'hésitant pas à parcourir hebdomadairement plusieurs
dizaines de kilomètres pour y
637 Site Internet :
http://www.biocoop.fr/pageinterieure/jeudecadre.htm
faire leurs achats de la semaine. Les produits que l'on
peut acheter dans ce véritable commerce biologique de détail
sont par exemple par catégorie :
É Produits frais : fruits, légumes,
lait, yaourt, oeuf, viande, poisson, plats préparés ;
É Boissons : eaux minérales,
bière (bière de sarrasin, d'épeautre, au chanvre),
digestif, vin rouge
et blanc, cidre, frenette, ortillette, chanvrette,
limonade, jus de fruits et de légumes, eau
minérale, thé, boisson aux céréales
(soja, avoine, riz) ;
É Epicerie salée : alimentation
bébé, pâtes, produits japonais (agar agar, kombu, algue de
mer, wakame, nori), conserves, condiments ;
É Epicerie sucrée : miel, pollen,
biscuit, desserts de soja, substitut du sucre (fructose, sirop de blé),
compotes, chocolat ;
É Petits déjeuners : biscottes,
pain, muesli, succédané de café (poudre de caroube,
yannoh), café, thé ;
É Produits Montignac ;
É Compléments alimentaires : spiruline,
guayapi, jus d'aloe vera, propolis "bio", gel de silice, aliments sans gluten
;
É Alimentation animale : terrine et croquettes
pour chien et chat ;
É Cosmétique et hygiène :
dentifrice, cire de jojoba, huile solaire, argile Rhassoul, lotion,
crème, shampooing naturel, huiles essentielles ;
É Non-alimentaire : insecticides "bio",
crème à récurer, lessive, assouplissant, gel wc,
savon, nettoie-vitre ;

Fig. 4.4 - La devanture du magasin Espace "bio" St. Charles
La force d'Espace "bio" est de négocier
lui-même avec les producteurs ou grossistes sans passer par une
quelconque centrale de distribution. En définitive, les tarifs
pratiqués sont très voisins de ceux de la grande
distribution. Le consommateur hésite moins à faire une
expérience d'achat, et rassuré par la certification "bio" et la
qualité des produits, est pris au jeu
et se fidélise.
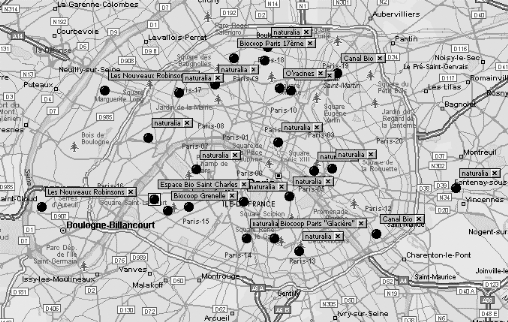
Fig. 4.5 - Les localisations des commerces de détail "bio"
à Paris et en région parisienne
4.1.3 La vente des produits biologiques sur Internet
Il n'est pas possible d'évoquer la distribution de
produits biologiques sans parler d'Internet qui selon certains chercheurs
représentent la quatrième révolution commerciale
après les boutiques, les grands magasins et le
libre-service638. Pour certains auteurs, ce nouveau mode
de distribution bouleversera demain notre façon de
consommer639. Non pas qu'Internet aura le
monopole de la distribution, mais tout au moins jouera-t-il dans
la même cour que les acteurs
638 VOLLE P. (2000) Du Marketing des Points de Vente
à Celui des Sites Marchands : Spécificités,
Opportunités
et Questions de Recherche, Revue Française du
Marketing, N°177/178, P.83.
639 MOATI P. (2001) L'avenir de la Grande
Distribution, Ed. Odile Jacob.
actuels de la grande distribution. En effet, une multitude de
sites de commerces électroniques proposant des produits biologiques ont
fleuri durant les années 1998 et 1999. Ces années de "vache
folle" et le faible investissement indispensable à la
création d'un site ont en effet stimulé à ce moment
les créateurs de tout poil. Le soufflet est bien vite retombé
car, en 2001, seuls restent, sur une centaine de commerces initialement
créés, au plus une dizaine d'acteurs,
la plupart étant adossée à des commerces de
détail bien réels et ayant pignon sur rue ce qui leur facilite
considérablement la logistique et les problèmes de stock.
Pourquoi cet effondrement des projets de commerces
"bio" sur Internet ? D'une part, les commandes n'étaient pas au
rendez-vous et presque au même moment en 2000, La Poste par laquelle
transitait la plupart des paquets alimentaires refusait d'assurer le
transport des produits frais ce qui a contraint sans détours un
grand nombre de sites à fermer. A l'heure actuelle, les
quelques sites Internet restant en lice et distribuant des produits
biologiques alimentaires sont essentiellement parisiens. Parmi eux, on trouve
:
É
www.Biodoo.com : le site de
commerce électronique du groupe Naturalia associé à
ces magasins.
É
www.epiceriebio.com : qui
distribue par La Poste des aliments "bio" conditionnés et des
produits d'hygiène naturels.
É www. espacebio.com : le site d'Espace "bio"
St. Charles. De l'aveu même du magasin, le site enregistre une seule
commande par jour et effectue donc un chiffre d'affaires annuel de quelques
dizaines de milliers de francs. Les paquets sont transportés en
triporteur électrique écologique du magasin jusqu'au domicile du
client.
É
www.chezemile.com : site
implanté à Houilles (78) spécialisé dans le "bio"
haut-de-gamme.
É
www.la-halle-au-bio.com :
spécialisé dans les produits biologiques frais.
É
www.natoora.com :
référence 500 produits et atteint un chiffre d'affaires de 2
millions de francs dans Paris intra-muros. Les produits sont acheminés
sous un délai de 24 heures au domicile du client dans un véhicule
électrique comportant des compartiments
réfrigérés.
É
www.vivrebio.com : site
distribuant les grandes marques d'aliments "bio" (Grillon d'Or,
Priméal, Joannusmolen, Borsa, Le Moulin Pivert, la Drôme
Provençale, Argiletz, Pierre Cattier).
www.biomarkets.com,
www.biosegur.co
m,
www.viridis.com sont d'autres
acteurs du "bio"
situé en province et d'importance moindre en terme de
chiffre d'affaires 640.
Ainsi, les sites Internet distribuant des produits
biologiques jouent dans l'immédiat un rôle négligeable
dans un secteur encore peu développé, d'autant que les
sites électroniques enregistrant un certain volume d'affaires sont ceux
d'implantations réelles pour lesquelles le commerce virtuel ne
constitue qu'une activité annexe et des profits secondaires.
Certains observateurs ont qualifié le commerce électronique
d'a-spatial641. Mais, bien au contraire, le
net fait apparaître par le truchement des liens,
des renvois et des bannières, une nouvelle
distance psychologique cette fois et non plus seulement
physique642. L'internaute qui "surfe", navigue de site en site et se
construit mentalement cette distance psychologique en se fondant
sur un sentiment de proximité qui dépend
de facteurs comme le partage d'une langue commune, la possibilité
de contact et de recours en cas de problème,... (les sites
régulièrement visités par un individu sont alors
considérés comme proches). Pour des raisons de différences
culturelles mais également de logistique et de livraison des produits
commandés, les distances physiques ne sont pas abolies dans le
cybercommerce qui n'est pas réellement global.
L'existence de sites adaptés à chaque pays
démontre ce fait (ex. amazon.fr, amazon.com,
640 BARAY J. (2002) Le Guide des Produits
Bio, Editions Grancher, Paris.
641 LORENTZ M. (1998) Le Commerce
Electronique, Les Editions de Bercy, Ministère de
l'Economie, des
Finances et de l'Industrie, p.15.
642 VOLLE P. (2000) Du Marketing des Points de Vente
à Celui des Sites Marchands : Spécificités,
Opportunités
et Questions de Recherche, Revue Française du
Marketing, N°177/178, P.86.
amazon.de). Le commerce électronique ne serait global que
si l'offre était la même pour tous
et si les clients provenaient du monde entier ce qui n'est
généralement pas le cas. Même si les nouvelles
technologies de l'information et de la communication (NTIC) d'une
manière générale devraient favoriser l'émergence
d'un marketing individualisé ou plus personnalisé (ou
marketing one to one), donc sans doute plus efficace, nul ne sait à
l'heure actuelle si ceux-
ci ne resteront dans l'avenir que de simples
améliorations technologiques de la vente par correspondance
à l'image du minitel ou s'ils deviendront de véritables
nouveaux canaux de distribution643.
La méfiance du consommateur à la fois
vis-à-vis d'Internet et des produits biologiques, le
problème de la sécurité du paiement
électronique et celui du transport feront que ces sites n'auront
dans l'avenir proche qu'une envergure commerciale limitée, à
moins que l'insécurité alimentaire atteigne un niveau tel que les
consommateurs se détournent soudainement de leurs modes traditionnels
d'achat pour en adopter d'autres. Un sondage effectué en ligne par le
site
www.edgdistribution.com
auprès d'internautes professionnels de la distribution, indique que
60 % des personnes interrogées, ne voient pas dans le
commerce électronique, "l'avenir de la grande distribution", (28 %
le voient comme tel et 12 % ne se prononcent pas). Les
spécialistes en prospective sentent bien les limites de la vente
virtuelle : "Faire ses courses
sur Internet n'est pas plus satisfaisant. Certes, le
consommateur n'a pas à se rendre en voiture
à l'hypermarché, mais il reste délicat
de choisir de bons produits frais ou de l'habillement sur
un écran d'ordinateur"644. De plus,
pour certains sites, le plus difficile est non pas encore de séduire la
clientèle, mais de se voir confier la production d'artisans
régionaux qui eux aussi, restent très méfiants face
à une distribution de leurs produits sur Internet : le "bio" est en
effet pour l'instant plus l'affaire de petits producteurs du terroir
que des grands industriels de l'agroalimentaire. La grande distribution
s'est, elle aussi, mise timidement au "bio". Mais, les
643 CLIQUET G. (2001) Rôle des NITIC dans
l'Evolution des Canaux de Distribution, Proche-Orient n°13 -
Revue de la Faculté de Gestion et de Management, Université
Saint-Joseph, Beyrouth, p.71-93
644 BOVET P. (2001) L'hypermarché, le Caddie
et le congélateur, Le Monde Diplomatique, Mars 2001, p.32.
mauvaises langues en particulier dans cette filière
n'hésitent pas à dire que 40 % de produits "bio" en plus dans
les rayons des hypermarchés en quelques mois n'est pas chose
normale d'autant que la demande dépassait déjà largement
l'offre. Ainsi, certains produits des grandes surfaces, étiquetés
"bio", ne seraient pas véritablement "bio". Les consommateurs sensibles
à cette appellation ne semblent plus se fonder seulement sur
l'étiquette AB mais aussi et surtout
sur l'identité du producteur ainsi que sur
l'origine du produit. Dans ce climat de méfiance, chacun souhaite
être rassuré sur ce qu'il achète. Les consommateurs boudent
plutôt la grande distribution dans le domaine du "bio", dont la
réputation associée à celle de l'industrie
agroalimentaire est quelque peu liée aux scandales alimentaires. Les
commerces placés sur ce marché de niche très actif que
sont les produits biologiques ont donc une véritable opportunité
pour se développer et ce déploiement ne passera que par des
réseaux de points de vente bien organisés et fonctionnant en
phase. La notion d'enseigne est importante, de même qu'une bonne
promotion car c'est sous cette bannière commune à tous les
magasins d'un réseau que le consommateur va peu à peu
acquérir l'envie d'acheter des produits sains sans risque et non
dénaturés. Qu'il fasse ses courses chez lui, en vacances ou sur
Internet, la marque, l'enseigne
est fondamentale pour enfin rassurer le client sur ce qu'il
achète et le convertir au "bio".
4.2 La mise en oeuvre du traitement du signal et du
modèle p-médian
4.2.1 La base de données utilisée
La société d'études de marché
et de consommation Consodata a réussi à se constituer,
en France, un panel d'enquêtes très important qui comprendrait 75
% des ménages français. Son succès est dû à
ses liens étroits avec la Poste : lorsqu'un nouveau ménage
s'installe, celui-ci reçoit en principe dans sa boîte aux lettres
peu de temps après un formulaire établi par cette
société, comprenant environ huit pages de questions sur ses
habitudes de consommation, ses marques préférées, ses
prévisions d'achat et sur ses intérêts pour certains
domaines (sport,
musique, informatique, nature,...). Pour inciter à
remplir et à renvoyer le questionnaire, les personnes
sondées se voient offrir des coupons de réduction sur leurs
achats. De nombreuses sociétés commerciales utilisent les
résultats de ces enquêtes pour réaliser des
opérations promotionnelles auprès de clients
déjà ciblés. En particulier, la société
de distribution de produits "bio", Espace "bio" St. Charles, a acquis la
base de données de ménages Consodata
de l'Ouest parisien, ayant manifesté un réel
intérêt pour les produits "bio", qu'ils soient déjà
consommateurs de ce type de produits ou qu'ils aient plus tard
l'intention éventuelle de se mettre aux produits "bio". C'est
à partir de cette base de données constituée
d'adresses de personnes anonymes, gracieusement mise à notre
disposition par Espace "bio" St. Charles, que nous avons pu
réaliser la présente étude d'implantation de
supermarchés "bio" à l'Ouest de Paris.
Celle-ci avait les caractéristiques suivantes:
|
?
|
1732
|
clients potentiels pour
|
Boulogne-Billancourt
|
(92100)
|
|
?
|
952
|
clients potentiels pour
|
Issy-Les-Moulineaux
|
(92130)
|
|
?
|
398
|
clients potentiels pour
|
Neuilly-Sur-Seine
|
(92200)
|
|
?
|
517
|
clients potentiels pour
|
Paris 7ème
|
(75007)
|
|
?
|
3456
|
clients potentiels pour
|
Paris 15ème
|
(75015)
|
|
?
|
1087
|
clients potentiels pour
|
Paris 16ème
|
(75016)
|
|
?
|
2069
|
clients potentiels pour
|
Paris 17ème
|
(75017)
|
soit 10 211 clients potentiels au total parmi lesquels
:
|
?
|
femmes mariées...........................
|
42 %
|
|
?
|
femmes célibataires...................
|
34 %
|
|
?
|
hommes......................................
|
24 %
|
La sur-représentation féminine dans cette base
provient sans doute du fait que, d'une part, les
femmes auront davantage le loisir de remplir un questionnaire
du fait de leur taux d'activité salariée moins fort que chez
les hommes, et d'autre part, la perspective de recevoir des coupons
de réduction sur des articles de secteurs aussi
variés que l'habillement, les cosmétiques ou
l'hygiène a sans doute plus d'impact sur la gente féminine.
Enfin, il apparaît, sans qu'aucune étude précise ne puisse
le confirmer, que les femmes sont plus sensibles pour
elles ou pour leurs enfants, à la santé, à
la beauté et à la forme et par voie de conséquence aux
produits "bio" qui sont censés mieux respecter l'être humain.
La zone analysée, à fort pouvoir d'achat,
a la particularité d'être divisée en deux par une
barrière naturelle constituée par le Bois de Boulogne.
Seules nous manquaient pour cette étude, les adresses de
consommateurs potentiels du VIIIème arrondissement
de Paris. Cependant, cet arrondissement a la particularité de
comporter une surface très importante de bureaux et en second lieu, de
nombreuses aires touristiques (ex. Arc de Triomphe, Champs Elysées) qui
limitent considérablement l'espace consacré à l'habitat.
Le VIIIème arrondissement où les emplacements
commerciaux sont rares et chers, est un secteur à très faible
potentiel pour le commerce de proximité, en témoigne le faible
nombre d'implantations d'épiceries et de supermarchés
traditionnels (voir carte suivante). Ainsi, le fait de ne pas
posséder de données relatives à cet arrondissement
ne devrait pas nous pénaliser outre
mesure.
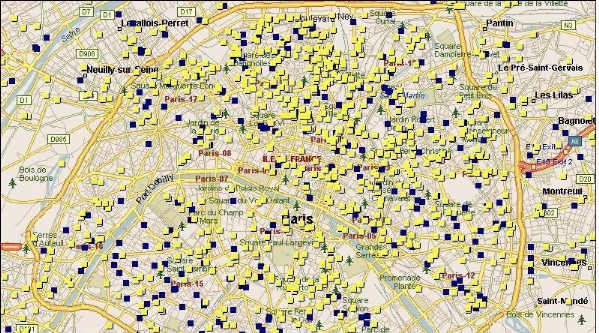
Fig. 4.6 - Les épiceries (en clair ou jaune) et les
supermarchés (en foncé ou bleu) à Paris
Source : CD Stratégie & localisation J.Baray -
Société Articque
Fig. 4.7 - La zone d'étude en gris foncé dans la
région parisienne
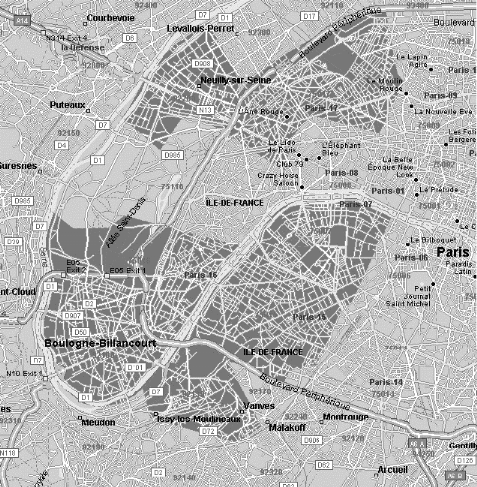
Fig. 4.8 - En gris foncé, la zone d'étude de
l'Ouest parisien
Ainsi que nous l'avons expliqué au chapitre trois, notre
méthode se décompose en une phase
de géocodage et de représentation des
données sur une carte, un filtrage, une phase de
délimitation de la zone de chalandise avec détermination des
centres de gravité et des surfaces des aires constitutives, puis la
résolution d'un modèle p-médian pour
déterminer la ou les localisations optimales.
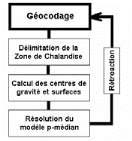
4.2.2 Le géocodage des données
Le géocodage des données a
été réalisé avec le logiciel MapPoint 2001
Europe développé par la société Microsoft. Ce
programme performant par ses capacités cartographiques,
recense 2,7 millions de kilomètres de voies urbaines
et
interurbaines dans toute l'Europe (données fournies par la
société Navigation Technologies).
Les fichiers peuvent être importés dans
MapPoint sous des formats variés (texte avec tabulation de
séparation, Access, Excel). Le logiciel permet également de
tracer le plus court chemin entre deux points en empruntant les voies de
circulation. Les clients sont repérés par des cercles, des
carrés ou d'autres symboles. Nous avons opté pour le
carré qui est la représentation la plus petite disponible et
qui s'insère au mieux dans le format en quadrillage des images
électroniques et de leur représentation électronique
matricielle. Le géocodage des
10211 clients par MapPoint a pris 6 minutes. Il a fallu
ensuite éliminer le fond de carte et le tracé des voies de
circulation ce qui est chose aisée avec un logiciel comme Photoshop
ou grâce à n'importe quel programme basique de traitement d'image.
Seule, la Seine a été laissée afin de permettre un
repérage cartographique. L'espace géographique analysé
s'inscrit dans un
rectangle de 8 kilomètres d'Est en Ouest sur 9,3
kilomètres du Nord au Sud.
Fig. 4.9 - Géocodage des 10 211 clients potentiels de
l'Ouest parisien
Voir Annexe A pour les cartes détaillées par
commune

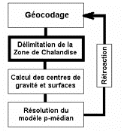
4.2.3 Le pré-traitement des données
Le pré-traitement des données de la carte
de points obtenue est destiné à homogénéiser
les parties texturées de manière à y
distinguer les formes de la zone de chalandise. Etant donné que le
nombre de clients potentiels est assez mince (environ 10 000), la
densité des points est relativement faible, surtout
dans les arrondissements à plus faible
population et potentiel réduit comme le
16ème arrondissement : les points-clients sont assez
espacés les uns des autres. Il convient pour
homogénéiser la répartition de la clientèle
et mieux distinguer les amas denses de clients constituant la zone de
chalandise, d'utiliser un filtre qui va relier les zones de clientèle
pratiquement adjacentes et combler les petites lacunes géographiques
(petits îlots dépourvus de clients). Le filtre de
dilatation vérifie ces conditions
en ce sens que si au moins quatre voisins d'un point
central blanc sont noirs alors cette transformation convertit ce point en
noir. La dilatation établit des connections entre des objets voisins
mais discontinus tout en lissant les objets de l'image (la dilatation peut
être comparée
à des tâches d'encre qui s'étalent
graduellement en étant absorbé par un papier buvard). Les autres
filtres non-morphologiques des types Nagao, moyenne, sigma ou
médian ne conviendraient pas bien dans notre cas puisque la carte
étudiée est très fragmentée en petits points (les
points clients) et que ces filtres n'agissent convenablement que sur des images
plus uniformes avec des objets plus contigus (voir §3.2.3 et exemple). Or,
on constate que dans sur
la carte ci-dessus, la densité des points varie dans
l'espace, mais n'est finalement pas encore suffisante pour distinguer les
formes pleines de la zone de chalandise. La dilatation étant ainsi une
transformation adaptée à notre problématique, nous l'avons
exécutée sur la cartographie des points géocodés
à l'aide du logiciel SCI développé par la
société américaine SCI Corp. pour la reconnaissance de
forme et l'imagerie scientifique. Mais, ce filtre se doit
d'être
appliqué de manière adéquate pour
réussir à joindre les parties isolées et distinguer sur la
carte
des aires homogènes et denses en terme de
clientèle. La dilatation peut en effet être pratiquée
par de multiples itérations successives (voir dessin du
chapitre 4.2.3.2 plus loin). L'effet de cette transformation sur le nombre
d'aires de la zone de chalandise apparaît clairement sur la figure
4.10. Logiquement, en établissant des connections entre
les aires voisines qui grossissent peu à peu, le nombre de
ces aires diminuent au fur et à mesure des dilatations
effectuées, comme on peut l'observer sur la figure 4.10.
Fig 4.10 - Nombre d'aires de la zone de chalandise par rapport au
nombre de dilatations pratiquées
Mais, ce graphe ne rend pas compte du
phénomène intéressant qui se déroule lors de
dilatations successives, à savoir, la formation d'aires
homogènes d'importance conséquente. Chaque dilatation
s'accompagne d'un grossissement des aires dont la surface progresse de
manière exponentielle. Ainsi, une aire qui a une surface de quelques
pixels la verra croître selon le carré du nombre de dilatations
pratiquées. Un schéma plus révélateur du processus
sous-jacent qui se déroule au cours de cette transformation consiste
à représenter le nombre d'aires ayant une taille "importante" en
fonction du nombre de dilatations pratiquées (les aires
supérieures à 500 pixels, suffisamment
grandes, sont en effet celles où la densité locale
correspond à la densité moyenne de la
zone - voir chapitre suivant). On remarque que le processus est en
escaliers avec des parties pour lesquelles l'apparition de grandes aires
croît de manière importante (partie A, C et E sur le
graphe), et d'autres parties de la courbe où ce nombre de
grandes aires reste stable quel que soit le nombre de dilatations
effectuées (parties
B et D essentiellement). Les parties C et E où la fonction
est croissante font en effet naître par
un remplissage progressif de l'espace, des connections
entre des aires qui étaient très rapprochées et qui
ont alors fusionné pour engendrer des aires de tailles plus importantes.
A la suite de ces transformations qui ont mis en évidence des
aires importantes d'équidensité importante de clients, les
autres segments B et D du graphe présentent une stabilité en
nombre d'aires par le fait que les aires les plus petites sont trop
éloignées les unes des autres pour donner naissance à
une aire plus grande même par remplissage du plan. Il faut
dépasser ces barrières en pratiquant de nombreuses
dilatations supplémentaires pour créer de nouvelles aires,
un peu comme si on devait rajouter pas seulement un peu mais beaucoup d'encre
sur une feuille de papier buvard pour voir toutes les taches
précédemment apparues, fondre en de plus imposantes.
Fig 4.11 - Nombre d'aires de la zone de chalandise de plus de 490
pixels en fonction du nombre de dilatations
Ces taches d'encre ou clients ne s'agglomèrent qui
si leur présence est suffisamment
importante sur le terrain pour que des liaisons puissent se
créer entre eux lors des dilatations successives. Le processus de
dilatation permet non seulement de lisser les formes, mais fait
apparaître les aires où la densité de clients
dépasse un certain niveau. Les aires très proches
les unes des autres au début ont fini par se
rejoindre en majorité et à former des aires
homogènes. Le processus de transformation ayant consisté à
effectuer au moins 6 dilatations
(de 6 à 10 dilatations) puis au moins 16 (de 16
à 20 dilatations) fait apparaître deux paliers correspondant
à des densités de clientèles différentes. La
partie F du graphe apparaît également comme un palier, mais
n'est en fait que le point où les dilatations successives ayant rempli
une grande partie du plan, amorce alors une décroissance en
nombre total d'aires, même les aires les plus grosses collant les unes
aux autres. Cette partie est moins intéressante dans l'immédiat
car au delà de 30 ou 40 dilatations, une grande partie du plan est
envahie par
les aires de chalandise difficilement
interprétables du moins en analyse de l'existant (poursuivre
le processus aussi loin ne conduirait de plus qu'à lier des aires qui au
départ n'était pas du tout voisines les unes des autres). En
accroissant ainsi la superficie des aires, on force artificiellement
l'étendue des aires de chalandise et de les faire
déborder de leurs limites initiales, et l'on ne se contente plus
seulement de remplir les interstices entre les points-clients. Une application
intéressante est de réaliser suffisamment de dilatations de
manière à se situer dans la zone F de la courbe et de
réaliser des prospectives d'extension des aires de chalandise
et de leur densification en terme de clientèle. Il faut
alors prendre une hypothèse de croissance
du marché local à court, moyen ou long
terme et répercuter cette vitesse sur le nombre de dilatations
effectuées (de la même manière qu'une tache d'encre se
répand plus ou moins vite
en fonction du support papier ou buvard qu'elle
imprègne).
Fig. 4.12 - Dilatation x 6 Dilatation x 30 Dilatation x 50



La figure précédente montre différentes
étapes de la dilatation. Une dilatation réitérée 50
fois
ayant absorbé toutes les aires petites ou grosses
montre un état de saturation du marché en nombre de clients. Les
seules régions encore vierges de clients (en blanc) sont pratiquement
celles ne comptant aucun habitant. Les formes pleines sans aucune
découpe indiquent une forte densité de la clientèle en
tout point où initialement il ne résidait seulement que quelques
rares clients. Sans doute, le phénomène de dilatation
correspond bien à la progression
classique du marché et à son cycle de vie du
moins jusqu'à la décroissance qui ne peut être
prévue par cette seule transformation (il faudrait alors utiliser la
transformation morphologique inverse d'érosion).
Mais, revenons sur ces deux paliers B et D qui
révèlent chacun les aires possédant une densité
de clients supérieure à un certain niveau. Le
premier correspond en fait à une densité de 1358 clients au
km² et la deuxième à un niveau de 1205 clients au km².
Ce qui signifie que dans le premier cas, la "tache" a absorbé
toutes les zones géographiques comportant au minimum
1358 clients/km² (niveau B) et 1205 clients/km² dans
le second cas (niveau D). Ainsi, nous retrouvons en fait deux
éléments de la zone de chalandise détectés
automatiquement, c'est-à- dire, la zone primaire correspondant au palier
B et la zone secondaire correspondant au palier
D (voir §1.1 pour les définitions des zones
primaire et secondaire). Si l'on observe sur les dessins des formes
dilatées suivantes, on remarque que ceux-ci diffèrent par l'ajout
des aires
2, 5, 6, 7, 8, 9, 14, 18, 21, 24 , 25 (numérotation du
2ème dessin) qui correspondent aux aires
de la zone secondaire de chalandise avec une densité de
clients comprise entre 1205 et 1358
clients/km2 (le nombre d'aires passant de 14 à 25) alors
que les aires 1, 3, 4, 10, 11, 12, 13,
15, 16, 17, 19, 20, 22 et 23 correspondent à la
zone primaire avec une densité de clients supérieure
à 1358 clients/kms² (sur le second dessin toujours).
Fig. 4.13 - Filtrage de points-clients par 10 dilatations
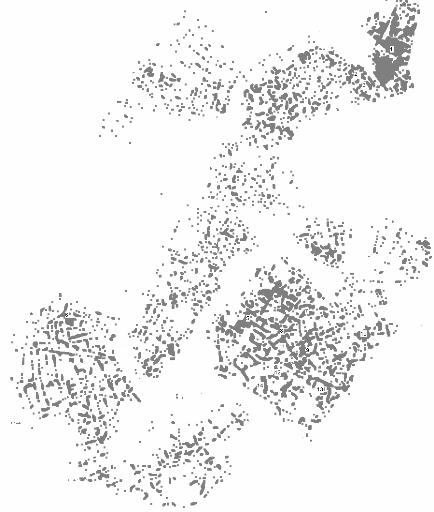
Fig. 4.14 - Filtrage de points-clients par 20 dilatations

Que l'on choisisse les cartes ayant subi 6, 7, 8, 9 ou 10
dilatations d'un côté pour l'analyse de
la zone primaire et possédant les mêmes aires ou
d'un autre côté de 16 à 20 dilatations pour
les zones primaires et secondaires ne change rien
pratiquement à la superficie globale de chaque aire (le remplissage
des interstices est plutôt limité à ce niveau, mais se
concentre à la frontière des aires). Cependant, nous
préférons dépasser l'amorce des paliers B et D en
choisissant les dilatations plus proches de la 10ème ou de
la 20ème que de la 6ème ou de la
10ème.
Il ne faut pas en effet oublié que le
phénomène de dilatation s'accompagne également
d'un
lissage des formes qui est prépondérant en ce qui
concerne les paliers B et D étant donné qu'il
n'y a plus de créations de connections entre les aires
d'importance. Ce lissage mettra mieux en évidence par la suite les
contours de la zone de chalandise. Ainsi, si la création de nouvelles
aires dans les zones A et C de la courbe nombre d'aires/dilatations s'est
accompagnée de la formation de connections entre des régions de
clientèle voisine, les paliers B et D favorisent plutôt l'ajout de
points en périphérie des aires et éventuellement au
voisinage des connections nouvellement formées pour avoir tendance d'une
manière générale à régulariser les
contours
de la zone de chalandise. Ainsi, nous retiendrons dans la suite
plutôt, la 10ème dilatation pour
la zone primaire et la 20ème dilatation pour
l'ensemble de la zone de chalandise (zone primaire
et secondaire) qui présentent des formes plus
régulières que celles des images de 6ème et de
la
16ème dilatation.
En résumé, nous dirons que le critère
fondamental qui nous permet de sélectionner telle ou telle région
comme faisant partie de la zone de chalandise porte essentiellement sur la
notion
de densité de clients révélatrice d'un
certain potentiel commercial. Les niveaux de densité de clientèle
correspondant aux caractéristiques de la zone de chalandise ne sont pas
déterminés aléatoirement ou de manière subjective
mais bel et bien par les dilatations successives qui font apparaître
cette zone à certaines étapes bien particulières du
processus de transformation
morphologique correspondant à des valeurs de
densité de clientèle précises. Partant de ces
principes, nous nous proposons donc d'introduire une
nouvelle définition de la zone de chalandise par rapport aux
nombreuses approches existantes (voir §1.2), fondée sur la
notion
de densité à savoir que : la zone de chalandise est
l'aire géographique d'influence où la densité
de clientèle dépasse un certain seuil.
Fig. 4.15 - Le filtrage par 20 dilatations superposé
à la carte des rues et aux points-clients

Ce seuil est de 1205 clients/km² dans notre exemple.
L'étape suivante de notre analyse sera de détecter les
frontières de la zone de chalandise sachant que la
transformation de dilatation nous a considérablement
facilité la tâche en faisant apparaître les aires
d'équidensité de clientèle. Les dilatations ont en
parallèle accentué leurs contours. Ces contours qui au
début étaient plutôt flous avec une évolution
graduelle de la densité en passant de l'extérieur vers
l'intérieur de la zone de chalandise sont devenus nets avec un
saut de valeurs en marche d'escalier (on passe de 0 à 1205
clients/km² en franchissant la frontière et en entrant dans la zone
de chalandise). L'opérateur de convolution et un filtre Sobel
nous permettra donc aisément de tracer les limites de cette zone.
4.2.3.1 La délimitation de la zone de
chalandise
La délimitation proprement dite a été
effectuée grâce à un filtrage par convolution de l'image
avec une matrice. Nous avons en l'occurrence le filtre Sobel mis en
oeuvre avec le logiciel de traitement d'image de la
société SCI. Pour rappel, le principe
mathématique d'une délimitation des formes
par filtrage et convolution est le suivant : les contours des aires
constitutives de la zone de chalandise sont détectés
à l'aide de deux convolutions de la matrice image par un
opérateur Sobel qui permet de générer des
dérivées horizontales et verticales. Le résultat est
la racine carrée de la somme des carrés des deux
matrices convoluées. Les matrices 3x3 des opérateurs Sobel
horizontaux et verticaux sont
données par :
|
1
|
2
|
1
|
1
|
0 -1
|
|
0
|
0
|
0
|
2
|
0 -2
|
-1 -2 -1 1 0 -1

Fig. 4.16 - Délimitation des aires constitutives de la
zone de chalandise
La carte 4.17 montre à titre d'exemple quel aurait
été le résultat de la délimitation selon la
méthode analogique (§1.3.2.1) qui sous-tend que
la zone de chalandise est à frontière
circulaire et qu'elle rassemble 80 % des clients 645.
Nous avons pris comme centre de la zone
de chalandise le centre de gravité de l'ensemble
des clients. Il apparaît clair que le cercle couvre très
largement un grand nombre d'aires comportant peu de clients et
d'aires non- habitées dont le Bois de Boulogne, ce qui rend
l'appréciation par cette méthode de la zone de chalandise
censée représenter les régions les plus riches en
clientèle très peu fiable.
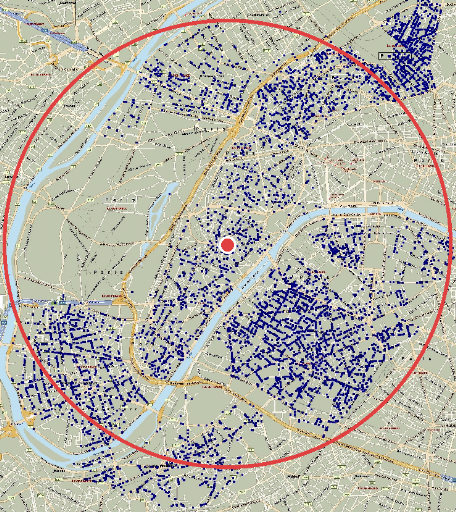
Fig. 4.17 - Délimitation de la zone de chalandise selon la
méthode analogique (cercle)
645 APPLEBAUM W. et GREEN H.L. (1974)
Determining Store Trade Areas, Handbook of Marketing
Research, edited by R. Ferber NY Mac Graw Hill, pp
4.313-4.323.
4.2.3.2 L'analyse de la zone de chalandise
Les aires délimitées sont alors
numérotées et analysées en termes
de superficie et de centres de gravité toujours avec le
logiciel SCI selon l'algorithme de parcours de l'image donné au chapitre
3. Le nombre total d'aires au départ était avant dilatation, de
1928 et l'on pourrait très bien résoudre le modèle
p-médian initial en prenant
comme noeuds le centre de gravité de toutes ces aires.
Le problème de localisation serait déjà simplifié
par rapport aux 10211 clients ou noeuds initiaux. Mais, on remarque que les
aires se divisent en deux catégories : les grandes aires qui comptent
plusieurs dizaines de clients et les nombreuses petites aires qui en compte
moins qu'une dizaine et souvent un ou deux. Or, si l'on s'en
réfère à notre définition
générale de la zone de chalandise à savoir, une
zone géographique possédant une densité de clients
élevée, les aires ne comptant que quelques clients ne
devraient logiquement pas vraiment lui appartenir. En effet, à
l'extrême, la densité locale de clientèle en un point de
l'espace géographique correspondant à un client unique est
infinie en théorie (la surface de ce point est nulle alors qu'il y a
présence d'un client, la densité
en clientèle est donc infinie). Mais, le fait que cette
densité locale soit infinie au niveau d'un client unique isolé
s'accompagne d'une faible densité de clientèle en moyenne au
voisinage de cette région qui ne compte pas d'autres clients à
proximité. Il faut de plus au minimum trois clients non alignés
pour définir une aire géographique digne de ce nom dans
laquelle on pourra définir une densité. Ainsi, tous les points
uniques ou même les petites aires n'indiquent pas finalement la
présence d'une grande densité de clientèle dans le
quartier, mais juste une concentration localisée de clients au niveau de
quelques habitations voisines sans aucun autre potentiel commercial autour. Ces
petites aires doivent donc être retirées de notre analyse de la
zone de chalandise.
Nous ferons ainsi abstraction des aires ne comptant qu'un client
et des petits rassemblements
isolés de quelques clients soit un client entouré
de quelques autres (voir le schéma suivant représentant 1 client
unique et un client entouré d'autres en configuration minimale soit 3
x
3), c'est-à-dire occupant un carré de surface
inférieure à celles de 25 clients juxtaposés (5 x
5). Compte-tenu de la densité de 1205 clients/km²,
cette surface minimum acceptable de 25
points-clients correspond donc à un carré de 150
mètres sur 150 mètres soit à 490 pixels sur
la carte dilatée (on trouve un client en moyenne environ
tous les trente mètres dans la zone
de chalandise et chaque client occupe alors 19,6 pixels
environ).


Fig. 4.18 - Aire d'1 point client, de 9 points-clients et de 25
points-clients
Si l'on compare l'éloignement moyen des aires, on
s'aperçoit de plus que celles-ci sont
séparées les unes des autres de 150
mètres et que les aires les plus petites sont encore
davantage isolées que les autres (par des
distances de 400 à 600 mètres pour des aires
inférieures à 40000 m²). Même si l'on ne connaît
pas précisément la distance que sont prêts à
parcourir les clients des magasins "bio", on peut considérer sans trop
se tromper que ce type
de commerce distribuant des produits alimentaires
courants appartient à la catégorie des magasins de
proximité. Toute personne connaissant quelque peu Paris et sa proche
banlieue n'ignore pas de plus que, compte-tenu des
difficultés de stationnement, les clients n'empruntent que
très rarement leur véhicule pour faire leurs courses. Les
statistiques montrent également que seuls 9% des clients des petits
commerces et des supermarchés situés
dans un tissu urbain font leurs courses en
voiture646. Ainsi, nous considérerons que les
magasins "bio" que nous cherchons à localiser,
s'adresseront en premier lieu à une clientèle de proximité
prête à parcourir quelques centaines de mètres à
pied ou en métro et que donc il sera préférable de
localiser un tel point de vente dans des aires isolées
contenant plus que quelques dizaines de clients. Cela n'exclut en rien les
cas courants de personnes qui, le plus souvent à cause de la
rareté de l'offre, se rendent dans des commerces "bio" à
plusieurs kilomètres de leur lieu d'habitation (certains clients
réguliers parcourent en effet plusieurs kilomètres une fois
par semaine pour faire leurs emplettes dans un supermarché "bio" selon
l'aveu même du directeur d'EspaceBio St. Charles).
Mais, l'argument le plus flagrant pour faire abstraction de
ces petites aires assez nombreuses réside surtout dans le fait que ce
saupoudrage de clients uniformément répartis en minuscules
clusters dans l'espace géographique correspond à un
éparpillement normal et équilibré de personnes
susceptibles d'acquérir des produits "bio", mais sans
véritable potentiel si l'on considère individuellement ces
regroupements. En l'occurrence, notre champ géographique d'analyse
est composé de deux éléments de clientèle
superposés : premièrement, ces clients
étalés de manière homogène dans
l'espace et isolés les uns des autres par des distances
646 BOVET P. (2001) L'hypermarché, le Caddie
et le congélateur, Le Monde Diplomatique, Données
fournies
par l'Ademe, Mars 2001, p. 32.
supérieures à 150 mètres et
deuxièmement, des aires atypiques importantes en surface et
à forte concentration de clients potentiels. La mesure de
l'autocorrélation spatiale en différentes zones du plan dans
lesquelles ne sont présentes que ces petits regroupements,
montrent en effet leur répartition aléatoire. On a
déterminé grâce au logiciel SCI, les
coordonnées des petits clusters dans ces régions ainsi que
leurs aires servant ultérieurement de pondération
(voir les trois régions sélectionnées sur
les dessins ci-dessous). Le logiciel Spatial647 mis au
point par le laboratoire de biologie de
l'université de Montréal nous a ensuite permis de calculer
de coefficient I de Moran648. Ce coefficient largement
utilisé dans la littérature pour mesurer la répartition
aléatoire ou non dans l'espace de variables géographiques a servi
par exemple pour évaluer le caractère dangereux de
certains tronçons de routes649 650, dans les
modèles de déplacement urbain651 ou même pour
les tissus cellulaires652. Une valeur positive
de l'indice de Moran montre une aurocorrélation spatiale
positive, une valeur négative, une autocorrélation
négative et une valeur nulle, une absence d'autocorrélation
spatiale.

Fig. 4.19 - Régions échantillons ne comptant que de
petites aires servant au calcul de l'indice de corrélation spatiale


Ce coefficient d'autocorrélation spatiale mesuré au
lieu i a pour expression :
647 Logiciel Spatial mis au point par
l'université de Montréal et le Professeur P.
Legendre -
http://biol10.biol.umontreal.ca/mnorton/stats.html
648 MORAN P. (1948) The Interpretation of Statistical
Maps, Journal of the Royal Statistical Society B, N°10,
1948, p. 243-251
649 FLAHAUT B. (2000) Impact de l'Aménagement
du Territoire sur la Sécurité Routière Durable : Analyse
de
la Situation Belge - Concentration Spatiale des Accidents
de la Route, Projet SSTC MD/10/042, Centre d'Analyse Spatiale et
Urbaine, Université Catholique de Louvain,
650 FLAHAUT B. (2001) L'autocorrélation
spatiale comme outil géostatistique d'identification des concentrations
spatiales des accidents de la route, CYBERGEO, n° 185
651 BANOS A. (2001) Enhancing mobility behavior
analysis using spatial interactive tools and computer
intensive methods, Geographic Information Sciences, Vol.
7, N° 1, pp. 35-41
652 SOKAL R., ODEN N., THOMSON B. (1998)
Local spatial autocorrelation in a biological model,
Geographical Analysis, Vol. 30, n° 4, pp.
331-353
I i =
Z i wij Z j et
j
Zi =
xi -
x ; Z j
= x j - x
l'indice de Moran global prenant alors pour forme :
I = I i
= Z i wij Z j
i i j
avec xi : la quantité mesurée au
point i qui évolue dans l'espace géographique, ici la
surface
des aires,
x : la valeur moyenne des xi,
wij : la distance pondérée entre le point i et le
point j,
Cet indice nous donne pour la première classe de
distances des aires les unes par rapport aux autres (l'indice a
été calculé par Spatial en considérant chaque
point par rapport à ses plus proches voisins) une valeur de
0,0304, donc très proche de zéro confirmant donc
l'hypothèse
de la répartition aléatoire de ces petites
aires. On remarquera aussi en observant la carte dilatée, que
les petites aires sont effectivement réparties de manière
homogène autour des aires plus importantes.
Le deuxième type d'aires au contraire massives
indique une irrégularité de l'espace et constitue la
véritable source d'un potentiel commercial pour les magasins
"bio" qui va véritablement influencer le positionnement des points de
vente. En imaginant, à la manière de Christaller, un espace
uniforme et infini dans lequel les clients seraient uniformément
répartis,
on se rend compte que ce manque d'"originalité" dans
ses caractéristiques fait que finalement, n'importe quel site dans ce
monde idéal en vaudrait un autre pour y fonder un commerce. S'il venait
à se constituer dans ce type d'espace socio-économique
utopique un ou plusieurs regroupements de clients potentiels, c'est
avec cette nouvelle donne qu'il faudrait compter pour y créer des
points de vente qui sans aucun doute, ne pourraient plus alors être
répartis aléatoirement. Notre raisonnement ne se fonde pas
sur la présence ou non de clients, mais plutôt sur les
variations de leurs densités de présence dans l'espace,
densités révélées par le
processus de dilatation précédemment
utilisé et par la délimitation des aires peuplées
de
clients ou zone de chalandise. Ainsi, les aires
importantes bénéficiant ultérieurement d'une
implantation commerciale seront assez bien centrées par rapport à
la clientèle marginale des aires plus petites qui pourra
fréquenter le magasin "bio", certes un peu plus éloigné,
mais tout
de même relativement proche de leur domicile. Le fait de
ne pas prendre en compte ces petites aires n'est donc également pas un
problème pour cette raison de symétrie (les grandes aires
à potentiel commercial ayant une densité élevée en
clientèle "baignent" en l'occurrence dans un milieu géographique
formé par ces petites aires de densité de clientèle aussi
homogène mais beaucoup plus faible). D'un autre côté, mais
cela n'est pas gênant, il nous faut aussi compter avec le manque de
capacité du logiciel de résolution du modèle
p-médian à notre disposition, que nous verrons plus tard.
Celui-ci ne permet en l'occurrence de ne résoudre que des modèles
limités à 50 noeuds. Ainsi, pour toutes ces raisons,
nous choisirons d'ignorer les aires de surface inférieure
à 2500 m² soit 490 pixels sur l'image (correspondant
à une aire de 150 mètres X 150 mètres et à
seulement 25 clients) dans notre recherche de localisation, le
potentiel commercial de clients vivant au sein de ces petites aires souvent
bien isolées étant trop faible pour être pris en compte
dans notre recherche de localisations commerciales. On a ainsi
détecté 25 aires d'importance et bien isolées où la
densité des clients potentiels est forte. Les aires d'importance sont
associées à des numéros sur la carte qui suit.
Fig. 4.20 - Numérotation et repérage du centre de
gravité des aires constitutives de la zone de chalandise

Nous obtenons ainsi le tableau de valeurs 4.1, où les
caractéristiques de chaque aire
sont détaillées.
|
AIRE
|
Superficie
|
X
|
Y
|
|
1
|
9138
|
812
|
105
|
|
2
|
517
|
631
|
117
|
|
3
|
971
|
736
|
151
|
|
4
|
730
|
757
|
175
|
|
5
|
638
|
568
|
206
|
|
6
|
754
|
604
|
226
|
|
7
|
1033
|
578
|
266
|
|
8
|
501
|
654
|
514
|
|
9
|
727
|
679
|
521
|
|
10
|
9809
|
599
|
673
|
|
11
|
943
|
631
|
639
|
|
12
|
2752
|
515
|
664
|
|
13
|
789
|
138
|
654
|
|
14
|
533
|
459
|
672
|
|
15
|
809
|
755
|
691
|
|
16
|
557
|
529
|
709
|
|
17
|
559
|
519
|
739
|
|
18
|
535
|
207
|
745
|
|
19
|
609
|
501
|
764
|
|
20
|
640
|
576
|
774
|
|
21
|
704
|
715
|
792
|
|
22
|
1781
|
667
|
806
|
|
23
|
726
|
543
|
798
|
|
24
|
536
|
593
|
803
|
|
25
|
533
|
146
|
805
|

















































Tableau 4.1 - Caractéristiques de chaque aire
La signification des paramètres du tableau 4.1,
mesurés en pixels est la suivante:
É superficie : superficie de l'aire en nombre de pixels
;
É X, Y : coordonnées du centre de gravité
de l'aire. L'origine est prise en haut et à gauche de
la carte, l'axe des Y étant orienté vers le bas et
l'axe des X vers la droite ;
É majeur, mineur : longueur des axes principaux de
l'ellipse exinscrite ;
É angle : angle en degrés de l'axe principal de
l'ellipse exinscrite (ellipse enveloppant l'aire).
Les 25 aires formeraient donc la zone de chalandise pour un ou
plusieurs points de vente de produits biologiques. La densité de clients
dans ces aires est pratiquement constante ce qui fait
que leur superficie est en définitive
révélatrice de la demande. C'est donc la superficie (niveau
de la demande) de chaque aire associée aux
coordonnées de leur centre de gravité (noeuds) qui formeront les
caractéristiques du réseau du modèle de
localisation-allocation.
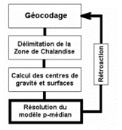
4.2.3.3 La construction et la résolution du
modèle p-médian correspondant
Le logiciel Sitation, utilisé pour résoudre
le modèle p-médian correspondant à notre
problématique, a été développé par le
Professeur Mark S. Daskin du Département d'ingénierie
industrielle de l'Université Northwestern à Evanston dans
l'Illinois. Daskin, auteur de plusieurs ouvrages de
références 653 est en outre un grand
spécialiste des modèles de
localisation-allocation.
Les paramètres que nous avons introduits dans le
modèle p-médian sont les coordonnées (X,
Y) des centres de gravité des noeuds à
partir desquels le logiciel Sitation calculera les distances
inter-noeuds en utilisant la distance euclidienne. Chaque noeud, centre
de gravité d'une aire, pourra constituer un emplacement
potentiel pour l'ouverture d'un point de vente "bio". Le potentiel de
l'aire est représenté par son importance en terme de superficie
(plus une aire est étendue, plus elle compte en principe de
clients potentiels, clients recensés dans l'enquête ou clients
n'ayant pas répondu au questionnaire). Nous avons associé
à chacun de
ces noeuds un coût d'ouverture qui est le prix moyen au
m² des surfaces commerciales (source:
chambre des notaires de Paris, prix au m² en 2000).
653 DASKIN M. S. (1995) Network and Discrete
Location: Models, Algorithms and Applications, John Wiley and Sons, Inc.,
New York.
AIRE Prix du m² Quartier ou Commune
1 11 755 F Paris 17ème
Epinettes
2 18 861 F Paris 17ème Plaine
Monceau
3 15 372 F Paris 17ème
Batignolles
4 15 372 F Paris 17ème
Batignolles
5 19 823 F Paris 17ème
Ternes
6 19 823 F Paris 17ème
Ternes
7 19 823 F Paris 17ème
Ternes
8 22 894 F Paris 7ème
Gros-Caillou
9 22 894 F Paris 7ème
Gros-Caillou
10 18 201 F Paris 15ème
Grenelle
11 18 201 F Paris 15ème
Grenelle

















































12 18 201 F Paris 15ème
Grenelle
13 15 000 F Boulogne-Billancourt
14 18 201 F Paris 15ème
Grenelle
15 16 107 F Paris 15ème
Necker
16 18 220 F Paris 15ème
Javel
17 18 220 F Paris 15ème
Javel
18 15 000 F Boulogne-Billancourt
19 18 220 F Paris 15ème
Javel
20 17 244 F Paris 15ème St.
Lambert
21 17 244 F Paris 15ème St.
Lambert
22 17 244 F Paris 15ème St.
Lambert
23 17 244 F Paris 15ème St.
Lambert
24 17 244 F Paris 15ème St.
Lambert
25 15 000 F Boulogne-Billancourt
Tableau 4.2 - Prix au m² par aire et quartier
correspondant
Il est demandé dans le logiciel Sitation un
coût au mile qui a été pris égal à
l'unité et une distance de couverture en miles (1 mile
anglo-saxon = 1609 mètres). Cette dernière est la distance
maximale qu'un client est prêt à parcourir pour se rendre à
un supermarché ou à un grand magasin distribuant des produits
"bio".

Fig. 4.21 - Fenêtre de saisie des paramètres de
distance et de coût dans le logiciel Sitation
Un entretien avec les responsables d'Espace "bio" nous
a permis de savoir que les clients n'hésitaient pas à venir
de loin (ex. Conflant Ste Honorine à Paris 15ème) pour effectuer
leurs courses étant donné que les prix du magasin sont
très abordables comparés à la moyenne du secteur et que
l'offre en produits "bio" est pléthorique. Ainsi, nous avons
considéré que tous
les clients recensés dans la base sont susceptibles de
se rendre aux points de vente à créer, chacun optant pour celui
le plus proche de son domicile. La distance de couverture a donc
été prise comme infinie (introduction d'un nombre très
élevé comme paramètre de couverture). Cette étape
de calcul suppose qu'il n'existe pas de concurrents en place dans ce
domaine à l'Ouest de Paris et que la société a
toute latitude de décision pour implanter son ou ses magasins
où bon lui semble en fonction du potentiel de clientèle. En
effet, Espace "bio" est, comme les autres magasins "bio", sur un segment de
marché bien à part bien que dérivé du commerce de
proximité traditionnel : les clients acquis à la philosophie
"bio" font en pratique exclusivement leurs courses dans ce
supermarché. Tous les noeuds, sans exclusion, ont
été
autorisés à recevoir un point de vente (Forced
Nodes).
Fig. 4.22 - Cartographie de la demande associée à
chaque noeud
(les bâtonnets représentent l'importance de la
demande)
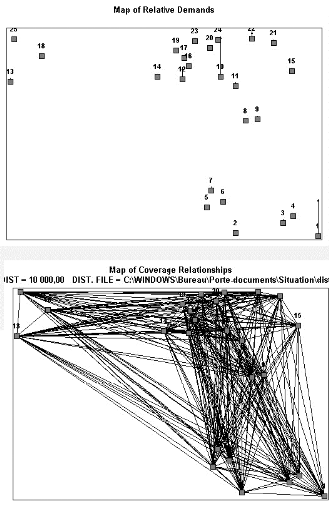
Fig. 4.23 - Cartographie de tous les noeuds et des
déplacements possibles pour effectuer ses achats
La figure 4.23 représente les 25 différents noeuds
qui tous comportent une certaine demande plus ou moins élevée et
peuvent être le siège d'accueil d'un point de vente.
L'enchevêtrement des liaisons entre les noeuds indique que les clients
habitant en un noeud sont susceptibles de
se rendre en un autre pour y faire leurs achats de
produits "bio" même si l'on sait par l'expérience que la
majorité des clients de ce type de magasin proviennent essentiellement
de leur quartier d'élection.
La question essentielle en suspend reste donc de savoir sur quels
noeuds porter son choix pour
la création de commerces "bio" sachant que l'on pourra
trouver réponse à cette question en faisant appel aux
traditionnelles heuristiques solutionnant les modèles de type
p-médian. Dans l'échelle la plus large de recherche, on
pourra essayer de placer de 1 magasin (approche minimaliste en terme
d'offre) à 25 magasins (approche maximaliste). Ce dernier cas est
trivial puisqu'il y a 25 noeuds possibles pour placer 25 points de vente,
chaque noeud accueillant alors son commerce, mais au moins servira-t-il
à vérifier la pertinence ultime de recherche de
localisations optimales par les heuristiques classiques. Ainsi, nous
prendrons connaissance dans le prochain chapitre des résultats de
localisation sachant que le modèle p-médian a été
résolu par plusieurs méthodes pour p variant de 1
à 25 points de vente à placer dont l'algorithme flou,
l'algorithme de voisinage, les multiplicateurs de Lagrange et
l'algorithme génétique. Ceci dit, cette phase initiale
d'élaboration et de résolution du modèle
p-médian n'est qu'une étape éventuellement
intermédiaire pour se plonger vers une connaissance de
localisations à un niveau plus fin. En effet, comme nous l'avons mis en
avant précédemment dans la description générale de
notre algorithme (voir chapitre 3.1), nous nous attendons à ce que la
précision insuffisante des localisations optimales obtenues
référencées par les 25 noeuds nécessite une
étape supplémentaire caractérisée par une
rétroaction du processus au niveau des noeuds retenus. Le même
processus de délimitation sera alors entrepris au niveau
de chacune des aires représentant ces noeuds
optimaux, mais à une échelle plus fine, de
manière à mettre en évidence des sous-aires
et d'élaborer des modèles p-médian secondaires
au sein de ces aires qui seront résolus par le
même type d'heuristiques. Il sera ainsi possible en analysant en
profondeur les aires optimales d'accéder à un niveau de
précision beaucoup plus élevée pour y placer des points de
vente.
Conclusion
En résumé, ce chapitre nous a conduit
à mettre en pratique notre méthode reposant sur le
traitement du signal pour élaborer un modèle p-médian en
partant d'une base de données de
10211 adresses de clients susceptibles d'acheter des
produits biologiques. Nous avons ainsi géocodé ces adresses
de manière à obtenir une carte des points de demande puis
traité la carte
par la transformation de dilatation adéquate de
manière à distinguer des aires homogènes de
clientèle, aires au nombre de 25. Ces aires atypiques par
rapport aux nombreuses aires minuscules et isolées qui
parsèment l'espace géographique, ont pour caractéristiques
d'être de taille importante et de receler un fort potentiel commercial.
Un filtre Sobel appliqué à la carte des aires homogènes
a alors permis de délimiter ces aires homogènes et donc
de cerner la zone de chalandise rassemblant la part la plus importante de la
clientèle concernée par l'achat
de produits biologiques. Les caractéristiques de ces
25 aires ont été obtenues par un sous- algorithme de
suivi de contour, et en particulier la surface de ces aires
révélant l'importance
de la demande et les coordonnées de leurs centres de
gravité. Ces deux paramètres ont permis d'élaborer un
réseau p-médian avec des noeuds correspondant aux centres de
gravité des aires
et le niveau de demande à la surface desdites aires.
Toutes ces étapes ont été obtenues avec rapidité et
sans difficulté grâce à des logiciels courants du
marché
Le prochain chapitre nous donnera l'occasion de
résoudre ce modèle avec les différents algorithmes
existants (algorithme flou, de voisinage, multiplicateurs de
Lagrange et
algorithme génétique) et d'examiner les
résultats.
Chapitre 5
Mise en oeuvre d'un système rapide d'aide
à la décision de localisation
Introduction
Le modèle p-médian ayant été
construit en particulier grâce aux puissantes fonctions
de filtrage du traitement du signal, nous débouchons alors
sur un problème classique
de résolution d'un modèle de
localisation-allocation. Ainsi, comme nous l'avons vu, les algorithmes
classiques d'un tel modèle sont bien connus :
l'algorithme flou, l'algorithme de voisinage, la résolution par les
multiplicateurs de Lagrange ou encore l'algorithme génétique.
Mais, appliqué à notre modèle d'une
complexité divisée par rapport au problème initial d'un
facteur 400, la résolution en sera d'autant plus rapide
(il y a avait en effet 10211 adresses au départ et nous
n'avons désormais plus qu'un réseau de 25 noeuds). Une ou
plusieurs régions géographiques appartenant à la zone de
chalandise parmi les 25, seront alors préconisées pour
être le siège d'implantations optimales de magasins de
produits biologiques. On pourra juger cependant que la précision
obtenue n'est pas suffisante puisqu'elle se cantonne à indiquer
seulement, parmi 25 quartiers, les plus intéressants. Nous montrerons
que cette précision peut être largement dépassée,
comme le prévoit notre algorithme. Le même processus de
dilatation, de filtrage sera réitéré au niveau des
quartiers préconisés afin d'obtenir de nouveaux modèles
p-médian plus fins qui seront ultérieurement résolus par
les mêmes heuristiques classiques. La précision atteindra, on le
verra alors, un positionnement au
niveau des voies de circulation à quelques numéros
de rue près.
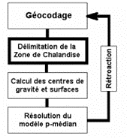
5.1 Résolution du modèle p-médian par
l'algorithme flou et l'algorithme de voisinage
Algorithme flou et algorithme de voisinage nous
donnent exactement les mêmes résultats quant aux localisations
optimales pour p variant de 1 à 25. Ils nous indiquent tout
d'abord que le noeud 10 est le plus indiqué pour
une
implantation unique. En ce qui concerne l'algorithme de
voisinage, une substitution est
pratiquée à la dernière itération
pour en améliorer les résultats. Ceux-ci sont
résumés dans le tableau suivant:
|
Nombre de
Localisations
|
Noeuds d'Implantation des Points de Vente
|
Fonction
Objectif
|
Distance
Maximale à Parcourir
|
|
2 loc.
|
1, 10
|
3205268
|
472
|
|
3 loc.
|
1, 10, 18
|
2512282
|
284
|
|
4 loc.
|
1, 6, 10, 18
|
1908833
|
172
|
|
5 loc.
|
1, 6, 10, 18, 22
|
1507518
|
172
|
|
6 loc.
|
1, 6, 10, 12, 18, 22
|
1177979
|
172
|
|
7 loc.
|
1, 6, 9, 10, 12, 18, 22
|
981793
|
145
|
|
8 loc.
|
1, 6, 9, 10, 12, 18, 22, 23
|
808933
|
145
|
|
9 loc.
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679238
|
145
|
|
10 loc.
|
1, 3, 7, 9, 10, 12, 15, 18, 22, 23
|
561933
|
114
|
|
11 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 18, 22, 23
|
471987
|
110
|
|
12 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
408799
|
110
|
|
13 loc.
|
1, 2, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
351929
|
86
|
|
14 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20,
22
|
302977
|
86
|
|
15 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22,
25
|
257139
|
57
|
|
16 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22,
25
|
212818
|
57
|
|
17 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21, 22,
25
|
177618
|
57
|
|
18 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21,
22, 23, 25
|
147852
|
57
|
|
19 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 23, 25
|
117471
|
41
|
|
20 loc.
|
1, 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20,
21, 22, 23, 25
|
91313
|
34
|
|
21 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
20, 21, 22, 23, 25
|
67953
|
34
|
|
22 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
19, 20, 21, 22, 23, 25
|
48579
|
34
|
|
23 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
25
|
30355
|
31
|
|
24 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 24,
23, 25
|
13026
|
26
|
|
25 loc.
|
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22,
23, 24, 25
|
0
|
0
|
Tableau 5.1 - Localisations optimales données par les
algorithmes flou et de voisinage
Fig. 5.1 - La mise en oeuvre de l'algorithme flou sur le logiciel
Sitation
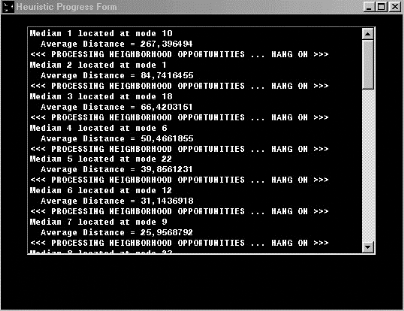
La distance moyenne à parcourir pour les clients en
fonction du nombre de magasins créés est donnée par le
graphique 5.2 :
Fig. 5.2 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts:
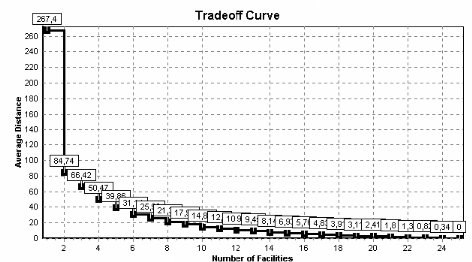
5.2 Résolution du modèle p-médian par
les multiplicateurs de Lagrange
Rappelons que les multiplicateurs de Lagrange sont des
variables à partir desquelles on construit une fonction
appelée lagrangien et notée L, fonction utilisée dans les
problèmes de recherche de l'extremum lié d'une fonction f
(optimisation sous contraintes). Dans ce type de problème
général, les variables xi sont astreintes à
vérifier m relations :
hk (x1,..., xi,..., xn) = 0
(pour k = 1,....., m)
Une condition nécessaire pour que f soit minimale
est qu'il existe m multiplicateurs de

Lagrange tels que :

Ces relations équivalent à l'annulation des
dérivées du premier ordre du lagrangien défini par :
Dans notre cas, la fonction à minimiser (voir §
2.2.1.2) est la fonction objectif relaxée par les
multiplicateurs de Lagrange i :
( ai dij + i ) xij +
i j i
i (1)(1)
et les contraintes sont :
xij = 1, i, (2)
i
xij yj, i, j, (3)
yj = p, (4)
j
xij, yj {0,1}, i, j (5)
où
ai : la demande au noeud i,
di,j : la distance du noeud i au noeud j,
p : le nombre d'activités à localiser,
xi,j = 1, si le noeud i est assigné à
l'activité j et 0 autrement,
yj = 1, si l'activité j est ouverte et 0 autrement.
Le nombre d'itérations a été fixé
à 400, la valeur minimale du paramètre lambda à
0,00000001
et le nombre d'échecs avant de modifier ce
paramètre (par pas de 0,3) à 36. Un algorithme
d'amélioration par substitution a été mis en oeuvre
ensuite pour en améliorer les résultats.
Les résultats obtenus ont été les
suivants:
|
Nombre de
Localisations
|
Noeuds d'Implantation des Points de Vente
|
Fonction
Objectif
|
Distance
Maximale à
Parcourir
|
|
2 loc.
|
1, 10
|
3205268
|
472
|
|
3 loc.
|
1, 10, 18
|
2512282
|
284
|
|
4 loc.
|
1, 6, 10, 18
|
1908833
|
172
|
|
5 loc.
|
1, 6, 10, 18, 22
|
1507518
|
172
|
|
6 loc.
|
1, 6, 10, 12, 18, 22
|
1177979
|
172
|
|
7 loc.
|
1, 6, 9, 10, 12, 18, 22
|
981793
|
145
|
|
8 loc.
|
1, 6, 9, 10, 12, 18, 22, 23
|
808933
|
145
|
|
9 loc.
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679238
|
145
|
|
10 loc.
|
1, 3, 7, 9, 10, 12, 15, 18, 22, 23
|
561933
|
114
|
|
11 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 18, 22, 23
|
471987
|
110
|
|
12 loc.
|
1, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
408791
|
110
|
|
13 loc.
|
1, 2, 3, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22
|
351929
|
86
|
|
14 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20,
22
|
302977
|
86
|
|
15 loc.
|
1, 2, 3, 6, 7, 9, 10, 12, 13, 15, 17, 18, 20, 22,
25
|
257139
|
57
|
|
16 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 22,
25
|
212818
|
57
|
|
17 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 15, 17, 18, 20, 21, 22,
25
|
177618
|
57
|
|
18 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 25
|
147237
|
41
|
|
19 loc.
|
1, 2, 3, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20, 21,
22, 23, 25
|
117471
|
41
|
|
20 loc.
|
1, 2, 3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18, 20,
21, 22, 23, 25
|
91313
|
34
|
|
21 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
20, 21, 22, 23, 25
|
67953
|
34
|
|
22 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17, 18,
19, 20, 21, 22, 23, 25
|
48579
|
34
|
|
23 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
25
|
30355
|
31
|
|
24 loc.
|
1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 16, 17,
18, 19, 20, 21, 22, 23,
24, 25
|
13026
|
26
|
|
25 loc.
|
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16,
17, 18, 19, 20, 21, 22,
23, 24, 25
|
0
|
0
|
Tableau 5.2 - Localisations optimales données par
l'algorithme des multiplicateurs de Lagrange
Pour 18 localisations, le noeud 14 a été choisi
à la place du 23, mais les résultats redeviennent
à nouveau équivalents aux noeuds choisis par
l'algorithme de voisinage ou l'algorithme flou pour 19 implantations à
créer : le choix de l'algorithme des multiplicateurs de Lagrange pour
18 localisations est néanmoins meilleur étant
donné que la fonction objectif (147 237 au lieu
de 147 852) est, dans ce cas, plus faible et que la distance
maximale à parcourir en moyenne par les consommateurs est
également moins importante (41 au lieu de 57).
Fig. 5.3 - Pour 4 localisations: aires de potentiel commercial
associées aux points de vente (en gras)
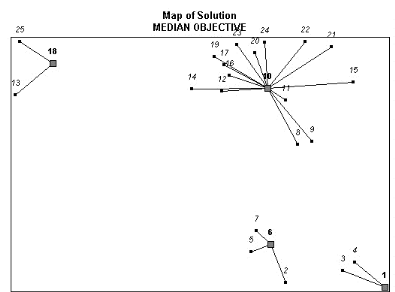
Le schéma précédent montre clairement
la supériorité stratégique de la localisation en 10
:
elle couvre nettement mieux les aires de clientèles que
les autres sites.
5.3 Résolution du modèle p-médian par
l'algorithme génétique
Le logiciel Sitation part d'une population de solutions
tirées au hasard. Au début, plusieurs ensembles de noeuds
répondant au problème sont sélectionnés
aléatoirement. La taille de la population de cet ensemble de solutions
du début a été prise à 50. Chaque solution est
codifiée sous forme de 0 et de 1 ce qui signifie qu'un noeud ayant
été sélectionné pour recevoir un site commercial
prend la valeur 1 et sinon 0 (le nombre de 1 dans chaque solution
correspond donc au nombre de sites à placer).
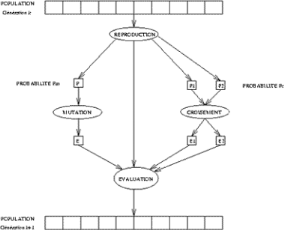
Fig. 5.4 - Schéma d'une itération de l'algorithme
génétique654
Ensuite, on a fixé à 200 le nombre
d'itérations possibles sachant qu'à chaque itération
s'effectue un croisement aléatoire entre des sous-ensembles de
ces solutions prises deux à deux avec une probabilité de 0,9
de se croiser et une prépondérance de ces croisements entre
les ensembles de solutions ayant la meilleure fonction
objectif (la plus faible). En parallèle au processus de croisement,
on fait intervenir une mutation dans un cas sur 400 (taux de
probabilité 0,25) : un zéro est alors transformé en un et
un en zéro de temps en temps.
En résumé, les paramètres pris pour faire
tourner l'algorithme génétique ont été les suivants
:
É Taille de population : 50
É Nombre d'itérations maximales : 200
É Probabilité de croisement : 0,9
É Probabilité de mutation : 0,25
La photo d'écran qui suit montre les étapes
franchies au départ par l'algorithme génétique pour
parvenir à une solution dans le cas de l'implantation de cinq points de
vente :
654
http://perso.wanadoo.fr/matt95/algogen/AGintro.htm
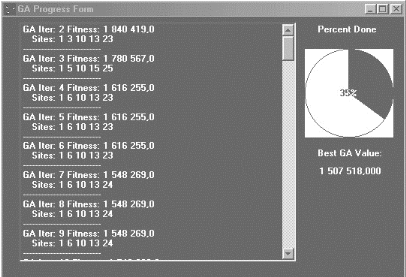
Fig. 5.5 - Etapes de recherche de l'algorithme de recherche avec
les localisations optimales provisoires obtenues
Au départ (voir fig. 5.5), on considère d'une
solution aléatoire : les noeuds 1, 3, 10, 13, 23 ont
été tirés au hasard pour 5 sites
commerciaux à placer. Puis, peu à peu, les solutions
s'améliorent pour se rapprocher de l'optimal. A la 9ème
itération, on obtient les noeuds 1, 6, 10,
13, 24 pour une fonction objective de 1 548 269. La solution
obtenue en définitive au bout de
20 itérations est de placer les points de vente aux
noeuds 1, 6, 10, 18, 22 conformément au résultat obtenu par
les autres algorithmes. Le processus est un peu plus long que par
les multiplicateurs de Lagrange qui ne prenaient que quelques secondes
pour parvenir à un résultat. Si la population initiale est de
50 au lieu de 200, la solution n'est trouvée qu'en 42 itérations
ce qui est logiquement plus long puisque le nombre de solutions passées
en revue à
la seconde est moindre qu'avec une population initiale
importante.
Avec les paramètres pris au départ, l'algorithme
génétique donne de moins bons résultats que l'algorithme
de voisinage ou l'algorithme par les multiplicateurs de Lagrange. La
solution obtenue au bout de 91 itérations est de placer les points de
vente aux noeuds 1, 3, 7, 9, 10, 12,
13, 22 et 23 pour une valeur de la fonction objectif de 684 927
au lieu des noeuds 1, 3, 7, 9,
10, 12, 18, 22, 23 pour une valeur de la fonction objectif plus
petite et meilleure de 679 238.
Le tableau suivant récapitule les résultats pour
une recherche de 9 localisations et montre la similitude en terme de
performance de l'algorithme par les multiplicateurs de Lagrange, de
l'algorithme flou et l'algorithme de voisinage.
|
Algorithme
|
Résultats
|
Fonction Objectif
|
Temps de Calcul
|
|
Multiplicateurs de Lagrange
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679 238
|
5 s
|
|
Voisinage
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679 238
|
5 s
|
|
Flou
|
1, 3, 7, 9, 10, 12, 18, 22, 23
|
679 238
|
5 s
|
|
Génétique
|
1, 3, 7, 9, 10, 12, 13, 22, 23
|
684 927
|
1 min
|
Tableau 5.3 - Comparatif des résultats de recherche de
localisations effectuée les différents algorithmes
5.4 Localisation améliorée des points de
vente au sein des aires de chalandise
imaginons qu'il s'agisse de créer 3 points de vente dans
l'Ouest parisien. Le premier, on l'a vu, est à implanter au sein de
l'aire
10 dans le XVème arrondissement. Le
deuxième, par ordre de
priorité est à placer dans l'aire 1
correspondant au quartier
Epinettes situé dans le 17ème
arrondissement de Paris. Le troisième doit se situer dans l'aire
18
de Boulogne-Billancourt.
Notre algorithme s'est déjà attaqué au
géocodage des adresses, au filtrage et à la délimitation
des aires constitutives de la zone de chalandise et à la
résolution du modèle p-médian par différents
algorithmes en prenant comme noeud les centres de gravité des aires pour
simplifier
le problème. Il reste éventuellement à
affiner la localisation de ces trois points de vente en focalisant notre
analyse au sein des aires 10, 1 et 18. Pour cela, nous allons
effectuer un processus de traitement du signal à titre d'exemple
sur les aires 10 et 1 en quelque sorte
passées à la loupe.
Localisation du point de vente au sein de l'aire 10 dans le
XVème arrondissement
Pour cela, effectuons le même traitement de filtrage, de
délimitations, d'analyse des sous-aires puis de résolution du
modèle p-médian au niveau de la sous-aire 10 correspondant au
quartier Grenelle / St. Lambert. La recherche d'une localisation plus
précise au sein de cette sous-aire
ne peut se faire sans tenir compte des clients
situés en son voisinage. Imaginons en effet qu'une localisation
idéale se situe sur le bord de la sous-aire 10. Dans ce cas,
ne pas tenir compte des clients potentiels des aires voisines fausserait
l'analyse et sans doute l'on passerait
à côté de cette solution
idéale. Pour éviter ainsi cet "effet de bord", nous
avons choisi d'incorporer dans l'analyse les sous-aires adjacentes à
l'aire 10 (aires 11, 12, 16, 20 et petits fragments non numérotés
à l'étape initiale).
Fig. 5.6 - L'aire 10 (bd de Grenelle) avec les aires les plus
proches
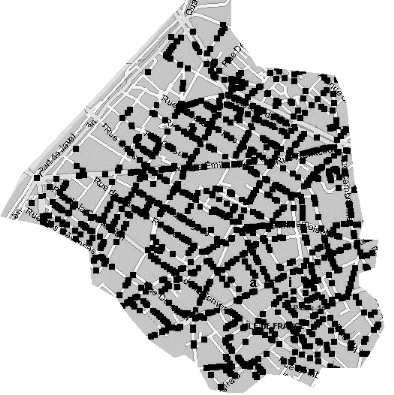
Fig. 5.7 - La zone d'analyse délimitée Fig. 5.8 -
et analysée en termes de sous-aires

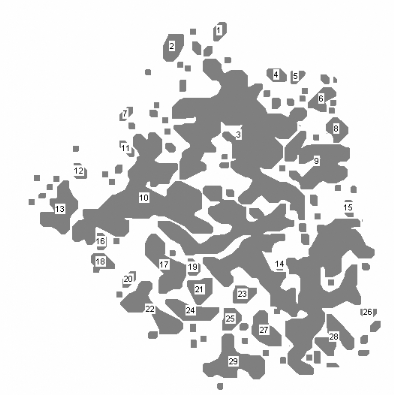
Fig. 5.9- Superposition des points-clients et des sous-aires
L'analyse des sous-aires appartenant à l'aire 10
réalisée par la même procédure de suivi de contour,
de calcul des coordonnées des centres de gravité et des
superficies nous donne les
résultats suivants (voir §3.3 pour la
procédure) :
|
Sous-aire
|
Superficie
|
X
|
Y
|
|
1
|
292
|
41
|
362
|
|
2
|
230
|
62
|
829
|
|
3
|
318
|
179
|
16650
|
|
4
|
368
|
100
|
409
|
|
5
|
395
|
101
|
276
|
|
6
|
428
|
132
|
727
|
|
7
|
168
|
151
|
232
|
|
8
|
449
|
172
|
680
|
|
9
|
422
|
215
|
3899
|
|
10
|
192
|
263
|
10792
|
|
11
|
169
|
197
|
270
|
|
12
|
106
|
228
|
326
|
|
13
|
80
|
279
|
1993
|
|
14
|
374
|
352
|
21702
|
|
15
|
465
|
277
|
259
|
|
16
|
135
|
321
|
273
|
|
17
|
219
|
353
|
2261
|
|
18
|
135
|
349
|
580
|
|
19
|
257
|
356
|
328
|
|
20
|
172
|
372
|
286
|
|
21
|
267
|
385
|
886
|
|
22
|
201
|
411
|
2210
|
|
23
|
324
|
391
|
619
|
|
24
|
255
|
414
|
1280
|
|
25
|
307
|
424
|
614
|
|
26
|
490
|
416
|
226
|
|
27
|
353
|
439
|
1227
|
|
28
|
446
|
448
|
1448
|
|
29
|
312
|
482
|
2603
|

























































Tableau 5.4 - Résultats d'analyse des sous-aires
appartenant à l'aire 10
Dans le tableau 5.4, la colonne Superficie s'identifiera à
la demande du réseau p-médian défini
par les coordonnées des centres de
gravité des sous-aires (avec un coût au m²
des emplacements de 18 201 F). Nous résolvons ce modèle par les
algorithmes classiques tels que ceux décrits à la première
étape. Ceux-ci nous indiquent les mêmes résultats.
Fig. 5.10 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts dans l'aire 10
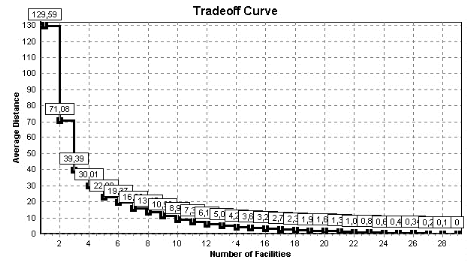
Fig. 5.11 - Pour 2 localisations: aires de potentiel commercial
associées aux points de vente (en gras)
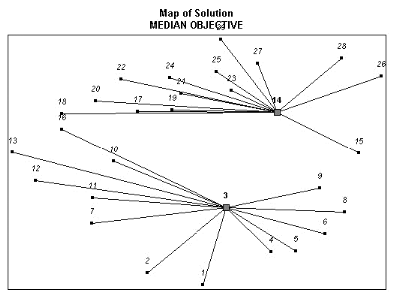
Le meilleur emplacement pour un point de vente semble être
dans la sous-aire 14 de l'aire 10.
Le tableau suivant donne les sous-aires à
privilégier si l'on veut implanter plus d'un magasin dans l'aire 10.
|
Nombre
de
Localisations
|
Noeuds d'Implantation des Points de
Vente
|
Fonction
Objectif
|
Distance
Maximale à Parcourir
|
|
2 localisations
|
3, 14
|
5 277 256
|
258
|
|
3 localisations
|
3, 10, 14
|
2 927 814
|
148
|
|
4 localisations
|
3, 10, 14, 24
|
2 227 803
|
146
|
Tableau 5.5 : Localisations optimales au sein de l'aire 10
Localisation du point de vente au sein de l'aire 1 dans le
17ème arrondissement
Procédons de même pour affiner la localisation de
notre deuxième point de vente au sein de l'aire 1 correspondant au
quartier Epinettes dans le 17ème arrondissement.
Fig. 5.12 - La sous-aire 1 du quartier Epinettes
(17ème arrondissement)
Pour cela, nous allons reprendre le même processus de
filtrage et de délimitation des aires de clients potentiels au niveau de
l'aire 1.
Fig. 5.13 - Représentations des points Fig. 5.14 -
délimitation et, Fig. 5.15 - numérotation des sous-aires

de l'aire 1,
Fig. 5.16 - Superposition des sous-aires et de la cartographie
Nous obtenons le même type de tableau de résultats
:
|
AIRE
|
Superficie
|
X
|
Y
|
Longueur
|
Majeur
|
Mineur
|
Angle
|
|
1
|
370
|
190
|
18
|
73
|
26
|
18
|
7
|
|
2
|
37548
|
150
|
186
|
1838
|
314
|
157
|
72
|
|
3
|
483
|
82
|
64
|
87
|
30
|
20
|
60
|
|
4
|
283
|
50
|
80
|
63
|
22
|
16
|
68
|
|
5
|
3718
|
199
|
334
|
345
|
77
|
62
|
87
|
|
6
|
1768
|
162
|
376
|
216
|
57
|
39
|
81
|











Tableau 5.6 - Résultats d'analyse des sous-aires
appartenant à l'aire 1
Le prix au m² des surfaces commerciales dans le quartier 1
(Epinettes - 17ème arrondissement)
est de 11 755 F.
Fig. 5.17 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts
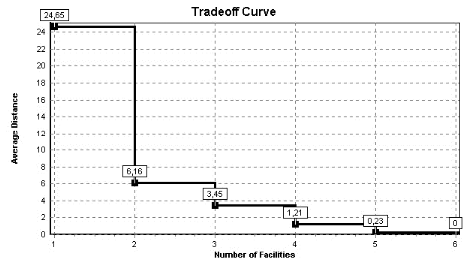
Les algorithmes nous donnent, pour la résolution
du modèle p-médian correspondant, une localisation à
privilégier dans la sous-aire 2 de l'aire 1. Pour plus d'un magasin
à implanter dans cette aire, il faudrait privilégier les
sous-aires indiquées dans le tableau 5.7 :
|
Nombre
de
Localisations
|
Noeuds d'Implantation des Points de Vente
|
Fonction
Objectif
|
Distance
Maximale à Parcourir
|
|
2 localisations
|
2, 5
|
271 956
|
173
|
|
3 localisations
|
2, 3, 5
|
152 486
|
117
|
|
4 localisations
|
2, 3, 5, 6
|
53 478
|
117
|
|
5 localisations
|
1, 2, 3, 5, 6
|
10 188
|
37
|
|
6 localisations
|
1, 2, 3, 4, 5, 6
|
0
|
0
|
Tableau 5.7 : Localisations optimales au sein de l'aire 1
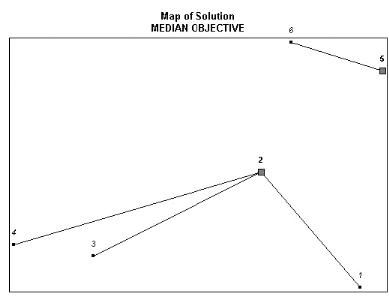
Fig. 5.18 - Pour 2 localisations: aires de potentiel commercial
associées aux points de vente en gras
De façon nette, le site commercial 2 implanté au
milieu de la plus grosse sous-aire s'accapare
la grande majorité du potentiel commercial avec les
sous-aires 1, 3 et 4 qui, pour en être le plus proches, sont
associées à ce potentiel.
Ceci dit, un facteur d'incertitude sur la viabilité de
l'emplacement détecté situé dans la sous- aire 2 du
quartier des Batignolles, apparaît par le fait que nous ne
possédons pas les adresses
des consommateurs potentiels du 18ème
arrondissement, arrondissement immédiatement à
l'Est
et en bordure de la zone d'analyse. Ainsi, à
cause de ce manque de données, l'étude de
localisation dans ce quartier pourra manquer de fiabilité
s'il apparaît qu'une zone de clientèle potentielle importante a
été involontairement ignorée : dans ce cas, le point de
vente semblera
être bien placé dans la sous-aire 2 alors qu'il
aurait dû être situé plus à l'Est voire dans le
18ème
arrondissement. D'un autre côté, le
18ème arrondissement est peut-être moins
intéressant que le
17ème étant donné
que le pouvoir d'achat de ses habitants est en moyenne plus faible
: il s'agirait d'étudier si leur niveau de revenus est
compatible avec l'habituelle chèreté des produits
biologiques qui apparaissent pour certains consommateurs presque comme
des produits de luxe.
Conclusion
Nous avons vu dans ce chapitre que notre méthode
était capable non seulement de rechercher
les localisations optimales de magasins, mais que l'on pouvait
également choisir le degré de précision de la
recherche, par exemple soit lors d'une première approche au
niveau grosso modo d'un quartier au sein d'une commune ou d'un
arrondissement, soit plus finement au niveau d'une rue. La rapidité
du processus de recherche dépend logiquement de la précision
souhaitée qui conditionne le nombre de boucles que l'algorithme
devra suivre ainsi que du nombre de localisations optimales
souhaitées.
D'un autre côté, toutes ces étapes
destinées à illustrer l'analyse conjointe traitement du signal /
algorithme p-médian nous serviront, tout au long du
chapitre suivant, à détailler les implications
managériales d'une telle démarche en particulier sur le
plan décisionnel. En particulier, notre recherche fait, pour
l'instant, abstraction de la concurrence. Il s'agit donc de vérifier
si les localisations optimales préconisées ne sont
pas déjà occupées par des commerces concurrents.
Le prochain chapitre permettra tout d'abord de récapituler les
avantages de notre méthode. Sa supériorité
apparaîtra encore plus clairement lorsque nous la comparerons aux
autres méthodes classiquement utilisées en recherche de
localisations
optimales.
Chapitre 6
Comparaison et implications managériales et
stratégiques
Introduction
L'intérêt de l'utilisation concomitante du
modèle p-médian et du traitement du signal dans la recherche de
localisations ne vaut que si cette approche apporte des avantages
comparativement aux méthodes traditionnelles. Nous verrons ainsi
dans ce chapitre que rapidité et précision sont bien les
maîtres-mots de notre algorithme qui recèlent encore
d'autres richesses sur le plan managérial.
Il est à noter que les résultats fournis par
notre démarche rationnelle méritent tout de même
d'être analysés de manière qualitative. En effet, quelle
que soit la méthode utilisée, les sites préconisés
ont un caractère théorique et ne correspondent parfois
pas à des emplacements faisables. La (ou les) rue(s)
relevée(s) ne présente(nt) par exemple pas
forcément d'emplacements commerciaux disponibles à l'achat ou
à la location. Les quartiers urbains ne sont peut-être pas en
adéquation avec l'activité prévue ou encore les sites sont
peut-être déjà occupés par la concurrence. C'est en
particulier lors de l'examen qualitatif minutieux des sites que la
précision obtenue quant à la localisation
géographique prend toute son importance, comme nous le verrons.
D'autre part, une fois cette étape franchie et que certains
sites effectivement faisables ont été définitivement
sélectionnés, il convient d'apprécier la zone de
chalandise des futurs points de vente et escompter leur chiffre d'affaires
(voir chapitre I). Ce même chiffre d'affaires d'ailleurs, s'il n'est pas
à la mesure de l'investissement, est capable de remettre en cause
l'ouverture du point de vente. Là encore, nous verrons que notre
méthode
est capable dans la foulée, de fournir par voie de
conséquence ces informations stratégiques.
Nous allons dans un premier temps récapituler quel type de
résultats aurait été fourni par une méthode de
recherche de localisation plus classique.
6.1 Comparaison des résultats de notre
algorithme avec ceux des méthodes traditionnelles de construction et
de résolution du p-médian
Comme nous l'avons vu précédemment, le
problème p-MP est réputé appartenir à la classe
ardue des problèmes connus comme étant NP-complets655
ce qui signifie que le nombre de
solutions à examiner en théorie est pour n noeuds
et p magasins à localiser est de :
n!
p! (n -
p)!
Pour 10 000 noeuds et par exemple 5 points de vente
"bio" à placer, nous aurions ainsi 83
milliards de milliards de solutions à passer en revue (83
x 1016) ce qui est impossible avec les systèmes informatiques
actuels.
Avec un algorithme du type recherche de voisinage qui
consiste à choisir au départ une configuration de
manière aléatoire, puis à effectuer une résolution
du 1-médian au niveau de chaque noeud d'implantation et des noeuds
voisins, le nombre de solutions à étudier est au minimum
de p x (n - p) avant de tomber sur un optimum éventuel, soit dans notre
exemple
10000 x (10000 - 5) ou pratiquement 100 millions de
configurations tout de même. L'algorithme génétique
est lui, programmé de manière à ne suivre qu'un
nombre limité d'itérations (par exemple 200 dans notre
étude de localisation). Ceci dit, sa procédure de
recherche de localisation a tout de même pris 4 minutes environ pour 25
noeuds et 10 points
de vente à placer pour en fin de compte n'atteindre
qu'un résultat imparfait. Si l'on considère que la durée
du processus suit une loi linéaire par rapport aux
combinaisons possibles, chercher 5 localisations du même niveau
d'optimalité pour 10 000 noeuds reviendrait à attendre 2,5
milliards d'années ! Ainsi, les algorithmes classiques de
résolution du p-médian
se révèlent dans l'impossibilité de
résoudre ce problème pris tel quel.
655 KARIV O et HAKIMI S.L. (1979) An Algorithmic
Approach to Network Location Problems, Part 2: The p- médians", SIAM
Jounal of Applied Mathematics 37, 539-560.
En revanche, grâce au traitement du signal, le
problème se réduit très simplement à 25 noeuds
et 5 points de vente. L'ensemble des configurations
d'implantation étant alors limité à 10 626,
il serait même possible de les examiner toutes
d'une manière exhaustive en retenant la solution
générant la meilleure fonction objectif.
En pratique, les spécialistes de la localisation
réalisent beaucoup d'approximations pour simplifier et tout de
même réussir à construire le modèle p-médian.
Dans notre cas, l'Ouest parisien aurait été découpé
très certainement en communes de périphérie, en
arrondissements
ou en quartiers tels que tout simplement
Boulogne-Billancourt, Issy-Les-Moulineaux, Neuilly-Sur-Seine, Paris
7ème, Paris 15ème, Paris
16ème, Paris 17ème. Il aurait alors
été assez facile de répartir les clients potentiels
selon leur code postal dans telle commune ou tel arrondissement. Chaque
élément de ce découpage aurait comporté un noeud
placé au centre du secteur géographique : les professionnels
choisissent en général un centre géographique parlant
comme la mairie ou l'église, ce lieu étant d'ailleurs choisi par
l'IGN pour repérer le secteur à partir de ses coordonnées
géographiques. Les distances auraient ensuite été
calculées
à vol d'oiseau et chaque noeud aurait reçu le
poids lié au nombre de clients potentiels habitant dans le secteur
correspondant. La chose se complique quand le découpage ne s'identifie
pas à des communes ou à des arrondissements bien
définis mais à des cellules plus petites (ex. quartier ou
pâté de maisons) ou encore à des zones à
cheval sur deux communes ou arrondissements: pour pouvoir exploiter la base
de données de Consodata par cette méthode classique, il aurait
alors fallu prendre tout à tour chacun des 10 000 clients et
l'affecter
manuellement à telle ou telle cellule ce qui constitue une
tâche herculéenne.
Dans le cas, le plus simple, on aurait eu :
|
?
|
un noeud pour
|
Boulogne-Billancourt
|
avec un poids de
|
1732
|
clients potentiels
|
|
?
|
un noeud pour
|
Issy-Les-Moulineaux
|
avec un poids de
|
952
|
clients potentiels
|
|
?
|
un noeud pour
|
Neuilly-Sur-Seine
|
avec un poids de
|
398
|
clients potentiels
|
|
?
|
un noeud pour
|
Paris 7ème
|
avec un poids de
|
517
|
clients potentiels
|
|
?
|
un noeud pour
|
Paris 15ème
|
avec un poids de
|
3456
|
clients potentiels
|
|
?
|
un noeud pour
|
Paris 16ème
|
avec un poids de
|
1087
|
clients potentiels
|
|
?
|
un noeud pour
|
Paris 17ème
|
avec un poids de
|
2069
|
clients potentiels
|
soit 7 noeuds et 10 211 clients potentiels au total.
En tenant compte des coordonnées des mairies
d'arrondissement et des communes de périphéries ainsi que du
prix de l'immobilier commercial, les paramètres des 7 noeuds à
entrer dans le modèle p-médian seront alors :













|
|
|
|
Commerciale au m²
|
|
1- Boulogne-Billancourt
|
1732
|
336
|
1549
|
15000
|
|
2- Issy-les-Moulineaux
|
952
|
788
|
1880
|
14615
|
|
3- Neuilly-sur-Seine
|
398
|
837
|
380
|
20000
|
|
4- Paris 7ème
|
517
|
1467
|
996
|
25081
|
|
5- Paris 15ème
|
3456
|
1255
|
1442
|
17443
|
|
6- Paris 16ème
|
1087
|
858
|
1001
|
21622
|
|
7- Paris 17ème
|
2069
|
1440
|
339
|
16453
|
Noeud Poids X Y Prix Surface
Tableau 6.1 - Analyse des arrondissements et des communes
appartenant à la zone étudiée
La mise en oeuvre de l'algorithme flou ou des coefficients de
Lagrange nous donne pour une localisation à placer, logiquement le plus
gros noeud également le plus central soit le noeud 5
(15ème arrondissement) et pour deux localisations
à placer les noeuds 5 et 7 en adéquation avec notre algorithme
qui conseillait de situer les deux magasins dans les
15ème et le 17ème
arrondissements.
Pour 3 magasins à placer, la résolution du
modèle p-médian nous indique les noeuds 1
(Boulogne-Billancourt), 5 (15ème arrondissement) et
7 (17ème arrondissement) : là encore, les
noeuds indiqués correspondent à ceux de notre
algorithme (aires 1, 10 et 18).
En revanche, pour 4 localisations, cette méthode
nous indique les noeuds 1 (Boulogne- Billancourt), 5
(15ème arrondissement), 6 (16ème
arrondissement) et 7 (17ème
arrondissement) : l'algorithme trop simpliste met en avant un nouvel
arrondissement, le 16ème, où réside
peu de potentiel alors qu'il y avait finalement possibilité de placer un
deuxième point de vente plus porteur à l'Ouest du
17ème arrondissement. Le 17ème
arrondissement a cela de particulier en effet qu'il compte
pratiquement le double de clients potentiels comparé au
16ème et que d'une forme longiligne, il est en
quelque sorte scindé en deux, avec à l'Ouest les beaux
quartiers
(avenue de la Grande Armée / Ternes) et bien plus à
l'Est des quartiers plus modestes (Guy
Môquet / Batignolles).
Nombre de points de vente à placer Noeuds solutions
2 5, 7
3 1,5, 7
4 1, 5, 6, 7
Tableau 6.2 - Noeuds solution avec un p-médian
classique
La méthode classique du p-médian a ici
ignoré cette répartition du 17ème en deux
pôles et a tout amalgamé. Notre algorithme au contraire a
respecté les frontières naturelles des aires de chalandise en
détectant les deux concentrations de clients potentiels et les
opportunités d'implantation. La méthode classique du
p-médian a le fort inconvénient de nécessiter le
jugement subjectif du manager qui doit lui-même découper
les secteurs en fonction de sa logique toute personnelle.
|
Noeuds solutions
|
|
Nombre de points de vente à placer
|
P-médian classique
|
Notre algorithme
|
|
2
|
15ème, 17ème
|
Paris 17ème Epinettes, Paris 15ème
Grenelle
|
|
3
|
ème ème ème
15 , 16 , 17 ,
Boulogne-Billancourt
|
Paris 17ème Epinettes, Paris
15ème Grenelle, Boulogne-Billancourt
|
|
4
|
ème ème
15 , 17 , Boulogne-
Billancourt
|
Paris 17ème Epinettes, Paris 15ème
Grenelle,
Boulogne-Billancourt, Paris
17ème Ternes
|
Tableau 6.3 - Comparatif des résultats entre notre
algorithme et l'utilisation classique du p-médian
L'algorithme à base de traitement du signal que
nous utilisons, détecte lui-même les aires
intéressantes sans introduire ce biais. Ce dernier ne s'arrête pas
là : comme nous l'avons vu, il
va se concentrer, sur les aires intéressantes,
dans une seconde phase pour y rechercher de manière plus
précise les emplacements les meilleurs, étape qu'ignore
totalement la méthode classique. Cela étant dit, les
résultats fournis ne dispensent pas le manager de leur analyse et
de leur interprétation qui doit en particulier tenir
compte de la présence de concurrents sur le terrain et des conditions
passées de leur implantation. C'est ce type d'analyse que nous allons
réaliser dans le chapitre suivant à partir des données que
nous venons de décrire.
6.2 Implications managériales et
stratégique : analyse des localisations existantes et choix d'une
nouvelle localisation
6.2.1 Vérifier la bonne localisation de magasins
existants
La résolution du modèle p-médian, au niveau
des 25 aires délimitées par traitement du signal, nous a
indiqué que, pour implanter 6 points de vente, il fallait choisir les
aires 10, 1, 18, 6, 12
et 9. Or, le tableau suivant nous montre de façon
étonnante que 5 aires sur les 6 premières aires
préconisées sont déjà occupées par un ou
plusieurs magasins "bio" (toutes sauf l'aire 18)
:
|
Groupe
|
Point de Vente
|
Rue
|
Code
Postal
|
Commune
|
Aire de
Rattachement
|
|
Naturalia
|
Naturalia
|
38 av de la Motte Picquet
|
75007
|
Paris
|
9
|
|
Naturalia
|
86 rue de Cambronne
|
75015
|
Paris
|
extrémité est de 10
|
|
Natur alia
|
25 r ue des Sablons
|
75016
|
Par is
|
|
|
Naturalia
|
26 rue Poncelet
|
75017
|
Paris
|
6
|
|
Naturalia
|
16 rue de Levis
|
75017
|
Paris
|
4
|
|
Biocoop
|
Biocoop Grenelle
|
44 Bd Degrenelle
|
75015
|
Paris
|
10
|
|
Biocoop Paris 17ème
|
153 Rue Legendre
|
75017
|
Paris
|
1
|
|
Les Nouveaux Robinsons
|
127 Av. Jean-Baptiste Clément
|
92100
|
Boulogne-Billancour t
|
|
|
Les Nouveaux Robinsons
|
14 Rue Des Gr avier s
|
92200
|
Neuilly-Sur -Seine
|
|
|
Espace Bio
|
Espace Bio Saint Charles
|
20 rue de l'Eglise
|
75015
|
Paris
|
12
|
Tableau 6.4 - les magasins "bio" de la région parisienne
et leur aire de rattachement
En particulier, l'aire 10 qui est la zone stratégiquement
la plus intéressante comporte déjà 2
implantations. On remarque que le groupe BioCoop occupe
déjà de façon judicieuse les aires
10 et 1 et que l'une des implantations de Naturalia se centre
aussi dans l'aire 10.
Plus précisément, nous avions mis en avant dans
l'aire 10, la sous-aire 14 qui a son centre de gravité au sud du Square
St. Lambert au niveau de l'avenue Lecourbe (n° 160 environ) : il
s'avère que le magasin Naturalia de cet arrondissement (86 rue
de Cambronne) se situe à moins de 200 mètres de cette
préconisation.
Fig. 6.1 - Le supermarché BioCoop (bd de Grenelle), le
supermarché Naturalia
(rue Cambronne) et notre préconisation (rue Lecourbe)
Au sein de l'aire 1 du 17ème
arrondissement, nous avons vu que la sous-aire 2 paraît la
plus conseillée: son centre de gravité est placé au milieu
de la rue Guy Môquet entre les avenues très passantes de Clichy
et de St. Ouen. Il s'avère que dans ce cas aussi, le point
de vente BioCoop dans ce quartier situé 153 rue Legendre est à
moins de 200 mètres de la localisation
que nous avons donnée !
Fig. 6.2 - Le supermarché BioCoop (rue Legendre) et le
2ième
emplacement préconisé par notre méthode (rue
Guy Môquet)
Mais comment BioCoop a-t-il procédé pour obtenir
ces emplacements de premier plan (aire
10/sous-aire 14 et aire 1/sous-aire 2) dans une ville
où les surfaces d'importance sont plutôt difficiles à
acquérir ? En fait, BioCoop Grenelle et BioCoop Paris 17ème
sont tous les deux d'anciens supermarchés G20 traditionnels
reconvertis depuis peu au "bio". Ainsi, non seulement ces magasins vont
s'attirer la forte clientèle potentielle des alentours sensible aux
produits biologiques, mais vont sans doute conserver une bonne partie de leur
ancien fonds de commerce.
6.2.2 Etendre son réseau de points de vente
Sans avoir à l'esprit une véritable
stratégie de développement mais en étant à
la recherche d'opportunités pour s'étendre, l'analyse nous
permet aussi de prévoir quel peut être le prochain emplacement
commercial à conquérir. Après les aires 10, 1, 18, 6, 12,
9, viennent les aires 22
et 23. Mais, à y regarder de plus près ces aires 22
et 23 assez petites sont très proches en fait
de la sous-aire 14 au sein de l'aire 10. Leur
intérêt pour localiser un nouveau point de vente
est donc moindre. Egalement, les aires venant tout de suite
après cette série et indiquées par
les algorithmes sont l'aire 7 (avenue des acacias proche de
l'avenue de la Grande Armée dans
le 17ème) et l'aire 3 (à la jointure
entre le bd Pereire et la rue de Rome dans le 17ème, proche
du Square des Batignolles). Ces aires ont cela de particulier
qu'à partir du 9-médian, elles remplacent et font
disparaître l'aire 6. Mais là encore, à cent mètres
de l'avenue des 1cacias, l'emplacement est occupé par Naturalia rue
Poncelet (sur une aire voisine), de même pour l'aire 3 où
se situe déjà à proximité un autre magasin
Naturalia (rue de Lévis - figures 6.3 et
6.4).
Fig. 6.3 - Le magasin Naturalia dans le 17ème (rue de
Lévis et rue Poncelet) et les emplacements préconisés
Il apparaît donc clairement qu'à l'Ouest de
Paris, les emplacements ayant le potentiel
commercial le plus fort sont tous occupés et
qu'à moins de se lancer dans une stratégie agressive de
localisation dans l'environnement immédiat des concurrents, il faut
chercher des sites à Paris extra-muros ou en province. En effet, les
prévisions limitées de développement
du "bio" justifient le fait qu'on ne puisse se contenter
d'emplacements de second ordre dans
Paris en espérant que la croissance du secteur
compensera la faiblesse de la localisation. De plus, s'il arrivait que la
demande en produits "bio" atteigne celle du commerce traditionnel de
détail, il serait fort probable que les supermarchés des
grandes chaînes occupant depuis longtemps d'excellents sites dans
Paris basculeraient automatiquement vers ce type d'offre
(éventuellement selon le même schéma que les
supermarchés G20 qui ont changé leur enseigne en
BioCoop).
Fig. 6.4 - 2 points de vente Naturalia du 16 rue de Lévis
et, Fig. 6.5 - du 26 rue Poncelet (XVIIème)


Pour ces raisons, l'aire 18 sur laquelle nous
revenons, paraît potentiellement assez intéressante. La
commune dans laquelle elle est située, Boulogne-Billancourt,
comporte presque le même niveau de clients potentiels (1732) que le
17ème arrondissement de Paris mais
ne présente qu'un seul magasin "bio", BioCoop-Les
Nouveaux Robinsons. En outre, ce
magasin n'est pas situé directement à
proximité de l'aire 18 que nous préconisons pour implanter
un nouveau point de vente, mais à l'Ouest de Boulogne-Billancourt en
bordure de Seine.
L'emplacement mis en avant par l'algorithme (pour le
3-médian) est placé au centre de gravité
de l'aire 18, soit approximativement au 40 route de la Reine
à Boulogne-Billancourt (figure
6.6). Il ne connaît aucune concurrence
géographiquement proche dans son secteur et se situe
en limite du 16ème arrondissement de
Paris, de l'Ouest du 15ème arrondissement et
d'Issy-les- Moulineaux, secteur à potentiel dans lesquels n'existe
également aucun magasin distribuant
des produits biologiques.
Fig. 6.6 - Le magasin BioCoop-Les Nouveaux Robinsons (rue
Clément)
à Boulogne-Billancourt et l'emplacement
préconisé (route de la Reine)
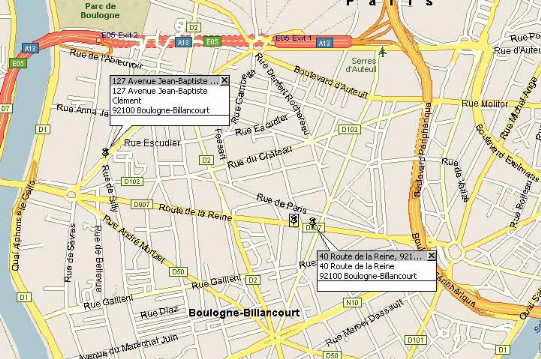
Nous constatons à travers cette étude
d'implantation que le traitement du signal associé au
modèle p-médian confirme l'optimalité d'implantation des
points de vente des deux groupes BioCoop et Naturalia ainsi que du
magasin Espace "bio" St. Charles. Les meilleures localisations
déterminées par l'algorithme sont cependant, à 150
mètres près, occupés pour la plupart par les points de
vente de ces réseaux. Après avoir donc constaté
une certaine saturation de l'offre "bio" dans l'Ouest de Paris, la
méthode a mis en exergue un autre emplacement viable de premier
choix, situé à Boulogne-Billancourt, proche de toutes les
aires
riches en clientèle potentielle et, malgré tout,
libre de toute concurrence.
6.2.3 Développer une stratégie de localisation
des réseaux de points de vente
Notre méthode permet, on l'a vu, de déterminer
les meilleures localisations sur un territoire pour un ensemble de
magasins. Or, la domination économique d'un territoire
nécessite également de tenir compte des sites
concurrents et d'élaborer une réelle stratégie
de développement dans le temps. Cette stratégie peut être
offensive et se traduire par l'extension
du réseau, la création de nouveaux points de
vente ou bien l'assimilation de points de vente concurrents. On parle alors de
stratégie d'évitement ou de stratégie de recherche de
concurrent selon que l'on souhaite exploiter des zones vierges de toute
concurrence ou bien au contraire aller à l'affrontement en
n'hésitant pas à se placer au plus proche des concurrents (voir
§3.4.2) sans exclure la possibilité de fermer les points de
vente les moins rentables (stratégie de
downsizing 656). La première approche
englobe les stratégies de remplissage et celles
d'expansion de marché. Elle peut être aussi
entièrement défensive, lorsque l'entreprise, face à des
difficultés économiques liées ou non à
l'action des compétiteurs est contrainte de restructurer son
réseau en fermant les points de vente engendreront le plus de
dettes et en relocalisant ou en regroupant éventuellement
des points de vente. Voyons comment concrètement, entreprendre
ce type de stratégies à partir de la méthode de traitement
du signal
et du modèle p-médian. Etant donné
que nous ne possédons pas le résultat et le chiffre
d'affaires des points de vente, il nous reste à raisonner sur des
hypothèses. Des stratégies de recherche de concurrents et
de prédation favoriseraient les implantations à
proximité immédiate de magasins "bio" appartenant à la
concurrence. En l'occurrence, pour ce qui est de
la distribution de produits "bio" dans l'Ouest parisien
qui nous préoccupe, on compte donc trois acteurs dans ce
secteur.
Rappelons tout d'abord, les forces en présence :
656 DAVIDSON W.R., SWEENEY D.J. et STAMPFL R.W.
(1988) Retailing Management, 6ème Ed., New York :
Wiley, cité par Cliquet G. dans Valeur Spatiale des
Réseaux et Stratégies d'Acquisition des Firmes de
Distribution, in Valeur, Marché et Organisation,
Ed. J-P. Brechet, Presses Académiques de l'Ouest., p.234.
Biocoop compte 4 implantations dans la zone analysée
soit:
É BioCoop Grenelle 44 Bd de Grenelle 75015
Paris
É BioCoop Paris 17ème 153 Rue
Legendre 75017 Paris
É Les Nouveaux Robinsons 127 Avenue Jean-Baptiste
Clément 92100 Boulogne-Billancourt
É Les Nouveaux Robinsons 14 Rue des Graviers 92200
Neuilly Sur Seine
Naturalia possède 5 implantations,
É 38 av de la Motte Picquet 75007 Paris
É 86 rue de Cambronne 75015 Paris
É 25 rue des Sablons 75016 Paris
É 26 rue Poncelet 75017 Paris
É 16 rue de Levis 75017 Paris
Et EspaceBio, une seule:
É EspaceBio 20 rue de l'Eglise 75015 Paris
Plaçons-nous donc plutôt dans une
stratégie plus classique qui viserait à occuper les zones
non encore exploitées comme une stratégie de type
évitement en concordance avec la première étape du
principe de différenciation minimale de Hotelling 657
(voir § 2.1.4). Le secteur "bio" est en effet encore en plein
développement et malgré un nombre d'implantations
déjà importants, il reste encore des places à prendre
(voir chapitre précédent avec la situation
de Boulogne-Billancourt). Si l'on recense les localisations
de ces magasins par groupe comparées aux localisations optimales
dans l'ordre déterminées par notre méthode, on obtient
le tableau 6.4.
|
Aires d'implantation
optimale
|
|
Naturalia
|
Biocoop
|
Espace Bio
|
|
Quartier Correspondant
|
|
|
10
|
Paris 15ème Grenelle Est
|
Oui
|
Oui
|
Non
|
|
1
|
Paris 17ème Epinettes
|
Oui
|
Oui
|
Non
|
|
18
|
Boulogne-Billancourt Est
|
Non
|
Partiellement
|
Non
|
|
6
|
Paris 17ème Ternes
|
Oui
|
Non
|
Non
|
|
12
|
Paris 15ème Grenelle Ouest
|
Non
|
Non
|
Oui
|
|
9
|
Paris 7ème Gros-Caillou
|
Oui
|
Non
|
Non
|
|
Nombre d'implantations optimales
|
4
|
2,5
|
1
|
Tableau 6.4 - Bilan des implantations des magasins "bio" dans les
aires optimales
Si l'on compte le nombre d'implantations optimales
occupées par chacun des réseaux, on observe que
Naturalia dépasse Biocoop avec respectivement 4 et 2,5
localisations
657 HOTELLING H. (1929) Stability in Competition,
The Economic Journal, vol. 39, p. 41-57.
stratégiquement intéressantes (le site de
Boulogne-Billancourt a été compté pour moitié
étant donné qu'il n'est pas exactement situé à
l'endroit de la localisation optimale mais à proximité tout de
même). On remarque également que, finalement, toutes les
aires comprennent au moins un magasin et que les aires 10 et 1 avec leurs
forts potentiels qui n'ont pas échappé aux deux concurrents,
possèdent chacune une implantations des deux principaux
groupes, Naturalia et Biocoop. Les produits biologiques sont en pleine
ascension et gagnent de plus en plus de notoriété dans la
population. La tendance actuelle des réseaux distribuant ces produits
est donc plutôt d'étendre leur
présence dans des zones géographiques encore
inexploitées. EspaceBio, avec son magasin unique, aura du mal à
développer un réseau de points de vente dans l'Est de la
région parisienne, puisque pratiquement toutes les aires
et quartiers comportent déjà une implantation concurrente.
Le chapitre précédent nous a montré que
Boulogne-Billancourt recelait encore une aire potentiellement
intéressante sans concurrence notable. Nous nous proposons
d'étudier tout d'abord le cas de l'extension des deux
réseaux principaux Naturalia et BioCoop dans le cadre d'une
stratégie d'expansion du marché en établissant des
têtes de pont et en évitant soigneusement la concurrence.
L'extension des réseau de distribution des
produits biologiques grâce à une stratégie d'expansion
du marché
Il s'agit d'examiner sur le terrain, quelles sont les
possibilités de Naturalia et de BioCoop d'agrandir leur
réseau dans un environnement favorable et, dans le cas positif, la
stratégie qu'il faudrait alors adopter. La création d'un
nouveau site dans l'aire 18 à Boulogne-Billancourt permettrait
à Naturalia d'améliorer sa couverture
géographique dans une aire où la concurrence ne fait
pas rage. Un nouveau site BioCoop dans cette aire 18 encore vierge
donnerait à ce réseau la possibilité de verrouiller
sa présence à Boulogne-Billancourt.
BioCoop occuperait les deux quartiers stratégiquement
importants de cette ville. Tout
nouveau concurrent devrait alors ensuite "se contenter
des miettes" et réaliser des efforts vraiment importants sur le
plan de la promotion pour asseoir sa notoriété en face
de ce concurrent majoritaire au niveau local. Mais, BioCoop n'est
connu à Boulogne-Billancourt que sous l'enseigne "Les Nouveaux
Robinsons". Pour vraiment bénéficier de la force du
réseau dans ce cadre et minimiser les conséquences d'une
implantation concurrente, il s'agirait donc en plus, que l'enseigne BioCoop
soit effectivement adoptée comme bannière commune dans tous les
points de vente du réseau.
D'autre part, on a vu (§ 6.2.1) que le BioCoop Paris
15ème Grenelle Est et BioCoop Paris 17ème
étaient d'anciens supermarchés G20 traditionnels
reconvertis récemment au "bio". Le risque pour Naturalia est qu'en
définitive, ces supermarchés classiques changent
graduellement d'enseigne et de type de produits en arborant l'enseigne BioCoop
et en distribuant alors les produits "bio" de ce groupement. Voici les adresses
de tous les supermarchés G20 de l'Ouest parisien :
É 6, rue Lakanal - Paris 15ème
É 269, rue Lecourbe - Paris 15ème
É 23-25 rue Georges Bernard Shaw - Paris 15ème
É 6-14 rue Belles Feuilles - Paris 16ème
É 22, rue Duban - Paris 16ème
É 41, rue st.ferdinand - Paris 17ème
É 175 avenue de Clichy - Paris 17ème
É 108, avenue du Gal de Gaulle - Neuilly sur Seine
Cette "réserve" d'espace foncier commercial convertible en
espace de vente de produits "bio"
est susceptible de menacer Naturalia dans les quartiers
où le réseau est bien implanté. Ainsi, nous avions
donné le 160 rue Lecourbe dans le 15ème
arrondissement comme emplacement optimal. Naturalia possède
en son voisinage (86 rue de Cambronne), un point de vente. Or, à
quelques centaines de mètres près, cohabite également au
269 rue Lecourbe, un supermarché G20 qui, s'il devenait "bio",
menacerait directement le magasin Naturalia. Egalement, le
supermarché G20 du 6, rue Lakanal ne se trouve qu'à un
pâté de maison du même magasin Naturalia. Ainsi, ce
magasin est entouré au sud-ouest, à l'ouest et au
nord-ouest, par une barrière de trois supermarchés G20
formant une ligne nord-sud 15ème arrondissement et
occupant une bonne partie de l'imposante aire 10. S'il
arrive qu'un jour, ces supermarchés deviennent des BioCoop,
Naturalia n'aurait plus qu'à se contenter de la maigre partie Est du
15ème arrondissement bordé par la
frontière naturelle des jardins de l'Ecole Militaire et un
arrondissement, le 7ème, moins riche en
clients potentiels car accueillant bon nombre d'administrations et
ambassades. Ainsi, Naturalia serait en position de faiblesse dans l'aire 10
possédant le marché de clients "bio" le plus important.
A l'Est du 17ème arrondissement (aire optimale
1) sont présents Naturalia et BioCoop. Certes,
le point de vente Naturalia est plus proche de la localisation
optimale que nous avions donnée (150 rue de Rome), mais BioCoop n'est
pas loin non plus avec son magasin rue Legendre. Pour étendre son
réseau, dans ce quartier peuplé, BioCoop aurait là encore
la possibilité de convertir le supermarché G20 de la rue
de Clichy, à la condition que le groupe arrive à
négocier un tel accord. La rue de Clichy a l'avantage
supplémentaire d'être un grand axe de circulation et de
commerce du nord de Paris, ce qui améliorerait la
visibilité d'un magasin "bio". Cette visibilité peut aussi
être un facteur important dans le succès commercial d'un
magasin. Ainsi, pour améliorer encore notre méthode, il faudrait
sans doute affecter un poids plus important aux noeuds du modèle
p-médian correspondant à des localisations potentielles
situées sur ou à proximité d'axes de
circulation importants, si l'on juge que cette
caractéristique peut jouer sur la performance des points de vente.
Par contre, Naturalia compte une implantation dans l'Ouest du
17ème (Paris 17ème Ternes - aire
optimale 6) contrairement à BioCoop. Mais, là
également, surprise, un supermarché G20 se situe également
dans ce quartier des Ternes commercialement intéressant
(supermarché G20,
41 rue St. Ferdinand, Paris 17ème).
Naturalia possède une implantation dans le
16ème arrondissement non identifiée en tant qu'aire
optimale (rue des Sablons) et où les consommateurs réputés
aisés et plus traditionnels sont moins enclins à acheter des
produits biologiques. Dans ce cas également, même si BioCoop
n'est pas présent, deux supermarchés G20 existent
bel et bien (6-14 rue Belles Feuilles et 22,
rue Duban). Neuilly-sur-Seine est habité par le même
type de consommateurs et dans cette ville, BioCoop a déjà un
magasin et G20, un supermarché.
En résumé, on remarque que, bien que BioCoop
possède moins d'implantations dans les aires optimales par rapport
à Naturalia, le fait que ce réseau ait réussi
à convertir déjà plusieurs supermarchés G20 en
supermarché "bio" à son enseigne pourrait lui donner une
supériorité inégalée s'il confirmait son expansion
via cet accord avec un réseau de distribution classique. Son nombre
d'implantations dans les aires intéressantes pourraient ainsi passer de
2,5 à 7,5
maximum (avec une augmentation des aires optimales où il
est présent de 3 à 4).
+
+
+
+
|
Aires
d'implantation
optimale
|
|
Naturalia
|
BioCoop
|
BioCoop
avec G20
|
Espace
Bio
|
|
Quartier Correspondant
|
|
|
10
|
Paris 15ème Grenelle Est
|
1
|
1
|
4
|
0
|
|
1
|
Paris 17ème Epinettes
|
1
|
1
|
2
|
0
|
|
18
|
Boulogne-Billancourt Est
|
0
|
0,5
|
0,5
|
0
|
|
6
|
Paris 17ème Ternes
|
1
|
0
|
1
|
0
|
|
12
|
Paris 15ème Grenelle Ouest
|
0
|
0
|
0
|
1
|
|
9
|
Paris 7ème Gros-Caillou
|
1
|
0
|
0
|
0
|
+
|
Nombre d'implantations optimales
|
4
|
2,5
|
7,5
|
1
|
=
+
|
Aire non-optimale
|
16ème arrondissement
|
1
|
0
|
1
|
0
|
|
Aire non-optimale
|
Neuilly-sur-Seine
|
0
|
1
|
2
|
0
|
+
|
Total d'implantations optimales
|
5
|
3,5
|
10,5
|
1
|
=
Tableau 6.6 - Bilan des implantations des magasins "bio" selon
les aires optimales et non-optimales
Comme les trois implantations de supermarchés G20
sont voisines de l'aire 12 (Paris 15ème
Grenelle Ouest) où est implanté le
supermarché unique EspaceBio, nul doute que la clientèle
de ce quartier viendrait également y faire ses courses.
Seul manquerait au réseau BioCoop un
magasin dans l'aire optimale 9 de Paris
7ème. L'expansion dans cette région pourrait
alors s'effectuer par une création pure d'un magasin. Le
réseau BioCoop pourra faire jouer au maximum la synergie de ces
implantations et accroître sa notoriété en faisant adopter
surtout pour son implantation importante de Boulogne-Billancourt, mais aussi
pour celle de Neuilly-
sur-Seine, son enseigne véritable au lieu de celle des
"Nouveaux Robinsons", nom de baptême donné par les
créateurs de ces deux commerces au temps où les magasins
ne faisaient pas encore partie d'un groupement. Cette enseigne
commune pourra par exemple donner l'opportunité d'une promotion
des magasins et de leurs produits dans les médias de masse au niveau
régional ou même national ce qui n'est actuellement pas possible
compte-tenu de la diversité des enseignes.
Naturalia, quant à lui, est loin d'être en
position de force. Sa stratégie d'expansion pourrait consister
d'abord à ouvrir un point de vente dans l'aire libre 18
à l'Est de Boulogne- Billancourt. L'aire 12 (Paris Grenelle
15ème Ouest), certes déjà occupée
par EspaceBio, pourrait aussi être une opportunité pour
Naturalia pour prendre en tenaille avec ses implantation
à l'Est de l'aire 10 (Paris 15ème Grenelle
Est) et dans l'aire 9 (Paris 7ème) le magasin
EspaceBio et les trois magasins G20 s'il advenait que ces derniers
passent à l'enseigne BioCoop. Les aires de chalandise effectives
de Naturalia prenant pour objet les clients réels des points de
vente empiéteraient donc largement à l'est et à l'ouest
sur celles de BioCoop malgré ses nouvelles implantations G20. Une
stratégie de communication offensive pourrait, si elle était
pratiquée sous peu, donnée en plus une avance
non-négligeable au réseau
des magasins Naturalia qui possèdent,
d'après les observations pratiquées sur le terrain,
l'inconvénient d'avoir des surfaces commerciales plus petites, du niveau
de celle de l'épicerie plutôt que de celui du
supermarché (contrairement aux supermarchés G20). Une autre
approche pourrait être de segmenter le marché et de se lancer sur
les produits "bio" haut de
gamme. Le réseau BioCoop semble, lui, en effet
plutôt privilégier la distribution de masse
tout comme le supermarché EspaceBio. Les clients des
nouveaux magasins BioCoop ne sont-
ils pas non plus en grande partie ceux des anciens
supermarchés G20 ? Passer de la distribution de produits
traditionnels aux produits "bio" permet aux BioCoop anciennement G20 de
familiariser la population souvent méfiante avec ce genre de produits ce
que n'a pas su faire Naturalia qui adresse ces produits à une
clientèle de connaisseurs. Une stratégie inverse pouvant
être adoptée par Naturalia serait de rechercher des commerces
traditionnels du style
de l'épicerie de quartier pouvant et souhaitant se
convertir au "bio" au moins graduellement,
en intégrant de plus en plus ce type de
produits dans leurs références jusqu'à adopter
officiellement l'enseigne Naturalia. Il existe en effet dans Paris une
multitude de petites épiceries souvent tenues par des
étrangers et ayant des heures d'ouverture assez souples
(jusqu'à minuit le soir et le dimanche) qui pourraient
éventuellement être fédérées en un
réseau. Encore faudrait-il étudier la bonne volonté de ces
commerçants indépendants vis-à-vis d'une telle offre et sa
faisabilité, puisque bon nombre de ces épiceries
s'approvisionnent déjà auprès de la centrale de
distribution Carrefour-Promodès.
Les supermarchés G20 du commerce traditionnel sont, nous
l'avons vu, bien complémentaires des implantations de BioCoop
puisque la fusion de ces deux réseaux pourraient amener au
groupe de distribution de produits "bio" une représentativité
intéressante dans toutes les aires stratégiques appartenant
à la zone de chalandise délimitée par la
méthode de traitement du signal. Il apparaît également
que les réseaux BioCoop et Naturalia ont un certain niveau de
complémentarité spatiale du fait qu'un magasin d'un réseau
est souvent présent dans une aire alors que l'autre n'en possède
pas. Leurs implantations dans certaines aires majeures sont très
voisines et donc directement concurrentes (aires 10 et 1). Cette
complémentarité pourrait
s'exercer dans les aires stratégiques 18
(Boulogne-Billancourt Est), 6 (Paris 17ème Ternes), 12
(Paris 15ème Grenelle Ouest), 9 (Paris
7ème Gros-Caillou) et dans les régions non
répertoriées comme majeures telles Paris 16ème
et Neuilly-sur-Seine.
Dans le cas de la fusion des deux groupes Naturalia et BioCoop
(voir tableau ci-dessous), la couverture géographique est excellente
puisque avec 9 magasins, l'ensemble possède une présence
dans toutes les aires stratégiques hormis l'aire 12 (Paris
15ème Grenelle Ouest ) occupée par EspaceBio et
dans le 16ème arrondissement et la commune de
Neuilly-sur-Seine, même si le nombre d'implantations dans les aires
optimales est légèrement inférieur comparé
à la configuration BioCoop + supermarchés
G20. Mais, cette fusion est assez improbable puisqu'elle condamne de
futurs conversions de supermarchés G20 en BioCoop (les
supermarchés G20 sont en général très proches
géographiquement des magasins Naturalia).
Ainsi, le groupe BioCoop apparaît, compte-tenu de la
qualité de ses implantations, en position
de supériorité face au réseau
Naturalia. Si de nouveaux supermarchés G20 passaient sous
l'enseigne BioCoop, Naturalia serait, d'autre part, menacé par
cette concurrence directe à proximité de ses sites. Etudions
maintenant le cas à la suite de tels changements d'enseignes. Naturalia,
assailli par cette nouvelle donne et en proie à des difficultés
économiques, serait conduit à réaliser des
économies importantes et à adopter une stratégie
défensive.
+
+
+
+
|
Aires
d'implantation
optimale
|
|
Naturalia
|
BioCoop
|
BioCoop
avec
Naturalia
|
Présence -
BioCoop avec
Naturalia
|
|
Quartier Correspondant
|
|
|
10
|
Paris 15ème Grenelle Est
|
1
|
1
|
2
|
Oui
|
|
1
|
Paris 17ème Epinettes
|
1
|
1
|
2
|
Oui
|
|
18
|
Boulogne-Billancourt Est
|
0
|
0,5
|
0,5
|
Oui
|
|
6
|
Paris 17ème Ternes
|
1
|
0
|
1
|
Oui
|
|
12
|
ème
Paris 15 Grenelle
Ouest
|
0
|
0
|
0
|
0
|
|
9
|
Paris 7ème Gros-Caillou
|
1
|
0
|
1
|
Oui
|
+
|
Nombre d'implantations optimales
|
4
|
2,5
|
6,5
|
Oui
|
=
+
|
Aire non-optimale
|
16ème arrondissement
|
1
|
0
|
1
|
Oui
|
|
Aire non-optimale
|
Neuilly-sur-Seine
|
0
|
1
|
1
|
Oui
|
+
|
Total d'implantations optimales
|
5
|
3,5
|
8,5
|
=
Tableau 6.7 - Comparaison des implantations optimales et
non-optimales des réseaux et de leur regroupement
Stratégie défensive et restructuration des
réseau de distribution des produits biologiques
Si l'on se réfère au tableau ci-dessous,
une fusion totale entre les supermarchés G20 et le groupe
BioCoop mènerait à une concurrence féroce principalement
dans l'aire 10 - Paris 15ème Grenelle Est) où un
magasin Naturalia ferait face à quatre supermarchés BioCoop, dans
l'aire
1 - Paris 17ème Epinettes (1 magasin
Naturalia contre 2 magasins BioCoop) et à Neuilly sur
Seine (1 magasin Naturalia contre 2 magasins BioCoop).
Naturalia ne conserverait le monopole de la distribution de produits "bio"
que dans l'aire 9 - Paris 7ème Gros-Caillou.
+
+
+
+
|
Aires
d'implantation
optimale
|
|
BioCoop
avec G20
|
Naturalia
|
Stratégie de
Naturalia
|
|
Quartier Correspondant
|
|
|
10
|
Paris 15ème Grenelle Est
|
4
|
1
|
A fermer
|
|
1
|
Paris 17ème Epinettes
|
2
|
1
|
A fermer
|
|
18
|
Boulogne-Billancourt Est
|
0,5
|
0
|
Créer un nouveau
site
|
|
6
|
Paris 17ème Ternes
|
1
|
1
|
Maintenir
|
|
12
|
Paris 15ème Grenelle Ouest
|
0
|
0
|
|
|
9
|
Paris 7ème Gros-Caillou
|
0
|
1
|
Maintenir
|
+
|
Nombre d'implantations optimales
|
7,5
|
4
|
3
|
=
+
|
Aire non-optimale
|
16ème arrondissement
|
1
|
1
|
Maintenir
|
|
Aire non-optimale
|
Neuilly-sur-Seine
|
2
|
0
|
|
+
|
Total d'implantations optimales
|
10,5
|
3,5
|
4
|
=
Tableau 6.8 - Comparaison des implantations optimales et
non-optimales de Naturalia avec le
regroupement G20/BioCoop et stratégie de réponse de
Naturalia
On peut miser sur le fait que ce réseau
verrait alors son chiffre d'affaires chuter fortement dans les aires 10
et 1 et que leurs deux points de vente ne deviennent bien moins rentables. Dans
le cas extrême de déficits importants pour ces magasins, la
stratégie de Naturalia serait
de fermer ces deux implantations et d'abandonner les
aires 10 et 1 à la concurrence. L'implantation dans l'aire 6 -
Paris 17ème Ternes pourrait être conservée car Naturalia
n'est au prise qu'avec un seul point de vente BioCoop-G20 dans une
aire somme toute importante. L'aire 18 de Boulogne-Billancourt
conserverait toujours son attrait et la réorganisation du
réseau Naturalia pourrait envisager la création d'un nouveau
point de vente dans ce segment
géographique vierge de concurrence. Les implantations des
aires 6 - Paris 17ème Ternes et 9 -
Paris 7ème Gros-Caillou pourrait
être conservées puisque, comme nous l'avons vu, elles ne
sont pas directement menacées. De même, le site de
Neuilly-sur-Seine serait susceptible d'être maintenu, même s'il
ne représente pas pour l'instant un gros potentiel de clients
pour les produits biologiques. Cette tendance peut néanmoins s'inverser
un jour, s'il arrive que ce type
de produits soit plus qu'une simple mode et conquiert l'assiette
de monsieur tout le monde.
Ainsi, nous constatons que l'utilisation conjointe du
traitement du signal et du modèle p- médian permet, suite
à la délimitation des aires de chalandise et à
l'identification des principales aires stratégiques
d'implantation, de planifier l'expansion d'un réseau de
distribution ou bien au contraire, de restructurer de tels réseaux
lorsque la nécessité s'en fait sentir. La simple comparaison des
implantations du réseau et de ses concurrents au sein de zones
géographiques de marché offre la possibilité
de juger de la pertinence d'une implantation à moyen terme. Il
aurait été bien entendu plus intéressant, dans cette
analyse, de connaître les résultats de chaque site, car certaines
aires sont sans doute susceptibles, compte tenu de leur important potentiel
commercial, d'accueillir un grand nombre de magasins sans que,
nécessairement, les uns ou les autres ne pâtissent trop de la
concurrence.
6.2.4 Déterminer la zone de chalandise de
magasins
L'utilisation conjointe du traitement du signal et du
modèle p-médian apparaît donc comme un moyen très
efficace pour détecter des opportunités d'implantation, chercher
des emplacements avec la perspective d'étendre son réseau
de magasins ou même pour s'assurer de la bonne localisation de
points de vente existants. La rapidité de la méthode, même
mise en oeuvre sur
un simple micro-ordinateur, ne fait aucun doute : la phase de
géocodage a pris 6 minutes pour
10 000 adresses, la phase de délimitation 30 secondes
tout comme celle de la résolution du modèle p-médian
pour 25 noeuds soit en tout, 7 minutes (si l'on ne tient pas
compte de la dizaine de minutes nécessaire pour transférer les
fichiers d'un logiciel à l'autre). Le processus
ne se contente pas de donner les meilleurs emplacements
commerciaux, il fournit par la même occasion les aires de chalandise
de ces points de vente, les aires de chalandise des autres points de
vente du réseau et celles des concurrents. Ainsi, nous avons
vu par exemple que BioCoop Grenelle se partage l'aire de chalandise
10 avec Naturalia Cambronne et que BioCoop Paris 17ème
rassemble l'essentiel de ses clients dans l'aire 1. Il sera
alors possible pour le manager suite à l'ouverture de son magasin, de
planifier immédiatement des actions marketing sur l'aire de chalandise
identifiée par cette méthode. Si un nouveau point de vente doit
ouvrir dans Boulogne-Billancourt au sein de l'aire 18 ainsi que nous l'avons
préconisé, il sera alors possible de considérer que
cette aire 18 correspondra à la zone de chalandise
principale de ce magasin et d'y effectuer les actions
promotionnelles adéquates (distribution
de prospectus dans les boîtes aux lettres, animation
commerciale dans les rues correspondant
à ces aires, création de panneaux publicitaires
dans cette zone) : l'aire 18 sera en effet la zone entourant le magasin dans
laquelle la densité de clients potentiels est la plus importante. Rien
n'empêche cependant d'effectuer des opérations marketing sur
les autres aires proches qui, elles aussi, peuvent receler des
potentialités commerciales. Nous avons vu que, proche de l'aire
18, à Issy-les-Moulineaux et dans le 16ème
arrondissement de Paris, il n'y avait pas, pour
l'instant, de magasins distribuant des produits biologiques :
étant donné que nous avons affaire
à du commerce de proximité, il sera possible de
considérer ces deux aires éloignées de l'aire
18 comme appartenant à la zone de chalandise
secondaire. La probabilité d'y trouver des consommateurs potentiels
sera plus faible, mais cependant non nulle étant donné qu'il
n'existe aucun concurrent, proche de ces secteurs, capable d'attirer à
lui ce potentiel.
6.2.5 Prévoir les ventes
Un troisième avantage découlant de
l'évaluation des zones de chalandise est de pouvoir
réaliser des prévisions de vente pour le (ou les) point(s) de
vente à créer. Ces prévisions se fondent sur le
modèle analogique décrit au chapitre 1 (§ 1.3.2.1).
Supposons que Naturalia décide d'étendre son réseau de
magasins en région parisienne et implante donc un point de vente dans
l'aire 18 à Boulogne-Billancourt. Remarquons que Naturalia
possède des implantations dans des aires similaires en 4, 6 et 9
(aires isolées dans lesquelles n'existe aucun autre concurrent). On peut
donc considérer que cette enseigne s'accapare, au sein de ces trois
aires, l'essentiel de la part de marché dans le domaine des
produits bio. D'autre part, on constate que les étendues de ces
aires, notées respectivement S4, S6 et S9 sont voisines (S4 =
730, S6 = 754 et S9 = 727). Or, nous
avons vu que les aires sont d'autant plus importantes en
surface que le nombre de clients potentiels qu'elles
intègrent est élevé, puisqu'elles sont
caractérisées par des densités de clientèle
similaires. Ainsi, en utilisant la méthode Analog, il sera possible
d'évaluer le chiffre d'affaires de la nouvelle implantation dans
l'aire 18 en postulant qu'il sera proportionnel au nombre de clients qui la
compose et donc à la surface de cette même aire (S18 = 535). Le
chiffre d'affaires au sein de l'aire 18 pourra être déduit des
aires 4, 6 et 9 par une règle de trois, considérant
tout simplement la moyenne des chiffres
d'affaires des trois magasins pondérés par la
surface relative de l'aire 18:
C18 =
1 S18 C4 +
S18 C6 +
S18 C9 ,
3 S 4
S 6 S9
C4, C6 et C9 étant
les chiffres d'affaires dans les aires 4, 6 et 9. En première
approximation,
compte tenu des surfaces annoncées et en supposant que les
chiffres d'affaires C4, C6 et C9
sont voisins, le chiffre d'affaires dans l'aire 18 sera alors 75
% de ceux des aires 4, 6 et 9.
La densité des clients potentiels étant
approximativement la même dans chacune de ces aires, leur surface est
directement proportionnelle à leur potentiel commercial (nombre de
clients du magasin) supposée être en relation directe avec
la performance du point de vente (chiffre d'affaires ou
résultat).
Grâce à la logique combinée du traitement du
signal et des modèles de localisation-allocation,
il est donc possible sous réserve de posséder les
données adéquates, de parvenir à construire
un réseau de points de vente en quelques minutes et
cela avec une grande précision. Le niveau d'analyse dépend de
l'échelle des données. Dans l'exemple
précédent, nous possédions une carte de France.
L'étude de localisation a donc été réalisée
à l'échelle de l'agglomération ou du département.
Dans le cas parisien des magasins de produits biologiques, nous nous
étions concentrés à l'échelle du quartier puis de
la rue. Une étude complète d'implantation visera en toute logique
à déterminer les meilleures villes, départements ou
régions puis se concentrera comme nous l'avons fait, sur ces aires
géographiques en y réalisant une micro-analyse locale. Mais,
même avec un niveau de précision pouvant atteindre la centaine de
mètres (au niveau
de la rue), un examen visuel et attentif des environs
permettra seul au niveau très local de placer vraiment très
précisément son point de vente, par exemple dans une rue de
préférence passante ou à un endroit offrant une bonne
visibilité, tout en tenant compte bien évidemment
des espaces commerciaux disponibles.
6.3 Les avantages immédiats apportés par
l'utilisation du traitement du signal en localisation commerciale
L'utilisation du traitement du signal dans le domaine de la
localisation commerciale du point
de vente engendre un certain nombre d'avantages
immédiats pour le manager en particulier lorsque ce domaine est
introduit au niveau de l'élaboration d'un modèle p-médian.
Parmi les avantages, on peut citer ceux-ci :
1- Le modèle p-médian, construit,
comme nous l'avons décrit, par les techniques de traitement
du signal, comprend une étape de
délimitation des aires de chalandise. La recherche de
localisations optimales s'accompagne par la même occasion de
l'identification de ces aires à différents niveaux (global,
local) à la fois concernant leurs limites et leurs
caractéristiques (étendue, nombre de clients,
fréquentation moyenne) ce qui peut constituer pour le
responsable marketing un avantage indéniable. L'analyse des aires de
chalandise est en effet susceptible de servir plus tard à la
réalisation d'opérations commerciales (exemples: mailing, ciblage
des campagnes de communication sur les quartiers). Le travail effectué
n'est donc pas seulement utile de manière ponctuelle lors de
l'implantation de points de vente, mais peut aussi servir pour la gestion
commerciale future du magasin.
2- Dans ce cadre, la rapidité et la
précision de calcul des méthodes de traitement du signal
comparées aux méthodes classiques de délimitation de
zones de chalandise décrites au chapitre 1, ne fait aucun
doute. Les méthodes de délimitation des zones de
chalandise par filtrage par exemple nous donnent un résultat
quasi-immédiat. Le gain de temps dans un processus de
décision d'implantation est appréciable d'autant que
souvent les décisions doivent être prises rapidement.
3- L'utilisation du traitement du signal pour
déterminer les noeuds et le niveau de la demande simplifie
considérablement la problématique du p-médian. Si on
délimite les aires de
chalandise par traitement du signal et que ce nombre
d'aires délimitées est de q pour un
nombre n de clients et p d'activités à placer, on
réduit donc le nombre de solutions à examiner
dans le modèle p-médian en le faisant passer de:
n!
p! (n -
p)!
(p activités à placer et n noeuds correspondant
chacun à un client)
q!
à: p! (q -
p)!
(p activités à placer et q noeuds correspondant
chacun à une aire)
le rapport entre le nombre de solutions à examiner dans
les deux cas est donc de:
n! (q -
q! (n -
p)!
p)!
Prenons l'exemple d'un réseau de 100 000 noeuds ou
clients et pour lequel on cherche à
localiser trois activités, et supposons que l'on obtienne
une délinéation en 20 aires, ce qui est tout à fait
plausible, alors le nombre de solutions à examiner est
divisé par 2,5 x 10 21 (le
20!
nombre de solutions à examiner est alors
3! (20
- 3)!
= 1140
ce qui pourrait même être
pratiqué de manière exhaustive sans passer par une
quelconque heuristique de résolution).
4- Les manipulations utilisées en
traitement du signal portent directement sur des images ou même des
cartes (les fichiers matriciels de ces images étant opaques pour
l'utilisateur) ce qui facilite considérablement les opérations
de calcul et les rend beaucoup plus simples pour l'utilisateur. Dans
les méthodes de construction et de résolution classiques
des modèles p- médian, les manipulations portent au contraire
sur des fichiers très volumineux (fichiers des noeuds/clients et des
distances inter-noeuds). Les résultats sont, de plus, dans notre
cas, visualisables à chaque étape: l'algorithme
devient alors plus attrayant et surtout plus démonstratif
vis-à-vis du responsable en charge des décisions de localisation.
La validité et la cohérence des opérations de
délimitation des zones de chalandise et de localisation peuvent
aussi être vérifiées plus facilement
grâce à un examen visuel direct sur les cartes.
5- Notre algorithme à base de
traitement du signal simplifie considérablement la recherche de
localisation en abordant le problème de manière globale
puis locale. La démarche entière constitue ainsi un
argumentaire direct pour le choix de telles ou telles localisations:
pourquoi
a-t-on choisi telle région ou aire de marché ?
Et dans cette ville, pourquoi a-t-on choisi tel quartier ou tel site ? La
réponse à ces questions est à chaque fois
donnée par les étapes correspondantes de l'algorithme et
par les cartes qui les accompagnent. Ces réponses correspondent
à chaque étape du processus de décision
d'implantation658. Les différents algorithmes
développés par le passé pour résoudre le
modèle p-médian peuvent d'autre part
être tous intégrés à notre algorithme
après la phase de filtrage.
6- La recherche d'une localisation par cet
algorithme progressif peut s'arrêter dès que le degré
de précision souhaité est atteint ou lorsque le
niveau d'information le plus bas (le plus local) a
été exploité. Les algorithmes de
résolution du p-médian ne connaissent pas en
général de temps limite de recherche et devaient
être stoppés lorsque la patience de l'utilisateur
était épuisée après quelques heures ou jours de
recherche pour trouver un extremum local un peu meilleur.
7- Cette méthode à base de
traitement du signal intègre à la fois l'étape de
modélisation du réseau et sa résolution. Elle constitue
donc une passerelle intéressante entre les logiciels de géocodage
et les algorithmes de résolution des problèmes de
localisation jusqu'à présent séparés par la phase
de modélisation plus ou moins bien réalisée. Ces
algorithmes nécessitent
en effet, d'une façon générale de
recevoir comme données d'entrée les coordonnées de chaque
noeud correspondant à chaque adresse de client ou bien à la
position géographique de zones (souvent administratives et pas
forcément logiques) regroupant un certain nombre de clients ainsi qu'une
évaluation de la demande dans ces zones pas forcément facile
à calculer. Dans
notre cas, les aires, caractérisées par une
densité forte et homogène de clients, sont identifiées
658 CLIQUET G., FADY A. BASSET G. (2002)
Management de la Distribution, Dunod, Paris.
par leurs centres de gravité (les noeuds du réseau
p-médian) et par leurs surfaces (les niveaux
de demande), toutes ces données servant à
"nourrir" un algorithme de résolution du modèle p- médian.
Ce n'est donc pas l'utilisateur qui choisit ses zones et manuellement
détermine leurs niveaux de demande pour enfin introduire
laborieusement toutes ces informations dans un logiciel de
résolution d'un modèle de localisation-allocation, mais
le processus qui, automatiquement, grâce au traitement du signal,
construit des aires rassemblant des densités identiques de clients,
puis calcule leurs caractéristiques pour élaborer dans la
foulée un modèle p-médian.
8- Comme nous l'avons vu dans l'exemple des
magasins de produits biologiques, le degré de précision de
notre algorithme est bon à la fois sur le plan de la
modélisation du réseau (obtention des noeuds et
caractéristiques du réseau) et concernant la résolution du
modèle en comparaison des méthodes existantes. En ce qui
concerne ces dernières, soit celles-ci regroupent les clients en des
zones administratives (les arrondissements dans l'exemple) et les
résultats obtenus sont susceptibles de devenir aberrants, soit l'on
considère que chaque client
est un noeud et alors il devient
particulièrement difficile de résoudre le modèle
p-médian correspondant compte-tenu de sa complexité (nombre de
noeuds très élevé). La partition de la clientèle
par des méthodes mathématiques comme la méthode des
plus proche voisins, en prenant ultérieurement le centre de
gravité des éléments de la partition comme noeud,
risque
de même de conduire à des erreurs dans
l'élaboration du réseau p-médian (voir §2.3.3). Ces
méthodes imposent en outre de connaître à l'avance le
nombre de zones à partitionner et l'on fait en pratique appel à
l'intuition pour fixer ce nombre.
Il est également intéressant de progresser
dans l'échelle de précision des localisations
recherchées au fur et à mesure que notre algorithme tourne en
boucle. En effet, on cherche à localiser les points de vente de
manière globale. Par exemple au niveau national, on
recherchera les régions ou départements les plus
intéressants (les quartiers les plus indiqués au
niveau d'une ville). Notre méthode concentre alors son
analyse au sein de ces régions pour y détecter les villes
potentiellement les plus prometteuses (les rues dans l'approche
urbaine). Ainsi, le processus reproduit finalement la démarche que tout
manager aurait mis en oeuvre pour rechercher empiriquement un ou plusieurs
emplacements optimaux. Dans la pratique, ce dernier n'aurait jamais
cherché en effet, à localiser ses points de vente directement au
niveau d'une rue alors qu'il souhaitait les placer au niveau de la France
entière. A chaque étape, la recherche est progressive et bien
adaptée au degré de précision géographique
escomptée dans
la localisation des activités. Cette
progressivité est importante également pour savoir
convaincre. Un manager qui, lorsqu'on lui demande de localiser ses magasins au
niveau de la France entière en utilisant les méthodes
existantes (méthodes de résolution directe du p-
médian où chaque client est un noeud) n'est capable que de citer
les rues où les implanter, ne peut pas être convaincant. Il lui
faudra dans un premier temps justifier le choix de telle région, puis
de telle commune et enfin de quartiers ou de rues
particulières. Notre méthode suit entièrement cette
logique de recherche et saura plus facilement réussir à
persuader une hiérarchie du choix judicieux des emplacements par
la visualisation de cartes d'échelles de plus en plus fines.
9- L'algorithme à base de traitement du
signal comprend un processus de filtrage qui permet
de lisser les imperfections de la base de
données d'adresses (fausses adresses ou adresses manquantes). Le
p-médian peut aussi pour la même raison être
résolu, si la base n'est pas complète mais comprend un
échantillon d'adresses.
10- Cet algorithme est capable de rechercher
des localisations optimales pour être au plus près
d'agrégats de clients et/ou d'optimiser les emplacements pour
occuper les lacunes dans lesquels la concurrence est faible avec
néanmoins des potentialités commerciales pour
l'activité considérée.
11- La simplicité du mode de
résolution de notre algorithme, effectuée par étapes en
degrés de précision croissants, permet d'envisager
l'utilisation de très grandes bases de données
comportant jusqu'à plusieurs millions d'adresses.
12- Enfin, notre algorithme peut être
appliqué à de nombreux autres modèles de localisation-
allocation (MCI, Multiloc, modèle p-centré, problèmes
de partition ou de cluster) pour résoudre des
problématiques variées. Il suffit alors d'utiliser à la
suite des étapes de géocodage
et de filtrage, les algorithmes classiques correspondant aux
modèles souhaités.
Le tableau 6.9 compare et résume les
différentes approches en recherche de localisations optimales
prenant pour fondement le modèle p-médian dans notre cas
d'étude.
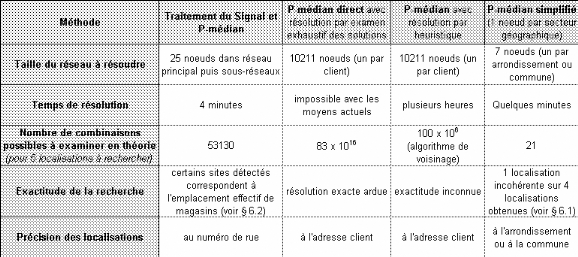
Tableau 6.9 - Caractéristiques des méthodes de
résolution du modèle p-médian dans notre cas de figure
On remarque bien que l'approche p-médian
alliée au traitement du signal combine les avantages de
rapidité et de précision. Cette précision est
maîtrisée, comme on l'a vu, puisque l'analyste peut choisir de
n'étudier que le réseau simplifié de 25 noeuds ou bien
améliorer la finesse des résultats de localisation en poussant la
recherche au sein des aires en en définissant
des sous-réseaux p-médian.
6.4 Limites et perspectives
Le modèle p-médian associé à une
phase de géocodage et à un traitement du signal même s'il
constitue un moyen véritablement performant pour localiser de
manière rapide et précise un échantillon de magasins,
ne constitue pas cependant une panacée universelle. Ainsi, les
emplacements détectés doivent comme on l'a souligné,
être examinés sur le terrain par l'oeil critique du
décideur. L'expertise issue de l'expérience n'est donc pas exclue
de la démarche,
au contraire 659 660 661.
La localisation préconisée dans l'aire 18, route de
la Reine à Boulogne-Billancourt correspond
par exemple à une voie très
commerçante et passagère avec concessionnaires automobiles
(Ford et Honda), grandes surfaces d'ameublement, magasins
spécialisés (moquettes, tapisseries) correspondant au style
de commerces présents au voisinage d'un hypermarché. Cette
aire pourra donc sans doute convenir à un supermarché de
produits biologiques. En revanche, l'emplacement situé rue des
Acacias (figure 6.5) dans le 17ème est de nature
totalement différente, car située à
proximité de la place de l'Etoile, dans une rue à
l'atmosphère plus feutrée.
Fig. 6.7 - L'emplacement préconisé dans le
XVIIème, rue des Acacias

659 LAPARRA L. (1995) L'implantation
d'hypermarché : comparaison de deux méthodes
d'évaluation du potentiel, Recherche et Applications en
Marketing, Vol. 10, Numéro 1, p. 69-79
660 CLARKE I. (2002) L'information
géographique dans les études de localisation commerciale : une
perspective managériale, in Le géomarketing : Méthodes
et Stratégies du Marketing Spatial, G. Cliquet éd.,
Hermès, Paris.
661 CLARKE I., HORITA M. et MACKANESS W.
(2002) Intuition et Evaluation des Sites Commerciaux :
Appréhender la Connaissance des Commerçants,
Stratégies de localisation des Entreprises Commerciales et Industrielles
: De Nouvelles Perspectives, p.107, Gérard Cliquet et Jean-Michel
Josselin éditeurs, De Boeck Université, à
paraître.
La politique marketing du réseau sera ainsi
déterminante dans le choix de la localisation selon
qu'elle voudra mettre en avant une clientèle par exemple
"haut de gamme" avec des tarifs en conséquence ou une clientèle
plus large.
Le p-médian ignorant les contraintes liées
à l'environnement pourra, dans certains cas, indiquer des
emplacements inacceptables situés par exemple au milieu d'un champ de
course
ou d'un jardin d'enfants. Il convient donc de ne pas prendre les
localisations suggérées au pied
de la lettre, mais de les appréhender en terme d'aire
ou de sous-aire et d'éventuellement d'aller repérer sur le
terrain des emplacements faisables au sein des aires. Le p-médian est en
effet capable d'intégrer des noeuds supplémentaires
correspondant à ces emplacements qui, de préférence,
se trouveront à proximité des centres de gravité des aires
homogènes définis dans notre algorithme (ce n'est donc plus
les centres de gravité des aires qui seront
représentés exactement par les noeuds du réseau
p-médian, mais ces emplacements faisables voisins de
ces centres et repérés sur le terrain).
Il est également possible, pour favoriser tantôt les
quartiers plus huppés, tantôt les quartiers à
pouvoir d'achat moyen ou même les zones purement commerciales sans
habitant, d'augmenter artificiellement leur potentiel, c'est-à-dire
le poids des noeuds correspondants, d'un certain pourcentage
prédéterminé afin d'intégrer cette
préférence. Il convient, d'une manière
générale, de ne pas oublier les autres critères
d'une bonne localisation qui sont aussi la visibilité et
l'accessibilité de l'emplacement ou encore la recherche du voisinage
d'autres enseignes (complémentaires ou concurrentes selon la nature
des produits) pour augmenter l'attraction du site662.
D'un autre côté, même si notre méthode
peut être utilisée de manière
concrète pour des cas pratiques d'études de localisation
ou de zones de chalandise, le fait d'avoir utilisé trois logiciels
différents (MapPoint, SCI et Sitation)
a amené quelques problèmes liés à la
différence de formats entre les fichiers utilisés par ces
662 MOATI P. et POUQUET L. (1998)
Stratégies de Localisation de la Grande Distribution et Impact
sur la
Mobilité des Consommateurs, Collection des Rapports
n°194, Crédoc, p.69.
logiciels (fichiers image de type MapPoint et bitmap)
ce qui a légèrement ralenti le temps global mis pour faire
l'étude. La mise au point d'un logiciel intégrant toutes les
fonctions de filtrage, de délimitation, d'analyse des zones de
chalandise et de calcul des localisations optimales par un sous-algorithme
de résolution d'un modèle de localisation-allocation rendrait
plus pratique l'utilisation de notre méthode.
D'autre part, dans notre exemple d'une boutique de produits
biologiques, nous sommes partis d'une base de données de clients
supposés avoir la même probabilité de fréquenter les
points
de vente. Sans doute, la réalité était
différente et ces clients étant plus ou moins attirés par
les produits biologiques, se rendront-ils plus ou moins souvent dans ce type de
magasin. Ceci dit,
le manager doit souvent composer avec une information
incomplète pour déterminer les meilleures localisations
possibles pour ces magasins et produire des prévisions de
vente. Notre démarche méthodologique peut tenir compte de
différences entre les clients en termes
de fréquentations ou de chiffre d'affaires
escomptés, si on a la chance de posséder ces informations
(quel montant chaque client prévoit-il de dépenser dans
un magasin "bio" installé à proximité de chez lui ?). Il
suffit pour cela de représenter les clients dans la phase de
géocodage par des points en niveaux de gris. Le traitement du signal
sera alors capable de délimiter les zones de chalandise en
intégrant ces différences de caractéristiques au sein de
la clientèle (voir notre exemple virtuel concernant les clients d'un
commerce dans la première partie). Il est également concevable en
théorie d'intégrer de la même manière des facteurs
de
perception du consommateur (cf. Modèle MCI663)
quant à une enseigne particulière ou quant
à certains types de produits et de comparer les
différences en termes de localisation préconisée par
le modèle p-médian et aussi en termes de prévisions de
ventes.
Une autre perspective future de recherche est celle
concernant les variations des zones de
chalandise au cours du temps. Comme on l'a vu dans le chapitre 1,
les formes des zones de
663 CLIQUET G. (1995) Implementing a Subjective MCI
Model: An Application to the Furniture Market,
European Journal of Operational Research 84, 279-291.
chalandise sont sujettes à des évolutions
saisonnières. Il serait intéressant d'évaluer grâce
au traitement du signal les caractéristiques de ces zones à
différentes époques de l'année, du mois
ou selon les différents jours de la semaine,
puis de construire et de résoudre le modèle p-
médian correspondant à chacune de ces zones. Sans doute,
les localisations optimales des magasins préconisées
seront-elles aussi variables dans le temps. La question sera alors de
savoir s'il s'agit de se décider pour une localisation moyenne
de tous les emplacements suggérés ou bien de retenir la
configuration engendrant pendant certaines périodes cruciales
de l'année, d'excellentes performances
commerciales. Cette étude, si elle portait sur une période
suffisante, permettrait également de cerner les évolutions et
migrations géographiques éventuelles des aires de chalandise et
de prévoir quelles seront les localisations intéressantes dans 2,
5, 10 ou 20 ans. Le suivi des contours de la zone de chalandise au cours du
temps donnerait sans doute en effet la possibilité d'extrapoler sa forme
à moyen ou long terme. Il suffirait de prendre conscience de
phénomènes de rétraction, de renflement ou de
déplacement
de la zone pour prévoir, à moins d'un
renversement des tendances, son devenir et donc de déterminer
les localisations optimales futures grâce à notre
méthode. Cette recherche nécessiterait sans doute de poser
des hypothèses quant aux vitesses de transformation de la zone de
chalandise et d'étudier éventuellement plusieurs
scénarios en comparant leurs similitudes et divergences: la
morphologie de cette zone va-t-elle se poursuivre au même rythme,
avec la même célérité et éventuellement
accélération, ou bien l'évolution subira-t-elle
un tassement ? Les réponses à ces questions
conditionneront les résultats de l'analyse de localisation et leur
qualité.
Enfin, nous l'avons déjà souligné,
le traitement du signal est susceptible d'apporter ses avantages de
rapidité et de précision aux autres modèles de
localisation-allocation que le p- médian comme le modèle
p-centré ou le modèle de couverture maximale. Le
p-centré est
utilisé pour placer des services d'urgence, des
hôpitaux ou des casernes de pompiers par
rapport à une population donnée et le modèle
de couverture maximale sert à localiser bureaux
de poste, trésorerie, mairie et plus
généralement administrations, services de proximité,
aéroports, station de métro ou de bus,... Une autre perspective
future de recherche est d'utiliser
le traitement du signal en association avec ces modèles
pour effectuer un bilan national ou par pays de l'adéquation de ces
services d'urgence ou de proximité par rapport à la population
sur
le plan de leur localisation. Cette étude constituerait,
sans aucun doute, un outil majeur pour
orienter les décisions des décideurs politiques
dans le domaine de l'aménagement du territoire.
Conclusion
Ce chapitre a été l'occasion de montrer
l'extrême rapidité de l'algorithme conciliant modèle p-
médian et traitement du signal. Cette méthode débouche en
quelques minutes sur des résultats probants de localisations
optimales avec une précision au niveau du numéro de rue,
alors même que la méthode classique du p-médian, utilisant
un découpage administratif des zones,
ne débouche que sur des résultats
aberrants. Vouloir considérer chaque adresse de client comme un
noeud indépendant conduit, d'un autre côté, à
un degré trop important de complexité du problème
dès que l'on cherche à localiser plus de deux points de
vente. L'analyse qualitative des résultats obtenus reste cependant
indispensable pour s'assurer de la faisabilité des emplacements sur
le plan de l'espace foncier disponible, de l'adéquation de
l'environnement avec l'activité prévue et pour s'assurer de
l'absence de concurrents notables dans les parages, à moins de vouloir
rechercher au contraire leur proximité pour jouer sur une synergie qui
augmenterait l'attractivité globale de l'ensemble commercial ou dans un
but de concurrence frontale. La zone de chalandise des points de vente
est calculée lors du fonctionnement de notre algorithme ce qui
constitue un avantage indéniable pour le manager
qui souhaite par la suite effectuer des prévisions de
chiffre d'affaires. Ces prévisions peuvent
en l'occurrence être extrapolées à partir du
calcul de la surface des aires constitutives de la zone de chalandise fournie
par notre méthode.
Un autre avantage indéniable est que le traitement
s'effectue directement sur des cartes, les résultats de localisation
obtenus étant alors beaucoup plus parlant et démonstratif
pour le professionnel. Celui-ci peut, en effet, s'assurer visuellement
que grosso modo, les sites préconisés se trouvent bien au
plus proche des concentrations de clients potentiels. Un tel
résultat aurait été néanmoins difficile, voire
impossible, à obtenir avec précision par simple observation ou
géométriquement compte tenu des paramètres en jeu
(nombre de clients
potentiels, nombre de magasins à localiser). Enfin,
même si ces clients ne constituent qu'une
fraction de l'ensemble des clients présents en
réalité sur le terrain, le résultat n'est pas
faussé puisque notre méthode aborde le problème de
localisation en termes de probabilités de présence de
clients potentiels. Le processus de filtrage a en effet tendance
à lisser les répartitions de clients dans l'espace et la
délimitation ultérieure de la zone de chalandise cerne
les aires d'équidensité de clients. La recherche
de localisations s'effectue donc dans l'espace des fréquences (la
fréquence des clients au niveau de la surface
géographique) et non simplement en fonctions des clients de la
base de données. D'où, le fait qu'une base
incomplète ne gêne pas cette recherche qui l'aborde sous l'aspect
d'un échantillon, mais encore faut-il que cet échantillon soit
représentatif et non biaisé par des erreurs manifestes
d'enquête. Ainsi, la combinaison du modèle p-médian et du
traitement du signal est tout indiquée pour la recherche de
localisations optimales d'un futur réseau de points de vente ou
même pour s'assurer de la bonne localisation de magasins existants. Cet
outil est très intéressant pour la gestion marketing quotidienne
du réseau. Il permet de s'assurer, jour après jour, de la bonne
localisation des points de vente en fonction des frontières de la zone
de chalandise qui, on le rappelle, évoluent dans le temps. Une nouvelle
simulation de l'algorithme sera effectuée, non plus en prenant la base
de données de clients potentiels, mais cette fois en utilisant une
base
de données de clients effectifs des magasins. Un
calcul de la position optimale des points de vente tenant compte de cette
saisonnalité pourrait être facilement effectué en moyennant
sur une période les coordonnées géographiques des
localisations préconisées par l'algorithme. Encore faut-il
accéder aux données décrivant la clientèle sur un
laps de temps suffisamment long, information assez facile à obtenir si
le réseau a su développer un système de cartes de
fidélité. Restent aussi les actions commerciales telles
que le publipostage qui peut être beaucoup plus facilement
planifié grâce à notre méthode. Si l'on veut
renforcer une clientèle existante, on privilégiera ainsi une
distribution de prospectus (ou tout autre mode de
promotion commerciale) dans les aires homogènes entourant
les points de vente considérés.
Au contraire, si l'on veut conquérir des parts de
marché, la distribution s'effectuera plutôt dans
les régions hors de ces aires.
Conclusion générale
Les profondes mutations des structures commerciales en
cette période de transition entre l'ancien et le nouveau
millénaire poussent les décideurs des grandes entreprises
à revoir, de nos jours, l'organisation des réseaux tant sur
le plan horizontal (fusions entre réseaux) que vertical
(apparition de nouveaux modes de distribution comme Internet).
Sur le plan horizontal tout d'abord, il s'agit d'apprécier
l'intérêt de tel point de vente qui se trouve par hasard
proche de tel autre anciennement concurrent mais désormais partenaire.
De fait, nous
ne sommes plus à l'heure actuelle dans
une phase de développement des surfaces commerciales mis
à part dans des filons comme les produits biologiques, mais plutôt
dans une logique d'optimisation des réseaux de vente existants. D'un
autre côté, sur le plan vertical, on cherche à
améliorer les logistiques d'approvisionnement des réseaux
de points de vente en marchandises en provenance des quatre coins du
monde, tout en développant de nouveaux centres de distribution
destinés à satisfaire les nouveaux
Internautes-consommateurs. Le secteur public n'échappe pas à la
règle et souhaite, sous la pression de contraintes budgétaires,
réorganiser son système hospitalier, ses
administrations territoriales et nationales, son éducation et
même son organisation de défense et de
sécurité (fermeture de casernes, ouverture de commissariat de
quartier).
L'algorithme général décrit dans cet
exposé, associant les principes du traitement du signal aux
modèles de localisation-allocation (p-médian,
p-centré, couverture maximale,...), a son mot à dire dans
toutes ces problématiques de localisation. Comme nous l'avons
vu, il se compose globalement de quatre phases. La phase 1
de géocodage consiste à exploiter une base de
données d'adresses de clients potentiels ou réels et à
représenter ces localisations sur une carte. La
représentation cartographique obtenue montre
grossièrement les zones géographiques où se
concentrent les clients par la forte densité des points s'y accumulant.
La phase 2 correspond à la délimitation de
ces zones denses de clients et donc à la zone de
chalandise (nous avons nommé dans notre
exposé ces zones denses de clientèle, aires de
chalandise). La distinction des aires de chalandise est
grandement facilitée en traitant au préalable la carte avec
un filtre qui a tendance à lisser les contours et/ou à tisser des
liaisons entre les zones géographiques les plus proches. Les aires de
chalandise apparaissent alors, avec des contours nets et peuvent ensuite
être délimitées par l'opérateur de
convolution
(§ 3.2.4). Lorsque les points clients sont
très éloignés les uns des autres, un filtre
morphologique de type dilatation ou de fermeture est alors tout
indiqué pour remplir les interstices et faire naître les
formes pleines des aires homogènes de chalandise. Lorsque
l'éparpillement des points clients se fait de manière
continue et qu'un simple lissage est nécessaire, il alors
souhaitable d'utiliser un filtre Nagao qui conserve les contours ou bien un
filtre médian (§ 3.2.3). On calculera dans la phase 3
les coordonnées des centres de gravité de chaque aire
délimitée dans la phase précédente de
manière à modéliser un réseau p-médian
(§
3.3) : les noeuds du réseau seront
représentés par les centres de gravité et les segments par
les distances routières ou par un indicateur d'éloignement
(temporel, kilométrique, généralisé...). Des
localisations potentielles supplémentaires pourront, d'autre part,
être introduites comme noeud, même si elles ne comptent pas de
clients. Il est possible de bâtir un réseau pondéré
et l'on affectera, dans ce cas, à chaque noeud, un poids
représentatif de l'importance de la clientèle ou de son
potentiel. Nous avons utilisé la surface de l'aire
homogène associée représentative de l'importance de la
clientèle locale comme pondération de chaque noeud dans notre
analyse de localisation des commerces "bio" de l'Ouest parisien
(§ 4.2.3.1). Dans la phase 4, le réseau
sera résolu sur la base du modèle p-médian
grâce aux algorithmes classiques de résolution et
d'amélioration (algorithmes de voisinage,
génétique, flou, multiplicateurs de Lagrange - § 2.2.1.2)
de manière à trouver les localisations optimales pour
les emplacements commerciaux. On aboutira donc au choix
de certains noeuds comme localisations optimales. Pour améliorer la
précision, on pourra, dans une étape supplémentaire
de rétroaction, réitérer le processus
d'identification d'aires homogènes en se concentrant cette
fois au niveau de chaque noeud et en augmentant l'échelle
d'analyse. Pour améliorer la finesse des localisations optimales,
l'examen d'aires de plus en plus petites est susceptible de se faire autant de
fois que souhaité sous réserve de l'existence d'un
nombre suffisant de clients ou d'emplacements potentiels à cette
échelle. Nous avons été ainsi conduit à
introduire une nouvelle définition de la zone de chalandise
fondée sur la notion de densité à la marge des nombreuses
approches existantes (§1.2), à savoir que la zone de
chalandise est l'aire géographique d'influence où la
densité de clientèle dépasse un certain seuil.
L'intérêt du traitement préalable à la
délimitation de la zone de chalandise, à savoir le
processus de dilatation dans l'analyse des magasins du secteur biologique,
permet justement de cerner les aires d'équidensité en terme de
clientèle. La distribution de la clientèle n'est pas
aléatoire, en général, ce qui se démontre
par un calcul d'autocorrélation, mais se fait selon des
regroupements ou clusters rassemblant une densité homogène de
clients. Nous avons mis en évidence deux seuils caractérisant les
zones d'équidensité des clients potentiels des produits "bio"
correspondant aux zones de chalandise primaire et secondaire (§ 4.2.3). Il
serait possible sans doute de distinguer d'autres seuils supplémentaires
de densité dans d'autres cas d'études. Cette approche, qui
considère les points du plan comme un signal discret à deux
dimensions, s'apparente entièrement aux méthodes
scientifiques de reconnaissance des objets et des formes. L'analyse des
images satellites utilise, depuis deux décennies sur le modèle de
notre étude, les filtres d'images réelles pour y détecter
les différents types de territoire, les forêts, les
déserts, les montagnes, les zones
inondées664. L'originalité de notre démarche a
été de montrer
que ces mêmes techniques peuvent être
utilisées sur des données virtuelles à savoir les bases
de données géomarketing transposées
sur une carte. Etant donné que le traitement des données
se fait indifféremment dans tout le plan, l'analyse ne
connaît pas de frontière méthodologique contrairement
aux logiciels actuels de géomarketing (d'ailleurs plutôt
des
664 MARCHIONNI D., CAVAYAS F., ROLLERI E. (1999)
Potentiel de Détection des Traits Structuraux d'un
Territoire Semi-Désertique sur des Images RADARSAT : Le
Cas du Macizo del Deseado, Argentina, Rapport
du Committee on Earth Observation Satellite.
logiciels de cartographie améliorée) qui,
du fait de leur mode de fonctionnement en dessin vectoriel et non sous
forme d'images composées de pixels, imposent des frontières
artificielles (les représentations vectorielles possèdent
à l'arrière plan une base de données de tous les
objets, rues, ronds-points, jardins publics,... sous forme de
coordonnées ce qui ne permet pas
de mettre en évidence des zones de chalandise coupant ces
objets).
Sur le plan de la gestion, notre méthode conciliant
traitement du signal et modèle p-médian recèle un grand
nombre d'avantages. Tout d'abord, nous l'avons souligné à
de multiples reprises, l'étude de localisation s'accompagne de
l'analyse de la zone de chalandise et de sa délimitation. Ainsi, on
pourra se rendre compte de l'importance du potentiel commercial
entourant le point de vente que l'on associe, dans notre méthode,
à l'aire de chalandise dont la surface connue révèle le
niveau de ce potentiel. Cependant, l'évaluation de la future
fréquentation du magasin nécessitera toujours une bonne
connaissance du secteur et du profil des clients, en particulier concernant la
distance maximale que ceux-ci sont prêts à parcourir pour s'y
rendre. La zone de chalandise, délimitée dans notre
étude, était une zone de chalandise de clients potentiels
puisque nous sommes partis d'une base de données de personnes
susceptibles d'acheter des produits biologiques. La même méthode
de délimitation pourra servir, après ouverture du ou des points
de vente et constitution d'une base de données
de clients réels cette fois, à définir
sur une carte la zone de chalandise réelle du magasin. Cette zone de
chalandise réelle sera très certainement composée de
fragments centrés autour du magasin de la zone de chalandise
potentielle préalablement déterminée. La comparaison des
deux types de zone de chalandise sera une indication précieuse
pour le manager sur la distance maximale que les clients sont prêts
à parcourir en mesurant la distance kilométrique
ou temporelle moyenne séparant le point de vente
et la frontière de la zone de chalandise réelle. La
gestion d'un réseau de points de vente sera riche
d'enseignement, puisqu'elle
apportera une certaine expérience en particulier sur
les habitudes de déplacement de la
clientèle, expérience pouvant être
transposée lors de la recherche de nouvelles localisations.
La bonne connaissance des clients d'une enseigne permettra
également de se constituer dans
les régions où l'on cherche à créer
de nouvelles surfaces commerciales, des bases de données
de clients potentiels correspondant à la segmentation
marketing mise en évidence.
La mise en oeuvre de notre méthode anticipe, d'autre
part, la phase de gestion quotidienne du point de vente : la
détermination très fine (au niveau de la rue) des
frontières de la zone de chalandise facilitera considérablement
la tâche du directeur commercial dans le ciblage
géographique des campagnes de promotion, que ces dernières
prennent la forme de prospectus distribués dans les boîtes aux
lettres, d'envois d'e-mail, ou encore de panneaux publicitaires à placer
aux endroits stratégiques,... Un avantage de la méthode combinant
traitement du signal
et modèle p-médian est en effet sa grande
précision à délimiter la zone de chalandise et dans une
étape ultérieure à spécifier les localisations
optimales en pratiquant un zoom au niveau des aires de chalandise les plus
intéressantes. Comme nous l'avons vu, les mêmes filtres et
traitements sont alors utilisés à un niveau local pour
accroître la finesse de l'analyse. Nos entretiens avec des
professionnels de la distribution de prospectus publicitaires comme les
dirigeants du groupe français leader Spir Communication qui offre des
prestation de services pour la grande distribution, nous ont confirmé
l'importance d'une délimitation précise de la zone de chalandise.
Alors que les logiciels du marché n'offre qu'une précision au
niveau du quartier ou des îlots (INSEE), notre méthode
reconnue par ces dirigeants cerne la zone de chalandise pratiquement au
niveau du numéro de rue. Les imprimés publicitaires sont en effet
distribués dans certaines aires préalablement définis
correspondant à la zone de chalandise du magasin dont on souhaite faire
la promotion. Le fait de cibler ces aires avec précision permet
d'engendrer des économies notables, puisque l'on évite ainsi de
remplir les boîtes aux lettres
de personnes hors zone et donc non concernées par
l'offre promotionnelle (économies de
prospectus et de frais de distribution). Ce géomarketing
très fin permet, d'autre part, de cibler
des aires de chalandise d'étendue limitée
(immeubles isolés, petit groupe de maisons recelant
de nombreux clients potentiels). Les efforts commerciaux se
centreront au sein de la zone de chalandise si l'on souhaite la renforcer
en terme de densité de clients ou au contraire, en dehors de
cette zone, si on souhaite l'étendre (en s'apercevant par
exemple que la zone de chalandise réelle est moins large que pour
d'autres points de vente similaires du réseau).
D'autre part, notre méthode met en évidence les
localisations optimales en une suite d'étapes logiques, ce qui n'est
pas sans intérêt pour les réseaux de points de
vente et dans le cadre général de la réticulation des
activités commerciales665. En particulier, en ce qui concerne
la réorganisation de réseaux, un processus intégré
de géocodage des clients, une délimitation des aires de
chalandise et la résolution d'un modèle de
localisation-allocation simplifié permettent
de se rendre très rapidement compte du double
emploi ou non de certains points de vente. Ainsi, la méthode est
aussi bien adaptée à des stratégies d'évitement
visant à rechercher des opportunités d'implantation dans les
aires lacunaires délaissées par la concurrence (§ 3.4.1)
qu'à une stratégie de recherche de concurrents ou
même de prédation dans laquelle on ira s'implanter
directement au voisinage des compétiteurs, quitte à se lancer
dans une guerre des prix effrénés (§ 3.4.2). La
méthode s'attaquera, dans le premier cas, plutôt à la
délimitation du complémentaire des aires où sont
implantés les concurrents (image inversée de la cartographie des
concurrents) et, dans l'autre cas, à la délimitation
directe de leurs aires d'implantation. Cette approche, en terme de
concurrence, est tout à fait conciliable avec l'approche client. Une
stratégie d'évitement cherchera donc les implantations les plus
éloignées des concurrents tout
en la croisant avec les implantations des clients, deux
modèles différents de réseau p-médian pouvant alors
être bâtis, l'un de concurrence, l'autre de clientèle.
Notre méthode est également rapide. Nous avons
montré, dans notre cas d'étude de magasins
de produits "bio", qu'un ensemble de 10211 clients
pouvait finalement se simplifier à un
665 CLIQUET G. (2000) Plural Form in Store
Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer
Research, vol. 10, n°4, pp 369-387.
réseau de 25 noeuds, tout en ayant dans le
même temps réussi à délimiter la zone de
chalandise et à la caractériser. La recherche de
localisations optimales en considérant les
10211 clients comme autant de noeuds d'un réseau
p-médian aurait pris sinon plusieurs jours
du moins plusieurs heures même avec les heuristiques
de résolution actuelle alors qu'avec notre méthode, il est
possible de parvenir à un résultat en quelques minutes.
Par voie de conséquence, cette méthode offre aussi
la possibilité de mesurer le potentiel des ventes de telle ou telle
région au niveau local, régional ou national selon le secteur
d'analyse
(§ 6.2.5). L'apparition d'un nouveau concurrent
dans la zone de chalandise donnera alors l'occasion de faire fonctionner
l'algorithme pour évaluer l'impact de son arrivée sur le chiffre
d'affaires du magasin : ce nouvel arrivant occupe-t-il une meilleure
localisation ? Quelle est la part du chiffre d'affaires qu'il ponctionnera
compte-tenu des clients habitant dans son environnement immédiat
? Est-il intéressant sur le plan des
bénéfices de changer d'emplacement par rapport au
coût que ce déménagement risque d'impliquer ?
N'est-il pas plus rentable de chercher à s'allier avec ce
concurrent ? Voilà à quel genre de questions, touchant la
gestion stratégique du point de vente, la mise en oeuvre de notre
algorithme peut répondre avec grande précision et
rapidité moyennant quelques petites règles de trois
supplémentaires et parfois une analyse qualitative. Sur le plan
de la logistique interne au réseau de vente (éventuellement
à la suite de son remodelage avec celui d'un concurrent par une
opération de fusion ou d'acquisition), la localisation adéquate
des centrales de distribution
ou des plates-formes de transport ou d'acheminement vers les
points de vente de détail pourra
être revue de la même manière en
faisant donc appel au traitement du signal et à un autre
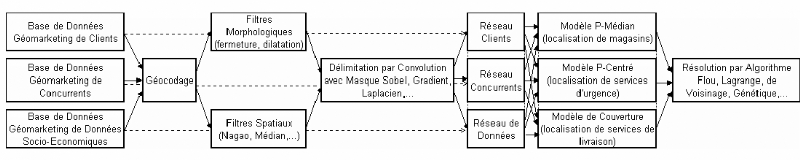
Fig. Conclusion.1- Les possibilités d'applications de la
méthode selon les données à traiter
525
modèle de localisation-allocation plus adapté
à cette problématique comme le p-centré (la
même méthodologie servira de la même
façon à localiser les grossistes indépendants par
rapport aux magasins de détail) : les points de vente joueront alors,
dans cette optique, le rôle des clients avec un certain niveau de
demande, clients approvisionnés par les centrales de
distribution
Ainsi, notre problématique de recherche apparaît
avoir trouvé une solution attractive à travers
ce nouvel outil qui possède une précision et une
rapidité indéniable. Les autres éléments que nous
avons cherché à améliorer étaient (voir
introduction) la démonstrativité et la capacité à
utiliser de grandes bases de données (les
datawarehouses) que les firmes n'exploitent actuellement pas
pleinement. Cette dernière contrainte est un autre des points forts de
notre méthode qui, justement nécessite l'introduction de
ces bases de géodonnées volumineuses. Comme on l'a dit au
départ, le traitement du signal serait sans intérêt pour
traiter des fichiers
ne comptant que quelques dizaines de clients puisque l'on
pourrait les introduire directement dans un modèle p-médian (sans
être capable d'ailleurs de cerner alors la zone de chalandise
correspondante). Les données géomarketing se doivent
justement d'être suffisamment nombreuses de manière à
constituer un signal à deux dimensions (dans le plan
géographique)
qui pourra être analysé par des filtres. Enfin,
la méthode à base de traitement du signal est
démonstrative, puisqu'elle permet de suivre, sur une succession
de cartes détaillées, le cheminement intellectuel
modélisé au sein d'un algorithme qui va indiquer la zone
de chalandise, puis les localisations optimales. Le manager non
aguerri à ces techniques "hermétiques" confirmera d'un
simple coup d'oeil les résultats obtenus, puisque, dans la
plupart des cas, les zones optimales d'implantation correspondent assez bien
aux lieux les plus
denses en clientèle.
Cependant, la méthode comporte un certain nombre
de limites. Outre le fait qu'il est assez difficile de se procurer les
bases de données de clients potentiels lorsque l'on cherche à
créer des points de vente, l'utilisation de filtres nécessite un
minimum de données. L'analyse d'une représentation spatiale de
quelques dizaines de clients ou de concurrents ne requiert pas les outils de
traitement du signal étant donné que dans ce cas, on peut
facilement construire un réseau p-médian en considérant
autant de noeuds qu'il y a de clients ou de concurrents et le résoudre
sans trop de difficultés par les méthodes traditionnelles.
Egalement, la détection de localisations optimales reste un exercice
théorique. Encore faut-il s'assurer par une visite sur
le terrain que les emplacements mis en évidence
correspondent effectivement à des sites viables et disponibles
à l'achat ou à la location. Une autre limite relatives aux
localisations commerciales trouvées vient du fait que l'on ne
considère dans la démarche que les adresses des clients, tout au
moins dans le cas pratique étudié des magasins de produits
biologiques. Sans doute, faudrait-il prendre en compte aussi tous leurs
déplacements et les endroits où ces clients potentiels
peuvent résider temporairement (lieux de travail par
exemple) qui constituent autant de lieux d'achats possibles. Il paraît
néanmoins difficile de constituer une volumineuse base de données
répertoriant tous les trajets d'un ensemble d'acheteurs probables
de certains produits ou services.
Sur le plan des perspectives de recherche, le
traitement du signal pourrait s'adapter à la localisation de bien
d'autres activités que celles des points de vente et de service à
travers le modèle p-médian. La figure
précédente (fig. Conclusion.1) montre les
possibilités variées d'applications théoriques de notre
méthode selon les données à traiter. Celles-ci peuvent
être, comme on l'a vu, des bases de données de clients
ou de concurrents ou bien même des données
socio-économiques. Rien n'empêche, en effet, d'utiliser notre
méthode pour délimiter non plus des zones de chalandise, mais par
exemple les zones de plein-emploi ou les quartiers rassemblant certaines
tranches de population pour des études à vocation
économique. La
phase suivante, après le géocodage, consistera de
la même façon à prétraiter ces données par
des filtres morphologiques ou bien spatiaux selon que les données
forment des points espacés
(le filtre de dilatation remplira les interstices pour
repérer les aires d'équidensité) ou bien des zones sans
discontinuité d'information. Suite à une délimitation des
aires homogènes par la désormais connue convolution, divers
modèles de localisation-allocation sont susceptibles d'être
appliqués. Outre le p-médian dédié surtout à
la localisation des points de vente et de service, le modèle
p-centré cherchant, non plus la proximité des clients mais les
sites les plus centraux, convient bien à la localisation de
services d'urgence (casernes de pompiers, commissariat, Samu). Le
modèle de couverture maximale préconise quant à lui, que
les sites possèdent une localisation optimale, si la distance maximale
qui les sépare des points-clients associés est minimisée.
Ainsi, à partir de ce site, l'on peut atteindre facilement tous les
clients, même les plus éloignés avec un coût minimum.
Le modèle de couverture maximale est donc bien adapté à la
localisation de services de livraison ou d'entrepôts. C'est en
particulier l'un des objectifs réservés à la suite
de cette recherche que de démontrer l'intérêt de
notre démarche méthodologique comparée aux autres
modèles de localisation-allocation, dans d'autres cas de figure
que la localisation d'activités commerciales, comme la logistique
de livraison de l'entreprise interne (localisation des centrales
de distribution) et externe (localisation des centres de livraison
des commandes Internet) ou la réorganisation spatiale des services
publics à l'échelon national. Une autre perspective de
recherche est d'appliquer notre démarche à la segmentation
de données statistiques. Les techniques de filtrages devraient en
effet être capables de délimiter des paquets de données
possédant une certaine similitude et les modèles de
localisation-allocation de spécifier les caractéristiques
les plus
marquantes de ces données.
Bibliographie
· ACHABAL D.D., GORR W.L. et MAHAJAN V. (1982)
Multiloc : A Multiple Store
Location Decision Model, Journal of Retailing, 58.
· APPLEBAUM W. (1952) Store Location Strategy
Classes, Preface, Addison-Wesley
Publishing Co.
· APPLEBAUM W. (1966) Method for determining Store Trade
Areas, Market Penetration and Potential Sales, Journal of Marketing
Research, 3.
· APPLEBAUM W. (1968) The Analog Method for Estimating
Potential Store Sales, Guide
to Store Location Research, Addison-Wesley,
Reading, Mass. by Kraus Reprint Ltd
Nendeln Lichtenstein in 1967.
· APPLEBAUM W. et COHEN S.B. (1961) The Dynamics
of Store Trading Areas and Market Equilibrium, Annals of the
Association of American Geographers n°51/1, reprinted with
permission of the original publishers by Kraus Reprint Ltd Nendeln
Lichtenstein in 1967.
· APPLEBAUM W. et GREEN H.L. (1974) Determining Store Trade
Areas, Handbook of
Marketing Research, edited by R. Ferber NY Mac Graw
Hill, pp 4.313-4.323.
· ARMSTRONG J.S. et BRODIE R.J. (1994) Effects of
Portfolio Planning Methods on
Decision Making : Experimental Results, International
Research Journal in Marketing
11, North-Holland.
· ARTLE A. (1959) Study in the Structure of
the Stockholm Economy : Towards a Framework for Projecting Metropolitan
Community Development, Business Research Institute, Stockholm School
Economics, Stockholm.
· AURIFEILLE J.M. (2000) A Bio-mimetic Approach to
Marketing Segmentation : Principles and Comparative Analysis, European
Journal of Economic and Social Systems
14 N°1, p. 93-108.
· AURIFEILLE J.M. (2001) Les algorithmes
génétiques, Conférence invitée à
l'IREIMAR, Institut de Recherche Européen sur les Institutions et les
Marchés, CNRS, Mars 2001.
· AURIFEILLE J.M. (2001) Conjoint fuzzy vs
non-fuzzy clustering : some empirical evidence using a genetic
algorithm optimization, Actes du 7ème congrès
international SIGEF, sept. 2001.
· BANOS A. (2001) Enhancing mobility behavior analysis
using spatial interactive tools and computer intensive methods,
Geographic Information Sciences, Vol. 7, N° 1, pp. 35-
41
· BARAY J. (2002) Le Guide des Produits Bio,
Editions Grancher, Paris.
· BEAUMONT J.R. (1987) Location-Allocation Models and
Central Place Theory, Spatial Analysis and Location-Allocation
Models, ed. Ghosh Avijit, Rushton Gerard, Van Nostrand
Reinhold.
· BEHBAHANI A. et HOZMAN H. (1998) La
Concentration dans le Secteur Bancaire, Mémoire de
maîtrise d'Economie mention Economie Internationale, Monnaie et Finance,
Université des Sciences Sociales de Toulouse.
· BINFORD T. (1971) Visual Perception by
Computer, IEEE Systems Science & Cybernetics Conference,
FA, Miami.
· BOUCHARD D.C. (1973) Location Patterns of Selected
Retail Activities in the Urban
Environment : Montreal, 1950-1970, Revue Géographie
Montréal, 27, p. 319-327.
· BOULANGER P., PERELMAN G. (1990) Le réseau et
l'Infini, Nathan, Paris, Cité par CLIQUET G. (2000) Plural Form in
Store Networks : A Model for Store Network Evolution, The
International Review of Retail, Distribution and Consumer Research,
vol.
10, n°4, pp 369-387.
· BOVET P. (2001) L'hypermarché, le Caddie et le
congélateur, Le Monde Diplomatique, Mars 2001, p.32.
· BRADACH J.L. (1998) Franchise
Organizations, Harvard Business School Press, Boston, Ma.
· BRADY J.E.M. (1977) The Pattern of Retailing in
Central Dublin, unpublished M.A. thesis, University College Dublin.
· BRICKLEY J.A., DARK F.H. (1987) The Choice of
Organizational Form : The Case of
Franchising, Journal of Financial Economics, 18,
401-20.
· BRIEC W., CLIQUET G. (1999) Plural Forms Versus
Franchise and Company-owned Systems : A DEA Approach of Hotel Chain
Performance, 28th EMAC Conference, Berlin, May, 11th-14th 5proceedings
on CD-ROM).
· BROWN S. (1992) Retail Location : A Micro-scale
Perspective, Ashgate, England.
· BRUNNER J. A. et MASON J. L. (1968) The Influence of
Driving Time Upon Shopping
Center Preference, Journal of Marketing Vol. 32.
· BUCKLIN L.P. (1971) Trade Areas Boundaries:
Some Issues in Theory and
Methodology, Journal of Marketing Research, 30-7.
· CANNY J. (1986) A Computational Approach to Edge
Detection, IEEE Transactions on
Pattern Analysis and Machine Intelligence, Vol. PAMI-8,
No. 6, pp. 679-698.
· CAP GEMINI / ERNST & YOUNG (2000) Etudes de Divers
Scenarii d'Organisation liés aux Hôpitaux du Chablais et de la
Riviera, Rapport Final pour le Département de la
Santé
/ Service Santé Public, p.3-16
· CAVES R.E. , MURPHY II W.F. (1976) Franchising :
Firms, Markets, and Intangible
Assets, Southern Economic Journal, 42, 572-86.
· CELLEUX G. et DIDAY E. (1980) L'analyse des
Données, Bulletin de liaison de la recherche en informatique et
automatique, INRIA.
· CHEN C.H. (1973) Statistical Pattern
Recognition, Editions Spartan Books, Rochelle
Park, N.J.
· CHERMANT J.L. et COSTER M. (1989) Précis
d'Analyse d'Images, Presses du CNRS.
· CHESNAUD C. (2001) Activité de Simag -
Développement en Recalage, Tracking et Reconstruction 3D, Aux
Frontières de l'Instrumentation et du Traitement d'Image,
Journée Thématique Organisée par le Pôle Optique et
Photonique Sud, Marseille, 20 mars
2001, p.11
· CHRISTALLER W. (1935) Die Zentralen Orte in
Süddeutschland, G.Fischer, Germany, Jena.
· CHURCH R.L. et SORENSEN P.A. (1995) A Comparison of
Strategies for Data Storage Reduction in Location-Allocation Problems, National
Center for Geographic Information and Analysis, Technical Report 95-4,
University of Santa Barbara, California.
· CLARKE I. (2002) L'information géographique
dans les études de localisation commerciale : une perspective
managériale, in Le géomarketing : Méthodes et
Stratégies
du Marketing Spatial, G. Cliquet éd.,
Hermès, Paris.
· CLARKE I., HORITA M. et MACKANESS W. (2002) Intuition
et Evaluation des Sites Commerciaux : Appréhender la Connaissance des
Commerçants, Stratégies de localisation des Entreprises
Commerciales et Industrielles : De Nouvelles Perspectives, p.107,
Gérard Cliquet et Jean-Michel Josselin éditeurs, De Boeck
Université, à paraître.
· CLIQUET G. (1990) La Mise en OEuvre du
Modèle Interactif de Concurrence Spatiale
(MICS) Subjectif, Recherche et Applications en Marketing
5 / 7, 3-18.
· CLIQUET G. (1997) Attraction Commerciale, Fondement de la
Modélisation en Matière
de Localisation Différentielle, Revue Belge de
Géographie, 121ème année.
· CLIQUET G. (2001) Rôle des NITIC dans
l'Evolution des Canaux de Distribution,
Proche-Orient n°13 - Revue de la Faculté de
Gestion et de Management, Université Saint- Joseph, Beyrouth,
p.71-93
· CLIQUET G. (1992) Le Management
Stratégique des Points de Vente, p.187-191, Ed.
Sirey.
· CLIQUET G. (1995) Implementing a Subjective MCI
Model: An Application to the
Furniture Market, European Journal of Operational Research
84, 279-291.
· CLIQUET G. (1998) Valeur Spatiale des Réseaux et
Stratégies d'Acquisition des Firmes
de Distribution, in Valeur, Marché et
Organisation, Ed. J-P. Brechet, Presses
Académiques de l'Ouest.
· CLIQUET G. (1998) Valeur Spatiale des Réseaux et
Stratégies d'Acquisition des Firmes
de Distribution, in Valeur, Marché et
Organisation, Ed. J-P. Brechet, Presses
Académiques de l'Ouest.
· CLIQUET G. (2000) Plural Form in Store Networks :
A Model for Store Network
Evolution, The International Review of Retail, Distribution
and Consumer Research, vol.
10, n°4, pp 369-387.
· CLIQUET G., FADY A. BASSET G. (2002) Management
de la Distribution, Dunod, Paris.
· CLIQUET G. (2002) Le Géomarketing :
Méthodes et Stratégies du Marketing Spatial,
Hermès, Paris.
· CONVERSE P.D. (1949) New Laws of Retail
Gravitation, Journal of Marketing 14, p.379-384.
· COOPER L.G. (1963) Location-Allocation Problems,
Operations Research 11, 331-341.
· COOPER L.G. et FINKBEINER C.T. (1983) A Composite
MCI Model for Integrating
Attribute and Importance Information, Advance in Consumer
Research, 109-113.
· COOPER L.G. et NAKANISHI M. (1983) Standardizing
Variables in Multiplicative
Choice Models, Journal of Consumer Research , 10,
96-108.
· CORNUEJOLS G., MARSHALL L.F. et NEMHAUSER G.L. (1977)
Location of Bank Accounts to Optimize Float: An Analytic Study of Exact and
Approximate Algorithms, Management Science, 23 (1pril), 789-810.
· CRASWELL N. et BAILEY P. (1999) Is it fair to evaluate
Web systems using TREC ad hoc, Department of Computer Science - CSIRO, The
Australian National University Pub.
· CRAUSAZ P.A., MUSY A., MATTEI A. (1999) GESREAU : GESREAU:
Ein Konzept
für ein Integriertes Management der Fliessgewässer,
Rapport de l'Hydram, Suisse, p.6
· DASKIN M. S. (1995) Network and Discrete
Location: Models, Algorithms and
Applications, John Wiley and Sons, Inc., New York.
· DAVIDSON W.R., SWEENEY D.J. et STAMPFL R.W. (1988)
Retailing Management,
6ème Ed., New York : Wiley,
cité par Cliquet G. dans Valeur Spatiale des Réseaux et
Stratégies d'Acquisition des Firmes de Distribution, in Valeur,
Marché et Organisation, Ed. J-P. Brechet, Presses
Académiques de l'Ouest, p.234.
· DE VOS (1973) The Use of Nearest-neighbour Methods,
Tijdschrift voor Economische en
Sociale Geografie, 64, p. 307-319.
· DELENDA J.F. (1970) EVEC : Une
Méthode d'Evaluation des Emplacements
Commerciaux, L.S.A. n° 335, sept. 1970, 57-61.
· DELOZIER M.W. et LEWISON D.M. (1986) Retailing,
2nd ed., Merill.
· DENG Y., ROSS L.S. et WATCHER S.M. (1999)
Employment Access, Residential
Location and Homeownership, Lusk Center for Real Estate Report,
Los Angeles.
· DENSHAM P.J. et RUSHTON G. (1992) A More Efficient
Heuristic for Solving Large p- median Problems, Papers in Regional Science:
The Journal of the RSAI 71/3, 307-329.
· DESMET P. (2001) Marketing Direct, 2ème
éd., Dunod, Paris.
· DIRICHLET, G. L. (1850), Über die Reduktion der
Positiven Quadratischen Formen mit
Drei Unbestimmten Ganzen Zahlen , Journal für die Reine
und Angewandte Mathematik
40, p. 216.
· DOUARD J.P. (2002) Géomarketing et
Localisation des Entreprises Commerciales, Stratégies de
localisation des Entreprises Commerciales et Industrielles : De Nouvelles
Perspectives, Gérard Cliquet et Jean-Michel Josselin
éditeurs, De Boeck Université, à paraître
p.120
· DRUMMEY G.L. (1984) Traditional Methods of Sales
Forecasting, in Store Location and
Store Assessment Research, R.L. Davies and D.S. Rogers
eds., Wicley, 279-299.
· DUDA R.O. et HART P.E. (1973) Pattern Classification
and Scene Analysis Editions J.
Wiley, New York, N.Y.
· FERBER R. (1958) Variations in Retail Sales Between
Cities, Journal of Marketing, 22, p.295-303.
· FILSER M. (1998) Taille critique et stratégie
du distributeur. Analyse théorique et implications
managériales, Décisions Marketing, Numéro : 15,
p.7-16.
· FLAHAUT B. (2000) Impact de l'Aménagement
du Territoire sur la Sécurité Routière Durable :
Analyse de la Situation Belge - Concentration Spatiale des Accidents
de la Route, Projet SSTC MD/10/042, Centre d'Analyse
Spatiale et Urbaine, Université Catholique de Louvain,
· FLAHAUT B. (2001) L'autocorrélation spatiale comme
outil géostatistique d'identification des concentrations spatiales des
accidents de la route, CYBERGEO, n° 185
· FOGG W. (1932) The Suq: a study in the human geography of
Morocco, Geography 12,
p. 257-258.
· FOSTER C. et LAMPKIN N. (1999) European Organic
Production Statistic 1993-96, Stuttgart, Hohenheim University.
· FOTHERINGHAM A. S. (1988) Market Share Analysis
Techniques : A review and Illustration of Current US Practice, in Store
Choice, Store Location and Market Analysis, Neil Wrigley, Routlege,
120-159.
· FRANCE TELECOM (2001) Rapport d'Activité de la
Société, Mars 2001.
· FREEMAN H. (1970) Boundary Encoding and Processing in
Picture and Processing and
Psychopictrorics, Lipkin B.S. and Rosenfeld A., Academic
Press, New York, p. 241-266.
· FU K.S. (1968) Sequential Methods in Pattern
Recognition and Machine Learning, Editions Academic Press, New York,
N.Y.
· GALVAO R.D. (1993) Use of Lagrangean Relaxation in
the Solution of Uncapacited
Facility Location Problems, Location Science 1,
57-70.
· GAUTSCHI D.A. (1981) Specification of Patronage
Models for Retail Center Choice,
Journal of Marketing Research, Vol. XVIII, 162-174.
· GETIS A. (1961) The Determination of the Location of
Retail Activities with the Use of a
Map Transformation, Economic Geography, p. 12-22.
· GHOSH A. (1984) Parameter Nonstationarity in Retail
Choice Models, Journal of
Business Research 12, 425-426.
· GHOSH A. et CRAIG C.S. (1984) A Location Allocation Model
for Facility Planning in a
Competitive Environment, Geographical Analysis, Vol. 16,
n°1, 39-51.
· GHOSH A. et McLAFFERTY S. (1987) Location Strategies
for Retail and Service Firms, Lexington Books.
· GHOSH A., CRAIG S. (1983) Formulating Retail
Location Strategy in a Changing
Environment, Journal of Marketing, 47, p. 56-68.
· GHOSH A., CRAIG S. (1991) Fransys : A Franchise
Distribution System Location
Model, Journal of Retailing, 67, p. 466-495.
· GHOSH A., RUSHTON G. (1987) Spatial Analysis and
Location-Allocation Models, Van Nostrand, Rheinhold, 1987.
· GHOSH A., TIBREWALA (1992) Optimal Timing and Location in
Competitive Markets,
Geographical Analysis, 24 (4): 317-334.
· GIBSON J.J. (1950) The Perception of the Visual
World, Editions Houghton-Miffin, Mass., Boston.
· GOLDBERG D.E. (1991) Genetic Algorithms,
Addison-Wesley, New York.
· GOLDBERG D.E. (1994) Algorithmes
Génétique, Exploration, Optimisation et
Apprentissage Automatique, Editions Addison-Wesley,
1994.
· GOLDBERG D.E. et LINGLE R. Jr. (1985) Alleles,
loci and the travelling salesman problem, Proceedings of an
International Conference on Genetic Algorithms, J.J.
Grefenstette (Ed.), LEA Pub, p 154-159.
· GOLDEN B, BODIN L., DOYLE T. et STEWART Jr.
(1980) Approximate Travelling
Salesman Algorithms, Operations Research, 28,
694-711.
· GOLDMAN 1J (1971) Optimal Center Location in Simple
Networks; Transportation
Science 5, 212-221.
· GOODSCHILD M.F. (1984) Ilacs : A
Location-Allocation Model for Retail Site
Selection, Journal of Retailing, 60, p. 84-100.
· GOODSCHILD M.F. et NORONHA V. (1983),
Location-Allocation for Small
Computers, University of Iowa, Monograph N°8.
· GREEN H.L. (Avril 1959) Correspondence with Applebaum
W. & Cohen S.B.
· GRUEN V. et SMITH L. (1960) Shopping Town USA:
The Planning of Shopping Centers, Reinhold Publishing Co., New
York.
· GUIDO P. (1971) Vérification Expérimentale
de la Formule de Reilly en Tant que Loi
d'Attraction des Supermarchés en Italie, Revue
Française de Marketing n°39, p. 101-107.
· GUPTA I. et DASGUPTA P. (2000) Report : Demand for
Curative Health Care in Rural India : Choose between Private, Public
and No Care, Programme on Research Development of the
National Council of Applied Economic Research sponsored by the
United Nations Development Programme, Dec. 2000.
· GUPTA R. (1996) Problems in Communication Network
Design and Location Planning; New Solution Procedures, PhD, Graduate
School of the Ohio State University.
· HADWIGER H. (1957) Vorlesung Über Inhalt,
Oberfläche und Isoperimetrie, Springer
Verlag, Berlin.
· HAKIMI S.L. (1965) Optimum Distribution of Switching
Centers in a Communication
Network and Some Related Graph Theoretic Problems, Operations
Research 13, 462-475.
· HALL M. et KNAPP J. et WINSTEN C. (1961) Distribution
in Great Britain and North
America, Oxford University Press, London.
· HANDLER G.Y. et MIRCHANDANI P.B. (1979)
Locations on Networks, MIT Press, Cambridge, MA.
· HERNADEZ T., BIASIOTTO M. (2001) The Survey of Corporate
Planning : Summary
Findings, Research Letter 2001-2, Centre for the Study of
Commercial Activity.
· HERNANDEZ J.A. (1998) The Role of Geographical
Information Systems Within Retail Location Decision Making, PhD
Thesis, The Manchester Metropolitan University Manchester.
· HOLLAND J.H. (1975) Adaptation in natural
and artificial systems, Ann Arbor: University of Michigan
Press.
· HOLLAND J.H. (1992) Les algorithmes
génétiques, revue Pour la Science, No 179, Sept.
1992, p. 44-51.
· HOLMBERG K., RÖNNQVIST M. et YUAN D. (1999)
An Exact Algorithm for the Capacitated Facility Location Problems with
Single Sourcing, European Journal of Operational research 113,
544-559.
· HORN B.K.P. (1975) The Psychology of Computer
Vision, Editeur P.Winston, NY.
· HORN B.K.P. (1986) Robot Vision, Editions MIT,
Press Mc Graw-Hill, NY.
· HOTELLING H. (1929) Stability in Competition, The
Economic Journal, vol. 39, p. 41-
57.
· HRUSCHKA H., FETTES W. et PROBST M. (2001) A
Neural Net-Multinomial Logit (NN-MNL) Model to Analyze Brand Choice.
In: Govaert, G., Janssen, J., Limnios, N. (eds.): Applied
Stochastic Models and Data Analysis, Volume 2. ASMDA,
Compiègne
2001, 555-560.
· HUBBARD R. (1978) A Review of Selected Factors
Conditioning Consumer Travel
Behavior, Journal of Consumer Research, vol. 5, june,
p.1-21.
· HUFF D. L. (1964) Defining and Estimating a Trading Area,
Journal of Marketing, Vol
28, p. 38.
· INGENE C. et LUSCH R. (1980) Market Selection
Decisions for Department Stores,
Journal of Retailing, 56, p.21-40.
· INGENE C. et YU (1981) Determinants of Retail Location in
SMSAs, Regional Science and Urban Economics 11, p.529-547.
· INGENE C.A. (1984) Structural Determinants of Market
Potential, Journal of Retailing, Vol.60 N°I, p.37-64.
· INRA (1999) L'agriculture Biologique en
France, Document du Groupe de Travail de l'Inra sur le Secteur
Biologique, Présidé par Guy Riba.
· ISADORE V.F. (1954) Retail Trade Analysis,
University of Wisconsin, Bureau of
Business Research and Service, Madison.
· ISARD W. (1956) Location and Space Economy, p.
254-287, New York.
· JAIN K. et MAHAJAN V. (1979) Evaluating the Competitive
Environment in Retailing Using Multiplicative Interactive Model, Research
in Marketing, Vol. 2, Jagdish Sheth ed., Greenwich, Conn.: JAI Press.
· JALLAIS J., ORSONY J. et FADY A. (1994)
Marketing du Commerce de Détail, Vuibert, Paris.
· JOHNSTON J. (1972) Econometric Methods,
McGraw-Hill, New York.
· JOHNSTON R.J. (1967) Land Use Changes in the Melbourne
CBD : 1857-1972, Troy, P.N., (ed), Urban Redevelopment in Australia,
Research School of Social Sciences, Urban Research Unit, Australian National
University, Canberra, p. 77-201.
· JOLIBERT A., ALEXANDRE D. (1981) L'utilisation du
modèle gravitaire généralisé dans la localisation
des agences bancaires, Techniques Economiques, 123, 31-44.
· KANE B.J. (1966) A Systematic Guide to Supermarket
Location Analysis, Fairchild, New
York.
· KARIV O. et HAKIMI S.L. (1979) An algorithmic Approach to
Location Problems, Part
1: The p-Centers, SIAM J. Math. 37, 513-538.
· KARIV O et HAKIMI S.L. (1979) An Algorithmic
Approach to Network Location
Problems, Part 2: The p-médians", SIAM Jounal of
Applied Mathematics 37, 539-560.
· KAUFMANN P.J., DONTHU N. et CHARLES M.B. (2000)
Multi-unit Retail Site Selection Processes : Incorporating Opening
Delays and Unidentified Competition, Journal of Retailing,
Vol.76(1), p. 113-127.
· KIMES S.E. et FITZSIMMONS (1990) Selecting
Profitable Hotel Sites at La Quinta
Motors Inn, Interfaces 20, Mars-Avril 12-20.
· KOENIG G. (1990) Management Stratégique :
Visions, Manoeuvres et Tactiques, Nathan.
· KOLEN A. et TAMIR A. (1990) Covering Problems,
Discrete Location Theory de
Mirchandani & Francis Chap. 6, Wiley & Sons.
· KOTLER P. (1971) Marketing Decision Making: A Model
Building Approach, New York: Holt, Rinehart & Winston.
|
·
|
LA POSTE SUISSE (2001) Communiqué de Presse
, http://www.poste.ch
|
|
|
·
|
LANE J.M. et RIESENFELF R.F. (janvier 1980) A Theoretical
Development for
|
the
|
Computer Generation and display of Piecewise Polynomial
Surfaces, IEEE Trans. on
PAMI, Vol. PAMI-2, No 1, p. 35-46.
· LAPARRA L. (1995) L'implantation d'hypermarché
: comparaison de deux méthodes d'évaluation du potentiel,
Recherche et Applications en Marketing, Vol. : 10, Numéro :
1,
p. 69-79
· LAULAJAINEN R. (1987) Spatial Strategies in
Retailing, Dordrecht, Holland, Reidel.
· LE MOIGNE J.L. (1990) La modélisation des
Systèmes Complexes, Bordas, Paris, 178p.
· LEE Y. (1979) A Nearest-neighbour Spatial Association
Measure for the Analysis of Firm
Interdependence, Environment and Planning A, 1, p.
169-176.
· LES ECHOS (2000) L'atlas des Régions Tome
1, Les Echos, réalisé en collaboration avec l'Insee.
· LES ECHOS (2001) Les Echos Magazine, parution du
28 août 2001.
· L'HEBDO (1998) Le "T"qui Vaut 20 Milliards de
Marks, L'Hebdo N°47, 21 novembre
1996
· LIM J. S. (1990) Two-Dimensional Signal and Image
Processing, Englewood Cliffs, NJ: Prentice Hall, pp. 478-488.
· LORD J.D. et OLSEN L.M. (1979) Market Area
Characteristics and Branch Bank
Performance, Journal of Bank Research 10, p. 102-110.
· LORENTZ M. (1998) Le Commerce Electronique, Les
Editions de Bercy, Ministère de l'Economie, des Finances et de
l'Industrie, p.15.
· LÖSCH A. (1940) Die Räumlische Ordnung der
Wirtschaft, Fischer, Iena.
· LUCE R. (1959) Individual Choice Behavior, New
York: John Wiley & Sons.
· MABILLOT V. (2000) Mises en Scène de
l'Interactivité : Représentations des Utilisateurs dans les
Dispositifs de Médiations Interactives, Thèse soutenue le
7 janvier 2000, Université de Lyon II, p.6
· MAHAJAN V., SHARMA S. et SRINIVAS D. (1985) An
Application of Portfolio Analysis for Identifying Attractive Retail
Locations, Journal of Retailing, vol.61, n°5, hiver 1985,
19-34.
· MALINVAUD E. (1980) Statistical Methods of
Econometrics, North Holland, New York.
· MARANZANA F.E (1964) On the Location of Supply
Points to Minimize Transport
Costs, Operational Research Quarterly, 15, 261-270.
· MARCHIONNI D., CAVAYAS F., ROLLERI E. (1999) Potentiel
de Détection des Traits Structuraux d'un Territoire
Semi-Désertique sur des Images RADARSAT : Le Cas du Macizo del
Deseado, Argentina, Rapport du Committee on Earth Observation
Satellite.
· MARKOWITZ H. (1952) Portfolio Selection, Journal of
Finance, Vol. 7, mars, p.77-91.
· MATHERON G. (1982) Les Applications
Idempotentes, Rapport du Centre de
Géostatistique et de Morphologie Mathématique
n°743, Ecole des Mines, Fontainebleau.
· Mc ROBERTS K.L. (1971) A Search Model for
Evaluating Combinatorially Explosive
Problems, Operations Research, 19, 1331-1349.
· MCKAY D.B. (1973) Spatial Measurement of Retail Store
Demand, Journal of Marketing
Research, 10, 4, p. 447-453.
· McLAFFERTY S.L. et GHOSH A. (1987) Optimal
Location and Allocation with Multipurpose Shopping, Spatial. Analysis
and Location-Allocation Models, ed. Ghosh Avijit, Rushton Gerard, Van
Nostrand Reinhold.
· MERCURIO J. (1984) Store Location Strategies,
dans Store Location and Store Assessment Research
cité par CLIQUET G. dans Valeur Spatiale des Réseaux
et Stratégies d'Acquisition des Firmes de Distribution, in Valeur,
Marché et Organisation, Ed. J-P. Brechet, Presses
Académiques de l'Ouest.
· MEYER F. (1978) IIème Symposium
Européen d'Analyse d'Images en Sciences des
Matériaux, Biologie et Médecine, 4-7 oct.
1977. Pract. Met., S8, p. 374, Caen, France.
· MINKOWSKI H. (1903) Mathematics Annals, Vol. 57,
p.447.
· MOATI P. (2001) L'avenir de la Grande
Distribution, Ed. Odile Jacob.
· MOATI P. et POUQUET L. (1998) Stratégies de
Localisation de la Grande Distribution et
Impact sur la Mobilité des Consommateurs, Collection
des Rapports n°194, Crédoc, p.53.
· MOATI P. et POUQUET L. (1998) Stratégies de
Localisation de la Grande Distribution et
Impact sur la Mobilité des Consommateurs, Collection
des Rapports n°194, Crédoc, p.69.
· MONROE K.B. et GUILTINAN J.P. (1975) A
Path-Analytic Exploration of Retail
Patronage Influences, Journal of Consumer Research 2,
19-28.
· MORAN P. (1948) The Interpretation of Statistical Maps,
Journal of the Royal Statistical
Society B, N°10, 1948, p. 243-251
· MURTY K.G. et DJANG P.A. (2000) The US Army National
Guard's Mobile Training Simulator Location and Routing Problem, US
Army Training and Doctrine Analysis Command, Dept. of IOE, University
of Michigan.
· NAGAO M., (1979) Edge Preserving Smoothing, CGIP,
vol. 9, p.394-407.
· NAKANISHI M. et COOPER L.G. (1974) Parameter
Estimate for Multiplicative
Competitive Interactive Model - Least Squares Approach,
Journal of Marketing Research,
11, 303-311.
· NAKANISHI M. et COOPER L.G. (1974) Parameter
Estimates for Multiplicative
Competitive Interaction Models: Least Square Approach,
Journal of Marketing Research
11: 303-311.
· NELSON R.L. (1958) The Selection of Retail
Locations, F.W. Dodge Corp, p.153, New
York.
· NEVIN J.R. et HOUSTON M.J. (1980) Image as a Component of
Attraction to Intraurban
Shopping Areas, Journal of Retailing, Vol. 56, No. 1,
pp.77-93.
· OKABE A., ASAMI Y. & MIKI F. (1985) Statistical
Analysis of the Spatial Association
of Convenience-good Stores by Use of a Random Clumping Model,
Journal of Regional
Science, 25, p. 11-28.
· ORSTOM (1998) Image Satellite et Milieux
Terrestre en Régions Arides et Tropicales, Editions de
l'Orstom, Bondy.
· PARKER A.J. (1973) The Structure and Distribution of
Grocery Shops in Dublin, Irish
Geography, 5, p. 625-630.
· PATRICK E.A. (1972) Fundamentals of Pattern
Recognition, Edition Prentice-Hall, Englewood Cliffs, N.J.
· PAVLIDIS T. (1977) Structural Pattern
Recognition, Editions Springer-Verlag, New
York, N.Y.
· PETERSON R.A. (1974) Trade Area Analysis Using Trend
Surface Mapping, Journal of
Marketing Research, Vol. XI, 338-42.
· PINDER D.A. & WITHERICK M.E. (1972) The
Principles, Practice and Pitfalls of
Nearest-neighbour Analysis in Linear Situations,
Geography, 57, p.277-288.
· POSTAIRE J.G. (1987) De l'Image à la
Décision, Editions Dunod-Informatique Bordas, Paris.
· PREWITT J.M.S. (1970) Picture Processing and
Psychopictories, Academic Press, p.75.
· REILLY W. J. (1931) The Law of Retail
Gravitation, W. Reilly ed, 285 Madison Ave, New York, NY.
· REVELLE C. et SWAIN R. (1970) Central Facilities Location,
Geographical Analysis, 2,
30-40.
· RIBEIRO FILHO G. et NOGUEIRA LORENA L.A.
(2000) Improvements On
Constructive Genetic Approaches To Graph Coloring, Sao
José Dos Campos, Spain.
· ROBERT-DEMONTROND P., THIEL D. (2002) Algorithmes
génétiques et stratégies spatiales des firmes de
distribution, in Stratégies de Localisation des
Entreprises Commerciales et Industrielles : De Nouvelles
Perspectives, G. Cliquet et J-M. Josselin éd., De Boeck
Université, Bruxelles.
· RODER W. (1975) A Procedure for Assessing Point Patterns
without Reference to Area
or Density, Professional Geographer, 27, p. 432-440.
· ROGER P. (1983) Description du Comportement
Spatial du Consommateur, Thèse de
Doctorat, Lille.
· ROGERS A. (1969) Quadrat Analysis of Urban Dispersion : 2.
case studies of urban retail systems, Environment and Planning, 1, p.
155-171.
· ROGERS A. (1974) Statistical Analysis of Spatial
Dispersion, Pion, London.
· ROGERS D.S. (1980) 5 ways to Evaluate a Store Location,
Store Location, 42-48.
· ROLLAND E., SCHILLING D.A. et CURRENT J.R. (1996) An
Efficient Tabu Procedure
for the p-Median Problem, European Journal of Operational
Research, 329-342.
· SCHOOLEY T. (2001) For some retailers,
drive-time is more important than location,
Pittsburgh Business Times, American City Business Journals, march
9, 2001, p.10.
· SCOTT A.J. (1971) Combinatorial Programming,
Spatial Analysis and Planning, London: Methuen and Company
Limited.
· SERRA J. (1982) Image Analysis and Mathematical
Morphology, Academic Press.
· SHACHAR A. (1967) Some Application of Geo-statistical
Methods in Urban Research,
Papers of the Regional Science Association, 18,
p.85-92.
· SIBLEY D. (1975) A Temporal Analysis of the
Distribution of the Distribution of Shops in
British Cities, unpublished Ph.D. thesis, University of
Cambridge.
· SMITH S.L.J. (1985) Location Pattern of Urban
Restaurants, Annals of Tourism
Research, 12, p. 581-602.
· SOKAL R., ODEN N., THOMSON B. (1998) Local spatial
autocorrelation in a biological model, Geographical Analysis, Vol. 30,
n° 4, pp. 331-353
· SORENSON A.D. (1970) A Comparative Study of the
Changing Patterns of Distribution
of Service Industries on Tyneside, Wearside and
Teeside, unpublished Ph.D. thesis, University of
Newcastle-upon-Tyne.
· STANLEY et SEWALL (1976) Image Inputs to a Probabilistic
Model: Predicting Retail
Potential, Journal of Marketing, 40 (July), 48-53.
· STANLEY et SEWALL (1976) Image Inputs to a Probabilistic
Model: Predicting Retail
Potential, Journal of Marketing, 40 (July), 48-53.
· STERNBERG (1979) Proc. 3rd Int. IEEE Comprac,
Chicago 1979.
· SYLVANDER B. (1999) Les Tendances de Consommation
de Produits Biologiques en France et en Europe : Conséquences sur
les Perspectives d'Evolution du Secteur. Colloque l'Agriculture Biologique
Face à Son Développement, Les enjeux Futurs, 6-8
déc. 1999, Lyon.
· TAILLARD E.D. (1996) Heuristic Methods for Large
Centroid Clustering Problems,
Technical Report Idsia 96-96, Idsia.
· TEITZ M.B. et BART P. (1968) Heuristic Methods for
Estimating Generalized Vertex
Median of a Weighted Graph, Operations Research, 16,
955-961.
· THIESSEN A.H. et ALTER J.C. (1911), Precipitation Averages
for Large Areas, Monthly
Weather Review, 39, p. 1082-1084.
· THIETARD Raymond-Alain (1988) La Stratégie
d'Entreprise, Mc Graw-Hill.
· TOU J.T. et GONZALEZ R.C. (1974) Pattern Recognition
Principles, Edition Addison- Wesley, Reading, Mass.
· TUKEY (1958) Bias and Confidence in Not-Quite
Large Samples, Annals of
Mathematical Statistics 29, p.614.
· UNI-Europa Finance (2000) L'impact des Fusions dans
le Secteur de la Banque et de l'Assurance, Rapport Interne
d'Entreprise, janvier 2000.
· University of Newcastle upon Tyne,
Agricultural Economics & Food Marketing Department (2001) Student
Ressources
http://www.ncl.ac.uk/aefm/student_resources/aef334/LeviStrauss.pdf
· VERAN L. (1991) La prise de Décisions dans les
Organisations : Prise de Décision et
Changement, Les Editions de l'Organisation.
· VOLLE P. (1999) Du Marketing des Points de
Vente à Celui des Sites Marchands : Spécificités,
Opportunités et Questions de Recherche, Cahier n°276,
Centre de Recherche DMSP, juin 1999.
· VOLLE P. (2000) Du Marketing des Points de
Vente à Celui des Sites Marchands : Spécificités,
Opportunités et Questions de Recherche, Revue Française
du Marketing, N°177/178.
· VON BERTALANFFY L. (1968) Théorie
générale des systèmes, Trad. fr. par J. B.
Chabrol., Dunod, Paris.
· WEBER A. (1909) Über den Standort der
Industrien, Tübingen, Traduction Anglaise de Friedrich (1929)
Theory of the Location of Industries, University of Chicago
Press, Chicago.
· WELLS W. et GUBAR G. (1966) The Life Cycle
Concept in Marketing Research,
Journal of Marketing Research, 3, p.355-363.
· WILSON (1971) A Family of Spatial Interaction Models, and
Associate Developments,
Environment and Planning A, vol. 3, 1-32.
· WING H.C. & LEE S.L. (1980) The
Characteristics and Locational Patterns of Wholesale and Service
Trades in the Central Area of Singapore, Singapore Journal
Geography, 1, p.23-36.
· WRIGHT P. et RIPS P.D. (1981) Retrospective Reports
on the Causes of Decisions,
Journal of Personality and Social Psychology 40,
601-614.
Table des Matières
Introduction
générale............................................................................................................
1
Partie I : La localisation commerciale multiple:
enjeux et théories............. 19
Chapitre 1 : Enjeux et pratiques de la localisation
commerciale ................................... 20
Introduction
...........................................................................................................................
21
1.1 Enjeux d'une bonne connaissance de la zone de chalandise
........................................... 24
1.2 Définir précisément la zone de
chalandise
...................................................................... 27
1.2.1 Variables façonnant l'étendue et la forme des
zones de chalandise ............................. 29
1.2.1.1 Variables intrinsèques au point de vente
................................................................... 30
1.2.1.2 Variables environnementales
....................................................................................
30
1.2.1.3 La variable
temporelle...............................................................................................
33
1.3 Méthodes traditionnelles de délimitation des
zones de chalandise ................................. 33
1.3.1 Approches subjectives : la méthode du temps de
conduite .......................................... 34
1.3.2 Approches normatives
..................................................................................................
36
1.3.2.1 La méthode analogique
.............................................................................................
36
1.3.2.2 La méthode par les modèles de
régression
................................................................ 38
1.3.2.3 La méthode par les surfaces enveloppantes
.............................................................. 40
1.3.2.4 La méthode des nuées dynamiques
...........................................................................
41
1.4 Inconvénients et limitations des méthodes
traditionnelles de délimitation ..................... 44
1.5 Les méthodes de localisation actuellement
utilisées ....................................................... 46
1.5.1 La méthode par les parts de marché et les
surfaces de vente ....................................... 48
1.5.2 La méthode analogique
................................................................................................
48
1.5.3 La méthode par le modèle de régression
multiple........................................................ 49
1.5.4 L'analyse discriminante
................................................................................................
52
1.5.5 La méthode du marché potentiel
..................................................................................
53
1.5.6 Le modèle p-médian
.....................................................................................................
53
Conclusion.............................................................................................................................
56
Chapitre 2 : Les théories de la localisation
.......................................................................
57
Introduction
...........................................................................................................................
58
2.1 Les modèles d'interaction spatiale
..................................................................................
60
2.1.1 La loi de
Hotteling........................................................................................................
60
2.1.2 La loi de Reilly et la formule du point de rupture
........................................................ 62
2.1.3 La méthode des secteurs proximaux et la
théorie des places centrales de
Christaller
..............................................................................................................................
64
2.1.4 Le modèle de
Huff........................................................................................................
69
2.1.5 Le modèle MCI
............................................................................................................
70
2.1.6 Le modèle MNL
...........................................................................................................
72
2.2 Les modèles de localisation multiple
..............................................................................
74
2.2.1 Les méthodes de localisation-allocation
...................................................................... 75
2.2.1.1 Formulation mathématique du p-MP
........................................................................ 80
2.2.1.2 Les algorithmes de résolution du p-MP
.................................................................... 83
2.2.2 Le modèle Multiloc
......................................................................................................
95
2.2.3 La méthode d'analyse de portefeuille
...........................................................................
97
2.2.4 Les autres modèles de localisation-allocation
.............................................................. 99
2.3 Limitations du modèle p-médian et de ses
méthodes actuelles de résolution ................ 99
2.3.1 Le modèle p-médian : une
réalité simplifiée
................................................................ 99
2.3.2 La complexité des méthodes de
résolution du p-médian
........................................... 102
2.3.3 L'analyse typologique : une solution imparfaite pour
simplifier la problématique
du p-MP
..........................................................................................................................
103
Conclusion...........................................................................................................................
111
Chapitre 3 : L'apport du traitement du signal dans le
modèle p-médian.................... 113
Introduction
.........................................................................................................................
114
3.1 Une nouvelle approche du p-MP par le traitement du signal :
premier aperçu d'un nouvel algorithme rapide de multilocalisation
d'activités ..........................................................
115
3.2 Méthodes de délimitation fondées sur le
traitement du signal et l'analyse d'image ...... 120
3.2.1 Introduction au traitement du signal et à l'analyse
d'image........................................ 121
3.2.2 Le géocodage et la représentation des
données géomarketing................................... 124
3.2.3 Le prétraitement des données par filtrage
.................................................................. 128
3.2.4 La délimitation des zones de chalandise par
traitement du signal ............................. 135
3.3 La construction du modèle p-médian :
détermination des centres de gravité, distances et
pondérations du modèle
p-médian..................................................................................
156
3.4 Approches stratégiques de la localisation
..................................................................... 165
3.4.1 La stratégie d'évitement ou rechercher les
zones non exploitées par la concurrence 172
3.4.2 La recherche de concurrents ou la
prédation..............................................................
174
3.4.3 Stratégie d'ouverture des points de vente
................................................................... 177
3.5 Un exemple de construction d'un modèle p-médian
par traitement du signal .............. 179
3.6 Utiliser toutes les sources d'informations commerciales
disponibles ........................... 184
Conclusion...........................................................................................................................
191
Partie II : La localisation d'un réseau
..................................................................
193
Chapitre 4 :Analyse d'un réseau de points
de vente de produits biologiques dans l'Ouest parisien
.............................................................................................................
194
Introduction
.........................................................................................................................
195
4.1 Le marché de la distribution des produits
biologiques.................................................. 196
4.1.1 Les produits biologiques : définition et importance
du marché ................................. 196
4.1.2 Le commerce de détail des produits biologiques en
France....................................... 199
4.1.3 La vente des produits biologiques sur
Internet........................................................... 205
4.2 La mise en oeuvre du traitement du signal et du modèle
p-médian ............................... 209
4.2.1 La base de données utilisée
........................................................................................
209
4.2.2 Le géocodage des données
.........................................................................................
213
4.2.3 Le pré-traitement des
données....................................................................................
215
4.2.3.1 La délimitation de la zone de chalandise
................................................................ 224
4.2.3.2 L'analyse de la zone de chalandise
..........................................................................
226
4.2.3.3 La construction et la résolution du modèle
p-médian correspondant...................... 234
Conclusion...........................................................................................................................
239
Chapitre 5 : Mise en oeuvre d'un système rapide
d'aide à la décision de localisation ....... 240
Introduction
.........................................................................................................................
241
5.1 Résolution du modèle p-médian par
l'algorithme flou et l'algorithme de voisinage ..... 242
5.2 Résolution du modèle p-médian par les
multiplicateurs de Lagrange .......................... 244
5.3 Résolution du modèle p-médian par
l'algorithme génétique .........................................
246
5.4 Localisation améliorée des points de vente au
sein des aires de chalandise ................. 249
Conclusion...........................................................................................................................
259
Chapitre 6 : Comparaison et implications
managériales et stratégiques..................... 260
Introduction
.........................................................................................................................
261
6.1 Comparaison des résultats de notre algorithme avec
ceux des méthodes traditionnelles de construction et de
résolution du
p-médian......................................................................
262
6.2 Implications managériales et stratégique :
analyse des localisations existantes et choix d'une nouvelle localisation
.............................................................................................
266
6.2.1 Vérifier la bonne localisation de magasins existants
................................................. 266
6.2.2 Etendre son réseau de points de
vente........................................................................
268
6.2.3 Développer une stratégie de localisation des
réseaux de points de vente .................. 271
6.2.4 Déterminer la zone de chalandise de magasins
.......................................................... 282
6.2.5 Prévoir les ventes
.......................................................................................................
284
6.3 Les avantages immédiats apportés par
l'utilisation du traitement du signal en localisation commerciale
...................................................................................................................
286
6.4 Limites et perspectives
..................................................................................................
292
Conclusion...........................................................................................................................
297
Conclusion générale
..........................................................................................................
300
Bibliographie......................................................................................................................
312
Table des matières
.............................................................................................................
332
Table des illustrations
.......................................................................................................
335
Tableaux
..............................................................................................................................
335
Figures
.................................................................................................................................
337
Annexe A : Cartes des clients géocodés par
arrondissement et communes de périphérie ...... 339
Annexe B : Répertoire français-anglais des
termes du traitement du signal et de
l'analyse automatique d'image
.........................................................................................
344
Table des illustrations
Figures
Introduction - Fig. 1: Scénarii de la
réorganisation de sites hospitaliers dans le canton de
Vaud...................... 5
Introduction - Fig. 2 : Notation des scénarii de la
réorganisation de sites hospitaliers dans le canton de Vaud 6
Introduction - Fig. 3 : Schéma d'un data warehouse
classique dans une entreprise ......................................... 10
Fig 1.1 - Exemple de détermination d'une zone de
chalandise par un logiciel commercial utilisant la méthode analogique
......................................................................................................................................
37
Fig. 2.1 - Le principe de différenciation
minimale...........................................................................................
61
Fig. 2.2 - Illustration de la formule du point de rupture
...................................................................................
63
Fig. 2.3 - Estimation d'une zone de chalandise par la
méthode du point de rupture ........................................
63
Fig. 2.4 - Les hexagones de la théorie des place centrales
...............................................................................
65
Fig. 2.5 - Etapes pour la détermination des secteurs
proximaux
...................................................................... 67
Fig. 2.6 - Répartition des commerces et de l'artisanat par
métier dans un souk marocain ............................... 68
Fig. 2.7 - Méthode de résolution du 1-médian
: étape
1...................................................................................
84
Fig. 2.8 - Méthode de résolution du 1-médian
: étape
2...................................................................................
84
Fig. 2.9 - Méthode de résolution du 1-médian
: étape
3...................................................................................
85
Fig. 2.10 - Méthode de résolution du
1-médian : étape 4
.................................................................................
85
Fig. 2.11 - Organigramme de l'algorithme
flou................................................................................................
86
Fig. 2.12 : La matrice de portefeuille appliquée à
l'Europe par le groupe Lévis Strauss .................................
98
Fig. 2.13 - Nombres d'articles traitant du p-médian par
année.......................................................................
103
Fig. 2.14 : Un exemple de 3 classes , et
identifiées par les variables x1, x2, x3
...................................... 104
Fig. 2.15- Partition des communes suisses en 23 cellules
représentées chacune par un centre urbain .......... 106
Fig. 2.16 - Les 76 villes représentées chacune par
un
cercle..........................................................................
106
Fig. 2.17 - Partition des 76 villes en 2 ensembles
..........................................................................................
107
Fig. 2.18 - Partition des 76 villes en 4 ensembles
..........................................................................................
108
Fig. 2.19 - Partition de 17 villes en 3
ensembles............................................................................................
108
Fig. 2.20 - Partition des 17 villes en 2 ensembles
..........................................................................................
109
Fig. 3.1 - Organigramme du nouvel algorithme proposé
...............................................................................
117
Fig. 3.2 - Exemple de représentation de clients sous forme
de pixels............................................................ 125
Fig. 3.3 - Exemple de localisation de clients associés
à leur fréquentation, sous forme d'un nuage de pixels en
niveaux de gris
.............................................................................................................................
126
Fig. 3.4 - Exemple de projection
cavalière.....................................................................................................
127
Fig. 3.5 - Exemple de lignes de niveaux
........................................................................................................
127
Fig. 3.6 - Exemple de représentation en code ternaire
...................................................................................
128
Fig. 3.7- 8 voisins adjacents à un point central
..............................................................................................
130
Fig. 3.8 - Adresses clients associées aux
fréquentations
................................................................................
131
Fig. 3.9 - La représentation traitée par 2 filtres
médians
................................................................................
131
Fig. 3.10 - Les 3 catégories des 9 configurations du
filtrage de Nagao sur lesquelles porte le calcul des moyennes
et des variances
............................................................................................................................
133
Fig. 3.11- Adresses clients associées aux
fréquentations
...............................................................................
134
Fig. 3.12 - La représentation traitée par 2 filtres
Nagao.................................................................................
134
Fig. 3.13 - Exemple de représentation histogramme des
valeurs f(x,y) des points d'une image .................... 136
Fig. 3.14 - Détermination d'un seuil de valeurs sur un
histogramme .............................................................
136
Fig. 3.15 - Exemples d'un histogramme et de son enveloppe
comportant plusieurs valeurs de seuils ........... 137
Fig. 3.16 - Adresses clients associées aux
fréquentations
..............................................................................
140
Fig. 3.17 - La représentation traitée par le
laplacien après 2 filtres médian
................................................... 140
Fig. 3.18 - L'image fi,j et le filtre
hi,j...............................................................................................................
141
Fig. 3.19- Adresses clients associées aux
fréquentations
..............................................................................
144
Fig. 3.20 - La représentation traitée par
filtres Sobel après 2 filtres médian (les contours sont
superposés à l'image filtrée par les 2 Nagao)
....................................................................................................
144
Fig. 3.21 - Exemple d'une dilatation
..............................................................................................................
149
Fig. 3.22- Exemple d'une
érosion...................................................................................................................
150
Fig. 3.23 - Image Initale, érosion, puis
dilatation...........................................................................................
150
Fig. 3.24 - En Noir: La Courbe Originale / En Gris: a courbe
transformée par dilatation ............................. 151
Fig. 3.25 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par dilatation ............................ 151
Fig. 3.26 - En Noir: La Courbe Originale / En Gris: la courbe
transformée par érosion................................ 152
Fig. 3.27 - En Noir: la courbe originale / En Gris: la courbe
transformée par fermeture ............................... 152
Fig. 3.28 - En Noir: la courbe originale / En Gris: la courbe
transformée par chapeau haut-de-Forme......... 153
Fig. 3.29 - Les 2 points et les 2 tangentes définissant
une courbe de Bézier cubique .................................... 154
Fig. 3.30 - Adresses clients associées aux
fréquentations
..............................................................................
155
Fig. 3.31 - Deux filtres
Nagao........................................................................................................................
155
Fig. 3.32 - Une dilatation
...............................................................................................................................
155
Fig. 3.33 - Une
érosion...................................................................................................................................
155
Fig. 3.34 - Une soustraction par rapport à l'image
filtrée (transformation du chapeau haut-de-forme) ......... 155
Fig. 3.35 - Un amincissement et une régularisation, des
contours (grâce aux courbes de Bézier) ................. 155
Fig. 3.36 - Exemple de Codage
Hexagonal....................................................................................................
157
Fig. 3.37 - Exemple de parcours d'une forme à
l'aide de l'algorithme destiné à extraire les
coordonnées du contour
...........................................................................................................................................................
158
Fig. 3.38 - Exemple de parcours de frontière de zone de
chalandise à l'aide de l'algorithme ....................... 159
Fig. 3.39 - Ensemble de clients potentiels
représentés par des points
............................................................ 161
Fig. 3.40 - Centre de gravité d'une zone de chalandise
délimitée
.................................................................. 161
Fig. 3.41 - Les centres des aires et ceux des points appartenant
à ces mêmes aires ....................................... 162
Fig. 3.42 - Type de Décisions prise par les
décideurs pour leur réseau de distribution
................................. 169
Fig. 3.43 - Adresses de magasins associées à leur
chiffre d'affaires
.............................................................. 173
Fig. 3.44 - Deux filtres
Nagao........................................................................................................................
173
Fig. 3.45 - Cartographie
inverse.....................................................................................................................
173
Fig. 3.46 - Cartographie inverse filtrée par deux filtres
Nagao ......................................................................
173
Fig. 3.47 - Délimitation des zones vides de concurrence
...............................................................................
174
Fig. 3.48 - Représentation des campings sur le territoire
national par des points .......................................... 176
Fig. 3.49 - Délimitation des zones d'implantation de
campings par filtre Sobel ............................................ 176
Fig. 3.50 - Numérotation des zones d'implantation de
campings ...................................................................
177
Fig. 3.51 - Adresses clients associées aux
fréquentations
..............................................................................
179
Fig. 3.52 - La délimitation des zones par filtres
médian et Sobel
................................................................... 179
Fig. 3.53 - Numérotation des aires de
chalandise...........................................................................................
180
Fig. 3.54 - Le p-médian modélisé
après délimitation de la zone de chalandise et calcul des centres
de gravité et fréquentations moyennes. La valeur de
fréquentation au sein des aires est ici prise comme valeur de
la demande aux noeuds.
................................................................................................................
182
Fig. 3.55 - L'aire 7 agrandie
...........................................................................................................................
183
Fig. 3.56 - L'aire 7 filtrée par un filtre médian
...............................................................................................
183
Fig. 3.57 - L'aire 7 délimitée par un filtre Sobel
............................................................................................
183
Fig. 3.58 - Les éléments de l'aire 7
numérotés après
délimitation..................................................................
184
Fig. 3.59 - Le réseau p-médian correspondant
à l'aire
7.................................................................................
184
Fig. 3.60 - Carte de France des densités de population en
2000 ....................................................................
186
Fig. 3.61 - La carte traitée par un filtre
médian..............................................................................................
186
Fig. 3.62 - puis délinée par filtre Sobel
..........................................................................................................
186
Fig. 3.63 - Les zones numérotées et
analysées
...............................................................................................
187
Fig. 3.64- Pour 10 localisations: zones de potentiel commercial
associées aux points de vente en gras ....... 189
Fig. 3.65 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts ................................ 190
Fig. 4.1 - Les magasins "bio" et boutiques de produits
diététiques en France par département en nombre ... 200
Fig. 4.2 - Les magasins "bio" et boutiques de produits
diététiques en France par département en
densités par
habitant.........................................................................................................................................
201
Fig. 4.3 - Les magasins "bio" et boutiques de produits
diététiques et naturels en Ile-de-France en densité
par
habitant.........................................................................................................................................
201
Fig. 4.4 - La devanture du magasin Espace "bio" St. Charles
....................................................................... 204
Fig. 4.5 - Les localisations des commerces de détail "bio"
à Paris et en région parisienne ...........................
205
Fig. 4.6 - Les épiceries et les supermarchés
à Paris
.......................................................................................
211
Fig. 4.7 - La zone d'étude en gris foncé dans la
région parisienne
................................................................. 212
Fig. 4.8 - En gris foncé, la zone d'étude de
l'Ouest
parisien...........................................................................
212
Fig. 4.9 - Géocodage des 10 211 clients potentiels de
l'Ouest parisien..........................................................
214
Fig. 4.10 - Nombre d'aires de la zone de chalandise par rapport
au nombre de dilatations pratiquées .......... 216
Fig. 4.11 - Nombre d'aires de la zone de chalandise > 490
pixels en fonction du nombre de dilatations ...... 217
Fig. 4.12 - Dilatation x 6-Dilatation x 30-Dilatation x 50
..............................................................................
219
Fig. 4.13 - Filtrage de points-clients par 10 dilatations
..................................................................................
220
Fig. 4.14 - Filtrage de points-clients par 20 dilatations
..................................................................................
221
Fig. 4.15 - Le filtrage par 20 dilatations superposée
à la carte des rues et aux points-clients ........................
223
Fig. 4.16 - Délimitation des aires constitutives de la
zone de chalandise ......................................................
225
Fig. 4.17 - Délimitation de la zone de chalandise selon la
méthode analogique (cercle) ............................... 226
Fig. 4.18 - Aire d'1 point client, de 9 points-clients et de 25
points-clients ................................................... 228
Fig. 4.19 - Régions ne comptant que de petites aires
servant au calcul de l'indice de corrélation spatiale .... 230
Fig. 4.20 - Numérotation et repérage du centre de
gravité des aires constitutives de la zone de chalandise.. 232
Fig. 4.21 - Fenêtre de saisie des paramètres de
distance et de coût dans le logiciel Sitation .........................
236
Fig. 4.22 - Cartographie de la demande associée à
chaque noeud ..................................................................
237
Fig. 4.23 - Cartographie de tous les noeuds et des
déplacements possibles pour effectuer ses achats............ 237
Fig. 5.1 - La mise en oeuvre de l'algorithme flou sur le logiciel
Sitation ....................................................... 243
Fig. 5.2 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts .................................. 243
Fig. 5.3 - Pour 4 localisations: zones de potentiel commercial
associées aux points de vente....................... 246
Fig. 5.4 - Schéma d'une itération de l'algorithme
génétique...........................................................................
247
Fig. 5.5 - Etapes de l'algorithme de recherche avec les
localisations optimales provisoires obtenues........... 248
Fig. 5.6 - L'aire 10 (bd de Grenelle) avec les aires les plus
proches .............................................................. 250
Fig. 5.7 - La zone d'analyse délimitée
............................................................................................................
251
Fig. 5.8 - Zone d'analyse analysée en termes de
sous-aires............................................................................
251
Fig. 5.9 - Superposition des points-clients et des sous-aires
..........................................................................
251
Fig. 5.10 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts dans l'aire 10 .......... 253
Fig. 5.11 - Pour 2 localisations: zones de potentiel commercial
associées aux points de vente (en gras) ..... 253
Fig. 5.12 - La sous-zone 1 du quartier Epinettes
(17ème
arrondissement)......................................................
254
Fig. 5.13 - Représentations des points de l'aire 1
...........................................................................................
255
Fig. 5.14 - Délimitation de l'aire 1
.................................................................................................................
255
Fig. 5.15 - Numérotation des sous-aires de l'aire 1
........................................................................................
255
Fig. 5.16 - Superposition des sous-aires et de la cartographie
....................................................................... 255
Fig. 5.17 - Distance moyenne à parcourir en fonction du
nombre de magasins ouverts ................................ 256
Fig. 5.18 - Pour 2 localisations: aires de potentiel commercial
associées aux points de vente en gras .......... 257
Fig. 6.1 - Le supermarché BioCoop (bd de
Grenelle), le supermarché Naturalia (rue Cambronne) et notre
préconisation (rue Lecourbe)
.......................................................................................................
267
Fig. 6.2 - Le supermarché BioCoop (rue Legendre) et le
2ième emplacement préconisé par notre méthode
(rue
Guy Môquet)
................................................................................................................................
268
Fig. 6.3 - Le magasin Naturalia dans le 17ème
(rues de Levis et Poncelet) et les emplacements préconisés
.. 269
Fig. 6.4 - Le point de vente Naturalia du 16 rue Levis
(XVIIème)
.................................................................. 270
Fig. 6.5 - Le point de vente Naturalia du 26 rue Poncelet
(XVIIème)
............................................................ 270
Fig. 6.6 - Le magasin BioCoop-Les Nouveaux
Robinsons (rue Clément) à Boulogne-Billancourt et
l'emplacement préconisé (route de la
Reine)................................................................................
271
Fig. 6.7 - L'emplacement préconisé dans le
XVIIème, rue des
Acacias........................................................... 292
Fig. Conclusion.1- Les possibilités d'applications de la
méthode selon les données à traiter
........................ 308
Fig. A.1 - Géocodage des 1732 clients potentiels de
Boulogne-Billancourt .................................................. 339
Fig. A.2 - Géocodage des 952 clients potentiels
d'Issy-Les-Moulineaux.......................................................
340
Fig. A.3 - Géocodage des 398 clients potentiels de
Neuilly-sur-Seine ..........................................................
340
Fig. A.4 - Géocodage des 517 clients potentiels de Paris
VIIème
....................................................................
341
Fig. A.5 - Géocodage des 3456 clients potentiels de Paris
XVème
................................................................. 342
Fig. A.6 - Géocodage des 1087 clients potentiels de Paris
XVIème
................................................................ 343
Tableaux
Tableau 3.1 - Paramètres géométriques des 12
aires de la zone de chalandise obtenus après délimitation ...
180
Tableau 3.2 - Paramètres marketing des 12 régions
de la zone de chalandise obtenus après délimitation .... 181
Tableau 3.3 : Les caractéristiques des 43 aires de
population détectées par traitement du signal..................
188
Tableau 4.1 - Caractéristiques de chaque zone
..............................................................................................
233
Tableau 4.2 - Prix au m² par zone et quartier
correspondant..........................................................................
235
Tableau 5.1 - Localisations optimales données par les
algorithmes flou et de voisinage .............................. 242
Tableau 5.2 - Localisations optimales données par
l'algorithme des multiplicateurs de Lagrange ................ 245
Tableau 5.3 - Comparatif des résultats de recherche de
localisations effectuée les différents algorithmes ... 249
Tableau 5.4 - Résultats d'analyse des sous-aires
appartenant à l'aire 10
........................................................ 252
Tableau 5.5 - Localisations optimales au sein de l'aire 10
.............................................................................
254
Tableau 5.6 - Résultats d'analyse des sous-aires
appartenant à l'aire 1
.......................................................... 256
Tableau 5.7 : Localisations optimales au sein de l'aire 1
...............................................................................
257
Tableau 6.1 - Analyse des arrondissements et des communes
appartenant à la zone étudiée ........................
264
Tableau 6.2 - Noeuds solution avev un p-médian classique
..........................................................................
265
Tableau 6.3 - Comparatif des résultats entre notre
algorithme et l'utilisation classique du p-médian............ 265
Tableau 6.4 - les magasins "bio" de la région parisienne
et leur aire de rattachement................................... 266
Tableau 6.5 - Bilan des implantations des magasins "bio" dans les
aires optimales ...................................... 273
Tableau 6.6 - Bilan des implantations des magasins "bio" selon
les aires optimales et non-optimales ......... 277
Tableau 6.7 - Comparaison des implantations optimales et
non-optimales des réseaux et de leur regroupement
..................................................................................................................................................
280
Tableau 6.8 - Comparaison des implantations optimales et
non-optimales de Naturalia avec le regroupement
G20/BioCoop et stratégie de réponse de Naturalia
................................................................... 281
Tableau 6.9 - Caractéristiques des méthodes de
résolution du modèle p-médian dans notre cas de figure ...
291
ANNEXES
ANNEXE A : cartes des clients géocodés par
arrondissement et communes de périphérie
Fig. A.1 - Géocodage des 1732 clients potentiels de
Boulogne-Billancourt

Fig. A.2 - Géocodage des 952 clients potentiels
d'Issy-Les-Moulineaux

Fig. A.3 - Géocodage des 398 clients potentiels de
Neuilly-sur-Seine
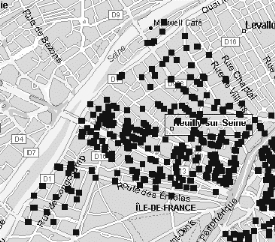
Fig. A.4 - Géocodage des 517 clients potentiels de Paris
VIIème
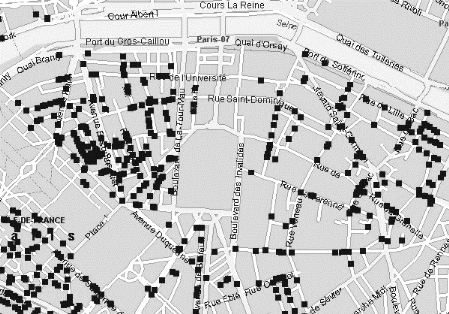
Fig. A.5 - Géocodage des 3456 clients potentiels de Paris
XVème
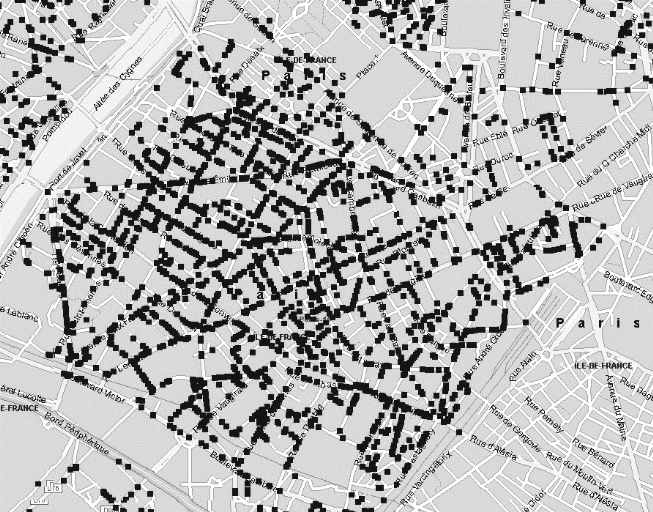
Fig. A.6 - Géocodage des 1087 clients potentiels de Paris
XVIème

ANNEXE B
REPERTOIREFRANCAIS-ANGLAISDES TERMESDU TRAITEMENTDU SIGNAL ET
DEL'ANALYSEAUTOMATIQUED'IMAGE
accentuation : enhancement
des contours : edge sharpening/enhancement du contraste :
contrast enhancement
de couleurs : colo(u)r enhancement de l'image : image enhancement
accentuer : to enhance
affaiblissement : fading, attenuation affichage : display
affichage en couleur : colo(u)r display de données : data
display
en ligne : raster display matriciel : raster display tramé
: raster display vectoriel : vector display afficher : to display
affine : affine
affiner (un modèle) : to enhance, to improve
agrandissement : enlargement, magnification, blow-up albedo spectral : spectral
albedo
algorithme : algorithm
de balayage par ligne : scan line algorithm
de compression non dégradant : lossless compression
algorithm
alias(s)age : aliasing
amélioration d'image : image improvement de contours :
edge enhancement
de contraste : contraste enhancement amincissement : thinning
amplificateur de brillance : image intensifier analyse
chromatique : colo(u)r analysis
en composantes principales : principal component analysis
des correspondances : correspondence analysis diachronique :
multidate analysis
discriminante : discriminent analysis factorielle : factor
analysis
de formes : pattern recognition/analysis/matching
granulométrique : grain-size analysis, particle-size analysis,
granulometry
de groupement : cluster analysis harmonique : harmonic
analysis
d'image (numérique) : (digital) image analysis, image
parsing
de mouvement : motion analysis multirésolution :
multiresolution analysis
de séquence d'images : image sequence analysis de texture
: texture analysis
animation : animation
anamorphose : anamorphosis (forme), stretching (gris)
antenne : antenna, dish (jargon)
synthétique, simulée : synthetic antenna
anti-aliasage : antialiasing
anticrénelage : antialiasing, dejagging
anti-halo : anthalation, grey-back (GB), gray-back (US)
aplatissement : flatness (courbe plane), oblateness (ellipsoide)
appariement : matching
de blocs : block-matching d'images : image-matching
apprentissage : learning
apprentissage-reconnaissance : training
approximation polygonale : polygonal approximation arborescence :
tree pattern
artefact : artifact arête : edge
asynchrinisme : asynchronism attributs : features
autocadrage : autoscaling autosimilarité : self-similarity
balayage : scanning
cavalier : directed beam scanning circulaire : circular
scanning
de trame : raster scanning balayeur (voir scanneur) : scanner
d'image : image scanner
linéaire : line-scanner
multispectral : multispectral scanner bande d'absorption :
absorption band base d'apprentissage : learning set
base de données-image (BDI) : image data base (IDB)
blanchiement (d'image) : lighter shading boîte englobante :
bounding box
brillance : brightness, brilliance, luminosity brouillage : blur,
smearing
bruit : noise
aléatoire : random noise erratique : Johnson noise
de fond : background noise furtif : stealth noise
d'image : image noise
de scintillement : flicker noise cadre : frame
canevas : pattern, control
capteur intelligent : smart sensor carreau : patch
carroyage : gridding, squaring
carte aéronautique : aeronautical chart, aviation map
chromoplèthe : chromopleth
couleur : colo(u)r map
d'état-major : ordonance survey map
infographique : computer map, computerized map de position :
location map
thématique : thematic map cartographie aérienne :
aerial mapping
assistée par ordinateur : computer-aided mapping
automatique : automatic mapping
radar : radar imagery causal (plur. causals) : causal cellule :
cell
adjacente : connected cell, adjacent cell cellule 2D : pixel
cellule 3D : voxel
centre de cliché : fiducial center/centre
centre de perspective : perspective center/centre centroïde
: centroid
chambre multibande : multiband camera champ : field
markovien : Markov random field lointain : far field
proche : near field chromaticité : chromaticity
chrominance : chrominance cible : target
manoeuvrante : maneuvering target circularité :
circularity
clarté : brilliance
classe spectrale : spectral class
classification automatique : automatic cluster analysis
dirigée : supervised classification
non dirigée : unsupervised classification classification
de couleurs : colo(u)r classification clignotement : blinking
cliniste (ligne de plus grande pente) : steepest slope line
(structure) clupéiforme : herringbone pattern codage en
couleur : colo(u)r coding
code-barre : bar code
coefficient de rétrodiffusion : backscattering coefficient
cohérent : coherent
coin : wedge
sensitométrique : step continuous wedge collecte :
gathering
coloriage : colo(u)r filling colorier : to paint compacité
: compaction
compactage d'image : image compression compensateur de mouvement
d'image : image motion compensator
compensation de contraste : contrast balancing composante
diffuse : diffuse component visuelle : visual component
composition colorée : colo(u)r composite compression (voir
compactage)
de données : data compression dégradante : lossy
compression
non dégradante : lossless compression
d'image : image compression
par valeur-longueur : run-length algorithm concave : concave
concavité : concavity concourant : intersecting
configuration : pattern
configurations contradictoires : contradictory patterns
connexité : connexity
contenu moyen d'information : average information content,
entropy
contiguïté : contiguity
contour : image contour, outline, edge contourer : to outline
contraste : contrast, gamma
mesure de - : contrast measurement moyen : average contrast
contre-jour : back lighting contre-plongé : tilt-up
convexe : convex
faiblement - : weakly convex convexité : convexity
convolution morphologique : morphological convolution
co-occurrence : co-occurrence
coordonnées d'image : photograph coordinates correction
d'éclairement : illumination correction de filé :
desmearing
corrélateur d'images : image correlator couleur
fausse-couleur : false colo(u)r réelle : true colo(u)r
complémentaire : complementary colo(u)r
modèle de - TSL (Teinte-Saturation-Luminance) :
Hue-Saturation-Value model (HSV)
primaire : primary colo(u)r soustractive : subtractive colo(u)r
spectrale : spectral colo(u)r
couloir exploré : (scan) swath coupage : clipping
couper-coller : cut and paste
couple stéréo(scopique) : stereopair courbure
moyenne : mean curvature totale : total curvature couverture :
surveying, coverage crayon optique : light pen
critère de rejet : reject criterium croissance de region :
region growth cycléament : circular feature débruitage :
enhancement
décimation : decimation/ resampling décompactage
d'image : image decompression
décomposition pyramidale : pyramidal decomposition
découpage : clipping
dédoublement : doubling défilement : scrolling
déflouage : deblurring
déformation d'image : image distortion
dégradation
d'image : image degradation degré de - : degree of
lossiness dégradé (de couleurs) : dithered
dégradée (image après compression) : lossy
délignage
demi-teinte (gris par juxtaposition de noir/blanc) :
halftone
densité : density
graphique : areal density (bits/cm2 ou /pouce2)
d'image : image density
de maillage : grid-cell density densitomètre :
densitometer
détail marquant/remarquable : salient feature
détecter : to detect, to sense
détection
de caractères : character detection
de contours : edge finding/detection de formes : shape
detection
de frontières : boundary finding/detection de mouvement :
motion detection d'obstacle : obstacle detection
de site : site detection déterministe : deterministic
détourage : clipping, scissoring détramage : unframeless
diamorphose : morphing différenciation : differentiation diffraction :
diffraction
diffusion : diffusion, scattering
vers l'arrière : backscattering, backward scattering
diffusométrie : scatterometry
dilatation : dila(ta)tion
géodésique : geodesic dila(ta)tion discrimination :
discrimination discriminer : to discriminate distorsion : distortion
d'échelles : scale distortion, length distortion
données numériques : digital data
données de terrain : ground data ébarbulage :
cliping, triming éblouissement : blooming échantillon : sample,
pixel échelle : scale
de gris : grey scale (GB), gray scale (US), neutral scale mise
à - : scaling
écho-fantome : ghost (echo) écho-mirage : angel
(echo) éclairement : illumination écrêtage : clipping
écriture : handwriting effet effect
de bord : edge effect
de scintillement : flicker effect effet-lacet : skew effect
effet
de bord : edge effect
de scintillement : flicker effect élagage (de
structures) : pruning élément
d'image : picture element, pixel (2D), voxel (3D), structurant :
structuring element
élimination
des faces arrières : back plane culling des surfaces
cachées : hidden suface élimination/removal
ellipsoïde
oblong/allongé : prolate ellipsoid aplati : oblate
ellipsoid encadrement : framing
encadrer : to frame ensemble flou : fuzzy set entropie :
entropy
méthode du maxium d': : maximum entropy method enveloppe
convexe : convex hull
épaississement : thickening éparsité :
sparsity
épreuve : print, hardcopy équidensité :
equidensity équidensitométrie : density slicing
équidistance des courbes : contour interval
équilibrage de couleurs : colo(u)r balance érodé :
eroded
ensemble des - ultimes : set of ultimate eroded érosion
euclidienne : Euclidean erosion géodésique :
geodesic/geodetic erosion érosion/dilatation : erosion/dila(ta)tion
(en) escalier : staircase, step function escalier
irrégulier : jaggies
estimée : estimate estompage : shading étalonnage :
calibration
étiquetage d'image : image labelling étirement des
contrastes : contrast stretching excentricité : eccentricity
excursion en fréquence : frequency swing extinction :
quench
extraction : extraction, detection and tracking (?)
de points caractéristiques : extraction of characteristic
points
facettage : facetisation fac-sim : hardcopy facteur : factor
d'échelle : scale factor de forme : form factor
sémiologique : semiologic factor fausse-couleur : false
colo(u)r fenêtrage : windowing, scissoring fenêtre : window,
frame
glissante : sliding window fermeture : closing
de contour : contour closing
morphologique : morphological closing
fil-de-fer (modélisation/répresentation) :
wireframe file : motion blur
filtrage : filtering
adapté : matched filtering spatial : spatial filtering
filtre : filter
d'accentuation : emphasis filter à contraste : contrast
filter
atténuateur : smooth filter (passe-bas, isotrope)
coupe-bande : band-elimination filter directionnel : directional filter
en éventail : fan filter
gradient : gradient filter (passe-haut, non isotrope)
gris, neutre : grey filter (GB), gray filter (US), neutral
density filter
laplacien : Laplacian filter (passe-haut, isotrope)
linéaire : linear filter
médian : median filter (coupe-haut) morphologique :
morphological filter non linéaire : nonlinear filter polaris(at)eur :
polarizing filter squelette : skeleton filter
tout pôle : allpole filter tout zéro : allzero
filter
flou (adj.) : blurred, hazy, not sharp, out of focus flou (subs.)
: blur, blurriness, blooming
artistique : soft focus focalisation : focusing
foncer : to deepen, to darken fonctionnelle-image : image
functional fond : background
fond de carte : base map
fondu enchaîné : cross fadé, fade over,
dissolved image fractale (subs. fem.) : fractal (image)
fractal, -ale, -als (adj.) : fractal frontière de cellule
: cell boundary fusion de données : data fusion
gamme de gris (voir coin) : step continuous wedge
généralisation (des cartes géographiques) : generalization
géométrie d'image : image geometry
gradient : gradient graphe : graph granulation : speckle
graphique : chart
grille de coordonnées : coordinates grid
(en) gris : grey-scale (GB), gray-scale (US)
grisé : halftone grappage : clustering
grossissement : magnification groupage : clustering hachurage :
hatching histogramme : bar chart
homogéneisation : homogenization, blending homotopie :
homotopy
icône : icon
iconocarte : image map
identification de structure : feature extraction îlot de
confiance : safe region, fiducial area image : image, picture
en couleur composée : composite colo(u)r image
d'écran : soft copy
fixe : still image, still médistancée : slant range
image
numérique, digitale : digital image numerisée,
digitalisée : digitized image de précharge : bias, offset image
secondaire : ghost image
de synthèse : image synthesis vidéo : soft copy
imagerie : imagery / imaging aérienne : aerial imagery
médicale : medical imaging imagette : subimage
imageur : imaging system/device incertitude : uncertainty
incrustation : inset, overlay
indice
de concavité : concavity index de déficit :
deficiency index
de forme : shape index/factor/parameter infographie : computer
graphics information : information
à information pauvre : poorly informed intensificateur
d'image : image intensifier interaction homme-machine : human computer
interpolation
de couleurs (improprement dit ``ombrage") : dithering de formes :
tweening
interpoler des formes : to tween invariant d'image : image
invariant (carte) isocouleur : chloropleth isodensitomètre : density
slicer isopérimètre : isoperimeter
isoligne : isoline, countour (line)
isosurface : isosurface isoplèthe : isopleth jacobien :
Jacobian
jaune-magenta-cyan (JMC ou CMJ) : cyan-magenta-
yellow, CMY krigeage : kriging kurtosis : kurtosis
lance de rayon (geophys.) : ray tracing/casting laplacien :
Laplacian
largeur de couloir : swath width legendage : annotation
libre parcours moyen : free mean path lignage : (voir
délignage)
ligne
de base : baseline cachée : hidden-line
de contour : contour (line) de crête : crest line
dentelée : jagged line
de partage des eaux : water divide, water parting de plus grande
pente : steepest slope line
des pourpres : purple boundary de référence :
baseline
lineament : linear feature, lineament lissage : smoothing
lobe : lobe
d'antenne : antenna lobe latéral : sidelobe
principal : main/major lobe secondaire : secondary/minor lobe
localisation de contours : edge localization maillage : mesh
maille : grid cell
manche a balai : joystick
masquage : clipping, masking, shielding masque : mask
matrice
de co-occurrences : co-occurrence matrix spectrale : spectral
matrix
mettre à l'échelle : to scale
mettre au point : to sharpen, to focus mise à l'echelle :
scaling
automatique : autoscaling mixage : mixing
pondéré : taper mixing (en) mode point : bit map
modèle : model
glissant : sliding model moindres carrés :
least-squares
moirage : interference pattern, watered effect moirure : moire
mosaïquage : mosaïcking, tessellation mosaïque :
image mosaic
motif : pattern
concordance / appariement de - : pattern matching multicapteur :
multisensor
multi-étiquetage : multilabelling multigrille : multigrid
multiéchelle : multiscale
niveau de gris : grey level (GB), gray level (US)
noeud de maillage : grid node
noir et blanc (image en -) : line art mode noircir : to
blacken
noircissement d'image : darker shading noyau de convolution :
convolution kernel
nuage de points : cluster of point représentation par -
:
scatter chartplot, dot-chart nuance
de couleur : hue de gris : shade
nuanciation : dithering
(objet) obombrant : shadow-casting (object)
octant : octant octronc : octree ombrage : shading
de Gouraud : Gouraud shading (lissage par
interpolation sur les valeurs sur ligne)
de Phong : Phong shading (lissage des valeurs sur les normales
à la ligne)
ombre : shadow
portée : cast shadow, geometric shadow ombrage :
shading
ondelette : wavelet
onduleur (d'image) : image inverter orientation : (image)
orientation osculateur : osculatory
plan -: osculation plane papillotage : blurring
paramètres de forme : shape parameters parasite :
glitch
parcelle : patch
parsage (analyse syntaxique) : image parsing partitionnement :
partitioning
pas-à-pas : step-by-step paysagisme : landscaping
pénombre : penumbra
périmètre spécifique : specific perimeter
perspective : perspective, outlook cavalière : cavalier perspective
photographie multibande : multispectral photography
photo-interprétation : photointerpretation
photostyle : light pen pistage : tracking
pivotement (d'image) : swivel
pixel : pixel, picture element, photosite, PEL (rare)
nombre de bits par - : pixel depth pixel-objet : obel
pixel 3D : voxel
de texture ou texel : texel plan de coupe : clipping plane
planche à clous (diagramme) : bed of nails, arrow plot,
stick plot
planéité : flatness
(surface) plissée : wrinkled surface pochage : shading,
toning
point de fuite : vanishing point point de vue : eye position
polygone en noeud-papillon : bowtie polygon poursuite :
tracking
pouvoir de résolution : resolving power pouvoir
séparateur : resolving power
prétraitement (d'image) : (image) preprocessing produit
moyen de variances : average product of variances
programmathèque : program library projection :
projection
conique : conic proj.
gnomonique : gnomonique proj. isométrique : isometric
proj. pyramidal : pyramidal
algorithme -: pyramidal algorithm représentation - :
pyramidal representation pyramide : pyramid
octaviée : octave-spaced pyramid quadrillage : gridding
quadrique : quadric surface quadtronc : quadtree
quantification vectorielle : vector quantization
(en) quinconce : five-spot pattern raccordement : seaming
radar : (vocabulaire à détailler)
radiosité : radiosity réalité
de terrain : ground truth virtuelle : virtual reality
recadrage : cropping
recalage : registration, matching de courbes : curve matching
d'images : image reseting/registering reconnaissance :
recognition
de formes (RDF) : pattern recognition (PR)
de caractères : character recognition de texte : text
recognition
reconstruction d'image : picture reconstruction redressement :
straightening
réduction (d'affichage) des couleurs : colo(u)r
quantization, colo(u)r reduction, colo(u)r selection
rééchantillonnage : resampling
réflexion : reflection
croisées : interreflections diffuse : diffuse reflection
spéculaire : specular reflection regroupement : gathering, fusion
relaxation : relaxation
stochastique : stochastic relaxation
remplissage de polygones : area filling, polygon-filling rendu :
rendering
des couleurs : colo(u)r rendition/rendering de solides :
rendering of solids
repère : system of coordinates
orthonorme direct : direct orthonormal system
représentation par frontières : boundary representation (BREP)
résolution de l'image : image resolution résolution
spectrale : spectral separability restauration d'image : image restoration
réticule : crosshair cursor
rétrodiffusion : backscattering rotationnel : curl,
rotational
rouge-vert-bleu (RVB) : red-green-blue, RGB
rugosité : roughness sautillement (d'image) : jitter
scalant : scaling
scannage : scanning scanner : to scan scanneur : scanner
scannogramme : scannogram scène : scene
en hyperfréquence : microwave scanner
multibande (SMB) : multispectral scanner (MSS)
naturelle : real-world scene scintillement : flicker
segment élémentaire : stroke segment visible :
visible segment segmentation : segmentation séquence : sequence
seuillage : thresholding seuiller : to threshold silhouettage :
outlining silhouette : silhouette
sommet (d'un polyèdre) : vertex (plur. vertices)
triédrique : trihedral vertex souris : mouse, trackball
sous-échantillonnage : subsampling sous-réseau :
subarray
soustraction de bruit : noise subtraction (?), noise
cancelling/reduction
squelettisation : skeletonization, thinning statistiques :
statistics
d'ordre supérieur : higher order statistics
sténopé : pinhole
stéréo : (vocabulaire à détailler)
structure : feature, structure suivi de ligne : tracing
suivi de contour : edge tracing/tracking superposition d'images :
image registration suppression : removal / removing
des surfaces cachées : hidden surface removal
suréchantillonage : supersampling
surexposition : over-exposure, overexposure surface
gauche : patch, curved surface de raccord : blend surface
réglée : ruled surface
survol d'images : browsing synchronisation
de la parole : speech synchronization synthèse d'images :
image synthesis tablette graphique : graphic tablet
tachèle : ground patch area
tamisée (lumière) : softened light, subdued light
tampon (de profondeur) en Z : Z-buffer
tectec (Tel ECrit, Tel ECran) : wysiwyg (acronyme de
``what you see is what you get").s teinte : hue
télédetection : remote sensing aérienne :
airborne remote sensing
spatiale : spaceborne remote sensing
aérospatiale : airborne and spaceborne remote sensing
temporal (adj.) : temporel, en temps
tessellation : tessellation
tesselle (pavé en motifs réguliers) : tesselated
texel (élément minimal de texture) : texel texton : texton
texturage : texture wrapping (plaquage d'une image 2D
sur un objet 3D)
texture : (image) texture
texture plane : planar texture enrobage/habillage de - : texture
wrapping texturé : textured
TFR : FFT
Tomao (tomographie assistée par ordinateur) :
compueetrized tomography tomographie : tomography
TOR (transformée en ondelette rapide)
tortuosité : tortuosity tracé
de courbes de niveau : contouring élastique : rubber
banding
de lignes : line drawing
de rayon : ray tracing/casting traceur (de courbes) : X-Y plotter
traînée : image motion
effet de -: drag effect
traitement d'image numérique : digital image processing
tramage : rasterization
trame : raster, screen transformation
en chapeau haut-de-forme : top-hat transform en distance :
distance transform
de Hough : Hough transform
de Karhunen-Loève : Karhunen-Loeve transform en ondelettes
: wavelet transform
en tout ou rien : hit or miss transform
valence : valence (nombre d'états significatifs distincts
que peut prendre un signal)
valeur de gris : greyness, grey value (GB), grayness, gray value
(US)
vision
monoculaire : monocular vision par ordinateur : computer
vision
robotique : robot vision / computer vision
visu (n.f.) ou visuel (n.m.) : display unit/device, monitor
visualisation : display
voile (de photo) : fog voisinage : neighbourhood
fonction de -: function of neighbourhood vraisemblance :
likelihood
vue perspective : perspective view zonage : zoning
zone
d'apprentissage : learning area de raccord : merge zone
- 1 -
| 


